Предельная
погрешность
О
появлении отдельной погрешности заранее
что–либо определенное сказать невозможно.
Однако, когда число этих погрешностей
возрастает, можно установить определенные
закономерности для всей совокупности
погрешностей данного ряда измерений.
Эти
закономерности можно выразить уравнением,
полученным К. Ф. Гауссом.
__
2
2
__ 2
2
y
= (1 / σ
√2π
)
e
– (li
–
a)
/
2σ
= (1 /σ
√2π
) e
– Δc
/
2σ
, (4.17)
где
y
– плотность распределения погрешностей;
σ
– параметр
уравнения, называемый стандартом, связан
со средней
квадратической
погрешностью соотношением
a
– параметр
уравнения, называемый математическим
ожиданием,
связан
с арифметической срединой соотношением
e
– основание натуральных логарифмов;
Δi
= li
– a
– случайная погрешность.
Это
уравнение называется законом
нормального распределения
погрешностей.
Уравнению
(4.17) соответствует колоколообразная
кривая, называемая кривой нормального
распределения (кривая Гаусса) (рисунок
4.1)
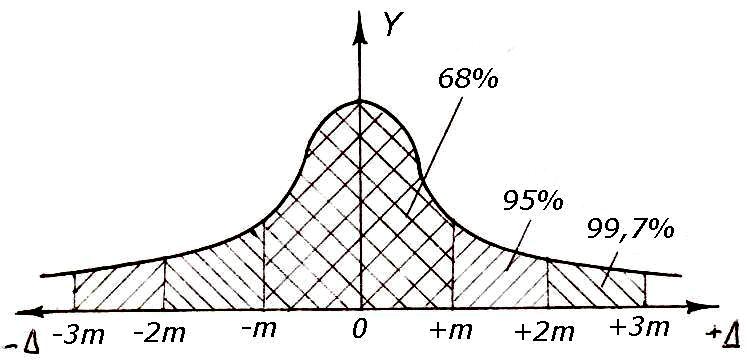
Рисунок
4.1 – Кривая Гаусса
Площадь
под кривой, ограниченная кривой и осью
абсцисс, принимают равной единице. Часть
этой площади, соответствующая какому-либо
отрезку оси абсцисс, дает, вероятность
попадания случайной погрешности в
данный интервал. При li
= a
или Δ = 0 получаем максимальное значение
ординаты кривой
__
Y
= 1 / σ √2π.
Из
рисунка 4.1 видно, что основная масса
погрешностей группируется около наиболее
вероятного значения погрешности Δi
= 0 (согласно четвертому свойству случайных
погрешностей, среднее арифметическое
из случайных погрешностей стремится к
нулю). Это положение обосновывает третье
свойство случайных погрешностей (малые
погрешности встречаются чаще, чем
большие). Второе свойство случайных
погрешностей о равном появлении
положительных и отрицательных ошибок
характеризуется симметричностью кривой
нормального распределения относительно
оси OY.
Теоретические
исследования и практика геодезических
измерений показывают, что в промежутках
от –m
до +m
попадает 68 % всех случайных погрешностей
(см. рисунок 4.1), в промежуток вдвое
больший (от –2m
до +2m)
попадает 95 % погрешностей, а в промежуток
втрое больший (от –3m
до +3m)
попадает 99,73 % погрешностей. Это означает,
что из 100 погрешностей измерений только
32 по абсолютной величине превзойдут
среднюю квадратическую погрешность m,
3 из 1000 погрешностей будет превышать
величину утроенной средней квадратической
погрешности ±3m.
Таким образом, за пределы ±3m
выходит лишь 0,27 % погрешностей измерений.
Поэтому в качестве предельной погрешности
Δпред
принимается утроенная средняя
квадратическая погрешность, т. е.
Δпред
= 3m.
(4.18)
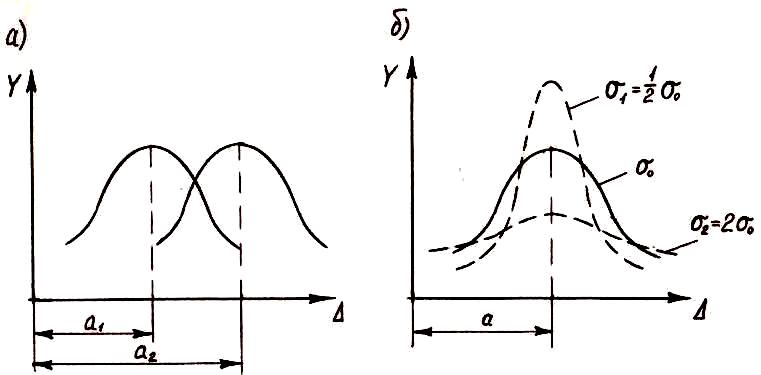
Рассмотрим
теперь сущность параметров a
и σ
в уравнении (4.17). Параметр a
называемый математическим ожиданием
и характеризует центр группирования
на кривой Гаусса, т. е. смещение центра
группирования вдоль оси абсцисс (рисунок
4.2, а)
при сохранении формы кривой. Если при
постоянном значении параметра a
будем изменять другой параметр σ
(называемый стандартом), характеризующий
точность измерений, а это возможно, если
мы меняем метод измерений или выполняем
их другими приборами. Тогда центр
группирования остается неизменным, а
форма кривой изменится. Она станет более
пологой, если точность измерений
уменьшается, и станет более крутой при
увеличении точности (рисунок 4.2, б).
Рисунок
4.2 – Смещение и изменение формы нормальной
кривой
Параметры
a
и σ заранее, до измерений, неизвестны.
Они получаются как результат большого
числа измерений. На практике вместо
параметров a
и σ мы получаем приближенные их значения:
арифметическую средину L,
вычисляемую по формуле (4.4), и среднюю
квадратическую погрешность m,
вычисляемую по формулам (4.5) или (4.15).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скачать с Depositfiles
1. Необходимые сведения из теории математической обработки геодезических измерений
1.1 Погрешности
Самые тщательные и точные результаты измерений не совпадают с истинными значениями измеряемых величин, т.е. содержат погрешности. Это подтверждается тем, что результаты измерения одной и той же величины, как правило, не совпадают друг с другом.
Причиной появления погрешностей является то обстоятельство, что как на измеряемый объект, так и на измерительный прибор, действует множество помех, как внешнего, так и внутреннего характера. Кроме того, на измерительный процесс оказывают влияние помехи со стороны среды, в которой выполняются измерения.
Вследствие указанных причин в результате измерений наблюдатель получает не истинное значение физической величины, а только какое-то приближение к ней.
Истинной погрешностью результата измерения
некоторой физической величины
называется разница между этим измерением и истинным значением
измеряемой физической величины, т.е.
(1.1).
По своему характеру погрешности делятся на два класса:
— грубые,
— неизбежные.
Грубые погрешности – это результат просчета во время измерений. Например, просчет на длину ленты при измерении расстояний или же на один сантиметр (дециметр) в отсчете по нивелирной рейке.
Неизбежные погрешности также в свою очередь делятся на два вида:
— систематические;
— случайные.
Систематические погрешности наиболее нежелательные при измерениях, потому что они имеют свойство накапливаться, существенно искажая результаты измерений. Поэтому всегда выбирают такую методику измерений, которая исключает систематические погрешности. Например, измеряя горизонтальный угол при двух положениях вертикального круга, исключают коллимационную погрешность теодолита. И т.д. Систематические погрешности будем обозначать через .
Случайные погрешности потому так и называются, что нельзя заранее предусмотреть в каждом конкретном случае измерений их величину и знак. Однако при многократных измерениях случайные погрешности подчиняются некоторым статистическим закономерностям, изучение которых позволяет существенно уменьшить их влияние на результаты измерений. Случайные погрешности будем обозначать через .
Истинная погрешность есть сумма случайной
и систематической
составляющих погрешности, т.е.
(1.2)
1.2. Среднее квадратическое отклонение случайной величины X
Среднее квадратическое отклонение или стандарт (сокращенно СКО) случайной величины
— это мера рассеивания или разбросанности значений случайной величины
относительно ее истинного значения
.
Применительно к измерениям случайная величина это не что иное, как измеренное значение
некоторой физической величины
, а
— это ее истинное значение
. Тогда разность
или
— это отклонение измеренного значения измеряемой величины от ее истинного значения. Ранее было отмечено, что такое отклонение называется истинной погрешностью
измеряемой величины.
В теории математической обработки геодезических измерений (сокращенно ТМОГИ) стандарт называется средней квадратической погрешностью (сокращенно СКП) измеряемой величины и обозначается буквой [2].
В случае присутствия в результатах измерений только случайных погрешностей или, что то же самое, в случае отсутствия в измерениях систематических погрешностей
, средняя квадратическая погрешность
вычисляется по формуле К.Ф. Гаусса
, (1.3)
где — это количество значений измеренной величины или, иначе, количество суммируемых истинных погрешностей
.
Средняя квадратическая погрешность зависит от числа значений случайных погрешностей
, просуммированных в формуле (1.3), однако при
ее значение практически не меняется с ростом числа
, и ее можно принимать за количественный показатель условий измерений.
Измерения, которые имеют одинаковые средние квадратические погрешности , называются равноточными.
1.3. Нормальный закон распределения случайной величины
Если взять достаточно большой ряд случайных значений какой-либо величины, то можно заметить, что некоторые из них встречаются чаще, а некоторые реже. Т.е. вероятности появления тех или иных случайных значений подчиняются некоторым закономерностям или, говорят, имеют некоторый закон распределения вероятностей. В общем случае значения различных случайных величин могут подчиняться различным законам распределения вероятностей появления этих значений. Наиболее распространенным из них является нормальный закон распределения.
Нормальное распределение, называемое также распределением Гаусса, — это распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно вфизике, геодезии, астрономии. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Случайные погрешности измеряемых величин также подчиняются нормальному закону распределения. Функция плотности вероятности нормального закона распределения имеет вид

где — это так называемое математическое ожидание случайной величины
.
Применительно к погрешностям, которые рассматривались в 1.1 и 1.2, — это истинная погрешность
результата измерения
,
— это систематическая составляющая
погрешности
, а разность
— это не что иное, как случайная погрешность
.
Случайная величина называется центрированной нормированной случайной величиной. Математическое ожидание этой величины равно
, а стандарт, или среднее квадратическое отклонение, равен
.
На рис. 1 показан график функции плотности вероятности нормального закона распределения.
Площадь фигуры, ограниченная сверху самой кривой, снизу — осью , а слева и справа вертикальными линиями с координатами
и
численно равна вероятности того, что измеренное значение случайной величины находится в интервале от
до
. Для значений
указанные вероятности будут составлять:
На основании этого можно сделать вывод, что для любых измерений всегда существует предельная или допустимая погрешность измеряемой величины, которую можно связать со средней квадратической погрешностью следующим соотношением:
, (1.5)
где — некоторая постоянная
|
|
|
Рис. 1. График функции плотности вероятности нормального закона распределения |
Многолетняя практика геодезических измерений показала, что параметр в зависимости от решаемой задачи, следует принимать равным 2 или 3. Поэтому предельную случайную погрешность измерения принимают равной удвоенной или утроенной средней квадратической погрешности
, (1.6)
или
. (1.7)
В общем случае точность измерений будет характеризоваться неравенствами
. (1.8)
Скачать с Depositfiles
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Человеку свойственно ошибаться. Это касается не только общих вопросов и знаний жизни. Но и распространяется на любые сферы его деятельности, в том числе в области геодезии. В ней все проводимые измерения выполняются с ошибками. Значительная часть работ в геодезическом производстве основывается на измерениях. А измерения — своего рода сравнение с какой-то эталонной или истинной величиной. Если понимать, что истинного значения в идеале не существует, то все сравнения в измерениях сводятся к сравнению с конкретно полученным значением и принятому, как верное. Одним из наиболее приближенных к истинному значению, считается среднее арифметическое.
Понятие погрешности, её абсолютная и относительная величины
Если переходить на понятие погрешности, то отклонение отдельного замера от среднего арифметического из выполненных измерений и считается абсолютной его ошибкой. Числовая форма погрешности не дает представления о качестве произведенного измерения. Для этого существует понятие относительной погрешности. Под ним понимают отношение значения собственно ошибки к замеренной величине. Применяется этот параметр в определении точности работ при линейных замерах в полигонометрических и теодолитных ходах.
В нивелирных ходах для его оценки точности существует так называемая приведенная погрешность. Это тоже своего рода относительный показатель. Только он подразумевает под собой отношение абсолютного значения ошибки к конкретному принятому значению определяемой величины (для нивелировок на 1 км хода).
Погрешности по источникам возникновения
При производстве геодезических работ после окончания каждой выполненной операции в полевых условиях можно говорить об ошибках. Присутствуют они и при проведении камеральных работ. Так при установке приборов в рабочее положение возникают отклонения в центрировании инструмента над центром знака. Также возникают неточности при выставлении прибора в отвесное состояние, когда выводим его цилиндрический уровень в верхнее горизонтальное положение и круглый уровень на середину. Следующими причинами возникновения погрешностей считаются визирование и снятие отсчетов в момент исполнения наблюдений. Влияние внешних условий окружающей среды: рефракция воздуха, дымка, туман, осадки, формирует еще одну группу ошибок. Помимо человеческого фактора и влияния внешней среды существуют конструктивные особенности приборов, с заложенными в них вероятностными составляющими точности измерений. Еще одной из причин возникновения погрешностей считается несовершенство методик их определений. Резюмируя выше сказанное, можно выделить следующий перечень ошибок по источникам их возникновения:
- инструментальные;
- индивидуальные;
- из-за условий окружающей среды;
- методические.
Погрешности по характеру действий
По данному признаку все ошибки можно разделить на следующие отклонения:
- грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
- систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
- случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;
Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.
Предельные и допустимые отклонения
При определенных факторах случайные ошибки по абсолютному значению своей величины не могут превышать определенного предела. Этот предел в геодезической и маркшейдерской практике имеет название предельной погрешности.
В строительном производстве нормативными документами введен термин предельного отклонения, который может иметь как положительное, так и отрицательное значения. Алгебраическая сумма этих параметров (предельных отклонений) имеет название допуска.
В геодезии крайние предельные значения отклонений, допускаемые нормативной документацией, называются допустимыми.
Средние, вероятные и средне квадратические погрешности
При различных оценках точности выполненных замеров применяются некоторые критерии случайных ошибок. К таким мерилам оценки относятся понятия:
- средне арифметического отклонения от всех случайных ошибок, имеющее название среднего уклонения;
- срединного отклонения, то есть находящегося в середине измеренного ряда по абсолютным значениям с учетом убывания и возрастания, именуемое вероятной ошибкой;
- средне квадратическое отклонение (СКО) – это параметр функции дисперсии (рассеивания) случайных величин результатов измерений. Он равен математическому ожиданию (среднему арифметическому значению) квадратов отклонений в измерениях от математического ожидания (среднего арифметического значения) результатов замеров.
Случайные погрешности подчиняются нормальному закону распределения и находятся в интервале от нуля до трех СКО. Большинство из них в пределах шестидесяти восьми процентов находятся в интервале до одного СКО. Девяносто пять процентов случайных величин попадает в интервал от нуля до двух СКО. Девяносто девять процентов случайных ошибок находится в интервале от нуля до трех СКО.
На основании этого в теоретических расчетах при предварительных оценках точности выполнения работ за предельные принимаются три средне квадратические ошибки. При геодезических и маркшейдерских работах на практике к расчетам принимаются двойные величины средне квадратических отклонений.