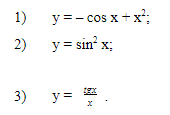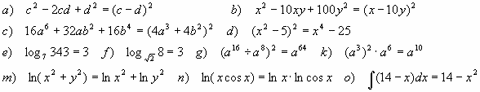Задания с ошибками для учителей

Для математики популярная поговорка «умные люди учатся на чужих ошибках» практически не работает, так как ошибка в большинстве случаев является необходимой и полезной, ведь она позволяет определить пробелы в знаниях школьника и своевременно их устранить. Главное – правильно относится к ошибке и ее правильно ее использовать.

Тем более обидно получать глупые ошибки, которые вызваны невнимательностью обучающихся, пропусками переменных, случайными потерями знаков, скобок и другими различными ляпами.

Для того чтобы снизить вероятность ошибок, необходимо использовать различные методики предупреждения типичных ошибок, что будет в итоге способствовать повышению уровня математической подготовки школьников.

Разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания

Организация работы обучающихся, направленной на анализ и исправление допущенных недочетов называется работой над ошибками. Ее основной целью является разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания. Правильно организованная работа обучающихся обеспечивает:

• дифференцированный подход к обучению;

• является профилактикой будущих ошибок;

• позволяет своевременно ликвидировать пробелы в знаниях и навыках детей;

• формирует умение систематизировать и обобщать, закреплять полученные знания.

Грамотный, творческий подход учителя к организации работы над ошибками создает условия для развития адекватного отношения обучающегося к ошибкам, умение работать с ними.

Можно говорить о том, что, после проведения работы над ошибками итоговая оценка отражает действительный уровень усвоения знаний и умений обучающихся. Существует практика, когда некоторые учителя практикуют выставление оценок за каждую проведенную работу. При этом, часто бывает, что после работы над ошибками, отметка за проверяемую работу повышается (как правило на один бал).

Обычно, работа над ошибками проводится в классе, под руководством учителя, но может проводиться и дома, возможно, под контролем родителей. Если учитель считает возможным дать выполнение работы над ошибками в качестве домашнего задания, он должен убедиться, что все обучающиеся знают и помнят основной алгоритм действий по выполнению работы. Целесообразно, каждому ребенку выдать памятку с порядком выполнения действий. Кроме этого, необходимо предварительно, на уроке провести общий анализ допущенных ошибок.

В классе, работу над ошибками проводят, как правило, после контрольных, самостоятельных или творческих работ. Работе над ошибками может быть посвящен, как весь урок, так и его часть. Это зависит от характера и количества видов ошибок, от уровня самостоятельности обучающихся и т.п. По усмотрению учителя возможны: фронтальная, групповая, парная, индивидуальная работа.

Основные этапы и формы организации работы над ошибками на уроке

При работе на уроке выделяют несколько основных этапов:

• консультация;

• коррекция знаний и умений;

• диагностика результатов;

• оценочная деятельность.

По усмотрению учителя возможны: фронтальная, групповая, индивидуальная работа.

Рассмотрим несколько вариантов проведения работы над ошибками

В начале урока, после проведения общего анализа проверенной работы, учитель просит поднять руку тех обучающихся, которые допустили ошибки при выполнении первого задания. К доске приглашается один из обучающихся, который будет выполнять и комментировать аналогичное задание у доски. Обучающийся определяется либо по его желанию, либо по решению учителя. Остальные обучающиеся выполняют работу у себя в тетрадях. Затем все самостоятельно решают задание проверочной работы. Таким образом, дети прорешивая аналогичное задание, прорабатывают ошибки, допущенные не только ими самими, но и остальными обучающимися. Такой подход целесообразен, когда в данном задании большинство обучающихся допустили ошибки.

Следующая форма работы используется, когда один, или несколько обучающихся допустили ошибки в задании, которое большинство обучающихся выполнили правильно. При данной форме организации урока один обучающийся выполняет работу над своими ошибками у доски, остальные обучающиеся исправляют свои недочеты в тетрадях или выполняют индивидуальные задания. С одной стороны, этот метод позволяет экономить время, затрачиваемое на данную деятельность, с другой — учитель не может контролировать деятельность других детей. Для исправления возникшей ситуации, нужно обеспечить каждому обучающемуся возможность обратиться к учителю за помощью, за консультацией.

Бывают ситуации, когда часть обучающихся выполнила проверочную работу на «отлично», т.е. возникает необходимость организовать деятельность этих обучающихся, и, одновременно организовать выполнение работы над ошибками остальными обучающимися. В этом случае, есть несколько вариантов организации работы на уроке.

Во-первых, «отличникам» можно предложить выполнение индивидуальных заданий повышенного или углубленного уровней, творческие задания, работу по подготовке, например, информационного сообщения к следующему уроку. С остальными обучающимися проводится работа над ошибками.

Во-вторых, обучающихся, показавших высокий уровень усвоения учебного материала, можно привлечь к консультированию других детей. В этом случае возможна организация групповой и (или) парной работы.

Имеют место случаи, когда педагог, в целях экономии времени, выделяет только типичные ошибки, допущенные обучающимися при выполнении проверочной работы, и на уроке проводят работу только таким видом ошибок. В этом случае работа организовывается фронтально, анализ и исправление типичных ошибок и недочетов выполняет весь класс вместе. При этом у доски работают обучающиеся по желанию, по очереди или по решению учителя, в зависимости от того, кто какие ошибки допустил.

Алгоритм действий по выполнению работы над ошибками

Алгоритм действий по проведению работы над ошибками определяется учителем самостоятельно, исходя из особенностей класса, общего уровня обученности и т.д.

Например, алгоритм действий обучающегося может выглядеть следующим образом:

1. просмотреть всю работу, обратить внимание на исправления учителя;
2. найти ошибку, выписать задание, в котором она допущена, проанализировать причину ее возникновения:

• ошибка в вычислении – перерешать;

• ошибка в применении формулы (правила, закона) — вспомнить нужную формулу (правило, закон) по данной теме, применить при решении;

• ошибка в построении рисунка – повторить материал в учебнике и выполнить рисунок правильно;

1. решить аналогичное задание

Памятка-помощник

В практике работы некоторых учителей встречается использование памяток, которые изготавливаются педагогом и раздаются каждому обучающемуся. Памятки могут быть индивидуальными. Работа с памятками выполняется под контролем педагога.

В памятке пронумерованы и записаны основные группы ошибок в виде:

Тема «….».

Примеры.

1.  
2.  
3. …

Если учитель планирует проводить работу над ошибками, с использованием памяток, то при проверке работы на полях тетради, напротив задания, в котором допущена ошибка, ставится номер, соответствующего задания в памятке. Это не только облегчает работу обучающихся, но и совершенствует систему обучения. Обучающийся неоднократно обращается к данной памятке, что способствует лучшему запоминанию учебного материала.

Проверка и подведение итогов работы над ошибками

В конце работы над ошибками необходимо провести проверку. Существует несколько форм ее организации.

• самопроверка;

• парная работа;

• групповая работа, когда «сильные» обучающиеся выступают в роли консультантов;

• фронтальная работа со всем классом.

Во всех случаях, необходимо обеспечить возможность каждому обучающемуся консультирования и помощи учителя, если возникают трудности.

В конце работы над ошибками, как и в конце любого урока, необходимо провести рефлексию. Дети анализируют свои ошибки, отмечают, как изменились собственные умения, отмечают моменты, которые остались не понятны, говорят о том, что вызвало трудности и высказывают свои предложения.

Следует отметить, что проведение работы над ошибками является обязательным и систематическим действием после каждой контрольной и проверочной работы. При этом необходимо обращать внимание и прорабатывать все ошибки, допущенные обучающимися, тщательно проводить отбор задач и примеров для отработки знаний и умений, для закрепления пройденного материала.

Превентивная деятельность учителя по предупреждению ошибок

Большая часть ошибок, допускаемых обучающимися, не связана с отсутствием или наличием знаний, хотя, конечно, доведение до уровня автоматизма ряда вычислительных операций позволяет существенно снизить вероятность появления ошибок. Однако при этом необходимо, чтобы обучающийся все равно руководствовался нужными правилами и постоянно сохранял концентрацию внимания.

Знание определенных правил нужно и для того, чтобы обучающийся мог проверить правильность решения и дать его обоснование. В тоже время многие школьники воспринимают курс алгебры в качестве набора правил, которые абсолютно не связаны между собой, поэтому они заучиваются исключительно для решения какой-то конкретной задачи, а по истечению незначительного промежутка времени просто забываются. В этой связи требуется организовывать процесс обучения правилам с использованием приемов, которые активизируют рефлексивную деятельность школьников по предупреждению и исправлению ошибок, возникающих при формальном усвоении правил.

Если процесс поиска и исправления ошибок сделать максимально поучительным для обучающихся, то анализ ошибок может стать эффективным средством для развития познавательного интереса к математике.

Наиболее распространенными ошибками являются:

• незнание или непонимание правил, формул и определений;

• неправильное применение формул или неумение правильно применять определения и правила;

• совершение вычислительных ошибок;

• невнимательное чтение условий задачи;

• отказ от использования свойств фигур при решении геометрических задач;

• неправильное раскрытие скобок;

• совершение логических ошибок при решении текстовых задач;

• применение формул сокращенного умножения.

К основным причинам совершения ошибок по математике относят:

• пропуски уроков, в результате чего появляются пробелы в знаниях;

• поверхностное изучение нового материала;

• повышенная усталость, вызванная чрезмерной нагрузкой или недостаточным сном, в результате чего понижается скорость мышления и снижается уровень внимания;

• неаккуратный почерк, из-за чего учитель часто не понимает, что написал обучающийся;

• скорость работы. При этом на появление ошибок влияет как высокая скорость работы, из-за которой обучающийся просто не стремиться вникнуть в суть задания, так и медленная. В последнем случае замедленная скорость мыслительных операций не позволяет обучающемуся в полной мере контролировать себя, а из-за «зависания» нужная информация просто удаляется из «оперативной памяти»;

• полное либо кратковременное переключение внимания с одной деятельности на другую;

• низкая мотивация, в результате которой теряется внимание и появляются ошибки.

Объяснение и предупреждение ошибок

Для предупреждения ошибок и сведения их к минимуму используются следующие профилактические мероприятия и действия:

• постоянный разбор наиболее распространенных ошибок в классе;

• предлагаемые обучающимся письменные задания должны быть максимально удобны для восприятия, то есть грамотно сформулированными и понятными;

• подбор заданий и упражнений, которые будут вызывать у детей интерес и повышенное внимание;

• учитель должен при объяснении нового материала стараться предугадать возможные ошибки обучающихся и разработать систему заданий, которые позволят правильно усвоить новые понятия;

• использование правил удобных для запоминания и исключающих двойную их трактовку.

Кроме того, учитель математики должен помнить, что систематическое и планомерное повторение является основным инструментом для ликвидации пробелов знаний.

Также рекомендуется при объяснении нового материала активно применять определения и теоремы, которые изучались ранее. Так, при изучении темы «Теоремы сложения» целесообразно организовать повторение ряда теоретических вопросов:

1. Изменение тригонометрических функций при возрастании и убывании аргумента.

2. Четные и нечетные функции.

3. Таблицы значений тригонометрических функций.

4. Знаки тригонометрических функций.

Дополнительно выполняются следующие задания:

1. Необходимо определить четность и нечестность тригонометрических функций:

1. Найдите область определения функции y = x2 – 6x + 10.

2. Определите, при каких значениях x, функции y = sin x и y = cos x принимают одинаковые значения?

Перед тем как приступить к изучению темы «Первообразная и интеграл», следует повторить все формулы дифференцирования. После этого обучающиеся выполняют самостоятельную работу (время решения – 10-15 минут), во время которой школьникам предлагаются карточки-задания, где «опущены» один-два компонента из формулы дифференцирования, а также приведены две функции, производные которых необходимо найти.

Затем проводиться проверка работы и анализ совершенных ошибок, что необходимо для выявления пробелов в знаниях и проведения работы по их устранению.

Список литературы:

1. Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
2. Амонашвили Ш.А. Воспитательная и образовательная функции оценки обучения школьников: Экспериментальное педагогическое исследование. – М.: Педагогика, 1984. – 296 с.
3. Бабанский Ю.К. Педагогика. М.: Просвещение, 1983.
4. Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
5. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
6. Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
7. Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
8. Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
9. Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
10. Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
11. Действующие учебники и учебные пособия по математике для средней школы.
12. Журналы «Математика в школе» за 1970-1990 гг.
13. Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
14. Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
15. Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
16. Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
17. Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
18. Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
19. Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
20. Рогановский, Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
21. Селевко, Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
22. Столяр, А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
23. Темербекова, А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
24. Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
25. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
26. Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
27. Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
28. Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
29. Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.

Статей и постов в интернете о типичных ошибках учителя довольно много. Но большей частью они касаются вопросов психологии или форм общения. Я хочу остановиться на педагогических ошибках, вопросах организации и проведения учебного занятия.

Надеюсь, эта статья пригодится не только начинающим, но и опытным учителям. Ошибки перечисляются в хаотичном порядке, без ранжирования и расстановки по степени важности.

Итак, каких ошибок следует избегать учителю на уроке?

Ошибка 1. Когда вы задаёте вопрос классу и тут же даёте высказаться добровольцам

Ученики по своему темпераменту, по способностям запоминания довольно разные. Дайте возможность ученикам сначала подумать. Тогда и поднятых рук будет больше, и ответы учеников глубже.

Ошибка 2. Когда урок превращается в мультимедийное шоу

Мультимедиа всегда носит вспомогательный характер. Не нужно становиться заложником красивых слайдов и впечатляющих обучающих видеороликов. Мы теряем минуты драгоценного педагогического общения, внезапного «прозрения» учеников и познания ими нового.

Ошибка 3. Монотонный урок

Когда весь урок выдержан в одном темпе. Когда ученики выполняют всего лишь одну учебную задачу. Если темп урока низкий, то ученики если не уснут, то потеряют всякий интерес к занятию. Если весь урок выдержан только в высоком темпе, — гарантирована быстрая утомляемость учеников. Может утомить ребят и выполнение лишь одной учебной задачи в течение всего занятия.

Ошибка 4. Жёсткая привязанность к сценарию, план-конспекту

Зачастую возникают различные обстоятельства, которые требуют изменения алгоритма занятия:

• Низкая работоспособность класса после выполнения контрольной работы по другому учебному предмету.
• Нет электричества, а у вас главным на уроке является мультимедийное сопровождение.
• Вы пришли в класс, где проектор «дышит на ладан».
• Завис компьютер, а вы, забыв о классе, упорно ждёте, когда откроется необходимый файл.

Лучше отказаться полностью от такого сценария, чем быть обречённым на неудачу.

Ошибка 5. Ученики работают в группах без индивидуальной подотчетности

Учитель разбил класс на группы, в которых ученики не знают своих задач и обязанностей. Одни ученики быстро берут на себя функции лидеров, а другие выбирают на какую руку облокотиться и спать с открытыми глазами и умным видом.

Ошибка 6. Ученики не усвоили учебный материал

По ходу урока учитель так и не выяснил, понятен ли был новый учебный материал, понятно ли вообще, о чём идёт речь на уроке. С первых минут урока учитель не обратил внимание, знакомы ли ученикам термины и понятия, которые посыпались от учителя, как из рога изобилия.

Ошибка 7. Учитель даёт слишком длинные и слишком частые тесты

Контроль знаний, обратная связь, — это, конечно, хорошо. Но этим не стоит злоупотреблять. Вместо системы обучения, учебный процесс превращается в натаскивание.

Ошибка 8. Урок проходит без чётких учебный целей и задач

Тема урока не объявлена. А если даже объявлена, то ученики не получили соответствующих инструкций и учебных задач. Это провальный урок.

Ошибка 9. Учитель не обращает внимание на учеников

Урок-лекция в школе неприемлема. Отсутствие диалога на уроке — катастрофа. Отсутствующие взгляды учеников — катастрофа. Учитель не проверил готовность учеников к учебной работе.

Ошибка 10. Учитель ведёт урок по бумажке

Учитель не держит в голове план урока. Плохо владеет содержанием. Постоянно заглядывает в план-конспект. Даже ходит по классу со своей тетрадью или очень модными в последнее время планшетами для бумаг или даже с электронными планшетами. Читает содержимое слайдов. Ученики теряют доверие к такому учителю. Диалог с учениками становится натянутым и отрывочным. Слабеет обратная связь с классом.

Конечно, ошибок может быть и больше. Каждый из нас знает свои слабые стороны. Но главное не врать самому себе. Признаться, что провалившийся урок — это прежде всего, моя вина, а не поведение учеников или их недостаточные знания и способности.

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.

«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.

Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:

• ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;

• ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

• ошибки, связанные с непониманием структуры теоремы;

• ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;

• ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

• Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.

• Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.

• Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

• Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА

• Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.

• При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)

Типичные ошибки:

20: (х+3)-20:х=20

• При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.

Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.

Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.

Ошибка 2. Пропуск этапа поиска решения.

Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.

Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)

Ошибка 3. Пропуск этапа исследования решения.

Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.

Ошибка 4. Смешение этапов анализа и поиска решения.

Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.

• Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.

На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»

И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.

Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.

2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.

Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.

Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.

Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;

• проверка правильности решения задач путём составления и решения задач, обратных к данной;

• оценка результата решения задачи с точки зрения здравого смысла;

• проверка аналитического решения графическим .

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Пусть решение ученика выглядит так: . Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:

“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.

Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.

Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.

Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.

Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.

Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.

Это можно сделать на следующем содержании материала:

1. Правоцирующие задачи.

Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.

Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.

Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.

Я использую такие разновидности провоцирующих задач:

1. условия, в которых навязывают неверный ответ;

2. условия, которые подсказывают неверный путь решения;

3. условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.

В качестве примера приведу задачи, побуждающие выбор неверного способа решения.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»

2.Задачи стандартные с нестандартным решением.

Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.

Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.

Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.

3. Проблемные задачи.

Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.

Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.

При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.

Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.

Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).

Найти два смежных угла, один из которых больше другого на прямой угол.

Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.

Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 316, значит, 0,310,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.

1. Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)

Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.

Основные методы решения логических задач:

• метод рассуждения;

• метод таблицы;

• метод граф;

• метод кругов Эйлера;

• комбинированный метод.

Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.

Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x², x³, x⁴, x⁵, x⁶, x⁷, x⁸, x⁹ в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.

	X5

Таблицы хорошо применять тогда, когда устанавливается соответствие между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Перед составлением таблиц отрабатываю правила их заполнения.

Например, в 5 классе знакомлю детей с задачей Пуассона (на переливание). Некто имеет 12 пинт сока (пинта- 0,57л) и желает подарить половину своему другу, но у него нет сосуда в 6 пинт, а есть два сосуда в 8 и 5 пинт. Каким образом можно налить 6 пинт сока в сосуд емкостью 8 пинт?

Решение.

Ходы	0	1	2	3	4	5	6	7
12 пинт	12	4	4	9	9	1	1	6
8 пинт	—	8	3	3	—	8	6	6
5 пинт	—	—	5	—	3	3	5	—

Логические связи, при помощи которых была выстроена общая схема решения задачи, помогут учащимся без труда решить подобного рода задачу.

Введение серии таких задач в содержание урока считаю необходимым. Это позволит стереть явную границу между занимательным и учебным материалом. Особенно целесообразно использовать задачи тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.

Для каждой задачи, которую предполагаю использовать на уроке, прежде выясняю: будет ли она интересна классу, органично ли войдет в структуру урока, будет ли ее использование эффективным. Практика показала: учебный навык, на формирование которого направлена та или иная задача, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.

При работе над провоцирующими, проблемными, логическими и стандартными с нестандартным решением задачами наиболее эффективной считаю групповую, парную, индивидуальную, фронтальную работу.

Приведу пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 часов. Однако после 2 часов пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?

Работа над задачей предполагает следующие действия учителя:

1. Предъявление задачи (читает учитель).

2. Определение вида задачи (творческая группа).

3. Выделение гипотез (индивидуальная самостоятельная работа).

4. Обмен мнениями (в творческой группе).

5. Формулировка предположительного ответа (в паре).

6. Проверка ответа на достоверность (фронтальная работа).

Или, задача. Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.

1. Предъявление задачи (творческие группы составляют задачи по готовому чертежу).

2. Выделение гипотез (работа в парах).

3. Обмен мнениями (фронтальная работа).

4. Формулировка предположительного ответа (индивидуальная работа).

5. Проверка ответа на достоверность (индивидуальная работа).

Обязательным этапом на уроке является устный и письменный счет. Целями устного счета являются, во-первых, совершенствование в вычислительных навыков, во-вторых, развитие творческого мышления учащихся.

На своих уроках я стараюсь разнообразить формы и методы устной работы:

— устный счет в начале, в середине, в конце урока;

• устная форма проверки домашнего задания;

• устная форма творческой работы;

• устные самостоятельная и контрольная работы;

• уроки устной работы.

Работая устно, воспитываю у учащихся навыки сознательного усвоения изучаемого материала, приучаю ценить и экономить время, развиваю желание поиска рациональных путей решения задачи. В этих целях использую такие приемы, развивающие творческие способности, как «Зашифрованные задания», «Найди ошибку», «Восстановление»,

«Выбор», «Задачи- сказки», детские презентации на устный счёт, математические листы с задачами, изготовленные самими учащимися, ребусы, кроссворды, которые учащиеся составляют самостоятельно.

Обязательно провожу подробный анализ результатов работы и коррекцию знаний. Объявляя количество набранных баллов, полученных за олимпиадное задание, называю ребят, которые представили самые «красивые» решения. При этом опираюсь на формулу «красивой» задачи по В.Г. Болтянскому: красивая задача = непредсказуемость + непредполагаемость +неожиданность + удивительная простота + простота + фантазия + революционный шаг + удивление + оптимизм + труд + …

Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.

Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека — способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи.

Поэтому решение текстовых задач — это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки».

Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.

Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.

Типичные ошибки учителей при проведении уроков математики в начальной школе

Идеальных уроков не бывает, и даже самые опытные педагоги не всегда могут провести без недочетов разные этапы занятия. Наши эксперты, авторы линий УМК по математике Ольга Муравина и Георгий Муравин, взяв за основу опубликованные в сети открытые уроки, определили самые распространенные ошибки преподавателей на уроках математики в начальных классах и рассказали как преодолеть трудности.

17 сентября 2018

Ошибки учителя на уроке математики

Этап «Самоопределение к деятельности»

1. Нечеткость в постановке целей и задач урока.

Формулируйте цели и задачи в деятельностной форме, например: «Сформировать умение делить двузначные числа на однозначные с остатком». Всегда знакомьте детей с планом урока: зная точно, какие будут темы и какие задания ждут в конце занятия, ученики лучше усваивают материал.

2. Нечеткость в формулировке метапредметных и личностных результатов обучения на этапах урока.

Также формулируйте их для ребят в деятельностной форме: «Ставить цели», «Классифицировать числа», «Проявлять интерес».

3. Затянутое начало урока.

Отводите не больше 5 минут на игровое мотивационное задание, если такое есть. Не ждите всех учеников — достаточно получить ответ от самых активных ребят. Также не тратьте слишком много драгоценного времени на обсуждение девиза урока.

Этап «Актуализация опорных знаний»

4. Нелогичная актуализация знаний: задания из разных разделов математики.

В начале урока выполняйте с ребятами только те задания, которые связаны с новой темой. Актуализация нужна для того, чтобы вспомнить базовые понятия, на которые будут опираться новые знания.

Этап «Постановка учебной задачи»

5. Отсутствие постановки проблемы или, наоборот, затянутость этого этапа.

Обязательно обсудите с детьми учебную задачу, но — быстро, с использованием наводящих вопросов. Не стоит предлагать ребятам сформулировать проблему на листочках: это сложно для детей и, тем более, для учеников начальной школы.

Этап «Изучение нового материала»

6. Работа исключительно на аудиалов.

Если учитель объясняет все устно (дает много занимательной наглядности, но мало учебной наглядности) — дети-визуалы и ребята с другими типами восприятия плохо усваивают информацию. Дублируйте все важное на доске, примеры решений прописывайте развернуто.

7. Отсутствие совместной работы.

Педагоги часто берут всю инициативу в свои руки, из-за чего ученики не производят собственный анализ. Подключайте детей к проговариванию нового материала. Если на доске представлен новый пример по теме, которая частично знакома детям, пусть ученики попробуют сами объяснить то, что видят.

Этап «Первичное закрепление»

8. Недостаточное внимание к алгоритму решения.

Часто алгоритм дается условно, проговаривается вскользь. Но алгоритм — это основа решения, порядок действий для достижения результата. Сформулируйте каждый шаг, зафиксируйте шаги на доске, проработайте их. Когда ученики выполняют задания по новой теме, лучше оставить алгоритм на доске.

9. Обилие фронтальной работы.

Так создается ошибочное впечатление, что все дети одинаково включены в рабочий процесс. Не пренебрегайте работой в тетрадях — она помогает определить эффективность урока, сократить домашнее задание, продемонстрировать родителям успехи и сложности в учебе ребенка.

Этап «Контроль и самоконтроль»

10. Разные задания при групповой работе.

Выдав группам разные задачи, после вы можете потратить слишком много времени на разбор решений. Лучше дать всем группам одну и ту же задачу по теме, и выделить больше времени на обсуждение ее решения.

Этап «Рефлексия деятельности и домашнее задание»

11. Затянутость рефлексии или, наоборот, отсутствие этого этапа.

Для быстрого подведения итогов вы можете предложить ученикам, например, листы самооценки.

12. Демонстрация двоечников.

После того как дети провели самооценку, предложите поднять руки только тем, кто получил «пять» и «четыре». Попросить двоечников показать себя классу — значит создать в конце урока некомфортную обстановку.

Дополнительно

13. Отсутствие описания при публикации открытого урока.

Выкладывая запись открытого урока в интернет, укажите ФИО, город, номер школы, класс, тему урока, учебник — это интересно вашим коллегам.

Учителю на вооружение

Издания корпорации «Российский учебник» составлены таким образом, чтобы помочь учителям избежать ошибок в преподавании математики и сделать каждый урок максимально продуктивным. Вы можете взять на вооружение некоторые пособия бесплатно прямо сейчас:

• Электронные формы учебников (содержание печатных изданий + интерактивные элементы) на сайте Lecta.ru по промокоду 5books.
• Рабочая программа по УМК «Математика. 1-4 классы», Г.К. Муравин, О.В. Муравина.
• Методическое пособие «Математика. 1 класс», О.В. Муравина.
• Методическое пособие
  «Математика. 2 класс», О.В. Муравина.
• Методическое пособие
  «Математика. 3 класс», О.В. Муравина.
• Методическое пособие
  «Математика. 4 класс», О.В. Муравина.

Советы начинающим педагогам. Анализ самых распространенных ошибок начинающего учителя

   Я хочу остановиться на педагогических ошибках, вопросах организации и проведения учебного занятия. Надеюсь, эта статья пригодится не только начинающим, но и опытным учителям.  Итак, каких ошибок следует избегать учителю на уроке?

Ошибка 1. Урок проходит без чётких учебный целей и задач

На уроке обязательно должна быть объявлена тема урока либо учителем, либо детьми. А также сформулированы дидактические задачи для ученика, а для учителя цель данного урока.

Ошибка 2 .  Монотонный урок. Когда весь урок выдержан в одном темпе. Когда ученики выполняют всего лишь одну учебную задачу. Если темп урока низкий, то ученики если не уснут, то потеряют всякий интерес к занятию. Если весь урок выдержан только в высоком темпе, — гарантирована быстрая утомляемость учеников.  Говорит только учитель, отсутствует диалог, обратная связь. В начальной школе нет уроков-лекций. Через каждые 10 миннут необходимо переключать внимание детей на другие задания. Задания должны быть разнообразными.

Ошибка 3. Учитель ведёт урок по бумажке или планшету.

Учитель не держит в голове план урока. Плохо владеет содержанием. Постоянно заглядывает в план-конспект. Даже ходит по классу со своей тетрадью или очень модными в последнее время планшетами для бумаг или даже с электронными планшетами. Читает содержимое слайдов. Ученики теряют доверие к такому учителю. Диалог с учениками становится натянутым и отрывочным. Слабеет обратная связь с классом.

Ошибка 4. Когда вы задаёте вопрос классу и тут же даёте высказаться детям, сразу поднявшим руки.

Ученики по своему темпераменту, по способностям запоминания довольно разные. Дайте возможность ученикам сначала подумать. Тогда и поднятых рук будет больше, и ответы учеников глубже.

Ошибка 5. Когда урок превращается в мультимедийное шоу

Мультимедиа всегда носит вспомогательный характер. Не нужно становиться заложником красивых слайдов и впечатляющих обучающих видеороликов. Есть нормы использования на уроке проектора, не более 15 минут. Это может быть в начале урока, в середине или в конце.

Ошибка 6. За урок не поставлено ни одной отметки. Урок нужно продумать так, что за урок можно было поставить 5-6 отметок (это минимум) . Для этого используем разные формы опроса: индивидуальные карточки, тесты, ответы у доски, оценивание ученика при работе в группах.  Я за сегодняшний урок поставила  13 отметок.

Ошибка 7. Жёсткая привязанность к сценарию, план-конспекту

Необходимо уметь перестроить урок при изменившихся обстоятельствах. Например,  нет электричества, а у вас главным на уроке является мультимедийное сопровождение или Вы пришли в класс, где проектор не включается или завис компьютер. Урок продумать надо так, чтоб его можно было провести и без проектора и компьютера.

Ошибка 8. Ученики работают в группах без четких инструкций и заданий.

Учитель разбил класс на группы, в которых ученики не знают своих задач и обязанностей. Задания в группах составлются с учетом включения каждого ученика в группе (т. е. вопросов должно быть для каждого ученика)

Ошибка 9. Учитель не знает, усвоили ли учебный материал ученики после проведенного урока.

По ходу урока учитель так и не выяснил, понятен ли был новый учебный материал, понятно ли вообще, о чём идёт речь на уроке.  Для этого необходимо проводить задания по усвоению темы. Самый удобный способ-это небольшой тест на первичное закрепление.