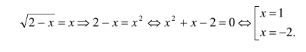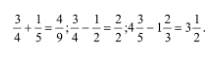Заданий с использованием метода ошибок

Метод проб и ошибок

в решении текстовых задач.

При решении текстовых задач многие учащиеся испытывают затруднения. Главная задача учителя научить решать ученика различные типы текстовых задач. Процесс решения текстовых задач развивает у учащихся логическое мышление, учат находить выход из проблем реальной жизни, дает почувствовать уверенность в своих силах.

Текстовые задачи можно разбить на два основных класса:

• текстовые арифметические задачи;

• текстовые задачи на составление уравнений.

Причем это разделение довольно условно. Многие текстовые арифметические задачи можно решить с помощью уравнений, а задачи на составление уравнений (систем уравнений) часто решают по действиям, а если это не получается, то используют метод проб и ошибок или метод перебора.

Мне бы хотелось продемонстрировать решение ряда задач этими методами.

Задача №1

Одна сторона прямоугольного участка земли на 3 м больше другой его стороны. Площадь участка равна 70 м². Найти размеры этого участка.

Пусть x м ширина участка, (x+3) м – длина участка, а площадь x·(x+3) м²,

что по условию задачи равно 70 м². Чтобы найти размеры участка надо составить уравнение x·(x+3)=70 и решить его. Но в 5^ом классе такие учащиеся решать еще не могут. Поэтому попробуем подобрать решение «экспериментально», так называемым методом проб и ошибок.

1. пусть x=4, т.е. 4·(4+3)=28, 28≠70;

2. x=6, т.е. 6·(6+3)=54, 54≠70;

3. x=7, т.е. 7·(7+3)=70, 70=70 верно.

Т.е. мы увидели, что метод проб и ошибок позволяет найти ответ даже в случае, когда математический модель представляет собой новый, не изученный еще объект. Но, решая задачи этим способом, следует помнить, что подбор одного решения не гарантирует полноты решения. Поэтому необходимы обоснования того, что найдены все возможные решения.

В нашей задаче, если бы x было больше 7,то x+310 и x·(x+3)70, если наоборот xx+3 x·(x+3)

Задачи для учащихся.

Переведи условие задачи на математический язык и найди решение методом проб и ошибок.

1. Площадь прямоугольника равна 68 дм², а длина больше ширины на 13 дм. Каковы стороны этого прямоугольника?

2. Ширина прямоугольника на 9 см меньше длины, а площадь равна 90 см². Найти стороны прямоугольника.

3. Найти периметр прямоугольника, площадь которого составляет 18 м², а ширина в 2 раза меньше длины.

4. Площадь прямоугольника равна 64 дм², а его длина в 4 раза больше ширины. Чему равен периметр прямоугольника?

5. Длину прямоугольника уменьшили на 3 см, а ширину увеличили на 4 см и получили квадрат. Найти сторону квадрата, если площадь прямоугольника равна 30 см².

6. После того как ширину прямоугольника увеличили на 1 м, а длину уменьшили на 5 м, получили квадрат. Чему равна площадь квадрата, если площадь прямоугольника 91 м².

7. Длина прямоугольника на 5 м больше ширины, а площадь составляет 24 м². каковы стороны этого прямоугольника?

8. Длину прямоугольника уменьшили в 2 раза, а ширину увеличили на 1 дм и получили квадрат. Найти сторону квадрата, если площадь прямоугольника 60 дм².

9. Найти периметр прямоугольника, у которого ширина на 4 см меньше длины, а площадь составляет 32 см².

10)Одна из сторон прямоугольника на 20 см больше другой. Если

большую сторону уменьшить в 3 раза, а меньшую сторону увеличить

в 2 раза, то площадь нового прямоугольника будет равна 200 см².

Найти стороны данного прямоугольника.

Метод перебора при

нахождении НОД.

Рассмотрим еще один метод – метод перебора. Т.к. предыдущий метод решения задач – метод проб и ошибок не дает уверенности в том, что найдены все искомые значения. Поэтому для обоснования полноты решения требуются дополнительные, иногда очень непростые рассуждения. В этом недостаток метода проб и ошибок. Но он исключен в методе полного перебора.

Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем «лобовой» перебор.

Задача. На экскурсию едут 252 ученика школы. Для них заказаны

несколько автобусов. Однако выяснилось, что если заказать

автобусы, вмещающие на 6 человек больше, то автобусов

потребуется на один меньше. Сколько больших автобусов надо

заказать?

Составим таблицу.

	Кол-во детей в одном автобусе	Количество автобусов	Общее кол-во детей
Большие автобусы	252 : x	x	252
Маленькие автобусы	252 : (x+1)	x+1	252

Т.к. по условию в большой автобус вмещается на 6 детей больше, чем в маленький, то разность 252 : x — 252 : (x+1) = 6. Значит решением задачи является число X, удовлетворяющее равенству: 252 : x — 252 : (x+1) = 6.

Но можно получить более простую математическую модель этой задачи, обозначив дополнительно буквой Y число детей, которых можно разместить в большом автобусе.

	Кол-во детей в одном автобусе	Количество автобусов	Общее кол-во детей
Большие автобусы	y	x	252
Маленькие автобусы	y-6	x+1	252

Очевидно, что в этом случае математической моделью задачи являются два равенства:

1. xy = 252;

2. (x+1)·(y-6) = 252.

Искомые числа x и y должны удовлетворять как первому, так и

второму равенству. Найдем эти числа x и y.

Из равенства xy = 252 можно заметить, что числа x и y не могут быть

больше, чем 252. Однако и в этом случае «лобовой» перебор потребовал бы рассмотрения огромного числа вариантов. Но более внимательный анализ первого равенства показывает, что числа x и y – это парные делители 252: при делении 252 на x получается y, и наоборот. Следовательно, достаточно рассмотреть лишь парные делители числа 252, причем для случая, когда y6 (y-60).

Составим таблицу:

+1

x	1	2	3	4	6	7	9	14	18	28	36
y	252	126	84	63	42	36	28	18	14	9	7

— 6

Анализ второго равенства позволяет еще больше сократить число возможных вариантов. Оно означает, что число (x+1) и (y-6) так же являются парными делителями 252. Из таблицы видно, что такими свойствами обладает только пара x=6, y=42.

Ответ: для экскурсии надо заказать 6 больших автобусов.

Задачи для учащихся.

1. Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 меньше исходного. Найти эти числа.

2. Сумма цифр двузначного числа равна 12. число, записанное теми же цифрами, но в обратном порядке, составляет ⁴ /₇ исходного числа. Найти эти числа.

3. Одно из двух натуральных чисел на 4 больше другого. Найди эти числа, если их произведение равно 96.

4. У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и трехместных лодок было у причала?

5. Прямоугольный газон обнесен изгородью, длинна которой 30 м. Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.

6. В несколько посылок упаковали 36 книг и 54 журнала, распределив их между посылками поровну. В каждой посылке книг на 2 меньше, чем журналов. Сколько получилось посылок?

7. Произведение двух натуральных чисел равно 72. Найти эти числа, если одно из них больше другого на 6.

8. На турбазе имеются палатки и домики, общее число которых равно 25. в каждом домике живут 4 человека, а в палатке – 2 человека. Сколько на турбазе палаток и сколько домиков, если всего на этой турбазе отдыхают 70 человек?

9. Прямоугольный участок земли обнесен забором, длина которого 40 м. Площадь участка 96 м². Найти длины сторон этого участка, если известно, что они выражаются натуральными числами.

Еще один тип задач, которые решаются методом перебора.

Задумано двузначное число, которое на 52 больше произведения своих цифр. Какое число задумано?

Пусть xy – задуманное двузначное число, где x – цифра десятков, а y – цифра единиц. Тогда их произведение равно xy. Само двузначное число можно записать как 10x+y. По условию 10x+y на 52 больше произведения своих цифр xy. Т.е. должно выполняться равенство 10x+y= xy+52, которое является математической моделью данной задачи.

Решается это уравнение методом перебора. Полный перебор можно провести, рассматривая последовательно все значения x от 1 до 9 и подбирая в каждом случае соответствующее значение y от 0 до 9.

Однако этот перебор можно сократить, если заметить, что первая часть данного равенства больше 52. Значит, и первая его часть, т.е. задуманное число, больше 52. Поэтому неизвестное число x не меньше 5, и можно рассматривать только пять значений x – от 5 до 9.

При x=5 будем иметь равенство 50+y=5y+52, оно невозможно, т.к. 50+yy+52.

При x=6 60+y=6y+52 | -y

60=5y+52

5y=8 невозможно для натурального y.

При x=7 70+y=7y+52

70=6y+52

6y=18

y=3 Число 73

При x=8 80+y=8y+52

80=7y+52

7y=28

y=4 Число 87

При x=9 90+y=9y+52

38=8y невозможно

Таким образом, задумано либо 73, либо 84.

Условие задачи не дает возможности ответить на этот вопрос. Поэтому два ответа: 73 или 84.

Задачи для учащихся.

Метод перебора используется при доказательстве общих утверждений, где необходимо вводить буквенные обозначения.

Например: Доказать, что сумма любых трех последовательных натуральных чисел делится на 3.

1 сл. 1,2,3 1+2+3=6, 6:3=2

2 сл. 5,6,7 5+6+7=18, 18:3=6

3 сл. 21,22,23 21+22+23=66 66:3=22

и т.д.

Возьмем произведение натурального числа и обозначим его n. Тогда следующие за ним два числа соответственно равны n+1 и n+2.

Их сумма: n+(n+1)+(n+2)=3n+3=3(n+1) делится на 3, т.к. один из множителей делится на 3.

Тренинг креативного мышления

Занятие № 1. Метод проб и ошибок

Цель занятия: познакомить студентов с понятием креативности и методом проб и ошибок.

1. Вводное тестирование экспериментальной группы.

2. Беседа со студентами.

Занятие, которое у нас с вами сегодня начинается, называется «Тренинг креативного мышления». Ежедневно мы слышим по телевизору, или в школе, или на улице слово креативность. Нам говорят вот это креативно, а вот это нет. Этот подход креативный, а вот этот обычный. Так что же такое креативность? Как вы считаете, что скрывается под словом тренинг креативного мышления?

Так, каждый из вас абсолютно в чем-то прав, под креативностью мы будем понимать способность человека к творчеству, способность создавать что-то оригинальное, казалось бы, из стандартной ситуации.

Нам с вами приходится ежедневно решать очень много всевозможных, разнообразных проблем. Задачи бывают не только, как наверное частенько вы считаете, математические, но и жизненные (бытовые, семейные, политические).

Ежедневно современному человеку приходится преодолевать всевозможные трудности, и при том, как можно эффективнее. А знать решение всех проблем, которые с нами могут случиться, невозможно.

Давайте попробуем сосчитать, сколько математических задач мы с вами решаем при обучении в колледже. Итак, предположим, что на занятии вы решаете 5 задач, а дома еще 3. На каждом году обучения в колледже вы посещаете около 140 занятий математики, тогда получаем, что в год мы решаем около 1120 задач. За первые 2 года обучения в колледже мы с вами решим 2240 задач. Отбросим 240 на праздники или случаи, когда вам не удалось решить задачу, получим 2 000 Можно даже вычесть еще 200 которые решили не самостоятельно. Итак, получаем что вы решили 1800 задач, то есть вы умеете решать около 1800 задач.

Казалось бы, вон как много, зачем нам уметь решать какие-то другие задачи и этого хватит. Ученые посчитали, что за свою жизнь человек решает около миллиона проблемных ситуаций. Так что, скажете вы, теперь, чтобы комфортно жить в будущем, нам в колледже придется научиться все их решать, так на это уйдет как раз всю жизнь, даже больше.

На самом деле, как хорошо было бы их уметь решать с помощью одного алгоритма или универсального механизма. Загрузил все данные нашей проблемы, и она выдает нам сразу решение. Такого алгоритма, конечно же, нет. А вот приемы и методы, которые нам часто помогают прийти к решению какой-либо проблемы, есть. И наша задача научится ими пользоваться в рамках нашего тренинга.

3. Прикладное упражнение.

Упражнение 1. Сейчас на парту будет выдано изображение чего-либо. Попробуйте в парах придумать название этой картинке, что как можно точнее отражает сюжет картинки. Потом мы с вами посмотрим, у кого оригинальнее получится. (Плавно подводит к преодолимым методам при придумывании названия картинке). (Пример фото «Микромир»)

4. Метод проб и ошибок.

Часто, когда мы с вами решаем, определенную задачу, мы выбираем самый легкий способ решения, просто перебираем все возможные варианты. Из всех вариантов оставляем только те, которые нам подходят. Такой метод решения, задач, когда происходит перебор всех вариантов решения, носит название — метод проб и ошибок. От начальных условий задачи мы движемся в «разных направлениях» стороны, своеобразно пытаясь найти решение, и только часть из направлений поиска оказываются успешными.

5. Упражнения математического характера.

Упражнение 2. В каком случае произведение двух натуральных чисел дает четное число.

Решение. Рассмотрим произведение двух натуральных чисел. И если учесть, что должно равняться четному числу, то . Достаточно рассмотреть три случая, когда числа оба четные, оба нечетные и одно четное второе нет. Тогда ответом будет любая пара натуральных чисел, одно из которых четное.

Упражнение 3. Сумма каких двух натуральных чисел равна их произведению?

Упражнение 4. Сумма каких двух натуральных чисел больше чем их произведение?

Упражнение 5. Могут ли числа 458, 523, 652 быть квадратами или кубами целого числа?

6. Подведение итогов.

Занятие № 2. Идеальный конечный результат

Цель занятия: познакомить студентов с принципом идеального конечного результата, как инструмента для продуктивного решения задачи.

1. Повторение. Метод проб и ошибок.

Представьте, что девочка Света собралась на дискотеку и думает, что ей надеть. Начинает подбирать себе платье. Первое — то, второе — то, третье, четвертое, шестое – вот это. И в итоге нашла себе платье. Все хорошо, она просто взяла и стала перебирать все возможные варианты, все имеющиеся у нее платья и в результате «наткнулась» на необходимое.

Такой метод, когда перед нами стоит проблема, мы называли в прошлом занятии Метод проб и ошибок. А теперь представьте, что у Светы не 10 платьев, а 100 или даже 1000 или и того больше. Тогда сколько ей понадобится времени, чтобы найти нужное платье. Час, два, неделю, а потом и дискотека закончится. Точно так при решении каких-либо задач очень неэффективно бывает перебирать все варианты, это может, пойти уйма времени.

Так, например, решая какое-либо уравнение нам легче его именно «решать», а не перебирать все варианты.

Поэтому, наверное, нам нужны какие-то способы, которые эффективно решают поставленные перед нами задачи. Один из них мы сегодня разберем.

2. Что такое ИКР?

— Приходилось ли вам когда-нибудь стрелять из спортивного лука? Смогли вы с первого раза попасть в мишень на расстоянии 50 метров?

— Наверное нет. Вряд ли.

— Не уверены? Да, для этого нужно тренироваться. Предположим, что вы хорошо натренированы. Тогда смогли бы попасть в мишень?

— Да, несомненно.

— А если предположить, что вам завязали глаза? Вы бы смогли попасть?

— Нет. Мы же не видим цели!

— Но цель перед вами. А если вас еще покрутить вокруг себя перед выстрелом? Вы будете стрелять наугад. И каковы будут ваши шансы попасть?

— Да кто же так стреляет, непонятно в какую сторону, и притом не видя цели.

— А как же тогда можно решить задачу, если решать ее, не видя цели?

Принцип идеального конечного результата (ИКР) — осуществляется в идеальных условиях, то есть требование системы выполняется при отсутствии ее самой. При этом, под системой понимается любая совокупность данных взаимосвязанных компонентов.

Учебные задачи для возможности самоконтроля часто обеспечены ответами к решению задачи. И многие студенты не удерживаются от соблазна сначала посмотреть правильный ответ, а потом решать задачу, получив своеобразный мысленный ориентир. Одним из таких ориентиров при решении проблем, и не только математических, служит ИКР.

3. Разбор прикладных упражнений.

Ситуация 1. Приехал студент — житель Севера на каникулы к дедушке. Пригласил его дед охотиться на медведя. Не хотел студент показаться трусом. Согласился. Пошли. Нашли берлогу. Разбудили медведя. Выскочил медведь из берлоги, бросился на них. Они — бежать. Бежит студент и думает: «У меня же ружье. И я — не трус ». Разворачивается и стреляет в медведя. Подходит тут к нему старый охотник и говорит: «Однако, плохой ты охотник. Зачем стрелял? Теперь бери его и тащи. Подошел бы к дому — там бы и убили ».

Этот пример заслуживает более детального разбора. Все дело в разном понимании главной функции. Для старого охотника главная функция — доставить добычу в дом. Для студента — проявить свою храбрость на охоте. И вероятно, старый охотник уже умел применять наш принцип, поскольку очень четко формулирует идеальный способ доставки добычи в дом — добыча САМА себя доставляет.

В природе также встречаются аналогичные примеры идеальности.

Ситуация 2. Рыбка-антенна. Обитает в морских глубинах, обычно лежит на дне и привлекает кусочком мясистой кожуры, которая болтается на кончике булавки, выступающей из верхней челюсти хищницы. Прежде чем наивная жертва осознает ошибку, она уже окажется в желудке охотника.

Ситуация 3. Растение росянка. Это небольшое растение можно найти на торфяных болотах. Его листья, собранные в розетку, покрытую красноватыми ловчими волосками-щупальцами с красной головкой наверху. Она выделяет липкую жидкость и поэтому покрыта росой. В центре листа волоски короткие, по краям — более длинные. Мухи, муравьи, привлеченные блеском капелек, попадают на лист и прилипают к нему. Жертва мечется, бьется и при этом задевает соседние волоски, сама себя все более запутывая. Край листа начинает медленно загибаться и накрывает свою добычу, которая тут же и переваривается.

Ситуация 4. Волшебная лампа Лавегрова. Вам потребуется очень много времени, чтобы найти выключатель в настольной лампе Адапсоп, созданной дизайнером Россом Лавегровом. Его просто нет. Чувствительный к прикосновению алюминиевый ободок плафона соединен с реостатом внутри — лампы, позволяет одним движением руки не только включать или выключать свет, но и менять его интенсивность от совсем приглушенного до максимально яркого.

Но все же это не совсем идеальный способ включения. А что если бы лампа сама себя включала в нужный момент?

Идеальный выключатель — выключателя нет, а его функция выполняется. Специальный датчик сам включает ночник при наступлении темноты, когда темнеет, а света нет, лампочка сама зажигается, а когда встает солнце — гаснет.

Ситуация 5. Плеер без плеера. Плеер от компании Evoltion Technologies имеет такой размер, что он просто вмещается в ухо, по форме он похож на простой наушник.

Вернемся к девочке Свете, которая собирается на дискотеку, для быстрого выбора ей достаточно вспомнить, что она собирается именно на дискотеку, тогда, например, спортивные варианты одежды уже сразу не подойдут и не стоит тратить на них время.

Задача 1. Дорожные знаки. Ночью дорожных знаков не видно, поскольку не освещаются. Только при достаточно близком приближении к ним, когда они освещены светом фар, можно разглядеть знак.

Противоречия. Знаки должны быть освещены, чтобы их было видно, и не должны быть освещены, поскольку неэкономно расходовать электроэнергию на их постоянное освещение.

ИКР. Когда знаки сами себя освещают в нужный момент при приближении автомобиля.

Решение. Дорожные знаки покрыты специальной люминофорной краской, которая начинает светиться при освещении ее даже слабым светом. Такие знаки видно издалека.

Задача 2. ИКР вокруг вас. Попробуйте привести свои примеры из живой природы или техники, окружающей вас.

4. Математические задачи.

Задача 3. Сумма каких двух натуральных чисел равна их произведению.

ИКР:

решение: , А значит целое. Но это число может быть целым только при. ответ:.

Задача 4. Сумма каких двух натуральных чисел больше чем их произведение.

ИКР:

решение: . так как .

тогда если тогда ().

если тогда

Ответ: Только в том случае, если одно из чисел является 1.

Задача 5. По разные стороны от прямого шоссе расположены два села. В каком месте на шоссе нужно построить автобусную остановку, чтобы расстояние от каждого села к ней была одинаковой? Шириной шоссе пренебрегать.

ИКР. Для решения воспользуемся принципом ИКР: соединим отрезком k (дорога) две точки A и B (две деревни). Если середина M в точности попадает на дорогу (l), то задача решена (рис. 1).

Решение. Рассмотрение случая, когда центр отрезка k не лежит на прямой l, подталкивает на мысль, что двигая прямую k, точка М помогает легко найти необходимую точку, восстановив к ней перпендикуляр и рассмотрев равнобедренные треугольники (рис. 2).

Конечно, следует сделать вывод о том, что задача не будет иметь решение, если отрезок k будет перпендикуляром к прямой l.

Задача 6. Задачи для самостоятельного решения.

1. Где надо построить автобусную остановку, если деревни расположены по одну сторону от шоссе?

2. Какое натуральное число больше его единиц в семь раз?

3. Какую последнюю цифру может иметь квадрат натурального числа?

4. Какую последнюю цифру может иметь куб натурального числа?

5. Найдите число, одна треть с одной четвертью которого составляет 21.

6. Полутреть — число 100. Что это за число?

7. Докажите, что если произведение нечетное, то и число m нечетное, и число n нечетное.

8. Докажите, что всякое нечетное число, не равное единице, есть разность квадратов двух каких-то чисел.

9. В комнате находятся 5 человек. Докажите, что найдутся 2 человека, которые сделают одинаковое число рукопожатий.

10. Сколько существует четырехзначных чисел с суммой цифр 34?

11. Петр решал пример 47, 48, 49, 58 и у него вышел ответ 1266. Покажите, что Петр где-то ошибся.

12. Сколько чисел от 1 до 100 ни делится, ни на 2, ни на 3?

5. Подведение итогов. Домашнее задание.

Прием «Зигзаг» на уроке: советы и рекомендации учителю

Прием «Зигзаг» придуман для тех случаев, когда требуется в короткий срок усвоить большой объем информации. Например, в некоторых программах для изучения той или иной темы отводится мало часов. А объем параграфов в учебниках не позволяет рассмотреть все их на уроке. Вот в таких случаях на выручку педагогу приходит прием «Зигзаг». 

Во-первых, он позволяет детально и в короткий срок освоить довольно большой объем информации.

• Во-вторых, усвоение материала происходит в интерактивной форме, то есть не учитель выдает готовое знание, а сами учащиеся.
• В-третьих, мобилизуется способность учащихся выделять главное из текста, систематизировать информацию.
• В-четвертых, развивается умение работать в группе, сообща.
• В-пятых, охваченным оказывается весь класс, здесь не будет пассивных учащихся.
• В-шестых, прием «Зигзаг» позволяет включать в работу и другие приемы ТРКМ, такие как «кластер«, «эссе», «сводные таблицы» и пр.

Алгоритм работы с приемом «Зигзаг» на уроке

Итак, условия заданы — требуется за урок освоить большой пласт материала.

• Текст изначально делится учителем на несколько частей (на сколько — см. условия ниже).
• Класс делится на группы с равным количеством участников. Например, на 5 групп по 5 учеников в каждой группе. Для удобства будем называть эти первичные группы рабочими. Текст должен быть поделен на столько частей, сколько участников в этой первичной группе.

Если текст слишком объемный, то можно разделить класс на три рабочие группы по 7 человек в каждой. Но не больше.

• Каждая группа получает один и тот же текст. Причем каждый участник рабочей группы получает по одному отрывку из текста. Эти отрывки можно пронумеровать или отметить разными цветами.
• Индивидуальная работа. Каждый ученик работает со своей частью текста — прорабатывает информацию, анализирует, составляет опорный конспект. Важно, чтобы из отрывка было взято все самое нужное. Задача ученика: представить своеобразную «выжимку», квинтэссенцию. Причем сделать это он может по-разному — составить кластер, таблицу, схему, инфографику и т.д.
• Следующий этап работы — групповой. Теперь учащиеся переходят к своим «коллегам». Составляются экспертные группы. То есть, в одной команде окажутся все те, кто получил отрывок № 1, в другой — те, кто получил отрывок № 2. Начинается этап обсуждения. Учащиеся обмениваются своими работами, мнениями, выбирают самый лучший вариант для презентации своей части текста.

Дополнительным заданием может быть составление вопросов по своему отрывку, которые покажут, насколько остальные поняли и усвоили материал. Причем вопросы тоже можно разнообразить — либо это просто вопросы, либо мини-тесты, либо какое-то практическое задание.

• После этого ребята возвращаются в свои рабочие группы, и начинается этап размышления. Каждый по очереди презентует свою часть текста. Будет это краткое изложение, кластер, таблица — это решено уже на стадии работы в экспертной группе. Таким образом, каждый из учеников получает сведения по всему тексту.
• Завершается «Зигзаг» общей работой всего класса. Каждую часть текста презентует один из экспертов по данному вопросу. В итоге происходит вторичное прослушивание материала. Остальные эксперты «дополняют» коллегу.

На этапе рефлексии учащиеся решают, чья презентация материала была наиболее точной и эффективной. А также намечают круг вопросов, которые требуют уточнений, пояснений. Итогом такой работы может стать совместный проект или презентация.

«Зигзаг-2», или облегченный вариант

Этот прием можно использовать для изучения текста меньшего объема или, например, при изучении художественного произведения. Так, прием «Зигзаг» можно использовать и в начальной школе, а его облегченный вариант и на уроках литературы.

В этом случае текст изучается каждым учеником полностью.

• Для деления на группы учитель изначально предлагает определенное количество вопросов.
• Получив свой вопрос, ученик отвечает на него, так же составляет график, кластер и проч.
• Далее также следует работа в экспертных группах, которая решит, чья презентация наиболее объективна.
• Работа в рабочих группах проводится, как и в «Зигзаге-1», только презентуются уже ответы на вопросы по тексту.
• Итоговая работа — общая. Один из экспертов каждой группы представляет свой вариант ответа на вопрос. Вторичное прослушивание еще больше закрепляет информацию в сознании учащихся.

Таким образом, за один урок можно освоить довольно большой пласт информации. Прием «Зигзаг» только на первый взгляд кажется громоздким и неудобным. На практике дети быстро втягиваются в процесс, так как работа в группах активизирует элемент соревнования.  

Метод «Фишбоун» (Рыбий скелет): что это такое, формы работы на уроке и примеры

34194

Одним из методических приемов, который можно использовать в группах, является прием «Фишбоун». Дословно он переводится с английского как «Рыбная кость» или «Скелет рыбы» и направлен на развитие критического мышления учащихся в наглядно-содержательной форме. Суть данного методического приема — установление причинно-следственных взаимосвязей между объектом анализа и влияющими на него факторами, совершение обоснованного выбора. Дополнительно метод позволяет развивать навыки работы с информацией и умение ставить и решать проблемы. Что такое фишбоун?

Диаграмма Исикавы

В основе Фишбоуна — схематическая диаграмма в форме рыбьего скелета. В мире данная диаграмма широко известна под именем Ишикавы (Исикавы) — японского профессора, который и изобрел метод структурного анализа причинно-следственных связей. Схема Фишбоун представляет собой графическое изображение, позволяющее наглядно продемонстрировать определенные в процессе анализа причины конкретных событий, явлений, проблем и соответствующие выводы или результаты обсуждения.

Схемы Фишбоун дают возможность:

• организовать работу участников в парах или группах;
• развивать критическое мышление;
• визуализировать взаимосвязи между причинами и следствиями;
• ранжировать факторы по степени их значимости.

С помощью схемы можно найти решение из любой рассматриваемой сложной ситуации, при этом возникают каждый раз новые идеи. Эффективным будет ее применение во время Мозгового штурма.

Нажмите для увеличения

Составление схемы Фишбоун

Схема Фишбоун может быть составлена заранее. С применением технических средств ее можно сделать в цвете. При их отсутствии используется обычный ватман либо ежедневный инструмент учителя — цветной мел.

В зависимости от возрастной категории учащихся, желания и фантазии учителя схема может иметь горизонтальный или вертикальный вид. Суть приема Фишбоун форма схемы не меняет, поэтому особо не имеет значения. Для младшего школьного возраста подойдет более естественная форма рыбы — горизонтальная. По завершению ее заполнения вместе с ребятами можно изобразить фигуру вдоль скелета и загадать желание, чтобы золотая рыбка и в дальнейшем помогала решить любую жизненную проблему.

Нажмите для увеличения

Схема включает в себя основные четыре блока, представленные в виде головы, хвоста, верхних и нижних косточек. Связующим звеном выступает основная кость или хребет рыбы.

• Голова — проблема, вопрос или тема, которые подлежат анализу.
• Верхние косточки (расположенные справа при вертикальной форме схемы или под углом 45 градусов сверху при горизонтальной) — на них фиксируются основные понятия темы, причины, которые привели к проблеме.
• Нижние косточки (изображаются напротив) — факты, подтверждающие наличие сформулированных причин, или суть понятий, указанных на схеме.
• Хвост — ответ на поставленный вопрос, выводы, обобщения.

Прием Фишбоун предполагает ранжирование понятий, поэтому наиболее важные из них для решения основной проблемы располагают ближе к голове. Все записи должны быть краткими, точными, лаконичными и отображать лишь суть понятий.

Применение метода Фишбоун на уроке

Схема Фишбоун может быть использована в качестве отдельно применяемого методического приема для анализа какой-либо ситуации, либо выступать стратегией целого урока. Эффективнее всего ее применять во время урока обобщения и систематизации знаний, когда материал по теме уже пройден и необходимо привести все изученные понятия в стройную систему, предусматривающую раскрытие и усвоение связей и отношений между ее элементами.

Так, учащимся предлагается информация (текст, видеофильм) проблемного содержания и схема Фишбоун для систематизации этого материала. Работу по заполнению схемы можно проводить в индивидуальной или групповой форме. Важным этапом применения технологии Фишбоун является презентация полученных результатов заполнения. Она должна подтвердить комплексный характер проблемы во взаимосвязи всех ее причин и следствий. Иногда при заполнении схемы учащиеся сталкиваются с тем, что причин обсуждаемой проблемы больше, чем аргументов, подтверждающих ее наличие. Это возникает вследствие того, что предположений и в жизни всегда больше, чем подтверждающих фактов. А потому некоторые нижние косточки могут так и остаться незаполненными. Далее в ходе урока учитель самостоятельно определяет действия — предлагает либо и далее исследовать проблему, либо попытаться определить ее решение.

Овладев технологией Фишбоун, учитель может с успехом ее применять на любом уроке. Наиболее популярной она является среди учителей-филологов либо историков. Этап урока с применением метода Фишбоун приобретает исследовательский характер.

Формы работы на уроке

• Индивидуальная работа. Всем учащимся раздается для анализа одинаковый текст и перед каждым ставится цель — заполнить схему «Рыбий скелет» на протяжении 10 минут. Затем проходит обсуждение результатов, обмен мнениями и заполнение общей схемы на доске.
• Работа в группах. Каждая из групп получает свой текст. Чтение текста происходит индивидуально, а его обсуждение – в группах. Общая схема Фишбоун заполняется на основе мнений групп.

Примеры использования технологии Фишбоун в обучении

Пример 1.

Фишбоун на уроке литературы при изучении повести Б. Полевого «Повесть о настоящем человеке» с применением межпредметных связей.

• Голова — легко ли совершить подвиг.
• Верхние косточки — герои смелые, хочется жить; нужно защищать Родину;
• Нижние косточки — мастерство летчика, выдержка героя, любовь к Родине.
• Хвост — каждый человек может стать героем, если он патриот.

После составления фишбоуна можно предложить учащимся обозначить части речи или выделить орфограммы в использованных словах (связь с русским языком), подготовить сообщение о великом летчике А. Мересьеве (связь с историей).

Пример 2.

Фишбоун на уроке истории по проблеме «Причины феодальной раздробленности Руси».

• Голова — причины феодальной раздробленности.
• Верхние косточки — стремление феодалов к независимости; усложнение социальной структуры; благоприятное внешнеполитическая обстановка.
• Нижние косточки — перестали делиться с Киевом; появилось дворянское сословие; отсутствие внешней угрозы.
• Хвост — феодальная раздробленность была неизбежной.
• Использование технологии Фишбоун развивает умения учащихся работать в группах, анализировать текст, выделять основные события и искать их причины, обобщать и делать выводы. Основная цель метода — стимулировать творческое и развивать критическое мышление детей, что отвечает главной задаче сегодняшней школы.

Прием кластер на уроке. Что это такое и как его использовать? Примеры

48183

Кластер — это графическая форма организации информации, когда выделяются основные смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними. Он представляет собой изображение, способствующее систематизации и обобщению учебного материала. 

Кластер как один из методов критического мышления

Современная система образования ориентирована на формирование у учеников самостоятельного мышления. Критическое мышление является педагогической технологией, стимулирующей интеллектуальное развитие учащихся. Кластер — один из его методов (приемов).

К особенностям критического мышления относят наличие трех стадий:

• вызов,
• осмысление,
• рефлексия.

На первом этапе происходит активизация, вовлечение всех участников коллектива в процесс. Целью является воспроизведение уже имеющихся знаний по данной теме, формирование ассоциативного ряда и постановка вопросов, на которые хочется найти ответы. На фазе осмысления организуется работа с информацией: чтение текста, обдумывание и анализ полученных фактов. На стадии рефлексии полученные знания перерабатываются в результате творческой деятельности и делаются выводы.

Прием кластера может применяться на любой из стадий.

• На этапе вызова дети высказывают и фиксируют все имеющиеся знания по теме, свои предположения и ассоциации. Он служит для стимулирования познавательной деятельности школьников, мотивации к размышлению до начала изучения темы.
• На стадии осмысления использование кластера позволяет структурировать учебный материал.
• На стадии рефлексии метод кластера выполняет функцию систематизирования полученных знаний.

Возможно применение кластера на протяжении всего урока, в виде общей стратегии занятия, на всех его стадиях. Так, в самом начале дети фиксируют всю информацию, которой они владеют. Постепенно, в ходе урока, в схему добавляются новые данные. Желательно выделять их другим цветом. Данный прием развивает умение предполагать и прогнозировать, дополнять и анализировать, выделяя основное.

Основные принципы составления кластера

Кластер оформляется в виде грозди или модели планеты со спутниками. В центре располагается основное понятие, мысль, по сторонам обозначаются крупные смысловые единицы, соединенные с центральным понятием прямыми линиями. Это могут быть слова, словосочетания, предложения, выражающие идеи, мысли, факты, образы, ассоциации, касающиеся данной темы. И уже вокруг «спутников» центральной планеты могут находиться менее значительные смысловые единицы, более полно раскрывающие тему и расширяющие логические связи. Важно уметь конкретизировать категории, обосновывая их при помощи мнений и фактов, содержащихся в изучаемом материале.

Правила оформления кластера на уроке

В зависимости от способа организации урока, кластер может быть оформлен на доске, на отдельном листе или в тетради у каждого ученика при выполнении индивидуального задания. Составляя кластер, желательно использовать разноцветные мелки, карандаши, ручки, фломастеры. Это позволит выделить некоторые определенные моменты и нагляднее отобразить общую картину, упрощая процесс систематизации всей информации.

Рекомендации по составлению кластера

Существует несколько рекомендаций по составлению кластера. При его создании не стоит бояться излагать и фиксировать все, что приходит на ум, даже если это просто ассоциации или предположения. В ходе работы неверные или неточные высказывания могут быть исправлены или дополнены. Учащиеся могут смело дать волю воображению и интуиции, продолжая работу до тех пор, пока не закончатся все идеи. Не стоит бояться значительного количества смысловых единиц, нужно попытаться составить как можно больше связей между ними. В процессе анализа все систематизируется и станет на свои места.

Применение метода кластер

Метод кластера может применяться практически на всех уроках, при изучении самых разных тем.

Форма работы при использовании данного метода может быть абсолютно любой: индивидуальной, групповой и коллективной. Она определяется в зависимости от поставленных целей и задач, возможностей учителя и коллектива. Допустимо перетекание одной формы в другую. Например, на стадии вызова, это будет индивидуальная работа, где каждый учащийся создает в тетради собственный кластер. По мере поступления новых знаний, в качестве совместного обсуждения пройденного материала, на базе персональных рисунков и с учетом полученных на уроке знаний, составляется общая графическая схема. Кластер может быть использован как способ организации работы на уроке, и в качестве домашнего задания. В последнем случае важно наличие у учащихся определенного опыта в его составлении.

Пример

В качестве примера приведем составление кластера на уроке обществознания при изучении темы «Монархия». В самом начале работы учащиеся высказывают все имеющиеся у них знания по данному вопросу, предположения и ассоциации. Например: форма правления, власть, глава государства, царь, монарх, единовластие. Учитель фиксирует их на доске. Далее следует чтение параграфа из учебника. В ходе ознакомления с материалом (или по результату прочтения), схема дополняется новыми фактами. Учитель дописывает их, используя цветной мел. Итогом урока должен стать анализ полученной картины, с обсуждением верности или неверности первоначальных суждений и обобщением полученной информации.

Достоинства и результаты применения приема

Применение кластера имеет следующие достоинства:

• он позволяет охватить большой объем информации;
• вовлекает всех участников коллектива в обучающий процесс, им это интересно;
• дети активны и открыты, потому что у них не возникает страха ошибиться, высказать неверное суждение.

В ходе данной работы формируются и развиваются следующие умения:

• умение ставить вопросы;
• выделять главное;
• устанавливать причинно-следственные связи и строить умозаключения;
• переходить от частностей к общему, понимая проблему в целом;
• сравнивать и анализировать;
• проводить аналогии.

Что дает применение метода кластера на уроках детям? Прием кластера развивает системное мышление, учит детей систематизировать не только учебный материал, но и свои оценочные суждения, учит ребят вырабатывать и высказывать свое мнение, сформированное на основании наблюдений, опыта и новых полученных знаний, развивает навыки одновременного рассмотрения нескольких позиций, способности к творческой переработке информации.

Выводы. Уроки с применением метода кластера дают ребятам возможность проявить себя, высказать свое видение вопроса, дают свободу творческой деятельности. В целом нетрадиционные технологии, использующиеся в образовательном процессе, повышают мотивацию учащихся, формируют обстановку сотрудничества и воспитывают в детях чувство собственного достоинства, дарят им ощущение творческой свободы.  

Восемь форм группового обучения учеников: одна голова хорошо, а две лучше

32«Одна голова хорошо, а две лучше» — таков девиз уроков, на которых мы используем групповую технологию обучения. Каждый преподаватель хочет, чтобы в его классе было как можно больше успешных  учеников.

В школу приходят разные дети: «способные» и «менее способные». И мы стремимся, чтобы ВСЕ они были активны на уроке. Но… возникает вопрос, как включить каждого ученика в урок. Эту проблему можно решить через использование групповой формы обучения. Группы могут быть однородными или дифференцированными. При этом каждый ученик является то учеником, то учителем;  то лидером, то ведомым. Основная цель каждого ученика: обучать других всему тому, что знаешь сам. В этом случае слабый ученик чувствует поддержку товарища, освобождается от боязни ошибиться, получить неправильный ответ.

Ребятам такая форма проведения урока нравится, потому, что:

• в результате постоянного повторения упражнений совершенствуются навыки логического мышления и понимания;
• дети учатся обсуждать, спорить, отстаивать свою точку зрения, учитывать мнение других;
• каждый чувствует себя раскованно, работает в индивидуальном темпе;
• повышается ответственность не только за свои успехи, но и за результаты коллективного труда;
• обсуждение одной информации с несколькими одноклассниками обеспечивает более прочное усвоение.

Существует много разновидностей групповой формы работы.

Обучение в командах

Схема реализации этого метода может быть представлена следующим образом: в начале урока учитель дает обзорную лекцию по новому материалу с акцентом на тех моментах, по которым команды будут выполнять индивидуальные задания. Лекция должна быть достаточно емкой по содержанию и одновременно практически-направленной. Рекомендуется использование наглядности, моделирования и учебных экспериментов.

Далее учащиеся работают в командах над конспектами лекции, помогая друг другу понять ее содержание. Учащиеся могут задавать друг другу вопросы, проясняя непонятные для себя моменты. Вопросы учителю разрешается задавать только тогда, когда никто из членов команды не может ответить на них. После проработки конспекта лекции учащиеся выполняют индивидуальные работы. На данном этапе помощь друг другу исключается, каждый член команды работает самостоятельно. Главная особенность данного метода заключается в системе оценки индивидуальных работ. Оценка осуществляется по прогрессивно-сравнительному признаку: учащийся может пополнить копилку команды только в том случае, если его оценка за данную работу выше средней его оценки за предыдущие работы. Команда, набравшая по итогам изучения темы наибольшее количество баллов, считается победившей: она заслуживает поощрения и внесения на специальную доску победителей.

Метод учебного турнира

Основная характеристика этого метода заключается в том, что после изучения нового материала в турнирном поединке встречаются учащиеся из разных команд с одинаковым уровнем учебных достижений. Как правило, такого рода турниры проводятся раз в неделю после изучения крупной учебной темы. Порядок проведения таков. Учащиеся из разных команд распределяются по уровню учебных достижений: сильные – первая подгруппа, средние – вторая подгруппа, слабые – третья подгруппа. Каждая подгруппа получает около тридцати пронумерованных карточек с вопросами, расположенных на столе в произвольном порядке в перевернутом виде. Каждый учащийся подгруппы поочередно выбирает карточку и отвечает на вопрос, записанный на ней. Отвечать можно как устно, так и письменно. Остальные члены подгруппы оценивают ответ, к примеру – по альтернативной шкале: правильно (1 балл) и неправильно (0 баллов). В случае спорной ситуации учащиеся прибегают к помощи учителя. В среднем на каждого учащегося приходится по три карточки. Таким образом, учителю необходимо подготовить к турниру около 90 карточек-вопросов трех уровней сложности. После турнира в подгруппах учащиеся возвращаются в свои команды и суммируют полученные баллы. Команда, набравшая наибольшее количество баллов, признается победительницей.

Метод командной поддержки индивидуального обучения

Суть этого метода заключается в предоставлении малым группам возможности продвигаться по учебной программе в индивидуальном темпе. Учащиеся работают в малых группах над индивидуальными заданиями, в процессе выполнения которых они могут обращаться друг к другу за советом, помощью и консультацией. Учащиеся также могут проверять работы друг у друга, помогать исправлять допущенные ошибки. Учитель, в свою очередь, наблюдает за работой групп, а также поочередно разъясняет новый учебный материал группам, которые закончили работать над индивидуальными заданиями по предыдущему материалу. Индивидуальные задания проверяются специально назначенными учителем учащимися – «мониторами» из разных групп. Они снабжаются листами-ответами для оперативной проверки индивидуальных работ. В это время учитель имеет возможность индивидуально работать с каждой малой группой. В конце недели подводится итог: сколько тем изучила каждая группа и каков суммарный учебный результат группы по индивидуальным заданиям.

Метод «американской мозаики» (Jigsaw)

Этот метод  реализуется по следующей схеме: команды формируются по 4–6 человек. Новый учебный материал делится на 4–6 частей, которые распределяются между членами команды, и каждый учащийся самостоятельно изучает свою часть. Затем члены разных команд, изучавшие одинаковую часть учебного материала, собираются вместе для 10–15-минутного обсуждения. После этого они возвращаются в свои команды, и каждый из них поочередно (согласно логике учебного материала) объясняет содержание своей части остальным членам команды. Уровень усвоения учебного материала каждым учащимся оценивается по результатам индивидуальной самостоятельной работы по всему новому материалу. Выигрывает та команда, которая набирает таким образом наибольший балл.

Метод кооперативного взаимообучения

Заключается в постоянной взаимопомощи и взаимоподдержке учащихся посредством взаимопроверок самостоятельных работ, совместного выполнения домашних заданий, пересказа друг другу изучаемого материала, взаимоисправления ошибок, совместной подготовки к зачетам и экзаменам и т.д. Данный метод может применяться в работе различных по форме учебных групп: формальных (сформированных по специальным критериям для решения конкретной учебной задачи), неформальных (укомплектованных по принципу симпатии или дружбы или просто по «территориальному принципу» – сидят за одной партой), базовых (сформированных для решения долгосрочных учебных задач на протяжении учебной четверти, полугодия).

Метод группового исследования

Особенность данного метода заключается в том, что группы, сформированные по неформальным признакам, исследуют какой-либо вопрос учебной темы с целью подготовки группового доклада и выступления перед всем классом. Вопросы по теме распределяются между командами так, чтобы в итоге выступлений охватить весь учебный материал новой темы. Внутри команды каждый учащийся исследует свою часть, собирая необходимый материал, предоставляет его в группу, и далее на основе собранных частей формируется общий доклад группы. За подготовленный доклад и выступление каждая команда получает групповую оценку.

Метод «кооп-кооп»

Этот метод очень близок по содержанию к методу группового исследования, но с одним лишь отличием: каждый член группы не просто сдает материал по своей части в команду, но и выступает перед ней с мини-докладом. После того, как сформирован окончательный доклад команды, спикер группы сначала выступает с ним перед командой, и только потом (с учетом изменений и корректив, внесенных членами группы и учителем) – перед всем классом. Дополнительно к этому учащиеся выполняют индивидуальную самостоятельную работу по всей теме. Итоговая оценка группы включает как общий балл за доклад, так и индивидуальные баллы за самостоятельную работу.

Лабораторный метод

Если в классе, например, 32 человека, то учащиеся рассчитываются с 1-го по 8-й, а затем формируют малые группы из «первых», «вторых», «восьмых». Цель учителя заключается в том, чтобы в укомплектованных по случайному признаку группах создать доброжелательную и плодотворную учебную атмосферу. Именно поэтому начало работы в таких группах рекомендуется организовывать с выявления общих интересов, с поиска общей цели, с формирования командного духа, и т.д.

Поисковый метод

Специфика данного метода заключается в формировании поисковых групп учащихся для решения какой-либо практически направленной учебной задачи или выполнения прикладного проекта. Реализация данного метода требует постановки заданий высокого уровня проблемности и предоставления малым группам полной самостоятельности в поисковой деятельности. Именно поэтому разрешается формирование групп по произвольному (зачастую неформальному) признаку, цель которых – провести мини-исследование, требующее творческого, изобретательского подхода, провести статистическую обработку результатов исследования, сформулировать новизну полученных результатов, оформить исследование в виде доклада, и, наконец, пройти «процедуру защиты» основных положений и результатов исследования.

Рассмотренные выше методы далеко не исчерпывают всего арсенала группового обучения. Это лишь наиболее популярные из них. Однако в целом они дают представление о процессуальных характеристиках такого обучения. Естественно, что их можно комбинировать и использовать в сочетании с традиционными методами. Более того, групповая  форма обучения – открытая и динамичная дидактическая система, она постоянно обогащается новыми находками учителей-практиков.

Приложение

Фрагменты урока «Решение тригонометрических уравнений».

Для проведения урока класс делится на три группы, отличающиеся по степени подготовленности учащихся. Все задания дифференцированы в зависимости от уровня группы (наиболее сложные задачи предлагаются III группе).

Задание 1. «Математическое лото».

Группам предлагается набор карточек с тригонометрическими уравнениями и значениями аргумента. Следует собрать лото по принципу домино, начиная с выделенной карточки.

Поощрительные очки получает группа, которая быстрее других правильно соберет лото.
Задания для 1 и 3 групп.

Задание 3. Учащимся каждой из групп предложены карточки с тремя группами заданий. На данном этапе следует внутри группы разработать способы решения двух первых уравнений и осуществить их представителями групп. По два участника групп, которые решали предложенные уравнения на доске, объясняют ход решения каждого. После выступления ребят подводится итог: при  решении тригонометрических уравнений следует выполнить, если это возможно,  разложение на множители.

Далее ученикам предлагается решить первое уравнение из своей индивидуальной карточки путем разложения на множители.

Примеры индивидуальных карточек для участников 2 и 3 групп.

2 группа                                                          3 вариант
Решите уравнения:
1. sin 2x + 2cos x = 1 + sin x
2. 2sin2x – 5cos x + 1 = 0
3. 9sin x – 10cos x = 0
4. 4sin2x + sin x×cos x – 3cos2x = 03 группа                                                          4 вариант
Решите уравнения:
1. sin3x×cos x – cos3х×sin x = 0,25
2. cos 4x + 3cos 2x = 1
3. 24sin x – 9cos x = 0
4. 3sin2х + 5sin x×cos x + 4cos2x = 1

Развитие критического мышления: приемы и методы стадии «Вызов»

В технологии РКМЧП урок строится по схеме: “Вызов” – “Осмысление” – “Рефлексия” и предполагает широкий набор методических приемов и стратегий ведения урока.

Первая фаза технологии развития критического мышления – “Вызов” или “Пробуждение”.

Задачи данной фазы:

1. Актуализация и обобщение имеющихся у учащегося знаний по данной теме.
2. Пробуждение познавательного интереса к изучаемой теме.
3. Обнаружение и осознание недостаточности наличных знаний.
4. Побуждение ученика к активной деятельности.

Функции стадии “Вызова”:

• мотивационная (побуждение к работе с новой информацией, стимулирование интереса к постановке и способам реализации цели);
• информационная (вызов на “поверхность” имеющихся знаний по теме);
• коммуникационная (бесконфликтный обмен мнениями).

Система приемов организации стадии “Вызова” включает в себя как способы организации индивидуальной работы, так и ее сочетание с парной и групповой работы.

На стадии “Вызова” уроков по технологии РКМЧП учитель может использовать следующие приемы:

• “Кластер”.
• Таблица “тонких” и “толстых” вопросов.
• Таблица “Знаю-хочу знать – узнал”.
• “Дерево предсказаний”.
• “Ромашка Блума”.
• “Верные и неверные утверждения”.
• “Верите ли вы?”.
• “Корзина идей”.
• Рассказ-предположение по “ключевым” словам.
• “Синквейн”.

Прием “Кластер” (гроздья) – выделение смысловых единиц текста и графическое оформление в определенном порядке в виде грозди. Такое оформление материала помогает обучающимся выяснить и понять, что можно сказать (устно и письменно) по данной теме. Этот прием может быть применен на стадии “Вызова”, когда систематизируется информация до знакомства с основным источником (текстом) в виде вопросов или заголовков смысловых блоков. (Приложение № 1. Пример 1, 2)

Прием “Таблица “толстых” и “тонких” вопросов”.

Таблица «толстых» и «тонких» вопросов может быть использована на любой из трех фаз урока: на стадии “Вызова” – это вопросы до изучения темы, на которые обучающиеся хотели бы получить ответы при изучении темы. Тонкие вопросы предполагают однозначный ответ. Толстые вопросы – это проблемные вопросы, предполагающие неоднозначные ответы. (Приложение № 1.Таблица 1)

Прием Таблица “Знаю. Хочу узнать. Узнал”. Таблица “ЗХУ”.

Этот прием графической организации материала поможет собрать уже имеющуюся по теме информацию, расширить знания по изучаемому вопросу, систематизировать их. Используется для актуализации имеющихся знаний и повышения мотивации к изучению нового на стадии “Вызова” с последующим возвратом к материалам на стадии “Рефлексии”. Ученикам до начала чтения фронтально предлагается вопрос: “Что вы знаете или думаете о теме нашего занятия?”. Все предлагаемые формулировки записываются в столбик «Знаю» для общего внимания без корректировки и без оценивания. Затем предлагается вопрос: “Что бы вы хотели узнать?” В столбик «Хочу узнать» записываются и эти формулировки. Записываются сведения, понятия, факты только своими словами, не цитируя учебник или иной текст, с которым работали. Записи остаются на доске до конца занятия.

На стадии “Рефлексии” осуществляется возврат к стадии вызова: вносятся корректировки в первый столбик высказываний и проверяются ответы на второй столбик вопросов. (Приложение № 1. Пример 3)

Прием “Дерево предсказаний”.  Этот прием помогает строить предположения по поводу развития сюжетной линии в рассказе, повести, тексте.

Правила работы с данным приемом: ствол дерева – тема, ветви – предположения, которые ведутся по двум направлениям – “возможно” и “вероятно” (количество ветвей не ограничено), и листья – обоснование этих предположений, аргументы в пользу того или иного мнения. (Приложение № 1.  Пример 4)

Прием “ Ромашка вопросов или ромашка Блума”.

«Ромашка» состоит из шести лепестков, каждый из которых содержит определенный тип вопроса. Таким образом, шесть лепестков – шесть вопросов:

1. Простые вопросы — вопросы, отвечая на которые, нужно назвать какие-то факты, вспомнить и воспроизвести определенную информацию: «Что?», «Когда?», «Где?», «Как?».

2. Уточняющие вопросы. Такие вопросы обычно начинаются со слов: «То есть ты говоришь, что…?», «Если я правильно понял, то …?», «Я могу ошибаться, но, по-моему, вы сказали о …?». Целью этих вопросов является предоставление обучающемуся возможностей для обратной связи относительно того, что он только что сказал. Иногда их задают с целью получения информации, отсутствующей в сообщении, но подразумевающейся.

3. Интерпретационные (объясняющие) вопросы. Обычно начинаются со слова «Почему?» и направлены на установление причинно-следственных связей. «Почему листья на деревьях осенью желтеют?». Если ответ на этот вопрос известен, он из интерпретационного «превращается» в простой. Следовательно, данный тип вопроса «срабатывает» тогда, когда в ответе присутствует элемент самостоятельности.

4. Творческие вопросы. Данный тип вопроса чаще всего содержит частицу «бы», элементы условности, предположения, прогноза: «Что изменилось бы …», «Что будет, если …?», «Как вы думаете, как будет развиваться сюжет в рассказе после…?».

5. Оценочные вопросы. Эти вопросы направлены на выяснение критериев оценки тех или иных событий, явлений, фактов. «Почему что-то хорошо, а что-то плохо?», «Чем один урок отличается от другого?», «Как вы относитесь к поступку главного героя?» и т.д.

6. Практические вопросы. Данный тип вопроса направлен на установление взаимосвязи между теорией и практикой: «Как можно применить …?», Что можно сделать из …?», «Где вы в обычной жизни можете наблюдать …?», «Как бы вы поступили на месте героя рассказа?».

На стадии «Вызова» учащиеся формулируют вопросы, а затем ищут на них ответы, используя материал учебника или других источников информации.

Прием “Верные и неверные высказывания”.

Обучающимся предлагается список утверждений, созданных на основе текста, который они в дальнейшем будут изучать. Учитель просит установить, верны ли данные утверждения, обосновывая свой ответ. После знакомства с основной информацией, возвращаемся к данным утверждениям, и ученики оценивают их достоверность, используя на уроке полученную информацию. (Приложение № 1. Пример 5)

Прием – Игра “ Верите ли вы?” или “Данетка”.

Учитель задает вопросы, на которые обучающиеся должны ответить “да” или “нет”. У каждого на парте таблица, как на доске. Учитель читает вопросы, а ученики ставят в первой строке плюс (да), если согласны с утверждением, и минус (нет), если не согласны. Вторая строка у вас пока останется пустой. В течение урока ученики обращаются к таблице и видят, насколько были правы. (Приложение № 1. Пример 6,7)

Прием “Корзина идей”

Это прием организации индивидуальной и групповой работы учеников на начальной стадии урока. Он позволяет выяснить все, что знают или думают ученики по обсуждаемой теме урока. На доске можно нарисовать значок корзины, в которой условно будет собрано все то, что все ученики вместе знают об изучаемой теме.

Обмен информацией проводится по следующей процедуре:

1. Задается прямой вопрос о том, что известно ученикам по той или иной проблеме.

2. Сначала каждый ученик вспоминает и записывает в тетради все, что знает по той или иной проблеме (строго индивидуальная работа, продолжительность 1–2 минуты).

3. Затем происходит обмен информацией в парах или группах. Ученики делятся друг с другом известным знанием (групповая работа). Время на обсуждение не более 3 минут. Это обсуждение должно быть организованным, например, ученики должны выяснить, в чем совпали имеющиеся представления, по поводу чего возникли разногласия.

4. Далее каждая группа по кругу называет какое-то одно сведение или факт, при этом, не повторяя ранее сказанного (составляется список идей).

5. Все сведения кратко в виде тезисов записываются учителем в “корзинке” идей (без комментариев), даже если они ошибочны. В корзину идей можно “сбрасывать” факты, мнения, имена, проблемы, понятия, имеющие отношение к теме урока. Далее в ходе урока эти разрозненные в сознании ребенка факты или мнения, проблемы или понятия могут быть связаны в логические цепи.

6. Все ошибки исправляются далее, по мере освоения новой информации. (Приложение № 1. Пример 8)

Прием “ Рассказ-предположение по “ключевым” словам”.

По ключевым словам нужно составить рассказ или расставить их в определенной последовательности, а затем, на стадии осмысления искать подтверждение своим предположениям, расширяя материал.

Прием “Написание синквейна”.   В переводе с французского слово “синквейн” означает стихотворение, состоящее из пяти строк, которое пишется по определенным правилам. Составление синквейна требует от ученика в кратких выражениях резюмировать учебный материал, информацию, что позволяет рефлексировать по какому-либо поводу. Это форма свободного творчества, но по определенным правилам. Составить синквейн ученики могут на стадии “Вызова”, затем, изучив информацию на уроке, составляется новый синквейн на стадии “Рефлексии”, сравнивая свои знания до урока и после изучения новой темы.

Правила написания синквейна:

На первой строчке записывается одно слово – существительное. Это и есть тема синквейна.

На второй строчке надо написать два прилагательных, раскрывающих тему синквейна.

На третьей строчке записываются три глагола, описывающих действия, относящиеся к теме синквейна.

На четвертой строчке размещается целая фраза, предложение, состоящее из нескольких слов, с помощью которого ученик высказывает свое отношение к теме. Это может быть крылатое выражение, цитата или составленная учеником фраза в контексте с темы.

Последняя строчка – это слово-резюме, которое дает новую интерпретацию темы, позволяет выразить к ней личное отношение. Понятно, что тема синквейна должна быть по – возможности, эмоциональной. (Приложение №1. Пример 9).

В случае успешной реализации фазы вызова у учебной аудитории возникает мощный стимул для работы на следующем этапе – этапе получения новой информации.

Описание активного метода обучения «Автобусная остановка»

Метод активного обучения. Мне кажется, что метод может использоваться как для детей младшего возраста, так и для детей старшего школьного возраста.

Метод «Автобусная остановка»

Цель: научиться обсуждать и анализировать заданную тему в малых группах. 
Группы: 5-7 человек 
Численность: весь класс 
Время: 20-25 мин. 
Материал: листы большого формата (ватман, плакат, блокнот ), фломастеры.

Проведение:   Учитель определяет количество обсуждаемых вопросов новой темы (оптимально 4-5). Участники разбиваются на группы по числу вопросов (5-7 человек в каждой). 
Группы распределяются по автобусным остановкам. На каждой остановке (на стене или на столе) расположен лист большого формата с записанным на нем вопросом по теме. Учитель ставит задачу группам – записать на листе основные моменты новой темы, относящиеся к вопросу. В течение 5 минут в группах обсуждаются поставленные вопросы и записываются ключевые моменты. Затем по команде учителя группы переходят по часовой стрелке к следующей автобусной остановке. Знакомятся с имеющимися записями и, при необходимости, дополняют их в течение 3 минут. Исправлять существующие записи, сделанные предыдущей группой нельзя. Затем следующий переход к новой автобусной остановке и еще 3 минуты на знакомство, обсуждение и добавление своих записей. Когда группа возвращается к своей первой остановке, она в течение 3 минут знакомится со всеми записями и определяет участника группы, который будет представлять материал. После этого каждая группа презентует результаты работы по своему вопросу. В завершении учитель резюмирует сказанное всеми группами, при необходимости вносит коррективы и подводит итоги работы. 
Примечание: Желательно организовать автобусные остановки (прикрепить листы с вопросами) в разных углах учебной комнаты, чтобы в процессе обсуждения группы не мешали друг другу. Вопросы изучаемой темы можно стилизовать под названия автобусных остановок.

Прием «Лови ошибку!», или Маленькие хитрости для больших успехов

Педагогический прием, выросший из реальных ошибок учителей, благодаря их же находчивости и креативности стал действенным и популярным. В чем суть приема «Лови ошибку!»? Как и зачем его использовать на уроке? Чем он хорош, есть ли недостатки в «ловле ошибок»?

Впервые идея была описана в книге А.А. Гина «Приемы педагогической техники». При объяснении нового материала или желая заострить внимание учащихся на проблемном месте в задании, педагог намеренно допускает ошибку (одну или несколько). Можно заранее оповестить детей о ее наличии. Обнаружив неточность, учащиеся вносят коррективы, оглашают правильный вариант.

Преимущества приема «Лови ошибку»:

• универсален, его применение возможно на уроках практически по всем школьным дисциплинам;
• приводит в тонус внимание, мыслительную деятельность учащихся;
• развивает аналитические способности;
• предоставляет поле для практического применения полученных знаний;
• заставляет взглянуть на получаемую информацию с долей скептицизма, порождает желание проверить надежность источников, сравнить с данными других ресурсов;
• воздействует на эмоциональную сферу учащихся, способствует более прочному усвоению учебного материала.

Недостатки приема «Лови ошибку!»

Их нет, если правила его применения не нарушены. Чтобы дети запомнили верный вариант, а не предложенный в тексте, усвоили «особо опасные места», то есть те, где может быть допущена неточность, необходимо соблюдение некоторых правил.

Инструкция по «Ловле ошибок»

Использовать такую хитрость, как ознакомление ребят с заведомо ложной информацией, содержащей неточности, искаженные факты, можно на любом этапе урока, в любом классе. Подготовка учителя должна быть обязательна. Важно учитывать способности учащихся, имеющиеся знания и опыт, необходимые для обнаружения ошибок, нахождения правильного варианта и аргументации своего выбора. Итак:

• Предупредите детей о наличии ошибок, неточностей, неверной информации в задании.
• Дайте установку найти определенное количество неверных пунктов, внести правки. При высоком уровне знаний у детей и большом опыте работы с подобными заданиями можно не указывать число ошибок в тексте.
• Применяя прием «Лови ошибку!» на уроке с младшими школьниками, намекните им с помощью мимики, жестов на месторасположение неточности.
• Составляя задание, продумайте с позиции ученика, по каким признакам он найдет ошибку, какие аргументы приведет в пользу своей точки зрения.
• Используйте прием в начале урока для активизации имеющихся знаний, в середине урока для повторения изученного материала, на этапе рефлексии с целью подведения итогов.
• Не переусердствуйте. Следуйте принципу «хорошего — понемногу».
• Обязательно после обнаружения ошибки, акцентируйте внимание детей на правильном варианте так, чтобы именно он отложился в сознании.
• Используйте доску, мультимедиа, карточки.
• Организуйте работу в парах, группах по обсуждению информации из текста, по корректировке. Результаты, проведенной работы в группах, оглашают избранные спикеры-представители.
• Индивидуальную форму приема «Лови ошибку» используйте в качестве контроля или работы с одаренными/ отстающими учащимися (здесь требуется индивидуальный подход в выборе степени сложности заданий).

Примеры применения приема «Лови ошибку» на уроках по разным предметам

Русский язык

Ошибки в правописании/ грамматике: «деревяное крыльцо» (деревянное).

Окружающий мир

Рассказ мальчика-фантазера: «И тут на меня налетела пчела, ужалила меня 100 раз, и полетела дальше» (Пчела жалит только однажды, после этого умирает)

Литература

«А.С. Пушкин величайший поэт серебряного века русской литературы» (золотого века)

Английский язык

What he has done? Нарушен порядок слов. (What has he done?)

Математика

10 – 4 × 2 = 12. Так будет, если сначала вычесть, а потом умножить — типичное «ошибкоопасное» место. Сначала умножение, потом вычитание. Правильный ответ: 2.

Фантазия учителя безгранична, разработать собственные дидактические материалы по своему предмету может каждый. А как вы «ловите ошибки»? Поделитесь в комментариях.

Технология АМО

Целями школьного образования, которые ставят перед школой государство, общество и семья, помимо приобретения определенного набора знаний и умений, являются раскрытие и развитие потенциала ребенка, создание благоприятных условий для реализации его природных способностей.

Теперь необходимо найти такие методы для эффективного и качественного обучения, такие формы организации процесса, которые способствовали бы развитию личности, повышению мобильности и обеспечили уверенное достижение поставленных новыми стандартами образовательных целей.

Такие методы существуют, и называются они активные методы обучения. В основе этих методов заложен игровой принцип обучения, их включение в образовательный процесс позволяет создать открытую, мотивирующую среду, как на уроке, так и во внеклассной работе.

Активные методы обучения – это методы, стимулирующие познавательную деятельность обучающихся. Строятся в основном на диалоге, предполагающем свободный обмен мнениями о путях разрешения той или иной проблемы. АМО характеризуются высоким уровнем активности учащихся. Возможности различных методов обучения в смысле активизации учебной и учебно-производственной деятельности различны, они зависят от природы и содержания соответствующего метода, способов их использования, мастерства педагога. Каждый метод активным делает тот, кто его применяет.

Активные методы обучения – это система методов, обеспечивающих активность и разнообразие мыслительной и практической деятельности учащихся в процессе освоения учебного материала. АМО строятся на практической направленности, игровом действе и творческом характере обучения, интерактивности, разнообразных коммуникациях, диалоге и полилоге, использовании знаний и опыта обучающихся, групповой форме организации их работы, вовлечении в процесс всех органов чувств, деятельностном подходе к обучению, движении и рефлексии.

Применение системы активных методов содействует достижению комплекса образовательных эффектов – обучения, воспитания, развития и социализации личности обучающегося.

По структуре, в соответствии с технологией,  образовательное мероприятие делится на логически связанные фазы и этапы.

Фаза 1. Начало образовательного мероприятия.

Этапы:

         Инициация (приветствие, знакомство).

         Вхождение или погружение в тему (определение целей урока).

         Определение ожиданий обучающихся (планирование личностного смысла урока и формирование безопасной образовательной среды).

Фаза 2. Работа над темой

Этапы:

         Интерактивная лекция (передача и объяснение педагогом новой информации).

         Проработка содержания темы (групповая, парная работа).

Фаза 3. Завершение образовательного мероприятия.

Этапы:

         Эмоциональная разрядка (разминка).

         Подведение итогов (рефлексия, анализ и оценка урока).

Каждый этап – это полноценный раздел образовательного мероприятия. Будучи логически связанными и взаимодополняя друг друга, фазы и этапы обеспечивают целостность и системность образовательного процесса. Для каждого этапа используются соответствующие активные методы.

К активным методам начала образовательного мероприятия относятся АМ приветствия и знакомства, целеполагания, выяснения ожиданий и опасений.

В начале урока или мероприятия  необходимо создать позитивную атмосферу в классе, установить хороший контакт с обучающимися. Для этого можно использовать активные методы приветствия.

Пример метода приветствия.

Метод «Поздоровайся глазами».

Ребята должны поздороваться с учителем и друг с другом не словами, а молча — глазами. При этом постараться глазами показать, какое у них сегодня настроение.

С этого упражнения можно начинать любой урок. Также на этом этапе можно использовать еще один метод «Поздоровайся локтями». Дети, выполняя задание, должны коснуться друг друга локтями, улыбнуться, сказать доброе слово.

А вот еще одна разновидность этого метода:

Учитель просит учеников встать в круг. Затем он предлагает им рассчитаться на первый-второй-третий и сделать следующее:

• Каждый «номер первый» складывает руки за головой так, чтобы локти были направлены в разные стороны;

• Каждый «номер второй» упирается руками в бедра так, чтобы локти также были направлены вправо и влево;

• Каждый «номер третий» нагибается вперед, кладет ладони на колени и выставляет локти в стороны.                                                                                                                                               Учитель говорит обучающимся, что на выполнение задания им дается только две минуты. За это время они должны поздороваться с как можно большим числом одноклассников, коснувшись друг друга локтями.

 Такие  забавные игры позволяют весело начать урок, размяться перед более серьезными упражнениями, способствуют установлению контакта между учениками в течение нескольких минут.

АМ выяснения целей, ожиданий и опасений.

Уяснение целей любого урока позволяет обучающемуся, во-первых, понять, каких результатов он должен достигнуть к моменту завершения урока, во-вторых, сосредоточиться на той деятельности, которая приводит к запланированным результатам. А в-третьих, эффективно начать погружение в изучаемый материал. Недаром методы целеполагания часто называют методами вхождения или погружения в тему. Ясное представление результатов, которых от него ожидают, помогает ребенку почувствовать себя уверенно, сконцентрироваться на ключевых моментах и активно включиться в работу.

В начале учебного года или четверти, на первом уроке по новому предмету или в начале новой темы очень важно определить: какие цели стоят перед обучающимися, что он сам ожидает от обучения, а также чего опасается. Выяснение возможных опасений обучающихся очень важно для создания безопасной, психологически комфортной обстановки в классе, в школе.

Такие методы, как «Разгадай кроссворд», «Инструментальный пазл», «Прогноз погоды», «Фруктовый сад», «Список покупок», «Разноцветные листы» и др. позволяют эффективно провести постановку целей урока и выяснение ожиданий и опасений обучающихся.

Пример АМ определения целей

Метод «Инструментальный  пазл».

На общем столе в произвольном порядке расположены следующие предметы: книга, блокнот, флэш-карта,  лазерный  диск, фотография, тетрадь для нот, зубная паста. Учитель озвучивает предметы.  Обучающимся предлагается найти лишний предмет и ответить на вопросы: «Почему этот предмет лишний? Для чего могут быть использованы оставшиеся предметы?»  (для хранения информации).

 Затем учитель спрашивает у класса: «Как вы думаете, какова тема сегодняшнего урока? Каковы цели нашего урока?»   (учащиеся формулируют тему урока, озвучивают цели, учитель при необходимости дополняет ответы ребят).

Пример АМ выяснения ожиданий и опасений

Метод «Прогноз погоды».

Заранее готовятся два плаката: на одном нарисовано яркое красивое улыбающееся Солнышко, на другом мрачная серая Туча. Обучающимся раздаются также заранее вырезанные из бумаги желтые солнышки и серые тучки.

Учитель предлагает обучающимся определить, что они ожидают от обучения и чего опасаются. Ожиданий и опасений может быть несколько. К числу ожиданий/опасений относятся формы и методы обучения, способы работы на уроках, атмосфера в классе, отношение учителей и одноклассников…

Свои ожидания ученикам предлагается написать на солнышках, а опасения —  на тучках. Те, кто записал, подходят к соответствующим плакатам и прикрепляют свои ожидания и опасения. После того как все ученики прикрепят свои солнышки и тучки, учитель озвучивает «прогноз погоды» на урок и подводит итог.

К активным методам работы над темой образовательного мероприятия относятся АМ презентации нового учебного материала (интерактивная лекция)  и АМ организации самостоятельной работы над темой.

АМ презентации учебного материала

В процессе обучения педагогу регулярно приходится сообщать новый материал обучающимся. Сегодня учителя нередко используют цифровые технологии. Мультимедийные презентации позволяют красочно и доступно рассказать ребятам об основных моментах рассматриваемой темы, но не всегда у педагога есть возможность воспользоваться техническими средствами. В этом случае не менее эффективным будет использование активных методов передачи информации — инпут, что в переводе с англ. означает «ввод информации» или «исходные данные». Общепринятым также является термин «интерактивная лекция».

Инпут представляет собой непродолжительное сообщение обучающимся новой информации, которая становится ориентиром и основой для их дальнейшей совместной работы над темой урока.

Инпут лучше разделять на несколько логических разделов. В конце каждого раздела нужно подвести итог, повторив ключевое положение, подчеркнув основную мысль сообщения или сделав иным способом акцент на самом важном материале. Монолог необходимо «разбавлять» демонстрационным материалом, т.е. визуализировать основные моменты темы.

Такие методы, как «Инфо-угадайка», «Инфо-шотик», «Кластер», «Научный эксперимент», «Золотой ключик» и др. позволяют эффективно сориентировать обучающихся в теме, сообщить информацию, необходимую для плодотворной самостоятельной работы, представить им основные направления движения для работы с новым материалом.

Пример АМ презентации учебного материала

Метод «Инфо-угадайка».

На стене прикреплен лист ватмана, в его центре указано название темы. Остальное пространство листа разделено на секторы, пронумерованные, но пока не заполненные. Начиная с сектора 1, учитель вписывает в сектор название раздела темы, о котором он сейчас начнет говорить в ходе сообщения. Обучающимся предлагается обдумать, о каких аспектах темы, возможно, далее пойдет речь в докладе. Затем учитель раскрывает тему, а в сектор вписываются наиболее существенные моменты первого раздела (можно записывать темы и ключевые моменты маркерами разных цветов). Они вносятся на плакат по ходу сообщения. Закончив изложение материала по первому разделу темы, учитель вписывает во второй сектор название второго раздела темы, и так далее.

Таким образом, наглядно и в четко структурированном виде представляется весь новый материал, выделяются его ключевые моменты. Существующие на момент начала презентации «белые пятна» по данной теме постепенно заполняются.

Этот метод изложения материала помогает обучающимся следить за аргументацией учителя и видеть актуальный в данный момент рассказа аспект темы. Отчетливое разделение общего потока информации способствует лучшему восприятию.            

Метод «Инфо-шотик».     Ребята разбиваются на группы, разбирают цветные маркеры (можно цветные ручки). Учитель демонстрирует мультимедийную презентацию, например, по теме «Основные компоненты компьютера и их функции». Учащиеся смотрят, слушают и записывают основное по секторам ватмана (склеенных листов), что считают важным.

 АМ организации самостоятельной работы над темой

При организации самостоятельной работы над новой темой важно, чтобы обучающимся было интересно всесторонне и глубоко проработать новый материал. Для работы над темой урока можно использовать методы «Ульи», «Визитные карточки», «Экспертиза» и др. Для проведения дискуссии и принятия решений – методы «Cветофор», «Приоритеты», «На линии огня». Для представления материала самостоятельной работы обучающихся – «Инфо-карусель», «Автобусная остановка», «Ярмарка».

Пример АМ организации самостоятельной работы над темой

Метод «Автобусная остановка»    Учитель определяет количество обсуждаемых вопросов новой темы. Участники разбиваются на группы по числу вопросов.

Группы распределяются по автобусным остановкам. На каждой остановке (на стене или на столе) расположен лист большого формата с записанным на нем вопросом по теме. Учитель ставит задачу группам – записать на листе основные моменты новой темы, относящиеся к вопросу. В течение 5 минут в группах обсуждаются поставленные вопросы и записываются ключевые моменты.

Затем по команде учителя группы переходят по часовой стрелке к следующей автобусной остановке. Знакомятся с имеющимися записями и, при необходимости, дополняют их в течение 3 минут и т.д. Исправлять существующие записи, сделанные предыдущей группой нельзя.

Когда группа возвращается к своей первой остановке, она в течение 3 минут знакомится со всеми записями и определяет участника группы, который будет представлять материал.

В завершении учитель резюмирует сказанное всеми группами, при необходимости вносит коррективы и подводит итоги работы.

Метод «На линии огня».  Ученики делятся на две команды. Одна команда отвечает за аргумент «за», другая за аргумент «против». Команды начинают дискуссию по предлагаемому преподавателем вопросу. Одни называют только доводы в пользу, другие – против этого. Каждый старается убедить противника в своей правоте. Через 2-4 минуты противники меняются местами и меняют аргументацию на противоположную.

Метод сигнальных карточек «Светофор».  Учащиеся показывают зеленую сигнальную карточку, если работа выполнена, красную – если нужна помощь.

Эффективно и эффектно завершить урок, внеклассное мероприятие, родительское собрание можно, применив АМ релаксации и АМ рефлексии.

Не стоит забывать о восстанавливающей релаксации на уроке. Ведь иногда нескольких минут достаточно, чтобы встряхнуться, весело и активно расслабиться, восстановить энергию. Активные методы релаксации позволят сделать это, не выходя из класса.

(Под тихую музыку). Закройте, пожалуйста, глаза. Наберите грудью побольше воздуха  и ощутите солоноватый запах моря. Морской воздух свежий и немного влажный. Вы слышите, как кричат чайки, и чувствуете себя сейчас совершенно спокойно и безмятежно. Потянитесь, выпрямитесь, откройте глаза и снова будьте здесь, свежи и полны бодрости.

Пример активных методов релаксации

Метод «Земля, воздух, огонь и вода».    Учитель просит обучающихся по его команде изобразить одно из состояний – воздух, землю, огонь и воду.

Воздух. Ученики начинает дышать глубже, чем обычно. Они встают и делают глубокий вдох, а затем выдох. Каждый представляет, что его тело, словно большая губка, жадно впитывает кислород из воздуха. Ученики делают несколько глубоких вдохов и выдохов. Можно предложить всем несколько раз зевнуть. Зевота – естественный способ компенсировать недостаток кислорода.

Земля. Теперь ученики должны установить контакт с землей, «заземлиться» и почувствовать уверенность. Учитель вместе с обучающимися начинает сильно давить на пол, стоя на одном месте, можно топать ногами и даже пару раз подпрыгнуть вверх. Можно потереть ногами пол, покрутиться на месте.

Огонь. Ученики активно двигают руками, ногами, телом, изображая языки пламени. Учитель предлагает всем ощутить энергию и тепло в своем теле, когда они двигаются подобным образом.

Вода. Эта часть упражнения составляет контраст с предыдущей. Ученики просто представляют себе, что комната превращается в бассейн, и делают мягкие, свободные движения в «воде», следя за тем, чтобы двигались суставы – кисти рук, локти, плечи, бедра, колени.

АМ подведения итогов урока (рефлексия, анализ и оценка урока)

Подведение итогов, обобщение результатов, выяснение впечатлений от обучения помогают учащимся еще раз «пропустить через себя» все произошедшее на уроке, оглянуться и оценить реализованные и приобретенные знания и умения, выявить успехи и неудачи, определить степень достижения целей (ожиданий) и четко понять – что дальше?

Не менее ценным является то, что у обучающегося появляется осознанность и осмысленность своих действий, появляется ясное понимание того, как вложенные усилия содействуют личным успехам, развитию, росту. Такое осознание способствует приобретению навыков самообразования и самосовершенствования, укрепляет мотивацию и уверенность ребят в собственных силах.

Для педагога подведение итогов и анализ результатов урока не менее важны, чем для обучающихся. Необходимо оценить не только действия и результаты обучающихся, но и свою работу, определить, что получилось хорошо, а что оказалось реализованным не до конца. Оценка проведенного урока и рефлексия помогают учителю совершенствовать свое мастерство, повышать качество проводимых уроков.

Для завершения образовательного мероприятия можно использовать такие АМ, как «Ресторан», «Все у меня в руках», Мухомор», Все дело в шляпе» и др.Эти методы позволяют эффективно, грамотно и интересно подвести итоги урока и завершить работу.

Метод «Ресторан».    Учитель предлагает ученикам представить, что сегодняшний день они провели в ресторане и теперь директор ресторана просит их ответить на несколько вопросов: 
— Я съел бы еще этого… 
— Больше всего мне понравилось… 
— Я почти переварил… 
— Я переел… 
— Пожалуйста, добавьте…

Метод «Все у меня в руках»

Учащиеся рисуют на листах бумаги свою руку, обводя ее контур, и вписывают внутри контура ответы на вопросы:

Большой палец – над этой темой я хотел еще бы поработать. Указательный палец – я узнал все, что хотел. Средний – мне совсем ничего не понравилось. Безымянный – психологическая атмосфера на уроке. Мизинец – мне захотелось…

Метод «Все дело в шляпе».     Учащиеся передают друг другу шляпу (другой предмет), по сигналу учителя тот, у кого осталась шляпа (другой предмет), анализирует свою работу на уроке или ставит оценку тем, кто работал у доски, и обосновывает ее.

Кроме освоения учебной информации, АМО позволяет так же эффективно в процессе урока и во внеклассной деятельности осуществлять воспитательный процесс. Работа в команде, совместная проектная и исследовательская деятельность, отстаивание своей позиции и толерантное отношение к чужому мнению, принятие ответственности за себя и команду формируют качества личности, нравственные установки и ценностные ориентиры школьника, отвечающие современным потребностям общества. Но и это еще не все возможности активных методов обучения. Параллельно с обучением и воспитанием, применение АМО в образовательном процессе обеспечивает становление и развитие у обучающихся так называемых мягких или универсальных навыков. К ним обычно относят способность принимать решения и умение решать проблемы, коммуникативные умения и качества, умения ясно формулировать сообщения и четко ставить задачи, умение выслушивать и принимать во внимание разные точки зрения и мнения других людей, лидерские умения и качества, умение работать в команде и др. А сегодня многие уже понимают, что, несмотря на свою мягкость, эти навыки в современной жизни играют ключевую роль, как для достижения успеха в профессиональной и общественной деятельности, так и для обеспечения гармонии в личной жизни. 

Прием «Бортовой журнал» — описание приема, алгоритм работы, примеры использования

Прием «Бортовой журнал» был разработан в рамках технологии развития критического мышления (ТРКМЧП). Он позволяет не только получить адекватную картину степени усвоения учениками материала, но и помогает ученикам развивать умение фиксировать информацию, используя графические способы, научиться оценивать свои сильные и слабые стороны, дает возможность наглядно представить заданную проблему. 

Прием «Бортовой журнал» охватывает все этапы урока, начиная от стадии вызова и заканчивая рефлексией.

Примеры оформления «бортовых журналов»

1. Простая форма бортового журнала

№	Что я знал по теме	Новое знание	Графическая форма

2. Более полная форма «бортового журнала»

ФИО ученика:

Тема:

Дата:

№	Ключевые понятия	Толкование	Графическая форма (рисунок, схема)
1.
2.

Оставшиеся вопросы:

1.

2.

Оценка:

Алгоритм работы с приемом

1. Учитель знакомит учеников с новой темой: кратко обрисовывает самые главные направления изучения темы, основные понятия темы, главные идеи.

Важно! Для приема «Бортовой журнал» лучше всего использовать темы, описывающие какую-то концепцию, идею принцип. Если же тема предполагает запоминание большого количества фактов, дат, терминов, то для нее лучше использовать другие технологии.

2. Ученики обсуждают идеи (в группах, парах), формулируют свое представление о том, какие понятия должны быть изучены, какие проблемы могут возникнуть при изучении темы.

3. Обсудив, ученики составляют план изучения новой темы или список основных понятий, которые наиболее полно отразят суть темы.

4. После осознания объема темы и ее сложности, ученики выбирают для себя тему эссе или сочинения, которые они будут писать после изучения проблемы урока. Можно предложить на выбор несколько тем, чтобы каждый ученик в процессе урока имел возможность определиться с выбором.

5. Составление ключевых вопросов по теме. Класс делится на группы, и каждая составляет свой список ключевых вопросов по теме. Потом списки обсуждаются и выделяются основные вопросы, которые должны быть изучены всеми.

6. Первичное заполнение бортового журнала. Лист разлиновывается на две части по вертикали. В левую часть записываются все вопросы и ключевые понятия темы.

7. Знакомство с новой темой. Выбор формы лекции — на усмотрение учителя. Это может быть привычная лекция, презентация, видеофильм и пр. Во время лекции ученики работают в правой части бортового журнала, фиксируя все новое, что они узнали, отмечая непонятное.

8. Первичная рефлексия. После лекции предлагается обсудить (в парах, в группах) первые впечатления. Ученики должны поработать со своим составленным списком вопросов и понятий: уточнить, добавить, зафиксировать новое знание.

9. Работа с графикой. На данном этапе задача учеников — отобразить новое знание в графической форме. Для этого можно использовать ранее изученные приемы: кластер, сводная таблица, понятийное колесо, фишбоун и пр. То есть, идет сжатие новое информации в опорный конспект.

10. Обсуждение построенных графических изображений. Здесь важно выявить взаимосвязь и вычленить главные понятия в теме. Поэтому обсуждение идет в максимально корректной форме: Что означает эта стрелочка? Почему информация расположилась по кругу? И т.д.

11. Практическое применение. На данном этапе учитель просит учеников соотнести новое знание с имеющимся практическим опытом: в какой жизненной ситуации может пригодиться новое знание, как его использовать на практике? Можно привести примеры из жизни, соотнести со сведениями из других уроков, описать свои воспоминания, которые появились во время прослушивания лекции.

12. Совершенствование опорного конспекта. На данном этапе ученики вновь возвращаются к своим графическим изображениям, соотносят первоначальный список вопросов и ключевых понятий. По итогам работы составляется первичный вывод: все ли понятия раскрыты, что осталось непонятым, что требуется уточнить, на все ли поставленные вопросы получены ответы. По итогам работы могут возникнуть дополнительные вопросы, которые также фиксируются в левой части бортового журнала.

13. Работа с дополнительными вопросами. На вопросы может отвечать учитель, а могут и ученики из составленной группы.

14. Рефлексия — обсуждение итогов работы. Примеры вопросов, по которым проводится этот этап: Что изменилось в вашем представлении по теме после изучения нового материала? Какие моменты лекции вы можете отметить как наиболее важные? Что вызвало затруднения? Какое из заданий было выполнить легче? Какие достоинства и недостатки исследований по теме вы можете указать? И др.

15. Самостоятельная письменная работа. По итогам урока ученики пишут эссе или сочинение на тему, которую они определили в начале урока. Работа может проводиться в классе. А может быть дана как домашнее задание.

Прием «Шесть шляп мышления» на уроке: как его применять?

Прием «Шесть шляп мышления» был впервые предложен английским психологом и писателем Эдвардом де Боно. Прием помогает развивать параллельное мышление, увидеть ситуацию с различных точек зрения, представить многогранность проблемы и выявить наиболее оптимальный путь ее решения. Технологию Боно уже взяли на вооружение такие ведущие мировые компании, как IBM, British Airways, Pepsico, Mary Key. А основоположники технологии развития критического мышления адаптировали прием «Шесть шляп» для обучения детей. 

Как работать с приемом «Шесть шляп мышления» на уроках

«Шесть шляп» — это прием групповой познавательной активности, который помогает рационально организовать изучение проблемы (текста, новой информации) и выявить разные стороны восприятия и оценки.

Алгоритм работы с приемом

1. Задается проблемная ситуация (вопрос, текст). Скажем сразу, что эта ситуация изначально должна быть многовариантной и не должна иметь однозначного ответа или решения.
2. Класс делится на шесть групп. Каждая выбирает себе одну шляпу (по жребию или по желанию).

Цвет шляпы определяет направление развития мысли:

• Белая — самая нейтральная. Поэтому участники этой группы оперируют только фактами. То есть доказывают, почему все произошло именно так, а не иначе.
• Желтая — солнечная, радостная, позитивная. Участники этой группы ищут выгоды предложенного решения, обрисовывают только положительные моменты.
• Черная — негативная, мрачная, отрицающая. Эта группа должна высказать сомнение, найти аргументы против.
• Красная — эмоции, страсть. Эта группа высказывает только эмоциональное восприятие заданной ситуации, без обоснования своих выводов.
• Зеленая — творческая, креативная. Участники этой группы предлагают новые решения заданной ситуации, которые могут быть самыми фантастическими и неожиданными.

А также:

• Синяя — нейтральная, оценочная. По сути, в этой группе собираются эксперты, аналитики, которые оценивают предложения всех групп и находят оптимальное решение.

Это эталон приема «Шесть шляп». Но каждый учитель может адаптировать стратегию, исходя из собственных планов и темы урока.

Примеры использования приема.   Предмет: Русский язык.

Тема: Лексика и развитие речи.

Заданная ситуация: сказка «Курочка Ряба». Ученикам предлагается рассказать сказку по-новому, в зависимости от цвета шляп.

• Белая — деловая речь, много терминов, точных фактов. Например, «Курица по кличке Ряба родилась в 2015 году и уже через 6 месяцев приобрела репродуктивную способность. Хозяева курицы — дед по имени Иванов Петр Алексеевич и его супруга Иванова Антонина Семеновна…».
• Желтая — в сказке должно быть много эпитетов, сравнений. Здесь употребляется речь художественная, образная.
• Черная — вполне возможно предложить составить сказку ужасов. Или написать сценарий для экранизации в жанре триллера.
• Красная — чувственная сказка. Это может быть сказка в стихах.
• Зеленая — креатив. Сказка должна иметь самый неожиданный конец. Или предложить рассказать сказку с использованием жаргона, либо представить ее в жанре пантомимы.
• Синяя — нейтральная. Участники этой группы будут представлять жюри.

Предмет: литература.

После изучения произведения, например, «Герой нашего времени», учитель предлагает для групп следующие задания:

• Белая — факты из истории создания произведения, объяснить поему выбрана именно такая структура, такой жанр.
• Желтая — найти аргументы, почему это произведение считается одним из лучших в русской классике.
• Черная — обосновать негативное восприятие главного героя. Либо доказать, что этот роман неактуален в наши дни.
• Красная — рассказать об эмоциях, чувствах и впечатлениях после прочтения произведения.
• Зеленая — доказать, что роман актуален в наши дни, чему он учит современных подростков.
• Синяя — эксперты.

Это лишь два варианта использования приема «Шесть шляп мышления» на уроках. По аналогии можно составить задания для групп и на уроках по другим предметам. Допустимо, что будет, например, не 6, а 4 шляпы. Обучение — дело творческое, так что при известной доли фантазии этот прием поможет разнообразить работу на уроке. 

ПОПС – формула как один из приемов для обучения устной инициативной речи

Современная жизнь отличается быстрыми темпами развития, высокой мобильностью, для молодого поколения появляется большое количество возможностей. Выйдя из стен школы, выпускник должен продолжить саморазвиваться и самосовершенствоваться, а для этого необходимо научиться определённым способам действий. Подготовка учеников к жизни закладывается в школе, поэтому требования к образованию сегодня меняют свои приоритеты: знаниевая составляющая уступает место развивающей. Меняются цели и содержание образования, появляются новые средства и технологии обучения, но при всём многообразии – урок остаётся главной формой организации учебного процесса.

Цель современного урока должна быть конкретной и измеряемой. Цель можно отождествить с результатом урока. Результатом урока является не успеваемость, не объем изученного материала, а приобретаемые УУД учащихся (способность применять знания, реализовывать собственные проекты, способность социального действия, т.е.). Вместе с этим, следует отметить, что такой подход на уроке не отрицает значения знаний, он акцентирует внимание на способности использовать полученные знания.

ПОПС-формула. Этот потрясающий по своему потенциалу интерактивный приём, направленный на рефлексию учащихся, создан профессором права Дэйвидом Маккойд-Мэйсоном. Перевёл её на русский язык Аркадий Гутников, вице-президент ассоциации «За гражданское образование», первый проректор Санкт-Петербургского Института права.

В результате перевода получилась аббревиатура ПОПС. Ценность этого технологического приёма заключается в том, что позволяет учащимся кратко и всесторонне выразить собственную позицию по изученной теме. Учителю необходимо знать, насколько качественно усвоен классом новый материал. Опросы, самостоятельные работы, тесты занимают или много времени, или не всегда позволяют оценить, насколько свободно владеет материалом ученик, насколько осознанно он воспринял его.

В данном случае учащимся предлагается написать четыре предложения, отражающие следующие четыре момента ПОПС — формулы:

П – позиция

О – объяснение (или обоснование)

П – пример

С – следствие (или суждение)

     Но этот приём не был бы технологичным, не обладал бы законченностью, если бы мы не предложили начало предложений.

Первое из предложений (позиция) должно начинаться со слов:

«Я считаю, что…».

Второе предложение (объяснение, обоснование своей позиции) начинается со слов:

«Потому что …».

Третье предложение (ориентированное на умение доказать правоту своей позиции на практике) начинается со слов:

«Я могу  доказать это на примере …».

И, наконец, четвертое предложение (следствие, суждение, выводы) начинается со слов:

«Исходя из этого, я делаю вывод о том, что…».

Пример. (по теме «Россия во второй половине XIX в»)

Я считаю, что отмена крепостного права в России была неизбежной.

Потому, что оно тормозило развитие всех сфер жизни общества.

Я могу доказать на примере того, что Россия значительно отставала от других стран по уровню жизни. Россия позорно проиграла Крымскую войну.

Исходя из этого, я делаю вывод, что эта реформа сыграла огромное значение в истории России и дала мощный толчок великим преобразованиям 1860-х годов.

Для того, чтобы задать общее направление рефлексии учащихся, учитель добавляет в первом предложении несколько слов, определяющих тему обсуждения.

Например.    «Я считаю, что Иван Грозный…»

                     «Я считаю, что правовое государство…»   и т.д.

Таким образом, мы получаем уникальную возможность в считанные минуты получить лаконичную информацию о степени «погружения» ученика в материал, о степени понимания происходящих процессов, о его нравственной оценке того или иного события, явления, факта.

А самое главное, мы предлагаем учащимся выразить собственное мнение, собственную позицию.

Ответ по ПОПС-формуле – это лаконичный и ёмкий ответ по законам риторики.

Мы предлагаем ученикам своеобразный каркас для устного ответа. Причём мы сразу нацеливаем ученика не на вызубренный ответ, а на высказывание собственной позиции: «Я считаю, что…» или «Мне кажется, что…», «Я думаю, что…», «На мой взгляд…».

Метод «Карусель», заключается в том, что учащиеся образуют два кольца: внутреннее и внешнее. Внутреннее кольцо — это сидящие неподвижно ученики, а во внутреннем  ученики через определенный промежуток времени  меняются. Например, детям внутреннего и внешнего кругов предлагается по несколько карточек с заданиями на одну орфограмму. Ученики внутреннего круга получают в первой карточке, например, следующее задание:

Обоснуйте, почему в словах деньки и пеньки написаны безударный гласный Е.

Объяснив свое задание однокласснику, который работает во внешнем круге, ученик внутреннего круга слушает объяснение своего оппонента, который получает задание типа:

«Помоги Незнайке вставить пропущенные буквы»: п…ля, м…ря, с…ды. Объясни, почему вставили такие буквы.

После смены партнера все учащиеся берут вторую карточку с аналогичным первому заданием и весь алгоритм повторяется заново.

Два, четыре – вместе»            Учащимся предлагается проблема или информация, которую они сначала отрабатывают самостоятельно, затем обговаривают в парах, далее объединяются в четверки. После принятия совместного решения в четверках происходит совместное обговаривание вопроса.

  «Микрофон»            Учащимся предлагается высказать свою точку зрения по поставленному вопросу или проблеме. По классу пускают предмет, имитирующий микрофон. Каждый, получивший такой «микрофон» обязан четко и лаконично изложить свою мысль и сделать вывод.

«Синтез идей».            Данное упражнение предусматривает выполнение группами поэтапно всех видов заданий урока: на отдельных листах бумаги первая группа выполняет первое задание, вторая – второе и т.д. После выполнения первая группа отдает свой листок для доработки второй группе, вторая – третьей и т.д. Когда доработанный листочек возвращается к «хозяевам», каждая группа презентует свои исследования с учетом дополнений одноклассников.

            Можно перед началом работы создать экспертную группу, которая будет оценивать продуктивность работы каждой группы.

«Мозговой штурм»            Для решения проблемного вопроса учащимся предлагается найти как можно больше путей, идей, предложений, каждое из которых фиксируется на доске или листе бумаги. После создания такого «Банка идей» проводится анализ и обговаривание.

Метод « ПРЕСС»

            Это упражнение развивает умение формулировать высказывание по определенному дискуссионному вопросу в сжатой форме, выразительно, аргументировано, лаконично. «Метод ПРЕСС» состоит из четырех этапов:

1.      – Высказывание собственной точки зрения («Я считаю, что…»)

2.      – Обоснование своей мысли («… Так как…»)

3.      – Примеры и аргументы для поддержания своей точки зрения («… например…»)

4.      – Обобщение, выводы («Итак…»).

     «Обучая – учусь».      Материал урока делится на отдельные блоки по количеству учащихся в классе. Учащиеся отрабатывают и обмениваются информацией, создавая временные пары, после чего происходит коллективное обговаривание и закрепление учебного материала.

«Выбери позицию»    Предлагается проблемный вопрос, две противоположные точки зрения и три позиции: «Да» (за первое предложение), «Нет» (за второе предложение), «Не знаю, не определил собственную позицию». Учащиеся класса выбирают определенную позицию, формируют три группы, обговаривают правильность своей позиции. Один или несколько членов каждой группы аргументируют свою позицию, после чего происходит коллективное обсуждение проблемы и понятие правильного решения.

«Карусель»             Учащиеся образуют  два кольца: «внутреннее и внешнее». «Внутренне кольцо» — это сидящие неподвижно ученики, а «внешнее»-ученики  через каждые небольшие промежутки времени меняются. Таким образом они успевают проговорить за несколько минут несколько тем. Например внутренний круг задает вопросы внешнему. Так можно повторять различные  темы.  Некоторое время каждая пара обменивается информацией, своими мыслями; после этого учащиеся внешнего круга перемещаются по кругу к следующему партнеру. Можно предварительно предложить учащимся подготовить вопросы по теме и провести по кругу опрос.

 «Совместный проект»            Группы работают над выполнением разных заданий одной темы. После завершения работы каждая группа презентует свои исследования, в результате чего все учащиеся знакомятся с темой в целом.

  «Броуновское движение» предполагает движение учеников по всему  классу с целью сбора информации по предложенной теме . Например: «Воспитание детей в казахской семье». В разных местах класса расположенны источники информации ( задания логического , творческого характера , презентации, видеофильмы и др.)

  «Дерево решений».   Класс делится на 3 или 4 группы с одинаковым количеством  учеников. Каждая группа обсуждает вопрос и делает  записи на своем «дереве» (лист ватмана), потом группы меняются местами и дописывают на деревьях соседей свои идеи.

Эти  техники могут «работать » на разных этапах урока.

Этап урока	% врем.	Методическая цель	Примерные методики
I. Мотивация	5%	Сконцентрировать внимание и вызвать интерес к изучению данной темы.	«Мозговой штурм» «Блицопрос» «Микрофон»
II. Оглашение темы задач	5%	Обеспечить понимание учащимися их деятельности, чего они должны достигнуть в результате урока, что его ожидает.	Через эпиграф Через слово Через название
III. Получение необходимой информации	5%	Инструктаж учащихся для выполнения задания.	Мини-лекция. Ознакомление с раздаточным материалом Презентация домашнего задания
IV. Интерактивное задание	60%	Практическое усвоение материала.	Стимуляция,  Дебаты,  Семинар, Работа в малых группах, «ПРЕСС», «Карусель», «Микрофон», «Снежный ком», «Защита проекта», «Аквариум»
V. Подведение итогов	25%	Обсуждение с целью закрепления материала.	«Большой круг»,  «ПРЕСС», «Неожиданное предложение», «Снежный ком»,   «Проект», «Творческое задание»

Алгоритм работы с приемом «Корзина идей»

По своему содержанию «Корзина идей» похожа на такие известные приемы, как «Мозговая атака» и «Кластер». В каждом случае предполагаются разные формы работы — и индивидуальная, и групповая, и каждый из приемов позволяет высказывать любые суждения — без их оценивания и анализа. Но, к примеру, кластер помогает лучше увидеть логические цепочки, в то время как «Корзина идей» всего лишь определяет «поле интересов». Если хотите, это «облако тегов», которые будут обсуждаться и анализироваться в процессе урока.

Итак, алгоритм работы с «Корзиной идей»:

• Объявляется тема урока.
• Индивидуальная работа. Каждый ученик тезисно записывает в тетради все, что ему известно по теме. Этот этап длится недолго — 2-3 минуты.
• Работа в парах или в группах. Учащиеся обмениваются информацией, выясняя, в чем совпали их мнения, а в чем возникли разногласия. Время проведения — 3 минуты.
• Работа с классом. На этом этапе каждая группа высказывает свое мнение по теме, приводит свои знания или высказывает идеи по данному вопросу. Причем ответы не должны повторятся. Все высказывания учитель кратко записывает на доске.

В «корзину» скидывается все, что имеет отношение к теме урока: идеи, имена, даты, факты, предположения, термины и т.д.

Важно! Предложения, предположения и идеи не критикуются и не оцениваются. На данном этапе идет просто сбор информации.

Обычно учителям трудно выступать нейтральным слушателем: мы привыкли поправлять, исправлять, указывать на ошибки. Отход от этого давления авторитета и есть одно из наиболее трудновыполнимых требований технологии критического мышления.

• Все идеи и предложения осмысливаются и анализируются в дальнейшем ходе урока. Постепенно из «корзины» должны исчезнуть все неправильные или некорректные утверждения, а остаться «выжимка» из верных.
• На этапе рефлексии можно снова обратиться к «Корзине идей», чтобы подвести итог урока.

Нюансы использования приема «Корзина идей»

• Прием ТРКМЧП «Корзина идей» можно использовать как для подготовки к восприятию большой по объему новой информации, так и для разрешения актуальных проблем, возникающих по ходу урока.
• Во время высказывания учащимися их идей и предположений, старайтесь требовать полных ответов. Таким образом, прием будет работать и для развития устной речи и навыков логического изложения.
• На этапе записи учителем идеи и мнений, записываются все, даже ошибочные и неверные. Никакой критики и анализа! Ваша цель: в ходе урока подвести учащихся к анализу своих ошибок.
• Если тема урока совершенно не известна, то можно попросить учащихся высказать свои предположения и домыслы — что они представляют и что они предполагают сегодня узнать.

«Плюсы» приема «Корзина идей»

Прием «Корзина идей» предлагается для проведения на этапе вызова. То есть на начальном этапе урока, когда происходит процесс актуализации знаний по теме — «вызываются» из памяти учащихся все, что имеет отношение к заявленной теме, происходит обобщение накопленного опыта и подготовка к восприятию нового материала. (Смотрите также другие приемы, используемые на этапе вызова: «Мозговой штурм», «Синквейн», «Да-нет», «Верю-не верю», «Кластер», «Отсроченная догадка»).

Здесь очень важно помочь ученикам самостоятельно определить цели урока. Ведь обычно учитель намечает цели и строит свой урок так, чтобы максимально приблизиться к достижению этих целей. При этом по умолчанию подразумевается, что учащиеся тоже знают эти цели или, в крайнем случае, учитель просто зачитывает их, ставя учащихся, так сказать, перед фактом.

Но психологи и ученые-дидакты отмечают, что процесс обучения гораздо эффективнее, если ученик сам определяет цель обучения и цель конкретного урока. Здесь, наряду с познавательной функцией работает и мотивация: это я хочу узнать, это мне интересно.

Вторая проблема, которая решается на стадии вызова с помощью приема «Корзина идей» — привлечение к работе всех учащихся. На обычном уроке этап актуализации знаний не всегда позволяет охватить всех учеников в классе. Многие пассивно отсиживаются, позволяя другим выполнить поставленную задачу. «Корзина идей» включает этап индивидуальной работы, что позволит даже самым пассивным внести лепту в общее дело.

Третий важный момент: в создании записей участвуют все — ведь одно из условий: термины и предлагаемые идеи не должны повторятся. То есть, каждый ученик не только внимательно выслушивает предложения других, но и попутно анализирует свои знания, отмечая, что он тоже знает, а что для него является незнакомым. Фиксируя свои пробелы, учащиеся в дальнейшем будут обращать внимание на исправление и корректировку своих ЗУН.

Прием охватывает сразу два вида деятельности учащихся: индивидуальный и групповой.

Примеры использования приема «Корзина идей» на уроках

Предмет: Литература

Тема урока: роман Ф. Достоевского «Преступление и наказание»

На первом этапе учащиеся кратко фиксируют в тетрадях, все, что им известно по теме.

На доске рисуется корзина (либо прикрепляется картинка). После обсуждения в группах в корзину попадают примерно следующее: русский писатель XIX в., преступление — это…, наказание — это…, Раскольников — главный герой, «Тварь я дрожащая или право имею?» и т.д.

Далее, в процессе урока каждое утверждение анализируется и осмысливается.

Предмет: история

Тема: Древний Египет

В «Корзину идей» могут попасть: «Египет — государство в Африке», «Египтяне использовали иероглифы», «Царь в Египте назывался фараон», «Египтяне строили пирамиды» и т.д.

Предмет: Окружающий мир

Тема: Почва

Один из важнейших понятий, которые должны быть усвоены в ходе этого урока — «Что такое почва?».

В корзину могут попасть такие предположения учащихся: это земля, это не вода и не воздух, это вещество, это место обитания животных и растений и т.д.

Этот пример показывает, как использовать прием ТРКМЧП «Корзина идей» в начальной школе для обсуждения одного из вопросов по новой теме, а не всей темы.

Прием «Корзина идей» позволяет быстро и в интерактивной форме подготовить учащихся к восприятию новой темы, помочь им увидеть взаимосвязь между темами, научиться видеть ошибки и исправлять их самостоятельно, анализируя свою работу и обобщая выводы. 

Два, четыре – вместе»            Учащимся предлагается проблема или информация, которую они сначала отрабатывают самостоятельно, затем обговаривают в парах, далее объединяются в четверки. После принятия совместного решения в четверках происходит совместное обговаривание вопроса.

Метод актуализации опорных знаний «Магазин»

Цель: актуализировать знания учащихся по ранее изученной теме, подвести учащихся к изучению нового материала.

Участники: все обучающиеся.

Необходимые материалы: предметные картинки с изображениями животных, фруктов, овощей, игрушек.

   Проведение: на доске картинки с изображениями предметов. Каждый ученик подходить к доске, произносит фразу: «Я покупаю машинку потому, что слово, обозначающее этот предмет, отвечает на вопрос что?» Или:«Я покупаю зайчика потому, что слово, обозначающее этот предмет, отвечает на вопрос кто?» Ученик, правильно задавший вопрос, забирает картинку.

Оценка результата: после покупки всех картинок подводится итог (чей ряд купил больше картинок).

Метод « ПРЕСС»  Это упражнение развивает умение формулировать высказывание по определенному дискуссионному вопросу в сжатой форме, выразительно, аргументировано, лаконично. «Метод ПРЕСС» состоит из четырех этапов:

 – Высказывание собственной точки зрения («Я считаю, что…»)

 – Обоснование своей мысли («… Так как…»)

  – Примеры и аргументы для поддержания своей точки зрения («… например…»)

 – Обобщение, выводы («Итак…»).       

 «Обучая – учусь».      Материал урока делится на отдельные блоки по количеству учащихся в классе. Учащиеся отрабатывают и обмениваются информацией, создавая временные пары, после чего происходит коллективное обговаривание и закрепление учебного материала.

«Выбери позицию»    Предлагается проблемный вопрос, две противоположные точки зрения и три позиции: «Да» (за первое предложение), «Нет» (за второе предложение), «Не знаю, не определил собственную позицию». Учащиеся класса выбирают определенную позицию, формируют три группы, обговаривают правильность своей позиции. Один или несколько членов каждой группы аргументируют свою позицию, после чего происходит коллективное обсуждение проблемы и понятие правильного решения.

Порядок выполнения логических операций в сложном логическом выражении:

1.
инверсия

2.
конъюнкция

3.
дизъюнкция

4.
импликация

5.
эквивалентность

• логическое
  выражение;

С
помощью логических переменных и символов
логических операций любое высказывание
можно формализовать, то есть
заменитьлогической формулой
(логическим выражением).

Логическое
выражение — это символическая запись
высказывания, состоящая из логических
величин (констант или переменных),
объединенных логическими операциями
(связками).

Связки
«НЕ», «И», «ИЛИ»заменяются логическими операциямиинверсия,конъюнкция,дизъюнкция. Это основные
логические операции, при помощи которых
можно записать любое логическое
выражение.

• массив;

Массив(в некоторыхязыках
программированиятакжетаблица,ряд) — набор однотипных
компонентов (элементов), расположенных
в памяти непосредственно друг за другом,
доступ к которым осуществляется поиндексу(индексам). В отличие отсписка,
массив является структурой с произвольным
доступом.

Размерностьмассива — количество индексов,
необходимое для однозначного доступа
к элементу массива.

Формаилиструктура массива— количество
размерностей и размер (протяжённость)
массива для каждой размерности, может
быть представлен одномерным массивом.

• сортировка
  массива;

Сортировкой
или упорядочением
массиваназывается расположение его элементов
по возрастанию (или убыванию). Если не
все элементы различны, то надо говорить
онеубывающем
(или невозрастающем)
порядке.

Вообще говоря, это
большая и сложная тема, в которой известно
много различных алгоритмов. Критерии
оценки эффективности этих алгоритмов
могут включать следующие параметры:

• количество шагов
  алгоритма, необходимых для упорядочения;

• количество
  сравнений элементов;

• количество
  перестановок, выполняемых при сортировке.

Примеры алгоритмов устойчивой сортировки

• Сортировка
  выбором—
  поиск наименьшего или наибольшего
  элемента и помещение его в начало или
  конец упорядоченного списка.

• Сортировка
  пузырьком—
  для каждой пары индексов производится
  обмен, если элементы расположены не по
  порядку.

• Сортировка
  перемешиванием

• Гномья
  сортировка
  — схожа с сортировкой пузырьком и
  сортировкой вставками.

• Сортировка
  вставками—
  Определяем, где текущий элемент должен
  находиться в упорядоченном списке, и
  вставляем его туда.

• Сортировка
  слиянием—
  выстраиваем первую и вторую половину
  списка отдельно, а затем объединяем
  упорядоченные списки.

• Сортировка
  с помощью двоичного дерева

• Сортировка Timsort—
  комбинированный алгоритм (используется
  сортировка
  вставками
  и сортировка
  слиянием).

• Сортировка
  подсчётом

• Блочная
  сортировка
  (Корзинная сортировка) — требуется
  O(k)
  дополнительной памяти и знание о природе
  сортируемых данных, выходящее за рамки
  функций «переставить» и «сравнить».

• подпрограмма.

Подпрограмма
— это отдельная функционально независимая
часть программы.

Подпрограммы
решают три важные задачи:

• избавляют от
  необходимости многократно повторять
  в тексте программы аналогичные фрагменты;

• улучшают структуру
  программы, облегчая ее понимание;

• повышают устойчивость
  к ошибкам программирования и непредвиденным
  последствиям при модификациях программы.

В языках
программирования высокого уровня
используется два типа подпрограмм:
процедуры
и функции.

• Функция — это
  подпрограмма специального вида, которая,
  кроме получения параметров, выполнения
  действий и передачи результатов работы
  через параметры имеет ещё одну
  возможность — она может возвращать
  результат.
  Вызов функции является, с точки зрения
  языка программирования, выражением,
  он может использоваться в других
  выражениях или в качестве правой части
  присваивания. Подробнее см. в статье
  Функция
  (программирование).

• Процедура —
  это независимая именованная часть
  программы, которую после однократного
  описания можно многократно вызвать по
  имени из последующих частей программы
  для выполнения определенных действий.

 Ответьте
на следующие содержательные вопросы:

Проанализируйте,
какие парадигмы программирования
поддерживаются в основной школе, и
заполните таблицу

Выходные данные учебника	Парадигма программирования	Язык программирования (система программирования)	Основные понятия (определения)

Приведите
список основных операторов языка
программирования Паскаль (Pascal
ABC).

Распределите
на две группы – описатели данных простого
типа и описатели данных составного типа
– приведенные ниже описатели типов:
real,
array,
string,
integer,
boolean,
set,
char,
file,
record.

Заполните
таблицу, в которой для каждой структуры
привести общий вид записи на языке
Паскаль и основные типы задач.

Следование	Ветвление	Выбор	Цикл

Объясните
смысл использования в программировании
логического типа данных. Приведите
примеры.

Сформулируйте
правила записи арифметических и
логических выражений на языке Паскаль.

Сформулируйте
алгоритм построения таблицы истинности
логического высказывания. Приведите
пример построения.

Объясните
смысл генерации случайных чисел. Как
она реализуется на языке Паскаль? Где
она может использоваться?

 Ответьте
на следующие методические вопросы:

Как
наиболее эффективно связать освоение
методов построения алгоритмов с освоением
языка программирования?

Какие
языки программирования наиболее подходят
для начального обучения программированию?

Почему
для успешного освоения программирования
ученику необходимо иметь представление
об архитектуре ЭВМ?

Как
объяснить ученикам, в чем заключается
разница между языками программирования
и системами программирования?

Какой
методический подход следует применять
при ознакомлении учеников с системой
программирования?

Приведите
систему типовых задач обработки
одномерных массивов.

Приведите
систему типовых задач обработки текстовой
информации (использование символьного
и строкового типов).

 Портфолио:

1)
конспект одного урока по теме;

2)
пять заданий
с использованием метода ошибок;

3)
материал по темам: «История развития
языков программирования», «Алгоритмы
сортировки массивов», «Процедуры и
функции», «Рекурсия».

4)
задача: «Запишите
с помощью разных операторов цикла
фрагменты программ, решающих задачу
вывода строчных букв латинского алфавита
в прямом и обратном порядке»
(оформить в виде текстового документа,
содержащего скриншоты текстов программ
в системе программирования и окна
выполнения программ; в окне программы
должна содержаться информация об
авторе-создателе программ).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для того чтобы систематизировать и квалифицировать ошибки, которые совершают обучающиеся в контрольных, самостоятельных и домашних работах, выделено 12 основных видов ошибок, благодаря которым можно понять основные причины появления затруднений.

Виды ошибок:

1. Решение даже не начато

2. Вычислительная ошибка в элементарном действии

3. Вычислительная ошибка в многошаговом действии

4. Установление неправильных связей между данными задачами

5. Неправильное понимание условий задачи

6. Ошибки при переписывании

7. Незнание алгоритмов математических действий

8. Неэквивалентные преобразования

9. Ошибки геометрических измерений

10. Незнание математических формул

11. Незнание законов арифметики

12. Логические ошибки

Все без исключения школьники совершают вычислительные ошибки. Для того чтобы снизить их количество в многошаговых арифметических действиях, необходимо обучать детей алгоритмам, которые позволяют разбивать сложные действия на более простые.

Однако для выделения элементарных действий предварительно следует установить уровень заданий, который будет доступен каждому обучающемуся. К такому уровню могут быть отнесены:

• вычитание/сложение однозначных или двузначных чисел без перехода единиц в старший разряд;

• вычитание однозначных или двузначных чисел при условии, что число единиц в соответствующем разряде уменьшаемого больше числа единиц в разряде вычитаемого;

• умножение однозначных чисел между собой и умножение на двузначные числа при условии, что последние остаются двузначными;

• деление однозначных чисел, а также деление двузначных чисел на однозначные, но при этом делитель является делителем числа единиц в каждом разряде.

Другие арифметические действия целесообразно разбивать на элементарные.

Достаточно сложными для детей являются текстовые задачи, так как они предполагают применение не только знаний, которые были получены на уроках, но и своего жизненного опыта. Наиболее распространенная ошибка – неиспользование части условия текстового задания. В целях исключения таких ошибок необходимо, чтобы дети обладали устойчивыми навыками по решению элементарных текстовых задач. При этом уровень сложности задачи не должен ставить обучающегося в безвыходное положение.

Что касается ошибок переписывания, то они в основном возникают в случаях, когда задания неинтересны обучающемуся. Как только они становятся значимыми для него, то количество ошибок при переписывании резко уменьшается.

Для того чтобы снизить количество ошибок, связанных со сложением и вычитанием обыкновенных дробей, необходимо более детальное изучение типовых примеров решения данного вида задач.

В ходе решений простейших уравнений обучающиеся часто сталкиваются с проблемой приведения эквивалентных преобразований. Самые распространенные ошибки – определение знака одночлена, когда он переносится в другую часть уравнения, а также непонимание сущности числового коэффициента переменной.

Ошибки, которые связаны с геометрическими измерениями, в большинстве случаев объясняются элементарным отсутствием навыков работы с линейкой и транспортиром. Проблема устраняется за счет постоянного применения на уроках этих инструментов. В целях профилактики необходимо, чтобы обучающиеся точно понимали, что такое точка отсчета и единица измерения. Кроме того, до начала практических измерений следует закрепить соотношения используемых единиц одной физической величины.

В 5 классе одним из самых трудных разделов является тема, посвященная прямоугольным параллелепипедам. И если обучающийся не знает формул объема, то он просто не сможет решить ни одной задачи. Однако и в самих заданиях этой темы можно выделить объективные трудности, ведь от обучающегося требуется, чтобы он усвоил единицы объема и взаимоотношения между ними. Очень часто более слабые обучающиеся просто не понимают, как между собой соотносятся кубические метры и сантиметры, а также кубические километры и кубические метры. Кроме того, для решения многих задач требуется наличие пространственного воображения, поэтому некоторые обучающиеся испытывают затруднения при решении задач, где требуется определить объем тел, изображенных на чертежах и рисунках. В целях профилактики таких ошибок рекомендуется больше уделять времени изучению моделей, которые должны быть доступны каждому обучающемуся. Особенно высоких результатов можно добиться, если применять разборные модели параллелепипедов.

В процессе изучения арифметики значительное количество ошибок связано с применением распределительного закона умножения. Обучающиеся, которые не усвоили этот закон, при умножении одночлена на многочлен делают только одно действие умножения, а остальную часть многочлена записывают без каких-либо необходимых изменений. Профилактика ошибки заключается в использовании схемы умножения, в которой стрелками соединяются все сомножители.

Реже всего встречаются логические ошибки, однако это, прежде всего, связано с тем, что обучающиеся пятых классов крайне мало решают таких задач. Поэтому профилактика таких задач предполагает, в первую очередь, увеличение количества таких задач в учебных пособиях для 5 класса.

Методы, направленные на предупреждение ошибок

Задачи-ловушки

Провоцирующие задачи, то есть задачи, которые подталкивают обучающегося к неправильному выбору, обладают крайне высоким развивающим потенциалом. При попадании в подготовленную «ловушку» обучающийся начинает испытывать досаду и смущение от того, что он не придал значения каким-либо нюансам и условиям задачи. В результате обучающийся испытывает сильное впечатление и надолго запоминает свои ошибочные действия, а в дальнейшем уже на подсознательном уровне старается не попадаться в аналогичные ситуации.

Кроме того, задачи-ловушки способствуют развитию критичности, учат детей внимательно анализировать информацию, проводить ее разностороннюю оценку. Одновременно и повышается и интерес к изучению математики.

Выделяют несколько основных видов провоцирующих задач:

• задачи, в которых условия навязывают получение неправильного ответа;

• задачи, где условия делают подсказку на неправильный алгоритм решения;

• задачи, в которых неоднозначность трактовки терминов, используемых оборотов, числовых и буквенных выражений выводят на неправильный путь решения;

• задачи, где обучающемуся необходимо что-то придумывать, строить, составлять и т.д. В итоге у обучающегося должны получиться такие математические объекты, которые не могут иметь места при заданных условиях;

• задачи, в которых условия допускают возможность «опровержения» семантически верного решения каким-либо нематематическим способом.

Задачи, условия которых навязывают неверный ответ

А. Задачи, навязывающие в явной форме один вполне определенный ответ.

Пример.

Сколько цифр потребуется, чтобы записать одинадцатизначное число?

На первый взгляд кажется, что ответ очевиден – «11 цифр». Однако по причине того, что десятичная система счисления использует только 10 цифр, то правильным ответом будет: «Одинадцатизначное число можно записать с помощью 0,1,2,3,4,5,6,7,8,9 или 10 цифр».

Б. Задачи, стимулирующие сделать выбор ответа из предложенной совокупности изначально неверных ответов.

Пример.

Какое из чисел 205, 206, 207, 208, 209, 210 является простым?

В большинстве случаев ученики называют 209 или 207, но это неверно, так как все числа являются составными. Правильный ответ: «Никакое».

В. Задачи, где предлагается сделать неправильный выбор из совокупности верных и неверных ответов.

В каком из вариантов пример решен неверно?

Г. Задачи, где условия не содержат неверных ответов в явном виде, но при этом каким-то образом указывают на него.

Пример.

Какое простое число следует за числом 200?

Напрашивается ответ: 201, ведь это число следующее – за числом 200. Однако ответ неправильный, ведь число 201 является составным. Правильный ответ – 211.

Задачи, побуждающие к выбору неверного способа решения

А. Задачи, в которых условия подталкивают обучающегося выполнить определенные действия с предложенными числами, однако на самом деле этого не требуется делать.

Пример.

Тройка лошадей проскакала 12 км. Сколько километров проскакала каждая лошадь?

Многие ученики делят 12 на 3 и получают ответ 4 км. Однако все лошади проскакали по 12 километров.

Б. Задачи, где условия подталкивают выполнить определенное действие, хотя на самом деле требуется выполнить обратное действие.

Пример.

У палки 2 конца. Если один из них отпилить, сколько концов получиться?

С ходу хочется ответить, что следует выполнить вычитание 2 – 1, что приводит к ответу «у палки один конец». На самом же деле количество концов останется неизменным – 2 или второй вариант правильного ответа – получится две палки, а значит, будет уже 4 конца.

В. Задачи, где условия подталкивают обучающегося выполнить действие определенным образом, хотя надо действовать по-другому и при этом выполнять более сложный расчет.

Пример.

На руках 10 пальцев. Сколько пальцев на 10 руках?

Большинство учеников сразу же перемножают 10 на 10. Однако у человека на руке 5 пальцев, поэтому надо 5 умножать на 10 и правильный ответ – число 50.

Г. Задачи, которые предлагают выполнить действия, которые в принципе невозможно выполнить.

Пример.

Двое пошли, 3 гриба нашли. Четверо пойдут, сколько грибов найдут?

Напрашивается последовательность действий:

1) 4:2 = 2,

2) 3х 2 = 6,

т.е. четверо вроде бы найдут 6 грибов. Однако же они могут вообще ничего не найти, поэтому правильный ответ: «Неизвестно».

Задачи, которые вынуждают придумывать, составлять, строить и др. несуществующие при заданных условиях математические объекты

Пример.

Придумайте простое трехзначное число, в записи которого употребляются лишь цифры 1 и 4.

Придумать такое число просто невозможно, так как любое число, удовлетворяющее условию задачи, будет кратно 3 и, соответственно, не является простым.

Задачи, которые вводят в заблуждение из-за неоднозначности трактовки терминов, буквенных и числовых выражений

Пример.

На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза?

Здесь имеется в виду, что надо совершать не математическое действие, а провести действие с листом бумаги. И если перевернуть листок, то с обратной стороны мы увидим число 909, которое как раз в 1,5 раза больше 606.

Задачи, где допускается возможность «опровержения» семантически верного решения нематематическим решением

Пример.

(Старинная задача). Крестьянин продал на рынке трех коз за 3 рубля. Спрашивается: «По чему каждая коза пошла?»

Очевидный ответ: «По одному рублю», но опровергается, так как козы по деньгам не ходят, а ходят по земле.

Логические ошибки

Возникновение логических ошибок связано с нарушениями основных принципов математических рассуждений.

Наиболее часто встречаются ошибки в определении понятия, например:

• квадратное уравнение с одним неизвестным – уравнение, которое содержит неизвестное второй степени;

• равносильные уравнения – уравнения, где корни первого уравнения выступают в роли корней второго уравнения;

• отрезок, которые соединяет середины сторон треугольника и равный половине его третьей стороны, называется средней линией треугольника;

• прямая, которая разделяет сторону треугольника пополам, называется медианой.

В данных примерах нарушено ключевое требование к установлению определения понятия, то есть наличие достаточных признаков объекта. Для профилактики появления таких ошибок требуется тщательная отработка определения понятий, в том числе с использованием метода сравнения объектов и различных примеров с опровержениями.

Для закрепления понятий целесообразно предложить детям решение следующих примеров:

1. Являются ли равносильными уравнения:

1. х – 2 = 0 и (х – 2) (х – 3) = 0;

2. х – 2 = 0 и х + 3 = 5;

1. Какие из нижеприведенных уравнений являются квадратными:

1. х2 – 3х + 2 = 0;

2. х3 – х2 + 3х = х3 – 2;

3. х3 + х2 – 3х = х3 – 2;

4. х2 – 4.

Ошибки при доказательстве теорем

При доказательстве теорем довольно часто обучающиеся используют искомое в качестве данного. Для предупреждения такой ошибки необходимо четко объяснять обучающимся, что дано и что требуется доказать.

Часто встречаются и логические ошибки в доказательстве утверждений, которые заключаются в неполной аргументации или пропуске аргументации.

Неполная дизъюнкция также является логической ошибкой и преимущественно допускается в вопросах и задач, которые связаны с исследованием.

Пример:

Необходимо установить сравнительную величину а3 и а2. Вместо того чтобы проверить все возможные значения буквы а, обучающийся начинает рассматривать значения выражений только при а > 1, в результате чего получает неполный ответ.

Много ошибок дети допускают в преобразованиях алгебраических выражений, что связано с применением необоснованной аналогии. Примером такой ошибки может служить следующее выражение: так как (a + b)c = ac + bc, то по аналогии (ab)c = ac(bc. Известно, что, если а = b, то ak = bk, отсюда по аналогии считают, что, если a > b, то ak > bk в любом случае; по аналогии с численными дробями обучающиеся иногда считают, что

Для профилактики ошибок необходимо обучающимся постоянно устно напоминать и демонстрировать примеры того, что аналогия выступает только как вспомогательное средство для установления истины и в каждом случае требует выполнения проверки и подтверждения логическим доказательством.

Наиболее распространенные ошибки, совершаемые обучающимися выпускных классов

Задание.

Очень часто обучающиеся применяют неверную формулу, даже не задумываясь над ней. Так, при определении того является ли число

использовании определения степени в похожих случаях обучающиеся могут вывести любую формулу действий со степенями. Аналогичным образом учитель может продемонстрировать ошибки в действиях со степенями.

Обучающимся также можно показать три варианта решения данного неравенства:

При выполнении тригонометрических заданий школьники часто сами придумывают формулы, к примеру: «sin 2 х = 2 sin x».

В таких случаях можно действовать двумя способами:

При этом учителю не требуется целенаправленно проводить исправление всех ошибочных утверждений обучающегося и рассказывать ему обо всех ошибках. Оптимальный вариант – обсудить ошибку всем классом и добиться того, чтобы все обучающиеся поняли причину ее появления и в дальнейшем не допускали ее. Как свидетельствует практический опыт, организация систематических проверок чужих записей позволяет сформировать у школьников привычку критически относиться и к своим записям.

Для этого отлично подходят задания, где надо найти ошибку в решении, например:

Процесс поиска и исправления ошибок самим обучающимся под руководством педагога является весьма поучительным для всех обучающимися, так как в ходе данного процесса изучение и анализ ошибок способствует развитию познавательного интереса к изучению математики.

Основные ошибки, обучающиеся допускают в следующих ситуациях:

• выполнение исследования функции на наименьшие и наибольшие значения;

• преобразование дробно-рациональных выражений, где содержится корень n-ой степени;

• вычисление площади криволинейной трапеции;

• решение показательных и логарифмических неравенств;

• изображение тел вращения при решении геометрических задач;

• построение графика функции, содержащей модуль;

• построение множества точек плоскости, которое должно удовлетворять заданному условию;

• теоретическое обоснование применяемых формул и фактов при выполнении задач по стереометрии;

• решение задач с параметром.

В целях повышения уровня учебных успехов обучающихся, а также в ходе подготовки к итоговой аттестации за курс старшей школы целесообразно повышенное внимание уделять следующим темам:

• углы в пространстве;

• комбинация тел;

• построение геометрических мест точек, удовлетворяющего установленным условиям;

• производная и ее применение при исследовании функции на отрезке;

• тригонометрические функции и их свойства;

• логарифмические и показательные неравенства;

• тождественные преобразования дробно-рациональных выражений, где содержится корень n-ой степени.

Целесообразно спланировать учебный процесс таким образом, чтобы учебный год в выпускных классах заканчивался повторением всего пройденного материала. При этом повторение должно быть нацелено на закрепление опорных знаний, подготовку к итоговому оцениванию знаний, а также формирование и развитие межпредметных связей с одновременным осознанием взаимосвязи с ранее пройденными темами.

При высоком уровне организации учителем работы учеников над типичными ошибками позволяет существенно повысить уровень обучения математике и способствует развитию логического мышления.

Особенность школьной программы состоит в том, что при оформлении упражнений используется не математический характер и существующие правила абсолютно не связаны с проверкой знаний. Особенно это остро ощущают сильные обучающиеся, которые справедливо раздражаются из-за того, что два незначительных недочета являются ошибкой.

Намного правильнее было бы, если к математическому тексту предъявлялось одно требование – ясное отражение логики решения. При этом должно быть абсолютно неважно, какие слова и выражения использовал обучающийся для объяснения своих действий. Кстати, именно такие правила используются в высших учебных заведениях, где преподаватель смотрит исключительно на логику решения задачи.

Например, по вузовским стандартам следующая записи

является полностью исчерпывающей и не предполагает какого-либо дополнительного словесного комментария. Ведь важно, чтобы обучающийся правильно преобразовал неравенство, а не использовал при объяснении фразу: «Так как основание логарифма меньше единицы, то функция убывает и знак неравенства меняется».

Современные экзамены по своему характеру максимально приближены к тестированию, поэтому к оформлению предъявляется всего одно требование – разборчивая запись ответа.

По теореме Виета х1 = 1, х2 = -2.

Проверка показывает, что х2 не удовлетворяет условию. Ответ: 1.

Данное решение в большинстве случаев оценивается положительно. В тоже время такая последовательность действий оставляет несколько неясностей:

1. Зачем нужно было искать ОДЗ, если он в решении не использовался.

2. Один из предложенных корней не удовлетворяет условию, поэтому надо выяснить, откуда он здесь появился.

3. Какие логические знаки необходимо применять для связывания сделанных записей.

4. В соответствии с каким математическим законом х1 и х2 являются значениями переменной х.

И если пункты 1, 2, 4 можно считать еще придирками, то отсутствие логических знаков (пункт 3) является уже серьезной ошибкой. Для справедливости стоит отметить, что такая ошибка присутствует во многих работах обучающихся.

Для сравнения можно привести другой вариант решения:

В связи с тем, что возведение в квадрат могло стать причиной появления посторонних корней, то требуется проверка.

Ответ: 1.

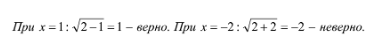
Если вместо первой импликации «(» ученик напишет «(», то это будет ошибкой. Если же любую из оставшихся эквиваленций «(» заменить на «(», то все останется верным.

В первом варианте решения обучающийся, скорее всего, просто не задумывался о логических связях записей и просто механически разделял записи с помощью «точки с запятой». И если бы «точка с запятой» использовалась только в одном определенном смысле, то было все нормально. Однако данный символ в работах школьников может быть заменой различных символов, в том числе:

• «равносильно»;

• «следовательно»;

• «и»/«или»;

• объединение и пересечение множеств.

Организация контроля и самоконтроля учебной деятельности обучающихся

При проверке работ педагог отмечает не только математические, но и грамматические, и стилистические ошибки. При этом учитель лично исправляет все ошибки, что является крайне неверным решением. Ведь если учитель исправил ошибку, то обучающийся просто соглашается с ней и успокаивается.

Для повышения уровня самостоятельной работы обучающегося необходимо, чтобы он сам выявил свою ошибку и разобрался, почему он ее совершил. Поэтому учителю достаточно просто указать место ошибки, для чего может использоваться определенная символьная система. Так, две черты обычно указывают на грубую ошибку, одна черта – случайная или негрубая ошибка, а волнистая линия – наличие какого-либо недочета.

При проверке домашних заданий учителю необходимо тщательно просматривать все проведенные обучающимся преобразования, вычисления и рассуждения. При этом все ошибки требуется систематизировать и выделить наиболее типичные и массовые. В первую очередь, выделяются наиболее грубые и принципиальные ошибки, которые связаны с нарушением основных математических законов.

Именно таким ошибкам и необходимо уделять повышенное внимание при проведении разбора в классе. Такой обзор нельзя ограничивать только сообщением ошибок каждого обучающегося, так как требуется произвести разбор ошибок и выявить причины, которые к ним привели. Для этих целей целесообразно привлекать и других обучающихся, которые допустили аналогичные ошибки.

Если какое-то задание вызвало затруднения у большинства обучающихся класса, то его надо разбирать максимально детально и при необходимости провести дополнительные упражнения.

Если ошибка не была массовой, то обучающемуся можно предложить произвести детальный ее разбор дома, внести все необходимые исправления и сделать отсылки на соответствующие правила.

Для повышения эффективности работы над ошибками нельзя откладывать проведение этого мероприятия, так как отсрочка неизбежно ведет к потере интереса учеников к разбору.

Для того чтобы исправить множество ошибок и предупредить их появление, крайне важно сформировать у обучающихся навыков самоконтроля, которые включают в себя две части:

• способность самостоятельно обнаруживать ошибки;

• умение самостоятельно объяснить ошибку и исправить ее.

Для поиска ошибок используются следующие приемы:

• проверка правильности проведенных вычислений и преобразований за счет выполнения обратного действия либо преобразования;

• проведение оценки полученного результата с точки зрения здравого смысла;

• осуществление проверки правильности решения за счет составления и решения задач, обратных решаемой задаче;

• проверка правильности решения с помощью графического способа.

Формированию навыков самоконтроля способствует и прием приближенной оценки ожидаемого результата, ведь установление возможных пределов планируемого результата позволяет не допустить недочеты в виде описок и пропуска цифр.

К примеру, обучающемуся надо решить следующую задачу: «За неделю завод выпустил 130 телевизоров, выполнив месячный план на 25%. Сколько телевизоров должен выпустить завод за месяц по плану».

Ученик написал 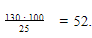Ошибку можно сразу вычислить, если перед решением школьник «включит» логику и прикинет «В течение недели было выпущено 130 телевизоров. Соответственно, за месяц будет выпущено больше 130 телевизоров, поэтому и ответ должен быть больше 130».

Система работы учителя математики по коррекции ошибок Достижение положительного эффекта от индивидуальных заданий объясняется тем, что обучающиеся их выполняют самостоятельно, в том числе и дома. В то же время индивидуальные задания должны составлять методически правильно и быть направлены на преодоление конкретных ошибок. Для этого от учителя требуется постоянное ведение учета основных затруднений обучающихся, для чего, например, может использоваться следующий вариант таблицы:

Список учащихся класса	Тема…	Примечание «+» — ошибка устранена; «-» — ошибка не устранена
Пробелы в знаниях	Классные индивидуальные задания	Домашние индивидуальные задания

Заполнение всех граф таблицы, за исключением первой, рекомендуется осуществлять карандашом. Пополнение списка ошибок ведется при проверке домашних заданий, самостоятельных и контрольных работ. Большинство ошибок повторяются из года в год, поэтому молодому педагогу рекомендуется ознакомиться с ними.

Ниже представлены наиболее распространенные ошибки.

При работе с десятичными дробями обучающиеся совершают ошибки в выделении целой части результата, к примеру:

а) 3,6 – 1,8 = 18;

б) 2 + 5,3 = 55;

в) 6,4 : 2 = 32.

Во время беседы с обучающимися, которые допускают такие ошибки, обычно выясняется, что они просто забыли поставить запятую. Устранение ошибки осуществляется в результате длительных тренировок.

Одна из самых типичных ошибок – деление десятичной дроби на десятичную. Деление обычно совершается без обращения внимания на запятые: 2,576: 11,2 = 23.

Для профилактики ошибок обучающимся предлагаются задания на карточках, где для каждого примера приведено соответствующее правило, но оно сформулировано с пропусками или полностью.

Примеры карточек.

Карточка №1. Чтобы сложить две десятичные дроби, надо:

1. сложить получившиеся числа, как складывают …;

2. записать слагаемые друг под другом так, чтобы запятая …;

3. уравнять число знаков … в слагаемых;

4. в полученной сумме поставить запятую под….

Задания.

1. В представленных числах уравняйте число знаков после запятой: 2,5; 0,25; 43, 1256; 325,1.

2. Выполните сложение дробей: 12,7 и 3,442; 0,237 и 10,44.

Карточка № 2.

Для того чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимание на …, а затем в результате отделить запятой… столько цифр, сколько их стоит после запятой… .

Задания.

1. В записи числа 1234567 отделите запятой справа:

   1. одну цифру;
   2. две цифры;
   3. шесть цифр;
   4. семь цифр.

В каком случае в результате получается число, которое больше 1, но меньше 2? больше 0, но меньше 1?

1. Найдите произведение чисел: 2,7 и 1,32.

Карточка № 3.

Чтобы разделить число на десятичную дробь, надо в делимом и в делителе перенести … вправо на столько цифр, сколько их после… в …, а потом выполнить деление на натуральное число.

Задания.

1. В записи 4,78: 0,8 подчеркните одной чертой делимое, а двумя – делитель.

2. В числах 1; 0,345; 30,25 перенесите запятую вправо на столько цифр, сколько их после запятой в числе 0,5.

3. Найдите частное чисел: 8,96 на 1,12.

Часто встречаются ошибки при совершении действий с обыкновенными дробями. В частности, при выполнении сложения (вычитания) дробей обучающиеся производят складывание (вычитание) числителей и знаменателей:

Складывая (вычитая) дроби, обучающиеся забывают умножить их числители на дополнительные множители:

Карточка № 5.

Известно, что вычитание проверяется и тем, что разность двух положительных чисел не может быть больше уменьшаемого.

1. Учитывая сказанное выше, установите, верен ли результат вычитания:

При умножении (делении) смешанного числа на десятичную дробь умножают (делят) отдельно целые части и отдельно дробные, а результаты записывают рядом, например:

Приемы работы по повышению качества работы по профилактике ошибок

Существует несколько основных правил, при руководстве которыми можно значительно снизить количество ошибок. При этом многие формулировки относятся к фольклорному жанру, но, тем не менее, дают объективное понимание какого-либо правила:

1. Правило ГАИ. Оно гласит, что большинство аварий случается при небольших скоростях. При переносе данного тезиса на математику получаем, что большинство ошибок возникают в самых простых ситуациях.

Для непопадания в такие ситуации обучающимся надо привить навык постоянной проверки правильности списывания условий задач, решения квадратных уравнений. А для выявления ошибки рекомендуется начинать ее искать с конца, что предполагает подстановку полученного результата в последнее действие и последовательное следование выше.

Правило закройщика: шов иголкой делается следующим образом: стежок вперед и назад, а потом еще вперед и опять назад.

В математике преобразования осуществляются аналогичным образом, то есть после совершения каждого перехода необходимо «оглянуться назад» и проверить полученный результат проведением обратного преобразования.

1. Правило программиста: работай блоками.

В программировании произвести отладку программы целиком невозможно, поэтому всю работу разбивают на небольшие автономные блоки, и затем по отдельности проверяется работоспособность каждого блока.

В математике этим правилом необходимо руководствоваться, прежде всего, при работе с громоздкими выражениями, то есть они разбиваются на несколько простых. При решении с каждым уравнением «разбираются» по отдельности.

Большинство приемов работы над ошибками не содержит методик диагностики выявления причин ошибок, а также не уделяется достаточного внимания работе по организации рефлексивной деятельности учеников и ее применения для предупреждения и исправления математических ошибок.

Еще один недостаток состоит в том, что работа над ошибками практически никак не контролируется, поэтому причины появления ошибок так и остаются не выясненными и повторяются снова и снова. Для повышения качества работы над ошибками необходимо обеспечивать большую самостоятельность учеников, так как это позволяет осуществлять более осознанный анализ ошибок и собственных действий при решении конкретной задачи.

В результате у обучающихся развивается логическое мышление, а также создаются благоприятные условия для лучшего усвоения новых знаний. Постепенно у детей развиваются и стремление самостоятельно разобраться в задаче, умение по планированию ее решения и навыки продумывания различных вариантов действий. Например, обучающийся отлично усвоил правило преобразования алгебраических выражений формулы квадрата суммы и разности двух чисел, однако, когда получает задание, где необходимо представить в виде многочлена (–х–5)2, он теряется.

В таких случаях обучающемуся надо предложить ответить на вопрос, что конкретно у него вызывает затруднение? Далее надо помочь ему преобразовать выражение таким образом, чтобы можно было использоваться одну из известных ему формул в том виде, в каком они представлены в учебнике.

Еще один пример неосознанного применения алгоритма:

Обучающемуся предлагается решить уравнение sin x = 1,2, он сразу же начинает искать его корни по уже отлично известной ему формуле и при этом совершенно не обращает внимания на недопустимые значения sin x. Для того чтобы помочь учащемуся разобраться в данной ситуации, рекомендуется продемонстрировать наглядное решение задачи на тригонометрическом круге.

Список литературы:

1. Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
2. Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
3. Гальперин П.Я. Методы обучения и умственное развитие ребенка. – М.: Изд-во Моск. Ун-та, 1985. – 45 с.
4. Гласс ДЖ., Стенли Дж. Сатистические методы в педагогике и психологии. Пер. С англ. – М.: Прогресс. – 1976. – 495 с.
5. Грабарь, И. И. Применение математической статистики в педагогических исследованиях. Непараметрические методы / И. И. Грабарь, К. А. Краснянская. – М.: Педагогика, 1977. – 136 с.
6. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
7. Груденов, Я. И. Изучения определений, аксиом, теорем / Я. И. Груденов. – М. Просвещение, 1984. – 95 с.
8. Груденов Я.И. Психологический анализ причин некоторых массовых ошибок учащихся// Журнал «Математика в школе» – 1981 г. – №3, с. 46-48.
9. Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
10. Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
11. Гуцанович С.А., Радьков А.М. Тестирование в обучении математике диагностико-дидактические основы. – Могилев, МГПИ им. А.А. Кулешова, 1995. – 203 с.
12. Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
13. Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
14. Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
15. Действующие учебники и учебные пособия по математике для средней школы.
16. Журналы «Математика в школе» за 1970-1990 гг.
17. Зайкин М.И., Колосова В.А. Провоцирующие задачи // Журнал «Математика в школе» – 1997 г. – №6, с. 32.
18. Запрудский Н. И. Современные школьные технологии: пособие для учителей. – 3-е изд. / Н. И. Запрудский. – Минск, 2006. – 288 с.
19. Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
20. Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
21. Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
22. Метельский Н.В. Пути совершенствования обучения математике: Проблемы современной, методики математики. – Минск: Университетское, 1989. – 160 с.
23. Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
24. Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
25. Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
26. Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
27. Рогановский Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
28. Селевко Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
29. Скобелев Г.Н. Контроль на уроках математики: Пособие для учителя. – Минск: Народная асвета, 1986. – 103 с.
30. Столяр А.А. Роль математики в гуманизации образования // Математика в школе. 1990. – № 6. – с. 5–7.
31. Столяр А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
32. Темербекова А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
33. Фарков А. В. Внеклассная работа по математике.
34. Фридман, Л. М. Как научиться решать задачи: пособие для учащихся / Л. М. Фридман, Е. Н. Турецкий – 2- изд. – М.: Просвещение, 1984. – 175 с.
35. Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
36. Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Журнал «Математика в школе» – 2000 г. – №4, с. 28.
37. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
38. Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
39. Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
40. Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
41. Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.