
ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .

1.Задачи теории ошибок измерений.
2.Сущность и виды измерений.
3.Ошибки измерений, их классификация и свойства.
4.Понятие о законах распределения ошибок.
5.Числовые характеристики точности измерений.

1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.

Теория ошибок измерений решает четыре основные задачи:
1.Изучение законов возникновения и распределения ошибок измерений и вычислений.
2.Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.

2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется
результатом измерения.

Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.

Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны- ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.

Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n—раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
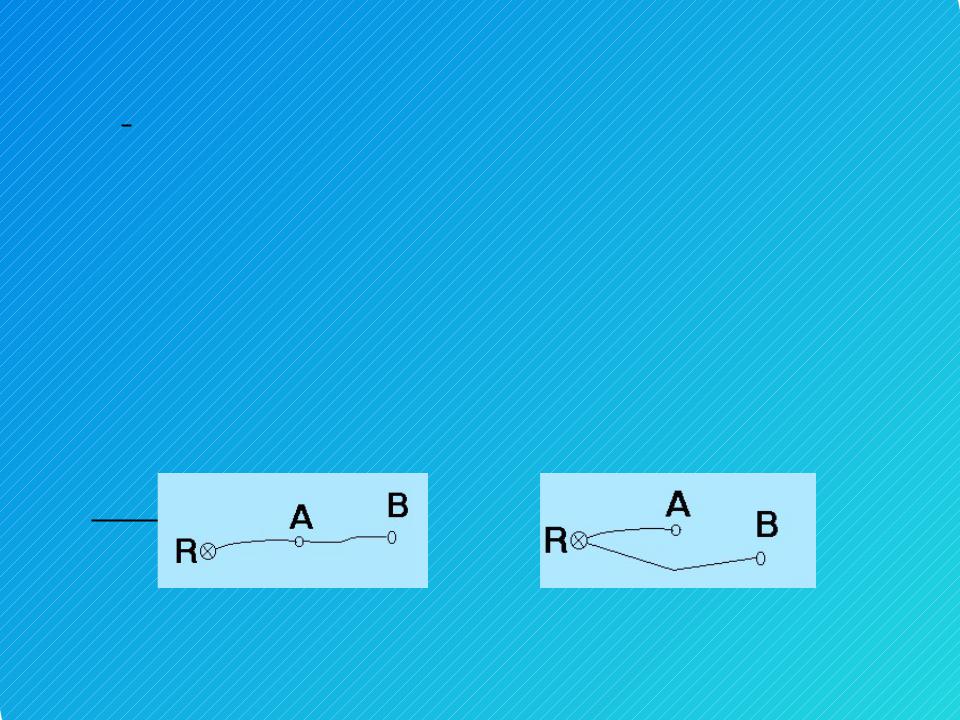
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут
(рис.2).
Соседние файлы в папке лекции по геодезии 2 курс
- #
- #
- #
29.02.20162.28 Mб32ЛЕКЦИЯ 13.pptx
- #
- #
- #
Насколько разнообразны виды геодезической деятельности, объекты и способы измерений, их количество, качество получаемых результатов, настолько разнообразен теоретический и математический аппарат, позволяющий все это выполнить. Если каждый из бывших студентов геодезическо-маркшейдерских специальностей вспомнит один из предметов под названием «МОМГИ», что означает математическая обработка маркшейдерско-геодезических измерений, то вспоминается ужас от обилия вновь вводимых критериев и понятий, набора новых способов вычислений с применением элементов до конца не доученных разделов высшей математики.
Сейчас попробуем целостно структурировать основы МОМГИ. После всех полевых наблюдений полученная информация не используется в том виде, в котором зафиксирована в первичной документации. Используя свои теоретические знания и практические умения, специалисты выполняют ее математическую обработку. Под этим понимается целый комплекс преобразований и вычислений, полученной при измерениях числовой информации, представляющей практическую ценность. Почти все вычислительные действия осуществляются в камеральных условиях, за исключением тех, которые предусмотрены методикой и исполняются в момент измерений для оценивания и сравнения полученных значений. Одной из специфических составляющих в математической обработке выступают погрешности, которые возникают изначально в моменты замеров и требующие определенного учета и преобразований. Все они имеют неизбежность находиться в неопределенных пределах искажения. Конечные результаты после их расчетов сопровождаются также неопределенными искажениями. Помимо этого, во многих способах и методах существуют в завершении работ контрольные измерения, приводящие к избыточным измерениям. Они влекут за собой возникновение различных значений одних и тех же величин. Кто из геодезистов и маркшейдеров с этим не сталкивался? Да, все.
Таким образом, можно сделать вывод, что основной задачей математической обработки можно считать нахождение однозначных значений величин наиболее приближенных к истинным. Наряду с этим на практике геодезические и маркшейдерские измерения решают следующие задачи:
- определение необходимой точности измерений для практических целей;
- выбор оптимальных средств и методов работ для достижения требуемой точности;
- установление необходимых допустимых параметров (критериев), которые давали бы возможность судить о достаточной точности выполненных работ;
- выбор способов и методик обработки проведенных измерений с целью получения оптимальных значений результатов;
- определение точности выполненных замеров и качественной характеристики полученных результатов.
Ориентировочный алгоритм вычислений
Существует определенный общий алгоритм вычислительных операций с целью получения результатов. Независимо от того какие виды работ выполнялись, математическая обработка, включает в себя следующие этапы:
- предварительную математическую обработку измеренных величин. Она включает проверку первичной документации, информации в ней, выявление грубых ошибок, определение средних измеренных параметров. Далее вычисление их невязок, оценка качества в пределах требуемой точности, введение поправок в измеренные параметры;
- уравнительные операции, включающие определение поправок в вычисляемые формулы;
- завершение вычислений, которые сводятся к окончательному получению результатов после выполнения математического определения уравненных значений величин.
- Окончательный анализ полученных результатов вычислений и оценка точности выполненных работ.
Такой алгоритм действует практически при создании всех геодезических сетей, при предварительном проектировании и по окончании их построения. Рассмотреть весь спектр возможностей математической обработки не возможно в одной статье из-за разных постановочных задач и путей их решения. Но каждый геодезист практически всегда использует в своей работе две основные геодезические задачи (прямую и обратную), которые требуют знаний теории погрешностей и двух различных способов их решения.
Прямая геодезическая задача в теории ошибок
Основной идеей ее является определение искомых координат неизвестных пунктов с использованием измеренных длин сторон и углов, при наличии известных координат на исходном геодезическом пункте. Прямая геодезическая задача решается, например при проложении теодолитного хода. При измерениях в нем линейных и угловых величин им сопутствуют получение целого ряда погрешностей. После вычислений можно записать функции измеренных величин в следующем виде:
yi =Fi (l1, l2, … , ln);
где l1, l2, … , ln – средние измеренные значения длин сторон,
Ряд известных погрешностей будет иметь такой вид: m1, m2, … , mn.
Истинные значения (Li) этой функции возникают при появлении взамен промеренных величин (l1, l2, … , ln).
Yi =F (L1, L1,…, Ln.),
Отсюда следует, что случайные ошибки определяются по формуле:
Е= yi — Yi,
Тогда СКП оцениваемой функции будет выглядеть:
M y =√[EE]/n
Числовые значения их определяются по формуле:
M2 yi = f21m21 + f22m22 + . . . + f2nm2n = ∑ f2im2i.
Эта формула одна из основополагающих в теории погрешностей и математической обработке в геодезии. Она имеет название формула переноса погрешностей. С ее помощью производится решение задач и оценка точности любых необходимых функций по известным среднеквадратическим отклонениям их независимых аргументов.
При решении прямой задачи стоит вопрос определения допустимых параметров. Для этого принимают истинные или измеренные с высокой точностью, или заранее известные, как верные. В замкнутом теодолитном ходе можно принять за такие условия сумму всех измеренных углов и приращений координат.
∑nj=1 β=180(n-2),
∑nj=1 Δ x=0,
∑nj=1 Δ γ=0.
где β1, β2, … , βn – средние значения измеренных углов;
n — количество углов.
Вследствие получения измерительных ошибок в углах и сторонах теодолитного хода, перечисленные выше три условия, как правило, не выполняются. Возникают угловые невязки (wβ) и невязки приращений (wx ; wy).
Функция измеренных угловых величин имеет общий вид:
yi=Fi (β1, β2, … , βn);
Тогда равенство измеренных и истинных величин приобретает такой вид:
yi=Fi (β1, β2, … , βn)=
То есть можно сделать вывод о том, что зная ошибки замеренных углов(mi), можно определить погрешности суммы углов (My). В то же время она считается среднеквадратической погрешностью (CКП) невязки измерений. Допустимое значение к ней устанавливается исходя из формулы.
wβдоп = k My,
где k — коэффициент кратности исходя из таблицы вероятности.
При выборе этого коэффициента, следует понимать следующее. Делая выбор в пользу единичного коэффициента следует, что все измеренные параметры с вероятностью более шестидесяти восьми процентов будут отсекаться. При выборе коэффициента равного двум, вероятность получения правильных замеренных параметров будет равна девяноста пяти процентам. А при выбранном коэффициенте три отсев грубых ошибок в промерах будет равен 0,3%. Вероятность допустимых отклонений возрастает до девяноста девяти процентов. В практике геодезических работ коэффициент кратности принимают от 2,0 до 2,5. В теоретических расчетах его выбирают равным трем (3,0).
Таким образом, обеспечиваются принципы необходимой точности и устанавливаются допуски, которые при контроле измеренных величин.
Обратная задача в теории ошибок
Основной целью решения этой задачи считается определение длин сторон и их дирекционных углов по известным координатам пунктов сети.
В теории погрешностей дополнительными определяемыми данными будут выступать отклонения конкретных величин, групповые и средние ошибки. При решении обратной геодезической задачи возможно установление средних ошибок отдельных конкретных измерений с целью обеспечения заданной точности какой-то функции замеренных величин. Такая задача обычно возникает при решении соединительных треугольников во время проведения ориентирований шахтных стволов, при выполнении предрасчета общей средней погрешности смыкания капитальных выработок и других работах. В зависимости от требуемой производственной необходимости выполняются проектные и расчетные работы с задаваемой и ожидаемой точностью (Mож). Допустимая погрешность (Mдоп) устанавливается и утверждается как предельная ошибка (Mпред). Среднеквадратическая погрешность (Mxyz) имеет связь с предельной через известный вероятностный коэффициент кратности (k):
Mож = Mдоп = Мпред = kMxyz ;
Коэффициент кратности считается своего рода степенью риска, которая устанавливается в расчетах маркшейдерских работ равным трем. Таким образом, получив общую среднеквадратическую ошибку, определяется требуемая точность выполнения полевых замеров отдельных параметров.
На чтение 9 мин Просмотров 1.6к. Опубликовано 03.10.2021
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)
где: ;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:
Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)
Величина (1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
по третьему свойству ошибок (1.26) можно написать:
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
или
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,
,
откуда ;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
откуда (1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)
Согласно (1.46) и (1.32) напишем:
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)
где pi – вес i-того элемента.




