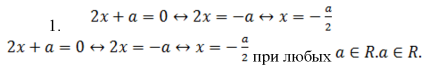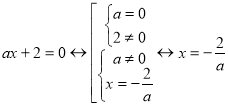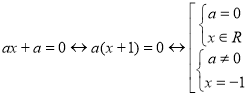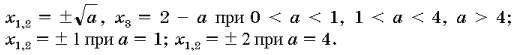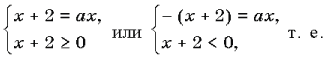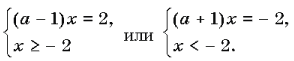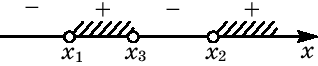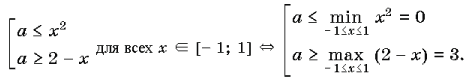Задачи с параметрами ошибки при решении

         Задачи с параметрами: трудности и
способы их преодоления.

                                                                                                              
Алейникова Т.В.

      
В связи с введением обязательного ЕГЭ по математике и отменой отдельных
вступительных экзаменов в ВУЗы существенно изменилась стратегия подготовки
выпускников к экзамену по предмету. Но подготовка учащихся к сдаче профильного
экзамена по математике не предполагает натаскивания на отдельные группы и типы
заданий, а требует научить выпускника мыслить в нестандартных ситуациях с
опорой на глубокие знания предмета.

  
Если обратиться к задачам с параметром, то для того, чтобы ученик мог
осмысленно выполнить все этапы решения, необходимо не только глубокое понимание
темы , но и немалый опыт решения таких задач. Поэтому знакомство с такими
задачами должно состояться не в 9,10,11 классах, а намного раньше, когда о
параметре, как таковом , вообще речи не ведется – в 5, 6 и 7классах. Работа с
задачами на исследование ситуаций, анализ вариаций, подбор значений по
поставленному условию – всё это приучает школьников к «многоразовости» задачи,
к умению выделить «пограничные» ситуации, что, впоследствии, мы и применяем при
решении задач с параметрами.

Итак,
вычленим основные проблемы, возникающие у учащихся при решении задач с
параметрами.

1.     Трудно
классифицировать задачу, отнести к какому-либо типу;

—
действительно, задачи исключительно разнообразны по материалу (тригонометрия,
логарифмы, КВУР, показательные, иррациональные уравнения, неравенства и прочее)
или по методам решения(графические или аналитические).

2. 
Трудность в понимании того, что такое параметр, что это – число, и какая буква
или буквы в условии являются параметром, а какие – нет.

—
обычно это проблема учащихся в младших классах или учащихся, никогда ранее не
встречавшихся с такой задачей

3.
Трудность в построении алгоритма решения (слишком много типов задач) и
понимании вопроса задачи: решать для всех значений параметра или для каких-то
отдельных.

4.
Трудность в отборе «пограничных»  значений параметра, то есть в умении найти в
задаче ситуацию, качественно отличающуюся от других.

—
действительно, часто при решении задачи графическим методом необходимо
вычленить эти «особые» случаи: графики имеют единственную общую
точку(пересечение прямых или касание прямой и кривой), или бесконечное
множество точек(совпадение участков).

5.
Трудность в построении графиков уравнений: с модулем, с параметром, в понимании
того что такое «пучок прямых», «семейство прямых», «распухающая окружность»,
окружность с подвижным  центром, или график квадратичной функции  или модуля,
вершина которых движется по некоторой прямой, заданной параметрами.

  
Все эти проблемы, несомненно, ставят задачу с параметром (на ЕГЭ — № 18) в
разряд особенно трудных, и без приобретения огромного опыта и знаний по этому
вопросу, ученикам очень сложно браться за её решение.

 
Как же постараться сузить эти проблемы и помочь учащимся освоить такие задачи,
пусть не всякие, но большинство?  Конечно, это пропедевтика очень многих
простейших понятий, связанных с функцией, уравнениями, преобразованиями
выражений. Огромная работа, которую надо начинать с 5-6 классов. Тем самым, к
концу 9, а затем уже 11 класса, учащиеся приобретут драгоценный опыт и
понимание таких задач.  Разберемся в каждой проблеме.

1.    
Классификация задачи:
учимся определять по какой теме задача, её тип(аналитическая или графическая).
Для этого обращаемся к главному вопросу: решить для всех значений параметра,
или задача с определенным условием (корни одного знака) или найти конкретное количество
решений, не находя сами решения.( в последнее время наиболее часто встречается)

Например:

1). При каких значениях
параметра k один из корней уравнения

(k² + k + 1)x² + (2k
– 3)x + k – 5 = 0 больше
1, а другой меньше 1?(задача условная, надо рассмотреть только случаи, удовлетворяющие
данному условию)

2).   В зависимости от значений параметра a
решить уравнение

   (a² – 1)x = 2a² +
a – 3. (Задача общего типа,  надо рассмотреть все возможные случаи.  Для
этого применяем метод «контрольных значений», т.е. тех значений
параметра, при которых качественно изменяется вся задача.

Рекомендации по
нахождению КЗ:

— для всех видов
уравнений: КЗ «нулевого типа» (КЗ0)- значение параметра, обращающее в ноль
старший коэффициент уравнения или неравенства.

x(1 – a) = –2.   КЗ0:
а
= 1

(p + 2)x² – 2(p + 3)x + p
+ 5 = 0.  КЗ0: р = — 2

у = ах — 3,  КЗ0: а = 0

— для КВУР: обращение в
ноль дискриминанта;

— для дробно-рационального
уравнения: обращение в ноль знаменателя уравнения;

— для иррациональных
уравнений(неравенств): «концевое» значение области существования корня;

— для логарифмов:
«концевое» значение области существования логарифма;

— прочие задачи, в которых присутствуют
ограничения на область допустимых значений.

3).  Найдите все значения параметра a, при
каждом из которых уравнение   имеет ровно три корня? (Графическая
задача, т.к.  нужно найти только количество корней, и в уравнении очевидны
функции, графики которых реально построить).

2.  Понимание, что параметр – это
действительное число. Думаю, чтобы решить эту проблему, надо приучать
учащихся к «параметрической» терминологии, начиная с 5 класса, где дети впервые
встречают понятие «линейное уравнение» и исследуют его на существование корней
в зависимости от коэффициентов (0·х = 0, 0·х = 2, 5·х = 2,

 а · х = 2). Потом такой список знаний
можно расширять, показывая, что целую группу однотипных математических задач мы
можем записывать, используя букву, которая заменяет повторяющееся число.

3. Построение алгоритма решения задачи.
Здесь мы можем только рекомендовать учащимся, с чего начать рассмотрение задачи
(понимание вопроса), какие значения предварительно отделить (КЗ) или какие
графики построить (отделить параметр от известной функции, если возможно),
какие значения параметра отбирать, исходя из условия задачи.

4. Отбор
«пограничных»  значений параметра. Эту проблему решаем опять же с
помощью контрольных значений и учим пониманию графических «обстоятельств» при
изображении графиков уравнений.

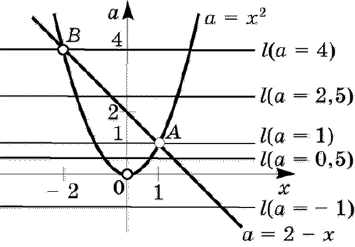
Пример: Найти все значения параметра а,
при которых графики функций имеют не менее 2-х общих точек.

« Пограничные
положения» одной их прямых «пучка» — это принадлежность ей точки В(4;0) и
касание с частью графика, левее прямой х = 4(парабола у = —  х² +
4х)

5.
Построении графиков уравнений (неравенств), графиков функций. Все
годы изучения алгебры и начал математического анализа мы занимаемся вопросами построения
графиков, постепенно усложняя функции, уравнения и преобразования. Ученик 11
класса должен владеть всеми этими методами на высоком уровне, т.к. это залог
решения задачи с параметром графическим способом. В активе учащихся должны быть
методы построения графиков с помощью преобразований  в системе координат,
графиков функций с модулем, графиков линейных уравнений. Уметь преобразовывать
уравнение окружности, получать совокупность уравнений и понимать, что
представляет её график. Это материал, изучаемый, в большей степени, в
профильных классах, но доступный и ученикам общеобразовательного профиля,
интересующимся математикой.

Пример:
3). При каком значении параметра а система имеет единственное решение?

 

(1)
при у ≠
2,  = у – 2, у = а(х – 6),
«пучок» прямых ℓ с центром в точке А(6: 0).

(2)
 — 7у –ху + 5х + 10 = 0; (либо КВУР относительно у, либо РМ с
помощью группировки)(7у = 5у + 2 у)

− 5) – х(у – 5) – 2(у – 5) = 0;

 5)(у – х -2) = 0;      график уравнения (2) – совокупность двух прямых.

(3)

1 случай: ℓǁМД,

а = 1, нет общих точек, не уд. усл.

2 случай: ℓǁВС,

а = 0,
1 общая точка, уд.усл.

3 случай: F(3;
5) ϵ ℓ,

5 = а(3 – 6), а = -5/3,

1 общая точка, уд.усл.

4 случай: (0;2) ϵ ℓ,

2 = а(0 -6), а = — 1/3,

1 общая точка, уд.усл.

Ответ: а = -5/3, а = — 1/3, 0

Для
преодоления всех проблем требуется ежедневная кропотливая работа учителя  с
учащимися по овладению общими знаниями математики в совершенстве. Только тогда
задача № 18 на ЕГЭ не будет казаться такой «пугающей и трудной»!

Литература:

1.    
Крамор В.С. Задачи с параметрами и методы
их решения /В.С. Крамор. – М.: ООО «Издательство Оникс»: ООО «Издательство «Мир
и образование», 2002

2.    
Решение всех экзаменационных задач по
алгебре и началам анализа за 11-й класс. Курсы «А», «В», «С», «Д»:
Учебно-практическое пособие к «Сборнику задач по алгебре и началам анализа для
проведения итоговой аттестации за курс средней школы»/ под. Ред. С.А.
Шестакова. – М.: издательство «Экзамен»,2003

3.    
Мордкович А.Г. Алгебра и начала анализа 11
класс. Задачник для общеобразовательных учреждений(профильный уровень)/ А.Г.
Мордкович и др., под ред. А.Г. Мордковича. –М.: Мнемозина, 2009

4.    
Горштейн П.И. Задачи с парметром. 3-е
издание, дополненное и переработанное/П.И. Горштейн, В.Б. Полонский, М.С. Якир
– М.: Илекса, Харьков: Гимназия, 2002

5.    
Иванов С.О. Математика. Учися решать
задачи с параметрами. Подготовка к ЕГЭ: задание С5/ С.О. Иванов, Е.А. Войта и
др.,  под ред. Ф.Ф.Лысенко, С.Ю. Калабухова –Ростов н/Д: Легион-М, 2011

Библиографическое описание:

Городничева, А. К. Причины сложности обучения решению задач с параметрами в школе и пути их преодоления / А. К. Городничева. — Текст : непосредственный // Молодой ученый. — 2022. — № 4 (399). — С. 324-326. — URL: https://moluch.ru/archive/399/88383/ (дата обращения: 12.06.2023).



Основными причинами здесь, безусловно, являются трудности, определяемые спецификой самой деятельности по решению этих задач: ее неалгоритмичность, необходимость комплексного использования знаний и умений, переноса их в новые условия. Важную роль играет также недостаточная разработанность методики введения теоретических вопросов, связанных с этими задачами, и, как следствие, обращение педагогов к чувственной основе действий, что выражается, например, в предложениях: «представьте, что параметр — это конкретное число, но не забывайте, что это переменная», «иногда удобно рассматривать уравнение с параметром как функцию», «для решения задачи необходимо выбрать управление значения параметра таким образом, что на полученных интервалах решение уравнения (неравенства) подчиняется алгоритму, но найти их сразу невозможно» и т. п.

Другой причиной является низкая эффективность методики обучения, основанной на группировке упражнений по видам выражений (линейные, квадратичные, целые, рациональные, дробно-рациональные, иррациональные, тригонометрические, логарифмические, экспоненциальные), так как в этом случае неправильно определяется стратегия решения для типа выражения. Например, меняя только положение параметра в структуре линейного уравнения, мы приходим к трем различным стратегиям его решения («последовательное преобразование», «интервальное исследование», «факторизация»).

Предлагаемая методика предполагает другой способ планирования содержания обучения, а именно по видам требований задач с параметром, так как различие между переменными (неизвестным и параметром), а следовательно и специфика задач проявляются лишь относительно заданной цели деятельности. Это дает следующую последовательность изучения уравнений и неравенств с параметром.

Таблица 1

Тема	Основное содержание
Уравнения и неравенства с параметром: основные понятия	Уравнение (неравенство) с двумя переменными, связь переменных, неизвестная и параметр, уравнение (неравенство) с параметром, область допустимых значений, область допустимых значений параметра, область возможных значений неизвестной, решение (а ; х), корень х(а), виды задач.
Задачи на нахождение множества корней уравнения (неравенства) зависимости от параметра	Критерии успешности решения, формула зависимости x(a) , контрольные значения параметра, условия выделения контрольных значений параметра, их связь с видом выражений
Задачи на нахождение значений параметра, удовлетворяющих условиям, на множество корней	Критерии успешности решения, виды условий, накладываемых на корни уравнения (неравенства), их роль в определении стратегии решения; приемы решения, их связь с видом выражений
Задачи, сводящиеся к решению уравнений и неравенств с параметром	Решение сюжетных, прикладных геометрических задач, на исследование свойств функции, сводящихся к уравнениям и неравенствам

Следует отметить, что традиционная схема обучения заключается в информировании учащихся об особенностях решения задач и организации деятельности по использованию этой информации. Однако в случае задач с конкретным параметром уточняется только методологическая информация (о критериях успешности, способах решения, условиях выбора управляющих значений и т. д.), а распространяются теоретические сведения и введенная терминология для уравнений и неравенств с одним Переменная. Поэтому здесь предпочтителен иной способ организации обучения, основанный не на усвоении подготовленной информации, а на вдумчивом анализе собственных трудностей и успехов в решении задач. Этот путь определяется спецификой характера методологического познания, которое относится к знанию рефлексивного типа (источником является не восприятие внешней действительности, а сознание внутреннего «Я»).

Психологи и педагоги обратились к категории рефлексивной деятельности относительно недавно в связи с задачами гуманизации образования, усиления его развивающей функции.

Психологи И. Н. Семенов и С. Ю. Степанов показали, что в мышлении можно выделить несколько иерархических уровней, высшими из которых являются уровни интеллектуальной и личностной рефлексии. Рефлексия выполняет в мышлении регулирующую функцию (планирует деятельность, контролирует выполнение программы, диагностирует трудности, корректирует образы и программы), а также интегрирующую функцию: помогает выявить и обобщить знания, содержащиеся в опыте. Именно вторая функция рефлексии делает эту деятельность воспитательно значимой.

Рефлексивные механизмы включаются только при интеллектуальных затруднениях, поэтому включение учащихся в рефлексивную деятельность необходимо начинать с осознания проблемы. Реализацию данного положения предлагается осуществлять по следующей схеме.

— Учитель предъявляет учащимся проблемную ситуацию, связанную с анализом их деятельности или оценкой результатов деятельности учителя.

— Учитель обсуждает с учащимися параметры анализа, демонстрирует круг возможных направлений осуществления действий, критерии их дорогой.

— Учитель дает учащимся возможность самостоятельно принимать решения.

Литература:

1. Виноградова, Л. В. Методика преподавания математики в средней школе [Текст] / Л. В. Виноградова- Ростов н/д: Феникс, 2005.- 252с..
2. Голубев, В. И. О параметрах — с самого начала [Текст] / В. И. Голубев, А. М. Гольдман, Г. В. Дорофеев // Репетитор. — 2007. — № 2 — с. 3–13..
3. Котухов, С. К. Различные способы решения задач с параметрами [Текст] // Мат. в шк.- 1998.-№ 6.- С. 9–12..
4. Колягин, Ю. М. Методика преподавания математики в средней школе: общая методика [Текст]: учеб. пособие для студентов физико- математических факультетов пед. институтов.- М.: Просвещение, 1975.- 462с..
5. Леонтович, А. В. Исследовательская деятельность школьников [Текст] / / Школьные
6. Пронина, Е. С. Линейные уравнения с параметрами: методические рекомендации [Текст] // Мат. в шк.- 2000. -№ 12.- С.3–5..
7. Савенков, А. И. Исследовательская деятельность учащихся [Текст] // Школьные технологии.- 2008.- № 1.- С. 11- 20. 21.
8. Цыпкин, А. Г. Справочник по методам решения задач по математике для средней школы [Текст] / А. Г. Цыпкин, А. И. Пинский. — 2-е издание, перераб. и доп. — М.: Наука, 2009. — 576 с..
9. Шахмейстер, А. Х. Уравнения и неравенства с параметрами [Текст]/ А. Х. Шахмейстер.-М.: Виктория плюс, 2010,-136с..
10. Шерстаков, С. В. Уравнения с параметром [Текст] / С. В. Шерстаков, Е. Н. Юрченко.- М.: Слог,1993.- 107с.. Шихалиев, Х. Ш. Уравнения и неравенства с параметрами [Текст] // Мат. в шк.- 1980.-№ 21.- С. 34- 35..
11. Ястребинецкий, Г. А. Задачи с параметрами [Текст] / Г. А. Ястребинецкий.- М.: Просвещение, 2006.- 128с.

Сайты, меню, вход, новости

Научно-образовательный форум школьников Республики Мордовия

Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ 

Секция: Математический калейдоскоп

Автор работы:	Ехлаков Д. Н.
	10 класс Лицей МГУ им. Н. П. Огарева
Руководитель работы:	Кубанцева А. В.
	учитель математики Лицей МГУ им Н. П. Огарева

Саранск

2021

СОДЕРЖАНИЕ

	Введение	3
1	Теоретическая часть	6
	1.1	Основные понятия	6
	1.2	Основные типы задач с параметром	7
	1.3	Методы решения задач с параметрами	9
2	Практическая часть
	2.1	Примеры решения задач с параметрами ЕГЭ по математике профильного уровня
	Заключение
	Список использованных источников

Введение

Задачи с параметрами являются одним из самых трудных разделов школьного курса математики, так как их решение связано с умением проводить сложные, разветвленные логические построения. В школе первые представления о параметре мы получаем при изучении прямой пропорциональности; линейной функции и линейного уравнения; при изучении квадратного уравнения и исследования количества его корней в зависимости от значений параметра.

Актуальность выбранной темы обусловлена тем, что затрагивает современную проблему, знакомую каждому выпускнику, а именно – решение задач единого государственного экзамена. Сдать ЕГЭ на высший балл – одно из самых актуальных желаний старшеклассников, так как это прямым образом влияет на шансы поступить в престижный ВУЗ и получение желаемой профессии. Добиться этого довольно непросто. Учебного времени не всегда хватает для углубленной подготовки к заданиям высокого уровня сложности, к одним из которых относятся уравнения и неравенства с параметрами.

Анализ предыдущих результатов ЕГЭ показывает, что школьники с большим трудом решают задания с параметром, а многие даже не приступают к ним. К решению задачи №18 из КИМ приступают лишь порядка 10% выпускников 11 классов. Причиной этого является отсутствие системы знаний по данной теме.

Статистика решения задачи №18 на ЕГЭ по профильной математике

Год	Проверяемые требования	Уровень сложности задания	Максимальный балл за выполнение задания	Средний процент выполнения
2017	Умение решать уравнения и неравенства, содержавшие параметр	Высокий уровень сложности	4	0,38
2018	1,2
2019	4,8
2020	2,4

В школьных учебниках по математике задач с параметрами недостаточно, к тому же, предлагаемые в них примеры слишком просты по сравнению с задачами из ЕГЭ. Поэтому исследование способов решения задач с параметрами является для меня одним из важных шагов в подготовке к единому государственному экзамену по математике профильного уровня. Рассматривая проблему решения 18-го задания по ЕГЭ, хочу определить самый рациональный способ, а точнее, наименее трудоемкий, менее время затратный и удобный метод решения задач с параметрами.

Цель работы заключается в исследование методов решения задач с параметрами и выявление наиболее рациональных, наименее трудоемких способов решения.

Для достижения поставленной цели необходимо решить следующие задачи:

1. познакомится с определением параметра и видами задач, содержащие параметры;
2. исследовать способы решения задач с параметрами и постараться выбрать из них для себя самые оптимальные;
3. приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике.

Гипотеза моего исследования заключается в том, что существуют общие методы решения заданий с параметрами, позволяющие решать задания разных видов.

Объект исследования: задания контрольно-измерительных материалов единого государственного экзамена по математике, содержащие параметр.

Предмет исследования: методы решения заданий с параметрами.

Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.

Практическая значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработка решения задач, содержащих параметры.

1. Теоретическая часть

1. Основные понятия

Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Что означает «решить задачу с параметром»? Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Одним из способов решения задания №18 из ЕГЭ является графический способ, поэтому следует повторить что такое функция, виды функций и их свойства. Понятие функции – одно из ключевых в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Другое определение – однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. Существует всего пять типов элементарных функций: степенные, показательные, тригонометрические, обратные тригонометрические.

1. Основные типы задач с параметрами

Выделяют основные 4 больших класса задач с параметрами:

• Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успехи при решении задач всех других основных типов.

• Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.

• Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
• Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых:

1) уравнение выполняется для любого значения переменной из заданного промежутка;

2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

Наиболее массовый класс задач с параметром – задачи с одной неизвестной и одним параметром.

1.3 Методы решения задач с параметром

В пособиях, посвященных задачам с параметрами, выделяют три метода решений:

• Аналитический метод: это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
• Графический метод: в зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).  
• Метод решения относительно параметра: при решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Иногда также применяется так называемый метод оценки для уравнений и неравенств, где функции, стоящие в левой и правой части, могут быть равны друг другу только в определенной точке, причем одна из них принимает в этой точке наименьшее значение, а другая – наибольшее.

При рассмотрении данных методов я пришел к выводу, что самые распространенные и удобные способы – это аналитический и графический. Рассмотрим их более подробно.

Графический способ. В зависимости от того, какая роль параметру отведена в задаче, можно соответственно выделить два основных графических приёма:

• первый – построение графика на координатной плоскости (х;у),
• второй – построение графика на координатной плоскости на (х;а).

На плоскости (х;у) или (х;а)  функция y=f(x;a) задаёт семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определёнными свойствами. Нас же в первую очередь будет интересовать с помощью какого преобразования плоскости (параллельный перенос, поворот и т.д.) можно перейти от одной прямой к какой-нибудь другой.

Разумеется, не всегда графический образ семейства y=f(x;a) описывается простым преобразованием. Графический метод — всего лишь одно из средств наглядности. Поэтому те случаи, когда результат «прочитан» с рисунка и вызывает сомнение, лучше подкрепить аналитически.

Алгоритм решения задачи с параметром графическим способом состоит из следующих шагов:

1. задачу с параметром будем рассматривать как функцию ; п
2. строим графический образ, т.е. Построим в одной системе координат графики обеих частей уравнения;
3. пересекаем полученное изображение прямыми, параллельными оси абсцисс;
4. считываем нужную информацию.

Если уравнение одной из фигур не зависит от изменяющегося параметра, то график этой фигуры неподвижен относительно системы координат. Если в уравнение другой фигуры входит параметр, то от его изменения зависит расположение и даже форма графика. Тогда суть решения уравнения состоит в определении числа точек пересечения графиков построенных уравнений, а значит в определении количества возможных решений в зависимости от конкретных числовых значений параметра.  Для усложнения заданий эти уравнения искусственно преобразуют, «камуфлируют». Понятно, что каждое семейство обладает определенными характерными свойствами, они-то и помогают решить задачу.  Приведем несколько примеров.  

Аналитический способ. Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Широкое распространение за последние годы в ходе государственной (итоговой) аттестации выпускников средней школы  в формате ЕГЭ и на вступительных экзаменах в вузы, предъявляющие повышенные требования к математической подготовке абитуриентов, получили задачи на расположения корней квадратного трехчлена на оси. Для данного типа задач свойствен аналитический метод решения.

Выделим два наиболее распространенных вида задач, связанных с применением графика квадратичной функции. Первый вид – задачи, в которых изучается расположение корней квадратного трехчлена относительно точки с абсциссой, равной m. Второй вид – задачи, в которых выясняется, как расположены корни квадратного трехчлена относительно отрезка.

Первый тип задач предусматривает три случая:

• оба корня меньше m;
• один корень меньше m, а другой больше;
• оба корня больше m.

Для каждого из этих случаев выполним соответствующий рисунок и запишем к нему систему неравенств при условии, что старший коэффициент квадратного трехчлена f (x) = ax2 + bx + c положительный.  В таблице приведена полная система случаев расположения корней уравнения в зависимости от значений выражений, зависящих от коэффициентов уравнения.

Расположение корней квадратного трехчлена относительно точки с абсциссой, равной  

	Один корень меньше m, а другой больше: Условие  обеспечивает положительный коэффициент перед  (направленность ветвей параболы вверх); Условие  обеспечивает: наличие корней квадратного трехчлена; расположение точки m между корнями.
	Оба корня больше m: Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие   обеспечивает расположение точки m левее отрезка между корнями.
	Оба корня меньше m:  Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями;   Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.

Рассмотрим расположение корней квадратного трёхчлена относительно отрезка. При этом возможны шесть случаев:

• корни квадратного трёхчлена находятся справа от отрезка;
• корни квадратного трёхчлена находятся слева от отрезка;
• больший корень находится внутри отрезка  
• меньший корень находится внутри отрезка;
• оба корня внутри отрезка;
• отрезок между корнями квадратного трехчлена

Изобразим геометрическую модель каждой из этих ситуаций и составим к каждой из них адекватную систему неравенств при условии, что старший коэффициент квадратичной функции y = ax2 + bx + c больше нуля.

Расположение корней квадратного трёхчлена относительно отрезка

	Корни квадратного трёхчлена находятся справа от отрезка: Условие  обеспечивает нахождение корней вне отрезка между корнями; Условие  обеспечивает наличие двух корней квадратного трёхчлена; Условие  обеспечивает расположение отрезка левее абсциссы вершины.
	Корни квадратного трёхчлена находятся слева от отрезка: Условие  обеспечивает расположение корней вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.
	Больший корень находится внутри отрезка: Условие  обеспечивает расположение точки m внутри отрезка между корнями; Условие  обеспечивает расположение корней вне отрезка меду корнями.
	Меньший корень находится внутри отрезка:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.
	Оба корня внутри отрезка: Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает расположение точки p вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение вершины параболы между концами отрезка.
	Отрезок между корнями квадратного трехчлена:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.

1. Практическая часть

2.1 Примеры решения задач с параметрами ЕГЭ по математике профильного уровня

В ходе исследования я понял, что наиболее универсальным и наглядными для меня оказались графический и аналитический способы решения задач с параметрами. Далее предлагаю провести разбор некоторых задач прошлых лет ЕГЭ по математике профильного уровня.

Пример №1.

Найдите все значения , при каждом из которых система неравенств  имеет хотя бы одно решение на отрезке [4; 5].

Преобразуем систему:  

Построим прямоугольную систему координат xOa. Изобразим множество точек, координаты которых удовлетворяют системе неравенств.

Гипербола  и график корня пересекаются в точке N(3; 2). Гипербола и прямая  пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.

Поскольку система должна иметь хотя бы одно решение на отрезке [4; 5], определим наименьшую и наибольшую ординаты проекции выделенного на рисунке четырехугольника на ось ординат.

Найдём координаты точки P:

 =>

 

Проекции точек P и M дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [4; 5] при  (выделено штриховкой на рисунке).

Ответ: (1;

Пример №2.

Найдите все значения , при каждом из которых имеет ровно три различных решения система уравнений

Первое уравнение системы является уравнением окружности с центром в точке  и радиусом 3. График функции  получается параллельным переносом на вектор  графика функции  Поскольку график функции  представляет собой прямой угол с вершиной в точке  и сторонами лежащими на прямых  и  выше оси абсцисс, график функции  также представляет собой прямой угол, но с вершиной в точке  и сторонами, параллельными прямым  Заметим, что прямая  на которой лежит вершина угла, является касательной к окружности.

Ровно три общие точки фигуры имеют в следующих случаях:

1. Вершина прямого угла лежит в точке  касания окружности и прямой , а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если .

2. Одна из сторон прямого угла пересекает окружность в двух точках, а другая касается окружности в точке  (второй случай) или в точке (третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник  является квадратом со стороной и диагональю . Тогда . Следовательно, для случая касания в точке  получаем  Для касания стороны угла и окружности в точке  аналогично получаем ещё одно значение параметра:  

При  или  прямой угол имеет не более двух общих точек с окружностью.

При  или  прямой угол имеет четыре общие точки с окружностью.

Ответ:

Пример №3.

Найдите все значения параметра  при каждом из которых уравнение  имеет хотя бы одно решение на интервале (0;

Обозначим в исходном уравнении  .

Пример №4.  

Найдите все значения , при каждом из которых уравнение меет ровно два различных корня на промежутке

Сделаем замену тогда получим: .

Выполним обратную замену:  =>  Дискриминант этого уравнения равенпоэтому оно при всех значениях  имеет ровно два различных корня. Положим  Так как  оба корня уравнения  принадлежат промежутку  тогда и только тогда, когда  и  то есть когда  и Значит, уравнение  имеет ровно два различных корня на промежутке  при

Ответ:

Пример №5.

Найдите все значения , при каждом из которых уравнение  имеет ровно один корень на отрезке

Преобразуем уравнение:  => Рассмотрим эти случаи:

Первый случай:  при условиях:

=>  

Число  лежит на отрезке  если  Тогда для первого случая получаем: .

Второй случай:  при условии :

 => =>

Число  лежит на отрезке , если  Тогда для второго случая получаем:

Корень  равен  если

Итак, исходное уравнение имеет ровно один корень на отрезке  при   

Ответ:   

Пример №6.

Найдите все значения , для каждого из которых уравнение  имеет единственное решение.

Аналитический способ решения:

;

Пусть   = t >0, тогда:  

(*)

Исходное уравнение будет иметь единственное решение:

1 случай: еcли уравнение (*) имеет единственное решение (D=0);

2 случай: если уравнение (*) имеет два корня (D>0), один из которых меньше нуля или равен нулю.

Пусть n=a+6, m=5+3|a|;

1 случай:

 =>  =>  =>  => ;

если a<0, то  => ; если a>0, то  => .

2 случай:

; ;

если n>m, то:

  ;

если n

; ;

 система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.

 =>  =>

или  =>  =>

или  =>   => система не имеет решений.

Ответ:  ;  ; .

Графический способ:

Преобразуем исходное уравнение:

 =>
 =>   или .

Построим графики функций   на координатной плоскости xOa:

На чертеже заметим, что система имеет единственное решение при ,  и . Найдём  и :

Если a>0, то:  => => .

Если а<0, то: =>  => .

Ответ:  ;  ; .

Важно помнить:

• при использовании только графического метода, так же, как и только аналитического, может быть допущена ошибка, поэтому необходимо последовательно и внимательно указывать ход своего решения. При возможности выполнить проверку полученного результата, применяя другой способ решения;
• ответ, полученный только с помощью графика, может быть сомнителен, поэтому необходимо подкрепить его с помощью аналитического вывода, что в первую очередь подтвердит правоту выбранного пути решения и полученный ответ.

Заключение

Работая над своей темой исследования, я провел большую работу: изучил литературу по выбранной теме; разобрался, что такое параметр и задачи с параметрами; познакомился с методами их решения.

Выполняя практическую часть, было решено много уравнений, неравенств и их систем, я приобрел опыт и научился решать определённый круг задач и пришёл к некоторым выводам.

Решение каждого задания требует к себе индивидуального подхода, но при этом задачи с параметрами чем-то похожи на детский конструктор. Разобрав много таких примеров, можно заметить, как решение «собирается» из мелких деталей – хорошо знакомых нам фактов.

Для себя я выделил два основных способа решения №18 из ЕГЭ: аналитический и графический.

Графический способ является наиболее наглядным, простым и доступным способом решения задач с параметрами. Если задачу с параметром можно нарисовать – рисуем. То есть применяем графический метод. Размытость в решение уравнения, неравенства или их системы с помощью графика, можно подкрепить аналитическим выводом, что поможет подтвердить правоту выбранного решения и ответа.

Сочетание аналитического способа решения с графической интерпретацией полученных результатов позволяет сделать процесс решения уравнений с параметрами более осознанным, способствуя при этом формированию элементов исследовательской деятельности.

Думаю, что данная работа будет интересна моим сверстникам. Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность.

Список использованных источников

В. Голубев, А. Гольдман,
Москва

О задачах с параметром

Первоначальные сведения

I. Что такое параметр?

Если вы вспомните некоторые основные уравнения
(например, kx+l=0, ax²+bx+c=0),
то обратите внимание, что при поиске их корней
значения остальных переменных, входящих в
уравнения, считаются фиксированными и заданными.
Все разночтения в существующей литературе
связаны с толкованием того, какими
фиксированными и заданными могут быть эти
значения остальных переменных.

Например, в уравнениях |x|=a–1
и ax=1 при a=0
равенства не выполняются при любых значениях
переменной x, а в уравнения

Предлагаемая методика предполагает другой способ планирования содержания обучения, а именно по видам требований задач с параметром, так как различие между переменными (неизвестным и параметром), а следовательно и специфика задач проявляются лишь относительно заданной цели деятельности. Это дает следующую последовательность изучения уравнений и неравенств с параметром.

Таблица 1

Тема	Основное содержание
Уравнения и неравенства с параметром: основные понятия	Уравнение (неравенство) с двумя переменными, связь переменных, неизвестная и параметр, уравнение (неравенство) с параметром, область допустимых значений, область допустимых значений параметра, область возможных значений неизвестной, решение (а ; х), корень х(а), виды задач.
Задачи на нахождение множества корней уравнения (неравенства) зависимости от параметра	Критерии успешности решения, формула зависимости x(a) , контрольные значения параметра, условия выделения контрольных значений параметра, их связь с видом выражений
Задачи на нахождение значений параметра, удовлетворяющих условиям, на множество корней	Критерии успешности решения, виды условий, накладываемых на корни уравнения (неравенства), их роль в определении стратегии решения; приемы решения, их связь с видом выражений
Задачи, сводящиеся к решению уравнений и неравенств с параметром	Решение сюжетных, прикладных геометрических задач, на исследование свойств функции, сводящихся к уравнениям и неравенствам

Следует отметить, что традиционная схема обучения заключается в информировании учащихся об особенностях решения задач и организации деятельности по использованию этой информации. Однако в случае задач с конкретным параметром уточняется только методологическая информация (о критериях успешности, способах решения, условиях выбора управляющих значений и т. д.), а распространяются теоретические сведения и введенная терминология для уравнений и неравенств с одним Переменная. Поэтому здесь предпочтителен иной способ организации обучения, основанный не на усвоении подготовленной информации, а на вдумчивом анализе собственных трудностей и успехов в решении задач. Этот путь определяется спецификой характера методологического познания, которое относится к знанию рефлексивного типа (источником является не восприятие внешней действительности, а сознание внутреннего «Я»).

Психологи и педагоги обратились к категории рефлексивной деятельности относительно недавно в связи с задачами гуманизации образования, усиления его развивающей функции.

Психологи И. Н. Семенов и С. Ю. Степанов показали, что в мышлении можно выделить несколько иерархических уровней, высшими из которых являются уровни интеллектуальной и личностной рефлексии. Рефлексия выполняет в мышлении регулирующую функцию (планирует деятельность, контролирует выполнение программы, диагностирует трудности, корректирует образы и программы), а также интегрирующую функцию: помогает выявить и обобщить знания, содержащиеся в опыте. Именно вторая функция рефлексии делает эту деятельность воспитательно значимой.

Рефлексивные механизмы включаются только при интеллектуальных затруднениях, поэтому включение учащихся в рефлексивную деятельность необходимо начинать с осознания проблемы. Реализацию данного положения предлагается осуществлять по следующей схеме.

— Учитель предъявляет учащимся проблемную ситуацию, связанную с анализом их деятельности или оценкой результатов деятельности учителя.

— Учитель обсуждает с учащимися параметры анализа, демонстрирует круг возможных направлений осуществления действий, критерии их дорогой.

— Учитель дает учащимся возможность самостоятельно принимать решения.

Литература:

1. Виноградова, Л. В. Методика преподавания математики в средней школе [Текст] / Л. В. Виноградова- Ростов н/д: Феникс, 2005.- 252с..
2. Голубев, В. И. О параметрах — с самого начала [Текст] / В. И. Голубев, А. М. Гольдман, Г. В. Дорофеев // Репетитор. — 2007. — № 2 — с. 3–13..
3. Котухов, С. К. Различные способы решения задач с параметрами [Текст] // Мат. в шк.- 1998.-№ 6.- С. 9–12..
4. Колягин, Ю. М. Методика преподавания математики в средней школе: общая методика [Текст]: учеб. пособие для студентов физико- математических факультетов пед. институтов.- М.: Просвещение, 1975.- 462с..
5. Леонтович, А. В. Исследовательская деятельность школьников [Текст] / / Школьные
6. Пронина, Е. С. Линейные уравнения с параметрами: методические рекомендации [Текст] // Мат. в шк.- 2000. -№ 12.- С.3–5..
7. Савенков, А. И. Исследовательская деятельность учащихся [Текст] // Школьные технологии.- 2008.- № 1.- С. 11- 20. 21.
8. Цыпкин, А. Г. Справочник по методам решения задач по математике для средней школы [Текст] / А. Г. Цыпкин, А. И. Пинский. — 2-е издание, перераб. и доп. — М.: Наука, 2009. — 576 с..
9. Шахмейстер, А. Х. Уравнения и неравенства с параметрами [Текст]/ А. Х. Шахмейстер.-М.: Виктория плюс, 2010,-136с..
10. Шерстаков, С. В. Уравнения с параметром [Текст] / С. В. Шерстаков, Е. Н. Юрченко.- М.: Слог,1993.- 107с.. Шихалиев, Х. Ш. Уравнения и неравенства с параметрами [Текст] // Мат. в шк.- 1980.-№ 21.- С. 34- 35..
11. Ястребинецкий, Г. А. Задачи с параметрами [Текст] / Г. А. Ястребинецкий.- М.: Просвещение, 2006.- 128с.

Сайты, меню, вход, новости

Научно-образовательный форум школьников Республики Мордовия

Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ 

Секция: Математический калейдоскоп

Автор работы:	Ехлаков Д. Н.
	10 класс Лицей МГУ им. Н. П. Огарева
Руководитель работы:	Кубанцева А. В.
	учитель математики Лицей МГУ им Н. П. Огарева

Саранск

2021

СОДЕРЖАНИЕ

	Введение	3
1	Теоретическая часть	6
	1.1	Основные понятия	6
	1.2	Основные типы задач с параметром	7
	1.3	Методы решения задач с параметрами	9
2	Практическая часть
	2.1	Примеры решения задач с параметрами ЕГЭ по математике профильного уровня
	Заключение
	Список использованных источников

Введение

Задачи с параметрами являются одним из самых трудных разделов школьного курса математики, так как их решение связано с умением проводить сложные, разветвленные логические построения. В школе первые представления о параметре мы получаем при изучении прямой пропорциональности; линейной функции и линейного уравнения; при изучении квадратного уравнения и исследования количества его корней в зависимости от значений параметра.

Актуальность выбранной темы обусловлена тем, что затрагивает современную проблему, знакомую каждому выпускнику, а именно – решение задач единого государственного экзамена. Сдать ЕГЭ на высший балл – одно из самых актуальных желаний старшеклассников, так как это прямым образом влияет на шансы поступить в престижный ВУЗ и получение желаемой профессии. Добиться этого довольно непросто. Учебного времени не всегда хватает для углубленной подготовки к заданиям высокого уровня сложности, к одним из которых относятся уравнения и неравенства с параметрами.

Анализ предыдущих результатов ЕГЭ показывает, что школьники с большим трудом решают задания с параметром, а многие даже не приступают к ним. К решению задачи №18 из КИМ приступают лишь порядка 10% выпускников 11 классов. Причиной этого является отсутствие системы знаний по данной теме.

Статистика решения задачи №18 на ЕГЭ по профильной математике

Год	Проверяемые требования	Уровень сложности задания	Максимальный балл за выполнение задания	Средний процент выполнения
2017	Умение решать уравнения и неравенства, содержавшие параметр	Высокий уровень сложности	4	0,38
2018	1,2
2019	4,8
2020	2,4

В школьных учебниках по математике задач с параметрами недостаточно, к тому же, предлагаемые в них примеры слишком просты по сравнению с задачами из ЕГЭ. Поэтому исследование способов решения задач с параметрами является для меня одним из важных шагов в подготовке к единому государственному экзамену по математике профильного уровня. Рассматривая проблему решения 18-го задания по ЕГЭ, хочу определить самый рациональный способ, а точнее, наименее трудоемкий, менее время затратный и удобный метод решения задач с параметрами.

Цель работы заключается в исследование методов решения задач с параметрами и выявление наиболее рациональных, наименее трудоемких способов решения.

Для достижения поставленной цели необходимо решить следующие задачи:

1. познакомится с определением параметра и видами задач, содержащие параметры;
2. исследовать способы решения задач с параметрами и постараться выбрать из них для себя самые оптимальные;
3. приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике.

Гипотеза моего исследования заключается в том, что существуют общие методы решения заданий с параметрами, позволяющие решать задания разных видов.

Объект исследования: задания контрольно-измерительных материалов единого государственного экзамена по математике, содержащие параметр.

Предмет исследования: методы решения заданий с параметрами.

Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.

Практическая значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработка решения задач, содержащих параметры.

1. Теоретическая часть

1. Основные понятия

Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Что означает «решить задачу с параметром»? Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Одним из способов решения задания №18 из ЕГЭ является графический способ, поэтому следует повторить что такое функция, виды функций и их свойства. Понятие функции – одно из ключевых в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Другое определение – однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. Существует всего пять типов элементарных функций: степенные, показательные, тригонометрические, обратные тригонометрические.

1. Основные типы задач с параметрами

Выделяют основные 4 больших класса задач с параметрами:

• Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успехи при решении задач всех других основных типов.

• Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.

• Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
• Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых:

1) уравнение выполняется для любого значения переменной из заданного промежутка;

2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

Наиболее массовый класс задач с параметром – задачи с одной неизвестной и одним параметром.

1.3 Методы решения задач с параметром

В пособиях, посвященных задачам с параметрами, выделяют три метода решений:

• Аналитический метод: это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
• Графический метод: в зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).  
• Метод решения относительно параметра: при решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Иногда также применяется так называемый метод оценки для уравнений и неравенств, где функции, стоящие в левой и правой части, могут быть равны друг другу только в определенной точке, причем одна из них принимает в этой точке наименьшее значение, а другая – наибольшее.

При рассмотрении данных методов я пришел к выводу, что самые распространенные и удобные способы – это аналитический и графический. Рассмотрим их более подробно.

Графический способ. В зависимости от того, какая роль параметру отведена в задаче, можно соответственно выделить два основных графических приёма:

• первый – построение графика на координатной плоскости (х;у),
• второй – построение графика на координатной плоскости на (х;а).

На плоскости (х;у) или (х;а)  функция y=f(x;a) задаёт семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определёнными свойствами. Нас же в первую очередь будет интересовать с помощью какого преобразования плоскости (параллельный перенос, поворот и т.д.) можно перейти от одной прямой к какой-нибудь другой.

Разумеется, не всегда графический образ семейства y=f(x;a) описывается простым преобразованием. Графический метод — всего лишь одно из средств наглядности. Поэтому те случаи, когда результат «прочитан» с рисунка и вызывает сомнение, лучше подкрепить аналитически.

Алгоритм решения задачи с параметром графическим способом состоит из следующих шагов:

1. задачу с параметром будем рассматривать как функцию ; п
2. строим графический образ, т.е. Построим в одной системе координат графики обеих частей уравнения;
3. пересекаем полученное изображение прямыми, параллельными оси абсцисс;
4. считываем нужную информацию.

Если уравнение одной из фигур не зависит от изменяющегося параметра, то график этой фигуры неподвижен относительно системы координат. Если в уравнение другой фигуры входит параметр, то от его изменения зависит расположение и даже форма графика. Тогда суть решения уравнения состоит в определении числа точек пересечения графиков построенных уравнений, а значит в определении количества возможных решений в зависимости от конкретных числовых значений параметра.  Для усложнения заданий эти уравнения искусственно преобразуют, «камуфлируют». Понятно, что каждое семейство обладает определенными характерными свойствами, они-то и помогают решить задачу.  Приведем несколько примеров.  

Аналитический способ. Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Широкое распространение за последние годы в ходе государственной (итоговой) аттестации выпускников средней школы  в формате ЕГЭ и на вступительных экзаменах в вузы, предъявляющие повышенные требования к математической подготовке абитуриентов, получили задачи на расположения корней квадратного трехчлена на оси. Для данного типа задач свойствен аналитический метод решения.

Выделим два наиболее распространенных вида задач, связанных с применением графика квадратичной функции. Первый вид – задачи, в которых изучается расположение корней квадратного трехчлена относительно точки с абсциссой, равной m. Второй вид – задачи, в которых выясняется, как расположены корни квадратного трехчлена относительно отрезка.

Первый тип задач предусматривает три случая:

• оба корня меньше m;
• один корень меньше m, а другой больше;
• оба корня больше m.

Для каждого из этих случаев выполним соответствующий рисунок и запишем к нему систему неравенств при условии, что старший коэффициент квадратного трехчлена f (x) = ax2 + bx + c положительный.  В таблице приведена полная система случаев расположения корней уравнения в зависимости от значений выражений, зависящих от коэффициентов уравнения.

Расположение корней квадратного трехчлена относительно точки с абсциссой, равной  

	Один корень меньше m, а другой больше: Условие  обеспечивает положительный коэффициент перед  (направленность ветвей параболы вверх); Условие  обеспечивает: наличие корней квадратного трехчлена; расположение точки m между корнями.
	Оба корня больше m: Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие   обеспечивает расположение точки m левее отрезка между корнями.
	Оба корня меньше m:  Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями;   Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.

Рассмотрим расположение корней квадратного трёхчлена относительно отрезка. При этом возможны шесть случаев:

• корни квадратного трёхчлена находятся справа от отрезка;
• корни квадратного трёхчлена находятся слева от отрезка;
• больший корень находится внутри отрезка  
• меньший корень находится внутри отрезка;
• оба корня внутри отрезка;
• отрезок между корнями квадратного трехчлена

Изобразим геометрическую модель каждой из этих ситуаций и составим к каждой из них адекватную систему неравенств при условии, что старший коэффициент квадратичной функции y = ax2 + bx + c больше нуля.

Расположение корней квадратного трёхчлена относительно отрезка

	Корни квадратного трёхчлена находятся справа от отрезка: Условие  обеспечивает нахождение корней вне отрезка между корнями; Условие  обеспечивает наличие двух корней квадратного трёхчлена; Условие  обеспечивает расположение отрезка левее абсциссы вершины.
	Корни квадратного трёхчлена находятся слева от отрезка: Условие  обеспечивает расположение корней вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.
	Больший корень находится внутри отрезка: Условие  обеспечивает расположение точки m внутри отрезка между корнями; Условие  обеспечивает расположение корней вне отрезка меду корнями.
	Меньший корень находится внутри отрезка:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.
	Оба корня внутри отрезка: Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает расположение точки p вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение вершины параболы между концами отрезка.
	Отрезок между корнями квадратного трехчлена:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.

1. Практическая часть

2.1 Примеры решения задач с параметрами ЕГЭ по математике профильного уровня

В ходе исследования я понял, что наиболее универсальным и наглядными для меня оказались графический и аналитический способы решения задач с параметрами. Далее предлагаю провести разбор некоторых задач прошлых лет ЕГЭ по математике профильного уровня.

Пример №1.

Найдите все значения , при каждом из которых система неравенств  имеет хотя бы одно решение на отрезке [4; 5].

Преобразуем систему:  

Построим прямоугольную систему координат xOa. Изобразим множество точек, координаты которых удовлетворяют системе неравенств.

Гипербола  и график корня пересекаются в точке N(3; 2). Гипербола и прямая  пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.

Поскольку система должна иметь хотя бы одно решение на отрезке [4; 5], определим наименьшую и наибольшую ординаты проекции выделенного на рисунке четырехугольника на ось ординат.

Найдём координаты точки P:

 =>

 

Проекции точек P и M дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [4; 5] при  (выделено штриховкой на рисунке).

Ответ: (1;

Пример №2.

Найдите все значения , при каждом из которых имеет ровно три различных решения система уравнений

Первое уравнение системы является уравнением окружности с центром в точке  и радиусом 3. График функции  получается параллельным переносом на вектор  графика функции  Поскольку график функции  представляет собой прямой угол с вершиной в точке  и сторонами лежащими на прямых  и  выше оси абсцисс, график функции  также представляет собой прямой угол, но с вершиной в точке  и сторонами, параллельными прямым  Заметим, что прямая  на которой лежит вершина угла, является касательной к окружности.

Ровно три общие точки фигуры имеют в следующих случаях:

1. Вершина прямого угла лежит в точке  касания окружности и прямой , а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если .

2. Одна из сторон прямого угла пересекает окружность в двух точках, а другая касается окружности в точке  (второй случай) или в точке (третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник  является квадратом со стороной и диагональю . Тогда . Следовательно, для случая касания в точке  получаем  Для касания стороны угла и окружности в точке  аналогично получаем ещё одно значение параметра:  

При  или  прямой угол имеет не более двух общих точек с окружностью.

При  или  прямой угол имеет четыре общие точки с окружностью.

Ответ:

Пример №3.

Найдите все значения параметра  при каждом из которых уравнение  имеет хотя бы одно решение на интервале (0;

Обозначим в исходном уравнении  .

Пример №4.  

Найдите все значения , при каждом из которых уравнение меет ровно два различных корня на промежутке

Сделаем замену тогда получим: .

Выполним обратную замену:  =>  Дискриминант этого уравнения равенпоэтому оно при всех значениях  имеет ровно два различных корня. Положим  Так как  оба корня уравнения  принадлежат промежутку  тогда и только тогда, когда  и  то есть когда  и Значит, уравнение  имеет ровно два различных корня на промежутке  при

Ответ:

Пример №5.

Найдите все значения , при каждом из которых уравнение  имеет ровно один корень на отрезке

Преобразуем уравнение:  => Рассмотрим эти случаи:

Первый случай:  при условиях:

=>  

Число  лежит на отрезке  если  Тогда для первого случая получаем: .

Второй случай:  при условии :

 => =>

Число  лежит на отрезке , если  Тогда для второго случая получаем:

Корень  равен  если

Итак, исходное уравнение имеет ровно один корень на отрезке  при   

Ответ:   

Пример №6.

Найдите все значения , для каждого из которых уравнение  имеет единственное решение.

Аналитический способ решения:

;

Пусть   = t >0, тогда:  

(*)

Исходное уравнение будет иметь единственное решение:

1 случай: еcли уравнение (*) имеет единственное решение (D=0);

2 случай: если уравнение (*) имеет два корня (D>0), один из которых меньше нуля или равен нулю.

Пусть n=a+6, m=5+3|a|;

1 случай:

 =>  =>  =>  => ;

если a<0, то  => ; если a>0, то  => .

2 случай:

; ;

если n>m, то:

  ;

если n

; ;

 система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.

 =>  =>

или  =>  =>

или  =>   => система не имеет решений.

Ответ:  ;  ; .

Графический способ:

Преобразуем исходное уравнение:

 =>
 =>   или .

Построим графики функций   на координатной плоскости xOa:

На чертеже заметим, что система имеет единственное решение при ,  и . Найдём  и :

Если a>0, то:  => => .

Если а<0, то: =>  => .

Ответ:  ;  ; .

Важно помнить:

• при использовании только графического метода, так же, как и только аналитического, может быть допущена ошибка, поэтому необходимо последовательно и внимательно указывать ход своего решения. При возможности выполнить проверку полученного результата, применяя другой способ решения;
• ответ, полученный только с помощью графика, может быть сомнителен, поэтому необходимо подкрепить его с помощью аналитического вывода, что в первую очередь подтвердит правоту выбранного пути решения и полученный ответ.

Заключение

Работая над своей темой исследования, я провел большую работу: изучил литературу по выбранной теме; разобрался, что такое параметр и задачи с параметрами; познакомился с методами их решения.

Выполняя практическую часть, было решено много уравнений, неравенств и их систем, я приобрел опыт и научился решать определённый круг задач и пришёл к некоторым выводам.

Решение каждого задания требует к себе индивидуального подхода, но при этом задачи с параметрами чем-то похожи на детский конструктор. Разобрав много таких примеров, можно заметить, как решение «собирается» из мелких деталей – хорошо знакомых нам фактов.

Для себя я выделил два основных способа решения №18 из ЕГЭ: аналитический и графический.

Графический способ является наиболее наглядным, простым и доступным способом решения задач с параметрами. Если задачу с параметром можно нарисовать – рисуем. То есть применяем графический метод. Размытость в решение уравнения, неравенства или их системы с помощью графика, можно подкрепить аналитическим выводом, что поможет подтвердить правоту выбранного решения и ответа.

Сочетание аналитического способа решения с графической интерпретацией полученных результатов позволяет сделать процесс решения уравнений с параметрами более осознанным, способствуя при этом формированию элементов исследовательской деятельности.

Думаю, что данная работа будет интересна моим сверстникам. Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность.

Список использованных источников

В. Голубев, А. Гольдман,
Москва

О задачах с параметром

Первоначальные сведения

I. Что такое параметр?

Если вы вспомните некоторые основные уравнения
(например, kx+l=0, ax²+bx+c=0),
то обратите внимание, что при поиске их корней
значения остальных переменных, входящих в
уравнения, считаются фиксированными и заданными.
Все разночтения в существующей литературе
связаны с толкованием того, какими
фиксированными и заданными могут быть эти
значения остальных переменных.

Например, в уравнениях |x|=a–1
и ax=1 при a=0
равенства не выполняются при любых значениях
переменной x, а в уравнения 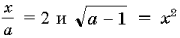при a=0
их левые части не определены. Есть авторы,
допускающие рассмотрение значения a=0
во всех приведенных случаях, и есть авторы,
исключающие его в двух последних, вводя понятие
допустимых значений переменной a.

Поскольку в школьных учебниках нет определения
параметра, мы предлагаем взять за основу
следующий его простейший вариант.

Определение. Параметром называется
независимая переменная, значение которой в
задаче считается заданным фиксированным или
произвольным действительным числом, или числом,
принадлежащим заранее оговоренному множеству.

Комментарий. Независимость параметра
заключается в его «неподчинении» свойствам,
вытекающим из условия задачи. Например, из
неотрицательности левой части уравнения |x|=a–1
не следует неотрицательность значений выражения
a–1, и если a–1<0,
то мы обязаны констатировать, что уравнение не
имеет решений.

 II. Что означает «решить задачу с
параметром»?

Естественно, это зависит от вопроса в задаче.
Если, например, требуется решить уравнение,
неравенство, их систему или совокупность, то это
означает предъявить обоснованный ответ либо для
любого значения параметра, либо для значения
параметра, принадлежащего заранее оговоренному
множеству.

Если же требуется найти значения параметра, при
которых множество решений уравнения,
неравенства и т. д. удовлетворяет объявленному
условию, то, очевидно, решение задачи и состоит в
поиске указанных значений параметра.

Более прозрачное понимание того, что означает
решить задачу с параметром, у читателя
сформируется после ознакомления с примерами
решения задач на последующих страницах.

III. Какие основные типы задач с
параметрами?

Тип 1. Уравнения, неравенства, их
системы и совокупности, которые необходимо
решить либо для любого значения параметра
(параметров), либо для значений параметра,
принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении
темой «Задачи с параметрами», поскольку
вложенный труд предопределяет успех и при
решении задач всех других основных типов.

Тип 2. Уравнения, неравенства, их
системы и совокупности, для которых требуется
определить количество решений в зависимости от
значения параметра (параметров).

Обращаем внимание на то, что при решении задач
данного типа нет необходимости ни решать
заданные уравнения, неравенства, их системы и
совокупности и т. д., ни приводить эти решения;
такая лишняя в большинстве случаев работа
является тактической ошибкой, приводящей к
неоправданным затратам времени. Однако не стоит
абсолютизировать сказанное, так как иногда
прямое решение в соответствии с типом 1 является
единственным разумным путем получения ответа
при решении задачи типа 2.

Тип 3. Уравнения, неравенства, их
системы и совокупности, для которых требуется
найти все те значения параметра, при которых
указанные уравнения, неравенства, их системы и
совокупности имеют заданное число решений (в
частности, не имеют или имеют бесконечное
множество решений).

Легко увидеть, что задачи типа 3 в каком-то
смысле обратны задачам типа 2.

Тип 4. Уравнения, неравенства, их
системы и совокупности, для которых при искомых
значениях параметра множество решений
удовлетворяет заданным условиям в области
определения.

Например, найти значения параметра, при
которых:

1) уравнение выполняется для любого значения
переменной из заданного промежутка;
2) множество решений первого уравнения
является подмножеством множества решений
второго уравнения и т. д.

Комментарий. Многообразие задач с
параметром охватывает весь курс школьной
математики (и алгебры, и геометрии), но
подавляющая часть из них на выпускных и
вступительных экзаменах относится к одному из
четырех перечисленных типов, которые по этой
причине названы основными.

Наиболее массовый класс задач с
параметром — задачи с одной неизвестной и
одним параметром. Следующий пункт указывает
основные способы решения задач именно этого
класса.

IV. Каковы основные способы (методы)
решения задач с параметром?

Способ I (аналитический). Это способ
так называемого прямого решения, повторяющего
стандартные процедуры нахождения ответа в
задачах без параметра. Иногда говорят, что это
способ силового, в хорошем смысле «наглого»
решения.

Комментарий. По мнению авторов,
аналитический способ решения задач с параметром
есть самый трудный способ, требующий высокой
грамотности и наибольших усилий по овладению им.

Способ II (графический). В
зависимости от задачи (с переменной x и
параметром a) рассматриваются графики или в
координатной плоскости (x; y), или в координатной
плоскости (x; a).

Комментарий. Исключительная наглядность и
красота графического способа решения задач с
параметром настолько увлекает изучающих тему
«Задачи с параметром», что они начинают
игнорировать другие способы решения, забывая
общеизвестный факт: для любого класса задач их
авторы могут сформулировать такую, которая
блестяще решается данным способом и с
колоссальными трудностями остальными способами.
Поэтому на начальной стадии изучения опасно
начинать с графических приемов решения задач с
параметром.

Способ III (решение относительно
параметра). При решении этим способом переменные
x и a принимаются равноправными и выбирается та
переменная, относительно которой аналитическое
решение признается более простым. После
естественных упрощений возвращаемся к исходному
смыслу переменных x и a и заканчиваем решение.

Перейдем теперь к демонстрации указанных
способов решения задач с параметром.

Задача 1. Для всех действительных
значений параметра a решите уравнение x³–(2–a)x²–ax–a(a–2)=0.

Решение. Исходное кубическое по x уравнение
является квадратным относительно a.
Поэтому, считая переменную x
параметром, перепишем это уравнение в виде
стандартного квадратного уравнения
относительно a, опуская промежуточные шаги по
раскрытию скобок и перегруппировке:

a²–(x²–x+2)a
– x³ + 2x² = 0.

Поскольку

x²–x+2=x²+(2–x) и –x³+2x²=x²(2–x),

то по обратной теореме Виета

a₁=x², a₂=2–x.

Поэтому исходное уравнение равносильно
совокупности уравнений

a=x² и a=2–x.

Первое уравнение преобразуется к виду x²=a,
откуда

(1): при a<0 решений нет;
(2): при a=0 единственное
решение x=0; при a>0
два решения
(3):

Второе уравнение совокупности имеет
единственное решение (5): x=2–a
для любого значения параметра a.

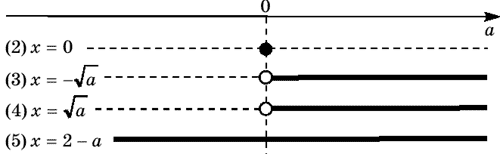
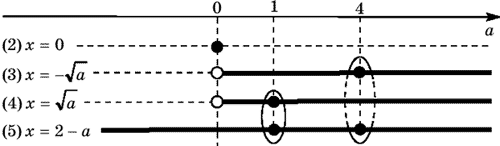
Комментарий 1. Многие учащиеся, доведя
решение до данного момента, испытывают трудности
в формировании общего ответа. Приведем удобный
прием представления полученных результатов для
дальнейшего продвижения в решении задачи. Будем
называть данный прием: «разверткой вдоль оси
параметра».

Изображаем ось параметра a
и отмечаем на ней граничные значения параметра,
которые фигурируют в ответах к каждому уравнению
совокупности. Все найденные решения уравнений
для тех значений параметра a,
при которых хотя бы одно решение существует,
выписываем в таблице слева (последовательно
сверху вниз). Сплошной линией, параллельной оси
параметра, указываем те промежутки значений
параметра, при которых полученное решение
существует. Заметим, что концы промежутков
изображаются «светлыми» точками в случае, когда
соответствующее решение не существует, а
«темными» точками — в противном случае.

Таблица 1

Данная развертка позволяет легко найти все
решения исходного уравнения для любого
действительного значения параметра: x=2–a
при a<0; x=0 или
x=2 при a=0; или или x=2–a
при a>0.

Комментарий 2. Возникает принципиальный
вопрос: является ли приведенный выше ответ
окончательным? С одной стороны, для поставленной
задачи ответ можно считать окончательным, если
допустить возможность повторения в ответе
одного и того же решения в различном виде.

Например, при a = 1 равенства и x = 2
– a определяют одно и то же значение переменной x=1,
а при a=4 равенства   и x=2–a
аналогично определяют одно значение x=–2.
Однако оставлять подобные повторения без
внимания обычно не принято, тем более, что при
других, особенно популярных в последнее время
постановках задач («Укажите количество
различных корней данного уравнения в
зависимости от параметра a» или «При каких
значениях параметра a уравнение имеет одно
решение?») игнорирование указанного
обстоятельства приводит к неверному ответу.

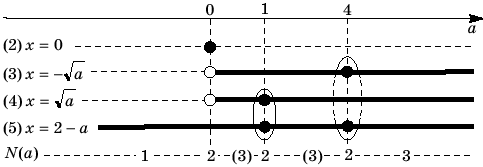
Полученные равенства (2)–(5) могут при некоторых
значениях параметра a
определять одно и то же значение переменной x.
Найдем указанные значения параметра. Поскольку
значения –
различны для всех a>0,
осталось выяснить, при каких значениях a
выполняются равенства Пусть  тогда первое уравнение приводится к виду t²+t–2=0,
откуда t=1 и t=–2
(не подходит, так как при a > 0), т. е.. Аналогично решая
второе уравнение, находим a=4.

Таблица 2

Полученный результат в таблице 2
проиллюстрирован следующим образом: линии
равенства (4) и (5) «сливаются» при a=1,
линии (3) и (5) «сливаются» при a=4.

Замечания. 1. При практическом
использовании «развертки по параметру»
таблицу 2 рекомендуем не воспроизводить, а
полученные «слияния» изображать в таблице 1.

2. Для изолированных значений параметра
естественно приводить числовые значения корней.

Используя таблицу 2, легко сформулировать
окончательный ответ задачи.

Ответ: x=2–a при a<0;
x₁=0, x₂=2 при a=0;

Задача 2. Для всех действительных
значений параметра a найдите число различных
корней уравнения (a–x²)(a+x–2)=0.

Замечание. Очевидно, что решение предыдущего
примера позволяет, в частности, получить ответ и
на поставленный вопрос. Для этого в таблицу 2
удобно ввести еще одну строчку, соответствующую
количеству различных корней по переменной x при
данном значении параметра a (в дальнейшем будем
обозначать указанное число различных корней
через N(a)). В этом случае таблица 2
будет выглядеть следующим образом.

Таблица 3

Количество различных корней для каждого
значения a совпадает с числом
пересечений соответствующей вертикальной линии
с приведенными ранее сплошными горизонтальными
линиями (или «темными» точками) с учетом
совпадений решений при найденных значениях
параметра. Например, при a=2
соответствующая вертикальная линия пересекает
сплошные горизонтальные три раза, а при a=4
она хотя и пересекает те же линии, но две из них
«сливаются», поэтому при a=4
количество различных корней равно двум, а не
трем, т. е. N(2)=3 и N(4)=2.

Ответ: уравнение имеет один корень при a<0;
два корня — при a=0, a=1,
a=4; три корня — при 0<a<1,
1<a<4, a > 4.

Укажем иной (достаточно популярный и
эффективный) способ решения данной задачи,
который с успехом может быть использован и при
решении задач других типов (включая и задачи типа
1). Предлагаемый способ основан на рассмотрении
множества точек плоскости с координатами (x; a),
для которых выполняются соответствующие
уравнения. Это множество точек обычно называют
графиком уравнения.

Решение. Исходное уравнение равносильно
совокупности a–x²=0 или a+x–2=0.
Поэтому построение искомого множества
точек — графика уравнения — сводится к
построению графиков a=x²
и a=2–x (рис. 1).

Рис. 1

Координаты точек пересечения графиков
определяются как решение системы уравнений 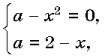решив которую
находим координаты (1; 1) точки A и (– 2; 4) —
точки B.

Понятно, что все точки параболы и прямой (и
только они) имеют координаты (x; a),
удовлетворяющие исходному уравнению. Поэтому
количество различных корней уравнения по
переменной x при каждом значении
параметра a=a₀ совпадает
с количеством точек пересечения прямой l,
задаваемой равенством a=a₀,
с построенным множеством точек.

Очевидно, что при a<0 прямая l
лежит в нижней полуплоскости и пересекает график
исходного уравнения (объединение точек параболы
и прямой) в одной точке, т. е. N(a)=1
при a<0. При a=0
прямая l касается параболы a=x²,
т. е. имеет с ней одну общую точку и пересекает
прямую a=2–x, поэтому N(0)=2.
При дальнейшем возрастании параметра a
от 0 до 1 (не включая значения 1) прямая l пересекает
график уравнения в трех точках, откуда N(a)=3
при 0<a<1. Аналогично
получаем N(1)=N(4)=2 и N(a)=3 при 1<a<4,
a>4.

Ответ: N(a)=1 при a<0;
N(a)=2 при a=0, a=1, a=4;
N(a)=3 при 0<a<1, 1<a<4,
a>4.

Комментарий. При решении рассмотренным
способом задач типа 1 при данном значении
параметра a₀ решениями
уравнения являются абсциссы точек пересечения
прямой a=a₀ с графиком
уравнения.

Задача 3. При каких значениях
параметра a уравнение |x+2|=ax
не имеет решений?

Решение 1. Для каждого значения параметра a
решим данное уравнение, после чего отберем те
значения параметра, при которых уравнение
решений не имеет.

На основании определения модуля заключаем, что
исходное уравнение равносильно совокупности
двух систем:

. 

или

Первая система имеет одно решение при т. е. при aЈ0
или a>1 и не имеет решений
при остальных значениях параметра. Вторая
система имеет одно решение т. е. при – 1<a<0
и не имеет решений при остальных значениях
параметра.

Объединяя решения систем, имеем: данное
уравнение имеет одно решение aЈ–1,
a=0, a>1; два решения Анализируя полученный
результат, определяем значения параметра a,
при которых уравнение не имеет решений.

Ответ: 0<aЈ1.

Замечание. Мы привели здесь решение задачи в
общем виде с целью повторной иллюстрации решения
задач типа 1 (рекомендуем для анализа полученных
решений составить таблицу «развертки вдоль оси
параметра», табл. 1–3).

Может показаться, что приведенное решение не
экономно и содержит много лишних ходов. Например,
кажется естественным после получения
совокупности двух систем сразу искать лишь те
значения параметра, при которых не имеет решений
каждая из систем, после чего найти значения
параметра, при которых обе системы не имеют
решений одновременно. Однако даже понимание
того, что требуется проделать в этом случае, уже
представляет собой определенную трудность для
ряда учащихся. Сказанное, разумеется, не
означает, что во всех аналогичных задачах
целесообразно выходить на более общую
постановку вопроса (выбор оптимального способа
решения зависит от конкретной задачи).

Решение 2. Приведем еще один вариант
использования графических представлений для
решения задач с параметрами.

Как известно, число решений уравнения f(х)=g(x)
совпадает с количеством точек пересечения
графиков функций y=f(x) и y=g(x),
построенных в одной системе координат.
Рассмотрим графики функций y=|x+2| и y=ax
(рис. 2). График первой функции не зависит от
параметра a; график второй
функции (правой части уравнения) принадлежит
семейству прямых, проходящих через начало
координат, — «подвижный» график. Поэтому
искомые значения параметра a
соответствуют тем прямым из указанного
семейства, которые не пересекают график функции y=|x+2|.

Рис. 2

При изменении параметра a от – Ґ до +Ґ
прямая y=ax поворачивается, начиная от
«вертикального» положения «слева» от оси
координат, против часовой стрелки вокруг начала
координат. Очевидно, что при aЈ0 прямая y=ax
пересекает по крайней мере один раз
«неподвижный» график y=|x+2|; при
дальнейшем возрастании параметра a
до момента a=1 (включительно)
прямая не имеет общих точек с «неподвижным»
графиком; при a>1 у графиков
снова появляется общая точка. Поэтому исходное
уравнение не имеет решений при 0<aЈ1.

Комментарий. В общем случае решение
уравнений предложенным способом состоит в
предварительном преобразовании уравнения к
одному из видов: f(x)=g(x; a) или f(x; a)=g(x;
a), после чего рассматриваются графики
обеих частей уравнения в одной системе
координат. При этом в первом случае изучается
взаимное расположение «неподвижного» графика
функции f и «подвижного» (в зависимости
от параметра) графика функции g, а во
втором случае оба графика «подвижны».

Выбор того или иного варианта предопределяется
как возможностью приведения исходного уравнения
к одному из видов, так и искусством работы с
графиками того, кто решает данное уравнение.

Для сравнения решите самостоятельно известную
задачу.

При каких значениях параметра a
уравнение x–a=2|2|x|– a²| имеет
ровно три различных корня?

Рассмотрите сначала графики функций f₁(x;
a)=x–a и g₁(x; a)=2|2|x|–a²|,
а затем графики функций f₂(x)=x
и g₂(x; a)=2| 2| x|–a²|+a.

Ответ: a=–2, a=–0,5.

Задача 4. Найдите все значения
параметра a, при каждом из
которых множество решений неравенства (a–x²)(a+x–2)<0
не содержит ни одного решения неравенства x²Ј1.

Замечание. Ниже приводятся три решения
данной задачи.

Первое из них традиционно для большинства
учащихся (обычно решение такого рода называют
прямым алгебраическим решением). Как правило,
попытки подобного решения характерны и для
начинающих овладевать методами решений задач с
параметрами, и для «опытных бойцов», которых не
смущает обилие технических трудностей.

Рекомендуем обратить самое пристальное
внимание на второе решение, поскольку приводимый
способ, во-первых, отличен от уже разобранных в
настоящей статье и, во-вторых, его можно
расценивать как достаточно самостоятельный и
эффективный метод решения широкого класса задач
с параметрами.

Третье решение проводится уже знакомым вам по
примерам 2 и 3 графическим способам.

Решение 1. Множитель (a–x²)
является квадратным трехчленом относительно x,
который не имеет корней при a<0,
имеет один корень при a=0 и
имеет два различных корня при a>0.
Второй множитель, линейный по переменной x,
имеет один корень при любом значении параметра a.
Поэтому в данной задаче целесообразно
рассмотреть три случая.

Случай 1. Пусть a<0; тогда
a–x²<0 при любом x,
а значит, исходное неравенство равносильно
неравенству a+x–2>0, т. е. x>2–a.

Комментарий. В этот момент возникает
основная логическая трудность, характерная для
данного способа решения задач типа 4: определение
тех значений параметра a<0, при которых
найденное множество решений, зависящее от
параметра, удовлетворяет условию задачи, т. е.
не содержит ни одного решения неравенства x²Ј1 (не содержит ни одного x
из отрезка [– 1; 1]).

Так как полученное множество решений
неравенства при a<0 есть
открытый луч (2–x; +Ґ),
то, очевидно, данный луч не содержит точек
отрезка [– 1; 1] тогда и только тогда, когда
начало луча лежит «правее» отрезка либо
совпадает с его правым концом, т. е.
выполняется условие 2–aі1,
которое, очевидно, истинно при всех
рассматриваемых значениях параметра a<0.

Таким образом показано, что все значения
параметра a<0 удовлетворяют
условию задачи, т. е. имеем «часть» общего
ответа: a<0.

Случай 2. Пусть a=0. В этом
случае исходное неравенство имеет вид (– x²)(x–2)<0,
решая которое получим x>2. Это
означает, что значение параметра a=0
удовлетворяет условию задачи: луч (2; + Ґ) не содержит точек отрезка
[– 1; 1], и мы имеем еще одну «часть» ответа:
a=0.

Комментарий. При разбиении решения задачи на
случаи в зависимости от параметра рекомендуем
все граничные значения параметра исследовать
непосредственной подстановкой в исходное
уравнение (неравенство, систему). Это полезно для
промежуточного контроля решения задачи.

Случай 3. Пусть a>0. Тогда
неравенство можно переписать в виде

   (A)

Комментарий. Ясно, что при фиксированном
значении a полученное неравенство легко решается
методом интервалов, однако в нашем случае (и это
характерно для задачи с параметрами!) процесс
упорядочения корней по возрастанию выделяется в
самостоятельный фрагмент решения.

Корень первого множителя при любом a>0
меньше корня второго множителя Корень третьего множителя
x₃=2–a в зависимости от a
может находиться как на промежутке от x₁
до x₂, так и вне его (слева
либо справа). Для определения возможных
вариантов сравним x₃ с x₁
и x₂.

Вариант 1. Пусть Полученное неравенство решаем как
квадратное относительно (t>0, так как в
рассматриваемом случае a>0): t²–t–2>0,
откуда t<–1 или t>2;
с учетом условия t>0 получаем, что
t>2. Возвращаясь к параметру a,
имеем неравенство т. е. a>4. Итак, для a>4
справедливо соотношение x₃<x₁<x₂,
следовательно, решая неравенство (A) методом
интервалов (рис. 3), находим решения

x₃<x<x₁, x>x₂, 
т. е.

Рис. 3.

Полученное множество решений не
содержит ни одной точки отрезка [– 1; 1] тогда и
только тогда, когда отрезок [– 1; 1] расположен
либо левее точки x₃=2–a,
либо между точками С учетом условия a>4
первая ситуация исключается, а вторая
определяется системой неравенств которая выполняется для
любого a>4. В итоге приходим
к выводу, что все значения параметра a>4
являются искомыми.

Вариант 2. Пусть x₃=x₁,
т. е. откуда a=4
и неравенство (A), принимая вид (x+2)²(x–2)>0,
имеет решение x>2, которое не
содержит точек отрезка [– 1; 1]. Следовательно,
значение a=4 — искомое.

Вариант 3. Пусть Решая соответствующую систему неравенств
получим, 1<t<2,
т. е. 1<a<4. При найденных
значениях параметра неравенство (A) имеет решение

x₁<x<x₃,  x>x₂,
т. е.

Рис. 4.

Следовательно, условию задачи удовлетворяют те
и только те значения параметра, при которых
отрезок [– 1; 1] расположен либо левее точки либо между
точками.
Поскольку первая ситуация, очевидно, невозможна то искомые
значения a определяются системой неравенств
aі3. С учетом того, что в данном
варианте рассматривались значения параметра a
от 1 до 4, получаем 3Јa<4.

Вариант 4. Пусть откуда a=1 и
неравенство (A) принимает вид (x+1)(x–1)²>0.
Решением последнего неравенства (рис. 4)
является объединение интервалов (–1;1)
и (1;+ Ґ), в котором
содержатся точки отрезка [– 1; 1]. Значит,
изучаемое значение параметра a=1
не удовлетворяет условию задачи.

Вариант 5. Пусть Решив полученное неравенство (квадратное
относительно ),
находим, что –2<t<1, т. е. 0<a<1
(напомним, что мы находимся в рамках
случая 3, определяемого условием a>0).
Неравенство (A) при полученных значениях
параметра (рис. 5) имеет решение

 

Найденное множество решений не содержит ни
одной точки отрезка [– 1; 1] тогда и только
тогда, когда этот отрезок расположен либо левее
точки либо
между точками
Ни та, ни другая ситуация невозможна ввиду
неотрицательности арифметического квадратного
корня. Следовательно, среди рассматриваемых
значений параметра 0<a<1
нет искомых.

Итак, после рассмотрения всех пяти возможных
вариантов получен ответ в случае 3: aі3.

Таким образом, окончательный ответ задачи
следующий: aЈ0, aі3.

Замечание к решению 1. При решении данным
способом практически всегда возникает
возможность продвигаться к поставленной цели с
существенно меньшими затратами времени, что
сопряжено, однако, с увеличением логических
трудностей. Например, в случаев 3 (a >
0) нашего решения можно было рассуждать
следующим образом.

Определив корни каждого множителя в неравенстве (A),
замечаем, что при значении параметра a<1
независимо от взаимного расположения корней в
окрестностях корней всегда найдется хотя бы одно решение
исходного неравенства из отрезка [– 1; 1]
(поскольку при переходе через корни x₁
и x₂ левая часть неравенства
(A) меняет знак), что не соответствует искомым
значениям параметра a.

Следовательно, осталось рассмотреть значения
параметра aі1.
Непосредственной проверкой легко убедиться, что
значение a=1 также не
удовлетворяет условию задачи. При a>1
корень корень а корень x₃=2–a<1.
Поэтому большим корнем левой части неравенства
(A) является x₂; значит, все
значения x из интервала (x₂;+ Ґ) не всегда являются
решениями неравенства (A). Поэтому неравенство (A)
не имеет ни одного решения из отрезка [– 1; 1]
тогда и только тогда, когда x₃Ј–1 (независимо (!) от
расположения корней x₁ и
x₃, (рис. 5, 6).

Рис. 5.

Рис. 6.

Итак, имеем 2–aЈ–1,
откуда aі3.

Решение 2. Основная идея решения: неравенство
(a – x²)(a+x–2)<0
будем рассматривать как неравенство
относительно параметра a и исследовать
полученный ответ (зависящий от x!) с целью
получения искомых значений параметра a.

Комментарий. Очевидно, сама идея
рассматриваемого метода предопределяет
ограничения по его использованию: во-первых,
далеко не всегда возможно решить уравнение
относительно параметра; во-вторых, в случае
возможности такого решения не всегда
целесообразно применение обсуждаемого способа в
силу возникновения в дальнейшем серьезных
технических и логических трудностей (оценка
подобных трудностей приходит, естественно, с
опытом решения такого рода задач).

Так как при любом x из отрезка [– 1;
1] справедливо соотношение x²Ј2–x, то при данных x исходное
неравенство как квадратное относительно a
равносильно неравенству a₁<a<a₂,
где a₁=x², a₂=2–x, т. е.
имеем x²<a<2–x для
любого xО[– 1; 1].     
(B)

Комментарий. Типичной трудностью при
решении задач предлагаемым способом является
осознание того, какому условию должны
удовлетворять искомые значения параметра для
вновь полученных уравнений (неравенств, систем).

В нашем случае задачу, равносильную исходной,
можно сформулировать следующим образом.

При каких значениях параметра a
двойное неравенство x²<a<2–x не
имеет ни одного решения из отрезка [–1;1]?

Чтобы понять, как действовать дальше, нужно для
конкретного значения параметра a=a₀
уметь ответить на вопрос: почему значение a₀
не является искомым? Очевидно, значение
параметра a₀ не
является искомым, если существует хотя бы одно
значение x₀ из отрезка [– 1;
1], при котором выполняется неравенство x₀²<a₀<2–x₀.
Следовательно, значение параметра a
является искомым тогда и только тогда, когда для
любого x из отрезка [– 1; 1] либо aЈx², либо aі2–x.

Найдем сначала все значения параметра a,
для которых при любом x из отрезка [– 1; 1]
имеет место неравенство aЈx².
Понятно, что если aЈx²
при любом x из отрезка [– 1; 1],
то это то же самое (!), что значение a
не больше наименьшего значения функции f(x)=x²
на этом отрезке. Поскольку наименьшее значение
функции f(x)=x² на отрезке [– 1;
1] равно 0, получаем aЈ0.

Теперь осталось найти все значения параметра a,
для которых при любом x из отрезка [– 1;
1] выполняется неравенство aі2–x. По аналогии с
предыдущими рассуждениями можно утверждать, что aі2–x для всех x из
отрезка [– 1; 1] тогда и только тогда,
когда a не меньше наибольшего
значения функции f(x)=2–x на отрезке
[–1;1]. Поскольку наибольшее значение
убывающей линейной функции f(x)=2–x
на отрезке [– 1; 1] равно ее значению в
точке x=–1, т. е. равно 3, то
искомые значения параметра aі3.

Объединяя полученные ответы, приходим к
окончательному ответу исходной задачи: aЈ0, aі3.

Комментарий. Обращаем особое внимание на
заключительный фрагмент решения задачи, который
характерен для многих задач с параметрами: мы
показали, что

Часто приходится иметь дело и с аналогичными
задачами: «Найти все значения параметра a,
при которых неравенство a<f(x) (или
неравенство a>g(x))
выполняется для любого x из заданного
множества X». Подобная постановка
вопроса у большинства учащихся вызывает
серьезные затруднения.

Приводим ответ на поставленный вопрос.

1. Неравенство a < f(x)
выполняется для любого x из множества X
тогда и только тогда, когда a меньше наименьшего
значения f(x) на множестве X
(если оно существует!), т. е.

2. Неравенство a>g(x)
выполняется для любого x из
множества X тогда и только тогда, когда a
больше наибольшего значения g(x) на
множестве X (если оно существует!),
т. е. 

На этом мы заканчиваем разбор отдельных
примеров и в заключение особо выделим важные, по
нашему мнению, соображения, которые необходимо
учитывать учащемуся при овладении темой «Задачи
с параметрами».

V. Заключительные рекомендации

1. Прежде чем приступить к решению задачи с
параметрами, советуем разобраться в ситуации для
конкретного числового значения параметра.
Например, возьмите значение параметра a=5
и ответьте на вопрос: является ли данное значение
a=5 искомым для задачи 4?
Неудачная попытка получения ответа на
поставленный вопрос, к сожалению, означает вашу
принципиальную неготовность решить задачу в
общем виде. В этом случае необходимо срочно
принять меры к овладению основными темами
школьного курса математики. Заметим, что
подстановка фиксированного значения параметра
позволяет во многих случаях нащупать путь
решения задачи.

2. Рекомендуем обратить ваше внимание на то,
что при решении задач с параметрами особую роль
играет обработка результатов, полученных на том
или ином этапе решения. Одной из удобных,
апробированных на практике форм организации
результатов, является представление их в
табличном виде (см. задачу 1). Советуем в первую
очередь обратить внимание на эту рекомендацию
тем, кто только начинает овладевать методами
решения задач с параметрами.

.