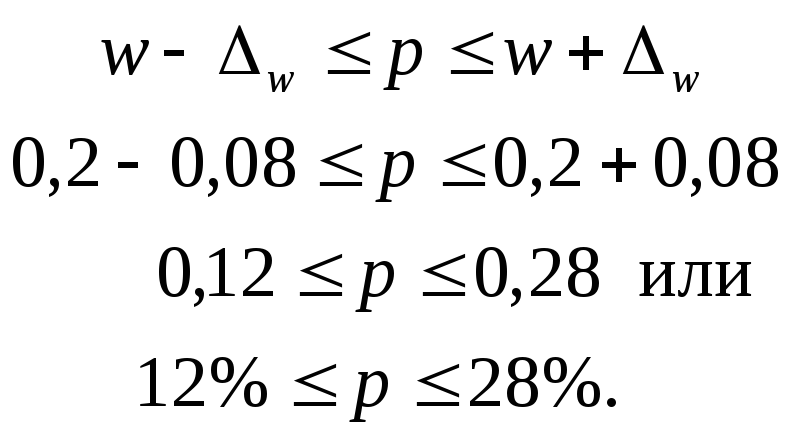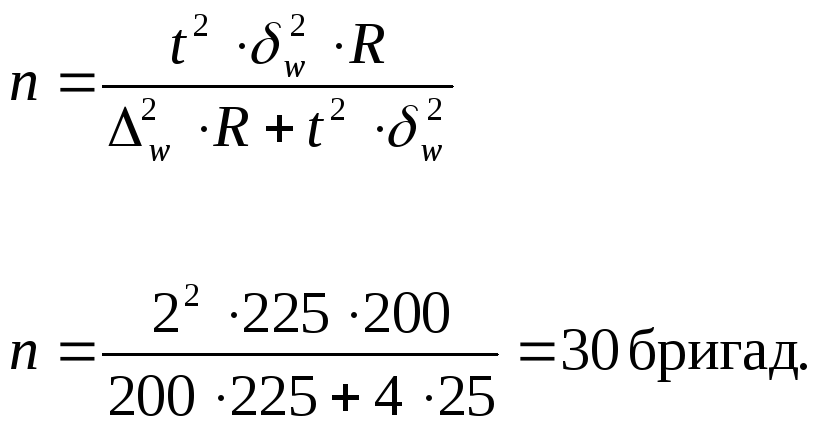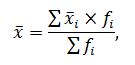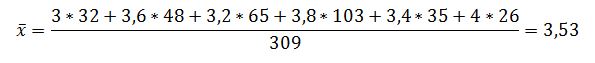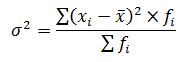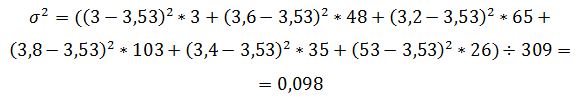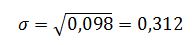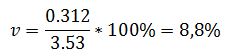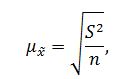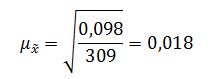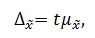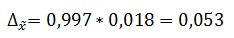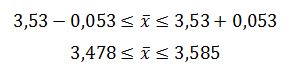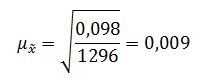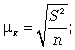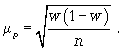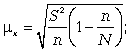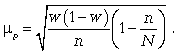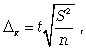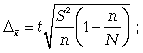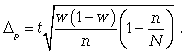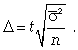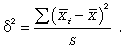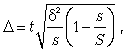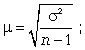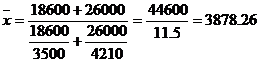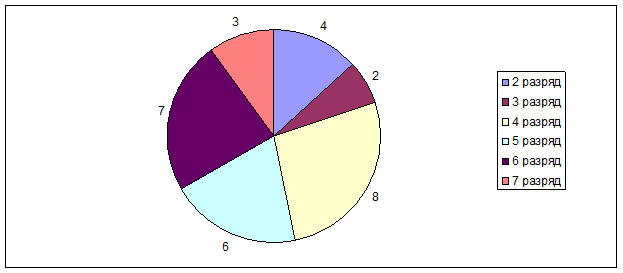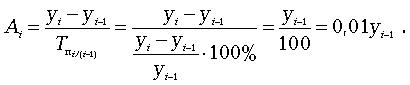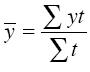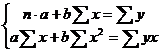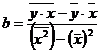Задачи на среднюю ошибку выборки

ВЫБОРОЧНЫЙ МЕТОД. РЕШЕНИЕ ТИПОВЫХ
ЗАДАЧ

Приступая к изучения
данной темы целесообразно вначале
ознакомиться с условными обозначениями
(приложение А), затем в процессе решения
задач, следует воспользоваться формулами
определения средней ошибки выборки,
дисперсии, необходимого объема выборки,
представленных в приложениях Б, В,Г.

Пример 1.

Из партии электроламп
взята 20%-ная случайная бесповторная
выборка для определения среднего веса
спирали.

Результаты выборки
следующие:

Определите: с
вероятностью
0,95 доверительные
пределы, в
которых лежит средний вес спирали, для
всей партии электроламп.

Решение.

Доверительные
интервалы для генеральной средней с
вероятностью Р:

Средний уровень
признака по выборке

найдем по формуле средней арифметической
взвешенной:

,

Предельную ошибку
при случайном бесповторном отборе
определим по формуле:

При вероятности
Р=0,95
t=1,96
(приложение Ж).

Для определения
выборочной дисперсии воспользуемся
формулой:

Доверительные
интервалы для генеральной средней с
вероятностью Р=0,95:

Таким образом, с
вероятностью 95% можно утверждать, что
средний вес спирали в генеральной
совокупности колеблется от 41,7 до 42,3 мг.

Пример 2.

На основе случайного
повторного выборочного обследования
в отделении связи города предполагается
определить долю писем частных лиц в
общем объеме отправляемой корреспонденции.
Никаких предварительных данных об
удельном весе этих писем в общей массе
отправляемой корреспонденции не имеется.

Определите:

• численность
  выборки, если результаты выборки
  необходимо дать с точностью до 1% и
  гарантировать это с вероятностью 0,95.

Решение.

По условию задачи
известны:

размер допустимой
(предельной) ошибки — _w=1%
или 0,01:

принята вероятность
– Р
= 0,95;

Необходимая
численность выборки при случайном
повторном отборе:

Так как значение
w
не дано, то следует ориентироваться на
наибольшую дисперсию, которой соответствует
значение w
= 0,5.

Таким образом,
чтобы с данной точностью определить
долю частных писем в общем объеме
отправляемой корреспонденции, необходимо
в порядке случайной выборки отобрать
9604 письма.

Пример 3.

В городе 500 тыс.
жителей. По материалам учета городского
населения было обследовано 50 тыс. жителей
методом случайного бесповторного
отбора. В результате обследования
установлено, что в городе 15% жителей
старше 60 лет.

Определите:

• с вероятностью
  0,683 пределы, в которых находится доля
  жителей в городе в возрасте старше 60
  лет

Решение.

Доверительные
интервалы для доли в генеральной
совокупности определяются:

По условию задачи,
выборочная доля w
= 15% (или w
= 0,15).

С вероятностью
0,683 определим предельную ошибку выборки
для доли альтернативного признака:

Определяем
доверительные интервалы

Таким образом, с
вероятностью 0,683 можно утверждать, что
доля жителей в возрасте старше 60 лет в
городе А
находятся в пределах 10% 
р

20%.

Пример 4.

В области, состоящей
из 20 районов, проводилось выборочное
обследование урожайности на основе
бесповторного отбора серий (районов).
Выборочные средние по районам составили
соответственно 14,5 ц/га;
16,0; 15,5; 15,0 и 14,0 ц/га.

Определите:

• с вероятностью
  0,954 пределы урожайности во всей области.

Решение.

Выборочная средняя

определяется по формуле средней
арифметической:

Межгрупповая
дисперсия определяется по формуле:

При вероятности
0,954 коэффициент доверия t
= 2. Предельная
ошибка серийной бесповторной выборки
определяется по формуле:

Доверительные
интервалы урожайности в области:

Таким образом,
урожайность в области с вероятностью
0,954 будет находиться в пределах от 14,45
до 15,55 ц/га.

Пример 5.

При проверке веса
импортируемого груза на таможне методом
случайной повторной выборки отобрано
200 изделий. В результате был установлен
средний вес изделия 30 г
при среднем квадратическом отклонении
4 г.

Определите:

• c
  вероятностью 0,9973 пределы, в которых
  находится средний вес изделий в
  генеральной совокупности.

Решение.

Рассчитаем
предельную ошибку выборки. Так, при
Р=0,9973,
t=3.

Определим пределы
генеральной средней:

или

Следовательно, с
вероятностью 0,9973 можно утверждать, что
средний вес изделий в генеральной
совокупности находится в пределах от
29,15 до 30,85 г.

Пример 6.

В 100 туристических
агентствах города предполагается
провести обследование среднемесячного
количества реализованных путевок
методом механического отбора. Какова
должна быть численность выборки, чтобы
с вероятностью 0,683 ошибка не превышала
3 путевок, если по данным пробного
обследования дисперсия составляет 225?

Решение.

Так как отбор
механический, численность выборки
определяется по формуле:

Рассчитаем
необходимый объем выборки:

Таким образом,
чтобы с данной точностью определить
среднемесячное количество реализованных
путевок, необходимо отобрать 20
туристических агентств.

Пример 7.

Произведено
выборочное наблюдение партии однородной
продукции для определения процента
изделий высшего сорта.

При механическом
способе отбора из партии готовых изделий
в 20000 единиц было обследовано 800 единиц,
из которых 640 изделий отнесены к высшему
сорту.

Определите:

• с вероятностью
  0,9973 возможный процент изделий высшего
  сорта во всей партии.

Решение.

В случае механического
отбора предельная ошибка определяется
по следующей формуле:

Границы генеральной
доли изделий высшего сорта:

Следовательно,
генеральная доля находится в пределах:

Таким образом, с
вероятностью 0,9973 можно утверждать, что
во всей партии от 76 до 84 % — продукция
высшего сорта.

Пример 8.

При обследовании
100 образцов изделий, отобранных из партии
в случайном порядке, оказалось 20
нестандартных.

Определите:

• с вероятностью
  0,954 пределы, в которых находится доля
  нестандартной продукции в партии.

Решение.

Чтобы определить
границы генеральной доли, необходимо
определить выборочную долю и ошибку
выборочной доли.

Рассчитаем долю
нестандартной продукции в выборочной
совокупности:

Предельная ошибка
выборочной доли с вероятностью 0,954
составит:

Доля нестандартной
продукции в генеральной совокупности
определяется по формуле:

Таким образом, с
вероятностью 0,954 можно утверждать, что
доля нестандартной продукции в партии
товара находится в пределах от 12 до 28%.

Пример 9.

200 ящиков деталей
упакованы по 40 шт. в каждом. Для проверки
качества деталей был проведен сплошной
контроль деталей в 20 ящиках (выборка
бесповторная). В результате контроля
установлено, что доля бракованных
деталей составляет 15%. Межсерийная
дисперсия равна 49.

Определите:

• с вероятностью
  0,9973 пределы, в которых находится доля
  бракованной продукции в партии ящиков.

Решение.

Определим среднюю
ошибку выборки:

Предельная ошибка
выборки для доли с вероятностью 0,9973
(t=3)
равна: _w
= 1,48 
3 = 4,44%.

Пределы в генеральной
совокупности:

Таким образом, с
вероятностью 0,9973 можно утверждать, что
доля бракованных деталей в партии будет
находиться в пределах от 10,59 до 19,41%.

Пример 10.

В районе 10 тыс.
семей. Из них 5 тыс. семей рабочих, 4 тыс.
семей работников сельского хозяйства,
1 тыс. семей служащих. Для определения
числа детей в семье была проведена
10%-ная типическая выборка, с отбором
единиц пропорционально численности
единиц типических групп. Внутри групп
применялся метод механического отбора.
Результаты выборки представлены в
таблице.

Определите:

• с вероятностью
  0,9973 пределы, в которых находится среднее
  число детей в семье в районе.

Решение.

Определим число
отобранных семей по типам семей:

где

Численность семей
в первой группе:

Численность семей
во второй группе:

Численность семей
в третьей группе:

Выборочная средняя
определяется
по формуле средней арифметической
взвешенной:

Определим среднюю
из внутригрупповых дисперсий:

Рассчитаем среднюю
ошибку выборочной средней типической
выборки:

С вероятностью
0,9973 (t
= 3) определим предельную ошибку
выборочной средней:

Доверительные
пределы определим по формуле:

Таким образом, с
вероятностью 0,9973 можно утверждать, что
в районе среднее число детей в семье
находится в пределах

Пример 11.

В акционерном
обществе 200 бригад рабочих. Планируется
проведение выборочного обследования
с целью определения удельного веса
рабочих, имеющих профессиональные
заболевания. Известно, что межсерийная
дисперсия доли равна 225.

Рассчитайте:

• с вероятностью
  0,683 необходимое количество бригад для
  обследования рабочих, если ошибка
  выборки не должна превышать 5%.

Решение.

Рассчитаем
необходимое количество бригад на основе
формулы объема серийной бесповторной
выборки:

Таким образом,
чтобы с заданной точностью определить
удельный вес рабочих, имеющих
профессиональные заболевания, необходимо
из 200 бригад обследовать 30 бригад.

Средняя из
внутригрупповых дисперсий определяется
по формуле:

Определим среднюю
ошибку выборочной доли:

Предельная ошибка
выборки для доли с вероятностью 0,683
(t
=
1)

Определим
доверительные интервалы:

или

Таким образом, с
вероятностью 0,683 можно утверждать, что
доля рабочих, не выполняющих норму
выработки на заводе колеблется от 2,45
до 5,15%.

ПРИЛОЖЕНИЕ А

Условные обозначения

ПРИЛОЖЕНИЕ Б

Определение средней ошибки выборки
при различных видах выборок

ПРИЛОЖЕНИЕ В

Определение дисперсий для различных
видов выборки

ПРИЛОЖЕНИЕ Г

Определение необходимого объема
выборки

Ошибка! Ошибка связи.

Соседние файлы в папке А Д

• #

  24.03.201569.63 Кб46123.xls

• #
• #
• #
• #
• #
• #

  24.03.201515.36 Кб65Лабораторная 1 , Алексеева Александра.xls

Задача

В результате случайной выборки взяты 309 проб молока на жирность. При этом получены следующие данные:

Средний процент жира в молоке	Число проб молока
3	32
3,6	48
3,2	65
3,8	103
3,4	35
4	26
Всего:	309

Определите:

1.  Средний процент жира в молоке и среднее квадратическое отклонение в данной выборочной совокупности; коэффициент вариации.

2.  С вероятностью 0,997 предельную ошибку выборки и величину генеральной средней.

3.  Величину средней ошибки выборочной совокупности, если объём выборки, т. е. количество проб молока, будет доведен до 1296 (при неизменном среднем квадратическом отклонении).

Решение

Средний процент жира в молоке определяется по формуле средней арифметической взвешенной:

где:   x_i – значение, полученное при i-той пробе;
f_i – число проб.

Средний процент жира равен:

Дисперсия вариационного ряда определяется по формуле:

Дисперсия равна:

Среднеквадратическое отклонение равно корню квадратному из дисперсии:

Коэффициент вариации равен отношению среднеквадратического отклонения к среднему значению:

Вывод: низкое значение коэффициента вариации говорит о количественной однородности совокупности.

Средняя ошибка выборки при случайном отборе определяется по формуле:

где:   S² – выборочная дисперсия;
n – объем выборки.

Средняя ошибка выборки равна:

Предельная ошибка выборки определяется по формуле:

где:   t – коэффициент доверия, для вероятности 0,997 равный 3.

Предельная ошибка выборки равна:

Доверительный интервал для среднего:

Вывод: генеральное среднее значение процента жира в молоке находится в пределах от 3,478% до 3,585%.

Если объем выборки будет доведен до 1296 проб молока, то величина средней ошибки выборки составит:

Вывод: увеличение объема выборки снижает среднюю ошибку, т.е. с ростом выборки измерения становятся точнее.

Задачи по статистике с решением — Выборочное наблюдение

Решения задач по выборочному наблюдению

Задача 1 по статистике

При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.

Решение.

В данном примере – случайный повторный отбор.

n=200

=30г

=4г — СКО

p=0,997, тогда t=3

Формула средней ошибки для случайного повторного отбора:

=0,84 г

г

Определяем величину средней ошибки.

Ответ: пределы в которых находится средний вес изделий: г

Задача 2

В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:

P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.

Число детей в семье, xi	0	1	2	3	4	5
Кол-во детей в семье	1000	2000	1200	400	200	200

Решение

2%-я выборка означает:

n=250000*0,02= 5000 семей было исследовано.

Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:

Найдем среднее число детей в выборочной совокупности:

ребенка

Определим дисперсию

ребенка – средняя величина ошибки

Т.к p = 0,954, то t = 2

ребенка

ребенка

Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.

Задача 3

С целью определения средней фактической продолжительности рабочего дня в гос. учреждении с численностью служащих 480 человек была проведена 25%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери рабочего времени достигали более 45 мин.в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.

Решение. Определим объем выборочной совокупности: n=480*0.25=120 чел.

Выборочная доля w по условию 10%.Учитывая, что показатели точности механической и собственно случайной бесповторной выборки определяются одинаково, а также то, что при P=0,683 t=1, предельная ошибка выборочной доли: =

Ответ: пределы в которых находится средняя доля % или: г

Т.о., с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6 до 12,4 %.

Задача 4 по статистике

В АО 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что дисперсия доли бесповторной выборки равна 225. с вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.

Численность выборки для бесповторного отбора:

бригад

Мода и медиана в статистике

Особый вид средних величин — структурные средние — применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.
В качестве структурных средних чаще всего используют показатели моды — наиболее часто повторяющегося значения признака — и медианы — величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой — не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется.
Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
,
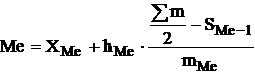
где XMe — нижняя граница медианного интервала;
hMe — его величина;
am/2- половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
SMe-1 — сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe — число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интер­вального ряда с равными интервалами величина моды определяется как
,
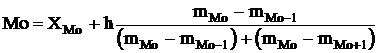
где  ХMo — нижнее значение модального интервала;
mMo — число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
mMo-1 — то же для интервала, предшествующего модальному;
mMo+1 — то же для интервала, следующего за модальным;
h — величина интервала изменения признака в группах.

Понятие об ошибке выборки. Методы расчета ошибки выборки

Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.
Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел.Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.
Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.
Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице.
Комбинированная выборка основана на сочетании нескольких способов выборки.
Многоступенчатая выборка есть образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать.
Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается.
Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.
Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки. Для иллюстрации можно предложить расчет ошибки выборки на примере простого случайного отбора.
Расчет средней ошибки повторной простой случайной выборки производится следующим образом:
cредняя ошибка для средней

cредняя ошибка для доли

Расчет средней ошибки бесповторной случайной выборки:
средняя ошибка для средней

средняя ошибка для доли

Расчет предельной ошибки  повторной случайной выборки:
предельная ошибка для средней

предельная ошибка для доли
где t — коэффициент кратности;
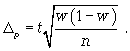
Расчет предельной ошибки бесповторной случайной выборки:
предельная ошибка для средней

предельная ошибка для доли

Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N — численность генеральной совокупности.
Что касается расчета ошибки выборки в других видах выборочного отбора (например, типической и серийной), то необходимо отметить следующее.
Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних. Так, в формуле предельной ошибки типической выборки учитывается средняя из групповых дисперсий, т.е.

При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии:

Серийная выборка, как правило, проводится как бесповторная, и формула ошибки выборки в этом случае имеет вид

где — межсерийная дисперсия; s — число отобранных серий; S — число серий в генеральной совокупности.
Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n < 30), которые могут иметь место в случаях нецелесообразности использования больших выборок.
При расчете ошибок малой выборки необходимо учесть два момента:
1) формула средней ошибки имеет вид

2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности Стьюдента, где Р = S (t, n), при этом Р определяется в зависимости от объема выборки и t.
В статистических исследованиях с помощью формулы предельной ошибки можно решать ряд задач.
1. Определять возможные пределы нахождения характеристики генеральной совокупности на основе данных выборки.
Доверительные интервалы для генеральной средней можно установить на основе соотношений

где — генеральная и выборочная средние соответственно; — предельная ошибка выборочной средней.
Доверительные интервалы для генеральной доли устанавливаются на основе соотношений
 
2. Определять доверительную вероятность, которая означает, что характеристика генеральной совокупности отличается от выборочной на заданную величину.
Доверительная вероятность является функцией от t, где

Доверительная вероятность по величине t определяется по специальной таблице.
3. Определять необходимый объем выборки с помощью допустимой величины ошибки:

Чтобы рассчитать численность п повторной и бесповторной простой случайной выборки, можно использовать следующие формулы:
(для средней при повторном способе);
(для средней при бесповторном способе);
(для доли при повторном способе);
(для доли при бесповторном способе).

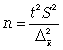
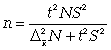
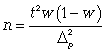
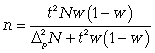
Задача 1

Определите индекс покупательской способности рубля, если в текущем году денежные средства на покупку товаров составили 860 млн. руб., денежные средства на оплату услуг 300 млн. руб. В планируемом году денежные средства на покупку товаров возрастут на 15% , денежные средства на оплату услуг увеличатся на 80 млн. рублей , цены на товары возрастут на 70% , ЦЕНЫ НА УСЛУГИ ВОЗРАСТУТ НА 20% Сделайте выводы.

Решение:

Рассчитаем планируемые показатели
Денежные средства на покупку товаров=860*1,15=989 млн. руб.
Денежные средства на оплату услуг=300+80=380 млн. руб.
Сведем все значения в таблицу.

Наименование	Денежные средства, млн. руб.	Цена
Текущий год	Планируемый год	Текущий год	Планируемый год
Товары	860	989	1	1,7
Услуги	300	380	1	1,2

Рассчитаем индекс цен.

Индекс покупательской способности рубля=1/Индекс цен
Индекс покупательской способности рубля=1/1,56=0,64

За счет повышения цены покупательская способность рубля снизилась  на 64%.

Задача 2

Рассчитайте среднюю выработку продавца по магазину по показателям:

секция	Дневная выработка продавца тыс. руб.	товарооборот тыс. руб.
1	3500	18600
2	4210	26000

Решение:
По формуле средней гармонической взвешенной:

Средняя выработка продавца по магазину равна 3878,26 тыс. руб.

Задача 3

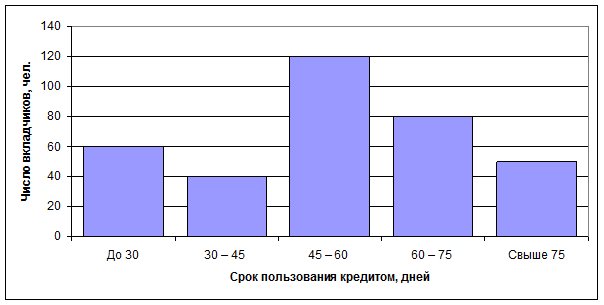
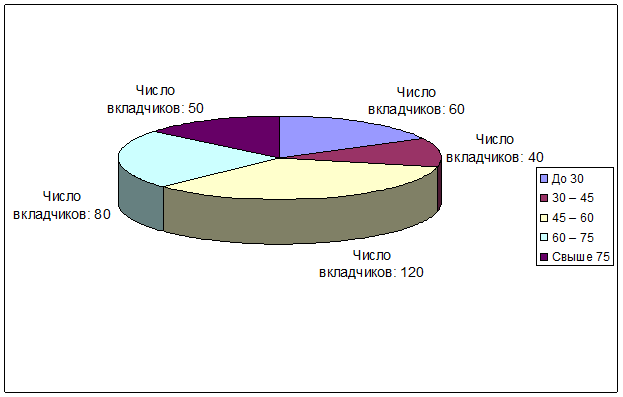
Для определения сроков пользования краткосрочным кредитом в коммерческом банке города была проведена 5% случайная бесповторная выборка лицевых счетов, в результате которой получено следующее распределение клиентов по сроку пользования кредитом (таблица 1):

Срок пользования кредитом (дней)	Число вкладчиков (чел.)
До 30	60
30 – 45	40
45 – 60	120
60 – 75	80
Свыше 75	50

По данным таблицы постройте не менее трёх видов статистических графиков, возможных для этого исследования.

Решение:

1) На основе данных задачи построим гистограмму распределения числа вкладчиков в зависимости от срока пользования кредитом.

Рис. 1. Гистограмма распределения числа вкладчиков
в зависимости от срока пользования кредитом

2) На основе данных задачи построим круговую диаграмму, отражающую число вкладчиков, имеющих различные сроки пользования кредитом, в общей их совокупности.

Рис. 2. Круговая диаграмма, отражающая число вкладчиков,
имеющих различные сроки пользования кредитом, в общей численности вкладчиков обследуемой совокупности.

3) На основе данных задачи построим диаграмму фигур-знаков, отражающую распределения числа вкладчиков в зависимости от срока пользования кредитом.
Одна фигура-знак  означает число вкладчиков от 10 человек.
Срок пользования кредитом до 30 дней:
Срок пользования кредитом от 30 до 45 дней:
Срок пользования кредитом от 45 до 60 дней:

Срок пользования кредитом  от 60 до 75 дней:

Срок пользования кредитом более 75 дней:

Срок пользования кредитом до 30 дней:

Рис. 3. Диаграмма фигур-знаков  распределения числа вкладчиков
в зависимости от срока пользования кредитом

Задача 4

В таблице 2 показано распределение рабочих монтажной бригады по уровню квалификации (разрядам).

Табельный номер	219	220	221	222	223	224	226	227	230	231	232	233	234	235	236
Разряд	4	4	7	6	4	6	4	5	2	4	2	5	2	5	6
Табельный номер	237	238	239	240	243	244	245	246	247	248	250	258	259	260	261
Разряд	2	5	4	6	7	3	7	6	4	6	3	5	4	6	5

Используя данные таблицы 2, выполните задания:

1. Сгруппируйте рабочих по разрядам, постройте новую группировочную таблицу.
2. Найдите моду, медиану и средний разряд рабочих данной бригады. Объясните, что означают полученные Вами значения средней величины, моды и медианы в данном исследовании.
3. Постройте круговую диаграмму распределения рабочих по уровню квалификации.
4. Найдите, какую долю составляют рабочие каждого разряда в общей численности рабочих бригады.

Решение:

1. Сгруппируем рабочих по разрядам:
Таблица 1

Разряд	2	3	4	5	6	7
Число рабочих	4	2	8	6	7	3

2. Модой (М0) в дискретном ряду распределения называется вариант, имеющий наибольшую частоту.
Варианты (хi) – разряды;
частоты (ni) – число рабочих, имеющих соответствующий разряд
В данном случае М0=4.
Медиана (Ме) – это значения варианта для которого значение накопленной частоты составляет не менее половины от общего числа наблюдений, а для следующего за ним варианта, значение накопленной частоты строго больше половины от общего числа наблюдений.
Рассчитаем накопленные частоты:
Таблица 2

Разряд (хi)	2	3	4	5	6	7
Число рабочих (ni)	4	2	8	6	7	3
Накопленная частота	4	6	14	20	27	30

Ме=5
Средний разряд рабочих найдем по формуле средней арифметической взвешенной:


Полученные значения средней величины, моды и медианы означают следующее: в квалификация рабочего монтажной бригады в среднем соответствует разряду уровня 4,6; наибольшее число рабочих в бригаде имеет 4-ый разряд; половина рабочих бригады имеет разряд не выше 5-го и половина – не ниже 5-го разряда.
3. Построим круговую диаграмму распределения рабочих по уровню квалификации.

Рис. 4.  Круговая диаграмма распределения рабочих по уровню квалификации
4. Рассчитаем, какую долю составляют рабочие каждого разряда в общей численности рабочих бригады по формуле:

Доля рабочих 2-го разряда в общей численности рабочих бригады составляет:
 или 13,3%
Доля рабочих 3-го разряда в общей численности рабочих бригады составляет:
 или 6,7%
Доля рабочих 4-го разряда в общей численности рабочих бригады составляет:
 или 26,7%
Доля рабочих 5-го разряда в общей численности рабочих бригады составляет:
 или 20%
Доля рабочих 6-го разряда в общей численности рабочих бригады составляет:
 или 23,3%
Доля рабочих 7-го разряда в общей численности рабочих бригады составляет:
 или 10%

Задача 5

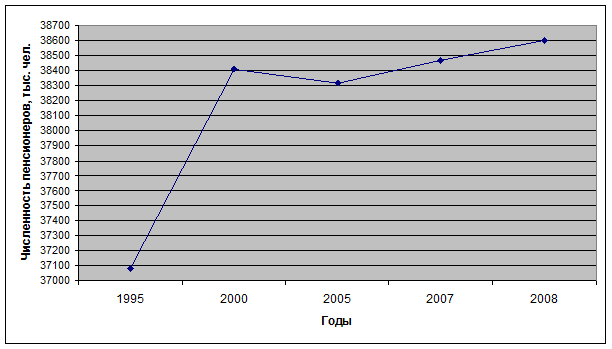
В таблице  имеются данные об общей численности пенсионеров РФ в исследуемые годы.

Используя данные таблицы 3, выполните задания:

1. Определите вид статистического ряда, представленного в таблице.
2. По данным таблицы определите основные показатели динамики.
3. Определите среднюю численность пенсионеров в исследуемый период. Обоснуйте  применённую Вами формулу.
4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.
5. Постройте парную линейную регрессию численности пенсионеров в исследуемый период.
6. Используя построенную модель регрессии, сделайте прогноз на 2010  год и сравните с реальной ситуацией. Данные о численности пенсионеров в 2010 году можно найти в СМИ. Не забудьте указать источник информации.

Решение:

1. Статистического ряд, представленный в таблице представляет собой ряд динамики.
2. По данным таблицы определите основные показатели динамики.
Важнейшим статистическим показателем анализа динамики  яв­ляется абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за оп­ределенный промежуток времени. Абсолютный прирост с пере­менной базой называют скоростью роста.
Абсолютные приросты вычисляются по формулам:
 (цепной)
 (базисный)
где yi — уровень сравниваемого периода; yi-1— уровень предшествующего периода; У0 — уровень базисного периода.
Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени ис­числяют темпы роста (снижения).
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда, выра­женный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности из­менения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым произ­водится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста вычисляются по формулам:
(цепной)
  (базисный)
Темпы  роста:
 (цепной)
  (базисный)
Темпы  прироста:
 (цепной)
  (базисный)
Абсолютное значение одного процента прироста Ai . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Данный показатель рассчитывают по формуле

Расчеты показателей оформим в таблице.
Таблица 3

Годы	Численность пенсионеров, тыс. чел.	Абсолютные приросты,                  тыс. чел.	Коэффициенты роста	Темпы роста, %	Темп прироста,      %	Абсолютное содержание 1% прироста, тыс. чел.
цеп	баз	цеп	баз	цеп	баз	цеп	баз
1995	37083	—	—	—	—	—	—	—	—	—
2000	38411	1328	1328	1,0358	1,0358	103,58	103,58	3,58	3,58	370,83
2005	38313	-98	1230	0,9974	1,0332	99,74	103,32	-0,26	3,32	384,11
2007	38467	154	1384	1,0040	1,0373	100,40	103,73	0,40	3,73	383,13
2008	38598	131	1515	1,0034	1,0409	100,34	104,09	0,34	4,09	384,67

3. Определим среднюю численность пенсионеров в исследуемый период. Средний уровень интервального ряда с разностоящими уровнями вычисляется по формуле средней арифметической взвешенной:

(тыс.чел.)
4. По данным таблицы постройте динамический график численности пенсионеров в исследуемый период.

Рис. 4.  Динамический график численности пенсионеров в исследуемый период
5. Постройте парную линейную регрессию численности пенсионеров в исследуемый период.
Х – номер года; Y – численность пенсионеров
Для расчета параметров а и b  линейной регрессии  решаем систему нормальных уравнений относительно а и b:

Из системы коэффициенты линейной регрессии a и b определяются по формулам:


Расчеты оформим в таблице:
Таблица 4

№ п/п	Х	Y	ХY	X2
1	1995	37083	73980585	3980025
2	2000	38411	76822000	4000000
3	2005	38313	76817565	4020025
4	2007	38467	77203269	4028049
5	2008	38598	77504784	4032064
Итого	10015	190872	382328203	20060163
Среднее значение	2003	38174,4	76465640,6	4012033

Уравнение парной линейную регрессии численности пенсионеров определяется формулой:

6. Используя построенную модель регрессии, сделаем прогноз на 2010  год
Данные о численности пенсионеров в 2010 году взяты из статистического сборника «Российский статистический ежегодник» — Стат.сб./Росстат. — М., 2011.
Численность пенсионеров в 2010 году составляла 39706 тыс. чел.
Прогноз численности пенсионеров на основе полученной модели составляет:
 (тыс.чел.)
Сравним прогнозные данные с реальной ситуацией: реальная численность пенсионеров в 2010 году превышает численность, полученную при расчете по уравнению парной регрессии, на 2,15% или 834 тыс. чел.

Задача по выборочному наблюдению

Проведено выборочное тестирование студентов факультета по экономическим дисциплинам. Численность факультета 850 студентов, объем выборки, сформированной методом бесповторного отбора — 24 студента. Результаты тестирования приведены в таблице. По этим данным определить выборочные средний балл, дисперсию и стандартное отклонение. Вычислить ошибку выборки, найти границы доверительного интервала, в котором окажется средняя генеральной совокупности с вероятностью 0,866 и 0,997.

№ п/п	Оценка  (в	№ п/п	Оценка  (в баллах)	№ п/п	Оценка  (в	№ п/п	Оценка  (в
	баллах)		баллах)		баллах)
1	112	7	105	13	98	19	95
2	95	8	108	14	95	20	115
3	119	9	110	15	111	21	94
4	98	10	101	16	115	22	105
5	112	11	117	17	130	23	121
6	95	12	99	18	104	24	111

Повторный и бесповторный отбор.
Ошибка выборки

Краткая теория

---

На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.

При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.

Выборка может осуществляться по схеме повторного и бесповторного
отбора.

В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.

Выборка может осуществляться отдельными единицами или сериями
(гнездами).

Собственно-случайная выборка

Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.

На основании приемов классической выборки решаются следующие
задачи:

а) определяются границы среднего значения показателя по генеральной
совокупности;

б) определяются границы доли признака по генеральной совокупности.

Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:

а) при повторном отборе:

б) при бесповторном отборе:

где

 – численность выборочной совокупности;

 – численность генеральной совокупности;

 – дисперсия признака;

 – критерий кратности ошибки: при

;
при

;
при

.

Значения

 
определяются

по таблице функции Лапласа.

Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:

где

 – среднее значение признака по выборочной
совокупности.

Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:

а) при повторном отборе:

при бесповторном отборе:

где

 – доля единиц совокупности с заданным
значением признака в обзей численности выборки,

 – дисперсия доли признака.

Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:

где

 – доля признака по генеральной совокупности.

Типическая (районированная) выборка

Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.

Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:

где

 – средняя из внутригрупповых дисперсий

 по каждой типичной группе.

При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:

где

 – численности единиц совокупности групп по выборке.

Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю

 из частных выборочных средних

.
Для случая пропорционального отбора это определяется по формуле:

При непропорциональном отборе средняя из  внутригрупповых дисперсий вычисляется по
формуле:

где

 – численность единиц групп по генеральной
совокупности.

Общая выборочная средняя в этом случае определяется по формуле:

Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:

Средняя дисперсия доли
признака из групповых дисперсий доли

 при
типической пропорциональной выборке вычисляется по формуле:

Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:

Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:

а средняя доля признака:

Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель

.

Серийная выборка

Серийная ошибка выборки
может применяться в двух вариантах:

а) объем серий различный

б) все серии имеют
одинаковое число единиц (равновеликие серии).

Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии

 и
производится отбор не единиц совокупности, а серий

. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки

 при
серийном отборе исчисляются по формулам:

а) при повторном отборе

б) при бесповторном отборе

где

 – число
серий в генеральной совокупности;

 – число
отобранных серий;

 – межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:

где

 –
среднее значение признака в каждой из отобранных серий;

 – межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:

Определение численности выборочной совокупности

При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.

Примеры решения задач

---

Задача 1

На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:

Группы рабочих по размеру заработной платы, тыс.р.	до 200	200-240	240-280	280-320	320 и выше	Итого
Число рабочих	33	35	47	45	40	200

На основании приведенных данных определите:

1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);

2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.

2) Выборочная дисперсия:

Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:

где

 —

аргумент функции Лапласа.  

Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:

Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:

Доля рабочих с з/п от 320 тыс.р.:

 

Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:

---

Задача 2

В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.

Решение

Численность
выборки можно найти по формуле:

В нашем случае:

Вывод к задаче

Таким образом численность
выборки должна составить 2661 чел.

---

Задача 3

С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:

Номер филиала	Средняя месячная заработная плата, руб.	Среднее квадратическое отклонение, руб.	Число сотрудников, чел.
1	870	40	30
2	1040	160	80
3	1260	190	140
4	1530	215	190

С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.

Решение

Предельная
ошибка выборочной средней:

Средняя
из внутригрупповых дисперсий:

Получаем:

Средняя
месячная заработная плата по всей совокупности филиалов:

Искомые
пределы средней месячной заработной платы:

Вывод к задаче

Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.