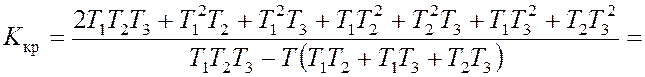Введение интеграла от ошибки в прямую цепь сау

15. Какими должны быть корни характеристического уравнения для устойчивости системы
• С отрицательной действительной частью
• Комплексно-сопряженные с положительными действительными частями
• С положительной действительной частью

16. Что такое принцип обратной связи
• Этот принцип предусматривает реакцию системы на несколько одновременно действующих входных воздействий, равных сумме реакций на каждое воздействие по отдельности
• Этот принцип предусматривает измерение возмущающих воздействий и результаты измерений учитываются при выработке управления, что позволяет повысить точность автоматической системы
• Этот принцип предусматривает, что реальные значения выхода объекта не учитываются управляющим устройством, что не позволяет обеспечить высокую точность управления
• Этот принцип предусматривает сравнение выхода с задаваемыми значениями при помощи канала обратной связи и элемента сравнения

17. Введение интеграла от ошибки в прямую цепь САУ
• Повышает степень астатизма системы
• Снижает устойчивость системы
• Увеличивает устойчивость системы

18. Какое звено называется запаздывающим
• Звено, в котором выходная величина воспроизводит без искажений и запаздываний входную величину
• Звено, выходная величина которого пропорциональна скорости изменения входной величины
• Звено, которое на выходе воспроизводит входной сигнал без искажений, однако с некоторым постоянным запаздыванием
• Звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величина стремится к новому установившемуся значению, совершившему затухающие колебания

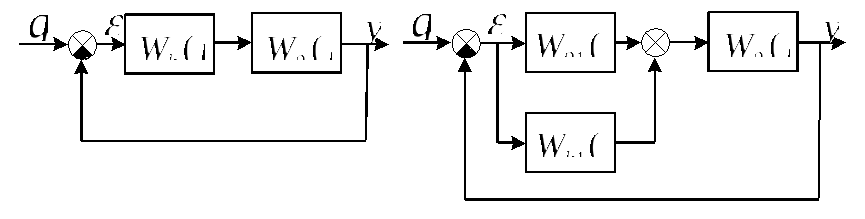
19. Системы, в которых помимо обратной главной связи существуют местные обратные связи, называются
• Многосвязные САУ
• Односвязные САУ
• Одноконтурные САУ
• Многоконтурные САУ

20. Как называется САУ несколькими регулируемыми величинами
• Многомерная САУ
• Одномерная САУ
• Система связанного регулирования
• Системы несвязанного регулирования

21. Система, которая установившемся режиме работы по отношению к заданному воздействию не имеет отклонение регулируемой величины от заданной называется
• Статическая
• Поисковая
• Астатическая
• Беспоисковая

Для того чтобы добиться желаемого
качества процесса управления, фактически
требуемой точности и качества переходного
процесса, существуют два пути. Первый
путь – изменение параметров системы
управления, и второй путь, – изменение
структуры системы, за счет введения
дополнительных звеньев. Введение
дополнительных, или корректирующих
звеньев, применяется в том случае, когда
изменением параметров не удается
добиться желаемых результатов.

Основная задача корректирующих
устройств заключается в повышении
точности системы управления и
обеспечении желаемого качества
переходного процесса.

Различают четыре основных вида
корректирующих устройств: последовательные
корректирующие устройства, параллельные
корректирующие устройства, корректирующие
устройства по возмущающему воздействию

и неединичные обратные связи.

8.1. Последовательные корректирующие
устройства

Последовательные корректирующие
устройства включатся последовательно
объекту управления в разомкнутую
цепь системы. Обобщенные структурные
схемы последовательной коррекции
показаны на рис.8.1.

Рис.8.1. Обобщенные
структурные схемы последовательной
коррекции

Таким образом, общая передаточная
функция разомкнутой цепи системы будет
иметь вид

(8.1)
,

где нуликами отмечены передаточные
функции заданной части системы.

8.1.1. Введение производной по ошибке
– простейший метод улучшения качества
переходного процесса. Структурное
введение коррекции показано на рис.8.2.

Рис.8.2. Введение
производной по ошибке

Технически это можно осуществить
различными устройствами, причем введение
производной можно осуществлять не в
чистом виде
,
а с инерционностью, например
,
потому, что реализовать идеальную
производную практически невозможно.

В случае идеального дифференцирующего
устройства передаточная функция
разомкнутой цепи будет иметь вид

, (8.2)

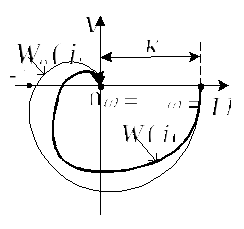
а соответствующая амплитудно-фазовая
характеристика разомкнутой части
представлена на рис.8.3.

Рис.8.3. АФЧХ

Существенным здесь является то, то при
введении производной как бы добавляется
положительная фаза. Вследствие этого
радиус-векторы АФЧХ поворачиваются
против часовой стрелки, увеличивая
тем самым запас устойчивости и
изменяя качество переходного процесса
при низменной добротности
.
В случае неидеального дифференцирования

этот факт несколько уменьшается
количественно, но качественно сохраняется.

Введение производной по ошибке также
улучшает стабилизирующие свойства
системы, за счет увеличения запаса по
фазе.

8.1.2. Увеличение общего коэффициента
усиления

разомкнутой цепи является методом
повышения точности системы
(уменьшаются все виды установившихся
ошибок). Но увеличение

ведет, как известно, к ухудшению условия
устойчивости (см. разд.5), а значит и
качества переходного процесса. Поэтому
часто приходится это делать одновременно
с введением производной.

8.1.3, Введение интеграла от ошибки
является методом создания или повышения
порядка астатизма системы, а значит
увеличения её точности.

Рис.8.4. Введение
интеграла от ошибки

Передаточная функция разомкнутой части
системы будет иметь вид

. (8.3)

Афчх такой
системы показана на рис.8.5.

Рис.8.5.
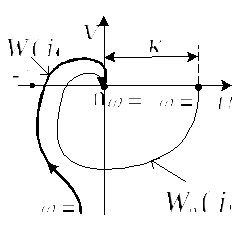
АФЧХ

Как видно, ухудшаются условия устойчивости,
вследствие поворота фазы на
,
а, следовательно, и качество процесса
управления. Иногда это может привести
и к неустойчивости системы.

8.1.4. Изодромное корректирующее
устройство имеет передаточную функцию
вида

,

объединяя в себе введение интеграла
и производной. Оно объединяет в себе
введение интеграла и производной и
позволяет избежать их недостатков, то
есть позволяет получить необходимый
порядок астатизма системы, сохраняя
устойчивость и качество процесса
управления. Техническое осуществление
изодромного устройства может быть
любым: механическим, электронным и пр.

Возможны и более сложные передаточные
функции последовательных корректирующих
устройств.

8.2. Параллельные корректирующие
устройства

Рассмотрим параллельные корректирующие
устройства в виде обратных связей.
Обобщенная структурная схема параллельных
корректирующих устройств представлена
на рис.8.6.

Рис.8.6. Параллельная
коррекция

Основные виды корректирующих обратных
связей следующие:

1. жесткая обратная связь (ЖОС)

;

1. инерционная жесткая обратная связь

;

1. гибкая обратная связь

;

1. инерционная гибкая обратная связь

.

Возможны и более сложные передаточные
функции корректирующих обратных связей.

Рассмотрим основные свойства этих
обратных связей на примерах.

8.2.1. Положительная жесткая обратная
связь (ПЖОС). Предположим, что ПЖОС
охватывает апериодическое звено первого
порядка.

Рис.8.7. ПЖОС

Передаточная функция охватываемой
части объекта имеет вид
,
а передаточная функция ОС –
,
соответственно. Тогда общая передаточная
функция этой части цепи будет иметь вид

или

,
где
,
. (8.4)

Следовательно, ПОС может служить для
увеличения коэффициента усиления.
Но надо иметь в виду, что одновременно
с этим увеличивается и постоянная
времени, то есть инерционность
звена. А при

звено становится неустойчивым.

8.2.2. Отрицательная жесткая обратная
связь (ОЖОС). При охвате ОЖОС
апериодического звена, получим

, (8.5)

где
,
.

Следовательно, ОЖОС уменьшает
инерционность звена, тем самым, улучшая
быстродействие системы, и может оказать
стабилизирующее действие. Уменьшение
коэффициента усиления системы

можно всегда скомпенсировать за счет
других звеньев.

При охвате интегрирующего звена
ОЖОС, то есть

, ,

получим

, (8.6)
где
,
.

Под действием ОЖОС интегрирующие
свойства звена теряются, и оно превращается
в апериодическое звено с коэффициентом
усиления, который определяется только
обратной связью. Постоянная времени

будет мала при больших коэффициентах
усиления
.

Рассмотренный способ применяется
практически в приводах, чтобы сделать
угол поворота на выходном валу двигателя
пропорциональным управляющему сигналу,
то есть напряжению.

Соседние файлы в папке ТАУ лекции

• #
• #
• #
• #
• #
• #
• #
• #

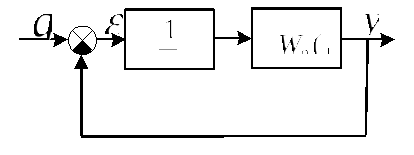
Поэтому возможность повышения точности исследуемой
САУ лишь за счет увеличения коэффициента усиления разомкнутой системы
ограничена, причем максимально допустимое значение K₀
должно быть меньше K_0кр в соответствии с требуемым запасом
устойчивости системы.

1.3. Введение производной

Введение производной от ошибки в закон регулирования
может быть осуществлено за счет использования прямой параллельной
корректирующей цепи с коэффициентом передачи k_п.

Передаточная функция разомкнутой скорректированной
системы в этом случае имеет вид

, гдеK=k₁(k₂+k_п)k₃ — общий коэффициент усиления;  —
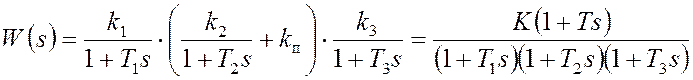
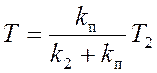
постоянная времени, определяющая уровень сигнала управления по производной.

Используя соотношение (2) или структурный признак
астатизма [1], нетрудно убедиться, что система осталась статической как по
задающему, так и по возмущающему воздействиям.

Характеристический полином замкнутой скорректированной
системы имеет вид

.

Отсюда
получаем условие для определения критического значения коэффициента усиления:

,

.                                         
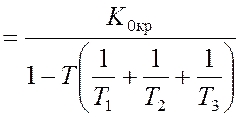
(5)

Из формулы (5) видно, что, вводя производную в закон
регулирования, можно значительно расширить границу увеличения коэффициента
усиления и, следовательно, уменьшить обе составляющие ошибки.

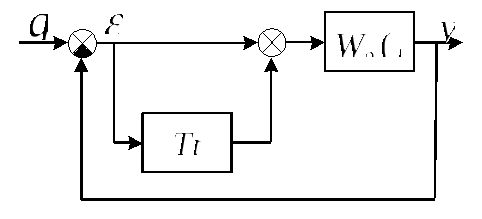
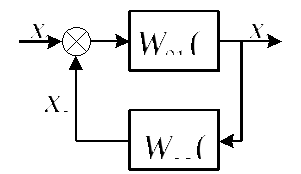
1.4. Введение гибкой обратной связи

При добавлении в цепь единичной обратной связи системы
дополнительного дифференцирующего звена с коэффициентом k’_ос (см. рис.1) передаточная функция обратной связи
примет вид

.

В этом случае
соответствующие передаточные функции замкнутой системы определяются по
соотношениям

, , .  (6)

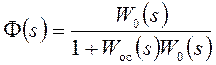
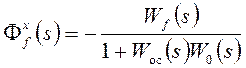
На
основе (6) получим характеристический полином замкнутой системы:

.

K_0кр определяется аналогично предыдущему подразделу.

1.5. Повышение порядка астатизма

При введении дополнительного идеального интегрирующего
звена (см. рис.1) повышается порядок астатизма системы. Передаточная
функция разомкнутой системы принимает вид

,       (7)

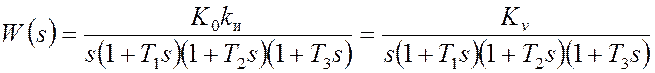
где
K_v = K₀k_и – новый коэффициент усиления разомкнутой системы, в
рассматриваемом случае называемый добротностью по скорости [1] и приобретающий
размерность с^-1. Ошибка системы в установившемся режиме работы может
быть определена на основе (2):

.                                    (8)

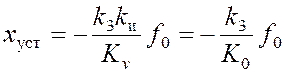
Из формулы (8) следует, что скорректированная САУ
стала астатической по задающему воздействию и осталась статической по отношению
к возмущающему воздействию. Кроме того, из этой формулы следует, что при введении
интеграла составляющая ошибки x_fможет
возрасти, так как при введении интеграла обычно уменьшается запас устойчивости
системы, что приводит к необходимости снижения коэффициента усиления.

На основе критерия Гурвица с учетом повышения степени
характеристического полинома можно найти условие устойчивости для данной
структурной схемы САУ:

              (9)

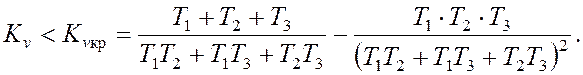
Нетрудно
убедиться, что здесь критическое значение коэффициента усиления значительно
меньше, чем при отсутствии интегрирующего звена.

Более эффективным является включение интегрирующего
звена в состав регулятора (интегральный закон регулирования). Если в отличие от
рис. 1 переместить интегратор до точки приложения возмущающего воздействия,
передаточная функция (7) и условие (9) сохранятся, но на основе (2) можно убедиться
в достижении теперь астатизма как по задающему, так и по возмущающему
воздействиям. При воздействиях рассматриваемого вида необходимость снижения
коэффициента усиления не повлияет на точность системы в установившемся режиме.

1.6. Повышение порядка астатизма введением изодромного
звена

Повысить порядок астатизма системы можно также путем
введения в прямую цепь изодромного звена (пропорционально-интегрального
регулятора) с передаточной функцией (см. рис.1)

.

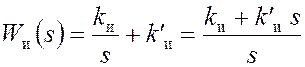
Передаточная функция разомкнутой системы принимает вид

, где K_v = K₀k_и – новый коэффициент усиления разомкнутой системы
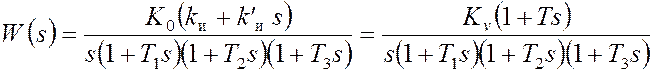
(добротность);  — новая постоянная времени.

Получить условие устойчивости для данной структуры 
САУ и убедиться, что значение критического коэффициента усиления здесь выше,
чем при введении в систему идеального интегратора, предлагается самостоятельно.
Здесь может быть полезно также использование частотного критерия устойчивости
Найквиста.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.