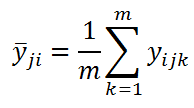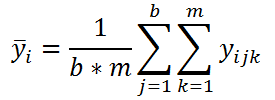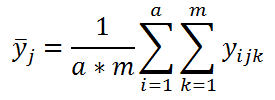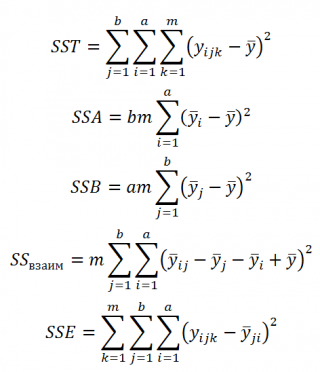Ранее был рассмотрен полностью рандомизированный эксперимент и связанный с ним однофакторный дисперсионный анализ. В настоящей заметке будет изучен двухфакторный дисперсионный анализ, в ходе которого одновременно оцениваются два фактора. Мы рассмотрим лишь ситуации, в которых выборки имеют одинаковый объем n‘. [1]
Применение статистики в этой заметке будет показано на сквозном примере. Предположим, что вы — руководитель производства в компании Perfect Parachute («Идеальный парашют»). Парашюты изготавливаются из синтетических волокон, поставляемых четырьмя разными поставщиками. Совершенно очевидно, что одной из основных характеристик парашюта является его прочность. Вам необходимо убедиться, что все поставляемые волокна обладают одинаковой прочностью. Более того, на фабрике используется два вида ткацких станков: Jetta и Turk. Можно ли утверждать, что парашюты, изготовленные на станке фирмы Jetta, так же прочны, как и парашюты, произведенные на станках компании Turk? Существует ли разница между прочностью парашютов, сотканных из синтетических волокон разных поставщиков на разных станках? Чтобы ответить на этот вопрос, следует разработать схему эксперимента, в ходе которого измеряется прочность парашютов, сотканных из синтетических волокон разных поставщиков на разных станках. Информация, полученная в ходе этого эксперимента, позволит определить, какой поставщик и какой тип станка обеспечивают наибольшую прочность парашютов.
Вследствие сложности вычислений, особенно при большом количестве уровней каждого фактора и реплик, для двухфакторного анализа следует применять либо Excel, либо специализированное программное обеспечение. В двухфакторном эксперименте факторы А и В считаются взаимодействующими, если эффект фактора А зависит от уровня фактора В. Напомним, что в полностью рандомизированном плане полная сумма квадратов (SST) подразделяется на межгрупповую сумму квадратов (SSA) и внутригрупповую сумму квадратов (SSW). В двухфакторном эксперименте с одинаковым количеством реплик в каждой ячейке полная вариация (SST) подразделяется на сумму квадратов, соответствующую фактору A (SSA), сумму квадратов, соответствующую фактору В (SSB), сумму квадратов, учитывающую взаимодействие факторов А и В (SSAB), и сумму квадратов, возникающую вследствие случайной ошибки (SSE) (рис. 1).
Рис. 1. Разделение полной вариации в двухфакторном эксперименте
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
В двухфакторном дисперсионном анализе применяются три разных критерия:
- Для проверки гипотезы об отсутствии эффекта фактора А
- Для проверки гипотезы об отсутствии эффекта фактора В
- Для проверки гипотезы об отсутствии эффекта взаимодействия факторов А и В (рис. 2).
Каждая из трех нулевых гипотез отклоняется, если при заданном уровне значимости α соответствующая F-статистика (см. последнюю колонку рис. 2) больше верхнего критического значения F-распределения FU.
Рис. 2. Дисперсионный анализ в двухфакторном эксперименте
Для иллюстрации двухфакторного дисперсионного анализа вернемся к нашему сценарию. Допустим, что, будучи руководителем производства, вы решили сравнить поставщиков синтетических волокон, и оценить, на каком из станков выпускаются более прочные парашюты: Jetta или Turk. Кроме того, необходимо определить, зависит ли разница между четырьмя поставщиками от типа станков, на которых производятся парашюты. Итак, необходимо разработать план эксперимента, в котором каждому поставщику и типу станка соответствует пять парашютов (рис. 3). Для проведения анализа пройдите по меню Данные → Анализ данных и выберите строку Двухфакторный дисперсионный анализ с повторениями.
Рис. 3. Двухфакторный дисперсионный анализ с повторениями в Пакете анализа Excel
На рис. 4 показаны результаты двухфакторного дисперсионного анализа данных: объем выборки, сумма, арифметическое среднее и дисперсия каждой комбинации типа станка и поставщика. В первых двух таблицах приведены результаты дисперсионного анализа для всех типов станка, а в третьей — для каждого поставщика. В сводной таблице дисперсионного анализа идентификатор df обозначает количество степеней свободы, SS — сумму квадратов, MS — среднее квадратичное отклонение, F — вычисленную F-статистику.
Рис. 4. Результат двухфакторного дисперсионного анализа прочности парашютов
Чтобы проанализировать эти результаты, сначала следует проверить, существует ли взаимодействие между факторами А (типами станка) и В (поставщиками). Если эффект взаимодействия является значительным, дальнейший анализ ограничивается лишь оценкой этого эффекта. С другой стороны, если эффект взаимодействия незначителен, необходимо сосредоточиться на главных эффектах — потенциальных различиях между типами станков (фактор А) и поставщиками (фактор В).
Чтобы определить наличие эффекта взаимодействия при уровне значимости, равном 0,05, применяется следующее решающее правило: нулевая гипотеза об отсутствии эффекта взаимодействия отклоняется, если вычисленное значение F-статистики (см. таблицу Дисперсионный анализ, строку Взаимодействие столбец F на рис. 4), больше верхнего критического значения F-распределения (там же, столбец F-критическое). Поскольку F = 0,01 < FU = 2,90, а р-значение равно 0,998, гипотеза Н0 не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что факторы станка и поставщика взаимодействуют друг с другом. Следовательно, необходимо проанализировать главные эффекты.
При заданном уровне значимости, равном 0,05, в основе проверки разности между двумя станками (фактор А) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение F-статистики больше верхнего критического значения F-распределения (см. таблицу Дисперсионный анализ, строку Выборка на рис. 4). Поскольку F = 0,81 < FU = 4,15, а р-значение равно 0,37 и больше уровня значимости α = 0,05, гипотеза Н0 не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что между прочностью парашютов, произведенных на разных станках, существует значимая разница.
При заданном уровне значимости, равном 0,05, в основе проверки разности между поставщиками (фактор В) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение F-статистики больше верхнего критического значения F-распределения (см. таблицу Дисперсионный анализ, строку Столбцы на рис. 4). Поскольку F = 5,20 > FU = 2,92, а р-значение равно 0,005 и меньше уровня значимости, гипотеза Н0 отклоняется. Следовательно, можно утверждать, что между прочностью парашютов, произведенных из волокна, приобретенного у разных поставщиков, существует значимая разница. [2]
Интерпретация эффектов взаимодействия
Чтобы лучше разобраться во взаимодействии факторов, следует построить график средних значений в ячейках (т.е. средних значений, соответствующих конкретным уровням факторов), как показано на рис. 5 (в качестве данных для построения графика использованы области В19:Е19 и В25:Е25 рис. 4). Из графика средней прочности для каждой комбинации станок–поставщик следует, что две линии, соответствующие разным станкам, проходят почти параллельно друг другу. Это означает, что разности между средними величинами прочности парашютов, произведенных на разных станках, практически одинаковы для всех четырех поставщиков. Иначе говоря, между этими двумя факторами нет связи, что полностью подтверждается F-критерием.
Рис. 5. График средних значений прочности парашютов в зависимости от станков и поставщиков
В чем проявляется эффект взаимодействия? В некоторых ситуациях определенные уровни фактора А могут оказаться связанными с конкретными уровнями фактора В. Например, предположим, что некоторые парашюты оказываются более прочными, если они сотканы из определенных волокон на станках Jetta, а другие — если они сотканы из волокон других поставщиков на станках Turk. Если бы это было правдой, линии на рис. 5 не были бы параллельными и взаимодействие между факторами было бы статистически значимым. Следовательно, в этих ситуациях разница между станками не будет одинаковой при разных поставщиках. Это усложняет интерпретацию главных эффектов, поскольку разности, соответствующие одному фактору (например, типу станка), не согласуются с другим фактором (например, поставщиком). Проиллюстрируем эту ситуацию следующим примером.
Пример.1. Интерпретация статистически значимых эффектов взаимодействия. Данные, приведенные на рис. 6а, характеризуют продолжительность работы подшипников под воздействием двух факторов: автоколебания и нагревания. Как влияют автоколебания и нагревание на продолжительность работы подшипников? Результаты двухфакторного дисперсионного анализа продолжительности работы подшипников, полученные с помощью Пакета анализа в Excel приведены на рис. 6б. Обратите внимание на то, что, кроме сводной таблицы дисперсионного анализа, Excel вычисляет среднее значение для каждой комбинации двух факторов: степени автоколебаний и нагревания, а также среднее значение для каждого уровня факторов. Для того чтобы проанализировать эти результаты, сначала необходимо определить, наблюдается ли статистически значимый эффект взаимодействия факторов автоколебания (фактор А) и нагревания (фактор В). При уровне значимости α = 0,05 нулевую гипотезу об отсутствии эффекта взаимодействия следует отклонить, поскольку p-значение равно 0,0018, т.е. меньше 0,05. Кроме того, F-статистика равна 53,78 и превышает величину 7,71 — верхнее критическое значение F-распределения с одной степенью свободы в числителе и четырьмя степенями свободы в знаменателе.
Рис. 6. (а) Продолжительность работы подшипников при автоколебании и нагревании; (б) Результаты двухфакторного дисперсионного анализа продолжительности работы подшипников
Значимый эффект взаимодействия между автоколебанием и нагреванием можно проследить на рис. 7. Поскольку графики средних значений продолжительности работы подшипников при слабом и сильном нагревании, соответствующие двум степеням автоколебаний, не параллельны, разности между средними значениями продолжительности работы при двух типах автоколебаний и двух степенях нагревания неодинаковы. Наличие эффекта взаимодействия факторов усложняет анализ основных эффектов. Теперь невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабых и сильных автоколебаниях, поскольку при разных степенях нагревания эта разность неодинакова. Аналогично невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабом и сильном нагревании, поскольку при разных степенях автоколебаний эта разность неодинакова.
Рис. 7. График средних значений продолжительности работы подшипников по ячейкам
Множественные сравнения
Если эффект взаимодействия факторов не важен, для множественного сравнения нескольких факторов можно применять процедуру Тьюки-Крамера.
Критический размах процедуры Тьюки-Крамера для фактора А
где QU — верхнее критическое значение распределения стьюдентизированного размаха, имеющего r степеней свободы в числителе и rc(n’ – 1) степеней свободы в знаменателе.
Критический размах процедуры Тьюки-Крамера для фактора B
где QU — верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и rc(n’ – 1) степеней свободы в знаменателе.
Применим процедуру Тьюки-Крамера к задаче о прочности парашютов (см. рис. 3). Анализ сводной таблицы дисперсионного анализа, представленной на рис. 4, показывает, что статистически значимым является лишь один главный эффект. При уровне значимости, равном 0,05, нет оснований утверждать, что между двумя типами станков (Jetta и Turk) существует значимая разница (фактор А), однако между четырьмя поставщиками (фактор В) эта разница существует. Таким образом, дальнейший анализ должен концентрироваться на разностях между поставщиками.
Поскольку компания, производящая парашюты, имеет четыре фирмы-поставщика, следует проверить 4(4 – 1)/2 = 6 пар поставщиков (рис. 8а). Вычислим модули разности между соответствующими средними значениями по выборкам отдельных поставщиков (рис. 8б).
Рис. 8. (а) Исходные данные о прочности парашютов; (б) попарные сравнения средних значений по выборкам отдельных поставщиков
Чтобы вычислить критический размах, обратимся к данным на рис. 4: MSE = 8,61, r = 2, с = 4, n’ = 5, rc(n’ – 1) = 32. При α = 0,05, с = 4 и rc(n’ – 1) = 32 по таблицам размаха (рис. 9) определим, что QU — верхнее критическое значение F-статистики с двумя степенями свободы в числителе и 32 степенями свободы в знаменателе — приближенно равно 3,84. Используя формулу (2), получаем:
Рис. 9. Критическое значение стьюдентизированного размаха QU; к сожалению, в Excel нет функции, рассчитывающей такой размах
Только одно значение разности между средними значениями (рис. 8б) больше 3,56. Статистически значимая разница существует лишь между первым и вторым поставщиком. Как и при однофакторном дисперсионном анализе, приходим к выводу, что средняя прочность парашютов, сотканных из волокон, приобретенных у первого поставщика, значительно ниже, чем у второго.
Предыдущая заметка Однофакторный дисперсионный анализ
Следующая заметка Блочный рандомизированный эксперимент
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 664–676
[2] К аналогичному выводу мы пришли и при проведении однофакторного дисперсионного анализа по поставщикам.
The reason behind this error is,
«The number of rows in the input dataset(x) are not matching with the corresponding rows in the labeled output dataset(y)».
Or probably, there is an issue while splitting the mnist dataset into a training and testing dataset.
The right way of fetching input and labeled dataset of training and testing dataset is:
mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
print("Training dataset:", train_images.shape, train_labels.shape)
print("Testing dataset:", test_images.shape, test_labels.shape)
Output: (The number of rows should be equal for the input and output set)
Training dataset: (60000, 28, 28) (60000,)
Testing dataset: (10000, 28, 28) (10000,)
Please check this attached gist for your reference.
В тех случаях,
когда в каждом классе дисперсионного
комплекса имеется лишь по одному
наблюдению, применяется так называемый
двухфакторный дисперсионный анализ
без повторности.
Пример.
Необходимо методом дисперсионного
анализа оценить влияние профиля цеха
и особенностей производственного
процесса на заболеваемость рабочих
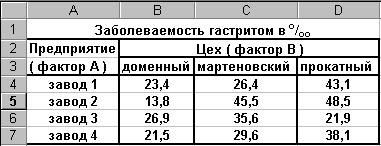
острым и хроническим гастритом. Исходные
данные представлены в таблице (Рисунок
6):
Рисунок
6
Согласно таблице
фактор А имеет 4 уровня (заводы 1-4), а
фактор В — 3 уровня (доменный, мартеновский
и прокатный цеха). В каждой группе имеется
только по одному наблюдению.
Для решения задачи
в MS Excel:
1.Сформируйте
таблицу с исходными данными (рисунок
6).
2.Выполните
команду Анализ
данных
из меню Сервис.
3.В соответствии
с условиями задачи выберите в появившемся
диалоговом окне метод «Двухфакторный
дисперсионный анализ без повторений»
и нажмите кнопку [OK].
4.В окне «Двухфакторный
дисперсионный анализ без повторений»
установите для входных данных следующие
параметры:
-
входной
интервал равен $B$4:$D$7, -
входной
диапазон не содержит метки, -
альфа
(уровень значимости равен
0,05),
5.Для параметров
вывода установите переключатель в
положение «Новый рабочий лист».
6.После завершения
настройки параметров нажмите кнопку
[OK].
Результаты
дисперсионного анализа будут представлены
на новом листе и состоять из двух таблиц.
В первой таблице для каждой строки и
каждого столбца исходной таблицы
приведены числовые параметры: количество
чисел, сумма, среднее и дисперсия.
Вторая часть
результатов представлена на рисунку
7.
Рисунок
7

Таким образом,
суммы квадратов, обусловленные влиянием
фактора А (источник вариации – «Строки»)
и фактора В (источник вариации –
«Столбцы»), равны 102,0 и 601,5,
соответственно, а остаточная сумма
квадратов («Погрешность») равна
597,0. Факторные дисперсии равны 34,0 (фактор
А) и 300,8 (фактор В), а остаточная дисперсия
— 99,5.
Основной
вывод из
полученных результатов заключается в
следующем:
Нет
оснований отвергать нулевую гипотезу
об отсутствии влияния каждого из
рассмотренных факторов на заболеваемость
рабочих гастритом, т.к. для обоих факторов
выполняется неравенство F<Fкр.
Принятие нулевой гипотезы подтверждается
и величинами значимостей, равными
0,797 для фактора А и 0,124 для фактора В.
Итак,
заболеваемость рабочих острым и
хроническим гастритом не зависит от
профиля цеха и номера завода.
Поэтому
нет смысла вычислять силу влияния
факторов.
5.Двухфакторный анализ с повторяющимися данными
Двухфакторный
дисперсионный анализ с повторениями
используется в том случае, когда в
каждой группе данных имеется более
одной выборkи. Он позволяет учесть как
влияние отдельных факторов, так и их
совместное действие на результативный
признак.
Примечание:
Проведение двухфакторного дисперсионного
анализа с повторениями в Excel
имеет
ограничение – все выборки должны быть
одинаковыми. Поскольку каждая строка
представляет повторение данных, то
каждая выборка должна содержать одно
и тоже количество строк.
Рассмотрим пример
применения двухфакторного дисперсионного
анализа с повторениями.
Исследуем
влияние формы токсического зоба (фактор
А), имеющего два уровня (узловая и
диффузная формы) и дозы мерказолила
(фактор В), имеющего три уровня (20 мг/сутки,
25 мг/сутки, 30 мг/сутки) и на длительность
устранения тиреотоксикоза. Статистический
комплекс представлен в Excel-таблице
(Рисунок 8). Числовые данные определяют
длительность выхода (в сутках) больных
из токсикоза для различных комбинаций
уровней двух факторов (в каждой из 6
подгрупп имеется по 3 наблюдения).
Для выполнения
расчетов двухфакторного комплекса:
1.Сформируйте
таблицу с исходными данными (Рисунок
8).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двухфакторный дисперсионный анализ с повторными измерениями в Excel рассмотрим на примере.
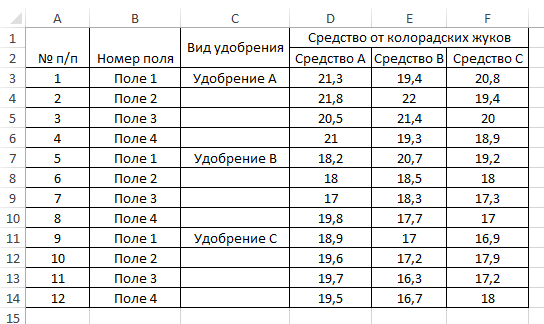
Ниже приведена статистика в виде таблицы об урожайности картофеля с 1 га. при применении разных видов удобрения и химических средств для борьбы с колорадскими жуками. На уровне значимости α=0.05 определить какие факторы влияют на урожайность картофеля.
| № п/п | Номер поля | Вид удобрения | Средство от колорадских жуков | ||
| Средство A | Средство B | Средство C | |||
| 1 | Поле 1 | Удобрение A | 21,3 | 19,4 | 20,8 |
| 2 | Поле 2 | 21,8 | 22 | 19,4 | |
| 3 | Поле 3 | 20,5 | 21,4 | 20 | |
| 4 | Поле 4 | 21 | 19,3 | 18,9 | |
| 5 | Поле 1 | Удобрение B | 18,2 | 20,7 | 19,2 |
| 6 | Поле 2 | 18 | 18,5 | 18 | |
| 7 | Поле 3 | 17 | 18,3 | 17,3 | |
| 8 | Поле 4 | 19,8 | 17,7 | 17 | |
| 9 | Поле 1 | Удобрение C | 18,9 | 17 | 16,9 |
| 10 | Поле 2 | 19,6 | 17,2 | 17,9 | |
| 11 | Поле 3 | 19,7 | 16,3 | 17,2 | |
| 12 | Поле 4 | 19,5 | 16,7 | 18 |
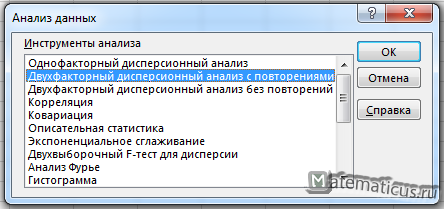
Итак, решаем данную задачу в Excel. Переходим на вкладку Данные -> Анализ данных. Выбираем однофакторный дисперсионный анализ c повторениями и жмём Ок.
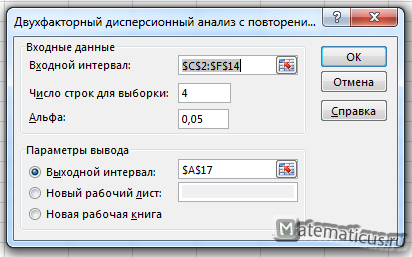
Во входном интервале ставим выбираем диапазон ячеек $C$2:$F$14, число строк для выборки указываем 4, альфа ставим 0,05 и в выходном интервале ячейку $A$17 и далее Ок.
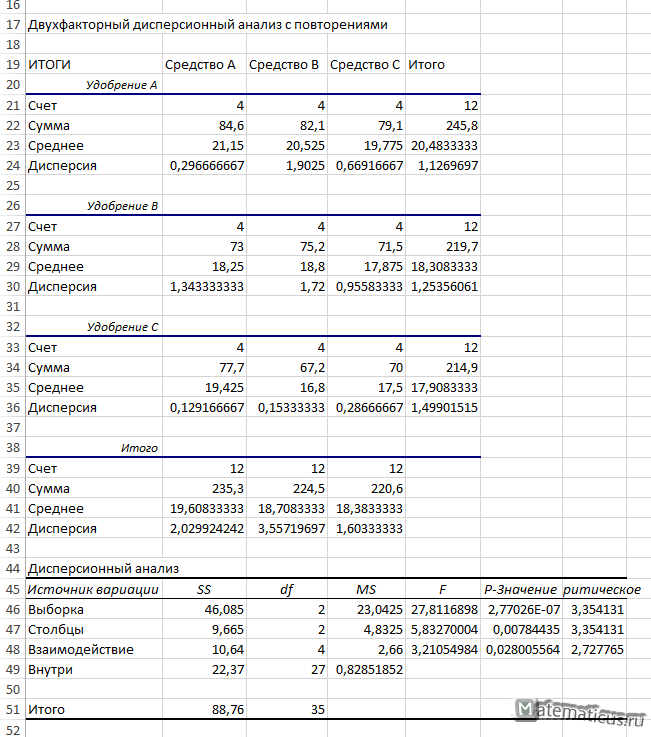
Получаем таблицу двухфакторного дисперсионного анализа с повторениями в Excel
| Двухфакторный дисперсионный анализ с повторениями | ||||
| ИТОГИ | Средство A | Средство B | Средство C | Итого |
| Удобрение A | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 84,6 | 82,1 | 79,1 | 245,8 |
| Среднее | 21,15 | 20,525 | 19,775 | 20,4833333 |
| Дисперсия | 0,296666667 | 1,9025 | 0,66916667 | 1,1269697 |
| Удобрение B | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 73 | 75,2 | 71,5 | 219,7 |
| Среднее | 18,25 | 18,8 | 17,875 | 18,3083333 |
| Дисперсия | 1,343333333 | 1,72 | 0,95583333 | 1,25356061 |
| Удобрение C | ||||
| Счет | 4 | 4 | 4 | 12 |
| Сумма | 77,7 | 67,2 | 70 | 214,9 |
| Среднее | 19,425 | 16,8 | 17,5 | 17,9083333 |
| Дисперсия | 0,129166667 | 0,15333333 | 0,28666667 | 1,49901515 |
| Итого | ||||
| Счет | 12 | 12 | 12 | |
| Сумма | 235,3 | 224,5 | 220,6 | |
| Среднее | 19,60833333 | 18,7083333 | 18,3833333 | |
| Дисперсия | 2,029924242 | 3,55719697 | 1,60333333 |
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Выборка | 46,085 | 2 | 23,0425 | 27,8116898 | 2,77026E-07 | 3,354131 |
| Столбцы | 9,665 | 2 | 4,8325 | 5,83270004 | 0,00784435 | 3,354131 |
| Взаимодействие | 10,64 | 4 | 2,66 | 3,21054984 | 0,028005564 | 2,727765 |
| Внутри | 22,37 | 27 | 0,82851852 | |||
| Итого | 88,76 | 35 |
Значение F-критерия фактора А — влияния удобрения на урожайность картофеля, Fнабл= 27.81, а Fкрит лежит в интервале (3.35; +∞). Fнабл не лежит в критической области, следовательно, принимаем, что удобрения влияют на урожайность картофеля.
Выборочный коэффициент детерминации для фактора — удобрения:
${R^2} = frac{{frac{{46,085}}{{36}}}}{{frac{{88,76}}{{36}}}} approx 0,52$
это означает, что 52% общей выборочной вариации урожайности картофеля зависит от удобрения.
Значение F-критерия фактора В — средство для борьбы с колорадскими жуками Fнабл= 5.83, а Fкрит=3,35. Fнабл находится в критической области, следовательно средство для борьбы с колорадскими жуками влияет на урожайность картофеля.
Выборочный коэффициент детерминации для фактора — средства для борьбы с колорадскими жуками равен:
${R^2} = frac{{frac{{9,665}}{{36}}}}{{frac{{88,76}}{{36}}}} approx 0,11$
11% общей выборочной вариации урожайности картофеля зависит от средства для борьбы с колорадскими жуками.
И в дополнении, найдём взаимодействие факторов Fкрит=2,73, a Fнабл=3,21. Так как Fнабл входит в интервал (2.73; +∞), значит полезность видов удобрения изменяется в зависимости от использования различных средств борьбы с колорадскими жуками.
5421
Пусть имеется случайная переменная
Y
, значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от 2-х факторов, значения которых мы можем контролировать, т.е. задавать с требуемой точностью. Покажем как методом дисперсионного анализа проверить гипотезу о наличии или отсутствии влияния указанных факторов на зависимую переменную
Y
.
Disclaimer
: Эта статья – о применении MS EXCEL для целей
Дисперсионного анализа, поэтому
данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения теории
Дисперсионного анализа
– плохая идея. Хорошая идея — найти в этой статье формулы MS EXCEL для проведения
Дисперсионного анализа.
Напомним, что
дисперсионный анализ
(ANOVA, ANalysis Of VAriance) позволяет
проверить гипотезу
о равенстве
средних значений
выборок (взяты ли выборки из одного распределения или из разных распределений). Данная задача возникает, например, когда необходимо исследовать зависимость некой
количественной
величины Y от одной или нескольких переменных (факторов), которые мы можем контролировать (устанавливать их значения). Действительно, если фактор оказывает влияние на зависимую переменную Y, то при разных уровнях фактора мы должны
в среднем
получать различные значения Y, т.е. мы должны получить «заметно отличающиеся»
средние значения выборок
. В статье будет показано, что значит
средние выборок
«заметно отличаются».
В этой статье рассмотрим метод дисперсионного анализа в случае двух факторов (Фактор А и Фактор В) (Two Factor ANOVA with Replication).
СОВЕТ
: Перед прочтением этой статьи рекомендуется освежить в памяти
Однофакторный дисперсионный анализ
.
Обозначения
Отдельные, заданные значения каждого фактора называются уровнями (
levels
) или испытаниями (
treatments
).
Уровни фактора А будем обозначать буквой j (j изменяется от 1 до
a
). Уровни фактора В будем обозначать буквой i (i изменяется от 1 до
b
). Каждой паре уровней факторов соответствует одна выборка, которая состоит из
m
измерений, каждое измерение будем обозначать буквой k (k от 1 до m). Таким образом, измеренные значения Y при уровне j фактора А и при уровне i фактора В будем обозначать y ijk . Всего выборок
a*b
.
Предполагается, что
дисперсии
всех выборок σ 2 неизвестны, но равны между собой.
Рассмотрим
двухфакторный дисперсионный анализ
при решении задачи.
Задача
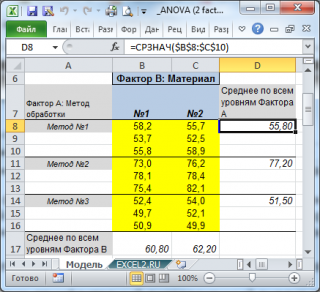
В компании, изготавливающей изделия путем механообработки, необходимо исследовать влияние на качество изделия двух факторов: Метода обработки поверхности детали, и Исходного материала детали (используется сталь с различным легированием).
Метод обработки представляет собой
фактор А
, который может принимать 3 значения (Метод 1, Метод 2, Метод 3), а Исходный материал
представляет собой
фактор В
, который может принимать 2 значения (№ 1, № 2). Качество изделий будем определять по количеству дефектных изделий в партии (это будет зависимой переменной Y).
Всего различных комбинаций 2-х факторов 6=3*2=a*b. Для каждой комбинации факторов было проведено по 3 измерения (т.е. m=3). Исходные данные приведены в файле примера .
Другими словами мы имеем 6 выборок по 3 значения в каждой. Средние этих выборок для каждой комбинации факторов ij можно вычислить по формуле:
Также для дальнейших вычислений нам потребуется вычислить еще несколько средних значений. Во-первых, вычислим среднее всех измерений, относящихся к каждому уровню i Фактора А:
Во-вторых, вычислим среднее всех измерений, относящихся к каждому уровню j Фактора В:
Взаимодействие факторов
Теперь, используя эти 6 средних значений, построим диаграмму, которая
состоит из 2-х рядов
.
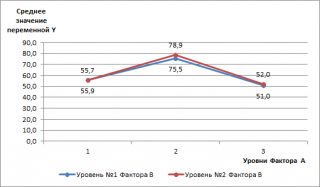
По оси Х (абсцисс) отложены уровни
Фактора А
, по оси ординат отложены средние значения переменной Y (среднее количество дефектов для заданных уровней факторов). Средние значения сгруппированы по 2-м уровням Фактора В (Синяя и красная линии. Каждая линия представляет собой отдельный ряд диаграммы).
Как видно из диаграммы – синяя и красная линии практически параллельны друг другу. Это означает, что взаимодействие между факторами практически отсутствует (они не влияют друг на друга). Действительно, выбор метода обработки никак не может влиять на выбор конкретного исходного материала.
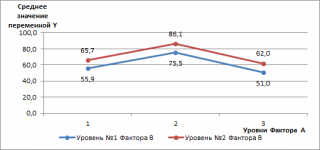
Вот еще одна диаграмма, демонстрирующая независимость 2-х факторов.
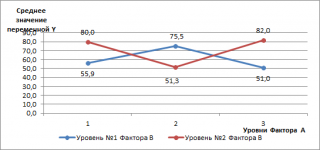
Обратная ситуация показана на диаграмме ниже, когда оба фактора взаимодействуют.
Из этой диаграммы видно, что при
уровне №1 фактора В
(синяя линия) количество дефектов сначала возрастает, затем снижается (когда мы переходим от метода №1 к №2, затем к №3). Мы наблюдаем диаметрально противоположную ситуацию при
уровне №2 фактора В
(красная линия): количество дефектов сначала снижается, а затем возрастает. В этом случае говорят о наличии взаимодействия факторов.
В случае взаимодействия факторов А и В, эффект от их взаимодействия может быть рассмотрен как некий
третий фактор АВ
. Чтобы пояснить это рассмотрим задачу анализа влияния на урожайность свеклы 2-х факторов:
Вид семян
и
Тип почвы
. Очевидно, что факторы
Вид семян
и
Тип почвы
не являются независимыми: можно утверждать, что для всех с/х культур на разных почвах разные типы семян дадут разную всхожесть. Различные комбинации
Вид семян
—
Тип почвы
могут сильно влиять на урожайность и поэтому взаимодействие факторов может вносить определенный вклад в разброс исходных данных.
Взаимодействие факторов было рассмотрено столь подробно, так как отсутствие или наличие взаимодействия принципиально влияет на ход
дисперсионного анализа
. При отсутствии взаимодействия влияние каждого фактора на переменную Y может быть рассмотрено по отдельности. При наличии взаимодействия анализировать влияние каждого фактора по отдельности нельзя. Альтернативным вариантом анализа в этом случае является
однофакторный дисперсионный анализ,
целью которого может быть поиск оптимального сочетания 2-х факторов.
Возвращаемся к диаграммам взаимодействия. Очевидно, что делать заключение о наличии или отсутствии взаимодействия факторов невозможно лишь по взаимному расположению линий на диаграмме. Для формулирования утверждения о взаимодействии требуется составить математическое выражение. Это выражение должно вычисляться на основании исходных данных, а результат должен сравниваться с неким критическим значением. Займемся этим в следующем разделе.
Определяем причины изменчивости исходных данных
По аналогии с однофакторным
дисперсионным анализом
общую изменчивость (разброс) значений Y относительно
общего среднего
(SST = Sum of Squares Total, общая сумма квадратов) определим как сумму нескольких компонентов, в данном случае 4-х:
SST=SSA+SSB+ SS взаим +SSE
- SSA – изменчивость, которую можно объяснить выбором метода обработки (фактор А)
- SSВ — изменчивость обусловленная выбором материала детали (фактор В)
- SS взаим — изменчивость обусловленная взаимодействием 2-х факторов
- SSE — ошибка модели (Error Sum of Squares).
SST и все 4 компонента вычисляются на основании имеющихся исходных данных:
Примечание
: Вычисления SST и всех 4-х компонентов выполнены в файле примера .
Также в
дисперсионном анализе
используется понятие
среднего квадрата отклонений
(Mean Square) или сокращенно MS. Соответственно для SST имеем MST=SST/(N-1), где N= a*b*m является общим количеством измерений (18). Для других SS степени свободы приведены в таблице ниже.
Таким образом, MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а делением на число
степеней свободы
(degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно (1) среднее значение (аналогично тому, как мы делали при
вычислении дисперсии
).
В случае
двухфакторного дисперсионного анализа
формируется 3
нулевых гипотезы
.
- Гипотеза Н 0 взаим об отсутствии взаимодействия Фактора А и Фактора В. Альтернативная гипотеза Н 1взаим формулируется о наличии взаимодействия.
- гипотеза Н 01 заключается в том, что уровень фактора А (метод обработки поверхности) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора А не отличаются статистически значимо (их различие может быть объяснено лишь случайностью выборок).
- гипотеза Н 0 2 заключается в том, что уровень фактора В (Исходный материал) не влияет на измеренные значения Y (количество дефектов), т.е. средние значения выборок, относящиеся к различным уровням Фактора В не отличаются статистически значимо.
Сначала тестируют гипотезу об отсутствии взаимодействия между факторами. Мы можем отклонить Н 0 взаим в пользу Н 1взаим при заданном
уровне значимости
α (альфа), если вычисленное значение тестовой статистики F= MS взаим /MSE больше F критич альфа – значения случайной величины F имеющей
распределение Фишера
с (b-1)*(a-1) и a*b*(m-1) степенями свободы.
Если взаимодействие между факторами отсутствует, то можно начинать тестировать гипотезы Н 01 и Н 0 2 . При наличии взаимодействия анализировать влияние каждого фактора по отдельности нельзя. Альтернативным вариантом анализа в этом случае является
однофакторный дисперсионный анализ
, целью которого может быть поиск оптимального сочетания 2-х факторов.
Чтобы проверить гипотезы необходимо вычислить значения тестовых статистик и сравнить их с соответствующими критическими значениями F крит ич , вычисленными для заданного уровня значимости
альфа
. Если вычисленное значение F 01 = MSА/MSE больше F 1крит ич , то нулевую гипотезу Н 0 1 об отсутствии влияния уровней Фактора А отклоняют. Аналогичные умозаключения справедливы и для Фактора В.
Проверить гипотезу Н 01 можно и через вычисление
p
-значения,
которое представляет собой вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 . Далее
p
-значение
сравнивают с уровнем значимости. Если
p
-значение
менее уровня значимости, то нулевую гипотезу отклоняют. Действительно, если вычисленное значение F 01 получить маловероятно, то это ставит под сомнение справедливость того, что случайная величина F 1 = MSА/MSE имеет
распределение Фишера
с
a
-1
и
a
*
b
*(
m
-1)
степенями свободы, а следовательно и саму нулевую гипотезу. В этом случае мы можем считать, что справедлива альтернативная гипотеза: уровни фактора А влияют на зависимую переменную Y.
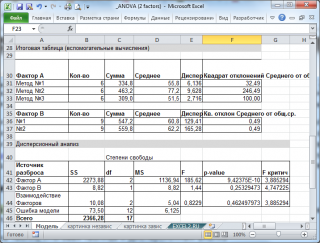
Вычисления в MS EXCEL
В файле примера приведено решение вышеуказанной задачи: вычислены средние значения выборок, суммы квадратов (SS), степеней свобод, средние квадратов отклонений (MS).
Для вычислений критических значений в MS EXCEL имеется специальная функция = F.ОБР.ПХ()
Формула для вычисления F 1критич = F.ОБР.ПХ(a-1; a*b*(m-1);альфа)
В MS EXCEL первое
p
-значение
(вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 ) можно вычислить по формуле:
= F.РАСП.ПХ((MSА/MSE; a-1; a*b*(m-1))
Второе
p
-значение
(вероятность того, что случайная величина F 2 = MSВ/MSE примет значение более F 0 2 ) вычисляется по аналогичным формулам.
В нашей задаче
p
-значения
получились 0,000 и 0,253, что значительно меньше обычно принимаемого в качестве
уровня значимости
0,05. Таким образом, обе нулевых гипотезы отклоняются.