В процессе тестирования программы 1 группа нашла 15 ошибок

В процессе тестирования
программы 1-я группа нашла 15 ошибок, 2-я
группа нашла 25 ошибок, общих ошибок было
5. Определить надёжность по простой
интуитивной модели.

4. Модель Коркорэна

Применение модели предполагает
знание следующих ее показателей:

• модель содержит изменяющуюся
  вероятность отказов для различных
  источников ошибок и соответственно
  разную вероятность их исправления;

• в модели используются такие
  параметры, как результат только N
  испытаний, в которых наблюдается N_i
  ошибок i-го типа;

• выявление в ходе N испытаний
  ошибки i-го типа появляется с вероятностью
  а_i.

Показатель уровня надежности R вычисляют
по следующей формуле:

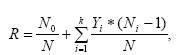
где N₀ —
число безотказных (или безуспешных)
испытаний, выполненных в серии из N
испытаний, k — известное число типов
ошибок, a_i
— вероятность выявления при тестировании
ошибки i-го
типа,

Y_i —
вероятность появления ошибок, при N_i
> 0, Y_i
= a_i,
при N_i =
0, Y_i =
0.

Пример 6.

Было проведено 100 испытаний
программы. 20 из 100 испытаний прошли
безуспешно, а в остальных случаях
получились следующие данные:

Оценить
надёжность по модели Коркорэна.

Пример 7. Было
проведено 100 испытаний программы. 20 из
100 испытаний прошли безуспешно, а в
остальных случаях получились следующие
данные:

Оценить
надёжность программы по модели Коркорэна.

Исходные данные:
N=	100
N0=	20
R=

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Подборка по базе: Самостоятельная работа по теме №4.docx, Практическая работа № 2.docx, Дипломная работа Набоких А.С..doc, Практическая работа №1.docx, Акзамова К.Н дипломная работа.docx, Титульный лист обж практическая работа слайды (1).rtf, Выпускная квалификационная работа на тему_Создание мультимедийно, Практическая работа по теме Распознавание математических понятий, Курсовая работа по бухгалтерскому финансовому учету Кудряшова А., Лабораторная работа 1.docx

Практическая работа

Факторы, определяющие надежность ИС

Модель Миллса. Простая интуитивная модель
Цель работы: научиться оценивать надежность ПС.

Практическая часть

Задачи по теме «Оценка надёжности ПО» Модель Миллса.

Задача 1.

Предположим в программе 12 собственных ошибки, внесём ещё 6 случайным обра­зом. В процессе тестирования было найдено 7 ошибок из рассеянных и 5 собственные. Найти надёжность по модели Миллса.

Задача 2.

Предположим в программе перед началом тестирования было 90 ошибок. Искусст­венно рассеяно 20 ошибок. В процессе тестовых прогонов было выявлено следующее ко­личество ошибок:

N 25 20 20 15 10 9 1

V 5 4 2 4 2 2 1

Оценить число возможно оставшихся ошибок в программе после каждого тестово­го прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.

Задача 3.

Предположим в программе перед началом тестирования было 100 ошибок. Искус­ственно рассеяно 15 ошибок. В процессе тестовых прогонов было выявлено следующее количество ошибок:

N 20 20 25 16 9 8 1

V 5 3 3 4 3 1 1

Оценит число возможно оставшихся ошибок в программе после каждого тестового прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.

Задача 4.

Предположим в программе перед началом тестирования было 80 ошибок. Искусст­венно рассеяно 30 ошибок. В процессе тестовых прогонов было выявлено следующее ко­личество ошибок:

N 30 15 15 13 10 10 1

V 5 3 3 4 3 1 1

Оценит число возможно оставшихся ошибок в программе после каждого тестового прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.

Простая интуитивная модель.

Задача 1.

В процессе тестирования программы 1-я группа нашла 15 ошибок, 2-я группа на­шла 25 ошибок, общих ошибок было 5. Определить надёжность по простой интуитивной модели.

Задача 2.

В процессе тестирования программы 1-я группа нашла 5 ошибок, 2-я группа нашла 2 ошибки, общих ошибок было 2. Определить надёжность по простой интуитивной модели.

Задача 3.

В процессе тестирования программы 1-я группа нашла 35 ошибок, 2-я группа на­шла 25 ошибки, общих ошибок было 20. Определить надёжность по простой интуитив­ной модели.

Задача 4.

В процессе тестирования программы 1-я группа нашла 5 ошибок, 2-я группа нашла 40 ошибок, общих ошибок было 5. Определить надёжность по простой интуи­тивной модели.

Контрольные вопросы

1. Дайте определение сложности программного средства.
2. Приведите классификацию динамических МНПС.