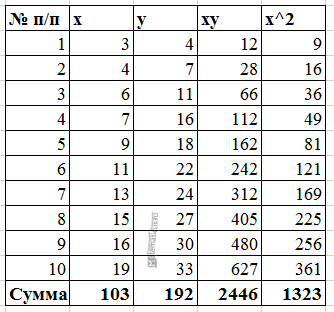
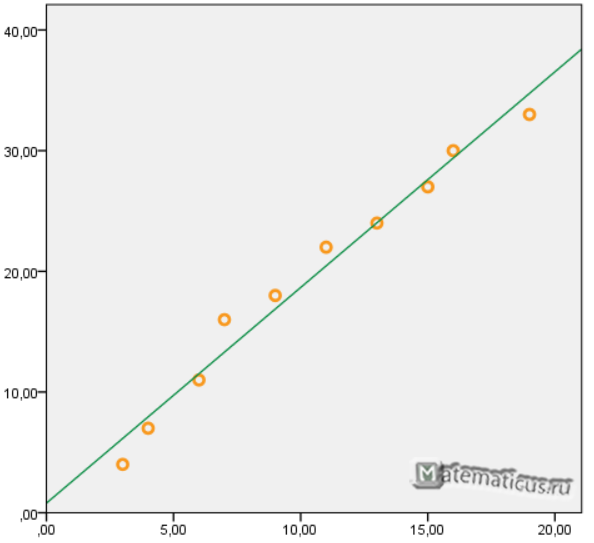
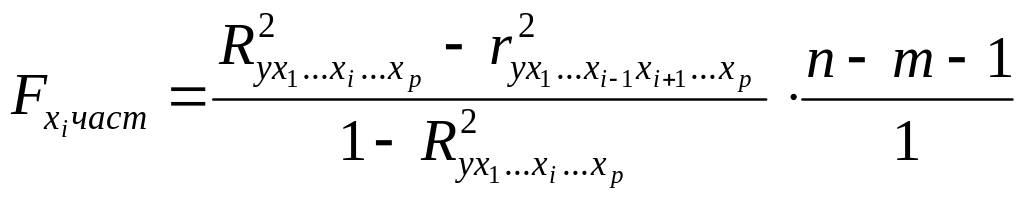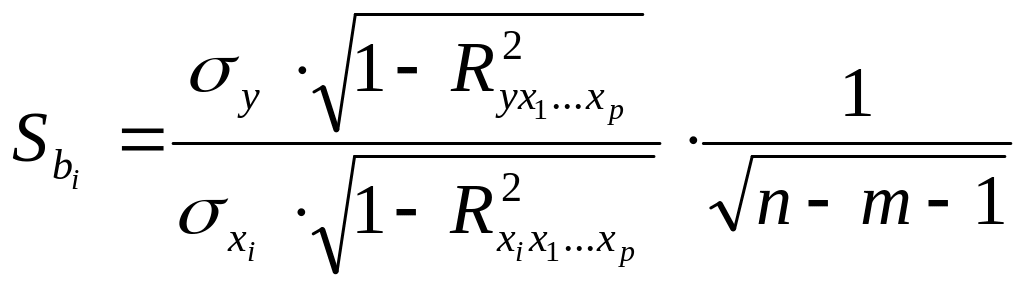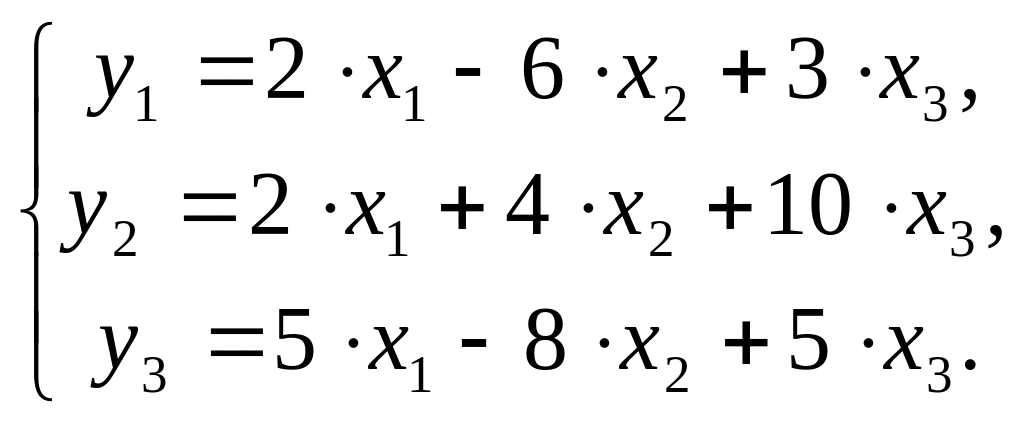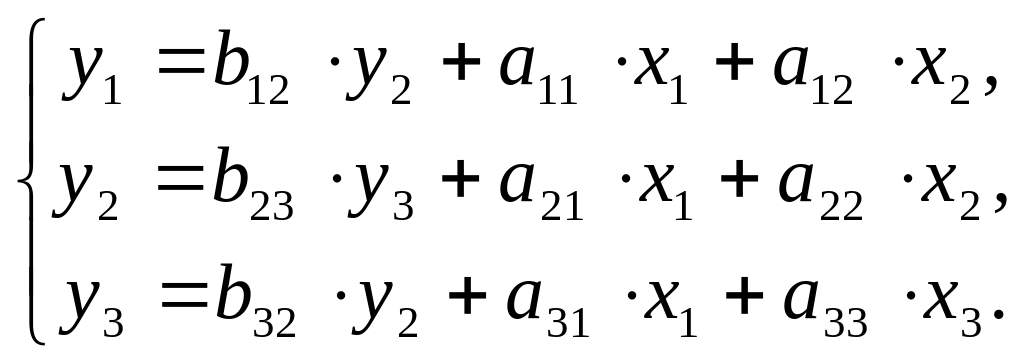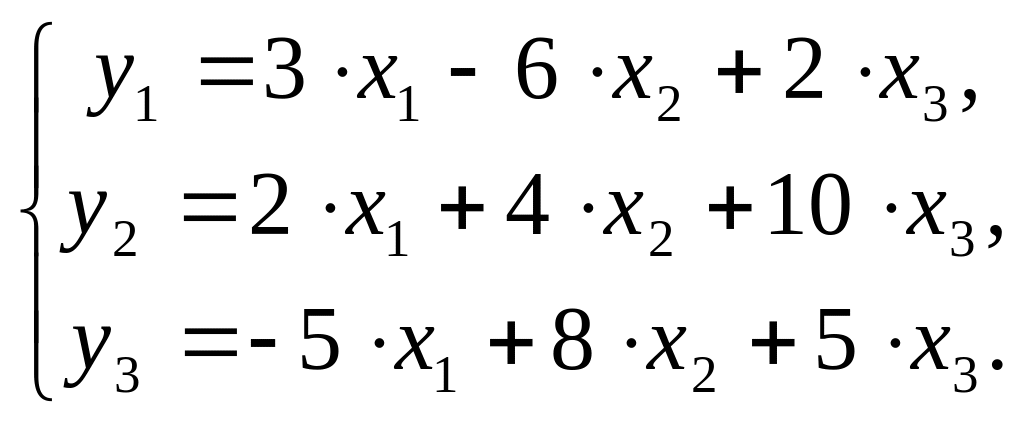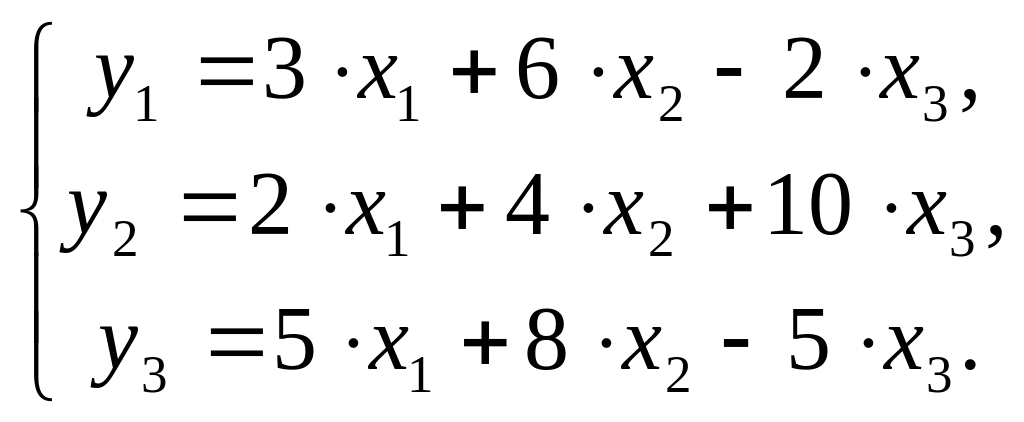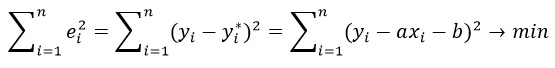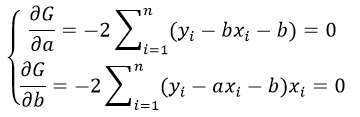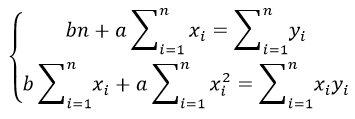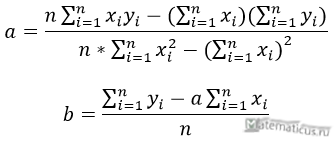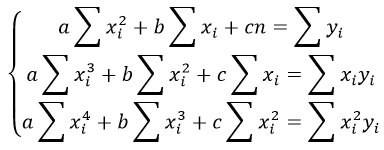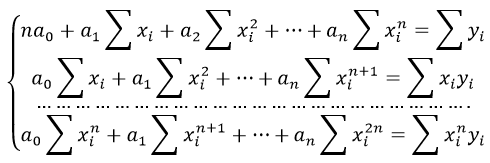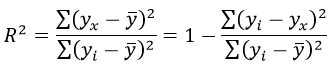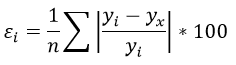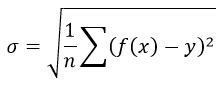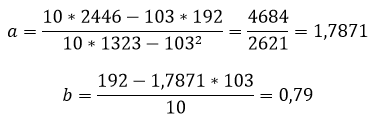Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.
Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:
1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).
- SST = Σ(y i – y ) 2
2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).
- SSE = Σ(ŷ i – y i ) 2
Между этими тремя показателями существует следующая зависимость:
SST = SSR + SSE
Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.
SSR, SST и R-квадрат
R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
Используя SSR и SST, мы можем рассчитать R-квадрат как:
R-квадрат = SSR / SST
Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:
R-квадрат = 137,5/156 = 0,8814
Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.
Расчет SST, SSR, SSE: пошаговый пример
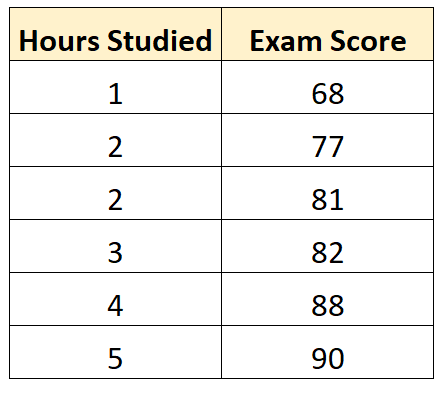
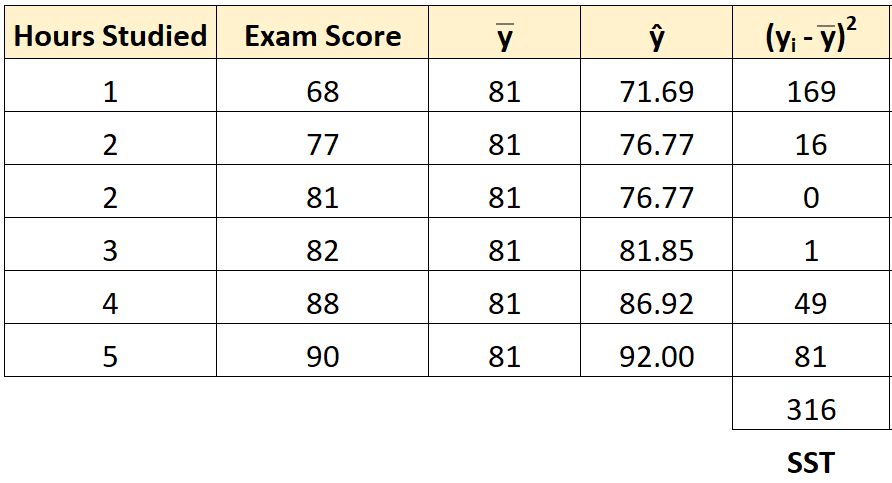
Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:
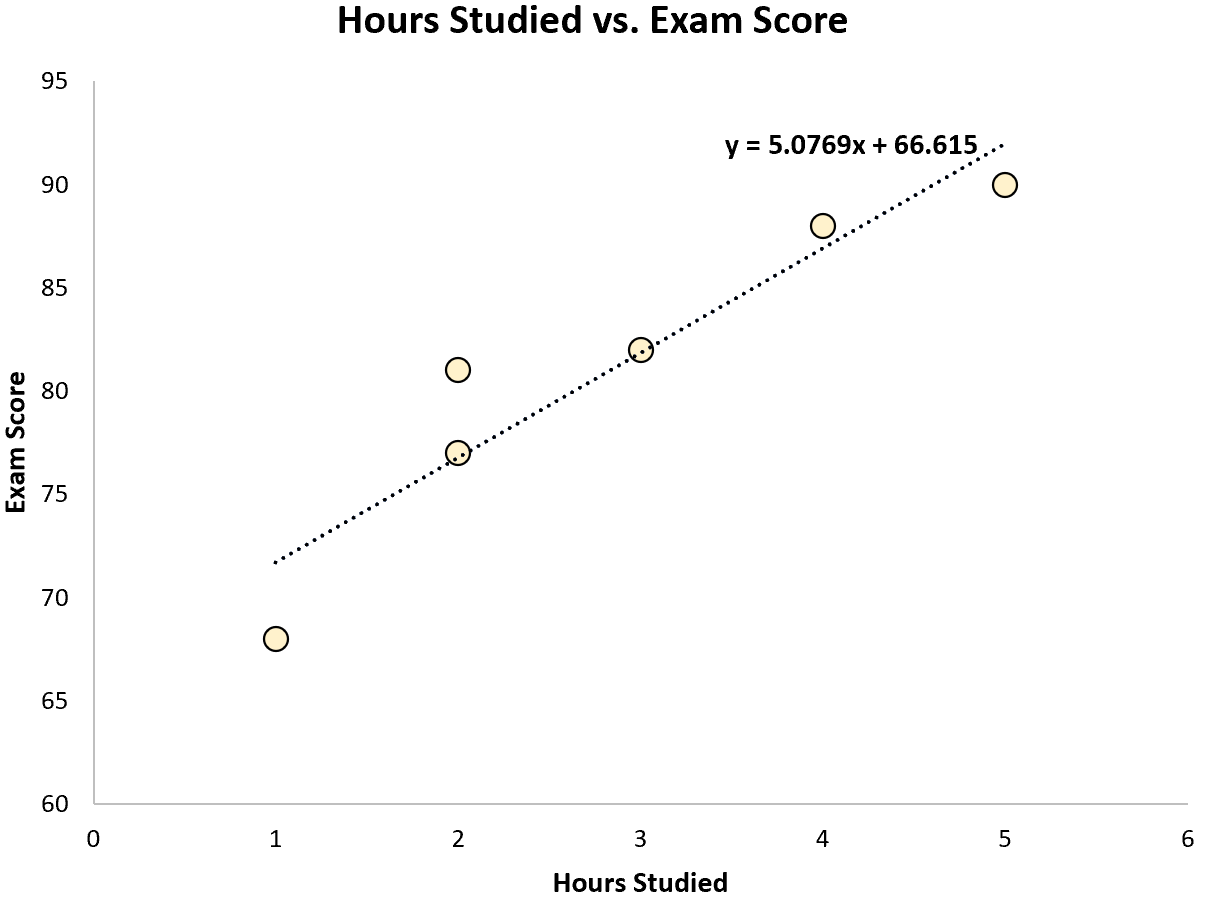
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:
Оценка = 66,615 + 5,0769 * (часы)
Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:
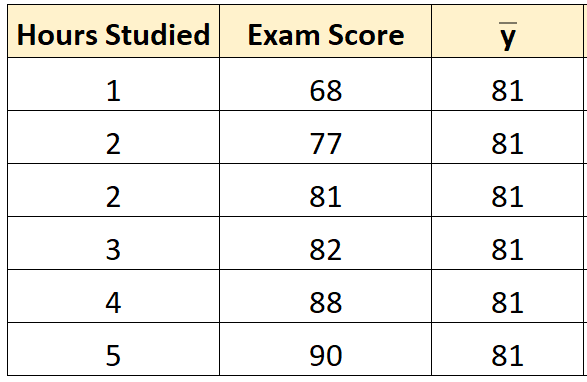
Шаг 1: Рассчитайте среднее значение переменной ответа.
Среднее значение переменной отклика ( y ) оказывается равным 81 .
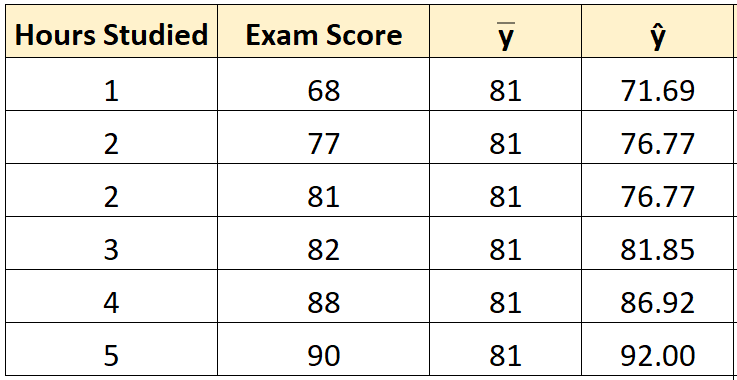
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.
Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.
Например, предполагаемая оценка экзамена для студента, который учился один час, такова:
Оценка = 66,615 + 5,0769*(1) = 71,69 .
Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:
Шаг 3: Рассчитайте общую сумму квадратов (SST).
Далее мы можем вычислить общую сумму квадратов.
Например, сумма квадратов для первого ученика равна:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:
Сумма квадратов получается 316 .
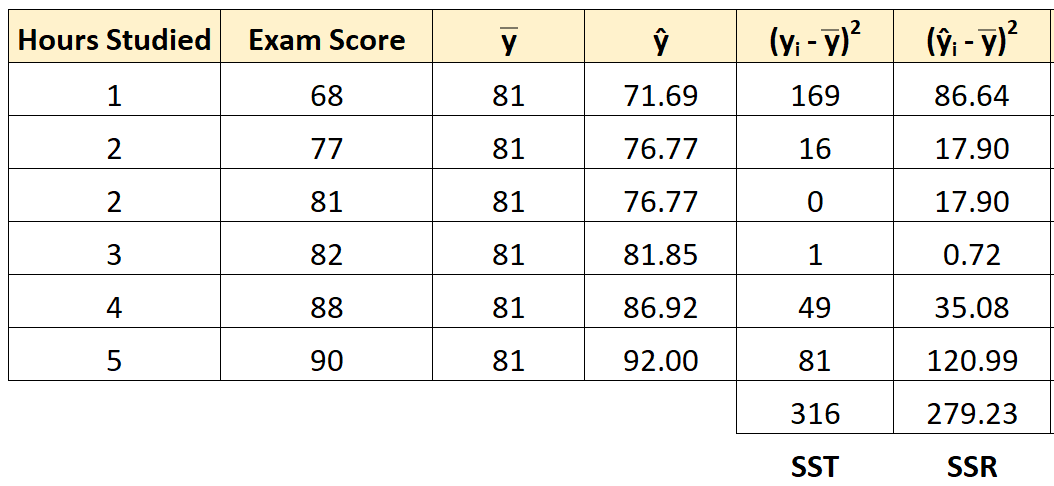
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).
Далее мы можем вычислить сумму квадратов регрессии.
Например, сумма квадратов регрессии для первого ученика равна:
(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .
Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:
Сумма квадратов регрессии оказывается равной 279,23 .
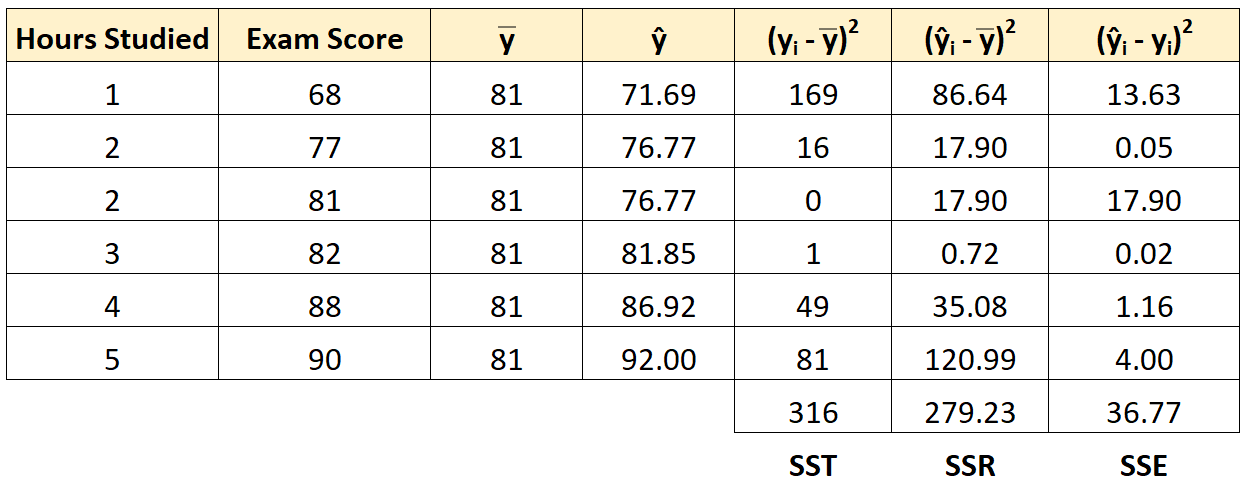
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).
Далее мы можем вычислить сумму квадратов ошибок.
Например, ошибка суммы квадратов для первого ученика:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:
Мы можем проверить, что SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:
- R-квадрат = SSR / SST
- R-квадрат = 279,23/316
- R-квадрат = 0,8836
Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.
Дополнительные ресурсы
Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:
Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE
Все курсы > Оптимизация > Занятие 4 (часть 2)
Во второй части занятия перейдем к практике.
Продолжим работать в том же ноутбуке⧉
Сквозной пример
Данные и постановка задачи
Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.
|
boston = pd.read_csv(‘/content/boston.csv’) |
При этом нам нужно будет решить две основные задачи:
Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.
- Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
- Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
- Этап 3. Обучим еще одну модель и посмотрим как изменится результат.
Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:
- Метод наименьших квадратов
- Метод градиентного спуска
Разделение выборки
Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.
Исследовательский анализ данных
Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, признаки в этом датасете количественные, за исключением переменной CHAS.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 506 entries, 0 to 505 Data columns (total 14 columns): # Column Non-Null Count Dtype — —— ————— —— 0 CRIM 506 non-null float64 1 ZN 506 non-null float64 2 INDUS 506 non-null float64 3 CHAS 506 non-null float64 4 NOX 506 non-null float64 5 RM 506 non-null float64 6 AGE 506 non-null float64 7 DIS 506 non-null float64 8 RAD 506 non-null float64 9 TAX 506 non-null float64 10 PTRATIO 506 non-null float64 11 B 506 non-null float64 12 LSTAT 506 non-null float64 13 MEDV 506 non-null float64 dtypes: float64(14) memory usage: 55.5 KB |
|
# мы видим, что переменная CHAS категориальная boston.CHAS.value_counts() |
|
0.0 471 1.0 35 Name: CHAS, dtype: int64 |
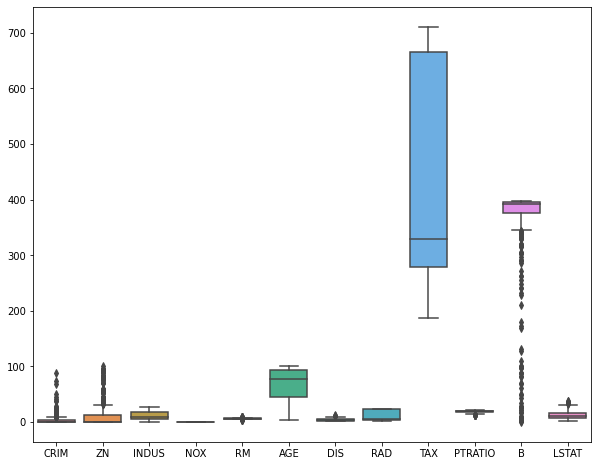
Посмотрим на распределение признаков с помощью boxplots.
|
plt.figure(figsize = (10, 8)) sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’])) plt.show() |
Посмотрим на распределение целевой переменной.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def box_density(x): # создадим два подграфика f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк ncols = 1, # и одного столбца sharex = True, # оставим только нижние подписи к оси x gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк figsize = (10,8)) # зададим размер графика # в первом подграфике построим boxplot sns.boxplot(x = x, ax = ax_box) ax_box.set(xlabel = None) # во втором — график плотности распределения sns.kdeplot(x, fill = True) # зададим заголовок и подписи к осям ax_box.set_title(‘Распределение переменной’, fontsize = 17) ax_kde.set_xlabel(‘Переменная’, fontsize = 15) ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15) plt.show() |
|
box_density(boston.iloc[:, —1]) |
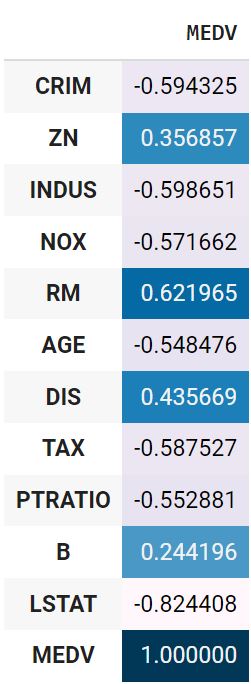
Посмотрим на корреляцию количественных признаков с целевой переменной.
|
boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient() |
Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def pbc(continuous, binary): # преобразуем количественную переменную в массив Numpy continuous_values = np.array(continuous) # классы качественной переменной превратим в нули и единицы binary_values = np.unique(binary, return_inverse = True)[1] # создадим две подгруппы количественных наблюдений # в зависимости от класса дихотомической переменной group0 = continuous_values[np.argwhere(binary_values == 0).flatten()] group1 = continuous_values[np.argwhere(binary_values == 1).flatten()] # найдем средние групп, mean0, mean1 = np.mean(group0), np.mean(group1) # а также длины групп и всего датасета n0, n1, n = len(group0), len(group1), len(continuous_values) # рассчитаем СКО количественной переменной std = continuous_values.std() # подставим значения в формулу return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) ) |
|
pbc(boston.MEDV, boston.CHAS) |
Обработка данных
Пропущенные значения
Посмотрим, есть ли пропущенные значения.
|
CRIM 0 ZN 0 INDUS 0 CHAS 0 NOX 0 RM 0 AGE 0 DIS 0 RAD 0 TAX 0 PTRATIO 0 B 0 LSTAT 0 MEDV 0 dtype: int64 |
Выбросы
Удалим выбросы.
|
from sklearn.ensemble import IsolationForest clf = IsolationForest(max_samples = 100, random_state = 42) clf.fit(boston) boston[‘anomaly’] = clf.predict(boston) boston = boston[boston.anomaly == 1] boston = boston.drop(columns = ‘anomaly’) boston.shape |
При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи
Масштабирование признаков
Приведем признаки к одному масштабу (целевую переменную трогать не будем).
|
boston.iloc[:, :—1] = (boston.iloc[:, :—1] — boston.iloc[:, :—1].mean()) / boston.iloc[:, :—1].std() |
Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).
Кодирование категориальных переменных
Даже после стандартизации переменная CHAS сохранила только два значения.
|
boston.CHAS.value_counts() |
|
-0.182581 389 5.463391 13 Name: CHAS, dtype: int64 |
Ее можно не трогать.
Построение модели
Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.
baseline-модель
|
X = boston.drop(‘MEDV’, axis = 1) y = boston[‘MEDV’] from sklearn.linear_model import LinearRegression model = LinearRegression() y_pred = model.fit(X, y).predict(X) |
Оценка качества
Диагностика модели, метрики качества и функции потерь
Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.
Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.
- Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
- Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.
MSE, RMSE, MAE, MAPE
MSE и RMSE
Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем вы ошибаетесь на 20-25 процентов.
В качестве практики напишем собственную функцию.
|
# параметр squared = True возвращает MSE # параметр squared = False возвращает RMSE def mse(y, y_pred, squared = True): mse = ((y — y_pred) ** 2).sum() / len(y) if squared == True: return mse else: return np.sqrt(mse) |
|
mse(y, y_pred), mse(y, y_pred, squared = False) |
|
(9.980044349414223, 3.1591208190593507) |
Сравним с sklearn.
|
from sklearn.metrics import mean_squared_error # squared = False дает RMSE mean_squared_error(y, y_pred, squared = False) |
MAE
Приведем формулу.
$$ MAE = frac{sum |y-hat{y}|}{n} $$
Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.
|
def mae(y, y_pred): return np.abs(y — y_pred).sum() / len(y) |
|
from sklearn.metrics import mean_absolute_error mean_absolute_error(y, y_pred) |
MAE часто используется при оценке качества моделей временных рядов.
MAPE
Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, выражая отклонение как долю от истинных ответов.
$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$
Это позволяет сравнивать модели с разными единицами измерения между собой.
|
def mape(y, y_pred): return 1/len(y) * np.abs((y — y_pred) / y).sum() |
|
from sklearn.metrics import mean_absolute_percentage_error mean_absolute_percentage_error(y, y_pred) |
Коэффициент детерминации
В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().
Также можно использовать функцию r2_score() модуля metrics.
|
from sklearn.metrics import r2_score r2_score(y, y_pred) |
Для скорректированного $R^2$ напишем собственную функцию.
|
def r_squared(x, y, y_pred): r2 = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum() n, k = x.shape r2_adj = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum() return r2, r2_adj |
|
(0.7965234359550825, 0.7965234359550825) |
Диагностика модели
Теперь проведем диагностику модели в соответствии с выдвинутыми выше допущениями.
Анализ остатков и прогнозных значений
Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
from scipy.stats import probplot from statsmodels.graphics.tsaplots import plot_acf from statsmodels.stats.stattools import durbin_watson def diagnostics(y, y_pred): residuals = y — y_pred residuals_mean = np.round(np.mean(y — y_pred), 3) f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3, ncols = 2, figsize = (12, 18)) # в первом подграфике построим график плотности sns.kdeplot(residuals, fill = True, ax = ax_rkde) ax_rkde.set_title(‘Residuals distribution’, fontsize = 14) ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’) ax_rkde.set(ylabel = ‘Density’) # во втором график нормальной вероятности остатков probplot(residuals, dist = ‘norm’, plot = ax_prob) ax_prob.set_title(‘Residuals probability plot’, fontsize = 14) # в третьем график остатков относительно прогноза ax_ry.scatter(y_pred, residuals) ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14) ax_ry.set(xlabel = ‘y_pred’) ax_ry.set(ylabel = ‘Residuals’) # автокорреляция остатков plot_acf(residuals, lags = 30, ax = ax_auto) ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14) ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’) ax_auto.set(ylabel = ‘Autocorrelation’) # на четвертом сравним прогнозные и фактические значения ax_yy.scatter(y, y_pred) ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], «k—«, lw = 1) ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14) ax_yy.set(xlabel = ‘y_true’) ax_yy.set(ylabel = ‘y_pred’) sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’) sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’) ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14) ax_ykde.set(xlabel = ‘y_true and y_pred’) ax_ykde.set(ylabel = ‘Density’) ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12}) plt.tight_layout() plt.show() |
Разберем полученную информацию.
- В целом остатки модели распределены нормально с нулевым средним значением
- Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
- Присутствует умеренная отрицательная корреляция
- График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
- Распределение прогнозных значений в целом повторяет распределение фактических.
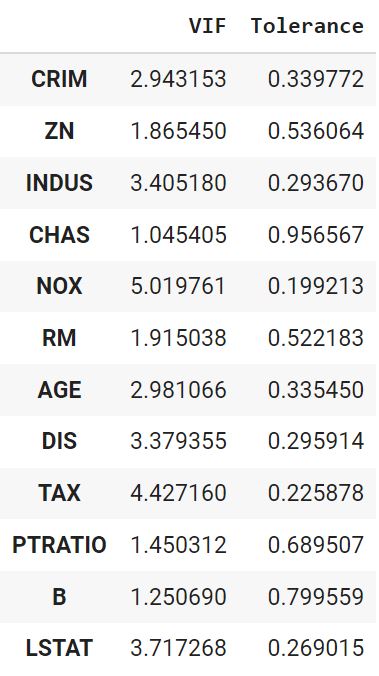
Мультиколлинеарность
Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def vif(df, features): vif, tolerance = {}, {} # пройдемся по интересующим нас признакам for feature in features: # составим список остальных признаков, которые будем использовать # для построения регрессии X = [f for f in features if f != feature] # поместим текущие признаки и таргет в X и y X, y = df[X], df[feature] # найдем коэффициент детерминации r2 = LinearRegression().fit(X, y).score(X, y) # посчитаем tolerance tolerance[feature] = 1 — r2 # найдем VIF vif[feature] = 1 / (tolerance[feature]) # выведем результат в виде датафрейма return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance}) |
|
vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns) |
Дополнительная обработка данных
Попробуем дополнительно улучшить некоторые из диагностических показателей.
VIF
Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.
|
vif(df = X, features = [‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’]) |
Показатели пришли в норму. Окончательно удалим RAD.
|
boston.drop(columns = ‘RAD’, inplace = True) |
Преобразование данных
Применим преобразование Йео-Джонсона.
|
from sklearn.preprocessing import PowerTransformer pt = PowerTransformer() boston = pd.DataFrame(pt.fit_transform(boston), columns = boston.columns) |
Отбор признаков
Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.
|
boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient() |
Также рассчитаем точечно-бисериальную корреляцию.
|
pbc(boston_t.MEDV, boston_t.CHAS) |
Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.
|
boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True) |
Повторное моделирование и диагностика
Повторное моделирование
Выполним повторное моделирование.
|
X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’]) y = boston_t.MEDV from sklearn.linear_model import LinearRegression model = LinearRegression() y_pred = model.fit(X, y).predict(X) |
Оценка качества и диагностика
Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.
|
(0.7546883769637166, 0.7546883769637166) |
Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.
Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.
Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.
Коэффициенты
Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.
|
model.intercept_, model.coef_ |
|
(9.574055157844797e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Обучение модели
Теперь, когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.
Векторизация уравнения
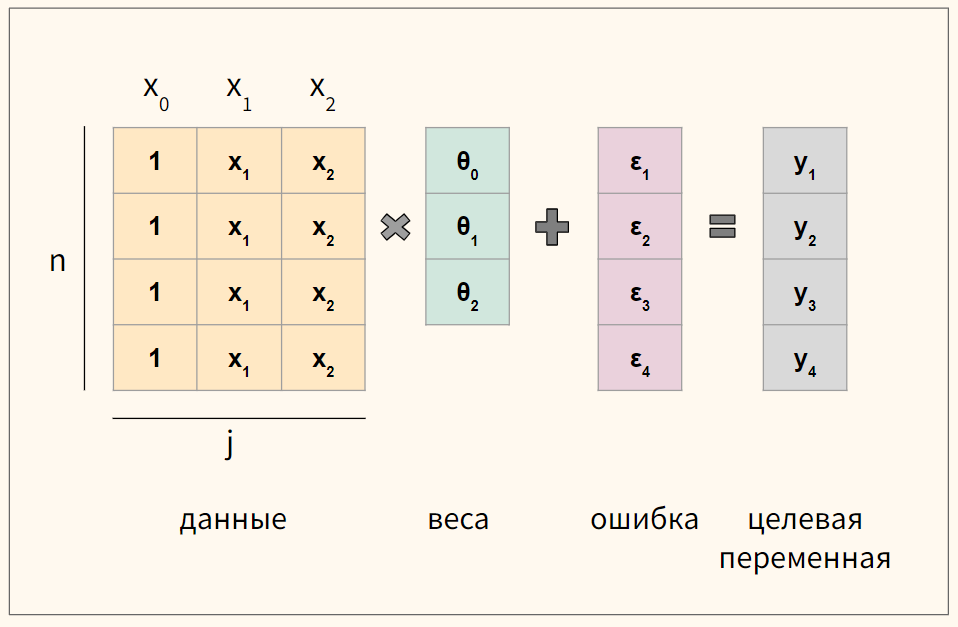
Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии
$$ y = begin{bmatrix} y_1 y_2 vdots y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j x_0 & x_1 & ldots & x_j vdots & vdots & vdots & vdots x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 theta_1 vdots theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 varepsilon_2 vdots varepsilon_n end{bmatrix} $$
где n — количество наблюдений, а j — количество признаков.
Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.
В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать записать уравнение через умножение матрицы на вектор.
$$ y = Xtheta + varepsilon $$
Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.
Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.
Функция потерь
Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.
$$ varepsilon = Xtheta-y $$
При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудалятся. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибку или L1 loss.
Абсолютная ошибка, L1 loss
При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).
$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$
Приведем пример такой функции на Питоне.
|
def L1(y_true, y_pred): return np.sum(np.abs(y_true — y_pred)) / y_true.size |
Помимо модуля ошибку можно возводить в квадрат.
Квадрат ошибки, L2 loss
В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).
$$ SSE = sum (y-Xtheta)^2 $$
Как мы уже говорили, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.
$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$
Ниже код на Питоне.
|
def L2(y_true, y_pred): return np.sum((y_true — y_pred) ** 2) / y_true.size |
На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# для построения графиков мы используем x вместо y_true, y_pred # в качестве входящего значения def mse(x): return x ** 2 def mae(x): return np.abs(x) plt.figure(figsize = (10, 8)) x_vals = np.arange(—3, 3, 0.01) plt.plot(x_vals, mae(x_vals), label = ‘MAE’) plt.plot(x_vals, mse(x_vals), label = ‘MSE’) plt.legend(loc = ‘upper center’, prop = {‘size’: 14}) plt.grid() plt.show() |
Как мы видим, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на ошибку, хотя де-факто большая часть значений такого уровня потерь не дали бы.
Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.
Функция Хьюбера
Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.
$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$
Представим ее на графике.
|
plt.figure(figsize = (10, 8)) def huber(x, delta = 1.): huber_mse = 0.5 * np.square(x) huber_mae = delta * (np.abs(x) — 0.5 * delta) return np.where(np.abs(x) <= delta, huber_mse, huber_mae) x_vals = np.arange(—3, 3, 0.01) plt.plot(x_vals, mae(x_vals), label = ‘MAE’) plt.plot(x_vals, mse(x_vals), label = ‘MSE’) plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’) plt.legend(loc = ‘upper center’, prop = {‘size’: 14}) plt.grid() plt.show() |
Также приведем код этой функции.
|
def huber(y_pred, y_true, delta = 1.0): # пропишем обе части функции потерь huber_mse = 0.5 * (y_true — y_pred) ** 2 huber_mae = delta * (np.abs(y_true — y_pred) — 0.5 * delta) # выберем одну из них в зависимости от дельта return np.where(np.abs(y_true — y_pred) <= delta, huber_mse, huber_mae) |
На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.
Метод наименьших квадратов
Нормальные уравнения
Для множественной линейной регрессии коэффициенты находятся по следующей формуле
$$ theta = (X^TX)^{-1}X^Ty $$
Давайте разбираться, как мы к ней пришли. Сумма квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T}varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)
$$ (y-Xtheta)^T(y-Xtheta) $$
Раскрываем скобки
$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$
Заметим, что $A^TB = B^TA$, тогда
$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$
$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$
Вспомним, что $(AB)^T = A^TB^T$, тогда
$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$
Теперь нужно найти частные производные этих функций
$$ nabla_{theta} J(theta) = y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$
После дифференцирования мы получаем следующую производную
$$ -2X^Ty+2X^TXtheta $$
Как мы помним, оптимум функции находится там, где производная равна нулю.
$$ -2X^Ty+2X^TXtheta = 0 $$
$$ -X^Ty+X^TXtheta = 0 $$
$$ X^TXtheta = X^Ty $$
Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.
$$ theta = (X^TX)^{-1}X^Ty $$
Замечу только, что по теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.
Код на Питоне
Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее функцией, которая добавляет столбец из единиц к признакам.
$$ h_{theta}(x) = theta X $$
|
def add_ones(x): # важно! изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
def h(x, theta): x = x.copy() add_ones(x) return np.dot(x, theta) |
Перейдем к функции, отвечающей за обучение модели.
$$ theta = (X^TX)^{-1}X^Ty $$
|
# строчную `x` используем внутри функций и методов класса # заглавную `X` вне функций и методов def fit(x, y): x = x.copy() add_ones(x) xT = x.transpose() inversed = np.linalg.inv(np.dot(xT, x)) thetas = inversed.dot(xT).dot(y) return thetas |
Обучим модель и выведем коэффициенты.
|
thetas = fit(X, y) thetas[0], thetas[1:] |
|
(9.3718435789647e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Примечание. Замечу, что не все матрицы обратимы, в этом случае они называются вырожденными (non-invertible, degenerate). В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().
Сделаем прогноз.
|
y_pred = h(X, thetas) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Создание класса
Объединим код в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
class ols(): def __init__(self): self.thetas = None def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def fit(self, x, y): x = x.copy() self.add_ones(x) xT = x.T inversed = np.linalg.inv(np.dot(xT, x)) self.thetas = inversed.dot(xT).dot(y) def predict(self, x): x = x.copy() self.add_ones(x) return np.dot(x, self.thetas) |
Создадим объект класса и обучим модель.
|
model = ols() model.fit(X, y) |
Выведем коэффициенты.
|
model.thetas[0], model.thetas[1:] |
|
(9.3718435789647e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274])) |
Сделаем прогноз.
|
y_pred = model.predict(X) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Оценка качества
Оценим качество через MAPE и $R^2$.
|
(0.7546883769637167, 0.7546883769637167) |
Мы видим, что результаты аналогичны.
Метод градиентного спуска
В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.
Нахождение градиента
Покажем расчет градиента на схеме.
В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).
Пошаговое построение модели
Начнем с функции гипотезы.
$$ h_{theta}(x) = theta X $$
|
def h(x, thetas): return np.dot(x, thetas) |
Объявим функцию потерь.
$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$
|
def objective(x, y, thetas, n): return np.sum((y — h(x, thetas)) ** 2) / (2 * n) |
Объявим функцию для расчета градиента.
$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$
где j — индекс признака.
|
def gradient(x, y, thetas, n): return np.dot(—x.T, (y — h(x, thetas))) / n |
Напишем функцию для обучения модели.
$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$
Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.
|
def fit(x, y, iter = 20000, learning_rate = 0.05): x, y = x.copy(), y.copy() # функцию add_ones() мы написали раньше add_ones(x) thetas, n = np.zeros(x.shape[1]), x.shape[0] loss_history = [] for i in range(iter): loss_history.append(objective(x, y, thetas, n)) grad = gradient(x, y, thetas, n) thetas -= learning_rate * grad return thetas, loss_history |
Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.
|
thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05) |
|
thetas[0], thetas[1:], loss_history[—1] |
|
(9.493787734953824e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274]), 0.1226558115181417) |
Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.
Прогноз
Сделаем прогноз.
|
def predict(x, thetas): x = x.copy() add_ones(x) return np.dot(x, thetas) |
|
y_pred = predict(X, thetas) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Создание класса
Объединим написанные функции в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
class gd(): def __init__(self): self.thetas = None self.loss_history = [] def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def objective(self, x, y, thetas, n): return np.sum((y — self.h(x, thetas)) ** 2) / (2 * n) def h(self, x, thetas): return np.dot(x, thetas) def gradient(self, x, y, thetas, n): return np.dot(—x.T, (y — self.h(x, thetas))) / n def fit(self, x, y, iter = 20000, learning_rate = 0.05): x, y = x.copy(), y.copy() self.add_ones(x) thetas, n = np.zeros(x.shape[1]), x.shape[0] # объявляем переменную loss_history (отличается от self.loss_history (?)) loss_history = [] for i in range(iter): loss_history.append(self.objective(x, y, thetas, n)) grad = self.gradient(x, y, thetas, n) thetas -= learning_rate * grad # записываем обратно во внутренние атрибуты, чтобы передать методу .predict() self.thetas = thetas self.loss_history = loss_history def predict(self, x): x = x.copy() self.add_ones(x) return np.dot(x, self.thetas) |
Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.
|
model = gd() model.fit(X, y, iter = 50000, learning_rate = 0.05) model.thetas[0], model.thetas[1:], model.loss_history[—1] |
|
(9.493787734953824e-16, array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128, -0.16878987, -0.18057055, -0.49319274]), 0.1226558115181417) |
|
y_pred = model.predict(X) y_pred[:5] |
|
array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788]) |
Оценка качества
|
(0.7546883769637167, 0.7546883769637167) |
Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.
Диагностика алгоритма
Работу алгоритма можно проверить с помощью кривой обучения (learning curve).
- Ошибка постоянно снижается
- Алгоритм остановится, после истечения заданного количества итераций
- Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)
Построим кривую обучения.
|
plt.plot(loss_history) plt.show() |
|
plt.plot(loss_history[:100]) plt.show() |
Она также позволяет выбрать адекватный коэффициент скорости обучения.
Подведем итог
Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.
Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.
Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно погружаться в способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.
Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.
Дополнительные материалы к занятию.
В
идеале, когда все точки лежат на прямой
регрессии, все остатки равны нулю и
значения Y
полностью вычисляются или объясняются
линейной функцией от Х.
Используя
формулу отклонений и отнимая
от обеих частей равенства, имеем
следующее.
Несложными
алгебраическими преобразованиями можно
показать, что суммы квадратов
складываются:
или
где

SS
обозначает «сумма квадратов» (Sum
of Squares), a T, R, Е— соответственно «общая»
(Total), «регрессионная» (Regression) и
«ошибки» (Error). С этими суммами
квадратов связаны следующие величины
степеней свободы.
Если
линейной связи нет, Y
не зависит от X
и дисперсия Y
оценивается значением выборочной
дисперсии.
Если
связь между X и Y
имеется, она может влиять на некоторые
разности значений Y.
Регрессионная
сумма квадратов, SSR, измеряет часть
дисперсии Y,
объясняемую линейной зависимостью.
Сумма квадратов ошибок, SSE
— это оставшаяся часть дисперсии Y,
или дисперсия Y,
не объясненная линейной зависимостью.
2.5 Коэффициент детерминации
Как
было указано в предыдущем разделе,
показатель SST измеряет общую вариацию
относительно Y,
а ее часть, объясненная изменением X,
соответствует SSR. Оставшаяся, или
необъясненная вариация, соответствует
SSE. Отношение объясненной вариации к
общей называется выборочным коэффициентом
детерминации и обозначается
Коэффициент
детерминации измеряет долю изменчивости
Y,
которую можно объяснить с помощью
информации об изменчивости (разнице
значений) независимой переменной X.
В
случае прямолинейной регрессии
коэффициент детерминации
равен квадрату коэффициента корреляции
.
В
регрессионном анализе коэффициенты
и
необходимо рассматривать отдельно, так
как они несут различную информацию.
Коэффициент корреляции выявляет не
только силу, но и направление линейной
связи. Следует отметить, что когда
коэффициент корреляции возводится в
квадрат, полученное значение всегда
будет положительным и информация о
характере взаимосвязи теряется.
Коэффициент
детерминации
измеряет силу взаимосвязи между Y и X
иначе, чем коэффициент корреляции
.
Значение
измеряет долю изменчивости Y, объясненную
разницей значений X. Эту полезную
интерпретацию можно обобщить на
взаимосвязь между Y и более чем одной
переменной X.
2.6 Проверка гипотез
Прямая
регрессии вычисляется по выборке пар
значений Х-Y. Статистическая модель
простой линейной регрессии предполагает,
что линейная связь величин X и Y имеет
место для всех возможных пар X-Y. Для
проверки гипотезы, что соотношение
истинно
для всех X и Y рассмотрим гипотезу:
,
Если
эта гипотеза справедлива, в генеральной
совокупности нет связи между значениями
X и Y. Если мы не можем опровергнуть
гипотезу, то, несмотря на ненулевое
значение вычисленного по выборке
углового коэффициента регрессионной
прямой, мы не имеем оснований гарантированно
утверждать, что значения X
и Y
взаимозависимы. Иными словами, нельзя
исключить возможность того, что
регрессионная прямая совокупности
горизонтальна.
Если
гипотеза
верна, проверочная статистика t со
значением
имеет t-распределение с количеством
степеней свободы df = n-2.
Здесь оценка стандартного отклонения
(или стандартная ошибка) равна
Для
выборки очень большого объема можно
отклонить гипотезу
и заключить, что между X и Y
есть линейная связь даже в тех случаях,
когда значение
мало (например, 10%). Аналогично для малых
выборок и очень большого значения
(например, 95%) можно сделать вывод, что
регрессионная зависимость имеет место.
Малое значение коэффициента детерминации
означает, что вычисленное уравнение
регрессии не имеет большого значения
для прогноза. С другой стороны, большое
значение
при очень малом объеме выборки не может
удовлетворить исследователя, и потребуются
дополнительные обоснования, чтобы
вычисленную функцию регрессии использовать
для целей прогноза. Такова разница между
статистической и практической значимостью.
В то же время вся собранная информация,
а также понимание сущности рассматриваемого
объекта будут необходимы, чтобы
определить, может ли вычисленная функция
регрессии быть подходящим средством
для прогноза.
Еще
один способ проверки гипотезы
возможен с помощью таблицы ANOVA. При
предположении, что статистическая
модель линейной регрессии правильна и
нулевая гипотеза
истинна, отношение
имеет
F-распределение со степенями свободы
df= 1, n-2.
Если гипотеза
истинна, каждая из величин MSR и MSE будет
оценкой
,
дисперсии слагаемого ошибки
в
статистической модели прямолинейной
регрессии. С другой стороны, если верна
гипотеза
,
числитель в отношении F стремится стать
большим, чем знаменатель. Большое
значение F согласуется с истинностью
альтернативной гипотезы.
Для
модели прямолинейной регрессии проверка
гипотезы
при альтернативе
основывается на отношении
с df= 1, n-2.
При уровне значимости
область отклонения гипотезы:.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Часть серии по |
| Регрессивный анализ |
|---|
 |
| Модели |
|
|
|
|
|
| Оценка |
|
|
|
|
| Фон |
|
|
В статистике и оптимизации ошибки и остатки являются двумя тесно связанными и легко путаемыми мерами отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». В ошибка (или же беспокойство) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинный значение интересующей величины (например, среднее значение генеральной совокупности), и остаточный наблюдаемого значения — это разница между наблюдаемым значением и по оценкам значение интересующей величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибки регрессии и остатки регрессии и где они приводят к концепции стьюдентизированных остатков.
Вступление
Предположим, что есть серия наблюдений из одномерное распределение и мы хотим оценить иметь в виду этого распределения (так называемый модель местоположения ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
А статистическая ошибка (или же беспокойство) — это величина, на которую наблюдение отличается от ожидаемое значение, последнее основано на численность населения из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся иметь в виду всего населения, обычно не наблюдается, и, следовательно, статистическая ошибка также не может быть обнаружена.
А остаточный (или подходящее отклонение), с другой стороны, является наблюдаемым оценивать ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка п люди. В выборочное среднее может служить хорошей оценкой численность населения иметь в виду. Тогда у нас есть:
- Разница между ростом каждого человека в выборке и ненаблюдаемой численность населения означает это статистическая ошибка, в то время как
- Разница между ростом каждого человека в выборке и наблюдаемым образец означает это остаточный.
Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, следовательно, остатки обязательно нет независимый. Статистические ошибки, с другой стороны, независимы, и их сумма в пределах случайной выборки равна почти наверняка не ноль.
Можно стандартизировать статистические ошибки (особенно нормальное распределение ) в z-оценка (или «стандартная оценка») и стандартизируйте остатки в т-статистический, или в более общем смысле стьюдентизированные остатки.
В одномерных распределениях
Если предположить нормально распределенный совокупность со средними μ и стандартное отклонение σ, и выбираем индивидуумов независимо, то имеем
и выборочное среднее
случайная величина, распределенная таким образом, что:
В статистические ошибки тогда
с ожидал значения нуля,[1] тогда как остатки находятся
Сумма квадратов статистические ошибки, деленное на σ2, имеет распределение хи-квадрат с п степени свободы:
Однако это количество не наблюдается, так как среднее значение для населения неизвестно. Сумма квадратов остатки, с другой стороны, наблюдается. Частное этой суммы по σ2 имеет распределение хи-квадрат только с п — 1 степень свободы:
Эта разница между п и п — 1 степень свободы дает Поправка Бесселя для оценки выборочная дисперсия популяции с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Примечательно, что сумма квадратов остатков и средние выборочные значения могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу расчетов, включающих t-статистика:
куда 


Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяется. Это удачно, потому что это означает, что даже если мы не знаемσ, мы знаем распределение вероятностей этого частного: оно имеет Распределение Стьюдента с п — 1 степень свободы. Поэтому мы можем использовать это частное, чтобы найти доверительный интервал заμ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».[3]
Регрессии
В регрессивный анализ, различие между ошибки и остатки тонкий и важный, и ведет к концепции стьюдентизированные остатки. При наличии ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от приспособленный функции — остатки. Если применима линейная модель, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам.[2] Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичность. Если все остатки равны или не разветвляются, они демонстрируют гомоскедастичность.
Однако возникает терминологическая разница в выражении среднеквадратичная ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатки, а не ненаблюдаемые ошибки. Если эту сумму квадратов разделить на п, количество наблюдений, результат — это среднее квадратов остатков. Поскольку это пристрастный Для оценки дисперсии ненаблюдаемых ошибок смещение устраняется путем деления суммы квадратов остатков на df = п − п — 1 вместо п, куда df это количество степени свободы (п минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует несмещенную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.[4]
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они такие же, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равны п − п — 1, где п — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать, разделив средний квадрат модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с).[5]
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) может отличаться даже если сами ошибки одинаково распределены. Конкретно в линейная регрессия где ошибки одинаково распределены, вариативность остатков входных данных в середине области будет выше чем изменчивость остатков на концах области:[6] линейные регрессии лучше подходят для конечных точек, чем средние. Это также отражено в функции влияния различных точек данных на коэффициенты регрессии: конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, необходимо скорректировать остатки на ожидаемую изменчивость остатки, который называется студенчество. Это особенно важно в случае обнаружения выбросы, где рассматриваемый случай чем-то отличается от другого случая в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другое использование слова «ошибка» в статистике
Термин «ошибка», как обсуждалось в предыдущих разделах, используется в смысле отклонения значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Средняя квадратичная ошибка или же среднеквадратичная ошибка (MSE) и Средняя квадратическая ошибка (RMSE) относятся к количеству, на которое значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).
Сумма квадратов ошибок (SSE или же SSе), обычно сокращенно SSE или SSе, относится к остаточная сумма квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой наименьших квадратов, когда коэффициенты регрессии выбираются таким образом, чтобы сумма квадратов была минимальной (т. Е. Ее производная равна нулю).
Точно так же сумма абсолютных ошибок (SAE) — сумма абсолютных значений остатков, которая минимизируется в наименьшие абсолютные отклонения подход к регрессу.
Смотрите также
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадратов
- Инновации (обработка сигналов)
- Неподходящая сумма квадратов
- Допустимая погрешность
- Средняя абсолютная ошибка
- Ошибка наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Студентизованный остаток
- Ошибки типа I и типа II
Рекомендации
- ^ Уэзерилл, Дж. Барри. (1981). Промежуточные статистические методы. Лондон: Чепмен и Холл. ISBN 0-412-16440-Х. OCLC 7779780.
- ^ а б Современное введение в вероятность и статистику: понимание, почему и как. Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005 г. ISBN 978-1-85233-896-1. OCLC 262680588.CS1 maint: другие (связь)
- ^ Брюс, Питер С., 1953- (2017-05-10). Практическая статистика для специалистов по данным: 50 основных концепций. Брюс, Эндрю, 1958- (Первое изд.). Севастополь, Калифорния. ISBN 978-1-4919-5293-1. OCLC 987251007.CS1 maint: несколько имен: список авторов (связь)
- ^ Steel, Robert G.D .; Торри, Джеймс Х. (1960). Принципы и процедуры статистики с особым акцентом на биологические науки. Макгроу-Хилл. п.288.
- ^ Зельтерман, Даниэль (2010). Прикладные линейные модели с SAS ([Online-Ausg.]. Ред.). Кембридж: Издательство Кембриджского университета. ISBN 9780521761598.
- ^ «7.3: Типы выбросов в линейной регрессии». Статистика LibreTexts. 2013-11-21. Получено 2019-11-22.
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Ред. Ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Получено 23 февраля 2013.
- Кокс, Дэвид Р.; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30 (2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Получено 23 февраля 2013.
- «Ошибки, теория», Энциклопедия математики, EMS Press, 2001 [1994]
внешняя ссылка
СМИ, связанные с Ошибки и остатки в Wikimedia Commons

В этой серии мы внимательно рассмотрим алгоритм машинного обучения и изучим плюсы и минусы каждого алгоритма. Мы рассмотрим алгоритмы вместе с математикой, лежащей в основе алгоритма.
Во-первых, давайте проясним некоторые основные термины, используемые в машинном обучении.
- Контролируемый алгоритм ML: Те алгоритмы, которые используют помеченные данные, известны как контролируемые алгоритмы ml. Контролируемые алгоритмы ml широко используются для двух задач: классификации и регрессии.
- Классификация: Когда задача состоит в том, чтобы классифицировать объекты выборки по определенным категориям (целевая переменная), тогда это называется классификацией. Например, определение того, является ли электронное письмо спамом или нет.
- Регрессия: когда задача состоит в том, чтобы предсказать непрерывную переменную (целевую переменную), тогда это называется регрессией. Например, прогнозирование цен на жилье.
- Неконтролируемый алгоритм ML: те алгоритмы, которые используют немаркированные данные, известны как неконтролируемые алгоритмы ml. Для кластеризации используется неконтролируемый алгоритм.
- Кластеризация: задача поиска групп в заданных немаркированных данных известна как кластеризация.
- Ошибка: разница между фактическим и прогнозируемым значением.
- Градиентный спуск: механизм обновления параметров модели таким образом, чтобы генерировать минимальное значение функции ошибки.
Что такое линейная регрессия в машинном обучении?
Линейная регрессия — это тип контролируемого алгоритма машинного обучения, который используется для прогнозирования непрерывной числовой переменной, известной как цель. Это один из самых простых алгоритмов машинного обучения. Он называется «линейным», потому что алгоритм предполагает, что взаимосвязь между входными характеристиками (также известными как независимые переменные) и выходной переменной (также известной как зависимая или целевая переменная) является линейной. Другими словами, алгоритм пытается найти прямую линию (или гиперплоскость в случае нескольких входных объектов), которая наилучшим образом соответствует данным.
Типы линейной регрессии:
Простая линейная регрессия:
Линейная регрессия известна как простая линейная регрессия, когда прогнозирование выходного значения выполняется с использованием одной входной функции. Мы можем провести линию между зависимыми и независимыми переменными в 2D-пространстве, когда задан один входной признак. здесь b0 — точка пересечения, b1 — коэффициент, x1, x2,…, xn — входные признаки, а y — выходная переменная.
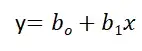
Множественная линейная регрессия:
Линейная регрессия известна как множественная линейная регрессия, когда прогнозирование выходной переменной выполняется с использованием нескольких входных признаков. Мы можем нарисовать плоскость между зависимой и независимой переменными в 3D-пространстве, когда заданы только два входных объекта. В более высоких измерениях визуализация становится затруднительной, но интуиция заключается в том, чтобы найти гиперплоскость в более высоких измерениях. здесь b0 — это перехват, а b1, b2, b3, ......., bn-1, bn известны как коэффициенты, а x1, x2,..., xn известны как входные характеристики, а y — переменная результата.
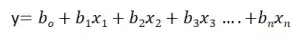
К этому моменту мы поняли, что линейная регрессия пытается построить линейную границу, но как она это делает?
Как он найдет идеальную линию, которая разделяет данные два класса?
Как указано в уравнении, b0 известен как перехват, а b1, b2,...., bn известны как коэффициенты линейной регрессии, и теперь цель состоит в том, чтобы найти ту линейную границу, которая минимизирует функцию ошибки. Функция ошибки представляет собой квадрат суммы разностей между прогнозируемыми и фактическими значениями целевой переменной. Если мы не сведем ошибку в квадрат, то положительные и отрицательные моменты будут компенсировать друг друга.
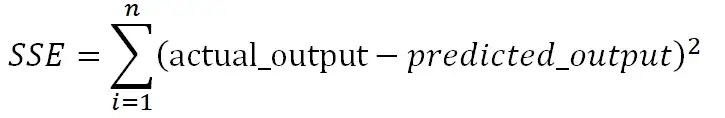
Нам нужно найти коэффициенты и перехваты для линейной регрессии таким образом, чтобы сумма квадратов ошибок (SSE) была минимизирована. Градиентный спуск — один из самых популярных методов, который используется для нахождения оптимальных коэффициентов для ml и алгоритмов глубокого обучения.
В приведенном ниже разделе мы обучим модель на базе данных страхования, где мы должны спрогнозировать расходы с учетом входных данных: возраст, пол, ИМТ, расходы на больницу, количество прошлых консультаций и т.д.
Реализация на Python:
Вы можете использовать библиотеку sklearn на python для обучения и тестирования модели линейной регрессии. Мы будем использовать набор данных insurance.csv для обучения модели линейной регрессии. Некоторые этапы предварительной обработки выполняются для описания данных, обработки пропущенных значений и проверки допущений линейной регрессии.
Шаг 1: Загрузите все необходимые библиотеки и наборы данных, используя библиотеку pandas.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF
from sklearn.metrics import classification_report
insurance=pd.read_csv('new_insurance_data.csv')
insurance.head()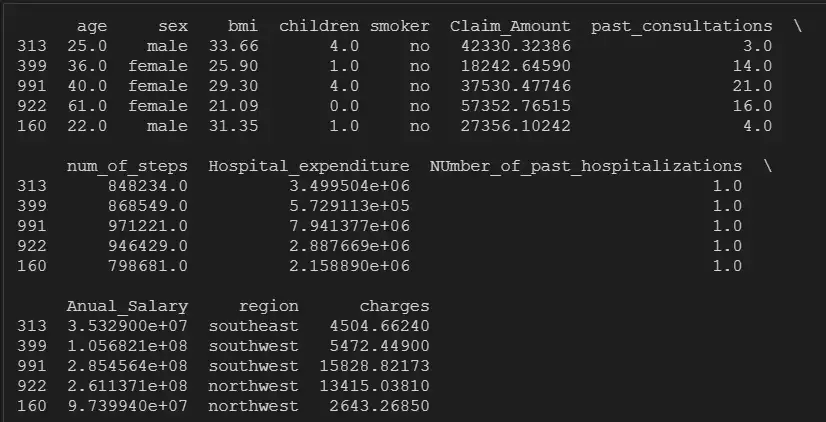
Шаг 2: Проверьте нулевые значения, форму и тип данных переменных:
# checks for non-null entries, size and datatype
insurance.info()
Мы можем отдельно проверить количество нулей для каждой функции, используя df.isna().sum():
insurance.isnull().sum()
# helps me to check for null values
Шаг 3. Заполните пропущенные значения
Мы можем заполнить недостающие значения объектов объектного типа, используя режим, а объектов целочисленного типа — среднее значение или медиану.
# calculating mode for object data type features which will be used to fill missing values.
# We have 3 features which are of object type
print(f"mode of sex feature: {insurance['sex'].mode()[0]}")
print(f"mode of region feature: {insurance['region'].mode()[0]}")
print(f"mode of smoker feature: {insurance['smoker'].mode()[0]}")
# describe() function will give the descriptive statistics for all numerical features
insurance.describe().transpose()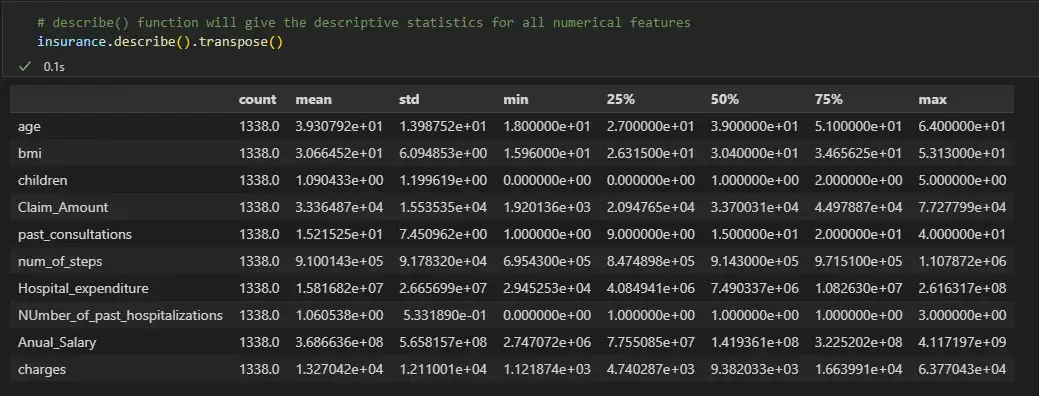
Мы видим, что для числовых признаков среднее и медиана почти одинаковы. Поэтому теперь мы заменим нулевые значения числовых признаков их медианой, а нулевые значения категориальных переменных — их режимом.
for col_name in list(insurance.columns):
if insurance[col_name].dtypes=='object':
# filling null values with mode for object type features
insurance[col_name] = insurance[col_name].fillna(insurance[col_name].mode()[0])
else:
# filling null values with mean for numeric type features
insurance[col_name] = insurance[col_name].fillna(insurance[col_name].median())
# Now the null count for each feature is zero
print("After filling null values:")
print(insurance.isna().sum())
Шаг 4: Анализ выбросов
Мы построим прямоугольную диаграмму для всех числовых характеристик, кроме целевых переменных зарядов.
i = 1
plt.figure(figsize=(16,15))
for col_name in list(insurance.columns):
# total 9 box plots will be plotted, therefore 3*3 grid is taken
if((insurance[col_name].dtypes=='int64' or insurance[col_name].dtypes=='float64') and col_name != 'charges'):
plt.subplot(3,3, i)
plt.boxplot(insurance[col_name])
plt.xlabel(col_name)
plt.ylabel('count')
plt.title(f"Box plot for {col_name}")
i += 1
plt.show()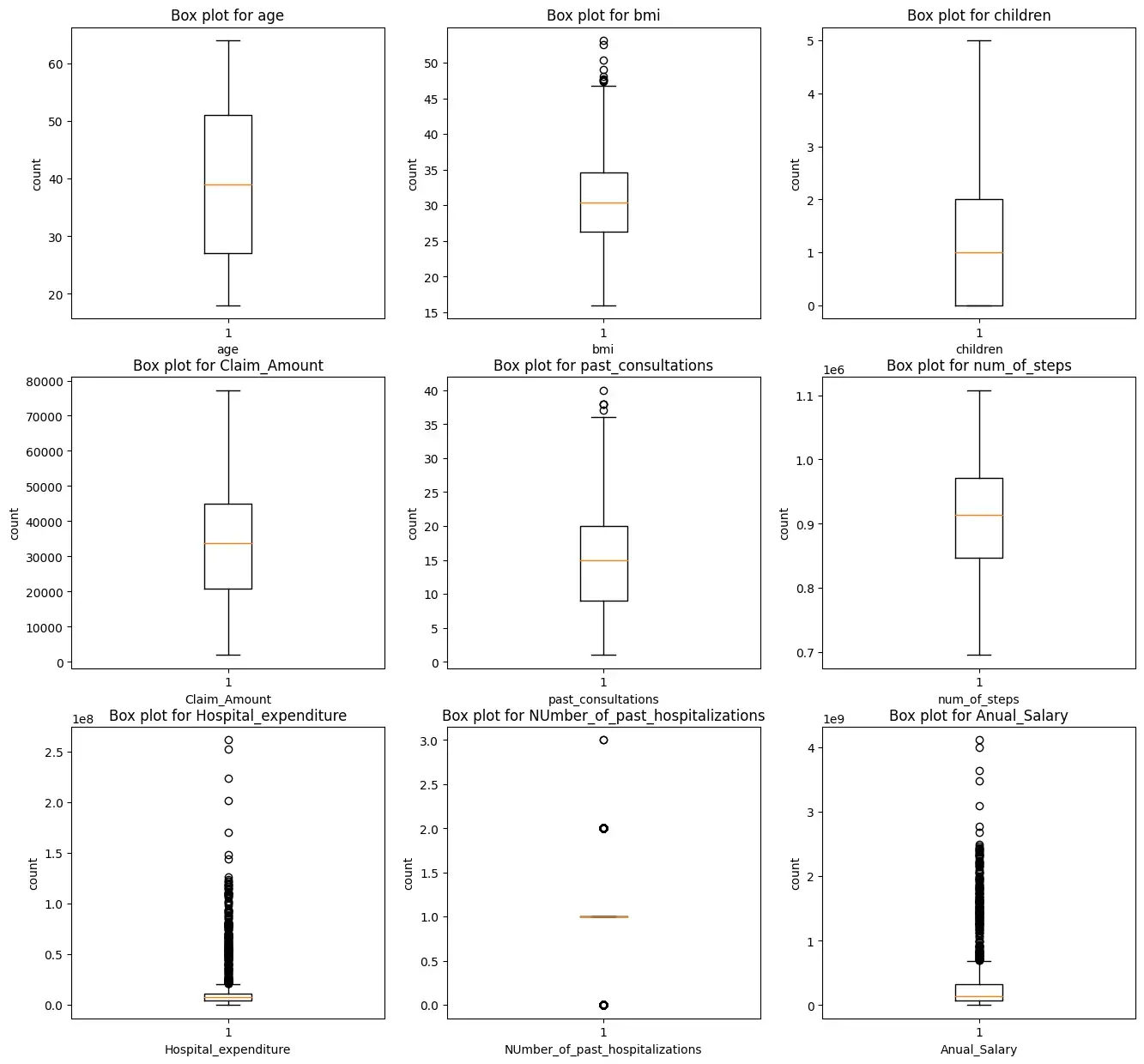
Мы видим, что характеристики ‘bmi’, ‘Hospital_expenditure’ и ‘Number_of_past_hospitalizations’ имеют выбросы. Мы удалим эти выбросы:
outliers_features = ['bmi', 'Hospital_expenditure', 'Anual_Salary', 'past_consultations']
for col_name in outliers_features:
Q3 = insurance[col_name].quantile(0.75)
Q1 = insurance[col_name].quantile(0.25)
IQR = Q3 - Q1
upper_limit = Q3 + 1.5*IQR
lower_limit = Q1 - 1.5*IQR
prev_size = len(insurance)
insurance = insurance[(insurance[col_name] >= lower_limit) & (insurance[col_name] <= upper_limit)]
cur_size = len(insurance)
print(f"dropped {prev_size - cur_size} rows for {col_name} due to presence of outliers")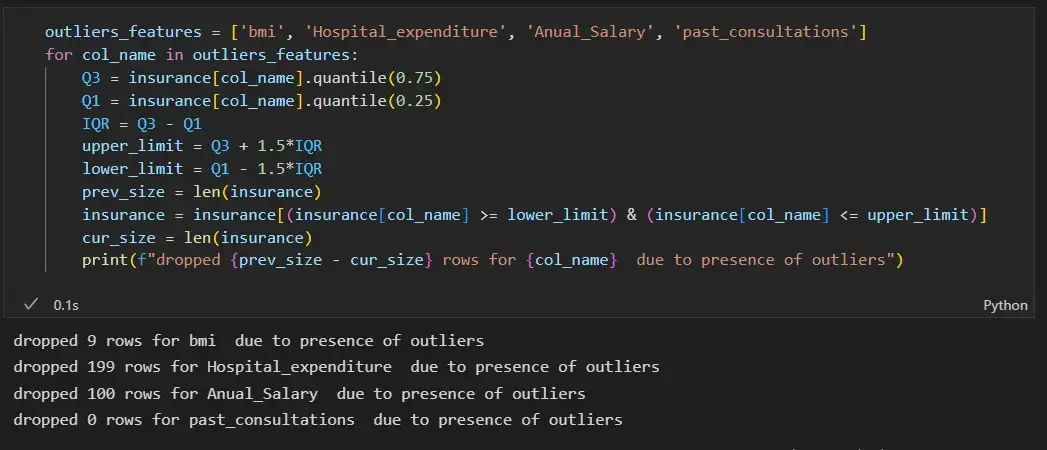
Шаг 5: Проверьте корреляцию:
Существует корреляция между age & charges, age & Anual_salary и т. д., поскольку их корреляция больше 0,5.
import seaborn as sns
sns.heatmap(insurance.corr(),cmap='gist_rainbow',annot=True)
plt.show()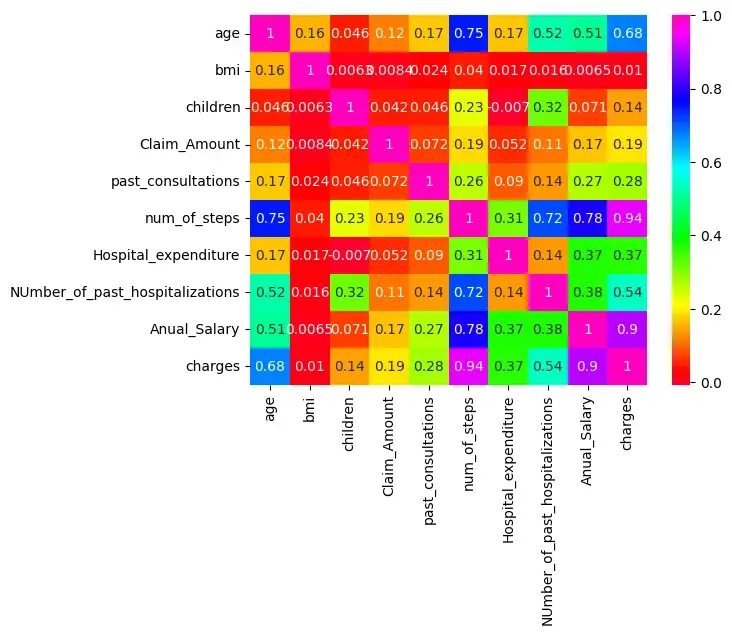
Мы проверим наличие мультиколлинеарности среди признаков:
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)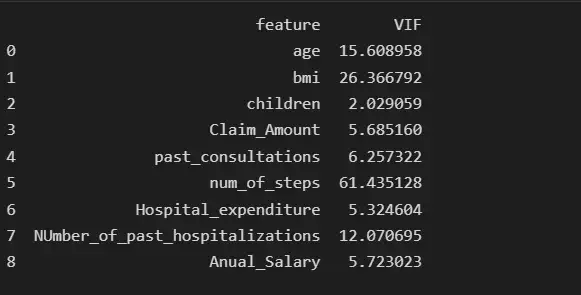
Мы видим, что функция num_of_steps имеет самую высокую коллинеарность, равную 61,43, поэтому мы удалим функцию num_of_steps и снова проверим оценку VIF.
# deleting num_of_steps feature
insurance.drop('num_of_steps', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)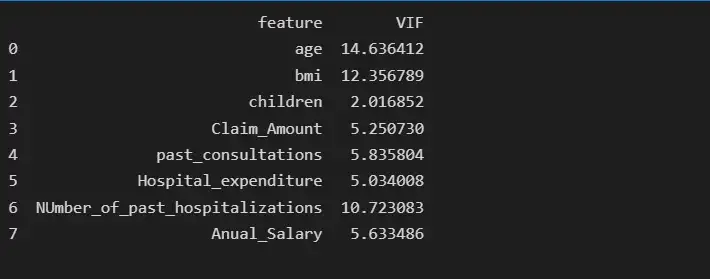
После удаления функции num_of_steps age имеет самую высокую коллинеарность, равную 14,63, поэтому мы удалим функцию age и снова проверим оценку VIF.
# deleting age feature
insurance.drop('age', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)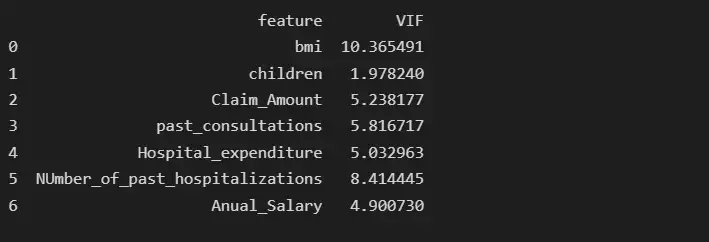
После удаления функции возраста BMI имеет самую высокую коллинеарность, равную 10,36, поэтому мы удалим BMI и снова проверим показатель VIF.
# deleting bmi feature
insurance.drop('bmi', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)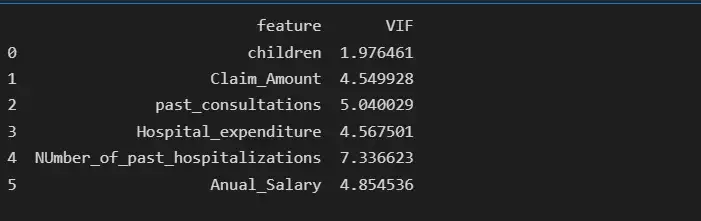
Шаг 6: Разделение входных функций и целевой переменной:
x=insurance.loc[:,['children','Claim_Amount','past_consultations','Hospital_expenditure','NUmber_of_past_hospitalizations','Anual_Salary']]
y=insurance.loc[:,'charges']
x_train, x_test, y_train, y_test=train_test_split(x,y,train_size=0.8, random_state=0)
print("length of train dataset: ",len(x_train) )
print("length of test dataset: ",len(x_test) )
Шаг 7: Обучение модели линейной регрессии на наборе поездов и ее оценка на тестовом наборе данных:
from sklearn.linear_model import LinearRegression
from sklearn.metrics import classification_report, recall_score, r2_score, f1_score, accuracy_score
model = LinearRegression()
# train the model
model.fit(x_train, y_train)
print("trained model coefficients:", model.coef_, " and intercept is: ", model.intercept_)
# model.intercept_ is b0 term in linear boundary equation, and model.coef_ is
# the array of weights assigned to ['children','Claim_Amount','past_consultations','Hospital_expenditure',
# 'NUmber_of_past_hospitalizations','Anual_Salary'] respectively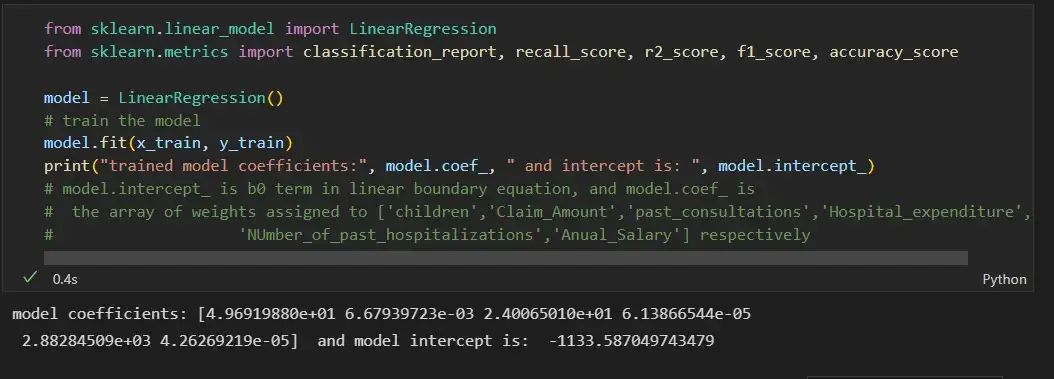
y_pred = model.predict(x_test)
error_pred=pd.DataFrame(columns={'Actual_data','Prediction_data'})
error_pred['Prediction_data'] = y_pred
error_pred['Actual_data'] = y_test
error_pred["error"] = y_test - y_pred
sns.distplot(error_pred['error'])
plt.show()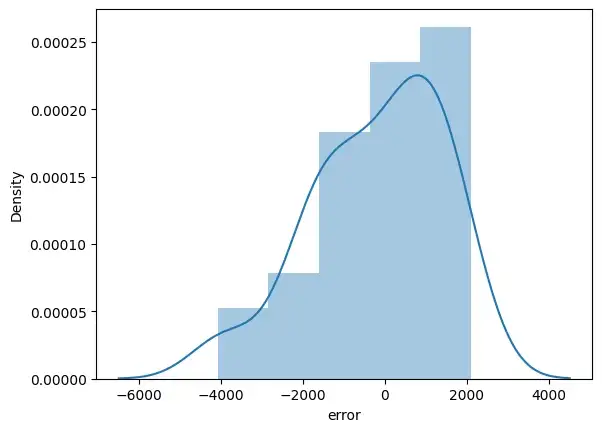
Мы можем построить остаточные графики между фактической целью и остатками или ошибками:
sns.scatterplot(x = y_test,y = (y_test - y_pred), c = 'g', s = 40)
plt.hlines(y = 0, xmin = 0, xmax=20000)
plt.title("residual plot")
plt.xlabel("actural target")
plt.ylabel("residula error")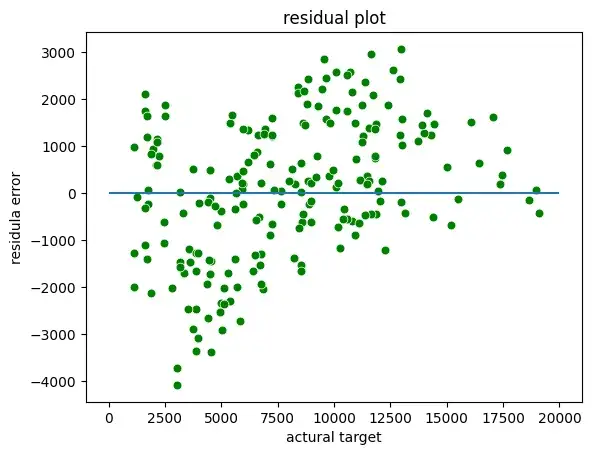
Оценка R-квадрата:
R-квадрат известен как коэффициент детерминации. R Squared — это статистическая мера, которая представляет долю дисперсии зависимой переменной, объясненную независимыми переменными в регрессии. Это значение находится в диапазоне от 0 до 1. Значение «1» указывает, что предиктор полностью учитывает все изменения в Y. Значение «0» указывает, что предиктор «x» не учитывает никаких изменений в «y». Значение R-Squared содержит три термина SSE, SSR и SST.
SSE — это сумма квадратов ошибок. Его также называют остаточной суммой квадратов (RSS).
SSR — это сумма квадратов регрессии.
SST (Сумма в квадрате) — это квадрат разницы между наблюдаемой зависимой переменной и ее средним значением.

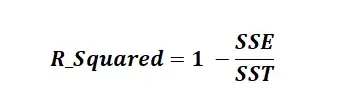
# check for model performance
print(f'r2 score of trained model: {r2_score(y_pred=y_pred, y_true= y_test)}')
Предположения линейной регрессии
- Линейная связь: линейная регрессия предполагает линейную связь между прогнозируемой переменной и независимой переменной. Вы можете использовать точечную диаграмму, чтобы визуализировать взаимосвязь между независимой переменной и зависимой переменной в 2D-пространстве.
- Небольшая мультиколлинеарность или отсутствие мультиколлинеарности между функциями: линейная регрессия предполагает, что функции должны быть независимыми друг от друга, т. Е. Никакой корреляции между функциями. Вы можете использовать функцию VIF, чтобы найти значение мультиколлинеарности признаков. Общее предположение гласит, что если значение признака VIF больше 5, то признаки сильно коррелированы.
- Однородность: линейная регрессия предполагает, что члены ошибок имеют постоянную дисперсию, т. е. разброс членов ошибок должен быть постоянным. Это предположение можно проверить, построив остаточную диаграмму. Если предположение нарушается, то точки образуют форму воронки, в противном случае они будут постоянными.
- Нормальность: линейная регрессия предполагает, что каждая функция данного набора данных следует нормальному распределению. Вы можете строить гистограммы и графики KDE для каждой функции, чтобы проверить, нормально ли они распределены или нет.
- Ошибка: линейная регрессия предполагает, что условия ошибки также должны быть нормально распределены. Вы можете строить гистограммы, а KDE строит графики ошибок, чтобы проверить, нормально ли они распределены или нет.
Вот ссылка GitHub для кода и набора данных.
В статистике и оптимизации ошибки и остатки тесно связаны и легко запутанные меры отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». ошибка (или возмущение ) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинного значения интересующей величины (например, среднего генерального значения), и остаток наблюдаемого значения представляет собой разность между наблюдаемым значением и оценочным значением представляющей интерес величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибками регрессии и остатками регрессии, и где они приводят к концепции студентизированных остатков.
Содержание
- 1 Введение
- 2 В одномерных распределениях
- 2.1 Замечание
- 3 Регрессии
- 4 Другие варианты использования слова «ошибка» в статистике
- 5 См. Также
- 6 Ссылки
- 7 Внешние ссылки
Введение
Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее этого распределения. (так называемая локационная модель ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
A статистическая ошибка (или нарушение ) — это величина, на которую наблюдение отличается от его ожидаемого значения, последнее основано на всей генеральной совокупности из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.
A невязка (или аппроксимирующее отклонение), с другой стороны, представляет собой наблюдаемую оценку ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. среднее значение выборки может служить хорошей оценкой среднего значения генеральной совокупности. Тогда у нас есть:
- Разница между ростом каждого человека в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой, тогда как
- разница между ростом каждого человека в выборке и наблюдаемой выборкой среднее — это остаток.
Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки не обязательно независимы. Статистические ошибки, с другой стороны, независимы, и их сумма в случайной выборке почти наверняка не равна нулю.
Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t-статистика или, в более общем смысле, стьюдентизированные остатки.
в одномерном распределении
Если мы предположим нормально распределенную совокупность со средним μ и стандартным отклонением σ и независимо выбираем людей, тогда мы имеем
- X 1,…, X n ∼ N (μ, σ 2) { displaystyle X_ {1}, dots, X_ {n} sim N ( mu, sigma ^ {2}) ,}
и выборочное среднее
- X ¯ = X 1 + ⋯ + X nn { displaystyle { overline {X}} = {X_ { 1} + cdots + X_ {n} over n}}
— случайная величина, распределенная так, что:
- X ¯ ∼ N (μ, σ 2 n). { displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}
Тогда статистические ошибки
- ei = X i — μ, { displaystyle e_ {i} = X_ {i} — mu, ,}
с ожидаемыми значениями нуля, тогда как остатки равны
- ri = X i — X ¯. { displaystyle r_ {i} = X_ {i} — { overline {X}}.}
Сумма квадратов статистических ошибок, деленная на σ, имеет хи -квадратное распределение с n степенями свободы :
- 1 σ 2 ∑ i = 1 nei 2 ∼ χ n 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.}
Однако это количество не наблюдается, так как среднее значение для генеральной совокупности неизвестно. Сумма квадратов остатков, с другой стороны, является наблюдаемой. Частное этой суммы по σ имеет распределение хи-квадрат только с n — 1 степенями свободы:
- 1 σ 2 ∑ i = 1 n r i 2 ∼ χ n — 1 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} r_ {i} ^ {2} sim chi _ {n-1} ^ { 2}.}
Эта разница между n и n — 1 степенями свободы приводит к поправке Бесселя для оценки выборочной дисперсии генеральной совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Замечание
Примечательно, что сумма квадратов остатков и выборочного среднего могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :
- T = X ¯ n — μ 0 S n / n, { displaystyle T = { frac {{ overline {X}} _ {n} — mu _ {0}} {S_ {n} / { sqrt {n}}}},}
где X ¯ n — μ 0 { displaystyle { overline {X}} _ {n} — mu _ {0}}


- Var (X ¯ n) = σ 2 n { displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}
Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения генеральной совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяет. Это удачно, потому что это означает, что, хотя мы не знаем σ, мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».
Регрессии
В регрессионном анализе различие между ошибками и остатками является тонким и важным, и приводит к концепции стьюдентизированных остатков. Для ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью. Если все остатки равны или не разветвляются, они проявляют гомоскедастичность.
Однако терминологическое различие возникает в выражении среднеквадратическая ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатков, а не ненаблюдаемых ошибок. Если эту сумму квадратов разделить на n, количество наблюдений, результатом будет среднее квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n, где df — число степеней свободы (n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они одинаковы, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равно n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с.).
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии , где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии соответствуют конечным точкам лучше среднего. Это также отражено в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, нужно скорректировать остатки на ожидаемую изменчивость остатков, что называется стьюдентизацией. Это особенно важно в случае обнаружения выбросов, когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другое использование слова «ошибка» в статистике
Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значение. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Среднеквадратичная ошибка или Среднеквадратичная ошибка (MSE) и Среднеквадратичная ошибка (RMSE) относятся к величине, на которую значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).
Сумма квадратов ошибок (SSE или SSe), обычно сокращенно SSE или SS e, относится к остаточной сумме квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой методом наименьших квадратов, где коэффициенты регрессии выбираются так, чтобы сумма квадратов минимально (т.е. его производная равна нулю).
Аналогично, сумма абсолютных ошибок (SAE) является суммой абсолютных значений остатков, которая минимизирована в наименьшие абсолютные отклонения подход к регрессии.
См. также
Портал математики
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадраты
- Инновация (обработка сигналов)
- Неподходящая сумма квадратов
- Погрешность
- Средняя абсолютная погрешность
- Погрешность наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Стьюдентизированная невязка
- Ошибки типа I и типа II
Ссылки
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Проверено 23 февраля 2013 г.
- Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 г.
- , Энциклопедия математики, EMS Press, 2001 [1994]
Внешние ссылки
СМИ, связанные с ошибками и остатками на Викимедиа Commons
Оценка значимости параметров уравнения парной линейной регрессии
Парная регрессия представляет собой регрессию между двумя переменными
—у и х, т.е. модель вида 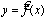
, где у — результативный признак,т.е зависимая переменная; х — признак-фактор.
Линейная регрессия сводится к нахождению уравнения вида 
Уравнение вида 
Построение линейной регрессии сводится к оценке ее параметров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его величина показывает
среднее изменение результата с изменением фактора на одну единицу.
Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а 0,
то относительное изменение результата происходит медленнее, чем изменение
проверка качества найденных параметров и всей модели в целом:
-Оценка значимости коэффициента регрессии (b) и коэффициента корреляции
-Оценка значимости всего уравнения регрессии. Коэффициент детерминации
Уравнение регрессии всегда дополняется показателем тесноты связи. При
использовании линейной регрессии в качестве такого показателя выступает
линейный коэффициент корреляции rxy. Существуют разные
модификации формулы линейного коэффициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy
≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем
ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к
линейной. Если r в точности =1или -1 все точки лежат на одной прямой.
Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и
в модели факторов.
МНК позволяет получить такие оценки параметров а и b, которых
сумма квадратов отклонений фактических значений результативного признака
(у) от расчетных (теоретических)

всего множества линий линия регрессии на графике выбирается так, чтобы сумма
квадратов расстояний по вертикали между точками и этой линией была бы
минимальной.
Решается система нормальных уравнений
ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия
Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен
нулю, т. е. b = 0, и следовательно, фактор х не оказывает
влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии.
Центральное место в нем занимает разложение общей суммы квадратов отклонений
переменной у от средне го значения у на две части —
«объясненную» и «необъясненную»:


отклонения объясненная регрессией
— остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степеней свободы, т.
е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для
образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий): 
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не
отличаются друг от друга. Для Н0 необходимо опровержение, чтобы
факторная дисперсия превышала остаточную в несколько раз. Английским
статистиком Снедекором разработаны таблицы критических значений F-отношений
при разных уровнях существенности нулевой гипотезы и различном числе степеней
свободы. Табличное значение F-критерия — это максимальная величина отношения
дисперсий, которая может иметь место при случайном их расхождении для данного
уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения
признается достоверным, если о больше табличного. В этом случае нулевая
гипотеза об отсутствии связи признаков отклоняется и делается вывод о
существенности этой связи: Fфакт > Fтабл Н0
Если же величина окажется меньше табличной Fфакт ‹, Fтабл
, то вероятность нулевой гипотезы выше заданного уровня и она не может быть
отклонена без серьезного риска сделать неправильный вывод о наличии связи. В
этом случае уравнение регрессии считается статистически незначимым. Но
Пример нахождения статистической значимости коэффициентов регрессии
Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: 
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:

где 
μa – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии: 
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий: 
Для линейного парного уравнения регрессии: 
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ( b =0) = t (r=0).
Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 69 | 124 | 4761 | 15376 | 8556 | 128.48 | 491.36 | 20.11 | 367.36 |
| 83 | 133 | 6889 | 17689 | 11039 | 141.4 | 173.36 | 70.56 | 26.69 |
| 92 | 146 | 8464 | 21316 | 13432 | 149.7 | 0.03 | 13.71 | 14.69 |
| 97 | 153 | 9409 | 23409 | 14841 | 154.32 | 46.69 | 1.73 | 78.03 |
| 88 | 138 | 7744 | 19044 | 12144 | 146.01 | 66.69 | 64.21 | 0.03 |
| 93 | 159 | 8649 | 25281 | 14787 | 150.63 | 164.69 | 70.13 | 23.36 |
| 74 | 145 | 5476 | 21025 | 10730 | 133.1 | 1.36 | 141.68 | 200.69 |
| 79 | 152 | 6241 | 23104 | 12008 | 137.71 | 34.03 | 204.21 | 84.03 |
| 105 | 168 | 11025 | 28224 | 17640 | 161.7 | 476.69 | 39.74 | 283.36 |
| 99 | 154 | 9801 | 23716 | 15246 | 156.16 | 61.36 | 4.67 | 117.36 |
| 85 | 127 | 7225 | 16129 | 10795 | 143.25 | 367.36 | 263.91 | 10.03 |
| 94 | 155 | 8836 | 24025 | 14570 | 151.55 | 78.03 | 11.91 | 34.03 |
| 1058 | 1754 | 94520 | 258338 | 155788 | 1754 | 1961.67 | 906.57 | 1239.67 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a — tтабл·S a; a + tтабл·Sa)
(0.4325;1.4126)
(b — tтабл·S b; b + tтабл·Sb)
(21.3389;108.3164)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Пример №2 . По территориям региона приводятся данные за 199Х г.;
| Среднедневная заработная плата, руб., у | ||
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.
| y 2 | x·y | y(x) | (y i — y ) 2 | (y-y(x)) 2 | (x i — x ) 2 | |y-y x |:y | |||
| 78 | 133 | 6084 | 17689 | 10374 | 148,77 | 517,56 | 248,7 | 57,51 | 0,1186 |
| 82 | 148 | 6724 | 21904 | 12136 | 152,45 | 60,06 | 19,82 | 12,84 | 0,0301 |
| 87 | 134 | 7569 | 17956 | 11658 | 157,05 | 473,06 | 531,48 | 2,01 | 0,172 |
| 79 | 154 | 6241 | 23716 | 12166 | 149,69 | 3,06 | 18,57 | 43,34 | 0,028 |
| 89 | 162 | 7921 | 26244 | 14418 | 158,89 | 39,06 | 9,64 | 11,67 | 0,0192 |
| 106 | 195 | 11236 | 38025 | 20670 | 174,54 | 1540,56 | 418,52 | 416,84 | 0,1049 |
| 67 | 139 | 4489 | 19321 | 9313 | 138,65 | 280,56 | 0,1258 | 345,34 | 0,0026 |
| 88 | 158 | 7744 | 24964 | 13904 | 157,97 | 5,06 | 0,0007 | 5,84 | 0,0002 |
| 73 | 152 | 5329 | 23104 | 11096 | 144,17 | 14,06 | 61,34 | 158,34 | 0,0515 |
| 87 | 162 | 7569 | 26244 | 14094 | 157,05 | 39,06 | 24,46 | 2,01 | 0,0305 |
| 76 | 159 | 5776 | 25281 | 12084 | 146,93 | 10,56 | 145,7 | 91,84 | 0,0759 |
| 115 | 173 | 13225 | 29929 | 19895 | 182,83 | 297,56 | 96,55 | 865,34 | 0,0568 |
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 3280,25 | 1574,92 | 2012,92 | 0,6902 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит:
tкрит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-ta)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Парная линейная регрессия. Задачи регрессионного анализа
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Уравнение парной линейной регрессии и метод наименьших квадратов
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:
- прямая парной линейной регрессии проходит через точку ;
- среднее значение отклонений равна нулю: ;
- значения и не связаны: .
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,
— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
—
остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .
Можем убедиться, что выполняется закономерность SSR = SST — SSE :
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.
Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .
Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .
Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Задачи регрессионного анализа
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,
где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
http://math.semestr.ru/corel/prim3.php
http://function-x.ru/statistics_regression1.html
Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.
Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:
1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).
- SST = Σ(y i – y ) 2
2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).
- SSE = Σ(ŷ i – y i ) 2
Между этими тремя показателями существует следующая зависимость:
SST = SSR + SSE
Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.
SSR, SST и R-квадрат
R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
Используя SSR и SST, мы можем рассчитать R-квадрат как:
R-квадрат = SSR / SST
Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:
R-квадрат = 137,5/156 = 0,8814
Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.
Расчет SST, SSR, SSE: пошаговый пример
Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:
Оценка = 66,615 + 5,0769 * (часы)
Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:
Шаг 1: Рассчитайте среднее значение переменной ответа.
Среднее значение переменной отклика ( y ) оказывается равным 81 .
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.
Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.
Например, предполагаемая оценка экзамена для студента, который учился один час, такова:
Оценка = 66,615 + 5,0769*(1) = 71,69 .
Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:
Шаг 3: Рассчитайте общую сумму квадратов (SST).
Далее мы можем вычислить общую сумму квадратов.
Например, сумма квадратов для первого ученика равна:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:
Сумма квадратов получается 316 .
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).
Далее мы можем вычислить сумму квадратов регрессии.
Например, сумма квадратов регрессии для первого ученика равна:
(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .
Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:
Сумма квадратов регрессии оказывается равной 279,23 .
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).
Далее мы можем вычислить сумму квадратов ошибок.
Например, ошибка суммы квадратов для первого ученика:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:
Мы можем проверить, что SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:
- R-квадрат = SSR / SST
- R-квадрат = 279,23/316
- R-квадрат = 0,8836
Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.
Дополнительные ресурсы
Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:
Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE
регрессии,
нелинейные по оцениваемым параметрам:
-
степенная
Портал математики
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадраты
- Инновация (обработка сигналов)
- Неподходящая сумма квадратов
- Погрешность
- Средняя абсолютная погрешность
- Погрешность наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Стьюдентизированная невязка
- Ошибки типа I и типа II
Ссылки
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Проверено 23 февраля 2013 г.
- Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 г.
- , Энциклопедия математики, EMS Press, 2001 [1994]
Внешние ссылки
СМИ, связанные с ошибками и остатками на Викимедиа Commons
Оценка значимости параметров уравнения парной линейной регрессии
Парная регрессия представляет собой регрессию между двумя переменными
—у и х, т.е. модель вида 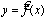
, где у — результативный признак,т.е зависимая переменная; х — признак-фактор.
Линейная регрессия сводится к нахождению уравнения вида 
Уравнение вида 
Построение линейной регрессии сводится к оценке ее параметров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его величина показывает
среднее изменение результата с изменением фактора на одну единицу.
Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а 0,
то относительное изменение результата происходит медленнее, чем изменение
проверка качества найденных параметров и всей модели в целом:
-Оценка значимости коэффициента регрессии (b) и коэффициента корреляции
-Оценка значимости всего уравнения регрессии. Коэффициент детерминации
Уравнение регрессии всегда дополняется показателем тесноты связи. При
использовании линейной регрессии в качестве такого показателя выступает
линейный коэффициент корреляции rxy. Существуют разные
модификации формулы линейного коэффициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy
≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем
ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к
линейной. Если r в точности =1или -1 все точки лежат на одной прямой.
Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и
в модели факторов.
МНК позволяет получить такие оценки параметров а и b, которых
сумма квадратов отклонений фактических значений результативного признака
(у) от расчетных (теоретических)

всего множества линий линия регрессии на графике выбирается так, чтобы сумма
квадратов расстояний по вертикали между точками и этой линией была бы
минимальной.
Решается система нормальных уравнений
ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия
Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен
нулю, т. е. b = 0, и следовательно, фактор х не оказывает
влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии.
Центральное место в нем занимает разложение общей суммы квадратов отклонений
переменной у от средне го значения у на две части —
«объясненную» и «необъясненную»:


отклонения объясненная регрессией
— остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степеней свободы, т.
е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для
образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий): 
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не
отличаются друг от друга. Для Н0 необходимо опровержение, чтобы
факторная дисперсия превышала остаточную в несколько раз. Английским
статистиком Снедекором разработаны таблицы критических значений F-отношений
при разных уровнях существенности нулевой гипотезы и различном числе степеней
свободы. Табличное значение F-критерия — это максимальная величина отношения
дисперсий, которая может иметь место при случайном их расхождении для данного
уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения
признается достоверным, если о больше табличного. В этом случае нулевая
гипотеза об отсутствии связи признаков отклоняется и делается вывод о
существенности этой связи: Fфакт > Fтабл Н0
Если же величина окажется меньше табличной Fфакт ‹, Fтабл
, то вероятность нулевой гипотезы выше заданного уровня и она не может быть
отклонена без серьезного риска сделать неправильный вывод о наличии связи. В
этом случае уравнение регрессии считается статистически незначимым. Но
Пример нахождения статистической значимости коэффициентов регрессии
Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: 
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:

где 
μa – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии: 
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий: 
Для линейного парного уравнения регрессии: 
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ( b =0) = t (r=0).
Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 69 | 124 | 4761 | 15376 | 8556 | 128.48 | 491.36 | 20.11 | 367.36 |
| 83 | 133 | 6889 | 17689 | 11039 | 141.4 | 173.36 | 70.56 | 26.69 |
| 92 | 146 | 8464 | 21316 | 13432 | 149.7 | 0.03 | 13.71 | 14.69 |
| 97 | 153 | 9409 | 23409 | 14841 | 154.32 | 46.69 | 1.73 | 78.03 |
| 88 | 138 | 7744 | 19044 | 12144 | 146.01 | 66.69 | 64.21 | 0.03 |
| 93 | 159 | 8649 | 25281 | 14787 | 150.63 | 164.69 | 70.13 | 23.36 |
| 74 | 145 | 5476 | 21025 | 10730 | 133.1 | 1.36 | 141.68 | 200.69 |
| 79 | 152 | 6241 | 23104 | 12008 | 137.71 | 34.03 | 204.21 | 84.03 |
| 105 | 168 | 11025 | 28224 | 17640 | 161.7 | 476.69 | 39.74 | 283.36 |
| 99 | 154 | 9801 | 23716 | 15246 | 156.16 | 61.36 | 4.67 | 117.36 |
| 85 | 127 | 7225 | 16129 | 10795 | 143.25 | 367.36 | 263.91 | 10.03 |
| 94 | 155 | 8836 | 24025 | 14570 | 151.55 | 78.03 | 11.91 | 34.03 |
| 1058 | 1754 | 94520 | 258338 | 155788 | 1754 | 1961.67 | 906.57 | 1239.67 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a — tтабл·S a; a + tтабл·Sa)
(0.4325;1.4126)
(b — tтабл·S b; b + tтабл·Sb)
(21.3389;108.3164)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Пример №2 . По территориям региона приводятся данные за 199Х г.;
| Среднедневная заработная плата, руб., у | ||
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.
| y 2 | x·y | y(x) | (y i — y ) 2 | (y-y(x)) 2 | (x i — x ) 2 | |y-y x |:y | |||
| 78 | 133 | 6084 | 17689 | 10374 | 148,77 | 517,56 | 248,7 | 57,51 | 0,1186 |
| 82 | 148 | 6724 | 21904 | 12136 | 152,45 | 60,06 | 19,82 | 12,84 | 0,0301 |
| 87 | 134 | 7569 | 17956 | 11658 | 157,05 | 473,06 | 531,48 | 2,01 | 0,172 |
| 79 | 154 | 6241 | 23716 | 12166 | 149,69 | 3,06 | 18,57 | 43,34 | 0,028 |
| 89 | 162 | 7921 | 26244 | 14418 | 158,89 | 39,06 | 9,64 | 11,67 | 0,0192 |
| 106 | 195 | 11236 | 38025 | 20670 | 174,54 | 1540,56 | 418,52 | 416,84 | 0,1049 |
| 67 | 139 | 4489 | 19321 | 9313 | 138,65 | 280,56 | 0,1258 | 345,34 | 0,0026 |
| 88 | 158 | 7744 | 24964 | 13904 | 157,97 | 5,06 | 0,0007 | 5,84 | 0,0002 |
| 73 | 152 | 5329 | 23104 | 11096 | 144,17 | 14,06 | 61,34 | 158,34 | 0,0515 |
| 87 | 162 | 7569 | 26244 | 14094 | 157,05 | 39,06 | 24,46 | 2,01 | 0,0305 |
| 76 | 159 | 5776 | 25281 | 12084 | 146,93 | 10,56 | 145,7 | 91,84 | 0,0759 |
| 115 | 173 | 13225 | 29929 | 19895 | 182,83 | 297,56 | 96,55 | 865,34 | 0,0568 |
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 3280,25 | 1574,92 | 2012,92 | 0,6902 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит:
tкрит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-ta)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Парная линейная регрессия. Задачи регрессионного анализа
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Уравнение парной линейной регрессии и метод наименьших квадратов
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:
- прямая парной линейной регрессии проходит через точку ;
- среднее значение отклонений равна нулю: ;
- значения и не связаны: .
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,
— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
—
остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .
Можем убедиться, что выполняется закономерность SSR = SST — SSE :
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.
Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .
Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .
Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Задачи регрессионного анализа
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,
где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
http://math.semestr.ru/corel/prim3.php
http://function-x.ru/statistics_regression1.html
Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.
Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:
1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).
- SST = Σ(y i – y ) 2
2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).
- SSE = Σ(ŷ i – y i ) 2
Между этими тремя показателями существует следующая зависимость:
SST = SSR + SSE
Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.
SSR, SST и R-квадрат
R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
Используя SSR и SST, мы можем рассчитать R-квадрат как:
R-квадрат = SSR / SST
Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:
R-квадрат = 137,5/156 = 0,8814
Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.
Расчет SST, SSR, SSE: пошаговый пример
Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:
Оценка = 66,615 + 5,0769 * (часы)
Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:
Шаг 1: Рассчитайте среднее значение переменной ответа.
Среднее значение переменной отклика ( y ) оказывается равным 81 .
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.
Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.
Например, предполагаемая оценка экзамена для студента, который учился один час, такова:
Оценка = 66,615 + 5,0769*(1) = 71,69 .
Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:
Шаг 3: Рассчитайте общую сумму квадратов (SST).
Далее мы можем вычислить общую сумму квадратов.
Например, сумма квадратов для первого ученика равна:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:
Сумма квадратов получается 316 .
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).
Далее мы можем вычислить сумму квадратов регрессии.
Например, сумма квадратов регрессии для первого ученика равна:
(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .
Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:
Сумма квадратов регрессии оказывается равной 279,23 .
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).
Далее мы можем вычислить сумму квадратов ошибок.
Например, ошибка суммы квадратов для первого ученика:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:
Мы можем проверить, что SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:
- R-квадрат = SSR / SST
- R-квадрат = 279,23/316
- R-квадрат = 0,8836
Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.
Дополнительные ресурсы
Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:
Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE
регрессии,
нелинейные по оцениваемым параметрам:
-
степенная
; -
показательная
; -
экспоненциальная
.
В парной регрессии
выбор вида математической функции может
быть осуществлен графическим, аналитическим
или экспериментальным методом.
Построение уравнения
регрессии сводится к оценке ее параметров.
Для оценки параметров регрессий обычно
используют метод наименьших квадратов
(МНК). МНК позволяет получить такие
оценки параметров, при которых сумма
квадратов отклонений фактических
значений результативного признака y
от теоретических
минимальна, т.е.
.
Для линейных и
нелинейных уравнений, приводимых к
линейным, решается следующая система
относительно b0
и b1:
.
Можно воспользоваться
готовыми формулами, которые вытекают
из этой системы:
.
Тесноту связи
изучаемых явлений оценивает:
-
линейный коэффициент
парной корреляции rxy
для
линейной регрессии (
):
;
-
индекс корреляции
для нелинейной регрессии(
):
.
Оценку
качества построенной модели даст
коэффициент (индекс) детерминации, а
также средняя ошибка аппроксимации.
Коэффициент
детерминации характеризует долю
дисперсии, объясняемую регрессией, в
общей дисперсии результативного признака
y:
.
Величина (1–R2)
характеризует
долю дисперсии у,
вызванную влиянием остальных не учтенных
в модели факторов.
Средняя ошибка
аппроксимации – среднее отклонение
расчетных значений результативного
признака от фактических:
.
Допустимый предел
значений
– не более 8-10%.
Оценивание качества
уравнения регрессии по F-критерию
Фишера состоит в проверке гипотезы H0
о статистической
незначимости уравнения регрессии и
показателя тесноты связи. Для этого
выполняется сравнение фактического
Fнабл
и критического (табличного) Fкр
значений
F-критерия
Фишера.
,
где n
– число единиц совокупности;
m
– число
параметров при переменной
х.
Fкр
– это
максимально возможное значение критерия
под влиянием случайных факторов при
данных степенях свободы (k1=m,
k2=n—m–1)
и уровне значимости α.
Уровень значимости α
– вероятность отвергнуть гипотезу при
условии что она верна. Обычно принимается
равной 0,05
или 0,01.
Если Fкр
< Fнабл,
то H0
– гипотеза о случайной природе оцениваемых
характеристик отклоняется и признается
их статистическая значимость и надежность.
Если Fкр
> Fнабл,
то гипотеза H0
не отклоняется и признается статистическая
незначимость и ненадежность уравнения
регрессии и показателя тесноты связи.
Для оценки
статистической значимости коэффициентов
регрессии рассчитываются t-критерий
Стьюдента и доверительные интервалы
каждого из показателей.
Выдвигается
гипотеза H0
о случайной
природе показателей, т.е. о незначимом
их отличии от нуля. Оценка значимости
коэффициентов регрессии с помощью
t-критерия
Стьюдента проводится путем сопоставления
их значений с величиной стандартной
ошибки:
.
Стандартные
ошибки параметров линейной регрессии
определяются по формулам:

где
– оценка остаточной дисперсии.
Сравнивая фактическое
и критическое (табличное) значение
t-статистики
– tкр
и tнабл
– принимаем
или отвергаем гипотезу H0.
tкр
определяется
из таблицы распределения Стьюдента для
уровня значимости α
и числа
степеней свободы df
= n—m-1.
Связь между
F-критерием
Фишера и t-статистикой
Стьюдента выражается равенством:
.
Если tкр
< |tнабл|,
то H0
отклоняется, т.е. bj
не случайно отличен от нуля и сформировался
под влиянием систематически действующего
фактора x.
Если tкр
> |tнабл|,
то гипотеза H0
не отклоняется и признается случайная
природа формирования bj.
Доверительным
интервалом называется такой интервал,
относительно которого можно с заранее
выбранной вероятностью утверждать, что
он содержит значения прогнозируемого
показателя.
Интервальная
оценка для коэффициентов β0
и β1
определяется по формулам:
.
Если в границы
доверительного интервала попадает
ноль, т.е. нижняя граница отрицательна,
а верхняя положительна, то оцениваемый
параметр принимается нулевым, так как
он не может одновременно принимать и
положительное, и отрицательное значения.
Прогнозное значение
yp
определяется путем подстановки в
уравнение регрессии
соответствующего (прогнозного) значения
xp.
Вычисляется средняя стандартная ошибка
прогноза:
;
и
строится доверительный интервал
прогноза:
.
Пример
1. По 10
хозяйствам района известны сведения о
дозах внесения удобрений на 1 га зерновых
(x)
и об урожайности зерновых культур (y):
Таблица 1.1– Исходные
данные для построения модели
|
Урожайность культур, |
26,4 |
21,1 |
21,9 |
38,1 |
19,2 |
28,6 |
19,4 |
35,2 |
24,1 |
32,3 |
|
Доза на |
3,4 |
3,1 |
3 |
5 |
2,8 |
4,1 |
2,5 |
5,3 |
2,9 |
4 |
Требуется:
1.
Для характеристики зависимости y
от x
рассчитать параметры следующих функций:
а) линейной;
б) степенной;
2. Оценить тесноту
связи изучаемых признаков.
3.
Оценить каждую модель через среднюю
ошибку аппроксимации и F-критерий
Фишера.
Решение:
а)
Для расчета
параметров b0
и b1
линейной регрессии
решаем
систему нормальных уравнений относительно
b0
и b1:

По
исходным данным рассчитываем Σy,
Σx,
Σxy,
Σx2,
Σy2.
Таблица 1.2 –
Определение параметров модели и оценка
её качества
|
№ |
x |
y |
xy |
x2 |
y2 |
|
|
Ai |
|
1 |
3,4 |
26,4 |
89,76 |
11,56 |
696,96 |
25,2 |
1,2 |
4,4 |
|
2 |
3,1 |
21,1 |
65,41 |
9,61 |
445,21 |
23,2 |
-2,1 |
10,1 |
|
3 |
3 |
21,9 |
65,70 |
9,00 |
479,61 |
22,6 |
-0,7 |
3,1 |
|
4 |
5 |
38,1 |
190,50 |
25,00 |
1451,61 |
35,9 |
2,2 |
5,8 |
|
5 |
2,8 |
19,2 |
53,76 |
7,84 |
368,64 |
21,2 |
-2,0 |
10,6 |
|
6 |
4,1 |
28,6 |
117,26 |
16,81 |
817,96 |
29,9 |
-1,3 |
4,5 |
|
7 |
2,5 |
19,4 |
48,50 |
6,25 |
376,36 |
19,2 |
0,2 |
0,8 |
|
8 |
5,3 |
35,2 |
186,56 |
28,09 |
1239,04 |
37,9 |
-2,7 |
7,6 |
|
9 |
2,9 |
24,1 |
69,89 |
8,41 |
580,81 |
21,9 |
2,2 |
9,1 |
|
10 |
4 |
32,3 |
129,20 |
16,00 |
1043,29 |
29,2 |
3,1 |
9,5 |
|
Итого |
36,1 |
266,3 |
1016,54 |
138,57 |
7499,49 |
266,3 |
0,0 |
65,6 |
|
Ср. знач. |
3,61 |
26,63 |
101,65 |
13,86 |
749,95 |
— |
— |
6,6 |
.
Решив
систему уравнений, получим следующие
значения параметров:
b1
= 6,66, b0
= 2,59.
Параметры
регрессии рассчитаем с помощью формул:
,
.
Уравнение
регрессии имеет вид:
.
С
увеличением дозы внесения удобрений
на 1 га зерновых на 1 ц д.в. урожайность
зерновых культур увеличивается на 6,66
ц/га.
Рассчитаем линейный
коэффициент парной корреляции:
.
Связь
между рассматриваемыми признаками
сильная, прямая.
Определим коэффициент
детерминации:
Вариация
результата на 90% объясняется вариацией
фактора x.
На долю прочих факторов, не учитываемых
в регрессии, приходится 10%.
Подставляя
в уравнение регрессии фактические
значения x,
определим
теоретические
(расчетные) значения
.
Найдем величину средней ошибки
аппроксимации:
.
Ошибка
аппроксимации показывает хорошее
соответствие расчетных и фактических
данных: среднее отклонение составляет
6,6 %.
Рассчитаем
F-критерий:
.
Fкр.
находим по таблице значений F-критерия
Фишера при уровне значимости
и степенях свободы k1=1,
k2=8:
Fкр=5,32.
Т.к.
Fкр<
Fнабл
(5,32 < 72), отклоняется гипотеза Н0
о случайной природе выявленной зависимости
и статистической незначимости параметров
уравнения и показателя тесноты связи.
б)
Построению
нелинейной модели
предшествует
процедура линеаризации переменных.
Линеаризация степенной модели
производится путем логарифмирования
обеих частей уравнения:
где
Y=lg
y,
X=lg
x,
В0=lg
b0.
Для расчетов
используем данные таблицы 1.3.
Таблица
1.3 – Определение параметров модели и
оценка её качества
|
№ |
X |
Y |
XY |
X2 |
Y2 |
|
|
Ai |
|
|
|
1 |
0,5315 |
1,4216 |
0,7556 |
0,2825 |
2,0210 |
25,2 |
1,2 |
1,5 |
4,6 |
0,1 |
|
2 |
0,4914 |
1,3243 |
0,6507 |
0,2414 |
1,7537 |
23,1 |
-2,0 |
4,1 |
9,6 |
30,6 |
|
3 |
0,4771 |
1,3404 |
0,6396 |
0,2276 |
1,7968 |
22,4 |
-0,5 |
0,3 |
2,4 |
22,4 |
|
4 |
0,6990 |
1,5809 |
1,1050 |
0,4886 |
2,4993 |
36,0 |
2,1 |
4,4 |
5,5 |
131,6 |
|
5 |
0,4472 |
1,2833 |
0,5738 |
0,2000 |
1,6469 |
21,0 |
-1,8 |
3,4 |
9,5 |
55,2 |
|
6 |
0,6128 |
1,4564 |
0,8924 |
0,3755 |
2,1210 |
30,0 |
-1,4 |
1,8 |
4,8 |
3,9 |
|
7 |
0,3979 |
1,2878 |
0,5125 |
0,1584 |
1,6584 |
18,9 |
0,5 |
0,2 |
2,4 |
52,3 |
|
8 |
0,7243 |
1,5465 |
1,1201 |
0,5246 |
2,3918 |
38,0 |
-2,8 |
7,9 |
8,0 |
73,4 |
|
9 |
0,4624 |
1,3820 |
0,6390 |
0,2138 |
1,9100 |
21,7 |
2,4 |
5,6 |
9,8 |
6,4 |
|
10 |
0,6021 |
1,5092 |
0,9086 |
0,3625 |
2,2777 |
29,3 |
3,0 |
9,1 |
9,3 |
32,1 |
|
Итого |
5,4455 |
14,1325 |
7,7974 |
3,0748 |
20,0766 |
265,7 |
0,6 |
38,2 |
65,9 |
407,9 |
|
Ср. знач. |
0,5446 |
1,4132 |
0,7797 |
0,3075 |
2,0077 |
— |
— |
— |
6,6 |
— |
Рассчитаем
значения параметров В0
и b1:
,
.
Получим
линейное уравнение:
.
Выполнив
его потенцирование, получим:
.
Подставляя
в данное уравнение фактические значения
x,
получаем
теоретические значения результата
.
По ним рассчитаем индекс корреляции
и среднюю ошибку аппроксимации
:
,
.

Так
как Fкр
< Fнабл
(5,32 < 76,6), отвергается гипотеза Н0
о статистической незначимости параметров
степенного уравнения.
Пример 2. По
10 территориям региона приводятся данные
за 200Х год (таблица 1.4).
Таблица 1.4 –
Исходные данные для построения модели
|
Себестоимость |
12,0 |
12,5 |
12,2 |
13,3 |
12,0 |
13,4 |
13,5 |
13,2 |
14,4 |
15,2 |
|
Объем производства |
310 |
322 |
325 |
330 |
340 |
382 |
384 |
328 |
380 |
386 |
Требуется:
1. Построить линейное
уравнение парной регрессии y
от x.
2. Рассчитать
линейный коэффициент парной корреляции.
3. Оценить
статистическую значимость параметров
регрессии с помощью t-критерия
Стьюдента.
4. Дать точечный
и интервальный прогноз себестоимости
единицы продукции с вероятностью 0,95,
принимая уровень объема производства
равным 370 ед.
Решение:
1. Для
расчета параметров уравнения линейной
регрессии строим расчетную таблицу
(таблица 1.5).
Таблица 1.5 Определение
параметров модели и оценка её качества
|
№ |
x |
y |
yx |
x2 |
y2 |
|
|
|
1 |
310 |
12,0 |
3720,0 |
96100 |
144,00 |
12,12 |
-0,12 |
|
2 |
322 |
12,5 |
4025,0 |
103684 |
156,25 |
12,45 |
0,05 |
|
3 |
325 |
12,2 |
3965,0 |
105625 |
148,84 |
12,53 |
-0,33 |
|
4 |
330 |
13,3 |
4389,0 |
108900 |
176,89 |
12,66 |
0,64 |
|
5 |
340 |
12,0 |
4080,0 |
115600 |
144,00 |
12,93 |
-0,93 |
|
6 |
382 |
13,4 |
5118,8 |
145924 |
179,56 |
14,07 |
-0,67 |
|
7 |
384 |
13,5 |
5184,0 |
147456 |
182,25 |
14,13 |
-0,63 |
|
8 |
328 |
13,2 |
4329,6 |
107584 |
174,24 |
12,61 |
0,59 |
|
9 |
380 |
14,4 |
5472,0 |
144400 |
207,36 |
14,02 |
0,38 |
|
10 |
386 |
15,2 |
5867,2 |
148996 |
231,04 |
14,18 |
1,02 |
|
Итого |
3487 |
131,7 |
46150,6 |
1224269 |
1744,43 |
131,7 |
— |
|
Ср.знач. |
348,7 |
13,17 |
4615,06 |
122426,9 |
174,443 |
— |
— |
;
.
Получено уравнение
регрессии:
.
С увеличением
объема производства на единицу,
себестоимость
единицы продукции возрастает в среднем
на 0,0272 д.е.
2.
Тесноту линейной связи оценивает
коэффициент корреляции:
;
.
Это означает, что
62% вариации себестоимости единицы
продукции (y)
объясняется вариацией фактора x
– объема производства.
3.
Оценку статистической значимости
параметров регрессии проведем с помощью
t-статистики
Стьюдента и путем расчета доверительного
интервала каждого из показателей.
Выдвигаем гипотезу
Н0
о статистически незначимом отличии
показателей от нуля: b0=b1=0.
tкр
для числа степеней свободы df=10-2=8
и α=0,05
составит 2,31.
Определим стандартные
ошибки
:
;
Тогда
Фактическое
значение t-статистики
для коэффициента b1
превосходит табличное значение
,
поэтому
гипотеза Н0
отклоняется, т.е.
b1
не случайно
отличен от нуля, а статистически значим.
Критическое
значение t-статистики
превосходит фактическое значение для
коэффициента b0
,
поэтому
гипотеза Н0
принимается, т.е.
b0
случайно
отличен от нуля и статистически незначим.
Рассчитаем
доверительный интервал для b0
и b1:
.
Анализ верхней и
нижней границ доверительных интервалов
приводит к выводу о том, что с вероятностью
p=1-α=0,95
параметр
b1,
находясь в указанных границах, не
принимает нулевых значений, т.е. является
статистически значимым и существенно
отличен от нуля. Параметр b0
является
статистически незначимым.
4.
Полученные оценки уравнения регрессии
позволяют использовать его для прогноза.
Точечный прогноз себестоимости при
прогнозном значении объема производства
хр=370
ед. составит:
д.е.
Чтобы получить
интервальный прогноз, найдем стандартную
ошибку прогноза:
Доверительный
интервал прогнозируемой себестоимости
составит:
,
т.е.
при объеме производства, равном 370 ед.,
себестоимость единицы продукции с
надежностью 0,95 находится в пределах от
12,04 д.е. до 15,46 д.е.
1.2 Контрольные задания
Задание к
задачам
1-10. Имеются
данные о
расходах населения на продукты питания
(y)
и доходах семьи (x),
ден. ед. для 8 районов.
1.
Для характеристики зависимости y
от x
рассчитайте параметры следующих функций:
а) линейной;
б) степенной;
2.Оцените
тесноту связи изучаемых признаков.
3.Оцените
каждую модель через среднюю ошибку
аппроксимации и F-критерий
Фишера.
Таблица 1.6 –
Исходные данные для моделирования
(варианты 1-10)
|
Задача |
Признак |
Значения признака |
|||||||
|
1 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
|
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
|
|
2 |
y |
95 |
125 |
185 |
225 |
260 |
270 |
325 |
350 |
|
x |
125 |
300 |
510 |
720 |
950 |
1150 |
1450 |
1861 |
|
|
3 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
|
x |
110 |
300 |
515 |
730 |
940 |
1100 |
1450 |
1850 |
|
|
4 |
y |
85 |
110 |
155 |
210 |
245 |
285 |
325 |
360 |
|
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
|
|
5 |
y |
80 |
100 |
130 |
165 |
200 |
255 |
300 |
345 |
|
x |
150 |
280 |
330 |
500 |
880 |
1050 |
1350 |
1800 |
|
|
6 |
y |
100 |
150 |
220 |
300 |
330 |
350 |
380 |
400 |
|
x |
200 |
280 |
350 |
600 |
750 |
1200 |
1400 |
1900 |
|
|
7 |
y |
85 |
110 |
155 |
210 |
245 |
285 |
325 |
360 |
|
x |
150 |
280 |
330 |
500 |
880 |
1050 |
1350 |
1800 |
|
|
8 |
y |
87 |
95 |
115 |
135 |
150 |
200 |
250 |
335 |
|
x |
180 |
200 |
250 |
310 |
650 |
980 |
1450 |
1750 |
|
|
9 |
y |
90 |
120 |
180 |
220 |
260 |
290 |
330 |
380 |
|
x |
200 |
280 |
350 |
600 |
750 |
1200 |
1400 |
1900 |
|
|
10 |
y |
87 |
95 |
115 |
135 |
150 |
200 |
250 |
335 |
|
x |
120 |
310 |
530 |
740 |
960 |
1180 |
1450 |
1870 |
Задание к задачам
11-20.
1. Определите
параметры уравнения парной линейной
регрессии и дайте интерпретацию
коэффициента регрессии.
2. Оцените тесноту
связи с помощью коэффициентов корреляции
и детерминации, проанализируйте их
значения.
3. С вероятностью
0,95 оцените статистическую значимость
параметров уравнения регрессии по
критерию Стьюдента.
4. Рассчитайте
прогнозное значение результата y,
если прогнозное значение фактора х
составит 1,062 от среднего уровня (
).
Определите доверительный интервал
прогноза (для
= 0,05).
Таблица 1.7– Исходные
данные для моделирования (варианты
11-20)
|
Задача |
Условие |
Функция |
|
11 |
Оцените зависимость среднедушевых |
|
|
12 |
Выявить и оценить зависимость |
|
|
13 |
Выявить и оценить зависимость между |
|
|
14 |
Выявить и оценить зависимость между |
|
|
15 |
Выявить и оценить зависимость расходов |
|
|
16 |
Выявить и оценить зависимость доходов
|
|
|
17 |
Выявить и оценить зависимость оборота |
|
|
18 |
Выявить и оценить зависимость между |
|
|
19 |
Выявить и оценить зависимость |
|
|
20 |
Выявить и оценить зависимость между |
|
Таблица 1.8 — Исходные
данные к задачам 11-17
-
Территории Северо-Западного федерального
округаСреднедушевые денежные расходы за
месяц, тыс. руб.Среднемесячная заработная плата
работающих в экономике, тыс. руб.
Прибыль за год, млрд руб.
Инвестиции в основной капитал в
2006 г., млрд. руб.Инвестиции в основной капитал в
предыдущем 2005 г., млрд руб.Валовой региональный продукт за год,
млрд руб.
Расходы консолидированных бюджетов
субъектов РФ, млрд руб.Доходы консолидированных бюджетов
субъектов РФ, млрд руб.
Валовой региональный продукт,
млрд руб.
Оборот розничной торговли за год,
млрд руб.
Среднегодовая численность экономически
активного населения, млн чел.y1
x1
y2
x2
x3
y4
y5
x5
(y6)x6
y7
x7
Республика
Карелия4,99
7,00
2,21
12,60
9,63
48,1
9,86
8,49
48,1
19,9
0,399
Республика
Коми
7,84
9,58
17,45
30,20
25,92
113,5
17,28
16,34
113,5
44,5
0,607
Архан-гельская
обл.5,26
7,85
8,60
30,50
31,60
107,6
18,78
18,28
107,6
35,7
0,763
Вологодская
обл.4,91
6,94
61,05
41,45
17,71
114,2
16,75
16,85
114,2
26,8
0,655
Калининградская
обл.4,69
6,21
5,76
18,11
14,87
51,3
9,71
9,32
51,3
22,7
0,502
Ленин-градская
обл.3,72
6,78
33,38
67,02
44,03
132,4
18,97
18,1
132,4
30,6
0,873
Мурманская обл.
7,10
10,40
16,22
13,53
13,70
81,6
13,68
12,42
81,6
161,9
2,483
Новгородская
обл.4,09
5,56
3,88
7,95
9,13
39,1
6,36
5,95
39,1
34,2
0,572
Псковская обл.
4,01
4,67
0,75
5,75
3,86
30,3
7,51
7,05
30,3
15,6
0,371
Таблица 1.9 — Исходные
данные к задачам 18-20
-
Территории Приволжского федерального
округаСреднедушевые денежные расходы за
месяц в 2006 г., тыс.руб.Среднемесячная начисленная заработная
плата работающих в экономике в 2006
г., тыс. руб.Прибыль за 2006 г., млн руб.
Инвестиции в основной капитал в 2006
г.,млрд. руб.
Расходование средств пенсионного
фонда за 2005 г. по субъектам РФ, млрд.
руб.Поступление средств в пенсионный
фонд по субъектам РФ за 2005 г., млрд.
руб.Валовой региональный продукт за
2005 г., млрд. руб.
y8
x8
y9
x9
y10
x10
y11
Республика
Башкортостан
4,62
5,5
43,4
62,4
19,7
17,3
279,7
Республика Марий Эл
2,48
3,9
0,6
5,8
3,5
2,6
24,6
Республика Мордовия
2,65
4,09
1,6
10,4
4,9
3,6
36,9
Республика Татарстан
4,78
5,55
70,0
86,6
18,9
17,8
319,1
Республика Удмуртия
3,4
5,16
6,4
15,4
7,9
7,3
97,7
Чувашская республика
3,12
4,06
3,0
14,2
6,4
5,1
50,2
Кировская обл.
3,69
4,55
3,2
9,5
8,7
6,6
62,4
Нижегородская обл.
4,71
5,17
24,2
48,5
21,8
17,5
222,4
Оренбургская обл.
3,34
4,87
19,8
27,7
11,1
8,8
125,2
Пензенская обл.
3,54
4,22
1,8
10,7
8,5
5,7
49,2
Пермская обл.
5,82
6,42
43,5
48,2
15,3
14,1
232,1
Самарская обл.
7,01
6,31
2,8
55,0
18,2
17,0
274,9
Саратовская обл.
3,51
4,49
8,3
23,8
13,9
10,3
131,3
Ульяновская обл.
3,43
4,47
1,4
11,3
7,6
5,7
58,3
2. Множественная регрессия
Множественная
регрессия
– уравнение
связи с несколькими переменными:
где y
– зависимая переменная (результативный
признак);
x1,
x2,
…, xp
– независимые переменные (факторы).
Для построения
уравнения множественной регрессии чаще
используются следующие функции:
-
линейная –
; -
степенная –
; -
экспонента –
; -
парабола второго
порядка –
.
Для оценки параметров
уравнения множественной регрессии
применяют метод наименьших квадратов
(МНК). Для линейных уравнений и нелинейных
уравнений, приводимых к линейным,
строится следующая система нормальных
уравнений:
Для ее решения
может быть применен метод определителей.
,
где ∆ – определитель
системы;
∆b0,
∆b1,
…, ∆bp
– частные определители, которые
получаются путем замены соответствующего
столбца матрицы определителя системы
данными левой части системы.
Другой вид уравнения
множественной регрессии – уравнение
регрессии в стандартизированном
масштабе:
,
где βi
– стандартизированные коэффициенты
регрессии;
–
стандартизированные
переменные.
К уравнению
множественной регрессии в стандартизированном
масштабе применим МНК. Стандартизированные
коэффициенты регрессии определяются
из следующей системы уравнений:
Связь коэффициентов
множественной регрессии bi
со
стандартизированными коэффициентами
βi
описывается
соотношением:
.
Параметр b0
определяется
как
.
Средние значения
коэффициентов эластичности рассчитываются
по формуле:
.
Тесноту совместного
влияния факторов на результат оценивает
индекс множественной корреляции:
.
Значение индекса
множественной корреляции лежит в
пределах от 0 до 1 и должно быть больше
или равно максимальному парному индексу
корреляции:
.
Индекс множественной корреляции для
уравнения в стандартизированном масштабе
можно записать в виде:
.
Коэффициент
(индекс) множественной детерминации
рассчитывается как квадрат индекса
множественной корреляции.
Для того, чтобы не
допускать возможного завышения тесноты
связи при небольших объемах выборок,
применяется скорректированный индекс
детерминации:
.
Чем больше m
(число параметров при переменных х),
тем сильнее различия
и
.
Одним из условий
построения уравнения множественной
регрессии является независимость
действия факторов. Считается, что две
переменные явно коллинеарны, т.е.
находятся между собой в линейной
зависимости, если парный коэффициент
корреляции
.
Если факторы коллинеарны, то они дублируют
друг друга и один из них рекомендуется
исключить из регрессии.
При наличии
мультиколлинеарности факторов, когда
более чем два фактора связаны между
собой линейной зависимостью, для ее
оценки может использоваться определитель
матрицы парных коэффициентов корреляции.
Чем ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и ниже
надежность результатов множественной
регрессии.
Частные коэффициенты
(или индексы) корреляции, измеряющие
влияние на y
фактора xi
при неизменном
уровне других факторов можно определить
по рекуррентной формуле:
.
Частные коэффициенты
корреляции изменяются в пределах от -1
до 1.
Порядок частного
коэффициента корреляции определяется
количеством факторов, влияние которых
исключается.
Значимость уравнения
множественной регрессии в целом
оценивается с помощью F-критерия
Фишера:
,
где m
– число параметров при переменных x;
p
– количество независимых переменных.
Непосредственному
расчету F-критерия
предшествует анализ дисперсии. Центральное
место в нем занимает разложение общей
суммы квадратов
отклонений переменной y
от среднего значения
на две части – «объясненную» и
«остаточную»:
Разделив каждую
сумму квадратов на соответствующее ей
число степеней свободы, получим дисперсию
на одну степень свободы D.
Сопоставляя
объясненную (факторную) и остаточную
дисперсии в расчете на одну степень
свободы, получим величину F-критерия
для проверки гипотезы Н0:
Dфакт=Dост
(F=Dфакт/Dост).
Частный F-критерий
оценивает статистическую значимость
присутствия каждого из факторов в
уравнении. В общем виде для фактора xi
частный
F-критерий
определяется по формуле:
.
Оценка значимости
коэффициентов регрессии с помощью
t-критерия
Стьюдента сводится к вычислению значения
,
где Sbi
– стандартная ошибка коэффициента
регрессии bi,
она определяется по следующей формуле:
.
При оценке параметров
уравнения регрессии по МНК делаются
определенные предпосылки (теорема
Гаусса-Маркова) относительно случайной
составляющей ε:
-
случайный характер
остатков; -
нулевая средняя
величина остатков, не зависящая от хi; -
гомоскедастичность
– дисперсия каждого отклонения εi
одинакова для всех значений х; -
отсутствие
автокорреляции остатков. Значения
остатков εi
распределены
независимо друг от друга;
остатки подчиняются
нормальному распределению.
Если распределение
остатков εi
не соответствует некоторым предпосылкам
МНК, то следует корректировать модель.
2.1. Решение типовых задач
Пример 1.
Торговое
предприятие имеет сеть, состоящую из
12 магазинов, информация о деятельности
которых представлена в таблице 2.1.
Требуется:
1. Построить линейное
уравнение множественной регрессии и
пояснить экономический смысл его
параметров.
2. Определить
стандартизованные коэффициенты
регрессии.
3. Рассчитать
частные коэффициенты эластичности,
сравнить их с β1
и β2,
пояснить различия между ними.
4. Определить парные
и частные коэффициенты корреляции, а
также множественный коэффициент
корреляции.
5. Провести
дисперсионный анализ для проверки
статистической значимости уравнения
множественной регрессии и его показателя
тесноты связи на уровне значимости
α=0,05.
6. С помощью частных
F-критериев
Фишера оценить, насколько целесообразно
включение в уравнение множественной
регрессии фактора х1
после фактора х2
и насколько целесообразно включение
х2
после х1.
7.
Оценить с помощью t-критерия
Стьюдента статистическую значимость
коэффициентов при переменных х1
и х2
множественного уравнения регрессии.
Таблица 2.1 –
Исходные данные для моделирования
|
Номер магазина |
Годовой |
Торговая площадь, |
Среднее число |
|
y |
x1 |
x2 |
|
|
1 |
19,76 |
0,24 |
8,25 |
|
2 |
38,09 |
0,31 |
10,24 |
|
3 |
40,95 |
0,55 |
9,31 |
|
4 |
41,08 |
0,48 |
11,01 |
|
5 |
56,29 |
0,78 |
8,54 |
|
6 |
68,51 |
0,98 |
7,51 |
|
7 |
75,01 |
0,94 |
12,36 |
|
8 |
89,05 |
1,21 |
10,81 |
|
9 |
91,13 |
1,29 |
9,89 |
|
10 |
91,26 |
1,12 |
13,72 |
|
11 |
99,84 |
1,29 |
12,27 |
|
12 |
108,55 |
1,49 |
13,92 |
Решение:
1.
Линейное уравнение множественной
регрессии y
от x1
и x2
имеет вид:
=b0+b1x1+b2x2.
Расчет его параметров
произведем в MS
Excel
с помощью инструмента анализа данных
Регрессия:
1) запишите
статистические данные в ячейки листа
Excel;
2)
в главном
меню выберете Сервис/Анализ
данных/Регрессия.
Щелкните по кнопке ОК;
3) заполните
диалоговое окно ввода данных и параметров
вывода (рис 2.1):

Рис. 2.1 — Диалоговое
окно ввода параметров инструмента
Регрессия
Входной интервал
Y
– диапазон, содержащий данные
результативного признака;
Входной интервал
Х – диапазон,
содержащий данные факторов независимого
признака;
Метки
– флажок, который указывает, содержит
ли первая строка названия столбцов или
нет;
Константа
– ноль – флажок, указывающий на наличие
или отсутствие свободного члена в
уравнении;
Выходной интервал
– достаточно указать левую верхнюю
ячейку будущего диапазона;
Новый рабочий
лист – можно
задать произвольное имя нового листа.
Чтобы получить
информацию и графики остатков, установите
соответствующие флажки в диалоговом
окне. Щелкните по кнопке ОК.

Рис. 2.2
— Результат
применения инструмента Регрессия
Столбец Коэффициенты
содержит
численные значения коэффициентов
регрессии:
.
При увеличении
торговой площади на 1 тыс. м2
годовой товарооборот увеличится на
61,6583 млн. руб. При увеличении среднего
числа посетителей на 1 тыс. чел. годовой
товарооборот увеличится на 2,2748 млн.
руб.
2.
Уравнение в стандартизированном масштабе
имеет вид:
.
Расчет β-коэффициентов
выполним, используя формулы для перехода
от βi
к bi:
.
Получим уравнение
.
3.
Для характеристики относительной силы
влияния x1
и x2
на y
рассчитаем средние коэффициенты
эластичности:
С увеличением
торговой площади x1
на 1% от ее среднего уровня годовой
товарооборот y
возрастает на 0,8% от своего среднего
уровня; при повышении среднего числа
посетителей в день х2
на 1% годовой товарооборот
y
возрастает на 0,35% от своего среднего
уровня. Очевидно, что сила влияния
торговой площади на годовой товарооборот
оказалась большей, чем сила влияния
среднего числа посетителей в день. К
аналогичным выводам о силе связи приходим
при сравнении модулей значений β1
и β2.
4. Матрицу
парных коэффициентов корреляции
переменных можно рассчитать, используя
инструмент анализа данных Корреляция.
Для этого:
1) в главном меню
последовательно выберете пункты
Сервис/Анализ
данных/Корреляция. Щелкните
по кнопке
ОК;
2) заполните
диалоговое окно ввода данных и параметров
вывода (рис 2.3);
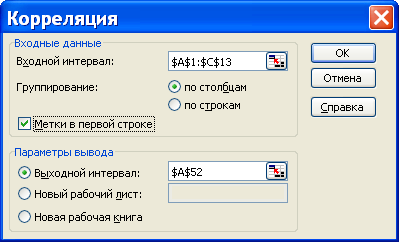
Рис. 2.3 —
Диалоговое
окно ввода параметров инструмента
Корреляция
3) результаты
вычислений представлены на рис. 2.4.

Рис. 2.4
— Матрица
коэффициентов парной корреляции
Линейные коэффициенты
частной корреляции рассчитаем по
формулам:


Из-за средней
межфакторной связи (
коэффициенты парной и частной корреляции
несколько отличаются: выводы о тесноте
и направлении связи на основе парных и
частных коэффициентов совпадают.
Значение линейного
коэффициента множественной корреляции
расположено в строке Множественный
R
таблицы
Регрессионная статистика (рис.
2.2):
Множественный
коэффициент детерминации (строка
R-квадрат):
Зависимость y
от x1
и x2
характеризуется как тесная, в которой
98,8% вариации годового товарооборота
определяется вариацией учтенных в
модели факторов: торговой площади и
среднего числа посетителей в день.
5.
Задача дисперсионного анализа состоит
в проверке гипотезы Н0
о статистической незначимости уравнения
регрессии в целом и показателя тесноты
связи. Анализ выполняется при сравнении
фактического и критического значений
F-критерия
Фишера.
Результаты
дисперсионного анализа представлены
в таблице Дисперсионный
анализ
(рис. 2.2). Столбец SS
содержит суммы квадратов отклонений,
столбец MS
– дисперсии на одну степень свободы.
Fкр.
находим по таблице значений F-критерия
Фишера при уровне значимости
и степенях свободы k1=2,
k2=9:
Fкр=4,26.
Так как Fнабл=384,2
> Fкр=4,26,
гипотеза Н0
о случайности различий факторной и
остаточной дисперсий отклоняется. Эти
различия существенны, статистически
значимы, уравнение надежно, значимо,
показатель тесноты связи надежен и
отражает устойчивую зависимость годового
товарооборота от торговой площади и
среднего числа
посетителей.
С вероятностью
0,95 делаем заключение о статистической
значимости уравнения в целом и показателя
тесноты связи, которые сформировались
под неслучайным воздействием факторов
x1
и x2.
6.
Частные F-критерии
– Fx1
и Fx2
оценивают статистическую значимость
присутствия факторов х1
и x2
в уравнении
множественной регрессии, оценивают
целесообразность включения в уравнение
одного фактора после другого фактора.

Fкр=5,12;
α=0,05.
Так как Fx1набл
> Fкр,
приходим к выводу о целесообразности
включения в модель фактора х1
после фактора х2.
Гипотезу Н0
о несущественности
прироста R2y
за счет включения дополнительного
фактора х1
отклоняем
и приходим к выводу о статистически
подтвержденной целесообразности
включения фактора х1
после фактора х2.

Так как Fx2набл
> Fкр,
гипотезу Н0
о несущественности
прироста R2y
за счет включения дополнительного
фактора х2
отклоняем
и приходим к выводу о статистически
подтвержденной целесообразности
включения фактора х2
после фактора х1.
7. Оценка
значимости коэффициентов b1
и b2
с помощью t-критерия
Стьюдента предполагает сопоставление
их значений с величиной их стандартных
ошибок:
.
Значения стандартных
ошибок и t-критерия
Стьюдента для коэффициентов регрессии
расположены в последней таблице вывода
итогов построения регрессии (рис. 2.2):
,
;
,
.
Табличное значение
t-критерия Стьюдента tкр
для числа степеней свободы df=12-3=9 и α=0,05
составит 2,26.
Сравнивая tкр
и tнабл,
приходим к выводу, что коэффициенты
регрессии b1
и b2
являются статистически значимыми и
надежными.
Несмотря на
полученную незначимость коэффициента
b0
(
),
принято оставлять константу в уравнении
регрессии для поглощения неучтенных в
модели факторов.
Интервальные
значения коэффициентов регрессии
составят (рис.2.2):
,
.
С вероятностью
0,95 истинная сила влияния переменной х1
на у
будет не меньше 55 и не больше 68,3; переменной
х2
– не меньше 0,96 и не больше 3,6.
Пример 2.
Имеются данные по странам (табл. 2.2).
Таблица 2.2 –
Исходные данные
|
Страна |
Индекс человеческого развития, у |
Ожидаемая продолжительность жизни |
Суточная калорийность питания |
|
Австрия |
0,904 |
77 |
3343 |
|
Австралия |
0,922 |
78,2 |
3001 |
|
Аргентина |
0,827 |
72,9 |
3136 |
|
Белоруссия |
0,763 |
68 |
3101 |
|
Бельгия |
0,923 |
77,2 |
3543 |
|
Бразилия |
0,739 |
66,8 |
2938 |
|
Великобритания |
0,918 |
77,2 |
3237 |
|
Венгрия |
0,795 |
70,9 |
3402 |
|
Германия |
0,906 |
77,2 |
3330 |
|
Греция |
0,867 |
78,1 |
3575 |
|
Дания |
0,905 |
75,7 |
3808 |
|
Египет |
0,616 |
66,3 |
3289 |
|
Израиль |
0,883 |
77,8 |
3272 |
|
Индия |
0,545 |
62,6 |
2415 |
|
Испания |
0,894 |
78 |
3295 |
|
Италия |
0,9 |
78,2 |
3504 |
|
Канада |
0,932 |
79 |
3056 |
|
Казахстан |
0,74 |
67,7 |
3007 |
|
Китай |
0,701 |
69,8 |
2844 |
|
Латвия |
0,744 |
68,4 |
2861 |
|
Нидерланды |
0,921 |
77,9 |
3259 |
|
Норвегия |
0,927 |
78,1 |
3350 |
Требуется:
1. Построить
уравнение множественной регрессии.
2. Провести
тестирование ошибок уравнения
множественной регрессии на
гетероскедастичность, применив тест
Гольдфельда-Квандта.
3. Определить, какое
уравнение лучше использовать для
прогноза: парную регрессию у
от х1
или множественную регрессию.
Решение:
1.
Расчет параметров линейного уравнение
множественной регрессии y
от x1
и x2
произведем с помощью инструмента анализа
данных Регрессия.
Уравнение регрессии
имеет вид:
.
Так как Fнабл
= 96,7 > Fкр
= 3,52, признается статистическая значимость
и надежность уравнения регрессии и
показателя тесноты связи (R2=0,91).
По t-критерию
Стьюдента параметры b0
и b1
статистически значимы и существенно
отличны от нуля (
).
Параметр b2
признается равным нулю, поскольку:
.
2.
Для оценки гетероскедастичности
используем метод Гольдфельда-Квандта.
Упорядочим n
= 22 наблюдений по мере возрастания
переменной х1.
Далее, исключив С
= 6 центральных наблюдений, разобьем
совокупность на две части по 8 наблюдений.
По каждой группе
наблюдений находим уравнение регрессии,
теоретические значения
,
остатки и их квадраты (табл. 2.3).
Таблица 2.3 –
Проверка линейной регрессии на
гетероскедастичность
|
Уравнение |
у |
х1 |
х2 |
|
ε |
ε2 |
|
|
0,545 |
62,6 |
2415 |
0,5635 |
-0,0185 |
0,00034 |
|
0,616 |
66,3 |
3289 |
0,6750 |
-0,0590 |
0,00348 |
|
|
0,739 |
66,8 |
2938 |
0,6841 |
0,0549 |
0,00301 |
|
|
0,74 |
67,7 |
3007 |
0,7094 |
0,0306 |
0,00094 |
|
|
0,763 |
68 |
3101 |
0,7188 |
0,0442 |
0,00196 |
|
|
0,744 |
68,4 |
2861 |
0,7266 |
0,0174 |
0,00030 |
|
|
0,701 |
69,8 |
2844 |
0,7644 |
-0,0634 |
0,00401 |
|
|
0,795 |
70,9 |
3402 |
0,8013 |
-0,0063 |
0,00004 |
|
|
Сумма |
S1=0,014084 |
|||||
|
|
0,883 |
77,8 |
3272 |
0,9010 |
-0,0180 |
0,00032 |
|
0,921 |
77,9 |
3259 |
0,9035 |
0,0175 |
0,00031 |
|
|
0,894 |
78 |
3295 |
0,9027 |
-0,0087 |
0,00008 |
|
|
0,867 |
78,1 |
3575 |
0,8851 |
-0,0181 |
0,00033 |
|
|
0,927 |
78,1 |
3350 |
0,9005 |
0,0265 |
0,00070 |
|
|
0,922 |
78,2 |
3001 |
0,9262 |
-0,0042 |
0,00002 |
|
|
0,9 |
78,2 |
3504 |
0,8916 |
0,0084 |
0,00007 |
|
|
0,932 |
79 |
3056 |
0,9355 |
-0,0035 |
0,00001 |
|
|
Сумма |
S2=0,00183 |
Находим отношение:
R = Smax/Smin
= 0,014084/0,00183 = 7,7. Сравним эту величину с
табличным значением F-критерия при
5%-ном уровне значимости и числе степеней
свободы
для каждой остаточной суммы квадратов:
Fкр
= 5,05.
Так как R
> Fкр,
то делаем вывод о наличии гетероскедастичности
остатков. Это означает, что для каждого
значения фактора х1
остатки εi
имеют неодинаковую дисперсию.
3.
Уравнение множественной регрессии y от
x1
и x2:
.
(1)
Построим уравнение
парной линейной регрессии у от х1:
.
(2)
Чтобы определить,
какое уравнение (1) или (2) лучше использовать
для прогноза, применим тест на выбор
«длинной» или «короткой» регрессии.
Определим для
каждого уравнения регрессии сумму
квадратов ошибок:
ESSUR
= 0,0229 – для «длинной» регрессии (1);
ESSR
= 0,0238 – для «короткой» регрессии (2).
Вычислим F-статистику:
,
где q
и k
– число переменных х
в «короткой» и «длинной» регрессии,
соответственно.
Критическая точка
распределения Фишера при уровне
значимости 0,05: Fкр(q,n-k-1)
= Fкр(1,19)
= 4,38.
Так как F < Fкр,
для прогноза лучше использовать
«короткую» модель, т.е. уравнение
регрессии (2).
2.1. Контрольные задания
Задание к задачам
1-20.
По данным об
экономических результатах деятельности
российских банков выполните следующие
задания:
1. Построить линейное
уравнение множественной регрессии и
пояснить экономический смысл его
параметров.
2. Определить
стандартизованные коэффициенты
регрессии.
3. Рассчитать
частные коэффициенты эластичности,
сравнить их с β1
и β2,
пояснить различия между ними.
4. Определить парные
и частные коэффициенты корреляции, а
также множественный коэффициент
корреляции.
5. Провести
дисперсионный анализ для проверки
статистической значимости уравнения
множественной регрессии и его показателя
тесноты связи на уровне значимости
α=0,05.
6. Рассчитать
частные F-критерии Фишера.
7. Оценить с помощью
t-критерия Стьюдента статистическую
значимость коэффициентов при переменных
х1
и х2
множественного уравнения регрессии.
Задачи 1, 11
Используйте
признаки: работающие активы, млн руб.,
собственный капитал, %, привлеченные
межбанковские кредиты, %.
Задачи 2, 12
Используйте
признаки: работающие активы, млн руб.,
собственный капитал, %, средства частных
лиц, %.
Задачи 3, 13
Используйте
признаки: работающие активы, млн руб.,
собственный капитал, %, средства
предприятий и организаций, %.
Задачи 4, 14
Используйте
признаки: работающие активы, млн руб.,
привлеченные межбанковские кредиты,
%, средства предприятий и организаций,
%.
Задачи 5, 15
Используйте
признаки: работающие активы, млн руб.,
собственный капитал, %, выпущенные ценные
бумаги, %.
Задачи 6, 16
Используйте
признаки: работающие активы, млн руб.,
привлеченные межбанковские кредиты,
%, выпущенные ценные бумаги, %.
Задачи 7, 17
Используйте
признаки: работающие активы, млн руб.,
средства частных лиц, %, средства
предприятий и организаций, %.
Задачи 8, 18
Используйте
признаки: работающие активы, млн. руб.,
средства частных лиц, %, выпущенные
ценные бумаги, %.
Задачи 9, 19
Используйте
признаки: кредиты предприятиям и
организациям, млн руб., собственный
капитал, %, средства частных лиц, %.
Задачи 10, 20
Используйте
признаки: кредиты предприятиям и
организациям, млн руб., средства
предприятий и организаций, %, выпущенные
ценные бумаги, %.
Таблица 2.4 — Исходные
данные
|
Банк |
Работающие активы, млн |
Собственный капитал, % |
Привлеченные межбанковские кредиты |
Средства частных лиц, % |
Средства предприятий и |
Выпущенные ценные бумаги, |
Кредиты частным лицам, |
Кредиты предприятиям и |
Акции, млн руб. |
Облигации, млн руб. |
|
к задачам 1-10 |
||||||||||
|
Сбербанк |
1917403 |
10 |
3 |
60 |
19 |
3 |
308437 |
1073255 |
13571 |
359499 |
|
Внешторгбанк |
426484 |
16 |
28 |
13 |
25 |
12 |
5205 |
189842 |
23152 |
50012 |
|
Газпромбанк |
362532 |
8 |
17 |
9 |
38 |
22 |
5084 |
207118 |
18660 |
35676 |
|
Альфа-банк |
186700 |
13 |
14 |
15 |
30 |
3 |
1361 |
138518 |
4505 |
8471 |
|
Банк Москвы |
157286 |
11 |
2 |
30 |
27 |
5 |
5768 |
90757 |
3026 |
24838 |
|
Росбанк |
151849 |
8 |
4 |
19 |
55 |
10 |
4466 |
62388 |
4474 |
5667 |
|
Промстройбанк |
85365 |
10 |
13 |
24 |
29 |
11 |
2719 |
45580 |
2781 |
18727 |
|
Уралсиб |
76617 |
16 |
15 |
22 |
19 |
10 |
8170 |
43073 |
6705 |
4026 |
|
Промсвязьбанк |
54848 |
9 |
14 |
11 |
46 |
11 |
822 |
32761 |
68 |
5250 |
|
Петрокоммерц |
53701 |
15 |
5 |
26 |
37 |
11 |
1693 |
23053 |
3561 |
9417 |
|
Номос-банк |
52473 |
11 |
24 |
6 |
17 |
24 |
476 |
28511 |
2126 |
9416 |
|
Зенит |
50666 |
14 |
19 |
10 |
36 |
17 |
421 |
25412 |
2743 |
8264 |
|
Транскредитбанк |
41332 |
9 |
7 |
8 |
46 |
27 |
993 |
18506 |
827 |
7350 |
|
Еврофинанс-Моснарбанк |
38245 |
15 |
18 |
5 |
22 |
37 |
171 |
18114 |
400 |
7949 |
|
Никойл |
36946 |
23 |
27 |
11 |
23 |
9 |
245 |
13117 |
9160 |
5231 |
|
Импэксбанк |
34032 |
13 |
9 |
37 |
20 |
11 |
3993 |
15047 |
4098 |
2584 |
|
Союз |
33062 |
13 |
10 |
8 |
34 |
31 |
3254 |
15507 |
3172 |
5187 |
|
Татфондбанк |
11949 |
22 |
8 |
20 |
27 |
18 |
544 |
9897 |
69 |
561 |
|
к задачам 11-20 |
||||||||||
|
БИН-банк |
32948 |
12 |
4 |
20 |
35 |
11 |
764 |
24980 |
17 |
2172 |
|
Россельхозбанк |
23863 |
21 |
10 |
14 |
23 |
29 |
1178 |
13953 |
102 |
1628 |
|
Собинбанк |
20905 |
25 |
7 |
15 |
24 |
19 |
1680 |
15405 |
18 |
322 |
|
Судостроительный банк |
18991 |
16 |
20 |
2 |
24 |
16 |
179 |
6811 |
20 |
950 |
|
Банк Санкт-Петербург |
18389 |
10 |
3 |
28 |
38 |
10 |
240 |
11911 |
140 |
2862 |
|
Авангард |
16070 |
19 |
22 |
12 |
19 |
21 |
727 |
11839 |
718 |
227 |
|
Кредитагропромбанк |
15332 |
9 |
2 |
14 |
46 |
21 |
3153 |
5334 |
40 |
622 |
|
Инвестсбербанк |
15326 |
17 |
4 |
26 |
34 |
16 |
3085 |
6249 |
814 |
1192 |
|
Пробизнесбанк |
13026 |
12 |
10 |
9 |
29 |
22 |
548 |
6913 |
794 |
680 |
|
Российский капитал |
10249 |
30 |
4 |
21 |
27 |
11 |
899 |
6971 |
51 |
484 |
|
БИН-банк |
32948 |
12 |
4 |
20 |
35 |
11 |
764 |
24980 |
17 |
2172 |
|
Россельхозбанк |
23863 |
21 |
10 |
14 |
23 |
29 |
1178 |
13953 |
102 |
1628 |
|
Собинбанк |
20905 |
25 |
7 |
15 |
24 |
19 |
1680 |
15405 |
18 |
322 |
|
Судстрой банк |
18990 |
16 |
20 |
2 |
24 |
16 |
179 |
6811 |
20 |
950 |
|
Банк Петербург |
18390 |
10 |
3 |
28 |
38 |
10 |
240 |
11911 |
140 |
2862 |
|
МБСП |
11889 |
13 |
8 |
13 |
46 |
14 |
295 |
5404 |
12 |
4676 |
|
Абсолют банк |
11831 |
12 |
29 |
10 |
21 |
17 |
639 |
7872 |
40 |
413 |
|
Центрокредит |
11674 |
29 |
8 |
5 |
29 |
13 |
364 |
5097 |
864 |
3438 |
3. Системы эконометрических уравнений
Сложные
экономические процессы описывают с
помощью системы взаимосвязанных
(одновременных) уравнений.
Различают несколько
видов систем уравнений:
1.
система независимых уравнений
– когда каждая зависимая переменная y
рассматривается как функция одного и
того же набора факторов
x:

2.
система
рекурсивных уравнений – когда
зависимая переменная y
одного
уравнения выступает в виде фактора x
в другом уравнении:

Для
решения этой системы и нахождения ее
параметров используется метод наименьших
квадратов.
3. система
взаимосвязанных уравнений
— когда одни и те же зависимые переменные
в одних уравнениях входят в левую часть,
а в других — в правую:

Такая
система уравнений называется структурной
формой модели (СФМ).
Эндогенные
переменные
– взаимозависимые переменные, которые
определяются внутри модели (системы)
y.
Экзогенные
переменные
– независимые переменные, которые
определяются вне системы x.
Предопределенные
переменные
– экзогенные и лаговые (за предшествующие
моменты времени эндогенные переменные
системы).
Коэффициенты
a
и b
при переменных – структурные
коэффициенты
модели.
Система
линейных функций эндогенных переменных
от всех предопределенных переменных
системы – приведенная
форма модели (ПФМ):
где δ – коэффициенты
приведенной формы модели.
С
позиции идентифицируемости структурные
модели можно подразделить на три вида:
идентифицируемые, неидентифицируемые
и сверхидентифицируемые.
Модель
идентифицируема, если все структурные
ее коэффициенты определяются однозначно,
единственным образом по коэффициентам
приведенной формы модели, т. е. если
число параметров структурной модели
равно числу параметров ПФМ.
Модель
неидентифицируема, если число приведенных
коэффициентов меньше числа структурных
коэффициентов, и в результате структурные
коэффициенты не могут быть оценены
через коэффициенты приведенной формы
модели.
Модель
сверхидентифицируема, если число
приведенных коэффициентов больше
числа структурных коэффициентов. В этом
случае на основе коэффициентов приведенной
формы можно получить два или более
значений одного структурного коэффициента.
Необходимое
условие идентификации
– выполнение счетного правила:
D+1=H
– уравнение идентифицируемо;
D+1<H
– уравнение неидентифицируемо;
D+1>H
– уравнение сверхидентифицируемо,
где
H
– число эндогенных переменных в
уравнении,
D
– число предопределенных переменных,
отсутствующих в уравнении, но присутствующих
в системе.
Достаточное
условие идентификации
– определитель матрицы, составленной
из коэффициентов при переменных,
отсутствующих в исследуемом уравнении,
не равен нулю, и ранг этой матрицы не
менее числа эндогенных переменных
системы без единицы.
Выполнение условия
идентифицируемости модели проверяется
для каждого уравнения системы.
Для
решения идентифицируемого уравнения
применяется косвенный метод наименьших
квадратов, для решения сверхидентифицируемых
– двухшаговый метод наименьших квадратов.
Косвенный
метод наименьших квадратов
состоит в следующем:
-
составляют
приведенную форму модели и определяют
численные значения параметров каждого
ее уравнения обычным МНК; -
путем
алгебраических преобразований переходят
от приведенной формы модели к уравнениям
структурной формы модели, получая тем
самым численные оценки структурных
параметров.
3.1. Решение типовых задач
Пример 1.
Требуется:
1. Оценить следующую
структурную модель на идентификацию:

2.
Исходя из приведенной формы модели
уравнений

найти
структурные коэффициенты модели.
Решение:
1.
Модель имеет
три эндогенные (y1,
y2,
y3)
и три экзогенные (x1,
x2,
x3)
переменные.
Проверим
каждое уравнение системы на необходимое
(Н) и достаточное (Д) условия идентификации.
Первое уравнение.
Н:
эндогенных переменных – 2 (y1,
y3),
отсутствующих
экзогенных – 1 (x2).
Выполняется
необходимое равенство: 2=1+1, следовательно,
уравнение точно идентифицируемо.
Д:
в первом уравнении отсутствуют y2
и x2.
Построим
матрицу из коэффициентов при них в
других уравнениях системы:
|
Уравнение |
Отсутствующие |
|
|
y2 |
x2 |
|
|
Второе |
-1 |
a22 |
|
Третье |
b32 |
0 |
Определитель
матрицы не равен 0, ранг матрицы равен
2; следовательно, выполняется достаточное
условие идентификации, и первое уравнение
точно идентифицируемо.
Второе уравнение.
Н:
эндогенных переменных – 3 (y1,
y2,
y3),
отсутствующих
экзогенных – 2 (x1,
x3).
Выполняется
необходимое равенство: 3=2+1, следовательно,
уравнение точно идентифицируемо.
Д:
во втором уравнении отсутствуют x1
и x3.
Построим матрицу из коэффициентов при
них в других уравнениях системы:
|
Уравнение |
Отсутствующие |
|
|
x1 |
x3 |
|
|
Первое |
a11 |
a13 |
|
Третье |
a31 |
a33 |
Определитель
матрицы не равен 0, ранг матрицы равен
2; следовательно, выполняется достаточное
условие идентификации, и второе уравнение
точно идентифицируемо.
Третье уравнение.
Н:
эндогенных переменных – 2 (y2,
y3),
отсутствующих
экзогенных – 1 (x2).
Выполняется
необходимое равенство: 2=1+1, следовательно,
уравнение точно идентифицируемо.
Д:
в третьем уравнении отсутствуют y1
и x2.
Построим матрицу из коэффициентов при
них в других уравнениях системы:
|
Уравнение |
Отсутствующие |
|
|
y1 |
x2 |
|
|
Первое |
-1 |
0 |
|
Третье |
b21 |
a22 |
Определитель
матрицы не равен 0, ранг матрицы равен
2; следовательно, выполняется достаточное
условие идентификации, и третье уравнение
точно идентифицируемо.
Следовательно,
исследуемая система точно идентифицируема
и может быть решена косвенным методом
наименьших квадратов.
2.
Вычислим
структурные коэффициенты модели:
1)
из третьего уравнения приведенной формы
выразим x2
(так как его нет в первом уравнении
структурной формы):
Данное
выражение содержит переменные y3,
x1
и x3,
которые нужны для первого уравнения
СФМ. Подставим полученное выражение x2
в первое
уравнение ПФМ:
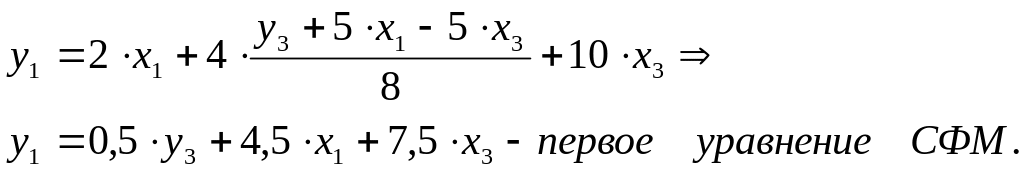
2)
во втором уравнении СФМ нет переменных
x1
и x3.
Структурные параметры второго уравнения
СФМ можно будет определить в два этапа:
Первый
этап: выразим
x1
в данном случае из первого или третьего
уравнения ПФМ. Например, из первого
уравнения:
Подстановка
данного выражения во второе выражение
ПФМ не решило бы задачу до конца, так
как в выражении присутствует x3,
которого нет в СФМ.
Выразим
x3
из третьего уравнения ПФМ:
Подставим
его в выражение x1:
Второй
этап:
аналогично, чтобы выразить x3
через искомые y1,
y3
и x2,
заменим в выражении x3
значение x1
на полученное из первого уравнения ПФМ:
Следовательно,
Подставим
полученные x1
и x3
во второе уравнение ПФМ:
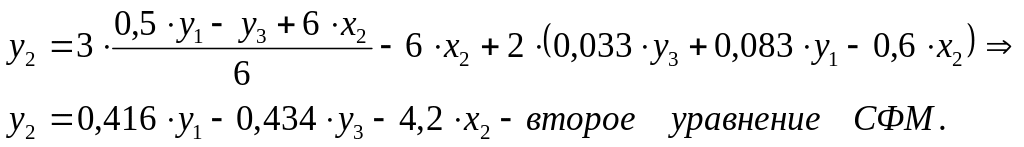
3)
из второго уравнения ПФМ выразим x2,
так как его нет в третьем уравнении СФМ:
Подставим полученное
выражение в третье уравнение ПФМ:
Таким образом, СФМ
примет вид:

Пример
2. Имеются
данные за 5 лет (табл. 3.1).
Таблица 3.1 –
Исходные данные
|
Номер года |
Годовое потребление |
Оптовая цена за |
Доход на душу |
Расходы по |
|
1 |
60 |
5,0 |
1300 |
60 |
|
2 |
62 |
4,0 |
1300 |
56 |
|
3 |
65 |
4,2 |
1500 |
56 |
|
4 |
62 |
5,0 |
1600 |
63 |
|
5 |
66 |
3,8 |
1800 |
50 |
Требуется:
Построить модель
вида
рассчитав
соответствующие структурные коэффициенты.
Решение:
Система одновременных
уравнений с двумя эндогенными и двумя
экзогенными переменными имеет вид
В каждом уравнении
две эндогенные и одна отсутствующая
экзогенная переменная из имеющихся в
системе. Для каждого уравнения данной
системы действует счетное правило 2 =
1+1. Это означает, что каждое уравнение
и система в целом идентифицированы.
Для определения
параметров такой системы применяется
косвенный метод наименьших квадратов.
С этой целью
структурная форма модели преобразуется
в приведенную форму:
в которой коэффициенты
при х определяются методом наименьших
квадратов.
Для нахождения
значений δ11 и δ12 запишем
систему нормальных уравнений:

При ее решении
предполагается, что х и у выражены
через отклонения от средних уровней,
т.е. матрица исходных данных составит:

Применительно к
ней необходимые суммы оказываются
следующими:
Система нормальных уравнений составит:
Решая ее, получим:
Первое уравнение
ПФМ:
.
Аналогично строим
систему нормальных уравнений для
определения коэффициентов δ21 и
δ22:

Следовательно,
Второе уравнение
ПФМ:
.
Приведенная форма
модели имеет вид:
из чего определяем
коэффициенты структурной модели:


Структурная форма
модели имеет вид:
3.2. Контрольные задания
Задание к задачам
1-20.
Имеются
структурная модель и приведенная форма
модели (таблица 3.1).
Требуется:
1.
Проверить структурную модель на
необходимое и достаточное условия
идентификации;
2.
Исходя из приведенной формы модели
уравнений, найти структурные коэффициенты
модели.
Таблица 3.2 –
Исходные данные
|
Вариант |
Структурная |
Приведенная |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
продолжение таблицы 3.1
|
Вариант |
Структурная |
Приведенная |
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
продолжение таблицы
3.2
|
Вариант |
Структурная |
Приведенная |
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
4. Временные ряды
Временной
ряд – это
совокупность значений какого либо
показателя за несколько последовательных
моментов или периодов времени.
Данные, представленные
в виде временных рядов, могут содержать
два вида компонент — систематическую
и случайную составляющие. Систематическая
составляющая является результатом
влияния постоянно действующих факторов.
Выделяют три основных систематических
компоненты временного ряда:
1) Тренд — это
систематическая линейная или нелинейная
компонента, плавно изменяющая во времени
(Т). Он описывает чистое влияние
долговременных факторов.
2) Циклическая
(сезонная) компонента (S).
Сезонность — это периодические колебания
уровней временного ряда в течение не
очень длительного периода (недели,
месяца, максимум — года). Цикличность
отражает повторяемость экономических
процессов в течение длительных периодов.
Систематические
составляющие могут одновременно
присутствовать во временном ряду.
Случайной
составляющей называется случайный шум,
или ошибка, воздействующая на временной
ряд нерегулярно (E).
Основными причинами случайного шума
могут быть факторы резкого и внезапного
воздействия , а также воздействие текущих
факторов, которое может быть связано,
например, с ошибками наблюдений.
Модель, в которой
временной ряд представлен как сумма
перечисленных компонент, называется
аддитивной
моделью временного ряда (Y=T+S+E).
Модель, в которой временной ряд представлен
как произведение перечисленных компонент,
называется мультипликативной
моделью временного ряда (Y=T∙S∙E).
Выбор одной из
двух моделей
проводится на основе анализа структуры
сезонных колебаний.
Если амплитуда колебаний приблизительно
постоянна, строят
аддитивную модель временного ряда, в
которой значения сезонной
компоненты предполагаются постоянными
для различных
циклов. Если амплитуда сезонных колебаний
возрастает или уменьшается, строят
мультипликативную модель временного
ряда,
которая ставит уровни ряда в зависимость
от значений сезонной
компоненты.
При наличии
тенденции и циклических колебаний
значения каждого последующего уровня
ряда зависят от предыдущих значений.
Корреляционную зависимость между
последовательными уровнями временного
ряда называют автокорреляцией
уровней
ряда.
Количественно ее
можно измерить с помощью линейного
коэффициента корреляции между уровнями
исходного временного ряда yt
и уровнями этого ряда, сдвинутыми на
несколько шагов во времени
yt—.
Число периодов,
по которым рассчитывается коэффициент
автокорреляции, называют лагом.
С увеличением лага число пар значений,
по которым рассчитывается коэффициент
автокорреляции, уменьшается. Максимальный
лаг должен быть не больше (n/4).
Коэффициент
автокорреляции уровней ряда первого
порядка, измеряющий зависимость между
соседними уровнями ряда yt
и yt-1,
т.е. при лаге 1, рассчитывается по формуле:
,
где
Аналогично
определяются коэффициенты автокорреляции
второго и более высоких порядков. Так,
коэффициент автокорреляции второго
порядка характеризует тесноту связи
между уровнями yt
и yt-2
и определяется по формуле:
,
где

Коэффициент
автокорреляции характеризует тесноту
только линейной связи текущего и
анализируемого уровней ряда. Поэтому
по коэффициенту автокорреляции можно
судить о наличии линейной (или близкой
к линейной) тенденции. Для некоторых
временных рядов, имеющих сильную
нелинейную тенденцию (например, параболу
или экспоненту), коэффициент автокорреляции
уровней исходного ряда может приближаться
к нулю.
Последовательность
коэффициентов автокорреляции уровней
первого, второго и т. д. порядков называют
автокорреляционной
функцией
временного ряда. График зависимости ее
значений от величины лага называется
коррелограммой.
При помощи анализа
автокорреляционной функции и коррелограммы
можно выявить структуру ряда.
Анализ структуры
можно проводить следующим образом:
-
если наиболее
высоким оказался коэффициент
автокорреляции первого порядка,
исследуемый ряд содержит только
тенденцию; -
если наиболее
высоким оказался коэффициент
автокорреляции порядка τ, ряд содержит
циклические колебания с периодичностью
в τ моментов времени; -
если ни один из
коэффициентов автокорреляции не
является значимым, можно сделать одно
из предположений относительно структуры
ряда:
-
ряд не содержит
тенденции и циклических колебаний, а
включает только случайную компоненту, -
ряд содержит
сильную нелинейную тенденцию.
Построение
аналитической функции для моделирования
тенденции (тренда) временного ряда
называют аналитическим
выравниванием временного ряда.
Для этого чаще всего применяются
следующие функции:
-
линейная
-
гипербола
-
экспонента
-
степенная
функция
-
парабола
второго и более высоких порядков
Параметры
трендов определяются обычным МНК, в
качестве независимой переменной
выступает время t=1,
2,…, n,
а в качестве зависимой переменной –
фактические уровни временного ряда yt.
Построение
аддитивной и мультипликативной моделей
сводится к расчету значений Т, S
и Е для каждого уровня ряда. Процесс
построения модели включает в себя
следующие шаги.
1) Выравнивание
исходного ряда методом скользящей
средней.
2)
Расчет значений сезонной компоненты
S.
3)
Устранение сезонной компоненты из
исходных уровней ряда и получение
выравненных данных (Т+Е) в аддитивной
или (Т∙Е) в мультипликативной модели.
4)
Аналитическое выравнивание уровней
(Т+Е) или (Т∙Е) и расчет значений Т с
использованием полученного уравнения
тренда.
5)
Расчет полученных по модели значений
(Т+S)
или (Т∙S).
6) Расчет абсолютных
и/или относительных ошибок.
Автокорреляция
в остатках
– корреляционная зависимость между
значениями остатков εt
за текущий и предыдущие моменты времени.
Для
определения автокорреляции остатков
используют критерий Дарбина-Уотсона и
расчет величины:

Выдвигается
гипотеза Н0
об отсутствии автокорреляции остатков.
Альтернативные гипотезы Н1
и Н1*
состоят, соответственно, в наличии
положительной или отрицательной
автокорреляции в остатках.
Далее
по специальным таблицам определяются
критические значения критерия
Дарбина-Уотсона dL
и dU
для заданного
числа наблюдений n,
числа независимых переменных модели k
и уровня значимости α.
По этим значениям числовой промежуток
[0;4] разбивают на пять отрезков.
Принятие
или отклонение каждой из гипотез с
вероятностью (1-α)
рассматривается на рис. 4.1.
0 dL
dU
2 4-dL
4-dU
4
Рис.
4.1. – Схема проверки гипотезы о наличии
автокорреляции
остатков
4.1. Решение типовых задач
Пример
1. Динамика
выпуска продукции Финляндии характеризуется
данными (млн. долл), представленными в
табл. 4.1.
Таблица 4.1 –
Исходные данные
|
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
|
Выпуск |
14150 |
14004 |
13088 |
12518 |
13471 |
13617 |
16356 |
20037 |
21748 |
23298 |
16570 |
23080 |
23981 |
23446 |
29658 |
38435 |
Требуется:
1.
Провести расчет параметров параболического
тренда. Построить графики ряда динамики
и тренда.
2.
Рассчитать критерий Дарбина-Уотсона.
Оценить полученный результат при 5%-ном
уровне значимости.
Решение:
1.
Параболический тренд имеет вид:
.
Определение
параметров тренда и построение графиков
осуществим с помощью «Мастера диаграмм»:
1)
введите исходные данные в ячейки листа
ПП Excel;
2)
на панели инструментов Стандартная
щелкните по кнопке Мастер
диаграмм;
3)
в окне «Тип диаграммы» из списка типов
выберете График;
вид графика – первый из списка.
4)
в окне «Источник данных диаграммы»
закладка Диапазон
данных
заполните поле Диапазон
(в нашем примере – Лист1!$A$1:$B$17);
закладка Ряд
заполните поле Подписи
оси Х (в нашем
примере – Лист1!$A$2:$A$17);
5)
в окне «Параметры диаграммы» заполните
параметры диаграммы на разных закладках;
6)
в окне «Размещение диаграммы» укажите
место размещения диаграммы;
7)
после построения графика ряда динамики
щелкните ПКМ на линии графика и в
контекстном меню выберете Добавить
линию
тренда;

в диалоговом окне «Линия тренда» выберете
вид линии тренда и задайте соответствующие
параметры (рис. 4.2);
9)
на рис. 4.3 представлены результаты
построения графиков ряда динамики и
параболического тренда.
Получили уравнение
параболического тренда:
.

Рис.
4.2 — Диалоговое окно параметров линии
тренда
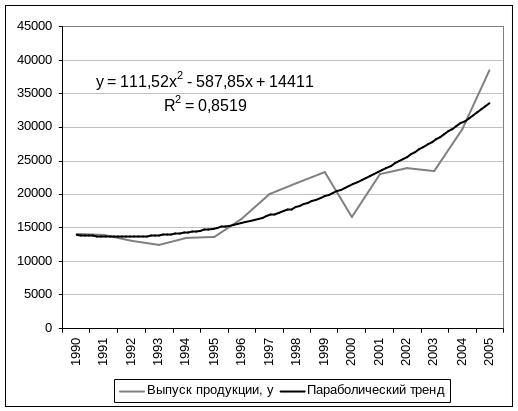
Рис.
4.3 — Графики ряда динамики и параболического
тренда
2.
Выровненные
значения ряда динамики
определим
путем подстановки фактических значений
t
(порядковый
номер года)
в уравнение
тренда:
Остатки
εt
рассчитываются по формуле
εt-1
– те же значения, что и εt,
но со сдвигом на один год.
Результаты
вычислений оформим в табл.4.2.
Критерий
Дарбина-Уотсона рассчитаем по формуле:

Таблица
4.2 – К расчету критерия Дарбина-Уотсона
|
№ |
|
εt |
εt-1 |
(εt— |
(εt— |
|
|
1 |
13934,7 |
215,3 |
— |
— |
— |
46367 |
|
2 |
13681,4 |
322,6 |
215,3 |
107,3 |
11511 |
104084 |
|
3 |
13651,1 |
-563,1 |
322,6 |
-885,8 |
784553 |
317115 |
|
4 |
13843,9 |
-1325,9 |
-563,1 |
-762,8 |
581849 |
1758064 |
|
5 |
14259,8 |
-788,8 |
-1325,9 |
537,2 |
288552 |
622127 |
|
6 |
14898,6 |
-1281,6 |
-788,8 |
-492,9 |
242921 |
1642550 |
|
7 |
15760,5 |
595,5 |
-1281,6 |
1877,1 |
3523467 |
354585 |
|
8 |
16845,5 |
3191,5 |
595,5 |
2596,1 |
6739476 |
10185800 |
|
9 |
18153,5 |
3594,5 |
3191,5 |
403,0 |
162417 |
12920646 |
|
10 |
19684,5 |
3613,5 |
3594,5 |
19,0 |
360 |
13057382 |
|
11 |
21438,6 |
-4868,6 |
3613,5 |
-8482,1 |
71945511 |
23702974 |
|
12 |
23415,7 |
-335,7 |
-4868,6 |
4532,9 |
20547092 |
112681 |
|
13 |
25615,8 |
-1634,8 |
-335,7 |
-1299,2 |
1687791 |
2672669 |
|
14 |
28039,0 |
-4593,0 |
-1634,8 |
-2958,2 |
8750888 |
21095833 |
|
15 |
30685,3 |
-1027,3 |
-4593,0 |
3565,8 |
12714716 |
1055243 |
|
16 |
33554,5 |
4880,5 |
-1027,3 |
5907,7 |
34901274 |
23819085 |
|
Итого |
317462,3 |
-5,3 |
-4885,8 |
4665,2 |
162882376 |
113467203 |
Фактическое
значение d
сравниваем с табличными значениями при
5%-ном уровне значимости. При n=16
лет и k=1
(число факторов) нижнее значение dL
равно 1,1, а верхнее dU
– 1,37. С вероятностью 0,95 принимается
гипотеза Н0
и можно считать, что автокорреляция в
остатках отсутствует. Следовательно,
уравнение регрессии может быть
использовано для прогноза.
Пример
2. Динамика
урожайности зерновых культур за 1996-2006
гг. характеризуется данными (ц/га),
представленными в табл. 4.3.
Таблица
4.3 — Урожайность зерновых культур за
1992-2006 гг.
|
Год |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
|
Урожайность, ц/га |
15,4 |
20,1 |
12 |
5,9 |
8,8 |
14,8 |
4,7 |
7 |
12,2 |
17 |
16,1 |
15,2 |
19,2 |
18,4 |
17,3 |
Требуется:
1.
Построить автокорреляционную функцию
временного ряда.
2.
Охарактеризовать структуру этого ряда.
Решение:
1.
Расчет
коэффициента автокорреляции первого
порядка для временного ряда урожайности
зерновых культур произведем в таблице
4.4.
Таблица 4.4 — Расчет
коэффициента автокорреляции первого
порядка
|
t |
|
|
|
|
|
|
|
|
1 |
15,4 |
— |
— |
— |
— |
— |
— |
|
2 |
20,1 |
15,4 |
6,62 |
2,06 |
13,621 |
43,8433 |
4,2318 |
|
3 |
12 |
20,1 |
-1,48 |
6,76 |
-9,991 |
2,1862 |
45,6590 |
|
4 |
5,9 |
12 |
-7,58 |
-1,34 |
10,177 |
57,4347 |
1,8033 |
|
5 |
8,8 |
5,9 |
-4,68 |
-7,44 |
34,822 |
21,8890 |
55,3961 |
|
6 |
14,8 |
8,8 |
1,32 |
-4,54 |
-6,003 |
1,7462 |
20,6376 |
|
7 |
4,7 |
14,8 |
-8,78 |
1,46 |
-12,792 |
77,0633 |
2,1233 |
|
8 |
7 |
4,7 |
-6,48 |
-8,64 |
55,993 |
41,9719 |
74,6990 |
|
9 |
12,2 |
7 |
-1,28 |
-6,34 |
8,110 |
1,6347 |
40,2318 |
|
10 |
17 |
12,2 |
3,52 |
-1,14 |
-4,024 |
12,4005 |
1,3061 |
|
11 |
16,1 |
17 |
2,62 |
3,66 |
9,587 |
6,8719 |
13,3747 |
|
12 |
15,2 |
16,1 |
1,72 |
2,76 |
4,746 |
2,9633 |
7,6018 |
|
13 |
19,2 |
15,2 |
5,72 |
1,86 |
10,626 |
32,7347 |
3,4490 |
|
14 |
18,4 |
19,2 |
4,92 |
5,86 |
28,826 |
24,2205 |
34,3061 |
|
15 |
17,3 |
18,4 |
3,82 |
5,06 |
19,326 |
14,6033 |
25,5747 |
|
Итого |
188,7* |
186,8 |
0,00 |
0,00 |
163,023 |
341,5636 |
330,3943 |
*) Сумма приведена
без значения 15,4 (затемненная ячейка).
Средние
составят:

Коэффициент
автокорреляции первого порядка:
Полученное значение
свидетельствует об отсутствии зависимости
между урожайностью зерновых культур
текущего и непосредственно предшествующего
годов.
Расчет коэффициента
автокорреляции второго порядка для
временного ряда урожайности зерновых
культур произведем в таблице 4.5.
Таблица 4.5 — Расчет
коэффициента автокорреляции второго
порядка
|
t |
|
|
|
|
|
|
|
|
1 |
15,4 |
— |
— |
— |
— |
— |
— |
|
2 |
20,1 |
— |
— |
— |
— |
— |
— |
|
3 |
12 |
15,4 |
-0,97 |
2,45 |
-2,371 |
0,9394 |
5,9837 |
|
4 |
5,9 |
20,1 |
-7,07 |
7,15 |
-50,518 |
49,9740 |
51,0675 |
|
5 |
8,8 |
12 |
-4,17 |
-0,95 |
3,977 |
17,3825 |
0,9098 |
|
6 |
14,8 |
5,9 |
1,83 |
-7,05 |
-12,914 |
3,3517 |
49,7567 |
|
7 |
4,7 |
8,8 |
-8,27 |
-4,15 |
34,349 |
68,3802 |
17,2544 |
|
8 |
7 |
14,8 |
-5,97 |
1,85 |
-11,020 |
35,6317 |
3,4083 |
|
9 |
12,2 |
4,7 |
-0,77 |
-8,25 |
6,349 |
0,5917 |
68,1260 |
|
10 |
17 |
7 |
4,03 |
-5,95 |
-23,999 |
16,2471 |
35,4483 |
|
11 |
16,1 |
12,2 |
3,13 |
-0,75 |
-2,360 |
9,8017 |
0,5683 |
|
12 |
15,2 |
17 |
2,23 |
4,05 |
9,026 |
4,9763 |
16,3714 |
|
13 |
19,2 |
16,1 |
6,23 |
3,15 |
19,603 |
38,8225 |
9,8983 |
|
14 |
18,4 |
15,2 |
5,43 |
2,25 |
12,198 |
29,4933 |
5,0452 |
|
15 |
17,3 |
19,2 |
4,33 |
6,25 |
27,051 |
18,7556 |
39,0144 |
|
Итого |
168,6* |
168,4 |
0,00 |
0,00 |
9,372 |
294,3477 |
302,8523 |
*) Сумма приведена
без значений 15,4 и 20,1 (затемненные ячейки).
Средние
составят:

Коэффициент
автокорреляции второго порядка:
Коэффициенты
автокорреляции третьего и четвертого
порядков рассчитаем в среде Excel
с помощью функции КОРРЕЛ при соответствующем
выборе диапазона значений.
Получаем r3=0,115
и r4=0,251.
Построим
автокорреляционную функцию и коррелограмму
временного ряда (табл. 4.6).
Таблица 4.6 —
Автокорреляционная функция и
коррелограмма ВР
|
Лаг |
Коэффициент |
Коррелограмма |
|
1 |
0,485 |
***** |
|
2 |
0,031 |
* |
|
3 |
0,115 |
* |
|
4 |
0,251 |
*** |
При анализе
временного ряда урожайности зерновых
культур наиболее высоким оказался
коэффициент автокорреляции уровней
первого порядка. Следовательно,
исследуемый ряд содержит только
тенденцию.
Пример 3.
Построить аддитивную модель временного
ряда потребления электроэнергии жителями
города за 18 кварталов, yt
(табл. 4.7).
Таблица 4.7 –
Потребление электроэнергии жителями
города,
млн. кВт∙ч
|
Номер квартала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
yt |
30 |
22 |
25 |
45 |
36 |
24 |
30 |
50 |
48 |
28 |
32 |
55 |
45 |
33 |
35 |
54 |
42 |
30 |
Решение:
Анализ значений
автокорреляционной функции (АКФ) и
коррелограммы (табл. 4.8) позволяет сделать
вывод о наличии в изучаемом временном
ряде линейной тенденции и сезонных
колебаний периодичностью в четыре
квартала.
Таблица 4.8 – АКФ
и коррелограмма временного ряда
потребления электроэнергии
|
Лаг |
Коэффициенты автокорреляции уровней |
Коррелограмма |
|
1 |
0,1802 |
** |
|
2 |
0,6115 |
****** |
|
3 |
0,1237 |
* |
|
4 |
0,919 |
********* |
|
5 |
0,0884 |
* |
|
6 |
0,7718 |
******** |
|
7 |
0,0208 |
|
|
8 |
0,8171 |
******** |
|
9 |
0,0698 |
* |
Объемы потребления
электроэнергии в осенне-зимний период
времени (I и IV кварталы) выше, чем весной
и летом (II и III кварталы).
По графику этого
ВР (рис. 4.4) можно установить наличие
приблизительно равной амплитуды
колебаний. Это свидетельствует о
возможном существовании аддитивной
модели временного ряда. Рассчитаем ее
компоненты.
Шаг 1.
Проведем выравнивание исходных уровней
ряда методом скользящей средней. Для
этого:
1) просуммируем
уровни ряда последовательно за каждые
четыре квартала со сдвигом на один
момент времени и определим условные
годовые объемы потребления электроэнергии
(гр.3 табл. 4.9);
2) разделив полученные
суммы на 4, найдем скользящие средние
(гр.4 табл. 4.9). Полученные таким образом
выравненные значения уже не содержат
сезонной компоненты;
3) приведем эти
значения в соответствие с фактическими
моментами времени, для чего найдем
средние значения из двух последовательных
скользящих средних, т.е. центрированные
скользящие средние (гр.5 табл. 4.9).
Таблица 4.9 –
Расчет оценок сезонной компоненты в
аддитивной модели
|
№ квартала, t |
Потребление электроэнергии, |
Итого по 4 кварталам |
Скользящая средняя по кварталам |
Центрированная скользящая |
Оценка сезонной компоненты |
|
1 |
30 |
||||
|
2 |
22 |
122 |
30,50 |
||
|
3 |
25 |
128 |
32,00 |
31,250 |
-6,250 |
|
4 |
45 |
130 |
32,50 |
32,250 |
12,750 |
|
5 |
36 |
135 |
33,75 |
33,125 |
2,875 |
|
6 |
24 |
140 |
35,00 |
34,375 |
-10,375 |
|
7 |
30 |
152 |
38,00 |
36,500 |
-6,500 |
|
8 |
50 |
156 |
39,00 |
38,500 |
11,500 |
|
9 |
48 |
158 |
39,50 |
39,250 |
8,750 |
|
10 |
28 |
163 |
40,75 |
40,125 |
-12,125 |
|
11 |
32 |
160 |
40,00 |
40,375 |
-8,375 |
|
12 |
55 |
165 |
41,25 |
40,625 |
14,375 |
|
13 |
45 |
168 |
42,00 |
41,625 |
3,375 |
|
14 |
33 |
167 |
41,75 |
41,875 |
-8,875 |
|
15 |
35 |
164 |
41,00 |
41,375 |
-6,375 |
|
16 |
54 |
161 |
40,25 |
40,625 |
13,375 |
|
17 |
42 |
||||
|
18 |
30 |
Шаг 2.
Найдем оценки сезонной компоненты как
разность между фактическими уровнями
ряда и центрированными скользящими
средними (гр.6 табл. 4.9).
Найдем (табл. 4.10)
средние за каждый квартал (по всем годам)
оценки сезонной компоненты Si.
Таблица 4.10 – Расчет
значений сезонной компоненты
в аддитивной
модели
|
Показатели |
№ квартала, |
|||
|
I |
II |
III |
IV |
|
|
Сезонная |
— |
— |
-6,250 |
12,750 |
|
Сезонная |
2,875 |
-10,375 |
-6,500 |
11,500 |
|
Сезонная |
8,750 |
-12,125 |
-8,375 |
14,375 |
|
Сезонная |
3,375 |
-8,875 |
-6,375 |
13,375 |
|
Итого |
15,000 |
-31,375 |
-27,500 |
52,000 |
|
Средняя оценка для |
5,000 |
-10,458 |
-6,875 |
13,000 |
|
Скорректированная |
4,833 |
-10,625 |
-7,041 |
12,833 |
В моделях с сезонной
компонентой обычно предполагается, что
сезонные воздействия за период взаимно
погашаются. В аддитивной модели это
выражается в том, что сумма значений
сезонной компоненты по всем кварталам
должна быть равна нулю.
Для данной модели
имеем:
.
Определим
корректирующий коэффициент:
.
Рассчитаем
скорректированные значения сезонной
компоненты как разность между ее средней
оценкой и корректирующим коэффициентом
k
(
).
Проверим условие равенства нулю суммы
значений сезонной компоненты:
.
Таким образом,
получены следующие значения сезонной
компоненты по кварталам года:
S1
= 4,833; S2
= -10,625; S3
= -7,041; S4
= 12,833.
Занесем полученные
значения в табл. 4.11 для соответствующих
кварталов каждого года (гр. 3).
Таблица 4.11 – Расчет
выровненных значений тренда и ошибок
в аддитивной
модели
|
t |
yt |
Si |
T+E=yt |
T |
T+S |
E=yt |
E2 |
|
1 |
30 |
4,833 |
25,167 |
30,756 |
35,589 |
-5,589 |
31,237 |
|
2 |
22 |
10,625 |
32,625 |
31,515 |
20,890 |
1,110 |
1,232 |
|
3 |
25 |
-7,041 |
32,041 |
32,274 |
25,233 |
-0,233 |
0,054 |
|
4 |
45 |
12,833 |
32,167 |
33,033 |
45,866 |
-0,866 |
0,750 |
|
5 |
36 |
4,833 |
31,167 |
33,792 |
38,625 |
-2,625 |
6,891 |
|
6 |
24 |
-10,625 |
34,625 |
34,551 |
23,926 |
0,074 |
0,005 |
|
7 |
30 |
-7,041 |
37,041 |
35,310 |
28,269 |
1,731 |
2,996 |
|
8 |
50 |
12,833 |
37,167 |
36,069 |
48,902 |
1,098 |
1,206 |
|
9 |
48 |
4,833, |
43,167 |
36,828 |
41,661 |
6,339 |
40,183 |
|
10 |
28 |
-10,625 |
38,625 |
37,587 |
26,962 |
1,038 |
1,077 |
|
11 |
32 |
-7,041 |
39,041 |
38,346 |
31,305 |
0,695 |
0,483 |
|
12 |
55 |
12,833 |
42,167 |
39,105 |
51,938 |
3,062 |
9,376 |
|
13 |
45 |
4,833 |
40,167 |
39,864 |
44,697 |
0,303 |
0,092 |
|
14 |
33 |
-10,625 |
43,625 |
40,623 |
29,998 |
3,002 |
9,012 |
|
15 |
35 |
-7,041 |
42,041 |
41,382 |
34,341 |
0,659 |
0,434 |
|
16 |
54 |
12,833 |
41,167 |
42,141 |
54,974 |
-0,974 |
0,949 |
|
17 |
42 |
4,833 |
37,167 |
42,900 |
47,733 |
-5,733 |
32,867 |
|
18 |
30 |
-10,625 |
40,625 |
43,659 |
33,034 |
-3,034 |
9,205 |
Шаг 3.
Элиминируем влияние сезонной компоненты,
вычитая ее значение из каждого уровня
исходного ряда.
Получим величины
T+E=Y– S, (гр. 4 табл. 4.11).
Эти значения
рассчитываются за каждый момент времени
и содержат только тенденцию и случайную
компоненту.
Шаг 4.
Определим компоненту Т данной модели.
Для этого проведем
аналитическое выравнивание ряда (Т+Е)
с помощью линейного тренда.
Результаты
аналитического выравнивания следующие:
Подставляя в это
уравнение значения t = 1, …, 18, найдем
уровни
для каждого момента времени (гр. 5 табл.
4.11).
График уравнения тренда приведен на
рис. 4.4.

Рис.4.4 – Потребление
электроэнергии жителями города
Шаг 5.
Найдем значения уровней ряда, полученные
по аддитивной модели. Для этого прибавим
к уровням тренда значения сезонной
компоненты для соответствующих кварталов.
Графически значения (Т+S) представлены
на рис. 4.4.
Шаг 6.
В соответствии с методикой построения
аддитивной модели расчет ошибки
производится по формуле
.
Численные значения абсолютных ошибок
приведены в гр. 7 табл. 4.11.
Сумма квадратов
абсолютных ошибок равна 148,05 (гр. 8 табл.
4.11). Общая сумма квадратов отклонений
уровней ряда от его среднего уровня
составляет 1867,778. Коэффициент детерминации
равен R2=0,9207.
Аддитивная модель
объясняет 92.07% общей вариации уровней
ряда потребления электроэнергии за
последние 18 кварталов.
4.2. Контрольные задания
Задачи
1-10. Динамика
выпуска продукции характеризуется
данными (млн. долл.), представленными в
табл. 4.3.
Требуется:
1.
Провести расчет параметров линейного,
степенного, экспоненциального и
параболического трендов.
2.
Выбрать наилучший вид тренда на основании
графического изображения и значения
коэффициента детерминации.
3.
Построить графики ряда динамики и
выбранного тренда.
4.
Рассчитать критерий Дарбина-Уотсона.
Оценить полученный результат при 5%-ном
уровне значимости.
5.
Сделать прогноз ряда на два ближайших
года.
Таблица
4.12 – Исходные данные по теме «Временные
ряды»
|
Задача |
Временные ряды |
|||||||||
|
1 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
|
1054 |
1104 |
1149 |
1291 |
1427 |
1505 |
1513 |
1635 |
1987 |
2306 |
|
|
2 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2367 |
2913 |
3837 |
5490 |
2202 |
6342 |
7665 |
8570 |
11172 |
14150 |
|
|
3 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14004 |
13088 |
12518 |
13471 |
13617 |
16356 |
20037 |
21748 |
23298 |
26570 |
|
|
4 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
23080 |
23981 |
23446 |
29658 |
39573 |
38435 |
39002 |
39020 |
40012 |
41005 |
|
|
5 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2467 |
3013 |
3837 |
5190 |
2200 |
6340 |
7660 |
8570 |
11072 |
14050 |
|
|
6 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14000 |
13080 |
12510 |
13470 |
13610 |
16350 |
20035 |
21745 |
23295 |
26570 |
|
|
7 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
|
1050 |
1100 |
1150 |
1290 |
1425 |
1505 |
1515 |
1635 |
1987 |
2306 |
Продолжение таблицы
4.12
|
8 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2365 |
2915 |
3840 |
5490 |
2202 |
6342 |
7663 |
8574 |
11175 |
14144 |
|
|
9 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14000 |
13091 |
12522 |
13474 |
13616 |
16354 |
20037 |
21745 |
23299 |
26572 |
|
|
10 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
23085 |
23980 |
23444 |
29657 |
39570 |
38435 |
39000 |
39020 |
40012 |
41010 |
|
|
11 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
|
1050 |
1104 |
1144 |
1291 |
1427 |
1508 |
1513 |
1635 |
1988 |
2303 |
|
|
12 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2377 |
2923 |
3847 |
5490 |
2212 |
6342 |
7655 |
8560 |
11072 |
14150 |
|
|
13 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14104 |
13188 |
12508 |
13471 |
13617 |
16356 |
20037 |
21728 |
23278 |
26550 |
|
|
14 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
23180 |
23881 |
23446 |
29558 |
39573 |
38535 |
39102 |
39020 |
40112 |
41005 |
|
|
15 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2467 |
3013 |
3837 |
5290 |
2200 |
6240 |
7660 |
8470 |
11172 |
14050 |
|
|
16 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14110 |
13080 |
12500 |
13470 |
13630 |
16550 |
20135 |
21755 |
23195 |
26550 |
|
|
17 |
1961 |
1962 |
1963 |
1964 |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
|
1150 |
1110 |
1350 |
1490 |
1425 |
1555 |
1515 |
1635 |
1977 |
2306 |
|
|
18 |
1971 |
1972 |
1973 |
1974 |
1975 |
1976 |
1977 |
1978 |
1979 |
1980 |
|
2385 |
2915 |
3820 |
5490 |
2262 |
6342 |
7633 |
8574 |
11375 |
14144 |
|
|
19 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
14025 |
13061 |
12522 |
13484 |
13416 |
16354 |
20437 |
21445 |
23229 |
26372 |
|
|
20 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
|
23085 |
23680 |
23444 |
28657 |
39570 |
35435 |
39320 |
39020 |
40312 |
41010 |
5. Контрольные вопросы по курсу
-
Предмет эконометрики
и сущность ее методов. С какими науками
она связана. -
Типы данных и
классы моделей. -
Этапы эконометрического
моделирования. -
Понятие парной и
множественной регрессии. -
Спецификация
эконометрических моделей. -
Погрешность
моделей. -
Смысл и оценка
параметров уравнения регрессии. -
Метод наименьших
квадратов. -
Линейный коэффициент
корреляции и коэффициент детерминации. -
Дисперсионный
анализ результатов регрессии. -
Оценка значимости
уравнения регрессии с помощью F-критерия
Фишера. -
Оценка значимости
параметров уравнения регрессии и
коэффициента корреляции по t-критерию
Стьюдента. -
Интервальная
оценка параметров регрессии. -
Интервальный
прогноз на основе уравнения регрессии. -
Нелинейная
регрессия. -
Оценивание
коэффициентов нелинейной регрессии. -
Показатели
корреляции для нелинейной регрессии. -
В чем смысл средней
ошибки аппроксимации и как она
определяется. -
Определение
коэффициентов эластичности по разным
видам регрессионных моделей. -
Предпосылки МНК.
Условия Гаусса-Маркова. -
Проверка 1 и 2
предпосылок МНК (графический метод). -
Проверка наличия
гомо- и гетероскедастичности остатков.
Метод Гольдфельда-Квандта. -
Проверка
автокоррелированности остатков. -
Линейные
регрессионные модели с гетероскедастичными
и автокоррелированными остатками -
Спецификация
модели множественной регрессии. -
Мультиколлинеарность
факторов и методы ее устранения. -
Оценка параметров
уравнения множественной регрессии. -
Тест на выбор
«длинной» или «короткой» регрессии. -
Множественная
корреляция. Коэффициенты частной
корреляции. -
Оценка надежности
результатов множественной регрессии
и корреляции. -
Обобщенный метод
наименьших квадратов. -
Метод максимального
правдоподобия. -
Способы построения
систем эконометрических уравнений. -
Структурная и
приведенная формы модели. -
Проблема
идентификации. Необходимое и достаточное
условия идентификации. -
Оценивание
параметров структурной модели. КМНК и
ДМНК. -
Основные элементы
временного ряда. -
Автокорреляция
уровней временного ряда и выявление
его структуры. -
Моделирование
тенденции временного ряда. -
Моделирование
сезонных и циклических колебаний.
Мультипликативная и аддитивная модели
временного ряда. -
Моделирование
тенденции ВР при наличии структурных
изменений. Тест Чоу. -
Стационарные и
нестационарные временные ряды. -
Модели нестационарных
временных рядов (AR,
MА,
ARIMA).
Библиографический список
-
Варюхин А.М.,
Панкина О.Ю., Яковлева А.В. Эконометрика:
Пособие для сдачи экзамена. – М.:
Юрайт-Издат, 2005. – 191 с. -
Гришин А.Ф.
Статистические модели в экономике /
А.Ф. Гришин, С.Ф. Котов-Дарти, В.Н. Ягунов.
– Ростов н/Д: «Феникс», 2005. – 344 с. -
Елисеева И.И.,
Юзбашев М.М. Общая теория статистики:
Учебник / Под ред. И.И. Елисеевой. – 5-е
изд., перераб. и доп. – М.: Финансы и
статистика, 2006. – 656 с. -
Кремер Н.Ш., Путко
Б.А. Эконометрика:Учебник для вузов /
Под ред. Проф. Н.Ш. Кремера. – М.:
ЮНИТИ-ДАНА, 2007. – 311 с. -
Луговская Л.В.
Эконометрика в вопросах и ответах:
учеб. пособие. – М.: ТК Велби, Изд-во
Проспект, 2005. – 208 с. -
Орлов А.И.
Эконометрика: Учебник для вузов / А.И.
Орлов.- 3-е изд., перераб. и доп. – М.:
Издательство «Экзамен», 2004. – 576 с. -
Практикум по
эконометрике: Учеб. пособие / И.И.
Елисеева, С.В. Курышева, Н.М. Гордеенко
и др.; Под ред. И.И. Елисеевой. – 2-е изд.,
перераб. и доп. – М.: Финансы и статистика,
2006. – 344 с. -
Статистическая
обработка и анализ экономических
данных / А.В. Каплан [и др.]. – Ростов
н/Д: Феникс, 2007. – 330 с. -
Тихомиров Н.П.,
Дорохина Е.Ю. Эконометрика: Учебник /
Н.П. Тихомиров, Е.Ю. Дорохина – М.:
Издательство «Экзамен», 2003. – 512 с. -
Тюрин Ю.Н. , Макаров
А.А. Анализ данных на компьютере / Под
ред. В.Э. Фигурнова. – 3-е изд., перераб.
и доп. – М.: ИНФРА-М, 2003. – 544 с.
Приложение 1
Таблица
значений F-критерия
Фишера при уровне значимости а
=
0,05
|
k1 k2 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
∞ |
|
1 |
161,45 |
199,50 |
215,72 |
224,57 |
230,17 |
233,97 |
238,89 |
243,91 |
249,04 |
254,32 |
|
2 |
18,51 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,37 |
19,41 |
19,45 |
19,50 |
|
3 |
10,13 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,84 |
8,74 |
8,64 |
8,53 |
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,77 |
5,63 |
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,53 |
4,36 |
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,84 |
3,67 |
|
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,41 |
3,23 |
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,12 |
2,93 |
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
2,90 |
2,71 |
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,74 |
2,54 |
|
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
2,95 |
2,79 |
2,61 |
2,40 |
|
12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,50 |
2,30 |
|
13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,77 |
2,60 |
2,42 |
2,21 |
|
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,70 |
2,53 |
2,35 |
2,13 |
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,29 |
2,07 |
|
16 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,59 |
2,42 |
2,24 |
2,01 |
|
17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,55 |
2,38 |
2,19 |
1,96 |
|
18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,51 |
2,34 |
2,15 |
1,92 |
|
19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,48 |
2,31 |
2,11 |
1,88 |
|
20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,45 |
2,28 |
2,08 |
1,84 |
|
21 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,42 |
2,25 |
2,05 |
1,81 |
|
22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,40 |
2,23 |
2,03 |
1,78 |
|
23 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,38 |
2,20 |
2,00 |
1,76 |
|
24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,36 |
2,18 |
1,98 |
1,73 |
|
25 |
4,24 |
3,38 |
2,99 |
2,76 |
2,60 |
2,49 |
2,34 |
2,16 |
1,96 |
1,71 |
Продолжение
приложения 1
|
k1 k2 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
∞ |
|
26 |
4,22 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,32 |
2,15 |
1,95 |
1,69 |
|
27 |
4,21 |
3,35 |
2,96 |
2,73 |
2,57 |
2,46 |
2,30 |
2,13 |
1,93 |
1,67 |
|
28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,44 |
2,29 |
2,12 |
1,91 |
1,65 |
|
29 |
4,18 |
3,33 |
2,93 |
2,70 |
2,54 |
2,43 |
2,28 |
2,10 |
1,90 |
1,64 |
|
30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,27 |
2,09 |
1,89 |
1,62 |
|
35 |
4,12 |
3,26 |
2,87 |
2,64 |
2,48 |
2,37 |
2,22 |
2,04 |
1,83 |
1,57 |
|
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,18 |
2,00 |
1,79 |
1,51 |
|
45 |
4,06 |
3,21 |
2,81 |
2,58 |
2,42 |
2,31 |
2,15 |
1,97 |
1,76 |
1,48 |
|
50 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,13 |
1,95 |
1,74 |
1,44 |
|
60 |
4,00 |
3,15 |
2,76 |
2,52 |
2,37 |
2,25 |
2,10 |
1,92 |
1,70 |
1,39 |
|
70 |
3,98 |
3,13 |
2,74 |
2,50 |
2,35 |
2,23 |
2,07 |
1,89 |
1,67 |
1,35 |
|
80 |
3,96 |
3,11 |
2,72 |
2,49 |
2,33 |
2,21 |
2,06 |
1,88 |
1,65 |
1,31 |
|
90 |
3,95 |
3,10 |
2,71 |
2,47 |
2,32 |
2,20 |
2,04 |
1,86 |
1,64 |
1,28 |
|
100 |
3,94 |
3,09 |
2,70 |
2,46 |
2,30 |
2,19 |
2,03 |
1,85 |
1,63 |
1,26 |
|
125 |
3,92 |
3,07 |
2,68 |
2,44 |
2,29 |
2,17 |
2,01 |
1,83 |
1,60 |
1,21 |
|
150 |
3,90 |
3,06 |
2,66 |
2,43 |
2,27 |
2,16 |
2,00 |
1,82 |
1,59 |
1,18 |
|
200 |
3,89 |
3,04 |
2,65 |
2,42 |
2,26 |
2,14 |
1,98 |
1,80 |
^,57 |
1,14 |
|
300 |
3,87 |
3,03 |
2,64 |
2,41 |
2,25 |
2,13 |
1,97 |
1,79 |
1,55 |
1,10 |
|
400 |
3,86 |
3,02 |
2,63 |
2,40 |
2,24 |
2,12 |
1,96 |
1,78 |
1,54 |
1,07 |
|
500 |
3,86 |
3,01 |
2,62 |
2,39 |
2,23 |
2,11 |
1,96 |
1,77 |
1,54 |
1,06 |
|
1000 |
3,85 |
3,00 |
2,61 |
2,38 |
2,22 |
2,10 |
1,95 |
1,76 |
1,53 |
1,03 |
|
oo |
3,84 |
2,99 |
2,60 |
2,37 |
2,21 |
2,09 |
1,94 |
1,75 |
1,52 |
1,00 |
Приложение
2
Критические
значения t-критерия
Стьюдента при уровне значимости 0,10,
0,05, 0,01 (двухсторонний)
|
Число степеней свободы |
a |
Число степеней свободы |
а |
||||
|
d.f. |
0,10 |
0,05 |
0,01 |
d.f. |
0,10 |
0,05 |
0,01 |
|
1 |
6,3138 |
12,706 |
63,657 |
18 |
1,7341 |
2,1009 |
2,8784 |
|
2 |
2,9200 |
4,3027 |
9,9248 |
19 |
1,7291 |
2,0930 |
2,8609 |
|
3 |
2,3534 |
3,1825 |
5,8409 |
20 |
1,7247 |
2,0860 |
2,8453 |
|
4 |
2,1318 |
2,7764 |
4,6041 |
21 |
1,7207 |
2,0796 |
2,8314 |
|
5 |
2,0150 |
2,5706 |
4,0321 |
22 |
1,7171 |
2,0739 |
2,8188 |
|
6 |
1,9432 |
2,4469 |
3,7074 |
23 |
1,7139 |
2,0687 |
2,8073 |
|
7 |
1,8946 |
2,3646 |
3,4995 |
24 |
1,7109 |
2,0639 |
2,7969 |
|
8 |
1,8595 |
2,3060 |
3,3554 |
25 |
1,7081 |
2,0595 |
2,7874 |
|
9 |
1,8331 |
2,2622 |
3,2498 |
26 |
1,7056 |
2,0555 |
2,7787 |
|
10 |
1,8125 |
2,2281 |
3,1693 |
27 |
1,7033 |
2,0518 |
2,7707 |
|
11 |
1,7959 |
2,2010 |
3,1058 |
28 |
1,7011 |
2,0484 |
2,7633 |
|
12 |
1,7823 |
2,1788 |
3,0545 |
29 |
1,6991 |
2,0452 |
2,7564 |
|
13 |
1,7709 |
2,1604 |
3,0123 |
30 |
1,6973 |
2,0423 |
2,7500 |
|
14 |
1,7613 |
2,1448 |
2,9768 |
40 |
1,6839 |
2,0211 |
2,7045 |
|
15 |
1,7530 |
2,1315 |
2,9467 |
60 |
1,6707 |
2,0003 |
2,6603 |
|
16 |
1,7459 |
2,1199 |
2,9208 |
120 |
1,6577 |
1,9799 |
2,6174 |
|
17 |
1,7396 |
2,1098 |
2,8982 |
∞ |
1,6449 |
1,9600 |
2,5758 |
Приложение
3
Значения
статистик Дарбина-Уотсона при 5%-ном
уровне значимости
|
n |
к1=1 |
kl=2 |
kl=3 |
kl=4 |
kl=5 |
|||||
|
dL |
du |
dL |
du |
dL |
dv |
dL |
du |
dL |
du |
|
|
6 |
0,61 |
1,40 |
— |
— |
— |
— |
||||
|
7 |
0,70 |
1,36 |
0,47 |
1,90 |
— |
— |
||||
|
8 |
0,76 |
1,33 |
0,56 |
1,78 |
0,37 |
2,29 |
||||
|
9 |
0,82 |
1,32 |
0,63 |
1,70 |
0,46 |
2,13 |
||||
|
10 |
0,88 |
1,32 |
0,70 |
1,64 |
0,53 |
2,02 |
||||
|
11 |
0,93 |
1,32 |
0,66 |
1,60 |
0,60 |
1,93 |
||||
|
12 |
0,97 |
1,33 |
0,81 |
1,58 |
0,66 |
1,86 |
||||
|
13 |
1,01 |
1,34 |
0,86 |
1,56 |
0,72 |
1,82 |
||||
|
14 |
1,05 |
1,35 |
0,91 |
1,55 |
0,77 |
1,78 |
||||
|
16 |
1,10 |
1,37 |
0,98 |
1,54 |
0,86 |
1,73 |
0,74 |
1,93 |
0,62 |
2,15 |
|
17 |
1,13 |
1,38 |
1,02 |
1,54 |
0,90 |
1,71 |
0,78 |
1,90 |
0,67 |
2,10 |
|
18 |
1,16 |
1,39 |
1,05 |
1,53 |
0,93 |
1,69 |
0,82 |
1,87 |
0,71 |
2,06 |
|
19 |
1,18 |
1,40 |
1,08 |
1,53 |
0,97 |
1,68 |
0,86 |
1,85 |
0,75 |
2,02 |
|
20 |
1,20 |
1,41 |
1,10 |
1,54 |
1,00 |
1,68 |
0,90 |
1,83 |
0,79 |
1,99 |
|
21 |
1,22 |
1,42 |
1,13 |
1,54 |
1,03 |
1,67 |
0,93 |
1,81 |
0,83 |
1,96 |
|
22 |
1,24 |
1,43 |
1,15 |
1,54 |
1,05 |
1,66 |
0,96 |
1,80 |
0,86 |
1,94 |
|
23 |
1,26 |
1,44 |
1,17 |
1,54 |
1,08 |
1,66 |
0,99 |
1,79 |
0,90 |
1,92 |
|
24 |
1,27 |
1,45 |
1,19 |
1,55 |
1,10 |
1,66 |
1,01 |
1,78 |
0,93 |
1,90 |
|
25 |
1,29 |
1,45 |
1,21 |
1,55 |
1,12 |
1,66 |
1,04 |
1,77 |
0,95 |
1,89 |
|
26 |
1,30 |
1,46 |
1,22 |
1,55 |
1,14 |
1,65 |
1,06 |
1,76 |
0,98 |
1,88 |
|
27 |
1,32 |
1,47 |
1,24 |
1,56 |
1,16 |
1,65 |
1,08 |
1,76 |
1,01 |
1,86 |
|
28 |
1,33 |
1,48 |
1,26 |
1,56 |
1,18 |
1,65 |
1,10 |
1,75 |
1,03 |
1,85 |
|
29 |
1,34 |
1,48 |
1,27 |
1,56 |
1,20 |
1,65 |
1,12 |
1,74 |
1,05 |
1,84 |
|
30 |
1,35 |
1,49 |
1,28 |
1,57 |
1,21 |
1,65 |
1,14 |
1,74 |
1,07 |
1,83 |
Приложение
4
Варианты заданий
для студентов заочного отделения
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
|
1 |
1 1 1 1 1 |
2 2 2 2 2 |
3 3 3 3 3 |
4 4 4 4 4 |
5 5 5 5 5 |
6 6 6 6 6 |
7 7 7 7 7 |
8 8 8 8 8 |
9 9 9 9 9 |
10 10 10 10 10 |
|
2 |
11 11 11 11 11 |
12 12 12 12 12 |
13 13 13 13 13 |
14 14 14 14 14 |
15 15 15 15 15 |
16 16 16 16 16 |
17 17 17 17 17 |
18 18 18 18 18 |
19 19 19 19 19 |
20 20 20 20 20 |
|
3 |
1 2 3 4 21 |
2 3 4 5 22 |
3 4 5 6 23 |
4 5 6 7 24 |
5 6 7 8 25 |
6 7 8 9 26 |
7 8 9 10 27 |
8 9 10 11 28 |
9 10 11 12 29 |
10 11 12 13 30 |
|
4 |
11 12 13 14 31 |
12 13 14 15 32 |
13 14 15 16 33 |
14 15 16 17 34 |
15 16 17 18 35 |
16 17 18 19 36 |
17 18 19 20 37 |
18 19 20 1 38 |
19 20 1 2 39 |
20 1 2 3 40 |
|
5 |
1 3 5 7 1 |
2 4 6 8 2 |
3 5 7 9 3 |
4 6 8 10 4 |
5 7 9 11 5 |
6 8 10 12 6 |
7 9 11 13 7 |
8 10 12 14 8 |
9 11 13 15 9 |
10 12 14 16 10 |
|
6 |
11 13 15 17 11 |
12 14 16 18 12 |
13 15 17 19 13 |
14 16 18 20 14 |
15 17 19 1 15 |
16 18 20 2 16 |
17 19 1 3 17 |
18 20 2 4 18 |
19 1 3 5 19 |
20 2 4 6 20 |
|
7 |
1 4 7 10 21 |
2 5 8 11 22 |
3 6 9 12 23 |
4 7 10 13 24 |
5 8 11 14 25 |
6 9 12 15 26 |
7 10 13 16 27 |
8 11 14 17 28 |
9 12 15 18 29 |
10 13 16 19 30 |
|
8 |
11 14 17 20 31 |
12 15 18 1 32 |
13 16 19 2 33 |
14 17 20 3 34 |
15 18 1 4 35 |
16 19 2 5 36 |
17 19 3 6 37 |
18 20 4 7 38 |
19 1 5 8 39 |
20 2 6 9 40 |
|
9 |
1 5 9 13 1 |
2 6 10 14 2 |
3 7 11 15 3 |
4 8 12 16 4 |
5 9 13 17 5 |
6 10 14 18 6 |
7 11 15 19 7 |
8 12 16 20 8 |
9 13 17 1 9 |
10 14 18 2 10 |
|
0 |
11 15 19 3 11 |
12 16 20 4 12 |
13 17 1 5 13 |
14 18 2 6 14 |
15 19 3 7 15 |
16 20 4 8 16 |
17 1 5 9 17 |
18 2 6 10 18 |
19 3 7 11 19 |
20 4 8 12 20 |
Вариант контрольной
работы для
студентов заочного отделения
содержит 5 заданий: 4 задачи (по темам
«Парная регрессия», «Множественная
регрессия», «Системы одновременных
уравнений», «Временные ряды») и 1
теоретический вопрос. Задания контрольной
работы должны выбираться студентами
по двум последним цифрам его учебного
номера (номер студенческого билета) в
соответствии с таблицей
выбора вариантов.
В первой колонке таблицы по вертикали
расположены цифры от 1 до 0, и каждая из
них – предпоследняя цифра личного
номера. В первой строке таблицы по
горизонтали также расположены цифры
от 1 до 0, и каждая из них – последняя
цифра личного номера Пересечения
вертикальных (А) и горизонтальных (Б)
линий определяют номера заданий
контрольной работы, записанные столбиком.
Например, если личный шифр студента
имеет две последние цифры 75, то он должен
выполнить номера 5 (тема 1), 8 (тема 2), 11
(тема 3), 14 (тема 4), 6 (вопрос).
Учебное издание
Алексей Фруминович
Рогачёв
Ольга Александровна
Заяц
Эконометрика
Учебное пособие
В авторской редакции
Компьютерная верстка О.А.Заяц
Подписано в печать 29.04.09 .
Формат 60-84 1/16.
Гарнитура Times.
Печать офсетная.Усл. печ. л. 5,0.
Тираж 100 экз. Заказ № ____.
Издательско-полиграфический комплекс
ВГСХА «Нива».
400002, Волгоград, пр-т. Университетский, 26
20
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R2:
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε<10%
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
16646