Материал из GIS-Lab
Перейти к: навигация,
поиск
| ГИС для преподавателей | Часть 6: Топология |

|
Цель: Понимание топологии векторных данных
Ключевые слова: Вектор, Топология, Правила Топологии, Топологические Ошибки, Радиус Поиска, Расстояние Замыкания, Простой Объект |
Обзор:
Топология регулирует пространственные отношения связности и соседства векторных объектов (точек, линий и полигонов) в ГИС. Топологические данные полезны для обнаружения и исправления ошибок оцифровки (например, две линии дорог не сходятся на месте перекрестка). Корректная топология необходима для проведения некоторых типов пространственного анализа, таких как сетевой анализ.
Представьте, что Вы поехали в Лондон. Сначала Вы планируете посетить Собор Святого Павла, а вечером поехать на Ковент Гарден за подарками. Смотря на лондонскую карту метро (на Рисунке 58), Вы ищете, как доехать от Собора до Ковент Гарден. Поиск требует топологическую информацию о том, где можно совершать пересадки. На карте метро топологические отношения связности показаны кружками. Пересадки на отмеченных станциях позволяют Вам перейти с одной ветки метро на другую.
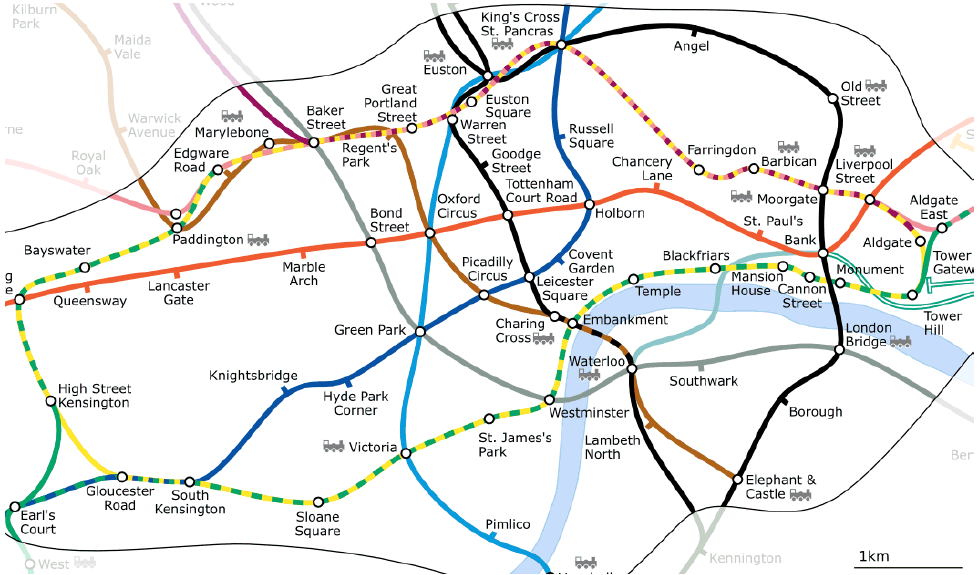
Рисунок 58: Топология сети лондонского метро.
Топологические ошибки
Существуют различные типа топологических ошибок, и они могут быть сгруппированы в соответствии с типами геометрии (полигоны или полилинии). Топологические ошибки с полигональными объектами включают незакрытые полигоны, разрывы между прилежащими полигонами, а также перекрывающиеся полигоны. Распространенной ошибкой для линейных объектов является то, когда их конечные вершины не совпадают в тех местах, где они должны совпадать (например, улицы на перекрестках). Подобные ошибки называются «недолетами», когда между линиями наблюдается разрыв, и «перелетами», когда одна линия пересекает другую и заканчивается чуть дальше (см. Рисунок 59).
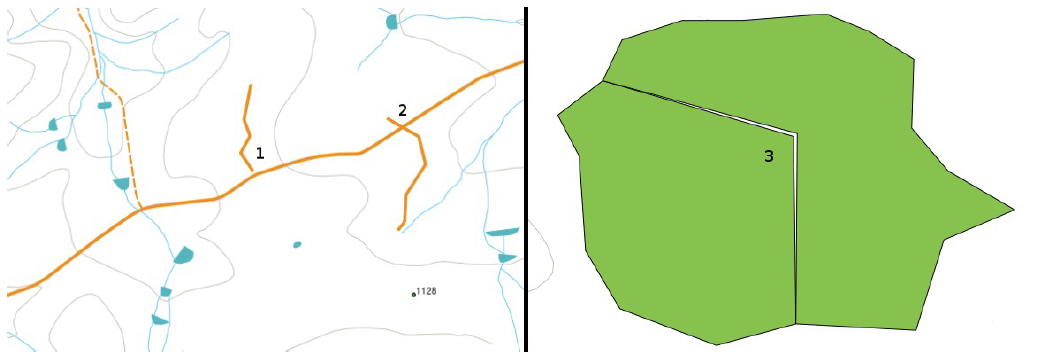
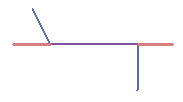
Рисунок 59: «Недолеты» (1) появляются, когда оцифрованные векторные линии, которые должны соединяться друг с другом, не соединяются.
«Перелеты» (2) происходят, когда одна линия заканчивается за другой линией, к которой должна быть присоединена. Когда вершины
двух полигонов на их границах не совпадают, появляются разрывы (3).
Результатами недолетов и перелетов являются так называемые «висячие узлы» в конце линий. Висячие узлы приемлемы в отдельных случаях, например для тупиковых улиц. Топологические ошибки нарушают отношения между объектами. Эти ошибки должны быть исправлены перед проведением таких типов анализа векторных данных, как сетевой анализ (т.е. поиск кратчайшего маршрута по дорожной сети) или измерения (т.е. выяснение длины рек). Помимо необходимости топологии в сетевом анализе и измерениях, существуют другие причины, почему следует иметь топологически корректные данные. Представьте, что Вы цифруете муниципальные границы Вашего района, и полигоны перекрываются или имеют разрывы. В случае таких ошибок Вы по-прежнему можете пользоваться инструментами измерений, но результаты будут некорректными. Полученная площадь будет неправильной, и будет непонятно, где именно находятся границы (например, в случае перекрывающихся полигонов принадлежность территории к двум муниципалитетам одновременно невозможна!).
Иметь топологически корректные данные важно не только для проведения собственного анализа, но и для других людей, которым Вы можете передать свои данные. Они могут не знать об ошибках и будут расценивать результаты своего анализа как правильные.
Правила топологии
К счастью, многие распространенные ошибки, происходящие при оцифровке, могут быть предотвращены с помощью правил топологии, внедренных во многие ГИС-приложения. Кроме некоторых специализированных форматов геоданных, топология обычно не применяется по умолчанию. Многие широко распространенные ГИС, такие как QGIS, определяют топологию как серию правил, которые могут быть выбраны пользователем и применены к векторным слоям. Следующий список включает некоторые примеры правил топологии, определяемых для объектов реального мира на векторной карте:
- Элементы муниципальной карты не должны перекрывать друг друга.
- Элементы муниципальной карты не должны иметь разрывов.
- Полигоны земельных участков должны быть замкнутыми. «Недолеты» и «перелеты» границ участков не позволяются.
- Горизонтали высот не должны пересекаться.
Топологические инструменты
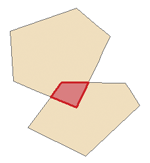
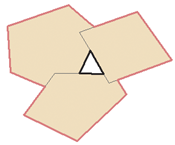
Многие ГИС-приложения имеют инструменты топологического редактирования. Например, в QGIS Вы можете включить топологическое редактирование для эффективного редактирования общих границ объектов полигональных слоев. ГИС-приложение обнаруживает общие границы объектов, и Вам достаточно будет передвинуть только одну вершину, в то время как приложение обновит вершину прилежащего полигона, как показано на Рисунке 60 (1). Другая опция топологического редактирования – установка ограничения на перекрытие полигонов (см. Рисунок 60 (2)). В QGIS, если Вы нарисуете новый полигон поверх существующего, приложение обрежет новый полигон по границе существующего.
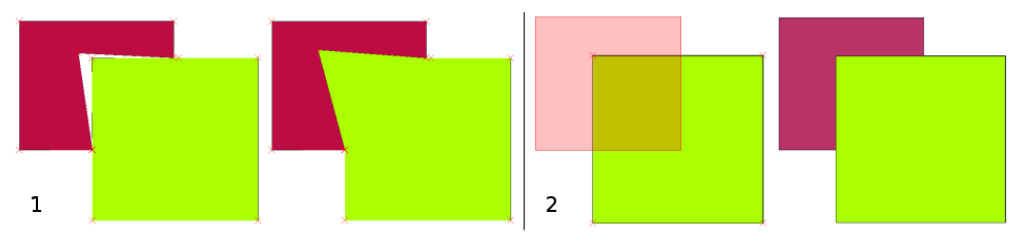
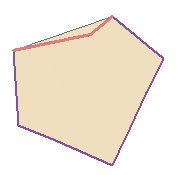
Рисунок 60: Топологическое редактирование. 1) Когда пользователь сдвигает вершину в углу бордового полигона, соответствующая вершина зеленого квадрата
автоматически следует за ней. 2) Чтобы избежать перекрытия полигонов, новый объект (бордовый) автоматически обрезается по границе существующего (зеленый).
Радиус замыкания
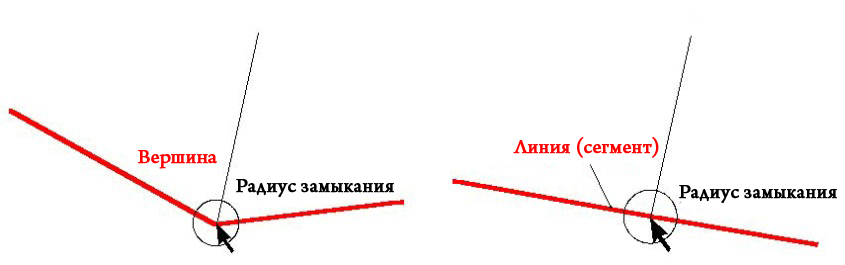
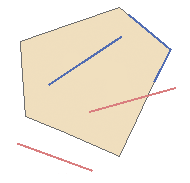
Радиус замыкания – это максимальный радиус поиска, который использует ГИС-приложение для стыковки инструмента редактирования с существующими вершинами или сегментами редактируемого слоя в ходе оцифровки (сегмент – это прямая линия, соединяющая две вершины полилинии или полигона). Если Ваш курсор находится внутри этого радиуса и Вы создаете новую вершину, ГИС-приложение стыкует ее к существующей вершине или сегменту (см. Рисунок 61). В противном случае вершина создается там, где был произведен клик мышью, независимо от существующих вершин.
Рисунок 61: Радиус замыкания (черный кружок) определяется в единицах измерения карты (например, в десятичных градусах)
для стыковки новой вершины к существующим вершинам или сегментам.
Радиус поиска
Радиус поиска – это расстояние, которое ГИС-приложение использует для поиска ближайшей к курсору вершины, когда Вы пытаетесь ее выделить для перетаскивания на карте. По сути, это почти то же самое, что и радиус замыкания, только для редактирования существующих вершин. Он также устанавливается в единицах измерения карты, и нужно попробовать разные значения, чтобы найти оптимальное. Если значение слишком большое, ГИС-приложение может при клике мышью выделить не ту вершину, которую Вы хотели выделить, просто потому что она тоже попала в радиус. Особенно эта проблема актуальна для объектов с большим количеством близко расположенных вершин. Если Вы укажете слишком маленькое значение, вершины вообще не будут выделяться, хотя будет казаться, что Вы подвели курсор прямо к вершине. Выбор оптимального радиуса поиска также зависит от чувствительности мышки и индивидуальных предпочтений пользователя.
О чем стоит помнить:
Топология – это сложное представление векторных данных. Топологические наборы данных хранятся в специальных файловых форматах, включающих описание отношений между объектами. В то же время, наиболее распространенные форматы геоданных являются «простыми», то есть хранят только геометрию и атрибуты. Они разработаны для быстрого отображения на карте и не расчитаны на топологический анализ (например, поиск кратчайшего пути). Многие ГИС-приложения могут отображать и топологические и простые данные, а некоторые могут также создавать и редактировать эти данные.
Что мы узнали?
Закрепим изученный материал:
- Топология описывает пространственные взаимоотношения соседствующих векторных объектов.
- В ГИС-приложениях за топологию отвечают топологические инструменты.
- Топологию можно использовать для выявления и исправления ошибок, возникших в ходе оцифровки.
- Корректная топология необходима для некоторых видов анализа, таких как сетевой анализ.
- Установка радиуса замыкания и радиуса поиска помогает нам производить топологически корректную оцифровку.
- Простые векторные данные не включают топологические правила, но они широко используются в ГИС-приложениях.
Попробуйте сами!
Ниже приведено несколько примеров практических заданий для Ваших учеников:
- Отметьте автобусные остановки на листе топографической карты и попросите учеников найти кратчайший маршрут между двумя остановками.
- Подумайте, как бы Вы создали векторные объекты в ГИС для представления топологической сети дорог в Вашем городе. Какие топологические правила важны в данном случае и какие инструменты QGIS могут использовать ученики, чтобы проверить топологическую корректность созданного набора данных?
Если у Вас нет компьютера:
Вы можете использовать карту автобусных или ж/д маршрутов и обсудить пространственные отношения и топологию с учениками.
Дополнительные материалы:
Книги:
- Сhang, Kang-Tsung (2006): Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. (ISBN 0070658986)
- DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. (ISBN 9814126195)
Веб-сайты:
- http://www.innovativegis.com/basis/primer/concepts.html
- http://en.wikipedia.org/wiki/Geospatial_topology
Руководство Пользователя QGIS включает более детальную информацию о топологическом редактировании.
Что дальше?
В следующем разделе мы изучим системы координат, чтобы понять, как географические данные о шарообразной Земле переносятся на плоские карты.
Основные модели гис-растровая и векторная.
В ГИС
происходит дискретизация—
преобразование реального географического
разнообразия в набор дискретных объектов.
|
Растровая модель данных |
Векторная модель данных |
(Аналогия- представление |
|
Разрешение- минимальная |
Местоположение и |
Топология.
Топология изучает пространственные
отношения, которые не изменяются при
любых непрерывных преобразованиях
пространства.
Пространственные отношения— это
такие отношения, с помощью которых
описывают пространственные взаимодействия
объектов (например: находиться
близко/далеко, соприкасаться, находиться).
Свойства топологии.
-
Топология
регулирует пространственные отношения
связности и соседства векторных
объектов(точек, линий и полигонов) в
ГИС. -
Топологические
данные полезны для обнаружения и
исправления ошибок оцифровки (например:
две линии дороги не пересекаются на
перекрестке). -
Корректная
топология необходима для проведения
некоторых типов пространственного
анализа (таких как сетевой анализ).
Топологические ошибки.
Топологические ошибки с линейными
объектами: конечные вершины не совпадают
в местах, где должны. Подобные ошибки
называются «недолётами» (если разрыв)
или «перелётами» (если пересекаются
линии и заканчиваются чуть дальше).
Доступно с лицензией Standard или Advanced.
- Правила для полигонов
- Правила для линий
- Правила для точек
Существует множество правил топологии, которые используются для управления геометрией объектов в базе геоданных, в зависимости от пространственных взаимоотношений, которые являются наиболее важными для поддержки в информационной системе вашей организации. Следует тщательно продумать, какие именно правила для ваших данных действительно нужны. Некоторые правила топологии управляют отношениями между объектами в одном классе объектов, а некоторые используются для управления пространственными отношениями между двумя различными классами объектов или подтипами объектов. Правила топологии могут быть настроены между подтипами объектов в одном или в нескольких классах объектов. Например, правило топологии может требовать, чтобы все объекты улиц соединялись с другими объектами улиц на обоих концах, за исключением тех случаев, когда улица относится к подтипу “тупик”.
Многие топологические правила можно применять к пространственным объектам баз геоданных. Хорошо продуманная база геоданных будет содержать только те правила, которые действительно необходимы в связи со спецификой данных организации.
Большинство ограничений, накладываемых правилами топологии имеют специальные предопределенные способы исправления, которые вы можете использовать для исправления ошибок. Однако, для некоторых ошибок предопределенных способов исправления не существует. Если вы обнаружили ошибки топологии, можно выделить ошибку на карте с помощью инструмента Исправить ошибки топологии (Fix Topology Error) 
Вы можете ознакомиться с правилами топологии на постере, доступном по ссылке Правила топологии баз геоданных в ArcGIS (ArcGIS Geodatabase Topology Rules) PDF.
Если эта ссылка не работает, вы можете открыть файл topology_rules_poster.pdf из директории Documentation в директории, в которую вы устанавливали ArcGIS. Для просмотра этого документа потребуется наличие установленного Adobe Reader.
Правила для полигонов
| Правило топологии | Описание правила | Возможные методы исправления | Примеры |
|---|---|---|---|
|
Должен превышать кластерный допуск |
Требуется, чтобы пространственный объект не схлопывался в процессе проверки. Это правило является обязательным для топологии и применяется для всех классов линейных и полигональных объектов. В случаях проверки этого правила исходная геометрия остаётся неизменённой. |
Удалить (Delete): Метод исправления Удалить удаляет полигональный объект, который был схлопнут в процессе проверки топологии, который проводился на основе значения кластерного допуска топологии. Исправление можно применять к одной или ко многим ошибкам типа Должен превышать кластерный допуск. |
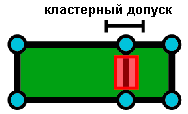
Любой полигональный объект вроде красного на этом рисунке, который схлопнулся бы при проверке топологии, что считается ошибкой. |
|
Не должны перекрываться |
Требуется, чтобы внутренние части полигонов не перекрывались. Полигоны могут иметь общие границы или вершины. Это правило используется в том случае, когда территория не может принадлежать одновременно нескольким полигонам. Оно может использоваться при моделировании административного деления и других взаимоисключающих классификаций, например при выделении типов растительного покрова. |
Вычитание (Subtract): Метод исправления Вычитание удаляет перекрывающуюся часть геометрии из каждого полигона, который вызвал ошибку, и оставляет промежуток на месте пересечения. Этот способ может быть применен к одной или нескольким выбранным ошибкам правила Не должны перекрываться. Слияние (Merge): Метод устранения ошибок Слияние добавляет перекрытие к одному из объектов, вызвавшему ошибку, и вычитает это перекрытие из другого. Вам необходимо указать объект, который получит область перекрытия, в диалоговом окне Слияние (Merge). Этот метод может быть применен только к одной ошибке правила Не должны перекрываться. Создать объект (Create Feature): При этом способе из геометрической формы, обозначенной как ошибка, создается новый полигональный объект, а из каждого из объектов, вызвавших ошибку, удаляется перекрывающаяся часть. При этом создается плоское представление геометрии объекта. Этот способ может быть применен к одной или нескольким выбранным ошибкам правила Не должны перекрываться. |
|
|
Не должны иметь пробелов |
Данное правило требует, чтобы не было пустых мест внутри полигонов или между граничащими полигонами. Все полигоны должны формировать область непрерывной поверхности. Ошибка будет всегда существовать на периметре этой области. Вы можете либо игнорировать эту ошибку, либо пометить ее как исключение. Используйте это правило для данных, которые должны полностью покрывать область. Например, полигоны почв не могут иметь пробелов или пустот, — они должны покрывать всю территорию. |
Создать объект (Create Feature): Создается новый объект из пустой области, которая полностью окружена полигонами (замкнутое кольцо из линий ошибок). Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Не должны иметь пробелов. Если вы выбрали два объекта ошибок и используете способ исправления Создать объект, в результате могут получиться два объекта — по одному полигональному объекту на кольцо. Если вы хотите получить в результате составной объект, вам нужно выбрать все новые объекты и указать Слияние (Merge) в меню Редактор. Обратите внимание, что внешняя граница класса объектов помечена как ошибка. Использование способа Создать объект для этой конкретной ошибки может привести к созданию перекрывающихся полигонов. Или, вы можете пометить внешнюю границу ошибки Не должны иметь пробелов как исключение. |
Вы можете использовать способ Создать объект, чтобы создать посередине новый полигон. Вы можете также использовать метод Создать объект или пометить ошибку на внешней границе как исключение. |
|
Не должны перекрываться с |
Требуется, чтобы внутренние части полигонов одного класса объектов (или подтипа) не перекрывались с внутренними частями полигонов другого класса объектов (или подтипа). Полигоны этих двух классов могут иметь общие ребра и вершины, или могут быть не связаны между собой. Это правило используется, когда территория не может одновременно принадлежать двум разным классам пространственных объектов. Например, при районировании земельных угодий важно, чтобы водные объекты не попали в площади районов, поэтому нужно отслеживать, чтобы полигональные объекты этих двух классов не перекрывались. |
Вычитание (Subtract): Метод исправления Вычитание удаляет перекрывающиеся части полигонов из исходных объектов, оставляя на месте перекрытия промежуток. Этот способ может быть применен к одной или нескольким выбранным ошибкам правила Не должны перекрываться с. Слияние (Merge): Метод устранения ошибок Слияние добавляет перекрытие к одному из объектов, вызвавшему ошибку, и вычитает это перекрытие из другого. Вам необходимо указать объект, который получит область перекрытия, в диалоговом окне Слияние (Merge). Этот способ применим только к одной ошибке для правила Не должны перекрываться с. |
|
|
Должны совмещаться с объектами другого класса |
Требуется, чтобы полигоны в одном классе объектов (или подтипе) имели общее покрытие территории с полигонами другого класса объектов (или подтипа). Область в первом классе объектов, не покрытая полигонами из другого класса пространственных объектов, является ошибкой. Это правило используется когда области одного типа, например, страны, должны быть покрыты другими областями, например, районами или субъектами. |
Вычитание (Subtract): Метод устранения ошибок Вычитание удаляет перекрывающийся участок из каждого объекта, который участвовал в ошибке, таким образом граница обоих объектов становится смежной. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Должны совмещаться с объектами класса. Создать объект (Create Feature): При этом способе вне области перекрытия будет образован новый полигональный объект из существующего полигона, так что границы каждого объекта из обоих классов будут совпадать. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Должны совмещаться с объектами класса. |
|
|
Должны совпадать друг с другом (Must Cover Each Other) |
Требуется, чтобы полигоны в одном классе объектов (или подтипе) имели общую площадь с полигонами другого класса объектов (или подтипа). У полигонов могут быть общие рёбра или вершины. Любая область, принадлежащая полигону из одного класса, которая одновременно не принадлежит полигонам другого класса, является ошибкой. Это правило используется, когда для одной территории представлено две системы классификации, и каждая территориальная единица, выделенная в одной системе, должна быть каким-то образом определена и в другой. Подобный случай возникает при работе с иерархическими системами объектов, например, бассейнами стока крупных рек и локальными водосборами. Также это правило может применяться при работе со связанными системами объектов, таких как типы почв и классы уклона поверхности. |
Вычитание (Subtract): Метод устранения ошибок Вычитание удаляет перекрывающийся участок из каждого объекта, который участвовал в ошибке, таким образом граница обоих объектов становится смежной. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Должны совпадать друг с другом. Создать объект (Create Feature): При этом способе вне области перекрытия будет образован новый полигональный объект из существующего полигона, так что границы каждого объекта из обоих классов будут совпадать. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Должны совпадать друг с другом. |
|
|
Должны совмещаться с |
Требуется, чтобы полигоны одного класса объектов (или подтипа) находились внутри полигонов другого класса объектов (или подтипа). У полигонов могут быть общие рёбра или вершины. Любая область, определенная в первом классе, должна быть покрыта областями объектов второго класса. Это правило используется, когда площадные объекты одного типа должны располагаться в пределах объектов другого типа. Оно полезно, когда моделируются территории, являющиеся частью более крупной окружающей области, например, территориальные единицы внутри лесов или участки внутри садовых товариществ. |
Создать объект (Create Feature): При этом способе вне области перекрытия будет образован новый полигональный объект из существующего полигона, так что границы каждого объекта из обоих классов будут совпадать. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Должны совмещаться с. |
|
|
Граница должна совмещаться с (Boundary Must Be Covered By) |
Это правило требует, чтобы границы полигональных объектов совпадали с линейными объектами другого класса пространственных объектов. Оно используется, когда требуется, чтобы линейные объекты отмечали границы площадных объектов. Обычно это необходимо, когда сама территория имеет один набор атрибутов, а ее граница — другой набор. Например, в базе геоданных могут храниться участки со своими границами. Каждый участок может быть определен одной или несколькими линиями, которые хранят информацию об их длине или дате съемки, и граница каждого участка должна полностью совпадать с этими линиями. |
Создать объект (Create Feature): При этом способе создается новый линейный объект из сегментов границы полигонального объекта, вызвавшего ошибку. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Граница должна совмещаться с. |
|
|
Граница должна совпадать с границей (полигон, полигон) |
Требуется чтобы границы полигонов в одном классе объектов (или подтипе) были покрыты границами полигонов в другом классе объектов (или подтипе). Это может быть полезно, когда полигоны в одном классе объектов, например, кварталы, состоят из нескольких полигонов из другого класса объектов, например, участков, и границы этих объектов должны совпадать. |
Нет |
|
|
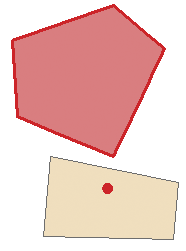
Содержит точку |
Это правило требует, чтобы полигоны одного класса пространственных объектов содержали хотя бы по одной точке из другого класса. Точки должны располагаться внутри полигона, а не на его границе. Это правило используется, когда необходимо, чтобы каждый полигон содержал хотя бы одну связанную точку, например, когда участок должен иметь указатель адреса. |
Создать объект (Create Feature): При этом способе создается новый точечный в центре полигонального объекта, вызвавшего ошибку. Создаваемый точечный объект гарантированно попадает в пределы полигонального объекта. Этот способ может быть применен к одной или нескольким выбранным ошибкам для правила Содержит точку. |
Верхний полигон является ошибкой, поскольку не содержит точку. |
|
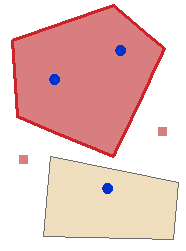
Содержит одну точку |
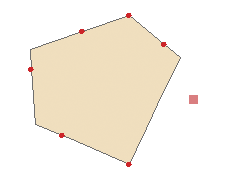
Требуется, чтобы каждый полигон содержал внутри один точечный объект и каждый точечный объект располагался в пределах одного полигона. Это правило используется, когда требуется обеспечить соответствие один к одному для полигональных и точечных объектов в разных классах объектов, например для границ субъектов и их столиц. Каждая точка должна быть расположена в пределах полигона и один полигон может содержать только одну точку. Точки должны располагаться внутри полигона, а не на его границе. |
Нет |
Верхний полигон является ошибочным, так как содержит внутри более одной точки. Точки за пределами полигонов также являются ошибками. |
Правила для полигонов
Правила для линий
| Правило топологии | Описание правила | Возможные методы исправления | Примеры |
|---|---|---|---|
|
Должен превышать кластерный допуск |
Требуется, чтобы пространственный объект не схлопывался в процессе проверки. Это правило является обязательным для топологии и применяется для всех классов линейных и полигональных объектов. В случаях проверки этого правила исходная геометрия остаётся неизменённой. |
Удалить (Delete): Метод исправления удаляет все объекты, длина которых меньше значения кластерного допуска топологии и они искажаются в процессе проверки топологии. Исправление можно применять к одной или ко многим ошибкам типа Должен превышать кластерный допуск. |
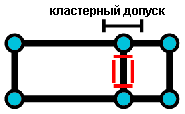
Любые линейные объекты, как красные линии на рисунке, которые схлопнутся при проверке топологии, считаются ошибкой. |
|
Не должны перекрываться |
Требуется, чтобы линии не перекрывались с линиями из того же класса объектов (или подтипа). Это правило используется, когда сегменты линий не должны дублироваться, например, в классе объектов водотоков. Линии могут пересекаться или соединяться, но не могут иметь общих сегментов. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Обратите внимание, что метод устранения ошибок Вычесть создает составные объекты, поэтому, если перекрывающиеся сегменты не расположены в начале или конце линейного объекта, то, возможно, потребуется воспользоваться командой Разделить на панели инструментов Расширенное редактирование, чтобы создать простые объекты. Этот способ может быть применен только к одной ошибке для правила Не должны перекрываться. |
|
|
Не должны пересекаться |
Требуется, чтобы линейные объекты из одного класса объектов (или подтипа) не пересекались или не накладывались друг на друга. Линии могут касаться конечными точками. Правило используется для изолиний, которые никогда не должны пересекаться, или в тех случаях, когда пересечения должны происходить только на концах линий, например, как в случае с сегментами улиц и перекрестками. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Обратите внимание, что метод устранения ошибок Вычесть создает составные объекты, поэтому, если перекрывающиеся сегменты не расположены в начале или конце линейного объекта, то, возможно, потребуется воспользоваться командой Разделить на панели инструментов Расширенное редактирование, чтобы создать простые объекты. Этот способ может быть применен только к одной ошибке для правила Не должны пересекаться. Разбить (Split): Метод разбивает линейные объекты, которые пересекают другие объекты, в точке их пересечения. Если две линии пересекаются в одной точке, применение этого способа в точке пересечения приведет к созданию четырех объектов. Атрибуты исходных объектов сохранятся для новых объектов. Если установлено правило разбиения, атрибуты присваиваются в соответствии с этим правилом. Этот способ может применяться к одной или нескольким ошибкам для правила Не должны пересекаться. |
|
|
Не должны пересекаться с |
Требуется, чтобы линейные объекты из одного класса объектов (или подтипа) не пересекали линии из другого класса объектов (или подтипа). Линии могут касаться конечными точками. Это правило используется, когда существуют линии в двух слоях, которые не должны пересекаться друг с другом, и пересечения могут происходить только в конечных точках, например, как в случае с железными дорогами или с улицами. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Обратите внимание, что метод устранения ошибок Вычесть создает составные объекты, поэтому, если перекрывающиеся сегменты не расположены в начале или конце линейного объекта, то, возможно, потребуется воспользоваться командой Разделить на панели инструментов Расширенное редактирование, чтобы создать простые объекты. Этот метод может применяться одновременно только к одной ошибке правила Не должны пересекаться с. Разбить (Split): Метод разбивает линейные объекты, которые пересекают другие объекты, в точке их пересечения. Если две линии пересекаются в одной точке, применение этого способа в точке пересечения приведет к созданию четырех объектов. Атрибуты исходных объектов сохранятся для новых объектов. Если установлено правило разбиения, атрибуты присваиваются в соответствии с этим правилом. Это исправление может быть применено к одной или к нескольких ошибкам правила Не должны пересекаться с. |
|
|
Не должны иметь висячих узлов |
Требуется, чтобы линейные объекты касались линейных объектов в том же классе объектов (или подтипе) двумя конечными точками. Конечная точка, не присоединенная к другой линии, называется висячим узлом. Это правило используется, когда линии должны образовывать замкнутые петли, например, тогда, когда они являются границами полигонов. Также правило можно использовать, если в классе пространственных объектов обычно линии соединяются между собой, например, как линии улиц. В таком случае, исключениями могут быть использованы, когда правило нарушается, но данные при этом правильные — например, в случае тупика улицы. |
Растянуть (Extend): Метод растягивает висячие концы линейного объекта, если они примыкают к другой линии в пределах кластерного допуска. Если на этом расстоянии не найдено объектов, то линия не будет растянута. При выборе нескольких ошибок, объекты, которые не могут быть растянуты, пропускаются. Ошибки объектов, которые не могут быть продлены до примыкания к другим объектам, остаются перечисленными в списке диалогового окна Инспектор ошибок (Error Inspector). Если значение расстояния 0, линии будут продолжены до любого объекта по прямой. Этот способ может быть применен к одной или нескольким ошибкам для правила Не должны иметь висячих узлов. Сократить (Trim): Этот метод сокращает висячий конец линии до точки пересечения линейных объектов в пределах кластерного допуска топологии. Если на этом расстоянии не найдено объектов, линия не будет ни сокращена, ни удалена, если заданное расстояние больше длины объекта, составляющего ошибку. Если значение расстояния равно 0, линии будут сокращаться, пока не достигнут точки пересечения. Если точка пересечения не обнаружена, объект не будет сокращен, и процесс продолжится для следующего ошибочного объекта. Этот способ может быть применен к одной или нескольким ошибкам для правила Не должны иметь висячих узлов. Замкнуть (Snap): Используется для замыкания линейных объектов к ближайшим линейным объектам в пределах указанного расстояния. Если на этом расстоянии не найдено линейных объектов, линия не будет замыкаться. Замыкание будет выполнено на ближайшем найденном объекте в пределах указанного расстояния. Сначала с целью замыкания идет поиск конечных точек, затем вершин, и наконец, ребер линейных объектов. Этот способ может быть применен к одной или нескольким ошибкам для правила Не должны иметь висячих узлов. |
|
|
Не должны иметь псевдоузлов |
Это правило требует, чтобы линия присоединялась как минимум к двум другим линиям каждой конечной точкой. Считается, что линия, которая присоединяется к одной линии или замыкается сама на себя, имеет псевдоузел. Это правило используется, когда линии должны образовывать замкнутые системы, такие как границы полигонов или когда линии моделируемых объектов логически должны соединяться с двумя другими линиями каждым концом, например, если они представляют сегменты в сети потоков, где как исключения будут отмечены начальные точки потоков первого порядка. |
Слияние к наибольшему (Merge To Largest): При этом способе геометрия короткой линии присоединяется к большей по длине линии. Сохраняются атрибуты большей по длине линии. Этот способ может быть применен к одной или нескольким ошибкам для правила Не должны иметь псевдоузлов. Слияние (Merge): Метод исправления Слияние добавляет геометрию линейного объекта к другому объекту, который стал причиной ошибки. Вы можете указать линию, с которой будет выполнено слияние. Этот способ может быть применен к одной ошибке для правила Не должны иметь псевдоузлов. |
|
|
Не должны пересекаться или касаться |
Требуется, чтобы линия в одном классе пространственных объектов (или подтипе) касалась линий в этом классе объектов только в конечных точках. Совпадение сегментов линий или любое пересечение не в конечной точке является ошибкой. Это правило полезно, когда линии должны быть соединены только в конечных точках, например, в случае с линиями лотов (съемочных участков), которые должны быть разбиты (только касаться конечных точек) линиями задних лотов и не могут перекрываться друг с другом. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Метод устранения ошибок Вычитание создает составные объекты, таким образом, если перекрывающиеся сегменты не располагаются в начале или конце линии, то, возможно, потребуется использовать команду Разделить (Explode) на панели инструментов Расширенное редактирование (Advanced Editing), чтобы создать простые объекты. Этот метод может использоваться только для одной выбранной ошибки правила Не должны пересекаться или касаться. Разбить (Split): Метод разбивает линейные объекты, которые пересекают другие объекты, в точке их пересечения. Если две линии пересекаются в одной точке, применение этого способа в точке пересечения приведет к созданию четырех объектов. Атрибуты исходных объектов сохранятся для новых объектов. Если установлено правило разбиения, атрибуты присваиваются в соответствии с этим правилом. Этот метод может использоваться для одной или нескольких ошибок правила Не должны пересекаться или касаться. |
|
|
Не должны пересекаться или касаться с |
Требуется, чтобы линии в одном классе объектов (или подтипе) касались линий в другом классе объектов (или подтипе) только в конечных точках. Совпадение сегментов линий или любое пересечение не в конечной точке является ошибкой. Это правило может быть полезным, когда линии из двух слоев должны соединяться только в конечных точках. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Метод устранения ошибок Вычитание создает составные объекты, таким образом, если перекрывающиеся сегменты не располагаются в начале или конце линии, то, возможно, потребуется использовать команду Разделить (Explode) на панели инструментов Расширенное редактирование (Advanced Editing), чтобы создать простые объекты. Этот метод исправления ошибок может быть применен только к одной выбранной ошибке правила Не должны пересекаться или касаться с. Разбить (Split): Метод разбивает линейные объекты, которые пересекают другие объекты, в точке их пересечения. Если две линии пересекаются в одной точке, применение этого способа в точке пересечения приведет к созданию четырех объектов. Атрибуты исходных объектов сохранятся для новых объектов. Если установлено правило разбиения, атрибуты присваиваются в соответствии с этим правилом. Этот метод исправления ошибок может быть применен к одной или нескольких выбранным ошибкам правила Не должны пересекаться или касаться с. |
|
|
Не должны перекрываться с |
Требуется, чтобы линия из одного класса объектов (или подтипа) не перекрывалась с линией из другого класса объектов (или подтипа). Правило используется, когда линии не могут проходить по одной территории, Например, дороги не должны перекрываться с железными дорогами или горизонтали подтипа понижения не могут перекрываться с другими типами горизонталей. |
Вычитание (Subtract): Метод удаляет перекрывающиеся сегменты линий и объекта, участвующего в ошибке. Вам надо выбрать пространственный объект, из которого будет удаляться ошибка. Если присутствуют дубли линейных объектов, выберите линейный объект, который вы хотите удалить, в диалоговом окне Вычитание. Метод устранения ошибок Вычитание создает составные объекты, таким образом, если перекрывающиеся сегменты не располагаются в начале или конце линии, то, возможно, потребуется использовать команду Разделить (Explode) на панели инструментов Расширенное редактирование (Advanced Editing), чтобы создать простые объекты. Этот способ может быть применен только к одной ошибке для правила Не должны перекрываться с. |
Совпадающий сегмент красной линии является ошибкой. |
|
Должны совмещаться с объектами другого класса |
Требуется, чтобы линии из одного класса объектов (или подтипа) были покрыты линиями из другого класса объектов (или подтипа). Это правило применяется при моделировании логически различных, но пространственно совпадающих линий, например таких, как маршруты и улицы. Объекты класса автобусных маршрутов не должны отделяться в пространстве от объектов класса улиц. |
Нет |
Когда пурпурные линии не совпадают — это ошибка. |
|
Должны совпадать с границей |
Это правило требует, чтобы линии совпадали с границами площадных объектов. Оно может использоваться для моделирования линейных объектов, таких как границы земельных участков, которые должны совпадать с ребрами полигональных объектов, в данном случае участков. |
Вычитание (Subtract): Метод удаляет сегменты линий, которые не совпадают с границей полигональных объектов. Если линейный объект не имеет общих линейных сегментов с границей полигонального объекта, он будет удален. Этот способ может применяться к одной или нескольким ошибкам для правила Должны совпадать с границами. |
|
|
Должны быть внутри |
Требуется, чтобы линейные объекты находились внутри площадного объекта. Это может быть полезно, когда линии должны частично или полностью находиться в пределах определенных границ и не могут располагаться за их пределами, например, государственные автомагистрали должны находиться в пределах границ субъектов, а реки должны находиться в пределах водосборных бассейнов. |
Удалить (Delete): Метод удаляет линейные объекты, которые располагаются за пределами полигональных объектов. Обратите внимание, что вы можете использовать инструмент Редактировать (Edit) и переместить линию в пределы полигона, если вы не хотите удалять этот объект. Этот метод исправления ошибок может быть применен к одной или нескольким ошибкам правила Должны быть внутри. |
|
|
Конечные точки должны совпадать с |
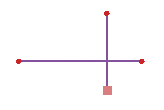
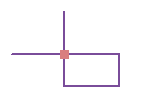
Это правило требует, чтобы конечные точки линейных объектов совпадали с точечными объектами из другого класса пространственных объектов. Это может быть полезно для моделирования случаев, когда специальные соединители должны использоваться для труб разного диаметра, или когда перекресток должен располагаться на пересечении улиц. |
Создать объект (Create Feature): При этом способе добавляется новый точечный объект на конце линейного объекта, вызвавшего ошибку. Этот способ может применяться к одной или нескольким ошибкам для правила Конечные точки должны совпадать с. |
Квадратик внизу указывает ошибку, поскольку с конечной точкой линии не совпадает точечный объект. |
|
Не должны перекрывать сами себя |
Это правило требует, чтобы у одного линейного объекта не было двух совпадающих сегментов. Линии могут пересекать или касаться сами себя, но не должны иметь совпадающих сегментов. Это правило будет полезно для улиц, когда сегменты могут касаться, но не допускается дублирования сегментов. |
Упростить (Simplify): Метод удаляет самопересекающиеся сегменты линий из объекта, вызвавшего ошибку. Применение этого способа может привести к созданию составных объектов, которые вы можете выявить при помощи правила Должны состоять из одной части. Метод исправления Упростить может быть применен к одной или нескольким ошибкам правила Не должны перекрывать сами себя. |
Этот отдельный линейный объект перекрывает сам себя, ошибка обозначена красной линией. |
|
Не должны пересекать сами себя |
Это правило требует, чтобы линии не пересекали себя и не имели совпадающих сегментов. Это правило применяется для изолиний, которые не должны самопересекаться. |
Упростить (Simplify): Метод удаляет самопересекающиеся сегменты линий из объекта, вызвавшего ошибку. Применение этого способа может привести к созданию составных объектов, которые вы можете выявить при помощи правила Должны состоять из одной части. Этот метод может быть использован для одной или нескольких ошибок правила Не должны пересекать сами себя. |
|
|
Должны состоять из одной части |
В соответствии с этим правилом каждая линия должна состоять из одной части. Оно используется, когда линейные объекты, такие как скоростные трассы, не могут иметь несколько частей. |
Разделить (Explode): Метод создает простые объекты из каждой части составного объекта, который стал причиной ошибки. Этот способ может применяться к одной или нескольким ошибкам для правила Должны состоять из одной части. |
Составные линии созданы из единственного скетча. |
Правила для линий
Правила для точек
| Правило топологии | Описание правила | Возможные методы исправления | Примеры |
|---|---|---|---|
|
Должны совпадать с (Must Coincide With) |
Требуется, чтобы точки в одном классе объектов (или подтипе) совпадали с точками в другом классе объектов (или подтипе). Это может быть полезно, когда точки должны быть покрыты другими точками, например, трансформаторы должны совпадать с питающими опорами, а точки обследования железной дороги должны совпадать со станциями. |
Замкнуть (Snap): Метод перемещает точечный объект из первого класса или подтипа к ближайшей точке во втором классе или подтипе, если второй объект располагается в пределах определенного расстояния. Если поблизости не будет найдено ни одного объекта в пределах указанного допуска, точка останется незамкнутой. Метод исправления Замкнуть может быть применен к одной или нескольким ошибкам правила Должны совпадать с. |
Красными квадратными маркерами показаны объекты, которые не совпадают с синими точками. |
|
Не должны совпадать (Must Be Disjoint) |
Требуется, чтобы точки располагались отдельно от других точек в пределах одного класса объектов (или подтипа). Любые точки, которые перекрываются, будут помечены как ошибки. Это может быть полезно для того, чтобы убедиться, что точечные объекты не совпадают и не дублируются в пределах одного класса или подтипу, например, города в слое с населенными пунктами, точки с номерами лотов участков и т.п. |
Нет |
Розовым отмечены точки, которые совпадают с синими точками, что является ошибкой. |
|
Должны совпадать с границей |
Это правило требует, чтобы точечные объекты размещались строго на границах полигональных объектов. Например, если эти точки формируют систему границ, как в случае с пограничными столбами, которые должны располагаться на ребрах полигонов. |
Нет |
Квадратик указывает ошибку, поскольку эта точка не лежит на границе полигона. |
|
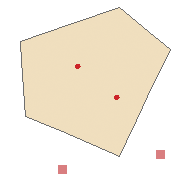
Должны быть полностью внутри |
Это правило требует, чтобы точечные объекты располагались внутри площадных объектов. Оно применяется, когда точки связаны с полигонами, как в случае со скважинами и бассейнами добычи или адресными точками и участками. |
Удалить (Delete): Метод удаляет точечные объекты, которые не находятся в пределах полигональных объектов. Обратите внимание, что вы можете использовать инструмент Редактировать (Edit), чтобы переместить точку в пределы полигона если вы не хотите удалять ее. Этот метод исправления ошибок может быть применен к одной или нескольким ошибкам правила Должны быть полностью внутри. |
Квадратики указывают ошибки, где точки находятся не внутри полигона. |
|
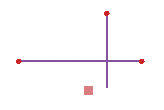
Должны совпадать с конечными точками |
Это правило требует, чтобы точечные объекты одного класса совпадали с конечными точками линий другого класса. Это правило похоже на правило Конечные точки должны совпадать с (Endpoint Must Be Covered By), в случаях когда оно нарушается, и точечный объект становится ошибкой, а не линия. |
Удалить (Delete): Метод удаляет точечные объекты, которые не совпадают с конечными точками линейных объектов. Вы можете замкнуть точку на линию, установив замыкание на ребра линейного слоя, Затем перемещая точку при помощи инструмента Редактировать. Этот способ может применяться к одной или нескольким ошибкам для правила Должны совпадать с конечными точками. |
Квадратик указывает ошибку, где точка не совпадает с конечной точкой линии. |
|
Точка должна лежать на линии |
Это правило требует, чтобы точки одного класса пространственных объектов размещались на линиях другого класса пространственных объектов. Точка может также лежать на конечной точке линии. Это правило может быть полезно для точечных объектов, которые должны следовать за линейными объектами, например автодорожные значки должны располагаться вдоль автомагистрали. |
Нет |
Квадратиками обозначены точки, не лежащие на линии. |
Правила для точек
Отзыв по этому разделу?
Материал из GIS-Lab
Перейти к: навигация,
поиск
| ГИС для преподавателей | Часть 6: Топология |

|
Цель: Понимание топологии векторных данных
Ключевые слова: Вектор, Топология, Правила Топологии, Топологические Ошибки, Радиус Поиска, Расстояние Замыкания, Простой Объект |
Обзор:
Топология регулирует пространственные отношения связности и соседства векторных объектов (точек, линий и полигонов) в ГИС. Топологические данные полезны для обнаружения и исправления ошибок оцифровки (например, две линии дорог не сходятся на месте перекрестка). Корректная топология необходима для проведения некоторых типов пространственного анализа, таких как сетевой анализ.
Представьте, что Вы поехали в Лондон. Сначала Вы планируете посетить Собор Святого Павла, а вечером поехать на Ковент Гарден за подарками. Смотря на лондонскую карту метро (на Рисунке 58), Вы ищете, как доехать от Собора до Ковент Гарден. Поиск требует топологическую информацию о том, где можно совершать пересадки. На карте метро топологические отношения связности показаны кружками. Пересадки на отмеченных станциях позволяют Вам перейти с одной ветки метро на другую.

Рисунок 58: Топология сети лондонского метро.
Топологические ошибки
Существуют различные типа топологических ошибок, и они могут быть сгруппированы в соответствии с типами геометрии (полигоны или полилинии). Топологические ошибки с полигональными объектами включают незакрытые полигоны, разрывы между прилежащими полигонами, а также перекрывающиеся полигоны. Распространенной ошибкой для линейных объектов является то, когда их конечные вершины не совпадают в тех местах, где они должны совпадать (например, улицы на перекрестках). Подобные ошибки называются «недолетами», когда между линиями наблюдается разрыв, и «перелетами», когда одна линия пересекает другую и заканчивается чуть дальше (см. Рисунок 59).
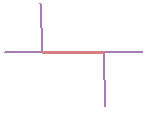
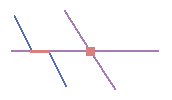
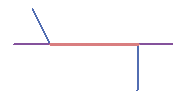
Рисунок 59: «Недолеты» (1) появляются, когда оцифрованные векторные линии, которые должны соединяться друг с другом, не соединяются.
«Перелеты» (2) происходят, когда одна линия заканчивается за другой линией, к которой должна быть присоединена. Когда вершины
двух полигонов на их границах не совпадают, появляются разрывы (3).
Результатами недолетов и перелетов являются так называемые «висячие узлы» в конце линий. Висячие узлы приемлемы в отдельных случаях, например для тупиковых улиц. Топологические ошибки нарушают отношения между объектами. Эти ошибки должны быть исправлены перед проведением таких типов анализа векторных данных, как сетевой анализ (т.е. поиск кратчайшего маршрута по дорожной сети) или измерения (т.е. выяснение длины рек). Помимо необходимости топологии в сетевом анализе и измерениях, существуют другие причины, почему следует иметь топологически корректные данные. Представьте, что Вы цифруете муниципальные границы Вашего района, и полигоны перекрываются или имеют разрывы. В случае таких ошибок Вы по-прежнему можете пользоваться инструментами измерений, но результаты будут некорректными. Полученная площадь будет неправильной, и будет непонятно, где именно находятся границы (например, в случае перекрывающихся полигонов принадлежность территории к двум муниципалитетам одновременно невозможна!).
Иметь топологически корректные данные важно не только для проведения собственного анализа, но и для других людей, которым Вы можете передать свои данные. Они могут не знать об ошибках и будут расценивать результаты своего анализа как правильные.
Правила топологии
К счастью, многие распространенные ошибки, происходящие при оцифровке, могут быть предотвращены с помощью правил топологии, внедренных во многие ГИС-приложения. Кроме некоторых специализированных форматов геоданных, топология обычно не применяется по умолчанию. Многие широко распространенные ГИС, такие как QGIS, определяют топологию как серию правил, которые могут быть выбраны пользователем и применены к векторным слоям. Следующий список включает некоторые примеры правил топологии, определяемых для объектов реального мира на векторной карте:
- Элементы муниципальной карты не должны перекрывать друг друга.
- Элементы муниципальной карты не должны иметь разрывов.
- Полигоны земельных участков должны быть замкнутыми. «Недолеты» и «перелеты» границ участков не позволяются.
- Горизонтали высот не должны пересекаться.
Топологические инструменты
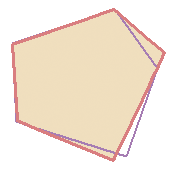
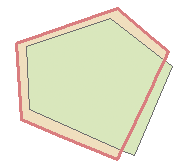
Многие ГИС-приложения имеют инструменты топологического редактирования. Например, в QGIS Вы можете включить топологическое редактирование для эффективного редактирования общих границ объектов полигональных слоев. ГИС-приложение обнаруживает общие границы объектов, и Вам достаточно будет передвинуть только одну вершину, в то время как приложение обновит вершину прилежащего полигона, как показано на Рисунке 60 (1). Другая опция топологического редактирования – установка ограничения на перекрытие полигонов (см. Рисунок 60 (2)). В QGIS, если Вы нарисуете новый полигон поверх существующего, приложение обрежет новый полигон по границе существующего.

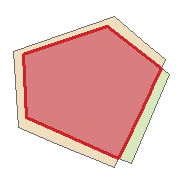
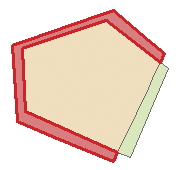
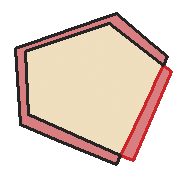
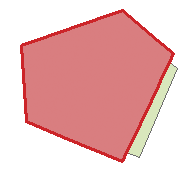
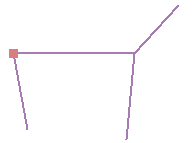
Рисунок 60: Топологическое редактирование. 1) Когда пользователь сдвигает вершину в углу бордового полигона, соответствующая вершина зеленого квадрата
автоматически следует за ней. 2) Чтобы избежать перекрытия полигонов, новый объект (бордовый) автоматически обрезается по границе существующего (зеленый).
Радиус замыкания
Радиус замыкания – это максимальный радиус поиска, который использует ГИС-приложение для стыковки инструмента редактирования с существующими вершинами или сегментами редактируемого слоя в ходе оцифровки (сегмент – это прямая линия, соединяющая две вершины полилинии или полигона). Если Ваш курсор находится внутри этого радиуса и Вы создаете новую вершину, ГИС-приложение стыкует ее к существующей вершине или сегменту (см. Рисунок 61). В противном случае вершина создается там, где был произведен клик мышью, независимо от существующих вершин.
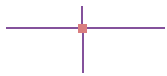
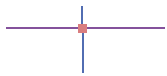
Рисунок 61: Радиус замыкания (черный кружок) определяется в единицах измерения карты (например, в десятичных градусах)
для стыковки новой вершины к существующим вершинам или сегментам.
Радиус поиска
Радиус поиска – это расстояние, которое ГИС-приложение использует для поиска ближайшей к курсору вершины, когда Вы пытаетесь ее выделить для перетаскивания на карте. По сути, это почти то же самое, что и радиус замыкания, только для редактирования существующих вершин. Он также устанавливается в единицах измерения карты, и нужно попробовать разные значения, чтобы найти оптимальное. Если значение слишком большое, ГИС-приложение может при клике мышью выделить не ту вершину, которую Вы хотели выделить, просто потому что она тоже попала в радиус. Особенно эта проблема актуальна для объектов с большим количеством близко расположенных вершин. Если Вы укажете слишком маленькое значение, вершины вообще не будут выделяться, хотя будет казаться, что Вы подвели курсор прямо к вершине. Выбор оптимального радиуса поиска также зависит от чувствительности мышки и индивидуальных предпочтений пользователя.
О чем стоит помнить:
Топология – это сложное представление векторных данных. Топологические наборы данных хранятся в специальных файловых форматах, включающих описание отношений между объектами. В то же время, наиболее распространенные форматы геоданных являются «простыми», то есть хранят только геометрию и атрибуты. Они разработаны для быстрого отображения на карте и не расчитаны на топологический анализ (например, поиск кратчайшего пути). Многие ГИС-приложения могут отображать и топологические и простые данные, а некоторые могут также создавать и редактировать эти данные.
Что мы узнали?
Закрепим изученный материал:
- Топология описывает пространственные взаимоотношения соседствующих векторных объектов.
- В ГИС-приложениях за топологию отвечают топологические инструменты.
- Топологию можно использовать для выявления и исправления ошибок, возникших в ходе оцифровки.
- Корректная топология необходима для некоторых видов анализа, таких как сетевой анализ.
- Установка радиуса замыкания и радиуса поиска помогает нам производить топологически корректную оцифровку.
- Простые векторные данные не включают топологические правила, но они широко используются в ГИС-приложениях.
Попробуйте сами!
Ниже приведено несколько примеров практических заданий для Ваших учеников:
- Отметьте автобусные остановки на листе топографической карты и попросите учеников найти кратчайший маршрут между двумя остановками.
- Подумайте, как бы Вы создали векторные объекты в ГИС для представления топологической сети дорог в Вашем городе. Какие топологические правила важны в данном случае и какие инструменты QGIS могут использовать ученики, чтобы проверить топологическую корректность созданного набора данных?
Если у Вас нет компьютера:
Вы можете использовать карту автобусных или ж/д маршрутов и обсудить пространственные отношения и топологию с учениками.
Дополнительные материалы:
Книги:
- Сhang, Kang-Tsung (2006): Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. (ISBN 0070658986)
- DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. (ISBN 9814126195)
Веб-сайты:
- http://www.innovativegis.com/basis/primer/concepts.html
- http://en.wikipedia.org/wiki/Geospatial_topology
Руководство Пользователя QGIS включает более детальную информацию о топологическом редактировании.
Что дальше?
В следующем разделе мы изучим системы координат, чтобы понять, как географические данные о шарообразной Земле переносятся на плоские карты.
Тип структуры в квантовой механике
A топологический солитон или «торон» возникает, когда две смежные структуры или пространства каким-либо образом находятся «не совпадают по фазе» друг с другом, что делает невозможным плавный переход между ними. Один из простейших и наиболее распространенных примеров топологического солитона встречается в старомодных спиральных телефонных шнурах телефонных трубок, которые обычно наматываются по часовой стрелке. Годы взятия трубки в руки могут привести к тому, что части шнура будут наматываться в противоположном направлении против часовой стрелки, и когда это произойдет, будет характерная большая петля, разделяющая два направления наматывания. Эта странно выглядящая петля перехода, которая не вращается ни по часовой, ни против часовой стрелки, является отличным примером топологического солитона. Независимо от того, насколько сложен контекст, все, что квалифицируется как топологический солитон, должно на каком-то уровне демонстрировать ту же простую проблему согласования, что и в примере скрученного телефонного кабеля.
Топологические солитоны легко возникают при создании кристаллических полупроводников, используемых в современной электронике, и в этом контексте их эффекты почти всегда вредны. По этой причине такие кристаллические переходы называются топологическими дефектами . Однако эта в основном твердотельная терминология отвлекает от богатых и интригующих математических свойств таких граничных областей. Таким образом, для большинства нетвердотельных контекстов предпочтительнее более позитивная и математически богатая фраза «топологический солитон».
Более подробное обсуждение топологических солитонов и связанных тем приведено ниже.
В математике и физике топологический солитон или топологический дефект является решением системы уравнения в частных производных или квантовой теории поля , гомотопически отличные от вакуумного решения.
Содержание
- 1 Обзор
- 2 Примеры
- 2.1 Уединенные волновые PDE
- 2.2 Лямбда-переходы
- 2.3 Космологические дефекты
- 2.3.1 Нарушение симметрии
- 2.4 Биохимия
- 2.5 Формальная классификация
- 3 Наблюдение
- 4 Конденсированное вещество
- 4.1 Устойчивые дефекты
- 5 Изображения
- 6 См. Также
- 7 Ссылки
- 8 Внешние ссылки
Обзор
существование топологического дефекта может быть продемонстрировал всякий раз, когда граничные условия влекут за собой существование гомотопически различных решений. Обычно это происходит из-за того, что граница, на которой заданы условия , имеет нетривиальную гомотопическую группу, которая сохраняется в дифференциальных уравнениях ; тогда решения дифференциальных уравнений топологически различны и классифицируются по их гомотопическому классу. Топологические дефекты не только устойчивы к небольшим возмущениям, но и не могут распадаться, устраняться или распутываться именно потому, что не существует непрерывного преобразования, которое отобразит их (гомотопически) в однородный или «тривиальный» решение.
Примеры
Топологические дефекты возникают в уравнениях в частных производных и, как полагают, вызывают фазовые переходы в физике конденсированного состояния.
Подлинность топологического дефекта зависит от природы вакуума, в который система будет стремиться, если истечет бесконечное время; ложные и истинные топологические дефекты можно различить, если дефект находится в ложном вакууме и истинном вакууме, соответственно.
УЧП уединенной волны
Примеры включают солитон или уединенную волну, которая возникает в точно решаемых моделях, таких как
- винтовые дислокации в кристаллических материалах,
- скирмион в квантовом поле. теории и
- топологические дефекты модели Весса – Зумино – Виттена.
Лямбда-переходы
Топологические дефекты в лямбда-переходах системы классов универсальности, включая:
- винтовые / краевые дислокации в жидких кристаллах,
- «трубках» магнитного потока, известные как флюксоны в сверхпроводниках, и
- вихри в сверхтекучие жидкости.
Космологические дефекты
Топологические дефекты космологического типа — это явления чрезвычайно высоких энергий, которые, как считается, нецелесообразно вызывать в физических экспериментах, связанных с Землей. Топологические дефекты, возникшие при формировании Вселенной, теоретически можно наблюдать без значительных затрат энергии.
Согласно теории Большого взрыва, Вселенная охлаждается из начального горячего плотного состояния, вызывая серию фазовых переходов, очень похожих на то, что происходит в системах с конденсированной материей, таких как как сверхпроводники. Некоторые теории великого объединения предсказывают образование устойчивых топологических дефектов в ранней Вселенной во время этих фазовых переходов.
Нарушение симметрии
Считается, что в зависимости от природы нарушения симметрии в ранней Вселенной в соответствии с механизмом Киббла-Зурека. Хорошо известными топологическими дефектами являются:
- Космические струны — это одномерные линии, которые образуются при нарушении осевой или цилиндрической симметрии.
- Доменные стенки, двумерные мембраны, образующиеся при дискретном симметрия нарушается при фазовом переходе. Эти стенки напоминают стенки пены с закрытыми ячейками, разделяющих вселенную на дискретные ячейки.
- Монополи, кубические дефекты, которые образуются при нарушении сферической симметрии, предположительно имеют магнитный заряд, северный или южный (и поэтому их обычно называют «магнитными монополями »).
- Текстуры образуются, когда более крупные и более сложные группы симметрии полностью нарушены. Они не так локализованы, как другие дефекты, и нестабильны.
- Скирмионы
- Дополнительные измерения и более высокие измерения.
Также возможны другие более сложные гибриды этих типов дефектов.
По мере того, как Вселенная расширялась и остывала, симметрии законов физики начали нарушаться в областях, которые распространяются со скоростью скорости света ; топологические дефекты возникают на границах прилегающих областей. Вещество, составляющее эти границы, находится в упорядоченной фазе, которая сохраняется после завершения фазового перехода в неупорядоченную фазу для окружающих областей.
Биохимия
Также были обнаружены дефекты в биохимии, особенно в процессе сворачивания белка.
Формальная классификация
Упорядоченный носитель определяется как область пространства, описываемая функцией f (r), которая присваивает каждой точке в области параметр порядка, а возможные значения пространства параметров порядка составляют пространство параметров порядка. Гомотопическая теория дефектов использует фундаментальную группу пространства параметров порядка среды для обсуждения существования, стабильности и классификации топологических дефектов в этой среде.
Предположим, R — параметр порядка. пространство для среды, и пусть G — группа Ли преобразований на R. Пусть H — подгруппа симметрии G для среды. Тогда пространство параметров порядка можно записать как фактор-группу Ли R = G / H.
Если G является универсальным покрытием для G / H, то можно показать, что π n (G / H) = π n − 1 (H), где π i обозначает i-ю гомотопическую группу.
Различные типы дефектов в среде могут быть охарактеризованы элементами различных гомотопических групп пространства параметров порядка.. Например, (в трех измерениях) линейные дефекты соответствуют элементам π 1 (R), точечные дефекты соответствуют элементам π 2 (R), текстуры соответствуют элементам π 3 (R). Однако дефекты, которые принадлежат к одному и тому же классу сопряженности π 1 (R), могут непрерывно деформироваться относительно друг друга, и, следовательно, отдельные дефекты соответствуют разным классам сопряженности.
Поэнару и Тулуза показали, что перекрестные дефекты запутываются тогда и только тогда, когда они являются членами отдельных классов сопряженности π 1 (R).
Наблюдение
Топологические дефекты не наблюдались астрономами; однако некоторые типы несовместимы с текущими наблюдениями. В частности, если бы доменные границы и монополи присутствовали в наблюдаемой Вселенной, они бы привели к значительным отклонениям от того, что могут видеть астрономы.
Из-за этих наблюдений образование дефектов в наблюдаемой Вселенной сильно ограничено, что требует особых обстоятельств (см. Инфляция (космология) ). С другой стороны, космические струны были предложены как обеспечивающие начальную «зародышевую» гравитацию, вокруг которой конденсировалась крупномасштабная структура космоса материи. Текстуры также безобидны. В конце 2007 года холодное пятно в космическом микроволновом фоне предоставило доказательства возможной текстуры.
Конденсированные материя
В физике конденсированного состояния теория гомотопических групп обеспечивает естественные условия для описания и классификации дефектов в упорядоченных системах. Топологические методы использовались в ряде задач теории конденсированного состояния. Поэнару и Тулуза использовали топологические методы для получения условия для линейных (струнных) дефектов в жидких кристаллах, которые могут пересекать друг друга без запутывания. Это было нетривиальное применение топологии, которое впервые привело к открытию своеобразного гидродинамического поведения в A-фазе сверхтекучего гелия -3.
Стабильные дефекты
Теория гомотопии глубоко связана со стабильностью топологических дефектов. В случае линейного дефекта, если замкнутый путь можно непрерывно деформировать в одну точку, дефект не является устойчивым, а в противном случае — устойчивым.
В отличие от космологии и теории поля, топологические дефекты в конденсированной среде наблюдались экспериментально. Ферромагнитные материалы имеют области магнитного выравнивания, разделенные доменными стенками. нематик и биаксиальный нематик жидкие кристаллы демонстрируют множество дефектов, включая монополи, струны, текстуры и т. Д.
Изображения

L знак равно ∂ μ ϕ ∂ μ ϕ — (ϕ 2-1) 2 { displaystyle { mathcal {L}} = partial _ { mu} phi partial ^ { mu} phi — left ( phi ^ {2} -1 right) ^ {2}}


См. Также
- Конденсированное вещество
- Дифференциальное уравнение
- Дислокация
- Квантовая механика
- Квантовая топология
- Квантовый вихрь
- Топологическая энтропия в физике
- Топологические возбуждения
- Топологические многообразие
- Топологический порядок
- Топологическая квантовая теория поля
- Топологическое квантовое число
- Топологическая теория струн
- Топология
- Векторный солитон
Ссылки
Внешние ссылки
- Cosmic Строки и другие топологические дефекты
- http://demonstrations.wolfram.com/SeparationOfTopologicalSingularities/
Слайд 2Топология
(от греч. topos — место) — раздел
математики, изучающий топологические свойства фигур,
т.е. свойства,
не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний.

Слайд 3Что такое топология ?
Одна из ключевых концепций
ГИС
В ГИС : топология – пространственные взаимоотношения
межу смежными и близлежащими объектами
Топология отражается в структуре данных
Топологические структуры более предпочтительны

Слайд 5Типы топологий
Линейно-узловые топологические отношения
Объектные топологии:
Внутриобъектные топологические
отношения.
Межобъектные топологические отношения:
Узловые топологические отношения.
Межобъектные топологические отношения в пределах одного слоя
Межслойные топологические отношения между объектами
Топологические межобъектные ресурсные связи
Концептуальные топологические отношения (отношения между классами объектов, или логические связи)

Слайд 6Внутриобъектная Топология
Полилинии, связность

Слайд 7Внутриобъектная топология
Полигоны, замкнутость
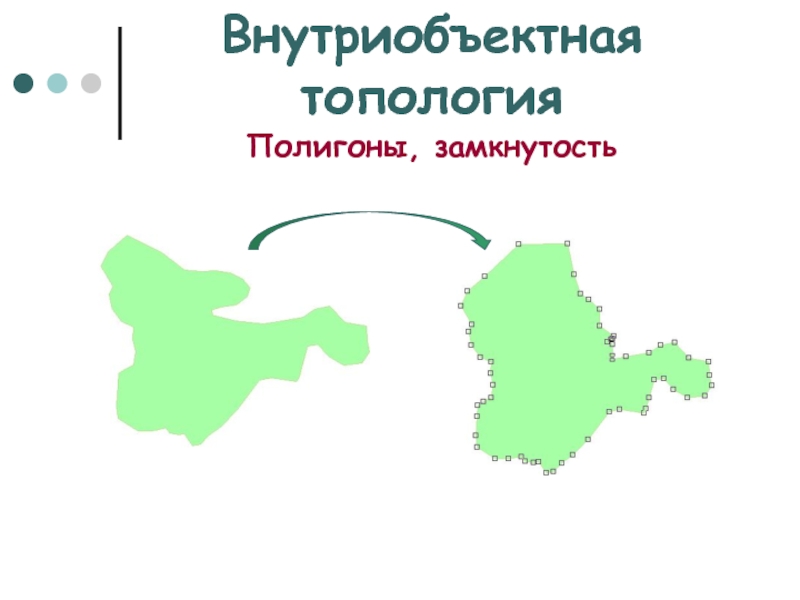
Слайд 8Внутриобъектная топология
нетопологические ГИС
Перемещение дуги
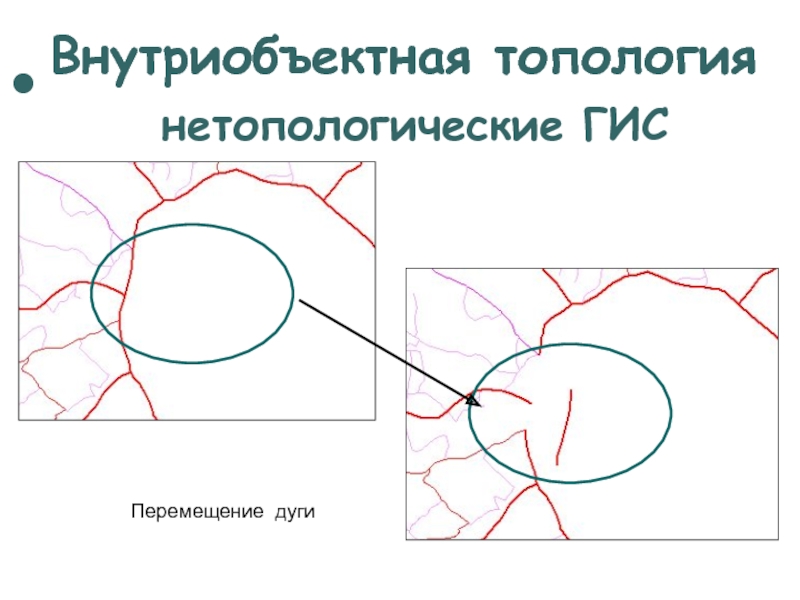
Слайд 9Внутриобъектная топология
нетопологические ГИС
Перемещение полигона
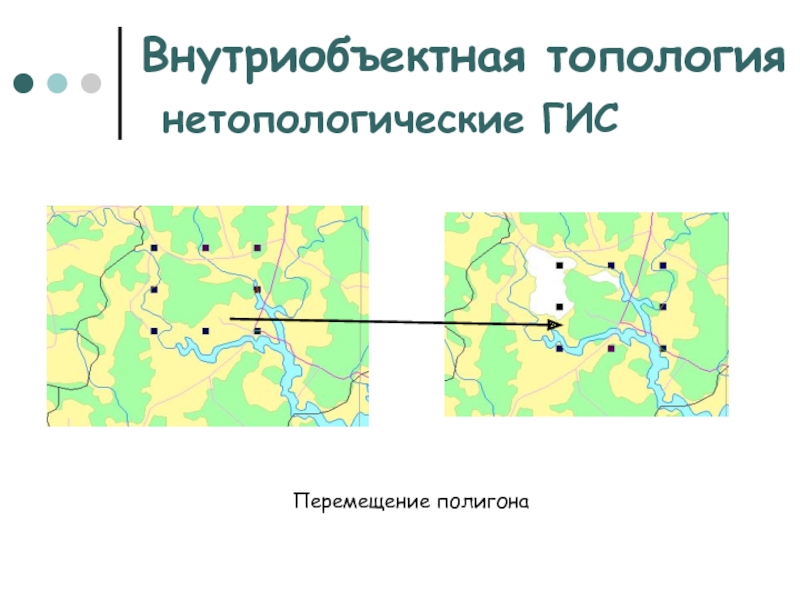
Слайд 10Топология объектов
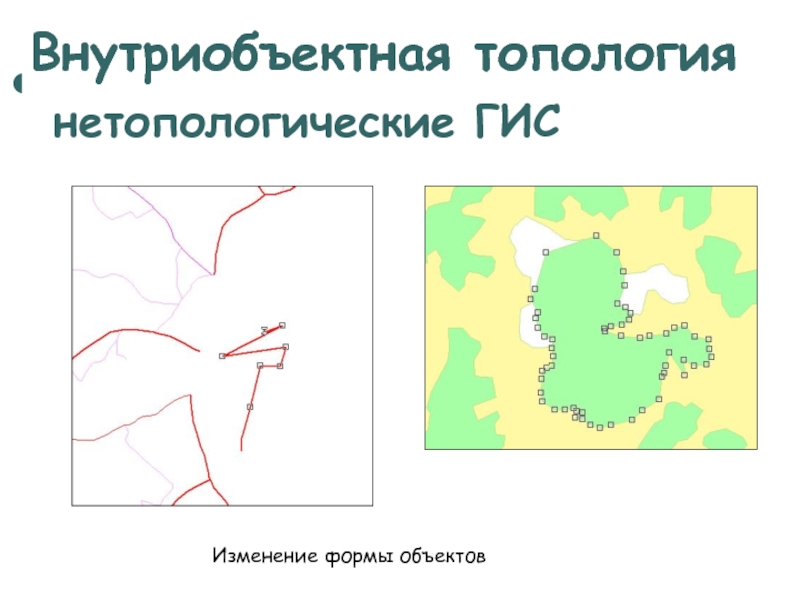
Изменение формы объектов
Внутриобъектная топология
нетопологические
ГИС
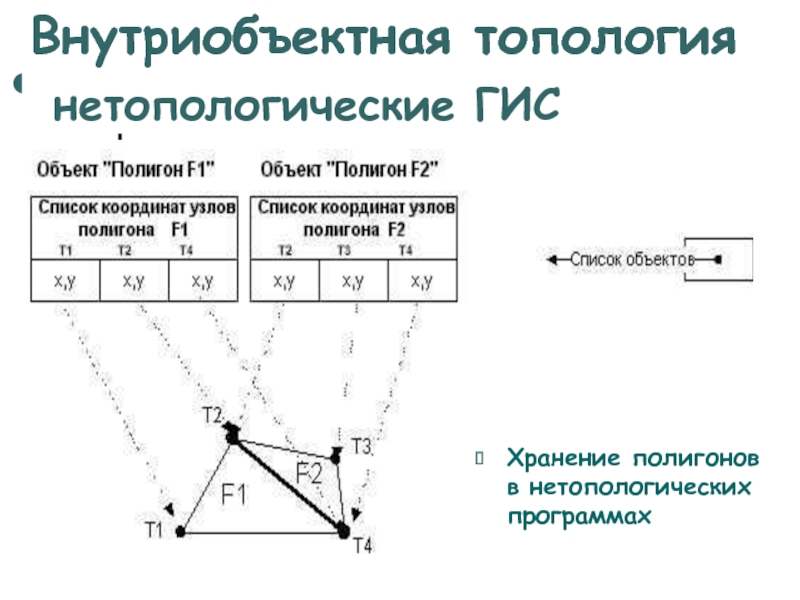
Слайд 11Топология
Хранение полигонов в нетопологических программах
Внутриобъектная топология
нетопологические ГИС
Слайд 12Программное обеспечение, поддерживающее только внутриобъектную топологию (нетопологические
ГИС)
MapInfo (MapInfo Corp., США);
AtlasGIS, ArcView (ESRI,
США);
«Панорама» (Ногинск);
И другие

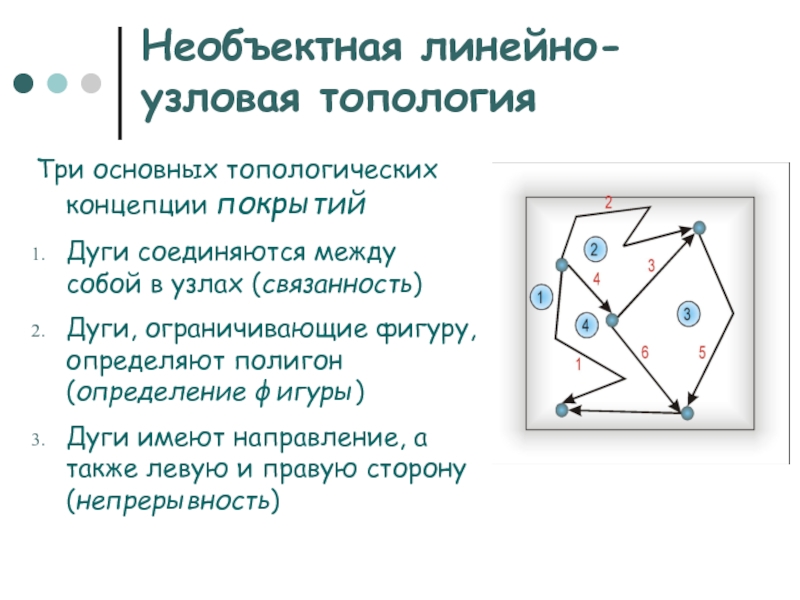
Слайд 13Необъектная линейно-узловая топология
Три основных топологических концепции покрытий
Дуги соединяются между собой в узлах (связанность)
Дуги,
ограничивающие фигуру, определяют полигон (определение фигуры)
Дуги имеют направление, а также левую и правую сторону (непрерывность)
Слайд 14Необъектная линейно-узловая топология
Сохранение местоположения всех узлов.
На
основе узлов определяются дуги.
Полигоны определяются дугами
путем их перечисления по часовой стрелке вокруг объекта.
Для каждой дуги можно определить, какой полигон находится слева и справа от направления ориентации.

Слайд 15Необъектная линейно-узловая топология
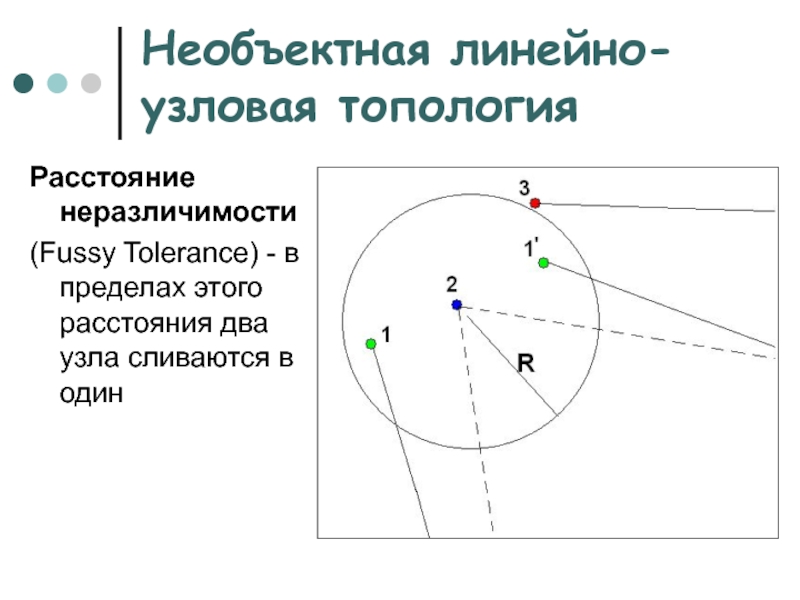
Расстояние неразличимости
(Fussy Tolerance) —
в пределах этого расстояния два узла сливаются
в один
Слайд 16Линейно-узловая топология
Хранение полигонов в программах с линейно-узловой
топологией

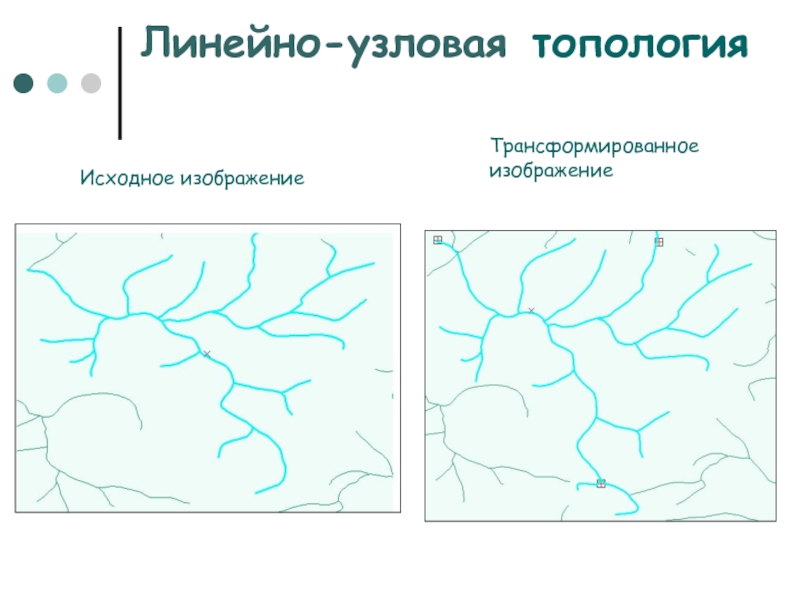
Слайд 17Линейно-узловая топология
Исходное изображение
Трансформированное изображение
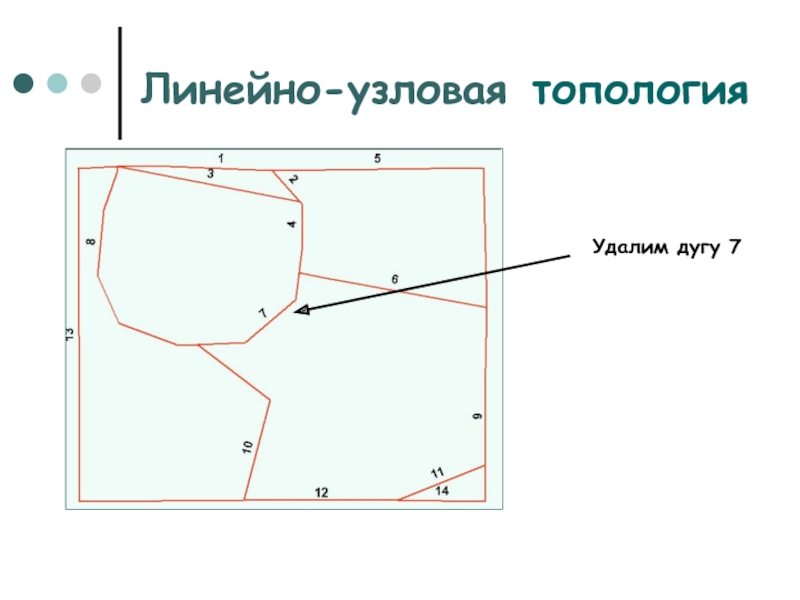
Слайд 19Линейно-узловая топология
Удалим дугу 7
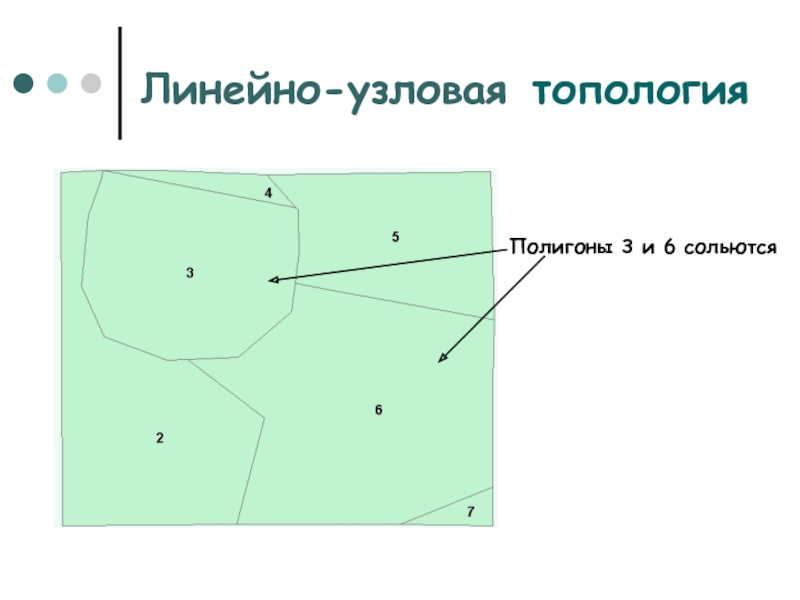
Слайд 20Линейно-узловая топология
Полигоны 3 и 6 сольются
Слайд 21Линейно-узловая топология
Результат удаления дуги
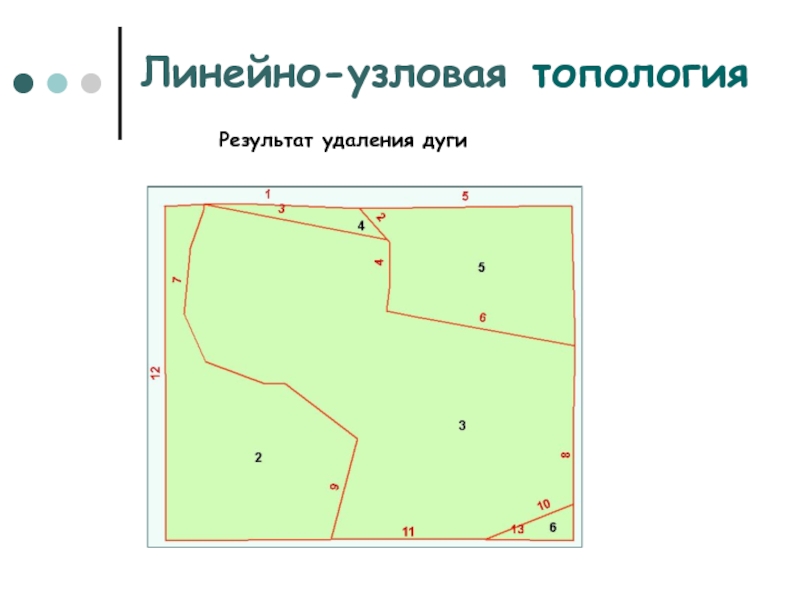
Слайд 22Топология линейно-узловая
Линейное покрытие — реки
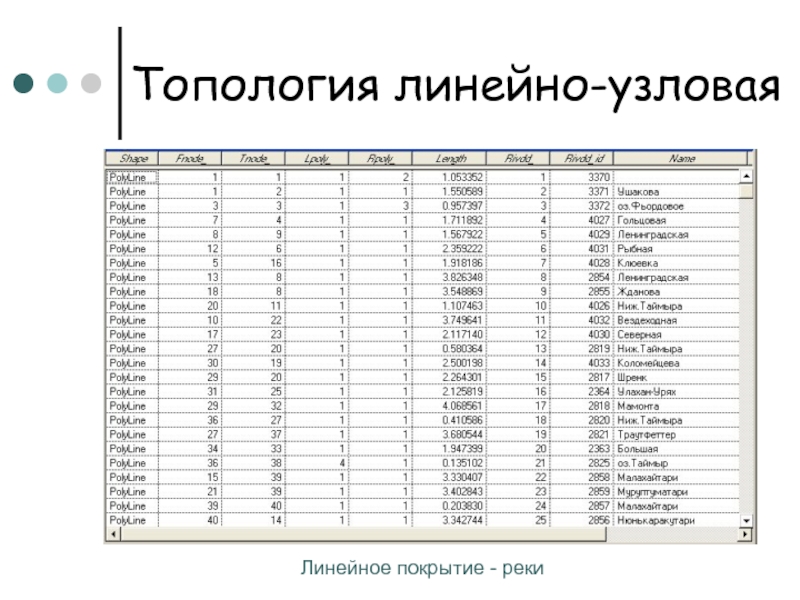
Слайд 23Топология линейно-узловая
Полигональное покрытие – градусная сетка

Слайд 24Получение общих границ объектов в нетопологических ГИС
при создании полигональной темы
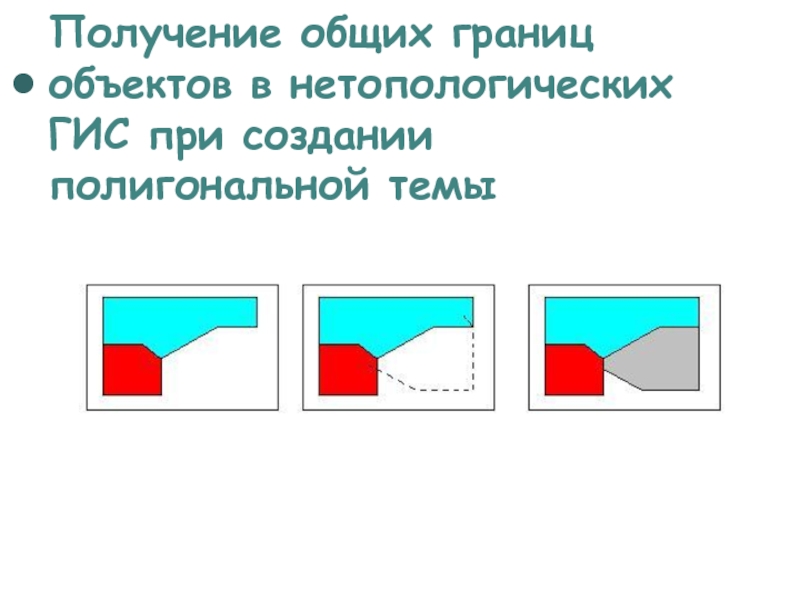
Слайд 25Топология
объектно-ориентированная модель данных — база геоданных
Слайд 27Классы объектов
Наборы классов объектов
База геоданных
Слайд 28Топология в БГД
Создается и хранится как новый
класс
базы геоданных
Хранит в себе:
Перечень участвующих в топологических отношениях классов (подтипов)
Кластерный допуск, ранги и правила
Имеющиеся топологические ошибки и исключения
Устанавливает и поддерживает требуемые пространственные взаимоотношения в момент проверки топологии

Слайд 30Топология БГД
Топологические правила
Домены
Отношения

Слайд 31Топология БГД
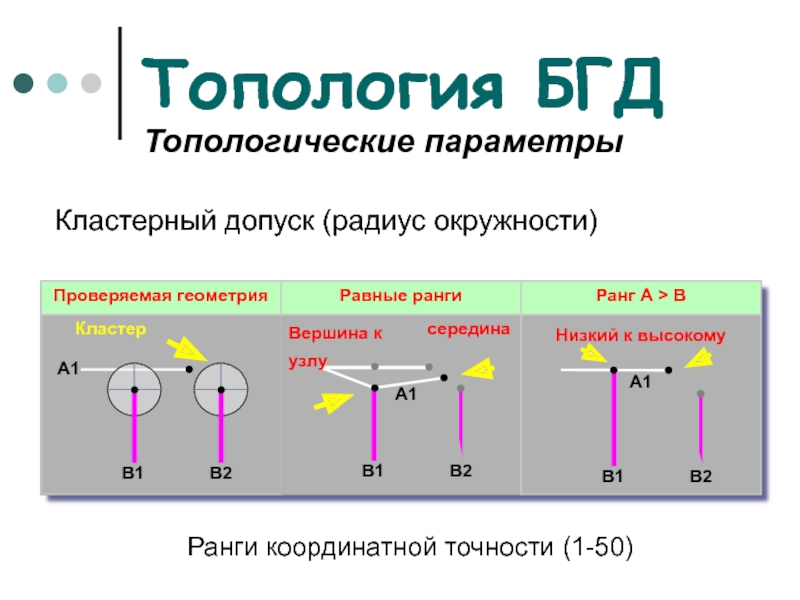
Топологические параметры
Кластерный допуск (радиус окружности)
Ранги координатной
точности (1-50)
Слайд 32ПРАВИЛА ТОПОЛОГИИ
Формулируются при создании топологии, контролируются при
проверке: 26 правил
Могут быть изменены в процессе
работы
Существуют для одного класса объектов или для отношений между классами объектов (можно подтипов)
ПРИМЕРЫ:
Участки…. Не должны иметь промежуточные пустоты
Линии водопровода … на концах должны совпадать с точками задвижек
Сформулированные правила можно сохранять и передавать для использования

Слайд 33
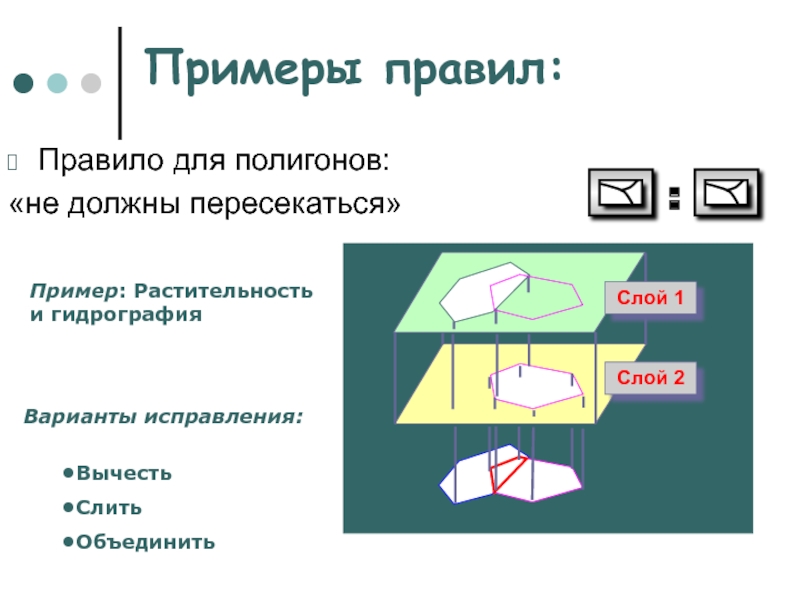
Примеры правил:
Правило для полигонов:
«не должны пересекаться»
Пример: Растительность
и гидрография
Варианты исправления:
Вычесть
Слить
Объединить
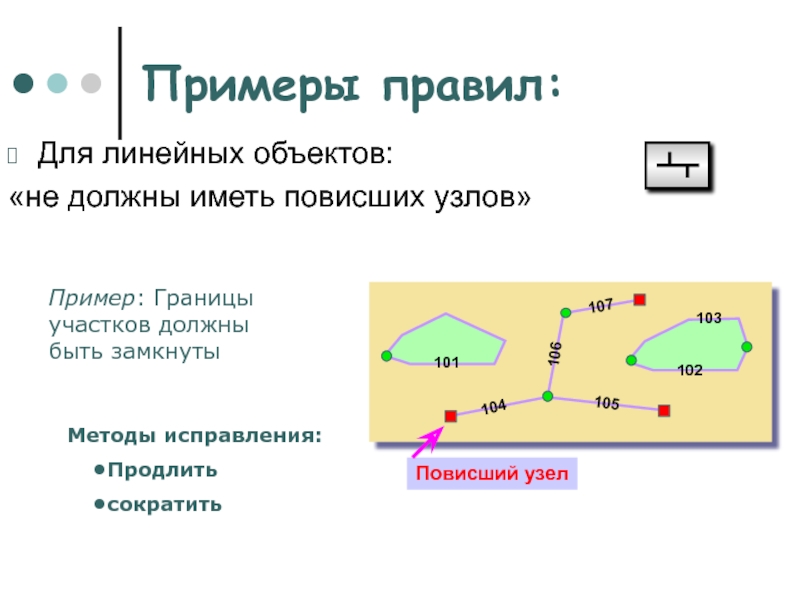
Слайд 34Примеры правил:
Для линейных объектов:
«не должны иметь повисших
узлов»
Повиcший узел
Пример: Границы участков должны быть замкнуты
Методы
исправления:
Продлить
сократить
Слайд 35Примеры правил:
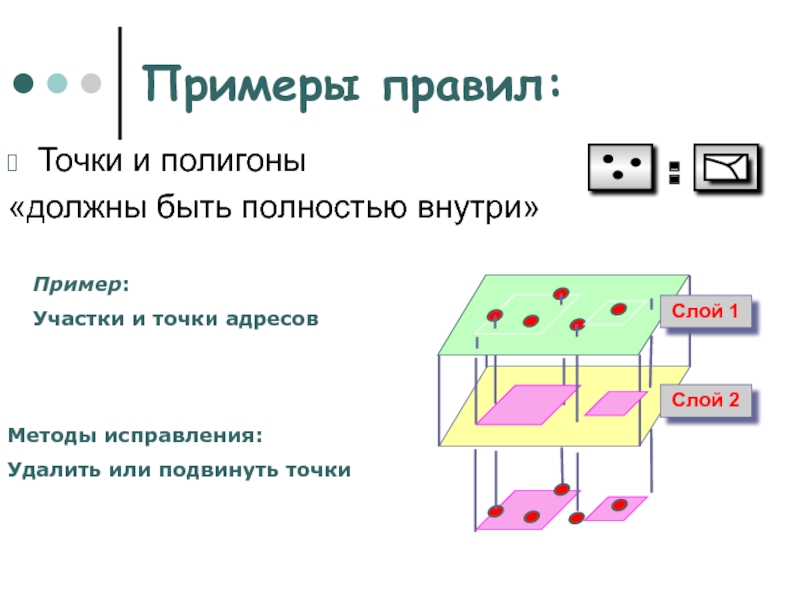
Точки и полигоны
«должны быть полностью внутри»
Пример:
Участки
и точки адресов
Методы исправления:
Удалить или подвинуть точки
Слайд 36Примеры правил:
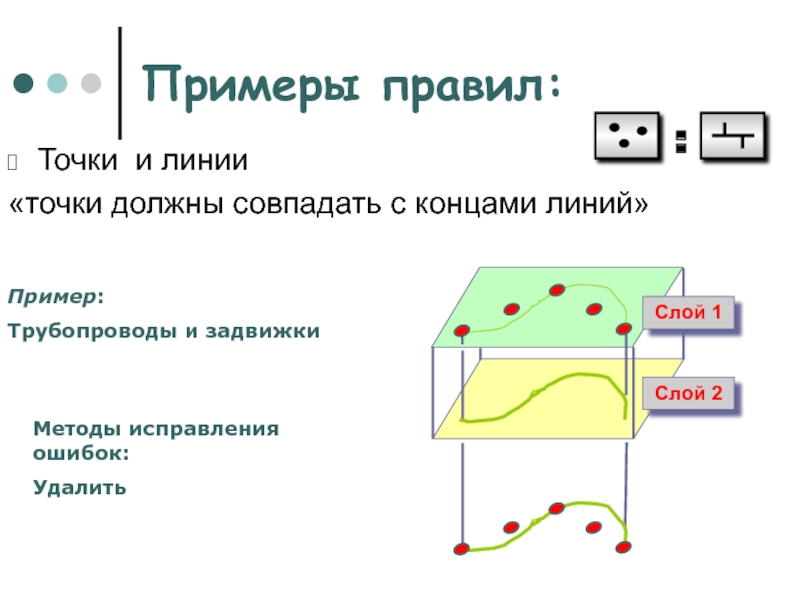
Точки и линии
«точки должны совпадать с
концами линий»
Слой 1
Слой 2
Пример:
Трубопроводы и задвижки
Методы исправления
ошибок:
Удалить
Слайд 37Примеры правил:
Модель данных – база геоданных
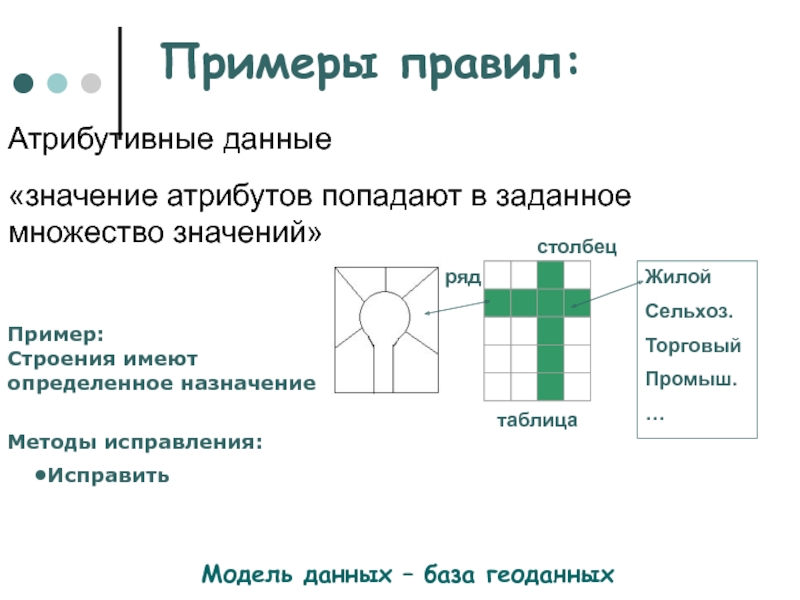
Атрибутивные данные
«значение
атрибутов попадают в заданное
множество значений»
Пример:
Строения имеют
определенное назначение
Методы исправления:
Исправить
Слайд 38Примеры правил:
Модель данных – база геоданных
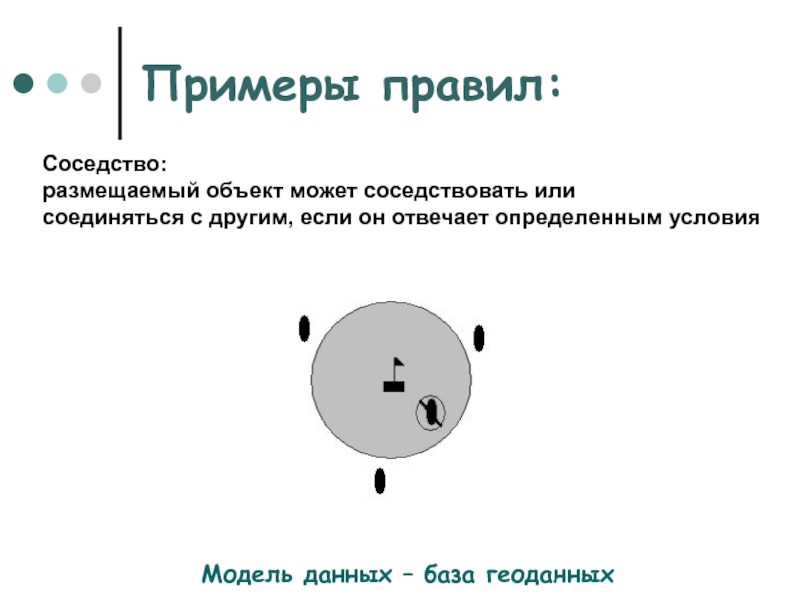
Соседство:
размещаемый объект
может соседствовать или
соединяться с другим, если
он отвечает определенным условия
Слайд 39Примеры правил:
Модель данных – база геоданных
геометрия пространственного
объекта соответствует
его логическому размещению
Слайд 40Как поступать с ошибками?
Игнорировать – это не
мешает использовать данные
Обозначить ошибку как исключение из
правила
Исправить ошибку предлагаемыми методами
Ошибки нельзя удалить: только исправить или отнести к исключению
Контроль за ошибками можно встроить в процесс работы : кто и когда контролирует

Слайд 47
Топология БГД
Создание топологии
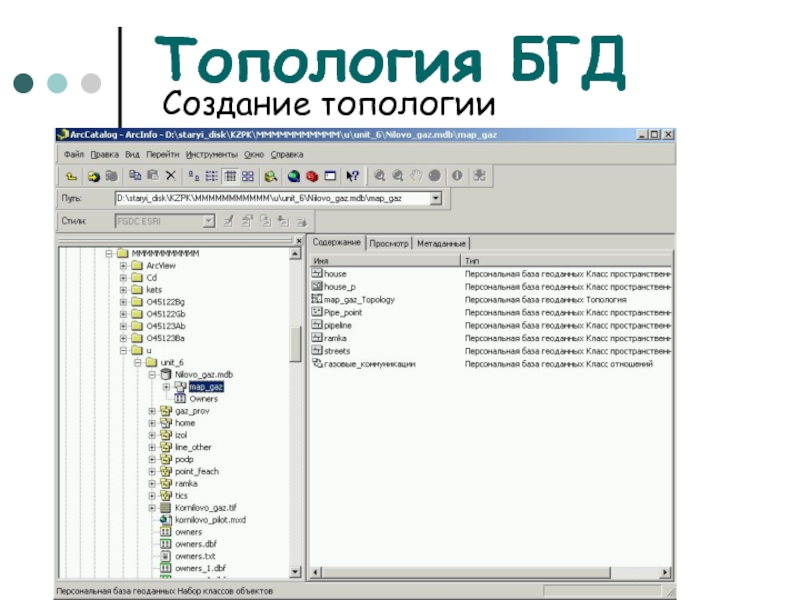
Слайд 48Топология БГД
Определение доменов
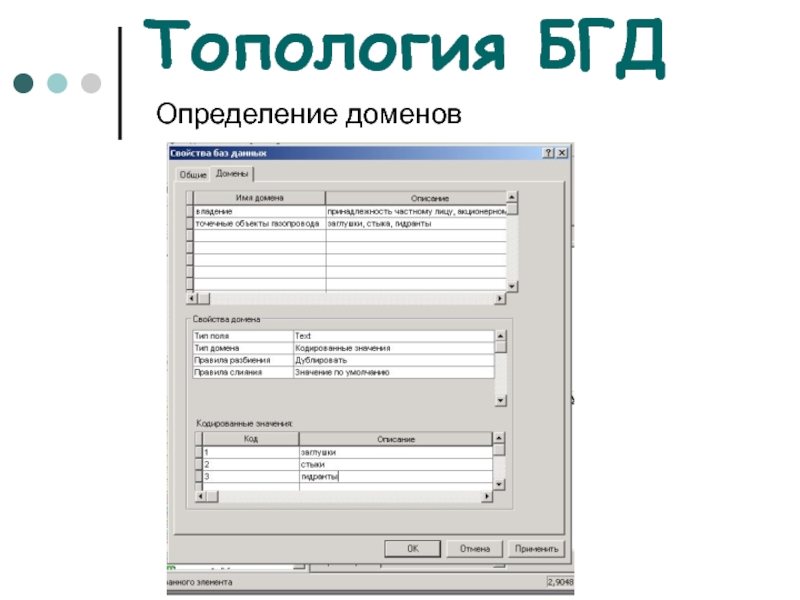
Слайд 50Топология БГД
Отношения слоя трубопроводы с точечными объектами
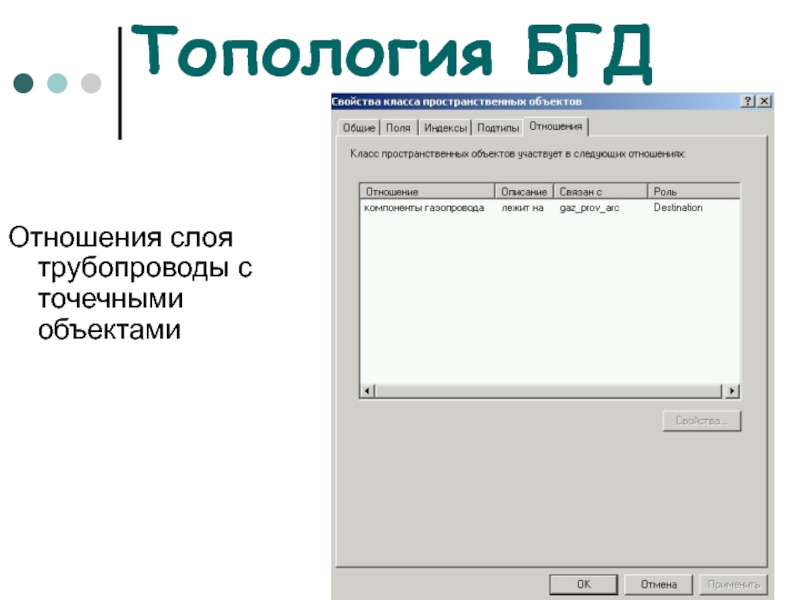
Слайд 51Топология БГД
Отношения слоя точечных объектов со слоем
трубопроводов
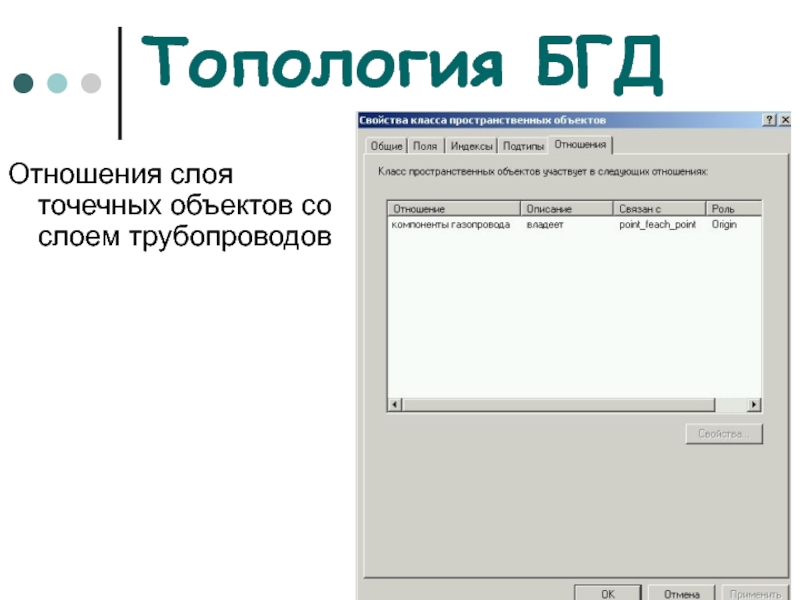
Слайд 52Топология
Выбираем ошибки
В меню нажимаем Растянуть
Указываем максимальное расстояние
Проверка
и исправление ошибок

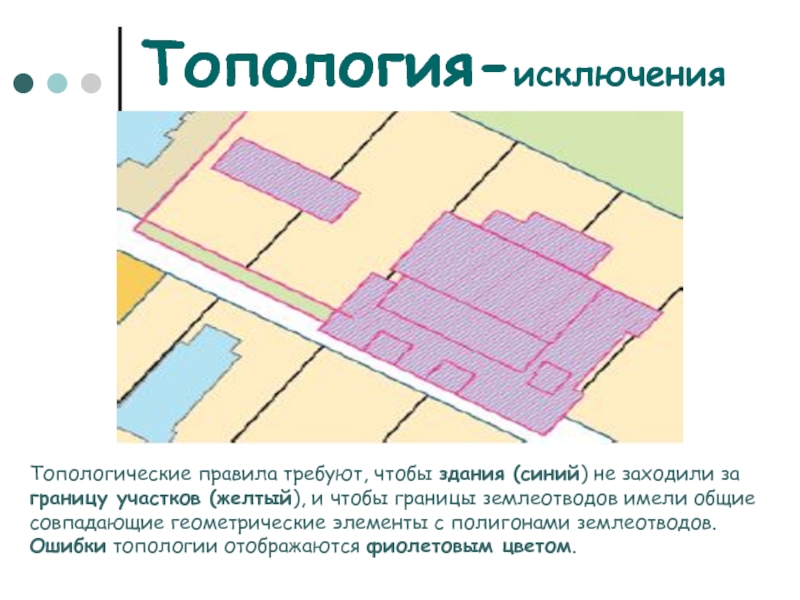
Слайд 53Топология-исключения
Топологические правила требуют, чтобы здания (синий) не
заходили за границу участков (желтый), и чтобы
границы землеотводов имели общие совпадающие геометрические элементы с полигонами землеотводов. Ошибки топологии отображаются фиолетовым цветом.
Слайд 54Создание топологии Проверка топологии
7
—
8
Building Geodatabases I (for
ArcEditor 8.3 and ArcInfo 8.3)
Copyright © 2003
ESRI. All rights reserved.
Create
topology
Создание
топологии
Cluster
tolerance
Кластерный
допуск
Ranks
РАНГИ
Rules
ПРАВИЛА
Validate
topology
Проверка
топологии
Edit
features
Редактироваине
объектов
Dirty
areas
Непроверенные
области
Fix
errors
Исправить
ошибки
Errors
ОШИБКИ
Exceptions
ИСКЛЮЧЕНИЯ
Make
exception
Отнести
К исключению
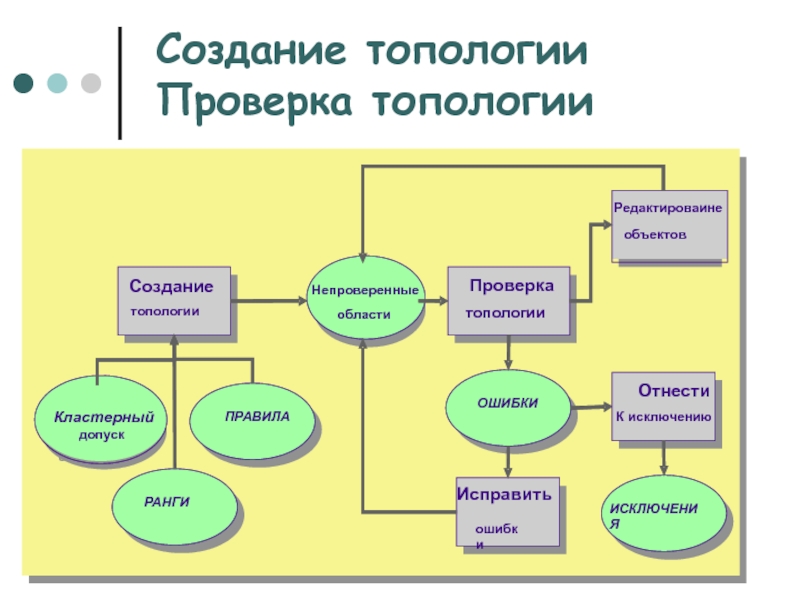
Рисунок 58: Топология сети лондонского метро.
Топологические ошибки
Существуют различные типы топологических ошибок, и они могут быть сгруппированы в соответствии с типами геометрии (полигоны или полилинии). Топологические ошибки с полигональными объектами включают незакрытые полигоны, разрывы между прилежащими полигонами, а также перекрывающиеся полигоны. Распространенной ошибкой для линейных объектов является то, когда их конечные вершины не совпадают в тех местах, где они должны совпадать (например, улицы на перекрестках). Подобные ошибки называются «недолетами», когда между линиями наблюдается разрыв, и «перелетами», когда одна линия пересекает другую и заканчивается чуть дальше (см. Рисунок 59).
Рисунок 59: «Недолеты» (1) появляются, когда оцифрованные векторные линии, которые должны соединяться друг с другом, не соединяются. «Перелеты» (2) происходят, когда одна линия заканчивается за другой линией, к которой должна быть присоединена. Когда вершины двух полигонов на их границах не совпадают, появляются разрывы (3).
Результатами недолетов и перелетов являются так называемые «висячие узлы» в конце линий. Висячие узлы приемлемы в отдельных случаях, например для тупиковых улиц. Топологические ошибки нарушают отношения между объектами. Эти ошибки должны быть исправлены перед проведением таких типов анализа векторных данных, как сетевой анализ (т. е. поиск кратчайшего маршрута по дорожной сети) или измерения (т. е. выяснение длины рек). Помимо необходимости топологии в сетевом анализе и измерениях, существуют другие причины, почему следует иметь топологически корректные данные. Представьте, что Вы цифруете муниципальные границы Вашего района, и полигоны перекрываются или имеют разрывы. В случае таких ошибок Вы по-прежнему можете пользоваться инструментами измерений, но результаты будут некорректными. Полученная площадь будет неправильной, и будет непонятно, где именно находятся границы (например, в случае перекрывающихся полигонов принадлежность территории к двум муниципалитетам одновременно невозможна!).
Иметь топологически корректные данные важно не только для проведения собственного анализа, но и для других людей, которым Вы можете передать свои данные. Они могут не знать об ошибках и будут расценивать результаты своего анализа как правильные.
Правила топологии
К счастью, многие распространенные ошибки, происходящие при оцифровке, могут быть предотвращены с помощью правил топологии, внедренных во многие ГИС-приложения. Кроме некоторых специализированных форматов геоданных, топология обычно не применяется по умолчанию. Многие широко распространенные ГИС, такие как QGIS, определяют топологию как серию правил, которые могут быть выбраны пользователем и применены к векторным слоям. Следующий список включает некоторые примеры правил топологии, определяемых для объектов реального мира на векторной карте:
•Элементы муниципальной карты не должны перекрывать друг друга.
•Элементы муниципальной карты не должны иметь разрывов.
•Полигоны земельных участков должны быть замкнутыми.
•«Недолеты» и «перелеты» границ участков не позволяются.
•Горизонтали высот не должны пересекаться.
Топологические инструменты
Многие ГИС-приложения имеют инструменты топологического редактирования. Например, в QGIS Вы можете включить топологическое редактирование для эффективного редактирования общих границ объектов полигональных слоев. ГИС-приложение обнаруживает общие границы объектов, и Вам достаточно будет передвинуть только одну вершину, в то время как приложение обновит вершину прилежащего полигона, как показано на Рисунке 60 (1). Другая опция топологического редактирования — установка ограничения на перекрытие полигонов (см. Рисунок 60 (2)). В QGIS, если Вы нарисуете новый полигон поверх существующего, приложение обрежет новый полигон по границе существующего.
Рисунок 60: Топологическое редактирование. 1) Когда пользователь сдвигает вершину в углу бордового полигона, соответствующая вершина зеленого квадрата автоматически следует за ней. 2) Чтобы избежать перекрытия полигонов, новый объект (бордовый) автоматически обрезается по границе существующего (зеленый).