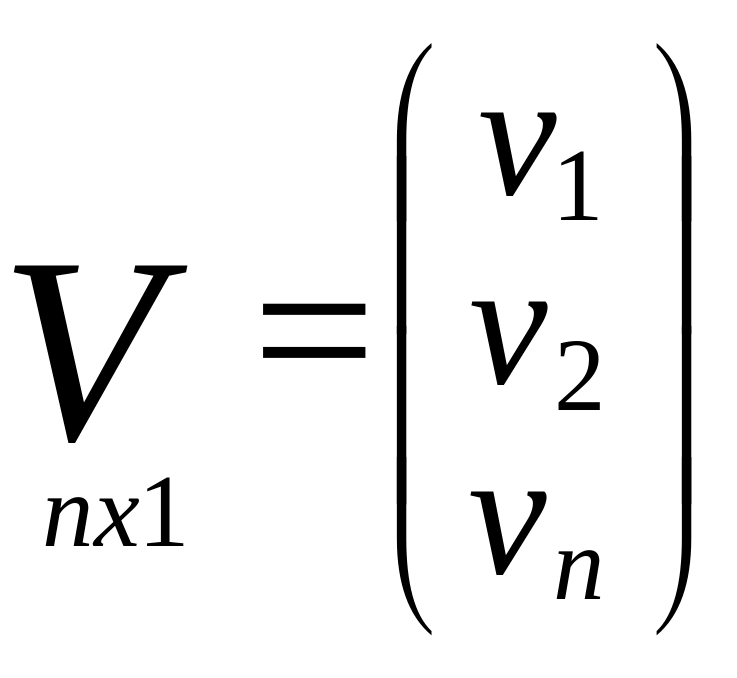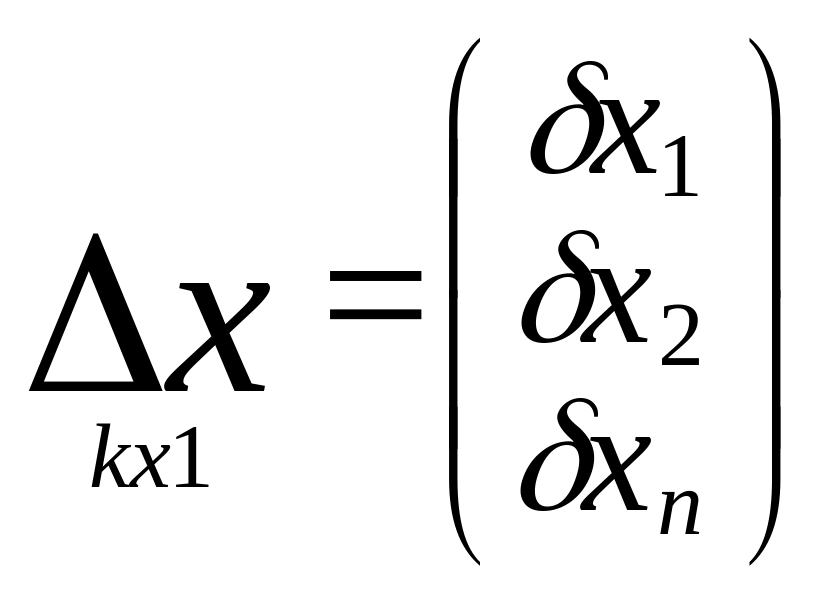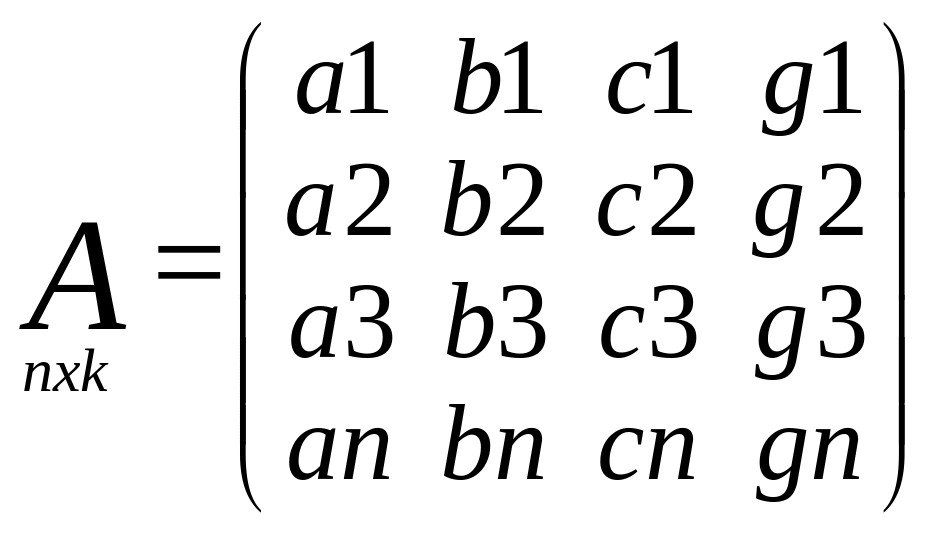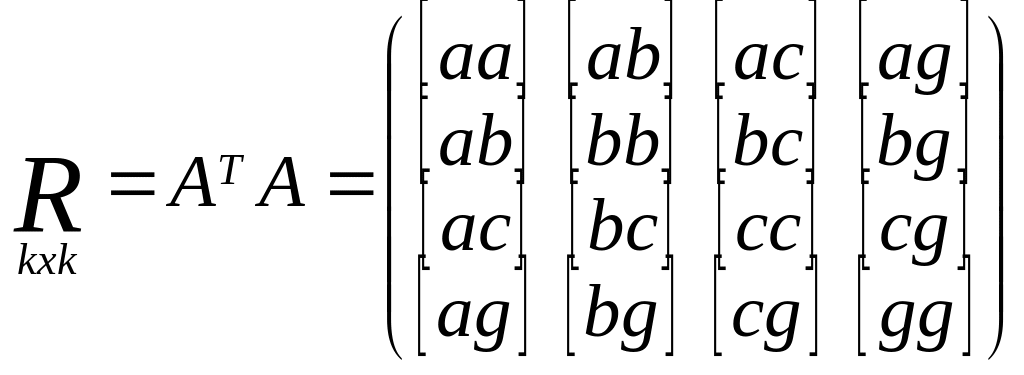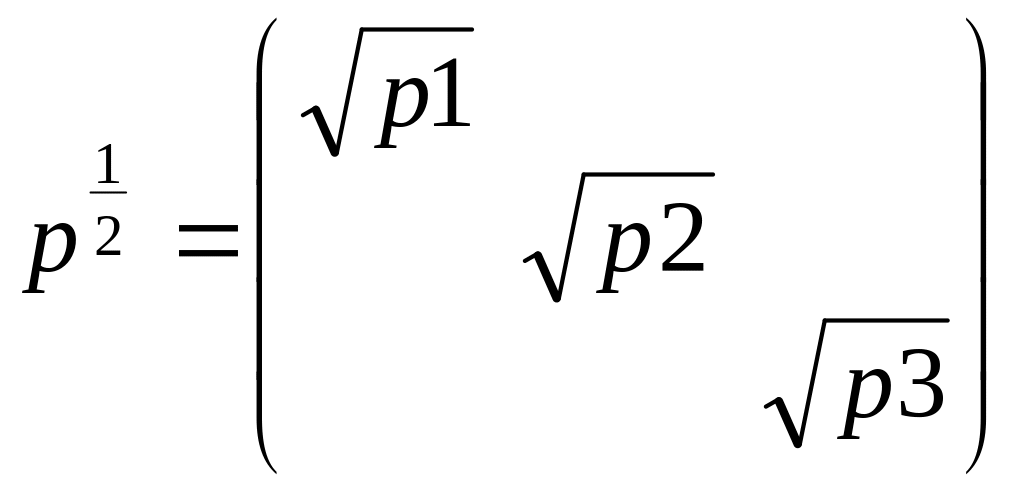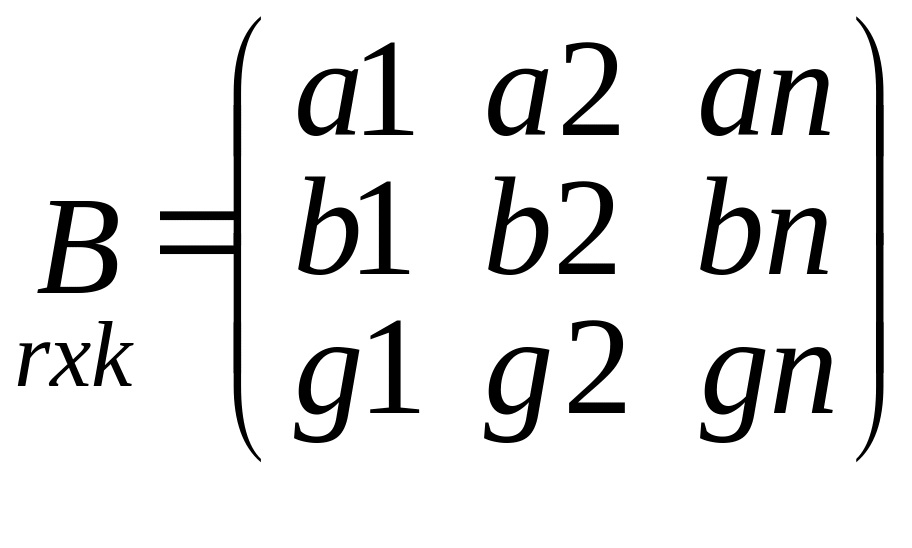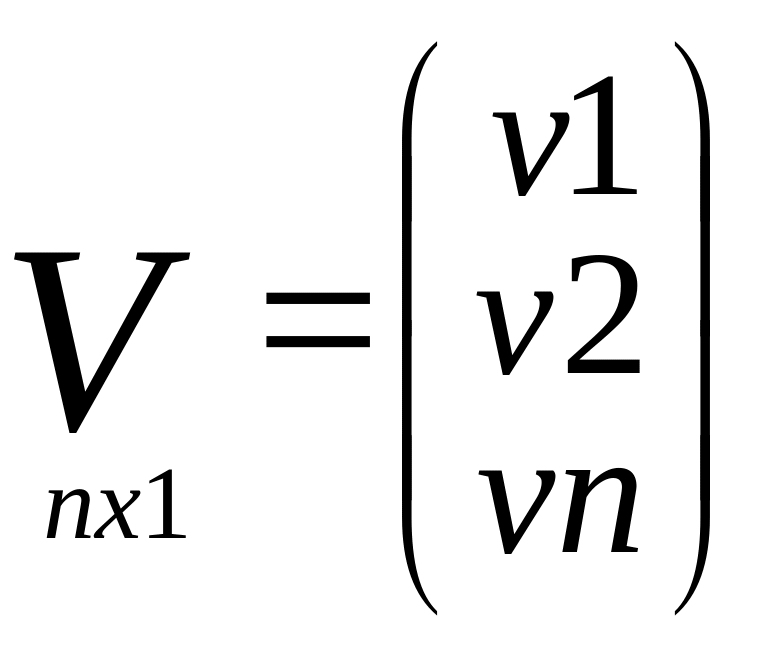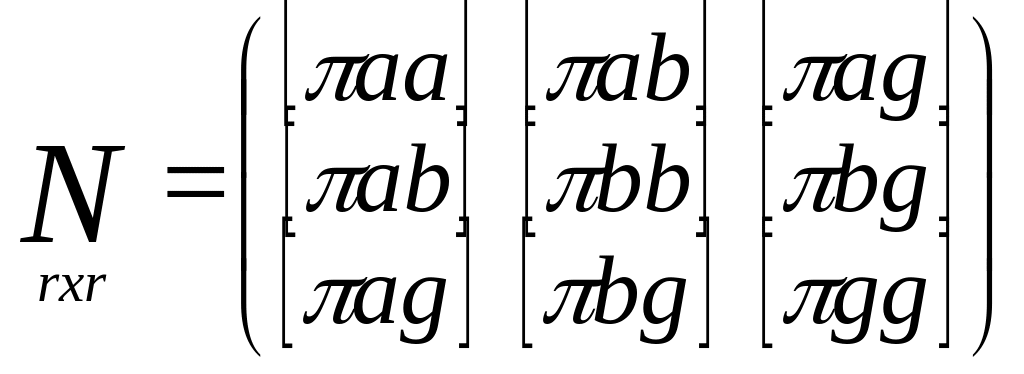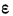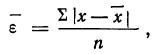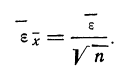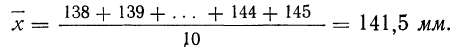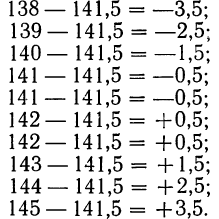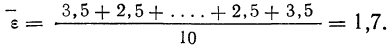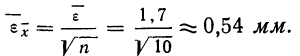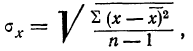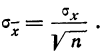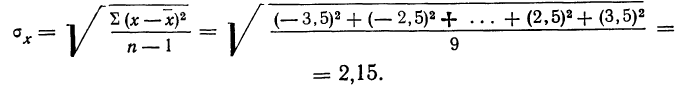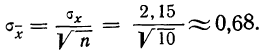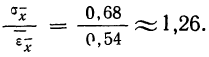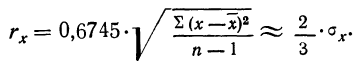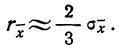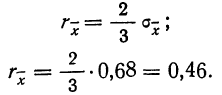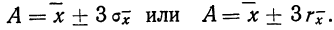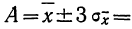Типы ошибок в теории ошибок - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Теория ошибок

Теория ошибок
– дисциплина, которая изучает законы
возникновения и распределения ошибок
измерений, а также методы их обработки.
Виды измерений: 1)полученные непосредственно
из измерения (длина линии при изм. мерной
летной) и косвенным путем (неприступные
расстояния); 2) необходимые
(назыв.минимальное
кол-во измерений, которое нужно выполнить
для определения искомой величины) и
избыточные
(назыв измерения в которых для контроля
всегда выполняются дополнительные
измерения) вычисл. по формуле : r=n-k,
где n
– общее число изм., k
– необходим число изм.; 3) равноточные
(измерения выполненные одним и тем же
инструментом, при одинаковых внешних
условиях, по одной и той же методике,
наблюдателями одинаковой опытности) и
неравноточные (если хотя бы одно из
условий равноточности нарушается это
приводит к неравноточности).

Ошибки измерений

Теория ошибок делит
ошибки на: грубые(возникают
при просчетах и промахах, теор.ош. их не
изучает), систематические
( назыв ошибки МО которых отлично от
нуля. Н.ошибка компарирования), случайные
(ошибки
измерений которых имеют различные знаки
и их МО равно 0). Св-ва случайных ошибок:
1) их МО равно нулю; 2) Положит и отриц
ошибки появляются равновозможно; 3)
Малые по абсолютной величине ошибки
появляются чаще чем большие; 4) Ошибки
не превосходят определенной величины
равной 3m.
Истинная
ошибка
измерения: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины. Истинное
значение практически никогда не известно.

Средняя
квадратическая ошибка

Это МО квадрата
истинной ошибки, т.е. нач момент второго
порядка:

.
Истинная ошибка состоит из: Δ=Θ+с;

.
Т.е. любая СКО содержит случайную и
систематическую составляющую.
Систематической ошибкой можно пренебречь
если ее величина равна:
,
Θ – случайная ошибка.

Равноточные
измерения

Условие: измерения
выполненные одним и тем же инструментом,
при одинаковых внешних условиях, по
одной и той же методике, наблюдателями
одинаковой опытности. Т.к. равноточность
подразумевает одинаковую точность
каждого измерения для хар-ки точности
любого одного измерения используют СКО
одного измерения. Наиболее надежным
значением из ряда равноточных измерений
будет среднее арифметическое, которое
вычисляется по формуле:

,
где х – результат измерения, n
– число изм.

Оценка точности
равноточных измерений

1) СКО одного
измерения.
Если известна истинная ошибка измерения
Δ, которая находиться по формуле: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины.

.СКО
одного измерения находим как: а) n>=30.
Формула Гаусса:

,
где

;
б) n<30.
Формула Бесселя:

.
2) При вычислении СКО удерживают две
значащих цифры. Для того чтобы убедиться
что этого достаточно вычислим СКО самой
СКО:

— если СКО вычислено по формулам Гаусса,

— -«»- по формулам Бесселя; 3) СКО среднего
арифметического: вычисляется по формулам:

,
где m
– CКО
одного измерения, n
– число измерений. 4) Кроме СКО для хар-ки
точности равн.измерний используют
среднюю и вероятную ошибку: Средняя
ошибка —

,
ν – уклонение ср.кв.значения. Для
вычисления вероятной ошибки r,
которая хар-ет середину ряда используют
или ряд истинных значений Δ, или уклонения
от среднего ν.
Эти величины берут по абсолютной величине
и выстраивают в порядке возвр. Вероятная
ошибка r
будет равна центральному значению из
полученного ряда если число измерений
нечетное или среднему из двух центральных
знач. при четном числе измерений.

Относительные
ошибки измерений Абсолютные

Абсолютными ошибками
назыв СКО, среднюю v,
вероятную r,
истинную Θ. Относительной ошибкой –
назыв. величину получаемую как отношение
ошибки измерения к результату измерения:
m_x/x.
В геодезии принято представлять
относительную ошибку в виде простой
дроби: 1/(х/m_x₎ И округлять
до целых сотых. В зависимости от того
какую точечную оценку использовали для
хар-ки точности различают относит.
истинная ош. – Δ/х, относит ср.кв.ош –
ν/х, относит вер-я ош – r/x.

СКО функции.
Принцип равного влияния

Если представить
ф-ю F(x)=F(x1,
x2…xn),
которую оцениваем как ф-ю измеренных
величин, то СКО ф-ии для некоррелированных
измерений
будет найдена как:

,
где

— частная производная оцениваемой ф-ии
по i-му
измерению. Если измерения коллерированы:

,
m_xi
m_xj
– коэф.кореляц между i-м
j-м
измерениями. Для определения СКО
отдельных аргументов применяют принцип
равного влияния. Суть принципа в том
что влияние каждого источника ошибок
на конечный результат применяют
одинаковым:

1)СКО алгебраической
суммы: F=x1±x2±..±xn,

— для неравноточных. Частный случай
когда измерения равноточны:

.
В этом случае формула приобретает вид:

2)Как СКО ф-ии
получают и СКО арифметической середины:

,

Неравноточные
измерения

Неравноточными
назыв измерения в которых каждое
измерение будет иметь свою отличную от
других СКО. Вычислить ошибку каждого
неравноточного измерения сложно, поэтому
для хар-ки неравноточ измерений применяют
относительную меру точности, которую
назыв.весом. Веса измерений обратны
квадратам СКО:

,
mi
– ско соотв измерения, с – произвольная
постоянная для данного ряда измерений.
При выборе с стараются чтобы вычисленные
веса измерений были близки к 1.Зная вес
всегда можно определить величину СКО
измерения:

.
При оценке точности заменяют с=μ².

Ошибка единицы
веса для ряда неравноточных измерений
играет ту же роль что и СКО одного
измерения для ряда равноточных:

.
Для вычисления ошибки единицы веса
используют формулу Гаусса:

— когда известно истинное значение,

— при n<30,

— при n>30.

Наиболее надежное
значение из ряда неравноточных измерений
и его оценка точности:

Наиболее надежным
будет ср.весовое

.
Эту величину так же назыв.общая
арифметич.середина. СКО среднего
весового:

.

Вес функции:

Формулы для
вычисления весов ф-ии получают из формул
для вычисления весов ф-ий разделив их
на μ².

Для некоррелированных
измерений:

.
Для коррелированных:

Задача уравнивания

Наличие в сети
избыточных измерений приводит к
неоднозначности определения неизвестных,
а значит возникает задача ур-я, которая
Состоит в определении наиболее надежных
значений неизвестных параметров и их
оценки точности. Мы решали такую задачу
при обработке измерения одной величины
в теории ошибок. Принципиальное отличие
задачи в том что в обработку включаются
разнородные величины. Существует два
вида ур-я: параметрический и корелантный.

Параметрический
способ ур-я

Х – истинное
значение неизвестного параметра, У –
истинное значение измеренной величины,
у – измеренное значение. Результаты
измерений всегда можно связать с какой
то ф-ей. Т.к. в общем случае ур-е (1) нелинейно
приведем его у линейному виду разложив
в ряд Тейлора

Порядок уравнивания
параметрическим способом

1) Выберем неизвестные
и обозначим их xj.
2)Составим у-е связей между измеренными
значениями и неизвестными У=φ(х).
3) Составим параметрическое у-е поправок
А∆х+L=V.
4)Находим приближенное значение
неизвестных и вычисляем свободные члены
параметрических у-ий поправок: φ(х⁽⁰⁾)-у=L.
5) Составим нормальное у-е R∆x+B=0,
R=A^TA,
b=A^TL.
6) Получим поправки из уравнивания
приближенным значением неизвестных
∆х=-R^-1b.
7) Вычислим уравненные значения неизвестных

.
Выполним оценку точности.

Запись матричных
выражений в параметрич.способе

Параметрич.у-е
поправок

V=A∆x+L

Для каждого измерения

Матрица поправок
изм.знач.

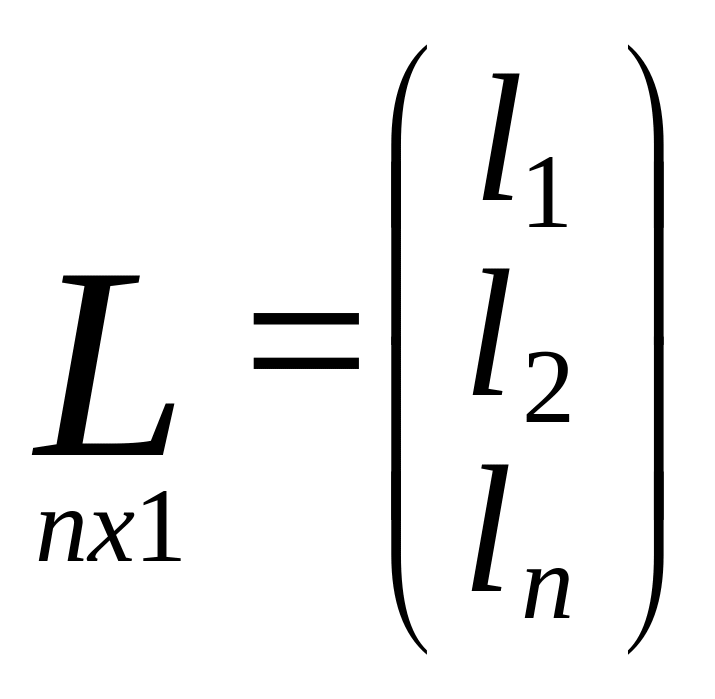
Матрица частных
произв.

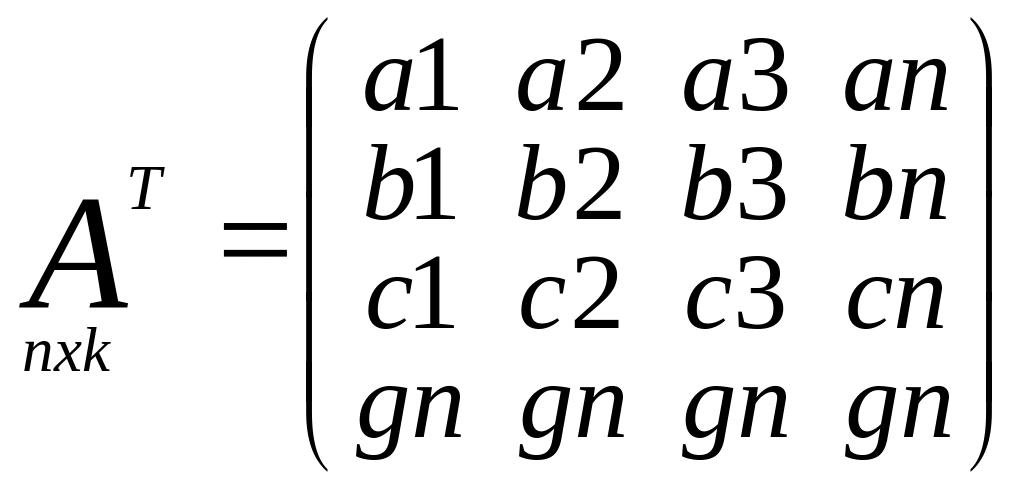
Матрица коэфиц.
норм.ур-й. Св-ва:
1) по диагонали стоят квадратичные коэф.,
они всегда положит. 2) не лиагональные
элементы симметричны относительно
главной диагонали.

Матрица свободных
членов нормальных ур-ий

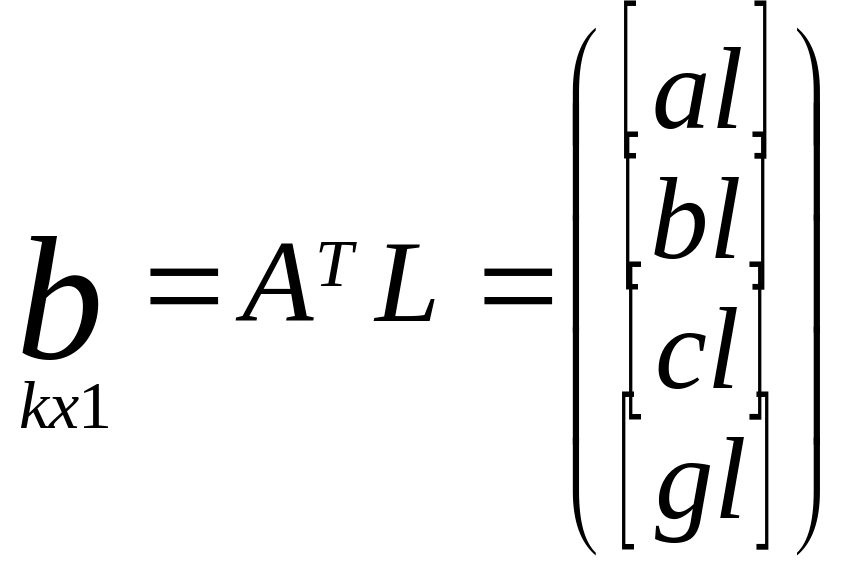
Номальные у-я для
4 неизвестных

R∆х+b=0

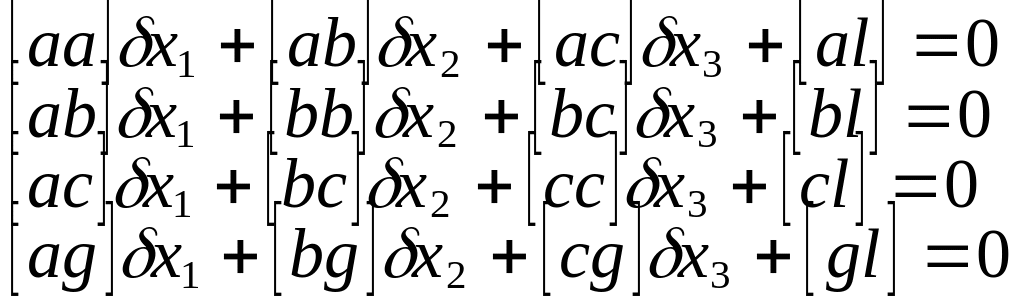
Способы решения
нормальных ур-ий

Прямой способ,
когда решения получают в виде: ax=b,
x=b/a.
При прямых способах мы можем заранее
указать кол-во операций. Приближенный
способ, когда решения получаем в виде:
ax+x-x-b=0,
xⁱ=(1-a)xⁱ^-1-b,
т.е. в каждом последующем приближении
I
используется значение неизвестного
xⁱ^-1полученное
в предыдущем приближении. В этом способе
мы заранее не можем описать кол-во
операций, но этот способ занимает меньше
памяти в ЭВМ.

Оценка точности
при параметрическом способе

а) оценка точности
неизвестных. Обратный вес уравненного
значения каждого неизвестного будет
равен соотв.диагональному элементу
обратной матрицы коэф.норм. ур-й
.В
матрице Q
по диагонали стоят обратные веса
неизвестных ее так же назыв. весовой
матрицей.

б) вычисление ошибки
единицы веса. При параметр. способе
ошибки единицы веса вычисляются по
формуле:
,
здесь v
может быть вычислено по формуле:

,
где n
– общее число изм., k
– число необходим изм., равное числу
определяемых неизвестных.

Ур-ие неравноточных
измерений

1)пусть измерения
неравноточны, чтобы привести их к
равноточному виду мы умножим их на
матрицу:

.
Получим у-е:

.
Решаем задачу также как и для равноточных
изм.: получим нормальное у-е и вектор
решения:

;

.
Из ур-я мы получим

,
чтобы получить величину V.
После ур-я разделим поправки:

2) для учета
неравноточных измерений во все алгоритмы
Гаусса ввести веса измерений и получит
алгоритмы в виде:

;

Коррелатный
способ ур-я

Сущность ур-я
коррелатным способом заключается в том
чт задачу нахождения минимума ф-ии
зависимых переменных [pv2]
решают способом Лагранжа, вводя
вспомогательные множители независимых
условных ур-ий. Приводит к тем же
результатам что и параметрический, но
иногда более выгоден.

Порядок ур-я
корелатным способом

1) Подсчитываем
число избыточных измерений в геод.сети.
Каждое избыточное измерение приводит
к возникновению независимого ксловного
у-я поправок. 2) Составляем у-е связей
между измеренными величинами которые
выражают какое-то математическое
соотношение: φ(У)=0;
3) Составляем условное у-е поправок:
BV+w=0;
4) Составляем нормальные у-я: Nk+w=0;
5)Получаем корелаты решив у-е любым
известным споcобом:
k=-N^-1w;
6) вычисляем поправки к измеренным
величинам: V=p^-1B^Tk;
7)Вычисляем уравненные значения измеренных
величин

;
По уравненным значениям измерений
вычисляем значения неизвестных; 9) Оценка
точности.

Подробная запись
матричных выражений

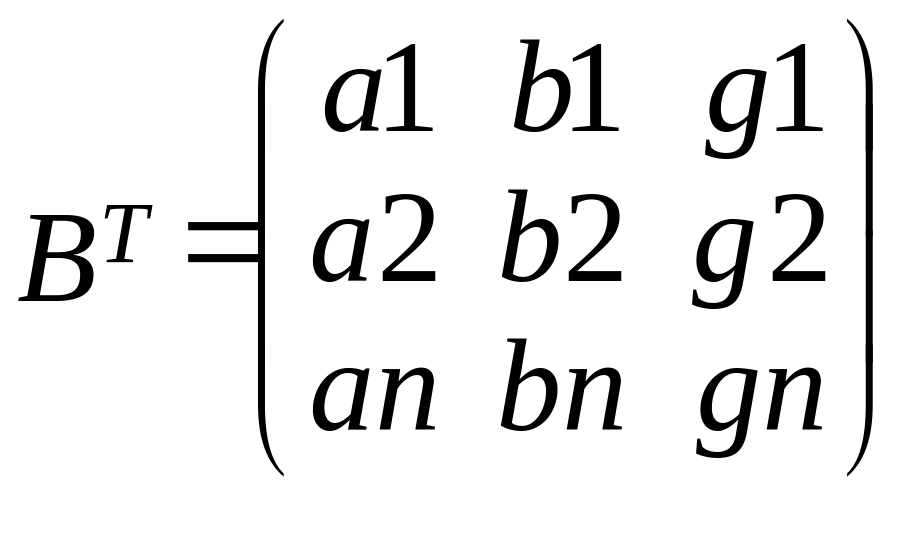
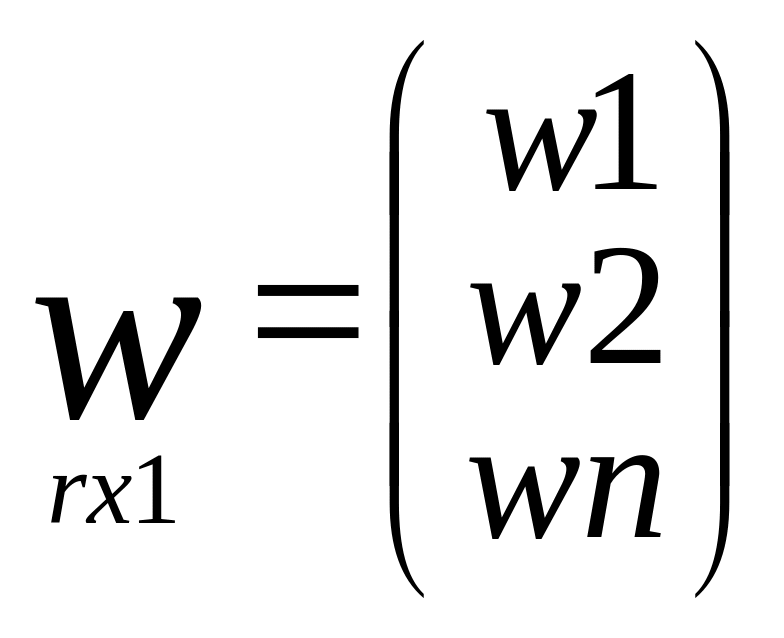
C
учетом у-я поправок:

Нормальные у-я в
подробной записи:

,
где

— обратный вес

Порядок обработки
ряда неравноточных измерений

1) Вычисляем общую
арифметич. середину:
,
где ε_i=x_i-x’,
x’=minx_i . 2)
Вычисялем уклонения v_i=х_о-х_точн
и выполняем контроль

,
где ошибка округления при вычислении

будет
.
3)Вычисляем [pv²]
с контролем:

.
4) Вычисляем μ, M,
m_μ,
m_M_bи строим
доверительные интервалы

Порядок обработки
ряда равноточных измерений

1.Вычисляем простую
арифметич. середину:
,
где ε_i=x_i-x’,
x’-
приближенное значение х (обычно
минимальное значение x_i).
2) Вычисляем отклонения v_i=
х_i-x_окр,
и выполняем контроль

,
где β – ошиюка округления х —

.
3) Вычисляем [v²]
с контролем:

.
4) Вычисляем m,
M,
m_m.
5)Cтроим
доверительные интервалы

;
;

Число нормальных
ур-й в параметрическом и корелатном
способе

В параметрическом
способе: это определенная система из k
линейных уравнений с k
неизвестными: R∆х+b=0.
В корелатном: в системе нормальных
уравнений число уравнений r
равно числу неизвестных.

Алгоритм гаусса.
Эквивалентные ур-я.

Система эквивалентных
у-й имеет вид:

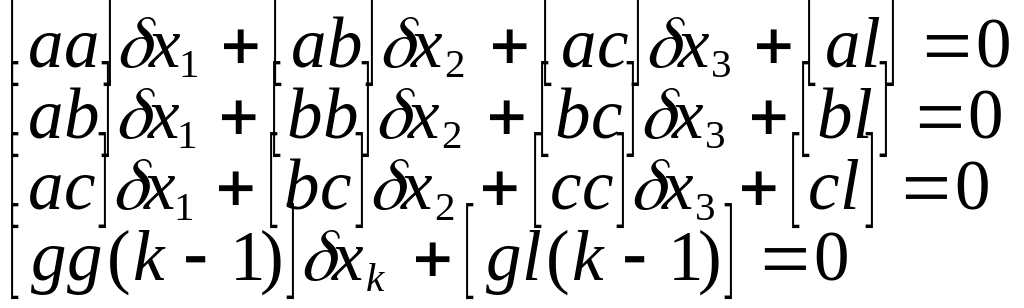
Алгоритм полученный
для вычисления коэффициентов в
экквивалентной системе, назыв алгоритмом
Гаусса. Первый сомножитель получается
как произведение первой буквы знаменателя
на первую букву раскрываемого алгоритма,
а второй как произведение второй буквы
знаменателя на его вторую букву

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Тео́рия оши́бок, раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. к. каждое измерение содержит некоторую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки постоянно либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на результаты измерений и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Например, в астрономии при измерении величины угла между направлением на светило и плоскостью горизонта систематическая ошибка является суммой двух ошибок: систематической ошибки, которую даёт прибор при отсчёте данного угла (инструментальная ошибка) и систематической ошибки, обусловленной преломлением лучей света в атмосфере (рефракция). Инструментальная ошибка учитывается с помощью таблицы или графика поправок для данного прибора; ошибку, связанную с рефракцией (для углов, меньших 80°), можно достаточно точно вычислить теоретически. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, как правило, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредсказуемым образом то в сторону уменьшения, то в сторону увеличения результата.

Теория ошибок занимается изучением лишь случайных и грубых ошибок. Основные задачи теории ошибок: определение законов распределения случайных ошибок, построение статистических оценок неизвестных величин по результатам измерений, вычисление погрешностей таких оценок и устранение грубых ошибок.

Пусть в результате nn независимых измерений некоторой неизвестной величины μmu получены значения X1,X2,…,XnX_1,X_2,dots,X_n. Разности

δ1=X1−μ, δ2=X2−μ, …, δn=Xn−μdelta_1=X_1-mu,, delta_2=X_2-mu, ,dots, , delta_n=X_n-muназываются истинными ошибками; в терминах вероятностной теории ошибок все δidelta_i рассматриваются как случайные величины, независимость измерений понимается как взаимная независимость случайных величин δ1,…,δndelta_1, dots, delta_n. При этом измерения называются равноточными (в широком смысле), если эти величины имеют одно и то же распределение. Т. о., истинные ошибки равноточных измерений суть независимые одинаково распределённые случайные величины. При этом математическое ожидание истинных ошибок b=Eδ1=…=Eδnb=text{E}delta_1=ldots =text{E}delta_n называется систематической ошибкой, а разности δ1−b,…,δn−bdelta_1-b,dots,delta_n-b – случайными ошибками. Отсутствие систематической ошибки означает, что b=0b=0, в этом случае δ1,…,δndelta_1,dots,delta_n суть случайные ошибки. Величину 1/(2σ)1/(sqrt{2}sigma), где σsigma – квадратичное отклонение ошибок δ1,…,δndelta_1,dots,delta_n, называют мерой точности (при наличии систематической ошибки мера точности есть 1/2(b2+σ2)1/sqrt{2(b^2+sigma^2)}. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений.

В качестве оценки неизвестной величины μ mu обычно берут арифметическое среднее из результатов измерений X1,…,XnX_1,dots,X_n:

X‾=1n∑i=1nXi,displaystyleoverline X=frac{1}{n}sum^n_{i=1}X_i,а разности Δ1=X1−X‾,…,Δn−X‾Delta_1=X_1- overline X, dots, Delta_n — overline X называются кажущимися ошибками. Выбор X‾overline X в качестве оценки для μmu основан на том, что при достаточно большом числе nn равноточных измерений, лишённых систематической ошибки, оценка X‾overline X с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины μmu (это связано с Законом больших чисел); оценка X‾overline X лишена систематической ошибки (оценки с таким свойством называются несмещёнными оценками); дисперсия этой оценки есть

DX‾=E(X‾−μ)2=σ2/n.text Doverline X=text E(overline X-mu)^2=sigma^2/n.Опыт показывает, что практически очень часто случайные ошибки имеют распределения, близкие к нормальным (это объясняется центральной предельной теоремой). В этом случае распределение величины X‾overline X мало отличается от нормального распределения с математическим ожиданием μmu и дисперсией σ2/nsigma^2/n. Если распределение величин δ1,…,δndelta_1,dots,delta_n в точности нормально, то дисперсия всякой другой несмещённой оценки для μmu, например медианы, не меньше DX‾text Doverline X. Если же распределение величин δ1,…,δndelta_1,dots,delta_n отлично от нормального, то последнее свойство может не иметь места.

Если дисперсия σ2sigma^2 отдельных измерений заранее неизвестна, то для её оценки пользуются величиной

s2=1n−1∑i=1nΔi2;displaystyle s^2=frac{1}{n-1}sum^n_{i=1}Delta^2_i;

s2s^2 – несмещённая оценка для σ2sigma^2, т. к. Es2=σ2text E s^2=sigma^2.

Если случайные ошибки δ1,…,δndelta_1,dots,delta_n имеют нормальное распределение, то отношение

t=(X‾−μ)nst=dfrac{(overline X -mu)sqrt{n}}{s}имеет распределение Стьюдента с n−1n-1 степенью свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства μ≈X‾mu approx overline X (см. Метод наименьших квадратов). Величина

χ2=(n−1)s2σ2chi^2=dfrac{(n-1)s^2}{sigma^2}при тех же предположениях имеет распределение хи-квадрат с n−1n-1 степенью свободы. Это позволяет оценить погрешность приближённого равенства σ≈ssigma approx s. Относительная погрешность ∣s−σ∣/s|s-sigma|/s не превосходит числа qq с вероятностью

ω=F(z2,n−1)−F(z1,n−1),omega=F(z^2,n-1)-F(z_1,n-1),
где F(z,n−1)F(z, n-1) – функция распределения хи-квадрат, а

z1=n−11+q,z2=n−11−q.z_1=dfrac{sqrt{n-1}}{1+q},quad z_2 = dfrac{sqrt{n-1}}{1-q}.

Дата публикации: 1 августа 2022 г. в 13:27 (GMT+3)

Источник

Введение

В теории и практике перевода проблема адекватности и точности относится к одной из наиболее обсуждаемых. Задача достижения разноуровневой эквивалентности при переводе на целевой язык требует от переводчика умения подбирать языковые единицы языка перевода, наиболее точно соответствующие исходному содержанию с точки зрения учета различных аспектов: исторических, грамматических, семантических, социокультурных, прагматических, стилистических и др. При анализе переводческих стратегий и решений исследователи нередко обращаются к понятию «ошибка», которое позволяет описать шаги переводчика, ведущие к утере, искажению содержания или его неверному представлению. Ошибки в этом случае становятся не только объектом научного изучения, но и инструментом обучения будущих переводчиков.

Уровень серьезности допускаемой переводчиком ошибки может варьироваться, а само ошибочное речевое действие может быть обусловлено различными факторами, связанными с языковыми компетенциями переводчика, со сложностью механизмов речепорождения, с влиянием экстралингвистических факторов, к числу которых относятся культурная дипломатия (culturaldiplomacy), юридические и профессиональные нормы, директивная политика в сфере перевода (например, какие произведения выбираются для перевода и на какие языки), психологическая установка переводчика (translator’sbias) и др.

Цель настоящей статьи заключается в том, чтобы уточнить место «переводческой ошибки» в общей системе научных представлений об ошибке, что предполагает сравнительный анализ концепций ошибки и их типологий в рамках различных гуманитарных дисциплин: философии, логики, лингвистики, лингводидактики и др.

Общее толкование ошибки как нарушения каких-либо законов, правил, схем, норм, логики (см., например, «Ошибка — неправильность в действиях, поступках, высказываниях, мыслях, погрешность» в «Толковом словаре русского языка» под ред. Д. Н. Ушакова) позволяет её рассматривать как результат девиантной деятельности или поведения (от лат. deviatio отклонение, англ. deviation; нем. Abweichung; Devianz), т. е. понятия, более широко применяемого в социологических и психологических исследованиях [1]. Девиантное (отклоняющееся) поведение индивида может проявляться в различных сферах его деятельности, и, следовательно, анализироваться с позиции широкого спектра научных дисциплин. Задачи настоящей статьи позволяют ограничить рассмотрение ошибки, как результата девиантного поведения индивида, сферой речемыслительной деятельности.

Логико-философский подход кошибке

С точки зрения философии и логики ошибка связана, прежде всего, с неправильным ходом мыслей в рассуждении [2]. Следуя аристотелевскому подходу, разграничившему два класса ошибок (ошибки «вне речи», т. е. ошибки в мышлении и «неправильности речи»), в логике выделяют две группы ошибок в зависимости от их причины: а) ошибки неформальные (ошибки, причиной которых служит неправильность в словесном выражении мысли); б) формальные ошибки (ошибки логические в собственном смысле) [3, С. 125–127]. Также в традиционной логике ошибки классифицируют как преднамеренные (софизмы) и непреднамеренные (паралогизмы). В свою очередь, формальные ошибки подразделяют на «Не следует» (от лат. Non sequitur); ошибки, связанные с вероятностью; количественные ошибки; ложные обобщения (от лат. Dictosimpliciter); безотносительные суждения (от лат. Ignoratioelenchi); каждые из которых имеют частные случаи. Неформальные ошибки также подвергаются более частной классификации. Так, к неформальным ошибкам относят оксюморон (соединение), омонимию (одноименность), эквивокацию, амфиболию (двусмысленность), ударение или произношение, форму выражения; которые, как и формальные ошибки, имеют частные случаи [4, с. 535–593].

Психологический подход кошибке

В рамках психологии девиантные проявления рассматриваются, прежде всего, в поведении и деятельности индивида или социальной группы (см., например, Словарь-справочник по социальной работе, 2008). Понятие ошибки связывается с «любой ситуацией, при которой некая цепочка ментальных или физических действий не достигает желанной цели, и эта неудача не может быть приписана случаю» [5, с. 31], что позволяет обобщенно выделить три вида ошибочной деятельности [ibid. Р. 113; цит. по [6]].

Психологический подход к изучению речевой деятельности выделяет такое явление как речевая ошибка (далее — РО), которое может быть представлено следующими разновидностями: ошибочное речевое действие; ошибочное программирование речевого действия; ошибочная операция; ошибка моторного программирования [7, с. 79]. При этом разграничиваются РО намеренные (используемые как средство достижения определенного стилистического эффекта) и РО случайные, а также РО, возникающие при освоении и использовании иностранного языка, в отличие от таковых при использовании родного. Наряду с термином «ошибка» ученые используют термин «отклонение» и «недочет», говоря о том, что отклонение — это не всегда ошибка, так как отклонение в речи может носить позитивный характер [8, с. 97].

Если первоначально РО интерпретировались как явления ненормальные, как нарушения языковых правил и немотивированные отступления от норм литературного языка: «Высокоорганизованная («хорошая») речь предполагает отсутствие речевых ошибок» [9, с. 5], то впоследствии ученые стали трактовать ошибки как естественное явление, свойственное и носителю языка, и человеку, изучающему данный язык. Это позволило считать РО своего рода инструментом оценки уровня коммуникативной компетенции языковой личности [10, с. 454; 11, с. 6]. З. Фрейд предлагал собственное понимание РО, согласно которому все несоответствия речевой норме были связаны с неспособностью полностью нейтрализовать влияние «подсознательного» (того, что человек думает, чувствует, скрывает и т. д.) в ходе процесса реализации программы высказывания [12].

В рамках современной традиции психологическая школа считает РО неотъемлемой частью генезиса речи, анализирует РО в контексте общего развития личности и рассматривает РО, способную возникать на различных этапах реализации программы высказывания, как инструмент отражения механизма речепорождения, интерференции мыслей, скрытых за речевым намерением, и самого высказывания [13].

Лингвистический подход кошибке

Девиантные явления в речи не остались без внимания лингвистов, для которых РО выступили в качестве объекта осмысления теоретического и прикладного анализа, что позволило разграничить РО, возникающие а) при овладении родным языком, б) при изучении иностранного языка, в) при осуществлении профессиональной деятельности (например, переводческой, педагогической, исследовательской).

Прежде всего, РО как объективация языковой девиации, была рассмотрена в контексте «норма» vs. «аномалия» и интерпретирована как материал, отражающий процессы развития коммуникативной компетенции личности и развития языковой системы в целом, ведь язык, будучи динамической системой, упрощается, отрицательный материал становится частью языковой нормы [14, с. 129–139; 15; 16]. «РО — это отклонение от языковой нормы, нарушение в употреблении единиц системно-структурного языкового строя в процессе речевой деятельности, обусловленное индивидуальными особенностями носителя языка: индивидуально-психологическими, социолингвистическими и др.». [13, с. 9]. Следовательно, РО может быть отделена от ошибки языковой [11, с. 8].

В рамках подхода «ошибка — нарушение правил (нормы)» предлагалось классифицировать РО на собственно речевые и несобственно речевые, т. е. фактические; при этом собственно РО должны были далее подразделяться на группы согласно типам правил языка [17] или видам речевой деятельности, с которой они связаны [9]. Так, С. Н. Цейтлин выделяла ошибки говорения (производства речи) и ошибки понимания (восприятия). Если выявить ошибки говорения не представляет трудности, поскольку они могут наблюдаться, то ошибки понимания выявить труднее. Тем не менее, связь между этими разновидностями ошибок неоспорима, так как процесс речепродуцирования неотделим от анализа речи [9, с. 14].

РО, вызванные расхождением между передаваемой и воспринятой мыслью, являются ошибками понимания. В зависимости от того, какое, с позиции субъекта восприятия, требование «нормированной» речи оказывается нарушенным, выделяют следующие типы РО: 1) ошибки, нарушающие ясность речи: смещение логического ударения, неправильное понимание значения словоформы, ошибочная смысловая связь слов, ошибочное смысловое разъединение слов; 2) ошибки, нарушающие коммуникативную точность речи: смешение слов, сходных по значению, по звучанию, по звучанию и значению, слов одного семантического поля; 3) ошибки, нарушающие требования краткости речи: лишние слова; 4) ошибки, нарушающие требования полноты речи: пропуск необходимого элемента речевой цепи, двойное использование зависимого элемента; 5) ошибки — нарушения логики: сопоставление несопоставимого, различение тождественного, выведение невыводимого, мнимое противопоставление [18]. Сигналом ошибки является семантическое противоречие в тексте, расхождение между передаваемой и воспринятой мыслью: если при первоначальном восприятии предложения у читателя возникает затруднение, побуждающее его повторно прочитывать фразу и искать правильный смысл, то предложение стилистически дефектно и должно быть исправлено.

РО говорящего (ошибки говорения) могут быть связаны с нарушениями смысловой стороны речи и на основании данного критерия подразделены на: 1) речевые нарушения, искажающие смысловую сторону речи и не имеющие языковой природы (фактические, логические, смысловые ошибки); 2) речевые нарушения, связанные с нечеткостью значения слова в языковом сознании говорящего или со сбоями в механизме выбора необходимого слова из семантического поля, ошибочное построение грамматических структур (семантические ошибки, аграмматизмы); 3) речевые нарушения, не искажающие смысловую сторону речи (нарушение сочетаемости, семантическая избыточность, смешение паронимов и пр.) [19].

Опора на системно-структурную модель языка позволяет распределить все РО на следующие типы: 1) лексические и фразеологические; 2) грамматические (морфологические и синтаксические) и стилистические; 3) орфоэпические, в т. ч. и связанные с дефектами речи; 4) логико-конструктивные, связанные с построением связной речи [20]. Важно отметить, что приведенные выше типы РО в одинаковой степени характерны для письменной и устной речи, однако устная речь может содержать и специфические РО, к числу которых относятся паузы, колебания, исправления, повторы, замещения, оговорки [20]. Подобный уровневый подход к классификации РО достаточно широко распространен в практике обучения иностранному или родному языку, так как он позволяет соотнести нарушения норм употребления языковых единиц, зафиксированных в конкретных случаях, с типами РО [13; 21; 22]. Очевидно, что данное распределение РО никак не учитывают причины и механизмы появления РО.

Психолингвистический подход к анализу РО позволил дополнить функционально-ориентированные классификации речевых нарушений, сосредоточившись на выявлении типов РО, характерных для каждого из четырех этапов процесса речепроизводства носителей родного языка и изучающих иностранный язык [23]. Так, наряду с РО, проявляющимися на каждом их этапов производства речи: 1) этапе планирования высказывания (conceptualization); 2) этапе грамматического оформления (grammaticalencoding); 3) этапе фонологического оформления (phonologicalencoding) и 4) этапе произнесения, артикулирования (articulation), выделяются РО, регистрируемые в процессе само-мониторинга и самокоррекции речи [24; 25; 26; 27; 28].

Выход за рамки собственно языковой формы расширил номенклатуру РО за счет введения дополнительных параметров разграничения. Так, в зависимости от причинвозникновения РО были подразделены на системные, просторечные и композиционные [29]. Учет положения о двух ступенях владения языком: ступени овладения строем языка (нормативный аспект) и ступени творческого владения языком (функционально-стилистический аспект), дал основание М. Н. Кожиной дифференцировать РО на стилистические и нестилистические [13, с. 12]. Позиция субъекта обучения отражена в классификации В. Е. Мамушина, основу которой составляет интерпретация ошибки как неверного действия, результат которого автор может самостоятельно обнаружить и устранить; в случае, когда обучающийся не осознает неправильность своих действий, в строгом смысле слова, для самого обучающегося ошибками не являются, т. к. у него нет выбора между нормативным и ненормативным явлениями. При такой трактовке РО являются: 1) ошибки, допущенные обучающимися в процессе усвоения кодифицированного варианта языка (причиной ошибки является незнание литературной нормы, методическая перспектива — ознакомление с нормами языка и речи); 2) ошибки, появившиеся в процессе развертывания высказывания при переходе внутренней речи в развернутую внешнюю речь (причина ошибки заключается в несформированности речевого самоконтроля, методическая перспектива — формирование и развитие умения осуществлять самоконтроль) [30].

Основанием для коммуникативной классификации РО стало нарушение смысловой стороны речи. К числу РО были отнесены: 1) речевые нарушения, искажающие смысловую сторону речи и не имеющие языковой природы (фактические, логические, смысловые ошибки); 2) речевые нарушения, связанные с нечеткостью значения слова в языковом сознании испытуемого или со сбоями в механизме выбора необходимого слова из семантического поля, ошибочное построение грамматических структур (семантические ошибки, аграмматизмы); 3) речевые нарушения, не искажающие смысловую сторону речи (нарушение сочетаемости, семантическая избыточность, смешение паронимов и пр.) [19].

В качестве критерия дифференциации РО в иных классификациях также выступили: принцип коммуникативной целесообразности употребленных языковых средств, их соответствия конкретной сфере общения, речевой ситуации, с учетом целей и задач общения, содержания высказывания, его жанра и т. д. [31]; принципы, отражающие основные операции речемыслительной деятельности и её результаты [32]; степень влияния «своей» языковой картины мира на функционирование языковой системы изучаемого иностранного языка [33] и др.

Взгляд на ошибки с позиции современного представления о языковой системе и о процессе формирования языковой компетенции (методология, опирающаяся на тетрахотомию «мышление — язык — речь — коммуникация») нашел отражение в классификации А. К. Григорьевой. Автор предлагает выделять четыре типа ошибок: ошибки мышления, ошибки языка, ошибки речи, ошибки коммуникации. При этом методологически разграничиваются ошибки языка как ошибки в языковой системе его носителей (идеальный объект) и ошибки в речи как материальное проявление языковых ошибок [34].

Общелингвистическое и психолингвистическое понимание типов ошибок и их механизмов, составляющее теоретическую основу формирующегося направления исследований — эрратологии, т. е. теории ошибок [35; 36], нашло свое отражение в переводоведении, а также в лингводидактике и дидактике перевода. Постоянное стремление повысить качество переводов (устных и письменных) заставляет педагогов, практикующих переводчиков, переводческие агентства и исследователей вновь и вновь обращаться к феномену ошибки, поскольку ошибка в переводе может служить критерием качества перевода, индикатором уровня владения иностранным языком и уровня профессиональной компетентности, «проблемных зон» в обучении переводу и иностранному языку т. д. Считается, что дальнейшее расширение предметного поля эрратологии будет способствовать уточнению и разрешению многих теоретических и прикладных вопросов переводоведения, например, разработке коррекционных методик преподавания перевода, изучение паралингвистических и экстралингвистических типов ошибок перевода и др. [37].

Одной из актуальных задач современного переводоведения является выработка максимально точного и непротиворечивого определения термина «переводческая ошибка», с чем непосредственно связана и типология подобных ошибок, а также степень их допустимости в переводах и соотношение с «переводческими находками» (термин В. В. Сдобникова, [38]). Известные определения термина «переводческая ошибка» (см., например, [39, с. 123; 40, с. 98]) представляют её как отклонение, неточность или несоответствие оригиналу, вызванные недостатком знания, опыта, профессиональной компетентности, внимания, понимания и т. п. [41, с. 514] переводчика и ведущие к нарушению нормы, снижению качества перевода и мешающие достижению цели перевода [42, с. 117].

Логический подход к РО в переводах представлен в классификации Д. М. Бузаджи, в которой переводческие ошибки были распределены на «апостериорные» (не возможные к идентификации без обращения к оригиналу) и «априорные» (заметные и без обращения к оригинальному тексту). В свою очередь, «априорные» ошибки подразделялись на синтетические (нарушающие предметную логичность) и аналитические (нарушающие понятийную логичность), последние, в сущности, были сведены к нарушениям норм словоупотребления и обозначались как РО [43]. Позднее априорные синтетические ошибки были разделены на фактические (нарушающие общую и специальную логичность) и ситуативные (нарушения частной логичности) [44].

Степень случайности появления ошибки в переводе учтена в делении всех переводческих несоответствий на а) ошибки произвольные, непредсказуемые или несистемные, которые могут появиться в речи как на родном, так и на иностранном языках (mistakes) и быть вызваны забывчивостью, усталостью, возбужденным состоянием и т. д., и б) ошибки предсказуемые, системные (errors) как различного рода ошибки переходного периода языковой компетенции [45, с. 148].

Е. В. Аликина подразделила переводческие ошибки на ошибки понимания и выражения, которые, по её мнению, обусловлены особенностями управления мыслительной деятельностью в процессе перевода [46]. В отдельную группу исследовательница выделила ошибки профессионального поведения переводчика в процессе устного последовательного перевода. К их числу относятся характеристики голоса (слишком тихий / слишком громкий), невербальные компоненты поведения (чрезмерное использование жестов), неумение справляться со стрессовой ситуацией и др. [47].

Обобщающая классификация переводческих ошибок, предложенная Л. Г Федюченко, опирается на аналогичное подразделение всех девиаций на ошибки, возникающие на этапе восприятия текста оригинала, и ошибки, возникающие на этапе воспроизведения текста [40, с. 100]. Материалом для анализа переводческих неудач послужили переводы студентов, обучающихся по программе дополнительного профессионального образования, что позволило автору классификации не только выделить разновидности ошибок восприятия и ошибок воспроизведения, но и сделать вывод о преобладании ошибок второго типа, который включает в себя фактические, лексические, грамматические, эстетические и формальные ошибки [40].

Одной из наиболее подробно разработанных таксономий переводческих ошибок является классификация М. А. Куниловской, в которой исследовательница учла отечественный и зарубежный опыт в области оценивания качества переводов как в профессиональной, так и академической среде [48]. Предложенная автором классификация переводческих ошибок была изначально создана для совершенствования практики обучения письменному переводу за счет внедрения автоматизированной программы проверки переведенных текстов с аннотированием обнаруженных отклонений и неточностей. Проверка переводов в электронном виде, с одной стороны, позволила максимально расширить реестр ошибок, распределенных на три основные категории: смысловые, языковые и оформительские/технические. С другой стороны, это дало возможность воссоздать для обучающихся реальные условия работы переводчика, в которых заказчики нередко оценивают качество переводов на основе «уникальных для каждого случая параметров прагматической приемлемости в принимающей культуре» [48, с. 144]. В этом случае переводческие ошибки могут квалифицироваться через понятие «профессиональные компетенции переводчика» (т. е. ошибки связаны с определенными компетенциями и степенью их сформированности), через «вес» ошибок, отражающий степень их «грубости», а значит влияния на приемлемость перевода, его понятность, а также на время, необходимое на устранение ошибок, например, критерии critical, major, minor или числовой показатель. Кроме того, в сфере профессионального перевода в особый тип могут быть выделены ошибки при переводе терминов, а также ошибки стиля, понимаемого как соответствие текста перевода принятым в принимающей культуре конвенциям [48, с. 147]. В разработанной М. А. Куниловской классификации обращает на себя внимание введение в три основные категории ошибок класса так называемых переводческих технологических ошибок, которые описывают нарушения процесса перевода (вольности, буквализмы), степень отклонения от содержания оригинала (искажения, неточности, неясности) и небинарные ошибки (многословность, неудачная формулировка). Методическая направленность всей классификации позволила автору включить в номенклатуру ошибок «нелинейные несоответствия» (например, несоответствие коммуникативной интенции автора и искажение коммуникативного намерения автора) и удачные переводческие решения.

Заключение

Подводя итог можно сказать, что задача классификации РО в целом и переводческих ошибок в частности не получила до настоящего времени однозначного решения. Многообразие предложенных классификаций РО и переводческих ошибок свидетельствует о многоаспектности анализируемого объекта и актуальности выработки относительно универсальной таксономии РО применительно к различным видам профессиональной деятельности (обучению языкам, переводческой практике, созданию программного обеспечения и др.).

На современном этапе наблюдается процесс трансформации функционального и интерпретативного потенциала РО: с одной стороны, РО выступает как индикатор и инструмент оценки уровня сформированности коммуникативной компетенции языковой личности, а с другой — как инструмент отлаживания, «настройки» процесса обучения и научения, корректировки и совершенствования образовательных программ.

Переводческая ошибка в этом общеметодологическом контексте приобретает статус ключевого критерия качества переводного текста и, следовательно, профессиональной компетентности переводчика. С этим связано расширение семантики термина «переводческая ошибка»: помимо всех компонентов содержательной структуры термина РО оно включает в себя и семы, отражающие девиантные проявления в профессиональной деятельности переводчика, т. е. нарушения в технологии перевода, в оформлении текста перевода, в профессиональном поведении и т. п. Таким образом, в теоретическом осмыслении переводческая ошибка выступает как результат неосознанного отступления переводчиком от предписанных норм, касающихся всех «включенных» в процесс перевода аспектов деятельности.

Литература:

Девиантное поведение. // Новая философская энциклопедия Института философии РАН. URL: http://iphras.ru/elib/3632.html (дата обращения: 28.11.2016).
Тетерлева Е. В., Попова Ю. К. Понятие ошибки в контексте различных научных дисциплин // Проблемы романо-германской филологии, педагогики и методики преподавания иностранных языков. — Пермь: ПГПУ, 2010. — С. 36–40.
Челпанов В. Г. Учебник логики. — М.: Научная Библиотека, 2010. — 128 с.
Аристотель. О софистических опровержениях // Сочинения в 4 томах. — М.: Мысль, 1978. Т. 2. С. 687
Reason J. L’erreur humaine. P.: PUF, 1993.
Дебренн М. Место межъязыковой девиатологии в общей теории ошибок //Компьютерная лингвистика и интеллектуальные технологии. Труды международной конференции «Диалог 2006» (Бекасово, 31 мая — 4 июня 2006 г.) / Под ред. Н. И. Лауфер, А. С. Нариньяни, В. П. Селегея. — М.: Изд-во РГГУ, 2006. — 642 с.
Леонтьев А. А. Некоторые проблемы обучения русскому языку как иностранному. — М.: Изд-во. Моск. гос. ун-та, 1970. — 88 с.
Красиков Ю. В. Теория речевых ошибок (на материале ошибок наборщика). —М.: Наука, 1980. — 124 с.
Цейтлин С. Н. Речевые ошибки и их предупреждение. М.,Просвещение, 1982. — 128 с.
Энциклопедический словарь-справочник. Выразительные средства русского языка и речевые ошибки и недочеты». — М.: Флинта: Наука, 2005. — 480 с.
Залевская А. А. Речевая ошибка как инструмент научного исследования // Вопросы психолингвистики. — 2009. —№ 9. — С. 6–22.
Фрейд З. Психопатология обыденной жизни. — М.: Азбука, 2013. — 224 с.
Голованова И. Ю. Проблема анализа речевых ошибок в контексте онтогенеза языковой компетенции:Автореф. дис…. канд. филол. наук. — Челябинск, 2004. — 22 с.
Бодуэн де Куртене И. А. Избранные труды по общему языкознанию. В 2-х т. — М.: Изд-во Ак. Наук СССР, 1963. — С. 129–139.
Арутюнова Н. Д. Аномалии в языке (к проблеме языковой «картины мира») // Вопросы языкознания. — 1987. — № 3. — С. 13–19.
Фрей А. Грамматика ошибок. — М.: КомКнига, 2006. — 304 с.
Фоменко Ю. В. Типы речевых ошибок. Учебное пособие. — Новосибирск: Изд-во НГПУ, 1994. — 60 с.
Мучник Б. С. Культура письменной речи: Формирование стилистического мышления: Пособие для учащихся 10–11-х классов средн. школ, гимназий.. — 2-е изд. — М.: Аспект Пресс, 1996. — 175 с.
Сивакова Ю. Н. Актуальные вопросы речевой культуры российских билингвов // Российская филология: традиции и современность// Российская филология: традиции и современность. Секция: Филологическое образование: сб. науч. докл. участников семинара ПАНИ, 20 нояб.1996 г. — СПб., 1997. — С. 138–144.
Тропина В. Г. Психолингвистические критерии предупреждения речевых ошибок студентов (нефилологических вузов) // Интерэкспо Гео-Сибирь. — 2011. — Том 6 — С. 250–255.
Титкова М. Ю. Классификация речевых ошибок школьников: вопрос и вариант решения // Вестник ВятГГУ. — 2015. — № 4. — С. 134–139.
Мильруд Р. П. Введение в лингвистику. Introduction to linguistics. — М.: Дрофа, 2005. — 136 с.
Kovač Mirjana M. Speech Errors in English as Foreign Language: A Case Study of Engineering Students in Croatia // English Language and Literature Studies. — 2011. — № 1. — С. 20–39.
Levelt W. J. M. Monitoring and self-repair in speech // Cognition. — 1983. — № 14. — С. 41–104.
George H. V. A model of error production // Second Language Learning. Contrastive Analysis. Error Analysis, and Related Aspects. — Univ. of Michigan, 1991
Postma A., Noordanus C. The production and detection of speech errors in silent, mouthed, noise-masked, and normal auditory feedback speech. // Language and Speech. — 1996. — № 39 (4). — С. 375–392.
Hohenberger, A., & Waleschkowski, E. Speech errors as evidence for language production processes — A historical journey from Meringer to Leuninger.// Poster presented at International Conference on Linguistic Evidence, University of Tübingen, Germany. — 2002. — С. 71–75.
Nooteboom S. G. Lexical bias revisited: Detecting, rejecting and repairing speech errors in inner speech // Speech Communication. — 2005. — № 47(1–2). — С. 43–58.
Цейтлин С. Н. Детская речь: инновации формообразования и словообразования (на материале современного русского языка): Автореф. дис. …д-ра филол. наук: 10.02.01/ ЛГПИ им. А. И. Герцена. — Л., 1989. — 32 с.
Мамушин В. Е. О характере и причинах речевых ошибок и об «ошибках» контроля (у школьников) // Русский язык в школе. — 1990. — № 1. — С. 45–49.
Арефьева С. А. К вопросу о стилистических ошибках в письменной речи учащихся // Русский язык в школе. — 2000. — № 2. — С. 23–25.
Кукушкина О. В. Основные типы речевых неудач в русских письменных текстах. — М.: Диалог-МГУ, 1998. — 288 с.
Беляева Е. В. Когнитивные механизмы возникновения речевых ошибок при усвоении русского языка в иноязычной аудитории: На материале ошибок китайских студентов: Автореф. дис..канд. филол. наук. Красноярск, 2004. — 188 с.
Григорьева А. К. Речевые ошибки и уровни языковой компетенции // Интеграция образования. — 2005. — № 1–2. — С. 209–216.
Шевнин А. Б. Эрратология и межъязыковая коммуникация // Вестник ВГУ, Серия: Лингвистика и межкультурная коммуникация. — 2004. — № 2. — С. 36–44.
Шевнин А. Б. Эрратология: теория ошибок и переводческих несоответствий // Вестник Южно-Уральского государственного университета. Серия: Лингвистика. — 2005. — № 11(51). — С. 11–113.
Лягушкина Н. В., Савитский И. В. Эрратологический анализ переводческих решений: теоретический и прикладной аспекты // Филологические науки. Вопросы теории и практики. — 2012. — № 4. — С. 86–90.
Сдобников В. В. Переводческие находки vs. переводческие ошибки // Вестник Нижегородского государственного лингвистического университета им. Н. А. Добролюбова. — 2009. — № 4. — С. 151–155.
Красильникова В. Г. Переводческие опыты Ю. А. Сорокина и проблемы профессионально ориентированного перевода // Вопросы психолингвистики. — 2016. —№ 3 (29). —С. 121–129.
Федюченко Л. Г. Экологический аспект перевода: переводческая ошибка // Вестник Тюменского государственного университета. Социально-экономические и правовые исследования. — 2012. — № 1. — С. 97–102.
Гарбовский Н. К. Теория перевода. М.: МГУ, 2004. — 544 с.
Аликина Е. В. Оценка качества устного последовательного перевода в реальной и учебной ситуации // Вестник Нижегородского государственного лингвистического университета им. Н. А. Добролюбова. —2011. —№ 13. —С. 114–123.
Бузаджи Д. М. Белые нитки. Логические аспекты перевода // Мосты. 2006. № 3. С. 36–47 // Думать вслух. Материалы о переводе [электронный ресурс]. URL: http://www.thinkaloud.ru/featureak.html (дата обращения: 01.05.2016).
Ланчиков В. К. Ошибки без кавычек // Мосты. 2008. № 2. С. 31–36 // Думать вслух. Материалы о переводе [электронный ресурс]. URL: http://www.thinkaloud.ru/featureak.html (дата обращения: 01.05.2016).
Куровский А. В., Хахалкина Т. В. Эрратологический аспект перевода зоонимов с английского языка на русский язык (на примере научных текстов по биологии) // Вестник Томского государственного педагогического университета. — 2013. — № 10. — С. 148–152.
Аликина Е. В. Введение в теорию и практику устного последовательного перевода. М., 2010. — 192 с.
Аликина Е. В., Швецова Ю. О. Формирование экстралингвистической компетентности будущих устных переводчиков // Современные проблемы науки и образования. —2012. —№ 2. —С. 189.
Куниловская М. А. Классификация переводческих ошибок для создания разметки в учебном параллельном корпусе RUSSIAN LEARNER TRANSLATOR CORPUS // Lingua Mobilis. — 2013. — № 1. — С. 141–158.

Основные термины (генерируются автоматически): ошибка, иностранный язык, смысловая сторона речи, нарушение, ошибка понимания, языковая система, классификация, ошибка говорения, речевая деятельность, родной язык.

Источник

Содержание:

Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (

Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.

Различают два вида ошибок измерения:

систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.

Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.

Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.

Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.

В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.

Средняя ошибка сводного результата измерения

Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:

где n — число измерений, х — численное значение отдельных измерений, — средняя арифметическая из результатов измерений.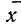

За меру точности соответствия принятой средней арифметической 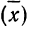истинному значению измеряемой величины (A) принимают среднюю ошибку сводного результата измерения, вычисляемую по формуле:

Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.

Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:

Найдем ошибки измерения:

Следовательно:

Теперь можно вычислить среднюю ошибку сводного результата измерения:

Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.

Средняя квадратическая ошибка

Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.

то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:

Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 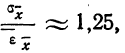если случайные ошибки подчиняются Гауссову закону нормального распределения.

Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:

Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:

Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:

Вероятная ошибка

За меру точности одного измерения иногда принимают вероятную ошибку:

Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:

Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:

Наиболее вероятные границы сводных результатов измерения

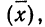
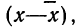
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них называемых в теории ошибок «кажущимися ошибками» позволяет произвести оценку точности соответствия средней арифметической неизвестному истинному значению измеряемой величины (A).

Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:

Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).

Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 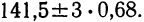Значит, истинное значение размера детали находится в границах от 141,5—2,04 до 141,5+2,04.

Методы математической статистики
Комбинаторика — правила, формулы и примеры
Классическое определение вероятности
Геометрические вероятности
Законы распределения случайных величин
Дисперсионный анализ
Математическая обработка динамических рядов
Корреляция — определение и вычисление

Источник