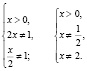Типы ошибок в математике 6 класс - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

План.

Введение.

Глава I. Психолого-дидактический анализ математических ошибок и
затруднений учащихся.

§ 1.
Психолого-педагогический и дидактико-методические причины типичных ошибок и
затруднений учащихся:

§ 1. 1. Сущность понятий
«типичная ошибка» и «познавательное

затруднение», сущность
математической ошибки, причины

появления ошибки.

§ 1. 2. О пользе и вреде ошибок.

§ 1. 3. Причины типичных ошибок
учащихся.

§ 1. 4. Причины познавательных затруднений в учебной деятельности школьников.

§ 2. Типичные ошибки и затруднения
учащихся при обучении математике в 5-6 классах.

Глава II. Пути и средства предупреждения и
преодоления ошибок и затруднений учащихся 5-6 классов.

§ 1. Методы и приемы обучения математике,
используемые учителем для предупреждения ошибок и затруднений.

§ 2. Контроль и самоконтроль учебной
деятельности школьников как средство выявления ошибок и затруднений.

§ 3. Система работы учителя математики
при коррекции ошибок учащихся 5-6 классов.

Приложение. Каталог статей из журнала
«Математика в школе»

за 1970-1990г.г., связанные с работой
над математическими ошибками; с анализом ошибок учащихся на вступительных экзаменах
в ВУЗ; с анализом ошибок, возникающих из недостатков программ и учебников; и
т.д.

Введение.

В настоящее время, также как
и раньше, существует проблема ошибок и затруднений учащихся при обучении
математике. Хотя в методике обучения математики к настоящему времени накоплен
опыт, разработано много различных методов профилактики и коррекции ошибок и
затруднений учащихся при обучении математике, но при этом школьники не
перестают делать ошибки. Плохо это или хорошо? Однозначного ответа нет. Ответ
будет зависеть от того, что мы понимаем под «ошибкой».

Методик обучения много. Но нет единой
теоретической основы. Одной из причин отсутствия в методике обучения математики
теоретической основы является слабая связь со смежными науками, особенно с
психологией.

Считаю, что и ошибка, и затруднение
напрямую связаны с психическими процессами человека. Поэтому в моей работе
много места будет уделяться психолого-педагогическим причинам ошибок и затруднений
учащихся.

Цель моей работы – выявить
необходимые условия, выполнение которых поможет уменьшить количество ошибок и
затруднений при обучении математике в 5-6 классах.

Исходя из цели, были поставлены
следующие задачи:

1. Изучение и классификация
ошибок и затруднений учащихся 5-6 классов при обучении математике.

2. Изучение и классификация
причин ошибок и затруднений учащихся при обучении математике.

3. Изучить опыт работы учителей
математики по предупреждению и коррекции ошибок и затруднений учащихся 5-6
классов при обучении математике.

Глава I. Психолого-дидактический анализ
математических

ошибок и затруднений
учащихся.

§ 1.
Психолого-педагогический и дидактико-методические причины

типичных
ошибок и затруднений учащихся:

Под ошибкой мы будем понимать результат
неправильного (ошибочного) действия.

Ошибочное действие – один из
существенных объектов психологии труда, педагогической психологии и психологии
управления; действие не достигшее цели. Ошибочное действие различают по
причине; по степени выраженности в зависимости от величины отклонения от нормы;
степени повторяемости; степени грубости в зависимости от этапа обучения, на
котором оно совершено; связи с другими ошибочными действиями в синдром
неуспеваемости.

Под сущностью ошибки следует понимать
некое объективное условие, требование, правило и т.п., которое нарушено или не
соблюдено, а под причиной появления ошибки – субъективные ситуации, состояния
или процессы, свойственные интеллектуальной сфере человека, которые повлекли
данное нарушение или несоблюдение.

Психологический анализ математических
ошибок школьников предполагает выявление механизма возникновения той или иной
ошибки в рамках какой-либо психологической концепции усвоения знаний,
формирования –умений и навыков.

Методический анализ ошибок предполагает
демонстрацию ошибки, выявление ее математической сущности, указание возможных
причин появления этой ошибки и характеристику сферы возможных ее проявлений.

Каждая ошибка характеризуется содержанием и причиной
возникновения (содержание лежит на поверхности явления, а причина ее скрыта в
его глубине).

Ошибки делятся на случайные и систематические, то есть
устойчивые. Случайными ошибками следует считать те, которые появляются
однократно, не систематически у одного-двух учащихся класса. К устойчивым (типичным)
ошибкам относятся те, которые появляются у одного и того же ученика (или
нескольких) неоднократно или те, которые появляются хотя и однократно, но у
многих учащихся.

Во второй половине XIX века господствовала ошибочная теория «недопущения ошибок» (Н. Кульман,
Ф. Флеров), согласно которой акцентирование внимание на ошибке повлечет за
собой упрощение ошибки в сознании школьников. Лозунгами этой теории были
следующие: «Ни одной ошибки для глаз!», «Ни одной ошибки для рук!».

Современная дидактика и частные методики доказывают, что
работа над ошибками не просто полезна, но и необходима, причем над типичными
ошибками должна проводиться фронтальная работа, а над случайными – индивидуальная.
Скорее всего, в начале «На ошибках учат», а затем уже «На ошибках учатся».

Сознательному усвоению знаний способствует глубокий анализ
самим учеником содержания каждой ошибки, которая была им допущена, выяснение
причин ее возникновения, теоретическое осмысление ее сути. «Как это не странно
звучит, — отмечает Н.М. Бескин, — ошибки в изучении не вредны, а полезны.
Они аналогичны симптомам болезни. По этим симптомам врач ставит диагноз. Точно
также и ошибки учащихся сигнализируют учителю, чего именно школьник не
понимает. Учитель мог это и не знать, а ошибка дает ему нужную информацию. От
учителя требуется умение понять неправильный ход мыслей ученика, который не
может объяснить, почему он пришел к такому результату». Любая ошибка должна
быть использована для более детального и глубокого проникновения в суть данного
правила, понятия, теоремы и т. д.

В каждой ошибке следует различать содержание и причину ее
возникновения. В содержание ошибки входит то, что объективно неверно,
неадекватно выполнено в действиях учащихся. Причина же появления ошибки – это
некоторое обстоятельство (или их совокупность), которое повлекло за собой
выполнение неадекватного действия учащегося. Содержание ошибки легко установить
по внешнему выражению действий учащегося (сужает или расширяет объем понятия,
неправильно произносит или пишет, неверно выполняет какое-то действие и т. д.).
Причина же ошибки, как правило, внешне себя не проявляет. Задача учителя –
определить исходные корни допущенной ошибки, что дает ему возможность верно
строить работу по ликвидации и предупреждению различного рода ошибок. «Учитель
должен не просто поправить ошибку, а выкорчевать ее. Для этого он должен понять
неправильный ход мыслей и заблуждений ученика, которые сам ученик не может
сформулировать».

Естественная
и зачастую единственная реакция учителя на ошибку ученика – сниженная оценка.
Нередко единственная реакция ученика на собственную ошибку – чувство досады…
из-за сниженной оценки. Как следствие из года в год ученики старших классов,
абитуриенты вузов, студенты младших курсов делают одни и те же ошибки…

Ученик работает у
доски и, уловив тень сомнения в глазах учителя, мгновенно стирает написанное.
Все, нет ошибки!.. Но примеры безошибочных решений учитель способен привести и
сам. А ученика пригласили к доске, в частности, затем, чтобы он ошибался.
Он интересен своими ошибками.

Чтобы перестать
делать ошибки, существует, по нашему мнению, только один путь: нужно делать ошибки,
находить ошибки и исправлять ошибки. Проще говоря, чтобы не
делать ошибок, нужно вволю наошибаться. Ошибка, «не убитая» в процессе
самостоятельной работы, «убивает» на контрольной или экзамене.

Ученики нередко
задают вопрос: «А можно здесь до множить на знаменатель (возвести в
квадрат, не делать проверки, сократить и т. п.)?» По существу, подобный вопрос
является попыткой переложить ответственность за решение на учителя. В
ответ уместно спросить: «Вы хотите, чтобы я вам разрешил или запретил
сделать то, о чем вы спросили? Сие не в моей власти. Так что адресуйте свой
вопрос самим себе!»

Ученик перестает
ошибаться только тогда, когда ответственность за полученный результат полностью
ляжет на него самого, когда появится ощущение, что только он сам – не приятель,
не учитель – может отыскать выход из создавшейся ситуации, что только от
качества его собственной работы зависит конечный результат.

Вспоминается расхожая
истина – умные люди учатся на чужих ошибках. Увы, в математике
приходится учиться в основном на собственных ошибках. Иными словами, если
ученик не ошибается, то он не учится.

Ошибка – вещь
необходимая и полезная. Нужно лишь правильно относиться к ошибке, умело и
грамотно ее использовать.

Не
знаешь алгебры – займись арифметикой.

Нередко ученик использует неверную формулу или, что еще хуже,
вообще не отдает себе отчета, чем именно он пользуется. Рассмотрим типичные
примеры.

Сколько бы учитель ни заставлял учеников повторять свойства
радикалов, рано или поздно кто-нибудь из них напишет нечто подобное.

Если учитель в очередной раз скажет: «Так нельзя!», то
долговременного эффекта это не даст. Подсказав или продиктовав некий факт, мы
загружаем оперативную память ученика. Последняя – как в компьютере – обновится
при новом включении… Чтобы информация попала в «долговременное запоминающее
устройство», необходимо добиться понимания, а в данном случае – осознания
учеником его ошибки. Для этой цели пригоден следующий почти универсальный
совет:

— Проверьте написанное вами равенство при каком-нибудь
значении х. Например, при х =1.

Важно, чтобы ученик сам написал

и получил абсурдный результат .

Полезен и иной тезис:

— Предложенное Вами
преобразование заметно упрощает теорему Пифагора:

Последнее
равенство опровергается и повседневной практикой: шагать по катетам все-таки
дальше, чем по гипотенузе.

Интересные
свойства рассматриваемой цепочки равенств еще не исчерпаны. При х = -1 получим

В
ошибочности первого равенства ученик уже убедился. Но, оказывается, и второе равенство
неверно.

Не стоит жалеть
времени на подробное обсуждение и исправление двух сделанных ошибок.

«Почленное
деление»:

И в данной
ситуации уместно дать ученику тот же совет:

—
Проверьте Ваше равенство, например при
х = 1:

После такого
конфуза ученик должен наконец понять, что не учитель, а арифметика не
позволяет делать подобные преобразования.

Не лишним будет и
еще одно наблюдение:

— Посмотрите, при каких значениях х
определено каждое из трех написанных выражений.

В первом
выражении х ¹-1, во втором – х ¹0, в последнем х – любое число. Тем самым все
выражения различны.

При работе с
«многоэтажными» дробями школьники делают отчаянно много ошибок. Например:

И снова нужно посоветовать
ученику проверить написанное при конкретных значениях переменных. Так,
при a=b=1 и с=2 получим

В результате ученик должен сделать вывод,
что при работе с «трехэтажными» выражениями лучше добавить скобки, чем
сравнивать длины обозначающих дроби «черточек»:

( К слову, последним правилом обычно
руководствуются программисты: «Лучше лишние скобки, чем лишние ошибки».) И,
разумеется, должна появиться верная запись

К сожалению, не редкость и арифметические
«фокусы»:

Не исключено, что написавший подобную нелепость
ученик в свое время получил пятерку за отменно вызубренное «правило деления
дроби на число». Правда, он так и не задумался, из каких соображений
предложено именно такое правило, в чем его смысл. Поэтому он не видит
никакой конкретики за исходной записью

Впрочем, никогда не поздно объяснить
человеку, что, отсыпав половину из мешка, наполненного на одну треть, нельзя, к
сожалению, наполнить его на две трети. ( В противном случае этим стоило бы
заняться.)

»Интересные преобразования» часто
встречаются при работе со степенями.

(1)

Это
изящное преобразование выполняется следующим образом: слегка удлиняется
«палочка» в показателе степени исходного выражения.

Если учитель в
очередной раз подскажет, что означает дробь в показатели степени, то это даст
лишь сиюминутный результат. Следует вернуть ученика от алгебры к арифметике
– заставить его самостоятельно проверять написанное при конкретных значениях
переменной. Например, при а=2 получится

Последнего
обычно достаточно, чтобы ученик вспомнил определение:

(2)

Если
же ученик так и не «пришел в себя», то можно дать еще один совет:

-Вся
алгебра держится на возможности проделать с обеими частями равенства одну и ту
же операцию. Попробуйте возвести обе части вашего равенства в квадрат:

Зная хоть
что-нибудь о свойствах степеней, ученик преобразует левую часть равенства

и
получит наконец возможность восстановить определение (2).

Автору
преобразования типа (1) встретилось недавно в работе абитуриента в следующей редакции:

Особенно много
«интересных преобразований» возникает в тригонометрии. Не найдя, какой
бы из имеющихся в шпаргалке формул, ученик начинает изобретать что-то
оригинальное. К наиболее ходовым изобретениям такого типа относятся «формулы»:

cos 2x = 2cos x, (3)

sin (x + y) = sin x + sin y. (4)

И снова следует
предложить ученику проверить написанные формулы при каких-либо «хороших»
значениях угла х: 0, В частности, «формула» (3) при
х =p/6
приводит к неверному равенству

Впрочем,
установить ошибочность формулы не так уж сложно. Заметно сложнее исправить
неверную формулу. Полезно предложить ученику следующую работу:

-Выпишите для
известных вам «хороших» углов значения cos 2x и cos x и поищите связь по табл.
1.

Таблица 1

х	0	p/6	p/4	p/3	p/2
cos 2x	1	1/2	0	-1/2	-1
cos x	1			1/2	0

В строке «cos 2x»
нет радикалов, а в строке «cos x» они есть. Вероятно, чтобы нащупать связь,
следует вместо cos x рассмотреть cos² x (см. табл. 2).

Таблица 2

cos 2x	1	1/2	0	-1/2	-1
сos² x	1	3/4	1/2	1/4	0

В строке значений
сos² x есть знаменатели 4, а среди значений cos 2x — только
половинки и целые. Видимо, значение сos² x нужно умножить на 2
(см. табл. 3).

Таблица 3

cos 2x	1	1/2	0	-1/2	-1
2сos² x	2	3/2	1	1/2	0

Теперь видно, что
все значения во второй строке больше соответствующих значений первой строки на
1. Следовательно, cos 2x = 2сos² x-1.

Поработаем теперь
с «формулой»(4).

При х = p/2 получим sin= sin + sin
y.

Придется
вспомнить формулу приведения: sin= cos y. Итак, рассматриваемая
формула привела к неверному равенству cos y = 1 + sin y. Последнее равенство
наталкивает на мысль, что в правой части формулы должен присутствовать еще и
cos y, а значит, и cos х. Попытаемся так составить формулу, чтобы она давала
верное равенство хотя бы для углов х=p/6 и y = p/3. Из значений

sin = ;
cos= ;
sin ;    cos ;
sin

Удается
получить верное равенство следующим способом (иного способа ученики автора до
сих пор не предлагали):

Тем самым

sin sin

Итак, формула
угадана:

sin (x + y) = sin x×cos y + cos x×sin y.

По поводу проведенных рассуждений уместно
сформулировать шуточную, но полезную теорему.

Предложение. Если правдоподобная
тригонометрическая формула выполнена для «хороших» углов p/6, p/4 p/3, то она верна.

Разумеется, существует масса других
способов восстановить ту или иную тригонометрическую формулу. Однако простейшим
с идейной точки зрения является вычисление значений тригонометрических функций
и поиск связи между найденными значениями. Подобную работу ученикам полезно
проделать еще до того, как они впервые познакомились с той или иной
формулой.

От радикала – к степени

Почти
всякий раз переход от записи с радикалом к записи со степенью сопровождается
стандартной ошибкой:

.
(5)

Ошибка
состоит в том, что написанная формула верна лишь для неотрицательных значений
переменной.

Проведем
рассуждение. Если формула (5) верна, то

Но а не
существует. Тем самым результат возведения числа –1 в степень 1/3 зависит не от
самой степени, а от ее записи. Иными словами, корректно
определить дробную степень отрицательного числа не удается.

Таким
образом, преобразование (5) приводит к потере отрицательных значений
переменной.

Например,
уравнения и х^2/3=1 неравносильны. В
первом уравнении х = ± 1, а во втором х = 1.

Лишь
немногие ученики понимают, что при переходе от записи с радикалом к записи со
степенью приходится пользоваться формулой

т. е.
рассматривать два случая – неотрицательные и отрицательные значения
подкоренного выражения.

Ошибки от непонимания

Приведенные
ниже записи являются небольшим фрагментом весьма обширной коллекции. Впрочем,
новые оригинальные экспонаты появляются крайне редко. В основном обновляются
старые:

;

a×b = 1 Û a = 1;

b = 1

= b Û
a = b² ;

a ³ 0

;

х² > 4 Þ х > 2;

a < b Þ a² < b²;

< 1 Û 1 < х;

> х Þ 2 – х > х²;

sin x + cos x = 1 Û ;

sin x + cos x = 1 Û (sin x + cos x)² = 1 Û sin 2x = 0;

sin x = ±

Едва
ли каждая из указанных записей нуждается в отдельном комментарии. Заметим
только, что последняя «формула» содержит ту же ошибку, что и «формула» . А между тем она частая гостья в записях
не только школьников но, увы, и учителей.

Особенно
много ошибок появляется в ситуациях, требующих от ученика не столько памяти,
сколько логики – умения рассуждать. В частности, школьники делают недопустимо
много ошибок при решении неравенств. Одна из причин состоит в том, что функциональная
точка зрения на неравенство – связь решения с монотонностью фигурирующих
в неравенстве функций – остается для них слишком абстрактной.

Определение.
Функция ¦(х) называется монотонно возрастающей на множестве МÌR, если a > b ¦(a) >¦(b).

Функция
¦(х) называется монотонно
убывающей на множестве МÌR, если
a < b ¦(a) < ¦(b).

В
частности, функция ¦(х) = х² возрастает на множестве М =[0 ; ¥). Следовательно,

a > b a² a²> b².

Иначе
говоря, неравенство, обе части которого неотрицательны, можно возводить в квадрат.

Та же функция ¦(х) = х²возрастает
на множестве М = (-¥ ; 0]. Следовательно,

a > b a² a²< b².

Иными
словами, если обе части неравенства неположительны, то при возведении в квадрат
следует сменить знак неравенства на противоположный.

Функция ¦(х) = х³
возрастает на множестве R. Следовательно,

a > b Û a³> b³.

Тем самым
любое неравенство можно возводить в куб.

Аналогично:
функция возрастает на множестве R. Следовательно,
при потенцировании по основанию 3 знак неравенства сохраняется:

a > b Û 3^a> 3^b.

Функция убывает на множестве М=(0;¥). Следовательно, при
логарифмировании по основанию 0,2 знак неравенства меняется на
обратный:

Проанализируем
следующие два примера из приведенных выше в списке ошибок.

Пример 1:

Введя в
рассмотрение функцию , можно переписать
неравенство

в виде f(x)
< f(1). Функция f(x) убывает на каждом из интервалов (- ¥;0), (0; ¥), но не является
убывающей на их объединении. Следовательно, переход f(x) < f(1) Û х > 1 справедлив лишь при
условии x > 0:

Случай x < 0
придется рассмотреть отдельно. Впрочем, несложно заметить, что при
x < 0 неравенство выполнено.

Пример 2:

Для решения
неравенства введем в рассмотрение функцию
. Неравенство примет вид f(x) > 0.

Функция f(x) является разностью убывающей и возрастающей f₂(x) = x функций и, следовательно, убывает
на всей своей области определения (- ¥; 2]. Кроме того, f(1) = 0. Суммируя сказанное, получим

Итак, исходное
неравенство равносильно системе

Рассмотрим причины математических ошибок и охарактеризуем эти
причины.

1) Причины, связанные с
психологическими факторами (ослабление психических функций: памяти, внимания,
мышления)

—
доминирование
ассоциативных связей над смысловыми;

—
интерференция
навыков, когда формирование одного навыка тормозится другим;

—
перенос
некоторых навыков в область таких задач, где их действие ограничено либо вовсе
исключено.

2) Причины, вытекающие из
недостатков учебных программ и учебников:

—
в текстах
учебников авторы предпринимают поспешный переход к абстрагированию и обобщению
при формировании у учащихся умения пользоваться правилами, алгоритмами и
умениями делать выводы;

—
алгоритмы,
правила вводятся в тексте учебников без рассмотрения необходимого числа
примеров;

—
увлечение
авторами учебников логической строгостью изложения учебного материала;

—
система
упражнений в учебнике не обеспечивает должной пропедевтической и закрепительной
работы.

3) Причины, обусловленные несовершенством организации
учебного процесса:

—
нет
работы учителя по предупреждению у учащихся стремления к автоматическому применению
изучаемых фактов;

—
у
учащихся не формируются такие умения как подведения объекта под понятие,
выведение следует из факта принадлежности объекта объему понятия, выделение
существенных признаков понятий;

—
у
учащихся не формируются навыки самоконтроля;

—
недостаточно
ведется подготовительная работа для сознательного усвоения учебного материала,
учителем не продумано его целесообразное закрепление в последующем;

—
слабо
ведется работа по повышению у учащихся вычислительной культуры;

—
неумение
учителем использовать наглядность не только с целью реализации ее иллюстративной
функции, но и учебно-познавательной.

1.
Влияние
мотивов деятельности и эмоций. В исследованиях Л.В.Занкова, Д.Н.Узнадзе,
А.А.Смирнова выявлено, что запоминание во многом зависит от
сознательного намерения, определенной направленности нашей деятельности
или от установок, т.е. неосознанных источников направленности на
запоминание. На основе этих исследований можно сформулировать следующие
закономерности:

I.1.
Установки
или направленность на полноту, точность, прочность, последовательность
запоминания материала вызывают определенные формы активной мыслительной
деятельности, что приводит соответственно к полному, точному, прочному,
последовательному запоминанию. Влияние этих установок на учащихся
усиливается по мере овладения ими приемами мыслительной деятельности.

I.2.
На
усвоение учебного материала большое влияние оказывают мотивы
деятельности учащихся, их интерес к изучаемой теме, к предмету, положительные
эмоции, осознание значимости, важности данного материала, устойчивые
интересы и потребности.

I.3.
Материал
относительно большого объема запоминается неохотно, с нежеланием.

2.
Существует
несколько закономерностей, характеризующих зависимость между пониманием и
запоминанием материала:

I.4.
Определенный
уровень понимания материала – необходимое условие его успешного запоминания.

I.5.
Если
материал плохо понят, то он запоминается неточно, и искажения не
замечаются человеком, либо может возникнуть иллюзия запоминания.

I.6.
Понимание
затрудняется, если установка на полноту и точность запоминания
появляется до осознания материала в целом. В остальных случаях
установка на запоминание, наоборот, способствует лучшему пониманию.

I.7.
Активная
мыслительная деятельность, направленная на понимание материала, может приводить
к его непроизвольному запоминанию.

Сформулируем более общее утверждение и назовем
его основной закономерностью памяти.

I.8.
Если
учащийся выполняет над материалом активную мыслительную деятельность и
эта деятельность способствует углубленному пониманию материала, тогда
происходит его успешное запоминание (произвольное или непроизвольное).

I.9.
Ведение
стимулирующих звеньев повышает эффективность запоминания материала.

Стимулирующим звеном условимся называть
промежуточный мыслительный процесс, который вводится между двумя другими
процессами, помогая устанавливать связи между ними и активизируя
мышление.

Например, нам надо вспомнить, какой знак имеют
значения функции . Обычно мы сначала
представляем график, а затем устанавливаем знак значения функции на
указанном интервале. Представление графика – промежуточный мыслительный
процесс, т.е. стимулирующее звено. В качестве стимулирующих звеньев
можно успешно использовать различные графики, схемы, таблицы, правила.

I.10.
Эффективному
запоминанию помогают следующие приемы мыслительной деятельности:
составление плана, выделение смысловых опорных пунктов, реконструкция
материала, соотнесение (т.е. увязывание изучаемого материала с прежними
знаниями и отдельных частей нового друг с другом), использование
стимулирующих звеньев, сравнение, обобщение, конкретизация, классификация,
систематизация, воспроизведение материала в реконструированном виде.

I.11.
Забывание
более интенсивно протекает сразу после изучения материала (в первый
день, первые часы и даже минуты), а затем оно замедляется –
закономерность Эббингауса.

I.12.
Повторение
путем разнообразной деятельности, сводящейся хотя бы к некоторой
реконструкции материала, эффективнее, чем его повторение в неизменном
виде.

I.13.
Рассредоточенное
по времени повторение эффективнее, чем концентрированное.

Но при этом необходимо соблюдать меру. Если повторение
растянуть на чрезмерно большой срок, то, по закономерности Эббингауса
часть материала забывается и приходится тратить много времени на
восстановление забытого.

Покажем, что за основу при построении группы
закономерностей формирования умений и навыков может быть принята
теория обобщенных ассоциаций.

П.А.Шеварев дал следующие определения:

1. Связь двух психических процессов
Р₁ и Р₂, при которых процесс Р₁ влечет
за собой возникновение процесса Р₂, называется ассоциацией. Обозначение
(Р₁;Р₂).

2. Ассоциация называется обобщенной,
если существенные компоненты одного или обоих ее членов могут
изменяться, и константной, если они всегда неизменны.

Закономерность формирования ассоциаций.

II.1.
Ассоциация
(Р₁;Р₂) образуется, если психические процессы Р₁
и Р₂ возникают по ходу деятельности и повторяются или
непосредственно друг за другом, или с участием стимулирующего звена М.
Если это звено в дальнейшем сохраняется, то образуется две ассоциации:
(Р₁;М), (М;Р₂).

Определение 3. Умения и навыки решения
мыслительных задач есть определенная система ассоциаций, преимущественно
обобщенных.

II.2.
Если
существенные компоненты двух психических процессов при их повторении друг
за другом изменяются, варьируются, может образоваться обобщенная
ассоциация; если они всегда неизменны – константная.

Определение 4. Ассоциация называется ошибочной,
если на основе ее проявления учащийся иногда решает задачи данного
типа верно, иногда ошибается либо она вообще не проявляется при
решении некоторых задач некоторого типа.

II.3.
Если в
процессе деятельности соблюдаются три условия:
1) учащийся выполняет задания одного типа;
2) в них неизменно повторяется некоторая особенность;
3) ее осознание не обязательно для получения верного результата,
то степень осознания данной особенности снижается, т.е. у учащегося образуется
ошибочная ассоциация.

II.4.
Проявление
ассоциации в процессе решения задачи сопровождается чувством
уверенности в правильности полученного результата, тем самым уменьшается
вероятность самоконтроля.

II.5.
Если
какая-либо особенность К, присущая отдельным задачам данного типа, не
отражена в системе упражнений, либо в рассматриваемых способах решения
задач, то у учащегося может образоваться ошибочная ассоциация, в состав
первого члена которой не входит осознание особенности К.

II.6.
Для
формирования обобщенной ассоциации требуется тем меньше тренировочных
упражнений, чем более учащийся развит и обогащен знаниями, умениями и
навыками, относящимися к данной области науки.

II.7.
Для
сохранения и упрочнения ассоциации рассредоточенное повторение эффективнее
концентрированного.

Условия активизации мыслительной деятельности
учащихся при решении задач:

II.8.
Ассоциации,
формируемые в процессе решения задач, оказываются тем более прочными и
устойчивыми, чем с большей мыслительной активностью, а значит, и
глубиной понимания решаются эти задачи.

II.9.
Использование
стимулирующих звеньев по ходу решения задач, активизируя мыслительную
деятельность, приводит тем самым к формированию прочных ассоциаций.

II.10.
Если
при изучении новой темы выполняются условия:
1) учащемуся предлагают задачи только одного типа;
2) их решения сводятся к одной и той же операции;
3) эту операцию (ее результат) учащемуся не надо выбирать среди других,
которые возможны в сходных ситуациях;
4) данные задач не являются для учащего непривычными;
5) он уверен в безошибочности своих действий,
то учащийся очень быстро, нередко при решении 2-й или 3-й задачи, перестает
применять изучаемые определения, теоремы, прекращает обосновывать решения
задач. Если хотя бы одно из перечисленных условий нарушается при
решении какой-то задачи, то учащийся начинает обосновывать решение этой
или одной-двух последующих задач.

Закономерности внимания и восприятия.

Определения. Внимание называется произвольным, если
оно поддерживается под влиянием сознательно поставленной цели и
волевых усилий; послепроизвольным, когда влияние сознательно поставленной
цели сохраняется, а волевые усилия отсутствуют; и непроизвольным, если
внимание поддерживается без сознательно поставленной цели и без
волевых усилий.

III.1.
Деятельность,
осуществляемая на основе произвольного внимания, требует значительных
усилий и быстро утомляет человека.

III.2.
Внимание
может возникнуть и усилиться под влиянием одного или нескольких из
следующих условий:
а) относительной интенсивности раздражителей;
б) их относительной новизны;
в) неожиданности их появления;
г) контраста между ними;
д) ожидания определенных событий или впечатлений;
е) положительных эмоций.

III.3.
Необходимыми
условиями длительного сохранения послепроизвольного внимания являются:
пассивность деятельности, наличие соответствующих знаний, умений и навыков.

III.4.
Достаточными
условиями длительного поддержания внимания (послепроизвольного и
произвольного) являются одно или несколько из следующих условий:
а) эта деятельность значима для человека;
б) у него имеется чувство ответственности за ее успешное завершение;
в) она совпадает с направлением постоянных интересов человека либо становится
для него интересной, увлекательной, хотя бы только в данный момент.

III.5.
Внимание
и интерес к деятельности усиливаются, если выполняется хотя бы одно
из следующих условий:
а) прилагаются активные умственные усилия;
б) углубляется понимание соответствующего материала;
в) возрастает уверенность;
г) возникают новые идеи, открытия.

III.6.
Внимание
может быть ослаблено при наличии одного или нескольких из следующих
условий:
а) задание непосильно, из-за чего теряется уверенность в возможности завершить
его выполнение;
б) работа совершается в чрезмерно быстром или слишком медленном темпе;
в) она сводится к однообразным операциям;
г) исчезает интерес к ней;
д) выполняемая работа слишком проста для человека.

III.7.
Внимание
облегчается, если выполняются условия:
а) мыслительная деятельность сопровождается соответствующей моторной
деятельностью;
б) объекты, которыми мы оперируем, воспринимаются зрительно.

Условия, позволяющие облегчать учащимся восприятие
учебного материала.

IV.1.
Восприятие
объектов облегчается, если они расположены в определенной системе,
требующей минимальных усилий со стороны наших органов чувств.
Восприятие объектов, расположенных хаотически, осуществляется неохотно.

IV.2.
Предварительная
подготовка к наблюдению, четко поставленная задача: как и в какой
последовательности вести наблюдения; прошлый опыт человека и его знания
значительно облегчают восприятие, делают его более богатым.

IV.3.
Активная
мыслительная деятельность в процессе наблюдения приводит к более
полному, богатому восприятию. При пассивном созерцании объекта от
внимания человека ускользают многие детали.

IV.4.
Легче
наблюдать единичные отличия среди многих черт сходства, чем наоборот.
Различие между объектами (ситуациями) привлекает к себе внимание более,
чем сходство.

При формировании умений поиска решения задачи
существенную помощь может оказывать следующая закономерность, приведенная
С.Л.Рубинштейном:

V.1.
Вероятность
вспоминания теоремы, нужной для решения задачи, возрастает при выполнении
двух условий:
а) теорема и данные задачи выражены в одних и тех же понятиях;
б) искомые и данные задачи сближены анализом и синтезом настолько, что
в оставшийся интервал как раз «укладывается» данная теорема, целиком
заполняя этот интервал.
(Аналогично при этих же условиях возрастает вероятность вспоминания
определений, аксиом, различных правил, законов и т.д.)

На основе исследований П.А.Шеварева
сформулирована следующая закономерность:

V.2.
а)
Последовательность мыслительных процессов (А;В;С;…;М), повторяющаяся при
решении однотипных задач, может свертываться до составной ассоциации
(А;М). В дальнейшем эта ассоциация в случае необходимости легко
«развертывается» в первоначальную цепь рассуждений.
б) Если ассоциация (А;М) образована без промежуточных рассуждений, то
вклинивать их в дальнейшем между процессами А и М бывает очень трудно.

V.3.
Мыслительные
операции можно целенаправленно формировать путем постепенного перехода
от развернутых внешних действий, заранее запрограммированных и
выполняемых в заданной последовательности, ко все более свернутым
умственным действиям.

Активизация мыслительной деятельности учащихся
при ознакомлении с теоретическим материалом.

V.4.
Активность
мыслительной деятельности по ходу ознакомления с материалом возрастает,
если одновременно учащийся выполняет конкретное задание, помогающее
глубже понять данный материал, и при этом соблюдаются следующие
условия:
1) поставленное задание направляет усилия учащегося на использование
определенного мыслительного приема;
2) учащийся обладает знаниями, необходимыми для выполнения этого задания,
и навыками применения данного приема;
3) этот прием соответствует содержанию материала, и чем в большей мере
соответствует, тем сильнее активизируется деятельность.

Примерно до 50-60 годов в
методической литературе анализ ошибок учащихся носил односторонний характер,
так как не учитывались психологические закономерности. Из-за их отсутствия
некоторые авторы пытались объяснить ошибки учащихся ссылками на законы физиологии.
Психологические закономерности для анализа ошибок одним из первых стал
использовать П.А. Шеварев, а в дальнейшем и другие авторы. В
психолого-дидактическом анализе ошибок, основанном уже на
психолого-дидактических закономерностях, учитываются и внутренние процессы
учебной деятельности учащихся, и внешние условия, влияющие на эти процессы.
Поэтому такой анализ позволяет более точно выявлять причины ошибок и намечать
меры по их предупреждению.

Однотипность упражнений.

Совокупность упражнений одного и
того же типа условимся называть однотипной системой упражнений. Известно,
что для формирования прочных навыков однотипные упражнения необходимы.
В то же время они приводят к механическому, неосознанному решению, к
ошибкам и т.д. Вероятно, из-за этого диалектического противоречия
наблюдаются противоположные методические подходы относительно реализации
принципа однотипности упражнений.

Авторы учебников и задачников
придерживаются часто самых противоположных точек зрения относительно
однотипности системы упражнений. Это можно объяснить отсутствием в
методике математики единых теоретических установок. Рассмотрим поэтому
данный вопрос на основе системы закономерностей. При изучении каждой темы
по математике учащиеся должны приобрести умения и навыки решения
задач. По закономерности II.1, это
возможно лишь при неоднократном решении задач данного типа. Известны,
правда, факты, когда у способных учащихся формируются прочные обобщенные
ассоциации при решении минимального числа однотипных задач, иногда
одной-двух. Однако таких способных учащихся в классе немного, а учить
надо всех. В соответствии с закономерностью II.6 количество однотипных задач можно уменьшить лишь
постепенно, по мере развития учащихся и накопления ими знаний и
навыков по данному предмету. Учителя по опыту знают (и это
соответствует закономерности II.6),
что при изучении новой темы слабоуспевающим учащимся требуется
выполнить большее число тренировочных упражнений, чем хорошо успевающим.
Но методика урока строится обычно так, что на дом всем учащимся
задают одинаковое число упражнений, а на самом уроке сильные учащиеся
успевают решить больше задач. Следовательно, вопреки закономерности II.6 слабоуспевающие учащиеся
упражняются меньше, и это – одна из причин их отставания и
замедленного развития. Такое расхождение между потребностью и
действительностью должно приводить к ослаблению внимания.

В домашнее задание по математике
включают обычно и совсем простые упражнения, и задачи чуть посложнее.
Рассмотрим теоретически, может ли слабоуспевающий учащийся осуществить
поиск решения задачи. Такое задание он не может выполнить на основе
послепроизвольного внимания, так как не знает приемов поиска решения
задачи (см. закономерность III.3).
Возникновение непроизвольного внимания к этому заданию также
маловероятно, поскольку активную мыслительную деятельность невозможно
осуществить без сознательно поставленной цели. Исключается также
возможность возникновения произвольного внимания, так как слабоуспевающему
учащемуся очень трудно сосредоточиться путем волевых усилий.
Следовательно, данное задание для него непосильно. Какие изменения в
поведении этих учащихся можно ожидать, если чередовать задачи знакомых
им типов? Поиск решения здесь осуществлять уже не надо, достаточно
вспомнить известный способ решения. Но это не всегда удается
слабоуспевающим учащимся, из-за чего теряется уверенность, а значит, ослабляется
внимание.

Чтобы обеспечить на уроках
устойчивое внимание всех учащихся и сформировать у них прочные умения
и навыки, необходимо непременно сохранить однотипность системы
упражнений, а для нейтрализации ее отрицательных последствий
одновременно использовать другие принципы.

Принцип непрерывного
повторения.

В однотипную систему упражнений
по новой теме с первого момента ее изучения включаются задачи из
предшествующих разделов. Цель их включения – устранение отрицательного
влияния закономерностей II.2 – II.5; II.10 и другие. При этом одновременно осуществляется
систематическое, непрерывное повторение изученного материала. Обозначим
условно такую систему в виде

Т₁,Т₂,Т₃,М₁,(М₂?),Т₄,Т₅,М₃,Т₆,Т₇,Т₈,К₁,Т₉,…,
(1)

где Т₁,Т₂,Т₃,…
— задачи одного типа по новой теме;

М₁,М₂,…, К₁,К₂,…
— задачи других типов из пройденных тем.

Условия применимости принципа
непрерывного повторения:

1. Последовательность
упражнений в системе (1) определяется не столько автором задачника,
сколько учителем. Только он может, учитывая уровень знаний и развитие
своих учащихся, при подготовке и по ходу урока изменять число задач
одного типа, следующих друг за другом.

2. Основная цель урока –
изучение новой темы. Поэтому большинство задач в системе (1) должно
быть по новой теме.

3. Главная цель использования
принципа непрерывного повторения – устранение отрицательного влияния
закономерностей Шеварева и II.10. Отсюда
вывод: из пройденных тем желательно подбирать такие упражнения, которые
по отдельным внешним признакам сходны с упражнениями новой темы.

4. Когда решаются
комбинированные задачи, насыщенные разнообразным материалом из
предшествующих разделов, принцип непрерывного повторения осуществляется
сам собой. Однако когда удается решать подряд много комбинированных
задач, то необходимость чередования задач различных типов ощущается
особенно остро.

5. При использовании принципа
непрерывного повторения общее число упражнений того или иного типа
фактически не уменьшается в сравнении с однотипной системой. Только
упражнения этого типа рассредоточиваются на более длительное время.

Контрпримеры.

Контрпримером условимся называть
любую задачу, которая помогает выявить, а значит, и устранить имеющиеся
у учащихся ошибочные ассоциации. В этом определении учитываются только
дидактические соображения.

В роли контрпримеров могут
выступать задачи с неполными или противоречивыми условиями и любые
другие упражнения, провоцирующие учащихся на ошибки. Мы именно
провоцируем, а учащиеся догадываются, что это своего рода игра. Они,
наоборот, стараются не ошибиться, внимание их усиливается.

Некоторые методисты и психологи
подчеркивают, что контрпримеры (или, по терминологии психологов,
«отрицательные примеры») предотвращают «скороспелые суждения» и на
начальных этапах изучения данной темы, и в дальнейшем.

На всех уроках без исключения,
где используются контрпримеры, наблюдается следующая характерная
особенность. Решение контрпримера, сопровождаемое анализом допущенной
ошибки, производит на учащихся столь сильное впечатление, что в классе
в момент обсуждения обычно не остается равнодушных и невнимательных.

Контрпримеры позволяют на
изучаемом математическом материале создавать на уроках игровые ситуации.
Сравним их с народными детскими играми «на внимательность». Контрпримеры
– это те самые «перевертыши», необходимость которых для детей многие
годы доказывал писатель К.И.Чуковский. детям читают: «Ехала деревня мимо
мужика», а они радостно сообщают взрослым о замеченных ошибках. В
контрпримере другое содержание – математическое, а игровая ситуация и
эмоции такого же типа. Только среди старших школьников или студентов
эти эмоции проявляются более сдержанно. Но всегда наблюдается
повышенный интерес, заостренное внимание и часто дружный смех, быстро
сменяющийся напряженной работой.

Следует учесть ряд существенных
организационных приемов. Как правило, контрпримеры решаются в классе под
наблюдением учителя и ошибки сразу анализируются. Тогда в памяти
учащихся сохраняется не сама ошибка, а ее анализ. По этой причине
нежелательно включать контрпримеры в домашнее задание. Если учитель
соблюдает игровые правила и по его внешнему поведению учащиеся не
могут догадаться, в какой момент дается контрпример, то они начинают
ожидать контрпримеры какую-то часть урока. Такое ожидание усиливает внимание
учащихся (III.2д). При систематическом
использовании контрпримеров напряженное внимание может перейти в
привычку. Таким путем развивается внимание учащихся. Разумеется,
контрпримеры используются не сами по себе. Они лишь изредка включаются
в систему упражнений.

Принцип сравнения.

Под принципом сравнения в
психолого-педагогической литературе понимают чередование упражнений на
прямые и обратные операции и любых других задач, когда желательно
показать их взаимосвязь, сходство и различия. Чтобы подчеркнуть важность
чередования упражнений, некоторые авторы используют термин
«перемежающееся противопоставление».

В зависимости от содержания
изучаемого материала, цели урока и других соображений учитель может
выбирать любой из трех принципов: непрерывного повторения, сравнения,
включения в систему упражнений контрпримеров. Каждый из этих принципов
в сочетании с однотипной системой позволяет ослабить ее недостатки и
сохранить ее положительное влияние.

Принцип сравнения удобно
использовать при одновременном изучении некоторых тем: сложения и
вычитания дробей, умножения и деления положительных и отрицательных
чисел, решения задач на нахождение дроби от данного числа и числа по
величине его дроби и т.д.

Систематическое включение
контрпримеров в систему упражнений приводит к тому, что, ожидая их,
учащиеся начинают все чаще и чаще контролировать свои результаты,
получаемые при решении задач, начинают постепенно выходить из-под
отрицательного влияния закономерностей Шеварева, II.5 и другие, все реже допускают
ошибки по невнимательности. Таким образом у них развиваются внимание,
самоконтроль.

Принцип полноты.

Условимся считать, что система
упражнений удовлетворяет принципу полноты, если совокупность ее задач и
способы их решения не способствуют формированию ошибочных ассоциаций и
позволяют учащимся глубоко усваивать все необходимые вопросы изучаемой
темы. Целесообразность использования принципа полноты непосредственно
следует из нескольких закономерностей: II.1;II.3, и в первую очередь из II.5.

Часто принцип полноты нарушается
учителями. Из-за медленного темпа работы на уроках, сокращения числа
уроков и по другим причинам многие учителя не успевают рассмотреть с
учащимися часть задач из школьных учебников. При этом далеко не
каждый учитель умеет отобрать задачи, не нарушая определенной целостной
системы, данной в учебнике. Чтобы уменьшить отрицательные последствия
такого отбора, можно предложить следующую рекомендацию. Внутри каждой
темы авторы учебников располагают упражнения несколькими блоками.
Отдельные блоки содержат минимальное число упражнений, необходимых для
изучения данной темы и расположенных в соответствии с определенными
принципами. Учитель выбирает столько блоков по теме, сколько задач его
учащиеся успевают решить на уроках и дома.

О соблюдении дидактических
принципов при построении системы упражнений.

Система упражнений должна
удовлетворять дидактическим принципам.

Задачи должны подбираться с
последовательным нарастанием трудности. Это требование обычно
выдерживается при изучении алгебры, но часто нарушается на уроках
геометрии. Использование задач по готовым чертежам позволяет соблюдать
дидактический принцип последовательного преодоления трудностей также и
на уроках геометрии.

Многие авторы подчеркивают, что
система упражнений должна содержать задачи, допускающие «изящные»
решения. Включая такие задачи, мы осуществляем дидактический принцип
индивидуального подхода. Обсуждение на уроках рациональных, «изящных»
способов решения задач, предложенных отдельными учащимися, повышает
интерес всего класса, усиливает внимание учащихся.

Особенно следует остановиться на
дидактическом принципе доступности. Нарушение дидактического принципа
доступности происходит в основном по двум причинам:

1) иногда из-за недостатков
самой программы, учебников, в которых сначала предлагают недоступные для
многих учащихся задачи, а затем рекомендуют опускать их;

2) часто из-за того, что
учителя не учитывают возможностей учащихся своих классов.

Решаемые на уроках задачи должны
быть доступными для всех учащихся (принцип доступности), но не
чрезмерно легкими для хорошо успевающих учащихся (принцип индивидуального
подхода).

Широко известны
серьезные трудности, которые испытывают учащиеся при решении задач.

Первая трудность состоит в
математизации предложенного текста, т.е. в составлении математической модели,
которая может представлять собой уравнение, неравенство или систему, диаграмму,
график, таблицу, функцию и т. д. Для того, чтобы перевести содержание задачи на
математический язык, учащемуся необходимо тщательно изучить и правильно
истолковать его, формализовать вопрос задачи, выразив искомые величины через
известные величины и введенные переменные. На этом пути проблемы, с которыми
сталкиваются учащиеся, носят различный характер. Иногда они связаны с
непониманием физических, химических, экономических терминов, законов,
зависимостей. Так, далеко не все четко осознают связь между расстоянием,
скоростью и временем при равномерном движении или между работой,
производительностью труда и временем и т. п. Ученики испытывают трудности в
определении скорости сближения объектов при движении навстречу или в одном
направлении, слабо ориентируются в движении по окружности, затрудняются в
выборе размерности.

Вторая трудность — составление
уравнений и неравенств, связывающих данные величины и переменные, которые
вводит учащийся.

Третья трудность состоит в том,
чтобы составить функцию (отношение), применительно к которой формулируется
вопрос задачи. Условно ее можно назвать функцией цели.

Четвертая трудность — это решение
полученной системы уравнений или неравенств желательно наиболее рациональным
методом.

§ 2. Типичные ошибки и
затруднения учащихся

при обучении математике в 5-6
классах.

5 класс

Тема	Ошибочно	Правильно
Вычислительные (арифметические ошибки, 5 кл.).	1) ₊356 2) _х326 3) _1224½12_ 2425 102 12 12 5985 ₊652 _24 326__ 24 4912 0 4) _ 458 ½9_ 45 5 8 (ост.)	1) ₊356 2) _х 326 3) _1224½12_ 2425 102 12__ 102 2781 ₊ 652 _2 326__ 0_ 33252 _24 24_ 0 4) _ 458 ½9_ 45 50 8 (ост.)
Действия с обыкновенными дробями и смешанными числами.
Десятичные дроби.	1)₊3,2 7 2) _х1,2 3 3) 1,257 : 3,2 5,9 2,5 3,8 6 6 1 5 1,257½3,2 2 4 6_ 3 0 7,5 4) _1,25½5_ 1 0_ 25 _25 25 0	1) ₊3,27 2) _х1,2 3 3) 12,57½32 5,90 2,5 9,17 61 5 4) 1,25½5__ 246__ 0 _ 0,25 0,307 5 1 2 1 0_ _ 25 25 0
Задачи на проценты.	Условие: найти 32 % от числа 1200. 1200 · 32 : 100 = 384 (непонимание сути, незнание определения процентов)	1200 : 100 · 32 = 384
Луч и прямая.	1) Луч А В 2) Луч ВА А В 3) Прямая А В 4) Прямой угол А В С 5) ÐАВС В С А	1) Луч А В 2) Луч АВ А В 3) Прямая А В 4) Прямой угол А В С 5) ÐВАС В А С
Единицы измерения.	1) 1 см²= 10 мм² 2) 1 м³ = 100 см³	1) 1 см²= 100 мм² 2) 1 м³ = 100000 см³

6 класс

Тема

Ошибочно

Правильно

Разложение на простые множители.

248 2

124 4

31 31

4 – составное число, поэтому оно не может входить в
разложение на простые множители.

248 2

124 2

62 2

31 31

Действия с обыкновенными
дробями с разными знаменателями.

Отношение пропорции.

Задача на обратную пропорциональную зависимость.

длина ширина

I 3,6 м 2,4 м

II 4,8 м х м

длина ширина

I 3,6 м х м

II 4,8 м 2,4 м

Положительные и отрицательные
числа.

1) – 5 + 3 = 2

2) (- 2) + (- 7) = 9

3) 6 – 10 = 4

4) – 2 – 7 = — 5

1) – 5 + 3 = — 2

2) (- 2) + (- 7) = — 9

3) 6 – 10 = — 4

4) – 2 – 7 = — 9

Решение уравнений.

1.
Раскрытие
скобок.

2.
Приведение
подобных.

3. Перенос слагаемых из одной части в другую

1) 5 – (х — 2) = 5 + х – 2

2) с – (- 2 + х) = с – 2 — х

1) 2х + х + 3 = 3х + 3 = 6х

2) 5 – 2х + 3 + х = 3х + 8

1) 2х + 7 + 3х = 2

2х + 3х = 2 + 7

2) 9х = 3

х = 9 : 3

х = 3

1) 5 – (х — 2) = 5 — х + 2

2) с – (- 2 + х) = с + 2 — х

1) 2х + х + 3 = 3х + 3

2) 5 – 2х + 3 + х = 8 — х

1) 2х + 7 + 3х = 2

2х + 3х = 2 — 7

2) 9х = 3

х = 3 : 9

х = 1/3

Координатная плоскость.

1.
Точки
на осях.

А(0;2) y

0
A x

А(0;2) y

0 x

Глава II. Пути и средства предупреждения и исправления ошибок и затруднений
учащихся 5-6 классов.

§ 1.
Методы и приемы обучения математике, используемые учителем для предупреждения
ошибок и затруднений.

На протяжении
1994 – 1998 г.г. автором были изучены более 4000 ошибок учащихся V классов. Для обработки и
классификации собирались ошибки, сделанные школьниками в контрольных,
самостоятельных и домашних работах по математике. Было выделено двенадцать
видов ошибок, которые могли дать ключ к пониманию причин затруднений учащихся.

Вид ошибки	1994 – 1995 гг.	1995 –1996 гг.	1996 – 1997 гг.	1997 –1998 гг.	всего
Решение даже не начато	37	38	23	40	128
Вычислительная ошибка в элементарном действии	54	39	44	28	156
Вычислительная ошибка в многошаговом действии	371	312	318	277	1278
Установление неправильных связей между данными задачами	175	160	136	106	577
Неправильное понимание условий задачи	209	132	152	249	742
Ошибки при переписывании	16	69	51	21	157
Незнание алгоритмов математических действий	72	66	94	57	289
Неэквивалентные преобразования	57	44	63	83	247
Ошибки геометрических измерений	19	22	61	17	119
Незнание математических формул	53	41	33	45	172
Незнание законов арифметики	48	59	38	63	208
Логические ошибки	9	13	10	9	41

Каждому школьнику
доводилось делать вычислительные ошибки. Если предложить пятикласснику умножить
устно 75 на 75, и ошибка будет гарантирована. Чтобы предотвратить
вычислительные ошибки в многошаговых арифметических действиях, мы должны
готовить детей к овладению алгоритмами, разбивающими сложные действия на
элементарные. Но для того, чтобы выделить элементарные действия, необходимо
установить уровень заданий, доступный любому учащемуся. К этому уровню могут
относиться: сложение однозначных или двузначных чисел без перехода единиц в
старший разряд; вычитание однозначных или двузначных чисел без перехода единиц
в старший разряд; вычитание однозначных или двузначных чисел при условии, что
число единиц в соответствующем разряде уменьшаемого больше числа единиц в
разряде вычитаемого; умножение однозначных чисел; умножение двузначных чисел на
однозначные, при котором нет необходимости проводить операции сложения и
произведение остается двузначным числом; деление однозначных чисел; деление
двузначных чисел на однозначные, при котором делитель является делителем числа
единиц в каждом разряде. Все остальные арифметические действия с помощью
алгоритмов должны разбиваться на элементарные.

Одним из наиболее
трудных разделов арифметики остаются текстовые задачи. Они требуют от школьника
применения не только знаний, полученных на уроках, но и использования
жизненного опыта. Большие трудности встречают учащиеся V классов при формализации текстовых
задач. Характерной ошибкой при решении текстовых задач с большим количеством
числовых данных является не использование части условия. Для предупреждения
подобных ошибок дети должны получить устойчивые навыки решения элементарных
текстовых задач. Кроме того, уровень сложности предлагаемых учащемуся задач не
должен ставить его в безвыходное положение.

Ошибки при
переписывании сначала казались непредсказуемыми. Соответственно, было
непонятно, как их классифицировать и какие меры принимать для профилактики. Как
только задания стали значимыми для ученика, как только стало возможным
использовать его жизненный опыт, то количество ошибок при переписывании резко
уменьшилось.

Некоторые разделы
математики V класса включают в себя
обязательное изучение специальных алгоритмов. Например, если сложение и
вычитание десятичных дробей не вызывает особых затруднений, то сложение и
вычитание обыкновенных дробей дается менее способным ученикам гораздо труднее.
Нередко при сложении 1/2 и 1/3 дети получают 2/5. И в этом ответе есть
какая-то логика (не хватает только знания алгоритма сложения обыкновенных
дробей). Для профилактики ошибок при работе с заданиями этих разделов
необходимо изучение типовых примеров решения подобных задач.

При решении
простейших уравнений школьники сталкиваются с необходимостью приведения
эквивалентных преобразований. Распространены ошибки в определении знака
одночлена при его переносе в другую часть уравнения, неоправданно меняются
знаки одночленов, не поменявших свое расположение относительно знака равенства.
Встречаются ошибки, связанные с непониманием сущности числового коэффициента
переменной.

Ошибки
геометрических измерений связаны с отсутствием навыков работы с линейкой и
(гораздо чаще) с транспортиром. Их количество увеличивается при использовании
прозрачных средств измерений. Для профилактики таких ошибок необходимо, чтобы
учащиеся усвоили понятия точки отсчета и единицы измерения. Надо до начала
практических измерений закрепить соотношения используемых единиц одной
физической величины.

Одним из трудных
разделов математики V класса является раздел, посвященный
изучению прямоугольных параллелепипедов. Учащийся, который не знает формул
объема, абсолютно не в состоянии решать соответствующие задачи. Однако в
заданиях этого раздела есть и объективные трудности. Ученик должен усвоить и
единицы объема, и их взаимоотношения между собой. Менее способные дети обычно
бывают неприятно поражены соотношениями кубических метров и кубических сантиметров,
кубических метров и кубических километров и т. п. Привычные для них названия
единиц (метры, сантиметры), приобретя дополнительное прилагательное, в разделе
объемов резко меняют свои отношения. Для решения некоторых заданий необходимо
пространственное воображение. Отдельным учащимся очень трудно решать задачи по
определению объема тел, представленных на рисунках и чертежах (особенно если
эти тела составлены из нескольких параллелепипедов). Для профилактики таких
ошибок необходимо проводить занятия с моделями, которые должны быть доступны
для исследования каждому ученику. Хорошие результаты могут принести занятия с
разборными моделями параллелепипедами.

При изучении
законов арифметики значительная часть ошибок приходится на распределительный
закон умножения. При умножении одночлена на многочлен не усвоившие
распределительный закон умножения учащиеся, делают только одно действие
умножения, а оставшуюся часть многочлена записывают без проведения необходимых
действий. Для профилактики таких ошибок полезно чертить схемы умножения,
соединяя стрелками все сомножители.

Наиболее редкие
логические ошибки. Несомненно, что это связано в первую очередь с тем, что
пятиклассникам не часто предлагаются логические задачи. Для профилактики
логических ошибок необходимо повысить число логических заданий в учебных
пособиях для V классов.

К задачам
провоцирующего характера будем относить все такие задачи, условия которых
содержат упоминания, указания, намеки или другие побудители, подталкивающие
учащихся к выбору ошибочного пути решения или неверного ответа. В методической
литературе такие задачи называют еще задачами-ловушками.

Дидактическая
ценность провоцирующих задач неоспорима – они служат действенным средством
предупреждения различного рода заблуждений или ошибок школьников. Попадая в
заранее подготовленную ловушку, ученик испытывает смущение, досаду, сожаление
от того, что не придал особого значения тем нюансам и условия, из-за которых он
угодил в неловкое положение. Простое сообщение о том, что учащиеся, как
правило, допускают в заданиях такого-то рода ошибки, несравнимо менее
действенно. Ибо оно, несмотря на общность (многие, большинство и т.п.) и
адресность (учащиеся такого-то класса), не является для конкретно взятого
ученика личностно значимым, поскольку, во-первых, события, о которых
сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых,
каждый из учащихся наивно полагает, что в число неудачников сам он не попадет.

Совершая
ошибку на глазах учителя или учащихся и осознавая провоцирующий характер учебной
ситуации, ученик испытывает сильнейшее впечатление, надолго запоминает
ошибочные действия и в дальнейшем на подсознательном уровне остерегается их.

Провоцирующие
задачи обладают высоким развивающим потенциалом. Они способствуют воспитанию
одного из важнейших качеств мышления – критичности, приучают к анализу
воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников
к занятием математикой.

Несмотря
на эти и другие положительные качества, феномен провоцирующих задач изучен
недостаточно.

При
самом первом рассмотрении полезно выделить следующие разновидности задач
провоцирующего характера:

I.
Задачи,
условия которых в той или в иной форме навязывают неверный ответ.

II. Задачи, условия которых тем
или иным способом подсказывают неверный путь решения.

III. Задачи, вынуждающие придумывать,
составлять, строить и т. п. Такие математические объекты, которые при заданных
условиях не могут иметь места.

IV. Задачи, вводящие в заблуждение из-за
неоднозначности трактовки терминов, словесных оборотов, буквенных или числовых
выражений.

V. Задачи, условия которых
допускают возможность «опровержения» семантически верного решения
синтаксическим или иным нематематическим способом.

I. Задачи, условия которых в
той или в иной форме навязывают неверный ответ.

1А.
Задачи, навязывающие в явной форме один вполне определенный ответ.

Пример.

Сколько цифр потребуется, чтобы записать двенадцатизначное число?

Навязывается
ответ: «12 цифр», но это не так, поскольку десятичная система счисления
обходится всего лишь десятью цифрами. Правильный ответ: «Двенадцатизначное
число можно записать с помощью одной, двух, трех, четырех, пяти, шести, семи,
восьми, девяти, десяти цифр».

1Б.
Задачи, побуждающие сделать выбор ответа из предложенной совокупности неверных
ответов.

Пример.

Какое из чисел 205, 206, 207, 208, 209, 210 является простым?

Чаще
всего учащиеся считают простым число 209 или 207, но это неверно. Все
записанные выше числа являются составными. Правильный ответ: «Никакое».

1В.
Задачи, побуждающие сделать неправильный выбор ответа из предложенной совокупности
верных и неверных ответов.

1Г.
Задачи, условия которых не содержат в явном виде неверного ответа, но
каким-либо образом указывают на него.

Пример.

Какое простое число следует за числом 200?

Напрашивается
ответ: 201, ведь это число следующее – за числом 200. Но этот ответ неверен,
так как число 201 – составное. На самом деле искомое число 211.

II. Задачи, побуждающие к
выбору неверного способа решения. Их тоже можно разделить на четыре типа.

2А.
Задачи, условия которых подталкивают решающего к тому, чтобы выполнить
какое-либо действие с заданными числами или величинами, тогда как выполнять это
действие вовсе не требуется.

Пример.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая
лошадь?

Хочется
выполнить деление 15:3 и тогда ответ – «5 км». На самом же деле деление
выполнять вовсе не требуется, поскольку каждая лошадь проскакала столько же,
сколько и вся тройка, т.е. 15 км.

2Б.
Задачи, условия которых подталкивают решающего к выполнению какого-то
определенного действия, тогда как выполнять нужно другое (зачастую обратное)
действие.

Пример.

У палки 2 конца. Если один из них отпилить, сколько концов получиться?

Сразу
кажется, что нужно выполнить вычитание 2 – 1 , что приводит к явно несуразному
ответу «у палки один конец». На самом деле нужно находить не разность 2 – 1 , а
сумму 2 + 2. Правильный ответ: «4 конца».

2В.
Задачи, условия которых подталкивают решающего к выполнению какого-то одного
или нескольких действий вполне определенным образом, тогда как выполнять
действия нужно иначе. Чаще всего, необходим более сложный расчет.

Пример.

На руках 10 пальцев. Сколько пальцев на 10 руках?

При
такой формулировке задачи решающему трудно преодолеть искушение выполнить
умножение 10 × 10, хотя легко непосредственно сосчитать реальное число пальцев на 10 руках,
т.е. у пяти человек: 10(10:2) = 50.

2Г.
Задачи, условия которых подталкивают решающего к выполнению какого-либо
действия или процедуры, тогда как выполнить их не представляется возможным в
принципе.

Пример.

Двое пошли, 3 гриба нашли. Четверо пойдут, сколько грибов найдут?

Напрашивается
последовательность действий:

1)
4:2 = 2, 2) 3× 2 = 6, т.е. четверо вроде бы найдут 6 грибов. Но они могут вообще ничего
не найти, если им не повезет. Правильный ответ: «Не известно».

III. Задачи, вынуждающие
придумывать, составлять, строить и т. п. несуществующие при заданных условиях
математические объекты.

Пример.

Придумайте простое трехзачное число, в записи которого употребляются лишь
цифры 1 и 4.

Придумать
такое число невозможно, поскольку любое число, удовлетворяющее условию задачи,
кратно 3 и, стало быть, не является простым.

IV. Задачи, вводящие в заблуждение из-за
неоднозначности трактовки терминов, словесных оборотов, буквенных и числовых
выражений.

Пример.

На
листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить
его в полтора раза?

Имеется
в виду не математическое «действие», а просто игра с бумажным листом. Если
перевернуть лист, на котором написано 606, то увидим запись 909, т.е. число,
которое в 1,5 раза больше, чем 606.

V. Задачи, допускающие
возможность «опровержения» семантически верного решения синтаксическим или иным
нематематическим решением.

Пример.

(Старинная
задача). Крестьянин продал на рынке трех коз за 3 рубля. Спрашивается: «По
чему каждая коза пошла?»

Очевидный
ответ: «По одному рублю», опровергается: козы по деньгам не ходят, а ходят по
земле.

Логические ошибки
возникают в результате нарушения основных принципов математических рассуждений.

Ошибки в определении понятия. Примеры.

1.
Равносильными уравнениями называются такие уравнения, когда корни первого уравнения
являются корнями второго уравнения.

2. Квадратное уравнение с одним
неизвестным – это уравнение, содержащее неизвестное во второй степени.

3. Прямая, делящая сторону треугольника
пополам, называется медианой.

4. Отрезок, соединяющий середины
сторон треугольника и равный половине третьей стороны, называется средней
линией треугольника.

Во всех приведенных примерах нарушено
основное требование к установлению определения понятия – наличие необходимых
достаточных признаков объекта. Мерой предупреждения таких ошибок являются в
первую очередь тщательная отработка определения понятия, в частности, с помощью
метода сравнения объектов, а кроме того, опровержение примерами. Так, для первого
примера ценными являются упражнения такого вида:

a) Являются ли равносильными уравнения
х – 2 = 0 и (х – 2 ) (х – 3) = 0?

b) Являются ли равносильными уравнения х
– 2 = 0 и х + 3 = 5?

И т.д.

Для второго
примера возможны упражнения такого вида:

Какие из приведенных уравнений
являются квадратными?

а) х² – 3х + 2 = 0; б) х³
+ х² – 3х = х³ – 2; в) х³ – х² +
3х = х³ – 2; г) х² – 4.

В третьем примере ошибка в
определении медианы стороны треугольника могла возникнуть в том случае, когда
при определении понятия не сопоставлялись проведенные различные отрезки в
треугольнике и прямые, делящие сторону треугольника пополам.

Ошибки при доказательстве теорем. Наиболее распространенной
ошибкой при доказательстве теорем является использование при доказательстве искомого
как данного. Предупредить такую ошибку можно только четким выяснением, что
дано, что надо доказать

Логической
ошибкой в доказательстве утверждений является неполная аргументация или пропуск
в аргументации. В курсе восьмилетней школы аргументация чаще всего допускается
учениками в доказательствах при решении задач, например при построении, реже
при доказательстве помещенных в учебнике теорем.

Логической ошибкой является неполная
дизъюнкция. Особенно часто эта ошибка допускается в вопросах и задачах, связанных
с исследованием.

Пример.

Требуется установить сравнительную
величину а³ и а²; вместо того чтобы исчерпать все
возможные значения буквы а, ученик рассматривает значение выражений при а >
1 и в результате получает неполный ответ.

Встречается много логических ошибок в
преобразованиях алгебраических выражений, когда ученики пользуются
необоснованной аналогией.

Известны распространенные ошибки
такого вида: так как (a + b)c = ac + bc , то по аналогии (ab)c = ac×bc; известно, что если а = b, то ak = bk, отсюда по аналогии считают,
что, если a > b, то ak > bk в любом случае; по аналогии
с численными дробями ученик иногда считает, что .
Предупредить эти ошибки или искоренить их можно постоянным напоминанием
школьникам (при этом не только словами, но и соответствующими примерами), что
аналогия может служить только вспомогательным средством для установления истины
и постоянно требует проверки и подтверждения логическим доказательством.

Чтобы не делать ошибок.

Известно
небольшое число правил, следуя которым можно заметно уменьшить
количество ошибок. Подобные формулировки принято относить к фольклору.
Однако познакомить с ними учеников небесполезно.

По поводу того,
где с наибольшей вероятностью может появиться ошибка, имеется неплохая
формулировка.

Правило ГАИ. Большинство аварий
происходит при небольшой скорости.

Иными словами,
ошибки чаще всего возникают в простых ситуациях.

В частности,
нужно с особой тщательностью проверять, верно ли списано условие
задачи, решено квадратное уравнение и т.п. Окончанию решения
задачи обычно уделяется минимум внимания – все трудности позади. Именно
в конце чаще всего появляются ошибки. Поэтому начинать поиск ошибки
лучше с конца.

Получив
неверный ответ, ученик обычно не знает, что с ним делать. На этот
случай есть мудрая пословица: Нет худа без добра. Лучше неверный
ответ, чем никакого.

Подставляя
полученное значение корня последовательно от конца к началу в каждое
из написанных соотношений, можно относительно быстро найти ошибочный переход.

Чтобы не
делать ошибок в преобразованиях, полезно учитывать два совета.

Правило
закройщика.
Вручную обычной иголкой шов делается так: стежок вперед и назад, еще
вперед и снова назад…

Выполнять
преобразования нужно также, как закройщик делает шов – после каждого
перехода нужно «оглянуться назад», проверить полученный результат обратным
преобразованием.

Например,
вынесли множитель за скобки – раскройте скобки и проверьте, получится
ли прежнее выражение.

Правило
программиста.
Работай блоками.

Невозможно
отлаживать программу в целом. Следует разбить работу на небольшие
автономные блоки и проконтролировать правильность каждого такого блока.

Сказанное
означает, в частности, что при работе с громоздким выражением полезно
разбить его на небольшие «блоки» и упростить каждый из них.

При решении
системы уравнений следует сначала разобраться с каждым уравнением в
отдельности.

Об ошибках в оформлении и «точке с запятой».

Сталкиваясь со
школьными «требованиями к оформлению», вузовский преподаватель приходит в
некоторое замешательство. Дело в том, что упомянутые требования носят внематематический
характер и практически не связаны с проверкой знаний. Последнее
особенно остро ощущают сильные, хорошо подготовленные ученики. Их
откровенно (и справедливо) раздражает неписанное правило: «Два недочета =
ошибка».

Единственное
требование к любому математическому тексту состоит в ясном отражении логики
решения задачи. При этом не играет роли, чертил ли автор текста поля,
писал ли какие-то слова типа «обозначим», «так как… то» или изложил
решение без слов – при помощи общеупотребительных символов.

Например, по
вузовским меркам запись

является
исчерпывающей и в словесном комментарии не нуждается. Важно, чтобы
школьник верно преобразовал неравенство, а не цитировал по памяти
полуграмотную фразу: «Так как основание логарифма меньше единицы, то
функция убывает и знак неравенства меняется».

Современный
экзамен по характеру часто приближается к тестированию. А в
таких условиях остается и вовсе одно единственное требование к
оформлению – разборчивая запись ответа.

Увлечение
оформительством мешает обратить внимание на вещи более серьезные.
Например, для уравнения нередко предлагается
следующее решение:

ОДЗ: 2 – х ³ 0; х £ 2.

По теореме
Виета х₁= 1, х₂ = -2.

Проверка
показывает, что х₂ не удовлетворяет условию. Ответ: 1.

Изложенное
решение обычно оценивается как верное. Однако предложенная последовательность
записей оставляет ряд неясностей:

1. ОДЗ в решении не использовалось.
Зачем нужно было ее искать?

2. Один из двух корней «не
удовлетворяет условию». Откуда же он взялся? Понимает ли ученик, что к
появлению постороннего корня привела не ошибка, а использованное при
решение возведение в квадрат?

3. Какими логическими знаками
следует связать сделанные записи?

4. Какой математический закон
обязывает считать х₁ и х₂ значениями переменной х?
(Ведь в геометрии, например, точки А и А₁ не имеют, вообще
говоря, ничего общего.) Разумеется, из контекста ясно, что обозначено
привычными символами х₁ и х₂ . Но зачем подменять
ясные математические записи околоматематическими условностями?

Указанные в
пункте 1,2 и 4 дефекты можно счесть не стоящими внимания придирками.
Но упомянутое в пункте 3 отсутствие логических знаков – это серьезная
ошибка. Впрочем, эта ошибка присутствует практически во всех работах
школьников и абитуриентов.

Приведем для
сравнения иную редакцию решения:

Поскольку
возведение в квадрат могло привести к появлению посторонних корней,
необходима проверка. Ответ: 1.

Если вместо
первой импликации «Þ» ученик напишет «Û», то это будет ошибкой. Если же
любую из оставшихся эквиваленций «Û» заменить на «Þ», то все останется
верным.

Автор первого
варианта решения, вероятно, просто не думал о логических связях сделанных
им записей и механически разделял их символом «точка с запятой».

Впрочем, если
бы «точка с запятой» употреблялась только в одном строго определенном
смысле, то все было бы не так плохо. Но на самом деле этот символ
в работах школьников может заменять символы «следовательно»,
«равносильно», «равносильно при дополнительных условиях», означать как
«и», так и «или», «объединение» или «пересечение» множеств. Нередки,
например, записи следующего типа: «».

В худшем для
ученика случае в подобных записях отмечается «недочет», но чаще всего
претензий не предъявляется. Стоит ли говорить о каких-то «ошибках в
оформлении», если из поля зрения выпадает главное – верное отражение
логики решения задач.

§
2. Контроль и самоконтроль учебной деятельности школьников как средство выявления
ошибок и затруднений.

Бесспорно, что
при проверке работ учитель обязан отмечать все ошибки учеников –
математические, стилистические и грамматические. Многие учителя исправляют
ошибки сами. Мы полагаем, что этого делать не следует; в том случае, когда
ошибка исправлена учителем, на долю ученика остается «согласиться» с
исправлением и успокоиться. Перестройка школы требует усиления самостоятельной
работы учащихся на всех этапах обучения. Важно, чтобы и при разборе ошибок
ученик сам установил, в чем его ошибка, умел найти источник возникновения ее и
пути исправления. Поэтому достаточно того, что учитель указывает место ошибки.
Практика такого подхода к исправлению ошибок в письменных работах достаточна
широка и оправдала себя. Для указания места ошибки вводятся условные знаки: для
грубых ошибок две черты, для негрубых и случайных – одна черта и для недочетов
– волнистая линия.

При домашнем анализе работ учитель не
может ограничиться только проверкой и сопоставлением ответов или беглым
просмотром хода рассуждений или последовательности преобразований. Надо
тщательно просматривать все преобразования, вычисления и рассуждения.
Результаты поспешной проверки работ могут поставить учителя в неприятное
положение. При анализе работ надо систематизировать ошибки и недочеты, выделить
типичные и массовые ошибки, в первую очередь принципиальные, грубые, связанные
с нарушением основных законов математике. На таких ошибках и должно быть
сосредоточено внимание учащихся при разборе ошибок в классе. Этот разбор никак
нельзя ограничивать сообщением каждому ученику его ошибок и проставленной за работу
оценки. Ошибки надо разбирать, при этом к разбору ошибок и причин, породивших
их, следует привлекать, учеников, в первую очередь допустивших ошибки и
пассивных в общей работе. Известно, что иногда достаточно перед учениками
поставить вопрос, можно ли так делать, как допустивший ошибку «спохватывается»
и сам указывает, в чем ошибка и как ее исправить. Таким образом, этап разбора
ошибок становится обучающим и мобилизующим мысль ученика.

Вопросы и задачи, вызвавшие
затруднения у многих учеников, необходимо особенно детально и тщательно
разбирать в классе, иногда следует даже провести дополнительные упражнения.
Если в классе проведен тщательный анализ ошибок (установлены источники их и
намечены пути их и намечены пути их исправления), то учитель может предложить
ученикам, допустившим ошибку, переделать задачу или внести нужные исправления,
не сопровождая их указаниями на соответствующие теоремы, правила, законы. Если
же ошибка не была массовой или явилась повторной, то рекомендуется предложить
ученику дома произвести детальный разбор ее, то есть внести исправления и
сделать нужные ссылки на соответствующие правила.

Анализ работ учитель должен провести
к очередному уроку по предмету и на этом уроке разобрать с учениками ошибки.
Отсрочка проверки и разбора работ в классе ведет к потере интереса учащихся к
разбору, часто разбор вклинивается в начатую уже работу по новой теме;
несвоевременно проставленные в журнале и дневнике оценки работ часто вызывают
законные упреки в адрес учителя со стороны классного руководителя и родителей.

§ 3. Система работы учителя
математики при коррекции ошибок учащихся 5-6 классов.

Положительный
эффект индивидуальных заданий несомненен, особенно домашних, так как ученики
выполняют их в основном самостоятельно. Просматривая индивидуальные работы
вместе с теми учащимися, которые их делали, нужно вовлекать ребят в беседу,
расспрашивая об испытанных трудностях, о примененных законах, определениях и т.
д.

Индивидуальные
задания должны быть составлены методически правильно и четко направлены на
преодоление конкретных ошибок. Чтобы справиться с такого рода методической
задачей, учителю необходимо постоянно вести учет основных затруднений учащихся.
Для этого можно использовать специальную тетрадку, разграфленную так, как
показано ниже.

Таблица

Список

учащихся

класса

Тема…

Примечание

«+» — ошибка

устранена;

«-» — ошибка

не устранена

Пробелы в

знаниях

Классные индивидуальные задания

Домашние индивидуальные
задания

Все графы таблицы, кроме
первой, заполняются карандашом, чтобы можно было стирать записи и заменять их
другими по мере преодоления ошибок. Список ошибок пополняется во время проверки
домашних заданий, самостоятельных и контрольных работ и при проведении зачета,
хотя ошибки в своем большинстве неоригинальны. По каждой теме они повторяются
из года в год. Молодому учителю будет полезно ознакомиться с ошибками, которые
учащиеся допускают при изучении математики в V — VI классах.

Ниже будут
перечислены типичные ошибки и указаны приемы их устранения, которые можно
реализовать в индивидуальных заданиях.

При выполнении
действий над десятичными дробями учащиеся допускают ошибки в выделении целой
части результата, например: 3,4 + 5,3 = 87; 4,2 — 1,8 = 24; 4,1* 1,1 = 451;
2,4 : 2 = 12.

При беседе с
учащимися, допустившими такую ошибку, выясняется, что они просто забыли
поставить запятую. Эта ошибка устраняется в результате длительных тренировок.

Самая типичная
ошибка допускается при делении десятичной дроби на десятичную: делят, не
обращая внимания на запятые, например так: 2,576 : 11,2 = 23. Обычно учащиеся
знают правило деления, но затрудняются различить делимое и делитель.

Для устранения
этих ошибок можно давать учащимся задания на карточках, в которых каждый пример
сопровождается тем или иным правилом, сформулированным полностью или с
пропусками.

Примеры некоторых
карточек.

Карточка №1. Чтобы сложить две
десятичные дроби, надо:

а) уравнять
число знаков … в слагаемых;

б) записать
слагаемые друг под другом так, чтобы запятая …;

в) сложить
получившиеся числа, как складывают …;

г) в
полученной сумме поставить запятую под … .

Задания.

1. Уравняйте
число знаков после запятой в следующих числах: 2,5; 0,25; 43, 1256; 325,1.

2. Сложите дроби
12,7 и 3,442; 0,237 и 10,44.

Карточка № 2.

Чтобы умножить дну
десятичную дробь на другую, надо выполнить умножение, не обращая внимание на
…, а затем в результате отделить запятой… столько цифр, сколько их стоит
после запятой… .

Задания.

1. В записи
1234567 отделите запятой справа: а) одну цифру; б) две цифры; в) шесть цифр;
г) семь цифр. В каком случае в результате получается число, которое больше 1,
но меньше 2 ? больше 0, но меньше 1?

2. Перемножьте
числа 2,7 и 1,32.

Карточка № 3.

Чтобы разделить
число на десятичную дробь, надо в делимом и в делителе перенести … вправо на
столько цифр, сколько их после… в …, а потом выполнить деление на
натуральное число.

Задания.

1. В записи 2,88
: 0,8 подчеркните одной чертой делимое, а двумя — делитель.

2. В числах 1;
0,05; 3,25 перенести запятую вправо на столько цифр, сколько их после запятой в
числе 0,5.

3. Разделите
2,576 на 1,12.

Наиболее
распространены ошибки в действиях обыкновенными дробями. Так, при сложении
(вычитании) дробей складывают (вычитают) числители и знаменатели:

Складывая
(вычитая) дроби, забывать умножить их числители на дополнительные множители:

Целую часть
прибавляют к числителю без приведения к общему знаменателю:

От целой части
отнимают числитель без приведения к общему знаменателю:

Учащимся,
допускающим такого рода промахи, можно предложить индивидуальные задания,
которые побуждают к поиску ошибок и установлению парадоксальности неверных
результатов.

Карточка № 4.

Сумма
положительных чисел не может быть равна одному из слагаемых. Не может она и
быть меньше какого-либо слагаемого.

1. Учитывая эти
свойства положительных чисел, объясните, в чем кроется ошибка следующего
действия:

а) б) 5 +

2. Среди данных
действий подчеркните верные, а неверные выпишите отдельно и исправьте:

а)

Карточка № 5.

Известно, что вычитание
проверяется и тем, что разность двух положительных чисел не может быть больше
уменьшаемого.

1. Учитывая
сказанное выше, установите, верен ли результат вычитания:

а) 3 — ; б)

2. В данных ниже
равенствах поставьте вместо квадратиков такие числа, чтобы равенства стали
верными:

а) ÿ = б) ÿ = в)
ÿ.

Ошибки при
умножении и делении смешанных чисел связаны с неумением превращать их в
неправильную дробь.

Умножают отдельно
целые и отдельно дробные части, например:

Делят целые части чисел, а дробную
часть первого числа просто переписывают:

Умножают (делят)
только дробные части чисел:

1) × 2)

При умножении
(делении) смешанного числа на десятичную дробь умножают (делят) отдельно целые
части и отдельно дробные, а результаты записывают рядом, например:

Для устранения
этих ошибок практикуют задания, в которых от учащихся требуются доказательства
ложности некоторых выводов.

Карточка № 6. Известно, что деление проверяется
умножением, а умножение – делением. Существуют и другие способы проверки. Они
основаны на том, что, например, произведение двух чисел, больших единицы, не
может быть меньше единицы, а частное от деления двух неравных чисел не может
быть равно единице.

1. Пользуясь этими правилами, что в
следующих действиях допущены ошибки. Исправьте результаты.

а) б)
в)

2. В
данных ниже равенствах вместо квадратиков вставьте нужные числа и объясните,
как они найдены:

а) ÿ = б)
ÿ =

Литература.

1. Азиев И.К. Индивидуальные
задания для устранения ошибок. // Журнал «Математика в школе»- 1993 г. — №5, с.
9.

2. Груденов Я.И. психологический
анализ причин некоторых массовых ошибок учащихся// Журнал «Математика в школе»-
1981 г. — №3, с. 46-48.

3. Груденов Я.И.
Психолого-дидактические основы методике обучения математики. –газета
«Математика», 1987 г. с. 91-96.

4. Зайкин М.И., Колосова В.А.
Провоцирующие задачи. // Журнал «Математика в школе»- 1997 г. — №6, с. 32.

5. Чаплыгин В.Ф. Некоторые
методические соображения по решению текстовых задач. // Журнал «Математика в
школе»- 2000 г. — №4, с. 28.

6. Шнейдерман М.В. Анализ ошибок
и затруднений учащихся V классов.// Журнал «Математика
в школе»- 1999 г. — №6, с. 21.

7. Ярский А.С. Что делать с
ошибками. // Журнал «Математика в школе»- 1998 г. — №2, с. 8-14.

8. Журналы «Математика в школе»
за 1970-1990 г.г.

Источник

«Предупреждение и устранение типичных ошибок и познавательных затруднений учащихся при обучении математике»

Содержание

Стр.

Введение………………………………………………………………………… 4

Глава I. Психолого-дидактический анализ математических ошибок и затруднений учащихся……………………………………………………………………….. 5

§ 1. Психолого-педагогический и дидактико-методические причины типичных ошибок и затруднений учащихся:

§ 1. 1. Сущность понятий «типичная ошибка» и «познавательное

затруднение», сущность математической ошибки, причины

появления ошибки………………………………………………… 5

§ 1. 2. О пользе и вреде ошибок.

§ 1. 3. Причины типичных ошибок учащихся.

§ 1. 4. Причины познавательных затруднений в учебной деятельности школьников.

§ 2. Типичные ошибки и затруднения учащихся при обучении математике в 5-6 классах………………………………………………………………… 32

Глава II. Пути и средства предупреждения и преодоления ошибок и затруднений учащихся 5-6 классов……………………………………………… 35

§ 1. Методы и приемы обучения математике, используемые учителем для предупреждения ошибок и затруднений…………………………………… 35

§ 2. Контроль и самоконтроль учебной деятельности школьников как средство выявления ошибок и затруднений…………………………………… 46

§ 3. Система работы учителя математики при коррекции ошибок учащихся 5-6 классов………………………………………………………………… 48

Список литературы……………………………………………………………….. 53

Введение.

В настоящее время, также как и раньше, существует проблема ошибок и затруднений учащихся при обучении математике. Хотя в методике обучения математики к настоящему времени накоплен опыт, разработано много различных методов профилактики и коррекции ошибок и затруднений учащихся при обучении математике, но при этом школьники не перестают делать ошибки. Плохо это или хорошо? Однозначного ответа нет. Ответ будет зависеть от того, что мы понимаем под «ошибкой».

Методик обучения много. Но нет единой теоретической основы. Одной из причин отсутствия в методике обучения математики теоретической основы является слабая связь со смежными науками, особенно с психологией.

Считаю, что и ошибка, и затруднение напрямую связаны с психическими процессами человека. Поэтому в моей работе много места будет уделяться психолого-педагогическим причинам ошибок и затруднений учащихся.

Цель моей работы – выявить необходимые условия, выполнение которых поможет уменьшить количество ошибок и затруднений при обучении математике в 5-6 классах.

Исходя из цели, были поставлены следующие задачи:

Изучение и классификация ошибок и затруднений учащихся 5-6 классов при обучении математике.
Изучение и классификация причин ошибок и затруднений учащихся при обучении математике.
Изучить опыт работы учителей математики по предупреждению и коррекции ошибок и затруднений учащихся 5-6 классов при обучении математике.

Глава I. Психолого-дидактический анализ математических

ошибок и затруднений учащихся.

§ 1. Психолого-педагогический и дидактико-методические причины

типичных ошибок и затруднений учащихся.

Под ошибкой мы будем понимать результат неправильного (ошибочного) действия.

Ошибочное действие – один из существенных объектов психологии труда, педагогической психологии и психологии управления; действие не достигшее цели. Ошибочное действие различают по причине; по степени выраженности в зависимости от величины отклонения от нормы; степени повторяемости; степени грубости в зависимости от этапа обучения, на котором оно совершено; связи с другими ошибочными действиями в синдром неуспеваемости.

Под сущностью ошибки следует понимать некое объективное условие, требование, правило и т.п., которое нарушено или не соблюдено, а под причиной появления ошибки – субъективные ситуации, состояния или процессы, свойственные интеллектуальной сфере человека, которые повлекли данное нарушение или несоблюдение.

Психологический анализ математических ошибок школьников предполагает выявление механизма возникновения той или иной ошибки в рамках какой-либо психологической концепции усвоения знаний, формирования –умений и навыков.

Методический анализ ошибок предполагает демонстрацию ошибки, выявление ее математической сущности, указание возможных причин появления этой ошибки и характеристику сферы возможных ее проявлений.

Каждая ошибка характеризуется содержанием и причиной возникновения (содержание лежит на поверхности явления, а причина ее скрыта в его глубине).

Ошибки делятся на случайные и систематические, то есть устойчивые. Случайными ошибками следует считать те, которые появляются однократно, не систематически у одного-двух учащихся класса. К устойчивым (типичным) ошибкам относятся те, которые появляются у одного и того же ученика (или нескольких) неоднократно или те, которые появляются хотя и однократно, но у многих учащихся.

Во второй половине XIX века господствовала ошибочная теория «недопущения ошибок» (Н. Кульман, Ф. Флеров), согласно которой акцентирование внимание на ошибке повлечет за собой упрощение ошибки в сознании школьников. Лозунгами этой теории были следующие: «Ни одной ошибки для глаз!», «Ни одной ошибки для рук!».

Современная дидактика и частные методики доказывают, что работа над ошибками не просто полезна, но и необходима, причем над типичными ошибками должна проводиться фронтальная работа, а над случайными – индивидуальная. Скорее всего, в начале «На ошибках учат», а затем уже «На ошибках учатся».

Сознательному усвоению знаний способствует глубокий анализ самим учеником содержания каждой ошибки, которая была им допущена, выяснение причин ее возникновения, теоретическое осмысление ее сути. «Как это не странно звучит, — отмечает Н.М. Бескин, — ошибки в изучении не вредны, а полезны. Они аналогичны симптомам болезни. По этим симптомам врач ставит диагноз. Точно также и ошибки учащихся сигнализируют учителю, чего именно школьник не понимает. Учитель мог это и не знать, а ошибка дает ему нужную информацию. От учителя требуется умение понять неправильный ход мыслей ученика, который не может объяснить, почему он пришел к такому результату». Любая ошибка должна быть использована для более детального и глубокого проникновения в суть данного правила, понятия, теоремы и т. д.

В каждой ошибке следует различать содержание и причину ее возникновения. В содержание ошибки входит то, что объективно неверно, неадекватно выполнено в действиях учащихся. Причина же появления ошибки – это некоторое обстоятельство (или их совокупность), которое повлекло за собой выполнение неадекватного действия учащегося. Содержание ошибки легко установить по внешнему выражению действий учащегося (сужает или расширяет объем понятия, неправильно произносит или пишет, неверно выполняет какое-то действие и т. д.). Причина же ошибки, как правило, внешне себя не проявляет. Задача учителя – определить исходные корни допущенной ошибки, что дает ему возможность верно строить работу по ликвидации и предупреждению различного рода ошибок. «Учитель должен не просто поправить ошибку, а выкорчевать ее. Для этого он должен понять неправильный ход мыслей и заблуждений ученика, которые сам ученик не может сформулировать».

Естественная и зачастую единственная реакция учителя на ошибку ученика – сниженная оценка. Нередко единственная реакция ученика на собственную ошибку – чувство досады… из-за сниженной оценки. Как следствие из года в год ученики старших классов, абитуриенты вузов, студенты младших курсов делают одни и те же ошибки…

Ученик работает у доски и, уловив тень сомнения в глазах учителя, мгновенно стирает написанное. Все, нет ошибки!.. Но примеры безошибочных решений учитель способен привести и сам. А ученика пригласили к доске, в частности, затем, чтобы он ошибался. Он интересен своими ошибками.

Чтобы перестать делать ошибки, существует, по нашему мнению, только один путь: нужно делать ошибки, находить ошибки и исправлять ошибки. Проще говоря, чтобы не делать ошибок, нужно вволю наошибаться. Ошибка, «не убитая» в процессе самостоятельной работы, «убивает» на контрольной или экзамене.

Ученики нередко задают вопрос: «А можно здесь до множить на знаменатель (возвести в квадрат, не делать проверки, сократить и т. п.)?» По существу, подобный вопрос является попыткой переложить ответственность за решение на учителя. В ответ уместно спросить: «Вы хотите, чтобы я вам разрешил или запретил сделать то, о чем вы спросили? Сие не в моей власти. Так что адресуйте свой вопрос самим себе!»

Ученик перестает ошибаться только тогда, когда ответственность за полученный результат полностью ляжет на него самого, когда появится ощущение, что только он сам – не приятель, не учитель – может отыскать выход из создавшейся ситуации, что только от качества его собственной работы зависит конечный результат.

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. Увы, в математике приходится учиться в основном на собственных ошибках. Иными словами, если ученик не ошибается, то он не учится.

Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, умело и грамотно ее использовать.

Не знаешь алгебры – займись арифметикой.

Нередко ученик использует неверную формулу или, что еще хуже, вообще не отдает себе отчета, чем именно он пользуется. Рассмотрим типичные примеры.

Сколько бы учитель ни заставлял учеников повторять свойства радикалов, рано или поздно кто-нибудь из них напишет нечто подобное.

Если учитель в очередной раз скажет: «Так нельзя!», то долговременного эффекта это не даст. Подсказав или продиктовав некий факт, мы загружаем оперативную память ученика. Последняя – как в компьютере – обновится при новом включении… Чтобы информация попала в «долговременное запоминающее устройство», необходимо добиться понимания, а в данном случае – осознания учеником его ошибки. Для этой цели пригоден следующий почти универсальный совет:

— Проверьте написанное вами равенство при каком-нибудь значении х. Например, при х =1.

Важно, чтобы ученик сам написал

и получил абсурдный результат .

Полезен и иной тезис:

Предложенное Вами преобразование заметно упрощает теорему Пифагора:

Последнее равенство опровергается и повседневной практикой: шагать по катетам все-таки дальше, чем по гипотенузе.

Интересные свойства рассматриваемой цепочки равенств еще не исчерпаны. При х = -1 получим

В ошибочности первого равенства ученик уже убедился. Но, оказывается, и второе равенство неверно.

Не стоит жалеть времени на подробное обсуждение и исправление двух сделанных ошибок.

«Почленное деление»:

И в данной ситуации уместно дать ученику тот же совет:

Проверьте Ваше равенство, например при х = 1:

После такого конфуза ученик должен наконец понять, что не учитель, а арифметика не позволяет делать подобные преобразования.

Не лишним будет и еще одно наблюдение:

Посмотрите, при каких значениях х определено каждое из трех написанных выражений.

В первом выражении х ≠-1, во втором – х ≠0, в последнем х – любое число. Тем самым все выражения различны.

При работе с «многоэтажными» дробями школьники делают отчаянно много ошибок. Например:

И снова нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a=b=1 и с=2 получим

В результате ученик должен сделать вывод, что при работе с «трехэтажными» выражениями лучше добавить скобки, чем сравнивать длины обозначающих дроби «черточек»:

( К слову, последним правилом обычно руководствуются программисты: «Лучше лишние скобки, чем лишние ошибки».) И, разумеется, должна появиться верная запись

К сожалению, не редкость и арифметические «фокусы»:

Не исключено, что написавший подобную нелепость ученик в свое время получил пятерку за отменно вызубренное «правило деления дроби на число». Правда, он так и не задумался, из каких соображений предложено именно такое правило, в чем его смысл. Поэтому он не видит никакой конкретики за исходной записью

Впрочем, никогда не поздно объяснить человеку, что, отсыпав половину из мешка, наполненного на одну треть, нельзя, к сожалению, наполнить его на две трети. ( В противном случае этим стоило бы заняться.)

»Интересные преобразования» часто встречаются при работе со степенями.

(1)

Это изящное преобразование выполняется следующим образом: слегка удлиняется «палочка» в показателе степени исходного выражения.

Если учитель в очередной раз подскажет, что означает дробь в показатели степени, то это даст лишь сиюминутный результат. Следует вернуть ученика от алгебры к арифметике – заставить его самостоятельно проверять написанное при конкретных значениях переменной. Например, при а=2 получится

Последнего обычно достаточно, чтобы ученик вспомнил определение:

(2)

Если же ученик так и не «пришел в себя», то можно дать еще один совет:

-Вся алгебра держится на возможности проделать с обеими частями равенства одну и ту же операцию. Попробуйте возвести обе части вашего равенства в квадрат:

Зная хоть что-нибудь о свойствах степеней, ученик преобразует левую часть равенства

и получит наконец возможность восстановить определение (2).

Автору преобразования типа (1) встретилось недавно в работе абитуриента в следующей редакции:

Особенно много «интересных преобразований» возникает в тригонометрии. Не найдя, какой бы из имеющихся в шпаргалке формул, ученик начинает изобретать что-то оригинальное. К наиболее ходовым изобретениям такого типа относятся «формулы»:

cos 2x = 2cos x, (3)

sin (x + y) = sin x + sin y. (4)

И снова следует предложить ученику проверить написанные формулы при каких-либо «хороших» значениях угла х: 0, В частности, «формула» (3) при х =π/6 приводит к неверному равенству

Впрочем, установить ошибочность формулы не так уж сложно. Заметно сложнее исправить неверную формулу. Полезно предложить ученику следующую работу:

-Выпишите для известных вам «хороших» углов значения cos 2x и cos x и поищите связь по табл. 1.

Таблица 1

х	0	π/6	π/4	π/3	π/2
cos 2x	1	1/2	0	-1/2	-1
cos x	1			1/2	0

В строке «cos 2x» нет радикалов, а в строке «cos x» они есть. Вероятно, чтобы нащупать связь, следует вместо cos x рассмотреть cos2 x (см. табл. 2).

Таблица 2

cos 2x	1	1/2	0	-1/2	-1
сos2 x	1	3/4	1/2	1/4	0

В строке значений сos2 x есть знаменатели 4, а среди значений cos 2x — только половинки и целые. Видимо, значение сos2 x нужно умножить на 2 (см. табл. 3).

Таблица 3

cos 2x	1	1/2	0	-1/2	-1
2сos2 x	2	3/2	1	1/2	0

Теперь видно, что все значения во второй строке больше соответствующих значений первой строки на 1. Следовательно, cos 2x = 2сos2 x-1.

Поработаем теперь с «формулой»(4).

При х = π/2 получим sin= sin + sin y.

Придется вспомнить формулу приведения: sin= cos y. Итак, рассматриваемая формула привела к неверному равенству cos y = 1 + sin y. Последнее равенство наталкивает на мысль, что в правой части формулы должен присутствовать еще и cos y, а значит, и cos х. Попытаемся так составить формулу, чтобы она давала верное равенство хотя бы для углов х=π/6 и y = π/3. Из значений

sin = ; cos= ; sin ; cos ; sin

Удается получить верное равенство следующим способом (иного способа ученики автора до сих пор не предлагали):

Тем самым

sin sin

Итак, формула угадана:

sin (x + y) = sin x⋅cos y + cos x⋅sin y.

По поводу проведенных рассуждений уместно сформулировать шуточную, но полезную теорему.

Предложение. Если правдоподобная тригонометрическая формула выполнена для «хороших» углов π/6, π/4 π/3, то она верна.

Разумеется, существует масса других способов восстановить ту или иную тригонометрическую формулу. Однако простейшим с идейной точки зрения является вычисление значений тригонометрических функций и поиск связи между найденными значениями. Подобную работу ученикам полезно проделать еще до того, как они впервые познакомились с той или иной формулой.

От радикала – к степени

Почти всякий раз переход от записи с радикалом к записи со степенью сопровождается стандартной ошибкой:

. (5)

Ошибка состоит в том, что написанная формула верна лишь для неотрицательных значений переменной.

Проведем рассуждение. Если формула (5) верна, то

Но а не существует. Тем самым результат возведения числа –1 в степень 1/3 зависит не от самой степени, а от ее записи. Иными словами, корректно определить дробную степень отрицательного числа не удается.

Таким образом, преобразование (5) приводит к потере отрицательных значений переменной.

Например, уравнения и х2/3=1 неравносильны. В первом уравнении х = ± 1, а во втором х = 1.

Лишь немногие ученики понимают, что при переходе от записи с радикалом к записи со степенью приходится пользоваться формулой

т. е. рассматривать два случая – неотрицательные и отрицательные значения подкоренного выражения.

Ошибки от непонимания

Приведенные ниже записи являются небольшим фрагментом весьма обширной коллекции. Впрочем, новые оригинальные экспонаты появляются крайне редко. В основном обновляются старые:

;

a⋅b = 1 ⇔ a = 1;

b = 1

= b ⇔ a = b2 ;

a ≥ 0

;

х2 • 4 ⇒ х • 2;

a • b ⇒ a2 • b2;

• 1 ⇔ 1 • х;

• х ⇒ 2 – х • х2;

sin x + cos x = 1 ⇔ ;

sin x + cos x = 1 ⇔ (sin x + cos x)2 = 1 ⇔ sin 2x = 0;

sin x = ±

Едва ли каждая из указанных записей нуждается в отдельном комментарии. Заметим только, что последняя «формула» содержит ту же ошибку, что и «формула» . А между тем она частая гостья в записях не только школьников но, увы, и учителей.

Особенно много ошибок появляется в ситуациях, требующих от ученика не столько памяти, сколько логики – умения рассуждать. В частности, школьники делают недопустимо много ошибок при решении неравенств. Одна из причин состоит в том, что функциональная точка зрения на неравенство – связь решения с монотонностью фигурирующих в неравенстве функций – остается для них слишком абстрактной.

Определение. Функция ƒ(х) называется монотонно возрастающей на множестве М⊂R, если a • b ƒ(a) •ƒ(b).

Функция ƒ(х) называется монотонно убывающей на множестве М⊂R, если a • b ƒ(a) • ƒ(b).

В частности, функция ƒ(х) = х2 возрастает на множестве М =[0 ; ∞). Следовательно,

a • b a2 a2 • b2.

Иначе говоря, неравенство, обе части которого неотрицательны, можно возводить в квадрат.

Та же функция ƒ(х) = х2 возрастает на множестве М = (-∞ ; 0]. Следовательно,

a • b a2 a2 • b2.

Иными словами, если обе части неравенства неположительны, то при возведении в квадрат следует сменить знак неравенства на противоположный.

Функция ƒ(х) = х3 возрастает на множестве R. Следовательно,

a • b ⇔ a3 • b3.

Тем самым любое неравенство можно возводить в куб.

Аналогично: функция возрастает на множестве R. Следовательно, при потенцировании по основанию 3 знак неравенства сохраняется:

a • b ⇔ 3a • 3b.

Функция убывает на множестве М=(0;∞). Следовательно, при логарифмировании по основанию 0,2 знак неравенства меняется на обратный:

Проанализируем следующие два примера из приведенных выше в списке ошибок.

Пример 1:

Введя в рассмотрение функцию , можно переписать неравенство

в виде f(x) < f(1). Функция f(x) убывает на каждом из интервалов (- ∞;0), (0; ∞), но не является убывающей на их объединении. Следовательно, переход f(x) < f(1) ⇔ х > 1 справедлив лишь при условии x > 0:

Случай x < 0 придется рассмотреть отдельно. Впрочем, несложно заметить, что при
x < 0 неравенство выполнено.

Пример 2:

Для решения неравенства введем в рассмотрение функцию . Неравенство примет вид f(x) > 0.

Функция f(x) является разностью убывающей и возрастающей f2(x) = x функций и, следовательно, убывает на всей своей области определения (- ∞; 2]. Кроме того, f(1) = 0. Суммируя сказанное, получим

Итак, исходное неравенство равносильно системе

Рассмотрим причины математических ошибок и охарактеризуем эти причины.

Причины, связанные с психологическими факторами (ослабление психических функций: памяти, внимания, мышления)

доминирование ассоциативных связей над смысловыми;
интерференция навыков, когда формирование одного навыка тормозится другим;
перенос некоторых навыков в область таких задач, где их действие ограничено либо вовсе исключено.

Причины, вытекающие из недостатков учебных программ и учебников:

в текстах учебников авторы предпринимают поспешный переход к абстрагированию и обобщению при формировании у учащихся умения пользоваться правилами, алгоритмами и умениями делать выводы;
алгоритмы, правила вводятся в тексте учебников без рассмотрения необходимого числа примеров;
увлечение авторами учебников логической строгостью изложения учебного материала;
система упражнений в учебнике не обеспечивает должной пропедевтической и закрепительной работы.

3) Причины, обусловленные несовершенством организации учебного процесса:

нет работы учителя по предупреждению у учащихся стремления к автоматическому применению изучаемых фактов;
у учащихся не формируются такие умения как подведения объекта под понятие, выведение следует из факта принадлежности объекта объему понятия, выделение существенных признаков понятий;
у учащихся не формируются навыки самоконтроля;
недостаточно ведется подготовительная работа для сознательного усвоения учебного материала, учителем не продумано его целесообразное закрепление в последующем;
слабо ведется работа по повышению у учащихся вычислительной культуры;
неумение учителем использовать наглядность не только с целью реализации ее иллюстративной функции, но и учебно-познавательной.

Влияние мотивов деятельности и эмоций. В исследованиях Л.В.Занкова, Д.Н.Узнадзе, А.А.Смирнова выявлено, что запоминание во многом зависит от сознательного намерения, определенной направленности нашей деятельности или от установок, т.е. неосознанных источников направленности на запоминание. На основе этих исследований можно сформулировать следующие закономерности:

Установки или направленность на полноту, точность, прочность, последовательность запоминания материала вызывают определенные формы активной мыслительной деятельности, что приводит соответственно к полному, точному, прочному, последовательному запоминанию. Влияние этих установок на учащихся усиливается по мере овладения ими приемами мыслительной деятельности.
На усвоение учебного материала большое влияние оказывают мотивы деятельности учащихся, их интерес к изучаемой теме, к предмету, положительные эмоции, осознание значимости, важности данного материала, устойчивые интересы и потребности.
Материал относительно большого объема запоминается неохотно, с нежеланием.

Существует несколько закономерностей, характеризующих зависимость между пониманием и запоминанием материала:

Определенный уровень понимания материала – необходимое условие его успешного запоминания.
Если материал плохо понят, то он запоминается неточно, и искажения не замечаются человеком, либо может возникнуть иллюзия запоминания.
Понимание затрудняется, если установка на полноту и точность запоминания появляется до осознания материала в целом. В остальных случаях установка на запоминание, наоборот, способствует лучшему пониманию.
Активная мыслительная деятельность, направленная на понимание материала, может приводить к его непроизвольному запоминанию.

Сформулируем более общее утверждение и назовем его основной закономерностью памяти.

Если учащийся выполняет над материалом активную мыслительную деятельность и эта деятельность способствует углубленному пониманию материала, тогда происходит его успешное запоминание (произвольное или непроизвольное).
Ведение стимулирующих звеньев повышает эффективность запоминания материала.

Стимулирующим звеном условимся называть промежуточный мыслительный процесс, который вводится между двумя другими процессами, помогая устанавливать связи между ними и активизируя мышление.

Например, нам надо вспомнить, какой знак имеют значения функции . Обычно мы сначала представляем график, а затем устанавливаем знак значения функции на указанном интервале. Представление графика – промежуточный мыслительный процесс, т.е. стимулирующее звено. В качестве стимулирующих звеньев можно успешно использовать различные графики, схемы, таблицы, правила.

Эффективному запоминанию помогают следующие приемы мыслительной деятельности: составление плана, выделение смысловых опорных пунктов, реконструкция материала, соотнесение (т.е. увязывание изучаемого материала с прежними знаниями и отдельных частей нового друг с другом), использование стимулирующих звеньев, сравнение, обобщение, конкретизация, классификация, систематизация, воспроизведение материала в реконструированном виде.
Забывание более интенсивно протекает сразу после изучения материала (в первый день, первые часы и даже минуты), а затем оно замедляется – закономерность Эббингауса.
Повторение путем разнообразной деятельности, сводящейся хотя бы к некоторой реконструкции материала, эффективнее, чем его повторение в неизменном виде.
Рассредоточенное по времени повторение эффективнее, чем концентрированное.

Но при этом необходимо соблюдать меру. Если повторение растянуть на чрезмерно большой срок, то, по закономерности Эббингауса часть материала забывается и приходится тратить много времени на восстановление забытого.

Покажем, что за основу при построении группы закономерностей формирования умений и навыков может быть принята теория обобщенных ассоциаций.

П. А. Шеварев дал следующие определения:

Связь двух психических процессов Р1 и Р2, при которых процесс Р1 влечет за собой возникновение процесса Р2, называется ассоциацией. Обозначение (Р1;Р2).
Ассоциация называется обобщенной, если существенные компоненты одного или обоих ее членов могут изменяться, и константной, если они всегда неизменны.

Закономерность формирования ассоциаций.

Ассоциация (Р1;Р2) образуется, если психические процессы Р1 и Р2 возникают по ходу деятельности и повторяются или непосредственно друг за другом, или с участием стимулирующего звена М. Если это звено в дальнейшем сохраняется, то образуется две ассоциации: (Р1;М), (М;Р2).

Определение 3. Умения и навыки решения мыслительных задач есть определенная система ассоциаций, преимущественно обобщенных.

Если существенные компоненты двух психических процессов при их повторении друг за другом изменяются, варьируются, может образоваться обобщенная ассоциация; если они всегда неизменны – константная.

Определение 4. Ассоциация называется ошибочной, если на основе ее проявления учащийся иногда решает задачи данного типа верно, иногда ошибается либо она вообще не проявляется при решении некоторых задач некоторого типа.

Если в процессе деятельности соблюдаются три условия:
1) учащийся выполняет задания одного типа;
2) в них неизменно повторяется некоторая особенность;
3) ее осознание не обязательно для получения верного результата,
то степень осознания данной особенности снижается, т.е. у учащегося образуется ошибочная ассоциация.
Проявление ассоциации в процессе решения задачи сопровождается чувством уверенности в правильности полученного результата, тем самым уменьшается вероятность самоконтроля.
Если какая-либо особенность К, присущая отдельным задачам данного типа, не отражена в системе упражнений, либо в рассматриваемых способах решения задач, то у учащегося может образоваться ошибочная ассоциация, в состав первого члена которой не входит осознание особенности К.
Для формирования обобщенной ассоциации требуется тем меньше тренировочных упражнений, чем более учащийся развит и обогащен знаниями, умениями и навыками, относящимися к данной области науки.
Для сохранения и упрочнения ассоциации рассредоточенное повторение эффективнее концентрированного.

Условия активизации мыслительной деятельности учащихся при решении задач:

Ассоциации, формируемые в процессе решения задач, оказываются тем более прочными и устойчивыми, чем с большей мыслительной активностью, а значит, и глубиной понимания решаются эти задачи.
Использование стимулирующих звеньев по ходу решения задач, активизируя мыслительную деятельность, приводит тем самым к формированию прочных ассоциаций.
Если при изучении новой темы выполняются условия:
1) учащемуся предлагают задачи только одного типа;
2) их решения сводятся к одной и той же операции;
3) эту операцию (ее результат) учащемуся не надо выбирать среди других, которые возможны в сходных ситуациях;
4) данные задач не являются для учащего непривычными;
5) он уверен в безошибочности своих действий,
то учащийся очень быстро, нередко при решении 2-й или 3-й задачи, перестает применять изучаемые определения, теоремы, прекращает обосновывать решения задач. Если хотя бы одно из перечисленных условий нарушается при решении какой-то задачи, то учащийся начинает обосновывать решение этой или одной-двух последующих задач.

Закономерности внимания и восприятия.

Определения. Внимание называется произвольным, если оно поддерживается под влиянием сознательно поставленной цели и волевых усилий; после произвольным, когда влияние сознательно поставленной цели сохраняется, а волевые усилия отсутствуют; и непроизвольным, если внимание поддерживается без сознательно поставленной цели и без волевых усилий.

Деятельность, осуществляемая на основе произвольного внимания, требует значительных усилий и быстро утомляет человека.
Внимание может возникнуть и усилиться под влиянием одного или нескольких из следующих условий:
а) относительной интенсивности раздражителей;
б) их относительной новизны;
в) неожиданности их появления;
г) контраста между ними;
д) ожидания определенных событий или впечатлений;
е) положительных эмоций.
Необходимыми условиями длительного сохранения послепроизвольного внимания являются: пассивность деятельности, наличие соответствующих знаний, умений и навыков.
Достаточными условиями длительного поддержания внимания (после произвольного и произвольного) являются одно или несколько из следующих условий:
а) эта деятельность значима для человека;
б) у него имеется чувство ответственности за ее успешное завершение;
в) она совпадает с направлением постоянных интересов человека либо становится для него интересной, увлекательной, хотя бы только в данный момент.
Внимание и интерес к деятельности усиливаются, если выполняется хотя бы одно из следующих условий:
а) прилагаются активные умственные усилия;
б) углубляется понимание соответствующего материала;
в) возрастает уверенность;
г) возникают новые идеи, открытия.
Внимание может быть ослаблено при наличии одного или нескольких из следующих условий:
а) задание непосильно, из-за чего теряется уверенность в возможности завершить его выполнение;
б) работа совершается в чрезмерно быстром или слишком медленном темпе;
в) она сводится к однообразным операциям;
г) исчезает интерес к ней;
д) выполняемая работа слишком проста для человека.
Внимание облегчается, если выполняются условия:
а) мыслительная деятельность сопровождается соответствующей моторной деятельностью;
б) объекты, которыми мы оперируем, воспринимаются зрительно.

Условия, позволяющие облегчать учащимся восприятие учебного материала.

Восприятие объектов облегчается, если они расположены в определенной системе, требующей минимальных усилий со стороны наших органов чувств. Восприятие объектов, расположенных хаотически, осуществляется неохотно.
Предварительная подготовка к наблюдению, четко поставленная задача: как и в какой последовательности вести наблюдения; прошлый опыт человека и его знания значительно облегчают восприятие, делают его более богатым.
Активная мыслительная деятельность в процессе наблюдения приводит к более полному, богатому восприятию. При пассивном созерцании объекта от внимания человека ускользают многие детали.
Легче наблюдать единичные отличия среди многих черт сходства, чем наоборот. Различие между объектами (ситуациями) привлекает к себе внимание более, чем сходство.

При формировании умений поиска решения задачи существенную помощь может оказывать следующая закономерность, приведенная С.Л.Рубинштейном:

Вероятность вспоминания теоремы, нужной для решения задачи, возрастает при выполнении двух условий:
а) теорема и данные задачи выражены в одних и тех же понятиях;
б) искомые и данные задачи сближены анализом и синтезом настолько, что в оставшийся интервал как раз «укладывается» данная теорема, целиком заполняя этот интервал.
(Аналогично при этих же условиях возрастает вероятность вспоминания определений, аксиом, различных правил, законов и т.д.)

На основе исследований П.А.Шеварева сформулирована следующая закономерность:

а) Последовательность мыслительных процессов (А;В;С;…;М), повторяющаяся при решении однотипных задач, может свертываться до составной ассоциации (А;М). В дальнейшем эта ассоциация в случае необходимости легко «развертывается» в первоначальную цепь рассуждений.
б) Если ассоциация (А;М) образована без промежуточных рассуждений, то вклинивать их в дальнейшем между процессами А и М бывает очень трудно.
Мыслительные операции можно целенаправленно формировать путем постепенного перехода от развернутых внешних действий, заранее запрограммированных и выполняемых в заданной последовательности, ко все более свернутым умственным действиям.

Активизация мыслительной деятельности учащихся при ознакомлении с теоретическим материалом.

Активность мыслительной деятельности по ходу ознакомления с материалом возрастает, если одновременно учащийся выполняет конкретное задание, помогающее глубже понять данный материал, и при этом соблюдаются следующие условия:
1) поставленное задание направляет усилия учащегося на использование определенного мыслительного приема;
2) учащийся обладает знаниями, необходимыми для выполнения этого задания, и навыками применения данного приема;
3) этот прием соответствует содержанию материала, и чем в большей мере соответствует, тем сильнее активизируется деятельность.

Примерно до 50-60 годов в методической литературе анализ ошибок учащихся носил односторонний характер, так как не учитывались психологические закономерности. Из-за их отсутствия некоторые авторы пытались объяснить ошибки учащихся ссылками на законы физиологии. Психологические закономерности для анализа ошибок одним из первых стал использовать П.А. Шеварев, а в дальнейшем и другие авторы. В психолого-дидактическом анализе ошибок, основанном уже на психолого-дидактических закономерностях, учитываются и внутренние процессы учебной деятельности учащихся, и внешние условия, влияющие на эти процессы. Поэтому такой анализ позволяет более точно выявлять причины ошибок и намечать меры по их предупреждению.

Однотипность упражнений.

Совокупность упражнений одного и того же типа условимся называть однотипной системой упражнений. Известно, что для формирования прочных навыков однотипные упражнения необходимы. В то же время они приводят к механическому, неосознанному решению, к ошибкам и т.д. Вероятно, из-за этого диалектического противоречия наблюдаются противоположные методические подходы относительно реализации принципа однотипности упражнений.

Авторы учебников и задачников придерживаются часто самых противоположных точек зрения относительно однотипности системы упражнений. Это можно объяснить отсутствием в методике математики единых теоретических установок. Рассмотрим поэтому данный вопрос на основе системы закономерностей. При изучении каждой темы по математике учащиеся должны приобрести умения и навыки решения задач. По закономерности II.1, это возможно лишь при неоднократном решении задач данного типа. Известны, правда, факты, когда у способных учащихся формируются прочные обобщенные ассоциации при решении минимального числа однотипных задач, иногда одной-двух. Однако таких способных учащихся в классе немного, а учить надо всех. В соответствии с закономерностью II.6 количество однотипных задач можно уменьшить лишь постепенно, по мере развития учащихся и накопления ими знаний и навыков по данному предмету. Учителя по опыту знают (и это соответствует закономерности II.6), что при изучении новой темы слабоуспевающим учащимся требуется выполнить большее число тренировочных упражнений, чем хорошо успевающим. Но методика урока строится обычно так, что на дом всем учащимся задают одинаковое число упражнений, а на самом уроке сильные учащиеся успевают решить больше задач. Следовательно, вопреки закономерности II.6 слабоуспевающие учащиеся упражняются меньше, и это – одна из причин их отставания и замедленного развития. Такое расхождение между потребностью и действительностью должно приводить к ослаблению внимания.

В домашнее задание по математике включают обычно и совсем простые упражнения, и задачи чуть посложнее. Рассмотрим теоретически, может ли слабоуспевающий учащийся осуществить поиск решения задачи. Такое задание он не может выполнить на основе послепроизвольного внимания, так как не знает приемов поиска решения задачи (см. закономерность III.3). Возникновение непроизвольного внимания к этому заданию также маловероятно, поскольку активную мыслительную деятельность невозможно осуществить без сознательно поставленной цели. Исключается также возможность возникновения произвольного внимания, так как слабоуспевающему учащемуся очень трудно сосредоточиться путем волевых усилий. Следовательно, данное задание для него непосильно. Какие изменения в поведении этих учащихся можно ожидать, если чередовать задачи знакомых им типов? Поиск решения здесь осуществлять уже не надо, достаточно вспомнить известный способ решения. Но это не всегда удается слабоуспевающим учащимся, из-за чего теряется уверенность, а значит, ослабляется внимание.

Чтобы обеспечить на уроках устойчивое внимание всех учащихся и сформировать у них прочные умения и навыки, необходимо непременно сохранить однотипность системы упражнений, а для нейтрализации ее отрицательных последствий одновременно использовать другие принципы.

Принцип непрерывного повторения.

В однотипную систему упражнений по новой теме с первого момента ее изучения включаются задачи из предшествующих разделов. Цель их включения – устранение отрицательного влияния закономерностей II.2 – II.5; II.10 и другие. При этом одновременно осуществляется систематическое, непрерывное повторение изученного материала. Обозначим условно такую систему в виде

Т1,Т2,Т3,М1,(М2?),Т4,Т5,М3,Т6,Т7,Т8,К1,Т9,…, (1)

где Т1,Т2,Т3,… — задачи одного типа по новой теме;

М1,М2,…, К1,К2,… — задачи других типов из пройденных тем.

Условия применимости принципа непрерывного повторения:

Последовательность упражнений в системе (1) определяется не столько автором задачника, сколько учителем. Только он может, учитывая уровень знаний и развитие своих учащихся, при подготовке и по ходу урока изменять число задач одного типа, следующих друг за другом.
Основная цель урока – изучение новой темы. Поэтому большинство задач в системе (1) должно быть по новой теме.
Главная цель использования принципа непрерывного повторения – устранение отрицательного влияния закономерностей Шеварева и II.10. Отсюда вывод: из пройденных тем желательно подбирать такие упражнения, которые по отдельным внешним признакам сходны с упражнениями новой темы.
Когда решаются комбинированные задачи, насыщенные разнообразным материалом из предшествующих разделов, принцип непрерывного повторения осуществляется сам собой. Однако когда удается решать подряд много комбинированных задач, то необходимость чередования задач различных типов ощущается особенно остро.
При использовании принципа непрерывного повторения общее число упражнений того или иного типа фактически не уменьшается в сравнении с однотипной системой. Только упражнения этого типа рассредоточиваются на более длительное время.

Контрпримеры.

Контрпримером условимся называть любую задачу, которая помогает выявить, а значит, и устранить имеющиеся у учащихся ошибочные ассоциации. В этом определении учитываются только дидактические соображения.

В роли контрпримеров могут выступать задачи с неполными или противоречивыми условиями и любые другие упражнения, провоцирующие учащихся на ошибки. Мы именно провоцируем, а учащиеся догадываются, что это своего рода игра. Они, наоборот, стараются не ошибиться, внимание их усиливается.

Некоторые методисты и психологи подчеркивают, что контрпримеры (или, по терминологии психологов, «отрицательные примеры») предотвращают «скороспелые суждения» и на начальных этапах изучения данной темы, и в дальнейшем.

На всех уроках без исключения, где используются контрпримеры, наблюдается следующая характерная особенность. Решение контрпримера, сопровождаемое анализом допущенной ошибки, производит на учащихся столь сильное впечатление, что в классе в момент обсуждения обычно не остается равнодушных и невнимательных.

Контрпримеры позволяют на изучаемом математическом материале создавать на уроках игровые ситуации. Сравним их с народными детскими играми «на внимательность». Контрпримеры – это те самые «перевертыши», необходимость которых для детей многие годы доказывал писатель К.И.Чуковский. детям читают: «Ехала деревня мимо мужика», а они радостно сообщают взрослым о замеченных ошибках. В контрпримере другое содержание – математическое, а игровая ситуация и эмоции такого же типа. Только среди старших школьников или студентов эти эмоции проявляются более сдержанно. Но всегда наблюдается повышенный интерес, заостренное внимание и часто дружный смех, быстро сменяющийся напряженной работой.

Следует учесть ряд существенных организационных приемов. Как правило, контрпримеры решаются в классе под наблюдением учителя и ошибки сразу анализируются. Тогда в памяти учащихся сохраняется не сама ошибка, а ее анализ. По этой причине нежелательно включать контрпримеры в домашнее задание. Если учитель соблюдает игровые правила и по его внешнему поведению учащиеся не могут догадаться, в какой момент дается контрпример, то они начинают ожидать контрпримеры какую-то часть урока. Такое ожидание усиливает внимание учащихся (III.2д). При систематическом использовании контрпримеров напряженное внимание может перейти в привычку. Таким путем развивается внимание учащихся. Разумеется, контрпримеры используются не сами по себе. Они лишь изредка включаются в систему упражнений.

Принцип сравнения.

Под принципом сравнения в психолого-педагогической литературе понимают чередование упражнений на прямые и обратные операции и любых других задач, когда желательно показать их взаимосвязь, сходство и различия. Чтобы подчеркнуть важность чередования упражнений, некоторые авторы используют термин «перемежающееся противопоставление».

В зависимости от содержания изучаемого материала, цели урока и других соображений учитель может выбирать любой из трех принципов: непрерывного повторения, сравнения, включения в систему упражнений контрпримеров. Каждый из этих принципов в сочетании с однотипной системой позволяет ослабить ее недостатки и сохранить ее положительное влияние.

Принцип сравнения удобно использовать при одновременном изучении некоторых тем: сложения и вычитания дробей, умножения и деления положительных и отрицательных чисел, решения задач на нахождение дроби от данного числа и числа по величине его дроби и т.д.

Систематическое включение контрпримеров в систему упражнений приводит к тому, что, ожидая их, учащиеся начинают все чаще и чаще контролировать свои результаты, получаемые при решении задач, начинают постепенно выходить из-под отрицательного влияния закономерностей Шеварева, II.5 и другие, все реже допускают ошибки по невнимательности. Таким образом у них развиваются внимание, самоконтроль.

Принцип полноты.

Условимся считать, что система упражнений удовлетворяет принципу полноты, если совокупность ее задач и способы их решения не способствуют формированию ошибочных ассоциаций и позволяют учащимся глубоко усваивать все необходимые вопросы изучаемой темы. Целесообразность использования принципа полноты непосредственно следует из нескольких закономерностей: II.1;II.3, и в первую очередь из II.5.

Часто принцип полноты нарушается учителями. Из-за медленного темпа работы на уроках, сокращения числа уроков и по другим причинам многие учителя не успевают рассмотреть с учащимися часть задач из школьных учебников. При этом далеко не каждый учитель умеет отобрать задачи, не нарушая определенной целостной системы, данной в учебнике. Чтобы уменьшить отрицательные последствия такого отбора, можно предложить следующую рекомендацию. Внутри каждой темы авторы учебников располагают упражнения несколькими блоками. Отдельные блоки содержат минимальное число упражнений, необходимых для изучения данной темы и расположенных в соответствии с определенными принципами. Учитель выбирает столько блоков по теме, сколько задач его учащиеся успевают решить на уроках и дома.

О соблюдении дидактических принципов при построении системы упражнений.

Система упражнений должна удовлетворять дидактическим принципам.

Задачи должны подбираться с последовательным нарастанием трудности. Это требование обычно выдерживается при изучении алгебры, но часто нарушается на уроках геометрии. Использование задач по готовым чертежам позволяет соблюдать дидактический принцип последовательного преодоления трудностей также и на уроках геометрии.

Многие авторы подчеркивают, что система упражнений должна содержать задачи, допускающие «изящные» решения. Включая такие задачи, мы осуществляем дидактический принцип индивидуального подхода. Обсуждение на уроках рациональных, «изящных» способов решения задач, предложенных отдельными учащимися, повышает интерес всего класса, усиливает внимание учащихся.

Особенно следует остановиться на дидактическом принципе доступности. Нарушение дидактического принципа доступности происходит в основном по двум причинам:

иногда из-за недостатков самой программы, учебников, в которых сначала предлагают недоступные для многих учащихся задачи, а затем рекомендуют опускать их;
часто из-за того, что учителя не учитывают возможностей учащихся своих классов.

Решаемые на уроках задачи должны быть доступными для всех учащихся (принцип доступности), но не чрезмерно легкими для хорошо успевающих учащихся (принцип индивидуального подхода).

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или систему, диаграмму, график, таблицу, функцию и т. д. Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные. На этом пути проблемы, с которыми сталкиваются учащиеся, носят различный характер. Иногда они связаны с непониманием физических, химических, экономических терминов, законов, зависимостей. Так, далеко не все четко осознают связь между расстоянием, скоростью и временем при равномерном движении или между работой, производительностью труда и временем и т. п. Ученики испытывают трудности в определении скорости сближения объектов при движении навстречу или в одном направлении, слабо ориентируются в движении по окружности, затрудняются в выборе размерности.

Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

Третья трудность состоит в том, чтобы составить функцию (отношение), применительно к которой формулируется вопрос задачи. Условно ее можно назвать функцией цели.

Четвертая трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным методом.

§ 2. Типичные ошибки и затруднения учащихся

при обучении математике в 5-6 классах.

5 класс

Тема	Ошибочно	Правильно
Вычислительные (арифметические ошибки, 5 кл.).	1) + 356 2) х326 3) _1224⏐12_ 2425 102 12 12 +652 _24 326__ 24 4912 0 4) _ 458 ⏐9_ 45 5 8 (ост.)	1) +356 2) х 326 3) _1224⏐12_ 2425 102 12__ 102 2781 + 652 _2 326__ 0_ 33252 _24 24_ 0 4) _ 458 ⏐9_ 45 50 8 (ост.)
Действия с обыкновенными дробями и смешанными числами.
Десятичные дроби.	1)+3,2 7 2) х1,2 3 3) 1,257 : 3,2 5,9 2,5 3,8 6 6 1 5 1,257⏐3,2 2 4 6_ 3 0 7,5 4) _1,25⏐5_ 1 0_ 25 _25 25 0	+3,27 2) х1,2 3 3) 12,57⏐32 5,90 2,5 9,17 61 5 4) 1,25⏐5__ 246__ 0 _ 0,25 0,307 5 1 2 1 0_ _ 25 25 0
Задачи на проценты.	Условие: найти 32 % от числа 1200. 1200 · 32 : 100 = 384 (непонимание сути, незнание определения процентов)	1200 : 100 · 32 = 384
Луч и прямая.	1) Луч А В 2) Луч ВА А В 3) Прямая А В 4) Прямой угол А В С 5) ∠АВС В С А	1) Луч А В 2) Луч АВ А В 3) Прямая А В 4) Прямой угол А В С 5) ∠ВАС В А С
Единицы измерения.	1 см2 = 10 мм2 1 м3 = 100 см3	1 см2 = 100 мм2 1 м3 = 100000 см3

6 класс

Тема

Ошибочно

Правильно

Разложение на простые множители.

248 2

124 4

31 31

4 – составное число, поэтому оно не может входить в разложение на простые множители.

248 2

124 2

62 2

31 31

Действия с обыкновенными дробями с разными знаменателями.

Отношение пропорции.

Задача на обратную пропорциональную зависимость.

длина ширина

I 3,6 м 2,4 м

II 4,8 м х м

длина ширина

I 3,6 м х м

II 4,8 м 2,4 м

Положительные и отрицательные числа.

– 5 + 3 = 2
(- 2) + (- 7) = 9
6 – 10 = 4
– 2 – 7 = — 5

1) – 5 + 3 = — 2

2) (- 2) + (- 7) = — 9

3) 6 – 10 = — 4

4) – 2 – 7 = — 9

Решение уравнений.

Раскрытие скобок.

Приведение подобных.

3. Перенос слагаемых из одной части в другую

5 – (х — 2) = 5 + х – 2
с – (- 2 + х) = с – 2 — х

2х + х + 3 = 3х + 3 = 6х
5 – 2х + 3 + х = 3х + 8

2х + 7 + 3х = 2

2х + 3х = 2 + 7

9х = 3

х = 9 : 3

х = 3

5 – (х — 2) = 5 — х + 2
с – (- 2 + х) = с + 2 — х

2х + х + 3 = 3х + 3
5 – 2х + 3 + х = 8 — х

2х + 7 + 3х = 2

2х + 3х = 2 — 7

9х = 3

х = 3 : 9

х = 1/3

Координатная плоскость.

Точки на осях.

А(0;2) y

0 A x

А(0;2) y

0 x

Глава II. Пути и средства предупреждения и исправления ошибок и затруднений учащихся 5-6 классов.

§ 1. Методы и приемы обучения математике, используемые учителем для предупреждения ошибок и затруднений.

На протяжении 2015-2016 г.г. автором были изучены более 1000 ошибок учащихся V классов. Для обработки и классификации собирались ошибки, сделанные школьниками в контрольных, самостоятельных и домашних работах по математике. Было выделено двенадцать видов ошибок, которые могли дать ключ к пониманию причин затруднений учащихся.

Вид ошибки	количество
Решение даже не начато	32
Вычислительная ошибка в элементарном действии	39
Вычислительная ошибка в многошаговом действии	320
Установление неправильных связей между данными задачами	144
Неправильное понимание условий задачи	186
Ошибки при переписывании	39
Незнание алгоритмов математических действий	73
Неэквивалентные преобразования	62
Ошибки геометрических измерений	29
Незнание математических формул	43
Незнание законов арифметики	52
Логические ошибки	11

Каждому школьнику доводилось делать вычислительные ошибки. Если предложить пятикласснику умножить устно 75 на 75, и ошибка будет гарантирована. Чтобы предотвратить вычислительные ошибки в многошаговых арифметических действиях, мы должны готовить детей к овладению алгоритмами, разбивающими сложные действия на элементарные. Но для того, чтобы выделить элементарные действия, необходимо установить уровень заданий, доступный любому учащемуся. К этому уровню могут относиться: сложение однозначных или двузначных чисел без перехода единиц в старший разряд; вычитание однозначных или двузначных чисел без перехода единиц в старший разряд; вычитание однозначных или двузначных чисел при условии, что число единиц в соответствующем разряде уменьшаемого больше числа единиц в разряде вычитаемого; умножение однозначных чисел; умножение двузначных чисел на однозначные, при котором нет необходимости проводить операции сложения и произведение остается двузначным числом; деление однозначных чисел; деление двузначных чисел на однозначные, при котором делитель является делителем числа единиц в каждом разряде. Все остальные арифметические действия с помощью алгоритмов должны разбиваться на элементарные.

Одним из наиболее трудных разделов арифметики остаются текстовые задачи. Они требуют от школьника применения не только знаний, полученных на уроках, но и использования жизненного опыта. Большие трудности встречают учащиеся V классов при формализации текстовых задач. Характерной ошибкой при решении текстовых задач с большим количеством числовых данных является не использование части условия. Для предупреждения подобных ошибок дети должны получить устойчивые навыки решения элементарных текстовых задач. Кроме того, уровень сложности предлагаемых учащемуся задач не должен ставить его в безвыходное положение.

Ошибки при переписывании сначала казались непредсказуемыми. Соответственно, было непонятно, как их классифицировать и какие меры принимать для профилактики. Как только задания стали значимыми для ученика, как только стало возможным использовать его жизненный опыт, то количество ошибок при переписывании резко уменьшилось.

Некоторые разделы математики V класса включают в себя обязательное изучение специальных алгоритмов. Например, если сложение и вычитание десятичных дробей не вызывает особых затруднений, то сложение и вычитание обыкновенных дробей дается менее способным ученикам гораздо труднее. Нередко при сложении 1/2 и 1/3 дети получают 2/5. И в этом ответе есть какая-то логика (не хватает только знания алгоритма сложения обыкновенных дробей). Для профилактики ошибок при работе с заданиями этих разделов необходимо изучение типовых примеров решения подобных задач.

При решении простейших уравнений школьники сталкиваются с необходимостью приведения эквивалентных преобразований. Распространены ошибки в определении знака одночлена при его переносе в другую часть уравнения, неоправданно меняются знаки одночленов, не поменявших свое расположение относительно знака равенства. Встречаются ошибки, связанные с непониманием сущности числового коэффициента переменной.

Ошибки геометрических измерений связаны с отсутствием навыков работы с линейкой и (гораздо чаще) с транспортиром. Их количество увеличивается при использовании прозрачных средств измерений. Для профилактики таких ошибок необходимо, чтобы учащиеся усвоили понятия точки отсчета и единицы измерения. Надо до начала практических измерений закрепить соотношения используемых единиц одной физической величины.

Одним из трудных разделов математики V класса является раздел, посвященный изучению прямоугольных параллелепипедов. Учащийся, который не знает формул объема, абсолютно не в состоянии решать соответствующие задачи. Однако в заданиях этого раздела есть и объективные трудности. Ученик должен усвоить и единицы объема, и их взаимоотношения между собой. Менее способные дети обычно бывают неприятно поражены соотношениями кубических метров и кубических сантиметров, кубических метров и кубических километров и т. п. Привычные для них названия единиц (метры, сантиметры), приобретя дополнительное прилагательное, в разделе объемов резко меняют свои отношения. Для решения некоторых заданий необходимо пространственное воображение. Отдельным учащимся очень трудно решать задачи по определению объема тел, представленных на рисунках и чертежах (особенно если эти тела составлены из нескольких параллелепипедов). Для профилактики таких ошибок необходимо проводить занятия с моделями, которые должны быть доступны для исследования каждому ученику. Хорошие результаты могут принести занятия с разборными моделями параллелепипедами.

При изучении законов арифметики значительная часть ошибок приходится на распределительный закон умножения. При умножении одночлена на многочлен не усвоившие распределительный закон умножения учащиеся, делают только одно действие умножения, а оставшуюся часть многочлена записывают без проведения необходимых действий. Для профилактики таких ошибок полезно чертить схемы умножения, соединяя стрелками все сомножители.

Наиболее редкие логические ошибки. Несомненно, что это связано в первую очередь с тем, что пятиклассникам не часто предлагаются логические задачи. Для профилактики логических ошибок необходимо повысить число логических заданий в учебных пособиях для V классов.

К задачам провоцирующего характера будем относить все такие задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. В методической литературе такие задачи называют еще задачами-ловушками.

Дидактическая ценность провоцирующих задач неоспорима – они служат действенным средством предупреждения различного рода заблуждений или ошибок школьников. Попадая в заранее подготовленную ловушку, ученик испытывает смущение, досаду, сожаление от того, что не придал особого значения тем нюансам и условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность (многие, большинство и т.п.) и адресность (учащиеся такого-то класса), не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадет.

Совершая ошибку на глазах учителя или учащихся и осознавая провоцирующий характер учебной ситуации, ученик испытывает сильнейшее впечатление, надолго запоминает ошибочные действия и в дальнейшем на подсознательном уровне остерегается их.

Провоцирующие задачи обладают высоким развивающим потенциалом. Они способствуют воспитанию одного из важнейших качеств мышления – критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятием математикой.

Несмотря на эти и другие положительные качества, феномен провоцирующих задач изучен недостаточно.

При самом первом рассмотрении полезно выделить следующие разновидности задач провоцирующего характера:

Задачи, условия которых в той или в иной форме навязывают неверный ответ.
Задачи, условия которых тем или иным способом подсказывают неверный путь решения.
Задачи, вынуждающие придумывать, составлять, строить и т. п. Такие математические объекты, которые при заданных условиях не могут иметь места.
Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов, словесных оборотов, буквенных или числовых выражений.
Задачи, условия которых допускают возможность «опровержения» семантически верного решения синтаксическим или иным нематематическим способом.

I. Задачи, условия которых в той или в иной форме навязывают неверный ответ.

1А. Задачи, навязывающие в явной форме один вполне определенный ответ.

Пример.

Сколько цифр потребуется, чтобы записать двенадцатизначное число?

Навязывается ответ: «12 цифр», но это не так, поскольку десятичная система счисления обходится всего лишь десятью цифрами. Правильный ответ: «Двенадцатизначное число можно записать с помощью одной, двух, трех, четырех, пяти, шести, семи, восьми, девяти, десяти цифр».

1Б. Задачи, побуждающие сделать выбор ответа из предложенной совокупности неверных ответов.

Пример.

Какое из чисел 205, 206, 207, 208, 209, 210 является простым?

Чаще всего учащиеся считают простым число 209 или 207, но это неверно. Все записанные выше числа являются составными. Правильный ответ: «Никакое».

1В. Задачи, побуждающие сделать неправильный выбор ответа из предложенной совокупности верных и неверных ответов.

1Г. Задачи, условия которых не содержат в явном виде неверного ответа, но каким-либо образом указывают на него.

Пример.

Какое простое число следует за числом 200?

Напрашивается ответ: 201, ведь это число следующее – за числом 200. Но этот ответ неверен, так как число 201 – составное. На самом деле искомое число 211.

II. Задачи, побуждающие к выбору неверного способа решения. Их тоже можно разделить на четыре типа.

2А. Задачи, условия которых подталкивают решающего к тому, чтобы выполнить какое-либо действие с заданными числами или величинами, тогда как выполнять это действие вовсе не требуется.

Пример.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Хочется выполнить деление 15:3 и тогда ответ – «5 км». На самом же деле деление выполнять вовсе не требуется, поскольку каждая лошадь проскакала столько же, сколько и вся тройка, т.е. 15 км.

2Б. Задачи, условия которых подталкивают решающего к выполнению какого-то определенного действия, тогда как выполнять нужно другое (зачастую обратное) действие.

Пример.

У палки 2 конца. Если один из них отпилить, сколько концов получиться?

Сразу кажется, что нужно выполнить вычитание 2 – 1 , что приводит к явно несуразному ответу «у палки один конец». На самом деле нужно находить не разность 2 – 1 , а сумму 2 + 2. Правильный ответ: «4 конца».

2В. Задачи, условия которых подталкивают решающего к выполнению какого-то одного или нескольких действий вполне определенным образом, тогда как выполнять действия нужно иначе. Чаще всего, необходим более сложный расчет.

Пример.

На руках 10 пальцев. Сколько пальцев на 10 руках?

При такой формулировке задачи решающему трудно преодолеть искушение выполнить умножение 10 ⋅ 10, хотя легко непосредственно сосчитать реальное число пальцев на 10 руках, т.е. у пяти человек: 10(10:2) = 50.

2Г. Задачи, условия которых подталкивают решающего к выполнению какого-либо действия или процедуры, тогда как выполнить их не представляется возможным в принципе.

Пример.

Двое пошли, 3 гриба нашли. Четверо пойдут, сколько грибов найдут?

Напрашивается последовательность действий:

1) 4:2 = 2, 2) 3⋅ 2 = 6, т.е. четверо вроде бы найдут 6 грибов. Но они могут вообще ничего не найти, если им не повезет. Правильный ответ: «Не известно».

III. Задачи, вынуждающие придумывать, составлять, строить и т. п. несуществующие при заданных условиях математические объекты.

Пример.

Придумайте простое трехзначное число, в записи которого употребляются лишь цифры 1 и 4.

Придумать такое число невозможно, поскольку любое число, удовлетворяющее условию задачи, кратно 3 и, стало быть, не является простым.

IV. Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов, словесных оборотов, буквенных и числовых выражений.

Пример.

На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза?

Имеется в виду не математическое «действие», а просто игра с бумажным листом. Если перевернуть лист, на котором написано 606, то увидим запись 909, т.е. число, которое в 1,5 раза больше, чем 606.

V. Задачи, допускающие возможность «опровержения» семантически верного решения синтаксическим или иным нематематическим решением.

Пример.

(Старинная задача). Крестьянин продал на рынке трех коз за 3 рубля. Спрашивается: «По чему каждая коза пошла?»

Очевидный ответ: «По одному рублю», опровергается: козы по деньгам не ходят, а ходят по земле.

Логические ошибки возникают в результате нарушения основных принципов математических рассуждений.

Ошибки в определении понятия. Примеры.

1. Равносильными уравнениями называются такие уравнения, когда корни первого уравнения являются корнями второго уравнения.

2. Квадратное уравнение с одним неизвестным – это уравнение, содержащее неизвестное во второй степени.

3. Прямая, делящая сторону треугольника пополам, называется медианой.

4. Отрезок, соединяющий середины сторон треугольника и равный половине третьей стороны, называется средней линией треугольника.

Во всех приведенных примерах нарушено основное требование к установлению определения понятия – наличие необходимых достаточных признаков объекта. Мерой предупреждения таких ошибок являются в первую очередь тщательная отработка определения понятия, в частности, с помощью метода сравнения объектов, а кроме того, опровержение примерами. Так, для первого примера ценными являются упражнения такого вида:

Являются ли равносильными уравнения х – 2 = 0 и (х – 2 ) (х – 3) = 0?
Являются ли равносильными уравнения х – 2 = 0 и х + 3 = 5?

И т.д.

Для второго примера возможны упражнения такого вида:

Какие из приведенных уравнений являются квадратными?

а) х2 – 3х + 2 = 0; б) х3 + х2 – 3х = х3 – 2; в) х3 – х2 + 3х = х3 – 2; г) х2 – 4.

В третьем примере ошибка в определении медианы стороны треугольника могла возникнуть в том случае, когда при определении понятия не сопоставлялись проведенные различные отрезки в треугольнике и прямые, делящие сторону треугольника пополам.

Ошибки при доказательстве теорем. Наиболее распространенной ошибкой при доказательстве теорем является использование при доказательстве искомого как данного. Предупредить такую ошибку можно только четким выяснением, что дано, что надо доказать

Логической ошибкой в доказательстве утверждений является неполная аргументация или пропуск в аргументации. В курсе восьмилетней школы аргументация чаще всего допускается учениками в доказательствах при решении задач, например при построении, реже при доказательстве помещенных в учебнике теорем.

Логической ошибкой является неполная дизъюнкция. Особенно часто эта ошибка допускается в вопросах и задачах, связанных с исследованием.

Пример.

Требуется установить сравнительную величину а3 и а2; вместо того чтобы исчерпать все возможные значения буквы а, ученик рассматривает значение выражений при а > 1 и в результате получает неполный ответ.

Встречается много логических ошибок в преобразованиях алгебраических выражений, когда ученики пользуются необоснованной аналогией.

Известны распространенные ошибки такого вида: так как (a + b)c = ac + bc , то по аналогии (ab)c = ac⋅bc; известно, что если а = b, то ak = bk, отсюда по аналогии считают, что, если a > b, то ak > bk в любом случае; по аналогии с численными дробями ученик иногда считает, что . Предупредить эти ошибки или искоренить их можно постоянным напоминанием школьникам (при этом не только словами, но и соответствующими примерами), что аналогия может служить только вспомогательным средством для установления истины и постоянно требует проверки и подтверждения логическим доказательством.

Чтобы не делать ошибок.

Известно небольшое число правил, следуя которым можно заметно уменьшить количество ошибок. Подобные формулировки принято относить к фольклору. Однако познакомить с ними учеников небесполезно.

По поводу того, где с наибольшей вероятностью может появиться ошибка, имеется неплохая формулировка.

Правило ГАИ. Большинство аварий происходит при небольшой скорости.

Иными словами, ошибки чаще всего возникают в простых ситуациях.

В частности, нужно с особой тщательностью проверять, верно ли списано условие задачи, решено квадратное уравнение и т.п. Окончанию решения задачи обычно уделяется минимум внимания – все трудности позади. Именно в конце чаще всего появляются ошибки. Поэтому начинать поиск ошибки лучше с конца.

Получив неверный ответ, ученик обычно не знает, что с ним делать. На этот случай есть мудрая пословица: Нет худа без добра. Лучше неверный ответ, чем никакого.

Подставляя полученное значение корня последовательно от конца к началу в каждое из написанных соотношений, можно относительно быстро найти ошибочный переход.

Чтобы не делать ошибок в преобразованиях, полезно учитывать два совета.

Правило закройщика. Вручную обычной иголкой шов делается так: стежок вперед и назад, еще вперед и снова назад…

Выполнять преобразования нужно также, как закройщик делает шов – после каждого перехода нужно «оглянуться назад», проверить полученный результат обратным преобразованием.

Например, вынесли множитель за скобки – раскройте скобки и проверьте, получится ли прежнее выражение.

Правило программиста. Работай блоками.

Невозможно отлаживать программу в целом. Следует разбить работу на небольшие автономные блоки и проконтролировать правильность каждого такого блока.

Сказанное означает, в частности, что при работе с громоздким выражением полезно разбить его на небольшие «блоки» и упростить каждый из них.

При решении системы уравнений следует сначала разобраться с каждым уравнением в отдельности.

Об ошибках в оформлении и «точке с запятой».

Сталкиваясь со школьными «требованиями к оформлению», вузовский преподаватель приходит в некоторое замешательство. Дело в том, что упомянутые требования носят вне математический характер и практически не связаны с проверкой знаний. Последнее особенно остро ощущают сильные, хорошо подготовленные ученики. Их откровенно (и справедливо) раздражает неписанное правило: «Два недочета = ошибка».

Единственное требование к любому математическому тексту состоит в ясном отражении логики решения задачи. При этом не играет роли, чертил ли автор текста поля, писал ли какие-то слова типа «обозначим», «так как… то» или изложил решение без слов – при помощи общеупотребительных символов.

Например, по вузовским меркам запись

является исчерпывающей и в словесном комментарии не нуждается. Важно, чтобы школьник верно преобразовал неравенство, а не цитировал по памяти полуграмотную фразу: «Так как основание логарифма меньше единицы, то функция убывает и знак неравенства меняется».

Современный экзамен по характеру часто приближается к тестированию. А в таких условиях остается и вовсе одно единственное требование к оформлению – разборчивая запись ответа.

Увлечение оформительством мешает обратить внимание на вещи более серьезные. Например, для уравнения нередко предлагается следующее решение:

ОДЗ: 2 – х ≥ 0; х ≤ 2.

По теореме Виета х1 = 1, х2 = -2.

Проверка показывает, что х2 не удовлетворяет условию. Ответ: 1.

Изложенное решение обычно оценивается как верное. Однако предложенная последовательность записей оставляет ряд неясностей:

ОДЗ в решении не использовалось. Зачем нужно было ее искать?
Один из двух корней «не удовлетворяет условию». Откуда же он взялся? Понимает ли ученик, что к появлению постороннего корня привела не ошибка, а использованное при решение возведение в квадрат?
Какими логическими знаками следует связать сделанные записи?
Какой математический закон обязывает считать х1 и х2 значениями переменной х? (Ведь в геометрии, например, точки А и А1 не имеют, вообще говоря, ничего общего.) Разумеется, из контекста ясно, что обозначено привычными символами х1 и х2 . Но зачем подменять ясные математические записи около математическими условностями?

Указанные в пункте 1,2 и 4 дефекты можно счесть не стоящими внимания придирками. Но упомянутое в пункте 3 отсутствие логических знаков – это серьезная ошибка. Впрочем, эта ошибка присутствует практически во всех работах школьников и абитуриентов.

Приведем для сравнения иную редакцию решения:

Поскольку возведение в квадрат могло привести к появлению посторонних корней, необходима проверка. Ответ: 1.

Если вместо первой импликации «⇒» ученик напишет «⇔», то это будет ошибкой. Если же любую из оставшихся эквиваленций «⇔» заменить на «⇒», то все останется верным.

Автор первого варианта решения, вероятно, просто не думал о логических связях сделанных им записей и механически разделял их символом «точка с запятой».

Впрочем, если бы «точка с запятой» употреблялась только в одном строго определенном смысле, то все было бы не так плохо. Но на самом деле этот символ в работах школьников может заменять символы «следовательно», «равносильно», «равносильно при дополнительных условиях», означать как «и», так и «или», «объединение» или «пересечение» множеств. Нередки, например, записи следующего типа: «».

В худшем для ученика случае в подобных записях отмечается «недочет», но чаще всего претензий не предъявляется. Стоит ли говорить о каких-то «ошибках в оформлении», если из поля зрения выпадает главное – верное отражение логики решения задач.

§ 2. Контроль и самоконтроль учебной деятельности школьников как средство выявления ошибок и затруднений.

Бесспорно, что при проверке работ учитель обязан отмечать все ошибки учеников – математические, стилистические и грамматические. Многие учителя исправляют ошибки сами. Мы полагаем, что этого делать не следует; в том случае, когда ошибка исправлена учителем, на долю ученика остается «согласиться» с исправлением и успокоиться. Перестройка школы требует усиления самостоятельной работы учащихся на всех этапах обучения. Важно, чтобы и при разборе ошибок ученик сам установил, в чем его ошибка, умел найти источник возникновения ее и пути исправления. Поэтому достаточно того, что учитель указывает место ошибки. Практика такого подхода к исправлению ошибок в письменных работах достаточна широка и оправдала себя. Для указания места ошибки вводятся условные знаки: для грубых ошибок две черты, для негрубых и случайных – одна черта и для недочетов – волнистая линия.

При домашнем анализе работ учитель не может ограничиться только проверкой и сопоставлением ответов или беглым просмотром хода рассуждений или последовательности преобразований. Надо тщательно просматривать все преобразования, вычисления и рассуждения. Результаты поспешной проверки работ могут поставить учителя в неприятное положение. При анализе работ надо систематизировать ошибки и недочеты, выделить типичные и массовые ошибки, в первую очередь принципиальные, грубые, связанные с нарушением основных законов математике. На таких ошибках и должно быть сосредоточено внимание учащихся при разборе ошибок в классе. Этот разбор никак нельзя ограничивать сообщением каждому ученику его ошибок и проставленной за работу оценки. Ошибки надо разбирать, при этом к разбору ошибок и причин, породивших их, следует привлекать, учеников, в первую очередь допустивших ошибки и пассивных в общей работе. Известно, что иногда достаточно перед учениками поставить вопрос, можно ли так делать, как допустивший ошибку «спохватывается» и сам указывает, в чем ошибка и как ее исправить. Таким образом, этап разбора ошибок становится обучающим и мобилизующим мысль ученика.

Вопросы и задачи, вызвавшие затруднения у многих учеников, необходимо особенно детально и тщательно разбирать в классе, иногда следует даже провести дополнительные упражнения. Если в классе проведен тщательный анализ ошибок (установлены источники их и намечены пути их и намечены пути их исправления), то учитель может предложить ученикам, допустившим ошибку, переделать задачу или внести нужные исправления, не сопровождая их указаниями на соответствующие теоремы, правила, законы. Если же ошибка не была массовой или явилась повторной, то рекомендуется предложить ученику дома произвести детальный разбор ее, то есть внести исправления и сделать нужные ссылки на соответствующие правила.

Анализ работ учитель должен провести к очередному уроку по предмету и на этом уроке разобрать с учениками ошибки. Отсрочка проверки и разбора работ в классе ведет к потере интереса учащихся к разбору, часто разбор вклинивается в начатую уже работу по новой теме; несвоевременно проставленные в журнале и дневнике оценки работ часто вызывают законные упреки в адрес учителя со стороны классного руководителя и родителей.

§ 3. Система работы учителя математики при коррекции ошибок учащихся 5-6 классов.

Положительный эффект индивидуальных заданий несомненен, особенно домашних, так как ученики выполняют их в основном самостоятельно. Просматривая индивидуальные работы вместе с теми учащимися, которые их делали, нужно вовлекать ребят в беседу, расспрашивая об испытанных трудностях, о примененных законах, определениях и т. д.

Индивидуальные задания должны быть составлены методически правильно и четко направлены на преодоление конкретных ошибок. Чтобы справиться с такого рода методической задачей, учителю необходимо постоянно вести учет основных затруднений учащихся. Для этого можно использовать специальную тетрадку, разграфленную так, как показано ниже.

Таблица

Список

учащихся

класса

Тема…

Примечание

«+» — ошибка

устранена;

«-» — ошибка

не устранена

Пробелы в

знаниях

Классные индивидуальные задания

Домашние индивидуальные задания

Все графы таблицы, кроме первой, заполняются карандашом, чтобы можно было стирать записи и заменять их другими по мере преодоления ошибок. Список ошибок пополняется во время проверки домашних заданий, самостоятельных и контрольных работ и при проведении зачета, хотя ошибки в своем большинстве неоригинальны. По каждой теме они повторяются из года в год. Молодому учителю будет полезно ознакомиться с ошибками, которые учащиеся допускают при изучении математики в V — VI классах.

Ниже будут перечислены типичные ошибки и указаны приемы их устранения, которые можно реализовать в индивидуальных заданиях.

При выполнении действий над десятичными дробями учащиеся допускают ошибки в выделении целой части результата, например: 3,4 + 5,3 = 87; 4,2 — 1,8 = 24; 4,1* 1,1 = 451; 2,4 : 2 = 12.

При беседе с учащимися, допустившими такую ошибку, выясняется, что они просто забыли поставить запятую. Эта ошибка устраняется в результате длительных тренировок.

Самая типичная ошибка допускается при делении десятичной дроби на десятичную: делят, не обращая внимания на запятые, например так: 2,576 : 11,2 = 23. Обычно учащиеся знают правило деления, но затрудняются различить делимое и делитель.

Для устранения этих ошибок можно давать учащимся задания на карточках, в которых каждый пример сопровождается тем или иным правилом, сформулированным полностью или с пропусками.

Примеры некоторых карточек.

Карточка №1. Чтобы сложить две десятичные дроби, надо:

а) уравнять число знаков … в слагаемых;

б) записать слагаемые друг под другом так, чтобы запятая …;

в) сложить получившиеся числа, как складывают …;

г) в полученной сумме поставить запятую под … .

Задания.

1. Уравняйте число знаков после запятой в следующих числах: 2,5; 0,25; 43, 1256; 325,1.

2. Сложите дроби 12,7 и 3,442; 0,237 и 10,44.

Карточка № 2.

Чтобы умножить дну десятичную дробь на другую, надо выполнить умножение, не обращая внимание на …, а затем в результате отделить запятой… столько цифр, сколько их стоит после запятой… .

Задания.

1. В записи 1234567 отделите запятой справа: а) одну цифру; б) две цифры; в) шесть цифр; г) семь цифр. В каком случае в результате получается число, которое больше 1, но меньше 2 ? больше 0, но меньше 1?

2. Перемножьте числа 2,7 и 1,32.

Карточка № 3.

Чтобы разделить число на десятичную дробь, надо в делимом и в делителе перенести … вправо на столько цифр, сколько их после… в …, а потом выполнить деление на натуральное число.

Задания.

1. В записи 2,88 : 0,8 подчеркните одной чертой делимое, а двумя — делитель.

2. В числах 1; 0,05; 3,25 перенести запятую вправо на столько цифр, сколько их после запятой в числе 0,5.

3. Разделите 2,576 на 1,12.

Наиболее распространены ошибки в действиях обыкновенными дробями. Так, при сложении (вычитании) дробей складывают (вычитают) числители и знаменатели:

Складывая (вычитая) дроби, забывать умножить их числители на дополнительные множители:

Целую часть прибавляют к числителю без приведения к общему знаменателю:

От целой части отнимают числитель без приведения к общему знаменателю:

Учащимся, допускающим такого рода промахи, можно предложить индивидуальные задания, которые побуждают к поиску ошибок и установлению парадоксальности неверных результатов.

Карточка № 4.

Сумма положительных чисел не может быть равна одному из слагаемых. Не может она и быть меньше какого-либо слагаемого.

1. Учитывая эти свойства положительных чисел, объясните, в чем кроется ошибка следующего действия:

а) б) 5 +

2. Среди данных действий подчеркните верные, а неверные выпишите отдельно и исправьте:

а)

Карточка № 5.

Известно, что вычитание проверяется и тем, что разность двух положительных чисел не может быть больше уменьшаемого.

1. Учитывая сказанное выше, установите, верен ли результат вычитания:

а) 3 — ; б)

2. В данных ниже равенствах поставьте вместо квадратиков такие числа, чтобы равенства стали верными:

а) • = б) • = в) •.

Ошибки при умножении и делении смешанных чисел связаны с неумением превращать их в неправильную дробь.

Умножают отдельно целые и отдельно дробные части, например:

⋅

Делят целые части чисел, а дробную часть первого числа просто переписывают:

Умножают (делят) только дробные части чисел:

1) ⋅ 2)

При умножении (делении) смешанного числа на десятичную дробь умножают (делят) отдельно целые части и отдельно дробные, а результаты записывают рядом, например:

⋅

Для устранения этих ошибок практикуют задания, в которых от учащихся требуются доказательства ложности некоторых выводов.

Карточка № 6. Известно, что деление проверяется умножением, а умножение – делением. Существуют и другие способы проверки. Они основаны на том, что, например, произведение двух чисел, больших единицы, не может быть меньше единицы, а частное от деления двух неравных чисел не может быть равно единице.

1. Пользуясь этими правилами, что в следующих действиях допущены ошибки. Исправьте результаты.

а) б) в)

2. В данных ниже равенствах вместо квадратиков вставьте нужные числа и объясните, как они найдены:

а) • = б) • =

Список литературы

Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе»- 1993 г. — №5, с. 9.
Груденов Я.И. психологический анализ причин некоторых массовых ошибок учащихся// Журнал «Математика в школе»- 1981 г. — №3, с. 46-48.
Груденов Я.И. Психолого-дидактические основы методике обучения математики. –газета «Математика», 1987 г. с. 91-96.
Зайкин М.И., Колосова В.А. Провоцирующие задачи. // Журнал «Математика в школе»- 1997 г. — №6, с. 32.
Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач. // Журнал «Математика в школе»- 2000 г. — №4, с. 28.
Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов.// Журнал «Математика в школе»- 1999 г. — №6, с. 21.
Ярский А.С. Что делать с ошибками. // Журнал «Математика в школе»- 1998 г. — №2, с. 8-14.
Журналы «Математика в школе» за 1970-1990 г.г.

Интернет-ресурсы

http://mat.1september.ru/view_article.php?ID=200900304
http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

— —

Источник

Контрольная работа по математике – это важное мероприятие, которое показывает, насколько хорошо ученик освоил материал по данному предмету. Однако, не все ученики успешно справляются с КР, из-за типичных ошибок. Рассмотрим их и способы их избежания.

Ошибка №1: Неправильное выполнение действий с дробями

Действия с дробями являются одним из самых сложных разделов математики в 6 классе, и часто ученики допускают ошибки при их выполнении. Самые распространенные ошибки – это неправильное сложение или вычитание дробей, а также умножение дроби на дробь.

Как избежать ошибки?

Не забывайте сокращать дроби
Проверяйте правильность выполнения действий
Убедитесь в правильности ответа путем приведения дроби к общему знаменателю

Ошибка №2: Ошибки при решении уравнений

Решение уравнений – это также один из сложных разделов математики в 6 классе, который требует особой внимательности при решении.

Как избежать ошибки?

Внимательно читайте условия уравнения
Не забывайте проверять правильность решения путем подстановки полученных значений обратно в уравнение
Используйте правильные методы решения уравнений

Ошибка №3: Неправильное округление результатов вычислений

Округление результатов вычислений – это еще один типичный и недопустимый вид ошибок на КР по математике.

Как избежать ошибки?

Убедитесь в правильности округления результата
Используйте правильные правила округления

Ошибка №4: Неправильное чтение графиков

Графики – это важное представление информации, которое требуется уметь анализировать и интерпретировать. Неправильное чтение графиков является еще одной типичной ошибкой на КР.

Как избежать ошибки?

Внимательно изучайте подписи осей и шкалы графиков
Проверяйте правильность установки значений на графике

Заключение

Избежание указанных выше ошибок поможет вам успешно справиться с контрольной работой по математике в 6 классе. Не забывайте также, что регулярное обучение и практика – это залог успешных результатов в учебе.

Источник

Примерные нормы оценок письменных работ по математике в 5-6 классах

Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Они обеспечивают единство требований к обучающимся со стороны всех учителей образовательного учреждения, сравнимость результатов обучения в разных классах. Применяя эти нормы, учитель должен индивидуально подходить к оценке каждой письменной работы учащегося, обращать внимание на качество выполнения работы в целом, а затем уже на количество ошибок и на их характер.

Содержание и объем материала, включаемого в контрольные письменные работы, а также в задания для повседневных письменных упражнений, определяются требованиями, установленными программой. Наряду с контрольными работами по отдельным разделам темы следует проводить итоговые контрольные работы по всей изученной теме.

По характеру заданий письменные работы могут состоять:

а) только из примеров; б) только из задач; в) из задач и примеров.

Контрольные работы, которые имеют целью проверку знаний, умений и навыков учащихся по целому разделу программы, а также по материалу, изученному за четверть (триместр) или за год, как правило, должны состоять из задач и примеров.

Оценка письменной работы определяется с учетом прежде всего ее общего математического уровня, оригинальности, последовательности, логичности ее выполнения, а также числа ошибок и недочетов и качества оформления работы. Ошибка, повторяющаяся в одной работе несколько раз, рассматривается как одна ошибка. За орфографические ошибки, допущенные учениками, оценка не снижается; об орфографических ошибках доводится до сведения преподавателя русского языка. Однако ошибки в написании математических терминов, уже встречавшихся школьникам класса, должны учитываться как недочеты в работе.

При оценке письменных работ по математике различают грубые ошибки, ошибки и недочеты. Полезно договориться о единой для всего образовательного учреждения системе пометок на полях письменной работы.

Грубыми в 5-6 классах считаются ошибки, связанные с вопросами, включенными в «Требования к уровню подготовки оканчивающих начальную школу» Образовательных стандартов, а также показывающие, что ученик не усвоил вопросы изученных новых

тем, отнесенные Стандартами основного общего образования к числу обязательных для усвоения всеми учениками. Так, к грубым относятся ошибки в вычислениях, свидетельствующие о незнании таблицы сложения или таблицы умножения, связанные с незнанием алгоритма письменного сложения и вычитания, умножения и деления на одно- или двузначное число и т.п., ошибки, свидетельствующие о незнании основных формул, правил и явном неумении их применять, о незнании приемов решения задач, аналогичных ранее изученным.

Примечание. Если грубая ошибка встречается в работе только в одном случае из нескольких аналогичных, то при оценке работы эта ошибка может быть приравнена к негрубой.

Примерами негрубых ошибок являются: ошибки, связанные с недостаточно полным усвоением текущего учебного материала, не вполне точно сформулированный вопрос или пояснение при решении задачи, неточности при выполнении геометрических построений и т. п.

Недочетами считаются нерациональные записи при вычислениях, нерациональные приемы вычислений, преобразований и решений задач, небрежное выполнение чертежей и схем, отдельные погрешности в формулировке пояснения или ответа в задаче. К недочетам можно отнести и другие недостатки работы, вызванные недостаточным вниманием учащихся, например: неполное сокращение дробей или членов отношения; обращение смешанных чисел в неправильную дробь при сложении и вычитании; пропуск наименований; пропуск чисел в промежуточных записях; перестановка цифр при записи чисел; ошибки, допущенные при переписывании, и т.п.

Оценка письменной работы по выполнению вычислительных заданий и алгебраических преобразований

Оценка «5» ставится за безукоризненное выполнение письменной работы, т.е.:

а) если решение всех примеров верное;

б) если все действия и преобразования выполнены правильно, без ошибок; все

записи хода решения расположены последовательно, а также

сделана проверка решения в тех случаях, когда это требуется.

Оценка «4» ставится за работу, в которай допущена одна (негрубая) ошибка или два-три недочета.

Оценка «3» ставится в следующих случаях:

а) если в работе имеется одна грубая ошибка и не более одной негрубой ошибки;

б) при наличии одной грубой ошибки и одного-двух недочетов;

в) при отсутствии грубых ошибок, но при наличии от двух до четырех (негрубых) ошибок;

г) при наличии двух негрубых ошибок и не более трех недочетов;

д) при отсутствии ошибок, но при наличии четырех и более недочетов;

е) если неверно выполнено неболее половины объема всей работы.

Оценка «2» ставится, когда число ошибок превосходит норму, при которой может быть выставлена положительная оценка, или

если правильно выполнено менее половины всей работы.

Оценка «1» ставится, если ученик совсем не выполнил работу.

Примечание. Оценка «5» может быть поставлена, несмотря на наличие одного-двух недочетов, если ученик дал

оригинальное решение заданий, свидетельствующее о его хорошем математическом развитии.

Оценка письменной работы на решение текстовых задач

Оценка «5» ставится в том случае, когда задача решена правильно: ход решения задачи верен, все действия и преобразования

выполнены верно и рационально; в задаче, решаемой с вопросами или пояснениями к действиям, даны точные и правильные

формулировки; в задаче, решаемой с помощью уравнения, даны необходимые пояснения; записи правильны, расположены

последовательно, дан верный и исчерпывающий ответ на вопросы задачи; сделана проверка решения (в тех случаях, когда это требуется).

Оценка «4» ставится в том случае, если при правильном ходе решения задачи допущена одна негрубая ошибка или два-три недочета.

Оценка «3» ставится в том случае, если ход решения правилен, но допущены:

а) одна грубая ошибка и не более одной негрубой;

б) одна грубая ошибка и не более двух недочетов;

в) три-четыре негрубые ошибки при отсутствии недочетов;

г) допущено не более двух негрубых ошибок и трех недочетов;

д) более трех недочетов при отсутствии ошибок.

Оценка «2» ставится в том случае, когда число ошибок превосходит норму, при которой может быть выставлена положительная оценка.

Оценка «1» ставится в том случае, если ученик не выполнил ни одного задания работы.

Примечания:

1. Оценка «5» может быть поставлена несмотря на наличие описки или недочета, если ученик дал оригинальное решение, свидетельствующее о его хорошем математическом развитии.

2. Положительная оценка «3» может быть выставлена ученику, выполнившему работу не полностью, если он безошибочно выполнил более половины объема всей работы.

Оценка комбинированных письменных работ по математике

Письменная работа по математике, подлежащая оцениванию, может состоять из задач и примеров (комбинированная работа). В таком случае преподаватель сначала дает предварительную оценку каждой части работы, а затем общую, руководствуясь следующим:

а) если обе части работы оценены одинаково, то эта оценка должна быть общей для всей работы в целом;

б) если оценки частей разнятся на один балл, например даны оценки «5» и «4» или «4» и «3» и т. п., то за работу в целом, как

правило, ставится балл, оценивающий основную часть работы;

в) если одна часть работы оценена баллом «5», а другая — баллом «3», то преподаватель может оценить такую работу в целом

баллом «4» при условии, что оценка «5» поставлена за основную часть работы;

г) если одна из частей работы оценена баллом «5» или «4»,а другая — баллом «2» или «1», то преподаватель может оценить

всю работу баллом «3» при условии, что высшая из двух данных

оценок поставлена за основную часть работы.

Примечание. Основной считается та часть работы, которая включает больший по объему или наиболее важный по значению материал по изучаемым темам программы.

Оценка текущих письменных работ

При оценке повседневных обучающих работ по математике учитель руководствуется указанными нормами оценок, но учитывает степень самостоятельности выполнения работ учащимися.

Обучающие письменные работы, выполненные учащимися вполне самостоятельно с применением ранее изученных и хорошо закрепленных знаний, оцениваются так же, как и контрольные работы.

Обучающие письменные работы, выполненные вполне самостоятельно, на только что изученные и недостаточно закрепленные правила, могут оцениваться менее строго.

Письменные работы, выполненные в классе с предварительным разбором их под руководством учителя, оцениваются более строго.

Домашние письменные работы оцениваются так же, как классная работа обучающего характера.

Устные ответы учащихся 5-6 классов.

Оценка устных ответов.

а) Ответ оценивается отметкой “5”, если учащийся:

1) полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником;

2) изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

3) правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

4) показал умение иллюстрировать теорию конкретными примерами, применять в новой ситуации при выполнении практического задания;

5) продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;

6) отвечая самостоятельно, без наводящих вопросов учителя.

Возможны 1-2 неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

б) Ответ оценивается отметкой “4”, если удовлетворяет в основном требованиям на оценку “5”, но при этом имеет один из недочетов:

1) в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

2) допущены 1-2 недочета при освещении основного содержания ответа, исправленные после замечания учителя;

3) допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

в) Ответ оценивается отметкой “3”, если:

1) неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программы;

2) имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

3) ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил обязательное задание.

г) Ответ оценивается отметкой “2”, если:

1) не раскрыто содержание учебного материала;

2) обнаружено незнание или не понимание учеником большей или наиболее важной части учебного материала;

3) допущены ошибки в определении понятия, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Источник

Задание «Проблемы,
типичные ошибки учащихся»

Вспоминается расхожая истина – умные люди
учатся на чужих ошибках. В математике приходится учиться, в основном, на
собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь
необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее
использовать.

Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти
ошибки.

Решая
уравнения и неравенства учащиеся допускают типичные ошибки:

·
Незнание
правил, определений, формул.

·
Непонимание
правил, определений, формул.

·
Неумение
применять правила, определения, формулы.

·
Неверное
применение формул.

·
Невнимательное
чтение условия и вопроса задания.

·
Вычислительные
ошибки.

·
Логические
ошибки

·
Раскрытие
скобок и применение формул сокращенного умножения.

Какие же проблемы, трудности общего
характера возникают у учащихся при изучении математики ( их несомненно можно
отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения
и неравенства»):

·
Пропуски
занятий приводят к незнанию материала, пробелам в знаниях.

·
Поверхностное,
невдумчивое восприятие нового материала приводят к непониманию его.

·
Недостаточная
мозговая деятельность приводит к неумению применять правила, определения и
формулы .

·
Неряшливый,
неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не
всегда сами понимают, что именно они написали.

·
Усталость. Чрезмерная
нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и,
как следствие, к многочисленным ошибкам.

·
Кратковременное
или полное переключение внимания с одной деятельности на другую (учебную или
внеучебную) приводит к утрате только что воспринятого материала, приходится все
начинать сначала.

·
Скорость
работы. Низкая
скорость выполнения мыслительных операций часто мешает ученику контролировать
себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь
одной частью задания удаляет из «оперативной памяти» информацию о другой, в
которой допускается не вынужденная ошибка. Скорость работы определяется
физиологией конкретного школьника и навыками выполнения тех или иных операций.

·
Мотивация.
Следствие низкой мотивации – потеря внимания и ошибка.

Ошибки, допускаемые обучающимися при решении уравнений
и неравенств, самые разнообразные: от неверного оформления решения до
ошибок логического характера.

1. Самая типичная ошибка состоит в том, что учащиеся
при решении уравнений и неравенств без дополнительных пояснений используют
преобразования, нарушающие равносильность, что приводит к потере корней
и появлению посторонних корней.

Предлагаю на конкретных примерах рассмотреть ошибки
подобного рода и определить способы их предупреждения и исправления, но прежде
всего хочу обратить внимание на следующую мысль: не надо бояться
приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться
потерять корни.

а) Решить уравнение:

log3(5 – x) = 3 – log3(–1 – x).

Это уравнение учащиеся очень часто решают следующим
образом.

log3(5 – x) = 3 –
log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)(
–1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x –
32 = 0,

х₁ = –4; x₂ = 8.

Учащиеся часто, не проводя дополнительных рассуждений,
записывают оба числа в ответ. Но как показывает проверка, число
x = 8 не является корнем исходного уравнения, так как при
x = 8 левая и правая части уравнения теряют смысл. Проверка
показывает, что число x = –4 является корнем заданного
уравнения.

б) Решить уравнение

х₁ = –4; x₂ = 8.

б) Решить уравнение dalin2.wmf

Область определения исходного уравнения задается системой

Для решения заданного уравнения перейдем к логарифму
по основанию x, получим

dalin4.wmf

Мы видим, что левая и правая части этого последнего
уравнения при x = 1 не определены, но это число является корнем
исходного уравнения (убедиться в этом можно путем непосредственной
подстановки). Таким образом, формальный переход к новому основанию привел
к потере корня. Чтобы избежать потери корня x = 1, следует
указать, что новое основание должно быть положительным числом, отличным от
единицы, и рассмотреть отдельно случай x = 1.

2. Целая группа ошибок, вернее сказать недочетов, состоит
в том, что учащиеся не уделяют должного внимания нахождению области
определения уравнений, хотя именно она в ряде случаев есть ключ
к решению.

3. Типичной ошибкой учащихся является то, что они не
владеют на нужном уровне определениями понятий, формулами, формулировками
теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.

Решить уравнение

Ученик предлагает следующее ошибочное решение этого
уравнения:

dalin9.wmf dalin11.wmf dalin13.wmf

х = –2.

Поверка показывает, что х = –2 не является
корнем исходного уравнения.

Напрашивается вывод, что заданное уравнение корней не
имеет.

Однако это не так. Выполнив подстановку х =
–4 в заданное уравнение, мы можем убедиться, что это корень.

Предлагаю проанализировать, почему произошла потеря
корня.

В исходном уравнении выражения х и х +
3 могут быть одновременно оба отрицательными или оба положительными, но
при переходе к уравнению х = –2.

Поверка показывает, что х = –2 не является
корнем исходного уравнения.

Напрашивается вывод, что заданное уравнение корней не
имеет.

Однако это не так. Выполнив подстановку х =
–4 в заданное уравнение, мы можем убедиться, что это корень.

Предлагаю проанализировать, почему произошла потеря
корня.

В исходном уравнении выражения х и х +
3 могут быть одновременно оба отрицательными или оба положительными, но
при переходе к уравнению dalin15.wmf эти же выражения
могут быть только положительными. Следовательно, произошло сужение области
определения, что и привело к потере корней.

Чтобы избежать потери корня, можно поступить следующим
образом: перейти в исходном уравнении от логарифма суммы к логарифму
произведения. Возможно в этом случае появление посторонних корней, но от
них, путем подстановки, можно освободиться.

4. Многие ошибки, допускаемые при решении уравнений
и неравенств, являются следствием того, что учащиеся очень часто пытаются
решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть
это на следующем примере.

Решить неравенство

Попытка решать это неравенство привычными
алгоритмическими способами не приведет к ответу. Решение здесь должно
состоять в оценке значений каждого слагаемого левой части неравенства
на области определения неравенства.

Найдем область определения неравенства:

dalin17.wmf

Для всех x из
промежутка (9;10] выражение имеет
положительные значения (значения показательной функции всегда положительны).

Для всех x из
промежутка (9;10] выражение ( x – 9) имеет положительные значения,
а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда
выражение

– (x – 9)
lg(x – 9) положительно или равно нулю.

Окончательно имеем x∈
(9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое,
стоящее в левой части неравенства, положительно (второе слагаемое может
быть равно нулю), а значит их сумма всегда больше нуля. Следовательно,
решением исходного неравенства является промежуток (9;10].

5. Одна из ошибок связана с графическим решением
уравнений.

Решить уравнение

имеет
положительные значения (значения показательной функции всегда положительны).

– (x – 9)
lg(x – 9) положительно или равно нулю.

5. Одна из ошибок связана с графическим решением
уравнений.

Решить уравнение

dalin19.wmf

Некоторые учащиеся, решая это уравнение графически (хочу
отметить, что его другими элементарными способами решить нельзя), получают лишь
один корень (он является абсциссой точки, лежащей на прямой y = x),
ибо графики функций

и и dalin21.wmf −

это графики взаимно обратных функций.

На самом деле исходное уравнение имеет три корня: один из
них является абсциссой точки, лежащей на биссектрисе первого координатного
угла y = x, другой корень и третий корень и третий корень dalin23.wmf Убедиться
в справедливости сказанного можно непосредственной подстановкой чисел и и dalin25.wmf в заданное уравнение.

Этот пример удачно иллюстрирует следующий вывод:
графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны»
(одна из них возрастает, а другая – убывает), и недостаточно
математически корректно в случае одномонотонных функций (обе либо
одновременно убывают, либо одновременно возрастают).

6. Ряд типичных ошибок связан с тем, что учащиеся не
совсем корректно решают уравнения и неравенства на основе функционального
подхода. Остановлюсь на типичных ошибки такого рода.

а) Решить уравнение x^х = x.

Функция, стоящая в левой части уравнения, –
показательно-степенная и раз так, то на основание степени следует
наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе
части заданного уравнения:

dalin28.wmf

dalin30.wmf или

Откуда имеем x = 1.

Логарифмирование не привело к сужению области
определения исходного уравнения. Но тем не менее произошла потеря двух корней
уравнения; непосредственным усмотрением мы находим, что x =
1 и x = –1 являются корнями исходного уравнения.

7. При решении неравенств с помощью подстановки мы
всегда сначала решаем новое неравенство относительно новой переменной,
и лишь в его решении делаем переход к старой переменной.

Школьники очень часто ошибочно делают обратный переход
раньше.Этого делать не следует.

8.Хочу привести пример еще одной ошибки, связанной
с решением неравенств.

Решите неравенство

Откуда имеем x = 1.

Школьники очень часто ошибочно делают обратный переход
раньше.Этого делать не следует.

8.Хочу привести пример еще одной ошибки, связанной
с решением неравенств.

Решите неравенство

dalin75.wmf .

Привожу ошибочное решение, которое очень часто
предлагают учащиеся.

Возведем обе части исходного неравенства в квадрат.
Будем иметь:

откуда получаем неверное числовое неравенство ,

откуда получаем неверное числовое неравенство dalin77.wmf , что позволяет сделать
вывод: заданное неравенство не имеет решений.

Однако полученный вывод неверен, например, при
х = 1000 имеем

, , dalin79.wmf , .

Полученное числовое неравенство верно, а значит
х = 1000 является решением.

Значит, заданное неравенство имеет решение, и, следовательно,
приведенное выше решение ошибочно.

Привожу правильное решение. Найдем область определения
исходного неравенства. Она задается системой

Полученное числовое неравенство верно, а значит
х = 1000 является решением.

Значит, заданное неравенство имеет решение, и, следовательно,
приведенное выше решение ошибочно.

Привожу правильное решение. Найдем область определения
исходного неравенства. Она задается системой

dalin81.wmf или

dalin83.wmf откуда .

Ясно, что на интервале (10;1000) нет решений, ибо
левая часть заданного неравенства при любом х из этого интервала не имеет
смысла.

Рассмотрим два случая.

а) .

Рассмотрим два случая.

а) dalin85.wmf , откуда х > 100. С учетом области определения
исходного неравенства имеем промежуток . Для всех х из этого промежутка левая часть
исходного неравенства неотрицательна (как значение арифметического квадратного
корня), а правая часть – отрицательна. Делаем вывод о том, что . Для всех х из этого промежутка левая часть
исходного неравенства неотрицательна (как значение арифметического квадратного
корня), а правая часть – отрицательна. Делаем вывод о том, что dalin87.wmf – решение заданного
неравенства.

б) , откуда , откуда dalin89.wmf . С учетом области определения исходного неравенства имеем
промежуток .
Для всех х из промежутка .
Для всех х из промежутка dalin91.wmf имеют смысл обе
части неравенства и они имеют неотрицательные значения, значит обе части
заданного неравенства мы можем возвести в квадрат. Будем иметь: , откуда , откуда dalin93.wmf . Это неверное числовое
неравенство позволяет сделать вывод: значения х из промежутка решениями исходного неравенства не
являются.

Ответ: решениями исходного неравенства не
являются.

Ответ: dalin95.wmf .

9. Типичная ошибка при решении уравнений, неравенств
и их систем состоит в том, что неверно преобразовываются выражения.

Большинство
ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение
некоторых вычислительных операций до автоматизма несколько снижает вероятность
их появления.

Необходимо
осуществлять процесс обучения правилам с помощью специальной модели с
использованием приема, активизирующего рефлексивную деятельность учащихся по
предупреждению и исправлению ошибок, которые возникают в результате формального
усвоения правил.

Самостоятельная
работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ
собственных действий по решению конкретной задачи, что оказывает благоприятное
влияние на качество получаемых знаний и стимулирует развитие логического
мышления.

Пример
неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет
его корни по хорошо известной формуле, не обращая внимания на недопустимые
значения sin x.

Для
исправления и предупреждения многих ошибок важно сформировать у школьников навыки
самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой
оценки ожидаемого результата.

Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок.

Систематические проверки чужих записей
формируют у ученика привычку критически относиться к своему решению. Для этого
подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления
ошибок самими учащимися под руководством учителя можно сделать поучительным для
учащихся.

Самоконтроль

Для исправления и предупреждения многих
ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят
из двух частей:

а) умения обнаружить ошибку;

б) умения её объяснить и исправить.

В процессе обучения применяются несколько
приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и
своевременно их исправить. К ним относятся:

·
проверка
вычисления и тождественного преобразования путём выполнения обратного действия
или преобразования;

·
проверка
правильности решения задач путём составления и решения задач, обратных к
данной;

·
оценка
результата решения задачи с точки зрения здравого смысла;

·
проверка
аналитического решения графическим способом.

Способы
исправления и предупреждения ошибок

Свести
ошибки к минимуму способствуют следующие профилактические меры:

Тексты письменных заданий должны быть
удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
Активная устная отработка основных
ЗУН, регулярный разбор типичных ошибок.
При объяснении нового материала
предугадать ошибку и подобрать систему заданий на отработку правильного усвоения
понятия. Акцентировать внимание на каждом элементе формулы, выполнение
разнотипных заданий позволит свести ошибочность к минимуму.
Подбирать задания, вызывающие
интерес, формирующие устойчивое внимание.
Прочному
усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для
запоминания, четкие алгоритмы, следуя которым заведомо придешь к
намеченной цели.

Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как
ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и
понимание последующего невозможно без знания предыдущего, отсюда неизбежность
повторения на каждом уроке. При объяснении нового материала следует использовать
ряд определений и теорем, которые были изучены ранее.

Источник