Типы ошибок случайные и систематические

Поскольку
выборка охватывает , как правило,
весьма незначительную часть генеральной
совокупности, то следует предполагать,
что будут иметь место различия между
оценкой и характеристикой генеральной
совокупности, которую эта оценка
отображает. Эти различия получили
название ошибок отображения или ошибок
репрезентативности. Ошибки
репрезентативности подразделяются
на два типа : систематические и случайные.

Систематические
ошибки —
это постоянное завышение или занижение
значения оценки по сравнению с
характеристикой генеральной совокупности
. Причиной появления систематической
ошибки является несоблюдение принципа
равновероятности попадания каждой
единицы генеральной совокупности в
выборку , то есть выборка формируется
из преимущественно «худших» ( или «
лучших») представителей генеральной
совокупности. Соблюдение принципа
равновозможности попадания каждой
единицы в выборку позволяет полностью
исключить этот тип ошибок .

Случайные
ошибки –
это меняющиеся
от выборки к выборке по знаку и величине
различия между оценкой и оцениваемой
характеристикой генеральной совокупности
. Причина возникновения случайных
ошибок- игра случая при формировании
выборки, составляющей лишь часть
генеральной совокупности. Этот тип
ошибок органически присущ выборочному
методу. Исключить их полностью нельзя,
задача состоит в том , чтобы предсказать
их возможную величину и свести их к
минимуму. Порядок связанных в связи
с этим действий вытекает из рассмотрения
трех видов случайных ошибок : конкретной
, средней и предельной.

2.2 Конкретная, средняя и предельная ошибки выборки

2.2.1
Конкретная
ошибка – это ошибка одной проведенной
выборки. Если средняя по этой выборке
(
) является оценкой для генеральной
средней (0
) и, если
предположить, что эта генеральная
средняя нам известна , то разница
=—0
и будет
конкретной ошибкой этой выборки. Если
из этой генеральной совокупности
выборку повторим многократно, то каждый
раз получим новую величину конкретной
ошибки :
…,
и так далее.
Относительно этих конкретных ошибок
можно сказать следующее: некоторые из
них будут совпадать между собой по
величине и знаку, то есть имеет место
распределение ошибок, часть из них
будет равна 0, наблюдается совпадение
оценки и параметра генеральной
совокупности;

2.2.2
Средняя ошибка
– это средняя квадратическая из всех
возможных по воле случая конкретных
ошибок оценки :
,
где— величина меняющихся конкретных
ошибок;частота
( вероятность ) встречаемости той или
иной конкретной ошибки. Средняя
ошибка выборки показывает насколько
в среднем можно ошибиться , если на
основе оценки делается суждение о
параметре генеральной совокупности.
Приведенная формула раскрывает
содержание средней ошибки, но она не
может быть использована для практических
расчетов, хотя бы потому, что предполагает
знание параметра генеральной совокупности
, что само по себе исключает необходимость
выборки.

Практические
расчеты средней ошибки оценки
основываются на той предпосылке, что
она ( средняя ошибка ) по сути является
средним квадратическим отклонением
всех возможных значений оценки. Эта
предпосылка позволяет получить алгоритмы
расчета средней ошибки, опирающиеся
на данные одной единственной выборки.
В частности средняя ошибка выборочной
средней может быть установлена на
основе следующих рассуждений. Имеется
выборка (
,…) состоящая изединиц. По выборке в качестве оценки
генеральной средней определена
выборочная средняя. Каждое значение(,…) , стоящее под знаком суммы, следует
рассматривать как независимую случайную
величину, поскольку при бесконечном
повторении выборки первая, вторая и
т.д. единицы могут принимать любые
значения из присутствующих в генеральной
совокупности. СледовательноПоскольку , как известно, дисперсия
суммы независимых случайных величин
равна сумме дисперсий , то.
Отсюда следует, что средняя ошибка для
выборочной средней будет равнаяи находится она в обратной зависимости
от численности выборки ( через корень
квадратный из нее ) и в прямой от среднего
квадратического отклонения признака
в генеральной совокупности. Это логично,
поскольку выборочная средняя является
состоятельной оценкой для генеральной
средней и по мере увеличения численности
выборки приближается по своему значению
к оцениваемому параметру генеральной
совокупности. Прямая зависимость
средней ошибки от колеблемости признака
обусловлена тем, что чем больше
изменчивость признака в генеральной
совокупности, тем сложнее на основе
выборки построить адекватную модель
генеральной совокупности. На практике
среднее квадратическое отклонение
признака по генеральной совокупности
заменяется его оценкой по выборке, и
тогда формула для расчета средней
ошибки выборочной средней приобретает
вид:,
при этом учитывая смещенность
выборочной дисперсии,
выборочное среднее квадратическое
отклонение рассчитывается по формуле=. Так как символомn
обозначена численность выборки. ,то
в знаменателе при расчете среднего
квадратического отклонения должна
использоваться не численность выборки
( n
), а так называемое число степеней
свободы (n-1).
Под числом степеней свободы понимается
число единиц в совокупности, которые
могут свободно варьировать ( изменяться
), если по совокупности определена
какая-либо характеристика. В нашем
случае , поскольку по выборке определена
ее средняя, свободно варьировать могут

единицы.

В
таблице 2.2 приведены формулы для
расчета средних ошибок различных
выборочных оценок . Как видно из этой
таблицы, величина средней ошибки по
всем оценкам находится в обратной связи
с численностью выборки и в прямой с
колеблемостью. Это можно сказать и
относительно средней ошибки выборочной
доли ( частости ). Под корнем стоит
дисперсия альтернативного признака,
установленная по выборке (
)

Приведенные
в таблице 2.2 формулы относятся к так
называемому случайному , повторному
отбору единиц в выборку. При других
способах отбора , о которых речь пойдет
ниже, формулы будут несколько
видоизменяться.

Таблица
2.2

Формулы для
расчета средних ошибок выборочных
оценок

Выборочные оценки	Формулы для расчета средней ошибки выборочной оценки
Выборочная средняя ( )
Выборочная дисперсия ( )
Выборочное среднее квадратическое отклонение ( s )
Выборочная доля (w )

2.2.3
Предельная ошибка выборки
Знание оценки и ее средней ошибки в
ряде случаев совершенно недостаточно
. Например , при использовании гормонов
при кормлении животных знать только
средний размер неразложившихся их
вредных остатков и среднюю ошибку,
значит подвергать потребителей продукции
серьезной опасности. Здесь настоятельно
напрашивается необходимость определения
максимальной ( предельной
ошибки ).
При использовании выборочного метода
предельная ошибка устанавливается не
в виде конкретной величины , а виде
равных границ

(
интервалов) в ту и другую сторону от
значения оценки.

Определение
границ предельной ошибки основывается
на особенностях распределения конкретных
ошибок . Для так называемых больших
выборок, численность которых более 30
единиц (
)
, конкретные ошибки распределяются в
соответствии с нормальным законом
распределения; при малых выборках () конкретные ошибки распределяются
в соответствии с законом распределения
Госсета

(
Стьюдента ). Применительно к конкретным
ошибкам выборочной средней функция
нормального распределения имеет
вид:
,
где— плотность вероятности появления тех
или иных значений,
при условии, что,
гдевыборочные средние;—
генеральная средняя,— средняя ошибка для выборочной
средней. Поскольку средняя ошибка
()
является величиной постоянной, то в
соответствии с нормальным законом
распределяются конкретные ошибки,
выраженные в долях средней ошибки, или
так называемых нормированных отклонениях
.

Взяв
интеграл функции нормального
распределения, можно установить
вероятность того , что ошибка будет
заключена в некотором интервале
изменения t
и вероятность того, что ошибка выйдет
за пределы этого интервала ( обратное
событие ). Например , вероятность того,
что ошибка не превысит половину средней
ошибки ( в ту и другую сторону от
генеральной средней ) составляет
0,3829, что ошибка будет заключена в
пределах одной средней ошибки — 0,6827,
2-х средних ошибок -0,9545 и так далее.

Взаимосвязь
между уровнем вероятности и интервалом
изменения t
( а в конечном счете интервалом
изменения ошибки ) позволяет подойти
к определению интервала ( или границ )
предельной ошибки, увязав его величину
с вероятностью осуществления..
Вероятность осуществления -это
вероятность того, что ошибка будет
находится в некотором интервале.
Вероятность осуществления будет
«доверительной» в том случае, если
противоположное событие ( ошибка будет
находится вне интервала ) имеет такую
вероятность появления, которой можно
пренебречь. Поэтому доверительный
уровень вероятности устанавливают,
как правило, не ниже 0,90 (вероятность
противоположного события равна 0,10 ).
Чем больше негативных последствий
имеет появление ошибок вне установленного
интервала, тем выше должен быть
доверительный уровень вероятности (
0,95; 0,99 ; 0,999 и так далее ).

Выбрав
доверительный уровень вероятности
по таблице интеграла вероятности
нормального распределения, следует
найти соответствующее значение t,
а затем используя выражение
=определить интервал предельной ошибки.
Смысл полученной величины в следующем
– с принятым доверительным уровнем
вероятности предельная ошибка выборочной
средней не превысит величину.

Для
установления границ предельной ошибки
на основе больших выборок для других
оценок ( дисперсии, среднего квадратического
отклонения, доли и так далее ) используется
выше рассмотренный подход, с учетом
того, что для определения средней
ошибки для каждой оценки используется
свой алгоритм.

Что
касается малых выборок () то, как уже говорилось, распределение
ошибок оценок соответствует в этом
случае распределениюt
— Стьюдента. Особенность этого
распределения состоит в том, что в
качестве параметра в нем , наряду с
ошибкой, присутствует численность
выборки ,вернее не численность выборки,
а число степеней свободы
При увеличении численности выборки
распределениеt-Стьюдента
приближается к нормальному, а при
эти распределения практически совпадают.
Сопоставляя значения величиныt-Стьюдента
и t
— нормального распределения при одной
и той же доверительной вероятности
можно сказать , что величина t-Стьюдента
всегда больше t
— нормального распределения, причем,
различия возрастают с уменьшением
численности выборки и с повышением
доверительного уровня вероятности.
Следовательно, при использовании малых
выборок имеют место по сравнению с
выборками большими , более широкие
границы предельной ошибки, причем , эти
границы расширяются с уменьшением
численности выборки и повышением
доверительного уровня вероятности.

Вопросы для
повторения

6-1.Какова
природа конкретной, средней и предельной
ошибок ?

6-2.Как
соблюсти принцип равновероятности
каждой единицы попасть в выборку при
выборочном устном опросе студентов ?

6-3 Каков источник
систематической ошибки ?

6-4.Какова
вероятность появления ошибки в 2.5 раза
превышающей среднюю?

6-5.Какие
различия в знаках ( + , — ) имеют
систематические и случайные ошибки?

6-6.Каковы основные
пути уменьшения средней и предельной
ошибки ?

6-7.При какой
выборочной доле имеет место ее наибольшая
ошибка ?

6-8.При какой доле
признака имеет место ее наименьшая
ошибка 7

6-9.При
каких выборках ( больших или малых )
при прочих равных условиях имеет место
большая предельная ошибка ?

Резюме по
модульной единице 2

Использование
выборочного метода неизбежно сопряжено
с появлением ошибок. Случайный характер
этих ошибок, нормальный или t
— Стьюдента закон их распределения
позволяет определить их средний и
предельный размер и видеть пути их
снижения

Модульная
единица 3 Типовые задачи решаемые на
основе выборочного метода

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

14. Виды погрешностей

Выделяют следующие виды погрешностей:

1) абсолютная погрешность;

2) относительна погрешность;

3) приведенная погрешность;

4) основная погрешность;

5) дополнительная погрешность;

6) систематическая погрешность;

7) случайная погрешность;

 инструментальная погрешность;

9) методическая погрешность;

10) личная погрешность;

11) статическая погрешность;

12) динамическая погрешность.

Погрешности измерений классифицируются по следующим признакам.

По способу математического выражения погрешности делятся на абсолютные погрешности и относительные погрешности.

По взаимодействию изменений во времени и входной величины погрешности делятся на статические погрешности и динамические погрешности.

По характеру появления погрешности делятся на систематические погрешности и случайные погрешности.

По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.

По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.

Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.

Абсолютная погрешность вычисляется по следующей формуле:

?Q_n =Q_n ?Q₀,

где AQ_n – абсолютная погрешность;

Q_n – значение некой величины, полученное в процессе измерения;

Q₀ – значение той же самой величины, принятое за базу сравнения (настоящее значение).

Абсолютная погрешность меры – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.

Относительная погрешность – это число, отражающее степень точности измерения.

Относительная погрешность вычисляется по следующей формуле:

где ?Q – абсолютная погрешность;

Q₀ – настоящее (действительное) значение измеряемой величины.

Относительная погрешность выражается в процентах.

Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.

Нормирующее значение определяется следующим образом:

1) для средств измерений, для которых утверждено номинальное значение, это номинальное значение принимается за нормирующее значение;

2) для средств измерений, у которых нулевое значение располагается на краю шкалы измерения или вне шкалы, нормирующее значение принимается равным конечному значению из диапазона измерений. Исключением являются средства измерений с существенно неравномерной шкалой измерения;

3) для средств измерений, у которых нулевая отметка располагается внутри диапазона измерений, нормирующее значение принимается равным сумме конечных численных значений диапазона измерений;

4) для средств измерения (измерительных приборов), у которых шкала неравномерна, нормирующее значение принимается равным целой длине шкалы измерения или длине той ее части, которая соответствует диапазону измерения. Абсолютная погрешность тогда выражается в единицах длины.

Погрешность измерения включает в себя инструментальную погрешность, методическую погрешность и погрешность отсчитывания. Причем погрешность отсчитывания возникает по причине неточности определения долей деления шкалы измерения.

Инструментальная погрешность – это погрешность, возникающая из—за допущенных в процессе изготовления функциональных частей средств измерения ошибок.

Методическая погрешность – это погрешность, возникающая по следующим причинам:

1) неточность построения модели физического процесса, на котором базируется средство измерения;

2) неверное применение средств измерений.

Субъективная погрешность – это погрешность возникающая из—за низкой степени квалификации оператора средства измерений, а также из—за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.

Погрешности по взаимодействию изменений во времени и входной величины делятся на статические и динамические погрешности.

Статическая погрешность – это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.

Динамическая погрешность – это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).

По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.

Основная погрешность – это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).

Дополнительная погрешность – это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.

Нормальные условия – это условия, в которых все значения влияющих величин являются нормальными либо не выходят за границы области нормальных значений.

Рабочие условия – это условия, в которых изменение влияющих величин имеет более широкий диапазон (значения влияющих не выходят за границы рабочей области значений).

Рабочая область значений влияющей величины – это область значений, в которой проводится нормирование значений дополнительной погрешности.

По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.

Аддитивная погрешность – это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).

Мультипликативная погрешность – это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.

Надо заметить, что значение абсолютной аддитивной погрешности не связано со значением измеряемой величины и чувствительностью средства измерений. Абсолютные аддитивные погрешности неизменны на всем диапазоне измерений.

Значение абсолютной аддитивной погрешности определяет минимальное значение величины, которое может быть измерено средством измерений.

Значения мультипликативных погрешностей изменяются пропорционально изменениям значений измеряемой величины. Значения мультипликативных погрешностей также пропорциональны чувствительности средства измерений Мультипликативная погрешность возникает из—за воздействия влияющих величин на параметрические характеристики элементов прибора.

Погрешности, которые могут возникнуть в процессе измерений, классифицируют по характеру появления. Выделяют:

1) систематические погрешности;

2) случайные погрешности.

В процессе измерения могут также появиться грубые погрешности и промахи.

Систематическая погрешность – это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки. В процессе нормирования систематической погрешности определяются границы ее допустимых значений. Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).

Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.

Способы исключения систематических погрешностей делятся на четыре вида:

1) ликвидация причин и источников погрешностей до начала проведения измерений;

2) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;

3) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);

4) определение пределов систематической погрешности в случае, если ее нельзя устранить.

Ликвидация причин и источников погрешностей до начала проведения измерений. Данный способ является самым оптимальным вариантом, так как его использование упрощает дальнейший ход измерений (нет необходимости исключать погрешности в процессе уже начатого измерения или вносить поправки в полученный результат).

Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы

Способ введения поправок базируется на знании систематической погрешности и действующих закономерностей ее изменения. При использовании данного способа в результат измерения, полученный с систематическими погрешностями, вносят поправки, по величине равные этим погрешностям, но обратные по знаку.

Способ замещения состоит в том, что измеряемая величина заменяется мерой, помещенной в те же самые условия, в которых находился объект измерения. Способ замещения применяется при измерении следующих электрических параметров: сопротивления, емкости и индуктивности.

Способ компенсации погрешности по знаку состоит в том, что измерения выполняются два раза таким образом, чтобы погрешность, неизвестная по величине, включалась в результаты измерений с противоположным знаком.

Способ противопоставления похож на способ компенсации по знаку. Данный способ состоит в том, что измерения выполняют два раза таким образом, чтобы источник погрешности при первом измерении противоположным образом действовал на результат второго измерения.

Случайная погрешность – это составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных измерений одной и той же величины. Появление случайной погрешности нельзя предвидеть и предугадать. Случайную погрешность невозможно полностью устранить, она всегда в некоторой степени искажает конечные результаты измерений. Но можно сделать результат измерения более точным за счет проведения повторных измерений. Причиной случайной погрешности может стать, например, случайное изменение внешних факторов, воздействующих на процесс измерения. Случайная погрешность при проведении многократных измерений с достаточно большой степенью точности приводит к рассеянию результатов.

Промахи и грубые погрешности – это погрешности, намного превышающие предполагаемые в данных условиях проведения измерений систематические и случайные погрешности. Промахи и грубые погрешности могут появляться из—за грубых ошибок в процессе проведения измерения, технической неисправности средства измерения, неожиданного изменения внешних условий.

Данный текст является ознакомительным фрагментом.

Разница между случайной и систематической ошибкой

Если ошибка не имеет какой-либо конкретной модели возникновения, она известна как случайная ошибка, которая также известна как несистематическая ошибка, и, следовательно, такие ошибки нельзя предсказать заранее, как неизбежную ошибку, тогда как систематическая ошибка — это ошибка, которая может возникнуть. из-за любой ошибки в измерении прибора ошибка или ошибка в использовании прибора экспериментатором и, следовательно, это ошибка, которой можно избежать.

Основное отличие состоит в том, что случайные ошибки в основном приводят к колебаниям, которые окружают истинное значение из-за трудностей при проведении измерений, тогда как систематические ошибки приводят к предсказуемым, а также постоянным отклонениям от истинного значения из-за проблем с калибровка оборудования.

Независимо от того, насколько осторожны при проведении экспериментов, скорее всего, будет ошибка, называемая экспериментальной ошибкой. Будь то из-за присущих ему проблем, связанных с проблемами с вашим оборудованием, точным выполнением измерений или полным предотвращением ошибки, это практически невозможно.

Чтобы противостоять упомянутой проблеме, ученые стараются изо всех сил классифицировать эти ошибки и пытаться количественно оценить любую неопределенность в измерениях, которые они делают. Выявление разницы между этими ошибками является жизненно важной частью обучения, позволяющего разрабатывать более эффективные эксперименты и пытаться свести к минимуму любые ошибки, которые действительно подкрадываются.

Инфографика случайных и систематических ошибок

Давайте посмотрим основные различия между случайной ошибкой и систематической ошибкой.

Ключевые отличия

Ключевые отличия заключаются в следующем:

• Случайная ошибка определяет себя как непредсказуемое нарушение, которое возникает в вашем эксперименте из-за неизвестного источника. При этом систематическая ошибка возникает из-за неисправности аппарата, который не построен.
• Случайная ошибка, как указано в приведенной выше таблице, возникает в обоих направлениях, тогда как систематическая ошибка возникает только в одном направлении. Систематические ошибки возникают из-за встроенной неисправности или ошибки аппарата; следовательно, он всегда дает аналогичную ошибку. Случайная ошибка, как упоминалось ранее, возникает из-за неизвестного источника, поэтому она возникает в любом направлении.
• Величина систематической ошибки будет оставаться постоянной или неизменной, потому что дефект, который присутствует в ней, встроен внутри устройства, и по сравнению с величиной случайной ошибки он имеет переменную величину.
• Ошибка 0 и неправильная калибровка прибора вызовут систематическую ошибку. Случайная ошибка возникает из-за параллакса или, как указано ранее в приведенной выше сравнительной таблице, из-за неправильного использования устройства.
• Случайная погрешность уменьшается или может быть минимизирована путем получения 2 или более показаний одного и того же эксперимента, в то время как систематическая ошибка может быть минимизирована путем тщательного проектирования конструкции устройства.
• Случайная ошибка сама по себе уникальна и не имеет конкретных типов, тогда как систематическая ошибка может быть разделена на три основных типа: ошибка среды, ошибка прибора и систематическая ошибка.
• Случайная ошибка не воспроизводится, с другой стороны, систематическая ошибка будет воспроизводимой, потому что дефект, как указано ранее, встроен в структуру устройства.

Сравнительная таблица случайных и систематических ошибок

Основа		Случайная ошибка		Систематическая ошибка
Основное определение		Это ошибки, которые колеблются из-за неопределенности или непредсказуемости, присущей вашему процессу измерения, или различий в величине, которую вы пытаетесь измерить.		Это происходит в основном из-за недостатков оборудования, то есть они обычно возникают из-за неправильной калибровки оборудования.
Величина ошибки		Величина ошибки меняется при каждом чтении.		Измеренное значение будет либо очень низким, либо очень высоким по сравнению с истинным значением.
Причины		1) Ошибка параллакса 2) Неправильное использование аппарата. 3) Ограничение инструмента, среды и т. Д.		1) Нулевая ошибка 2) Неправильная калибровка
Методы минимизации		Повторно снимая показания.		1) За счет улучшения конструкции аппарата. 2) Ошибка нуля может быть уменьшена путем вычитания из ошибки нуля полученного показания.
Направление ошибки		Это происходит с обеих сторон		Это происходит только в одном направлении.
Подтипы ошибок		Подтипов нет.		Есть 3 подтипа — a. Инструмент b. Систематическая ошибка c. Среда.
Воспроизводимо ли это		Этот вид ошибки не воспроизводится		Этот вид ошибки воспроизводится
С точки зрения стоимости		Цена — это комбинация стоимости, которая в основном связана с производством.		Затраты снижаются, когда они сравниваются со стоимостью с точки зрения стоимости.

Вывод

Случайная ошибка в основном возникает из-за каких-либо нарушений, происходящих в вашем окружении, таких как колебания или перепады давления, температуры или из-за наблюдателя, который может принимать неправильные или неправильные показания. Систематическая ошибка, возможно, также возникает из-за механической конструкции аппарата.

Случайных ошибок по существу нельзя избежать, а систематических ошибок можно избежать. Ученые не могут делать точных масштабов или измерений, какими бы умелыми они ни были.

Систематические ошибки, возможно, трудно обнаружить, и это связано с тем, что все, что вы измеряете, будет неверным или неверным на ту же величину, и вы, возможно, вообще не осознаете, что существует проблема. Перед использованием необходимо правильно откалибровать оборудование, и да, тогда вероятность систематических ошибок будет намного меньше.

• Разница между случайной ошибкой и систематической ошибкой

Разница между случайной ошибкой и систематической ошибкой

Ошибка определяется как разница между фактическим или истинным значением и измеренным значением. Измерение количества или стоимости основано на каком-то стандарте. Измерение любого количества осуществляется путем сравнения его с производным стандартом, который не является полностью точным. Чтобы понять ошибки в измерении, следует понимать два термина, которые определяют ошибку, и они являются истинным значением и измеренным значением. Истинное значение невозможно выяснить, оно может быть определено по среднему значению бесконечного числа. Измеренное значение определяется как оценочное значение истинного значения путем взятия нескольких измеренных значений. Ошибка не должна быть перепутана с ошибкой, ошибки можно избежать, но ошибки не избежать, но их можно минимизировать. Так что ошибка не является ошибкой его части измерительной обработки. Измерение — это разница между измеренным значением количества и его истинным значением. мы обсудим случайную ошибку и систематическую ошибку. Погрешности измерения делятся на два обширных класса ошибок.

1. Случайная ошибка
2. Систематическая ошибка

Случайная ошибка:

Случайная ошибка — это не что иное, как колебания в измерении, которые в основном наблюдаются путем проведения нескольких испытаний данного измерения. Как следует из названия, эта ошибка происходит совершенно случайно. Они непредсказуемы и не могут быть воспроизведены путем повторения эксперимента снова. Так что каждый раз это дает разные результаты. Случайная ошибка варьируется от наблюдения к другому. При случайной ошибке колебание может быть как отрицательным, так и положительным. Не всегда возможно определить источник случайной ошибки. Случайная ошибка происходит из-за фактора, который не может или не будет контролироваться. Случайная ошибка влияет на достоверность результатов. Некоторые из возможных источников или причин случайных ошибок перечислены ниже.

• Наблюдение: ошибка в суждении наблюдателя.
• Небольшие помехи: Небольшие помехи могут привести к ошибкам измерения, например
• Колеблющиеся условия: Некоторое изменение температуры во времени или в окружающей среде может привести к ошибке в измерении.
• Качество: Некоторое время, когда качество объекта, измерение которого должно быть выполнено, не определено должным образом, приводит к ошибке.

Ошибка может быть уменьшена, если взять число чтений, а затем найти среднее или среднее значение чтения.

Систематическая ошибка:

Систематическая ошибка — это когда одна и та же ошибка присутствует во всех показаниях. Систематическая ошибка предсказуема и обычно постоянна или пропорциональна истинному значению. Таким образом, систематическая ошибка повторяется каждый раз, и это приводит к ошибкам согласованности. Если мы повторим эксперимент, мы получим одну и ту же ошибку каждый раз. Систематические ошибки возникают из-за неправильной калибровки прибора. Систематическая ошибка влияет на точность результата. Систематическая ошибка также называется нулевой ошибкой, положительной или отрицательной ошибкой. Некоторые из возможных источников или причин систематической ошибки перечислены ниже.

• Инструментальная ошибка: оборудование, используемое для измерения объекта, может быть не совсем точным.
• Экологическая ошибка: ошибка возникает из-за изменений условий окружающей среды, таких как влажность, давление, температура и т. Д.
• Наблюдательная ошибка: ошибка в записи данных, также называемая человеческими ошибками. После выявления систематической ошибки она может быть в некоторой степени уменьшена. Систематическая ошибка может быть сведена к минимуму путем регулярной калибровки оборудования, использования элементов управления и сравнения значений со стандартным значением.

Сравнение между случайными ошибками и значением систематической ошибки (инфографика)

Ниже приведено 8 основных различий между случайной ошибкой и систематической ошибкой

Ключевые различия между случайной ошибкой и систематической ошибкой

Давайте обсудим некоторые основные различия между случайной ошибкой и систематической ошибкой

• Случайная ошибка непредсказуема и возникает из-за неизвестных источников, тогда как систематическая ошибка является предсказуемой и возникает из-за дефекта прибора, который используется для измерения.
• Случайная ошибка возникает в обоих направлениях, тогда как систематическая ошибка возникает только в одном направлении.
• Случайная ошибка не может быть устранена, но большинство систематических ошибок может быть уменьшено.
• Случайная ошибка является уникальной и не имеет определенного типа, тогда как систематическая ошибка имеет 3 типа, как указано в таблице выше.
• Систематическую ошибку трудно обнаружить, это происходит из-за одних и тех же результатов каждый раз и не осознает, что проблема вообще существует, тогда как случайную ошибку легко обнаружить из-за разных результатов каждый раз.

Сравнительная таблица случайных ошибок и систематических ошибок

Ниже приведено 8 лучших сравнений между случайной ошибкой и систематической ошибкой.

Основное сравнение между случайной ошибкой и систематической ошибкой	Случайная ошибка	Систематическая ошибка
Определение	Это происходит из-за неопределенных изменений в окружающей среде и колеблется каждый раз при измерении.	Это постоянная ошибка и остается неизменной для всех измерений.
Свести к минимуму	Путем многократного взятия показаний и расчета среднего или среднего из повторных показаний.	Сравнивая значение со стандартным значением и улучшая структуру оборудования.
Величина ошибки	Каждый раз дают другой результат, который меняется каждый раз.	Результат остается неизменным или постоянным каждый раз.
Направление ошибки	Это происходит в обоих направлениях.	Это происходит в том же направлении.
Подтип ошибки	Нет подтипов	Подтипы Инструмент, Среда и Систематическая Ошибка.
воспроизводимый	Невоспроизводимый.	Воспроизводимые.
Значение	Цена представляет собой сочетание стоимости.	Затраты снижаются, когда они сравниваются со стоимостью в стоимостном выражении.
Пример ошибки	Время реакции, погрешность измерения из-за недостаточной точности, погрешность параллакса (если каждый раз смотреть под случайным углом)	Ошибка шкалы, ошибка нуля, ошибка параллакса (если диск виден под тем же углом)

Выводы

Таким образом, случайная ошибка в основном возникает из-за каких-либо возмущений в окружающей среде, таких как колебания или различия в давлении, температуре или из-за наблюдателя, который может принять неправильные показания, в то время как систематическая ошибка возникает из-за механической структуры прибора. Случайная ошибка не может быть предотвращена, в то время как систематическая ошибка может быть предотвращена. Полное устранение обеих ошибок невозможно. Основное различие между случайными ошибками и систематическими ошибками заключается в том, что случайная ошибка в основном приводит к колебаниям, тогда как систематические ошибки приводят к предсказуемому и последовательному результату. При работе с промышленными приборами важно, чтобы оператор тщательно следил за экспериментом, чтобы погрешность измерения могла быть уменьшена.

Рекомендуемые статьи

Это было руководство к разнице между случайной ошибкой и систематической ошибкой. Здесь мы также обсудим различия между случайной ошибкой и систематической ошибкой с помощью инфографики и сравнительной таблицы. Вы также можете взглянуть на следующие статьи, чтобы узнать больше.

1. Экономический рост против экономического развития
2. Бухгалтерский учет и финансовый менеджмент
3. Покупка активов против покупки акций
4. Ангел Инвестор против Венчурного Капитала

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

1. Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
2. Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась  погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому  значению.

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

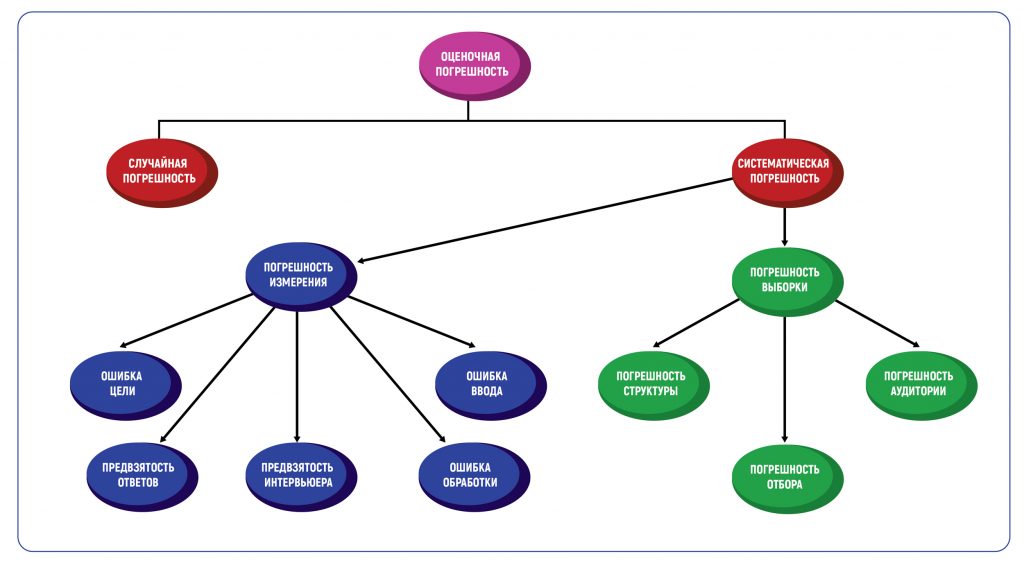
Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения. 

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

• Знайте свою аудиторию.
  Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
• Разделите аудиторию на группы.
  Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
• Увеличьте размер выборки.
  Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть  или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

• Предварительно протестируйте.
  Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
• Проводите выборку случайным образом.
  Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
• Тренируйте команду интервьюеров и наблюдателей.
  Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
• Всегда выполняйте проверку сделанных записей.
  Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок  не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.