Типичные ошибки в математике это - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Авторы
Файлы
Литература

Далингер В.А.

1 Омский государственный педагогический университет

1. Асанов Р.А. Работа над ошибками при обучении математике // Из опыта преподавания математики в школе. – М.: Просвещение, 1978. – С. 23-48.

2. Бескин Н.М. Роль задач в преподавании математики // Математика в школе. – 1992. – № 4-5. – С. 3-4.

3. Высоцкий И.Р., Ященко И.В. Типичные ошибки в преподавании теории вероятностей и статистики // Математика в школе. – 2014. – № 5. – С. 32-43.

4. Далингер В.А. Анализ типичных ошибок, допускаемых в курсе алгебры и начал анализа // Математика в школе. – 1998. – № 6. – С. 13-18.

5. Далингер В.А. Типичные ошибки по математике на вступительных экзаменах и как их не допускать. – Омск: Изд-во Омского ИУУ, 1991. – 129 с.

6. Далингер В.А. Начала математического анализа. Типичные ошибки, их причины и пути предупреждения: учебное пособие. – Омск: Изд-во ООО «Издатель-Полиграфист», 2002. – 158 с.

7. Далингер В.А. Совершенствование процесса обучения математике на основе целенаправленной реализации внутрипредметных связей: монография. – Омск: Изд-во ОИПКРО, 1993 г. – 323 с.

8. Далингер В.А., Тарасова О.А. Причины типичных ошибок, допускаемых учащимися в процессе изучения математики и самоконтроль как средство организации рефлексии по предупреждению ошибок // Научные исследования: информация, анализ, прогноз: монография / под общ. ред. проф. О.И. Кирикова. – Книга 2. – Воронеж: Изд-во ВГПУ, 2004. – С. 216-143.

9. Зеленский А.С., Панфилов И.И. Различные способы решения задач С 5 ЕГЭ: сравнительный анализ, ошибки и недочеты, оценивание // Математика в школе. – 2013. – № 8. – С. 15-23.

10. Зеленский А.С., Панфилов И.И. Задачи с параметром на ЕГЭ – 2014: способы решения, ученические ошибки и недочеты // Математика в школе. – 2014. – № 7. – С. 17-24.

11. Зеленский А.С. Формирование навыков самоконтроля у старшеклассников // Математика в школе. – 2014. – № 9. – С. 26-30.

12. Лында А.С. Самостоятельная работа и самоконтроль учебной деятельности старших школьников. – М.: Изд-во МОПИ, 1972. – 198 с.

13. Матизен В. Найдем ошибку // Квант. – 1980. – № 10. – С. 43-46.

14. Рыжик В.И. Формирование потребностей в самоконтроле при обучение математике // Математика в школе. – 1980. – № 3. – С. 7-11.

15. Самсонов П.И. Анализ ошибок выпускников школ на ЕГЭ по математике в 2014 году: от анализа к предупреждению // Математика в школе. – 2014. – №8. – С. 3-7; Математика в школе. – 2014. – № 9. – С. 3-10.

16. Шашкина М.Б., Якименко М.Ш. Типичные ошибки при решении заданий С 3 на ЕГЭ в 2010-2011 гг. // Математика в школе. – 2011. – № 9. – С. 11-17.

17. Ягунова Е.Б. Ошибки по невнимательности. Работа над ошибками // Компьютерные инструменты в школе. – 2012. – № 1. – С. 9-16.

Ошибки делятся на случайные и систематические, то есть устойчивые. Случайными ошибками следует считать те, которые появляются однократно, не систематически у одного-двух обучающихся. К устойчивым (типичным) ошибкам относятся те, которые появляются у одного и того же обучающегося (или у нескольких) неоднократно, или те, которые появляются хотя и однократно, но у многих обучающихся. Типичные ошибки имеют массовый характер, высокую частоту «встречаемости» в работах обучающихся.

К типичным ошибкам по математике можно, например, отнести: ассоциативный перенос методов решения уравнений на неравенства, неверное применение метода декомпозиции неравенства, потеря решений при выполнении заданий на решение уравнений и неравенств, неверное определение вида геометрической фигуры, тавтология в рассуждениях и т.д.

Особо рассмотрим такой пример типичной ошибки по математике. При решении логарифмических уравнений и неравенств учащиеся используют свойства логарифмов:

;

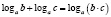
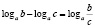
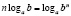
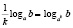
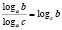
Но анализ практики показывает, что большинство учащихся не знают или не до конца осознают условия применения этих формул.

Если мы читаем формулы слева направо, то обязательно подразумеваем, что все аргументы логарифмов и все основания положительны, основания логарифмов не равны единице.

Но если мы запишем, например, формулу 1 справа налево: 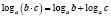, то положительным должно быть произведение (то есть числа и должны быть одного знака). Значит, учащиеся должны иметь в виду формулу: , .

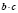
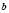
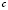
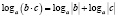
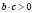
Следовательно, мы имеем дело не с одной формулой, а с двумя, причем каждая из них имеет свою область определения, что и важно учитывать при решении.

Эти рассуждения имеют место и для многих других формул.

Приведем еще примеры типичных ошибок учащихся:

на вопрос «Чему равны точные значения 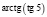и arcsin(sin10)?», учащиеся дают неверный ответ: , arcsin(sin10)=10, ссылаясь на то, что мы имеем дело со взаимно обратными функциями (верные ответы будут соответственно такими: ; );

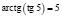
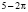
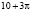
учащиеся ошибочно считают, что при решении иррациональных уравнений надо опасаться возведения обеих частей уравнения в четную степень, − могут появиться посторонние корни, и не стоит опасаться возведения в нечетную степень; если появляются посторонние корни, то они обязательно окажутся в той области, которая, после преобразований исходного уравнения, добавится к его области определения;

учащиеся ошибочно считают, что при решении систем уравнений методом деления одного уравнения системы на другое, не происходит потери решений (хотя это не так; например, при решении этим методом системы

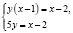
получаем решение 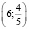, в то время как и пара также является решением);

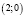
учащиеся неверно записывают ответ в случае решения систем тригонометрических уравнений (в записи ответов к двум уравнениям системы используется одна и та же буква);

учащиеся ошибочно считают, что если числа 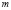и являются корнями квадратного уравнения, то они исчерпывают все множество корней этого уравнения (ошибочность этого утверждения демонстрируют решения двух таких задач: 1. Найдите числа и такие, что корни уравнения есть числа и (Ответ: или ) и 2. При каких и числа и являются корнями уравнения ? (Ответ: или или ));

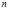
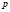
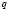
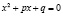
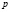
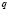
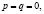
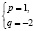
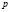
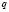
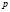
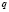
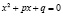
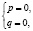
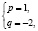
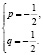
при решении логарифмических уравнений путем перехода к новому основанию, учащиеся, как правило, забывают наложить ограничения на это новое основание, а если и осуществили это действие, то забывают проверить те значения неизвестной, которые входили в прежнюю область ограничения, но оказались выброшенным из области определения нового основания;

при решении дробно-рациональных неравенств (со знаком нестрогого неравенства) учащиеся в ответ забывают записать изолированные решения (те, которые обращают в ноль числитель дроби);

при решении уравнений вида 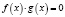учащиеся всегда пользуются утверждением: «произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю», хотя есть уравнения, при решении которых следует пользоваться утверждением: «произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю, а другой при этом имеет смысл».

Большинство ошибок связаны, как правило, с формализмом в знаниях учащихся, которые внешне проявляется следующим образом: отрыв формы от содержания; неумение применять теорию на практике; преобладание памяти над пониманием; господство трафарета, шаблона.

Заметим, что во второй половине XIX века господствовала ошибочная теория «недопущения ошибок» (Н. Кульман, Ф. Флеров), согласно которой акцентирование внимания на ошибке повлечет за собой упрочение ошибки в сознании обучающихся. Лозунгами этой теории были следующие: «Ни одной ошибки для глаз!», «Ни одной ошибки для рук!».

Современная дидактика и частные методики доказывают, что работа над ошибками не просто полезна, но и необходима, причем над типичными ошибками должна проводиться фронтальная работа, а над случайными – индивидуальная. Скорее всего, вначале «На ошибках учат», а затем уже «На ошибках учатся». Любая ошибка должна быть использована для более детального и глубокого проникновения в суть каждого правила, понятия, теоремы и т.д.

В каждой ошибке следует различать содержание и причину ее возникновения. В содержание ошибки входит то, что объективно неверно, неадекватно выполнено в действиях обучающихся.

Причина же появления ошибки – это некоторое обстоятельство (или их совокупность), которое повлекло за собой выполнение неадекватного действия обучающимся.

Содержание ошибки легко установить по внешнему выражению действия обучающихся (сужает или расширяет объем понятия, неправильно произносит или пишет, неверно выполняет какое-то действие и т.д.). Причина же ошибка, как правило, внешне себя не проявляет. Задача учителя определить исходные корни допущенной ошибки, что даст ему возможность верно строить работу по ликвидации и предупреждению различного рода ошибок.

П.И. Самсонов замечает, что, судя по допускаемым учащимися ошибкам на ЕГЭ по математике, можно «с уверенностью говорить о недостаточной методической работе в школе, о недостаточной дидактической гибкости учителя. А ведь за этими недоработками стоит будущее ученика!» [15, с. 3-4].

Высказанной мысли созвучны слова Н.М. Бескина: «Как это ни странно звучит, ошибки в процессе изучения не вредны, а полезны. Они аналогичны симптомам болезни. По этим симптомам врач ставит диагноз. Точно так же ошибки учащихся сигнализируют учителю, чего именно школьник не понимает. Учитель мог этого и не знать, а ошибка дает ему нужную информацию. От учителя требуется умение понять неправильный ход мыслей ученика, который не может объяснить, почему он пришел к такому результату. … Учитель должен не просто поправить ошибку, а выкорчевать ее. Для этого он должен понять неправильный ход мыслей и заблуждений ученика, который сам ученик не может сформулировать» [2, с. 3].

Укажем причины типичных математических ошибок учащихся (да они имеют место и по другим учебным дисциплинам):

• причины, связанные с психологическими факторами (ослабление психических функций у обучающихся: внимания, памяти, мышления);

• причины, обусловленные недостатками учебных программ и учебников;

• причины, обусловленные несовершенством организации учебного процесса;

• причины, обусловленные невладением обучающимися на требуемом уровне синтаксисом и семантикой математического языка.

В наших учебных пособиях [5, 6], монографии [7] и статьях [4, 8] приведены примеры типичных ошибок обучающихся по математике и указаны их причины.

В данной статье укажем какие типичные ошибки учащиеся допустили в ЕГЭ по математике в 2014 году при выполнении заданий раздела С.

При решении задачи С 1 (тригонометрическое уравнение) типичными ошибками были:

• ошибки в применении формул приведения;

• ошибки из-за незнания формул тригонометрии;

• ошибка, допущенные в записи корней тригонометрического уравнения;

• ошибки в преобразовании выражений со степенью;

• выполнение преобразования уравнения, ведущее к потере корней.

При решении задания С 2 (стереометрическая задача на нахождение угла между плоскостью основания треугольной пирамиды и плоскостью, проходящей через три заданные точки) типичными были следующие ошибки:

• неверное определение искомого угла;

• неверное определение вида фигуры;

• использовались необоснованные выводы.

При решении задания С 3 (решение системы неравенств, одно из которых показательной, а другое логарифмическое) были допущены такие типичные ошибки:

• потеря части решения неравенства;

• неверное преобразование неравенств;

• не учитывались условия существования решения неравенств;

• ошибки в записи числового промежутка;

• нет четкого понимания сути понятий «система» и «совокупность»;

• неверное применение метода декомпозиции;

• ошибки в преобразовании показательного и логарифмического неравенств;

• ошибки при выполнении тождественных преобразований степенных и логарифмических выражений.

При выполнении задания С 4 (планиметрическая задача с элементами доказательства) были допущены такие типичные ошибки:

• неверное определение центра описанной окружности;

• ошибки в формулировании утверждения;

• неверное определение вида четырехугольника;

• из рассмотрения частных случаев делается общее заключение.

• При выполнении задания С 5 (логарифмическое уравнение с параметром) типичными ошибками были:

• неверно формулируется условие после замены переменной;

• ошибки в нахождении корней квадратного уравнения;

• не учтен возможный случай равенства корней 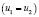, что привело к потере условия ;

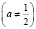
• использованы неравносильные преобразования при переходе от одного уравнения к другому;

• неверно решены рациональные неравенства;

• неполное исследование свойств новой переменной.

При решения задания С 6 (задача целочисленной арифметики) учащиеся допустили следующие типичные ошибки:

• сужен круг поиска необходимых значений;

• ошибка в формулировании свойства чисел;

• проводится неверное обобщение.

Следует заметить, что при выполнении всех шести задач раздела С были допущены речевые ошибки. Например, «угол между плоскостями есть угол между двумя перпендикулярами, проведенными к линии их пересечения», «наложим ОДЗ», «разобьем неравенство на интервалы», «число 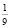− число нечетное», «число − число четное», «меньше чисел нет, поэтому быть не может» и др.

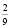
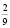
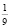
Практика показывает, что очень важно воспитывать и развивать у школьников навыки самоконтроля для того, чтобы каждый из них мог бы проводить диагностику своего решения задач.

Стихийно, сам по себе самоконтроль у ученика не рождается. Самоконтролю следует обучать специально.

Анализ причин типичных ошибок по математике показывает, что это как раз и есть ошибки, связанные с недостаточным или полным отсутствием самоконтроля.

Для проведения учащимися самоконтроля правильности проведенного решения задачи им можно дать на вооружение весьма простые средства, которые позволят установить неправильность решения задачи. Примеры таких средств читатель найдет в работах [11, 12, 13, 14].

Библиографическая ссылка

Далингер В.А. ТИПИЧНЫЕ ОШИБКИ УЧАЩИХСЯ ПО МАТЕМАТИКЕ И ИХ ПРИЧИНЫ // Современные наукоемкие технологии. – 2014. – № 12-1.
– С. 94-97;

URL: https://top-technologies.ru/ru/article/view?id=34851 (дата обращения: 11.06.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Математика — наука непростая, и учащиеся часто допускают ошибки при ее изучении.

В статье мы проведем анализ типичных ошибок при изучении математики и дадим советы, как их избежать.

Кстати, мы уже писали о самых распространенных ошибках в ЕГЭ по математике. Подписывайтесь на наш Telegram-канал, чтобы не пропустить новые публикации. Еще там вы найдете интересные предложения для вашей учебы.

Нужна помощь?

Доверь свою работу кандидату наук!

Какие бывают ошибки в математике

Ошибки в математике допускают все: и учащиеся, и даже сами преподаватели. Однако, эти ошибки носят разный характер.

Есть два вида ошибок:

типичные (устойчивые);
случайные.

Типичные ошибки — это системные ошибки, которые появляются у многих учащихся одновременно. К таким ошибкам можно отнести неправильно понятые формулы или условия их применения, правила решения уравнений и т.д. Например, если на контрольной половина класса допустила одинаковую ошибку, значит эта ошибка типичная. В этом случае преподаватель понимает, что ученики неправильно поняли материал. Такие ошибки опасны — если преподаватель вовремя не заметит, а ученики запомнят неправильный вариант, то будут допускать в этом месте ошибку и приходить к неверному результату.

Случайные ошибки — это ошибки, которые появляются однократно, у одного-двух учащихся. Случайных ошибок в работе может быть много и, как правило, их допускают из-за невнимательности или спешки. К таким ошибкам можно отнести просчеты в вычислениях, упущения в формулах и т.д.

Типичные ошибки в математике

Чтобы одолеть математику, нужно много времени. Неудивительно, что при ее изучении и школьники, и студенты часто допускают ошибки.

Мы не будем разбирать конкретные ошибки в вычислениях, ведь для каждого уровня математики они свои. Мы разберемся в характерных общих ошибках при изучении этого предмета.

Допускать пробелы в знаниях

С каждым классом математика становится сложнее. Но есть базовые знания, без которых не обойтись. И, если неправильно понять какой-то материал, скорее всего это отрицательно скажется на учебе в целом: если один раз неправильно выучите, потом будете делать ошибку везде, где сталкиваетесь с этим материалом. Такая недопонятая информация, как снежный ком, будет нарастать все больше и мешать продвигаться дальше.

Зазубривать теорию

В математике важно знать формулы и теоремы. Но просто зазубрить теоретическую информацию недостаточно, надо уметь применять ее на практике. К тому же, если просто заучить материал и не понимать, что заучили, вы быстро забудете зазубренное. Так что всю теорию в математике обязательно надо закреплять на практике.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы.

Перескакивать от простого к сложному

Очень часто учащиеся, после того как почувствуют силы и уверенность в математике, начинают хвататься за более сложный уровень, пропуская, на их взгляд, легкую информацию. В математике такой подход не работает, ведь чтобы был результат, этот предмет надо изучать систематично, не опуская даже на первый взгляд простые и очевидные вещи.

Списывать домашнее задание

Все знают, что списывать не совсем хорошо. Однако, одно дело, когда ученик списал домашнее задание из решебника из-за нехватки времени, и совсем другое, если он списал из-за незнания или непонимания материала. В математике в непонятных темах надо разбираться сразу, потому что, как мы писали выше, с каждым годом все сложнее будет наверстать упущенное.

Заниматься нерегулярно

Для математики нужна постоянная практика. Если вы всерьез хотите изучать математику, или этот предмет вам важен при поступлении, то изучайте его регулярно. Наш мозг устроен так, что информация, которая не совсем понятна или малоизученна, быстро забывается. Лучше, чтобы в изучении математики была систематичность. Это касается не только самостоятельного изучения, но и занятий с репетиторами.

Делать упор только на алгебру или геометрию

В математике нет менее или более важных дисциплин, большинство информации в ней тесно переплетается. Например, без алгебраических знаний нельзя понять некоторые геометрические задачи и наоборот.

Посмотри примеры работ и убедись, что мы поможем на совесть!

Теперь вы знаете главные ошибки при изучении математики. Старайтесь их избегать, и у вас все обязательно получится. А если появятся вопросы и трудности, обращайтесь в студенческий сервис. Наши специалисты помогут в решении любых учебных задач.

Источник

Ошибки учащихся при изучении математики,

их предупреждение и объяснение

Автор работы:

Дука Наталья Ивановна

учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________

Аннотация

В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.

Тезисы

В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.

Иногда ученики используют неверную формулу, не задумываясь над ней.

Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ,

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают ошибки, но просто забывают формулы, например формулу

an am = an+m.

Пример ошибки на свойство степени: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2.

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С». Треугольник, описанный в условии задачи, не существует.

Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.

В газете «Математика» предлагается уравнение и к нему ответ:1. Приведенное решение неверное, так как приводит к потере корней.

Вступление

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.

Причины ошибок, допускаемых учащимися при изучении математики

Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок? Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.

Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Выполняя математические задания, учащиеся допускают типичные ошибки:

Незнание правил, определений, формул.
Непонимание правил, определений, формул.
Неумение применять правила, определения, формулы.
Неверное применение формул.
Невнимательное чтение условия и вопроса задания.
Вычислительные ошибки.
Не использование свойств фигур при решении геометрических задач.
Логические ошибки при решении текстовых задач.
Раскрытие скобок и применение формул сокращенного умножения.

Какие причины ошибок по математике?

Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не всегда сами понимают, что именно они написали.
Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.

Работа над ошибками

В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена

(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком они предложены в учебнике. Другой пример неосознанного применения алгоритма: получив уравнение

sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
проверка правильности решения задач путём составления и решения задач, обратных к данной;
оценка результата решения задачи с точки зрения здравого смысла;
проверка аналитического решения графическим способом.

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Ученик написал = 52, ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .

Объяснение и предупреждение ошибок

Свести ошибки к минимуму способствуют следующие профилактические меры.

Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:

1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.

А также выполнить задания:

1. Определите четность и нечетность тригонометрической функции:

а) y = – cos x + x2; б) y = sin2 x; в) y = .
2. Найдите область определения функции y = x2 – 6x + 10.

3. При каких значениях x функции y = sin x и y = cos x принимают одинаковые значения?

Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.

Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение arcsin (sin).

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. По определению . Следовательно, число arcsin(sin) должно принадлежать промежутку , число этому промежутку не принадлежит. Имеем: arcsin (sin) = arcsin (sin)) = arcsin (sin ) = arcsin =

Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о. Можно исправить ошибку следующим образом: учитывая, что 90о 90о для любого и arctg (tgх) = х при

х arctg (tg130о) = arctg (tg180о 50о) = arctg (tg( 50о)) = 50о. Существует второй способ решения. Пусть arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о. По условию равенства тангенсов имеем х = 130о + k, где kZ. Учитывая область определения функции у = arctg х, где х(90О; 90О), при k = 1 х = 130о 180о = 50о.

Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin() = 2, т. к. 2.

Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил = х+2. Во-первых, учащиеся забывают, что , во-вторых, опять ошибочная аналогия с формулой = , где Применение «формулы =» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой = , где и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден совет: вычислите по тому алгоритму, который только что применили, имеем = и по действиям 2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.

Можно предложить учащимся проверить себя, взяв, например, значение х = 2 но ;

при х = –2 но .

Делаем вывод: преобразование выполнено неверно, формула «=» не существует и

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2, получим , с другой стороны , тогда 2= В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»: . И, разумеется, должна появиться верная запись .

an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.

Ещё пример ошибки: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением

=. Здесь же можно предложить другой способ

Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «», но допустили следующую ошибку «=х». Верное решение Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у = при х0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х24, х2,

(х-2)(х+2)0, . Третий способ графический.

х24 при .

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin 2sin , /2 = 21/2 или вспомнить определение sin х на тригонометрическом круге. Наглядно хорошо видно, что sin 2х 2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.

Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении»:

Анализ работ ГИА и ЕГЭ

Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:

преобразовании дробно-рациональных выражений, содержащих корень

n-ой степени

исследовании функций на наибольшее и наименьшее значения;
решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
вычислении площади криволинейной трапеции;
построении графика функции с модулем;
изображении тел вращения в геометрической задаче;
теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
построении множества точек плоскости, удовлетворяющего заданному условию;
решении задач с параметром.

Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:

комбинация тел;
углы в пространстве;
производная и её применение к исследованию функции на отрезке;
построение ГМТ, удовлетворяющего заданным условиям;
логарифмические и показательные неравенства;
тригонометрические функции и их свойства;
тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.

Ошибки в учебниках и методической литературе

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С».

Решение.

ВD – биссектриса АВС =

∠ВDС = ∠С ВDС равнобедренный ВD = DС =

Отсюда СD =

Ответ:

Решим задачу вторым способом.

ВЕ – высота АВС. Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:

АВ2 – АЕ2 = ВD2 – DЕ2,

302 – (20 + х)2 = 162 – х2,

900 – 400 – 40х – х2 = 256 – х2,

40х = 244,

х = 6,1.

ВЕ высота и медиана DЕ = СЕ СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.

Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С и ∠АВD = ∠DВС. Найдем величины ∠DВС, ∠ВDС, ∠С.

АD2 = АВ2 + ВD2 – 2 cos ∠AВD

cos ∠AВD =

Тогда ∠АВD 38,5о. ∠DВС = ∠АВD 38,5о.

Аналогично cos ∠ADВ =

Тогда ∠АDВ = 180о – 67,59о ∠ВDС 67,59о. Из ВDС

∠С = 180о – 38,05о – 67,59о = 74,36о,

Отсюда следует, что ∠ВDС ∠С и треугольник DВС неравнобедренный.

Значит, задача составлена некорректно: треугольник, описанный в условии задачи, не существует.

Возможны два корректных варианта задачи:

Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С.

В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.

Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30. АD = 20, ВD = 16.

∠ВDС ∠С, в этом случае из треугольника DВС по теореме синусов получаем

В действующем учебнике задача № 536 имеет вид:

Отрезок BD является биссектрисой треугольника АВС. а) Найдите АВ, если ВС = 9 см, АD = 7,5 см, DС = 4,5 см. б) Найдите DС, если АВ = 30. АD = 20, ВD = 16.

Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).

Цитируем: «Прочитай, объясни и проверь записи.

190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»

Проверяем 20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.

Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее), т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.

Предлагаем верные записи:

190 : 20 = 190 : 10 : 2 = 9 ( 1 д. остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).

В газете «Математика» предлагается уравнение и к нему ответ:1. Предложено решение уравнения по следующей схеме:

af(x)bg(x) = apbp

Приведенное решение неверное, так как приводит к потере корней. данное уравнение следует решать по схеме:

a f(x) b g(x) = a p b p a f(x)– р b q – g(x)

Вернемся к данном уравнению.

= 40 2 3

Заключение

Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.

Литература

Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
2-98 Ярский А. С, «Что делать с ошибками»
Хэкало С. П. «Корни терять нельзя» 5-98
Игнатенко В. З. «Сюрпризы биссектрисы» 5-98

Интернет-ресурсы

http://mat.1september.ru/view_article.php?ID=200900304
http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

Источник

10 основных ошибок, допускаемых в ЕГЭ по математике

Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.

Б. Шоу

Обзор основных ошибок

Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.

https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view

http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf

Профильный уровень

Задание	Процент выполнения	Типичные ошибки
1	90%	Неумение читать условие и непонимание процентов
2	95%	Невнимательное чтение условия и непонимание единиц измерения
3	88%	Невнимательное чтение условия
4	89%	Невнимательное чтение условия
5	91%	Ошибки в свойствах степеней
6	65%	Непонимание математической записи угла и неверное чтение чертежа
7	54%	Невнимательное чтение условия
8	57%	Отсутствие базовых пространственных представлений и знаний соотношений
9	47%	Ошибки в определении знака тригонометрической функции
10	65%	Невнимательное чтение условия или непонимание текста
11	36%	Невнимательное чтение условия
12	38%	Непонимание алгоритма исследования функции с помощью производной
13	36%	Неумение и небрежность отбора корней тригонометрического уравнения с помощью единичной окружности
14	6%	Неумение доказывать, непонимание взаимосвязи элементов геометрической конструкции, ошибки в теоретических фактах
15	15%	Невнимательное чтение математической записи неравенства, непонимание алгоритма решения совокупностей и систем логарифмических неравенств, забыт знаменатель при решении дробно-рационального неравенства, небрежность при изображении множества решений на координатной прямой
16	3%	Неверное понимание логики построения доказательства, ошибки в построении чертежа
17	11%	Неверное составление модели задачи (непонимание взаимосвязи величин) и вычислительные ошибки
18	3,5%	Недостаточная сформированность графического метода решения – отсутствие объяснений и обоснований, отсутствие ответа на поставленный вопрос
19	3,5%	Непонимание того, что на вопрос «Может ли…?» нужно давать аргументированное решение, а не ответ «да» или «нет»

Базовый уровень

Основные факторы, вызывающие ошибки:

недостаточный уровень понимания условия при чтении задания,
вычислительные ошибки,
недостаточная развитость наглядных геометрических представлений.

Анализ 10 типичных ошибок на примерах заданий ЕГЭ

Задачи на проценты – непонимание механизма начисления процентов.

В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.

Пример:

При решении этого задания 6% участников экзамена посчитали, что если цена была повышена на 25%, то для нахождения старой цены нужно новую цену понизить на 25%. В действительности же новая цена составляет 125% от старой цены, а узнать нужно, сколько рублей соответствуют 100%.

В более сложной экономической задаче требуется понимание механизма начисления простых и сложных процентов, обоснованное применение формул, выбор правильного способа решения. Типичные ошибки здесь связаны с неверным составлением модели задачи, непониманием взаимосвязи величин, непониманием того, что важен не только ответ, но и способ решения задачи.

Невнимательное чтение условия.

К сожалению, это самая распространенная ошибка согласно анализу типичных ошибок ЕГЭ, проведенному ФИПИ.

Конечно, многое здесь можно списать на волнение и психологическое напряжение. Даже самые подготовленные ученики на экзамене могут растеряться, переволноваться или поспешить в решении более простых заданий. Однако факт остается фактом, и при подготовке к экзаменам на него нужно обратить внимание.

Примеры:

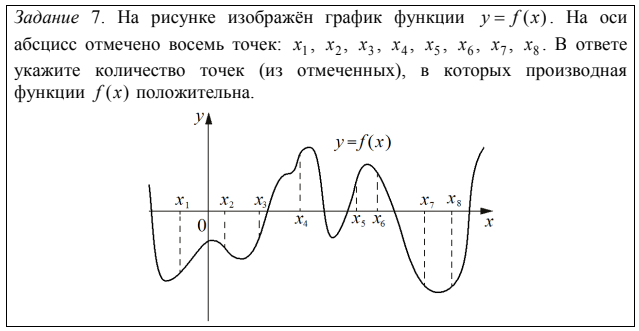
Почти 24% участников экзамена указали количество точек, в которых значение функции (а не ее производной) положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительное значение.

Около 2,5% участников экзамена нашли вероятность выбора подтекающего насоса, не обратив внимания на частицу «не» в условии.

Практико-ориентированные задания базового и повышенного уровня – непонимание текста задачи.

Кроме ошибок, связанных с невнимательным чтением условия, на первое место здесь выходит непонимание текста задачи, незнание единиц измерения величин, неумение работать с формулами. Многие выпускники даже не приступают к технически не сложным практико-ориентированным задачам повышенного уровня.

Пример:

Выполнение задания – около 57%. Отмечается, что 8% участников не дали никакого ответа; 6% решили, что чем ближе, тем лучше; 4% решили, что лампочку нужно поместить в середину разрешенного интервала, а еще 4,5% решили, что самый главный параметр – это фокус.

Вычислительные ошибки.

Привычка вычислять все с помощью калькулятора, вплоть до таблицы умножения и действий с круглыми числами доставляет учащимся немало проблем на экзамене. Отсутствие навыков быстрого счета в уме или на бумаге часто приводит к тому, что участники экзамена допускают грубые ошибки в элементарных примерах. «Слабые» места многих старшеклассников – это дроби, отрицательные числа, элементарные преобразования выражений, т.е. проблемы, накопившиеся с 5 класса.

Ошибки в теоретических фактах.

Незнание необходимых для решения задач теоретических фактов, как по алгебре, так и по геометрии, существенно снижает процент выполнения большинства заданий как базового, так и повышенного уровня сложности.

Примеры:

Около 8% выпускников не дали никакого ответа; 38% ошиблись в формуле боковой поверхности конуса, а еще 12% в формуле его объема. Отмечается, что процент выполнения этого задания существенно ниже, чем, например, формально гораздо более сложного задания с полным решением на решение уравнения и осуществление отбора корней. Это означает, что низкий процент выполнения заданий по стереометрии вызван именно существенными проблемами в ее преподавании.

В задании 5 проверялось умение решать показательные и логарифмические уравнения. Из семи процентов выпускников, не справившихся с заданием, 2% ошиблись в свойствах степеней.

Незнание алгоритмов и методов решения.

Знание алгоритмов и методов решения проверялось во многих заданиях экзаменационной работы. Например, в задании 12 требовалось продемонстрировать понимание алгоритма исследования функции с помощью производной, а в заданиях 5,13,15 знание общих и частных методов решения уравнений и неравенств.

Пример:

Ненулевые баллы получило около 15% участников экзамена. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок при решении дробно-рационального неравенства (забыт знаменатель).

Неверное чтение чертежей, непонимание взаимосвязи элементов геометрической конструкции, отсутствие базовых пространственных представлений, ошибки в построении чертежа.

В преподавании геометрии очень важным является не только умение решать вычислительные задачи с геометрическим содержанием (по формулам), но и формировать геометрические представления о фигурах (телах). При отсутствии базовых пространственных представлений сложно ожидать высокого процента выполнения стереометрического задания с полным решением.

Пример:

Отмечается, что около 10% участников экзамена при решении этой задачи неверно определили углы по их записи (перепутали буквы или не понимают, какая из букв в записи угла соответствует его вершине). Около 5% участников «увидели» прямоугольный треугольник ACD, а еще 3% — равносторонний треугольник ABD.

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. В целом при решении геометрических задач более половины выпускников продемонстрировали отсутствие знания взаимосвязей элементов геометрической конструкции и соотношений между величинами пространственных фигур.

Неумение доказывать, обосновывать.

К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Оба задания содержали два пункта. В первом пункте задание доказать, а во втором пункте вычислить. Основной проблемой оказалось выполнение первого пункта. Участники экзамена продемонстрировали неумение доказывать. При этом много встречается различного рода логических ошибок. Наибольшие затруднения участники испытывали при оформлении доказательства.

Пример:

Типичные ошибки связаны с непониманием логики построения доказательства. Например, доказательство начинается так: «Пусть точка О является серединой отрезка СК…». Т.е. в начале доказательства уже допускается факт, который и требуется доказать.

Задания 18 и 19 высокого уровня сложности предназначены для конкурсного отбора в ВУЗы с повышенными требованиями к математической подготовке абитуриентов. Это задания на комбинацию различных методов. Для успешного их выполнения, кроме прочих математических знаний, необходим высокий уровень математической культуры, который предполагает, в частности, умение обосновывать выбранные методы и способы решения.

Примеры:

Ненулевые баллы при решении этого задания получило около 17% участников экзамена. Многие выпускники попробовали исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не качественный ответ «да» или «нет».

Ненулевые баллы при решении этого задания получило около 3% участников экзамена. Основной проблемой оказалось применение графического метода, который, как показали работы участников экзамена, не достаточно сформирован. Без объяснений и обоснований на координатной плоскости отмечаются графики, и считывается множество значений параметра. Во многих случаях на координатной плоскости обозначено много верных объектов, а ответа на поставленный вопрос так и не последовало.

Задания по тригонометрии требуют тщательности решения.

Представленные в экзаменационной работе задания по тригонометрии не относятся к числу самых сложных, однако их выполнение требует тщательности решения, аккуратности, внимания, знания большого количества теоретических фактов и умения их применять на практике.

Примеры:

Выполнение задания – около 34%. Типичные ошибки связаны в первую очередь с определением знака тригонометрической функции – почти 12% участников экзамена потеряли знак «минус». Еще 22% решили, что ответ ожидается «хорошим» — 1 или 2.

Задание 13 проверяло умение решать тригонометрические уравнения и производить отбор корней. Основной проблемой первого пункта оказалось неумение вводить новую переменную (ошибки в свойствах степеней), незнание формул решения простейшего тригонометрического уравнения. При выполнении второго пункта участники продемонстрировали неумение или небрежность отбора корней.

Отсутствие навыков математического моделирования.

Способность к построению и исследованию простейших математических моделей проверяется в заданиях 11 (текстовая задача) и 17 (текстовая задача с экономическим содержанием). Текстовые задачи, как правило, являются стандартными задачами на составление уравнений курса алгебры 8 класса. В экономической задаче требуется верно построить математическую модель и исследовать ее. Важную роль при этом играет сюжетная, практико-ориентированная часть условия. При составлении математических моделей основные ошибки являются следствием непонимания взаимосвязи величин. Так, например, в задачах на движение около 10% участников экзамена продемонстрировали непонимание движения по реке – собственную скорость умножили на время движения.

Задачи с ошибками как форма работы на уроке.

Одной из форм работы на уроках является поиск и исправление ошибок. «Задачи с ошибками» являются заданиями творческого типа, они приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д.

Мой опыт преподавания показывает, что такие задания нравятся учащимся и являются достаточно эффективным способом совершенствования навыков решения задач.

Методика работы с задачами с ошибками может быть следующей:

1 этап: Индивидуальная, парная или групповая работа, в зависимости от уровня подготовленности учащихся, по поиску и исправлению ошибок. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.

2 этап: Совместное обсуждение ошибок.

3 этап: Снова индивидуальная или парная работа – составление памятки «Советы ученику, решающему задачу».

4 этап: Проверка результатов и подведение итогов учителем.

Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.

Мои рекомендации:

Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.

У меня старое издание 1996 года, но есть и более поздние издания этой книги.

Раздел 7 этого пособия так и называется: «Учимся на чужих ошибках».

http://math4school.ru/rabota_nad_oshibkami.html

Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.

Источник

02.03.2020

Статья: «Государственная итоговая аттестация по математике. Типичные ошибки и методические приемы их устранения»

В данной статье рассматриваются типичные ошибки, которые допускают учащиеся на ОГЭ по математике. На конкретных примерах разобраны возможные ошибки и рассмотрены пути их предупреждения. Автор делится со своими методическими приемами в работе со слабоуспевающими учащимися. Материал может заинтересовать учителей математики.

Оценить

1399

Содержимое разработки

Статья: «Государственная итоговая аттестация по математике. Типичные ошибки и методические приемы их устранения»

Бушкова Марина Григорьевна

Муниципальное общеобразовательное учреждение

Школа с. Белоярск

учитель математики

В математике приходится учиться в основном на собственных ошибках. Не ошибается тот, кто ничего не делает. Ошибка – вещь необходимая и полезная. Необходимая и полезная, но не на экзамене. На экзамене ученик должен показать хорошие результаты, чтобы затем продолжить образование на следующей ступени обучения. Задача учителя — в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, что будет способствовать повышению качества математической подготовки учащихся. Я.А. Коменский писал: «Любая ошибка превращается из маленького снежка в большой снежный ком, если на эту ошибку сразу не реагировал учитель при непременном привлечении самого учащегося к ее осознанию и последующему труду, направленному на ее полное преодоление».

Типичные ошибки учащихся:

незнание правил, определений, формул;

непонимание правил, определений, формул;

неумение применять правила, определения, формулы;

неверное применение формул;

невнимательное чтение условия и вопроса задания;

вычислительные ошибки;

неиспользование свойств фигур при решении геометрических задач;

логические ошибки при решении текстовых задач;

раскрытие скобок и применение формул сокращенного умножения.

Причины ошибок по математике:

пропуски занятий приводят к незнанию материала, пробелам в знаниях;

поверхностное, невдумчивое восприятие нового материала приводят к непониманию его;

недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы;

неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам (учащиеся не всегда сами понимают, что именно они написали);

усталость, чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам;

кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала;

низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки;

«зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается ошибка.

низкая мотивация: следствие низкой мотивации – потеря внимания и ошибка.

Ошибки, допускаемые учениками на экзамене по математике, я бы условно разделила на три категории: технические; глупые, обидные, сделанные на ровном месте; содержательные.

Технические ошибки связаны с неправильным заполнением бланков ответов. При проверке пробных диагностических и тренировочных работ, первое, что бросается в глаза, – это неграмотное заполнение бланка с кратким ответом.

Есть смысл показать ученикам презентацию, в которой показано то, как нельзя заполнять бланки.

К заданиям, где требуется установить соответствие, а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б1В3», или «2,1,3», или «2;1;3», или «2 1 3» вместо верного «213».

Нередко ученики в бланк ответов вписывают единицы измерения, что нельзя делать (единицы длины, веса, градус).

Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.

В некоторых работах наблюдаем, как числа написаны небрежно: иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9. Данное замечание относится и к записи решения задач с развернутым ответом – иногда просто невозможно понять, что написано учеником.

Некоторые ученики в черновиках пишут настолько неаккуратно, что из-за этого на пустом месте теряют знаки или числа. Почему-то вычисления в столбик и деление уголком многие выполняют в черновиках стыдливо мелким шрифтом где-то сбоку, будто боятся, что кто-то заметит их за этим постыдным занятием. Приучайте работать учеников в своих черновиках разумно. Это поможет избежать ненужных, досадных ошибок.

Самые частые и обидные ошибки дети совершают в том, что, как им кажется, они знают.

Во избежание обидных ошибок следует обращать внимание учащихся на указания, написанные курсивом или записанные в скобках.

Пример. Найдите корни уравнения х² + 7х – 8 = 0

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

В этом примере формирование ответа у многих учеников может вызвать затруднение. Полученные корни: -9 и 2. В соответствии с указанием ученики должны записать -92.

Отрабатываем материал с опорой на теорию. Рассмотрим задание на числовые неравенства.

Какие из следующих утверждений верны при любых значениях a и b, удовлетворяющих условию а > b?

a – 3 > b – 2

a² > b²

5a > 5b

a – b>—2

Как чаще всего решают такие задачи? Выбирают какие-то конкретные значения a и b, а затем начинают подставлять их в утверждения. В большинстве случаев такой способ годится, но не всегда. Надежнее пользоваться свойствами неравенств.

Давайте подставим значения а = 6, b =2, ведь 6 >2. Проверим первое утверждение:

6 – 3 > 2-2; 3 > 0. Получили верное неравенство. Ученики в таком случае поставят «+» и будут уверены в своей правоте.

Однако, если взять пару чисел а = 3,5 и b =3, то получится неверное равенство: 3,5 — 3 > 3-2; 0,5 > 1.

Оказывается, это неравенство верно, но не при любых значениях а и b. Поэтому ставим «- «.

Как нужно действовать, чтобы избежать ошибки?

Из того, что а > b, следует а – b > 0. Неравенство а – 3 > b – 2 преобразуем: а – b > 1. Думаем: всегда ли верно это неравенство? Этого гарантировать мы не можем, так как нельзя же утверждать, что, если а > b , то разность этих чисел всегда > 1. Например, при а = 1,2 и b = 1 разность а – b = 1,2 — 1 = 0,2 < 1.

Проверим второе утверждение. 6² > 2², 36 > 4. Но если взять а = — 6, b = — 10, то получим неверное равенство: 36 > 10. Когда мы взяли отрицательные числа, то все сломалось. Это утверждение верно, но не при любых значениях. В этом утверждении мы также вынуждены поставить «- «.

Третье утверждение верно всегда, так как, если обе части неравенства умножить на положительное число, то получится равносильное неравенство.

Четвертое утверждение верно всегда. По условию а – b > 0, но 0 > — 2. Следовательно, тем более, а – b > -2.

Как наши дети применяют формулы сокращенного умножения? Можно встретить такие решения: (а + b)² = а² + b²; (а – b)² = а² — b². Удвоенное произведение членов пропускают. Придумывают несуществующие формулы, например, а² + b² = (а – b)(a+b).

Что с этим делать? Учить, доводить до автоматизма, учить применять эти формулы в 7 классе, продолжать работу в 8-9 классах. Включать упражнения на применение этих формул на этапе повторение пройденных материалов на уроках.

Самые глупые и обидные ошибки связаны с банальной невнимательностью. Во многих случаях учащиеся невнимательно или не до конца читают текст задачи, отвечают не на поставленный вопрос. Чаще всего это задачи на чтение графиков, теорию вероятности.

Пример. На экзамене 25 билетов, Иван не выучил 7 из них. Найдите вероятность того, что ему попадется выученный билет.

Ответ: 0,28.

Этот ошибочный ответ объясняется тем, что ученик невнимательно прочитал вопрос задачи.

Необходимо приучать учеников проверять, отвечает ли полученный ответ на вопрос, поставленный в задаче. Можно пару раз самому учителю допустить ошибку и спровоцировать их на обсуждение данной проблемы.

Итак, добиваемся от учеников внимательного чтения условия задачи

Необходимо приучать учеников детально прорабатывать каждое задание, делать проверки. Некоторые ученики стараются перескакивать через несколько шагов вычислений, делая их в уме. Но в условиях экзамена лучше посчитать надежнее, расписав несколько лишних действий, чем провести их в уме, рискуя сделать ошибку. Если ученик все сделает верно, это сэкономит 5 с из 4 часов. Если ученик приучен делать проверки в вычислениях, это поможет ему избежать на экзамене досадных ошибок. Цена ошибки – драгоценные баллы.

Ошибки нужно изучать, выявлять наиболее устойчивые, вести учет. Работать над формированием навыков самоконтроля, приучая учащихся к проверке вычислений и преобразований путем обратного действия, к оценке результата решения задачи с точки зрения здравого смысла.

Пример. Решить уравнение 58 – 11х – 8 = 0

58 – 11х – 8 = 0

-11х = 58 + 8

-11х = 66

х = 66 : (-11)

х = -6

Приучаем детей делать проверку:

-58 — 11(-6) – 8 = 0

-58 + 66 -8 = 0

0 = 0

При упрощении дробно-рациональных выражений зачастую подводит «коварный» минус. При вычитании многочлена ученики не меняют знаки членов, тем самым приводят решение в тупик, теряют время и получают неверный ответ.

Пример. Найти значение выражения при а = 78, с = 21.

Приведем пример неверного решения:

Как избежать ошибку?

После «минуса» многочлен сначала лучше записать в скобках, а затем эти скобки раскрыть:

Задания по геометрии учащимися решаются с меньшей успешностью.

Определение сosα, sinα, tgα, ctgα- больная тема. Ученики плохо запоминают определение, а в стрессовой ситуации путают эти определения. Можно применить секреты для запоминания.

Начнем с определения сosα. Слово «косинус» созвучно со словом «коснуться». Значит, в определении косинуса фигурирует катет, который касается угла, то есть сosα — это отношение катета, прилежащего к углу, к гипотенузе. Для sinα остается отношение противоположного катета к гипотенузе.

Слово «тангенс» созвучно со словом «там» (далеко), то есть – это отношение противоположного (дальнего) катета к прилежащему катету.

Таких секретов для лучшего запоминания в математике много, и мы, учителя, щедро делимся с учениками этими секретами.

В задачах по геометрии в работе со слабоуспевающими при отработке конкретного задания не стоит показывать все вариации решений. На мой взгляд, лучше выбрать самый оптимальный способ решения, сформулировать его на этапе изучения нового материала с учениками и пользоваться этим способом вплоть до сдачи экзамена. Дело в том, что малейшее отступление от алгоритма сбивает слабых учеников с толку, они теряют уверенность, допускают ошибки.

Пример. Тема «Теорема Пифагора» применяется на ОГЭ в практических геометрических задачах. В этом году эта теорема может быть использована в одном из практико-ориентированных заданий №№ 1-5.

В работе со слабоуспевающими детьми отрабатываю следующую схему применения теоремы Пифагора:

Записать формулу:	с² = а² + b²
Подставить числовые значения:	17² = 15² + b²
Вычислить квадраты чисел:	289 = 225 + b²
Поменять левую и правую части уравнения местами, чтобы переменная оказалась в левой части уравнения:	225 + b² = 289

Выразитьb²:	b² = 289 – 225
Вычислить значение выражения в правой части уравнения:	b² = 64
Вычислитьb:	b= = 8

Многократное использование одной и той же схемы позволит даже самым слабым ученикам справиться с заданием. Пусть будет один способ, но надежный.

Самые частые ошибки в ГИА по математике связаны с дробями и отрицательными числами — такие результаты из года в год отмечают специалисты из федеральной группы разработчиков ГИА по математике. То есть «слабым местом» оказались темы, которые ученики проходят в 5-7 классах.

Чтобы перед экзаменом не терять время на ликбез, необходимо отрабатывать материал на этапе его изучения. Много сил и энергии учитель тратит на работу со слабоуспевающими учениками. В работе с ними помимо математических правил необходимы особые приемы, личные придумки, и у каждого учителя их немало.

Даю совет слабоуспевающим ученикам: перед тем как начать работу, напишите таблицу умножения. Пусть она будет перед глазами.

Но даже написание таблицы в черновике нужно отрабатывать с учеником при подготовке к экзамену. Пусть он на консультации вам несколько раз продемонстрирует умение составления таблицы умножения.

Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Пример. Расположить числа 0,66; 0,066; 0,606; 0,0606 в порядке возрастания.

Очень важно, как ученики оформляют решение в черновиках. Сильные ученики буквально устно могут выполнить это задание. А вот слабых и невнимательных учеников желательно приучать к строгим схемам.

Одна из схем может выглядеть следующим образом:

Записать числа столбиком:	0,66 0,066 0,606 0,0606
Уравнять количество знаков после запятой:	0,66 = 0,6600 0,066 = 0,0660 0,606 = 0,6060 0,0606 = 0,0606
Сравнить числа, невзирая на запятые, и присвоить каждому числу порядковый номер (в порядке возрастания):	0,66 = 0,6600 6600 (4) 0,066 = 0,0660 660 (2) 0,606 = 0,6060 6060 ( 3) 0,0606 = 0,0606 606 (4)
С новой строки записать числа в их первоначальном виде в этом порядке:	0,606; 0,066; 0,606; 0,66.
Выбрать правильный вариант ответа:	Ответ:

Тщательное прорабатывание решения – залог успеха.

Лучшему усвоению математического материала помогут некоторые ассоциативные картинки. Математика должна ожить в образах.

В работе со слабоуспевающими учениками необходимо использовать универсальные способы решения. Например, у них возникают большие проблемы при нахождении НОЗ, при сокращении дробей, при внесении множителя за знак корня. Во всех перечисленных случаях поможет разложение на простые множители.

Пример: Найти значение выражения .

Пример .

Итак, учащиеся с низким уровнем обученности:

•выполняют задания по образцу;

•с проработкой;

•многократным повторением правил и формул;

• методы и приемы отрабатывают до автоматизма.

Разберем некоторые ошибки в заданиях ОГЭ с развернутым решением.

В задачах на проценты необходимо акцентировать внимание на необходимости определить стопроцентную величину, только после этого выбирать способ решения.

Пример. Вишня стоит 120 рублей за килограмм, а черешня – 150 рублей за килограмм. На сколько процентов черешня дороже вишни?

Как могут дети решить такую задачу? Некоторым учащимся кажется, что 150 руб. – 100%, что неверно. Ключевое утверждение к таким задачам: за 100% принимают ту величину, с которой сравнивают другие величины.

В нашей задаче стоимость черешни сравнивается со стоимостью вишни. Следовательно, 100% — 120 руб.

Полезно разобрать эту же задачу с другим вопросом.

Пример. Вишня стоит 120 рублей за килограмм, а черешня – 150 рублей за килограмм. На сколько процентов вишня дешевле черешни?

Решение. В этой задаче стоимость вишни сравнивается со стоимостью черешни. Следовательно, 150 руб. – 100%.

В качестве еще одного примера рассмотрим задачу, предлагаемую в 9-ом классе для развернутого ответа

Задача: «На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей за час делает первый рабочий?».

Решение одного из учеников: ; х = 25; х = -9,5 (не подходит).

Ответ: 25 деталей.

Комментарий. Приведенный ответ совпадает с верным. Уравнение по условию задачи составлено верно, если принять, что x – это число деталей, которые изготавливает за час первый рабочий. Но если учащийся не говорит, что принимается за x, то проверить правильность составления уравнения невозможно: в зависимости от того, какую величину приняли за x, получим различные уравнения. К сожалению, эксперт вынужден будет поставить 0 баллов. Заметим, что при арифметической ошибке при решении верно составленного уравнения решение оценивается неполным баллом.

Иногда ученики приводят пояснение к составлению уравнения в форме таблицы – это выбор учащегося, но при этом сам учащийся должен понимать, что его запись должна быть понятна не только ему, но и проверяющему. Думаем, размышляющий ученик здесь согласится, что запись решения текстовой задачи с помощью составления уравнения следует начинать словами: «Пусть x – это…».

В случае арифметического решения задачи (по действиям) необходимо давать пояснения каждому действию. Иначе получаем, что ученик складывает, вычитает, умножает, делит числа, в итоге получает некоторое число, которое записывает в ответ. Это число, конечно, может и совпадать с верным ответом, но верны ли при этом размышления? Подчеркнем, эксперт не должен додумывать за ученика, он проверяет верность решения.

Кроме того, если составленное уравнение – дробно-рациональное, необходимо указать О.Д.З.

Задание 23. Основным условием положительной оценки за решение задания № 23 является верное построение графика. Верное построение графика включает в себя: масштаб, содержательная таблица значений или объяснение построения, выколотая точка обозначена в соответствии с ее координатами.

Комментарий: график построен неверно – отсутствует выколотая точка. В соответствии с критериями – 0 баллов.

Оценка эксперта: 0 баллов.

При проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.

Перед учителем математики стоит задача: научить всех учащихся, подготовить их к прохождению ГИА, создать базу для дальнейшего образования. Но его терпение, тактичные и доброжелательные отношения ко всем ученикам, искренняя заинтересованность в их успехах является основой выполнения этой нелегкой задачи.

Чем ученики больше знают — тем меньше стресс и больше уверенность в себе и своих силах. Очень важна аксиома: больше знаешь – меньше боишься, меньше боишься — больше веришь в победу, веришь в победу — значит победишь. Задача педагогов и родителей заставить поверить в это учеников.

Список литературы:

Дука Н. И. Методическая разработка. Ошибки учащихся при изучении математики, их предупреждение и объяснение. // сайт Социальная сеть работников образования.nsportal.ru/20.08.2013.

Сайт Сдам ГИА: Решу ОГЭ. математика

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/399296-statja-gosudarstvennaja-itogovaja-attestacija

«Свидетельство участника экспертной комиссии»

Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!

Источник

Библиографическая ссылка

Какие бывают ошибки в математике

Типичные ошибки в математике

Допускать пробелы в знаниях

Зазубривать теорию

Перескакивать от простого к сложному

Списывать домашнее задание

Заниматься нерегулярно

Делать упор только на алгебру или геометрию

Статья: «Государственная итоговая аттестация по математике. Типичные ошибки и методические приемы их устранения»

Возможно, вам также будет интересно: