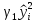Скрипт в R для этого примера
Данные для этого примера.
Гетероскедастичность — это типичная «болезнь» пространственных данных, поэтому лучше по умолчанию исходить из того, что она в вашей модели есть. Тем не менее, иногда бывает полезно уметь аккуратно проверить её наличие. Для этого можно использовать два традиционных подхода: графический анализ данных и формальные статистические тесты.
Один из способов выявления гетероскедастичности при помощи графического анализа состоит в том, чтобы построить диаграммы рассеяния, в каждой из которых по оси ординат стоит зависимая переменная, а по оси абсцисс — один из регрессоров. Если, разглядывая подобную диаграмму, вы видите нечто похожее на рисунок 2.3б, то у вас есть гетероскедастичность, связанная с соответствующим регрессором. Другой вариант состоит в анализе графика остатков регрессии. Отсортируйте остатки по возрастанию какой-либо объясняющей переменной и постройте их график. Если разброс остатков вокруг нуля равномерен (как, например, на рис. 5.1), то можно заключить, что гетероскедастичность, связанная с этим регрессором, в данных отсутствует. Если же на графике остатков явно видно, что их разброс вокруг нуля зависит от значения регрессора (как, например, на рис. 5.2), значит, гетероскедастичность есть.
Рисунок 5.1. Поведение остатков регрессии говорит в пользу гомоскедастичности
Рисунок 5.2. Поведение остатков регрессии говорит в пользу гетероскедастичности
Анализ графиков не всегда позволяет сделать однозначный вывод по поводу наличия или отсутствия гетероскедастичности, поэтому помимо него могут быть полезны соответствующие формальные статистические тесты. Ниже приводятся два наиболее часто используемых в настоящее время теста.
Тест Бреуша — Пагана
Тестируемая гипотеза в данном тесте состоит в том, что гетероскедастичности в модели нет:
(H_{0}:{sigma_{1}^{2} = ldots = sigma_{n}^{2}})
Альтернативная гипотеза — дисперсия случайной ошибки (varepsilon_{i}) некоторым образом зависит от группы переменных:
(H_{1}:{sigma_{i}^{2} = {gamma_{0} + gamma_{1}}}{z_{i}^{(1)} + ldots + gamma_{p}}z_{i}^{(p)})
Здесь (z_{i}^{(1)},z_{i}^{(2)},ldots,z_{i}^{(p)}) — набор переменных, которые предположительно влияют на дисперсию случайной ошибки. Обычно в качестве таких переменных берутся регрессоры из исходной модели, а также их квадраты.
Процедура осуществления теста устроена так: сначала при помощи обычного МНК оценивается исходная модель (для которой мы хотим проверить отсутствие гетероскедастичности) и вычисляются соответствующие остатки (e_{i}). Далее вычисляется вспомогательное значение ({{overset{sim}{sigma}}^{2} = frac{1}{n}}{sum e_{i}^{2}}). После этого необходимо оценить вспомогательное уравнение, в котором справа стоят переменные, потенциально влияющие на дисперсию случайной ошибки:
({frac{e_{i}^{2}}{{overset{sim}{sigma}}^{2}} = {gamma_{0} + gamma_{1}}}{z_{i}^{(1)} + ldots + gamma_{p}}{z_{i}^{(p)} + u_{i}})
Далее вычисляется расчетное значение тестовой статистики по простой формуле: половина от объясненной суммы квадратов во вспомогательном уравнении.
Если верна нулевая гипотеза, то указанная статистика асимптотически имеет распределение Хи-квадрат с (p) степенями свободы. Поэтому, если расчетное значение больше критического значения, взятого из таблиц распределения (chi^{2}) с (p) степенями свободы для выбранного исследователем уровня значимости, то следует отвергнуть нулевую гипотезу и заключить, что в данных есть гетероскедастичность (необходимые таблицы доступны, например, в приложении к главе 6). В противном случае можно сделать вывод в пользу гомоскедастичности.
Тест Уайта
Тестируемая гипотеза в данном тесте снова состоит в том, что гетероскедастичности в модели нет:
(H_{0}:{sigma_{1}^{2} = ldots = sigma_{n}^{2}})
Альтернативная гипотеза — дисперсия случайной ошибки (varepsilon_{i}) произвольным (возможно, нелинейным) образом зависит от переменных модели.
Процедура теста устроена так: сначала при помощи обычного МНК оценивается исходная модель (для которой мы хотим проверить отсутствие гетероскедастичности) и вычисляются соответствующие остатки (e_{i}). После этого необходимо оценить вспомогательное уравнение, в котором слева стоит (e_{i}^{2}), а справа — константа, регрессоры исходного уравнения, их квадраты и попарные произведения1.
Далее вычисляется расчетное значение тестовой статистики по следующей формуле
({left( {R^{2}mathit{во}mathit{вспомогательном}mathit{уравнении}} right) ast n}.)
Если верна нулевая гипотеза, то указанная статистика асимптотически имеет распределение Хи-квадрат с (p) степенями свободы ((p) — число регрессоров во вспомогательном уравнении). Поэтому, если расчетное значение больше критического значения, взятого из таблиц распределения (chi^{2}) с (p) степенями свободы для выбранного исследователем уровня значимости, то следует отвергнуть нулевую гипотезу и заключить, что в данных есть гетероскедастичность. В противном случае можно сделать вывод в пользу гомоскедастичности2.
Закончить обсуждение вопроса выявления гетероскедастичности следует предостережением по поводу ложной гетероскедастичности. Ложной гетероскедастичностью называется ситуация, при которой формальные тесты указывают на наличие гетероскедастичности, однако в действительности дело вовсе не в ней, а в неверной спецификации уравнения. Хорошим примером может служить рисунок 4.5б, на котором представлена нелинейная зависимость между парой переменных. Если при этом ошибочно оценить линейную регрессию (соответствующая прямая линия изображена на рисунке), то статистические тесты будут говорить в пользу гетероскедастичности, так как поведение остатков технически будет зависеть от значения регрессора (см. нижний график на этом же рисунке). Однако в действительности гетероскедастичности в модели нет, а есть только нелинейная связь между переменными.
Важно различать истинную и ложную гетероскедастичность, так как они приводят к совершенно разным последствиям. Истинная гетероскедастичность не вызывает смещения оценок коэффициентов модели, в то время как ошибочная спецификация уравнения регрессии вызывает его, то есть является гораздо более серьезной проблемой.
Пример 5.3. Оценка эффективности использования удобрений (окончание)
Для модели, оцененной в примере 5.1, осуществите тест Уайта, используя пятипроцентный уровень значимости. Интерпретируйте полученные результаты.
Решение:
Результаты оценки вспомогательного уравнения для осуществления теста Уайта представлены ниже.
Тест Уайта на гетероскедастичностьМНК, использованы наблюдения 1-200
Зависимая переменная: квадраты остатков регрессии, оцененной в примере 5.1
Коэффициент Ст. ошибка t-статистика P-значение
--------------------------------------------------------------------
const -2270,16 5654,83 -0,4015 0,6886
FUNG1 0,482935 108,468 0,004452 0,9965
FUNG2 -150,789 95,3876 -1,581 0,1158
GIRB 1,82902 98,0229 0,01866 0,9851
INSEC 129,035 72,6436 1,776 0,0775 *
LABOUR 2,05511 4,84800 0,4239 0,6722
YDOB1 30,5354 43,6171 0,7001 0,4849
YDOB2 3,43369 50,1279 0,06850 0,9455
квадрат_FUNG1 0,0956897 0,0549105 1,743 0,0833 *
FUNG1*FUNG2 0,0294522 0,0492979 0,5974 0,5510
FUNG1*GIRB -0,0332633 0,0480171 -0,6927 0,4895
FUNG1*INSEC 0,0229300 0,0554156 0,4138 0,6796
FUNG1*LABOUR -0,00259087 0,00348456 -0,7435 0,4582
FUNG1*YDOB1 0,0104778 0,0246791 0,4246 0,6717
FUNG1*YDOB2 -0,0536699 0,0501448 -1,070 0,2861
квадрат_FUNG2 0,0919819 0,0646201 1,423 0,1565
FUNG2*GIRB -0,0931636 0,0529473 -1,760 0,0803 *
FUNG2*INSEC -0,0878293 0,0548646 -1,601 0,1113
FUNG2*LABOUR -0,00520969 0,00419928 -1,241 0,2165
FUNG2*YDOB1 0,0829467 0,0471221 1,760 0,0802 *
FUNG2*YDOB2 -0,0118900 0,0437395 -0,2718 0,7861
квадрат_GIRB -0,0598434 0,0581283 -1,030 0,3048
GIRB*INSEC -0,0361947 0,0561232 -0,6449 0,5199
GIRB*LABOUR 0,00279620 0,00413522 0,6762 0,4999
GIRB*YDOB1 0,0287539 0,0384965 0,7469 0,4562
GIRB*YDOB2 0,0537695 0,0489420 1,099 0,2735
квадрат_INSEC -0,0406052 0,0570708 -0,7115 0,4778
INSEC*LABOUR -0,00562133 0,00477862 -1,176 0,2412
INSEC*YDOB1 0,0367439 0,0296061 1,241 0,2163
INSEC*YDOB2 -0,0599689 0,0474392 -1,264 0,2080
квадрат_LABOUR -0,000342326 0,000950427 -0,3602 0,7192
LABOUR*YDOB1 -0,00130669 0,00215676 -0,6059 0,5454
LABOUR*YDOB2 0,00492378 0,00240166 2,050 0,0419 **
квадрат_YDOB1 -0,0176598 0,00913794 -1,933 0,0550 *
YDOB1*YDOB2 -0,0352604 0,0255207 -1,382 0,1690
квадрат_YDOB2 0,0194422 0,0232499 0,8362 0,4042
Неисправленный R-квадрат = 0,280856
Тестовая статистика: n*R-квадрат = 56,171138,
р-значение = P(Хи-квадрат(35) > 56,171138) = 0,013059
В учебных целях мы привели оцененное уравнение полностью, хотя обычно в этом нет нужды, так как для осуществления теста достаточно знать только количество переменных в этом уравнении, его R-квадрат и число наблюдений. Обратите внимание, что число регрессоров тут действительно велико из-за добавления квадратов и попарных произведений переменных из исходного уравнения.
В нашем случае P-значение для осуществляемого теста (представленное в самом низу таблицы с результатами) составляет 0,013. Это меньше, чем 0,05. Поэтому при уровне значимости 5% следует отвергнуть нулевую гипотезу данного теста. Напомним, что нулевая гипотеза теста Уайта состоит в том, что в модели нет гетероскедастичности. Следовательно, отвергая её, мы должны заключить: в нашем случае в данных наблюдается гетероскедастичность.
-
Обратите внимание, что добавлять нужно только такие квадраты и попарные произведения, включение которых в модель не приводит к чистой мультиколлинеарности. Например, квадраты фиктивных переменных добавлять не стоит, так как они будут принимать в точности такие же значения, что и исходные переменные ((0^{2} = 0) и (1^{2} = 1)).↩︎
-
В XX веке для выявления гетероскедастчиности использовался широкий спектр альтернативных тестов: Голдфелда — Квандта, Спирмена, Глейзера и Парка. Они остались за рамками этой книги, поскольку в современных исследованиях применяются редко.↩︎
Проверка на наличие гетероскедастичности
Случайные отклонения принимают произвольные значения некоторых вероятностных распределений. Но, несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо меньшим, положительным либо отрицательным, не должно быть причины, вызывающей большие отклонения при одних наблюдениях и меньшие при других. Если дисперсии случайных составляющих неодинаковы в разных наблюдениях: σ 2 ui ≠ σ 2 u σ const, i, j = 1;n (i ≠ j), говорят, что имеет место гетероскедастичность (т. е. неодинаковый разброс случайных составляющих).
Гомоскедастичность подразумевает одинаковую дисперсию остатков при каждом значении фактора.
Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка — курсовая работа
Министерство образования Республики Беларусь
Белорусский Государственный Университет
Кафедра Экономической и институциональной экономики
По дисциплине «Эконометрика и прогнозирование»
«Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка»
Студентка третьего курса
Отделения «Экономическая теория»
Волкова Ольга Александровна
Абакумова Юлия Георгиевна
Построение базовой регрессионной модели и оценка её качества
Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка
Устранение гетероскедастичности в модели
Список использованных источников
Вся история развития человечества неразрывно связана с изменениями динамики численности и воспроизводства населения. Современные очень высокие темпы роста численности населения мира в решающей степени определяются темпами его увеличения в развивающихся странах.
Современный «взрыв» населения в развивающихся странах имеет существенные особенности. Главная особенность заключается в том, что если в Европе быстрый рост населения был обусловлен в первую очередь социально-экономическими изменениями, т.е. следовал за экономическим ростом и изменениями в социальной сфере, то в развивающихся странах мы наблюдаем прямо противоположную картину: быстрый рост населения значительно опережает их экономическое и социальное развитие, усугубляя тем самым и без того ложные проблемы занятости, социальной сферы, обеспечения продовольствием, экологии.
Наряду с наблюдаемым во второй половине XX века демографическим взрывом проявился и демографический кризис, затронувший в первую очередь развитые страны мира.
Суть современного демографического кризиса заключается не только в резком ухудшении развития народонаселения, что выражается в резком уменьшении темпов роста численности населения в развитых странах, а в некоторых из них и снижении этого показателя за нулевую отметку, но и в определенном кризисе института семьи, в некотором ухудшении качества развития населения, в демографическом старении.
Наблюдаемая в развитых странах мира тенденция к резкому падению рождаемости значительно ниже уровня, обеспечивающего простое воспроизводств населения, ведет к значительному демографическому старению, сокращению трудовых ресурсов и увеличению «экономической нагрузки» на экономически активное население, на старение населения или увеличение доли пожилых и старых людей.
Итак, изменение показателя общей численности населения происходит под воздействием целого ряда прямых и косвенных факторов. В своей работе я бы хотела рассмотреть влияние показателей рождаемости, смертности и численности пожилого населения в разных странах мира на общую численность населения этих стран.
Такой выбор обусловлен, в первую очередь, целью моей работы – проверка регрессионной модели на гетероскедастичность (т.к. эта проблема в большей степени присуща пространственным данным и редко встречается во временных рядах).
Таким образом построенная мною модедь содержит следующие объясняющие переменные:
X1 – численность рожденных детей за 2007г. (чел.),
X2 – численность умерших за 2007г. (чел),
Х3 – численность населения в возрасте от 65 лет и старше (чел.), и объясняемую переменную:
Y – общая численность населения на начало 2008г. (чел.).
Статистические данные по странам взяты за период 2007г, влияющие на общую численность населения начала 2008г. (Таблица 1)
| Страны | Общая численность населения на начало года | X1- численность рожненных детей за 2007г. | X2 — смертность за 2007г. | X3 — численность населения старше 65 лет за 2007г. |
| Бельгия | 10666866 | 120663 | 374.0553 | 1824034.086 |
| Болгария | 7640238 | 75349 | 693.2108 | 1321761.174 |
| Чехия | 10381130 | 114632 | 355.3592 | 1484501.59 |
| Дания | 5475791 | 64082 | 256.328 | 837796.023 |
| Германия | 82221808 | 682700 | 2594.26 | 16279917.98 |
| Эстония | 1340935 | 15775 | 78.875 | 229299.885 |
| Ирландия | 4419859 | 70623 | 261.3051 | 490604.349 |
| Греция | 11214992 | 110048 | 418.1824 | 2085988.512 |
| Испания | 45283259 | 488335 | 1806.8395 | 7562304.253 |
| Франция | 63753140 | 816500 | 3102.7 | 10328008.68 |
| Италия | 59618114 | 563236 | 2140.2968 | 11864004.69 |
| Кипр | 794580 | 8529 | 52.8798 | 97733.34 |
| Латвия | 2270894 | 23273 | 202.4751 | 388322.874 |
| Литва | 3366357 | 32346 | 190.8414 | 525151.692 |
| Люксембург | 483799 | 5477 | 9.8586 | 67731.86 |
| Венгрия | 10045000 | 97600 | 575.84 | 1597155 |
| Мальта | 410584 | 3871 | 25.1615 | 56660.592 |
| Нидерланды | 16404282 | 180882 | 741.6162 | 2378620.89 |
| Австрия | 8331930 | 76250 | 282.125 | 1408096.17 |
| Польша | 38115641 | 387873 | 2327.238 | 5107495.894 |
| Португалия | 10617575 | 102492 | 348.4728 | 1836840.475 |
| Румыния | 21528627 | 214728 | 2576.736 | 3207765.423 |
| Словения | 2025866 | 19636 | 60.8716 | 322112.694 |
| Словакия | 5400998 | 54424 | 331.9864 | 642718.762 |
| Финляндия | 5300484 | 58729 | 158.5683 | 874579.86 |
| Швеция | 9182927 | 103421 | 258.5525 | 1597829.298 |
| Великобритания | 61185981 | 770651 | 3467.9295 | 9789756.96 |
| Турция | 70586256 | 1361000 | 29533.7 | 4658692.896 |
| Исландия | 314321 | 4508 | 6.3112 | 36775.557 |
| Норвегия | 4737171 | 58459 | 181.2229 | 691626.966 |
| Швейцария | 7591414 | 74440 | 290.316 | 1229809.068 |
При практическом проведении регрессионного анализ модели с помощью МНК необходимо обращать внимание на проблемы, связанные с выполнимостью свойств случайных отклонений модели, т.к. свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса-Маркова), т.к. при их нарушении МНК может давать оценки с плохими статистическими свойствами.
Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: т.е. D( εi ) = D( εj ) = σ 2 для любых наблюдений i и j. Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
Наличие гетероскедастичности может привести к снижению эффективности оценок, полученных по МНК, к смещению дисперсий, к ненадежности интервальных оценок, получаемых на основе соответствующих t- и F-статистик. Таким образом, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключения по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно можно признать статистически значимыми коэффициенты, которые таковыми не являются. Причиной гетероскедастичности могут быть выбросы (резко выделяющиеся наблюдения), ошибки спецификации модели, ошибки в преобразовании данных, ассиметрия распределения какой-либо из объясняющих переменных. Чаще всего, появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако обычно приходиться решать эту проблему уже после построения уравнения регрессии. Не существует какого-либо однозначного метода определения гетероскедастичности. Существует довольно большое количество тестов и критериев, наиболее популярными и наглядными из которых являются: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфельда-Квандта и тест Уайта. Моя работа посвящена исследованию поледних двух тестов.
Алгоритм этого теста заключается в том, что сперва оценивается исходная модель и определяются остатки εi , затем строится вспомогательно уравнение регрессии и определяется его коэффициент детерминации, произведение n*R^2 сравнивается со значением χ^2- распределения и делается вывод о наличии или об отсутствии гетероскедастичности.
Парк в свою очередь предложил следующую функциональную зависимость:
1) Оцениваем исходное уравнение и определяем ei .
2) Оцениваем уравнение
Проверяем статистическую значимость коэффициента β уравнения на основе статистики
Если β значим, то гетероскедастичность. Если нет, то гомоскедастичность.
1) Оценивается исходная модель и определяются остатки
2) Оценивается регрессия

Если
При установлении присутствия гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Сначала можно попробовать устранить возможную причину гетероскедастичности, скорректировав исходные данные, затем попробовать изменить спецификацию модели, а в случае, если не помогут эти меры, использовать метод взвешенных наименьших квадратов.
Далее в работе проведем довольно полный анализ базовой модели, включая непосредственно тесты на обнаружение гетероскедастичности.
1. Построение базовой регрессионной модели и оценка её качества
По данным Таблицы 1 построим исходную модель с помощью пакета Eviews3.1. Получим следующее уравнение построенной модели:
Population – общая численность населения на начало 2008г. (чел.),
Birth – численность рожденных детей за 2007г. (чел.),
Mortality – численность умерших за 2007г. (чел),
Old – численность населения в возрасте от 65 лет и старше (чел.).
Проверим на значимость коэффициенты уравнения регрессии. Для этого оценим t-статистику:
Используем в данном случае уровень значимости 
Значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.
Продолжая оценивать общее качество модели, используем критерий Фишера:
Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна. Поскольку значение F-наблюдаемого велико, можно сделать предположение о наличии мультиколлинеарности, что будет проверено мною в дальнейшем.
Оценим также распределение остатков в модели:
P (J-B) = 0,06, следовательно присутствует нормальное распределение остатков.
Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.
1) Первоначально воспользуемся тестомБреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:
Запишем значение 
Приведем результаты теста с lag = 1:
Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше
а P-вероятность статистики Бреуша-Годфри больше уровня значимости
( 
2) Воспользуемся также тестом Дарбина-Уотсона:
Приведем значение статистики:
Значения критических точек


Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-Wв данном случае близко к 2.
Выполним проверку регрессионной модели на мультиколлинеарность.
Построим корреляционную матрицу коэффициентов:
Найдем частные коэффициенты корреляции:
Делаем вывод о наличии высокой зависимости (коллинеарности) между переменными в каждом из трех случаев. Следовательно в модели присутствует мультиколлинеарность. Эта проблема оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели.
2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка
Переходим непосредственно к основной теме курсвой — проверяем модель на наличие гетероскедастичности. Для этого первоначально проведем тест Вайта и оценим его результаты:
Т.к. значение P- вероятности в обоих случаях теста Уайта (nocrossterms/ crossterms) меньше уровня значимости
( 
то принимаем гипотезу о наличии гетероскедастичности в модели.
Дополнительно можно использовать графический анализ ряда остатков, который подтверждает вывод о наличии гетероскедастичности, т.к. график имеет выбросы и не укладывается в полосу постоянной ширины, параллельную оси ОХ (-1000000,1000000).
Таким образом, в этой модели мы имеем две проблемы – мультиколлинеарность и гетероскедастичность, в связи с чем нельзя доверять статистическим выводам и оценкам качества регрессионной модели.Продолжим дальнейший анализ модели с помощью теста Парка. Данный тест не предполагает особой свободы выбора и мы строим три регрессионные модели натуральных логарифмов остатков базовой модели на натуральные логарифмы каждой объясняющей переменной отдельно.
Представим вспомогательную модель 1 теста Парка:
Запишем уравнение вспомогательной модели 1:
Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику:
Найдем критическое значение t-статистики на уровне значимости
( 
После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Birth в следствие того, что коэффициент 
Представим вспомогательную модель 2 теста Парка:
Запишем уравнение вспомогательной модели 2:
Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику. Найдем критическое значение t-статистики на уровне значимости ( 

После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Mortality в следствие того, что коэффициент 
Представим вспомогательную модель 3 теста Парка:
Запишем уравнение вспомогательной модели 2:
Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику. Найдем критическое значение t-статистики на уровне значимости ( 
После проведенного теста можно сделать вывод о наличии гетероскедастичности по переменной Old в следствие того, что коэффициент 
Оценив каждую переменную по тесту парка в отдельности подтверждаем выводы сделанные ранее по тесту Вайта о гетероскедастичности исходной модели.
Теперь используем тест Бреуша-Пагана для окончательного подтвержения гетероскедастичности. Для начала строим временной ряд квадратов остатков, деленных на величину
а затем строим для него саму регрессионную модель.
Находим необходимые для анализа параметры вспомогательной регрессии:
Делаем вывод об очевидном присутствии в модели гетероскедастичности, так как

Устранение гетероскедастичности в модели
После проведения тестовВайта, Бреуша-Пагана-Годфри и Парка было выявлено очевидное наличие проблемы гетероскедастичности остатков в базовой модели регрессии. Приступим к ее устранению при помощи веса, выбранного соответственно тесту Бреуша-Пагана. Предпологаем форму выявленной гетероскедастичности:
Вес:
Оцененная с помощью метода взвешанных наименьших квадратов базовая регрессия выглядит следующим образом:
Получим следующее уравнение построенной модели-NEW:
Где переменные, скорректированные на вес:
PopulationNEW – общая численность населения на начало 2008г. (чел.),
cNEW – константа базовой модели, деленная на вес,
BirthNEW – численность рожденных детей за 2007г. (чел.),
MortalityNEW – численность умерших за 2007г. (чел),
OldNEW – численность населения в возрасте от 65 лет и старше (чел.).
Проверим на значимость коэффициенты уравнения регрессии. Для этого оценим t-статистику. Используем в данном случае уровень значимости 
Если значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. Лишь одна переменная, являющаяся в прошлой базовой модели константой в данном случае незначима, что логично, ведь она не имеет реального смысла, т.е. не описывает реальным образом объясняемую переменную. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.
Продолжая оценивать общее качество модели, используем критерий Фишера:
Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна.
Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.
1) Первоначально воспользуемся тестомБреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:
Запишем значение 
Приведем результаты теста с lag = 1:
Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше
а P-вероятность статистики Бреуша-Годфри больше уровня значимости
( 
2) Воспользуемся также тестом Дарбина-Уотсона:
Приведем значение статистики:
Значения критических точек


Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-Wв данном случае близко к 2.
Проверим скорректированную модель на наличие гетероскедастичности с помощью теста Вайта
Т.к. значение P- вероятности в обоих случаях теста Уайта (nocrossterms/ crossterms) больше уровня значимости
( 
и Obs* R-squared превышает
то принимаем гипотезу об отсутствии гетероскедастичности в модели (гомоскедастичность).
В моей курсовой работе я построила регрессионную модель по реальным данным. Я разбиралась с моделью зависимости общей численности населения от показателей рождаемости, смертности и численности пожилого населения, их влиянием друг на друга и на объясняемую переменную. Так как целью моей работы являлось проверить, как работают на практике тесты Уайта и Бреуша-Пагана-Годфри и Парка, то я использовала пространственные данные, которые позволяют наиболее наглядно проиллюстрировать проблему гетероскедастичности и способы ее устранения.
В работе достаточно наглядно продемонстрирована работа тестов для выявления гетероскедастичности, также удалось решить задачу с выбором веса для ВНК.
В ходе курсовой работы мне удалось скорректировать модель с помощью метода взвешенных наименьших квадратов, правильно подобрав вес при помощи теста Бреуша-Пагана, поскольку тест Вайта, к примеру, не дает нам точного ответа на вопрос о весе для ВНК. Построенная в конце моего исследования модель-NEW значима и является качественной, остатки ее в свою очередь гомоскедастичны.
Список использованных источников:
1. Бородич С.А. Вводный курс эконометрики: Учеб. пособие. – Мн.; БГУ, 2000. – 209, 227, 245 с.
2. Бородич С.А. Эконометрика: Учеб. пособие. – Мн.; Новое знание, 2006. – 237, 238 с.
3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.; ИНФРА-М, 1997.
http://www.zinref.ru/000_uchebniki/04600_raznie_4/997_05_economica_teoria_referati_05/193382.htm
17 авг. 2022 г.
читать 2 мин
Тест Уайта используется для определения наличия гетероскедастичности в регрессионной модели.
Гетероскедастичность относится к неравному разбросу остатков на разных уровнях переменной отклика в регрессионной модели, что нарушает одно из ключевых предположений линейной регрессии о том, что остатки одинаково разбросаны на каждом уровне переменной отклика.
В этом руководстве объясняется, как выполнить тест Уайта в R, чтобы определить, является ли гетероскедастичность проблемой в данной регрессионной модели.
Пример: Тест Уайта в R
В этом примере мы подберем модель множественной линейной регрессии, используя встроенный набор данных R mtcars.
Как только мы подгоним модель, мы будем использовать функцию bptest из библиотеки lmtest , чтобы выполнить тест Уайта, чтобы определить, присутствует ли гетероскедастичность.
Шаг 1: Подберите регрессионную модель.
Во-первых, мы подгоним регрессионную модель, используя mpg в качестве переменной отклика и disp и hp в качестве двух независимых переменных.
#load the dataset
data(mtcars)
#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)
#view model summary
summary(model)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.735904 1.331566 23.083 < 2e-16 ***
disp -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
Шаг 2: Проведите тест Уайта.
Далее мы будем использовать следующий синтаксис для выполнения теста Уайта, чтобы определить, присутствует ли гетероскедастичность:
#load lmtest library
library(lmtest)
#perform White's test
bptest(model, ~ disp*hp + I(disp^2) + I(hp^2), data = mtcars)
studentized Breusch-Pagan test
data: model
BP = 7.0766, df = 5, p-value = 0.215
Вот как интерпретировать вывод:
- Тестовая статистика X 2 = 7,0766 .
- Степеней свободы 5 .
- Соответствующее значение p равно 0,215 .
В тесте Уайта используются следующие нулевая и альтернативная гипотезы:
- Null (H 0 ) : присутствует гомоскедастичность.
- Альтернатива ( HA ): присутствует гетероскедастичность.
Поскольку p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что в регрессионной модели присутствует гетероскедастичность.
Что делать дальше
Если вы не можете отвергнуть нулевую гипотезу теста Уайта, то гетероскедастичность отсутствует, и вы можете приступить к интерпретации результатов исходной регрессии.
Однако если вы отвергаете нулевую гипотезу, это означает, что в данных присутствует гетероскедастичность. В этом случае стандартные ошибки, показанные в выходной таблице регрессии, могут быть ненадежными.
Есть несколько распространенных способов решить эту проблему, в том числе:
1. Преобразуйте переменную ответа.
Вы можете попробовать выполнить преобразование переменной ответа, например, взять логарифм, квадратный корень или кубический корень из переменной ответа. Как правило, это может привести к исчезновению гетероскедастичности.
2. Используйте взвешенную регрессию.
Взвешенная регрессия присваивает вес каждой точке данных на основе дисперсии ее подобранного значения. По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок. Когда используются правильные веса, это может устранить проблему гетероскедастичности.
Тестирование ошибки спецификации уравнения регрессии
Как
уже отмечалось, среди предпосылок МНК
присутствует предпосылка о нулевом
математическом ожидании остатков
регрессионной модели и, если при этом
остатки и регрессоры независимы, оценки
параметров уравнения регрессии будут
несмещёнными. Тестирование предположения
о том, что в рамках нормальной линейной
модели M(
= 0, (i
=
1,2,…,n)
осуществляется на основе критерия Рэмси
RESET
(Ramsey̕
s
Regression
Equation
Specification
Error
Test).
При
помощи этого критерия можно выявить:
•
наличие
пропущенных переменных (т.е. невключение
в правую часть уравнения некоторых
существенных переменных);
•
неправильную
функциональную форму представления
переменных (например, использование
логарифмов переменных вместо их уровней);
•
наличие
корреляции между объясняющими переменными
и остатками уравнения регрессии.
Рассмотрим
идею этого теста, реализованного в
пакете EViews.
В этом тесте сначала оценивается исходная
модель и по ней находятся расчётные
значения зависимой переменной

(i=1,…,n).
Затем
оценивается вспомогательная модель, в
которую помимо исходных переменных
включаются несколько слагаемых вида

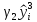

Например,
исходная модель имеет вид
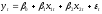
Тогда вспомогательная модель будет
вида
+


В
рамках этой модели проверяется гипотеза
H0
:


Эту
гипотезу можно тестировать с помощью
обычного F-теста.
Обычно этот тест применяется при
небольших значениях r
=1,2,3.
Идея
этого теста заключается в том, что
добавлением нелинейных членов в уравнение
регрессии не удаётся улучшить его
качество.
2.2.6. Учёт некоторых нарушений стандартных предположений о модели
Рассмотрим
кратко один из вариантов решения проблем,
возникающих при наличии автокорреляции
и гетероскедастичности в остатках
регрессионных уравнений. Как уже
отмечалось, в этих случаях МНК-оценки
параметров уравнений регрессии будут
состоятельными и несмещёнными, но
несостоятельными и смещёнными могут
оказаться ошибки этих оценок. В связи
с этим одним из методов коррекции
статистических выводов состоит в
использовании обычных МНК-оценок, со
скорректированными стандартными
ошибками этих оценок, с учётом их
автокорреляции и гетероскедастичности
.
Рассмотрим
эти два случая по отдельности. Предположим,
что после оценивания параметров модели
каким-либо методом было выяснено, что
имеет место гетероскедастичность
остатков этой модели при отсутствии
какой-либо автокорреляции. Поскольку
сами оценки при этом будут несмещёнными,
то для верных статистических выводов
достаточно будет скорректировать
стандартные ошибки этих оценок. Одним
из вариантов получения скорректированных
на гетероскедастичность стандартных
ошибок

предложен Уайтом и реализован в ряде
пакетов анализа статистических данных,
в том числе и вEViews.
При этом удовлетворительные свойства
скорректированной оценки Уайта (White
estimator
или White
standard
errors)
гарантируются только при большом
количестве наблюдений.
Оценка
Уайта строится на основе явного выражения
для ковариационной матрицы вектора
оценок коэффициентов линейной
эконометрической модели, в которой
ошибки хотя и имеют нулевые математические
ожидания, но не являются одинаково
распределёнными, т. е. с разными
дисперсиями, но взаимно независимы.
Тогда ковариационная матрица остатков
примет вид Cov(
=diag(
т. е. на главной диагонали проставлены
дисперсии остатков (для каждого остатка
своя дисперсия), а вне диагонали – нули
(какая-либо автокорреляция отсутствует).
Для оценки этихn
дисперсий имеется всего n
наблюдений. Тем не менее можно получить
состоятельную оценку этой ковариационной
матрицы, заменив неизвестные дисперсии
ошибок, на квадраты остатков, полученных
в результате оценки модели обычным МНК.
Это приводит к оценке Уайта.
Понятно,
что это не единственный вариант
корректировки последствий
гетероскедастичности остатков уравнения
регрессии. Иногда достаточно изменить
вид зависимости или преобразовать
переменные (например, перейти к логарифмам
объясняемых переменных вместо их
исходных значений).
Пусть
теперь имеем более сложный случай, когда
остатки не только гетероскедастичны,
но и автокоррелированы. Поскольку
последствия автокорреляции в остатках
аналогичны уже рассмотренным в случае
их гетероскедастичности, можно
воспользоваться аналогичной процедурой
коррекции статистических выводов и при
автокоррелированных остатках.
Один
из вариантов получения скорректированных
на автокоррелированность и
гетероскедастичность значений
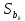
и реализован, например, в EViews,
при этом удовлетворительные свойства
оценки Ньюи –
Веста
(Newey
–
West
estimate
или Newey
–
West
standard
errors)
как и в предыдущем случае гарантируются
при большом количестве наблюдений. От
предыдущего случая этот вариант поведения
остатков отличается ещё и тем, что
ковариационная матрица остатков не
является диагональной (предполагается
автокорреляция остатков, причём не
обязательно только первого порядка),
но и в этом случае авторам удалось
получить состоятельную оценку указанной
ковариационной матрицы.
Следует
отметить, что автокореляция в остатках
может появиться и потому, что при выборе
объясняющих переменных была пропущена
значимая переменная, и её влияние на
зависимую переменную будет отражаться
на поведении остатков. Кроме того,
автокорреляция в остатках может появиться
и при не правильном выборе вида
зависимости. Ясно, что в этих случаях
простой коррекцией ошибок оценок не
обойтись. Необходимо провести более
тщательный анализ при определении
спецификации уравнения регрессии.
Подобные ошибки в спецификации уравнения
регрессии вряд ли удастся нейтрализовать
описанными методами.
Пример
2.
Тестирование предпосылок МНК
Проиллюстрируем
вышеизложенные положения на условном
примере, в котором описывается зависимость
пятилетних процентных ставок (r60)
от одномесячных (r1),
квартальных (r3)
, полугодовых (r6)
и годовых (r12)
процентных ставок (данные взяты из М.
Вербик, 2008). На рисунке 2.6 приведены
графики этих переменных.
Рисунок
2.6 – Графики динамики анализируемых
переменных
На
рисунке 2.6 видим, что анализируемые
переменные изменяются во времени почти
параллельно, что может быть причиной
их коллинеарности, в чём действительно
убеждаемся, просмотрев матрицу парных
коэффициентов корреляции (рисунок 2.7).
Все коэффициенты корреляции между
независимыми переменными оказались
больше 0,9. В этом случае «доверять»
коэффициентам уравнения не рекомендуется.
Рисунок
2.7. – Матрица парных коэффициентов
корреляции
Рисунок
2.8 – «Полное» уравнение регрессии
Рисунок
2.9 – Уравнение регрессии с исключённой
переменной
Как
известно, мультиколлинеарность искажает
смысл коэффициентов регрессии и делает
их неустойчивыми. «Полное» уравнение
регрессии не позволяет проследить
последствия мультиколлинеарноси. Разве
что малое значение статистики Дарбина
–
Уотсона
указывает на наличие автокорреляции
первого порядка (рисунок 2.8). Но относить
этот факт на счёт мультиколлинеарности
вряд ли корректно.
Попробуем
проверить устойчивость коэффициентов
регрессии, удалив из регрессии одну из
переменных. Пусть это будет r3
(рисунок 2.9). Как видим, действительно
коэффициенты «сокращённого» уравнения
существенно отличаются от коэффициентов
исходного уравнения. Кроме того, что
коэффициенты значимо отличаются от их
исходных значений по величине, сменился
даже знак коэффициента при переменной
r1.
При этом точность уравнения регрессии
с исключённой переменной значимо не
изменилась. Разве что уменьшилось
значение статистики Дарбина –
Уотсона,
что означает, что имеет место существенная
автокорреляция первого порядка.
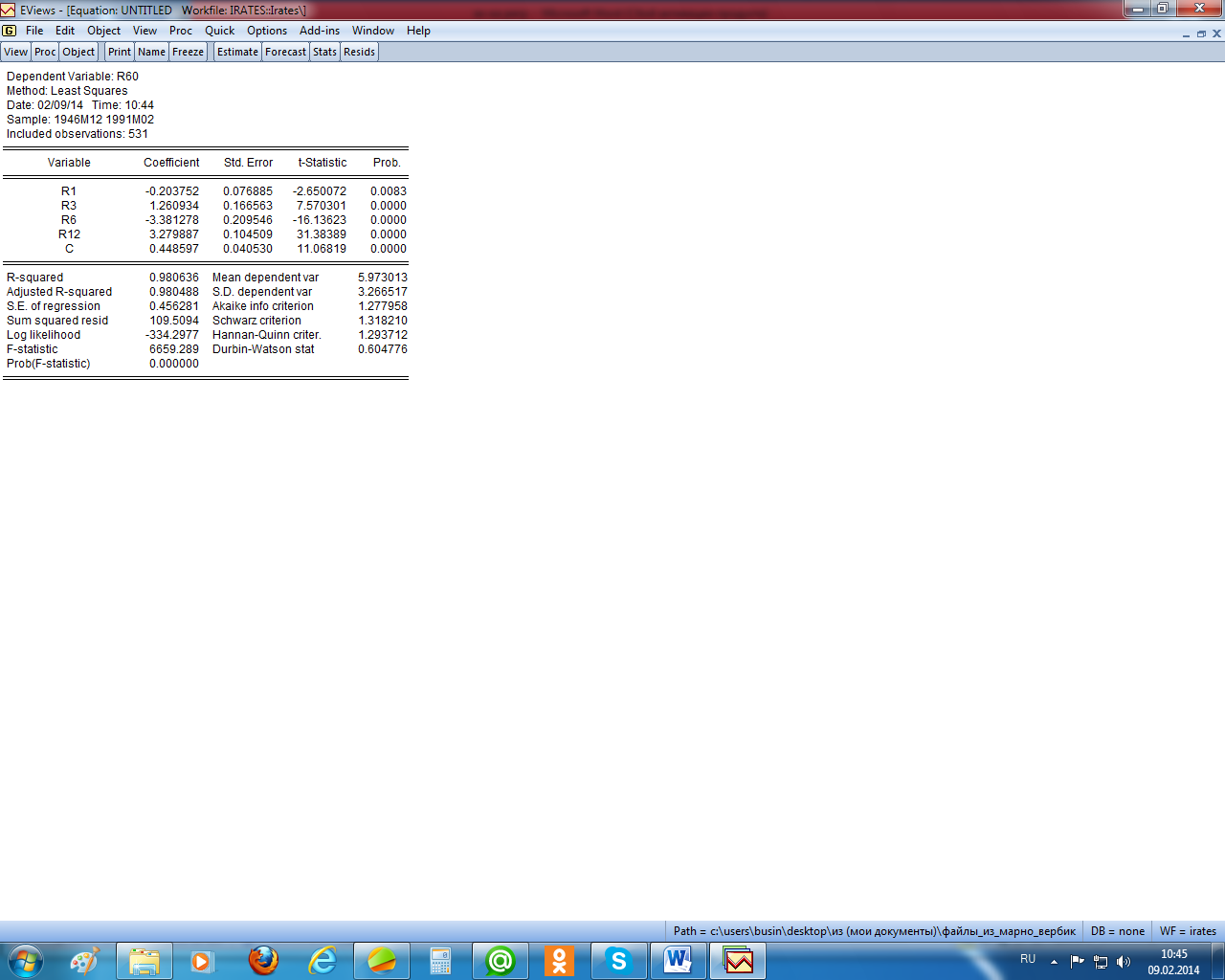
Рисунок
2.10 – Графики остатков, фактических и
расчётных значений зависимой переменной
На
рисунке 2.10 чётко просматривается наличие
автокорреляции и гетероскедастичности
остатков. Протестируем эти остатки по
всем предпосылкам МНК.
Рисунок
2.11 – Гистограмма остатков регрессии и
тест Jarque
–
Bera
Сначала
проверим их на нормальный закон
распределения (рисунок 2.11). Тест Jarque
–
Bera
показывает, что гипотезу о нормальном
законе следует отклонить, т. к. расчётный
уровень значимости (Probability)
меньше 0,05. У этого распределения
асимметрия отрицательна – более
«тяжёлый» левый хвост распределения,
а эксцесс значимо больше трёх – более
островершинное распределение по
сравнению с нормальным. Как уже отмечалось,
значимое влияние на свойство оценок
этот факт не оказывает.
Рисунок
2.12 – Тест Breusch
– Godfrey
на автокорреляцию остатков
Протестируем
остатки на автокорреляцию на основе
теста Breusch
– Godfrey
(рисунок 2.12). На второй строчке отчёта
о тесте Obs*-squared
– это nR2,
расчётный уровень значимости для
статистики теста – это Prob.
Chi-Square
(4). Для тестирования по этому тесту было
выбрано 4 лаговых значения для остатков,
т. е. тестировалась автокорреляция до
4–го
порядка. Prob.
Chi-Square(4)
= 0,0, что меньше 0,05, значит гипотеза об
отсутствии автокорреляции отклоняется.
Просматривая
уравнение теста, видим, что имеется
автокорреляция первого и четвёртого
порядков, т. к. коэффициенты при RESID(–1)
и RESID(–4)
значимо отличаются от нуля 0 (расчётный
уровень значимости для них меньше 0,05).
Автокорреляция
первого порядка была видна и на основе
статистики
Дарбина
–
Уотсона, а здесь выяснилось, что ещё
имеется автокорреляция более высокого
порядка.
Протестируем
остатки на гетероскедастичность по
тесту Уайта (Heteroskedasticity
Test
White
– рисунок 2.13). В нашем случае nR2
= 96,46, расчётный уровень значимости
меньше 0,05, следовательно, гипотезу о
гомоскедастичности остатков отклоняем
и по уравнению теста видим, что остатки
зависят от произведений переменных r1,
r12
и от r6,
r12,
а также от r122.
Далее,
протестируем уравнение регрессии на
ошибку спецификации по Ramsey
RESET-тесту
(рисунок 2.14). Как видим, F-статистика
теста равна 7,7 и расчётный уровень
значимости (Probability)
равен 0,0. Следовательно, гипотеза об
отсутствии ошибки спецификации
отклоняется. Из уравнения теста видно,
что добавление двух нелинейных членов
в уравнение регрессии несколько улучшило
качество исходного уравнения (хоть и
не значимо, но увеличились R2
и
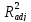
уменьшился информационный критерий
Шварца). Хотя автокорреляция в остатках
усилилась (статистика Дарбина–
Уотсона
приблизилась к нулю).
Рисунок
2.13 – Тест White
на гетероскедастичность остатков
регрессии
Рисунок
2.14 – Ramsey
RESET-тест
RESET-тест
не указывает на конкретный тип ошибочной
классификации. Это дело исследователя.
В нашем случае высокий уровень
автокоррелированности остатков может
указывать на пропуск в уравнении
регрессии значимой независимой
переменной.
Проиллюстрируем
далее коррекцию стандартных ошибок
МНК-оценок в случае их гетероскедастичности
и автокоррелированности.
Если
оценки гетероскедастичны, но в них
отсутствует какая-либо автокорреляция,
то, как отмечалось, скорректировать их
стандартные ошибки с учётом
гетероскедастичности можно, используя
стандартные ошибки в форме Уайта. Чтобы
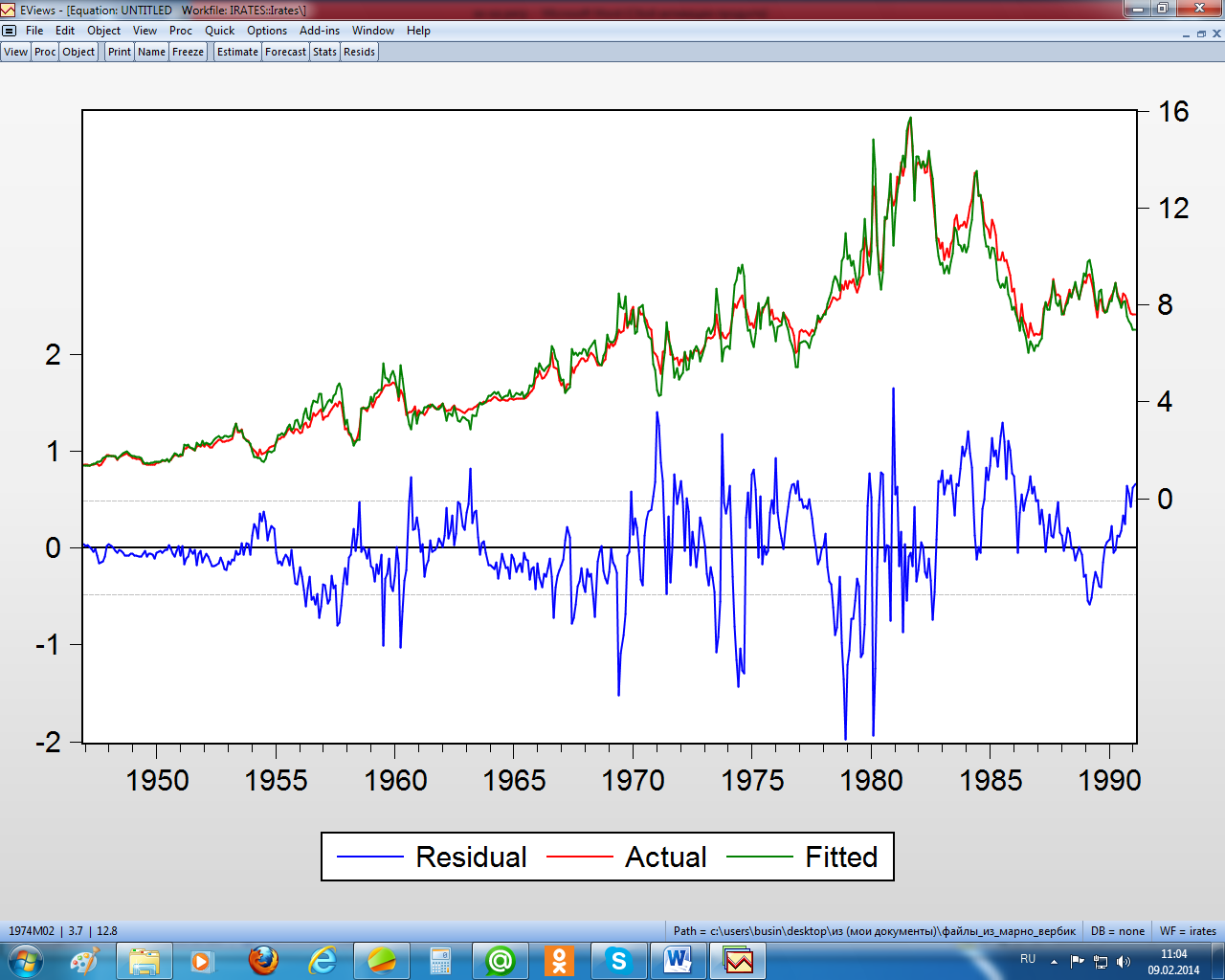
реализовать эту процедуру в EViews,
надо в окне специализации уравнения
регрессии выбрать заставку «Options»
и там выбрать в позиции «Coefficient
covariance
matrix»
нужный метод (рисунок 2.15).
После
выбора метода «White»
получим (рисунок 2.16). Как видим на этом
рисунке, стандартные ошибки были
пересчитаны и стали больше по сравнению
с аналогичными, вычисленными при
использовании обычного МНК (рисунок
2.9). Значимость параметров при этом не
изменилась.
А
теперь проведём корректировку отклонений
с помощью метода Ньюи –
Веста.
Здесь кроме гетероскедастичности
предполагается ещё и автокорреляция
остатков (см. рисунок 2.17).
Как
видим, коррекция в этом случае оказалась
более существенной, что привело даже к
изменению значимости параметров –
коэффициент при r1
оказался незначимым.
Рисунок
2.15 – Выбор процедур коррекции стандартных
отклонений
Рисунок
2.16 – Стандартные ошибки в форме Уайта
Рисунок
2.17 – Стандартные ошибки в форме Ньюи –
Веста
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вглядываясь в зеркала или еще раз о проблеме гетероскедастичности
Время на прочтение
2 мин
Количество просмотров 1.3K
Секунда теории
Гетероскедастичность – это ситуация, когда ошибка регрессии не удовлетворяет условию гомоскедастичности, т.е. дисперсия этой самой ошибки непостоянно. Это приводит при использовании метода наименьших квадратов к разным неприятным эффектам смещения значений оценок, что ставит под сомнение смысл всей проделанной на основании данного уравнения регрессии работы.
В странствиях по CRAN-у попался пакет skedastic, в котором реализованы 25 разных тестов гомоскедастичности – о нем и поговорим.
О тестах
Вдумчивый разбор математического основания всех реализованных тестов – это дело статьи в специализированном журнале, дело данной заметки – посмотреть, как они работают.
Возьмем из пакета UsingR данные о бриллиантах diamond и посмотрим уравнение регрессии (цена зависит от веса)
library(tidyverse)
library(ggplot2)
library(skedastic)
library(AER)
library(gvlma)
library(UsingR)
data(diamond)
ggplot(data = diamond, aes(x=carat, y=price)) + geom_point()
model_1 <- lm(price~carat, data=diamond)
summary(model_1)
gvlma(model_1)
ggplot(data = diamond, aes(x=carat, y=model_1$residuals)) + geom_point() + ylab("Error of model")На графике видна классическая линейная зависимость. Соответствующая модель значима и даже (по версии пакета gvlma) все условия Гаусса-Маркова выполняются
График ошибок говорит о том же самом:
Есть значительные основания полагать, что гетероскедастичности тут нет. Теперь посмотрим на результаты применения пакета skedastic (во всех тестах нулевая гипотеза: есть гомоскедастичность; при уровне значимости меньше заданного, допустим, 0.05, она будет отвергнута):
Собственно, тесты почти единодушны: 24 из 25 (кроме теста Хонды) указали, что нулевая гипотеза не может быть отвергнута, значит, можно смело говорить про гомоскедастичность.
Эксперимент
Самое интересное, правда, другое – вопрос о том, насколько эти тесты определяют гетероскедастичность, когда у нас она есть. Создадим искусственный датафрейм по формуле y = ax+b+e(1+s|x|) при разных значениях s. При s=0 у нас классическая гомоскедастичность (ошибки происходят из нормального распределения), при s=1 – классическая гетероскедастичность (когда дисперсия ошибок растет при увеличении х по модулю). Логично предположить, что нормальное поведение теста в этих случаях – обратная пропорциональность p-значения от значения s. Каждый тест проводился 100 раз на разных значениях a и b, его результаты потом усреднялись. Соответствующие графики представлены ниже:
Собственно, тестов, определяющий данный вид гетероскедастичности, всего 4 (из 25): Диблази-Боуманна, Уайта, Юса и Чжоу. Это говорит о том, что даже если вам тесты показали, что у вас все хорошо, это не значит, что оно так и есть. И это также повод внимательно посмотреть и определить области эффективности этих тестов.
Все материалы, в т.ч. статьи авторов-изобретателей тестов, есть на https://github.com/acheremuhin/Heteroscedacity