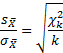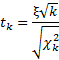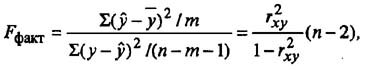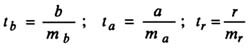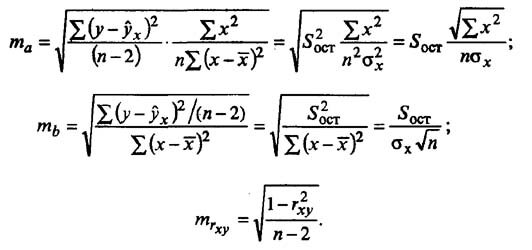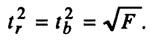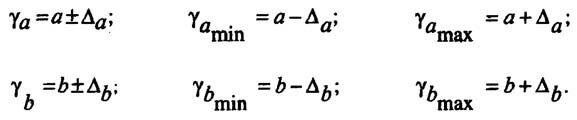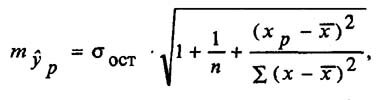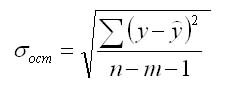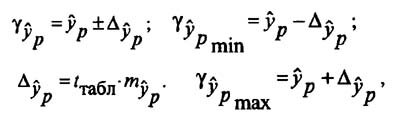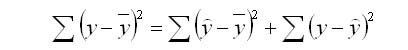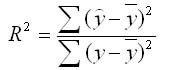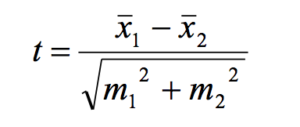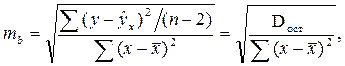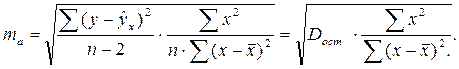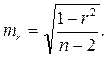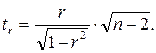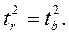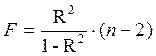Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
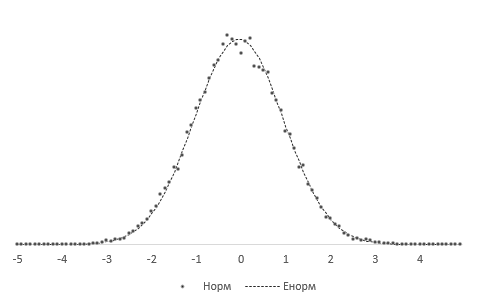
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
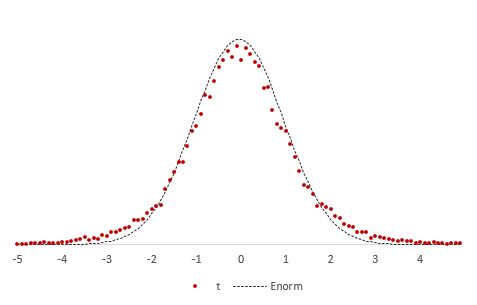
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
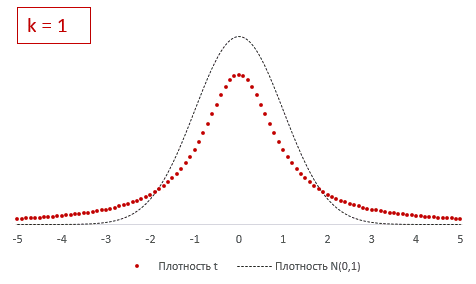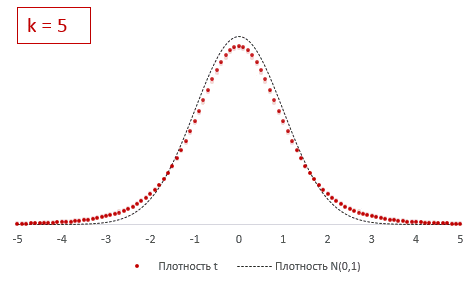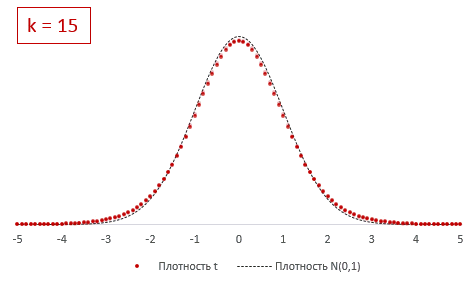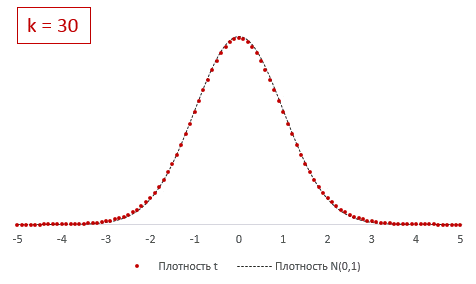
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
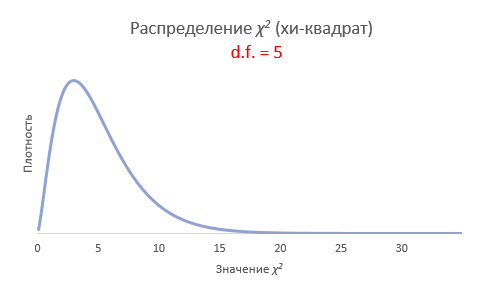
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
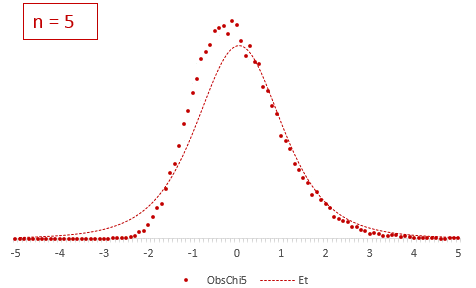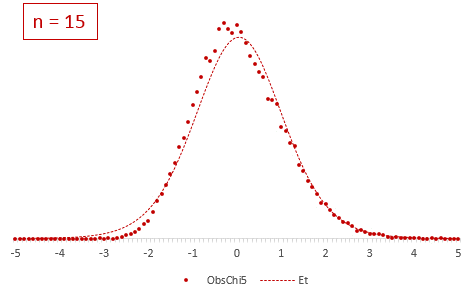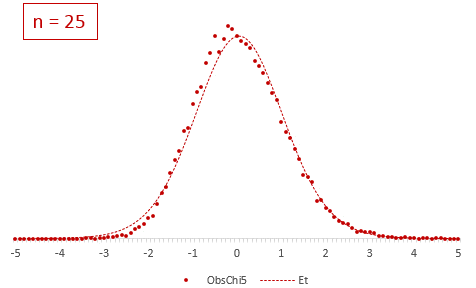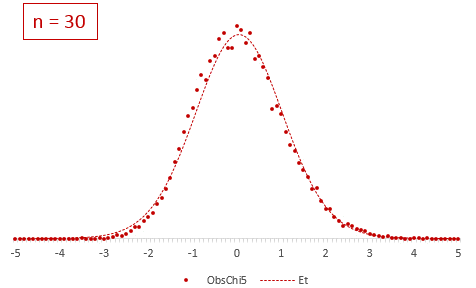
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
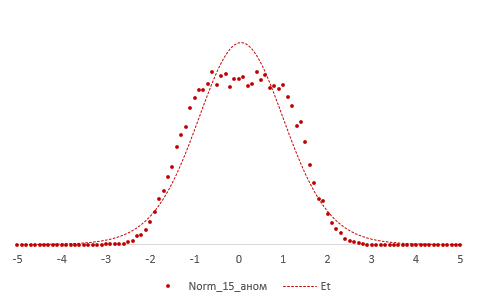
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
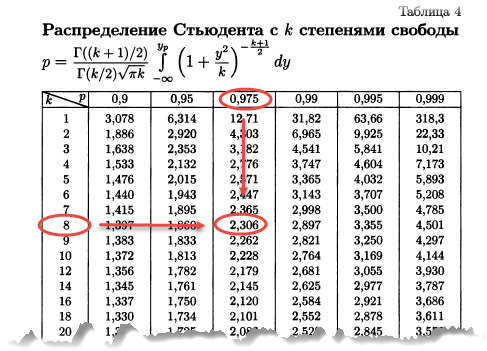
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
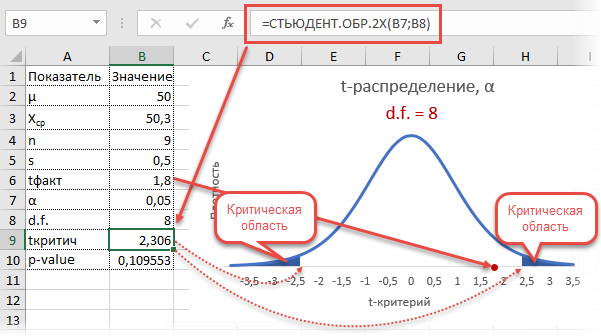
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
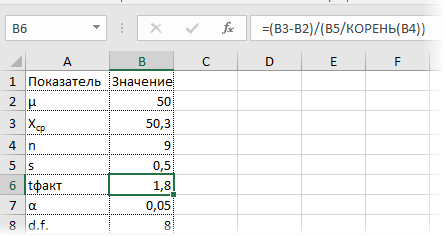
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
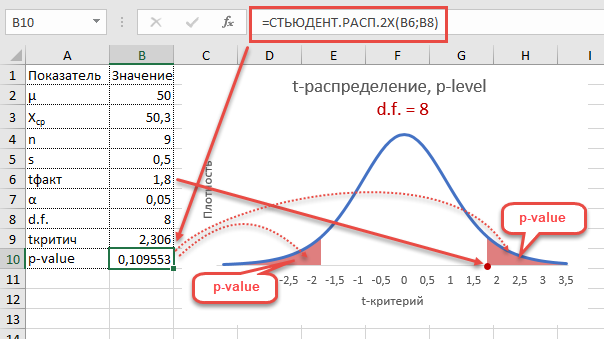
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
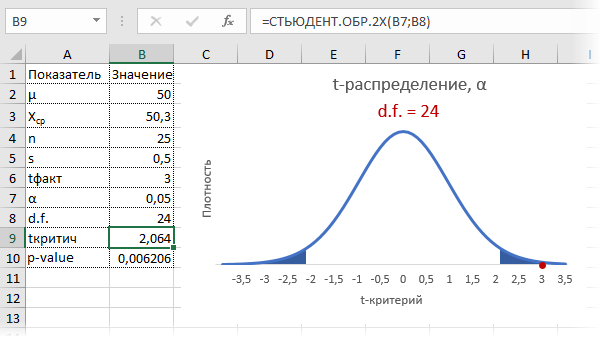
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
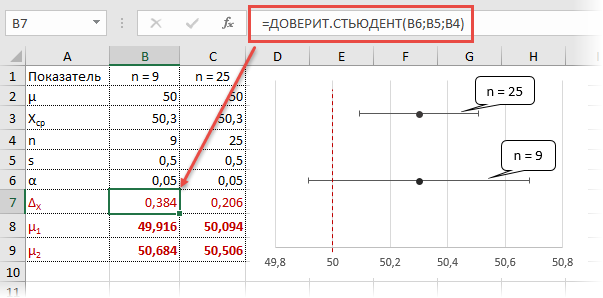
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
Как видно из табл.1
наибольшей популярностью при проверке
гипотез о равенстве двух генеральных
средних (математических ожиданий)
пользуется t-критерий
Стьюдента. Частота применения данного
критерия в разных журналах отличается
друг от друга не очень значительно.
Например, в 11-ти выпусках БЭБМ за 1997г.
t-критерий использован в
114 статьях, тогда как корреляционный и
дисперсионный анализ применен всего
лишь в 15 публикациях, критерий
Колмогорова-Смирнова — в одной статье,
парная линейная регрессия — в трех
статьях, точный критерий Фишера — в трех
статьях и т.д. В 56 статьях этих выпусков,
в которых использовалось выражение «p
< 0,05», вообще не упоминался
использованный статистический критерий.
При чтении статей БЭБМ складывается
впечатление, что большинство авторов
данного журнала знают и используют лишь
единственный статистический критерий
— t-критерий Стьюдента.
Критерий Стьюдента был разработан
английским химиком У.Госсетом, когда
он работал на пивоваренном заводе
Гиннеса и по условиям контракта не имел
права открытой публикации своих
исследований. Поэтому публикации своих
статей по t-критерию
У.Госсет сделал в 1908г. в журнале
«Биометрика» под псевдонимом
«Student», что в переводе
означает «Студент». В отечественной
же литературе принято писать «Стьюдент».
Коварная простота вычисления t-критерия
Стьюдента, а также его наличие в
большинстве статистических пакетов и
программ привели к широкому использованию
этого критерия даже в тех условиях,
когда применять его нельзя. В течение
3-х лет нами был проведен опрос более
250 медиков и биологов, занятых научными
исследованиями. Им задавался единственный
вопрос: «Каковы достаточные и
необходимые условия использования
t-критерия Стьюдента при
сравнении групповых средних»? Ни один
из опрашиваемых не смог полностью и
правильно ответить на него. Примерно
50% говорили о нормальности распределения,
однако не могли при этом объяснить, как
реально проверить нормальность
распределения. Впрочем, очевидно и 250
статистиков не смогли бы внятно объяснить,
чем, например, эритроциты отличаются
от лейкоцитов. Этот пример иллюстрирует,
что прикладная статистика является не
менее узкоспециальной областью
профессиональной деятельности, нежели
медицина и биология.
Рассмотрим более подробно
особенности использования статистического
критерия t-Стьюдента.
Наиболее часто t-критерий
используется в двух случаях. В первом
случае его применяют для проверки
гипотезы о равенстве генеральных средних
двух независимых, несвязанных выборок
(так называемый двухвыборочный
t-критерий). В этом случае
есть контрольная группа и опытная
группа, состоящая из разных пациентов,
их количество в группах может быть
различно. Во втором же случае используется
так называемый парный t-критерий,
когда одна и та же группа объектов
порождает числовой материал для проверки
гипотез о средних. Поэтому эти выборки
называют зависимыми, связанными.
Например, измеряется содержание
лейкоцитов у здоровых животных, а затем
у тех же самых животных после облучения
определенной дозой излучения. В обоих
случаях должно выполняться требование
нормальности распределения исследуемого
признака в каждой из сравниваемых групп.
Из всех 877 проанализированных публикаций,
в которых был использован t-критерий
Стьюдента, упоминание о проверке
нормальности распределения исследуемых
признаков было только в 5 статьях. Более
того, лишь в единичных работах был
проведен достаточно детальный анализ
распределения вероятностей исследуемых
количественных признаков, и на этом
основании было принято аргументированное
решение о выборе статистического
критерия [17-18]. Наши личные исследования
показали, что 50-70% наиболее часто
упоминаемых в публикациях по кардиологии
и радиобиологии количественных
показателей не подчиняются нормальному
распределению. Для проверки гипотезы
о нормальности распределения (основной
гипотезы) может быть использован целый
набор так называемых критериев согласия:
критерий асимметрии и эксцесса,
Dn-критерий Колмогорова,
Хи-квадрат — критерий Пирсона, Омега-квадрат
критерий, критерий Шапиро-Уилки, и т.д.
Предположим, применив один из этих
критериев, мы установили, что исследуемый
признак подчиняется нормальному
распределению в каждой из групп сравнения.
Однако это требование является
необходимым, но не достаточным для
применения t-критерия
Стьюдента. Следующее требование, которое
должно выполняться, это равенство
генеральных дисперсий в сравниваемых
группах. Как известно из курса статистики,
для проверки гипотезы о равенстве двух
генеральных дисперсий нормально
распределенных совокупностей используются
такие критерии, как F-критерий
Фишера, критерий Кохрана, критерий
Вальда и т.д. Для многих статей, в которых
был использован двухвыборочный t-критерий
Стьюдента и приведены объемы выборок
и среднеквадратичные отклонения,
примерно в 50% случаев проверка равенства
генеральных дисперсий дала отрицательный
результат.
Проверка гипотезы о генеральных
средних двух групп с неравными дисперсиями
в математической статистике называется
проблемой Беренса-Фишера и имеет в
настоящее время только приближенные
решения. Подробное изложение проблемы
Беренса-Фишера можно найти в /19,с.258/,
/20,с.235/, /21,с.190/, /12,с.93/. Почему так важно
требование равенства дисперсий в
сравниваемых группах? Не вдаваясь в
детали этой проблемы, отметим, что чем
больше различаются между собой дисперсии
и объемы выборок, тем сильнее отличается
распределение «вычисляемого t-критерия»
от распределения истинного «t-критерия
Стьюдента». При этом различную величину
имеет как сам t-критерий,
так и такой параметр этих распределений,
как число степеней свободы. В свою
очередь число степеней свободы сказывается
на величине достигнутого (критического)
уровня значимости (р < …. ) определяемого
для вычисленной величины t-критерия.
Во многих статистических пакетах
величина t-критерия
вычисляется для двух случаев: 1) дисперсии
равны; 2) дисперсии неравны. При этом
предполагается, что в обоих случаях
требование нормальности распределения
выполняется. Для случая неравных
дисперсий существует несколько наиболее
популярных приближенных решений,
например критерии Кохрана-Кокса,
Саттерзвайта, Уэлча, Гронау и т.д.
Пренебрежение авторами публикаций,
приведенными выше условиями допустимости
использования t-критерия
Стьюдента, приводит к существенному
искажению результатов проверки гипотез
о равенстве средних. На рисунке приведены
графики зависимости величины t-критерия
Стьюдента для случая равных (t=)
и неравных генеральных дисперсий (t|=),
а также отвечающие им значения достигнутых
уровней значимости ( p <
) в зависимости от величины разности D
между генеральными средними.
Как
видно из этого рисунка, достигнутый
уровень значимости (p
< ) для случая неравных дисперсий ( Р
|= ) всегда выше, чем для случая равных
дисперсий (Р =). Величина ( Р |= ) определялась
с использованием аппроксимаций критерия
Беренса-Фишера по Уэлчу, Саттерзвайту,
Гронау и Кохрану-Коксу. Отличия значений
( Р |= ) для этих аппроксимаций наблюдались
в 3-4-ом знаках. Значения Рн/п были получены
для непараметрических критериев
Вилкоксона, Краскела-Валлиса и Манна-Уитни
с помощью статистических пакетов SGWIN
2.1, PRISM
2.01, SPSS
7.53, SAS
6.04 и STATISTICA
5.1. О том, сколь сильно могут отличаться
при этом как значения самого t-критерия,
так и достигнутого уровня значимости
р < , можно судить по результатам
выполненного нами анализа реальных
данных полученных в отделении ИБС НИИ
Кардиологии Томского отделения РАМН.
В табл. 2 приведены итоги проверки гипотез
о равенстве средних в двух группах с
помощью t-критерия
Стьюдента для случая равных дисперсий,
и для случая неравных дисперсий
Условные обозначения
к табл.2.
Х21
— отношение iR
(периода изометрического расслабления)
к длительности RR
при пробе с дипиридамолом (ПД) перед
началом лечения.
Z9
— толщина межжелудочковой перегородки
после лечения, мм.
Z14
— конечный систолический объем в покое
после лечения, мл.
Z15
— ударный объем в покое после лечения,
мл.
Z16
— фракция выброса в покое после лечения,
усл. ед.
А5
— наличие (отсутствие) депрессии сегмента
ST
при ВЭМ.
А6
— наличие (отсутствие) депрессии сегмента
ST
при ПД.
А7 — наличие (отсутствие)
обызвествления коронарных артерий.
А10 — наличие
(отсутствие) нарушений сердечного ритма.
А12 — наличие
(отсутствие) нарушений сердечного ритма
при ПД.
Таблица 2 Результаты
проверки гипотез о равенстве групповых
средних различными критериями.
|
Исследуемая |
Z9 |
Z15 |
X21 |
Z14 |
Z16 |
X21 |
Z9 |
|
Группирующая |
A5 |
A7 |
A5 |
A12 |
A7 |
A10 |
A6 |
|
Значения |
10,17 |
141,7 |
0,14 |
37,4 |
0,77 |
1,24 |
8,10 |
|
Величина |
2,94 |
1,98 |
2,69 |
1,57 |
2,23 |
2,09 |
1,84 |
|
Величина |
1,76 |
2,54 |
2,03 |
2,93 |
1,85 |
1,73 |
1,77 |
|
Величина |
0,0048 |
0,0138 |
0,0107 |
0,1235 |
0,0297 |
0,0401 |
0,0714 |
|
Величина |
0,1049 |
0,0665 |
0,0755 |
0,0307 |
0,0830 |
0,1229 |
0,0851 |
|
Величина |
0,1059 |
0,0693 |
0,0797 |
0,0482 |
0,0866 |
0,1259 |
0,0879 |
|
Значение |
9,29 |
2,57 |
2,71 |
4,55 |
2,00 |
1,59 |
5,23 |
|
Величина |
0,0000 |
0,023 |
0,055 |
0,24 |
0,10 |
0,30 |
0,0000 |
Таким образом, для исследованных
нами переменных принятие или отклонение
гипотезы о равенстве генеральных средних
в группах во многом определяется
результатом проверки гипотезы о равенстве
генеральных дисперсий. Предположим,
что проверка основной гипотезы подтвердила
нормальность исследуемых нами переменных
в обеих сравниваемых группах. Далее,
зададимся уровнем значимости равным
0,05 , т.е. для критериев с достигнутым
уровнем значимости р<0,05 нулевую
гипотезу о равенстве будем отклонять,
а при р>0,05 гипотезу о равенстве будем
принимать. В этом случае, для толщины
межжелудочковой перегородки Z9
мы должны принять гипотезу о равенстве
средних в подгруппах по А5 для неравных
дисперсий, и отклонить эту гипотезу при
равных дисперсиях. Аналогичные
неоднозначные выводы получены и для
других пар признаков. Только для пары
Z9 — А6 нулевая гипотеза о
равенстве средних принимается для всех
трех случаев. Проведенная нами проверка
еще для 50 аналогичных пар признаков
показала, что для 43 пар принятие или
отклонение гипотезы о равенстве групповых
средних непосредственно зависело от
результата проверки гипотезы о дисперсиях.
Напомним, что мы предположили нормальность
распределения количественной переменной
в обеих группах. Дальнейшая проверка
50 исследуемых кардиологических признаков
показала, что нормальность распределения
наблюдалась в обеих группах у 8 признаков,
в одной из групп — у 19, и отсутствовала
в обеих группах у 31 признака. В таких
ситуациях допустимо применение только
непараметрических критериев, таких как
Ван дер Вардена, Краскела-Валлиса,
Манна-Уитни, Вилкоксона, критерия знаков
и т.д.
В табл.3 приведены результаты
проверки гипотезы о равенстве групповых
средних для признака Х21 (группирующий
признак А5) с помощью нескольких
непараметрических критериев. Проверка
гипотез производилась с помощью пакетов
SGWIN 2.1, PRISM
2.01, SPSS 7.53, SAS
6.04 и STATISTICA 5.1 .
Таблица 3. Результаты
проверки гипотез о равенстве групповых
средних непараметрическими критериями.
|
Критерий |
Критерий |
Критерий |
Критерий |
|
|
Достигнутый |
0,0321 |
0,0307 |
0,0224 |
0,0307 |
В проанализированных нами статьях
непараметрические критерии, такие как
критерий Вилкоксона, Манна-Уитни,
Сиджела-Тьюки, медианный критерий,
критерий знаков и т.д. были использованы
примерно в 1% статей. Отметим, что в
большинстве это были статьи по
радиобиологии и радиоэкологии.
Итак, корректное применение
t-критерия Стьюдента для
двух групп требует обязательной
нормальности распределения исследуемой
количественной переменной в обеих
группах и столь же обязательного
равенства дисперсий в сравниваемых
совокупностях. Поэтому в тех статьях,
где проверка гипотез о равенстве двух
средних производилась с помощью
t-критерия Стьюдента, и
нет упоминания критериев проверки
нормальности распределения и равенства
дисперсий, можно достаточно основательно
предполагать некорректное использование
авторами публикации данного критерия,
а стало быть, и сомнительность декларируемых
ими выводов.
Достаточно часто встречается
и такая ошибка, как использование
t-критерия Стьюдента при
сравнении двух долей (пропорций). Другая
частая ошибка — применение t-критерия
Стьюдента для проверки гипотез о
равенстве трех и более групповых средних.
Например, для случая трех групп попарно
сравнивают группы 1-2, 1-3 и 2-3 с одним и
тем же уровнем значимости, например
р=0,05. Такой прием недопустим, поскольку
в этом случае принимаемый критический
уровень значимости, равный, например
5% , неравномерно распределяется между
тремя парами групп. В результате этого
авторы также получают ложные выводы о
равенстве либо неравенстве средних
значений в сравниваемых группах. В том
случае, когда необходимо осуществить
проверку статистической гипотезы о
равенстве генеральных средних для трех
и более групп, необходимо применять так
называемую общую линейную модель,
реализованную в процедуре однофакторного
дисперсионного анализа с фиксированными
эффектами. Часто этот метод называют
сокращенно ANOVA (Analysis
of Variance —
анализ отклонений, вариаций). Теория
метода, разработанная английским
статистиком Р.Фишером, с многочисленными
примерами его приложения дана в
/12,19-22/. Если в результате применения
процедуры ANOVA гипотеза о
равенстве всех трех (или более) генеральных
средних отклоняется, то вполне возможно,
что часть групповых средних равна между
собой, а другие средние не равны. Для
такого более тонкого анализа используют
методы линейных контрастов, называемые
также методами множественных сравнений.
Такие методы сравнения позволяют
проверить гипотезы о равенстве между
собой отдельных пар групповых средних.
Наиболее часто для этой цели используют
методы сравнения Шеффе, Тьюки, Бонферони,
Дункана, Габриеля, REGWF,
SNK, LSD и т.д.
/12,19-22/. Отметим, что дисперсионный анализ
для подобной цели был использован всего
лишь в 4% работ. Примеры использования
дисперсионного анализа с применением
методов множественных сравнений имеются
в [12,19-22]. О малоизвестности данного
метода в среде кардиологов говорит не
только мизерная частота его упоминания
в публикациях, но и следующий известный
авторам реальный факт. Два исследователя
одного из НИИ Томского отделения РАМН
направили в английский журнал статью,
которая была возвращена на доработку,
с предложением применить метод ANOVA.
Полгода авторы статьи потратили на то,
чтобы установить, что ANOVA
— это дисперсионный анализ, которому
уже более 60 лет.
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
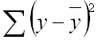
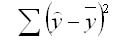
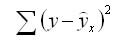
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Т-критерий Стьюдента (t-тест) простым языком
Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.
При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:
Этапы статистического вывода (statistic inference)
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.
Видео-версия статьи
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:
Условия применения статистического критерия т-теста (критерия Стьюдента)
— данные распределялись по закону нормального распределения;
— данные были количественными;
— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).
В итоге Мы определились с тем, что это будет t-критерий Стьюдента.
Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:
Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.
Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (mr).
Давайте остановимся на том, что же значат эти значения:
— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;
— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;
— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки (mr=).
Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.
Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.
Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.
Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.
Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.
На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Расчет доверительных интервалов и прогнозов для линейного уравнения регрессии
Как правило, в линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков.
Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии b средняя ошибка оценки вычисляется как:
где Dост – остаточная дисперсия на одну степень свободы.
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
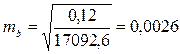
Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Они определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью точности, соответствующей заданному уровню значимости α (α – вероятность отвергнуть правильную гипотезу при условии, что она верна, обычно принимается равной 0,05 или 0,01).
Для оценки статистической значимости коэффициента линейной регрессии и линейного коэффициента парной корреляции, а также для расчета доверительных интервалов b, применяется t – критерий Стьюдента.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 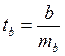
В рассматриваемом примере фактическое значение t-критерия для коэффициента регрессии составило:
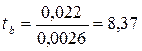
Этот же результат получим, извлекая квадратный корень из найденного F-критерия, т.е.
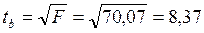
Действительно, справедливо равенство 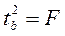
При 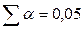
Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют вид:
Если границы интервала имеют разные знаки, т.е. в эти границы попадает ноль, то оцениваемый параметр принимается нулевым.
Доверительный интервал для коэффициента регрессии определяется как 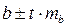
0,022 ± 2,16·0,0026 = 0,022 ± 0,0057, т.е.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 ≤ b ≤ 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра а определяется по формуле:
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 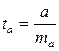
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует, что в парной линейной регрессии 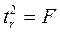
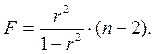
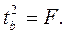
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
В рассматриваемом примере tr совпало с tb. Величина tr =8,37 значительно превышает табличное значение 2,16 при а=0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалом прогноза с достаточно большой вероятностью.
Точечный прогноз заключается в получении прогнозного значения yp, которое определяется путем подстановки в уравнение регрессии
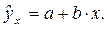
Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. верхней и нижней границы ypmin, ypmax интервала, содержащего точную величину для прогнозного значения
(ypmin 2 – индекс детерминации;
n – число наблюдений;
m – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m — 1) – число степеней свободы для остаточной суммы квадратов.
Для степенной функции 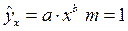
Для параболы второй степени y=a + b·x + c·x 2 + ε m=2 и 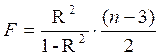
Для оценки качества построенной модели используется также средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у— ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения берутся величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у=20, а для второго у=50, ошибка аппроксимации составит 25% для первого наблюдения и 20% — для второго.
Поскольку (у— ) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
.
Для нашего примера представим расчет средней ошибки аппроксимации в таблице 4.
Пример нахождения доверительных интервалов коэффициентов регрессии
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Постройте уравнение зависимости экспорта нефти от цены на нефть.
3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.
4. Оцените полученные результаты, выводы оформите в аналитической записке.
Таблица 5
Цена нефти марки Urals (Россия), долл/барр.
Экспорт нефти и нефтепродуктов, млн.т.
Решение:
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 119 | 298.12 | 14161 | 88875.53 | 35476.28 | 219.63 | 232120.8 | 6160.56 | 24362.01 |
| 203 | 481.03 | 41209 | 231389.86 | 97649.09 | 521.16 | 89328.76 | 1610.26 | 5196.01 |
| 281 | 539.12 | 78961 | 290650.37 | 151492.72 | 801.15 | 57979.42 | 68658.51 | 35.01 |
| 305 | 653.57 | 93025 | 427153.74 | 199338.85 | 887.3 | 15961.59 | 54628.94 | 895.01 |
| 381 | 987.66 | 145161 | 975472.28 | 376298.46 | 1160.11 | 43160.41 | 29738.57 | 11218.34 |
| 363 | 1252.85 | 131769 | 1569633.12 | 454784.55 | 1095.5 | 223673.03 | 24760.35 | 7729.34 |
| 389 | 1276.88 | 151321 | 1630422.53 | 496706.32 | 1188.83 | 246980.01 | 7753.57 | 12977.01 |
| 387 | 1396.70 | 149769 | 1950770.89 | 540522.9 | 1181.65 | 380430.93 | 46248.04 | 12525.34 |
| 315 | 952.03 | 99225 | 906361.12 | 299889.45 | 923.19 | 29625.58 | 831.49 | 1593.34 |
| 217 | 619.96 | 47089 | 384350.4 | 134531.32 | 571.41 | 25583.74 | 2356.85 | 3373.67 |
| 149 | 384.40 | 22201 | 147763.36 | 57275.6 | 327.32 | 156427.5 | 3258.23 | 15897.01 |
| 192 | 516.59 | 36864 | 266865.23 | 99185.28 | 481.67 | 69336.98 | 1219.24 | 6902.84 |
| 3301 | 9358.91 | 1010755 | 8869708.45 | 2943150.82 | 9358.91 | 1570608.75 | 247224.62 | 102704.92 |
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.4906
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)
Статистическая значимость коэффициента регрессии b не подтверждается (1.46 Fkp, то коэффициент детерминации статистически значим.
Доверительные интервалы для зависимой переменной
Уравнение тренда имеет вид y = at 2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
Для наших данных система уравнений имеет вид (см. таблицу).
Получаем a0 = -11.37, a1 = 88.47, a2 = 2151.09
Уравнение тренда: y = -11.37t 2 +88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая
| t | y | t 2 | y 2 | x ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y | t 3 | t 4 | t 2 y |
| 1 | 2225.3 | 1 | 4951960.09 | 2225.3 | 2228.19 | 65.6099 | 8.352 | 16 | 6431.117 | 1 | 1 | 2225.3 |
| 2 | 2254.9 | 4 | 5084574.01 | 4509.8 | 2282.55 | 462.25 | 764.5225 | 9 | 62347.985 | 8 | 16 | 9019.6 |
| 3 | 2332.3 | 9 | 5439623.29 | 6996.9 | 2314.17 | 9781.21 | 328.6969 | 4 | 42284.599 | 27 | 81 | 20990.7 |
| 4 | 2365.8 | 16 | 5597009.64 | 9463.2 | 2323.05 | 17529.76 | 1827.5625 | 1 | 101137.95 | 64 | 256 | 37852.8 |
| 5 | 2295.4 | 25 | 5268861.16 | 11477 | 2309.19 | 3844 | 190.1641 | 0 | 31653.566 | 125 | 625 | 57385 |
| 6 | 2303.9 | 36 | 5307955.21 | 13823.4 | 2272.59 | 4970.25 | 980.3161 | 1 | 72135.109 | 216 | 1296 | 82940.4 |
| 7 | 2166.7 | 49 | 4694588.89 | 15166.9 | 2213.25 | 4448.89 | 2166.9025 | 4 | 100859.885 | 343 | 2401 | 106168.3 |
| 8 | 2080.4 | 64 | 4328064.16 | 16643.2 | 2131.17 | 23409 | 2577.5929 | 9 | 105621.908 | 512 | 4096 | 133145.6 |
| 9 | 2075.9 | 81 | 4309360.81 | 18683.1 | 2026.35 | 24806.25 | 2455.2025 | 16 | 102860.845 | 729 | 6561 | 168147.9 |
| 45 | 20100.6 | 285 | 44981997.26 | 98988.8 | 20100.51 | 89317.2199 | 11299.312 | 60 | 625332.964 | 4050 | 30666 | 1235751.2 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 4.8518
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L — период упреждения; уn+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; Tтабл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79
K1 = 247.4924
1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49
K2 = 261.9213
1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45
K3 = 278.0099
1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67
K4 = 295.4871
1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15
K5 = 314.1213
1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается
Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.895):
(a — tтабл·Sa; a + tтабл·Sa)
(-20.5642;-2.1758)
(b — t табл·Sb; b + tтаблS·b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.
Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i — e i-1 ) 2 |
| 2225.3 | 2228.19 | -2.89 | 8.3521 | 0 |
| 2254.9 | 2282.55 | -27.65 | 764.5225 | 613.0576 |
| 2332.3 | 2314.17 | 18.13 | 328.6969 | 2095.8084 |
| 2365.8 | 2323.05 | 42.75 | 1827.5625 | 606.1444 |
| 2295.4 | 2309.19 | -13.79 | 190.1641 | 3196.7716 |
| 2303.9 | 2272.59 | 31.31 | 980.3161 | 2034.01 |
| 2166.7 | 2213.25 | -46.55 | 2166.9025 | 6062.1796 |
| 2080.4 | 2131.17 | -50.77 | 2577.5929 | 17.8084 |
| 2075.9 | 2026.35 | 49.55 | 2455.2025 | 10064.1024 |
| 11299.3121 | 24689.8824 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Остаточная сумма квадратов
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где – случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
http://math.semestr.ru/corel/prim1.php
http://ecson.ru/economics/econometrics/zadacha-3.raschyot-parametrov-regressii-i-korrelyatsii-s-pomoschju-excel.html