С увеличением объема выборки уменьшается ошибка регрессии - ErrorsMaster.ru

5.1. Классическая линейная регрессионная модель. Предпосылки метода наименьших квадратов

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но, являясь лишь оценками, они не позволяют сделать вывод, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности, насколько близки оценки b0 и b1 коэффициентов своим теоретическим прототипам β0 и β1, как близко оцененное значение yi к условному матема-

тическому ожиданию M(Y X = xi), насколько надежны найденные оценки. Для ответа на эти вопросы необходимы определенные дополнительные исследования.

Как следует из соотношения (4.6), значения уi зависят от значений xi и случайных отклонений εi. Следовательно, переменная Y является случайной величиной, напрямую связанной с εi. Это означает, что до тех пор, пока не будет определенности в вероятностном поведении εi, мы не сможем быть уверенными в качестве оценок. Действительно, можно показать, что оценки коэффициентов регрессии − случайные величины, зависящие от случайного члена в уравнении регрессии.

Рассмотрим модель парной линейной регрессии

Пусть на основе выборки из n наблюдений оценивается регрессия

Как показано в формуле (4.14),

b =	Sxy	,	(5.3)

1	S2x

что означает, что коэффициент b1 также является случайным. В самом деле, значение выборочной ковариации Sxy зависит от того, какие значения принимают X и Y. Если Х можно рассматривать как экзогенный фактор, значения которого известны, то значения Y зависят от случайной составляющей εi. Теоретически коэффициент b1 можно разложить на неслучайную и случайную составляющие.

Sxy = COV(X, β0 + β1Х + ε) = COV(X, β0) + COV(X, β1Х) + COV(X, ε).

Sxy = β1 S2x + COV( X, ε).

(5.4)

112

Здесь использовались правила вычисления ковариации:

COV(X, β0) = 0, т. к. β0 = const, COV(X, β1Х) = β1COV( X, Х) = β1 S2x .

Следовательно,

b	=	Sxy	= β1 +	S	xе	.	(5.5)

1	S2x		S2x

Здесь β1 − постоянная величина (истинное значение коэффициен-

та регрессии), Sxе − случайная компонента. Аналогичный результат

S2x

можно получить и для коэффициента b0. Отметим при этом, что на практике такое разложение осуществить невозможно, поскольку неизвестны истинные значения β0 и β1, а также значения отклонений для всей генеральной совокупности.

Итак, мы показали, что свойства оценок коэффициентов регрессии, а следовательно, и качество построенной регрессии существенно зависят от свойств случайной составляющей. Доказано, что для получения по МНК наилучших результатов необходимо, чтобы выполнялся ряд предпосылок относительно случайного отклонения.

Предпосылки МНК (условия Гаусса−Маркова)

10. Математическое ожидание случайного отклонения εi равно нулю: M(εi) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения. Отметим, что выполнимость M(εi) = 0 влечет выполнимость

M(Y X = = xi) = β0 + β1xi.

20. Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = σ2 для любых наблюдений i и j.

Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастич-

ностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).

113

Поскольку D(εi) = M(εi − M(εi))2 = M(еi2 ) , то данную предпосылку

можно переписать в форме: M(еi2 ) = σ2.

Причины невыполнимости данной предпосылки и проблемы, связанные с этим, подробно рассматриваются в главе 8.

30. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.

Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Другими словами, величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Выполнимость данной предпосылки влечет следующее соотношение:

		0,		если i ≠ j;
уе е					(5.6)
j	= cov(еi ,еj ) =	2
i		,	если i = j.
		у

Поэтому, если данное условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнимости предпосылки 10 соотношение (5.6) может быть переписано в виде: M(εi εj) = 0 (i ≠ j).

Причины невыполнимости данной предпосылки и проблемы, связанные с этим, подробно рассматриваются в главе 9.

40. Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически при условии, что объясняющие переменные не являются случайными в данной модели.

Данное условие предполагает выполнимость следующего соотношения:

уеixi = cov(εi, xi) = M((εi − M(εi))(xi − M(xi))) = M(εi(xi − M(xi))) =

=M(εi xi) − M(εi) M(xi) = M(εi xi) = 0.

Следует отметить, что выполнимость данной предпосылки не столь критична для эконометрических моделей.

50. Модель является линейной относительно параметров.

114

Теорема Гаусса−Маркова. Если предпосылки 1о − 5о выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1.Оценки являются несмещенными, т. е. M(b0 ) = в0 , M(b1) = в1 . Это вытекает из того, что M(еi ) = 0 и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2.Оценки состоятельны, т. к. дисперсия оценок параметров при

возрастании	числа	n наблюдений стремится к нулю:
D(b	0	) →0	, D(b ) →0. Другими словами, при увели-
	n→∞	1	n→∞

чении объема выборки надежность оценок увеличивается (b0 наверняка близко к β0, b1 − близко к β1).

3.Оценки эффективны, т. е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.

Ванглоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.

Если предпосылки 2о и 3о нарушены, т. е. дисперсия отклонений непостоянна и (или) значения е i , еj связаны друг с другом, то свойст-

ва несмещенности и состоятельности сохраняются, но свойство эффективности − нет.

Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения. Например:

•объясняющие переменные не являются случайными величинами;

•случайные отклонения имеют нормальное распределение;

•число наблюдений существенно больше числа объясняющих переменных;

•отсутствуют ошибки спецификации;

•отсутствует совершенная мультиколлинеарность.

5.2.Анализ точности определения оценок коэффициентов регрессии

Всилу случайного отбора элементов в выборку случайными яв-

ляются также оценки b0 и b1 коэффициентов β0 и β1 теоретического уравнения регрессии. Их математические ожидания при выполнении

предпосылок об отклонениях εi равны соответственноM(b0 ) = в0 ,

115

M(b1) = в1 . При этом оценки тем надежнее, чем меньше их разброс

вокруг β0 и β1, т. е. чем меньше дисперсии D(b0) и D(b1) оценок. Надежность получаемых оценок, очевидно, тесно связана с дисперсией случайных отклонений εi. Фактически D(εi) является дисперсией D(Y X = xi) переменной Y относительно линии регрессии (дисперсией Y, очищенной от влияния X). Полагая, что измерения − равноточные, можно считать, что все эти дисперсии равны между собой

(предпосылка 20) D(εi) = уе2 = σ2.

Приведем формулы связи дисперсий коэффициентов D(b0) и D(b1) с дисперсией σ2 случайных отклонений εi. Для этого представим формулы определения коэффициентов а и b в виде линейных функций относительно значений Y:

b	= ∑(xi − x)(yi − y)	= ∑(xi − x)yi − y∑(xi − x)
1	∑(xi − x)2	∑(xi − x)2	∑(xi − x)2

b	= ∑(xi − x)(yi − y)	= ∑(xi − x)yi , т. к. ∑(xi −
1	∑(xi − x)2	∑(xi − x)2

x ) = 0.

Введя обозначение ci =		(xi − x)	, имеем:
	∑(xi − x)2
			b1 = ∑ ciyi.							(5.7)
По аналогии имеем:
b	0	= y − b x =	∑ yi	− ∑c	y	x = ∑(	1 − c	x)y	.

	1			n	i	i		n	i	i

Обозначив di =	1 − ci x , имеем:
		n	b0 = ∑ diyi.							(5.8)

Так как предполагается, что дисперсия Y постоянна и не зависит от значений X, то ci и di можно рассматривать как некоторые постоянные. Следовательно,

D(b1) = D(∑ ciyi) = σ2 ∑ ci2 =

у2

(5.9)

∑(xi − x)2

2ci x

D(b0) = D(∑ diyi) = σ

∑ di

= σ

∑(

− cix )

= σ

∑(

−

+ ci

) =

116

2	1		x 2	2	1		x2	у2 ∑ xi2
= σ	(		− 0 +		) = σ	( n	+		) =	. (5.10)
n	∑ (xi − x)2	∑(xi − x)2	n∑(xi − x)2

Из соотношений (5.10), (5.11) очевидны следующие выводы.

•Дисперсии b0 и b1 прямо пропорциональны дисперсии случайного отклонения σ2. Следовательно, чем больше фактор случайности, тем менее точными будут оценки.

•Чем больше число n наблюдений, тем меньше дисперсии оценок. Это вполне логично, т. к. чем большим числом мы располагаем, тем вероятнее получение более точных оценок.

•Чем больше дисперсия (разброс значений ∑(хi − x )2) объясняющей переменной, тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменений объясняющей переменной, тем точнее будут оценки (тем меньше доля случайности в их определении).

Наглядное обсуждение этих выводов проведем чуть позже на основе следующих рассуждений.

В силу того, что случайные отклонения εi по выборке определены быть не могут, при анализе надежности оценок коэффициентов регрессии они заменяются отклонениями ei = yi − b0 − b1xi значений yi

переменной Y от оцененной линии регрессии. Дисперсия случайных отклонений D(εi) = σ2 заменяется ее несмещенной оценкой

∑e2

∑(yi

− b0 − b1xi)

(5.11)

− 2

Тогда

n − 2

D(b ) ≈ S2 =

(5.12)

∑(xi − x)2

S2∑ xi2

= x

D(b0 ) ≈ Sb0

Sb1 .

(5.13)

∑ei2

n ∑(xi − x)2

S2 =

− необъясненная дисперсия (мера разброса зависимой пе-

n − 2

ременной вокруг линии регрессии). Отметим, что корень квадратный

из необъясненной дисперсии, т. е. S =	∑e2	, называется стандарт-
i
	n − 2

ной ошибкой оценки (стандартной ошибкой регрессии).

117

Sb	=	Sb2	и Sb =	Sb2	− стандартные отклонения случайных ве-
	0	0	1	1

личин b0 и b1, называемые стандартными ошибками коэффициентов регрессии.

Объяснение данных соотношений имеет весьма наглядную графическую интерпретацию.

Коэффициент b1 определяет наклон прямой регрессии. Чем больше разброс значений Y вокруг линии регрессии, тем больше (в среднем) ошибка определения наклона прямой регрессии. Действительно, если такой разброс совсем отсутствует (еi = 0 ), то прямая оп-

ределяется однозначно и ошибки при определении b и a не будет вовсе ( ∑ei = 0 S2 = 0 Sb0 = Sb1 = 0). Например, на рис. 5.1, а все наблюдаемые точки лежат на одной прямой ( ∑ei2 = 0). Тогда через лю-

бой набор точек проводится одна и та же прямая. На рис. 5.1, б точки не лежат на одной прямой, но для трех точек прямая регрессии будет такой же (хотя отклонения от линии регрессии существенны), как и на рис. 5.1, а. Однако при исключении из рассмотрения любой из указанных трех точек прямые регрессии будут существенно отличаться друг от друга ((1, 2), (1, 3), (2, 3)). Следовательно, значительно различаются их углы наклона, а значит, стандартная ошибка Sb1 коэффици-

ента регрессии b1 будет существенной.

Y		Y
	3		3

	2	1
1
			2
а	X	б	X

Рис. 5.1

В знаменателе дроби (5.12), определяющей значение S2b1 , стоит сумма ∑(хi − x )2 квадратов отклонений xi от среднего значения x . Эта сумма велика (а следовательно, вся дробь мала, и дисперсия S2b1 оцен-

118

ки меньше), если регрессия определяется на широком диапазоне значений переменной X.

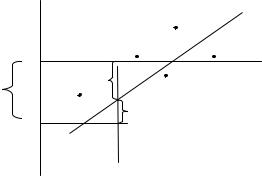
Например, на рис. 5.2 через пары точек (1, 3) и (2, 3) проведена одна и та же прямая. Но диапазон (1, 3) шире диапазона (2, 3). Если вместо точки 3 рассмотреть либо точку 3а, либо 3б (т. е. при случайном изменении выборки), то наклон прямой для пары (1, 3) изменится значительно меньше, чем для пары (2, 3).

Y
		3а
		2
1		3б
0		X
	Рис. 5.2
		2	2	∑ xi2
Дисперсия свободного члена уравнения регрессии Sb0	= Sb1	n
	Sb2
пропорциональна дисперсии	. Действительно, чем сильнее меняет-
	1
ся наклон прямой, проведенной через данную точку (x, y) , тем больше

разброс значений свободного члена, характеризующего точку пересечения этой прямой с осью OY.

Кроме того, разброс значений свободного члена тем больше, чем

больше средняя величина x 2 . Это связано с тем, что при больших по модулю значениях X даже небольшое изменение наклона регрессионной прямой может вызвать большое изменение оценки свободного члена, поскольку в этом случае в среднем велико расстояние от точек наблюдений до оси OY.

На рис.5.3 через пары точек (1, 2) и (3, 4) проходит одна и та же прямая, пересекающая ось OY в точке (0, b0). Для второй из этих пар значения переменной X больше по абсолютной величине (при одинаковом диапазоне изменений X и Y), чем для первой. Если в этих парах точки 1 и 3 изменить на одну и ту же величину (новые точки 1а, 3а), то углы наклона новых прямых (1а, 2) и (3а, 4) будут одинаковы. Но сво-

119

бодный член b01 для первой прямой будет существенно меньше отличаться от b0, чем свободный член b02 для второй прямой.

Y			•3a	4•
b02
				•
				3
b01		1a	2	•
	•
b0		• 1


0				X
				Рис. 5.3

5.3. Проверка гипотез относительно коэффициентов линейного уравнения регрессии

Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Поэтому коэффициенты эмпирического уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. При проведении статистического анализа перед исследователем зачастую возникает необходимость сравнения эмпирических коэффициентов регрессии b0 и b1 с некоторыми теоретически ожидаемыми значениями β0 и β1 этих коэффициентов. Данный анализ осуществляется по схеме статистической проверки гипотез, которая подробно проанализирована в разделе 3.4.

Для проверки гипотезы

H0: b1 = β1,

H1: b1 ≠ β1

используется статистика

t =	b1 − в1	,	(5.14)

	Sb
1

которая при справедливости H0 имеет распределение Стьюдента с числом степеней свободы ν = n − 2, где n − объем выборки. Следовательно, H0: b1 = β1 отклоняется на основании данного критерия, если

Тнабл. =	b1 − в1		≥ tб	,	(5.15)
Sb
				,n−2
		2
	1

120

где α − требуемый уровень значимости. При невыполнении (5.15) cчитается, что нет оснований для отклонения H0.

Наиболее важной на начальном этапе статистического анализа построенной модели все же является задача установления наличия линейной зависимости между Y и X. Эта проблема может быть решена по той же схеме:

H0: b1 = 0, H1: b1 ≠ 0.

Гипотеза в такой постановке обычно называется гипотезой о статистической значимости коэффициента регрессии. При этом, ес-

ли H0 принимается, то есть основания считать, что величина Y не зависит от Х. В этом случае говорят, что коэффициент b1 статистически незначим (он слишком близок к нулю). При отклонении H0 коэффициент b1 считается статистически значимым, что указывает на наличие определенной линейной зависимости между Y и X. В данном случае рассматривается двусторонняя критическая область, т. к. важным является именно отличие от нуля коэффициента регрессии, и он может быть как положительным, так и отрицательным.

Поскольку в данном случае полагается, что β1 = 0, то формально значимость оцененного коэффициента регрессии b1 проверяется с помощью анализа отношения его величины к его стандартной ошибке

Sb1 = S2b1 . В случае выполнения исходных предпосылок модели эта

дробь имеет распределение Стьюдента с числом степеней свободы ν = = n − 2, где n − число наблюдений. Данное отношение называется t-

статистикой.

t =	b1 =	b1	.	(5.16)

	Sb1	Sb2
		1

Для t-статистики проверяется нулевая гипотеза о равенстве ее нулю. Очевидно, t = 0 равнозначно b1 = 0, поскольку t пропорциональна b1. Фактически это свидетельствует об отсутствии линейной связи между X и Y.

По аналогичной схеме на основе t-статистики проверяется гипо-

теза о статистической значимости коэффициента b0:
t =	b0 =	b .	(5.17)
	Sb0	Sb20
		121

Отметим, что для парной регрессии более важным является анализ статистической значимости коэффициента b1, т. к. именно в нем скрыто влияние объясняющей переменной Х на зависимую переменную Y.

Для примера 4.1.

∑ e2

∑ (y

− b

− b x

35.3

1 i

= 0.0023.

n(x2 − x2 )

n(n − 2)(x2 − x2 )

12 10 125.25

Sb1

= 0.0023 = 0.0485.

= 0.9339

= 19.2557.

Sb1

0.0485

Критическое значение при уровне значимости α = 0.05 равно tкр. = t

,n−2

= t0.025;10 = 2.228.

Сравним модуль наблюдаемого значения tb1

= 19.2557 с критическим

значением t0.025;0.8 . Поскольку tb1

= 19.2557 > 2.228 = tкр., то нулевая гипотеза

{t = 0} должна быть отвергнута в пользу альтернативной при выбранном уровне

значимости. Это подтверждает статистическую значимость коэффициента регрес-

сии b1.

Аналогично проверяется статистическая значимость коэффициента b0:


S2b0			S2 ∑ xi2	= S2b1	= 0.0023 15884.75 = 36.5349 .
=		x2

	n(x2 − x2 )

Sb0	=	36.5349 = 6.044.
tb0	=		b0	= 3.699 = 0.612 .
Sb0
		6.044

Так как t b0 = 0.612 < 2.228 = tкр., то гипотеза о статистической незначимо-

сти коэффициента b0 не отклоняется. Это означает, что в данном случае свободным членом уравнения регрессии можно пренебречь, рассматривая регрессию как

Y = b1X.

При оценке значимости коэффициента линейной регрессии на начальном этапе можно использовать следующее “грубое” правило, позволяющее не прибегать к таблицам.

Если стандартная ошибка коэффициента больше его модуля ( t < 1 ), то коэффициент не может быть признан значимым, т. к. доверительная вероятность здесь при двусторонней альтернативной гипотезе составит менее чем 0.7.

Если 1 < t < 2, то найденная оценка может рассматриваться как

122

относительно (слабо) значимая. Доверительная вероятность в этом случае лежит между значениями 0.7 и 0.95.

Если 2 < t < 3, то это свидетельствует о значимой линейной связи между X и Y. В этом случае доверительная вероятность колеблется от 0.95 до 0.99.

Наконец, если t > 3, то это почти гарантия наличия линейной связи.

Конечно, в каждом конкретном случае играет роль число наблюдений. Чем их больше, тем надежнее при прочих равных условиях выводы о значимости коэффициента. Однако для n >10 предложенное “грубое” правило практически всегда работает.

5.4. Интервальные оценки коэффициентов линейного уравнения регрессии

Как отмечалось в параграфе 5.2, базовыми предпосылками МНК является предположение о нормальном распределении отклонений εi с нулевым математическим ожиданием и постоянной дисперсией, т. е.

еi N(0,у2 ) . Естественность этого предположения обосновывается

хорошо известной в теории вероятностей центральной предельной теоремой (ЦПТ), которую можно сформулировать следующим образом.

Если СВ представляет собой сумму очень большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то рассматриваемая СВ имеет распределение, близкое к нормальному.

Но случайное отклонение εi как раз и отражает влияние на независимую величину тех переменных, которые не включены в модель. Таких переменных обычно очень много, причем их индивидуальное влияние достаточно мало (иначе, их необходимо было учесть в модели). Следовательно, при рассмотрении случайных отклонений мы попадаем практически в условия ЦПТ. Тогда можно заключить, что εi

(i = 1, n ) имеют нормальное распределение с M(еi ) = 0 , у2 (еi ) = у2 . Это позволяет получать не только наилучшие линейные несмещенные точечные оценки (BLUE) b0 и b1 коэффициентов β0 и β1 линейного уравнения регрессии, но и находить их интервальные оценки, что дает определенные гарантии точности.

Указанные выше предположения позволяют утверждать, что СВ b0 и b1 имеют нормальные распределения. Действительно, как извест-

123

но, линейная комбинация нормально распределенных СВ является нормально распределенной СВ. Но, как показано в формулах (5.7), (5.8), коэффициенты b1 и b0 могут быть представлены в виде:

b1 = ∑ci yi , b0 = ∑di yi ,

где ci, di − постоянные.

Другими словами, b1 и b0 являются линейными комбинациями yi. В свою очередь yi по формуле (4.6) является линейной комбинацией εi (при этом считается, что β0, β1 и xi − константы или неслучайные величины). Тогда b1 и b0 через yi являются линейными функциями от εi, имеющими нормальное распределение. Следовательно, b1 и b0 также распределены нормально.

Как отмечалось ранее, M(b0 ) = в0 ,

M(b1) = в1 .

D(b ) ≈ S2

∑(xi − x)2

D(b

) ≈ S2

S2∑ xi2

где S2 =

∑ei2

n ∑(xi − x)2

n − 2

Следовательно, b0 N(β0, D(b0)), b1 N(β1, D(b1)).

Тогда, как отмечалось выше, статистики

tb =

b0 − в0

b1 − в1

(5.18)

S(b1 )

S(b0 )

имеют распределение Стьюдента с числом степеней свободы ν = n − 2. Далее для определения 100(1 − α)%-ного доверительного интервала по таблицам критических точек распределения Стьюдента по доверительной вероятности γ =1 − α и числу степеней свободы ν определяют

критическое значение t б , удовлетворяющее условию

2,n−2

< t б

) =1 − б .

(5.19)

,n−2

Подставив каждую из формул (5.18) в (5.19), получаем

P(−t б

b0 − в0

< t б

) =1 − б ;

,n−2

S(b0 )

,n−2

(5.20)

b1 − в1

P(−t б

< t б

) =1 − б .

,n−2

S(b1)

,n−2

После преобразований выражений, стоящих в скобках, имеем:

124

P(b0 − t б

S(b0 ) < в0 < b0 + t

S(b

0 )) =1 − б ,

(5.21)

,n−2

P(b1 − t б

,n−2S(b1) < в1 < b1 + t

,n−2S(b1)) =1 − б .

(5.22)

C учетом (5.12), (5.13) получаем

P(b0 − tб

S2 ∑ xi2

< в0

S2 ∑ xi2

,n−2

n∑(x

− x)2

< b0 + t

,n−2

n∑

− x)2 ) = 1− б ; (5.23)

P(b1 − tб

< в1

,n −2

∑(x

− x)2

< b1 + t

,n−

∑(x

− x)2 ) = 1− б .

(5.24)

Соотношения (5.23), (5.24) определяют доверительные интервалы

S(b0 );

b0 + t б

− t

S(b0 )

(5.25)

,n−2

− t

S(b );

b + t

(5.26)

S(b ) ,

,n−2

которые с надежностью (1 − α) накрывают определяемые параметры

β0 и β1.

Для примера 4.1 95%-ные доверительные интервалы для коэффициентов будут следующими:

(3.699 − 2.228 6.044; 3.699 + 2.228 6.044) = (−9.767; 17.165); (0.9339 − 2.228 0.0485; 0.9339 + 2.228 0.0485) = (0.826; 1.042).

Фактически доверительный интервал определяет значения теоретических коэффициентов регрессии β0 и β0, которые будут приемлемыми с надежностью (1 − α) при найденных оценках b0 и b1.

5.5. Доверительные интервалы для зависимой переменной

Одной из центральных задач эконометрического моделирования является предсказание (прогнозирование) значений зависимой переменной при определенных значениях объясняющих переменных. Здесь возможен двоякий подход: либо предсказать условное математическое ожидание зависимой переменной при определенных значениях объясняющих переменных (предсказание среднего значения), либо прогнозировать некоторое конкретное значение зависимой переменной (предсказание конкретного значения).

125

Предсказание среднего значения. Пусть построено уравнение парной регрессии yi = b0 + b1xi , на основе которого необходимо пред-

сказать условное математическое ожидание M(Y X = xp) переменной Y при X = xp. В данном случае значение yp = b0 + b1xp является оцен-

кой M(Y X = xp). Тогда естественным является вопрос, как сильно может уклониться модельное среднее значение yp , рассчитанное по

эмпирическому уравнению регрессии, от соответствующего условного математического ожидания. Ответ на этот вопрос дается на основе интервальных оценок, построенных с заданной надежностью (1 − α) при любом конкретном значении xp объясняющей переменной.

Чтобы построить доверительный интервал, покажем, что СВ Yp

имеет нормальное распределение с конкретными параметрами. Используя формулы (5.7), (5.8), имеем:

Yp = b0 + b1xp = ∑ diyi + (∑ ciyi)xp = ∑(di + cixp)yi.

Следовательно, Yp является линейной комбинацией нормальных СВ и, значит, сама имеет нормальное распределение.

M( Yp ) = M(b0 + b1xp) = M(b0) + M(b1)xp = β0 + β1xp ,	(5.27)
D( Y ) = D(b0	+ b1xp) = D(b0) + D(b1) x2	+ 2cov(b0, b1) xp
p	p

(здесь используем формулы: D(X + Y) = D(X) + D(Y) + 2cov(X, Y); D(cX) = c2D(X); cov(X, bY) = b cov(X, Y)).

cov(b0, b1) = M[(b0 − M(b0))(b1 − M(b1))] = M[(b0 − β0)(b1 − β1)] =

= M[( y − b1x − ( y − в1x ))(b1 − β1)] = − x M[(b1 − β1)(b1 − β1)] =

= − x D(b1) = − x

у2

∑(xi

− x)2

у2

∑ xi2

у2

−2 x

у2

D( Yp ) =

xp =

n∑(xi − x)2

∑(xi

− x)2

∑

(xi − x)2

у2

(x − xp )2

[ x

− 2xxp + xp

] = σ

(5.28)

∑(x

− x)2

∑(x

− x)2

∑e2

Подставив вместо σ

ее несмещенную оценку S

, получим

n − 2

выборочную исправленную дисперсию S2( Yp ) рассматриваемой СВ.

126

Тогда СВ

Т =	Yp − (в0)+ в1xp )	(5.29)
	S(Yp )

имеет распределение Стьюдента с числом степеней свободы ν = n − 2. Следовательно, по таблице критических точек распределения Стьюдента по требуемому уровню значимости α и числу степеней свободы

ν = n − 2 можно определить критическую точку t б , удовлетворяю-

2,n−2

щую условию P(

< t б

) =1 − б . С учетом (5.29) имеем:

,n−2

)

− (в

+ в

)

< t

= 1 − α.

(5.30)

S(Yp )

,n−2

После алгебраических преобразований получим:

P(b0 +b1xp− t б

,n−2

S( Yp )<β0+β1xp<b0+b1xp+ t б

,n−2

S( Yp )) =1−α.

(5.31)

Таким образом, доверительный интервал для M(Y X = xp) = β0 + β1xp имеет вид:

(x − xp )2

b0 + b1xp − t

,n−2 S

; b0 +b1xp+ t

,n−2 S

∑(xi − x)2

(5.32)

Доверительный интервал

для M(Y X = xp)

Y = b0 + b1X

)

127

Для проверки гипотезы

Н0 : M(Y X = xp) = yp; Н1 : M(Y X = xp) ≠ yp

используется следующая статистика:

T =	M(Y	X = xp ) − yp		,	(5.33)

S	1	+	(x − xp )2

	n	∑(xi − x)2

имеющая распределение Стьюдента с числом степеней свободы ν =

=n−2. Поэтому Н0 отклоняется, если Тнабл. ≥ t б	( α − требуемый
		,n−2
2

уровень значимости).

Предсказание индивидуальных значений зависимой переменной.

На практике иногда более важно знать дисперсию Y, чем ее средние значения или доверительные интервалы для условных математических ожиданий. Это позволяет определить допустимые границы для конкретного значения Y.

Пусть нас интересует некоторое возможное значение у0 переменной Y при определенном значении xp объясняющей переменной Х. Предсказанное по уравнению регрессии значение Y при X = xp составляет yp. Если рассматривать значение у0 как СВ Y0, а yp − как СВ

Yp, то можно отметить, что					(x − xp )2
2			2	1
Y0 N(β0 + β1xp, σ	), а	Yp N(b0 + b1xp, σ			+	).
	n	∑(x		− x)2
					i

СВ Y0 и Yp являются независимыми, а следовательно, СВ U = Y0 − Yp имеет нормальное распределение с

M(U) = 0 и D(U) = σ

(x − xp )2

∑

− x)2

Но тогда можно показать, что

СВ

Y0 − Yp

− xp )2

∑(xi − x)2

имеет распределение Стьюдента с числом степеней свободы ν = n − 2. На основании этого можно сделать вывод, что

128

P ( − tб

Y0 − Yp

< tб

) = 1 − α.

(5.34)

(x − xp )2

,n−2

,n −2

∑(xi − x)2

Таким образом, интервал

(x − xp )2

b0 + b1xp m t

1+ n

(5.35)

,n−2

∑(xi − x)2

определяет границы, за пределами которых могут оказаться не более 100α % точек наблюдений при X = xp. Заметим, что данный интервал шире доверительного интервала для условного математического ожидания (на рис. 5.4 границы этого интервала отмечены пунктирной линией).

Проводя анализ построенных интервалов, несложно заметить, что наиболее узкими они будут при Хp = x . По мере удаления Хp от среднего значения доверительные интервалы расширяются (см. рис. 5.4). Поэтому необходимо достаточно осторожно экстраполировать полученные результаты на прогнозные области. С другой стороны, с ростом числа наблюдений n эти интервалы сужаются к линии регрессии при n → ∞.

По данным из примера 4.1 рассчитаем 95 %-ный доверительный интервал для условного математического ожидания M(Y X = xp) при Х = 160. Воспользовавшись формулой (5.32), рассчитаем границы интервала:

3.699+ 0.9339 160 ± 2.228 1.8788	1	+	(125.25 −160)	2	.
12	2102.1875

Таким образом, доверительный интервал для среднего значения Y при Х = 160 имеет вид: (149.728; 156.5193). Другими словами, среднее потребление при доходе 160 с вероятностью 95 % будет находиться в интервале (149.728; 156.5193).

Рассчитаем границы интервала, в котором будет сосредоточено не менее 95% возможных объемов потребления при неограниченно большом числе наблюдений при уровне дохода Х = 160. Для этого воспользуемся формулой (5.35).


3.699 + 0.9339 160 ± 2.228 1.8788 1+		1	+	(125.25 −160)	2	.
12	2102.1875

Тогда интервал, в котором будут находиться, по крайней мере, 95 % индивидуальных объемов потребления при доходе Х = 160, имеет вид: (147.4898; 158.7082). Нетрудно заметить, что он включает в себя доверительный интервал для условного среднего потребления.

129

5.6. Проверка общего качества уравнения регрессии. Коэффициент детерминации R2

После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии. Очевидно, если все точки лежат на построенной прямой, то регрессия Y на X “идеально” объясняет поведение зависимой переменной. В реальной жизни такая ситуация практически не встречается. Обычно поведение Y лишь частично объясняется влиянием переменной Х. Возможные соотношения между двумя переменными имеют наглядную графическую интерпретацию в виде так называемой диаграммы Венна (рис. 5.5).

Y	X	Y	X	Y	X
	а		б		в
	Y	X		Y = X
		г		д
			Рис. 5.5

На рис. 5.5, а Х никак не влияет на Y. На каждом следующем рисунке влияние Х все усиливается. Наконец, на рис. 5.5, д значения Y целиком определяются значениями Х.

Суммарной мерой общего качества уравнения регрессии (соответствия уравнения регрессии статистическим данным) является коэффициент детерминации R2. В случае парной регрессии коэффициент детерминации будет совпадать с квадратом коэффициента корреляции. В общем случае коэффициент детерминации рассчитывается по формуле:

2		∑ei2
R	= 1 −		.	(5.36)
∑(yi − y )2

130

Поясним смысл коэффициента детерминации. Пусть эмпирическое уравнение регрессии имеет вид:

Тогда наблюдаемые (реальные) значения уi, i = 1, 2, … , n отличаются от модельных yi на величину ei:

		уi = yi	+ ei .		(5.38)
Соотношение (5.38) можно переписать в следующем виде:
	уi − y = ( yi − y ) + (уi	− yi ),	(5.39)
т. е.	уi − y =	ki	+	еi,

где (уi − y ) − отклонение i-й (наблюдаемой) точки от среднего значения y зависимой переменной Y; ki − отклонение i-й точки на линии регрессии от y ; еi − отклонение i-й точки от модельного значения yi ,

определяемого по линии регрессии. Все отклонения рассчитываются по оси зависимой переменной (см. рис. 5.6).

yi ei

X xi

Рис. 5.6

Возведем обе части равенства (5.39) в квадрат и просуммируем полученные значения по объему выборки n:

∑(yi − y )2	)	)	(5.40)
= ∑(yi − y )2 +	2∑((yi − y ) ei ) + ∑ei2 .

Можно показать, что ∑((y)i − y ) ei ) = 0 (доказательство опускаем для упражнения). Тогда справедливо следующее соотношение:

∑(yi − y)2 = ∑ ki2 + ∑ei2 .

(5.41)

131

Очевидно, ∑(yi − y)2 − общая (полная) сумма квадратов может

интерпретироваться как	мера	общего разброса (рассеивания) пере-
менной Y относительно	y .	∑ ki2	)
= ∑(yi − y )2 − объясненная сумма

квадратов, интерпретируемая как мера разброса, объяснимого с по-

мощью регрессии. ∑ei2	)
= ∑(yi − yi )2 − остаточная (необъясненная)

сумма квадратов, являющаяся мерой остаточного, необъясненного уравнением регрессии разброса (разброса точек вокруг линии регрессии).

Разделив (5.41) на левую его часть, получим:

∑ ki2

∑ei2

∑ ki2

∑ei2

1 =

= 1−

(5.42)

∑(yi

− y )2

∑(yi − y )2

∑ ki2

Вводя

обозначение R

получаем соотношение

∑(yi − y )2

(5.36). При этом очевидно, что коэффициент детерминации R2

опре-

деляет долю разброса зависимой переменной, объяснимую регрессией

Y на X.

∑e2

i 2 определяет долю разброса зависимой переменной,

∑(yi − y )

необъясненную регрессией Y на X.

Из проведенных рассуждений следует, что в общем случае справедливо соотношение 0 ≤ R2 ≤ 1. Возможные условия нарушения неравенства R2 ≥ 0 рассмотрены чуть ниже.

Нетрудно заметить, что если между величинами Х и Y существует значимая линейная связь, то ∑ei2 существенно меньше, чем ∑ (yi − y )2 . Действительно, МНК позволяет найти прямую, для которой ∑ei2 минимальна, а прямая Y = y является одной из возможных линий, для которых выполняется условие y = b0 + b1x . Поэтому зна-

чение числителя вычитаемой из единицы дроби в (5.36) меньше, чем значение ее знаменателя (иначе, выбираемой по МНК линией регрессии была бы прямая Y = y ). Следовательно, в этом случае коэффици-

ент детерминации R2 близок к единице.

Таким образом, коэффициент детерминации R2 является мерой, позволяющей определить, в какой степени найденная прямая регрес-

132

сии дает лучший результат для объяснения поведения зависимой переменной Y, чем горизонтальная прямая Y = y .

Следовательно, чем теснее линейная связь между Х и Y, тем ближе коэффициент детерминации R2 к единице (рис. 5.5, д). Чем слабее такая связь, тем R2 ближе к нулю (рис. 5.5, а).

Однако не следует абсолютизировать высокое значение R2, т. к. коэффициент детерминации может быть близким к единице просто в силу того, что обе исследуемые величины Х и Y имеют выраженный временной тренд, не связанный с их причинно-следственной зависимостью. В экономике обычно такой тренд имеет объемные показатели (ВНП, ВВП, доход, потребление). А темповые и относительные показатели (темпы роста, производительность, ставка процента) не всегда имеют тренд. Поэтому при оценивании регрессий по временным рядам объемных показателей (например, зависимость потребления от дохода или спроса от цены) величина R2 может быть весьма близкой к единице. Но это не обязательно свидетельствует о наличии значимой линейной связи между исследуемыми показателями, а может означать лишь то, что поведение зависимой переменной нельзя описать уравнением Y = y .

Если уравнение регрессии строится по перекрестным данным, а не по временным рядам, то коэффициент детерминации R2 для него обычно не превышает 0.6 – 0.7. Аналогичные значения R2 обычно получаются и для регрессий по временным рядам, если они не имеют выраженного тренда (темп инфляции от уровня безработицы, темпы прироста выпуска от темпов прироста затрат ресурсов и т. п.).

Естественно, возникает вопрос, какое значение R2 можно считать удовлетворительным. Точную границу приемлемости (статистической значимости) R2 для всех случаев сразу указать невозможно. Нужно обращать внимание на объем выборки, число объясняющих переменных, наличие трендов и содержательную интерпретацию. R2 может оказаться даже отрицательным. Обычно это случается для линейных уравнений регрессии, в которых отсутствует свободный член Y = ∑ bjX j . Оценивая такое уравнение по МНК, мы вынуждены рас-

сматривать лишь те прямые (гиперплоскости), которые проходят через начало координат (рис. 5.7). Значение R2 получается отрицательным тогда, когда разброс значений зависимой переменной вокруг линии Y = y меньше, чем вокруг любой из прямых (гиперплоскостей),

проходящих через начало координат.

133

Y	Y = bX

	Y = b0 + b1X
Y = y
x	X
	Рис. 5.7

Из рис. 5.7 видно, что разброс наблюдаемых значений переменной Y относительно прямой Y = y существенно меньше разброса от-

носительно прямой Y = bX . Отрицательное значение R2 свидетельствует о целесообразности добавления в уравнение Y = ∑ bjX j свобод-

ного члена (Y = b0 + b1X, см. рис. 5.7).

Схему анализа общего качества уравнения регрессии на основе коэффициента детерминации мы подробно обсудим в разделе 6.7.

Проиллюстрируем связь между коэффициентом детерминации R2 для парного уравнения регрессии и выборочным коэффициентом корреляции rxy.

∑ k2

)

− y)2

∑(b

+ b x

− (b

+ b x))2

∑(y

R =

= ∑(yi — y )2

∑(yi — y )2

= b

∑(x

— x))2

∑(x

− x)(y

− y) 2

∑(x

— x))2

∑(yi — y )

∑

(xi − x)

∑(yi — y )

(∑ (xi

− x)(yi − y))

∑ (xi

− x)(yi − y)

= r2 .

∑ (xi − x) ∑ (yi — y )

∑ (xi − x)

∑

(yi — y )

Рассчитаем коэффициент детерминации R2 для примера 4.1.

R2 = 1 −

∑ ei2

= 1 −

35.3

= 0.983.

2108.6668

∑ (yi

− y )2

Столь высокое значение коэффициента детерминации свидетельствует о высоком

общем качестве построенного уравнения регрессии. R2 = 0.983 ≈ (0.9914)2 = r2

(неточности в данном случае связаны с округлением вычислений).

134

Вопросы для самопроверки

1.Перечислите предпосылки МНК, каковы последствия их выполнимости либо невыполнимости?

2.В чем суть наилучших линейных несмещенных оценок (BLUE)?

3.Как определяются стандартные ошибки регрессии и коэффициентов регрессии?

4.Опишите схему проверки гипотез о величинах коэффициентов регрессии.

5.В чем суть статистической значимости коэффициентов регрессии?

6.Опишите “грубое” правило анализа статистической значимости коэффициентов регрессии.

7.Приведите схему определения интервальных оценок коэффициентов регрессии.

8.Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной?

9.В чем суть предсказания индивидуальных значений зависимой переменной?

10.Объясните суть коэффициента детерминации.

11.В каких пределах изменяется коэффициент детерминации?

12.Дайте определения следующих понятий: а) оценка коэффициента регрессии; б) стандартная ошибка регрессии;

в) статистическая значимость коэффициента; г) общая (объясненная, необъясненная) сумма квадратов отклонений; д) коэффициент детерминации;

е) интервальная оценка коэффициента регрессии.

13.Объясните, какое из указанных утверждений истинно, ложно, не определено. а) Предпосылки МНК являются обязательным условием построения линейной регрессионной модели.

б) Теоретическим обоснованием МНК является теорема Гаусса–Маркова.

в) Оценки коэффициентов регрессии будут иметь нормальное распределение, если случайные отклонения распределены нормально.

г) В любой линейной регрессионной модели, построенной по МНК, справед-

лива формула ∑ei = 0.

д) Построение интервальных оценок для коэффициентов регрессии основано на том, что эти оценки имеют нормальное распределение.

е) Чем больше стандартная ошибка регрессии, тем точнее оценки коэффициентов.

ж) Условная средняя СВ и среднее значение СВ являются по сути одним и тем же.

з) 90 %-ный доверительный интервал для условного математического ожидания зависимой переменной определяет область возможных значений для 90 % наблюдений за зависимой переменной при соответствующем уровне объяс-

няющей переменной.

и) 0 ≤ R2 ≤ 1.

135

к) Для парной линейной регрессии коэффициент корреляции превосходит коэффициент детерминации.

14.По наблюдениям за 150 фирмами в отрасли стремятся построить регрессионную модель Y = β0 + β1X + ε и оценить коэффициенты β0 и β1 по МНК. Здесь

Х − прибыль фирм, Y − затраты на обновление основного капитала.

а) Если прибыль у всех фирм будет одинаковой, возможно ли построение уравнения регрессии?

б) Если условные дисперсии затрат Y при различных прибылях различны, то мы не можем быть уверены в найденных оценках (да; нет; нет определенного ответа).

в) Если прибыль фирм не имеет нормального распределения, то использование МНК нецелесообразно (да; нет; нет определенного ответа).

г) Если условия Гаусса–Маркова выполнены, то для определения оценок коэффициентов мы обязаны использовать МНК, т. к. в этом случае полученные оценки будут наилучшими линейными несмещенными оценками.

15.С увеличением объема выборки

а) увеличивается точность оценок; б) уменьшается ошибка регрессии;

в) расширяются интервальные оценки; г) уменьшается коэффициент детерминации;

д) увеличивается точность прогноза по модели. (Да; нет; не определено. Ответ поясните).

16.При оценке парной линейной регрессии Y = β0 + β1X + ε по МНК получена завышенная оценка b1 коэффициента β1. Какая оценка в этом случае более вероятна для коэффициента β0: завышенная, заниженная или несмещенная? Ответ поясните графически.

Упражнения и задачи

1.Имеются данные за 10 лет по прибылям (Х и Y) двух компаний:

Х (%)	19.2	15.8	12.5	10.3	5.7	−5.8	−3.5	5.2	7.3	6.7
Y (%)	20.1	18.0	10.3	12. 5	6.0	−6.8	−2.8	3.0	8.5	8.0

а) Постройте регрессионную модель Y = b0 + b1X + e.

б) Оцените статистическую значимость коэффициентов регрессии. в) Оцените коэффициент детерминации R2 данного уравнения.

г) Постройте регрессионную модель Y = bX + u.

д) Приведите формулы расчета коэффициента b, его стандартной ошибки Sb и стандартной ошибки регрессии S (обратите внимание на число степеней свободы при расчете данной оценки).

е) Значимо или нет различаются коэффициенты b1 и b? ж) Какую из построенных моделей вы предпочтете?

з) Можно ли на основе построенных регрессий утверждать, что прибыль одной из компаний является следствием прибыли другой?

136

2.	Для прогноза возможного объема экспорта на основе ВНП предложено ис-
	пользовать линейную регрессионную модель. При этом используются дан-
	ные с 1989 по 1998 г.

	Годы		89	90	91	92	93	94		95		96		97	98

	ВНП		1000	1090	1150	1230	1300	1360	1400	1470	1500	1580

	Экспорт		190	220	240	240	260	250		280		290	310	350

	а) Сформулируйте соответствующую регрессионную модель, дав интерпре-
	тацию ее параметров;
	б) рассчитайте на основе имеющихся данных оценки параметров модели;
	в) рассчитайте стандартную ошибку регрессии;
	г) рассчитайте стандартные ошибки коэффициентов;
	д) рассчитайте 90 %-ные и 95 %-ные доверительные интервалы для теорети-
	ческих коэффициентов регрессии;
	е) проанализируйте статистическую значимость коэффициентов при уров-
	нях значимости α = 0.1 и α = 0.05;
	ж) оцените коэффициент корреляции между ВНП и экспортом;
	з) дайте прогнозы по объему экспорта на 2000 и 2003 гг.;
	и) рассчитайте 95 %-ные доверительные интервалы для этих прогнозов;
	к) рассчитайте коэффициент детерминации и сравните его с коэффициентом
	корреляции;
	л) какие предпосылки относительно случайного отклонения модели
	необходимы для обоснованности выводов по предыдущим пунктам?
	м) сделайте выводы по построенной модели.
3.	Имеется информация за семь лет относительно среднего дохода и среднего
	потребления (млн руб.):

				Годы		91	92	93	94		95		96			97
			Доход ( I )	14.56 15.70	16.30	18.50	20.34	21.70	23.50
		Потребление (С)	12.00	12.70	13.00	15.50	16.70	17.30	20.00

а) Оцените коэффициенты линейной регрессии C = b0 + b1X + e по МНК; б) проинтерпретируйте найденные коэффициенты;

в) проверьте статистическую значимость коэффициентов при уровне значи-

мости α = 0.05;

г) рассчитайте 95 %-ные доверительные интервалы для теоретических коэффициентов регрессии;

д) спрогнозируйте потребление при доходе I = 25.00; постройте доверительный интервал для данного прогноза;

е) оцените коэффициенты регрессии C = b0 + b1X + e, проведя прямую через крайние точки наблюдений;

ж) оцените коэффициенты регрессии C = b0 + b1X + e, проведя прямую через средние значения для пары крайних значений (91, 92) и (96, 97);

137

з) являются ли оценки, найденные в пунктах е) и ж), несмещенными оценками теоретических коэффициентов регрессии β0, β1; и) сравните построенные три регрессии на основе стандартных ошибок регрессий и сделайте выводы;

к) насколько изменится потребление, если доход вырастет на 3 млн руб.

4. Проводится анализ взаимосвязи количества населения (POP) и количества практикующих врачей (МЕD).

Годы	81	82	83	84	85	86	87	88	89	90

POP(млн чел.)	10.0	10.3	10.4	10.55	10.6	10.7	10.75	10.9	10.9	11.0

MED(тыс.чел)	12.1	12.6	13.0	13.8	14.9	16.0	18.0	20.0	21.0	22.0

а) Оцените по МНК коэффициенты линейного уравнения регрессии

MEDt = b0 + b1POP.

б) Существенно ли отличаются от нуля найденные коэффициенты?

в) Рассчитайте коэффициент корреляции rpop;med; существенно ли он отличен от нуля?

г) Если прогнозное количество населения в 1995 г. составит 11.5 млн, каково ожидаемое количество врачей? Рассчитайте 99 %-ный доверительный интервал для данного предсказания.

д) Если население вырастет на 0.8 млн, насколько изменится количество врачей?

е) Рассчитайте коэффициент детерминации R2 для построенного уравнения, сравните его с коэффициентом корреляции, найденным в пункте в).

ж) Сделайте вывод по построенной модели.

5.Пусть имеются следующие наблюдения за переменными Х и Y:

Х	0	0	2	2

Y	0	2	0	2

а) Постройте эмпирическое уравнение регрессии Y = b0 + b1X + e и изобразите его на корреляционном поле.

б) Постройте эмпирическое уравнение регрессии Y = bX + v и изобразите его на корреляционном поле.

в) Рассчитайте коэффициенты детерминации для обоих уравнений. г) Каковы выводы из построенных моделей.

6.По 10 наблюдениям за СВ Х и Y получены следующие данные:

∑ xi = 1700; ∑ yi = 1100; ∑ xiyi = 204400; ∑ xi2 = 316000; ∑ yi2 = 135000.

Предполагая, что предпосылки МНК выполнены, оцените а) коэффициенты b0 и b1;

138

б) стандартные ошибки коэффициентов; в) 90 и 99 %-ные доверительные интервалы для коэффициентов β0 и β1;

г) можно ли на основе построенных доверительных интервалов принять гипотезу Н0: β1 = 0;

д) коэффициент детерминации R2.

7.По данным 15-летних наблюдений построена следующая регрессионная модель:

ВНПt = −787.4723+ 8.0863M1t	+ et
se	= (	…	) (0.2197)	R2 = 0.9912.
t	=	(−10.0)	( … ),

ВНП − валовой национальный продукт (в млрд $), M1 − денежная масса. а) заполните скобки; б) оцените статистическую значимость коэффициентов регрессии;

в) оцените общее качество уравнения регрессии; г) по утверждениям монетаристов, денежная масса имеет существенное по-

ложительное влияние на ВНП. Находит ли это подтверждение по построенной регрессии?

д) каков смысл отрицательного свободного члена?

е) предложение денег в году после интервала наблюдений планируется на уровне 550 млрд $. Каково прогнозное значение ВНП на данный год?

ж) в каком интервале будет лежать прогнозируемое значение ВНП с надежностью 95 %.

8.По данным за 9 лет построена следующая эмпирическая регрессия:

)	+ 0.888xt ,
yt = −70.85	R2 = 0.685,
t = (−5.89) (5.9),

где Y − индекс цен оптовой торговли; Х − процент использования производственных мощностей.

а) Совпадает ли знак коэффициента b1 с ожидаемым априори?

б) Как трактуется угловой коэффициент данного уравнения регрессии? в) Оцените значимость коэффициентов.

г) Существенно или нет коэффициент b1 отличается от единицы? д) Оцените качество модели.

9.Наблюдаются две переменные Х и Y помесячно в течение года. Имеется следующая информация:

x = 122.167 ; y = 125.25;	∑(xi − x )2 = 2135.679;
∑(yi − y )2 = 2216.168;	∑(xi − x )(yi − y ) = 2115.

Рассчитайте а) по МНК коэффициенты парного линейного уравнения регрессии;

б) стандартную ошибку регрессии; в) стандартные ошибки коэффициентов регрессии;

139

г) коэффициент детерминации; д) оцените качество построенного уравнения регрессии и статистическую значимость коэффициентов.

10. Пусть построена следующая регрессия:

Y = 150 + 5Х,

se = (20) (1.2), R2 = 0.87,

где xt = zt / zt−1 − темп роста показателя Z. Как изменится регрессия, если в качестве переменной Х использовать темп прироста показателя Z (%):

xt = (zt − zt−1) / zt−1.

11.Рассматривается зависимость объема (Y) потребления импортируемых благ

внекоторой стране от персонального располагаемого дохода (Х). По 25-лет- ним данным построена следующая регрессия:

Y = −250.15 + 0.2941Х	R2 = 0.9215.
se = ( 25.832)	( … )
t = ( … )	(15.275)

а) Заполните скобки.

б) Проинтерпретируйте коэффициенты регрессии.

в) Будет ли отклонена гипотеза о равенстве нулю коэффициентов регрессии? Какие тесты вы использовали и почему?

г) Можно ли считать, что коэффициент b1 не отличается существенно от 0.3? д) Можно ли вычислить коэффициент детерминации (при предположении, что он не известен) по имеющимся данным?

140

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Увеличение — объем — выборка

Cтраница 2

Размах увеличивается с увеличением объема выборки. Это естественно, поскольку вероятность появления больших отклонений в большой выборке возрастает.
[16]

Например, с увеличением объема выборки обследования частота поступления деталей с тем или иным состоянием постепенно стабилизируется, приближаясь к какому-то постоянному значению. При этом выявляются так называемые статистические закономерности или устойчивость поступления деталей, когда невозможно заранее предсказать, с каким именно сочетанием дефектов поступает на контроль-сортировку та или иная деталь, но можно предсказать вероятность этого события по результатам обследования большого количества таких деталей.
[18]

Итак, при увеличении объема выборки п выборочная средняя стремится по вероятности к генеральной средней, а это и означает, что выборочная средняя есть состоятельная оценка генеральной средней. Из сказанного следует также, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.
[19]

Понятие эффективности связано с увеличением объема выборки, при котором один критерий становится столь же мощным, как и другой.
[20]

Тем более что не всякое увеличение объема выборки может дать существенное повышение ее точности.
[21]

Сыть частично устранены за счет увеличения объема выборки, рекомендованного Шухартом. Однако увеличение объема выборок ке всегда целесообразно по другим причинам.
[22]

Это означает, что при увеличении объема выборки дисперсия оценок параметров регрессии стремится к нулю, то есть оценки параметров регрессии являются состоятельными.
[23]

Особенно резко снижается ошибка при увеличении объема выборки с 1 до 10 и затем с 10 до 30 единиц наблюдений. Поэтому размер выборки на первоначальных этапах исследования целесообразно устанавливать в пределах 10 — 30 единиц наблюдений. Дальнейшее увеличение численности выборки сопровождается менее заметным снижением ошибки, и во многих исследованиях этот путь повышения репрезентативности выборочного наблюдения оказывается дорогостоящим.
[25]

В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки.
[26]

Для повышения точности измерений за счет увеличения объема выборки целесообразно автоматизировать обработку проб, используя поточные хроматографы и ЭВМ.
[27]

Оценка называется состоятельной, если с увеличением объема выборки она стремится ( по вероятности) к оцениваемому параметру.
[28]

Это явление не может быть устранена путем увеличения объема выборки или удачного выбора алгоритма решения системы ( И), поскольку оно связано со значениями оцениваемых параметров, а не с объемом выборки или сходимостью алгоритмов.
[29]

Мере усиления корреляционной связи и уменьшаются с увеличением объема выборок и интервалов между изделиями, попадающими в выборки.
[30]

Страницы:

Источник

Если коэффициент регрессии является несущественным, то для него выполняются условия ….(несколько правильных ответов)
1. стандартная ошибка превышает половину значения параметров
2. расчетное значение t- критерия Стьюдента меньше табличного
1. Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
МНК
2Нелинейная модель, линейная относительно параметров

4Нелинейная модель внутренние нелинейные

3Нелинейная модель нелинейная относительно параметров (внутренне линейная)
1.Термин эконометрика был введен (Фришем)
2.Формулой определяется _________ показателя (средняя арифметическая величина)
3.Часть зависимой переменной в регрессионной модели, которая полностью объясняется значением регрессора (уравнение регрессии)
4.Остаток регрессионной модели представляет собой оценку (случайной ошибки)
5. Экономические модели относятся к классу ___________ экономико-математических моделей (стохастических)
6.Найти среднюю урожайность пшеницы с 1 га за три года: 60ц, 49ц, 41ц. (55)
7.Эконометрика — это . (наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.)
8.Стохастическая связь между признаками, выраженная в том, что средняя величина одного признака увеличивается с возрастанием другого, называется. ( автокорреляцией)
9 Как изменяется средняя арифметическая, если все веса уменьшить в А раз?( Увеличивается)
10.Основные стадии экономико-статистического исследования включают: а) сбор первичных данных, б) статистическая сводка и группировка данных, в) контроль и управление объектами статистического изучения, г) анализ статистических данных (а, б, г)

11.Медиана в ряду распределения с четным числом членов ряда равна (полусумме двух срединных членов)

12.Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим . (тесноту и форму зависимости между признаками)
13.К ошибкам спецификации относится . ( неправильный выбор той или иной математической функции)
14.При использовании метода Монте-Карло результаты наблюдений генерируются с помощью (датчика случайных чисел)
15.По какой формуле производится вычисление средней величины в интервальном ряду? (Средняя арифметическая взвешенная)
16.Назовите основные виды ошибок регистрации: а) случайные; б) систематические; в) ошибки репрезентативности; г) расчетные (а,б,в)
17.Число степеней свободы определяется . (числом свободы независимого варьирования признака (переменной, фактора))
18.Формализация закономерностей общей эконометрической теории является одним из принципов . эконометрической модели (спецификации)
19.Часть зависимой переменной в регрессионной модели, которая не может быть объяснена значением регрессора (случайное возмущение)

20.Корреляция подразумевает наличие связи между . (переменными)

21.Принцип спецификации модели, лежащий в основании классификации: экономические модели; эконометрические модели (включение случайных возмущений)
22.Дисперсия — это отношение (среднего квадратичного отклонения к средней арифметической величине)

23.Для описания тесноты (силы) связи между зависимой переменной и фактором (факторами) проводят расчет. (коэффициент корреляции)

24.Среднее квадратичное отклонение (показывает в среднем, на сколько отклоняются значения показателя от среднего значения)

25.Значение признака, повторяющееся с наибольшей частотой, называется (модой)

26.Случайная составляющая характеризует ( отклонение модельного значения результирующей переменной от наблюдаемого)

27.Укажите правильные варианты ответов относительно числа переменных включаемых в уравнение регрессии(несколько зависимых и одна не зависимая переменных, одна зависимая и несколько независимых переменных)

28.Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно . ( 10%)

29.Верификация модели заключается в( сопоставлении модельных и реальных данных)

30.Этап параметризации модели включает в себя.. (оценку параметров модели)

31.определяется _________ показателей x и y.( Ковариация)

32.В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно . (сумме)

33.Один из этапов построения экономической модели, на котором проверяются статистические свойства построенной модели, называется. (верификацией модели.)

34.По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются на (эндогенные и экзогенные)

35.Коэффициент корреляции это: (относительная мера взаимосвязи переменных)

.Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено . (неоднородностью выборки)

37. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой.. (спецификации)

38Средне квадратическое отклонение исчисляется как (корень квадратный из дисперсии)

39.Разность фактического и теоретического значений результирующей переменной регрессионной модели называется. (остатком)

40.Статистический показатель дает оценку свойства изучаемого явления: (количественную)

41.Под верификацией модели понимается (проверка адекватности модели)

42.Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапе (спецификация модели)

43.Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,25 (3,5)

44.Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетом (ошибки выборки)

45.Принцип спецификации модели, лежащий в основании классификации: статические модели; динамические модели (датирование переменных)

46.Средняя арифметическая величина — это отношение( суммы значений показателя к объему совокупности)

47.Экономические модели относятся к классу ___________ экономико-математических моделей (стохастических)

48.Средняя геометрическая — это: (корень из произведения индивидуальных показателей)

49.При анализе взаимосвязи признаков в экономической модели используют корреляционное отношение, подсчитанное на основе( аналитической группировки)

50.Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените? (средняя арифметическая)

51.Причинами нарушения предпосылок МНК могут являться .. (наличие неучтенного в уравнении существенного фактора ,наличие в уравнении фиктивных переменных.)

52.Модель, содержащая фиктивную переменную, относится к ____ модели. (Регрессионной)

53.МНК позволяет получить состоятельные и несмещенные оценки параметров системы: (независимых уравнений)

При каком значении линейного коэффициента корреляции связь между признаками Y и X можно считать тесной (сильной)( 0,975)

54.С увеличением объема выборки длина доверительного интервала индивидуального значения эндогенной переменной (уменьшается)

55.Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R 2 для модели парной регрессии равен: (единице)

Задачи и тесты по эконометрике

19.1. Рассматривается следующая модель:

t, =с, + i, + d =ao+a | р+8

где Q- количество товара, р- цена товара, w — заработная плата, 8 и в — случайные отклонения, удовлетворяющие предпосылкам МНК.

Пусть имеются следующие наблюдения:
- а) Какие из переменных являются экзогенными, а какие — эндогенными?; б) Представьте систему в приведенном виде; в) Определите по МНК коэффициенты приведенных уравнений; г) совпадают ли знаки найденных коэффициентов с предполагаемыми теоретически?; д) на основе найденных приведенных коэффициентов по КМНК определите структурные коэффициенты для функции спроса; е) можно ли по МНК оценить структурные коэффициенты для функции предложения? Если да, то как?
- 19.3. Рассматривается следующая система одновременных уравнений:
- а) Выделите экзогенные и эндогенные переменные в данной модели;
- б) Пусть по статистическим данным в момент времени t получены следующие результаты: ?q’=l 10, Xp 2 =5O,Xi 2 =ioo,Xi 2 =ioo,Xq-p=ioo,Xqi=9O,Xpi=ioo.
На основе МНК найдите оценку параметра ар в) Найдите оценку параметра а, на основе КМНК по методу ДМНК. г)Сравнитс найденные оценки.

19.4. К системе уравнений вида

приведен КМНК и для коэффициентов приведенной формы

получены следующие оценки: сц=2,2; Cj ₂=0,4; c₂i=0,08; с₂₂=-0,5.

Найдите оценки ДМНК, примененного к структурной модели.

19.5. Дана следующая структурная модель:

‘ У2 = ^21У| ^^2зУз + а 22 Х 2

,Уз = ^32^2 “*? Я зН1 + а ЗЗ Х 3

а) Оценить данную систему на идентификацию, б) Исходя из следующей приведенной формы модели

найти структурные коэффициенты модели.

19.6. Изучается модель вида

где y_t — валовой национальный доход, y_t.i — ВНП предшествующего года, c_t — личное потребление, d_r конечный спрос.

Имеется информация за девять лет:___________________________________________

Для данной модели была получена система приведенных уравнений:

Требуется: 1) Провести идентификацию модели. 2) Рассчитать параметры первого уравнения структурной модели.
- 19.7. Применив необходимое и достаточное условие идентификации определите идентифицировано ли каждое из уравнений модели. Определите метод оценки параметров и запишите приведенную форму модели:
- 1. Модель денежного рынка:
где R- процентная ставка, Y- ВВП, М-денежная масса, I-внутренние инвестиции, t-текущий период.

2. Макроэкономическая модель (модель Клейна)

где С- потребление, 1-инвестиции, Y-доход, Т-налоги, К-запас капитала.

3. Модель протекционизма Сальватора (упрошенная версия):

Ма ] +Ь1₂N_t+b 13S t+b 14 Ef. 1 + ?j

где M- доля импорта в ВВП; N- общее число прошений об освобождении от таможенных пошлин; S- число удовлетворительных прошений об освобождении от таможенных пошлин; Е- фиктивная переменная, равная 1 для тех лет, в которую курс доллара на международных валютных рынках был искусственно завышен, и 0 — для всех остальных лет; Y- реальный ВВП, Х-реальный объем чистого экспорта.

4.Гипотетическая модель экономики:

где совокупность потребления, Y-совокупный доход, I-инвсстиции, Т- налоги, G- государственные доходы ( все в период t).

Тесты по эконометрике.
- 1. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой.
- а) измерения; б) выборки; в) линеаризации; г) спецификации.
- 2. Отбор факторов в эконометрическую модель множественной регрессии может быть осуществлена на основе.
- а) значение коэффициентов автокорреляции уровней ряда различных порядков;
- б) матрицы парных коэффициентов корреляции;
- в) сравнения коэффициентов «чистой» регрессии;
- г) сравнения остаточной дисперсии до и после включения фактора в модель.
- ( Укажите не менее двух вариантов)
- 3. Для оценки заработной платы некоторого работника используется следующая модель
стаж его работы на данном предприятии; D— количество лет, потраченных работником на профессиональное обучение ( в том числе и повышение квалификации ); С,- переменная, принимающая значение 1, если у работника есть дети и 0 если нет; S,переменная имеющая значение 1, если работник мужчина и 0, если женщина; W, — количество должностей, который сменил работник на различных предприятиях в течении последнего года. Сколько факторов необходимо представить в модели фиктивными переменными? Выведите ответ.
- 4. Для уравнения множественной регрессииy-a + h_ix_] + b₂x₂ + Ь₃х₃ + ?построено частное уравнение видау = а—Ь_хх_<+Ь₂х₂ + Ь₃х₃ + ?,в которомх₂и х₃.
- а) приравнены к 1; б) закреплены на неизменном уровне; в) являются изменяемыми факторными переменными; не оказывают существенное влияние на у .
- 5. Метод наименьших квадратов применим к уравнениям регрессии.
- а) которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду;
- б) которые отражают линейную зависимость между двумя экономическими показателями; в) которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду; г) нелинейного вида.
- 6. Если предпосылки метода наименьших квадратов нарушены, то.
- а) коэффициент регрессии является несущественным; б) полученное уравнение статистически не значимо; в) оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности; г) коэффициент корреляции является несущественным.
- 7. Несмещенность оценки характеризуется. (Укажите не менее двух вариантов)
- а) зависимостью от объема выборки значения математического ожидания остатков;
- б) максимальной дисперсией остатков;
- в) отсутствием накопления остатков при большом числе выборочных оцениваний;
- г) равенством нулю математического ожидания остатков.
- 8. Обобщенный МНК применяется в случае.
- а) наличия в модели фиктивных переменных; б) наличия в модели мультиколлинеарности; в) наличия в остатках гстсросксдастичности или автокорреляции; г) наличия в модели незначимых оценок.
- 9. Для значимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии видау = а + Ь_х ? х_х + Ь, -х₂+?.Парными коэффициентами корреляции могут быть
- а) г_хх ; б) R ; в) г ; r)7?J .
- 10. Критическое (табличное) значение F-критерия является пороговым значением для определения.
- а) доли дисперсии зависимой переменной, не объясняемой с помощью построения модели, а вызванной влиянием случайных воздействий ;
- б) статистической значимости построения моделей;
- в) доли дисперсии зависимой переменной, объясняемой с помощью построенной модели;
- г) значимости (существенности) моделируемой связи между зависимой переменной и совокупностью независимых переменных эконометрической модели.
- 11. Если коэффициент регрессии является несущественным, то его значение приравнивается
- а) к нулю и соответствующий фактор включается в модель;
- б) к табличному значению и соответствующий фактор не включается в модель;
- в) к нулю и соответствующий фактор не включается в модель;
- г) к единице и не влияет на результат.
- 12. Пусть зависимость выпуска (Y) от затрат капитала (К) и труда (L) описывается функцией Кобба-ДугласаY = АК а L p. Тогда.
- а) эластичность выпуска по затратам труда равна а; б) эластичность выпуска по затратам труда равна 0; в) эластичность выпуска по затратам капитала равна 0; г) эластичность выпуска по затратам капитала равна а.
- (Укажите не менее двух вариантов).
- 13.Установите соответствие между названием модели и видом ее уравнения:
- 1. гипербола а) у = а + Ь_х • х, + с • х₂ + d • х₃ + г
- 2. парабола третьего порядка б) у = a + b_x -х + с -х 2 +d -х 3 + ?
- 3. многофакторная в) у = а + Ь-х + ?
4. линейная г) у = al Ь?
- (Укажите соответствие для каждого нумерованного элемента задания).
- 14.Линеаризация экспоненциальной зависимости У = а₀-Х 0 ’ ?? (кривой Энгеля,
отражающей зависимость спроса от уровня семейных доходов) основана на.
- а) разложение функции в ряд; б) дифференцирование функции по параметрам;
- в) интегрировании функции по параметрам; г) логарифмировании и замене преобразованной переменной.
- 15. Относительные отклонения расчётных значений результирующего признака от его наблюдаемых значений используются при расчете.
- а) параметров регрессии; б) t-критерия Стыодента; в) средней ошибки аппроксимации;
- г) коэффициента эластичности.
- 16. Факторы, описывающие трендовую компоненту временного ряда характеризуются.
- а) долговременным воздействием на экономический показатель;
- б) периодическим воздействием на величину экономического показателя;
- в) возможностью расчета значения компонента с помощью аналитической функции от времени; г) случайным воздействием на уровень временного ряда.
- (Укажите не менее двух вариантов ответа).
- 17. Область значений автокорреляционной функции представляет собой промежуток.
- а) (-1,1); б) [-1,0]; в) [-1,1]; г) [0,1].
- 18. Построение модели временного ряда может быть осуществлено с использованием.
- а) критерия Дарбина-Уотсона; б) аддитивной модели; в) мультипликативной модели;
- г) метода последовательных разностей.
- 19. При моделировании временных рядов экономических показателей необходимо учитывать характер уровней исследуемых показателей.
- а) конструктивный; б) аналитический; в) независящий от времени; г) стохастичный.
- 20. Для оценки коэффициентов структурной формы моделей не применяют метод
- а) косвенный; б) трёхшаговый; в) двухшаговый; г) обычный.
- 21. Согласно предпосылке теоремы Гаусса-Маркова дисперсии случайных возмущений в уравнениях наблюдений должны быть.
- а) равными; б) различными; в) нулевыми; г) случайными.
- 22. Если справедлива гипотеза //„:b = 0, относительно коэффициентаbмодели парной регрессии, то независимая переменнаяхявляется.
- а) значимой; б) незначимой; в) необходимой; г) желательной.
- 23. Для оценки точности оптимального прогноза зависимой переменной, нужно знать.
- а) прогнозное значение зависимой переменной; б) оценку дисперсии случайного возмущения; в) параметры модели; г) коэффициент детерминации.
- 24. Наличие незначащей объясняющей переменной в функции регрессии влечет.
- а) неадекватность модели; б) неравенство нулю математических ожиданий случайных возмущений;
- в) некоррелированность независимых переменных; г) снижение точности коэффициентов регрессии.
- 25. Если в модели присутствуют лаговые зависимые переменные, то это.
- а) линейная модель; б) нелинейная модель; в) модель со случайными возмущениями; г) динамическая модель.
- 26. Состояние экономики в момент времени t описывается следующими характеристиками: У,- валовой внутренний продукт, С,-уровень потребления, /,-величина инвестиций,G, —
государственные расходы, Т, -величина налогов, R_t -реальная ставка процентов. При этом величина инвестиций зависит от реальной ставки процента в предыдущем периоде, то есть в системе к предопределенным переменным системы относится лаговая экзогенная переменная. Приведенное утверждение справедливо для модели.

а) b o +Ь Y i + Ь 2 R :-l + ? 2

T,) + t ‘ A = Ь 0 +b r Y , +b 2- R ,

В ) i Л = + Ь ‘ К + Ь 2 ‘ R , + ^,-1

источники:

http://topuch.ru/dlya-poiska-nujnogo-otveta-najimaem-ctrlf-i-vvodim-nujnij-vopr/index.html

http://ozlib.com/983321/ekonomika/zadachi_testy_ekonometrike

Источник

Данная статья открывает цикл публикаций, посвященных общим проблемам выбора и практического применения методов статистического анализа в клинических исследованиях. Мнения о ценности такого (статистического) подхода к оценке результатов исследования колеблются в диапазоне от «отсутствие грамотного статистического анализа приводит к утрате научной ценности исследования в целом» до «статистика — это некие «фантики», которыми принято декорировать исследование для пущей привлекательности и наукообразия». Последнее утверждение верно в той мере, в какой манипуляция статистикой или добросовестное заблуждение при выборе метода действительно могут изменить результат исследования, иногда на прямо противоположный. Однако необходимо отдавать себе отчет в том, что это проблема не статистики, а добросовестности и (или) полноты знания проблемы со стороны исследователя.

В эпоху доказательной медицины, в которую мы, хорошо ли, плохо ли, проживаем, статистический анализ, наряду с эпидемиологическим подходом к проведению исследования, стал обязательным элементом любой клинической работы, претендующей на звание научной. Раз так, а это именно так, то знание (в прагматически необходимом объеме!) статистики становится неотъемлемым элементом подготовки каждого научного сотрудника и обязательным квалификационным признаком состоявшегося специалиста. Однако на практике дела обстоят не настолько хорошо.

Последнее, к сожалению, становится все более и более заметно для авторов настоящей публикации, которые на протяжении многих лет являются рецензентами ряда ведущих отечественных журналов анестезиолого-реаниматологической тематики. Растущее количество работ с досадными, иногда нелепыми ошибками, допущенными по незнанию или недоразумению, заставляет каждый раз вновь обращаться к вопросам планирования исследования вообще и правилам проведения статистического анализа в частности.

Ряд ошибок, допущенных на этапе планирования, как мины замедленного действия, «срабатывают» в тот момент, когда менять что-либо уже поздно. Уже рекрутировано достаточное количество пациентов, и вдруг становится очевидно, что необходимо было мониторировать еще и «этот» показатель, без которого исследование «рассыпается», становится малоинформативным и бездоказательным. Рано или поздно авторы оказываются перед дилеммой: прервать исследование и начать все заново (жалко: столько сил и средств уже потрачено!) или продолжить, отдавая себе отчет в том, что цель достигнута быть не может, а единственное, что остается — это рассчитывать на получение некоего суррогата сомнительного качества. Именно поэтому крайне необходимым является проведение тщательного анализа предстоящей работы на этапе планирования, определение цели и задач, формулировка первичной, вторичной и т.д. конечных точек, адекватных поставленной цели; подбор методов не из арсенала того, «что у нас есть», а в соответствии с тем, «что необходимо, чтобы ответить на главный вопрос исследования». Жесткое соблюдение протокола и наличие CRF (Case Report Form — форма наблюдения за пациентом) являются абсолютными признаками качественного планирования. Все это в комплексе позволяет определить метод статистического анализа не «после», а еще «до» начала исследования, хотя некоторые коррективы, по-видимому, неизбежны (например, сообразно различному характеру распределения данных).

Маленькая иллюстрация вышесказанного. Допустим, вы собираетесь исследовать эффективность и безопасность разработанного Вами метода анестезии. Сделать это Вы планируете на основе анализа интраоперационных изменений уровня артериального давления (АД) и динамики активности ряда ферментов, обычно используемых для предварительной оценки функции некоторых органов и систем (аспартатаминотрансферазы — АсАТ, аланинаминотрансферазы — АлАТ, лактатдегидрогеназы — ЛДГ и т.д.). Вы справедливо полагаете, что для изучения летальности или частоты встречаемости жизнеугрожающих осложнений понадобится многосотенная, а то и многотысячная выборка, что нереально в рамках вашего учреждения, на что уйдут многие годы, и к окончанию работы либо «осел сдохнет», либо… далее по известной притче.

В итоге Вы получаете какой-то статистически значимый результат, например, тот, что уровень АД на неких, выбранных Вами, дискретных точках оказался несколько выше в контрольной группе, а значение некоторых ферментов — ниже. Радостно потирая руки, Вы пишете, что разработали более совершенный метод анестезии. Вся беда заключается в том, что полученный Вами результат говорит лишь о том, что наблюдается некоторое влияние метода на уровень АД в определенных фиксированных точках (и еще стоит подумать, положительное ли?), и уменьшается активность некоторых ферментов, что может указывать на меньший риск развития органной недостаточности, не более того. Утверждать, что предложенный Вами метод эффективнее и безопаснее существующих, без изучения частоты осложнений, летальности, времени пребывания в палате интенсивной терапии и других клинических исходов — невозможно.

Означает ли это, что проделанная Вами работа бессмысленна? Вовсе нет. Вы показали хотя бы то, что предложенный метод интересен, и следует подумать о его дальнейшем изучении. Можно ли рекомендовать предложенный Вами метод для широкого клинического применения? Увы, нет — недостаточно оснований. Таким образом, если Вы сформулировали цель исследования как «изучение эффективности и безопасности…», то Вы ее не достигли. И не могли достичь, так как выбрали методы, не отвечающие поставленной цели.

Авторы настоящей статьи осознают, насколько предложенный пример условен, ограничен и не детализирован, хотя и типичен. Тем не менее представляется, что он позволяет указать на один из многих «подводных камней», которые ждут исследователя на этапе планирования работы. В этой связи многие ученые обоснованно полагают, что время и усилия, затраченные на планирование, должны быть сопоставимы со временем и усилиями при выполнении работы. Только такой подход если и не гарантирует качество исследования, то определенно создает к тому серьезные предпосылки.

Первая, но далеко не единственная, проблема, которую необходимо решить до начала исследования — определение размера выборки. В отечественной и зарубежной литературе описано множество методик определения оптимального объема выборки, однако отсутствует четко установленная единая методология их применения.

Цель данной статьи — попытка предоставить неискушенному читателю общие сведения и один из возможных алгоритмов действия при определении размера выборки в ходе организации клинического исследования.

Варианты ошибок и их последствия

Ошибка в определении размера выборки одинаково нежелательна как в меньшую, так и в большую сторону.

При выборке меньшего объема мы с большей долей вероятности можем столкнуться с ошибками первого и второго родов. Для понимания сути таких ошибок нам необходимо ввести понятие нулевой гипотезы. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что между двумя явлениями не существует никакой связи. В действительности нулевая гипотеза похожа на презумпцию невиновности. Мы всегда изначально считаем, что экспериментальная стратегия никак не может повлиять на исходы группы (то есть эффективность экспериментальной стратегии равна эффективности плацебо или отсутствию вмешательства, что зависит от дизайна исследования). Теперь вернемся к возможным ошибкам. Ошибкой первого рода называется отказ от правильной нулевой гипотезы (например, мы установили, что препарат эффективен, хотя в действительности его эффект такой же, как у плацебо). Ошибкой второго рода называется принятие неправильной нулевой гипотезы (например, мы установили, что препарат неэффективен, хотя в действительности он оказывает значительный положительный эффект).

При выборке большего объема (по сравнению с необходимым) большее количество больных будет подвергнуто неоправданному риску при испытании нового препарата или методики. А это недопустимо в соответствии со стандартами GCP (Good Clinical Practice) [1]. Кроме того, в случае избыточно большой выборки возможно обнаружение несуществующих в генеральной совокупности взаимосвязей, что вновь является ошибкой первого рода [2].

Важность определения объема выборки можно проиллюстрировать на следующем «доведенном до абсурда» примере. Скажем, Вы запланировали исследование, при котором в экспериментальной и контрольной группах по одному пациенту. Пациент контрольной группы получает плацебо, в то время как пациент экспериментальной группы получает препарат, об эффективности которого мы ничего не знаем. Если мы зададимся целью проанализировать летальность в таком исследовании, то обнаружим, что возможны 4 варианта развития событий.

Представим, что пациент контрольной группы умирает, а пациент экспериментальной группы выздоравливает. Вы даете абсолютно обоснованное заключение, что «все пациенты контрольной группы умерли, а все пациенты, которым применен тестируемый препарат, поправились, следовательно, методика эффективна». Интересно не то, что Вы с большой долей вероятности выдали ошибочное заключение, а то, что Вы, возможно, и правы. Дело в том, что объем выборки, в данном случае, не позволяет сделать никакого заключения вовсе!

Теперь представим, что оба больных поправились или оба погибли. Следуя простой логике, должно появиться заключение об отсутствии положительного эффекта у тестируемого препарата. Здесь Вы также обоснованно можете заключить, что препарат не отличается от плацебо. Но вся проблема снова в том, что объем выборки не позволяет сделать никакого заключения.

Вариант «пациент контрольной группы выжил, пациент экспериментальной группы погиб» приведет к рекомендации не использовать препарат (запрет) ввиду безусловного вреда здоровью. Но мы ведь с Вами понимаем, что ни о какой достоверности подобного заключения речи быть не может.

Остается удивительным, насколько люди не готовы допустить вероятность подобных ошибок при размере выборки в 15—20—30 человек. Мало того, иногда 100—200 и более пациентов недостаточно для обоснованного заключения. Очень многое, как будет показано далее, зависит от выбора первичной конечной точки, гетерогенности групп, возможных bias (перевод с английского — смещение в исходах, связанное с влиянием субъективного фактора) и т.д.

Пренебрегая предварительным расчетом размера выборки, авторы никогда не могут быть уверены в статистической значимости полученного результата [3]. Однако некоторые обзоры наглядно демонстрируют, что далеко не все исследователи понимают важность обозначенной проблемы [4, 5].

Определение объема выборки

Исследователь, ставящий перед собой цель определить размер выборки планируемого исследования, должен свободно оперировать следующими понятиями:

— Статистическая мощность (1-β), под которой понимают вероятность отклонить неверную нулевую гипотезу. Чем выше мощность статистического теста, тем меньше вероятность совершить ошибку второго рода. При планировании исследования желаемая мощность, как правило, принимается равной 0,8—0,9.

— Уровень статистической значимости (α) — вероятность ошибки первого рода — допускаемая исследователем вероятность ошибочного отклонения верной нулевой гипотезы (гипотезы об отсутствии различия между группами, об отсутствии взаимосвязи признаков и т.д.). Это постоянная величина, которая произвольно принимается автором за допустимую границу значимости полученных результатов. Именно с этой величиной будет производиться сравнение полученных данных. Как правило, за величину уровня значимости принимаются значения 0,05; 0,01 или 0,001.

— p-уровень значимости — рассчитанная в ходе статистического анализа вероятность ошибочного отклонения некоторой предполагаемой гипотезы. Если рассчитанный p-уровень меньше принятого уровня значимости (α), то предполагаемая гипотеза (нулевая гипотеза) отклоняется. Чем меньше p-уровень значимости, тем более значимой является тестовая статистика.

— Генеральная совокупность — совокупность всех возможных объектов данного рода, для которых будут справедливы результаты проведенного исследования. Скажем, вы исследуете эффективность препарата для лечения ишемической болезни сердца (ИБС) у пожилых пациентов. В этом случае генеральной совокупностью будут все пациенты с установленным диагнозом ИБС старшей возрастной группы.

— Выборка — часть генеральной совокупности (например, используя вышеприведенный пример, — пожилые пациенты с ИБС), полученная путем отбора. По результатам анализа выборки делают выводы о всей популяции (генеральной совокупности), что правомерно в случае, если отбор был случайным. Ввиду того, что случайный отбор из популяции осуществить практически невозможно, необходимо стремиться к тому, чтобы выборка была репрезентативна по отношению ко всей совокупности (популяции).

— Гетерогенность в таком случае относится к выборке. Гетерогенный означает неоднородный по составу (в противоположность понятию «гомогенный»). Чем менее гетерогенна выборка, тем менее выраженным является «разброс» значений изучаемого показателя в исходе, тем меньшие отличия, обнаруженные в результате исследования, могут иметь статистическую значимость. Обратная сторона этого утверждения заключается в том, что достаточно гомогенную выборку можно получить только ценой ужесточения критериев включения/исключения. Следовательно, полученный результат можно будет экстраполировать на ограниченную группу пациентов. В качестве примера: вы можете ограничить выборку пациентов, в которой планируете изучать эффективность нового препарата для лечения ИБС, вводя следующие критерии включения: возраст от 65 до 80 лет; впервые выявленная ИБС, «не получавшие ранее кардиотропной терапии». Но тогда и обнаруженный эффект (в случае его выявления) можно будет распространить только на выделенную когорту больных. Проведенное исследование не позволит вам рекомендовать тестируемый препарат у пациентов с «ИБС в анамнезе» или у пациентов в возрасте 40—50 лет и т.д.

Определение размера выборки всегда является неким компромиссом между необходимой мощностью исследования и возможностью ее практической реализации с учетом имеющихся ресурсов.

Метод расчета размера выборки во многом зависит от объема знаний о характеристиках изучаемого параметра.

Еще раз вынуждены оговориться: все примеры, иллюстрирующие данную статью, в той или иной мере условны; необходимо с пониманием отнестись к тому, что строгое и детальное описание настоящего (а не выдуманного) клинического примера займет слишком много места и, скорее всего, отвлечет от предмета обсуждения настоящей статьи.

Начнем с самого неприятного случая: нам ничего не известно ни о генеральной совокупности, ни о параметре, который мы собираемся изучать. Например, мы изобрели новый метод анестезии, который не имеет даже близкого аналога (изобретение эфирного наркоза, открытие хлороформа, более близкий пример — ксенон) и работа будет проходить в клинике, проводящей уникальные операции в гериатрии. Первичной конечной точкой исследования выбрана 28-дневная летальность. Допустим, что никто и никогда не изучал летальность после выбранного типа операций, тем более в гериатрии, т.е. Вам неизвестны характеристики основного изучаемого параметра (среднее (медиана) и разброс данных) и невозможно предположить эффективность нашего метода по сравнению с известным (т.е. какая летальность будет при применении нашего метода относительно летальности при использовании эталонного метода анестезии). Это достаточно редкая ситуация, так как:

— если неизвестна летальность при точно такой же операции, как у нас, то, скорее всего, есть какой-то очень близкий аналог;

— если неизвестна летальность, предположим, у лиц «90 лет и старше», то известна у лиц «пожилого и старческого возраста» («60 лет и старше»);

— и даже такой, несомненно, новый анестетик, как ксенон, можно как-то, в первом приближении (при оценке анальгетической активности, например), соотнести с закисью азота.

Следует иметь в виду, что всегда предпочтительнее иметь хотя бы крайне ненадежный ориентир в размере выборки, чем не иметь никакого, так как при использовании рекомендованных в этой ситуации методов объем выборки, как правило, получается завышенным.

Но, допустим, мы имеем дело с истинно «пилотным» исследованием — никто и никогда ничего похожего не изучал. В таком случае планирование объема выборки возможно исключительно с использованием табличных методов (табл. 1—4), не требующих от исследователя информации о распределении изучаемых параметров. Выбор алгоритма из предложенных четырех будет определяться особенностями исследования и/или пожеланиями авторов [6]:

— методика К.А. Отдельновой [7] требует информации о желаемом уровне значимости и «уровне точности» исследования (см. табл. 1);

— метод В.И. Паниотто [8] требует от исследователей лишь информации об объеме генеральной совокупности (см. табл. 2);

— методика N. Fox [9] определяет объем выборки в зависимости от требуемой величины возможной ошибки (см. табл. 3);

— и наиболее «продвинутый» способ определения объема выборки, предложенный S. Das, K. Mitra, M. Mandal [10], принимает на входе информацию о предполагаемой величине эффекта, мощности и уровне значимости исследования (см. табл. 4).

Таблица 1. Определение требуемого размера выборки по методике К.А. Отдельновой [7]

Уровень значимости	Уровень точности
ориентировочное знакомство	исследование средней точности	исследование повышенной точности
0,05	44	100	400
0,01	100	225	900

Примечание. Уровень значимости: безразмерная величина, указан размер выборки как абсолютное значение количества пациентов в группе.

Таблица 2. Определение требуемого размера выборки по методике В.И. Паниотто [8]

Объем генеральной совокупности (единиц)	500	1000	2000	3000	4000	5000	10000	100000	∞
Объем выборки (единиц)	222	286	333	350	360	370	385	398	400

Таблица 3. Определение объема выборки по методике N. Fox [9]

Величина допускаемой ошибки, %	Объем выборки, единиц
10	88
5	350
3	971
2	2188
1	8750

Таблица 4. Способ определения объема выборки, предложенный S. Das, K. Mitra, M. Mandal [10]

Величина различий (между контрольной и основной группами)	Мощность (1-β)	Уровень значимости (α)	Размер выборки, единиц
0,2	80	0,5	586
0,2	80	0,1	773
0,2	90	0,5	746
0,4	80	0,5	146
0,4	80	0,1	193
0.4	90	0,5	186
0,6	80	0,5	65
0,6	80	0,1	86
0,6	90	0,5	83

Еще пример. Другая ситуация несколько лучше: операции, которые выполняются в клинике, не уникальны; летальность и ее разброс при эталонном методе анестезии известны, однако отсутствует информация о характеристиках распределения изучаемых количественных параметров, влияющих на летальность в генеральной совокупности, а предлагаемая методика действительно аналогов не имеет. В такой ситуации можно продолжать пользоваться «табличными» методами, но предпочтительнее все же взять на вооружение статистические формулы (Приложение: см. табл. 5, формулы 3—15). Последний подход позволит получить искомый показатель с большей точностью и, вероятно, использовать меньший объем выборки. Например, изучается послеоперационная летальность пациентов группы высокого риска (возраст 60 лет и старше, наличие хронических заболеваний) при применении нового метода анестезии. Необходимо определить объем выборки с принимаемым исследователем уровнем значимости 0,05 и предельно допустимой ошибкой 5%. Так как информация о распределении количественных параметров, влияющих на летальность, неизвестна, подходящей является формула 4 (см. Приложение, табл. 5). Допустим, что по данным литературы, 28-дневная летальность среди пациентов старшего возраста при применении стандартной анестезии составляет 9%, а исследователи предполагают, что предлагаемая ими методика позволит уменьшить обсуждаемый показатель в полтора раза (т.е. летальность может составить около 6%). Критическое значение нормального стандартного распределения при заданном уровне значимости α=0,05 принято равным 1,96. В соответствии с имеющимися условиями, для последующего сравнения летальности в контрольной и основной группах объем каждой выборки рассчитывается следующим образом:

Это означает, что для решения поставленной исследователем задачи достаточно сформировать выборку, включающую по 126 пациентов в основной и в контрольной группах.

Третий пример — вам известны все необходимые параметры: исходная летальность, характеристики распределения изучаемых параметров в генеральной совокупности; операции рутинные, кроме того, предлагаемый метод является близким аналогом другого, эффективность которого является секретом Полишинеля. Как и в предыдущем примере, изучается послеоперационная летальность у пациентов группы высокого риска (возраст 60 лет и старше, наличие хронических заболеваний) при применении нового метода анестезии, однако теперь исследователи имеют информацию практически обо всех влияющих на летальность факторах, распределение параметров соответствует нормальному закону, известен также объем генеральной совокупности (например, 1000 пациентов с равной вероятностью входят в группу риска в календарном году). Тогда в соответствии с формулой 17:

Как видим, в связи с появлением дополнительной информации необходимый объем выборки снизился со 126 до 112 пациентов.

Возможно, вы обратили внимание, что, в соответствии с формулой 17, при увеличении объема генеральной совокупности необходимый объем выборки также увеличивается. В этой связи бытует распространенное заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки. Проще говоря, исследователь попадает в ловушку: с одной стороны, чем больше больных с искомой патологией (или операцией) проходит через стационар, тем быстрее можно набрать достаточное количество пациентов. С другой стороны, увеличение размера генеральной совокупности (количества больных с искомой патологией, проходящих лечение или оперируемых в клинике) влечет за собой необходимость увеличения размера выборки (количества больных, рекрутируемых в исследование). Ложный вывод: чем реже встречается в клинике какая-то патология или тип оперативного вмешательства, тем быстрее можно выполнить исследование — меньшая выборка будет признана достаточной. Однако эта закономерность (чем больше генеральная совокупность, тем больше должен быть объем выборки) справедлива лишь отчасти (а вывод и вовсе вводит в заблуждение), и то лишь в ситуации, когда объем выборки сопоставим с размером генеральной совокупности. Возникает дилемма: сколько должно продолжаться проспективное исследование, чтобы объем выборки был репрезентативен по отношению ко всей совокупности пациентов, но в то же время исследование не продолжалось бы бесконечно долго.

Иными словами, как определить ту точку, когда погоня за точностью перестает реально влиять на результат и становится, скорее всего, самоцелью.

В соответствии с исследованием В.И. Паниотто [8], с ростом объема выборки значение получаемой ошибки уменьшается все медленнее (см. рисунок). Так, при объеме выборки 400 человек предельная ошибка для доли встречаемости признака 50% составит ±5%, а при объеме 1000 человек — ±3%. То есть возникает ситуация, когда при определенном объеме выборки дальнейшее ее увеличение не дает значительного выигрыша в точности.

Зависимость ошибки выборки от ее объема при 95% доверительном уровне.

Иная ситуация возникает, если изучаемая когорта пациентов имеет низкую распространенность в популяции, а критерии формирования выборки достаточно жесткие (что ограничивает подходящий контингент пациентов). Тогда все отобранные в ходе проспективного исследования пациенты, составляющие генеральную совокупность, будут попадать в исследуемую выборку, т.е. они будут сопоставимы по размеру.

В нашем примере, в соответствии с рисунком, при уровне летальности 9% и объеме выборки 50 человек предельная ошибка будет составлять примерно 10%. Для клинических исследований это недопустимо низкий уровень точности. Увеличение выборки до 200 человек приведет к уменьшению предельной ошибки до 4%, а при объеме выборки 400 пациентов ошибка составит всего 3%. Исходя из требований к клиническим исследованиям точность, при которой ошибка составляет 4%, считается допустимой, поэтому размер выборки можно ограничить 200 больными. Увеличивать объем выборки в два раза, по-видимому, в таком случае нецелесообразно.

Таким образом, в похожих ситуациях исследователи могут планировать продолжительность проспективного исследования исходя из требуемого и допустимого уровня ошибки.

Следует принять во внимание, что для медицинских исследований допустимой ошибкой считается 5%, если же удается получить результат с точностью до 1%, то исследование можно признать крайне убедительным.

Однако даже самое тщательное планирование не позволяет получить размер выборки, гарантирующий получение статистически значимого результата. Два приема используются порознь или вместе:

— автоматическое увеличение размера выборки на 10—15% по отношению к расчетному (особенно популярно при одноцентровых исследованиях небольшой мощности);

— коррекция размера выборки после получения первых данных о показателях, необходимых для более точного математического анализа.

Чем менее точно определен размер выборки при планировании (что не всегда является дефектом работы составителя плана, но, как показано выше, может быть и следствием отсутствия необходимых данных), тем насущнее становится необходимость коррекции данного показателя после появления первичных, предварительных данных, характеризующих исследуемый показатель и его изменения в результате предпринятых воздействий. Как правило, проведение повторного, уточняющего расчета размера выборки планируется до начала исследования и проводится после набора 50—75% от первоначально определенного количества больных.

Некоторые дополнительные замечания относительно определения размера выборки

Принято использовать два подхода к структурированию выборки — вероятностный и детерминированный (стратифицированный) [11]. Первый связан с формированием случайной выборки в процессе рандомизации (каждый элемент выборки включается с равной, ненулевой вероятностью); при использовании второго подхода элементы выборки отбираются субъективно в случае, если они отвечают целям исследования — выборка, основывается на неких частных предпочтениях или суждениях исследователя (например, ограничения по полу, возрасту, массе тела и т.д.).

Вероятностная выборка во многих случаях является предпочтительной, однако ее реализация в практической медицине может быть ограничена. Использование же детерминированного подхода в общем случае предполагает и использование иного математического аппарата или эмпирической методики [12].

Отдельную сложность представляет планирование объема выборки в условиях несоответствия распределения генеральной совокупности нормальному закону, а также при необходимости формирования различных по численности опытной и контрольной групп. Значительная вариабельность характеристик генеральной совокупности, а также многообразие вариантов клинических исследований предъявляют определенные требования к используемым методам планирования объема выборки.

Математический подход к определению размера выборки

Все математические методы определения объема выборки можно классифицировать на несколько групп:

— табличные методы, не требующие априорного представления об изучаемом факторе и о характеристиках генеральной совокупности (совокупности всех объектов или наблюдений, которые подлежат изучению). Описаны ранее;

— методы, требующие от исследователя некоторого представления об изучаемом признаке (количественный, порядковый (шкала), номинальный и т.д.);

— методы, требующие предварительной информации как о признаке, так и о генеральной совокупности (ее размере, нормальности распределения данных).

В медицине и анестезиологии-реаниматологии, в частности, авторы нередко сталкиваются с ситуацией, при которой невозможно оценить распределение исследуемого признака в генеральной совокупности и потому приходится использовать табличные методы при планировании объема выборки. Размер выборки может быть уточнен по мере получения предварительных результатов исследования, что сделает возможным использование математических формул. Это, в свою очередь, в некоторых случаях позволяет снизить риск необоснованного применения тестируемой методики у большего количества больных и уменьшить материальные затраты и нагрузку на медицинский персонал.

Экспертный подход к планированию объема выборки

Как отмечено ранее, в процессе набора данных возможен момент, когда большее количество данных (наблюдений) не обязательно приводит к большему количеству информации. А поскольку качественные исследования очень трудоемки, анализ значительной по размерам выборки может занять много времени, а зачастую и просто будет нецелесообразен [5]. Как правило, для непрерывной оценки размера выборки при проведении клинических исследований используется концепция насыщения выборки данными, позволяющая принимать обоснованные решения о необходимости прекращения процесса набора данных или о продолжении исследования.

Принципы определения насыщенности данных

В зарубежной литературе предложено несколько принципов, относящихся к концепции «насыщенности» в планировании исследования [13]. Согласно J. Francis и соавт., прежде всего необходимо учесть, какого размера будет выборка по завершении первого этапа исследования, чтобы определить основу для прогрессивных суждений о насыщенности данными и оценить наблюдаемую тенденцию, в том числе методами экстраполяции. Объем выборки будет зависеть от особенностей организации исследования, разнообразия выборки и способа ее формирования. Второй принцип заключается в том, что исследователи должны заранее знать продолжительность всего исследования (время набора данных). Важно также, чтобы методы насыщения данных были подробно описаны в тексте статьи, и коллеги имели возможность оценить доказательную базу исследования [13].

Концепция насыщения является в настоящее время спорной ввиду наличия более объективных методик оценки размера выборки [14]. В частности, указывается на тот факт, что для получения представления о размере выборки и мощности исследования приходится делать большое количество допущений. Информацию, необходимую для оценки объема выборки, получают либо из результатов собственных предыдущих исследований (пилотных исследований), либо из источников литературы. Возможны ситуации, при которых исследователь не имеет ни того, ни другого. Тем не менее необходимо заранее знать минимальную величину эффекта, которая в данном исследовании будет считаться достаточной, и на ее основании можно будет сделать предположение о мощности исследования.

Обсуждение

Определение размера выборки — важнейший этап планирования научной работы. Кроме того, это не просто формальный пункт, обязательный к исполнению по прихоти какого-то чиновника от науки. Это инструмент, позволяющий, с одной стороны, не делать лишнюю работу, с другой,— не сомневаться по окончании этой работы при получении отрицательного результата: «что это, реальное отсутствие эффекта или что «не хватило буквально каких-то …дцать больных»? Действительно, задача не так проста, как может показаться, но, соблюдая предложенный алгоритм, можно получить искомый результат с известной точностью [15—26].

Несколько полезных замечаний:

— при анализе пилотных исследований и сопоставимых работ других авторов необходимо обратить внимание не только на схожесть дизайна, но и на факторы, которые послужили причиной разброса данных. К таким факторам можно отнести демографические сведения о пациентах (половозрастные характеристики, прогностические факторы и т.д.), методы сбора информации, погрешности инструментальных и лабораторных методов исследования и прочее;

— необходимо помнить и о том, что мощность исследования зависит не только и не столько от объема выборки, сколько от предполагаемой величины эффекта и разброса данных. Возможно определение объема выборки исходя из априорных представлений об анализируемых параметрах, однако эмпирический подход является субъективным и проигрывает при равных условиях математическому подходу;

— возможны ситуации, при которых исследователь в силу определенных обстоятельств (финансовых, этических, организационных) не способен увеличить или изменить численность групп. В такой ситуации необходимо учитывать, что размер выборки не является единственным фактором качества исследования. И по сей день подходы к анализу объема выборки расширяются. В частности, показано использование однофакторного дисперсионного анализа ANOVA для определения объема выборки [15].

Таким образом, грамотному исследователю доступен широкий функционал математических методов определения требуемого объема выборки, руководствуясь которым в совокупности с собственным опытом и эмпирической методикой можно оптимально спланировать исследование и получить статистически обоснованные выводы.

Заключение

На современном этапе развития науки отсутствует четко установленная, единая методология определения минимально необходимого объема выборки для клинических исследований. В данной работе представлены наиболее часто применяемые методы определения необходимого объема выборки, которые могут быть применены при планировании исследований. Результатом анализа стало формирование единого алгоритма, позволяющего выбрать наиболее подходящую методику определения искомого показателя.

Приложение

Методы, требующие информации о типе анализируемого признака. Эта группа методов определения объема выборки зависит от ряда факторов: вида признаков, связанности выборок, количества предполагаемых групп и подхода к их формированию — вероятностного или детерминированного (стратифицированного). Формулы для расчетов приведены в табл. 5 (формулы 3—15). Использование приведенных формул дает значительно меньшие объемы выборок по сравнению с методами, не требующими информации о характеристиках распределения и типе анализируемого фактора, однако в некоторых случаях это может привести к неоправданному занижению необходимого объема выборки [6].

Таблица 5. Выбор метода планирования объема выборки (математический подход)

Нет информации о признаке/информация неполная Нет информации о генеральной совокупности	Есть информация о признаке. Нет информации о генеральной совокупности	Есть информация о признаке Есть информация о генеральной совокупности (распределение соответствует нормальному закону)	Есть информация о признаке. Есть информация о генеральной совокупности (распределение не соответствует нормальному закону)
Две выборки: односторонние тесты	Две выборки: двусторонние тесты	Одна выборка (вероятностный подход)	Одна выборка (детерминированный подход)	Одна выборка (погрешность измерений)	Одна выборка (вероятностный подход)	Одна выборка (детерминированный подход)
Методика К.А. Отдельновой [6, 7]	Количественный признак [24]: (3)	Количественный признак [25]: (7) (8)	Количественный признак [26]: (11)	Количественный признак [26]: (13)	[20] (15)	Количественный признак [26]: (16)	Количественный признак [26]: (18)	Лог-нормальное распределение, Hale W. E. [22]: (20)
Методика В.И. Паниотто [8]	Качественный признак [25]: (4)	Качественный признак [25]: (9) (10)	Оценка доли (частоты признака) [26]: (12)	Оценка доли (частоты признака) [26]: (14)		Номинальный/порядковый признак [26]: (17)	Качественный признак [26]: (19)	Распределение Пуассона [21]: (21)
Метод Монте-Карло [23]
Методика N. Fox [9] и S. Das, K. Mitra, M. Mandal [10]	Известна численность одной из групп [17]: (5)	Примечание. * — Использовать в случае несвязанных выборок; для связанных выборок расчет обеих групп проводить по формулам 7 и 9; n — рассчитанный объем выборки; N — объем генеральной совокупности; ????² — критическое значение критерия Стьюдента при соответствующем уровне значимости; d² — предельно допустимая ошибка (минимальная, клинически значимая величина различий, которую необходимо обнаружить, как правило — 5%); ???? — стандартное отклонение признака, который будет изучаться в исследовании (????²— дисперсия); ???? — доля случаев, в которых встречается анализируемый признак; Q — доля случаев, в которых не встречается анализируемый признак (100—????); Zα, — критические значения нормального стандартного распределения для заданных α и β; α/2 — желаемый уровень значимости; 1-β — желаемая мощность; p — доля признака в группе; σ⁽^d^{^}²⁾ — средняя внутригрупповая дисперсия, pq^d — средняя внутригрупповая дисперсия; X — среднее арифметическое изучаемого признака; E — погрешность измерения прибора
Определение Х выборки [6]: (1)	Сравнение долей (частот признаков) [24]: (6)
Определение выборки [16]: (2)	Номограммы [6, 18, 19]

Возможны ситуации, при которых оценить некоторые характеристики признака (такие как среднее арифметическое, стандартное отклонение) определить невозможно по причине отсутствия пилотного исследования или сопоставимых исследований в литературе — в данном случае возможно определение параметров с использованием расчетных формул (см. табл. 5, формулы 1—2). Эти формулы требуют наличия экспертных навыков и опыта у исследователя для предварительного определения размаха вариабельности исследуемого признака. Расчет размаха признака основывается на предположении о том, что расстояние между максимальным и минимальным значениями признака приблизительно равно шести стандартным отклонениям, что вытекает из правила трех сигм, и отсюда возможно определение стандартного отклонения (см. табл. 5, формула 2). В частности, если распределение генеральной совокупности соответствует нормальному закону, ее размах приблизительно равен 6σ, а следовательно, стандартное отклонение приблизительно равно одной шестой диапазона [16].

Весьма распространенной является задача планирования объема для последующего сравнения медианного значения определенного параметра между выборками в случае, если распределение признака уже известно, а информация о всей генеральной совокупности еще не получена. Например, необходимо определить объем выборки при сравнении уровня С-реактивного белка (СРБ) в одной группе пациентов с разлитым фибринозно-гнойным перитонитом в 1-е сутки и через 7 суток. Различия считаются статистически значимыми при уровне p<0,05, предельно допустимая ошибка равна 5%. По результатам предварительного (пилотного) исследования известно, что стандартное отклонение σ в первой группе составило 11,5, во второй — 16,2, а разница средних значений уровня СРБ в группах (X1—X2) по модулю составила 2. Так как СРБ является количественным параметром, выборки зависимы (связанные), а объем генеральной совокупности неизвестен, подходящими являются формулы 3 и 7. Однако в связи с тем, что стандартные отклонения в двух выборках различны, воспользуемся формулой 4, так как она учитывает стандартные отклонения обеих выборок.

(4)

Отметим, что при уменьшении разницы X1—X2 (например, в пилотном исследовании ввиду неэффективной терапии уровень СРБ снизился менее чем на 1 единицу) объем выборки будет увеличиваться, что необходимо для выявления незначительных различий в уровне СРБ.

Ввиду финансовых, этических или иных соображений возможна ситуация, при которой требуется формирование различных по объему основной и контрольной групп [17]. Такое часто встречается в обсервационном исследовании или в рандомизированном контролируемом исследовании с неравной рандомизацией. Разработан математический аппарат, позволяющий оценить требуемую численность одной группы при известной фиксированной численности другой группы для формирования заключения о наличии/отсутствии статистически значимых различий между ними (см. табл. 5, формула 5).

Актуальной является задача определения объема выборки для дальнейшей оценки (сравнения) долей (частот встречаемости) признаков в одной или нескольких группах с использованием хи-квадрат критерия Пирсона — для этого случая также представлено несколько методик. Первая связана с использованием критических значений стандартного нормального распределения для оценки объема выборки (см. табл. 5, формулы 6, 12, 14). Вторая методика предполагает использование номограмм [18, 19]. Номограмма представляет собой диаграмму с двумя осями: осью стандартизованной разности и осью величины мощности; на пересечении приведенной прямой с необходимым уровнем значимости находится требуемый объем выборки. Расчет стандартизованной разности предполагает расчет отношения разности средних арифметических значений признака между группами к стандартному отклонению анализируемого признака, а уровень мощности в клинических исследованиях принимается, как правило, равным 0,8—0,9 [6]. В случае связанных выборок стандартизованная разность умножается на 2. В некоторых ситуациях может потребоваться расчет объема выборки с учетом прямой погрешности измерения прибора [20]. Тогда становится возможным заменить t-статистику Стьюдента на Z-оценку стандартного нормального распределения (см. табл. 5, формула 15).

Методы, требующие предварительной информации о виде признака и о генеральной совокупности. Наилучшая ситуация с точки зрения планирования объема выборки возникает при наличии информации о типе признака и о характеристиках распределения совокупности, при этом предпочтительно наличие нормально распределенных данных. В таком случае возможно использование статистических формул с учетом подхода к формированию выборки и использованием t-статистики (см. табл. 5, формулы 16—19). Этот математический аппарат широко описан в литературе, однако он неприменим к данным, распределение которых отлично от нормального [21]. Достаточно давно известен подход к планированию размера выборки для данных, распределение которых близко к лог-нормальному [22] (см. табл. 5, формула 20). По результатам исследования B. Cundill и N. Alexander, описанный выше подход к анализу лог-нормального распределения хорошо работал и для рассмотренных отрицательных биномиальных и гамма-распределений и превосходил по качеству методы, используемые при нормально распределенных данных [21]. Тем не менее он показал лишь незначительное преимущество для пуассоновского распределения, в связи с чем авторами предложен отдельных подход к расчету объема выборки для частного случая — Пуассоновского распределения данных (см. табл. 5, формула 21). В качестве альтернативного подхода к планированию объема выборки описано использование методов Монте-Карло, в частности, модели подтверждающего факторного анализа и модели роста [23]. В исследованиях данные генерируются из совокупности с гипотетическими значениями параметров, выбирается большое количество наблюдений и для каждого образца оценивается модель; значения параметров и стандартные ошибки усредняются по выборкам. Для определения объема выборки требуется соблюдение трех критериев. Первый критерий остановки алгоритма срабатывает в случае отклонения параметров и стандартных ошибок более 10% для любого параметра в модели. Второй критерий — стандартное смещение ошибки для параметра, для которого оценивается мощность, не превышает 5%. Третий критерий — оценка доверительных интервалов находится в интервале между 0,91 и 0,98. В случае, если эти три условия выполнены, размер выборки выбирается так, чтобы мощность была близка к 0,80. В целом такой подход может быть использован и при соответствии распределения совокупности нормальному закону.

Авторы заявляют об отсутствии конфликта интересов.

Источник

Тесты по дисциплине

ТЕСТ №1

1. Коэффициент корреляции, равный нулю, означает, что между переменными:

а) линейная связь отсутствует;

б) существует линейная связь;

в) ситуация не определена.

2. Коэффициент корреляции, равный 1, означает, что между переменными:

а) линейная связь отсутствует;

б) существует линейная связь;

в) функциональная зависимость;

г) ситуация не определенна.

В регрессионном анализе обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием

Y = <р(Xj,…,xk), являющимся функцией от аргументов xj, и с постоянной, от аргументов дисперсией о2 :

а) не зависящей;

б) зависящей.

Статистика Дарбина Уотсона (DW) вычисляется по формуле:

Z (et et_i)2

t=2

Z et2

б)

Z (et et-i)2

t=2

Zyt2

t=1

Z (yt yt-1)2

t=2

Zyt2

В модели lnY = во + (3X+ є коэффициент в имеет смысл:

а) абсолютного прироста;

б) темпа роста;

в) темпа прироста.

При анализе эластичности спроса по цене целесообразно использовать следующую модель:

а) линейную;

б) полиномиальную;

в) логарифмическую;

г) степенную;

д) экспоненциальную.

Использование обычного Евклидова расстояния оправдано в следующих случаях (выберите необходимые варианты):

а) наблюдения берутся из генеральной совокупности, имеющей многомерное

нормальное распределение с ковариационной матрицей вида а Ек, т.е. компоненты Х взаимно независимы и имеют одну и ту же дисперсию, где Ек единичная матрица;

б) наблюдения берутся из генеральной совокупности, имеющей биномиальное

распределение;

в) компоненты вектора наблюдений Х неоднородны по физическому смыслу и

при классификации используются с определенным весом;

г) компоненты вектора наблюдений Х однородны по физическому смыслу и

одинаково важны для классификации;

д) признаковое пространство совпадает с геометрическим пространством;

е) совпадение признакового пространства с геометрическим пространством необязательно.

Академиком А.Н.Колмогоровым было предложено:

а) «обобщенное расстояние» между классами;

б) расстояние, измеряемое по принципу «ближайшего соседа»;

в) расстояние, измеряемое по принципу «дальнего соседа»;

г) расстояние, измеряемое по «центрам тяжести» групп;

д) расстояние, измеряемое по принципу «средней связи».

Производственная функция Кобба Дугласа с учетом технического прогресса имеет вид:

а) Qt = Aхeet хК? хLet;

б) Q = A х К а х Le х eє;

в) Q = A х K а х L1~a х ee = A х (f)a х L х ee.

10. Оценки неизвестных параметров A, а и в в производственной функции Кобба

Дугласа можно найти с помощью:

а) метода наименьших квадратов;

б) принципа «ближнего соседа»;

а) дисконтированием множителей.

ТЕСТ №2

1. Двумерная корреляционная модель определяется параметрами (вставьте

необходимое слово):

а) тремя;

б) пятью;

в) семью.

2. Коэффициент регрессии определяется по формуле: а) /? = р—=— коэффициент регрессии y на x;

б) M [ ^. ^ ] = р,;

Ox Oy

12/3,4…, k

3. Если вектор ошибок имеет постоянную дисперсию, то это явление называется:

а) гомоскедастичностью;

б) гетероскедастичностью;

в) ситуация не определена.

4. С увеличением объема выборки:

а) увеличивается точность оценок;

б) уменьшается ошибка регрессии;

в) расширяются интервальные оценки;

г) уменьшается коэффициент детерминации.

При анализе издержек Y от объемы выпуска X целесообразно использовать следующую модель:

а) линейную;

б) полиномиальную;

в) логарифмическую;

г) степенную;

д) экспоненциальную.

Модель Y = в0 + Pln X+ є используется, когда необходимо исследовать влияние:

а) процентного изменения независимой переменной на абсолютное изменение

зависимой переменной;

б) процентного изменения независимой переменной на процентное изменение

зависимой переменной;

в) абсолютное изменения независимой переменной на абсолютное изменение

зависимой переменной.

Наиболее употребительными расстояниями и мерами близости между классами объектов являются (выберите необходимый вариант):

а) расстояние, измеряемое по принципу «ближайшего соседа»;

б) расстояние, измеряемого по принципу «дальнего соседа»;

в) расстояние, измеряемое по принципу «родственной связи»;

г) расстояние, измеряемое по «центрам тяжести» групп;

д) расстояние, измеряемое по принципу «незначимой связи»;

е) расстояние, измеряемое по принципу «средней связи»;

ж) расстояние, измеряемое по принципу «значимой связи».

Расстояние, измеряемое по принципу «ближайшего соседа» находится по формуле:

а) Ре (Хг, Xj ) =

У(xu xji) ;

б) pmm (Si, Sm ) = тin р(xi, xj);

в) pmax (Sl, Sm ) = 111ax p(^ , x} );

д) pl,(m,g) = p(S1, S(m,q)) = ap1m + + Wmq + 6(p1m pq X

е) Рср (S, Sm) = — P( x, x]).

9. Параметры а и в в производственной функции Кобба Дугласа называют:

а) коэффициентами эластичности;

б) коэффициентами корреляции;

в) коэффициентами автокорреляции.

10. Коэффициенты эластичности показывают, на какую величину в среднем изменится Q, если а или в увеличить соответственно:

а) на один процент;

б) на единицу своего измерения.

ТЕСТ №3

1. Коэффициент регрессии показывает:

а) на сколько единиц своего измерения увеличится (в>0) или уменьшится (в<0)

в среднем y(My/x), если x увеличить на единицу своего измерения;

б) долю дисперсии одной случайной величины, обусловленную вариацией другой;

в) на сколько % увеличится (в>0) или уменьшится (в<0) в среднем y(My/x), если x увеличится на 1 %.

Коэффициент регрессии изменяется в пределах от:

а) -1 до 1;

б) 0 до 1;

min

Po.Pi—.Pk

в) принимает любое значение.

Квадратичная форма

Q=(Y XP) ) (Y Xf) = __(y; у,)

і=і

соответствует :

а) методу максимального правдоподобия;

б) методу наименьших квадратов;

в) методу «дальнего соседа»;

г) методу «средней связи»;

д) двухшаговому методу наименьших квадратов.

4. На главной диагонали ковариационной матрицы в выражении S(b) = S (XTX)-1 находятся:

а) дисперсии коэффициентов регрессии;

б) средние значения коэффициентов регрессии;

в) коэффициенты корреляции;

г) квадраты коэффициентов корреляции.

5. При анализе производственной функции целесообразно использовать следующую

модель:

а) линейную;

б) полиномиальную;

в) логарифмическую;

г) степенную;

д) экспоненциальную.

Модели lnY = fP + PPX+ є Y = /Зо + ffln X+ є называются:

а) линейными;

б) полулогарифмическими;

в) логарифмическими.

Расстояние, измеряемое по принципу «дальнего соседа «, находится по формуле:

а) Ре (Хг, xj ) =

1=1

б) pmin (S1, Sm ) = ПІІП s p(X, , Xj );

в) pmax (S1 > Sm ) = ЇПЗЗС s p(x, , Xj );

Д) Pl,(»,,) = P(S1, S(m,q)) = aPlm + PP1q + Wmq + p q );

5. Расстояние, измеряемое по «центрам тяжести » групп, находится по формуле:

а) P£ (X,, Xj ) = ^	1=1

В) Pmax(S1, Sm ) =

Д) P ,(m,q) = P(S1, S(m,q)) = af>tm + Pftq + YPmq + 6(P1m Pq );
Є) Pop (S1, Sm ) =

9. Если a + в = 1, то уровень эффективности:

а) не зависит от масштабов производства;

б) зависит от масштабов производства.

10. Если a + в < 1, то средние издержки, рассчитанные на единицу продукции:

а) растут по мере расширения масштабов производства;

б) убывают по мере расширения масштабов производства.

ТЕСТ №4

В двумерной модели для вывода о независимости признаков х и y в генеральной совокупности достаточно проверить значимость:

а) только коэффициента корреляции;

б) коэффициента корреляции и регрессии;

в) коэффициента корреляции, детерминации и регрессии.

Значимость частных и парных коэффициентов корреляции проверяется с помощью:

а) нормального закона распределения;

б) t-критерия Стъюдента;

в) F-критерия;

г) таблицы Фишера Иейтса.

В регрессионном анализе Xj рассматриваются как:

а) неслучайные величины;

б) случайные величины;

в) любые величины.

Для оценки вектора в наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор b, который минимизирует:

а) сумму отклонений наблюдаемых значений у; от модельных значений y;

б) сумму квадратов отклонения наблюдаемых значений у; от модельных значений yt.

Если в модели Y = во + в ln X+ є положить Y = GNP (валовой национальный продукт), а X=M (денежная масса), то из формулы:

GNP = во + вІпМ + є, следует, что если увеличить предложение денег М на ,

тоВНПвырастет на 0,01 в:

а) 1%;

б) 1 измерения.

Для получения качественных оценок уравнений регрессии необходимо выполнение следующих предпосылок МНК (выберите необходимые пункты):

а) отклонения є должны быть нормально распределенными случайными величинами с нулевым математическим ожиданием и постоянной дисперсией;

б) отклонения Єї не должны коррелировать друг с другом;

в) отклонения є должны иметь показательный закон распределения.

Расстояние, измеряемое по принципу «средней связи», находится по формуле:

а) Ре (xi, xj ) =

1=1

б) pmm(S1 > Sm ) = mІП р(^ , x} );

в) pmax (S 1 > Sm ) = max s p(^ , x} );

д) pl,(m,g) = p(S1 > S(m,q)) = ap1m + Pftq + Wmq + 6(p1m plg X

е) pср.(S1, Sm ) = IZ p( xi , xj ).

11 nm xi«Slxj<=Sm

Кластерный анализ позволяет проводить:

а) группировку объектов;

б) группировку признаков;

в) группировку объектов и группировку признаков.

Если а + в> 1, то средние издержки, рассчитанные на единицу продукции:

а) растут по мере расширения масштабов производства;

б) убывают по мере расширения масштабов производства.

10. Исходя из априорных соображений значения а и в должны удовлетворять условиям:

а) 0<а<1 и 0< в<1;

б) -1<а<1 и -1< в<1;

в) -1<а<1 и 0< в<1.

ТЕСТ №5

Коэффициент корреляции считается значимым с вероятностью ошибки а если:

а) 1;набл по модулю будет больше, чем 1кр,

б) не имеет значения;

в) 1;набл по модулю будет меньше, чем 1;кр.

Матрица R парных коэффициентов корреляции является (выберите необходимые пункты):

а) обратной;

б) транспонированной;

в) симметричной;

г) положительно определенной.

3. В каких пределах изменяется множественный коэффициент корреляции:

а) от 0 до 1;

б) от -1 до 0;

в) от -1 до 1;

г) от 0 до 10.

4. В каких пределах изменяется коэффициент детерминации:

а) от 0 до 1;

б) от -1 до 0;

в) от -1 до 1;

г) от 0 до 10.

5. В хорошо подобранной модели остатки должны (выберите необходимые пункты):

а) иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией;

б) не коррелировать друг с другом;

в) иметь экспоненциальный закон распределения;

г) хаотично разбросаны;

д) форма и вид распределения не важен.

6. Неправильный выбор функциональной формы или объясняющих переменных называется:

а) ошибками спецификации;

б) ошибками прогноза;

в) гетероскедастичностью.

7. С какой целью производят нормирование признаков:

а) с целью устранения влияния различных единиц измерения;

б) с целью уменьшить признаковое пространство;

в) с целью упрощения расчетов.

8. Хемминговорасстояние вычисляется по формуле:

а) Ре (Хг, xj ) =

б) рВе (Хг, Xe )

1=1

9. Коэффициент а интерпретируется как:

а) эластичность по труду;

б) эластичность по капиталу;

в) эластичность замещения.

10. Для определения параметров и вида производственной функции пользуются

следующими видами данных:

а) динамическими рядами;

б) данными одновременных наблюдений (пространственной информацией);

в) динамическими рядами и пространственной информацией.

ТЕСТ №6

1. С помощью данной формулыr12/34 k =—. 12 можно определить:

а) множественный коэффициент корреляции (£-2)-го порядка между факторами

X1 и X2;

б) частный коэффициент корреляции (&-2)-го порядка между факторами X1 и X2;

в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.

2. С помощью данной формулы r 1/2 3 k =r 1 =

1 можно определить:

R11

а) множественный коэффициент корреляции (£-2)-го порядка между факторами

X1 и X2;

б) частный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2;

в) парный коэффициент корреляции (£-2)-го порядка между факторами X1 и X2.

Коэффициент детерминации это:

а) квадрат парного коэффициента корреляции;

б) квадрат частного коэффициента корреляции;

в) квадрат множественного коэффициента корреляции.

Метод максимального правдоподобия лучше работает на…, где он, как правило, дает оценки с минимальной дисперсией:

а) больших выборках;

б) малых выборках;

в) любых выборках.

Модель вида Y = AKaLe носит название:

а) функции Энгеля;

б) функции Кобба Дугласа;

в) лог-линейной модели;

г) степенной модели.

Модель вида Yt = Y0(1+r/ носит название:

а) функции Энгеля;

б) функции Кобба Дугласа;

в) лог-линейной модели;

г) степенной модели.

В задаче классификации данное расстояние применяется в тех случаях, когда каждой компоненте xi вектора наблюдений Xудается приписать некоторый «вес «, пропорционально степени важности признака.

а) Хеммингово расстояние;

б) «взвешенное» Евклидово пространство;

в) обычное Евклидово расстояние.

Иерархические (древообразные) процедуры являются наиболее распространенными (в смысле реализации на ЭВМ) алгоритмами кластерного анализа, они бывают … типов:

а) 2;

б) 3;

в) 5;

г) любых.

Если производство, эффективность которого не зависит от масштабов и описывается производственной функцией Кобба Дугласа, то с ростом параметра а параметр в:

а) растет;

б) уменьшается;

в) остается неизменным;

г) растет или уменьшается.

10. Если производство, эффективность которого растет по мере его укрупнения, описывается производственной функцией Кобба Дугласа, то параметры модели удовлетворяют соотношению:

а) a+f<1;

б) a+f=1;

в) a+f=0;

г) a+f>1.

ТЕСТ №7

Уравнение My / X My = f3yX (X Mx) :

а) прямая регрессии y на x;

б) прямая регрессии X на y.

Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой:

а) коэффициент детерминации;

б) парный коэффициент корреляции;

в) частный коэффициент корреляции;

г) множественный коэффициент корреляции.

3. Оценки максимального правдоподобия и метода наименьших квадратов:

а) могут не совпадать;

б) совпадают;

в) никогда не совпадают.

В матричной форме регрессионная модель имеет вид: Y = Xf + є,

где Y:

а) матрица, размерности [n x (k+1)];

б) случайный вектор-столбец размерности (n x 1).

Какой смысл у коэффициентов регрессии в логарифмических регрессионных моделях:

а) показывают процентное изменение Y для данного процентного изменения X;

б) показывают абсолютное изменение Y для данного процентного изменения X;

в) показывают процентное изменение Y для данного абсолютного изменения X.

Изменяются ли свойства случайного отклонения при преобразовании уравнения регрессии:

а) да;

б) нет;

в) случайное отклонение не зависит от вида уравнения регрессии

В … процедурах начальным является разбиение, состоящее из n одноэлементных

классов, а конечным из одного класса; в наоборот (вставьте необходимые буквы):

а) агломеративных, дивизимных;

б) дивизимных, агломеративных;

в) дисконтированных, агломеративных.

Большинство программ, реализующих алгоритм иерархической классификации, предусматривает графическое представление результатов классификации в виде:

а) дендрограммы;

б) длок-схемы;

в) графиков показателей.

В задачах многомерной классификации объектов а, в, 8 и у являются:

а) числовыми коэффициентами;

б) коэффициентами эластичности.

10. В производственной функции Кобба-Дугласа параметр в соответствует коэффициенту:

а) корреляции;

б) вариации;

в) эластичности;

г) детерминации.

ТЕСТ №8

Величина, рассчитанная по формуле r = ——Х-У-, является оценкой:

sxsy

а) коэффициента детерминации;

б) парного коэффициента корреляции;

в) частного коэффициента корреляции;

г) множественного коэффициента корреляции.

Выборочный коэффициент корреляции r по абсолютной величине:

а) не превосходит единицы;

б) не превосходит нуля;

в) принимает любые значения.

В матричной форме регрессионная модель имеет вид: Y = Хв + є,

где X:

а) матрица, размерности [n x (k+1)];

б) случайный вектор-столбец размерности (n x 1).

В матричной форме регрессионная модель имеет вид: Y = Хв+ є,

где є :

а) матрица, размерности [n x (k+1)] ошибок наблюдений (остатков);

б) случайный вектор-столбец размерности (n x 1) ошибок наблюдений (остатков).

5. Отметьте основные виды ошибок спецификации:

а) отбрасывание значимой переменной;

б) добавление незначимой переменной;

в) низкое значение коэффициента детерминации;

г) выбор неправильной формы модели.

Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена:

а) да;

б) нет;

в) ситуация не определена.

В задачах многомерной классификации объектов при а=в=-8=1/2и у=0 расстояние между классами определяется по принципу:

а) «дальнего соседа»;

б) «средней связи»;

в) «ближайшего соседа».

В задачах многомерной классификации объектов при а=в=8=1/2 и у=0 расстояние между классами определяется по принципу:

а) «дальнего соседа»;

б) «средней связи»;

в) «ближайшего соседа».

Получены две производственные функции Кобба Дугласа, имеющие равные значения параметров а и в, но различающиеся по параметру А. В каком случае первое производство более эффективно, чем второе:

а) Аі<А2;

б) Аі>А2;

в) Аі=А2;

г) Аі^А2.

10. В матричном виде структурная формы системы одновременных эконометрических уравнений имеет следующий вид: Byt + Txt = et:

а) да, это так;

б) нет;

в) данное уравнение не является структурной формой системы одновременных

эконометрических уравнений.

ТЕСТ №9

1. Есть ли необходимость при определении с надежностью у доверительного интервала для значимого парного или частного коэффициентов корреляции использовать Z-преобразование Фишера и предварительно устанавливать интервальную оценку для Z:

а) нет;

б) да;

в) ситуация не определена.

2. Для проверки значимости какого коэффициента

1 2

Fнабл = k 1

n ■

«(1 )

рассчитывают :

а) коэффициента детерминации;

б) парного коэффициента корреляции;

в) частного коэффициента корреляции;

г) множественного коэффициента корреляции.

Компоненты вектора є i :

а) независимы между собой;

б) зависимы между собой;

в) имеют нормальный закон распределения с нулевым математическим ожиданием (Мє i =0) и неизвестной дисперсией а2 (De i = а2).

На практике при построении регрессионных моделей рекомендуется, чтобы n превышало k не менее, чем:

а) в два раза;

б) в три раза;

в) не имеет значения.

Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению:

а) t-статистики;

б) F-статистики;

в) коэффициента детерминации.

Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения є i, а именно, к их математическому ожиданию Мєі и дисперсии Dei:

а) Мє=1; в) МЄі=0;

Dei=a2; Dei=a2;

б) Мєі=0; г) Мєі=1;

Dei=1; Dei=0

а) «дальнего соседа»;

б) «средней связи»;

в) «ближайшего соседа».

8. В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа «ближайшего соседа'»:

а) 2; в) 6;

б) 5; г) 7.

9. Если M є t1 є t2 = 0 при t1 ф 12 и t1,12 = 1,2,…, n, то случайные ошибки регрессии:

а) зависимы между собой;

б) независимы между собой;

с) ситуация не определена.

10. Если дисперсия ошибки постоянна Мє2 = а2 = а1 и не зависит от t и Xt,

то это свидетельствует о:

а) гомоскедастичности остатков;

б) гетероскедастичности остатков.

ТЕСТ №10

1. Известно, что при фиксированном значении X3 между величинами X1 и X2 существует положительная связь. Какое значение может принять частный коэффициент корреляции р12/3?

а) -0,8;

б) 0;

в) 0,4;

г) 1,3.

По результатам n=20 наблюдений получен частный коэффициент корреляции r12/3=0,8. Определите, чему при уровне значимости a=0,05 равна разность между наблюдаемым (r12/3) и критическим (гкр) значениями коэффициентов корреляции:

а) -0,513;

б) 0, 357;

в) 0, 700;

г) 0,133.

На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше , то

считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включать только один из показателей Xj или Xe. Вставьте недостающее значение.

а) 0,3;

б) 0,5;

в) 0,6;5;

г) 0,8;

д) 0,9;

е) другое значение.

4. Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез

H0: в=0, где j=1,2,…k, используют:

а) нормальный закон распределения;

б) t-критерий;

в) распределение Фишера.

5. Двойная логарифмическая модель является линейной относительно ее переменных:

а) утверждение истинно;

б) утверждение ложно;

в) утверждение не определено.

Коэффициенты двойной логарифмической модели определяют эластичность зависимой переменной по соответствующим определяющим переменным:

а) утверждение истинно;

б) утверждение ложно;

в) утверждение не определено.

В кластер S1 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера S1, если исходить из принципа » дальнего соседа»:

а) 2; в) 6;

б) 5; г) 7.

В условиях гетероскедастичности случаных остатков оценки коэффициентов, полученные по методу наименьших квадратов, будут:

а) несмещенными; в) эффективными; д) надежными;

б) смещенными; г) неэффективными; е) ненадежными.

Условием гетероскедастичности является:

а) независимость значений = <J2t от t и xt;

б) зависимость значений Мє2 = a2t от t и xt;

в) ситуация не определена.

10. Систему yt = B~lTxt + B~1є( одновременных уравнений называют рекурсивной,

если выполняются следующие условия (выберите необходимые условия):

а) Матрица значений эндогенных переменных является нижней треугольной

матрицей, т. е. в ij = 0 при j>i и (3 ц = 1;

б) случайные ошибки независимы между собой, т. е. aii > 0, аij = 0 при j ,

где i,j=1,2,…,G;

в) каждое ограничение на структурные коэффициенты относится к отдельному

уравнению.

Источник

Увеличение — объем — выборка

Задачи и тесты по эконометрике

Варианты ошибок и их последствия

Определение объема выборки

Некоторые дополнительные замечания относительно определения размера выборки

Математический подход к определению размера выборки

Экспертный подход к планированию объема выборки

Принципы определения насыщенности данных

Обсуждение

Заключение

Приложение

Тесты по дисциплине

Возможно, вам также будет интересно: