Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
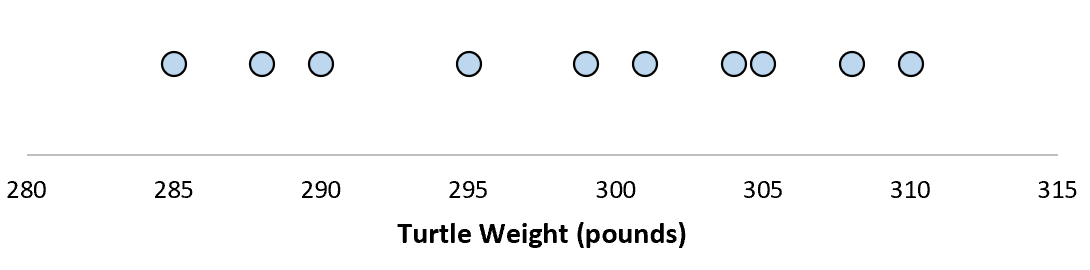
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
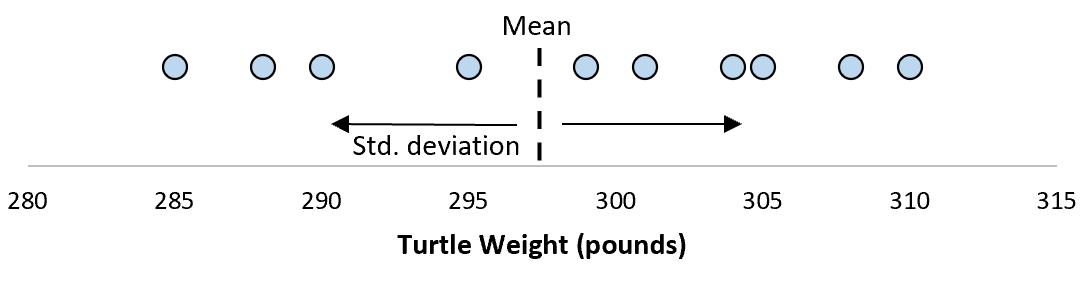
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
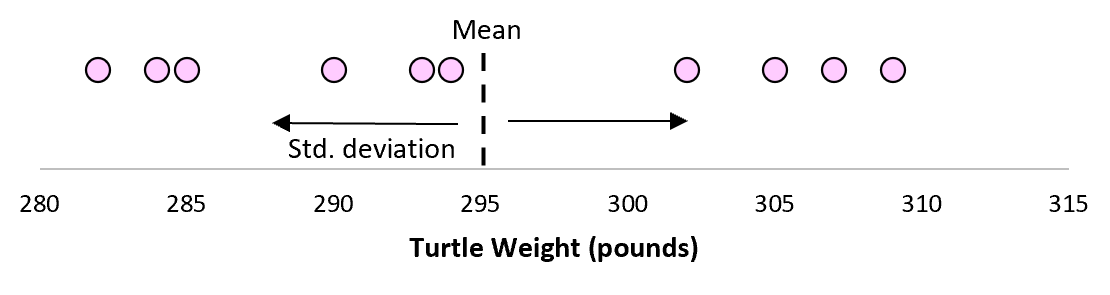
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
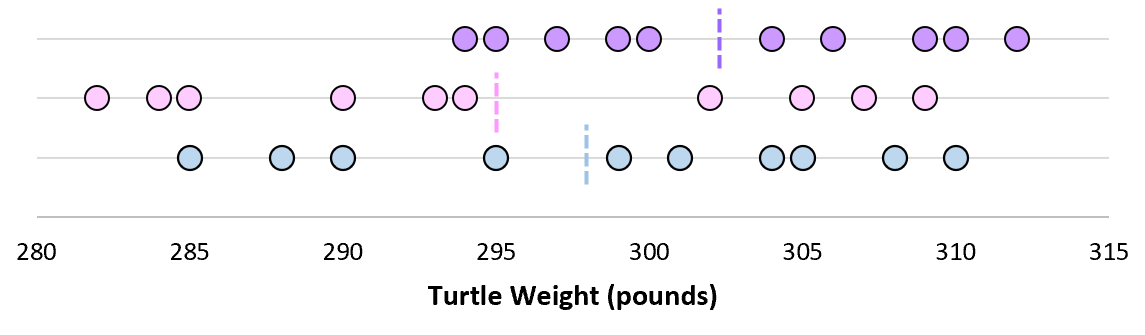
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
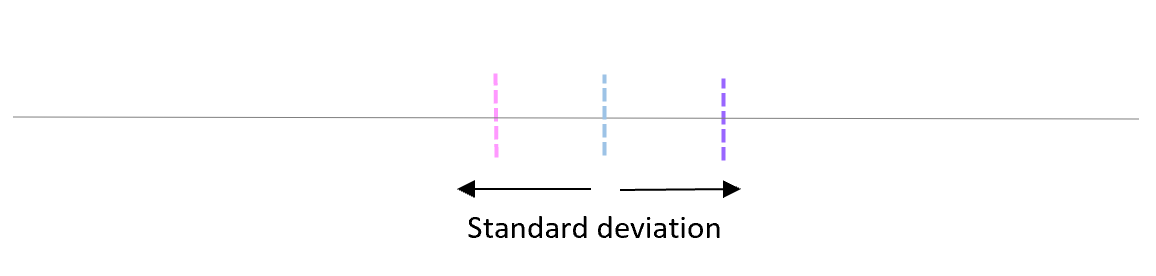
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.
Ключевые выводы
- Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
- Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
- SEM берет SD и делит его на квадратный корень из размера выборки.
SEM против SD
Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD – это разброс отдельных значений данных.
Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM – это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).
Расчет стандартного отклонения
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.
Вступление
стандарт D (SD) а также S tandard Е rror (SE) по-видимому, аналогичные терминологии; однако они концептуально настолько разнообразны, что они используются почти взаимозаменяемо в статистической литературе. Каждому термину обычно предшествует символ плюс-минус (+/-), который указывает на то, что они определяют симметричное значение или представляют диапазон значений. Неизменно оба выражения появляются со средним (средним) набором измеренных значений.
Интересно, что SE не имеет ничего общего со стандартами, с ошибками или с сообщением научных данных.
Подробный взгляд на происхождение и объяснение SD и SE покажет, почему профессиональные статистики и те, кто использует это сдержанно, оба склонны ошибаться.
Стандартное отклонение (SD)
SD является описательный статистика, описывающая распространение распределения. Как метрика, это полезно, когда данные обычно распределяются. Однако это менее полезно, когда данные сильно искажены или бимодальны, потому что они не очень хорошо описывают форму распределения. Как правило, мы используем SD при представлении характеристик образца, поскольку мы намерены описывать насколько данные изменяются по среднему значению. Другая полезная статистика для описания распространения данных — это межквартильный диапазон, 25-й и 75-й процентили и диапазон данных.
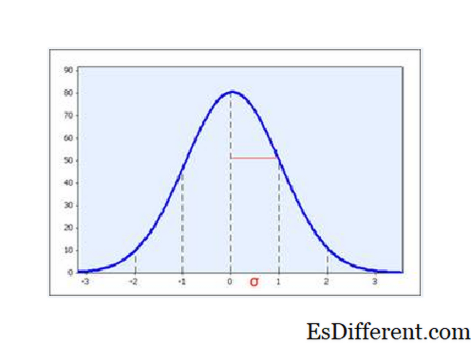
Рисунок 1. SD является мерой распространения данных. Когда данные являются образцом из нормально распределенного распределения, тогда ожидается, что две трети данных будут находиться в пределах 1 стандартного отклонения среднего значения.
Разница заключается в описательный статистика также, и она определяется как квадрат стандартного отклонения. Обычно это не сообщается при описании результатов, но это более математически приемлемая формула (a.k.a. сумма квадратов отклонений) и играет роль в вычислении статистики.
Например, если у нас есть две статистики п & Q с известными отклонениями вар (П) & вар (Q) , то дисперсия суммы Р + Q равна сумме дисперсий: вар (P) + вар (Q) , Теперь очевидно, почему статистикам нравится говорить об отклонениях.
Но стандартные отклонения имеют важное значение для распространения, особенно когда данные обычно распределяются: среднее значение интервала +/- 1 SD можно ожидать захвата 2/3 образца, а среднее значение интервала + — 2 SD можно ожидать захвата 95% образца.
SD дает представление о том, насколько индивидуальные ответы на вопрос меняются или «отклоняются» от среднего. SD рассказывает исследователю, насколько распространены ответы: сосредоточены ли они вокруг среднего или разбросаны по всему миру? Все ваши респонденты оценили ваш продукт в середине шкалы, или кто-то одобрил его, а некоторые отклонили его?
Рассмотрим эксперимент, в котором респондентам предлагается оценивать продукт по ряду атрибутов по 5-балльной шкале. Среднее значение для группы из десяти респондентов (обозначаемое «A» через «J» ниже) для «хорошей стоимости за деньги» составляло 3,2 с SD 0,4, а среднее значение для «надежности продукта» составляло 3,4 с SD 2,1.
На первый взгляд (смотря только на средства), казалось бы, надежность была оценена выше стоимости. Но более высокий SD для надежности может указывать (как показано ниже в распределении), что ответы были очень поляризованы, где большинство респондентов не имели проблем с надежностью (с оценкой атрибута «5»), но меньший, но важный сегмент респондентов, проблема надежности и оценили атрибут «1». Однако, глядя на среднее значение, он говорит только часть истории, однако чаще всего это то, на что ориентируются исследователи. Распределение ответов важно учитывать, и SD обеспечивает ценную описательную меру этого.
| ответчик | Хорошая ценность для денег | Надежность продукта |
| 3 | 1 | |
| В | 3 | 1 |
| С | 3 | 1 |
| D | 3 | 1 |
| Е | 4 | 5 |
| F | 4 | 5 |
| г | 3 | 5 |
| ЧАС | 3 | 5 |
| я | 3 | 5 |
| J | 3 | 5 |
| Имею в виду | 3.2 | 3.4 |
| Std. Девиация | 0.4 | 2.1 |
Первый опрос: респонденты оценивают продукт по пятибалльной шкале
Два очень разных распределения ответов на 5-балльную рейтинговую шкалу могут дать одно и то же значение. Рассмотрим следующий пример, показывающий значения ответа для двух разных оценок.
В первом примере (Рейтинг «A») SD равен нулю, потому что ВСЕ ответы были точно средним значением. Индивидуальные ответы не отклонялись от среднего.
В рейтинге «B», хотя среднее значение группы одинаково (3.0) в качестве первого распределения, стандартное отклонение выше. Стандартное отклонение 1.15 показывает, что индивидуальные ответы в среднем * были чуть более 1 балла от среднего.
| ответчик | Рейтинг «A» | Рейтинг «B» |
| 3 | 1 | |
| В | 3 | 2 |
| С | 3 | 2 |
| D | 3 | 3 |
| Е | 3 | 3 |
| F | 3 | 3 |
| г | 3 | 3 |
| ЧАС | 3 | 4 |
| я | 3 | 4 |
| J | 3 | 5 |
| Имею в виду | 3.0 | 3.0 |
| Std. Девиация | 0.00 | 1.15 |
Второй опрос: респонденты оценивают продукт по пятибалльной шкале
Другой способ взглянуть на SD — это построить распределение как гистограмму ответов. Распределение с низким SD будет отображаться как высокая узкая форма, в то время как большая SD будет обозначаться более широкой формой.
SD обычно не указывает «правильно или неправильно» или «лучше или хуже» — более низкая SD не обязательно более желательна. Он используется исключительно как описательная статистика. Он описывает распределение по отношению к среднему.
T echnical disclaimer, относящийся к SD
Думая о том, что SD как «отклонение» — это отличный способ концептуально понять его смысл. Тем не менее, он фактически не рассчитывается как среднее (если бы это было так, мы бы назвали это «отклонениями»). Вместо этого он «стандартизирован» — несколько сложный метод вычисления значения с использованием суммы квадратов.
Для практических целей вычисление не имеет значения. Большинство программ табуляции, электронных таблиц или других инструментов управления данными будут вычислять SD для вас. Более важно понять, что передает статистика.
Стандартная ошибка
Стандартная ошибка — это выведенный статистика, которая используется при сравнении выборочных средств (средних) по группам населения. Это мера точность от среднего значения выборки. Среднее значение выборки — это статистическая информация, полученная из данных, имеющих базовое распределение. Мы не можем визуализировать его так же, как и данные, поскольку мы выполнили один эксперимент и имеем только одно значение. Статистическая теория говорит нам о том, что среднее значение выборки (для большого, более выбранного образца и в нескольких условиях регулярности) приблизительно нормально распределено. Стандартное отклонение этого нормального распределения — это то, что мы называем стандартной ошибкой.
Фигура 2. Распределение в нижней части распределяет данные, тогда как распределение сверху — это теоретическое распределение среднего значения выборки. SD 20 является мерой распространения данных, тогда как SE of 5 является мерой неопределенности вокруг среднего значения выборки.
Когда мы хотим сравнить средства исходов от эксперимента с двумя образцами Лечения A против лечения B, нам нужно оценить, насколько точно мы измерили средства.
На самом деле нас интересует, насколько точно мы измерили разницу между этими двумя средствами. Мы называем эту меру стандартной ошибкой разности. Вы не можете быть удивлены, узнав, что стандартная ошибка разницы в средствах выборки является функцией стандартных ошибок средств:
Теперь, когда вы поняли, что стандартная ошибка среднего (SE) и стандартное отклонение распределения (SD) — это два разных зверя, вам может быть интересно, как они запутались в первую очередь. Хотя они принципиально отличаются друг от друга, они имеют математическую форму:
, где n — количество точек данных.
Обратите внимание, что стандартная ошибка зависит от двух компонентов: стандартного отклонения выборки и размера выборки N , Это делает интуитивный смысл: чем больше стандартное отклонение выборки, тем менее точным может быть наша оценка истинного среднего.
Кроме того, большой размер выборки, чем больше информации мы имеем о населении, тем точнее мы можем оценить истинное значение.
SE является показателем надежности среднего значения. Небольшой SE является показателем того, что среднее значение выборки является более точным отражением фактического значения популяции. Более большой размер выборки обычно приводит к меньшему SE (тогда как SD не зависит напрямую от размера выборки).
Большинство исследовательских исследований включает в себя выборку из населения. Затем мы делаем выводы о популяции из результатов, полученных из этого образца. Если был сделан второй образец, результаты, вероятно, были бы точно совпадают с первым образцом. Если среднее значение для атрибута рейтинга составляло 3,2 для одного образца, это может быть 3,4 для второго образца того же размера. Если бы мы собирали бесконечное количество выборок (равного размера) из нашей популяции, мы могли бы отображать наблюдаемые средства как распределение. Затем мы могли бы вычислить среднее значение всех наших образцов. Это означало бы равное истинное значение популяции. Мы также можем рассчитать SD распределения средств выборки. SD этого распределения средств выборки является SE каждого отдельного образца.
Таким образом, мы имеем самое значительное наблюдение: SE является SD среднего значения.
| Образец | Имею в виду |
| первый | 3.2 |
| второй | 3.4 |
| третий | 3.3 |
| четвёртая | 3.2 |
| пятые | 3.1 |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| Имею в виду | 3.3 |
| Std. Девиация | 0.13 |
Таблица, иллюстрирующая взаимосвязь между SD и SE
Теперь ясно, что если SD этого распределения помогает нам понять, насколько далека среднее значение выборки от истинной совокупности, то мы можем использовать это, чтобы понять, насколько точна какая-либо индивидуальная выборка по отношению к истинному среднему значению. В этом суть SE.
На самом деле, мы набрали только один образец из нашего населения, но мы можем использовать этот результат для оценки надежности нашего наблюдаемого образца.
На самом деле, SE говорит нам, что мы можем быть на 95% уверены, что наше наблюдаемое среднее значение выборки плюс или минус примерно 2 (на самом деле 1,96). Стандартные ошибки от населения.
В приведенной ниже таблице показано распределение ответов от нашей первой (и единственной) выборки, используемой для наших исследований. SE 0,13, будучи относительно небольшим, дает нам указание на то, что наше среднее значение относительно близко к истинному среднему для нашей общей популяции. Предел погрешности (с доверием 95%) для нашего среднего значения (примерно) в два раза превышает это значение (+/- 0,26), сообщая нам, что истинное среднее значение, скорее всего, составляет от 2,94 до 3,46.
| ответчик | Рейтинг |
| 3 | |
| В | 3 |
| С | 3 |
| D | 3 |
| Е | 4 |
| F | 4 |
| г | 3 |
| ЧАС | 3 |
| я | 3 |
| J | 3 |
| Имею в виду | 3.2 |
| Std. заблуждаться | 0.13 |
Резюме
Многие исследователи не понимают различия между стандартным отклонением и стандартной ошибкой, хотя они обычно включаются в анализ данных. Хотя фактические расчеты для стандартного отклонения и стандартной ошибки выглядят очень схожими, они представляют собой две очень разные, но взаимодополняющие меры. SD рассказывает нам о форме нашего распределения, насколько близки значения отдельных данных от среднего значения. SE рассказывает нам, насколько близка наша выборка к истинному средству общей популяции.Вместе они помогают обеспечить более полную картину, чем может сказать нам только одно значащее.
Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.
Ключевые выводы
- Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
- Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
- SEM берет SD и делит его на квадратный корень из размера выборки.
SEM против SD
Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD — это разброс отдельных значений данных.
Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM — это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).
Расчет стандартного отклонения
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.
Автор:
Laura McKinney
Дата создания:
7 Апрель 2021
Дата обновления:
6 Июнь 2023
Содержание
- Сравнительная таблица
- Определение стандартного отклонения
- Определение стандартной ошибки
- Ключевые различия между стандартным отклонением и стандартной ошибкой
- Вывод

Стандартная ошибка используется для измерения статистической точности оценки. Он в основном используется в процессе проверки гипотез и оценки интервала.
Это две важные концепции статистики, которые широко используются в области исследований. Разница между стандартным отклонением и стандартной ошибкой основана на различии между описанием данных и их выводом.
Сравнительная таблица
| Основа для сравнения | Стандартное отклонение | Стандартная ошибка |
|---|---|---|
| Имея в виду | Стандартное отклонение подразумевает меру отклонения набора значений от их среднего. | Стандартная ошибка означает меру статистической точности оценки. |
| Статистика | Описательный | Логический |
| Меры | Насколько наблюдения отличаются друг от друга. | Насколько точно среднее значение выборки соответствует истинному среднему значению генеральной совокупности. |
| Распределение | Распределение наблюдения относительно нормальной кривой. | Распределение оценки относительно нормальной кривой. |
| Формула | Корень квадратный из дисперсии | Стандартное отклонение, деленное на квадратный корень из размера выборки. |
| Увеличение размера выборки | Дает более конкретную меру стандартного отклонения. | Уменьшает стандартную ошибку. |
Определение стандартного отклонения
Стандартное отклонение — это мера разброса ряда или расстояния от стандарта. В 1893 году Карл Пирсон ввел понятие стандартного отклонения, которое, несомненно, является наиболее часто используемой мерой в научных исследованиях.
Это квадратный корень из среднего квадрата отклонений от их среднего значения. Другими словами, для данного набора данных стандартное отклонение — это среднеквадратичное отклонение от среднего арифметического. Для всего населения он обозначается греческой буквой «сигма (σ)», а для выборки — латинской буквой «s».
Стандартное отклонение — это мера, которая количественно определяет степень дисперсии набора наблюдений. Чем дальше точки данных от среднего значения, тем больше отклонение в наборе данных, что означает, что точки данных разбросаны по более широкому диапазону значений и наоборот.
Определение стандартной ошибки
Вы могли заметить, что разные выборки одинакового размера, взятые из одной и той же совокупности, дадут разные значения рассматриваемой статистики, т.е. выборочное среднее. Стандартная ошибка (SE) представляет собой стандартное отклонение различных значений выборочного среднего. Он используется для сравнения выборочных средних по совокупности.
Короче говоря, стандартная ошибка статистики — это не что иное, как стандартное отклонение ее выборочного распределения. Он играет большую роль в проверке статистических гипотез и интервальной оценке. Это дает представление о точности и достоверности сметы. Чем меньше стандартная ошибка, тем больше однородность теоретического распределения и наоборот.
- Формула: Стандартная ошибка для выборочного среднего = σ / √n
Где, σ — стандартное отклонение совокупности
Ключевые различия между стандартным отклонением и стандартной ошибкой
Приведенные ниже моменты существенны с точки зрения разницы между стандартным отклонением:
- Стандартное отклонение — это мера, которая оценивает степень вариации набора наблюдений. Стандартная ошибка измеряет точность оценки, т. Е. Является мерой изменчивости теоретического распределения статистики.
- Стандартное отклонение — это описательная статистика, тогда как стандартная ошибка — это выводимая статистика.
- Стандартное отклонение измеряет, насколько отдельные значения отличаются от среднего значения. Напротив, насколько близко среднее значение выборки к среднему значению генеральной совокупности.
- Стандартное отклонение — это распределение наблюдений относительно нормальной кривой. В отличие от этого, стандартная ошибка — это распределение оценки относительно нормальной кривой.
- Стандартное отклонение определяется как квадратный корень из дисперсии. И наоборот, стандартная ошибка описывается как стандартное отклонение, деленное на квадратный корень из размера выборки.
- Когда размер выборки увеличивается, это дает более конкретную меру стандартного отклонения. В отличие от стандартной ошибки, когда размер выборки увеличивается, стандартная ошибка имеет тенденцию к уменьшению.
Вывод
В целом стандартное отклонение считается одним из лучших показателей дисперсии, который измеряет отклонение значений от центрального значения. С другой стороны, стандартная ошибка в основном используется для проверки надежности и точности оценки, поэтому чем меньше ошибка, тем выше ее надежность и точность.
Термин «статистика» означает практику анализа и сбора числовых данных, которые предоставляются в больших количествах. Есть несколько статистических исследований, в том числе биология, финансы, психология, инженерия и многие другие.
Статистические исследования полезны для сбора и анализа любых данных в числовой форме.
Стандартное отклонение и стандартная ошибка являются двумя наиболее распространенными показателями, которые используются в области статистики. Основной мотив стандартного отклонения и стандартной ошибки — показать результаты статистического анализа и характеристики выборочных данных.
Стандартное отклонение и стандартная ошибка немного сбивают с толку, но они отличаются друг от друга во многих терминах.
Основные выводы
- Стандартное отклонение измеряет разброс точек данных вокруг среднего значения, а стандартная ошибка оценивает изменчивость среднего значения выборки.
- Чем больше размер выборки, тем меньше стандартная ошибка, но размер выборки не влияет на стандартное отклонение.
- Стандартное отклонение подходит для анализа отдельных точек данных, а стандартная ошибка используется для оценки точности выборочных средних.
Стандартное отклонение против стандартной ошибки
Разница между стандартным отклонением и стандартной ошибкой заключается в том, что они оба различаются по своим статистическим помехам. Стандартное отклонение помогает рассредоточить отдельные значения данных. Он показывает точность среднего значения, которое представляет выборочные данные. В то время как стандартная ошибка основана на статистических помехах данных выборки.
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.
Вступление
стандарт D (SD) а также S tandard Е rror (SE) по-видимому, аналогичные терминологии; однако они концептуально настолько разнообразны, что они используются почти взаимозаменяемо в статистической литературе. Каждому термину обычно предшествует символ плюс-минус (+/-), который указывает на то, что они определяют симметричное значение или представляют диапазон значений. Неизменно оба выражения появляются со средним (средним) набором измеренных значений.
Интересно, что SE не имеет ничего общего со стандартами, с ошибками или с сообщением научных данных.
Подробный взгляд на происхождение и объяснение SD и SE покажет, почему профессиональные статистики и те, кто использует это сдержанно, оба склонны ошибаться.
Стандартное отклонение (SD)
SD является описательный статистика, описывающая распространение распределения. Как метрика, это полезно, когда данные обычно распределяются. Однако это менее полезно, когда данные сильно искажены или бимодальны, потому что они не очень хорошо описывают форму распределения. Как правило, мы используем SD при представлении характеристик образца, поскольку мы намерены описывать насколько данные изменяются по среднему значению. Другая полезная статистика для описания распространения данных — это межквартильный диапазон, 25-й и 75-й процентили и диапазон данных.
Рисунок 1. SD является мерой распространения данных. Когда данные являются образцом из нормально распределенного распределения, тогда ожидается, что две трети данных будут находиться в пределах 1 стандартного отклонения среднего значения.
Разница заключается в описательный статистика также, и она определяется как квадрат стандартного отклонения. Обычно это не сообщается при описании результатов, но это более математически приемлемая формула (a.k.a. сумма квадратов отклонений) и играет роль в вычислении статистики.
Например, если у нас есть две статистики п & Q с известными отклонениями вар (П) & вар (Q) , то дисперсия суммы Р + Q равна сумме дисперсий: вар (P) + вар (Q) , Теперь очевидно, почему статистикам нравится говорить об отклонениях.
Но стандартные отклонения имеют важное значение для распространения, особенно когда данные обычно распределяются: среднее значение интервала +/- 1 SD можно ожидать захвата 2/3 образца, а среднее значение интервала + — 2 SD можно ожидать захвата 95% образца.
SD дает представление о том, насколько индивидуальные ответы на вопрос меняются или «отклоняются» от среднего. SD рассказывает исследователю, насколько распространены ответы: сосредоточены ли они вокруг среднего или разбросаны по всему миру? Все ваши респонденты оценили ваш продукт в середине шкалы, или кто-то одобрил его, а некоторые отклонили его?
Рассмотрим эксперимент, в котором респондентам предлагается оценивать продукт по ряду атрибутов по 5-балльной шкале. Среднее значение для группы из десяти респондентов (обозначаемое «A» через «J» ниже) для «хорошей стоимости за деньги» составляло 3,2 с SD 0,4, а среднее значение для «надежности продукта» составляло 3,4 с SD 2,1.
На первый взгляд (смотря только на средства), казалось бы, надежность была оценена выше стоимости. Но более высокий SD для надежности может указывать (как показано ниже в распределении), что ответы были очень поляризованы, где большинство респондентов не имели проблем с надежностью (с оценкой атрибута «5»), но меньший, но важный сегмент респондентов, проблема надежности и оценили атрибут «1». Однако, глядя на среднее значение, он говорит только часть истории, однако чаще всего это то, на что ориентируются исследователи. Распределение ответов важно учитывать, и SD обеспечивает ценную описательную меру этого.
| ответчик | Хорошая ценность для денег | Надежность продукта |
| 3 | 1 | |
| В | 3 | 1 |
| С | 3 | 1 |
| D | 3 | 1 |
| Е | 4 | 5 |
| F | 4 | 5 |
| г | 3 | 5 |
| ЧАС | 3 | 5 |
| я | 3 | 5 |
| J | 3 | 5 |
| Имею в виду | 3.2 | 3.4 |
| Std. Девиация | 0.4 | 2.1 |
Первый опрос: респонденты оценивают продукт по пятибалльной шкале
Два очень разных распределения ответов на 5-балльную рейтинговую шкалу могут дать одно и то же значение. Рассмотрим следующий пример, показывающий значения ответа для двух разных оценок.
В первом примере (Рейтинг «A») SD равен нулю, потому что ВСЕ ответы были точно средним значением. Индивидуальные ответы не отклонялись от среднего.
В рейтинге «B», хотя среднее значение группы одинаково (3.0) в качестве первого распределения, стандартное отклонение выше. Стандартное отклонение 1.15 показывает, что индивидуальные ответы в среднем * были чуть более 1 балла от среднего.
| ответчик | Рейтинг «A» | Рейтинг «B» |
| 3 | 1 | |
| В | 3 | 2 |
| С | 3 | 2 |
| D | 3 | 3 |
| Е | 3 | 3 |
| F | 3 | 3 |
| г | 3 | 3 |
| ЧАС | 3 | 4 |
| я | 3 | 4 |
| J | 3 | 5 |
| Имею в виду | 3.0 | 3.0 |
| Std. Девиация | 0.00 | 1.15 |
Второй опрос: респонденты оценивают продукт по пятибалльной шкале
Другой способ взглянуть на SD — это построить распределение как гистограмму ответов. Распределение с низким SD будет отображаться как высокая узкая форма, в то время как большая SD будет обозначаться более широкой формой.
SD обычно не указывает «правильно или неправильно» или «лучше или хуже» — более низкая SD не обязательно более желательна. Он используется исключительно как описательная статистика. Он описывает распределение по отношению к среднему.
T echnical disclaimer, относящийся к SD
Думая о том, что SD как «отклонение» — это отличный способ концептуально понять его смысл. Тем не менее, он фактически не рассчитывается как среднее (если бы это было так, мы бы назвали это «отклонениями»). Вместо этого он «стандартизирован» — несколько сложный метод вычисления значения с использованием суммы квадратов.
Для практических целей вычисление не имеет значения. Большинство программ табуляции, электронных таблиц или других инструментов управления данными будут вычислять SD для вас. Более важно понять, что передает статистика.
Стандартная ошибка
Стандартная ошибка — это выведенный статистика, которая используется при сравнении выборочных средств (средних) по группам населения. Это мера точность от среднего значения выборки. Среднее значение выборки — это статистическая информация, полученная из данных, имеющих базовое распределение. Мы не можем визуализировать его так же, как и данные, поскольку мы выполнили один эксперимент и имеем только одно значение. Статистическая теория говорит нам о том, что среднее значение выборки (для большого, более выбранного образца и в нескольких условиях регулярности) приблизительно нормально распределено. Стандартное отклонение этого нормального распределения — это то, что мы называем стандартной ошибкой.
Фигура 2. Распределение в нижней части распределяет данные, тогда как распределение сверху — это теоретическое распределение среднего значения выборки. SD 20 является мерой распространения данных, тогда как SE of 5 является мерой неопределенности вокруг среднего значения выборки.
Когда мы хотим сравнить средства исходов от эксперимента с двумя образцами Лечения A против лечения B, нам нужно оценить, насколько точно мы измерили средства.
На самом деле нас интересует, насколько точно мы измерили разницу между этими двумя средствами. Мы называем эту меру стандартной ошибкой разности. Вы не можете быть удивлены, узнав, что стандартная ошибка разницы в средствах выборки является функцией стандартных ошибок средств:
Теперь, когда вы поняли, что стандартная ошибка среднего (SE) и стандартное отклонение распределения (SD) — это два разных зверя, вам может быть интересно, как они запутались в первую очередь. Хотя они принципиально отличаются друг от друга, они имеют математическую форму:
, где n — количество точек данных.
Обратите внимание, что стандартная ошибка зависит от двух компонентов: стандартного отклонения выборки и размера выборки N , Это делает интуитивный смысл: чем больше стандартное отклонение выборки, тем менее точным может быть наша оценка истинного среднего.
Кроме того, большой размер выборки, чем больше информации мы имеем о населении, тем точнее мы можем оценить истинное значение.
SE является показателем надежности среднего значения. Небольшой SE является показателем того, что среднее значение выборки является более точным отражением фактического значения популяции. Более большой размер выборки обычно приводит к меньшему SE (тогда как SD не зависит напрямую от размера выборки).
Большинство исследовательских исследований включает в себя выборку из населения. Затем мы делаем выводы о популяции из результатов, полученных из этого образца. Если был сделан второй образец, результаты, вероятно, были бы точно совпадают с первым образцом. Если среднее значение для атрибута рейтинга составляло 3,2 для одного образца, это может быть 3,4 для второго образца того же размера. Если бы мы собирали бесконечное количество выборок (равного размера) из нашей популяции, мы могли бы отображать наблюдаемые средства как распределение. Затем мы могли бы вычислить среднее значение всех наших образцов. Это означало бы равное истинное значение популяции. Мы также можем рассчитать SD распределения средств выборки. SD этого распределения средств выборки является SE каждого отдельного образца.
Таким образом, мы имеем самое значительное наблюдение: SE является SD среднего значения.
| Образец | Имею в виду |
| первый | 3.2 |
| второй | 3.4 |
| третий | 3.3 |
| четвёртая | 3.2 |
| пятые | 3.1 |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| Имею в виду | 3.3 |
| Std. Девиация | 0.13 |
Таблица, иллюстрирующая взаимосвязь между SD и SE
Теперь ясно, что если SD этого распределения помогает нам понять, насколько далека среднее значение выборки от истинной совокупности, то мы можем использовать это, чтобы понять, насколько точна какая-либо индивидуальная выборка по отношению к истинному среднему значению. В этом суть SE.
На самом деле, мы набрали только один образец из нашего населения, но мы можем использовать этот результат для оценки надежности нашего наблюдаемого образца.
На самом деле, SE говорит нам, что мы можем быть на 95% уверены, что наше наблюдаемое среднее значение выборки плюс или минус примерно 2 (на самом деле 1,96). Стандартные ошибки от населения.
В приведенной ниже таблице показано распределение ответов от нашей первой (и единственной) выборки, используемой для наших исследований. SE 0,13, будучи относительно небольшим, дает нам указание на то, что наше среднее значение относительно близко к истинному среднему для нашей общей популяции. Предел погрешности (с доверием 95%) для нашего среднего значения (примерно) в два раза превышает это значение (+/- 0,26), сообщая нам, что истинное среднее значение, скорее всего, составляет от 2,94 до 3,46.
| ответчик | Рейтинг |
| 3 | |
| В | 3 |
| С | 3 |
| D | 3 |
| Е | 4 |
| F | 4 |
| г | 3 |
| ЧАС | 3 |
| я | 3 |
| J | 3 |
| Имею в виду | 3.2 |
| Std. заблуждаться | 0.13 |
Резюме
Многие исследователи не понимают различия между стандартным отклонением и стандартной ошибкой, хотя они обычно включаются в анализ данных. Хотя фактические расчеты для стандартного отклонения и стандартной ошибки выглядят очень схожими, они представляют собой две очень разные, но взаимодополняющие меры. SD рассказывает нам о форме нашего распределения, насколько близки значения отдельных данных от среднего значения. SE рассказывает нам, насколько близка наша выборка к истинному средству общей популяции.Вместе они помогают обеспечить более полную картину, чем может сказать нам только одно значащее.
Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.
Ключевые выводы
- Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
- Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
- SEM берет SD и делит его на квадратный корень из размера выборки.
SEM против SD
Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD — это разброс отдельных значений данных.
Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM — это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).
Расчет стандартного отклонения
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.
Автор:
Laura McKinney
Дата создания:
7 Апрель 2021
Дата обновления:
6 Июнь 2023
Содержание
- Сравнительная таблица
- Определение стандартного отклонения
- Определение стандартной ошибки
- Ключевые различия между стандартным отклонением и стандартной ошибкой
- Вывод

Стандартная ошибка используется для измерения статистической точности оценки. Он в основном используется в процессе проверки гипотез и оценки интервала.
Это две важные концепции статистики, которые широко используются в области исследований. Разница между стандартным отклонением и стандартной ошибкой основана на различии между описанием данных и их выводом.
Сравнительная таблица
| Основа для сравнения | Стандартное отклонение | Стандартная ошибка |
|---|---|---|
| Имея в виду | Стандартное отклонение подразумевает меру отклонения набора значений от их среднего. | Стандартная ошибка означает меру статистической точности оценки. |
| Статистика | Описательный | Логический |
| Меры | Насколько наблюдения отличаются друг от друга. | Насколько точно среднее значение выборки соответствует истинному среднему значению генеральной совокупности. |
| Распределение | Распределение наблюдения относительно нормальной кривой. | Распределение оценки относительно нормальной кривой. |
| Формула | Корень квадратный из дисперсии | Стандартное отклонение, деленное на квадратный корень из размера выборки. |
| Увеличение размера выборки | Дает более конкретную меру стандартного отклонения. | Уменьшает стандартную ошибку. |
Определение стандартного отклонения
Стандартное отклонение — это мера разброса ряда или расстояния от стандарта. В 1893 году Карл Пирсон ввел понятие стандартного отклонения, которое, несомненно, является наиболее часто используемой мерой в научных исследованиях.
Это квадратный корень из среднего квадрата отклонений от их среднего значения. Другими словами, для данного набора данных стандартное отклонение — это среднеквадратичное отклонение от среднего арифметического. Для всего населения он обозначается греческой буквой «сигма (σ)», а для выборки — латинской буквой «s».
Стандартное отклонение — это мера, которая количественно определяет степень дисперсии набора наблюдений. Чем дальше точки данных от среднего значения, тем больше отклонение в наборе данных, что означает, что точки данных разбросаны по более широкому диапазону значений и наоборот.
Определение стандартной ошибки
Вы могли заметить, что разные выборки одинакового размера, взятые из одной и той же совокупности, дадут разные значения рассматриваемой статистики, т.е. выборочное среднее. Стандартная ошибка (SE) представляет собой стандартное отклонение различных значений выборочного среднего. Он используется для сравнения выборочных средних по совокупности.
Короче говоря, стандартная ошибка статистики — это не что иное, как стандартное отклонение ее выборочного распределения. Он играет большую роль в проверке статистических гипотез и интервальной оценке. Это дает представление о точности и достоверности сметы. Чем меньше стандартная ошибка, тем больше однородность теоретического распределения и наоборот.
- Формула: Стандартная ошибка для выборочного среднего = σ / √n
Где, σ — стандартное отклонение совокупности
Ключевые различия между стандартным отклонением и стандартной ошибкой
Приведенные ниже моменты существенны с точки зрения разницы между стандартным отклонением:
- Стандартное отклонение — это мера, которая оценивает степень вариации набора наблюдений. Стандартная ошибка измеряет точность оценки, т. Е. Является мерой изменчивости теоретического распределения статистики.
- Стандартное отклонение — это описательная статистика, тогда как стандартная ошибка — это выводимая статистика.
- Стандартное отклонение измеряет, насколько отдельные значения отличаются от среднего значения. Напротив, насколько близко среднее значение выборки к среднему значению генеральной совокупности.
- Стандартное отклонение — это распределение наблюдений относительно нормальной кривой. В отличие от этого, стандартная ошибка — это распределение оценки относительно нормальной кривой.
- Стандартное отклонение определяется как квадратный корень из дисперсии. И наоборот, стандартная ошибка описывается как стандартное отклонение, деленное на квадратный корень из размера выборки.
- Когда размер выборки увеличивается, это дает более конкретную меру стандартного отклонения. В отличие от стандартной ошибки, когда размер выборки увеличивается, стандартная ошибка имеет тенденцию к уменьшению.
Вывод
В целом стандартное отклонение считается одним из лучших показателей дисперсии, который измеряет отклонение значений от центрального значения. С другой стороны, стандартная ошибка в основном используется для проверки надежности и точности оценки, поэтому чем меньше ошибка, тем выше ее надежность и точность.
Термин «статистика» означает практику анализа и сбора числовых данных, которые предоставляются в больших количествах. Есть несколько статистических исследований, в том числе биология, финансы, психология, инженерия и многие другие.
Статистические исследования полезны для сбора и анализа любых данных в числовой форме.
Стандартное отклонение и стандартная ошибка являются двумя наиболее распространенными показателями, которые используются в области статистики. Основной мотив стандартного отклонения и стандартной ошибки — показать результаты статистического анализа и характеристики выборочных данных.
Стандартное отклонение и стандартная ошибка немного сбивают с толку, но они отличаются друг от друга во многих терминах.
Основные выводы
- Стандартное отклонение измеряет разброс точек данных вокруг среднего значения, а стандартная ошибка оценивает изменчивость среднего значения выборки.
- Чем больше размер выборки, тем меньше стандартная ошибка, но размер выборки не влияет на стандартное отклонение.
- Стандартное отклонение подходит для анализа отдельных точек данных, а стандартная ошибка используется для оценки точности выборочных средних.
Стандартное отклонение против стандартной ошибки
Разница между стандартным отклонением и стандартной ошибкой заключается в том, что они оба различаются по своим статистическим помехам. Стандартное отклонение помогает рассредоточить отдельные значения данных. Он показывает точность среднего значения, которое представляет выборочные данные. В то время как стандартная ошибка основана на статистических помехах данных выборки.
Хотите сохранить эту статью на потом? Нажмите на сердечко в правом нижнем углу, чтобы сохранить в свой собственный блок статей!
В статистике стандартное отклонение выражает количество членов определенной группы, которое отличается от значения среднего значения той же группы. Карл Пирсон был первым, кто использовал стандартное отклонение в письменной форме для своих лекций.
Этот термин был впервые использован в 1894 году. Термин «стандартное отклонение» использовался для замены альтернативных названий, использовавшихся ранее для тех же идей.
В статистике стандартная ошибка называется приблизительным стандартным отклонением, которое включается в статистическую выборку. Вариация, включенная в стандартную ошибку, находится между средним значением, рассчитанным на основе совокупности, и другим точным значением, которое принято.
Если расчет среднего включает больше точек данных, то стандартная ошибка будет меньше.
Сравнительная таблица
| Параметры сравнения | Стандартное отклонение | Стандартная ошибка |
|---|---|---|
| Смысл | Мера дисперсии от среднего по набору данных. | Мера оценки посредством ее статистической точности. |
| Обозначает изменчивость | В пределах выборки. | В популяции, среди нескольких выборок. |
| Тип | Описательная статистика. | Выведенный статистика. |
| Распределение | Наблюдение касается нормальной кривой. | Оценка связана с нормальной кривой. |
| Расчет | Путем извлечения квадратного корня из дисперсии. | Деление стандартного отклонения на квадратный корень из размера выборки. |
Что такое стандартное отклонение?
Вариация указывает на отклонение значений, находящихся в среднем. В результате степень вариации обозначается мерами вариации. Что касается показателей вариации, стандартное отклонение является одним из наиболее распространенных показателей.
Для удобного математического анализа люди предпочитают стандартное отклонение, поскольку оно полностью основано на всех значениях, будь то самое высокое или самое низкое.
Стандартное отклонение называется мерой отклонения от среднего по набору данных. Его основной мотив — измерить абсолютную изменчивость любого распределения.
Если дисперсия или изменчивость выше, стандартное отклонение слишком велико. В результате величина отклонения также будет больше. Стандартное отклонение обозначается σ (сигма).
Когда дело доходит до финансовых условий, стандартное отклонение используется в таких сделках, как взаимные фонды, акции и другие. Стандартное отклонение используется для измерения рисков, связанных с инвестиционным инструментом.
Это полезно для инвесторов, потому что дает им математическую основу для принятия решений на финансовом рынке для своих инвестиций.
Стандартное отклонение можно рассчитать с помощью программного обеспечения, используемого для статистического анализа, а также вручную. Для окончательного результата вам нужно пройти несколько шагов, например найти среднее значение, а затем найти отклонение каждой оценки.
Далее квадратное отклонение и находим сумму квадратов. Затем перейдите к дисперсии и найдите ее, а затем найдите из нее квадратный корень.
Что такое стандартная ошибка?
В математике стандартная ошибка используется для измерения изменчивости статистики. SE — это его сокращенная форма. Это помогает сделать приближение стандартной ошибки в данной выборке.
Он оценивает точность, согласованность и эффективность выборки, или можно сказать, что он измеряет, как представить распределение выборки, точно представляющее совокупность.
Среднее или среднее значение рассчитывается при наличии выборочной совокупности. Стандартная ошибка помогает компенсировать любые случайные неточности, связанные со сбором образцов.
Когда собирается несколько выборок, это создает разницу между переменными, поскольку среднее значение каждой выборки немного отличается друг от друга. Разница рассчитывается как стандартная ошибка.
Стандартная ошибка полезна как в статистике, так и в экономике. Когда дело доходит до финансовых терминов, это полезно в области, связанной с эконометрикой. В этом исследователь использует стандартную ошибку для выполнения гипотеза тестирование и регрессионный анализ.
Тогда как в выведенный статистика Стандартная ошибка является основой для создания доверия интер.
Стандартная ошибка рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки. Если в расчете среднего значения больше точек данных, стандартная ошибка будет меньше.
В результате данные будут более репрезентативными для истинного среднего значения. Если в данных обнаружены заметные несоответствия, это означает, что стандартная ошибка велика.
Основные различия между стандартным отклонением и стандартной ошибкой
- Стандартное отклонение не зависит от случайной выборки, потому что это типичное отклонение от среднего. Но стандартная ошибка зависит от случайной выборки, потому что от ожидаемого значения это типичное отклонение.
- Что касается увеличения размера выборки, стандартное отклонение дает его конкретную меру. С другой стороны, в стандартной ошибке она уменьшается.
- Стандартное отклонение упоминается как выборочная статистика, поскольку его статистика включает значения, полученные из выборки. В то время как стандартная ошибка упоминается как параметр совокупности, в котором параметр является значением и описывает всю совокупность.
- Стандартное отклонение измеряет количество наблюдений, которые отличаются друг от друга, тогда как стандартная ошибка измеряет точность среднего значения выборки до Средняя численность населения.
- Когда дело доходит до расчета доверительного интервала, связанного с генеральной совокупностью, стандартное отклонение не рассчитывается через него. С другой стороны, стандартная ошибка делает это.
Рекомендации
- https://www.sciencedirect.com/science/article/pii/S0022103113000668
- https://www.jstor.org/stable/2729411
Эмма Смит имеет степень магистра английского языка в колледже Ирвин-Вэлли. Она работает журналистом с 2002 года, пишет статьи об английском языке, спорте и праве. Подробнее обо мне на ней био страница.