В данной главе мы изучим инструмент, который позволяет анализировать ошибку алгоритма в зависимости от некоторого набора факторов, влияющих на итоговое качество его работы. Этот инструмент в литературе называется bias-variance decomposition — разложение ошибки на смещение и разброс. В разложении, на самом деле, есть и третья компонента — случайный шум в данных, но ему не посчастливилось оказаться в названии. Данное разложение оказывается полезным в некоторых теоретических исследованиях работы моделей машинного обучения, в частности, при анализе свойств ансамблевых моделей.
Некоторые картинки в тексте кликабельны. Это означает, что они были заимствованы из какого-то источника и при клике вы сможете перейти к этому источнику.
Вывод разложения bias-variance для MSE
Рассмотрим задачу регрессии с квадратичной функцией потерь. Представим также для простоты, что целевая переменная $y$ — одномерная и выражается через переменную $x$ как:
$$
y = f(x) + varepsilon,
$$
где $f$ — некоторая детерминированная функция, а $varepsilon$ — случайный шум со следующими свойствами:
$$
mathbb{E} varepsilon = 0, , mathbb{V}text{ar} varepsilon = mathbb{E} varepsilon^2 = sigma^2.
$$
В зависимости от природы данных, которые описывает эта зависимость, её представление в виде точной $f(x)$ и случайной $varepsilon$ может быть продиктовано тем, что:
-
данные на самом деле имеют случайный характер;
-
измерительный прибор не может зафиксировать целевую переменную абсолютно точно;
-
имеющихся признаков недостаточно, чтобы исчерпывающим образом описать объект, пользователя или событие.
Функция потерь на одном объекте $x$ равна
$$
MSE = (y(x) — a(x))^2
$$
Однако знание значения MSE только на одном объекте не может дать нам общего понимания того, насколько хорошо работает наш алгоритм. Какие факторы мы бы хотели учесть при оценке качества алгоритма? Например, то, что выход алгоритма на объекте $x$ зависит не только от самого этого объекта, но и от выборки $X$, на которой алгоритм обучался:
$$
X = ((x_1, y_1), ldots, (x_ell, y_ell))
$$
$$
a(x) = a(x, X)
$$
Кроме того, значение $y$ на объекте $x$ зависит не только от $x$, но и от реализации шума в этой точке:
$$
y(x) = y(x, varepsilon)
$$
Наконец, измерять качество мы бы хотели на тестовых объектах $x$ — тех, которые не встречались в обучающей выборке, а тестовых объектов у нас в большинстве случаев более одного. При включении всех вышеперечисленных источников случайности в рассмотрение логичной оценкой качества алгоритма $a$ кажется следующая величина:
$$
Q(a) = mathbb{E}_x mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2
$$
Внутреннее матожидание позволяет оценить качество работы алгоритма в одной тестовой точке $x$ в зависимости от всевозможных реализаций $X$ и $varepsilon$, а внешнее матожидание усредняет это качество по всем тестовым точкам.
Замечание. Запись $mathbb{E}_{X, varepsilon}$ в общем случае обозначает взятие матожидания по совместному распределению $X$ и $varepsilon$. Однако, поскольку $X$ и $varepsilon$ независимы, она равносильна последовательному взятию матожиданий по каждой из переменных: $mathbb{E}_{X, varepsilon} = mathbb{E}_{X} mathbb{E}_{varepsilon}$, но последний вариант выглядит несколько более громоздко.
Попробуем представить выражение для $Q(a)$ в более удобном для анализа виде. Начнём с внутреннего матожидания:
$$
mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2 = mathbb{E}_{X, varepsilon}[f(x) + varepsilon — a(x, X)]^2 =
$$
$$
= mathbb{E}_{X, varepsilon} [ underbrace{(f(x) — a(x, X))^2}_{text{не зависит от $varepsilon$}} +
underbrace{2 varepsilon cdot (f(x) — a(x, X))}_{text{множители независимы}} + varepsilon^2 ] =
$$
$$
= mathbb{E}_X left[
(f(x) — a(x, X))^2
right] + 2 underbrace{mathbb{E}_varepsilon[varepsilon]}_{=0} cdot mathbb{E}_X (f(x) — a(x, X)) + mathbb{E}_varepsilon varepsilon^2 =
$$
$$
= mathbb{E}_X left[ (f(x) — a(x, X))^2 right] + sigma^2
$$
Из общего выражения для $Q(a)$ выделилась шумовая компонента $sigma^2$. Продолжим преобразования:
$$
mathbb{E}_X left[ (f(x) — a(x, X))^2 right] = mathbb{E}_X left[
(f(x) — mathbb{E}_X[a(x, X)] + mathbb{E}_X[a(x, X)] — a(x, X))^2
right] =
$$
$$
= mathbb{E}_Xunderbrace{left[
(f(x) — mathbb{E}_X[a(x, X)])^2
right]}_{text{не зависит от $X$}} + underbrace{mathbb{E}_X left[ (a(x, X) — mathbb{E}_X[a(x, X)])^2 right]}_{text{$=mathbb{V}text{ar}_X[a(x, X)]$}} +
$$
$$
+ 2 mathbb{E}_X[underbrace{(f(x) — mathbb{E}_X[a(x, X)])}_{text{не зависит от $X$}} cdot (mathbb{E}_X[a(x, X)] — a(x, X))] =
$$
$$
= (underbrace{f(x) — mathbb{E}_X[a(x, X)]}_{text{bias}_X a(x, X)})^2 + mathbb{V}text{ar}_X[a(x, X)] + 2 (f(x) — mathbb{E}_X[a(x, X)]) cdot underbrace{(mathbb{E}_X[a(x, X)] — mathbb{E}_X [a(x, X)])}_{=0} =
$$
$$
= text{bias}_X^2 a(x, X)+ mathbb{V}text{ar}_X[a(x, X)]
$$
Таким образом, итоговое выражение для $Q(a)$ примет вид
$$
Q(a) = mathbb{E}_x mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2 = mathbb{E}_x text{bias}_X^2 a(x, X) + mathbb{E}_x mathbb{V}text{ar}_X[a(x, X)] + sigma^2,
$$
где
$$
text{bias}_X a(x, X) = f(x) — mathbb{E}_X[a(x, X)]
$$
— смещение предсказания алгоритма в точке $x$, усреднённого по всем возможным обучающим выборкам, относительно истинной зависимости $f$;
$$
mathbb{V}text{ar}_X[a(x, X)] = mathbb{E}_X left[ a(x, X) — mathbb{E}_X[a(x, X)] right]^2
$$
— дисперсия (разброс) предсказаний алгоритма в зависимости от обучающей выборки $X$;
$$
sigma^2 = mathbb{E}_x mathbb{E}_varepsilon[y(x, varepsilon) — f(x)]^2
$$
— неустранимый шум в данных.
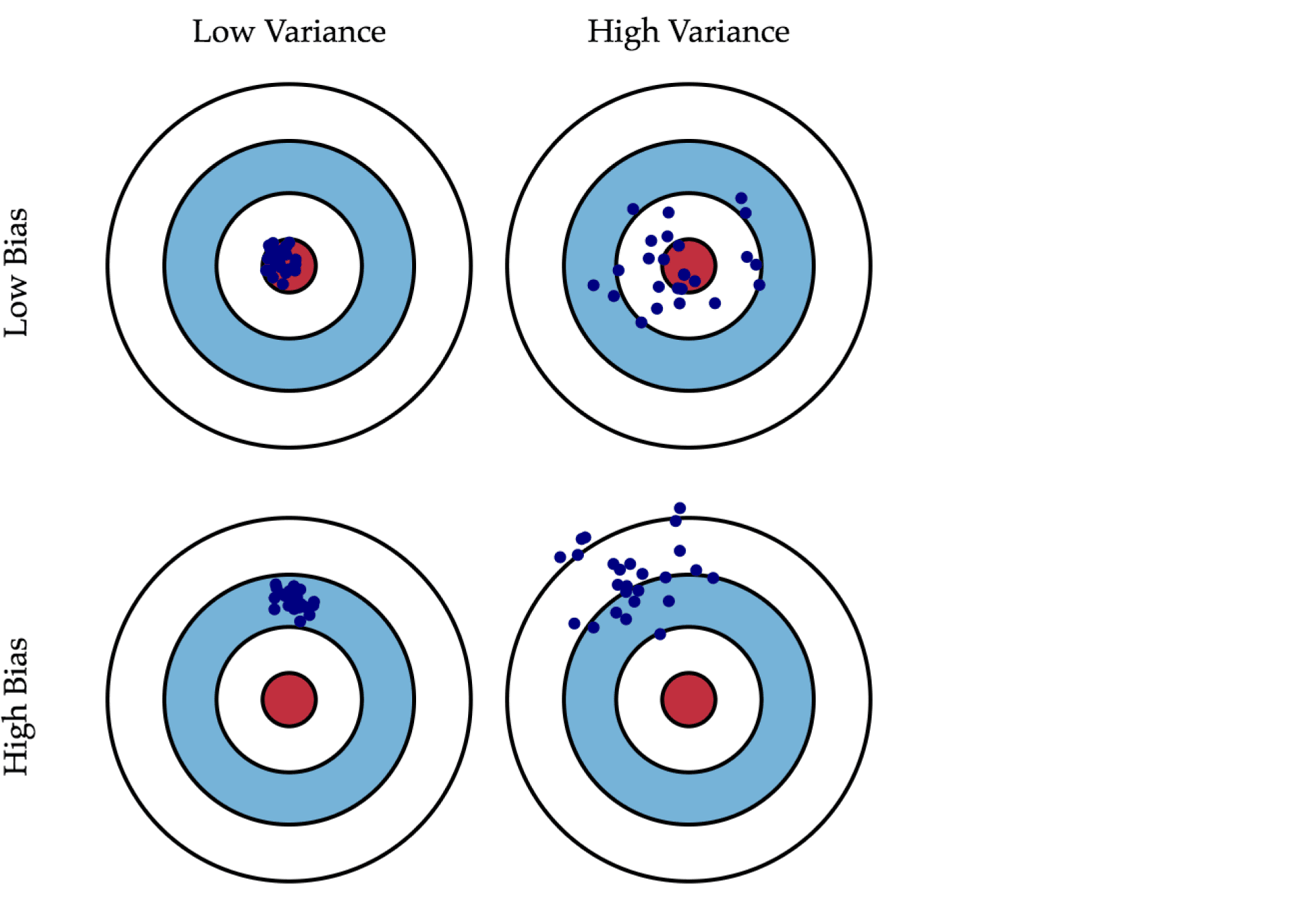
Смещение показывает, насколько хорошо с помощью данного алгоритма можно приблизить истинную зависимость $f$, а разброс характеризует чувствительность алгоритма к изменениям в обучающей выборке. Например, деревья маленькой глубины будут в большинстве случаев иметь высокое смещение и низкий разброс предсказаний, так как они не могут слишком хорошо запомнить обучающую выборку. А глубокие деревья, наоборот, могут безошибочно выучить обучающую выборку и потому будут иметь высокий разброс в зависимости от выборки, однако их предсказания в среднем будут точнее. На рисунке ниже приведены возможные случаи сочетания смещения и разброса для разных моделей:
Синяя точка соответствует модели, обученной на некоторой обучающей выборке, а всего синих точек столько, сколько было обучающих выборок. Красный круг в центре области представляет ближайшую окрестность целевого значения. Большое смещение соответствует тому, что модели в среднем не попадают в цель, а при большом разбросе модели могут как делать точные предсказания, так и довольно сильно ошибаться.
Полученное нами разложение ошибки на три компоненты верно только для квадратичной функции потерь. Для других функций потерь существуют более общие формы этого разложения (Domigos, 2000, James, 2003) с похожими по смыслу компонентами. Это позволяет предполагать, что для большинства основных функций потерь имеется некоторое представление в виде смещения, разброса и шума (хоть и, возможно, не в столь простой аддитивной форме).
Пример расчёта оценок bias и variance
Попробуем вычислить разложение на смещение и разброс на каком-нибудь практическом примере. Наши обучающие и тестовые примеры будут состоять из зашумлённых значений целевой функции $f(x)$, где $f(x)$ определяется как
$$
f(x) = x sin x
$$
В качестве шума добавляется нормальный шум с нулевым средним и дисперсией $sigma^2$, равной во всех дальнейших примерах 9. Такое большое значение шума задано для того, чтобы задача была достаточно сложной для классификатора, который будет на этих данных учиться и тестироваться. Пример семпла из таких данных:
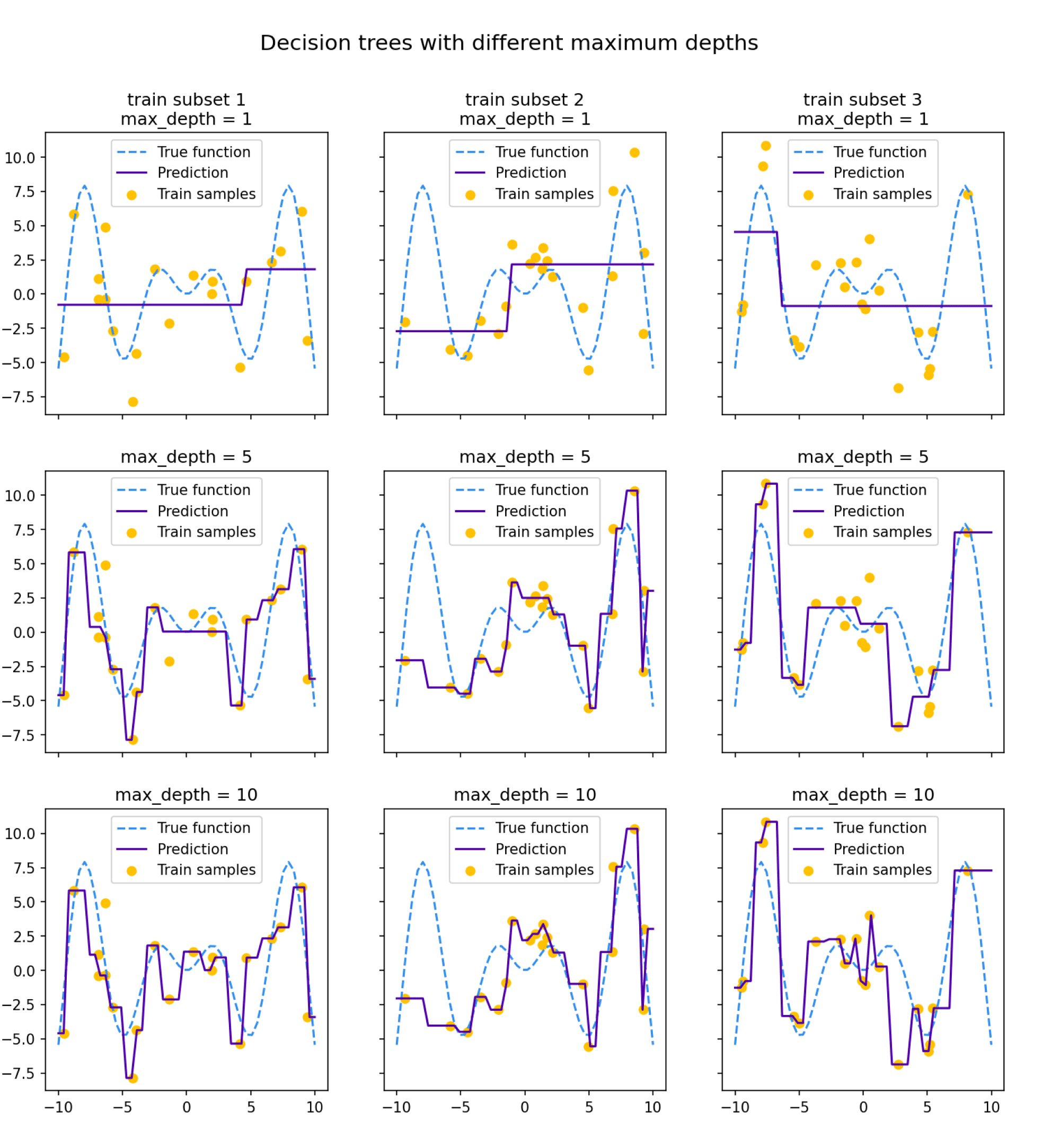
Посмотрим на то, как предсказания деревьев зависят от обучающих подмножеств и максимальной глубины дерева. На рисунке ниже изображены предсказания деревьев разной глубины, обученных на трёх независимых подвыборках размера 20 (каждая колонка соответствует одному подмножеству):
Глядя на эти рисунки, можно выдвинуть гипотезу о том, что с увеличением глубины дерева смещение алгоритма падает, а разброс в зависимости от выборки растёт. Проверим, так ли это, вычислив компоненты разложения для деревьев со значениями глубины от 1 до 15.
Для обучения деревьев насемплируем 1000 случайных подмножеств $X_{train} = (x_{train}, y_{train})$ размера 500, а для тестирования зафиксируем случайное тестовое подмножество точек $x_{test}$ также размера 500. Чтобы вычислить матожидание по $varepsilon$, нам нужно несколько экземпляров шума $varepsilon$ для тестовых лейблов:
$$
y_{test} = y(x_{test}, hat varepsilon) = f(x_{test}) + hat varepsilon
$$
Положим количество семплов случайного шума равным 300. Для фиксированных $X_{train} = (x_{train}, y_{train})$ и $X_{test} = (x_{test}, y_{test})$ квадратичная ошибка вычисляется как
$$
MSE = (y_{test} — a(x_{test}, X_{train}))^2
$$
Взяв среднее от $MSE$ по $X_{train}$, $x_{test}$ и $varepsilon$, мы получим оценку для $Q(a)$, а оценки для компонент ошибки мы можем вычислить по ранее выведенным формулам.
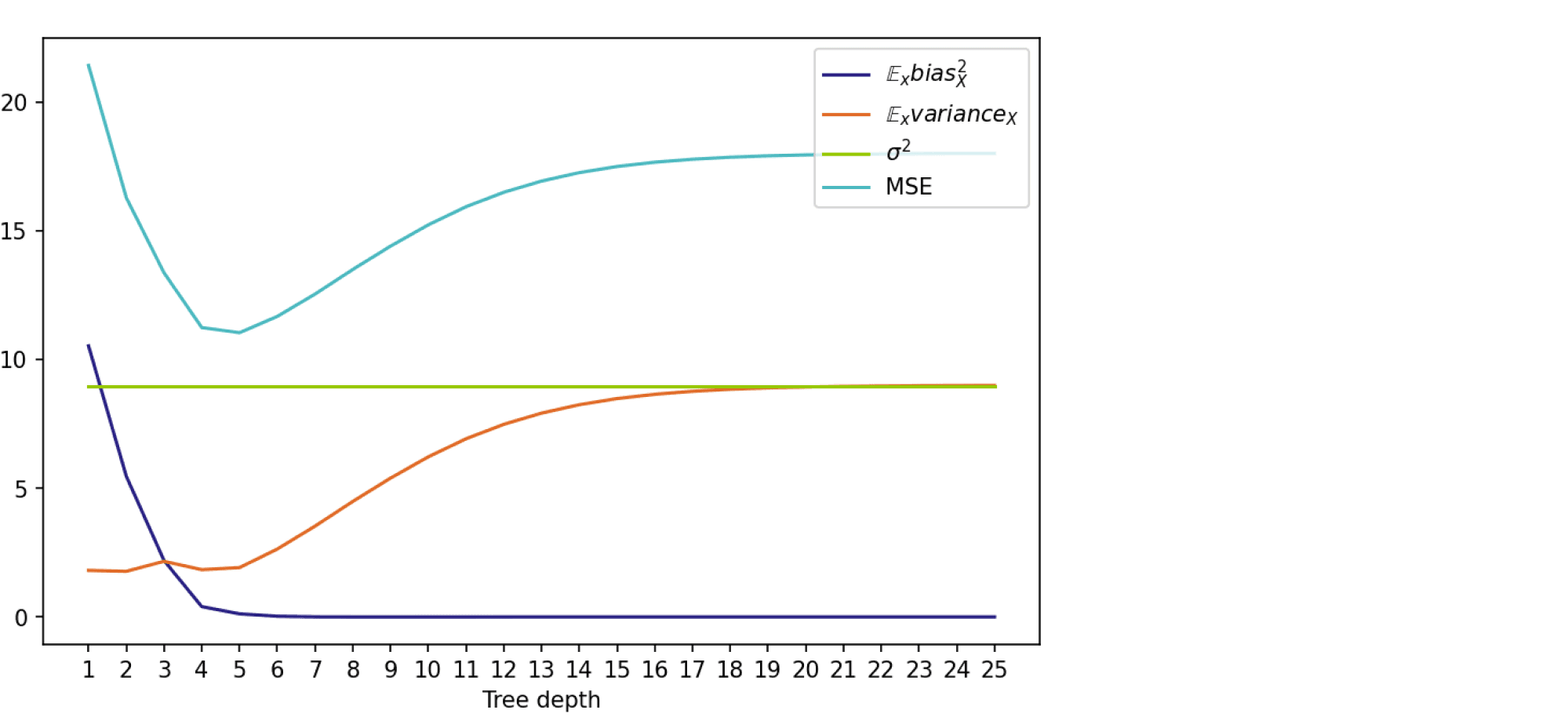
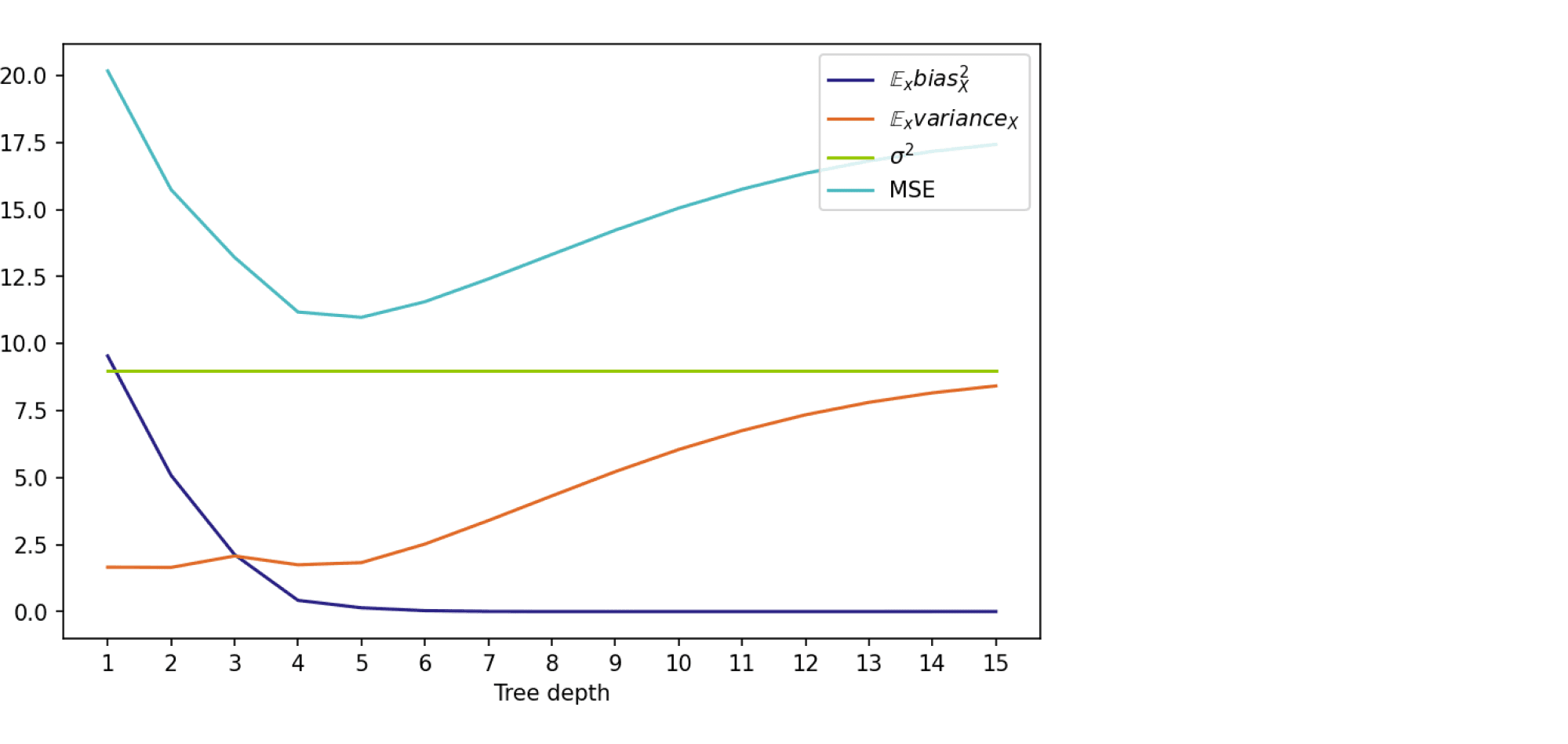
На графике ниже изображены компоненты ошибки и она сама в зависимости от глубины дерева:
По графику видно, что гипотеза о падении смещения и росте разброса при увеличении глубины подтверждается для рассматриваемого отрезка возможных значений глубины дерева. Правда, если нарисовать график до глубины 25, можно увидеть, что разброс становится равен дисперсии случайного шума. То есть деревья слишком большой глубины начинают идеально подстраиваться под зашумлённую обучающую выборку и теряют способность к обобщению:
Код для подсчёта разложения на смещение и разброс, а также код отрисовки картинок можно найти в данном ноутбуке.
Bias-variance trade-off: в каких ситуациях он применим
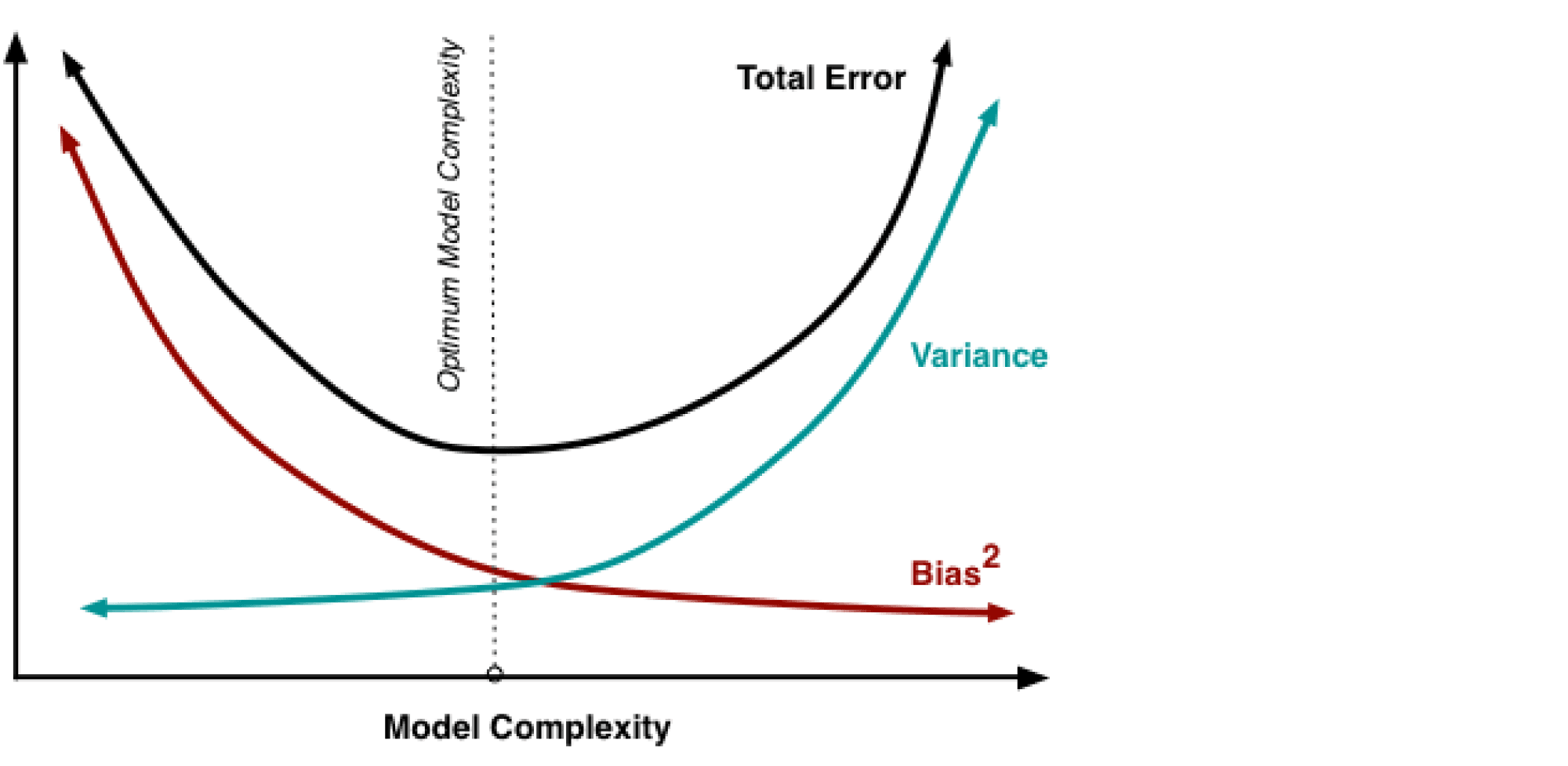
В книжках и различных интернет-ресурсах часто можно увидеть следующую картинку:
Она иллюстрирует утверждение, которое в литературе называется bias-variance trade-off: чем выше сложность обучаемой модели, тем меньше её смещение и тем больше разброс, и поэтому общая ошибка на тестовой выборке имеет вид $U$-образной кривой. С падением смещения модель всё лучше запоминает обучающую выборку, поэтому слишком сложная модель будет иметь нулевую ошибку на тренировочных данных и большую ошибку на тесте. Этот график призван показать, что существует оптимальная сложность модели, при которой соблюдается баланс между переобучением и недообучением и ошибка при этом минимальна.
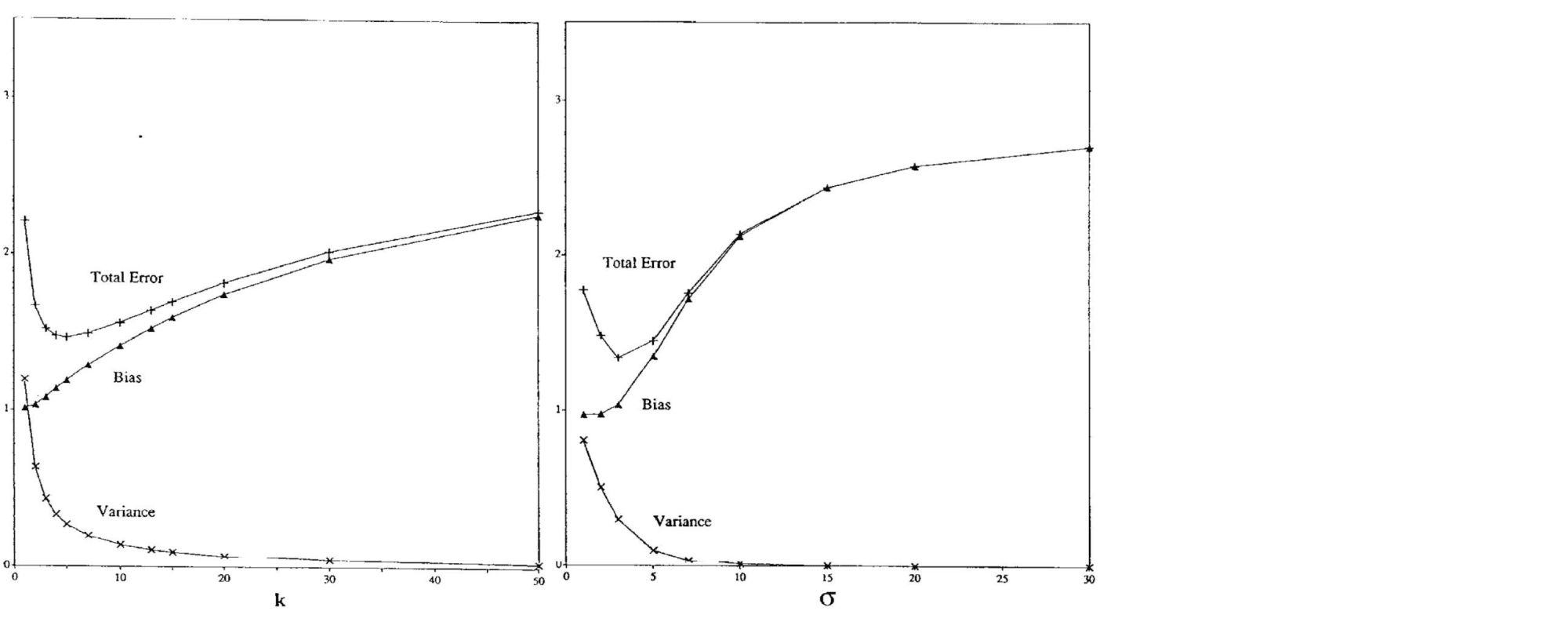
Существует достаточное количество подтверждений bias-variance trade-off для непараметрических моделей. Например, его можно наблюдать для метода $k$ ближайших соседей при росте $k$ и для ядерной регрессии при увеличении ширины окна $sigma$ (Geman et al., 1992):
Чем больше соседей учитывает $k$-NN, тем менее изменчивым становится его предсказание, и аналогично для ядерной регрессии, из-за чего сложность этих моделей в некотором смысле убывает с ростом $k$ и $sigma$. Поэтому традиционный график bias-variance trade-off здесь симметрично отражён по оси $x$.
Однако, как показывают последние исследования, непременное возрастание разброса при убывании смещения не является абсолютно истинным предположением. Например, для нейронных сетей с ростом их сложности может происходить снижение и разброса, и смещения. Одна из наиболее известных статей на эту тему — статья Белкина и др. (Belkin et al., 2019), в которой, в частности, была предложена следующая иллюстрация:
Слева — классический bias-variance trade-off: убывающая часть кривой соответствует недообученной модели, а возрастающая — переобученной. А на правой картинке — график, называемый в статье double descent risk curve. На нём изображена эмпирически наблюдаемая авторами зависимость тестовой ошибки нейросетей от мощности множества входящих в них параметров ($mathcal H$). Этот график разделён на две части пунктирной линией, которую авторы называют interpolation threshold. Эта линия соответствует точке, в которой в нейросети стало достаточно параметров, чтобы без особых усилий почти идеально запомнить всю обучающую выборку. Часть до достижения interpolation threshold соответствует «классическому» режиму обучения моделей: когда у модели недостаточно параметров, чтобы сохранить обобщающую способность при почти полном запоминании обучающей выборки. А часть после достижения interpolation threshold соответствует «современным» возможностям обучения моделей с огромным числом параметров. На этой части графика ошибка монотонно убывает с ростом количества параметров у нейросети. Авторы также наблюдают похожее поведение и для «древесных» моделей: Random Forest и бустинга над решающими деревьями. Для них эффект проявляется при одновременном росте глубины и числа входящих в ансамбль деревьев.
В качестве вывода к этому разделу хочется сформулировать два основных тезиса:
- Bias-variance trade-off нельзя считать непреложной истиной, выполняющейся для всех моделей и обучающих данных.
- Разложение на смещение и разброс не влечёт немедленного выполнения bias-variance trade-off и остаётся верным и для случая, когда все компоненты ошибки (кроме неустранимого шума) убывают одновременно. Этот факт может оказаться незамеченным из-за того, что в учебных пособиях часто разговор о разложении дополняется иллюстрацией с $U$-образной кривой, благодаря чему в сознании эти два факта могут слиться в один.
Список литературы
- Блог-пост про bias-variance от Йоргоса Папахристудиса
- Блог-пост про bias-variance от Скотта Фортмана-Роу
- Статьи от Домингоса (2000) и Джеймса (2003) про обобщённые формы bias-variance decomposition
- Блог-пост от Брейди Нила про необходимость пересмотра традиционного взгляда на bias-variance trade-off
- Статья Гемана и др. (1992), в которой была впервые предложена концепция bias-variance trade-off
- Статья Белкина и др. (2019), в которой был предложен double-descent curve
Сегодня дадим немного объяснений стандартных для машинного обучения понятий: смещение, разброс, переобучение и недообучение. Как всегда, всё объясним просто (но нужна будет математическая подготовка), на картинках, с примерами (в данном случае на модельных задачах). Все рисунки и эксперименты авторские, в конце, по традиции, изюминка – в чём при объяснении этих понятий Вас обманывают на курсах по ML и в учебниках;)
Ниже обсудим несколько фундаментальных понятий машинного обучения. Первое – переобучение (overfitting) – явление, когда ошибка на тестовой выборке заметно больше ошибки на обучающей. Это главная проблема машинного обучения: если бы такого эффекта не было (ошибка на тесте примерно совпадала с ошибкой на обучении), то всё обучение сводилось бы к минимизации ошибки на тесте (т.н. эмпирическому риску).
Второе – недообучение (underfitting) – явление, когда ошибка на обучающей выборке достаточно большая, часто говорят «не удаётся настроиться на выборку». Такой странный термин объясняется тем, что недообучение при настройке алгоритмов итерационными методами (например, нейронных сетей методом обратного распространения) можно наблюдать, когда сделано слишком маленькое число итераций, т.е. «не успели обучиться».
Третье – сложность (complexity) модели алгоритмов (допускает множество формализаций) – оценивает, насколько разнообразно семейство алгоритмов в модели с точки зрения их функциональных свойств (например, способности настраиваться на выборки). Повышение сложности (т.е. использование более сложных моделей) решает проблему недообучения и вызывает переобучение.
Сначала опишем на примере, как проявляется проблема выбора сложности и почему возникает переобучение. Для начала рассмотрим задачу регрессии. Для простоты будем считать, что это регрессия от одного признака x. Целевая зависимость y(x) известна в конечном наборе точек. На рис. 1 показана выборка для зависимости вида y = sin(4x) + шум, на рис. 2 для зашумлённой пороговой зависимости.
На рисунках показаны также решения указанных задач полиномиальной регрессией с разными степенями полиномов. Видно, что в обеих задачах полином первой степени явно плохо подходит для описания целевой зависимости, второй – достаточно хорошо её описывает, хотя ошибки есть и на обучающей выборке, седьмой – идеально проходит через точки обучающей выборки, но совсем не похож на «естественную функцию» и существенно отклоняется от целевой зависимости в остальных точках.
Если попробовать решить задачу полиномами различной степени, то мы получим рис. 3 (он построен для первой задачи, но во второй картина аналогичная). Видно, что с увеличением степени ошибка на обучающей выборке падает, а на тестовой (мы взяли очень мелкую сетку отрезка [0, 1]) – сначала падает, потом возрастает.
Попробуем разобраться, в чём дело с теоретической точки зрения (сейчас немного математики). Наша целевая зависимость имеет вид
Мы строим алгоритм (в нашем случае полином фиксированной степени) a=a(x), посмотрим чему равно математическое ожидание квадрата отклонения ответа алгоритма от истинного значения:
Здесь важно понимать, как берутся матожидания (т.е., по сути, интегрирования) в приведённых выше формулах. Мы считаем, что обучающая выборка выбирается случайно из некоторого распределения, настроенный алгоритм тоже случаен, поскольку зависит от выборки, настройка алгоритма также может быть стохастической. Таким образом, матожидание берётся по всем данным (обучающим выборкам) и настройкам алгоритма, а сами формулы записываются в конкретной точке x:
При желании, можно проинтегрировать полученные формулы и по всем объектам (точнее, по какому-то распределению всех объектов) и получить уже смещение и разброс модели алгоритмов как таковой.
Разбросом (variance) мы назвали дисперсию ответов алгоритмов Da, а смещением (bias) – матожидание разности между истинным ответом и выданным алгоритмом: E(f – a). Мы получили, что ошибка раскладывается на три составляющие. Первая связана с шумом в самих данных, а вот две остальные связаны с используемой моделью алгоритмов. Понятно, что разброс характеризует разнообразие алгоритмов (из-за случайности обучающей выборки, в том числе шума, и стохастической природы настройки), а смещение – способность модели алгоритмов настраиваться на целевую зависимость. Проиллюстрируем это. На рис. 4-5 – показаны различные полиномы первой степени, они настроены на разных обучающих выборках. В точке x=0.5 ответы алгоритмов являются случайными величинами, они немного «разбросаны» (есть variance), а также они сильно смещены (есть bias) относительно правильного ответа (который, кстати, даже если нам и известен, то с точностью до шума).
На рис. 6-7 изображены уже полиномы второй степени (настроенные на тех же выборках). В точке x=0.5 у них сильно меньше смещение и чуть меньше разброс. Видно, что они совсем неплохо описывают целевую зависимость во всех точках.
Часто разброс и смещение иллюстрируют такими картинками – рис. 8. Если провести аналогию, что алгоритм – это игрок в дартс, то самый лучший игрок будет иметь небольшое смещение и разброс – его дротики ложатся кучно «в яблочко», если у игрока большое смешение, то они сгруппированы около другой точки, а если большой разброс, то они ложатся совсем не кучно. Эта аналогия понятна, но может сбить с толку. Например, известно, что спортсменов учат стрелять кучно, поскольку нужного смещения легко добиться (например, целясь повыше). С алгоритмами машинного обучения всё сложнее. Смещение нельзя просто «подвинуть», приходится переходить к другой (например, более сложной модели), а у неё может быть уже другой разброс.
Ещё важный момент: спортсмен может повысить точность целясь выше/ниже/правее/левее, а для алгоритма нет таких понятий. Напомним, что разброс и смещение мы вводили в конкретной точке. Если изменить смещение в этой точке, то модель будет по-новому вести себя и в остальных. Если же усреднить смещение, точнее его квадрат, по всем точкам, то мы получим просто число (оно не указывает, как менять модель, чтобы уменьшить ошибку).
Теперь рассмотрим самую частую иллюстрацию, которую приводят при объяснении разброса и смещения, см. рис. 9. Она полностью согласуется с рис. 3. При увеличении сложности модели (например, степени полинома) ошибка на независимом контроле сначала падает, потом начинает увеличиваться. Обычно это связывают с уменьшением смещения (в сложных моделях очень много алгоритмов, поэтому наверняка найдутся те, которые хорошо описывают целевую зависимость) и увеличением разброса (в сложных моделях больше алгоритмов, а следовательно, и больше разброс).
Для простых моделей характерно недообучение (они слишком простые, не могут описать целевую зависимость и имеют большое смещение), для сложных – переобучение (алгоритмов в модели слишком много, при настройке мы выбираем ту, которая хорошо описывает обучающую выборку, но из-за сильного разброса она может допускать большую ошибку на тесте). Теперь рассмотрим задачу классификации. Отметим, что для неё тоже есть результат о разложении ошибки на шум, разброс и смещение. На рис. 10-12 показаны результаты экспериментов в задаче с двумя классами (стандартная задача «два полумесяца») и моделью k ближайших соседей (kNN) при разных k. Результат также согласуется с рис. 9, если учесть, что изображена точность, а не ошибка, и сложность алгоритма ~ 1/k. Возникает вопрос, а почему так вводится сложность для kNN? Ведь при разных k эти алгоритмы Всё очень просто: часто сложность как раз и логично формализовать как 1/variance. На рис. 11 показаны разделяющие поверхности метода 1NN для разных выборок, которые описывают одну и ту же целевую зависимость. Они очень сильно отличаются друг от друга. А разделяющие поверхности kNN при больших k, см. рис 12, различаются существенно меньше. И чем выше k, тем стабильней результат. В этом смысле это очень простые алгоритмы: то, как они разделяют классы, меньше зависит от исходных данных, т.е. по определению ответ алгоритма 9NN в каждой точке зависит от 9и ближайших соседей, а по факту он практически не меняется от выборки к выборке (при варьировании обучения). Теперь покажем, в чём не правы стандартные учебники и учебные курсы по машинному обучению. Проведём эксперименты по оцениванию разброса и смещения в модельных задачах. На рис. 13-14 приведены результаты для задачи с целевой зависимостью «ступенька», а на рис. 15-16 для задачи с целевой зависимостью «sin(4x)». Очевидно, что степень полинома – очень естественная мера сложности для полиномиальной регрессии. Но полученные рисунки немного отличаются от рис. 9: Почему так происходит? Одна их причин в том, что «сложность модели», если мы хотим видеть красивые графики монотонных и унимодальных функций, правильнее определять для конкретных данных! Например, ступенчатая функция нечётная (с точностью до смещения) и для восстановления такой целевой зависимости лучше подходят полиномы с нечётной старшей степенью. Кстати, если использовать полиномиальную регрессию с L2-регуляризацией, то на рис. 16 смещение начинает вести себя «по классике»: убывать при увеличении степени полинома. П.С. Дальше возникают естественные вопросы: как найти оптимальную сложность модели, как решать задачу сложными моделями и не переобучаться (используют же нейросети). Но это тема для отдельного поста… Просьба к читателям – давать отклики в комментариях. Этот материал будет использован, в том числе, в рамках нового курса на ВМК МГУ, а также в книжке, которую автор уже и не надеется закончить… Поэтому любые замечания по формулировкам, корректности выводов и т.п. будут полезны. Удачи!
Пусть 




— квадрат смещения.
— разброс.
— неустранимый шум.
Более короткая запись:

Доказательство[]
Подробно доказательство проводится тут
Bias-Variance decomposition c усреднением по всем объектам[]
Более подробно почитать про это можно тут
Связь Bias-Variance decomposition и алгоритмов обучения[]
Смещение алгоритма показывает, насколько хорошо алгоритм приближает реальную зависимость между данными и откликами. Разбор показывает, насколько сильно может меняться ответ в зависимости от выборки, то есть насколько сильно изменится алгоритм при изменениях в выборке.
Алгоритмы с маленьким смещением — как правило, сложные алгоритмы, например, решающее дерево.
Алгоритмы с большим смещением — как правило, простые алгоритмы, например, линейные классификаторы.
Алгоритмы с маленькой дисперсией — как правило, простые алгоритмы.
Алгоритмы с большой дисперсией — как правило, сложные алгоритмы.
Также, высокая дисперсия показывает то, что алгоритм, скорее всего переобучен, а высокое смещение — что недообучен.
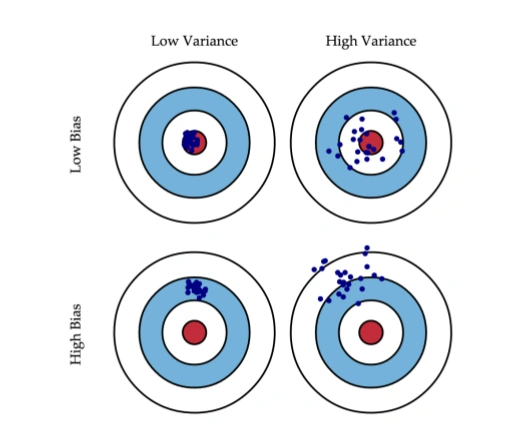
Чтобы оценить производительность модели в наборе данных, нам нужно измерить, насколько хорошо прогнозы модели соответствуют наблюдаемым данным.
Для регрессионных моделей наиболее часто используемой метрикой является среднеквадратическая ошибка (MSE), которая рассчитывается как:
MSE = (1/n)*Σ(y i – f(x i )) 2
куда:
- n: общее количество наблюдений
- y i : значение отклика i -го наблюдения
- f(x i ): прогнозируемое значение отклика i -го наблюдения.
Чем ближе прогнозы модели к наблюдениям, тем меньше будет MSE.
Однако нас интересует только тестовая MSE — MSE, когда наша модель применяется к невидимым данным. Это потому, что мы заботимся только о том, как модель будет работать с невидимыми данными, а не с существующими данными.
Например, хорошо, если модель, предсказывающая цены на фондовом рынке, имеет низкое среднеквадратичное отклонение на исторических данных, но мы действительно хотим иметь возможность использовать эту модель для точного прогнозирования будущих данных.
Получается, что тест MSE всегда можно разложить на две части:
(1) Дисперсия: относится к величине, на которую изменилась бы наша функция f , если бы мы оценили ее, используя другой обучающий набор.
(2) Смещение: Относится к ошибке, возникающей при аппроксимации реальной проблемы, которая может быть чрезвычайно сложной, гораздо более простой моделью.
Написано математическими терминами:
СКО теста = Var( f̂( x0)) + [Bias( f̂( x0))] 2 + Var(ε)
СКО теста = дисперсия + погрешность 2 + неустранимая ошибка
Третье слагаемое, неустранимая ошибка, — это ошибка, которую нельзя уменьшить с помощью какой-либо модели просто потому, что всегда существует некоторый шум в отношениях между набором объясняющих переменных и переменной отклика .
Модели с высоким смещением , как правило, имеют низкую дисперсию.Например, модели линейной регрессии, как правило, имеют высокое смещение (предполагает простую линейную связь между независимыми переменными и переменной отклика) и низкую дисперсию (оценки модели не будут сильно меняться от одной выборки к другой).
Однако модели с низким смещением , как правило, имеют высокую дисперсию.Например, сложные нелинейные модели, как правило, имеют низкое смещение (не предполагает определенной связи между независимыми переменными и переменной отклика) с высокой дисперсией (оценки модели могут сильно меняться от одной обучающей выборки к другой).
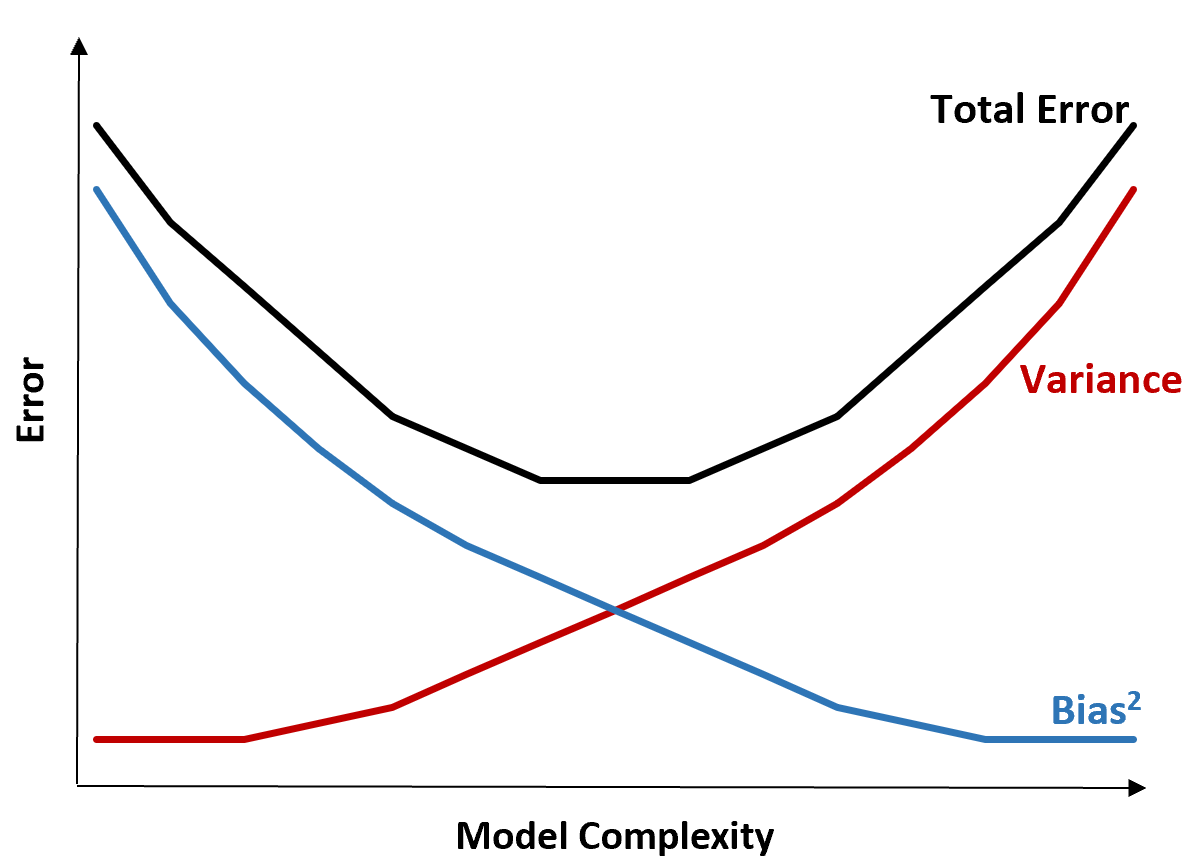
Компромисс смещения и дисперсии
Компромисс между смещением и дисперсией относится к компромиссу, который имеет место, когда мы решаем снизить смещение, что обычно увеличивает дисперсию, или уменьшить дисперсию, что обычно увеличивает смещение.
Следующая диаграмма предлагает способ визуализации этого компромисса:
Общая ошибка уменьшается по мере увеличения сложности модели, но только до определенного момента. После определенного момента дисперсия начинает увеличиваться, и общая ошибка также начинает увеличиваться.
На практике нас интересует только минимизация общей ошибки модели, а не обязательно минимизация дисперсии или систематической ошибки. Оказывается, чтобы минимизировать общую ошибку, нужно найти правильный баланс между дисперсией и погрешностью.
Другими словами, нам нужна модель, которая достаточно сложна, чтобы фиксировать истинную связь между независимыми переменными и переменной отклика, но не слишком сложна, чтобы находить шаблоны, которых на самом деле не существует.
Когда модель слишком сложна, она подгоняет данные. Это происходит потому, что слишком сложно найти закономерности в обучающих данных, которые просто вызваны случайностью. Этот тип модели, вероятно, будет плохо работать с невидимыми данными.
Но когда модель слишком проста, она не соответствует данным. Это происходит потому, что предполагается, что истинная связь между объясняющими переменными и переменной отклика более проста, чем она есть на самом деле.
Способ выбора оптимальных моделей в машинном обучении состоит в том, чтобы найти баланс между смещением и дисперсией, чтобы мы могли минимизировать ошибку тестирования модели на будущих невидимых данных.
На практике наиболее распространенным способом минимизации тестовой MSE является использование перекрестной проверки .
Регрессия как задача машинного обучения
38 мин на чтение
(55.116 символов)
Постановка задачи регрессии
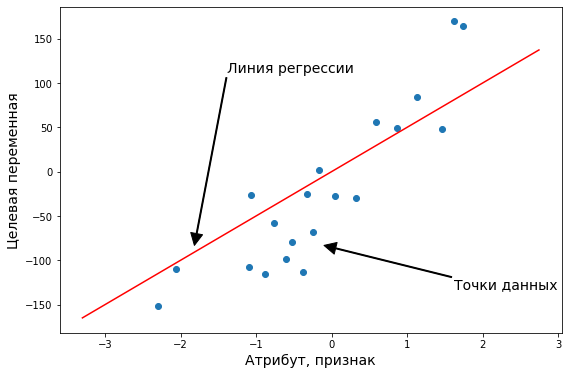
Источник: Analytics Vidhya.
Задача регрессии — это одна из основных задач машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, наборы данных для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (dependent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Так же надо сказать, что иногда регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия почти не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Линейная регрессия с одной переменной
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y.
Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$б которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно, или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Возведение в квадрат в этой формуле нужно для того, чтобы положительные отклонения не компенсировали отрицательные. Можно было бы для этого брать, например, абсолютное значение, но эта функция не везде дифференцируема, а это станет нам важно позднее.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
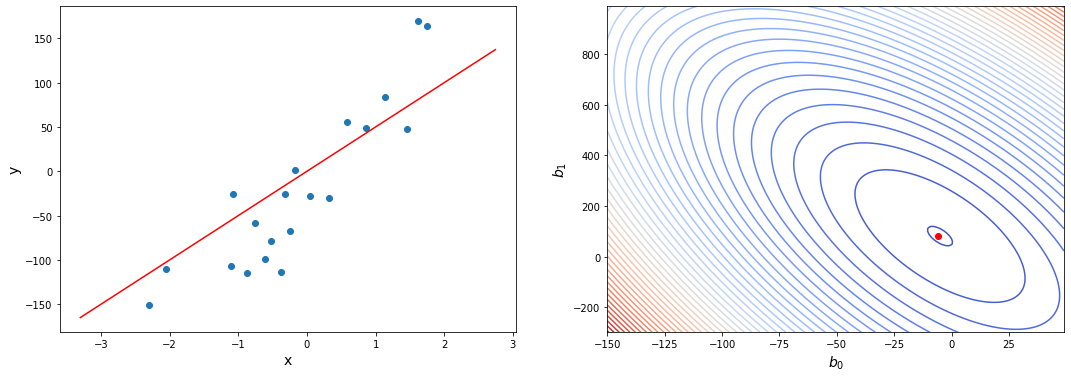
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
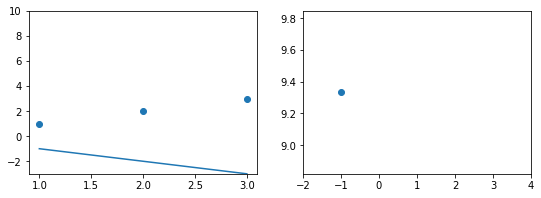
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
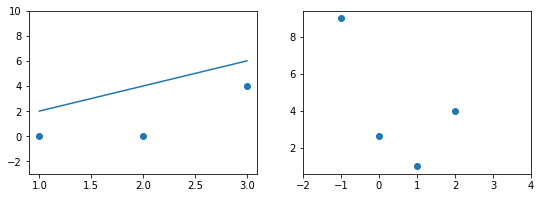
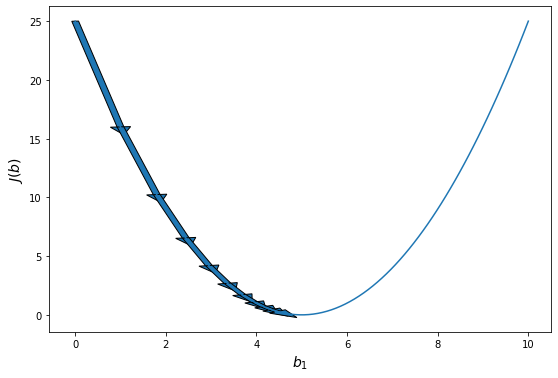
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
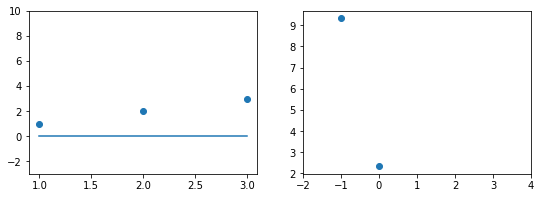
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
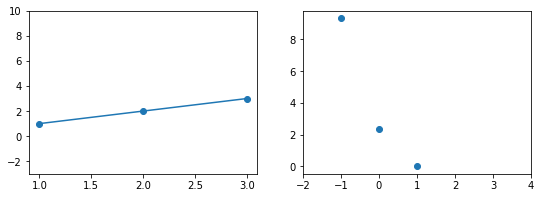
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
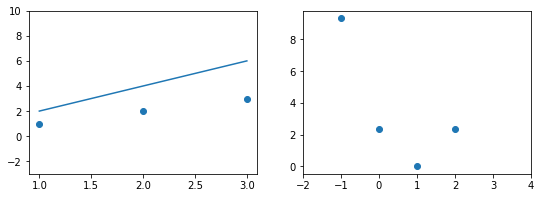
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
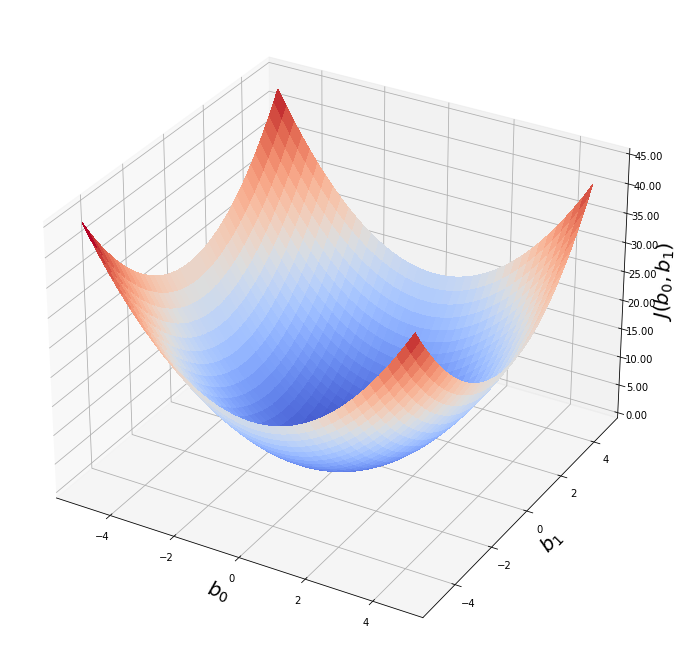
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
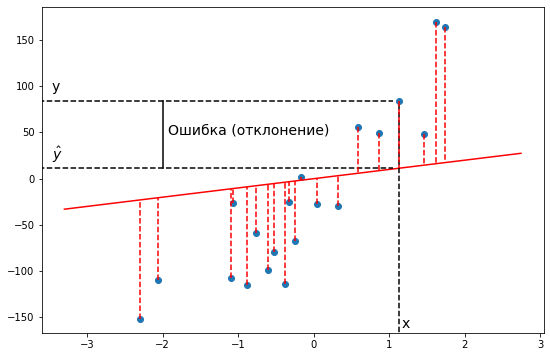
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска.
Это происходит при помощи производной функции ошибки. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит, от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
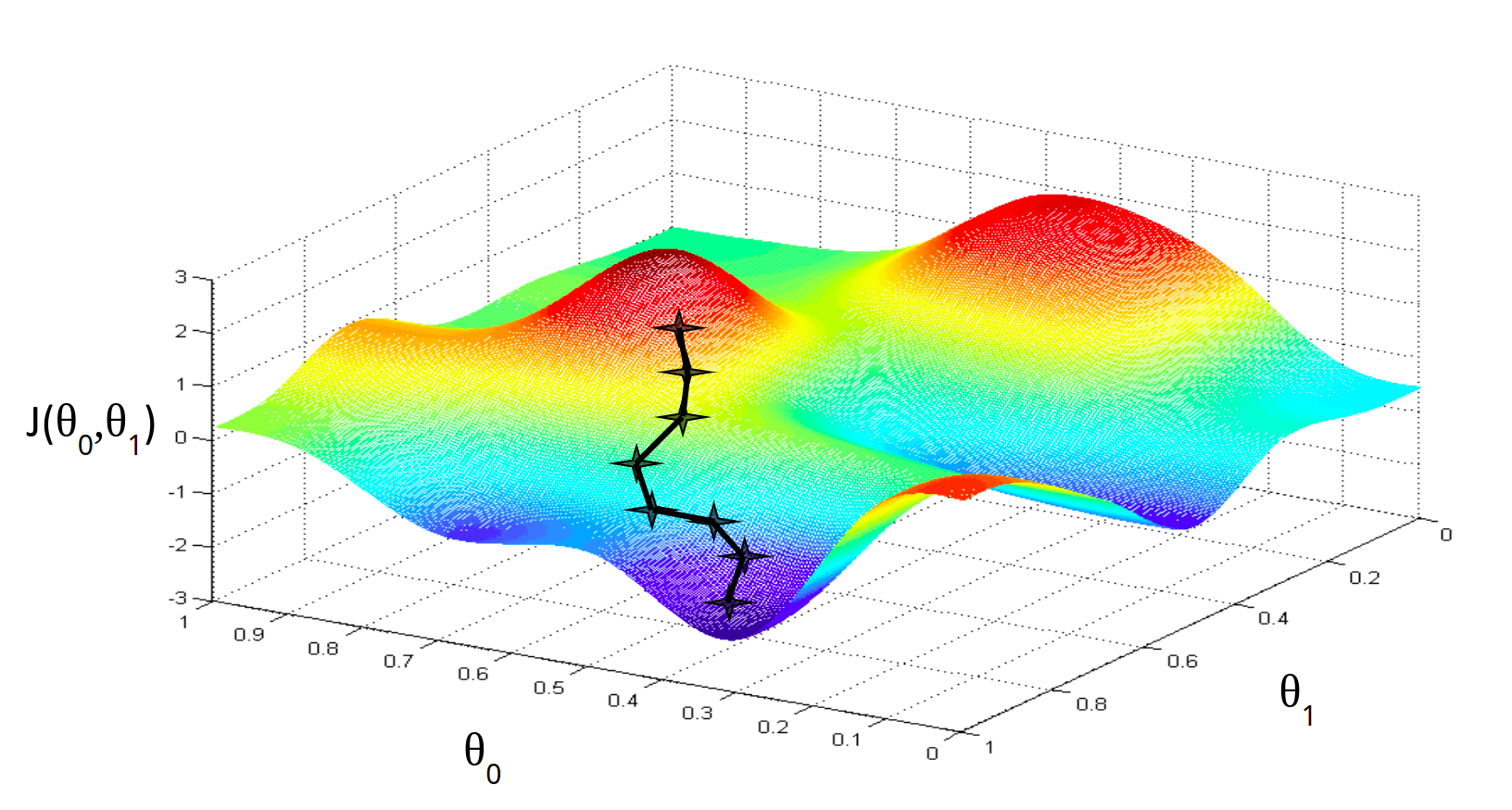
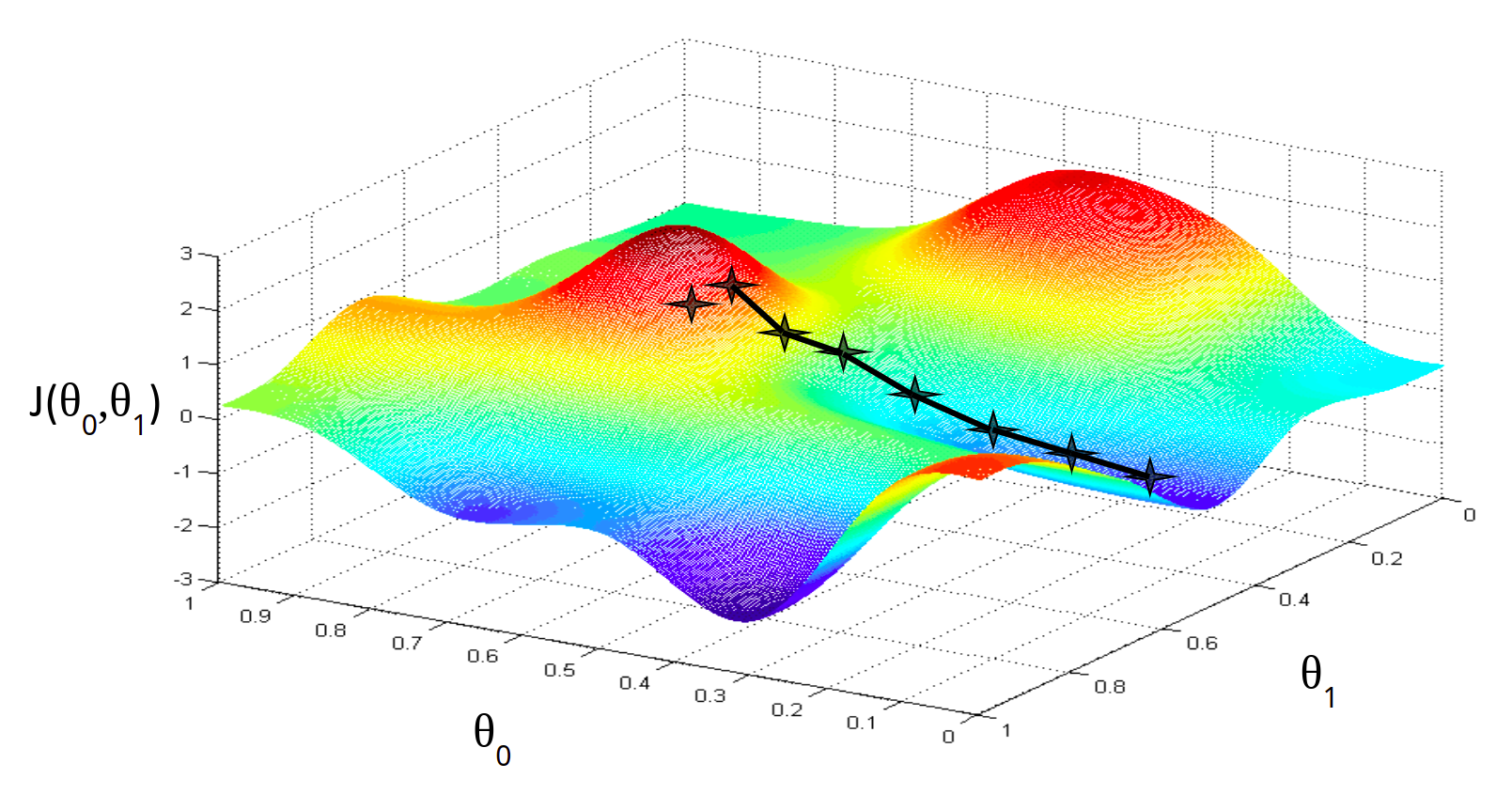
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки:
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Целевая переменная не нормируется.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Источник: Wikimedia.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данном разделе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данного раздела предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
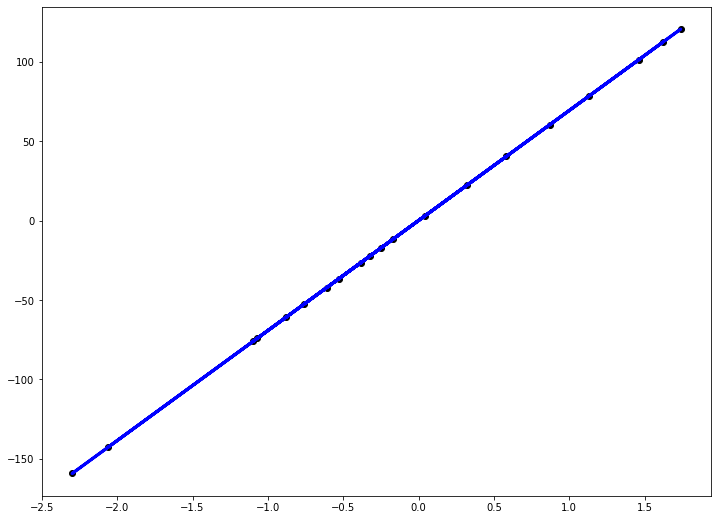
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
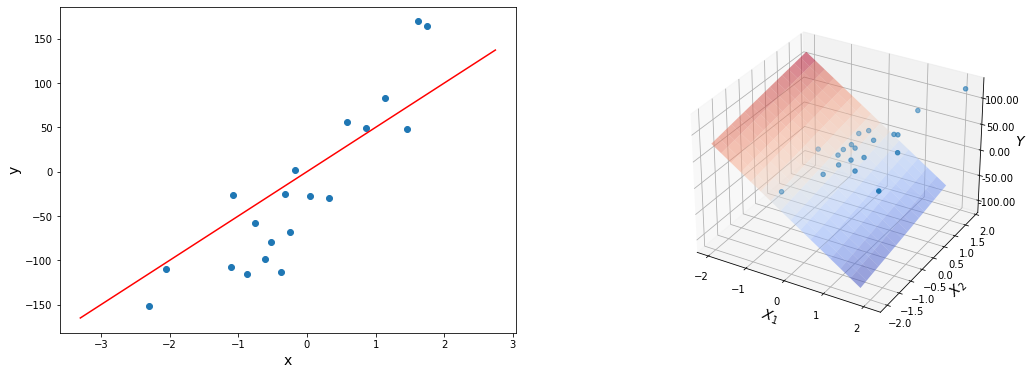
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
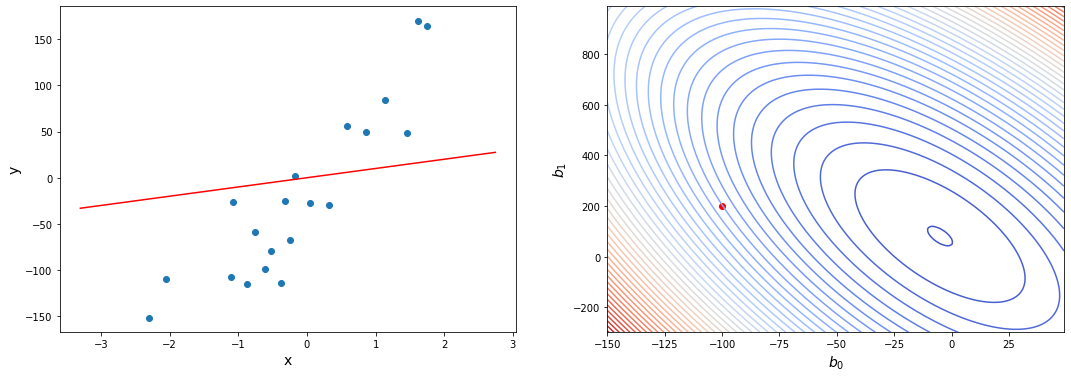
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
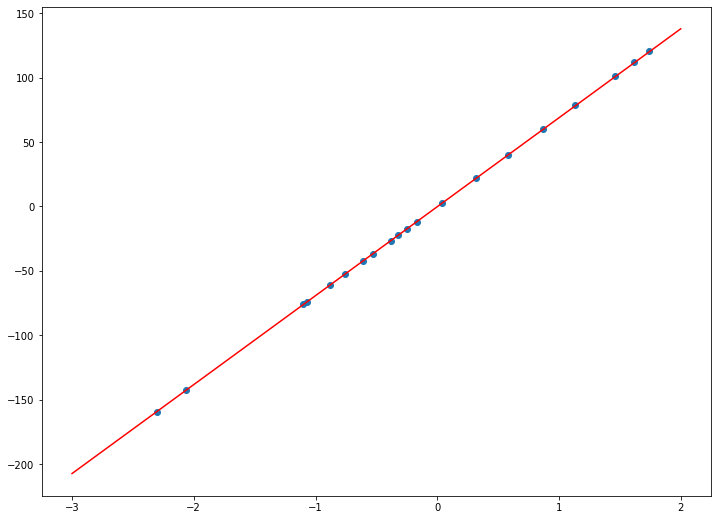
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
В данной главе мы изучим инструмент, который позволяет анализировать ошибку алгоритма в зависимости от некоторого набора факторов, влияющих на итоговое качество его работы. Этот инструмент в литературе называется bias-variance decomposition — разложение ошибки на смещение и разброс. В разложении, на самом деле, есть и третья компонента — случайный шум в данных, но ему не посчастливилось оказаться в названии. Данное разложение оказывается полезным в некоторых теоретических исследованиях работы моделей машинного обучения, в частности, при анализе свойств ансамблевых моделей.
Некоторые картинки в тексте кликабельны. Это означает, что они были заимствованы из какого-то источника и при клике вы сможете перейти к этому источнику.
Вывод разложения bias-variance для MSE
Рассмотрим задачу регрессии с квадратичной функцией потерь. Представим также для простоты, что целевая переменная $y$ — одномерная и выражается через переменную $x$ как:
$$
y = f(x) + varepsilon,
$$
где $f$ — некоторая детерминированная функция, а $varepsilon$ — случайный шум со следующими свойствами:
$$
mathbb{E} varepsilon = 0, , mathbb{V}text{ar} varepsilon = mathbb{E} varepsilon^2 = sigma^2.
$$
В зависимости от природы данных, которые описывает эта зависимость, её представление в виде точной $f(x)$ и случайной $varepsilon$ может быть продиктовано тем, что:
-
данные на самом деле имеют случайный характер;
-
измерительный прибор не может зафиксировать целевую переменную абсолютно точно;
-
имеющихся признаков недостаточно, чтобы исчерпывающим образом описать объект, пользователя или событие.
Функция потерь на одном объекте $x$ равна
$$
MSE = (y(x) — a(x))^2
$$
Однако знание значения MSE только на одном объекте не может дать нам общего понимания того, насколько хорошо работает наш алгоритм. Какие факторы мы бы хотели учесть при оценке качества алгоритма? Например, то, что выход алгоритма на объекте $x$ зависит не только от самого этого объекта, но и от выборки $X$, на которой алгоритм обучался:
$$
X = ((x_1, y_1), ldots, (x_ell, y_ell))
$$
$$
a(x) = a(x, X)
$$
Кроме того, значение $y$ на объекте $x$ зависит не только от $x$, но и от реализации шума в этой точке:
$$
y(x) = y(x, varepsilon)
$$
Наконец, измерять качество мы бы хотели на тестовых объектах $x$ — тех, которые не встречались в обучающей выборке, а тестовых объектов у нас в большинстве случаев более одного. При включении всех вышеперечисленных источников случайности в рассмотрение логичной оценкой качества алгоритма $a$ кажется следующая величина:
$$
Q(a) = mathbb{E}_x mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2
$$
Внутреннее матожидание позволяет оценить качество работы алгоритма в одной тестовой точке $x$ в зависимости от всевозможных реализаций $X$ и $varepsilon$, а внешнее матожидание усредняет это качество по всем тестовым точкам.
Замечание. Запись $mathbb{E}_{X, varepsilon}$ в общем случае обозначает взятие матожидания по совместному распределению $X$ и $varepsilon$. Однако, поскольку $X$ и $varepsilon$ независимы, она равносильна последовательному взятию матожиданий по каждой из переменных: $mathbb{E}_{X, varepsilon} = mathbb{E}_{X} mathbb{E}_{varepsilon}$, но последний вариант выглядит несколько более громоздко.
Попробуем представить выражение для $Q(a)$ в более удобном для анализа виде. Начнём с внутреннего матожидания:
$$
mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2 = mathbb{E}_{X, varepsilon}[f(x) + varepsilon — a(x, X)]^2 =
$$
$$
= mathbb{E}_{X, varepsilon} [ underbrace{(f(x) — a(x, X))^2}_{text{не зависит от $varepsilon$}} +
underbrace{2 varepsilon cdot (f(x) — a(x, X))}_{text{множители независимы}} + varepsilon^2 ] =
$$
$$
= mathbb{E}_X left[
(f(x) — a(x, X))^2
right] + 2 underbrace{mathbb{E}_varepsilon[varepsilon]}_{=0} cdot mathbb{E}_X (f(x) — a(x, X)) + mathbb{E}_varepsilon varepsilon^2 =
$$
$$
= mathbb{E}_X left[ (f(x) — a(x, X))^2 right] + sigma^2
$$
Из общего выражения для $Q(a)$ выделилась шумовая компонента $sigma^2$. Продолжим преобразования:
$$
mathbb{E}_X left[ (f(x) — a(x, X))^2 right] = mathbb{E}_X left[
(f(x) — mathbb{E}_X[a(x, X)] + mathbb{E}_X[a(x, X)] — a(x, X))^2
right] =
$$
$$
= mathbb{E}_Xunderbrace{left[
(f(x) — mathbb{E}_X[a(x, X)])^2
right]}_{text{не зависит от $X$}} + underbrace{mathbb{E}_X left[ (a(x, X) — mathbb{E}_X[a(x, X)])^2 right]}_{text{$=mathbb{V}text{ar}_X[a(x, X)]$}} +
$$
$$
+ 2 mathbb{E}_X[underbrace{(f(x) — mathbb{E}_X[a(x, X)])}_{text{не зависит от $X$}} cdot (mathbb{E}_X[a(x, X)] — a(x, X))] =
$$
$$
= (underbrace{f(x) — mathbb{E}_X[a(x, X)]}_{text{bias}_X a(x, X)})^2 + mathbb{V}text{ar}_X[a(x, X)] + 2 (f(x) — mathbb{E}_X[a(x, X)]) cdot underbrace{(mathbb{E}_X[a(x, X)] — mathbb{E}_X [a(x, X)])}_{=0} =
$$
$$
= text{bias}_X^2 a(x, X)+ mathbb{V}text{ar}_X[a(x, X)]
$$
Таким образом, итоговое выражение для $Q(a)$ примет вид
$$
Q(a) = mathbb{E}_x mathbb{E}_{X, varepsilon} [y(x, varepsilon) — a(x, X)]^2 = mathbb{E}_x text{bias}_X^2 a(x, X) + mathbb{E}_x mathbb{V}text{ar}_X[a(x, X)] + sigma^2,
$$
где
$$
text{bias}_X a(x, X) = f(x) — mathbb{E}_X[a(x, X)]
$$
— смещение предсказания алгоритма в точке $x$, усреднённого по всем возможным обучающим выборкам, относительно истинной зависимости $f$;
$$
mathbb{V}text{ar}_X[a(x, X)] = mathbb{E}_X left[ a(x, X) — mathbb{E}_X[a(x, X)] right]^2
$$
— дисперсия (разброс) предсказаний алгоритма в зависимости от обучающей выборки $X$;
$$
sigma^2 = mathbb{E}_x mathbb{E}_varepsilon[y(x, varepsilon) — f(x)]^2
$$
— неустранимый шум в данных.
Смещение показывает, насколько хорошо с помощью данного алгоритма можно приблизить истинную зависимость $f$, а разброс характеризует чувствительность алгоритма к изменениям в обучающей выборке. Например, деревья маленькой глубины будут в большинстве случаев иметь высокое смещение и низкий разброс предсказаний, так как они не могут слишком хорошо запомнить обучающую выборку. А глубокие деревья, наоборот, могут безошибочно выучить обучающую выборку и потому будут иметь высокий разброс в зависимости от выборки, однако их предсказания в среднем будут точнее. На рисунке ниже приведены возможные случаи сочетания смещения и разброса для разных моделей:
Синяя точка соответствует модели, обученной на некоторой обучающей выборке, а всего синих точек столько, сколько было обучающих выборок. Красный круг в центре области представляет ближайшую окрестность целевого значения. Большое смещение соответствует тому, что модели в среднем не попадают в цель, а при большом разбросе модели могут как делать точные предсказания, так и довольно сильно ошибаться.
Полученное нами разложение ошибки на три компоненты верно только для квадратичной функции потерь. Для других функций потерь существуют более общие формы этого разложения (Domigos, 2000, James, 2003) с похожими по смыслу компонентами. Это позволяет предполагать, что для большинства основных функций потерь имеется некоторое представление в виде смещения, разброса и шума (хоть и, возможно, не в столь простой аддитивной форме).
Пример расчёта оценок bias и variance
Попробуем вычислить разложение на смещение и разброс на каком-нибудь практическом примере. Наши обучающие и тестовые примеры будут состоять из зашумлённых значений целевой функции $f(x)$, где $f(x)$ определяется как
$$
f(x) = x sin x
$$
В качестве шума добавляется нормальный шум с нулевым средним и дисперсией $sigma^2$, равной во всех дальнейших примерах 9. Такое большое значение шума задано для того, чтобы задача была достаточно сложной для классификатора, который будет на этих данных учиться и тестироваться. Пример семпла из таких данных:
Посмотрим на то, как предсказания деревьев зависят от обучающих подмножеств и максимальной глубины дерева. На рисунке ниже изображены предсказания деревьев разной глубины, обученных на трёх независимых подвыборках размера 20 (каждая колонка соответствует одному подмножеству):
Глядя на эти рисунки, можно выдвинуть гипотезу о том, что с увеличением глубины дерева смещение алгоритма падает, а разброс в зависимости от выборки растёт. Проверим, так ли это, вычислив компоненты разложения для деревьев со значениями глубины от 1 до 15.
Для обучения деревьев насемплируем 1000 случайных подмножеств $X_{train} = (x_{train}, y_{train})$ размера 500, а для тестирования зафиксируем случайное тестовое подмножество точек $x_{test}$ также размера 500. Чтобы вычислить матожидание по $varepsilon$, нам нужно несколько экземпляров шума $varepsilon$ для тестовых лейблов:
$$
y_{test} = y(x_{test}, hat varepsilon) = f(x_{test}) + hat varepsilon
$$
Положим количество семплов случайного шума равным 300. Для фиксированных $X_{train} = (x_{train}, y_{train})$ и $X_{test} = (x_{test}, y_{test})$ квадратичная ошибка вычисляется как
$$
MSE = (y_{test} — a(x_{test}, X_{train}))^2
$$
Взяв среднее от $MSE$ по $X_{train}$, $x_{test}$ и $varepsilon$, мы получим оценку для $Q(a)$, а оценки для компонент ошибки мы можем вычислить по ранее выведенным формулам.
На графике ниже изображены компоненты ошибки и она сама в зависимости от глубины дерева:
По графику видно, что гипотеза о падении смещения и росте разброса при увеличении глубины подтверждается для рассматриваемого отрезка возможных значений глубины дерева. Правда, если нарисовать график до глубины 25, можно увидеть, что разброс становится равен дисперсии случайного шума. То есть деревья слишком большой глубины начинают идеально подстраиваться под зашумлённую обучающую выборку и теряют способность к обобщению:
Код для подсчёта разложения на смещение и разброс, а также код отрисовки картинок можно найти в данном ноутбуке.
Bias-variance trade-off: в каких ситуациях он применим
В книжках и различных интернет-ресурсах часто можно увидеть следующую картинку:
Она иллюстрирует утверждение, которое в литературе называется bias-variance trade-off: чем выше сложность обучаемой модели, тем меньше её смещение и тем больше разброс, и поэтому общая ошибка на тестовой выборке имеет вид $U$-образной кривой. С падением смещения модель всё лучше запоминает обучающую выборку, поэтому слишком сложная модель будет иметь нулевую ошибку на тренировочных данных и большую ошибку на тесте. Этот график призван показать, что существует оптимальная сложность модели, при которой соблюдается баланс между переобучением и недообучением и ошибка при этом минимальна.
Существует достаточное количество подтверждений bias-variance trade-off для непараметрических моделей. Например, его можно наблюдать для метода $k$ ближайших соседей при росте $k$ и для ядерной регрессии при увеличении ширины окна $sigma$ (Geman et al., 1992):
Чем больше соседей учитывает $k$-NN, тем менее изменчивым становится его предсказание, и аналогично для ядерной регрессии, из-за чего сложность этих моделей в некотором смысле убывает с ростом $k$ и $sigma$. Поэтому традиционный график bias-variance trade-off здесь симметрично отражён по оси $x$.
Однако, как показывают последние исследования, непременное возрастание разброса при убывании смещения не является абсолютно истинным предположением. Например, для нейронных сетей с ростом их сложности может происходить снижение и разброса, и смещения. Одна из наиболее известных статей на эту тему — статья Белкина и др. (Belkin et al., 2019), в которой, в частности, была предложена следующая иллюстрация:
Слева — классический bias-variance trade-off: убывающая часть кривой соответствует недообученной модели, а возрастающая — переобученной. А на правой картинке — график, называемый в статье double descent risk curve. На нём изображена эмпирически наблюдаемая авторами зависимость тестовой ошибки нейросетей от мощности множества входящих в них параметров ($mathcal H$). Этот график разделён на две части пунктирной линией, которую авторы называют interpolation threshold. Эта линия соответствует точке, в которой в нейросети стало достаточно параметров, чтобы без особых усилий почти идеально запомнить всю обучающую выборку. Часть до достижения interpolation threshold соответствует «классическому» режиму обучения моделей: когда у модели недостаточно параметров, чтобы сохранить обобщающую способность при почти полном запоминании обучающей выборки. А часть после достижения interpolation threshold соответствует «современным» возможностям обучения моделей с огромным числом параметров. На этой части графика ошибка монотонно убывает с ростом количества параметров у нейросети. Авторы также наблюдают похожее поведение и для «древесных» моделей: Random Forest и бустинга над решающими деревьями. Для них эффект проявляется при одновременном росте глубины и числа входящих в ансамбль деревьев.
В качестве вывода к этому разделу хочется сформулировать два основных тезиса:
- Bias-variance trade-off нельзя считать непреложной истиной, выполняющейся для всех моделей и обучающих данных.
- Разложение на смещение и разброс не влечёт немедленного выполнения bias-variance trade-off и остаётся верным и для случая, когда все компоненты ошибки (кроме неустранимого шума) убывают одновременно. Этот факт может оказаться незамеченным из-за того, что в учебных пособиях часто разговор о разложении дополняется иллюстрацией с $U$-образной кривой, благодаря чему в сознании эти два факта могут слиться в один.
Список литературы
- Блог-пост про bias-variance от Йоргоса Папахристудиса
- Блог-пост про bias-variance от Скотта Фортмана-Роу
- Статьи от Домингоса (2000) и Джеймса (2003) про обобщённые формы bias-variance decomposition
- Блог-пост от Брейди Нила про необходимость пересмотра традиционного взгляда на bias-variance trade-off
- Статья Гемана и др. (1992), в которой была впервые предложена концепция bias-variance trade-off
- Статья Белкина и др. (2019), в которой был предложен double-descent curve