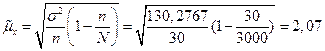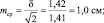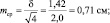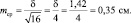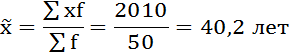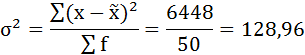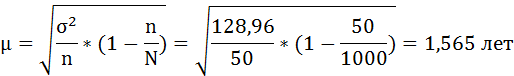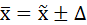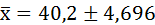Рассчитать среднюю ошибку выборки среднего возраста - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Результаты выборочного обследования незанятого населения

Возраст, лет	до 25	25-35	35-45	45-55	55 и более
Численность лиц данного возраста	15	37	71	45	22

С вероятностью
0,954 определите границы:

а) среднего возраста
незанятого населения;

б) доли
(удельного веса) лиц, моложе 25 лет, в
общей численности незанятого населения.

Решение.
Для определения средней ошибки выборки
нам необходимо прежде всего рассчитать
выборочную среднюю величину и дисперсию
изучаемого признака, данные для расчета
которых приведены в табл.

Таблица
7.2

Расчет среднего возраста незанятого населения и дисперсии

Возраст,
лет x

Численность
лиц данного возраста f

Середина

интервала x

x²f

До 25

25-35

35-45

45-55

55 и более

300

1110

2840

2250

1320

6000

33300

113600

112500

79200

Итого

190

—

7820

344600

Средняя ошибка
выборки составит:

года.

Определим
с вероятностью 0,954 (t
=
2) предельную ошибку выборки:

года.

Установим
границы генеральной средней: 41,2 — 1,6
5
41,2+1,6 или:

39.6
42.8

Таким
образом, на основании проведенного
выборочного обследования с вероятностью
0,954 можно заключить, что средний возраст
незанятого населения, ищущего работу,
лежит в пределах от 40 до 43 лет.

Для
ответа на вопрос, поставленный в пункте
«б» данного примера, по выборочным
данным определим долю лиц в возрасте
до 25 лет и рассчитаем дисперсию доли:

Рассчитаем среднюю
ошибку выборки:

Предельная ошибка
выборки с заданной вероятностью составит:

Определим границы
генеральной доли:

или

Следовательно,
с вероятностью 0,954 можно утверждать,
что доля лиц в возрасте до 25 лет в общей
численности незанятого населения
находится в пределах от 3,9 до 1 1,9%.

При
расчете средней ошибки собственно-случайной
бесповторной выборки необходимо
учитывать поправку на бесповторность
отбора:

где
N
— объем (число единиц) генеральной
совокупности/

Необходимый
объем собственно-случайной
повторной выборки
определяется по формуле:

Если отбор
бесповторный, то формула приобретает
следующий вид:

Полученный
на основе использования этих формул
результат всегда округляется в большую
сторону до целого значения.

Пример.
Необходимо определить, сколько учащихся
первых классов школ района необходимо
отобрать в порядке собственно-случайной
бесповторной выборки, чтобы с вероятностью
0,997 определить границы среднего роста
первоклассников с предельной ошибкой
2 см. Известно, что всего в первых классах
школ района обучается 1100 учеников, а
дисперсия роста по результатам
аналогичного обследования в другом
районе составила 24.

Решение.
Необходимый объем выборки при уровне
вероятности 0,997 (t
= 3) составит:

Таким
образом, для получения данных о среднем
росте первоклассников с заданной
точностью необходимо обследовать 52
школьника.

Механическая
выборка.
Данная выборка заключается в отборе
единиц из общего списка единиц генеральной
совокупности через равные интервалы в
соответствии с установленным процентом
отбора. При решении задач на определение
средней ошибки механической выборки,
а также необходимой ее численности,
следует использовать приведенные выше
формулы, применяемые при собственно-случайном
бесповторном отборе.

Типическая
выборка.
Эта выборка применяется в тех случаях,
когда единицы генеральной совокупности
объединены в несколько крупных типичных
групп. Отбор единиц в выборку производится
внутри этих групп пропорционально их
объему на основе использования
собственно-случайной или механической
выборки (при наличии необходимой
информации отбор также может производиться
пропорционально вариации изучаемого
признака в группах).

Средняя ошибка
типической выборки определяется по
формулам:

(повторный отбор);

(бесповторный
отбор),

где
—
средняя из внутригрупповых дисперсией.

Пример

В
целях изучения доходов населения по
трем районам области сформирована
2%-ная выборка, пропорциональная
численности населения этих районов.
Полученные результаты представлены в
табл. 7.3.

Таблица
7.3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пример выполнения расчетного задания по статистике

Имеются следующие выборочные данные службы занятости о времени поиска работы 30 безработными одного из районов города (выборка 1%-ная, механическая):

№ п/п	Возраст безработного, Лет	Время поиска работы, Мес.	№ п/п	Возраст безработного, Лет	Время поиска работы, Мес.
1	37	8,7	16	60	11,3
2	53	9,4	17	21	5,6
3	18	5,1	18	33	7,5
4	25	6,9	19	29	7,2
5	33	7,9	20	42	8,3
6	32	7,8	21	17	5,3
7	48	8,5	22	44	8,4
8	61	10,4	23	41	7,9
9	29	7,8	24	26	7,4
10	39	8,4	25	30	7,9
11	28	7,9	26	41	8,1
12	35	8,5	27	47	8,7
13	52	9,4	28	27	7,5
14	36	8,7	29	23	6,7
15	48	8,9	30	57	10,0

Задание 1

По исходным данным:

1) постройте Статистический ряд распределения по признаку возраст безработного, образовав 4 группы с равными интервалами;

2) графическим методом и путем расчетов определите значения Моды и Медианы полученного ряда распределения;

3) рассчитайте характеристики интервального ряда распределения: Среднюю арифметическую, Среднее квадратическое отклонение, Коэффициент вариации.

Сделайте выводы по результатам выполнения пунктов 1, 2, 3 задания;

4) вычислите Среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитанным в п. 3 для интервального ряда распределения. Объясните причину их расхождения.

Задание 2

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1) ошибку выборки среднего возраста безработных в районе и границы, в которых будет находиться средний возраст безработных в целом по району;

2) ошибку выборки доли безработных в районе в возрасте до 50 лет и границы, в которых будет находиться генеральная доля.

Выполнение задания 1

1.1. Построение интервального ряда распределения безработных по возрасту

Для построения интервального вариационного ряда, характеризующего распределение безработных по возрасту, необходимо вычислить Величину и границы интервалов ряда.

При построении ряда с равными интервалами величина интервала H определяется по формуле

, (1)

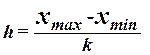
Где – наибольшее и наименьшее значения признака в исследуемой совокупности, K – число групп интервального ряда.

Число групп K задается в условии задания или рассчитывается по формуле Г. Стерджесса

K=1+3,322 Lg N, (2)

Где N – число единиц совокупности. По условиям задания k=4.

Определение величины интервала по формуле (1) при заданных K = 4:

XmaX = 61 год, Xmin = 17 лет

Лет.

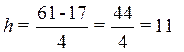
При H = 11 границы интервалов ряда распределения имеют следующий вид (табл. 2):

Таблица 2

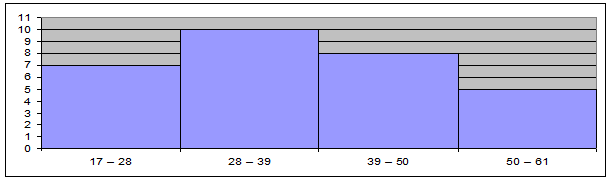
Номер группы	Возраст безработного, лет
1	17 – 28
2	28 – 39
3	39 – 50
4	50 – 61

Для построения интервального ряда необходимо подсчитать число безработных, входящих в каждую группу (Частоты групп). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов. Отнесение таких единиц к одной из двух смежных групп рекомендуется осуществлять По принципу полуоткрытого интервала. Т. к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и Нижняя, и Верхняя границы.

Процесс группировки единиц совокупности по признаку Возраст безработного представлен во вспомогательной (разработочной) таблице 3 (графа 4 этой таблицы необходима для построения аналитической группировки в Задании 2).

Таблица 3

Разработочная таблица для построения интервального ряда распределения и аналитической группировки

Возраст безработного, лет	Середина интервала	Частота
17 – 28	22,5	7
28 – 39	33,5	10
39 – 50	44,5	8
50 – 61	55,5	5
	Всего	30

На основе групповых итоговых строк «Всего» табл. 3 формируется итоговая табл. 4, представляющая Интервальный ряд распределения безработных по возрасту.

Таблица 4

Распределение безработных по возрасту

I	Возраст безработного, лет	Середины интервалов	Частота (nI)	Частость (доля), ni/n	Накопленная частота (Sj)	Накопленная частость
1	17-28	22,5	7	0,2333	7	23%
2	28-39	33,5	10	0,3333	17	57%
3	39-50	44,5	8	0,2667	25	83%
4	50-61	55,5	5	0,1667	30	100%
		Всего (n)	30

Помимо частот групп в абсолютном выражении в анализе интервальных рядов используются ещё три характеристики ряда, приведенные в графах 4 – 6 табл. 1.4. Это Частоты групп в относительном выражении, Накопленные (кумулятивные) частоты Sj, Получаемые путем последовательного суммирования частот всех предшествующих (j-1) интервалов, и Накопленные частости, рассчитываемые по формуле .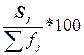

Вывод. Анализ интервального ряда распределения изучаемой совокупности безработных показывает, что распределение безработных по возрасту не является равномерным: преобладают безработные в возрасте от 28 до 39 лет (это 10 безработных, доля которых составляет 33%), почти в два раза меньше (17%) старшая возрастная группа (от 50 лет до 61 года); группы от 17 до 28 лет и от 39 до 50 лет отличаются не так заметно (23% и 27% соответственно).

1.2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов

Мода и медиана являются Структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку.

Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности[1]. В интервальном вариационном ряду модой приближенно считается Центральное значение модального интервала (имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).

Рис. 1 Определение моды графическим методом

Конкретное значение моды для интервального ряда рассчитывается по формуле:

(3)

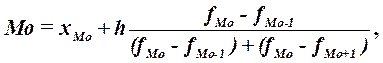
Где ХМo – нижняя граница модального интервала,

H –величина модального интервала,

FMo – частота модального интервала,

FMo-1 – частота интервала, предшествующего модальному,

FMo+1 – частота интервала, следующего за модальным.

Согласно табл.1.3 модальным интервалом построенного ряда является интервал 28 – 39 лет, так как его частота максимальна (f2 = 10).

Расчет моды по формуле (3):

Вывод. Для рассматриваемой совокупности безработных наиболее распространенный возраст характеризуется средней величиной 34,4 года.

Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.

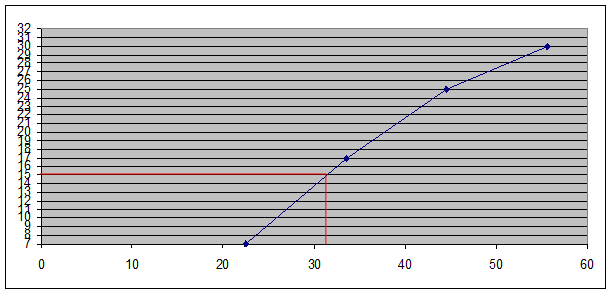
Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 5, графа 5).

Рис. 2. Определение медианы графическим методом

Конкретное значение медианы для интервального ряда рассчитывается по формуле:

, (4)

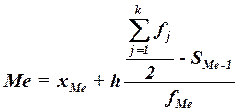
Где ХМе– нижняя граница медианного интервала,

H – величина медианного интервала,

– сумма всех частот,

FМе – частота медианного интервала,

SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.

Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости) из табл. 5 (графа 5). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота Впервые равна полусумме всех частот или превышает ее (т. е. все предшествующие накопленные частоты меньше этой величины).

В демонстрационном примере медианным интервалом является интервал 28 – 39 лет, так как именно в этом интервале накопленная частота Sj = 17 впервые превышает величину, равную половине численности единиц совокупности (=).

Расчет значения медианы по формуле (4):

33,5 года

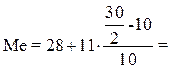
Вывод. В рассматриваемой совокупности, половина безработных имеют возраст в среднем не более 33,5 лет, а другая половина – не менее 33,5 лет.

1.3. Расчет характеристик ряда распределения

Для расчета характеристик ряда распределения , σ, σ2, Vσ на основе табл. 5 строится вспомогательная табл. 6 ( – середина j-го интервала).

Таблица 6

Расчетная таблица для нахождения характеристик ряда распределения

Возраст безработного, лет	Середина интервала,	Частота. Fj
1	2	3	4	5	6	7
17-28	22,5	7	157,5	-15,033	226,001	1582,01
28-39	33,5	10	335	-4,0333	16,2678	162,678
39-50	44,5	8	356	6,96667	48,5344	388,276
50-61	55,5	5	277,5	17,9667	322,801	1614,01
Итого		30	1126			3746,97

Расчет средней арифметической взвешенной:

лет (5)

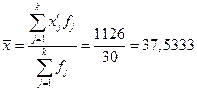
Расчет дисперсии:

(6)

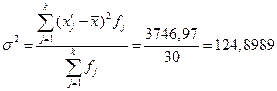
Расчет среднего квадратического отклонения:

Расчет коэффициента вариации:

(7)

Вывод. Анализ полученных значений показателей и σ говорит о том, что средний возраст безработных составляет 37,5333 лет, отклонение от среднего возраста в ту или иную сторону составляет в среднем 11,1758 лет (или 29,78%), наиболее характерные значения среднего возраста безработных находятся в пределах от 26,3575 до 48,7092 (диапазон ).

Значение Vσ = 29,78% не превышает 33%, следовательно, вариация возраста в исследуемой совокупности безработных незначительна и совокупность по данному признаку качественно однородна. Расхождение между значениями , Мо и Ме незначительно (=37,5333 лет, Мо=34,4 года, Ме=33,5 лет), что подтверждает вывод об однородности по возрасту совокупности безработных. Таким образом, найденное среднее значение возраста безработных (37,5333 лет) является типичной, надежной характеристикой исследуемой совокупности безработных.

1.4. Вычисление средней арифметической по исходным данным

Для расчета применяется формула средней арифметической простой:

(8)

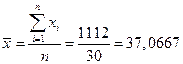
Причина расхождения средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по формуле (8) средняя определяется по фактическим значениям исследуемого признака для всех 30-ти безработных, а по формуле (5) средняя вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).

Задание 2

По результатам выполнения задания 1 с вероятностью 0,683 определите:

Выполнение Задания 3

1. Определение ошибки выборки для Среднего возраста безработных в районе и границы, в которых будет находиться генеральная средняя

Применение выборочного метода наблюдения всегда связано с Установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, т. е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину ε, которую называют Ошибкой выборки (ошибкой репрезентативности).

Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок — среднюю и предельную .

Средняя ошибка выборки – это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т. е. от своего математического ожидания M[].

Величина средней ошибки выборки рассчитывается Дифференцированно (по различным формулам) в зависимости от Вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка выборочной средней определяется по формуле

, (15)

Где – общая дисперсия выборочных значений признаков,

N – число единиц в генеральной совокупности,

N – число единиц в выборочной совокупности.

Предельная ошибка выборки определяет границы, в пределах которых будет находиться генеральная средняя:

, (16)

Где – выборочная средняя,

– генеральная средняя.

Границы задают Доверительный интервал генеральной средней, т. е. случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют Доверительной вероятностью Или Уровнем надёжности.

В экономических исследованиях чаще всего используются доверительные вероятности Р= 0,954, Р= 0,997, Реже Р= 0,683.

В математической статистике доказано, что предельная ошибка выборки кратна средней ошибке µ с Коэффициентом кратности T (Называемым также Коэффициентом доверия), который зависит от значения доверительной вероятности Р. Для предельной ошибки выборочной средней это теоретическое положение выражается формулой

(17)

Значения T вычислены заранее для различных доверительных вероятностей Р и Протабулированы (таблицы функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р Значения T задаются следующим образом (табл. 15):

Таблица 15

Доверительная вероятность P	0,683	0,866	0,954	0,988	0,997	0,999
Значение T	1,0	1,5	2,0	2,5	3,0	3,5

По условию демонстрационного примера выборочная совокупность насчитывает 30 безработных, выборка 1% механическая, следовательно, Генеральная совокупность включает 3000 безработных. Выборочная средняя , дисперсия определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 16:

Таблица 16

Р	T	N	N
0,683	1	30	3000	36,8	130,2767

Расчет средней ошибки выборки по формуле (15):

Расчет предельной ошибки выборки по формуле (17):

Определение по формуле (16) доверительного интервала для генеральной средней:

36,8-2,0736,8+2,07,

34,73 лет 38,87 лет.

Вывод. На основании проведенного выборочного обследования среднего возраста безработных в районе с вероятностью 0,683 можно утверждать, что для генеральной совокупности безработных средний возраст находится в пределах от 34,73 лет до 38,87 лет.

2. Определение ошибки выборки для Доли безработных в районе в возрасте до 50 лет и границы, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

, (18)

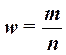
Где M – число единиц совокупности, обладающих заданным свойством;

N – общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки доли единиц, обладающих заданным свойством, рассчитывается по формуле

, (19)

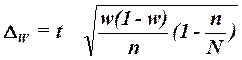
Где W – доля единиц совокупности, обладающих заданным свойством;

(1-W) – доля единиц совокупности, не обладающих заданным свойством,

N – число единиц в генеральной совокупности,

N– число единиц в выборочной совокупности.

Предельная ошибка выборки определяет границы, в пределах которых будет находиться генеральная доля Р единиц, обладающих заданным свойством:

(20)

По условию Задания 3 исследуемым свойством является не Превышение среднего возраста безработных 50 лет.

Число безработных с заданным свойством определяется из табл. 3 (графа 3):

M=25

Расчет выборочной доли по формуле (18):

Расчет по формуле (19) предельной ошибки выборки для доли:

Определение по формуле (20) доверительного интервала генеральной доли:

0,8333-0,0677<=p<=0,8333+0,0677

Или

76,56% <= p<=90,10%

Вывод. С вероятностью 0,683 можно утверждать, что в генеральной совокупности безработных доля безработных в возрасте до 50 лет будет находиться в пределах от 77% до 90%.

[1] Если в дискретном ряду все варианты встречаются одинаково часто, то в этом случае мода отсутствует. Могут быть распределения, где не один, а два (или более) варианта имеют наибольшие частоты. Тогда ряд имеет две (или более) моды, распределение является бимодальным (или многомодальным), что указывает на качественную неоднородность совокупности по изучаемому признаку.

< Предыдущая		Следующая >

Источник

11.2. Оценка результатов выборочного наблюдения

11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ().

В теории выборочного наблюдения выведены формулы для определения , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.

Например, если применяется повторная собственно случайная выборка, то определяется как:

— при оценивании среднего значения признака;

— если признак альтернативный, и оценивается доля.

При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):

— для среднего значения признака;

— для доли.

Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.

Предельная ошибка выборки ( Delta ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.

Уровень предельной ошибки выборки зависит от следующих факторов:

степени вариации единиц генеральной совокупности;
объема выборки;
выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
уровня доверительной вероятности.

Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Таблица
11.2.

Значение доверительной вероятности P	0,683	0,954	0,997
Значение коэффициента доверия t	1,0	2,0	3,0

Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

Ошибки выборки при различных видах отбора

Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.

Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ()

где $sigma^{2}$ — дисперсия признака в выборочной совокупности.

Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.

Таблица
11.4.

Уровень фондоотдачи, руб.	До 1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0-2,2	2,2 и выше	Итого
Количество предприятий	13	15	17	15	16	14	90

В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:

По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:

Таблица
11.5.

Результаты наблюдения	Расчетные значения
уровень фондоотдачи, руб., x_i	количество предприятий, f_i	середина интервала, x_i^xb4	x_i^xb4f_i	x_i^xb4²f_i
До 1,4	13	1,3	16,9	21,97
1,4-1,6	15	1,5	22,5	33,75
1,6-1,8	17	1,7	28,9	49,13
1,8-2,0	15	1,9	28,5	54,15
2,0-2,2	16	2,1	33,6	70,56
2,2 и выше	14	2,3	32,2	74,06
Итого	90	—	162,6	303,62

Выборочная средняя

Выборочная дисперсия изучаемого признака

Определяем среднюю ошибку повторной случайной выборки
Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.

Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.

Предельная ошибка выборки с вероятностью 0,954 равна
$delta_{x}= tmu_{x}= 2*0.035 = 0.07$
Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.

Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

$delta_{x}= tmu_{x}= 2*0.027 = 0.054$

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.

По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:

рассчитаем выборочную долю.

Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда

m = 60, n = 90, w = m/n = 60 : 90 = 0,667;

рассчитаем дисперсию доли в выборочной совокупности

$sigma_{w}^{2}= w(1 - w) = 0,667(1 - 0,667) = 0,222$ ;

средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

зададим доверительную вероятность и определим предельную ошибку выборки.

При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

$delta_{x}= tmu_{x}= 3*0.04 = 0.12$

установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.

Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда

N₁ + N₂ + … + N_i + … + N_k = N.

Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки

n₁ + n₂ + … + n_i + … + n_k = n.

Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.

Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:

n = n_i · N_i/N

где n_i — количество извлекаемых единиц для выборки из i-й типической группы;

n — общий объем выборки;

N_i — количество единиц генеральной совокупности, составивших i-ю типическую группу;

N — общее количество единиц генеральной совокупности.

Отбор единиц внутри групп происходит в виде случайной или механической выборки.

Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

Таблица
11.6.
Формулы для расчета средней ошибки выборки () при использовании типического отбора, пропорционального объему типических групп

Здесь $sigma^{2}$ — средняя из групповых дисперсий типических групп.

Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:

Таблица
11.7.

Номер курса	Всего студентов, чел., N_i	Обследовано в результате выборочного наблюдения, чел., n_i	Среднее число посещений библиотеки одним студентом за семестр, x_i	Внутригрупповая выборочная дисперсия, $sigma_{i}^{2}$
1	650	33	11	6
2	610	31	8	15
3	580	29	5	18
4	360	18	6	24
5	350	17	10	12
Итого	2 550	128	8	—

Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:

общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
количество единиц, отобранных из каждой типической группы:

аналогично для других групп:

n₂ = 31 (чел.);

n₃ = 29 (чел.);

n₄ = 18 (чел.);

n₅ = 17 (чел.).

Проведем необходимые расчеты.

Выборочная средняя, исходя из значений средних типических групп, составит:
Средняя из внутригрупповых дисперсий
Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

$delta_{x} = tmu_{x} = 2*0.334 = 0.667$
Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.

Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

$delta_{MB}= tmu_{MB}$

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.

Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.

Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.

Среднее значение признака в выборке равно
Значение среднего квадратического отклонения составляет
Средняя ошибка выборки:
Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
Предельная ошибка выборки:
$delta_{MB}= tmu_{MB}=2,365*0,344 = 0,81356 ~ 0,81 (ч)$
Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.

11.2.2. Определение численности выборочной совокупности

Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):

вид предполагаемой выборки;
способ отбора (повторный или бесповторный);
выбор оцениваемого параметра (среднего значения признака или доли).

Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.

Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.

Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.

При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.

Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.

2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал

Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:

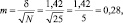
11.wmf (2.1)

где δ –	стандартное отклонение;
N –	число наблюдений или объем выборки, шт.

Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 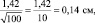12.wmf а если увеличить до 10000 шт., то в 10 раз, до 0,014 см.

Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:

при объеме выборки N = 2 ошибка будет

13.wmf

при объеме выборки N = 4 ошибка будет

14.wmf

при объеме выборки N = 16 ошибка будет

15.wmf

Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 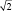16.wmf = в 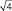1,41 раза; при выборках из 4 шт. –
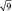
в 17.wmf = в 2 раза; при выборках из 9 шт. – в 18.wmf = в 3 раза и т.д.

Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.

Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.

Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 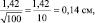19.wmf а ее отнесение к средней высоте сеянцев 5,0 см, выражаемое в %, дает нам так называемую точность опыта: 0,14/5,0×100 = 2,8 %. В биологии точность опыта ±2–3 % считается высокой, ±5 % – достаточной, а ±6–7 % – пониженной, но это весьма упрощенное представление о планировании эксперимента.

Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта

Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.

Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?

Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:

хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см

хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.

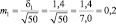
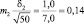
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 20.wmf и 21.wmf и пределы колебаний возможных значений средних будут:

хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;

хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.

2_1.tif

Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)

Снова вынесем эти пределы на график (рис. 2.2).

2_2.tif

Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки

Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?

Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).

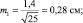
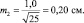
При выборках из 25 штук сеянцев, получаем две ошибки: 22.wmf 23.wmf Тогда пределы значений для этих двух выборочных средних для уровня прогноза в 95 % будут:

хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;

хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.

Выносим эти пределы опять на график (рис. 2.3).

2_3.tif

Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)

Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

На заводе, где число рабочих составляет 1000 человек, было проведено выборочное обследование возраста рабочих. Методом случайного бесповторного отбора было отобрано 50 человек. Результаты обследования следующие:

Возраст рабочих (лет)	до 30	30 – 40	40 – 50	50 – 60	свыше 60
Число рабочих	8	22	10	6	4

С вероятностью 0,997 определите предел, в котором находится средний возраст рабочих завода.

Решение:

1. Рассчитаем средний возраст рабочих завода в выборочной совокупности. Все расчёты оформим в таблицу.

Возраст рабочих (лет)	Число рабочих (f)	Среднее значение интервала (х)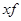
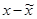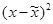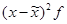до 30	8	25	200	-15,2	231,04	1848,3
30 – 40	22	35	770	-5,2	27,04	594,88
40 – 50	10	45	450	4,8	23,04	230,4
50 – 60	6	55	330	14,8	219,04	1314,2
свыше 60	4	65	260	24,8	615,04	2460,2
Итого:	50	—	2010	—	—	6448

Средняя выборочная в данном случае будет рассчитываться по формуле средней арифметической взвешенной:

2. Рассчитаем дисперсию выборочной совокупности:

3. Средняя ошибка выборки составит:

4. С вероятностью 0,997 рассчитаем предельную ошибку выборочной средней.

Δ = μ * t

t — коэффициент доверия.

Значение коэффициента доверия t определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения и берётся из готовых таблиц.

Наиболее часто встречающиеся в задачах подобного рода значения t:

Вероятность Р	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

При Р = 0,997, t = 3.

Δ = 1,565 * 3 = 4,696 лет.

5. Определим пределы, в которых находится средний возраст рабочих завода.

Генеральная средняя (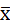) находится в пределах

40,2 — 4,696 ˂ ˂ 40,2 + 4,696.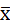

35,5 ˂ 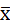˂ 44,9

С вероятностью 0,997 можно утверждать, что средний возраст рабочих завода находится в пределах 35,5 ˂ 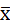˂ 44,9 лет.

Источник

11.2. Оценка результатов выборочного наблюдения

11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Например, если применяется повторная собственно случайная выборка, то определяется как:

— при оценивании среднего значения признака;

— если признак альтернативный, и оценивается доля.

При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):

— для среднего значения признака;

— для доли.

Уровень предельной ошибки выборки зависит от следующих факторов:

степени вариации единиц генеральной совокупности;
объема выборки;
выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
уровня доверительной вероятности.

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Таблица
11.2.

Значение доверительной вероятности P	0,683	0,954	0,997
Значение коэффициента доверия t	1,0	2,0	3,0

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

Ошибки выборки при различных видах отбора

Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.

Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ()

где $sigma^{2}$ — дисперсия признака в выборочной совокупности.

Таблица
11.4.

Уровень фондоотдачи, руб.	До 1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0-2,2	2,2 и выше	Итого
Количество предприятий	13	15	17	15	16	14	90

По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:

Таблица
11.5.

Результаты наблюдения	Расчетные значения
уровень фондоотдачи, руб., x_i	количество предприятий, f_i	середина интервала, x_i^xb4	x_i^xb4f_i	x_i^xb4²f_i
До 1,4	13	1,3	16,9	21,97
1,4-1,6	15	1,5	22,5	33,75
1,6-1,8	17	1,7	28,9	49,13
1,8-2,0	15	1,9	28,5	54,15
2,0-2,2	16	2,1	33,6	70,56
2,2 и выше	14	2,3	32,2	74,06
Итого	90	—	162,6	303,62

Выборочная средняя

Выборочная дисперсия изучаемого признака

Определяем среднюю ошибку повторной случайной выборки
Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.

Предельная ошибка выборки с вероятностью 0,954 равна
$delta_{x}= tmu_{x}= 2*0.035 = 0.07$
Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

$delta_{x}= tmu_{x}= 2*0.027 = 0.054$

рассчитаем выборочную долю.

m = 60, n = 90, w = m/n = 60 : 90 = 0,667;

рассчитаем дисперсию доли в выборочной совокупности

$sigma_{w}^{2}= w(1 - w) = 0,667(1 - 0,667) = 0,222$ ;

средняя ошибка выборки при использовании повторной схемы отбора составит

зададим доверительную вероятность и определим предельную ошибку выборки.

$delta_{x}= tmu_{x}= 3*0.04 = 0.12$

установим границы для генеральной доли с вероятностью 0,997:

Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда

N₁ + N₂ + … + N_i + … + N_k = N.

n₁ + n₂ + … + n_i + … + n_k = n.

n = n_i · N_i/N

где n_i — количество извлекаемых единиц для выборки из i-й типической группы;

n — общий объем выборки;

N_i — количество единиц генеральной совокупности, составивших i-ю типическую группу;

N — общее количество единиц генеральной совокупности.

Отбор единиц внутри групп происходит в виде случайной или механической выборки.

Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

Здесь $sigma^{2}$ — средняя из групповых дисперсий типических групп.

Таблица
11.7.

Номер курса	Всего студентов, чел., N_i	Обследовано в результате выборочного наблюдения, чел., n_i	Среднее число посещений библиотеки одним студентом за семестр, x_i	Внутригрупповая выборочная дисперсия, $sigma_{i}^{2}$
1	650	33	11	6
2	610	31	8	15
3	580	29	5	18
4	360	18	6	24
5	350	17	10	12
Итого	2 550	128	8	—

Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:

общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
количество единиц, отобранных из каждой типической группы:

аналогично для других групп:

n₂ = 31 (чел.);

n₃ = 29 (чел.);

n₄ = 18 (чел.);

n₅ = 17 (чел.).

Проведем необходимые расчеты.

Выборочная средняя, исходя из значений средних типических групп, составит:
Средняя из внутригрупповых дисперсий
Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

$delta_{x} = tmu_{x} = 2*0.334 = 0.667$
Доверительные границы для среднего значения признака в генеральной совокупности:

Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.

Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

$delta_{MB}= tmu_{MB}$

Среднее значение признака в выборке равно
Значение среднего квадратического отклонения составляет
Средняя ошибка выборки:
Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
Предельная ошибка выборки:
$delta_{MB}= tmu_{MB}=2,365*0,344 = 0,81356 ~ 0,81 (ч)$
Доверительный интервал для среднего значения признака в генеральной совокупности:

11.2.2. Определение численности выборочной совокупности

вид предполагаемой выборки;
способ отбора (повторный или бесповторный);
выбор оцениваемого параметра (среднего значения признака или доли).

Таблица
11.8.
Формулы для определения численности выборочной совокупности

При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.

Источник