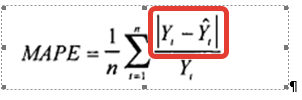17 авг. 2022 г.
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является MAPE , что означает среднюю абсолютную ошибку в процентах .
Формула для расчета MAPE выглядит следующим образом:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать и легко объяснить. Например, значение MAPE, равное 11,5%, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 11,5%.
Чем ниже значение MAPE, тем лучше модель способна прогнозировать значения. Например, модель с MAPE 2% более точна, чем модель с MAPE 10%.
Как рассчитать MAPE в Excel
Чтобы рассчитать MAPE в Excel, мы можем выполнить следующие шаги:
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
Шаг 2: Рассчитайте абсолютную процентную ошибку для каждой строки.
Напомним, что абсолютная процентная ошибка рассчитывается как: |фактический-прогноз| / |фактическое| * 100. Мы будем использовать эту формулу для расчета абсолютной процентной ошибки для каждой строки.
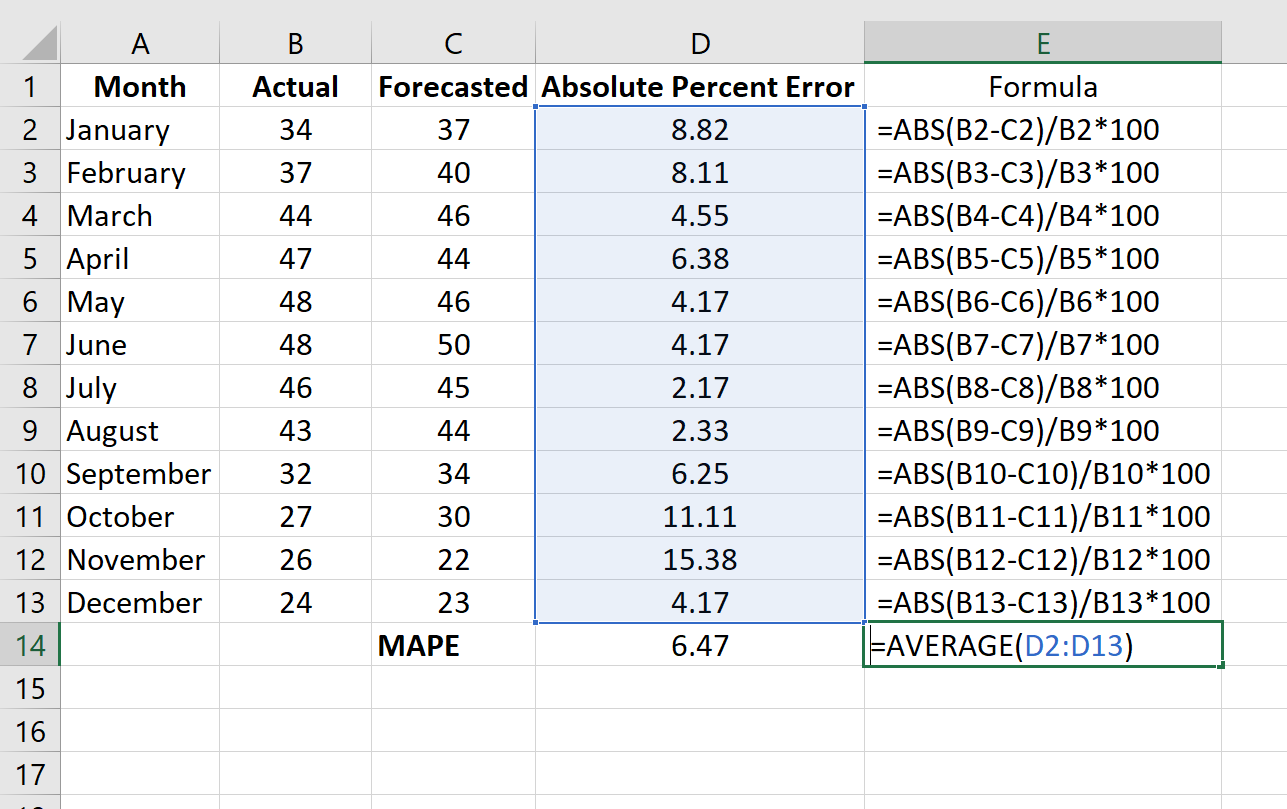
Столбец D отображает абсолютную процентную ошибку, а столбец E показывает формулу, которую мы использовали:
Повторим эту формулу для каждой строки:
Шаг 3: Рассчитайте среднюю абсолютную ошибку в процентах.
Рассчитайте MAPE, просто найдя среднее значение в столбце D:
MAPE этой модели оказывается равным 6,47% .
Примечание по использованию MAPE
Хотя MAPE легко вычислить и легко интерпретировать, его использование имеет несколько потенциальных недостатков:
1. Поскольку формула для расчета абсолютной процентной ошибки |фактический-прогноз| / |фактическое| это означает, что он будет неопределенным, если какое-либо из фактических значений равно нулю.
2. MAPE не следует использовать с данными небольшого объема. Например, если фактический спрос на какой-либо товар равен 2, а прогноз равен 1, значение абсолютной процентной ошибки будет |2-1| / |2| = 50%, что создает впечатление, что ошибка прогноза довольно высока, несмотря на то, что прогноз отличается всего на одну единицу.
Другим распространенным способом измерения точности прогнозирования модели является MAD — среднее абсолютное отклонение. О том, как посчитать MAD в Excel, читайте здесь .
Дополнительные ресурсы
Что считается хорошей ценностью для MAPE?
Как рассчитать SMAPE в Excel
Как рассчитать MAE в Excel
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Где:
- Yt – фактический объем продаж за анализируемый период;
- Ŷt — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷt;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
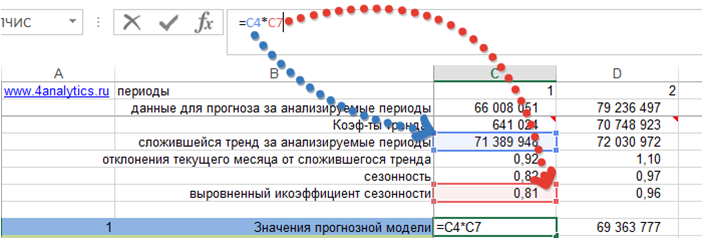
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
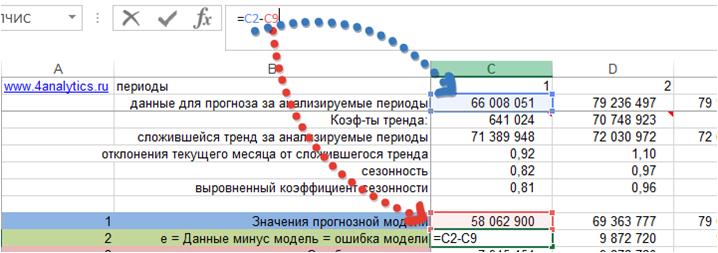
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
e — Ошибка прогноза — это разность между значениями временного ряда (фактом продаж) и моделью прогноза:
e= Yt — Ŷt
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
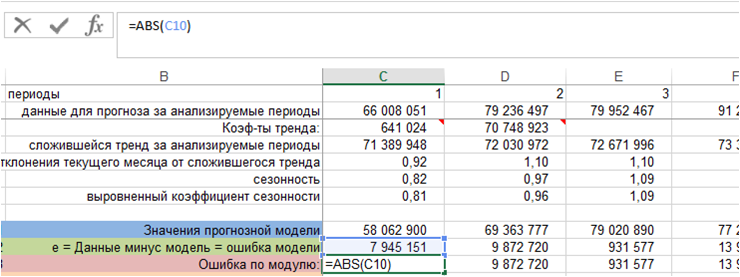
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
4. Определяем абсолютную ошибку.
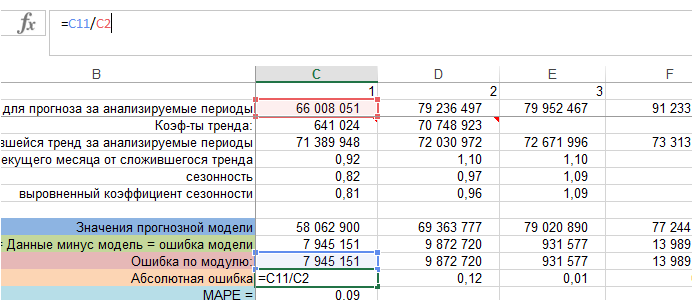
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
Получили абсолютную ошибку для каждого периода фактических продаж. В формуле MAPE — это:
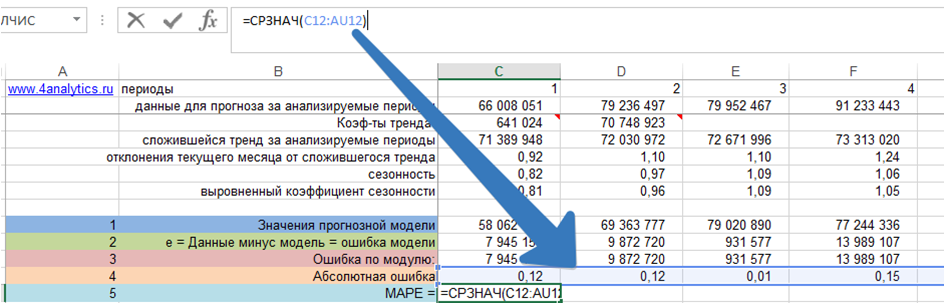
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Скачать файл с примером расчета MAPE – средней абсолютной ошибки.
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Об этом подробнее можете почитать в нашей статье на сайте http://novoforecast.com/novo-forecast/instruktsiya/item/rost-tochnosti-prognoza-rost-pribyli.html
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
In statistics, we often use Forecasting Accuracy which denotes the closeness of a quantity to the actual value of that particular quantity. The actual value is also known as the true value. It basically denotes the degree of closeness or a verification process that is highly used by business professionals to keep track records of their sales and exchanges to maintain the demand and supply mapping every year. There are various methods to calculate Forecasting Accuracy.
So, one of the most common methods used to calculate the Forecasting Accuracy is MAPE which is abbreviated as Mean Absolute Percentage Error. It is an effective and more convenient method because it becomes easier to interpret the accuracy just by seeing the MAPE value.
In this article, we are going to see how to calculate Mean Absolute Percentage Error, MAPE in Excel.
The formula to calculate MAPE is :
The above formula can be interpreted as the average value of Absolute Percentage Error (APE) of all the observations in the data set.
Note: The actual value can’t be zero. We can observe from the above formula that if the Actual value becomes zero, it will be undefined.
Example:
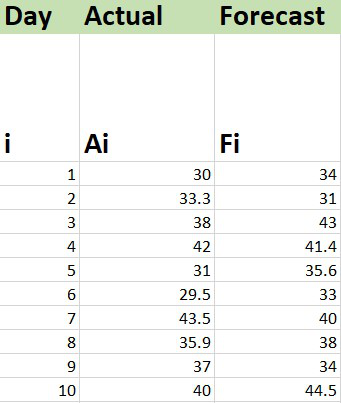
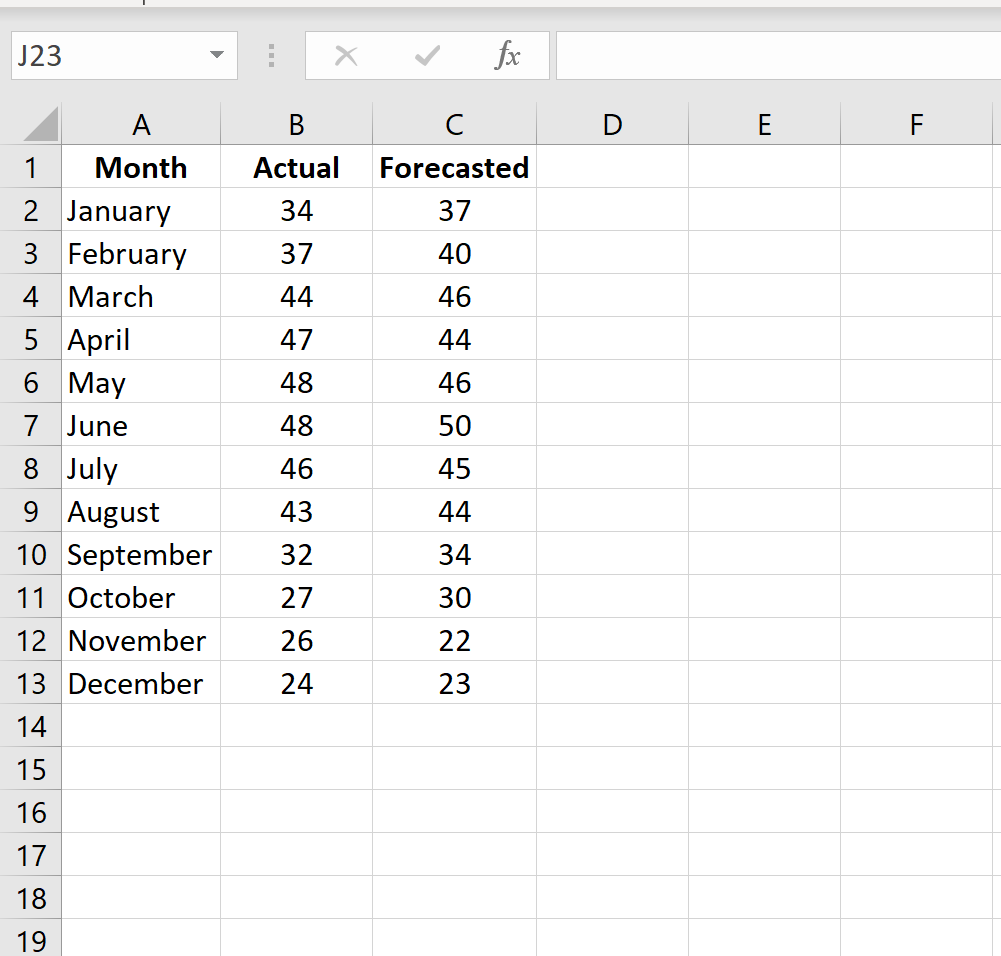
Consider the dataset shown below :
Calculation of MAPE in Excel:
The functions needed for formulas in Excel are-
ABS : To calculate the absolute value.
AVERAGE : To calculate the mean.
The steps are :
1. Insert the data set in the Excel sheet.
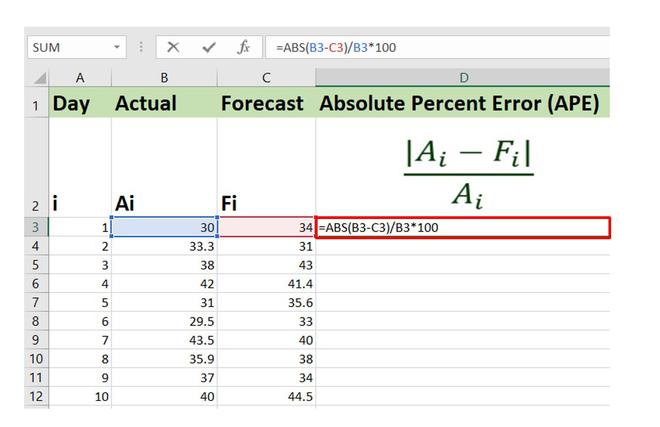
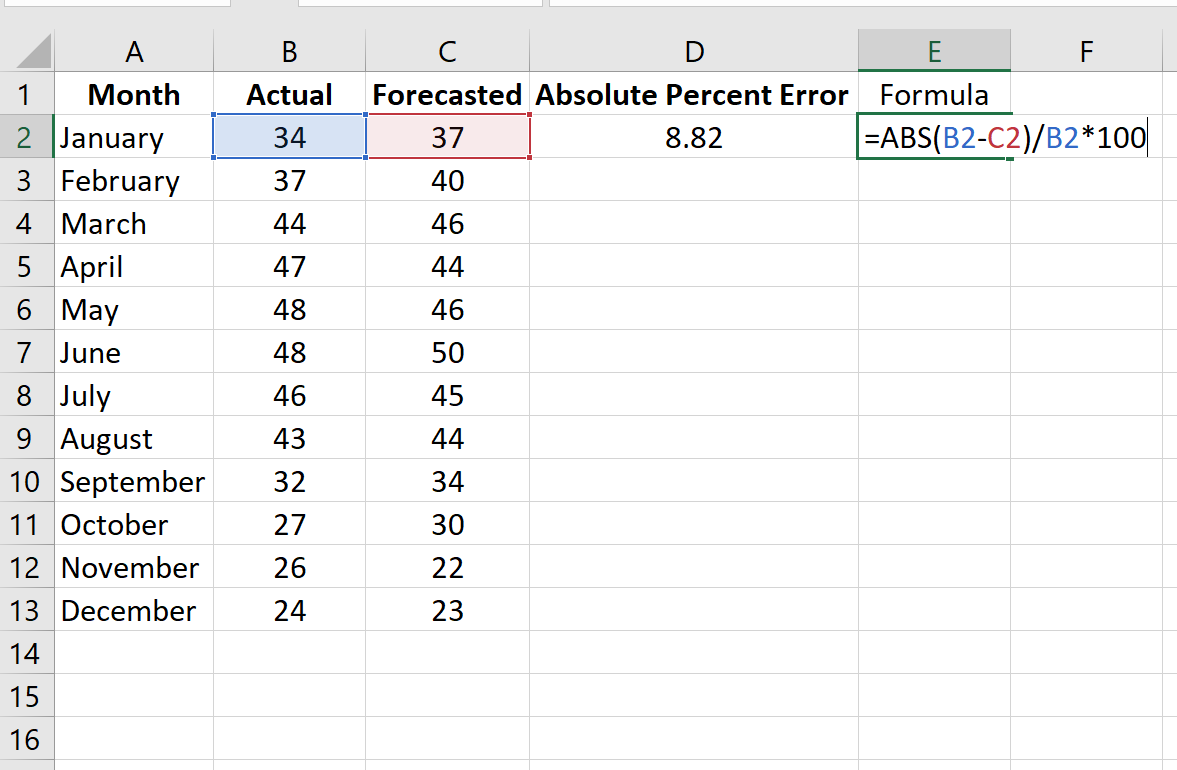
2. Calculate APE for each individual observation using Excel Formula. The formula will be :
=ABS(Cell_No_Act-Cell_No_Fore)/Cell_No_Act*100 where ABS : Used to calculate the absolute value Cell_No_Act : Cell number where Actual value is present Cell_No_Fore : Cell number where Forecast value is present
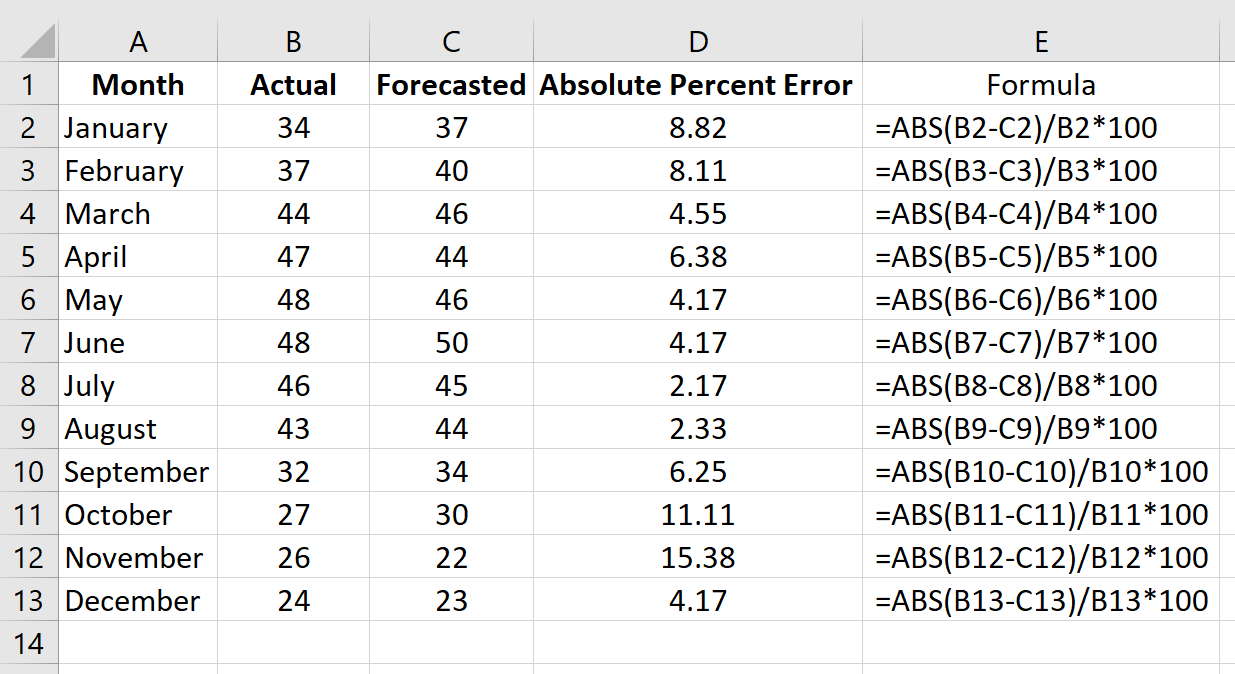
Similarly, you can write the formulas for the other entries and get the APE for all the records.
APE
3. Now, simply we need to find the average or the mean value for all these values in order to calculate MAPE.
The formula to find average value in Excel is :
=AVERAGE(Cell_Range)
The value of MAPE for the given data set is 9.478% approximately. Therefore, we can say that the average difference between the actual value and forecasted value is 9.478%.
MAPE
Last Updated :
09 Jul, 2021
Like Article
Save Article
Измерение точности ваших инструментов прогнозирования может помочь вам делать более точные прогнозы в будущем. SMAPE, или симметричная средняя абсолютная процентная ошибка, — это один из расчетов, который вы можете использовать для проверки точности ваших методов прогнозирования. Знание того, что представляет собой формула SMAPE и преимущества ее использования, поможет вам принимать лучшие финансовые решения. В этой статье мы обсудим, что такое формула SMAPE, рассмотрим, почему она важна, и рассмотрим четыре метода ее использования для расчетов.
Что такое формула SMAPE?
Формула SMAPE — это расчет, который можно выполнить для нахождения симметричной средней абсолютной процентной ошибки. Вот что означают буквы более подробно:
-
СимметричноеУравнение, которое сравнивает как прогнозы, которые превышают, так и прогнозы, которые ниже фактического результата.
-
Значение: Указание на то, что вы используете эту формулу для вычисления средней разницы вместо одной измеренной разницы.
-
Абсолют: Вычисление, которое выводит только положительные числа, поскольку использует символ абсолютного значения |x|.
-
Процент: Ссылка на то, что это уравнение выводит разницу между сделанным вами прогнозом и реальным результатом для предсказанного события в виде части числа 100.
-
Ошибка: Разница между прогнозируемым результатом и тем, что произошло в действительности.
Формула SMAPE имеет вид:
SMAPE = 1n x ?(|Прогноз — Факт| ((|Актуальный + Прогноз|) 2) x 100
Где:
-
n — размер выборки.
-
? это символ, который означает сумму.
-
|x| — символы, обозначающие абсолютную величину, которая является расстоянием от нуля.
-
Прогноз — это предсказание, которое вы сделали относительно исхода события.
-
Факт — это реальный результат события.
-
100 преобразует результат остальной части уравнения в процент.
Почему формула SMAPE важна?
Формула SMAPE важна, потому что она может помочь вам скорректировать ваши расчеты, чтобы сделать более точные прогнозы для бизнеса, личных финансов или фондового рынка. SMAPE также важен при использовании с другими измерениями точности прогнозирования, такими как MAPE и WMAPE — что означает взвешенную среднюю абсолютную процентную ошибку — поскольку эти уравнения нацелены на конкретные различия между прогнозом и фактическими измерениями.
Как использовать формулу SMAPE
Использование формулы SMAPE может потребовать некоторой практики, но четыре приведенных ниже метода помогут вам освоить ее:
Метод первый: Расчет SMAPE вручную
Этот метод может занять больше времени, чем следующие три, но вы часто можете узнать, как произвести расчет и какие шаги необходимо предпринять, чтобы последующие методы рассчитали его правильно. Вы также можете рассчитать SMAPE вручную, если у вас есть относительно небольшой объем данных, для которых вы хотите найти SMAPE, например, пять записей или меньше. Вот шаги для вычисления SMAPE вручную:
1. Соберите данные для заполнения уравнения
Первый шаг для расчета SMAPE — собрать нужные данные и заполнить разделы уравнения. Может быть полезно собрать необходимую информацию в таблицу, так как она поможет разделить нужные вам данные. Например, в таблице ниже приведены данные по фактическому количеству продаж в сравнении с прогнозируемыми цифрами:
Фактические продажи Прогнозные продажи
2. Рассчитайте SMAPE для каждой записи в таблице
Получив начало уравнения, вы можете рассчитать индивидуальный SMAPE для каждой записи в таблице. Чтобы найти индивидуальную ценность каждой записи, вы можете использовать приведенную ниже формулу:
SMAPEI = (|Forecast — Actual| ((|Actual| + |Forecast|) 2)
Это означает, что вычисления для каждой записи следующие:
-
(|5 — 5| ((|5| + |5|) 2) = 0 (10 2) = 0 5 = 0
-
(|10 — 15| ((|15| + |10| 2) = 5 (25 2) = 5 12.5 = 0.4
-
(|8 — 11| ((|11| + |8| 2) = 3 (19 2) = 3 9.5 = 0.32
-
(|11 — 2| ((|2| + |11| 2) = 9 (13 2) = 9 6.5 = 1.38
Еще раз, может быть полезно использовать таблицу для записи результата каждой записи, как показано ниже:
Фактические продажи Прогноз продаж Индивидуальный SMAPE
| 5 | 5 | 0.00 |
| 15 | 10 | 0.40 |
| 11 | 8 | 0.32 |
| 2 | 11 | 1.38 |
3. Рассчитайте среднее значение для отдельных значений SMAPE
После расчета индивидуальных значений SMAPE вы можете рассчитать среднее значение, сложив их вместе и разделив на общее количество значений. Например:
(0.00 + 0.40 + 0.32 + 1.38) 4 = 0.53
4. Умножьте результат предыдущих шагов на 100
Последним шагом для расчета SMAPE по формуле является умножение значения на 100 для получения процента. Для этого возьмите абсолютное среднее значение набора данных и умножьте его на 100. Например:
0.53 x 100 = 53%
5. Используйте SMAPE для изменения методов прогнозирования
Вы можете использовать найденный SMAPE, чтобы определить, насколько близки ваши модели прогнозирования к фактическим результатам ваших данных. Например, значение 2% означает, что разница между вашими методами прогнозирования и полученными реальными данными относительно невелика. Высокий показатель SMAPE, например 53%, означает, что вы можете улучшить свои модели прогнозирования, чтобы сделать их более точными и в дальнейшем сэкономить на расходах.
Метод 2: Вычисление SMAPE в Excel
Этот метод дает возможность быстро рассчитать SMAPE большой выборки данных с помощью функций в программе Excel. Ниже приведены шаги, которые помогут вам рассчитать SMAPE:
1. Ввести данные в электронную таблицу Excel
Первый шаг к нахождению SMAPE в Excel — это ввод фактических и прогнозных точек данных в электронную таблицу. Например, вы можете отобразить три точки данных в ячейках A2 — B4 как:
A B
| 1 | Прогноз | Фактический |
| 2 | 10 | 12 |
| 3 | 15 | 14 |
| 4 | 5 | 7 |
После ввода данных в электронную таблицу вы можете рассчитать SMAPE для отдельных наборов данных, выбрав пустую ячейку и введя функцию:
=ABS(A2-B2)((ABS(B2)+ABS(A2))2
Где:
-
=ABS — это функция, которая вычисляет абсолютное значение.
-
A2 — ячейка для примера данных прогноза.
-
B2 — ячейка для фактических данных примера.
Как только вы найдете SMAPE для одной пары точек данных, вы можете навести курсор на правую нижнюю часть ячейки с вычислениями, пока ваш курсор не примет вид символа плюса, а затем нажмите и перетащите ячейку вниз. Например, если вы поместили расчет в ячейку C2, вы можете перетащить его на ячейки C3 и C4, чтобы сделать расчет для ячеек A3, A4, B3 и B4. Ниже приведена таблица, в которой представлены результаты вычислений:
A B C
| 1 | Прогноз | Фактический | Индивидуальный SMAPE |
| 2 | 10 | 12 | 0.18 |
| 3 | 15 | 14 | 0.07 |
| 4 | 5 | 7 | 0.33 |
Вы можете рассчитать итоговый SMAPE набора данных, введя формулу в пустую ячейку, например, в ячейку C5:
=SUM(C2:C4)COUNT(C2:C4)
Эта функция вычисляет среднее значение отдельных расчетов SMAPE. Получив число из этого расчета, вы можете умножить его на 100, чтобы получить значение всего набора данных. Например, приведенные выше значения дают результат 0.19. Вы можете умножить это значение на 100, чтобы получить 19%, что и будет вашим окончательным значением.
Метод третий: Вычисление SMAPE в Python
Третий способ использования формулы SMAPE — это использование языка программирования Python. Чтобы использовать SMAPE, вы можете создать пользовательскую функцию в программе. Ниже приведены шаги по созданию функции и ее использованию в Python:
1. PIP установить numpy
Для вычисления SMAPE в Python необходим дополнительный пакет numpy. Чтобы установить пакет, вы можете ввести в первую строку Python следующее:
pip install numpy
Этот пакет позволяет Python работать с различными частями формулы SMAPE и может помочь вам рассчитать ее на языке программирования.
2. Импортируйте numpy как np
После установки numpy вы можете импортировать его в Python. Для этого можно ввести следующую команду во вторую строку Python, чтобы позволить ему получить доступ к частям пакета, необходимым для использования формулы SMAPE:
import numpy as np
Эта команда указывает Python, что любая ссылка на «np» в следующих командах импорт ссылается на пакет numpy.
3. Определить SMAPE
Третий шаг к использованию формулы SMAPE в Python заключается в определении формулы. Вы можете использовать формулу «определить» команда в третьей строке командной строки в Python. Формула для определения SMAPE имеет вид:
def smape(actual,forecast): return 100len(actual) * np.sum(2 * np.абс(прогноз — факт) (np.abs(actual) + np.abs(forecast)))
Эта команда указывает Python определить SMAPE, ссылаясь на значения фактического и прогнозного, а затем произвести расчет, используя эти значения.
4. Введите данные для фактических и прогнозных показателей
После ввода определения SMAPE в Python вы можете определить, какими будут фактические и прогнозные значения. Вы можете сделать это, перейдя на следующую пустую строку и набрав:
Фактический = np.array([значение 1, значение 2, значение 3, …])
Прогноз = np.array([значение 1, значение 2, значение 3, …])
Где:
-
np. это ссылка на пакет numpy.
-
array — это команда, которая сообщает Python, что это связанный набор чисел.
-
значение — это место, где вы вводите значения фактических и прогнозных показателей.
5. Рассчитайте SMAPE и распечатайте результаты
После того, как вы определили, каковы ваши массивы для прогноза и фактических значений, вы можете рассчитать SMAPE, используя созданное вами определение. Для этого можно использовать следующую команду:
result = smape(actual, forecast)
После того как Python вычислит результат SMAPE, вы можете распечатать его с помощью одной команды, записанной как:
print(«SMAPE :», результат)
Это печатает результат SMAPE на основе значений, которые вы ввели для фактических и прогнозных значений.
Четвертый метод: Вычисление SMAPE в R
Вычисление SMAPE в R эффективно, поскольку язык имеет функцию для SMAPE, включенную в базовую программу. Приведенные ниже шаги помогут вам использовать формулу SMAPE в R:
1. Открыть библиотеку метрик
Первым шагом для расчета SMAPE в языке программирования R является открытие библиотеки метрик пакета. Чтобы открыть пакет, вы можете набрать «library (Metrics)» введите метрики в программу и нажмите «Введите» на клавиатуре. Это даст программе понять, что вы хотите использовать один из инструментов метрики из этого пакета.
2. Определить фактические и прогнозные значения
После открытия пакета метрик вы можете определить значения для фактических и прогнозных данных, набрав команды, приведенные ниже:
фактический <- c(значение 1, значение 2, …)
прогноз <- c(значение 1, значение 2, …)
Эти две команды сообщают программе значения как прогнозных, так и фактических данных, чтобы она могла рассчитать SMAPE.
3. Вычислите SMAPE
Последним шагом для вычисления формулы SMAPE в R является использование команды для запуска вычисления. Команда для SMAPE имеет следующий вид:
smape(actual, forecast)
Это запустит расчет в R и выведет число, основанное на ваших фактических и прогнозных данных.
Обратите внимание, что ни один из продуктов или компаний, упомянутых в этой статье, не связан с Indeed.
Бизнес-профессионалы, специалисты по данным и финансовым аналитикам, а также бухгалтеры используют модели прогнозирования, чтобы предсказать, как все изменится в течение определенного периода. Чтобы обеспечить точность своих моделей, эти специалисты измеряют, насколько модель похожа на фактические данные. Для этого они могут использовать средневзвешенную абсолютную процентную ошибку или WMAPE. Знание того, что такое WMAPE и как его рассчитать, может помочь вам делать более точные прогнозы будущих данных и финансовых тенденций. В этой статье мы обсудим, что такое WMAPE, рассмотрим способы его использования и рассмотрим, как рассчитать WMAPE для выборки данных.
Что такое средневзвешенная абсолютная ошибка в процентах?
Средневзвешенная абсолютная процентная ошибка, обычно называемая WMAPE, представляет собой способ измерения точности финансовых и статистических прогнозов по сравнению с фактическими или реальными результатами для выборки. Например, если вы предсказали, что продадите пять автомобилей, и действительно продали пять автомобилей в этот день, то ваш WMAPE будет равен 0 %, поскольку в вашем прогнозе не было ошибок. Если бы вы продали три автомобиля, то ваш WMAPE составил бы 66,6%, потому что в прогнозе был указан один результат, а реальный результат был другим. Различные части WMAPE:
-
Взвешенный: это означает, что есть компонент, по которому вы измеряете результат расчета.
-
Среднее: это означает, что ваш результат для этого расчета является средним показателем точности ваших прогнозов.
-
Абсолют: это означает, что независимо от того, был ли реальный результат больше или меньше прогноза, ваш расчет даст положительное число.
-
Процент: это означает, что результат вашего расчета представлен в процентном формате для простоты использования.
-
Ошибка: это означает, что результат вашего расчета является мерой разницы между вашим прогнозом и вашим реальным результатом.
Как используется средневзвешенная абсолютная процентная ошибка?
Вы можете использовать WMAPE для исследования средней ошибки ваших прогнозов с течением времени по сравнению с тем, что происходит на самом деле. Как правило, вы используете WMAPE для сравнения прогнозов за более длительный период, потому что это показывает общую тенденцию правильности ваших прогнозов, а не конкретный день или час. Вы также можете использовать WMAPE в сочетании с другими измерениями прогнозирования, чтобы получить представление о точности и скорости отклика ваших моделей данных.
Как рассчитывается средневзвешенная абсолютная ошибка в процентах?
Формула для расчета WMAPE:
(1/n) x Σ(|Факт. — Прогноз|) x 100 / |Факт.| = WMAPE
Где части формулы:
-
n = размер выборки
-
Σ = сумма всех значений в скобках
-
|х| = символы, представляющие абсолютное значение чисел между ними
-
Факт = реальная стоимость за данный период
-
Прогноз = ожидаемое значение для данного периода
Например, если у вас есть следующие прогнозируемые и фактические значения:
Прогноз**Фактический**53101555Следующие шаги могут помочь вам найти WMAPE для вашего набора данных:
1. Найдите все значения для |Факт — Прогноз|
Чтобы найти эти значения, вы можете ввести каждое значение прогнозируемого и фактического в уравнение. Например:
|3 — 5| = 2
|15 -10| = 5
|5 — 5| = 0
Это удовлетворяет части формулы |Факт — Прогноз| и может помочь вам рассчитать вес каждого значения. Примечательно, что в первом уравнении используются символы абсолютных значений |x| и преобразует отрицательное число два в значение положительного числа два. Это связано с тем, что символы абсолютного значения заботятся о расстоянии числа от нуля, а не о его реальном значении. Здесь минус два — это два от нуля.
2. Разделите каждое значение на фактическое значение.
После того как вы рассчитали абсолютные значения фактических и прогнозируемых данных, вы можете разделить эти данные на фактическое значение. Например:
2/3 = 0,66
5/15 = 0,33
0 / 5 = 0
Это удовлетворяет части уравнения /|Actual|. Каждый из результатов вычислений является положительным числом из-за использования символов абсолютного значения. Это может помочь вам рассчитать вес для каждого значения в вашем наборе данных.
3. Умножить на 100 и разделить на фактическое значение
После того, как вы нашли результаты своих предыдущих расчетов, вы можете умножить каждый из них на 100. Это гарантирует, что все ваши значения находятся в той же шкале, что и фактические значения, удовлетворяет части уравнения x 100 и может помочь вам определить каждое значение. масса. Например:
0,66 х 100 = 66
0,33 х 100 = 33
0 х 100 = 0
После того, как вы завершили приведенные выше расчеты, вы можете разделить каждый результат на исходное фактическое значение. Например:
66/3 = 22
33/15 = 2,2
0 / 5 = 0
Эти числа представляют веса каждого вычисления, которые используются в следующих шагах. Для этого шага вы также можете присвоить веса на основе важных моментов в вашем наборе данных. Например, если понедельник — лучший день продаж на неделе, а все остальные дни равны, то понедельнику можно присвоить вес, равный шести, а другим дням — один. Это означает, что понедельник имеет 60% веса, а все остальные дни имеют 10% веса.
4. Рассчитать сумму фактических значений и сумму весов
Теперь, когда вы вычислили веса каждого набора значений, вы можете вычислить сумму фактических значений. Вы можете сделать это, добавив каждое фактическое значение к другим. Например:
3 + 15 + 0 = 18
После того, как вы подсчитали сумму фактических значений, вы можете сложить свои веса. Например:
22 + 2,2 = 24,2
5. Рассчитайте средневзвешенную абсолютную процентную ошибку.
Наконец, вы можете рассчитать средневзвешенную абсолютную процентную ошибку, разделив сумму весов на сумму фактических значений. Например:
24,2/18 = 1,34
Преобразованное в проценты, это значение составляет 1,34%, что равно средневзвешенной абсолютной процентной ошибке значений. Это относительно низкая процентная ошибка, означающая, что модели прогнозирования были почти на 100% точными.


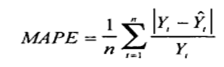 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: