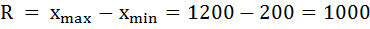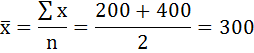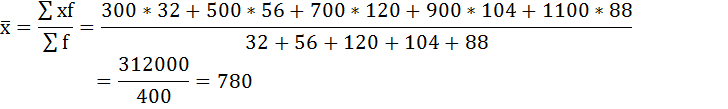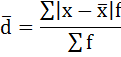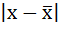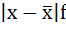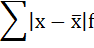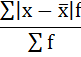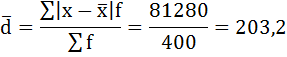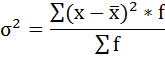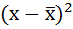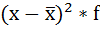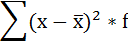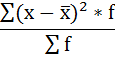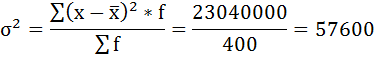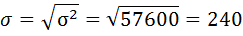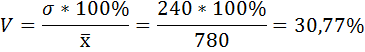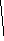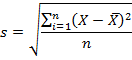Рассчитать среднее и его ошибку и коэффициент вариации - ErrorsMaster.ru

On-line калькулятор, который выполняет расчеты среднего арифметического показателя, Дисперсии, Вариации, Среднеквадратичного отклонения, удобный в использовании. Для получения правильного результата необходимо правильно заполнить предложенную таблицу.

Такой онлайн калькулятор станет незаменимым помощником для осуществления математических расчетов. Указав нужные значения вам достаточно нажать кнопку «Расчет» и незамедлительно появится правильный результат. Простота в использовании делает калькулятор незаменимым и популярным. Им легко пользоваться на работе, дома, во время учебы. Он не требует выполнения сложных действий. Вы сможете сделать все вычисления для всех нужных величин.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также

Источник

По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:

Размер вклада, руб.	До 400	400 — 600	600 — 800	800 — 1000	Свыше 1000
Число вкладчиков	32	56	120	104	88

Определите:

1) размах вариации;

2) средний размер вклада;

3) среднее линейное отклонение;

4) дисперсию;

5) среднее квадратическое отклонение;

6) коэффициент вариации вкладов.

Решение:

Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.

Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.

Размер вклада, руб.	200 — 400	400 — 600	600 — 800	800 — 1000	1000 — 1200
Число вкладчиков	32	56	120	104	88

1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:

Размах вариации размера вклада равен 1000 рублей.

2) Средний размер вклада определим по формуле средней арифметической взвешенной.

Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.

Среднее значение первого интервала будет равно:

второго — 500 и т. д.

Занесём результаты вычислений в таблицу:

Размер вклада, руб.	Число вкладчиков, f	Середина интервала, х	xf
200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
Итого	400	—	312000

Средний размер вклада в Сбербанке города будет равен 780 рублей:

3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:

Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:

1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).

2. Определяются абсолютные отклонения вариант от средней:

3. Полученные отклонения умножаются на частоты:

4. Находится сумма взвешенных отклонений без учёта знака:

5. Сумма взвешенных отклонений делится на сумму частот:

Удобно пользоваться таблицей расчётных данных:

Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.

4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

Расчёт дисперсии в интервальных рядах распределения производится по формуле:

Порядок расчёта дисперсии в этом случае следующий:

1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).

2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:

4. Умножают квадраты отклонений на веса (частоты):

5. Суммируют полученные произведения:

6. Полученная сумма делится на сумму весов (частот):

Расчёты оформим в таблицу:

5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:

6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:

По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

Источник

ОБЩИЕ ЗАМЕЧАНИЯ

Чтобы
получить представление о размахе
модификационной изменчивости изучаемого
признака (например, длины или ширины
листовой пластинки вяза), необходимо
составить вариационный
ряд. С этой
целью измеряют, например, длину и ширину
50 листовых пластинок вяза с точностью
до 1 мм и получают варианты
– возможные значения изучаемого
признака, которые обозначают буквой Х
или Y:

Полученные варианты располагают в
порядке их возрастания (см. образец
представления данных в табл.9). Так, в
вышеприведенном примере длина листа
варьирует от 81 до 101, а ширина – от 63 до
83 мм, и в возрастающем порядке варианты
записаны в табл.5. Каждое значение
признака встречается неодинаковое
число раз. Число, указывающее, сколько
раз повторяется каждое значение признака
в данном вариационном ряду, называется
частотойи обозначается буквойf.

Таким
образом, вариационный ряд представляет
собой такой ряд данных, в котором указаны
значения варьирующего признака в порядке
возрастания или убывания, а также
соответствующие их частоты. Из
представленных данных видно, что чаще
всего встречаются варианты, находящиеся
в середине ряда, реже – в начале и в
конце ряда.

Таблица
5

Два вариационных ряда, характеризующих
длину и ширину листьев вяза

Длина листа, мм (варианты Х)	Число листьев (частоты f)	Ширина листа, мм (варианты Y)	Число листьев (частоты f)
81	2	63	2
83	7	65	7
86	10	67	10
87	12	71	12
88	10	75	10
95	7	77	5
101	2	81	2
		83	2

n=∑f=50n=∑f=50

Имея
вариационный ряд, можно получить
достаточно полную характеристику
изучаемого признака. Для этого необходимо
вычислить следующие статистические
показатели: среднюю арифметическую,
стандартное отклонение (или среднее
квадратическое отклонение), коэффициент
вариации, или изменчивости, ошибку
средней арифметической.

Средняя арифметическаяхарактеризует величину признака всей
совокупности изучаемых растений и
обозначается буквойх.
Вычисляют среднюю арифметическую
вариационного ряда по формуле:

∑ Х^.f

х =—————;

где:
х
– средняя арифметическая,

f
– частота встречаемости варианта,

Х
– варианты,

∑ —
знак суммы,

n
– сумма частот, то есть общий объем
выборки.

Для подсчетов следует воспользоваться
табл. 5. Таким образом, средняя арифметическая
длины листа равна 87,88 мм. Эта величина
наиболее характерна для данной выборки.

Для
характеристики вариационных рядов
большое значение имеют также следующие
средние величины: мода
– Мо и медиана
– Ме. Модальным называется класс,
обладающий наибольшей частотой; значение
его называется модой. В нашем примере
модальным является класс со средним
значением 87.

Медианой
называется значение варианты, находящейся
посередине вариационного ряда, т.е.
разделяющей его пополам. В данном случае
медиана совпадает с модой и равна 87. При
четном числе классов, как в другом
вариационном ряду – ширина листовой
пластинки, нужно сложить значение
вариант двух центральных классов и
сумму их разделить пополам. Таким
образом, в нашем примере медиана
соответствует значению73.

В
ряде случаев рассчитывают не среднюю
арифметическую, а среднюю геометрическую
по следующей формуле:

log
x_геом
=1/n · (log x₁
+ log x₂
+ log x₃
+ …+ log x_n)
.

По
значению log
x_геом
затем определяется величина x_геом.

Основным критерием для применения
средней геометрической является
возрастание данного признака не путем
арифметического прибавления к
первоначальному значению какой-то
величины, а в геометрической прогрессии
(например, при изучении темпов роста
организмов или популяции).

Таблица 6

Вычисление
средней арифметической, моды и медианы
длины листа вяза

Длина листа, мм (Х)	Число листьев (f)	X·f	X -x	(X -x)²	(X -x)²·f
81	8	162	-6,88	47,33	378,64
83	17	581	-4,88	23,81	404,77
86	26	860	-1,88	3,53	91,78
87	28	1044	-0,88	0,77	21,56
88	14	880	0,12	0,01	0,14
95	7	665	7,12	50,69	354,83
101	2	202	13,12	172,13	344,26
	n=Σf=50	Σ=4394			Σ=1595,98

∑ Хf
4394

х
= ——— = ——- = 87,88; Мо = 87; Ме = 87.

n
50

Средняя
арифметическая не отражает степени
изменчивости признака у данной группы
особей, сорта и т.д. Для характеристики
изменчивости используют стандартное
(среднее квадратическое) отклонение.
Оно обозначается буквой σ; это число
выражается в тех же единицах, что и
средняя арифметическая. Стандартное
отклонение вычисляем по формуле:

 (Х-х)^2.f
1595,98

σ
= 
————— = 
——— = 
32,571= 5,71
(мм).

n-1
49

Это означает, что по длине каждый лист
в среднем отличается от средней
арифметической х
на 5,71 мм.

Стандартное отклонение иногда называют
ошибкой отдельного варианта, так как,
зная значение х и
σ для данного вариационного ряда, можно
определить, относится ли данная особь
к этому ряду. Она может относиться к
данному ряду с вероятностью 99%, если ее
отклонение от средней арифметической
не превышает 3σ. В рассматриваемом
примерех = 87,88; σ =
5,71, наибольшее значение варианта равно
101, наименьшее – 81. Отклонение составит
101 — 87,88=+13,12; 81- 87,88= — 6,88.

Так как отклонения наибольшего и
наименьшего вариантов от средней
арифметической не превышают 3σ, то есть
17,13, то все особи относятся к данному
вариационному ряду. Следовательно,
пределы модификационной изменчивости
определяются значениями х3σ.

Для сравнения изменчивости разных
признаков у особей одной выборки
(например, у растений одного сорта) или
изменчивости одного и того же признака
у разных сортов, а также, чтобы иметь
возможность судить о степени выровненности
изучаемого материала, вычисляют
коэффициент вариации(V):

V
= — 
100%.

х

В нашем примере:

5,71

V
= ——- 
100% = 6,5%.

87,88

Чтобы сравнить размах изменчивости
различных признаков у растений одного
и того же сорта, следует вычислить
стандартное отклонение (σ) и коэффициент
вариации (V) для этих
признаков.

Чем
больше коэффициент вариации того или
иного признака, тем более он изменчив
под действием внешних условий.

Ошибка
средней арифметической
обозначается S__х.
Она показывает, какую допустили ошибку,
считая, что средняя арифметическая
выборки равна средней арифметической
генеральной совокупности. Ошибку средней
арифметической вычисляют по формуле:

S__х= ——— .

В нашем примере:

5,71

S__х= ——— = 0,81
(мм).

После вычисления ошибки средней
арифметической можем сказать, что у
вяза, изучавшегося нами, средняя длина
листа равна 87,880,81мм.

Данные, полученные в результате
статистического изучения тех или иных
признаков, заносят в сводную таблицу
(табл.7).

Таблица 7

Изменчивость признаков листовой
пластинки вяза

Растение	Изучаемый признак	Статистический показатель
х	σ	V	S__х	х S__х
Вяз	Длина листа, мм	87,88	5,71	6,5	0,81	87,880,81
Ширина листа, мм
Количество крупных жилок

При определении степени взаимосвязи
двух случайных величин, XиY, вычисляюткоэффициент
корреляции(r) по
следующей формуле:

 (x_i
– x)
· (y_i
— y)

r = ——————————

  (x_i-x)²·(y_i-y)²

Если величина rимеет знак
«+», то корреляционная связь – положителная,
если знак «-» — то связь отрицательная.
Считается, что:

при r0,3 –
корреляция отсутствует,

при 0,3 r0,5 –
корреляция слабая,

при 0,5 r0,7 –
корреляция средняя,

при 0,7 r0,9 –
корреляция сильная,

при 0,9 r1,0 –
корреляция значительная.

Для удобства расчета данные заносят в
следующую таблицу:

Таблица 8

Представление данных для вычисления
коэффициента корреляции

Номер пары	x_i	y_i	x_i-x	(x_i–x)²	y_i-y	(y_i–y)²	(x_i–x) · * (y_i–y)
1
2
…
n
	 x_i= …	 y_i= …		(x_i– x)²= …		(y_i – y)²= …	(x_i– x) *(y_i – y)= …

ПОДГОТОВКА
К ЗАНЯТИЮ (ОСУЩЕСТВЛЯЕТСЯ ЛАБОРАНТОМ).
Летом необходимо собрать листья вяза
с одного
дерева и
высушить их между листами бумаги под
прессом.

ЗАДАНИЕ. Замерьте длину, ширину и
число крупных зубчиков листовой пластинки
вяза. Измерения проводить с точностью
до 1 мм.

Запишите данные по всем трём признакам
для каждого листа отдельнов виде
единой таблицы по следующему образцу:

Таблица 9

Образец представления первичных данных
по изменчивости листьев вяза

Длина листа, мм	81	81	83	…
Ширина листа, мм	63	63	65	…
Количество зубчиков	19	19	21	…

Рассчитайте средние арифметические,
определите моды и медианы для каждого
из трёх признаков. Данные представьте
в виде трёх отдельных таблиц (по аналогии
с табл. 6).

Рассчитайте стандартное отклонение,
коэффициент вариации, ошибку средней
арифметической по каждому из показателей.
Данные представьте в виде таблиц (по
аналогии с табл.7).

Сформулируйте и запишите вывод о степени
изменчивости и сравните размах
модификационной изменчивости каждого
из признаков.

Представьте в виде двух отдельных
таблиц (по аналогии с табл. данные для
расчёта коэффициентов корреляции между
длиной листа (x) и числом
зубчиков (z), а также между
длиной (x) и шириной листа
(y). Рассчитайте коэффициенты
корреляции между этими двумя парами
признаков.

Запишите этот расчет и сделайте письменное
заключение о наличии и степени взаимосвязи
двух пар признаков (длины листа и
количества зубчиков; длины и ширины
листа).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

5.1. Методические рекомендации и решения типовых задач

Вариация
– это изменение (колеблемость) значений
признака в пределах изучаемой совокупности
при переходе от одного объекта (группы
объектов), или от одного случая к другому.
Абсолютные и относительные показатели
вариации, характеризующие колеблемость
значений варьирующего признака,
позволяют, в частности, измерить степень
связи и взаимозависимости между
признаками, определить степень
однородности совокупности, типичности
и устойчивости средней, определить
величину погрешности выборочного
наблюдения, статистически оценить закон
распределения совокупности и т. п.

В этой теме
необходимо уяснить сущность (смысл),
назначение и способы вычисления каждого
показателя вариации, рассматриваемого
в курсе теории статистики: размах
вариации, среднее линейное отклонение,
средний квадрат отклонений (дисперсию),
среднее квадратическое отклонение,
относительные коэффициенты вариации
(коэффициент осцилляции, коэффициент
среднего линейного отклонения, коэффициент
вариации).

Размах вариации
(R)
представляет
собой разность между максимальным
(х_max)
и минимальным (х_min)
значениями признака в совокупности (в
ряду распределения):

R
= х_max
— х_min.
(5.1)

Мерой других
показателей вариации является разность
не между крайними значениями признака,
а средняя разность между каждым значением
признака и средней величиной этих
признаков. Разность между отдельным
значением признака и средней называют
отклонением.

Среднее линейное
отклонение
вычисляется по следующим формулам:

по индивидуальным
(несгруппированным) данным

;
(5.2)

по вариационным
рядам (сгруппированным данным)

.
(5.3)

Так как алгебраическая
сумма отклонений индивидуальных значений
признака от средней (согласно нулевому
свойству) всегда равна нулю, то при
расчете среднего линейного отклонения
используется арифметическая сумма
отклонений, взятая по модулю, т.е.
.

Среднее линейное
отклонение имеет ту же размерность, что
и признак, для которого оно исчисляется.

Дисперсия и
среднее квадратическое отклонение.
Среднее линейное отклонение относительно
редко применяется для оценки вариации
признака. Поэтому обычно вычисляются
дисперсия (²)
и среднее квадратическое отклонение
().
Эти показатели применяются не только
для оценки вариации признака, но и для
измерения связи между ними, для оценки
величины ошибки выборочного наблюдения
и других целей.

Дисперсия признака
рассчитывается по формулам:

по первичным данным

; (5.4)

по вариационным
рядам

. (5.5)

Среднее
квадратическое отклонение
представляет собой корень квадратный
из дисперсии:

по первичным данным

; (5.6)

по вариационным
рядам

. (5.7)

Среднее квадратическое
отклонение так же, как и среднее линейное
отклонение, имеет ту же размерность,
что и сам исходный признак.

Дисперсию можно
определить и как разность между средним
квадратом вариантов и квадратом их
средней величины, т. е.
.
(5.8)

В этом случае по
первичным данным дисперсия равна:

(5.9)

Применительно к
сгруппированным данным, расчет дисперсии
этим способом в развернутом виде
представим в таком виде:

. (5.10)

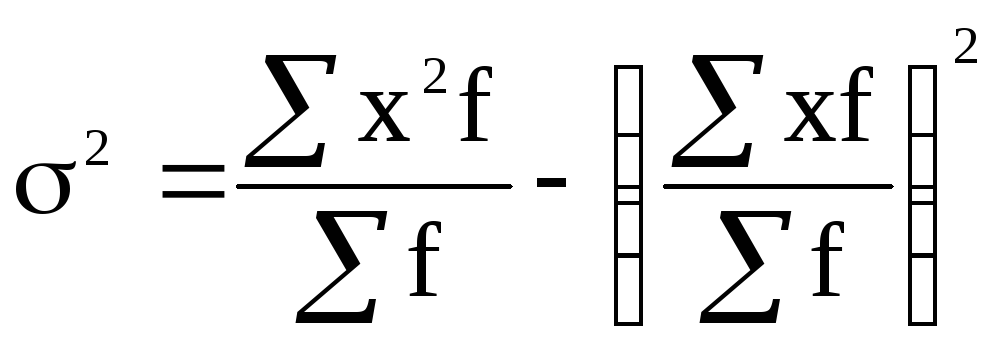
Для рядов
распределения с равными интервалами
значение дисперсии можно вычислить,
применяя способ условных моментов, т.
е.

, (5.11)

где
— первый условный момент; (5.12)

— второй условный момент. (5.13)

Среднее квадратическое
отклонение по способу условных моментов
определяется по формуле:

(5.14)

Преобразуя выражение
расчета дисперсии по способу условных
моментов, получим формулу вида:
(5.15)

На основе одних и
тех же исходных данных получим одинаковое
значение дисперсии.

Относительные
показатели вариации вычисляются как
отношение ряда абсолютных показателей
вариации к их средней арифметической
и выражаются в процентах:

коэффициент
осцилляции —
; (5.16)

коэффициент
относительного линейного отклонения
—
; (5.17)

коэффициент
вариации —
. (5.18)

Задача 1.
Рассмотрим способы расчета показателей
вариации на основе данных табл. 5.1.

Таблица 5.1.Исходные
данные для расчета показателей вариации

Затраты времени на производство деталей мин	Количество деталей, шт. (f)	Середина интервала (х)	xf					х²	х²f
1	2	3	4	5	6	7	8	9	10	11	12	13
до 10	10	9	90	-4,2	42	17,64	176,4	81	810	-2	-20	40
10-12	10	11	110	-2,2	22	4,84	48,4	121	1210	-1	-10	10
12-14	50	13	650	-0,2	10	0,04	2,0	169	8450	0	0	0
14-16	20	15	300	1,8	36	3,24	64,8	225	4500	1	20	20
16 и выше	10	17	170	3,8	38	14,44	144,4	289	2890	2	20	40
Итого	100	—	1320	—	148	—	436	—	17860		10	110

; к = 2

Приведенный ряд
распределения ранжированный, поэтому
здесь легко найти минимальное значение
признака, оно равно 8 мин. (10 — 2), и
максимальное, равное 18 мин. (16 + 2). Значит,
размах вариации признака в этом ряду
составит 10 мин., т. е.

R
= x_max
– x_min
= 18 – 8 = 10 мин.

Вычислим среднее
линейное отклонение. Прежде всего
необходимо вычислить среднюю величину
.
Все вычисления будем вести в табличной
форме (табл. 5.1.), отводя для каждой
вычислительной операции графу в таблице.

Поскольку исходные
данные представлены рядом распределения,
то

мин.

Покажем способы
расчета дисперсии:

а) обычным способом
(по определению):

;

б) как разность
между средним квадратом и квадратом
средней величины:

Для определения
величины дисперсии по этой формуле
необходимо вычислить средний квадрат
вариантов признака по формуле:

;

²=178,6
– (13,2)²=4,36;

в) по способу
условных моментов:

;

г) на основе
преобразования формулы расчета дисперсии
по способу условных моментов имеем:

Дисперсия – число
отвлеченное, не имеющее единиц измерения.

Среднее квадратическое
отклонение вычислим путем извлечения
корня квадратного из дисперсии:

мин.

По способу условных
моментов величину среднего квадратического
отклонения определим так:

мин.

Вычислим относительные
показатели вариации:

Основным относительным
показателем вариации является коэффициент
вариации (V).
Он используется для сравнительной
оценки меры колеблемости признаков,
выраженных в различных единицах
измерения.

Наряду с вариацией
количественных признаков может
наблюдаться и вариация качественных
признаков (в частности альтернативной
изменчивости качественных признаков).
В этом случае каждая единица изучаемой
совокупности либо обладает каким-то
свойством, либо нет (например, каждый
взрослый человек либо работает, либо
нет). Наличие признака у единиц совокупности
обозначают 1, а отсутствие –0; долю же
единиц совокупности, обладающих изучаемым
признаком, обозначают p,
а не обладающих им – q.
Дисперсия альтернативного признака
определяется по формуле:

; (5.19)

p
+ q
= 1 (5.20)

Если, например,
доля поступивших в университет равна
30%, а не поступивших – 70%, то дисперсия
равна 0,21(0,3 · 0,7). максимальное значение
произведения pq
равно 0,25 (при условии, когда одна половина
единиц обладает данным признаком, а
другая половина нет: (0,5 · 0,5 = 0,25).

Способ разложения
общей дисперсии.
Для оценки влияния различных факторов,
определяющих колеблемость индивидуальных
значений признака, воспользуемся
разложением общей дисперсии на
составляющие: на так называемую групповую
дисперсию и среднюю из внутригрупповых
дисперсий:

, (5.21)

где
– общая дисперсия, характеризующая
вариацию признака как результат влияния
всех факторов, определяющих индивидуальные
различия единиц совокупности.

Вариацию признака,
обусловленную влиянием фактора,
положенного в основу группировки,
характеризует межгрупповая дисперсия
²,
которая является мерой колеблемости
частных средних по группам
вокруг общей средней и исчисляется по
формуле:

, (5.22)

где n_j
– число единиц совокупности в каждой
группе;

j
– порядковый номер группы.

Вариацию признака,
обусловленную влиянием всех прочих
факторов, кроме группировочного
(факторного), характеризует в каждой
группе внутригрупповая дисперсия:

, (5.23)

где i
– порядковый номер x
и f
в пределах каждой группы.

По совокупности
в целом средняя из внутригрупповых
дисперсий определяется по формуле:

(5.24)

Отношение
межгрупповой дисперсии ²
к общей
даст коэффициент детерминации:

(5.25)

который характеризует
долю вариации результативного признака,
обусловленную вариацией факторного
признака, положенного в основание
группировки.

Показатель,
полученный как корень квадратный из
коэффициента детерминации, называется
коэффициентом эмпирического корреляционного
отношения, т.е.:

(5.26)

Он характеризует
тесноту связи между результативным и
факторным (положенным в основу группировки)
признаками. Численное значение
коэффициента эмпирического корреляционного
отношения имеет два знака: .
При решении вопроса о том, с каким знаком
его следует брать, необходимо иметь
ввиду: если вариация факторного и
результативного признаков идет синхронно
в одном и том же направлении (возрастает
или убывает), то корреляционные отношение
берется со знаком плюс; если же изменение
этих признаков идет в противоположных
направлениях, то оно берется со знаком
минус.

Для вычисления
групповых и межгрупповых дисперсий
можно применять любой из описанных выше
способов исчисления среднего квадрата
отклонений.

Задача 2.
Вычислим все названные дисперсии по
исходным данным табл. 5.2.

Таблица 5.2.
Распределение
посевной площади озимой пшеницы по
урожайности

Номер участка	Урожайность, ц/га (х)	Посевная площадь, га (f)	xf	x²	x²f
1	2	3	4	5	6
1	20	80	1600	400	32000
2	22	50	1100	484	24200
3	25	20	500	625	12500
4	28	50	1400	784	39200
5	30	100	3000	900	90000
6	35	80	2800	1225	98000
7	38	50	1900	1444	72200
8	40	70	2800	1600	112000
Итого		500	15100	x	480100

Вычислим среднюю
урожайность озимой пшеницы по всем
участкам (общая средняя):

ц/га.

Общую дисперсию
найдем по формуле:

В гр. 6 табл. 5.2.
вычислим значения для расчета среднего
квадрата вариантов признака:

Находим общую
дисперсию:

Урожайность зависит
от многих факторов (качество почвы,
размер внесения органических и минеральных
удобрений, качество семян, сроки сева,
уход за посевами и др.) Общая дисперсия
в данном случае измеряет колеблемость
урожайности за счет всех факторов.

Задача 3.
Разобьем совокупность участков на две
группы: I
группа – посевные площади, на которых
не вносились органические удобрения;
II
– площади, на которых они вносились. К
первой группе отнесем участки 1-4, а ко
второй – 4-8. По данным этих групп
рассчитаем остальные из необходимых
нам дисперсий, используя уже произведенные
в табл. 5.2. вычисления.

Таблица 5.3. Расчетные
данные для вычисления межгрупповой и
групповых дисперсий

Номер участка	Урожайность, ц/га (х)	Посевная площадь, га (f)	xf	x²	x²f	Номер участка	Урожайность, ц/га (х)	Посевная площадь, га (f)	xf	x²	x²f
1	20	80	1600	400	32000	5	30	100	3000	900	90000
2	22	50	1100	484	24200	6	35	80	2800	1225	98000
3	25	20	500	625	12500	7	38	50	1900	1444	72200
4	28	50	1400	784	39200	8	40	70	2800	1600	112000
Итого		200	4600	x	107900	Итого		300	10500	x	372200

Определяем:

для I группы:	для II группы:
а) групповую среднюю	а) групповую среднюю
ц/га;	ц/га;
б) средний квадрат вариантов признака	б) средний квадрат вариантов признака
;	;
в) групповую дисперсию	в) групповую дисперсию
.	.

Определяем среднюю
из групповых дисперсий:

Находим межгрупповую
дисперсию:

Средняя из групповых
дисперсий измеряет колеблемость признака
за счет всех прочих факторов, кроме
положенного в основание группировки
(разграничения на группы), а межгрупповая
– за счет именно этого фактора. Сумма
этих дисперсий должна дать общую
дисперсию, а именно:

Отношение
межгрупповой дисперсии к общей в нашем
примере даст следующее значение
коэффициента детерминации:

,
или 71,8%,

т. е. вариация
урожайности озимой пшеницы на 71,8% зависит
от вариации размеров внесения органических
удобрений. Остальные же 28,2% вариации
урожайности зависит от влияния всех
остальных факторов, кроме размеров
внесения органических удобрений.

Коэффициент
эмпирического корреляционного отношения
составит:

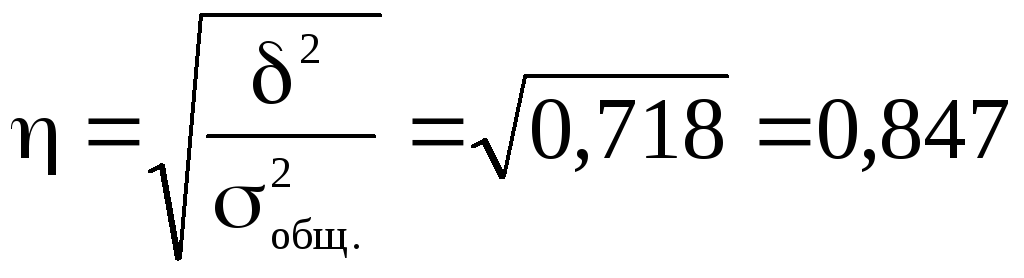
Это говорит о том,
что внесение органических удобрений
оказывает весьма существенное влияние
на урожайность.

Статистические
характеристики асимметрии и эксцесса.
Выяснение общего характера распределения
предполагает оценку степени его
однородности, а также вычисление
показателей асимметрии и эксцесса.

Величина показателя
асимметрии может быть положительной
(правосторонняя асимметрия) и отрицательной
(левосторонняя асимметрия). Существует
следующее соотношение между показателями
центра распределения: при правосторонней
асимметрии —
;
при левосторонней асимметрии —.

Коэффициент
асимметрии исчисляется по формуле:

, (5.27)

где М₃
– центральный момент третьего порядка,
который в вариационных интервальных
рядах с равновеликими интервалами
определяется через систему условных
моментов по выражению:

. (5.28)

Значение 
в системе стандартных условных моментов
исчисляется по формуле:

. (5.29)

Оценка степени
существенности показателя асимметрии
дается с помощью его среднеквадратической
ошибки:

. (5.30)

Если отношение
,
асимметрия существенна, и распределение
признака в генеральной совокупности
не является симметричным. Если отношение,
асимметрия несущественна, ее наличие
может быть объяснено влиянием случайных
обстоятельств.

Для симметричных
распределений рассчитывается показатель
экцесса (островершинности):

. (5.31)

Четвертый центральный
момент (М₄)
вычисляется по уравнению:

М₄
= m₄
– 4m₃m₁
+ 6m₂m²₁
– 3m⁴₁. (5.32)

Средняя квадратическая
ошибка эксцесса рассчитывается по
формуле

(5.33)

Если отношение
,
то следует предложить, что эксцесс
свойствен распределению признака в
генеральной совокупности и наоборот.

Задача 4.
Покажем способы расчета коэффициентов
асимметрии и эксцесса по данным табл.
5.4.

Таблица 5.4.
Исходные данные для вычисления
коэффициентов асимметрии и эксцесса

Затраты времени производство детали, мин.	Количество деталей, шт. (f)	Середина интервала, (х)
1	2	3	4	5	6	7	8
до 10	10	9	-2	-20	40	-80	160
10-12	10	11	-1	-10	10	-10	10
12-14	50	13	0	0	0	0	0
14-16	20	15	1	20	20	20	20
16 и	10	17	2	20	40	80	160
Итого	100	x	x	10	110	10	350

Вычислим значения
условных моментов:

На основе комбинации
первого, второго и третьего условных
моментов исчислим третий центральный
момент:

М₃
= 0,1-31,10,1+2(0,1)³=-0,228.

Значение среднего
квадратического отклонения вычислим
по формуле:

Определим коэффициент
асимметрии:

Наличие знака
минус при коэффициенте свидетельствует
о левосторонней асимметрии.

Вычислим величину
средней квадратической ошибки коэффициента
асимметрии:

Критерий t_AS
вычислим по формуле:

Поскольку t_AS

3, то это свидетельствует о несущественности
асимметрии распределения деталей по
затратам времени на их изготовление.

Для расчета
коэффициента эксцесса вычислим значение
четвертого центрального момента:

М₄
= 3,5 – 4 
0,1 
0,1 + 6 
1,1 (0,1)²
– 3(0,1)⁴
= 3,5256.

Определим коэффициент
эксцесса:

Величина
среднеквадратической ошибки эксцесса
составит:

Критерий t_ЕХ
определим по формуле:

Так как t_EX

3, то наличие эксцесса не свойственно
распределению признака в генеральной
совокупности.

Ошибка коэффициента вариации
[c.106]

При проведении диагностики нижнего пояса резервуара на внутренней поверхности не было обнаружено видимых локальных повреждений металла типа язв и питтингов. По-видимому, в данном случае имела место равномерная коррозия, и предварительный коэффициент вариации глубин коррозионного разрушения V был принят равным 0,2. С учетом условий эксплуатации величины доверительной вероятности оценки у и допустимой относительной ошибки расчета 5 считали равными 0,95 и 0,1 соответственно. По параметрам у, б, V с помощью
[c.213]

Проведенные исследования показывают, что при коэффициенте вариации сроков службы, меньшем 0,35, вполне возможна замена распределения Вейбулла нормальным с теми же математическим ожиданием и дисперсией, Ошибка в вычислении числа восстановлений или интенсивности их при такой замене практически отсутствует. Кроме того, как показывают наблюдения, сроки службы многих машин (автомобилей, тракторов, комбайнов и др,) имеют распределения, близкие к нормальному.
[c.31]

Во второй группе источников неточностей эксперимента столь же незакономерно могут вносить погрешности и влиять па коэффициент вариации распределения ошибки при отборе проб картерного масла и расчета износа. Эти ошибки устраняются системой контроля. Например, наибольшая ошибка в определении износа, связанная с отбором пробы объемом 20 мл, заключается в том, что промывка отборного трубопровода и крана проводится недостаточно, в результате чего в пробу попадает масло, наполнившее трубопровод в предшествующий проводимому отбору пробы. Для устранения этой ошибки проводится операция отбора последовательно двух проб, первая (нечетная) из которых ложная . Регистрацию обеих проб осуществляет оператор, выполнивший отбор, а взвешивание и последующие операции — другой (обычно следующей смены), который выполняет операцию упаковки, регистрирует отправку на анализ действительной пробы и слив ложной в картер двигателя. Для осуществления отбора проб масла двигатель был оборудован пробоотборным краном в масляной магистрали, скорость перемещения в которой смазывающей жидкости составляла около 2—2,5 м/с.
[c.51]

В технических задачах критерием пренебрежимой малости отбрасываемой величины обычно считается значение последней, меньшее 1—2% результата. В некоторых задачах ошибками измерения пренебрегают, если полное поле практического рассеяния результатов измерения, т. е. 6а, меньше чем 5—10% значения измеряемой величины (коэффициент вариации порядка 1—2%).
[c.212]

Относительная величина средней квадратичной ошибки w, выраженная в процентах, называется коэффициентом вариации
[c.29]

Так как выборочный коэффициент вариации оказался больше первоначально принятого Уш то при п = 11 фактическая ошибка будет больше = 0,02.
[c.45]

Пусть далее по результатам испытания п = 11 -1- 9 = 20 образцов выборочный коэффициент вариации а = 0,045. Определяем по формуле (2.76) ожидаемую с вероятностью Р = 0,9 максимальную относительную ошибку оценки среднего значения предела прочности
[c.45]

Коэффициент вариации разрушающ,его напряжения, вычисленный по средней квадратической ошибке, равен ш = 18%, а средняя арифметическая ошибка р=18,3%.
[c.98]

При статистической обработке остальных результатов вычислялись средние арифметические значения измеряемых величин Жср, средние квадратичные ошибки отдельных измерений Ох, квадратичные ошибки средних арифметических tq, коэффициент вариации V. Окончательный результат измерений полагали А = = (Та + Хер, а предельные отклонения — равными 3Wx- В табл. 6.1 приведены результаты обработки при определении коэффициента к , модуля El и коэффициента Ui.
[c.239]

Результаты статистической обработки числа Fo/Fo p при Кр = = 0,5 и числе измерений п = 10 таковы среднее арифметическое значение = 0,444 средняя квадратичная ошибка отдельного измерения = 0,058, квадратичная ошибка среднего арифметического tq = 0,0184 коэффициент вариации V = 13%.
[c.247]

Тип образца V, кг-см/см Коэффициент вариации, % Относи- тельная ошибка, %
[c.130]

Выполненные авторами методики исследования показали, что наибольшее влияние на функцию интенсивности ремонтов оказывает величина М. Влияние второго параметра распределения сроков службы а на функцию интенсивности ремонтов зависит от его относительной величины — коэффициента вариации V, и может быть заметным только на начальном участке вычисляемых функций для отдельных элементов. Что же. касается такой многоэлементной системы, какой является парк автомобилей, то, как выяснилось, изменение величины V в пределах от 0,1 до 0,3 в вычисление функции интенсивности ремонтов заметной ошибки не вносит. Исследованиями установлено также, что при одних и тех же значениях М п V вид закона распределения сроков службы мало влияет на величину искомых функций. Так, при коэффициенте вариации, меньшем 0,35, вполне допустима замена закона Вейбулла нормальным законом. Ошибка при вычислениях интенсивности ремонтов при такой замене практически отсутствует. На этом основании в перспективных расчетах вполне допустимо обходиться такими распределениями, которые более удобны для вычислений. Настоящей методикой предусмотрено, выполнение расчетов с использованием данных о функции
[c.385]

Часто величины и называются соответственно генеральной и выборочной дисперсиями, а а и S — стандартной или среднеквадратичной ошибкой (сокращенно стандартом). Относительную величину стандарта называют иногда коэффициентом вариации ф, %,
[c.34]

В качестве примера можно указать, что при надежности у=0,01 и относительной ошибке 6=0,05 в определении среднего логарифма долговечности потребное число образцов в зависимости от коэффициента вариации составляет [c.77]

Поправка (1 -Ь дИ) учитывает также и возможные ошибки при определении средней интенсивности изнашивания а, вызванные ограниченным количеством наблюдений, и рассеивание его результатов, так как на величину среднеквадратического отклонения < , а следовательно, и коэффициент вариации V оказывает влияние число опытов (наблюдений) п.
[c.168]

Нередко представляется желательным определить, каково должно быть число образцов К, чтобы средний параметр X был найден с заданной относительной ошибкой 5 при известном коэффициенте вариации V для вероятности а. Для
[c.585]

При доверительной вероятности р = 0,95, относительной ошибке в определении средней наработки до отказа б =0,10 и коэффициенте вариации V = 0,462 число объектов наблюдения для закона распределения Вейбулла необходимо не менее N — 64.
[c.243]

При 14 интервалах, 11 степенях свободы и 1—р = 0,050, критерий х = 4,570 число объектов наблюдения при р = 0,95 и ошибке б = 0,1 составляет N = 51 коэффициент вариации v = 0,417.
[c.251]

Обработка полученных данных проводится по ГОСТ 14359-69, действие которого продлено до 1983 г. Она состоит в расчете основных статистических характеристик достоверности полученных результатов-среднего арифметического (или логарифмического), стандартного отклонения и стандартного отклонения среднего значения, вероятного отклонения искомого, коэффициента вариации и относительной ошибки.
[c.66]

Выбирая доверительный интервал при измерении данного параметра, следует руководствоваться, с одной стороны, средней квадратичной ошибкой (или коэффициентом вариации У ), а с другой стороны — точностью самого метода измерений (аппаратуры, датчиков, способа расшифровки). Если систематическую погрешность измерений, определяемую лишь классом точности аппаратуры (а не вариацией самой измеряемой величины), обозначить б, то доверительный интервал будет
[c.64]

Число объектов наблюдения N определяют в зависимости от относительной ошибки А среднего значения / р исследуемой случайной величины (наработка до первого отказа, ресурс, срок службы и т. п.) с доверительной вероятностью р и ожидаемой величины коэффициента вариации Уа. Значения А, взаимосвязаны.
[c.158]

Исходные данные предельная относительная ошибка 8 доверительная вероятность д предполагаемый коэффициент вариации V распределения наработок между отказами предполагаемый коэффициент вариации Kg распределения времени восстановления.
[c.570]

Оценка разности между коэффициентами вариации. Разность между коэффициентами вариации сравниваемых групп, извлеченных из нормально распределяющихся совокупностей, можно оценить с помощью критерия Стьюдента. Приближенной оценкой разности Сю —Си2 = с со служит ее отношение к своей ошибке, которая равна корню квадратному из суммы ошибок коэффициентов вариации сравниваемых групп, т. е.
[c.126]

На основании уравнений (2) и (3) и с учетом того, что для нормального закона распределения и распределения Вейбулла параметры распределения и коэффициент вариации связаны однозначно [26], составлены [8, 9] графики (рис. 3, а и б), позволяющие приближенно рассчитать объем партии N для первичных испытаний при малом объеме предварительной информации о надежности. Ошибка при планировании испытаний по предлагаемо-
[c.14]

Определить количество клиновых вентиляторных ремней, которые необходимо испытать для определения их среднего ресурса с доверительной вероятностью р=0,9 и предельной относительной ошибкой 6=0,1. Для клиновых ремней характерны отказы из-за трещин резины слоя сжатия, расслоения, остаточной деформации (удлинения). По табл. 4 и уравнению (1) определяем наиболее вероятное значение параметра Вейбулла й=2,74-3,2 и коэффициента вариации 11=0,35- 0,4. По графику на рис. 3 находим iV=33-b38.
[c.17]

На рис. 7.5 а приведен средний вертикальный профиль оптической толщины т для Х==10,6 мкм до высоты 30 км. Здесь же приведено среднее значение коэффициента поглощения на уровне земли (/1 = 0). На рис. 7.6 6 дан профиль стандартного отклонения ат. Величина сгх характеризует ошибку в определении т, связанную с вариациями температуры и влажности. Из рис. 7.5 6 следует, что на высоте 22 км сгт достигает значения 0,15 и далее с высотой не изменяется. Ошибка в определении пропускания слоя О— 30 км составляет 15 %.
[c.221]

Систематические ошибки возникают за счет погрешностей априорного расчета профиля дифференциального коэффициента поглощения Ах(Я), которые зависят от многих факторов, таких как вариаций давления, температуры и влажности по трассе зондирования, нестабильности длины волны и ширины спектра излучения, поглощения другими газами, доплеровского уширения спектра эхо-сигнала за счет хаотического движения молекул воздуха, флуоресценции. К перечисленным факторам следует отнести и сдвиг центра линии поглощения Н2О давлением воздуха. Оценим его влияние при решении обратной задачи зондирования.
[c.199]

Максимальные ошибки определения профиля коэффициента Даэ(Уе, г)/аэ(Уо, г) в процентах, вызванные вариациями частоты лазерного излучения Ve около центральной частоты го линии поглощения Н2О 694,38 нм. Модель атмосферы —
[c.145]

Относительная величина среднеквадратичной ошибки-в процентах называется коэффициентом вариации, а интервал значений от х—Ал до х+Дж —доверительным интервалом. Знание доверительной вероятности позволяет оценить степень надежности полученного результата. Обычно ограничиваются доверительной вероятностью, )авной 0,9 или 0,95. Она рассчитывается по формуле «аусса для разных значений доверительного интервала. Эти значения приводятся в виде таблиц, помещенных, например, в [Л. 30]. Среднеквадратичной ошибке соответствует доверительная вероятность 0,69, удвоенной ошибке 0,95 и утроенной ошибке 0,997.
[c.42]

Если после дополнительных испытаний девяти образцов выборочный коэффициент вариации оказался бы существенно выше 0,051, а величина максимальной ошибки, подсчитанная по формуле (2.76), была бы неприемлемо высокой, то следовало бы вновь йкйрректировать объем испытаний с учетом полученного значения после дополнительных испытаний коэффициента вариации н т. д.
[c.45]

Наиболее полно сопротивление усталости характеризуется кривыми усталости, получаемыми для различных вероятностей разрушения с заданной точностью и принятым значением уровня значимости (надежности). Такие характеристики требуют испытания большого числа образцов (или деталей) на нескольких уровнях напряжений. Число испытуемых образцов п на каждом уровне напряжений зависит от величины рассеяния, характеризуемого коэффициентом вариации F=SIgJv/lgЛ (отношение среднего квадратического отклонения логарифма долговечности к среднему значению) и принятыми односторонними значениями урорня значимости у (характеризует надежность), и точности, характеризуемой величиной относительной ошибки б, равной отношению абсолютной ошибки Д к среднему значению 1 N.
[c.76]

В связи с этим Лайн для получения достоверных данных рекомендует производить до 10 испытаний манжет в одинаковых условиях. Шнюрле и Уппер проводили по 4—10 испытаний манжет для получения каждой точки на графике изучаемой зависимости [141]. Статистический анализ показывает [43], что при коэффициенте вариации 0,1—0,2 и допустимой относительной ошибке измеряемого параметра 0,1, при доверительной вероятности 0,95 необходимо проводить 6—18 испытаний резинотехнических деталей.
[c.57]

Число объектов наблюдения опредляется по заданной величине относительной ошибки 6, доверительной вероятности р и коэффициенту вариации V = 1 (по табл. 12). При б = 0,15, Р = 0,80 и V = 1 число объектов наблюдения N = 45.
[c.248]

При диагностировании нижнего пояса резервуара, выполненном изнутри, не было обнаружено видимых локальных повреждений металла поверхности в виде явных язв и питтингов. Па этом основании было признано, что в данном случае имела место слабая неравномерность коррозионного повреждения, и был принят предварительный коэффициент вариации глубин коррозионного разрушения V = 0,2. Исходя из условий эксплуатации, в данном случае приняты следующие величины доверительной вероятности оценки (у) и допустимой относительной ошибки расчета (б) у = 0,95 и б = 0,1. По трем принятым параметрам — у, б, V — из табл. 4.6 было выбрано минимальное число необходимых измерений — = 13. Измерения ульт-
[c.211]

Методы численного решения систем типа (3.39) будут подробно нами рассматриваться в п. 4.2, а сейчас лишь напомним, что в основе этой системы лежат предположения о сферичности рассеивающих частиц и априорное задание показателя преломления аэрозольного вещества т = т —т»1 в пределах зондируемого слоя [ЯьЯг]. В силу этого изложенная выше теория многочастотного касательного зондирования приводит к вычислительным схемам обращения оптических данных, применимых при тех же исходных допущениях, что и в методе многочастотного лазерного зондирования. Это обусловлено единством методологического подхода к теории оптического зондирования рассеивающей компоненты атмосферы. Вместе с тем необходимо обратить внимание на то обстоятельство, что требования к выполнению указанных выше допущений существенно различны для указанных двух методов. Действительно, уравнения теории касательного зондирования относительно локальных оптических характеристик светорассеяния являются интегральными, причем первого рода, и поэтому вариации бРех (то же самое бт и б/)ц), обусловленные ошибками Ат в задании подходящих значений т, слабо сказываются на значении интегралов (3.24). В силу этого схемы обращения в методе касательного зондирования более устойчивы к неопределенностям при априорном задании соответствующих оптических операторов в (3.39). В локационных задачах оптические сигналы Р %1,г) прямо пропорциональны значениям аэрозольных коэффициентов обратного рассеяния (Зя(Я/, г), и поэтому вариации бРяг связанные с Дт, непосредственно сказываются на точности интерпретации оптических данных.
[c.166]

Производные в ЭТИХ формулах являются функциями координат и могут быть получены на основании формул (22.37) и (22.38). Они должны быть вычислены для невозмущепной траектории снаряда. Однако этот метод приводит к дифференциальным уравнениям с переменными коэффициентами, которые не могут быть проинтегрированы в замкнутой форме. При полетах в области пространства шириной порядка нескольких сотен миль коэффициенты могут быть вычислены в точках самой траектории с точностью, достаточной для наших целей. Это дает следующие уравнения для определения возмущений в положении снаряда, вызываемых вариациями ускорения силы тяги и ошибками акселерометров [c.668]

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

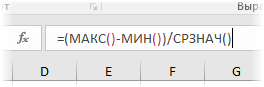
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

From Wikipedia, the free encyclopedia

In probability theory and statistics, the coefficient of variation (CV), also known as relative standard deviation (RSD),^{[citation needed]} is a standardized measure of dispersion of a probability distribution or frequency distribution. It is often expressed as a percentage, and is defined as the ratio of the standard deviation sigma to the mean (or its absolute value, |mu | ). The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R,^{[citation needed]} by economists and investors in economic models, and in neuroscience.

Definition[edit]

The coefficient of variation (CV) is defined as the ratio of the standard deviation sigma to the mean , ${displaystyle c_{rm {v}}={frac {sigma }{mu }}.}$ ^[1]

It shows the extent of variability in relation to the mean of the population.
The coefficient of variation should be computed only for data measured on scales that have a meaningful zero (ratio scale) and hence allow relative comparison of two measurements (i.e., division of one measurement by the other). The coefficient of variation may not have any meaning for data on an interval scale.^[2] For example, most temperature scales (e.g., Celsius, Fahrenheit etc.) are interval scales with arbitrary zeros, so the computed coefficient of variation would be different depending on the scale used. On the other hand, Kelvin temperature has a meaningful zero, the complete absence of thermal energy, and thus is a ratio scale. In plain language, it is meaningful to say that 20 Kelvin is twice as hot as 10 Kelvin, but only in this scale with a true absolute zero. While a standard deviation (SD) can be measured in Kelvin, Celsius, or Fahrenheit, the value computed is only applicable to that scale. Only the Kelvin scale can be used to compute a valid coefficient of variability.

Measurements that are log-normally distributed exhibit stationary CV; in contrast, SD varies depending upon the expected value of measurements.

A more robust possibility is the quartile coefficient of dispersion, half the interquartile range ${displaystyle {(Q_{3}-Q_{1})/2}}$ divided by the average of the quartiles (the midhinge), ${displaystyle {(Q_{1}+Q_{3})/2}}$ .

In most cases, a CV is computed for a single independent variable (e.g., a single factory product) with numerous, repeated measures of a dependent variable (e.g., error in the production process). However, data that are linear or even logarithmically non-linear and include a continuous range for the independent variable with sparse measurements across each value (e.g., scatter-plot) may be amenable to single CV calculation using a maximum-likelihood estimation approach.^[3]

Examples[edit]

In the examples below, we will take the values given as randomly chosen from a larger population of values.

The data set [100, 100, 100] has constant values. Its standard deviation is 0 and average is 100, giving the coefficient of variation as 0 / 100 = 0

The data set [90, 100, 110] has more variability. Its standard deviation is 10 and its average is 100, giving the coefficient of variation as 10 / 100 = 0.1

The data set [1, 5, 6, 8, 10, 40, 65, 88] has still more variability. Its standard deviation is 32.9 and its average is 27.9, giving a coefficient of variation of 32.9 / 27.9 = 1.18

In these examples, we will take the values given as the entire population of values.

The data set [100, 100, 100] has a population standard deviation of 0 and a coefficient of variation of 0 / 100 = 0

The data set [90, 100, 110] has a population standard deviation of 8.16 and a coefficient of variation of 8.16 / 100 = 0.0816

The data set [1, 5, 6, 8, 10, 40, 65, 88] has a population standard deviation of 30.8 and a coefficient of variation of 30.8 / 27.9 = 1.10

Estimation[edit]

When only a sample of data from a population is available, the population CV can be estimated using the ratio of the sample standard deviation to the sample mean :

${displaystyle {widehat {c_{rm {v}}}}={frac {s}{bar {x}}}}$

But this estimator, when applied to a small or moderately sized sample, tends to be too low: it is a biased estimator. For normally distributed data, an unbiased estimator^[4] for a sample of size n is:

${displaystyle {widehat {c_{rm {v}}}}^{*}={bigg (}1+{frac {1}{4n}}{bigg )}{widehat {c_{rm {v}}}}}$

Log-normal data[edit]

In many applications, it can be assumed that data are log-normally distributed (evidenced by the presence of skewness in the sampled data).^[5] In such cases, a more accurate estimate, derived from the properties of the log-normal distribution,^[6]^[7]^[8] is defined as:

${displaystyle {widehat {cv}}_{rm {raw}}={sqrt {mathrm {e} ^{s_{rm {ln}}^{2}}-1}}}$

where ${displaystyle {s_{rm {ln}}},}$ is the sample standard deviation of the data after a natural log transformation. (In the event that measurements are recorded using any other logarithmic base, b, their standard deviation s_b , is converted to base e using ${displaystyle s_{rm {ln}}=s_{b}ln(b),}$ , and the formula for ${displaystyle {widehat {cv}}_{rm {raw}},}$ remains the same.^[9]) This estimate is sometimes referred to as the «geometric CV» (GCV)^[10]^[11] in order to distinguish it from the simple estimate above. However, «geometric coefficient of variation» has also been defined by Kirkwood^[12] as:

${displaystyle mathrm {GCV_{K}} ={mathrm {e} ^{s_{rm {ln}}}!!-1}}$

This term was intended to be analogous to the coefficient of variation, for describing multiplicative variation in log-normal data, but this definition of GCV has no theoretical basis as an estimate of ${displaystyle c_{rm {v}},}$ itself.

For many practical purposes (such as sample size determination and calculation of confidence intervals) it is $s_{ln} ,$ which is of most use in the context of log-normally distributed data. If necessary, this can be derived from an estimate of ${displaystyle c_{rm {v}},}$ or GCV by inverting the corresponding formula.

Comparison to standard deviation[edit]

Advantages[edit]

The coefficient of variation is useful because the standard deviation of data must always be understood in the context of the mean of the data.
In contrast, the actual value of the CV is independent of the unit in which the measurement has been taken, so it is a dimensionless number.
For comparison between data sets with different units or widely different means, one should use the coefficient of variation instead of the standard deviation.

Disadvantages[edit]

When the mean value is close to zero, the coefficient of variation will approach infinity and is therefore sensitive to small changes in the mean. This is often the case if the values do not originate from a ratio scale.
Unlike the standard deviation, it cannot be used directly to construct confidence intervals for the mean.
CVs are not an ideal index of the certainty of measurement when the number of replicates varies across samples because CV is invariant to the number of replicates while the certainty of the mean improves with increasing replicates. In this case, standard error in percent is suggested to be superior.^[13]

Applications[edit]

The coefficient of variation is also common in applied probability fields such as renewal theory, queueing theory, and reliability theory. In these fields, the exponential distribution is often more important than the normal distribution.
The standard deviation of an exponential distribution is equal to its mean, so its coefficient of variation is equal to 1. Distributions with CV < 1 (such as an Erlang distribution) are considered low-variance, while those with CV > 1 (such as a hyper-exponential distribution) are considered high-variance^{[citation needed]}. Some formulas in these fields are expressed using the squared coefficient of variation, often abbreviated SCV. In modeling, a variation of the CV is the CV(RMSD). Essentially the CV(RMSD) replaces the standard deviation term with the Root Mean Square Deviation (RMSD). While many natural processes indeed show a correlation between the average value and the amount of variation around it, accurate sensor devices need to be designed in such a way that the coefficient of variation is close to zero, i.e., yielding a constant absolute error over their working range.

In actuarial science, the CV is known as unitized risk.^[14]

In Industrial Solids Processing, CV is particularly important to measure the degree of homogeneity of a powder mixture. Comparing the calculated CV to a specification will allow to define if a sufficient degree of mixing has been reached.^[15]

Laboratory measures of intra-assay and inter-assay CVs[edit]

CV measures are often used as quality controls for quantitative laboratory assays. While intra-assay and inter-assay CVs might be assumed to be calculated by simply averaging CV values across CV values for multiple samples within one assay or by averaging multiple inter-assay CV estimates, it has been suggested that these practices are incorrect and that a more complex computational process is required.^[16] It has also been noted that CV values are not an ideal index of the certainty of a measurement when the number of replicates varies across samples − in this case standard error in percent is suggested to be superior.^[13] If measurements do not have a natural zero point then the CV is not a valid measurement and alternative measures such as the intraclass correlation coefficient are recommended.^[17]

As a measure of economic inequality[edit]

The coefficient of variation fulfills the requirements for a measure of economic inequality.^[18]^[19]^[20] If x (with entries x_i) is a list of the values of an economic indicator (e.g. wealth), with x_i being the wealth of agent i, then the following requirements are met:

Anonymity – c_v is independent of the ordering of the list x. This follows from the fact that the variance and mean are independent of the ordering of x.
Scale invariance: c_v(x) = c_v(αx) where α is a real number.^[20]
Population independence – If {x,x} is the list x appended to itself, then c_v({x,x}) = c_v(x). This follows from the fact that the variance and mean both obey this principle.
Pigou–Dalton transfer principle: when wealth is transferred from a wealthier agent i to a poorer agent j (i.e. x_i > x_j) without altering their rank, then c_v decreases and vice versa.^[20]

c_v assumes its minimum value of zero for complete equality (all x_i are equal).^[20] Its most notable drawback is that it is not bounded from above, so it cannot be normalized to be within a fixed range (e.g. like the Gini coefficient which is constrained to be between 0 and 1).^[20] It is, however, more mathematically tractable than the Gini coefficient.

As a measure of standardisation of archaeological artefacts[edit]

Archaeologists often use CV values to compare the degree of standardisation of ancient artefacts.^[21]^[22] Variation in CVs has been interpreted to indicate different cultural transmission contexts for the adoption of new technologies.^[23] Coefficients of variation have also been used to investigate pottery standardisation relating to changes in social organisation.^[24] Archaeologists also use several methods for comparing CV values, for example the modified signed-likelihood ratio (MSLR) test for equality of CVs.^[25]^[26]

Examples of misuse[edit]

Comparing coefficients of variation between parameters using relative units can result in differences that may not be real. If we compare the same set of temperatures in Celsius and Fahrenheit (both relative units, where kelvin and Rankine scale are their associated absolute values):

Celsius: [0, 10, 20, 30, 40]

Fahrenheit: [32, 50, 68, 86, 104]

The sample standard deviations are 15.81 and 28.46, respectively. The CV of the first set is 15.81/20 = 79%. For the second set (which are the same temperatures) it is 28.46/68 = 42%.

If, for example, the data sets are temperature readings from two different sensors (a Celsius sensor and a Fahrenheit sensor) and you want to know which sensor is better by picking the one with the least variance, then you will be misled if you use CV. The problem here is that you have divided by a relative value rather than an absolute.

Comparing the same data set, now in absolute units:

Kelvin: [273.15, 283.15, 293.15, 303.15, 313.15]

Rankine: [491.67, 509.67, 527.67, 545.67, 563.67]

The sample standard deviations are still 15.81 and 28.46, respectively, because the standard deviation is not affected by a constant offset. The coefficients of variation, however, are now both equal to 5.39%.

Mathematically speaking, the coefficient of variation is not entirely linear. That is, for a random variable , the coefficient of variation of is equal to the coefficient of variation of only when b=0 . In the above example, Celsius can only be converted to Fahrenheit through a linear transformation of the form ax+b with bneq 0 , whereas Kelvins can be converted to Rankines through a transformation of the form .

Distribution[edit]

Provided that negative and small positive values of the sample mean occur with negligible frequency, the probability distribution of the coefficient of variation for a sample of size of i.i.d. normal random variables has been shown by Hendricks and Robey to be^[27]

${displaystyle mathrm {d} F_{c_{rm {v}}}={frac {2}{pi ^{1/2}Gamma {left({frac {n-1}{2}}right)}}};mathrm {e} ^{-{frac {n}{2left({frac {sigma }{mu }}right)^{2}}}{frac {{c_{rm {v}}}^{2}}{1+{c_{rm {v}}}^{2}}}}{frac {{c_{rm {v}}}^{n-2}}{(1+{c_{rm {v}}}^{2})^{n/2}}}sideset {}{^{prime }}sum _{i=0}^{n-1}{frac {(n-1)!,Gamma left({frac {n-i}{2}}right)}{(n-1-i)!,i!,}}{frac {n^{i/2}}{2^{i/2}left({frac {sigma }{mu }}right)^{i}}}{frac {1}{(1+{c_{rm {v}}}^{2})^{i/2}}},mathrm {d} c_{rm {v}},}$

where the symbol ${textstyle sideset {}{^{prime }}sum }$ indicates that the summation is over only even values of , i.e., if is odd, sum over even values of and if is even, sum only over odd values of .

This is useful, for instance, in the construction of hypothesis tests or confidence intervals.
Statistical inference for the coefficient of variation in normally distributed data is often based on McKay’s chi-square approximation for the coefficient of variation ^[28]^[29]^[30]^[31]^[32]^[33]

Alternative[edit]

According to Liu (2012),^[34]
Lehmann (1986).^[35] «also derived the sample distribution of CV in order to give an exact method for the construction of a confidence interval for CV;» it is based on a non-central t-distribution.^{[incomprehensible]}

Similar ratios[edit]

Standardized moments are similar ratios, ${mu_k}/{sigma^k}$ where $mu _{k}$ is the k^th moment about the mean, which are also dimensionless and scale invariant. The variance-to-mean ratio, , is another similar ratio, but is not dimensionless, and hence not scale invariant. See Normalization (statistics) for further ratios.

In signal processing, particularly image processing, the reciprocal ratio (or its square) is referred to as the signal-to-noise ratio in general and signal-to-noise ratio (imaging) in particular.

Other related ratios include:

References[edit]

^ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
^ «What is the difference between ordinal, interval and ratio variables? Why should I care?». GraphPad Software Inc. Archived from the original on 15 December 2008. Retrieved 22 February 2008.
^ Odic, Darko; Im, Hee Yeon; Eisinger, Robert; Ly, Ryan; Halberda, Justin (June 2016). «PsiMLE: A maximum-likelihood estimation approach to estimating psychophysical scaling and variability more reliably, efficiently, and flexibly». Behavior Research Methods. 48 (2): 445–462. doi:10.3758/s13428-015-0600-5. ISSN 1554-3528. PMID 25987306.
^ Sokal RR & Rohlf FJ. Biometry (3rd Ed). New York: Freeman, 1995. p. 58. ISBN 0-7167-2411-1
^ Limpert, Eckhard; Stahel, Werner A.; Abbt, Markus (2001). «Log-normal Distributions across the Sciences: Keys and Clues». BioScience. 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.
^ Koopmans, L. H.; Owen, D. B.; Rosenblatt, J. I. (1964). «Confidence intervals for the coefficient of variation for the normal and log normal distributions». Biometrika. 51 (1–2): 25–32. doi:10.1093/biomet/51.1-2.25.
^ Diletti, E; Hauschke, D; Steinijans, VW (1992). «Sample size determination for bioequivalence assessment by means of confidence intervals». International Journal of Clinical Pharmacology, Therapy, and Toxicology. 30 Suppl 1: S51–8. PMID 1601532.
^ Julious, Steven A.; Debarnot, Camille A. M. (2000). «Why Are Pharmacokinetic Data Summarized by Arithmetic Means?». Journal of Biopharmaceutical Statistics. 10 (1): 55–71. doi:10.1081/BIP-100101013. PMID 10709801. S2CID 2805094.
^ Reed, JF; Lynn, F; Meade, BD (2002). «Use of Coefficient of Variation in Assessing Variability of Quantitative Assays». Clin Diagn Lab Immunol. 9 (6): 1235–1239. doi:10.1128/CDLI.9.6.1235-1239.2002. PMC 130103. PMID 12414755.
^ Sawant,S.; Mohan, N. (2011) «FAQ: Issues with Efficacy Analysis of Clinical Trial Data Using SAS» Archived 24 August 2011 at the Wayback Machine, PharmaSUG2011, Paper PO08
^ Schiff, MH; et al. (2014). «Head-to-head, randomised, crossover study of oral versus subcutaneous methotrexate in patients with rheumatoid arthritis: drug-exposure limitations of oral methotrexate at doses >=15 mg may be overcome with subcutaneous administration». Ann Rheum Dis. 73 (8): 1–3. doi:10.1136/annrheumdis-2014-205228. PMC 4112421. PMID 24728329.
^ Kirkwood, TBL (1979). «Geometric means and measures of dispersion». Biometrics. 35 (4): 908–9. JSTOR 2530139.
^ ^a ^b Eisenberg, Dan (2015). «Improving qPCR telomere length assays: Controlling for well position effects increases statistical power». American Journal of Human Biology. 27 (4): 570–5. doi:10.1002/ajhb.22690. PMC 4478151. PMID 25757675.
^ Broverman, Samuel A. (2001). Actex study manual, Course 1, Examination of the Society of Actuaries, Exam 1 of the Casualty Actuarial Society (2001 ed.). Winsted, CT: Actex Publications. p. 104. ISBN 9781566983969. Retrieved 7 June 2014.
^ «Measuring Degree of Mixing — Homogeneity of powder mix — Mixture quality — PowderProcess.net». www.powderprocess.net. Archived from the original on 14 November 2017. Retrieved 2 May 2018.
^ Rodbard, D (October 1974). «Statistical quality control and routine data processing for radioimmunoassays and immunoradiometric assays». Clinical Chemistry. 20 (10): 1255–70. doi:10.1093/clinchem/20.10.1255. PMID 4370388.
^ Eisenberg, Dan T. A. (30 August 2016). «Telomere length measurement validity: the coefficient of variation is invalid and cannot be used to compare quantitative polymerase chain reaction and Southern blot telomere length measurement technique». International Journal of Epidemiology. 45 (4): 1295–1298. doi:10.1093/ije/dyw191. ISSN 0300-5771. PMID 27581804.
^ Champernowne, D. G.; Cowell, F. A. (1999). Economic Inequality and Income Distribution. Cambridge University Press.
^ Campano, F.; Salvatore, D. (2006). Income distribution. Oxford University Press.
^ ^a ^b ^c ^d ^e Bellu, Lorenzo Giovanni; Liberati, Paolo (2006). «Policy Impacts on Inequality – Simple Inequality Measures» (PDF). EASYPol, Analytical tools. Policy Support Service, Policy Assistance Division, FAO. Archived (PDF) from the original on 5 August 2016. Retrieved 13 June 2016.
^ Eerkens, Jelmer W.; Bettinger, Robert L. (July 2001). «Techniques for Assessing Standardization in Artifact Assemblages: Can We Scale Material Variability?». American Antiquity. 66 (3): 493–504. doi:10.2307/2694247. JSTOR 2694247. S2CID 163507589.
^ Roux, Valentine (2003). «Ceramic Standardization and Intensity of Production: Quantifying Degrees of Specialization». American Antiquity. 68 (4): 768–782. doi:10.2307/3557072. ISSN 0002-7316. JSTOR 3557072. S2CID 147444325.
^ Bettinger, Robert L.; Eerkens, Jelmer (April 1999). «Point Typologies, Cultural Transmission, and the Spread of Bow-and-Arrow Technology in the Prehistoric Great Basin». American Antiquity. 64 (2): 231–242. doi:10.2307/2694276. JSTOR 2694276. S2CID 163198451.
^ Wang, Li-Ying; Marwick, Ben (October 2020). «Standardization of ceramic shape: A case study of Iron Age pottery from northeastern Taiwan». Journal of Archaeological Science: Reports. 33: 102554. doi:10.1016/j.jasrep.2020.102554. S2CID 224904703.
^ Krishnamoorthy, K.; Lee, Meesook (February 2014). «Improved tests for the equality of normal coefficients of variation». Computational Statistics. 29 (1–2): 215–232. doi:10.1007/s00180-013-0445-2. S2CID 120898013.
^ Marwick, Ben; Krishnamoorthy, K (2019). cvequality: Tests for the equality of coefficients of variation from multiple groups. R package version 0.2.0.
^ Hendricks, Walter A.; Robey, Kate W. (1936). «The Sampling Distribution of the Coefficient of Variation». The Annals of Mathematical Statistics. 7 (3): 129–32. doi:10.1214/aoms/1177732503. JSTOR 2957564.
^ Iglevicz, Boris; Myers, Raymond (1970). «Comparisons of approximations to the percentage points of the sample coefficient of variation». Technometrics. 12 (1): 166–169. doi:10.2307/1267363. JSTOR 1267363.
^ Bennett, B. M. (1976). «On an approximate test for homogeneity of coefficients of variation». Contributions to Applied Statistics Dedicated to A. Linder. Experientia Supplementum. 22: 169–171. doi:10.1007/978-3-0348-5513-6_16. ISBN 978-3-0348-5515-0.
^ Vangel, Mark G. (1996). «Confidence intervals for a normal coefficient of variation». The American Statistician. 50 (1): 21–26. doi:10.1080/00031305.1996.10473537. JSTOR 2685039..
^ Feltz, Carol J; Miller, G. Edward (1996). «An asymptotic test for the equality of coefficients of variation from k populations». Statistics in Medicine. 15 (6): 647. doi:10.1002/(SICI)1097-0258(19960330)15:6<647::AID-SIM184>3.0.CO;2-P. PMID 8731006.
^ Forkman, Johannes (2009). «Estimator and tests for common coefficients of variation in normal distributions» (PDF). Communications in Statistics – Theory and Methods. 38 (2): 21–26. doi:10.1080/03610920802187448. S2CID 29168286. Archived (PDF) from the original on 6 December 2013. Retrieved 23 September 2013.
^ Krishnamoorthy, K; Lee, Meesook (2013). «Improved tests for the equality of normal coefficients of variation». Computational Statistics. 29 (1–2): 215–232. doi:10.1007/s00180-013-0445-2. S2CID 120898013.
^ Liu, Shuang (2012). Confidence Interval Estimation for Coefficient of Variation (Thesis). Georgia State University. p.3. Archived from the original on 1 March 2014. Retrieved 25 February 2014.
^ Lehmann, E. L. (1986). Testing Statistical Hypothesis. 2nd ed. New York: Wiley.

External links[edit]

cvequality: R package to test for significant differences between multiple coefficients of variation

From Wikipedia, the free encyclopedia

Definition[edit]

The coefficient of variation (CV) is defined as the ratio of the standard deviation sigma to the mean , ${displaystyle c_{rm {v}}={frac {sigma }{mu }}.}$ ^[1]

Measurements that are log-normally distributed exhibit stationary CV; in contrast, SD varies depending upon the expected value of measurements.

Examples[edit]

In the examples below, we will take the values given as randomly chosen from a larger population of values.

The data set [100, 100, 100] has constant values. Its standard deviation is 0 and average is 100, giving the coefficient of variation as 0 / 100 = 0

The data set [90, 100, 110] has more variability. Its standard deviation is 10 and its average is 100, giving the coefficient of variation as 10 / 100 = 0.1

The data set [1, 5, 6, 8, 10, 40, 65, 88] has still more variability. Its standard deviation is 32.9 and its average is 27.9, giving a coefficient of variation of 32.9 / 27.9 = 1.18

In these examples, we will take the values given as the entire population of values.

The data set [100, 100, 100] has a population standard deviation of 0 and a coefficient of variation of 0 / 100 = 0

The data set [90, 100, 110] has a population standard deviation of 8.16 and a coefficient of variation of 8.16 / 100 = 0.0816

The data set [1, 5, 6, 8, 10, 40, 65, 88] has a population standard deviation of 30.8 and a coefficient of variation of 30.8 / 27.9 = 1.10

Estimation[edit]

When only a sample of data from a population is available, the population CV can be estimated using the ratio of the sample standard deviation to the sample mean :

${displaystyle {widehat {c_{rm {v}}}}={frac {s}{bar {x}}}}$

${displaystyle {widehat {c_{rm {v}}}}^{*}={bigg (}1+{frac {1}{4n}}{bigg )}{widehat {c_{rm {v}}}}}$