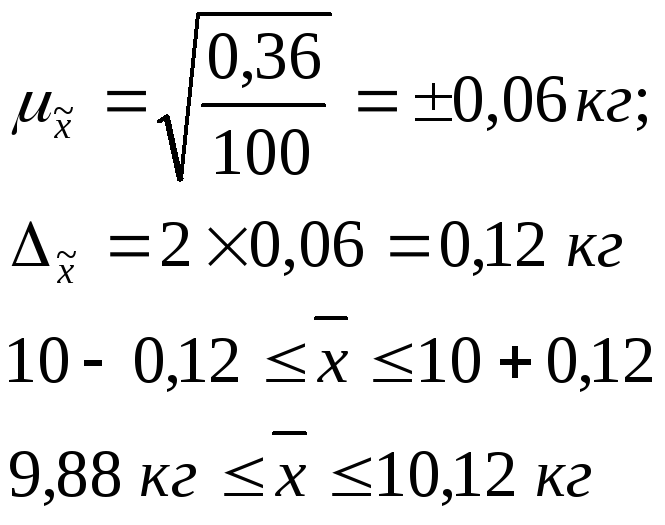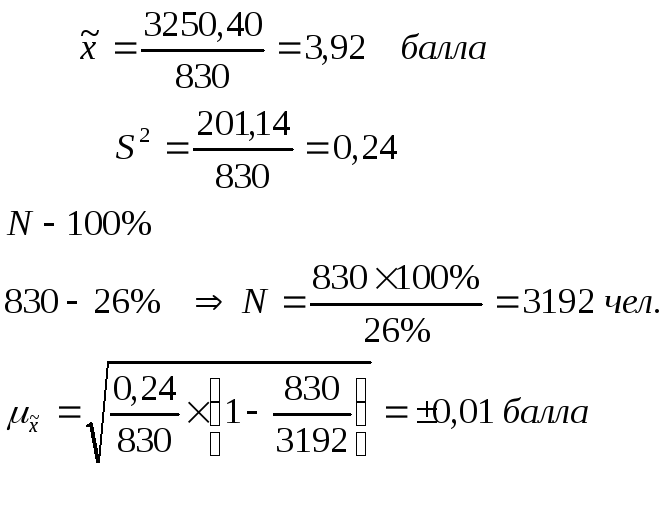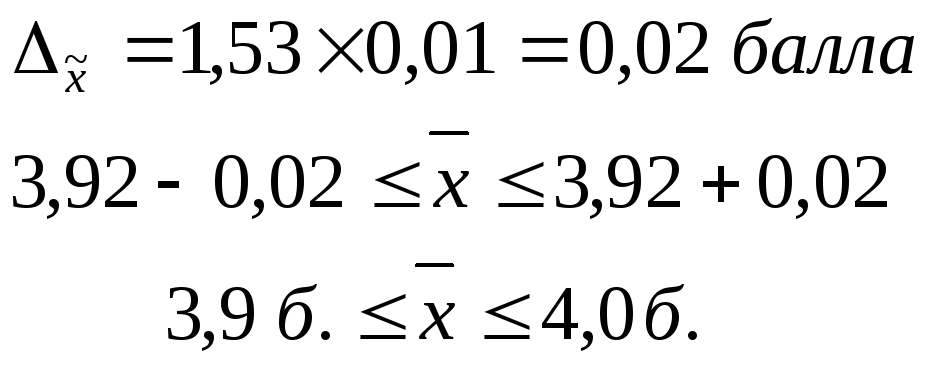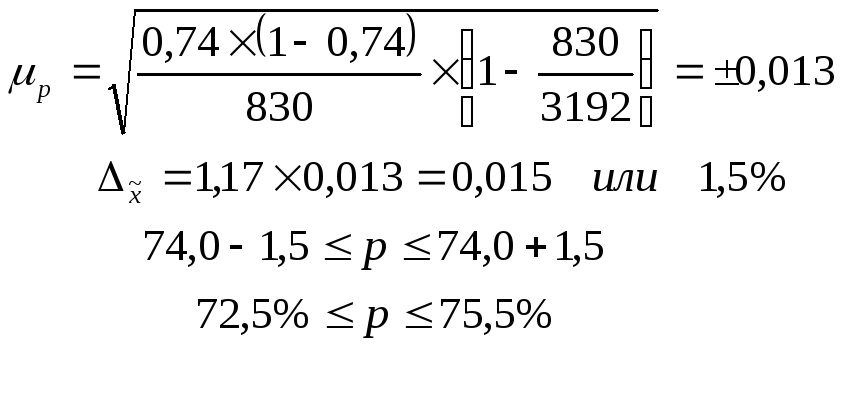Рассчитайте предельную ошибку среднего веса изделия

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. Готовое решение: Заказ №9697

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. Тип работы: Задача

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.Статус:  Выполнен (Зачтена преподавателем ВУЗа)

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. Предмет: Экономика

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. Дата выполнения: 23.10.2020

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. Цена: 229 руб.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Описание и исходные данные задания, 50% решения + фотография:

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

Задача № 3

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии остались не обследованными 2400 изделий. Уровень гарантийной вероятности 0,997.

Решение:

Рассчитаем среднюю ошибку выборочной средней:

где    σ — среднее квадратическое отклонение;

Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г.

  • По УР имеются данные о количестве зарегистрированных разводов 1998 г.    1999 г.    2000 г.    2001 г.    2002 г.    2003 г.    2004 г.    2005 г.    2006 г. 3599    4081    5044    6154    7373    6709    5369    4849    5416 
  • Имеются следующие данные по предприятию: Вид    Изменение количества произведенной продукции, %    Производственные затраты, млн. руб. продукции        Базисный период    Отчетный период № 1    – 10    180    175 № 2    + 20    1 
  • Имеются следующие отчетные данные 24 заводов одной из отраслей промышленности: Номер завода    Среднегодовая стоимость основных производственных фондов, млн. руб.    Валовая продукция в сопоставимых ценах 
  • Имеются следующие данные о строительстве жилья в Приволжском федеральном округе в 2005 году: Субъект РФ    Ввод в действие жилья в сельской местности, тыс. м2    Ввод в действие жилых домов, тыс. м2 
Источник

Решение типовых задач

Задача 1.

При случайном повторном отборе было
установлено, что средний вес товара в
выборочной совокупности, состоящей из
100 изделий, оказался равным 10 кг при
среднем квадратическом отклонении 0,6
кг. С вероятностью, равной 0,954 определите,
в каких пределах заключен средний вес
товара в генеральной совокупности.

Решение:

Для того, чтобы определить предел
среднего веса товара в генеральной
совокупности необходимо воспользоваться
следующей формулой:

По данным задачи среднее значение
признака в совокупности
=10
кг, среднее квадратическое отклонение
S = 0,6 кг, следовательно
дисперсия S² = 0,6² = 0,36;
объем выборочной совокупности n
= 100 изделий.

Также известно, что вероятность Р =
0,954. Если известна вероятность Р, то по
таблице Лапласа (прил.1) можно найти t.
В данной задаче при заданной вероятности
коэффициент t = 2,0.

Среднее значение признака в выборке
известно, но для расчета доверительного
интервала не хватает предельной ошибки
выборки, которая определяется по формуле:

.

Согласно условию задачи для обследования
применяется случайный повторный отбор,
поэтому расчет средней ошибки выборки
будет осуществляться по формуле:
.

По данным расчетам видно, что выборочная
средняя отличается от генеральной
средней на ± 0,12 кг.

Задача 2.

Имеются следующие данные о распределении
студентов нашего техникума по среднему
баллу успеваемости в результате
выборочного 26%-ного собственно-случайного
бесповторного отбора:

Группы
студентов по успеваемости, баллы

до 3,2

3,2 – 3,6

3,6 – 4,0

4,0 – 4,4

4,4 и более

Количество
студентов, чел.

91

125

211

258

145

Определить:

  1. доверительный интервал, в котором с
    вероятностью 0, 874 находится средний
    балл успеваемости студентов;

  2. доверительный интервал, в котором лежит
    доля студентов с баллом успеваемости
    3,6 и выше, гарантируя результат с
    вероятностью 0,758.

Решение:

1. Прежде чем начать конкретный расчет
в данной задаче необходимо написать
все формулы, которые нам потребуются
для решения по порядку.

Нам необходимо рассчитать доверительный
интервал для среднего значения признака:

Для того, чтобы определить данный
интервал необходимо знать среднее
значение признака
и
предельную ошибку
.
Их определяют по формулам:

.

Чтобы узнать предельную ошибку необходимо
рассчитать среднюю ошибку, которая в
данном случае при собственно-случайном
бесповторном отборе будет определяться
по следующей формуле:

.

Прежде чем рассчитать среднюю ошибку
выборки нужно определить дисперсию:

Теперь можно оформлять решение. Для
простоты можно оформить решение в
таблице, которая является аналогом той,
которая составлялась ранее при расчете
показателей вариации:

Таблица 40

Исходные и расчетные данные

Т.к. вероятность Р=0,874, то по таблице
Лапласа (см.приложение) можно определить
t. В нашей задаче t=1,53.
Теперь можно определить предельную
ошибку выборки и построить доверительный
интервал:

По данным расчетам видно, что размер
расхождений между величиной среднего
балла успеваемости студентов, полученного
в выборочной совокупности и генеральной
в условиях одинаковой точности единичных
наблюдений составляет ± 0,02 балла. Т.е.
генеральная средняя находится в
доверительном интервале [3,9 ; 4,0].

2.Для определения доверительного
интервала, в котором лежит доля студентов
с баллом успеваемости 3,6 и выше, гарантируя
результат с вероятностью 0,758, необходимо
воспользоваться следующими формулами.

Прежде всего, нам изначально нужно
определить доверительный интервал для
доли:

Для того, чтобы определить доверительный
интервал необходимо определить выборочную
долю w и предельную ошибку
доли
.

Для определения доли необходимо выбрать
те частоты, у которых средний балл свыше
3,6:

.

Предельная ошибка выборки для доли
определяется по формуле:

,

Для того чтобы рассчитать предельную
ошибку теперь необходимо определить
среднюю ошибку для доли:

По таблице Лапласа при помощи заданной
вероятности Р=0,758 можно определить
коэффициент кратности t,
он будет равен 1,17.

Теперь преступим к конкретным расчетам:

По данным расчетам видно, что размер
расхождений между долей студентов со
средним баллом успеваемости 3,6 и выше,
полученного в выборочной совокупности
и генеральной в условиях одинаковой
точности единичных наблюдений составляет
± 1,5%. Т.е. генеральная доля находится в
доверительном интервале [72,5 ; 75,5].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Главная » Учебные материалы » Статистика » Решения задач » Несколько классов/семестров » Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий. Уровень

Для студентов по предмету СтатистикаРассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее

2022-03-182022-03-18СтудИзба

Описание

Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий. Уровень гарантийной вероятности – 0,932.

Характеристики решённой задачи

Учебное заведение

Неизвестно

Качество

Идеальное компьютерное

Список файлов

  • Задача.docx 55,46 Kb

Картинка-подпись

Комментарии

Сопутствующие материалы

В ходе эксперимента измерялись характеристики x и y. Представить результаты измерений графически. Найти выборочный коэффициент корреляции этих величин. Что можно сказать о зависимости этих двух величин? Построить уравнение линейной регрессии y от x.

Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы: Размер зарплаты, тыс. руб.до 5,05,0-7,57,5-10,010,0-12,5свыше 12,5 Число рабочих, чел.1515256530 Определите среднюю месячную зарплату рабочих цеха

Численность населения составляла на 1 января 460 тыс. человек. За год родилось 5 тыс. человек, умерло 23 тыс. человек. За год прибыло 5 тыс. человек и выбыло 23 тыс. человек. Численность женщин в возрасте 15-49 лет: на начало года – 156 тыс. человек;

Известны данные о результатах проверки исполнения местных бюджетов населенных пунктов на конец 3-го квартала в трех регионах. В случайном бесповторном порядке в каждом из регионов было отобрано 10% населенных пунктов (серийный отбор). Таблица 1 Проц

При исследовании форм выплаты заработной платы получены следующие данные о ее доле, начисленной в форме наличных выплат в кредитный организациях. Данные получены методом 10%-ного механического отбора: Таблица 3 Данные по организациям Номер организаци

1. Используя результаты расчетов, выполненных в задании №2, и полагая, что эти данные получены при помощи собственно-случайного 10-ти процентного бесповторного отбора, определить: а) пределы, за которые с доверительной вероятностью 0,954 не выйдет ср

Свежие статьи

Популярно сейчас

Ответы на популярные вопросы

То есть уже всё готово?

Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.

А я могу что-то выложить?

Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.

А если в купленном файле ошибка?

Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!

Отзывы студентов

Добавляйте материалы
и зарабатывайте!

Продажи идут автоматически

560

Средний доход
с одного платного файла

Обучение Подробнее

Источник

Заказ №38717

Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий. Уровень гарантийной вероятности – 0,932.

Решение:

Средняя ошибка выборки для бесповторной выборки определяется по формуле:          N n n x 1 2 ~   , где  — среднее квадратическое отклонение в выборке; n – объем выборочной совокупности; N – объем генеральной совокупности; N n — доля выборки. Объем генеральной совокупности N = 400 + 1600 = 2000 изделий. Расчет средней ошибки выборки: 0,447 2000 400 1 400 102 ~         x    Предельная ошибка выборки рассчитывается по формуле: х x ~  t ~ , где t – коэффициент доверия, зависящий от вероятности Р, с которой можно гарантировать определенные размеры предельной ошибки.

 Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий.

Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий.

Рассчитайте предельную ошибку среднего веса изделий, если при собственно-случайной бесповторной выборки 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось необследованными 1600 изделий.

  • Предприниматель Николай Надеждин зафрахтовал у морского пароходства в г. Новороссийске грузовое судно на один рейс из Морокко в Россию для перевозки апельсинов. По договору перед погрузкой трюмы судна должны были быть чистыми и свободными от постороннего
  • Из содержания ч. 2 ст. 265 УК РФ следует, что в подготовительной части судебного разбирательства председательствующий устанавливает личность подсудимого, а затем выясняет, вручена ли подсудимому и когда именно копия обвинительного заключения или обвинительного акта, постановления прокурора об изменении обвинения. При этом судебное разбирательство уголовного дела не может быть начато ранее 7 суток со дня вручения обвиняемому копии обвинительного заключения или обвинительного акта, постановления об изменении обвинения.
  • Решением суда города Вильгельмсхафен (Германия) был расторгнут брак между гражданами Российской Федерации Л. и М., проживавшими на момент рассмотрения данного дела на территории Германии. Л. обратилась в компетентный суд Российской Федерации с возражениями относительно признания на территории Российской Федерации решения иностранного суда, которое не подлежало принудительному исполнению.
  • Предприниматель Николай Надеждин зафрахтовал у морского пароходства в г. Новороссийске грузовое судно на один рейс из Морокко в Россию для перевозки апельсинов. По договору перед погрузкой трюмы судна должны были быть чистыми и свободными от постороннего груза.
  • В соответствии со ст. 281 УПК РФ, оглашение показаний потерпевшего и свидетеля, ранее данных при производстве предварительного расследования или судебного разбирательства, а также демонстрация фотографических негативов и снимков, диапозитивов, сделанных в ходе допросов, воспроизведение аудио- и (или) видеозаписи
  • Выручка от реализации продукции составила 19421 тыс. руб., себестоимость – 16124 тыс. руб., коммерческие расходы – 2200 тыс. руб., управленческие расходы – 405 тыс. руб., проценты к получению – 10 тыс. руб., проценты к уплате – 48 тыс. руб., прочие доходы – 81 тыс. руб., налог на прибыль составляет 24%.
  • Популяция включает в себя М особей. Ежегодно человеком изымается Х особей.
  • Рассчитайте убыток от обесценения. Показатели Значение показателя, тыс. долл. Комп. 1 Комп. 2 Комп. 3 Комп. 4 Комп. 5 Первоначальная стоимость ОС 1200 1200 1200 900 Первоначальная стоимость
  • Определите выработку (В) продукции на одного работающего в натуральном и денежном выражении на основе следующих данных: 1) годовой объем выпуска продукции предприятия – 2000 тыс. шт.; 2) годовой объем валовой продукции – 250 млн. руб.;
  • Смешаны 20 мл 0.2 М раствора нитрата серебра и 30 мл 0.1 М раствора йодида калия. Изобразите строение частиц зола. Ответ обоснуйте.
  • Определите общую жесткость (Ж) воды по массе содержащихся в воде солей.
  • Согласно ст. 64 УПК РФ, при наличии обстоятельств, предусмотренных статьями 61 и 63 УПК РФ, судье может быть заявлен отвод участниками уголовного судопроизводства. Отвод судье заявляется до начала судебного следствия, а в случае рассмотрения уголовного дела судом с участием присяжных заседателей — до формирования коллегии присяжных заседателей.
  • Грузинский бизнесмен Ш. обратился в российский суд с ходатайством о разрешении принудительного исполнения на территории Российской Федерации заочного решения Потийского городского суда Грузии, вступившего в законную силу, о взыскании ущерба с должника М., проживающего на территории Российской Федерации.
  • В течение последних 18 месяцев компания, специализирующаяся на инвестиционной недвижимости, строит новое здание кинокомплекса. По состоянию на 31 декабря 2016 года строительство приближается к завершению.
Источник

Понравилась статья? Поделить с друзьями:
  • Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости
  • Рассуждения как бы я могла исправить свои ошибки
  • Рассуждением кажущимся правильным но содержащим скрытую логическую ошибку
  • Рассуждение правильное на вид но содержащее преднамеренную логическую ошибку
  • Рассуждение кажущееся правильным но содержащее скрытую логическую ошибку