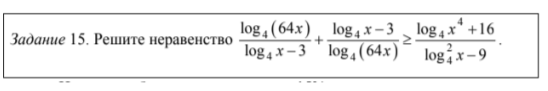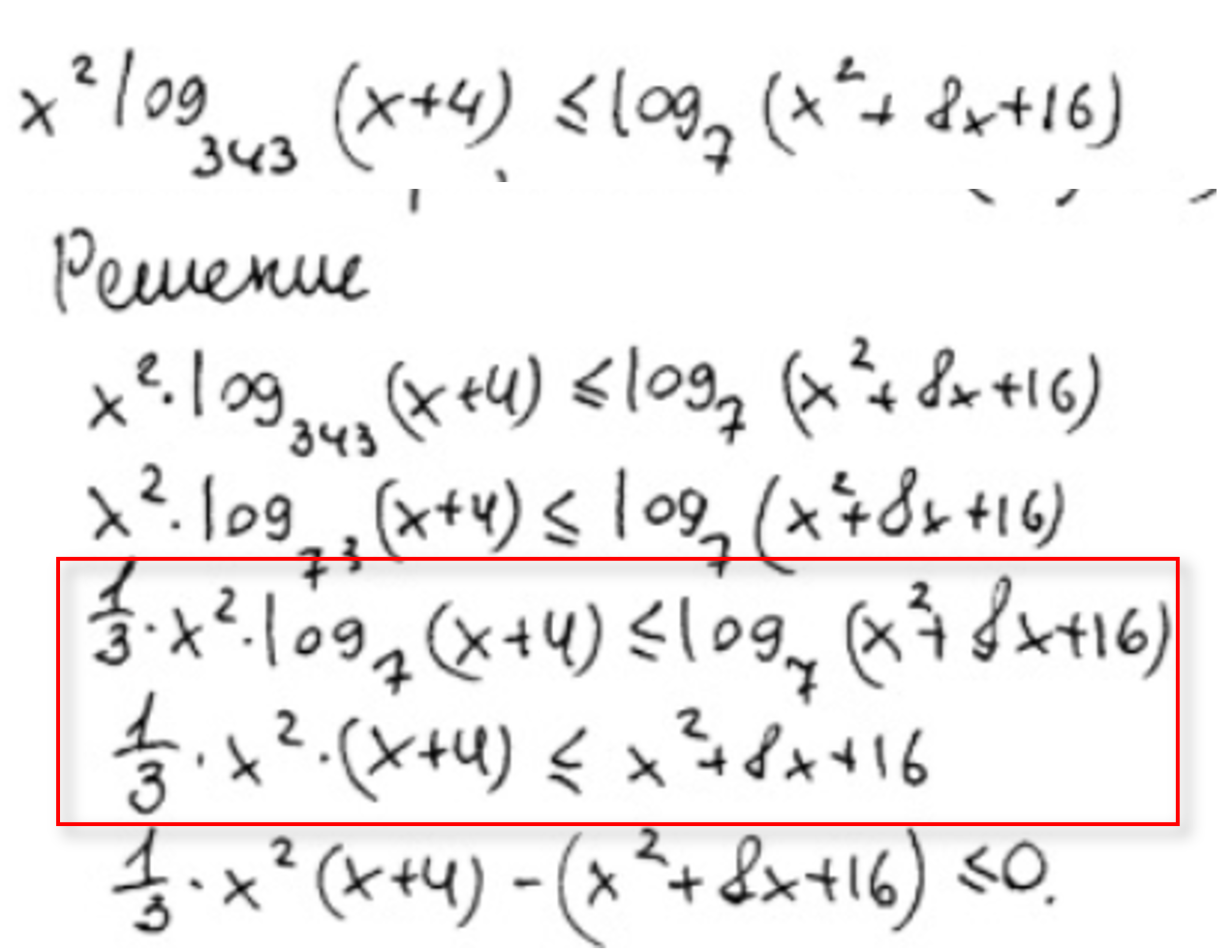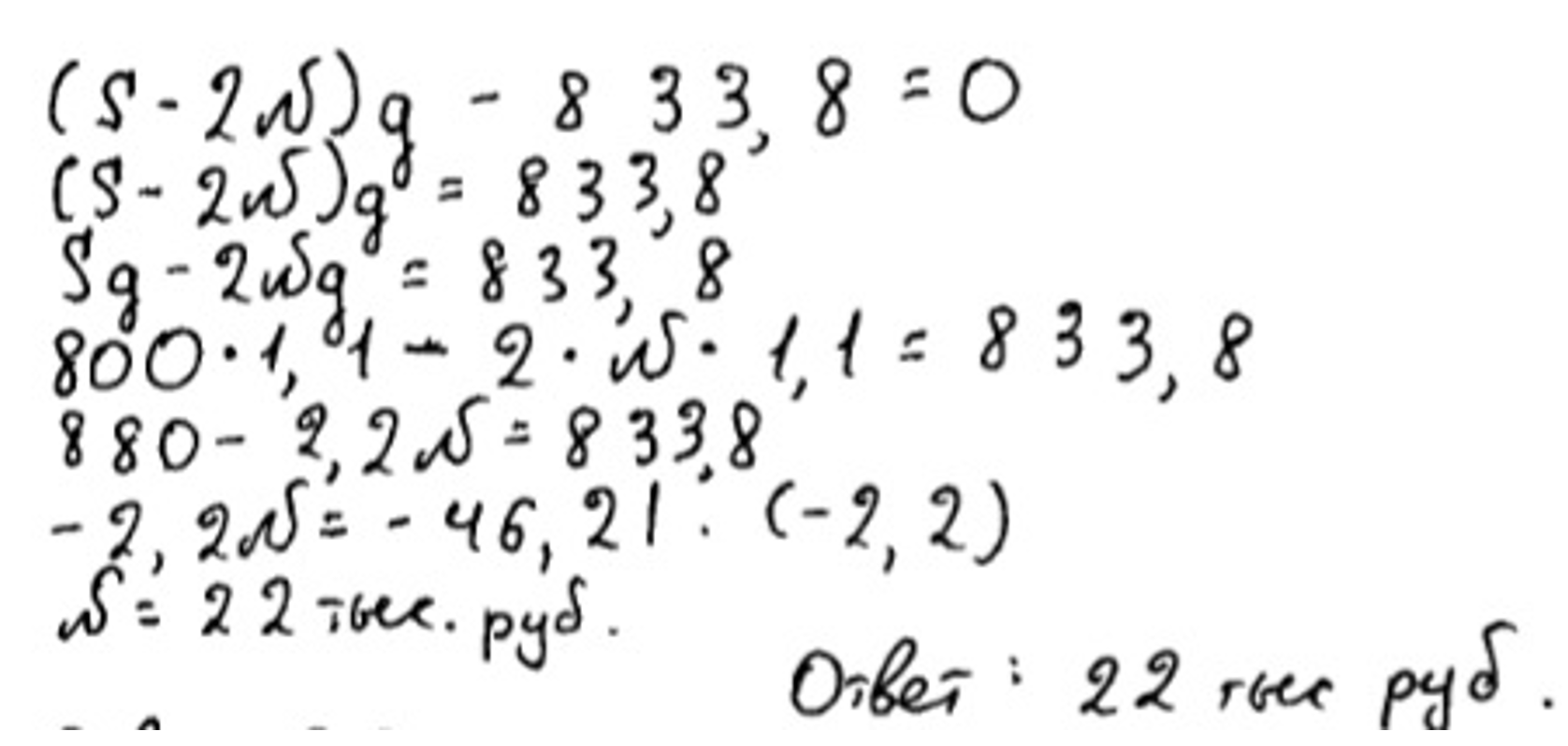Распространенные ошибки в решении математики

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

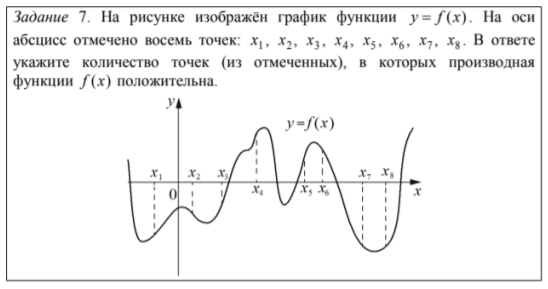
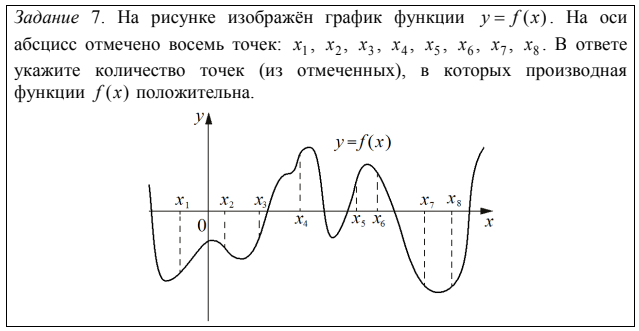
Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

Например:

В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях. 

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях. 

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями. 

Например:

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник. 

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления. 

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей. 

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи. 

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

1. Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
2. Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
3. Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
4. Задание 8 – ошибаются в наглядном решении. 
5. Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
6. Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

• прочтите условие;
• выпишите данные величины, сделайте рисунок в геометрическом задании;
• установите и запишите отношения и взаимосвязи между известными данными;
• выпишите что найти, ответ на какой вопрос нужно дать;
• определите тип задания;
• сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок. 

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

• сориентироваться в условии,
• обдумать и спланировать ее решение,
• понять уровень ее сложности и решить, откладывать ли ее решение напоследок. 

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.

И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.

В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.

Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.

Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.

Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.

Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…

Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:

Уравнения

Основные ошибки:

1) неправильное использование формул приведения.

При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

2) незнание свойств четных и нечетных функций.  Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

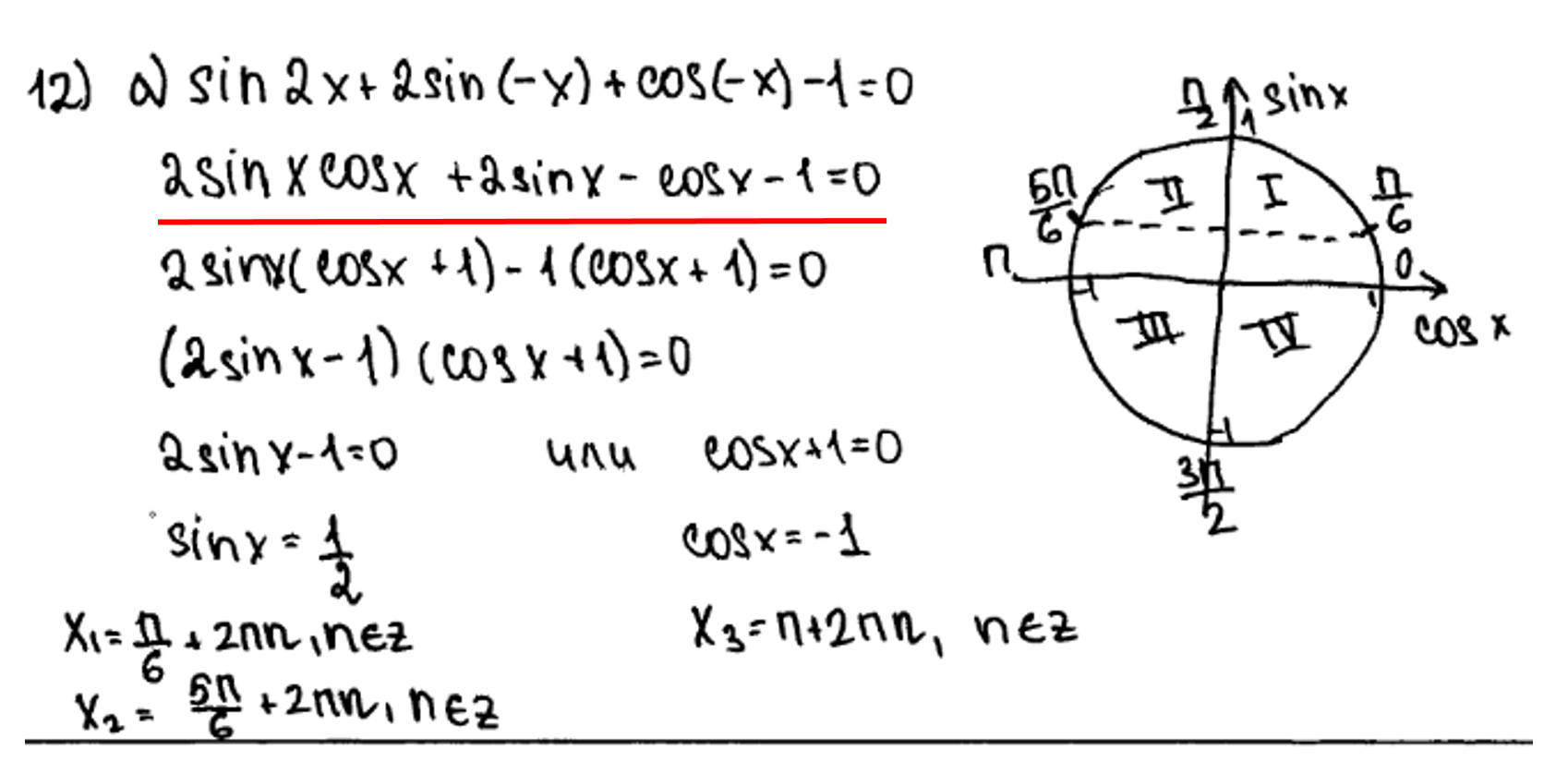
2) незнание свойств четных и нечетных функций.  Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус.  Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида  – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус.  Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида  .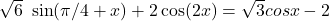

Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.

Неравенства

С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.

1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.

Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.

2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.

Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

.

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

3) Неравносильный переход от неравенства к системе неравенств.

Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.

4) Ошибки при использовании свойств логарифмов.

Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.

Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.

Экономические задачи

В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования   – с дифференцированными платежами, аннуитентными или иная форма кредитования.

Могу выделить несколько основных ошибок.

1)Неверное построение математической модели, связанное с неверным определением формы кредитования.

Для лучшего понимания начну с условия задачи.

В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:

– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года

– размер платежей в 2027 и 2028 годах одинаковый

– к июлю 2029 года долг выплачивается полностью.

Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?

Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2  по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

.

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2  по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: . Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату: .

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

—  25 января с 2021 по 2026 года долг возрастает на 10 процентов;

—  25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.

Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.

В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.

PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый  модуль, и расписанные все значения параметра и т.д и т.д.

В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.

На этом мой краткий обзор подошел к концу. Я желаю удачи и сил  всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!

Все, что не убивает, делает нас сильнее!

P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Ошибки учащихся при изучении математики,

их предупреждение и объяснение

Автор работы:

Дука Наталья Ивановна

учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________

Аннотация

В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.

Тезисы

В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

          Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

          Пример неосознанного применения алгоритма: получив уравнение  sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.  

Иногда ученики используют неверную формулу, не задумываясь  над ней.

Например, определяя, является ли число  рациональным,  ученик пишет:  =   и получает неверный ответ,

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают  ошибки,  но просто  забывают  формулы,  например  формулу

an am = an+m.

Пример ошибки на свойство степени:  . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу .

Встречаются  ошибки от непонимания. Большинство учащихся, решая  впервые  неравенство х24, приводят неверное решение х2.

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого  подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Учебный  год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была  приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС,  если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С». Треугольник, описанный в  условии задачи, не существует.

Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.

В газете «Математика» предлагается уравнение   и к нему ответ:1. Приведенное решение неверное, так как приводит к потере  корней.

Вступление

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики  не могут объяснить, чем  вызваны эти ошибки.

Причины ошибок, допускаемых учащимися при изучении математики

Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок?  Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.

Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Выполняя математические задания, учащиеся допускают типичные ошибки:

• Незнание правил, определений, формул.
• Непонимание правил, определений, формул.
• Неумение применять правила, определения, формулы.
• Неверное применение формул.
• Невнимательное чтение условия и вопроса задания.
• Вычислительные ошибки.
• Не использование свойств фигур при решении геометрических задач.
• Логические ошибки при решении текстовых задач.
• Раскрытие скобок и применение формул сокращенного умножения.

Какие причины ошибок по математике?

• Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
• Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
• Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
• Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся  не всегда сами понимают, что именно они написали.
• Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
• Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
• Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
• Мотивация. Следствие низкой мотивации  – потеря внимания и ошибка.

Работа над ошибками

В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена

(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком  они предложены в учебнике. Другой  пример неосознанного применения алгоритма: получив уравнение

sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
• проверка правильности решения задач путём составления и решения задач, обратных к данной;
• оценка результата решения задачи с точки зрения здравого смысла;
• проверка аналитического решения графическим способом.

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Ученик написал  = 52,  ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .

Объяснение и предупреждение ошибок

Свести ошибки  к минимуму способствуют следующие профилактические меры.

• Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
• Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
• При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
• Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
• Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:

1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.

А также выполнить задания:

1.  Определите четность и нечетность тригонометрической функции:

а)  y  =  – cos x + x2;    б)  y = sin2 x;    в) y = .
2.  Найдите область определения функции   y  =  x2 – 6x + 10.

3. При каких значениях x функции   y = sin x и  y = cos x принимают одинаковые значения?

Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.

Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение  arcsin (sin).

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. По определению . Следовательно, число arcsin(sin) должно принадлежать промежутку , число   этому промежутку не принадлежит. Имеем: arcsin (sin) =  arcsin (sin)) = arcsin (sin ) = arcsin =

Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.  Можно исправить ошибку следующим образом: учитывая, что  90о 90о  для  любого   и    arctg (tgх) = х при

х   arctg (tg130о) = arctg (tg180о  50о) = arctg (tg( 50о)) =  50о. Существует второй способ решения.  Пусть  arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о.  По условию равенства тангенсов  имеем х = 130о + k,  где kZ. Учитывая область определения функции у = arctg х, где х(90О; 90О),  при  k = 1  х = 130о 180о =  50о.

Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin() = 2, т. к.  2.

Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число  рациональным,  ученик пишет:  =   и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил  = х+2. Во-первых, учащиеся забывают, что , во-вторых, опять ошибочная аналогия с формулой = , где  Применение «формулы =» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой =  ,  где и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден  совет: вычислите по тому алгоритму, который только что применили, имеем =  и по действиям  2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.

Можно предложить учащимся проверить себя, взяв, например,  значение   х = 2   но   ;

при  х = –2   но .

Делаем вывод: преобразование выполнено неверно, формула «=» не существует и  

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2,  получим  , с другой стороны  , тогда  2= В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»: . И, разумеется, должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают  ошибки,  но просто  забывают  формулы,  например  формулу

an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.

Ещё пример ошибки:  . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением

=. Здесь же можно предложить другой способ

Необходимо в результате записать формулу .

Встречаются  ошибки от непонимания. Большинство учащихся, решая  впервые  неравенство х24, приводят неверное решение х2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «», но допустили следующую ошибку «=х». Верное решение Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у =  при х0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х24,  х2,

(х-2)(х+2)0, .  Третий  способ графический.

х24 при  .

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin 2sin , /2 = 21/2 или вспомнить определение sin х на тригонометрическом круге.  Наглядно хорошо видно, что sin 2х 2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.

у

Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки.  Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого  подходят задания типа «найди ошибку в решении»:

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Анализ работ ГИА и ЕГЭ

Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:

• преобразовании дробно-рациональных выражений,  содержащих  корень

n-ой степени

• исследовании функций на наибольшее и наименьшее значения;
• решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
• вычислении площади криволинейной трапеции;
• построении графика функции с модулем;
• изображении тел вращения в геометрической задаче;
• теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
• построении множества точек плоскости, удовлетворяющего заданному условию;
• решении задач с параметром.

          Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:

• комбинация тел;
• углы в пространстве;
• производная и её применение к исследованию функции на отрезке;
• построение ГМТ, удовлетворяющего заданным условиям;
• логарифмические и показательные неравенства;
• тригонометрические функции и их свойства;
• тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.

           Учебный  год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.

Ошибки в учебниках и методической литературе

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была  приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС,  если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С».

Решение.

ВD – биссектриса АВС   =  

∠ВDС = ∠С  ВDС равнобедренный  ВD = DС   =

Отсюда СD  =  

Ответ:  

Решим задачу вторым способом.

ВЕ – высота АВС.  Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:  

АВ2  –  АЕ2  =  ВD2 – DЕ2,

302  –  (20 + х)2  = 162 – х2,  

900 – 400 – 40х – х2  = 256 – х2,

40х  = 244,  

х  =  6,1.

  ВЕ высота и медиана DЕ = СЕ  СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.

Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С  и  ∠АВD = ∠DВС.  Найдем величины  ∠DВС, ∠ВDС, ∠С.

АD2  =  АВ2 + ВD2 – 2  cos ∠AВD   

cos ∠AВD =

Тогда   ∠АВD 38,5о.    ∠DВС = ∠АВD 38,5о.

Аналогично   cos ∠ADВ =

Тогда    ∠АDВ = 180о  – 67,59о  ∠ВDС  67,59о.     Из  ВDС

∠С = 180о – 38,05о – 67,59о  = 74,36о,

Отсюда следует, что   ∠ВDС  ∠С  и  треугольник   DВС неравнобедренный.

Значит, задача составлена некорректно: треугольник, описанный в  условии задачи, не существует.

Возможны два корректных варианта задачи:

1. Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С.

В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.

1. Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30.  АD = 20,  ВD = 16.

∠ВDС  ∠С, в этом случае из треугольника DВС по теореме синусов получаем

В действующем учебнике задача № 536 имеет вид:

Отрезок BD является биссектрисой треугольника АВС. а)  Найдите АВ, если ВС = 9 см,  АD = 7,5 см,  DС = 4,5 см.   б)  Найдите  DС,  если  АВ = 30. АD = 20,  ВD = 16.

        Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).

        Цитируем: «Прочитай, объясни и проверь записи.

190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»

        Проверяем    20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится  в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.

        Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее),  т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.

        Предлагаем верные записи:

 190 : 20 = 190 : 10 : 2 = 9 ( 1 д.  остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).

В газете «Математика» предлагается уравнение   и к нему ответ:1. Предложено решение  уравнения  по следующей  схеме:

af(x)bg(x) = apbp

Приведенное решение неверное, так как приводит к потере  корней. данное уравнение следует решать по схеме:

a f(x) b g(x) = a p b p    a  f(x)– р b q – g(x) 

Вернемся к данном уравнению.

 = 40    2 3   

Заключение

Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при  изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема  приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.

Литература

1. Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
2.  2-98 Ярский А. С, «Что делать с ошибками»
3.  Хэкало С. П. «Корни терять нельзя» 5-98
4.  Игнатенко В. З. «Сюрпризы биссектрисы» 5-98

Интернет-ресурсы

1. http://mat.1september.ru/view_article.php?ID=200900304
2. http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
3. http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
4. http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
5. http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

10 основных ошибок, допускаемых в ЕГЭ по математике

Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.

Б. Шоу

1. Обзор основных ошибок

Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.

https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view

http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf

Профильный уровень

Базовый уровень

Основные факторы, вызывающие ошибки:

• недостаточный уровень понимания условия при чтении задания,

• вычислительные ошибки,

• недостаточная развитость наглядных геометрических представлений.

1. Анализ 10 типичных ошибок на примерах заданий ЕГЭ

Задачи на проценты – непонимание механизма начисления процентов.

В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.

Пример:

.

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

—  25 января с 2021 по 2026 года долг возрастает на 10 процентов;

—  25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.

Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.

В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.

PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый  модуль, и расписанные все значения параметра и т.д и т.д.

В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.

На этом мой краткий обзор подошел к концу. Я желаю удачи и сил  всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!

Все, что не убивает, делает нас сильнее!

P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Ошибки учащихся при изучении математики,

их предупреждение и объяснение

Автор работы:

Дука Наталья Ивановна

учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________

Аннотация

В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.

Тезисы

В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

          Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

          Пример неосознанного применения алгоритма: получив уравнение  sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.  

Иногда ученики используют неверную формулу, не задумываясь  над ней.

Например, определяя, является ли число  рациональным,  ученик пишет:  =   и получает неверный ответ,

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают  ошибки,  но просто  забывают  формулы,  например  формулу

an am = an+m.

Пример ошибки на свойство степени:  . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу .

Встречаются  ошибки от непонимания. Большинство учащихся, решая  впервые  неравенство х24, приводят неверное решение х2.

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого  подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Учебный  год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была  приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС,  если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С». Треугольник, описанный в  условии задачи, не существует.

Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.

В газете «Математика» предлагается уравнение   и к нему ответ:1. Приведенное решение неверное, так как приводит к потере  корней.

Вступление

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики  не могут объяснить, чем  вызваны эти ошибки.

Причины ошибок, допускаемых учащимися при изучении математики

Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок?  Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.

Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Выполняя математические задания, учащиеся допускают типичные ошибки:

• Незнание правил, определений, формул.
• Непонимание правил, определений, формул.
• Неумение применять правила, определения, формулы.
• Неверное применение формул.
• Невнимательное чтение условия и вопроса задания.
• Вычислительные ошибки.
• Не использование свойств фигур при решении геометрических задач.
• Логические ошибки при решении текстовых задач.
• Раскрытие скобок и применение формул сокращенного умножения.

Какие причины ошибок по математике?

• Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
• Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
• Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
• Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся  не всегда сами понимают, что именно они написали.
• Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
• Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
• Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
• Мотивация. Следствие низкой мотивации  – потеря внимания и ошибка.

Работа над ошибками

В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена

(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком  они предложены в учебнике. Другой  пример неосознанного применения алгоритма: получив уравнение

sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
• проверка правильности решения задач путём составления и решения задач, обратных к данной;
• оценка результата решения задачи с точки зрения здравого смысла;
• проверка аналитического решения графическим способом.

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Ученик написал  = 52,  ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .

Объяснение и предупреждение ошибок

Свести ошибки  к минимуму способствуют следующие профилактические меры.

• Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
• Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
• При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
• Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
• Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:

1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.

А также выполнить задания:

1.  Определите четность и нечетность тригонометрической функции:

а)  y  =  – cos x + x2;    б)  y = sin2 x;    в) y = .
2.  Найдите область определения функции   y  =  x2 – 6x + 10.

3. При каких значениях x функции   y = sin x и  y = cos x принимают одинаковые значения?

Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.

Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение  arcsin (sin).

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. По определению . Следовательно, число arcsin(sin) должно принадлежать промежутку , число   этому промежутку не принадлежит. Имеем: arcsin (sin) =  arcsin (sin)) = arcsin (sin ) = arcsin =

Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.  Можно исправить ошибку следующим образом: учитывая, что  90о 90о  для  любого   и    arctg (tgх) = х при

х   arctg (tg130о) = arctg (tg180о  50о) = arctg (tg( 50о)) =  50о. Существует второй способ решения.  Пусть  arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о.  По условию равенства тангенсов  имеем х = 130о + k,  где kZ. Учитывая область определения функции у = arctg х, где х(90О; 90О),  при  k = 1  х = 130о 180о =  50о.

Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin() = 2, т. к.  2.

Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число  рациональным,  ученик пишет:  =   и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил  = х+2. Во-первых, учащиеся забывают, что , во-вторых, опять ошибочная аналогия с формулой = , где  Применение «формулы =» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой =  ,  где и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден  совет: вычислите по тому алгоритму, который только что применили, имеем =  и по действиям  2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.

Можно предложить учащимся проверить себя, взяв, например,  значение   х = 2   но   ;

при  х = –2   но .

Делаем вывод: преобразование выполнено неверно, формула «=» не существует и  

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2,  получим  , с другой стороны  , тогда  2= В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»: . И, разумеется, должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают  ошибки,  но просто  забывают  формулы,  например  формулу

an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.

Ещё пример ошибки:  . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением

=. Здесь же можно предложить другой способ

Необходимо в результате записать формулу .

Встречаются  ошибки от непонимания. Большинство учащихся, решая  впервые  неравенство х24, приводят неверное решение х2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «», но допустили следующую ошибку «=х». Верное решение Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у =  при х0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х24,  х2,

(х-2)(х+2)0, .  Третий  способ графический.

х24 при  .

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin 2sin , /2 = 21/2 или вспомнить определение sin х на тригонометрическом круге.  Наглядно хорошо видно, что sin 2х 2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.

у

Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки.  Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого  подходят задания типа «найди ошибку в решении»:

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Анализ работ ГИА и ЕГЭ

Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:

• преобразовании дробно-рациональных выражений,  содержащих  корень

n-ой степени

• исследовании функций на наибольшее и наименьшее значения;
• решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
• вычислении площади криволинейной трапеции;
• построении графика функции с модулем;
• изображении тел вращения в геометрической задаче;
• теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
• построении множества точек плоскости, удовлетворяющего заданному условию;
• решении задач с параметром.

          Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:

• комбинация тел;
• углы в пространстве;
• производная и её применение к исследованию функции на отрезке;
• построение ГМТ, удовлетворяющего заданным условиям;
• логарифмические и показательные неравенства;
• тригонометрические функции и их свойства;
• тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.

           Учебный  год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.

Ошибки в учебниках и методической литературе

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была  приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС,  если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С».

Решение.

ВD – биссектриса АВС   =  

∠ВDС = ∠С  ВDС равнобедренный  ВD = DС   =

Отсюда СD  =  

Ответ:  

Решим задачу вторым способом.

ВЕ – высота АВС.  Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:  

АВ2  –  АЕ2  =  ВD2 – DЕ2,

302  –  (20 + х)2  = 162 – х2,  

900 – 400 – 40х – х2  = 256 – х2,

40х  = 244,  

х  =  6,1.

  ВЕ высота и медиана DЕ = СЕ  СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.

Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С  и  ∠АВD = ∠DВС.  Найдем величины  ∠DВС, ∠ВDС, ∠С.

АD2  =  АВ2 + ВD2 – 2  cos ∠AВD   

cos ∠AВD =

Тогда   ∠АВD 38,5о.    ∠DВС = ∠АВD 38,5о.

Аналогично   cos ∠ADВ =

Тогда    ∠АDВ = 180о  – 67,59о  ∠ВDС  67,59о.     Из  ВDС

∠С = 180о – 38,05о – 67,59о  = 74,36о,

Отсюда следует, что   ∠ВDС  ∠С  и  треугольник   DВС неравнобедренный.

Значит, задача составлена некорректно: треугольник, описанный в  условии задачи, не существует.

Возможны два корректных варианта задачи:

1. Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30,  АD = 20,  ВD = 16  и  ∠ВDС = ∠С.

В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.

1. Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30.  АD = 20,  ВD = 16.

∠ВDС  ∠С, в этом случае из треугольника DВС по теореме синусов получаем

В действующем учебнике задача № 536 имеет вид:

Отрезок BD является биссектрисой треугольника АВС. а)  Найдите АВ, если ВС = 9 см,  АD = 7,5 см,  DС = 4,5 см.   б)  Найдите  DС,  если  АВ = 30. АD = 20,  ВD = 16.

        Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).

        Цитируем: «Прочитай, объясни и проверь записи.

190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»

        Проверяем    20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится  в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.

        Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее),  т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.

        Предлагаем верные записи:

 190 : 20 = 190 : 10 : 2 = 9 ( 1 д.  остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).

В газете «Математика» предлагается уравнение   и к нему ответ:1. Предложено решение  уравнения  по следующей  схеме:

af(x)bg(x) = apbp

Приведенное решение неверное, так как приводит к потере  корней. данное уравнение следует решать по схеме:

a f(x) b g(x) = a p b p    a  f(x)– р b q – g(x) 

Вернемся к данном уравнению.

 = 40    2 3   

Заключение

Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при  изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема  приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.

Литература

1. Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
2.  2-98 Ярский А. С, «Что делать с ошибками»
3.  Хэкало С. П. «Корни терять нельзя» 5-98
4.  Игнатенко В. З. «Сюрпризы биссектрисы» 5-98

Интернет-ресурсы

1. http://mat.1september.ru/view_article.php?ID=200900304
2. http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
3. http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
4. http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
5. http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

10 основных ошибок, допускаемых в ЕГЭ по математике

Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.

Б. Шоу

1. Обзор основных ошибок

Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.

https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view

http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf

Профильный уровень

Базовый уровень

Основные факторы, вызывающие ошибки:

• недостаточный уровень понимания условия при чтении задания,

• вычислительные ошибки,

• недостаточная развитость наглядных геометрических представлений.

1. Анализ 10 типичных ошибок на примерах заданий ЕГЭ

Задачи на проценты – непонимание механизма начисления процентов.

В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.

Пример:

При решении этого задания 6% участников экзамена посчитали, что если цена была повышена на 25%, то для нахождения старой цены нужно новую цену понизить на 25%. В действительности же новая цена составляет 125% от старой цены, а узнать нужно, сколько рублей соответствуют 100%.

В более сложной экономической задаче требуется понимание механизма начисления простых и сложных процентов, обоснованное применение формул, выбор правильного способа решения. Типичные ошибки здесь связаны с неверным составлением модели задачи, непониманием взаимосвязи величин, непониманием того, что важен не только ответ, но и способ решения задачи.

Невнимательное чтение условия.

К сожалению, это самая распространенная ошибка согласно анализу типичных ошибок ЕГЭ, проведенному ФИПИ.

Конечно, многое здесь можно списать на волнение и психологическое напряжение. Даже самые подготовленные ученики на экзамене могут растеряться, переволноваться или поспешить в решении более простых заданий. Однако факт остается фактом, и при подготовке к экзаменам на него нужно обратить внимание.

Примеры:

Почти 24% участников экзамена указали количество точек, в которых значение функции (а не ее производной) положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительное значение.

Около 2,5% участников экзамена нашли вероятность выбора подтекающего насоса, не обратив внимания на частицу «не» в условии.

Практико-ориентированные задания базового и повышенного уровня – непонимание текста задачи.

Кроме ошибок, связанных с невнимательным чтением условия, на первое место здесь выходит непонимание текста задачи, незнание единиц измерения величин, неумение работать с формулами. Многие выпускники даже не приступают к технически не сложным практико-ориентированным задачам повышенного уровня.

Пример:

Выполнение задания – около 57%. Отмечается, что 8% участников не дали никакого ответа; 6% решили, что чем ближе, тем лучше; 4% решили, что лампочку нужно поместить в середину разрешенного интервала, а еще 4,5% решили, что самый главный параметр – это фокус.

Вычислительные ошибки.

Привычка вычислять все с помощью калькулятора, вплоть до таблицы умножения и действий с круглыми числами доставляет учащимся немало проблем на экзамене. Отсутствие навыков быстрого счета в уме или на бумаге часто приводит к тому, что участники экзамена допускают грубые ошибки в элементарных примерах. «Слабые» места многих старшеклассников – это дроби, отрицательные числа, элементарные преобразования выражений, т.е. проблемы, накопившиеся с 5 класса.

Ошибки в теоретических фактах.

Незнание необходимых для решения задач теоретических фактов, как по алгебре, так и по геометрии, существенно снижает процент выполнения большинства заданий как базового, так и повышенного уровня сложности.

Примеры:

Около 8% выпускников не дали никакого ответа; 38% ошиблись в формуле боковой поверхности конуса, а еще 12% в формуле его объема. Отмечается, что процент выполнения этого задания существенно ниже, чем, например, формально гораздо более сложного задания с полным решением на решение уравнения и осуществление отбора корней. Это означает, что низкий процент выполнения заданий по стереометрии вызван именно существенными проблемами в ее преподавании.

В задании 5 проверялось умение решать показательные и логарифмические уравнения. Из семи процентов выпускников, не справившихся с заданием, 2% ошиблись в свойствах степеней.

Незнание алгоритмов и методов решения.

Знание алгоритмов и методов решения проверялось во многих заданиях экзаменационной работы. Например, в задании 12 требовалось продемонстрировать понимание алгоритма исследования функции с помощью производной, а в заданиях 5,13,15 знание общих и частных методов решения уравнений и неравенств.

Пример:

Ненулевые баллы получило около 15% участников экзамена. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок при решении дробно-рационального неравенства (забыт знаменатель).

Неверное чтение чертежей, непонимание взаимосвязи элементов геометрической конструкции, отсутствие базовых пространственных представлений, ошибки в построении чертежа.

В преподавании геометрии очень важным является не только умение решать вычислительные задачи с геометрическим содержанием (по формулам), но и формировать геометрические представления о фигурах (телах). При отсутствии базовых пространственных представлений сложно ожидать высокого процента выполнения стереометрического задания с полным решением.

Пример:

Отмечается, что около 10% участников экзамена при решении этой задачи неверно определили углы по их записи (перепутали буквы или не понимают, какая из букв в записи угла соответствует его вершине). Около 5% участников «увидели» прямоугольный треугольник ACD, а еще 3% — равносторонний треугольник ABD.

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. В целом при решении геометрических задач более половины выпускников продемонстрировали отсутствие знания взаимосвязей элементов геометрической конструкции и соотношений между величинами пространственных фигур.

Неумение доказывать, обосновывать.

К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Оба задания содержали два пункта. В первом пункте задание доказать, а во втором пункте вычислить. Основной проблемой оказалось выполнение первого пункта. Участники экзамена продемонстрировали неумение доказывать. При этом много встречается различного рода логических ошибок. Наибольшие затруднения участники испытывали при оформлении доказательства.

Пример:

Типичные ошибки связаны с непониманием логики построения доказательства. Например, доказательство начинается так: «Пусть точка О является серединой отрезка СК…». Т.е. в начале доказательства уже допускается факт, который и требуется доказать.

Задания 18 и 19 высокого уровня сложности предназначены для конкурсного отбора в ВУЗы с повышенными требованиями к математической подготовке абитуриентов. Это задания на комбинацию различных методов. Для успешного их выполнения, кроме прочих математических знаний, необходим высокий уровень математической культуры, который предполагает, в частности, умение обосновывать выбранные методы и способы решения.

Примеры:

Ненулевые баллы при решении этого задания получило около 17% участников экзамена. Многие выпускники попробовали исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не качественный ответ «да» или «нет».

Ненулевые баллы при решении этого задания получило около 3% участников экзамена. Основной проблемой оказалось применение графического метода, который, как показали работы участников экзамена, не достаточно сформирован. Без объяснений и обоснований на координатной плоскости отмечаются графики, и считывается множество значений параметра. Во многих случаях на координатной плоскости обозначено много верных объектов, а ответа на поставленный вопрос так и не последовало.

Задания по тригонометрии требуют тщательности решения.

Представленные в экзаменационной работе задания по тригонометрии не относятся к числу самых сложных, однако их выполнение требует тщательности решения, аккуратности, внимания, знания большого количества теоретических фактов и умения их применять на практике.

Примеры:

Выполнение задания – около 34%. Типичные ошибки связаны в первую очередь с определением знака тригонометрической функции – почти 12% участников экзамена потеряли знак «минус». Еще 22% решили, что ответ ожидается «хорошим» — 1 или 2.

Задание 13 проверяло умение решать тригонометрические уравнения и производить отбор корней. Основной проблемой первого пункта оказалось неумение вводить новую переменную (ошибки в свойствах степеней), незнание формул решения простейшего тригонометрического уравнения. При выполнении второго пункта участники продемонстрировали неумение или небрежность отбора корней.

Отсутствие навыков математического моделирования.

Способность к построению и исследованию простейших математических моделей проверяется в заданиях 11 (текстовая задача) и 17 (текстовая задача с экономическим содержанием). Текстовые задачи, как правило, являются стандартными задачами на составление уравнений курса алгебры 8 класса. В экономической задаче требуется верно построить математическую модель и исследовать ее. Важную роль при этом играет сюжетная, практико-ориентированная часть условия. При составлении математических моделей основные ошибки являются следствием непонимания взаимосвязи величин. Так, например, в задачах на движение около 10% участников экзамена продемонстрировали непонимание движения по реке – собственную скорость умножили на время движения.

1. Задачи с ошибками как форма работы на уроке.

Одной из форм работы на уроках является поиск и исправление ошибок. «Задачи с ошибками» являются заданиями творческого типа, они приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д.

Мой опыт преподавания показывает, что такие задания нравятся учащимся и являются достаточно эффективным способом совершенствования навыков решения задач.

Методика работы с задачами с ошибками может быть следующей:

1 этап: Индивидуальная, парная или групповая работа, в зависимости от уровня подготовленности учащихся, по поиску и исправлению ошибок. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.

2 этап: Совместное обсуждение ошибок.

3 этап: Снова индивидуальная или парная работа – составление памятки «Советы ученику, решающему задачу».

4 этап: Проверка результатов и подведение итогов учителем.

Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.

Мои рекомендации:

1. Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.

У меня старое издание 1996 года, но есть и более поздние издания этой книги.

Раздел 7 этого пособия так и называется: «Учимся на чужих ошибках».

1. http://math4school.ru/rabota_nad_oshibkami.html

Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.

Решение задач по математике может быть сложным и требовать много времени и усилий. Но порой мы делаем ошибки, которые могут привести к неправильному решению. В этой статье мы рассмотрим топ-10 ошибок, которые чаще всего допускаются при решении задач по математике, и как их можно избежать.

Ошибка 1: Неправильное чтение условия задачи

Одной из самых распространенных ошибок является неправильное чтение или неполное понимание условия задачи. Чтобы ее избежать, необходимо внимательно и тщательно изучить каждую деталь условия задачи и понять, что от вас требуется.

Ошибка 2: Несоответствие данных условию задачи

Еще одна распространенная ошибка – это использование неверных данных при решении задачи. Чтобы этого избежать, нужно перепроверять каждый шаг, который вы делаете, и убедиться, что он соответствует условиям задачи.

Ошибка 3: Недостаточное использование информации

Часто при решении задач мы не используем всю информацию, которая нам доступна. Для того чтобы избежать этой ошибки, нужно уделять особое внимание каждой детали, которая была предоставлена в условии задачи.

Ошибка 4: Неправильный выбор формулы

Если вы выбрали не ту формулу или не правильно применили формулу из учебника, то в результате получите неправильный ответ. Поэтому проверьте правильность выбранной формулы и убедитесь, что она соответствует условию задачи.

Ошибка 5: Неправильно поставленные знаки

Еще одна распространенная ошибка – это неправильно поставленные знаки. Например, если вы поставили плюс вместо минуса, то получите неправильный ответ. Проверяйте каждый знак и убедитесь, что он правильно поставлен.

Ошибка 6: Неправильно решенное уравнение

Неправильно решенное уравнение – это еще одна распространенная ошибка. Внимательно рассмотрите каждый шаг, который вы сделали при решении уравнения, и убедитесь, что он правильный.

Ошибка 7: Неверное округление

Если вы неправильно округляете результат, то в конечном итоге получите неправильный ответ. Убедитесь, что вы используете правильное количество знаков после запятой при округлении.

Ошибка 8: Недостаточное количество времени на задачу

Недостаточное количество времени на задачу – это еще одна распространенная проблема. Чтобы избежать этой ошибки, необходимо правильно планировать свое время на решение задач, и убедиться, что у вас есть достаточно времени для каждой задачи.

Ошибка 9: Неспособность критически мыслить

Критическое мышление – это ключевой навык для решения математических задач. Если вы не можете анализировать информацию, то вы будете допускать ошибки. Упражняйте свой разум и старайтесь анализировать каждый вопрос, который задан в условии задачи.

Ошибка 10: Недостаточно практики

Для того чтобы стать лучшим в решении математических задач, вам нужно много практиковаться. Если вы не тренируете свой ум, то никогда не достигнете того уровня, который хотели бы достичь. Порой даже небольшая дополнительная практика может сделать бОльшую разницу в решении задач.

Заключение

Избегайте этих распространенных ошибок при решении задач по математике, и вы сможете повысить свой успех в этой области. Не забывайте, что ключевой навык – это критическое мышление и много практики. Старайтесь улучшить свои навыки, и вы обязательно достигнете желаемого результата.