Примеры кодов с исправлением ошибок - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 63K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ( $A$ , $B$ , $C$ , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (). Ошибки при передаче будем подчёркивать.

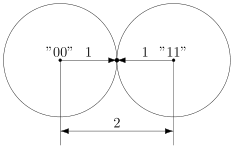
Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$ . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$begin{aligned} A &to 0,\ B &to 1. end{aligned}$

Передача по каналу, в котором возникла ошибка будет записана так:

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$ .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$begin{aligned} A &to 00,\ B &to 11. end{aligned}$

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

Какие выводы мы можем сделать, когда получили $01$ ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$ . А может, во втором, и была передана $A$ .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Проверим в деле:

Получили $010$ . Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$ . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$ .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$ , а получили $001$ . Видно, что эта цепочка больше похожа на исходные $000$ , чем на $111$ . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$ . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, , так как все цифры в соответствующих позициях равны, а вот .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
Расстояние в обе стороны одинаково.
Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

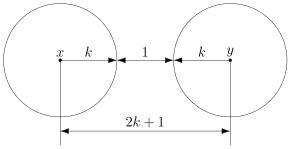
Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$ ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$ , мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$ . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$d_{min} geqslant 2k+1.$

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned}$

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

	A	B	C	D
A	—	3	3	4
B	3	—	4	3
C	3	4	—	3
D	4	3	3	—

Минимальное расстояние $d_{min}=3$ , а значит , откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned}$

Минимальное расстояние получилось для символа $A$ , значит вероятнее всего передавался именно он:

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned}$

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

Это свойство прямо следует из определения.

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

Математически равенство всех трёх цифр можно записать как систему:

$left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right.$

Или, если воспользоваться свойствами сложения в GF(2), получаем

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Или

$left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right.$

В матричном виде эта система будет иметь вид

где

$H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}.$

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$ ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}.$

Соответствующая система имеет вид:

$left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right.$

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right.$

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned}$

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$a_1 x^{(1)}+a_2 x^{(2)},$

где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$(a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG.$

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned}$

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0.$

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$ , а было отправлено кодовое слово $v$ . Тогда вектор ошибки по определению

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$begin{aligned} v &= x + e,\ x &= v + e. end{aligned}$

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

И заметим следующее

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100).$

Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Для
того, чтобы код исправлял ошибки,
необходимо увеличить его минимальное
кодовое расстояние.

Пример.
Трёхразрядный код состоит из двух
допустимых комбинаций 000 и 111. В случае
одиночной ошибки для первого кодового
набора возможные кодовые наборы
001,010,100, для второго – 011,101,110. У каждого
допустимого кодового набора “свои”
недопустимые кодовые наборы. Его
минимальное кодовое расстояние d_min
равно 3.

Если
ошибка одиночная, то удается определить
её местоположение и исправить её, так
как каждая ошибка приводит к недопустимому
кодовому набору, соответствующему
только одному из допустимых кодовых
наборов.

Определение.
Код называется
кодом с исправлением ошибок, если всегда
из неправильного кодового набора можно
получить правильный кодовый набор
(например, коды Хэмминга).

Если
d_min= 3, то любая
одиночная ошибка переводит допустимый
кодовый набор в недопустимый, находящийся
на расстоянии, равном 1, от исходного
кодового набора, и на расстоянии, равном
2, от любого другого допустимого кодового
набора. Поэтому в коде с d_min= 3 можно
исправить любую одиночную ошибку или
обнаружить любую двойную ошибку. Если
d_min= 4, то можно
исправить любую одиночную ошибку и
обнаружить любую двойную или обнаружить
тройную ошибку.

Основное
свойство кода – возможность обнаруживать
и выделять местоположение ошибочных
разрядов. Когда местоположение ошибки
определено, то осуществляют замену
ошибочного разряда на его дополнение.

5.2.1. Основные принципы построения кодов Хэмминга с исправлением ошибок

К
каждому набору из m
информационных разрядов (сообщению)
присоединяются k
разрядов p₁,
p₂,
…p_k
проверки на чётность.
Каждому
из (m+k)
присваивается десятичное значение
позиции, начиная со значения 1 для
старшего разряда и кончая значением
(m+k)
для младшего разряда.
Производится
k
проверок на чётность числа единиц в
выбранных разрядах каждого кодового
набора. Результат каждой проверки на
чётность записывается как 1 или 0 в
зависимости от того, обнаружена ошибка
или нет.
По
результатам проверок строится двоичное
число c_k
_…
c₂c₁,
равное десятичному значению, присвоенному
местоположению ошибочного разряда,
если произошла ошибка, и нулю при её
отсутствии. Это число называется номером
позиции ошибочного разряда.

Число
разрядов k
должно быть достаточно большим для
указания положения любой из (m+k)
возможных одиночных ошибок. Так как
m+k+1-количество
возможных событий, 2^k
– максимальное количество кодовых
комбинаций, то k
должно удовлетворять неравенству 2^k
m+k+1.

Определим
максимальное значение m
для заданного количества k.Обозначим
количество разрядов в коде n=
m+k.

Таблица 15

n	1	2…3	4…7	8…15	16…31	32…63
m	0	0…1	1…4	4…11	11…26	26…57
k	1	2…2	3…3	4…4	5…5	6…6

Определим
теперь позиции, которые необходимо
проверить в каждой из k
проверок. Если в кодовой комбинации
ошибок нет, то контрольное число двоичное
c_k_…
c₂c₁содержит
только 0. Если в первом разряде контрольного
числа стоит 1, то в результате первой
проверки обнаружена ошибка.

Таблица 16

№ позиции возможной ошибки	Двоичный эквивалент
0	00000
1	00001
2	00010
3	00011
4	00100
5	00101
6	00110
7	00111
8	01000
9	01001

Окончание
таблицы 16

№ позиции возможной ошибки	Двоичный эквивалент
10	01010
11	01011
12	01100
13	01101
14	01110
15	01111
16	10000
17	10001
18	10010
…	…

Из
табл. 16 двоичных эквивалентов для номера
позиции возможной ошибки видно, что в
первую проверяемую группу разрядов
входят 1,3,5,7,9, 11,13,15, 17 и т.д., во вторую –
2,3,6,7,10,11,14,15,18 и т.д.

Таблица
17

Проверка	Проверяемые разряды
1	1,3,5,7,9, 11,13,15, 17 …
2	2,3,6,7,10,11,14,15,18 …
3	4,5,6,7, 12,13,14, 15 …
4	8,9,10,11, 12,13,14, 15 …
…	…

Разряды,
номера которых кратны степеням 2:
1,2,4,8,16…, встречаются в каждой проверяемой
группе один раз. Удобно использовать
эти разряды в качестве контрольных, а
остальные – информационных разрядов.

Пример.
Пусть исходное сообщение 00111. Количество
информационных разрядов m=5.
Количество контрольных разрядов k=4.
Длина кода Хэмминга равна 9. Построим
код Хэмминга для исходного сообщения.

Номер позиции	1	2	3	4	5	6	7	8	9
Исходное сообщение			0		0	1	1		1
1-я контрольная группа	0		0		0		1		1
2-я контрольная группа		0	0			1	1
3-я контрольная группа				0	0	1	1
4-я контрольная группа								1	1
Код Хэмминга	0	0	0	0	0	1	1	1	1

Код
Хэмминга для десятичных цифр в
двоично-десятичном коде 8421 приведен в
табл. 18.

Таблица
18

Десятичная цифра	p₁	p₂	m₁	p₃	m₂	m₃	m₄
0	0	0	0	0	0	0	0
1	1	1	0	1	0	0	1
2	0	1	0	1	0	1	0
3	1	0	0	0	0	1	1
4	1	0	0	1	1	0	0
5	0	1	0	0	1	0	1
6	1	1	0	0	1	1	0
7	0	0	0	1	1	1	1
8	1	1	1	0	0	0	0
9	0	0	1	1	0	0	1

Рассмотрим
способ выявления положения ошибки и её
исправления.

Пример.
Пусть передана последовательность
1000011. Из-за ошибки в третьем разряде
принято сообщение 1010011. Положение ошибки
можно определить, выполняя 3 проверки
на четность.

Номер позиции	1	2	3	4	5	6	7	c_i
Сообщение	1	0	1	0	0	1	1
1-я проверка на четность	1		1		0		1	1
2-я проверка на четность		0	1			1	1	1
3-я проверка на четность				0	0	1	1	0
Исправленное сообщение	1	0	0	0	0	1	1

Полученный
номер позиции c₃c₂c₁=
011, т.е. ошибка в третьем разряде.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

In coding theory, burst error-correcting codes employ methods of correcting burst errors, which are errors that occur in many consecutive bits rather than occurring in bits independently of each other.

Many codes have been designed to correct random errors. Sometimes, however, channels may introduce errors which are localized in a short interval. Such errors occur in a burst (called burst errors) because they occur in many consecutive bits. Examples of burst errors can be found extensively in storage mediums. These errors may be due to physical damage such as scratch on a disc or a stroke of lightning in case of wireless channels. They are not independent; they tend to be spatially concentrated. If one bit has an error, it is likely that the adjacent bits could also be corrupted. The methods used to correct random errors are inefficient to correct burst errors.

Definitions[edit]

A burst of length ℓ^[1]

Say a codeword is transmitted, and it is received as Then, the error vector is called a burst of length ell if the nonzero components of are confined to ell consecutive components. For example, is a burst of length

Although this definition is sufficient to describe what a burst error is, the majority of the tools developed for burst error correction rely on cyclic codes. This motivates our next definition.

A cyclic burst of length ℓ^[1]

An error vector is called a cyclic burst error of length ell if its nonzero components are confined to ell cyclically consecutive components. For example, the previously considered error vector , is a cyclic burst of length , since we consider the error starting at position and ending at position . Notice the indices are -based, that is, the first element is at position .

For the remainder of this article, we will use the term burst to refer to a cyclic burst, unless noted otherwise.

Burst description[edit]

It is often useful to have a compact definition of a burst error, that encompasses not only its length, but also the pattern, and location of such error. We define a burst description to be a tuple where is the pattern of the error (that is the string of symbols beginning with the first nonzero entry in the error pattern, and ending with the last nonzero symbol), and is the location, on the codeword, where the burst can be found.^[1]

For example, the burst description of the error pattern is . Notice that such description is not unique, because describes the same burst error. In general, if the number of nonzero components in is , then will have different burst descriptions each starting at a different nonzero entry of . To remedy the issues that arise by the ambiguity of burst descriptions with the theorem below, however before doing so we need a definition first.

Definition. The number of symbols in a given error pattern is denoted by

A corollary of the above theorem is that we cannot have two distinct burst descriptions for bursts of length ${displaystyle {tfrac {1}{2}}(n+1).}$

Cyclic codes for burst error correction[edit]

Cyclic codes are defined as follows: think of the symbols as elements in $mathbb {F} _{q}$ . Now, we can think of words as polynomials over ${displaystyle mathbb {F} _{q},}$ where the individual symbols of a word correspond to the different coefficients of the polynomial. To define a cyclic code, we pick a fixed polynomial, called generator polynomial. The codewords of this cyclic code are all the polynomials that are divisible by this generator polynomial.

Codewords are polynomials of degree . Suppose that the generator polynomial g(x) has degree . Polynomials of degree that are divisible by g(x) result from multiplying g(x) by polynomials of degree . We have ${displaystyle q^{n-r}}$ such polynomials. Each one of them corresponds to a codeword. Therefore, for cyclic codes.

Cyclic codes can detect all bursts of length up to . We will see later that the burst error detection ability of any (n,k) code is bounded from above by . Cyclic codes are considered optimal for burst error detection since they meet this upper bound:

Theorem (Cyclic burst correction capability) — Every cyclic code with generator polynomial of degree can detect all bursts of length

The above proof suggests a simple algorithm for burst error detection/correction in cyclic codes: given a transmitted word (i.e. a polynomial of degree ), compute the remainder of this word when divided by g(x) . If the remainder is zero (i.e. if the word is divisible by g(x) ), then it is a valid codeword. Otherwise, report an error. To correct this error, subtract this remainder from the transmitted word. The subtraction result is going to be divisible by g(x) (i.e. it is going to be a valid codeword).

By the upper bound on burst error detection (), we know that a cyclic code can not detect all bursts of length . However cyclic codes can indeed detect most bursts of length . The reason is that detection fails only when the burst is divisible by g(x) . Over binary alphabets, there exist ${displaystyle 2^{ell -2}}$ bursts of length ell . Out of those, only ${displaystyle 2^{ell -2-r}}$ are divisible by g(x) . Therefore, the detection failure probability is very small ( ${displaystyle 2^{-r}}$ ) assuming a uniform distribution over all bursts of length ell .

We now consider a fundamental theorem about cyclic codes that will aid in designing efficient burst-error correcting codes, by categorizing bursts into different cosets.

Burst error correction bounds[edit]

Upper bounds on burst error detection and correction[edit]

By upper bound, we mean a limit on our error detection ability that we can never go beyond. Suppose that we want to design an (n,k) code that can detect all burst errors of length A natural question to ask is: given and , what is the maximum ell that we can never achieve beyond? In other words, what is the upper bound on the length ell of bursts that we can detect using any (n,k) code? The following theorem provides an answer to this question.

Theorem (Burst error detection ability) — The burst error detection ability of any (n,k) code is

Now, we repeat the same question but for error correction: given and , what is the upper bound on the length ell of bursts that we can correct using any (n,k) code? The following theorem provides a preliminary answer to this question:

Theorem (Burst error correction ability) — The burst error correction ability of any (n,k) code satisfies ${displaystyle ell leqslant n-k-log _{q}(n-ell )+2}$

A stronger result is given by the Rieger bound:

Definition. A linear burst-error-correcting code achieving the above Rieger bound is called an optimal burst-error-correcting code.

Further bounds on burst error correction[edit]

There is more than one upper bound on the achievable code rate of linear block codes for multiple phased-burst correction (MPBC). One such bound is constrained to a maximum correctable cyclic burst length within every subblock, or equivalently a constraint on the minimum error free length or gap within every phased-burst. This bound, when reduced to the special case of a bound for single burst correction, is the Abramson bound (a corollary of the Hamming bound for burst-error correction) when the cyclic burst length is less than half the block length.^[3]

Theorem (Abramson’s bounds) — If ${displaystyle 1leqslant ell leqslant {tfrac {1}{2}}(n+1)}$ is a binary linear -burst error correcting code, its block-length must satisfy:

${displaystyle nleqslant 2^{n-k-ell +1}-1.}$

Proof

For a linear (n,k) code, there are $2^{k}$ codewords. By our previous result, we know that

${displaystyle 2^{k}leqslant {frac {2^{n}}{n2^{ell -1}+1}}.}$

Isolating , we get ${displaystyle nleqslant 2^{n-k-ell +1}-2^{-ell +1}}$ . Since and must be an integer, we have ${displaystyle nleqslant 2^{n-k-ell +1}-1}$ .

Remark. is called the redundancy of the code and in an alternative formulation for the Abramson’s bounds is ${displaystyle rgeqslant lceil log _{2}(n+1)rceil +ell -1.}$

Fire codes^[3]^[4]^[5][edit]

While cyclic codes in general are powerful tools for detecting burst errors, we now consider a family of binary cyclic codes named Fire Codes, which possess good single burst error correction capabilities. By single burst, say of length ell , we mean that all errors that a received codeword possess lie within a fixed span of ell digits.

Let p(x) be an irreducible polynomial of degree over $mathbb {F} _{2}$ , and let be the period of p(x) . The period of p(x) , and indeed of any polynomial, is defined to be the least positive integer such that ${displaystyle p(x)|x^{r}-1.}$ Let ell be a positive integer satisfying and not divisible by , where is the period of p(x) . Define the Fire Code by the following generator polynomial:

${displaystyle g(x)=left(x^{2ell -1}+1right)p(x).}$

We will show that is an ell -burst-error correcting code.

Lemma 1 — ${displaystyle gcd left(p(x),x^{2ell -1}+1right)=1.}$

Lemma 2 — If p(x) is a polynomial of period , then ${displaystyle p(x)|x^{k}-1}$ if and only if

Proof

If , then ${displaystyle x^{k}-1=(x^{p}-1)(1+x^{p}+x^{2p}+dots +x^{k/p})}$ . Thus, ${displaystyle p(x)|x^{k}-1.}$

Now suppose ${displaystyle p(x)|x^{k}-1}$ . Then, . We show that is divisible by by induction on . The base case follows. Therefore, assume . We know that p(x) divides both (since it has period )

${displaystyle x^{p}-1=(x-1)left(1+x+dots +x^{p-1}right)quad {text{and}}quad x^{k}-1=(x-1)left(1+x+dots +x^{k-1}right).}$

But p(x) is irreducible, therefore it must divide both ${displaystyle (1+x+dots +x^{p-1})}$ and ${displaystyle (1+x+dots +x^{k-1})}$ ; thus, it also divides the difference of the last two polynomials, ${displaystyle x^{p}(1+x+dots +x^{p-k-1})}$ . Then, it follows that p(x) divides ${displaystyle (1+x+cdots +x^{p-k-1})}$ . Finally, it also divides: ${displaystyle x^{k-p}-1=(x-1)(1+x+dots +x^{p-k-1})}$ . By the induction hypothesis, , then .

A corollary to Lemma 2 is that since ${displaystyle p(x)=x^{p}-1}$ has period , then p(x) divides $x^{k}-1$ if and only if .

Theorem — The Fire Code is ell -burst error correcting^[4]^[5]

If we can show that all bursts of length ell or less occur in different cosets, we can use them as coset leaders that form correctable error patterns. The reason is simple: we know that each coset has a unique syndrome decoding associated with it, and if all bursts of different lengths occur in different cosets, then all have unique syndromes, facilitating error correction.

Proof of Theorem[edit]

Let ${displaystyle x^{i}a(x)}$ and ${displaystyle x^{j}b(x)}$ be polynomials with degrees ${displaystyle ell _{1}-1}$ and ${displaystyle ell _{2}-1}$ , representing bursts of length $ell _{1}$ and $ell _{2}$ respectively with ${displaystyle ell _{1},ell _{2}leqslant ell .}$ The integers i,j represent the starting positions of the bursts, and are less than the block length of the code. For contradiction sake, assume that ${displaystyle x^{i}a(x)}$ and ${displaystyle x^{j}b(x)}$ are in the same coset. Then, ${displaystyle v(x)=x^{i}a(x)+x^{j}b(x)}$ is a valid codeword (since both terms are in the same coset). Without loss of generality, pick . By the division theorem we can write: for integers and . We rewrite the polynomial v(x) as follows:

${displaystyle v(x)=x^{i}a(x)+x^{i+g(2ell -1)+r}=x^{i}a(x)+x^{i+g(2ell -1)+r}+2x^{i+r}b(x)=x^{i}left(a(x)+x^{b}b(x)right)+x^{i+r}b(x)left(x^{g(2ell -1)}+1right)}$

Notice that at the second manipulation, we introduced the term ${displaystyle 2x^{i+r}b(x)}$ . We are allowed to do so, since Fire Codes operate on $mathbb {F} _{2}$ . By our assumption, v(x) is a valid codeword, and thus, must be a multiple of g(x) . As mentioned earlier, since the factors of g(x) are relatively prime, v(x) has to be divisible by ${displaystyle x^{2ell -1}+1}$ . Looking closely at the last expression derived for v(x) we notice that ${displaystyle x^{g(2ell -1)}+1}$ is divisible by ${displaystyle x^{2ell -1}+1}$ (by the corollary of Lemma 2). Therefore, ${displaystyle a(x)+x^{b}b(x)}$ is either divisible by ${displaystyle x^{2ell -1}+1}$ or is . Applying the division theorem again, we see that there exists a polynomial d(x) with degree delta such that:

${displaystyle a(x)+x^{b}b(x)=d(x)(x^{2ell -1}+1)}$

Then we may write:

${displaystyle {begin{aligned}delta +2ell -1&=deg left(d(x)left(x^{2ell -1}+1right)right)\&=deg left(a(x)+x^{b}b(x)right)\&=deg left(x^{b}b(x)right)&&deg(a(x))=ell _{1}-1<2ell -1\&=b+ell _{2}-1end{aligned}}}$

Equating the degree of both sides, gives us ${displaystyle b=2ell -ell _{2}+delta .}$ Since ${displaystyle ell _{1},ell _{2}leqslant ell }$ we can conclude which implies and . Notice that in the expansion:

${displaystyle a(x)+x^{b}b(x)=1+a_{1}x+a_{2}x^{2}+dots +x^{ell _{1}-1}+x^{b}left(1+b_{1}x+b_{2}x^{2}+dots +x^{ell _{2}-1}right).}$

The term ${displaystyle x^{b}}$ appears, but since , the resulting expression ${displaystyle d(x)(x^{2ell -1}+1)}$ does not contain ${displaystyle x^{b}}$ , therefore and subsequently ${displaystyle a(x)+x^{b}b(x)=0.}$ This requires that b=0 , and . We can further revise our division of j-i by to reflect that is . Substituting back into v(x) gives us,

${displaystyle v(x)=x^{i}b(x)left(x^{j-1}+1right).}$

Since ${displaystyle deg(b(x))=ell _{2}-1<ell }$ , we have . But p(x) is irreducible, therefore b(x) and p(x) must be relatively prime. Since v(x) is a codeword, ${displaystyle x^{j-1}+1}$ must be divisible by p(x) , as it cannot be divisible by ${displaystyle x^{2ell -1}+1}$ . Therefore, j-i must be a multiple of . But it must also be a multiple of , which implies it must be a multiple of but that is precisely the block-length of the code. Therefore, j-i cannot be a multiple of since they are both less than . Thus, our assumption of v(x) being a codeword is incorrect, and therefore ${displaystyle x^{i}a(x)}$ and ${displaystyle x^{j}b(x)}$ are in different cosets, with unique syndromes, and therefore correctable.

Example: 5-burst error correcting fire code[edit]

With the theory presented in the above section, consider the construction of a -burst error correcting Fire Code. Remember that to construct a Fire Code, we need an irreducible polynomial p(x) , an integer ell , representing the burst error correction capability of our code, and we need to satisfy the property that
is not divisible by the period of p(x) . With these requirements in mind, consider the irreducible polynomial ${displaystyle p(x)=1+x^{2}+x^{5}}$ , and let . Since p(x) is a primitive polynomial, its period is ${displaystyle 2^{5}-1=31}$ . We confirm that is not divisible by . Thus,

${displaystyle g(x)=(x^{9}+1)left(1+x^{2}+x^{5}right)=1+x^{2}+x^{5}+x^{9}+x^{11}+x^{14}}$

is a Fire Code generator. We can calculate the block-length of the code by evaluating the least common multiple of and . In other words, . Thus, the Fire Code above is a cyclic code capable of correcting any burst of length or less.

Binary Reed–Solomon codes[edit]

Certain families of codes, such as Reed–Solomon, operate on alphabet sizes larger than binary. This property awards such codes powerful burst error correction capabilities. Consider a code operating on $mathbb {F} _{2^{m}}$ . Each symbol of the alphabet can be represented by bits. If is an (n,k) Reed–Solomon code over $mathbb {F} _{2^{m}}$ , we can think of as an ${displaystyle [mn,mk]_{2}}$ code over ${displaystyle mathbb {F} _{2}}$ .

The reason such codes are powerful for burst error correction is that each symbol is represented by bits, and in general, it is irrelevant how many of those bits are erroneous; whether a single bit, or all of the bits contain errors, from a decoding perspective it is still a single symbol error. In other words, since burst errors tend to occur in clusters, there is a strong possibility of several binary errors contributing to a single symbol error.

Notice that a burst of errors can affect at most symbols, and a burst of can affect at most symbols. Then, a burst of can affect at most symbols; this implies that a -symbols-error correcting code can correct a burst of length at most .

In general, a -error correcting Reed–Solomon code over $mathbb {F} _{2^{m}}$ can correct any combination of

${displaystyle {frac {t}{1+lfloor (l+m-2)/mrfloor }}}$

or fewer bursts of length , on top of being able to correct -random worst case errors.

An example of a binary RS code[edit]

Let be a RS code over $mathbb{F}_{2^8}$ . This code was employed by NASA in their Cassini-Huygens spacecraft.^[6] It is capable of correcting symbol errors. We now construct a Binary RS Code from . Each symbol will be written using ${displaystyle lceil log _{2}(255)rceil =8}$ bits. Therefore, the Binary RS code will have ${displaystyle [2040,1784,33]_{2}}$ as its parameters. It is capable of correcting any single burst of length .

Interleaved codes[edit]

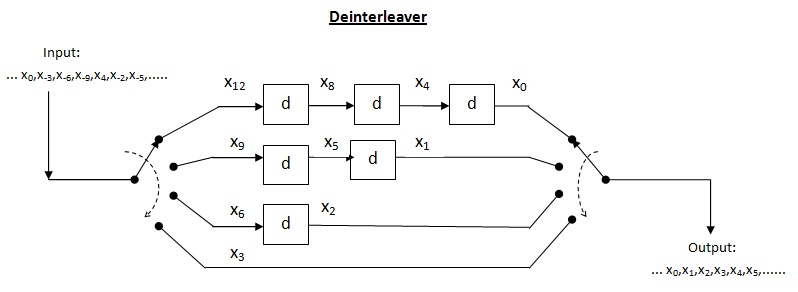
Interleaving is used to convert convolutional codes from random error correctors to burst error correctors. The basic idea behind the use of interleaved codes is to jumble symbols at the transmitter. This leads to randomization of bursts of received errors which are closely located and we can then apply the analysis for random channel. Thus, the main function performed by the interleaver at transmitter is to alter the input symbol sequence. At the receiver, the deinterleaver will alter the received sequence to get back the original unaltered sequence at the transmitter.

Burst error correcting capacity of interleaver[edit]

Illustration of row- and column-major order

Block interleaver[edit]

The figure below shows a 4 by 3 interleaver.

An example of a block interleaver

The above interleaver is called as a block interleaver. Here, the input symbols are written sequentially in the rows and the output symbols are obtained by reading the columns sequentially. Thus, this is in the form of array. Generally, is length of the codeword.

Capacity of block interleaver: For an block interleaver and burst of length the upper limit on number of errors is ${displaystyle {tfrac {ell }{M}}.}$ This is obvious from the fact that we are reading the output column wise and the number of rows is . By the theorem above for error correction capacity up to the maximum burst length allowed is For burst length of , the decoder may fail.

Efficiency of block interleaver (): It is found by taking ratio of burst length where decoder may fail to the interleaver memory. Thus, we can formulate gamma as

${displaystyle gamma ={frac {Mt+1}{MN}}approx {frac {t}{N}}.}$

Drawbacks of block interleaver : As it is clear from the figure, the columns are read sequentially, the receiver can interpret single row only after it receives complete message and not before that. Also, the receiver requires a considerable amount of memory in order to store the received symbols and has to store the complete message. Thus, these factors give rise to two drawbacks, one is the latency and other is the storage (fairly large amount of memory). These drawbacks can be avoided by using the convolutional interleaver described below.

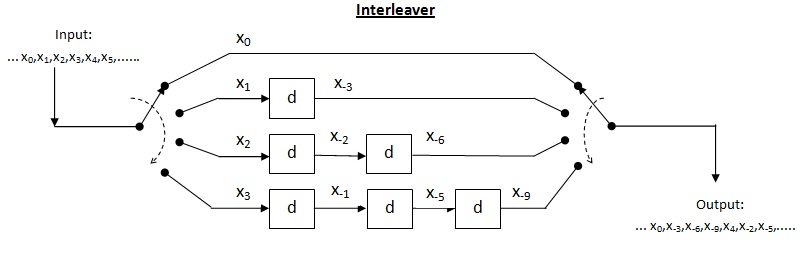
Convolutional interleaver[edit]

Cross interleaver is a kind of multiplexer-demultiplexer system. In this system, delay lines are used to progressively increase length. Delay line is basically an electronic circuit used to delay the signal by certain time duration. Let be the number of delay lines and be the number of symbols introduced by each delay line. Thus, the separation between consecutive inputs = symbols. Let the length of codeword Thus, each symbol in the input codeword will be on distinct delay line. Let a burst error of length ell occur. Since the separation between consecutive symbols is the number of errors that the deinterleaved output may contain is ${displaystyle {tfrac {ell }{nd+1}}.}$ By the theorem above, for error correction capacity up to , maximum burst length allowed is For burst length of decoder may fail.

An example of a convolutional interleaver

An example of a deinterleaver

Efficiency of cross interleaver (): It is found by taking the ratio of burst length where decoder may fail to the interleaver memory. In this case, the memory of interleaver can be calculated as

${displaystyle (0+1+2+3+cdots +(n-1))d={frac {n(n-1)}{2}}d.}$

Thus, we can formulate gamma as follows:

${displaystyle gamma ={frac {(nd+1)(t-1)+1}{{frac {n(n-1)}{2}}d}}.}$

Performance of cross interleaver : As shown in the above interleaver figure, the output is nothing but the diagonal symbols generated at the end of each delay line. In this case, when the input multiplexer switch completes around half switching, we can read first row at the receiver. Thus, we need to store maximum of around half message at receiver in order to read first row. This drastically brings down the storage requirement by half. Since just half message is now required to read first row, the latency is also reduced by half which is good improvement over the block interleaver. Thus, the total interleaver memory is split between transmitter and receiver.

Applications[edit]

Compact disc[edit]

Without error correcting codes, digital audio would not be technically feasible.^[7] The Reed–Solomon codes can correct a corrupted symbol with a single bit error just as easily as it can correct a symbol with all bits wrong. This makes the RS codes particularly suitable for correcting burst errors.^[5] By far, the most common application of RS codes is in compact discs. In addition to basic error correction provided by RS codes, protection against burst errors due to scratches on the disc is provided by a cross interleaver.^[3]

Current compact disc digital audio system was developed by N. V. Philips of The Netherlands and Sony Corporation of Japan (agreement signed in 1979).

A compact disc comprises a 120 mm aluminized disc coated with a clear plastic coating, with spiral track, approximately 5 km in length, which is optically scanned by a laser of wavelength ~0.8 μm, at a constant speed of ~1.25 m/s. For achieving this constant speed, rotation of the disc is varied from ~8 rev/s while scanning at the inner portion of the track to ~3.5 rev/s at the outer portion. Pits and lands are the depressions (0.12 μm deep) and flat segments constituting the binary data along the track (0.6 μm width).^[8]

The CD process can be abstracted as a sequence of the following sub-processes:

Channel encoding of source of signals
Mechanical sub-processes of preparing a master disc, producing user discs and sensing the signals embedded on user discs while playing – the channel
Decoding the signals sensed from user discs

The process is subject to both burst errors and random errors.^[7] Burst errors include those due to disc material (defects of aluminum reflecting film, poor reflective index of transparent disc material), disc production (faults during disc forming and disc cutting etc.), disc handling (scratches – generally thin, radial and orthogonal to direction of recording) and variations in play-back mechanism. Random errors include those due to jitter of reconstructed signal wave and interference in signal. CIRC (Cross-Interleaved Reed–Solomon code) is the basis for error detection and correction in the CD process. It corrects error bursts up to 3,500 bits in sequence (2.4 mm in length as seen on CD surface) and compensates for error bursts up to 12,000 bits (8.5 mm) that may be caused by minor scratches.

Encoding: Sound-waves are sampled and converted to digital form by an A/D converter. The sound wave is sampled for amplitude (at 44.1 kHz or 44,100 pairs, one each for the left and right channels of the stereo sound). The amplitude at an instance is assigned a binary string of length 16. Thus, each sample produces two binary vectors from ${displaystyle mathbb {F} _{2}^{16}}$ or 4 ${displaystyle mathbb {F} _{2}^{8}}$ bytes of data. Every second of sound recorded results in 44,100 × 32 = 1,411,200 bits (176,400 bytes) of data.^[5] The 1.41 Mbit/s sampled data stream passes through the error correction system eventually getting converted to a stream of 1.88 Mbit/s.

Input for the encoder consists of input frames each of 24 8-bit symbols (12 16-bit samples from the A/D converter, 6 each from left and right data (sound) sources). A frame can be represented by ${displaystyle L_{1}R_{1}L_{2}R_{2}ldots L_{6}R_{6}}$ where ${displaystyle L_{i}}$ and $R_{i}$ are bytes from the left and right channels from the $i^{th}$ sample of the frame.

Initially, the bytes are permuted to form new frames represented by ${displaystyle L_{1}L_{3}L_{5}R_{1}R_{3}R_{5}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}}$ where ${displaystyle L_{i},R_{i}}$ represent -th left and right samples from the frame after 2 intervening frames.

Next, these 24 message symbols are encoded using C2 (28,24,5) Reed–Solomon code which is a shortened RS code over ${displaystyle mathbb {F} _{256}}$ . This is two-error-correcting, being of minimum distance 5. This adds 4 bytes of redundancy, ${displaystyle P_{1}P_{2}}$ forming a new frame: ${displaystyle L_{1}L_{3}L_{5}R_{1}R_{3}R_{5}P_{1}P_{2}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}}$ . The resulting 28-symbol codeword is passed through a (28.4) cross interleaver leading to 28 interleaved symbols. These are then passed through C1 (32,28,5) RS code, resulting in codewords of 32 coded output symbols. Further regrouping of odd numbered symbols of a codeword with even numbered symbols of the next codeword is done to break up any short bursts that may still be present after the above 4-frame delay interleaving. Thus, for every 24 input symbols there will be 32 output symbols giving . Finally one byte of control and display information is added.^[5] Each of the 33 bytes is then converted to 17 bits through EFM (eight to fourteen modulation) and addition of 3 merge bits. Therefore, the frame of six samples results in 33 bytes × 17 bits (561 bits) to which are added 24 synchronization bits and 3 merging bits yielding a total of 588 bits.

Decoding: The CD player (CIRC decoder) receives the 32 output symbol data stream. This stream passes through the decoder D1 first. It is up to individual designers of CD systems to decide on decoding methods and optimize their product performance. Being of minimum distance 5 The D1, D2 decoders can each correct a combination of errors and erasures such that .^[5] In most decoding solutions, D1 is designed to correct single error. And in case of more than 1 error, this decoder outputs 28 erasures. The deinterleaver at the succeeding stage distributes these erasures across 28 D2 codewords. Again in most solutions, D2 is set to deal with erasures only (a simpler and less expensive solution). If more than 4 erasures were to be encountered, 24 erasures are output by D2. Thereafter, an error concealment system attempts to interpolate (from neighboring symbols) in case of uncorrectable symbols, failing which sounds corresponding to such erroneous symbols get muted.

Performance of CIRC:^[7] CIRC conceals long bust errors by simple linear interpolation. 2.5 mm of track length (4000 bits) is the maximum completely correctable burst length. 7.7 mm track length (12,300 bits) is the maximum burst length that can be interpolated. Sample interpolation rate is one every 10 hours at Bit Error Rate (BER) ${displaystyle =10^{-4}}$ and 1000 samples per minute at BER = $10^{-3}$ Undetectable error samples (clicks): less than one every 750 hours at BER = $10^{-3}$ and negligible at BER = $10^{-4}$ .

References[edit]

^ ^a ^b ^c ^d Coding Bounds for Multiple Phased-Burst Correction and Single Burst Correction Codes
^ The Theory of Information and Coding: Student Edition, by R. J. McEliece
^ ^a ^b ^c Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print
^ ^a ^b Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print
^ ^a ^b ^c ^d ^e ^f Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print
^ quest.arc.nasa.gov https://web.archive.org/web/20120627022807/http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt. Archived from the original on 2012-06-27.
^ ^a ^b ^c Algebraic Error Control Codes (Autumn 2012) – Handouts from Stanford University
^ McEliece, Robert J. The Theory of Information and Coding: A Mathematical Framework for Communication. Reading, MA: Addison-Wesley Pub., Advanced Book Program, 1977. Print

Источник

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

где n – количество символов закодированного сообщения (результата кодирования);
m – количество проверочных символов, добавляемых при кодировании;
k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

1 1 0 0 0 1 0 0 | 1

Здесь R=8/9=0,88

И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.

Классификация помехоустойчивых кодов

Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.

По используемому алфавиту:

Двоичные. Оперируют битами.
Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.

Блочные коды делятся на

Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

n — количество символов на входе.
k — количество символов на выходе.
t — кратность исправляемых ошибок.
Отношение k/n — скорость кода.
G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:

Достоверность vs полоса пропускания.
Мощность vs полоса пропускания.
Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

Источник

Корректирующие коды «на пальцах»

Каналы с ошибкой

Код с утроением

Расстояния между кодами

Окрестности

Сколько ошибок может исправить код?

Интерлюдия: поле GF(2)

Проверяем корректность

Кодирование

Ошибка по синдрому

Что же дальше?

5.2.1. Основные принципы построения кодов Хэмминга с исправлением ошибок

Definitions[edit]

Burst description[edit]

Cyclic codes for burst error correction[edit]

Burst error correction bounds[edit]

Upper bounds on burst error detection and correction[edit]

Further bounds on burst error correction[edit]

Fire codes[3][4][5][edit]

Proof of Theorem[edit]

Example: 5-burst error correcting fire code[edit]

Binary Reed–Solomon codes[edit]

An example of a binary RS code[edit]

Interleaved codes[edit]

Burst error correcting capacity of interleaver[edit]

Block interleaver[edit]

Convolutional interleaver[edit]

Applications[edit]

Compact disc[edit]

See also[edit]

References[edit]

Исправление ошибок в помехоустойчивом кодировании

Параметры помехоустойчивого кодирования

Контроль чётности

Классификация помехоустойчивых кодов

Код Хэмминга

Декодирование кода Хэмминга

Расстояние Хэмминга

Помехоустойчивые коды

Компромиссы при использовании помехоустойчивых кодов

Необходимость чередования (перемежения)

Возможно, вам также будет интересно:

Fire codes^[3]^[4]^[5][edit]