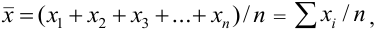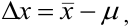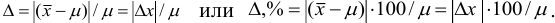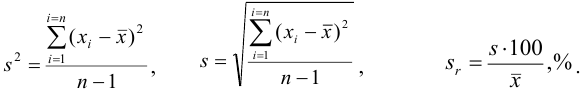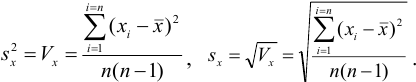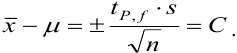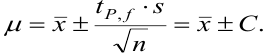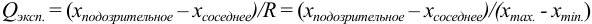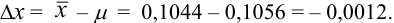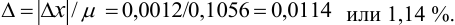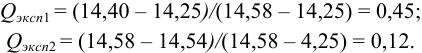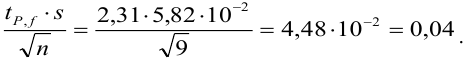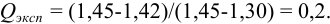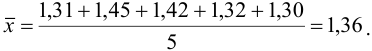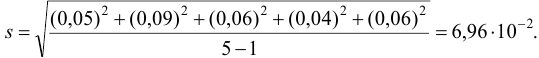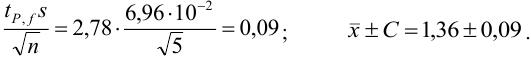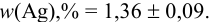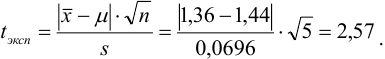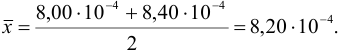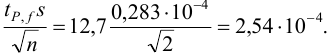Для
выявления ошибок и их численной оценки
(особенно при разработке новых
аналитических методик) количественный
анализ повторяют несколько раз, т.е.
проводят параллельные
определения. Под
параллельными определениями понимают
получение нескольких результатов
единичных определений для одной и той
же пробы в одинаковых условиях.
Пусть
μ
— истинное
значение определяемой величины; Х1,
Х2,
…, Хi,
…, …, Хn
— измеренные
(единичные) значения определяемой
величины — результаты единичных
определений; п- общее
число единичных определений.
Под
единичным определением понимают
однократное проведение всей
последовательности операций,
предусмотренных методикой анализа.
Результат единичного определения- это
значение содержания определяемого
компонента, найденное при единичном
определении.
Иногда
(часто) вместо истинного значения
определяемой величины μ
используют действительное
значение содержания а
(или просто
действительное
значение а),
под которым
подразумевают экспериментально
полученное или расчетное значение
определяемого содержания, настолько
близкое к истинному, что для данной цели
может быть использовано вместо него.
Тогда величина

есть
среднее
арифметическое (среднее) из
результатов единичных определений.
Считается, что х–
— наиболее вероятное значение определяемой
величины, более вероятное, чем каждое
отдельное значение Хi.
Под
правильностью
результата
анализа понимают качество анализа,
отражающее близость к нулю разности
между средним арифметическим и истинным
μ
(или действительным а)
значением определяемой величины:

Другими
словами, правильность результата анализа
отражает близость полученного среднего
значения х–
к истинному (или действительному)
значению определяемой величины.
Воспроизводимость
результата
анализа характеризует степень близости
результатов единичных определений Хi,
друг к другу.
Правильность
и воспроизводимость результата анализа
зависят от различного типа ошибок.
1.4.2. Классификация ошибок количественного анализа.
Ошибки
количественного анализа условно
подразделяют
на систематические,
случайные и грубые.
Грубые
ошибки,
обусловленные
несоблюдением методики анализа, очевидны.
Они устраняются при повторном проведении
анализа с соблюдением всех требуемых
условий, предусмотренных методикой
анализа.
а)
Систематическая ошибка
Различают:
систематическую
ошибку и
процентную
систематическую ошибку.
Систематическая
ошибка результата
анализа Δ0
— это статистически значимая разность
между средним х–
и действительным а
(или истинным
μ)
значениями содержания компонента:

Систематическая
ошибка результата анализа может быть
больше нуля, меньше нуля или равна нулю.
Процентная
систематическая ошибка (относительная
величина систематической ошибки) —
это систематическая ошибка, выраженная
в процентах от действительного значения
а
(или истинного
значения μ)
определяемой величины:
δ
= (х–
– а)∙100%
/ а
или δ = (х–
– μ)•100% / μ (1.3)
Для
относительной величины систематической
ошибки вместо символа 5 используют
также обозначение Δ0
%.
Систематическая
ошибка характеризует правильность
результатов анализа; поэтому правильность
анализа можно определить так же, как
качество анализа, отражающее близость
к нулю систематической ошибки.
Систематические
ошибки обусловлены либо постоянно
действующими причинами (и поэтому они
повторяются при многократном проведении
анализа), либо изменяются по постоянно
действующему закону, который можно
учесть.
Так,
например, процентная систематическая
ошибка (Δс/с)•100% фотометрических
определений (с
— концентрация,
Δс — систематическая ошибка определения
концентрации фотометрическим методом)
минимальна в интервале изменений
оптической плотности А
от А
≈ 0,2 до А
≈ 0,8 и
составляет (Δс/с)•100% < 0,4%.
Источники
систематических ошибок. Невозможно
с исчерпывающей полнотой перечислить
все источники систематических ошибок.
Основными являются следующие.
Методические
— обусловлены
особенностями методики анализа. Например,
аналитическая реакция прошла не до
конца; имеются потери осадка вследствие
его частичной растворимости в растворе
или при его промывании; наблюдается
соосаждение примесей с осадком, вследствие
чего масса осадка возрастает, и т.д.
Инструментальные
— обусловлены
несовершенством используемых приборов
и оборудования. Так, например,
систематическая ошибка взвешивания на
лабораторных аналитических весах
составляет ±0,0002 г. Систематическая
ошибка в титриметрических методах
анализа вносится вследствие неточности
калибровки бюреток, пипеток, мерных
колб, цилиндров, мензурок и т.д.
Индивидуальные
— обусловлены
субъективными качествами аналитика.
Так, например, дальтонизм может влиять
на определение конечной точки титрования
при визуальной фиксации изменения
окраски индикатора.
В
конечном итоге правильность результатов
анализа определяется наличием или
отсутствием именно систематических
ошибок.
Существуют способы
выявления систематических ошибок.
а)
Использование стандартных, образцов.
Общий состав
стандартного образца должен быть близким
к составу анализируемой пробы, а
содержание определяемого компонента
в стандартном образце должно быть точно
известно.
Анализ
стандартного образца — наиболее надежный
способ выявления наличия или отсутствия
систематической ошибки и оценки
правильности результата анализа.
б) Анализ
исследуемого объекта другими методами.
Исследуемый
объект анализируют методом или методами,
которые не дают систематической ошибки
(метрологически аттестованы), и сравнивают
результаты анализа с данными, полученными
при анализе того же объекта с использованием
оцениваемой методики или не аттестованного
оборудования. Сравнение позволяет
охарактеризовать правильность оцениваемой
методики анализа.
в)
Метод добавок или метод удвоения —
используют при отсутствии стандартных
образцов и метрологически аттестованной
методики (метода) анализа.
Анализируют
образец, используя оцениваемую методику.
Затем удваивают массу анализируемой
пробы или увеличивают (уменьшают) массу
в иное число раз, снова находят содержание
определяемого компонента в уже новой
пробе и сравнивают результаты анализов.
Должна выполняться определенная
закономерность (например, пропорциональность).
б)
Случайные ошибки.
Случайные
ошибки показывают отличие результатов
параллельных определений друг от друга
и фактически характеризуют воспроизводимость
анализа. Причины
случайных ошибок однозначно указать
невозможно. При многократном повторении
анализа они или не воспроизводятся, или
имеют разные численные значения и даже
разные знаки.
Случайные
ошибки можно оценить методами
математической статистики, если
выявлены и устранены систематические
ошибки (или систематические ошибки
меньше случайных).
ЭТАПЫ
КОЛИЧЕСТВЕННОГО ХИМИЧЕСКОГО АНАЛИЗА
Наука
об измерениях, методах и средствах
обеспечения их единства
и способах достижения требуемой точности
называется метрологией.
Количественный
химический анализ, целью которого
является
определение содержания веществ в разных
объектах, может
рассматриваться как измерительная
процедура, характеризующаяся
рядом специфических особенностей.
Количественный
химический анализ, прежде всего, является
многостадийным процессом, включающим
ряд этапов и стадий. При выполнении
химического анализа с помощью любого
метода можно выделить следующие
основные этапы:
— постановка
аналитической задачи;
— выбор метода
анализа;
— выполнение
анализа;
— оценка качества
анализа;
— принятие решений
по результатам анализа.
При
постановке аналитической задачи
необходимо дать характеристику объекта
анализа, указать химическую формулу
определяемого
компонента, возможный интервал его
содержаний, требуемую
точность и продолжительность анализа.
Выбор
метода анализа определяется поставленной
аналитической
задачей и техническими возможностями
аналитической лаборатории.
Этап,
связанный непосредственно с проведением
химического
анализа, наиболее трудоемок и включает
ряд стадий, представленных на рис. 5.2.
Методика
анализа включает
подробное описание последовательности
и условий проведения всех стадий анализа.
Точное следование
методике анализа позволяет выполнить
анализ с минимальными
погрешностями на каждой стадии и получить
правильный
результат анализа.
Первая
стадия химического анализа — отбор
средней
(представительной)
пробы. Это
небольшая часть анализируемого объекта,
средний
состав и свойства которой должны быть
идентичны во всех
отношениях среднему составу и свойствам
объекта анализа. Содержание
определяемого компонента в анализируемой
пробе должно
отражать среднее содержание этого
компонента во всем исследуемом
объекте, т. е. анализируемая проба должна
быть представительной.
Погрешность в отборе пробы часто
определяет общую
погрешность химического анализа. Не
оценив погрешность на
этой стадии, нельзя говорить о правильности
определения компонента
в анализируемом объекте.
Подготовка
пробы к анализу включает ряд сложных
операций, например, такие как высушивание
пробы, разложение (вскрытие)
пробы,
устранение влияния мешающих компонентов.
В зависимости
от цели анализа, природы объекта и
выбранного метода могут быть использованы
разные модификации и комбинации этих
операций.
В правильном проведении химического
анализа роль подготовки
пробы настолько велика, что химик-аналитик
должен каждый
раз оценивать необходимость включения
операций пробоподготовки
в методику анализа, их влияние на общую
погрешность анализа.
После
отбора и подготовки пробы наступают
стадии химического
анализа, на которых определяют количество
компонента. С
этой целью измеряют аналитический
сигнал. В
большинстве методов им является среднее
из измерений физической величины на
заключительной стадии анализа,
функционально связанной с содержанием
определяемого компонента. Это
может быть сила тока, ЭДС системы,
оптическая плотность, интенсивность
излучения и т.д. В отдельных методах
анализа возможно непосредственное
определение содержания. Например, в
гравиметрическом методе иногда прямо
измеряют массу определяемого компонента.
При
определении количества компонента
измеряют величину аналитического
сигнала. Затем рассчитывают содержание
компонента с использованием функциональной
зависимости аналитического
сигнала от содержания: у =
f(с),
которая устанавливается расчетным или
опытным путем и может быть представлена
в виде формулы, таблицы или графика.
Содержание может быть выражено абсолютным
количеством определяемого компонента
в молях, в единицах массы или через
соответствующие концентрации.
При
измерении аналитического сигнала
учитывают наличие полезного аналитического
сигнала, являющегося функцией содержания
определяемого компонента, и аналитического
сигнала фона, обусловленного
примесями определяемого компонента и
мешающими компонентами в растворах,
растворителях и матрице образца, а также
«шумами» в
измерительных приборах, усилителях
и другой аппаратуре. Эти шумы не имеют
отношения к определяемому компоненту,
но накладываются на его собственный
аналитический сигнал. Задача аналитика
состоит в том, чтобы максимально снизить
величину аналитического сигнала фона
и, главное, сделать минимальными его
колебания.
Обычно
аналитический сигнал фона учитывают в
контрольном
(холостом) опыте, когда
через все стадии химического анализа
проводится проба, не содержащая
определяемого компонента. Полезным при
этом будет аналитический сигнал, равный
разности измеренного сигнала и
аналитического сигнала фона.
На
основании существующей зависимости
между аналитическим сигналом и содержанием
находят концентрацию определяемого
компонента. Обычно при этом используют
методы
градуированного графика, стандартов
или
добавок. Описанные
в литературе другие способы определения
содержания компонента, как правило,
являются модификацией этих трех методов.
Наиболее
распространен метод
градуировочного графика: в
координатах (аналитический сигнал –
содержание компонента) строят график
с использованием образцов сравнения с
разными и точно известными уровнями
содержания компонента (концентрация
С).
Затем, измерив
величину аналитического сигнала в
пробе, находят содержание определяемого
компонента по градуировочному графику
(рис. 5.3).
В
методе
стандартов измеряют
аналитический сигнал в образце
сравнения (стандартном образце) с
известным содержанием компонента и в
анализируемой пробе: Уст
= sСст
и ух
= sСХ,
где s-коэффициент
пропорциональности.
Если
определенное в идентичных условиях
значение s
заранее известно, то можно провести
расчет по формуле Сх
= Ух/S.
Обычно же используют соотношение Уст/УХ
= Сст/СХ,
откуда
Иногда
работают с двумя стандартными образцами,
в которых содержание компонента
отличается от предполагаемого содержания
в анализируемой пробе в одном случае в
меньшую, в другом — в большую сторону.
Этот вариант метода стандартов называют
методом
ограничивающих растворов.
Содержание определяемого компонента
рассчитывают по формуле

Если
при определении малых количеств
компонента нужно учесть
влияние матрицы образца на величину
аналитического сигнала,
то часто используют
методы добавок — расчетный
или графический.
При
определении содержания расчетным
методом берут
две аликвоты
раствора анализируемой пробы. В одну
из них вводят добавку
определяемого компонента известного
содержания. В обеих
пробах измеряют аналитический сигнал
— ух
и
ух+доб—
Неизвестную
концентрацию определяемого компонента
рассчитывают
по формуле
где
Vдоб
и Сдоб
— объем и концентрация добавленного
раствора определяемого компонента; V
— аликвота
анализируемой пробы.
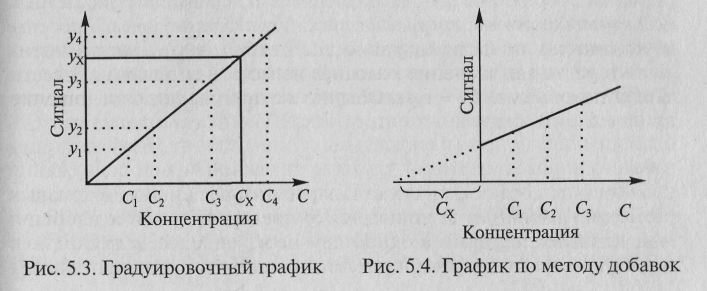
При
определении содержания компонента
графическим
методом
берут
п
аликвот
анализируемой пробы: 1, 2, 3, …, п.
Во
2-ю, …, п-ю
аликвоты
вводят известные, возрастающие, количества
определяемого
компонента. Во всех аликвотах измеряют
аналитический сигнал
и строят график в координатах аналитический
сигнал -содержание
определяемого компонента, приняв за
условный нуль содержание
определяемого компонента в аликвоте
без добавки (аликвота 1). Экстраполяция
полученной прямой до пересечения с
осью абсцисс дает отрезок слева от
условного нуля координат, величина
которого в выбранном масштабе и единицах
измерения соответствует
Сх
определяемого компонента (рис. 5.4).
Метод
стандартов и метод добавок применимы
для линейной градуировочной функции.
Метод градуировочного графика допускает
использование как линейной, так и
нелинейной функций аналитический
сигнал—содержание. В последнем случае
требуется большее число экспериментальных
данных, и результат определения содержания
компонента бывает, как правило, менее
точным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Слайд 1ЛЕКЦИЯ 17
на тему «Метрологические основы аналитической
химии»

Слайд 2План:
1. Метрология как наука. Правильность и воспроизводимость.
2.
Классификация ошибок количественного анализа.
3. Методы проверки
правильности результатов анализа.
4. Некоторые понятия математической статистики и их использование в количественном анализе. Доверительный интервал и доверительная вероятность
5. Пример статистической обработки и представления результатов количественного анализа.
Литература: Харитонов Ю.Я. Аналитика. Кн. 2, гл.1, §1.4-1.7.

Слайд 31. Метрология как наука. Правильность и воспроизводимость.
Под
параллельными определениями понимают получение нескольких результатов единичных
определений для одной пробы практически в одинаковых условиях.
При проведении химического анализа обычно не ограничиваются единичным определением, а проводят несколько параллельных определений (как правило, 3-5) для одной и той же пробы в одинаковых условиях. Средний результат параллельных определений называют результатом анализа и обозначают через с или х. Отклонение результатов анализа от истинного содержания определяемого компонента (µ) называют погрешностью (или ошибкой) определения.

Слайд 4
Пусть μ — истинное значение определяемой величины;
х1,х2,хi..хn — измеренные (единичные) значения определяемой величины
результаты единичных определений; п — общее число единичных определений.
Под единичным определением понимают однократное проведение всей последовательности операций, предусмотренных методикой анализа.
Результат единичного определения — это значение содержания определяемого компонента, найденное при единичном определении.

Слайд 5
Часто вместо истинного значения определяемой величины μ
используют действительное значение содержания а (или просто
дейcтвительнoe значение а), под которым подразумевают экспериментально полученное или расчетное значение определяемого содержания, настолько близкое к истинному, что для данной цели может быть использовано вместо него. Тогда величина
хср.= (х1+х2+…+хп) / п = (∑хі) / п (1)
есть среднее арифметическое (среднее) из результатов единичных определений. Считается, что хср. — наиболее вероятное значение определяемой величины, более вероятное, чем каждое
отдельное значение хi.

Слайд 6 Правильностью измерений называют качество измерений, отражающее близость
к нулю систематических погрешностей.
Под правuльностью результата
анализа понимают качество анализа, отражающее близость к нулю разности между средним арифметическим и истинным μ (или действительным а) значением определяемой величины:
хср.- μ →0 или хср.- а →0
при n → ∞ при n → ∞

Слайд 7
2. Классификация ошибок количественного анализа
Ошибки количественного анализа
условно подразделяют на систематические, случайные и грубые.

Слайд 8А. Систематические ошибки
Систематические погрешности являются следствием устойчивых отклонений результатов
анализа от истинных величин. Погрешность измерений, которая при повторных измерениях остается постоянной или закономерно изменяется, называется систематической погрешностью.
Различают: систематическую ошибку и процентную систематическую ошибку.
Систематическая ошибка результата анализа Δo — это статистически значимая разность между средним хср. и действительным а (или истинным μ) значениями содержания определяемого компонента:
Δo = хср.- а или Δo = хср. — μ. (2)
Систематическая ошибка результата анализа может быть больше нуля, меньше нуля или равна нулю.
Процентная систематическая ошибка (относительная величина систематической ошибки) — это систематическая ошибка, выраженная в процентах от действительного значения а (или истинного значения μ) определяемой величины:

Слайд 10Источники систематических ошибок
Методические — обусловлены особенностями методики
анализа.
Инструментальные — обусловлены несовершенством используемых приборов
и оборудования.
Индивидуальные — обусловлены субъективными качествами аналитика.
Так, например, дальтонизм может влиять на определение конечной точки титрования при визуальной фиксации изменения окраски индикатора.
Правильность результатов анализа определяется наличием или отсутствием систематических ошибок.

Слайд 11Б. Случайные ошибки
Погрешность, которая при повторных измерениях
изменяется случайным образом, называется случайной погрешностью измерений. Причины их возникновения многообразны, и исключить их полностью невозможно.
Промах – это погрешность, резко искажающая результат анализа и обычно легко обнаруживаемая, вызванная, как правило, небрежностью или некомпетентностью аналитика.
Случайные ошибки показывают отличие результатов параллельных определений друг от друга и характеризуют воспроизводимость анализа.

Слайд 12
3. Методы проверки правильности результатов анализа
Аналитический сигнал
– среднее результатов измерений физической величины на
заключительном этапе анализа, функционально связанное с содержанием определяемых компонентов.
В качественном химическом анализе – изменение агрегатного состояния или внешнего вида вещества в результате химической реакции.
При определении количества компонента измеряется величина аналитического сигнала: масса осадка, сила тока, интенсивность линии спектра и т.д.
Затем рассчитывают содержание компонента с использованием функциональной зависимости аналитический сигнал–содержание: у = f(c), которая устанавливается расчетным или опытным путем и может быть представлена в виде формулы, таблицы или графика.

Слайд 13
На основании существующей зависимости между измеренным аналитическим
сигналом и содержанием находят концентрацию определяемого компонента.
Обычно при этом используют методы градуировочного графика, стандартов или добавок.
1). Метод градуировочного графика:

Слайд 152). Метод добавок
При определении содержания компонента методом
добавок берут п аликвот анализируемой пробы: 1,
2, 3, …, п. В аликвоты 2, 3, …, п вводят известные, возрастающие количества определяемого компонента. Во всех аликвотах измеряют аналитический сигнал – содержание определяемого компонента, приняв за условный нуль содержание определяемого компонента в аликвоте без добавки (аликвота 1).

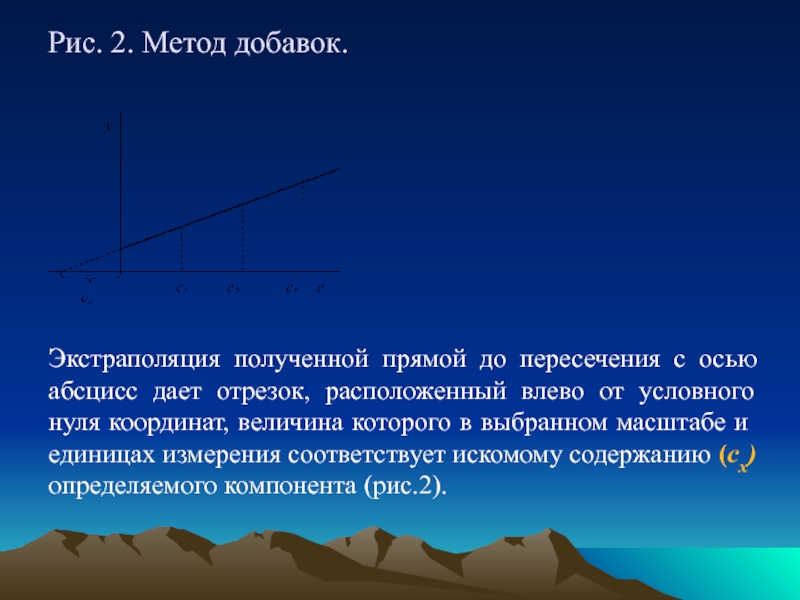
Слайд 16Рис. 2. Метод добавок.
Экстраполяция полученной прямой до
пересечения с осью абсцисс дает отрезок, расположенный
влево от условного нуля координат, величина которого в выбранном масштабе и единицах измерения соответствует искомому содержанию (сх) определяемого компонента (рис.2).
Слайд 17Во всех рассмотренных способах используют образцы сравнения
(эталоны), т.е. образцы, пробы, растворы с точно
установленным содержанием компонента.
Методы анализа, использующие образцы сравнения – это так называемые относительные методы химического анализа.
Абсолютных (безэталонных) методов в аналитической химии немного – например, методы гравиметрии, прямой кулонометрии, некоторые варианты радиохимических методов.

Слайд 20Если число наблюдений велико, величина S стремится
к некоторому постоянному значению σ, которое можно
назвать статистическим пределом S:
σ = lim S
n→∞
Этот предел называют стандартным отклонением, а квадрат этой величины – дисперсией измерений. Таким образом, в условиях аналитического определения обычно находят выборочное среднее x, а не генеральное среднее µ и выборочное стандартное отклонение S , а не σ.

Слайд 23Доверительная вероятность Р — вероятность нахождения действительного
значения определяемой величины а в пределах доверительного
интервала. Изменяется от 0 до 1 или (что то же самое) от 0% до 100%.
В фармацевтическом анализе при контроле качества лекарственных препаратов доверительную вероятность чаще всего принимают равной Р = 0,95 = 95% и обозначают как P0,95. При оценке правильности методик или методов анализа доверительную вероятность обычно считают равной Р = 0,99 = 99%.

Слайд 24
_
Полуширину доверительного интервала Δx находят по формуле:
_
Δx = tP, f s /√n
где tP, f — коэффициент нормированных отклонений (коэффициент Стьюдента, функция Стьюдента, критерий Стьюдента), который зависит от доверительной вероятности Р и числа степеней свободы f = n — 1, т. е. от числа п проведенных определений.
Численные значения tP, f рассчитаны для различных возможных величин Р и n и табулированы в справочниках.
Чем больше п, тем меньше tP, f Однако при n > 5 уменьшение tP, f уже сравнительно невелико, поэтому на практике обычно считают достаточным проведение пяти параллельных определений (n= 5).

Слайд 255. Пример статистической обработки и представления результатов
количественного анализа.
Пусть содержание определяемого компонента в анализируемом
образце, найденное в пяти параллельных единичных определениях (п = 5), оказалось равным, %: 3,01; 3,04; 3,08; 3,16 и 3,31. Известно, что систематическая ошибка отсутствует.
Требуется провести статистическую обработку результатов количественного анализа (оценить их воспроизводимость) при доверительной вероятности, равной Р = 0,95.

Слайд 28Относительная (процентная) ошибка среднего результата ε:
_
_
ε = (Δx
/x) ·100%.
Итоговая таблица

Слайд 29Оценка правильности результатов анализа — проблема значительно
более трудная, чем оценка воспроизводимости.
Для оценки
правильности необходимо сравнение результата измерения с истинным значением. Строго говоря, такое значение никогда не может быть известно. Однако для практических целей можно вместо истинного использовать любое значение, систематическая погрешность которого пренебрежимо мала. Если при этом и случайная погрешность также пренебрежимо мала, то такое значение можно считать точной величиной (константой) и постулировать в качестве истинного. Величина, принимаемая за истинное значение, называется действительной величиной и обозначается a

Слайд 30Важнейшие способы получения информации о действительном (или,
по крайней мере, не содержащем систематической погрешности)
значении содержания определяемого компонента в анализируемом образце состоят в следующем:

Слайд 31Данные независимого анализа. Образец анализируют повторно, используя
другую методику анализа, о которой известно (из
опыта практического применения), что она не содержит систематической погрешности.

Слайд 322. Способ «введено — найдено». В этом
случае аналитик сам готовит для анализа образец
с известным содержанием определяемого компонента. Полученный результат («найдено») сравнивают с заданным содержанием («введено»).

Слайд 333. Использование стандартных образцов. В качестве объекта
анализа выбирают подходящий СО, а данные о
содержании определяемого компонента берут из паспорта СО.
После получения тем или иным способом независимых данных о содержании определяемого компонента их необходимо сравнить с результатами, полученными с помощью проверяемой методики.

Слайд 34Чувствительность, селективность и их характеристики
Точность результатов анализа
в целом и ее отдельные составляющие, правильность
и воспроизводимость, могут сильно изменяться в зависимости от состава образца. При уменьшении содержания определяемого компонента или при увеличении содержания посторонних компонентов точностные характеристики непрерывно ухудшаются, и с какого-то момента определение, а затем и обнаружение компонента оказывается вообще невозможным. Работоспособность методики в таких «экстремальных», неблагоприятных для анализа условиях характеризуют еще два важнейших понятия химической метрологии — чувствительность и селективность.

Слайд 35Чувствительность.
Традиционно под «чувствительностью» понимают возможность обнаружения
или определения при помощи данной методики малых
содержаний вещества («методика высокочувствительна» — значит, она позволяет работать в области очень низких концентраций). Простейшей численной величиной, характеризующей эту возможность, служит коэффициент чувствительности (S).

Слайд 36Однако знание одной лишь величины S не
позволяет ответить на вопрос, насколько низкие содержания
можно определять с помощью той или иной методики. Во-первых, коэффициент чувствительности — величина размерная, поэтому сопоставление коэффициентов чувствительности для принципиально разных (различающихся природой аналитического сигнала) методов невозможно. Во-вторых, сопоставление значений S даже одинаковой размерности имеет смысл действительно только «при прочих равных условиях», т.е. в первую очередь при одинаковой точности измерения аналитических сигналов. В то же время эта точность может меняться от методики к методике. Поэтому для характеристики чувствительности используют еще две величины, называемые пределом обнаружения и пределом определения.

Слайд 37Предел обнаружения (cmin) — это наименьшее содержание
вещества, которое может быть обнаружено по данной
методике с заданной степенью достоверности. Таким образом, предел обнаружения (как это и следует из названия) характеризует методику с точки зрения возможностей качественного анализа.

Слайд 38Для характеристики возможностей методики с точки зрения
количественного анализа используют величину, называемую пределом определения
clim. Предел определения — это минимальное содержание компонента, которое можно определить с заданной степенью точности, характеризуемой предельно допустимой величиной относительного стандартного отклонения

Слайд 39Селективность. Под селективностью (или избирательностью) понимают возможность
определения данного вещества в присутствии посторонних компонентов.
Численной характеристикой селективности служит коэффициент селективности ki,J

Слайд 40Заключение
Аналитическая химия – это наука о методах
и средствах получения информации о составе вещества.
Но любая информация представляет интерес только тогда, когда известно, насколько она достоверна. Оценка достоверности результатов – это неотъемлемая часть химического анализа, это задача не менее важная и ответственная, чем само их получение. В данном пособии рассмотрены лишь некоторые, наиболее простые, но вместе с тем и наиболее распространенные приемы, используемые для оценки качества результатов химического анализа. На практике контроль качества результатов химического анализа часто оказывается достаточно сложным. Это связано со спецификой химического анализа – многостадийной косвенной измерительной процедуры, которая включает не только операцию измерения как таковую, но и предварительные этапы пробоотбора и пробоподготовки, а также градуировку. Отдельную задачу представляет собой обеспечение качества результатов химического анализа, достижение необходимой точности. Ее решение требует множества мер не только научного, но и организационного характера. Эти мероприятия, устанавливаемые законодательно, разрабатывают и проводят в жизнь специальные отраслевые, национальные и межгосударственные службы.

Слайд 41Изучением всех вопросов, связанных с измерением химических
величин, методами и средствами обеспечения их единства,
контроля и обеспечения качества результатов химического анализа занимается специальный раздел аналитической химии – химическая метрология. Основные правила и законы химической метрологии едины для всех методов анализа. Знание химической метрологии, умение правильно обрабатывать, оценивать и интерпретировать результаты химического анализа и, шире, любого химического эксперимента – одна из важных составляющих подготовки химика-исследователя.

Классификация и оценка погрешностей количественного анализа
По способу вычисления различают абсолютную 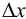

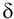
Если среднее арифметическое значение 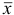
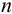
то абсолютную погрешность выражают как
где 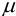
Относительная погрешность может быть выражена в долях или процентах и обычно не имеет знака:
По происхождению погрешности делят на систематические, случайные и промахи (грубые ошибки).
Погрешность определения, обусловленная постоянно действующей причиной, неизменная во всех измерениях, сохраняющая знак от опыта к опыту или закономерно изменяющаяся, называется систематической погрешностью. Погрешность, случайным образом изменяющаяся от опыта к опыту, называется случайной погрешностью. Грубые погрешности или промахи резко искажают результат анализа, вызываются небрежностью и обычно легко обнаруживаются.
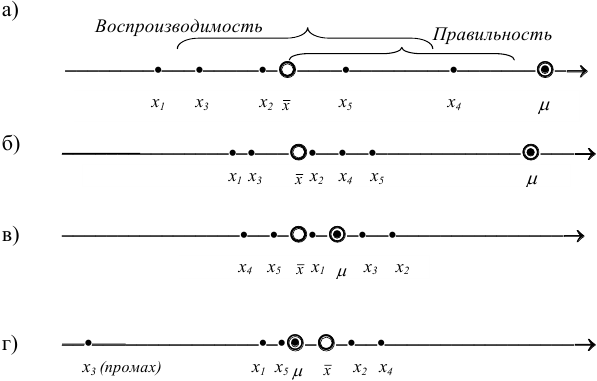
Рис. 9.1. Воспроизводимость и правильность химического анализа. Результаты: а) невоспроизводимы и неправильны; б) воспроизводимы, но неправильны; в) воспроизводимы и правильны; г) воспроизводимы и правильны, но есть промах.
С систематическими погрешностями связана правильность анализа, со случайными погрешностями — воспроизводимость. Правильность и воспроизводимость являются метрологическими характеристиками анализа и входят в понятие «точность анализа».
Воспроизводимость результатов анализа характеризует рассеяние единичных результатов относительно среднего.
Правильность характеризует отклонение полученного результата от истинного и показывает, насколько близка к нулю систематическая погрешность. Систематические погрешности выявляют и устраняют. Если же устранение невозможно, то при постоянном значении систематической погрешности ее учитывают, вводя поправку. Для выявления используют различные приемы и методы, например “введено — найдено”, анализ стандартного образца, “двойной или тройной добавки”.
Оценка случайных погрешностей проводится методами математической статистики. В обычной практике выполняют ограниченное число параллельных измерений п (обычно 3-5), называемое выборочной совокупностью данных или просто выборкой (в отличие от генеральной совокупности — при 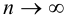
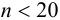
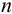
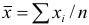
Характеристики случайной погрешности (воспроизводимости) для выборки: выборочная дисперсия 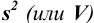
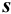
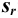
С ними связаны дисперсия среднего 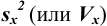
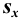
При обработке данных химического анализа определяют границы доверительного интервала 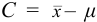
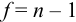
Доверительный интервал (С) — это интервал значений, в котором для данного вида распределения случайных величин (при отсутствии систематических погрешностей), при заданной доверительной вероятности Р и числе степеней свободы 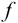
Доверительная вероятность попадания величины внутрь доверительного интервала в химическом анализе принята равной 0,95 или 95 %. Это означает, что в рассчитанный интервал попадут 95 из 100 значений. Коэффициенты 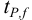
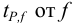
Оценка промахов (выбраковка результатов). Перед обработкой данных методами математической статистики необходимо выявить промахи и исключить их из числа обрабатываемых результатов. Для выявления промахов используют различные критерии, в частности, 

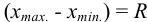
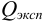
и сравнивают с критическим значением 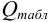
Если 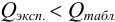
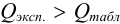

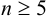
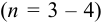
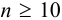
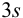
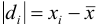
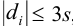
Пример 9.1.
Контрольный раствор соли кальция имеет концентрацию 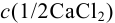
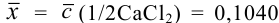
Решение:
Абсолютная погрешность результата:
Относительная погрешность:
Пример 9.2.
При определении содержания аскорбиновой кислоты в пробе картофеля по новой методике пробоподготовки получены следующие результаты (мг/100 г): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,49. Оцените:
а) наличие грубых погрешностей (промахов);
б) воспроизводимость результатов анализа.
Решение:
а) наличие промахов оценим по 

Из табл. 9 приложения при 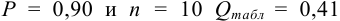
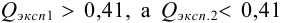
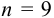
б) после исключения промаха найдем среднее и характеристики воспроизводимости: дисперсию 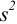
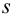
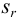
Пример 9.3.
Используя условия примера 9.2 и считая, что содержание аскорбиновой кислоты для той же пробы картофеля, определенное по стандартной методике составляет 14,58 мг/100 г, рассчитайте доверительный интервал и установите, свидетельствуют ли полученные результаты о наличии систематической погрешности при работе по новой методике?
Решение:
Для расчета доверительного интервала при числе степеней свободы 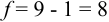
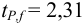
Находим полуширину доверительного интервала, оставляя значащие цифры:
Таким образом, среднее содержание аскорбиновой кислоты лежит в границах
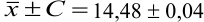
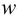
Пример 9.4.
При анализе стандартного образца, содержащего 1,44 % 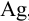
Решение:
Проверим наличие грубых погрешностей по 

Для 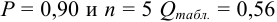

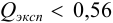
Находим среднее значение из пяти определений:
Вычисляем стандартное отклонение:
По табл. 8 приложения для 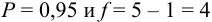
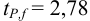
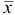
Результат представляем в виде:
Наличие систематической погрешности можно выявить, как в предыдущем примере, проверяя попадает ли истинное значение содержания серебра в доверительный интервал. В данном случае для 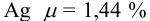
Ответить на вопрос задачи о присутствии систематической погрешности можно, используя критерий Стьюдента и сравнивая вычисленное значение 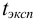
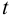
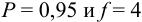
Поскольку 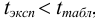
Пример 9.5.
При определении ванадия были получены результаты: 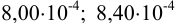
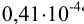
Решение:
Находим среднее значение:
Вычислим стандартное отклонение:
По табл. 8 приложения находим 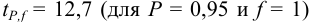
Требуется же получить доверительный интервал с полушириной 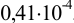
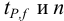
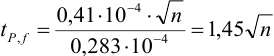
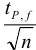
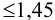
При 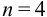
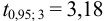
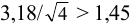
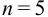
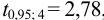
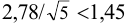
Таким образом, для сужения границ доверительного интервала до 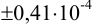
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:
Классификация ошибок количественного анализа способы их выявления
Статистическая обработка результатов химического эксперимента
Метрологические характеристики методов и результатов, которые получают при статистической обработке экспериментальных данных, позволяют проводить оценку и сравнение как экспериментальных методик, так и анализируемых объектов, и на этом основании решать прикладные задачи, связанные с определением статистической достоверности результатов исследований.
Ошибки в количественном анализе
Любое измерение имеет определенную ошибку, связанную с точностью измерительной аппаратуры, особенностями метода и случайными причинами. Во время анализа возникают ошибки при выполнении отдельных операций (взятии навески, растворении и т. д.).
Ошибки в количественном анализе делятся на систематические, случайные и промахи.
Систематические ошибки вызывают однотипные (одного знака) отклонения от истинного значения. Они зависят от особенностей данного метода анализа (методические ошибки), неточности измерений (инструментальные ошибки), недостаточной чистоты реагентов (реактивная ошибка), индивидуальных особенностей самого аналитика. Их можно выявить, уменьшить или внести поправки.
Случайные погрешности не имеют определенного знака, в их появлении отсутствуют любые закономерности. Их нельзя устранить введением каких-либо поправок, но они могут быть значительно уменьшены при повышении тщательности работы и увеличении числа параллельных определений.
Промахи — это грубые погрешности, возникающие при неверных измерениях, расчетах, неправильных записях и т. д. При обработке экспериментальных данных результаты с грубыми ошибками должны быть выявлены и отброшены.
По способу выражения погрешности количественных определений делят на абсолютные и относительные.
Абсолютной ошибкой (ΔХi) называют разность между полученным результатом (Xi) и истинным значением величины (μ), которую определяют как ΔХi = Xi — μ. При этом в большинстве случаев среднее выборки ( X ) является лучшей оценкой истинного значения измеряемой величины (μ):
Относительной ошибкой называется отношение абсолютной ошибки к истинному значению определяемой величины, выраженное в процентах:
Правильность, воспроизводимость и точность анализа
Правильность анализа показывает близость результата или среднего арифметического нескольких результатов X к истинному значению. Обычно ее обозначают погрешностью ДХ. Правильность анализа указывает на его качество, то есть практическое отсутствие систематической ошибки.
Воспроизводимость анализа определяют близостью параллельно полученных результатов и обозначают величиной отклонения полученных результатов от их среднеарифметического значения. Воспроизводимость анализа зависит от случайных ошибок.
Точность анализа отображает приближение к нулю ошибок всех видов.
Основные статистические характеристики, их вычисление. Проверка однородности выборки
Выборкой называют совокупность статистически эквивалентных результатов. Например, ряд результатов, полученных при параллельных определениях любого вещества в пробе.
Результаты, полученные при статистической обработке выборки, будут достоверны в том случае, если выборка однородна, то есть в полученных результатах анализа отсутствуют грубые ошибки.
Оценку однородности выборки удобно проводить по ^-критерию, если число опытов не превышает 10. Для этого все полученные результаты размещают в порядке возрастания: Xv X2, . X.
Источник
§ 13. Ошибки в количественном анализе
С какой бы тщательностью ни проводилось то или иное количественное определение, полученный результат, как правило, всегда
несколько отличается от действительного содержания определяемого вещества, т. е. содержит некоторую ошибку.
По своему характеру ошибки анализа подразделяются на: 1) систематические ошибки; 2) случайные ошибки; 3) промахи.
Систематические ошибки. Систематическими ошибками называют погрешности, одинаковые по знаку, происходящие от определенных причин, влияющих на результат либо в сторону увеличения,- либо в сторону уменьшения его. Систематические ошибки можно обычно предусмотреть и устранить их или же ввести соответствующие поправки. Отметим следующие виды систематических ошибок.
Ошибки методические. Эти ошибки зависят от особенностей применяемого метода анализа, например от не вполне количественного протекания реакции, на которой основано определение, от частичной растворимости осадка, от соосаждения вместе с ним различных посторонних примесей, от частичного разложения или улетучивания осадка при прокаливании, от гигроскопичности прокаленного осадка, от течения наряду с. основной реакцией каких-либо побочных реакций, искажающих результаты титриметрических определений, от свойств примененного при титровании индикатора и т. д. Методические ошибки составляют наиболее серьезную причину искажения результатов количественных определений, устранить их трудно.
Ошибки, зависящие от применяемых приборов и реактивов. Сюда относятся, например, ошибки, связанные с неравноплечестью или недостаточной точностью весов, с употреблением непроверенных разновесок или сосудов для точного измерения объемов. К этой же категории относятся ошибки, происходящие в результате загрязнения раствора продуктами разрушения стекла или фарфора, из которых сделана применяемая при анализе посуда; ошибки, происходящие от присутствия в употребляемых реактивах определяемого элемента или веществ, мешающих определению.
Ошибки оперативные. Оперативные ошибки происходят от неправильного или недостаточно тщательного выполнения аналитических операций. Сюда относится, например, недостаточное промывание осадков, приводящее к постоянному завышению результатов, иногда — излишнее промывание осадков, приводящее к систематическим потерям. Систематические ошибки появляются также в результате недостаточной или чрезмерной продолжительности прокаливания осадков, недостаточно тщательного перенесения осадков из стакана в тигель, неправильного способа выливания растворов из пипеток и т. п.
Ошибки индивидуальные. Эти ошибки зависят от индивидуальных особенностей самого аналитика, например от его неспособности точно улавливать момент перемены окраски при
титровании, и г. д. К индивидуальным ошибкам следует отнести также так называемые психологические ошибки, заключающиеся в некоторой предвзятости, часто встречающейся у студентов. Например, при повторных взвешиваниях или титрованиях из двух смежных делений шкалы весов или бюретки * студент нередко старается брать не то деление, которое ближе подходит к определяемым массе или объему, а то, которое более совпадает со сделанными ранее определениями. Разумеется, это только снижает точность результатов анализа, а подчас может сделать их и вовсе неприемлемыми. Поэтому нужно поставить себе за правило— быть как можно объективное и не допускать никакой предвзятости при оценке результатов опыта.
Ошибки, зависящие от применяемых приборов и реактивов, оперативные и индивидуальные, могут быть учтены и сведены до ничтожно малых величин.
Случайные ошибки. Случайными называются неопределенные по величине и знаку ошибки, в появлении каждой из которых не наблюдается какой-либо закономерности. Они могут быть, например, вызваны изменением температуры, влажности воздуха, случайными потерями вещества и т. п.
Случайные ошибки происходят при всяком измерении, и в том числе при любом аналитическом определении, как бы тщательно оно ни проводилось. Наличие их сказывается в том, что повторные определения того или иного элемента в данном образце, выполненные одним и тем же методом, дают, как правило, не одинаковые, а несколько различающиеся между собой результаты.
В отличие от систематических ошибок случайные ошибки не могут быть учтены или устраненены введением каких-либо поправок. Однако они могут быть значительно уменьшены при увеличении числа параллельных определений (см. ниже). Влияние случайных ошибок на результат анализа может быть учтено теоретически, путем обработки результатов, полученных в серии параллельных определений данного элемента, с помощью методов математической статистики (см. § 14).
Промахи. Промахами называются грубые ошибки, сильно искажающие результат анализа. Сюда относятся, например, ошибки, зависящие от неправильного подсчета разновесок или отсчета по шкале весов при взвешивании, от неправильного отсчета по шкале бюретки при титровании, от проливания части раствора или просыпания части осадка при определении и т. п. Из-за промахов результат данного определения становится неверным, и потому он отбрасывается при выводе среднего из серии параллельных определений.
* Бюреткой называется измерительный сосуд для жидкостей, которым пользуются при титровании.
Правильность и точность (воспроизводимость) анализа. Под
правильностью в анализе понимают близость полученного результата к истинному значению. Точность результата — это его воспроизводимость, которая характеризуется разбросом ряда отдельных измерений, проведенных одним и тем же методом. Разброс оценивается по отношению к среднему результату измерений или к истинному значению определяемой величины.
Следовательно, анализ считается выполненным тем более точно, чем меньше результаты параллельных определений различаются между собой, т. е. чем выше воспроизводимость.
Следует заметить, что эта терминология не является общепринятой. Так, до сих пор вместо термина точность в химической литературе часто применяют термин воспроизводимость, а вместо термина правильность пользуются термином точность. В частности, такая терминология была принята и в первом издании настоящего учебника. Недостатком ее является расхождение с терминологией, общепринятой в метрологии и математической статистике. Такое расхождение является тем более недопустимым, что в настоящее время применение методов математической статистики при обработке результатов анализов становится все более необходимым в практике. В соответствии с этим в ряде работ, посвященных вопросу об учете влияния случайных ошибок на результат анализа, устаревшая терминология заменена терминологией, применяемой в математической статистике и метрологии. Считая это вполне целесообразным, автор ввел новую терминологию в настоящий учебник.
Нетрудно понять, что хорошая точность анализа не может служить доказательством его правильности. Чтобы убедиться в этом, рассмотрим следующий пример. Положим, что при ряде повторных титрований равных объемов исследуемого раствора щелочи раствором соляной кислоты были израсходованы весьма близкие между собой объемы ее; это указывает на хорошую точность выполнения анализа. Однако для получения окончательного результата анализа необходимо по затраченному объему раствора HCl и его концентрации вычислить из уравнения реакции соответствующее количество определяемой щелочи. Если концентрация раствора HCl была в свое время определена неверно, то эта ошибка в качестве постоянной систематической ошибки отразится на всех результатах отдельных определений и, несмотря на хорошую воспроизводимость, полученные результаты будут совершенно неправильными.
Таким образом, по точности результата анализа можно судить о его правильности только при отсутствии систематических ошибок. Но, не переоценивая значения точности, не следует все же забывать, что хорошая точность свидетельствует об отсутствии сколько-нибудь значительных случайных ошибок при выполнении анализа. Такие ошибки (и даже промахи) могут быть у самого опытного и добросовестного аналитика, поэтому всякое определение, как правило, проводят по крайней мере дважды, из двух навесок вещества (параллельные определения). Анализ считают
выполненным удовлетворительно лишь при условии хорошей воспроизводимости результатов отдельных определений; из этих данных берут среднее арифметическое, которое и принимают за окончательный результат анализа.
В математической теории ошибок доказывается, что ошибка среднего арифметического из п определений в Yn раз меньше ошибки единичного определения. Однако это справедливо только при условии, если ошибки являются случайными, и поэтому значения их колеблютсяГ в обе стороны от значения измеряемой величины, т. е. они меньше или больше ее.
Между тем при анализе могут встретиться случаи, когда соответствующие ошибки имеют только один знак. Например, результаты взвешивания какого-либо гигроскопичного вещества будут всегда больше, но не меньше истинной массы. Понятно, что среднее арифметическое будет больше отклоняться от истинного значения массы вещества, чем наименьшая из полученных масс. Очевидно, что ошибки, с которыми здесь имеют дело, не являются в действительности случайными, а носят систематический характер.
Ошибки количественных определений, как и при любых других измерениях, можно выражать различно. По способу выражения они разделяются на абсолютные и относительные.
В большинстве случаев интерес представляет не абсолютная, а относительная ошибка определения.
Абсолютная ошибка. Разность между полученным результатом и истинным (или наиболее достоверным) значением определяемой величины, выраженная в абсолютных единицах, называется абсолютной ошибкой. Допустим, что в кристаллическом хлориде бария было найдено 14,70% кристаллизационной воды. Из формулы BaCl2 •2H2O легко вычислить, что в действительности хлорид бария должен содержать 14,75% кристаллизационной воды. Следовательно, абсолютная ошибка определения (D) равна:
D = 14,70 — 14,75 = — 0,05%
Относительная ошибка. Отношение абсолютной ошибки к истинному значению определяемой величины называется относительной ошибкой. Чаще всего ее выражают в процентах, умножая указанное отношение на 100. Например, в рассматриваемом случае относительная ошибка (D0) равна:
Очевидно, что при такой же величине абсолютной ошибки относительная ошибка будет тем меньше, чем больше истинное значение определяемой величины. Так, если ту же абсолютную ошибку (±0,05%) мы сделали бы при определении бария в ВаС12-2Н20,
то, поскольку содержание его. равно 56,20%. относительная ошибка в этом случае равнялась бы:
Если истинное значение определяемой величины неизвестно, то вместо него берут среднее арифметическое (х) из результатов проделанных определений и сравнивают с ним каждый из результатов (лгг). Полученные величины (d — х — Xi) называются отклонениями от среднего значения отдельных результатов. По ним можно (как это будет подробнее разъяснено в § 14) судить о точности результатов анализа. Отклонения,от среднего значения можно представить также либо в абсолютных единицах, либо в относительных, принимая за 100% величину соответствующего среднего значения.
Влияние ошибок отдельных измерений на результат анализа. При количественных определениях приходится проводить несколько отдельных измерений, например взятие навески и определение массы полученного осадка (или объема раствора реактива, израсходованного на реакцию при объемных определениях) и т. д. При вычислении результата анализа ошибки отдельных измерений так или иначе складываются и обусловливают ошибку всего анализа. -Как именно’ происходит суммирование ошибок отдельных измерений, зависит от того, какие математические действия проводятся с соответствующими величинами при вычислении результатов анализа.
Приведенные ниже формулы иллюстрируют правила сложения ошибок в различных случаях:
г = пху Дг = Д* + Ay (а>
г — п(ху) Дг = Дл — Ay (б)
г = п(х±у) Дг = п Ax ± у- Ay^ (s)
т = пхауь Ar = а Ax + Ь Ay (г)
Здесь Ax и Ay — относительные ошибки отдельных измерений величин хну; Ar — относительная ошибка результата вычисления (г); п — фактор, практически свободный от ошибки (такими факторами являются, например, атомные и молекулярные веса, ошибка которых ничтожна по сравнению с другими ошибками).
Рассмотрим пример, иллюстрирующий применение приведенных формул. Положим, что навеска 0,5000 г какого-либо вещества растворена в воде и объем полученного раствора доведен до 250,0 мл. Требуется вычислить концентрацию (С) данного вещества в растворе. Она, очевидно, равна:
где g—навеска, г; V—объем раствора, мл.
Вычислим, с какой точностью определена эта концентрация, если взвешивание проводилось на аналитических весах с точностью до ±0,0002 г, а измерение объема раствора содержит ошибку, равную +0,5 мл. Относительная ошибка взвешивания в данном случае равна:
Относительная ошибка при измерении объема составляет
Отсюда, применяя формулу (б), получим:
ДС = Ag — Д V = + 0,04 — (+ 0,2)
Следовательно, относительная ошибка, допущенная при приготовлении раствора заданной концентрации (0,002000 г!мл), колеблется в пределах от —0,16% до —0,24% (в зависимости от того, какой знак имеет ошибка взвешивания Ag при взятии навески).
Компенсация ошибок. Из формулы (б) (см. выше, мелкий’ шрифт) видно, что если при вычислении результатов анализа одну из измеренных величин приходится делить на другую, то ошибки отдельных измерений могут частично или. полностью компенсировать друг друга. Такая компенсация ошибок весьма выгодна, и нужно стараться выполнять определения так, чтобы она имела место. Именно поэтому необходимо все взвешивания проводить на одних и тех же весах с одним и тем же набором разновесок. Ведь при вычислении результатов анализа придется найденное по массе осадка количество определяемого элемента делить на величину взятой навески. Будет происходить тем большая компенсация ошибок взвешивания, чем идентичнее были условия этих взвешиваний. Выше говорилось также, что именно вследствие компенсаций ошибок (взвешивание на одних и тех же весах) можно во многих случаях не считаться с неравноплечестью весов, а также не вводить поправок на взвешивание в воздухе.
Источник
Классификация методов анализа. Метрологические характеристики методов анализа. Погрешности: абсолютная и относительная, их классификация. Правильность, сходимость, воспроизводимость и точность результатов анализа
При аналитических определениях исследователь всегда допускает определенные погрешности. Случайные и систематические погрешности можно объяснить следующими причинами:
1. Исследуемые вещества неоднородны. Отдельные небольшие части пробы могут иметь неодинаковый состав. Следует уметь правильно взять среднюю пробу.
2. Все необходимые для анализа величины, например, массу осадка, объем титранта, оптическую плотность и т.д. можно измерить только с ограниченной точностью.
3. В процессе анализа исследуемые пробы подвергаются химической обработке. Как правило, все химические реакции считаются равновесными и, несмотря на то, что исследователи стараются выбрать реакции, практически смещенные в сторону продуктов, все же всегда имеют место явления, создающие случайные и систематические погрешности. Например, это могут быть различные солевые эффекты, явления соосаждения и другие, препятствующие полноте протекания реакций.
Существует два фактора, по которым аналитик судит о своих результатах:
1) воспроизводимость полученных результатов;
2) соответствие их содержанию в пробе (правильность результатов).
Воспроизводимость зависит от случайной погрешности, правильность — от систематической погрешности.
Погрешность титриметрического метода анализа определяется в основном погрешностью измерения объема и непосредственно зависит от величины капли, объем которой составляет в среднем 0,04 мл. При тщательном титровании можно снимать доли капли, например, половину, тогда абсолютная погрешность измерения объема составит ± 0,02 мл, а относительная (при объеме, пошедшем на титрование, 20 мл):
Поэтому, чтобы не снижать точность результатов, расчеты следует производить с ошибкой, не превышающей 0,1%. Для этого все численные величины при расчетах (объемы раствора, молекулярные массы, эквиваленты, навески и т.д.) должны быть выражены четырьмя значащими цифрами.
Например:
1) V = 19,53, а не 19,5 мл.
2) С(H2SO4) = 0,1010, а не 0,101 моль/л.
3) Т(H2SO4) = 0,004900, а не 0,0049 г/мл.
4) 1/2М(H2SO4) = 49,04, а не 49 г/моль.
Цель всех аналитических исследований — нахождение результата, наиболее близкого к истинному содержанию в пробе.
Общую погрешность метода можно оценить только с привлечением методов математической статистики. Эти методы исходят из идеализированного представления о бесконечно большом числе измерений. Исследователь же имеет дело с небольшим числом измерений, они называются выборкой. При оценке результатов анализа часто пользуются средним арифметическим значением. Прежде чем рассчитать среднее арифметическое значение результатов, они должны быть оценены на предмет выявления промахов, т.е. грубых отклонений. Нельзя без предварительной оценки отбросить кажущиеся неподходящими значения. Промахи или грубые отклонения устанавливаются по «размаху варьирования».
Размах варьирования — это разница между двумя крайними значениями: максимальным и минимальным. Далее вычисляют Q критерий, который определяется отношением:
где Х1 — подозрительно выделяющееся значение,
Х2 — значение, ближайшее по величине к подозрительному.
Вычисленную величину Q сопоставляют с табличным значением (таблицы обычно приведены в учебниках). Наличие грубого промаха доказано, если Q>Qтабл., при данном числе определений n и выбранной доверительной вероятности P.
Доверительная вероятность (Р) — это соответствие экспериментального результата истинной величине и обычно принимается равной 95%.
Для систематической обработки определяют ряд метрологических характеристик:
1. Среднее арифметическое — .
Эта величина при большом числе определений наиболее соответствует истинному значению.
2. Доверительный интервал.
Для ограниченного числа измерений истинное значение определяемой величины находится в пределах определенного интервала от среднего арифметического X, т.е. в пределах ±X. Этот интервал называют доверительным и рассчитывают по методу, известному как метод Стьюдента.
Им предложено простое уравнение, связывающее доверительную вероятность (Р) и число определений (n) с доверительным интервалом.
X=t•S(),
где: t — коэффициент Стьюдента для заданных n и Р. Эта величина берется из справочных таблиц.
S() — функция от среднего арифметического значения, среднее квадратичное отклонение среднего арифметического.
3. Среднее квадратичное отклонение среднего арифметического.
Эта метрологическая характеристика, используемая для расчета доверительного интервала, связана со средним квадратичным отклонением отдельного результата и числом определений n соотношением:
где: S(X) — среднее квадратичное отклонение отдельного результата,
n — число определений.
4. Среднее квадратичное отклонение отдельного результата рассчитывают по формуле:
где: Хi — отдельный результат,
— среднее арифметическое значение n определений,
n — число определений.
Пример расчета.
Данные определения действующей субстанции в пробе лекарственного препарата представлены в таблице.
|
№ |
X(%) |
Xi- |
(X-)2 |
|
1 |
96,6 |
+0,6 |
0,36 |
|
2 |
95,4 |
-0,6 |
0,36 |
|
3 |
95,5 |
-0,5 |
0,25 |
|
4 |
96,5 |
+0,5 |
0,25 |
|
5 |
96,1 |
+0,1 |
0,01 |
|
6 |
95,9 |
-0,1 |
0,01 |
|
7 |
94,1 |
Проверим на промах величину, наиболее отличающуюся от результатов всей серии — 94,1%.
Табличные значения Q для n=7 и Р=95% — 0,480, следовательно, это значение является промахом и не включается в расчет среднего арифметического значения.