В
выборочном наблюдении используются
понятия «генеральная совокупность» —
изучаемая совокупность единиц, подлежащая
изучению по интересующим исследователя
признакам, и «выборочная совокупность»
— случайно выбранная из генеральной
совокупности некоторая ее часть. К
данной выборке предъявляется требование
репрезентативности, т.е. при изучении
лишь части генеральной совокупности
полученные выводы можно применять ко
всей совокупности.
Характеристиками
генеральной и выборочной совокупностей
могут служить средние значения изучаемых
признаков, их дисперсии и средние
квадратические отклонения, мода и
медиана и др. Исследователя могут
интересовать и распределение единиц
по изучаемым признакам в генеральной
и выборочной совокупностях. В этом
случае частоты называются соответственно
генеральными и выборочными.
Система
правил отбора и способов характеристики
единиц изучаемой совокупности составляет
содержание выборочного метода, суть
которого состоит в получении первичных
данных при наблюдении выборки с
последующим обобщением, анализом и их
распространением на всю генеральную
совокупность с целью получения достоверной
информации об исследуемом явлении.
Репрезентативность
выборки обеспечивается соблюдением
принципа случайности отбора объектов
совокупности в выборку. Если совокупность
является качественно однородной, то
принцип случайности реализуется простым
случайным отбором объектов выборки.
Простым случайным отбором называют
такую процедуру образования выборки,
которая обеспечивает для каждой единицы
совокупности одинаковую вероятность
быть выбранной для наблюдения для любой
выборки заданного объема. Таким образом,
цель выборочного метода — сделать вывод
о значении признаков генеральной
совокупности на основе информации
случайной выборки из этой совокупности.
2.1. Генеральная и выборочная совокупности.
Пусть
требуется изучить совокупность однородных
объектов относительно некоторого
качественного или количественного
признака, характеризующего эти объекты.
Например, если имеется партия деталей,
то качественным признаком может служить
стандартность детали, а
количественным—контролируемый размер
детали.
Иногда
проводят сплошное обследование, т. е.
обследуют каждый из объектов совокупности
относительно признака, которым
интересуются. На практике, однако,
сплошное обследование применяют
сравнительно редко. Например, если
совокупность содержит очень большое
число объектов, то провести сплошное
обследование физически невозможно.
Если обследование объекта связано с
его уничтожением или требует больших
материальных затрат, то проводить
сплошное обследование практически не
имеет смысла. В таких случаях случайно
отбирают из всей совокупности ограниченное
число объектов и подвергают их изучению.
Различают генеральную и выборочную
совокупности:
Генеральной
совокупностью называют совокупность
всех мысленно возможных объектов данного
вида, над которыми проводятся наблюдения
с целью получения конкретных значений
случайной величины, или совокупность
результатов всех мыслимых наблюдений,
проводимых в неизменных условиях над
одной из случайных величин, связанных
с данным видом объектов.
Замечание:
Часто генеральная совокупность содержит
конечное число объектов. Однако если
это число достаточно велико, то иногда
в целях упрощения вычислений допускают,
что генеральная совокупность состоит
из бесчисленного множества объектов.
Такое допущение оправдывается тем, что
увеличение объема генеральной совокупности
(достаточно большого объема) практически
не сказывается на результатах обработки
данных выборки.
Выборочной
совокупностью называют часть отобранных
объектов из генеральной совокупности.
Объемом
совокупности (выборочной или генеральной)
называют число объектов этой совокупности.
Например, если из 1000 деталей отобрано
для обследования 100 деталей, то объем
генеральной совокупности N = 1000, а объем
выборки п =100.
Число
объектов генеральной совокупности N
значительно превосходит объем выборки
n .
18
3.
Расчет объема и ошибки выборки
Из
всех вопросов, которые задают сотрудникам
знаменитого Института опросов
общественного мнения Гэллапа, самым
популярным является такой: как вы можете,
проинтервьюировав 1000 человек, судить
о том, что думают 250 млн. американцев.
Для
ответа на этот вопрос нужно упомянуть
не только высокую квалификацию и огромный
практический опыт сотрудников, но и
использование ими статистики и математики.
Если методы опроса не основаны на науке,
результаты могут ввести вас в заблуждение.
В
статистике приняты следующие разграничения
объемов выборки. Объем выборки, достаточный
для взаимопогашения случайностей и
получения статистических характеристик
закономерного характера, равен 30. Выборка
такого объема называется малой. Характер
распределения значений признака в малых
выборках приближается к нормальному с
ростом числа испытаний. Минимальный
объем выборки, позволяющий получить
средние значения признака с указанием
доверительных вероятностей, равен 5.
Выборки такого объема называются
сверхмалыми. Распределение значений
признака в таких выборках характеризуется
распределением Стьюдента. Но чаще всего
в социологии имеют дело с гораздо большим
объемом выборки.
При
планировании выборочного обследования
наступает момент, когда нужно решить,
сколько человек опрашивать, т.е. каким
должен быть объем выборки. Это решение
чрезвычайно важно, поскольку слишком
большая выборка потребует излишних
затрат, а слишком маленькая понизит
качество результатов.
Объем
выборки — общее число единиц наблюдения,
включенных в выборочную совокупность.
Поскольку
выборочная совокупность — это часть
генеральной совокупности, отобранная
с помощью специальных методов, — важно,
чтобы эта часть не искажала представления
о целом, т.е. репрезентировала его.
Социологов, часто проводящих эмпирические
исследования, постоянно волнует вопрос
о том, как много надо опрашивать человек,
чтобы получить достоверную информацию?
Специалисты
считают, что наилучшая выборка — не
обязательно большая. Конечно, чем больше
объем выборки, тем выше точность ее
результатов. Однако даже огромная
выборка не гарантирует успеха, если
генеральная совокупность «плохо
перемешана», т.е. является неоднородной.
Однородной считается такая совокупность,
в которой контролируемый признак
распределен равномерно, не образует
пустот или сгущений. В этом случае,
опросив нескольких человек, можно
получить точную информацию о распределении
этого признака в генеральной совокупности.
Таким
образом, на репрезентативность данных
влияют не количественные характеристики
выборочной совокупности (ее объем), а
качественные характеристики генеральной
совокупности — степень ее однородности.
В
социологии еще не придумано единой и
четкой формулы, используя которую можно
рассчитать оптимальный объем выборочной
совокупности, — такой формулы просто
не существует в природе. И объясняется
это весьма просто. Дело в том, что
определение объема выборочной совокупности
— проблема не столько статистическая,
сколько содержательная. Иными словами,
объем выборочной совокупности зависит
от множества факторов, в том числе от
целей и задач, теоретической модели,
гипотез и методов исследования, степени
однородности генеральной совокупности,
наконец, требующейся точности получаемой
информации.
Надо
всегда помнить, что каждый процент
прироста точности информации в
исследовании приводит к резкому
увеличению расходов на его проведение.
Знаменитый институт Гэллапа, на протяжении
многих десятилетий проводящий опросы
в США, выявил, что при общенациональной
выборке в 100 человек — ошибка выборки
будет в пределах ±11%; 200 человек — ±8%; 400
— ±6%; 600 — ±5%; 750 — ±4%; 1000 — ±4%; 1500 — ±3%; 4000
человек — +2%. Именно поэто-му он проводит
общенациональные опросы в США на выборке
в 1500-2000 человек. Как видно, он предпочитает
увеличение ошибки на 1% многократному
увеличению стоимости исследования.
Практика
показывает, что для многих социологов
обоснование объема выборки является
камнем преткновения, несмотря на
значительное количество литературы,
посвященной выборочным
методам
и, в частности, расчету объема выборки.
Причин несколько: 1) дефицит специальной
литературы на периферии; 2) нехватка
времени для самообразования; 3) неумение
пользоваться математическим аппаратом.
В связи с этим возникает необходимость
без сложных математических формул
изложить стратегию и тактику обоснования
объема выборки.
Процедура
расчета объема выборки — цепь бесконечных
компромиссов между стремлением к
точности и ограниченностью ресурсов,
дефицитом времени и неполнотой сведений
об изучаемом явлении. Вместе с тем это
наука и искусство, познание которых
доступно каждому человеку. Однако для
этого нужно знать стратегии расчета
объема выборки (предварительного
расчета, последовательной и комбинированной
стратегии), а также факторы, влияющие
на объем выборки (объем генеральной
совокупности, варьирование ответов
респондентов, точность оценивания,
характер предполагаемого распределения
ответов, метод исследования, процедура
обработки).
Стратегия
предварительного расчета состоит в
том, что объем выборки определяется до
проведения основного исследования. В
наиболее простом случае можно
воспользоваться уже наработанным
опытом, например, института Гэллапа,
где используется объем выборки
приблизительно в 1500—2000 человек. Для
среднестатистического отечественного
исследования объема выборки — примерно
400—600 человек.
Для
расчета объема случайной выборки надо
знать желаемую точность оценивания,
величину риска получаемого ответа и
степень изменчивости ответа. Традиционно
точность оценивания принимают за 5%, а
величину риска — за 0,95. Иными словами,
если по данным выборочного исследования
60% опрошенных удовлетворены работой,
то можно утверждать, что в генеральной
совокупности доля удовлетворенных
составит от 55 до 65% в 95% случаев, а в 5%
случаев такая доля может выйти за этот
интервал.
Стратегия
последовательного расчета объема
выборки. При расчете объема выборки
желательно знать разброс оценок и
некоторые другие параметры. Однако
они-то, как правило, неизвестны. Для того
чтобы не допустить ошибки, лучше
предположить, что они максимальны. Плата
за наше незнание — разбухание объема
выборки сверх необходимого и дополнительные
финансовые и временные затраты (приходится
опрашивать большее число людей). Для
сохранения затрат применяется
последовательная стратегия — объем
выборки не рассчитывается заранее, а
ставится в зависимость от конечных
результатов исследования. Например,
опрашивают 100 человек, затем устанавливают
величину разброса оценок и уже в
зависимости от этого рассчитывают
необходимый объем выборки. Если
оказывается, что 100 человек достаточно,
то исследование заканчивается. В
противном случае добирается необходимое
количество респондентов, но не до
бесконечности. Известен пример из
практики Дж. Гэллапа, который в начале
своей карьеры активно экспериментировал
с объемами выборки. В 1936 г. американцам
был задан вопрос: «Хотели бы вы
возобновления закона о восстановлении
национальной промышленности?» Выяснился
странный парадокс: Дж. Гэллап вначале
опросил 500 человек и замерил ошибку
выборки, а затем последовательно
наращивал число респондентов до 30 тыс.
К своему сожалению, он обнаружил, что
прибавление 29,5 тыс. опрошенных увеличило
точность информации менее чем на 1%.
Следовательно, опрос можно было прекращать
уже при 500 опрошенных. Этот пример
показывает, что, применяя последовательную
стратегию, можно добиваться значительного
снижения необходимого числа наблюдений
по сравнению с предварительным расчетом
объема выборки.
Однако
стратегия последовательного расчета
объема выборки приносит желаемый
результат лишь в том случае, если социолог
может производить необходимые расчеты
в ходе самого опроса, например телефонного,
с применением компьютерных систем.
Социолог вводит ответы респондента в
свой персональный компьютер, с него
результаты сразу поступают на компьютер
руководителя исследования, обрабатываются,
и на экране дисплея выдается информация
не только об одномерных частотах,
распределенных по тому или иному вопросу,
но и о требуемом объеме выборки.
Если
существует опасность, что объем выборки
может оказаться катастрофически большим,
надо совместить оба вида стратегии —
предварительную и последовательную,
т.е. применить комбиниро- ванную стратегию.
Рассчитывая выборку по предварительной
стратегии, получаем верхние допустимые
значения для последовательной стратегии
или, иначе говоря, ту величину объема
выборки, при достижении которой
прекращается опрос по последовательной
стратегии.
Наиболее
обоснованный и корректный подход к
определению объема выборки основан на
расчете доверительных интервалов, в:
основе которого лежит ряд базовых
понятий математической статистики
(вариация, среднее квадратическое
отклонение, доверительный интервал,
средняя квадратическая ошибка).
Для
расчета необходимого размера выборки
в количественном исследовании чаще
всего используют два статистических
понятия — доверительный интервал и
доверительную вероятность. Доверительный
интервал представляет собой заранее
задаваемую вами погрешность выборки.
Например, если вы задаете доверительный
интервал в 3% и конкретный ответ на
конкретный вопрос исследования составит
48%, это значит, что даже при проведении
опроса всей генеральной совокупности
реальное значение попадет в интервал
между 45 (48-3) и 51% (48 + 3). Доверительная
вероятность показывает, насколько вы
можете быть уверены в полученных
результатах, в том, что характеристики
выборки соответствуют характеристикам
всей генеральной совокупности -иными
словами, с какой вероятностью случайный
ответ попадет в доверительный интервал.
Обычно используют доверительную
вероятность 95 и 99%. Чаще всего используется
95% — этого вполне достаточно в подавляющем
большинстве исследований. Если объединить
доверительную вероятность и доверительный
интервал, то можно сказать, что ответы
на вопрос с 95%-ной вероятностью попадут
в интервал между 45 и 51%.
Весьма
полезна следующая приблизительная
оценка надежности результатов выборочного
обследования. Повышенная надежность
допускает ошибку выборки до 3%, обыкновенная
— от 3 до 10% (доверительный интервал
распределений на уровне 0,03-0,1), приближенная
— от 10 до 20%, ориентировочная — от 20 до
40%, а прикидочная — более 40%33.
На
основе этих понятий с учетом ряда
предположений выводятся формулы расчета
объема выборки, которые предполагают,
что репрезентативность гарантируется
путем использования корректных
вероятностных процедур формирования
выборки.
В
ряде случаев в качестве главного
аргумента при определении объема выборки
используется стоимость проведения
обследования. Так, в бюджете маркетинговых
исследований предусматриваются затраты
на проведение определенных обследований,
которые нельзя превышать, и очевидно,
что ценность получаемой информации не
принимается при этом в расчет. Однако
в ряде случаев и малая выборка может
дать достаточно точные результаты.
Исследовательская
практика подсказывает следующее правило:
объем выборки должен обеспечивать не
менее 100 наблюдений для каждой
первостепенной и не менее 20—50 наблюдений
для каждой второстепенной классификационной
составляющей. Первостепенные
классификационные составляющие
соответствуют наиболее критичным, а
второстепенные — наименее критичным
ячейкам перекрестной классификации,
принятой в данном исследовании34.
Теоретические расчеты и практика
доказывают, что для получения достоверных
данных о мнении и предпочтениях населения
такого крупного города, как Санкт-Петербург,
достаточно опросить 700—800 человек. Однако
большинство опросов населения здесь
проходят на выборках объемом до 1,5 тыс.
человек.
Ошибка
выборки
Как
мы уже знаем, репрезентативность —
свойство выборочной совокупности
представлять характеристику генеральной.
Если совпадения нет, говорят об ошибке
репрезентативности — мере отклонения
статистической структуры выборки от
структуры соответствующей генеральной
совокупности. Предположим, что средний
ежемесячный семейный доход пенсионеров
в генеральной совокупности составляет
2 тыс. руб., а в выборочной — 6 тыс. руб.
Это означает, что социолог опрашивал
только зажиточную часть пенсионеров,
а в его исследование вкралась ошибка
репрезентативности. Иными словами,
ошибкой репрезентативности называется
расхождение между двумя совокупностями
— генеральной, на которую направлен
теоретический интерес социолога и
представление о свойствах которой он
хочет получить в конечном итоге, и
выборочной, на которую направлен
практический интерес социолога, которая
выступает одновременно как объект
обследования и средство получения
информации о генеральной совокупности.
Наряду
с термином «ошибка репрезентативности»
в отечественной литературе можно
встретить другой — «ошибка выборки».
Иногда они употребляются как синонимы,
а иногда «ошибка выборки» используется
вместо «ошибки репрезентативности»
как количественно более точное понятие.
Ошибка
выборки — отклонение средних характеристик
выборочной совокупности от средних
характеристик генеральной совокупности.
На
практике ошибка выборки определяется
путем сравнения известных характеристик
генеральной совокупности с выборочными
средними. В социологии при обследованиях
взрослого населения чаще всего используют
данные переписей населения, текущего
статистического учета, результаты
предшествующих опросов. В качестве
контрольных параметров обычно применяются
социально-демографические признаки.
Сравнение средних генеральной и
выборочной совокупностей, на основе
этого определение ошибки выборки и ее
уменьшение называется контролированием
репрезентативности. Поскольку сравнение
своих и чужих данных можно сделать по
завершении исследования, такой способ
контроля называется апостериорным,
т.е. осуществляемым после опыта.
В
опросах Института Дж. Гэллапа
репрезентативность контролируется по
имеющимся в национальных переписях
данным о распределении населения по
полу, возрасту, образованию, доходу,
профессии, расовой принадлежности,
месту проживания, величине населенного
пункта. Всероссийский центр изучения
общественного мнения (ВЦИОМ) использует
для подобных целей такие показатели,
как пол, возраст, образование, тип
поселения, семейное положение, сфера
занятости, должностной ста- туе
респондента, которые заимствуются в
Государственном комитете по статистике
РФ. В том и другом случае генеральная
совокупность известна. Ошибку выборки
невозможно установить, если неизвестны
значения переменной в выборочной и
генеральной совокупностях.
Специалисты
ВЦИОМ обеспечивают при анализе данных
тщательный ремонт выборки, чтобы
минимизировать отклонения, возникшие
на этапе полевых работ. Особенно сильные
смещения наблюдаются по параметрам
пола и возраста. Объясняется это тем,
что женщины и люди с высшим образованием
больше времени проводят дома и легче
идут на контакт с интервьюером, т.е.
являются легко достижимой группой по
сравнению с мужчинами и людьми
«необразованными»35.
Ошибка
выборки обусловливается двумя факторами:
методом формирования выборки и размером
выборки.
Ошибки
выборки подразделяются на два типа —
случайные и систематические. Случайная
ошибка — это вероятность того, что
выборочная средняя выйдет (или не выйдет)
за пределы заданного интервала. К
случайным ошибкам относят статистические
погрешности, присущие самому выборочному
методу. Они уменьшаются при возрастании
объема выборочной совокупности.
Второй
тип ошибок выборки — систематические
ошибки. Если социолог решил узнать
мнение всех жителей города о проводимой
местными органами власти социальной
политике, а опросил только тех, у кого
есть телефон, то возникает предумышленное
смещение выборки в пользу зажиточных
слоев, т.е. систематическая ошибка.
Таким
образом, систематические ошибки —
результат деятельности самого
исследователя. Они наиболее опасны,
поскольку приводят к довольно значительным
смещениям результатов исследования36.
Систематические ошибки считаются
страшнее случайных еще и потому, что
они не поддаются контролю и измерению.
Репрезентативность
(от франц. représentatif — представляющий
собой что-либо, показательный) в
статистике, главное свойство выборочной
совокупности, состоящее в близости её
характеристик (состава, средних величин
и др.) к соответствующим характеристикам
генеральной совокупности, из которой
отобрана (с соблюдением определённых
правил) выборочная (см. Выборочное
наблюдение). Суждение о степени Р.
выносится на основании рассмотрения
выборочной совокупности в двух
направлениях. Во-первых, она сравнивается
с генеральной совокупностью в отношении
всех признаков, зафиксированных как в
той, так и в другой. Так, для суждения о
Р. совокупности семей, отобранных для
наблюдения семейных бюджетов, сравнивают
их распределение по уровню заработной
платы работников с аналогичным
распределением по общим статистическим
данным или (при отсутствии общих данных
о распределении) сравнивают средние
уровни заработной платы и т. д. Во-вторых,
суждение о степени Р. может быть вынесено
на основании колеблемости исследуемых
характеристик в выборочной совокупности.
Так, если по данным обследования семейных
бюджетов, например, душевое потребление
хлеба от семьи к семье колеблется гораздо
меньше, чем потребление мяса, то это
даёт основание считать Р. данной выборки
в отношении потребления хлеба большей,
чем в отношении мяса.
Р.
измеряется «ошибкой репрезентативности»,
т. е. разностью между характеристиками
выборочной и генеральной совокупностей.
Однако фактическая (действительная)
величина указанной разности остаётся
неизвестной, вследствие чего мерой Р.
служит определяемая по правилам
математической статистики её вероятная
величина или же средняя квадратическая
её возможных значений (см. также Выборочный
метод).
Проблема
репрезентативности выборки
Задача
индуктивной статистики – определять,
достаточно ли велика разность между
средними двух распределений для того,
чтобы можно было объяснить ее действие
независимой переменной, а не случайностью,
связанной с малым объемом выборки,
отсутствием репрезентативности.
Основная
проблема репрезентативности выборки
– величина и верность образцов. Величина
представленности образцов зависит от
степени однородности целого (чем
однороднее целое, тем меньше требуется
образцов); от численности категорий и
классов, на которые подразделяются
результаты исследования (чем их больше,
тем больше должно быть образцов); от
количества работников, привлеченных к
исследованию; от финансирования.
Выборки
называются статистически однородными,
если их распределения сходны, а различия
между ними пренебрежимо малы. В противном
случае, когда различия велики, а сходство
пренебрежимо мало, выборки статистически
неоднородны.
В
некоторых случаях исследователю
приходится проверять гипотезы об
однородности (неоднородности) через
параметры, делая определенные допущения
о виде распределения. Это делается не
просто путем проверки сходства или
различия средних арифметических
значений, но с учетом того, что все
распределения (кроме Пуассона) имеют
два или больше параметров, к примеру,
нормальное распределение Гаусса и
гамма-распределение, которым следуют
многие психологические и педагогические
явления, являются двухпараметрическими.
Поэтому вместо простой гипотезы о
сходстве (различии) двух функций
распределения необходимо проверять
сложную гипотезу о сходстве двух средних
арифметических и одновременно о сходстве
двух дисперсий. Только такая гипотеза
может быть адекватной в этом случае.
Объём
выборки — число случаев, включённых в
выборочную совокупность. Из статистических
соображений рекомендуется, чтобы число
случаев составляло не менее 30—35.
Ошибки
выборки
При
любом статистическом наблюдении
(сплошном и выборочном) могут встретиться
ошибки двух видов: регистрации и
репрезентативности. Ошибки регистрации
могут иметь случайный и систематический
характер. Случайные ошибки складываются
из множества различных неконтролируемых
причин, носят непреднамеренный характер
и обычно по совокупности уравновешивают
друг друга (например, изменения показателей
прибора при температурных колебаниях
в помещении).
Систематические
ошибки тенденциозны, так как нарушают
правила отбора объектов в выборку
(например, отклонения в измерениях при
изменении настройки измерительного
прибора).
Пример.
Для оценки социального положения
населения в городе предусмотрено
обследовать 25% семей. Если при этом выбор
каждой четвертой квартиры основан на
ее номере, то существует опасность
отобрать все квартиры только одного
типа (например, однокомнатные), что
обеспечит систематическую ошибку и
исказит результаты; выбор же номера
квартиры по жребию более предпочтителен,
так как ошибка будет случайной.
Ошибки
репрезентативности присущи только
выборочному наблюдению, их невозможно
избежать и они возникают в результате
того, что выборочная совокупность не
полностью воспроизводит генеральную.
Значения показателей, получаемых по
выборке, отличаются от показателей этих
же величин в генеральной совокупности
(или получаемых при сплошном наблюдении).
Ошибка
выборочного наблюдения есть разность
между значением параметра в генеральной
совокупности и ее выборочным значением.
Для среднего значения количественного
признака она равна: , а для доли
(альтернативного признака) — .
Ошибки
выборки свойственны только выборочным
наблюдениям. Чем больше эти ошибки, тем
больше эмпирическое распределение
отличается от теоретического. Параметры
эмпирического распределения и являются
случайными величинами, следовательно,
ошибки выборки также являются случайными
величинами, могут принимать для разных
выборок разные значения и поэтому
принято вычислять среднюю ошибку.
Средняя
ошибка выборки есть величина , выражающая
среднее квадратическое отклонение
выборочной средней от математического
ожидания. Эта величина при соблюдении
принципа случайного отбора зависит
прежде всего от объема выборки и от
степени варьирования признака: чем
больше и чем меньше вариация признака
(следовательно, и значение ), тем меньше
величина средней ошибки выборки .
Соотношение между дисперсиями генеральной
и выборочной совокупностей выражается
формулой:
т.е.
при достаточно больших можно считать,
что . Средняя ошибка выборки показывает
возможные отклонения параметра выборочной
совокупности от параметра генеральной.
В табл. 9.2 приведены выражения для
вычисления средней ошибки выборки при
разных методах организации наблюдения.
Ошибки
выборки
Рассмотрим
подробно перечисленные выше способы
формирования выборочной совокупности
и возникающие при этом ошибки
репрезентативности.
Собственно-случайная
выборка основывается на отборе единиц
из генеральной совокупности наугад без
каких-либо элементов системности.
Технически собственно-случайный отбор
проводят методом жеребьевки (например,
розыгрыши лотерей) или по таблице
случайных чисел.
Собственно-случайный
отбор «в чистом виде» в практике
выборочного наблюдения применяется
редко, но он является исходным среди
других видов отбора, в нем реализуются
основные принципы выборочного наблюдения.
Рассмотрим некоторые вопросы теории
выборочного метода и формулы ошибок
для простой случайной выборки.
19
2.
Типы и методы выборки
Типами
выборки называются основные разновидности
статистической выборки: случайная
(вероятностная) и неслучайная
(невероятностная). Вместо термина «тип
выборки» часто употребляют слова «вид»
и «разновидность», что также правильно.
Тип выборки говорит о том, как люди
попадают в выборочную совокупность,
объем выборки сообщает о том, какое их
количество туда попало.
Методом
выборки будем называть способ построения
того типа выборки, название которого
этот метод носит, например метод
вероятностной выборки. В социологии
методом называют основной способ сбора,
обработки или анализа данных; правила
и процедуры, с помощью которых
устанавливается связь между фактами,
гипотезами и теориями.
Для
каждого типа выборки разработаны свои
математические аппараты и процедуры.
Так, в простой случайной выборке все
элементы из списка людей, составляющих
основу выборки, пронумеровываются и с
помощью таблицы случайных чисел из них
отбирается искомая совокупность.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные определения
Понятие выборки используется, когда надо изучить какие-либо свойства совокупности объектов. Свойства объектов можно разделить на качественные и количественные.
Пример 1
Пусть нам необходимо изучить совокупность партии сметаны. Тогда качественным признаком может служить срок её годности, а количественным процент содержания жиров в данной сметане.
Совокупность или выборка может быть разделена на генеральную и выборочную.
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 4 500 ₽
Определение 2
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
С понятием совокупности также связано понятие объема данной совокупности.
Определение 3
Объем совокупности — число объектов этой совокупности.
Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.
Пример 2
Пусть из партии 100 пачек масла для исследования выбрано 10 пачек. Тогда объем генеральной совокупности $N=100$, а объем выборки $n=10$.
Примечание 1
Исходя из первых двух определений, очевидно, что всегда выполняется неравенство $N>n$
«Генеральная и выборочная совокупности, выборки» 👇
Помимо этих двух совокупностей выделяют также репрезентативную или представительную выборку.
Определение 4
Репрезентативная (представительная) выборка — выборка, в которой все объекты выбраны случайно и генеральной совокупности, то есть каждый объект генеральной совокупности имеет одинаковую вероятность попасть в выборку.
Выборка также может быть повторной и бесповторной.
Определение 5
Повторная выборка — выборка, при которой выбранный объект возвращается обратно в генеральную совокупность перед выбором следующего объекта для исследования.
Определение 6
Бесповторная выборка — выборка, при которой объект не возвращается обратно в генеральную совокупность перед выбором очередного объекта для исследования.
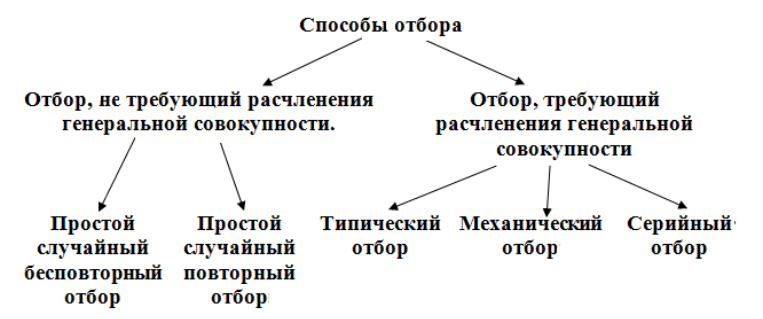
Способы отбора
Рассмотрим теперь различные способы отбора (схема 1).
Рисунок 1. Способы отбора.
Разберемся теперь с каждым понятием по отдельности.
Определение 7
Простой случайный бесповторный отбор — отбор, при котором объекты из генеральной совокупности выбираются по одному и не возвращаются обратно в генеральную совокупность.
Определение 8
Простой случайный повторный отбор — отбор, при котором объекты из генеральной совокупности выбираются по одному и возвращаются обратно в генеральную совокупность.
Определение 9
Типический отбор — отбор, при котором выборка производится не из всей генеральной совокупности, а из каждой его части по отдельности.
Пример 3
К примеру, если сметана произведена на трех разных заводах, то выборка делается по каждому заводу отдельно.
Определение 10
Механический отбор — отбор, при котором генеральная совокупность делится на такое количество групп сколько объектов для исследования необходимо выбрать.
Пример 4
Пусть из партии 100 пачек масла нужно для исследования отобрать $10%$. Тогда выбирается по одной пачке из каждых 10 пачек масла.
!!! Отметим, что при таком отборе выборка не всегда получается репрезентативной.
Определение 11
Серийный отбор — отбор, при котором выборка происходит из генеральной совокупности не по одному, а сериями.
!!! На практике часто применяется комбинированный отбор, при котором используются сразу несколько видов отборов, перечисленных выше.
Формулы, связанные с понятием выборки
Введем несколько формул:
- Генеральная средняя при повторной выборке:
Отметим, что $sum{N_i}=N$
- Генеральная средняя при бесповторной выборке:
- Выборочная средняя при повторной выборке:
Отметим, что $sum{n_i}=n$
- Выборочная средняя при бесповторной выборке:
- Ошибка репрезентативности:
Пример задачи на нахождение ошибки репрезентативности
Пример 5
Пусть в магазине 20 видов глазированных сырков. Средняя цена 1 вида сырка составляет 10,4 рублей. Сырков с начинкой из этих видов составляет $25%$ и средняя цена каждого вида с начинкой равняется 11 рублей. Найти ошибку репрезентативности данной выборки.
Решение:
Ошибка репрезентативности:
[triangle =overline{x}-overline{X}]
10,4 — это генеральная средняя величина, то есть $overline{X}=10,4$.
Так как сырки с начинкой составляют $25%$, то сырков с начинкой$20cdot 0,25=5$ видов.
Тогда выборочная средняя $overline{x}=11$.
Получаем:
[triangle =overline{x}-overline{X}=11-10,4=0,6]
Ответ: 0,6.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Поговорим о том, что такое выборка и генеральная совокупность, чем они отличаются, и возможно ли определить генеральную совокупность при ограниченном наборе данных.
Давайте представим, что у нас стоит задача получить количественные данные (quantitative data) о росте всех мужчин в России. Когда мы говорим о количественных данных, мы всегда говорим о каком-нибудь числовом значении. Приступив к делу, можем начать опрашивать мужчин на улице, помещая полученные данные, к примеру, в Python-список:
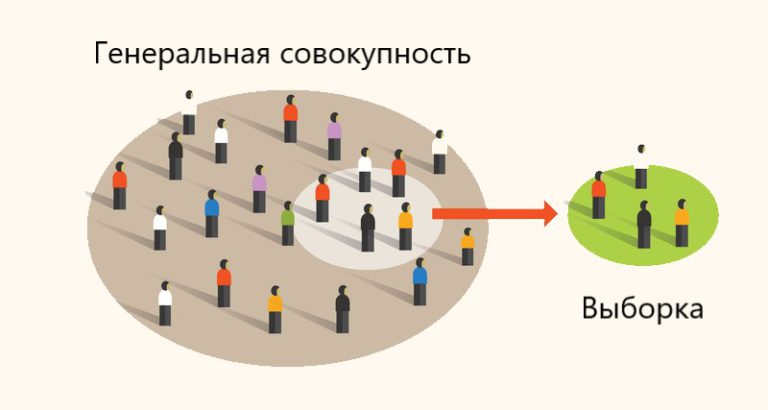
# данные по 1000 респондентов в сантиметрах [185.0, 179.0, 186.0, 195.0, 178.0, 178.0, 196.0, 188.0, 175.0, 185.0, 175.0, 175.0, 182.0, 161.0, 163.0, 174.0, 170.0, 183.0, 171.0, 166.0, 195.0, 178.0, 181.0, 166.0, 175.0, 181.0, 168.0, 184.0, 174.0, 177.0, 174.0, 199.0, 180.0, 169.0, 188.0, 168.0, 182.0, 160.0, 167.0, 182.0, 187.0, 182.0, 179.0, 177.0, 165.0, 173.0, 175.0, 191.0, 183.0, 162.0, 183.0, 176.0, 173.0, 186.0, 190.0, 189.0, 172.0, 177.0, 183.0, 190.0, 175.0, 178.0, 169.0, 168.0, 188.0, 194.0, 179.0, 190.0, 184.0, 174.0, 184.0, 195.0, 180.0, 196.0, 154.0, 188.0, 181.0, 177.0, 181.0, 160.0, 178.0, 184.0, 195.0, 175.0, 172.0, 175.0, 189.0, 183.0, 175.0, 185.0, 181.0, 190.0, 173.0, 177.0, 176.0, 165.0, 183.0, 183.0, 180.0, 178.0, 166.0, 176.0, 177.0, 172.0, 178.0, 184.0, 199.0, 182.0, 183.0, 179.0, 161.0, 180.0, 181.0, 205.0, 178.0, 183.0, 180.0, 168.0, 191.0, 188.0, 188.0, 171.0, 194.0, 166.0, 186.0, 202.0, 170.0, 174.0, 181.0, 175.0, 164.0, 181.0, 169.0, 185.0, 171.0, 195.0, 172.0, 177.0, 188.0, 168.0, 182.0, 193.0, 164.0, 182.0, 183.0, 188.0, 168.0, 167.0, 185.0, 183.0, 183.0, 183.0, 173.0, 182.0, 183.0, 173.0, 199.0, 185.0, 168.0, 187.0, 170.0, 188.0, 192.0, 172.0, 190.0, 184.0, 188.0, 199.0, 178.0, 172.0, 171.0, 172.0, 179.0, 183.0, 183.0, 188.0, 180.0, 195.0, 177.0, 207.0, 186.0, 171.0, 169.0, 185.0, 178.0, 187.0, 185.0, 179.0, 172.0, 165.0, 176.0, 189.0, 182.0, 168.0, 182.0, 184.0, 171.0, 182.0, 181.0, 169.0, 184.0, 186.0, 191.0, 191.0, 166.0, 171.0, 185.0, 185.0, 185.0, 219.0, 186.0, 191.0, 190.0, 187.0, 177.0, 188.0, 172.0, 178.0, 175.0, 181.0, 203.0, 161.0, 187.0, 164.0, 175.0, 191.0, 181.0, 169.0, 173.0, 187.0, 173.0, 182.0, 180.0, 173.0, 201.0, 186.0, 160.0, 182.0, 173.0, 189.0, 172.0, 179.0, 185.0, 189.0, 168.0, 177.0, 175.0, 173.0, 198.0, 184.0, 167.0, 189.0, 201.0, 190.0, 165.0, 175.0, 193.0, 173.0, 184.0, 188.0, 171.0, 179.0, 148.0, 170.0, 177.0, 168.0, 196.0, 166.0, 176.0, 181.0, 194.0, 166.0, 192.0, 180.0, 170.0, 185.0, 182.0, 174.0, 181.0, 176.0, 181.0, 187.0, 196.0, 168.0, 201.0, 160.0, 178.0, 186.0, 183.0, 174.0, 178.0, 175.0, 174.0, 188.0, 184.0, 173.0, 189.0, 183.0, 188.0, 186.0, 172.0, 174.0, 187.0, 186.0, 180.0, 181.0, 193.0, 174.0, 185.0, 178.0, 178.0, 191.0, 188.0, 188.0, 193.0, 180.0, 187.0, 177.0, 183.0, 179.0, 181.0, 186.0, 172.0, 201.0, 170.0, 168.0, 192.0, 188.0, 186.0, 186.0, 180.0, 171.0, 181.0, 173.0, 190.0, 179.0, 172.0, 177.0, 184.0, 174.0, 172.0, 182.0, 182.0, 175.0, 175.0, 182.0, 166.0, 166.0, 173.0, 178.0, 183.0, 195.0, 189.0, 178.0, 180.0, 170.0, 180.0, 177.0, 183.0, 172.0, 185.0, 195.0, 179.0, 184.0, 187.0, 176.0, 182.0, 180.0, 181.0, 172.0, 180.0, 185.0, 195.0, 190.0, 202.0, 172.0, 189.0, 182.0, 202.0, 172.0, 172.0, 174.0, 159.0, 175.0, 172.0, 182.0, 183.0, 199.0, 190.0, 174.0, 171.0, 185.0, 167.0, 198.0, 192.0, 175.0, 163.0, 194.0, 179.0, 192.0, 164.0, 174.0, 180.0, 180.0, 175.0, 186.0, 169.0, 179.0, 181.0, 185.0, 187.0, 169.0, 165.0, 193.0, 183.0, 173.0, 196.0, 181.0, 192.0, 181.0, 201.0, 198.0, 178.0, 190.0, 186.0, 194.0, 170.0, 187.0, 191.0, 162.0, 168.0, 160.0, 177.0, 187.0, 195.0, 181.0, 196.0, 166.0, 163.0, 179.0, 184.0, 180.0, 159.0, 179.0, 167.0, 187.0, 184.0, 171.0, 175.0, 169.0, 179.0, 190.0, 170.0, 185.0, 175.0, 172.0, 179.0, 170.0, 174.0, 168.0, 200.0, 180.0, 173.0, 182.0, 179.0, 178.0, 186.0, 188.0, 175.0, 174.0, 177.0, 157.0, 165.0, 194.0, 196.0, 178.0, 186.0, 183.0, 211.0, 191.0, 179.0, 170.0, 164.0, 182.0, 172.0, 166.0, 174.0, 169.0, 197.0, 189.0, 180.0, 195.0, 181.0, 171.0, 195.0, 185.0, 170.0, 178.0, 171.0, 166.0, 189.0, 199.0, 166.0, 186.0, 173.0, 175.0, 174.0, 171.0, 180.0, 172.0, 183.0, 179.0, 178.0, 171.0, 174.0, 188.0, 185.0, 170.0, 181.0, 188.0, 163.0, 185.0, 173.0, 186.0, 172.0, 162.0, 164.0, 180.0, 183.0, 171.0, 186.0, 163.0, 179.0, 168.0, 173.0, 180.0, 171.0, 176.0, 190.0, 174.0, 188.0, 169.0, 185.0, 194.0, 155.0, 172.0, 186.0, 178.0, 184.0, 174.0, 181.0, 178.0, 192.0, 183.0, 183.0, 176.0, 175.0, 176.0, 184.0, 176.0, 183.0, 201.0, 189.0, 177.0, 192.0, 176.0, 160.0, 170.0, 161.0, 176.0, 180.0, 197.0, 183.0, 178.0, 188.0, 158.0, 182.0, 188.0, 165.0, 191.0, 183.0, 176.0, 186.0, 203.0, 182.0, 182.0, 175.0, 172.0, 188.0, 171.0, 181.0, 175.0, 185.0, 183.0, 190.0, 175.0, 177.0, 170.0, 176.0, 184.0, 188.0, 171.0, 189.0, 194.0, 184.0, 199.0, 172.0, 168.0, 162.0, 195.0, 187.0, 179.0, 183.0, 169.0, 204.0, 181.0, 181.0, 187.0, 185.0, 182.0, 172.0, 185.0, 199.0, 193.0, 196.0, 175.0, 170.0, 179.0, 181.0, 191.0, 163.0, 195.0, 178.0, 176.0, 170.0, 163.0, 188.0, 181.0, 167.0, 167.0, 177.0, 197.0, 177.0, 165.0, 178.0, 177.0, 153.0, 179.0, 178.0, 187.0, 198.0, 191.0, 177.0, 169.0, 206.0, 181.0, 180.0, 180.0, 182.0, 179.0, 174.0, 175.0, 180.0, 175.0, 173.0, 181.0, 177.0, 195.0, 153.0, 191.0, 192.0, 159.0, 177.0, 176.0, 166.0, 172.0, 169.0, 198.0, 189.0, 193.0, 187.0, 169.0, 175.0, 185.0, 168.0, 187.0, 178.0, 176.0, 187.0, 184.0, 176.0, 192.0, 169.0, 186.0, 186.0, 177.0, 183.0, 167.0, 189.0, 178.0, 175.0, 190.0, 173.0, 166.0, 164.0, 186.0, 167.0, 198.0, 159.0, 197.0, 182.0, 179.0, 175.0, 184.0, 180.0, 191.0, 181.0, 182.0, 176.0, 179.0, 183.0, 163.0, 167.0, 187.0, 182.0, 178.0, 180.0, 183.0, 175.0, 172.0, 182.0, 170.0, 184.0, 163.0, 190.0, 185.0, 183.0, 190.0, 197.0, 190.0, 162.0, 167.0, 174.0, 180.0, 185.0, 173.0, 182.0, 172.0, 174.0, 166.0, 171.0, 166.0, 170.0, 191.0, 171.0, 206.0, 185.0, 182.0, 171.0, 187.0, 174.0, 181.0, 206.0, 179.0, 191.0, 173.0, 180.0, 198.0, 174.0, 198.0, 187.0, 174.0, 186.0, 190.0, 186.0, 164.0, 173.0, 178.0, 179.0, 186.0, 182.0, 167.0, 184.0, 186.0, 186.0, 191.0, 188.0, 185.0, 179.0, 163.0, 184.0, 182.0, 183.0, 167.0, 169.0, 191.0, 180.0, 187.0, 180.0, 180.0, 189.0, 175.0, 181.0, 175.0, 176.0, 177.0, 182.0, 175.0, 193.0, 171.0, 178.0, 176.0, 194.0, 182.0, 190.0, 165.0, 183.0, 189.0, 181.0, 191.0, 175.0, 194.0, 203.0, 176.0, 176.0, 195.0, 196.0, 175.0, 176.0, 177.0, 167.0, 171.0, 170.0, 172.0, 180.0, 182.0, 196.0, 170.0, 190.0, 178.0, 180.0, 187.0, 169.0, 184.0, 182.0, 185.0, 183.0, 205.0, 174.0, 175.0, 174.0, 174.0, 174.0, 192.0, 194.0, 174.0, 172.0, 185.0, 174.0, 186.0, 182.0, 165.0, 195.0, 198.0, 174.0, 176.0, 183.0, 183.0, 187.0, 200.0, 178.0, 172.0, 166.0, 173.0, 180.0, 198.0, 175.0, 182.0, 180.0, 192.0, 205.0, 175.0, 175.0, 190.0, 187.0, 198.0, 186.0, 176.0, 186.0, 191.0, 188.0, 185.0, 191.0, 192.0, 194.0, 186.0, 178.0, 181.0, 192.0, 172.0, 184.0, 176.0, 180.0, 193.0, 182.0, 180.0, 166.0, 187.0, 186.0, 202.0, 177.0, 182.0, 182.0, 196.0, 179.0, 183.0, 186.0, 182.0, 176.0, 182.0, 191.0, 170.0, 181.0, 173.0, 192.0, 165.0, 174.0, 184.0, 196.0, 179.0, 174.0, 199.0, 166.0, 158.0, 184.0, 175.0, 170.0, 187.0, 182.0, 174.0, 167.0, 189.0, 187.0, 179.0, 198.0, 169.0, 165.0, 173.0, 180.0, 182.0, 178.0, 184.0, 167.0, 194.0, 179.0, 191.0, 183.0, 185.0, 186.0, 184.0, 186.0, 193.0, 182.0, 187.0, 179.0, 194.0, 173.0, 198.0, 180.0, 166.0, 181.0, 173.0, 188.0, 173.0, 176.0, 161.0, 175.0, 156.0, 164.0, 188.0, 188.0, 184.0, 170.0, 180.0, 180.0, 168.0, 195.0, 189.0, 178.0, 180.0, 182.0, 160.0, 178.0, 173.0, 170.0, 177.0, 198.0, 186.0, 174.0, 186.0]Опросив тысячу респондентов, можем ли мы сказать, что полученные результаты полностью отражают фактические показатели роста всех российских мужчин? Нет, не можем, ведь мы же не измеряли рост каждого человека. То есть на первый взгляд задача кажется нереализуемой.
По сути, те мужчины, которых удалось измерить, попали в выборку (sample). А все российские мужчины — это генеральная совокупность (population).
Но можно ли вообще хоть как-то определить генеральную совокупность, имея ограниченный набор данных? На самом деле, да. Существует теоретическое обоснование этой возможности и называется оно Центральной предельной теоремой.
Центральная предельная теорема
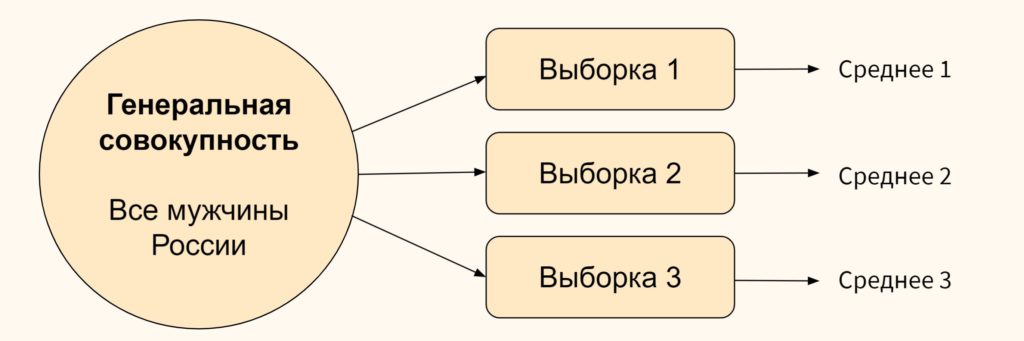
Central Limit Theorem говорит, что при множественном выборочном сборе данных среднее средних всех полученных выборок (распределение средних) станет стремиться к среднему генеральной совокупности. Давайте рассмотрим, как это может выглядеть на практике.
Возьмем несколько выборок из одной генеральной совокупности и узнаем среднее из каждой выборки.
Теперь посчитаем среднее арифметическое средних наших выборок. Мы получим новое среднее значение, которое станет стремиться к среднему генеральной совокупности (для обозначения используется греческая буква μ, «мю»).
Что из этого всего следует? На самом деле, очень важная вещь: по факту мы получили возможность сказать что-либо определенное про ту величину, которую в принципе невозможно охватить измерением.
По материалам сайта https://www.dmitrymakarov.ru/intro/.