Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.
Что такое P-значение
P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.
Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.
Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.
Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.
Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном
- Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
- Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
- Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.
Статистическая значимость
Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.
Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.
Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.
Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.
Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.
Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.
Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.
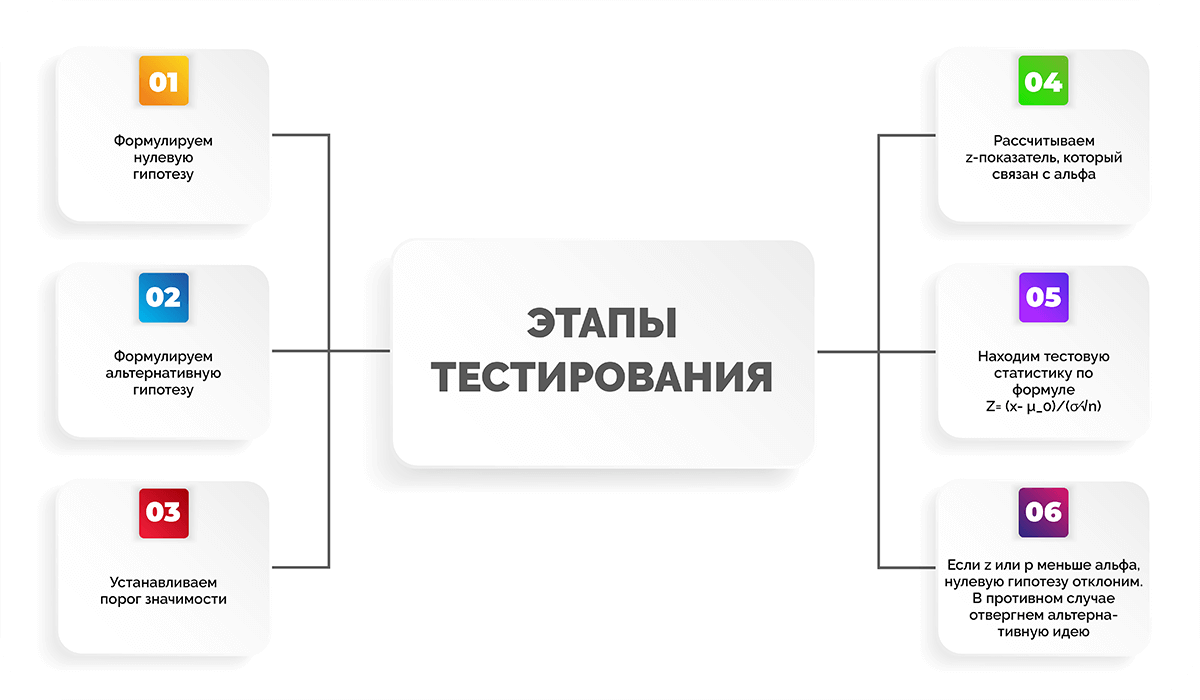
Все тестирование можно разделить на несколько этапов:
- Формулируем нулевую гипотезу.
- Формулируем альтернативную гипотезу.
- Устанавливаем порог значимости.
- Рассчитываем z-показатель, который связан с альфа.
- Находим тестовую статистику по формуле
.
- Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.
Порог вероятности
В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.
Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.
Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.
Доверительные уровни
Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.
Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.
|
Доверительный уровень |
Стандартное отклонение (z-оценка) |
Вероятность (p-уровень) |
|
90% |
< -1,65 или > +1,65 |
< 0,10 |
|
95% |
< -1,96 или > +1,96 |
< 0,05 |
|
99% |
< -2,58 или > +2,58 |
< 0,01 |
Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.
Проверка статистических гипотез
Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).
Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.
Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии
Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.
В статистике применяется рандомизация и нормализация нулевой гипотезы.
Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.
Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.
Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.
Подход p-value к проверке гипотез
Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.
Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.
Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.
Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».
Как рассчитать P-value
Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.
Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.
Как рассчитать p-значение, используя тестовую статистику
Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.
Левосторонний эксперимент:
P-value = cdf (x)
Правосторонний эксперимент:
P-value = 1 – cdf (x)
Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}
Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.
Пошаговый алгоритм расчета p-значения
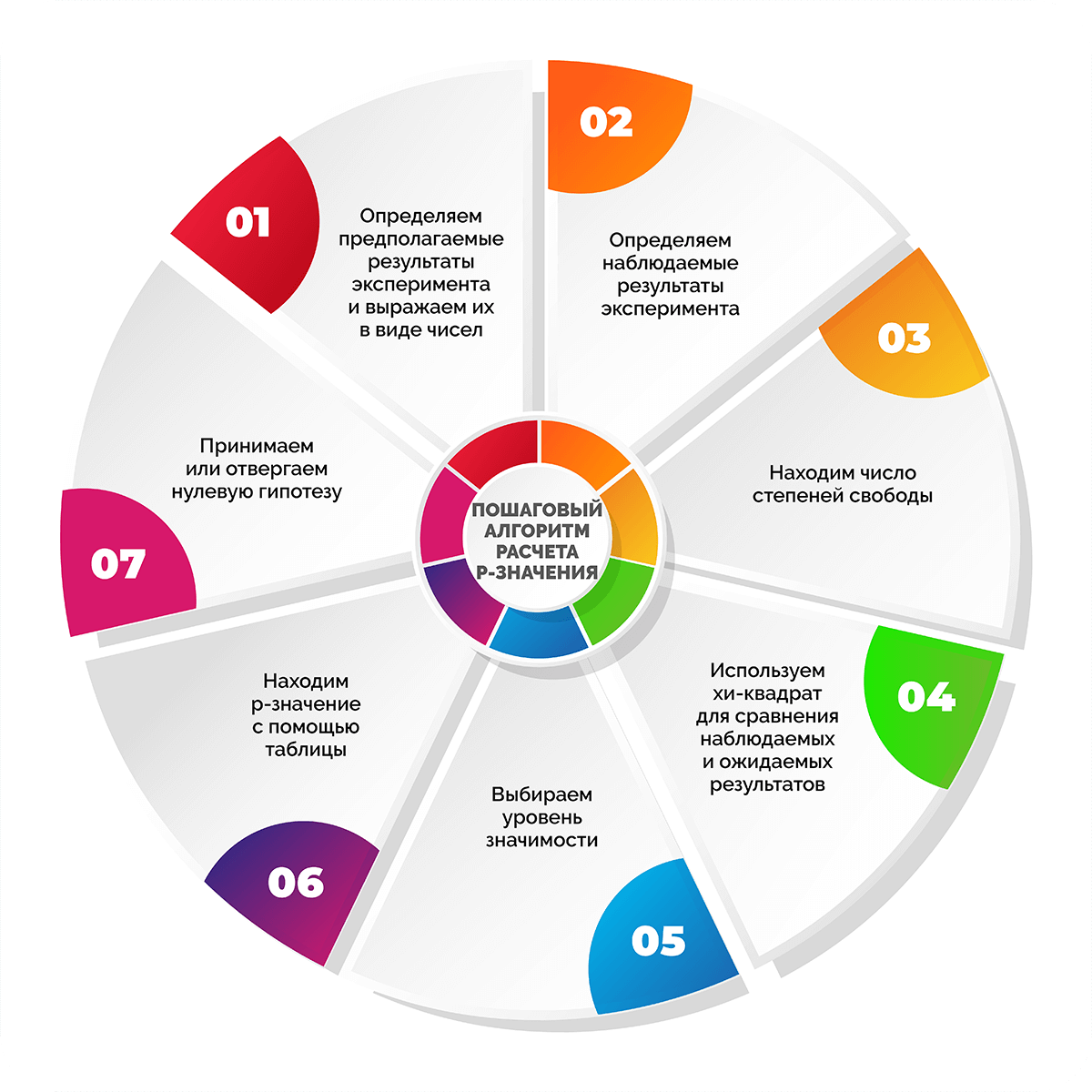
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел
Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.
Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.
Шаг 2. Определяем наблюдаемые результаты эксперимента
Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.
Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.
Шаг 3. Находим число степеней свободы
Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.
Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.
В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.
Число степеней свободы = 2 – 1 = 1.
Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.
Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов
Хи-квадрат (х2) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.
где:
о – наблюдаемое значение;
е – ожидаемое значение.
Подставляем наши цифры в уравнение и учитываем, что 
х2 = ((220 – 200)2/200) + ((80 – 100)2/100) = ((20)2/200)) + ((-20)2/100) = (400/200) + (400/100) = 2 + 4 = 6.
Шаг 5. Выбираем уровень значимости
Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.
Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.
В нашем случае примем статистическую значимость, равную 0,05.
Шаг 6. Находим p-значение с помощью таблицы
Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.
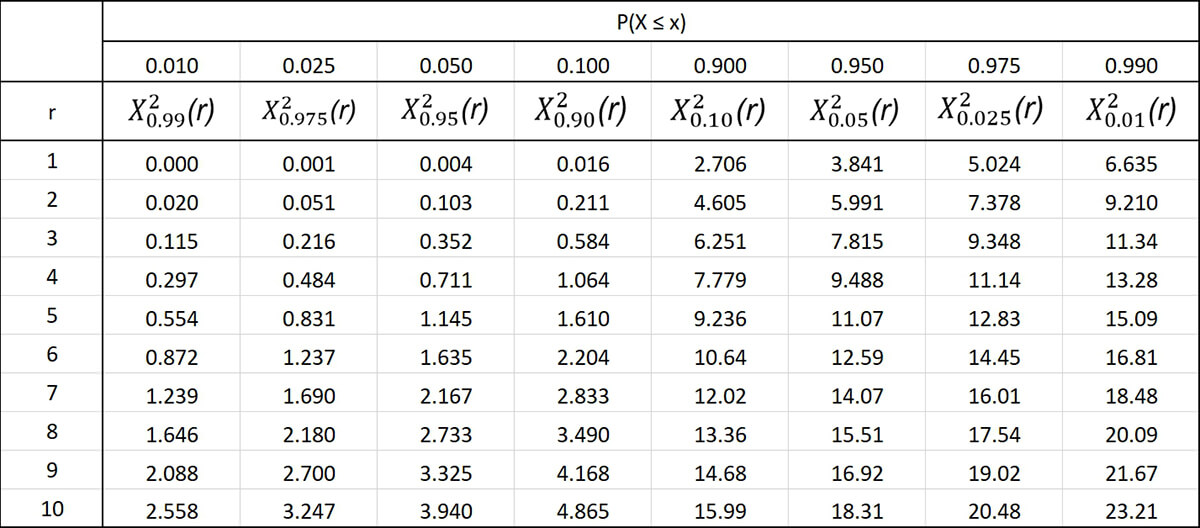
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.
Шаг 7. Принимаем или отвергаем нулевую гипотезу
Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.
В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.
Как интерпретировать P-значение
P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.
- Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
- Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.
Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.
P-значение – это…
- вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
- вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.
Что нужно помнить о P-значениях
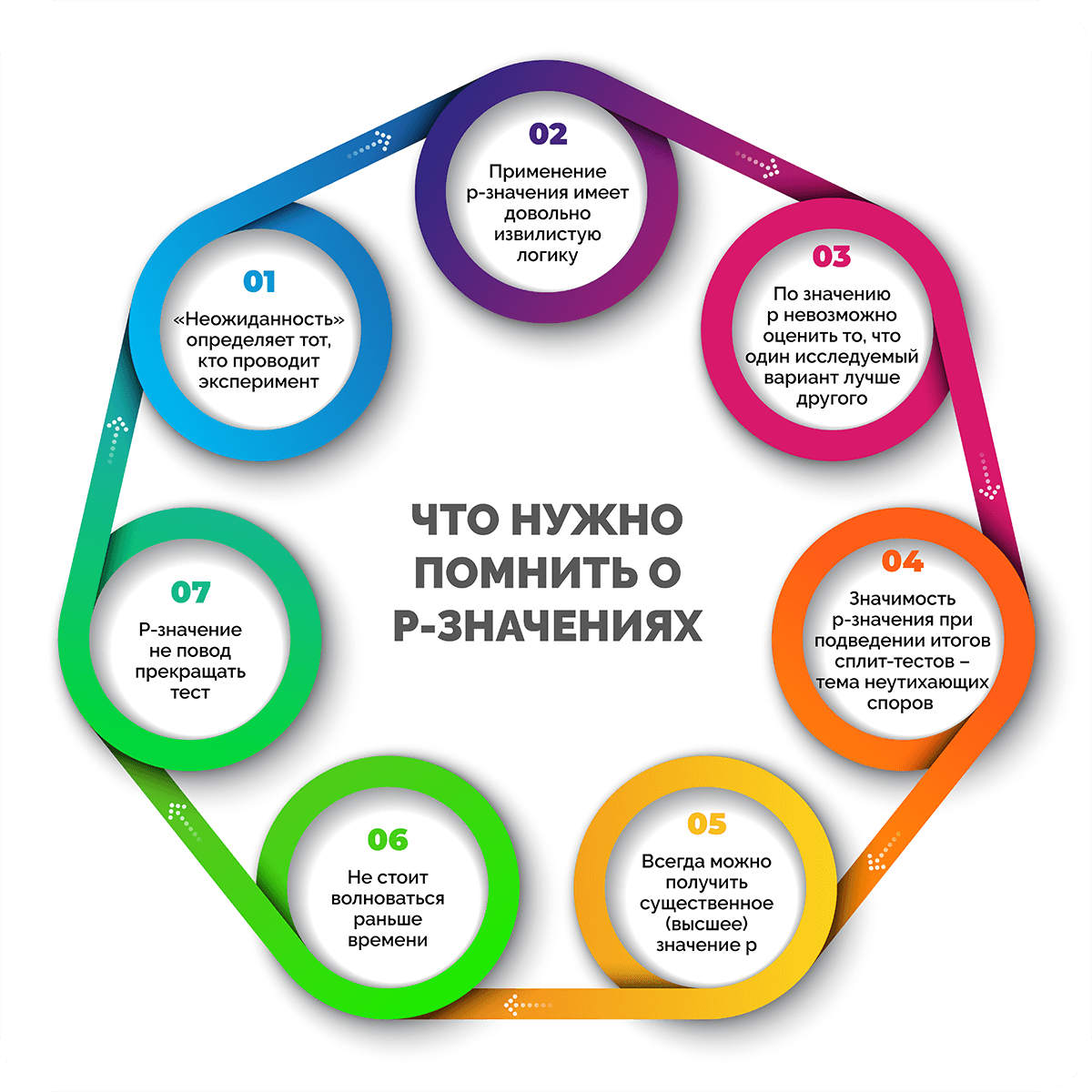
- «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
- Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
- По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
- Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
- Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
- Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
- P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.
Примеры интерпретации P-значений
На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.
По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.
Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.
Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.
Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.
Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.
Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.
Часто задаваемые вопросы
P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.
Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.
Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.
Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:
- При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
- Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.
Заключение
Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Что такое p-value?
P-значение (англ. P-value) — величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-значения является альтернативой классической процедуре проверки через критическое значение распределения.
Обычно P-значение равно вероятности того, что случайная величина с данным распределением (распределением тестовой статистики при нулевой гипотезе) примет значение, не меньшее, чем фактическое значение тестовой статистики. Википедия.
Иначе говоря, p-значение – это наименьшее значение уровня значимости (т.е. вероятности отказа от справедливой гипотезы), для которого вычисленная проверочная статистика ведет к отказу от нулевой гипотезы. Обычно p-значение сравнивают с общепринятыми стандартными уровнями значимости 0,005 или 0,01.
Например, если вычисленное по выборке значение проверочной статистики соответствует p = 0,005, это указывает на вероятность справедливости гипотезы 0,5%. Таким образом, чем p-значение меньше, тем лучше, поскольку при этом увеличивается «сила» отклонения нулевой гипотезы и увеличивается ожидаемая значимость результата.
Интересное объяснение этого есть на Хабре.
Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value).
О чём говорит p-value?
Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры). В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.
Примеры про p-value
Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верное утверждение:
1.Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
2. Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
3. Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
4. Вероятность случайно получить такие различия равняется 0.04.
5. Все утверждения неверны.
Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value.
Давайте разберём все ответы по порядку:
Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.
Это уже более интересное утверждение. Всё дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».
А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.
Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или ещё более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!
Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.
Как найти p-value?
Источник.
1. Определите ожидаемые в вашем эксперименте результаты
Обычно когда ученые проводят эксперимент, у них уже есть идея того, какие результаты считать «нормальными» или «типичными». Это может быть основано на экспериментальных результатах прошлых опытов, на достоверных наборах данных, на данных из научной литературы, либо ученый может основываться на каких-либо других источниках. Для вашего эксперимента определите ожидаемые результаты, и выразите их в виде чисел.
Пример: Например, более ранние исследования показали, что в вашей стране красные машины чаще получают штрафы за превышение скорости, чем синие машины. Например, средние результаты показывают предпочтение 2:1 красных машин перед синими. Мы хотим определить, относится ли полиция точно так же предвзято к цвету машин в вашем городе. Для этого мы будем анализировать штрафы, выданные за превышение скорости. Если мы возьмем случайный набор из 150 штрафов за превышение скорости, выданных либо красным, либо синим автомобилям, мы ожидаем, что 100 штрафов будет выписано красным автомобилям, а 50 синим, если полиция в нашем городе так же предвзято относится к цвету машин, как это наблюдается по всей стране.
2. Определите наблюдаемые результаты вашего эксперимента
Теперь, когда вы опредили ожидаемые результаты, необходимо провести эксперимент, и найти действительные (или «наблюдаемые») значения. Вам снова необходимо представить эти результаты в виде чисел. Если мы создаем экспериментальные условия, и наблюдаемые результаты отличаются от ожидаемых, то у нас есть две возможности – либо это произошло случайно, либо это вызвано именно нашим экспериментом. Цель нахождения p-значения как раз и состоит в том, чтобы определить, отличаются ли наблюдаемые результаты от ожидаемых настолько, чтобы можно было не отвергать «нулевую гипотезу» – гипотезу о том, что между экспериментальными переменными и наблюдаемыми результатами нет никакой связи.
Пример: Например, в нашем городе мы случайно выбрали 150 штрафов за превышение скорости, которые были выданы либо красным, либо синим автомобилям. Мы определили, что 90 штрафов были выписаны красным автомобилям, и 60 синим. Это отличается от ожидаемых результатов, которые равны 100 и 50, соответственно. Действительно ли наш эксперимент (в данном случае, изменение источника данных с национального на городской) привел к данному изменению в результатах, или наша городская полиция относится предвзято точно так же, как и в среднем по стране, а мы видим просто случайное отклонение? P-значение поможет нам это определить.
3. Определите число степеней свободы вашего эксперимента
Число степеней свободы — это степень изменяемости вашего эксперимента, которая определяется числом категорий, которые вы исследуете. Уравнение для числа степеней свободы – Число степеней свободы = n-1, где «n» это число категорий или переменных, которые вы анализируете в своем эксперименте.
Пример: В нашем эксперименте две категории результатов: одна категория для красных машин, и одна для синих машин. Поэтому в нашем эксперименте у нас 2-1 = 1 степень свободы. Если бы мы сравнивали красные, синие и зеленые машины, у нас было бы 2 степени свободы, и так далее.
4. Сравните ожидаемые и наблюдаемые результаты с помощью критерия хи-квадрат
Хи-квадрат (пишется «x2») это числовое значение, которое измеряет разницу между ожидаемыми и наблюдаемыми значениями эксперимента. Уравнение для хи-квадрата следующее x2 = Σ((o-e)2/e), где «o» это наблюдаемое значение, а «e» это ожидаемое значение. Суммируйте результаты данного уравнения для всех возможных результатов (смотри ниже).
Заметьте, что данное уравнение включает оператор суммирования Σ (сигма). Другими словами, вам необходимо подсчитать ((|o-e|-.05)2/e) для каждого возможного результата, и сложить полученные числа, чтобы получить значение критерия хи-квадрат. В нашем примере у нас два возможных результата – либо машина, получившая штраф красная, либо синяя. Поэтому мы должны посчитать ((o-e)2/e) дважды – один раз для красных машин, и один раз для синих машин.
Пример: Давайте подставим наши ожидаемые и наблюдаемые значения в уравнение x2 = Σ((o-e)2/e). Помните, что из-за оператора суммирования нам необходимо посчитать ((o-e)2/e) дважды – один раз для красных автомобилей, и один раз для синих автомобилей. Мы выполним эту работу следующим образом:
x2 = ((90-100)2/100) + (60-50)2/50)
x2 = ((-10)2/100) + (10)2/50)
x2 = (100/100) + (100/50) = 1 + 2 = 3.
5. Выберите уровень значимости
Теперь, когда мы знаем число степеней свободы нашего эксперимента, и узнали значение критерия хи-квадрат, нам нужно сделать еще одну вещь перед тем, как мы найдем наше p-значение. Нам нужно определить уровень значимости. Говоря простым языком, уровень значимости показывает, насколько мы уверены в наших результатах. Низкое значение для значимости соответствует низкой вероятности того, что экспериментальные результаты получились случайно, и наоборот. Уровни значимости записываются в виде десятичных дробей (таких как 0.01), что соответствует вероятности того, что экспериментальные результаты мы получили случайно (в данном случае вероятность этого 1%).
По соглашению, ученые обычно устанавливают уровень значимости своих экспериментов равным 0.05, или 5%.[2] Это означает, что экспериментальные результаты, которые соответствуют такому критерию значимости, только с вероятностью 5% могли получиться чисто случайно. Другими словами, существует 95% вероятность, что результаты были вызваны тем, как ученый манипулировал экспериментальными переменными, а не случайно. Для большинства экспериментов 95% уверенности наличия связи между двумя переменными достаточно, чтобы считать, что они «действительно» связаны друг с другом.
Пример: для нашего примера с красными и синими машинами, давайте последуем соглашению между учеными, и установим уровень значимости в 0.05.
6. Используйте таблицу с данными распределения хи-квадрат, чтобы найти ваше p-значение
Ученые и статисты используют большие таблицы для вычисления p-значения своих экспериментов. Данные таблицы обычно имеют вертикальную ось слева, соответствующую числу степеней свободы, и горизонтальную ось сверху, соответствующую p-значению. Используйте данные таблицы, чтобы сначала найти число ваших степеней свободы, затем посмотрите на ваш ряд слева направо, пока не найдете первое значение, большее вашего значения хи-квадрат. Посмотрите на соответствующее p-значение вверху вашего столбца. Ваше p-значение находится между этим числом и следующим за ним (тем, которое находится левее вашего).
Таблицы с распределением хи-квадрат можно получить из множества источников (вот по этой ссылке можно найти одну из них).
Пример: Наше значение критерия хи-квадрат было равно 3. Так как мы знаем, что в нашем эксперименте всего 1 степень свободы, выберем самую первую строку. Идем слева направо по данной строке, пока не встретим значение, большее 3, нашего значения критерия хи-квадрат. Первое, которое мы находим это 3.84. Смотрим вверх нашего столбца, и видим, что соответствующее p-значение равно 0.05. Это означает, что наше p-значение между 0.05 и 0.1 (следующее p-значение в таблице по возрастанию).
7. Решите, отклонить или оставить вашу нулевую гипотезу
Так как вы определили приблизительное p-значение для вашего эксперимента, вам необходимо решить, отклонять ли нулевую гипотезу вашего эксперимента или нет (напоминаем, это гипотеза о том, что экспериментальные переменные, которыми вы манипулировали не повлияли на наблюдаемые вами результаты). Если ваше p-значение меньше, чем ваш уровень значимости – поздравляем, вы доказали, что очень вероятна связь между переменными, которыми вы манипулировали и результатами, которые вы наблюдали. Если ваше p-значение выше, чем ваш уровень значимости, вы не можете с уверенностью сказать, были ли наблюдаемые вами результаты результатом чистой случайности или манипуляцией вашими переменными.
Пример: Наше p-значение находится между 0,05 и 0,1. Это явно не меньше, чем 0,05, поэтому, к сожалению, мы не можем отклонить нашу нулевую гипотезу. Это означает, что мы не достигли минимум 95% вероятности того, чтобы сказать, что полиция в нашем городе выдает штрафы красным и синим автомобилям с такой вероятностью, которая достаточно сильно отличается от средней по стране.
Другими словами, существует 5-10% шанс, что наблюдаемые нами результаты – это не последствия смены места (анализа города, а не всей страны), а просто случайность. Так как мы потребовали точности меньше чем 5%, мы не можем сказать что мы уверены в том, что полиция нашего города менее предвзято относится к красным автомобилям – существует небольшая (но статистически значимая) вероятность, что это не так.
В статистике p-значения обычно используются при проверке гипотез для t-тестов, тестов хи-квадрат, регрессионного анализа, дисперсионного анализа и множества других статистических методов.
Несмотря на то, что это так распространено, люди часто неправильно интерпретируют p-значения, что может привести к ошибкам при интерпретации результатов анализа или исследования.
В этом посте объясняется, как понять и интерпретировать p-значения понятным и практичным способом.
Проверка гипотезы
Чтобы понять p-значения, нам сначала нужно понять концепцию проверки гипотез .
Проверка гипотезы — это формальный статистический тест, который мы используем, чтобы отвергнуть или не отвергнуть какую-либо гипотезу. Например, мы можем предположить, что новое лекарство, метод или процедура дает некоторые преимущества по сравнению с текущим лекарством, методом или процедурой.
Чтобы проверить это, мы можем провести проверку гипотезы, в которой мы используем нулевую и альтернативную гипотезы:
Нулевая гипотеза.Между новым и старым методом нет никакого эффекта или разницы.
Альтернативная гипотеза.Между новым и старым методом существует некоторый эффект или разница.
Значение p показывает, насколько правдоподобна нулевая гипотеза с учетом данных выборки. В частности, если предположить, что нулевая гипотеза верна, p-значение говорит нам о вероятности получения эффекта, по крайней мере, такого же большого, как тот, который мы фактически наблюдали в выборке данных.
Если p-значение проверки гипотезы достаточно низкое, мы можем отклонить нулевую гипотезу. В частности, когда мы проводим проверку гипотезы, мы должны с самого начала выбрать уровень значимости. Обычный выбор уровней значимости: 0,01, 0,05 и 0,10.
Если p-значения меньше нашего уровня значимости, мы можем отклонить нулевую гипотезу.
В противном случае, если p-значение равно или превышает наш уровень значимости, мы не можем отвергнуть нулевую гипотезу.
Как интерпретировать P-значение
Определение p-значения в учебнике:
P-значение — это вероятность наблюдения выборочной статистики, которая по крайней мере столь же экстремальна, как и ваша выборочная статистика, при условии, что нулевая гипотеза верна.
Например, предположим, что завод заявляет, что производит шины, средний вес которых составляет 200 фунтов. Аудитор выдвигает гипотезу о том, что истинный средний вес шин, произведенных на этом заводе, отличается от 200 фунтов, поэтому он проводит проверку гипотезы и обнаруживает, что p-значение теста равно 0,04. Вот как интерпретировать это p-значение:
Если фабрика действительно производит шины со средним весом 200 фунтов, то 4% всех аудитов получат эффект, наблюдаемый в выборке, или больше из-за случайной ошибки выборки. Это говорит нам о том, что получение выборочных данных, которые сделал аудитор, было бы довольно редким, если бы завод действительно производил шины, средний вес которых составлял 200 фунтов.
В зависимости от уровня значимости, используемого в этой проверке гипотезы, аудитор, скорее всего, отклонит нулевую гипотезу о том, что истинный средний вес шин, произведенных на этом заводе, действительно составляет 200 фунтов. Выборочные данные, полученные им в ходе аудита, не очень согласуются с нулевой гипотезой.
Как не следует интерпретировать P-значение
Самое большое заблуждение относительно p-значений состоит в том, что они эквивалентны вероятности совершить ошибку, отклонив истинную нулевую гипотезу (известную как ошибка типа I).
Есть две основные причины, по которым p-значения не могут быть частотой ошибок:
1. P-значения рассчитываются на основе предположения, что нулевая гипотеза верна и что разница между данными выборки и нулевой гипотезой просто вызвана случайностью. Таким образом, p-значения не могут сказать вам вероятность того, что ноль является истинным или ложным, поскольку он на 100% верен, исходя из точки зрения вычислений.
2. Хотя низкое значение p указывает на то, что ваши выборочные данные маловероятны при условии, что нулевое значение истинно, значение p по-прежнему не может сказать вам, какой из следующих случаев более вероятен:
- Нуль является ложным
- Нуль верен, но вы получили нечетную выборку
Что касается предыдущего примера, вот правильный и неправильный способ интерпретации p-значения:
- Правильная интерпретация: если предположить, что завод производит шины со средним весом 200 фунтов, вы получите наблюдаемую разницу, которую вы получили в своей выборке, или более значительную разницу в 4% аудитов из-за ошибки случайной выборки.
- Неверная интерпретация: если вы отвергаете нулевую гипотезу, существует 4%-ная вероятность того, что вы делаете ошибку.
Примеры интерпретации P-значений
Следующие примеры иллюстрируют правильные способы интерпретации p-значений в контексте проверки гипотез.
Пример 1
Телефонная компания утверждает, что 90% ее клиентов довольны их услугами. Чтобы проверить это утверждение, независимый исследователь собрал простую случайную выборку из 200 клиентов и спросил их, довольны ли они своим сервисом, на что 85% ответили утвердительно. Значение p, связанное с данными выборки, оказалось равным 0,018.
Правильная интерпретация p-значения: если предположить, что 90% клиентов действительно удовлетворены их обслуживанием, исследователь получит наблюдаемую разницу, которую он действительно получил в своей выборке, или более экстремальную разницу в 1,8% аудитов из-за ошибки случайной выборки. .
Пример 2
Компания изобретает новый аккумулятор для телефонов. Компания утверждает, что эта новая батарея будет работать как минимум на 10 минут дольше, чем старая. Чтобы проверить это утверждение, исследователь берет простую случайную выборку из 80 новых батарей и 80 старых батарей. Новые батареи работают в среднем 120 минут при стандартном отклонении 12 минут, а старые батареи работают в среднем 115 минут при стандартном отклонении 15 минут. Значение p, полученное в результате теста на разницу в средних значениях населения, равно 0,011.
Правильная интерпретация p-значения: если предположить, что новая батарея работает столько же или меньше времени, чем старая батарея, исследователь получит наблюдаемую разницу или более крайнюю разницу в 1,1% исследований из-за случайной ошибки выборки.
Определение статистической значимости
Статистическая значимость – это вероятность того, что наблюдение не вызвано ошибкой выборки. Это подразумевает, что наблюдение имеет определенную причину. Следовательно, чтобы считать наблюдение статистически значимым, оно должно пройти тестирование.
Чтобы доказать статистическую значимость, набор данных должен отклонить нулевую гипотезу. Нулевая гипотеза. абсолютная истина и всегда прав. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Читать далее. Чтобы доказать ошибочность нулевой гипотезы, p-значение наблюдения должно быть меньше уровня значимости. p-valueP-valueP-Value, или значение вероятности, является решающим фактором для нулевой гипотезы для вероятности того, что предполагаемый результат окажется истинным, будет принят или отклонен, и принятия альтернативного результата в случае отклонения предполагаемых результатов. . Читать дальше — это вероятность того, что наблюдение вызвано случайными факторами.
Оглавление
- Определение статистической значимости
- Понимание уровней статистической значимости
- Тест статистической значимости (P-значение)
- #1 – Статистическая проверка гипотез
- # 2 — Статистически значимое значение p
- Расчет статистической значимости
- Статистическая и практическая значимость
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Статистическая значимость показывает, что наблюдение вызвано конкретной причиной, а не случайным фактором.
- Уровень значимости представлен α. Исследователь устанавливает его значения и обычно составляет 0,01, 0,05 или 0,1.
- Нулевая гипотеза предполагает, что исследование ложно. Однако альтернативная гипотеза, являющаяся предположением исследователя, может оказаться верной, отвергнув нулевую гипотезу.
- Условное значение α = 0,05. Следовательно, если значение p для набора данных ≤ 0,05, то результат статистически значим. Если p-значение > 0,05, то исследование может быть статистически незначимым.
Понимание уровней статистической значимости
Статистическая значимость широко применяется исследователями в качестве инструмента количественного исследования для принятия решений. Этот инструмент применяется в различных областях, таких как бизнес, маркетинг, реклама, инвестиции и финансы.
Следующие два фактора определяют значимость.
- Размер образца: Количество наблюдений в огромной степени влияет на уровень значимости. Большой набор данных (обязательно рандомизированная выборка) часто устраняет ошибку выборкиОшибка выборкиФормула ошибки выборки используется для расчета статистической ошибки, которая возникает, когда человек, проводящий тест, не выбирает выборку, которая представляет всю рассматриваемую совокупность. Формула для ошибки выборки = Z x (σ /√n)подробнее.
- Размер эффекта: Корреляция между двумя наборами данных или переменными называется размером эффекта. Больший эффект sizeEffect SizeEffect size измеряет интенсивность взаимосвязи между двумя наборами переменных или групп. Он рассчитывается путем деления разницы между средними значениями, относящимися к двум группам, на стандартное отклонение. Это статистическая концепция. Следовательно, она подразумевает, что два разных исследования показывают очень похожие значения. Больший размер эффекта указывает на то, что данные статистически более значимы.
Значение альфа (α) представляет собой статистическую значимость. Традиционное значение альфы составляет 0,05, что составляет 5%. Он служит 95% порогом значимости. Это означает, что вероятность точности результата составляет 95%.
Для достижения статистической значимости должно выполняться хотя бы одно из заданных условий:
- Значение p должно быть ниже значения альфа.
- Значения нулевой гипотезы не должны иметь места в доверительном интервале.
Доверительный интервал Доверительный интервал Доверительный интервал относится к степени неопределенности, связанной с конкретной статистикой, и часто используется вместе с пределом погрешности. Доверительный интервал = среднее значение выборки ± критический фактор × стандартное отклонение выборки. read more относится к гарантированному диапазону, в который попадают фактические значения. Для p-значения 0,05, то есть 5%, оставшиеся 95% считаются доверительным интервалом.
Например, в июне 2020 г. ОСИНА Испытание не достигло статистической значимости по своей основной конечной точке. Об этом сообщило агентство Рейтер.
Тест статистической значимости (P-значение)
Статистическая значимость включает в себя нахождение результата и его проверку. Набор данных должен успешно отвергнуть нулевую гипотезу.
#1 – Статистическая проверка гипотез
Гипотеза – это предположение исследователя. Исследователи предполагают, что они получат тот или иной результат еще до проведения теста. Это предположение основано на взаимосвязи между различными переменными или наборами данных.
Два типа гипотез, используемых для анализа данных, следующие:
- Нулевая гипотеза: Теперь, если теория, предложенная исследователями, неверна, гипотеза исследователя считается недействительной. Это обозначается H0.
- Альтернативная гипотеза: Однако, если теория исследователя оказывается верной, она называется альтернативной гипотезой. Обозначается H1.
# 2 — Статистически значимое значение p
Значение p обозначает значение вероятности, то есть вероятность результата, являющегося результатом случайности или совпадения, а не фактов. Таким образом, уровень статистической значимости можно анализировать с помощью p-значения, которое находится в диапазоне от 0 до 1. Статистический результат считается точным, когда p-значение равно или меньше 0,05. Другими словами, вероятность того, что данные были получены случайно или случайно, составляет всего 5%.
Таким образом, тестирование приведет к следующим двум возможностям.
- p-значение ≤ 0,05: значение p, равное или меньшее 0,05, указывает на то, что нулевая гипотеза, вероятно, ложна. Таким образом, есть шансы, что результат будет более статистически значимым.
- р-значение > 0,05: Напротив, значение, превышающее 0,05, означает, что нулевая гипотеза кажется вероятной, и результат может быть статистически незначимым.
Расчет статистической значимости
Рассмотрим следующую задачу на основе гипотетического сценария. Самуэль, владелец парка развлечений, хочет, чтобы гости проводили больше времени в парке. Среднее время, проведенное 20 посетителями парка, составляет 199 минут. Сэмюэл решает установить новые аттракционы. Для теста порог значимости принят равным 5%, среднее значение выборки равно 200 минутам, а стандартное отклонение равно 200 минутам. На основе полученных данных проведите тест значимости для Сэмюэля.
Данные:
- µ = 199 минут
- п = 20
- µ остается 199 минут до установки новых аттракционов
- µ > 199 минут после установки новых аттракционов
- α = 5% или 0,05
- х = 200 минут
- σ = 200 минут
Расчет
Мы будем применять z-тест здесь,
Z = (x̄ — μ) / √ (σ2 / n)
Z = (200 – 199) / √(200 / 20)
Z = 1/3,16228
Z = 0,31623 = 0,3
Теперь давайте определим z-оценку или p-значение для данной z-таблицы:
Z0,000,10,20,30,40,00,500000,503990,507980,511970,51595
Таким образом, p-значение равно 0,51197.
Здесь, p-значение > α, т.е.., 0,51197 > 0,05
Следовательно, нулевая гипотеза может быть верной, и результат не является статистически значимым.
В качестве альтернативы пользователи могут выбирать из различных онлайн-калькуляторов для проведения тестов значимости.
Статистическая и практическая значимость
Статистическая значимость исключает случайное совпадение и указывает на то, что данные являются результатом определенной причины. Однако практическая значимость обнаруживает величину этого эффекта и его актуальность в реальном мире.
В то время как исследователи используют размер выборки и p-значение для установления статистической значимости, размер эффекта наборов данных указывает на практическую значимость.
Таким образом, получение статистической значимости без определения практической значимости было бы не очень полезным.
Часто задаваемые вопросы (FAQ)
Что такое статистическая значимость в исследованиях?
Тесты значимости широко используются в научных, экономических и медицинских исследованиях для определения надежности результатов тестов путем анализа шансов на истинность нулевой гипотезы.
Как определить статистическую значимость?
Шаги для расчета значимости следующие.
1. Найдите нулевую и альтернативную гипотезы, т. е. H0 и H1.
2. Предположим порог значимости или уровень значимости (α).
3. Получите образец и данные для проведения теста.
4. Запустите статистические тесты, такие как z-тест, T-тест, ANOVA или Chi-Square.
5. Проверьте, являются ли данные статистически значимыми, определив p-значение.
6. Интерпретируйте результат или завершите исследование.
Почему значимо значение p, равное 0,05?
Значение p, равное 0,05, представляет собой альфа, т.е. порог статистической значимости. Это граница вероятности, поэтому любое значение, выходящее за ее пределы, считается статистически незначимым. Если p-значение превышает 5%, это указывает на то, что более 5% значений вызваны случайностью. В результате набор данных нельзя использовать в качестве существенного доказательства причинно-следственной связи.
Рекомендуемые статьи
Это было Руководство по статистической значимости и ее значению. Здесь мы обсуждаем тесты значимости (значение p) и то, как понять его уровни, а также примеры и расчеты. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:
- Проверка гипотезы
- Степени свободы
- Тест хи-квадрат в Excel
Not to be confused with the P-factor.
In null-hypothesis significance testing, the p-value[note 1] is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct.[2][3] A very small p-value means that such an extreme observed outcome would be very unlikely under the null hypothesis. Even though reporting p-values of statistical tests is common practice in academic publications of many quantitative fields, misinterpretation and misuse of p-values is widespread and has been a major topic in mathematics and metascience.[4][5] In 2016, the American Statistician Association (ASA) made a formal statement that «p-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone» and that «a p-value, or statistical significance, does not measure the size of an effect or the importance of a result» or «evidence regarding a model or hypothesis.»[6] That said, a 2019 task force by ASA has issued a statement on statistical significance and replicability, concluding with: «p-values and significance tests, when properly applied and interpreted, increase the rigor of the conclusions drawn from data.»[7]
Basic concepts[edit]
In statistics, every conjecture concerning the unknown probability distribution of a collection of random variables representing the observed data 
As our statistical hypothesis will, by definition, state some property of the distribution, the null hypothesis is the default hypothesis under which that property does not exist. The null hypothesis is typically that some parameter (such as a correlation or a difference between means) in the populations of interest is zero. Our hypothesis might specify the probability distribution of 

The p-value is used in the context of null hypothesis testing in order to quantify the statistical significance of a result, the result being the observed value of the chosen statistic 
Loosely speaking, rejection of the null hypothesis implies that there is sufficient evidence against it.
As a particular example, if a null hypothesis states that a certain summary statistic 



Definition and interpretation[edit]
Definition[edit]
Probability under the null hypothesis of obtaining a real-valued test statistic at least as extreme as the one obtained[edit]
Consider an observed test-statistic 




Interpretations[edit]
p-value as the statistic for performing significance tests[edit]
In a significance test, the null hypothesis 



In 2018, a group of statisticians led by Daniel Benjamin proposed the adoption of the 0.005 value as standard value for statistical significance worldwide.[8]
The p-value is a function of the chosen test statistic 



Different p-values based on independent sets of data can be combined, for instance using Fisher’s combined probability test.
Distribution[edit]
When the null hypothesis is true, if it takes the form 
The distribution of p-values for a group of studies is sometimes called a p-curve.[11] A p-curve can be used to assess the reliability of scientific literature, such as by detecting publication bias or p-hacking.[11][12]
For composite hypothesis[edit]
In parametric hypothesis testing problems, a simple or point hypothesis refers to a hypothesis where the parameter’s value is assumed to be a single number. In contrast, in a composite hypothesis the parameter’s value is given by a set of numbers. For example, when testing the null hypothesis that a distribution is normal with a mean less than or equal to zero against the alternative that the mean is greater than zero (variance known), the null hypothesis does not specify the probability distribution of the appropriate test statistic. In the just mentioned example that would be the Z-statistic belonging to the one-sided one-sample Z-test. For each possible value of the theoretical mean, the Z-test statistic has a different probability distribution. In these circumstances (the case of a so-called composite null hypothesis) the p-value is defined by taking the least favourable null-hypothesis case, which is typically on the border between null and alternative.
This definition ensures the complementarity of p-values and alpha-levels. If we set the significance level alpha to 0.05, and only reject the null hypothesis if the p-value is less than or equal to 0.05, then our hypothesis test will indeed have significance level (maximal type 1 error rate) 0.05. As Neyman wrote: “The error that a practising statistician would consider the more important to avoid (which is a subjective judgment) is called the error of the first kind. The first demand of the mathematical theory is to deduce such test criteria as would ensure that the probability of committing an error of the first kind would equal (or approximately equal, or not exceed) a preassigned number α, such as α = 0.05 or 0.01, etc. This number is called the level of significance”; Neyman 1976, p. 161 in «The Emergence of Mathematical Statistics: A Historical Sketch with Particular Reference to the United States»,»On the History of Statistics and Probability», ed. D.B. Owen, New York: Marcel Dekker, pp. 149-193. See also «Confusion Over Measures of Evidence (p’s) Versus Errors (a’s) in Classical Statistical Testing», Raymond Hubbard and M. J. Bayarri, The American Statistician, August 2003, Vol. 57, No 3, 171—182 (with discussion). For a concise modern statement see Chapter 10 of «All of Statistics: A Concise Course in Statistical Inference», Springer; 1st Corrected ed. 20 edition (September 17, 2004). Larry Wasserman.
Usage[edit]
The p-value is widely used in statistical hypothesis testing, specifically in null hypothesis significance testing. In this method, before conducting the study, one first chooses a model (the null hypothesis) and the alpha level α (most commonly .05). After analyzing the data, if the p-value is less than α, that is taken to mean that the observed data is sufficiently inconsistent with the null hypothesis for the null hypothesis to be rejected. However, that does not prove that the null hypothesis is false. The p-value does not, in itself, establish probabilities of hypotheses. Rather, it is a tool for deciding whether to reject the null hypothesis.[13]
Misuse[edit]
According to the ASA, there is widespread agreement that p-values are often misused and misinterpreted.[3] One practice that has been particularly criticized is accepting the alternative hypothesis for any p-value nominally less than .05 without other supporting evidence. Although p-values are helpful in assessing how incompatible the data are with a specified statistical model, contextual factors must also be considered, such as «the design of a study, the quality of the measurements, the external evidence for the phenomenon under study, and the validity of assumptions that underlie the data analysis».[3] Another concern is that the p-value is often misunderstood as being the probability that the null hypothesis is true.[3][14]
Some statisticians have proposed abandoning p-values and focusing more on other inferential statistics,[3] such as confidence intervals,[15][16] likelihood ratios,[17][18] or Bayes factors,[19][20][21] but there is heated debate on the feasibility of these alternatives.[22][23] Others have suggested to remove fixed significance thresholds and to interpret p-values as continuous indices of the strength of evidence against the null hypothesis.[24][25] Yet others suggested to report alongside p-values the prior probability of a real effect that would be required to obtain a false positive risk (i.e. the probability that there is no real effect) below a pre-specified threshold (e.g. 5%).[26]
That said, in 2019 a task force by ASA had convened to consider the use of statistical methods in scientific studies, specifically hypothesis tests and p-values, and their connection to replicability.[7] It states that «Different measures of uncertainty can complement one another; no single measure serves all purposes.», citing p-value as one of these measures. They also stress that p-values can provide valuable information when considering the specific value as well as when compared to some threshold. In general, it stresses that «p-values and significance tests, when properly applied and interpreted, increase the rigor of the conclusions drawn from data.»
Calculation[edit]
Usually, 
For the important case in which the data are hypothesized to be a random sample from a normal distribution, depending on the nature of the test statistic and the hypotheses of interest about its distribution, different null hypothesis tests have been developed. Some such tests are the z-test for hypotheses concerning the mean of a normal distribution with known variance, the t-test based on Student’s t-distribution of a suitable statistic for hypotheses concerning the mean of a normal distribution when the variance is unknown, the F-test based on the F-distribution of yet another statistic for hypotheses concerning the variance. For data of other nature, for instance categorical (discrete) data, test statistics might be constructed whose null hypothesis distribution is based on normal approximations to appropriate statistics obtained by invoking the central limit theorem for large samples, as in the case of Pearson’s chi-squared test.
Thus computing a p-value requires a null hypothesis, a test statistic (together with deciding whether the researcher is performing a one-tailed test or a two-tailed test), and data. Even though computing the test statistic on given data may be easy, computing the sampling distribution under the null hypothesis, and then computing its cumulative distribution function (CDF) is often a difficult problem. Today, this computation is done using statistical software, often via numeric methods (rather than exact formulae), but, in the early and mid 20th century, this was instead done via tables of values, and one interpolated or extrapolated p-values from these discrete values[citation needed]. Rather than using a table of p-values, Fisher instead inverted the CDF, publishing a list of values of the test statistic for given fixed p-values; this corresponds to computing the Quantile function (inverse CDF).
Example[edit]
Testing the fairness of a coin[edit]
As an example of a statistical test, an experiment is performed to determine whether a coin flip is fair (equal chance of landing heads or tails) or unfairly biased (one outcome being more likely than the other).
Suppose that the experimental results show the coin turning up heads 14 times out of 20 total flips. The full data 

This probability is the p-value, considering only extreme results that favor heads. This is called a one-tailed test. However, one might be interested in deviations in either direction, favoring either heads or tails. The two-tailed p-value, which considers deviations favoring either heads or tails, may instead be calculated. As the binomial distribution is symmetrical for a fair coin, the two-sided p-value is simply twice the above calculated single-sided p-value: the two-sided p-value is 0.115.
In the above example:
- Null hypothesis (H0): The coin is fair, with Pr(heads) = 0.5
- Test statistic: Number of heads
- Alpha level (designated threshold of significance): 0.05
- Observation O: 14 heads out of 20 flips; and
- Two-tailed p-value of observation O given H0 = 2 × min(Pr(no. of heads ≥ 14 heads), Pr(no. of heads ≤ 14 heads)) = 2 × min(0.058, 0.978) = 2*0.058 = 0.115.
The Pr (no. of heads ≤ 14 heads) = 1 — Pr(no. of heads ≥ 14 heads) + Pr (no. of head = 14) = 1 — 0.058 + 0.036 = 0.978; however, the symmetry of this binomial distribution makes it an unnecessary computation to find the smaller of the two probabilities. Here, the calculated p-value exceeds .05, meaning that the data falls within the range of what would happen 95% of the time, if the coin were fair. Hence, the null hypothesis is not rejected at the .05 level.
However, had one more head been obtained, the resulting p-value (two-tailed) would have been 0.0414 (4.14%), in which case the null hypothesis would be rejected at the .05 level.
Multistage experiment design[edit]
The difference between the two meanings of «extreme» appear when we consider a multistage experiment for testing the fairness of the coin. Suppose we design the experiment as follows:
- Flip the coin twice. If both comes up heads or tails, end the experiment.
- Else, flip the coin 4 more times.
This experiment has 7 types of outcomes: 2 heads, 2 tails, 5 heads 1 tail…, 1 head 5 tails. We now calculate the p-value of the «3 heads 3 tails» outcome .
If we use the test statistic 

If we consider every outcome that has equal or lower probability than «3 heads 3 tails» as «at least as extreme», then the p-value is exactly 
However, suppose we have planned to simply flip the coin 6 times no matter what happens, then the second definition of p-value would mean that the p-value of «3 heads 3 tails» is exactly 1.
Thus, the «at least as extreme» definition of p-value is deeply contextual, and depends on what the experimenter planned to do even in situations that did not occur.
History[edit]
P-value computations date back to the 1700s, where they were computed for the human sex ratio at birth, and used to compute statistical significance compared to the null hypothesis of equal probability of male and female births.[27] John Arbuthnot studied this question in 1710,[28][29][30][31] and examined birth records in London for each of the 82 years from 1629 to 1710. In every year, the number of males born in London exceeded the number of females. Considering more male or more female births as equally likely, the probability of the observed outcome is 1/282, or about 1 in 4,836,000,000,000,000,000,000,000; in modern terms, the p-value. This is vanishingly small, leading Arbuthnot that this was not due to chance, but to divine providence: «From whence it follows, that it is Art, not Chance, that governs.» In modern terms, he rejected the null hypothesis of equally likely male and female births at the p = 1/282 significance level. This and other work by Arbuthnot is credited as «… the first use of significance tests …»[32] the first example of reasoning about statistical significance,[33] and «… perhaps the first published report of a nonparametric test …»,[29] specifically the sign test; see details at Sign test § History.
The same question was later addressed by Pierre-Simon Laplace, who instead used a parametric test, modeling the number of male births with a binomial distribution:[34]
In the 1770s Laplace considered the statistics of almost half a million births. The statistics showed an excess of boys compared to girls. He concluded by calculation of a p-value that the excess was a real, but unexplained, effect.
The p-value was first formally introduced by Karl Pearson, in his Pearson’s chi-squared test,[35] using the chi-squared distribution and notated as capital P.[35] The p-values for the chi-squared distribution (for various values of χ2 and degrees of freedom), now notated as P, were calculated in (Elderton 1902), collected in (Pearson 1914, pp. xxxi–xxxiii, 26–28, Table XII).
The use of the p-value in statistics was popularized by Ronald Fisher,[36][full citation needed] and it plays a central role in his approach to the subject.[37] In his influential book Statistical Methods for Research Workers (1925), Fisher proposed the level p = 0.05, or a 1 in 20 chance of being exceeded by chance, as a limit for statistical significance, and applied this to a normal distribution (as a two-tailed test), thus yielding the rule of two standard deviations (on a normal distribution) for statistical significance (see 68–95–99.7 rule).[38][note 3][39]
He then computed a table of values, similar to Elderton but, importantly, reversed the roles of χ2 and p. That is, rather than computing p for different values of χ2 (and degrees of freedom n), he computed values of χ2 that yield specified p-values, specifically 0.99, 0.98, 0.95, 0,90, 0.80, 0.70, 0.50, 0.30, 0.20, 0.10, 0.05, 0.02, and 0.01.[40] That allowed computed values of χ2 to be compared against cutoffs and encouraged the use of p-values (especially 0.05, 0.02, and 0.01) as cutoffs, instead of computing and reporting p-values themselves. The same type of tables were then compiled in (Fisher & Yates 1938), which cemented the approach.[39]
As an illustration of the application of p-values to the design and interpretation of experiments, in his following book The Design of Experiments (1935), Fisher presented the lady tasting tea experiment,[41] which is the archetypal example of the p-value.
To evaluate a lady’s claim that she (Muriel Bristol) could distinguish by taste how tea is prepared (first adding the milk to the cup, then the tea, or first tea, then milk), she was sequentially presented with 8 cups: 4 prepared one way, 4 prepared the other, and asked to determine the preparation of each cup (knowing that there were 4 of each). In that case, the null hypothesis was that she had no special ability, the test was Fisher’s exact test, and the p-value was 
Fisher reiterated the p = 0.05 threshold and explained its rationale, stating:[42]
It is usual and convenient for experimenters to take 5 per cent as a standard level of significance, in the sense that they are prepared to ignore all results which fail to reach this standard, and, by this means, to eliminate from further discussion the greater part of the fluctuations which chance causes have introduced into their experimental results.
He also applies this threshold to the design of experiments, noting that had only 6 cups been presented (3 of each), a perfect classification would have only yielded a p-value of 
In later editions, Fisher explicitly contrasted the use of the p-value for statistical inference in science with the Neyman–Pearson method, which he terms «Acceptance Procedures».[43] Fisher emphasizes that while fixed levels such as 5%, 2%, and 1% are convenient, the exact p-value can be used, and the strength of evidence can and will be revised with further experimentation. In contrast, decision procedures require a clear-cut decision, yielding an irreversible action, and the procedure is based on costs of error, which, he argues, are inapplicable to scientific research.
[edit]
The E-value corresponds to the expected number of times in multiple testing that one expects to obtain a test statistic at least as extreme as the one that was actually observed if one assumes that the null hypothesis is true.[44] The E-value is the product of the number of tests and the p-value.
The q-value is the analog of the p-value with respect to the positive false discovery rate.[45] It is used in multiple hypothesis testing to maintain statistical power while minimizing the false positive rate.[46]
The Probability of Direction (pd) is the Bayesian numerical equivalent of the p-value.[47] It corresponds to the proportion of the posterior distribution that is of the median’s sign, typically varying between 50% and 100%, and representing the certainty with which an effect is positive or negative.
See also[edit]
- Student’s t-test
- Bonferroni correction
- Counternull
- Fisher’s method of combining p-values
- Generalized p-value
- Harmonic mean p-value
- Holm–Bonferroni method
- Multiple comparisons problem
- p-rep
- p-value fallacy
Notes[edit]
- ^ Italicisation, capitalisation and hyphenation of the term vary. For example, AMA style uses «P value», APA style uses «p value», and the American Statistical Association uses «p-value».[1]
- ^ The statistical significance of a result does not imply that the result also has real-world relevance. For instance, a medicine might have a statistically significant effect that is too small to be interesting.
- ^ To be more specific, the p = 0.05 corresponds to about 1.96 standard deviations for a normal distribution (two-tailed test), and 2 standard deviations corresponds to about a 1 in 22 chance of being exceeded by chance, or p ≈ 0.045; Fisher notes these approximations.
References[edit]
- ^ «ASA House Style» (PDF). Amstat News. American Statistical Association.
- ^ Aschwanden C (2015-11-24). «Not Even Scientists Can Easily Explain P-values». FiveThirtyEight. Archived from the original on 25 September 2019. Retrieved 11 October 2019.
- ^ a b c d e Wasserstein RL, Lazar NA (7 March 2016). «The ASA’s Statement on p-Values: Context, Process, and Purpose». The American Statistician. 70 (2): 129–133. doi:10.1080/00031305.2016.1154108.
- ^ Hubbard R, Lindsay RM (2008). «Why P Values Are Not a Useful Measure of Evidence in Statistical Significance Testing». Theory & Psychology. 18 (1): 69–88. doi:10.1177/0959354307086923. S2CID 143487211.
- ^ Munafò MR, Nosek BA, Bishop DV, Button KS, Chambers CD, du Sert NP, et al. (January 2017). «A manifesto for reproducible science». Nature Human Behaviour. 1: 0021. doi:10.1038/s41562-016-0021. PMC 7610724. PMID 33954258. S2CID 6326747.
- ^ Wasserstein, Ronald L.; Lazar, Nicole A. (2016-04-02). «The ASA Statement on p -Values: Context, Process, and Purpose». The American Statistician. 70 (2): 129–133. doi:10.1080/00031305.2016.1154108. ISSN 0003-1305. S2CID 124084622.
- ^ a b Benjamini, Yoav; De Veaux, Richard D.; Efron, Bradley; Evans, Scott; Glickman, Mark; Graubard, Barry I.; He, Xuming; Meng, Xiao-Li; Reid, Nancy M.; Stigler, Stephen M.; Vardeman, Stephen B.; Wikle, Christopher K.; Wright, Tommy; Young, Linda J.; Kafadar, Karen (2021-10-02). «ASA President’s Task Force Statement on Statistical Significance and Replicability». CHANCE. Informa UK Limited. 34 (4): 10–11. doi:10.1080/09332480.2021.2003631. ISSN 0933-2480.
- ^ Benjamin, Daniel J.; Berger, James O.; Johannesson, Magnus; Nosek, Brian A.; Wagenmakers, E.-J.; Berk, Richard; Bollen, Kenneth A.; Brembs, Björn; Brown, Lawrence; Camerer, Colin; Cesarini, David; Chambers, Christopher D.; Clyde, Merlise; Cook, Thomas D.; De Boeck, Paul; Dienes, Zoltan; Dreber, Anna; Easwaran, Kenny; Efferson, Charles; Fehr, Ernst; Fidler, Fiona; Field, Andy P.; Forster, Malcolm; George, Edward I.; Gonzalez, Richard; Goodman, Steven; Green, Edwin; Green, Donald P.; Greenwald, Anthony G.; Hadfield, Jarrod D.; Hedges, Larry V.; Held, Leonhard; Hua Ho, Teck; Hoijtink, Herbert; Hruschka, Daniel J.; Imai, Kosuke; Imbens, Guido; Ioannidis, John P. A.; Jeon, Minjeong; Jones, James Holland; Kirchler, Michael; Laibson, David; List, John; Little, Roderick; Lupia, Arthur; Machery, Edouard; Maxwell, Scott E.; McCarthy, Michael; Moore, Don A.; Morgan, Stephen L.; Munafó, Marcus; Nakagawa, Shinichi; Nyhan, Brendan; Parker, Timothy H.; Pericchi, Luis; Perugini, Marco; Rouder, Jeff; Rousseau, Judith; Savalei, Victoria; Schönbrodt, Felix D.; Sellke, Thomas; Sinclair, Betsy; Tingley, Dustin; Van Zandt, Trisha; Vazire, Simine; Watts, Duncan J.; Winship, Christopher; Wolpert, Robert L.; Xie, Yu; Young, Cristobal; Zinman, Jonathan; Johnson, Valen E. (1 September 2017). «Redefine statistical significance». Nature Human Behaviour. 2 (1): 6–10. doi:10.1038/s41562-017-0189-z. eISSN 2397-3374. PMID 30980045. S2CID 256726352.
- ^ Bhattacharya B, Habtzghi D (2002). «Median of the p value under the alternative hypothesis». The American Statistician. 56 (3): 202–6. doi:10.1198/000313002146. S2CID 33812107.
- ^ Hung HM, O’Neill RT, Bauer P, Köhne K (March 1997). «The behavior of the P-value when the alternative hypothesis is true». Biometrics (Submitted manuscript). 53 (1): 11–22. doi:10.2307/2533093. JSTOR 2533093. PMID 9147587.
- ^ a b Head ML, Holman L, Lanfear R, Kahn AT, Jennions MD (March 2015). «The extent and consequences of p-hacking in science». PLOS Biology. 13 (3): e1002106. doi:10.1371/journal.pbio.1002106. PMC 4359000. PMID 25768323.
- ^ Simonsohn U, Nelson LD, Simmons JP (November 2014). «p-Curve and Effect Size: Correcting for Publication Bias Using Only Significant Results». Perspectives on Psychological Science. 9 (6): 666–681. doi:10.1177/1745691614553988. PMID 26186117. S2CID 39975518.
- ^ Nuzzo R (February 2014). «Scientific method: statistical errors». Nature. 506 (7487): 150–152. Bibcode:2014Natur.506..150N. doi:10.1038/506150a. PMID 24522584.
- ^ Colquhoun D (November 2014). «An investigation of the false discovery rate and the misinterpretation of p-values». Royal Society Open Science. 1 (3): 140216. arXiv:1407.5296. Bibcode:2014RSOS….140216C. doi:10.1098/rsos.140216. PMC 4448847. PMID 26064558.
- ^ Lee DK (December 2016). «Alternatives to P value: confidence interval and effect size». Korean Journal of Anesthesiology. 69 (6): 555–562. doi:10.4097/kjae.2016.69.6.555. PMC 5133225. PMID 27924194.
- ^ Ranstam J (August 2012). «Why the P-value culture is bad and confidence intervals a better alternative». Osteoarthritis and Cartilage. 20 (8): 805–808. doi:10.1016/j.joca.2012.04.001. PMID 22503814.
- ^ Perneger TV (May 2001). «Sifting the evidence. Likelihood ratios are alternatives to P values». BMJ. 322 (7295): 1184–1185. doi:10.1136/bmj.322.7295.1184. PMC 1120301. PMID 11379590.
- ^ Royall R (2004). «The Likelihood Paradigm for Statistical Evidence». The Nature of Scientific Evidence. pp. 119–152. doi:10.7208/chicago/9780226789583.003.0005. ISBN 9780226789576.
- ^ Schimmack U (30 April 2015). «Replacing p-values with Bayes-Factors: A Miracle Cure for the Replicability Crisis in Psychological Science». Replicability-Index. Retrieved 7 March 2017.
- ^ Marden JI (December 2000). «Hypothesis Testing: From p Values to Bayes Factors». Journal of the American Statistical Association. 95 (452): 1316–1320. doi:10.2307/2669779. JSTOR 2669779.
- ^ Stern HS (16 February 2016). «A Test by Any Other Name: P Values, Bayes Factors, and Statistical Inference». Multivariate Behavioral Research. 51 (1): 23–29. doi:10.1080/00273171.2015.1099032. PMC 4809350. PMID 26881954.
- ^ Murtaugh PA (March 2014). «In defense of P values». Ecology. 95 (3): 611–617. doi:10.1890/13-0590.1. PMID 24804441.
- ^ Aschwanden C (7 March 2016). «Statisticians Found One Thing They Can Agree On: It’s Time To Stop Misusing P-Values». FiveThirtyEight.
- ^ Amrhein V, Korner-Nievergelt F, Roth T (2017). «The earth is flat (p > 0.05): significance thresholds and the crisis of unreplicable research». PeerJ. 5: e3544. doi:10.7717/peerj.3544. PMC 5502092. PMID 28698825.
- ^ Amrhein V, Greenland S (January 2018). «Remove, rather than redefine, statistical significance». Nature Human Behaviour. 2 (1): 4. doi:10.1038/s41562-017-0224-0. PMID 30980046. S2CID 46814177.
- ^ Colquhoun D (December 2017). «The reproducibility of research and the misinterpretation of p-values». Royal Society Open Science. 4 (12): 171085. doi:10.1098/rsos.171085. PMC 5750014. PMID 29308247.
- ^ Brian E, Jaisson M (2007). «Physico-Theology and Mathematics (1710–1794)». The Descent of Human Sex Ratio at Birth. Springer Science & Business Media. pp. 1–25. ISBN 978-1-4020-6036-6.
- ^ Arbuthnot J (1710). «An argument for Divine Providence, taken from the constant regularity observed in the births of both sexes» (PDF). Philosophical Transactions of the Royal Society of London. 27 (325–336): 186–190. doi:10.1098/rstl.1710.0011. S2CID 186209819.
- ^ a b Conover WJ (1999). «Chapter 3.4: The Sign Test». Practical Nonparametric Statistics (Third ed.). Wiley. pp. 157–176. ISBN 978-0-471-16068-7.
- ^ Sprent P (1989). Applied Nonparametric Statistical Methods (Second ed.). Chapman & Hall. ISBN 978-0-412-44980-2.
- ^ Stigler SM (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 225–226. ISBN 978-0-67440341-3.
- ^ Bellhouse P (2001). «John Arbuthnot». In Heyde CC, Seneta E (eds.). Statisticians of the Centuries. Springer. pp. 39–42. ISBN 978-0-387-95329-8.
- ^ Hald A (1998). «Chapter 4. Chance or Design: Tests of Significance». A History of Mathematical Statistics from 1750 to 1930. Wiley. p. 65.
- ^ Stigler SM (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. p. 134. ISBN 978-0-67440341-3.
- ^ a b Pearson K (1900). «On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling» (PDF). Philosophical Magazine. Series 5. 50 (302): 157–175. doi:10.1080/14786440009463897.
- ^ Inman 2004.
- ^ Hubbard R, Bayarri MJ (2003), «Confusion Over Measures of Evidence (p′s) Versus Errors (α′s) in Classical Statistical Testing», The American Statistician, 57 (3): 171–178 [p. 171], doi:10.1198/0003130031856, S2CID 55671953
- ^ Fisher 1925, p. 47, Chapter III. Distributions.
- ^ a b Dallal 2012, Note 31: Why P=0.05?.
- ^ Fisher 1925, pp. 78–79, 98, Chapter IV. Tests of Goodness of Fit, Independence and Homogeneity; with Table of χ2, Table III. Table of χ2.
- ^ Fisher 1971, II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment.
- ^ a b Fisher 1971, Section 7. The Test of Significance.
- ^ Fisher 1971, Section 12.1 Scientific Inference and Acceptance Procedures.
- ^ «Definition of E-value». National Institutes of Health.
- ^ Storey JD (2003). «The positive false discovery rate: a Bayesian interpretation and the q-value». The Annals of Statistics. 31 (6): 2013–2035. doi:10.1214/aos/1074290335.
- ^ Storey JD, Tibshirani R (August 2003). «Statistical significance for genomewide studies». Proceedings of the National Academy of Sciences of the United States of America. 100 (16): 9440–9445. Bibcode:2003PNAS..100.9440S. doi:10.1073/pnas.1530509100. PMC 170937. PMID 12883005.
- ^ Makowski D, Ben-Shachar MS, Chen SH, Lüdecke D (10 December 2019). «Indices of Effect Existence and Significance in the Bayesian Framework». Frontiers in Psychology. 10: 2767. doi:10.3389/fpsyg.2019.02767. PMC 6914840. PMID 31920819.
Further reading[edit]
- Denworth L (October 2019). «A Significant Problem: Standard scientific methods are under fire. Will anything change?». Scientific American. 321 (4): 62–67 (63).
The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields. There is growing determination to reform statistical analysis… Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining «significant» results.
- Elderton WP (1902). «Tables for Testing the Goodness of Fit of Theory to Observation». Biometrika. 1 (2): 155–163. doi:10.1093/biomet/1.2.155.
- Fisher RA (1925). Statistical Methods for Research Workers. Edinburgh, Scotland: Oliver & Boyd. ISBN 978-0-05-002170-5.
- Fisher RA (1971) [1935]. The Design of Experiments (9th ed.). Macmillan. ISBN 978-0-02-844690-5.
- Fisher RA, Yates F (1938). Statistical tables for biological, agricultural and medical research. London, England.
- Stigler SM (1986). The history of statistics : the measurement of uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
- Hubbard R, Armstrong JS (2006). «Why We Don’t Really Know What Statistical Significance Means: Implications for Educators» (PDF). Journal of Marketing Education. 28 (2): 114–120. doi:10.1177/0273475306288399. hdl:2092/413. S2CID 34729227. Archived from the original (PDF) on May 18, 2006.
- Hubbard R, Lindsay RM (2008). «Why P Values Are Not a Useful Measure of Evidence in Statistical Significance Testing» (PDF). Theory & Psychology. 18 (1): 69–88. doi:10.1177/0959354307086923. S2CID 143487211. Archived from the original (PDF) on 2016-10-21. Retrieved 2015-08-28.
- Stigler S (December 2008). «Fisher and the 5% level». Chance. 21 (4): 12. doi:10.1007/s00144-008-0033-3.
- Dallal GE (2012). The Little Handbook of Statistical Practice.
- Biau DJ, Jolles BM, Porcher R (March 2010). «P value and the theory of hypothesis testing: an explanation for new researchers». Clinical Orthopaedics and Related Research. 468 (3): 885–892. doi:10.1007/s11999-009-1164-4. PMC 2816758. PMID 19921345.
- Reinhart A (2015). Statistics Done Wrong: The Woefully Complete Guide. No Starch Press. p. 176. ISBN 978-1593276201.
- Benjamini, Yoav; De Veaux, Richard D.; Efron, Bradley; Evans, Scott; Glickman, Mark; Graubard, Barry I.; He, Xuming; Meng, Xiao-Li; Reid, Nancy; Stigler, Stephen M.; Vardeman, Stephen B.; Wikle, Christopher K.; Wright, Tommy; Young, Linda J.; Kafadar, Karen (2021). «The ASA President’s Task Force Statement on Statistical Significance and Replicability». Annals of Applied Statistics. 15 (3): 1084–1085. doi:10.1214/21-AOAS1501.
- Benjamin, Daniel J.; Berger, James O.; Johannesson, Magnus; Nosek, Brian A.; Wagenmakers, E.-J.; Berk, Richard; Bollen, Kenneth A.; Brembs, Björn; Brown, Lawrence; Camerer, Colin; Cesarini, David; Chambers, Christopher D.; Clyde, Merlise; Cook, Thomas D.; De Boeck, Paul; Dienes, Zoltan; Dreber, Anna; Easwaran, Kenny; Efferson, Charles; Fehr, Ernst; Fidler, Fiona; Field, Andy P.; Forster, Malcolm; George, Edward I.; Gonzalez, Richard; Goodman, Steven; Green, Edwin; Green, Donald P.; Greenwald, Anthony G.; Hadfield, Jarrod D.; Hedges, Larry V.; Held, Leonhard; Hua Ho, Teck; Hoijtink, Herbert; Hruschka, Daniel J.; Imai, Kosuke; Imbens, Guido; Ioannidis, John P. A.; Jeon, Minjeong; Jones, James Holland; Kirchler, Michael; Laibson, David; List, John; Little, Roderick; Lupia, Arthur; Machery, Edouard; Maxwell, Scott E.; McCarthy, Michael; Moore, Don A.; Morgan, Stephen L.; Munafó, Marcus; Nakagawa, Shinichi; Nyhan, Brendan; Parker, Timothy H.; Pericchi, Luis; Perugini, Marco; Rouder, Jeff; Rousseau, Judith; Savalei, Victoria; Schönbrodt, Felix D.; Sellke, Thomas; Sinclair, Betsy; Tingley, Dustin; Van Zandt, Trisha; Vazire, Simine; Watts, Duncan J.; Winship, Christopher; Wolpert, Robert L.; Xie, Yu; Young, Cristobal; Zinman, Jonathan; Johnson, Valen E. (1 September 2017). «Redefine statistical significance». Nature Human Behaviour. 2 (1): 6–10. doi:10.1038/s41562-017-0189-z. eISSN 2397-3374. PMID 30980045. S2CID 256726352.
External links[edit]
Wikimedia Commons has media related to P-value.
- Free online p-values calculators for various specific tests (chi-square, Fisher’s F-test, etc.).
- Understanding p-values, including a Java applet that illustrates how the numerical values of p-values can give quite misleading impressions about the truth or falsity of the hypothesis under test.
- StatQuest: P Values, clearly explained on YouTube
- StatQuest: P-value pitfalls and power calculations on YouTube
- Science Isn’t Broken — Article on how p-values can be manipulated and an interactive tool to visualize it.
В этой статье рассмотрим тему p-значений в статистике. Информация пригодится всем, кто занимается анализом данных и статистическими сведениями.
Определение простыми словами
P value – это вероятность того, что случайное значение величины с данным распределением (тестовой статистики при нулевой гипотезе) будет принимать значение, не менее фактического. Представляет собой наибольший показатель уровня значимости (вероятности отказа от того, что предположение верно), для которого вычислительная проверочная статистика ведет к отказу от нулевой гипотезы. Это – некая «жизнеспособность нулевого предположения».
Чтобы далее этот вопрос был более понятным, стоит рассматривать его на наглядном примере. А именно – на связи пристрастия к кровавым играм и агрессивностью в реальной жизни.
Уровни
P-значения бывает нескольких уровней. В зависимости от соответствующего показателя делается выбор относительно того, является ли показатель статистически значимым или нет:
- P-значения ≤0,05 – обычный уровень статистической значимости. Он интерпретируется как «получение статически значимого результата». Часто помечается одной звездочкой. Это «традиционная» отметка при анализе.
- P-значения ≤0,01 – высокая статистическая значимость. Может быть интерпретирована как «обнаружение выраженной закономерности». Обозначает тесную связь между несколькими переменными, если подразумевается уровень значимости корреляционного коэффициента. На письме имеет обозначение в виде двух звездочек.
- P-значения ≤0,001 – высокий уровень статистической значимости. Обозначение – три звездочки.
Есть результаты, которые могут быть описаны как близкие к статистическим. В них P-значение примерно равно 0,05. Они указывают на то, что существует тенденция к формированию той или иной закономерности.
Если показатель статистической значимости будет более 0,1, то это будет свидетельствовать о полученном результате, который не имеет статистической «важности». Пример – когда подразумевается сравнение выборок. Полученный показатель p-значения более 0,1, указывает на то, что статистически значимые различия между ними отсутствуют.
Обычно для анализа соответствующий элемент выступает одним из основополагающих. Уровень p-значимости (value) указывает на вероятность ошибки при выявлении закономерностей. Чем меньше данная величина, тем ниже вероятность «сбоя». И тем более статистически значимым выступает полученный результат.
Как определить
P-значения используются для того, чтобы определить, попадают ли итоговые результаты эксперимента в диапазон значений, являющийся нормальным для заданной величины. Определить значимость поможет специальная таблица. Воспользоваться ей можно, если просчитать х-квадрат:
- Определить ожидаемые итоги. Обычно ученые при анализе и экспериментах уже знают, какие значимости являются «типичными» или «нормальными». Выводы базируются на ранее проведенных опытах, достоверных наборах информации, а также на научной литературе. Иногда происходит ссылка на сторонние источники. Ожидания должны быть выражены числами.
- Определить наблюдаемые результаты. Для этого необходимо провести эксперимент и найти действительные (наблюдаемые) параметры. Они тоже должны быть представлены в виде чисел. Специальная таблица поможет представить информацию в более удобной форме. При экспериментальных условиях и отличии «ожидания» от «реальности» действуют две теории. Первая – это вызвано одним конкретным экспериментом. Вторая – ситуация случайна. P-значения как раз помогут определить, отличаются ли наблюдения от ожиданий настолько, чтобы опровергнуть нулевую гипотезу.
- Определить число степеней свободы значимости эксперимента. Так называется степень изменяемости исследования, которая выражается числом исследуемых категорий. Рассчитывается по формуле n-1. Здесь n – число категорий или переменных, анализируемых во время теста.
- Сравнить ожидания и реально наблюдаемые результаты. Для этого используется хи-квадрат (x2). Это значение (не статистическое), измеряющее разницу между ожиданием и реальностью. Уравнение будет таким: Сумма((o-e)2/e), где o – наблюдение, e – ожидаемые показатели. Необходимо просуммировать результаты уравнения для всех возможных итогов.
- Выбрать уровень статистической значимости (values). После обнаружения степеней свободы эксперимента и расчета значения критерия хи-квадрата, необходимо определить значение p. От него будет зависеть значимость полученных наблюдений. Записывается значение p в виде десятичных дробей.
- Использовать список с данными распределения хи-квадрата. Определить p-значение поможет специальная таблица. Она имеет вертикальную ось слева. Это – соответствие числу степеней свободы. Также имеется горизонтальная ось, расположенная сверху. Она указывает на p-значения. Сначала здесь требуется обнаружить степени свободы, затем – посмотреть на ряд слева-направо. Остановиться необходимо при первом параметре, превышающем хи-квадрат. Теперь потребуется посмотреть в верхнюю часть столбца. Там будет p-значение (value). Оно расположено между соответствующим число и тем, что расположено левее.
Остается принять решение, что делать с полученными статистическими значимостями далее – оставлять нулевую гипотезу или нет. Если итоговый параметр меньше уровня значимости – связь между переменными вероятна. Когда показатель p-значения находится между 0,05 и 0,1, он не может быть отклонен.
Наглядный пример
Чтобы лучше понять выбранное направление, стоит изучить наглядный пример. В ходе исследований были получены такие итоги относительно связи агрессивности в жизни и пристрастия к кровавым компьютерным играм:
Две группы школьников поделены по степени агрессивности через стандартный t-тест. Заветный уровень value менее 0,05. Пример – 0,04. Существуют несколько предположений:
- Компьютерные игры являются основной причиной агрессивного поведения. Вероятность этого составляет 96%.
- Шанс того, что игры и агрессия не связаны – 0,04.
- Если показатель более 0,05, то агрессивность и компьютерные кровавые игры никак не связаны между собой.
- Случайное получение соответствующей разницы составляет 0,04.
- Все утверждения не являются верными.
Последний вариант является наиболее грамотным. Но многочисленные исследования указывают на то, что интерпретация итоговых данных даже опытными аналитиками бывает ошибочна. Из-за этого приходится производить расчеты и пользоваться специальными таблицами.
Как лучше изучать статистические показатели
Статистика – целая наука, которая изучается в ВУЗах. Здесь можно посмотреть краткий видео-курс по рассмотренному ранее направлению. Освоить его удается не только при помощи высшего образования и самообучения. На помощь приходят специализированные компьютерные курсы.
Обычно они проводятся дистанционно, что помогает совмещать обучение с обыденной жизнью. Человека с нуля обучают статистике, математике, а при желании – основам работы с Big Data и разработки программного обеспечения на любом языке.
К преимуществам курсов относят:
- грамотно составленные программы, поданные понятным языком;
- спектр направлений – удастся подобрать курс не только по конкретной тематике, но и в зависимости от имеющегося первоначального багажа знаний;
- совместимость с работой, обычными делами и семьей – уроки разрешено просматривать в записи с любого устройства;
- полностью дистанционное обучение;
- помощь в формировании портфолио;
- интересные практические и домашние задачки.
Пример – курсы от образовательного центра OTUS. На протяжении всего времени обучения пользователю будет предложено постоянное кураторство опытными специалистами. Пользователи смогут обратиться за помощью к ним, если какие-то моменты не понятны.
В конце обучения будет выдан электронный сертификат установленного образца. Он поможет подтвердить полученные во время обучения навыки и умения.
Интересуют курсы по системному анализу и не только? Огромный выбор обучающих онлайн-программ по востребованным IT-направлениям есть в Otus!


 .
.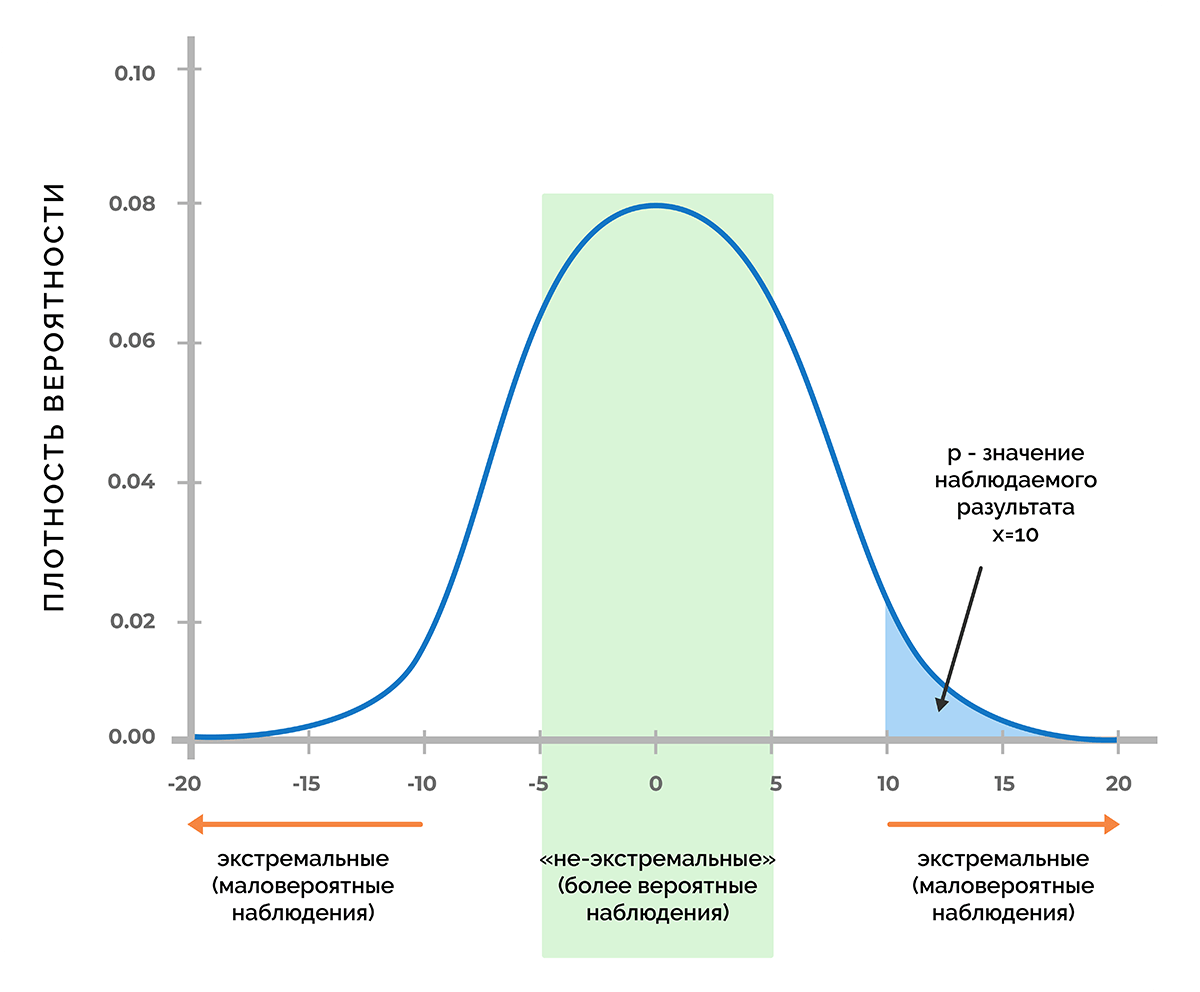




![{displaystyle {begin{aligned}&Pr(14{text{ heads}})+Pr(15{text{ heads}})+cdots +Pr(20{text{ heads}})\&={frac {1}{2^{20}}}left[{binom {20}{14}}+{binom {20}{15}}+cdots +{binom {20}{20}}right]={frac {60,!460}{1,!048,!576}}approx 0.058end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2c59548d359fb637177e73515aea16368929436)



