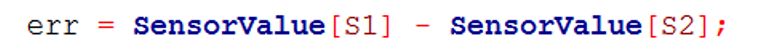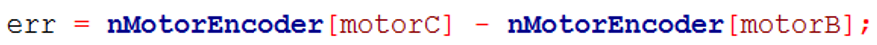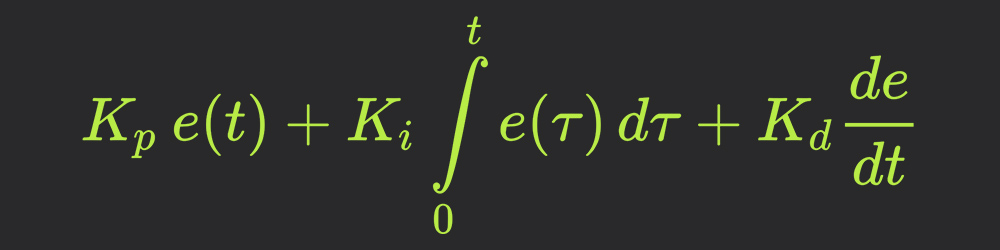Ошибка в пропорциональном регуляторе это

Регуляторы простым языком

Введение

Кому рекомендовано: всем, кто изучает робототехнику от полугода и испытывает трудности с применением регуляторов, а также для тех, кто хочет разобраться глубже с данным вопросом.

Рекомендуемый возраст: от 11 до 99 лет.

Бывают случаи, когда учащиеся даже избегают их применения, применяя костыли в своих решения. Но робототехника без регуляторов приводит в тупик – это факт. Регуляторы — это слишком сложно – это заблуждение. Конечно, существуют регуляторы со сложным устройством, однако есть и простые. 

Нашим подопытным будет робот, собранный из набора Lego Mindstorms EV3. Будем учить его ездить по линии, вдоль стен, а как же выполнять другие задачи, где применяются регуляторы. Нам помогут среды программирования TrikStudio и RobotC. 

Градус сложности в данной статье от начала к концу возрастает в несколько раз, поэтому рекомендуется изучить всё постепенно, лучше даже с перерывами, а не съедать материал целиком.

Определение

Регулятор – это устройство, выполняющее задачу поддержания объекта управления в определённом состоянии. Регулятор получает информацию о состоянии объекта управления с помощью датчиков и вырабатывает управляющее воздействие для того, чтобы его корректировать.

Пример: паяльник с регулятором температуры.  Давайте будем считать, что жало паяльника – это объект управления. Получая информацию от датчика температуры, программа определяет с какой интенсивностью необходимо задействовать нагревательный элемент. Таким образом с точностью до градуса можно задавать нужную температуру для комфортной работы, крайне удобная штука.

Регуляторы часто встречаются в повседневной жизни: кондиционер поддерживает температуру в помещении, стиральная машина умеет поддерживать скорость вращения барабана с помощью специальных датчиков – энкодеров, кулер в компьютере тоже имеет регулятор, так скорость его вращения зависит от температуры нагревания процессора.

Есть и более сложные устройства, например, в ракеты, которые регулируют направление движения с помощью множества датчиков. Гироскутеры удерживают равновесие тоже с помощью регуляторов, которые ориентируются на гироскоп и акселерометр.

Но есть и совсем простой бытовой пример – регулятор уровня воды в бачке унитаза. Принцип прост: если в бачке уровень воды ниже определённой планки — клапан открывается, если наоборот, выше – клапан закрывается. Это пример релейного двухпозиционного регулятора. С него и начнём…
 

Релейный регулятор

Релейный регулятор – это тип регуляторов, который может вырабатывать ограниченное количество вариантов (положений регулятора) движения, обычно от 2 до 4. Говоря проще – он не умеет работать плавно. Если, например, количество положений в регуляторе 2, то такой регулятор называют двухпозиционный, если 3, то трёхпозиционный и т.д.

Попробуем построить релейный регулятор для робота, который движется по линии. Начнём с самого простого – двигаться по границе черной линии на одном датчике освещенности. 

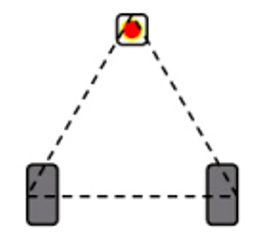
Конструкция робота: тележка с танковым управлением, спереди которой есть датчик освещенности. Желательно, чтобы ведущие колёса и датчик, образовывали собой равносторонний треугольник, тогда движение будет наиболее стабильным.

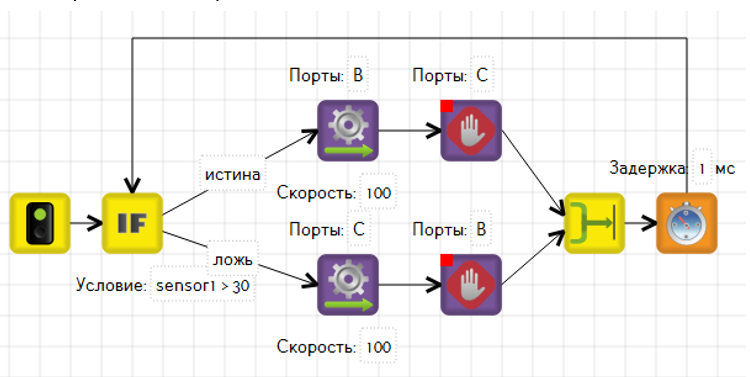
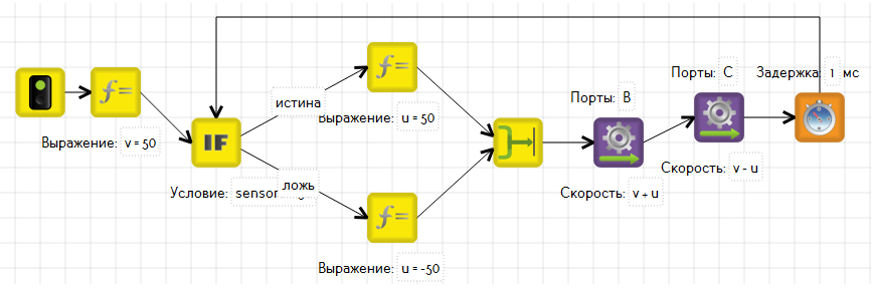
Робот должен двигаться по границе линии, находясь датчиком между белым и чёрным. Построим двухпозиционный релейный регулятор, который заставит робота поворачивать вправо, когда датчик находится над белым, и поворачивать влево, когда датчик находится над чёрным.

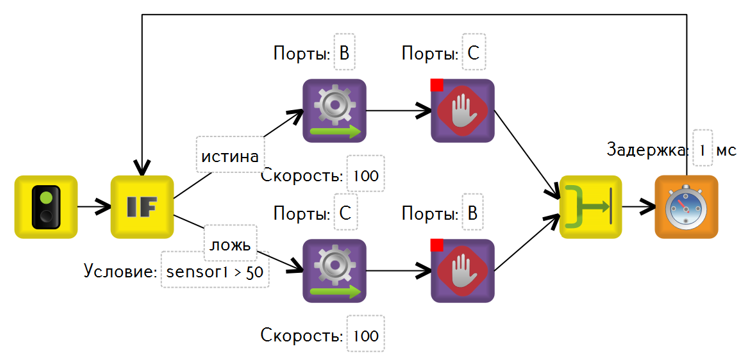
Рассмотрим программу. Она зациклена, и в начале цикла каждый раз происходит проверка датчика света, над белым он или над чёрным.

Для этого мы использовали блок «если». Данный блок направляет программу по двум возможным путям. Куда пойдёт программа, вверх или вниз, зависит от того, является ли условие в блоке «если» истиной. 

Sensor1 > 50. Почему 50? Разберёмся откуда взялось это число, и почему для разных роботов оно может быть разным. 50 – это желаемое состояние, то пороговое значение, которое видит датчик, когда находится ровно между белым и черным. Давайте называть его «серым». Переход от белого к черному и наоборот, для датчика освещенности происходит не мгновенно, а по мере того, насколько много в его области действия черного или белого.  Для отладчика TrikStudio это значение всегда 50, а для реального робота оно зависит от показания датчика на белом и на чёрном, и будет являться их средним арифметическим. Например, робот видит на белом 46, а на чёрном 12. Тогда значение серого на реальном роботе будет (46+12)/2 = 29. 

Таким образом, всё что меньше серого – это черное, а всё что больше – белое. Если робот на белом, то есть условие

 «Sensor1 > 50» — истина, то следует повернуть направо, запустив левый мотор вперёд, а правый остановив. Если робот на чёрном, то есть условие ложно, то необходимо поворачивать в другом направлении. 

Любой регулятор, это цикл, который повторяется с большой частотой. Чтобы не заставлять контроллер работать 100% времени, сделаем минимальную задержку по времени. Пока это время идёт, моторы работают, а процессор отдыхает. Таким образом программа делает 1000 итераций в секунду.

В итоге мы получаем робота, который умеет поворачивать направо и налево. Это как водитель, который выкручивает руль всегда до упора, и не может ехать прямо. 

 Усложним нашу программу, добавив третье действие – движение вперёд, и определим для него условие. Пусть робот едет вперёд, если отклонение от значения серого не превысило 5 пунктов. Предположим, что значение серого – 29. Это значит, что если значение датчика больше чем 29-5, и меньше, чем 29+5, то необходимо двигаться вперёд. Получился классический трёхпозиционный релейный регулятор. Движение вперёд позволяет быстрее преодолевать прямые участки, поскольку поворот – это остановка одно из моторов, а значит движение на повороте замедлено.

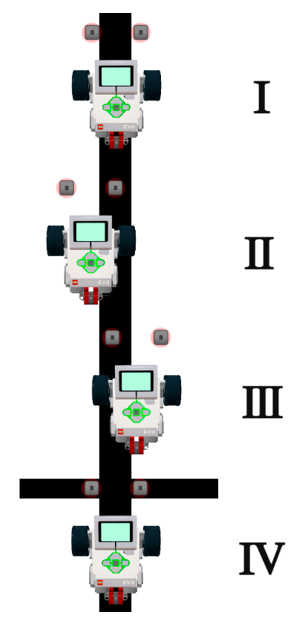
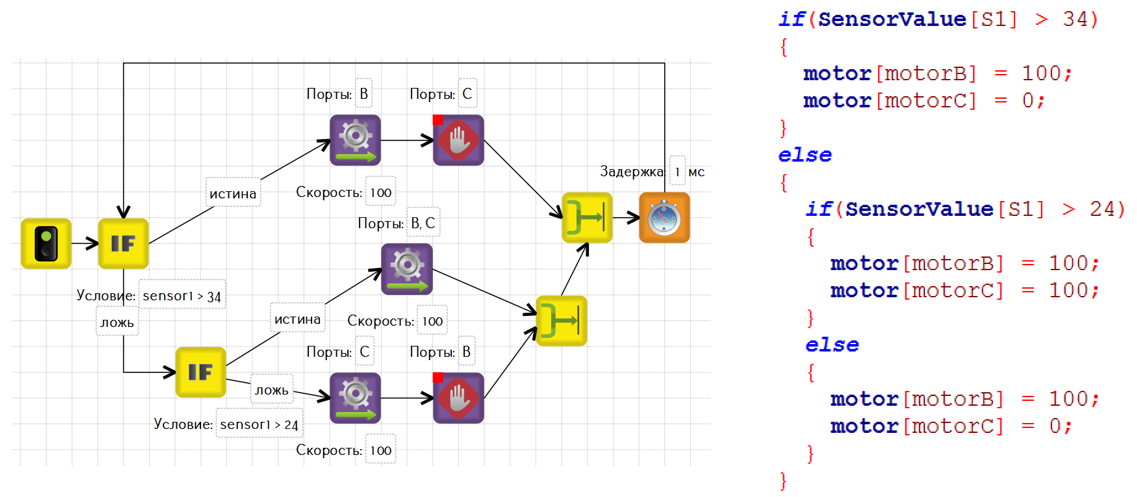
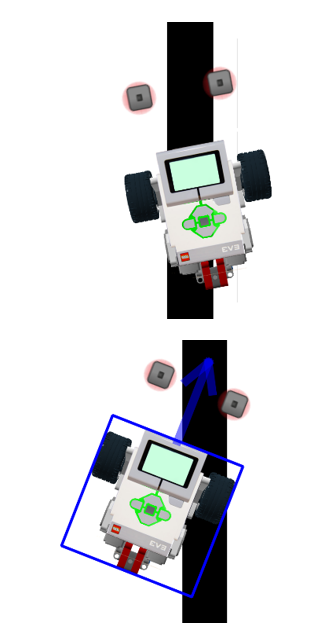
И, наконец, попробуем сделать четырёхпозиционный регулятор для робота с двумя датчиками освещенности. Для этого необходимо определить значения серого для обоих датчиков. Пусть оно будет 40 и 34.  

На картинке представлены 4 возможных положения робота относительно линии и, соответственно, в программе есть 4 варианта поведения робота. Сперва программа проверяет первый датчик, и если он на белом, то проверяется второй датчик, и если он тоже на белом, то робот едет прямо, а если второй на чёрном – поворачивает направо. Если первый датчик показал черное, то так же проверяется второй, и если второй датчик показал белое – то необходимо повернуть влево, а если второй тоже на чёрном, то пусть робот поедет прямо, сбавив скорость.

 Если заменить остановку моторов на движение с низкой скоростью, то можно добиться более плавного поворота. Но если сделать скорость более медленного мотора быстрее, то робот может не вписаться в резкий поворот. Найдите оптимальное решение при выборе скорости для вашей трассы. 

А вот пример применения релейного регулятора для движения вдоль стены. Для этого определим, на каком расстоянии необходимо двигаться. Пусть оно будет равно 30 сантиметрам. Отдаляясь от стены более чем на 30 см, робот будет пытаться приблизиться к ней, выполняя поворот направо, и наоборот, двигаться влево, если оказался ближе. Эта программа удивительным образом похожа на движение по линии. Это демонстрация того, что одни и те же алгоритмы могут быть применены к разным задачам. 

Попробуйте составить трёхпозиционный регулятор для движения вдоль стены. А если поставить робота в коридор и снабдить вторым датчиком расстояния, то можно двигаться на двух датчиках по знакомому алгоритму на четырёхпозиционном регуляторе.

Пропорциональный регулятор (П-регулятор)

Пропорциональный регулятор – это регулятор, в котором управляющее воздействие пропорционально отклонению. Говоря проще – чем сильнее робот (наш объект управления), отклонился от желаемого значения, тем сильнее он будет поворачивать, чтобы скорректировать своё отклонение. 

Чтобы понять работу данного регулятора, раскроем некоторые термины.

Пропорциональность. Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным. Например: x = y * 2. y всегда больше чем x в 2 раза, значит эти числа пропорциональны.

Отклонение – величина, характеризующая насколько сильно отличается текущее значение датчика(ов) от желаемого состояния. 

Управляющее воздействие – сила с которой объект корректирует отклонение.

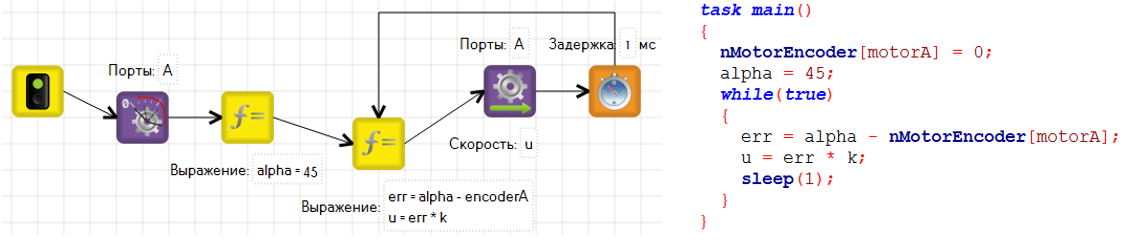
Попробуем применить пропорциональный регулятор для управления положением мотора. Мотор должен не просто повернуться на заданный угол, но и зафиксироваться в данном положении, сопротивляясь внешнему воздействию. Мотор, снабженный энкодером может справиться с этой задачей.

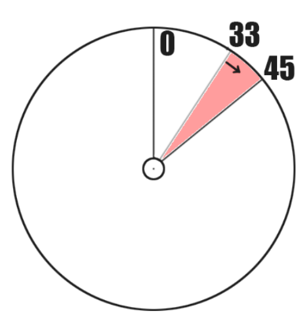
Зададим желаемый угол, пусть он будет 45 градусов.

Переменные

alpha – значение желаемого положения мотора.

k – усиливающий коэффициент 

err – отклонение(ошибка)

u – управляющее воздействие

Переменная err находит угол, на который мотор отклоняется от желаемого значения. Предположим сейчас энкодер показывает 33 градуса. Тогда ошибка будет равна 45 – 33 = 12. Следовательно, управляющее воздействие будет 12 * 4 = 48. Это заставит мотор двигаться вперёд, что будет приближать его к отметке 45 градусов. Если энкодер превысил значение 45, то ошибка станет отрицательной, что приведёт к его вращению в противоположную сторону. 

Таким образом мотор будет сопротивляться внешнему воздействию. Чем сильнее отклонился мотор и чем больше величина коэффициента k, тем сильнее сопротивление. Высокий коэффициент приведёт к дрожанию мотора, поскольку он будет вновь и вновь проскакивать желаемое значение. Это состояние называется перерегулирование. 

Изменяя угол alpha можно заставить мотор совершать точные движения и фиксироваться заданном положении. Это позволяет искусно решать задачи с захватом объектов, манипуляторами, поворотными башнями и т.д.

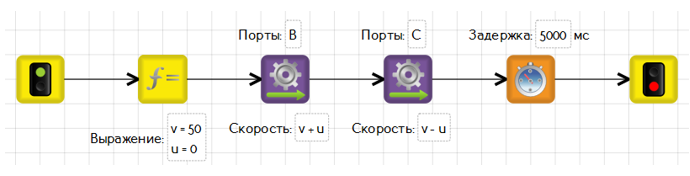
Применим пропорциональный регулятор для движения по линии. Начнём с того, как робот будет управляться. В командах запуска моторов мы используем две переменные: v – базовая скорость моторов, u – управляющее воздействие. Чтобы понять, как влияют на движение эти переменные, поэкспериментируйте с их различными значениями. 

Переменная v определяет, с какой скоростью робот поедет вперёд или назад в зависимости от знака. При положительной скорости – вперёд, назад при отрицательной. Переменная u задаёт резкость поворота, а от её знака зависит его направление. При положительном управляющем воздействии ускоряется мотор В и замедляется мотор С – поворот вправо, при отрицательном u соответственно наоборот робот поворачивает влево. Вот так выглядит релейный двухпозиционный регулятор, если управлять роботом с помощью переменных v и u:

Если с управлением разобрались, давайте построим уже пропорциональный регулятор для движения по линии на одном датчике освещенности. Вспомним расположение робота на линии. 

Переменные:

grey – значение серого для датчика освещенности.

k – усиливающий коэффициент

v – базовая скорость

err – отклонение(ошибка)

u – управляющее воздействие

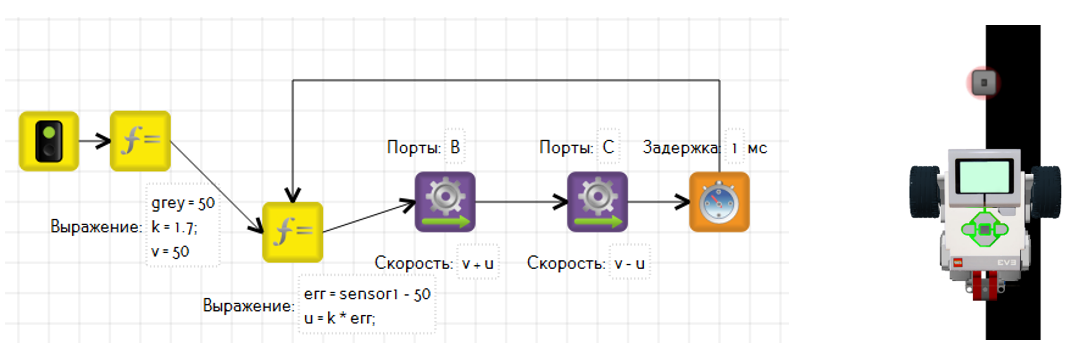
Что делают переменные v и u мы разобрали ранее, а в переменную grey запишем значение серого. 

Переменная err – это отклонение(ошибка) от желаемого значения. Когда текущее значение датчика (sensor1) превышает значение grey, ошибка становится положительной, когда они равны, то ошибка равна нулю, а когда sensor1 меньше grey, ошибка — отрицательная.

Теперь надо заставить робота поворачивать в нужную сторону. Сделаем так, чтобы управляющее воздействие зависело от ошибки. Но если просто приравнять их, то может возникнуть проблема, когда роботу не хватит силы управляющего воздействия, чтобы преодолеть крутой поворот. Для этого воспользуемся усиливающим коэффициентом k. Чем сильнее значение этого коэффициента, тем сильнее робот реагирует на отклонение. При слишком большом коэффициенте может возникнуть эффект перерегулирования, характеризующийся раскачиванием робота.

Допустим, что значение серого (grey) – 35. Рассмотрим примеры расположения робота на линии и его реакцию на отклонение:

Датчик света слегка сместился влево, и его значение выросло до 42. Это значит, что ошибка (err) будет равна 42 – 35 = 7. При коэффициенте (k) равном 2, управляющее воздействие (u) будет равно 7 * 2 = 14. При базовой скорости (v) 50, на мотор В будет подана скорость 50 + 14 = 64, а на мотор С 50 – 14 = 36. То есть робот плавно поворачивает направо, поскольку не сильно отклонился влево. 

Во втором примере робот сильно заехал датчиком на чёрное. Его значение стало равно 18. Теперь ошибка равна 18 – 35 = -17. При отрицательной ошибке управляющее воздействие тоже будет отрицательным и станет равным -17 * 2 = -34. При данном управляющем воздействии моторы получат значения В: 50 + (-34) = 16 и С: 50 – (-34) = 84, что заставит робота резко повернуть влево.

Вывод: чем сильнее отклонился робот, тем сильнее его реакция.

Поэкспериментируйте над значениями коэффициента и скорости робота. Найдите те оптимальные значения этих величин, при которых робот проходит линию наиболее быстро и плавно, при этом вписываясь во все повороты. Помните, что отладка – важнейшая часть работы, и большая часть времени при работе над созданием эффективных роботов посвящена именно ей. 

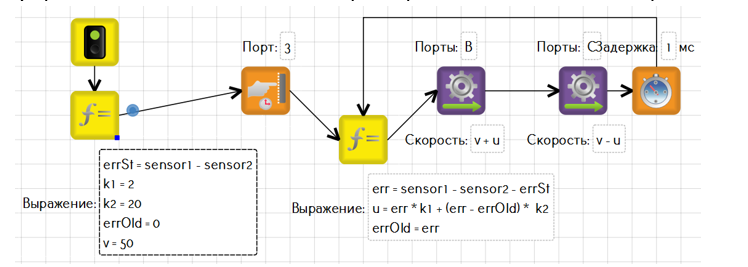
Теперь попробуем с двумя датчиками освещенности. Установим их по обе стороны от линии так, чтобы края области охвата датчиков (красные круги) соприкасались с границей линии. 

Ошибка вычисляется с помощью нахождения разности показания датчиков: err = Sensor1 – Sensor2. Желаемое значение разности между датчиками – ноль. Отличие в написании программы заключается лишь в том, как находится ошибка. Теперь нам не обязательно знать значение серого.

Однако далеко не всегда оба датчика будут показывать одинаковые значения на белом поле. Чаще всего значение имеют небольшие различия, а иногда и значительные. Робот с такими датчиками, например, не сможет ехать прямо, находясь на белом поле. А при движении по лини можно заметить, что один из датчиков (тот, который ярче) частично наезжает на черную линию.

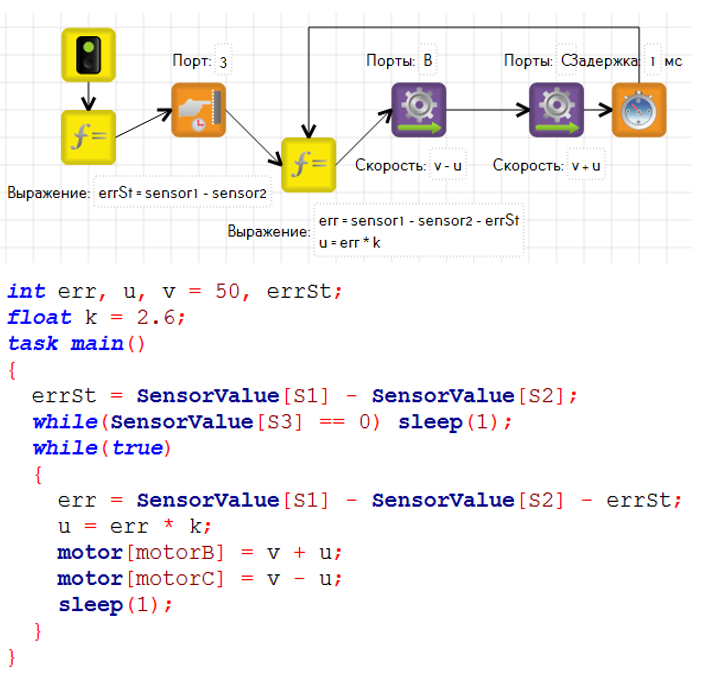
Чтобы этого избежать, необходимо найти так называемую статическую ошибку. Она находится один раз при запуске робота на белом полигоне и вычитается из динамической ошибки (err). 

П-регулятор можно применить для синхронизации скорости моторов. В таком случае нам потребуются показания энкодеров вместо датчиков света. Все остальные действия остаются прежними.

П-регулятор, как и релейный, может быть применён для множества задач. Попробуйте применить его, например, для движения вдоль стены. 

Для закрепления, еще раз пройдём по порядку все действия программы в цикле:

• Вычислениеошибки (err = sensor1 – grey или err = sensor1 – sensor2).
• Вычисление управляющего воздействия (u = err * 2).
• Подача управляющего воздействия на моторы (B: v + u, C: v – u).
• Не забываем про маленькую задержку по времени (1 миллисекунда).

Вычисление ошибки, подача управления на моторы и задержка характерны почти для всех регуляторов. Задача конкретно П-регулятора здесь в том, чтобы управляющее воздействие было пропорционально ошибке.

Пропорционально-дифференциальный регулятор (ПД-регулятор)

Вовсе не обязательно обладать знаниями в области высшей математики, чтобы применять дифференциальный или интегральный регуляторы. Достаточно понимать его принцип работы и предназначение. Учащиеся 7-х классов (а некоторые гораздо раньше) осознанно и с успехом применяют их в своих роботах, особенно там, где необходима высокая скорость и стабильность работы. 

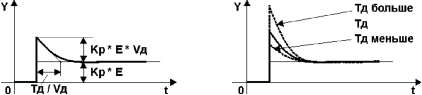
Зачем нужна Д-составляющая в регуляторе? Ответ – препятствовать перерегулированию. Как мы узнали ранее, существует проблема раскачивания при применении

 П-регулятора. Особенно сильно это проявляется на больших скоростях, ведь для быстрой скорости необходимо интенсивнее реагировать на повороты, повышая коэффициент усиления (k) П-регулятора, что неизбежно приводит к раскачиванию(перерегулированию). 

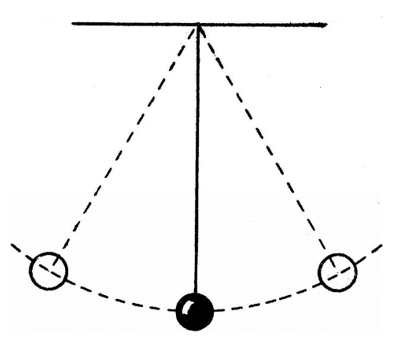
Взглянем на маятник. Он тоже раскачивается. Ему, как и скоростному роботу, нужно время, чтобы стабилизироваться. Для маятника в качестве П-регулятора выступает земная гравитация. Действительно, чем сильнее он отклонился от вертикального (желаемого) положения, тем сильнее гравитация пытается его вернуть. Но ничего не получается, он вновь и вновь проскакивает середину… Что, если погрузить его в воду? Сопротивление воды даст нужный эффект, ведь оно замедляет его движение. Маятник опускается на середину и фиксируется в этом положении. Давайте попробуем применить это на роботе, который движется по линии.

Принцип работы дифференциального регулятора заключается в том, что он определяет скорость изменения ошибки и создаёт управляющее воздействие пропорционально этой скорости. Говоря проще – робота нужно заставить сопротивляться изменениям ошибки. Скорость, как известно, можно найти зная расстояние и время. 

Посчитать скорость изменения ошибки можно, найдя разность текущей ошибки (err) и той ошибки, которая была в предыдущем цикле (errOld), а значит время известно – это задержка (1 миллисекунда). Чтобы запомнить предыдущую ошибку, присвоим её значение переменной errOld после всех вычислений. Таким образом, после обновления err, мы сможем знать и новую и старую ошибку. Так как скорость изменения отклонения (err – errOld) расчитывается в миллисекундах, то соответственно, значения получаются очень маленькие. Будьте внимательны выставляя задержку в цикле, так как её величина напрямую влияет на силу Д-регулятора. Действительно, значения датчиков вряд ли могли сильно измениться спустя всего 1 миллисекунду. А значит необходим усиливающий коэффициент (k2) достаточный, чтобы оказать влияние на управляющее воздействие. Полученное значение складывается вместе с управляющим воздействием пропорционального регулятора err * k1. Эти два регулятора работают бок о бок, но вовсе не обязательно, что их знаки будут совпадать.

Рассмотрим примеры действия ПД-регулятора при коэффициентах k1 = 2, k2 = 20. 

Пример 1: Робот правым датчиком заехал на черную линию и продолжает двигаться влево, а это значит, что ошибка увеличивается. Значение текущей ошибки равно 15, а предыдущей равно 13. П-регулятор заставляет робота поворачивать вправо с силой 15 * 2 = 30, а Д-регулятор с силой (15 – 13) * 20 = 40. Их сила складывается, значит общее управляющее воздействие равно 70. Робот будет поворачивать вправо.

Пример 2: Робот всё еще слева от линии, значит ошибка положительная, однако направление его движения изменилось – он движется вправо. Ошибка уменьшается, а значит дифференциальный регулятор должен заставлять робота поворачивать влево. Пусть ошибка равна 12, а предыдущая равна 15. В этом случае сила П-регулятора равна 12 * 2 = 24, а Д-регулятора (12-15) * 20 = -60. Суммарное управляющее воздействие 24 + (-60) = -36. Робот будет поворачивать влево.

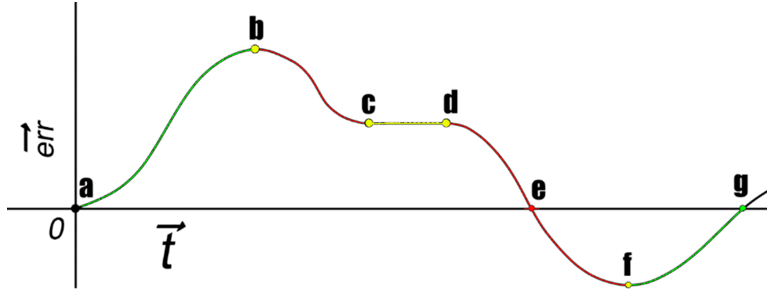
Чтобы глубже понять поведение ПД-регулятора, можно представить ошибку на графике. Везде, где график находится над нулевой отметкой – ошибка положительная, а значит действие П-регулятора будет иметь положительный знак. Знак Д-регулятора зависит от того, движется ли график вверх или идёт на спад. Его сила зависит от того, насколько резко происходит подъём или спад.

На отрезках ab и fg, в те моменты, когда график идёт «в гору» знак Д-регулятора положительный.

На отрезках bc и df при «скатывании» вниз знак Д-регулятора отрицательный.

На ровном отрезке cd, и в пиковых точках b и f значение Д-регулятора нулевое, поскольку в эти моменты не происходит изменений ошибки.

Интегральный регулятор. ПИД-регулятор

  Интегральная составляющая ПИД-регулятора обеспечивает значительное управляющее воздействие в случаях, когда объект упрвления(робот) длительное время (например 0.5 секунды) находится в состояни ошибки. Управляющее воздействие И-регулятора тем сильнее, чем дольше робот не может вернуться в состояние нулевой ошибки. 

Задача И-регулятора – вернуть объект в желаемое состояние в тех случаях, когда управляющего воздействия П-составляющей недостаточно. 

Рассмотрим простой пример: робот движется по круговой линии. На П или ПД-регуляторе он не может поддерживать ошибку в состоянии близкой к 0, поскольку при нулевой ошибке он движется прямо. При движении правый датчик частично заезжает на черную линию и создаёт ошибку, необходимую для обеспечения поворота. Попробуем сделать так, чтобы робот стабилизировался на нулевом положении.

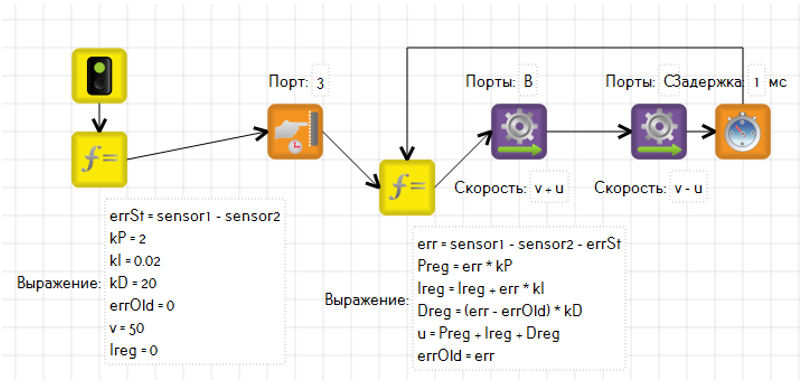
Принцип работы И-регулятора заключается в постоянном накапливании значений ошибки. Этот процесс так и называется – интегрирование. Создадим переменную I, в которую будем суммировать настоящую ошибку в каждом цикле: Ireg = Ireg + err. Коэффициент для И-составляющей будет очень мал, поскольку суммирование происходит каждую миллисекунду, и, скажем, если робот будет в течение секунды получать ощибку равную 10, то при коэффициенте 1 мы получим гигантское управляющее воздействие 10*1000 = 10000. Пусть коэффициент будет 0,02. Может возникнуть вопрос: а не будет ли переменная Ireg со временем разрастаться до огромных значений, ведь мы

 постоянно прибавляем? Ответ: переменная Ireg увеличивается только при положительной ошибке, при отрицательной ошибке происходит её уменьшение. Значит она может разрастись в обе стороны, но только в случае, если робот застрял в состоянии ошибки надолго.

Для удобства восприятия, давайте разложим ПИД-регулятор на 3 отдельные его составляющие. Подпишем коэффициенты (kP, kD, kI).

Preg = err * kP

Ireg = I + err * kI

Dreg = (err – errOld) * kD

u = Preg + Ireg + Dreg

Следует помнить, что интегральный регулятор, как и дифференциальный, имеет прямую зависимость от времени задержки. Чем меньше задержка, тем чаще производится действие сложения, и тем быстрее она будет накапливаться. 

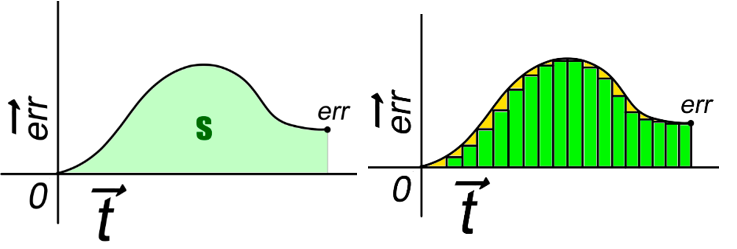
Давайте отразим работу И-регулятора на графике ошибки. Первое, что необходимо знать – интеграл – это площадь под графиком. Каждый зелёный столбик – это величина ошибки, которая была накоплена регулятором за время

 работы программы. 

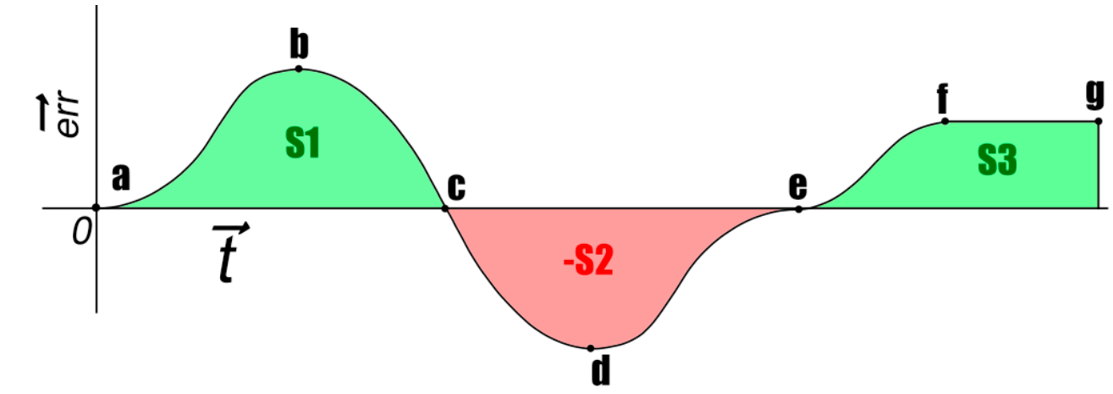
Рассмотрим график ошибки и значения И-составляющей для каждой выделенной точки на этом графике.

В точке a значение И-составляющей равно нулю. 

В точке b оно положительное, поскольку при положительной ошибке оно накапливалось за промежуток времени от a до b.

В точке c оно так же положительное.

В точке d – всё еще положительное, поскольку площадь S1 больше чем кусок площади S2 до точки d. 

Предположим, что площади S1 и S2 равны, хоть в реальной жизни, это маловероятно. Тогда в точке e значение вновь возвратится в ноль.

И далее в точках f и g снова положительное.

Попробуем более грамотно посчитать значение интегральной и дифференциальной составляющих, учитывая, что задержа по времени (будем называть её deltaT, или dT) влияет на расчет величин управляющего воздействия.

Известно, что в TrikStudio и RobotC время исчисляется в миллисекундах. В физике больше любят секунды, так что давайте переведём всё в них.

Тогда dT будет равна 0.001 сек. Тогда задержку по времени, будем выполнять так: sleep(dT * 1000), то есть получим значение 1 при dT равной 0.001.

Значение П-составляющей от времени не зависит, а значит ничего не изменится: err * kP

Значение Д-составляющей получится следующее: kD * (err-errOld) / dT. Всё как учили по физике: скорость равна частному от изменения на время. Помним, что теперь измерение ведётся в секундах, так что стоит изменить kD, уменьшив его в 1000 раз.

Значение И-составляющей: Ireg + err * dT * kI. Увеличиаем kI в 1000 раз.

Итог: изменяя задержку в цикле, теперь мы не создадим помех в работе ПИД-регулятора.

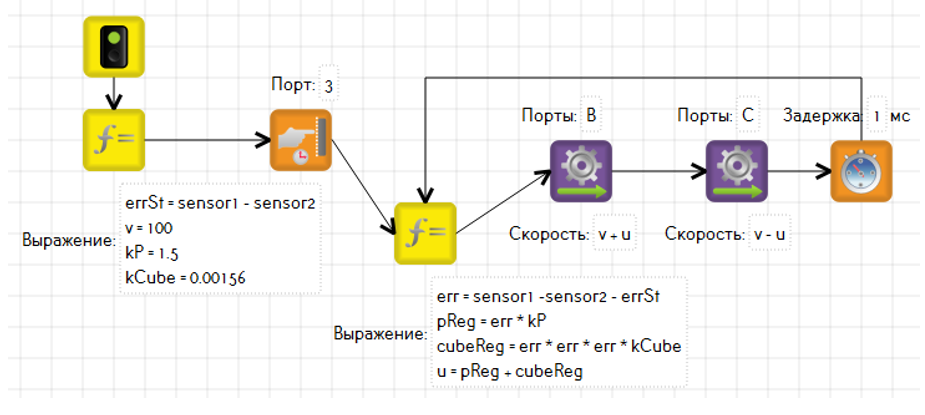
Кубический регулятор

Достаточно простой регулятор, в котором управляющее воздействие пропорционально ошибке, возведённой в куб. 

Его применение актуально там, где, периодически, необходимо вырабатывать очень большое управляющее воздействие, при этом сохраняя плавность работы в условиях небольших значений ошибки. Пример: движение по линии, в которой есть участки с резкими поворотами и прямые участки, либо участки с очень плавными поворотами.

Важно правильно подобрать коэффициент для кубического регулятора, ведь число, возведённое в куб может выдать огромные значения. Давайте вычислим минимальную и максимальную ошибку. Рассмотрим классическое движение по линии на двух датчиках света.

Минимальная ошибка — это разность минимального значения правого датчика и максимального значения левого. Максимальная ошибка – соответственно будет равна разности белого для первого датчика и черного для второго.

Пусть диапазон ошибки будет от -40, до 40 единиц. Нам нужно, чтобы кубический регулятор выработал при максимальной ошибке значение 100.

Посчитаем, чему будет равно управляющее воздействие при коэффициенте 1 и ошибке 40. 40*40*40 = 64000. Многовато! Узнаем, во сколько раз это больше чем 100 и разделим на это число наш коэффициент.

64000 / 100 = 640, значит нам необходим коэффициент  или около 0.00156.

Управляющее воздействие при ошибке менее 10 не превысит даже единицы! При ошибке, равной 20 – около 12, при 30 – около 42, при 40 – 100.

Кубический регулятор практически никак не будет реагировать на малые отклонения. Эффективнее всего использовать кубический регулятор в паре с П-регулятором или ПД-регулятором. Они отлично дополняют друг друга! 

ПИД регулятор – один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: специальные печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков. Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Это всё ПИД регулятор. Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но, чтобы грамотно синтезировать такой регулятор, нужно быть гораздо больше чем “семи пядей” во лбу, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам ПИД регулятор универсален для почти любого процесса.

Система управления

---

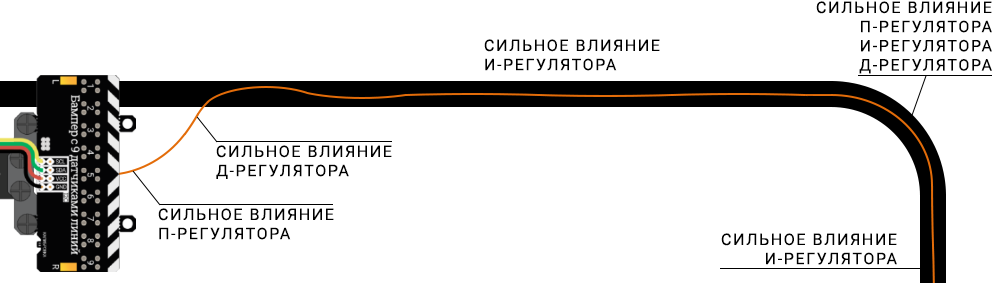
Прежде чем переходить непосредственно к пиду, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет и находится в центре системы. Регулятор в данном понимании – математический алгоритм или часть программы, которая крутится на микроконтроллере. Регулятор, как алгоритм, работает с обычными числами. Объект управления – это девайс, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число. Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180, потому что регулятору без разницы чем управлять. В объекте управления у нас стоит датчик, с которого регулятор получает управляемую величину, то есть текущий сигнал с датчика. Это – обратная связь, которая и даёт возможность системе ирчно поддержать заданное значение. В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает установку (уставку), то есть число, к которому он должен привести текущее значение с датчика. Установка может задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками, да хоть смской или голосовым вводом. Регулятору это неважно, для него это просто цифра. Задача регулятора состоит в том, чтобы сравнивать текущее значение с установкой и выдавать управляющий сигнал на управляющее устройство. То есть в программе это будет выглядеть условно так: регулятор получил установку, регулятор получил значение с датчика, регулятор выполнил вычисления и выдал нам управляющий сигнал, опять же число. Если это шим – мы его подаём через функцию генерации шим. Есть ещё один момент – регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования.  

Под капотом у ПИД регулятора

---

ПИД регулятор состоит из трёх составляющих: пропорциональной P, интегрирующей I и дифференциирующей D, формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство, обозначим его как out.

out = P*kP + I*kI + D*kD

kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы. Тут есть ещё один момент: любой коэффициент может быть равен нулю, и в таком случае обнуляется вся его компонента. То есть регулятор можно превратить в П, ПИ, ПД, и прочие сочетания. Разные системы требуют разного подхода, именно поэтому ПИД регулятор такой универсальный. В дальнейшем будем пользоваться следующими названиями переменных:

• out – выход с регулятора (управляющий сигнал)
• setpoint – установка (заданное значение)
• input – вход (значение с датчика)
• err – ошибка регулирования
• dt – период вычисления и регулирования

P составляющая

---

Пропорциональная составляющая предоставляет собой разность текущего значения с датчика и установки.

P = setpoint - input

Данная разность называется ошибкой регулирования, то есть насколько далеко находится система от заданного значения. Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент kP тут влияет роль усиления ошибки и настраивается вручную. Но в то же время, если система пришла к заданной величине, ошибка станет равной нулю, и управляющий сигнал тоже! Другими словами, п регулятор никогда не сможет привести к заданному значению, всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной. P составляющая исправляет ошибку в текущий момент времени.

I составляющая

---

Интегральная составляющая просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.

I = I + (setpoint - input) * dt

В самом регуляторе это ещё умножается на коэффициент kI, которым настраивается резкость данной составляющей. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. I составляющая исправляет прошлые, накопившиеся ошибки.

D составляющая

---

Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.

err = setpoint - input
D = (err - prevErr) / dt
prevErr = err

Фактически D составляющая реагирует на изменение сигнала с датчика, и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку. Коэффициент д позволяет настроить вес, или резкость данной компенсации, как и остальные коэффициенты регулируют свои составляющие. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, такие как квадрокоптер или шпиндель станка под переменной нагрузкой. D составляющая исправляет возможные будущие ошибки, анализируя скорость.

Настройка регулятора

---

Для настройки регулятора нужно варьировать коэффициенты:

• При увеличении kP увеличивается скорость выхода на установленное значение, увеличивается управляющий сигнал. Чисто математически система не может прийти ровно к заданному значению, так как при приближении к установке П составляющая пропорционально уменьшается. При дальнейшем увеличении kP реальная система теряет устойчивость и начинаются колебания.
• При увеличении kI растёт скорость компенсации накопившейся ошибки, что позволяет вывести систему точно к заданному значению с течением времени. Если система медленная, а kI слишком большой – интегральная сумма сильно вырастет и произойдёт перерегулирование, которое может иметь характер незатухающих колебаний с большим периодом. Поэтому интегральную сумму в алгоритме регулятора часто ограничивают, чтобы она не могла увеличиваться и уменьшаться до бесконечности.
• При увеличении kD растёт стабильность системы, она не даёт системе меняться слишком быстро. В то же время kD может стать причиной неадекватного поведения системы и постоянных скачков управляющего сигнала, если значение с датчика шумит. На каждое резкое изменение сигнала с датчика Д составляющая будет реагировать изменением управляющего сигнала, поэтому сигнал с датчика нужно фильтровать (читай урок по фильтрам).

Вот так выглядит процесс стабилизации при изменении коэффициентов: 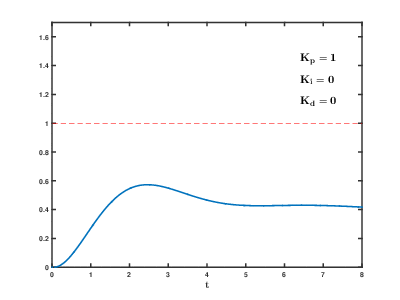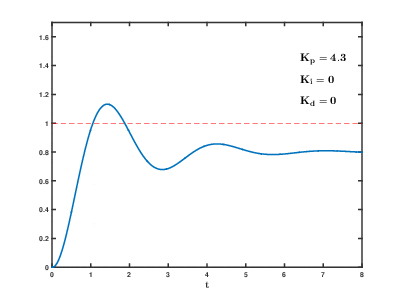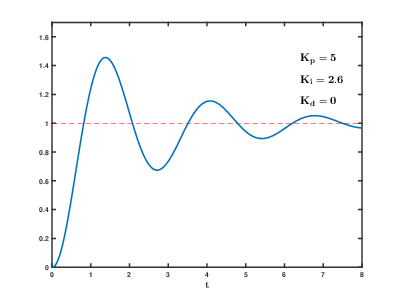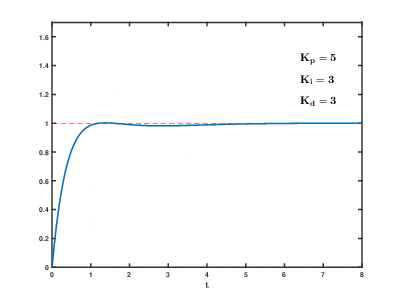  Настройка регулятора – дело не очень простое. Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в 0. Плавно увеличиваем kP до появления незатухающих колебаний. Значение kP, при котором они появились, запишем и обозначим как kP1. Далее замеряем период колебаний системы в секундах, обозначим как T. Итоговые коэффициенты получим так:

• kP = 0.6 * kP1
• kI = kP / T * 2 * dt
• kD = kP * T / 8 / dt

Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:

• kP: 0.6*20=12
• kI: 12/3*2*0.05=0.4
• kD: 12*2/8/0.05=60

На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.

Реализация на C++

---

Соединяя все рассмотренные выше уравнения, получим:

// (вход, установка, п, и, д, период в секундах, мин.выход, макс. выход)
int computePID(float input, float setpoint, float kp, float ki, float kd, float dt, int minOut, int maxOut) {
  float err = setpoint - input;
  static float integral = 0, prevErr = 0;
  integral = constrain(integral + (float)err * dt * ki, minOut, maxOut);
  float D = (err - prevErr) / dt;
  prevErr = err;
  return constrain(err * kp + integral + D * kd, minOut, maxOut);
}

Это готовая функция, которая принимает значение с датчика, установку, три коэффициента и время, а также ограничение выхода с регулятора. Как пользоваться этой функцией: функция должна вызываться с некоторым периодом, причем длительность этого периода нужно будет передать в функцию в секундах. Если попроще, можно использовать задержку. Но делать так не рекомендуется, лучше сделать таймер на миллис и работать с ним. Функция возвращает управляющий сигнал, то есть можно подать его например как ШИМ. Период dt имеет такой смысл: чем инерционнее у нас система, тем реже можно вычислять пид. Например для обогрева комнаты период можно поставить 1 секунду или больше, а для контроля за оборотами двигателя надо будет поставить пару десятков миллисекунд, то есть около сотни раз в секунду.

Библиотеки

---

• GyverPID – моя библиотека со встроенным тюнером коэффициентов
• QuickPID – хорошая библиотека с интересными возможностями (оптимизация интегральной суммы, смешанный режим пропорционально ошибке/измерению)
• sTune – тюнер коэффициентов, несколько алгоритмов

Видео

---

Полезные страницы

---

• Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
• Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
• Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
• Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
• Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
• Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
• Поддержать автора за работу над уроками
• Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])

В данном разделе приведены описания алгоритмов работы и законы регулирования непрерывных П-, ПИ-, ПД-, ПИД-регуляторов с различными структурами выходного сигнала — аналоговым выходом, дискретным (импульсным) выходом или ШИМ-выходом (широтно импульсным модулированным сигналом).

Классификация систем автоматического регулирования (САР) приведена в таблице 1 в «Классификация систем автоматического регулирования».

Типовые регуляторы и регулировочные характеристики

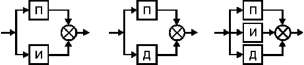
Для регулирования объектами управления, как правило, используют типовые регуляторы, названия которых соответствуют названиям типовых звеньев (описание типовых звеньев представлено в разделе 2.4):

1. П-регулятор, пропорциональный регулятор
   Передаточная функция П-регулятора: W_п(s) = K₁. Принцип действия заключается в том, что регулятор вырабатывает управляющее воздействие на объект пропорционально величине ошибки (чем больше ошибка Е, тем больше управляющее воздействие Y).
2. И-регулятор, интегрирующий регулятор
   Передаточная функция И-регулятора: W_и(s) = К₀/s. Управляющее воздействие пропорционально интегралу от ошибки.
3. Д-регулятор, дифференцирующий регулятор
   ПередаточнаяфункцияД-регулятора: W_д(s) = К₂*s. Д-регуляторгенерирует управляющее воздействие только при изменении регулируемой веричины: Y= K2 * dE/dt.

   На практике данные простейшие П, И, Д регуляторы комбинируются в регуляторы вида ПИ, ПД, ПИД (см. рис.1):

Рисунок 1 — Виды непрерывных регуляторов

В зависимости от выбранного вида регулятор может иметь пропорциональную характеристику (П), пропорционально-интегральную характеристику (ПИ), пропорционально-дифференциальную характеристику (ПД) или пропорционально-интегральную (изодромную) характеристику с воздействием по производной (ПИД-регулятор).

1. ПИ-регулятор, пропорционально-интегральный регулятор (см. рис.3.18.а)
   ПИ-регулятор представляет собой сочетание П- и И-регуляторов. Передаточная функция ПИ-регулятора: W_пи(s) = K₁ + K₀/s.
2. ПД-регулятор, пропорционально-дифференциальный регулятор (см. рис.3.18.б)
   ПД-регулятор представляет собой сочетание П- и Д-регуляторов. Передаточная функция ПД-регулятора: W_пд(s) = K₁ + K₂ s.
3. ПИД-регулятор, пропорционально-интегрально-дифференциальный регулятор (см. рис.3.18.в)

ПИД-регулятор представляет собой сочетание П-, И- и Д-регуляторов. Передаточная функция ПИД-регулятора: W_пид(s) = K₁ + K₀ / s + K₂ s.

Наиболее часто используется ПИД-регулятор, поскольку он сочетает в себе достоинства всех трех типовых регуляторов.

Структурные схемы непрерывных регуляторов

В данном разделе приведены структурные схемы непрерывных регуляторов с аналоговым выходом -рис.2, с импульсным выходом — рис.3 и с ШИМ (широтно импульсным модулированным) выходом -рис.4.

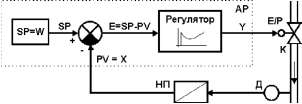
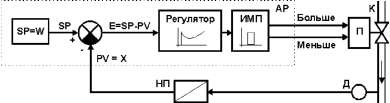
В процессе работы система автоматического регулирования АР (регулятор) сравнивает текущее значение измеряемого параметра Х, полученного от датчика Д, с заданным значением (заданием SP) и устраняет рассогласование регулирования E (B=SP-PV). Внешние возмущающие воздействия Z также устраняются регулятором. Работа приведенных структурных схем отличается методом формирования выходного управляющего сигнала регулятора.

Непрерывный регулятор с аналоговым выходом

Структурная схема непрерывного регулятора с аналоговым выходом приведена на рис.2.

Выход Y регулятора АР (например, сигнал 0-20мА, 4-20мА, 0-5мА или 0-10В) воздействует через электропневматический преобразователь Е/Р сигналов (например, с выходным сигналом 20-100кПа) или электропневматический позиционный регулятор на исполнительный элемент К (регулирующий орган).

Рисунок 2 — Структурная схема регулятора с аналоговым выходом

где:
АР — непрерывный ПИД-регулятор с аналоговым выходом,
SP — узел формирования заданной точки,
PV=X- регулируемый технологический параметр,
Е — рассогласование регулятора,
Д — датчик,
НП — нормирующий преобразователь (в современных регуляторах является входным устройством)
Y — выходной аналоговый управляющий сигнал Е/Р — электропневматический преобразователь,
К — клапан регулирующий (регулирующий орган).

Непрерывный регулятор с импульсным выходом

Структурная схема непрерывного регулятора с импульсным выходом приведена на рис.3.

Выходные управляющие сигналы регулятора — сигналы Больше и Меньше (транзистор, реле, симистор) через контактные или бесконтактные управляющие устройства (П) воздействуют на исполнительный элемент К (регулирующий орган).

Рисунок 3 — Структурная схема регулятора с импульсным выходом

где:
АР — непрерывный ПИД-регулятор с импульсным выходом,
SP — узел формирования заданной точки,
PV=X- регулируемый технологический параметр,
Е — рассогласование регулятора,
Д — датчик,
НП — нормирующий преобразователь (в современных регуляторах является входным устройством) ИМП — импульсный ШИМ модулятор, преобразующий выходной сигнал Y в последовательность импульсов со скважностью, пропорциональной выходному сигналу: Q=Y/100. Сигналы Больше и Меньше — управляющие воздействия,
П — пускатель контактный или бесконтактный,
К — клапан регулирующий (регулирующий орган).

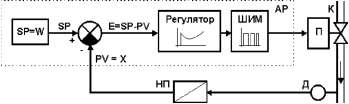
Непрерывный регулятор с ШИМ (широтно импульсным модулированным) выходом

Структурная схема непрерывного регулятора с ШИМ (широтно импульсным модулированным) выходом приведена на рис.4.

Выходной управляющий сигнал регулятора (транзистор, реле, симистор) через контактные или бесконтактные управляющие устройства (П) воздействуют на исполнительный элемент К (регулирующий орган).

Непрерывные регуляторы с ШИМ выходом широко применяются в системах регулирования температуры, где выходной управляющий симисторный элемент (или твердотельное реле, пускатель) воздействуют на термоэлектрический нагреватель ТЭН, или вентилятор.

Рисунок 4 — Структурная схема регулятора с ШИМ выходом

АР — непрерывный ПИД-регулятор с импульсным ШИМ выходом,
SP — узел формирования заданной точки,
PV=X- регулируемый технологический параметр,
Е — рассогласование регулятора,
Д — датчик,
НП — нормирующий преобразователь (в современных регуляторах является входным устройством) ШИМ — импульсный ШИМ модулятор, преобразующий выходной сигнал Y в последовательность импульсов со скважностью, пропорциональной выходному сигналу: Q=Y/100.
П — пускатель контактный или бесконтактный,
К — клапан регулирующий (регулирующий орган).

Согласование выходных устройств непрерывных регуляторов

Выходной сигнал регулятора должен быть согласован с исполнительным механизмом и исполнительным устройством.

В соответствии с видом привода и исполнительным механизмом необходимо использовать выходное устройство непрерывного регулятора соответствующего типа, см. таблицу 1.

Таблица 1 — Согласование выходных устройств непрерывных регуляторов

Выходное устройство непрерывного регулятора	Тип выходного устройства	Закон регулирования	Исполнительный механизм или устройство	Вид привода	Регулирующий орган
Аналоговый выход	ЦАП с выходом 0-5мА, 0-20мА, 4-20мА, 0-10В	П-, ПИ-,ПД-, ПИД-закон	Преобразователи и позиционные регуляторы электро-пневматические и гидравлические	Пневматические исполнительные приводы (с сжатым воздухом в качестве вспомогательной энергии) и электропневматические преобразователи сигналов или электропневматические позиционные регуляторы, электрические (частотные привода)
Импульсный выход	Транзистор, реле, симистор	П-, ПИ-, ПД-, ПИД-закон	Контактные (реле) и бесконтактные (симисторные) пускатели	Электрические приводы (с редуктором), в т. ч. реверсивные
ШИМ выход	Транзистор, реле, симистор	П-, ПИ-, ПД-, ПИД-закон	Контактные (реле) и бесконтактные (симисторные) пускатели		Термоэлектрический нагреватель(ТЭН) и др.

Реакция регулятора на единичное ступенчатое воздействие

Одной из динамических характеристик обьекта управления является его переходная характеристика -реакция обьекта на единичное ступенчатое воздействие (см. Динамические характеристики), например, изменение заданной точки регулятора.

В данном разделе приведены переходные процессы системы управления при единичном ступенчатом изменении заданной точки при использовании регуляторов с различным законом регулирования.

Если на вход регулятора подается скачкообразная функция изменения заданной точки — см. рис. 5, то на выходе регулятора возникает реакция на единичное ступенчатое воздействие в соответствии с характеристикой регулятора в функции времени.

Рисунок 5 — Единичное ступенчатое воздействие скачкообразная функция изменения заданной точки регулятора

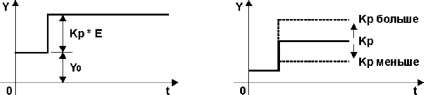
П-регулятор, реакция на единичное ступенчатое воздействие

Параметрами П-регулятора являются коэффициент усиления Кр и рабочая точка Y₀. Рабочая точка Y₀ определяется как значение выходного сигнала, при котором рассогласование регулируемой величины равно нулю. При влиянии возмущающих воздействий возникает, в зависимости от Y₀, отклонение регулирования.

Рисунок 6 — П-регулятор. Реакция на единичное ступенчатое воздействие

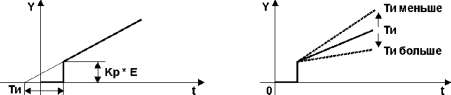
ПИ-регулятор, реакция на единичное ступенчатое воздействие

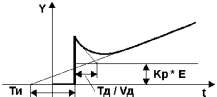
В отличие от П-регулятора у ПИ-регулятора, благодаря интегральной составляющей, исключается отклонение регулирования.

Параметром интегральной составляющей является время интегрирования Ти.

Рисунок 7 — ПИ-регулятор. Реакция на единичное ступенчатое воздействие

ПД-регулятор, реакция на единичное ступенчатое воздействие

У ПД-регуляторов пропорциональная составляющая накладывается на затухающую дифференциальную составляющую.

Д-составляющая определяется через усиление упреждения Уд и время дифференцирования Тд.

Рисунок 8 — ПД-регулятор. Реакция на единичное ступенчатое воздействие

ПИД-регулятор, реакция на единичное ступенчатое воздействие

Б лагодаря дополнительному подключению Д-составляющей ПИД-регулятор достигает улучшения динамического качества регулирования.

См. ПИ-регулятор, ПД-регулятор.

Рисунок 9 — ПИД-регулятор. Реакция на единичное ступенчатое воздействие

Классический ПИД-регулятор

Простейшая система автоматического регулирования с обратной связью показана на рисунке. В ней блок R называют регулятором (от слова Regulator), P — объектом регулирования (от слова Process), r — управляющим воздействием или уставкой (reference), e — сигналом рассогласования или ошибки (error), u — выходной величиной регулятора, y — регулируемой величиной.

Частный случай ПИД-регулятора — пропорциональный или П-регулятор: u(t)=K·e(t). С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку (статическая ошибка e0 — постоянная ошибка в установившемся режиме системы; см. рис. ниже).

С увеличением пропорционального коэффициента K статическая ошибка e0 уменьшается, время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается.

Чтобы убрать статическую ошибку в установившемся режиме, в регулятор вводят интегральный канал с коэффициентом усиления Ki, так что:

Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется.

Однако за счет интегрального канала обеспечивается нулевая ошибка e0 в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.

С увеличением коэффициента интегральной составляющей ПИ-регулятора Ki время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается, время регулирования tр увеличивается.

Для ускорения переходных процессов добавляют дифференциальный канал с коэффициентом усиления Kd:

Распространена также другая модификация выражения (1.01):

где t — время; K — пропорциональный коэффициент (безразмерный), Ti — постоянная интегрирования (размерность времени) и Td — постоянная дифференцирования (размерность времени) регулятора. Такой регулятор называют ПИД-регулятором.

Регуляторы этого типа очень хорошо зарекомендовали себя в практических задачах. Кроме того, иногда используются ПД-регуляторы (пропорционально-дифференциальные), у которых нет интегрального канала.

Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденцию ее изменения, и принять превентивные меры. Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений.

С увеличением коэффициента дифференциальной составляющей ПИД-регулятора Kd перерегулирование σ уменьшается, время регулирования tр уменьшается.

	При увеличении коэффициентов
	Kp	Ki	Kd
Время нарастания tн
Пере- регулирование σ
Время регулирования tр
Статическая ошибка e0
— Увеличивается. — Уменьшается. — Устраняется. — Нет определенной тенденции (No definite Trend). Незначительное изменение.

Для устойчивого объекта можно выбрать коэффициенты регулятора опытным путем, выполняя эксперименты с реальным объектом. Предложено несколько методов решения этой задачи, например, правила Зиглера-Никольса (Ziegler J. G. — Nichols N. B.), Коэна-Куна (Cohen O.H. – Coon O.A.) или CHR (Chien K. L. — Hrones J. A. — Reswick J. B.).

Список используемой литературы

1. Поляков К.Ю., Теория автоматического управления для чайников, Санкт-Петербург, 2008 г.
2. Востриков А.С., Французова Г.А., Теория автоматического регулирования. 2003 г.
3. Глушков В.М., Амосов Н.М., Артеменко И.А. Энциклопедия кибернетики. Том 2. Киев, 1974 г.
4. Теория автоматического управления: Учеб. для вузов по спец. Автоматика и телемеханика. В 2-х ч. Ч. I. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др.; Под ред. А. А. Воронова.—2-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 367 с.
5. Денисенко В.В., Энциклопедия АСУ ТП, bookasutp.ru
6. Dew Toochinda, Scilab Ninja. Control Engineering with Scilab, Scilab Control Engineering Basics, scilab.ninja/study-modules/scilab-control-engineering-basics/ 

У нас на сайте Вы можете приобрести качественные частотные преобразователи. Подробности тут

В этом уроке

• И-регулятор и за что он отвечает
• Настройка регулятора
  
• Управление машинкой с помощью ПИД-регулятора

Видео версия урока

Общие сведения о ПИД-регуляторе:

В прошлом уроке мы разобрались с работой ПД-регулятора.

П-регулятор указывает машине повернуть в сторону линии. Чем дальше линия от центра бампера, итем сильнее ошибка отличается от 0, тем круче поворот машины.

Недостатком П-регулятора является то, что он не может работать на больших скоростях.

Для борьбы с указанным недостатком в одном регуляторе совмещают пропорциональную (П) и дифференциальную (Д) составляющую, получается ПД-регулятор.

Дифференциальная составляющая (от лат. differentia – разность) — это разность между текущей и предыдущей ошибкой.

Ошибки для Д-регулятора берутся через одинаковые интервалы времени, значит разность между текущей и предыдущей ошибкой, является скоростью изменения ошибки.

Чем выше скорость изменения ошибки, тем сильнее влияние Д-регулятора.

Д-регулятор выполняет сразу две задачи: он помогает П-регулятору справиться с резкими поворотами и превращает крутой въезд на линию в более пологим.

Недостатком Д-регулятора является его чувствительность к шумам (некорректным данным).

Недостатком ПД-регулятора является то, что он не может справиться с маленькими ошибками. Это выражается в незначительных отклонениях при движении по прямой линии и отклонении к внешнему краю линии при движении по дугам или поворотам трассы.

Для борьбы с указанными недостатками в одном регуляторе совмещают пропорциональную (П), интегральную (И) и дифференциальную (Д) составляющую, получается ПИД-регулятор.

Интегральная составляющая (от лат. integra – составной) — это сумма нескольких последних ошибок.

Количество ошибок в сумме определяет скорость реакции И-регулятора:

• Малое количество ошибок приведёт к тому, что их сумма будет мала для воздействия;
• Большое количество ошибок придаст воздействию существенную инерционность;
• В примере ниже мы будем использовать сумму из 10 последних ошибок.

И-регулятор позволяет исправить статические и слабые ошибки, а также избавиться от нежелательного воздействия шумов на Д-регулятор.

И-регулятор помогает ПД-регулятору выровнять центр бампера с центром линии как на прямых участках, так и на поворотах.

Пример: представим, что машина едет по дуге, и бампер выдаёт ошибку 0,5. П-регулятор слабо доворачивает вправо, — этого хватает для движения по линии, но ошибка сохраняется на прежнем уровне до завершения поворота. Значит, весь путь центр бампера был смещён от центра линии. Сумма из 10 ошибок по 0,5 уже равна 5, и И-регулятор поможет П-регулятору скорректировать путь так, что центр бампера пройдёт по центру линии на протяжении всей дуги.

Пример: предположим, что на линии трассы появилась царапина, — это будет шумом для Д-регулятора, который резко среагирует, и машина «дёрнется» на линии. Но И-регулятор сгладит воздействие Д-регулятора, так как изменение всего 1 из 10 ошибок является незначительным.

Поведение составляющих ПИД-регулятора:

Поведение составляющих ПД-регулятора было рассмотрено в предыдущем уроке. Ниже представлена картинка движения машины по линии с ПД-регулятором:

Как видно из картинки выше, у ПД-регулятора есть два слабых места: на прямой линии машина едет с небольшими отклонениями, и на повороте видно отклонение центра бампера от центра линии.

После добавления интегральной составляющей, картинка станет такой:

И-регулятор накапливает ошибки и оценивает их сумму. Это позволяет ему справляться со статическими или слабыми ошибками. Теперь машина едет по прямой и на повороте ровнее

Код ПИД-регулятора:

float ERR[10] = {0,0,0,0,0,0,0,0,0,0};                 // Определяем массив последних ошибок
                                                       //
void loop(){                                           //
     i++;     if( i>=10 ){ i=0; }                      // Переходим к следующему элементу массива «ERR»
     ERR[i] = bum.getErrPID();                         // Получаем текущую ошибку
     SUM    = 0; for( auto a:ERR ){ SUM+=a; }          // Получаем сумму последних ошибок
     P      = ERR[i]            * kP;                  // Определяем пропорциональную составляющую регулятора
     I      = SUM               * kI;                  // Определяем интегральную составляющую регулятора
     D      = ( ERR[i]-ERR[j] ) * kD;                  // Определяем дифференциальную составляющую регулятора
     PID    = P + I + D;                               // Получаем результат ПИД-регулятора
     j      = i;                                       // Сохраняем номер элемента массива «ERR» в котором хранится текущая ошибка,
}                                                      // на следующем проходе цикла она станет предыдущей ошибкой

• До цикла определяем массив ERR для хранения 10 последних ошибок;
• Предполагается, что остальные переменные кода также объявлены;
• Первая строка цикла увеличивает значение i на 1, со сбросом в 0 при достижении 10;
• Вторая строка сохраняет текущую ошибку в элемент ERR[i];
• Третьей строкой мы получаем в переменную SUM сумму последних 10 ошибок;
• Следующие три строки определяют составляющие ПИД регулятора;
• Предпоследняя строка получает результат PID как сумму составляющих P + I + D;
• Последней строкой значение i сохраняется в j. Значит, при каждом новом проходе цикла элемент ERR[i] хранит текущую ошибку, а ERR[j]  хранит предыдущую ошибку.

Настройка ПИД-регулятора:

• Настройка ПИД-регулятора сводится к поиску коэффициентов для пропорциональной, интегральной и дифференциальной составляющих.
• Сброс любого из коэффициентов в 0 приводит к отключению его составляющей:
• Спрос kP в ПИД-регуляторе приведёт к получению ИД-регулятора;
• Спрос kI в ПИД-регуляторе приведёт к получению ПД-регулятора;
• Спрос kD в ПИД-регуляторе приведёт к получению ПИ-регулятора.
• Получаем П-регулятор, сбросив в 0 коэффициенты kI и kD.
• Подбираем значение kP, при котором бампер машины или не покидает линию трассы на всех её поворотах, или находится как можно ближе к линии на поворотах. При этом машина может «вилять» на прямых участках трассы — это нормально. Во время настройки допускается немного снизить скорость машины, но её прийдётся вновь повысить в следующем пункте.
• Постепенно увеличиваем значение kD, получая ПД-регулятор. При этом машина будет всё меньше «вилять» на прямых участках трассы и лучше проходить крутые повороты:
• Слишком высокий kD приведёт к тому, что машина начнёт «дрожать» на прямой линии;
• Слишком низкий kD не избавит от «виляний» машины на прямых участках и не улучшит прохождение крутых поворотов;
• Оптимальным является kD, при котором бампер машины не покидает линию на всех поворотах трассы. При этом машина не «виляет» и не «дрожит» на прямых участках;
• После настройки kD можно снизить kP, если это не ухудшит движение машины;
• Постепенно увеличиваем значение kI, получая ПИД-регулятор, уменьшая отклонение центра бампера от центра линии как на прямых участках трассы, так и на поворотах:
• Слишком высокий kI похож на перерегулировку kP — машина начнёт «вилять»;
• В процессе настройки kI можно снизить подобранные ранее kP и kD.
• Коэффициенты kP, kI и kD являются константами, только если машина движется с одной скоростью.

• Обычно kD > kP, так как разность ошибок меньше одной ошибки, значит, коэффициент больше.
• Обычно kI < kP, так как сумма ошибок больше одной ошибки, значит, коэффициент меньше.

Скетч для одной скорости:

Скорость колёс в скетче задаётся функцией setSpeed() в процентах.
Выберем скорость машины, равную 60%. Именно эту скорость мы и указываем обоим колёсам.
Предположим, что при kI = 0, kD = 0, kP = 8 машина не покидает повороты трассы.
Предположим, что при kI = 0, kD = 14.4, kP = 8 машина перестала «вилять» на прямых участках.
Предположим, что при kI = 0.1, kD = 14.4, kP = 8 бампер не покидает центр линии на поворотах.

#include <Wire.h>                                 // Подключаем библиотеку для работы с аппаратной шиной I2C
#include <iarduino_I2C_Motor.h>                   // Подключаем библиотеку для работы с мотором  I2C-flash
#include <iarduino_I2C_Bumper.h>                  // Подключаем библиотеку для работы с бампером I2C-flash
                                                  //
iarduino_I2C_Motor mot_R (0x0A);                  // Объявляем объект mot_R для правого мотора, указав адрес модуля на шине I2C
iarduino_I2C_Motor mot_L (0x0B);                  // Объявляем объект mot_L для правого мотора, указав адрес модуля на шине I2C
iarduino_I2C_Bumper bum(0x0C);                    // Объявляем объект bum  для работы с бампером I2C-flash, указав адрес модуля на шине I2C
                                                  //
float   speed   = 60;                             // Скорость машины в %
float   kP      = 8;                              // Коэффициент пропорциональной составляющей
float   kI      = 0.1;                            // Коэффициент интегральной составляющей
float   kD      = 14.4;                           // Коэффициент дифференциальной составляющей
float   ERR[10] = {0,0,0,0,0,0,0,0,0,0};          // Определяем массив последних ошибок
uint8_t i;                                        // Объявляем переменную указывающую на элемент массива «ERR» хранящий текущую ошибку
                                                  //
void setup(){                                     //
     mot_R.begin();                               // Инициируем работу с левым  мотором I2C-flash
     mot_L.begin();                               // Инициируем работу с правым мотором I2C-flash
     bum.begin();                                 // Инициируем работу с бампером I2C-flash
     mot_R.setDirection(true);                    // Указываем правому мотору, что его вращение должно быть прямым (по часовой стрелке при положительных скоростях)
     mot_L.setDirection(false);                   // Указываем левому мотору, что его вращение должно быть обратным (против часовой стрелки при положительных скоростях)
}                                                 //
                                                  //
void loop(){                                      //
           i++;     if( i>=10 ){ i=0; }           // Переходим к следующему элементу массива «ERR»
           ERR[i] = bum.getErrPID();              // Получаем текущую ошибку
     float SUM    = 0; for(auto j:ERR){SUM+=j;}   // Получаем сумму последних ошибок
     float P      = ERR[i]                 * kP;  // Определяем пропорциональную составляющую регулятора
     float I      = SUM                    * kI;  // Определяем интегральную составляющую регулятора
     float D      = (ERR[i]-ERR[(i+9)%10]) * kD;  // Определяем дифференциальную составляющую регулятора
     float PID    = P + I + D;                    // Получаем результат ПИД-регулятора
     mot_R.setSpeed( speed - PID, MOT_PWM );      // Устанавливаем скорость правого мотора
     mot_L.setSpeed( speed + PID, MOT_PWM );      // Устанавливаем скорость левого  мотора
}

Немного пояснений к коду loop():

• Текущая ошибка сохраняется в элемент ERR[i];
• Цикл for(auto j:ERR) проходит по всем элементам массива ERR, копируя их значения в переменную j. В теле цикла выполняется суммирование всех значений в SUM;
• Запись ERR[(i+9)%10] равносильна записи ERR[i-1] , только при i=0 получим ERR[9]. Эта запись позволяет получить предыдущую ошибку.

Скетч для диапазона скоростей:

В предыдущем скетче все коэффициенты были найдены для скорости 60%. Если уменьшить скорость движения машины speed с 60% до 30%, то найденные ранее коэффициенты будут слишком велики, и мы получим перерегулирование.

Выход из положения — найти коэффициенты для минимальной и максимальной скоростей машины, после чего вывести формулы зависимости коэффициентов от скорости. Мы уже так делали в предыдущих уроках с коэффициентами kP и kD. Коэффициент kI обычно столь мал, что не сильно зависит от скорости.

Теперь можно написать скетч, у которого скорость можно менять от 20 до 60%:

#include <Wire.h>                                 // Подключаем библиотеку для работы с аппаратной шиной I2C
#include <iarduino_I2C_Motor.h>                   // Подключаем библиотеку для работы с мотором I2C-flash
#include <iarduino_I2C_Bumper.h>                  // Подключаем библиотеку для работы с бампером I2C-flash
                                                  //
iarduino_I2C_Motor mot_R (0x0A);                  // Объявляем объект mot_R для правого мотора, указав адрес модуля на шине I2C
iarduino_I2C_Motor mot_L (0x0B);                  // Объявляем объект mot_L для правого мотора, указав адрес модуля на шине I2C
iarduino_I2C_Bumper bum(0x0C);                    // Объявляем объект bum  для работы с бампером I2C-flash, указав адрес модуля на шине I2C
                                                  //
float   speed   = 60;                             // Скорость машины в %.
float   kP      = 3 + 0.125*(speed-20);           // Коэффициент пропорциональной составляющей
float   kI      = 0.1;                            // Коэффициент интегральной составляющей
float   kD      = speed*speed/250;                // Коэффициент дифференциальной составляющей
float   ERR[10] = {0,0,0,0,0,0,0,0,0,0};          // Определяем массив последних ошибок
uint8_t i;                                        // Объявляем переменную, указывающую на элемент массива «ERR», который хранит текущую ошибку
                                                  //
void setup(){                                     //
     mot_R.begin();                               // Инициируем работу с левым  мотором I2C-flash
     mot_L.begin();                               // Инициируем работу с правым мотором I2C-flash
     bum.begin();                                 // Инициируем работу с бампером I2C-flash
     mot_R.setDirection(true);                    // Указываем правому мотору, что его вращение должно быть прямым (по часовой стрелке при положительных скоростях)
     mot_L.setDirection(false);                   // Указываем левому мотору, что его вращение должно быть обратным (против часовой стрелки при положительных скоростях)
}                                                 //
                                                  //
void loop(){                                      //
           i++;     if( i>=10 ){ i=0; }           // Переходим к следующему элементу массива «ERR»
           ERR[i] = bum.getErrPID();              // Получаем текущую ошибку
     float SUM    = 0; for(auto j:ERR){SUM+=j;}   // Получаем сумму последних ошибок
     float P      = ERR[i]                 * kP;  // Определяем пропорциональную составляющую регулятора
     float I      = SUM                    * kI;  // Определяем интегральную составляющую регулятора
     float D      = (ERR[i]-ERR[(i+9)%10]) * kD;  // Определяем дифференциальную составляющую регулятора
     float PID    = P + I + D;                    // Получаем результат ПИД-регулятора
     mot_R.setSpeed( speed - PID, MOT_PWM );      // Устанавливаем скорость правого мотора
     mot_L.setSpeed( speed + PID, MOT_PWM );      // Устанавливаем скорость левого  мотора
}

Этот скетч отличается от предыдущего только тем, что значения kP и kD определены не числами, а формулами.

При изменении значений скорости speed в пределах от 20% до 60%, будут автоматически пересчитываться коэффициенты kP и kD, и машина продолжит корректно двигаться по линии

Итак, мы получили ПИД-регулятор — зачастую самый оптимальный способ регулирования. При грамотной настройке можно добиться невероятно точной и в то же время быстрой езды. Обязательно «поиграйтесь» с коэффициентами, если Вы этого еще не делали.

Недостаток ПИД-регулятора:

• ПИД-регулятор настраивается дольше, чем П-регулятор или ПД-регулятор, так как нужно подобрать все три коэффициента;
• ПД-регулятор позволяет развивать более высокую скорость, чем ПИД-регулятор.