Ошибка в ошибке софизм пример

Математические софизмы

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

1. Введение

Математика — один из наших любимых школьных предметов. Он нам нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.

Тема нашей работы «Софизмы в нашей жизни». Мы выбрали эту тему для своего проекта не случайно. Как-то вечером папа задал мне вопрос: «Саша, а ты знаешь, что 6 = 7? Мне стало интересно. Папа с легкостью доказал это равенство.

Вот как это было: 6=7.

Запишем верное равенство: 42 +12 — 54 = 49 +14 – 63.

Вынесем общий множитель за скобки: 6(7 + 2 – 9) = 7(7 + 2 – 9)

Разделим обе части на общий множитель (7 + 2 – 9).

Получим, что 6 = 7 , что и требовалось доказать. Где ошибка? Ведь этого быть не может. Папа сказал, что есть такое понятия, как софизм. Так я определился с темой проекта. Катя сама выбрала тему из списка, который был предложен учителем математики. Для нее понятие софизм тоже было неизвестно, поэтому она решила узнать, что означает это незнакомое и интересное слово.

В процессе работы мы выяснили, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой (например, 34 =7), так и то, что прямой угол равен тупому.
Эта тема сейчас актуальна, потому что софизм — это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад.

Цель: узнать, что такое софизмы и научиться находить ошибку в софизмах.

Задачи:

1. Познакомиться с историей софизмов.

2. Узнать, какие бывают софизмы. Классификация софизмов.

3. Понять, как найти ошибку в софизмах?

4. Разбор софизмов.

5. Составить анкету для обучающихся, познакомить одноклассников с результатами работы.

6. Составить рекомендации для нахождения ошибок в софизмах.

Гипотеза: софизмы — тренировка для ума.

Объект и предмет исследования: софизмы

Методы исследования:

1. Анализ литературы и информации, полученной из Интернет источников

2. Обсуждение темы с учителем, родными и одноклассниками

3. Анкетирование одноклассников

4. Анализ и обобщение полученных данных.

2. Теоретическая часть

Что такое софизмы?

Софизм (от греч. — мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.

Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами.

2.2. История возникновения софизмов

Мы изучили историю возникновения софизмов. Софистика – это искусство ведения спора. Она вошла в моду в Греции в V веке до нашей эры. Имея в этом выгоду или просто интерес, многие умные и хитрые люди строго логически доказывали, что черное – это белое, истина – это ложь, добро – это зло и т.д. Так появились софизмы – формально кажущиеся правильными, но по существу ложными умозаключениями. Эти рассуждения могут быть истинны в каждой отдельной части, но неверные в целом.

Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку, ухищрение или головоломку. Речь идет о «доказательстве», направленном на формально – логическое установление абсурдного положения. В основном математические софизмы строятся на неверном словоупотреблении, на неточности формулировок, на скрытом выполнении невозможных действий, на незаконных обобщениях.

Систематический анализ софизмов был дан впервые Аристотелем   (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т.е. в мышлении. Каков бы ни был софизм, он обязательно содержит замаскированные ошибки. Часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применения теорем, формул и правил.

Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.

Софист – это:

1. Человек, прибегающий к софизмам для доказательства заведомо неверных мыслей, положений.

2. В древней Греции первоначальный мудрец, знаток, потом платный учитель философии, красноречия, искусства спора, а также — философ, расходившийся с общепринятыми взглядами в вопросах религии и морали и обвинявшийся противниками в пользовании софизмами.

Наиболее серьезную роль сыграли математические софизмы, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элеи. Например, одна из них: «В каждый момент времени летящая стрела неподвижна. Значит, она неподвижна во все моменты времени, и ее движение никогда не сможет начаться».

В истории развития математики софизмы способствовали повышению строгости в рассуждениях и более глубокому пониманию понятий и методов математики.

2.3. Классификация ошибок в софизмах

Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.

Софисты в своих рассуждениях использовали разные ошибки, такие как:

Логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство. Но закон Моисеев потерял свою силу, следовательно, воровство не запрещено»,   или «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа;

Терминологические ошибки – неправильное употребление слов или построение предложения. Например, «Все углы треугольника равны 180 градусам» в смысле «Сумма углов треугольника равна 180 градусам».  

Ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные! 

Практическая часть

3.1. Разбор математических софизмов

Рассмотрим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Математические софизмы делятся на 4 вида: арифметические, алгебраические, геометрические, логические. Мы рассмотрим некоторые из них.

Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. 
Дважды два – пять (2 * 2 = 5)
Доказательство:
Пусть исходное соотношение — очевидное равенство:
4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой части (1) равенства, и мы получим:
4*(1:1)=5*(1:1) (2)
Разложим число 4 на произведение 2 *2
(2*2)* (1:1)=5*(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в в частном, множитель можно выносить либо из суммы, либо из разности.

Один рубль не равен ста копейкам
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: необходимо переходить к единым единицам измерения.

Софизм «5 = 6»

Докажем, что 5 =6. С этой целью возьмем числовое равенство 35 + 10- 45 = 42 + 12 — 54. Вынесем общий множитель левой и правой части за скобки. Получим 5(7 + 2 — 9) = 6 (7 + 2 — 9). Разделим обе части этого равенства на общий множитель (7 + 2 — 9). Получаем 5=6. В чем ошибка?

Ошибка: нельзя делить на равенство (7 + 2 — 9), т. к. (7 + 2 — 9)= 0. Ма знаем еще из начальной школы, что на 0 делить нельзя.

Таки образом, можно доказать равенство любых разных двух чисел.

Софизм «Пропавший рубль»

Три подруги зашли в кафе выпить по чашке кофе7 Выпили. Официант принес им счет на 30 рублей. Подруги заплатили по 10 рублей и вышли. Однако хозяин кафе решил сделать скидку посетительницам, сказав что кофе стоит 25 рублей. Официант взял деньги и побежал доганять подруг, но пока он бежал, подумал, что им будет трудно делить 5 рублей, ведь их трое, поэтому решил отдать им по 1 рублю, а 2 рубля оставить себе. Так и сделал.

Что же получилось? Подруги заплатили по 9 рублей. 9 . 3 = 27 рублей, да 2 рубля осталось у официанта. А где же еще 1 рубль?

Ошибка. Задача сформулирована так, чтобы запутать читателя. Подруги заплатили 27 рублей, из этой суммы 25 рублей осталось у хозяина кафе, а 2 рубля у официанта. И никакого пропавшего рубля!

Логические софизмы

Софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Приведем некоторые примеры:

Полный стакан равен пустому

Рассмотрим стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану наполовину пустому.

Увеличивая обе части равенства вдвое, получим, что стакан полный равен

стакану пустому. Где ошибка?

Ясно, что приведенное рассуждение неверно, так как в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации его применение бессмысленно, т.к. пустое увеличить вдвое не возможно.

Софизм учебы

Данным софизмом является песенка, сочиненная английскими студентами:

The more you study, the more you know

The more you know, the more you forget

The more you forget, the less you know

The less you know, the less you forget

The less you forget, the more you know

So why study?

Перевод:

Чем больше учишься, тем больше знаешь.

Чем больше знаешь, тем больше забываешь.

Чем больше забываешь, тем меньше знаешь.

Чем меньше знаешь, тем меньше забываешь.

Но чем меньше забываешь, тем больше знаешь.

Так для чего учиться?

Это стихотворение можно смело назвать логическим софизмом!

Геометрические софизмы

Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Софизм «Загадочное исчезновение» (Приложение 1). У нас есть произвольный прямоугольник на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?

Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.

Примеры софизмов приведены в Приложении 2.

Работая над проектом, мы составили рекомендации по нахождению ошибок в софизмах (Приложение 3).

3.2. Анкетирование

Мы провели анкетирование среди обучающихся 7 классов на знание софизмов. В анкетировании приняло участие 40 человек. Были заданы следующие вопросы:

1. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы «Два равно трём»?

«Да» – 24 человека, 60 %

2. Знакомо ли вам понятие «софизм»?

«Да» — 10 человек, 25 %

3. Хотелось ли вам познакомиться с софизмами?

«Да» — 36 человек, 90 %.

Анкетирование показало, что немногим ребятам известно понятие «софизм». 90 % обучающихся хотели бы больше узнать о софизмах. Мы выступим перед ребятами с нашим проектом.

Заключение

Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться. К концу работы над проектом ошибки стали находиться быстрее. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свою речь.

Вообще, решение софизмов – интересное и познавательное занятие. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Работая над проектом, мы составили рекомендации по разбору софизмов (Приложение 3). Наш проект будет полезен людям, которые начинают работать с софизмами с целью развития свих интеллектуальных способностей.

Мы считаем, наш проект актуален и имеет практическое применение. Задачи выполнены, цель достигнута.
Решение софизмов тренируют наш мозг, то есть наша гипотеза верна.

Действительно, софизмы являются тренировкой для ума.

Информационные источники

«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.

«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.

Т.Н. Михеева. Софизмы

«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.

«Парадоксы науки». Автор: А.К.Сухотин. Издательство «Молодая гвардия», 1978 г.

Приложение 1

«Загадочное исчезновение»

Приложение 2

Лекарства

«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».

Девушка — не человек

Доказательство от противного. Допустим, девушка – человек. Девушка – молодая, значит девушка – молодой человек. Молодой человек – это парень. Противоречие. Значит девушка — не человек.

Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.

Разговор софиста и любителя спорить

Софист: “Может ли мёд быть сладким и несладким одновременно?”

Любитель: “нет”

Софист: “ А мёд сладкий?”

Любитель: “Да”

Софист: “А мёд желтый?”

Любитель: “Да”

Софист: “А жёлтый — значит сладкий?”

Любитель: “Нет”

Софист: “Значит мёд сладкий и несладкий одновременно!”

Не знаешь то, что знаешь

— Знаешь ли ты то, о чём я хочу тебя спросить?
— Нет.
— Знаешь ли ты, что добродетель есть добро?
— Знаю.
— Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.

Примеры геометрических софизмов, которые можно услышать на уроке геометрии:

— Смежные углы равны 180 градусам;

— Накрест лежащие углы равны.

Приложение 3

Рекомендации по нахождению ошибок в софизмах

Внимательно прочитать условие предложенной вам задачи.
Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
 

Установить темы, которые отражены в софизме. Обучающиеся, учителя привыкли, что задания, предлагаемые в учебнике, не содержат ошибок в условии, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
 

Воспроизвести вслух точные формулировки утверждений. Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие. 
 

Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности. Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма.
 

Проверять преобразования. После каждого перехода проверить полученный результат обратным действием. Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».

Просмотров работы: 12722

1. Логические софизмы.

Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может
быть сведён к нарушению правил силлогизма. Наиболее типичными источниками
логических софизмов являются следующие нарушения правил силлогизма:

§ 
Вывод с отрицательной меньшей посылкой в первой фигуре: «Все люди
суть разумные существа, жители планет не суть люди, следовательно, они не суть
разумные существа»;

§ 
Вывод с утвердительными посылками во второй фигуре: «Все,
находящие эту женщину невинной, должны быть против наказания её; вы —
против наказания её, значит, вы находите её невинной»;

§ 
Вывод с отрицательной меньшей посылкой в третьей фигуре: «Закон
Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно,
воровство не запрещено»;

§ 
Особенно распространённая ошибка употребление среднего термина в
большой и в меньшей посылке не в одинаковом значении: «Все металлы — простые
вещества, бронза — металл: бронза — простое вещество» (здесь в
меньшей посылке слово «металл» употреблено не в точном химическом значении
слова, обозначая сплав металлов): отсюда в силлогизме получаются четыре
термина.

2. Терминологические софизмы.

Грамматические, терминологические и
риторические источники софизмов выражаются:

§ 
В неточном или неправильном словоупотреблении и построении фразы.
Например,  «Все углы треугольника » в том смысле, что «каждый угол ».

§ 
Более сложные софизмы проистекают из неправильного построения
целого сложного хода доказательств, где логические ошибки являются
замаскированными неточностями внешнего выражения. Например, начав доказывать
некоторый тезис, постепенно в ходе доказательства переходят к доказательству
другого положения, сходного с тезисом.

3. Психологические софизмы.

Психологические причины софизмов бывают
троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей
предполагается взаимодействие между 2 лицами, читателем и автором или лектором
и слушателем, или двумя спорящими. Убедительность софизма поэтому предполагает
два фактора: α — психические свойства одной и β — другой из
обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости
того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от
различных особенностей обеих индивидуальностей.

4.
Интеллектуальные софизмы.

Интеллектуальные причины софизма
заключаются в преобладании в уме лица, поддающегося софистике, ассоциаций по
смежности над ассоциациями по сходству, в отсутствии развития способности
управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному
словоупотреблению, бедности фактических знаний по данному предмету, лености в
мышлении (ignava ratio) и т. п. Обратные качества, разумеется,
являются наиболее выгодными для лица, защищающего софизм: обозначим первые
отрицательные качества через ,
вторые соответствующие им положительные через .

Как было сказано ранее, в математических
софизмах чаще всего используются «запрещенные действия» либо не учитываются
условия применимости теорем, формул или правил. Часто понимание людьми ошибок в
софизме ведет к пониманию математики в целом, развивает логику и навыки
правильного мышления. Поиск ошибки в софизме ведет к ее пониманию и осознанию,
а осознавая ошибку, человек имеет больше шансов ее не допустить. Также, в
истории развития математики софизмы способствовали повышению точности
формулировок и более глубокому пониманию понятий математики.

Математические софизмы делятся на арифметические,
алгебраические, геометрические и логические.

Рассмотрим несколько примеров
алгебраических софизмов, в которых ошибки намеренно скрытые в уравнениях и
числовых выражениях.

1. Всякое число равно своему удвоенному значению.

Запишем очевидное для любого числа a
тождество
a² — a² = a² — a², вынесем a в левой части за скобку, а правую
часть разложим на множители по формуле разности квадратов, получим a(a – a)
= (a + a)(a — a).Разделив обе части на (a – a),
получим a = a + a,
или a=2a.

Итак, всякое число равно своему удвоенному
значению.
Здесь ошибочен переход к равенству
a=2a. В самом деле, число a-a, на которое делится равенство a(a – a)
= (a + a)(a — a) равно нулю. А мы прекрасно знаем, что
на ноль делить нельзя.

2. Чётное число равно нечётному.

Возьмём произвольное чётное число 2n, где n-любое целое число, и
запишем тождество ,

в справедливости которого нетрудно убедиться,
раскрыв скобки. 

Прибавив к обеим частям этого тождества ,
перепишем его в следующем виде: , или
в таком:,

откуда следует, что ,
или 2n=2n+1, что означает
равенство чётного числа нечётному.  Однако из равенства квадратов не следует
равенство величин.

3.

 

 

4. Сумма
любых двух одинаковых чисел равна нулю.

Возьмём
произвольное не равное нулю число a и напишем уравнение x=a. Умножая обе его части на (-4а),
получим -4ах=. Прибавляя к обеим частям последнего равенства  и
перенеся член  влево с противоположным знаком,
получим , откуда, замечая, что слева стоит полный
квадрат, имеем , или х-2а=х. Заменяя в последнем равенстве х
на равное ему число а, получим а-2а=а, или -а=а, откуда 0=а+а, т. е. сумма двух произвольных
одинаковых чисел а равна 0.

Однако,
когда мы имеем полный квадрат , то /х-2а/=/х/, а так x=a, то 2а-x=x.

5. Все
числа равны между собой.

Возьмем любые два числа х, у. Рассмотрим тождество х2 – 2ху +у2 =у2 – 2ху +х2.  Имеем (х — у)2 = (у – х)2. Отсюда х-у = у-х или 2х= 2у, а, значит, х = у.

Ошибка заключается в том, что из равенства (х — у)2 = (у – х)2 следует, что, а это равенство
справедливо для любых чисел у,
х.

6. 1=0.

Возьмем уравнение x-a=0. Разделив обе его части
на х-а, получим х-а/х-а=0/х-а. Откуда
сразу же получаем требуемое равенство 1=0.

Однако в данном софизме используется
распространенная ошибка, а именно деление на 0.

7. Всякое число равно своему удвоенному
значению.

Запишем очевидное для любого числа а
тождество 2а-2а= 2а-2а. Вынесем
а в левой части за скобку, а правую часть разложим на множители по формуле
разности квадратов, получив: а(а-а)=(а+а)(а-а)
(1)

Разделив обе части на а-а, получим а=а+а, а=2а.

В данном софизме вновь используется
деление на нуль неравенства (1) (а-а=0
).

8. Если одно число больше другого, то эти
числа равны.

Возьмем два произвольных числа Х и У, такие, что Х > У , и другие три произвольных числа а, b и с , сумма которых равна d , т.е. а+ b
+ c = d . Умножив обе части
этого равенства на Х , а затем на У , получим: Хa+Хb+Хc=Хd,
Уa+Уb+Уc=Уd. Сложив почленно эти равенства получим Хa + Хb + Хc + Уd = Уa + Уc
+ Уb + Хd . Перенося здесь Уd  вправо, а  Хd влево, имеем Хa+Хb+ХcХd=Уa+Уb+УcУd.

Вынося слева число Х ,
а справа число У за скобки, придем к соотношению m(a+b+cd)=n(a+b+cd). 
(1)

Разделив обе части последнего равенства на ( a + b + c d ) , находим, что, У=Х.

Ошибка, как и в предыдущих примерах
заключается в делении на 0,
то есть на ( a + b + c d
).

9. Любое число а равно меньшему
числу b. 

Начнем с равенства    а = b +
c.

Умножив обе его части на a — b, получим  а² — аb = аb + аc — b²
— be.
Перенесем ас в левую часть:  а² — аb — аc = аb — b² — be
 и разложим на множители:  а(а — b — c) = b(а — b — c).
Разделив обе части равенства на а — b — c, найдем  а = b,
  что и требовалось доказать.

Арифметические софизмы – это
числовые выражения, имеющие неточность или ошибку, не заметную с первого
взгляда. Рассмотрим некоторые из арифметических софизмов.

1. Дважды два – пять.

Пусть исходное соотношение — очевидное
равенство: 4:4= 5:5 (1) .

Вынесем за скобки общий множитель каждой
чести (1) равенства, и мы получим: 4*(1:1)=5*(1:1). (2)

Разложим число 4 на произведение 2 *2.

(2*2)* (1:1)=5*(1:1).  (3)

Наконец, зная, что 1:1=1, мы из соотношения
(2) устанавливаем: 2*2=5.

Ошибка заключается в том, что нельзя было
выносить множитель за скобки в уравнение (2).

2. Один рубль не равен ста копейкам.

Известно, что любые два неравенства можно
перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd. 

Применим это положение к двум очевидным
равенствам 1 р.=100 коп, (1)

10р.=10*100коп. (2) 

Перемножая эти равенства почленно, получим 10 р.=100000 коп.

Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не
равен ста копейкам.

Ошибка, допущенная в этом софизме, состоит
в нарушении правил действия с именованными величинами: все действия,
совершаемые над величинами, необходимо совершать также и над их размерностями.

3. Число, равное другому числу,
одновременно и больше, и меньше его.

Возьмем два положительных равных числа a и b и напишем для них следующие
неравенства: 

a > — b и b
> — b. 

Перемножив оба этих неравенства почленно,
получим неравенство a·b>b·b. 

Разделим его на b (это
законно, т.к. b>0),
получим a > b. 

Записав же два других столь же бесспорных
неравенства:

b > — a и  a
> — a.

Перемножив оба этих неравенства почленно,
получим неравенство b·a > a·a. 

Разделив на a>0, придем к b > a. 

Итак, число a, равное числу b,
одновременно и больше, и меньше его. 

Ошибка заключается в неправильном
почленном перемножении, вследствие которого место выражений a>-b; b>-a получились выражения a>b; a .

4. 1=2.

Никто не станет возражать, что 3-1=6-4.
Умножим обе части равенства на (-1): 1-3=4-6, прибавим к обеим частям
равенства одно и тоже число, (9/4):1-3+9/4=4-6 +9/4.

Замечаем, что обе части равенства
представляют собой квадраты разностей: (1-3/2)2=(2-3/2)2.

Извлечем из обеих частей квадратный
корень: 1-3/2=2-3/2, и теперь к каждой части прибавим 3/2, имеем 1=2.

Не менее интересными являются
геометрические софизмы, которые основаны на ошибках связанных с геометрическими
фигурами и действиями над ними. В качестве примера, рассмотрим следующие
софизмы.

 1. Спичка вдвое длиннее телеграфного
столба.

Пусть, а дм — длина спички и
b дм — длина столба. Разность между b и a обозначим через c
. Имеем b — a = c, b = a + c. Перемножаем два эти равенства по частям,
находим: 2b — ab = ca + 2c. Вычтем из обеих частей bc. Получим: 2b-
ab — bc = ca + 2c — bc, или b(b — a — c) = — c(b — a — c), откуда b
= — c, но c = b — a, поэтому b = a — b, или a = 2b. 

Тем не менее, в выражении b(b-a-c)=(-c)*(b-a-c)
производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит,
спичка не может быть вдвое длиннее телеграфного столба.

2. Хорда, не проходящая через центр
окружности, равна диаметру.

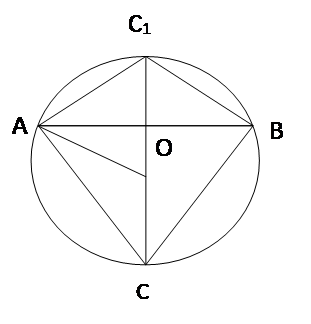
Пусть в окружности приведен диаметр АВ. Через точку В проведем любую хорду ВЕ, не проходящую через
центр, затем через середину этой хорды D и точку А проведем новую хорду АС. Наконец, точки Е и С соединим отрезком прямой. Рассмотрим ∆АВD и ∆ЕDС.

В этих треугольниках: ВD = DЕ (по построению), А=Е (как вписанные, опирающиеся на одну и
ту же дугу).

Кроме того,  ВDА=ЕDC (как вертикальные). Если же сторона и
два угла одного треугольника соответственно равны стороне и двум углам другого
треугольника, то такие треугольники равны. Значит, ∆ ВDА= ∆ЕDC , а в равных треугольниках
против равных углов лежат равные стороны. Поэтому, АВ=ЕС. 

По теореме о признаке равенства
треугольника:

Если сторона и два прилежащих к ней угла
одного треугольника соответственно равны стороне и двум прилежащим к ней углам
другого треугольника, то такие треугольники равны.

А в
нашем случае, А не прилежит к стороне ВD .

Ошибка заключается в неправильном
применении теоремы о равенстве треугольников (равны 2 угла , не прилежащие к
одной стороне).

3. Тор.

 

 Один из наиболее
впечатляющих софизмов топологии заключается в том, что тор (поверхность
 бублика), если его поверхность растягивать (не разрывая при этом), можно
вывернуть наизнанку  через любую сколь угодно малую дырочку. Никакой
проблемы здесь нет. Но уж если тор  действительно можно вывернуть
наизнанку, то следует  обратить внимание и еще на один, пожалуй, даже
более удивительный факт.  Если тор вывернуть наизнанку, то кажется, что
кольца, нарисованные на его поверхности, расцепляются.

  На наружной
стороне тора проведем меридиан (рис, вверху). На внутренней стороне того же
тора проведем параллель. Обе эти окружности, очевидно, сцеплены между собой.
Вывернем теперь тор наизнанку через дырочку в его поверхности. Как видно из
нижнего рисунка, первая окружность перейдет с наружной поверхности тора внутрь,
а вторая — наружу, и обе окружности окажутся расцепленными. Очевидно, что это
нарушает фундаментальный топологический закон, который гласит: разделить две
сцепленные замкнутые кривые можно, лишь разорвав одну из кривых и протащив
через место разрыва вторую.

4. Из точки на прямой
можно опустить два перпендикуляра.

Попытаемся «доказать», что через
точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра.

С этой целью
возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на
диаметрах, построим полуокружности.

Пусть эти полуокружности
пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с
точкой В.

Угол АЕВ прямой, как вписанный,
опирающийся на диаметр; угол ВDС также прямой. Следовательно, ВЕ
перпендикулярна АС и ВD перпендикулярна АС. Через точку В проходят два
перпендикуляра к прямой АС.

Особый интерес с момента
зарождения математики, как одной из фундаментальных наук, вызывали логические
софизмы. Логические софизмы — софизмы, ошибки которых заключаются в
неправильных рассуждениях.

1. Софизм Кратила.

Диалектик Гераклит, провозгласив
тезис «все течет», пояснял, что в одну и ту же реку (образ природы) нельзя
войти дважды, ибо когда входящий будет входить в следующий раз, на него будет
течь уже другая вода. Его ученик Кратил, сделал из утверждения учителя другие
выводы: в одну и ту же реку нельзя войти даже один раз, ибо пока ты входишь,
она уже изменится. Поэтому Кратил предлагал не называть вещи, а указывать на
них: пока произносишь название, вещь уже станет иной.

2. Полупустое и полуполное.

Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное

Однако полупустое не является половиной
чего либо пустого, а является чем либо наполовину наполненным.

3. Вор.

Вор не желает приобрести ничего дурного. Приобретение
хорошего есть дело хорошее. Следовательно, вор желает хорошего.

4. Не знаешь то, что знаешь.

«Знаешь ли ты, о чём я хочу тебя
спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». —
«Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».

5. Лекарства.

«Лекарство, принимаемое больным,
есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно
принимать как можно больше».

6. Отец — собака.

«Эта собака имеет детей, значит,
она — отец. Но это твоя собака. Значит, она твой отец. Ты её бьёшь, значит, ты
бьёшь своего отца и ты — брат щенят».

Как видно из приведённых выше
софизмов, найти ошибки в них не очень сложно, зная основные математические
законы и их доказательства. Однако можно выделить несколько основных способов
нахождения ошибки в софизме:

§    
Внимательно прочитать условие предложенной вам задачи. Начинать
поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах
абсурдный результат, получается, из-за противоречивых или неполных данных в
условии, неправильного чертежа, ложного первоначального предположения, а далее
все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
Все привыкли, что задания, предполагаемые в различной литературе, не содержат
ошибок в условии и, поэтому, если получается неверный результат, то ошибку они
ищут непременно по ходу решения.

§    
Установите области знаний (темы), которые отражены в софизме,
предложенных преобразованиях. Софизм может делиться на несколько тем, которые
потребуют детального анализа каждой из них.

§    
Выясните, соблюдены ли все условия применимости теорем, правил,
формул, соблюдена ли логичность. Некоторые софизмы построены на неверном
использовании определений, законов, на «забывании» условий применимости. Очень
часто в формулировках, правилах запоминаются основные, главные фразы и
предложения, всё остальное упускается. И тогда второй признак равенства
треугольников превращается в признак «по стороне и двум углам».

§    
Проверяйте результаты преобразования обратным действием.

§    
Часто следует разбить работу на небольшие блоки и
проконтролировать правильность каждого такого блока.

Можно бесконечно говорить о софизмах в
целом и о математических софизмах в частном. Из года в год появляются новые
софизмы, некоторые из них могут остаться в истории, о многих быстро забудут.
Ведь софизмы — это смесь математики и логики, поэтому они помогают не только
развивать логику, но и лучше понимать математику в целом. В современном мире
есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не
зная, что это такое. Есть же и такие люди, которые целенаправленно изучают
софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или
просто развить свои навыки логики и правильности рассуждений.

Поначалу может показаться, что существует
мало софизмов, или, что они не используются в жизни, то есть бесполезны. Но это
не так. Существует огромное множество разных видов софизмов. И математические
софизмы – всего лишь небольшая их часть. За свою жизнь человек слышит десятки
софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что
вообще означает слово софизм.

Понять софизм, то есть решить его,
получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходится по
многу раз их внимательно перечитывать, вдумываться и всматриваться. В ходе
написания данной работы и доказательства софизмов, приведённых в ней, ошибки
стали находиться быстрее. Хорошо развитое логическое мышление может помочь не
только в решении задач, но и в обычной жизни.

О математических софизмах можно говорить
бесконечно много, как и о математике в целом. Изо дня в день рождаются новые
парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один
день

Вообще, решение софизмов – интересное и
познавательное занятие. Им можно заниматься как целенаправленно, так и в
свободное время для собственного удовольствия. Изучение
математических софизмов раскрывает еще одну страничку в математике, позволяет
прикоснуться к тому, с чем сталкивались далекие предки, к теме, которая имеет
исторические корни.

Литература

1.    
Брадис В. М., Минковский В. Л., Харчева Л. К. Ошибки
в математических рассуждениях. 3 изд.: М., 1967.

2.    
Дёмин
Р. Н. Собрание «задач» Ричарда
Софиста как контекст для
«парадоксов» древнекитайской школы имен // Вестник РХГА № 6, СПб., 2005.

3.     Ивин А. А.. Логика.: М. —
Издательство «Знание», Изд. 2-е,  1998. 

4.    
Интернет источник Timerl@n.

5.    
Интернет
источник http://www.rchgi.spb.ru/Pr/vest_6.htm.

6.    
Неркарарян К. В., Софизмы и парадоксы, 1 издание, 2001.

Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа №8 г. Белорецк

муниципального района Белорецкий район

Республики Башкортостан

III МЕЖРЕГИОНАЛЬНАЯ НАУЧНО – ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ

«ЕВРОПА – АЗИЯ. ОТКРЫВАЯ ГОРИЗОНТЫ»

Направление исследования: «Математика»

Тема: «Математические софизмы»

Автор работы: Кривошеева Екатерина Игоревна, обучающаяся 6 А класса МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ

Руководитель: Лукманова Гульсина Хакимовна, учитель математики МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ

2018

Оглавление

Введение…………………………………………………………………..3 стр.

ГЛАВА 1 Исторические условия возникновения софизмов ………..…5 стр. 1.1 Понятие софизма. Из истории возникновения софизмов…….…5 стр. 1.2 Классификация математических софизмов.………..…………..……7 стр.

Выводы по главе 1…………………………………………………….8 стр.

ГЛАВА 2 Исследование в сфере учебной деятельности

2.1 Классификация ошибок и их причины….. ………………………9 стр.

2.2 Анализ ошибок учащихся по математике…………………….….9 стр.

Выводы по главе 2……………………………………………………10 стр.

Заключение…………………………………..……………………………11 стр.

Список источников литературы и интернет – ресурсов.………….…..12 стр. Приложение «Классификация математических софизмов с примерами » Приложение «Классификация ошибок и их причин» Приложение «Результаты исследования»

Приложение «Анализ ошибок учащихся по математике»

Приложение «Анкета»

Введение

«Правильно понятая ошибка — путь к открытию»

И. П. Павлов

Знаменитый комик Чарли Чаплин сказал: «Способность думать, подобно игре на скрипке или рояле, требует ежедневной практики». Невозможно с этим не согласиться! Мыслительная деятельность человека − своеобразный инструмент, пользуясь которым, можно добиться духовных, нравственных, научных высот. Такое понятие, как «софизм» бесспорно свидетельствует о блестяще развитом уме и логике владеющего им человека.

Актуальность исследования. Наше общество развивается большими темпами, и все больше требуются техники, инженеры, ученые, знания которых базируются на точных науках: математика, физика, химия. Но эти науки надо не только знать, но и понимать. Для лучшего усвоения математики существуют софизмы. Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме — это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.

Целью настоящей работы как раз является показать значимость математических софизмов при изучении математики, их роль в формировании полноценной личности, способной адаптироваться в условиях современного общества.

Гипотеза: если неточно знать формулировки определений, математические формулы, правила и условия, при которых они выполняются, а также не анализировать построение чертежа к геометрической задаче, то можно получить абсурдные результаты, противоречащие общепринятым представлениям.

Задачи исследования:

• Узнать, что называют софизмами и выяснить исторические условия возникновения софизмов; выяснить, какие виды математических софизмов бывают;

• Рассмотреть влияние софизмов в математике, проанализировать и классифицировать ошибки в работах учащихся по математике;

• Научиться самой обосновывать свои ошибки и познакомить своих одноклассников с софизмами и показать, что они встречаются чаще, чем они думают, просто они об этом не задумываются.

Предмет исследования: математические софизмы.

Объект исследования: ошибки учащихся в работах по математике.

В ходе исследования решались следующие проблемные вопросы:

1. Как появились софизмы?

2. Какие виды математических софизмов бывают?

3. В каких заданиях и как делают «математические» ошибки учащиеся?

4. Как использование софизмов помогает в понимании математики?

5. Как научиться «видеть» ошибки?

Чтобы достичь своей цели, использовались такие методы исследования: изучение литературы, сбор информации, анкетирование учащихся, обработка данных, составление таблиц и диаграмм, просмотр сайтов в Интернете.

Практическая значимость: тема исследования я считаю, значима, так как понимание математики пригодится в жизни и в первую очередь для успешной учебы в школе, надо не только точно знать правила и формулы, но уметь находить свои ошибки и ошибочные рассуждения.

ГЛАВА 1 Исторические условия возникновения софизмов 1.1 Понятие софизма. Из истории софизмов.

Софизмы… Редко кто встречался с этим понятием в жизни.

В самом начале своей работы, мы выяснили, а знают ли другие школьники о софизмах. Поэтому провели с руководителем анкету, на вопросы которой ответили 40 учеников 6 классов. И я выяснила, что практически с понятием софизмов они не знакомы. Тогда мы привели примеры известных софизмов: «Дважды два равно пяти» или хотя бы: «Два равно трем». И снова лишь 17% опрошенных ответили, что слышали о них, 27 % — считают, что встречались с софизмами на уроках математики, 30 % считают, что в повседневной действительности встречаются с софизмами.

Так что же это такое?

Софизм — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.

Софизм — (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. (Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.)

Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.

Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашла ошибку в софизме, значит, ты ее осознала, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.

Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.

Софизмы появились в Древней Греции. Они тесно связаны с философской деятельностью софистов. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса.

Аристотель называл софизмами «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению.

Вот один из древних софизмов («рогатый»), приписываемый Эвбулиду: «Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога». Здесь маскируется двусмысленность большей посылки. Если она мыслится универсальной: «Всё, что ты не терял…», то вывод логически безупречен, но неинтересен, поскольку очевидно, что большая посылка ложна; если же она мыслится частной, то заключение не следует логически. Последнее, однако, стало известно лишь после того, как Аристотель создал логику.

Этапы возникновения софизмов

1. Первая в истории проба проведения «логической профилактики» в математике принадлежит гениальному древнегреческому математику — Эвклиду. Он был автором первого из известных сборников математических софизмов и парадоксов (сборник «Псевдарий»).

2. Софистам идейно противостоял знаменитый греческий философ Сократ. Дискуссия между софистами и Сократом о существовании объективной истины зародилась приблизительно в V в. до н.э.

3. Наши дни: появление мысли о том, что человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искуснее замаскирована ошибка, тем больше удовлетворения приносит он тому, кто разгадал его, так как это — маленькое открытие и прекрасная школа, культура математических вычислений.

1.2 Классификация математических софизмов

Распределим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики.

В этом разделе работы я рассмотрю три типа математических софизмов: алгебраические, геометрические и арифметические (Приложение 1)

Арифметические софизмы — числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

Пример: «Число, которое равно другому числу, и больше его, и меньше одновременно».

Алгебраические софизмы — намеренно скрытые ошибки в уравнениях и числовых выражениях. Пример: «Дважды два равно пяти».

Геометрические софизмы — это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними. Пример: «Спичка вдвое длиннее телеграфного столба».

Выводы по главе 1

Софизмы есть смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.

Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика — это целая наука, а именно математические софизмы — это лишь часть одного большого течения.

Очень важно, чтобы человек умел выявлять свои и чужие ошибки, учился избегать их.

ГЛАВА 2 Исследование в сфере учебной деятельности

2.1 Классификация ошибок и их причин.

Основные ошибки в математических софизмах (Приложение 2)

• Деление на 0;

• Неправильные выводы из равенства дробей;

• Неправильное извлечение квадратного корня из квадрата выражения;

• Нарушения правил действия с именованными величинами;

• Путаница с понятиями “равенства” и “эквивалентность” в отношении множеств;

• Не правильное использование теорем;

• Проведение преобразований над математическими объектами, не имеющими смысла;

• Неравносильный переход от одного неравенства к другому;

• Выводы и вычисления по неверно построенным чертежам;

• Ошибки, возникающие при операциях с бесконечными рядами и предельным переходом.

2.2 Анализ ошибок учащихся по математике

Чтобы показать и подтвердить значимость софизмов в жизни, мы провели исследовательскую работу в сфере учебной деятельности (Приложение 3, 5).

Данная работа была направлена: на развитие умения находить ошибку, анализировать и устранять ее; на развитие логического мышления; на формирование математической грамотности учащихся.

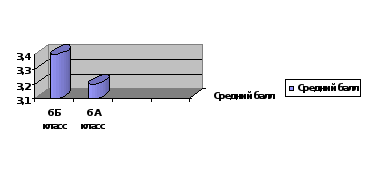
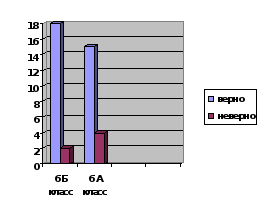
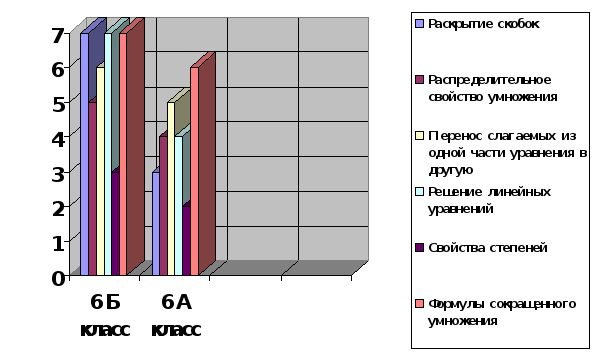
Исследование проводилось среди учащихся шестых классов. В 6 Б классе был проведен урок – презентация, посвященный алгебраическим софизмам по теме «Распределительное свойство умножения», а в 6 А данного урока не проводилось. Затем по этой теме была проведена самостоятельная работа. По итогам самостоятельных работ средние баллы в каждом из классов разошлись. В 6 Б классе средний балл был равен – 3,4, а в 6 А классе – 3,2. Только два учащихся (10%) 6 Б класса допустили ошибку по данной теме, когда в 6 А ошибки допустили 4 человека (21%). Все полученные данные мы оформили в виде диаграмм (приложение 3), которые наглядно показали нам различия по уровню усвоения темы самостоятельной. Таким образом, проанализировав полученные результаты, мы сделали вывод, что ученики, разобравшие варианты возможных ошибок, научились находить и устранять их. Ученики, не получившие данной информации, допустили различные ошибки по данной теме.

Также в своей работе мы провели анализ ошибок в работах учащихся 6 классов по математике. Как я уже отмечала ранее, неточное знание формулировок, правил и условий, при которых эти правила выполняются, приводят учащихся к неправильным, а иногда и абсурдным результатам.

В настоящем исследовании рассмотрели некоторые ошибки из контрольных работ обучающихся по математике (приложение 4).

Выводы по главе 2:

По результатам анализа ошибок, допущенных учащимися 6 классов в тестовых работах по математике, можно сделать вывод, что поверхностное изучении теории (а чаще её незнание) приводит к абсурдным результатам. Софизмы наглядно показывают, почему это происходит.

Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.

Заключение

Исследовать софизмы действительно очень интересно и необычно. Порой сама попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научиться грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку.

В своей работе мы доказали, что софизмы являются не просто интеллектуальным мошенничеством, а важным двигателем человеческой мысли. Показали практическое применение софизмов и их актуальность и в наше время. Мы рассмотрели математические софизмы с точки зрения их важности для изучения математики. Вот почему имеет первостепенное значение глубокое изучение школьной математики. И математические софизмы вам покажут, как важно строго соблюдать правила и формулировки теорем при логических умозаключениях.

«Решайте задачи и не бойтесь трудностей. Преодоление их вам доставит не только глубокое удовлетворение, но и большую радость, так как «в математике есть своя красота, как в поэзии и музыке» (Н.Е.Жуковский).

«Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным». Б. Паскаль

Список источников литературы и интернет ресурсов:

1. Ахманов А.С., Логическое учение Аристотеля, М., 1960г.

2. Брадис В.М., Минковский В.Л., Еленев Л.К., Ошибка в математических рассуждениях, 3 изд., М., 1967г.

3. Брутян Г., Паралогизм, софизм и парадокс//Вопросы философии, 1959г. № 1 с. 56-66.

4. Гарднер Мартин. Математические головоломки и развлечения.М.: Оникс, 1994г.

5. Глейзер Г.И. История математики в школе. М.:Просвещение, 1982г.

6. Кордемский Б.А. Великие жизни в математике. М.:Просвещение, 1995г.

7. Р.Курант, Г.Роббинс. Что такое математика? М.-.МЦНМО, 2004

8. Морозов И.А., О научном значении математических софизмов// Известия научного института им. П.Ф.Лесгафта, Пг., 1919г., с. 193-207.

9. Л.Ф.Пичурин. За страницами учебника алгебры. М. -.Просвещение, 1991г.

10. Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.

11. Софизмы http://sophisms.ucoz.ru/index/geometricheskie_sofizmy/0-9 (15.10.18г)

12. Софизмы http://sofizmy.narod.ru/ (20.10.18г)

Приложение 1

Классификация математических софизмов с примерами

Алгебраические софизмы. Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Приведем примеры таких софизмов.

1. «Сочетательное и переместительное свойства алгебраической суммы не имеют места» Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е. S=1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 +… (1)

И попробуем найти значение этой суммы. Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е. S=1 — (1 — 1) — (1 — 1) -…=1 – 0 – 0 — …= 1

Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда S= -1 +1 – 1 + 1 – 1 + 1 — …= -1 +(1-1)+(1-1)+…=-1+0+0+…= -1.

Итак, по-разному переставляя слагаемые суммы (1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых, а сочетательное и переместительное свойства алгебраической суммы не имеют места.

Где ошибка??? Данное свойство суммы может оказаться неверным, если некоторые члены суммы сгруппированы иначе.

2. «Дважды два равно пяти»

Имеем числовое равенство (верное): 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5, или 2 * 2=5.

Где ошибка? Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4:4=5:5.

3. «Отрицательное число больше положительного»

Возьмем два положительных числа а и с. Сравним два отношения:

а: (-с) и -а : с

Они равны, так как каждое из них равно –(а:с). Можно составить пропорцию:

а: (-с) = (-а) : с

Но, если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего.

В нашем случае а -с, следовательно, должно быть -ас, т.е. отрицательное число больше положительного.

Где ошибка??? Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.

« Спичка вдвое длиннее телеграфного столба»

 Пусть  а дм— длина спички и b дм — длина столба. Разность между b и  a  обозначим через c . Имеем  b — a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b² — ab = ca + c². Вычтем из обеих частей bc. Получим: b²— ab — bc = ca + c² — bc, или b(b — a — c) = — c(b — a — c), откуда b = — c, но c = b — a, поэтому b = a — b, или a = 2b.    

Где ошибка??? В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

Арифметические софизмы. Арифметика — (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы? Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Приведем примеры таких софизмов.

1. « 4 руб. = 40000 коп.» Возьмём верное равенство: 2руб.=200 коп. и возведём его по частям в квадрат. Мы получим: 4 руб.=40 000 коп. В чем ошибка?

В чем ошибка? Возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.

2.«Один рубль не равен ста копейкам»

Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. если a=b, c=d, то ac=bd.

Применим это положение к двум очевидным равенствам

1 р.=100 коп, (1) 10р.=10*100коп.(2)

перемножая эти равенства почленно, получим 10 р.=100000 коп. (3)

и, наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам.

Где ошибка??? Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 р. =100 000 к . , которое после деления на 10 дает

1 р. = 10 000 коп., (*) а не равенство 1р=10 000 к, как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство 1р.=100 коп.

1. «Число, равное другому числу, одновременно и больше, и меньше его»

Возьмем два произвольных положительных равных числа А и В и напишем для них следующие очевидные неравенства:

А-В и В-В. (1) Перемножив оба этих неравенства почленно, получим неравенство А*ВВ*В, а после его деления на В, что вполне законно, ведь В0, придем к выводу, что АВ. (2) Записав же два других столь же бесспорных неравенства В-А и А-А (3)

Аналогично предыдущему получим, что В*АА*А, а разделив на А0, придем к неравенству АВ. (4) Итак, число А, равное числу В, одновременно и больше, и меньше его.

Где ошибка??? Здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств.

Проделаем правильные преобразования неравенств. Запишем неравенство (1) в виде А+В0, В+В0. Левые части этих неравенств положительны, следовательно, умножая почленно оба эти неравенства (А+В)(В+В)0, или А-В, что представляет собой просто верное неравенство.

Аналогично предыдущему, записывая неравенства (3) в виде (В+А)0, А+А0, получим просто верное неравенство В-А.

Приложение 2

Классификация ошибок и их причин

Логические ошибки. Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может быть сведён к нарушению правил силлогизма. (Силлогизм — тонкий, хитрый ход (для подтверждения или доказательства чего-либо)).

Терминологические ошибки. Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы (всякое quaternio terminorum предполагает такое словоупотребление);

В устную речь математиками введены такие слова как «сумма», «произведение», «разность». Так — сумма произведения два на два и пятерки, а — удвоенная сумма двух и пяти.

Более сложные софизмы проистекают из неправильного построения целого сложного хода доказательств, где логические ошибки являются замаскированными неточностями внешнего выражения. Всякое беспорядочное следование мыслей представляет частный случай этой ошибки.

Психологические причины. Бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма поэтому предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.

Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софизму, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignava ratio) и т. п. Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм.

Аффективные причины ошибок. Сюда относятся трусость в мышлении — боязнь опасных практических последствий, вытекающих от принятия известного положения; надежда найти факты, подтверждающие ценные для нас взгляды, побуждающая нас видеть эти факты там, где их нет, любовь и ненависть, прочно ассоциировавшиеся с известными представлениями, и т. д. Желающий обольстить ум своего соперника софист должен быть не только искусным диалектиком, но и знатоком человеческого сердца, умеющим виртуозно распоряжаться чужими страстями для своих целей

Волевые причины. При обмене мнений мы воздействуем не только на ум и чувства собеседника, но и на его волю. Во всякой аргументации (особенно устной) есть элемент волевой — императивный — элемент внушения. Категоричность тона, не допускающего возражения, определённая мимика и т. п. () действуют неотразимым образом на лиц, легко поддающихся внушению, особенно на массы. С другой стороны, пассивность () слушателя особенно благоприятствует успешности аргументации противника. Таким образом, всякий софизм предполагает взаимоотношение между шестью психическими факторами: . Успешность софизма определяется величиной этой суммы, в которой составляет показатель силы диалектика, есть показатель слабости его жертвы. Прекрасный психологический анализ софистики даёт Шопенгауэр в своей «Эристике» (перев. кн. Д. Н. Цертелева). Само собой разумеется, что логические, грамматические и психологические факторы теснейшим образом связаны между собой; поэтому софизм, представляющий, например, с логической точки зрения quaternio ter.

Приложение 3

Результаты исследования

Средний балл выполнения самостоятельной работы

в 6 классах

Диаграмма 1 Средний балл выполнения самостоятельной работы

в 6 классах

Классификация ошибок в работах учащихся 6 классов

Диаграмма 2 Классификация ошибок в работах учащихся 6 классов

Приложение 4

Анализ ошибок учащихся по математике

6 класс Выражения, тождества, уравнения

1.Ученики знают распределительное свойство умножения относительно сложения и вычитания.

Правило: а(b + с) = ab + ас а(b — с) = аb — ас.

Ошибки: — 2(а + 4) = -2а + 8; — 2(а — 4) = -2а — 8.

«Минус» и «плюс» в формулах сыграли плохую роль после того, как ученики познакомились с отрицательными числами. Надо быть внимательными.

2.Правила раскрытия скобок все знают, а при применении забывают и выполняют его только для первого слагаемого.

Правило: + (а -b + с) = а — b + с; -(а-b- с) = -а + b — с.

Ошибки: — (5a + b- х) =-5а+ b- х.

3.Правило переноса слагаемых из одной части уравнения в другую.

Правило: при переносе слагаемых из одной части уравнения в другую их знаки меняются на противоположные. 5х — 7 = 2x + 9;

Ошибки: 5х + 2x = 9 — 7.

4.Решение линейного уравнения. Привычка из начальной школы большее число делить на меньшее «заставляет» при решении уравнений учащихся совершать ошибку, а надо всего то знать правило нахождения неизвестного множителя или правило деления обеих частей уравнения на одно и то же, отличное от нуля число. Правило ах = b; (а не равно 0) х = Ошибки: 6х =2; х = 3

5. Правило: при раскрытии скобок с применением распределительного свойства умножения нужно каждое слагаемое умножить на число.

2х — 5(х + 2) = 2х — 5х — 10;

Ошибки: 2х — 5(х + 2) = 2х — 5х +10.

Приложение 5

Анкета (Перед уроком – презентацией)

1. Укажите ваш возраст.
2. Укажите ваш пол.
3. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем»?
4. Знакомо ли вам понятие «Софизм»?

(После урока – презентации)

1. Постарайся дать определение этого понятия самостоятельно.
2. Надо ли знакомить учащихся на уроках с софизмами?
3. Как ты думаешь, для чего нужны софизмы?
4. Хотел бы ты больше узнать о софизмах?
5. Как ты считаешь, какую роль для тебя может сыграть более глубокое знакомство с софизмами?

26

Читайте также

7.7. Паралогизмы, софизмы и парадоксы

7.7. Паралогизмы, софизмы и парадоксы
Логические ошибки бывают непреднамеренные и преднамеренные. Первые из них возникают из-за неосознаваемого нарушения правил логики и называются паралогизмами. В переводе с древнегреческого паралогизм означает не правильное

2. Софизмы

2. Софизмы
Софизм обычно определяется как умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.Хорошим примером софизма является ставший знаменитым еще в

4.9. Софизмы

4.9. Софизмы
Если объективной истины нет, считали софисты, тогда главное для победы в любом споре – это искусное владение приемами подтверждения и опровержения чего угодно, среди которых важное место занимают софизмы, в которых, как мы уже знаем, различными способами

Исторические софизмы доктринерской школы немецких коммунистов[114]

Исторические софизмы доктринерской школы немецких коммунистов[114]
(…) Не таково мнение доктринерской школы социалистов, или скорее государственных коммунистов Германии, школы, основанной несколько раньше 1848 г. и оказавшей – надо признать это – крупные услуги делу

СОФИЗМЫ КАК ПРОБЛЕМЫ

СОФИЗМЫ КАК ПРОБЛЕМЫ
Употребление софизмов с целью обмана заставляет относиться к ним с осуждением. Неприязнь с софистике как систематическому использованию мошеннических приемов велика и вполне оправданна. Но эта неприязнь не должна заслонять тот факт, что софизмы

55. Софизмы

55. Софизмы
Раскрывая данный вопрос, необходимо сказать, что любой софизм является ошибкой.В отличие от логической ошибки, возникающей непроизвольно и являющейся следствием невысокой логической культуры, софизм является преднамеренным нарушением логических правил.

ЛЕКЦИЯ № 23 Софизмы. Логические парадоксы

ЛЕКЦИЯ № 23
Софизмы. Логические парадоксы

1. Софизмы. Понятие, примеры
Раскрывая данный вопрос, необходимо сказать, что любой софизм является ошибкой. В логике выделяют также паралогизмы. Отличие этих двух видов ошибок состоит в том, что первая (софизм) допущена умышленно,

1. Софизмы. Понятие, примеры

1. Софизмы. Понятие, примеры
Раскрывая данный вопрос, необходимо сказать, что любой софизм является ошибкой. В логике выделяют также паралогизмы. Отличие этих двух видов ошибок состоит в том, что первая (софизм) допущена умышленно, вторая же (паралогизм) — случайно.

Глава 6 СОФИЗМЫ

Глава 6 СОФИЗМЫ

СОФИЗМ — ИНТЕЛЛЕКТУАЛЬНОЕ МОШЕННИЧЕСТВО!
Софизмы обычно трактуются вскользь и с очевидным осуждением. И в самом деле, стоит ли задерживаться и размышлять над такими, к примеру, рассуждениями: «Сидящий встал; кто встал, тот стоит; следовательно, сидящий

СОФИЗМЫ И ЗАРОЖДЕНИЕ ЛОГИКИ

СОФИЗМЫ И ЗАРОЖДЕНИЕ ЛОГИКИ
Очень многие софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т. д. Эти софизмы кажутся особенно наивными и

Кто не делится найденным, подобен свету в дупле секвойи (древняя индейская пословица)

Библиографическая запись:
Софизмы. Понятие, примеры. Логические парадоксы. Понятие, примеры. — Текст : электронный // Myfilology.ru – информационный филологический ресурс : [сайт]. – URL: https://myfilology.ru//169/sofizmy-ponyatie-primery-logicheskie-paradoksy-ponyatie-primery/ (дата обращения: 29.01.2023)

02.09.2016, 52844 просмотра.

Софизмы в математике

Секция: Математические науки.

Автор: Шеметова Анастасия, Глазунова Екатерина, 8  класс
МБОУ «СОШ №18».

Научный руководитель: Лукьянова Ольга Георгиевна, учитель
математики МБОУ «СОШ №18».

Г. Миасс

Челябинская
область

Оглавление

Введение

I.
Софизм и история его возникновения

1.1. Софизм и софистика

1.2. Экскурс в историю

II.
Математические софизмы и их классификация

2.1. Софизмы и типичные ошибки в
них

2.2. Математические софизмы

2.3. Разбор математических
софизмов

2.4. Логические софизмы

2.5. Источники софизмов

III.    «Софизмы из наших школьных тетрадей»

Заключение

Список литературы

Приложение 1.

Приложение 2. Арифметические софизмы

Приложение 3. Алгебраические софизмы

Приложение 4. Геометрические софизмы

В
математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.

И. Ньютон

Введение

У ученых есть такое свойство — поставят в
тупик все человечество, а потом целое поколение или даже несколько поколений с
трудом из него выбираются, проявляя чудеса изобретательности и изворотливости.
И одним из средств не только учёных, но и любознательных остроумных людей,
любящих ставить окружающих в тупик, является «софизм». Нас заинтересовал факт
глубокой древности зарождения софизмов и популярности их у ученых.

Актуальность: Наверное,
каждый человек хоть раз в жизни слышал фразу: «Дважды два равно пяти» или «Два
равно трем». Что они обозначают? Кто их выдумал? Имеют ли они какое-нибудь
логическое объяснение или же это лишь вымысел? Чтобы ответить на эти и подобные
им вопросы, мы в своей работе рассматриваем математические софизмы. Математический софизм – удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
Поэтому нам представляется актуальным изучение ошибок в софизмах, потому что их
понимание ведёт к пониманию математике в целом, помогает развивать логику и
навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее
осознал, а осознание ошибки предупреждает от ее повторения в дальнейших
математических рассуждениях.

Цель: изучение типичных ошибок, которые возникают у учащихся
в процессе изучения математики, их причин и способов  предупреждения на примере
математических софизмов.

Задачи:

1.    
изучить понятие софизма и историю его возникновения;

2.    
рассмотреть виды софизмов и дать классификацию их ошибок;

3.    
составить сборник разбора задач на софизмы по различным разделам
математики для 6 — 9 классов.

Гипотеза исследования: если в процессе обучения математике целенаправленно
и систематически организовывать работу учащихся над типичными ошибками, на
примере софизмов, то это будет способствовать повышению качества математической
подготовки учащихся.

I. Софизм и история его возникновения

1.1. Софизм и софистика

Софизм в
переводе с греческого означает дословно: уловка, выдумка или мастерство. Этим
термином называют утверждение, являющееся ложным, но не лишенным элемента
логики, за счет чего при поверхностном взгляде на него кажется верным.
Софизмы основаны на сознательном и преднамеренном обмане, нарушении логики.

Софизм — преднамеренная ошибка, совершаемая с целью запутать
противника и выдать ложное суждение за истинное.

Софистика –
направление философии, которое возникло в V — IV вв. до н.э. в Греции и
стало очень популярным в Афинах.

1.2. Экскурс в историю

Во
второй половине V века до н.э. в Греции появились софисты. Софистами называли
группу древнегреческих философов достигших большого искусства в логике. Они
появились во время становления демократии в Афинах и на подвластных Афинам
территориях. Софисты — это мудрецы, но мудрецы особого рода. Этих мудрецов
истина не интересовала. Они были, как правило, платными «учителями мудрости».
Их нанимали политики для того, чтобы организовать свою предвыборную компанию, в
частности, переспорить оппонентов на собрании, а также для того, чтобы выиграть
судебное дело. В Греции софистами называли и простых ораторов —
философов-учителей, задачей которых было научить своих учеников «мыслить,
говорить и делать». Одним из представителей
софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а
это и есть гражданское искусство» (приложение 1, рис. 1).

Чтобы выйти победителем в словесном
поединке, софисты часто пользовались тем, что противник недостаточно глубоко
знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен, и
поэтому не в состоянии отличить ложь от истины. В результате словесного
поединка противник должен был согласиться с доводами софиста и признать себя
побежденным, хотя истина, казалось, была на его стороне. Софизмы существуют и
обсуждаются более двух тысячелетий, причем острота их обсуждения не снижается с
годами. Если софизмы — всего лишь хитрости и словесные уловки, выведенные на
чистую воду еще Аристотелем, то долгая их история и устойчивый интерес к ним
непонятны. Однако софизмы существовали задолго до философов-софистов, а
наиболее известные и интересные были сформулированы позднее в сложившихся под
влиянием Сократа философских школах.(Приложение 1,рис.2)

Термин «софизм» впервые ввел Аристотель
(приложение 1, рис.3), охарактеризовавший софистику как мнимую, а не
действительную мудрость. К софизмам им были отнесены и «апории Зенона» (внешне парадоксальные рассуждения
на тему о движении и множестве), направленные
против движения и множественности вещей, и рассуждения собственно софистов, и
все те софизмы, которые открывались в других философских школах. Это говорит о
том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то
обычным для многих школ античной философии. Аристотель называл софизмом «мнимые
доказательства», в которых обоснованность заключения кажущаяся и обязана чисто
субъективному впечатлению, вызванному недостаточностью логического анализа.
Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана
с хорошо замаскированной ошибкой, с использованием, например, «неразрешённых»
или даже «запрещённых» правил или действий.

Современный софизм, основной задачей
которого является манипуляция общественным сознанием, существует в
многочисленных формах. Современные софисты, прежде всего, — специалисты по
пиару. Работа, которых заключается в навязывании обществу тех или иных
политических деятелей.

В обычном и распространенном понимании
софизм — это умышленный обман, основанный на нарушении правил. Но обман тонкий
и завуалированный. Цель софизма – выдать ложь за истину.

В нашей работе мы рассматриваем
математические софизмы.

II. Математические софизмы и их классификация

2.1. Софизмы и типичные ошибки в
них

Математический софизм — удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.

История математики полна неожиданных и
интересных софизмов, разрешение которых порой служило толчком к новым
открытиям. Математические софизмы приучают  внимательно и настороженно
продвигаться вперед, тщательно следить за точностью формулировок, правильностью
записи чертежей, за законностью математических операций. Поиск и нахождение
ошибок в софизме способствует пониманию математики в целом и развивает
логическое мышление.

К типичным ошибкам
в софизмах относятся:

·       запрещенные
действия;

·       пренебрежение условиями
теорем, формул и правил;

·       ошибочный чертеж;

·       опора на ошибочные
умозаключения.

Нередко, ошибки,
допущенные в софизме, настолько умело скрыты, что даже опытный математик не
сразу их выявит. Именно в этом и проявляется связь математики и философии в
софизмах.

2.2. Математические софизмы

Математические
софизмы делятся на:

1. Арифметические софизмы — это числовые
выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

Пример: « Дважды два — пять!».

Возьмем в качестве исходного соотношения
следующее очевидное равенство: 4:4= 5:5. После вынесения за скобки общего
множителя из каждой части равенства будем иметь: 4∙(1:1)=5∙(1:1)
или (2∙2)(1:1)=5(1:1) Наконец, зная, что 1:1=1, из соотношения 4(1:1)=5(1:1)
устанавливаем: 4=5, 2∙2=5. 

Ошибка.

Распределительный закон умножения применяется
только для сложения и вычитания:     ав + ас = а(в + с).

2. Алгебраические
софизмы —
намеренно скрытые ошибки в уравнениях и числовых выражениях.

Алгебра — один из больших разделов
математики, принадлежащий наряду с арифметикой и геометрией к числу старейших
ветвей этой науки. Задачи, а также методы алгебры отличаются от других отраслей
математики.

Приёмы
эти заключаются обычно в составлении и решении уравнений.

Пример: «Любое отрицательное число больше
положительного, имеющего то же абсолютное значение».

Этот софизм основан на очевидной истине:
«Если в равенстве числитель левой дроби больше знаменателя в n раз, то и в
правой части равенства соотношение внутри дроби будет таким же».

Напишем следующие равенства:

  и    и  ; т.е.  .

Другими словами, если в левой части
равенства + a > — a, то и в правой части равенства должно соблюдаться то же
соотношение.

Т.е. – a > + a.

Ошибка.

Чтобы получить из равенства +a > -a
равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить
знак неравенства (–a<+a).

3.Геометрические софизмы – это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость,
абсурд или противоречивое утверждение, связанное с геометрическими фигурами и
действиями над ними.

Пример: «Из точки на прямую можно
опустить два перпендикуляра.»

 .

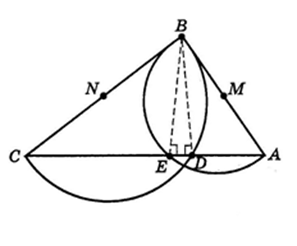
Другими словами, если в левой части
равенства + a > — a, то и в правой части равенства должно соблюдаться то же
соотношение.

Т.е. – a > + a.

Ошибка.

Чтобы получить из равенства +a > -a
равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить
знак неравенства (–a<+a).

3.Геометрические софизмы – это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость,
абсурд или противоречивое утверждение, связанное с геометрическими фигурами и
действиями над ними.

Пример: «Из точки на прямую можно
опустить два перпендикуляра.»

Рассмотрим
треугольник АВС.

Разделим стороны АВ и ВС пополам точками M
и N. На этих сторонах, как на диаметрах, опишем окружности с центрами в точках
M и N. Окружности пересекут сторону АС в точках D и E.

Углы
AEB и BDC опираются на диаметры АВ и ВС соответственно, значит они прямые.

Следовательно, отрезки BD и BE, исходящие
из точки В, будут перпендикулярны, стороне АС, следовательно, из точки В можно
опустить два перпендикуляра на сторону АС.

Ошибка.

Действительно, опустив из B перпендикуляр
на AC , получим два прямоугольных треугольника, гипотенузами которых будут
стороны BC и AB, и если вокруг этих треугольников описать окружности, их
гипотенузы будут диаметрами. Неправильный чертеж. Известно,
что окружности, построенные на двух сторонах треугольника как на диаметрах,
пересекаются в одной точке, лежащей на третьей стороне.

2.3. Разбор математических софизмов

В математических софизмов выделяются 6 основных
ошибок:

1. Деление на 0.

Софизм №1 «Пять равно шести».

Возьмем тождество 35+10-45=42+12-54.

В каждой части вынесем за скобки общий
множитель:

5(7+2-9)=6(7+2-9).

Теперь, получим, что 5=6.  

Ошибка.

При делении верного равенства
5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое
равенство можно делить только на число, отличное от 0.

Софизм №2 «Уравнение x-a=0 не имеет
корней».

Дано уравнение x –a = 0. Разделив обе
части этого уравнения на x-a, получим, что 1 = 0. Поскольку это равенство
неверное, то это означает, что исходное уравнение не имеет корней.   

 Ошибка.

Поскольку x = a – корень уравнения, то,
разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому
получили неверное равенство 1=0.(x—a=0 -на ноль делить нельзя).

2. Неправильные выводы из равенства дробей;

Софизм №3 «Отклонение от алгоритма может
привести к приобретению посторонних корней данного уравнения».

3. Неправильное извлечение квадратного корня из
квадрата выражения.

Софизм №4  

3. Неправильное извлечение квадратного корня из
квадрата выражения.

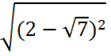
Софизм №4   = = =  =2-

 Ошибка.

  При
вычислении квадратного корня  2-

 Ошибка.

  При
вычислении квадратного корня  2- < 0

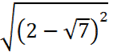
  =  = =  =ç2- =ç2- ç= — 2

4. Нарушения правил действия с величинами.

Софизм №5 «Один метр не равен ста
сантиметрам».

Известно, что любые два равенства можно
перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d,
то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр  =
100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно,
получим 10 метров  = 100000 сантиметров  и, разделив последнее равенство на 10,
получим, что 1  метр  = 10000 сантиметров .

Ошибка.

 Она состоит в нарушении правила действий
с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.

«Один рубль не равен ста копейкам».

Возьмем верное равенство: 2р. = 200к. и
возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.

Ошибка.

Здесь надо вспомнить, что
возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не
величины.

5. Проведение преобразований над математическими
объектами, не имеющими смысла.

Софизм №6 «Два
неодинаковых натуральных числа равны между собой».

Решим систему двух уравнений:

— 2

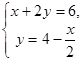
4. Нарушения правил действия с величинами.

Софизм №5 «Один метр не равен ста
сантиметрам».

Известно, что любые два равенства можно
перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d,
то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр  =
100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно,
получим 10 метров  = 100000 сантиметров  и, разделив последнее равенство на 10,
получим, что 1  метр  = 10000 сантиметров .

Ошибка.

 Она состоит в нарушении правила действий
с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.

«Один рубль не равен ста копейкам».

Возьмем верное равенство: 2р. = 200к. и
возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.

Ошибка.

Здесь надо вспомнить, что
возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не
величины.

5. Проведение преобразований над математическими
объектами, не имеющими смысла.

Софизм №6 «Два
неодинаковых натуральных числа равны между собой».

Решим систему двух уравнений:

.

Сделаем это
подстановкой у из 2-го уравнения в 1-е, получаем х+8-х=6, откуда
8=6.

Ошибка

Уравнение (2)
можно записать как х+2у=8, так, что исходная система запишется в виде: .

В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.

Графически это
означает, что прямые у=3-.

В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.

Графически это
означает, что прямые у=3- и у=4- параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.

6. Неравносильный переход от одного неравенства к
другому.

Софизм №7 «Если А
больше В, то А всегда больше, чем 2В».

Возьмем два произвольных
положительных числа А и В, такие, что А>В. Умножив это неравенство на В,
получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим
неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А).
(1)

После деления обеих частей
неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому
неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к
примеру, что из неравенства 6>5 следует, что 6>10.

Ошибка.

Здесь совершен неравносильный
переход от неравенства (1) к неравенству (2). Действительно, согласно условию А
> В, поэтому В – А < 0.Это означает, что обе части неравенства (1)
делятся на отрицательное число. Но согласно правилу преобразования неравенств
при делении или умножении неравенства на одно и то же отрицательное число знак
неравенства необходимо изменить на противоположный. С учетом сказанного из
неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к
которому почленно исходное неравенство В<А, получим просто исходное
неравенство А+В<В+2А.

7. Выводы и вычисления по неверно построенным чертежам;

 параллельны и не совпадают. Перед
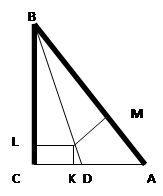
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.

6. Неравносильный переход от одного неравенства к
другому.

Софизм №7 «Если А
больше В, то А всегда больше, чем 2В».

Возьмем два произвольных
положительных числа А и В, такие, что А>В. Умножив это неравенство на В,
получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим
неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А).
(1)

После деления обеих частей
неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому
неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к
примеру, что из неравенства 6>5 следует, что 6>10.

Ошибка.

Здесь совершен неравносильный
переход от неравенства (1) к неравенству (2). Действительно, согласно условию А
> В, поэтому В – А < 0.Это означает, что обе части неравенства (1)
делятся на отрицательное число. Но согласно правилу преобразования неравенств
при делении или умножении неравенства на одно и то же отрицательное число знак
неравенства необходимо изменить на противоположный. С учетом сказанного из
неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к
которому почленно исходное неравенство В<А, получим просто исходное
неравенство А+В<В+2А.

7. Выводы и вычисления по неверно построенным чертежам;

Софизм
№8  ∟С=90, ВД — биссектриса угла СВА, СК=КА, ОК перпендикулярна СА, О —
точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС.

∟С=90, ВД — биссектриса ∟ СВА,
СК=КА, ОК ^ СА, О —
точка пересечения прямых ОК и ВД, ОМ ^ АВ, ОL ^
ВС.

Имеем: D
LВО=D МВО, ВL = ВМ, ОМ = ОL = СК = КА,

 D КОА=D ОМА (ОA- общая сторона, КА = ОМ,  ∟ ОКА и

 ∟ ОМА — прямые), ∟ ОАК =
∟ МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и
потому ВА = ВС

     Ошибка.

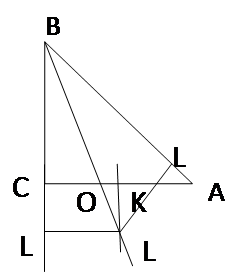Рассуждения о
том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка
пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к
катету АС, находится вне треугольника АВС.

2.4. Логические софизмы

Один из видов
математических софизмов является логический софизм.

Пример № 1: «Полупустое или полуполное».

Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное

Ошибка.

Полупустое не является половиной чего либо
пустого, а является чем либо наполовину наполненным.

Пример
№2: «Когда
же учиться?»

1. По ночам занятий нет, половина суток свободна.

Остаётся: 365-182=183 дня. 2.

2. В школе ученики занимаются половину дня, значит, вторая
половина (или четвёртая часть суток) может быть свободна.
Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы
приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.

Итого остаётся 137-37=100 дней.

4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние
(7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.

5. Итак, школьники заняты в году 100-100=0 дней. Когда же
учиться?!

2.5. Источники софизмов

Источниками
софизмов может выступать терминология, которая используется во время спора.
Многие слова имеют несколько смыслов (доктор может быть врачом или же научным
сотрудником, имеющим ученую степень), за счет чего и происходит нарушение
логики. Софизмы в математике, например, основаны на изменении чисел путем
перемножения их и последующего сравнения исходных и полученных данных.
Неправильное ударение тоже может быть оружием софиста, ведь множество слов при
изменении ударения меняют и смысл. Построение фразы иногда очень запутанно,
как, например, «два умножить на два плюс пять». В данном случае непонятно
имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма
произведения двоек и пятерки.

Разбор и
решение любого рода математических задач, а в особенности нестандартных,
помогает развивать смекалку и логику. Математические софизмы относятся именно к
таким задачам.

III.          
«Софизмы из наших школьных тетрадей»

Цель практической работы: проанализировать наши тетради для
контрольных работ по  математике,  выявить софизмы и найти  ошибки, заключенные
в них.

Известная истина гласит «Умные люди учатся
на чужих ошибках». В математике приходится учиться, в основном, на собственных
ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и
полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики  не могут объяснить, чем  вызваны эти ошибки.

С помощью задач,
содержащих противоречие в условии, можно предупредить ошибки учащихся,
связанные с работой над математическими объектами, которые не существуют при
заданных условиях.  Если учащиеся решают задачу, работая с несуществующими
объектами, то происходит выход за границы применяемости теоремы, свойства и
т.д. Эти ошибки возникают по той причине, что большинство учебных задач
содержит информацию непротиворечивую и приводящую к единственному решению.

Софизм	Ошибка
№1

Рассуждения о
том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка
пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к
катету АС, находится вне треугольника АВС.

2.4. Логические софизмы

Один из видов
математических софизмов является логический софизм.

Пример № 1: «Полупустое или полуполное».

Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное

Ошибка.

Полупустое не является половиной чего либо
пустого, а является чем либо наполовину наполненным.

Пример
№2: «Когда
же учиться?»

1. По ночам занятий нет, половина суток свободна.

Остаётся: 365-182=183 дня. 2.

2. В школе ученики занимаются половину дня, значит, вторая
половина (или четвёртая часть суток) может быть свободна.
Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы
приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.

Итого остаётся 137-37=100 дней.

4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние
(7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.

5. Итак, школьники заняты в году 100-100=0 дней. Когда же
учиться?!

2.5. Источники софизмов

Источниками
софизмов может выступать терминология, которая используется во время спора.
Многие слова имеют несколько смыслов (доктор может быть врачом или же научным
сотрудником, имеющим ученую степень), за счет чего и происходит нарушение
логики. Софизмы в математике, например, основаны на изменении чисел путем
перемножения их и последующего сравнения исходных и полученных данных.
Неправильное ударение тоже может быть оружием софиста, ведь множество слов при
изменении ударения меняют и смысл. Построение фразы иногда очень запутанно,
как, например, «два умножить на два плюс пять». В данном случае непонятно
имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма
произведения двоек и пятерки.

Разбор и
решение любого рода математических задач, а в особенности нестандартных,
помогает развивать смекалку и логику. Математические софизмы относятся именно к
таким задачам.

III.          
«Софизмы из наших школьных тетрадей»

Цель практической работы: проанализировать наши тетради для
контрольных работ по  математике,  выявить софизмы и найти  ошибки, заключенные
в них.

Известная истина гласит «Умные люди учатся
на чужих ошибках». В математике приходится учиться, в основном, на собственных
ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и
полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики  не могут объяснить, чем  вызваны эти ошибки.

С помощью задач,
содержащих противоречие в условии, можно предупредить ошибки учащихся,
связанные с работой над математическими объектами, которые не существуют при
заданных условиях.  Если учащиеся решают задачу, работая с несуществующими
объектами, то происходит выход за границы применяемости теоремы, свойства и
т.д. Эти ошибки возникают по той причине, что большинство учебных задач
содержит информацию непротиворечивую и приводящую к единственному решению.

Софизм	Ошибка
№1   — 10 × ×  = 11 – 10  ×  ×  =  =  =  = 0,8	Неправильный   порядок действий:  — 10 — 10 ×  = 11 – 10   = 11 – 10  ×  = 11 — 10  = 11 — 10  = 11 — 10 = 11 – 10 ×0,8 = 11 – 8 = 3
№2  = 11 – 10 ×0,8 = 11 – 8 = 3
№2  —  =  =  —  = = =	Нарушение правил приведения дробей к общему знаменателю:	Нарушение правил приведения дробей к общему знаменателю:  —  =    =     ==   =
№3		Нарушение правил сокращения дробей:   Нарушение правил сокращения дробей:
№4  +  +  = x2 ОДЗ: все числа, кроме 2.  —  —  = x2  Умножим обе части уравнение на x-2 2 — 3x — 2 = x2(x — 2) Разложили на множители квадратный трёхчлен 2 — 3x — 2 = x2(x — 2) Разложили на множители квадратный трёхчлен 2 — 3x – 2 = 2(x — 2) (x +  ) = = (x — 2) (2x + 1) (x — 2) (2x + 1) = x2 (x — 2) Разделим обе части уравнения на х — 2,получим 2x + 1 = x2 X2 -2x -1 =0 Д=4+4=8 X1= ) = = (x — 2) (2x + 1) (x — 2) (2x + 1) = x2 (x — 2) Разделим обе части уравнения на х — 2,получим 2x + 1 = x2 X2 -2x -1 =0 Д=4+4=8 X1= == 1+= 1+ X2=1- Корни удовлетворяют ОДЗ. Ответ: 1- Корни удовлетворяют ОДЗ. Ответ: 1-; 1+.	Ошибка: при делении уравнения  (x-2)(2x+1)=x2 (x-2) , на x-2произошла потеря корня Верное решение: x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х — 2=0 или x2 — 2x — 1=0 x = 2 или x1=1 + .	Ошибка: при делении уравнения  (x-2)(2x+1)=x2 (x-2) , на x-2произошла потеря корня Верное решение: x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х — 2=0 или x2 — 2x — 1=0 x = 2 или x1=1 +  и x2=1 —   Уравнение имеет три корня: 2; 1 +   Уравнение имеет три корня: 2; 1 + ; 1 — . Но 2 — не удовлетворяет ОДЗ. Ответ: 1 + . Но 2 — не удовлетворяет ОДЗ. Ответ: 1 + ; 1 — .
№5 .
№5   =  = 66 =46656	Верное решение:  = 66 =46656	Верное решение: =  = == =22=4 Ошибка:  =22=4 Ошибка: *    Правило: при умножении степеней с одинаковым основанием, показатели складываются, а основание остаётся прежним.
№6 Периметр треугольника равен 6, его стороны относятся как 1:2:3. Чему равна его средняя по величине сторона.	Задача провоцирует учащихся на то, чтобы дать ответ 2. При этом не выполняется неравенство треугольника.
Правило: при умножении степеней с одинаковым основанием, показатели складываются, а основание остаётся прежним.
№6 Периметр треугольника равен 6, его стороны относятся как 1:2:3. Чему равна его средняя по величине сторона.	Задача провоцирует учащихся на то, чтобы дать ответ 2. При этом не выполняется неравенство треугольника.
№7В окружность радиуса 8 см вписан равнобедренный треугольник АВС. Радиус ОА образует с основанием АВ треугольника АВС угол в 30º. Найдите боковую сторону треугольника.	Известные элементы (радиус окружности и угол, образуемый радиусом ОА с основанием АВ вписанного равнобедренного треугольника), заданные в условии этой задачи, определяют две сложные фигуры: а) окружность центра О радиуса 8 см и вписанный в эту окружность остроугольный равнобедренный треугольник АВС; б) та же окружность и вписанный в нее тупоугольный равнобедренный треугольник АВС1.

Заключение

Исторические
сведения о софистике и софистах помогли нам разобраться, откуда же все-таки
началась история софизмов. Вначале  мы думали, что софизмы бывают исключительно
математические. Причем в виде конкретных задач, но, начав исследование в этой
области, мы поняли, что софистика — это целая наука, а именно математические
софизмы — это лишь часть большого течения.

Разбор софизмов
развивает логическое мышление, помогает сознательному усвоению изучаемого
материала, воспитывая вдумчивость, наблюдательность, критическое отношение к
тому, что изучается. Кроме того, разбор софизмов увлекателен. Мы с большим
интересом  воспринимали софизмы, чем труднее софизм, тем большее удовлетворение
доставляет его разбор. Порой сам попадаешься на уловки софиста.

Гипотеза, которую
мы ставили в начале работы «Если в процессе обучения математике целенаправленно и
систематически организовывать работу учащихся над типичными ошибками, на примере
софизмов, то это будет способствовать повышению качества математической подготовки
учащихся», подтвердилась.

Благодаря знанию
софизмов  можно научиться искать ошибки в рассуждениях других, научится
грамотно строить свои рассуждения и логические объяснения. Когда ребенок раз
притронется к горячему предмету, то впоследствии он постарается этого не
делать. Он будет много осторожнее. Так, изучающий математику, впоследствии
проявит больше осторожности, чтобы не повторить осознанную ошибку.   Значит, математические софизмы заставляют внимательно
и настороженно продвигаться вперед, тщательно следить за точностью
формулировок, правильностью записей и чертежей, за допустимостью обобщений, за
законностью выполняемых операций. Все это нужно и полезно. Только очень сухого
человека не может увлечь интересный софизм. Как приятно бывает обнаружить
ошибку в математическом софизме и тем как бы восстановить истину в ее правах.
Математические софизмы показали нам, как важно строго соблюдать правила и
формулировки теорем при логических умозаключениях.

Нам
было очень интересно работать над данной темой. Мы создали сборник «Софизмы из
наших школьных тетрадей».

Задания,
предложенные нами в работе, можно использовать как на уроках алгебры и
геометрии, так и на внеклассных мероприятиях.

Список
литературы

1.     «Софисты»
под редакцией  Б.С. Чернышева

2.     «Софизмы. Алгебра.
Геометрия. Тригонометрия» под редакцией Т.Н. Михеевой

3.     http://gamzatovasm.ru/node/88 — Алгебраические
софизмы

4.     http://reshit.ru/sofizm — Геометрические
софизмы

5.     http://sophisms.ucoz.ru/index/arifmeticheskie_sofizmy/0-6 — Арифметические софизмы

6.     http://referatwork.ru/category/logika/view/131832_sofizmy — Логические софизмы

7.      https://ru.wikipedia.org/wiki/Апории_Зенона — Апории Зенона

Приложения

Приложение 1.

 Рис. 1 Протагор

 Рис. 1 Протагор

Рис.
2 Сократ

  Рис. 3 Аристотель

Приложение 2.
Арифметические софизмы

1.
Верно ли равенство 7 = 8?

35 +
14 – 49 = 40 + 16 — 56

7(5 +
2 — 7)=8(5 + 2 — 7)

Следовательно,
7 = 8

Ошибка.

Обе части равенства разделили на (5 + 2 — 7),
но нарушено правило, что на «0» делить нельзя (5 + 2 – 7 = 0)

2.

Некто
утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы
последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же
чисел, но взятых в обратном порядке (от 1 до 9):

9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9

8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2

Будем
последовательно вычитать числа второй строки из чисел первой. Например, так как
9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь
нетрудно установить,

8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.

Итак,
45 – 45 = 45.

Ошибка состоит в том,
что занимаемую единицу возводили в ранг десятка.

3.Меньшее число больше, чем большее».

Очевидно,что7 > 5 и что – 8 = — 8

Тогда:7 – 8 > 5 — 8 или – 1 > — 3

Это не противоречит основному понятию об
отрицательных величина, на основании которого мы считаем меньшей ту
отрицательную величину, численное значение которой больше, и наоборот.

Умножим обе части последнего неравенства на (- 4).

Получим (-1)*(-4)>(-3)*(-4) или 4 > 12

Ошибка.

При умножении неравенства на отрицательное
число, знак неравенства изменяется на противоположный.

Приложение 3. Алгебраические софизмы

1.«Отрицательное число больше положительного».

Возьмем два положительных
числа а и с. Сравним два отношения:  Рис. 3 Аристотель

Приложение 2.
Арифметические софизмы

1.
Верно ли равенство 7 = 8?

35 +
14 – 49 = 40 + 16 — 56

7(5 +
2 — 7)=8(5 + 2 — 7)

Следовательно,
7 = 8

Ошибка.

Обе части равенства разделили на (5 + 2 — 7),
но нарушено правило, что на «0» делить нельзя (5 + 2 – 7 = 0)

2.

Некто
утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы
последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же
чисел, но взятых в обратном порядке (от 1 до 9):

9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9

8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2

Будем
последовательно вычитать числа второй строки из чисел первой. Например, так как
9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь
нетрудно установить,

8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.

Итак,
45 – 45 = 45.

Ошибка состоит в том,
что занимаемую единицу возводили в ранг десятка.

3.Меньшее число больше, чем большее».

Очевидно,что7 > 5 и что – 8 = — 8

Тогда:7 – 8 > 5 — 8 или – 1 > — 3

Это не противоречит основному понятию об
отрицательных величина, на основании которого мы считаем меньшей ту
отрицательную величину, численное значение которой больше, и наоборот.

Умножим обе части последнего неравенства на (- 4).

Получим (-1)*(-4)>(-3)*(-4) или 4 > 12

Ошибка.

При умножении неравенства на отрицательное
число, знак неравенства изменяется на противоположный.

Приложение 3. Алгебраические софизмы

1.«Отрицательное число больше положительного».

Возьмем два положительных
числа а и с. Сравним два отношения:  и

Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию:

Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию:  

Но если в пропорции предыдущий член первого отношения больше последующего,
то предыдущий член второго отношения также больше своего последующего. В нашем
случае а > — с, следовательно, должно быть –а > с, т.е. отрицательное
число больше положительного.

Ошибка.

Данное свойство пропорции может оказаться неверным, если некоторые
члены пропорции отрицательны.

2. « Если
одно число больше другого, то эти числа равны»

Возьмем два
произвольных числа т и п, такие, что m > n , и другие три произвольных числа а, b и с, сумма которых
равна d, т.е. а + b + c = d. Умножив обе части этого равенства на n, а затем на
m, получим:

ma + mb + mc
= md, na + nb + nc = nd.

Сложив почленно равенства: 

ma + mb + mc
= md и nd = na
+ nb + nc

 получим: ma + mb + mc + nd = na + nc + nb + md.

Перенося здесь nd вправо, а md влево, имеем

ma + mb + mc
– md = na + nb + nc — nd.

Вынося слева число m, а справа число n за скобки,
придем к соотношению m (a + b + c — d) = n (a + b + c — d).

Разделив обе части последнего равенства на

(a + b + c — d), находим, что m = n.

Ошибка.

a + b + c – d =0, на ноль делить нельзя.

4.    
«Любое число равно нулю»

Возьмем произвольное положительное число а и
рассмотрим сумму х бесконечного числа слагаемых, равных а: х = а + а + а + а +…
Очевидно, что мы можем представить эту сумму как х = а + (а + а + а +….) в
которой сумма, стоящая в скобках, также равна х как сумма бесконечного числа слагаемых,
равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0.

Ошибка допущена в равенстве (1) , в котором бесконечная сумма чисел
а обозначена конечным числом х.

4.

Решим систему двух
уравнений:

Сделаем это подстановкой у из 2го
уравнения в 1, получаем х + 8 — х = 6, откуда

8 = 6

Ошибка.

Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде:

Сделаем это подстановкой у из 2го
уравнения в 1, получаем х + 8 — х = 6, откуда

8 = 6

Ошибка.

Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде:

В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.

Графически это
означает, что прямые у=3 —  и у = 4
— и у = 4
— параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.

5.     «Если “a” больше “b”, то “a” всегда больше,
чем “2b”»

Возьмем два
произвольных положительных числа a и b, такие, что a > b. Умножив это
неравенство на b, получим новое неравенство:

ab > bb, а отняв от обеих
его частей a·a, получим
неравенство:

ab—aa > bb — aa, которое
равносильно следующему: a(b—a) > (b+a)(b—a).(1)

После деления обеих частей неравенства (1)
на b—a получим, что a > b+a (2),

Прибавив к этому неравенству почленно
исходное неравенство a> b, имеем

2a >
2b + a,
откуда a > 2b.

Итак, если a > b, то a > 2b.

Ошибка совершена при
переходе от равенства (1) к (2).

Т.к. a > b, то b — a<0,
следовательно, при делении неравенства (1) на b – a, мы должны
поменять знак неравенства на противоположный.

6.«Единица равна двум»

Простым вычитанием легко убедиться в
справедливости равенства

1 — 3 = 4-6.

Добавив к обеим частям этого равенства
число ⁹/₄, получим новое равенство

1 — 3 + ⁹/₄ = 4 — 6
+ ⁹/₄,

в котором, как нетрудно заметить, правая и
левая части представляют собой полные квадраты, т. е. (1 — ³/₂)=(2 — ³/₂)

Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство: 1 — ³/₂ 
=2 — ³/₂

откуда следует, что    1=2.

Ошибка.

По определению =(2 — ³/₂)

Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство: 1 — ³/₂ 
=2 — ³/₂

откуда следует, что    1=2.

Ошибка.

По определению представляет собой некоторое
неотрицательное число, которое, будучи возведено в квадрат, даст х. Ясно, что
этому определению удовлетворяют два числа, а именно х и -х. Итак, если число х
неотрицательно (х ≥ 0), то= х; если же число х отрицательно (х<0), то есть число –х положительно, то = х; если же число х отрицательно (х<0), то есть число –х положительно, то = — x. Отсюда заключаем, что  (свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.

7.    
«Всякое
число равно своей половине.»

Запишем очевидное для любого числа a
тождество a²— a²= a²— a²,где
а — любое число.

Вынесем a в левой части за скобку,
а правую часть разложим на множители по формуле разности квадратов, получим

a(a – a) = (a + a)(a — a).

Разделив обе части на a — a, получим a = a + a, или a=2a.

Разделим на 2 и получим а
= а/2

Ошибка.

Мы делим обе части на ноль, а деление на
ноль запрещено

Приложение 4. Геометрические софизмы

1.  (свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.

7.    
«Всякое
число равно своей половине.»

Запишем очевидное для любого числа a
тождество a²— a²= a²— a²,где
а — любое число.

Вынесем a в левой части за скобку,
а правую часть разложим на множители по формуле разности квадратов, получим

a(a – a) = (a + a)(a — a).

Разделив обе части на a — a, получим a = a + a, или a=2a.

Разделим на 2 и получим а
= а/2

Ошибка.

Мы делим обе части на ноль, а деление на
ноль запрещено

Приложение 4. Геометрические софизмы

1. , а длина всякой окружности равна ее
диаметру.

Построим
на отрезке МN  как на диаметре окружность. Радиус окружности обозначим через . Тогда длина окружности будет
равна: . Тогда длина окружности будет
равна:

Поделим
MO и NO пополам точками

Поделим
MO и NO пополам точками  и  и построим новые окружности с центрами в
этих точках радиусами   и построим новые окружности с центрами в
этих точках радиусами .

Найдем
длины новых окружностей:

Сумма
их длин будет равна

Сумма
их длин будет равна

т.е.
равна длине большой окружности C.

Таким
же образом будем строить окружности и далее и находить сумму их длин.

Так,
сумма длин окружностей  и  и . и будет равна

Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны

Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны  и т.д. При этом сумма длин всех этих
окружностей всегда будет равна .

Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна.

Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна.

С
другой стороны, сумма длин этих окружностей постоянна и равна , следовательно,, следовательно,

Из
этого равенства получаем   или, деля на  или, деля на  :

Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна

Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна  . Пусть  — длина малой
окружности — длина малой
окружности,
— ее радиус. Как бы такая окружности ни была мала, всегда имеем  или

 или

Отсюда
видим, что эта бесконечно-малая окружность никогда не будет равна своему
диаметру ,
что следовало бы из результата софизма.

2.« Отрезки параллельных прямых, заключенные между сторонами
угла, равны»

Рассмотрим произвольный угол с
вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки
которых АВ и CD заключены между сторонами этого угла.

Как известно параллельные
прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ :
CE = BE : DE,

Откуда АЕ·DE = BE·CE

Умножив обе части последнего
равенства на отличную от нуля разность (АВ –CD), запишем

AE·DE·AB — AE·DE·CD = AE·DE·CD
— BE·CE·CD,

или

AB(AE·DE — BE·CE) = CD(AE·DE —
BE·CE)

Разделив обе части последнего равенства на (AE·DE — BE·CE), получим
равенство АВ=CD.

что следовало бы из результата софизма.

2.« Отрезки параллельных прямых, заключенные между сторонами
угла, равны»

Рассмотрим произвольный угол с
вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки
которых АВ и CD заключены между сторонами этого угла.

Как известно параллельные
прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ :
CE = BE : DE,

Откуда АЕ·DE = BE·CE

Умножив обе части последнего
равенства на отличную от нуля разность (АВ –CD), запишем

AE·DE·AB — AE·DE·CD = AE·DE·CD
— BE·CE·CD,

или

AB(AE·DE — BE·CE) = CD(AE·DE —
BE·CE)

Разделив обе части последнего равенства на (AE·DE — BE·CE), получим
равенство АВ=CD.

 

Ошибка.

AE·DE — BE·CE=0

3.Все треугольники равнобедренные.

Рассмотрим
произвольный ∆АВС (рис.2).

Проведем
в нем биссектрису угла B и серединный перпендикуляр к стороне АС. Точку их
пересечения обозначим через О.

Из
точки O опустим перпендикуляр OD на сторону АВ и перпендикуляр ОЕ на сторону
ВС. Очевидно, что ОА = ОС и OD = ОЕ. Но тогда ∆AOD = ∆СОЕ по катету и
гипотенузе. Поэтому ∟DAO = ∟ЕСО. В то же время ∟ОАС = ∟ОСА,
так как ∆АОС -равнобедренный.

Получаем:
∟ВАС = ∟DAO + ∟ОАС = ∟ЕСО + ∟ОСА = ∟ВСА

Итак, угол ВАС равен углу ВСА, поэтому ∆АВС — равнобедренный:
АВ=ВС.

Ошибка. При построения чертежа. Серединный перпендикуляр к
стороне и биссектриса противоположного ей угла для не равнобедренного
треугольника, пересекаются вне этого треугольника.

Приложение 4.

Логические софизмы.

1.
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше.
Значит, лекарств нужно принимать как можно больше».

Ошибка. При построения чертежа. Серединный перпендикуляр к
стороне и биссектриса противоположного ей угла для не равнобедренного
треугольника, пересекаются вне этого треугольника.

Приложение 4.

Логические софизмы.

1.
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше.
Значит, лекарств нужно принимать как можно больше».

2. Одна
песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+1
песчинка – тоже не куча. Следовательно, никакое число песчинок не образует кучу
песка. К этому парадоксу можно сделать следующий комментарий: метод полной
математической индукции нельзя применять, как показывает парадокс, к объёмно
неопределённым понятиям, каковым является понятие «куча песка».

3.
Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна
существовать курица, но ведь курица может вылупиться только из яйца, а значит,
первичным является именно оно.

3.
Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна
существовать курица, но ведь курица может вылупиться только из яйца, а значит,
первичным является именно оно.

4.«Может ли
всемогущий маг создать камень, который не сможет поднять?»

Если не может – значит, он не всемогущий.
Если может – значит, всё равно не всемогущий, т.к. он не может поднять это
камень.

6.В мире нет ни одного человека,
говорящего на моем языке; или короче: ни одного человека, говорящего; или еще
короче: ни одного человека.

6.В мире нет ни одного человека,
говорящего на моем языке; или короче: ни одного человека, говорящего; или еще
короче: ни одного человека.

Скачано с www.znanio.ru

1. Софизмы. Понятие, примеры

Раскрывая данный вопрос, необходимо сказать, что любой софизм является ошибкой. В логике выделяют также паралогизмы. Отличие этих двух видов ошибок состоит в том, что первая (софизм) допущена умышленно, вторая же (паралогизм) — случайно. Паралогизмами изобилует речь многих людей. Умозаключения, даже, казалось бы, правильно построенные, в конце искажаются, образуя следствие, не соответствующее действительности. Паралогизмы, несмотря на то что допускаются неумышленно, все же часто используются в своих целях. Можно назвать это подгонкой под результат. Не осознавая, что делает ошибку, человек в таком случае выводит следствие, которое соответствует его мнению, и отбрасывает все остальные версии, не рассматривая их. Принятое следствие считается истинным и никак не проверяется. Последующие аргументы также искажаются для того, чтобы больше соответствовать выдвинутому тезису. При этом, как уже было сказано выше, сам человек не сознает, что делает логическую ошибку, считает себя правым (более того, сильнее подкованным в логике).

В отличие от логической ошибки, возникающей непроизвольно и являющейся следствием невысокой логической культуры, софизм является преднамеренным нарушением логических правил. Обычно он тщательно маскируется под истинное суждение.

Допущенные умышленно, софизмы преследуют цель победить в споре любой ценой. Софизм призван сбить оппонента с его линии размышлений, запутать, втянуть в разбор ошибки, которые не относятся к рассматриваемому предмету. С этой точки зрения софизм выступает как неэтичный способ (и при этом заведомо неправильный) ведения дискуссии.

Существует множество софизмов, созданных еще в древности и сохранившихся до сегодняшнего дня. Заключение большей части из них носит курьезный характер. Например, софизм «вор» выглядит так: «Вор не желает приобрести ничего дурного; приобретение хорошего есть дело хорошее; следовательно, вор желает хорошего». Странно звучит и следующее утверждение: «Лекарство, принимаемое больным, есть добро; чем больше делать добра, тем лучше; значит, лекарство нужно принимать в больших дозах». Существуют и другие известные софизмы, например: «Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит», «Сократ — человек; человек — не то же самое, что Сократ; значит, Сократ — это нечто иное, чем Сократ», «Эти кутята твои, пес, отец их, тоже твой, и мать их, собака, тоже твоя. Значит, эти кутята твои братья и сестры, пес и сука — твои отец и мать, а сам ты собака».

Такие софизмы нередко использовались для того, чтобы ввести оппонента в заблуждение. Без такого оружия в руках, как логика, соперникам софистов в споре было нечего противопоставить, хотя зачастую они и понимали ложность софистических умозаключений. Споры в Древнем мире зачастую заканчивались драками.

При всем отрицательном значении софизмов они имели обратную и гораздо более интересную сторону. Так, именно софизмы стали причиной возникновения первых зачатков логики. Очень часто они ставят в неявной форме проблему доказательства. Именно с софизмов началось осмысление и изучение доказательства и опровержения. Поэтому можно говорить о положительном действии софизмов, т. е. о том, что они непосредственно содействовали возникновению особой науки о правильном, доказательном мышлении.

Известен также целый ряд математических софизмов. Для их получения числовые значения тасуются таким образом, чтобы из двух разных чисел получить одно. Например, утверждение, что 2 х 2 = 5, доказывается следующим образом: по очереди 4 делится на 4, а 5 на 5. Получается результат (1:1) = (1:1). Следовательно, четыре равно пяти. Таким образом, 2 х 2 = 5. Такая ошибка разрешается достаточно легко — нужно лишь произвести вычитание одного из другого, что выявит неравенство двух этих числовых значений. Также опровержение возможно записью через дробь.

Как раньше, так и теперь софизмы используются для обмана. Приведенные выше примеры достаточно просты, легко заметить их ложность и не обладая высокой логической культурой. Однако существуют софизмы завуалированные, замаскированные так, что отличить их от истинных суждений бывает очень проблематично. Это делает их удобным средством обмана в руках подкованных в логическом плане мошенников.

Вот еще несколько примеров софизмов: «Для того чтобы видеть, нет необходимости иметь глаза, так как без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет, поэтому ясно, что глаза не являются необходимыми для зрения» и «Что ты не терял, то имеешь; рога ты не терял, значит, у тебя рога». Последний софизм является одним из самых известных и часто приводится в качестве примера.

Можно сказать, что софизмы вызываются недостаточной самокритичностью ума, когда человек хочет понять пока недоступное, не поддающееся на данном уровне развития знание.

Бывает и так, что софизм возникает как защитная реакция при превосходящем противнике, в силу неосведомленности, невежества, когда спорящий не проявляет упорство, не желая сдавать позиций. Можно говорить о том, что софизм мешает ведению спора, однако такую помеху не стоит относить к значительным. При должном умении софизм легко опровергается, хотя при этом и происходит отход от темы рассуждения: приходится говорить о правилах и принципах логики.

Данный текст является ознакомительным фрагментом.