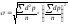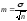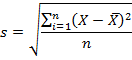Ошибка среднего квадратического отклонения это

From Wikipedia, the free encyclopedia

In statistics, the mean squared error (MSE)^[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.^[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.^[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).^{[citation needed]} For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.

Definition and basic properties[edit]

The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.

Predictor[edit]

If a vector of predictions is generated from a sample of data points on all variables, and is the vector of observed values of the variable being predicted, with hat{Y} being the predicted values (e.g. as from a least-squares fit), then the within-sample MSE of the predictor is computed as

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

In other words, the MSE is the mean ${textstyle left({frac {1}{n}}sum _{i=1}^{n}right)}$ of the squares of the errors ${textstyle left(Y_{i}-{hat {Y_{i}}}right)^{2}}$ . This is an easily computable quantity for a particular sample (and hence is sample-dependent).

In matrix notation,

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}(e_{i})^{2}={frac {1}{n}}mathbf {e} ^{mathsf {T}}mathbf {e} }$

where $e_{i}$ is ${displaystyle (Y_{i}-{hat {Y_{i}}})}$ and is the column vector.

The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,^[4] and is computed as

${displaystyle operatorname {MSE} ={frac {1}{q}}sum _{i=n+1}^{n+q}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter theta is defined as^[1]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}$

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator is derived as a sample statistic and is used to estimate some population parameter, then the expectation is with respect to the sampling distribution of the sample statistic.

The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.^[5]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} ({hat {theta }},theta )^{2}.}$

Proof of variance and bias relationship[edit]

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}$

An even shorter proof can be achieved using the well-known formula that for a random variable , ${textstyle mathbb {E} (X^{2})=operatorname {Var} (X)+(mathbb {E} (X))^{2}}$ . By substituting with, , we have

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}$

But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.

In regression[edit]

In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,^[6] but whose limitation is related to known distribution of the data.

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).^[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.

In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.

Examples[edit]

Mean[edit]

Suppose we have a random sample of size from a population, $X_{1},dots ,X_{n}$ . Suppose the sample units were chosen with replacement. That is, the units are selected one at a time, and previously selected units are still eligible for selection for all draws. The usual estimator for the is the sample average

$overline{X}=frac{1}{n}sum_{i=1}^n X_i$

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

${displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}$

where $sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

${displaystyle S_{n-1}^{2}={frac {1}{n-1}}sum _{i=1}^{n}left(X_{i}-{overline {X}}right)^{2}={frac {1}{n-1}}left(sum _{i=1}^{n}X_{i}^{2}-n{overline {X}}^{2}right).}$

This is unbiased (its expected value is $sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

${displaystyle operatorname {MSE} (S_{n-1}^{2})={frac {1}{n}}left(mu _{4}-{frac {n-3}{n-1}}sigma ^{4}right)={frac {1}{n}}left(gamma _{2}+{frac {2n}{n-1}}right)sigma ^{4},}$

where $mu _{4}$ is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for $sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

${displaystyle S_{a}^{2}={frac {n-1}{a}}S_{n-1}^{2}={frac {1}{a}}sum _{i=1}^{n}left(X_{i}-{overline {X}},right)^{2}}$

then we calculate:

${displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}$

This is minimized when

$a=frac{(n-1)gamma_2+n^2+n}{n} = n+1+frac{n-1}{n}gamma_2.$

For a Gaussian distribution, where , this means that the MSE is minimized when dividing the sum by a=n+1 . The minimum excess kurtosis is ,^[a] which is achieved by a Bernoulli distribution with p = 1/2 (a coin flip), and the MSE is minimized for ${displaystyle a=n-1+{tfrac {2}{n}}.}$ Hence regardless of the kurtosis, we get a «better» estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit; this is a simple example of a shrinkage estimator: one «shrinks» the estimator towards zero (scales down the unbiased estimator).

Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be $S^2_{n-1}.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean, $overline{X}=frac{1}{n}sum_{i=1}^n(X_i)$	$operatorname{MSE}(overline{X})=operatorname{E}((overline{X}-mu)^2)=left(frac{sigma}{sqrt{n}}right)^2$
${displaystyle theta =sigma ^{2}}$	= the unbiased estimator of the population variance, $S^2_{n-1} = frac{1}{n-1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n-1})=operatorname{E}((S^2_{n-1}-sigma^2)^2)=frac{2}{n - 1}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n} = frac{1}{n}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n})=operatorname{E}((S^2_{n}-sigma^2)^2)=frac{2n - 1}{n^2}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n+1} = frac{1}{n+1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n+1})=operatorname{E}((S^2_{n+1}-sigma^2)^2)=frac{2}{n + 1}sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter theta with perfect accuracy, is ideal (but typically not possible).

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).

Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.

In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Squared error loss is one of the most widely used loss functions in statistics^{[citation needed]}, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.^[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.

Criticism[edit]

The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.^[10]

Like variance, mean squared error has the disadvantage of heavily weighting outliers.^[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

Источник

Среднее
квадратическое отклонение
характеризует среднее отклонение
всех вариант вариационного ряда от
средней арифметической
величины. Поскольку отклонения вариант
от средней,
имеют значения с «+» и «-», то при
суммировании
они взаимоуничтожаются. Чтобы избежать
этого, отклонения возводятся
во вторую степень, а затем, после
определенных вычислений,
производится обратное действие —
извлечение корня квадратного. Поэтому
среднее отклонение именуется
квадратическим.

Среднее
квадратическое отклонение определяют
по формуле:

(отклонение
d
— это разность между каждой вариантой
и средней величиной, т. е. d
= V-M;
р –частота; количество вариант n
(при числе наблюдений менее 30 сумма
делится
на n-1);

При
вычислении среднеквад. отклонения по
способу
моментов используется следующая формула.
Т.о.
, формула вычисления сред. отклонения
по способу моментов будет читаться как
корень квадратный
из
разности момента второй степени и
квадрата момента первой степени.
Результаты
вычисления сред. отклонения обычным
способом и способом моментов идентичны.
Однако, как указывалось
выше, второй способ значительно убыстряет
и упрощает
расчеты. Итак,
нахождение сред. отклонения позволяет
судить о характере однородности
исследуемой группы наблюдений. Если
величина среднеквад. отклонения
небольшая, то
это свидетельствует о достаточно высокой
однородности изучаемого
явления. Среднюю арифметическую в таком
случае следует признать
вполне характерной для данного
вариационного ряда. Однако
слишком малая величина сигмы заставляет
думать об искусственном
подборе наблюдений. При очень большой
сигме средняя арифметическая в меньшей
степени характеризует вариационный
ряд,
что говорит о значительной вариабельности
изучаемого признака
или явления или о неоднородности
исследуемой группы. Значение:
Определение
среднеквад. отклонения представляет
немалую ценность для медицинской науки
и практики. При диагностике
отдельных заболеваний очень важно
оценить на основании конкретных
исследований, какие признаки проявляются
у соответствующей
группы больных относительно одинаково,
с небольшими колебаниями,
а для каких признаков характерны большие
индивидуальные
колебания. Очень широко используется
это свойство при оценке
физического развития отдельных групп
населения, при выработке
стандартов школьной меб.

Ошибка
репрезентативности (сред.
ошибка сред. арифметич.)

Чтобы
определить степень точности выборочного
наблюдения, необходимо оценить величину
ошибки, которая может
случайно произойти в процессе выборки.
Такие ошибки носят название
случайных ошибок репрезентативности
т.
Они
фактически являются разностью
между средними числами, полученными
при выборочном статистическом
наблюдении, и аналогичными величинами,
которые были бы
получены при сплошном исследовании
того же объекта (т. е. при исследовании
генеральной совокупности).
Ошибки
репрезентативности вытекают из самой
сущности выборочного
исследования. С помощью ошибок
репрезентативности числовые характеристики
выборочной совокупности распространяются
на всю генеральную совокупность, то
есть она характеризуется с учетом
определенной погрешности. Величины
ошибок репрезентативности определяются
как объемом
выборки, так и разнообразием признака.
Чем больше число наблюдений,
тем меньше ошибка, чем больше изменчив
признак, тем больше
величина статистической ошибки.
На
практике для определения средней ошибки
выборки в статистических
исследованиях пользуются следующей
формулой:

(где
m
— ошибка репрезентативности;
σ
— среднее квадратическое отклонение;

n
— число наблюдений в выборке (при числе
наблюдений менее 30
в подкоренное выражение вносится
значение п-1)).

Размер
средней ошибки прямо пропорционален
среднему квадратичному отклонению, т.
е. вариабельности изучаемого
признака, и обратно пропорционален
корню квадратному из
числа наблюдений

Билет 25

Источник

From Wikipedia, the free encyclopedia

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

Definition and basic properties[edit]

Predictor[edit]

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

In matrix notation,

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}(e_{i})^{2}={frac {1}{n}}mathbf {e} ^{mathsf {T}}mathbf {e} }$

where $e_{i}$ is ${displaystyle (Y_{i}-{hat {Y_{i}}})}$ and is the column vector.

${displaystyle operatorname {MSE} ={frac {1}{q}}sum _{i=n+1}^{n+q}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter theta is defined as^[1]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}$

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} ({hat {theta }},theta )^{2}.}$

Proof of variance and bias relationship[edit]

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}$

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}$

In regression[edit]

Examples[edit]

Mean[edit]

$overline{X}=frac{1}{n}sum_{i=1}^n X_i$

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

${displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}$

where $sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

${displaystyle S_{n-1}^{2}={frac {1}{n-1}}sum _{i=1}^{n}left(X_{i}-{overline {X}}right)^{2}={frac {1}{n-1}}left(sum _{i=1}^{n}X_{i}^{2}-n{overline {X}}^{2}right).}$

This is unbiased (its expected value is $sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

${displaystyle operatorname {MSE} (S_{n-1}^{2})={frac {1}{n}}left(mu _{4}-{frac {n-3}{n-1}}sigma ^{4}right)={frac {1}{n}}left(gamma _{2}+{frac {2n}{n-1}}right)sigma ^{4},}$

where $mu _{4}$ is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for $sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

${displaystyle S_{a}^{2}={frac {n-1}{a}}S_{n-1}^{2}={frac {1}{a}}sum _{i=1}^{n}left(X_{i}-{overline {X}},right)^{2}}$

then we calculate:

${displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}$

This is minimized when

$a=frac{(n-1)gamma_2+n^2+n}{n} = n+1+frac{n-1}{n}gamma_2.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean, $overline{X}=frac{1}{n}sum_{i=1}^n(X_i)$	$operatorname{MSE}(overline{X})=operatorname{E}((overline{X}-mu)^2)=left(frac{sigma}{sqrt{n}}right)^2$
${displaystyle theta =sigma ^{2}}$	= the unbiased estimator of the population variance, $S^2_{n-1} = frac{1}{n-1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n-1})=operatorname{E}((S^2_{n-1}-sigma^2)^2)=frac{2}{n - 1}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n} = frac{1}{n}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n})=operatorname{E}((S^2_{n}-sigma^2)^2)=frac{2n - 1}{n^2}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n+1} = frac{1}{n+1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n+1})=operatorname{E}((S^2_{n+1}-sigma^2)^2)=frac{2}{n + 1}sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter theta with perfect accuracy, is ideal (but typically not possible).

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Criticism[edit]

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

From Wikipedia, the free encyclopedia

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

Definition and basic properties[edit]

Predictor[edit]

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

In matrix notation,

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}(e_{i})^{2}={frac {1}{n}}mathbf {e} ^{mathsf {T}}mathbf {e} }$

where $e_{i}$ is ${displaystyle (Y_{i}-{hat {Y_{i}}})}$ and is the column vector.

${displaystyle operatorname {MSE} ={frac {1}{q}}sum _{i=n+1}^{n+q}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter theta is defined as^[1]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}$

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} ({hat {theta }},theta )^{2}.}$

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

$overline{X}=frac{1}{n}sum_{i=1}^n X_i$

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

${displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}$

where $sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

${displaystyle S_{n-1}^{2}={frac {1}{n-1}}sum _{i=1}^{n}left(X_{i}-{overline {X}}right)^{2}={frac {1}{n-1}}left(sum _{i=1}^{n}X_{i}^{2}-n{overline {X}}^{2}right).}$

This is unbiased (its expected value is $sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

${displaystyle operatorname {MSE} (S_{n-1}^{2})={frac {1}{n}}left(mu _{4}-{frac {n-3}{n-1}}sigma ^{4}right)={frac {1}{n}}left(gamma _{2}+{frac {2n}{n-1}}right)sigma ^{4},}$

where $mu _{4}$ is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for $sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

${displaystyle S_{a}^{2}={frac {n-1}{a}}S_{n-1}^{2}={frac {1}{a}}sum _{i=1}^{n}left(X_{i}-{overline {X}},right)^{2}}$

then we calculate:

This is minimized when

$a=frac{(n-1)gamma_2+n^2+n}{n} = n+1+frac{n-1}{n}gamma_2.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean, $overline{X}=frac{1}{n}sum_{i=1}^n(X_i)$	$operatorname{MSE}(overline{X})=operatorname{E}((overline{X}-mu)^2)=left(frac{sigma}{sqrt{n}}right)^2$
${displaystyle theta =sigma ^{2}}$	= the unbiased estimator of the population variance, $S^2_{n-1} = frac{1}{n-1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n-1})=operatorname{E}((S^2_{n-1}-sigma^2)^2)=frac{2}{n - 1}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n} = frac{1}{n}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n})=operatorname{E}((S^2_{n}-sigma^2)^2)=frac{2n - 1}{n^2}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n+1} = frac{1}{n+1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n+1})=operatorname{E}((S^2_{n+1}-sigma^2)^2)=frac{2}{n + 1}sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter theta with perfect accuracy, is ideal (but typically not possible).

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Criticism[edit]

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

Стандартное
отклонение для оценки обозначается S_e
и рассчитывается по формуле
среднеквадратичного отклонения:

Величина стандартного
отклонения характеризует точность
прогноза.

Вариант
5. Возвращаясь к данным нашего примера,
рассчитаем значение S_e:

Предположим,
необходимо оценить значение Y для
конкретного значения независимой
переменной, например, спрогнозировать
объем продаж при затратах на рекламу в
объеме 10 тыс. долл. Обычно при этом также
требуется оценить степень достоверности
результата, одним из показателей которого
является доверительный интервал для
Y.

Граница доверительного
интервала для Y при заданной величине
X рассчитывается следующим образом:

где
Х_p
– выбранное значение независимой
переменной, на основе которого выполняется
прогноз. Обратите внимание: t – это
критическое значение текущего уровня
значимости. Например, для уровня
значимости, равного 0,025 (что соответствует
уровню доверительности двухстороннего
критерия, равному 95%) и числа степеней
свободы, равного 10, критическое значение
t равно 2, 228 (см. Приложение II). Как можно
увидеть, доверительный интервал – это
интервал, ограниченный с двух сторон
граничными значениями предсказания
(зависимой переменной).

Вариант
6. Для нашего примера расходов на рекламу
в размере 10 тыс. долл. интервал предсказания
зависимой переменной (объема продаж) с
уровнем доверительности в 95% находится
в пределах [10,5951; 21,8361]. Его границы
определяются следующим образом (обратите
внимание, что в Варианте 2 Y’=16,2156):

Из приведенного
расчета имеем: для заданных расходов
на рекламу в объеме 10 тыс. долл., объем
продаж изменяется в диапазоне от 10,5951
до 21,8361 тыс. долл. При этом:
10,5951=16,2156-5,6205 и 21,8361=16,2156+5,6205.

3. Стандартное отклонение для коэффициента регрессии Sb и t-статистика

Значения
стандартного отклонения для коэффициентов
регрессии S_b
и значение статистики тесно взаимосвязаны.
S_b
рассчитываются как

Или в сокращенной
форме:

S_b
задает интервал, в который попадают.
Все возможные значения коэффициента
регрессии. t-статистика
(или t-значение)
– мера статистической значимости
влияния независимой переменной Х на
зависимую переменную Y
определяется путем деления оценки
коэффициента b
на его стандартное отклонение S_b.
Полученное значение затем сравнивается
с табличным (см. табл. В Приложении II).

Таким
образом, t-статистика
показывает, насколько велики величина
стандартного отклонения для коэффициента
регрессии (насколько оно больше нуля).
Практика показывает, что любое t-значение,
не принадлежащее интервалу [-2;2], является
приемлемым. Чем выше t-значение,
тем выше достоверность коэффициента
(т.е. точнее прогноз на его основе). Низкое
t-значение
свидетельствует о низкой прогнозирующей
силе коэффициента регрессии.

Вариант
7. S_b
для нашего примера равно:

t-статистика
определяется:

Так
как t=3,94>2,
можно заключить,
что
коэффициент
b
является
статистически
значимым.
Как
отмечалось раньше,
табличное
критическое
значение (уровень отсечения)
для 10 степеней свободы равно
2,228
(см.
табл.
в
Приложении
11).

Обратите
внимание:

—
t-значения
играют большую
роль для коэффициентов
множественной регрессии
(множественная
модель описывается
с помощью
нескольких
коэффициентов
b);

—
R²
характеризует
общее согласие (всего
«леса»
невязок
на
диаграмме
разброса),
в
то время как
t-значение
характеризует
отдельную
независимую переменную
(отдельное
«дерево»
невязок).

В
общем случае
табличное
t-значение
для
заданных
числа
степеней свободы и уровня
значимости используется,
чтобы:

—
установить
диапазон
предсказания:
верхнюю
и нижнюю границы
для прогнозируемого
значения при заданном значении
независимой
переменной;

-установить
доверительные
интервалы
для
коэффициентов
регрессии;

—
определить
уровень
отсечения
для t-теста.

РЕГРЕССИОННЫЙ
АНАЛИЗ С ПРИМЕНЕНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ
MS EXCEL

Электронные
таблицы,
такие
как Excel,
имеют
встроенную
процедуру
регрессионного
анализа,
легкую
в
применении.

Регрессионный
анализ
с помощью
MS Ехсеl
требует
выполнения
следующих
действий:

—
выберите
пункт
меню
«Сервис
— Надстройки»;

—
в
появившемся
окне отметьте
галочкой
надстройку
Analysis
ToolPak
–
VBA нажмите
кнопку
ОК.

Если
в списке Analysis
ToolPak
—
VВА
отсутствует,
выйдите
из MS Ехсеl
и добавьте эту надстройку,
воспользовавшись
программой
установки Мiсrosоft
Office.
Затем
запустите Ехсеl
снова
и повторите
эти действия.
Убедившись,
что
надстройка
Analysis
ToolPak
—
VВА
доступна,
запустите
инструмент
регрессионного
анализа,
выполнив
следующие
действия:

—
выберите
пункт меню «Сервис
—
Анализ»
данных;

—
в появившемся окне выберите
пункт
«Регрессия»
и
нажмите
кнопку
ОК.
На
рисунке 16.3
показано окно ввода данных для
регрессионного
анализа.

Рисунок 16.3 – Окно
ввода данных для регрессионного анализа

Таблица
16.2
показывает
выходной
результат
регрессии,
содержащий
описанные
выше статистические
данные.

Примечание:
для
того чтобы получить
поточечный
график
(ХY график),
используйте
«Мастер
Диаграмм»
MS
Excel.

Получаем:
Y’
= 10,5386
+ 0,563197
Х (d
виде
Y’
=
а
+
bХ)
с R²=0,608373=60,84%.

Все
полученные
данные
ответствуют
данным,
рассчитанным
вручную.

Таблица 16.2 –
Результаты регрессионного анализа

в
электронных таблицах MS
Excel

Вывод итогов
Регрессионная статистика
Множественный R	0,7800
R-квадрат	0,6084
Нормированный R-квадрат	0,5692
Стандартная ошибка	2,3436
Наблюдения	12
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	85,3243	85,3243	15,5345	0,0028
Остаток	10	54,9257	5,4926
Итого	11	140,2500
	Коэффи-циенты	Стандарт-ная ошибка	t-статистика	Р- значение*	Нижние 95%	Верхние 95%
Свободный член	10,5836	2,1796	4,8558	0,0007	5,7272	15,4401
Линейный коэффициент	0,563197	0,1429	3,9414	0,0028	0,2448	0,8816
*Р – значение для переменной X, равное 0,0028 показывает, что истинное значение переменной коэффициента с 0,28%-ной вероятностью равна нулю, что предполагает высокую точность прогнозируемого значения, равного 0б563197.

Таблица
16.3 показывает выходной результат
регрессии, полученный с применением
популярного программного обеспечения
Minitab
для статистического анализа.

Таблица
16.3 – Результаты регрессионного анализа
Minitab

Анализ регрессии Уравнение регрессии: FO=10,6+0,563DLH
Прогнозируемые параметры	Коэффициент	Стандартное отклонение	t-значение	P
Константа	10,584	2,180	4,86	0,000
DLH	0,5632	0,1429	3,94	0,003
s=2,344	R-квадрат=60,8%	R-квадрат (нормированный)=56,9%
Анализ отклонений
Показатель	DF	SS	MS	F	P
Регрессия	1	85,324	85,324	15,53	0,003
Отклонение	10	54,926	5,493
Итого	11	140,250

ВЫВОДЫ

C
помощью регрессионного анализа
устанавливается
зависимость
между
изменениями
независимых
переменных
и
значениями зависимой
переменной.
Регрессионный
анализ
— популярный
метод для прогнозирования
продаж.
В
этой
главе обсуждался
широко
распространенный
способ
оценки значений,
так
называемый
метод
наименьших
квадратов.
Метод
наименьших
квадратов
рассматривался
применительно
к
модели
простой
регрессии
Y
=
а
+ bх.
Обсуждались
различные
статистические
коэффициенты,
характеризующие
добротность
и надежность
уравнения
(согласие
модели)
и помогающие установить
доверительный
интервал.

Показано
применение
электронных
таблиц MS Ехсеl для
проведения
регрессионного
анализа
шаг за шагом.
С
помощью электронных
таблиц
можно не только составить
уравнение
регрессии,
но
и рассчитать статистические
коэффициенты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

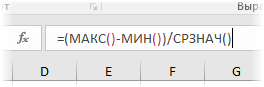
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

Загрузить PDF

Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.

1

Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
2

Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
3

Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
4

Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
5

Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
6

Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.

Реклама

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
  Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
  Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
  Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
  Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.

Советы

Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.

Об этой статье

Эту страницу просматривали 48 054 раза.

Была ли эта статья полезной?

Статистические данные

Слово статистика образовано от латинского status, которое обозначает состояние. От этого корня произошли слова stato (государство), statistica (сумма знаний о государстве). Математическая статистика — наука, которая изучает методы сбора и обработки информации, представленной в численном виде. Эта информация появляется как результат экспериментов. Во многом математическая статистика опирается на теорию вероятностей, которая позволяет оценить точность и надёжность заключений, сделанных на основании изучения ограниченных статистических данных.

Метод не исследует сущность процессов, а формулирует и описывает их количественную сторону. Термином генеральная совокупность обозначается общность всех объектов, относительно которых необходимо сделать выводы при изучении научной проблемы. Выборочная совокупность или выборка — множество объектов, отобранных из генеральной совокупности для исследования. Основные цели математической статистики:

указание способов сбора и систематизации статистических данных;
определение закона распределения случайной величины;
поиск неопределённых параметров;
проверка подлинности выдвинутых гипотез.

Главный метод математической статистики — выборочный метод, состоящий в исследовании представительной выборочной совокупности для получения достоверной характеристики генеральной. Отбор объектов в выборку производится случайно, а исследуемое свойство должно обладать статистической устойчивостью, то есть иметь высокую частоту повторений при многократных испытаниях.

Выборочный метод сокращает время и трудоёмкость исследований, так как изучение всей совокупности оказывается более тяжёлым или невозможным. Математическая статистика выявляет закономерности массовых явлений и предсказывает появление внешних влияний.

Размах вариации

Вариация — это различия значений признака у единиц исследуемой совокупности. Она образуется из-за того, что индивидуальные значения формируются при различных условиях. Выборка должна быть представительной, чтобы по результатам её исследований можно было сделать правильные выводы о характеристиках всей совокупности.

Количественная репрезентативность достигается при использовании достаточного числа наблюдений в выборке, которое может обеспечить получение достоверных результатов. Качественная репрезентативность заключается в одинаковой структуре выборочной и генеральной совокупностей по признакам, имеющим влияние на получение конечного результата. К абсолютным показателям вариации относятся:

размах, R;
среднее линейное отклонение, a;
среднеквадратичное отклонение, σ (сигма);
дисперсия, D.

Размах вариации показывает абсолютную разницу между максимумом и минимумом значений признака:

R = x max — x min, где x — значения признака.

Основным недостатком показателя R можно назвать то обстоятельство, что колебания значений признака могут вызываться случайными причинами и искажать характерный для исследуемой совокупности размах.

Показатели отклонения

Существуют показатели вариации, учитывающие все значения величин, а не только наибольшие или наименьшие. Одним из них можно назвать среднее линейное отклонение — показатель, характеризующий меру разброса значений. Сначала требуется определить точку отсчёта разброса. Как правило, ею становится среднее арифметическое значение, входящее в исследование величин. Потом необходимо измерить, отклонение от среднего для каждого значения. Все отклонения вычисляются по модулю и определяется среднее значение уже среди них. Формула для расчёта отклонения:

a = Σ ⁿ i=1 (x — x̅) / n, где:

a — среднее линейное отклонение;
n — количество значений в исследуемой совокупности;
x — анализируемый показатель;
x̅ — среднее значение показателя.

СКО характеризует разброс значений относительно среднего математического ожидания. Оно измеряется в единицах измерения само́й величины. Существует правило, согласно которому для нормально распределённых данных диапазон разброса 997 значений из 1 тыс. составляет три сигмы от средней арифметической, [x̅ — 3σ; x̅ + 3σ].

Коэффициент вариации

Квадратичное отклонение — это абсолютная оценка меры разброса. Для того чтобы сравнить величину разброса с самими значениями величины, необходимо применить относительный показатель — коэффициент вариации:

V = σ / x̅, где σ — стандартное отклонение из выборки, x̅ — среднее арифметическое.

Коэффициент вариации измеряется в процентах. Показатель полезен для сравнивания однородности разных процессов.

Математическое ожидание — среднее значение случайной величины. Для дискретной выборки оно определяется по формуле:

M (X)= Σ ⁿi=1 xi ⋅ pi, где xi — случайные значения, pi — их вероятность.

Дисперсией называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

D (X) = M (X²) — (M (X))²

Для дискретной случайной величины формула приобретает вид:

D (X) = Σ ⁿi=1 xi² ⋅ pi — M (X)².

Среднеквадратическое отклонение или стандартный разброс — это корень квадратный из дисперсии, формула которого имеет вид:

σ(X) = √ D (X).

Дисперсия и стандартный разброс — взаимозависимые характеристики. Стандартная ошибка среднего — величина, которая характеризует квадратическое отклонение выборочного среднего, рассчитанного по выборке размера из генеральной совокупности. Величина ошибки SDx̅ зависит от дисперсии генеральной совокупности и объёма выборки и рассчитывается по формуле:

SDx̅ = σ / √ n, где σ — величина стандартного разброса генеральной совокупности, а n — объём выборки.

Статистическая закономерность — это количественная форма проявления причинной связи. Она возникает как результат воздействия большого числа причин, действующих либо постоянно, либо только временами. Существует ряд статистических критериев, которые позволяют сравнивать экспериментально полученное распределение с нормальным, полученным в теории. Погрешность измерения — отклонение измеренного значения величины от действительного, являющиеся характеристикой точности измерения. Вместе с полученным результатом должна указываться погрешность измерений.

Пример расчёта

Пример расчёта по формулам для среднеквадратичного отклонения и дисперсии при решении следующей задачи по теории вероятностей: для выполнения ремонтных работ рабочему необходима краска определённого цвета. В городе имеется четыре строительных магазина, в каждом из которых эта краска может находиться в продаже с вероятностью 0,41. Записать закон распределения количества посещаемых магазинов. Рассчитать дисперсию и среднеквадратичное отклонение случайной величины. Обход заканчивается после того, как необходимая краска будет куплена или после посещения всех четырёх магазинов.

x = 1 — краска куплена в первом магазине.

p (1) = 0,41.

x = 2 — краски не нашлось в первом магазине, но она была во втором.

p (2) = (1 — 0,41) · 0,41 = 0,59 · 0,41 = 0,242.

x = 3 — краски не нашлось в двух первых магазинах, но она была в третьем.

p (3) = (1 — 0,41)² · 0,41 = 0,59² · 0,41 = 0,143.

x = 4 — краски не было в первых трёх магазинах, рабочий зашёл в четвёртый магазин, купил краску или просто закончил обход.

p (4) = 0,59³ · 0,41 + 0,59⁴ = 0,205.

Закон распределения:

xi	1	2	3	4
p (X)	0,41	0,242	0,143	0.205

Математическое ожидание: M (X) = 1 · 0,41 + 2 · 0.242 + 3 · 0,143 + 4 · 0,205 = 2,143.

Дисперсия: D (X) = Σ ⁿi=1 xi² ⋅ pi — M (X)² = 1² · 0,41 + 2² · 0,242 + 3² · 0,143 + 4² · 0,205 — 2,143² = 1,353.

Стандартное отклонение: σ(X) = √ D (X) = √1,353 = 1,163.

Ответ: Дисперсия 1,353; квадратическое отклонение 1,163.

Для вычисления среднеквадратичного отклонения в онлайн-калькуляторе достаточно внести в таблицу значения случайной величины xi и их количество.

Среднеквадратичное отклонение применяется для определения погрешности при проведении последовательных измерений. Эта характеристика играет важную роль для сравнения изучаемого процесса с теоретически предсказанным. Если СКО велико, то полученные результаты или метод их получения нужно проверить.

Стандартное отклонение и стандартная ошибка: в чем разница?

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

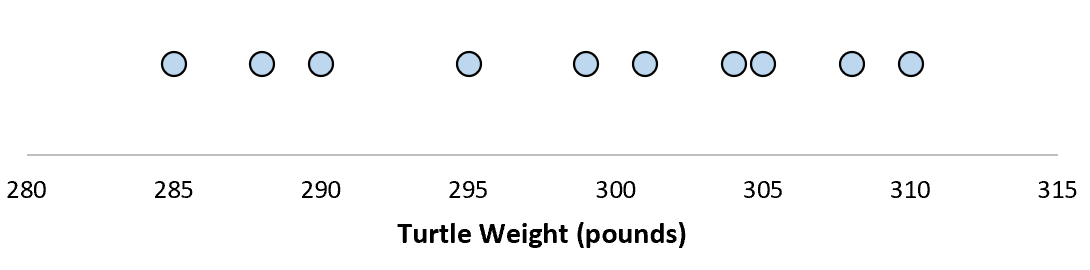
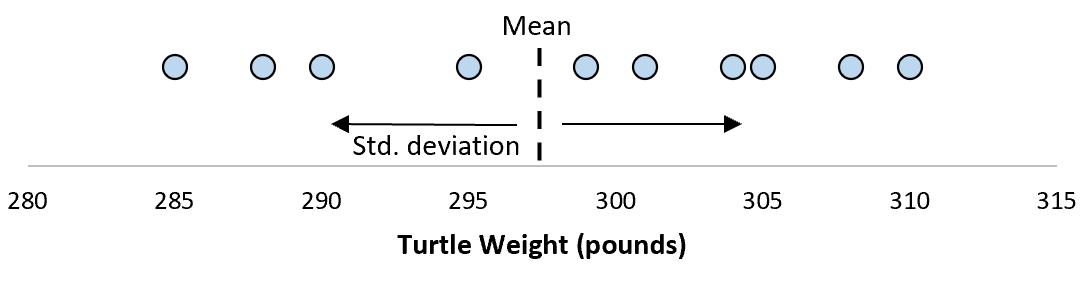
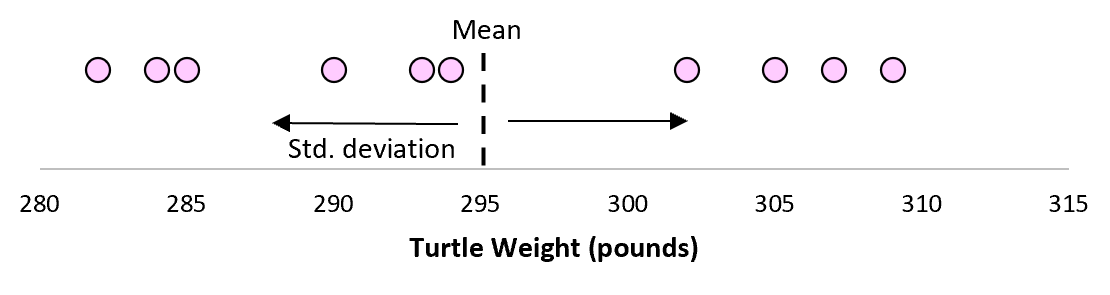
Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

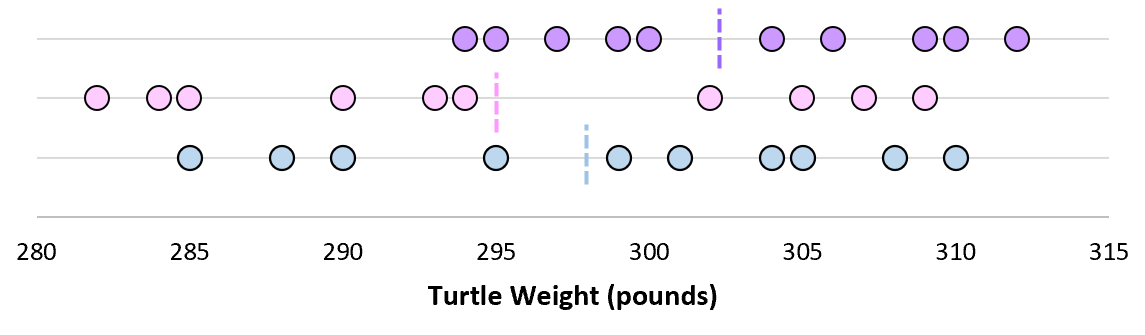
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

s: стандартное отклонение выборки
n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

среднеквадратическое отклонение,
среднее квадратическое отклонение,
среднеквадратичное отклонение,
квадратичное отклонение,
стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

в финансах в качестве меры волатильности,
в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

А -> (19 + 21 + 19+ 21) / 4 = 20
Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

стандартное отклонение компании A = 1,
стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

стандартное отклонение формула, среднее квадратичное отклонение формула, среднеквадратическое отклонение формула, среднее квадратическое отклонение формула

Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с «n–1»),
полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

Вычесть среднее значение из каждого числа
Возвести каждый результат в квадрат (так получатся квадраты разностей)
Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Где:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Правило трёх сигм

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

Формулы вычисления стандартного отклонения sigma сигма стандартное отклонение в эксель excel

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Формулы вычисления стандартного отклонения sigma сигма стандартное отклонение в эксель excel

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

при <10% выборка слабо вариабельна,
при 10% – 20 % — средне вариабельна,
при >20 % — выборка сильно вариабельна.

Узнайте также про:

Корреляции,
Метод Крамера,
Метод наименьших квадратов,
Теорию вероятностей
Интегралы.

Источник

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

Коэффициент вариации

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

при <10% выборка слабо вариабельна,
при 10% – 20 % — средне вариабельна,
при >20 % — выборка сильно вариабельна.

Узнайте также про:

Корреляции,
Метод Крамера,
Метод наименьших квадратов,
Теорию вероятностей
Интегралы.

Источник

MSE как среднее дистанций между предсказаниями и реальными наблюдениями

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = frac{1}{9} × 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

import sklearn
from sklearn.metrics import mean_squared_error

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]

Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:

mean_squared_error(y_true, y_pred)

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

496.0

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Автор оригинальной статьи: @mmoshikoo

Фото: @tobyelliott

Источник

Статистика

Контур Статистиков Глоссарий Обозначение Журналы Списки тем Статьи Категория Математический портал

В среднеквадратичное отклонение (RMSD) или же Средняя квадратическая ошибка (RMSE) является часто используемой мерой различий между значениями (значениями выборки или генеральной совокупности), прогнозируемыми моделью или оценщик и наблюдаемые значения. RMSD представляет собой квадратный корень из второго образец момент различий между прогнозируемыми значениями и наблюдаемыми значениями или среднее квадратичное этих различий. Эти отклонения называются остатки когда вычисления выполняются над выборкой данных, которая использовалась для оценки и называется ошибки (или ошибки предсказания) при вычислении вне выборки. RMSD служит для агрегирования величин ошибок в прогнозах за разное время в единую меру предсказательной силы. RMSD — это мера точность, чтобы сравнивать ошибки прогнозирования разных моделей для определенного набора данных, а не между наборами данных, так как это зависит от масштаба.^[1]

Среднеквадратичное отклонение всегда неотрицательно, и значение 0 (почти никогда не достигается на практике) указывает на точное соответствие данным. В общем, более низкое RMSD лучше, чем более высокое. Однако сравнения между разными типами данных будут недопустимыми, поскольку мера зависит от масштаба используемых чисел.

RMSD — это квадратный корень из среднего квадрата ошибок. Влияние каждой ошибки на RMSD пропорционально величине квадратичной ошибки; таким образом, большие ошибки имеют непропорционально большое влияние на RMSD. Следовательно, RMSD чувствителен к выбросам.^[2]^[3]

Формула

RMSD оценщик относительно оцениваемого параметра theta определяется как квадратный корень из среднеквадратичная ошибка:

$operatorname {RMSD} ( hat { theta}) = sqrt { operatorname {MSE} ( hat { theta})} = sqrt { operatorname {E} (( hat { theta} - тета) ^ 2)}.$

Для объективный оценщик, RMSD — это квадратный корень из дисперсии, известный как стандартное отклонение.

RMSD прогнозируемых значений на время т из регресс зависимая переменная ${ displaystyle y_ {t},}$ с переменными, наблюдаемыми за Т раз, вычисляется для Т различные прогнозы как квадратный корень из среднего квадратов отклонений:

${ displaystyle operatorname {RMSD} = { sqrt { frac { sum _ {t = 1} ^ {T} ({ hat {y}} _ {t} -y_ {t}) ^ {2} } {T}}}.}$

(Для регрессий на данные поперечного сечения, нижний индекс т заменяется на я и Т заменяется на п.)

В некоторых дисциплинах RMSD используется для сравнения различий между двумя вещами, которые могут различаться, ни одна из которых не принимается в качестве «стандарта». Например, при измерении средней разницы между двумя временными рядами $x_ {1, t}$ и $x_ {2, t}$ , формула принимает вид

${ displaystyle operatorname {RMSD} = { sqrt { frac { sum _ {t = 1} ^ {T} (x_ {1, t} -x_ {2, t}) ^ {2}} {T }}}.}$

Нормализация

Нормализация RMSD облегчает сравнение наборов данных или моделей с разными масштабами. Хотя в литературе нет согласованных средств нормализации, обычно выбирают среднее значение или диапазон (определяемый как максимальное значение минус минимальное значение) измеренных данных:^[4]

$mathrm {NRMSD} = frac { mathrm {RMSD}} {y_ max -y_ min}$ или же ${ displaystyle mathrm {NRMSD} = { frac { mathrm {RMSD}} { bar {y}}}}$

Это значение обычно называют нормированное среднеквадратичное отклонение или же ошибка (NRMSD или NRMSE) и часто выражается в процентах, где более низкие значения указывают на меньшую остаточную дисперсию. Во многих случаях, особенно для небольших выборок, на диапазон выборки, вероятно, влияет размер выборки, что затрудняет сравнения.

Другой возможный способ сделать RMSD более полезным средством сравнения — разделить RMSD на межквартильный размах. При делении RMSD на IQR нормализованное значение становится менее чувствительным к экстремальным значениям целевой переменной.

${ displaystyle mathrm {RMSDIQR} = { frac { mathrm {RMSD}} {IQR}}}$ куда ${ displaystyle IQR = Q_ {3} -Q_ {1}}$

с ${ displaystyle Q_ {1} = { text {CDF}} ^ {- 1} (0,25)}$ и $Q_3 = text {CDF} ^ {- 1} (0,75),$ где CDF⁻¹ это квантильная функция.

При нормировании на среднее значение измерений член коэффициент вариации RMSD, CV (RMSD) может использоваться, чтобы избежать двусмысленности.^[5] Это аналогично коэффициент вариации с RMSD вместо стандартное отклонение.

${ displaystyle mathrm {CV (RMSD)} = { frac { mathrm {RMSD}} { bar {y}}}.}$

Некоторые исследователи рекомендовали использовать Средняя абсолютная ошибка (MAE) вместо среднеквадратичного отклонения. MAE обладает преимуществами в интерпретируемости перед RMSD. MAE — это среднее абсолютных значений ошибок. MAE принципиально легче понять, чем квадратный корень из среднего квадрата ошибок. Более того, каждая ошибка влияет на MAE прямо пропорционально абсолютному значению ошибки, что не относится к RMSD.^[2]

Приложения

В метеорология, чтобы увидеть, насколько эффективно математический модель предсказывает поведение атмосфера.
В биоинформатика, то среднеквадратичное отклонение позиций атомов — мера среднего расстояния между атомами наложенный белки.
В дизайн лекарств на основе структуры, RMSD является мерой разницы между кристаллической конформацией лиганда конформация и стыковка прогноз.
В экономика, RMSD используется, чтобы определить, подходит ли экономическая модель экономические показатели. Некоторые эксперты утверждают, что RMSD менее надежен, чем относительная абсолютная ошибка.^[6]
В экспериментальная психология, RMSD используется для оценки того, насколько хорошо математические или вычислительные модели поведения объясняют эмпирически наблюдаемое поведение.
В ГИС, RMSD является одним из показателей, используемых для оценки точности пространственного анализа и дистанционного зондирования.
В гидрогеология, RMSD и NRMSD используются для оценки калибровки модели подземных вод.^[7]
В визуализация науки, RMSD является частью пиковое отношение сигнал / шум, показатель, используемый для оценки того, насколько хорошо метод восстановления изображения работает по сравнению с исходным изображением.
В вычислительная нейробиология, RMSD используется для оценки того, насколько хорошо система изучает данную модель.^[8]
В спектроскопия ядерного магнитного резонанса белков, RMSD используется как мера для оценки качества полученного пучка конструкций.
Материалы для Приз Netflix были оценены с использованием RMSD на основе нераскрытых «истинных» значений тестового набора данных.
При моделировании энергопотребления зданий RMSE и CV (RMSE) используются для калибровки моделей по измеренным характеристикам здания.^[9]
В Рентгеновская кристаллография, RMSD (и RMSZ) используется для измерения отклонения внутренних координат молекулы от значений библиотеки ограничений.

Смотрите также

Среднеквадратичное значение
Средняя абсолютная ошибка
Среднее абсолютное отклонение
Среднее знаковое отклонение
Среднеквадратичное отклонение
Квадратные отклонения
Ошибки и неточности в статистике

Definition and basic properties[edit]

Predictor[edit]

Estimator[edit]

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

Variance[edit]

Gaussian distribution[edit]

Interpretation[edit]

Applications[edit]

Loss function[edit]

Criticism[edit]

See also[edit]

Notes[edit]

References[edit]

Definition and basic properties[edit]

Predictor[edit]

Estimator[edit]

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

Variance[edit]

Gaussian distribution[edit]

Interpretation[edit]

Applications[edit]

Loss function[edit]

Criticism[edit]

See also[edit]

Notes[edit]

References[edit]

Definition and basic properties[edit]

Predictor[edit]

Estimator[edit]

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

Variance[edit]

Gaussian distribution[edit]

Interpretation[edit]

Applications[edit]

Loss function[edit]

Criticism[edit]

See also[edit]

Notes[edit]

References[edit]

3. Стандартное отклонение для коэффициента регрессии Sb и t-статистика

Дисперсия

Свойства дисперсии

Среднеквадратичное (стандартное) отклонение

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Коэффициент вариации

Расчет коэффициента вариации в Excel

Коэффициент осцилляции

Советы

Об этой статье

Была ли эта статья полезной?

Статистические данные

Размах вариации

Показатели отклонения

Коэффициент вариации

Пример расчёта

Стандартное отклонение и стандартная ошибка: в чем разница?

Пример: стандартное отклонение против стандартной ошибки

Какой смысл использовать стандартную ошибку?

Когда использовать стандартное отклонение против стандартной ошибки

Использование и интерпретация величины среднеквадратического отклонения

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Пример 2 (с S)

Пример 2 (с S)

Дисперсия и стандартное отклонение

Правило трёх сигм

Правило трёх сигм

Стандартное отклонение в excel