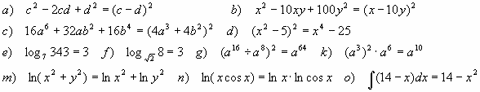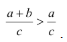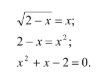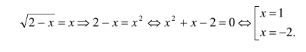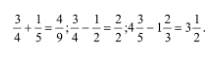Ошибка при решении элементарной задачи - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

В связи с техническими работами в центре обработки данных, часть прикреплённых файлов в настоящее время недоступна.

Ошибка при решении элементарной задачистатья

Статья опубликована в журнале из списка RSCI Web of Science

Информация о цитировании статьи получена из

Scopus

Статья опубликована в журнале из перечня ВАК

Статья опубликована в журнале из списка Web of Science и/или Scopus

Дата последнего поиска статьи во внешних источниках: 6 апреля 2016 г.

Автор:

Сурдин В.Г.
Журнал:
Вестник Российской академии наук (ранее: Вестник Академии наук СССР)
Том:
72
Номер:
6
Год издания:
2002
Издательство:
Наука: МАИК «Наука/Интерпериодика»
Местоположение издательства:
М.
Первая страница:
543
Последняя страница:
544
Добавил в систему:
Сурдин Владимир Георгиевич

Источник

Решение — элементарная задача

Cтраница 2

Сначала для решения элементарных задач каждого блока получают исходную информацию определенной структуры, характерную только для данного блока. Далее определяются элементарные задачи, для решения которых используется указанная информация или полученные на ее основании промежуточные данные вплоть до формирования бухгалтерских записей.
[16]

Задачу поиска неисправностей разбивают на ряд подзадач, которые, в свою очередь, сводятся к некоторым элементарным задачам. Эвристическая программа решения элементарных задач строится путем анализа очевидных свойств причинно-следственных связей: циклограммы работы оборудования, взаимосвязи между отдельными единицами отказов и признаков их возникновения. Эвристическую программу установления места ( причины) отказа составляют на основе процедур анализа граф-дерева логических суждений.
[18]

Каждому допустимому значению k соответствуют два электронных состояния с антипараллельными спинами. Этот результат аналогичен решению элементарной задачи квантовой механики о частице в потенциальном ящике.
[19]

Как бы ни был сложен процесс, подлежащий расчету, он всегда может быть разбит на элементарные процессы, и полное решение всегда будет результатом решений целого ряда элементарных задач. Поэтому ошибки, допускаемые при решении элементарных задач, определяют точность расчета в целом. Эти ошибки слагаются из ошибок, которые допущены при получении экспериментальных данных, положенных в основу построения диаграммы, и ошибок, допущенных при построении и отсчетах на диаграмме.
[20]

Пусть теперь искомые функции заданы на пересекающихся в точке О отрезках ОА и 0В акустических характеристик разных семейств ( рис. 3.8.2), причем значения этих функций при подходе к точке О вдоль разных характеристик совпадают. Для получения сетки характеристик и значений искомых функций в ее узловых точках процедура решения элементарной задачи метода характеристик используется совершенно аналогично тому, как это было сделано в гл.
[21]

По этой методике вся оценирае-мая работа делится на относительно небольшие самостоятельные части или единицы работ. Разбиение продолжается до тех пор, пока не будет ясно, какие шаги и способности потребуются для решения элементарной задачи. Далее каждая элементарная составляющая оценивается с учетом стоимости с получением итога стоимости по всему ПО.
[22]

При подготовке 3-го издания учебник был подвергнут детальной переработке. Объем его сокращен по сравнению с предыдущими изданиями за счет исключения вспомогательного материала описательного характера, примеров решения элементарных задач, некоторых справочных данных.
[23]

Блок 01 концентрирует все бухгалтерские записи за отчетный месяц на уровне синтетических счетов и объектов аналитического учета. Они поступают в блок из следующих источников: первичных документов, в которых хозяйственные операции описаны в денежном выражении и закодированы в соответствии с номенклатурой кодов синтетических счетов и объектов аналитического учета; других блоков, в которых бухгалтерские записи сформированы автоматически по итогам произведенных группировок и расчетов при решении соответствующих элементарных задач; бухгалтерские записи формируются автоматически в самом блоке 01 при решении элементарных задач.
[24]

Обратным методом называют процедуру, состоящую в том, что частное решение считается известным заранее ( или угадано) и затем выясняется, какая именно задача при этом может быть решена. Это означает, что исходя из решения проверяют, какие могут быть удовлетворены граничные условия, и в результате получают возможные виды нагрузок. Такой способ, который предполагает наличие известной интуиции, привел к решению многочисленных элементарных задач.
[26]

С моделированием и имитацией посредством вычислительных машин непосредственно связываются такие задачи обработки информации, как ее сбор и накопление, получение информации, ее обработка и анализ. Это обусловливается тем, что моделирование с помощью вычислительной машины, хотя и может иметь некоторые черты качественного анализа, представляет собой вычислительную задачу. В зависимости от вида решаемой задачи обработка информации может иметь различный характер, начиная от решения элементарных задач вплоть до таких, в которых получение результата требует выполнения большого числа операций с громадным массивом чисел.
[27]

Таким образом, понятие обобщенной функции позволяет приписать некоторый вполне определенный смысл сумме ряда, который в обычном смысле расходится. То же самое относится и ко многим расходящимся интегралам. С этим обстоятельством приходится часто встречаться в квантовой теории поля и ряде других областей теоретической физики. Впрочем, такая ситуация возникает уже при решении элементарных задач математической физики с помощью метода Фурье.
[28]

Страницы:

Источник

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.

«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.

Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:

ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;
ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

ошибки, связанные с непониманием структуры теоремы;
ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;
ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.
Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.
Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.
Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА

Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.
При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)

Типичные ошибки:

20: (х+3)-20:х=20

При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.

Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.

Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.

Ошибка 2. Пропуск этапа поиска решения.

Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.

Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)

Ошибка 3. Пропуск этапа исследования решения.

Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.

Ошибка 4. Смешение этапов анализа и поиска решения.

Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.

Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.

На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»

И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.

Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.

2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.

Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.

Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.

Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

Информация о цитировании статьи получена из

Scopus

Статья опубликована в журнале из перечня ВАК

Статья опубликована в журнале из списка Web of Science и/или Scopus

Дата последнего поиска статьи во внешних источниках: 6 апреля 2016 г.

Автор:

Сурдин В.Г.
Журнал:
Вестник Российской академии наук (ранее: Вестник Академии наук СССР)
Том:
72
Номер:
6
Год издания:
2002
Издательство:
Наука: МАИК «Наука/Интерпериодика»
Местоположение издательства:
М.
Первая страница:
543
Последняя страница:
544
Добавил в систему:
Сурдин Владимир Георгиевич

Источник

Решение — элементарная задача

Cтраница 2

Страницы:

Источник

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;
ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

ошибки, связанные с непониманием структуры теоремы;
ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;
ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.
Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.
Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.
Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.
При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

Типичные ошибки:

20: (х+3)-20:х=20

При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

Ошибка 2. Пропуск этапа поиска решения.

Ошибка 3. Пропуск этапа исследования решения.

Ошибка 4. Смешение этапов анализа и поиска решения.

Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Например: Найти ошибки:

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
проверка правильности решения задач путём составления и решения задач, обратных к данной;
оценка результата решения задачи с точки зрения здравого смысла;
проверка аналитического решения графическим .

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Пусть решение ученика выглядит так: . Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:

“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.

Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.

Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.

Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.

Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.

Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.

Это можно сделать на следующем содержании материала:

Правоцирующие задачи.

Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.

Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.

Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.

Я использую такие разновидности провоцирующих задач:

условия, в которых навязывают неверный ответ;
условия, которые подсказывают неверный путь решения;
условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.

В качестве примера приведу задачи, побуждающие выбор неверного способа решения.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»

2.Задачи стандартные с нестандартным решением.

Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.

Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.

Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.

3. Проблемные задачи.

Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.

Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.

При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.

Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.

Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).

Найти два смежных угла, один из которых больше другого на прямой угол.

Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.

Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 316, значит, 0,310,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.

Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)

Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.

Основные методы решения логических задач:

метод рассуждения;
метод таблицы;
метод граф;
метод кругов Эйлера;
комбинированный метод.

Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.

Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x², x³, x⁴, x⁵, x⁶, x⁷, x⁸, x⁹ в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.


	X⁵

Таблицы хорошо применять тогда, когда устанавливается соответствие между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Перед составлением таблиц отрабатываю правила их заполнения.

Например, в 5 классе знакомлю детей с задачей Пуассона (на переливание). Некто имеет 12 пинт сока (пинта- 0,57л) и желает подарить половину своему другу, но у него нет сосуда в 6 пинт, а есть два сосуда в 8 и 5 пинт. Каким образом можно налить 6 пинт сока в сосуд емкостью 8 пинт?

Решение.

Ходы	0	1	2	3	4	5	6	7
12 пинт	12	4	4	9	9	1	1	6
8 пинт	—	8	3	3	—	8	6	6
5 пинт	—	—	5	—	3	3	5	—

Логические связи, при помощи которых была выстроена общая схема решения задачи, помогут учащимся без труда решить подобного рода задачу.

Введение серии таких задач в содержание урока считаю необходимым. Это позволит стереть явную границу между занимательным и учебным материалом. Особенно целесообразно использовать задачи тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.

Для каждой задачи, которую предполагаю использовать на уроке, прежде выясняю: будет ли она интересна классу, органично ли войдет в структуру урока, будет ли ее использование эффективным. Практика показала: учебный навык, на формирование которого направлена та или иная задача, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.

При работе над провоцирующими, проблемными, логическими и стандартными с нестандартным решением задачами наиболее эффективной считаю групповую, парную, индивидуальную, фронтальную работу.

Приведу пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 часов. Однако после 2 часов пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?

Работа над задачей предполагает следующие действия учителя:

Предъявление задачи (читает учитель).
Определение вида задачи (творческая группа).
Выделение гипотез (индивидуальная самостоятельная работа).
Обмен мнениями (в творческой группе).
Формулировка предположительного ответа (в паре).
Проверка ответа на достоверность (фронтальная работа).

Или, задача. Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.

Предъявление задачи (творческие группы составляют задачи по готовому чертежу).
Выделение гипотез (работа в парах).
Обмен мнениями (фронтальная работа).
Формулировка предположительного ответа (индивидуальная работа).
Проверка ответа на достоверность (индивидуальная работа).

Обязательным этапом на уроке является устный и письменный счет. Целями устного счета являются, во-первых, совершенствование в вычислительных навыков, во-вторых, развитие творческого мышления учащихся.

На своих уроках я стараюсь разнообразить формы и методы устной работы:

— устный счет в начале, в середине, в конце урока;

устная форма проверки домашнего задания;
устная форма творческой работы;
устные самостоятельная и контрольная работы;
уроки устной работы.

Работая устно, воспитываю у учащихся навыки сознательного усвоения изучаемого материала, приучаю ценить и экономить время, развиваю желание поиска рациональных путей решения задачи. В этих целях использую такие приемы, развивающие творческие способности, как «Зашифрованные задания», «Найди ошибку», «Восстановление»,

«Выбор», «Задачи- сказки», детские презентации на устный счёт, математические листы с задачами, изготовленные самими учащимися, ребусы, кроссворды, которые учащиеся составляют самостоятельно.

Обязательно провожу подробный анализ результатов работы и коррекцию знаний. Объявляя количество набранных баллов, полученных за олимпиадное задание, называю ребят, которые представили самые «красивые» решения. При этом опираюсь на формулу «красивой» задачи по В.Г. Болтянскому: красивая задача = непредсказуемость + непредполагаемость +неожиданность + удивительная простота + простота + фантазия + революционный шаг + удивление + оптимизм + труд + …

Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.

Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека — способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи.

Поэтому решение текстовых задач — это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки».

Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.

Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.

Источник

ЛИТЕРАТУРА

Арифметика

1. Андронов И. К- и Брадис В. М. Арифметика. Книга представляет собою обстоятельное изложение курса элементарной арифметики; предназначена как пособие для учителей. Книга может быть прочитана с пользой учащимися старших классов средней школы, готовящимся к экзаменам в высшие учебные заведения.

2. Брадис В. М. — Теоретическая арифметика. Книга предназначена как пособие для пединститутов.

3. Филичев С. В. и Чекмарев Я- Ф. — Сборник задач по арифметике. Пособие для педагогических училищ.

Алгебра

1. Новоселов С. И. — Специальный курс элементарной ал-

гебры, «Советская наука», 1958. Книга представляет собою подробный курс элементарной алгебры, предназначенный для студентов университетов и педагогических институтов. Изложение дано на высоком научном уровне. Книгу можно рекомендовать, в первую очередь, для поступающих на механико математический, физические и физико-математические факультеты университетов и педагогических институтов.

2. Новоселов С. И. — Алгебра и элементарные функции.

Учпедгиз, 1954. В книге изложены почти все принципиальные вопросы школьного курса алгебры и тригонометрии. Книга написана на высоком научном уровне и хотя предназначена как пособие для учителей, но может быть использована учащимися старших классов средней школы.

3. Моденов П. С. Сборник задач по специальному курсу элементарной математики, «Советская наука», 1957. В книге дано большое число задач и вопросов (примерно 10000) по всем разделам элементарной математики; даны многочисленные образцы методов решения.

4. Пржевальский Е. — Сборник алгебраических задач. Учпедгиз, 1941. Книга несколько устарела, однако в ней содержится большой набор задач на тождественные преобразования, на решение уравнений и неравенств.

5. Барыбин К. С. и Исаков А. К — Сборник задач по элементарной математике. Пособие для учителей восьмых классов. В сборнике дан хороший заданный материал» расположенный в последовательности, предусмотренной школьно. программой.

6. Баранова И. В. и Ляпин С. Е.— Задачи на доказательство по алгебре. Пособие для учителей. Учпедгиз, 1954. Книга может оказать существенную помощь при изучении темы «Неравенства».

7. Давыдов А. К- Сборник задач по алгебре и элементарным функциям. Пособие для учительских и педагогических институтов. Книга приспособлена к теоретическому курсу С. И. Новоселова. Алгебра и элементарные функции.

8. Моденов П. С. — Сборник задач по математике (с анализом ошибок, допущенных поступавшими в высшие учебные, заведения). «Советская наука», 1954. Книга содержит боль шой набор примеров и задач по всем разделам элементарной алгебры. Автор дает указания по ряду принципиально важных вопросов, связанных с решением и исследованием примеров и задач. Этот материал окажет существенную помощь при самостоятельном изучении предмета.

9. Обер П. и Папелье Г. — Упражнения по элементарной

алгебре (перевод с французского). Учпедгиз, 1940. Книга содержит богатый заданный материал по следующим разделам тождественные преобразования рациональных и иррациональных выражений, решение и исследование уравнений. В сборнике содержится много текстовых задач. Упражнения и за дачи снабжены подробными решениями. Весьма тщательно выполнены исследования решений примеров и задач с параметрическими данными. Книга окажет большую помощь пр самостоятельном изучении элементарной алгебры.

Геометрия

1. Перепелкин Д. И. —Курс элементарной геометрии, т. I

Геометрия на плоскости. Гостехиздат, 1948; т. II— Геометрия в пространстве. Гостехиздат. 1949. В книге дано подробное и высоконаучное изложение элементарной геометрии. Книга предназначена для студентов педагогических инст; тутов, но может быть рекомендована также готовящимся экзаменам в высшие учебные заведения, в первую очередь поступающим на механико-математические, физические и физико-математические факультеты университетов и пединститутов.

2. Адамар Ж — Элементарная геометрия, т. Г — Планиметрия. Учпедгиз, 1952; т. II — Стереометрия. Учпедгиз, 1952. Книга является наиболее полным курсом элементарной геометрии. Может служить для справок. Готовиться по ней к экзаменам в высшие учебные заведения трудно, ввиду очень большого объема. Книга содержит, помимо очень большого фактического материала по геометрии, богатый набор интересных задач.

3. Делонэ Б. Н. и Житомирский О. К.—Задачник по

геометрии. Гостехиздат, 1949. Очень интересная книга, содержащая помимо большого числа удачно подобранных задач! и решения к ним. Очень хорошо представлены задачи по стереометрии.

Александров И. И. — Геометрические задачи на построение и методы их решения. Учпедгиз, 1954. В этой книге читатель найдет много трудных и интересных задач на построение (на плоскости); в книге изложены и методы решения. Книга очень полезна для развития навыков геометрии, однако в ней много трудных задач, решение которых потребует большого напряжения.

Д з ы к П. Г. — Сборник геометрических задач по комбинации геометрических тел. Учпедгиз, 1936. В книге предложены задачи по стереометрии, в основном на вычисление. Решение почти всех задач требует хорошего пространственного представления, так как комбинации геометрических тел, рассматриваемых автором, почти всегда сложны. Для решения многих задач нужно предварительно производить (во многих случаях) достаточно сложные построения в пространстве.

Адлер А. — Теория геометрических построений. Учпедгиз, 1940. Классическое руководство по теории геометрических построений.

Тригонометрия

Новоселов С. И. — Специальный курс тригонометрии, «Советская наука», 1957. В книге дано подробное и весьма полное изложение вопросов тригонометрии. Книга написана на высоком научном уровне и может быть, в первую очередь, рекомендована, поступающим на механико-математические, физические и физико-математические факультеты университетов и пединститутов.

Новоселов С. И. — Обратные тригонометрические функции. Учпедгиз, 1947. Книга содержит подробное изложение теории обратных тригонометрических функций, а также содержит много задач по этому вопросу. Ко многим задачам даны подробные решения.

Источник

Для того чтобы систематизировать и квалифицировать ошибки, которые совершают обучающиеся в контрольных, самостоятельных и домашних работах, выделено 12 основных видов ошибок, благодаря которым можно понять основные причины появления затруднений.

Виды ошибок:

Решение даже не начато
Вычислительная ошибка в элементарном действии
Вычислительная ошибка в многошаговом действии
Установление неправильных связей между данными задачами
Неправильное понимание условий задачи
Ошибки при переписывании
Незнание алгоритмов математических действий
Неэквивалентные преобразования
Ошибки геометрических измерений
Незнание математических формул
Незнание законов арифметики
Логические ошибки

Все без исключения школьники совершают вычислительные ошибки. Для того чтобы снизить их количество в многошаговых арифметических действиях, необходимо обучать детей алгоритмам, которые позволяют разбивать сложные действия на более простые.

Однако для выделения элементарных действий предварительно следует установить уровень заданий, который будет доступен каждому обучающемуся. К такому уровню могут быть отнесены:

вычитание/сложение однозначных или двузначных чисел без перехода единиц в старший разряд;
вычитание однозначных или двузначных чисел при условии, что число единиц в соответствующем разряде уменьшаемого больше числа единиц в разряде вычитаемого;
умножение однозначных чисел между собой и умножение на двузначные числа при условии, что последние остаются двузначными;
деление однозначных чисел, а также деление двузначных чисел на однозначные, но при этом делитель является делителем числа единиц в каждом разряде.

Другие арифметические действия целесообразно разбивать на элементарные.

Достаточно сложными для детей являются текстовые задачи, так как они предполагают применение не только знаний, которые были получены на уроках, но и своего жизненного опыта. Наиболее распространенная ошибка – неиспользование части условия текстового задания. В целях исключения таких ошибок необходимо, чтобы дети обладали устойчивыми навыками по решению элементарных текстовых задач. При этом уровень сложности задачи не должен ставить обучающегося в безвыходное положение.

Что касается ошибок переписывания, то они в основном возникают в случаях, когда задания неинтересны обучающемуся. Как только они становятся значимыми для него, то количество ошибок при переписывании резко уменьшается.

Для того чтобы снизить количество ошибок, связанных со сложением и вычитанием обыкновенных дробей, необходимо более детальное изучение типовых примеров решения данного вида задач.

В ходе решений простейших уравнений обучающиеся часто сталкиваются с проблемой приведения эквивалентных преобразований. Самые распространенные ошибки – определение знака одночлена, когда он переносится в другую часть уравнения, а также непонимание сущности числового коэффициента переменной.

Ошибки, которые связаны с геометрическими измерениями, в большинстве случаев объясняются элементарным отсутствием навыков работы с линейкой и транспортиром. Проблема устраняется за счет постоянного применения на уроках этих инструментов. В целях профилактики необходимо, чтобы обучающиеся точно понимали, что такое точка отсчета и единица измерения. Кроме того, до начала практических измерений следует закрепить соотношения используемых единиц одной физической величины.

В 5 классе одним из самых трудных разделов является тема, посвященная прямоугольным параллелепипедам. И если обучающийся не знает формул объема, то он просто не сможет решить ни одной задачи. Однако и в самих заданиях этой темы можно выделить объективные трудности, ведь от обучающегося требуется, чтобы он усвоил единицы объема и взаимоотношения между ними. Очень часто более слабые обучающиеся просто не понимают, как между собой соотносятся кубические метры и сантиметры, а также кубические километры и кубические метры. Кроме того, для решения многих задач требуется наличие пространственного воображения, поэтому некоторые обучающиеся испытывают затруднения при решении задач, где требуется определить объем тел, изображенных на чертежах и рисунках. В целях профилактики таких ошибок рекомендуется больше уделять времени изучению моделей, которые должны быть доступны каждому обучающемуся. Особенно высоких результатов можно добиться, если применять разборные модели параллелепипедов.

В процессе изучения арифметики значительное количество ошибок связано с применением распределительного закона умножения. Обучающиеся, которые не усвоили этот закон, при умножении одночлена на многочлен делают только одно действие умножения, а остальную часть многочлена записывают без каких-либо необходимых изменений. Профилактика ошибки заключается в использовании схемы умножения, в которой стрелками соединяются все сомножители.

Реже всего встречаются логические ошибки, однако это, прежде всего, связано с тем, что обучающиеся пятых классов крайне мало решают таких задач. Поэтому профилактика таких задач предполагает, в первую очередь, увеличение количества таких задач в учебных пособиях для 5 класса.

Методы, направленные на предупреждение ошибок

Задачи-ловушки

Провоцирующие задачи, то есть задачи, которые подталкивают обучающегося к неправильному выбору, обладают крайне высоким развивающим потенциалом. При попадании в подготовленную «ловушку» обучающийся начинает испытывать досаду и смущение от того, что он не придал значения каким-либо нюансам и условиям задачи. В результате обучающийся испытывает сильное впечатление и надолго запоминает свои ошибочные действия, а в дальнейшем уже на подсознательном уровне старается не попадаться в аналогичные ситуации.

Кроме того, задачи-ловушки способствуют развитию критичности, учат детей внимательно анализировать информацию, проводить ее разностороннюю оценку. Одновременно и повышается и интерес к изучению математики.

Выделяют несколько основных видов провоцирующих задач:

задачи, в которых условия навязывают получение неправильного ответа;
задачи, где условия делают подсказку на неправильный алгоритм решения;
задачи, в которых неоднозначность трактовки терминов, используемых оборотов, числовых и буквенных выражений выводят на неправильный путь решения;
задачи, где обучающемуся необходимо что-то придумывать, строить, составлять и т.д. В итоге у обучающегося должны получиться такие математические объекты, которые не могут иметь места при заданных условиях;
задачи, в которых условия допускают возможность «опровержения» семантически верного решения каким-либо нематематическим способом.

Задачи, условия которых навязывают неверный ответ

А. Задачи, навязывающие в явной форме один вполне определенный ответ.

Пример.

Сколько цифр потребуется, чтобы записать одинадцатизначное число?

На первый взгляд кажется, что ответ очевиден – «11 цифр». Однако по причине того, что десятичная система счисления использует только 10 цифр, то правильным ответом будет: «Одинадцатизначное число можно записать с помощью 0,1,2,3,4,5,6,7,8,9 или 10 цифр».

Б. Задачи, стимулирующие сделать выбор ответа из предложенной совокупности изначально неверных ответов.

Пример.

Какое из чисел 205, 206, 207, 208, 209, 210 является простым?

В большинстве случаев ученики называют 209 или 207, но это неверно, так как все числа являются составными. Правильный ответ: «Никакое».

В. Задачи, где предлагается сделать неправильный выбор из совокупности верных и неверных ответов.

В каком из вариантов пример решен неверно?

Г. Задачи, где условия не содержат неверных ответов в явном виде, но при этом каким-то образом указывают на него.

Пример.

Какое простое число следует за числом 200?

Напрашивается ответ: 201, ведь это число следующее – за числом 200. Однако ответ неправильный, ведь число 201 является составным. Правильный ответ – 211.

Задачи, побуждающие к выбору неверного способа решения

А. Задачи, в которых условия подталкивают обучающегося выполнить определенные действия с предложенными числами, однако на самом деле этого не требуется делать.

Пример.

Тройка лошадей проскакала 12 км. Сколько километров проскакала каждая лошадь?

Многие ученики делят 12 на 3 и получают ответ 4 км. Однако все лошади проскакали по 12 километров.

Б. Задачи, где условия подталкивают выполнить определенное действие, хотя на самом деле требуется выполнить обратное действие.

Пример.

У палки 2 конца. Если один из них отпилить, сколько концов получиться?

С ходу хочется ответить, что следует выполнить вычитание 2 – 1, что приводит к ответу «у палки один конец». На самом же деле количество концов останется неизменным – 2 или второй вариант правильного ответа – получится две палки, а значит, будет уже 4 конца.

В. Задачи, где условия подталкивают обучающегося выполнить действие определенным образом, хотя надо действовать по-другому и при этом выполнять более сложный расчет.

Пример.

На руках 10 пальцев. Сколько пальцев на 10 руках?

Большинство учеников сразу же перемножают 10 на 10. Однако у человека на руке 5 пальцев, поэтому надо 5 умножать на 10 и правильный ответ – число 50.

Г. Задачи, которые предлагают выполнить действия, которые в принципе невозможно выполнить.

Пример.

Двое пошли, 3 гриба нашли. Четверо пойдут, сколько грибов найдут?

Напрашивается последовательность действий:

1) 4:2 = 2,

2) 3х 2 = 6,

т.е. четверо вроде бы найдут 6 грибов. Однако же они могут вообще ничего не найти, поэтому правильный ответ: «Неизвестно».

Задачи, которые вынуждают придумывать, составлять, строить и др. несуществующие при заданных условиях математические объекты

Пример.

Придумайте простое трехзначное число, в записи которого употребляются лишь цифры 1 и 4.

Придумать такое число просто невозможно, так как любое число, удовлетворяющее условию задачи, будет кратно 3 и, соответственно, не является простым.

Задачи, которые вводят в заблуждение из-за неоднозначности трактовки терминов, буквенных и числовых выражений

Пример.

На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза?

Здесь имеется в виду, что надо совершать не математическое действие, а провести действие с листом бумаги. И если перевернуть листок, то с обратной стороны мы увидим число 909, которое как раз в 1,5 раза больше 606.

Задачи, где допускается возможность «опровержения» семантически верного решения нематематическим решением

Пример.

(Старинная задача). Крестьянин продал на рынке трех коз за 3 рубля. Спрашивается: «По чему каждая коза пошла?»

Очевидный ответ: «По одному рублю», но опровергается, так как козы по деньгам не ходят, а ходят по земле.

Логические ошибки

Возникновение логических ошибок связано с нарушениями основных принципов математических рассуждений.

Наиболее часто встречаются ошибки в определении понятия, например:

квадратное уравнение с одним неизвестным – уравнение, которое содержит неизвестное второй степени;
равносильные уравнения – уравнения, где корни первого уравнения выступают в роли корней второго уравнения;
отрезок, которые соединяет середины сторон треугольника и равный половине его третьей стороны, называется средней линией треугольника;
прямая, которая разделяет сторону треугольника пополам, называется медианой.

В данных примерах нарушено ключевое требование к установлению определения понятия, то есть наличие достаточных признаков объекта. Для профилактики появления таких ошибок требуется тщательная отработка определения понятий, в том числе с использованием метода сравнения объектов и различных примеров с опровержениями.

Для закрепления понятий целесообразно предложить детям решение следующих примеров:

Являются ли равносильными уравнения:

х – 2 = 0 и (х – 2) (х – 3) = 0;
х – 2 = 0 и х + 3 = 5;

Какие из нижеприведенных уравнений являются квадратными:

х2 – 3х + 2 = 0;
х3 – х2 + 3х = х3 – 2;
х3 + х2 – 3х = х3 – 2;
х2 – 4.

Ошибки при доказательстве теорем

При доказательстве теорем довольно часто обучающиеся используют искомое в качестве данного. Для предупреждения такой ошибки необходимо четко объяснять обучающимся, что дано и что требуется доказать.

Часто встречаются и логические ошибки в доказательстве утверждений, которые заключаются в неполной аргументации или пропуске аргументации.

Неполная дизъюнкция также является логической ошибкой и преимущественно допускается в вопросах и задач, которые связаны с исследованием.

Пример:

Необходимо установить сравнительную величину а3 и а2. Вместо того чтобы проверить все возможные значения буквы а, обучающийся начинает рассматривать значения выражений только при а > 1, в результате чего получает неполный ответ.

Много ошибок дети допускают в преобразованиях алгебраических выражений, что связано с применением необоснованной аналогии. Примером такой ошибки может служить следующее выражение: так как (a + b)c = ac + bc, то по аналогии (ab)c = ac(bc. Известно, что, если а = b, то ak = bk, отсюда по аналогии считают, что, если a > b, то ak > bk в любом случае; по аналогии с численными дробями обучающиеся иногда считают, что

Для профилактики ошибок необходимо обучающимся постоянно устно напоминать и демонстрировать примеры того, что аналогия выступает только как вспомогательное средство для установления истины и в каждом случае требует выполнения проверки и подтверждения логическим доказательством.

Наиболее распространенные ошибки, совершаемые обучающимися выпускных классов

Задание.

Очень часто обучающиеся применяют неверную формулу, даже не задумываясь над ней. Так, при определении того является ли число

использовании определения степени в похожих случаях обучающиеся могут вывести любую формулу действий со степенями. Аналогичным образом учитель может продемонстрировать ошибки в действиях со степенями.

Обучающимся также можно показать три варианта решения данного неравенства:

При выполнении тригонометрических заданий школьники часто сами придумывают формулы, к примеру: «sin 2 х = 2 sin x».

В таких случаях можно действовать двумя способами:

При этом учителю не требуется целенаправленно проводить исправление всех ошибочных утверждений обучающегося и рассказывать ему обо всех ошибках. Оптимальный вариант – обсудить ошибку всем классом и добиться того, чтобы все обучающиеся поняли причину ее появления и в дальнейшем не допускали ее. Как свидетельствует практический опыт, организация систематических проверок чужих записей позволяет сформировать у школьников привычку критически относиться и к своим записям.

Для этого отлично подходят задания, где надо найти ошибку в решении, например:

Процесс поиска и исправления ошибок самим обучающимся под руководством педагога является весьма поучительным для всех обучающимися, так как в ходе данного процесса изучение и анализ ошибок способствует развитию познавательного интереса к изучению математики.

Основные ошибки, обучающиеся допускают в следующих ситуациях:

выполнение исследования функции на наименьшие и наибольшие значения;
преобразование дробно-рациональных выражений, где содержится корень n-ой степени;
вычисление площади криволинейной трапеции;
решение показательных и логарифмических неравенств;
изображение тел вращения при решении геометрических задач;
построение графика функции, содержащей модуль;
построение множества точек плоскости, которое должно удовлетворять заданному условию;
теоретическое обоснование применяемых формул и фактов при выполнении задач по стереометрии;
решение задач с параметром.

В целях повышения уровня учебных успехов обучающихся, а также в ходе подготовки к итоговой аттестации за курс старшей школы целесообразно повышенное внимание уделять следующим темам:

углы в пространстве;
комбинация тел;
построение геометрических мест точек, удовлетворяющего установленным условиям;
производная и ее применение при исследовании функции на отрезке;
тригонометрические функции и их свойства;
логарифмические и показательные неравенства;
тождественные преобразования дробно-рациональных выражений, где содержится корень n-ой степени.

Целесообразно спланировать учебный процесс таким образом, чтобы учебный год в выпускных классах заканчивался повторением всего пройденного материала. При этом повторение должно быть нацелено на закрепление опорных знаний, подготовку к итоговому оцениванию знаний, а также формирование и развитие межпредметных связей с одновременным осознанием взаимосвязи с ранее пройденными темами.

При высоком уровне организации учителем работы учеников над типичными ошибками позволяет существенно повысить уровень обучения математике и способствует развитию логического мышления.

Особенность школьной программы состоит в том, что при оформлении упражнений используется не математический характер и существующие правила абсолютно не связаны с проверкой знаний. Особенно это остро ощущают сильные обучающиеся, которые справедливо раздражаются из-за того, что два незначительных недочета являются ошибкой.

Намного правильнее было бы, если к математическому тексту предъявлялось одно требование – ясное отражение логики решения. При этом должно быть абсолютно неважно, какие слова и выражения использовал обучающийся для объяснения своих действий. Кстати, именно такие правила используются в высших учебных заведениях, где преподаватель смотрит исключительно на логику решения задачи.

Например, по вузовским стандартам следующая записи

является полностью исчерпывающей и не предполагает какого-либо дополнительного словесного комментария. Ведь важно, чтобы обучающийся правильно преобразовал неравенство, а не использовал при объяснении фразу: «Так как основание логарифма меньше единицы, то функция убывает и знак неравенства меняется».

Современные экзамены по своему характеру максимально приближены к тестированию, поэтому к оформлению предъявляется всего одно требование – разборчивая запись ответа.

По теореме Виета х1 = 1, х2 = -2.

Проверка показывает, что х2 не удовлетворяет условию. Ответ: 1.

Данное решение в большинстве случаев оценивается положительно. В тоже время такая последовательность действий оставляет несколько неясностей:

Зачем нужно было искать ОДЗ, если он в решении не использовался.
Один из предложенных корней не удовлетворяет условию, поэтому надо выяснить, откуда он здесь появился.
Какие логические знаки необходимо применять для связывания сделанных записей.
В соответствии с каким математическим законом х1 и х2 являются значениями переменной х.

И если пункты 1, 2, 4 можно считать еще придирками, то отсутствие логических знаков (пункт 3) является уже серьезной ошибкой. Для справедливости стоит отметить, что такая ошибка присутствует во многих работах обучающихся.

Для сравнения можно привести другой вариант решения:

В связи с тем, что возведение в квадрат могло стать причиной появления посторонних корней, то требуется проверка.

Ответ: 1.

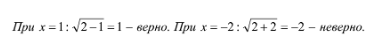
Если вместо первой импликации «(» ученик напишет «(», то это будет ошибкой. Если же любую из оставшихся эквиваленций «(» заменить на «(», то все останется верным.

В первом варианте решения обучающийся, скорее всего, просто не задумывался о логических связях записей и просто механически разделял записи с помощью «точки с запятой». И если бы «точка с запятой» использовалась только в одном определенном смысле, то было все нормально. Однако данный символ в работах школьников может быть заменой различных символов, в том числе:

«равносильно»;
«следовательно»;
«и»/«или»;
объединение и пересечение множеств.

Организация контроля и самоконтроля учебной деятельности обучающихся

При проверке работ педагог отмечает не только математические, но и грамматические, и стилистические ошибки. При этом учитель лично исправляет все ошибки, что является крайне неверным решением. Ведь если учитель исправил ошибку, то обучающийся просто соглашается с ней и успокаивается.

Для повышения уровня самостоятельной работы обучающегося необходимо, чтобы он сам выявил свою ошибку и разобрался, почему он ее совершил. Поэтому учителю достаточно просто указать место ошибки, для чего может использоваться определенная символьная система. Так, две черты обычно указывают на грубую ошибку, одна черта – случайная или негрубая ошибка, а волнистая линия – наличие какого-либо недочета.

При проверке домашних заданий учителю необходимо тщательно просматривать все проведенные обучающимся преобразования, вычисления и рассуждения. При этом все ошибки требуется систематизировать и выделить наиболее типичные и массовые. В первую очередь, выделяются наиболее грубые и принципиальные ошибки, которые связаны с нарушением основных математических законов.

Именно таким ошибкам и необходимо уделять повышенное внимание при проведении разбора в классе. Такой обзор нельзя ограничивать только сообщением ошибок каждого обучающегося, так как требуется произвести разбор ошибок и выявить причины, которые к ним привели. Для этих целей целесообразно привлекать и других обучающихся, которые допустили аналогичные ошибки.

Если какое-то задание вызвало затруднения у большинства обучающихся класса, то его надо разбирать максимально детально и при необходимости провести дополнительные упражнения.

Если ошибка не была массовой, то обучающемуся можно предложить произвести детальный ее разбор дома, внести все необходимые исправления и сделать отсылки на соответствующие правила.

Для повышения эффективности работы над ошибками нельзя откладывать проведение этого мероприятия, так как отсрочка неизбежно ведет к потере интереса учеников к разбору.

Для того чтобы исправить множество ошибок и предупредить их появление, крайне важно сформировать у обучающихся навыков самоконтроля, которые включают в себя две части:

способность самостоятельно обнаруживать ошибки;
умение самостоятельно объяснить ошибку и исправить ее.

Для поиска ошибок используются следующие приемы:

проверка правильности проведенных вычислений и преобразований за счет выполнения обратного действия либо преобразования;
проведение оценки полученного результата с точки зрения здравого смысла;
осуществление проверки правильности решения за счет составления и решения задач, обратных решаемой задаче;
проверка правильности решения с помощью графического способа.

Формированию навыков самоконтроля способствует и прием приближенной оценки ожидаемого результата, ведь установление возможных пределов планируемого результата позволяет не допустить недочеты в виде описок и пропуска цифр.

К примеру, обучающемуся надо решить следующую задачу: «За неделю завод выпустил 130 телевизоров, выполнив месячный план на 25%. Сколько телевизоров должен выпустить завод за месяц по плану».

Ученик написал 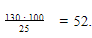Ошибку можно сразу вычислить, если перед решением школьник «включит» логику и прикинет «В течение недели было выпущено 130 телевизоров. Соответственно, за месяц будет выпущено больше 130 телевизоров, поэтому и ответ должен быть больше 130».

Система работы учителя математики по коррекции ошибок Достижение положительного эффекта от индивидуальных заданий объясняется тем, что обучающиеся их выполняют самостоятельно, в том числе и дома. В то же время индивидуальные задания должны составлять методически правильно и быть направлены на преодоление конкретных ошибок. Для этого от учителя требуется постоянное ведение учета основных затруднений обучающихся, для чего, например, может использоваться следующий вариант таблицы:

Список учащихся класса	Тема…	Примечание «+» — ошибка устранена; «-» — ошибка не устранена
Пробелы в знаниях	Классные индивидуальные задания	Домашние индивидуальные задания

Заполнение всех граф таблицы, за исключением первой, рекомендуется осуществлять карандашом. Пополнение списка ошибок ведется при проверке домашних заданий, самостоятельных и контрольных работ. Большинство ошибок повторяются из года в год, поэтому молодому педагогу рекомендуется ознакомиться с ними.

Ниже представлены наиболее распространенные ошибки.

При работе с десятичными дробями обучающиеся совершают ошибки в выделении целой части результата, к примеру:

а) 3,6 – 1,8 = 18;

б) 2 + 5,3 = 55;

в) 6,4 : 2 = 32.

Во время беседы с обучающимися, которые допускают такие ошибки, обычно выясняется, что они просто забыли поставить запятую. Устранение ошибки осуществляется в результате длительных тренировок.

Одна из самых типичных ошибок – деление десятичной дроби на десятичную. Деление обычно совершается без обращения внимания на запятые: 2,576: 11,2 = 23.

Для профилактики ошибок обучающимся предлагаются задания на карточках, где для каждого примера приведено соответствующее правило, но оно сформулировано с пропусками или полностью.

Примеры карточек.

Карточка №1. Чтобы сложить две десятичные дроби, надо:

сложить получившиеся числа, как складывают …;
записать слагаемые друг под другом так, чтобы запятая …;
уравнять число знаков … в слагаемых;
в полученной сумме поставить запятую под….

Задания.

В представленных числах уравняйте число знаков после запятой: 2,5; 0,25; 43, 1256; 325,1.
Выполните сложение дробей: 12,7 и 3,442; 0,237 и 10,44.

Карточка № 2.

Для того чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимание на …, а затем в результате отделить запятой… столько цифр, сколько их стоит после запятой… .

Задания.

В записи числа 1234567 отделите запятой справа:
1. одну цифру;
2. две цифры;
3. шесть цифр;
4. семь цифр.

В каком случае в результате получается число, которое больше 1, но меньше 2? больше 0, но меньше 1?

Найдите произведение чисел: 2,7 и 1,32.

Карточка № 3.

Чтобы разделить число на десятичную дробь, надо в делимом и в делителе перенести … вправо на столько цифр, сколько их после… в …, а потом выполнить деление на натуральное число.

Задания.

В записи 4,78: 0,8 подчеркните одной чертой делимое, а двумя – делитель.
В числах 1; 0,345; 30,25 перенесите запятую вправо на столько цифр, сколько их после запятой в числе 0,5.
Найдите частное чисел: 8,96 на 1,12.

Часто встречаются ошибки при совершении действий с обыкновенными дробями. В частности, при выполнении сложения (вычитания) дробей обучающиеся производят складывание (вычитание) числителей и знаменателей:

Складывая (вычитая) дроби, обучающиеся забывают умножить их числители на дополнительные множители:

Карточка № 5.

Известно, что вычитание проверяется и тем, что разность двух положительных чисел не может быть больше уменьшаемого.

1. Учитывая сказанное выше, установите, верен ли результат вычитания:

При умножении (делении) смешанного числа на десятичную дробь умножают (делят) отдельно целые части и отдельно дробные, а результаты записывают рядом, например:

Приемы работы по повышению качества работы по профилактике ошибок

Существует несколько основных правил, при руководстве которыми можно значительно снизить количество ошибок. При этом многие формулировки относятся к фольклорному жанру, но, тем не менее, дают объективное понимание какого-либо правила:

Правило ГАИ. Оно гласит, что большинство аварий случается при небольших скоростях. При переносе данного тезиса на математику получаем, что большинство ошибок возникают в самых простых ситуациях.

Для непопадания в такие ситуации обучающимся надо привить навык постоянной проверки правильности списывания условий задач, решения квадратных уравнений. А для выявления ошибки рекомендуется начинать ее искать с конца, что предполагает подстановку полученного результата в последнее действие и последовательное следование выше.

Правило закройщика: шов иголкой делается следующим образом: стежок вперед и назад, а потом еще вперед и опять назад.

В математике преобразования осуществляются аналогичным образом, то есть после совершения каждого перехода необходимо «оглянуться назад» и проверить полученный результат проведением обратного преобразования.

Правило программиста: работай блоками.

В программировании произвести отладку программы целиком невозможно, поэтому всю работу разбивают на небольшие автономные блоки, и затем по отдельности проверяется работоспособность каждого блока.

В математике этим правилом необходимо руководствоваться, прежде всего, при работе с громоздкими выражениями, то есть они разбиваются на несколько простых. При решении с каждым уравнением «разбираются» по отдельности.

Большинство приемов работы над ошибками не содержит методик диагностики выявления причин ошибок, а также не уделяется достаточного внимания работе по организации рефлексивной деятельности учеников и ее применения для предупреждения и исправления математических ошибок.

Еще один недостаток состоит в том, что работа над ошибками практически никак не контролируется, поэтому причины появления ошибок так и остаются не выясненными и повторяются снова и снова. Для повышения качества работы над ошибками необходимо обеспечивать большую самостоятельность учеников, так как это позволяет осуществлять более осознанный анализ ошибок и собственных действий при решении конкретной задачи.

В результате у обучающихся развивается логическое мышление, а также создаются благоприятные условия для лучшего усвоения новых знаний. Постепенно у детей развиваются и стремление самостоятельно разобраться в задаче, умение по планированию ее решения и навыки продумывания различных вариантов действий. Например, обучающийся отлично усвоил правило преобразования алгебраических выражений формулы квадрата суммы и разности двух чисел, однако, когда получает задание, где необходимо представить в виде многочлена (–х–5)2, он теряется.

В таких случаях обучающемуся надо предложить ответить на вопрос, что конкретно у него вызывает затруднение? Далее надо помочь ему преобразовать выражение таким образом, чтобы можно было использоваться одну из известных ему формул в том виде, в каком они представлены в учебнике.

Еще один пример неосознанного применения алгоритма:

Обучающемуся предлагается решить уравнение sin x = 1,2, он сразу же начинает искать его корни по уже отлично известной ему формуле и при этом совершенно не обращает внимания на недопустимые значения sin x. Для того чтобы помочь учащемуся разобраться в данной ситуации, рекомендуется продемонстрировать наглядное решение задачи на тригонометрическом круге.

Список литературы:

Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
Гальперин П.Я. Методы обучения и умственное развитие ребенка. – М.: Изд-во Моск. Ун-та, 1985. – 45 с.
Гласс ДЖ., Стенли Дж. Сатистические методы в педагогике и психологии. Пер. С англ. – М.: Прогресс. – 1976. – 495 с.
Грабарь, И. И. Применение математической статистики в педагогических исследованиях. Непараметрические методы / И. И. Грабарь, К. А. Краснянская. – М.: Педагогика, 1977. – 136 с.
Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
Груденов, Я. И. Изучения определений, аксиом, теорем / Я. И. Груденов. – М. Просвещение, 1984. – 95 с.
Груденов Я.И. Психологический анализ причин некоторых массовых ошибок учащихся// Журнал «Математика в школе» – 1981 г. – №3, с. 46-48.
Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
Гуцанович С.А., Радьков А.М. Тестирование в обучении математике диагностико-дидактические основы. – Могилев, МГПИ им. А.А. Кулешова, 1995. – 203 с.
Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
Действующие учебники и учебные пособия по математике для средней школы.
Журналы «Математика в школе» за 1970-1990 гг.
Зайкин М.И., Колосова В.А. Провоцирующие задачи // Журнал «Математика в школе» – 1997 г. – №6, с. 32.
Запрудский Н. И. Современные школьные технологии: пособие для учителей. – 3-е изд. / Н. И. Запрудский. – Минск, 2006. – 288 с.
Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
Метельский Н.В. Пути совершенствования обучения математике: Проблемы современной, методики математики. – Минск: Университетское, 1989. – 160 с.
Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
Рогановский Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
Селевко Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
Скобелев Г.Н. Контроль на уроках математики: Пособие для учителя. – Минск: Народная асвета, 1986. – 103 с.
Столяр А.А. Роль математики в гуманизации образования // Математика в школе. 1990. – № 6. – с. 5–7.
Столяр А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
Темербекова А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
Фарков А. В. Внеклассная работа по математике.
Фридман, Л. М. Как научиться решать задачи: пособие для учащихся / Л. М. Фридман, Е. Н. Турецкий – 2- изд. – М.: Просвещение, 1984. – 175 с.
Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Журнал «Математика в школе» – 2000 г. – №4, с. 28.
Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.

Источник