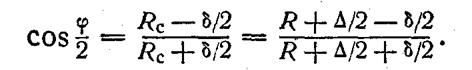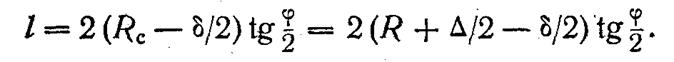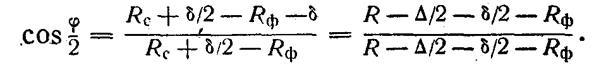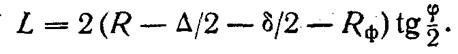Расчёт эквидистантного
контура.
Эквидистанта –
кривая равноудалённая от другой кривой.


r
траектория
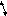
x
хэ‘
Эквидистантный
контур состоит из кривых параллельных
кривым основного программного контура
и представляет собой геометрическое
место точек, равноудалённых от основного
контура.
Здесь
r –
это, например
радиус фрезы rф.
Для
прямой: хэ
= х0
r
sin
уэ
= у0
r
cos
dy
где
= arctg
— угол
наклона касательной (в точке (х0,
у0)).
dx
или,
так как dx/dy = tg
= k = const , то
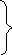
хэ
= х0
r
k/1+k2
если
F(x0,
y0)
– прямая
____
то F(xэ,
уэ)
– так же прямая.
уэ
= у0
r
k/1+k2
«+»
– при внутренней обработке.
«-»
— при наружной обработке.
Для
кривых 2 – го порядка.
F(x, y) = 0
F(x)
Xэ
= X0
r
cos ( arctg )
F(x)
F(x)
Yэ
= Y0
r sin ( arctg )
, где
F(x)
F
F
—
частные
производные.
х
у
r
– условный
радиус инструмента.
Если
программный контур является прямой или
окружностью, то расчёт эквидистанты
прост.
Если
же при сопряжении участков в контуре
имеются изломы, то расчёт усложняется.
Эквидистанта
эллипса является кривой 8 – го порядка,
расчёт которой затруднителен.
Расчёт эквидистанты
при сопряжении 2-х прямых.
Х

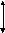

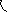
L1
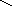
L2

A
– точка
сопряжения L1
и L2.
A’
– точка
сопряжения эквидистанты.
Для
упрощения расчётов повернём исходный
контур на угол
относительно точки А.
Из
рассматриваемого
АСВ и
ВДЕ получим выражение для смещений
точки А.
у0
= z

Д

А
В t

H
L2
C
_______
z
/ cos
+ r
ctg
= (r L2
r
L2
– H2)/H
где
«+» — если
— острый
«-»
— если
— тупой.
Условие
для определения остроты угла :
если
L <
L0
то
— острый,
L
> L0
то
— тупой.
________
где
L0
=
L12
+ L22
_______________________
L
= (Х1
— Х2)2
+ (Y1
— Y2)2
В
ЧПУ задача расчёта эквидистанты может
решаться:
-
На
этапе подготовки УП. -
В
процессе функционирования УЧПУ (то
есть в реальном масштабе времени).
1
способ) Не требует введения в устройство
ЧПУ дополнительных алгоритмов и программ
и применяется при подготовке УП для
обработки сложных объёмных деталей на
многокоординатных станках, то есть
когда алгоритм расчёта эквидистанты
гораздо сложнее алгоритмов интерполяции
(эквидистантный контур рассчитывается
на внешней ЭВМ).
2
способ) Позволяет реализовывать
безэквидистантное программирование
станков. Он предполагает программную
реализацию алгоритмов автоматического
расчёта эквидистанты и коррекции УП
непосредственных устройств ЧПУ.
Безэквидистантное
программирование позволяет: обрабатывать
сопряжённые детали по одной УП;
использовать не верный инструмент
(важен тип);
производить черновую и чистовую обработку
по одной программе;
повышать точность обработки за счёт
коррекции, расчёт эквидистанты по
реальному размеру инструмента, а также
с учётом реального износа инструмента.
Управление контурной
скоростью.
По технологическим
причинам в системе ЧПУ требуется
поддержание постоянства контурной
скорости в каждой точке программирования
траектории.
Основное
содержание этой задачи в разложении
вектора скорости на составляющие в
декартовой системе координат:
а)
Для прямой.
Vy

Vx
b

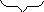
= VkTkcos(arctg(b/a))
= Lтcos
Lт
Vy
= VkTksin(arctg(b/a))
= Lтsin
a
Vx
= L
_____
_____
a2
+ b2
b
Vy
= Lт
______
______
a2
b2
Vk
– контурная
скорость.
Тк
– время интерполяционного цикла.
видно,
что Vx
= const
Vy
= const
б)
Для окружности.
Vk


у)
Vx
R
C(x,y)
Vkt
Vx
=
X
________
Xc2
+ Yc2
Vkt
Vy
=
Y
_______
Хс2+Yc2
где
t
– время
пересчёта Vx,
Vy.
Устройства
ЧПУ целесообразно для расчёта и коррекции
эквидистанты, используются те же
алгоритмы, что и при решении интерполяционных
задач (любые из методов 4-х групп
рассмотренных ранее) вводя соответствующие
начальные условия.
Динамика контурных
систем ЧПУ.
Основные
показатели СЧПУ:
-
Быстродействие
– для сокращения времени на холостые
перемещения в позиционных режимах. Это
важно для станков с большим количеством
перемещений, скоростей перемещений 20
м/мин
и более.
В
разгона
tразгона
tторможения
надо снижать
Быстродействие
ограничивается прочностными
характеристиками механизмов, динамикой
контуров положения приводов.
-
Точность
– оценивается величиной контурной
ошибки, при воспроизведении
устройств программной траектории д.
б. в
минимуме
=0.
Отсутствие
установленных ошибок при позиционировании.
Точность
обеспечивается:
а)
Диапазоном регулирования по скорости
Дc0
=
10000 и более.
б)
Введением астатизма в алгоритм
управления.
в)
Использование комбинированного
управления.
г)
Качество переходных процессов. Требуется
обеспечить
отсутствие
перерегулирования G = 0%, однако возникают
скоростные
ошибки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4. Аппроксимация контура (при необходимости). Аппроксимация
— это представление сложного геометрического элемента участками более простых
геометрических элементов. Например, линейная аппроксимация дуги окружности —
это замена её участками прямых линий. Необходимость выполнения аппроксимации
определяется типом интерполятора имеющегося в системе управления данного
оборудования. Интерполятор — это устройство, которое обеспечивает перемещение
инструмента относительно детали из одной опорной точки в другую в соответствии
с законом, заложенным в него. Интерполяторы бывают линейными или
линейно-круговыми. Если интерполятор линейный, весь контур детали, а,
следовательно, и эквидистанту, необходимо представить только участками прямых
линий. Расчёт координат промежуточных опорных точек выполнится с учётом радиуса
дуги и допуском на аппроксимацию, который может составлять одну треть от
допуска на обработку. Если интерполятор линейно-круговой, траектория движения
инструмента может включать как участки прямых линий, так и дуги окружностей.
18
Пример аппроксимация дуги участками прямых линий (рис. 2.3.). При
наличие в системе управления только линейного интерполятора, криволинейные
участки обрабатываемого контура, в частности дуги окружностей, приходится
аппроксимировать участками прямых линий. В этом случае можно использовать
следующие рекомендации.
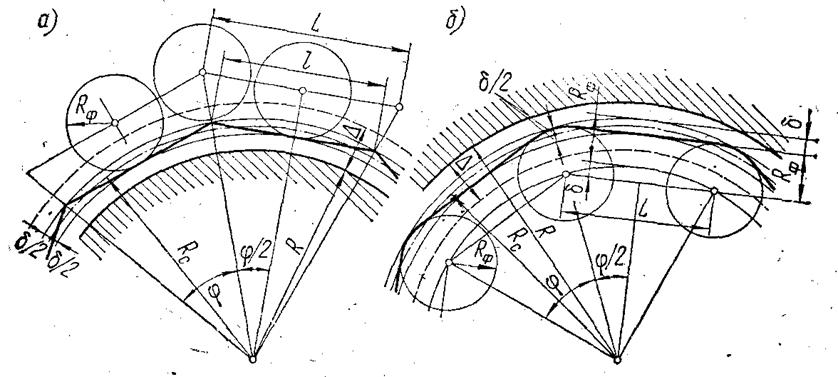
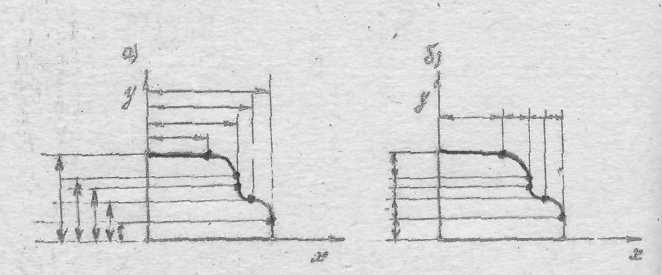
Рис. 2.3. Аппроксимация контура окружности ломаной линией и
построение траектории движения инструмента при фрезеровании выпуклого (а) и
вогнутого (б) контуров.
Промежуточные опорные точки на дуге определяются для каждого отрезка ломаной
линии, которой аппроксимируется дуга окружности. При фрезеровании плоского
контура, очерченного дугами окружностей, можно выделить два характерных случая:
обработка выпуклого контура (рис. 2.3. а) и обработка вогнутого контура (рис.
2.3 б). Контур имеет номинальный радиус R при
одностороннем расположении поля допуска. При обработке выпуклого контура
траектория движения центра фрезы выбирается такой, при которой фреза формирует
поверхность с размером, соответствующим середине поля допуска Δ на обработку.
Величина этого среднего размера Rc = R +Δ/2. Так как допуск на
аппроксимацию не должен превышать величины δ= (0,1—0,3)Δ, то заменяющая ломаная
линия должна уложиться в круговую полосу шириной ± δ/2 (от радиуса Rc — δ/2 до радиуса Rc
+ δ/2). Как следует из рис. 2.3 а, в этом случае косинус половины
центрального угла одного звена ломаной линии равен:
19
Тогда длина одного звена ломаной линии на обработанной
поверхности (величина огранки) определится так:
Соответственно длина одного звена ломаной траектории центра
фрезы (расстояние между соседними опорными точками) будет равна:
где Rф—радиус фрезы.
При обработке вогнутого контура с номинальным радиусом R, в случае одностороннего расположения поля допуска Δ
(см. рис. 2.3 б) радиус фрезы Rф должен быть
меньше радиуса обрабатываемого контура. При условиях, аналогичных тем, которые
были приняты в предыдущем случае, косинус половины центрального угла одного
звена ломаной траектории движения центра фрезы определяется по формуле:
Длина
звена ломаной траектории фрезы
5. Заполнение расчётных таблиц. Следует иметь в
виду, что координаты опорных точек, рассчитанные для записи управляющей
программы, могут отображаться в абсолютной системе отсчёта, когда все размеры
задаются от одной, единой базы, или в относительной системе отсчёта, когда
следующая опорная точка задаётся от предыдущей опорной точки, (эта система
записи координат называется иногда «запись по приращениям»). Примеры
представления размеров в абсолютной и в относительной системе координат
показаны на рис. 2.4.
20
Рис. 2.4. Примеры представления размеров детали:
а) в абсолютной системе координат;
б) в относительной системе координат (по
приращению).
В процессе расчёта опорных точек накапливается большой
объём информации: координаты опорных точек, рассчитанные в абсолютной системе
отсчёта (Таблица 2.1), а, при необходимости, пересчитанные в относительную
систему отсчёта (Таблица 2.2); координаты центра окружностей (Таблица 2.3);
параметры круговой интерполяции I, G, K (Таблица 2.4) и
т. п. Для лучшей организации этой информации, вся она заносится в таблицы,
примеры которых представлены ниже.
(Таблица 2.1)
Координаты опорных точек на эквидистанте
в
абсолютной системе отсчёта.
|
Опорная точка |
X |
Y |
Опорная точка |
X |
Y |
|
О |
0 |
0 |
9 |
229 |
120 |
|
Твх. |
-9 |
130 |
10 |
206,75 |
91,8 |
|
1 |
-9 |
145 |
11 |
117,67 |
79,73 |
|
2 |
25 |
179 |
12 |
111,91 |
75,88 |
|
3 |
54,2 |
162,42 |
13 |
79,41 |
15,88 |
|
4 |
54,92 |
161,94 |
14 |
60 |
6 |
|
5 |
182,78 |
143,67 |
15 |
37,7 |
21,13 |
|
6 |
182,92 |
143,66 |
16 |
-6,59 |
132,43 |
|
7 |
183,49 |
143,84 |
17 |
-9 |
145 |
|
8 |
200 |
149 |
Твых. = 18 |
-9 |
160 |
21
(Таблица 2.2)
Координаты опорных точек на эквидистанте в относительной
системе отсчёта, т.е. координаты i-ой точки, относительно (i-1)-ой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Как вычислить эквидистанту?
Автор Николай, 18.02.16, 13:32:35
« предыдущая — следующая »
0 Пользователей и 1 гость просматривают эту тему.
Как посчитать точки, образующие край канавки от фрезы, как на рисунке?
Фреза движется по траектории:
X1 = 0
Y1 = R
For t = 0 To 2 * Pi + 0.05 Step dt
‘Синусоида на окружности
X = (R + (E * Sin(t * (Z)))) * Sin(t)
Y = (R + (E * Sin(t * (Z)))) * Cos(t)
ksDocument2D.ksLineSeg X, Y, X1, Y1, 1
X1 = X
Y1 = Y
Next t
Расписываюсь в математическом бессилии…
Ang:=Angle(X1,Y1,X,Y);
XeN:=X+r*CosD(Ang-90);
YeN:=Y+r*SinD(Ang-90);
XeV:=X+r*CosD(Ang+90);
YeV:=Y+r*SinD(Ang+90);

Вячеславу Никонову.
Наверное, немного не в ту тему написал, но сегодня, используя Компас График, не смог построить эквидистанту к линии, построенной из 10000 соединённых между собой отрезков.
А вот и предложение: Чтоб Компас График смог!
Задача сугубо практическая. Пытаюсь решить её с помощью API.
Вот Борис Николаевич подкинул формулы, попробую разобраться…
Делается легко, соединяете отрезки в контур и строите эквидистанту.
И программным способом получилось!
Немного подправил ваши формулы под VB:
‘Построение канавок
Ang = Atn((Y1 — Y) / (X1 — X)) ‘Угол касательной к синусоиде
‘Наружная канавка
XeN = (X — rC * Cos(Ang — Pi / 2))
YeN = Y — rC * Sin(Ang — Pi / 2)
XeV = X1 — rC * Cos(Ang — Pi / 2)
YeV = Y1 — rC * Sin(Ang — Pi / 2)
и т.д.
Отчётливо видны подрезания углов, что и требовалось выявить.
P.S.
Что-то не нашёл, как соединить отрезки в контур…
Цитата: Николай от 19.02.16, 15:49:50
Отчётливо видны подрезания углов, что и требовалось выявить.
Конфликт радиусов кривизны базовой линии (переменная величина вдоль линии) и расстояния до эквидистантного контура. Очевидно же…
- Форум пользователей ПО АСКОН
-
►
Профессиональные вопросы -
►
Раздел с ограниченным доступом -
►
2D: черчение и оформление -
►
Как вычислить эквидистанту?
Эквидистанта — Вычисление координат 202—204 Элементы геометрические зубчатого колеса 217 [c.586]
Вычисление координат эквидистанты для кулачка механизма с вращающимся коромыслом должно быть произведено по другим формулам. [c.203]
Процесс вычисления координат эквидистанты по формулам (8.56) — (8.61) тот же, что и в предыдущем случае. [c.204]
Наибольшая доля расчета программ приходится на вычисление координат опорных точек профиля и на расчет эквидистанты, поэтому круговая интерполяция сама по себе в ряде случаев может и не дать желаемого эффекта. Вместе с тем широкое внедрение автоматического программирования делает обе системы интерполяции почти равноценными с точки зрения удобства программирования. [c.96]
ППП Система ускоренной подготовки управляющих программ для станков с ЧПУ на базе АРМ-М предназначен для подготовки управляющих перфолент, графической интерпретации результатов расчетов эквидистан-ты, а также исправления ошибок, обнаруженных при прохождении задачи. Программы пакета обеспечивают вычисление координат точек и параметров окружностей обработкой геометрической и технологической информации ускоренный контроль построения эквидистанты на этапе вычисления координат опорных точек отображением на экране графического дисплея УПГИ масштабирование чертежа эквидистанты для отображения на экране УПГИ получение структуры трехмерного представления графической информации локализацию параметров в отдельных программах пакета для получения необходимой информации при моделировании обработки детали и корректировке отдельных элементов во время работы системы. [c.80]
|
|
От: |
vitz |
|
| Дата: | 23.03.04 11:14 | ||
| Оценка: |
Поделитесь опытом по этому поводу.
Если можно пару ссылочек.
Особенно интересует случай когда радиус кривизны меньше эквидистантного расстояния.
… << RSDN@Home 1.1.3 stable >>
Re: Построение эквидистанты
|
|
От: |
VNG |
https://organicmaps.app/ |
| Дата: | 23.03.04 15:32 | ||
| Оценка: |
Здравствуйте, vitz, Вы писали:
V>Поделитесь опытом по этому поводу.
Для каких кривых нужно?
V>Если можно пару ссылочек.
V>Особенно интересует случай когда радиус кривизны меньше эквидистантного расстояния.
Не совсем понятно. Если радиус кривизны меньше эквидистантного расстояния, то полученная эквидистантная кривая не будет того-же порядка
гладкости, что и исходная кривая (грубо говоря будет иметь точки излома). Нормально ли это?
… << RSDN@Home 1.1.3 beta 1 >>
Re[2]: Построение эквидистанты
|
|
От: |
vitz |
|
| Дата: | 23.03.04 16:11 | ||
| Оценка: |
Здравствуйте, VNG, Вы писали:
В принципе суть заключается в том, что нужно сформировать плоский контур с учетом припуска по заданному без припуска.
Кривая есть кубический сплайн.
А вот по по поводу нормальности и хотелось узнать.
Как я понимаю мы смещаем опорные точки на эквидистантное расстояние вдоль нормали к производной в этих точках?
А во как поступить с малым радиусом кривизны слегка не понятно.
… << RSDN@Home 1.1.3 stable >>
Re[3]: Построение эквидистанты
|
|
От: |
VNG |
https://organicmaps.app/ |
| Дата: | 23.03.04 16:49 | ||
| Оценка: |
Здравствуйте, vitz, Вы писали:
V>Здравствуйте, VNG, Вы писали:
V>В принципе суть заключается в том, что нужно сформировать плоский контур с учетом припуска по заданному без припуска.
V>Кривая есть кубический сплайн.
Эквидистантная кривая к кубическому сплайну — это будет уже не кубический сплайн, а кривая более высокой степени.
V>А вот по по поводу нормальности и хотелось узнать.
V>Как я понимаю мы смещаем опорные точки на эквидистантное расстояние вдоль нормали к производной в этих точках?
Вообще-то нет. Сместив по нормали только опорные точки сплайна мы не получим сплайн, эквидистантный исходному.
Как я уже говорил эквидистантой будет более сложная кривая.
V>А во как поступить с малым радиусом кривизны слегка не понятно.
См. выше.
… << RSDN@Home 1.1.3 beta 1 >>
Re[4]: Построение эквидистанты
|
|
От: |
vitz |
|
| Дата: | 24.03.04 08:02 | ||
| Оценка: |
Здравствуйте, VNG, Вы писали:
VNG>Эквидистантная кривая к кубическому сплайну — это будет уже не кубический сплайн, а кривая более высокой степени.
Ну так а можно привести алгоритм получения данной кривой или ткнуть носом в нужное место.
… << RSDN@Home 1.1.3 stable >>
Re[5]: Построение эквидистанты
|
|
От: |
VNG |
https://organicmaps.app/ |
| Дата: | 24.03.04 09:21 | ||
| Оценка: |
Здравствуйте, vitz, Вы писали:
V>Здравствуйте, VNG, Вы писали:
VNG>>Эквидистантная кривая к кубическому сплайну — это будет уже не кубический сплайн, а кривая более высокой степени.
V>Ну так а можно привести алгоритм получения данной кривой или ткнуть носом в нужное место.
Алгоритм может быть такой.
Возьми параметрическое уравнение твоего сплайна, что-то типа x(t) = …, y(t) = …
Можно найти вектор касательной к этому сплайну:
( x'(t) / sqrt(x'(t)^2 + y'(t)^2), y'(t) / sqrt(x'(t)^2 + y'(t)^2) )
sqrt — корень квадратный
x'(t) — производная
Из него можно получить вектор нормали к сплайну, пусть это будет n(t) = (Xn(t), Yn(t))
Теперь можно получить параметрическое уравнение эквидистантной кривой:
Xэ(t) = x(t) + S*Xn(t)
Yэ(t) = y(t) + S*Yn(t)
S — расстояние эквидистанты.
Алгоритм конечно в лоб и конечное уравнение будет содержать иррациональность, но может чем поможет.
… << RSDN@Home 1.1.3 beta 1 >>
Re[6]: Построение эквидистанты
|
|
От: |
vitz |
|
| Дата: | 24.03.04 10:53 | ||
| Оценка: |
Здравствуйте, VNG, Вы писали:
VNG>Алгоритм может быть такой.
VNG>Возьми параметрическое уравнение твоего сплайна, что-то типа x(t) = …, y(t) = …
VNG>Можно найти вектор касательной к этому сплайну:
VNG>( x'(t) / sqrt(x'(t)^2 + y'(t)^2), y'(t) / sqrt(x'(t)^2 + y'(t)^2) )
VNG>sqrt — корень квадратный
VNG>x'(t) — производная
VNG>Из него можно получить вектор нормали к сплайну, пусть это будет n(t) = (Xn(t), Yn(t))
VNG>Теперь можно получить параметрическое уравнение эквидистантной кривой:
VNG>Xэ(t) = x(t) + S*Xn(t)
VNG>Yэ(t) = y(t) + S*Yn(t)
VNG>S — расстояние эквидистанты.
Это все конечно понятно (уж больно шото напоминает),
но все же что делать с петлями которые получаются на эквидистанте:
нужно делать разрыв, но как
… << RSDN@Home 1.1.3 stable >>
Re[7]: Построение эквидистанты
|
|
От: |
VNG |
https://organicmaps.app/ |
| Дата: | 24.03.04 14:12 | ||
| Оценка: |
Здравствуйте, vitz, Вы писали:
V>Здравствуйте, VNG, Вы писали:
VNG>>Алгоритм может быть такой.
VNG>>Возьми параметрическое уравнение твоего сплайна, что-то типа x(t) = …, y(t) = …
VNG>>Можно найти вектор касательной к этому сплайну:
VNG>>( x'(t) / sqrt(x'(t)^2 + y'(t)^2), y'(t) / sqrt(x'(t)^2 + y'(t)^2) )
VNG>>sqrt — корень квадратный
VNG>>x'(t) — производная
VNG>>Из него можно получить вектор нормали к сплайну, пусть это будет n(t) = (Xn(t), Yn(t))
VNG>>Теперь можно получить параметрическое уравнение эквидистантной кривой:
VNG>>Xэ(t) = x(t) + S*Xn(t)
VNG>>Yэ(t) = y(t) + S*Yn(t)
VNG>>S — расстояние эквидистанты.
V>Это все конечно понятно (уж больно шото напоминает),
V>но все же что делать с петлями которые получаются на эквидистанте:
V>нужно делать разрыв, но как
Так все таки. Что тебе нужно получить?
— точное уравнение эквидистантной кривой — это уже описано выше
или
— кривую близкую к эквидистантной, без петель и сохраняющую порядок гладкости сплайна — в этом случае я не знаю, что можно сделать
Может ты бы поподробнее описал задачу, что именно тебе надо делать с использованием эквидистантных сплайнов.
… << RSDN@Home 1.1.3 beta 1 >>
Re[8]: Построение эквидистанты
|
|
От: |
vitz |
|
| Дата: | 24.03.04 16:33 | ||
| Оценка: |
Здравствуйте, VNG, Вы писали:
Вообще то требуется построить для плоской детали (корпус судна) контур с учетом припуска.
В оригинале контур состоит из прямых, дуг и сплайнов, с прямыми и дугами вроде просто, а вот со слайнами выходит загвоздка.
В принципе достаточно построить близкий к эквидистантной кривой сплайн.
В случае с петлями я думаю нужно получить точку пересечения и исходя из этого построить два сплайна отбросив точки в петле
(возможно для этого случая подойдет )
Вобщем спасибоньки за совет.
… << RSDN@Home 1.1.3 stable >>
Re[9]: Построение эквидистанты
|
|
От: |
VNG |
https://organicmaps.app/ |
| Дата: | 24.03.04 16:53 | ||
| Оценка: |
Здравствуйте, vitz, Вы писали:
V>Здравствуйте, VNG, Вы писали:
V>Вообще то требуется построить для плоской детали (корпус судна) контур с учетом припуска.
V>В оригинале контур состоит из прямых, дуг и сплайнов, с прямыми и дугами вроде просто, а вот со слайнами выходит загвоздка.
V>В принципе достаточно построить близкий к эквидистантной кривой сплайн.
V>В случае с петлями я думаю нужно получить точку пересечения и исходя из этого построить два сплайна отбросив точки в петле
Кажется мне, что найти точку самопересечения эквидистантной кривой будет не очень просто
Здесь можно попробовать так:
В исходном сплайне найти участки, где кривизна больше, либо равна величине смещения. Это тоже не просто, но можно каким-нибудь приближенным методом. Очевидно, что участок сплайна можно представить одним сплайном.
Для каждого такого участка строим эквидистанту. В итоге при суммировании участков мы получим примерно эквидистантную кривую к исходному сплайну и без петель.
V>(возможно для этого случая подойдет )
V>Вобщем спасибоньки за совет.
Пожалуйста
… << RSDN@Home 1.1.3 beta 1 >>


- Переместить
- Удалить
- Выделить ветку
Пока на собственное сообщение не было ответов, его можно удалить.
Как вычислить эквидистанту?
Автор Николай, 18.02.16, 13:32:35
« предыдущая — следующая »
0 Пользователей и 1 гость просматривают эту тему.
Как посчитать точки, образующие край канавки от фрезы, как на рисунке?
Фреза движется по траектории:
X1 = 0
Y1 = R
For t = 0 To 2 * Pi + 0.05 Step dt
‘Синусоида на окружности
X = (R + (E * Sin(t * (Z)))) * Sin(t)
Y = (R + (E * Sin(t * (Z)))) * Cos(t)
ksDocument2D.ksLineSeg X, Y, X1, Y1, 1
X1 = X
Y1 = Y
Next t
Расписываюсь в математическом бессилии…
Ang:=Angle(X1,Y1,X,Y);
XeN:=X+r*CosD(Ang-90);
YeN:=Y+r*SinD(Ang-90);
XeV:=X+r*CosD(Ang+90);
YeV:=Y+r*SinD(Ang+90);

Вячеславу Никонову.
Наверное, немного не в ту тему написал, но сегодня, используя Компас График, не смог построить эквидистанту к линии, построенной из 10000 соединённых между собой отрезков.
А вот и предложение: Чтоб Компас График смог!
Задача сугубо практическая. Пытаюсь решить её с помощью API.
Вот Борис Николаевич подкинул формулы, попробую разобраться…
Делается легко, соединяете отрезки в контур и строите эквидистанту.
И программным способом получилось!
Немного подправил ваши формулы под VB:
‘Построение канавок
Ang = Atn((Y1 — Y) / (X1 — X)) ‘Угол касательной к синусоиде
‘Наружная канавка
XeN = (X — rC * Cos(Ang — Pi / 2))
YeN = Y — rC * Sin(Ang — Pi / 2)
XeV = X1 — rC * Cos(Ang — Pi / 2)
YeV = Y1 — rC * Sin(Ang — Pi / 2)
и т.д.
Отчётливо видны подрезания углов, что и требовалось выявить.
P.S.
Что-то не нашёл, как соединить отрезки в контур…
Цитата: Николай от 19.02.16, 15:49:50
Отчётливо видны подрезания углов, что и требовалось выявить.
Конфликт радиусов кривизны базовой линии (переменная величина вдоль линии) и расстояния до эквидистантного контура. Очевидно же…
- Форум пользователей ПО АСКОН
-
►
Профессиональные вопросы -
►
Раздел с ограниченным доступом -
►
2D: черчение и оформление -
►
Как вычислить эквидистанту?
Доброго всем.
Уважаемые форумчане столкнулся с такой проблемой.
есть 2 окружности R500 и R400 с известными центрами. к ним проведена касательная.
Контур задан из т1, лежащей на окружности R500 в точку 2 на R400. T3 и T4 — точки касания прямой и окружностей.
беда в том, что при обработке на станке в этих местах происходит «преломление» контура. На выходе видим ситуацию как на картинке в красном кружке. причем ситуация имеет место в обеих точках перехода.
вот выдержка из программы
N1810 G0 X200 Z514.494
N1820 G1 G41 X197.3 Z514.494 F0.45 ;подход с коррекцией в Т1
N1821 G3 X183.357 Z619.282 CR=550 F0.3 ;R550 в Т3
N1880 G1 X166.26 Z1093.591 F0.45 ;конус в Т4
N1881 G3 X166 Z1108 CR=400 ;R400 в Т2
N1860 G40 X210 F2
полное впечатление, что при расчете траектории станок не может дотянуться заданным радиусом в конечную точку окружности и смещает ее центр. Отсюда и происходит зарез.
пробовал программировать с указанием центра окружности
N1810 G0 X200 Z514.494
N1820 G1 G41 X197.3 Z514.494 F0.45 ;подход с коррекцией в Т1
N1821 G3 X183.357 Z619.282 I=AC(639.095) K=AC(733) F0.3 ;R550 в Т3
N1880 G1 X166.26 Z1093.591 F0.45 ;конус в Т4
N1881 G3 X166 Z1108 I=AC(566) K=AC(1108) ;R400 в Т2
N1860 G40 X210 F2
получаю ошибку «Ошибка конечной точки окружности».
в общем «концов» пока найти не могу. С этой стойкой мало общался, может чего не так делаю? помогите чем можете))
Токарный ЧПУ Sinumerik 840D
Расчёт эквидистантного
контура.
Эквидистанта –
кривая равноудалённая от другой кривой.


r
траектория
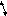
x
хэ‘
Эквидистантный
контур состоит из кривых параллельных
кривым основного программного контура
и представляет собой геометрическое
место точек, равноудалённых от основного
контура.
Здесь
r –
это, например
радиус фрезы rф.
Для
прямой: хэ
= х0
r
sin
уэ
= у0
r
cos
dy
где
= arctg
— угол
наклона касательной (в точке (х0,
у0)).
dx
или,
так как dx/dy = tg
= k = const , то
хэ
= х0
r
k/1+k2
если
F(x0,
y0)
– прямая
____
то F(xэ,
уэ)
– так же прямая.
уэ
= у0
r
k/1+k2
«+»
– при внутренней обработке.
«-»
— при наружной обработке.
Для
кривых 2 – го порядка.
F(x, y) = 0
F(x)
Xэ
= X0
r
cos ( arctg )
F(x)
F(x)
Yэ
= Y0
r sin ( arctg )
, где
F(x)
F
F
—
частные
производные.
х
у
r
– условный
радиус инструмента.
Если
программный контур является прямой или
окружностью, то расчёт эквидистанты
прост.
Если
же при сопряжении участков в контуре
имеются изломы, то расчёт усложняется.
Эквидистанта
эллипса является кривой 8 – го порядка,
расчёт которой затруднителен.
Расчёт эквидистанты
при сопряжении 2-х прямых.
Х


L1
L2

A
– точка
сопряжения L1
и L2.
A’
– точка
сопряжения эквидистанты.
Для
упрощения расчётов повернём исходный
контур на угол
относительно точки А.
Из
рассматриваемого
АСВ и
ВДЕ получим выражение для смещений
точки А.
у0
= z

Д

А
В t

H
L2
C
_______
z
/ cos
+ r
ctg
= (r L2
r
L2
– H2)/H
где
«+» — если
— острый
«-»
— если
— тупой.
Условие
для определения остроты угла :
если
L <
L0
то
— острый,
L
> L0
то
— тупой.
________
где
L0
=
L12
+ L22
_______________________
L
= (Х1
— Х2)2
+ (Y1
— Y2)2
В
ЧПУ задача расчёта эквидистанты может
решаться:
-
На
этапе подготовки УП. -
В
процессе функционирования УЧПУ (то
есть в реальном масштабе времени).
1
способ) Не требует введения в устройство
ЧПУ дополнительных алгоритмов и программ
и применяется при подготовке УП для
обработки сложных объёмных деталей на
многокоординатных станках, то есть
когда алгоритм расчёта эквидистанты
гораздо сложнее алгоритмов интерполяции
(эквидистантный контур рассчитывается
на внешней ЭВМ).
2
способ) Позволяет реализовывать
безэквидистантное программирование
станков. Он предполагает программную
реализацию алгоритмов автоматического
расчёта эквидистанты и коррекции УП
непосредственных устройств ЧПУ.
Безэквидистантное
программирование позволяет: обрабатывать
сопряжённые детали по одной УП;
использовать не верный инструмент
(важен тип);
производить черновую и чистовую обработку
по одной программе;
повышать точность обработки за счёт
коррекции, расчёт эквидистанты по
реальному размеру инструмента, а также
с учётом реального износа инструмента.
Управление контурной
скоростью.
По технологическим
причинам в системе ЧПУ требуется
поддержание постоянства контурной
скорости в каждой точке программирования
траектории.
Основное
содержание этой задачи в разложении
вектора скорости на составляющие в
декартовой системе координат:
а)
Для прямой.
Vy

Vx
b

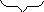
= VkTkcos(arctg(b/a))
= Lтcos
Lт
Vy
= VkTksin(arctg(b/a))
= Lтsin
a
Vx
= L
_____
_____
a2
+ b2
b
Vy
= Lт
______
______
a2
b2
Vk
– контурная
скорость.
Тк
– время интерполяционного цикла.
видно,
что Vx
= const
Vy
= const
б)
Для окружности.
Vk


у)
Vx
R
C(x,y)
Vkt
Vx
=
X
________
Xc2
+ Yc2
Vkt
Vy
=
Y
_______
Хс2+Yc2
где
t
– время
пересчёта Vx,
Vy.
Устройства
ЧПУ целесообразно для расчёта и коррекции
эквидистанты, используются те же
алгоритмы, что и при решении интерполяционных
задач (любые из методов 4-х групп
рассмотренных ранее) вводя соответствующие
начальные условия.
Динамика контурных
систем ЧПУ.
Основные
показатели СЧПУ:
-
Быстродействие
– для сокращения времени на холостые
перемещения в позиционных режимах. Это
важно для станков с большим количеством
перемещений, скоростей перемещений 20
м/мин
и более.
В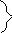
разгона
tразгона
tторможения
надо снижать
Быстродействие
ограничивается прочностными
характеристиками механизмов, динамикой
контуров положения приводов.
-
Точность
– оценивается величиной контурной
ошибки, при воспроизведении
устройств программной траектории д.
б. в
минимуме
=0.
Отсутствие
установленных ошибок при позиционировании.
Точность
обеспечивается:
а)
Диапазоном регулирования по скорости
Дc0
=
10000 и более.
б)
Введением астатизма в алгоритм
управления.
в)
Использование комбинированного
управления.
г)
Качество переходных процессов. Требуется
обеспечить
отсутствие
перерегулирования G = 0%, однако возникают
скоростные
ошибки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4. Аппроксимация контура (при необходимости). Аппроксимация
— это представление сложного геометрического элемента участками более простых
геометрических элементов. Например, линейная аппроксимация дуги окружности —
это замена её участками прямых линий. Необходимость выполнения аппроксимации
определяется типом интерполятора имеющегося в системе управления данного
оборудования. Интерполятор — это устройство, которое обеспечивает перемещение
инструмента относительно детали из одной опорной точки в другую в соответствии
с законом, заложенным в него. Интерполяторы бывают линейными или
линейно-круговыми. Если интерполятор линейный, весь контур детали, а,
следовательно, и эквидистанту, необходимо представить только участками прямых
линий. Расчёт координат промежуточных опорных точек выполнится с учётом радиуса
дуги и допуском на аппроксимацию, который может составлять одну треть от
допуска на обработку. Если интерполятор линейно-круговой, траектория движения
инструмента может включать как участки прямых линий, так и дуги окружностей.
18
Пример аппроксимация дуги участками прямых линий (рис. 2.3.). При
наличие в системе управления только линейного интерполятора, криволинейные
участки обрабатываемого контура, в частности дуги окружностей, приходится
аппроксимировать участками прямых линий. В этом случае можно использовать
следующие рекомендации.
Рис. 2.3. Аппроксимация контура окружности ломаной линией и
построение траектории движения инструмента при фрезеровании выпуклого (а) и
вогнутого (б) контуров.
Промежуточные опорные точки на дуге определяются для каждого отрезка ломаной
линии, которой аппроксимируется дуга окружности. При фрезеровании плоского
контура, очерченного дугами окружностей, можно выделить два характерных случая:
обработка выпуклого контура (рис. 2.3. а) и обработка вогнутого контура (рис.
2.3 б). Контур имеет номинальный радиус R при
одностороннем расположении поля допуска. При обработке выпуклого контура
траектория движения центра фрезы выбирается такой, при которой фреза формирует
поверхность с размером, соответствующим середине поля допуска Δ на обработку.
Величина этого среднего размера Rc = R +Δ/2. Так как допуск на
аппроксимацию не должен превышать величины δ= (0,1—0,3)Δ, то заменяющая ломаная
линия должна уложиться в круговую полосу шириной ± δ/2 (от радиуса Rc — δ/2 до радиуса Rc
+ δ/2). Как следует из рис. 2.3 а, в этом случае косинус половины
центрального угла одного звена ломаной линии равен:
19
Тогда длина одного звена ломаной линии на обработанной
поверхности (величина огранки) определится так:
Соответственно длина одного звена ломаной траектории центра
фрезы (расстояние между соседними опорными точками) будет равна:
где Rф—радиус фрезы.
При обработке вогнутого контура с номинальным радиусом R, в случае одностороннего расположения поля допуска Δ
(см. рис. 2.3 б) радиус фрезы Rф должен быть
меньше радиуса обрабатываемого контура. При условиях, аналогичных тем, которые
были приняты в предыдущем случае, косинус половины центрального угла одного
звена ломаной траектории движения центра фрезы определяется по формуле:
Длина
звена ломаной траектории фрезы
5. Заполнение расчётных таблиц. Следует иметь в
виду, что координаты опорных точек, рассчитанные для записи управляющей
программы, могут отображаться в абсолютной системе отсчёта, когда все размеры
задаются от одной, единой базы, или в относительной системе отсчёта, когда
следующая опорная точка задаётся от предыдущей опорной точки, (эта система
записи координат называется иногда «запись по приращениям»). Примеры
представления размеров в абсолютной и в относительной системе координат
показаны на рис. 2.4.
20
Рис. 2.4. Примеры представления размеров детали:
а) в абсолютной системе координат;
б) в относительной системе координат (по
приращению).
В процессе расчёта опорных точек накапливается большой
объём информации: координаты опорных точек, рассчитанные в абсолютной системе
отсчёта (Таблица 2.1), а, при необходимости, пересчитанные в относительную
систему отсчёта (Таблица 2.2); координаты центра окружностей (Таблица 2.3);
параметры круговой интерполяции I, G, K (Таблица 2.4) и
т. п. Для лучшей организации этой информации, вся она заносится в таблицы,
примеры которых представлены ниже.
(Таблица 2.1)
Координаты опорных точек на эквидистанте
в
абсолютной системе отсчёта.
|
Опорная точка |
X |
Y |
Опорная точка |
X |
Y |
|
О |
0 |
0 |
9 |
229 |
120 |
|
Твх. |
-9 |
130 |
10 |
206,75 |
91,8 |
|
1 |
-9 |
145 |
11 |
117,67 |
79,73 |
|
2 |
25 |
179 |
12 |
111,91 |
75,88 |
|
3 |
54,2 |
162,42 |
13 |
79,41 |
15,88 |
|
4 |
54,92 |
161,94 |
14 |
60 |
6 |
|
5 |
182,78 |
143,67 |
15 |
37,7 |
21,13 |
|
6 |
182,92 |
143,66 |
16 |
-6,59 |
132,43 |
|
7 |
183,49 |
143,84 |
17 |
-9 |
145 |
|
8 |
200 |
149 |
Твых. = 18 |
-9 |
160 |
21
(Таблица 2.2)
Координаты опорных точек на эквидистанте в относительной
системе отсчёта, т.е. координаты i-ой точки, относительно (i-1)-ой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.