При передаче по каналу связи информация
подвергается воздействию различного
рода помех: широко известные флуктуационные,
гармонические и импульсные помехи.
Флуктуационная помехапредставляет
собой напряжение, меняющееся во
времени случайным образом (рис. 6.5,а).
Причина появления ее—тепловые шумы
линии, элементов аппаратуры и т. д.
Гармоническая помеха (рис. 6.5,б)
приближенно описывается синусоидальным
колебанием:Uпом
=Vsin(t+).
Эти помехи возникают, как правило, в
самой аппаратуре из-за паразитного
проникновения в канал различных несущих
колебаний.
.
Рис. 6.5. Различные виды помех
Импульсной
помехойназывается помеха, пиковое
значение которой соизмеримо с амплитудой
полезного сигнала или превышает ее.
Типичный вид одиночной импульсной
помехи показан на рис. 6.5,в.Импульсные
помехи обычно появляются пачками, по
несколько помех в пачке (рис. 6.5,г).Характер процесса появления пачек во
времени и отдельных помех внутри одной
пачки существенно изменяется от канала
к каналу и даже в одном канале в различные
периоды времени.
По типу
источников импульсные помехи можно
разделить на три основные группы:
естественного происхождения,
промышленные, возникающие в аппаратуре.
К
помехам естественного происхожденияв первую очередь следует отнести
атмосферные помехи, основным источником
которых являются грозовые разряды,
хаотически возникающие во многих
участках земного шара. Каждый такой
разряд создает несколько мощных
импульсов электрического тока.
Источники
промышленных помехмногочисленны.
К ним относятся различные коллекторные
электрические машины, двигатели,
аппараты, линии электропередачи,
электросварка.
Кроме классификации
помех по характеру воздействия на
передаваемое сообщение, их классифицируют
по поведению во времени. Флуктуационные
и гармонические помехи действуют
непрерывно в течение длинных отрезков
времени. Их можно назвать постоянно
действующими. В отличие от них
импульсные помехи действуют на сигнал
только в отдельные моменты. Помехи
такого типа называютсясосредоточенными
во времени.
В
результате действия помех в канале
связи информация, передаваемая по
этому каналу, искажается, принятое
сообщение будет отличаться от переданного,
т. е. сообщение принимается с ошибкой.
Возникновение ошибок — случайный
процесс, и предсказать появление их
заранее, до эксперимента, можно только
статистически, т. е. указывая вероятности
того, что ошибка либо произойдет, либо
нет. При этом вероятность ошибки может
не зависеть от значения передаваемого
элементарного символа 0 или 1, т. е.
среди неправильно принятых сигналов
одинаково часто встречаются как 1, так
и 0. Канал связи с такими ошибками
называется симметричным каналом.
Условно такой канал показан на рис. 6.6.
Здесь входными являются символы 0 и 1.
Возможными выходными символами также
будут 0 и 1. Вероятностиp1,
Р2определяют вероятность
неискаженной передачи символов 0 и 1
соответственно, а вероятности (1—Р1),
(1—Р2)—вероятность трансформации
символов. При Р1=Р2 канал
является симметричным.
Рис. 6.6.. Канал с искажениями. Рис.
6.7. Канал со стиранием
Другим
примером канала связи с помехами может
служить так называемый канал со
стиранием (рис. 6.7). На вход такого
канала поступают двоичные символы,
которые с вероятностью Р передаются
правильно и с вероятностью (1—Р)
стираются (стертые символы условно
обозначены через х).Таким образом,
если на вход канала поступают символы
0 и 1, то на выходе получаются три различных
символа: 0, 1,x.В этом
канале предполагается отсутствие
трансформации символов. Такое предположение
на практике не всегда оправдывается.
Поэтому используется модель стирающего
канала, в которой допустима трансформация
символов (рис. 6.8).
Рис.6.8.
Канал со стиранием и трансформацией
символов
Если
условия передачи ряда последовательных
символов не зависят один от другого, то
такой канал называется каналом без
памяти. Если же условия передачи
символа зависят от предыдущих состояний
канала, канал называетсяканалом с
памятью.
Итак,
в результате действия помех в каналах
связи при передаче сообщений возникают
ошибки. В зависимости от количества
разрядов передаваемой последовательности,
принимаемых с ошибками, различают
однократные, двукратные и т. д.
ошибки. Кроме этого имеют местопачки
ошибок (участок последовательности,
начинающийся и заканчивающийся ошибочно
принятыми элементами. Внутри пачки
могут быть и правильно принятые элементы).
Знание характера распределения ошибок
в канале связи позволяет правильно
выбрать метод передачи сообщений по
данному каналу.
Если
ошибки, возникающие в передаваемом
сообщении, происходят независимо одна
от другой, их распределение подчиняется
биномиальному закону. В этом случае
предполагается, что вероятность поражения
каждого символа Pэ
передаваемой последовательности
является величиной постоянной. Тогда
вероятность безошибочного его приема
— (1—Pэ), а вероятность
распределения ошибок при передаче
последовательности изn
символов
P=CinPiэ
(1-Pэ)n-i,
где
i—кратность ошибки в
последовательности, 0in;Cin—
число сочетаний изnпоi,
Cin=[n(n-1)(n-2)…(n-i+1)]/i!
Каждый
член суммы в формуле (206) характеризует
вероятность появления i‑кратной
ошибки в передаваемой последовательности.
Соседние файлы в папке конспект ТИ
- #
23.02.20151.26 Mб454.doc
- #
- #
- #
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
Когда
информация передается между различными
частями компьютера, или с Земли на Луну
и обратно, или просто оставляется на
запоминающем устройстве, существует
вероятность того, что полученный двоичный
код не тождественней исходному коду.
Частицы пыли или жира на магнитном
носителе или сбой схемы могут привести
к неправильной записи или к неправильному
чтению данных. Кроме того, фоновое
излучение некоторых устройств может
привести к изменению кода, хранящегося
в оперативной памяти машины.
Для
решения таких проблем было разработано
большое количество методов кодирования,
позволяющих обнаружить и даже исправить
ошибки. Сегодня эти методы включены во
внутренние составляющие вычислительных
машин и не видны пользователю. Тем не
менее их наличие является важным и
составляет значительную часть научных
исследований. Поэтому мы рассмотрим
некоторые из этих методов, обеспечивающих
надежность современного компьютерного
оборудования.
Контрольный
разряд четности. Простой метод обнаружения
ошибок основывается на том принципе,
что если известно, что обрабатываемый
двоичный код должен содержать нечетное
число единиц, а полученный код содержит
четное число единиц, то произошла ошибка.
Для того чтобы использовать этот принцип,
нам нужна система, в которой каждый код
содержит нечетное число единиц. Этого
легко достичь, добавив дополнительный
разряд, контрольный разряд соответствия
(parity bit), на место старшего разряда.
(Следовательно, каждый 8-битовый код
ASCII станет 9-битовым, а 16-битовой
дополнительный код станет 17-битовым.)
В каждом случае мы присваиваем этому
разряду значение 1 или 0, так чтобы весь
код содержал нечетное число единиц.
Например, ASCII-код буквы А становится
101000001 (контрольный разряд четности 1), а
код буквы F становится 001000110 (контрольный
разряд четности 0) (рис. 1.28). Хотя 8-битовый
код А содержит четное число единиц, а
8-битовый код F — нечетное, 9-битовый код
этих символов содержит нечетное
количество единиц. Теперь, когда мы
модифицировав нашу систему кодирования,
код с четным числом единиц будет означать,
что произошла ошибка и что обрабатываемый
двоичный код — неправильный.
Рисунок
1 — ASCII-коды букв А и F, измененные для
проверки на нечетность
Система
контроля, описанная выше, называется
контролем нечетности (odd parity), так как
мы построили нашу систему таким образом,
что каждый код содержит нечетное число
единиц. Существует также метод-антипод
— контроль четности (even parity). Б таких
системах каждый двоичный код содержит
четное число единиц, и, следовательно,
об ошибке говорит появление кода с
нечетным числом единиц.
Сегодня
использование контрольных разрядов
четности в оперативной памяти компьютера
довольно распространено. Хотя мы
говорили, что ячейка памяти машин состоит
из восьми битов, на самом деле она состоит
из девяти битов, один из которых
используется в качестве контрольного
бита. Каждый раз, когда 8-битовый код
передается в запоминающую схему, схема
добавляет контрольный бит соответствия
и сохраняет получающийся 9-битовый код.
Если код уже был получен, схема проверяет
его на четность. Если в нем нет ошибки,
память убирает контрольный бит и
возвращает 8-битовый код. В противном
случае память возвращает восемь
информационных битов с предупреждением
о том, что возвращенный код может не
совпадать с исходным кодом, помещенным
в память.
Длинные
двоичные коды часто сопровождает набор
контрольных битов четности, которые
образуют контрольный байт. Каждый разряд
в байте соответствует определенной
последовательности битов, находящейся
в коде. Например, один контрольный бит
может соответствовать каждому восьмому
биту кода, начиная с первого, а другой
может соответствовать каждому восьмому
биту, начиная со второго. В этом случае
больше вероятность обнаружить скопление
ошибок в какой-либо области исходного
кода, поскольку они будут находиться в
области действия нескольких контрольных
битов четности. Разновидностью
контрольного байта являются такие схемы
для обнаружения ошибок, как контрольная
сумма и циклический избыточный код.
Коды
с исправлением ошибок. Хотя использование
контрольного разряда четности и позволяет
обнаружить ошибку, но не дает возможности
исправить ее. Многие удивляются тому,
что коды с исправлением ошибок построены
таким образом, что с их помощью можно
не только найти ошибку, но и исправить
ее. Интуиция подсказывает нам, что мы
не сможем исправить ошибку в полученном
сообщении, не зная информацию, которая
в нем содержится. Однако простой
корректирующий код представлен на рис.
2.
Рисунок
2 – Коды с исправлением ошибок
Для
того чтобы понять, как работает этот
код, определим сначала расстояние
Хемминга (Hamming distance) между двумя кодами
как число различающихся разрядов. Это
расстояние названо в честь Р. В. Хемминга
(R. W. Hamming), который первым стал исследовать
коды с исправлением ошибок, поняв
ненадежность релейных машин в 40-х годах
XX века. Например, расстояние Хемминга
между кодами символов А и В равно четырем
(см. рис. 1.29), а расстояние Хемминга между
В и С равно трем. Важное свойство этой
системы кодирования состоит в том, что
расстояние Хемминга между любыми двумя
кодами больше или равно трем. Поэтому
если один бит в коде будет изменен,
ошибку можно будет обнаружить, так как
результат не будет допустимым кодом.
(Для того чтобы код выглядел, как другой
допустимый код, мы должны изменить по
меньшей мере три бита.)
Кроме
того, если появится ошибка в коде (см.
рис. 1.29), мы сможем понять, как выглядел
исходный код. Расстояние Хемминга между
измененным кодом и исходным будет равно
единице, а между ним и другими допустимыми
кодами — по меньшей мере двум. Для того
чтобы расшифровать сообщение, мы просто
сравниваем каждый полученный код с
кодами в системе до тех пор, пока не
найдем код, находящийся на расстоянии,
равном единице, от исходного кода. Это
и будет правильный символ. Например,
предположим, что мы получили код 010100.
Если мы сравним его с другими кодами,
то получим таблицу расстояний (рис. 3).
Следовательно, мы можем сделать вывод,
что был послан символ D, так как между
его кодом и полученным кодом наименьшее
расстояние.
Рисунок
3 – Расшифровка кодов 010100 с использованием
кодов из рисунка 2
Вы
увидите, что использование этой системы
(коды на рис. 2) позволяет обнаружить до
двух ошибок в одном коде и исправить
одну. Если мы создадим систему, в которой
расстояние Хемминга между любыми двумя
кодами будет равно самое меньшее пяти,
мы сможем обнаружить до четырех ошибок
в одном коде и исправить две. Конечно,
создание эффективной системы кодов с
большими расстояниями Хемминга
представляет собой непростую задачу.
В действительности, она является частью
раздела математики, который называется
алгебраической теорией кодов и входит
в линейную алгебру и теорию матриц.
Методы
исправления ошибок широко применяются
для того, чтобы повысить надежность
компьютерного оборудования. Например,
они часто используются ii дисководах
для магнитных дисков большой емкости,
чтобы уменьшить вероятность того, что
изъян на магнитной поверхности диска
разрушит данные. Кроме того, главное
различие между форматом первоначальных
компакт-дисков, которые использовались
для звукозаписей, и более поздним
форматом, который используется для
хранения данных в компьютере, состоит
в степени исправления ошибок. Формат
CD-DA включает в себя возможности исправления
ошибок, которые сводят частоту появления
ошибок к одной ошибке на два компакт-диска.
Этого достаточно для звукозаписи, но
компании, использующие компакт-диски
для поставки программного обеспечения
покупателям, сказали бы, что наличие
дефектов в 50 процентах дисков — слишком
много. Поэтому в компакт-дисках для
хранения данных применяются дополнительные
возможности исправления ошибок,
сокращающие вероятность появления
ошибки до одной ошибки на 20 000 дисков.
Соседние файлы в папке Комплект Информатика
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 5
Проверка правильности передачи данных
- Причины возникновения ошибок
- Классификация методов защиты от ошибок
- Групповые методы
- мажоритарный
- блок с количественной характеристикой
- Помехоустойчивое кодирование
- Системы передачи с обратной связью
- решающая
- информационная
- Групповые методы
Проблема обеспечения безошибочности (достоверности) передачи информации в
сетях имеет очень большое значение. Если при передаче обычной телеграммы в
тексте возникает ошибка или при разговоре по телефону слышен треск, то в
большинстве случаев ошибки и искажения легко обнаруживаются по смыслу. Но при
передаче данных одна ошибка (искажение одного бита) на тысячу переданных
сигналов может серьезно отразиться на качестве информации.
Существует множество методов обеспечения достоверности передачи информации
(методов защиты от ошибок), отличающихся по используемым для их реализации
средствам, по затратам времени на их применение на передающем и приемном
пунктах, по затратам дополнительного времени на передачу фиксированного объема
данных (оно обусловлено изменением объема трафика пользователя при реализации
данного метода), по степени обеспечения достоверности передачи информации.
Практическое воплощение методов состоит из двух частей — программной и
аппаратной. Соотношение между ними может быть самым различным, вплоть до почти
полного отсутствия одной из частей. Чем больше удельный вес аппаратных средств
по сравнению с программными, тем при прочих равных условиях сложнее
оборудование, реализующее метод, и меньше затрат времени на его реализацию, и
наоборот.
Причины возникновения ошибок
Выделяют две основные причины возникновения ошибок при передаче информации в
сетях:
- сбои в какой-то части оборудования сети или возникновение
неблагоприятных объективных событий в сети (например, коллизий при
использовании метода случайного доступа в сеть). Как правило, система
передачи данных готова к такого рода проявлениям и устраняет их с помощью
предусмотренных планом средств; - помехи, вызванные внешними источниками и атмосферными явлениями. Помехи
— это электрические возмущения, возникающие в самой аппаратуре или
попадающие в нее извне. Наиболее распространенными являются флуктуационные
(случайные) помехи. Они представляют собой последовательность импульсов,
имеющих случайную амплитуду и следующих друг за другом через различные
промежутки времени. Примерами таких помех могут быть атмосферные и
индустриальные помехи, которые обычно проявляются в виде одиночных импульсов
малой длительности и большой амплитуды. Возможны и сосредоточенные помехи в
виде синусоидальных колебаний. К ним относятся сигналы от посторонних
радиостанций, излучения генераторов высокой частоты. Встречаются и смешанные
помехи. В приемнике помехи могут настолько ослабить информационный сигнал,
что он либо вообще не будет обнаружен, либо будет искажен так, что «единица»
может перейти в «нуль», и наоборот.
Трудности борьбы с помехами заключаются в беспорядочности, нерегулярности и в
структурном сходстве помех с информационными сигналами. Поэтому защита
информации от ошибок и вредного влияния помех имеет большое практическое
значение и является одной из серьезных проблем современной теории и техники
связи.
Классификация методов защиты от ошибок
Среди многочисленных методов защиты от ошибок выделяются три группы методов:
групповые методы, помехоустойчивое кодирование и методы защиты от ошибок в
системах передачи с обратной связью.
Групповые методы
Из групповых методов получили широкое применение мажоритарный метод,
реализующий принцип Вердана, и метод передач информационными блоками с
количественной характеристикой блока.
- Мажоритарный метод
- Суть этого метода, давно и широко используемого в телеграфии,
состоит в следующем. Каждое сообщение ограниченной длины передается
несколько раз, чаще всего три раза. Принимаемые сообщения запоминаются,
а потом производится их поразрядное сравнение. Суждение о правильности
передачи выносится по совпадению большинства из принятой информации
методом «два из трех». Например, кодовая комбинация 01101 при
трехразовой передаче была частично искажена помехами, поэтому приемник
принял такие комбинации: 10101, 01110, 01001. В результате проверки по
отдельности каждой позиции правильной считается комбинация 01101.- Передача блоками с количественной характеристикой
- Этот метод также не требует перекодирования информации. Он
предполагает передачу данных блоками с количественной характеристикой
блока. Такими характеристиками могут быть: число единиц или нулей в
блоке, контрольная сумма передаваемых символов в блоке, остаток от
деления контрольной суммы на постоянную величину и др. На приемном
пункте эта характеристика вновь подсчитывается и сравнивается с
переданной по каналу связи. Если характеристики совпадают, считается,
что блок не содержит ошибок. В противном случае на передающую сторону
поступает сигнал с требованием повторной передачи блока. В современных
телекоммуникационных вычислительных сетях такой метод получил самое
широкое распространение.
Помехоустойчивое (избыточное) кодирование
Этот метод предполагает разработку и использование корректирующих
(помехоустойчивых) кодов. Он применяется не только в телекоммуникационных сетях,
но и в ЭВМ для защиты от ошибок при передаче информации между устройствами
машины. Помехоустойчивое кодирование позволяет получить более высокие
качественные показатели работы систем связи. Его основное назначение заключается
в обеспечении малой вероятности искажений передаваемой информации, несмотря на
присутствие помех или сбоев в работе сети.
Существует довольно большое количество различных помехоустойчивых кодов,
отличающихся друг от друга по ряду показателей и прежде всего по своим
корректирующим возможностям.
К числу наиболее важных показателей корректирующих кодов относятся:
- значность кода n, или длина
кодовой комбинации, включающей информационные символы (m)
и проверочные, или контрольные, символы (К):
n = m
+ K
(Значения
контрольных символов при кодировании определяются путем контроля на четность
количества единиц в информационных разрядах кодовой комбинации. Значение
контрольного символа равно 0, если количество единиц будет четным, и равно 1
при нечетном количестве единиц); - избыточность кода Кизб,
выражаемая отношением числа контрольных символов в кодовой комбинации к
значности кода: Кизб = К/
n;
- корректирующая способность кода Ккс, представляющая
собой отношение числа кодовых комбинаций L,
в которых ошибки были обнаружены и исправлены, к общему числу переданных
кодовых комбинаций M в фиксированном объеме
информации: Ккс =
L/ M
Выбор корректирующего кода для его использования в данной компьютерной сети
зависит от требований по достоверности передачи информации. Для правильного
выбора кода необходимы статистические данные о закономерностях появления ошибок,
их характере, численности и распределении во времени. Например, корректирующий
код, обнаруживающий и исправляющий одиночные ошибки, эффективен лишь при
условии, что ошибки статистически независимы, а вероятность их появления не
превышает некоторой величины. Он оказывается непригодным, если ошибки появляются
группами. При выборе кода надо стремиться, чтобы он имел меньшую избыточность.
Чем больше коэффициент Кизб, тем менее эффективно используется
пропускная способность канала связи и больше затрачивается времени на передачу
информации, но зато выше помехоустойчивость системы.
В телекоммуникационных вычислительных сетях корректирующие коды в основном
применяются для обнаружения ошибок, исправление которых осуществляется путем
повторной передачи искаженной информации. С этой целью в сетях используются
системы передачи с обратной связью (наличие между абонентами дуплексной связи
облегчает применение таких систем).
Системы передачи с обратной связью
Системы передачи с обратной связью делятся на системы с решающей обратной
связью и системы с информационной обратной связью.
- Системы с решающей обратной связью
- Особенностью систем с решающей обратной связью (систем с
перезапросом) является то, что решение о необходимости повторной передачи
информации (сообщения, пакета) принимает приемник. Здесь обязательно применяется
помехоустойчивое кодирование, с помощью которого на приемной станции
осуществляется проверка принимаемой информации. При обнаружении ошибки на
передающую сторону по каналу обратной связи посылается сигнал перезапроса, по
которому информация передается повторно. Канал обратной связи используется также
для посылки сигнала подтверждения правильности приема, автоматически
определяющего начало следующей передачи.- Системы с информационной обратной связью
- В системах с информационной обратной связью передача информации
осуществляется без помехоустойчивого кодирования. Приемник, приняв информацию по
прямому каналу и зафиксировав ее в своей памяти, передает ее в полном объеме по
каналу обратной связи передатчику, где переданная и возвра0щенная информация
сравниваются. При совпадении передатчик посылает приемнику сигнал подтверждения,
в противном случае происходит повторная передача всей информации. Таким образом,
здесь решение о необходимости повторной передачи принимает передатчик.
Обе рассмотренные системы обеспечивают практически одинаковую достоверность,
однако в системах с решающей обратной связью пропускная способность каналов
используется эффективнее, поэтому они получили большее распространение.
Сайт управляется системой uCoz
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной 


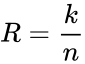
Если исходные 
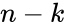
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует 



Это значит, что операция кодирования соответствует умножению исходного 
Пусть 


Минимальное расстояние и корректирующая способность
-
Основная статья: Расстояние Хемминга
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 
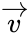


Минимальное расстояние Хемминга 
, округляем «вниз», так чтобы
.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 

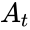



Таким образом получив искажённый код из 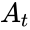

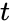
Поясним на примере. Предположим, что есть два кодовых слова 










Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 





Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 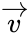
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 


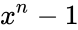
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному 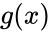
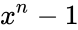
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 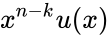
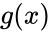
Таким образом, вид полинома 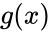
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | 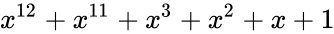
|
| CRC-16 | 16 | 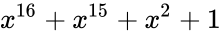
|
| CRC-CCITT | 16 | 
|
| CRC-32 | 32 | 
|
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома 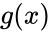
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды
Файл:ECC NASA standard coder.png
Свёрточный кодер (
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
-
Основная статья: Граница Хэмминга
Пусть имеется двоичный блоковый 
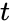
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки
Имеется викиучебник по теме:
Обнаружение и исправление ошибок
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обнаружение и исправление ошибок. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Проверка правильности передачи данных
Проблема обеспечения безошибочности (достоверности) передачи информации в сетях имеет очень большое значение. Если при передаче обычной телеграммы в тексте возникает ошибка или при разговоре по телефону слышен треск, то в большинстве случаев ошибки и искажения легко обнаруживаются по смыслу. Но при передаче данных одна ошибка (искажение одного бита) на тысячу переданных сигналов может серьезно отразиться на качестве информации.
Существует множество методов обеспечения достоверности передачи информации (методов защиты от ошибок), отличающихся по используемым для их реализации средствам, по затратам времени на их применение на передающем и приемном пунктах, по затратам дополнительного времени на передачу фиксированного объема данных (оно обусловлено изменением объема трафика пользователя при реализации данного метода), по степени обеспечения достоверности передачи информации. Практическое воплощение методов состоит из двух частей — программной и аппаратной. Соотношение между ними может быть самым различным, вплоть до почти полного отсутствия одной из частей. Чем больше удельный вес аппаратных средств по сравнению с программными, тем при прочих равных условиях сложнее оборудование, реализующее метод, и меньше затрат времени на его реализацию, и наоборот.

Причины возникновения ошибок
Выделяют две основные причины возникновения ошибок при передаче информации в сетях:
- сбои в какой-то части оборудования сети или возникновение неблагоприятных объективных событий в сети (например, коллизий при использовании метода случайного доступа в сеть). Как правило, система передачи данных готова к такого рода проявлениям и устраняет их с помощью предусмотренных планом средств;
- помехи, вызванные внешними источниками и атмосферными явлениями. Помехи — это электрические возмущения, возникающие в самой аппаратуре или попадающие в нее извне. Наиболее распространенными являются флуктуационные (случайные) помехи. Они представляют собой последовательность импульсов, имеющих случайную амплитуду и следующих друг за другом через различные промежутки времени. Примерами таких помех могут быть атмосферные и индустриальные помехи, которые обычно проявляются в виде одиночных импульсов малой длительности и большой амплитуды. Возможны и сосредоточенные помехи в виде синусоидальных колебаний. К ним относятся сигналы от посторонних радиостанций, излучения генераторов высокой частоты. Встречаются и смешанные помехи. В приемнике помехи могут настолько ослабить информационный сигнал, что он либо вообще не будет обнаружен, либо будет искажен так, что «единица» может перейти в «нуль», и наоборот.
Трудности борьбы с помехами заключаются в беспорядочности, нерегулярности и в структурном сходстве помех с информационными сигналами. Поэтому защита информации от ошибок и вредного влияния помех имеет большое практическое значение и является одной из серьезных проблем современной теории и техники связи.

Классификация методов защиты от ошибок
Среди многочисленных методов защиты от ошибок выделяются три группы методов: групповые методы, помехоустойчивое кодирование и методы защиты от ошибок в системах передачи с обратной связью.
Групповые методы
Из групповых методов получили широкое применение мажоритарный метод, реализующий принцип Вердана, и метод передач информационными блоками с количественной характеристикой блока.
Мажоритарный метод Суть этого метода, давно и широко используемого в телеграфии, состоит в следующем. Каждое сообщение ограниченной длины передается несколько раз, чаще всего три раза. Принимаемые сообщения запоминаются, а потом производится их поразрядное сравнение. Суждение о правильности передачи выносится по совпадению большинства из принятой информации методом «два из трех». Например, кодовая комбинация 01101 при трехразовой передаче была частично искажена помехами, поэтому приемник принял такие комбинации: 10101, 01110, 01001. В результате проверки по отдельности каждой позиции правильной считается комбинация 01101.
Передача блоками с количественной характеристикой Этот метод также не требует перекодирования информации. Он предполагает передачу данных блоками с количественной характеристикой блока. Такими характеристиками могут быть: число единиц или нулей в блоке, контрольная сумма передаваемых символов в блоке, остаток от деления контрольной суммы на постоянную величину и др. На приемном пункте эта характеристика вновь подсчитывается и сравнивается с переданной по каналу связи. Если характеристики совпадают, считается, что блок не содержит ошибок. В противном случае на передающую сторону поступает сигнал с требованием повторной передачи блока. В современных телекоммуникационных вычислительных сетях такой метод получил самое широкое распространение.

Помехоустойчивое (избыточное) кодирование
Этот метод предполагает разработку и использование корректирующих (помехоустойчивых) кодов. Он применяется не только в телекоммуникационных сетях, но и в ЭВМ для защиты от ошибок при передаче информации между устройствами машины. Помехоустойчивое кодирование позволяет получить более высокие качественные показатели работы систем связи. Его основное назначение заключается в обеспечении малой вероятности искажений передаваемой информации, несмотря на присутствие помех или сбоев в работе сети.
Существует довольно большое количество различных помехоустойчивых кодов, отличающихся друг от друга по ряду показателей и прежде всего по своим корректирующим возможностям.
К числу наиболее важных показателей корректирующих кодов относятся:
- значность кода n , или длина кодовой комбинации, включающей информационные символы ( m) и проверочные, или контрольные, символы (К): n = m + K
(Значения контрольных символов при кодировании определяются путем контроля на четность количества единиц в информационных разрядах кодовой комбинации. Значение контрольного символа равно 0, если количество единиц будет четным, и равно 1 при нечетном количестве единиц); - избыточность кода Кизб, выражаемая отношением числа контрольных символов в кодовой комбинации к значности кода: Кизб = К/ n ;
- корректирующая способность кода Ккс, представляющая собой отношение числа кодовых комбинаций L , в которых ошибки были обнаружены и исправлены, к общему числу переданных кодовых комбинаций M в фиксированном объеме информации: Ккс = L / M
Выбор корректирующего кода для его использования в данной компьютерной сети зависит от требований по достоверности передачи информации. Для правильного выбора кода необходимы статистические данные о закономерностях появления ошибок, их характере, численности и распределении во времени. Например, корректирующий код, обнаруживающий и исправляющий одиночные ошибки, эффективен лишь при условии, что ошибки статистически независимы, а вероятность их появления не превышает некоторой величины. Он оказывается непригодным, если ошибки появляются группами. При выборе кода надо стремиться, чтобы он имел меньшую избыточность. Чем больше коэффициент Кизб, тем менее эффективно используется пропускная способность канала связи и больше затрачивается времени на передачу информации, но зато выше помехоустойчивость системы.
В телекоммуникационных вычислительных сетях корректирующие коды в основном применяются для обнаружения ошибок, исправление которых осуществляется путем повторной передачи искаженной информации. С этой целью в сетях используются системы передачи с обратной связью (наличие между абонентами дуплексной связи облегчает применение таких систем).

Системы передачи с обратной связью
Системы передачи с обратной связью делятся на системы с решающей обратной связью и системы с информационной обратной связью.
Системы с решающей обратной связью Особенностью систем с решающей обратной связью (систем с перезапросом) является то, что решение о необходимости повторной передачи информации (сообщения, пакета) принимает приемник. Здесь обязательно применяется помехоустойчивое кодирование, с помощью которого на приемной станции осуществляется проверка принимаемой информации. При обнаружении ошибки на передающую сторону по каналу обратной связи посылается сигнал перезапроса, по которому информация передается повторно. Канал обратной связи используется также для посылки сигнала подтверждения правильности приема, автоматически определяющего начало следующей передачи.
Системы с информационной обратной связью В системах с информационной обратной связью передача информации осуществляется без помехоустойчивого кодирования. Приемник, приняв информацию по прямому каналу и зафиксировав ее в своей памяти, передает ее в полном объеме по каналу обратной связи передатчику, где переданная и возвра0щенная информация сравниваются. При совпадении передатчик посылает приемнику сигнал подтверждения, в противном случае происходит повторная передача всей информации. Таким образом, здесь решение о необходимости повторной передачи принимает передатчик.
Обе рассмотренные системы обеспечивают практически одинаковую достоверность, однако в системах с решающей обратной связью пропускная способность каналов используется эффективнее, поэтому они получили большее распространение.
Источник
Способы контроля правильности передачи данных
Управление правильностью (помехозащищенностью) передачи информации выполняется с помощью помехоустойчивого кодирования. Различают коды, обнаруживающие ошибки, и корректирующие коды, которые дополнительно к обнаружению еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности. Устранение ошибок с помощью корректирующих кодов (такое управление называют Forward Error Control) реализуют в симплексных каналах связи. В дуплексных каналах достаточно применения кодов, обнаруживающих ошибки (Feedback or Backward Error Control), так как сигнализация об ошибке вызывает повторную передачу от источника. Это основные методы, используемые в информационных сетях.
Простейшими способами обнаружения ошибок являются контрольное суммирование, проверка на нечетность. Однако они недостаточно надежны, особенно при появлении пачек ошибок. Поэтому в качестве надежных обнаруживающих кодов применяют циклические коды. Примером корректирующего кода является код Хемминга.
В коде Хемминга вводится понятие кодового расстояния d (расстояния между двумя кодами), равного числу разрядов с неодинаковыми значениями. Возможности исправления ошибок связаны с минимальным кодовым расстоянием dmin. Исправляются ошибки кратности r = ent(dmin–1)/2 и обнаруживаются ошибки кратности dmin–1 (здесь ent означает “целая часть”). Так, при контроле на нечетность dmin=2 и обнаруживаются одиночные ошибки. В коде Хемминга dmin=3. Дополнительно к информационным разрядам вводится L=log2K избыточных контролирующих разрядов, где К – число информационных разрядов, L округляется до ближайшего большего целого значения. L-разрядный контролирующий код есть инвертированный результат поразрядного сложения (т.е. сложения по модулю 2) номеров тех информационных разрядов, значения которых равны 1.
Пример 1. Пусть имеем основной код 100110, т.е. К = 6. Следовательно, L = 3 и дополнительный код равен
010 # 011 # 110= 111,
где # – символ операции поразрядного сложения, и после инвертирования имеем 000. Теперь вместе с основным кодом будет передан и дополнительный. На приемном конце вновь рассчитывается дополнительный код и сравнивается с переданным. Фиксируется код сравнения (поразрядная операция отрицания равнозначности), и если он отличен от нуля, то его значение есть номер ошибочно принятого разряда основного кода. Так, если принят код 100010, то рассчитанный в приемнике дополнительный код равен инверсии от 010 # 110 = 100, т.е. 011, что означает ошибку в третьем разряде.
Пример 2. Основной код 1100000, дополнительный код 110 (результат инверсии кода 110 # 111 =001). Пусть принятый код 1101000, его дополнительный код 010, код сравнения 100, т.е. ошибка в четвертом разряде.
К числу эффективных кодов, обнаруживающих одиночные, кратные ошибки и пачки ошибок, относятся циклические коды (CRC – Cyclic Redundance Code). Они высоконадежны и могут применяться при блочной синхронизации, при которой выделение, например, бита нечетности было бы затруднительно.
Один из вариантов циклического кодирования заключается в умножении исходного кода на образующий полином g(Х), a декодирование – в делении на g(Х). Если остаток от деления не равен нулю, то произошла ошибка. Сигнал об ошибке поступает на передатчик, что вызывает повторную передачу.
Образующий полином есть двоичное представление одного из простых множителей, на которые раскладывается число Xn–1, где Xnобозначает единицу в n-м разряде, n равно числу разрядов кодовой группы. Так, если n=10 и Х=2, то Xn–1=1023=11·93, и если g(X) = 11 или в двоичном коде 1011, то примеры циклических кодов Ai·g(X) чисел Aiв кодовой группе при этом образующем полиноме можно видеть в табл. 2.2.
Основной вариант циклического кода, широко применяемый на практике, отличается от предыдущего тем, что операция деления на образующий полином заменяется следующим алгоритмом: 1) к исходному кодируемому числу А справа приписывается К нулей, где К – число битов в образующем полиноме, уменьшенное на единицу; 2) над полученным числом А(2К) выполняется операция О, отличающаяся от деления тем, что на каждом шаге операции вместо вычитания выполняется поразрядная операция “исключающее ИЛИ”; 3) полученный остаток В и есть CRC – избыточный K-разрядный код, который заменяет в закодированном числе С приписанные справа К нулей, т.е.
На приемном конце над кодом С выполняется операция О. Если остаток не равен нулю, то при передаче произошла ошибка и нужна повторная передача кода А.
Пример 3. Пусть А = 1001 1101, образующий полином 11001.
Так как К = 4, то А(2К)=100111010000. Выполнение операции О расчета циклического кода показано на рис. 2.7.
Рис. 2.7. Пример получения циклического кода
Положительными свойствами циклических кодов являются малая вероятность необнаружения ошибки и сравнительно небольшое число избыточных разрядов.
Общепринятое обозначение образующих полиномов дает следующий пример:
g(X) = Xl6 + Х l2 + Х5+ 1,
что эквивалентно коду 1 0001 0000 0010 0001.
Наличие в сообщениях избыточности позволяет ставить вопрос о сжатии данных, т.е. о передаче того же количества информации с помощью последовательностей символов меньшей длины. Для этого используются специальные алгоритмы сжатия, уменьшающие избыточность. Эффект сжатия оценивают коэффициентом сжатия:
где n – число минимально необходимых символов для передачи сообщения (практически это число символов на выходе эталонного алгоритма сжатия); q – число символов в сообщении, сжатом данным алгоритмом. Так, при двоичном кодировании n равно энтропии источника информации. Часто степень сжатия оценивают отношением длин кодов на входе и выходе алгоритма сжатия.
Наряду с методами сжатия, не уменьшающими количество информации в сообщении, применяются методы сжатия, основанные на потере малосущественной информации.
Сжатие данных осуществляется либо на прикладном уровне с помощью программ сжатия, называемых архиваторами, либо с помощью устройств защиты от ошибок (УЗО) непосредственно в составе модемов.
Очевидный способ сжатия числовой информации, представленной в коде ASCII, заключается в использовании сокращенного кода с четырьмя битами на символ вместо восьми, так как передается набор, включающий только 10 цифр, символы “точка”, “запятая” и “пробел”.
Среди простых алгоритмов сжатия наиболее известны алгоритмы RLE (Run Length Encoding). В них вместо передачи цепочки из одинаковых символов передаются символ и значение длины цепочки. Метод эффективен при передаче растровых изображений, но малополезен при передаче текста.
К методам сжатия относят также методы разностного кодирования, поскольку разности амплитуд отсчетов представляются меньшим числом разрядов, чем сами амплитуды. Разностное кодирование реализовано в методах дельта-модуляции и ее разновидностях.
Предсказывающие (предиктивные) методы основаны на экстраполяции значений амплитуд отсчетов, и если выполнено условие
то отсчет должен быть передан, иначе он является избыточным; здесь Аrи Ар– амплитуды реального и предсказанного отсчетов; d – допуск (допустимая погрешность представления амплитуд).
Иллюстрация предсказывающего метода с линейной экстраполяцией представлена на рис. 2.8. Здесь точками показаны предсказываемые значения сигнала. Если точка выходит за пределы “коридора” (допуска d), показанного пунктирными линиями, то происходит передача отсчета. На рис. 2.8 передаваемые отсчеты отмечены темными кружками в моменты времени t1, t2, t4, t7. Если передачи отсчета нет, то на приемном конце принимается экстраполированное значение.
Рис. 2.8. Предиктивное кодирование
Методы MPEG (Moving Pictures Experts Group) используют предсказывающее кодирование изображений (для сжатия данных о движущихся объектах вместе со звуком). Так, если передавать только изменившиеся во времени пиксели изображения, то достигается сжатие в несколько десятков раз. Методы MPEG становятся мировыми стандартами для цифрового телевидения.
Для сжатия данных об изображениях можно использовать также методы типа JPEG (Joint Photographic Expert Group), основанные на потере малосущественной информации (не различимые для глаза оттенки кодируются одинаково, коды могут стать короче). В этих методах передаваемая последовательность пикселей делится на блоки, в каждом блоке производится преобразование Фурье, устраняются высокие частоты, передаются коэффициенты разложения для оставшихся частот, по ним в приемнике изображение восстанавливается.
Другой принцип воплощен в фрактальном кодировании, при котором изображение, представленное совокупностью линий, описывается уравнениями этих линий.
Более универсален широко известный метод Хаффмена, относящийся к статистическим методам сжатия. Идея метода, – часто повторяющиеся символы нужно кодировать более короткими цепочками битов, чем цепочки редких символов. Недостаток метода заключается в необходимости знать вероятности символов. Если заранее они не известны, то требуются два прохода: на одном в передатчике подсчитываются вероятности, на другом эти вероятности и сжатый поток символов передаются к приемнику. Однако двухпроходность не всегда возможна.
Этот недостаток устраняется в однопроходных алгоритмах адаптивного сжатия, в которых схема кодирования есть схема приспособления к текущим особенностям передаваемого потока символов. Поскольку схема кодирования известна как кодеру, так и декодеру, сжатое сообщение будет восстановлено на приемном конце.
Обобщением этого способа является алгоритм, основанный на словаре сжатия данных. В нем происходит выделение и запоминание в словаре повторяющихся цепочек символов, которые кодируются цепочками меньшей длины.
Интересен алгоритм “стопка книг”, в котором код символа равен его порядковому номеру в списке. Появление символа в кодируемом потоке вызывает его перемещение в начало списка. Очевидно, что часто встречающиеся символы будут тяготеть к малым номерам, а они кодируются более короткими цепочками 1 и 0.
Кроме упомянутых алгоритмов сжатия существует ряд других алгоритмов, например LZ-алгоритмы (алгоритмы Лемпеля–Зива). В LZ-алгоритме используется следующая идея: если в тексте сообщения появляется последовательность из двух ранее уже встречавшихся символов, то эта последовательность объявляется новым символом, для нее назначается код, который при определенных условиях может быть значительно короче исходной последовательности. В дальнейшем в сжатом сообщении вместо исходной последовательности записывается назначенный код. При декодировании повторяются аналогичные действия и поэтому становятся известными последовательности символов для каждого кода.
Статьи к прочтению:
- Способы организации и их особенности
- Способы организации высокопроизводительных процессоров. ассоциативные процессоры. конвейерные процессоры. матричные процессоры
Телекоммуникация Часть 6: Способы контроля
Похожие статьи:
Информация в локальных сетях, правило, пересдается отдельным и порциями, кусками, называемыми в различных источниках пакетами кадрами пли блоками….
Процессы передачи или приема информации в вычислительных сетях могут быть привязаны к определенным временным отметкам, т.е. один из процессов может…
Источник
Лекция 5
Проверка правильности передачи данных
- Причины возникновения ошибок
- Классификация методов защиты от ошибок
- Групповые методы
- мажоритарный
- блок с количественной характеристикой
- Помехоустойчивое кодирование
- Системы передачи с обратной связью
- решающая
- информационная
- Групповые методы
Проблема обеспечения безошибочности (достоверности) передачи информации в
сетях имеет очень большое значение. Если при передаче обычной телеграммы в
тексте возникает ошибка или при разговоре по телефону слышен треск, то в
большинстве случаев ошибки и искажения легко обнаруживаются по смыслу. Но при
передаче данных одна ошибка (искажение одного бита) на тысячу переданных
сигналов может серьезно отразиться на качестве информации.
Существует множество методов обеспечения достоверности передачи информации
(методов защиты от ошибок), отличающихся по используемым для их реализации
средствам, по затратам времени на их применение на передающем и приемном
пунктах, по затратам дополнительного времени на передачу фиксированного объема
данных (оно обусловлено изменением объема трафика пользователя при реализации
данного метода), по степени обеспечения достоверности передачи информации.
Практическое воплощение методов состоит из двух частей — программной и
аппаратной. Соотношение между ними может быть самым различным, вплоть до почти
полного отсутствия одной из частей. Чем больше удельный вес аппаратных средств
по сравнению с программными, тем при прочих равных условиях сложнее
оборудование, реализующее метод, и меньше затрат времени на его реализацию, и
наоборот.
Причины возникновения ошибок
Выделяют две основные причины возникновения ошибок при передаче информации в
сетях:
- сбои в какой-то части оборудования сети или возникновение
неблагоприятных объективных событий в сети (например, коллизий при
использовании метода случайного доступа в сеть). Как правило, система
передачи данных готова к такого рода проявлениям и устраняет их с помощью
предусмотренных планом средств; - помехи, вызванные внешними источниками и атмосферными явлениями. Помехи
— это электрические возмущения, возникающие в самой аппаратуре или
попадающие в нее извне. Наиболее распространенными являются флуктуационные
(случайные) помехи. Они представляют собой последовательность импульсов,
имеющих случайную амплитуду и следующих друг за другом через различные
промежутки времени. Примерами таких помех могут быть атмосферные и
индустриальные помехи, которые обычно проявляются в виде одиночных импульсов
малой длительности и большой амплитуды. Возможны и сосредоточенные помехи в
виде синусоидальных колебаний. К ним относятся сигналы от посторонних
радиостанций, излучения генераторов высокой частоты. Встречаются и смешанные
помехи. В приемнике помехи могут настолько ослабить информационный сигнал,
что он либо вообще не будет обнаружен, либо будет искажен так, что «единица»
может перейти в «нуль», и наоборот.
Трудности борьбы с помехами заключаются в беспорядочности, нерегулярности и в
структурном сходстве помех с информационными сигналами. Поэтому защита
информации от ошибок и вредного влияния помех имеет большое практическое
значение и является одной из серьезных проблем современной теории и техники
связи.
Классификация методов защиты от ошибок
Среди многочисленных методов защиты от ошибок выделяются три группы методов:
групповые методы, помехоустойчивое кодирование и методы защиты от ошибок в
системах передачи с обратной связью.
Групповые методы
Из групповых методов получили широкое применение мажоритарный метод,
реализующий принцип Вердана, и метод передач информационными блоками с
количественной характеристикой блока.
- Мажоритарный метод
- Суть этого метода, давно и широко используемого в телеграфии,
состоит в следующем. Каждое сообщение ограниченной длины передается
несколько раз, чаще всего три раза. Принимаемые сообщения запоминаются,
а потом производится их поразрядное сравнение. Суждение о правильности
передачи выносится по совпадению большинства из принятой информации
методом «два из трех». Например, кодовая комбинация 01101 при
трехразовой передаче была частично искажена помехами, поэтому приемник
принял такие комбинации: 10101, 01110, 01001. В результате проверки по
отдельности каждой позиции правильной считается комбинация 01101.- Передача блоками с количественной характеристикой
- Этот метод также не требует перекодирования информации. Он
предполагает передачу данных блоками с количественной характеристикой
блока. Такими характеристиками могут быть: число единиц или нулей в
блоке, контрольная сумма передаваемых символов в блоке, остаток от
деления контрольной суммы на постоянную величину и др. На приемном
пункте эта характеристика вновь подсчитывается и сравнивается с
переданной по каналу связи. Если характеристики совпадают, считается,
что блок не содержит ошибок. В противном случае на передающую сторону
поступает сигнал с требованием повторной передачи блока. В современных
телекоммуникационных вычислительных сетях такой метод получил самое
широкое распространение.
Помехоустойчивое (избыточное) кодирование
Этот метод предполагает разработку и использование корректирующих
(помехоустойчивых) кодов. Он применяется не только в телекоммуникационных сетях,
но и в ЭВМ для защиты от ошибок при передаче информации между устройствами
машины. Помехоустойчивое кодирование позволяет получить более высокие
качественные показатели работы систем связи. Его основное назначение заключается
в обеспечении малой вероятности искажений передаваемой информации, несмотря на
присутствие помех или сбоев в работе сети.
Существует довольно большое количество различных помехоустойчивых кодов,
отличающихся друг от друга по ряду показателей и прежде всего по своим
корректирующим возможностям.
К числу наиболее важных показателей корректирующих кодов относятся:
- значность кода n, или длина
кодовой комбинации, включающей информационные символы (m)
и проверочные, или контрольные, символы (К):
n = m
+ K
(Значения
контрольных символов при кодировании определяются путем контроля на четность
количества единиц в информационных разрядах кодовой комбинации. Значение
контрольного символа равно 0, если количество единиц будет четным, и равно 1
при нечетном количестве единиц); - избыточность кода Кизб,
выражаемая отношением числа контрольных символов в кодовой комбинации к
значности кода: Кизб = К/
n;
- корректирующая способность кода Ккс, представляющая
собой отношение числа кодовых комбинаций L,
в которых ошибки были обнаружены и исправлены, к общему числу переданных
кодовых комбинаций M в фиксированном объеме
информации: Ккс =
L/ M
Выбор корректирующего кода для его использования в данной компьютерной сети
зависит от требований по достоверности передачи информации. Для правильного
выбора кода необходимы статистические данные о закономерностях появления ошибок,
их характере, численности и распределении во времени. Например, корректирующий
код, обнаруживающий и исправляющий одиночные ошибки, эффективен лишь при
условии, что ошибки статистически независимы, а вероятность их появления не
превышает некоторой величины. Он оказывается непригодным, если ошибки появляются
группами. При выборе кода надо стремиться, чтобы он имел меньшую избыточность.
Чем больше коэффициент Кизб, тем менее эффективно используется
пропускная способность канала связи и больше затрачивается времени на передачу
информации, но зато выше помехоустойчивость системы.
В телекоммуникационных вычислительных сетях корректирующие коды в основном
применяются для обнаружения ошибок, исправление которых осуществляется путем
повторной передачи искаженной информации. С этой целью в сетях используются
системы передачи с обратной связью (наличие между абонентами дуплексной связи
облегчает применение таких систем).
Системы передачи с обратной связью
Системы передачи с обратной связью делятся на системы с решающей обратной
связью и системы с информационной обратной связью.
- Системы с решающей обратной связью
- Особенностью систем с решающей обратной связью (систем с
перезапросом) является то, что решение о необходимости повторной передачи
информации (сообщения, пакета) принимает приемник. Здесь обязательно применяется
помехоустойчивое кодирование, с помощью которого на приемной станции
осуществляется проверка принимаемой информации. При обнаружении ошибки на
передающую сторону по каналу обратной связи посылается сигнал перезапроса, по
которому информация передается повторно. Канал обратной связи используется также
для посылки сигнала подтверждения правильности приема, автоматически
определяющего начало следующей передачи.- Системы с информационной обратной связью
- В системах с информационной обратной связью передача информации
осуществляется без помехоустойчивого кодирования. Приемник, приняв информацию по
прямому каналу и зафиксировав ее в своей памяти, передает ее в полном объеме по
каналу обратной связи передатчику, где переданная и возвра0щенная информация
сравниваются. При совпадении передатчик посылает приемнику сигнал подтверждения,
в противном случае происходит повторная передача всей информации. Таким образом,
здесь решение о необходимости повторной передачи принимает передатчик.
Обе рассмотренные системы обеспечивают практически одинаковую достоверность,
однако в системах с решающей обратной связью пропускная способность каналов
используется эффективнее, поэтому они получили большее распространение.
Сайт управляется системой uCoz
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

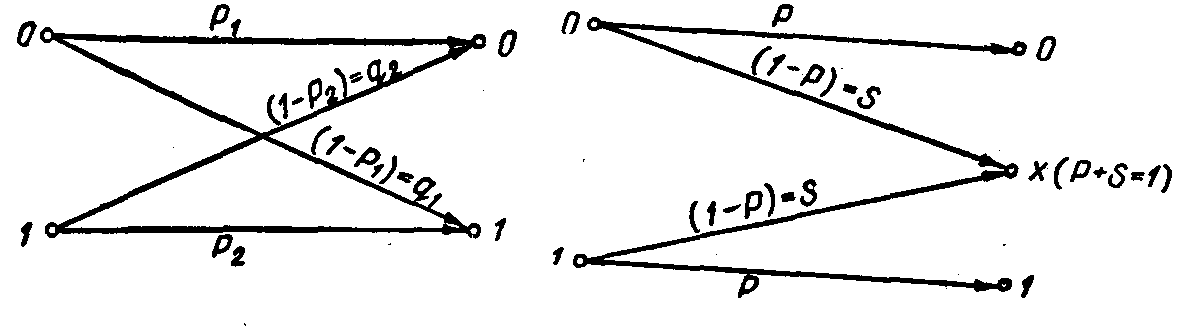

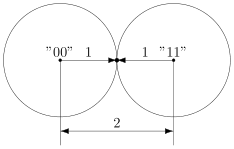

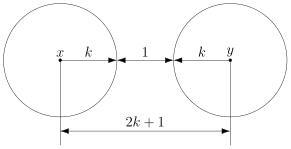

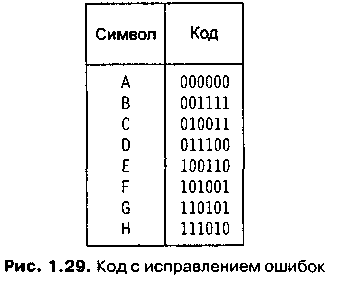


 , округляем «вниз», так чтобы
, округляем «вниз», так чтобы  .
.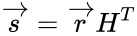 , где
, где 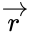 — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.













