Ошибка первого рода уровень статистической значимости

Выдвинутая
гипотеза может быть правильной или
неправильной, поэтому возникает
необходимость ее проверки. Поскольку
проверку производят статистическими
методами, ее называют статистической.
В итоге статистической проверки гипотезы
в двух случаях может быть принято
неправильное решение, т. е. могут быть
допущены ошибки двух родов.

Ошибка
первого рода состоит
в том, что будет отвергнута правильная
гипотеза.

Ошибка
второго рода состоит
в том, что будет принята неправильная
гипотеза.

Вероятность
совершить ошибку первого рода принято
обозначать через ;
ее называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0.05 или 0.01. Если, например, принят
уровень значимости, равный 0.05, то это
означает, что в пяти случаях из ста мы
рискуем допустить ошибку первого рода
(отвергнуть правильную гипотезу).

Пусть
дана выборка из
неизвестного совместного распределения,
и поставлена бинарная задача проверки
статистических гипотез:

где —нулевая
гипотеза,
а —альтернативная
гипотеза.
Предположим, что задан статистический
критерий

,

31. Статистический критерий проверки нулевой гипотезы.

Для
проверки нулевой гипотезы используют
специально подобранную случайную
величину, точное или приближенное
распределение которой известно. Эту
величину обозначают через U или Z, если
она распределена нормально, F или v2 – по
закону Фишера-Снедекора, T – по закону
Стьюдента, c² – по закону «хи квадрат»
и т. д. Все эти случайные величины
обозначим через К.

Статистическим
критерием (или
просто критерием)
называют случайную величину К, которая
служит для проверки нулевой гипотезы.

Для
проверки гипотезы по данным выборок
вычисляют частные значения входящих
в критерий величин, и таким образом
получают частное (наблюдаемое) значение
критерия.

Наблюдаемым
значением Кнабл назначают
значение критерия, вычисленное по
выборкам.

32. Критическая область. Область принятия гипотезы, критические точки.

После
выбора определенного критерия множество
всех его возможных значений разбивают
на два непересекающихся подмножества,
одно из которых содержит значения
критерия, при которых нулевая гипотеза
отвергается, а другое – при которых
она принимается.

Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.

Областью
принятия гипотезы (областью допустимых
значений) называют совокупность
значений критерия, при которых
гипотезу принимают.

Основной
принцип проверки статистических гипотез
можно сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
области принятия гипотезы – гипотезу
принимают.

Так
как критерий K – одномерная случайная
величина, то все ее возможные значения
принадлежат некоторому интервалу и,
соответственно, должны существовать
точки, разделяющие критическую область
и область принятия гипотезы. Такие
точки называются критическими точками.

Различают
одностороннюю (правостороннюю и
левостороннюю) и двустороннюю критические
области.

Правосторонней
называют критическую область, определяемую
неравенством ,
где–
положительное число.

Левосторонней
называют критическую область, определяемую
неравенством ,
где–
отрицательное число.

Двусторонней
называют критическую область, определяемую
неравенствами ,
где.
В частности, если критические точки
симметричны относительно нуля,
двусторонняя критическая область
определяется неравенствамиили
равносильным неравенством.
Различия между вариантами критических
областей иллюстрирует следующий
рисунок.

Рис.
1. Различные варианты критических
областей a) правосторонняя, b) левосторонняя,
с) двусторонняя

Резюмируя,
сформулируем этапы проверки статистической
гипотезы:

Формулируется
нулевая гипотеза ;
Определяется критерий K, по значениям
которого можно будет принять или
отвергнутьи
выбирается уровень значимости;
По уровню значимости определяется
критическая область; По выборке
вычисляется значение критерия K,
определяется, принадлежит ли оно
критической области и на основании
этого принимаетсяили.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Проверка статистических гипотез

  1. Понятие о статистической гипотезе
  2. Уровень значимости при проверке гипотезы
  3. Критическая область
  4. Простая гипотеза и критерии согласия
  5. Критерий согласия (X^2) Пирсона
  6. Примеры

п.1. Понятие о статистической гипотезе

Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.

Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.

Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).

В результате проверки гипотезы возможны 4 исхода:

Верная гипотеза
(H_0) (H_1)
Принятая гипотеза (H_0) True Negative
(H_0) принята верно		 False Negative
(H_0) принята неверно
Ошибка 2-го рода
(H_1) False Positive
(H_0) отвергнута неверно
(H_1) принята неверно
Ошибка 1-го рода		 True Positive
(H_0) отвергнута верно
(H_1) принята верно

Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».

Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»

Уровень значимости при проверке гипотезы

Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.

Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.

Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.

В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).

Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:

Уровень
значимости (p)		 Решение о гипотезе (H_0) Вывод для гипотезы (H_1)
(pgt 0,1) (H_0) не может быть отклонена Статистически достоверные доказательства не обнаружены
(0,5lt pleq 0,1) Истинность (H_0) сомнительна, неопределенность Доказательства обнаружены на уровне статистической тенденции
(0,01lt pleq 0,05) Отклонение (H_0), значимость Обнаружены статистически достоверные (значимые) доказательства
(pleq 0,01) Отклонение (H_0), высокая значимость Доказательства обнаружены на высоком уровне значимости

Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).

Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.

п.3. Критическая область

Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.

Различают 3 вида критических областей

Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется

п.4. Простая гипотеза и критерии согласия

Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).

Например:
Простая гипотеза и критерии согласия
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]

Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.

К критериям согласия относятся:

  • Критерий Колмогорова-Смирнова;
  • Критерий (X^2) Пирсона;
  • Критерий (omega^2) Смирнова-Крамера-фон Мизеса

п.5. Критерий согласия (X^2) Пирсона

Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид: Критерий согласия X^2 Пирсона
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).

Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).

Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Критерий согласия X^2 Пирсона
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Критерий согласия X^2 Пирсона
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)

Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:

Очки, (x_i) 1 2 3 4 5 6
Частота, (f_i) 8 12 13 7 12 8

Не является ли кубик фальшивым?

Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:

(x_i) 1 2 3 4 5 6 ∑
(f_i) 8 12 13 7 12 8 60
(m_i) 10 10 10 10 10 10 60
(f_i-m_i) -2 2 3 -3 2 -2 —
(frac{(f_i-m_i)^2}{m_i}) 0,4 0,4 0,9 0,9 0,4 0,4 3,4

Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Критерий согласия X^2 Пирсона $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2lt X_{кр}^2 $$ На уровне значимости α=0,05 принимается гипотеза (H_0) про равномерное распределение.
Значит, с вероятностью 95% кубик не фальшивый.

п.6. Примеры

Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:

Очки, (x_i) 1 2 3 4 5 6
Частота, (f_i) 8 12 13 7 10 22

Не является ли кубик фальшивым?

Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:

(x_i) 1 2 3 4 5 6 ∑
(f_i) 8 12 13 7 10 22 72
(m_i) 12 12 12 12 12 12 72
(f_i-m_i) -4 0 1 -5 -2 10 —
(frac{(f_i-m_i)^2}{m_i}) 1,333 0,000 0,083 2,083 0,333 8,333 12,167

Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Пример 1 $$ X_{кр}^2approx 11,1 $$ Получается, что: $$ X_e^2gt X_{кр}^2 $$ На уровне значимости α=0,05 гипотеза (H_0) про равномерное распределение не принимается.
Значит, с вероятностью 95% кубик фальшивый.

Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:

Число попаданий, (x_i) 0 1 2 3 4 5 6 7
Количество участков, (f_i) 229 211 93 35 7 0 0 1

Проверялась гипотеза (H_0) — стрельба случайна.

Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:

(x_i) 0 1 2 3 4 5 6 7 ∑
(f_i) 229 211 93 35 7 0 0 1 576
(x_if_i) 0 211 186 105 28 0 0 7 537

$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:

(x_i) 0 1 2 3 4 5 6 7 ∑
(f_i) 229 211 93 35 7 0 0 1 576
(p_i) 0,39365 0,36700 0,17107 0,05316 0,01239 0,00231 0,00036 0,00005 0,99999
(m_i) 226,7 211,4 98,5 30,6 7,1 1,3 0,2 0,0 576,0
(f_i-m_i) 2,3 -0,4 -5,5 4,4 -0,1 -1,3 -0,2 1,0 —
(frac{(f_i-m_i)^2}{m_i}) (результат) 0,02 0,00 0,31 0,63 0,00 1,33 0,21 34,34 36,84

Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
Пример 2
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.

Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:

Число попаданий, (x_i) 0 1 2 3 4-7
Количество участков, (f_i) 229 211 93 35 8

Проверялась гипотеза (H_0) — стрельба случайна.

Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.

(x_i) 0 1 2 3 4,375 ∑
(f_i) 229 211 93 35 8 576
(x_if_i) 0 211 186 105 35 537

$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:

(x_i) 0 1 2 3 4,375 ∑
(f_i) 229 211 93 35 8 576
(p_i) 0,3937 0,3670 0,1711 0,0532 0,0121 0,9970
(m_i) 226,7 211,4 98,5 30,6 7,0 574,2
(f_i-m_i) 2,3 -0,4 -5,5 4,4 1,0 —
(frac{(f_i-m_i)^2}{m_i}) 0,02 0,00 0,31 0,63 0,16 1,12

Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
Пример 3
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.

И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.

Правильный ответ – в Примере 3.
Стрельба случайна.

Внимание!Критерий согласия (X^2) чувствителен к низкочастотным (редким) событиям и может ошибаться на таких выборках. Поэтому низкочастотные события нужно либо отбрасывать, либо объединять с другими событиями. Эта процедура называется коррекцией Йетса.
Источник

Материал из MachineLearning.

(Перенаправлено с Статистический тест)

Перейти к: навигация, поиск

Содержание

  • 1 Методика проверки статистических гипотез
  • 2 Альтернативная методика на основе достигаемого уровня значимости
  • 3 Типы критической области
  • 4 Ошибки первого и второго рода
  • 5 Свойства статистических критериев
  • 6 Типы статистических гипотез
  • 7 Типы статистических критериев
    • 7.1 Критерии согласия
    • 7.2 Критерии сдвига
    • 7.3 Критерии нормальности
    • 7.4 Критерии однородности
    • 7.5 Критерии симметричности
    • 7.6 Критерии тренда, стационарности и случайности
    • 7.7 Критерии выбросов
    • 7.8 Критерии дисперсионного анализа
    • 7.9 Критерии корреляционного анализа
    • 7.10 Критерии регрессионного анализа
  • 8 Литература
  • 9 Ссылки

Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.

Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.

Методика проверки статистических гипотез

Пусть задана случайная выборка x^m = (x_1,ldots,x_m) — последовательность m объектов из множества X.
Предполагается, что на множестве X существует некоторая неизвестная вероятностная мера mathbb{P}.

Методика состоит в следующем.

  1. Формулируется нулевая гипотеза H_0 о распределении вероятностей на множестве X. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая H_0 и альтернативная H_1. Иногда альтернатива не формулируется в явном виде; тогда предполагается, что H_1 означает «не H_0». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.
  2. Задаётся некоторая статистика (функция выборки) T:: X^m to mathbb{R}, для которой в условиях справедливости гипотезы H_0 выводится функция распределения F(T) и/или плотность распределения p(T). Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика T. Вывод функции распределения F(T) при заданных H_0 и T является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для F(T); в статистических пакетах имеются готовые вычислительные процедуры.
  3. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число alpha in [0,1]. На практике часто полагают alpha=0.05.
  4. На множестве допустимых значений статистики T выделяется критическое множество Omega_alpha наименее вероятных значений статистики T, такое, что mathbb{P}{TinOmega_alphaleft|H_0right.} = alpha. Вычисление границ критического множества как функции от уровня значимости alpha является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
  5. Собственно статистический тест (статистический критерий) заключается в проверке условия:

Итак, статистический критерий определяется статистикой T
и критическим множеством Omega_alpha, которое зависит от уровня значимости alpha.

Замечание.
Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна.
Тому есть две причины.

Альтернативная методика на основе достигаемого уровня значимости

Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.

Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия T:

p(T) = min { alpha:: TinOmega_alpha },

где
Omega_alpha — критическая область критерия.

Другая интерпретация:
достигаемый уровень значимости p(T) — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем T.

Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается.
В частности, его можно сравнивать с фиксированным уровнем значимости;
тогда альтернативная методика будет эквивалентна классической.

Типы критической области

Обозначим через t_alpha значение, которое находится из уравнения F(t_alpha) = alpha, где F(t) = mathbb{P}left{ T<t right} — функция распределения статистики T.
Если функция распределения непрерывная строго монотонная,
то t_alpha есть обратная к ней функция:

t_alpha = F^{-1}(alpha).

Значение t_alpha называется также alpha—квантилем распределения F(t).

На практике, как правило, используются статистики T с унимодальной (имеющей форму пика) плотностью распределения.
Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения.
Поэтому чаще всего возникают критические области одного из трёх типов:

  • Левосторонняя критическая область:
определяется интервалом Omega_alpha = (-infty,, t_alpha).
пи-величина: p(T) = F(T).
  • Правосторонняя критическая область:
определяется интервалом Omega_alpha = (t_{1-alpha},,+infty).
пи-величина: p(T) = 1-F(T).
  • Двусторонняя критическая область:
определяется двумя интервалами Omega_alpha = (-infty,, t_{alpha/2}) cup (t_{1-alpha/2},,+infty);
пи-величина: p(T) = min left{ 2F(T),; 2(1-F(T)) right}.

Ошибки первого и второго рода

  • Ошибка первого рода или «ложная тревога» (англ. type I error, alpha error, false positive) — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода:
alpha = mathbb{P}left{ TinOmega_alpha | H_0 right}.
  • Ошибка второго рода или «пропуск цели» (англ. type II error, beta error, false negative) — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:
beta(H_1) = mathbb{P}left{ TnotinOmega_alpha | H_1 right}.
  Верная гипотеза
 H_0   H_1 
Результат
 применения 
критерия 		 H_0  H_0 верно принята H_0 неверно принята 
(Ошибка второго рода)
 H_1  H_0 неверно отвергнута 
(Ошибка первого рода) 		H_0 верно отвергнута

Свойства статистических критериев

Мощность критерия:
1 - beta(H) = mathbb{P}left{ TinOmega_alpha | H right} — вероятность отклонить гипотезу H_0, если на самом деле верна альтернативная гипотеза H.
Мощность критерия является числовой функцией от альтернативной гипотезы H.

Несмещённый критерий:
1-beta(H) geq alpha
для всех альтернатив H
или, что то же самое,
mathbb{P}left{ TinOmega_alpha | H right} geq mathbb{P}left{ TinOmega_alpha | H_0 right}
для всех альтернатив H.

Состоятельный критерий:
beta(H) to 0 при mtoinfty для всех альтернатив H.

Равномерно более мощный критерий.
Говорят, что критерий с мощностью 1-beta(H) является равномерно более мощным, чем критерий с мощностью 1-beta'(H), если выполняются два условия:

  1. beta(H_0) = beta'(H_0);
  2. beta(H_1) leq beta'(H_1) для всех рассматриваемых альтернатив H_1neq H_0, причём хотя бы для одной альтернативы неравенство строгое.

Типы статистических гипотез

  • Простая гипотеза однозначно определяет функцию распределения на множестве X. Простые гипотезы имеют узкую область применения, ограниченную критериями согласия (см. ниже). Для простых гипотез известен общий вид равномерно более мощного критерия (Теорема Неймана-Пирсона).
  • Сложная гипотеза утверждает принадлежность распределения к некоторому множеству распределений на X. Для сложных гипотез вывести равномерно более мощный критерий удаётся лишь в некоторых специальных случаях.

Типы статистических критериев

В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.

Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.

  • Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.
  • Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.

Критерии согласия

Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.

  • Критерий Колмогорова-Смирнова
  • Критерий хи-квадрат (Пирсона)
  • Критерий омега-квадрат (фон Мизеса)

Критерии сдвига

Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.

  • Критерий Стьюдента
  • Критерий Уилкоксона-Манна-Уитни

Критерии нормальности

Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.

  • Критерий Шапиро-Уилка
  • Критерий асимметрии и эксцесса

Критерии однородности

Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.

Критерии симметричности

Критерии симметричности позволяют проверить симметричность распределения.

  • Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
  • Критерий знаков
  • Коэффициент асимметрии

Критерии тренда, стационарности и случайности

Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.

Критерии выбросов

Критерии дисперсионного анализа

Критерии корреляционного анализа

Критерии регрессионного анализа

Литература

  1. Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
  2. Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006. — 816 с.

Ссылки

  • Statistical hypothesis testing — статья в англоязычной Википедии.
Источник

При работе со статистическим отчетом, научной статьей или диссертацией Вы постоянно сталкиваетесь таким термином, как уровень значимости или альфа (ошибка первого рода), чаще всего этот уровень задается относительно 5% или вероятности р=о,05. Решение о достоверности различий или «статистически значимых различиях» принимается относительно этого порогового значения. В данной статье мы предлагаем читателю разобраться в том, почему так важен этот уровень и что он значит в практическом смысле.

Определение (словарь Дж. М. Ласта):

ОШИБКА ТИПА I (ERROR TYPE I; син. alpha-error — ошибка альфа)

ошибочное отклонение нулевой гипотезы, т.е. утверждение о том, что различия существуют, тогда как их нет.

Немного о смысле уровня значимости и достовернности различий

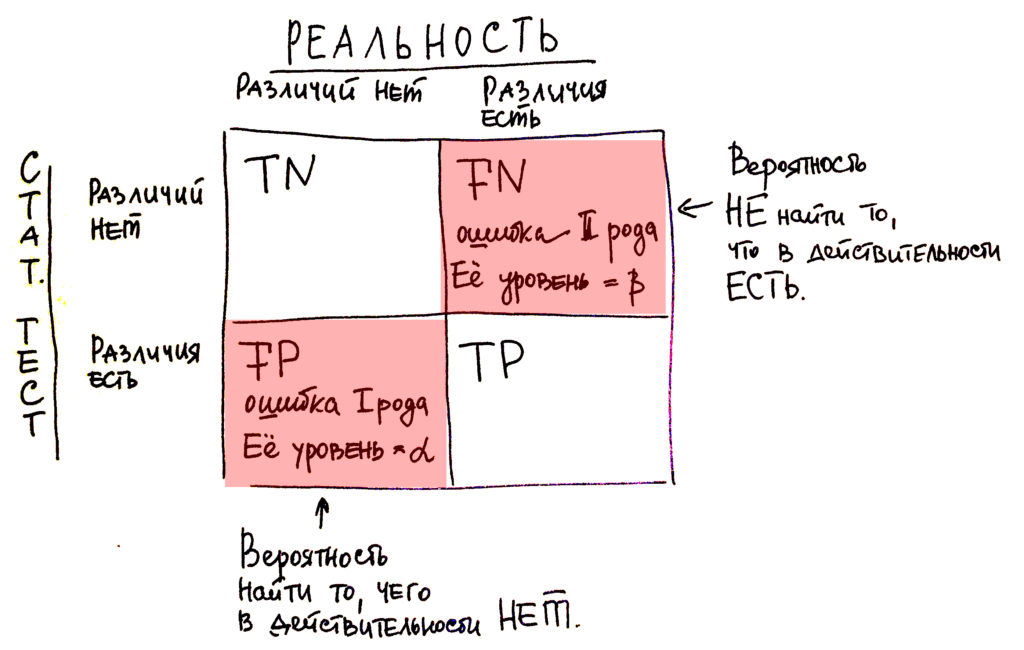
Для понимания темы статистических ошибок мы перейдем к простейшей матрице соотношения статистики  (что она нам говорит по результатам статистических тестов) и реальности. Так вот, предположим, что статистика нам говорит о существовании связей, о существовании различий. В реальности же они также существуют, тогда мы считаем этот результат правильным положительным или truth positive (ТР). Например, статистика нам говорит об отсутствии связей, об отсутствии различий, а в реальности же они действительно существуют. Такая ситуация называется ложноотрицательной или false-negative (FN). Соответственно существуют ситуации, когда статистика нам говорит о существовании каких-то определенных взаимосвязей или о существовании различий, которые в реальности не существуют. Тогда это называется  ложноположительной или false-positive (FP). И последний случай касается отсутствия по данным статистических тестов того, чего в действительности не существует, различий в действительности нет. И эта ситуация именуется как truth negative (TN) или ложноотрицательный результат.

Рисунок 1. Матрица соотношения реальность-результаты статистического теста. TN (true negative) — верноотрицательный, FN (false negative) — ложноотрицательный, FP (false positive) — ложноположительный, TP (true positive) — верно позитивный.

Так вот, как видно из этой матрицы, у нас существуют 2 ситуации, в которых мы можем ошибаться: это false-positive и truth negative. Это как раз два типа ошибок, о которых я говорил в начале этого блока: о ложноотрицательной ошибке и ложноположительной. Что на самом деле это значит?

Что в какой-то ситуации мы можем пересмотреть, а в какой-то – недосмотреть.

Пересмотреть, то есть найти то, чего в действительности нет, это является false-positive – это ошибка первого рода.

Или недосмотреть, то есть упустить то, что в действительности существует в реальности, но по данным статистических тестов мы чего-то не находим – это ложноотрицательный результат или ошибка второго рода.

Давайте нанесем те термины, которые, возможно, вы уже слышали – «уровень достоверности», «достоверные различия». Что это за слово такое «достоверность»? Оно относится как раз к ошибке первого рода и обозначается буквой α. Вы наверняка знаете обозначение уровня в р=0,05. Уровень достоверности в 0,05 как раз является критическим значением для результатов большинства статистических тестов ( 5 %). Мы делаем вывод относительно этих 5 %. Что в практическом смысле это значит? Что в 95 % мы находим различия, которые действительно существуют, и в 5 % даем себе возможность переобнаружить то, чего в действительности не существует в реальности.

Что касается ошибки второго рода, то здесь это уже не 5 %. И мы задаем либо 20, либо 10 %, что-то в этом диапазоне, это ошибка в 0,2; в 0,1. И как раз мы подходим к следующему чрезвычайно важному статистическому понятию как «мощность исследования». Мощность исследования это: (1 – β), где β это ошибка второго рода. Если стандартный уровень ошибки это 0,2 и 0,1, то мы получаем, что мощность исследования в норме составляет 0,8 или 0,9 (чаще, конечно, 0,8).

NB! по уровню значимости

Уровень значимости, то есть ошибки первого рода составляет чаще всего относительно уровня в 5 %, это уровень той ошибки, при которой мы даем возможность себе «перенайти» то, что в действительности не существует. В ошибке второго рода мы даем себе определенный люфт до 20 % не обнаружить того, что в действительности существует, то есть когда статистические тесты нам скажут, что чего-то нет, а в реальности эти различия существуют.

Автор: Кирилл Мильчаков

Источник

Понравилась статья? Поделить с друзьями:
  • Ошибка первого рода статистика это
  • Ошибка переведите рычаг в положение p шкода октавия а7
  • Ошибка первого рода ошибка второго рода это
  • Ошибка переадресации google search console
  • Ошибка первого рода математическая статистика