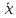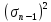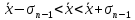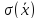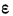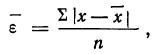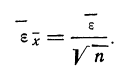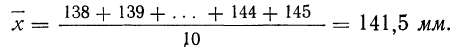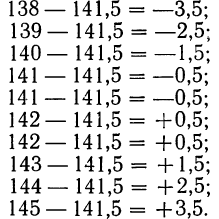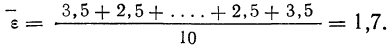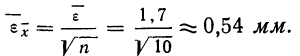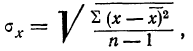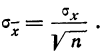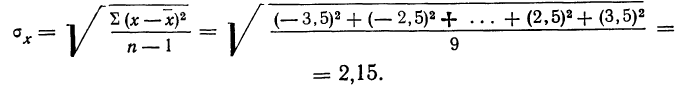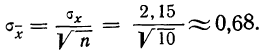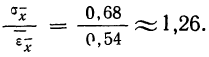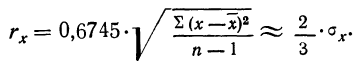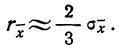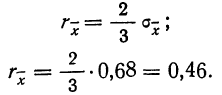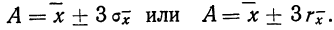Определение случайной ошибки
Если
исходить из предположения, что все
систематические ошибки учтены, то в
качестве результата измерения можно
рассматривать наиболее вероятное
значение соответствующей случайной
величины. Чтобы найти это наиболее
вероятное значение или хотя бы оценить
его точность нужно знать распределение
случайной величины.
Анализ
различных случайных величин, как
изучаемых теоретически, так и вычисляемых
на основании опытов, показывает
существование одного наиболее часто
встречающегося распределения, называемого
нормальным или распределением Гаусса.
Распределение
Гаусса получено на основе следующих
двух допущений:
1)
окончательная ошибка любого измерения
представляет собой результат большого
числа очень малых величин, распределенных
случайным образом;
2)
положительные и отрицательные отклонения
относительно истинного значения
равновероятны; и имеет
вид рис. 1 (где f(x)
плотность вероятности,
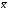
наиболее вероятное значение).
рис. 1
Кривая,
изображенная на рис.1. непрерывна,
т.е. описывает совокупность, содержащую
бесконечное множество измерений, Это
так называемая генеральная совокупность,
из которой для исследования берутся
некоторые конечные выборки.
Погрешность
прямых, многократных, равноточных
измерений
одной и той же физической
величины
Рассмотрим
выборку из n отсчетов,
содержащую значения x1,
x2, x3,
…, xn
полученные при повторных измерениях
одной и той же величины. Допустим, что
эти отсчеты составляют некоторую часть
бесконечной нормально распределенной
совокупности с неизвестным истинным
значением.
Из
свойства нормального распределения
случайных величин следует, что наиболее
вероятное значение
равно среднему арифметическому значению
полученных n отсчетов

Таким
образом, в качестве результата измерений
величины x нужно брать
не числа x1, x2,
x3, …, xn,
а число
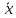
Погрешность
этого результата будет значительно
меньше, но не следует думать, что
будет в точности равно истинному
значению, так как
играет роль центра рассеяния.
Из
эксперимента мы можем найти только
отклонения отсчетов хi,
от среднего
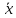
Эти отклонения мы обозначим через
Δxi:

Выборочной
дисперсией
(или s2) измерения
называют величину

Квадратный
корень из выборочной дисперсии, т.е.
величину
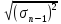
называют среднеквадратичной
погрешностью одного измерения:

Среднеквадратичная
погрешность характеризует степень
разброса единичных измерений относительно
x: в интервал
попадает примерно половина всех отсчетов
хi.
Среднеквадратичное
отклонение среднего значения
можно вычислить по формуле
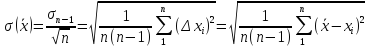
Так
как обычно число измерений n
существенно меньше, чем требуется, то
истинное значение x
лежит в доверительном интервале
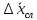
определяемом условием (6), с определенной
доверительной вероятностью α.

где

коэффициент Стьюдента; n
— объем выборки.
Значение
коэффициента Стьюдента берется из
таблицы 1. При выполнении лабораторных
работ доверительная вероятность обычно
выбирается равной 0,95 (95%)
Условие
(6) представляет собой абсолютную
случайную ошибку измерений.
Тогда
результат измерения величины x
будет находиться в интервале значений
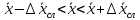
Относительная
погрешность измерений равна
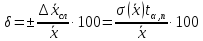
Таблица 1.
Коэффициенты
Стьюдента (часть таблицы,
полный
вариант см. приложение)
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
|
|
α |
||||||||||||
|
0.9 |
6.31 |
2.92 |
2.35 |
2.13 |
2.02 |
1.94 |
1.89 |
1.86 |
1.83 |
1.81 |
1.72 |
|
|
0.95 |
12.7 |
4.3 |
3.18 |
2.78 |
2.57 |
2.45 |
2.36 |
2.31 |
2.26 |
2.23 |
2.09 |
|
|
0.99 |
63.66 |
9.92 |
5.84 |
4.6 |
4.03 |
3.71 |
3.5 |
3.36 |
3.25 |
3.17 |
2.85 |
|
|
0.999 |
636.6 |
31.6 |
12.94 |
8.61 |
6.86 |
5.96 |
5.41 |
5.04 |
4.78 |
4.59 |
3.85 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ
И УПРАВЛЕНИЯ ИМЕНИ К.Г. РАЗУМОВСКОГО»
(Первый казачий университет)
Сибирский казачий институт технологий и управления (филиал)
ФГБОУ ВО «МГУТУ имени К.Г. Разумовского
(Первый казачий университет)»
Кафедра проектирования и автоматизации производств
МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Конспект лекций
для студентов всех направлений полготовки
Омск
2015 г.
Оглавление
Раздел 1. Эксперимент как предмет исследования 4
Тема 1.1. Введение 4
Тема 1.2. Ошибки измерений и их оценка 9
Раздел 2. Случайные величины 13
Тема 2.1. Дискретные случайные величины 13
Тема 2.2. Непрерывные случайные величины 15
Тема 2.3. Основные законы распределения НСВ 16
2.3.1. Равномерный закон распределения 16
2.3.2. Показательный (экспоненциальный) закон распределения 17
2.3.3. Нормальное распределение 19
Раздел 3. Статистическая обработка экспериментальных данных 26
Тема 3.1. Выборочный метод 26
Тема 3.2. Интервальные оценки 26
Тема 3.3. Интервальная оценка математического ожидания
при известной дисперсии 28
Тема 3.4. Проверка статистических гипотез 32
3.4.1. Понятие статистической гипотезы 32
3.4.2. Понятие статистического критерия 34
Тема 3.5. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона 36
Раздел 4. Представление результатов эксперимента 41
Тема 4.1. Дисперсионный анализ. 41
4.1.1. Основные понятия 41
4.1.2. Постановка задачи 43
Тема 4.2. Однофакторный дисперсионный анализ 45
Раздел 5. Элементы корреляционного анализа 50
Тема 5.1. Основные понятия 50
Тема 5.2. Виды зависимости 52
Тема 5.3. Линейный коэффициент корреляции 54
Раздел 6. Элементы регрессионного анализа 57
Тема 6.1. Основные понятия 57
Тема 6.2. Парная линейная регрессионная модель 58
Тема 6.3. Нахождение уравнения линейной регрессии 61
Тема 6.4. Сравнительный анализ основных видов обработки экспериментальных данных 66
Рекомендуемая литература 68
4.1. Основная литература 68
4.2. Дополнительная литература 68
4.3. Методическая литература 69
Раздел 1. Эксперимент как предмет исследования
Тема 1.1. Введение
Методы исследования. Понятие наблюдения и эксперимента. Пассивный и активный эксперименты. Цель эксперимента.
Специфика работы инженера требует владения современной измерительной аппаратурой, знания основных приемов и способов измерений, обработки и интерпретации экспериментально полученных данных.
Цель дисциплины «Методы обработки экспериментальных данных» — изучение основ обработки, анализа и интерпретации экспериментальных данных.
Эксперимент — (от лат. experimentum — проба, опыт) — метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления действительности.
Эмпирический (с греч.) – основанный на опыте.
При изучении технических, экономических и других систем могут использоваться теоретические и эмпирические методы исследования.
Методы исследования
теоретические эмпирические
Каждое из этих направлений обладает относительной самостоятельностью, имеет свои достоинства и недостатки. В общем случае, теоретические методы в виде математических моделей позволяют описывать и объяснять взаимосвязи элементов изучаемой системы или объекта в относительно широких диапазонах изменения переменных величин.
Пример. Исследование функции по ее уравнению с помощью диф. анализа.
Пример. Вычисление вероятности того, что в 10 бросках монеты «герб» выпадет ровно 7 раз по формуле Бернулли.
Однако при построении теоретических моделей неизбежно введение каких-либо ограничений, допущений, гипотез и т.п. Поэтому возникает задача оценки достоверности (адекватности) полученной модели реальному процессу или объекту. «Теория поверяется практикой». Для этого проводится экспериментальная проверка разработанных теоретических моделей.
Практика является решающей основой научного познания. В ряде случаев именно результаты экспериментальных исследований дают толчок к теоретическому обобщению изучаемого явления. Экспериментальное исследование дает более точное соответствие между изучаемыми параметрами. Но не следует и преувеличивать результаты экспериментальных исследований, которые справедливы только в пределах условий проведенного эксперимента.
Таким образом, теоретические и экспериментальные исследования дополняют друг друга и являются составными элементами процесса познания окружающего нас мира.
Управленческое, инженерное или даже бытовое решение, как правило, опирается на анализ эмпирических сведений, содержащих в себе информацию, необходимую для его принятия. В простейших ситуациях анализ имеющихся сведений может быть осуществлен непосредственно автором решения в соответствии с его профессиональной подготовкой, опытом, интуицией, даром предвидения и т.п.
Пример. В обыденной жизни: анализируя время, затраченное на проезд к институту в течение нескольких дней, студент может установить оптимальное время поездки.
Пример.
Однако сложные ситуации, в том числе характеризуемые большим объемом данных, часто противоречивых, с не всегда известной степенью взаимодействия, что характерно для большинства реальных явлений и процессов, не позволяют достаточно глубоко проникнуть в их суть только средствами не вооруженного современными математико-вычислительными методами человеческого разума.
Результаты эксперимента для инженера-исследователя были и остаются главным критерием при решении практических задач и при проверке теоретических гипотез. Однако при этом важно не только умело спланировать и поставить эксперимент, но и грамотно обработать его результаты. Этому вопросу часто не уделяется должного внимания, и нередки случаи, когда результаты дорогостоящих экспериментов не подвергают даже простейшей обработке; при этом, как следствие, теряется огромное количество полезной информации. Как правило, результаты экспериментальных исследований нуждаются в определенной математической обработке.
Следует также подчеркнуть, что обработке экспериментальных данных с целью построения моделей «сложных систем» (эмпирических зависимостей) должна предшествовать предварительная обработка, содержание которой, в основном, состоит в отсеивании грубых погрешностей измерений и в проверке соответствия распределения результатов нормальному закону. Следует помнить, что только после выполнения предварительной обработки можно с наибольшей эффективностью, а главное корректно, использовать более сложные экспериментально-статистические методы, позволяющие получать математические модели даже таких процессов, строгое детерминированное описание которых вообще отсутствует.
В настоящее время процедура обработки экспериментальных данных достаточно хорошо формализована и исследователю необходимо только ее правильно использовать. Круг вопросов, решаемых при обработке результатов эксперимента, не так уж велик.
Целью эксперимента является:
• определение качественной и количественной связи между исследуемыми параметрами,
• оценка численного значения какого-либо параметра. В некоторых случаях вид зависимости между переменными величинами известен по результатам теоретических исследований. Как правило, формулы, выражающие эти зависимости, содержат некоторые постоянные, значения которых и необходимо определить из опыта.
• проверка выдвинутых гипотез
• и некоторые другие
Однозначно определить неизвестную функциональную зависимость между переменными невозможно даже в том случае, если бы результаты эксперимента не имели ошибок. Тем более не следует этого ожидать, имея результаты эксперимента, содержащие различные ошибки измерения. Поэтому следует четко понимать, что целью математической обработки результатов эксперимента является не нахождение истинного характера зависимости между переменными или абсолютной величины какой-либо константы, а представление результатов наблюдений в виде наиболее простой формулы с оценкой возможной погрешности ее использования.
В последние годы наблюдается широкое применение современных информационных технологий во всех сферах человеческой деятельности, в том числе, при обработке результатов эксперимента. На вооружении математиков, экономистов, инженеров оказались многочисленные пакеты прикладных программ (например, Statistica, Mathcad, MatLab, Matematica и др.). Однако крайне важно, чтобы пользователь этих пакетов не оказался механическим приложением к ним, слепо использующим возможности современных вычислительных систем без глубокого погружения и проникновения в сущность соответствующих математических. Творческий подход к решению прикладных задач невозможен без фундаментальной подготовки специалиста в области математико-статистических методов.
Основой всего естествознания является наблюдение и эксперимент.
Определение. Наблюдение — это систематическое, целенаправленное восприятие того или иного объекта или явления без воздействия на него. Наблюдение позволяет получить первоначальную информацию по изучаемому объекту или явлению.
Определение. Эксперимент — метод изучения объекта, когда исследователь активно и целенаправленно воздействует на него путем создания искусственных или естественных условий, необходимых для выявления соответствующих свойств.
Достоинствами эксперимента по сравнению с наблюдением реального явления или объекта является:
1. Возможность изучения в «чистом виде», без влияния побочных факторов, затемняющих основной процесс;
2. В экспериментальных условиях можно получить результат более быстро и точно;
3. При эксперименте можно проводить испытания столько раз, сколько это необходимо.
Тема 1.2. Ошибки измерений и их оценка
Типы измерений. Абсолютная и относительная погрешность измерения.
Выполнение любых научных исследований связано с измерением различных физических величин и последующей математической обработкой полученных данных.
Определение. Под измерением понимают сравнение измеряемой величины с другой величиной, принятой за единицу измерения.
Различают два типа измерений: прямые и косвенные.
типы измерений
прямые косвенные
Определение. Прямые измерения – такие, при которых измеряется непосредственно интересующая нас физическая величина. При прямом измерении величина сравнивается непосредственно со своей единицей меры. Значение измеряемой величины отсчитывается при этом по соответствующей шкале прибора.
Пример. (длина, интервал времени, масса, температура и т.д.).
• Измерение микрометром линейного размера,
• промежутка времени при помощи часовых механизмов,
• температуры — термометром,
• силы тока – амперметром и т.п.
Определение. Косвенные измерения – такие, при которых измеряемая величина определяется (вычисляется) по результатам измерений других величин, связанных с измеряемой величиной определенной функциональной зависимостью.
Пример.
• измерение скорости по пройденному пути и затраченному времени,
• измерение плотности тела по измерению массы и объема,
• температуры при резании по электродвижущей силе,
• величины силы — по упругим деформациям и т.п.
При измерении любой физической величины производят проверку и установку соответствующего прибора, наблюдение их показаний и отсчет. Даже при использовании очень точных и чувствительных приборов и наилучших условий проведения эксперимента во всяком измерении содержится ошибка (погрешность), характер и причины которых могут быть различными. Общая черта измерений – невозможность получения истинного значения измеряемой величины, поскольку результат эксперимента или измерения всегда содержит какую-то ошибку (погрешность).
Это объясняется как точностью самого измерения, так и природой измеряемых объектов, тем, что измерительные средства основаны на определенном методе измерения, точность которого конечна. При изготовлении прибора задается класс точности. Его погрешность определяется точностью делений шкалы прибора. Если шкала линейки нанесена через 1 мм, то точность отсчета 0,5 мм не изменить, даже если применим лупу для рассматривания шкалы. Аналогично происходит измерение и при использовании других измерительных средств.
Кроме приборной погрешности на результат измерения влияет еще ряд объективных и субъективных причин, обуславливающих появление ошибки измерения. Поэтому одной из важнейших задач математической обработки результатов эксперимента и является оценка истинного значения измеряемой величины по данным эксперимента с возможно меньшей ошибкой.
Поэтому, чтобы указать, насколько полученный результат близок к истинному значению, вместе с ним указывают ошибку измерения. Оценка ошибок необходима, т. к. не зная, каковы они, нельзя сделать определенных выводов из эксперимента.
Если погрешность мала, то ею можно пренебречь. Однако при этом неизбежно возникают два вопроса: во-первых, что понимать под малой погрешностью, и, во-вторых, как оценить величину погрешности. То есть, и результаты эксперимента нуждаются в определенном теоретическом осмыслении. Поэтому правильная оценка проведенных измерений и расчетов позволяет выяснить степень достоверности полученных данных.
Обычно рассчитывают абсолютную и относительную ошибку (погрешность) измерения.
погрешность измерения
Абсолютная Относительная
Определение. Абсолютная погрешность измерения — разность между результатом измерения хi и истинным значением измеряемой величины х:
i
Выражена в единицах измеряемой величины x.
Однако абсолютная погрешность зачастую не отражает качества измерений.
Пример. Действительно, абсолютная погрешность 1 метр при измерении расстояния от Земли до Луны свидетельствует о высоком качестве измерения, та же погрешность совершенно неприемлема при измерении роста человека.
Пример. При измерении длины детали получен ряд значений (мм): l1=10,55; l2=10,57;…; ln=10,56. Вычислено среднее значение lср=10,56 мм. В этом случае погрешности: Δl1= -0,01 мм; Δl2= +0,01 мм;…; Δln= 0 мм – являются абсолютными погрешностями.
Значение только абсолютной погрешности не позволяет в полной мере оценить качество проводимых измерений. Сравним два результата измерений детали: длины (100) мм и толщины (2) мм. Хотя граница абсолютной погрешности в обоих случаях одинакова, качество измерений в первом случае выше.
Поэтому для более объективной характеристики качества измерений вводят относительную погрешность.
Определение. Относительная погрешность измерения δ равна отношению абсолютной погрешности ΔХ к значению величины х, получаемой в результате измерения:
или .
Это отношение безразмерно, и используется как в абсолютном, так и в процентном выражении. Работая с относительной погрешностью, выраженной в процентах, достаточно записать результат с двумя значащими цифрами.
Относительная ошибка характеризует качество измерений. Высокой точности измерения соответствует малое значение относительной погрешности. Наоборот, существенная относительная погрешность характеризует малую точность.
Пример. При измерении длины детали были вычислены среднее значение lср=10,00 мм и абсолютная погрешность Δl=0,01 мм. В этом случае относительная погрешность составляет δ=0,001 или δ%=0,1%.
Определение. Точностью измерения называют величину, обратную относительной ошибке: 1/δ.
Раздел 2. Случайные величины
Тема 2.1. Дискретные случайные величины
Закон распределения вероятностей дискретной случайной величины. Математическое ожидание и дисперсия дискретной случайной величины. Биномиальный закон распределения вероятностей. Распределение Пуассона. Моделирование дискретной случайной величины.
МО – среднее наивероятнейшее значение СВ
Основные законы распределения ДСВ
Биномиальное распределение
Биномиальное распределение – закон распределения дискретной случайной величины Х, представляющей собой число m наступлений события А в серии n независимых испытаний, в каждом из которых событие может произойти с одной и той же вероятностью р. Вероятности вычисляют по формуле Бернулли (где q = 1 — p):
1
…
m
…
n
…
…
Для биномиального распределения: M(X) = np, D(X) = npq.
Пример 4. Построить ряд распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,6. Найти среднее число попаданий и дисперсию. Случайная величина Х – число попаданий в корзину при трех бросках, имеет биномиальный закон распределения.
1
2
3
0,064
0,288
0,432
0,216
Контроль: 0,064+0,288+0,432+0,216=1
M(X)= 3·0,6 = 1,8
D(X) = 3·0,6·0,4 = 0,72
σ(X) = 0,85
Закон Пуассона
Во многих задачах практики приходится иметь дело со случайными величинами, распределенными по своеобразному закону, который называется законом Пуассона.
Рассмотрим прерывную случайную величину X, которая может принимать только целые, неотрицательные значения: О, 1, 2 …, причем последовательность этих значений теоретически не ограничена. Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение k, выражается формулой
где λ — некоторая положительная величина, называемая параметром закона Пуассона.
Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а. Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики — математическое ожидание и дисперсию — случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Тема 2.2. Непрерывные случайные величины
Функция распределения. Плотность распределения вероятностей. Математическое ожидание и дисперсия непрерывной случайной величины. Законы распределения вероятностей: нормальный, показательный, равномерный. Моделирование непрерывной случайной величины.
2.2.1. Функция распределения. Плотность распределения вероятностей
Распределение выступает в роли исчерпывающей характеристики случайной величины. Закон распределения можно задать в виде функционального выражения, графика, таблицы или каким-то другим способом. При любом варианте задания устанавливается связь между вероятностью того, что результат однократного измерения случайной величины попадет в заданный интервал возможных значений, и шириной этого интервала.
2.2.2. Математическое ожидание и дисперсия непрерывной случайной величины
Распределение содержит наиболее полную информацию о случайной величине, однако пользоваться им не всегда удобно. Оперируя результатами проведенного эксперимента, вместо функции распределения лучше иметь привычные числовые величины – ими являются среднее значение и дисперсия.
Тема 2.3. Основные законы распределения НСВ
2.3.1. Равномерный закон распределения
В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.
Определение. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.
Пример. Примеры случайных величин, имеющих равномерное распределение – время ожидания автобуса, ошибка при взвешивании, измерении.
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению.
Пример. Измерения проводят линейкой с ценой деления 1 мм. Показания измерений округляют до ближайшего целого значения. а) Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,1 мм. б) Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х, равномерно распределенной в интервале [0; 1].
а) Р(0,1<Х<0,9) = (0,9 — 0,1) / (1 — 0) = 0,8, т.е. 80%.
б) МХ = (0 + 1)/ 2 = 0,5; DX = (1 — 0)2 /12 = 0,08 и σ(Х) = 0,29.
2.3.2. Показательный (экспоненциальный) закон распределения
Определение. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ>0, если ее плотность вероятности имеет вид:
Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Показательное распределение определяется одним параметром, в этом его преимущество перед другими распределениями.
Пример. Примеры случайных величин, имеющих показательное распределение – период времени работы прибора между поломками, затраты времени на обслуживание одного станка.
Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
Пусть элемент начинает работать и по истечении времени t происходит отказ. Обозначим через T непрерывную СВ – длительность времени безотказной работы элемента.
Функция распределения:
F(t) = P(T
5)=0,5
Если нужно производить вычисления для нормальной величины, ее нормируют.
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m и на участок от α до β.
—
вероятность того, что нормальная СВ попадет в интервал (α;β)
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания:
—
Вероятность попадания случайной величины в интервал, симметричный относительно математического ожидания
Пример. Случайная величина Х распределена нормально с параметрами =8 и =3. Найти вероятность того, что случайная величина попадет в интервал [12,5; 14].
Решение.
Р(12,5<Х<14) = = Ф(2) – Ф(1,5) = 0,4772 – 0,4332 = 0,0440, т.е. с вероятностью 4,4% случайная величина попадет в заданный интервал.
Пример. Диаметр изготовляемой на станке детали – нормальная случайная величина со стандартом =2 мм. Какова вероятность брака, если бракуются детали, диаметр которых отклоняется от нормы (математического ожидания) более, чем на 3,5 мм?
Решение.
P(Δd>3,5)=1-P(Δd ≤3,5)
P(Δd ≤3,5)== 2Ф(1,75)=0,9198
P(Δd>3,5)=1-0,9198=0,0802
Пример. Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м); среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).
Решение. Ошибка измерения есть случайная величина X, подчиненная нормальному закону с параметрами m = 1,2 и = 0,8. Нужно найти вероятность попадания этой величины на участок от =—1,6 до = + 1,6.
По формуле имеем:
Р (—1,6 < X < 1,6) = Ф* (0,5) — Ф* (—3,5).
Пользуясь таблицами функции Ф* (х), найдем:
Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,
откуда
Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913 = 0,691.
Очевидно, что вероятность абсолютного отклонения нормальной СВ не зависит от ее МО, а зависит только от . Можно вычислить:
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигм». Из «правила трех сигм» вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения .
Смысл этих соотношений заключается в установлении связи между шириной интервала ± Δx вокруг m и вероятностью попадания измеренного значения случайной величины в этот интервал, если величина распределена по нормальному закону. Так, результат измерения с вероятностью 68% попадет в интервал [m– , m+ ], т.е. примерно каждое третье измерение даст результат за пределами этого интервала. За пределами интервала [m-2, m+2] окажется один результат из двадцати, а для интервала [m-3, m+3] – только один из трехсот. Значит, интервал ±3 вокруг m является почти достоверным, так как подавляющее большинство отдельных результатов многократного измерения случайной величины окажется сосредоточенным именно в нем. Отсюда следует правило «трех сигм»: практически достоверно, что значения нормальной случайной величины Х заключены в интервале или, другими словами, отклонения более чем утроенный стандарт, (3) практически невозможны.
Опережая ход изложения, заметим, что часто используемое при измерениях правило 3, или правило трех стандартов, основано на указанном свойстве нормального распределения. С учетом проведенного выше анализа, можно установить наличие промаха в результате отдельного измерения, а значит, отбросить его, если результат измерения более чем на 3 отличается от измеренного среднего значения случайной величины.
Нормальное распределение является наиболее изученным, поэтому его стараются использовать при рассмотрении величин, подчиняющихся другим распределениям. Если при обработке экспериментальных данных точно не известно распределение СВ, ее считают приближенно подчиненной нормальному закону. В дальнейших расчетах, например, при проверке гипотезы, различия между распределениями могут быть учтены.
Раздел 3. Статистическая обработка экспериментальных данных
Тема 3.1. Выборочный метод
Во многих экспериментах исход опыта зависит от такого большого количества факторов, что статистические методы исследования являются практически единственными для исследования. Даже если сами исследуемые величины не являются случайными, в результате проведения опыта допускаются погрешности измерений, случайные ошибки.
Тема 3.2. Интервальные оценки
Оценки, рассматриваемые ранее, выражались одним числом и поэтому назывались точечными. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. В этом случае необходимо пользоваться интервальными оценками. Кроме того, в ряде задач требуется не только найти для оцениваемого параметра числовое значение, но оценить его точность и надежность. Такого рода задачи очень важны при малом числе наблюдений, так как конечная оценка в значительной мере является случайной и приближенная замена на может привести к серьезным ошибкам.
Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Задачу интервального оценивания в самом общем виде можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что этот интервал покроет (накроет) оцениваемый параметр.
Для определения точности оценки в математической статистике пользуются доверительными интервалами, а для определения надежности — доверительными вероятностями. Раскроем сущность этих понятий.
Определение. Доверительным интервалом для параметра называется такой интервал, относительно которого можно с заранее выбранной вероятностью (близкой к единице), утверждать, что он содержит неизвестное значение параметра .
Пусть по данным выборки изучается некоторый параметр θ. Пусть — несмещенная оценка параметра θ. Требуется оценить возможную при этом ошибку. По определенным правилам находят такое число , чтобы выполнялось соотношение:
(1)
.
Равенство означает, что интервал [], где = , а = , заключает в себе оцениваемый параметр с вероятностью .
Определение. Вероятность , с которой выполняется неравенство (1), называют доверительной вероятностью или надежностью интервальной оценки, а значение — уровнем значимости.
Нижняя и верхняя граница доверительного интервала и определяются по результатам наблюдений, следовательно, сам доверительный интервал является случайной величиной. В связи с этим говорят, что доверительный интервал покрывает оцениваемый параметр с вероятностью .
Выбор определяется конкретными условиями решаемой задачи. Надежность принято выбирать равной 0,95; 0,99; 0,999 – тогда событие, состоящее в том, что интервал [], покрывает параметр будет практически достоверным.
При этом число характеризует точность интервальной оценки: чем меньше , тем оценка точнее и наоборот.
Заданная надежность указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен, лишь в 5% случаев он может выйти за границы доверительного интервала.
Тема 3.3. Интервальная оценка математического ожидания
при известной дисперсии
На практике часто встречаются нормально распределенные случайные величины (или стремящиеся к нормальному). Рассмотрим интервальные оценки для параметров нормального распределения.
Пусть случайная величина Х распределена по нормальному закону, причем математическое ожидание m неизвестно, а дисперсия известна. Требуется оценить неизвестное математическое ожидание. По наблюдениям найдем точечную оценку математического ожидания. Зададимся вероятностью и найдем такое число , чтобы выполнялось соотношение:
.
Доказано, что построение доверительного интервала в этом случае осуществляется по формуле:
,
где – значение стандартной нормальной величины, соответствующее надежности , а – функция Лапласа. Очевидно, что увеличение надежности приводит к увеличению функции и соответственно увеличению параметра t, что в свою очередь увеличивает величину . То есть увеличение надежности оценки ведет к снижению ее точности (увеличению погрешности).
При этом точность оценки математического ожидания равна:
Очевидно, что с увеличением объема выборки n величина погрешности уменьшается, т.е. точность оценки повышается. Эта формула позволяет определить необходимый объем выборки для оценки математического ожидания с наперед заданной точностью и надежностью:
.
Для вычисления значения можно воспользоваться статистической функцией НОРМСТОБР(1– α) мастера функций, где .
Пример. СВ Х имеет нормальное распределение с известным средним квадратическим отклонением Найти доверительные интервалы для оценки неизвестного математического ожидания по выборочной средней = 4,1, если объем выборки = 36, и задана надежность оценки
Решение.
,
По таблице: t=1,96
Доверительный интервал: -0.98=3.12, +0,98=5,08
Т.о., значения неизвестного параметра удовлетворяют неравенству: 3,12 , нулевую гипотезу отвергают.
В принятии гипотезы следует проявлять осторожность. Можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями и др.
Рассмотрим один из способов вычисления теоретических частот и проверки гипотезы.
Ход проверки гипотезы по критерию Пирсона:
1. Построить точечное распределение выборки.
2. Вычислить выборочную среднюю и выборочное среднее квадратическое отклонение
3. Нормировать случайную величину Х:
4. По таблице найти значения функции .
5. Вычислить теоретические частоты:
.
где h – длина интервала или шаг.
6. Вычислить
7. Сравнить и и сделать вывод.
Пример 1. В таблице представлены изменения выработки в % на одного основного рабочего. Проверить гипотезу, что выработка рабочих цеха распределена по нормальному закону при уровне значимости 0,05.
Выработка, %
94-100
100-106
106-112
112-118
118-124
124-130
130-136
136-142
Число рабочих
5
7
9
20
28
18
8
5
Найдем середины интервалов. Первоначально определяем характеристики: ; . В предположении, что выработка рабочих цеха распределена нормально, вычисляем теоретические частоты:
i
xi
ni
zi
φ(zi)
ni’
1
97
5
-2,19
0,0363
2,15
3,78
2
103
7
-1,59
0,1127
6,68
0,02
3
109
9
-1,01
0,2396
14,19
1,89
4
115
20
-0,41
0,3668
21,73
0,14
5
121
28
0,18
0,3925
23,25
0,97
6
127
18
0,77
0,2966
17,57
0,1
7
133
8
1,36
0,1582
9,37
0,20
8
139
5
1,95
0,0596
3,53
0,61
Σ
100
98,46
7,62
1. .
2. Согласно критерию критическая область W – правосторонняя: .
3. Т.к. нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
4. Вывод: предположение о том, что выработка рабочих цеха распределена нормально, согласуется с данными исследования.
Задача 9. В сборочном цехе время вынужденных простоев в течение смены представлено распределением:
хi, мин
15
20
25
30
35
40
45
50
55
ni
6
13
38
74
106
85
30
10
4
При уровне значимости 0,05 проверить гипотезу о нормальном распределении времени вынужденных простоев по критерию согласия Пирсона.
Задача 12. В механическом цехе была проанализирована выработка рабочих за смену и эмпирическое распределение выборки приведено в таблице:
хi – хi+1
3-8
8-13
13-18
18-23
23-28
28-33
33-38
ni
6
8
15
40
16
8
7
Используя критерий Колмогорова, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении выработки рабочих за смену с эмпирическим распределением выборки.
Раздел 4. Представление результатов эксперимента
с помощью корреляционного и регрессионного анализа
Тема 4.1. Дисперсионный анализ.
Основы дисперсионного анализа. Однофакторный дисперсионный анализ. Коэффициент детерминации. Двухфакторный дисперсионный анализ без повторений. Реализация дисперсионного анализа в пакете Exel.
4.1.1. Основные понятия
При проверке нулевых гипотез предполагалось, что наблюдаемый разброс результатов связан со случайными причинами, которые поддерживаются на одном и том же уровне.
При проведении типичного эксперимента приходится иметь дело с большим количеством факторов, влияющих на изучаемую случайную величину. Перейдем к рассмотрению задачи обработки результатов эксперимента, в которой один или несколько факторов заданным образом могут изменяться. Эти изменения могут повлиять на результаты эксперимента и необходимо установить степень такого изменения, его количественные и качественные характеристики.
В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как факторы, независимые переменные, а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.
Определение. Переменные, значения которых определяются с помощью измерений в ходе эксперимента, называются зависимыми переменными. Переменные, которыми можно управлять при проведении эксперимента, называются факторами или независимыми переменными.
Фактор может быть количественным (скорость резания, размер заготовки, и т.п.) или качественным (модель станка, марка инструментального материала и т.п.).
Будем обозначать:
F – независимая переменная, фактор, причина, влияющая на результат
Х – зависимая переменная, отклик, наблюдаемый признак — результат эксперимента
Пример. Х — балл, набранный при тестировании, F — методы обучения, или время на подготовку, или способ тестирования, позволяющие разделить наблюдения на группы или классифицировать.
Пример. Х – производительность труда, F – стаж работы.
Пример. Х – зарплата работника, F – уровень образования.
Определение. Дисперсионный анализ — это статистический метод обработки данных эксперимента, который применяется для исследования влияния одного или нескольких факторов на одну зависимую количественную переменную (отклик).
Дисперсионный анализ — от латинского Dispersio – рассеивание / на английском Analysis Of Variance – ANOVA.
Дисперсионный анализ – анализ изменчивости (вариации) признака Х под влиянием каких-либо контролируемых переменных факторов. Следует подчеркнуть, что в отличие от регрессионного анализа в ДА оценивается лишь влияние фактора в целом (влияет или нет) и не выясняются количественные соотношения.
Родоначальником метода дисперсионного анализа в 20 – х годах ХХ века является английский статистик и генетик, один из основоположников математической статистики Роналд Эйлмер Фишер (1890-1962 г.г.), применивший его впервые в задачах биологической и, в частности, сельскохозяйственной статистики. Поэтому классическим примером здесь является исследование зависимости урожая.
Пример. X — вес урожая некоторой культуры, F1 — характер почвы, F2 — способ ее обработки, F3 – освещенность, F4 – температура и т.д.
В дисперсионном анализе устанавливается факт зависимости или независимости исследуемой случайной величины от одного или нескольких факторов. Сами факторы могут быть как количественными, так и качественными.
Пример. Можно, например, поставить вопрос, зависит ли количество дорожно-транспортных происшествий (ДТП) от цвета автомобилей? Здесь фактор – цвет автомобиля – является качественным. Можно поставить другой вопрос: зависит ли количество ДТП от возраста водителя? Здесь фактор – возраст водителя – является количественным.
В настоящее время дисперсионный анализ является мощным орудием обработки самых различных наблюдений.
Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными.
По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).
Дисперсионный анализ в зависимости от количества факторов
однофакторный
изучается влияние одного фактора на результаты эксперимента
двухфакторный
при изучении влияния двух факторов
многофакторный
позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие
При проведении ДА предполагается, что выполняются следующие условия:
1 Результаты наблюдений признака Х являются независимыми случайными величинами, имеющими нормальный закон распределения.
2 Случайные ошибки наблюдений подчиняются нормальному закону распределения.
3 Входные исследуемые факторы Fi влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной. (Это предположение обычно оправдывается, если в ходе эксперимента для получений наблюдений используется одна и та же методика, одни и те же приборы.)
4 Эксперименты равноточны.
Проверка данных условий перед проведением ДА обязательна.
Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным. Строго говоря, перед тем, как применять дисперсионный анализ, мы должны убедиться в нормальности распределения результативного признака.
4.1.2. Постановка задачи
Пусть X – некоторая случайная величина, распределенная нормально, на которую влияет фактор F. В процессе эксперимента фактор поддерживаются на n уровнях. На каждом уровне фактора проводится по m испытаний. Значение m может быть одинаковым или разным для каждого из уровней. Результаты всех измерений представляют в виде таблицы, которую называют матрицей наблюдений.
Требуется выяснить, какие из этих факторов являются существенными в смысле влияния на величину X и какие – несущественными.
Выдвигается гипотеза H0: все групповые выборочные средние одинаковы при допущении, что групповые генеральные дисперсии хотя и неизвестны, но одинаковы. Эта гипотеза эквивалентна предположению, что ни один из факторов не влияет на величину X.
Альтернативной или конкурирующей гипотезой H1 является предположение, что хотя бы один фактор влияет на величину X.
Требуется с помощью сравнения (анализа) дисперсий проверить гипотезу.
Принимая решение H0, отвергаем влияние на X одновременно всех факторов. Принимая решение H1, признаём, что на величину X оказывает существенное влияние хотя бы один фактор.
Сущность дисперсионного анализа заключается в разделении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F — критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.
Общая дисперсия
Факторная дисперсия
Дисперсия, обусловленная влиянием факторов
Остаточная дисперсия
Дисперсия, обусловленная случайной ошибкой
Тема 4.2. Однофакторный дисперсионный анализ
Итак, начнем рассмотрение дисперсионного анализа с простейшего случая, когда исследуется действие только одной переменной (одного фактора). Исследователя интересует, как изменяется определенный признак в разных условиях действия этой переменной. Например, как изменяется время решения задачи при разных условиях мотивации испытуемых (низкой, средней, высокой) или при разных способах предъявления задачи (устно, письменно, в виде текста с графиками и иллюстрациями), в разных условиях работы с задачей (в одиночестве, в одной комнате с экспериментатором, в одной комнате с экспериментатором и другими испытуемыми) и т.п. В первом случае переменной, влияние которой исследуется, является мотивация, во втором — степень наглядности, в третьем — фактор публичности.
Пусть на нормально распределенный признак Х воздействует фактор F, который имеет n постоянных уровней. Пусть число наблюдений на каждом уровне одинаково и равно m. Пусть наблюдалось mn значений xij признака X, где
m – число испытаний
n – число уровней фактора
i – номер испытания, i=1, 2 ,… m
j – номер уровня фактора, j=1, 2, … n
Результаты наблюдений представлены в таблице.
Номер испытания
Уровни фактора F
F1
F2
…
F n
1
х11
х12
х1 n
2
х21
х22
х2 n
…
…
…
…
m
х m 1
х m 2
хq n
Групповая средняя
гр1
гр2
гр n
Требуется на уровне значимости α проверить нулевую гипотезу о равенстве всех групповых средних, т. е. установить, значимо или незначимо различаются выборочные средние.
Необходимо вычислить:
— групповая средняя
—
сумма квадратов наблюдаемых значений признака на уровне Fj
—
сумма наблюдаемых значений признака на уровне Fj
Sобщ. = —
общая сумма квадратов отклонений наблюдаемых значений признака от общей средней
S факт. = —
факторная сумма квадратов отклонений групповых средних от общей средней, характеризует рассеяние между группами
Sост. = Sобщ. — Sфакт. –
остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, характеризует рассеяние внутри группы
— общая дисперсия
— факторная дисперсия
— остаточная дисперсия
Далее применяется критерий Фишера – Снедекора, по которому для
S2 факт. и S2 ост. необходимо вычислить величину:
—
наблюдаемое значение критерия Фишера
По таблице критических точек распределения критерия Фишера – Снедекора по заданному уровню значимости α и числам степеней свободы k1 и k2 находят критическую точку Fкр.( α, k1, k2), где
k1 – число степеней свободы числителя
k2 — число степеней свободы знаменателя
Если Fнабл. < Fкр. – нет оснований отвергнуть нулевую гипотезу, т.е. различие групповых средних незначимо, фактор не оказывает существенное влияние на случайную величину Х и им можно пренебречь. Влияние фактора нужно признать незначимым, так как он не сумел существенно увеличить случайный разброс наблюдений.
Если Fнабл. > Fкр. – нулевую гипотезу отвергают, т.е. различие групповых средних значимо, фактор оказывает существенное влияние на случайную величину Х и его нужно учитывать. Это различие может быть вызвано только влиянием фактора, которое нужно признать значимым.
Пример1. На предприятии проверяется зависимость производительности труда Х от технологического процесса F. Проведено по 4 измерения Х при трех различных технологиях производства (изменялась последовательность выполнения операций). Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний приведены в таблице.
Номер испытания
i
Уровни фактора F
F1
F2
F3
1
38
20
21
2
36
24
22
3
35
26
31
4
31
30
34
гр.j
35
25
27
Решение. Составим расчетную таблицу.
n=3, m=4
Номер испытания
i
Уровни фактора F
Сумма
Σ
F1
F2
F3
xi1
x2 i1
xi2
x2 i2
xi3
x2 i3
1
38
1444
20
400
21
441
2
36
1296
24
576
22
484
3
35
1225
26
676
31
961
4
31
961
30
900
34
1156
P1=4926
P2=2552
P3=3042
ΣP=
10520
R1=140
R2=100
R3=108
ΣR= 348
R2 1=
19600
R2 2=
10000
R2 3=
11664
ΣR2= 41264
Sобщ.=10520-3482/12=428
Sфакт.=41264/4-3482/12=224
S 2факт.=224/2=112
Sост.=428-224=204
S 2ост.=204/3*3=22,67
112/22,67=4,94
Число степеней свободы для S 2факт=2, а для S 2ост.=9. По таблице находим:
F кр.(0,05; 2;9)=4,26
F набл.> F кр., след., нулевая гипотеза о равенстве групповых средних отвергается. Т.е., групповые средние в целом различаются значимо и фактор оказывает существенное влияние на результат. Т.е., последовательность операций значимо влияет на производительность труда.
Пример 2. Исследуется зависимость процентного содержания брака (величина X) среди изделий, изготовленных за единицу времени, от температуры окружающей среды (фактор F). Был произведён подсчёт количества бракованных изделий для пяти интервалов времени при трёх различных температурах окружающей среды. Результаты измерений представлены в следующей таблице.
Процент брака при повышенной температуре
2,5
3,3
2,4
3,0
2,6
Процент брака при нормативной температуре
2,4
3,2
2,2
2,7
2,3
Процент брака при пониженной температуре
2,6
3,4
3,0
3, 1
2,8
Методом дисперсионного анализа проверить гипотезу о влиянии температуры среды на процентное содержание брака среди изготовленных изделий.
Решение. Пусть уровень фактора F1 соответствует повышенной температуре, F2 – нормативной температуре, F3 – пониженной температуре. Все вычисления проведём по формулам (8.3) в одной таблице.
Раздел 5. Элементы корреляционного анализа
Тема 5.1. Основные понятия
Исследования, как в научной, так и прикладной области, носят, как правило, комплексный характер. В этом случае изучается не одна характеристика исследуемого объекта, а целая совокупность показателей. В ряде случаев между показателями – случайными величинами — обнаруживается взаимосвязь, зависимость, которую необходимо оценить, чтобы иметь возможность управлять ими, делать прогнозы.
Различают функциональную, статистическую и корреляционную зависимости.
Определение. Функциональной называется взаимосвязь, при которой каждому значению одного показателя соответствует строго определенное значение другого.
Например, средняя скорость V движения автомобиля на расстояние S связана со временем движения t: V = S / t. Функциональная зависимость между экспериментальными величинами встречается редко.
Определение. Статистической (стохастической, вероятностной) называется взаимосвязь, при которой изменение одной из величин вызывает изменение распределения другой.
При этом одному значению первого показателя может соответствовать несколько значений второго показателя. В качестве примера можно привести зависимость веса человека от его роста. Одному значению роста может соответствовать несколько значений веса.
Среди статистических зависимостей наибольший интерес представляют корреляционные зависимости.
Определение. Корреляционной называется зависимость, при которой с изменением одной из величин изменяется среднее значение другой.
Или иначе, корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием (средним значением) другой.
Термин «корреляция» впервые ввел французский палеонтолог Ж. Кювье, изучающий восстановление облика животного по найденным частям. В статистику этот термин был введен Френсисом Гальтоном, англ. психологом. Однако точную формулу для подсчёта коэффициента корреляции разработал его ученик — математик и биолог — Карл Пирсон (1857 – 1936).
Корреляция – взаимосвязь. Регрессия — зависимость.
Величина Х – независимая переменная, значения которой известны, величина У – зависимая переменная, значения которой нужно предсказать, оценить.
Пример. Пусть У – урожай зерна, Х – количество внесенных удобрений. С одинаковых по площади участков земли при равных удобрениях получают различный урожай, т.е. У не является функцией Х. Это объясняется различными случайными факторами: погодными условиями, осадками, и т.д. Но средний урожай является функцией от количества удобрений, т.е Х и У связаны корреляционной зависимостью.
Пример. Зависимость между средним баллом по результатам сессии и количеством часов, затраченных на подготовку к экзаменам.
Пример. Х- рост, У – вес человека.
Пример. Х- стаж работы, У – производительность труда. Зависимость существует, но без дополнительного исследования нельзя сказать, сколько времени работник потратит на выполнение задания, т.к. на У влияют многие другие факторы, строго учесть которые невозможно.
Пример. У усадка материалов, Х – продолжительность тепловой обработки.
Пример. У – прочность шва, Х – параметры строчки.
Пример. У – покупательский спрос на модель, Х – ее цвет или фасон.
Пример. Зависимость недельной выручки от продажи товара от числа посетителей магазина. Если удается установить такую зависимость и построить ее регрессионную модель, то можно использовать ее для прогноза.
= 2,423+0,00873х – уравнение регрессии.
0,00873 – коэффициент линии регрессии, означает, что каждый новый посетитель магазина в среднем увеличивает выручку на 0,00873 ден. ед.
2,423 – это значение у при х=0, т.е. это результат влияния на выручку других факторов (скидок, стоимости, обслуживания и т.д.).
Корреляционный анализ позволяет определить количественную зависимость результативного признака от изучаемых факторов. Дает возможность установить наличие, силу и форму связи между величинами.
Регрессионный анализ позволяет установить, как в среднем изменяется случайная величина с изменением неслучайных величин; позволяет установить влияние изучаемых факторов на результативный признак.
Тема 5.2. Виды зависимости
Пусть изучается система количественных признаков Х и У. Пусть в результате п опытов получено п пар чисел (xi, yi). При исследовании корреляции начинают с графического анализа полученных данных. Корреляционное поле (или диаграмма рассеяния) является графической зависимостью между результатами измерений двух переменных. Для ее построения исходные данные наносят на график, отображая каждую пару значений (xi,yi) в виде точки с координатами xi и yi в прямоугольной системе координат.
Визуальный анализ корреляционного поля позволяет сделать предположение о форме взаимосвязи двух исследуемых показателей. По форме взаимосвязи корреляционные зависимости принято разделять на линейные и нелинейные. При линейной зависимости огибающая корреляционного поля близка к эллипсу. Выявление формы статистической зависимости необходимо для выбора метода оценки тесноты (силы) взаимосвязи.
Линейная взаимосвязь двух случайных величин состоит в том, что при увеличении одной случайной величины другая случайная величина имеет тенденцию возрастать (или убывать) по линейному закону.
Определение. Корреляция является положительной, если увеличение значения одной переменной приводит к увеличению значения второй (см. рис. 1). Корреляция является отрицательной, если увеличение значения одной переменной приводит к уменьшению значения второй.
Зависимость может и не иметь направленности: в этом случае линейная корреляция отсутствует.
положительная
отрицательная
отсутствует
Рис. 2. Теснота взаимосвязи
Рис. 1. Направленность взаимосвязи
Задачи корреляционного анализа:
— установление наличия корреляционной связи между величинами
— количественная оценка тесноты этой связи
Теснота взаимосвязи может быть оценена качественно по ширине корреляционного поля – чем меньше его ширина, тем больше теснота и сильнее зависимость (см. рис. 2). В качестве количественной меры связи используют линейный коэффициент корреляции, корреляционное отношение и ранговый коэффициент корреляции.
Тема 5.3. Линейный коэффициент корреляции
Коэффициент корреляции Пирсона r применяется для измерения тесноты связи между переменными X и Y при линейной зависимости, когда пара признаков распределены нормально или близко к нормальному. Отличие коэффициента корреляции от нуля характеризует не только наличие связи, но и силу связи.
Основные свойства линейного коэффициента корреляции:
• Коэффициент корреляции принимает значения на отрезке [-1; 1], т.е.
-1 r 1
Чем ближе r к 0, тем слабее корреляция. Чем ближе r к 1, тем сильнее корреляция.
Значение коэффициента корреляции r
Сила связи между Х и У
(0; 0,3)
слабая
(0,3; 0,5)
умеренная
(0,5; 0,7)
заметная
(0,7; 0,9)
достаточно тесная
(0,9; 0,99)
весьма тесная
• Если переменные X и Y умножить на одно и то же число, то коэффициент корреляции не изменится.
• Если , то корреляционная связь между X и Y представляет собой линейную зависимость.
• Если , то линейной корреляционной связи между X и Y нет (а нелинейная может существовать).
• Коэффициент корреляции характеризует только линейную связь.
В теории разработаны и на практике применяются различные модификации формул расчета линейного коэффициента корреляции. Одна из наиболее распространенных формул, применяемых, если каждая пара чисел встречается по одному разу:
—
линейный коэффициент корреляции,
где
— среднее выборочное значение х
— среднее выборочное значение у
— среднее квадратическое отклонение x
— среднее квадратическое отклонение y
Так как линейный коэффициент корреляции вычисляется по данным выборки, то, его называют выборочным (в отличие от генерального коэффициента корреляции rген) и он является случайной величиной.
Если каждое значение двух и более случайных величин встречается только один раз, Exel позволяет определять линейный коэффициент корреляции с помощью функции КОРРЕЛ или режима Корреляция. Для этого в Анализе данных нужно выбрать значение Корреляция. В результате откроется диалоговое окно, в котором задать определенные параметры: диапазон ячеек входных данных; группирование (по строкам или столбцам); флажок метки (если есть заголовок) и новый рабочий лист или ячейки для выходного интервала.
Пример. При исследовании связи между производительностью труда Y и уровнем механизации работ X на предприятии были получены данные, представленные в таблице. Имеется ли линейная корреляционная связь между переменными?
Y, т/ч
32
30
36
40
41
47
56
54
60
55
61
67
69
76
X, %
20
24
28
30
31
33
34
37
38
40
41
43
45
48
Y, т/ч
X, %
Т.к. r = 0,96 и tнабл = =11,86 > tкр=tдв(0,05;12) = 2,18,
Y, т/ч
1
линейный коэффициент корреляции значим и между производительностью труда и уровнем механизации имеется весьма тесная линейная корреляционная связь.
X, %
0,960317
1
Пример. Проводится исследование спроса на некоторый вид товара. Пробные продажи показали следующие данные о зависимости дневного спроса от цены:
Х – цена, ден. ед.
У – спрос, ед. товара
i
xi
yi
1
3,5
8,1
2
4,6
9,4
3
5,8
11,3
4
4,2
6,9
5
5,2
9,7
Cумма
23,3
45,4
Коэффициент корреляции довольно близок к 1, следовательно, связь между величинами довольно тесная, т.е. х оказывает линейное влияние на у.
Раздел 6. Элементы регрессионного анализа
Тема 6.1. Основные понятия
При обработке экспериментальных данных часто возникает задача установления зависимости между исследуемыми величинами.
Основная цель регрессионного анализа состоит в определении связи между некоторой характеристикой Y наблюдаемого явления или объекта и величинами х1, х2, …, хn, которые обусловливают, объясняют изменения Y. Переменная Y называется зависимой переменной (откликом), влияющие переменные х1, х2, …, хn называются факторами (регрессорами).
Задачи регрессионного анализа:
— установление формы зависимости,
— подбор уравнения (модели) регрессии,
— оценка параметров уравнения регрессии
В зависимости от типа выбранного уравнения различают:
Регрессия
линейная нелинейная
квадратичная, экспоненциальная, логарифмическая и т.д.
В зависимости от числа взаимосвязанных признаков различают:
Регрессия
парная множественная
Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками – множественной (многофакторной) регрессией.
Таким образом, корреляционный анализ позволяет сделать вывод о силе взаимосвязи между парами данных х и у, а регрессионный анализ используется для прогнозирования одной переменной (у) на основании другой (х). Иными словами, в этом случае пытаются выявить причинно-следственную связь между анализируемыми совокупностями.
Тема 6.2. Парная линейная регрессионная модель
Линейную регрессию следует ожидать во многих исследованиях. Пропорциональная зависимость величин часто вытекает из математических или физических представлений, исследователь почти всегда представляет, с какой формой зависимости он имеет дело. Предварительный анализ зависимости можно выяснить графически. В сложных случаях, когда зависимость заведомо будет нелинейной, изучение линейной регрессии можно использовать, как первый этап исследования с тем, чтобы потом внести в нее необходимые поправки.
На первом этапе регрессионного анализа данные наблюдений или эксперимента представляют графически.
Зависимость между переменными Х и Y изображают точками на координатной плоскости (х, y) и соединяют их ломаной линией. Этот ломаный график называется эмпирической линией регрессии Y по Х. По виду эмпирической линии регрессии делают предположение о виде (форме) зависимости переменной Y от Х. В данном случае логично предположить линейную зависимость.
Рис. 1.
Если вид функции в уравнении регрессии выбран, то для оценки неизвестных параметров используется метод наименьших квадратов (МНК). Согласно методу неизвестные параметры функции выбираются таким образом, чтобы сумма квадратов отклонений экспериментальных (эмпирических) значений yi от их расчетных (теоретических) значений была минимальной, т.е.
где – значение, вычисленное по уравнению регрессии
– отклонение (ошибка, остаток);
n – количество пар исходных данных.
Рис. 2. Понятие отклонения
(линейная регрессия)
Пусть Х и У связаны линейной зависимостью, тогда искомое уравнение регрессии имеет вид:
y=kx+b,
где k и b – неизвестные параметры, которые нужно найти.
k — коэффициент регрессии (показатель наклона линии линейной регрессии). Коэффициент регрессии показывает, на сколько единиц в среднем изменяется переменная Y при изменении переменной Х на одну единицу.
Пусть для отыскания уравнения произведено n независимых испытаний и получены n пар чисел: (х1; у1); (х2; у2); … (хn; уn). Рассмотрим простейший случай, когда каждая пара значений наблюдалась по одному разу.
С помощью метода наименьших квадратов получают формулы, по которым можно вычислять параметры линейной регрессии:
— коэффициент регрессии
— свободный член
Направление связи между переменными определяется на основании знака коэффициента регрессии. Если знак коэффициента регрессии положительный, связь зависимой переменной с независимой будет положительной. Если знак коэффициента регрессии отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).
Для анализа общего качества уравнения регрессии используют коэффициент детерминации R2, называемый также квадратом коэффициента множественной корреляции. Коэффициент детерминации (мера определенности) всегда находится в пределах интервала [0;1]. Если значение R2 близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R2 близкое к нулю, означает плохое качество построенной модели.
Коэффициент детерминации R2 показывает, на сколько процентов найденная функция регрессии описывает связь между исходными значениями Y и Х. На рис. 3 показана – объясненная регрессионной моделью вариация и — общая вариация. Соответственно, величина показывает, сколько процентов вариации параметра Y обусловлены факторами, не включенными в регрессионную модель.
При высоком значении коэффициента детерминации 75%) можно делать прогноз для конкретного значения в пределах диапазона исходных данных. При прогнозах значений, не входящих в диапазон исходных данных, справедливость полученной модели гарантировать нельзя. Это объясняется тем, что может проявиться влияние новых факторов, которые модель не учитывает.
Оценка значимости уравнения регрессии осуществляется с помощью критерия Фишера. При условии справедливости нулевой гипотезы критерий имеет распределение Фишера с числом степеней свободы , (для парной линейной регрессии р = 1). Если нулевая гипотеза отклоняется, то уравнение регрессии считается статистически значимым. Если нулевая гипотеза не отклоняется, то признается статистическая незначимость или ненадежность уравнения регрессии.
Тема 6.3. Нахождение уравнения линейной регрессии
Для проведения регрессионного анализа:
1. Построить график исходных данных и визуально приближенно определить характер зависимости между величинами и вид функции регрессии.
2. Определить коэффициенты функции регрессии.
3. Оценить силу найденной регрессионной зависимости с помощью коэффициента детерминации.
4. Сделать прогноз 75%) или сделать вывод о невозможности прогнозирования с помощью найденного уравнения регрессии.
Для удобства вычислений используют вспомогательную таблицу.
Пример. В механическом (швейном) цехе анализируется структура себестоимости продукции и доля покупных комплектующих. Было отмечено, что стоимость комплектующих зависит от времени их поставки. В качестве наиболее важного фактора, влияющего на время поставки, выбрано пройденное расстояние. Провести регрессионный анализ данных о поставках:
Расстояние, миль
3,5
2,4
4,9
4,2
3,0
1,3
1,0
3,0
1,5
4,1
Время, мин
16
13
19
18
12
11
8
14
9
16
Построенные точки не находятся точно на линии: помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Но эти точки собраны вдоль прямой линии, поэтому можно предположить линейную положительную связь между параметрами.
1. Вычислим суммы, необходимые для расчета коэффициентов уравнения линейной регрессии и коэффициента детерминации R2:
№
1
3,5
16
12,25
56,00
15,22
2,63
5,76
2
2,4
13
5,76
31,20
12,30
1,70
0,36
3
4,9
19
24,01
93,10
18,95
28,59
29,16
4
4,2
18
17,64
75,60
17,09
12,15
19,36
5
3,0
12
9,00
36,00
13,89
0,08
2,56
6
1,3
11
1,69
14,30
9,37
17,88
6,76
7
1,0
8
1,00
8,00
8,57
25,27
31,36
8
3,0
14
9,00
42,00
13,89
0,09
0,16
9
1,5
9
2,25
13,50
9,90
13,67
21,16
10
4,1
16
16,81
65,60
16,82
10,36
5,76
Σ
28,9
136
99,41
435,30
–
112,42
122,40
; ; ; .
Искомая регрессионная зависимость имеет вид:
.
Определяем направление связи между переменными: знак коэффициента регрессии положительный, следовательно, связь также является положительной, что подтверждает графическое предположение.
3. Вычислим коэффициент детерминации:
или 92%.
Таким образом, линейная модель объясняет 92% вариации времени поставки, что означает правильность выбора фактора (расстояния). Не объясняется 8% вариации времени, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
4. Проверим значимость уравнения регрессии:
Т.к. – уравнение регрессии (линейной модели) статистически значимо.
6. Решим задачу прогнозирования. Поскольку коэффициент детерминации R2 имеет достаточно высокое значение и расстояние 2 мили, для которого надо сделать прогноз, находится в пределах диапазона исходных данных, то можно сделать прогноз:
мин.
Пример. Рассматривается зависимость между прочностью образцов льняной пряжи У и влажностью воздуха Х.
№ пп
х
у
Х2
ху
1.
36
2
1296
72
2.
38
2,5
1444
95
3.
40
2,3
1600
92
4.
58
2,8
3364
162,4
5.
70
3,1
4900
217
6.
80
3,1
6400
248
7.
82
3,2
6724
262,4
8.
93
3,0
9649
279
497
22,0
34377
1427,8
У=0,018х+1,67 – зависимость прочности от влажности
Пример. Анализируется связь между разрывной нагрузкой У и удлинением при растяжении трикотажного полотна Х.
№ пп
хi, %
уi, даН
xi-
1.
37
3
-2,9
-1,4
4,06
8,41
1,96
2.
40
5
0,1
0,6
0,06
0,01
0,36
3.
43
6
3,1
1,6
4,96
9,61
2,56
4.
46
5
6,1
0,6
3,66
37,21
0,36
5.
45
6
5,1
1,6
8,16
26,01
2,56
6.
33
3
-6,9
-1,4
9,66
47,61
1,96
7.
41
3
1,1
-1,4
-1,54
1,21
1,96
8.
48
7
8,1
2,6
21,06
65,61
6,76
9.
37
5
-2,9
0,6
-1,74
8,41
0,36
10.
43
5
3,1
0,6
1,86
9,61
0,36
11.
31
2
-8,9
-2,4
21,36
79,21
5,76
12.
37
4
-2,9
-0,4
1,16
8,41
0,16
13.
35
3
-4,9
-1,4
6,86
24,01
1,96
14.
40
4
0,1
-0,4
-0,04
0,01
0,16
15.
42
5
2,1
0,6
1,26
4,41
0,36
Σ
598
66
-0,5
80,8
329,75
27,6
Пример. Рассматривается зависимость между обхватом груди Х и ростом У у мужчин некоторого города.
Решите самостоятельно.
№ пп
Обхват груди, см х
Рост, см у
Х2
ху
1.
91
160
2.
95
169
3.
97
162
4.
99
168
5.
92
164
6.
96
164
7.
100
165
8.
100
169
9.
97
159
10.
101
170
11.
97
171
12.
95
165
13.
102
171
14.
98
166
15.
101
172
16.
99
175
17.
103
170
18.
104
181
19.
104
176
20.
83
175
Тема 6.4. Сравнительный анализ основных видов обработки экспериментальных данных
Вид анализа
Основные
характеристики
Дисперсионный анализ
Корреляционный анализ
Регрессионный анализ
Цель
Исследование влияния одного или нескольких факторов на одну зависимую количественную переменную.
Установление наличия корреляционной связи между величинами, количественная оценка тесноты этой связи
Установление формы зависимости между величинами Х и У, подбор уравнения (модели) регрессии, оценка параметров уравнения регрессии
Разновидности
Однофакторный, двухфакторный, многофакторный
Линейная – нелинейная, положительная — отрицательная
парная — множественная линейная — нелинейная
Условия проведения анализа
1. Признак Х является нормальной СВ
2. Случайные ошибки наблюдений подчиняются нормальному закону распределения.
3.Дисперсия наблюдений остается постоянной.
4. Эксперименты равноточны.
Пара признаков Х и У распределены нормально или близко к нормальному
Пара признаков Х и У распределены нормально или близко к нормальному
Постановка задачи
Пусть на нормально распределенный признак Х воздействует фактор F, который имеет n постоянных уровней. Требуется проверить нулевую гипотезу о равенстве всех групповых средних, т. е. установить, значимо или незначимо различаются выборочные средние. Эта гипотеза эквивалентна предположению, что фактор не влияет на величину X.
Пусть изучается система количественных признаков Х и У. Пусть в результате п опытов получено п пар чисел (xi, yi). Требуется установить наличие, силу и форму связи между величинами
Пусть произведено n независимых испытаний и получены n пар чисел(xi, yi). Требуется найти уравнение регрессии, оценить силу найденной регрессионной зависимости с помощью коэффициента детерминации, Сделать прогноз (R^2≥75%) или сделать вывод о невозможности прогнозирования с помощью найденного уравнения регрессии
Основные вычисляемые величины
—
наблюдаемое значение критерия Фишера
—
линейный коэффициент корреляции
— уравнение линейной регрессии
Результат анализа (вывод)
Если Fнабл. < Fкр. – нет оснований отвергнуть нулевую гипотезу, т.е. различие групповых средних незначимо, фактор не оказывает существенное влияние на случайную величину Х и им можно пренебречь.
Если Fнабл. > Fкр. – нулевую гипотезу отвергают, т.е. различие групповых средних значимо, фактор оказывает существенное влияние на случайную величину Х и его нужно учитывать.
Чем ближе r к 0, тем слабее корреляция. Чем ближе r к 1, тем сильнее корреляция.
Уравнение регрессии, оценка его значимости, прогноз
Рекомендуемая литература
4.1. Основная литература
1. Вуколов Э.А. Основы статистического анализа.-М.: ИД Форум: Инфра-М, 2008 – Гриф МО.
2. Петров Ю. П., Петров И. А. Введение в теорию инженерных расчетов, учитывающую вариации параметров исследуемых объектов, 2014 г.
3. Голубева, Н.В. Математическое моделирование систем и процессов: Учебное пособие — СПб.: Лань, 2013.- 192с.: ил.
4. Рогов В.А. Методика и практика технических экспериментов: учеб пособ.- М.: Издательский центр «Академия», 2005.
5. Общий курс высшей математики для экономистов: учебник для втузов/ Под. ред. В.И. Ермакова.-М.: Инфра-М, 2004.-656 с. – Гриф МО.
6. Кремер, Н.Ш. Теория вероятности и математическая статистика [Текст]. — М.: Юнити, 2007 – Гриф МО.
4.2. Дополнительная литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пос. — М.: Высш. шк., 2005.
2. Яворский В.А. Планирование научного эксперимента и обработка экспериментальных данных. Учебно-методическое пособие. – М.: МФТИ, 2006. – 24 с. (http://www.twirpx.com/file/136115/)
3. Ходасевич Г.Б. Обработка экспериментальных данных на ЭВМ: обработка одномерных массивов. Учебное пособие. – СПб.: ГУ Телекоммуникаций, 2008 – 60 с. (http://dvo.sut.ru/libr/opds/i130hod2/index.htm)
4. Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного эксперимента. Учебное пособие. – Екатеринбург: Уральский ГТУ, 2004. – 257 с.
5. Жедь О.В. Методические разработки к лабораторному практикуму по дисциплине «Математические методы обработки экспериментальных данных» — М.: РУДН, Кафедра Технологии машиностроения, 2012, 142 с. CD-диск.
6. Жедь О.В. Методические указания по программному обеспечению лабораторного практикума дисциплины «Математические методы обработки экспериментальных данных». — М.: РУДН, Кафедра Технологии машиностроения, 2012, 56 с. CD-диск.
4.3. Методическая литература
1. Борисевич В.И. Случайные события и случайные величины. Учебное пособие для студентов всех специальностей.
2. Борисевич В.И. Элементы математической статистики. Учебное пособие для студентов всех специальностей.
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 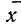
За меру точности соответствия принятой средней арифметической 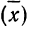
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 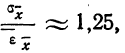
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 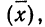
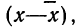
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 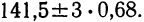
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление