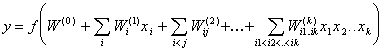Характер приближений в информационных моделях
Специфичность информационных моделей проявляется не только в способах их синтеза, но и характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении системы и ее информационной модели возникают вследствие свойств экспериментальных данных.
- Информационные модели ab initio являются неполными. Пространства входных и выходных переменных не могут, в общем случае, содержать все параметры, существенные для описания поведения системы. Это связано как с техническими ограничениями, так и с ограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются требования на объем необходимых экспериментальных данных для построения модели (об этом см. ниже). Эффект опущенных (скрытых) входных параметров может нарушать однозначность моделируемой системной функции F.
- База экспериментальных данных, на которых основывается модель G рассматривается, как внешняя данность. При этом, в данных всегда присутствуют ошибки разной природы, шум, а также противоречия отдельных измерений друг другу. За исключением простых случаев, искажения в данных не могут быть устранены полностью.
- Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задачи. Как следствие, получаемые модели будут обладать неодинаковой достоверностью и точностью в различных областях изменения параметров.
- Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери информации, отказа измеряющих датчиков, невозможности проведения полного набора анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки, ухудшает свойства модели.
Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам информационных моделей.
Ошибка обучения и ошибка обобщения
Итак, при информационном подходе требуемая модель G системы F не может быть полностью основана на явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в соответствии с заданным критерием, настолько близко, насколько возможно. Алгоритмически, обучение означает подстройку внутренних параметров модели (весов синаптических связей в случае нейронной сети) с целью минимизации ошибки модели 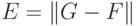
Прямое измерение указанной ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента не известна. Однако возможно получение ее оценки:
где суммирование по X проводится по некоторому конечному набору параметров X, называемому обучающим множеством. При использовании базы данных наблюдений за системой, для обучения может отводиться некоторая ее часть, называемая в этом случае обучающей выборкой. Для обучающих примеров X отклики системы Y известны7С учетом описанных выше особенностей экспериментальных данных.
. Норма невязки модельной функции G и системной функции Y на множестве X играет важную роль в информационном моделировании и называется ошибкой обучения модели.
Для случая точных измерений (например, в некоторых задачах классификации, когда отношение образца к классу не вызывает сомнений) однозначность системной функции для достаточно широкого класса G моделей гарантирует возможность достижения произвольно малого значения ошибки обучения EL. Нарушение однозначности системной функции в присутствии экспериментальных ошибок и неполноты признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В этом случае предельная достижимая ошибка обучения может служить мерой корректности постановки задачи и качества класса моделей G.
В приложениях пользователя обычно интересуют предсказательные свойства модели. При этом главным является вопрос, каковым будет отклик системы на новое воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая моделью G на данных, не использовавшихся при обучении, называется ошибкой обобщения модели EG.
Основной целью при построении информационной модели является уменьшение именно ошибки обобщения, поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее выбранных точках (а в них значения отклика системы известны и без всякой модели!). Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка обучения соответствует прямому запоминанию обучающей информации, а малая ошибка обобщения — формированию понятий и навыков, позволяющих распространить ограниченный опыт обучения на новые условия. Последнее значительно более ценно при проектировании нейросетевых систем, так как для непосредственного запоминания информации лучше приспособлены не нейронные устройства компьютерной памяти.
Важно отметить, что малость ошибки обучения не гарантирует малость ошибки обобщения. Классическим примером является построение модели функции (аппроксимация функции) по нескольким заданным точкам полиномом высокого порядка. Значения полинома (модели) при достаточно высокой его степени являются точными в обучающих точках, т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут значительно отличаться от аппроксимируемой функции, следовательно ошибка обобщения такой модели может быть неприемлемо большой.
Поскольку истинное значение ошибки обобщения не доступно, в практике используется ее оценка. Для ее получения анализируется часть примеров из имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта выборка примеров называется тестовой выборкой. Ошибка обобщения оценивается, как норма уклонения модели на множестве примеров из тестовой выборки.
Оценка ошибки обобщения является принципиальным моментом при построении информационной модели. На первый взгляд может показаться, что сознательное не использование части примеров при обучении может только ухудшить итоговую модель. Однако без этапа тестирования единственной оценкой качества модели будет лишь ошибка обучения, которая, как уже отмечалось, мало связана с предсказательными способностями модели. В профессиональных исследованиях могут использоваться несколько независимых тестовых выборок, этапы обучения и тестирования повторяются многократно с вариацией начального распределения весов нейросети, ее топологии и параметров обучения. Окончательный выбор «наилучшей» нейросети выполняется с учетом имеющегося объема и качества данных, специфики задачи, с целью минимизации риска большой ошибки обобщения при эксплуатации модели.
Каталог статей
- Выбор модели, переоснащение и недооборудование
- Ошибка обучения и ошибка обобщения
- Выбор модели
- Набор для проверки
- K-кратная перекрестная проверка
- Недостаточное и переобучение
- Сложность модели
- Подгонка полинома
- Снижение веса
- L2 регуляризация
- Pytorch реализация снижения веса
- dropout
- Реализация отсева в Pytorch
- Исчезающий градиент и взрывной градиент
- Произвольно инициализировать параметры модели
- Случайная инициализация PyTorch по умолчанию
- Ксавье случайная инициализация
- резюме
Выбор модели, переоснащение и недооборудование
Ошибка обучения и ошибка обобщения
Ошибка обучения (ошибка обучения) относится к ошибке, которую модель показывает в наборе данных обучения.
Ошибка обобщения — это ожидаемая ошибка модели для любой выборки тестовых данных, которая часто приближается к ошибке в наборе тестовых данных.
Чтобы вычислить ошибку обучения и ошибку обобщения, вы можете использовать функции потерь, представленные ранее, такие как функция потерь квадрата, используемая в линейной регрессии, и функция потерь кросс-энтропии, используемая в регрессии softmax.
Следовательно, ожидаемая ошибка обучения меньше или равна ошибке обобщения. То есть, как правило, параметры модели, полученные из набора обучающих данных, сделают производительность модели на наборе обучающих данных лучше или равной производительности на наборе тестовых данных. Поскольку ошибку обобщения невозможно оценить по ошибке обучения, слепое уменьшение ошибки обучения не означает, что ошибка обобщения будет уменьшена.
Модели машинного обучения должны быть направлены на уменьшение ошибок обобщения.
Выбор модели
Набор для проверки
Набор тестов можно использовать только один раз после выбора всех гиперпараметров и параметров модели. Вы не можете использовать тестовые данные для выбора моделей, таких как параметры настройки.
Зарезервируйте часть данных вне набора обучающих данных и набора тестовых данных для выбора модели. Эта часть данных называется набором данных проверки, или для краткости набором данных проверки.
K-кратная перекрестная проверка
Поскольку набор данных проверки не участвует в обучении модели, слишком расточительно резервировать большой объем данных проверки, когда данных обучения недостаточно. Один из способов улучшить
K
K
Сложите перекрестную проверку (
K
K
-кратная перекрестная проверка). в
K
K
При перекрестной проверке сверток мы разбиваем исходный набор обучающих данных на
K
K
Наборы субданных, которые не пересекаются, мы делаем
K
K
Вторичное обучение и проверка модели. Каждый раз мы используем набор дополнительных данных для проверки модели и других
K
−
1
K-1
Наборы вспомогательных данных для обучения модели. На это
K
K
При обучении и проверке набор дополнительных данных, используемых для проверки модели, каждый раз отличается. Наконец, мы
K
K
Ошибка суб-обучения и ошибка проверки усредняются отдельно.
Недостаточное и переобучение
- Первый тип заключается в том, что модель не может получить более низкую ошибку обучения.Мы называем это явление недостаточным соответствием;
- Другой тип заключается в том, что ошибка обучения модели намного меньше, чем ее ошибка на наборе тестовых данных.Мы называем это явление переобучением. На практике нам приходится иметь дело с недооборудованием и переоборудованием одновременно, насколько это возможно. Хотя существует множество факторов, которые могут вызвать эти две проблемы подгонки, здесь мы сосредоточимся на двух факторах: сложности модели и размере обучающего набора данных.
Сложность модели

Рисунок 3.4 Влияние сложности модели на недостаточное и переобучение
Еще один важный фактор, влияющий на недостаточную и избыточную подгонку, — это размер набора обучающих данных. Вообще говоря, если количество выборок в наборе обучающих данных слишком мало, особенно когда количество параметров модели (по элементам) меньше, вероятность переобучения выше. Кроме того, ошибка обобщения не увеличивается по мере увеличения количества выборок в наборе обучающих данных. Поэтому в пределах допустимого диапазона вычислительных ресурсов мы обычно надеемся, что набор обучающих данных будет больше, особенно когда сложность модели высока, например, модель глубокого обучения с большим количеством слоев.
Подгонка полинома

Нормальная посадка

Недостаточное оснащение

Переоснащение
Снижение веса
В предыдущем разделе мы наблюдали явление переобучения, то есть ошибка обучения модели намного меньше, чем ее ошибка на тестовом наборе. Хотя увеличение набора обучающих данных может уменьшить переобучение, получение дополнительных обучающих данных часто обходится дорого. В этом разделе представлен общий метод решения проблем с переобучением: снижение веса.
L2 регуляризация
Снижение веса эквивалентно
L
2
L_2
Регуляризация нормы (регуляризация). Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением. Сначала опишем
L
2
L_2
Нормализация регуляризации, а затем объясните, почему это также называется снижением веса.
L
2
L_2
Добавлена регуляризация нормы на основе исходной функции потерь модели.
L
2
L_2
Нормальный штрафной срок для получения функции, которую необходимо минимизировать для обучения.
L
2
L_2
Штраф за норму относится к произведению суммы квадратов каждого элемента весового параметра модели и положительной константы. Возьмите функцию потерь линейной регрессии из раздела 3.1 (линейная регрессия)
ℓ
(
w
1
,
w
2
,
b
)
=
1
n
∑
i
=
1
n
1
2
(
x
1
(
i
)
w
1
+
x
2
(
i
)
w
2
+
b
−
y
(
i
)
)
2
ell(w_1, w_2, b) = frac{1}{n} sum_{i=1}^n frac{1}{2}left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right)^2
Например, где
w
1
,
w
2
w_1, w_2
Весовой параметр,
b
b
Параметр отклонения, образец
i
i
Вход
x
1
(
i
)
,
x
2
(
i
)
x_1^{(i)}, x_2^{(i)}
С этикеткой
y
(
i
)
y^{(i)}
, Количество образцов
n
n
. Использовать векторные весовые параметры
w
=
[
w
1
,
w
2
]
boldsymbol{w} = [w_1, w_2]
Средства с
L
2
L_2
Новая функция потерь нормального штрафного члена имеет вид
ℓ
(
w
1
,
w
2
,
b
)
+
λ
2
n
∥
w
∥
2
,
ell(w_1, w_2, b) + frac{lambda}{2n} |boldsymbol{w}|^2,
Где гиперпараметры
λ
>
0
lambda > 0
. Когда все весовые параметры равны 0, срок штрафа самый маленький. когда
λ
lambda
Когда он больше, штрафной член имеет большую долю в функции потерь, что обычно приближает элемент изученного весового параметра к 0. когда
λ
lambda
Если установлено значение 0, штраф не действует. В приведенной выше формуле
L
2
L_2
Норма в квадрате
∥
w
∥
2
|boldsymbol{w}|^2
После раскладывания
w
1
2
+
w
2
2
w_1^2 + w_2^2
. С
L
2
L_2
После штрафного члена нормы в небольшом пакетном стохастическом градиентном спуске мы будем использовать веса в разделе линейной регрессии.
w
1
w_1
с
w
2
w_2
Метод итерации изменен на
w
1
←
(
1
−
η
λ
∣
B
∣
)
w
1
−
η
∣
B
∣
∑
i
∈
B
x
1
(
i
)
(
x
1
(
i
)
w
1
+
x
2
(
i
)
w
2
+
b
−
y
(
i
)
)
,
w
2
←
(
1
−
η
λ
∣
B
∣
)
w
2
−
η
∣
B
∣
∑
i
∈
B
x
2
(
i
)
(
x
1
(
i
)
w
1
+
x
2
(
i
)
w
2
+
b
−
y
(
i
)
)
.
begin{aligned} w_1 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_1 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_1^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right),\ w_2 &leftarrow left(1- frac{etalambda}{|mathcal{B}|} right)w_2 — frac{eta}{|mathcal{B}|} sum_{i in mathcal{B}}x_2^{(i)} left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b — y^{(i)}right). end{aligned}
видимый,
L
2
L_2
Вес заказа регуляризации нормы
w
1
w_1
с
w
2
w_2
Умножьте число меньше 1, а затем вычтите градиент без штрафа. следовательно,
L
2
L_2
Регуляризация нормы также называется снижением веса. Ослабление веса увеличивает ограничение модели, которое необходимо изучить, штрафуя параметры модели большими абсолютными значениями, что может быть эффективным при переобучении. В реальных сценариях мы иногда добавляем сумму квадратов элементов отклонения к сроку штрафа.
Pytorch реализация снижения веса
%matplotlib inline
import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append(".")
import d2lzh_pytorch as d2l
print(torch.__version__)
1.3.1
def fit_and_plot_pytorch(wd):
# Ослабьте весовые параметры. Названия веса обычно заканчиваются на вес
net = nn.Linear(num_inputs, 1)
nn.init.normal_(net.weight, mean=0, std=1)
nn.init.normal_(net.bias, mean=0, std=1)
optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # Затухание весовых параметров
optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr) # Неправильное затухание параметра отклонения
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y).mean()
optimizer_w.zero_grad()
optimizer_b.zero_grad()
l.backward()
# Вызвать пошаговую функцию в двух экземплярах оптимизатора, чтобы обновить вес и смещение соответственно
optimizer_w.step()
optimizer_b.step()
train_ls.append(loss(net(train_features), train_labels).mean().item())
test_ls.append(loss(net(test_features), test_labels).mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('L2 norm of w:', net.weight.data.norm().item())
dropout
Расчетное выражение многослойного персептрона имеет вид
h
i
=
ϕ
(
x
1
w
1
i
+
x
2
w
2
i
+
x
3
w
3
i
+
x
4
w
4
i
+
b
i
)
h_i = phileft(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_iright)
Вот
ϕ
phi
Есть функция активации,
x
1
,
…
,
x
4
x_1, ldots, x_4
Вход, скрытый блок
i
i
Весовой параметр
w
1
i
,
…
,
w
4
i
w_{1i}, ldots, w_{4i}
, Параметр отклонения
b
i
b_i
. Когда для этого скрытого слоя используется метод отбрасывания, скрытые блоки этого уровня будут отброшены с определенной вероятностью. Пусть вероятность отбрасывания равна
p
p
, То есть
p
p
Вероятность
h
i
h_i
Будет очищено, есть
1
−
p
1-p
Вероятность
h
i
h_i
Разделит на
1
−
p
1-p
Сделайте растяжку. Вероятность отбрасывания — это гиперпараметр метода отбрасывания. В частности, пусть случайная величина
ξ
i
xi_i
Вероятности быть 0 и 1 равны
p
p
с
1
−
p
1-p
. При использовании метода отбрасывания мы вычисляем новый скрытый блок
h
i
′
h_i’
h
i
′
=
ξ
i
1
−
p
h
i
h_i’ = frac{xi_i}{1-p} h_i
из-за
E
(
ξ
i
)
=
1
−
p
E(xi_i) = 1-p
,следовательно
E
(
h
i
′
)
=
E
(
ξ
i
)
1
−
p
h
i
=
h
i
E(h_i’) = frac{E(xi_i)}{1-p}h_i = h_i
которыйМетод discard не меняет ожидаемое значение входных данных.。

Многослойный перцептрон с использованием метода отбрасывания для скрытого слоя
Реализация отсева в Pytorch
net = nn.Sequential(
d2l.FlattenLayer(),
nn.Linear(num_inputs, num_hiddens1),
nn.ReLU(),
nn.Dropout(drop_prob1),
nn.Linear(num_hiddens1, num_hiddens2),
nn.ReLU(),
nn.Dropout(drop_prob2),
nn.Linear(num_hiddens2, 10)
)
for param in net.parameters():
nn.init.normal_(param, mean=0, std=0.01)
Исчезающий градиент и взрывной градиент
Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению. Предположим, что слой
L
L
Многослойного перцептрона
l
l
Этаж
H
(
l
)
boldsymbol{H}^{(l)}
Весовой параметр
W
(
l
)
boldsymbol{W}^{(l)}
, Выходной слой
H
(
L
)
boldsymbol{H}^{(L)}
Весовой параметр
W
(
L
)
boldsymbol{W}^{(L)}
. Для удобства обсуждения параметр отклонения не рассматривается, а функции активации всех скрытых слоев устанавливаются как отображение идентичности.
ϕ
(
x
)
=
x
phi(x) = x
. Данный ввод
X
boldsymbol{X}
, Первый из многослойных персептронов
l
l
Вывод слоя
H
(
l
)
=
X
W
(
1
)
W
(
2
)
…
W
(
l
)
boldsymbol{H}^{(l)} = boldsymbol{X} boldsymbol{W}^{(1)} boldsymbol{W}^{(2)} ldots boldsymbol{W}^{(l)}
. В это время, если количество слоев
l
l
Больше,
H
(
l
)
boldsymbol{H}^{(l)}
Расчет может ослабнуть или взорваться. Например, предположим, что входные и весовые параметры всех слоев являются скалярными. Например, весовые параметры равны 0,2 и 5, а выход 30-го слоя многослойного персептрона является входом.
X
boldsymbol{X}
Соответственно и
0.
2
30
≈
1
×
1
0
−
21
0.2^{30} approx 1 times 10^{-21}
(Затухание) и
5
30
≈
9
×
1
0
20
5^{30} approx 9 times 10^{20}
Продукт (взрыв). Точно так же, когда слоев больше, расчет градиента более подвержен затуханию или взрыву.
Произвольно инициализировать параметры модели
Случайная инициализация PyTorch по умолчанию
Есть много способов случайной инициализации параметров модели. использоватьtorch.nn.init.normal_()Сделайте модельnetВесовые параметры использования метода случайной инициализации нормального распределения. Однако в PyTorchnn.ModuleВ параметрах модуля принята более разумная стратегия инициализации (для конкретного метода выборки различных типов слоев см.Исходный код), поэтому нам вообще не нужно рассматривать.
Ксавье случайная инициализация
Существует также более часто используемый метод случайной инициализации, называемый случайной инициализацией Xavier [1].
Предположим, что количество входов полностью связанного слоя равно
a
a
, Количество выходов
b
b
, Случайная инициализация Xavier сделает каждый элемент весового параметра в этом слое случайным образом выборкой с равномерным распределением
U
(
−
6
a
+
b
,
6
a
+
b
)
.
Uleft(-sqrt{frac{6}{a+b}}, sqrt{frac{6}{a+b}}right).
Его конструкция в основном учитывает, что после инициализации параметров модели на дисперсию выходных данных каждого слоя не должно влиять количество входов уровня, а на дисперсию градиента каждого слоя не должно влиять количество выходных данных уровня.
резюме
- Регуляризация добавляет штрафной член к функции потерь модели, чтобы уменьшить значения изученных параметров модели, что является распространенным методом борьбы с переобучением.
- Снижение веса эквивалентно
L
2
L_2
Регуляризация нормы обычно приближает изученные весовые параметры к 0. - Снижение веса можно пропустить через оптимизатор
weight_decayУкажите гиперпараметры. - Вы можете определить несколько экземпляров оптимизатора, чтобы использовать разные итерационные методы для разных параметров модели.
- Мы можем справиться с переобучением, используя метод discard.
- Метод отбрасывания используется только при обучении модели.
- Типичными проблемами, связанными с численной стабильностью глубинных моделей, являются затухание и взрыв. Когда нейронная сеть имеет большое количество слоев, численная стабильность модели имеет тенденцию к ухудшению.
- Обычно нам нужно случайным образом инициализировать параметры модели нейронной сети, например весовые параметры.
Машинное обучение — это построение моделей на основе некоторых заданных выборочных данных, также известных как данные обучения, с последующим использованием этой модели для прогнозирования и принятия решений на основе новых, неизвестных данных. Следовательно, можно сказать, что машинное обучение — это изучение и использование правил, присущих обучающим данным. Здесь возникает проблема — как мы можем быть уверены, что правила, которые модель извлекла из обучающих данных, применимы к новым, невидимым данным? Эта статья будет первой в серии статей, посвященных теории обобщения в машинном обучении. В этой статье будет четко определена проблема обучения.
Определение ошибки обобщения
Поскольку эта серия статей посвящена пониманию ошибки обобщения и тому, как ее минимизировать, важно сначала определить, что это такое. Проще говоря, ошибка обобщения — это мера того, насколько хорошо модель машинного обучения работает (то есть прогнозирует) на ранее невидимых данных. Значит, чем он меньше — тем лучше. Это также называется ошибкой вне выборки, которая будет подробнее объяснена далее в этой статье. Разобравшись с этим, давайте начнем.
Изучение правил
Давайте представим, что у нас есть набор данных D, который состоит из нескольких выборок — каждая выборка состоит из некоторых наблюдений и их результатов. Это наши обучающие данные, и мы хотим, чтобы наша модель научилась предсказывать на их основе. Чтобы это стало возможным, нам нужно найти функцию f, которую мы будем называть целевой функцией. Интуитивно целевую функцию можно сравнить с хорошо известной математической функцией f (x) — функция определяет выход на основе входных данных. Легко, не правда ли? Что ж, одна проблема — целевая функция нам неизвестна и всегда будет!
Поскольку целевая функция неизвестна, кроме как внутри нашего образца, как мы можем узнать, является ли наша приближенная функция хорошей? Любая функция, которая согласуется с целевой функцией внутри D, может быть правильной! Каждая из этих возможных функций называется гипотезой, а набор возможных функций называется классом гипотез, H.
Если наша целевая функция f неизвестна, мы не можем исключить какие-либо значения «f» за пределами D, нашего данного обучающего набора. Что мы можем сделать, так это использовать вероятность, чтобы сделать вывод о том, что находится вне D, используя только D. Это будет интуитивно объяснено с помощью примеров. Если вы ничего не знаете о неравенстве Хёффдинга, рекомендуется сначала прочитать мою статью об этом, поскольку она будет очень актуальна в следующем разделе.
Хёффдинг спасает положение
Теперь мы увидим, как вероятность может помочь нам оценить нашу целевую функцию f, просто используя наш образец набора данных D. Начнем с простого примера.
Мы рассматриваем коробку — внутри нее находятся синие и желтые шары. Важным моментом является то, что мы не можем заглянуть внутрь коробки — она закрыта для наших глаз. Однако мы можем проводить с ним эксперименты. Для этого нам сначала нужно определить некоторые вещи — нам нужно определить вероятность выбрать синий или желтый шар.
- P (собирая желтый шар) = µ
- P (взятие синего шара) = 1 — µ
Помните, что µ — это просто имя переменной, поскольку мы не знаем фактическую вероятность выбрать желтый шар! Теперь самое интересное — мы можем залезть в коробку и взять образец. Выбираем N шаров независимо друг от друга. Затем мы наблюдаем долю желтых шаров в нашей выборке, эта фракция будет называться v.
Тогда возникает вопрос на миллион долларов — может ли этот образец рассказать нам что-нибудь о нашем неизвестном дистрибутиве в коробке? Абсолютно! Если выборка достаточно велика — тогда v, вероятно, будет близко к µ! Мы можем описать это следующим знакомым уравнением:
Другими словами, уравнение говорит, что по мере роста размера выборки N становится экспоненциально маловероятным, что v отклонится от µ больше, чем наш «допуск», ε. Обратите внимание, что на границу влияет только размер N образца, а не размер «рамки». «Коробка» может быть большой или маленькой, конечной или бесконечной, и мы все равно получаем ту же границу, когда используем тот же размер выборки. Если мы выберем ε маленьким, чтобы v было хорошим приближением к µ, нам понадобится больший размер выборки N. Стоит отметить следующее: µ не влияет на нашу границу вероятности! Теперь мы увидим, почему именно это интересно.
От коробки к обучению
В нашем примере с рамкой µ было неизвестным — в нашей обучающей ситуации это целевая функция f. Мы можем использовать коробку в качестве прямого примера — это может быть немного техническим, и нам нужно будет понять важное определение:
- Пространство ввода, X: «Пространство ввода» — это всего лишь все возможные поля ввода. В нашем случае поле является нашим входным пространством — мы не знаем, насколько оно велико, мы можем просто сказать, что оно содержит n точек. В нашем случае каждая точка x представляет собой желтый или синий шар.
Желтые шары — это точки, в которых наш h (x) получает правильное значение в соответствии с целевой функцией f (x). Итак, если h (x) совпадает с f (x), то мяч окрашивается в желтый цвет. Если шары окрашены в синий цвет, наша гипотеза не согласуется с целевой функцией. Теперь есть вероятность, связанная с коробкой — цвет, который получает каждая точка, нам не известен, поскольку неизвестно f. Однако, если мы выберем x случайным образом в соответствии с некоторым распределением вероятностей P во входном пространстве X, мы знаем, что x будет желтым с некоторой вероятностью, назовем его µ, и синим с вероятностью 1 — µ.
Независимо от значения µ пространство X теперь ведет себя как в примере с прямоугольником. Проблема обучения теперь сводится к проблеме ящика при предположении, что входные данные в D выбираются независимо в соответствии с некоторым распределением P на X, нашем входном пространстве. Любой P будет транслироваться в некоторый µ в эквивалентном блоке. Поскольку µ может быть неизвестным, то P тоже может быть неизвестным. Теперь нам нужно изменить некоторые обозначения.
- E_in (h) — v: Мы называем это in-sample of h, Ein (h), потому что мы пытаемся увидеть ошибку аппроксимации цели функции с помощью h.
- E_out (h) — µ: Out of sample — это то, чего мы не видели — это ошибка обобщения, которая эквивалентна µ.
Это можно напрямую перевести в неравенство Хёффдинга — вместо того, чтобы аппроксимировать разницу между mu и v, мы пытаемся аппроксимировать разницу между E_in и E_out.
Обучение или проверка?
Теперь вопрос в следующем: это обучение или проверка? Это больше похоже на проверку, чем на фактическое обучение, поскольку мы просто проверяем жизнеспособность единственной выбранной гипотезы, а не ищем оптимальную. К счастью, это решаемо.
Нам просто нужно применить описанную выше идею к нескольким блокам вместо одного — мы можем сказать, что каждый блок является гипотезой для нашей целевой функции, и мы хотим найти хорошую — до того, как у нас был один единственный блок, и мы должны были проверьте, кажется ли это вероятным с нашим образцом из целевой функции. На этот раз у нас может быть много ящиков, и нам нужно проверить все из них, чтобы определить, какой из них наиболее вероятен. На этот раз мы обобщаем на конечное число ящиков.
Однако у нас есть одна проблема — неравенство Хёффдинга не применимо к нескольким коробкам! У нас есть предположение с помощью неравенства Хёффдинга, что функция гипотез фиксируется до набора данных. С несколькими гипотезами, то есть с учетом всего набора гипотез, алгоритм обучения выбирает окончательную гипотезу g на основе D. Это означает, что она выбирается после создания набора данных. Как это решить?
Ослабление ограничений
Способ обойти это — попытаться связать P | E_in (g) — E_out (g) | ›Ε | таким образом, чтобы это не зависело от конкретной выбранной гипотезы. Способ сделать это — взять объединение всех оценок вероятностей для всех гипотез в наборе гипотез, H.
Тогда мы получим следующее неравенство:
Обратной стороной является то, что неравенство является фактором M более свободным, чем оценка для одной гипотезы, и будет иметь смысл только в том случае, если M, наше количество гипотез в H, конечно. Но не отчаивайтесь — в следующих статьях мы увидим, что мы можем улучшить эту границу!
Заключение
Вывод таков: мы видим, что да, обучение возможно! Принятие вероятностной точки зрения позволяет сделать вывод о возможности обучения. Не требуется даже конкретного распределения вероятностей или даже знания того, какое из них используется. Единственное необходимое предположение — это то, что примеры в наших выборочных данных созданы независимо. Нам также нужно только оценить, насколько хорошо наша выбранная гипотеза g соответствует целевой функции f. Это причина того, что «Неравенство» Хёффдинга так удачно сочетается.
Использованная литература:
— — — — — — — — — — — — — — — — — — — — — — — — —
[1] H-S. Лин, М. Магдон-Исмаил, Ю. С. Абу-Мостафа, Обучение на основе данных — краткий курс (2012).
[2] Я. Син, Понимание ошибки обобщения в машинном обучении (2018), https://medium.com/@yixinsun_56102/understanding-generalization-error-in-machine-learning-e6c03b203036
From Wikipedia, the free encyclopedia
For supervised learning applications in machine learning and statistical learning theory, generalization error[1] (also known as the out-of-sample error[2] or the risk) is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data. Because learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about predictive ability on new data. Generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of a machine learning algorithm is visualized by plots that show values of estimates of the generalization error through the learning process, which are called learning curves.
Definition[edit]
In a learning problem, the goal is to develop a function 





![I[f]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8213b3ec4b7c34969992d3f12dd96b830c9082ef)




where 


Without knowing the joint probability distribution 
![I[f]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8213b3ec4b7c34969992d3f12dd96b830c9082ef)


An algorithm is said to generalize if:
Of particular importance is the generalization error ![{displaystyle I[f_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a7111bafb06436dbb5c6bdd88aaad9f689133c2)

![{displaystyle I[f_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a7111bafb06436dbb5c6bdd88aaad9f689133c2)
That is, the goal is to characterize the probability 



For many types of algorithms, it has been shown that an algorithm has generalization bounds if it meets certain stability criteria. Specifically, if an algorithm is symmetric (the order of inputs does not affect the result), has bounded loss and meets two stability conditions, it will generalize. The first stability condition, leave-one-out cross-validation stability, says that to be stable, the prediction error for each data point when leave-one-out cross validation is used must converge to zero as 

These conditions can be formalized as:
Leave-one-out cross-validation Stability[edit]
An algorithm 




and 


Expected-leave-one-out error Stability[edit]
An algorithm 




with 


For leave-one-out stability in the 
with 

Algorithms with proven stability[edit]
A number of algorithms have been proven to be stable and as a result have bounds on their generalization error. A list of these algorithms and the papers that proved stability is available here.
Relation to overfitting[edit]
This figure illustrates the relationship between overfitting and the generalization error I[fn] — IS[fn]. Data points were generated from the relationship y = x with white noise added to the y values. In the left column, a set of training points is shown in blue. A seventh order polynomial function was fit to the training data. In the right column, the function is tested on data sampled from the underlying joint probability distribution of x and y. In the top row, the function is fit on a sample dataset of 10 datapoints. In the bottom row, the function is fit on a sample dataset of 100 datapoints. As we can see, for small sample sizes and complex functions, the error on the training set is small but error on the underlying distribution of data is large and we have overfit the data. As a result, generalization error is large. As the number of sample points increases, the prediction error on training and test data converges and generalization error goes to 0.
The concepts of generalization error and overfitting are closely related. Overfitting occurs when the learned function 


The amount of overfitting can be tested using cross-validation methods, that split the sample into simulated training samples and testing samples. The model is then trained on a training sample and evaluated on the testing sample. The testing sample is previously unseen by the algorithm and so represents a random sample from the joint probability distribution of 

Many algorithms exist to prevent overfitting. The minimization algorithm can penalize more complex functions (known as Tikhonov regularization), or the hypothesis space can be constrained, either explicitly in the form of the functions or by adding constraints to the minimization function (Ivanov regularization).
The approach to finding a function that does not overfit is at odds with the goal of finding a function that is sufficiently complex to capture the particular characteristics of the data. This is known as the bias–variance tradeoff. Keeping a function simple to avoid overfitting may introduce a bias in the resulting predictions, while allowing it to be more complex leads to overfitting and a higher variance in the predictions. It is impossible to minimize both simultaneously.
References[edit]
- ^ Mohri, M., Rostamizadeh A., Talwakar A., (2018) Foundations of Machine learning, 2nd ed., Boston: MIT Press
- ^ Y S. Abu-Mostafa, M.Magdon-Ismail, and H.-T. Lin (2012) Learning from Data, AMLBook Press. ISBN 978-1600490064
- ^ Mohri, M., Rostamizadeh A., Talwakar A., (2018) Foundations of Machine learning, 2nd ed., Boston: MIT Press
- ^ a b c Mukherjee, S.; Niyogi, P.; Poggio, T.; Rifkin., R. M. (2006). «Learning theory: stability is sufficient for generalization and necessary and sufficient for consistency of empirical risk minimization» (PDF). Adv. Comput. Math. 25 (1–3): 161–193. doi:10.1007/s10444-004-7634-z. S2CID 2240256.
Further reading[edit]
- Olivier, Bousquet; Luxburg, Ulrike; Rätsch, Gunnar (eds.). Advanced Lectures on Machine Learning. pp. 169–207. ISBN 978-3-540-23122-6. Retrieved 10 December 2022.
- Bousquet, Olivier; Elisseeff, Andr´e (1 March 2002). «Stability and Generalization». The Journal of Machine Learning Research. 2: 499–526. doi:10.1162/153244302760200704. Retrieved 10 December 2022.
- Mohri, M., Rostamizadeh A., Talwakar A., (2018) Foundations of Machine learning, 2nd ed., Boston: MIT Press.
- Moody, J.E. (1992), «The Effective Number of Parameters: An Analysis of Generalization and Regularization in Nonlinear Learning Systems», in Moody, J.E., Hanson, S.J., and Lippmann, R.P., Advances in Neural Information Processing Systems 4, 847-854.
- White, H. (1992b), Artificial Neural Networks: Approximation and Learning Theory, Blackwell.
В данной главе обсуждаются
нейросетевые методы построения моделей сложных систем, основанные на
экспериментальных данных. Подробно рассмотрены постановки типовых задач
информационного моделирования (прямых, обратных и смешанных). Изложение
сопровождается модельными иллюстрациями и примерами реальных практических
применений.
Сложные системы
Рассмотрим
систему, состоящую из некоторого числа компонент. Для определенности будем
иметь в виду, скажем, терминал крупного океанского порта, обслуживающий
разгрузку судов портовыми кранами, и отправку грузов автомобильным и
железнодорожным транспортом. Нашей конечной целью будет построение модели системы, описывающей ее
поведение, и обладающей предсказательными свойствами. Модель способна во многих
приложениях заменить собой исследуемую систему.
Каждая из компонент системы
имеет свои свойства и характер поведения в зависимости от собственного
состояния и внешних условий. Если все возможные проявления системы сводятся к сумме проявлений ее компонент, то
такая система является простой, несмотря на то, что число ее компонент может
быть велико. Для описания простых систем традиционно применяются методы анализа, состоящие в последовательном
расчленении системы на компоненты и построении моделей все более простых
элементов. Таковым в своей основе является метод математического
моделирования [1], в котором модели описываются в форме уравнений, а
предсказание поведения системы основывается на их решении.
Современные технические
системы (например, упомянутый выше порт, инженерные сооружения, приборные
комплексы, транспортные средства и др.) приближаются к такому уровню сложности,
когда их наблюдаемое поведение и свойства не сводятся к простой сумме свойств
отдельных компонент. При объединении компонент в систему возникают качественно новые свойства, которые не
могут быть установлены посредством анализа
свойств компонент.
В случае терминала порта
небольшие отклонения в производительности работы кранов, малые изменения или
сбои графика движения железнодорожных составов, отклонения в степени загрузки и
в графике прибытия судов могут вызвать качественно новый режим поведения порта,
как системы, а именно затор. Образование затора вызывает обратное воздействие
на режимы работы компонент, что может привести к серьезным авариям и т.д. Состояние затора не может быть в полной мере
получено на основе отдельного анализа, например, свойств одного крана. Однако в
рамках системы обычный режим работы этого крана может приводить к состоянию
затора.
Такие системы, в которых при
вычленении компонент могут быть потеряны принципиальные свойства, а при добавлении
компонент возникают качественно новые свойства, будем называть сложными. Модель сложной системы,
основанная на принципах анализа, будет неустранимо неадекватной изучаемой
системе, поскольку при разбиении системы на составляющие ее компоненты теряются
ее качественные особенности.
Принципы информационного кибернетического моделирования
Возможным
выходом из положения является построение модели на основе синтеза компонент. Синтетические модели являются практически
единственной альтернативой в социологии, долгосрочных прогнозах погоды, в
макроэкономике, медицине. В последнее время синтетические информационные модели
широко используются и при изучении технических и инженерных систем. В ряде
приложений информационные и математические компоненты могут составлять единую
модель (например, внешние условия описываются решениями уравнений
математической физики, а отклик системы — информационной моделью).
Основным принципом
информационного моделирования является принцип «черного ящика«. В противоположность аналитическому подходу,
при котором моделируется внутренняя структура
системы, в синтетическом методе «черного ящика» моделируется внешнее функционирование системы. С точки зрения
пользователя модели структура системы спрятана в черном ящике, который
имитирует поведенческие особенности системы.
Кибернетический принцип
«черного ящика» был предложен [2] в рамках теории идентификации
систем, в которой для построения модели системы предлагается широкий
параметрический класс базисных функций или уравнений, а сама модель синтезируется путем выбора параметров из
условия наилучшего, при заданной функции ценности, соответствия решений
уравнений поведению системы. При этом структура системы никак не отражается в
структуре уравнений модели.
Функционирование системы в
рамках синтетической модели описывается чисто информационно, на основе данных экспериментов или наблюдений над
реальной системой. Как правило, информационные модели проигрывают формальным
математическим моделям и экспертным системам1 по степени «объяснимости» выдаваемых результатов, однако
отсутствие ограничений на сложность моделируемых систем определяет их важную
практическую значимость.
Типы информационных моделей
Можно выделить несколько
типов2 информационных моделей, отличающихся по характеру запросов к ним.
Перечислим лишь некоторые из них:
- Моделирование отклика системы на внешнее воздействие
- Классификация внутренних состояний системы
- Прогноз динамики изменения системы
- Оценка полноты описания системы и сравнительная информационная значимость параметров системы
- Оптимизация параметров системы по отношению к заданной функции ценности
- Адаптивное управление системой
В этом разделе изложение
будет основываться на моделях первого из указанных типов.
Пусть X — вектор, компоненты которого соответствуют количественным
свойствам системы, X’ — вектор
количественных свойств внешних воздействий. Отклик системы может быть описан
некоторой (неизвестной) вектор-функцией
F: Y = F(X,X’), где Y — вектор отклика. Задачей моделирования является идентификация системы, состоящая в
нахождении функционального отношения, алгоритма или системы правил в общей
форме Z=G(X,X’), ассоциирующей каждую пару векторов (X,X’) с вектором Z таким образом, что Z и Y
близки в некоторой метрике, отражающей цели моделирования. Отношение Z=G(X,X’),
воспроизводящее в указанном смысле функционирование системы F, будем называть информационной моделью системы F.
Нейронные сети в информационном моделировании
Искусственные нейронные сети (ИНС)
являются удобным и естественным базисом для представления информационных
моделей. Нейросеть может быть достаточно формально определена [3], как
совокупность простых процессорных элементов (часто называемых нейронами), обладающих полностью
локальным функционированием, и объединенных однонаправленными связями
(называемыми синапсами). Сеть
принимает некоторый входной сигнал3 из внешнего мира, и пропускает его сквозь себя с преобразованиями в
каждом процессорном элементе. Таким образом, в процессе прохождения сигнала по
связям сети происходит его обработка, результатом которой является определенный
выходной сигнал. В укрупненном виде
ИНС выполняет функциональное соответствие между входом и выходом, и может
служить информационной моделью G
системы F.
Определяемая нейросетью
функция может быть произвольной при
легко выполнимых требованиях к структурной сложности сети и наличии
нелинейности в переходных функциях нейронов [4]. Возможность представления
любой системной функции F с наперед
заданной точностью определяет нейросеть, как компьютер общего назначения. Этот компьютер, в сравнении с машиной фон
Неймана, имеет принципиально другой способ организации вычислительного процесса
— он не программируется с
использованием явных правил и кодов в соответствии с заданным алгоритмом, а обучается посредством целевой
адаптации синаптических связей (и, реже, их структурной модификацией и
изменением переходных функций нейронов) для представления требуемой функции.
В гипотетической ситуации,
когда функция системы F известна или
известен алгоритм ее вычисления при произвольных значениях аргументов, машина
фон Неймана наилучшим средством для моделирования (состоящего в вычислении F), и необходимость в информационных
моделях отпадает.
При моделировании реальных
сложных технических систем значения системной функции F получаются на основе экспериментов или наблюдений, которые
проводятся лишь для конечного параметров X.
При этом значения как Y так и Х измеряются приближенно, и подвержены
ошибкам различной природы (см. ниже). Целью моделирования является получение
значений системных откликов при произвольном изменении X. В этой ситуации может быть успешно применена информационная
(статистическая) модель G исследуемой
системы F.
Информационные модели могут
строиться на основе традиционных методов непараметрической
статистики Данная наука позволяет строить обоснованные модели систем в
случае большого набора экспериментальных данных (достаточного для
доказательства статистических гипотез о характере распределения) и при
относительно равномерном их распределении в пространстве параметров. Однако при
высокой стоимости экспериментальных данных, или невозможности получения
достаточного их количества (как, например, при построении моделей тяжелых
производственных аварий, пожаров и т.п.), их высокой зашумленности, неполноте и
противоречивости, нейронные модели оказываются более предпочтительными.
Нейронная сеть оказывается избирательно чувствительной в областях скопления
данных, и дает гладкую интерполяцию в остальных областях.
Эта особенность нейросетевых
моделей основывается на более общем принципе — адаптивной кластеризации данных.
Одной из первых сетей, обладающих свойствами адаптивной кластеризации была
карта самоорганизации Т. Кохонена [5,6]. Задачей нейросети Кохонена является
автоматизированное построение отображения набора входных векторов высокой
размерности в карту кластеров меньшей размерности, причем, таким образом что
близким кластерам на карте отвечают близкие друг к другу входные вектора в
исходном пространстве. Таким образом, при значительном уменьшении размерности
пространства сохраняется топологический порядок расположения данных. При замене
всех векторов каждого кластера его центроидом достигается высокая степень
сжатия информации при сохранении ее структуры в целом4.
Карты Кохонена применяются в
основном, для двух целей. Первая из них — наглядное упорядочивание
многопараметрической информации. На практике обычно используются одномерные и
двумерные карты. Кластеры, задаваемые узлами карты, содержат группы в некотором
смысле похожих наблюдений, которым может быть приписан групповой семантический
смысл. Одним из новых эффективных применений сети Кохонена является построение
тематической карты электронных сообщений в глобальных компьютерных сетях. При
помощи такой карты пользователь получает возможность свободной навигации в
бесконечном потоке сообщений, в соответствии с индивидуальным кругом интересов5. В применении к моделированию технических систем, карты Кохонена могут
использоваться для выявления различий в режимах поведения системы, при этом
могут выявляться аномальные режимы. Важно, что при этом могут быть обнаружены
неожиданные скопления близких данных, последующая интерпретация которых
пользователем может привести к получению нового
знания об исследуемой системе.
Вторая группа технических
применений связана с предобработкой данных. Карта Кохонена группирует близкие
входные сигналы X, а требуемая
функция Y=G(X) строится на основе
применения обычной нейросети прямого распространения (например, многослойного
персептрона или линейной звезды Гроссберга) к выходам нейронов Кохонена. Такая
гибридная архитектура была предложена Р. Хехт-Нильсеном [7,8], она получила
название сети встречного распространения.
Нейроны слоя Кохонена обучаются без учителя, на основе самоорганизации, а
нейроны распознающих слоев адаптируются с учителем итерационными методами. При
использовании линейных выходных нейронов значения их весов могут быть получены
безитерационно, непосредственным вычислением псевдо-обратной матрицы по
Муру-Пенроузу.
Сеть встречного
распространения дает кусочно-постоянное представление модели Y=G(X), поскольку при вариации вектора X в пределах одного кластера на слое
соревнующихся нейронов Кохонена возбуждается один и тот же нейрон-победитель. В
случае сильно зашумленных данных, такое представление обладает хорошими
регуляризирующими свойствами. При этом процедура обучения сети встречного
распространения заметно быстрее, чем, например, обучение многослойного
персептрона стандартным методом обратного распространения ошибок [9].
Другой альтернативой
традиционным многослойным моделям является переход к нейросетям простой
структуры, но с усложненными процессорными элементами. В частности, можно
рассмотреть нейроны высоких порядков, активирующим сигналом для которых
является взвешенная сумма входов, их попарных произведений, произведений троек
и т.д., вплоть до порядка k.
Каждый процессорный элемент k-го порядка способен выполнить не
только линейное разделение областей в пространстве входов, но также и
произвольное разделение, задаваемое поли-линейной функцией нескольких
аргументов. Семейство решающих правил, определяемых нелинейным нейроном
значительно богаче, чем множество линейно разделимых функций. На Рис. 1
приведен пример решающего правила, задаваемого одним нейроном второго порядка, для классической линейно
неразделимой задачи «исключающее ИЛИ«.
 |
| Рис.1 Решающее правило для задачи «исключающее ИЛИ». |
Важным достоинством нейронов
высокого порядка является возможность строить нейросетевые модели без скрытых
слоев, воспроизводящие широкий класс функций6. Такие нейроархитектуры не требуют длительного итерационного обучения,
оптимальные веса даются решением уравнений регрессии. Другой отличительной
чертой является возможность эффективной аппаратной (электронной или оптической)
реализации корреляций высокого порядка. Так, например, существуют нелинейные
среды, оптические свойства которых определяются полиномиальной зависимостью от
амплитуды электрического поля световой волны. Потенциально, устройства,
основанные на таких средах, могут обеспечить высокие скорости вычислений со
свойственной оптическим компьютерам супер-параллельностью вычислений.
В этой главе описанные и
другие нейроархитектуры будут применены к модельным и реалистичным задачам
информационного моделирования сложных инженерных систем.
Характер приближений в информационных моделях
Специфичность
информационных моделей проявляется не только в способах их синтеза, но и
характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении
системы и ее информационной модели возникают вследствие свойств
экспериментальных данных.
- Информационные модели ab initio являются неполными.
Пространства входных и выходных переменных не
могут, в общем случае, содержать все
параметры, существенные для описания поведения системы. Это связано как с
техническими ограничениями, так и с ограниченностью наших представлений о
моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются
требования на объем необходимых экспериментальных данных для построения модели
(об этом см. ниже). Эффект опущенных (скрытых) входных параметров может
нарушать однозначность моделируемой системной функции F. - База экспериментальных данных, на которых основывается модель G
рассматривается, как внешняя данность. При этом, в данных всегда
присутствуют ошибки разной природы, шум, а также противоречия отдельных
измерений друг другу. За исключением простых случаев, искажения в данных не
могут быть устранены полностью. - Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных
задачи. Как следствие, получаемые модели будут обладать неодинаковой
достоверностью и точностью в различных областях изменения параметров. - Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери
информации, отказа измеряющих датчиков, невозможности проведения полного набора
анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки,
ухудшает свойства модели.
Такие особенности в данных и
в постановке задач требуют особого отношения к ошибкам информационных моделей.
Ошибка обучения и ошибка обобщения
Итак, при информационном
подходе требуемая модель G системы F не может быть полностью основана на
явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в
соответствии с заданным критерием,
настолько близко, насколько возможно. Алгоритмически, обучение означает
подстройку внутренних параметров модели (весов синаптических связей в случае
нейронной сети) с целью минимизации ошибки
модели .
Прямое измерение указанной
ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента
не известна. Однако возможно получение ее оценки:
,
где суммирование по X проводится по некоторому конечному
набору параметров X, называемому обучающим множеством. При использовании
базы данных наблюдений за системой, для обучения может отводиться некоторая ее
часть, называемая в этом случае обучающей
выборкой. Для обучающих примеров X
отклики системы Y известны7. Норма невязки модельной функции G
и системной функции Y на множестве X играет важную роль в
информационном моделировании и называется ошибкой
обучения модели.
Для случая точных измерений
(например, в некоторых задачах классификации, когда отношение образца к классу
не вызывает сомнений) однозначность системной функции для достаточно широкого
класса G моделей гарантирует
возможность достижения произвольно малого значения ошибки обучения EL. Нарушение однозначности
системной функции в присутствии экспериментальных ошибок и неполноты
признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В
этом случае предельная достижимая ошибка обучения может служить мерой
корректности постановки задачи и качества класса моделей G.
В приложениях пользователя
обычно интересуют предсказательные свойства модели. При этом главным является
вопрос, каковым будет отклик системы на новое
воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее
общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая
моделью G на данных, не
использовавшихся при обучении, называется ошибкой
обобщения модели EG.
Основной целью при
построении информационной модели является уменьшение именно ошибки обобщения,
поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее
выбранных точках (а в них значения отклика системы известны и без всякой модели!).
Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка
обучения соответствует прямому
запоминанию обучающей информации, а малая ошибка обобщения — формированию понятий и навыков,
позволяющих распространить ограниченный опыт обучения на новые условия.
Последнее значительно более ценно при проектировании нейросетевых систем, так
как для непосредственного запоминания информации лучше приспособлены не
нейронные устройства компьютерной памяти.
Важно отметить, что малость
ошибки обучения не гарантирует
малость ошибки обобщения. Классическим примером является построение модели
функции (аппроксимация функции) по нескольким заданным точкам полиномом
высокого порядка. Значения полинома (модели) при достаточно высокой его степени
являются точными в обучающих точках,
т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут
значительно отличаться от аппроксимируемой функции, следовательно ошибка
обобщения такой модели может быть неприемлемо большой.
Поскольку истинное значение
ошибки обобщения не доступно, в практике
используется ее оценка. Для ее получения анализируется часть примеров из
имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта
выборка примеров называется тестовой
выборкой. Ошибка обобщения оценивается, как норма уклонения модели на
множестве примеров из тестовой выборки.
Оценка ошибки обобщения
является принципиальным моментом при построении информационной модели. На
первый взгляд может показаться, что сознательное не использование части
примеров при обучении может только ухудшить итоговую модель. Однако без этапа
тестирования единственной оценкой качества модели будет лишь ошибка обучения,
которая, как уже отмечалось, мало связана с предсказательными способностями
модели. В профессиональных исследованиях могут использоваться несколько
независимых тестовых выборок, этапы обучения и тестирования повторяются
многократно с вариацией начального распределения весов нейросети, ее топологии
и параметров обучения. Окончательный выбор «наилучшей» нейросети выполняется
с учетом имеющегося объема и качества данных,
специфики задачи, с целью минимизации риска большой ошибки обобщения при
эксплуатации модели.
Прямые, обратные и комбинированные задачи информационного моделирования
При
формулировании постановки информационной задачи предсказания реакции
исследуемой системы при ее известном состоянии на заданные внешние воздействия,
т.е. получения величин Y при заданных
X исследователь имеет дело с прямой задачей. Прямая задача является
типичной при моделировании поведения системы, если запросы к информационной
модели носят характер что-если.
Другим важным классом
информационных задач являются обратные
задачи. Целью обратной задачи выступает получение входных величин X, соответствующих наблюдаемым значениям
выходов Y. При моделировании сложных
систем соответствующий запрос к модели формулируется, как поиск внешних
условий, которые привели к реализовавшемуся отклику системы.
Для большинства приложений
чисто обратные задачи встречаются относительно редко, так как обычно имеются
дополнительные сведения о системе. Например, кроме измеренного отклика, могут
быть известны переменные состояния системы и часть параметров воздействия. В
этом случае задача относится к классу комбинированных
задач: по известным значениям части компонент входного X и выходного Y векторов
восстановить оставшиеся неизвестные компоненты.
В общем случае моделируемая
системная функция может быть представлена в виде (X,Y)=F (X, Y). В этом случае
комбинированный вектор (X,Y) рассматривается одновременно, как
входной и выходной. В этом смысле, произвольная задача допускает
комбинированную постановку.
Некорректность обратной задачи
Отличительная особенность
обратных и комбинированных задач состоит в том, что они обычно являются некорректно поставленными[10], и поэтому
требуют специализированных методов поиска приближенных решений. Согласно
Ж.Адамару, для корректности постановки задачи необходимо:
- существование решения при всех допустимых исходных данных;
- единственность данного решения;
- устойчивость решения к изменениям (малым) исходных данных.
Рассмотрим характер
возможных нарушений данных условий при решении модельной обратной задачи.
Пусть имеется три
исследуемых систем, описываемых кусочно-линейными функциями одной переменной y=F(x) на отрезке [0..1]. Системы
отличаются друг от друга величиной скачка h
системной функции (см Рис.2). Прямая задача состоит в построении приближения G к функции F, с использованием пар значений {xi, yi=s(xi)},
где xi — конечный набор Na случайных равномерно распределенных на [0..1] точек. Обратная задача
заключается в нахождении функции, аппроксимирующей соотношения xi(yi). В зависимости от величины скачка моделируемой
функции можно выделить три варианта.
Система A (h=0). Модель является
линейной: y=x. Для прямой задачи
легко получить исчезающую ошибку обучения EL
» 0, и малую8 ошибку обобщения EG.
Для обратной задачи получаются такие же результаты, так она при точных значения {xi, yi}
не содержит некорректности. Задачи с решениями, корректными на всей области
определения и множестве значений, будем называть безусловно корректными. Корректность постановки обратной задачи для
системы А определяется существованием однозначной и непрерывной функции F-1.
 |
| Рис. 2. Модельные системы с различными величинами скачка системной функции. |
Система B (0<h<1). Прямая задача
в этом случае также хорошо определена, и при использовании достаточно богатого
множества базисных функций можно произвольно уменьшить ошибку обучения (EL » 0) при хорошем обобщении. Обратная задача характеризуется наличием на
множестве значений областей с однозначной (y
> 0.5+0.5h; y < 0.5-0.5h) и
неоднозначной (y Î [0.5-0.5h, 0.5+0.5h]) обратной функцией. В областях
однозначности функции могут быть получены произвольно точные результаты для
обратной задачи. Однако в отрезке нарушения однозначности ошибка обучения (и
ошибка обобщения) останется конечной, поскольку противоречие в данных,
полученных из разных ветвей обратной функции, не устранимо. Значение ошибки
обобщения пропорционально длине отрезка неоднозначности h. Такие задачи, корректное (единственное и устойчивое) решение
которых может быть получено только для некоторой подобласти множества значений,
будем называть условно (или частично) корректными9.
Система C (h=1). Прямая задача
по-прежнему корректно поставлена, требуемое обучение и обобщение может быть
достигнуто (EL » 0). Однако ситуация качественно меняется для случая обратной задачи.
Обратная функция двузначна на всем множестве значений, информация о ее значении
минимальна. Обратная задача полностью некорректно поставлена.
Что общего между всеми этими
примерами? В каждом из них ошибка обобщения при решении обратной задачи не
может быть меньше значения, определяемого размером области неоднозначности h, который, таким образом, может
рассматриваться, как мера некорректности задачи. В случае, если для решения
обратной задачи используется метод со стабилизирующими свойствами (например, с
малым числом свободных параметров по сравнению с числом обучающих примеров),
будет получено гладкое решение с ненулевой ошибкой обучения, определяемой
параметром h.
Заметим, что прямая задача
является безусловно корректной только при полном отсутствии шума в обучающих
данных. При наличии случайных компонент в значениях X имеется целое «облако» решений прямой задачи, причем
размер облака пропорционален величине шума. Таким образом, нарушается
единственность решения прямой задачи, и она становится некорректно
поставленной.
Регуляризация в нейросетевых моделях
Классическим методом решения
некорректных задач является метод регуляризации А.Н.Тихонова [10]. Суть метода
состоит в использовании дополнительных априорных
предположений о характере решения. Обычно в качестве таковых используются
требования максимальной гладкости функции, представляющей решение задачи.
Данный принцип полностью соответствует идее бритвы
Оккама, согласно которой следует предпочесть простейшее из возможных
решений, если нет указаний на необходимость использования более сложного
варианта.
В приложении к нейросетевые
моделям, регуляризирующие методы сводятся к оптимизации функционала ошибки (в
простейшем случае — суммы квадратов уклонений модели от экспериментальных
значений) с аддитивной добавкой, исчезающей по мере улучшения свойств гладкости
функции:
.
Здесь j — регуляризирующий функционал, l — неотрицательная константа регуляризации.
Замечательной особенностью
нейросетевых моделей (аппроксимаций системной функции на основе конечного
набора наблюдений) являются их внутренние регуляризирующие свойства,
позволяющие получать малые ошибки обобщения. Полезность регуляризирующих
свойств нейронных сетей проявляется в ситуациях, когда экспериментальные данные
о системе содержат внутреннюю избыточность. Избыточность позволяет представить
совокупность данных моделью, содержащей меньшее число параметров, чем имеется
данных. Таким образом, нейросетевая модель сжимает
экспериментальную информацию, устраняя шумовые компоненты и подчеркивая
непрерывные, гладкие зависимости.
Следует отметить, что в
случае полностью случайных отображений построение модели с малой ошибкой
обобщения не возможно. Достаточно
рассмотреть простой пример, в котором аппроксимируется отображение фамилий
абонентов телефонной сети (вектор входов X)
в номера их телефонов (вектор выходов Y).
При любой схеме построения обобщающей модели предсказание номера телефона
нового абонента по его фамилии представляется абсурдным.
Имеется обширная научная
библиография, посвященная обоснованию оптимального выбора нейроархитектур и
переходных функций нейронов исходя из различных видов регуляризирующих
функционалов j (см., например [11] и цитируемую там литературу). Практическая
направленность данной главы не позволяет изложить математические детали. Одним
из продуктивных подходов к построению нейросетей с хорошими обобщающими
свойствами является требование убывания высоких гармоник Фурье переходных
функций. Различные законы убывания приводят к локальным сплайн-методам и
нейросетям с радиальными базисными функциями.
В случае сигмоидальной
переходной функции абсолютная величина коэффициентов Фурье10 асимптотически быстро убывает. Это свойство отчасти объясняет
регуляризирующие свойства популярных многослойных сетей с такими переходными
функциями.
Рассмотрим особенности
регуляризированных решений обратных задач моделирования описанных систем A, B и
C. Обучающая выборка в расчетах содержала 200 пар x-y, в которых величина x
случайно равномерно распределена на отрезке [0,1], а значение y определяется моделируемой функцией.
Расчеты проведены для нейросети с обратным распространением ошибки и нейросети
встречного распространения. Еще 500 случайных примеров служили для оценки
ошибки обобщения. В трех сериях расчетов величины y из обучающей выборки нагружались внешней шумовой компонентой с
амплитудой 0%, 10% и 50% соответственно. Обучение проводилось на обратной
зависимости x(y), т.е. величины y
использовались в качестве входов, а x
— выходов нейросети.
Проведенные расчеты
преследовали следующие основные цели:
- выяснение возможности получения оценки некорректности задачи из наблюдений за ошибкой
обучения и обобщения, - изучение роли шума и его влияния на точность оценки степени некорректности,
Результаты
моделирования приведены на Рис. 3 — 7.
 |
| Рис. 3 Зависимость ошибки обучения EL (кружки) и ошибки обобщения EG (точки) от степени некорректности h обратной задачи при различных уровнях шума |
На Рис. 3 представлено
изменение ошибки обучения (и практически совпадающей с ней ошибки обобщения)
при росте скачка моделируемой функции. Ошибка при различных уровнях шума прямо
пропорциональна величине скачка, определяемого параметром некорректности h. Для сильно некорректной задачи (h=1) результаты полностью не зависят от
шума в данных. Теоретически, для неограниченного обучающего набора для
моделируемых систем имеется точное (линейное) решение, минимизирующее
среднеквадратичное уклонение, которое в предельном случае (h=1) дает значение ошибки 0.25. Расчетное значение на Рис.3 в этом
наихудшем случае близко к данной теоретической величине.
Таким образом, скейлинг
ошибки обучения выявляет степень некорректности задачи независимо от
присутствия аддитивного шума в обучающих данных. Данные шум может быть вызван
как неточностью измерений, так и эффектом «скрытых» параметров,
неучтенных в модели.
На следующем рисунке
приведено регуляризованное решение предельно некорректной задачи (h=1), даваемое нейронной сетью с
обратным распространением, обученной на зашумленных данных.
 |
| Рис. 4. Регуляризованное решение (точки) предельно некорректной обратной задачи, полученное при помощи нейросети с обратным распространением ошибки на зашумленных данных (кружки). |
Решение отвечает минимуму
среднеквадратичного уклонения от обучающих данных, что является типичным для
сетей с сигмоидальными функциями.
Укажем явно, в чем состоит
характер априорных предположений, принимаемых при построении нейросетевых
моделей. Единственное предположение (которого оказывается достаточно для
регуляризации) состоит в указании базисной архитектуры нейросети с ограничением ее структурной сложности.
Последнее существенно, т.к., например, при неограниченном увеличении числа
нейронов на скрытом слое, сеть способна достаточно точно запомнить дискретный
обучающий набор. При этом вместо гладкого решения (Рис.4) будет получено
«пилообразное» решение, колеблющееся между двумя ветвями обратной
функции, проходя через все обучающие точки.
Дифференцированная оценка степени корректности обратной задачи на основе кластерного
анализа сетью Кохонена
Обратная
задача может считаться условно корректной, если в признаковом пространстве выходных
переменных имеются области, где обратное отображение однозначно (как в случае
системы B с промежуточными значениями скачка h). Для рассмотренных в предыдущем пункте однопараметрических
систем области корректности могут быть выявлены при графическом представлении
экспериментальных данных. Отделение областей условной корректности в
многомерных пространствах параметров является качественно более сложной
задачей. В этом разделе предлагается исследовать возможности нейросетевых
алгоритмов адаптивной кластеризации данных для дифференциальных оценок областей
условной корректности.
При произвольном
распределении точек в многомерном пространстве задача таксономии (т.е. разделения всех точек на несколько компактных
групп, называемых кластерами) является достаточно сложной, несмотря на то, что
имеется целый ряд методов ее решения. Ситуация дополнительно усложняется в
важном практическом случае, когда число кластеров заранее не известно.
На классе нейросетевых
алгоритмов также предложено несколько подходов [5,6, 12-13]. Классическим
является предложенный Т.Кохоненом [5] алгоритм построения самоорганизующейся карты, которая представляет собой отображение
многомерного распределения точек на двумерную решетку с регулярным соседством
между узлами. При этом близким узлам на карте отвечают близкие вектора в
исходном многомерном пространстве, т.е. сохраняется не только структура
разбиения точек на кластеры, но и отношения топологической близости между ними.
Если для приложений
достаточно только оценки плотности распределения точек по кластерам с
сохранением лишь ближнего порядка в
кластеризации, то такое разбиение может быть выполнено более эффективно на
основе модели «нейронного газа»
[12-13], в которой соседство узлов не фиксировано, а динамически меняется по
мере улучшения кластеризации. В относительно недавней модификации метода,
получившей название «расширяющийся
нейронный газ» [13], переменными являются не только отношения
соседства, но и число нейронов-кластеров.
В данной главе более
подробно рассматриваются приложения более часто используемой карты Кохонена.
Метод дифференциальной оценки степени некорректности задачи
Основная идея предлагаемого
метода дифференциальной оценки степени некорректности обратной или
комбинированной задачи состоит в реализации следующего плана:
- Построить распределение векторов обучающей выборки по кластерам, содержащим близкие по
величине параметров наблюдения. Кластеризация ведется по выходным компонентам Y
для чисто обратной задачи, или по совокупности входных и выходных компонент
(X,Y) для комбинированного отображения (X,Y)=F(X,Y); - Провести обучение набора (по числу кластеров) малых нейросетей с обратным
распространением на данных каждого кластера, оценить ошибку обучения (и, если в
распоряжении имеется достаточно данных, ошибку обобщения). Провести набор
статистики по результатам обучения нескольких вариантов с различными
реализациями случайной инициализации весов. Для получения несмещенных оценок
следует учесть, что кластеры могут содержать разное число векторов; - Поставить в соответствие каждому кластеру данных количественную степень
некорректности отображения в области данного
кластера. В качестве нее может выступать величина, пропорциональная локальной
ошибке обучения для данного кластера; - Выбрать неприемлемый уровень некорректности (в простейшем случае при помощи порогового
правила) для построения гибридной системы, аналогичной малым экспертам [4],
которая дает регуляризованное решение с локальной оценкой точности в областях с
«малой» некорректностью, и предупреждает пользователя о плохой
обусловленности задачи, если запрос относится к области «сильной»
некорректности.
Важно отметить, что в данном
подходе пользователь получает для каждого запроса к нейросетевой модели адекватную локальную точность
получаемого результата, и корректный
отказ в выдаче результата в области высокой нерегулярности задачи. Поскольку
карта Кохонена дает высокую степень наглядности при изучении распределения
экспериментальных данных, то распределение степени некорректности по ней
представляет богатый материал для понимания особенностей модели и ее
параметров. Неоднородности в «раскраске» карты могут отвечать
различным режимам поведения инженерной установки или прибора. При моделировании
технических систем это часто может служить указанием на нежелательные (или
аварийные!) соотношения параметров при эксплуатации.
Пример выявления области некорректности в модельной задаче
Для иллюстрации
предлагаемого метода рассмотрим его применение к уже использовавшимся модельным
системам A, B и C. Для простоты рассмотрения (и снижения числа необходимых
вычислений) можно применить упрощенный алгоритм получения оценки
некорректности. Для этого вместо использования набора малых экспертов
ограничимся одним персептроном (без скрытых слоев), входы которого замкнуты на
выходы нейронов карты Кохонена, а число выходов совпадает с размерностью
признакового пространства выходов задачи. Такая гибридная нейроархитектура,
называемая сетью встречного
распространения, предложена Р.Хехт-Нильсеном [7-8].
Каждый кластер
соревновательного слоя Кохонена в сети встречного распространения включает в
себя несколько векторов обучающего множества. Предъявление на вход нейросети
некоторого вектора вызывает соревнование в слое Кохонена, при этом в результате
остается активным лишь один нейрон, возбуждение которого затормозило все
остальные нейроны. Выход победившего нейрона (нормированный на единицу)
воспринимается персептроном, в итоге формируется вектор выходов нейросети в
целом. Нужно отметить, что все входные вектора в пределах одного кластера
неразличимы (т.к. им всем соответствует один и тот же победитель), поэтому
выходы сети встречного распространения не изменятся, если при смене входных
векторов не произойдет переход от одного кластера к другому. Таким образом,
нейронная сеть встречного распространения дает кусочно-постоянное приближение к моделируемой функции.
Уклонение кусочно-постоянной
поверхности от значений выходных векторов обучающей выборки, соответствующих
входам в пределах заданного кластера принимается за оценку степени
некорректности в области этого кластера11.
 |
| Рис. 5. Гладкое регуляризованное решение (кружки) сетью с обратным распространением ошибки для слабо некорректной задачи двузначного отображения, заданного дискретным набором примеров (точки). |
На Рис. 5 и 6 приведено
сравнения гладкого регуляризованного решения, определяемого многослойной сетью
с обратным распространением, и решения, получаемого при помощи нейросети
встречного распространения. Расчеты проведены для системы B для случая относительно
слабой некорректности с малым значением величины скачка h.
Легко заметить совершенно
различный характер регуляризации, даваемый этими моделями. Уклонение решения от
точек обучающего множества в многослойной сети с гладкими переходными функциями
охватывает более широкую область, чем собственно область некорректности
(0.4<Y<0.6). Кривая решения и
ошибка гладко распространяются в область, где поведение моделируемой системы
регулярно.
В случае сети встречного
распространения, напротив, регуляризованное решение содержит минимальные ошибки в области регулярности (разбиение на
кластеры заметно только вблизи Y=0 и Y=1). Решение же в области
многозначности функции не является регуляризованным — кластеры со значениями
обеих ветвей обратной функции хаотически перепутаны.
Полезность того или иного
представления решения может определиться только в контексте конкретного
приложения. Для системы, предупреждающей о высокой ошибке решения в области
некорректности, по-видимому, следует предпочесть результат сети встречного
распространения (Рис. 6), так искажения решения в областях, где это решение
имеет смысл, минимальны.
 |
| Рис. 6. Кусочно-постоянное в области регулярности решение некорректной обратной задачи, полученное с помощью сети встречного распространения (см. подпись и обозначения на Рис.5). |
Обратимся теперь к изучению
возможности автоматического выделения области некорректности. В нейронной сети
встречного распространения кластеры, расположенные в области некорректности
задачи будут содержать близкие вектора, для которых значения моделируемой
функции относятся к разным ветвям неоднозначности. Персептрон выходного слоя
нейросети в этом случае будет обучаться среднему значению на векторах кластера,
поэтому ошибка обучения останется конечной.
В приведенном примере, при h=0.2, теоретическое значение предельной
ошибки обучения (среднеквадратичное уклонение) для данных одного кластера равно
0.1. Распределение ошибки по кластерам, наблюдаемое в расчетах, приведено на Рис. 7. Область некорректности может быть
легко автоматически выделена при помощи простого решающего правила.
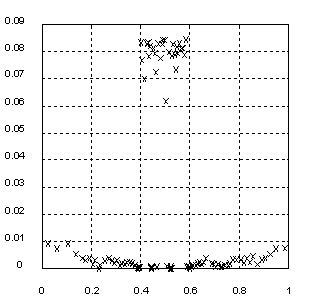 |
| Рис. 7. Распределение ошибки обучения по пространственным кластерам Карты самоорганизации Кохонена с легко выделяемой областью некорректности задачи. |
Подведем некоторые итоги
рассмотрения модельных задач. Можно выделить два основных пути применения
нейронных сетей встречного распространения для решения обратных и
комбинированных некорректно поставленных задач.
Во-первых, слой
самоорганизующихся нейронов карты Кохонена позволяет получить локальную
дифференциальную оценку степени некорректности задачи и пространственное
распределение ошибки обобщения, делаемой сетью. Кластерное разложение одинаково
легко выполняется в признаковых пространствах любой размерности.
Алгоритм кластеризации
Кохонена легко обобщается на случай наличия пропусков в данных. Поскольку для
отнесения некоторого вектора к кластеру требуется лишь вычислить Евклидово
расстояние между этим вектором и текущим приближением к центроиду кластера, и найти
кластер с минимальным расстоянием, то при наличии пропущенных компонент в
векторе расстояние можно вычислять по имеющимся компонентам. Это эквивалентно
поиску ближайшего кластера в подпространстве известных компонент. Замечательно,
что сеть встречного распространения может обучаться даже если в каждом обучающем векторе имеются
пропущенные компоненты. При этом не требуется заполнения пропусков
искусственными значениями.
Второй прикладной аспект
состоит в том, что в областях корректности задачи решение, даваемое сетью
встречного распространения является весьма точным. Это связано с локальным
характером обучения в пределах каждого кластера, и, соответственно отсутствием
эффектов равномерного распределения ошибки по кластерам. В этом смысле,
регуляризующий эффект сети встречного распространения меньше, нежели у
традиционной многослойной сети с обратным распространением.
Прикладное информационное моделирование в задаче
оценки риска при эксплуатации сложной инженерной системы
Сложные
инженерные устройства при воздействии внешних факторов могут демонстрировать
разнообразное нелинейное поведение. С точки зрения эксплуатации таких систем
отклик может отвечать нормальному режиму работы, а также аномальным и аварийным
режимам. В последнем случае требуется принятие специальных мер для снижения
риска последствий инцидента.
Задача информационного
моделирования при оценке риска12 для объекта при внешнем нагружении состоит в необходимости
предсказания его поведения в обычных и аномальных условиях.
Описание инженерной системы
Примером задачи оценки риска
является эксплуатация контейнера для перевозки или хранения промышленных
отходов (например, делящиеся материалы в отработанных твэлах атомных
электростанций, или токсичные химические вещества). В качестве аномального
внешнего воздействия требуется рассмотрение пожара с различными параметрами.
Отклик контейнера (измеряемый оценкой сохранности содержимого и не
проникновением его во внешнюю среду) может изменяться в зависимости от текущего
состояния системы, например, степенью возможных повреждений в аварийных
условиях.
Рассмотрим относительно
простую и полезную с практической точки зрения модель, основанную на данных
измерений параметров контейнера при различных условиях пожара. Фактически,
построенная модель основывалась на результатах численного моделирования, а не на
реальных данных. Это, однако, не снижает ценность рассмотрения, поскольку в
численных расчетах удается учесть широкий спектр пожаров для одного и того же
контейнера. Неопределенность в коэффициентах, описывающих теплофизические
свойства материалов, а также численные эффекты, вносят шум в используемые
данные, приближая условия моделирования к реальным. В сложившейся практике
нейросетевого моделирования данные такого рода называют реалистичными (в отличие от искусственных
и реальных данных).
База собранных данных
содержит 8 параметров, описывающих контейнер и условия пожара. Признаковое
пространство входов состоит из 6 переменных — одной переменной состояния контейнера (экспертная оценка степени
повреждения контейнера) и пяти параметров
воздействия (свойств пожара).
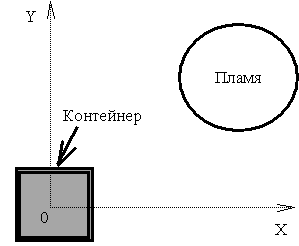 |
| Рис. 8. Схема расположения контейнера и области, охваченной пламенем. |
Параметры пожара включают
две координаты области пламени, диаметр этой области, температуру пожара и его
длительность.
Двумя выходными переменными
являются максимальное значение температуры внутри контейнера на протяжении
всего пожара, а также отрезок времени, в течении которого температура внутри
контейнера превышала некоторое пороговое значение, соответствующее критическому
уровню возможного повреждения содержимого контейнера.
Нейросетевая информационная модель системы
Информационная модель
отклика контейнера строилась на основе сети встречного распространения и
многослойной сети с обучением по методу обратного распространения ошибки. Были
рассмотрены прямая, обратная и комбинированная задачи.
Нейронная сеть для прямой
задачи содержит 6 входов и 2 оцениваемых выхода. Прямая задача для данного
приложения позволят ответить на следующие вопросы:
- Какова будет максимальная температура внутри контейнера при известных параметрах
пожара? - Превысит или нет внутренняя температура заданное критическое значение? Если да, то как
долго система будет находиться в критических условиях? - Что отвечает большему риску повреждения содержимого контейнера: короткий, но
высокотемпературный пожар, или длительная умеренная тепловая нагрузка?
Обратная задача
соответствует оценке параметров внешнего воздействия по измерениям отклика
системы. Тепловой режим внутри контейнера при этом контролируется датчиками
температуры. Запросы к обратной модели носят диагностический характер:
- Какова длительность и температура пламени?
- Как далеко от контейнера произошел пожар, и каков был размер пламени?
- Какова фактическая степень повреждения контейнера?
Наиболее интересная
комбинированная задача рассматривает часть параметров как известные, а
остальные, как неизвестные. При обучении нейросети комбинированной задаче
множества переменных, используемых как входные и как выходные, могут частично
или полностью перекрываться.
Комбинированная задача
отвечает на все запросы прямой и обратной задач, но имеет дополнительные
возможности:
- Оценка состояния контейнера по внешним и внутренним измерениям.
- Каковы наитяжелейшие условия пожара, при которых контейнер еще сохраняет содержимое?
Обратную и комбинированную
задачи следует рассматривать, как некорректно поставленные.
Область возможных значений
физических параметров ограничивалась максимальными температурами пожара
(достигаемыми при горении обогащенного топлива), расстояниями и размерами пламени,
при которых теплопередача контейнеру приводит к температуре около 200оС
(типичный порог для пожаро-сигнализирующих датчиков). Длительность пожара
ограничивалась значением 1 час.
После введения всех
ограничений данные из базы данных были линейным преобразованием приведены в
«серый» формат [0..1].
Интегральная оценка корректности модели
На первом этапе в
предлагаемой технологии исследовалась корректность задачи на всей области
значений параметров. С этой целью последовательно выбирались семь параметров из
восьми, включенных в модель. Эти параметры считались известными, а оставшийся
восьмой параметр — неизвестным. Таким образом, каждый из параметров по очереди
тестировался, как неизвестный. При моделировании определялась ошибка обучения
многослойной сети с обратным распространением. Все расчеты проводились для
нейросетей большого13 размера, поэтому полученная ошибка связывается только с
некорректностью задачи. Был использован следующий вид функции ошибки
(называемой процентом среднего квадрата ошибки14):
Численное моделирование
показало, что обе прямые задачи,
когда неизвестными считались выходные переменные задачи — максимальная
температура внутри контейнера и длительность периода превышения заданного
уровня температуры, являются корректно поставленными. Значение ошибки обучения
не превышало 1%. Напротив, все шесть
обратных/комбинированных задач оказались некорректными с ошибкой обучения
масштаба 25-35%. Данные результат является принципиальным для планирования
последующих экспериментов с информационной моделью: попытки оценки решения
обратных задач на всей области значений (без дифференциального анализа
корректности) будут неудачными.
Прикладная нейросетевая модель для прямой задачи
Для
выбора эффективной нейросетевой модели для (корректно поставленной) прямой
задачи была изучена зависимость ошибки обучения и обобщения от объема
используемых при обучении данных и числа свободных весовых параметров в
нейронной сети.
 |
| Рис. 9. Области на плоскости «температура пламени» — «длительность пожара», в которых максимальная температура внутри контейнера превышает значения 200, 500 и 800oC. |
Для приложений требуется
компактная и быстрая нейросетевая модель, легко обучаемая и имеющая невысокую
ошибку обобщения. Данные требования в некоторой мере противоречивы, поэтому был
суммирован опыт большого числа компьютерных экспериментов. Были обнаружены
следующие особенности:
- Степень обобщения улучшается лишь на 50-80% при росте объема базы обучающих данных (и
соответственно, затрат на обучение!) в 3-4 раза. Следовательно, можно избежать
больших объемов данных. - Использование нейронных сетей с число свободных параметров, близким к числу записей в базе
данных приводит к ошибке обобщения, в 10 раз большей, чем ошибка обучения. В
этом случае предсказательные возможности системы не велики. - Подходящая нейронная сеть для прямой задачи характеризуется 10-15 нейронами на скрытом
слое с масштаба 100 синаптическими связями, обученная на базе данных из 300-500
записей, она показывает ошибку обучения 2-3% при ошибке обобщения до 5%.
На основе выбранной
нейросетевой модели было проведено обучение нейросети и исследован ряд
информационных запросов к ней.
Первая серия запросов была
выполнена для определения области температур и длительностей пожара, при
которых содержимое контейнера не перегревается. Рассматривались пожары,
происходящие в непосредственной близости к контейнеру и имеющие диаметр до 15
м. Изолинии температур внутри контейнера показаны на Рис.9. Расчеты
соответствуют трем различным значениям нагрева содержимого 200, 500 и 800oC.
Данные результаты в применении к конкретным образцам контейнеров могут
составить основу технических требований к противопожарным службам. Так,
например, кривая 200oC показывает параметры, при которых срабатывают
типичные температурные датчики. Если критическим для эксплуатации оказывается
режим превышения 500oC при температуре пламени 800oC, то,
как следует из Рис.9, контейнер способен выдерживать такую нагрузку в течение
22 мин.
 |
| Рис. 10. Зависимость длины промежутка времени (в минутах), в течении которого температура внутри контейнера превышала критический уровень, от расстояния до эпицентра пожара (в метрах) для двух значений диаметра пламени (15 и 20 м). |
Вторая рассмотренная задача
связана с изучением зависимости тепловых условий внутри системы от расстояния
до эпицентра пожара. На Рис. 10 представлена зависимость длительности
закритического нагрева (в минутах) от расстояния до области пожара (в метрах).
Длительность пожара составляла 1 час. Интересно отметить, что наблюдается
некоторое промежуточное значения расстояния до пожара, при котором
теплопередача к контейнеру максимальна15.
На основе данной модели
может быть исследовано множество других практических вопросов. Поскольку при
анализе запросов нейронная сеть работает только в режиме прямого ненагруженного
функционирования, время выполнения запросов минимально.
Возможности регуляризации обратной задачи
Займемся теперь
рассмотрением обратной и комбинированной задач. Как мы уже убедились на основе
расчетов, эти задачи обладают ярко выраженной некорректностью, связанной с
неустранимой неоднозначностью обратной функции, поэтому интерес представляет
возможность лишь их частичной регуляризации.
 |
| Рис. 11. Распределение ошибок обучения по кластерам карты Кохонена. Ошибка на данных каждого кластера пропорциональна размеру соответствующего квадрата. |
Для исследований была
выбрана комбинированная задача определения диаметра пламени по остальным
параметрам пожара и измерениям внутри контейнера. Эта задача имеет минимальную
ошибку обучения (22%) при использовании данных из всей области параметров. Для
данной задачи был выполнен кластерный анализ на основе сети встречного
распространения. Слой Кохонена представлял собой карту из 5×5=25 нейронов. Рис.
11 отражает распределение ошибки обучения сети по кластерам карты, определяемым
нейронами Кохонена.
Результирующее распределение
ошибок близко к равномерному, однако имеются две области (кластеры 1-2 и 4-3 в матричных обозначениях)
с относительно малыми ошибками. Эти кластеры определяют области частичной
регулярности задачи в 7-мерном пространстве параметров.
Наиболее регулярной является
область кластера 1-2. Анализ значений параметров, отвечающих центроиду данного
кластера, позволяет заключить, что наименьшая ошибка определения диаметра
пламени путем решения обратной задачи достигается для высокотемпературных
(около 1000oC), длительных (более получаса) пожаров при
промежуточных расстояниях до эпицентра (масштаба диаметра пламени).
Следующий шаг исследований
состоял в классификации записей в базе данных по построенным кластерам
обученной сети Кохонена. Из полного набора измерений около 2.5% данных
оказалось относящимися к наиболее регулярному кластеру 1-2. Эти данные были
использованы для обучения многослойной сети с обратным распространением с 7
входами и одним выходом. Результирующая ошибка регуляризованного решения
составила лишь 8.5%, что приблизительно в три раза меньше ошибки обучения на
полном наборе векторов.
Результаты описанных
исследований могут быть обобщены в нейросетевую
технологию решения обратных и комбинированных задач:
- Для данной комбинированной задачи оценивается степень ее некорректности по ошибке
обучения нейронной сети с обратным распространением, использующей известные
параметры в качестве входов, а запрашиваемые параметры в качестве оцениваемых
выходов. - Если указанная ошибка мала (имеется сходимость нейросетевой аппроксимации), то
построенная нейросеть дает искомое решение. Следует далее оценить ошибку
обобщения, исходя из априорных теоретических соображений о сложности нейросети,
или на основе прямых вычислений с использованием тестовых данных. При
недостаточном качестве обобщения можно попытаться уменьшить число нейронов в
скрытых слоях нейросети и применить алгоритмы удаления наименее значимых
связей. - В случае неприемлемо больших ошибок обучения применяется уже описанная технология
дифференциальной оценки степени некорректности задачи. После кластерного
анализа данных на основе сети Кохонена16 оценивается распределение ошибок обучения в пространстве параметров
модели. Далее строится система малых экспертов, использующих данных отдельных
кластеров, или строится более укрупненная оценка на основе сети встречного
распространения.
Промышленная нейросетевая
модель, созданная по данной технологии будет содержать материнскую сеть
Кохонена и семейство малых сетей-экспертов с обратным распространением ошибки.
Такая системная модель предоставляет пользователю
- семейство решений для прямых задач
- регуляризованное решение обратных и комбинированных некорректно поставленных задач с оценкой
точности, в областях значений параметров с малой локальной степенью
некорректности задачи, либо - диагностическое сообщение о невозможности уверенного прогноза вследствие принадлежности вектора
пользовательского запроса области сильной неустранимой нерегулярности задачи.
Предлагаемый подход к
нейросетевому моделированию сложных технических систем относительно прост в
реализации и непосредственно соответствует ежедневным информационным потребностям инженеров, связанных с эксплуатацией
таких систем.
Итоги
Подведем
итоги этой главы. Нейронные сети являются естественным инструментом для
построения эффективных и гибких информационных моделей инженерных систем.
Различные нейроархитектуры отвечают различным практическим требованиям.
Сети двойственного
функционирования с обратным распространением ошибки и сети встречного
распространения обладают хорошими обобщающими свойствами и дают количественные
решения для прямых информационных задач.
Внутренние регуляризирующие
особенности нейронных сетей позволяют решать также обратные и комбинированные
задачи с локальной оценкой точности.
Для некорректно поставленных задач моделирования предложена нейросетевая
информационная технология построения гибридной нейроархитектуры, содержащей
кластеризующую карту Кохонена и семейство сетей с обратным распространением,
обучаемых на данных индивидуальных кластеров. В этой технологии выявляются
области частичной корректности задачи, в которых дается решение с высокой
локальной точностью. Для остальных областей признакового пространства нейросеть
автоматически корректно отвергает
пользовательские запросы.
В работе рассмотрены примеры
применения методики решения обратных задач к моделированию отклика сложной
инженерной системы — промышленного контейнера на внешние аномальные условия
(тепловая нагрузка вследствие пожара). Результаты исследований могут быть использованы
для технических рекомендаций и требований к противопожарным службам и ресурсам.
Автор благодарен В.В.Легонькову
и Л.И.Шибаршову за полезные обсуждения и консультации.
Литература
- Марчук Г.И. Методы вычислительной математики. 3-е изд., М.:Наука,1989
- Винер Н. Кибернетика, или Управление и связь в животном и машине. пер. с
англ., 2-е изд., М, 1968. - P. Wasserman, Neurocomputing.Theory and practice,
Nostram Reinhold, 1990. (Рус. перевод. Ф.Уоссермэн. Нейрокомпьютерная
техника. М. Мир, 1992). - Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. Н. Наука, 1996.
- T. Kohonen, «Self-organized formation of topologically correct feature maps», Biological
Cybernetics, Vol. 43, pp.59-69, 1982. - T. Kohonen, Self-Organizing Maps, Springer, 1995.
- R. Hecht-Nielsen, «Counterpropagation networks», Applied Optics, Vol. 23, No. 26, pp.
4979-4984, 1987. - R. Hecht-Nielsen, «Counterpropagation networks», Proc. First IEEE Int.
Conf. on Neural Networks. eds. M.Candill, C.Butler, Vol. 2, pp.19-32, San
Diego, CA: SOS Printing. 1987. - D. E. Rummelhart, G. E. Hinton, R. J. Williams, «Learning
representations by back-propagating errors», Nature, Vol.323, pp.533-536, 1986. - Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. 2 изд. М. Наука, 1979.
- F.Girosi, M.Jones, and T.Poggio. «Regularization Theory and Neural Networks
Architectures». Neural Computation, Vol.7, pp.219-269, 1995. - T.M. Martinetz, S.G. Berkovich, K.J. Schulten. «Neural-gas
network for vector quantization and its application to time-series
prediction», IEEE Transactions on
Neural Networks, Vol. 4, No. 4, p.558-569, 1993. - B.Fritzke. «A growing neural gas networks learns topologies», In Advances in Neural
Information Processing Systems 7, eds. G.Tesauro, D.S.Touretzky, T.K.Leen, MIT Press,
Cambridge MA, pp.625-632, 1995.
1 Информационные модели,
основанные на логически прозрачных
нейронных сетях, предложенные в [4], в некоторой степени отражают
причинно-следственные взаимоотношения между параметрами модели
2 Границы между типами
моделей являются весьма условными
3 Под сигналом в широком
смысле может понимается вектор состояний входов нейросети.
4 При этом, конечно, часть
информации теряется. Однако, это не очень принципиально, например, при сжатии
изображений.
5 Электронный адрес
интерактивной карты Кохонена WEBSOM с сообщениями по тематике нейронных сетей,
разработанной в университете в Хельсинки группой самого Т.Кохонена, в сети Интернет:
http://websom.hut.fi
6 Нужно заметить, что класс
нейросетей без скрытых слоев не является полным
в смысле возможности приближения произвольной функции. Так, для представления
решающих правил для двух переменных все многообразие функций сводится лишь к
Паде (1,1)-приближениям (гиперболам).
7 С учетом описанных выше
особенностей экспериментальных данных.
8 Это достигается, например,
использованием нейронной сети без скрытых слоев с произвольной переходной
функцией нейронов, имеющей близкий к линейному участок изменения.
9 В книге [1], стр. 563,
условно-корректными названы задачи, в
постановку которых добавлено априорное предположение о существовании решения на
некотором компакте. Для данного решения должна быть доказана теорема
единственнности. В нашем рассмотрении в качестве такого компактного множества
выступают отрезки, на которых обратная функция однозначна.
10 Имеется в виду интеграл
Фурье в смысле главного значения (интеграл от квадрата сигмоидальной функции,
очевидно, расходится).
11 Центры кластеров задают
разбиение признакового пространства на многогранники
Вороного (в двумерном случае — на ячейки
Дирихле). Все точки в пределах одного многогранника ближе к центроиду
соответствующего кластера, чем ко всем остальным кластерам.
12 Проблема оценивания самой
величины риска при этом остается за рамками данного рассмотрения. Одним из
методов вычисления риска при известных из информационного или математического
моделирования режимах работы системы является взвешивание вероятностей реализации
различных режимов с экспертными оценками их последствий. Далее управление
эксплуатацией системы состоит в минимизации риска.
13 Для определения
необходимого числа нейронов на скрытом слое была выполнена серия расчетов с
увеличивающимся размером сети. Далее использовалось полученное предельное
значение (для нашей базы данных из ~9000 примеров потребовалось 30 нейронов).
14 Исходный английский термин
— squared error percentage.
15 Наличие конечного
расстояния, при котором теплопередача максимальна, подтверждается простыми
геометрическими соотношениями для однородно изотропно излучающего источника
конечных размеров.
16 Сеть Кохонена здесь
предпочтительнее других алгоритмов кластеризации, так как при образовании
относительно больших областей корректности, они будут представлены макрокластером пространственно близких
нейронов.
| Предыдущая | Оглавление | Следующая |

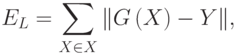











![{displaystyle I[f]=int _{Xtimes Y}V(f({vec {x}}),y)rho ({vec {x}},y)d{vec {x}}dy,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dbb449f1246d2d43f7913fdce840176d89eaceb)
![{displaystyle I_{n}[f]={frac {1}{n}}sum _{i=1}^{n}V(f({vec {x}}_{i}),y_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ebbb7c212127a833303ad4ebc28b8249204f3bb)
![{displaystyle lim _{nrightarrow infty }I[f]-I_{n}[f]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c05fa4b3ba87ee702f09fde44ed49d570c921361)
![{displaystyle P_{G}=P(I[f_{n}]-I_{n}[f_{n}]leq epsilon )geq 1-delta _{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d68caa5402a52609e73c853af11069095cc00b6c)

![{displaystyle forall iin {1,...,n},mathbb {P} _{S}left{left|I[f_{S}]-{frac {1}{n}}sum _{i=1}^{N}Vleft(f_{S^{i}},z_{i}right)right|leq beta _{EL}^{(n)}right}geq 1-delta _{EL}^{(n)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f0055901b3111a9b60b2532bb3d7905884787cd)
![{displaystyle mathbb {E} _{S,z}[|V(f_{S},z)-V(f_{S^{i}},z)|]leq beta _{H}^{(n)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06cc4ccaa28eae9dd8c93319e4304c66a93f9845)