Содержание
- «Элемент не может быть повернут в эту позицию»
- Вариант 1: установить на наклонную опорную плоскость
- Вариант 2: создать поворот внутри семейства болта:
- Вариант 3: установка на вертикальную плоскость
- Как развернуть последние углы кубика Рубика — Шаг 7
- Как повернуть уголы кубика Рубика 3х3
- Поворот угла третьего слоя кубика Рубика
«Элемент не может быть повернут в эту позицию»
…а также немного информации о рабочих плоскостях и способах поворота элементов в семействах.
Последнее время не первый раз встречаю такой вопрос, решил написать.
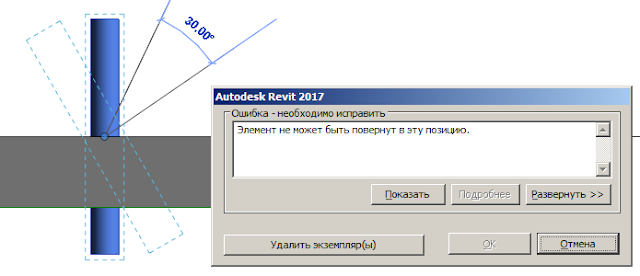
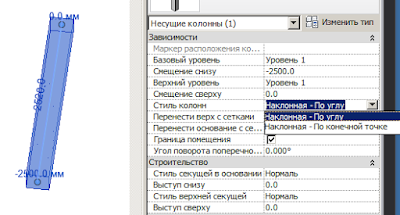
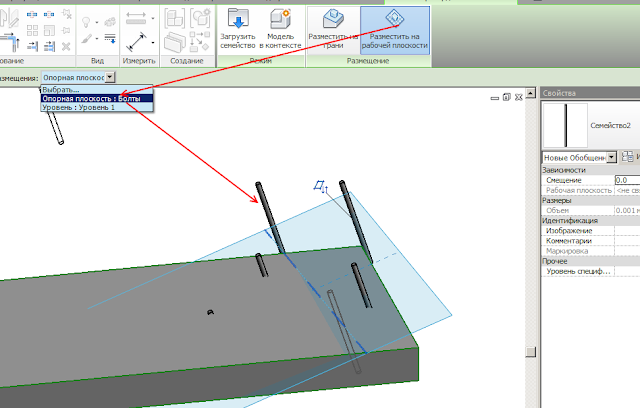
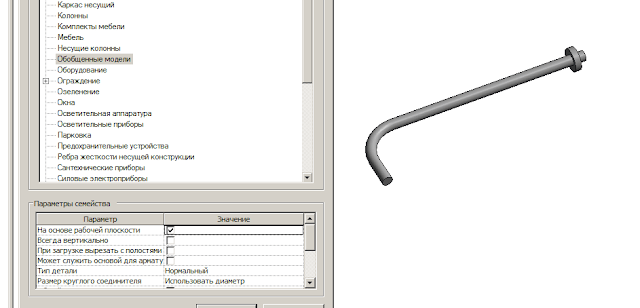
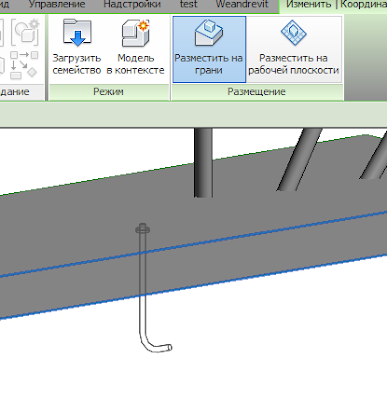
Сделали мы, например, семейство фундаментного болта, а затем хотим установить его не вертикально, а под углом. Переходим на разрез, пытаемся повернуть — и получаем ругательство:
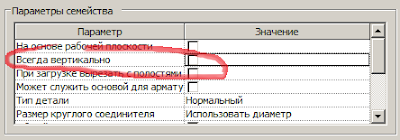
Можно даже найти в свойствах семейства опцию «Всегда вертикально», но сообщение всё равно будет вылезать.
Когда первый раз столкнулся с проблемой много лет назад — тоже подумал: «Что за глупое ограничение!».
Но сейчас (и уже не первый раз) понимаю, что ограничения появились неспроста, и они отражают саму суть логики программы. Итак, в чем же особенность? Дело в том, что Ревит — параметрическая САПР, основанная на рабочих плоскостях.
«Параметрический» — значит, что в элементы могут передаваться какие-то значения (параметры) и эти элементы автоматически изменяются (удлиняются, поворачиваются, изменяют конфигурацию) в зависимости от этих параметров, по определенным зависимостям.
«Основанный на рабочих плоскостях» — означает, что геометрические параметры в основном работают с плоскостями, а не с точками или прямыми, и параметризация осуществляется за счет перемещения плоскостей.
Например, в Ревите вообще нет 3D-элементов, которые бы «висели в воздухе»: у элемента всегда есть «Основа» или «Рабочая плоскость».
Фактически, единственные элементы, которые действительно «висят в воздухе» — это оси, уровни и опорные плоскости.
Благодаря этому можно, например, изменить высоту первого этажа (переместить выше уровень второго этажа) и быть уверенным, что все элементы на этих этажах также передвинутся на нужную высоту.
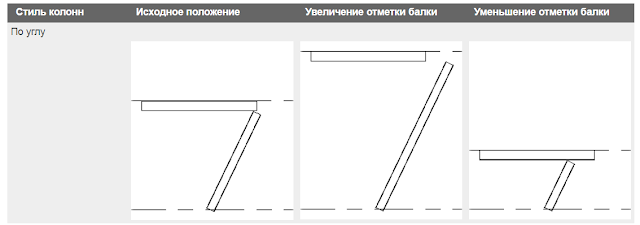
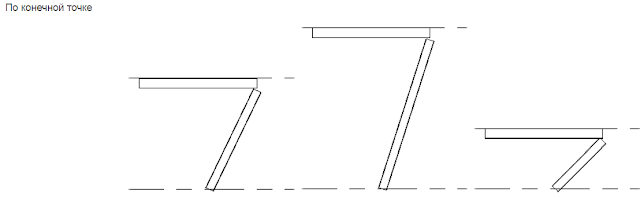
Проблема параметризации рабочими плоскостями — в том, она имеет однозначное решение только в случае ортогональных плоскостей. Простой пример — вертикальные и наклонные колонны. Колонна — объект «На базе двух уровней» — для неё указывается нижний и верхний уровень. Что будет происходить, если изменится высота уровня? Для вертикальной колонны — всё просто: увеличится высота колонны.
Но для наклонной колонны всё сложнее. В этом случае есть выбор:
— сохранить угол, под которым расположена колонна;
— сохранить положение точек начала и конца колонны в плане.
Статья в справке:
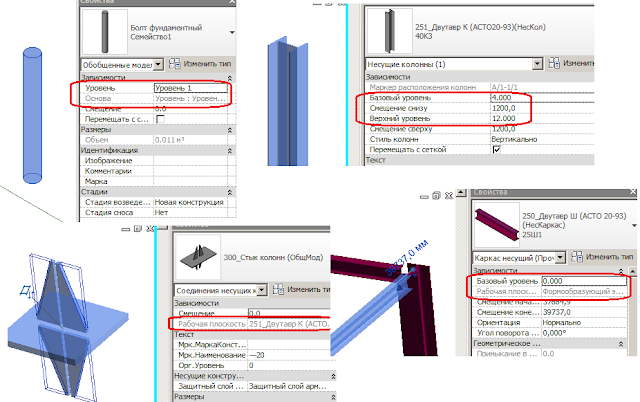
Вариант 1: установить на наклонную опорную плоскость
Вариант 2: создать поворот внутри семейства болта:
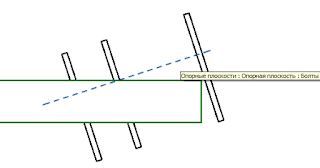
Привяжем начальную точку вспомогательной линии к пересечению опорных плоскостей:
Нажимайте Tab, чтобы выбрать не всю линию, а её конечную точку.
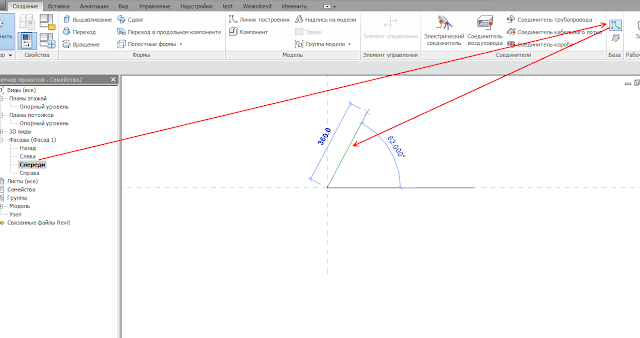
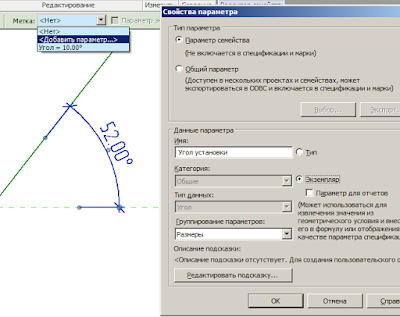
Создадим параметр угла поворота:
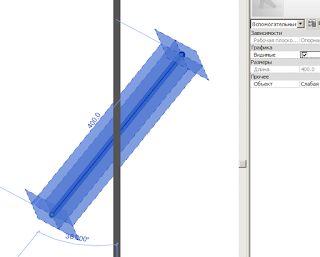
«Вспомогательная линия» — интересный объект. Она имеет 4 плоскости, которые можно использовать в качестве рабочих плоскостей для размещения элементов.
Укажу нижнюю плоскость вспомогательной линии в качестве рабочей плоскости:
Создаю элемент выдавливания:
Обратите внимание, эскиз выдавливания теперь создается в плоскости вспомогательной линии.
Загружаю семейство в проект и проверяю работу:
Вариант 3: установка на вертикальную плоскость
Идея простая. Если мы можем вращать элементы только в плоскости, на которую установили элемент, а повернуть нам надо в вертикальной плоскости — установим болт на вертикальную плоскость.
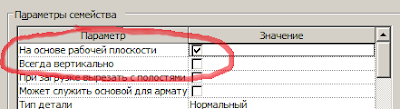
Для этого семейство болта сделаем «Лежащим на боку» 🙂
Включим «На основе рабочей плоскости» и отключим «Всегда вертикально».
В проекте нам понадобится вертикальная рабочая плоскость. Можно использовать вертикальную боковую грань фундамента, создать в плане именованную опорную плоскость, или использовать в качестве рабочей плоскости одну из осей.
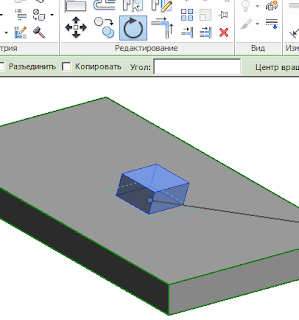
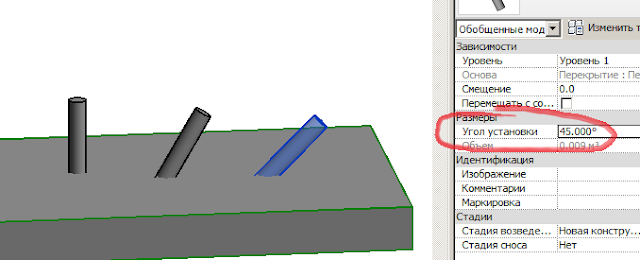
Я установлю на грань фундамента:
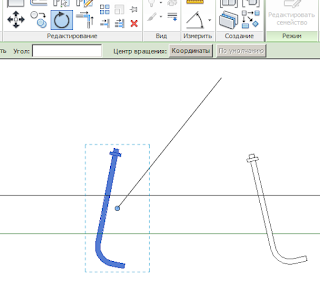
Теперь этот болт можно вращать инструментом «Повернуть» так, как нам нужно:
Каждый из способов в чем-то удобен, каком применять — выбирайте по ситуации.
Рабочие плоскости — может быть, проклятье Ревита, но задачи вполне можно решать, если научиться с ними работать.
Удачи!
Всем привет! Тут мой блог об Autodesk Revit, а на самом деле — просто блокнот, куда я записываю свои идеи.
Надеюсь, что информация окажется полезной и интересной.
Источник
Как развернуть последние углы кубика Рубика — Шаг 7
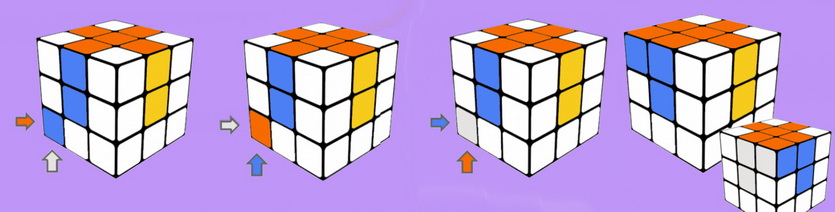
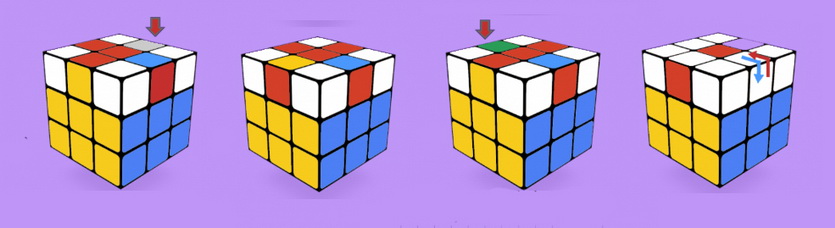
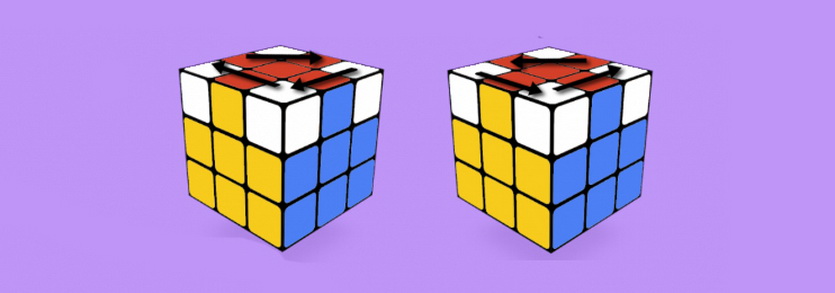
В начале этого этапа все угловые кубики верхней грани должны находится на своих местах, при этом они могут быть неправильно повёрнуты. Данная формула развернет угловые кубики по часовой стрелке.
Смотри иллюстрацию ниже.
Как повернуть уголы кубика Рубика 3х3
В конце данного этапа по сборке головоломки 3×3, ваш куб будет полностью собран!
Смотри картинку головоломки в сборе.

В зависимости от того, как у вас был разобран рубик 3х3, у вас могут быть варианты по расположению боковых элементов последней грани:
- Два угловых кубика повёрнуты неправильно. 3×3
- Два противоположенных угловых кубика повёрнуты неправильно.
- Три детали повернуты неправильно.
- Все четыре элемента повернуты неправильно.
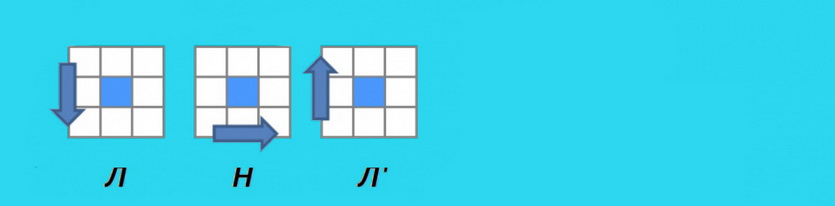
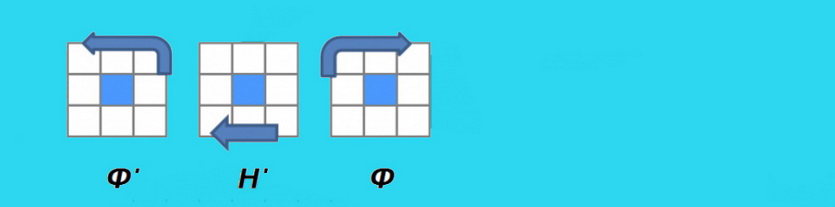
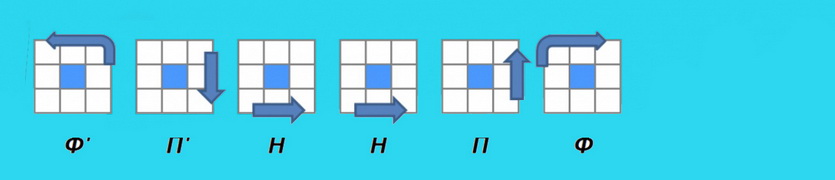
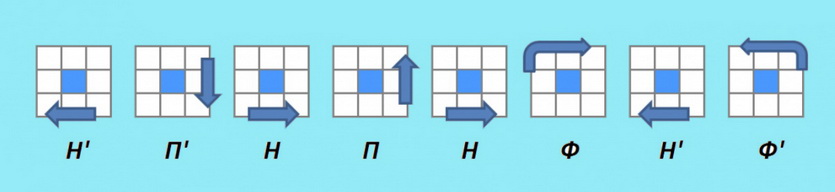
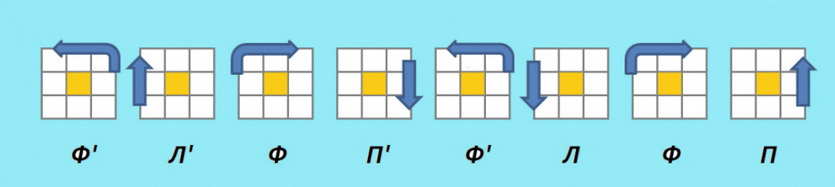
Поворот угла третьего слоя кубика Рубика
Данная формула предназначена, для поворота угловой детали по часовой стрелке.
Важно!
Этот алгоритм надо повторять до тех пор, пока правый кубик верхней грани, не повернётся правильным образом!
Далее поверните верхнюю грань и повторяйте формулу, до тех пор пока угловая деталь не будет правильно сориентирована.
Поверните верхнюю грань один раз:
Поверните верхнюю грань два раза:
При выполнении данной формулы, может создаться впечатление, что все запуталось. Не пугайтесь. Если повторить последовательность действий ещё несколько раз, то всё встанет на свои места.
Не огорчайтесь, если у вас не получилось собрать головоломку с первого раза. Я и сам не сразу всё понял, но теперь могу собрать его менее чем за 2 минуты, не глядя в формулы. Они уже в моей голове.
Вернее не в голове — руки сами помнят алгоритмы.
И знайте, лучший способ отблагодарить нас, это поделиться ссылкой на наш сайт с друзьями!
Если Вы смогли собрать головоломку Рубика, нажмите — Я собрал кубик 3×3!
Источник
Шаг 7.
В последнем этапе нашей инструкции, мы расскажем Вам, как развернуть углы последнего слоя кубика Рубика 3х3 одной формулой.
В начале этого этапа все угловые кубики верхней грани должны находится на своих местах, при этом они могут быть неправильно повёрнуты. Данная формула развернет угловые кубики по часовой стрелке.
Смотри иллюстрацию ниже.
Как повернуть уголы кубика Рубика 3х3
В конце данного этапа по сборке головоломки 3×3, ваш куб будет полностью собран!
Смотри картинку головоломки в сборе.
В зависимости от того, как у вас был разобран рубик 3х3, у вас могут быть варианты по расположению боковых элементов последней грани:
- Два угловых кубика повёрнуты неправильно. 3×3
- Два противоположенных угловых кубика повёрнуты неправильно.
- Три детали повернуты неправильно.
- Все четыре элемента повернуты неправильно.
Поворот угла третьего слоя кубика Рубика
Данная формула предназначена, для поворота угловой детали по часовой стрелке.
Смотри рисунок.
Важно!
Этот алгоритм надо повторять до тех пор, пока правый кубик верхней грани, не повернётся правильным образом!
Далее поверните верхнюю грань и повторяйте формулу, до тех пор пока угловая деталь не будет правильно сориентирована.
Поверните верхнюю грань один раз:
и / или
Поверните верхнюю грань два раза:
При выполнении данной формулы, может создаться впечатление, что все запуталось. Не пугайтесь. Если повторить последовательность действий ещё несколько раз, то всё встанет на свои места.
Не огорчайтесь, если у вас не получилось собрать головоломку с первого раза. Я и сам не сразу всё понял, но теперь могу собрать его менее чем за 2 минуты, не глядя в формулы. Они уже в моей голове.
Вернее не в голове — руки сами помнят алгоритмы.
И знайте, лучший способ отблагодарить нас, это поделиться ссылкой на наш сайт с друзьями!
Если Вы смогли собрать головоломку Рубика, нажмите — Я собрал кубик 3×3!
Предупреждение: «Элемент слегка отклонился от оси и может вызвать неточности».
Причина: это предупреждение отображается при наличии элементов, отклоненных на угол величиной от 1x(10^-9) до 0,2 градуса от горизонтального или вертикального направления либо от направления, составляющего угол 45 градусов с горизонтальным и вертикальным направлениями.
Данная проблема может возникнуть при создании эскизов или повороте элементов с отключенной угловой привязкой. Причинами также могут служить:
- Создание элемента на основе слегка отклоненных граней или линий.
- Выравнивание элемента по слегка отклоненной вспомогательной линии.
- Расчленение импортированных объектов AutoCAD, содержащих слегка отклоненные линии.
- Создание граней перекрытия из формообразующих элементов со слегка отклоненной геометрией.
- Привязка концов определяющих линий к слегка отклоненным вспомогательным линиям (например, импортированные чертежи или две невыровненные колонны).
- Привязка концов определяющих линий к вспомогательным линиям, имеющим правильное расположение в их собственном контексте, однако линия между ними слегка отклонена (например, привязка к двум разным сеткам потолка).
Отклонение от оси необходимо устранить, так как в Revit размеры можно создавать только между строго параллельными линиями, а соединять и разрезать геометрические объекты можно только в том случае, если их грани строго параллельны и не содержат даже небольших зазоров, которые могут быть вызваны отклонением элементов от осей.
Решение: в зависимости от причин возникновения, существует несколько способов решения этой проблемы:
- Перетащите концы отклоненных элементов и выполните их привязку к оси.
- Повторите операцию поворота с включенной угловой привязкой.
- Если неточности обусловлены существующими элементами, исправьте их и повторите действие.
- Если источником ошибок являются импортированные данные, следует исправить их в исходных приложениях, а затем повторно импортировать.

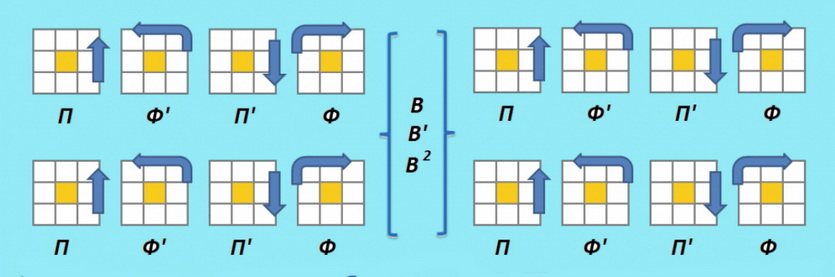
В верхней оси могут находиться два, три или четыре угловых кубика, неправильно развернутых. Если имеется два угловых кубика, неправильно развернутых, выполним следующее решение тем или иным способом, в зависимости от нашего случая.
ПРОЧИТАТЬ ПЕРЕД ПЕРЕДВИЖЕНИЕМ КУБИКОВ!
Очень важно: Этот шаг не такой простой, как предыдущие, однако, и не очень сложный. До его выполнения тебе надо кое-что знать. В Случае 1 есть несколько подслучаев, поэтому прежде всего, определи, какой подслучай твой. Для этого шага, выполни первую серию передвижений. Затем осуществи передвижения, изображенные на красном фоне, соответствующие твоему случаю. Наконец, следуй последней фазе передвижений.
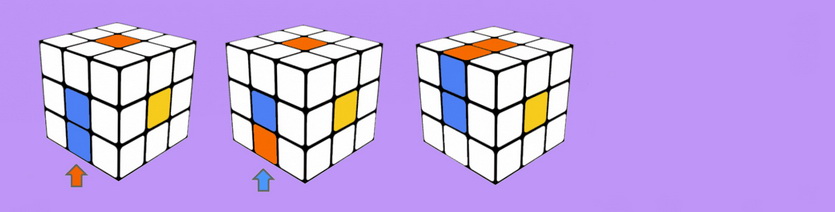
Случай 1: (Сперва прочитай информацию выше) Два угловых кубика неправильно развернуты
«Ближайший» угловой кубик должен быть перемещен по часовой стрелке.
Случаи 2 и 3: Три угловых кубика неправильно развернуты
Если три угловых кубика развернуты неправильно, расположи кубик Рубика так, как изображено на картинках и следуй первому из вышеуказанных решений, поворачивая только два угловых кубика. Затем следуй решению, в соответствии с твоим случаем.
Случай 4: Все угловые кубики неправильно развернуты
Если все четыре угловых кубика развернуты неправильно, применяй первое из вышеуказанных решений. Затем — решение, в соответствии с твоим случаем.

- Как быстро и правильно настроить кубик Рубика?
- Как избежать основных ошибок при настройке кубика?
- Как определить, что Ваш кубик требует настройки?
- Практические советы и лайфхаки настройки.
Обо всём расскажем в этой статье.
Очень важно уметь правильно настроить кубик Рубика, ведь от этого зависит скорость Вашей сборки и получаемое удовольствие.
Как понять, что ваша головоломка требует настройки:
- Грани вращаются очень медленно, с трудом.
- Кубик разваливается при сборке.
- Куб плохо режет углы, или вообще не режет.
- Вращение слишком быстрое и неконтролируемое.
Если при сборке Вы заметили что-либо из выше сказанного, то вам обязательно необходимо настроить кубик Рубика.
Как правильно настроить кубик Рубика
Внутри каждой из сторон кубика расположены болты, их 6, как и сторон. В кубиках 3х3, 5х5, 7х7 и 9х9 эти болты расположены под съёмной крышкой в центре граней.
В кубиках 2х2, 4х4, 6х6 и 8х8, болты расположены прямо между центрами куба.
Теперь, когда вы нашли болты на своей головоломке, необходимо взять отвёртку (обычную, а лучше специальную) и раскрутить или закрутить винты:
— Чтобы грани вращались быстрее, раскрутите болты, против часовой стрелки.
— Если необходимо больше контроля или грани вращаются очень быстро, закрутите винты, по часовой стрелке.
Настраивать кубик Рубика необходимо так, чтобы вам было комфортно его вращать.
Ошибки начинающих
На первый взгляд, правильно настроить кубик Рубика очень просто. Но есть некоторые основные ошибки при настройке куба:
- Слишком сильно раскрученный кубик
При сильной раскрутке, куб становится »рыхлый» и начинает разваливаться при сборке. В этом случае надо закрутить болтики обратно.
- Неравномерно настроенные болты
Бывает такое, что одна грань вращается очень быстро, а вторая очень медленно. Это значит, что вы не равномерно настроили свою головоломку. Как узнать, что ваш куб настроен равномерно, расскажем чуть ниже.
- Слишком сильно затянутые болты
Некоторым людям кажется, что чем больше контроля, тем лучше. Но это не совсем верно. Контроль – это хорошо, но он обязательно должен сочетаться с хорошей скоростью. Поэтому не стоит сильно затягивать болты, в надежде, что от этого ваши сборки будут быстрее.
Как проверить равномерность настройки кубика Рубика.
Как мы говорили выше, бывает такое, что одна сторона крутится быстро, другая медленнее. Это происходит из-за того, что один болт
затянут сильнее, чем другой. Чтобы это исправить необходимо, провести небольшой тест:
Возьмите кубик двумя руками так, как показано на фото, и начните растягивать две стороны кубика в противоположные стороны (не сильно).
Вы увидите, что между гранями образовались две щели. Вам необходимо посмотреть, чтобы эти щели были одинаковые по размеру. Если это не так, значит, куб настроен не равномерно и его надо, настроить повторно.
Подведём итоги:
Очень важно правильно настроить кубик Рубика.
Если Вы внимательно прочли статью, то настройка кубика займёт у Вас не более 10-15 минут.
Необходимо отметить, что если Вы собираете обычный бюджетный кубик, то, как бы правильно Вы его не настраивали, он не сможет крутиться, как скоростные профессиональные кубы.
Невозможно сделать из обычного куба, скоростной.
Настройка кубика Рубика нужна не для этого. Она нужна для того, чтобы Вам было удобнее со своей головоломкой, ведь у всех куберов свои предпочтения в сборке, кто-то любит быстрые кубы, кто-то более медленные, но контролируемые.
Хотите приобрести себе крутой куб — наш интернет-магазин Закубиком предоставляет вам огромный выбор головоломок на любой вкус и цвет!
19 мая 1974 года венгерский скульптор и архитектор Эрно Рубик изобрел знаменитую головоломку — кубик Рубика.
Когда и как был изобретен кубик Рубика?

В качестве первых испытателей головоломки выступали друзья Рубика и студенты Академии.
В 1975 Рубик получил патент на своё изобретение. Однако выпуск опытной промышленной партии кубиков состоялся лишь в конце 1977-го. Первым производителем кубика был небольшой будапештский кооператив, выпустивший кубик как новогоднюю игрушку под Рождество 1978 года.
Однажды кубик Рубика в руках официанта увидел немецкий предприниматель Тибор Лакзи. Увлекающийся математикой Лакзи пришёл в восхищение от игрушки и занялся её продвижением вместе с Томом Кремером — успешным изобретателем игр.
В результате их стараний в начале 1980 началось настоящее «кубическое» нашествие. В то время было выпущено около 100 миллионов «легальных кубиков» и еще больше — подделок.
За какое время можно собрать «Кубик Рубика»?
Люди, увлекающиеся скоростной сборкой кубика Рубика, называются спидкуберами (от английского «speed» — скорость). А сама скоростная сборка — спидкубинг. Официальные соревнования по скоростной сборке кубика Рубика регулярно проводятся Всемирной ассоциацией кубика.
Нынешний рекорд скоростной сборки кубика был установлен Мэтсом Волком, он собрал кубик за 5,55 секунды. Действующий мировой рекорд принадлежит Феликсу Земдегсу и составляет 5,66 секунд. Его неофициальный рекорд составляет 4,79 секунды.
Как собрать кубик Рубика?
Перед тем, как начать собирать кубик Рубика, рекомендуется разобрать его на детали и собрать заново, чтобы убедиться, что кубик сложен правильно.
Способ для начинающих
1. крест в первом слое;
2. углы первого слоя;
3. рёбра среднего слоя;
4. крест в последнем слое;
5. расстановка рёбер последнего слоя;
6. расстановка углов последнего слоя;
7. разворот углов последнего слоя.
Начинающим следует, помимо видео, иметь перед глазами инструкцию, чтобы было проще собрать головоломку.
Урок 1
Урок 2
Метод Джессики Фридрих
На данный момент одним из самых популярных методов скоростной сборки является метод Джессики Фридрих. В этой сборке не нужно запоминать большое количество формул, главное понять принцип.
Этапы сборки:
1. Сборка креста на одной из сторон.
2. Сборка первого слоя одновременно со вторым.
3. Ориентация элементов верхнего слоя.
4. Перестановка элементов верхнего слоя.
Видео
Метод Валерия Морозова (интуитивный)
Задача этого метода — не давать готовые формулы для заучивания, а показать принципы сборки.
Схема сборки:
1. Собрать 8 угловых элементов.
2. 4 рёберных элемента в среднем слое собираются в крест на любой из боковых граней.
3. 8 остальных рёберных элементов собираются в правильные пары.
4. 6 центров устанавливаются каждый на свою грань.
Видео
Метод полос
Метод для сборки кубика 5×5, рассчитан на начинающих, которые умеют как минимум собирать 3×3.
Для продвинутых
Как собрать кубик Рубика за 31 ход.
Кажется, что Кубик Рубика существовал всегда. Однако его изобрел в 1975 году венгерский скульптор Эрнё Рубик, а головоломке понадобилось меньше 50 лет, чтобы завоевать мир.
Шутка ли: по всему миру продано 450 миллионов копий головоломки, как официальных, так и поддельных (оригинал запатентован, поэтому выпускается определенными тиражами).
Такой популярности не добивались не то что спиннеры. Вероятно, кубик Рубика может поспорить с шахматами и другими древнейшими играми-головоломками-таймкиллерами.
Почему кубик Рубика стал таким популярным?
Секрет популярности прост: кубик Рубика является детской игрушкой только на первый взгляд. На деле это серьезная математическая задача по комбинаторике, воплощенная в форме.
Что такое кубик Рубика известно всем. Что такое собрать его? Это означает привести его в исходное состояние, когда каждая грань заполнена одним цветом. Для этого необходимо менять местами раскрашенные квадраты до полного успеха.
Каждый отдельный случай — одно из 43 252 003 274 489 856 000 состояний кубика Рубика. Ещё раз, округленно: 43,3 18 , или чуть больше 43 квинтиллионов различных вариантов. Каждый может участвовать в конкретном решении.
С учетом центральных элементов, число возможных вариантов текущего состояния кубика Рубика равно 88,5*10 21 . Архив интернета на март 2019 года составляет 45*10 15 байт, или 45 петабайт.
По этой причине у кубика нет однозначного решения: оно требует слишком объемных расчетов, и подчиняется только комбинаторике как подразделу математической статистики. Впрочем, вероятность той или иной конфигурации можно оценить.
Поскольку элементы повторяемы, и для сбора головоломки достаточно собрать по цвету все грани, возможно создать алгоритм, который приведет к правильному решению.
Огромное число возможных решений привело к тому, что все существующие алгоритмы срабатывают только для бОльшей части (80-98%) начальных состояний. Иногда их приходится комбинировать.
Тем не менее, существуют наиболее распространенные, простые и понятные без серьезных математических выкладок (хотя совсем без них не обойдется): именно они позволяют собирать затейливую головоломку чаще всего.
Как умные люди собирают кубик Рубика?
Для сборки или приведения кубика к виду с гранями одного цвета существует несколько официально разработанных методик:
Последний гарантирует, что кубик рано или поздно будет собран и достаточно прост в освоении. Поэтому его сегодня и рассмотрим, оставив прочие варианты для фанатов.
Важно: если кубик упал и рассыпался, то неправильный «ремонт» приведет к невозможности собрать головоломку.
Для ускорения процесса можно воспользоваться Решателем кубика Рубика. Помогает, хотя в некоторых случаях предложенные компьютером варианты не приведут к положительному итогу.
Из чего состоит кубик Рубика. Важно знать, прежде чем собирать
Внутри кубика Рубика прячется крестовидный каркас, на котором закреплены подвижные и статичные элементы головоломки.
- Центры — 6 шт. Один цвет, всегда остаются на своем месте.
- Ребра — 12 шт. Крайние элементы с двумя цветами.
- Углы — 8 шт. Угловые элементы с тремя цветами.
- Грань — совокупность 9 элементов, которые можно вращать одновременно.
Для записи алгоритмов используют упрощенные наименования базовых элементов, которые определяются наблюдателем (человеком, который проводит сборку) относительно самого себя:
- Ф — фасад
- Т — тыл
- П — правая грань
- Л — левая грань
- В — верх
- Н — низ
- С — средний слой
В формуле каждый символ соответствует повороту указанного элемента на 90° по часовой стрелке: Ф, Т, П, Л, В, Н. Поворот против часовой определяет штрих: Ф’, Т’, П’, Л’, В’, Н’. Цифра после буквы обозначает количество повторов операции.
Пример: формула НП’Ф’В2
1. Повернуть нижнюю грань на 90° по часовой (вправо).
2. Повернуть правую грань на 90° против часовой (на себя).
3. Повернуть фасадную грань на 90° против часовой.
4. Повернуть правую грань на 90° по часовой (на себя) дважды, или один раз на 180°.
Все формулы (повороты) выполняются до тех пор, пока не будет получен удовлетворяющий (показанный на рисунке) результат.
Поехали, начинаем собирать кубик Рубика. Инструкция далее.
1. Начинаем. Объемный крест
На первом этапе сборки необходимо определить основной цвет, цвет верхней грани, он же цвет центрального выбранного элемента.
Важно: от выбора цвета дальнейшее решение не зависит.
Далее необходимо поднять элементы того же цвета, чтобы получить так называемый «крест верхней грани»:
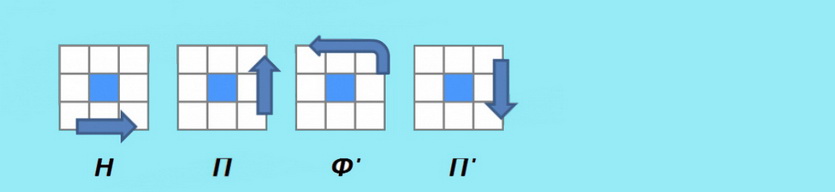
1.1 НПФ’П’ — если угловой кубик на нижней грани (поворот боковой грани и несколько поворотов нижней)
1.2 ФФ — если угловой кубик на боковой грани (поворот нижней грани).
Сборка первой части дает понимание процесса и в целом не зависит от формул — эта часть решается без применения комбинаторики простыми вращениями.
2. Продолжаем. Сторона
Для сборки верхней грани нужно поставить 4 угловых кубика выбранного цвета на свои места. В этом случае возможно несколько «фасадов», так как угловой кубик может быть развернут 3 способами относительно граней.
Возможно 3 ситуации, для каждой из которых применяется собственный алгоритм:
2.1 ЛН’Л’ – если кубик выбранного цвета на боковой грани
2.2 Ф’Н’Ф — если кубик выбранного цвета на фронтальной грани
2.3 (Ф’П’)Н2(ПФ) — если кубик выбранного цвета на нижней грани
3. Следующее. Пояс
Этап предполагает 2 возможных раскладки и 2 формулы, с помощью которых необходимо собрать второй от верхней грани слой (пояс).
После последней операции кубик для перестановки в этой находится под центральным элементом фасадной грани. Его нужно вывести на фасад так, чтобы цвет центрального и углового элементов совпадали.
Используется 2 основных алгоритма:
3.1 (НЛН’Л’)(Н’Ф’НФ) — если элемент идет на левую грань
3.2 (Н’П’НП)(НФН’Ф’) — если элемент идет на правую грань
Если нужный кубик находится в среднем слое, необходимо применить любой алгоритм до тех пор, пока кубик не окажется на нижней грани.
4. Теперь – выставка рёбер
Важно: данный этап требует перевернуть кубик на 180° от себя, так, чтобы нижняя грань оказалась вверху, а прочие остались на своих местах.
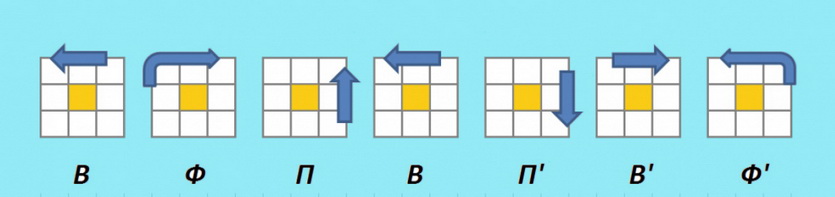
На данном этапе необходимо правильно выставить с помощью единственной формулы рёберные кубики, за счет чего на нижней грани окажется 2 кубика верного цвета.
4.1 (ВФП)В(П’В’Ф’)
5. Делаем согласованный крест
После этапа 3 возможны 3 базовых начальных позиции, применив к которым формулы этапа, получится необходимая сборка. Если текущая ситуация не подходит ни под один из вариантов, необходимо выполнить алгоритм 5.3 дважды.
Для каждой базовой ситуации имеется свой алгоритм решения? который сводится к повторению одной комбинации:
5.1 (ПС)4 В (ПС)4 В’
5.2 (ПС)4 В’ (ПС)4 В
5.3 (ПС)4 В2 (ПС)4 В2
Внимание: поворот средней грани «С» осуществляется с нижней стороны.
6. Затем – расстановка углов
На этом этапе снова нужно перевернуть, переориентировать кубик таким образом, чтобы в левом дальнем углу верхней грани оказался подходящий по цвету угловой кубик.
Выбор алгоритма зависит от конкретной ситуации и остаётся за «игроком»:
6.1 (П’Ф’Л’Ф)(ПФ’ЛФ) — прямой алгоритм
6.2 (Ф’Л’ФП’)(Ф’ЛФП) — обратный алгоритм
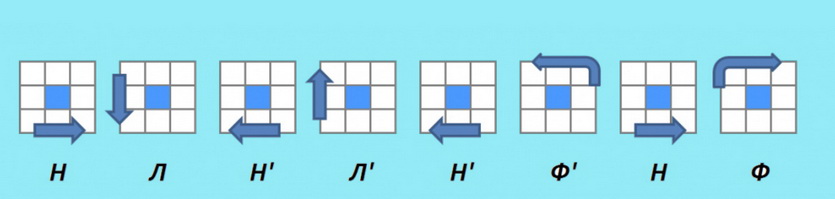
7. Теперь разворот углов
Заключительный этап сборки самый ответственный, поскольку неправильная сборка (выполнение алгоритма) приведет к нарушению конструкции и откату на несколько шагов назад.
В зависимости от сложившейся комбинации, необходимо применить один из алгоритмов, которые сводятся к одному:
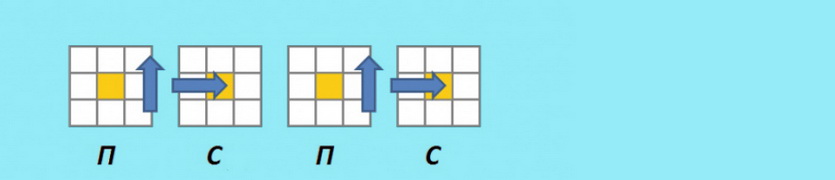
7.1 (ПФ’П’Ф)2 В (ПФ’П’Ф)2
7.2 (ПФ’П’Ф)2 В’ (ПФ’П’Ф)2
7.3 (ПФ’П’Ф)2 В2 (ПФ’П’Ф)2
Каждый выполняется в 2 этапа: первая половина до правильной ориентации углового кубика, вторая половина (после поворота) до возвращения порядка в нижних слоях.
Ура, почти всё. Завершение сборки
Завершается сборка единственным поворотом последней собранной грани на 90° по/против часовой в зависимости от текущей ситуации.
Кубик Рубика собран!
А есть способы проще?
Нет, если вы не гений-рекордсмен. Вначале надо научиться собирать правильно.
Каждый из этапов сборки осуществляется строго из базового положения. Причем, в некоторых случаях кубик необходимо привести к базовому положению самостоятельно, переориентировав его либо повторно выполнив текущий (предыдущий) алгоритм.
Важен не только алгоритм конкретной операции, но и общая последовательность сборки. В противном случае нарушается строй решения задачи и возможен непредсказуемый вариант.
Остаётся ответить самому себе на вопрос: зачем собирать кубик Рубика?
Для основной массы населения планеты ответ очевиден. В отличие от спиннеров и других простых способов занять руки кубик Рубика позволяет тренировать не только руки, но и ум.
Решение (сборка) кубика вслепую невозможны. Вероятность этого события намного меньше, чем появление разумных инопланетян на Земле, начало Звездных войн или самостоятельное возрождение динозавров.
Так что руки в ноги — и за кубиком!


Шаг 7.
В последнем этапе нашей инструкции, мы расскажем Вам, как развернуть углы последнего слоя кубика Рубика 3х3 одной формулой.
В начале этого этапа все угловые кубики верхней грани должны находится на своих местах, при этом они могут быть неправильно повёрнуты. Данная формула развернет угловые кубики по часовой стрелке.
Смотри иллюстрацию ниже.
Как повернуть уголы кубика Рубика 3х3
В конце данного этапа по сборке головоломки 3×3, ваш куб будет полностью собран!
Смотри картинку головоломки в сборе.
В зависимости от того, как у вас был разобран рубик 3х3, у вас могут быть варианты по расположению боковых элементов последней грани:
- Два угловых кубика повёрнуты неправильно. 3×3
- Два противоположенных угловых кубика повёрнуты неправильно.
- Три детали повернуты неправильно.
- Все четыре элемента повернуты неправильно.
Поворот угла третьего слоя кубика Рубика
Данная формула предназначена, для поворота угловой детали по часовой стрелке.
Смотри рисунок.
Важно!
Этот алгоритм надо повторять до тех пор, пока правый кубик верхней грани, не повернётся правильным образом!
Далее поверните верхнюю грань и повторяйте формулу, до тех пор пока угловая деталь не будет правильно сориентирована.
Поверните верхнюю грань один раз:
и / или
Поверните верхнюю грань два раза:
При выполнении данной формулы, может создаться впечатление, что все запуталось. Не пугайтесь. Если повторить последовательность действий ещё несколько раз, то всё встанет на свои места.
Не огорчайтесь, если у вас не получилось собрать головоломку с первого раза. Я и сам не сразу всё понял, но теперь могу собрать его менее чем за 2 минуты, не глядя в формулы. Они уже в моей голове.
Вернее не в голове — руки сами помнят алгоритмы.
И знайте, лучший способ отблагодарить нас, это поделиться ссылкой на наш сайт с друзьями!
Если Вы смогли собрать головоломку Рубика, нажмите — Я собрал кубик 3×3!
АЛГОРИТМЫ СБОРКИ КУБИКА РУБИКА
Ключевые слова: кубик Рубика, алгоритм, теория
групп, Python, скорость сборки, число Бога, оптимальный алгоритм, теория
графов.
Аннотация: В данной статье будут рассмотрены
различные алгоритмы для сборки кубика Рубика. Они реализованы на Python 3.6 со
стандартными библиотеками. Данные алгоритмы основаны на теории групп, теории
графов и комбинаторике. Все сборки кубика произведены на одном компьютере. В
данной статье рассматриваются четыре алгоритма для сборки.
Key words: Rubiks Cube, algorithm, group theory, Python,
assembly speed, number of God, optimal algorithm , graph theory.
Annotation: Different algorithms of Rubiks cube assembly
will be considered here. This algorithms are realized by Python 3.6 with
standard libraries. Given algorithms are based on group theory, graph theory
and combinatorics. All cube’s assemblies done with one computer. In this
article four algorithms of assembly are considered.
Кубик Рубика – это головоломка, созданная
венгерским архитектором Эрнё Рубиком в 1974 году. Для создания любого алгоритма
необходимо понимать саму структуру данной головоломки. Кубик Рубика состоит из
21
детали: 1 центральная ( 6 центральных
квадратов), 8 угловых( 3 квадрата в углах куба), 12 боковых( 2 квадрата между
центрами). Кубик покрашен в 6 различных цветов, по количеству граней. Суть
головоломки состоит в том, чтобы собрать (на 1 грани 1 цвет) кубик.
Рис.1 Эрнё Рубик.
Алгоритмы, которые существуют в настоящее
время для сборки Кубика, основаны на теории графов, теории групп, теории
вычислимости и комбинаторике. В этой статье для обозначения последовательности
поворотов граней кубика Рубика 3×3×3 используется «нотация Сингмастера»,
разработанная Дэвидом Сингмастером и опубликованная им в 1981 году. Сборка куба
происходит в метрике QTM, грани поворачиваются только на 90 градусов.
Буквы L , R , F , B , U , D обозначают поворот
на 90° по часовой стрелке левой (left), правой (right), передней (front), задней
(back), верхней (up) и нижней (down) граней соответственно. Знак « ’ »
обозначает поворот против часовой стрелки.
Как уже говорилось ранее, алгоритмы сборки
основываются на теории групп. Группа кубика Рубика — подгруппа симметрической
группы S48, элементы которой соответствуют преобразованиям кубика Рубика. Под
преобразованием подразумевается эффект поворота любой из граней или
последовательности поворотов граней.
Группа кубика Рубика G определяется как
подгруппа S 48, порождаемая поворотами шести граней на 90°:
G = ⟨ L , F , R , B , U , D ⟩
Порядок группы G равен:
| G | = 8 ! ⋅ 12 ! ⋅ 38 ⋅ 212
3 ⋅ 2 ⋅ 2
= 43 252 003 274 489 856 000 = 227 ⋅
3 14 ⋅ 5 3 ⋅ 72 ⋅ 11.
По сути – это количество всех возможных
комбинаций цветов кубика.
G не является абелевой группой, так как,
например, F R ≠ R F. Другими словами, не все пары элементов коммутируют.
В июле 1981 года Jesper C. Gerved и Torben
Maack Bisgaard доказали, что группа кубика Рубика содержит элементы 73
различных порядков от 1 до 1260, и нашли число элементов каждого возможного
порядка
Группа кубика Рубика содержит циклические
подгруппы порядков
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15,
16, 18, 20, 21, 22, 24, 28, 30, 33,
35, 36, 40, 42, 44, 45, 48, 55, 56, 60, 63,
66, 70, 72, 77, 80, 84, 90, 99, 105, 110,
112, 120, 126, 132, 140, 144, 154, 165, 168,
180, 198, 210, 231, 240, 252, 280, 315,
330, 336, 360, 420, 462, 495, 504, 630, 720,
840, 990, 1260.
Одним из самых популярных современных методов
сборки кубика Рубика является метод FTM. Этот метод состоит из 4 шагов:
1. Собрать на верхней грани крест
2. Собрать верхнюю грань
3. Собрать на боковой грани 2
верхних слоя
4. Собрать нижний слой
На всех этих четырех шагах существуют
определенные ограничения при поворотах граней куба. Этот метод так же описывается
на основе теории групп, он менее эффективен чем другие методы, но очень прост
для освоения человеком. Именно этот метод используют люди, собирающие кубик на
скорость.
Не смотря на простоту для человека, этот метод
трудоемок для написания кода не менее, чем другие, более эффективные методы. Мы
рассмотрим две реализации данного метода.
Первая, и самая простая реализация – это
интуитивный метод. Существует определенная последовательность действий и
закономерность для каждого из этапов этого метода.
Для первого этапа мы ищем боковые квадраты
верхней грани на остальных гранях. В связи с закономерностями сборки кубика они
могут присутствовать только на боковых квадратах граней. Обнаруживая их по
одному, мы ставим их на место, так чтобы не сдвинуть квадраты, которые уже
присутствуют на верхней грани. Для таких действий есть определенная
последовательность поворотов: F U’ R U. Далее начинаем этап с начала для поиска
еще одного квадрата.
После этого, при помощи определенных
комбинаций мы делаем так, чтобы квадраты на боковых элементах совпадали с
квадратами боковых граней.
Для выполнения второго этапа сперва необходимо
установить местоположение наших угловых элементов. После того как мы найдем
угловой элемент, существует несколько вариантов развития событий:
1. Угловой элемент на месте, но он
повернут неверно. Тогда проворачиваем его при помощи следующей комбинации (
угол смотрит на нас и находится справа): R’ D’ R D
2. Угловой элемент на нижней грани.
Проворачиваем нижнюю грань, до тех пор, пока цвета углового элемента не будут
совпадать с цветами боковых соседних. После этого повторяем комбинацию из 1-го
варианта.
3. Угловой элемент на верхней
грани, но не на своем месте, тогда размещаем кубик, как в первом варианте,
после этого выполняем комбинацию R’ D’ RD. И переходим ко второму варианту.
Рис.2 Положения кубика во время сборки методом FTM
После этого переходим к третьему этапу. Сперва
перевернем куб, так чтобы нижняя грань стала сверху. Начинаем движение по
боковым элементам. Ищем боковой элемент между передней и правой гранью.
Существует 3 варианта местоположения бокового элемента:
1. Боковой элемент на месте, но
неправильно повернут. Поворачиваем куб, так чтобы один из квадратов элемента
был справа, а другой спереди. После этого поворачиваем элемент при помощи
комбинации до того, как куб будет сложен: U R U’ R’U’ F’ U F
2. Боковой элемент находится между
другими гранями. Поворачиваем куб относительно элемента так как в первом.
Производим комбинацию U R U’ R’U’ F’ U F, после этого проворачиваем верхнюю грань,
до тех пор , пока элемент не встанет над левой гранью. После этого делаем
комбинацию из первого.
3. Боковой элемент сверху. Делаем
2-й Четвертый этап состоит из нескольких подразделов:
1. Собрать сверху правильный крест.
Сперва просто получим сверху крест. Делаем 1,2 или 3 раза(до креста) F R U R’
U’ F’. После этого делаем правильный крест. Вращаем верхний слой, чтобы
какие-либо ДВА ребра совпали по цветам с центрами из среднего слоя. Может
получиться одна из двух ситуаций. Если стоят неправильно два противолежащих
угла, то делаем R U R’ U R U2 R’. Если два собранных ребра, стоят под углом,
два остальных нужно поменять местами комбинацией, при этом кубик держим, чтобы
угол смотрел от вас и вправо R U R’ U R U2 R’ U.
2. Расставить углы верхнего слоя по
местам. Сперва надо несколько раз сделать комбинацию U R U’ L’ U R’ U’ L. После
этого один из угловых элементов станет на место. Три несобранных угла нужно
перемещать по часовой стрелке до его сборки. Собранным углом нужно повернуть к
себе и справа, U R U’ L’ U R’ U’ L.
Куб собран. При помощи компьютерного алгоритма
куб собирается за 170-220 шагов, при этом затрачивается от 0,6 до 1,2 секунды.
Человек собирает
этот куб за 70-150 ходов в нотации
Сингмастера, потому что он также использует логические выводы по ходу сборки, в
отличии от машинального подхода компьютера, который просто однообразно
перебирает ходы.
Также FTM-сборку можно реализовать
генетическим методом. Несмотря на более низкую эффективность этот метод
представляет интерес как пример саморазвивающейся системы, которая отбрасывает
наименее слабые генерации, и представляет пример эволюции.
Он движется по тем же шагам что и простой FTM.
В данном случае шаг(обычный поворот грани) называется геном. Новые гены
генерируются случайно, при этом прибавляясь к геному алгоритма сборки. Важным
параметром мутации является максимальное возможное число генов, которые будут
добавлены во время следующей мутации. Это важное число, которое регулирует, на
сколько сложную модификацию Куб сможет сгенерировать за один раз. После мутации
Куба считается его фитнесс, а затем и фитнесс всех остальных кубов. Наиболее
эффективный геном на определенный момент выживает и передается как основа для
дальнейших мутаций.
Основная особенность состоит в том, что
максимальное количество генов (шагов) приходится увеличивать до 30 раз, из-за
того, что последний этап является намного сложнее первых, и ради решения задачи
приходится пренебрегать сложностью решения. Это необходимо, чтобы избегать
генетических ям, и не прекращать поиск на некотором локальном максимуме. В
среднем этот алгоритм решает куб за 300 — 400 шагов, и за 2 – 4 минуты, что
проигрывает даже обычному наивному методу, недаром Скиена советует использовать
алгоритм имитации отжига вместо генетического алгоритма везде, где это
возможно. Единственное что в нем привлекает – это
симуляция эволюционного процесса.
Один из самых эффективных алгоритмов сборки, а
также самым популярным машинным алгоритмом является алгоритм Коцембы. Он
основывается на алгоритме М. Тистлетуэйта. Тистлеуэйт предложил ограничить
сборку куба до четырех этапов, а Коцемба и вовсе до двух:
𝐺0 = ⟨ U , D , L , R , F , B ⟩
𝐺1 = ⟨ U , D , 𝐿2 , 𝑅 2, 𝐹2, 𝐵2 ⟩
𝐺2 = { 1 }
Наглядное описание группы 𝐺1
можно получить, если произвести следующую разметку:
• Все этикетки U и D пометить
знаком «+».
• Этикетки F и B на рёберных
элементах FR, FL, BL, BR пометить знаком «-».
• Все остальные этикетки оставить
без меток.
Тогда все конфигурации группы 𝐺1
будут иметь одну и ту же разметку (совпадающую с разметкой на собранном
кубике).
Рис.3 Разметка куба по методу Коцембы.
Отмеченные квадраты будут на месте после первого этапа алгоритма.
Решение состоит из двух этапов. На первом
этапе заданная конфигурация x ∈ 𝐺0 переводится последовательностью ходов 𝑆1 в
некоторую конфигурацию X′ ∈ 𝐺1. Иными словами, задача первого этапа — восстановить разметку,
соответствующую начальной конфигурации, игнорируя цвета этикеток. Эта сборка
производится путем обхода графа в определенной последовательности.
Просто проанализировав обычный обход графа в
глубину мы получим, что при таком лобовом подходе объем просматриваемых
вариантов был бы слишком велик. Так, первый ход можно сделать 6Х3=18 способами
(любую из шести граней можно повернуть на один из трех углов — 180°, ±90°), на
втором и каждом из следующих ходов число способов равно 15, так как нет смысла
дважды подряд поворачивать одну грань. Таким образом, возникает «дерево
вариантов», от каждой ветви которого отходят пять следующих ветвей. (На самом
деле, начиная с определенного момента некоторые ветви будут срастаться, потому
что разные цепочки ходов могут порождать одинаковые преобразования кубика.)
Число цепочек ходов длины, не превосходящей n, равно сумме геометрической
прогрессии 18(1+15+…+15n-1).
Между прочим, только при n=18 это число
превысит общее число N со- стояний кубика, а значит, заведомо найдутся
состояния, которые нельзя упорядочить меньше чем за 18 ходов.
В действительности, из-за сращивания ветвей
дерева вариантов число 18 можно еще увеличить.
Для сокращения обхода Коцемба догадался
использовать фильтры. Они хранят информацию о цепочках, например, из 7 ходов.
Алгоритм порождает первые два хода, и проходит через фильтр на 7 ходов, если
это состояние не отсеется, то включается фильтр на 6 ходов и т.д.
На втором этапе конфигурация
X′ ∈ 𝐺1 переводится последовательностью ходов 𝑆2 в
начальную конфигурацию. При этом повороты боковых граней на ±90° не
используются, благодаря чему разметка автоматически сохраняется.
Склейка последовательностей ходов 𝑆1
и 𝑆2 является субоптимальным решением к исходной конфигурации.
Для поиска решений на каждом из двух этапов
применяется алгоритм IDA* с эвристическими функциями, основанными на стоимостях
решения соответствующих подзадач.
Задача первого этапа сводится к поиску пути в
пространстве с тремя координатами из разметки с координатами (x1, y1, z1) в
разметку (0, 0, 0):
1. Ориентация x1 восьми угловых
элементов (2187 значений)
2. Ориентация y1 двенадцати
рёберных элементов (2048 значений)
3. Расстановка z1 четырёх рёберных
элементов FR, FL, BL и BR (495 значений)
Рассмотрим три подзадачи поиска пути из
разметки (x1, y1, z1) в разметки (x1’, y1’, 0), (x1’, 0, z1’), (0, y1’, z1’).
Значение эвристической функции h1, используемой на первом этапе, равно
максимальной из стоимостей решения этих подзадач. Стоимости решения подзадач
предварительно вычисляются и хранятся в виде баз данных с шаблонами.
Задача второго этапа сводится к поиску пути в
пространстве с тремя координатами из конфигурации (x2, y2, z2) в конфигурацию
(0, 0, 0):
1. Перестановка x2 восьми угловых
элементов (40320 значений)
2. Перестановка y2 восьми рёберных
элементов верхней и нижней граней (40320 значений)
3. Перестановка z2 четырёх рёберных
элементов среднего слоя (24 значения)
Рассмотрим три подзадачи поиска пути из
конфигурации (x2, y2, z2) в конфигурации (x2’, y2’, 0), (x2’, 0, z2’), (0, y2’,
z2’). Значение эвристической функции h2, используемой на втором этапе, равно
максимальной из стоимостей решения этих подзадач.
В алгоритме применяются дополнительные
оптимизации, направленные на увеличение быстродействия и уменьшение памяти,
занимаемой таблицами. Данный алгоритм был реализован на языке Python.
Он является достаточно быстрым, и в то же время эффективным по количеству
ходов. Он решает куб в среднем за 22-30 ходов, и в тоже время не более чем за
1,8
секунды.
Этот алгоритм несомненно является крайне
эффективным, в особенности для специальных машин «Cube solver’ов» , так как он
быстро дает краткое решение. Но этот алгоритм не подходит для поиска алгоритма
бога(кратчайшего решения).
Рис.4 Cubesolver , созданный на базе
конструктора LEGO Mindstorm.
Суть сборки состоит в том , чтобы собрать куб
за минимальное количество времени и ходов, поэтому следует рассмотреть алгоритм
для нахождения числа Бога для кубика.
Лучшим алгоритмом для этой цели является
алгоритм Корфа. Алгоритм Коцембы позволяет быстро находить короткие, субоптимальные
решения. Тем не менее, может потребоваться значительное время, чтобы доказать
оптимальность найденного решения. Был необходим специализированный алгоритм
поиска оптимальных решений.
В 1997 году Ричард Корф опубликовал алгоритм,
позволявший оптимально решать произвольные конфигурации кубика Рубика. Десять
выбранных случайным образом конфигураций были решены не более чем в 18 ходов
FTM[55][56].
Совсем недавно, в 2010 году группа
программистов из Google, совместно с Гербертом Коцембой , доказали что любой
куб можно решить не более чем за 20 ходов. Они использовали модифицированный
алгоритм Корфа, и исследовали 55 888 296 уникальных множеств состояний куба. На
это потребовалось 35 лет компьютерного времени Google.
Собственно алгоритм Корфа работает следующим
образом. В первую очередь определяются подзадачи, достаточно простые для того,
чтобы осуществить полный перебор. Были использованы следующие три подзадачи
1. Состояние головоломки
определяется только восемью угловыми кубиками, положения и ориентации рёбер
игнорируются.
2. Состояние головоломки
определяется шестью из 12 рёберных кубиков, другие кубики игнорируются.
3. Состояние головоломки определяется другими шестью
рёберными кубиками.
Количество ходов, необходимое для решения
каждой из этих подзадач, является нижней оценкой количества ходов, необходимого
для полного решения. Произвольно заданная конфигурация кубика Рубика решается с
помощью алгоритма IDA*, использующего эту оценку в качестве эвристики.
Стоимости решения подзадач хранятся в виде баз данных с шаблонами.
Хотя этот алгоритм будет всегда находить
оптимальные решения, он не позволяет напрямую определить, как много ходов может
потребоваться в худшем случае.
Этот алгоритм самый медленный. Исполнение
программы на моем компьютере занимает от 2 минут и более, так как он исследует
буквально все ходы данного решения, и находит самое оптимальное.
В результате мы получили, что наиболее
эффективным, с точки зрения машины, вариантом сборки кубика, является сборка
методом Коцембы. Она одновременно является быстрой и эффективной, выдавая
погрешность лишь в пределе 5 ходов. Второй по эффективности – это метод Корфа,
и на последнем месте, ожидаемо находиться наивный метод. Таким образом
математическими методами можно ускорить решения как этой, так и других подобных
задач.
Cписок литературы:
1) Объяснение алгоритма Коцембы от
его создателя(англ.) // kociemba.org пуб. Сайт Герберта Коцембы.
URL:kociemba.org/math/imptwophase.html
2) В. Дубровский, А. Калинин
Новости кубологии (рус.) // Квант. — 1992. — № 11. — С. 52 — 56.
3) David Joyner. Adventures in Group Theory:
Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys. — Second edition.
// JHU Press, 2008. — 328 p. — ISBN 0-801-89726-2, 978-0-801-89726-9.
4) Сборка Кубика Рубика
генетическим алгоритмом //harbhabr.ru: ежедн. интернет издание. URL:
https://habrahabr.ru/post/260965/
Not knowing the details of the cube or the app, I’d say there are two main possibilities:
- a single corner piece was forcibly twisted into one of the two unsolvable configurations. (This is pretty common, and often happens by accident on loose speed cubes.)
To determine if this is the case, first solve any 7 corner pieces, and then fix by forcibly twisting the remaining piece into the correct orientation.
- Some stickers have been swapped.
To determine if this is the case, one at a time, move each corner piece to its correct place and orientation. (The correct place and orientation can be determined by the centre pieces of the sides: those cannot be moved wrt. each other.) If you find a corner piece for which there is no place where you can match all three centre colours perfectly, then this is the case.
There’s a common (may happen accidentally if you drop the cube so that some centre caps pop out) special case that’s easy to fix:
- if you can match all the three colours but not the order of the colours, and this happens on every corner piece, then you have a mirrored centre block. Fix by choosing a pair of opposing sides, then pry off the cap on the centre piece on those sides, and swap them.
Otherwise, you’ll probably need to take the cube apart, solve it piecewise as far as you can, and then try to find the minimum number of stickers you need to swap in order to make a solvable cube.
(To take a cube apart, rotate the top layer 45 degrees, and pop the middle piece of an edge out by pushing a flat head screw driver or something similar under it. The rest of the pieces should come apart easily after that.)
For more detailed instructions, please solve the cube as far as you are able to, and then post photos showing all the sides.