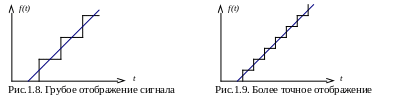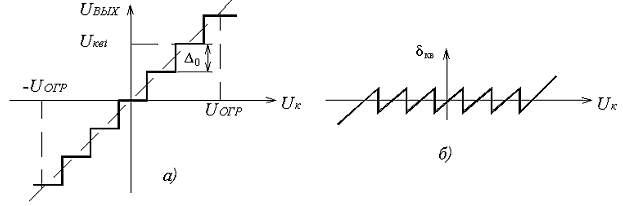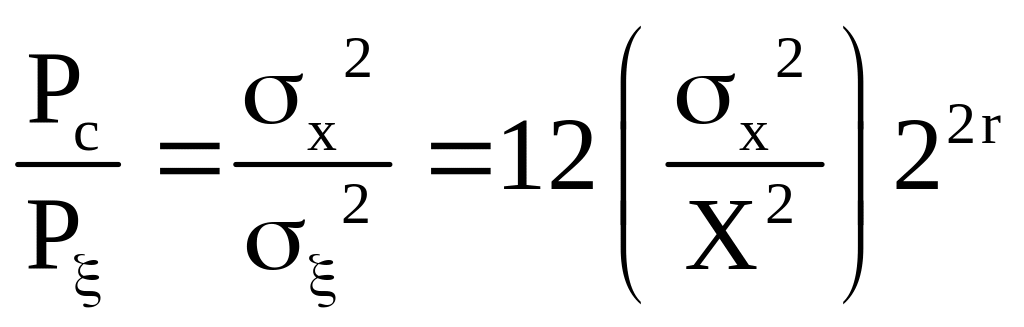-
Квантование сообщений по уровню
Квантованием по уровню называют
дискретизацию множества значений
непрерывного сигнала по уровню, то есть
по амплитуде параметра. Идея квантования
по уровню заключается в следующем. Весь
диапазон возможных изменений сигнала
(функции) разбивается на N различимых
величин – уровней квантования. В
результате квантования сигнала каждое
из его значений данного интервала
округляется до некоторого уровня.
Порогами квантования называются
величины, при сравнении с которыми
исходного непрерывного сигнала в
процессе квантования определяется его
принадлежность к уровню квантования.
Величина, представляющая собой разность
между двумя соседними уровнями, называется
шагом квантования. Замена исходных
значений функции соответствующими
дискретными значениями – уровнями
квантования – вносит ошибку квантования,
называемую шумом квантования.
Существует три способа квантования:
1-й способ квантования — путем
соотнесения исходного значения сигнала
с ближайшим значением уровня. Информационная
система содержит устройство квантования,
которое выполняет операцию квантования
непрерывного сигнала по уровню. В
процессе такой операции отдельное
значение исходного непрерывного сигнала
соотносится с одним из возможных значений
уровней; если исходное значение
оказывается в пределах двух соседних
порогов квантования, то это значение
заменяется уровнем квантования,
заключенным между данными порогами. В
этом случае квантование происходит по
методу соотнесения с ближайшим значением
уровня. Этот способ квантования
аналогичен округлению чисел до ближайшего
целого. При таком способе вместо исходного
непрерывного сигнала мы получим
квантованный сигнал, представленный
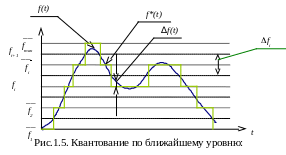
временной диаграммой на рис.1.5.
f(t) — исходный непрерывный сигнал;
f *(t) — квантованный
сигнал;
fi , fi+1 ,… —
значения соседних порогов квантования
(пунктир);
fi — шаг квантования,
fi =
fi+1 — fi;
—
значения уровней квантования (сплошные
линии).
Таким образом, очевидно, что в процессе
квантования неизбежно возникает
принципиальная или методическая ошибка
квантования — шум квантования; ее
величина для момента времени t
определяется в виде
Для этого способа ошибка квантования
не превышает половины шага квантования
, а ее значения могут быть разных знаков
±∆f(t).
2
-й
способ квантования — путем соотнесения
исходного значения с ближайшим снизу
значением уровня. В этом случае i-е
пороговое значение совпадает со значением
(i+1)-го уровня. Данный способ аналогичен
округлению числа до ближайшего целого
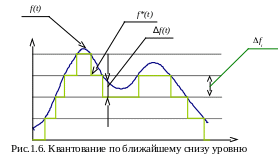
снизу. Соответствующая временная
диаграмма представлена на рис.1.6.
Ошибка квантования всегда положительна
(f(t) > 0) и не
превышает величину шага квантования
(
).
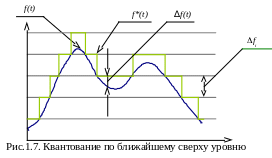
3-й способ квантования — путем
соотнесения исходного значения с
ближайшим сверху
значением уровня. Пороги и уровни
совпадают по номерам и значениям. Шум
квантования всегда отрицательный
(f(t)< 0) и не
превышает величину шага квантования
(
i).
Этот способ аналогичен округлению числа
до ближайшего целого сверху.
С
оответствующая
временная диаграмма представлена на
рис.1.7.
Равномерным квантованием называется
такое квантование, при котором шаг
квантования
есть постоянная величина. В большинстве
случаев применяется равномерное
квантование.
Шаг квантования выбирается исходя из
необходимой точности передачи сигнала.
Если же при этом существуют внешние
помехи, то необходимо, чтобы амплитуда
помех не превышала половины шага
квантования, тогда возможно будет
восстановить заданный уровень, так как
воздействие помехи не выведет значение
сообщения за зону, соответствующую
данному уровню квантования. Кроме
уровней выделяют пороги квантования.
При равномерном квантовании расстояние
между двумя соседними порогами равняется
шагу квантования.
Из трех способов квантования первый
дает минимальную среднюю ошибку
квантования при одном и том же шаге
квантования, поэтому на практике часто
используется именно этот способ.
Для более точного отображения исходного
сигнала необходимо увеличивать число
уровней, т. е. уменьшать шаг квантования
(рис. 1.8-1.9).
Однако бесконечное уменьшение шага
квантования физически невозможно, а
формально не имеет смысла, так как мы
опять возвращаемся к непрерывному
сигналу. Уменьшать шаг до бесконечности
невозможно также из-за влияния помех.
Сообщения по мере передачи по каналам
связи или по мере хранения в памяти
искажаются под воздействием помех,
поэтому на приемной стороне или при
считывании сигнала должен находиться
еще один квантователь. Этот квантователь,
как и исходный квантователь сигналов,
для опознавания сигнала должен соотносить
реальный сигнал с возможными значениями
уровней. Для некоторых значений это
соответствие может быть неправильным
и на приемной стороне могут быть ложные
восприятия соседних уровней. Таким
образом, исходный сигнал, поступающий
от источника непрерывных сигналов, в
системе квантования по уровню искажается
из-за самого квантования и, кроме того,
под воздействием помех, как показано
на рис.1.10.
Временные диаграммы:
Увеличение шага квантования в системе
квантования, при неизменном уровне
помех, приводит к подавлению помех,
поэтому самый простой способ защиты
квантованного сигнала от помех —
увеличение шага квантования. Однако
при этом мы увеличиваем шум квантования,
т.е. вносим погрешность за счет грубого
квантования.
Различают следующие две модели помех
(два типа помех):
a) аддитивные помехи формируют смесь
сигнала с помехой путем алгебраического
суммирования их амплитуд:
f
сп(t)=
f*(t) fп(t) , где
fn(t) — амплитуда помехи;
б) мультипликативные помехи формируют
смесь сигнала с помехой путем перемножения
их значений:
f
сп(t)=k
f*(t) fп(t)
, где k — масштабный коэффициент.
(При имитации работы системы квантования
на лабораторных работах моделируются
аддитивные помехи.)
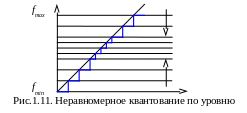
Кроме равномерного квантования, в
некоторых случаях используют неравномерное
квантование, при котором шаг квантования
∆fi — переменная величина
в зависимости от номера уровня: ∆fi
= fi+1 — fi. В
некоторых диапазонах изменения сигнала,
для уточнения его значений, шаг квантования
делают меньше.
Такая система применяется тогда, когда
возникает необходимость отображать
значения сигнала в некоторых диапазонах
точнее, чем за их пределами, как это
показано на рис.1.11.
При построении устройства для равномерного
квантования необходимо:
1) определить диапазон изменения сигнала;
2) определить шаг квантования.
При определении шага квантования следует
учитывать:
— желаемую точность отображения сигнала;
— влияние помех, величина которых ставит
ограничения на минимальную величину
шага квантования.
При равномерном квантовании число
уровней квантования определяется
диапазоном изменения сигнала и величиной
шага квантования в виде:
nmax= (fmax —
fmin) / ∆f ,
где fmax, fmin –
максимальное и минимальное возможные
значения сигнала в
данной информационной системе.
Если известен характер изменения помех,
то минимальную величину шага квантования
можно определить численно. При
моделировании часто имитируется
случайная помеха с нормальным (гауссовым)
распределением, закон которого
характеризуется двумя параметрами m
и б, где m — математическое
ожидание (величина постоянной составляющей
помехи); б — среднеквадратическое
отклонение — СКО ( интенсивность случайной
составляющей помехи).
Изображенная на рис. 1.12. гауссова помеха
имеет постоянную составляющую со знаком
+.
Обычно в системах передачи данных помеха
бывает именно нормально распределенной
с нулевым математическим ожиданием.
Помеха может быть рассеяна более или
менее сильно, но площадь под кривой
распределения должна быть одинаковой
и соответствовать вероятности достоверного
события — единице. Степень рассеивания
случайной величины (помехи) определяется
значением среднеквадратического
отклонения б.
При наложении такой помехи на квантованный
сигнал последний становится случайной
величиной fсп(t) с
математическим ожиданием, равным его
уровню
(m
=
),
и среднеквадратическим отклонением
помехи (б = бn), как показано
на рис.1.13.
Рис.1.13.
Плотность распределения смеси fсп
квантованного сигнала с гауссовой
помехой: _ __ __
fi , fi-1 , fi+1
— данный, нижний и верхний
соседние уровни квантования;
fi , fi+1 —
соседние пороги квантования
Площади под кривой распределения за
пределами пороговых значений fi
и fi+1 данного уровня
составляют вероятность искажения
квантованного сигнала (ВИКС). Предположим,
что допустимая ВИКС = 0,01 и нам нужно
определить шаг квантования. Если известен
закон распределения или характер помехи
и его параметры, то можно решить обратную
задачу — определить значения порогов
квантования. Таким образом, шаг квантования
подбирается с учетом помех двумя разными
способами:
— экспериментально (или методом подбора);
— численно, аналитически, если известен
характер помех.
Итак, система квантования должна
содержать один квантователь на выходе
источника непрерывных сигналов, а другой
— на входе приемника сигналов; между
ними располагается канал связи, где на
передаваемый сигнал воздействуют
помехи.
(В составе лабораторного программного
пакета функцию источника непрерывного
сигнала и функцию квантователя имитируют
специальные подпрограммы. Подпрограмма
источника формирует сразу весь массив
значений, а подпрограмма-квантователь
обрабатывает сигнал поэлементно. События
в канале связи имитируются не полностью
— квантованный сигнал деформируется
только помехами. Помехи аддитивные,
случайные и нормально распределенные).
Эффективность работы системы квантования
определяется степенью искажения формы
исходного сигнала. Если передается не
непрерывный сигнал, а сразу квантованный
или дискретный, то эффективность работы
системы может определяться также
частотой правильной передачи отсчетных
сообщений.
Целью квантования по уровню является
замена бесконечного множества непрерывных
сообщений (значений параметра) конечным
множеством дискретных значений. При
этом становится возможным кодирование
конечного множества дискретных сообщений,
которое осуществляется кодовыми словами
на основе алфавита меньшего объема.
Значительным преимуществом системы
квантования по уровню является возможность
применения ее на протяженных линиях
связи с промежуточными приемными
пунктами. В этом случае применение такой
системы позволяет избежать накопления
помехи в процессе передачи сигнала по
участкам, так как на каждом промежуточном
пункте производится приведение сигнала
к первоначальному квантованному уровню.
В результате этого единственная помеха,
которая остается в сигнале к моменту
его прихода на конечный пункт — это шум
квантования, который принципиально не
устраним. Квантование сообщений позволяет
обеспечить их длительное хранение без
искажений в аналоговых запоминающих
устройствах путем периодического
считывания, квантования и записи данного
сообщения на прежнее место с помощью
одного и того же блока квантования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки квантования
В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).
Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.
Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой
е
=B–А= F(А)
–А.
Шаг квантования
Q
=
2–b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.
Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
eус=
Fус(А) –А.
Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2–b
<еус
0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0еус
< 2–b,
а в дополнительном коде эта ошибка
неположительна: 0еус
> –2–b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxeус
< 2–b
=Q.
Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,аb+1…ат
и величиной
,
гдеаi–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления еoк
=
fок(А)–
А
при всех способах кодирования лежит в
пределах
–2–(b+1)
<
еoк
< 2–(b+1)
(1.11)
и, следовательно,
max<2–b
= Q/2.
(1.12)
В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.
(nT)
x(nT)
e(nT)
Рис. 3. Линейная модель квантования
сигналов:
(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);
x(nT) —квантованный
b-разрядный
цифровой сигнал;
e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.
Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.
Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).
Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) e
и дисперсия
ошибки квантованияе
определяются
по формулам:
=E(е)
=,
=
=
=E(е2)
–,
где ре
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:
=
=
В логарифмическоммасштабе
=
Лекция 2
В настоящее время во всём мире развивается цифровая форма передачи сигналов: цифровая телефония, цифровое кабельное телевидение, цифровые системы коммутации и системы передачи, цифровые сети связи. Качество цифровой связи значительно выше, чем аналоговой, так как цифровые сигналы гораздо более помехоустойчивы: нет накопления шумов, легко обрабатываются, цифровые сигналы можно «сжимать», что позволяет в одной полосе частот организовать больше каналов с высокой скоростью передачи и отличным качеством.
Цифровой сигнал – это последовательность импульсов. Общепринято импульсную последовательность представлять как чередование двух символов: 0 и 1. «Binary Digit» – «двоичная цифра». Отсюда и пошло понятие бит, то есть одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале определяется понятием байт [1].
При передаче цифровых сигналов вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени (в секунду).
Для передачи непрерывных сообщений цифровыми методами необходимо произвести преобразование этих сообщений в дискретные, которое осуществляется путём дискретизации непрерывных сигналов во времени и квантования их по уровню, и преобразования квантованных отсчётов в цифровой сигнал [6].
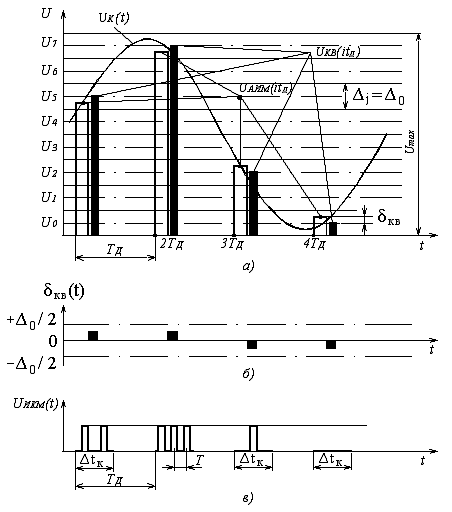
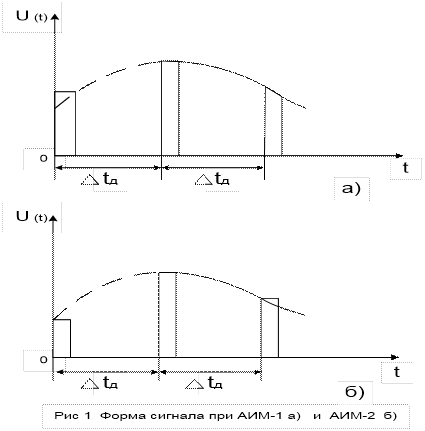
Дискретизация сигналов заключается в замене непрерывного сообщения uк(t) последовательностью его отсчётов, то есть последовательностью импульсов, модулированных по амплитуде (смотри рисунок 5.1, а). Частота дискретизации Fд выбирается из условия (4.4.1). Полученный аналоговый АИМ сигнал uАИМ(iTд), где i = 1, 2, 3 …, приведённый на рисунке 5.1, а, затем подвергается операции квантования, которая состоит в замене отсчётов мгновенных значений сигнала uАИМ (iTд) дискретными значениями u0, u1, u2 … u7 разрешённых уровней uкв (iTд). В процессе квантования мгновенные значения АИМ сигнала уровней uАИМ(iTд) заменяются ближайшими разрешёнными уровнями сигнала uкв(iTд) (смотри рисунок 5.1, а).
Рисунок 5.1. Принцип ИКМ: а – дискретизация; б – ошибка квантования; в – цифровой сигнал с ИКМ
Такое преобразование первичных сигналов можно называть квантованной амплитудно-импульсной модуляцией (КАИМ). Особенностью такого сигнала является то, что все его уровни можно пронумеровать и тем самым свести передачу КАИМ-сигнала к передаче последовательностей номеров уровней, которые этот сигнал принимает в моменты i∙tд.
Расстояние между ближайшими разрешёнными уровнями квантования (u0 … u7 на рисунке 5.1, а) ∆ называется шагом квантования. Шкала квантования называется равномерной, если все шаги квантования равны между собой ∆j = ∆0 [5].
Если в момент взятия i-го отсчёта мгновенное значение непрерывного сообщения uк(ti) удовлетворяет условию
uj – ∆j/2 ≤ uАИМ(iTд) ≤ uj + ∆j/2, (5.1)
то квантованному импульсу uкв(iTд) присваивается амплитуда разрешённого uj уровня квантования (смотри рисунок 5.1, а). При этом возникает ошибка квантования δкв, представляющая разность между передаваемой квантованной величиной uкв(iTд) и истинным значением непрерывного сигнала в данный момент времени uАИМ(iTд) (смотри рисунок 5.1, б):
δкв(iTд) = uкв(iTд) – uАИМ(iTд). (5.2)
Как следует из рисунков 5.1, б и (5.1), ошибка квантования лежит в пределах
–∆0/2 ≤ δкв ≤ ∆0/2. (5.3)
Амплитудная характеристика квантующего устройства при равномерной шкале квантования приведена на рисунке 5.2, а. Она имеет ступенчатую форму, и при изменении непрерывного сообщения uк(t) и соответствующего ему АИМ сигнала uАИМ(iTд) в пределах одной ступени выходной сигнал остаётся постоянным, а при достижении границы этой ступени изменяется скачком на величину шага квантования. При этом ошибка квантования зависит от uк(t) и имеет вид, изображённый на рисунке 5.2, б.
Рисунок 5.2. Амплитудная характеристика квантователя (а) и зависимость ошибки квантования от амплитуды импульсов (б)
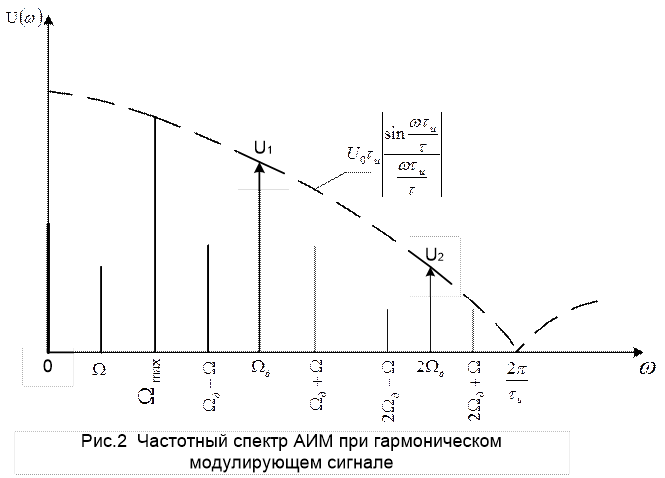
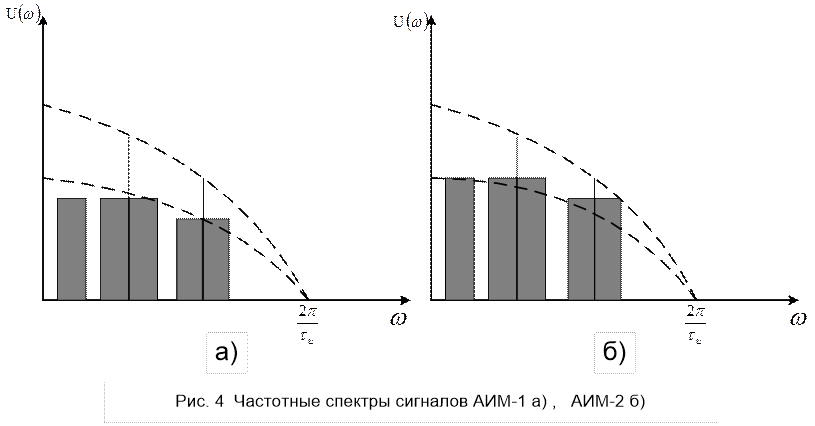
Как следует из рисунка 5.2, б, из-за нелинейности амплитудной характеристики квантователя ошибка квантования δкв представляет собой функцию с большим числом резких скачков, частота следования которых существенно выше частоты исходного сообщения uк(t), то есть при квантовании происходит расширение спектра сигнала. При этом соседние боковые полосы будут накладываться друг на друга и в полосу пропускания ФНЧ на выходе канала попадут составляющие спектра искажений от квантования, распределение которых в полосе ФНЧ считается равномерным. Поскольку практически все дискретные значения непрерывного сообщения находятся в пределах зоны квантования от –uогр до +uогр, то при равномерной шкале квантования ∆j = ∆0 и тогда:
Ркв = (1/12) ∆20. (5.4)
Из выражения (5.4) видно, что при равномерной шкале квантования мощность шума квантования не зависит от уровня квантуемого сигнала и определяется только шагом квантования ∆0.
Рассмотрим теперь кодирование и декодирование сигналов. Следующий шаг в преобразовании сигнала состоит в переводе квантованного АИМ-сигнала в цифровой. Эта операция называется кодированием АИМ-сигнала. Кодом называется закон, устанавливающий соответствие между квантованной амплитудой и структурой кодовой группы [8].
Различают равномерный и неравномерный коды. Если все кодовые группы состоят из равного числа символов, то код называется равномерным. Если же кодовые группы состоят из различного числа символов, то код называется неравномерным. В системах передачи с импульсно-кодовой модуляцией, как правило, используется равномерный двоичный код.
Для определения структуры двоичной кодовой комбинации на выходе кодера в простейшем случае необходимо в двоичном коде записать амплитуду АИМ отсчётов, выраженную в шагах квантования
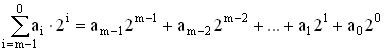
где ai = {0,1} – состояние соответствующего разряда комбинации; 2i – вес соответствующего разряда в шагах квантования.
Если в десятичной системе «вес» каждой позиции числа равен числу десять в некоторой степени, то в двоичной системе вместо числа десять используют число два. «Веса» первых тринадцати позиций двоичного числа имеют следующие значения:
Таблица – 5.1
|
212 |
211 |
210 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
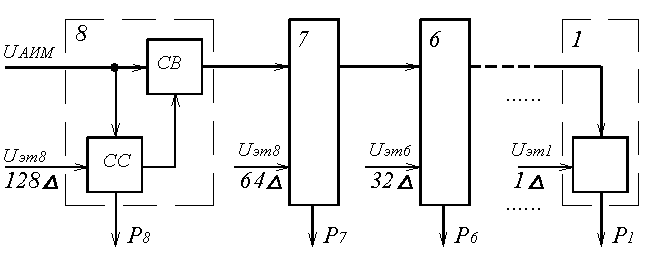
По принципу действия кодеры делятся на кодеры счётного типа, матричные, взвешивающего типа и другие. Наиболее часто используются кодеры взвешивающего типа, простейшим из которых является кодер поразрядного взвешивания (рисунок 5.3), реализующий функцию (5.5) с формирования натурального двоичного кода [5]. Принцип работы такого кодера заключается в уравновешивании кодируемых АИМ отсчётов суммой эталонных напряжений. Схема линейного кодера поразрядного взвешивания содержит восемь ячеек (при m = 8), обеспечивающих формирование значения коэффициента аi соответствующего разряда (5.5). В состав каждой ячейки (за исключением последней, соответствующей младшему по весу разряду) входит схема сравнения СС и схема вычитания СВ.
Схема сравнения обеспечивает сравнение амплитуды поступающего АИМ сигнала с эталонными сигналами, амплитуды которых равны весам соответствующих разрядов
Uэт8 = 27∆ = 128∆; Uэт7 = 26∆ = 64∆; … Uэт1 = 20∆ = 1∆.
Если на входе ССi амплитуда поступающего АИМ сигнала равна или превышает Uэтi, то на выходе схемы сравнения формируется «1», а в СВi из входного сигнала вычитается Uэтi, после чего он поступает на вход следующей ячейки. Если же амплитуда АИМ сигнала на входе ССi меньше Uэтi, то на выходе ССi формируется «0» и АИМ сигнал проходит через СВi без изменений. После окончания процесса кодирования текущего отсчёта на выходе кодера получается восьмиразрядный параллельный код, кодер устанавливается в исходное состояние и начинается кодирование следующего отсчёта.
Рисунок 5.3. Линейный кодер поразрядного действия
Если, например, на вход кодера поступил АИМ отсчёт с амплитудой UАИМ = 185∆, то СС8 формирует Р8 = 1 и на вход седьмой ячейки поступил сигнал с амплитудой UАИМ = 185∆ – 128∆ = 57∆. На выходе СС7 сформируется Р7 = 0 и на вход шестой ячейки кодера поступит сигнал с той же амплитудой UАИМ = 57∆. На выходе СС6 сформируется Р6 = 1 и на вход следующей ячейки поступит сигнал с амплитудой UАИМ = 57∆ – 32∆ = 25∆ и так далее. В результате будет сформирована кодовая комбинация 10111001.
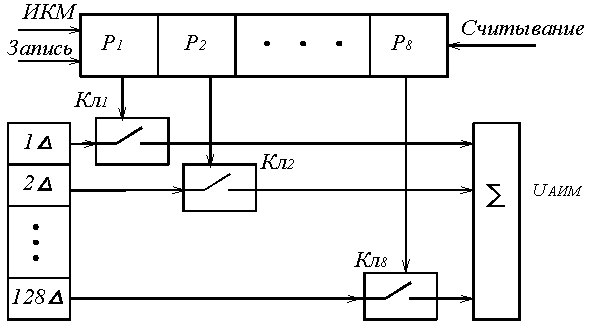
В процессе декодирования сигнала m – разрядные кодовые комбинации преобразуются в АИМ отсчёты соответствующей амплитуды [4]. Сигнал на выходе декодера получается в результате суммирования эталонных сигналов Uэтi тех разрядов кодовой комбинации, значения которых равно 1 (рисунок 5.4). Так, если на вход декодера поступила кодовая комбинация 10111001, то амплитуда АИМ отсчёта на его выходе будет равна UАИМ = 128∆ + 32∆ + 16∆ + 8∆ + 1∆ = 185∆.
В линейном декодере (рисунок 5.4) под воздействием управляющих сигналов, поступающих от генераторного оборудования, в регистр сдвига записывается очередная восьмиразрядная кодовая комбинация. В момент прихода импульса считывания замыкаются только те ключи Кл1 … Кл8, которые соответствуют разрядам, имеющим значения «1». В результате в сумматоре объединяются соответствующие эталонные напряжения и на его выходе получается соответствующая амплитуда АИМ отсчёта.
Рисунок 5.4. Линейный декодер взвешивающего типа
Рассмотренная схема кодера (рисунок 5.3) поразрядного взвешивания содержит большое число схем сравнения, которые являются относительно сложными устройствами. На практике чаще используется кодер взвешивающего типа с одной схемой сравнения и цепью обратной связи, содержащей декодер. Как следует из выражения (5.4), мощность шума квантования при линейном кодировании будет равной при различных амплитудах квантованных сигналов. Для синусоидальных сигналов отношение сигнал/шум квантования, рассчитывается по формуле:
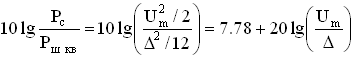
где Um – амплитуда квантуемого сигнала.
Из формулы видно, что для слабых входных сигналов это отношение гораздо хуже, чем для сигналов большой амплитуды. Для устранения этого недостатка было предложено использовать неравномерное квантование, то есть изменять шаг квантования пропорционально изменению амплитуды входного сигнала.
Для кодирования с неравномерной шкалой квантования могут быть использованы:
- прямое нелинейное кодирование, при котором кодер сочетает в себе функции аналого-цифрового преобразования (АЦП) и компрессора;
- аналоговое компандирование, при котором компрессирование сигнала осуществляется перед линейным кодером и экспандирование сигнала после линейного декодера;
- преобразование на основе линейного кодирования, при котором кодирование сигнала осуществляется в линейном кодере с большим числом разрядов с последующим цифровым компандированием [5].
Переменную величину шага квантования можно получить с помощью устройства с нелинейной амплитудной характеристикой (рисунок 5.5) (которая называется компрессором, поскольку сжимает динамический диапазон входного сигнала) и равномерного квантователя (смотри рисунок 5.2). На приёмной стороне осуществляется расширение динамического диапазона экспандером, имеющим характеристику, противоположную компрессору, что обеспечивает линейность системы передачи. Совокупность операций сжатия динамического диапазона компрессором и расширение его экспандером называется компадированием сигнала.
В настоящее время в системах ВРК с ИКМ применяется характеристика компадирования типа А (рисунок 5.5).
Рисунок 5.5. Характеристика компрессирования типа А
На этом рисунке сегментированная характеристика компрессии типа А для положительных сигналов (для отрицательных сигналов характеристика имеет аналогичный вид). Общее число сегментов характеристики Nс = 16, однако четыре центральных сегмента (по два в положительной и отрицательной областях) имеют одинаковый шаг квантования и фактически образуют один сегмент, вследствие чего число сегментов равно Nс = 13. Поэтому такая характеристика получила название типа А = 87.16/13. В центральном сегменте (Nс =1 или 2) значение ∆0 минимально (то есть равно ∆0) и соответствует равномерной двенадцатиразрядной шкале (m = 12), а в каждом последующем сегменте к краям характеристики шаг квантования увеличивается вдвое.
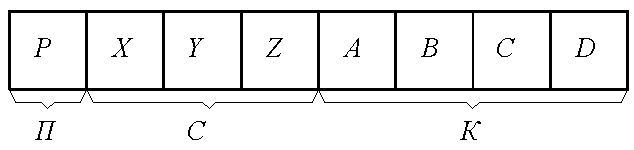
Представление ИКМ сигнала восьмиразрядными кодовыми комбинациями использует формат «знак – абсолютное значение», где один разряд отображает полярность АИМ сигнала П, а остальные – определяют его абсолютное значение. Семь разрядов, отображающих абсолютное значение, подразделяются на определитель номера сегмента С из трёх разрядов и определитель шага квантования К из четырёх разрядов (рисунок 5.6).
Рисунок 5.6. Формат восьмиразрядной ИКМ комбинации
Для реализации такого кодера необходимо задать величины эталонных напряжений для нижней границы каждого сегмента и при кодировании внутри сегмента (таблица 5.2).
Схемы и принцип действия нелинейных кодеков взвешивающего типа в основном те же, что и у линейных кодеков. Отличие заключается в последовательности включения эталонных напряжений в процессе кодирования исходного сигнала [5].
Таблица 5.2. Эталонные напряжения для нелинейного кодека
|
Номер сегмента Nс |
Эталонное напряжение нижней границы сегмента |
Эталонные напряжения при кодировании в пределах сегмента |
|||
|
8∆i(A) |
4∆i(B) |
2∆iI(С) |
∆i(D) |
||
|
0 |
0 |
8∆0 |
4∆0 |
2∆0 |
1∆0 |
|
1 |
16∆0 |
8∆0 |
4∆0 |
2∆0 |
1∆0 |
|
2 |
32∆0 |
16∆0 |
8∆0 |
4∆0 |
2∆0 |
|
3 |
64∆0 |
32∆0 |
16∆0 |
8∆0 |
4∆0 |
|
4 |
128∆0 |
64∆0 |
32∆0 |
16∆0 |
8∆0 |
|
5 |
256∆0 |
128∆0 |
64∆0 |
32∆0 |
16∆0 |
|
6 |
512∆0 |
256∆0 |
128∆0 |
64∆0 |
32∆0 |
|
7 |
1024∆0 |
512∆0 |
256∆0 |
128∆0 |
64∆0 |
Таким образом, максимальный шаг квантования (в седьмом сегменте) в 64 раза превышает минимальный шаг квантования, а отношение сигнал/шум квантования (для максимального значения синусоидального сигнала) может быть определено по выражению (5.6) и составит: для второго сегмента
Рс – Рш кв = 7.78 + 20lg(А/∆) = 7.78 + 20 lg(32∆0/∆0) = 37.88 дБ;
Для седьмого сегмента
Рс – Рш кв = 7.78 + 20 lg(2048∆0/64∆0) = 37.88 дБ.
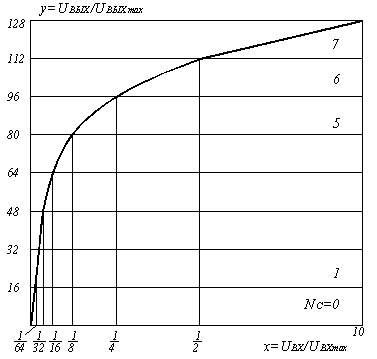
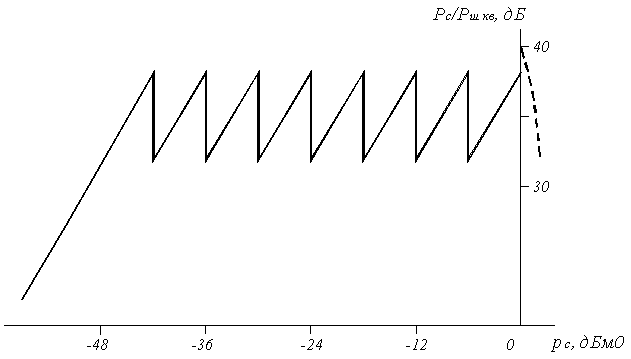
Зависимость отношения сигнал/шум квантования от уровня входного сигнала при компадировании по закону А = 87.6/13 приведена на рисунке 5.7. Для сигналов в пределах нулевого и первого сегментов осуществляется равномерное квантование с шагом ∆0, поэтому Рс – Рш кв увеличивается с ростом рс. При переходе ко второму сегменту шаг квантования увеличивается в два раза, вследствие чего Рс – Рш кв резко уменьшается на 6 дБ, а затем в пределах данного сегмента возрастает с ростом рс, поскольку внутри сегмента осуществляется равномерное квантование. После попадания сигнала в зону ограничения отношение сигнал/шум резко уменьшается за счёт перегрузки кодера.
Рисунок 5.7. Зависимость Рс/Рш кв = f(рс)
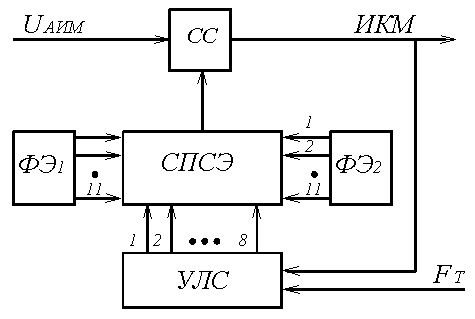
На рисунке 5.8 представлена упрощённая схема нелинейного кодера взвешивающего типа, реализующего прямое кодирование АИМ сигнала.
Рисунок 5.8. Нелинейный кодер взвешивающего типа
Кодирование осуществляется за восемь тактовых интервалов, в каждом из которых формируется один из символов кодовой комбинации (рисунок 5.6). В первом такте определяется знак поступившего на вход кодера отсчёта. Если отсчёт положительный, то в знаковом разряде формируется «1» и к схеме переключения и суммирования эталонов СПСЭ подключается формирователь положительных эталонных напряжений ФЭ1, в противном случае формируется «0» и к схеме подключается ФЭ2. Затем происходит формирование кода номера сегмента методом деления их числа пополам (рисунок 5.9).
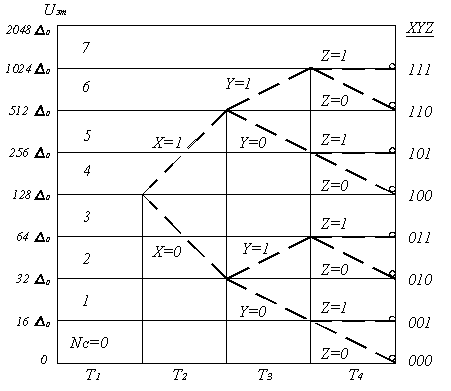
Рисунок 5.9. Алгоритм формирования кода номера сегмента
Во втором такте управляющая логическая схема УЛС и СПСЭ обеспечивают подачу на вход схемы сравнения эталонного сигнала Uэт = 128 ∆0, соответствующего нижней границе четвёртого (среднего) сегмента. Если амплитуда отсчёта UАИМ ≥ Uэт = 128 ∆0, то принимается решение, что амплитуда отсчёта попадёт в один из четырёх вышележащих сегментов и формируется очередной символ X = 1, который по цепи обратной связи поступает на вход УЛС. В противном случае принимается решение, что амплитуда отсчёта попадает в один из нижележащих сегментов и формируется X = 0.
В третьем такте в зависимости от значения предыдущего символа X уточняется номер сегмента, в который попадает амплитуда кодируемого отсчёта. Если X = 1, то УЛС и СПСЭ подают на вход СС эталонное напряжение Uэт = 512 ∆0, соответствующего нижней границе шестого сегмента. При этом, если UАИМ ≥ Uэт = 512 ∆0 то принимается решение, что отсчёт попадает в один из двух вышележащих сегментов и формируется очередной символ Y = 1. В противном случае, если UАИМ ≤ Uэт = 512 ∆0, принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.
Если же X = 0, то УЛС с помощью СПСЭ обеспечивает подачу на вход СС эталонного напряжения Uэт = 32 ∆0, соответствующего нижней границе второго сегмента. Если UАИМ ≥ Uэт = 32 ∆0, то принимается решение, что отсчёт попадает во второй и третий сегменты и формируется Y = 1. Если UАИМ ≤ Uэт = 32 ∆0, то принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.
В четвёртом такте аналогичным образом формируется символ Z и окончательно формируется код номера сегмента. В результате, после четырёх тактов кодирования, сформируется четыре символа восьмиразрядной кодовой комбинации PXYZ (рисунок 5.6) и к СС подключается одно из восьми эталонных напряжений, соответствующих нижней границе сегмента, в котором находится кодируемый отсчёт.
В оставшихся четырёх тактах последовательно формируются символы ABCD кодовой комбинации, значения которых зависят от номера шага квантования внутри сегмента, соответствующего амплитуде кодируемого отсчёта. Поскольку внутри любого сегмента осуществляется равномерное квантование, то процесс кодирования реализуется, как и в линейных кодерах взвешивающего типа, путём последовательного включения эталонных напряжений соответствующих данному сегменту (таблица 5.2).
Практикум на применение нелинейного кодера при компадировании по закону А = 87.6/13:
Например, если на вход кодера поступил положительный отсчёт с амплитудой UАИМ = 889 ∆0, то после первых четырёх тактов сформируются символы PXYZ = 1110 и к СС подключится эталонное напряжение Uэт = 512 ∆0, соответствующее нижней границе шестого сегмента, поскольку кодируемый сигнал находится в этом сегменте. В пятом такте к этому эталонному сигналу добавляется максимальное эталонное напряжение Uэт = 256 ∆0, соответствующее символу А в определителе шага квантования К (рисунок 5.6) шестого сегмента (таблица 5.2). Так как UАИМ > Uэт = (512 +256) ∆0, то формируется символ А = 1 и это эталонное напряжение остаётся включенным. В шестом такте подключается эталонное напряжение соответствующее символу В в определителе шага квантования Uэт = 128 ∆0 и так как UАИМ > Uэт = (512 +256 + 128) ∆0, то на выходе СС формируется символ В = 1 и это эталонное напряжение остаётся включенным. В седьмом такте подключается эталонное напряжение соответствующее символу С в определителе шага квантования Uэт = 64 ∆0 и так как UАИМ < Uэт = (512 +256 + 128 + 64) ∆0, то на выходе СС формируется символ С = 0. В восьмом такте вместо Uэт = 64 ∆0 подключается эталонное напряжение соответствующее символу D в определителе шага квантования Uэт = 32 ∆0 и так как UАИМ < Uэт = (512 +256 + 128 + 32) ∆0, то на выходе СС формируется символ D = 0 и это эталонное напряжение отключается и на этом процесс кодирования очередного отсчёта заканчивается. При этом на выходе кодера сформирована кодовая комбинация PXYZABCD = 11101100, соответствующая амплитуде уравновешивающего АИМ сигнала на входе СС UАИМ = 896 ∆0. Разница между входным и уравновешивающим АИМ сигналами на входах СС представляет ошибку квантования δкв = UАИМ – UАИМ = 7∆0.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Если
кодовая комбинация содержит r
разрядов, то число дискретных уровней
выходного сигнала квантователя равно
.
Для
взаимно однозначного соответствия весь
диапазон изменения входного сигнала
X
= x
max
– x
min
должен быть разбит на такое же количество
уровней.
Величина
интервала разбиения – шаг
квантования
– представляет собой значение аналоговой
величины, на которую отличаются уровни
входного сигнала, представленные двумя
соседними кодовыми комбинациями.
При
наиболее распространенном равномерном
квантовании шаг квантования равен
(1.12)
Характеристикой
квантования
называется зависимость квантованного
значения
от значения непрерывной величины x.
Типичная
характеристика
квантователя
с постоянном шагом квантования
приведена на рисунке 1.16.

Рисунок 1.16 –
Характеристика квантования при постоянном
шаге квантования
На
рисунке 1.17 приведена временная диаграмма
работы квантователя, где точками отмечены
квантованные значения, и временная
диаграмма ошибки квантования
.
Временная последовательность ошибок
квантования случайного сигнала
представляет собой случайный процесс
с равномерным законом распределения.
Этот случайный процесс называют шумом
квантования.

Рисунок
1.17 – Временные зависимости сигналов
на входе (x)
и выходе (
)
квантователя
и
ошибки квантования
Из
рисувнка видно, что абсолютное значение
ошибки квантования не превышает Δ/2.
Закон
распределения этого случайного процесса
приведен на рисунке 1.18.

Рисунок 1.18 –
Плотность вероятности шума квантования
Определим дисперсию шума квантования

После подстановки
(2.1) в последнее соотношение получим
(1.13)
Из
(1.13) следует, что дисперсия шума квантования
зависит от характеристик квантователя
и не зависит от уровня сигнала.
Определим отношение сигнал/шум на выходе квантователя
,
где
Pc—
мощность сигнала,
–
мощность шума,
—
среднеквадратическое значение сигнала.
Это отношение в
децибелах равно
(1.14)
Из последнего соотношения
видно, что
-
каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ. -
с
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
1.6.
Квантователи с переменным шагом
квантования
(нелинейные
квантователи)
Недостаток
линейного квантователя, связанный с
уменьшением отношения сигнал/шум
квантования при уменьшении уровня
сигнала, можно устранить, если уменьшать
шаг квантования по мере уменьшения
уровня сигнала.
Характеристика
квантования с переменным шагом квантования
приведена на рисунке 1.19.
Такую
характеристику можно получить, если
последовательно включить нелинейный
преобразователь и линейный квантователь
(рисунок 1.19)
Чтобы
устранить нелинейные искажения,
обусловленные введением нелинейного
преобразователя, после квантователя
используют второй нелинейный
преобразователь квантованного сигнала
с характеристикой, обратной характеристике
первого. С помощью первого осуществляют
компрессию сигнала, а с помощью второго
– его экспандирование. В целом описанная
операция называется компандированием.
Результирующая сквозная характеристика
системы «компрессор-экспандер» остается
линейной.
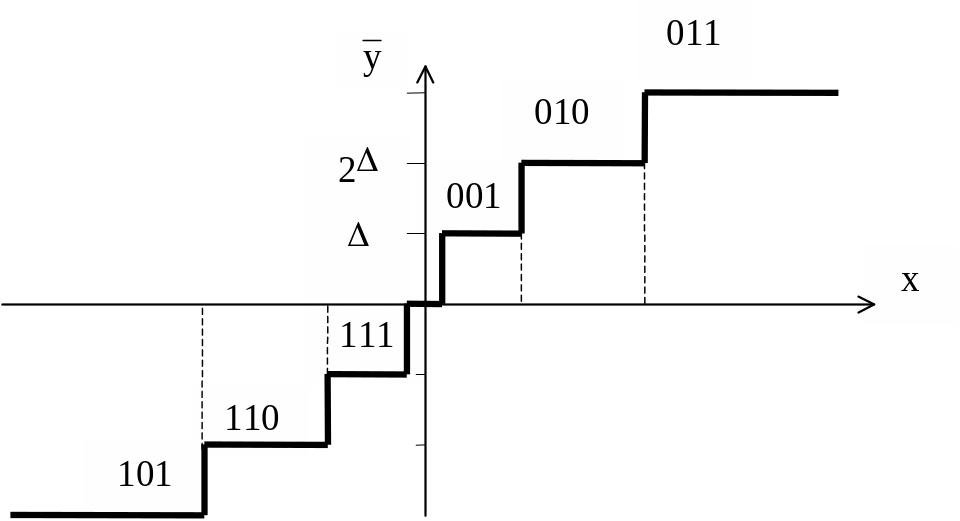
Рисунок
1.19 – Характеристика квантования при
переменном шаге квантования
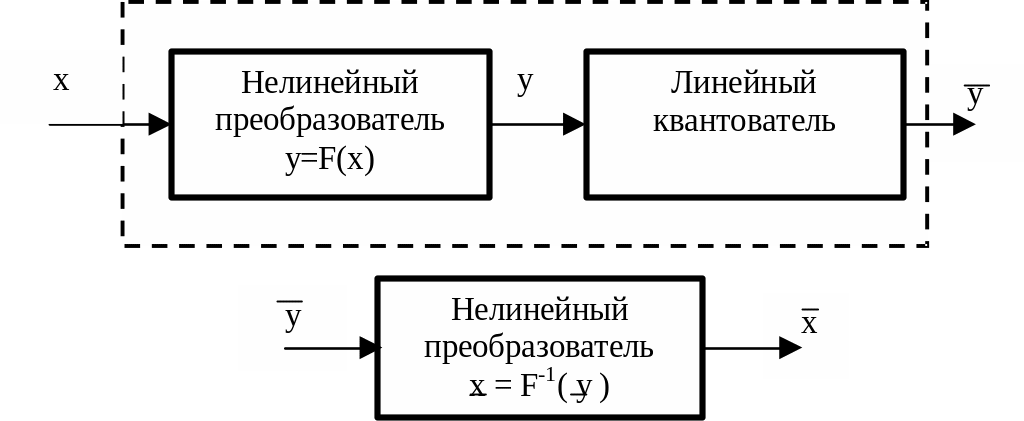
Рисунок
1.20 –Система «компрессор-экспандер»
В настоящее время
используются два закона компандирования:
μ-закон
(1.15) и А – закон (1.16):
(1.15)
где
=255,
,
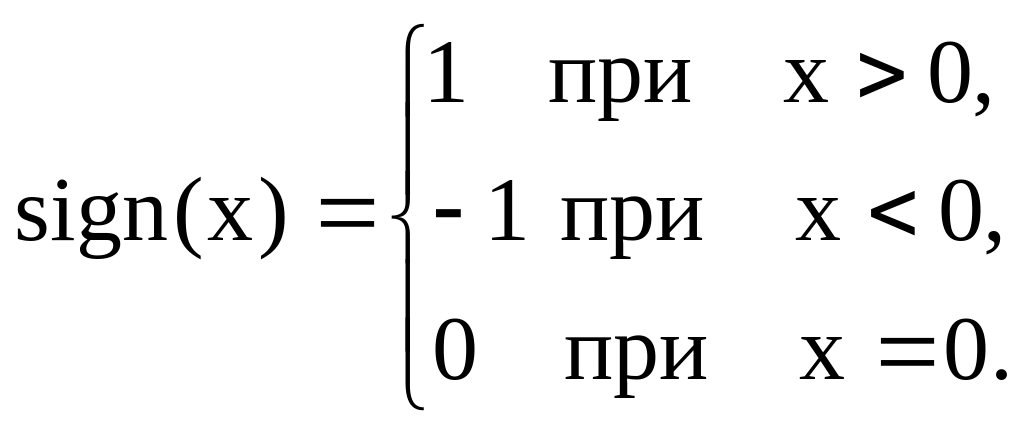
(1.16)
где
A
= 87.6.
Заключение
При дискретизации
аналогового сигнала возникают два
эффекта, касающиеся спектра сигнала:
-
Эффект
размножения спектра аналогового
сигнала, -
Эффект
наложения сгустков спектра дискретного
сигнала друг на друга.
Эффект
наложения спектров приводит к искажению
дискретного сигнала и невозможности
точного восстановления аналогового
сигнала из дискретного.
Спектр дискретного
сигнала представляет собой периодическую
функцию частоты, период которой равен
частоте дискретизации.
Если дискретизации
подвергается периодический аналоговый
сигнал с линейчатым спектром, то
размножение спектра осуществляется по
закону:
при
где
F
– частота спектральной составляющей
аналогового сигнала.
Амплитуды
спектральных составляющих дискретного
сигнала пропорциональны соответствующим
составляющим спектра аналогового
сигнала.
Размножение
спектра апериодического аналогового
сигнала осуществляется по этому же
закону, если рассматривать в качестве
F
характерные частоты непрерывного
спектра аналогового сигнала.
Эффект
наложения спектров при дискретизации
отсутствует, если выполняется условие
,
где
Fmax
– максимальная частота спектра
аналогового сигнала.
Если
дискретизации подвергается узкополосный
модулированный сигнал, а результатом
последующей цифровой обработки должно
быть выделение модулирующего сигнала,
то частота дискретизации может быть
выбрана существенно меньше, чем 2Fmax.
В этом случае
необходимо выполнить условия:
,
где
—
ширина спектра аналогового сигнала,
,
где
,
а f0
– частота несущей аналогового сигнала.
При
выполнении последнего условия частота
несущей, приведенная в интервал частот
от нуля до половины частоты дискретизации
(интервал Котельникова), равна четверти
частоты дискретизации.
Необходимость
квантования дискретного сигнала связана
с тем, что в вычислительных устройствах
значение сигнала должно быть представлено
числом конечной разрядности.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Разность
между квантованным значением и значением
отсчета дискретного сигнала называется
ошибкой квантования. Временная
последовательность ошибок квантования
случайного сигнала представляет собой
случайный процесс с равномерным законом
распределения. Этот случайный процесс
называют шумом
квантования.
В
квантователе с постоянным шагом
квантования (линейном квантователе)
отношение сигнал/шум квантования зависит
от количества разрядов квантователя,
уровня сигнала и диапазона квантователя.
Каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ.
С
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
Последнее
обстоятельство является недостатком
линейного квантователя, который
устраняется в квантователе с переменным
шагом квантования (нелинейном квантователе)
за счет уменьшения шага квантования по
мере уменьшения абсолютного значения
уровня входного сигнала квантователя.
Контрольные
вопросы и задачи по теме №1:
1.
Что такое дискретизация аналогового
сигнала? Начертите временные диаграммы
синусоидального сигнала на входе и
выходе дискретизатора в случае, когда
частота синусоидального колебания
меньше половины частоты дискретизации.
2. Начертите
спектральные диаграммы синусоидального
сигнала на входе и выходе дискретизатора
в случае, когда частота синусоидального
колебания меньше половины частоты
дискретизации.
3.В
чем сущность эффекта наложения спектров?
Каким образом можно уменьшить ошибку
наложения?
4.Начертите
амплитудный спектр дискретной синусоиды,
если частота аналогового синусоидального
колебания на входе дискретизатора выше
частоты дискретизации.
5.
Из каких условий выбирается частота
дискретизации модулированного колебания,
если результатом последующей цифровой
обработки должно быть выделение
модулирующего колебания?
6.
Дискретизация синусоидального колебания
,
где f0=20МГц,
осуществляется с частотой FД
= 16 МГц. Чему равна частота дискретной
синусоиды?
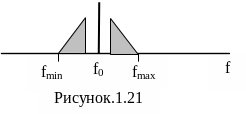
7.
На входе аналогового ФНЧ действует
последовательность прямоугольных
импульсов. АЧХ фильтра показана на
рисунке 1.21. Выходной сигнал фильтра
подается на дискретизатор. Частота
дискретизации равна 20 кГц. Возникнет
ли эффект наложения спектров при
дискретизации?

8.
На входе дискретизатора действует
сигнал
,
где
F1=1
МГц, F2
= 2 МГц.
Частота дискретизации FД
= 8 МГц. Чему равен максимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
9.
На входе дискретизатора действует
сигнал
,
где F=1
МГц, f0
= 15 МГц.
Частота дискретизации FД
= 12 МГц. Чему равен минимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
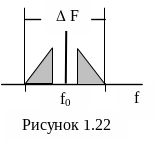
10.На
рисунке 1.22 приведен спектр аналогового
сигнала. Начертите в относительном
масштабе спектр сигнала после дискретизации
в пределах интервала Котельникова (от
0 до половины частоты дискретизации),
если f0=28МГц,
fmin=25МГц,
fmax=31МГц,
а частота дискретизации равна FД=
16 МГц.
11.
На входе демодулятора действует
модулированный аналоговый сигнал,
спектр которого симметричен относительно
частоты несущей f0
= 445кГц (рисунок 1.22). Ширина спектра
.
При каком из двух значений частоты
дискретизации отсутствует эффект
наложения спектров: FД=20кГц,
FД=21кГц?
12. Поясните
сущность операции квантования дискретных
сигналов. Что такое шаг квантования?
Как зависит шаг квантования при
равномерном (линейном) квантовании от
количества разрядов и диапазона
квантователя?
13.
Дайте определение характеристике
квантования. Начертите характеристику
линейного квантователя.
14. Поясните механизм
возникновения шума квантования. Начертите
график вероятностного распределения
шума квантования. Как связана дисперсия
шума квантования с шагом квантования
и количеством разрядов квантователя
при равномерном квантовании?
15.
Как зависит отношение сигнал/шум на
выходе равномерного квантователя от
количества разрядов, диапазона
квантователя и среднеквадратичного
уровня входного сигнала?
16.
Начертите характеристику квантования
квантователя с неравномерным шагом
квантования (нелинейного квантователя).
17.Поясните сущность
алгоритма функционирования нелинейного
квантователя, состоящего из входного
нелинейного преобразователя и линейного
квантователя. Каким образом устраняются
нелинейные искажения выходного сигнала
при использовании нелинейного
квантователя?
18.Чем
отличается зависимость отношения
сигнал/шум на выходе нелинейного
квантователя от среднеквадратичного
уровня входного сигнала от аналогичной
зависимости для линейного квантователя?
19.
Отношение сигнал/шум на выходе линейного
квантователя равно 40 дБ. Каким станет
это отношение, если количество разрядов
увеличить на два при неизменном уровне
входного сигнала и неизменном диапазоне
квантователя?
Контрольная
карта ответов
Номер
ответа соответствует номеру контрольного
вопроса в предыдущем разделе.
6.
F
= f0
–FД
= 20-16 = 4 МГц
7.
FД
= 20 кГц, Fmax
= 8 кГц. Так как FД>
2 Fmax,
то эффект наложения не возникнет.
8.
Максимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 4 МГц
9.
Минимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 2 МГц.
10.

11.
Эффект наложения отсутствует при частоте
дискретизации FД
=20 кГц.
19.
Отношение сигнал/шум станет равным 52
дБ.
Список
литературы по теме № 1:
1.
В.Г.Иванова, А.И.Тяжев. Цифровая обработка
сигналов и сигнальные процессоры / Под
редакцией д.т.н., профессора Тяжева А.И.
— Самара, 2008г.
2.Куприянов
М.С., Матюшкин Б.Д. Цифровая обработка
сигналов: процессоры, алгоритмы, средства
проектирования. –2-е изд., перераб. и
доп.- СПб.: Политехника, 1999. –592с.
:
ил.
3.Л.Р.Рабинер,
Р.В.Шафер. Цифровая обработка речевых
сигналов. – М.: Радио и связь, 1981. – 495с.:
ил.
4.
А.И. Солонина, Д.А.
Улахович, С.М. Арбузов, Е.Б. Соловьёва.
Основы цифровой обработки сигналов.-
Изд. 2-е испр. и перераб. – СПб.: БХВ-Петербург,
2005.-768с.: ил.
5.А.Б.
Сергиенко. Цифровая обработка сигналов.
– СПб.: Питер, 2002.-2002.-608с.: ил.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда я был в Питере, и мы сидели в кабаке, у нас с товарищами 



Поскольку дельта икс у нас совершенно чёткая, или скорее равная отрезкам оцифровки, то производная значения снятого с АЦП будет нынешнее значение минус предыдущее, делённое на период квантования: df/dt=(f(t1) -f(t2))/(t1 -t2). Для опытов я выбрал функцию гармонического синуса sin(x). В дальнейшем проверил и на остальных функциях, но это самая красивая и в нашем случае самая актуальная.
Изначальный график для экспериментов
Для начала я составил таблицу, над которой начал издеваться. Первая строчка [ t= ] — это время от старта работы условного АЦП, который наращивается с шагом квантования (последняя строчка). Вторая — [ SIN(t) ]синус вычесленный от этого кванта времени, формула которого примитивна: =SIN(B1). Третья — [ dSIN(t)/dt ] это численное нахождение производной. Формула её проста: =(C2-B2)/C5 (первая ячейка). Предпоследняя строчка это [ COS(t) ], это нахождения косинуса от перменной t. Она нужна для того, чтобы сравнивать с истинным значением косинуса вычисленную производную (если помните, производная синуса — это косинус). Последняя строка — это квантование, т.е. проще говоря шаг изменения t. Внизу строиться график, который строит гибкую линию по точкам. Сейчас у нас выбран самый оптимальный шаг квантования 0,5 . Здесь всё ясно, дальше я двух разделах покажу сначала ошибки квантования, и следственные ошибки производных, затем ошибки дифференцирования при ошибочных входных данных. Если ваш мозг не вспух и вы готовы дальше пуститься в дебри математики и электроники,
Ошибки квантования
Как видно из самой первой картинки, производная практически полностью соответствует графику косинуса. Если мы ещё уменьшим «частоту дискретизации», или в нашем случае шаг до dt=0,1, то получим вообще практически совпадающие кривые, которые я проиллюстрирую ниже:
Полученный график с шагом 0,1
Как видно, при этом шаге квантования график производной (фиолетовая кривая), практически полностью совпадает с графиком косинуса (красная кривая). Маркерами показанны точки квантования. В этом случае всё ясно, но давайте увеличим шаг, от 0,5 до 1
Полученный график с шагом 1
Видно, что производная, да и все графики начинают «плыть».
Продолжим увеличение квантования до 2:
Полученный график с шагом 2
Всё начинает плыть и уходить, но ещё отдалённо напоминает синус. Однако уже видно, что численно рассчитанная производная СОВЕРШЕННО не соответствует своему значению. Да и вообще находится в противофазе. Напоследок возьмём квантование равное 5 (в 10 раз больше исходного).
Полученный график с шагом 10
Видно что в этом случае мы наблюдаем полную ересь. И в данном случае можно сказать, что высокие частоты и шумы, могут хорошо подпортить реальное значение производной. Теперь же посмотрим как влияет погрешность снятого сигнала, на численный рассчёт производной.
Численное вычисление производной, при неточности снятого сигнала (шумах, наводках, высших гармониках)
Добавим теперь в формулу вычисления синуса некоторую погрешность снятия сигнала, для этого прибавим к формуле вычисления синуса некоторое случайное число: =SIN(C1)+СЛЧИС()*0,1 . Данная формула внесёт 10% погрешность от амплитудного значения в вычисление сигнала, просто добавляя некоторое случайное число от нуля до 0,1. Я покажу несколько вариантов с разной погрешностью. Сначала покажем сигнал с 5% погрешностью:
Полученный график с погрешностью 5%
Как видно из графика, ни на синус, ни на производную такая погрешность не оказывает должного влияния. Возьмём тогда погрешность в 10%
Полученный график с погрешностью 10%
Вот, ярко видно, что на графике синуса погрешность сказалось мало. А вот на графике производной очень даже, в особенности хорошо раскорячило её концы. На последок покажу что будет если построить график производной с 20% погрешностью:
Полученный график с погрешностью 20%
График отдалённо напоминает косинус. Видно куча убеганий и прочего. Надо учитывать, что это ПСЕВДОслучайная велечина, в реальной жизни всё может быть гораздо хуже. Но всё же лучше смоделировать данные фишки, чтобы представлять себе что же может твориться на АЦП.
Вывод: Считать численно производную по снятым значениям с АЦП можно и нужно. Но необходимо оценивать уровень внешних помех, которые могут влиять на сигнал, и очень сильно его портить. Желательно использовать фильтрацию сигнала, выделяя полезный сигнал. Филтрация может быть как аналоговая, так цифровая. Мне даже показали прекрасную формульную замену аналоговой фильтрацией прекрасной програмкой на си. И разумеется мы должны себе ЧЁТКО представлять какой сигнал цифруем, и не цифровать сигнал на пределах возможностей АЦП. 5 точек на период, как показала практика — не самый плохой вариант!
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png
Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png
Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods.
First, a random signal is created that spans the range of the quantizer.
Next, the signal is quantized, respectively, with rounding methods ‘fix’, ‘floor’, ‘ceil’, ‘nearest’, and ‘convergent’, and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error will be computed with ERRPDF, the theoretical mean of the quantization error will be computed with ERRMEAN, and the theoretical variance of the quantization error will be computed with ERRVAR.
Uniformly Distributed Random Signal
First we create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizers that we will look at.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero.
Notice that with ‘fix’ rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Floor: Round Towards Minus Infinity.
Floor rounding is often called truncation when used with integers and fixed-point numbers that are represented in two’s complement. It is the most common rounding mode of DSP processors because it requires no hardware to implement. Floor does not produce quantized values that are as close to the true values as ROUND will, but it has the same variance, and small signals that vary in sign will be detected, whereas in ROUND they will be lost.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Ceil: Round Towards Plus Infinity.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Round: Round to Nearest. In a Tie, Round to Largest Magnitude.
Round is more accurate than floor, but all values smaller than eps(q) get rounded to zero and so are lost.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Convergent: Round to Nearest. In a Tie, Round to Even.
Convergent rounding eliminates the bias introduced by ordinary «round» caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Comparison of Nearest vs. Convergent
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error p.d.f. of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error p.d.f. of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Note that the error p.d.f. of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Plot Helper Function
The helper function that was used to generate the plots in this example is listed below.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods.
First, a random signal is created that spans the range of the quantizer.
Next, the signal is quantized, respectively, with rounding methods ‘fix’, ‘floor’, ‘ceil’, ‘nearest’, and ‘convergent’, and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error will be computed with ERRPDF, the theoretical mean of the quantization error will be computed with ERRMEAN, and the theoretical variance of the quantization error will be computed with ERRVAR.
Uniformly Distributed Random Signal
First we create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizers that we will look at.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero.
Notice that with ‘fix’ rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Floor: Round Towards Minus Infinity.
Floor rounding is often called truncation when used with integers and fixed-point numbers that are represented in two’s complement. It is the most common rounding mode of DSP processors because it requires no hardware to implement. Floor does not produce quantized values that are as close to the true values as ROUND will, but it has the same variance, and small signals that vary in sign will be detected, whereas in ROUND they will be lost.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Ceil: Round Towards Plus Infinity.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Round: Round to Nearest. In a Tie, Round to Largest Magnitude.
Round is more accurate than floor, but all values smaller than eps(q) get rounded to zero and so are lost.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Convergent: Round to Nearest. In a Tie, Round to Even.
Convergent rounding eliminates the bias introduced by ordinary «round» caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Comparison of Nearest vs. Convergent
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error p.d.f. of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error p.d.f. of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Note that the error p.d.f. of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Plot Helper Function
The helper function that was used to generate the plots in this example is listed below.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
Задание №1
Рассмотрите вопросы, связанные с принципом построения цифровых систем передачи ЦСП с ВРК ИКМ-ВД.
1. Составьте структурную схему, поясняющую принцип построения ЦСП с ИКМ-ВД для заданного числа телефонных каналов. Кратко укажите назначение всех узлов и этапы аналого-цифрового преобразования АЦП в тракте передачи и цифро-аналогового преобразования ЦАП в тракте приема.
2. Рассчитайте тактовую частоту fт, длительность канального интервала Тки, длительность цикла Ти, длительность сверхцикла Тсц.
3. Постройте диаграмму временного цикла, сверхцикла, канального интервала, разрядного интервала.
4. Заполните рисунок 1 по мере выполнения заданий 2, 3, 4, 5 данной домашней работы.
Исходные данные:
|
Число ТЛФ каналов |
Fg, кГц |
m |
Передача СУВ |
|
|
18 |
8 |
8 |
За один цикл передаются СУВ для двух ТЛФ каналов |
|
1. 3 этапа аналого-цифрового преобразования АЦП на передаче:
a. Дискретизация по времени;
b. Квантование по уровню;
c. Кодирование.
Назначение узлов схемы:
ФНЧ передачи – фильтр нижних частот – выделение ограниченного спектра частот из сигнала;
М – канальный амплитудно-импульсный модулятор – осуществляет дискретизацию передаваемых сигналов во времени;
ГОпр и ГОпер – генераторное оборудование – посылает канальные импульсы для управления модуляторами, на передаче и приеме СУВ для дискретизации сигналов управления и взаимодействия, обеспечивает правильный порядок следования циклов в сверхцикле и кодовых групп в цикле передачи и приема;
ЗГ – задающий генератор – формирует гармоничный высокостабильный сигнал с частотой равной или кратной fт;
ВТЧ – выделитель тактовой частоты – для синхронной и синфазной работы ГО;
Пер СУВ – передатчик сигналов управления и взаимодействия – дискретизация СУВ, передаваемых по телефонным каналам для управления приборами АТС,
Пер СС – передатчик синхросигнала – для передачи синхросигнала цикловой синхронизации;
Кодер – преобразование амплитуды АИМ сигнала в 8-ми разрядную кодовую комбинацию, квантование по уровню и кодирование;
УО – устройство объединения – объединение кодовых групп каналов выхода кодера, кодирование сигналов СУВ и кодовой группы синхросигнала в циклы и сверхциклы;
ПК пер – преобразователь кода передачи – преобразование однополярного ИКМ сигнала в биполярный сигнал, удобный для передачи по линейному тракту;
РЛ – линейный регенератор – для периодического восстановления ИКМ сигнала в процессе передачи по линии связи;
РС – станционный регенератор – восстановление ИКМ сигнала на приемной станции;
ПК пр – преобразователь кода – преобразует биполярный сигнал в однополярный;
Пр СС – приемник синхросигналов – правильное декодирование и распределение сигналов по своим телефонным каналам и каналам передачи СУВ;
УР – устройство разделения – разделяет кодовые группы ТЛФ каналов и СУВ;
Пр СУВ – приемник групповых сигналов управления и взаимодействия – распределяет СУВ по своим каналам;
Декодер – преобразует групповой ИКМ сигнал в групповой АИМ сигнал; для преобразования 8-ми разрядной кодовой комбинации в амплитуду КАИМ сигнала;
ВС – временной селектор – обеспечивает выделение отсчетов своего канал из группового АИМ сигнала;
ФНЧ приема – восстановление непрерывного исходного сигнала из последовательности его АИМ отсчетов.
Тактовая частота рассчитывается по формуле:
Fт=Fд?m?Nки, (кГц),где Fд =8 кГц – частота дискретизации ТЛФ сигнала; m=8 – разрядность кодовой комбинации; Nки – число канальных интервалов в цикле системы; складывается из числа ТЛФ каналов, одного канального интервала для системы синхронизации и одного КИ для передачи сигналов управления и взаимодействия между АТС СУВ.
FТ=8?(18+2) ?8?103=1280 (кГц).
Длительность тактового (разрядного) интервала рассчитывается по формуле:
Тт=, мкс
Тт==0,781 (мкс).
Длительность импульса рассчитывается по формуле:
?=, мкс
?==0,39 (мкс).
Длительность канального интервала рассчитывается по формуле:
Тки= Тт?m, мкс
Тки=0,781?8=6,248 (мкс).
Длительность цикла рассчитывается по формуле:
Тц=Тки?Nки, мкс
Тц=6,248 ?20=124,96 (мкс).
Длительность сверхцикла рассчитывается по формуле:
S=+1
S=+1=10.
Диаграмма временных цикла, сверхцикла, канального интервала и разрядного интервала:
4. Упрощенная структурная схема ЦСП с ИКМ-ВД: см. приложение №1.
Задание №2
1. Составьте схему построения генераторного оборудования ГОпер или ГОпр для заданного числа ТЛФ каналов. Укажите назначение элементов схемы.
2. Укажите отличие ГОпер от ГОпр; с помощью чего обеспечивается синхронная и синфазная работа ГОпер и ГОпр; назначение сигналов «Установка по циклу» и «Установка по сверхциклу».
3. Рассчитайте частоты импульсных последовательностей, управляющих работой АИМ или временных селекторов ВС, кодера или декодера, передатчика или приемника СУВ.
4. Рассчитанные значения Fт, Fк, Fр, Fц проставьте на упрощенной структурной схеме ЦСП с ИКМ-ВД.
Исходные данные:
|
ГО |
Число ТЛФ каналов |
Число канальных интервалов, Nки |
Число циклов в сверхцикле, S |
|
|
ГОпер |
18 |
20 |
10 |
|
1. Структурная схема ГО передачи:
Назначение элементов схемы:
ЗГ – задающий генератор – формирует гармоничный высокостабильный сигнал с частотой равной или кратной fт;
ФТП – формирователь тактовой последовательности – вырабатывает основную импульсную последовательность с частотой следования fт;
РР – распределитель разрядный – формирует m импульсных последовательностей. Число разрядных импульсов, формирующих РР, равно числу разрядов в кодовой комбинации;
РК – распределитель канальный – формирует управляющие канальные импульсные последовательности КИ0, КИ1, …, КИn, где n – число канальных интервалов в цикле;
РЦ – распределитель цикловой – формирует цикловые импульсные последовательности Ц0, Ц1, …, ЦS, где s – число циклов в сверхцикле.
В соответствии с рекомендациями МККТТ относительная нестабильность частоты ЗГ должна быть не хуже 10-5, поэтому в ЗГ используется кварцевая стабилизация частоты.
2. В отличие от ГОпер, в ГОпр используется выделитель тактовой частоты системы устройств тактовой синхронизации (для обеспечения синхронной и синфазной работы передающей и приемной станции).
Для подстройки генераторного оборудования по циклам и сверхциклам используются сигналы «Установка по циклу» и «Установка по сверхциклу». Это дает возможность подстраивать ГО одной станции в режим цикловой и сверхцикловой синхронизации с ГО другой станции.
Тактовая частота рассчитывается по формуле:
Fт=Fд?m?Nки, кГц
Fт=8?(18+2) ?8?103=1280 (кГц).
Частота следования разрядных импульсов рассчитывается по формуле:
Fр=, кГц, где m – число разрядов в кодовой комбинации
Fр==160 (кГц).
Частота следования канальных импульсных последовательностей (частота дискретизации) рассчитывается по формуле:
Fк=Fд=, кГц, где Nku – число канальных интервалов в цикле передачи
Fк=Fд==8 (кГц).
Частота следования цикловых импульсных последовательностей рассчитывается по формуле:
Fц=, Гц, где S – число циклов в сверхцикле
Fц==800 (Гц).
Задание №3.
1. Начертите структурную схему нелинейного кодера. Кратко поясните: 3 этапа кодирования, назначение всех узлов кодера.
2. выполните операцию нелинейного кодирования. Рассчитайте ошибку квантования.
3. На упрощенной структурной схеме ЦСП с ИКМ-ВД на выходе кодера приведите полученную в результате кодирования кодовую 8-разрядную комбинацию.
Для кодирования используется нелинейный кодер взвешивающего типа с характеристикой компрессии А – 87,6/13.
Значение амплитуды отсчета АИМ-сигнала в у. е. – «+130».
1. Назначение кодера – для преобразования амплитуды отсчета АИМ-сигнала в соответствующую 8-разрядную кодовую комбинацию.
3 этапа кодирования:
a) Кодирование полярности (результат записывается в первом разряде);
b) Кодирование номера сегмента, выбор основного эталонного тока (результат записывается во 2, 3, 4 разрядах;
c) Кодирование уровня квантования внутри выбранного сегмента, выбор дополнительного эталонного тока (результат записывается в 5, 6, 7, 8 разрядах).
Назначение элементов схемы:
Компаратор определяет знак разности между амплитудами токов кодируемого отсчета и эталона (Ic и Iэт);
Цифровой регистр служит для записи решений компаратора после каждого такта кодирования и формирования структуры кодовой группы;
Генератор эталонов (ГЭТ(+) и ГЭТ()) формирует полярность и величины эталонов, количество формируемых эталонов равно 11, их значения – 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 усл. ед.
ПК преобразует параллельный код в последовательный, считывая состояние выходов 1 … 8 ЦР;
ГОпер управляет работой узлов кодера;
БКЭ – блок выбора и коммутации эталонных токов – для подключения выбранных ГЭТ, а также для подключения выбранных эталонных токов по сигналам от ключей;
КЛ – компрессирующая логика – для коммутации поступающего от ЦР семиразрядного регистра (без первого символа полярности) в П-разрядный двоичный код для управления разрядами выбранного ГЭТ.
Структурная схема нелинейного кодера: см. приложение №2.
1-й этап – кодирование полярности – 130>0 > 1;
2-й этап – кодирование номера сегмента, выбор основного эталонного тока –
130>128 > 1130<512 > 0130<256 > 0 |
> 4 сегмент (ОЭ для 4 сегмента – 128) |
|
3-й этап – кодирование уровня квантования внутри выбранного сегмента, выбор дополнительного эталонного тока: ОЭ -128, ДЭ -64, 32, 16, 8
130<128+64 > 0
130<128+32 > 0
130<128+16 > 0
130<128+8 > 0
Шаг квантования равен последнему эталону – 8
Ошибка квантования: ?кв=130-128=2, не должна превышать 0,5?
|
Опред. полярности |
Выбор основного эталонного тока, Iосн.эт. |
Вкл. Iосн.эт. |
Дополнительные эталонные токи, Iдоп.эт. |
|||||||
|
Разряды кодирования |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
Iэт. |
1 |
128 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
|
|
Iаим ? Iэт. |
130>0 |
130128>0 |
130-512<0 |
130-256<0 |
130 – (128 +64) <0 |
130 – (128+32) <0 |
130 – (128+16) <0 |
130 – (128+8) <0 |
||
|
Состояние выхода компаратора |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
Запись решения в ЦР |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
Шаг квантования |
8 |
|||||||||
|
Ошибка квантования, |
2 |
|||||||||
|
1-й этап |
2-й этап |
3-й этап |
||||||||
При неравномерном квантовании шаг квантования изменяется в допустимых пределах амплитудных значений квантуемых сигналов, возрастая с увеличением уровня сигнала. Абсолютная ошибка квантования возрастает с увеличением уровня сигнала, но ее относительное значение, т.е. отношение сигнал-ошибка квантования, не изменяется. Использование неравномерного квантования позволяет выровнять отношение сигнал-ошибка квантования во всем диапазоне сигналов, а, следовательно, сократить число шагов квантования в 2 … 4 раза по сравнению с равномерным квантованием до Мкв.=128 … 256, что требует семи разрядов кодовой группы.
Вывод: преимущество кодера с неравномерной шкалой квантования заключается в передаче сигналов с необходимым качеством.
Задание №4
1. Начертите структурную схему нелинейного декодера. Кратко поясните три этапа декодирования, назначение всех узлов декодера.
2. Выполните операцию нелинейного декодирования.
3. Укажите назначение эталона коррекции.
Исходные данные: кодовая комбинация – 11000000.
1. Назначение декодера – для преобразования 8-разрядной кодовой комбинации в соответствующую амплитуду отсчета АИМ-сигнала.
3 этапа декодирования:
1-й этап – по символу записанному в 1-м разряде, выбирается ГЭТ. Если записана «1», то выбирается ГЭТ(+), если «0» ГЭТ().
2-й этап – по кодовой комбинации, записанной во 2, 3 и 4-м разрядах, выбирается эталонный ток Iосн.эт..
3-й этап – из четырех дополнительных эталонных токов данного Iосн.эт. выбираются те, в чьих разрядах записаны «1».
В конце добавляется эталон коррекции, равный половине шага квантования данного сегмента.
Структурная схема нелинейного декодера: см. приложение №3.
Назначение элементов схемы:
ЦР – служит для принятия кодовой группы ИКМ-сигнала и формирования на выходе в виде 8-разрядного параллельного двоичного кода.
ГОпр – управляет работой узлов декодера.
ГЭТ – формирует полярность и величины эталонов, количество формируемых эталонов равно 11, их значения – 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 у. е.
БКЭ – для подключения выбранного ГЭТ1 или ГЭТ2, а также для подключения выбранных эталонных токов по сигналу от ЭЛ.
ЭЛ – экспандирующая логика – для коммутации 7-разрядного кода (без первого символа полярности сигнала), поступившего от ЦР, в 12-разрядный двоичный код для управления разрядами выбранного ГЭТ.
2. Кодовая комбинация – 1100000.
1-й этап – выбираем ГЭТ:
«1» > ГЭТ(+);
2-й этап – выбираем основной эталонный ток:
100 > 4-й сегмент > ОЭ – 128, ДЭ – 64, 32, 16, 8;
3-й этап – из ДЭ выбираем те, в чьих разрядах стоит «1». Т.к. в ДЭ нет разрядов со значением «1», выбираем последний и определяем шаг квантования:
?=8, эталон коррекции равен 0,5?=4.
128+4=132 (у. е.) – полученный КАИМ-сигнал.
Эталон коррекции применяется для уменьшения искажения при декодировании.
Задание №5
1. Приведите три требования к линейным кодам. Укажите достоинства и недостатки заданного линейного кода.
2. Постройте заданную цифровую последовательность в кодах:
Однополярном со скважностью Q=2 (ВН);
Однополярном со скважностью Q=1 (МБВН);
Двухполярном ЧПИ;
Двухполярном КВП-3 (МЧПИ).
Исходные данные:
|
Цифровая последовательность |
Тип линейного кода |
|
|
1110000110000101000010101 |
МБВН (NRZ) |
|
1. Три требования к линейным кодам:
– Энергетический спектр сигнала должен ограничиваться сверху и снизу, быть достаточно узким, располагаться на сравнительно низких частотах и не содержать постоянной составляющей.
– В составе спектра должна быть составляющая fт.
– Сигнал должен быть представлен в коде, содержащем информационную избыточность.
Линейный код МБВН (NRZ) – однополярный, со скважностью Q=1, так называемый сигнал с импульсами, затянутыми на тактовый интервал.
«+»:
Спектр линейного сигнала расположен в НЧ области, поэтому малы МСИ-1 и переходные помехи;
Схема генератора проще, чем у ЧПИ.
«»:
В спектре есть постоянный ток и мощные НЧ составляющие, поэтому велики МСИ-1;
Возможен сбой УТС из-за большой серии нулей;
В коде нет избыточности, поэтому нельзя контролировать ошибки;
В спектре нет fр, поэтому схема УТС сложнее, чем у ВН.
Список использованной литературы
1. Скалин Ю.В., Финкевич А.Д., Бернштейн А.Г. цифровые системы передачи. М.: Радио и связь, 1987
2. Цифровые системы передачи. Контрольные задания, методические указания по их выполнению и задание на курсовой проект для студентов заочных отделений по специальности 2005 – «Многоканальные телекоммуникационные системы».
Страницы работы
Фрагмент текста работы
1 вопрос : Процесс амплитудно-импульсной модуляции .
Форма и спектр сигналов АИМ 1
и АИМ 2
При амплитудно-импульсной модуляции (АИМ) по закону
модулирующего сигнала изменяется амплитуда импульсов , а длительность и частота
следования остаются постоянными .
Различают амплитудно-импульсную модуляцию первого (АИМ-1) и
второго (АИМ- 2) рода .
При АИМ-1 амплитуда импульса изменяется в
пределах его длительности в соответствии с огиба- ющей непрерывного сигнала . При
АИМ-2 амплитуда импульса в пределах его длительности пос тоянна и
соответствует значению модулирующего сигнала в момент начала отсчета .
Частотный спектр АИМ-1 для однополярных прямоугольных
импульсов длительностью , модурованных синусоидальным сигналом с частотой
показан
на рисунке 2 .
Как видно, в отличие от немодулированной импульсной
последовательности ( рис 3 ) в спектре по- являются боковые частоты
дисретизации и её гармоник , а также спектр модулирующего сигнала .
Таким образом задача восстановления непрерывного сигнала из
последовательности его дискрет- ных отсчетов заключается в фильтрации спектра
модулирующего сигнала с помощью ФНЧ с частотой
среза .
При дискретизации сложного сигнала со сплошным спектром
частотные спектры сигналов АИМ1,
АИМ2 будут содержать все составляющие модулирующего сигнала
и боковые полосы частот около частоты дискретизации и её гармоник . При этом следует
обратить внимание на различие час- тотных спектров АИМ-1 и АИМ-2 .
Спектральный состав сигналов АИМ-2 по своей структуре не
отличается от структуры спектра сигналов АИМ-1 , однако при АИМ-2 изменение
спектральных составляющих модулирующего сигнала и боковых полос зависит от длительности
импульса , что в принципе приводит к
амплитудно-частотным искажениям демодулированного из АИМ-2
сигнала при (рис.4).
В реальных ЦСП и спектры совпадают
практически полностью, а амплитудно-частот –ные искажения при демодуляции
сигналов АИМ-2 незначительны .
2 вопрос : Квантование сигнала по уровню. Принцип
равномерного и неравномерного кван- тования сигнала. Шумы квантования . Способы
их уменьшения.
Квантование — замена бесконечного множества
значений напряжения сигнала конечным множеством дисретных (квантованных) значений .
Единица измерения — уровень квантования .
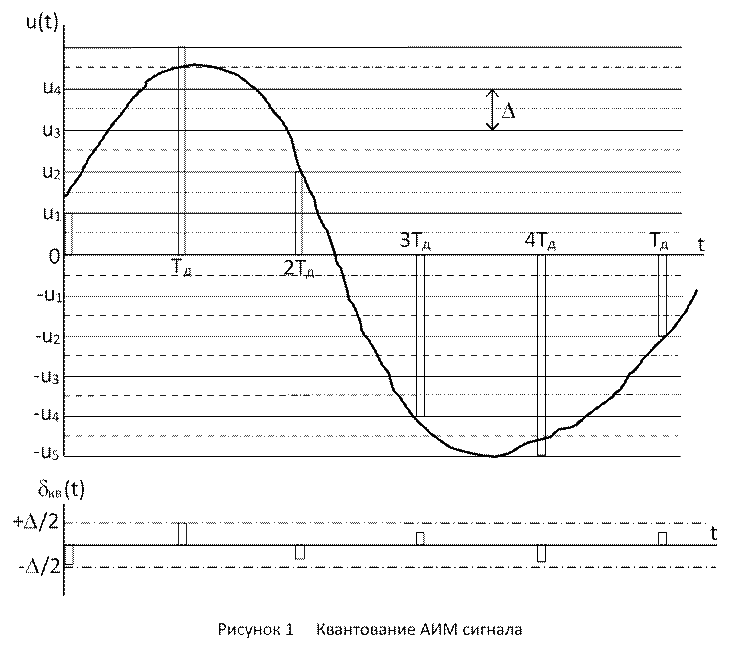 |
Расстояние между двумя ближайшими разрешенными уровнями
квантования (D) называется шагом
квантования и обозначается D
.
Импульсы квантованного по времени АИМ сигнала, заменяются
импульсами, амплитуда которых совпадает с ближайшим допустимым уровнем квантования
.Квантованный по амплитуде сигнал можно записать в виде последовательности
цифр, характеризующих высоту импульсов этого сигнала в условных единицах (шагах квантования) . Квантование
сигналов сопровождается определенной погрешностью, которая тем меньше, чем меньше шаг
квантования .
Разность между исходным и квантованным сигналами называется шумом
квантования .
Максимальная ошибка квантования не должна превышать половины
шага квантования .
Равномерное квантование.
Квантование называется равномерным в том случае, если шаг
квантования в допустимых пределах возможных амплитудных значений сигнала остается постоянным .
Квантование сигналов сопровождается определенной
погрешностью, которая тем меньше, чем меньше шаг квантования .
Разность между исходным и квантованным сигналами называется шумом
квантования .
Максимальная ошибка квантования не должна превышать половины
шага квантования .
Кроме шумов квантования различают ещё и шумы
ограничения, которые
Похожие материалы
- Структурная схема РРЛ СЦИ
- Тестовые задания с дисциплины «Цифровые системы передачи»
- Изучение структуры, принципа действия и работы корреляционного приемника
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.