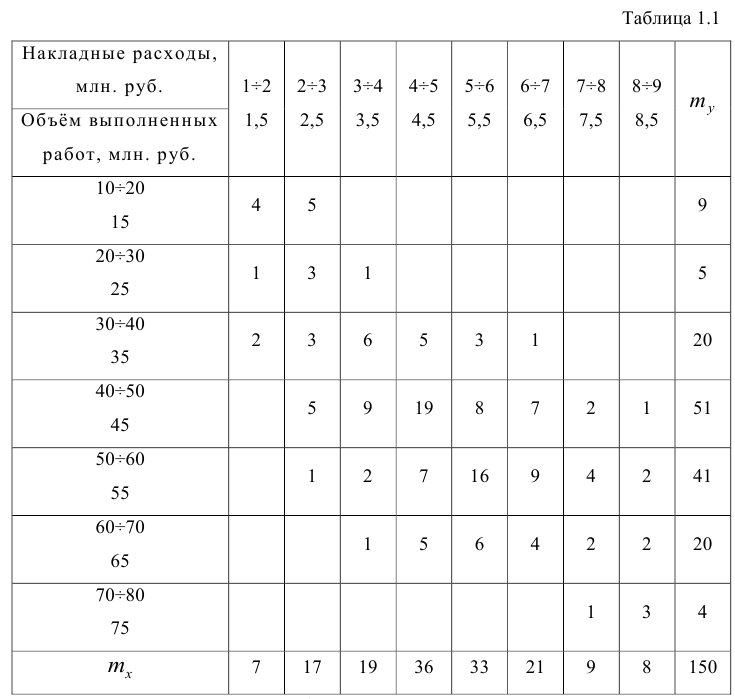
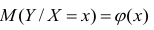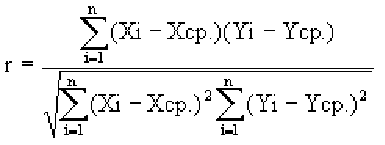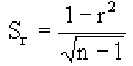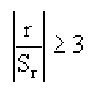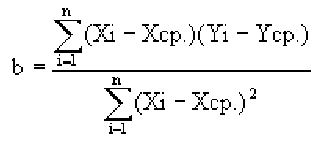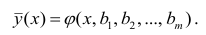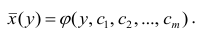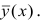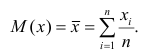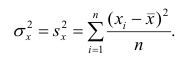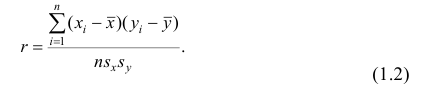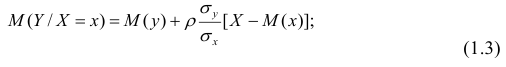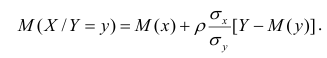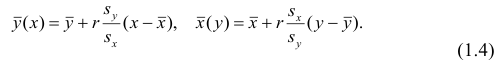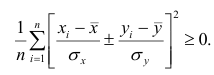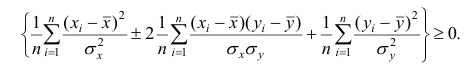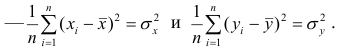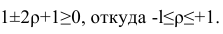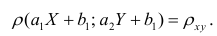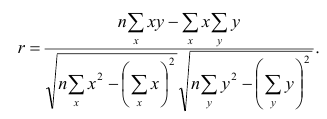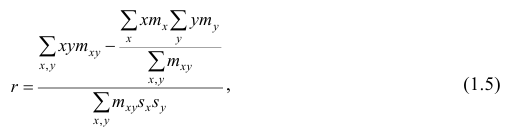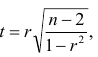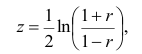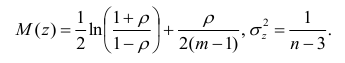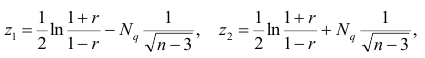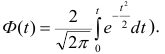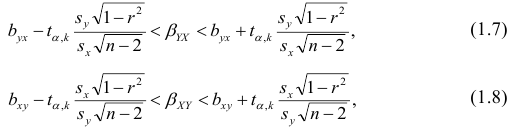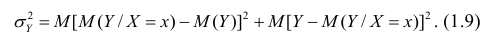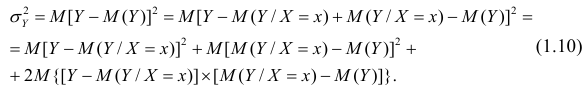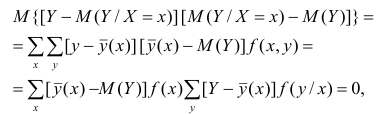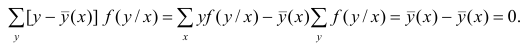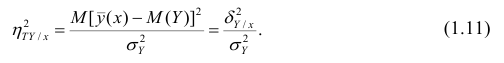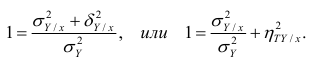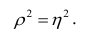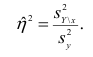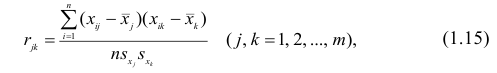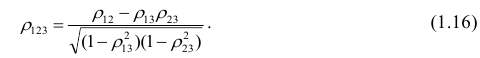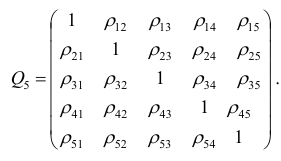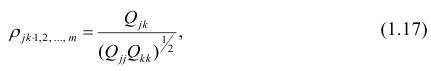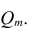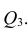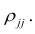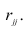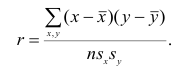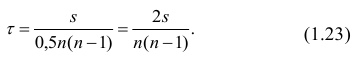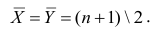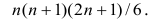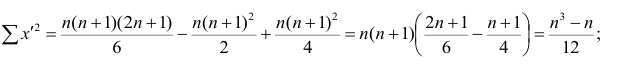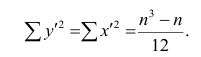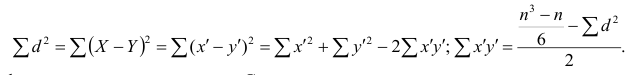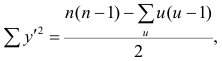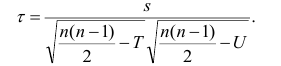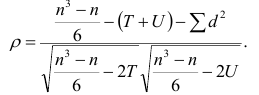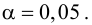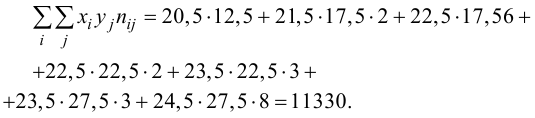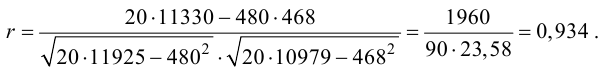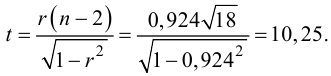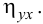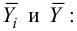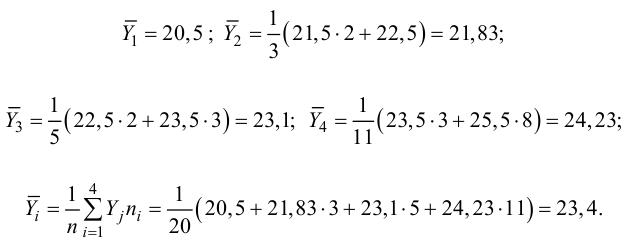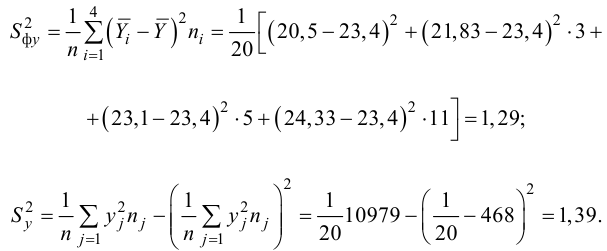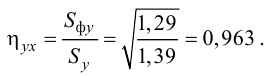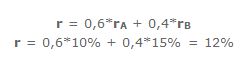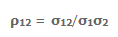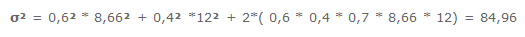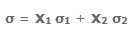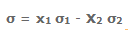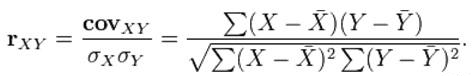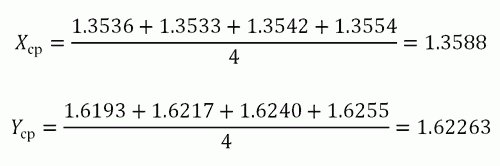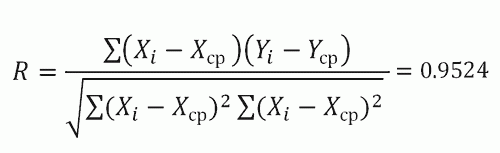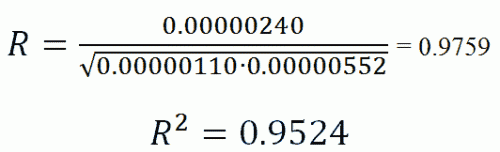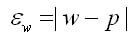Затем каждую из величин Σfxyax перемножаем на условные отклонения ряда у для данной строки (ay) и результаты записываем в графу 17. Суммируя полученные произведения, получаем величину Σ(Σfxyax)ay=417.
Теперь в нашем распоряжении имеются все необходимые величины для вычисления r по формуле:
Величина полученного коэффициента корреляции говорит об умеренной тесноте связи исследованных признаков, а знак свидетельствует о прямом характере этой связи.
Иногда при наличии линейной связи можно, используя коэффициент корреляции, оценить влияние признака-фактора на результативный признак. Для этого применяется квадрат коэффициента корреляции, называемый коэффициентом детерминации (r2). Если выразить коэффициент детерминации в процентах, то он покажет долю влияния данного факториального признака на результативный. Например, коэффициент корреляции между ростом и весом детей равен +0,75, тогда коэффициент детерминации будет: rxy2=0,752=0,56. Если принять все факторы, влияющие на вес тела, за 100%, то на долю роста приходится 56%.
Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют сред-
нюю ошибку коэффициента корреляции. При достаточно большом числе на-
блюдений (больше 100) средняя ошибка коэффициента корреляции (тr) вычисляется по формуле:
|
1− r |
2 |
|||
|
mr |
= |
xy |
(1.37) |
|
|
n |
||||
где n — число парных наблюдений.
В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:
|
1− r 2 |
|||
|
mr = |
xy |
(1.38) |
|
|
n −1 |
|||
66

С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (rxy>=3mr). Обычно это отношение коэффициента корреляции (rху) к его средней ошибке (тr) обозначают буквой t и называют критерием достоверности:
|
tr |
= |
rxy |
(1.39) |
|
|
mr |
||||
Если tr >= 3, то коэффициент корреляции достоверен. В рассмотренном выше примере число наблюдений 142, а коэффициент корреляции 0,68. Тогда
|
mr |
= |
1− rxy2 |
1−(0,68)2 |
||
|
n |
= |
142 |
= 0,045 |
||
|
r |
|||||
|
tr = |
= |
0,68 |
=15 , |
||
|
mr |
0,045 |
||||
т. е. коэффициент корреляции вполне достоверен.
В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, т. е. для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции (тr) определяется по формуле:
|
1− r 2 |
|||
|
mr = |
xy |
(1.40) |
|
|
n − 2 |
|||
Значения критерия tr оцениваются по таблице t Стьюдента при числе степеней свободы v = п — 2. Если величина tr больше табличного значения t05, то коэффициент корреляции признается надежным с доверительной вероятностью больше 95%. Например, имеется коэффициент корреляции, равный +0,72 при числе наблюдений 28. Тогда
mr = 1−(0,72)2 = ±0,019 28 −2
tr = 0,0190,72 = 35,9
Полученное значение tr = 35,9 значительно больше табличного t01 = 2,779, следовательно, полученному коэффициенту корреляции можно доверять с высокой степенью вероятности (>99%).
В медицинской практике нередко возникает необходимость сравнить между собой два выборочных коэффициента корреляции и определить, существенна ли разница между ними. Ввиду того, что распределение коэффициента корреляции отличается от нормального, для оценки значимости различия между двумя коэффициентами корреляции рекомендуется использовать величину Z,
67

предложенную Р. Фишером. Величины Z, соответствующие различным значениям коэффициента корреляции, представлены в табл. 1.38.
Например, при исследовании тесноты связи между ростом и весом девочек и мальчиков было установлено, что у мальчиков коэффициент корреляции равен 0,5, а у девочек — 0,7. При этом обследовано 20 мальчиков и 30 девочек. Можно ли считать, что у девочек сильнее выражена связь между ростом и весом, чем у мальчиков? Для решения этого вопроса переведем значение наших коэффициентов корреляции (r) в величины Z. Находим по таблице, что r = 0,5 соответствует Z = 0,5493, а для r = 0,7 соответствует Z = 0,8673. Ошибка разности вычисляется по формуле:
|
mz |
= |
n1 |
1 |
+ |
1 |
= |
1 |
+ |
1 |
= 0,10 = 0,316 |
|
−3 |
n2 −3 |
20 −3 |
30 −3 |
Вычисляем критерий значимости различий:
|
tz |
= |
z1 − z2 |
= |
0,8673 −0,5493 |
= |
0,3188 |
=1,005 |
|
|
mz |
0,316 |
0,316 |
||||||
Разность признается значимой, если tz ≥ 3. В нашем примере tz < 3; следовательно, на основании полученных коэффициентов корреляции нельзя делать вывод о более выраженной связи между ростом и весом у девочек.
Таблица 1.38 — Таблица величин Z
|
r |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,90 |
1,4722 |
1,5275 |
1,5890 |
1,6584 |
1,7380 |
1,8318 |
1,9459 |
2,0923 |
2,2976 |
2,6467 |
|
0,80 |
1,0986 |
1,1270 |
1,1568 |
1,1881 |
1,2212 |
1,2562 |
1,2933 |
1,3101 |
1,3758 |
1,4219 |
|
0,70 |
0,8673 |
0,8872 |
0,9076 |
0,9287 |
0,9505 |
0,9730 |
0,9962 |
1,0203 |
1,0454 |
1,0714 |
|
0,60 |
0,6931 |
0,7089 |
0,7250 |
0,7414 |
0,7582 |
0,7753 |
0,7623 |
0,8107 |
0,8291 |
0,8480 |
|
0,50 |
0,5493 |
0,5627 |
0,5763 |
0,5901 |
0,6042 |
0,6184 |
0,6328 |
0,6475 |
0,6625 |
0,6777 |
|
0,40 |
0,4236 |
0,4356 |
0,4477 |
0,4599 |
0,4722 |
0,4847 |
0,4973 |
0,5101 |
0,5230 |
0,5361 |
|
0,30 |
0,3045 |
0,3205 |
0,3316 |
0,3428 |
0,3541 |
0,3654 |
0,3769 |
0,3884 |
0,4001 |
0,4118 |
|
0,20 |
0,2027 |
0,2132 |
0,2237 |
0,2342 |
0,2448 |
0,2554 |
0,2661 |
0,2769 |
0,2877 |
0,2986 |
|
0,10 |
0,1003 |
0,1104 |
0,1205 |
0,1307 |
0,1409 |
0,1511 |
0,1614 |
0,1717 |
0,1820 |
0,1923 |
|
0,00 |
0,0000 |
0,0100 |
0,0200 |
0,0300 |
0,0400 |
0,0501 |
0,0600 |
0,0701 |
0,0802 |
0,0902 |
1.8.5 Определение тесноты связи между качественными признаками
При изучении зависимости качественных признаков используется коэффициент сопряженности. Для определения тесноты связи в случае альтернативной изменчивости двух сопоставляемых признаков имеющиеся данные сводятся в четырехпольную таблицу, и коэффициент сопряженности вычисляется по формуле:
|
C1 = |
ad −bc |
(1.41) |
|
(a +c)(b + d)(a +b)(c + d) |
68

Если ранее по данным этой таблицы был вычислен критерий χ2, то коэффициент сопряженности вычисляется по формуле:
|
C1 = |
χ2 |
= |
χ2 |
(1.42) |
|
a +b +c + d |
n |
Например, требуется установить, имеется ли связь между степенью тяжести ревматизма и эффективностью тонзиллэктомии (табл. 1.39).
Таблица 1.39 — Эффективность тонзиллэктомии в зависимости от симптоматики ревматизма
|
Симптоматика ревматизма |
Результат лечения |
Итого |
|||
|
успешное |
неэффективное |
||||
|
Больные, имевшие изменения со |
9 |
26 |
|||
|
cтороны сердца и суставов. |
|||||
|
Больные, имевшие изменения |
8 |
16 |
|||
|
только со cтороны сердца . . |
|||||
|
Всего |
25 |
17 |
42 |
||
Коэффициент сопряженности изменяется в пределах от +1 до -1 и оценивается аналогично коэффициенту корреляции.
При сопоставлении качественных признаков, имеющих три и больше групп, для определения тесноты связи, пользуются коэффициентом средней квадратичной сопряженности Пирсона:
и коэффициентом взаимной сопряженности Чупрова:
|
K = |
φ2 |
(1.44) |
|
(k1 −1) (k2 −1) |
где k1 — число групп по столбцам;
k2 — число групп по строкам таблицы;
ϕ2 + 1 — равно о сумме отношений квадратов частот каждой клетки таблицы к произведению итогов строк и соответствующих итогов столбцов
|
2 |
||||||||
|
ϕ2 |
+ 1 = |
∑ |
mxy |
(1.45) |
||||
|
m |
m |
|||||||
|
x |
||||||||
|
y |
Пример. Вычислим коэффициент средней квадратической сопряженности Пирсона между гистологической структурой и типом роста опухоли по данным таблицы 1.40.
Находим значение ϕ2 + 1:
69

|
φ |
2 |
+1 |
= |
∑ |
mxy2 |
= |
112 |
+ |
62 |
+ |
22 |
+ |
2 |
2 |
+ |
32 |
+ |
10 |
2 |
+ |
12 |
+ |
12 |
+ |
32 |
+ |
|||||||||||||||||||||||||||||||||||
|
mx |
my |
20 |
21 |
33 21 |
14 |
21 |
6 |
21 |
20 |
15 |
33 |
15 |
14 15 |
6 |
15 |
20 |
12 |
||||||||||||||||||||||||||||||||||||||||||||
|
+ |
52 |
+ |
32 |
+ |
12 |
+ |
12 |
+ |
72 |
+ |
32 |
+ |
12 |
+ |
52 |
+ |
2 |
2 |
+ |
4 |
2 |
+ |
22 |
=1,47 |
|||||||||||||||||||||||||||||||||||||
|
33 12 |
14 12 |
6 12 |
20 12 |
33 11 |
14 11 |
33 6 |
14 6 |
20 |
8 |
33 |
6 |
6 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
Отсюда находим ϕ2 =1,47 – 1 = 0,47.
Коэффициент средней квадратичной сопряженности Пирсона:
C1 = 
Коэффициент взаимной сопряженности Чупрова равняется
|
K = |
0,47 |
= |
0,47 |
= |
0,47 |
= 0,12 = 0,348 |
|
(4 |
−1) (6 −1) |
3 5 |
15 |
Полученный коэффициент К также свидетельствует о наличии связи между рассматриваемыми признаками.
Таблица 1.40 — Зависимость между гистологической структурой опухоли и типом ее роста
|
Гистологическая |
Тип роста опухоли (х) |
Итого |
|||
|
структура (у) |
экзофит- |
язвенно- |
диффузно- |
переход- |
(my) |
|
ный |
инфиль- |
инфильтра- |
ный |
||
|
тративный |
тивный |
||||
|
Аденокарцинома |
11(mxy) |
6 |
2 |
2 |
21 |
|
Cr. simplex……… |
3 |
10 |
1 |
1 |
15 |
|
Солидный рак…… |
3 |
5 |
3 |
1 |
12 |
|
Слизистый……… |
1 |
7 |
3 |
─ |
11 |
|
Фиброзный рак… |
─ |
1 |
5 |
─ |
6 |
|
Смешанные формы |
2 |
4 |
─ |
2 |
8 |
|
Всего (mx)……… |
20 |
33 |
14 |
6 |
73 |
При применении коэффициента сопряженности С1 следует учитывать, что он всегда меньше 1 и теоретическая его величина зависит от числа строк и столбцов таблицы. Поэтому вычисление коэффициента С1 правомочно только тогда, когда каждый из сопоставляемых признаков имеет не менее 5 градаций (таблица 5×5 групп). Коэффициент Чупрова, который всегда меньше коэффициента С1 не имеет этого ограничения.
Достоверность выборочного коэффициента взаимной сопряженности оценивается с помощью критерия χ2. Полученная величина χ2=nϕ2 сопоставляется с табличными значениями χ2 при числе степеней свободы v=(k —1)(k2-1) и р = 0,05.
70
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нужна помощь в написании работы?
Главная проблема регистрации результатов наблюдения – категоризация поведенческих актов и параметров поведения. Помимо этого наблюдатель должен уметь точно устанавливать отличие по поведенческому акту одной категории от другой. Соблюдение операциональной валидности при проведении исследования методом наблюдения всегда вызывает наибольшие сложности. Влияние субъекта исследования – наблюдателя, его индивидуально-психологических особенностей также чрезвычайно велико. При такой фиксации поведения наблюдаемых индивидов можно избежать субъективной оценки, используя (если это позволяют условия) средства регистрации (аудио- или видеозапись). Но субъективную оценку нельзя исключить на этапе вторичной кодировки и интерпретации результатов. Тогда здесь требуется участие экспертов, чьи мнения и оценки “обрабатываются”; вычисляется коэффициент согласованности; к рассмотрению принимаются лишь те случаи, в отношении которых проявляется наибольшая согласованность мнений экспертов.
Какие же конкретные недостатки метода наблюдения нельзя в принципе исключить? В первую очередь, все ошибки, допущенные наблюдателем.
Искажение восприятия событий тем больше, чем сильнее наблюдатель стремится подтвердить свою гипотезу. Он устает, адаптируется к ситуации и перестает замечать важные изменения, делает ошибки при записях и т. д. и т. п. А. А. Ершов (1977) выделяет следующие типичные ошибки наблюдения:
1.Гало-эффект. Обобщенное впечатление наблюдателя ведет к грубому восприятию поведения, игнорированию тонких различий.
2. Эффект снисхождения. Тенденция всегда давать положительную оценку происходящему.
3. Ошибка центральной тенденции. Наблюдатель стремится давать усредненную оценку наблюдаемому поведению.
4. Ошибка корреляции. Оценка одного признака поведения дается на основании другого наблюдаемого признака (интеллект оценивается по беглости речи).
5. Ошибка контраста. Склонность наблюдателя выделять у наблюдаемых черты, противоположные собственным.
6. Ошибка первого впечатления. Первое впечатление об индивиде определяет восприятие и оценку его дальнейшего поведения.
Однако наблюдение является незаменимым методом, если необходимо исследовать естественное поведение без вмешательства извне в ситуацию, когда нужно получить целостную картину происходящего и отразить поведение индивидов во всей полноте.
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость

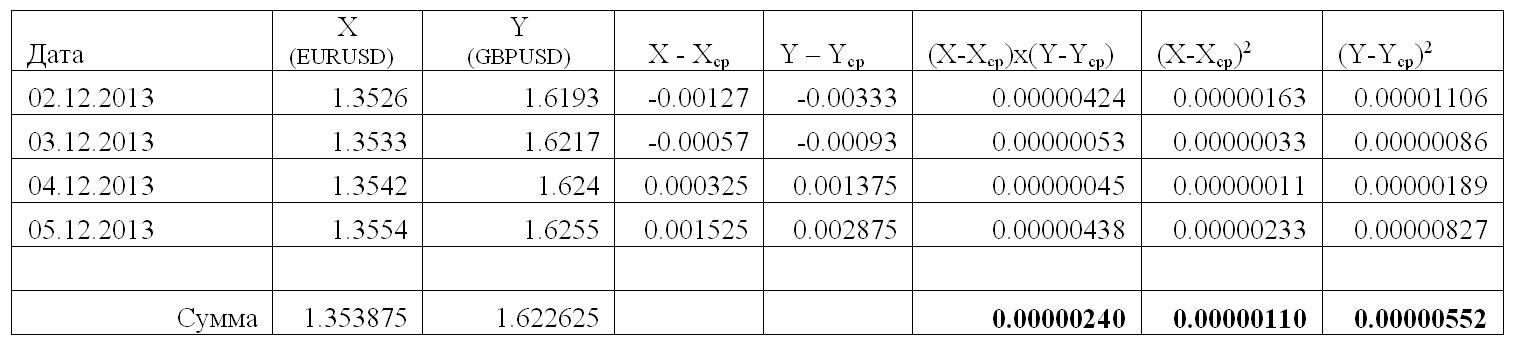
Затем каждую из величин Σfxyax перемножаем на условные отклонения ряда у для данной строки (ay) и результаты записываем в графу 17. Суммируя полученные произведения, получаем величину Σ(Σfxyax)ay=417.
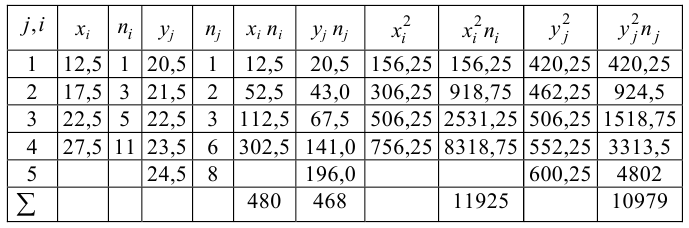
Теперь в нашем распоряжении имеются все необходимые величины для вычисления r по формуле:
Величина полученного коэффициента корреляции говорит об умеренной тесноте связи исследованных признаков, а знак свидетельствует о прямом характере этой связи.
Иногда при наличии линейной связи можно, используя коэффициент корреляции, оценить влияние признака-фактора на результативный признак. Для этого применяется квадрат коэффициента корреляции, называемый коэффициентом детерминации (r2). Если выразить коэффициент детерминации в процентах, то он покажет долю влияния данного факториального признака на результативный. Например, коэффициент корреляции между ростом и весом детей равен +0,75, тогда коэффициент детерминации будет: rxy2=0,752=0,56. Если принять все факторы, влияющие на вес тела, за 100%, то на долю роста приходится 56%.
Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют сред-
нюю ошибку коэффициента корреляции. При достаточно большом числе на-
блюдений (больше 100) средняя ошибка коэффициента корреляции (тr) вычисляется по формуле:
|
1− r |
2 |
|||
|
mr |
= |
xy |
(1.37) |
|
|
n |
||||
где n — число парных наблюдений.
В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:
|
1− r 2 |
|||
|
mr = |
xy |
(1.38) |
|
|
n −1 |
|||
66

С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (rxy>=3mr). Обычно это отношение коэффициента корреляции (rху) к его средней ошибке (тr) обозначают буквой t и называют критерием достоверности:
|
tr |
= |
rxy |
(1.39) |
|
|
mr |
||||
Если tr >= 3, то коэффициент корреляции достоверен. В рассмотренном выше примере число наблюдений 142, а коэффициент корреляции 0,68. Тогда
|
mr |
= |
1− rxy2 |
1−(0,68)2 |
||
|
n |
= |
142 |
= 0,045 |
||
|
r |
|||||
|
tr = |
= |
0,68 |
=15 , |
||
|
mr |
0,045 |
||||
т. е. коэффициент корреляции вполне достоверен.
В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, т. е. для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции (тr) определяется по формуле:
|
1− r 2 |
|||
|
mr = |
xy |
(1.40) |
|
|
n − 2 |
|||
Значения критерия tr оцениваются по таблице t Стьюдента при числе степеней свободы v = п — 2. Если величина tr больше табличного значения t05, то коэффициент корреляции признается надежным с доверительной вероятностью больше 95%. Например, имеется коэффициент корреляции, равный +0,72 при числе наблюдений 28. Тогда
mr = 1−(0,72)2 = ±0,019 28 −2
tr = 0,0190,72 = 35,9
Полученное значение tr = 35,9 значительно больше табличного t01 = 2,779, следовательно, полученному коэффициенту корреляции можно доверять с высокой степенью вероятности (>99%).
В медицинской практике нередко возникает необходимость сравнить между собой два выборочных коэффициента корреляции и определить, существенна ли разница между ними. Ввиду того, что распределение коэффициента корреляции отличается от нормального, для оценки значимости различия между двумя коэффициентами корреляции рекомендуется использовать величину Z,
67

предложенную Р. Фишером. Величины Z, соответствующие различным значениям коэффициента корреляции, представлены в табл. 1.38.
Например, при исследовании тесноты связи между ростом и весом девочек и мальчиков было установлено, что у мальчиков коэффициент корреляции равен 0,5, а у девочек — 0,7. При этом обследовано 20 мальчиков и 30 девочек. Можно ли считать, что у девочек сильнее выражена связь между ростом и весом, чем у мальчиков? Для решения этого вопроса переведем значение наших коэффициентов корреляции (r) в величины Z. Находим по таблице, что r = 0,5 соответствует Z = 0,5493, а для r = 0,7 соответствует Z = 0,8673. Ошибка разности вычисляется по формуле:
|
mz |
= |
n1 |
1 |
+ |
1 |
= |
1 |
+ |
1 |
= 0,10 = 0,316 |
|
−3 |
n2 −3 |
20 −3 |
30 −3 |
Вычисляем критерий значимости различий:
|
tz |
= |
z1 − z2 |
= |
0,8673 −0,5493 |
= |
0,3188 |
=1,005 |
|
|
mz |
0,316 |
0,316 |
||||||
Разность признается значимой, если tz ≥ 3. В нашем примере tz < 3; следовательно, на основании полученных коэффициентов корреляции нельзя делать вывод о более выраженной связи между ростом и весом у девочек.
Таблица 1.38 — Таблица величин Z
|
r |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,90 |
1,4722 |
1,5275 |
1,5890 |
1,6584 |
1,7380 |
1,8318 |
1,9459 |
2,0923 |
2,2976 |
2,6467 |
|
0,80 |
1,0986 |
1,1270 |
1,1568 |
1,1881 |
1,2212 |
1,2562 |
1,2933 |
1,3101 |
1,3758 |
1,4219 |
|
0,70 |
0,8673 |
0,8872 |
0,9076 |
0,9287 |
0,9505 |
0,9730 |
0,9962 |
1,0203 |
1,0454 |
1,0714 |
|
0,60 |
0,6931 |
0,7089 |
0,7250 |
0,7414 |
0,7582 |
0,7753 |
0,7623 |
0,8107 |
0,8291 |
0,8480 |
|
0,50 |
0,5493 |
0,5627 |
0,5763 |
0,5901 |
0,6042 |
0,6184 |
0,6328 |
0,6475 |
0,6625 |
0,6777 |
|
0,40 |
0,4236 |
0,4356 |
0,4477 |
0,4599 |
0,4722 |
0,4847 |
0,4973 |
0,5101 |
0,5230 |
0,5361 |
|
0,30 |
0,3045 |
0,3205 |
0,3316 |
0,3428 |
0,3541 |
0,3654 |
0,3769 |
0,3884 |
0,4001 |
0,4118 |
|
0,20 |
0,2027 |
0,2132 |
0,2237 |
0,2342 |
0,2448 |
0,2554 |
0,2661 |
0,2769 |
0,2877 |
0,2986 |
|
0,10 |
0,1003 |
0,1104 |
0,1205 |
0,1307 |
0,1409 |
0,1511 |
0,1614 |
0,1717 |
0,1820 |
0,1923 |
|
0,00 |
0,0000 |
0,0100 |
0,0200 |
0,0300 |
0,0400 |
0,0501 |
0,0600 |
0,0701 |
0,0802 |
0,0902 |
1.8.5 Определение тесноты связи между качественными признаками
При изучении зависимости качественных признаков используется коэффициент сопряженности. Для определения тесноты связи в случае альтернативной изменчивости двух сопоставляемых признаков имеющиеся данные сводятся в четырехпольную таблицу, и коэффициент сопряженности вычисляется по формуле:
|
C1 = |
ad −bc |
(1.41) |
|
(a +c)(b + d)(a +b)(c + d) |
68

Если ранее по данным этой таблицы был вычислен критерий χ2, то коэффициент сопряженности вычисляется по формуле:
|
C1 = |
χ2 |
= |
χ2 |
(1.42) |
|
a +b +c + d |
n |
Например, требуется установить, имеется ли связь между степенью тяжести ревматизма и эффективностью тонзиллэктомии (табл. 1.39).
Таблица 1.39 — Эффективность тонзиллэктомии в зависимости от симптоматики ревматизма
|
Симптоматика ревматизма |
Результат лечения |
Итого |
|||
|
успешное |
неэффективное |
||||
|
Больные, имевшие изменения со |
9 |
26 |
|||
|
cтороны сердца и суставов. |
|||||
|
Больные, имевшие изменения |
8 |
16 |
|||
|
только со cтороны сердца . . |
|||||
|
Всего |
25 |
17 |
42 |
||
Коэффициент сопряженности изменяется в пределах от +1 до -1 и оценивается аналогично коэффициенту корреляции.
При сопоставлении качественных признаков, имеющих три и больше групп, для определения тесноты связи, пользуются коэффициентом средней квадратичной сопряженности Пирсона:
и коэффициентом взаимной сопряженности Чупрова:
|
K = |
φ2 |
(1.44) |
|
(k1 −1) (k2 −1) |
где k1 — число групп по столбцам;
k2 — число групп по строкам таблицы;
ϕ2 + 1 — равно о сумме отношений квадратов частот каждой клетки таблицы к произведению итогов строк и соответствующих итогов столбцов
|
2 |
||||||||
|
ϕ2 |
+ 1 = |
∑ |
mxy |
(1.45) |
||||
|
m |
m |
|||||||
|
x |
||||||||
|
y |
Пример. Вычислим коэффициент средней квадратической сопряженности Пирсона между гистологической структурой и типом роста опухоли по данным таблицы 1.40.
Находим значение ϕ2 + 1:
69

|
φ |
2 |
+1 |
= |
∑ |
mxy2 |
= |
112 |
+ |
62 |
+ |
22 |
+ |
2 |
2 |
+ |
32 |
+ |
10 |
2 |
+ |
12 |
+ |
12 |
+ |
32 |
+ |
|||||||||||||||||||||||||||||||||||
|
mx |
my |
20 |
21 |
33 21 |
14 |
21 |
6 |
21 |
20 |
15 |
33 |
15 |
14 15 |
6 |
15 |
20 |
12 |
||||||||||||||||||||||||||||||||||||||||||||
|
+ |
52 |
+ |
32 |
+ |
12 |
+ |
12 |
+ |
72 |
+ |
32 |
+ |
12 |
+ |
52 |
+ |
2 |
2 |
+ |
4 |
2 |
+ |
22 |
=1,47 |
|||||||||||||||||||||||||||||||||||||
|
33 12 |
14 12 |
6 12 |
20 12 |
33 11 |
14 11 |
33 6 |
14 6 |
20 |
8 |
33 |
6 |
6 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
Отсюда находим ϕ2 =1,47 – 1 = 0,47.
Коэффициент средней квадратичной сопряженности Пирсона:
C1 = 
Коэффициент взаимной сопряженности Чупрова равняется
|
K = |
0,47 |
= |
0,47 |
= |
0,47 |
= 0,12 = 0,348 |
|
(4 |
−1) (6 −1) |
3 5 |
15 |
Полученный коэффициент К также свидетельствует о наличии связи между рассматриваемыми признаками.
Таблица 1.40 — Зависимость между гистологической структурой опухоли и типом ее роста
|
Гистологическая |
Тип роста опухоли (х) |
Итого |
|||
|
структура (у) |
экзофит- |
язвенно- |
диффузно- |
переход- |
(my) |
|
ный |
инфиль- |
инфильтра- |
ный |
||
|
тративный |
тивный |
||||
|
Аденокарцинома |
11(mxy) |
6 |
2 |
2 |
21 |
|
Cr. simplex……… |
3 |
10 |
1 |
1 |
15 |
|
Солидный рак…… |
3 |
5 |
3 |
1 |
12 |
|
Слизистый……… |
1 |
7 |
3 |
─ |
11 |
|
Фиброзный рак… |
─ |
1 |
5 |
─ |
6 |
|
Смешанные формы |
2 |
4 |
─ |
2 |
8 |
|
Всего (mx)……… |
20 |
33 |
14 |
6 |
73 |
При применении коэффициента сопряженности С1 следует учитывать, что он всегда меньше 1 и теоретическая его величина зависит от числа строк и столбцов таблицы. Поэтому вычисление коэффициента С1 правомочно только тогда, когда каждый из сопоставляемых признаков имеет не менее 5 градаций (таблица 5×5 групп). Коэффициент Чупрова, который всегда меньше коэффициента С1 не имеет этого ограничения.
Достоверность выборочного коэффициента взаимной сопряженности оценивается с помощью критерия χ2. Полученная величина χ2=nϕ2 сопоставляется с табличными значениями χ2 при числе степеней свободы v=(k —1)(k2-1) и р = 0,05.
70
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
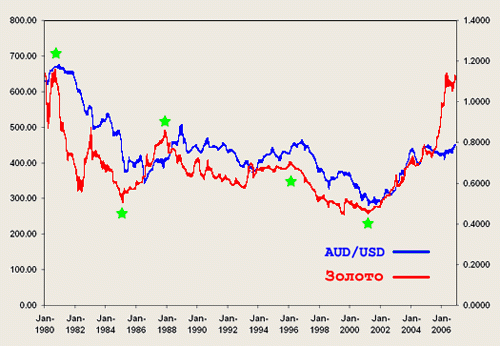
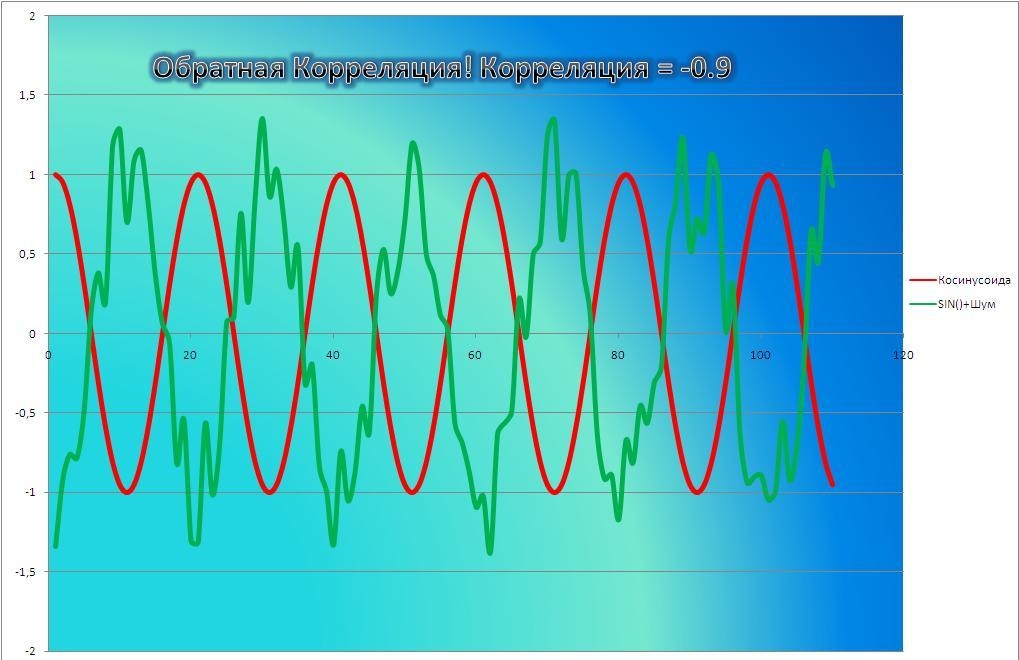
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
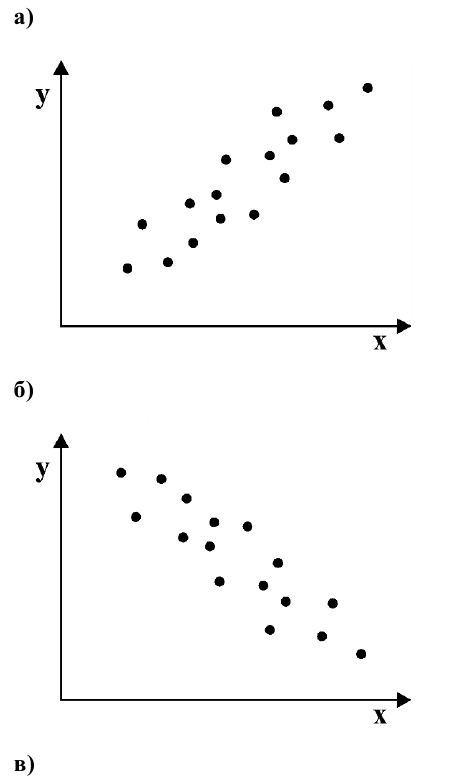
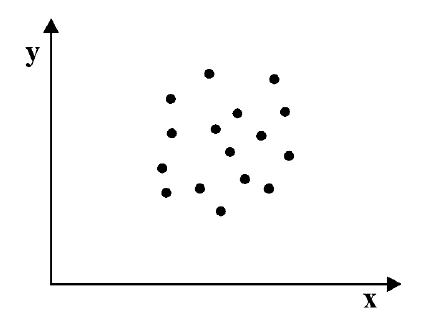
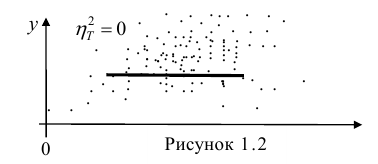
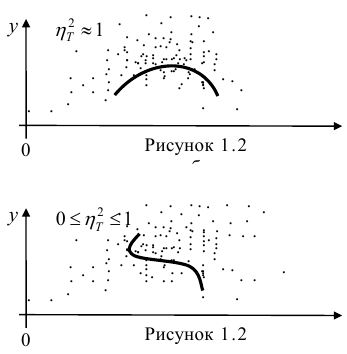
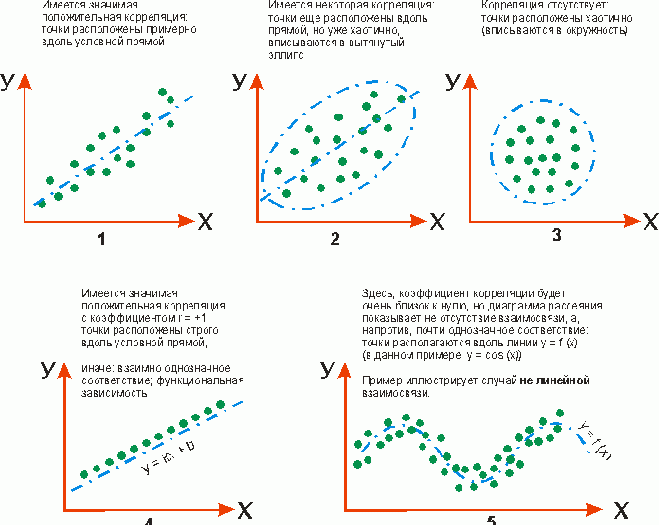
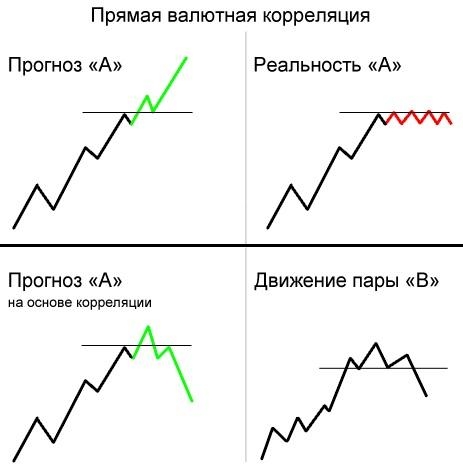
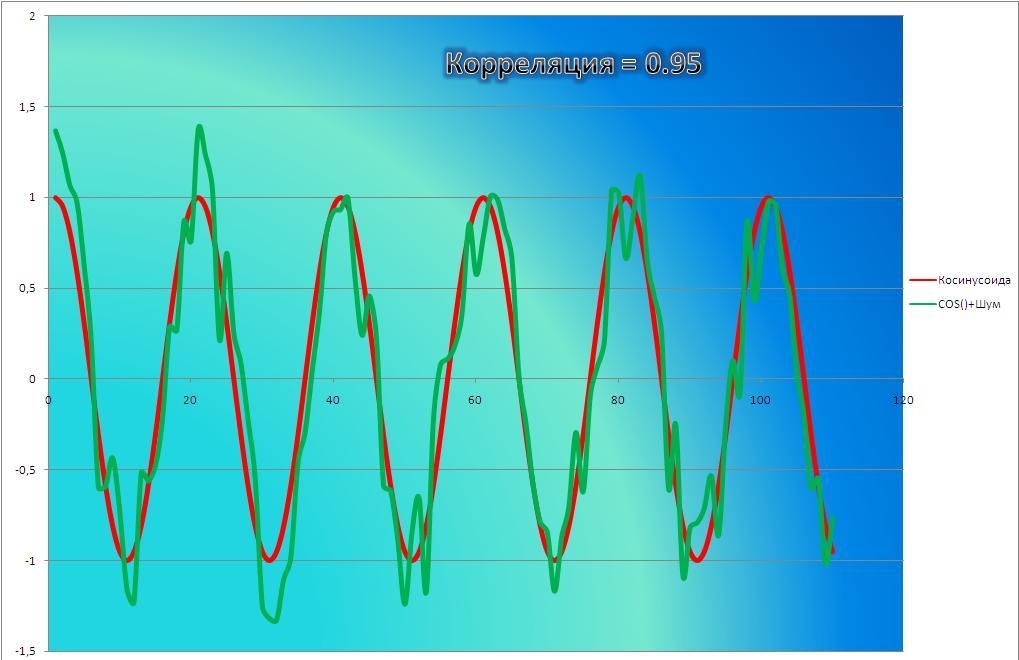
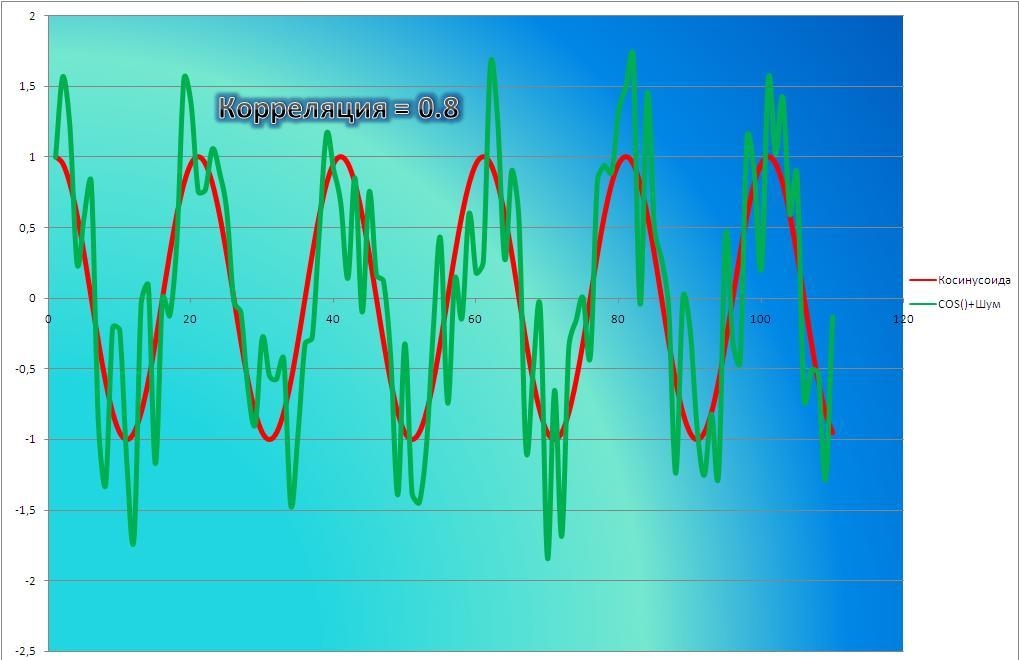
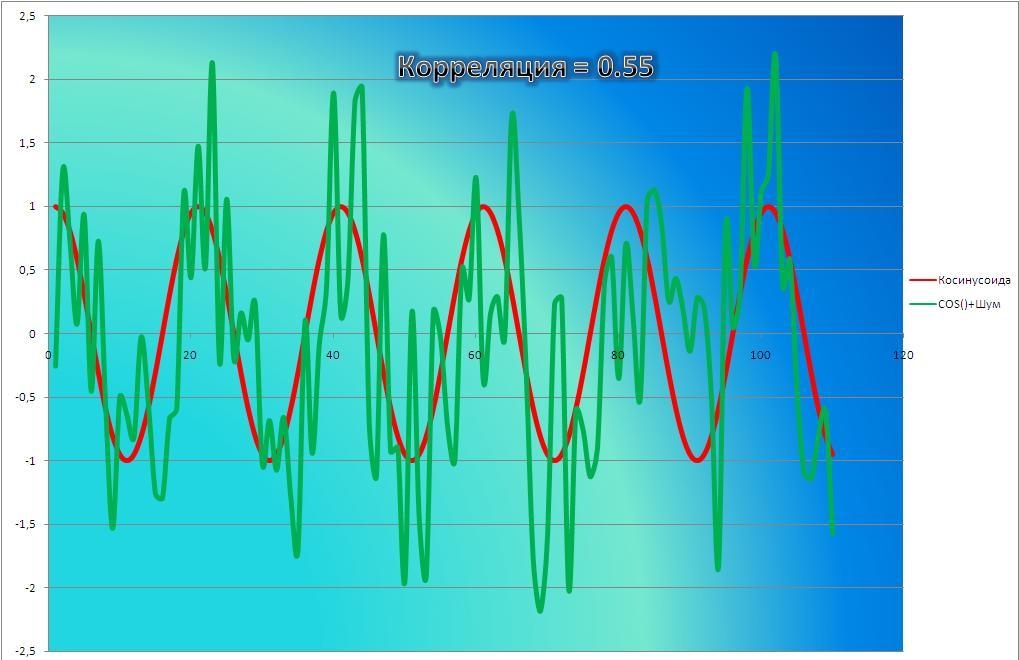
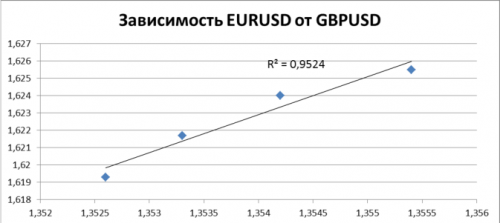
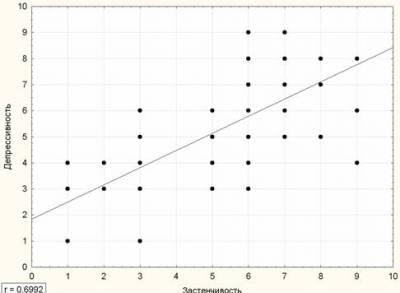
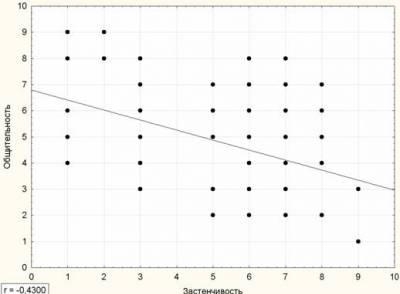
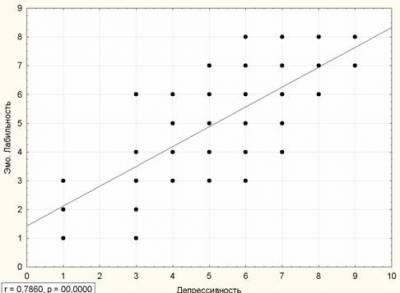
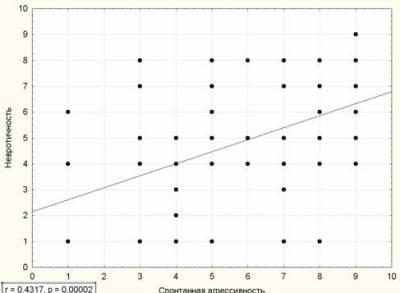
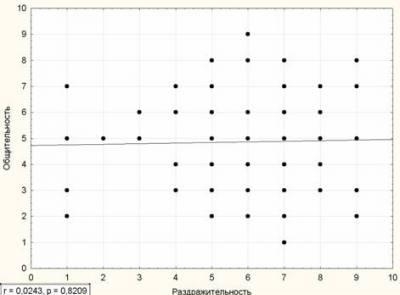
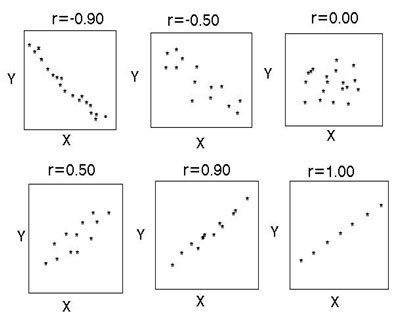
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 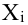
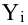
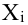
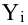
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: 
Коэффициент r мы считаем в Excel, с помощью функции 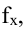
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:
Связь нельзя считать случайной, если:
В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 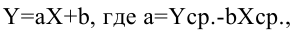
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 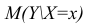
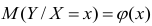
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
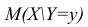
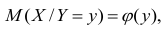
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек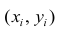
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
Аналогично определяется кривая регрессии X по Y (X на Y):
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее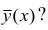
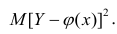
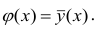
Если рассеивание вычисляется относительно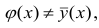
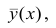
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
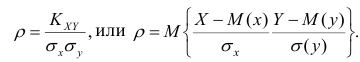
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 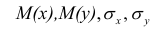
математического ожидания является среднее арифметическое, т.е.
Оценкой дисперсии служит выборочная дисперсия, т.е.
Тогда выборочный коэффициент корреляции
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
функция регрессии X на Y — следующий вид:
Выражения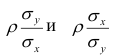
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 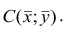
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
Возведём выражение под знаком суммы в квадрат:
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что
Таким образом, окончательно получаем
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 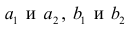
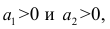
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 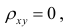
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
где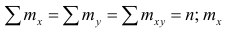
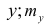
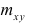
Из формулы (1.2) очевидно, что 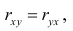
Поле корреляции. Вычисление оценок параметров двумерной модели
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 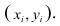
Пару случайных чисел 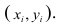
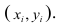
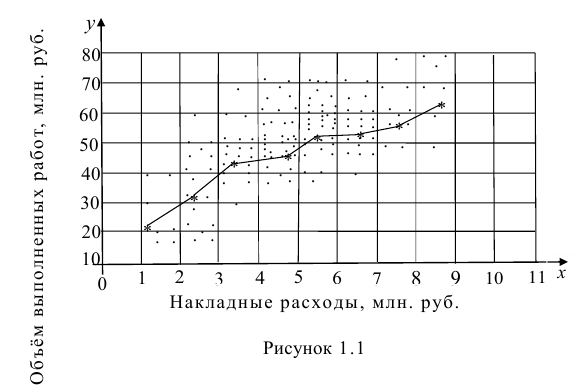
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 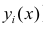
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 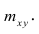
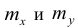
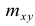
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
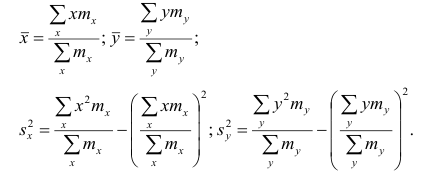
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 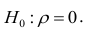
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 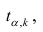
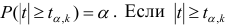
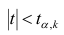
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
В этом, случае доверительный интервал для римеетвид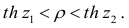
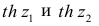
где 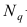
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
где 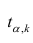
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 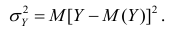
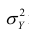
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 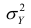
Первое слагаемое обозначим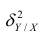
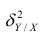
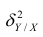
Покажем, что 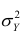
Для простоты полагаем распределение дискретным. Имеем
так как при любом х справедливо равенство
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 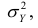
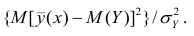
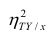
Разделив обе части равенства (1.9) на 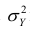
Из последней формулы имеем
Поскольку 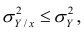
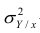
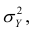
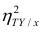
Все сделанные выводы справедливы и для 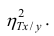
следует, что 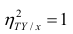
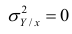
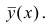
Далее, из равенства (1.12) следует, что 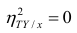
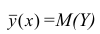
Аналогичными свойствами обладает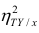
Часто используют величину
Считают, что она не может быть отрицательной. Значения величины 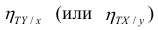
Значения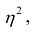
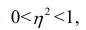
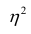
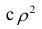
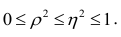
Разность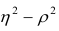
При вычислении 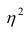
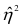
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 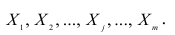
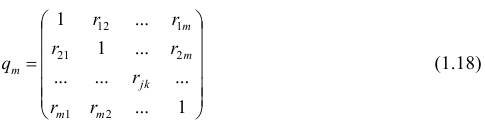
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 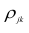
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
где 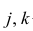
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между 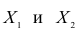
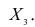
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 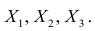
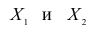
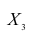
корреляции и имеет вид
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при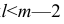
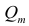
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
Для определения частного коэффициента корреляции второго порядка, например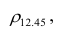
вычеркнув из исходной матрицы 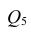
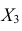
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
где 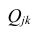
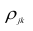
матрицы 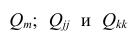
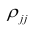
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
Формула выборочного частного коэффициента корреляции имеет вид
где 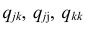
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 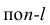
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции
где 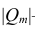
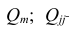
дополнение к элементу
Квадрат коэффициента множественной корреляции 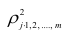
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 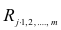
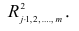
где 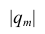
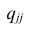
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
Пусть 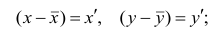
что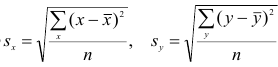
В зависимости от того, что принять за меру различия между величинами 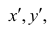
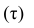
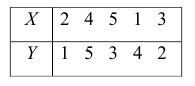
Введём следующую меру различия между объектами: будем считать 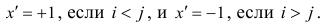
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как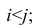
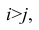
Рассмотрим формулу ( 1 .22). В нашем случае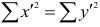
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.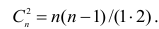
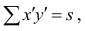
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 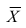
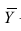
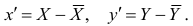
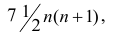
Тогда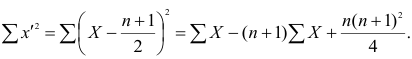
чисел натурального ряда равна
Тогда
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину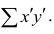
Коэффициент корреляции рангов Спирмэна
У коэффициентов 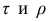
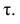
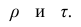
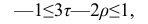
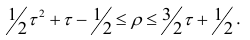
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму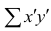
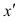
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 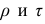
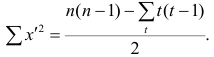
где t и u—число связанных пар в последовательностях.
Обозначая 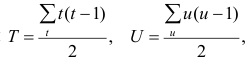
Аналогично находим выражение для р. Только в этом случае
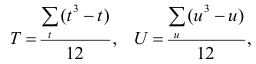
последовательностях, а
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации
где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
Пример:
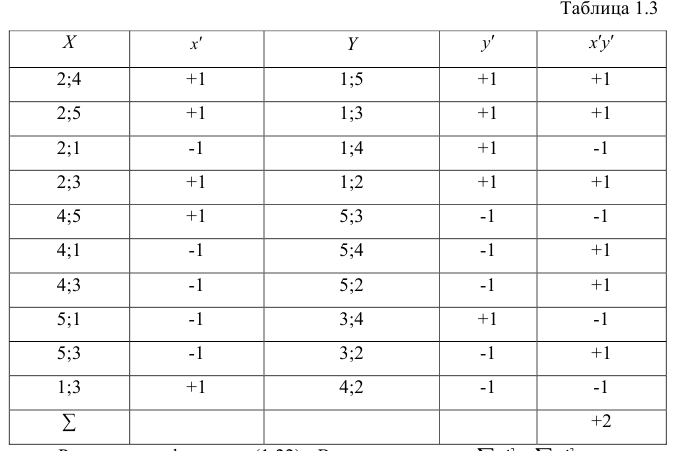
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне
Решение. Для вычислений составим таблицу. Находим суммы
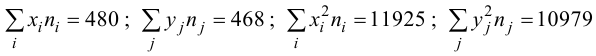
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
Проверим значимость 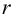
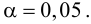
По таблице распределения П6 Стьюдента 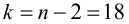
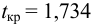
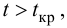
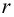
Пример:
Для данных табл. 13 найти корреляционное отношение
Для вычисления эмпирического корреляционного отношения найдем групповые средние
Тогда
Вычисляем корреляционное отношение
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ
Если вы где-то читаете фразу вида «оказалось, что у данных событий корреляция вот такая вот», то примерно в 99,99% случаев, если прямо не оговорено иного, речь идёт о коэффициенте корреляции Пирсона. «Дефолт-корреляция» — это он.
Причём пользуются им далеко не только безграмотные журналисты, но и в целом довольно грамотные учёные. Что, на мой взгляд, весьма странно, ибо область его осмысленного применения сильно уже, чем область его фактического использования.
По этой причине мне хотелось бы рассказать, какими способами при помощи «дефолт-корреляции» можно сделать множество совершенно неправильных, однако весьма наукообразных и кажущихся весьма правдоподобными выводов.
Но для начала о том…
Что такое «коэффициент корреляции Пирсона»?
Вполне понятно, что для несведущих это — особая научная магия, однако довольно обидно, что для многих сведущих дела обстоят аналогично. «Я же биолог, а не математик — зачем мне лезть в эти тонкости?» — обычное дело.
Положим, у нас есть некие два предполагаемых процесса, для каждого из которых мы замеряем какой-то параметр, обычно называемый в данном случае «величиной». В результате у нас появляется набор пар чисел.
Предполагая заодно, что эти процессы не только существуют, но и как-то связаны, мы предполагаем же, что эта связь должна численно проявиться в сделанных нами измерениях. То есть из полученных пар чисел мы каким-то образом можем получить сведения о наличии или отсутствии связи.
Однако связи бывают разной степени жёсткости, поэтому желательно получать не бинарное «да» или «нет», а что-то типа непрерывной по пространству состояний оценки «силы связи».
И вот, встречайте, коэффициент корреляции Пирсона.
Я понимаю, что на этом месте очень многие испугались, что и дальше всё будет столь же непонятным. Какие-то страшные буковки в страшных комбинациях, всё такое.
Признаться, я тоже не особо-то люблю математический вариант записи. Мне «программистский» кажется гораздо более понятным. Поэтому я попытаюсь следовать именно ему.
Есть такое понятие «математическое ожидание величины», для краткости называемое «матожиданием». В простейшем случае его смысл крайне прост: это среднее арифметическое от всех полученных значений.
Получили мы какой-то набор измерений, представленный тут в виде списка
Потом мы просуммировали их все, поделили на количество чисел в этом списке — и вот оно, среднее арифметическое.
Далее мы найдём для каждого числа из списка его отклонение от матожидания.
…и получим, таким образом, список отклонений. Список отклонений каждого из значений от среднего арифметического по всему этому списку.
То же самое можно проделать и с другим списком, в котором находятся измерения второго параметра, измеренного одновременно с первым.
Например, мы у каждого пациента в палате померили температуру. И, кроме того, зафиксировали, сколько таблеток аспирина он сегодня принял. И теперь по вышеуказанной процедуре построим список отклонений температуры каждого пациента от средней температуры пациентов и соответствующий ему список отклонений количества принятых пациентом таблеток аспирина от среднего принятого их количества.
Да, тут уже и так есть суровые подозрения о множестве натяжек, но мы всё-таки не остановимся и предположим, что если температура как-то связана с приёмом аспирина, то должны быть связаны между собой и эти самые отклонения.
Например, если приём аспирина приводит к росту температуры, то мы будем видеть следующее.
Если пациент выпил больше таблеток, чем другие, то его температура отклоняется от средней в бо́льшую сторону.
Если пациент выпил меньше таблеток, чем другие, то его температура отклоняется от средней в меньшую сторону.
То есть оба отклонения — в одну и ту же сторону.
Если мы перемножим попарно все отклонения, то все произведения будут положительными.
И наоборот: если приём аспирина понижает температуру, то все произведения отклонений будут отрицательными.
Иными словами, у нас получилась некая величина, которая обладает чудесным свойством: для прямой связи явлений она положительная, а для обратной — отрицательная.
Однако что с ней будет, если явления не связаны?
Навскидку, с ней будет — «когда как».
Но ведь если явления действительно не связаны, то на большом количестве измерений приблизительно в равной мере должны быть распределены оба варианта: положительное произведение отклонений и отрицательное. Если их просуммировать, то, видимо, получится что-то около нуля. Причём, тем ближе к нулю, чем больше было измерений.
Собственно, вышевведённая функция «матожидание» именно это и делает: суммирует. Потом, правда, ещё делит на количество измерений, но для обнаруженного свойства это не так важно: ведь деление на положительное число не меняет знак результата и не может превратить ноль в не ноль или наоборот.
Поэтому вот он, критерий: ковариация.
Или, если расположить все формулы рядом…
Да, так несколько длиннее, чем в оригинальном определении, но зато и лучше понятно, что происходит.
Теперь, в общем, остался последний момент. Ковариация, увы, может иметь произвольную величину, а потому, для того, чтобы сделать по ней вывод о связи между списками, надо ещё знать максимальное её значение именно для этих величин.
Однако, по счастью, оное можно вычислить в общем виде.
Для этого введём ещё одну интересную величину — выведенную из списка квадратов отклонений от среднего.
Это, как можно видеть, корень из матожидания квадратов отклонений от среднего. Оно так и называется «среднеквадратическое отклонение».
Так вот, можно показать, что ковариация по своей абсолютной величине не превышает произведения среднеквадратических отклонений по этим двум спискам.
Ну а так как среднеквадратическое отклонение по построению всегда положительно, то можно заключить, что
или
В общем, если за меру взаимосвязи взять такую «нормированную величину», то она получится очень удобной и очень универсальной: будет показывать, связаны ли величины между собой, давая для прямой связи единицу, для обратной — минус единицу, а для несвязанных величин — ноль…
…думали они.
Но ага, щаз.
Всё очень удобно и универсально, однако в вышеприведённых рассуждениях есть изрядное количество изъянов, которые — ввиду очевидного удобства и универсальности полученной «меры взаимосвязей» — очень удобно игнорировать, и от этого иметь универсальный способ для поточной генерации совершенно неверных, но зато наукообразных выводов.
Впрочем, надо отметить, что процесса «нормировки» это не касается — со знаменателем всё зашибись, а способ стрельбы себе в ногу кроется в числителе. Да и в самом подходе в целом.
Поэтому, хотя для проформы я тут и привёл полное рассуждение, вскрываемые далее явления вызваны ковариацией и именно на способ её вычисления следует обратить особое внимание.
Выстрел номер один: Ньютон всё наврал
Предположим, некий физик усомнился в законе всемирного тяготения. И решил — в полном соответствии с научным методом — проверить, что тела и правда притягиваются по определённому закону.
Для этого он заказал себе очень точные приборы и сделал экспериментальную установку, в центре которой размещено массивное тело, на любом расстоянии от которого можно размещать другие тела и замерять воздействующую на них силу.
Со всей тщательностью физик измерил силу, действующее на тело, отнесённое от центра на самые разные расстояния. Запротоколировал данные. А потом посчитал корреляцию между координатой изображённого тут зелёным тела и действующей на него силой.
Хм. Ньютон вроде бы утверждал, что сила тяготения однозначно связана с расстоянием между центрами объектов. Почему же мы тут получаем не единицу, а что-то меньшее? Ну ладно, это, быть может, погрешность измерений. Всё равно ведь понятно, что определённо между расстоянием по оси икс и действующей силой есть заметная обратная связь.
На беду, у этого физика были свои личные подозрения об устройстве мира. «Вдруг», — думал он — «миру не всё равно, с какой стороны расположено тело?». Надо попробовать размещать тела не только справа, но и слева.
Правда, прибор для измерения силы умел измерять только её абсолютную величину, но ничего страшного: ведь если есть взаимосвязь между двумя величинами, то между величиной и модулем второй тоже должна быть взаимосвязь.
Поэтому физик провёл второй эксперимент: помещая теперь тело не только справа, но иногда и слева от центра.
В результате, его подозрения оправдались: теперь корреляция координаты с абсолютной величиной силы уже не просто отличалась от единицы или минус единицы…
Она стала нулевой.
Что же тут произошло?
Сейчас, подождите, сначала мы посмотрим на ещё один способ стрельбы в собственные конечности.
Выстрел номер два: хаос энергоснабжения
Однажды физик обнаружил у себя дома удивительный артефакт: электрическую розетку.
Про розетки он слышал, что в них есть электрический ток, которым как раз и питаются электроприборы. А у тока есть напряжение. Которое, вроде бы, в розетках переменное. Так вот, интересно, связано ли это переменное напряжение со временем? Или же, напротив, оно там совершенно хаотичное и меняется как попало?
Для ответа на этот вопрос физик собрал хитрую схему из компьютера и вольтметра, которая через равные промежутки времени измеряет напряжение в сети.
Если связь есть, — рассуждал физик, — то я её таким образом обнаружу. И он был прав: таким образом её действительно можно обнаружить. Причём для этого даже не обязательно быть физиком.
Но на беду и этот физик тоже решил не доверяться интуиции, а вычислить связь автоматически. Для этого он посчитал корреляцию измеренных напряжений с теми моментами времени, когда они были измерены.
Как вы думаете, что в результате получил физик?
Не спешите с ответом…
Не спешите…
Wait…
Wait…
Here it comes…
Физик получил случайную величину от минус до плюс единицы.
В зависимости от того, как встали звёзды, физик мог «выяснить», что напряжение связано со временем прямой или обратной связью, или же, что оно со временем вообще не связано.
Но как?! Как совершенно логичный математический коэффициент может привести к столь абсурдному результату?
Сбитый прицел номер один
Чтобы понять, откуда в мире берётся такая фигня, мы временно, для простоты забудем про знаменатель.
Расположенная в числителе ковариация — это среднее арифметическое произведений отклонений.
Отклонений от чего?
От среднего.
Когда первый физик меряет силу, в зависимости от координаты, слева и справа в симметричных точках у него получаются одинаковые силы. Они отклонены от средней силы совершенно идентично, какой бы эта сила ни была.
Средняя же координата — 0. Отклонения от неё в симметричных точках равны по абсолютной величине, но противоположны по знаку.
Пусть в точке 1 отклонение силы от среднего равно dF1. Тогда в точке −1 будет такое же отклонение dF1. Но вот отклонения в координатах будут уже 1 и −1. Если мы перемножим отклонения, то получим…
| Координата | dx | dF | dx*dF |
|---|---|---|---|
| 1 | 1 | dF1 | dF1 |
| −1 | −1 | dF1 | −dF1 |
С точки зрения ковариации, эти симметричные значения просто взаимно уничтожаются.
Поскольку же физик приблизительно равномерно измерял силы слева и справа, то в среднем все измерения взаимно уничтожились.
Вот как выглядит график произведений отклонений, в зависимости от координаты.
Если случайным образом набрать с него точек, то сумма значений в них будет приблизительно равна нулю. И, следовательно, будет равна нулю ковариация.
И чем больше точек мы возьмём, тем она ближе к нулю. Что наверняка будет убеждать физика, что тут нет никакой ошибки или случайности: чем больше измерений он производит, тем более очевидно, что корреляция — нулевая.
И это при том, что наличие связи между координатой и действующей силой видно невооружённым глазом.
Быть может, ошибка была в том, что физик измерял абсолютную величину силы? Быть может, стоило ему измерить силу с учётом направления, всё получилось бы правильно?
О да, в этом случае корреляция была бы не нулевой, а ранее упомянутыми −0,68. Ведь в этом случае произведения симметричных отклонений не уничтожали бы друг друга.
Только это всё равно был бы ошибочный результат. Просто вывод, сделанный по нему, случайно совпал бы с правильным.
Ведь предположим, что Ньютон действительно наврал, и тела, расположенные справа, притягиваются, но вот расположенные слева — отталкиваются. В этом случае, напротив, игнорирование направления силы дало бы ненулевую корреляцию, а вот его учёт — нулевую.
И в одном из двух вариантов по-прежнему можно было бы сделать вывод об отсутствии взаимосвязи при реальном её наличии.
Причём с правильным совпадал бы вывод, сделанный по тому методу, по которому в другом случае получался бы вывод, не совпадающий с правильным.
Таким образом, в рамках данного метода в обязательном порядке надо сделать выбор между вариантами, заранее зная правильный ответ, — иначе можно выбрать тот вариант, который приводит к ошибке.
То есть это сам метод ошибочен. С его помощью невозможно сделать правильный вывод, не зная его заранее.
Сбитый прицел номер два
Аналогичная история происходит и со вторым физиком: он измеряет процесс, в котором взаимно уничтожаются произведения отклонений от среднего, хотя сам процесс при этом вполне закономерен.
Я для примера взял колебания вокруг нуля, однако это только для наглядности: коэффициент корреляции зависит не от величины, а от её отклонения от среднего, поэтому «без разницы», где расположено это среднее.
Здесь мы тоже наблюдаем симметрию. И эта симметрия с неизбежностью приводит к тому, что на некотором отрезке — кратном двойному периоду колебаний — сумма произведений отклонений взаимно уничтожается. И фактически на корреляцию будет оказывать влияние только тот «хвостик», который останется после последнего обнуления.
Вот как для данного фрагмента будет вести себя корреляция — в зависимости от того момента, когда физик остановил измерения.
Поскольку момент начала и конца измерений зависит только от стечения обстоятельств, физик в реальности высчитывает случайное число, а вовсе не «надёжный показатель связи между явлениями».
Правда, тут выручает то, что одна из величин — время — неограниченно растёт с ростом количества измерений, а вторая величина — напряжение — ограничена определённым диапазоном. В результате, расположенное в знаменателе среднеквадратическое отклонение времени увеличивается до сколь угодно большой величины быстрее, а потому корреляция стремится к нулю с увеличением отрезка времени, на котором проводятся измерения.
Это позволяет уверенно «доказывать» независимость абсолютно любой ограниченной диапазоном величины от времени, а не просто диагностировать наличие или отсутствие связи, в зависимости от того, как звёзды встали.
Хотя, конечно, и тут есть шанс выбрать периодичность замеров, слегка некратную периодичности колебаний, и снова тщательно вычислить случайное число. Например, напряжение в сети колеблется со слегка плавающей частотой: 50 раз в секунду. Поэтому проведение измерений с интуитивно напрашивающейся частотой раз в секунду — серьёзная заявка на успех.
В общем, если физику повезёт, и он замерит много периодов колебаний, не попав при этом в нужную «слегка некратность», он обнаружит на них близкую к нулю корреляцию. После чего сделает ошибочный вывод, что связи между временем и напряжением нет.
Если не повезёт, то результат вообще будет случайным числом, и тут уже, разумеется, никакой ошибки не будет.
Шутка.
В любом случае, вывод ошибочен. Даже если он случайно совпадёт с правильным — ведь ошибочен сам метод его получения.
Но иллюзия о научном обнаружении наличия или отсутствия связи в обоих случаях вполне может сохраниться.
Hold your fire №1 and №2
Первые два примера демонстрируют штуку, которую надо помнить в обязательном порядке: введённая нами «мера взаимосвязи» не универсальна. Сделанные при её построении рассуждения относились только к линейным зависимостям одной величины от другой.
Грубо говоря, это работает только тогда, когда предполагается зависимость…
Если же зависимость иная, то, вообще говоря, коэффициент корреляции может оказаться произвольным.
Да-да, не нулевым, а произвольным.
Ведь даже при очень хорошем случае — при убывании одной величины при возрастании другой — первый физик уже получил странный результат. Ещё до того, как он начал пробовать помещать тело не только справа, но и слева, при наличии совершенно однозначной и непериодической зависимости, полученный им коэффициент корреляции уже заметно отличался от −1.
И дело тут не в погрешности измерений. Дело в том, что даже зависимость
достаточно нелинейна для коэффициента корреляции. Уже на ней результат опасно близок к «хм, возможно, на силу влияет что-то ещё». Да, это, конечно, не −0,1, но всё-таки −0,68 — это и не чистая минус единица. Всё выглядит так, будто бы тут не совсем детерминированная связь.
Так какие же заключения можно сделать, вычислив коэффициент корреляции?
Если она нулевая, значит ли это, что величины не связаны?
Два примера показывают, что нет, нельзя.
А если она ненулевая, значит ли это, что зависимость есть?
Второй пример показывает, что и это тоже совершенно не обязательно: ведь вполне возможно и даже весьма вероятно на, например, периодическом процессе получить случайное число, довольно существенно отличающееся от нуля.
Иными словами, исследователь откуда-то должен знать заранее, что тут либо линейная зависимость, либо вообще никакой, чтобы сделать более-менее правильный вывод.
Но откуда он может это знать до исследований? Только из других исследований. Где анализ делался другими методами. Например, основывался на вдумчивом разглядывании графиков или распределений, формированием на их основе гипотезы о функции, связывающей две величины, и последующей экспериментальной проверке того, что эта функция и правда именно такая, поскольку с её помощью удаётся предсказать значение второй величины, зная первую.
Но если это всё уже проделано, то зачем ему вообще считать корреляцию? У него же уже есть более надёжные результаты.
Может быть, коэффициент корреляции можно использовать как первое приближение? Как оценку связи навскидку?
Хороша же такая оценка, которая при весьма вероятных закономерностях даёт случайное число, и приводит, таким образом, к совершенно разным выводам — в зависимости от расположения звёзд.
То есть в сухом остатке оказывается, что единственное, что можно сделать при помощи корреляции — это вывод об отсутствии одной и той же линейной на всём отрезке взаимосвязи между величинами.
Именно об отсутствии — ведь даже о наличии такой взаимосвязи вывод сделать нельзя (см. «случайное число»).
И именно что линейной на всём отрезке, поскольку при фрагментарно линейной вполне возможно взаимное уничтожение произведений отклонений.
Причём натолкнуться на такое может совсем даже не только усомнившийся в законе всемирного тяготения физик. Ровно так же хлебнуть полную чашу горя может медик, решивший выяснить связь температуры тела пациента с самочувствием пациента. При нормальной температуре — 36,6 °C — самочувствие, видимо, наилучшее. При повышении температуры оно ухудшается. Однако и при понижении температуры оно тоже ухудшается…
Чувствуете схожесть ситуации с экспериментами первого физика? О да, и с корреляцией будет тоже: при симметричности оценок слева и справа от нормальной температуры корреляция окажется близкой к нулю. Из чего медик сможет заключить, что связи между температурой и самочувствием нет.
И ровно то же самое будет с лекарством, у которого есть оптимальная доза приёма: при этой дозе результаты будут наилучшими, но вот при меньшей и при большей они будут хуже, что тоже приведёт к чисто техническому занулению коэффициента корреляции.
И вы думаете, на этом проблемы с коэффициентом кончились?
Ага. Щаз.
Выстрел номер три: неубедительный экстрасенс
Однажды к группе заинтересованных в изучении паранормальных явлений пришёл человек, обладающий удивительной способностью — он абсолютно безошибочно умел угадывать выпавшее на кубиках.
Правда, по воле паранормальных сил эта способность у него была выражена в весьма странной форме: если кто-то собирался бросить четыре кубика, то Космос тут же шептал экстрасенсу сумму выпавшего на них в тридцатой степени. Увы, экстрасенс был безграмотен (он просто слушал голос Космоса), а потому извлекать корень тридцатой степени не умел.
Впрочем, паранормологи этого делать тоже не умели: ни извлекать корень тридцатой степени, ни возводить в тридцатую степень. Однако они предположили, что его предсказания всё равно должны коррелировать с суммой выпавшего на кубиках (которую они считать всё-таки умели) — ведь между числом и его тридцатой степенью имеется однозначная математическая связь.
Не поленившись, паранормологи провели 10 000 испытаний. Не было никаких сомнений в том, что такого вполне достаточно для исключения любых случайностей.
Но результат их разочаровал: предсказания экстрасенса имели корреляцию с суммой выпавшего на кубиках всего 0,2. Такой вшивой корреляции явно недостаточно, чтобы подтвердить экстрасенсорные способности. 0,5 ещё куда ни шло, но вот 0,2…
В результате экстрасенс был изгнан и высмеян.
Сбитый прицел номер три
Я специально придумал этот пример, чтобы развеять сомнения, будто бы «дефолт-корреляция» может не срабатывать только при попытках измерять связь времени и состояния, но вот для неких случайных событий она всегда подходит.
О нет. И данные паранормологи тому примером.
На самом деле они прогнали экстрасенса, который совершенно правильно угадал в 100% случаев. Да-да, он ни разу не ошибся.
Однако проведи они даже миллион испытаний, всё равно корреляция была бы всё столь же низкой. Ибо я не зря сказал о том, что корреляция более-менее корректно отображает только линейную связь между величинами.
Здесь же наблюдался аналог того, что произошло с первым физиком, только в гипертрофированной форме: корреляция была не просто несколько подозрительной, а существенно ниже порогового уровня достоверности.
Случайно угадать все сто тысяч раз тридцатую степень суммы выпавшего на четырёх кубиках столь нереально, что такое вряд ли можно рассматривать всерьёз, но корреляция при этом утверждает, что экстрасенс как бы не угадывал.
Как бы утверждает.
Hold your fire №3
На самом же деле, совершенно не зря в справочниках пишут, что всё это осмыслено только при гауссовом распределении случайных величин. И зря так многие это либо не читают, либо игнорируют в своей практической деятельности.
«Гауссово» распределение подразумевает концентрацию основной массы результатов измерений вокруг некоторой величины (того самого «матожидания» или «среднего»). Причём чем дальше от неё случай, тем меньше раз мы его должны встречать.
Имеющаяся же в формуле корреляции σ — среднеквадратическое отклонение — характеризует в этом случае «ширину» данного колокола.
Негауссовость одного или обоих распределений — залог получения очень низкой корреляции даже при очевидной прямой взаимосвязи величин.
В данном случае сумма выпавшего на четырёх кубиках имела распределение, близкое к гауссову, но вот возведение результата в тридцатую степень убило даже намёк на гауссовость, что не замедлило сказаться на результате.
И не помогли даже 10 000 испытаний.
В реальных же исследованиях испытаний вполне может быть штук 100, например. И негауссовость распределения там может быть существенно менее экстремальной, но всё равно пагубно сказаться на результатах.
Выстрел номер четыре: убедительный экстрасенс
К тем же самым паранормологам через некоторое время пришёл ещё один посетитель. Он тоже имел паранормальную связь с кубиками, но его метод был проще: он бросал один кубик, а потом предлагал экспериментатору бросить второй. Благодаря тому, что в его руках была заключена особая магия, первый бросок кубика мистическим образом влиял на всю ситуацию в целом.
О нет, выпавшее на втором кубике он не брался предсказать, однако утверждал, что первый бросок окажет очень сильное влияние на второй бросок, суть коего влияния он, впрочем, не брался объяснить. Но предлагал просто взять и посчитать корреляцию выпавшего на первом кубике с суммой выпавшего на двух кубиках.
Первые сто испытаний повергли паранормологов в шок и трепет: корреляция действительно оказывалась весьма нехилой: 0,75.
Правда, они всё-таки усомнились, не было ли тут простого везения. Однако, проделав привычные для них 10 000 испытаний, они с удивлением отметили, что корреляция упала, но не так, чтобы очень сильно. Всё-таки 0,7 — это весьма неплохо. Согласно всем справочникам, это уже тянет на термин «высокая корреляция».
Определённо у этого экстрасенса был талант — оставалось только понять, каким способом из его предсказаний можно извлекать сведения о том, что выпадет на втором кубике…
Сбитый прицел номер четыре
…и правильный ответ: никаким. Нет никакого способа предсказать, что именно там выпадет. И даже, внезапно, нет никакого способа предсказать сумму.
Да-да, корреляция — высокая, однако всё, что можно сказать про сумму, это то, что она будет лежать на отрезке от выпавшего на первом кубике плюс один до выпавшего на первом кубике плюс шесть. Что было вполне понятно и безо всяких экстрасенсов.
Но никаких случайных совпадений — корреляция, правда, получится примерно вот такая.
Hold your fire №4
Разумеется, выпавшее на первом кубике влияет на сумму, поскольку оно входит туда как слагаемое. Однако корреляция показала всего лишь линейную связь первого со вторым. Выпавшего на первом кубике и случайной величины, полученной прибавлением к уже выпавшему второй случайной величины.
Но сколь же легко очароваться большим значением коэффициента и сделать вывод, который вовсе из него не следует: первый кубик как-то влияет на второй. Или даже, наоборот: ещё не брошенный второй кубик как-то влияет на первый.
Или хотя бы, что из результата броска первого кубика можно узнать что-то ещё, кроме и так очевидного.
Ах, сколько же раз такого рода эксперименты приводят к восторженным публикациям — причём не только в обычной прессе, но даже и во вполне научной.
Временами ничто не отделяет добросовестного биолога от того, чтобы путём сотен замеров открыть удивительный факт: все муравьи планеты строят муравейники, длина окружности основания которых примерно втрое больше диаметра этого основания.
Кажется, будто бы выполнение некого «научного» ритуала обязательно должно давать правильные результаты, даже если при этом не понимать сути этого ритуала, оправдывая фразами вида «я же паранормолог, а не математик».
Математика как бы работает сама. Ведь она же математика. Математика не обманывает.
И да, математика не обманывает — обманывают её трактовки.
Выстрел номер пять: хороший способ вызвать дождь
Как-то раз антрополог наблюдал за обычным городским жителем (конечно же, с его, этого жителя, согласия). И через некоторое время он заметил удивительную закономерность: если этот житель брал с собой зонт, то в этот день шёл дождь.
Конечно, так случалось не каждый раз: иногда объект наблюдения брал зонт, но дождь не шёл, иногда не брал, но дождь всё равно шёл, — однако слишком часто наличие зонта с наличием дождя и отсутствие зонта с отсутствием дождя случались одновременно.
Антрополог, как настоящий учёный, конечно, не доверился таким «навскидочным» оценкам, а вместо этого стал каждый день тщательно протоколировать свои наблюдения.
Через год он приписал событиям «взят зонт» и «был дождь» число 1, событиям «не взял зонт» и «не было дождя» число 0, и посчитал корреляцию по своим протоколам.
Корреляция была очень высокой: 0,95. Эти два события однозначно были связаны.
Гордый собой антрополог написал статью «Как вызывать дождь», в которой убедительно — по трём с половиной сотням наблюдений — доказывал, что именно вот этот житель управляет дождями по месту своего проживания. При помощи ношения зонта.
К сожалению, эту статью отказались печатать, ссылаясь на то, что как-то это всё неубедительно звучит.
Подумав некоторое время, антрополог пришёл к мысли, что наверно всё наоборот: это дождь управляет взятием зонта этим жителем. Просто данный гражданин способен видеть будущий дождь своим внутренним зрением. И, увидев будущий дождь, берёт с собой зонт — даже если на улице сейчас пока ещё нет никакого дождя. Если, конечно, не забыл с утра внутренним зрением посмотреть в будущее.
Ведь однозначно, столь высокая корреляция не может быть результатом случайности.
К сожалению, эту статью в журнал тоже не взяли, поскольку тамошние скептики не поверили в реальности внутреннего футуристического зрения, несмотря на столь яркие доказательства существования оного.
Однако антрополог не отчаялся. Подумав ещё, он сделал финальный вывод: существует мистическая незримая сила, которая вызывает дожди и одновременно с тем побуждает отдельных граждан брать с собой зонт. Поиском этой силы срочно следует заняться, поскольку она перевернёт все представления о мироздании.
В этот раз Фортуна улыбнулась антропологу: под это дело был создан специальный институт и много лет всевозможные учёные мужи пытались найти эту силу, под чутким руководством данного антрополога, которого хоть и не сделали директором, но всё-таки сделали замом. Вот так добро победило зло.
Сбитый прицел номер пять
Если коэффициент корреляции показал реальную связь одной величины с другой (а не случайное число, как это было со вторым физиком), это всё равно никак не доказывает, что одно явление вызывается другим. Даже если этим способом с самого начала хотели доказать наличие таковой связи, что многим почему-то кажется гарантией верности выводов.
Вполне может быть так, что первое явление не вызывается вторым, и при этом даже второе явление не вызывается первым.
В этих случаях говорят: «может быть, что есть некое третье явление, вызывающее оба два», — но и это в ряде случаев скорее вводит в заблуждение, нежели помогает. Ведь правда может быть такое явление, но на этом всё равно возможные варианты не кончаются.
И уж, тем более, никто не гарантирует, что именно то «третье явление», которое предположил кто-то там, и есть то самое искомое.
Улыбнувшаяся антропологу Фортуна, в это время со спины показывала человечеству средний палец, ибо не было никакой внешней мистической силы. Гражданин просто утром смотрел прогноз погоды, и, если там обещался дождь, брал с собой зонт.
Может показаться, что, ну ладно, пусть не мистическая сила, но всё-таки третье явление, вызывающее первые два, тут есть.
Предположим, есть. Но какое?
Прогноз погоды вызывает дождь?
Или ещё не случившийся дождь вызывает прогноз?
Ну Ok, не сам дождь, а атмосферное давление, скорость и направление ветра, наличие водоёмов и т. п. вызывают и дождь, и прогноз?
Однако мы могли бы убедиться, что, вообще говоря, данного жителя побуждают взять зонт сами опубликованные прогнозы, а вовсе не физические явления. Для этого надо было бы просто попросить тот источник, в котором он эти прогнозы читает, некоторое время публиковать неправильные прогнозы. И тем самым воочию узреть, что зонт берётся, если в прогнозе написано, что будет дождь, а вовсе не если какие-то физические параметры указывают на его высокую вероятность.
То есть некого одного «третьего явления», вызывающие первые два, не существует. Вместо этого есть целый набор явлений, состоящих друг с другом в весьма непростых отношениях.
Долгое время некая служба делала прогнозы, ориентируясь на ряд параметров. Их метод правда работал, поэтому их прогнозам начали доверять. Настолько, что некоторые даже стали игнорировать положение вещей, опираясь только на сказанное этой службой. И теперь слова этой службы побуждают этих людей брать зонт. И они достаточно долгое время брали бы его, даже если бы данные метеорологи поголовно сошли бы с ума и начали бы строить прогнозы на основе рисунка кофейной гущи.
Хотя в прошлом связь между явлениями через общую «третью силу» была, сейчас её уже нет. Но по инерции всё продолжает работать.
Выстрел номер шесть — прибытие автобуса
Один психолог наблюдал за ещё одним гражданином. И выяснил, что каждый раз, когда тот гражданин приходит на остановку, не позже, чем через пять минут, к ней приезжает автобус. Причём всё время один и тот же.
Естественно, предположение о том, что приход на остановку именно этого человека вызывает приезд этого автобуса, психолог сразу же отверг, как слишком абсурдное.
Но его заинтересовало, может ли быть верно обратное: что приезд этого автобуса вызывает приход этого человека на остановку? Это выглядело очень правдоподобным.
С согласия этого человека психолог начал за ним наблюдать. Оказалось, что этот человек каждый будний день встаёт в одно и то же время, за полчаса собирается и завтракает, а потом идёт на остановку.
Все введённые психологом способы измерить корреляцию данных событий указывали на одно и то же: связь тут очень жёсткая. Совершенно точно приезд этого автобуса вызывает приход человека на остановку. Точнее, не сам приезд, а знание о приезде.
Именно под приезд данного автобуса (время прибытия которого этот человек, видимо, вычислил на стихийной серии экспериментов) данный человек подстроил свой распорядок дня, учтя, разумеется, время на «успеть собраться».
Это вам не дождь, вызывающий зонт, тут всё тип-топ. Вон, даже читатели этой статьи сейчас думают: «А здесь-то что не так с выводами?!»
Сбитый прицел номер шесть
А с выводами здесь тоже не так всё.
Все способы подсчёта корреляции действительно могут показать однозначную линейную взаимосвязь. Совершенно честно. Без ошибок. И даже другие, не дефолтные, коэффициенты корреляции её покажут. И всё может казаться вообще очевидным. Но и в этом случае вполне возможны неверные выводы.
Дело в том, что описанный гражданин не вычислял время прибытия автобуса. И никогда не видел расписания. И не подстраивал под него свой график.
Он по городскому навигатору узнал время поездки от дома до работы, а потом поставил будильник на красивое круглое число, позволяющее ему успевать на работу. Ну, на девять утра, например.
Полчаса ему хватало на сборы, после этого он выходил на улицу, и — ну надо же — именно в это время приходил данный автобус. Да, вот так вот удачно совпало расписание.
Впрочем, там, в этом расписании, автобусы вообще ходили раз в пять минут, поэтому не совпасть оно просто не могло: округления времени будильника до красивого числа с запасом хватало на покрытие даже максимального ожидания — пяти минут. Приходи этот автобус на две минуты раньше, ну так этот человек ездил бы на следующем. И точно так же каждый раз успевал бы вовремя.
Да, можно понатягивать сову на глобус и выстроить какую-то отмазку про «третье явление». Ну, там, «третьим явлением в данном случае оказывается всё человеческое общество, где людей на работу развозит общественный транспорт, а потому какие-то работники автобусного парка составили правильное расписание с достаточно частым движением автобусов и так далее». Однако всё это совершенно не помогает понять то самое, что хотел понять психолог: почему этот человек так делает? Что его побуждает поступать именно так? Какая сила?
И в данном случае реальной «силой» оказалось «я попробовал почти наугад, оно сработало, поэтому я и дальше так делал».
Сравните это с нарисованной психологом картиной, согласно которой этот человек, как стихийный, но добросовестный исследователь, вычислял расписание автобуса, рассчитывал свои действия, составлял план… в общем, явно был кем-то не тем, кем оказался на самом деле.
И вся эта стройная теория отлично подтверждалась всеми возможными корреляциями и даже, вроде бы, правдоподобными рассуждениями.
Возможно даже, услышав о реальном положении вещей непосредственно от самого наблюдаемого, психолог всё равно решил бы сохранить свой вариант описания, добавив модификацию «он всё равно планирует, только подсознательно». И даже, не исключено, построил бы целую теорию подсознательного планирования, столь же хорошо подкреплённую высокими корреляциями, как и его первоначальный вывод.
Hold your fire №5 and №6
Мораль последних двух историй в том, что никакой статистический показатель сам по себе не может подтвердить нравящуюся вам теорию. Теории подтверждаются только совокупностью показателей в рамках правильно построенной серии экспериментов.
Серии, а не одного эксперимента — пусть даже с большим числом данных.
Какими бы ни оказались все подсчитанные вами статистические показатели, они лишь дают вам некоторую почву для размышлений и предположений. Для гипотез, а не для «теорий», о которых многие любят на первом же этапе заявлять.
Первый эксперимент — первый. По его результатам вам надо сформулировать гипотезу и в следующих экспериментах проверять, правда ли она даёт сбывающиеся прогнозы.
Намеренное в первом эксперименте — это ведь данные, на которых строится гипотеза. На этих данных нельзя проверить, правда ли гипотеза работает: ведь именно на них вы её построили — ясен пень, на них она будет работать. Так будет с любой гипотезой — даже с неверной.
При сбывшихся же прогнозах на новых экспериментах уже правда появится «статистическое доказательство»: ведь предположенная вами зависимость одной величины от другой правда позволяет делать прогнозы на тех данных, которые мы на момент её введения в качестве гипотезы ещё не получили. Вот это доказывает реальность связи, а не просто высокая корреляция.
Более того, мало повторить тот же эксперимент и убедиться, что и второй раз сработало. Сработало или нет, но надо всё это проверить и в других условиях тоже. Ведь реальная теория не может описывать один частный случай — она должна распространяться на довольно обширную область возможных вариантов.
Но и на этом всё не кончается: даже если эта гипотеза правда даёт сбывающиеся прогнозы на широкой области, всё равно на следующих экспериментах надо ещё проверить, что все альтернативные гипотезы на них не срабатывают. В ином случае окажется, что вы доказали не верность именно вашей гипотезы, а лишь верность довольно обширного множества гипотез, включая вашу.
Заметьте, в пунктах пять и шесть исследователи имели дело именно с таким случаем: полученные ими данные укладывались в несколько совершенно разных гипотез. И для окончательного вывода исследователям следовало экспериментально доказать, что в других случаях одна из гипотез срабатывает, а все остальные — нет. И именно по этой причине она стала бы наиболее вероятным объяснением наблюдаемого и заслужила бы звания «теории». А без этого она не «теория», но «одна из возможных гипотез».
Hold your fire now
Собственно, можно догадаться, какие эмоции я испытываю, читая очередную статью, где исследователи замерили две величины, посчитали корреляцию между ними и уже называют это «открытием» и «построением новой теории». О нет, на данном этапе вы ещё не сделали открытие. Вы получили какой-то намёк и первую порцию данных, которые потом, если вы не бросите это занятие и будете ставить корректные серии экспериментов с корректным же анализом результатов, возможно, приведут к открытию.
Увы, сейчас вся мировая наука медленно, но верно, движется в направлении безудержной генерации «теорий» на ровном месте, что в основном провоцируется специфическим подходом к оценке работы учёного.
Считается, что учёный отчитывается за свою работу строго публикациями в журналах. И что эти публикации должны следовать с определённой плотностью, иначе а-я-яй, плохо работал. При этом журналы имеют тенденцию публиковать те работы, где заявлено о «прорывах», «успехах» и «новых теориях», а вовсе не о «проверили — не работает»
И даже статьи, где измерено что-то полезное, зачастую получают низкий приоритет, если в них не содержится заявлений или хотя бы намёков на тему «мы с первой попытки поняли, как всё устроено».
Естественно, в данном эволюционном процессе преимущество получает стратегия высасывания «открытий» из пальца. Что фактически приводит к отсеву добросовестных учёных в пользу недобросовестных, а также склоняет всех учёных к подтасовке результатов исследований и фабрикации недостоверных выводов.
Метод незатейлив: взяли как можно больше данных, посчитали попарные корреляции всего со всем, нашли ту, которая — пусть даже случайно — «высокая», приписали к ней тот вариант объяснения, который первым пришёл в голову или просто понравился, и вот уже публикация об «открытии».
Даже странно, что всё ещё так мало статей, создаваемых на основании данных с сайта «Ложные корреляции». Давно уже пора построить стройную теорию о том, почему количество выпущенных за год фильмов с Николасом Кейджем так тесно связано с количеством утонувших в этом году в бассейне.
Тут, вон, не только корреляция 66%, но и даже сходство в графиках видно невооружённым глазом.
Кто-то обязательно должен объяснить всё это.
И тем более, объяснить, почему количество потребляемого на душу населения маргарина на 99,26% коррелирует с интенсивностью разводов в Майне.
Геодезия и геоинформатика
УДК 519.2:528.1
О КОРРЕЛЯЦИИ ФУНКЦИЙ СЛУЧАЙНЫХ ОШИБОК ИЗМЕРЕНИЙ
Наталья Борисовна Лесных
Сибирская государственная геодезическая академия, 630108, Россия, г. Новосибирск,
ул. Плахотного, 10, кандидат технических наук, ведущий научный сотрудник, тел. (383)343-18-53
Владимир Евгеньевич Мизин
Сибирская государственная геодезическая академия, 630108, Россия, г. Новосибирск,
ул. Плахотного, 10, кандидат технических наук, старший преподаватель кафедры геодезии, тел. (383)344-36-60, e-mail: ssga221@mail.ru
Исследована корреляция повторных определений координат пунктов полигонометрического хода как функций случайных ошибок измерений.
Ключевые слова: корреляция, координаты, анализ, разности, ошибки, функции.
CORRELATION OF ACCIDENTAL MEASUREMENT ERRORS FUNCTIONS
Natalya B. Lesnykh
Siberian State Academy of Geodesy, 630108, Russia, Novosibirsk, 10 Plakhotnogo St., Ph. D., leading researcher, tel. (383)343-18-53
Vladimir E. Mizin
Siberian State Academy of Geodesy, 630108, Russia, Novosibirsk, 10 Plakhotnogo St., Ph. D., senior lecturer, Department of Geodesy, tel. (383)344-36-60, e-mail: ssga221@mail.ru
The authors investigate correlation of repeated determinations of polygon traverse points coordinates as functions of random measurement errors.
Key words: correlation, coordinates, analysis, differences, errors, functions.
Корреляционная (вероятностная) связь между случайными величинами возникает тогда, когда имеются общие факторы, влияющие на значения этих величин. Показателем тесноты линейной связи между случайными величинами системы X!, Х2, …, Хп служит коэффициент корреляции
Г, j =
д j
a ja j
(1)
где k j =M {[X j -M (Xj )]•[Xj -M (Xj)]} — корреляционный момент пары X, Xj; a j, a j — средние квадратические отклонения Xj и X j. Для независимых (некоррелированных) случайных величин kt , = rz , = 0 .
21
Геодезия и геоинформатика
Случайные, нормально распределенные ошибки измерений А, и А’ некор-релированы (независимы), имеют математическое ожидание M (А)=0 и дисперсию ст2 =М {А-M (А)}2 =М (А2), M (А-А’) = M (А) • M (А’) = 0.
Проверим наличие корреляционной связи для некоторых функций случайных ошибок измерений, содержащих одинаковые коэффициенты при соответствующих ошибках. Рассмотрим систему двух случайных величин, заданную
вектором F —
f ‘j
Ковариационная матрица системы определяется формулой:
KF =M {[ F-M (F)] • [ F-M (F )]т} =M
f» М (f)_
If’ _ М (f ‘)_ (
‘(. fт f ,m)-( M (f )m m (. f r)
О > J О J> J
Для функций f = < а2 А 2 >={а/ Ai} и f = а2 А2 >
ая А я ая Ая
■{aA,}, где
Qi —
постоянные коэффициенты, M {аг Аг } = {аг М (Аг )} = 0; М(f) = М(f’) = 0
является дисперсионной матрицей.
и KF = М
К f) (fm f’ m Гст2 0 ^ CT f 0
fl. f ‘J ■yj J ) 0 ст f’ l f J
Здесь ст2 = М(f • f m), ст2> = М(f’ • f’m), kff’ = M(f • f ‘m)=0 — корреляционный момент пары случайных величин f и f.
Для функций:
f={аА(а) +^А6)} и f={^А^’ + Ь,А’ъ }, (i = 1 2> •••, я); (2)
M(f)={ а1М(А(а))+Ь,М(А{Ь ))}=0, М( f)=0;
( а,А«> + Ь^
kf = М
а„Ая) + Ья АЬЯ) J
(а1Аа(1) +Ь1АЬ(1) … аяА’а(я) + ЬяАЬ(я))
}=0
функции f и f’ некоррелированы.
22
Геодезия и геоинформатика
Для функций накопленных случайных ошибок измерений
A! A’,
V II A1 + A2 V” S II Л. A1+A2 >
A1 + A2 + … + An A1+A2 +…+An
‘ Ai «
M < A1 +A2 • (a1 a1+a2 . .. A1 + A2 + … + An )
KA1 + A2 + An у
(3)
функции f и f’ также некоррелированы, M(f) = 0, M(f) = 0.
Разности повторных определений координат полигонометрического хода содержат информацию о стабильности пунктов геодезической основы при мониторинге инженерного сооружения. Если координаты, вычисленные по результатам независимых повторных измерений, некоррелированы, предельно допустимое значение их разностей можно определить по формуле [1]:
Кред. = * • mx -&■ (4)
На моделях ходов полигонометрии 4-го класса исследована корреляционная связь между координатами пунктов, полученными по результатам повторных, независимых измерений углов и сторон.
Представим разности координат d(x), d(y) как функции их истинных случайных ошибок Ax, Ay, A’x, Ay:
d(x)=x-Х=X + Ax-X-AX = Ax-AX; d(y)=y-y’=Ay-Ay.
Истинные ошибки координат можно получить через истинные ошибки приращений:
A dx =A S)cos a i
(5)
Случайные ошибки дирекционных углов и координат являются функциями накопленных аргументов — случайных ошибок измеренных углов и приращений координат соответственно:
j=1
A x° =IA dx)
j=1
j=1
(6)
23
Геодезия и геоинформатика
Функции (5), (6) аналогичны (2), (3) и теоретически не коррелированны с результатами их повторных определений. Проверим это утверждение экспериментально. Оценка коэффициента корреляции вычисляется по формуле:
[5.x -5.x’]
rx, x’ — — ,
ax ’ax’ (n — 1)
(7)
где 5xt = xi — x, Mx = x = [x]/ n — оценка математического ожидания,
ax=yJ[5×2]/n -1 — оценка среднего квадратического отклонения.
Значимость 7xx>, Ту у устанавливалась с использованием функции z Фишера для доверительной вероятности 0(t) = 0,997, t = 3 [2].
Характеристики ходов полигонометрии и оценки коэффициентов корреляции истинных ошибок координат первого и второго циклов наблюдений представлены в табл. 1.
Таблица 1
Корреляция повторных определений координат
Варианты 1 2 3 4 5
Характери- стики a =170°- 195° s = 300 м, n = 20, op = 2” os = 2 см a = 170-195° s = 500 м, n = 20, op = 2” os = 3 см a = 85-96° s = 300 м, n = 20, op = 2” os = 2 см a = 85-96° s = 300 м, n = 20, op = 2” os = 2 см a = 10-180° s = 300 м, n = 20, op = 2” os = 2см
rx, x’ -0,237 -0,583 -0,379 -0,984 0,963
r 2 — Г1 1,199 0,944 1,127 0,064 0,141
Корреляция — — — + +
ry, у’ -0,993 -0,980 -0,229 -0,288 0,230
r 2 — ri 0,029 0,077 1,203 1,178 1,202
Корреляция + + — — —
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
В четырех случаях из десяти между координатами первого и второго циклов установлено наличие корреляционной связи. Почему некоторые функции (5) оказались коррелированы? Вероятностно-статистический анализ закона распределения [3-5] ошибок приращений координат Л^, Adx>, Л^у, Л^’, выполненный по каждому из пяти вариантов хода, выявил несоответствие распределения коррелированных рядов ошибок нормальному закону.
24
Геодезия и геоинформатика
В частности, критерием равенства средних, статистика которого
|Д-м (Д)|
3 а / 4п ’
(8)
установлено существенное отклонение оценки математического ожидания случайных ошибок приращений координат от нуля, что противоречит теоретическим предпосылкам некоррелированности координат (табл. 2).
Закон распределения
Таблица 2
№ 1 2 4 5
Критерии Д dy Д dy’ Д dy Ady’ Д dx Д dx’ Д dx Д dx’
Д (см) -0,80 0,68 -2,82 2,07 -0,98 0,72 -0,53 -1,27
а (см) 0,70 0,43 1,48 1,50 0,47 0,30 1,40 1,46
t э 5,1 7,1 8,5 6,2 9,3 10,8 1,67 3,89
Рб > tэ) 6 ■ 10-5 9 ■ 10-7 7 ■ 10-8 6 ■ 10-6 2 ■ 10-6 2 ■ 10-9 0,08 9 ■ 10-4
Три свойства ± — — — — — + ±
Знак «-» в табл. 2 означает, что свойства случайных ошибок не выполняются.
В формулах (5), в зависимости от значения дирекционного угла, преобладают слагаемые Дs cos а, Дs sin а или (-s • sin а / р) • Да, (s • cos а / р) • Да. Закон распределения первого слагаемого соответствует закону случайных, нормально распределенных ошибок Дs с математическим ожиданием M (Дs)=0 и оценкой математического ожидания, несущественно отличающейся от нуля. Ошибки дирекционных углов второго слагаемого являются функциями накопленных аргументов — случайных ошибок угловых измерений (6). Подобные функции могут на значительном протяжении сохранять один и тот же знак и вследствие этого, по своим статистическим свойствам не совпадать со свойствами случайных, нормально распределенных ошибок измерений.
Представим эту ситуацию в табл. 3 примерами из варианта 1.
Закон распределения преобладающего слагаемого в формулах ошибок приращений координат определил закон распределения суммы слагаемых. В формулах Дdx преобладает первое слагаемое. Ошибки Adx распределены нормально, как и случайные ошибки Дs, оценка математического ожидания Дdx пренебрегаемо мало отличается от нуля, между результатами повторных определений координат корреляционной связи не установлено.
25
Геодезия и геоинформатика
Таблица 3
Слагаемые формул ошибок приращений координат
а А* Аdx (см) Аdy (см)
Ascosа -(dy / Р»)Аа Д5 sin а (dx / р»)Да
170 0 0,93 -0,256 -0,023 0,045 -0,133
195 1,05 4,878 0,040 1,308 -0,146
170 4,02 0,699 -0,102 -0,123 -0,576
175 6,06 0,936 -0,077 -0,082 -0,878
190 8,85 1,093 0,224 0,193 -1,268
В формулах Ady преобладает, в основном, второе слагаемое. Закон распределения ошибок A dy, как и Да, не является нормальным, среднее арифметическое Ady существенно отличается от нуля, что и привело к значительному увеличению оценки коэффициента корреляции Гу у’.
Появление в полигонометрическом ходе невязок, близких к предельным значениям, свидетельствует о накоплении ошибок одного знака и возможном искажении случайных свойств в рядах истинных ошибок дирекционных углов и координат.
Очевидно, исследование устойчивости пунктов геодезической основы требует комплексного подхода и не может быть ограничено единственно расчетом допустимого значения разности повторных определений координат [2, 6-10].
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Мизин В. Е. Допустимые значения разностей повторных определений координат полигонометрического хода // ГЕО-Сибирь-2011. VII Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). — Новосибирск: СГГА, 2011. Т. 3, ч. 2. — С. 42-45.
2. Мизин В. Е. Корреляционный анализ разностей повторных наблюдений геодезической основы при мониторинге линейных объектов // Изв. вузов. Геодезия и аэрофотосъемка. — 2011. — № 3. — С. 26-28.
3. Лесных Н. Б. Законы распределения случайных величин в геодезии: монография. -Новосибирск: СГГА, 2005. — 128 с.
4. Лесных Н. Б. Объекты статистического анализа в геодезии: монография. — Новосибирск: СГГА, — 2010. — 128 с.
5. Лесных Н. Б., Мизин В. Е. Сравнительная характеристика результатов двух статистических методов анализа разностей повторных измерений // Вестник СГГА. — Новосибирск: СГГА, 2012. — Вып. 1 (17). — С. 41-46.
6. Мизин В. Е. Оценка точности геодезических измерений при мониторинге линейных объектов // ГЕО-Сибирь-2006. Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 24-28 апреля 2006 г.). — Новосибирск: СГГА, 2006. Т. 2, ч. 1. — С. 91-94.
26
Геодезия и геоинформатика
7. Мизин В. Е. Проектирование полигонометрического хода методом моделирования // ГЕО-Сибирь-2010. VI Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2010 г.). — Новосибирск: СГГА, 2010. Т. 1, ч. 1. — С. 123-126.
8. Мизин В. Е. Предрасчет точности координат полигонометрического хода для целей мониторинга земель линейных объектов // ГЕО-Сибирь-2010. VI Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2010 г.). — Новосибирск: СГГА, 2010. Т. 2, ч. 1. — С. 127-130.
9. Мизин В. Е. О систематических ошибках повторных // ГЕО-Сибирь-2011. VII Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). — Новосибирск: СГГА, 2011. Т. 3, ч. 2. — С. 38-41.
10. Лесных Н. Б. Две ошибки проверки гипотезы об отсутствии систематических влияний // ГЕО-Сибирь-2010. VI Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2010 г.). — Новосибирск: СГГА, 2010. Т. 1, ч. 1. — С. 85-90.
Получено 15.06.2013
© Н. Б. Лесных, В. Е. Мизин, 2013
27
Для каждого трейдера важно понимать, что мы работаем с торговыми инструментами, состоящими из пары валют. В отличие от фондового рынка, где, как правило, каждый торговый инструмент это всего лишь одна индивидуальная единица, на Форекс используется измерение стоимости одной валюты в единицах другой. При этом мы не редко можем наблюдать, визуальную схожесть в движении нескольких валютных пар. Это может быть связано с тем, что обе пары могут содержать одну и ту же валюту в обоих случаях. Например, можно говорить о корреляции валютных пар EUR/USD и USD — CHF с отрицательным значением К.
Одним из способов использования корреляции пар в торговле является устранение расхождения инструментов. Например, трейдер выбрал для своей работы две валютные пары, которые коррелируют с К = 0.8. В этом случае, при наблюдении за движением подопытных, человек заметит, что К время от времени меняется, то несколько увеличиваясь, то несколько уменьшаясь. Тем не менее, средние значения коэффициента все равно находятся в диапазоне 0.7<К<0.8.
Как только на рынке наступит ситуация, что К<0.4, например, то это будет означать наличие лишь частичного соответствия в движении обоих инструментов. То есть, при росте одной пары рост другой окажется весьма ограничен. Но, помня о том, что в целом эти инструменты коррелируют с К=0.7 или 0.8, мы можем использовать данный разрыв себе на пользу, открыв позиции в сторону сближения пар.
Нахождение подобных ситуаций и дальнейшее их использование затрудняется непостоянностью значения К. Мы можем не верно толковать новые значения коэффициента, принимая из за ожидаемый нами разрыв, но позже может оказаться, что это новое значение данного коэффициента, которое теперь станет постоянным на определенное время. Существуют специальные корреляционные индикаторы, помогающие трейдерам наблюдать за схождением и расхождением инструментов, а другими словами, за изменениями текущих значений К.
Сложно переоценить значимость коэффициента корреляции в рыночной торговле. Его использование позволяет смотреть на трейдинг более глобально, учитывая движения пар, относительно друг друга. Еще одной областью применения коэффициента стало хеджирование. Желая снизить риски в своей торговле, спекулянты могут проводить хеджирование не только на разных рынках, но и с помощью коррелирующих инструментов. Таким образом, происходит частичное хеджирование.
Для начала разберемся в самой сути такого понятия, как арбитраж. Это несколько логически связанных сделок, направленных на извлечение прибыли из разницы в ценах на одинаковые или связанные активы в одно и то же время на разных рынках (пространственный арбитраж), либо на одном и том же рынке в разные моменты времени (временно́й арбитраж, обычная биржевая спекуляция). Выделяют эквивалентный арбитраж — операции с комбинацией составных или производных активов (опционов, биржевых индексов) и обычных контрактов, когда между теоретически эквивалентными комбинациями на практике возникает разница цен.
Упрощенно арбитраж выглядит следующим образом: торгуются пары или группы инструментов, суммарная стоимость которых должна быть равна определенной величине, исходя из природы инструментов. Например: акции одной и той же компании на различных торговых площадках, группа инструментов входящих в индекс и фьючерс на индекс. При отклонении стоимости корзины от расчетной величины, совершается сделка. Трейдеры-арбитражеры сглаживают дисбаланс цен на родственных» инструментах.
Коэффициент корреляции (Correlation coefficient) — это
В первоначальном виде арбитраж возник на заре развития вторичных (региональных) бирж, когда один итот же актив торговался на разных площадках по разным ценам и с 44 каждым годом разрыв этой цены стремительно сокращался, а вместе с ним скорость арбитражных стратегий и их объем.
Сегодня существует в качестве межбиржевого варианта, когда актив торгуется на биржах разных стран, например на токийской и нью-йоркской, лондонской и франкфуртской. А также на NYSE и NASDAQ в качестве арбитража разных активов, например двух-трех акций из одного сектора.
В основе арбитража лежит такое понятие, как корреляция. корреляция, если простыми словами — это взаимосвязь двух или более событий, т.е. когда происходит одно, то вероятно (статистически подтверждено) и другое. Когда-то корреляции на рынке были невыраженными в моменте, они были растянуты во времени. Вот к примеру, как рассуждают экономисты/аналитики: «Если индекс доллара упадет, цена на нефть должна расти…» или «Если индекс SNP упадет, цена на золото должна вырасти или наоборот…», ну это как бы простые причинно-следственные связи. Однако совершенно очевидно, что если все так просто, то все бы с легкостью зарабатывали, чего, как мы все прекрасно знаем, не происходит. Пример самой жесткой корреляции — это пары типа Евро/Доллар. Они намертво связаны между собой. Малейшее изменение цены одного приводит к мгновенному изменению цены другого. Тут, понятно, корреляция обратная и речь идет о торгуемых инструментах, например, на СМЕ. И данная корреляция действительна в обе стороны. Есть же, например, бумаги, которые сами «ничего не решают», но есть у них «старший», который и скажет, куда им «идти». А есть ситуации, в которых таких «старших» два и более, вот тут совсем все интересно становится.
Когда речь заходит о корреляциях, в том смысле, в каком я их понимаю, неизбежно возникает вопрос: «а кто главный (ведущий)?». Для этого введем понятие «Поводырь» — это будет любой торгуемый инструмент, изменение цены которого приведет к какой-либо реакции того, за которым мы наблюдаем (торгуем).
Основные поводыри для Американского фондового рынка следующие (в порядке убывания силы глобального влияния):
1. Фьючерсный контракт на индекс SNP 500 — главный поводырь, самый влиятельный, нет ни одного ликвидного инструмента, на который бы не оказало влияние изменение цены фьючерсного контракта хотя бы на тик, реакция есть всегда. Вопрос о первичности (кто за кем «ходит»), индекс или фьючерс, всегда рождает много споров, но нас, спекулянтов, скальперов, волнует только одно — кто из них быстрее. Я могу ответственно заявить, что фьючерсный контракт — быстрее, изменчивее (в разы) и главнее в данном контексте.
2. Фьючерс на нефть марки Light Sweet — углеводороды, что тут еще сказать. Сильное влияние оказывает на некоторые сектора, на отдельные индустрии, связанные с нефтедобычей и нефтепереработкой, а также на те отрасли, где существенная статья издержек — топливо и ГСМ, например авиакомпании. Сам актив несколько зависим от Индекса доллара.
3. Фьючерсный контракт на золото (и другие драг. металлы) — Au рулит по-прежнему, ибо мировое «золотое плечо» уже вылезло за все допустимые рамки, не дам источник, но цитату приведу: «В мире обещания продать золото, больше в 100 раз, чем самого золота», как-то так. Т.е. это и мерило ценности некоторых валют, и надежный (однако!) для многих актив, и инструмент хеджирования рисков и еще много чего полезного делает. Также как и нефть, оказывает серьезное влияние на компании, занимающиеся золотодобычей, переработкой, реализацией и прочим. Сам по себе поводырь зависим (в моменте) от Индекса доллара.
4. Индекс доллара — с появлением евро все сильнее стал подвержен колебаниям, связанным с проблемами в Еврозоне, также изменчив за счет спекулятивных действий в торгуемой валютной паре евро/доллар. Сам зависим от макроэкономической статистики, стоимости облигаций (и наоборот тоже, тут уже сложный аналитический расклад, который данной статьи никак не касается, тем более, я не аналитик и тем более, не экономист, а спекулянт. Оказывает влияние на многие товарные фьючерсы, расчет по которым ведется в долларах Соединенных Штатов.
Поводырем вторичным (а иногда и первичным) может также являться акция, которая в данный момент самая сильная/слабая в секторе/индустрии, которая сама по себе является более весомой в индексе из всего сектора. Например, если $C (Citigroup) измениться резко в цене на полпроцента, это мгновенно скажется на остальных акциях, связанных с банковской деятельностью и с финансами, не так сильно отразиться на $JPM и $BAC, но точно «дернет» $BBT и $PNC, к примеру, а уж $FAZ и $FAS отреагируют как следует, по взрослому, с резким изменением котировок и объемом. А вот обратное не будет иметь такого влияния. Если $PNC или какой-нибудь банк Испании или Ирландии не обрушиться на пару процентов, то никто из «толстых» не заметит, однако по цепочке может привести к некоей корректировке на графике. Скажем так, $PNC также входит в состав портфеля, торгуемого в виде ETF $FAZ ($FAS), так вот сильное его ($PNC) изменение приведет к неминуемому (но небольшому) изменению цены индекса, что, закономерно, приведет к корректировке даже $C и $BAC, первого на несколько центов, а второго, возможно, ни на сколько, разве стакан уплотниться в «сильную» сторону. Это один из вариантов, комбинаций может быть очень много. На графике видно, как акции вторичные стоят в рэйндже, пока сильнейшие представители сектора «смотрят» в разные стороны, и как послушно они «идут» за всеми, если направление сильных совпадает:
На графике изображены: SPY — SPDR S&P 500 (белая линия), C — Citigroup, Inc., JPM — JP Morganand Co., BAC — Bank of America Corp Corporation, GS — The Goldman Sachs Group, Inc., BBT — BB&T Corporation, PNC — PNC Financial Services Group Inc.
Теперь давайте рассмотрим какой-нибудь самый необычный пример. Вот Авиакомпании. Например $UAL или $DAL или $LCC, не входят в состав индекса SNP 500 и тем более DJIA, однако довольно объемны, имеют высокую капитализацию, в целом привязаны к рынку, как таковому, но главное — зависят от цен на топливо. И не нужно рассказывать, что у них все поставки фьючерсные, с фиксированной ценой на пару лет вперед и прочее, это все так, но откройте их график минутный и понаблюдайте, что происходит, когда нефть очень резко изменяется в цене. А теперь добавьте сюда индекс доллара, который влияет на них самих, т.к. Цены их услуг — они в долларахи сама нефть зависит от него (доллара), ну и SNP 500, который частенько идет в противоход нефти… Вот их (акции авиакомпаний) разрывает в разные стороны. А еще помню день был, когда у $LCC отчет случился и нефть с рынком в разные стороны… Вот остальных трепало! График выглядел интересно. Вот пример за эту неделю, $LCC валится на растущей черного золота и растущем фьючерсе, и отрастает на падающей черного золота (тикер $USO):
На графике изображены: SPY — SPDR S&P 500 (белая линия), USO — United States Oil, UAL — United Continental Holdings, Inc., LCC — US Airways Group, Inc., DAL — Delta Air Lines Inc.
Также, для дальнейшего понимания написанного мною, потребуется ввести еще один термин — «Драйвер», под которым понимается некое событие, которое сильно влияет на поведение торгуемого актива, либо, что немаловажно, поводыря, за которым мы также наблюдаем, это может быть новость в компании, отчет, понижение/повышение рейтинга или новость, касающаяся сектора в целом, макроэкономическая статистика, изменение ставки вложения инвистиций и другие. Т.е. драйверы глобальные влияют на фьючерсные контракты (поводыри, описанные выше), а те, в свою очередь, на торгуемые инструменты и т.д.
Теперь вопрос: почему акции так одинаково ходят и кто за всем этим стоит? Да все, особенно скальперы, роботы-скальперы, люди-скальперы. Роботы-арбитражеры в первую очередь, а также алгоритмы, котирующие акцию (читай маркетмейеры). Ведь иначе невозможно было бы такую массу акций заставить двигаться более менее одинаково, речь, понятно, внутри дня. Потому что, если мы взглянем на большие таймфреймы, то выясниться, что многие сектора живут своей отдельной жизнью. Вот например, график месячный, с 2000 года:
На нем изображены: XLK — Technology Select Sector SPDR, XLF — Financial Select Sector SPDR, XLP — customer Staples Select Sector SPDR, XLE — energy Select Sector SPDR, XLV — Health Care Select Sector SPDR, XLI — Industrial Select Sector SPDR, XLB — Materials Select Sector SPDR, XLU — Utilities Select Sector SPDR, XLY — customer Discret Select Sector SPDR, SPY — SPDR S&P 500 (белая линия).
Ютилитис какие слабенькие. Интересно, они рванут вверх, за ростом фьючерсного контракта или на малейшем его откате шлёпнутся еще ниже? Разброс относительно $SPY приличный. А вот, что на меньших масштабах времени, дневка, за 2012 год:
Действующие лица те же. В общем есть некое понимание, что графики похожи, но одни сильнее рынка в целом, а другие слабее, в абсолютном выражении, при расчете на начало года. Это все глобально, на год, а вот на месяц:
Действующие лица те же. Меня же в торговле интересует арбитраж внутридневной, график — от пятиминутного до минутного:
Или, например, технологический сектор в пятницу (14.09.2012), смотрите, как на откатах фьючерсного контракта вниз они «валяться» и «стоят» на его росте, между прочим — это и есть входы в шорт:
На графике изображены: SPY — SPDR S&P 500 (белая линия), T — AT&T, Inc., VZ — Verizon Communications Inc., XLK — Technology Select Sector SPDR.
Это, что касательно фьючерсного контракта SNP 500 (на графиках, для моего удобства показан не сам фьючерс, а ETF на индекс SNP 500, учитывая, что график — линия, различий нет совсем). А вот пример акций нефтяной индустрии, в сравнении с черным золотом:
На графике изображены: USO — United States Oil, XOM — Exxon Mobil Corporation, SLB — Schlumberger Limited, CVX — Chevron. Или, например, «золотые» акции, в сравнении, понятно, с золотом:
На графике изображены: GLD — SPDR gold Shares, NEM — Newmont mining industry Corp., KGC — Kinross gold Corporation, ABX — Barrick gold Corporation.
Однако, график — одно, а стакан с лентой (LEVEL II + Time & sales) — совсем другое дело (кстати, именно это и позволяет торговать $SPY, опираясь на фьючерс). Показать в картинках, что происходит и какая реакция — сложно, потому распишу немного словами. Что можем видеть на ведомых, если на ведущих есть большое движение? В первую очередь — изменение котировки без сделок, оно и понятно, акции скоррелированы, а торговать-то некому, ибо акции не первого эшелона, но машинки-котировщики будут исправно двигать биды с оферами, в след за «старшим» братом, держа при этом некий спред, обычно больше 3-4 ц. Если же движение общее, не только на сильных акциях, а на всем рынке в целом, то может произойти сильное движение, с объемом, и с еще большим расширением спреда в противоположную от него (движения) сторону. Например, нефть ($USO) улетела вверх на полпроцента за секунду, в $SLB будет расширен спред в сторону оферов (ASK), чтобы продать повыше, а потом закрыться пониже, поднимая биды (BID). Это один из десятков сценариев, понятно, что всегда есть вариации, но уловить общее можно, если тщательно понаблюдать и проанализировать поведение акций и их поводырей.
Стиль торговли таким образом называется «арбитраж», торгуется, как правило, минимум два инструмента, причем часто в разные стороны, но можно торговать один, рассматривая другие инструменты, как поводырей. Стиль сегодня очень роботизирован, но и для «мануальных скальперов» еще есть место.
Сложим все варианты арбитража в одну табличку и определим четыре варианта действий (простым языком, не пинайте, но так понятно всем будет): что отросло и главное — продавать, а что недоросло — покупать; что упало и главное — покупать, а что недоупало — продавать; что отросло и главное — не трогать, а что недоросло — продавать; что упало и главное — не трогать, а что недоупало — покупать.
Имея ввиду торговлю одного инструмента, чаще поступают так, торгуя по тренду сектора (индустрии): что не главное и отросло сильно — продавать, в случае, когда главное — «стоит и смотрит» вниз (было на вебинаре, кто помнит, $TCK); что не главное и упало сильно — покупать, в случае, когда главное — «стоит и смотрит» вверх.
Еще более кратко сам процесс можно описать так: определяем глобально (по секторам), кто сильный, кто слабый — по дневке; смотрим внутри сектора (на дневках) между акциями тоже самое; смотрим внутри дня на акции (по тренду сектора), опираясь на фьючерсный контракт (+ другие поводыри).
Коэффициент корреляции (Correlation coefficient) — это
Теперь, как определить «главного» в секторе/индустрии. Те, кто первый в столбце, те и рулят, как правило. НО!!! В случае, если нет глобальных новостей по сектору или если нет отчетов у разных акций из этого сектора. Т.е. их главенство имеет место быть в самый скучный понедельник, а не в день статистики, запасов газа, безработицы да еще с отчетом старших акций.
Вычисление коэффициента корреляции портфеля
Итак, перейдем к вычислению средней доходности, дисперсии и стандартного отклонения для портфеля акций, состоящего на 60% из акций А и на 40% из акций В. Мы предполагаем, что доходность по каждой из акций А и В — это случайные величины Rа и Rв. Среднее значение доходности акции А равно 10%, со стандартным отклонением 8,66%. Среднее значение доходности акции В равно 15%, со стандартным отклонением 12%.
Коэффициент корреляции (Correlation coefficient) — это
Теперь нас интересует, каково будет среднее значение доходности портфеля и стандартное отклонение для портфеля. Вопрос средней доходности портфеля решается просто. А вот стандартное отклонение — показатель уровня изменчивости доходности портфеля, не отражает средней изменчивости доходности его компонентов (акций). Причина в том, что диверсификация снижает изменчивость, так как цены различных акций изменяются неодинаково. Во многих случаях снижение стоимости одной акции компенсируется ростом цены на другую.
Ожидаемая доходность нашего портфеля равна средневзвешенной ожидаемых значений доходностей отдельных акций:
Для того, чтобы найти дисперсию и стандартное отклонение доходности портфеля, мы должны знать значения ковариации акций А и В. Ковариация служит для измерения степени совместной изменчивости двух акций. Общая формула вычисления ковариации:
Из формулы видно, что ковариация любой акции с ней самой равна ее дисперсии. В задачах, значение ковариации двух активов будет дано. Или, вместо нее будет дано значение коэффициента корреляции — безразмерной величины, которая стандартизует ковариацию для облегчения сравнения, и принимает значения от -1 до 1. Пусть нам дано, что коэффициент корреляции акций А и В равен 0,7. Формула коэффициента корреляции:
В большинстве случаев, изменение акций происходит в одном направлении. В этом случае коэффициент корреляции и, соответственно, ковариация, положительны. Если акции изменяются соверженно не связанно, тогда коэффициент корреляции и ковариация равны нулю. Если акции изменяются в противоположных направляения — коэффициент корреляции и ковариация отрицательны. Для нахождения дисперсии портфеля, нам надо заполнить матрицу:
Эта матрица очень похожа на матрицу ковариаций. Заполнив матрицу, надо просто сложить полученные в ней величины и найдем дисперсию портфеля:
Вычислим дисперсию портфеля:
Стандартное отклонение равно квадратному корню из дисперсии, то есть:
Легко подсчитать, что только в том случае, если коэффициент корреляции двух акций равен +1, то стандартное отклонение портфеля равно средневзвешенному стандартных отклонений доходности отдельных акций:
Если же коэффициент корреляции равен -1, то стандартное отклонение портфеля равно:
и можно было бы добиться, изменяя пропорции X1 и X2 акций в портфеле, чтобы стандартное отклонение портфеля было равно нулю. К сожалению, в реальности, отрицательная корреляция акций практически не встречается.
Коэффициент корреляции (Correlation coefficient) — это
Применение линейного коэффициента корреляции в трейдинге
Коллеги, добрый день! В настоящей статье я хочу предложить вашему вниманию небольшое исследование, посвященное одному из статистических показателей — линейному коэффициенту корреляции. А также поделюсь некоторыми соображениями по его применению в трейдинге на примере акций Лукойла.
Коэффициент корреляции (Correlation coefficient) — это
Для начала позвольте небольшой экскурс в историю возникновения показателя корреляции (да возблагодарим Википедию!): Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение либо коэффициент корреляции. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
Линейный коэффициент корреляции (далее ЛКК) (коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле:
Коэффициент корреляции изменяется в пределах [-1…+1]. Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Итак, коллеги, ЛКК определяет: во-первых, наличие связи между двумя потоками данных, во-вторых, силу этой связи (сила связи определяется приближением абсолютного значения ЛКК к единице), в-третьих, направление этой связи (прямая — ЛКК больше единицы или обратная — ЛКК меньше единицы). Важным и необходимым условием для расчета ЛКК является наличие двух одинаковых по количеству данных потоков данных. Так же в общем случае считается, что значения ЛКК можно считать достоверным, если в расчете участвует поток из более, чем 30 пар данных.
Коэффициент корреляции (Correlation coefficient) — это
В Excel расчет значения ЛКК реализован через функцию «КОРРЕЛ()». Пример наличия корреляции: Положительная корреляция: температура окружающего воздуха и продажи летней одежды. Чем теплее на улице, тем больше покупаем летних вещей. Рост температуры — рост продаж. Отрицательная корреляция: та же самая температура окружающего воздуха, но продажи уже зимней одежды. Чем холоднее на улице, тем больше покупаем зимних теплых вещей. Снижение температуры — рост продаж.
Примеры применения ЛКК в трейдинге. Области применения ЛКК в трейдинге достаточно широки. Например, долго считалось, что при падении фондовых рынков в целом растет спрос на золото. То есть между динамикой фондовых рынков и динамикой цен на золото существует обратная корреляционная зависимость. Другой пример. Рост котировок нефти и рост рынков, вес «нефтянки» в которых высок и является значимым. К таким рынкам относится и фондовый рынок России. Но в последние несколько лет, а именно в основном начиная с 2007 года, такие зависимости явно изменились. И либо сильно ослабли, либо исчезли совсем.
У приведенных выше примеров есть одна общая особенность: они построены строго на двух потоках данных, как того и требует формула расчета ЛКК. Тем не менее, в одной из книг, посвященных теории управления капиталом (а именно, Р.Винс «Математика управления капиталом») я нашел интересный подход к построению ЛКК на массиве, состоящем только из одного потока данных. Это может быть, например, непрерывный поток исходов в системных сделках или поток цен какой-то одной акции. О таком методе построения ЛКК ниже.
Коэффициент корреляции (Correlation coefficient) — это
Торговая стратегия, построенная на коэффициенте корреляции
Итак, давайте исследуем, например, поток цен на акции Лукойла (LKOH). Составим поток из недельных свечей. Мне удалось найти архив, начиная с 01.01.2001 и по сей день, то есть поток из почти 600 недельных свечей за десять с половиной лет. Исследовать будем не свечи в целом, а, например, максимальные цены в каждой свечей. Таким образом, перед нами непрерывный поток из 600 данных — максимальные цены в каждой торговой неделе, начиная с 01 января 2001 года. Кроме этих данных, пока никакие другие данные нам не нужны.
На рисунке показана динамика максимальных недельных цен в акциях LKOH. Расчет ЛКК должен дать ответы на вопросы: Есть ли зависимость между максимальными ценами двух любых соседних недель. Если зависимость есть, то какова ее направленность? Коллеги, если упростить, то вопрос можно сформулировать так: Если на истекшей неделе Лукойл обновил свой недельный максимум по сравнению с предыдущей неделей, то можем ли мы ожидать продолжения роста и на будущей неделе? Для расчета ЛКК поток данных требует некоторой трансформации. Составим таблицу:
В таблице на рисунке в последнем столбце, построенном на основе данных столбца «High цена», логика расчета следующая: если максимум текущей недели выше, чем максимум предыдущей недели, то в ячейке стоит значение 1. В противном случае значение равно 0. Таким образом, поток цен преобразован в поток единиц и нулей. Далее произведем расчет ЛКК на основе данных столбца «Обновление High цены». Поскольку для расчета ЛКК необходимо два потока данных, то сделаем следующее:
Как видно из рисунка, поток 2 «сдвинут» относительно потока 1 на один период. Таким образом, из одного потока данных получено два. И теперь смысл расчета ЛКК заключается в выяснении связи между двумя соседними значениями выборки. В нашем случае — максимальными ценами соседних недель (текущей и предыдущей). Теперь собственно по расчету ЛКК. Расчет произведем двумя способами: Охватим весь период выборки (600 недель).
Начиная с 30й недели выборки (август 2001 года) для каждой недели рассчитаем значение ЛКК по последним 30 неделям. То есть для каждой недели рассчитаем т.н. «скользящее» значение ЛКК с периодом n=30 (по аналогии со скользящей средней), поскольку при n>30 в общем случае значение ЛКК считается значимым. Результаты расчетов отражены на рисунке:
Выводы по рисунка: На протяжении всего периода выборки у акций Лукойла наблюдается неярко выраженная положительная корреляция между максимальными ценами соседних недель (красная линия графика с ЛКК = +0,1). То есть факт обновления максимальной цены на текущей неделе по сравнению с предыдущей позволяет сделать предположение о том, что на следующей неделе в сравнении с текущей вероятность обновления максимума выше вероятности НЕобновления максимума.
Коэффициент корреляции (Correlation coefficient) — это
ЛКК, построенное по последним 30 неделям (синяя линия на графике), изменяется в диапазоне от -0,35 (сильная отрицательная корреляция) до +0,6 (очень сильная положительная корреляция). Самый продолжительный период, в течение которого корреляция между недельными максимумами была положительная — это период с мая 2004 года до августа 2007 года. В этот период обновление максимумов на прошлой неделе в большинстве случаев приводило к обновлению максимумов в течение текущей недели. Именно в этот период акции Лукойла агрессивно росли.
Самый продолжительный период, в течение которого корреляция между недельными максимумами была отрицательная — это период с августа 2007 года по июль 2011 года. В этот период недельной обновление максимумов на прошлой неделе в большинстве случаев не приводило к обновлению максимумов в течение текущей недели. И наоборот, НЕобновление недельных максимумов в течение текущей недели в большинстве случае приводило к росту на следующей неделе. В этот период акции Лукойла «запилило» от максимумов весной 2008 года до низов в июле 2009 года.
В точках, где синяя линия находится выше красной, корреляция между недельными максимумами выше средней за период и имеет прямую направленность. В таких точках при обновлении недельных максимумов на текущей неделе наиболее вероятно обновление максимумов в течение следующей недели. В точках, где синяя линия находится ниже красной, корреляция между недельными максимумами ниже средней за период и имеет в основном обратную направленность. В таких точках, в отличие от ситуации п.5, наиболее вероятно обновление максимумов в течение следующей недели при НЕобновлении недельных максимумов текущей недели.
Коллеги, на основании последних двух выводов у меня сформировалась идея тестирования стратегии, построенной на принципах такого парного корреляционного эффекта.
Коэффициент корреляции (Correlation coefficient) — это
Торговля ациями по коэффициенту корреляции
Стратегия, построенная на принципах автокорреляции. Общее описание стратегии. Принципы стратегии: тестируемый инструмент — акции Лукойла (LKOH) на недельном ТФ за период с 01.01.2001 по 31.07.2012; типы совершаемых сделок — исключительно Long; время удержания позиции — вход на Open недельной свечи, выход на Close этой же свечи. Таким образом, удержание позиции строго в течение торговой недели без ухода в бумагах на выходные; внешние факторы — цены на нефть, мировые новости, динамика западных рынков и проч. — не учитываются; внутренние факторы — внутрикорпоративные новости, дивидендные отсечки и проч. — не учитываются.
Принципы формирования сигналов: Методом тестирования определяется некое критическое скользящее значение линейного коэффициента корреляции (далее — ЛККкр) по 30 периодам. Покупка Вариант 1. Если текущее значение ЛКК ВЫШЕ критического значения и на текущей неделе ПРОИЗОШЛО обновление максимума по сравнению с прошлой неделей, то на Open следующей недели происходит покупка. Срок удержания позиции — не позднее Close недели открытия позиции.
Покупка Вариант 2. Если текущее значение ЛКК НИЖЕ критического значения и на текущей неделе НЕ ПРОИЗОШЛО обновление максимума по сравнению с прошлой неделей, то на Open следующей недели происходит покупка. Срок удержания позиции — не позднее Close недели открытия позиции. Во всех остальных случаях — вне позиции (cash). Таким образом, для принятия решения о входе/невходе в позицию необходима информация о максимальных ценах последних 30ти недель. И ничего более сверх этого.
Коэффициент корреляции (Correlation coefficient) — это
Само решение принимается в промежутке между закрытием торговой недели и открытием следующей торговой недели. В случае формирования торгового сигнала трейдеру необходимо находиться в рынке утром первого дня торговой недели для открытия позиции и вечером последнего дня торговой недели для выхода из бумаг. Для тестирования такой стратегии вполне хватило возможностей Excel. У недельного Лукойла критическим значением ЛКК оказалось значение 0,15. Приведу пару примеров для иллюстрации:
Пример 1.
Сигнал от 25.06.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1855 (>0,15) и обновлен максимум предыдущей недели (1805 руб. > 1765 руб.). На основании этого на Open свечи 02.07.12 совершена покупка по 1804 руб. Позиция закрыта на Close свечи 02.07.12, то есть 06.07.12, по цене 1825 руб. Рентабельность сделки составила +1,2% при периоде удержания позиции 5 сессий.
Сигнал от 02.07.12. В данном случае так же выполнены оба условия покупки: ЛККкр=0,2472 (>0,15) и обновлен максимум предыдущей недели (1857 руб. > 1805 руб.). На основании этого на Open свечи 09.07.12 совершена покупка по 1826 руб. Позиция закрыта на Close свечи 09.07.12, то есть 13.07.12, по цене 1818 руб. Рентабельность сделки составила -0,4% при периоде удержания позиции 5 сессий.
Пример 2.
Сигнал от 07.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1098 (<0,15) и НЕ обновлен максимум предыдущей недели (1700 руб. < 1802 руб.). На основании этого на Open свечи 14.05.12 совершена покупка по 1684 руб. Позиция закрыта на Close свечи 14.05.12, то есть 18.05.12, по цене 1594 руб. Рентабельность сделки составила -5,4% при периоде удержания позиции 5 сессий.
Сигнал от 14.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1258 (<0,15) и НЕ обновлен максимум предыдущей недели (1684 руб. < 1700 руб.). На основании этого на Open свечи 21.05.12 совершена покупка по 1602 руб. Позиция закрыта на Close свечи 21.05.12, то есть 25.05.12, по цене 1639 руб. Рентабельность сделки составила +2,3% при периоде удержания позиции 5 сессий.
Коэффициент корреляции (Correlation coefficient) — это
Сигнал от 21.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1336 (<0,15) и НЕ обновлен максимум предыдущей недели (1602 руб. < 1684 руб.). На основании этого на Open свечи 28.05.12 совершена покупка по 1647 руб. Позиция закрыта на Close свечи 28.05.12, то есть 01.06.12, по цене 1742 руб. Рентабельность сделки составила +5,8% при периоде удержания позиции 5 сессий.
Back-testing стратегии. В данном разделе приведу результаты тестирования стратегии в сравнении со стратегией «Buy&Hold» (B&H).
На рисунке показана динамика дохода тестируемой стратегии в сравнении с принципом B&H. За точку отчета (0%) принята цена акций Лукойла в начале января 2001 года (270 руб.). Как видно, принцип B&H опережал стратегию в течение 2001-2008 гг. Падение ранка в 2008 году сравняло результаты обоих стратегий до уровня примерно +200% к старту. Затем, начиная с 2009 года, обе стратегии показали примерно одинаковые результаты и на сегодня корреляционная стратегия незначительно опережает по доходности принцип B&H.
Как видно из профилей графиков, волатильность (риск) принципа B&H гораздо выше волатильности тестируемой стратегии. Размер среднегодовой доходности тестируемой стратегии составляет 20% годовых на всем периоде тестирования.
Риск-менеджмент, основанный на коэффициенте корреляции
Покупка по Варианту 1 (ЛККкр >0,15 + новый максимум)
Из 600 недель тестового периода сигналы по Варианту 1 возникли в 109 случаях (19% потока или каждая пятая неделя). Из 109 сигналов 74 отработали в плюс (68%, или два из трех сигналов). Средний результат положительного исхода равен по модулю среднему результату отрицательного исхода (38 руб./акция) Общий положительный результат потока сигналов сформирован за счет превышения в 2 раза количества положительных исходов над отрицательными исходами.
Коэффициент корреляции (Correlation coefficient) — это
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +26 руб./акция, Размер ожидаемого убытка -13 руб./акция, Общий ожидаемый результат +13 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 24 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-11 руб.;+38 руб.], Максимальная серия подряд убыточных сигналов составила 2 сигнала с максимальным риском не более 178 руб./акция. В нынешних ценах это около 9% торгового депозита.
Покупка по Варианту 2 (ЛККкр <0,15 + нет нового максимума)
Фактически покупки по варианту 2 — это покупки против падения рынка. Поэтому показатели риска и волатильности выше, нежели по варианту 1. Из 600 недель тестового периода сигналы по Варианту 2 возникли в 190 случаях (33% потокаили каждая третья неделя). Из 190 сигналов 91 отработали в плюс (48% или половина сигналов). Средний результат положительного исхода равен +66 руб./акция, а отрицательного исхода -50 руб./акция. Общий положительный результат потока сигналов сформирован за счет превышения размера средней прибыли над средним убытком.
Коэффициент корреляции (Correlation coefficient) — это
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +32 руб./акция, Размер ожидаемого убытка -26 руб./акция, Общий ожидаемый результат +6 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 49 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-44 руб.;+55 руб.], Максимальная серия подряд убыточных сигналов составила 6 сигналов с максимальным риском 187 руб./акция. В нынешних ценах это около 10% торгового депозита. Стратегия в целом:
Из 600 недель тестового периода сигналы по стратегии в целом возникли в 299 случаях (53% потока или каждая вторая неделя). Из 299 сигналов 165 отработали в плюс (55% или более половины сигналов). Средний результат положительного исхода равен +53 руб./акция, а отрицательного исхода -47 руб./акция. Общий положительный результат потока сигналов сформирован как за счет превышения количества положительных исходов над отрицательными исходами, так и за счет превышения размера средней прибыли над средним убытком.
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +29 руб./акция, Размер ожидаемого убытка -21 руб./акция, Общий ожидаемый результат +8 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 55 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-47 руб.;+63 руб.], Максимальная серия подряд убыточных сигналов составила 6 сигналов с максимальным риском 187 руб./акция. В нынешних ценах это около 10% торгового депозита при доходности 20% годовых.
В целом стратегия показала неплохой тренд-следящий результат, а так же оказалась достаточно устойчива в условиях падения 2008 года. Особенно, если учесть усилия трейдера по следованию сигналам. Коллеги, за сим пока все по описанию линейной корреляции и ее применении в трейдинге.
Коэффициент корреляции валютных пар
Рассмотрим такое явление, как межвалютная корреляция на Форексе. Данная методика может существенно повысить понимание рыночных процессов, а также улучшить качество ваших краткосрочных и среднесрочных прогнозов. Существует две разновидности межвалютной корреляции, которые могут помочь в работе трейдера. Рассмотрим подробнее.
Коэффициент корреляции (Correlation coefficient) — это
Корреляция — это статистический термин, означающий наличие взаимосвязанных тенденций изменений между двумя рядами данных. В нашем случае Валютная корреляция — это взаимосвязь между историческими данными курсов одной валютной пары. Или изменения курса одной пары могут быть взаимосвязанными с изменениями другой пары. Данная взаимосвязь чаще всего имеет фундаментальное экономическое обоснование и уходит корнями в особенности всемирного хозяйства. Проще говоря, есть две валютных пары: A/B и C/D. Если между ними есть корреляция, при росте курса A/B может стабильно наблюдаться или рост кусра C/D (тогда это прямая корреляция) или его падение (тогда корреляция буде обратной).
Выше мы говорили о двух разновидностях. Это скользящая и прямая корреляция. Прямая корреляция валютных пар — явление, полезное для повышения точности прогнозов. Даже торгуя на одном инструменте, вы можете повысить точность прогнозирования, применяя анализ нескольких валютных пар. Вернемся к нашим A/B и C/D, допустим, вы торгуете инструментом A/B. Известно, что эти валютные пары в прямой корреляции, то есть вверх и вниз идут синхронно. Ваш технический анализ показал, что пара A/B должна падать. Соответственно, если теханализ пары C/D говорит об обратном, есть повод усомниться в достоверности сигнала. Если же всё совпало, — вы можете с большей уверенностью открывать позицию. Получается, зная взаимосвязи, можно уменьшить количество случайных сигналов. Однако нужно помнить, что корреляционный анализ работает на относительно больших масштабах (в лучшем случае на часовых или получасовых графиках). Если ваша торговая стратегия базируется на «минутках», эти данные могут только помешать.
Следующий вид корреляции — скользящая. Суть в том, что взаимосвязь проявляется на сдвинутом по временной шкале наборе данных. То есть изменение курса пары A/B сейчас является предвестником изменения пары C/D в будущем. Если собрать информацию, достаточно детальную для формирования торговой стратегии, наличие таких корреляций может очень существенно повысить точность. Фактически, у вас появляется инструмент базового прогнозирования курса.
Как анализировать корреляцию?
Чтобы отыскать корреляционную связь, можно пользоваться существующими утилитами из Интернета (которые не сложно найти в Гугле по запросу «корреляция валют форекс») или делать всё руками, в старом добром экселе. Там есть такая замечательная функция КОРРЕЛ, которая показывает корреляцию двух выбранных множеств данных. Берем курсы нескольких инструментов, копируем исторические данные в Эксель и ищем корреляцию. Чтобы искать прямую корреляцию, необходимо выделять два совпадающих по временному промежутку набора данных. Чтобы искать скользящую взаимосвязь, сдвигаем множество вправо или влево на несколько периодов. Корреляция более 0.5 свидетельствует о прямой взаимосвязи, менее 0.5 — об обратной взаимосвязи, в пределах от -0.5 до 0.5 — об отсутствии взаимосвязи. Эти границы более чем условны, следует проверять их на практике…
Коэффициент корреляции (Correlation coefficient) — это
Для того чтобы легче было понять взаимосвязи и соотношение с числом коэффициента корреляции я подготовил рисунки, которые наглядно показывают коэффициент и визуальное сходство двух рядов. В качестве примера взяты рад косинуса и зашумлённый ряд косинусоиды, от амплитуды зашумления зависит коэффициент корреляции:
А здесь пример обратной корреляции валют. Как видим когда одна расчёт другая падает! Как EUR/USD и USD — CHF:
Текущая корреляция наиболее популярных валютных пар. Нужно понимать, что корреляция между валютами не является постоянной, рынок постоянно меняется. Приведенные здесь данные являются примерными, точную информацию нужно рассчитывать самостоятельно. Рассмотрим, как коррелирует с другими инструментами наиболее популярный среди трейдеров инструмент EUR/USD: прямая корреляция с: AUD — USD, BP/USD, NZD — USD; обратная корреляция с: USD-JPY, USD / CHF, USD — CAD.
Еще один любимый нашими трейдерами инструмент — «йенадоллар», USD/JPY. Взгялем на него: прямая: Доллар / Франк, USD / CAD; обратная: EUR/USD, AUS/USD,GBP/USD,NZD/USD. Что касается скользящей корреляции, ловить ее довольно сложно. К примеру, часто цена на золото опережает или немного отстает от GBP — USD. Но такую взаимосвязь нужно рассчитывать чуть ли не для каждого отдельного торгового дня.
Изменение коэффициента корреляции ценовых графиков
В качестве примера корреляции двух пар с положительным К, можно вспомнить о EUR/USD и EUR / JPY. В обоих случаях мы покупаем EUR и продаем вторую валюту. Некоторые пары движутся относительно друг друга, но со временем К может меняться. Например, чтобы определить для своей работы две коррелирующие между собой валютные пары, достаточно найти такую из всего ассортимента, предоставляемого ДЦ, которая бы имела очень низкую волатильность. В 2012 году в качестве такого инструмента вполне могла бы выступать EUR/CHF. Не каждый день ширина ее движения на рынке превышала бы 30 пунктов, что можно считать малой величиной, относительно аналогичных показателей других пар.
Данную валютную пару можно без труда разложить на две пары, используя для этого ту валюту, которая “разбавит” выбранный нами инструмент. Для этого мы берем USD, который позволит представить нам EUR/CHF, как EUR/USD*USD/CHF. Действительно, если перемножить две новых долларовых пары, то в результате мы вновь получаем исследуемую нами EUR/CHF. Данное преобразование говорит о том, что обе пары будут коррелировать между собой, так как их произведение будет демонстрировать значения пары EUR/CHF, а они относительно малы, о чем говорили в самом начале примера.
Коэффициент корреляции (Correlation coefficient) — это
Для уверенной торговли необходимо иметь четкое представление не только об особенностях отдельных инструментов торговли, но и об их взаимодействии друг с другом. Существуют целые торговые стратегии, построенные с использованием К. Могут применяться даже наложения одного ценового графика на другой, для выявления аналогий в движениях цены. Коэффициент может периодически рассчитываться заново, учитывая последние изменения в поведении ценовых графиков.
Коэффициент корреляции в анализе инвестиционного портфеля
Согласно Марковицу, любой инвестор должен основывать свой выбор исключительно на ожидаемой доходности и стандартном отклонении при выборе портфеля. Таким образом, осуществив оценку различных комбинаций портфелей, ондолжен выбрать «лучший», исходя из соотношения ожидаемой доходности и стандартного отклонения этих портфелей. При этом соотношение доходность-риск портфеля остается обычным: чем выше доходность, тем выше риск.
Также, прежде чем приступить к формированию портфеля, необходимо дать определение термину «эффективный портфель». Эффективный портфель — это портфель, который обеспечивает: максимальную ожидаемую доходность для некоторого уровня риска, или минимальный уровень риска для некоторой ожидаемой доходности.
В дальнейшем будем находить эффективные портфели в среде Excel в соответствии со вторым принципом — с минимальным уровнем риска для любой ожидаемой доходности. Для нахождения оптимального портфеля необходимо определить допустимое множество соотношений «риск-доход» для инвестора, которое достигается путем построения минимально-дисперсионной границы портфелей, т.е. границы, на которой лежат портфели с минимальным риском при заданной доходности.
граница src=»/pictures/investments/img1996892_Minimalno_dispersionnaya_granitsa.gif» style=»width: 600px; height: 373px;» title=»Минимально — дисперсионная граница» />
На рисунке выше жирной линией отображена «эффективная граница», а большими точками отмечены возможные комбинации портфелей.
Эффективная граница — это граница, которая определяет эффективное множество портфелей. Портфели, лежащие слева от эффективной границы применить нельзя, т.к. они не принадлежат допустимому множеству. Портфели, находящиеся справа (внутренние портфели) и ниже эффективной границы являются неэффективными, т.к. существуют портфели, которые при данном уровне риска обеспечивают более высокую доходность, либо более низкий риск для данного уровня доходности.
Коэффициент корреляции (Correlation coefficient) — это
Для построения минимально-дисперсионной границы и определения «эффективной границы» нам будут необходимы значения ожидаемых доходностей, рисков (стандартных отклонений) и ковариации активов. Имея эти данные можно приступить к нахождению «эффективных портфелей».
Начнем с расчета ожидаемой доходности портфеля по формуле:
где Хi — доля i-ой бумаги в портфеле, E(ri) — ожидаемая доходность i-ой бумаги. А затем определим дисперсию портфеля, в формуле которой используется двойное суммирование:
И как следствие найдем стандартное отклонение портфеля, которое является квадратным корнем из дисперсии. Для наглядности приведем пример построения эффективной границы при помощи Microsoft Excel, а точнее при помощи встроенного в него компонента Поиск решения.
Зададим долю каждого актива в нашем первоначальном портфеле пропорционально их количеству. Следовательно, доля каждого актива в портфеле составит 1/3, т.е. 33%. Общая доля должна равняться 1, как для портфелей,в которых разрешены «короткие» позиции, так и для тех, в которых запрещены. Сам Марковиц запрещает открывать «короткие» позиции по активам, входящим в портфель, однако современная портфельная это разрешает. Если «короткие» позиции разрешены, то доля по активу будет отображена как -0.33 и средства, вырученные от его продажи, должны быть вложены в другой актив, таким образом, доля активов в портфеле в любом случае будет равняться 1.
Рассчитаем ожидаемую доходность, дисперсию и стандартное отклонение средневзвешенного портфеля:
Как видно из таблицы, для определения дисперсии портфеля нужно просто просуммировать данные в ячейках B19-D19, а квадратный корень из значения ячейки C21 даст нам стандартное отклонение портфеля в ячейке C22. Произведение долей бумаг на их ожидаемую доходность даст нам ожидаемую доходность нашего портфеля, которая отражена в ячейке C23. Окончательный результат средневзвешенного портфеля представлен ниже.
Средняя (ожидаемая) месячная доходность средневзвешенного портфеля 0,28% при риске 6,94%. Теперь можноприменить тот самый второй принцип, о котором было написано выше, т.е. обеспечить минимальный риск при заданном уровне доходности. Для этого воспользуемся функцией «Поиск Решений» из меню «Сервис». Если нет, значит надо открыть «Сервис» выбрать «Надстройки» и установить «Поиск решений». Запускаем «Поиск решений», в пункте «Установить указанную ячейку» указываем ячейку С22, которую будем минимизировать за счет изменения долей бумаг в портфеле, т.е. варьированием значений в ячейках A16-A18. Далее надо добавить два условия, а именно:
— сумма долей должна равняться 1, т.е. ячейка A19 = 1;
— задать доходность, которая нас интересует, к примеру, доходность 0.28% (ячейка С23), которая получилась при расчете средневзвешенного портфеля.
Так как мы запрещаем наличие «коротких» позиций по бумагам в меню «Параметры» надо установить галочку «Неотрицательные значения». Вот так должно выглядеть:
В результате мы получаем:
Итак, задав «Поиск решений» найти минимальное стандартное отклонение при заданной ожидаемой доходности в 0,33% мы получили оптимальный портфель, состоящий на 83% из РАО ЕЭС, на 17% из Лукойла и на 0% из Ростелекома. Несмотря на то, что уровень доходности тот же, что и при средневзвешенном портфеле, риск снизился.
Парный трейдинг и коэффициент корреляции
Понятие корреляция лежит в основе многих прибыльных торговых стратегий валютного рынка. В качестве примера можно привести парный трейдинг, основанный на корреляции валютных пар, позволяющий получить стабильную высокую прибыль на разных коррелирующих инструментах (об этом мы писали в предыдущих статьях) и торгового робота Octopus Arbitrage, его реализующего. В этой статье мы попытаемся просто и доступно объяснить суть корреляции и показать, как это можно применить на практике для парного трейдинга.
Почему было решено посвятить этой теме отдельную статью? Дело вот в чем. Несмотря на то, что корреляция нашла широкое практическое применение, доступное объяснение найти весьма трудно.
Как говорил Альберт Эйнштейн «если ты не можешь объяснить шестилетнему ребенку, чем ты занимаешься, значит, ты шарлатан». К сожалению, математики, пишущие учебные материалы этого принципа не придерживаются. Как только открываешь их талмуды, желая понять достаточно простые вещи, например, корреляция, так на тебя злобно смотрят четырехэтажные формулы, тройные интегралы и двухстраничные доказательства с применением огромного количества матерных слов незнакомых терминов. Самые стойкие засыпают через три минуты прочтения. Менее стойкие — через пять секунд созерцания этой «математической гармонии» создают облако пыли от захлопывающегося талмуда или нажимают крестик в правом верхнем углу экрана.
Корреляция — величина, характеризующая взаимную зависимость двух случайных величин, X и Y, безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением… Итак, что такое корреляция? По сути, корреляция показывает, насколько сильно связаны между собой величины. Если взять две произвольные величины, они могут быть сильно связаны между собой, никак не связаны, или слабо связаны.
Рассмотрим пример. Насколько связаны между собой количество прибыли, которую заработал трейдер за торговую сессию от количества выпитых им чашек кофе за тот же период? Т.е. имеем две величины: количество кружек кофе и прибыль.
Простой и наглядный способ анализа корреляции — загнать эти данные в Microsoft Excel и построить график. Стандартными средствами Excel можно вывести линию тренда, а также коэффициент корреляции R2. Как определяется коэффициент корреляции, поговорим чуть позже, пока лишь скажем, что эта величина изменяется от 0 до 1. При этом 0 — показывает, что связи нет вообще, а 1 — самая сильная связь, какая может быть. Линия тренда при отсутствии связи будет направлена параллельно оси X, при максимально сильной связи — под углом 45 градусов.
Ну что ж, похоже количество выпитого кофе на получение прибыли трейдером не влияет никак. Коэфициент корреляции R2 всего лишь 0,0289, линия тренда почти горизонтальна. Почему так? Возможно, помимо выпитого кофе существует множество факторов, оказывающих куда более существенное влияния на получение прибыли: факторы рынка, работа ДЦ, особенности выбранной торговой стратегии, личные качества трейдера и т.д.
Теперь разберем другой пример. Рассмотрим связь между валютными парами EUR/USD и GBP / USD. Были взяты скользящие средние дневных цен с 2 по 5 декабря 2013 года. Было взято четыре точки для простоты дальнейшего объяснения расчетов. Как правило, для подобных расчетов, точек нужно брать больше.
Теперь, аналогично, предыдущему примеру на основании этих данных построим график в Excel.
Так, здесь видно, что зависимость гораздо сильнее, так как R2 близко к единице, а линия тренда расположена почти под 45о. Можно сказать, что величины здесь коррелируют. Теперь рассмотрим, как рассчитывается коэффициент R. Здесь, к сожалению, без формул не обойтись. Однако, на самом деле, все заумные формулы можно свести к уровню седьмого класса средней школы. Для начала определимся, что у нас есть две «случайные» величины. Обозначим EURUSD как X, а GBPUSD как Y.
Далее хочу отметить, что большинство понятий, математической статистики базируются на среднем значении выборки. Проще говоря, на среднем арифметическом, т.е. сумма всех элементов, поделенная на их число. Вычислим среднее для величин X и Y.
Далее, приведем формулу расчета R2. В ней нет ничего сложного, как может показаться на первый взгляд. Здесь просто используются вычисленные нами средние арифметические:
Подставив выделенное в формулу получаем:
Таким образом, мы получили, посчитав «вручную», то, что автоматически делает Excel. Коэффициент R2 называется еще «коэффициентом Пирсона». Корреляция по EURUSD и GBPUSD, на самом деле, достаточно сильная, на это конечно есть фундаментальные причины, рассмотрение которых находится за рамками этой статьи.
Как корреляцию можно использовать для получения прибыли? Ярким примером может послужить стратегия парного трейдинга. Стратегия подразумевает, что большую часть времени выбранные валютные пары двигаются в рынке синхронно, но расхождения в поведении курсов происходят достаточно часто и каждое значительное рассогласование можно использовать для извлечения прибыли. Когда валютные пары расходятся на определенное количество пунктов: открываются две сделки, на одной паре — продажа, на другой — покупка. Когда пары возвращаются «друг к другу», позиции закрываются и прибыль фиксируется на одной или обеих позициях.
При расхождении инструментов открываются встречные позиции, при возвращении корреляции в исходное положение, встречные ордера закрываются, прибыль фиксируется на одной или обеих позициях
Безусловно, в нашей статье, описаны только основные принципы корреляции и парного трейдинга, поняв которые можно четко уяснить суть. Однако, для того, чтобы получать прибыль на FOREX, одних этих знаний недостаточно. Необходимо использовать специальные индикаторы, понимать расхождение каждой из пар и многое другое. Сколько трейдеров уже набили себе шишек на этом пути!
Коэффициент корреляции (Correlation coefficient) — это
Кроме того, необходимо постоянно быть «в рынке», двадцать четыре часа в сутки, семь дней в неделю, чтобы «не проспать», когда разойдется или же наоборот сойдется корреляция. При этом для устойчивого получения прибыли необходимо использовать не две валютные пары, а больше. Трейдер просто физически не сможет этого сделать. Как же здесь быть?
К счастью, есть уникальный торговый советник Octopus Arbitrage. Правильно настроив его и установив на нескольких парах, от трейдера, как правило, больше ничего не требуется. Все остальное сделает робот. Уникальный алгоритм позволит получать достойную прибыль при минимальных просадках, трейдер просто наблюдает за ростом депозита. Как говорится: «Вкалывают роботы — счастлив человек».
Коэффициент корреляции в психологических исследованиях
Коэффициент корреляции является одним из самых востребованых методов математической статистики в психологических и педагогических исследованиях. Формально простой, этот метод позволяет получить массу информации и сделать такое же количество ошибок. В этой статье мы рассмотрим сущность коэффициента корреляции, его свойства и виды. Слово correlation (корреляция) состоит из приставки «co-», которая обозначает совместность происходящего (по аналогии с «координация») и корня «relation», переводится как «отношение» или «связь» (вспомним public relations — связи с общественностью). Дословно correlation переводится как взаимосвязь.
Коэффициент корреляции — это мера взаимосвязи измеренных явлений. Коэффициент корреляции (обозначается «r») рассчитывается по специальной формуле и изменяется от -1 до +1. Показатели близкие к +1 говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной. Показатели близкие к -1 свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются.
Пример. На большой выборке был проведён тест FPI. Проанализируем взаимосвязи шкал Общительность, Застенчивость, Депрессивность. Начнем с Застенчивости и Депрессивности. Для наглядности, задаём систему координат, на которой по X будет застенчивость, а по Y — депрессивность. Таким образом, каждый человек из выборки исследования может быть изображен точкой на этой системе координат. В результате расчетов, коэффициент корреляции между ними r=0,6992.
Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны. Построим аналогичный график для Застенчивости и Общительности.
Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…). Если бы точки были расположены хаотично, коэффициент корреляции приближался бы к 0.
Коэффициент корреляции отражает степень приближенности точек на графике к прямой. Приведём примеры графиков, отражающих различную степень взаимосвязи (корреляции) переменных исследования. Сильная положительная корреляция:
Слабая положительная корреляция:
Нулевая корреляция:
В подписи у каждого графика кроме значения r есть значение p. p — это вероятность ошибки, о которой будет рассказано отдельно.
Источники и ссылки
ru.wikipedia.org — свободная энциклопедия Википедия
ru.math.wikia.com — математическая энциклопедия
vocabulary.ru — национальная психологическая энциклопедия
basegroup.ru — технологии анализа данных
investpark.ru — портал инвестора ИнвестПарк
megafx.ru — сайт для начинающих на рынке Форекс
psyfactor.org — центр практической психологии
learnspss.ru — сайт профессиональной обработки даных
exceltip.ru — блог о программе Microsoft Excel
economyreview.ru — информационные системы и технологии в экономике
aup.ru — аминистративно-управленческий портал
math-pr.com — решение задач и примеров по высшей математике
neerc.ifmo.ru — Викиконспекты
exponenta.ru — образовательный математический сайт
edu.jobsmarket.ru — курсы повышения квалификации в России и за рубежом
quans.ru — анализ и исследование рынка
Частные коэффициенты регрессии
Ошибки относительно линейной регрессии
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Приближенные частные линейные регрессии
Частные коэффициенты регрессии
8. Обобщим теперь соотношения линейной регрессии на случай p величин. Для p совместно нормальных величин xi с нулевым средним и дисперсиями математическое ожидание величины x1 при условии, что x2, …, xp фиксированы, как видно из выражения в экспоненте распределения, равно
. (17)
Коэффициент регрессии x1 по xj при фиксированных остальных p-2 величинах будем обозначать или, короче
, где q символизирует совокупность величин, отличных от указанных первичными индексами, а индекс у q служит для различения этих совокупностей. Коэффициенты
называются частными коэффициентами регрессии.
Следовательно, мы имеем
. (18)
Сравнивая (18) с (17), получаем для многомерного нормального случая

Аналогично, коэффициент регрессии xj по x1 при фиксированных остальных переменных есть

Таким образом, поскольку C1j=Cj1, то из (6), (19) и (20) получаем

— очевидное обобщение соотношения (17). Соотношения (19) и (20) показывают, что коэффициент не симметричен относительно x1 и xj, как и следовало ожидать от коэ ффициента зависимости. Подобно(5) и (6), (19) и (20) являются определениями частных коэффициентов регрессии в общем случае.
Ошибки относительно линейной регрессии
9. Назовем ошибкой (эту величину часто называют «остатком» (residual) но мы будем проводить различие между ошибками (errors) относительно линейных регрессий в генеральной совокупности и остатками, возникающими при подгонке регрессий к выборочным данным) порядка (p-1) величину
.
Ее среднее равно нулю, а дисперсия равна
.
так что является дисперсией ошибки величины x1 относительно регрессии. Из (18) немедленно получаем


Если брать математическое ожидание в два этапа, фиксируя вначале x2, …, xp, то условное математическое ожидание от второго члена в (23) будет равно, согласно (18), нулю. Таким образом,

Дисперсия ошибки (24) не зависит от фиксируемых значений x3, …, xp, если только от них не зависят коэффициенты .
В этом случае условное распределение величины x1 называется гомоскедастическим (homoscedastic) (или гетероскедастическим (heteroscedastic) в противном случае). Это постоянство дисперсии ошибок делает интерпретацию регрессий и корреляций более простой.
Например, в нормальном случае условные дисперсии и ковариации, полученные при фиксировании множества величин, не зависят от значений, в которых последние фиксированы (см. (14)).
В других случаях при интерпретациях мы должны надлежащим образом учитывать обнаруженную гетероскедастичность, тогда, возможно, частные коэффициенты регрессии лучше всего рассматривать как показатели зависимости, усредненные по всевозможным значениям фиксированных величин.
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Если даны p величин, то мы можем изучать корреляцию между любыми двумя из них, когда среди оставшихся зафиксированы значения произвольного подмножества величин. Аналогично, можно интересоваться регрессией произвольной величины относительно любого подмножества из оставшихся величин. С возрастанием p число всевозможных коэффициентов становится очень большим.
Если некоторый коэффициент содержит k вторичных индексов, то говорят, что он имеет порядок k. Так, порядок p12.34 равен 2, порядок p12.3 — единице, порядок p12 — нулю, тогда как β12.678 имеет порядок 3, а — порядок 4. В наших нынешних обозначениях коэффициенты линейной регрессии β1 и β2 должны быть записаны в виде β12 и β21 соответственно. Они имеют порядок нуль, как и обычная дисперсия σ2.
В 4 и 7 мы уже видели, как любой коэффициент корреляции первого порядка может быть выражен через коэффициенты нулевого порядка. Теперь будут получены более общие результаты такого сорта для коэффициентов всех типов.
11. Из (24) и (19) имеем

откуда
.
Пользуясь символом q, введенным в 8, получаем
, (26)
и аналогично, если 1 заменить любым другим индексом.
Точно таким же путем можно получить более общий результат

который сводится к (26) при l=m. Соотношение (27) применимо в случае, когда вторичные индексы одной величины включают в себя первичные индексы другой.
Если, с другой стороны, оба множества вторичных индексов не содержат l и m, то обозначим через r общее множество вторичных индексов. Ковариация двух ошибок xl.r, xm.r связана с их корреляцией и дисперсиями соотношениями:

что согласуется с уже найденным соотношением (21). Присоединяя множество индексов r к обеим величинам xl, xm, мы попросту должны сделать то же самое со всеми их коэффициентами.
12. Теперь можно использовать (26) для получения соотношения между дисперсиями ошибок различных порядков. Обозначая |D| корреляционный определитель всех величин, кроме x2. Тогда, имеем из (26)
(где индекс q-2 обозначает множество q без x2) и
,
откуда
. (29)
По определению |D|=C22, а согласно обобщенной теореме Якоби об определителях
, (30)
так как D11 является дополнительным минором для в C. Таким образом, используя (30), получаем из (29)

или, учитывая (6), находим
. (32)
Соотношение (32) является обобщением двумерного результата, который может быть представлен в виде
.
13. Соотношение (32) дает нам возможность выразить дисперсию ошибки порядка (p-1) через дисперсию ошибки и коэффициент корреляции порядка (p-2). Если мы теперь вновь воспользуемся (32) для того, чтобы выразить , то тем же путем найдем, что
.
Применяя последовательно (32) и записывая более полно индексы, получаем
. (33)
В (33), очевидно, не играет роли порядок вторичных индексов у σ1.23…p; мы их можем переставить так, как пожелаем. Например, для простоты в силу (26) можно написать
. (34)
В (34) индексы, отличные от 1, допускают перестановку. Соотношение (34) позволяет нам выразить дисперсию ошибки порядка s через дисперсию ошибки нулевого порядка и s коэффициентов корреляции, порядок которых принимает значения от нуля до (s-1).
14. Перейдем теперь к коэффициентам регрессии. Перепишем (15) для ковариации между x1 и x2 при фиксированном xp:
.
Присоединяя повсюду индексы 3, …, (p-1), имеем
. (35)
Используя определение (28) коэффициента регрессии как отношения ковариации к дисперсии, т.е.
,
и обозначим через r множество 3, …, (p-1), находим из (35)
,
или
. (36)
Если в (36) положить x1≡x2, то получим
, (37)
другую форму соотношения (32). Таким образом, из (36) и (37) имеем
. (38)
Это и есть требуемая формула для выражения коэффициента регрессии через некоторые коэффициенты следующего более низкого порядка. Повторно применяя (38), найдем представление любого коэффициента регрессии в терминах коэффициентов нулевого порядка.
Наконец, используя (21), из (38) получаем соотношение
, (39)
обобщающее (5) путем присоединения множества индексов r.
Приближенные частные линейные регрессии
15. В нашем изложении, начиная с 8, мы занимались точно линейными регрессионными зависимостями типа (18). Рассмотрим теперь вопрос подгонки регрессионных соотношений этого типа к наблюденным совокупностям, регрессии которых почти никогда не бывают точно линейными.
С помощью тех же рассуждений мы приходим к методу наименьших квадратов. Мы выбираем поэтому так, чтобы минимизировать сумму квадратов уклонений n наблюдений от подгоняемой регрессии:

где «иксы» измеряются от своих средних значений и предполагается n>p. Решение имеет вид
, (41)
где матрица X составлена из наблюдений над p-1 величинами x2, …, xp, а x1 — вектор наблюдений величины x1. Соотношение (41) можно переписать в виде
, (42)
где Vp-1 — матрица рассеяния для x2, …, xp, а M — вектор ковариаций между x1 и xj (j=2, …, p). Таким образом,
. (43)
Поскольку |Vp-1| есть минор V11 матрицы рассеяния V всех p величин, то (Vp-1)jl представляет собой дополнительный минор для
в V, так что сумма в правой части (43) является алгебраическим дополнением для (-σ1j) в V. Поэтому (43) представляется в виде
. (44)
Соотношение (44) совпадает с (19). Таким образом, мы приходим к заключению, что аппроксимация по методу наименьших квадратов дает те же коэффициенты регрессии, что и в случае точной линейной регрессии.
Из этого следует, что все результаты данной главы остаются в силе, когда для наблюденных совокупностей мы подгоняем регрессии по методу наименьших квадратов.
Связанные определения:
Выборочный коэффициент корреляции
Корреляционный анализ
Корреляция
Коэффициент корреляции
Линейная регрессия
Логистическая регрессия
Матрица плана
Метод наименьших квадратов
Независимый признак
Некоррелированный
Общая линейная модель
Регрессия
В начало
Содержание портала
В научных исследованиях часто возникает необходимость в нахождении связи между результативными и факторными переменными (урожайностью какой-либо культуры и количеством осадков, ростом и весом человека в однородных группах по полу и возрасту, частотой пульса и температурой тела и т.д.).
Вторые представляют собой признаки, способствующие изменению таковых, связанных с ними (первыми).
Понятие о корреляционном анализе
Существует множество определений термина. Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.
Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.
Понятие о ложности корреляции
При проведении корреляционного анализа необходимо учитывать, что его можно провести по отношению к любой совокупности признаков, зачастую абсурдных по отношению друг к другу. Порой они не имеют никакой причинной связи друг с другом.
В этом случае говорят о ложной корреляции.
Задачи корреляционного анализа
Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.
Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:
- выявление факторов, оказывающих наибольшее влияние на результативный признак;
- выявление неизученных ранее причин связей;
- построение корреляционной модели с ее параметрическим анализом;
- исследование значимости параметров связи и их интервальная оценка.
Связь корреляционного анализа с регрессионным
Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.
Условия использования метода
Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.
Метод корреляционного анализа часто не ограничивается нахождением тесноты связи между исследуемыми величинами. Иногда он дополняется составлением уравнений регрессии, которые получают с помощью одноименного анализа, и представляющих собой описание корреляционной зависимости между результирующим и факторным (факторными) признаком (признаками). Этот метод в совокупности с рассматриваемым анализом составляет метод корреляционно-регрессионного анализа.
Условия использования метода
Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.
Правила отбора факторов корреляционного анализа
При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.
Отображение результатов
Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.
Трехмерное представление диаграммы разброса (рассеивания)
Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.
Трехмерное представление диаграммы разброса (рассеивания)
Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.
Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.
Оценка тесноты связи
Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.
Оценка тесноты связи
Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.
Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.
Исходные данные для корреляционного анализа
|
Профессиональная группа |
курение |
смертность |
|
Фермеры, лесники и рыбаки |
77 |
84 |
|
Шахтеры и работники карьеров |
137 |
116 |
|
Производители газа, кокса и химических веществ |
117 |
123 |
|
Изготовители стекла и керамики |
94 |
128 |
|
Работники печей, кузнечных, литейных и прокатных станов |
116 |
155 |
|
Работники электротехники и электроники |
102 |
101 |
|
Инженерные и смежные профессии |
111 |
118 |
|
Деревообрабатывающие производства |
93 |
113 |
|
Кожевенники |
88 |
104 |
|
Текстильные рабочие |
102 |
88 |
|
Изготовители рабочей одежды |
91 |
104 |
|
Работники пищевой, питьевой и табачной промышленности |
104 |
129 |
|
Производители бумаги и печати |
107 |
86 |
|
Производители других продуктов |
112 |
96 |
|
Строители |
113 |
144 |
|
Художники и декораторы |
110 |
139 |
|
Водители стационарных двигателей, кранов и т. д. |
125 |
113 |
|
Рабочие, не включенные в другие места |
133 |
146 |
|
Работники транспорта и связи |
115 |
128 |
|
Складские рабочие, кладовщики, упаковщики и работники разливочных машин |
105 |
115 |
|
Канцелярские работники |
87 |
79 |
|
Продавцы |
91 |
85 |
|
Работники службы спорта и отдыха |
100 |
120 |
|
Администраторы и менеджеры |
76 |
60 |
|
Профессионалы, технические работники и художники |
66 |
51 |
Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.
С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.
Использование ПО при проведении корреляционного анализа
Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих параметров с использованием функций:
1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ [CORREL](массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.
Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.
Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».
После указания исходных данных получаем график.
2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).
3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.
В заключение
Использование в научных исследованиях метода корреляционного анализа позволяет определить связь между различными факторами и результативными показателями. При этом необходимо учитывать, что высокий коэффициент корреляции можно получить и из абсурдной пары или множества данных, в связи с чем данный вид анализа нужно осуществлять на достаточно большом массиве данных.
После получения расчетного значения r его желательно сравнить с r критическим для подтверждения статистической достоверности определенной величины. Корреляционный анализ может осуществляться вручную с использованием формул, либо с помощью программных средств, в частности MS Excel. Здесь же можно построить диаграмму разброса (рассеивания) с целью наглядного представления о связи между изучаемыми факторами корреляционного анализа и результативным признаком.
Ошибки в статистике
Ошибки в статистике (сплошных и выборочных) могут возникнуть ошибки двух видов: репрезентативности и регистрации.
Ошибки репрезентативности характерны только для выборочного наблюдения и возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Они определяются как расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном сплошном наблюдении с одинаковой степенью точности.
Ошибки регистрации могут иметь случайный, систематический и непреднамеренный характер.
Случайные ошибки часто уравновешивают друг друга, так как они не имеют преимущественного направления в сторону преувеличения (преуменьшении) значения изучаемого показателя. Данные ошибки имеют объективный характер и возникают в следствии случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. В результате и структуры этих совокупностей чаще всего не совпадают. Научным обоснованием случайных ошибок являются теория вероятностей и ее предельные теоремы.
Систематические ошибки направлены в одну сторону в результате предумышленного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения.
Ошибка выборки в статистике
Ошибка выборки или ошибка репрезентативности определяется как разница между значением показателя, который был получен по выборке, и генеральным параметром. Она характерна только для выборочных наблюдений. Чем больше значение этой ошибки, тем в большей степени выборочные показатели отличаются от соответствующих им генеральных показателей.
Ошибку выборки часто определяют по формулам:
1. Для среднего количественного признака:
где первое — среднее значение признака в генеральной совокупности или генеральная средняя;
второе — выборочная средняя.
2. Для доли (альтернативного признака):
где w — выборочная доля;
р — генеральная доля, или доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности.
Ошибки выборки возникают вследствие двух причин из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки) и в результате случайного отбора (случайные ошибки). Выборки являются случайными величинами и могут принимать разные значения.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.