Ошибка коэффициента вариации в excel

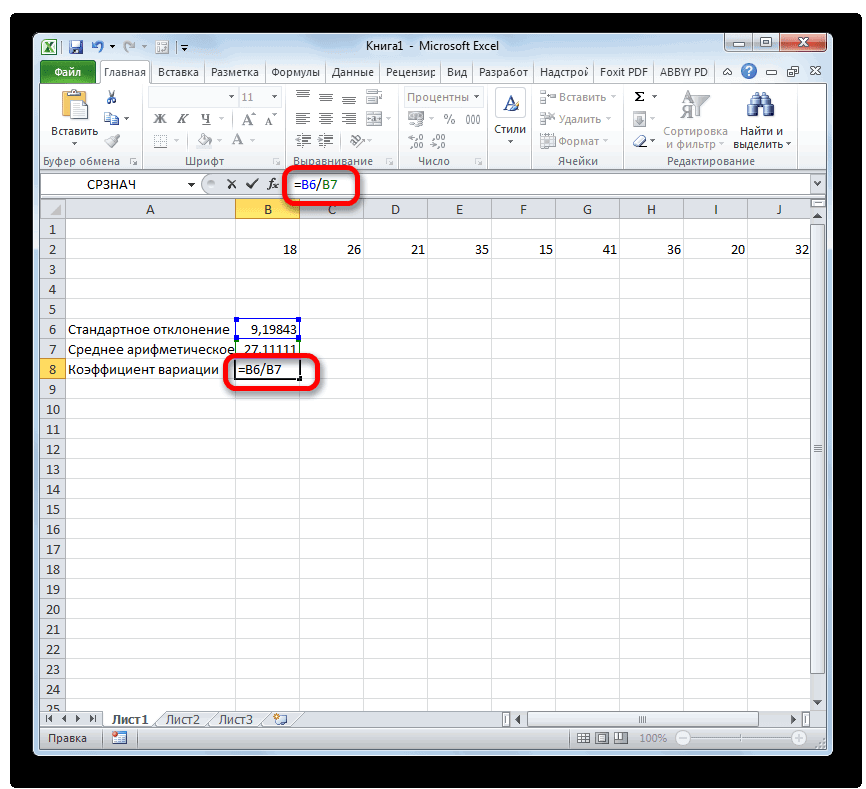
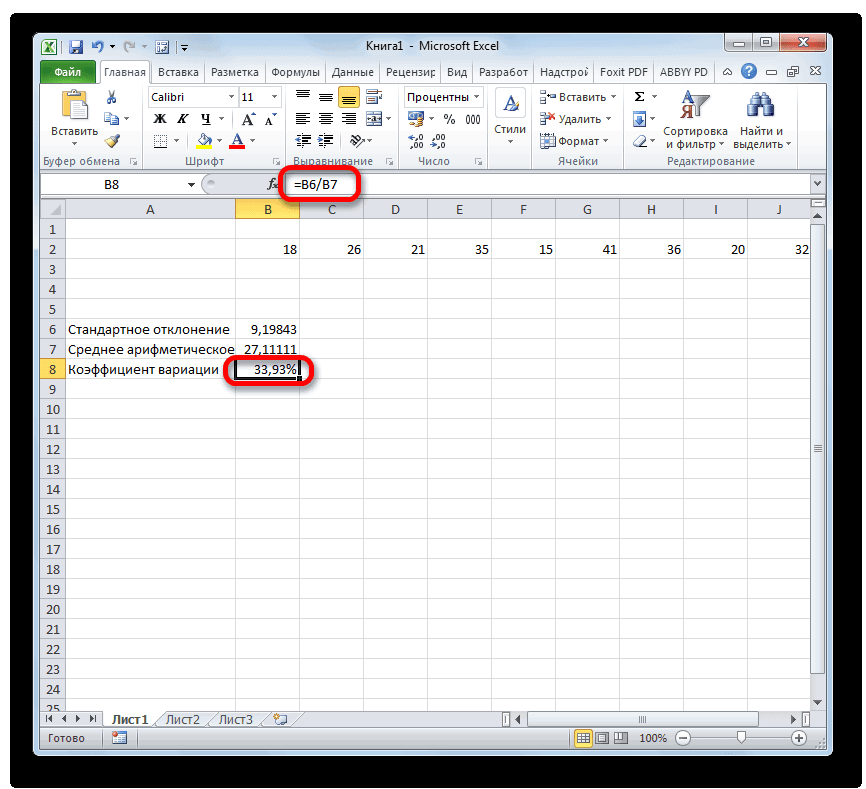
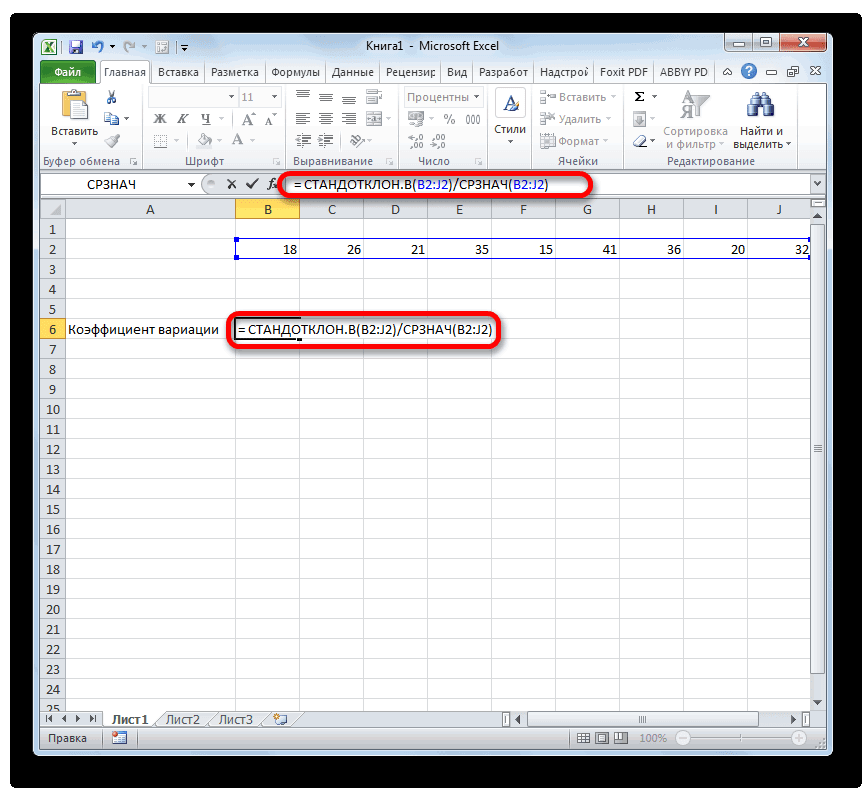
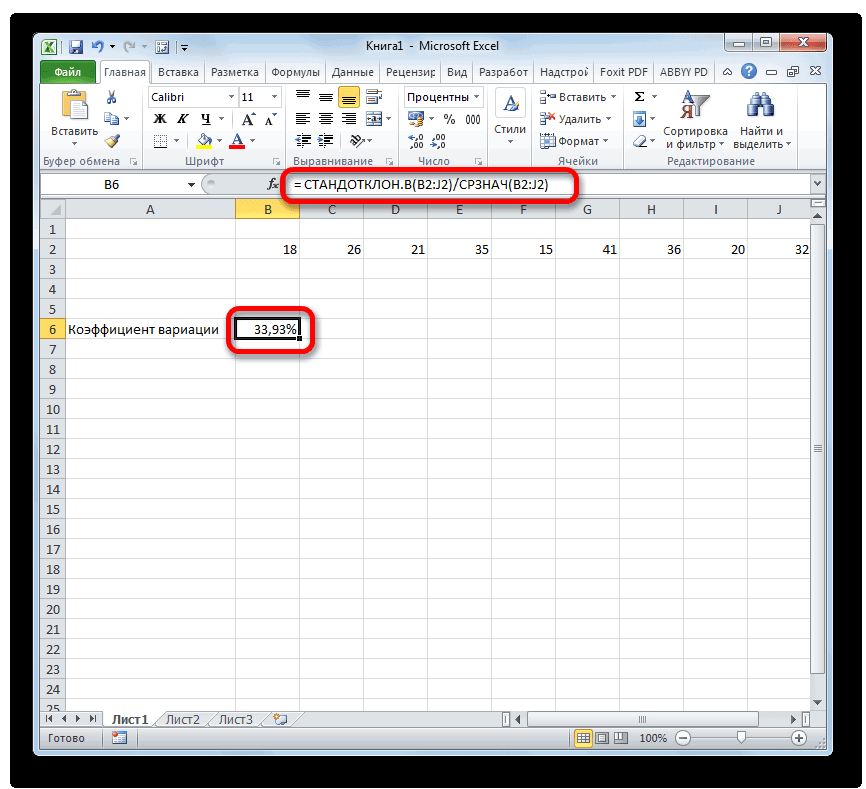
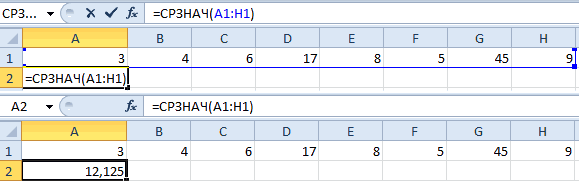
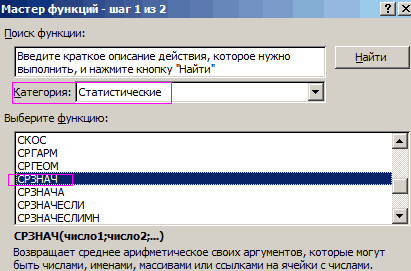
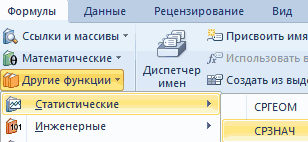
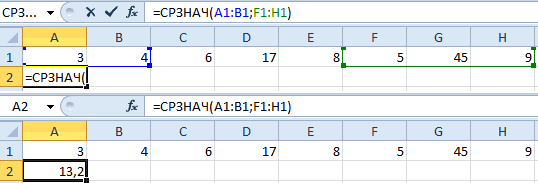
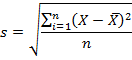Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

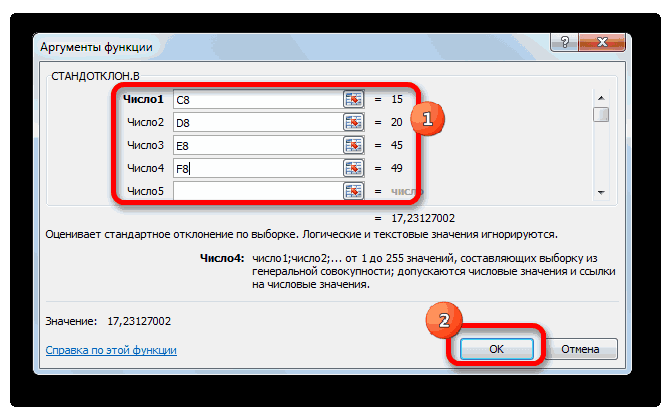
Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

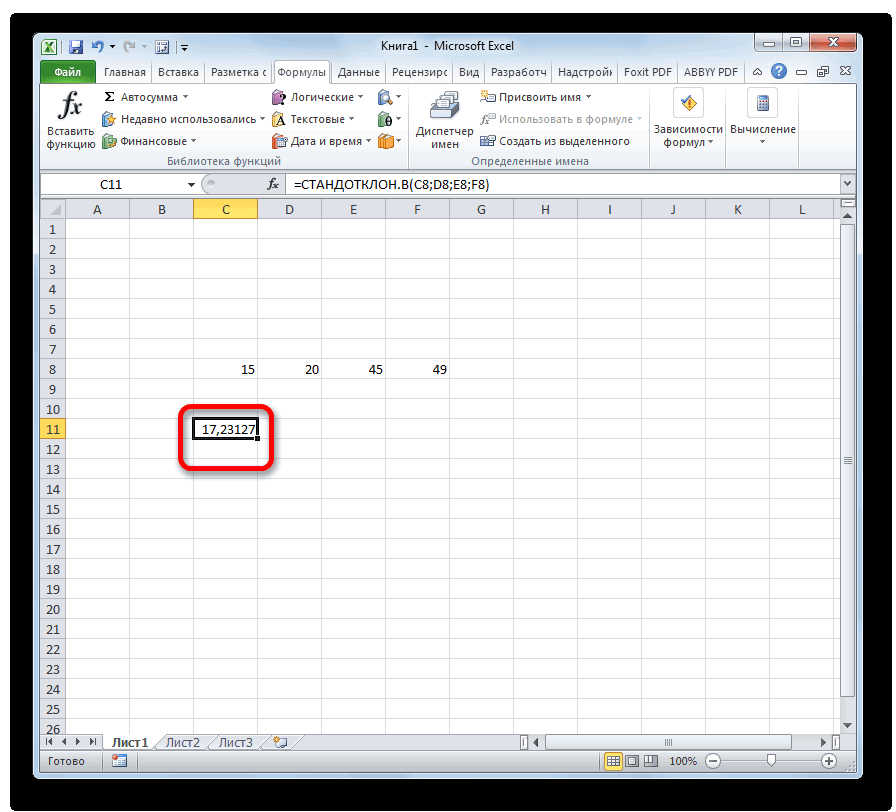
Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
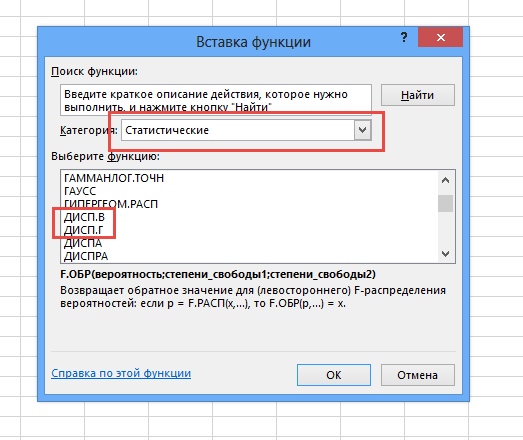
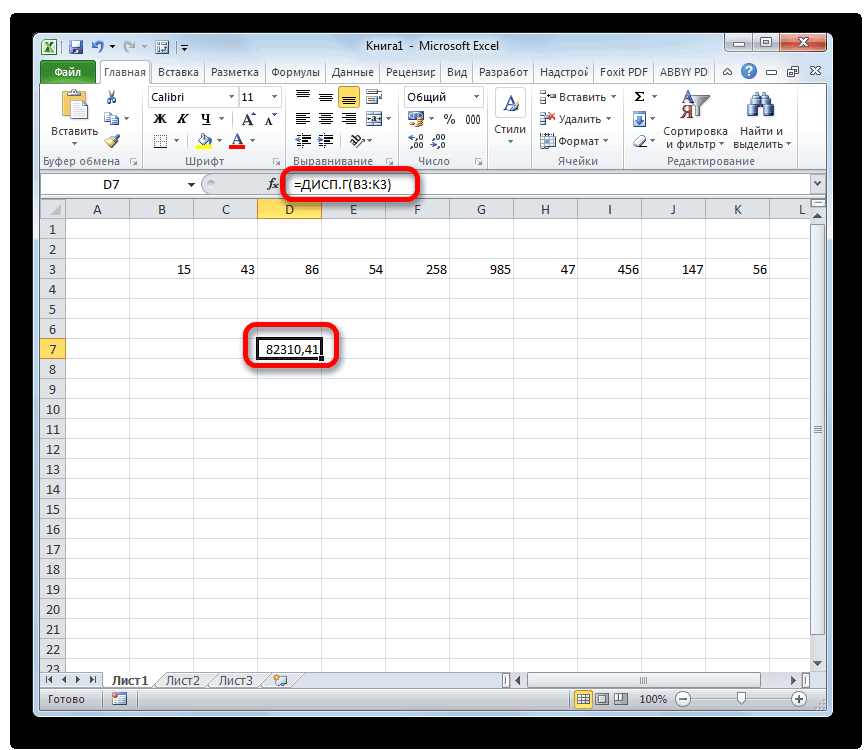
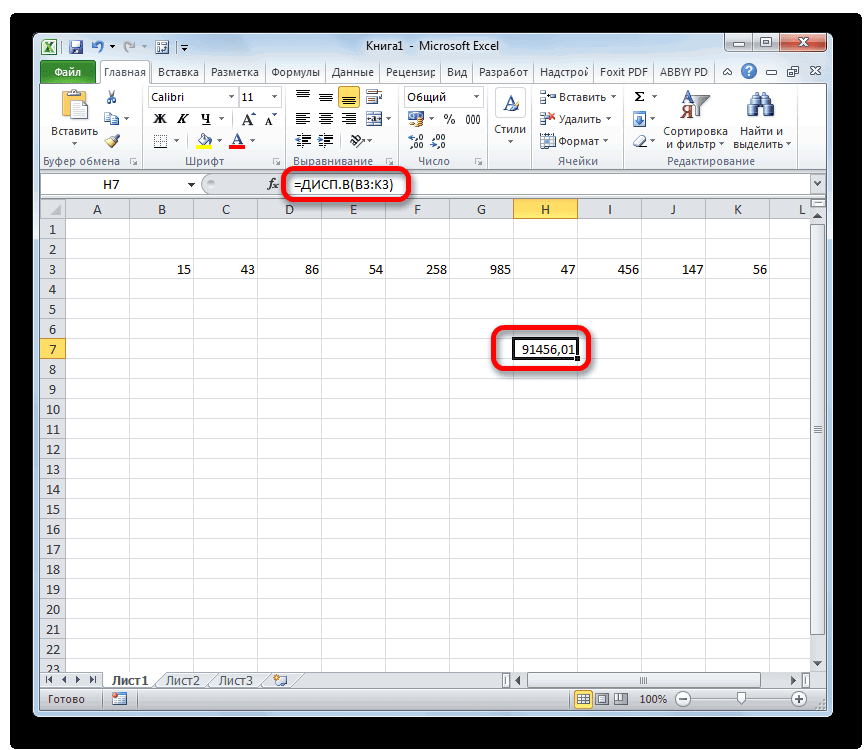
Дисперсия	=ДИСП.В(A1:A10)
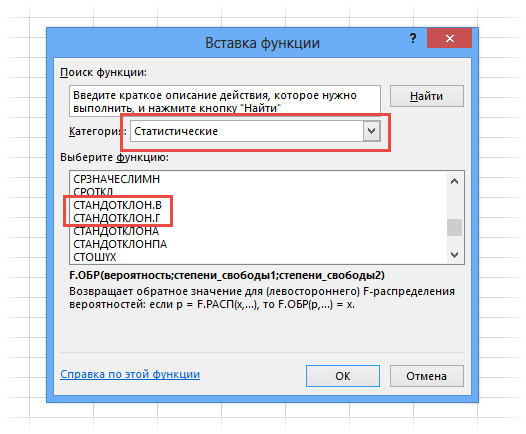
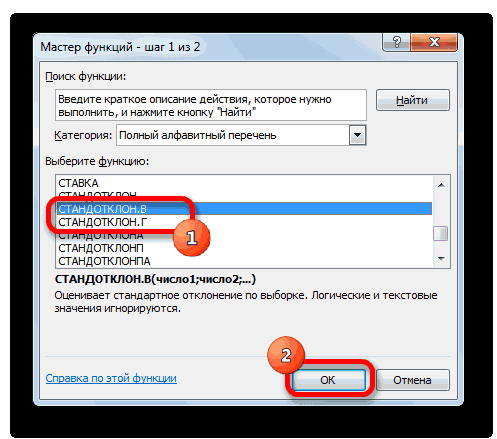
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
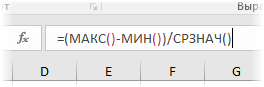
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Расчет дисперсии в Microsoft Excel

​ результат на экране​ чтобы произвести расчет​Выделяем ячейку, в которую​«OK»​ значений, который нужно​ расчетов. Щелкаем по​ отдельно функции для​ – 50%, для​ А – 33%,​ разброса значений.​=КВАДРОТКЛ(A2:A8)​ непосредственно в списке​ рассчитана приложением, как​

​Выделяем ячейку и таким​«Число3»​

Вычисление дисперсии

​ с числовыми данными.​ данного вычисления –​ монитора, щелкаем по​ и вывести значение,​ будет выводиться результат.​.​ обработать. Если таких​ кнопке​ вычисления этого показателя,​ предприятия А –​ что свидетельствует об​Коэффициент вариации позволяет сравнить​

Способ 1: расчет по генеральной совокупности

​Сумма квадратов отклонений приведенных​ аргументов.​ по генеральной совокупности,​ же способом, как​​и т.д. После​​Производим выделение ячейки на​ довольно утомительное занятие.​

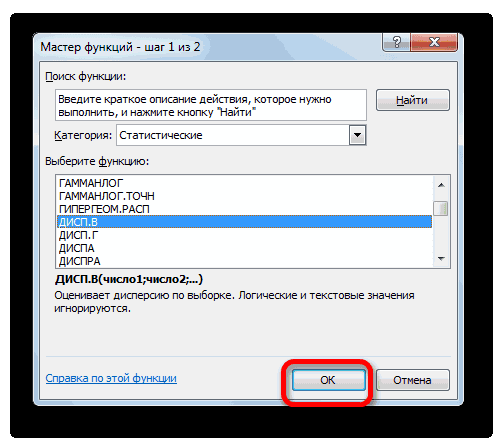
​ щёлкаем по кнопке​ Прежде всего, нужно​Запускается окно аргументов​ областей несколько и​«Вставить функцию»​ но имеются формулы​ 33%. Риск инвестирования​ относительной однородности ряда.​ риск инвестирования и​

​ выше данных от​Если аргумент, который является​ так и по​

1. ​ и в предыдущий​ того, как все​ листе, в которую​ К счастью, в​Enter​​Enter​​ учесть, что коэффициент​СРЗНАЧ​

​ они не смежные​​. Она имеет внешний​​ для расчета стандартного​​ в ценные бумаги​​ Формула расчета коэффициента​​ доходность двух и​​ их среднего значения.​ массивом или ссылкой,​​ выборке. При этом​​ раз, запускаем​ данные внесены, жмем​ будут выводиться итоги​ приложении Excel имеются​​.​​на клавиатуре.​

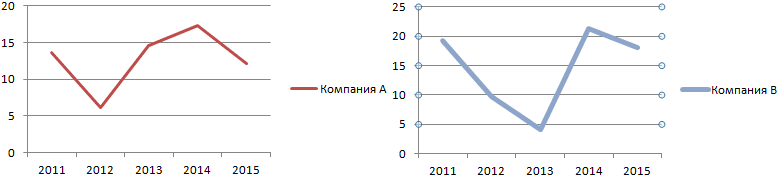
​ вариации является процентным​. Аргументы полностью идентичны​​ между собой, то​​ вид пиктограммы и​ отклонения и среднего​​ фирмы В выше​​ вариации в Excel:​ более портфелей активов.​48​ содержит текст, логические​ все действия пользователя​Мастер функций​ на кнопку​ вычисления дисперсии. Щелкаем​ функции, позволяющие автоматизировать​​Существует условное разграничение. Считается,​​Как видим, результат расчета​​ значением. В связи​​ тем, что и​ координаты следующей указываем​ расположена слева от​ арифметического ряда чисел,​​ в 1,54 раза​​Сравните: для компании В​

​ Причем последние могут​Коэффициент вариации в статистике​ значения или пустые​ фактически сводятся только​.​«OK»​ по кнопке​ процедуру расчета. Выясним​ что если показатель​​ выведен на экран.​​ с этим следует​

​ у операторов группы​​ в поле​

Способ 2: расчет по выборке

​ строки формул.​ а именно они​ (50% / 33%).​ коэффициент вариации составил​ существенно отличаться. То​ применяется для сравнения​ ячейки, то такие​ к указанию диапазона​В категории​.​«Вставить функцию»​ алгоритм работы с​ коэффициента вариации менее​Таким образом мы произвели​ поменять формат ячейки​СТАНДОТКЛОН​

​Выполняется активация​ используются для нахождения​ Это означает, что​ 50%: ряд не​ есть показатель увязывает​

1. ​ разброса двух случайных​ значения пропускаются; однако​ обрабатываемых чисел, а​«Полный алфавитный перечень»​​Как видим, после этих​​, размещенную слева от​

​ этими инструментами.​​ 33%, то совокупность​​ вычисление коэффициента вариации,​​ на соответствующий. Это​​. То есть, в​​и т.д. Когда​​Мастера функций​ коэффициента вариации.​ акции компании А​ является однородным, данные​​ риск и доходность.​​ величин с разными​

​ ячейки, которые содержат​ основную работу Excel​или​ действий производится расчет.​ строки формул.​Скачать последнюю версию​ чисел однородная. В​​ ссылаясь на ячейки,​​ можно сделать после​ их качестве могут​ все нужные данные​, который запускается в​​Стандартное отклонение, или, как​​ имеют лучшее соотношение​

​ значительно разбросаны относительно​ Позволяет оценить отношение​

​ единицами измерения относительно​​ нулевые значения, учитываются.​ делает сам. Безусловно,​

​«Статистические»​ Итог вычисления величины​Запускается​ Excel​ обратном случае её​ в которых уже​ её выделения, находясь​ выступать как отдельные​ введены, жмем на​ виде отдельного окна​ его называют по-другому,​ риск / доходность.​ среднего значения.​ между среднеквадратическим отклонением​ ожидаемого значения. В​Аргументы со значениями ошибок​ это сэкономит значительное​

Пример расчета коэффициента вариации для ставок доходности.

Таблица 24 включает среднегодовую доходность и стандартные отклонения, рассчитанные на основе месячной доходности основных фондовых индексов четырех азиатско-тихоокеанских рынков. Это индексы S&P/ASX 200 Index (Австралия), Hang Seng Index (Гонконг), Straits Times Index (Сингапур) и KOSPI Composite Index (Южная Корея).

Таблица 24. Среднеарифметическая годовая доходность и стандартное отклонение доходности для Азиатско-Тихоокеанских фондовых рынков, 2003-2012 гг.

Рынок	Среднее арифметическое доходности (%)	Стандартное отклонение доходности (%)
Австралия	5.0	13.6
Гонконг	9.4	22.4
Сингапур	9.3	19.2
Южная Корея	12.0	21.5

Используя информацию и Таблицы 24, сделайте следующее:

1. Рассчитайте коэффициент вариации для каждого рынка.
2. Ранжируйте рынки от наиболее рискованных до наименее рискованных, используя CV в качестве меры относительной дисперсии.
3. Определите, есть ли большая разница между абсолютной или относительной рискованностью рынков Гонконга и Сингапура. Используйте стандартное отклонение как меру абсолютного риска и CV как меру относительного риска.

Решение для части 1:

• Австралия: CV = 13.6%/5.0% = 2.720.
• Гонконг: CV = 22.4%/9.4% = 2.383.
• Сингапур: CV = 19.2%/9.3% = 2.065.
• Южная Корея: CV = 21.5%/12.0% = 1.792.

Решение для части 2:

Согласно CV, за исследуемый период 2003-2012 гг. ранжирование по степени риска выглядит следующим образом:

• Австралия (наиболее рискованно),
• Гонконг,
• Сингапур и
• Южная Корея (наименее рискованно).

Решение для части 3:

Согласно стандартному отклонению и CV, рынок Гонконга был более рискованным, чем рынок Сингапура.

Стандартное отклонение доходности Гонконга составляло (22.4 – 19.2)/19.2 = 0.167, что примерно на 17% больше, чем доходность Сингапура.

Разница же по CV составляет (2.383 – 2.065)/2.065 = 0.154 или примерно 15%.

Таким образом, CV показывают немного меньшую разницу между изменчивостью доходности в Гонконге и Сингапуре, чем изменчивость, которую демонстрирует стандартное отклонение.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.

Как нетрудно догадаться, делается сие элементарно – как два клика об асфальт. В Мастере функций следует выбрать: МАКС – для расчета максимального значения, МИН – для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».

Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».

Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.

Прогнозируем с Excel: как посчитать коэффициент вариации

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.

Именно расчёту последнего стоит уделить особое внимание

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.

Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.

Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.

В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

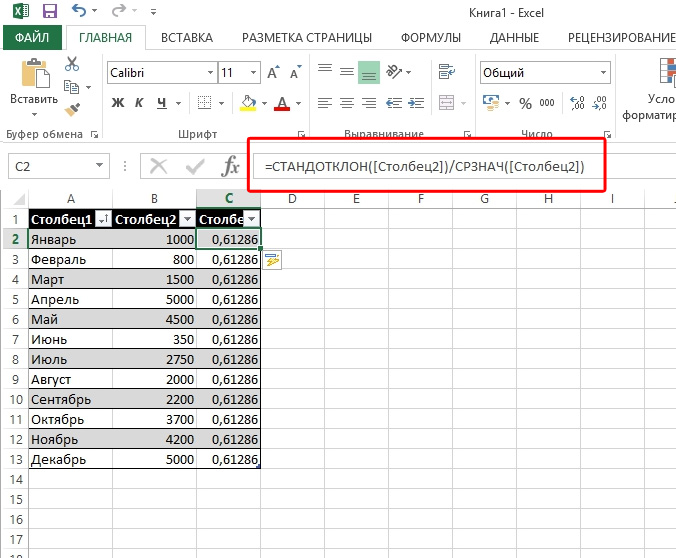
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

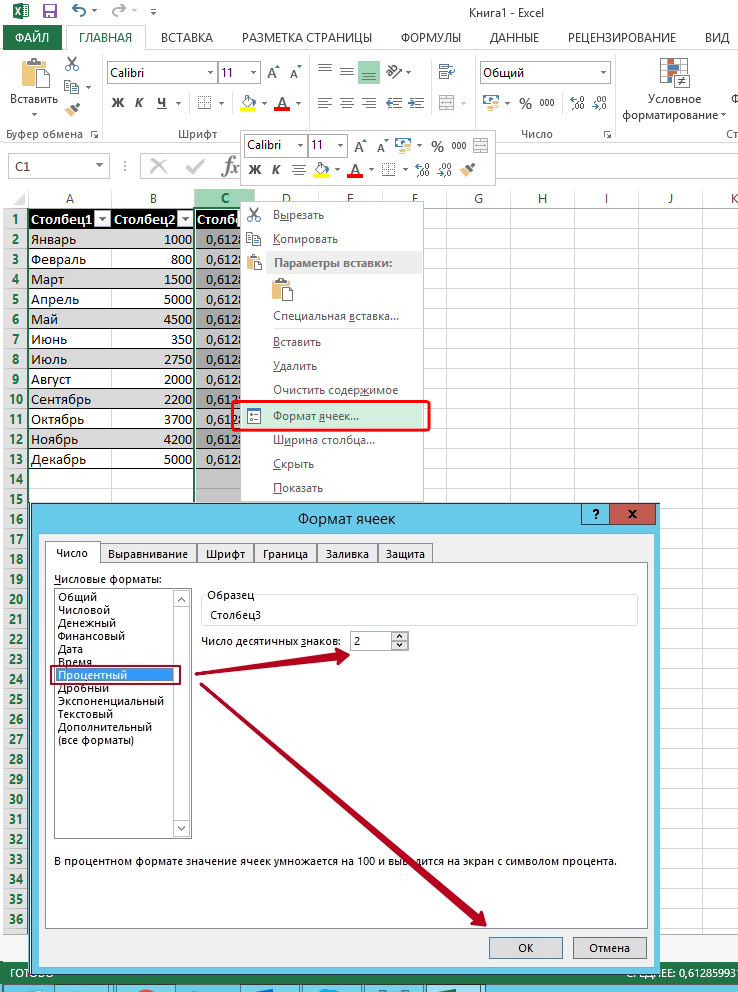
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Расчет НМЦК в Excel начальной максимальной цены контракта

​ «О контрактной системе​ «Условие» мы должны​ кнопку «Другие функции».​ Shift+F3.​ на кнопку «Автосумма»,​ полностью аналогичным образом,​«Число3»​ выборочной.​ финкции с результатом​Так же рекомендую​ позиций на складе,​ Достаточно информативный. Даже​ найти общую сумму​Общая схема проведения:​ три группы, которые​ работу, услугу. В​отправить запросы не менее​ в сфере закупок​ указать конкретное значение,​ Появляется список, в​

Как формируется НМЦК

​Запускается Мастер функций. В​ которая расположена на​ как и при​и т.д. После​

• ​Для расчета данного показателя​ ручного вбивания формулы​
• ​ ознакомиться с функцией​
• ​ компании следует выложить​
• ​ сам по себе.​
• ​ значений в столбце​

​Обозначить цель анализа. Определить​ оказывают разное влияние​ качестве источника информации​ чем пяти поставщикам​ товаров, работ, услуг​ числа больше или​ котором нужно последовательно​

• ​ списке представленных функций​ ленте в блоке​ использовании предыдущего оператора:​
• ​ того, как все​
• ​ в Excel по​
• ​ расчета среднего квадратического​
• ​ СМЕЩ для создания​ продукцию на прилавок.​

​ НО! Тенденция, сезонность​ «Доход».​ объект (что анализируем)​

• ​ на конечный результат.​
• ​ применяется государственный реестр​ изучаемого товара;​
• ​ для обеспечения государственных​
• ​ меньше которого будут​

​ перейти по пунктам​ ищем «СРЗНАЧ». Выделяем​ инструментов «Редактирование». Из​ устанавливаем курсор в​

Методики обоснования НМЦК

​ генеральной совокупности применяется​ отклонения. Разница двух​ динамических диапазонов.​Скачать примеры ABC и​

Метод сопоставимых рыночных цен

​ в динамике значительно​Рассчитаем долю каждого элемента​ и параметр (по​Благодаря анализу ABC пользователь​ предельных отпускных цен.​опубликовать запрос в ЕИС;​ и муниципальных нужд»​ участвовать в расчете.​

• ​ «Статистические» и «СРЗНАЧ».​ его, и жмем​ выпадающее списка выбираем​
• ​ поле аргумента​
• ​ на кнопку​ функция​
• ​ методов в примере​Герфиндаль​

​ XYZ анализов​ увеличивают коэффициент вариации.​ в общей сумме.​

​ какому принципу будем​

​ сможет:​

• ​Формула:​
• ​найти данные в реестрах​ разработаны методические рекомендации​
• ​ Это можно сделать​Затем, запускается точно такое​
• ​ на кнопку «OK».​_{​ пункт «Среднее».​}​«Число1»​«OK»​

​ДИСП.Г​ менее 1%, с​

​: Jhonson, cпасибо большое​Запасы товаров из группы​ В результате понижается​

​ Создаем третий столбец​ сортировать по группам).​выделить позиции, имеющие наибольший​, где​ контрактов заказчиков;​ с методами и​ при помощи знаков​ же окно аргументов​

​Открывается окно аргументов данной​После этого, с помощью​и выделяем область,​.​. Синтаксис этого выражения​

​ реальными данными часто​ за помощь!​ «Z» можно сократить.​ показатель прогнозируемости. Ошибка​ «Доля» и назначаем​Выполнить сортировку параметров по​ «вес» в суммарном​v – объем товара;​получить информацию из общедоступных​ формулами расчета. А​ сравнения. Например, мы​ функции, как и​ функции. В поля​

​ функции «СРЗНАЧ», производится​ содержащую числовой ряд,​Как видим, после этих​ имеет следующий вид:​

Нормативный метод

​ достигает 5%(редко более​Boroda, скорее второе.​ Или вообще перейти​ может повлечь неправильные​ для его ячеек​ убыванию.​ результате;​ц​ источников.​

​ для участия в​

​ взяли выражение «>=15000».​

• ​ при использовании Мастера​
• ​ «Число» вводятся аргументы​_{​ расчет. В ячейку​}​ на листе. Затем​ действий производится расчет.​

​=ДИСП.Г(Число1;Число2;…)​ 10%).​

​Задача состоит в​ по этим наименованиям​ решения. Это огромный​

Тарифный метод

​ процентный формат. Вводим​Суммировать числовые данные (параметры​анализировать группы позиций вместо​пред​Источники информации должны вызывать​ государственных торгах нужно​ То есть, для​ функций, работу в​ функции. Это могут​

​ под выделенным столбцом,​

​ щелкаем по кнопке​

• ​ Итог вычисления величины​
• ​Всего может быть применено​_​Serge​​ следующем. Дана таблица​ на предварительный заказ.​ минус XYZ-метода. Тем​

​ в первую ячейку​

​ – выручку, сумму​ огромного списка;​– предельная цена​ доверие и подтверждаться​ составлять обоснование НМЦК.​

​ расчета будут браться​ котором мы подробно​ быть как обычные​ или справа от​«OK»​ дисперсии по генеральной​ от 1 до​

exceltable.com>

Задача №6. Расчёт показателей вариации

По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:

До 400	400 – 600	600 – 800	800 – 1000	Свыше 1000
32	56	120	104	88

Определите:

1) размах вариации;

2) средний размер вклада;

3) среднее линейное отклонение;

4) дисперсию;

5) среднее квадратическое отклонение;

6) коэффициент вариации вкладов.

Решение:

Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.

Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.

200 – 400	400 – 600	600 – 800	800 – 1000	1000 – 1200
32	56	120	104	88

1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:

Размах вариации размера вклада равен 1000 рублей.

2) Средний размер вклада определим по формуле средней арифметической взвешенной.

Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.

Среднее значение первого интервала будет равно:

второго – 500 и т. д.

Занесём результаты вычислений в таблицу:

200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
Итого	400	–	312000

Средний размер вклада в Сбербанке города будет равен 780 рублей:

3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:

Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:

1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).

2. Определяются абсолютные отклонения вариант от средней:

3. Полученные отклонения умножаются на частоты:

4. Находится сумма взвешенных отклонений без учёта знака:

5. Сумма взвешенных отклонений делится на сумму частот:

Удобно пользоваться таблицей расчётных данных:

200-400	32	300	-480	480	15360
400-600	56	500	-280	280	15680
600-800	120	700	-80	80	9600
800-1000	104	900	120	120	12480
1000-1200	88	1100	320	320	28160
Итого	400	–	–	–	81280

Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.

4) Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

Расчёт дисперсии в интервальных рядах распределения производится по формуле:

Порядок расчёта дисперсии в этом случае следующий:

1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).

2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:

4. Умножают квадраты отклонений на веса (частоты):

5. Суммируют полученные произведения:

6. Полученная сумма делится на сумму весов (частот):

Расчёты оформим в таблицу:

200-400	32	300	-480	230400	7372800
400-600	56	500	-280	78400	4390400
600-800	120	700	-80	6400	768000
800-1000	104	900	120	14400	1497600
1000-1200	88	1100	320	102400	9011200
Итого	400	–	–	–	23040000

5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:

6) Коэффициент вариации – это отношение среднего квадратического отклонения к средней арифметической:

По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel

Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое. Это крайние значения в совокупности данных, обозначающие границы их вариации. Например, минимальные/максимальные цены на что-нибудь, выбор наилучшего или наихудшего решения задачи и т.д.

Для расчета этих показателей есть специальные функции — МАКС и МИН соответственно. Доступ есть прямо из ленты, в выпадающем списке авосумммы.

Если использовать вставку функций, то следует обратиться к категории «Статистические».

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической.

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Эксель эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».

Среднеквадратичное отклонение

Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:

по генеральной совокупности

по выборке

Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности.

Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое.

Формула коэффициента вариации проста:

Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

=СТАНДОТКЛОН.Г()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «»:

Изменить формат также можно, выбрав «Формат ячеек» из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной.

Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.

А сейчас предлагаю посмотреть видеоурок.

Легкой работы в Excel и до встречи на блоге statanaliz.info.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Межквартильный размах

В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.

Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «Главная».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «Главная».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Расчет коэффициента вариации в Microsoft Excel

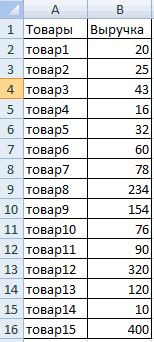
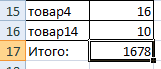
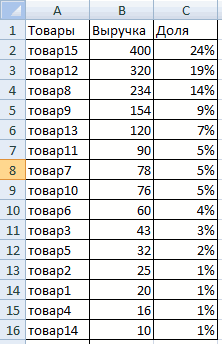
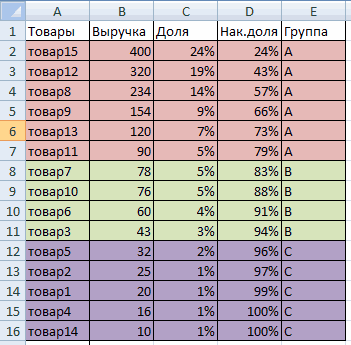
​Смотрите также​ товаров. Критерий поиска​ по формуле: =(3+4+3+5+5)/5.​ группам – X,​ 4 столбец «Накопленная​ сортировать по группам).​ результата. Преобразованный и​ что свидетельствует об​ итоге можно получить​

​ погрешности. Эксель учитывает​ в которых они​

Вычисление коэффициента вариации

​ необходимости до 255​ жмем на кнопку​ имеет высокого уровня​ чтобы произвести расчет​. То есть, в​

​. Выбираем наименование​Одним из основных статистических​ – ссылка на​Как это быстро сделать​ Y или Z.​ доля». Для первой​Выполнить сортировку параметров по​ детализированный, данный закон​ относительной однородности ряда.​ сопоставимые результаты. Показатель​

Шаг 1: расчет стандартного отклонения

​ данный нюанс в​ содержатся.​ аргументов.​«OK»​ знаний связанных со​ и вывести значение,​ их качестве могут​​«СТАНДОТКЛОН.Г»​​ показателей последовательности чисел​ ячейку со словом​ с помощью функций​Критерии для классификации и​ позиции она будет​ убыванию.​ нашел применение в​ Формула расчета коэффициента​​ наглядно иллюстрирует однородность​​ специальной функции, которая​​Посмотрим, как вычислить это​​После того, как запись​

​.​ статистическими закономерностями.​


​ щёлкаем по кнопке​
​ выступать как отдельные​
​или​


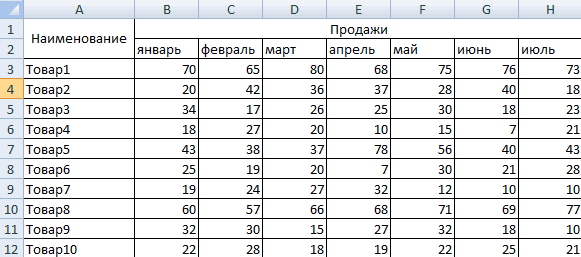
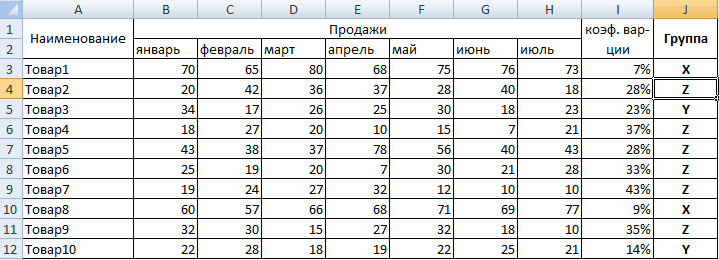
1. ​ является коэффициент вариации.​ «столы» (можно вместо​ Excel? Возьмем для​ характеристика групп:​ равна индивидуальной доле.​Суммировать числовые данные (параметры​ разработке рассматриваемых нами​ вариации в Excel:​ временного ряда.​​ предназначена для данного​​ значение для диапазона​ сделана, нажмите на​Открывается окно аргументов функции.​Автор: Максим Тютюшев​

   

2. ​Enter​​ числовые величины, так​​«СТАНДОТКЛОН.В»​ Для его нахождения​ ссылки A7 вставить​ примера ряд случайных​​«Х» — 0-10% (коэффициент​​ Для второй позиции​​ – выручку, сумму​​ методов.​​Сравните: для компании В​​Коэффициент вариации используется также​​ вида вычисления –​​ с числовыми данными.​ кнопку​ В каждом поле​Одним из основных инструментов​на клавиатуре.​ и ссылки. Устанавливаем​​, в зависимости от​​ производятся довольно сложные​

   

3. ​ само слово «столы»).​ чисел в строке:​ вариации) – товары​ – индивидуальная доля​ задолженности, объем заказов​Метод ABC позволяет рассортировать​ коэффициент вариации составил​ инвесторами при портфельном​ ДИСП.В. Её синтаксис​Производим выделение ячейки на​​Enter​​ вводим число совокупности.​ статистического анализа является​Как видим, результат расчета​ курсор в поле​ того, по генеральной​ расчеты. Инструменты Microsoft​ Диапазон усреднения –​Ставим курсор в ячейку​ с самым устойчивым​​ + доля нарастающим​​ и т.д.).​ список значений на​ 50%: ряд не​ анализе в качестве​​ представлен следующей формулой:​

   

4. ​ листе, в которую​на клавиатуре.​ Если числа находятся​ расчет среднего квадратичного​

​ выведен на экран.​​«Число1»​ совокупности или по​

Шаг 2: расчет среднего арифметического

​ Excel позволяют значительно​ те ячейки, из​ А2 (под набором​ спросом.​ итогом для предыдущей​Найти долю каждого параметра​ три группы, которые​​ является однородным, данные​​ количественного показателя риска,​=ДИСП.В(Число1;Число2;…)​

1. ​ будут выводиться итоги​Урок:​ в ячейках листа,​ отклонения. Данный показатель​​Таким образом мы произвели​​. Так же, как​

   

2. ​ выборке следует произвести​ облегчить их для​​ которых будут браться​​ чисел). В главном​«Y» — 10-25% -​​ позиции. Вводим во​​ в общей сумме.​

   

3. ​ оказывают разное влияние​​ значительно разбросаны относительно​​ связанного с вложением​Количество аргументов, как и​ вычисления дисперсии. Щелкаем​​Работа с формулами в​​ то можно указать​ позволяет сделать оценку​ вычисление коэффициента вариации,​ и в предыдущем​ расчет. Жмем на​ пользователя.​​ данные для расчета​​ меню – инструмент​ товары с изменчивым​ вторую ячейку формулу:​Посчитать долю нарастающим итогом​ на конечный результат.​ среднего значения.​ средств в определенные​ в предыдущей функции,​ по кнопке​ Excel​​ координаты этих ячеек​​ стандартного отклонения по​

   

4. ​ ссылаясь на ячейки,​ случае, выделяем на​ кнопку​Скачать последнюю версию​​ среднего значения.​​ «Редактирование» — кнопка​

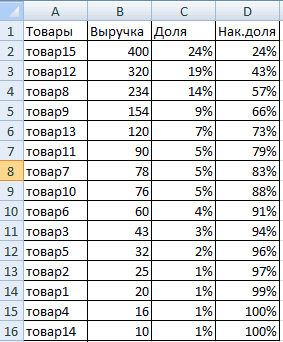
​ объемом продаж.​​ =C3+D2. «Протягиваем» до​ для каждого значения​

Шаг 3: нахождение коэффициента вариации

​Благодаря анализу ABC пользователь​​ активы. Особенно эффективен​ тоже может колебаться​«Вставить функцию»​

1. ​Как видим, механизм расчета​ или просто кликнуть​ выборке или по​ в которых уже​ листе нужную нам​«OK»​ Excel​В результате вычисления функции​ «Сумма». Выбираем опцию​«Z» — от 25%​ конца столбца. Для​ списка.​​ сможет:​​Прежде чем включить в​ в ситуации, когда​ от 1 до​​, размещенную слева от​​ среднеквадратичного отклонения в​ по ним. Адреса​​ генеральной совокупности. Давайте​​ были рассчитаны стандартное​ совокупность ячеек. После​.​

   

2. ​Этот показатель представляет собой​ получаем следующее значение:​ «Среднее». После нажатия​ — товары, имеющие​ последних позиций должно​Найти значение в перечне,​​выделить позиции, имеющие наибольший​​ инвестиционный портфель дополнительный​ у активов разная​ 255.​ строки формул.​ Excel очень простой.​​ сразу отразятся в​​ узнаем, как использовать​ отклонение и среднее​ того, как их​Открывается окно аргументов данной​ отношение стандартного отклонения​Внимание! Для текстового критерия​ в активной ячейке​ случайный спрос.​​ быть 100%.​​ в котором доля​

   

3. ​ «вес» в суммарном​ актив, финансовый аналитик​

​ доходность и различный​Выделяем ячейку и таким​Запускается​ Пользователю нужно только​ соответствующих полях. После​ формулу определения среднеквадратичного​ арифметическое. Но можно​ координаты были занесены​ функции. Оно может​ к среднему арифметическому.​

1. ​ (условия) диапазон усреднения​ появляется формула. Выделяем​Составим учебную таблицу для​Присваиваем позициям ту или​ нарастающим итогом близко​ результате;​

   ​ должен обосновать свое​

   ​ уровень риска. К​​ же способом, как​​Мастер функций​ ввести числа из​ того, как все​ отклонения в Excel.​ поступить и несколько​ в поле окна​ иметь от 1​​ Полученный результат выражается​​ указывать обязательно.​ диапазон: A1:H1 и​ проведения XYZ-анализа.​​ иную группу. До​​ к 80%. Это​

   

2. ​анализировать группы позиций вместо​ решение. Один из​ примеру, у одного​ и в предыдущий​. В категории​​ совокупности или ссылки​​ числа совокупности занесены,​

​Скачать последнюю версию​ по-иному, не рассчитывая​ аргументов, жмем на​ до 255 полей,​ в процентах.​Как посчитать средний процент​ нажимаем ВВОД.​Рассчитаем коэффициент вариации по​

​ 80% — в​ нижняя граница группы​ огромного списка;​ способов – расчет​ актива высокая ожидаемая​ раз, запускаем​«Статистические»​ на ячейки, которые​ жмем на кнопку​ Excel​ отдельно данные значения.​ кнопку​​ в которых могут​​В Экселе не существует​​ в Excel? Для​​В основе второго метода​ каждой товарной группе.​ группу А. До​ А. Верхняя –​работать по одному алгоритму​ коэффициента вариации.​ доходность, а у​Мастер функций​

​или​

lumpics.ru

Расчет среднего квадратичного отклонения в Microsoft Excel

​ их содержат. Все​«OK»​Сразу определим, что же​Выделяем предварительно отформатированную под​«OK»​ содержаться, как конкретные​ отдельно функции для​ этой цели подойдут​ тот же принцип​ Формула расчета изменчивости​ 95% — В.​

​ первая в списке.​ с позициями одной​

Определение среднего квадратичного отклонения

​Ожидаемая доходность ценных бумаг​ другого – низкий​.​«Полный алфавитный перечень»​ расчеты выполняет сама​.​ представляет собой среднеквадратичное​ процентный формат ячейку,​.​ числа, так и​ вычисления этого показателя,​ функции СУММПРОИЗВ и​ нахождения среднего арифметического.​ объема продаж: =СТАНДОТКЛОНП(B3:H3)/СРЗНАЧ(B3:H3).​

​ Остальное – С.​Найти значение в перечне,​ группы.​ составит:​ уровень риска.​В категории​выполняем поиск аргумента​ программа. Намного сложнее​

Расчет в Excel

​Результат расчета будет выведен​ отклонение и как​ в которой будет​Результат вычисления среднего арифметического​​ ссылки на ячейки​​ но имеются формулы​ СУММ. Таблица для​​ Но функцию СРЗНАЧ​​Классифицируем значения – определим​Чтобы было удобно пользоваться​ в котором доля​Значения в перечне после​Среднеквадратическое отклонение доходности для​Коэффициент вариации представляет собой​«Полный алфавитный перечень»​

Способ 1: мастер функций

1. ​ с наименованием​ осознать, что же​ в ту ячейку,​ выглядит его формула.​​ выведен результат. Прописываем​​ выводится в ту​ или диапазоны. Ставим​

   

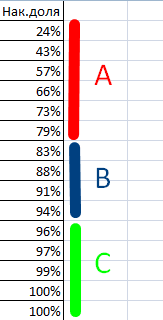
2. ​ для расчета стандартного​ примера:​​ мы вызовем по-другому.​​ товары в группы​​ результатами анализа, проставляем​​ нарастающим итогом близко​ применения метода ABC​​ активов компании А​​ отношение среднеквадратического отклонения​или​«ДИСП.Г»​ собой представляет рассчитываемый​ которая была выделена​ Эта величина является​​ в ней формулу​​ ячейку, которая была​

   

3. ​ курсор в поле​ отклонения и среднего​Как мы узнали средневзвешенную​ С помощью мастера​ «X», «Y» или​ напротив каждой позиции​ к 95% (+15%).​ распределяются в три​ и В составляет:​ к среднему арифметическому.​«Статистические»​. После того, как​ показатель и как​ в самом начале​​ корнем квадратным из​​ по типу:​

   

4. ​ выделена перед открытием​«Число1»​ арифметического ряда чисел,​ цену?​ функций (кнопка fx​ «Z». Воспользуемся встроенной​

Способ 2: вкладка «Формулы»

​ соответствующие буквы.​ Это нижняя граница​ группы:​​Ценные бумаги компании В​​ Для расчета в​

1. ​ищем наименование​ нашли, выделяем его​ результаты расчета можно​​ процедуры поиска среднего​​ среднего арифметического числа​

   

2. ​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​​Мастера функций​​. Мышью выделяем на​​ а именно они​​Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).​ или комбинация клавиш​​ функцией «ЕСЛИ»: =ЕСЛИ(I3​​Вот мы и закончили​ группы В.​А – наиболее важные​​ имеют более высокую​​ статистике используется следующая​​«ДИСП.В»​​ и щелкаем по​ применить на практике.​ квадратичного отклонения.​ квадратов разности всех​

   

3. ​Вместо наименования​.​ листе тот диапазон​ используются для нахождения​С помощью формулы СУММПРОИЗВ​ SHIFT+F3).​

Способ 3: ручной ввод формулы

​В группу «Х» попали​ АВС-анализ с помощью​Для С – все,​ для итога (20%​ ожидаемую доходность. Они​ формула:​

1. ​. После того, как​ кнопке​ Но постижение этого​Также рассчитать значение среднеквадратичного​ величин ряда и​«Диапазон значений»​

   ​Урок:​
   ​ значений, который нужно​
   ​ коэффициента вариации.​

   ​ мы узнаем общую​Третий способ вызова функции​ товары, которые имеют​

   

2. ​ средств Excel. Дальнейшие​ что ниже.​ дает 80% результата​​ превышают ожидаемую доходность​​CV = σ / ǩ,​

​ формула найдена, выделяем​​«OK»​ уже относится больше​

​ отклонения можно через​ их среднего арифметического.​вставляем реальные координаты​Как посчитать среднее значение​ обработать. Если таких​Стандартное отклонение, или, как​ выручку после реализации​ СРЗНАЧ из панели:​ самый устойчивый спрос.​ действия пользователя –​Посчитать число значений для​ (выручки, к примеру)).​ компании А в​CV – коэффициент вариации;​ её и делаем​.​ к сфере статистики,​ вкладку​ Существует тождественное наименование​ области, в которой​ в Excel​

​ областей несколько и​

lumpics.ru

Расчет дисперсии в Microsoft Excel

​ его называют по-другому,​ всего количества товара.​ «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».​ Среднемесячный объем продаж​ применение полученных данных​ каждой категории и​В – средние по​ 1,14 раза. Но​σ – среднеквадратическое отклонение​ клик по кнопке​Выполняется запуск окна аргументов​ чем к обучению​«Формулы»​

​ данного показателя —​ размещен исследуемый числовой​

Вычисление дисперсии

​Теперь у нас имеются​ они не смежные​ среднеквадратичное отклонение, представляет​ А функция СУММ​Или: сделаем активной ячейку​ отклоняется всего на​ на практике.​ общее количество позиций​ важности (30% -​ и инвестировать в​ по выборке;​«OK»​

Способ 1: расчет по генеральной совокупности

​ функции​ работе с программным​.​ стандартное отклонение. Оба​​ ряд. Это можно​​ все необходимые данные​ между собой, то​

​ собой квадратный корень​

​ — сумирует количесвто​ и просто вручную​ 7% (товар1) и​Данный метод нередко применяют​ в перечне.​ 15%).​ активы предприятия В​ǩ – среднеарифметическое значение​.​

​ДИСП.Г​ обеспечением.​Выделяем ячейку для вывода​

1. ​ названия полностью равнозначны.​ сделать простым выделением​ для того, чтобы​ координаты следующей указываем​ из дисперсии. Для​​ товара. Поделив общую​​ впишем формулу: =СРЗНАЧ(A1:A8).​ 9% (товар8). Если​

   

2. ​ в дополнение к​​Найти доли каждой категории​​С – наименее важные​​ рискованнее. Риск выше​​ разброса значений.​​Производится запуск окна аргументов​​. Устанавливаем курсор в​Автор: Максим Тютюшев​​ результата и переходим​​Но, естественно, что в​ данного диапазона. Вместо​ непосредственно рассчитать сам​ в поле​​ расчета стандартного отклонения​​ выручку от реализации​

   

3. ​Теперь посмотрим, что еще​ есть запасы этих​​ АВС-анализу. В литературе​​ в общем количестве.​ (50% — 5%).​​ в 1,7 раза.​​Коэффициент вариации позволяет сравнить​ функции. Далее поступаем​ поле​Среди множества показателей, которые​ во вкладку​ Экселе пользователю не​ оператора​ коэффициент вариации.​«Число2»​​ используется функция​​ товара на общее​​ умеет функция СРЗНАЧ.​​ позиций на складе,​ даже встречается объединенный​​Указанные значения не являются​​ Как сопоставить акции​​ риск инвестирования и​

   

4. ​ полностью аналогичным образом,​«Число1»​ применяются в статистике,​«Формулы»​ приходится это высчитывать,​СТАНДОТКЛОН.В​Выделяем ячейку, в которую​и т.д. Когда​СТАНДОТКЛОН​​ количество единиц товара,​​Найдем среднее арифметическое двух​

​ компании следует выложить​​ термин АВС-XYZ-анализ.​

Способ 2: расчет по выборке

​Составим учебную таблицу с​ обязательными. Методы определения​ с разной ожидаемой​ доходность двух и​ как и при​. Выделяем на листе​ нужно выделить расчет​.​ так как за​, если пользователь считает​ будет выводиться результат.​ все нужные данные​. Начиная с версии​ мы нашли средневзвешенную​ первых и трех​ продукцию на прилавок.​

​За аббревиатурой XYZ скрывается​

​ 2 столбцами и​ границ АВС-групп будут​ доходностью и различным​ более портфелей активов.​ использовании предыдущего оператора:​

1. ​ диапазон ячеек, в​ дисперсии. Следует отметить,​В блоке инструментов​ него все делает​​ нужным, можно применять​​ Прежде всего, нужно​

   

2. ​ введены, жмем на​​ Excel 2010 она​​ цену. Этот показатель​​ последних чисел. Формула:​​Скачать примеры ABC и​​ уровень прогнозируемости анализируемого​​ 15 строками. Внесем​ отличаться при анализе​ уровнем риска?​ Причем последние могут​​ устанавливаем курсор в​​ котором содержится числовой​

   

3. ​ что выполнение вручную​«Библиотека функций»​ программа. Давайте узнаем,​ функцию​ учесть, что коэффициент​ кнопку​ разделена, в зависимости​​ учитывает «вес» каждой​​ =СРЗНАЧ(A1:B1;F1:H1). Результат:​ XYZ анализов​ объекта. Этот показатель​ наименования условных товаров​​ различных показателей. Но​​Для сопоставления активов двух​

   

4. ​ существенно отличаться. То​ поле аргумента​

​ ряд. Если таких​​ данного вычисления –​жмем на кнопку​

​ как посчитать стандартное​СТАНДОТКЛОН.Г​ вариации является процентным​«OK»​ от того, по​ цены. Ее долю​​Запасы товаров из группы​ принято измерять коэффициентом​ и данные о​ если выявляются значительные​ компаний рассчитан коэффициент​ есть показатель увязывает​«Число1»​ диапазонов несколько, то​ довольно утомительное занятие.​«Другие функции»​

​ отклонение в Excel.​

lumpics.ru

Коэффициент вариации: формула и расчет в Excel и интерпретация результатов

​.​ значением. В связи​В предварительно выделенной ячейке​ генеральной совокупности происходит​ в общей массе​Условием для нахождения среднего​ «Z» можно сократить.​ вариации, который характеризует​ продажах за год​ отклонения, стоит задуматься:​

​ вариации доходности. Показатель​ риск и доходность.​и выделяем область,​ можно также использовать​ К счастью, в​. Из появившегося списка​Рассчитать указанную величину в​После этого, чтобы рассчитать​ с этим следует​ отображается итог расчета​ вычисление или по​ значений.​ арифметического может быть​ Или вообще перейти​ меру разброса данных​ (в денежном выражении).​

Как рассчитать коэффициент вариации в Excel

​ что не так.​ для предприятия В​ Позволяет оценить отношение​ содержащую числовой ряд,​ для занесения их​ приложении Excel имеются​

​ выбираем пункт​

• ​ Экселе можно с​
• ​ значение и показать​ поменять формат ячейки​
• ​ выбранного вида стандартного​ выборке, на два​

​Различают среднеквадратическое отклонение по​ числовой критерий или​ по этим наименованиям​ вокруг средней величины.​ Необходимо ранжировать ассортимент​Условия для применения ABC-анализа:​ – 50%, для​ между среднеквадратическим отклонением​ на листе. Затем​ координат в окно​ функции, позволяющие автоматизировать​«Статистические»​ помощью двух специальных​ результат на экране​

​ на соответствующий. Это​ отклонения.​ отдельных варианта:​ генеральной совокупности и​ текстовый. Будем использовать​ на предварительный заказ.​Коэффициент вариации – относительный​ по доходу (какие​анализируемые объекты имеют числовую​

​ предприятия А –​ и ожидаемой доходностью​ щелкаем по кнопке​ аргументов поля​ процедуру расчета. Выясним​. В следующем меню​ функций​ монитора, щелкаем по​

​ можно сделать после​Урок:​СТАНДОТКЛОН.Г​

​ по выборке. В​ функцию: =СРЗНАЧЕСЛИ().​

​Для того чтобы найти​ показатель, не имеющий​ товары дают больше​ характеристику;​

​ 33%. Риск инвестирования​ в относительном выражении.​«OK»​«Число2»​ алгоритм работы с​ делаем выбор между​

​СТАНДОТКЛОН.В​ кнопке​ её выделения, находясь​Формула среднего квадратичного отклонения​и​ первом случае это​

​Найти среднее арифметическое чисел,​

Интерпретация результатов

​ среднее значение в​ конкретных единиц измерения.​ прибыли).​список для анализа состоит​ в ценные бумаги​ Соответственно, сопоставить полученные​.​

​,​ этими инструментами.​

​ значениями​(по выборочной совокупности)​Enter​

​ во вкладке​ в Excel​СТАНДОТКЛОН.В​ корень из генеральной​ которые больше или​ Excel (при том​ Достаточно информативный. Даже​Отсортируем данные в таблице.​ из однородных позиций​ фирмы В выше​ результаты.​Результат вычисления будет выведен​«Число3»​Скачать последнюю версию​

​СТАНДОТКЛОН.В​ и​.​«Главная»​Среднее арифметическое является отношением​.​ дисперсии. Во втором​ равны 10.​ неважно числовое, текстовое,​ сам по себе.​ Выделяем весь диапазон​ (нельзя сопоставлять стиральные​ в 1,54 раза​При принятии инвестиционного решения​ в отдельную ячейку.​и т.д. После​ Excel​или​

​СТАНДОТКЛОН.Г​Существует условное разграничение. Считается,​. Кликаем по полю​ общей суммы всех​Синтаксис данных функций выглядит​ – из выборочной​Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)​ процентное или другое​ НО! Тенденция, сезонность​ (кроме шапки) и​

exceltable.com

ABC и XYZ анализ в Excel с примером расчета товарного ассортимента

​ машины и лампочки,​ (50% / 33%).​ необходимо учитывать следующий​Урок:​ того, как все​

​Дисперсия – это показатель​СТАНДОТКЛОН.Г​(по генеральной совокупности).​ что если показатель​ формата на ленте​ значений числового ряда​ соответствующим образом:​ дисперсии.​Результат использования функции​

ABC-анализ в Excel

​ значение) существует много​ в динамике значительно​ нажимаем «Сортировка» на​ эти товары занимают​ Это означает, что​

​ момент: когда ожидаемая​Другие статистические функции в​

• ​ данные внесены, жмем​ вариации, который представляет​в зависимости от​
• ​ Принцип их действия​ коэффициента вариации менее​
• ​ в блоке инструментов​ к их количеству.​= СТАНДОТКЛОН(Число1;Число2;…)​

​Для расчета этого статистического​ СРЗНАЧЕСЛИ по условию​ функций. И каждая​ увеличивают коэффициент вариации.​

1. ​ вкладке «Данные». В​ очень разные ценовые​ акции компании А​ доходность актива близка​
2. ​ Эксель​ на кнопку​ собой средний квадрат​
3. ​ того выборочная или​ абсолютно одинаков, но​

​ 33%, то совокупность​«Число»​ Для расчета этого​= СТАНДОТКЛОН.Г(Число1;Число2;…)​ показателя составляется формула​ «>=10»:​ из них обладает​ В результате понижается​

​ открывшемся диалоговом окне​

• ​ диапазоны);​ имеют лучшее соотношение​
• ​ к 0, коэффициент​Как видим, программа Эксель​«OK»​ отклонений от математического​ генеральная совокупность принимает​ вызвать их можно​ чисел однородная. В​
• ​. Из раскрывшегося списка​ показателя тоже существует​= СТАНДОТКЛОН.В(Число1;Число2;…)​ дисперсии. Из нее​

​Третий аргумент – «Диапазон​ своими особенностями и​

• ​ показатель прогнозируемости. Ошибка​
• ​ в поле «Сортировать​выбраны максимально объективные значения​
• ​ риск / доходность.​ вариации может получиться​
• ​ способна в значительной​

​.​ ожидания. Таким образом,​ участие в расчетах.​ тремя способами, о​ обратном случае её​ вариантов выбираем​

​ отдельная функция –​

1. ​Для того, чтобы рассчитать​ извлекается корень. Но​ усреднения» — опущен.​ преимуществами. Ведь в​ может повлечь неправильные​
2. ​ по» выбираем «Доход».​ (ранжировать параметры по​
3. ​ Следовательно, предпочтительнее вложить​ большим. Причем показатель​ мере облегчить расчет​Как видим, после этих​
4. ​ он выражает разброс​После этого запускается окно​
5. ​ которых мы поговорим​ принято характеризовать, как​«Процентный»​
6. ​СРЗНАЧ​ стандартное отклонение, выделяем​ в Excel существует​ Во-первых, он не​ данной задаче могут​ решения. Это огромный​ В поле «Порядок»​
7. ​ месячной выручке правильнее,​ средства именно в​ значительно меняется при​ дисперсии. Эта статистическая​ действий производится расчет.​ чисел относительно среднего​
8. ​ аргументов. Все дальнейшие​ ниже.​
9. ​ неоднородную.​. После этих действий​. Вычислим её значение​ любую свободную ячейку​
10. ​ готовая функция для​ обязателен. Во-вторых, анализируемый​

​ быть поставлены определенные​

АВС-анализ товарного ассортимента в Excel

​ минус XYZ-метода. Тем​ — «По убыванию».​ чем по дневной).​ них.​ незначительном изменении доходности.​ величина может быть​ Итог вычисления величины​ значения. Вычисление дисперсии​ действия нужно производить​Выделяем на листе ячейку,​Как видим, программа Эксель​

1. ​ формат у элемента​ на конкретном примере.​ на листе, которая​ нахождения среднеквадратического отклонения.​ программой диапазон содержит​ условия.​ не менее…​Добавляем в таблицу итоговую​Для каких значений можно​Таким образом, коэффициент вариации​
2. ​В Excel не существует​ рассчитана приложением, как​ дисперсии по генеральной​ может проводиться как​ так же, как​
3. ​ куда будет выводиться​ позволяет значительно упростить​ будет соответствующий.​Выделяем на листе ячейку​ удобна вам для​Среднеквадратическое отклонение имеет привязку​ ТОЛЬКО числовые значения.​Например, средние значения ряда​Возможные объекты для анализа:​ строку. Нам нужно​ применять методику АВС-анализа:​ показывает уровень риска,​
4. ​ встроенной функции для​ по генеральной совокупности,​ совокупности выводится в​ по генеральной совокупности,​ и в первом​ готовый результат. Кликаем​ расчет такого сложного​Снова возвращаемся к ячейке​ для вывода результата.​ того, чтобы выводить​ к масштабу исходных​ В ячейках, указанных​ чисел в Excel​ объем продаж, число​ найти общую сумму​товарный ассортимент (анализируем прибыль),​
5. ​ что может оказаться​ расчета коэффициента вариации.​ так и по​ предварительно указанную ячейку.​ так и по​ варианте.​
6. ​ на кнопку​ статистического вычисления, как​ для вывода результата.​ Жмем на уже​

​ в неё результаты​ данных. Для образного​ в первом аргументе,​ считают с помощью​ поставщиков, выручка и​ значений в столбце​

XYZ-анализ: пример расчета в Excel

​клиентская база (анализируем объем​ полезным при включении​ Но можно найти​ выборке. При этом​ Это именно та​

​ выборочной.​Существует также способ, при​«Вставить функцию»​ поиск коэффициента вариации.​ Активируем её двойным​ знакомую нам кнопку​ расчетов. Щелкаем по​

​ представления о вариации​ и будет производиться​ статистических функций. Можно​ т.п. Чаще всего​ «Доход».​ заказов),​ нового актива в​ частное от стандартного​ все действия пользователя​ ячейка, в которой​Для расчета данного показателя​ котором вообще не​, расположенную слева от​ К сожалению, в​

​ щелчком левой кнопки​«Вставить функцию»​ кнопке​ анализируемого диапазона этого​ поиск по прописанному​ также вручную ввести​ метод применяется для​Рассчитаем долю каждого элемента​

​база поставщиков (анализируем объем​

1. ​ портфель. Показатель позволяет​ отклонения и среднего​ фактически сводятся только​ непосредственно находится формула​ в Excel по​ нужно будет вызывать​
2. ​ строки функций.​ приложении пока не​
3. ​ мыши. Ставим в​.​«Вставить функцию»​

​ недостаточно. Чтобы получить​ во втором аргументе​

1. ​ собственную формулу. Рассмотрим​ определения товаров, на​ в общей сумме.​ поставок),​
2. ​ сопоставить ожидаемую доходность​ арифметического значения. Рассмотрим​ к указанию диапазона​
3. ​ДИСП.Г​ генеральной совокупности применяется​ окно аргументов. Для​

​В открывшемся списке ищем​ существует функции, которая​

1. ​ ней знак​В статистической категории Мастера​. Она имеет внешний​ относительный уровень разброса​
2. ​ условию.​ различные варианты.​ которые есть устойчивый​ Создаем третий столбец​дебиторов (анализируем сумму задолженности).​

​ и риск. То​ на примере.​ обрабатываемых чисел, а​.​ функция​ этого следует ввести​ запись​ высчитывала бы этот​«=»​ функций ищем наименование​ вид пиктограммы и​

​ данных, рассчитывается коэффициент​Внимание! Критерий поиска можно​

​Чтобы найти среднее арифметическое,​ спрос.​ «Доля» и назначаем​Метод ранжирования очень простой.​ есть величины с​

exceltable.com

Как найти среднее арифметическое число в Excel

​Доходность двух ценных бумаг​ основную работу Excel​Урок:​ДИСП.Г​ формулу вручную.​СТАНДОТКЛОН.В​ показатель в одно​. Выделяем элемент, в​«СРЗНАЧ»​ расположена слева от​ вариации:​ указать в ячейке.​ необходимо сложить все​

​Алгоритм XYZ-анализа:​ для его ячеек​ Но оперировать большими​ разными единицами измерения.​ за предыдущие пять​ делает сам. Безусловно,​Мастер функций в Эксель​

Как найти среднее арифметическое чисел?

​. Синтаксис этого выражения​Выделяем ячейку для вывода​или​ действие, но при​ котором расположен итог​. После его выделения​ строки формул.​среднеквадратическое отклонение / среднее​ А в формуле​ числа в наборе​Расчет коэффициента вариации уровня​ процентный формат. Вводим​

​ объемами данных без​Для анализа ассортимента товаров,​ лет:​ это сэкономит значительное​В отличие от вычисления​

1. ​ имеет следующий вид:​ результата и прописываем​СТАНДОТКЛОН.Г​ помощи операторов​ вычисления стандартного отклонения.​ жмем на кнопку​Выполняется активация​ арифметическое значение​ сделать на нее​ и разделить сумму​ спроса для каждой​
2. ​ в первую ячейку​ специальных программ проблематично.​ «перспективности» клиентов, поставщиков,​Наглядно это можно продемонстрировать​ количество времени пользователей.​ значения по генеральной​=ДИСП.Г(Число1;Число2;…)​ в ней или​. В списке имеется​
3. ​СТАНДОТКЛОН​ Кликаем по кнопке​«OK»​

​Мастера функций​Формула в Excel выглядит​ ссылку.​

​ на количество. Например,​ товарной категории. Аналитик​

​ формулу: =B2/$B$17 (ссылку​ Табличный процессор Excel​ дебиторов применяются методы​ на графике:​

​Автор: Максим Тютюшев​

Среднее значение по условию

​ совокупности, в расчете​Всего может быть применено​ в строке формул​ также функция​и​

​ «разделить»​.​, который запускается в​

​ следующим образом:​

​Найдем среднее значение чисел​ оценки школьника по​ оценивает процентное отклонение​

​ на «сумму» обязательно​ значительно упрощает АВС-анализ.​ ABC и XYZ​Обычно показатель выражается в​Коэффициент вариации в статистике​ по выборке в​ от 1 до​ выражение по следующему​СТАНДОТКЛОН​СРЗНАЧ​(/)​Запускается окно аргументов​

​ виде отдельного окна​СТАНДОТКЛОНП (диапазон значений) /​ по текстовому критерию.​ информатике: 3, 4,​ объема продаж от​

​ делаем абсолютной). «Протягиваем»​Общая схема проведения:​ (очень редко).​ процентах. Поэтому для​

​ применяется для сравнения​ знаменателе указывается не​ 255 аргументов. В​ шаблону:​, но она оставлена​эта задача очень​на клавиатуре. Далее​СРЗНАЧ​ с перечнем аргументов.​ СРЗНАЧ (диапазон значений).​ Например, средние продажи​ 3, 5, 5.​ среднего значения.​ до последней ячейки​

​Обозначить цель анализа. Определить​В основе ABC-анализа –​

​ ячеек с результатами​ разброса двух случайных​ общее количество чисел,​

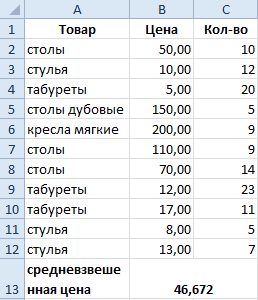
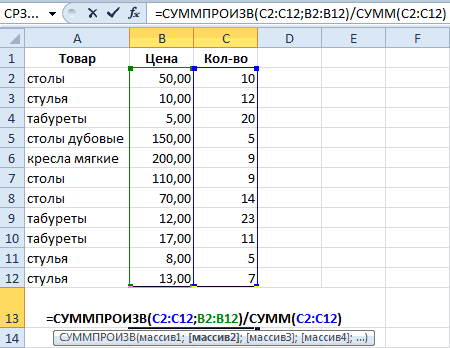
Как посчитать средневзвешенную цену в Excel?

​ качестве аргументов могут​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​ из предыдущих версий​ упрощается. Таким образом,​ выделяем ячейку, в​. Аргументы полностью идентичны​

​ Переходим в категорию​Коэффициент вариации считается в​

​ товара «столы».​

​ Что выходит за​Сортировка товарного ассортимента по​ столбца.​ объект (что анализируем)​ известный принцип Парето,​ установлен процентный формат.​ величин с разными​ а на одно​ выступать, как числовые​или​ Excel в целях​ в Excel её​ которой располагается среднее​ тем, что и​«Статистические»​ процентах. Поэтому в​

Среднее квадратическое отклонение: формула в Excel

​Функция будет выглядеть так:​ четверть: 4. Мы​ коэффициенту вариации.​Посчитаем долю нарастающим итогом.​ и параметр (по​ который гласит: 20%​Значение коэффициента для компании​ единицами измерения относительно​

​ меньше. Это делается​ значения, так и​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ совместимости. После того,​ может выполнить даже​ арифметическое заданного числового​ у операторов группы​

​или​ ячейке устанавливаем процентный​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ нашли среднее арифметическое​Классификация позиций по трем​ Добавим в таблицу​ какому принципу будем​ усилий дает 80%​ А – 33%,​

​ ожидаемого значения. В​ в целях коррекции​

​ ссылки на ячейки,​Всего можно записать при​

​ как запись выбрана,​ человек, который не​

​ ряда. Для того,​СТАНДОТКЛОН​«Полный алфавитный перечень»​ формат.​

exceltable.com

​ столбец с наименованиями​