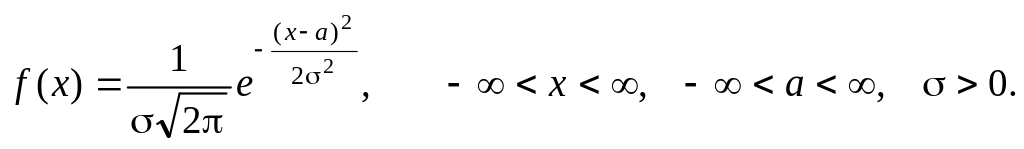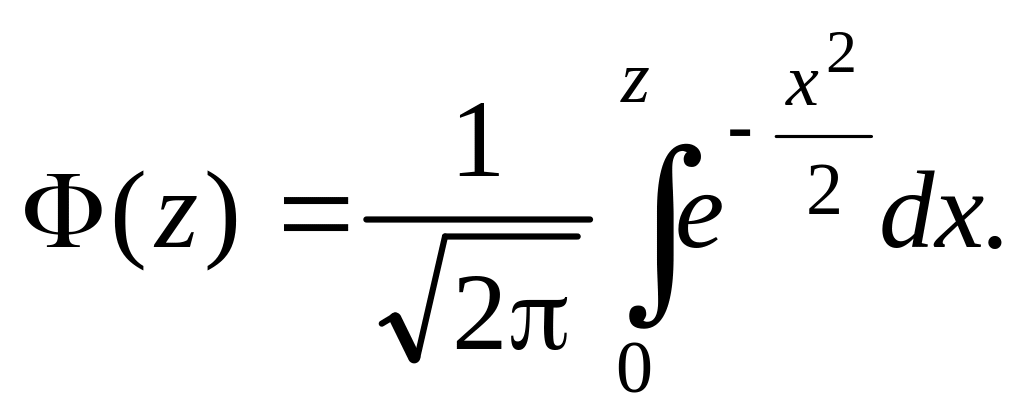Нормальным
называется распределение непрерывной
случайной величины, дифференциальная
функция (плотность распределения)
которой имеет вид
(5.17)
Параметр а
является математическим ожиданием
случайной величины, параметр
– ее средним квадратическим отклонением.
Нормальное распределение с указанными
параметрами обозначается
Интегральная
функция нормального распределение
нормированной случайной величины N(0,
1) имеет вид
(5.18)
Вероятность
попадания случайной величины
в интервал
равна
приращению интегральной функции Лапласа:
где
а
Отсюда
Вероятность
заданного отклонения случайной величины
от ее математического ожидания вычисляется
как удвоенная функция Лапласа:
.
Для нормального
распределения асимметрия и эксцесс
равны нулю, а мода и медиана совпадают
с математическим ожиданием, т.е. равны
а.
-
Измерение
дальности до объекта сопровождается
случайной ошибкой, подчиненной
нормальному закону со средним
квадратическим отклонением
= 100 м. Найти: а) вероятность того, что
измеренная дальность не превзойдет
истинной более чем на 150 м ; б) вероятность
измерения дальности с ошибкой, не
превосходящей по абсолютной величине
150 м.
Пусть случайная
величина Х – случайная ошибка
измерения дальности. По условию она
распределена по закону N(0,
100).
а) Событие А =
измеренная дальность
не превзойдет истинной
означает, что ошибка измерения Х
150. Тогда искомая вероятность
Из таблицы значений
функции
(табл.
2 Приложений) находим:
Значит,
б) Вероятность
заданного отклонения
где
Отсюда
-
Случайная
величина Х
распределена
по закону N(10;
2). Найти вероятность того, что в
результате испытания она примет
значение из интервала (12, 14). -
Деталь,
изготовленная автоматом, считается
годной, если отклонение ее размера Х
от номинала
не превышает 10 мк. Точность изготовления
детали характеризуется средним
квадратическим отклонением .
Считая, что
= 5 мк и Х
подчиняется закону N(a,
),
определить процент выпускаемых годных
изделий. -
Химический
завод выпускает серную кислоту
номинальной плотности 1,84 г/см3.
Известно, что плотность 99,9% всех
реактивов лежит в интервале (1,82; 1,86).
Найти вероятность того, что партия
кислоты удовлетворяет стандарту, если
для этого достаточно, чтобы ее плотность
не отклонялась от номинала более чем
на 0,01 г/см3. -
Случайное
отклонение размера детали от номинала
имеет параметры а
= 0 и
= 5 мк. Сколько необходимо изготовить
деталей, чтобы с вероятностью не менее
0,9 среди них была хотя бы одна годная,
если для этого отклонение размера от
номинала должно быть не более 2 мк? -
Случайная
величина Х
– годовая
процентная ставка потребительского
кредита – подчинена закону нормальному
распределения с параметрами а
= 12,0% и
= 1,75%. Найти вероятность того, что в
текущем году процентная ставка не
превысит 15,5%. -
Размер
отчислений предприятия в социальные
и культурные фонды зависит от текущей
прибыли и является величиной случайной,
подчиненной закону N(27,
6). Найти доверительный интервал для
случайной величины отчислений при
заданной вероятности
= 0,95. -
Размер
потребительского кредита есть величина
случайная, подчиненная нормальному
распределению с параметрами а
= = 45 тыс.руб. и
= 12 тыс.руб. Найти вероятность того, что
очередной кредит будет выдан на сумму
не менее чем в 30 тыс.руб. -
Улов
тихоокеанской камбалы (в тоннах)
является величиной случайной, подчиненной
закону N(2,4;
0,6). Найти доверительный интервал, в
котором с вероятностью 0,9 окажется
очередное значение улова. -
Нагрузка,
испытываемая ваерным канатом при
донном тралении, является величиной
случайной, подчиненной нормальному
распределению с параметрами а
= 4,8 тс и
= 1,75 тс. При заданной вероятности 0,98
найти разрывную прочность каната, если
запас прочности должен быть не менее
трех.
61
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Гость
Какова должна быть срединная ошибка (вероятное отклонение)
Имеется в виду среднее квадратическое отклонение. Задача стандартная. Решайте.
ProLL
Да я уже понял это и задачу вроде как решил, но ошибка у меня получилась 20/1,96 = 10,2 А в книге, из которой я брал задачу, есть ответ и он равен 6,9… Вот теперь не пойму, где я ошибся
Распиши. Символы можно вставить из Ворда и скопировать сюда
ProLL
Всё, уже разобрался с задачей) Спасибо
Гость
пожалуйста розпишите решения задачи
Радиодальномер
Cтраница 1
Радиодальномеры предназначены для измерения линейных координат летательного аппарата: наклонной дальности и высоты. Функционирование дальномера основано на измерении промежутка времени между излучаемым и принимаемым сигналами или параметров сигнала, связанных с этим промежутком времени.
[1]
Радиодальномер, состоящий из самолетного запросчика и наземного ответчика, служит для определения дальности до аэродрома, и обеспечения полета самолетов по орбитам вокруг аэродрома, используемых в качестве зон ожидания.
[2]
Радиодальномеры позволяют определить расстояние между радиостанцией, находящейся на судне ( задающая станция), и двумя отражающими радиостанциями на берегу и таким образом определять местонахождение судна в плохую видимость.
[3]
Радиодальномер, как любая радиотехническая система, находится под влиянием различных воздействий, которые мы разделим, как уже неоднократно поступали раньше, на управляющие и возмущающие.
[4]
Радиодальномеры — приборы для измерения расстояний с помощью радиоволн. Они позволяют измерять расстояния в сотни километров с точностью до стотысячных долей измеряемого расстояния и нашли широкое применение в радионавигации, геодезии и гидрографии.
[5]
Радиодальномер — прибор для измерения расстояний по скорости и времени прохождения радиоволн вдоль измеряемой линии и обратно после их отражения от конечной точки этой линии. При использовании непрерывных колебаний измерение расстояний производится фазовым методом. Мандельштамом и Н. Д. Папалекси, основаны на определении числа радиоволн, укладывающихся вдоль измеряемого расстояния; применяются в радионавигации, геодезии и гидрографии.
[6]
Радиодальномерами называют приборы, состоящие из двух прпемо-передающих радиостанций, снабженные устройствами для измерения времени прохождения радиосигналов при распространении их от одного пункта до другого. Радиостанции помещают в пунктах, расстояние между которыми необходимо измерить.
[7]
Ошибка радиодальномера подчинена нормальному закону. Систематической ошибки радиодальномер не дает.
[8]
В радиодальномерах и других устройствах с аппаратурой селекции движущихся объектов требование к стабильности частоты следования импульсов и их длительности определяется типом и характеристиками применяемых устройств компенсации сигналов, отраженных от неподвижных объектов.
[9]
В радиодальномере с двойным интегратором ( рис. 11 — 21 а) наряду с координатой дальности можно получить напряжение, пропорциональное скорости изменения дальности до цели.
[10]
Принцип работы радиодальномеров и радиовысотомеров определяется параметрами сигналов, несущих информацию о дальности. Наиболее широко применяются импульсные дальномеры с ответчиком и частотные высотомеры.
[11]
Постоянная поправка радиодальномера должна быть взята та, которая соответствует паре станций, участвовавших в измерении данной линии.
[12]
При помощи радиодальномера произведено 16 измерений одного и того же расстояния.
[13]
Для схемы импульсного радиодальномера найдите выражение, определяющее установившуюся ошибку при движении цели с постоянным ускорением а, при наличии в системе одного ( рис. 9.11) и двух ( рис. 9.15) интеграторов.
[15]
Страницы:
1
2
3
4
. . ,Хп точечную оценку параметра р биномиального распределениягде Х( — число появлений события в /-м опыте (/ = 1, 2,. . . , /г), т — количество испытаний в одном опыте.У к а з а н и е . Приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка.475. Случайная величина X (число появлений события А ъ т независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределениечисла появлений события в 10 опытах по 5 испытанийв каждом (в первой строке указано число Xi появленийсобытия А в одном опыте; во второй строке указаначастота л,- — количество опытов, в которых наблюдалосьXi появлений события Л):X,.л,.О512213141Найти методом моментов точечную оценку параметра рбиномиального распределения.У к а з а н и е .
Использовать решение задачи 474.476. Найти методом моментов по выборке х^, Xg, . . . ,Хп точечную оценку неизвестного параметра X показательного распределения, плотность которого f{x) = Xe-‘^^(х>0).477. Случайная величина X (время работы элемента)имеет показательное распределение f{x) = Xe-^ (х^О).Ниже приведено эмпирическое распределение среднеговремени работы п = 2 0 0 элементов (в первой строке при165ведено среднее время х^ работы элемента в часах; во второй строке указана частота щ—количество элементов»проработавших в среднем Х/ часов):Xi 2,5 7,5 12,5 17,5 22,5 27,5л^ 133 45 15421Найти методом моментов точечную оценку неизвестного параметра показательного распределения.У к а з а н и е .
Использовать решение задачи 476.478. Найти методом моментов точечную оценку параметра р (вероятности) геометрического распределенияP(X = Xi) = {}—pY»’^-pf где X/—число испытаний, произведенных до появления события; р—вероятность появления события в одном испытании.У к а з а н и е . Принять во внимание, что М(X) = 1/р (см. задачу 222).479. Найти методом моментов оценку параметра ргеометрического распределения Р{Х = х^) = {1—ру^’^-р^если в четырех опытах событие появилось соответственнопосле двух, четырех, шести и восьми испытаний.480. Найти методом моментов по выборке х^, х,, …»Хп точечные оценки неизвестных параметров а и р гамма-распределения, плотность которого/(^) = ра^хга+1)^^^»^^ ( а > — 1 . Р > 0 , х > 0 ) .Р е ш е н и е .
Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретическиймомент первого порядка Vi начальному эмпирическому моменту первого порядка Ml и центральный теоретический момент второго порядка fis центральному эмпирическому моменту второго порядка т^;Учитывая, что Vi = Ai(X), Мг^х^^ ^ia=Z>(X), m^^D^, имеемГЛ1(Х)=7,.*.Математическое ожидание и дисперсия гамма-распределения соответственно равны Л1 (Х) = (а+1)Р» D(X)=(aH-l)p* (см.
задачу 302), поэтому (^) можно записать в виде/(а+1)р=7„Ua+1)P*=I>B.Решив эту систему, окончателыю^ получим искомые JFOчeчныeоценки ненэтестяых параметров: а*=(х^)^/0,^—1, ^*=0^/х^’16в481. Случайная величина X (уровень воды в реке посравнению с номиналом) подчинена гамма-распределению,плотность которого определяется параметрами а и Э(а>—1, р>0):Ниже приведено распределение среднего уровня воды поданным /г = 45 паводков (в первой строке указан средний уровень воды х^ (см); во второй строке приведеначастота п^- — количество паводков со средним уровнемводы JC,):Xi 37,5 62,5 87,5 112,5 137,5 162,5 187,5 250 350п ^ 1 3 6 7754 8 4Найти методом моментов точечные оценки неизвестныхпараметров а и р рассматриваемого гамма-распределения.Р е ш е н и е . Используем точечные оценки параметров гаммараспределения (см.
задачу 480):OC*=(7B)VZ)B-1,Р*=^ВМВ.ППо заданному распределению легко найдем выборочную среднююи выборочную дисперсию: х^=1&6, DB = 6782.Подставив эти числа в формулы (*), окончательно получимискомые точечные оценки неизвестных параметров рассматриваемогогамма-распределения: а* =3,06, р* =40,86.482. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению.Испытания пяти элементов дали следующие наработки(время работы элемента в часах до отказа): 50, 75, 125, 250,300. Найти методом моментов точечные оценки неизвестных параметров а и р , которыми определяется гаммараспределение.У к а з а н и е .
Использовать решение задачи 480. Учесть, чтообъем выборки п = 5 мал, поэтому в формулах для вычисления параметров а и р вместо выборочной дисперсии подставить исправленную дисперсию s^ = ‘Lni(Xi—х^)^/(п — 1).483. Найти методом моментов по выборке лг^, Xg, .
. . ,Хп точечные оценки неизвестных параметров а и о нормального распределения, плотность которого/(л:) = —i=e-<^-«>V(2a«).У к а з а н и е . Приравнять начальный теоретический моментпервого порядка и центральный теоретический момент второго порядка соответствующим эмпирическим моментам.167484. Случайная величина X (отклонение контролируемого размера изделия от номинала; подчинена нормальному закону распределения с неизвестными параметрамиа и о.
Ниже приведено эмпирическое распределение отклонения от номинала п = 200 изделий (в первой строкеуказано отклонение х^- (мм); во второй строке приведеначастота п,- — количество изделий, имеющих отклонение Xf):Xi 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3п^ 6926 25 30 26 21 24 2085Найти методом моментов точечные оценки неизвестныхпараметров а и о нормального распределения.У к а з а н и е .
Использовать задачу 483.485. Найти методом моментов по выборке х^, дг^, …»х„ точечные оценки параметров а и b равномерного распределения, плотность которого / (х) = 1/(6—а) (6 > а).У к а з а н и е . Использовать решения задач 313, 315.486. Случайная величина X (ошибка измерения дальности радиодальномером) подчинена равномерному закону распределения с неизвестными параметрами а и Ь.Ниже приведено эмпирическое распределение среднейошибки л = 200 измерений дальности (в первой строкеуказана средняя ошибка л:,-; во второй строке указаначастота п^—количество измерений, имеющих среднююошибку АГ/):л:,.
3 5 7 9 11 13 15 17 19 21п^ 21 16 15 26 22 14 21 22 18 25Найти методом моментов точечные оценки неизвестныхпараметров а и Ь равномерного распределения.У к а з а н и е . Использовать задачу 485.487. Найти методом моментов по выборке х^, х^, . . . ,л:„ точечные оценки неизвестных параметров Х^ и Яд«двойного распределения» Пуассона1*Х= Xf) = -оГ •Х^’е~^«;1h «о* •Х^’е~^«i— »где х^ — число появлений события в п^ испытаниях Х^ иЯа—положительные числа, причем X2>^i.Р е ш е н и е . Если случайная величина Z распределена по законуПуассона с параметром X, то ее начальные теоретические моменты168первого и второго порядка соответственно равны (см.
задачи 207,227):Vi = Af(Z)==^,Найдем начальные теоретические моменты первого и второгопорядка рассматриваемой случайной величины X, учитывая соотношения (*):Vi = M (X) = A,,/2 + X2/2=(Xi + X2)/2,V2=Af(X2) = (l/2)(^i + A?)+(l/2)(X2 + ^ l ) = V i + ( > . ? + X i ) / 2 .Отсюда/Xi + X2 = 2vbXf + X| = 2v2 —2vi.Решив эту систему относительно неизвестных параметров, принявво внимание, что Лг > Ki, получим:^i = vi —Kv2-—Vi —V?, X2 = V i + K Va —Vi —V?.488. Случайная величина X распределена по «двойному» закону Пуассона:1 Xfe-^*1 Ц^e-^*Р (2С = X:) == «7Г •iЬ 7Г «i•Ниже приведено эмпирическое распределение числапоявлений события в л = 327 испытаниях (в первойстроке указано число х,- появлений события; во второйстроке приведена частота n^• — количество испытаний,в которых появилось Х/ событий):X,.
О 1 2 3 4 5 6 7 8 9 10п^ 28 47 81 67 53 24 13 8 3 2 1Найти методом моментов точечные оценки неизвестных параметров Х^ и К^ «двойного распределения» Пуассона.У к а з а н и е . Использовать решение задачи 487. Вычислить повыборке начальные эмпирические моменты первого и второго порядков:Ml = ( 2 niXi)/n, Af 2 = ( 2 ^i^b/^§ 3. Метод наибольшего правдоподобияМетод наибольшего правдоподобия точечной оценки неизвестныхпараметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров.А. Дискретные случайные величины.
Пусть X—дискретная случайная величина, которая в результате «опытов приняла возможные значения Xi, х^, . . . , л:„. Допустим, что вид закона распределения величины X задан, но неизвестен параметр в , которым оп169ределяетсяэтотзакон;требуетсянайтиего точечную оценкуОбозначим вероятность того, что в результате испытания величина X примет значение Xi через p(Xi 0 ) .Функцией правдоподобия дискретной ‘случайной величины Xназывают функцию аргумента 0 :ЦхиХ2, …,Хп 0) = p(-ti; е)’Р(Х2 в)…р(Хп).Оценкой наибольшего правдоподобия параметра 0 называюттакое его значение 0*, при котором функция правдоподобия достигает максимума.Функции L и In L достигают максимума при одном и том жезначении 0 , поэтому вместо отыскания максимума функции L ищут,что удобнее, максимум функции In L.Логарифмической функцией правдоподобия называют функцию InL.Точку максимума функции InL аргумента 0 можно искать, например, так:1 и чd InL1.
Его решение имеет вид ш Ьг аг 2(1пЬ вЂ” 1па) 158 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Нетрудно проверить, что при фиксированных значениях а и Ь, в силу условия О < а < Ь < +со справедливы соотношения Р(а < Х < Ь) = Фо( ) Фо(-) — +О Ь а Р1а <Х <Ь) =Фо( — ) Фо( ) — + О. Позтому вероятность Р(а < Х < Ь) при (Ь2 2) 2(1п Ь вЂ” 1па) принимает максимальное значение. Вопросы и задачи 4.1. Дайте определение случайной величины. 4.2. Что называют законом распределения (вероятностей) случайной величины? 4.3.
Дайте определение функции распределения (вероятностей). Перечислите и докажите свойства функции распределе- 4.4. Как, зная функцию распределения, найти вероятность попадания случайной величины в заданный интервал? 4.5. Какие свойства должна иметь некоторая функция для того, чтобы она могла быть функцией распределения? 4.6. Какую случайную величину называют дискретной? Приведите примеры дискретных случайных величин.
4.7. Что называют рядом распределения дискретной случайной величины? Как еще можно задать закон распределения дискретной случайной величины? Волросм иэалачя 159 4.8. Какой вид имеет функция распределения дискретной случайной величины? 4.9. Какое распределение называют биномиальным? 4.10. Какое распределение называют распределением Пуассона? 4.11.
Какое распределение называют геометрическим распределением? 4.12. Какую случайную величину называют непрерывной? Приведите примеры непрерывный случайных величин. 4.13. Дайте определение плотности распределения (вероятностей). Перечислите и докажите свойства плотности распределения. Существует ли плотность распределения у дискретной случайной величины? 4.14. Как, зная плотность распределения, найти вероятность попадания случайной величины в заданный интервал? 4.15. Чем различаются графики функций распределения дискретной и непрерывной случайных величин? 4.18. Какое распределение называют равномерным? 4.17.
Какое распределение называют экспоненциальным (показательным)? 4.18. Какое распределение называют нормальным? 4.19. Как выглядит график плотности нормального распределения? 4.20. Что называют интегралом Лапласа? Как, пользуясь таблицей значений интеграла Лапласа, вычислить вероятность попадания нормально распределенной случайной величины в некоторый интервал? 4.21. Какое распределение называют распределением Вейбулла? 160 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.22.
Какое распределение называют гамма-распределением? 4.23. Из партии в 10 деталей, среди которых две бракованные, наудачу выбирают три детали. Найдите закон распределения числа бракованных деталей среди выбранных. Постройте функцию распределения. Ответ: 4.24. Вероятность приема самолетом радиосигнала при каждой передаче равна 0,7. Найдите ряд распределения и функцию распределения числа Х принятых сигналов при шестикратной передаче. Ответ: Ряд распределения и функцию распределения случайной величины Х легко построить, зная, что Р(Х = з) = =Со1(0,7)'(0,3)о ‘, 4 =0,6. 4.25.
Найдите закон распределения случайной величины Х вЂ” числа таких бросаний трех игральных костей, в каждом из которых ровно на двух костях появится по 2 очка, если общее число бросаний равно 15. Ответ: Р(Х=з)=С11зр’Чы ‘, 4=0,15, где р=Сз(1/6)~(5/6) = = 5/72 я~ 0,0694. 4.26. В течение часа на станцию скорой помощи поступает случайное число Х вызовов, распределенное по закону Пуассона с параметром Л = 5. Найдите вероятность того, что в течение часа поступит: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов. О, С.Сз-с 7/15 Р(Х з) зз 4=0,1,2; Р(х) = С1зо 14/15 1, х<0; х Е (О, 1]; х Е (1, 2]; х > 2.
161 Вопросы и задачи Ответ: а) Р1Х =2) =5эе ~/2! 0,086; б) Р(Х < 2) = (5о/О! + 51/1! + 5э/2!)е а — 0,127; в) Р1Х ) 2) = 1 — Р1Х < 2) = 1 — (5е/О!+ 51/1!)е ~ 0,041. 4.27. Число вызовов, поступающих на АТС (автоматическая телефонная ставция) каждую минуту, распределено по закону Пуассона с параметром Л = 1,5. Найдите вероятность того, что за минуту поступит: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов. Ответ: а) 0,12551; б) 0,77687; в) 0,98143.
4.28. В приборный отсек космического корабля за время полета попадает случайное число частиц, распределенное по закону Пуассона с параметром Л, причем вероятность попасть в блок управления, расположенный в отсеке космического корабля, для каждой иэ этих частиц равна р. Определите вероятность попадания в блок: а) ровно й частиц; б) хотя бы одной частицы. Ответ: а) (Лр)»е «и/й!; 6) 1 — е ~’з. 4.29. По цели производят серию независимых выстрелов до первого попадания.
Даны вероятность р попадания в цель при одном выстреле и запас патронов и. Найдите ряд распределения и функцию распределения числа Х израсходованньп~ патронов. рд’ ‘, з’=б;и:Т (9=1-р); Ответ: Р1Х =з) = ! 9 ~ Ф=п. 4.30. Летательный аппарат, по которому ведется стрельба, состоит из двух различных по уязвимости частей. Аппарат выходит из строя при одном попадании в первую часть или трех попаданиях во вторую.
Стрельба ведется до поражения летательного аппарата. Постройте ряд распределения и функцию 6 — той 162 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ распределения числа попаданий Х в летательный аппарат, которое понадобится для его поражения, если каждый попаюпий в аппарат снаряд с вероятностью 0,3 поражает первую часть и с вероятностью 0,7 — вторую. О т в е т: Р(Х = 1) = 0,3; Р [Х = 21 = 0,21; Р(Х = 3) = 0,49.
4.31. Непрерывная случайная величина Х распределена по экспоненцизльному закону с параметром А = 0,2. Найдите вероятность попадания этой случайной величины в интервал (О, 2). Ответ: 1 — е е4 я~ 0 33. 4.32. Длительность времени Х безотказной работы элемента имеет экспоненцизльное распределение с параметром Л = = 0,02 ч 1. Вычислите вероятность того, что за время $ = 100 ч элемент: а) выйдет из строя; б) будет исправно работать. Ответ: а) 1 — е з ж0,865; б) е з 0,135. 4.33. Случайная величина Х имеет нормальное распределение с параметрами гп = 2 и и = 1. Определите вероятность попадания случайной величины в интервал (1, 5).
Ответ: 0,83999. 4.34. Случайная величина Х распределена по нормальному закону с параметрами т = 4 и и = 1. Определите вероятность попадания случайной величины Х в интервал (6, 8). Ответ: 0,0227. 4.35. Случайная величина Х имеет нормальное распределение с параметрами т и и. Вычислите вероятность попадания случайной величины в интервал (пз — 4о’, т). Ответ: 0,499971. 4.36.
Случайная величина Х подчинена нормальному закону распределения с тп = О. Вероятность попадания случайной величины в интервал (-0,3, 0,3) равна 0,5. Найдите среднее квадратичное отклонение и. Ответ: о 0,44. 153 Воиросьг и задачи 4.3Т. Измерительный прибор имеет систематическую погрешность 5 м. Случайные погрепности подчиняются нормальному закону со средним квадратическим отклонением, равным 10 м. Какова вероятность того, что погрешность измерения не превзойдет по абсолютному значению 5 м? Ответ: 0,3413.
4.38. Измерение дальности до объекта сопровождается случайными погрешностями, подчиняющимися нормальному закону со средним квадратичным отклонением, равным 50 м. Систематическая погрешность отсутствует. Найдите: а) вероятность измерения дальности с погрешностью, не превосходящей по абсолютному значению 100 м; б) вероятность того, что измеренная дальность не превзойдет истинной. Ответ: а) 0,9545; б) 0,5. 4.39.
Высотомер имеет случайную и систематическую погрешности. Систематическы погрешность равна 20 м. Случайная погрешность распределена по нормальному закону. Какую среднюю квадратичную погрешность должен иметь прибор, чтобы с вероятностью 0,9452 погр~пность измерения высоты бь|ла меньше 10 му Ответ: 50 м. 4.40. Случайны величина Х распределена по нормальному закону с математическим ожиданием пз и средним квадратичным отклонением о. Определите абсциссы и ординаты точек перегиба кривой плотности распределения. Ответ: шло; е 1~з/(а~(2~г). 4.41. Нормально распределенная случайная величина Х имеет математическое ожидание, равное нулю.
Найдите среднее квадратичное отклонение а,при котором вероятность попадания случайной величины в интервал (5, 10) была бы наибольшей. О: = ~/75Д2) 2). 164 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.42. Время Х (в часах) безотказной работы электрической лампочки имеет распределение Вейбулла с параматрами а = = 0,02 и ~3 = 0,5. Определите вероятность того, что лампочка проработает не менее 10000 ч. Ответ: Р(Х ) 100001 =е ~Ли~сесе -0,14. 4.43. Время Х (в месяцах) безотказной работы некоторой системы, состоящей из одного основного и двух резервных элементов, имеет гамма-распределение с параматрами у = 3 и А = 0,05. Найдите вероятность того, что система проработает не менее 5 лет.
О т в е т: Р 1Х ) 60) = е з(1+ 3 = Зз/2) и 0,42, 5. МНОГОМЕРНЫЕ СЛ’У ЧАЙНЫЕ ВЕЛИЧИНЫ В прикладных задачах обычно приходится рассматривать не одну случайную величину, а несколько случайных величин, одновременно измеряемых (наблюдаемых) в эксперименте. При этом с каждым элементпарным всходом ат е Й бывает связан набор числовых значений некоторых количественных параметров. В этой главе мы обобщим ранее полученные результаты на совокупность из нескольких случайных величин, задзвных на одном и том же веролптностпном простпранстпве. 5.1. Многомерная случайная величина.
Совместная функция распределения Определение 5.1. Совокупность случайныя величин Хт = Хт(от), …, Х„= Х„(ы), заданных на одном и том же веролтпностпном простпранстпве (Й,З,Р), называют многомерной (и-мерной) случайной величиной или тт-мерным случайным еектпором. При этом сами случайные величины Хт, Хт,, Х„называют коордннатптьнн случайного вектпора. В частности, при и = 1 говорят об одномерной, при и = 2 — двумерной с.аучайной еелнчнне (или двумерном случайном вектпоре). Для и-мерного случайного вектора воспользуемся обозначе. пнями (Хм …, Х„) и Х = (Хт, …, Х„). В случае двумерных и трехмерных случайных векторов наряду с обозначениями (Хм Хз) и (Хы Хг, Хз) будем испольэовать также обозначения (Х, У) и (Х, У, Я).
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
|
0 / 0 / 0 Регистрация: 28.05.2014 Сообщений: 2 |
|
|
1 |
|
Измерение дальности до объекта сопровождается систематическими и случайными ошибками28.05.2014, 23:55. Показов 4334. Ответов 2
Измерение дальности до объекта сопровождается систематическими и
0 |
|
831 / 678 / 101 Регистрация: 11.11.2012 Сообщений: 1,800 |
|
|
29.05.2014, 12:58 |
2 |
|
Измерение дальности до объекта сопровождается систематическими и это значит, что мат. ожидание равно 20
Случайная ошибка подчиняется нормальному закону со вот второй параметр — сигма
Найти вероятность Р(-100<Х<100)=? решается по простой формуле для нормального закона
0 |
|
0 / 0 / 0 Регистрация: 28.05.2014 Сообщений: 2 |
|
|
29.05.2014, 13:20 [ТС] |
3 |
|
Да по этой формуле решается
0 |