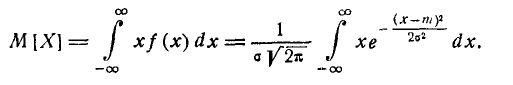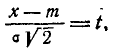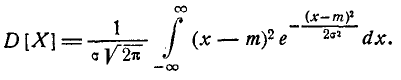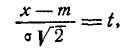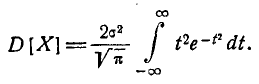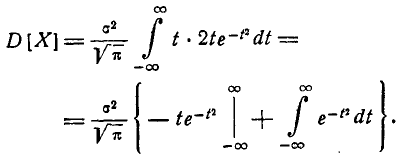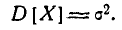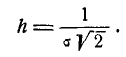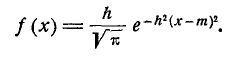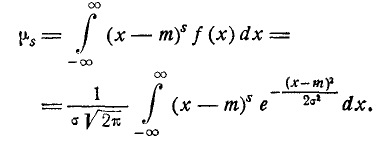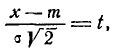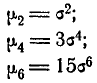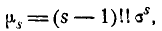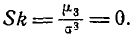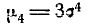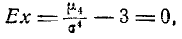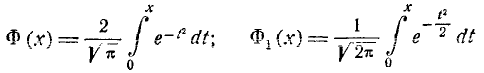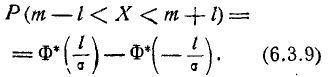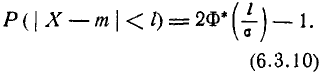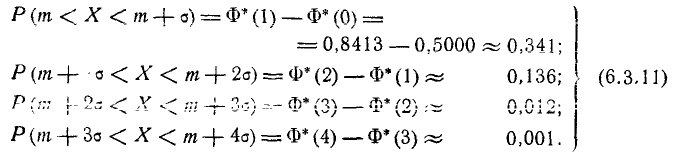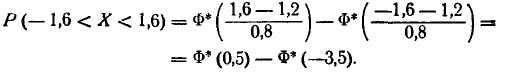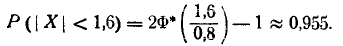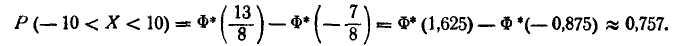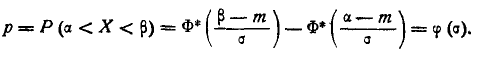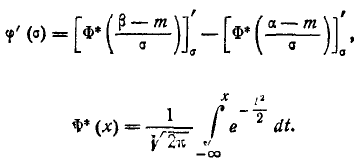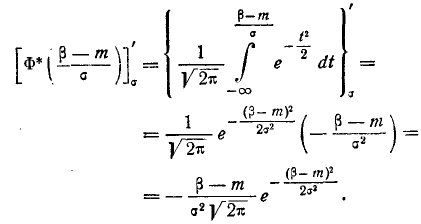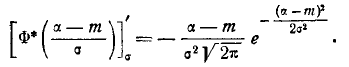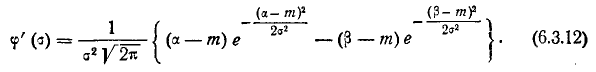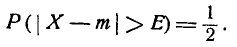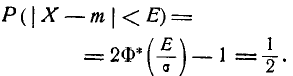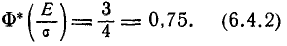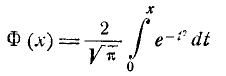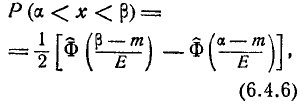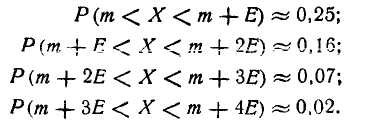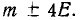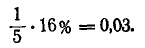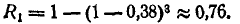Ошибка измерений подчиняется нормальному закону при - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

§ 6. ТЕОРЕМЫ ЛЯПУНОВА И ЛАПЛАСА.

6.2. Основной закон ошибок.

Когда мы производим некоторое измерение, то на его результат влияет большое количество факторов, которые
порождают ошибки измерений. Ошибки измерений в основном можно подразделить на три группы: 1) грубые ошибки; 2) систематические ошибки;
3) случайные ошибки.

Грубые ошибки возникают от невнимательности при чтении показателей прибора, неправильной записи показаний,
неправильном использовании прибора. Эти ошибки могут быть исключены соблюдением правил измерения.

Систематические ошибки искажают обычно результат измерения в определенную сторону. Они происходят, например,
от несовершенства приборов, от личных качеств наблюдателя и могут быть устранены соответствующими поправками.

Случайные ошибки вызываются большим числом отдельных причин, не поддающихся точному учету и действующих в
каждом отдельном случае различным образом. Эти ошибки возникают от незаметных механических причин, из-за изменения параметров
измерительных приборов, зависящих от метеорологических условий, и т. д. Каждая из этих причин в отдельности порождает при измерении ничтожную
ошибку . Складываясь, эти ничтожно малые ошибки порождают суммарную ошибку , которой уже нельзя пренебречь.
Эта суммарная ошибка v есть случайная величина, являющаяся суммой огромного числа незначительных, независимых друг от друга случайных
величин и имеет, согласно следствию из теоремы Ляпунова, нормальное распределение.

Предполагая измерение свободным от грубых и систематических
ошибок, можно считать, что возможный результат измерения есть случайная величина , математическое ожидание
которой равно истинному значению а измеряемой величины: (см. Теорему Ляпунова).
Так как суммарная ошибка подчиняется нормальному закону распределения, то возможный результат
измерения также подчиняется нормальному закону распределения (см. § 4, п. 3).
В этом заключается основной закон ошибок.

Дальше…

Источник

В
законе ошибок, который мы сейчас
рассмотрим, проявляется всеобщая
связь и взаимообусловленность явлений
в природе, проявляется

объективно
существующая закономерность, связь
между величиной

ошибки и частотой
ее появления при систематическом
повторении опытов.

Нам известно, что
случайные события при большом числе их
повторения обнаруживают определенную
закономерность. Так происходит и со
случайными ошибками.

При
большом числе измерений появление
случайных ошибок подчиняется
определенному закону, который выражает
зависимость между величиной ошибки и
частотой ее появления. Из теории
вероятностей также известно, что при
достаточно большом числе опытов частота
события очень мало отличается от
вероятности события. На основании этого
можно сказать, что между величиной
случайной ошибки и вероятностью ее
получения также существует определенная
зависимость.

Зависимость
между величиной случайной ошибки и
вероятностью ее получения называется
законом случайных ошибок.

Ошибки
могут подчиняться различным законам.
Наибольший интерес для нас представляет
так называемый нормальный
закон ошибок,
так как этому закону подчиняются ошибки
большинства измерений (измерение
дальности разными способами, измерение
углов, измерение скорости движения
и т. п.). Этому же закону подчиняется и
рассеивание траекторий.

В
огневой практике встречается другой
закон ошибок — закон равной вероятности.
Ошибки, которые подчиняются этому
закону, получаются при округлении от
счетов, считываемых со шкал приборов.

Закономерности
случайных ошибок можно выявить опытным
путем. Для этого надо произвести измерения
какой-либо величины, учесть величины
полученных ошибок и установить частоту
их появления. Чем больше число полученных
ошибок, тем меньше будет различий между
частотой и вероятностью, тем точнее
можно выявить закон ошибок.

Положим,
что произведено 100 измерений одного и
того же расстояния глазомерно. Пусть
истинное расстояние равно 1000 м (получено
путем измерения более точным способом).
Определим ошибки всех результатов
измерения и данные сведем в таблицу,
где ошибки сгруппированы через каждые
100 м в большую и в меньшую сторону.

Таблица № 2.

Зависимости величин
ошибок и их частоты

Величина ошибок в метрах	Отрицательные ошибки	Положительные ошибки
от 301 до 400 м	от 201 до 300 м	от 101 до 200 м	от0 до 100 м	от0 до 100 м	от 101 до 200 м	от 201 до 300 м	от 301 до 400 м	более 400 м
Кол-во ошибок	3	8	14	26	23	15	8	2	1
Частота получения ошибок	3% .	8%	14%	26%	23%	15%	8%	2%	1%

Численное
распределение ошибок в пределах 100 м

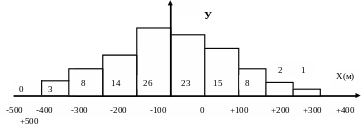
На
основании данных этой таблицы построим
график зависимости между величиной
ошибки и частотой ее появления. Для
этого на горизонтальной оси (рис.
от точки 0 в обе стороны отложим в условном
масштабе ошибки величиной 100 м.

По
вертикальной оси 0У
отложим то же в условном масштабе частоты
появления этих ошибок, выраженных в
процентах. Получаем ряд прямоугольников,
площади которых наглядно характеризуют
частоты появления ошибок в заданных по
величине и знаку пределах.

Рис.
8. График распределения ошибок 100
измерений.

Для
примера мы взяли только 100 ошибок. Это
число не является

достаточно большим,
чтобы можно было полностью установить
закономерности появления случайных
ошибок. Однако и в этом случае некоторые
выводы можно сделать. Так, например, из
рис. 8 видно, что ошибки меньшие по
величине появляются чаще, а ошибки
большие по величине появляются реже.
Кроме того, имеется основание сказать,
что число ошибок в большую и меньшую
стороны примерно одинаково.

Рассмотрим
опытные данные еще одного ряда многократных
измерений расстояний глазомером. В
предыдущем примере мы взяли сто ошибок,
полученных при измерении одного и того
же расстояния, и все полученные ошибки
выразили в метрах. Теперь возьмем опытные
данные измерения разных расстояний.
Практикой установлено, что ошибки
определения расстояний глазомером
по своей величине прямо пропорциональны
измеряемым расстояниям. На основании
этого величину ошибок всех измерений
можно выражать не в метрах, а в процентах
по отношению к истинным значениям
измеряемых расстояний.

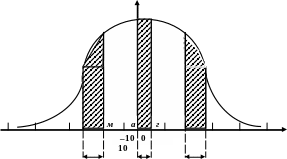
Для
обработки и группирования получаемых
ошибок подготовим график. Часть
этого графика показана на рис. 9. В правой
части графика будем группировать ошибки
положительные, а в левой — отрицательные.
По горизонтальной оси в обе стороны от
точки 0 в условном масштабе отложим
ошибки, выраженные в процентах.

Х(%)

•
•

-9 –8 –7 –6 –5 –4 –3
–2 –1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14 +15 +16

Рис.
9. Построение графика распределения
ошибок после опытов.

Порядок
группирования ошибок поясним на примере.
Истинное расстояние до цели Х₀
= 747 м (измерено наиболее точным способом
— мерной лентой). Результат отдельного
измерения Х₁=850
м; тогда σ₁=850-747=+103
м, что составляет
.
Эту ошибку отмечаем в графике в точке
«а».

До
второй цели истинное расстояние Х₀
= 685 м. Ошибка результата отдельного
измерения Х₂
= 640 м; σ₂=640-685=-45
м, что составляет

.
Эту ошибку отмечаем в графике в точке
«б».

Положим, что нам
удалось собрать достаточно большое
число ошибок и сгруппировать их на
графике указанным выше способом. По
данным числа полученных ошибок,
приходящихся на каждую группу, в
произвольном масштабе восстановим
ординаты, и вершины ординат соединим
плавной кривой АБВ, которая показывает
зависимость между величиной ошибки (в
процентах), ее знаком и частотой появления
(рис. 10).

Так как мы взяли
большое число опытов, при котором частота
мало отличается от вероятности, то
кривая АБВ характеризует зависимость
между величиной ошибки, ее знаком и
вероятностью ее появления. Иначе говоря,
кривая АБВ характеризует закон ошибок.
Из рис. 10 видно, что ошибки измерения
расстояний не выходят за пределы АВ,
следовательно, вероятность получения
ошибки в этих пределах является
достоверным событием и равна 1
(единице) или 100%. Поэтому площадь,
ограниченную кривой АБВ, принимаем
равной 1 или 100%.

Б
б в

л
е

к
ж

А
и
м з В
Х(%)

-40
–30 –20 20 30
40 50

-25%
-20% 0 +5% 20% 25%

Рис.
10. График закона ошибок из опыта.

Вероятность получения
ошибки в каких-либо меньших пределах

будет
меньше 1 или 100% во столько раз, во сколько
площадь, ограниченная соответствующими
ординатами и частью кривой, меньше
всей

площади, ограниченной кривой
АБВ. На основании этого мы можем

сравнивать
вероятности получения ошибок в каких-либо
заданных пределах, для чего нужно
сравнить площади, соответствующие этим
пределам.

Рассматривая
рис. 10 можно установить следующие
положения, характеризующие нормальный
закон ошибок.

I.
С
увеличением ошибки вероятность ее
появления уменьшается и, наоборот, чем
меньше ошибка, тем больше вероятность
ее появления.

Так,
вероятность получения ошибки в пределах
от 0 до +5% больше вероятности получения
ошибки в пределах от +20% до +25% во столько
раз, во сколько площадь абвг
больше площади дежз
(рис. 10).

II.
Равные
по абсолютной величине, но разные по
знаку ошибки равновероятны.

Например,
вероятность получения ошибки в пределах
от -20% до -25% равна вероятности получения
ошибки в пределах от +20% до +25%, так как
площадь иклм
равна площади дежз
(рис. 10).

III.
Для
каждого способа измерения существует
свой предел ошибок. Вероятность получения
ошибки вне этого предела столь мала,
что ее считают равной нулю.

Ошибки,
превышающие по своей величине этот
предел, настолько маловероятны, что ими
обычно пренебрегают. В зависимости от
требуемой точности в нашем примере
пределом ошибок можно считать или 50%,
или 40% истинной величины

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Нормальным называют распределение вероятностей непрерывной случайной величины

, плотность которого имеет вид:

где

–
математическое ожидание,

–
среднее квадратическое отклонение

Вероятность того, что

примет
значение, принадлежащее интервалу

где

– функция Лапласа:

Вероятность того, что абсолютная
величина отклонения меньше положительного числа

В частности, при

справедливо
равенство:

Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:

, где

Правило трех сигм

Преобразуем формулу:

Положив

. В итоге получим

если

, и, следовательно,

, то

то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.

Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.

На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.

Смежные темы решебника:

Таблица значений функции Лапласа
Непрерывная случайная величина
Показательный закон распределения случайной величины
Равномерный закон распределения случайной величины

Пример 2

Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.

а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.

б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?

в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину

В нашем
случае получаем:

б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:

Пусть событие

– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм

– ошибка не
превзошла 5 мм;

– ошибка не
превзошла 15 мм

в)
Для заданной нормальной величины получаем следующее правило трех сигм:

Ошибка высотометра будет лежать в интервале:

Функция плотности вероятностей:

График плотности распределения нормально распределенной случайной величины

Функция распределения:

График функции
распределения нормально распределенной случайной величины

Задача 1

Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?

Задача 2

Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?

Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).

Задача 3

Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

Задача 5

Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.

Задача 6

Заданы
математическое ожидание a_x=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.

Задача 7

Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см².
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.

Задача 8

Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.

Задача 9

Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).

а) Написать
плотность распределения вероятностей и функцию распределения.

б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).

в) Определить
приближенно минимальное и максимальное значения случайной величины X.

г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.

a=5; σ=1.3;
α=4; β=6

Задача 10

Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σ_x=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.

Задача 11

Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.

Задача 12

Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.

а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.

б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?

в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.

Задача 13

Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 14

Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?

Задача 15

Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.

Задача 16

В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).

Задача 17

Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:

а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;

б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.

Задача 18

Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?

Задача 19

Случайная
величина X~N(1,2²). Найти P{2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 20

Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.

Задача 21

Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.

Задача 21

Найти
вероятность попадания снарядов в интервал (α₁=10.7; α₂=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.

Задача 22

Плотность
вероятности распределения случайной величины имеет вид

Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).

Задача 23

Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)

Задача 24

Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.

Задача 25

В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.

Задача 26

Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.

Источник

Нормальный закон распределения и его параметры:

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.

Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.

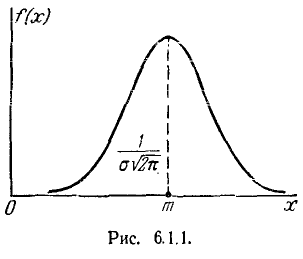
Нормальный закон распределения характеризуется плотностью вероятности вида:

(6.1.1)

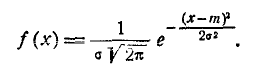
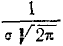
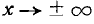
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная , соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина — среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.

Применяя замену переменной

имеем:

(6.1.2)

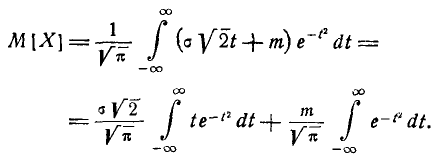
Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:

(6.1.3)

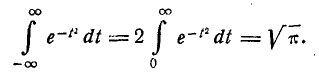
Следовательно, М[Х] = m

т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:

Применив снова замену переменной

имеем:

Интегрируя по частям, получим:

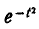
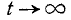
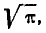
Первое слагаемое в фигурных скобках равно нулю (так как При убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно откуда

Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.

Выясним смысл параметров m и нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.

Размерность центра рассеивания—та же, что размерность случайной величины X.

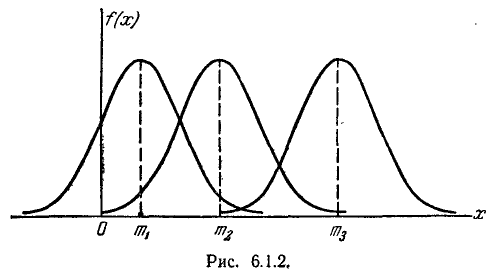
Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна ; при увеличении максимальная ордината уменьшается. Так как площадь

кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует

самому большому, а кривая /// — самому малому значению . Изменение параметра равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.

Размерность параметра , естественно, совпадает с раpмерноcтью случайной величины X.

В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению :

Размерность меры точности обратна размерности случайной величины.

Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде:

Моменты нормального распределения

Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно .

Выведем общие формулы для центральных моментов любого порядка.

По определению:

Делая замену переменной

получим:

(6.2.1)

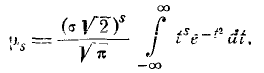
Применим к выражению (6.2.1) формулу интегрирования по частям: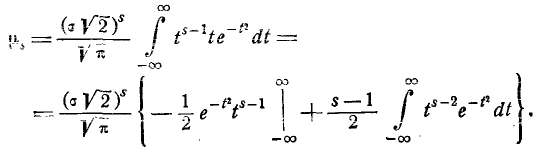

Имея в виду, что первый член внутри скобок равен нулю, получим: 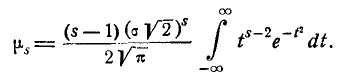(6.2.2)

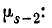
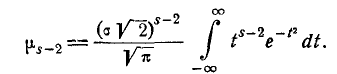
Из формулы (6.2.1) имеем следующее выражение для (6.2.3)

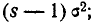
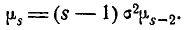
Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем следовательно,

(6.2.4)

Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 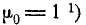и можно вычислить центральные моменты всех порядков. Так как то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.

Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:

и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:

где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона то асимметрия его также равна нулю:

Из выражения четвертого момента

имеем:

‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.

т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m, , на участок от а до Для вычисления этой вероятности воспользуемся общей формулой

(6.3.1)

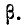
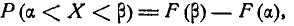
где F (х)— функция распределения величины X.

Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, . Плот- Плотность распределения величины X равна:

(6.3.2)

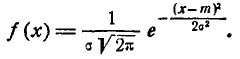
Отсюда находим функцию распределения

(6.3.3)

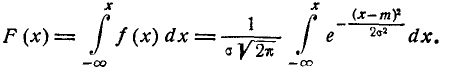
Сделаем в интеграле (6.3.3) замену переменной

(6.3.4)

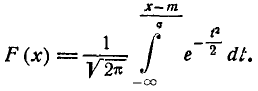
и приведем его к виду:

(6.3.4)

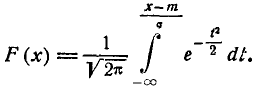
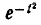
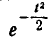
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения или (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:

и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции

(6.3.5)

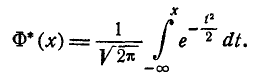
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0, =1.

Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)

Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и через нормальную функцию распределения Ф*(х). Очевидно,

(6.3.6)

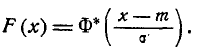
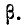
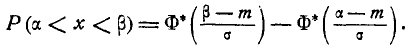
Теперь найдем вероятность попадания случайной величины X на участок от а до Согласно формуле (6.3.1)

(6.3.7)

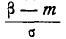
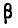
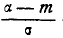
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: есть расстояние от правого конца участка до центра рассеивания, выраженное в средних квадратических отклонениях; — такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.

Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:

-неубывающая функция

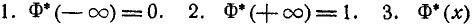
Кроме того, из симметричности нормального распределения с параметрами m = 0, =1 относительно начала координат следует, что

ф* (— х)=1— Ф* (х). (6.3.8)

Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц

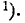
Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.

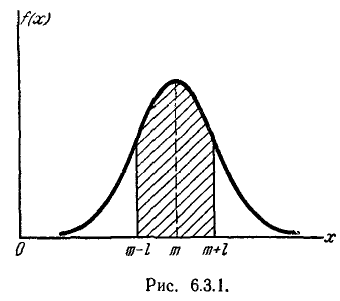
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7):

Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:

Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной (рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.

По формуле (6.3.7) находим:

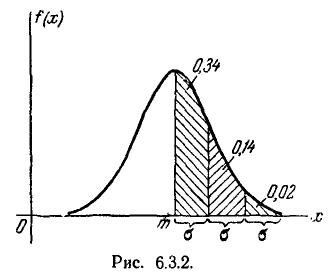
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.

Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.

Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З.

Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения .

Пример:

Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м) среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).

Решение:

Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и = 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до = + 1,6. По формуле (6.3.7) имеем:

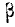
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:

Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,

откуда Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913 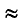0,691.

Пример:

Найти ту же вероятность, что в предыдущем примере, но при условии, что систематической ошибки нет.

Решение:

По формуле (6.3.10), полагая l=1.6, найдем:

Пример:

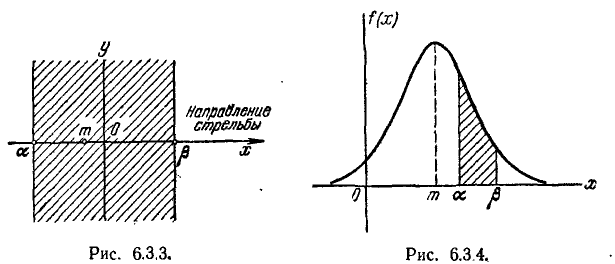
По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде, прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно = 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.

Решение:

Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения X (другая координата Y нам безразлична). Случайная величина X распределена по нормальному закону

с параметрами m = —3, = 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до = 4-10. Применяя формулу (6.3.7), имеем:

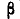
Пример:

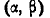
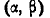
Имеется случайная величина Х, нормально распределенная, с центром рассеивания m (рис. 6.3.4) и некоторый участок оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок достигала максимума?

Решение:

Имеем:

Продифференцируем эту функцию величины :

Применяя правило дифференцирования интеграла по переменной, входящей в его предел, получим:

Аналогично

Для нахождения экстремума положим:

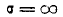
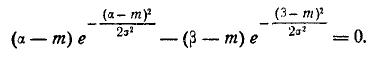
При это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия (6.3.13)

Уравнение (6.3.13) можно решить численно или графически.

6.4. Вероятное (срединное) отклонение

В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой Е (иногда В).

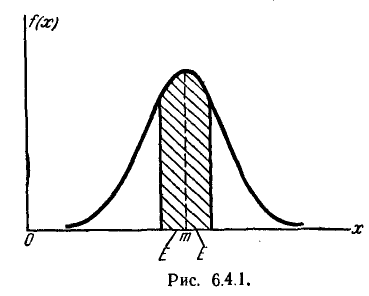
Вероятным (срединным) отклонением случайной величины X, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.

Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение Е — это половина длины участка оси абсцисс, симметричного относительно точки m, на кото- который опирается половина площади кривой распределения.

Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».

Рассмотрим случайную величину X, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания m меньше чем на Е, по определению вероятного отклонения Е, равна

(6.4.1)

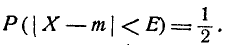
Вероятность того, что она отклонится от m больше чем на Е, тоже равна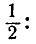

Таким образом, при большом числе опытов в среднем половина значений случайной величины X отклонится от m больше чем на Е, а половина — меньше. Отсюда и термины «срединная ошибка», «срединное отклонение».

Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего rвадратического отклонения . Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:

Отсюда

По таблицам функции Ф* (х) можно найти такое значение аргумента х, при котором она равна 0,75. Это значение аргумента приближенно равно 0,674; отсюда

(6.4.3)

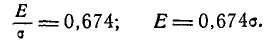
Таким образом, зная значение , можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:

(6.4.4)

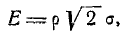
где р — такое значение аргумента, при котором одна из форм интеграла вероятностей — так называемая функция Лапласа

— равна половине. Численное значение величины р приближенно равно 0,477.

В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой . В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.

Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность нормального распределения записывается в виде:

(6.4.5)

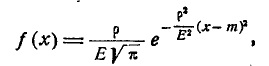
а вероятность попадания на участок от а до 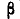чаще всего записывается в виде:

где

— так называемая приведенная функция Лапласа.

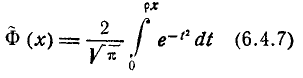
Сделаем подсчет, аналогичный выполненному в предыдущем п° для среднего квадратического отклонения : отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим:

Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке

Пример:

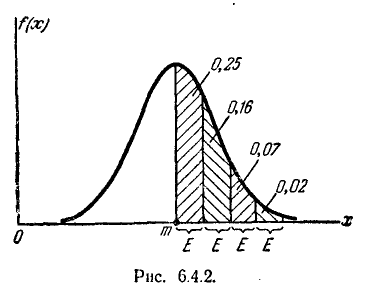
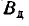
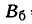
Самолет-штурмовик производит обстрел колонны войск противника, ширина которой’ равна 8 м. Полет — вдоль колонны, прицеливание— по средней линии колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо но направлению полета. Главные вероятные отклонения: по направлению полета = 15 м, в боковом направлении = 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:

25%, 16%, 7%, 2%,

оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.

Решение:

Для решения задачи достаточно рассмотреть одну координату точки попадания — абсциссу X в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания m = 2 и вероятным отклонением 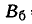=Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:

0,4-25% =0,1.

Влево от центра рассеивания цель занимает участок б м. Это — целое вероятное отклонение E м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна:

Таким образом, вероятность попадания в колонну приближенно равна:

0,1+0,25 + 0,03 = 0,38.

Вероятность хотя бы одного попадания при трех выстрелах равна:

Закон нормального распределения случайных величин

Смотрите также:

Решение заданий и задач по предметам:

Теория вероятностей
Математическая статистика

Дополнительные лекции по теории вероятностей:

Случайные события и их вероятности
Случайные величины
Функции случайных величин
Числовые характеристики случайных величин
Законы больших чисел
Статистические оценки
Статистическая проверка гипотез
Статистическое исследование зависимостей
Теории игр
Вероятность события
Теорема умножения вероятностей
Формула полной вероятности
Теорема о повторении опытов
Определение законов распределения случайных величин на основе опытных данных
Системы случайных величин
Нормальный закон распределения для системы случайных величин
Вероятностное пространство
Классическое определение вероятности
Геометрическая вероятность
Условная вероятность
Схема Бернулли
Многомерные случайные величины
Предельные теоремы теории вероятностей
Оценки неизвестных параметров
Генеральная совокупность

Источник

2. Пусть [math]X[/math]— ошибка измерения, [math]sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = Pleft( {left| X right| < 2} right) = Pleft( {left| {frac{X}{sigma }} right| < frac{2}{sigma }} right) = Phi left( {0.2} right) — Phi left( { — 0.2} right) = 2 cdot Phi left( {0.2} right) — 1 = 2 cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]Phi left( x right)[/math] отличается от функции, которую использовал Alexdemath

3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]Pleft( {X < 15} right) = intlimits_0^{15} {lambda cdot e^{ — lambda x} dx} = 1 — e^{ — 15lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]pleft( t right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]Pleft( {X < 15} right) = 1 — Pleft( {X > 15} right) = 1 — intlimits_{15}^infty {pleft( t right)dt} = 1 — intlimits_{15}^infty {frac{t}{t}pleft( t right)dt} geqslant 1 — frac{1}{{15}}intlimits_0^infty t pleft( t right)dt = 1 — frac{8}{{15}} = frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.

Источник