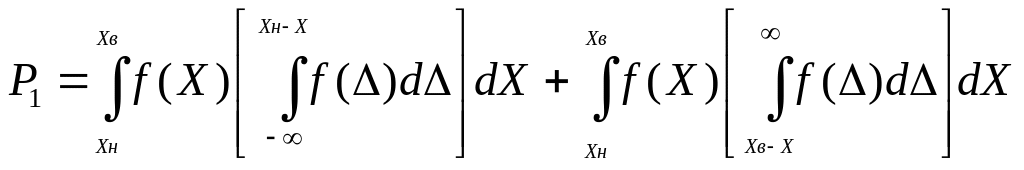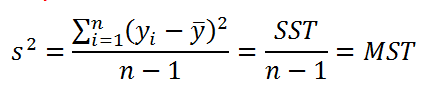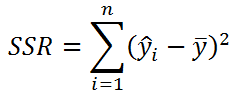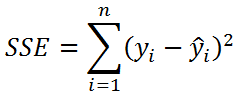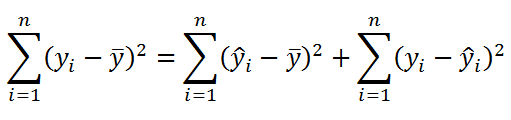С чего начинается
статистическое исследование — с
теоретического построения
гипотез или с эмпирического анализа? В
действительности теория и практика
обогащают друг друга, и подобные вопросы
возникают. Поэтому мы будем
рассматривать вопрос о проверке гипотез
с двух точек зрения. С одной стороны, мы
можем предположить, что сначала идет
теория и что цель эксперимента
заключается в выяснении ее применимости.
Это приведет к проверке гипотезы
о значимости. С другой стороны, мы можем
сначала провести эксперимент
и затем определить, какие из теоретических
гипотез соответствуют результатам
эксперимента. Это приводит к построению
доверительных интервалов.
Вам уже известна
логика, лежащая в основе построения
критериев значимости
и доверительных интервалов и описанная
в вводном курсе статистики. Поэтому
вы уже знакомы с большинством понятий,
используемых в регрессионном
анализе. Однако один вопрос может
оказаться для вас новым — это использование
односторонних критериев. Такие критерии
используются в регрессионном
анализе очень часто. В самом деле, они
являются, или должны быть,
более обычными здесь, чем традиционно
используемые в учебниках двусторонние
критерии. Поэтому важно, чтобы вы поняли
целесообразность их
применения, и путь к этому состоит из
последовательности небольших аналитических
шагов. Ни один из них не должен представлять
трудности, но следует
иметь в виду, что если вы попытаетесь
сократить свой путь, или, еще хуже,
сделаете попытку свести всю процедуру
к механическому использованию
нескольких формул, вы столкнетесь с
большими трудностями.
Формулирование нулевой гипотезы
Начнем с допущения
о том, что теория предшествует эксперименту
и что вы уже
имеете в виду некоторую гипотетическую
связь или зависимость. Например,
вы можете считать, что темп общей инфляции
в экономике (p,
в %) зависит от
темпа инфляции, вызванной ростом
заработной платы (w,
в %), и что эта
зависимость описывается линейным
уравнением:
(2.61)
где p1
и р2
— параметры, а u
— случайный член. Далее вы можете
построить гипотезу о том, что без учета
эффектов, вносимых случайным членом,
общая инфляция
увеличивается в той же степени, что и
инфляция, вызванная ростом
заработной платы. В этих условиях вы
можете сказать, что гипотеза, которую
вы собираетесь проверять, известная
как ваша нулевая
гипотеза и
обозначенная
H0,
состоит в том, что β2
равняется единице. Мы также определяем
альтернативную
гипотезу, обозначаемую
Н1,
которая представляет заключение. которое
делается в том случае, если экспериментальная
проверка указала на ложность
H0.
В данном случае эта гипотеза состоит в
том, что
.
Две гипотезы
сформулированы с использованием
следующих обозначений:
H0:β2=1;
H1:β2≠1.
В этом конкретном
случае, если мы действительно считаем,
что общая инфляция равна инфляции,
вызванной ростом заработной платы, мы
делаем попытку
защитить нулевую гипотезу H0,
подвергнув ее максимально строгой
проверке и
надеясь, что она не будет опровергнута.
Однако на практике более обычным
является построение нулевой гипотезы,
которая затем будет проверяться
с помощью альтернативной гипотезы,
которая предполагается верной Например,
рассмотрим простую функцию заработка:
(2.62)
где EARNINGS
— часовой
заработок в долларах, a
S
— число
законченных лет обучения.
Исходя из вполне разумных теоретических
оснований, вы предполагаете, что
заработок зависит от продолжительности
обучения, но ваша теория
недостаточно «сильна», чтобы можно было
определить конкретное значение
для β2.
Тем не менее, вы можете установить
наличие зависимости величины
заработка от S,
используя
для этого обратную процедуру, когда в
качестве нулевой
гипотезы принимается утверждение о
том, что величина заработка не
зависит от
S,
т.е. что β2
равняется нулю. Альтернативная гипотеза
заключается в
том, что величина β2
не равняется нулю, иными словами, что
величина S
влияет на
размер заработка. Если вы можете
отвергнуть нулевую гипотезу, то вы
таким образом устанавливаете наличие
зависимости, по крайней мере в
общих чертах.
С использованием введенной системы
обозначений, ваши нулевая
и альтернативная гипотезы примут вид
H0:
β2
= 0 и Н1:
β2
≠ 0
соответственно.
Последующий анализ
касается модели парной регрессии
(2.65)
Он будет относиться
только к коэффициенту наклона β2,
но точно такие ж с процедуры
применимы и к постоянному члену β1
Возьмем общий случай, в
котором в
нулевой гипотезе утверждается, что β2
равно некоторому конкретному значению,
например
,
и альтернативная гипотеза состоит в
том, что β2
не равно этому
значению (H0:
β2
=
,;
Н1:
β2
≠
).
Вы можете предпринять попытку
отклонить или подтвердить нулевую
гипотезу, в зависимости от того что
вам необходимо в данном случае. Будем
считать, что предпосылки в разделе
2.2 выполнены.
Вывод следствии
гипотезы
Если гипотеза H0
верна, то значения b2,
полученные
в ходе регрессионного анализа,
будут иметь распределение с математическим
ожиданием
и дис-
Персией
.
Теперь мы вводим допущение, что случайный
член и
имеет нормальное
распределение. Если это так, то величина
b2
будет также
нормально
распределена, как показано на рис. 2.6.
Сокращение «sd»
на рисунке соответствует величине
стандартного отклонения оценки b2
т.е.
.
Учитывая структуру нормального
распределения, большинство
оценок параметра b2
будет
находиться в пределах двух стандартных
отклонений от
(если гипотеза H0
:β2 =
верна).
Сначала мы допустим,
что знаем величину стандартного
отклонения величины
b2.
Это наиболее
нереалистичное допущение, и мы позднее
отбросим его. На
практике же значение этого отклонения
(так же, как и неизвестные значения
параметров (β1
и β2)
подлежит оценке. Можно, тем не менее,
упростить обсуждение,
предположив, что точное значение
отклонения известно, и, следовательно,
у нас есть возможность построить график,
показанный на рис. 2.6.
Проиллюстрируем
это на примере модели связи общей
инфляции и инфляции,
вызванной ростом заработной платы
(2.61). Предположим, что некоторым
образом мы знаем, что стандартное
отклонение величины b2
составляет
0,1. Тогда, если
нулевая гипотеза H0:
β2
= 1 верна, то оценки коэффициентов
регрессии будут распределены так, как
это показано на рис. 2.7. Из этого рисунка
можно видеть, что при справедливости
нулевой гипотезы оценки будут находиться
приблизительно между 0,8 и 1,2.
Сопоставимость,
случайность и уровень значимости
Теперь приступим
к главному. Предположим, что мы взяли
фактическую выборку
из наблюдений общей инфляции и инфляции,
вызванной ростом заработной платы, и
построили оценку β2,
используя для этого регрессионный
анализ. Если
оценка близка к единице, то мы должны
быть полностью удовлетворены
нулевой гипотезой, так как она и результат
оценивания для выборки
совместимы друг с другом. Предположим,
с другой стороны, что оценка значительно
отличается от единицы. Допустим,
например, что она равна 0,7. Это
составит три стандартных отклонения
вниз от 1,0. Если нулевая гипотеза верна,
то вероятность того, что отличие b2
от среднего
достигнет трех стандартных
отклонений в положительную или
отрицательную сторону, составляет лишь
0,0027, т.е. очень низка.

Рисунок 2.6.
Структура
нормального распределения оценки b2
в единицах стандартных отклонений от
математического ожидания

Рисунок 2.7. Пример
распределения величины b2
(модель связи общей инфляции и
инфляции, вызванной ростом заработной
платы)
Исходя из этого
вызывающего беспокойство результата,
вы можете прийти к одному из двух
выводов:
-
Вы можете продолжать
считать, что ваша нулевая гипотеза H0:
(β2
= 1 верна и
что эксперимент дал случайный результат.
Вы допускаете, что вероятность
получения такого низкого значения для
b2
является
очень небольшой. но,
тем не менее, она имеет место в 0,27%
случаев, и вы допускаете, что это именно
тот случай. -
Вы можете сделать
вывод о том, что гипотеза противоречит
результат) оценивания
регрессии. Вы не удовлетворяетесь
объяснением, данным в
пункте 1, так
как вероятность очень мала, и понимаете,
что наиболее правдоподобным
объяснением является то, что величина
β2
вовсе не равняется единице. Другими
словами, вы принимаете альтернативную
гипотезу H1:
β2≠
1.
Каким образом вы
определите, когда необходимо выбрать
первый вывод, а когда
— второй? Очевидно, что чем меньше
вероятность получения регрессии,
подобной той, которую вы получили при
условии правильности вашей гипотезы,
тем больше вероятность вашего отказа
от гипотезы и тем очевиднее переход
ко второму выводу. Насколько малой
должна быть указанная вероятность
для выбора второго вывода?
На этот вопрос нет
и не может быть определенного ответа.
В большинстве работ
по экономике за критический уровень
берется 5 или 1%. Если выбирается
уровень 5%, то переключение на второй
вывод происходит в том случае. когда
при истинности нулевой гипотезы
вероятность получения столь экстремального
значения для b2
составляет
менее 5%. В этом случае говорят, что
нулевая
гипотеза должна быть отвергнута при
5%-ном уровне
значимости.
Это происходит в том случае, когда
величина b2
отстоит от величины
более чем на 1,96 стандартного
отклонения. Если вы посмотрите на таблицу
нормального распределения (табл. А.1 в
Приложении А), то вы увидите, что
вероятность того,
что величина b2
будет
превосходить среднее значение на более
чем 1,96 стандартного отклонения, составляет
2,5%, и, аналогичным образом, вероятность
того, что эта величина будет более чем
на 1,96 стандартного отклонения ниже
среднего значения, также составляет
2,5%. Общая вероятность того, что данная
величина отстоит от математического
ожидания более чем на 1,96 стандартного
отклонения, составляет, таким образом,
5%. Мы можем обобщить это решающее
правило в математической форме, полагая,
что нулевая гипотеза отвергается, если:
z> 1,96 или z<
-1,96, (2.64)
где z — число
стандартных отклонений между регрессионной
оценкой и гипотетическим значением
для β2:
(2,65)
Нулевая гипотеза не будет отвергнута,
если
-1,96 <z<
1,96. (2.66)
Это условие можно записать с помощью
величин b2
и
,
подставив выражение для z
из уравнения (2.65):
-1,96 ≤
≤
1,96. (2.67)
Умножив все части
неравенства на стандартное отклонение
величины b2
можно получить
-1,96 s.d.(b2)
≤ b2
—
≤
1,96 s.d.(b2), (2.68)
а из этого соотношения
можно получить следующее:
—
1,96 s.d.(b2)
<b2<
+
1,96 s.d.(b2). (2.69)
Уравнение (2.69) дает
множество значений для величины b2,
которые не
приводят к
отказу от конкретной нулевой гипотезы
о том, что β2
=
.
Это множество
значений получило название области
принятия гипотезы для
b2
при 5%-ном
уровне значимости. В нашем примере
модели связи общей инфляции и
инфляции, вызванной ростом заработной
платы, где s.d.(b2)
равняется
0,1, можно
отвергнуть гипотезу при уровне значимости
в 5%, если величина b2
находится
выше или ниже гипотетического среднего
значения на величину более
0,196, т.е. выше 1,196 или ниже 0,804. Таким
образом, область принятия гипотезы
включает значения величины b2
от 0,804 до
1,196. Это показано не-затененной
областью на рис. 2.8

Рисунок 2.8.
Область
принятия гипотезы для величины Ь2
при 5%-ном уровне значимости
Аналогичным образом
считается, что нулевая гипотеза должна
быть отвергнута
при уровне значимости в 1%, если гипотеза
подразумевает, что вероятность
получения столь экстремального значения
для величины b2
составляет
менее 1%. Это
происходит тогда, когда величина b2
отстоит на
более чем 2.58
стандартного
отклонения вверх или вниз от гипотетического
значения величины β2, т.е. когда
z
> 2,58 или z<
-2,58.
(2
.70)
Вставка 2.4.
Ошибки I
и II
рода в повседневной жизни
Проблема избежать
допущения ошибок I
и II
рода известна всем. Типичным примером
этого является расследование уголовного
преступления. Если за нулевую
гипотезу принять то, что подсудимый
невиновен, то ошибка I
рода происходит
тогда, когда суд присяжных признает его
виновным. Ошибка II
рода имеет место
в том случае, когда суд присяжных ошибочно
оправдывает виновного подсудимого.
Опять возвратившись
к таблице нормального распределения,
вы может видеть,
что вероятность того, что величина b2
будет более
чем на 2,58 стандартного
отклонения отстоять вверх от своего
математического ожидания, составляет
0,5%, и та же самая вероятность для
нахождения этой величины ниже
своего
математического ожидания более чем на
2,58 стандартного отклонения.
Таким образом, общая вероятность
получения столь экстремальных значений
составляет 1 %. В нашем примере вы
отвергнете нулевую гипотезу о том что
β2
= 1, если оценка коэффициента регрессии
будет находиться выше 1.258 или ниже
0,742.
Можно задаться
вопросом, почему исследователи обычно
представляют
результаты при уровнях значимости 5 и
1%. Почему недостаточно ограничиться
только одним уровнем? Причина заключается
в том, что обычно делается
попытка найти баланс между риском
допущения ошибок I
и II
рода.
Ошибка I
рода имеет место в том случае, когда вы
отвергаете истинную нулевую
гипотезу. Ошибка II
рода возникает тогда, когда вы не
отвергаете ложную гипотезу.
Очевидно, что чем
ниже критическая вероятность, тем меньше
риск получения
ошибок I
рода. Если вы используете уровень
значимости, равный 5%, то
вы будете отвергать истинную гипотезу
в 5% случаев. Если уровень значимости
составляет 1%, то вы будете делать ошибку
I
рода в 1% случаев. Таким образом,
в этом отношении 1%-ный уровень значимости
более надежен. Если вы
отвергли гипотезу на этом уровне, вы
почти наверняка были вправе сделать
это. Именно по этой причине 1%-ный уровень
значимости описывается как «более
высокий» в сравнении с 5%-ным уровнем.
В то же время, если
нулевая гипотеза ложна, то чем выше ваш
уровень значимости,
тем шире ваша область принятия гипотезы,
тем выше вероятность того, что вы не
отвергнете ее, и тем выше риск допущения
ошибки II
рода. Таким
образом, вы оказываетесь перед дилеммой.
Если вы будете настаивать на
очень высоком уровне значимости, то
столкнетесь с относительно высоким
риском допущения ошибки II
рода, если гипотеза окажется ложной.
Если вы выбираете низкий уровень
значимости, то оказываетесь перед
относительно
высоким риском допущения ошибки I
рода, если гипотеза истинна.
Большинство людей
выбирают достаточно простую форму
обеспечения гарантий
и осуществляют проверку на обоих уровнях
значимости, представляя результаты
каждой такой проверки. На самом деле
часто нет никакой необходимости
непосредственно ссылаться на оба
результата. Так как величина b2
должна
быть более «экстремальной» для гипотезы,
отвергаемой при 1 %-ном уровне
значимости, чем при 5%-ном, и если вы
отклоняете ее при 1 %-ном уровне,
то из этого автоматически следует, что
вы отклоните ее и при уровне значимости
в 5%, и нет необходимости упоминать об
этом. Если же вы не отвергаете
гипотезу при уровне значимости в 5%, то
из этого автоматически следует,
что вы не отвергнете ее и при 1 %-ном
уровне значимости. Только в одном случае
вы должны представить оба результата:
если гипотеза отвергается на 5%-ном,
но не на 1%-ном уровне значимости.
t
-ТЕСТЫ
До сих пор мы считали,
что стандартное отклонение величины
b2
известно.
Однако на
практике это допущение нереально. Это
можно показать на примере
стандартной ошибки для величины b2
взятой из
уравнения (2.44). Это приводит
к двум изменениям процедуры проверки
гипотез. Во-первых, величина
z
определяется
на основе использования стандартной
ошибки с.о.(b2)
вместо
стандартного отклонения s.d.(b2)
и носит название t-статистики:
(2.71)
Во-вторых, критические
уровни t
определяются
величиной, имеющей так называемое
t-распределение
вместо нормального распределения. Мы
не будем
вдаваться в причины этого или даже
описывать t-распределение
математически. Достаточно будет
сказать, что оно родственно нормальному
распределению, а его точная форма
зависит от числа степеней свободы в
регрессии, и
оно все лучше аппроксимируется нормальным
распределением по мере увеличения
числа степеней
свободы. Вы,
конечно, уже встречали понятие
t—распределения
во вводном курсе статистики. В табл. А.2
Приложения А представлены критические
значения для t,
сгруппированных
по уровням значимости и числу
степеней свободы.
Оценивание каждого
параметра в уравнении регрессии поглощает
одну степень
свободы в выборке. Отсюда число степеней
свободы равняется числу наблюдений
в выборке минус число оцениваемых
параметров. Параметрами являются
постоянный член (при условии, что он
введен в модель регрессии) и коэффициенты
при независимых переменных. В
рассматриваемом случае парной регрессии
оцениваются только два параметра β1
и β2,
поэтому число степеней
свободы составляет (п
— 2). Следует
подчеркнуть, что когда мы перейдем к
множественному регрессионному анализу,
потребуется более общее выражение.
Критическое значение
для t,
которое мы обозначим как tкрит
, заменит
число 1,96 в
уравнении (2.67). Задача t-теста
состоит в том, чтобы сравнить t-статистику
и tкрит
. Таким образом,
условие того, что оценка регрессии не
должна приводить
к отказу от нулевой гипотезы HQ:
β2
=
,
будет следующим:

(2.72)
Следовательно, мы
имеем правило для принятия решения: H0
отвергается, если
,
и она не
отвергается, если
,
где
—
абсолютная величина (модуль) значения
t.
Примеры
В разделе 1.6 была
оценена регрессия величины заработка
на число лет обучения
по данным Всеамериканского опроса
молодежи, распечатка для которой
приведена в табл. 2.6. В первых двух ее
столбцах указаны названия переменных,
здесь это S
и свободный член (Stata
обозначает его как _cons),
и оценки их
коэффициентов. В третьем столбце
приведены соответствующие стандартные
ошибки. Предположим, что одна из задач
оценивания регрессии состояла
в подтверждении нашей догадки о том,
что размер заработка зависит от
продолжительности полученного
образования. Соответственно, мы формируем
нулевую гипотезу Н0:
β2
= 0, и затем пытаемся опровергнуть ее.
Соответствующая
t-cтатистика,
вычисленная по формуле (2.71), есть оценка
коэффициента, деленная на ее
стандартную ошибку:
(2.73)
Так как в выборку
включено 540 наблюдений, и мы оценили два
параметра, то
число степеней свободы составляет 538.
В табл. А.2 отсутствуют критические
значения t
для 538 степеней свободы, но мы знаем, что
они должны быть меньше,
чем соответствующие критические значения
для 500 степеней свободы,
так как критическое значение есть
убывающая функция числа степеней
свободы.
Критическое значение для 500 степеней
свободы при 5%-ном уровне значимости
равняется 1,965. Следовательно, мы можем
с уверенностью отвергнуть
H0,
сделав вывод о том, что продолжительность
обучения влияет на размер
заработка. Если этот критерий описать
словами, то верхний и нижний 1.5%-ные
«хвосты» t-распределения
при 538 степенях свободы начинаются со
стандартных
отклонений (1,965 вверх и вниз) от его
математического ожидания,
равного нулю. Коэффициент регрессии,
который по оценкам находится в пределах
1,965 стандартного отклонения от
гипотетического значения, не приводит
к отказу от последнего. В рассматриваемом
случае расхождение будет
эквивалентно 10,59 стандартного отклонения,
и мы приходим к выводу о том,
что результат регрессии противоречит
нулевой гипотезе. Конечно, поскольку
мы используем уровень значимости 5% в
качестве основы
для проверки гипотезы, существует 5%-ный
риск допустить ошибку I
рода. В этом случае мы могли бы снизить
риск до 1% за счет применения уровня
значимости в 1 %. Критическое значение
для / при 1 % -ном уровне зна-чимости
с 500 степенями свободы составляет 2,586.
Поскольку /-статистика превышает
это число, мы видим, что можно легко
отказаться от нулевой гипотезы
также и на этом уровне значимости.
Таблица 2.6
|
EARNINGS S |
|||||||
|
Sourse |
SS |
df |
MS |
Number of |
= |
540 |
|
|
F(1,538) |
= |
112.15 |
|||||
|
Model |
19321.5589 |
1 |
19321.5589 |
Prob>F |
= |
0.0000 |
|
|
R-squared |
= |
0.1725 |
|||||
|
92688.6722 |
538 |
172.283777 |
Adj |
= |
0.1710 |
||
|
Total |
112010.231 |
539 |
207.811189 |
RootMSE |
= |
13.126 |
|
|
EARNINGS |
Coef. |
Std. Err. |
t |
P>|t| |
[95%Conf. |
Interval] |
|
|
S |
2.455321 |
.2318512 |
10.59 |
0.000 |
1.999876 |
2.910765 |
|
|
_cons |
-13.93347 |
3.219851 |
-4.33 |
0.000 |
-20.25849 |
-7.608444 |
Отметим, что если
5%- и 1 %-ный тесты приводят к одному и тому
же выводу,
то нет необходимости представлять
результаты обоих, и если это сделать,
то это может
быть расценено как некомпетентность.
По этому вопросу прочтите
внимательно Вставку 2.5 о представлении
результатов оценивания регрессии.
Процедура установления
взаимосвязи между зависимой и объясняющей
переменными
путем высказывания, а затем отклонения
нулевой гипотезы H0:
β2
= 0, используется очень часто. Соответственно
все серьезные регрессионные программы
автоматически выводят t-статистику
для этого специального
случая; иными словами, коэффициент
делится на его стандартную ошибку.
Данное отношение
часто обозначается как «t-статистика».
В приведенной распечатке
результатов значения t-статистики
для постоянного члена и коэффициента
наклона показаны в среднем столбце.
Если, однако, нулевая
гипотеза определяет некоторое ненулевое
значение величины
β2,
то необходимо использовать более общее
выражение (2.71),
Вставка 2.5.
Описание результатов проверок по
t-критерию
Предположим, что
имеет место теоретическая зависимость

и нулевая и
альтернативная гипотезы имеют вид H0:
β2
=
, H1:
β2
≠
.
Если для β2
по выборочным данным получена оценка
b2,
то области принятия и отклонения
гипотез для 5%- и 1%-ного уровней значимости
могут быть в общем виде представлены
левой частью рис. 2.9.
Правая часть рисунка
показывает те же самые области для
конкретного примера
модели связи общей инфляции и инфляции,
вызванной ростом заработной
платы; при этом нулевая гипотеза будет
иметь вид β2
= 1. Нулевая гипотеза не
будет отклонена при уровне значимости
5%, если величина bг
находится в
пределах 2,101
стандартной ошибки от единицы, т.е. в
диапазоне 0,29-1,21, и она
не будет отклонена при уровне значимости
1 %, если величина b2
находится в
пределах 2,878 стандартного отклонения
от единицы, т.е. в диапазоне между 0,71
и 1,29.
Из рис. 2.9 можно
видеть, что существует три типа зон
принятия решений:
-
зона, где величина
b2
настолько
далека от гипотетической величины (β
2, что
нулевая гипотеза отклоняется как при
5%~ном, так и при 1%-ном уровнях значимости; -
зона, где величина
b2
достаточно
далека от гипотетической величины (β
2, чтобы
нулевая гипотеза была отклонена при
5%-ном, но не при 1%-ном уровне значимости; -
зона, где величина
b2
достаточно
близка к гипотетической величине (β
2, чтобы
нулевая гипотеза не была отклонена ни
при одном из двух рассматриваемых
уровней значимости.
На основании схемы
можно проверить, что если нулевая
гипотеза отклоняется
при 1%-ном уровне значимости, то она
автоматически отклоняется и при 5%-ном
уровне значимости. Следовательно, в
случае I
необходимо заявить лишь
об отклонении гипотезы при 1%-ном уровне.
Заявлять об ее отклонении при
5%-ном уровне нет необходимости. Это
равнозначно тому, чтобы сделать заявление
о возможности взятия прыгуном высоты
в 2 м, а затем, в качестве дополнения,
заявить о его возможности взять высоту
в 1,5 м. Аналогичным образом, для случая
3
вам необходимо сделать только заявление
о том, что в этом конкретном
случае гипотеза не будет отклонена при
5%-ном уровне значимости.
Отсюда автоматически следует, что она
не будет отклонена и при 1%-ном уровне,
и дополнение к этому заявлению имело
бы тот же эффект, как если бы к заявлению
о том, что прыгун в высоту не может взять
высоту в 1,5 м, было добавлено
утверждение о его неспособности взять
высоту в 2 м. Лишь в случае 2
нужно (и
желательно) представить результаты
обеих проверок.
Заметим, что если
вы обнаружили, что нулевую гипотезу
можно отвергнуть при
5%г-ном уровне значимости, то не нужно
на этом останавливаться. Вы обнаружили,
что нулевая гипотеза может быть отвергнута
при данном уровне значимости,
но остается 5% шансов совершить ошибку
I
рода. Вы должны также выполнить тест
при уровне значимости 1%. Если вы
обнаружили, что нулевая гипотеза
может быть отвергнута и при этом уровне
значимости, то это и есть результат,
который нужно приставить. Риск ошибки
I
рода составляет теперь только
1%, и ваш вывод будет намного более
убедительным. Это — случай 1, описанный
выше. Если вы не можете отвергнуть
гипотезу на 1%-ном уровне, то вы
пришли к случаю 2
и
должны
представить результаты обоих тестов.
а t-статистика
вычисляется вручную. Например, вновь
рассмотрим модель связи общей
инфляции и инфляции, вызванной ростом
заработной платы (2.61),
и предположим, что выбранная модель
оказалась следующей (в скобах —
стандартные ошибки):
(2.74)
(0.05) (0.10)
Если теперь
исследовать гипотезу о том, что общая
инфляция равна инфляции,
вызванной ростом заработной платы, то
наша нулевая гипотеза будет состоять
в том, что коэффициент при w
равен 1,0.
Соответствующая t-статистика
примет вид:
(2.75)
Если в выборке
содержится, скажем, 20 наблюдений, то
количество степеней
свободы составит 18, а критическое
значение для t
на 5%-ном уровне значимости
составит 2,101. Абсолютная величина
t-статистики
меньше этого числа, поэтому в данном
случае мы не отвергаем нулевую гипотезу.
Оценка, равная
0,82, меньше гипотетического значения
1,00, но не настолько меньше, чтобы
исключить возможность правильности
нулевой гипотезы. И последнее замечание
о представлении результатов оценивания
регрессии: некоторые авторы
помещают t-статистику
в скобках под коэффициентом вместо
стандарт ной
ошибки. Это нужно тщательно проверять,
а представляя свои результаты следует
ясно указать, какую из двух величин вы
приводите.
|
Общий случай |
Решение |
Пример зависимости общей инфляции |
|
Отклонить Н0 при |
||
|
|
1,29 |
|
|
Отклонить Н0 при |
||
|
|
1,21 |
|
|
При уровне значимости 5% или 1% гипотеза |
1,00 |
|
|
|
0,79 |
|
|
Отклонить Н0 при |
||
|
|
0,71 |
|
|
Отклонить Н0 при |
Рисунок 2.9.
Представление результатов проверки
гипотез по f-критерию
(суждения в
скобках представлять не нужно)
Значения р
Пятый столбец
результатов расчетов в табл. 2.6,
озаглавленный Р
>t,
представляет
альтернативный подход к описанию
значимости коэффициентов регрессии.
Числа в этом столбце показывают значения
р для
каждого коэффициента.
Это вероятности получения соответствующих
значений t-статистку
если нулевая
гипотеза Н0:
(β2
= 0 верна. Значение p
меньшее, чем 0,01, означает,
что эта вероятность меньше, чем 1%, что,
в свою очередь, означает, что
нулевая
гипотеза была бы отклонена при 1%-ном
уровне значимости; значение
p
между 0,01 и 0,05 означает, что нулевая
гипотеза была бы отклонена при
5%-ном уровне
значимости, но не при 1%-ном. Величина p,
равная или превышающая
0,05, свидетельствует, что нулевая гипотеза
не была бы отклонена при 5%-ном уровне
значимости.
Подход, основанный
на значениях p
более информативен, чем подход, основанный
на задании с 5%- и 1%-ного уровня значимости,
поскольку он дает точную
вероятность ошибки I
рода, если нулевая гипотеза верна.
Например, в табл.
2.6 для функции заработка, приведенной
выше, значение р
для коэффициента
наклона равно 0,0000, что означает, что
вероятность получения t-статистики
10,59 или больше составляет здесь менее
чем 0,005%. Следовательно мы
отвергнем гипотезу о равенстве нулю
коэффициента наклона при 1%-н: уровне
значимости. В действительности мы
отвергли бы здесь ее и при yровне
значимости 0,1%
(см. следующий подраздел). Выбор между
подходом, основанным
на значении р,
и подходом с
заданием уровня значимости 5%(1%) может
быть основан на негласном соглашении.
Так, в медицинской литературе
используются значения p,
в то время как в экономической литературе
обычно применяются
оценки 5%- и 1%-ного уровня значимости.
Вставка 2.6.
Терминология принятия (отклонения)
гипотезы
В этом подразделе
было показано, что следует отклонить
нулевую гипотезу, если t-статистика
больше, чем tкрит,
или меньше, чем — tкрит,
и не следует отклонять
эту гипотезу, если t-статистика
находится между t
и tкрит.
Почему «не отклонять»,
к чему это усложнение? Не было бы проще
сказать, что вы принимаете
гипотезу, если абсолютная величина t
-статистики меньше, чем
tкрит.
Аргументом против
использования «термина «принять»
является то, что вы способны «принять»
несколько взаимоисключающих гипотез
в одно и то же время.
Так, в примере с зависимостью между
общей инфляцией и инфляцией. вызванной
ростом заработной платы, вй не могли бы
отклонить нулевую гипотезуH0:
β2
= 0,9 или нулевую гипотезу H0:
β2
= 0,8. Логично утверждать, что вы не
отклоняете эти нулевые гипотезы, а также
нулевую гипотезу HQ;
β2
= 1, рассмотренную
выше, но практически бессмысленно
заявлять, что вы одновременно
принимаете все три гипотезы. В следующем
подразделе вы увидите, что можно
определить целый ряд гипотез, которые
не могут быть отклонены в результате
данного эксперимента, поэтому было бы
неосторожно выбрать одну из них как
«принятую».
Тесты с
уровнем значимости 0,1%
Если значение
t-статистики
очень велико, то следует проверить,
отвергается ли нулевая гипотеза при
уровне значимости 0,1%. Если возможно,
следует представить
результат такого теста, поскольку он
дает возможность отвергнуть
нулевую гипотезу с минимальным риском
допущения ошибки I
рода.
Вчера мне в очередной раз пришлось объяснять почему DataScientist-ы не используют ошибки первого и второго рода и зачем же ввели полноту и точность. Вот прямо заняться нам нечем, лишь бы новые критерии вводить.
И если ошибка второго рода выражается просто:
где Π — это полнота;
то вот ошибка первого рода весьма нетривиально выражается через полноту и точность (см.ниже).
Но это лирика. Самый важный вопрос:
Почему в DataScience используют полноту и точность и почти никогда не говорят об ошибках первого и второго рода?
Кто не знает или забыл — прошу под кат.
Бизнес-задача
Так как Хабр — это блог IT-шников, постараюсь по минимуму использовать мат.абстракции и рассказывать сразу на примере. Предположим, что мы решаем задачу Fraud-мониторинга в ДБО условного банка Roga & Copyta, сокращённо R&C.
Предположим, что у мы разработали некую автоматизированную экспертную систему (ЭС), определяющую для каждой платёжной транзакции: является ли данная транзакция мошеннической (fraud, F) или легитимной (genuine, G).
Необходимо определить «хорошие» критерии оценки качества системы и дать формулы расчета этих критериев.
Так как Roga & Copyta — это хоть и маленький, но всё же банк, то в нём работают люди меркантильные и ничего кроме денег их не интересует. Поэтому разрабатываемые критерии должны максимально прозрачно показывать: насколько выгодно им использовать нашу ЭС? Может быть выгодно установить ЭС конкурентов?
События и вероятности
Для каждой транзакции могут быть определены четыре события:
- Fr (fraud real) — событие того, что транзакция в действительности окажется мошеннической;
- Gr (genuine real) — событие того, что транзакция в действительности окажется легитимной;
- F — событие того, что ЭС «определит» транзакцию как мошенническую;
- G — событие того, что ЭС «определит» транзакцию как легитимную
Очевидно, что Fr и Gr — несовместные события; аналогично F и G — несовместные. По этой причине разумно рассматривать четыре вероятности:
Аббревиатуры читаются так:
- tn — true negative
- fn — false negative
- fp — false positive
- tp — true positive
Мы можем рассматривать условные вероятности:
Так же нам будут интересны и «обратные» условные вероятности:
Например вероятность означает следующее:
Какова вероятность того, что транзакция действительно окажется мошеннической, если ЭС «определила» это событие как мошенническое.
Не следует путать с
, которое можно определить словами:
Какова вероятность того, что ЭС «назовёт» транзакцию мошеннической, если данная транзакция действительно мошенническая.
Аналогично можно определить словами и другие условные вероятности.
Вспомним определения
В статистике любят говорить о нулевой гипотезе (H0) и альтернативной (H1) гипотезе. Обычно под нулевой гипотезой определяют «естественное» состояние. В случае фрод-мониторинга «естественным» состоянием является то, что транзакция легитимная. Это действительно разумно, хотя бы по той причине, что количество мошеннических транзакций гораздо меньше количества легитимных.
Поэтому за нулевую гипотезу примем Gr, а за альтернативную Fr.
Ошибки первого (O1) и второго (O2) рода определяются так:
Словами
Ошибка первого рода (O1) — это вероятность того, что ЭС «определит» транзакцию как мошенническую, при условии, что она легитимная.
Ошибка второго рода (O2) — это вероятность того, что ЭС «определит» транзакцию как легитимную, при условии, что она мошенническая.
Замечание: часто ошибку первого рода называют false positives а ошибку второго рода как false negatives. В том числе, таковы определения в википедии. Это верно по сути. Но
и
. Очень многие новички в DataScience делают такую ошибку и путаются.
Полнота (П) и точность (Т) по определению:
Т.е. полнота — это вероятность того, что ЭС «определит» транзакцию мошеннической, при условии, что она действительно мошенническая. А точность — это вероятность того, что транзакция действительно мошенническая, при условии, что ЭС «определила» транзакцию как мошенническую.
Полноту и точность можно выразить через tp, fp, fn следующим образом:
Вывод формул
Выводим тупо в лоб.
Для полноты:
Для точности:
Следует заметить, что именно эти формулы очень частно приводят в качестве определения полноты и точности. Тут вопрос во вкусе. Можно сказать, что квадрат — это прямоугольник, у которого все стороны равны и доказать, что ромб с прямым углом — это квадрат. А можно наоборот. Например, когда я учился в школе, у меня квадрат определяли как ромб с прямым углом и доказывали, что прямоугольник с равными сторонами — это квадрат.
Но все же определение полноты как и точности как T
мне кажется более правильным. Сразу понятно в чем физический смысл этих величин. Понятно, зачем они нужны.
Бизнес-смысл полноты и точности
Предположим, что для Roga & Copyta мы создали систему с полнотой в 80% и точностью в 10%.
Предположим, что без ЭС банк теряет на мошенничестве 1 миллиард тугриков (₮) в год. Это значит, что благодаря ЭС они смогут предотвратить хищение на сумму в 800 миллионов ₮. Останется еще 200 миллионов ₮ — это ущерб банку (или клиентам банка), который не смогла предотвратить ЭС.
А что на счет точности в 10%? Данная величина значит, что из 100 сработок ЭС только 10 будут попадать по цели, а в остальных случаях мы приостановим легитимные транзакции. Хорошо это или плохо?
Во-первых при остановки транзакции банк совершает какие-либо действия. Например звонит клиентам с просьбой подтвердить операции.
Во-вторых заблокировать легитимные транзакции тоже не всегда хорошая идея. Представьте, что вы сидите с девушкой в ресторане, просите счёт, оплачиваете картой… А тут бах… ЭС ошибочно подсчитала что вы — мошенник… Наверное не очень удобно будет перед барышней… Но мы, чтобы не усложнять, пока опустим эту проблему.
Итак, предположим один звонок стоит 1000 ₮. Так же предположим что средний чек хакера у нас составляет 100 тысяч ₮.
Так как мы предотвращаем мошенничества на 800 миллионов ₮, то в среднем у нас будет 8000 правильных мошеннических сработок. Но 8000 — это, судя по точности, лишь 10%; следовательно всего мы позвоним 80000 раз. Умножаем эту цифру на стоимость одного звонка (1000 ₮) и получаем аж 80 миллионов ₮!
Итоговый ущерб в год для банка R&C равен: 200 + 80 = 280 миллионов ₮. Но без ЭС банк терял бы один один миллиард. Следовательно выгода R&C составляет 720 миллионов тугриков.
нюанс
Следует различать полноту и точность по количеству транзакций и по суммам. Это четыре разные величины. Здесь я «смешал все в кучу», что, конечно не верно! ;)) Будем считать что полнота и точность 80% и 10% как по количеству транзакций, так и по денежным суммам.
Бизнес-смысл ошибок первого и второго рода
Ошибка второго рода элементарно выводится через полноту:
Вывод формулы элементарен (см. следующий параграф)
Поэтому что считать — полноту или упущенный фрод (ошибка второго рода) особой разницы не представляет.
А что на счет ошибки первого рода?
Это вероятность того, что ЭС назовёт мошеннической операцией транзакцию, при условии что она легитимная. Проблема в том, что легитимных транзакций существенно больше мошеннических. Есть банки, в которых более 50 платёжных транзакций в секунду… И это совсем не предел.
R&C — банк небольшой, там всего пять платёжных транзакций в секунду. Давайте посчитаем, сколько это в сутки:
В прошлом параграфе мы узнали, что в R&C 80000 сработок в год, это значит что в сутки в среднем 80000 / 365 = 219,17 сработок. Из них только 10% попали в цель (такова точность), то есть 22. Значит остальные — подлинные: 432000 — 22 = 431978.
Так как полнота 80%, то из этих 22 мы только 4.4 будем упускать.
Значит ошибка первого рода:
Слишком маленькая величина! Бизнес не любит такие числа. Так же сложнее, чем для точности высчитать пользу и ущерб для бизнеса. И есть еще одна проблема:
через ошибку первого рода, можно косвенно понять об объемах платёжных операций в банке!
Что касается точности, то такой проблемы нет. Специалисты из отдела безопасности R&C знают об объемах мошенничества. Они узнают о допустимой нагрузке на контактный центр у самой главной девочки + спрашивают руководство банка о желаемой полноте. Зная абсолютную нагрузку, желаемую полноту и объем фрода можно без труда вычислить приемлемую точность. Эти две цифры вписываются в техническое задание (или тендер).
Разработчику выдают выборку из мошеннических транзакций и легитимных. Если выборка репрезентативна, этих данных достаточно.
«Неправильность» точности с точки зрения чистой математики
Если объем транзакций увеличится в два раза, то точность уменьшится. Если объем мошенничества увеличится в два раза, то точность так же будет больше… С ошибкой первого рода такой проблемы нет, поэтому с точки зрения «чистой математики», эта величина гораздо более «правильная»…
Но на практике, если и резко увеличивается объем мошенничества, то как правило это фрод нового типа и ЭС просто не обучена его ловить… Точность останется той же (а вот полнота уменьшиться, т.к. появится фрод, который мы не умеем ловить). Что касается увеличения количества легитимных транзакций — то это увеличение постепенное и никаких «рывков» не будет.
Поэтому на практике точность — замечательный, понятный для бизнеса критерий оценки качества ЭС.
Вывод ошибок первого рода и второго рода из полноты и точности
Но может быть существует изящная формула вывода ошибки первого рода через точность?
Вот с ошибкой второго рода как все красиво:
Вывод формулы
К сожалению с O1 так изящно не получится. Вот отношение через точность (Т) и полноту (П):
Вывод формулы
Эй! Ты что такой ленивый! А ну давай сам попробуй!
Я сегодня плохо спал, Павел! Ну покажи!
Из и
можно составить выражение:
Откуда следует:
Уже из этого отношения легко получить формулу для O1
Заключение
Точность и полнота «не хуже» и «не лучше» чем ошибки первого и второго рода. Всё зависит от задачи. Мы же не едим столовой ложкой торт, а чайной борщ? Хотя это возможно.
Точность и полнота более понятные критерии качества. Ими легче оперировать. С помощью них просто вычислить предотвращённый ущерб в задаче фрод-мониторинга.
Если вы обнаружили описку или грамматическую ошибку — прошу написать в личку.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
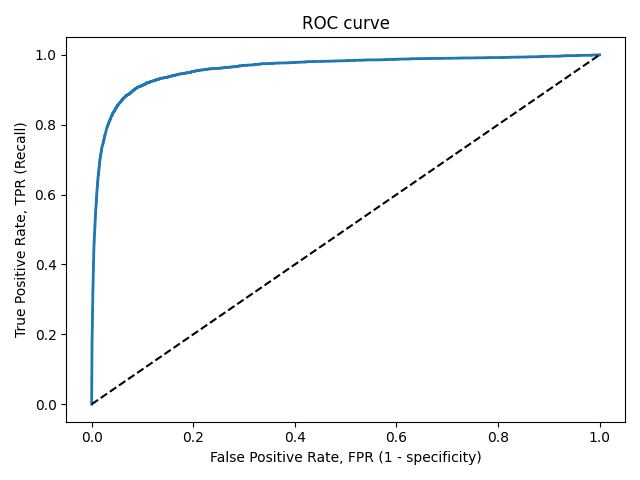
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
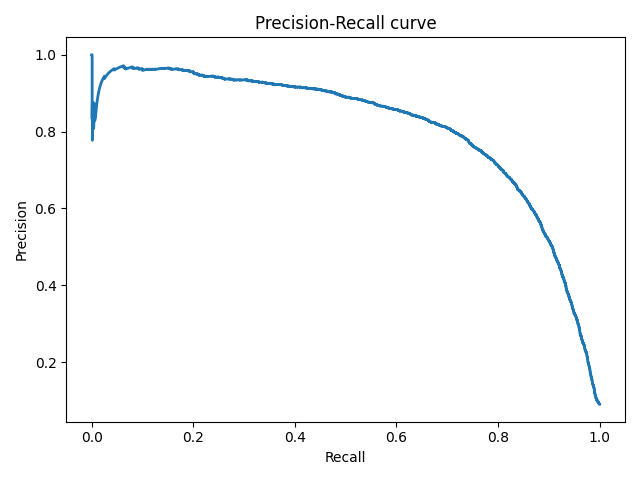
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Оши́бка пе́рвого ро́да (α-ошибка, ложноположительное заключение) — ситуация, когда отвергнута верная нулевая гипотеза (b) (об отсутствии связи между явлениями или искомого эффекта).
Оши́бка второ́го ро́да (β-ошибка, ложноотрицательное заключение) — ситуация, когда принята неверная нулевая гипотеза.
В математической статистике (b) это ключевые понятия задач проверки статистических гипотез (b) . Данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Определения
Пусть дана выборка из неизвестного совместного распределения , и поставлена бинарная задача проверки статистических гипотез:
где — нулевая гипотеза (b) , а — альтернативная гипотеза (b) . Предположим, что задан статистический критерий
- ,
сопоставляющий каждой реализации выборки одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
- Распределение выборки соответствует гипотезе , и она точно определена статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , и она точно определена статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .
Во втором и четвёртом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно[1][2].
| Верная гипотеза | |||
|---|---|---|---|
| Результат применения критерия |
верно принята | неверно принята (Ошибка второго рода) |
|
| неверно отвергнута (Ошибка первого рода) |
верно отвергнута |
О смысле ошибок первого и второго рода
Из определения выше видно, что ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы и , то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.
С учётом вышесказанного, ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием. Если, например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня, то принятая гипотеза не верна, а следовательно совершена ошибка первого рода. Слово «ложноположительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (то есть показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т. п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием. Человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов). Данные примеры указывают на совершение ошибки второго рода. Слово «ложноотрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (то есть показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т. п.
Так как с ростом вероятности ошибки первого рода обычно уменьшается вероятность ошибки второго рода, и наоборот, настройка принимающей решение системы должна представлять собой компромисс. Где именно находится точка получаемого такой настройкой баланса, зависит от оценки последствий при совершении обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез (b) называют уровнем значимости (b) и обычно обозначают греческой буквой (отсюда название -ошибка).
Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, она обозначается греческой буквой (отсюда название -ошибка). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле Таким образом, чем выше мощность критерия, тем меньше вероятность совершить ошибку второго рода.
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности (b) критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объёма, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев (b) это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости (b) , которым задаются при проверке статистических гипотез (b) . Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация (b)
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций (b) . Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность (b) ). В данном контексте возможны следующие нежелательные ситуации[3]:
- когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода);
- когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода).
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама (b) ошибочно классифицирует легитимное email (b) -сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1 % до 30 %. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1 % хорошей почты оценивается как незначительный, для других же потеря даже 0,1 % является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное (b) программное обеспечение ошибочно классифицирует безвредный файл как вирус (b) . Неверное обнаружение может быть вызвано особенностями эвристики (b) , либо неправильной сигнатурой вируса (b) в базе данных. Подобные проблемы могут происходить также и с антитроянскими (b) и антишпионскими (b) программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (b) (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска (b) , когда поисковый алгоритм (b) анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков (b) , многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря (b) . Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование (b) ) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов (b) может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности (b) в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т. п. (см. обнаружение взрывчатых веществ (англ.) (рус. (b) , металлодетекторы (b) ).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического (b) сканирования, использующих распознавание радужной оболочки (b) или сетчатки (b) глаза, черт лица (b) и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении[4].
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом (b) и тестированием (b) :
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау (b) ).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию (b) и гипотиреоз (b) , помимо других врождённых аномалий (b) . Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии[5].
Простые анализы крови, используемые для скрининга потенциальных доноров (b) на ВИЧ (b) и гепатит (b) , имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография (b) ). В США уровень ошибок первого рода в маммограммах достигает 15 %, это самый высокий показатель в мире[6]. Самый низкий уровень наблюдается в Нидерландах (b) , 1 %[7].
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании (b) . Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам велоэргометрии (b) при выявлении коронарного атеросклероза (b) , хотя известно, что велоэргометрия выявляет только те затруднения кровотока в коронарной артерии (b) , которые вызваны стенозом (b) .
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70 %, то многие отрицательные результаты теста окажутся ложными. (См. теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными[8].
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений (b) и привидений (b) для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т. д.), которое имеет обычное объяснение.[9]
См. также
- Статистическая значимость (b)
- Атака второго рода (b)
- Случаи ложного срабатывания систем предупреждения о ракетном нападении (b)
- ROC-кривая (b)
- Коррекция на множественное тестирование (b)
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения». — С. 26Архивная копия от 9 ноября 2018 на Wayback Machine (b)
- ↑ Easton V. J., McColl J. H.Statistics Glossary: Hypothesis Testing.Архивная копия от 24 сентября 2011 на Wayback Machine (b)
- ↑ Moulton R. T. Network Security (англ.) // Datamation. — 1983. — Vol. 29, iss. 7. — P. 121—127.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. )
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную (b) маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90—95 % женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (b) (высокий порог снижает статистическую эффективность (b) теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS)Архивировано 28 марта 2005 года. (недоступная ссылка с 13-05-2013 [3546 дней]) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research)Архивировано 14 июня 2006 года. (недоступная ссылка с 13-05-2013 [3546 дней] — история).
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
Ошибки первого и второго рода
Ошибки первого рода (false positives) и ошибки второго рода (false negatives) — ключевые понятия задач проверки статистических гипотез. Они используются также и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет).
Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным результатом — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранности данных, а с другой стороны — обеспечивать доступ пользователей к этим данным. В этом контексте возможны следующие нежелательные ситуации:
когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус.
Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п.
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение
Источник: https://ru.wikipedia.org/wiki/Ошибки_первого_и_второго_рода
18
766
-
Ошибки первого и второго рода при проверке гипотез.
шибки первого рода (англ. type
I
errors,
α
errors,
false
positives)
и ошибки
второго рода (англ. type
II
errors,
β
errors,
false
negatives)
в математической
статистике —
это ключевые понятия задач проверки
статистических гипотез. Тем не менее,
данные понятия часто используются и в
других областях, когда речь идёт о
принятии «бинарного» решения (да/нет)
на основе некоего критерия (теста,
проверки, измерения), который с некоторой
вероятностью может давать ложный
результат.
[Править]Определения
Пусть дана выборка
из
неизвестного совместного распределения
,
и поставлена бинарная задача проверки
статистических гипотез:
где
— нулевая
гипотеза,
а
— альтернативная
гипотеза.
Предположим, что задан статистический
критерий
,
сопоставляющий каждой
реализации выборки
одну
из имеющихся гипотез. Тогда возможны
следующие четыре ситуации:
-
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
.
Во втором и четвертом случае
говорят, что произошла статистическая
ошибка, и её называют ошибкой
первого и второго рода соответственно. [1][2]
|
Верная гипотеза |
|||
|
Результат
применения
критерия |
верно |
(Ошибка второго рода) |
|
|
(Ошибка первого рода) |
верно |
[Править]о смысле ошибок первого и второго рода
Как видно из вышеприведённого
определения, ошибки
первого и второго рода являются
взаимно-симметричными, то есть если
поменять местами гипотезы
и
,
то ошибки
первого рода превратятся
в ошибки
второго рода и
наоборот. Тем не менее, в большинстве
практических ситуаций путаницы не
происходит, поскольку принято считать,
что нулевая
гипотеза
соответствует
состоянию «по умолчанию» (естественному,
наиболее ожидаемому положению вещей) —
например, что обследумый человек здоров,
или что проходящий через рамку
металлодетектора пассажир не имеет
запрещённых металлических предметов.
Соответственно, альтернативная
гипотеза
обозначает
противоположную ситуацию, которая
обычно трактуется как менее вероятная,
неординарная, требующая какой-либо
реакции.
С учётом этого ошибку
первого рода часто
называют ложной
тревогой, ложным
срабатыванием илиложноположительным срабатыванием —
например, анализ крови показал наличие
заболевания, хотя на самом деле человек
здоров, или металлодетектор выдал сигнал
тревоги, сработав на металлическую
пряжку ремня. Слово «положительный» в
данном случае не имеет отношения к
желательности или нежелательности
самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний, иногда дают
положительный результат (т. е. показывают
наличие заболевания у пациента), когда,
на самом деле пациент этим заболеванием
не страдает. Такой результат называется
ложноположительным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «ложное срабатывание», «ложная
тревога» и т. п. В информационных
технологиях часто используют английский
термин false positive без перевода.
Из-за возможности ложных срабатываний
не удаётся полностью автоматизировать
борьбу со многими видами угроз. Как
правило, вероятность ложного срабатывания
коррелирует с вероятностью пропуска
события (ошибки второго рода). То есть,
чем более чувствительна система, тем
больше опасных событий она детектирует
и, следовательно, предотвращает. Но при
повышении чувствительности неизбежно
вырастает и вероятность ложных
срабатываний. Поэтому чересчур
чувствительно (параноидально) настроенная
система защиты может выродиться в свою
противоположность и привести к тому,
что побочный вред от неё будет превышать
пользу.
Соответственно, ошибку
второго рода иногда
называют пропуском
события или ложноотрицательным срабатыванием —
человек болен, но анализ крови этого не
показал, или у пассажира имеется холодное
оружие, но рамка металлодетектора его
не обнаружила (например, из-за того, что
чувствительность рамки отрегулирована
на обнаружение только очень массивных
металлических предметов).
Слово «отрицательный» в данном случае
не имеет отношения к желательности или
нежелательности самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний иногда дают
отрицательный результат (т. е. показывают
отсутствие заболевания у пациента),
когда, на самом деле пациент страдает
этим заболеванием. Такой результат
называется ложноотрицательным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «пропуск события», и т. п. В
информационных технологиях часто
используют английский термин false negative
без перевода.
Степень чувствительности системы защиты
должна представлять собой компромисс
между вероятностью ошибок первого и
второго рода. Где именно находится точка
баланса, зависит от оценки рисков обоих
видов ошибок.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
8 июля 2021 г.
При проверке гипотез нулевая гипотеза — это гипотеза по умолчанию, которая утверждает, что между переменными нет статистической значимости. Исследователь проверяет нулевую гипотезу, чтобы увидеть, достаточно ли статистической значимости, чтобы опровергнуть ее, и это иногда приводит к ошибке типа 1 или типа 2. Если вы занимаетесь проверкой гипотез как частью своей работы, важно понимать, как ошибки типа 1 и типа 2 могут повлиять на ваши результаты.
В этой статье мы объясним, что такое ошибки типа 1 и типа 2, рассмотрим, как они могут возникнуть, обсудим их важность в исследованиях и приведем примеры, которые помогут вам понять эти концепции.
Ошибки типа 1 и типа 2 относятся к неправильным определениям нулевой гипотезы, но они различаются тем, что исследователь считает верным или ложным в отношении гипотезы. Ошибка 1-го типа, также называемая ложноположительной, возникает, когда исследователь отвергает нулевую гипотезу, которая является истинной, и решает, что существует статистически значимое различие, которого не существует. Ошибка типа 2 является обратной ошибкой типа 1. Также известная как ложный отрицательный результат, она возникает, когда исследователь не отвергает нулевую гипотезу, когда альтернативная гипотеза верна.
Например, в судебном деле нулевая гипотеза будет заключаться в том, что обвиняемый невиновен, пока его вина не будет доказана, а альтернативная гипотеза будет состоять в том, что он виновен. Есть четыре возможных исхода в отношении истинного характера дела:
-
Истинно отрицательный: признан невиновным в суде и невиновен на самом деле.
-
Ложное срабатывание: признан виновным в суде, но на самом деле невиновен.
-
Ложноотрицательный: признан невиновным в суде, но на самом деле виновен.
-
Истинно положительный: признан виновным в суде и фактически виновен
В приведенном выше примере второй и третий результаты являются ошибками типа 1 и типа 2 соответственно. В случае ложного срабатывания присяжные ошибочно отвергают нулевую гипотезу, утверждающую, что подсудимый невиновен. В случае ложноотрицательного результата они ошибочно не отвергают нулевую гипотезу.
Почему возникают ошибки первого рода?
Есть два фактора, которые обычно способствуют возникновению ошибок 1-го рода:
Шанс
Проверка гипотез никогда не бывает стопроцентной, поэтому всегда есть возможность сделать неверные выводы на основе имеющихся данных. Как правило, данные поступают из выборочной совокупности, относительно небольшой выборки лиц, предназначенных для обозначения более широкой демографической группы. Иногда данные, генерируемые выборочными совокупностями, искажают выводы, которые не обязательно отражают интересы всего населения. Это переменная, которую исследователи не могут контролировать, но они могут помочь смягчить ее, выбрав более крупные выборки.
Злоупотребление служебным положением
Иногда ошибки 1-го рода возникают из-за неправильной исследовательской практики. Например, исследователи могут неосознанно исказить результаты теста, завершив его слишком рано. Им может показаться, что у них достаточно данных, хотя стандартная практика рекомендует продолжить тест. В качестве альтернативы они могут сделать вывод, несмотря на то, что им не удалось достичь соответствующего уровня статистической значимости. Исследователи могут избежать выводов типа 1, связанных с злоупотреблением служебным положением, если будут следовать протоколам исследований и обеспечивать надежность своей практики.
Почему возникают ошибки второго рода?
Основным фактором, способствующим возникновению ошибок 2-го рода, является размер выборки. Чем больше размер выборки, тем больше вероятность обнаружения различий в статистическом тесте. Например, если вы хотите проверить, относятся ли студенты колледжа положительно или отрицательно к определенному продукту, группа из трех человек может выразить только два к одному разнообразию или вообще ничего не сказать. Для сравнения, выборка из 1000 человек с большей вероятностью вызовет широкий спектр мнений и, таким образом, более точно отразит большую часть населения.
Какова важность ошибок типа 1 по сравнению с ошибками типа 2?
Ошибки типа 1 и типа 2 являются значительными из-за последствий, которые они имеют в реальных приложениях. Ошибки типа 1 обычно приводят к ненужному использованию ресурсов без какой-либо выгоды. Например, если исследователь-медик совершает ошибку 1-го рода в отношении эффективности нового лечения, он может подтвердить ошибочность исследований и методов, что может привести к созданию лекарства, не приносящего облегчения.
Ошибки 2-го типа важны тем, что могут помешать выделению ресурсов и выполнению необходимых действий. Например, при скрининге пациента на наличие заболевания ложноотрицательный результат может свидетельствовать о том, что пациент здоров, хотя на самом деле он нуждается в медицинском вмешательстве.
Примеры ошибок типа 1 и типа 2
Рассмотрим эти примеры ошибок типа 1 и типа 2, чтобы помочь вам понять, что они из себя представляют:
Пример ошибки 1 рода
Медицинский исследователь проверяет эффективность домашнего средства от головной боли. Нулевая гипотеза состоит в том, что домашнее средство не влияет на головную боль, в то время как альтернативная гипотеза состоит в том, что оно лечит головную боль. Исследователь набирает выборку из 20 пациентов с хроническими головными болями и назначает лекарство половине из них в течение одного месяца. Половина, не получающая лекарство, продолжает страдать от хронических головных болей, в то время как у шести человек из оставшейся половины головные боли прекратились.
На основании вышеизложенного исследователь отвергает нулевую гипотезу. Однако, учитывая небольшое количество тех, кто испытал облегчение, могут возникнуть сомнения относительно того, было ли это лекарство или посторонний фактор, который улучшил состояние шести участников. Если эти шесть участников использовали другие средства от головной боли вместе с тестируемым средством, вполне вероятно, что исследователь совершил ошибку 1-го типа.
Пример ошибки 2 рода
Интернет-магазин хочет знать, могут ли изменения дизайна его веб-сайта помочь увеличить продажи. Нулевая гипотеза состоит в том, что изменения дизайна не влияют на продажи, а альтернативная гипотеза говорит об обратном. Продавец проводит A/B-тестирование, в ходе которого сравниваются две версии сайта, существующая версия и обновленная версия. Три дня мониторят продажи на основе существующей версии. Затем в течение следующих трех дней они представляют новую версию и смотрят, как она повлияет на продажи. По истечении шести дней они не видят значительных изменений в показателях продаж.
Однако возможно, что увеличение периодов наблюдения для каждой версии сайта привело бы к статистически значимой разнице. Если бы розничный продавец отслеживал продажи в течение одного месяца каждый и заметил увеличение продаж во втором месяце, он совершил бы ошибку второго рода, ошибочно приняв нулевую гипотезу.
В
практике большое распространение
получил так называемый допусковый
контроль,
суть которого состоит в определении
путем измерения или испытания значения
контролируемого параметра объекта и
сравнение полученного результата с
заданными граничными допустимыми
значениями. Частным случаем допускового
контроля является поверка средств
измерений, в процессе которой исследуется
попадание погрешностей средства
измерений в допустимые пределы. По
расположению зоны контролируемого
состояния различают допусковый контроль
состояний:
• ниже
допускаемого значения Х
< Хдн;
• выше
допускаемого значения Х
> Хдв;
• между
верхним и нижним допускаемыми значениями
Хдн< Х
< Хдв.
Результатом
контроля является не число, а одно из
взаимоисключающих утверждений:
• «контролируемая
характеристика (параметр) находится в
пределах допускаемых значений»,
результат контроля
— «годен»;
• «контролируемая
характеристика (параметр) находится за
пределами допускаемых значений»,
результат контроля
—»не
годен » или «брак».
Для
определенности примем, что решение
«годен» должно приниматься, если
выполняется условие Хдн
Х
Xвд,
где
X, Хдн, Xдв
— истинное значение и допускаемые
верхнее и нижнее значения контролируемого
параметра. На самом же деле с допускаемыми
значениями Хд и Хд сравнивается не
истинное значение Х (поскольку оно
неизвестно), а его оценка Хо, полученная
в результате измерений. Значение Х
отличается от Х на величину погрешности
измерения: Хо
= Хо+ А.
Решение «годен» при проведении
контроля принимается в случае выполнения
неравенства ХднХоХдв.
Отсюда следует, что при допусковом
контроле возможны четыре исхода.
-
Принято
решение «годен», когда значение
контролируемого параметра находится
в допускаемых пределах, т.е. имели место
события ХднХХдв
, ХднХоХдв.
Если известны плотности вероятностей
законов распределения f(X)
контролируемого параметра Х и погрешности
его измерения f(А),
то при взаимной независимости тих
законов и заданных допустимых верхнем
и нижнем значениях параметра вероятность
события «годен» .
2.
Принято решение «брак», когда
значение контролируемого параметра
находится вне пределов допускаемых
значений, т.е. имели место события Х
< Хдн или
Х >
Хдв и Хо< Хдн или Хо> Хдв. При оговоренных
допущениях вероятность события «негоден»
или «брак»
-
Принято
решение «брак», когда истинное
значение контролируемого параметра
лежит в пределах допускаемых значений,
т.е. Хо<Хдн или Хо>Хдв и Хдн
Х Хдв
и забракован исправный объект. В этом
случае принято говорить, что имеет
место ошибка
I рода. Ее
вероятность
4.
Принято решение «годен», когда
истинное значение контролируемого
параметра лежит вне пределов допускаемых
значений, т.е. имели место события Х
< Хдн или
Х>Хдв и ХднХо<Хдв
и неисправный объект признан годным. В
этом случае говорят, что произошла
ошибка
II рода,
вероятность которой
Очевидно,
что ошибки I
и
II родов
имеют разное значение для изготовителей
и потребителей (заказчиков) контролируемой
продукции
[26]. Ошибки
I рода ведут
к прямым потерям изготовителя, так как
ошибочное признание негодным в
действительности годного изделия
приводит к дополнительным затратам на
исследование, доработку и регулировку
изделия. Ошибки
II рода
непосредственно сказываются на
потребителе, который получает
некачественное изделие. При нормальной
организации отношений между потребителем
и производителем брак, обнаруженный
первым из них, приводит к рекламациям
и ущербу для изготовителя.
Рассмотренные
вероятности Рг, Рнг, Р1, и Р2 при массовом
контроле партии изделий характеризуют
средние доли годных, негодных,
неправильно забракованных и неправильно
пропущенных изделий среди всей
контролируемой их совокупности. Очевидно,
что Рг+Ргн+Р1+Р2=
1.
Достоверность
результатов допускового контроля
описывается различными показателями,
среди которых наибольшее распространение
получили вероятности ошибок
I (Р1
) и
II (Р2
) родов
и риски изготовителя и заказчика
(потребителя):
Одна
из важнейших задач планирования контроля
— выбор
оптимальной точности измерения
контролируемых параметров. При завышении
допускаемых погрешностей измерения
уменьшается стоимость средств измерений,
но увеличиваются вероятности ошибок
при контроле, что в конечном итоге
приводит к потерям. При занижении
допускаемых погрешностей стоимость
средств измерений возрастает,
вероятность ошибок контроля уменьшается,
увеличивает себестоимости выпускаемой
продукции. Очевидно, что существует
некоторая оптимальная точность,
соответствующая минимуму суммы потерь
от брака и стоимости контроля.
Приведенные
формулы позволяют осуществить
целенаправленный поиск таких значений
погрешности измерения, которые бы при
заданных верхнем и нижнем значениях
контролируемого параметра обеспечили
бы допускаемые значения вероятностей
ошибок
I и
II родов
(Р1д и Р2д
) или
соответствующих рисков. Этот поиск
производится путем численного или
графического интегрирования. Следовательно,
для рационального выбора точностных
характеристик средств измерений,
используемых при проведении контроля,
каждом конкретном случае должны быть
заданы допускаемые значения Р1д и Р2д.
3.7.
Метод импульсной рефлектометрии для
контроля протяженных объектов.
Метод
импульсной рефлектометрии, называемый
также методом
отраженных импульсов
или локационным
методом, базируется на распространении
импульсных сигналов в двух- и многопроводных
системах.
Сущность
метода импульсной рефлектометрии
заключается в следующих операциях:
-
Зондировании
трубопроводной системы импульсами
напряжения. -
Приеме импульсов,
отраженных от места повреждения и
неоднородностей волнового сопротивления. -
Выделении отражений
от места повреждений на фоне помех
(случайных и отражений от неоднородностей
трубопроводов). -
Определении
расстояния до повреждения по временной
задержке отраженного импульса
относительно зондирующего.
Упрощенная
структурная схема измерений с помощью
импульсного рефлектометра приведена
на рисунке 3.
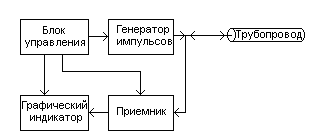
Рис.3. Упрощенная
структурная схема измерений.
С
генератора импульсов зондирующие
импульсы подаются в трубопровод.
Отраженные импульсы поступают с
трубопровода в приемник, в котором
производятся необходимые преобразования
над ними. С выхода приемника преобразованные
сигналы поступают на графический
индикатор. Все блоки импульсного
рефлектометра функционируют по сигналам
блока управления. На графическом
индикаторе рефлектометра воспроизводится
рефлектограмма трубопровода — реакция
трубопровода на зондирующий импульс.
Образование
рефлектограммы трубопровода легко
проследить по диаграмме, приведенной
на рисунке 4. Здесь осью ординат является
ось расстояния, а осью абсцисс — ось
времени.
В левой
части рисунка показан трубопровод из
двух секций с согласующим устройством
и коротким замыканием, а в нижней части
— рефлектограмма этого трубопровода.
Анализируя рефлектограмму трубопровода,
оператор получает информацию о наличии
или отсутствии в ней повреждений и
неоднородностей.

Рис.4. Пример
рефлектограммы с двумя неоднородностями
в трубопроводе.
Например, по
приведенной рефлектограмме можно
сделать несколько выводов:
-
На рефлектограмме,
кроме зондирующего импульса, есть
только два отражения: отражение от
согласующего устройства и отражение
от короткого замыкания. Это свидетельствует
о хорошей однородности трубопровода
от начала до согласующего устройства
и от согласующего устройства до короткого
замыкания. -
Выходное
сопротивление рефлектометра согласовано
с волновым сопротивлением трубопровода,
так как переотраженные сигналы, которые
при отсутствии согласования располагаются
на двойном расстоянии, отсутствуют. -
Повреждение имеет
вид короткого замыкания, так как
отраженный от него сигнал изменил
полярность. -
Короткое замыкание
полное, так как после отражения от него
других отражений нет. -
Линия имеет большое
затухание, так как амплитуда отражения
от короткого замыкания много меньше,
чем амплитуда зондирующего сигнала.
Если
выходное сопротивление рефлектометра
не согласовано с волновым сопротивлением
трубопровода, то в моменты времени 2*
tм,
4* tм
и т.д. будут наблюдаться переотраженные
сигналы от согласующего устройства,
убывающие по амплитуде, а в моменты
времени 2*
tх,
4*tх
и т.д. — переотражения от места короткого
замыкания.
Основную
сложность и трудоемкость при методе
отраженных импульсов представляет
выделение отражения от места повреждения
на фоне помех.
Важное
значение для метода импульсной
рефлектометрии имеет отношение между
напряжением и током введенной в систему
электромагнитной волны, которое одинаково
в любой точке трубопровода. Это
соотношение:
Z
= U/I
имеет размерность
сопротивления и называется волновым
сопротивлением трубопровода.
При использовании метода импульсной
рефлектометрии в трубопроводную систему
контроля посылают зондирующий импульс
и измеряют интервал tх — время двойного
пробега этого импульса до места
повреждения (неоднородности волнового
сопротивления). Расстояние до места
повреждения рассчитывают по выражению:
Lx
= tx*V/2
,
где
V
— скорость распространения импульса в
трубопровода.
Отношение
амплитуды отраженного импульса Uо к
амплитуде зондирующего импульса Uз
обозначают коэффициентом отражения p:
p
= Uo/Uз = (Z1
— Z)
/ (Z1
+ Z),
где:
Z
— волновое сопротивление трубопровода
до места повреждения (неоднородности),
Z1
— волновое сопротивление трубопровода
в месте повреждения (неоднородности).
Отраженный
сигнал появляется в тех местах
трубопровода, где волновое сопротивление
отклоняется от своего среднего значения:
согласующие устройства, изгибах
трубопроводов, в месте обрыва, короткого
замыкания и т.д.
Если
выходное сопротивление импульсного
рефлектометра отличается от волнового
сопротивления измеряемого трубопровода,
то в месте подключения рефлектометра
к трубопровода возникают переотражения.
Переотражения
— это отражения от входного сопротивления
рефлектометра отраженных сигналов,
которые пришли к месту подключения
рефлектометра из трубопровода.
В
зависимости от соотношения входного
сопротивления рефлектометра и волнового
сопротивления трубопровода изменяется
полярность и амплитуда переотражений,
которая может оказаться соизмеримой с
амплитудой отражений. Поэтому перед
измерением рефлектометром обязательно
нужно выполнить операцию согласования
выходного сопротивления рефлектометра
с волновым сопротивлением трубопровода.
Примеры
рефлектограммы трубопровода с
переотражением без согласования
выходного сопротивления с трубопроводом
и с согласованием приведены на рис. 5 и
6:
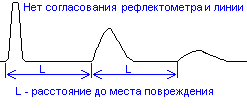
Рис.5. Рефлектограмма
трубопровода в отсутствие согласования.
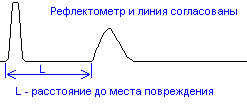
Рис.6. Рефлектограмма
трубопровода при согласовании.
При
распространении вдоль трубопровода
импульсный сигнал затухает. Затухание
трубопровода определяется ее геометрической
конструкцией и выбором материалов для
проводников и изоляции и является
частотно-зависимым. Следствием
частотной зависимости является изменение
зондирующих импульсов при их распространении
по трубопроводу: изменяется не только
амплитуда, но и форма импульса —
длительности фронта и среза импульса
увеличиваются («расплывание”
импульса). Чем длиннее трубопроводная
система, тем больше “расплывание” и
меньше амплитуда импульса. Это затрудняет
точное определение расстояния до
повреждения.
Примеры
рефлектограмм трубопроводов без
затухания и с затуханием показаны на
рисунке 7.


Рис.7. Влияние
затухания трубопровода на вид
рефлектограммы в отсутствие согласования.
Для
более точного измерения необходимо
правильно, в соответствии с длиной и
частотной характеристикой затухания
трубопровода, выбирать параметры
зондирующего импульса в рефлектометре.
Критерием правильного выбора является
минимальное «расплывание» и
максимальная амплитуда отраженного
сигнала.
Если при подключенном
трубопроводе на рефлектограмме
наблюдается только зондирующий импульс,
а отраженные сигналы отсутствуют, то
это свидетельствует о точном согласовании
выходного сопротивления рефлектометра
с волновым сопротивлением трубопровода,
отсутствии повреждений и наличии на
конце трубопровода нагрузки равной
волновому сопротивлению трубопровода
(Рис.8).

Рис.8. Рефлектограмма
при идеальном согласовании.
Вид
отраженного сигнала зависит от характера
повреждения или неоднородности. Например,
при обрыве отраженный импульс имеет ту
же полярность, что и зондирующий, а при
коротком замыкании отраженный импульс
меняет полярность (Рис.9).

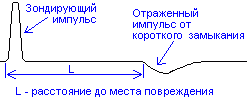
Рис.9. Рефлектограммы
при обрыве и коротком замыкании.
В
идеальном случае, когда отражение от
повреждения полное и затухание
отсутствует, амплитуда отраженного
сигнала равна амплитуде зондирующего
импульса.
Рассмотрим два
случая эквивалентных схем повреждений,
которые наиболее часто встречаются на
практике: шунтирующая
утечка
и продольное
сопротивление.
Пусть
место повреждения трубопровода
представляет собой
шунтирующую утечку
Rш:
С изменением
сопротивления утечки от нуля (соответствует
короткому замыканию) до бесконечности
(соответствует исправности трубопровода),
при положительном зондирующем импульсе
отраженный импульс имеет отрицательную
полярность и изменяется по амплитуде
от максимального значения до нулевого,
в соответствии с выражением:
p=
(Z1
— Z)
/ (Z1
+ Z)
= — Z
/ (Z+2*Rш),
где:
Rш
— сопротивление шунтирующей утечки,
Z1
— волновое сопротивление трубопровода
в месте повреждения, определяется
выражением:
Z1
= (Z*R
ш) / (Z
+ Rш)
Так,
например, при коротком замыкании (Rш=0)
получаем:
p
= -1
В
этом случае сигнал отражается полностью
с изменением полярности.
При отсутствии
шунтирующей нагрузки (Rш=
)
имеем:
p
= 0
Сигнал
не отражается вообще.
При
изменении Rш
от 0 до
амплитуда отраженного сигнала уменьшается
от максимального значения до нулевого,
сохраняя отрицательную полярность (см.
рисунок).
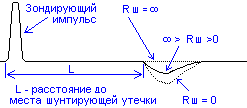
Рис.10. Рефлектограмма
при наличии шунта.
Если
эквивалентная схема места повреждения
трубопровода имеет вид включения
продольного сопротивления (например,
нарушение спайки), то с изменением
величины продольного сопротивления
отраженный импульс изменяется по
амплитуде, оставаясь той же полярности
что и зондирующий импульс.
Выражение для коэффициента отражения
при наличии включения продольного
сопротивления
будет иметь вид:
p
= (Z1
— Z)
/ (Z1
+ Z)
= 1 / (1+2*Z/Rп),
где:
Rп
— продольное сопротивление,
Z1
— волновое сопротивление трубопровода
в месте включения продольного повреждения,
определяемое выражением:
Z1
= Rп + Z
В
случае обрыва жилы (Rп=
)
получаем
коэффициент отражения:
р = 1.
Это
означает, что сигнал отражается полностью
без изменения полярности.
При нулевом
значении продольного сопротивления
(Rп=0)
имеем:
р = 0
С
игнал
не отражается вообще.
При
изменении Rп
от
до
0 отраженный сигнал уменьшается по
амплитуде от максимального значения
до нулевого, без изменения полярности.
Рис.11. Рефлектограмма
— влияние продольного сопротивления.
Разрешающая
способность —
это минимальное расстояние между двумя
неоднородностями волнового сопротивления
при котором отраженные от них сигналы
еще наблюдаются как отдельные сигналы.
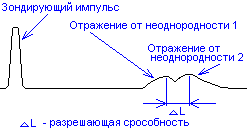
Рис.12. Рефлектограмма
— отражение от двух близких неоднородностей.
На рисунке 11
отраженные от двух неоднородностей
импульсы еще наблюдаются раздельно.
Зондирующие импульсы
распространяются в кабельных линиях
по определенным волновым каналам.
Импульсный
сигнал распространяется в трубопроводе
с определенной скоростью, которая
зависит от типа диэлектрика и определяется
выражением:
где
с
— скорость света,
g
— коэффициент укорочения электромагнитной
волны в трубопровода,
ε
— диэлектрическая проницаемость материала
изоляции трубопровода.
Коэффициент
укорочения
показывает, во сколько раз скорость
распространения импульса в трубопроводе
меньше скорости распространения в
воздухе.
В любом рефлектометре
перед измерением расстояния нужно
установить коэффициент укорочения.
Точность измерения расстояния до места
повреждения зависит от правильной
установки коэффициента укорочения.
По соотношению величин
отражения от повреждения и напряжения
помех все отражения можно разделить на
простые
и сложные.
Простое
повреждение — это такое повреждение
кабельной трубопровода, при котором
амплитуда отражения от места повреждения
больше амплитуды помех.
Сложное
повреждение — это такое повреждение,
для которого амплитуда отражения от
места повреждения меньше или равна
амплитуде помех.
По
источникам возникновения помехи бывают
асинхронные
(аддитивные)
и синхронные.
Асинхронные
помехи
не связаны с зондирующим сигналом и
неоднородностями кабельной трубопровода
и вызваны наводками от соседних кабельных
трубопроводов, от оборудования, транспорта
и различной аппаратуры.
Пример рефлектограммы трубопровода с
асинхронными помехами показан на рисунке
13.
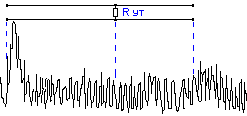
Рис.13. Рефлектограмма
трубопровода с асинхронными помехами.
На рефлектограмме
асинхронные помехи полностью закрывают
отражение от повреждения. Это отражение
невозможно рассмотреть на фоне помех.
Эффективными
методами отстройки от асинхронных помех
являются аналоговая
фильтрация
и цифровое
накопление сигнала.
Сущность цифрового
накопления
заключается в том, что одну и туже
рефлектограмму считывают несколько
раз и вычисляют среднее значение. В
связи с тем, что асинхронные помехи
носят случайный характер, после цифрового
накопления их уровень значительно
снижается.
Пример
предыдущей рефлектограммы трубопровода,
«очищенной» в результате цифрового
накопления рефлектометром, приведен
на рисунке.

Рис.14. Рефлектограмма
с асинхронными помехами после цифровой
очистки.
На
этой рефлектограмме можно легко выделить
сигнал, отраженный от места утечки.
Синхронные
помехи связаны с зондирующим сигналом
и являются отражениями зондирующего
сигнала от неоднородностей волнового
сопротивления трубопровода (отражения
от согласующих устройств, неоднородностей
трубопроводов технологического характера
и др.).
В принципе трубопроводы
не предназначены для передачи коротких
импульсных сигналов, используемых при
методе импульсной рефлектометрии.
Поэтому этим системам контроля
трубопроводов присуще большое количество
синхронных помех. Пример рефлектограммы
трубопровода с синхронными помехами
показан на рисунке.
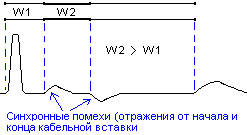
Рис.11. Рефлектограмма
трубопровода с синхронными помехами.
Синхронные
помехи можно существенно уменьшить
посредством сравнения
или
дифференциального
анализа.
При сравнении
накладывают
рефлектограммы двух трубопроводов
(неповрежденного и поврежденного),
проложенных по одной трассе.
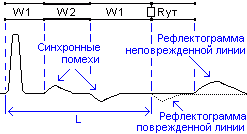
Наложение
двух рефлектограмм позволяет быстро
обнаружить начальную точку их различия,
по которой и определяют расстояние L до
повреждения.
При
дифференциальном
анализе рефлектограммы поврежденного
и неповрежденного трубопроводов
вычитают, как показано на рисунке ниже
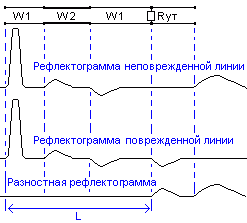
Из
рисунка видно, что при вычитании все
синхронные помехи компенсируются. По
разностной рефлектограмме легко
обнаружить отражение от места повреждения
и определить расстояние L
до него.
При
измерении качества трубопровода методом
импульсной рефлектометрии асинхронные
и синхронные помехи присутствуют на
рефлектограмме одновременно.
Асинхронные
помехи (кроме помех импульсного
характера), как правило, имеют одинаковые
величины, независимо от того, с какого
конца кабельной трубопровода ведется
измерение рефлектометром.
Синхронные
помехи при измерении с разных концов
кабеля имеют различную величину, в
зависимости от многих факторов: длины
кабельной трубопровода, затухания
импульсных сигналов, удаленности места
повреждения и мест неоднородностей
волнового сопротивления трубопровода,
точности согласования выходного
сопротивления импульсного рефлектометра
с волновым сопротивлением трубопровода
и других факторов. Поэтому отраженный
сигнал от одной и той же неоднородности
может иметь различные величины при
измерении с разных концов трубопровода.
Если
хотя бы предположительно известно, к
какому концу кабельной трубопровода
ближе может быть расположено место
повреждения, то для измерений нужно
выбирать именно этот конец кабельной
трубопровода. В других случаях желательно
проводить измерения последовательно
с двух концов трубопровода.
Следует учитывать, что даже такие
повреждения как «короткое замыкание»
и «обрыв», дающие максимальные
отражения зондирующего сигнала, не
всегда можно легко обнаружить на фоне
помех. Например, при большом затухании
и больших неоднородностях волнового
сопротивления трубопровода амплитуда
отражения от удаленного повреждений
типа “короткое замыкание” или “обрыв”
зачастую бывает меньше, чем отражения
от близко расположенных неоднородностей
волнового сопротивления. Поэтому такие
повреждения являются сложным для
обнаружения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
Что такое значимость уравнения регрессии что такое ошибка первого или второго рода нулевая гипотеза
77-1. Как проверить гипотезу о нулевом значении теоретического коэффициента регрессии?
Для проверки нулевой гипотезы H0 о равенстве нулю некоторого коэффициента регрессионного уравнения (H0:β2=0, H0: β2≠0) необходимо сравнить фактическое значение статистики, найденное по формуле с критическим значением t-статистики Стьюдента для выбранного уровня значимости, то есть со значением двусторонней (1-α) квантили t-статистики Стьюдента с n-k степенями свободы. Величина α характеризует допустимый уровень вероятности ошибиться, отвергнув нулевую гипотезу, когда она верна.
Если фактическое значение t-статистики Стьюдента больше критического значения статистики, то нулевая гипотеза отвергается для данного уровня значимости α, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости α. В случае отвержения нулевой гипотезы для уровня значимости говорят, что коэффициент β регрессионного уравнения значим на уровне значимости α (или, говорят, что оценка коэффициента β значимо отличается от нуля), и соответствующий ему регрессор объясняет вариацию зависимой переменной. В противном случае говорят, что коэффициент незначим на уровне значимости α.
Второй способ проверки гипотезы – сравнить p-значение (фактическую вероятность принятия нулевой гипотезы данного коэффициента регрессии) с выбранным уровнем значимости. Если выполняется условие p |t критич|, то гипотеза H0 отвергается, если меньше, то подтверждается
79. Что такое p-значение (p-value, обозначаемое в программе EViews как Prob.) для
статистического критерия?
Метод p-value («метод значения вероятность») p-value = Prob – вероятность того, что случайно будет получен результат лучше, чем у нас (тот, что рассчитан). Если p-value маленький, то это хорошо, а если большой, то плохо.
80. В чем заключается техника работы с p-значением при проверке гипотез?
Смотрим значение prob. в таблице с результатами регрессии и сравниваем с 0,01 и 0,05.
Иначе коэффициент (уравнение) не значим.
81. Как рассчитать p-значение в случае, если невозможно получить доступ к эконометрической программе, или в ней не предусмотрен его расчет?
Открываем таблицу t-распределения, смотрим ряд для нашего числа степеней свободы. Если в нем есть значение t-статистики для рассматриваемого параметра, то уровень значимости (верх таблицы) будет как раз искомым значением p. Если значение t-статистики располагается между двумя табличными, то на основе значений для двух табличных можно приближенно рассчитать искомое по формуле , где t – значение t-статистики, t1 – первое из табличных значений, t2 – второе (большее, правее первого в ряду), а p1 и p2 – значения p соответственно для первого и второго табличных значений t-статистики.
82. Что такое ошибки первого и второго рода в проверке гипотез о коэффициентах регрессии?
Ошибка I рода состоит в том, что мы отвергаем Н0, когда на самом деле она истина.
Ошибка II рода имеет место в случае, если мы принимаем Н0, когда она ложна.
83. Какова связь ошибок первого и второго рода при проверке гипотез о коэффициентах регрессии?
При уменьшении вероятности ошибки 1ого рода увеличивается вероятность ошибки 2ого рода.
84. Что такое мощность критерия?
Мощность критерия (теста)- это вероятность допустить ошибку II рода (β), то есть принять ложную гипотезу. Вычисляется по формуле (1 − β). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода. Используя односторонний критерий вместо двустороннего, можно получить большую мощность при любом уровне значимости. Нужно, однако, помнить, что выигрыш в мощности будет получен только в условиях, когда использование одностороннего критерия оправдано.
Пример нахождения статистической значимости коэффициентов регрессии
Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: 
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:

где 
μa – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии: 
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий: 
Для линейного парного уравнения регрессии: 
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ( b =0) = t (r=0).
Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 69 | 124 | 4761 | 15376 | 8556 | 128.48 | 491.36 | 20.11 | 367.36 |
| 83 | 133 | 6889 | 17689 | 11039 | 141.4 | 173.36 | 70.56 | 26.69 |
| 92 | 146 | 8464 | 21316 | 13432 | 149.7 | 0.03 | 13.71 | 14.69 |
| 97 | 153 | 9409 | 23409 | 14841 | 154.32 | 46.69 | 1.73 | 78.03 |
| 88 | 138 | 7744 | 19044 | 12144 | 146.01 | 66.69 | 64.21 | 0.03 |
| 93 | 159 | 8649 | 25281 | 14787 | 150.63 | 164.69 | 70.13 | 23.36 |
| 74 | 145 | 5476 | 21025 | 10730 | 133.1 | 1.36 | 141.68 | 200.69 |
| 79 | 152 | 6241 | 23104 | 12008 | 137.71 | 34.03 | 204.21 | 84.03 |
| 105 | 168 | 11025 | 28224 | 17640 | 161.7 | 476.69 | 39.74 | 283.36 |
| 99 | 154 | 9801 | 23716 | 15246 | 156.16 | 61.36 | 4.67 | 117.36 |
| 85 | 127 | 7225 | 16129 | 10795 | 143.25 | 367.36 | 263.91 | 10.03 |
| 94 | 155 | 8836 | 24025 | 14570 | 151.55 | 78.03 | 11.91 | 34.03 |
| 1058 | 1754 | 94520 | 258338 | 155788 | 1754 | 1961.67 | 906.57 | 1239.67 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a — tтабл·S a; a + tтабл·Sa)
(0.4325;1.4126)
(b — tтабл·S b; b + tтабл·Sb)
(21.3389;108.3164)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Пример №2 . По территориям региона приводятся данные за 199Х г.;
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (y i — y ) 2 | (y-y(x)) 2 | (x i — x ) 2 | |y-y x |:y |
| 78 | 133 | 6084 | 17689 | 10374 | 148,77 | 517,56 | 248,7 | 57,51 | 0,1186 |
| 82 | 148 | 6724 | 21904 | 12136 | 152,45 | 60,06 | 19,82 | 12,84 | 0,0301 |
| 87 | 134 | 7569 | 17956 | 11658 | 157,05 | 473,06 | 531,48 | 2,01 | 0,172 |
| 79 | 154 | 6241 | 23716 | 12166 | 149,69 | 3,06 | 18,57 | 43,34 | 0,028 |
| 89 | 162 | 7921 | 26244 | 14418 | 158,89 | 39,06 | 9,64 | 11,67 | 0,0192 |
| 106 | 195 | 11236 | 38025 | 20670 | 174,54 | 1540,56 | 418,52 | 416,84 | 0,1049 |
| 67 | 139 | 4489 | 19321 | 9313 | 138,65 | 280,56 | 0,1258 | 345,34 | 0,0026 |
| 88 | 158 | 7744 | 24964 | 13904 | 157,97 | 5,06 | 0,0007 | 5,84 | 0,0002 |
| 73 | 152 | 5329 | 23104 | 11096 | 144,17 | 14,06 | 61,34 | 158,34 | 0,0515 |
| 87 | 162 | 7569 | 26244 | 14094 | 157,05 | 39,06 | 24,46 | 2,01 | 0,0305 |
| 76 | 159 | 5776 | 25281 | 12084 | 146,93 | 10,56 | 145,7 | 91,84 | 0,0759 |
| 115 | 173 | 13225 | 29929 | 19895 | 182,83 | 297,56 | 96,55 | 865,34 | 0,0568 |
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 3280,25 | 1574,92 | 2012,92 | 0,6902 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит:
tкрит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-ta)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Проверка значимости регрессии с помощью дисперсионного анализа (F-тест)
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Проведем проверку значимости простой линейной регрессии с помощью процедуры F -тест.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Процедуру F -теста рассмотрим на примере простой линейной регрессии , когда прогнозируемая переменная Y зависит только от одной переменной Х.
Чтобы определить может ли предложенная модель линейной регрессии быть использована для адекватного описания значений переменной Y, дисперсию наблюдаемых данных анализируют методом Дисперсионного анализа (ANOVA for Simple Regression) . Дисперсия данных разбивается на компоненты, которые затем используются в F -тесте для определения значимости регрессии.
F -тест для проверки значимости регрессии НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения F -теста требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
Можно, конечно, рассмотреть F -тест формально:
- вычислить на основании выборки значение тестовойFстатистики;
- сравнить полученное значение со значением, соответствующему заданному уровню значимости ;
- в зависимости от соотношения этих величин принять решение о значимости вычисленной линейной регрессии
В этой статье ставится более амбициозная задача – разобраться в самом подходе, на котором основан F -тест . Сначала введем несколько определений, которые используются в процедуре F -теста , затем рассмотрим саму процедуру.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части .
Определения, необходимые для F -теста
Согласно определению дисперсии , дисперсия выборки прогнозируемой переменной Y определяется формулой:
В формуле используется ряд сокращений:
- SST (Total Sum of Squares) – это просто компактное обозначение Суммы Квадратов отклонений от среднего (такое сокращение часто используется в зарубежной литературе).
- MST (Total Mean Square) – Среднее Суммы Квадратов отклонений (еще одно общеупотребительное сокращение).
Примечание : Необходимо иметь в виду, что с одной стороны величины MST и SST являются случайными величинами, вычисленными на основании выборки, т.е. статистиками . Однако с другой стороны, при проведении регрессионного анализа по данным имеющейся выборки вычисляются их конкретные значения. В этом случае величины MST и SST являются просто числами.
Значение n-1 в вышеуказанной формуле равно числу степеней свободы ( DF ) , которое относится к дисперсии выборки (одна степень свободы у n величин yi потеряна в результате наличия ограничения 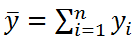
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов дисперсионного анализа в различных прикладных статистических программах (в том числе и в надстройке Пакет анализа, инструмент Регрессия ).
Значение SST, характеризующую общую изменчивость переменной Y, можно разбить на 2 компоненты:
- Изменчивость объясненную моделью (Explained variation), обозначается SSR
- Необъясненную изменчивость (Unexplained variation), обозначается SSЕ
Известно , что справедливо равенство:
Величинам SSR и SSE также сопоставлены степени свободы . У SSR одна степень свободы , т.к. она однозначно определяется одним параметром – наклоном линии регрессии a (напомним, что мы рассматриваем простую линейную регрессию ). Это очевидно из формулы:
Примечание: Очевидность наличия только одной степени свободы проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы величины SSR имеет специальное обозначение: DFR (для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1) . По аналогии с MST, отношение этих величин также часто обозначают MSR = SSR / DFR .
У SSE число степеней свободы равно n -2 , которое обозначается как DFE (или DFRES — residual degrees of freedom). Двойка вычитается, т.к. изменчивость переменной yi имеет 2 ограничения, связанные с оценкой 2-х параметров линейной модели ( а и b ): ŷi=a*xi+b
Отношение этих величин также часто обозначают MSE = SSE / DFE .
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Примечание : Напомним, что MSE (Mean Square of Errors) является оценкой дисперсии s 2 ошибки, подробнее см. статью про линейную регрессию , раздел Стандартная ошибка регрессии .
Число степеней свободы обладает свойством аддитивности: DFT = DFR + DFE . В этом можно убедиться, составив соответствующее равенство n -1=1+( n -2)
Наконец, определившись с определениями, переходим к рассмотрению самой процедуры F -тест .
Процедура F -теста
Сущность F -теста при проверке значимости регрессии заключается в том, чтобы сравнить 2 дисперсии : объясненную моделью (MSR) и необъясненную (MSE). Если эти дисперсии «примерно равны», то регрессия незначима (построенная модель не позволяет объяснить поведение прогнозируемой Y в зависимости от значений переменной Х). Если дисперсия, объясненная моделью (MSR) «существенно больше», чем необъясненная, то регрессия значимая .
Примечание : Чтобы быстрее разобраться с процедурой F -теста рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х нормальных распределений (т.е. двухвыборочный F-тест для дисперсий ).
Чтобы пояснить вышесказанное изобразим на диаграммах рассеяния 2 случая:
- регрессия значима (в этом случае имеем значительный наклон прямой) и
- регрессия незначима (линия регрессии близка к горизонтальной прямой).
На первой диаграмме показан случай, когда регрессия значима:
- Зеленым цветом выделены расстояния от среднего значения до линии регрессии , вычисленные для каждого хi. Сумма квадратов этих расстояний равна SSR;
- Красным цветом выделены расстояния от линии регрессии до соответствующих точек наблюдений . Сумма квадратов этих расстояний равна SSЕ.
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
В случае значимой регрессии точки наблюдений будут находиться вдоль линии регрессии. Их разброс вокруг этой линии описываются ошибками регрессии, которые были минимизированы посредством процедуры МНК . Очевидно, что разброс точек относительно линии регрессии значительно меньше, чем относительно горизонтальной линии, соответствующей среднему значению Y.
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
Понятно, что если вычисленное на основании выборки значение MSR/MSE будет существенно больше некоторого критического значения, то регрессия значима, если нет, то не значима. Очевидно, что это значение должно быть больше 1, но как определить это критическое значение статистически обоснованным методом ?
Вспомним, что для формулирования статистического вывода (т.е. значима регрессия или нет) используют проверку гипотез . Для этого формулируют 2 гипотезы: нулевую Н 0 и альтернативную Н 1 . Для проверки значимости регрессии в качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. наклон прямой a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Примечание : Даже если связи между переменными нет (a=0), то вычисленная на основании данных выборки оценка наклона — величина а , из-за случайности выборки будет близка, но все же отлична от 0.
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
- MSR/MSE будет близко к 1;
- Случайная величина F = MSR/MSE будет иметь F-распределениесо степенями свободы 1 (в числителе) и n-2 (знаменателе). F является тестовой статистикой для проверки значимости регрессии.
Примечание : MSR и MSE являются случайными величинами (т.к. они получены на основе случайной выборки). Соответственно, выражение F=MSR/MSE, также является случайной величиной, которая имеет свое распределение, среднее значение и дисперсию .
Ниже приведен график плотности вероятности F-распределения со степенями свободы 1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Если нулевая гипотеза верна, то значение F 0 =MSR/MSE, вычисленное на основании выборки, должно быть около ее среднего значения (т.е. около 1,04). Если F 0 будет существенно больше 1 (чем больше F0 отклоняется в сторону больших значений, тем это маловероятней), то это будет означать, что F не имеет F-распределение , а, следовательно, нулевую гипотезу нужно отклонить и принять альтернативную, утверждающую, что связь между переменными есть (значима).
Обычно предполагают, что если вероятность, того что F -статистика приняла значение F0 составляет менее 5%, то это событие маловероятно и нулевую гипотезу необходимо отклонить. 5% — это заданный исследователем уровень значимости , который может быть, например, 1% или 10%.
Значение статистики F0 может быть вычислено на основании выборки:
Вычисления в MS EXCEL
В MS EXCEL критическое значение для заданного уровня значимости F1-альфа, 1, n-2 можно вычислить по формуле = F.ОБР(1- альфа;1; n-2) или = F.ОБР.ПХ(альфа;1; n-2) . Другими словами требуется вычислить верхний альфа-квантиль F-распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
В случае простой регрессии значение F0 также равно квадрату t-статистики, которую мы использовали при проверке двусторонней гипотезе о равенстве 0 коэффициента регрессии .
Проверку значимости регрессии можно также осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что случайная величина F примет значение F0 (это и есть p-значение), затем сравнивают p-значение с заданным уровнем значимости . Если p-значение больше уровня значимости, то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL для проверки гипотезы используя p -значение используйте формулу = F.РАСП.ПХ(F0;1;n-2) файл примера , где показано эквивалентность всех подходов проверки значимости регрессии).
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Таблица, которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
http://math.semestr.ru/corel/prim3.php
http://statistica.ru/theory/oshibki-pri-proverke-gipotez-moshchnost/
http://excel2.ru/articles/proverka-znachimosti-regressii-s-pomoshchyu-dispersionnogo-analiza-f-test







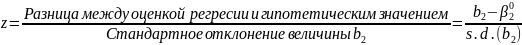

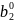









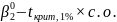

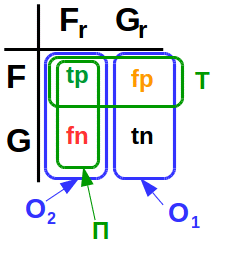
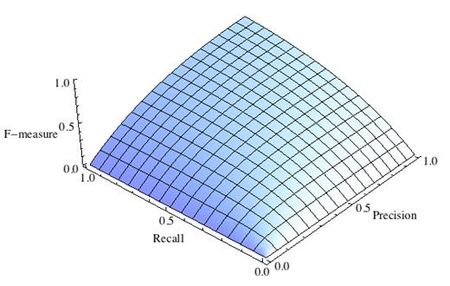
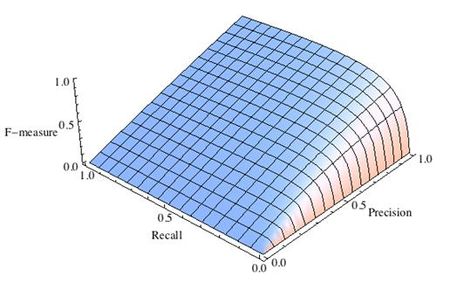
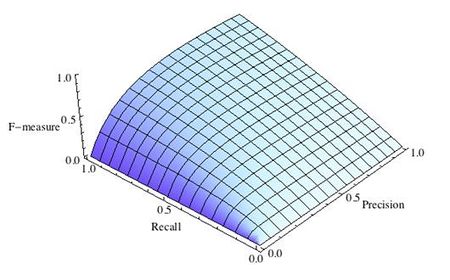

 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.