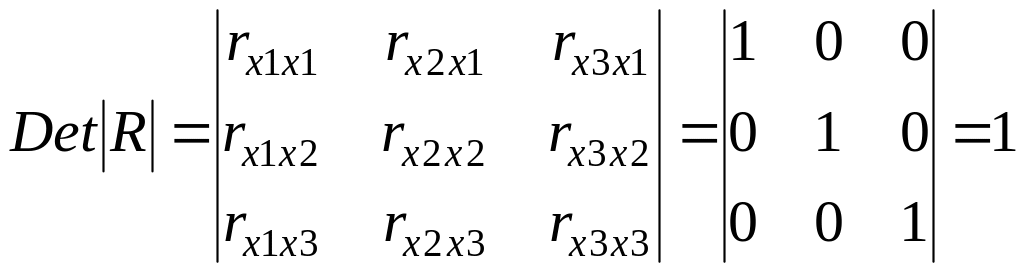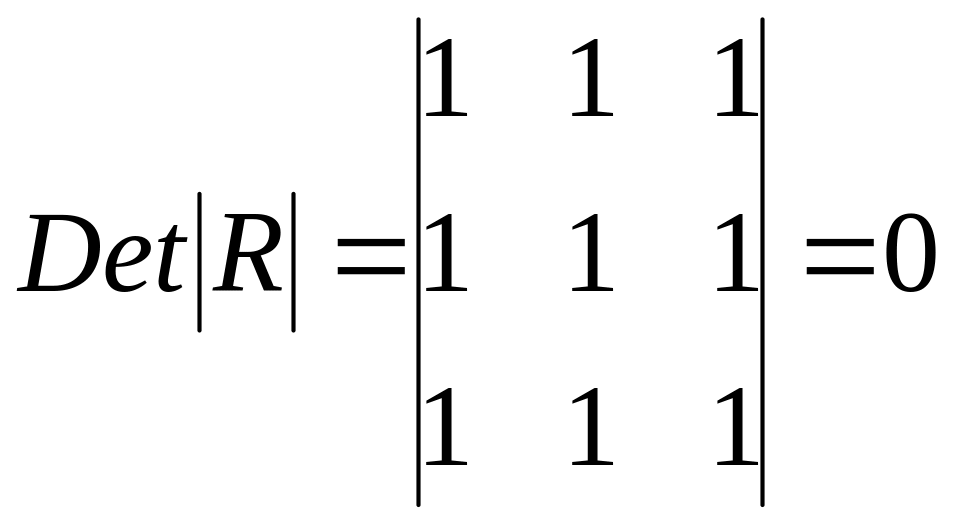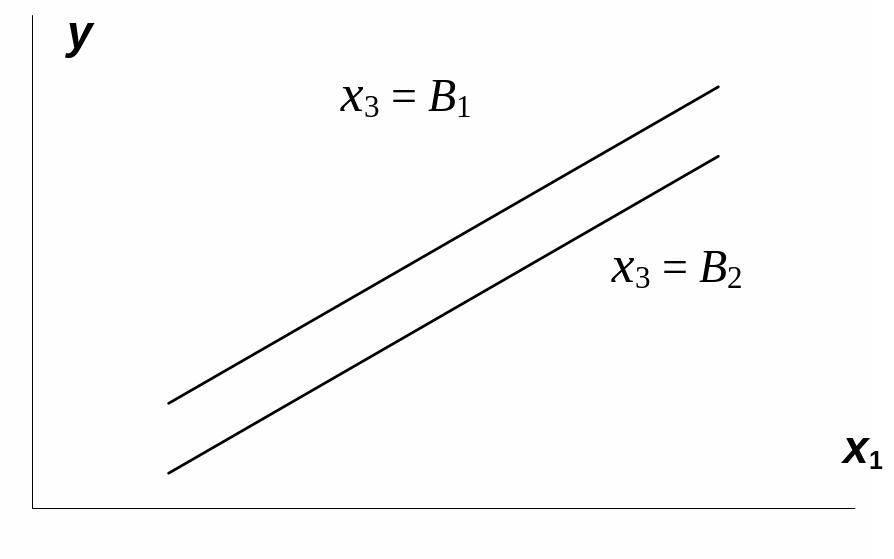From Wikipedia, the free encyclopedia
For broader coverage of this topic, see Approximation.
«Absolute error» redirects here. Not to be confused with Absolute deviation.
Graph of 

The approximation error in a data value is the discrepancy between an exact value and some approximation to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value).
An approximation error can occur for a variety of reasons, among them a computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm).
In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates the extent to which errors in the input of the algorithm will lead to large errors of the output; numerically stable algorithms to not yield a significant error in output when the input is malformed and vice versa. [1]
Formal definition[edit]
Given some value v and its approximation vapprox, the absolute error is
[2][3]
where the vertical bars denote the absolute value.
If 
and the percent error (an expression of the relative error) is [3]
An error bound is an upper limit on the relative or absolute size of an approximation error.[4]
Generalizations[edit]
|
This section needs expansion. You can help by adding to it. (April 2023) |
These definitions can be extended to the case when 

Examples[edit]
Best rational approximants for π (green circle), e (blue diamond), ϕ (pink oblong), (√3)/2 (grey hexagon), 1/√2 (red octagon) and 1/√3 (orange triangle) calculated from their continued fraction expansions, plotted as slopes y/x with errors from their true values (black dashes)
- v
- t
- e
As an example, if the exact value is 50 and the approximation is 49.9, then the absolute error is 0.1 and the relative error is 0.1/50 = 0.002 = 0.2%. As a practical example, when measuring a 6 mL beaker, the value read was 5 mL. The correct reading being 6 mL, this means the percent error in that particular situation is, rounded, 16.7%.
The relative error is often used to compare approximations of numbers of widely differing size; for example, approximating the number 1,000 with an absolute error of 3 is, in most applications, much worse than approximating the number 1,000,000 with an absolute error of 3; in the first case the relative error is 0.003 while in the second it is only 0.000003.
There are two features of relative error that should be kept in mind. First, relative error is undefined when the true value is zero as it appears in the denominator (see below). Second, relative error only makes sense when measured on a ratio scale, (i.e. a scale which has a true meaningful zero), otherwise it is sensitive to the measurement units. For example, when an absolute error in a temperature measurement given in Celsius scale is 1 °C, and the true value is 2 °C, the relative error is 0.5. But if the exact same approximation is made with the Kelvin scale, a 1 K absolute error with the same true value of 275.15 K = 2 °C gives a relative error of 3.63×10−3.
Instruments[edit]
In most indicating instruments, the accuracy is guaranteed to a certain percentage of full-scale reading. The limits of these deviations from the specified values are known as limiting errors or guarantee errors.[6]
See also[edit]
- Accepted and experimental value
- Condition number
- Errors and residuals in statistics
- Experimental uncertainty analysis
- Machine epsilon
- Measurement error
- Measurement uncertainty
- Propagation of uncertainty
- Quantization error
- Relative difference
- Round-off error
- Uncertainty
References[edit]
- ^ Weisstein, Eric W. «Numerical Stability». mathworld.wolfram.com. Retrieved 2023-06-11.
- ^ Weisstein, Eric W. «Absolute Error». mathworld.wolfram.com. Retrieved 2023-06-11.
- ^ a b «Absolute and Relative Error | Calculus II». courses.lumenlearning.com. Retrieved 2023-06-11.
- ^ «Approximation and Error Bounds». www.math.wpi.edu. Retrieved 2023-06-11.
- ^ Golub, Gene; Charles F. Van Loan (1996). Matrix Computations – Third Edition. Baltimore: The Johns Hopkins University Press. p. 53. ISBN 0-8018-5413-X.
- ^ Helfrick, Albert D. (2005) Modern Electronic Instrumentation and Measurement Techniques. p. 16. ISBN 81-297-0731-4
External links[edit]
- Weisstein, Eric W. «Percentage error». MathWorld.
From Wikipedia, the free encyclopedia
For broader coverage of this topic, see Approximation.
Graph of 

The approximation error in a data value is the discrepancy between an exact value and some approximation to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value).
An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm).
In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm.
Formal definition[edit]
One commonly distinguishes between the relative error and the absolute error.
Given some value v and its approximation vapprox, the absolute error is
where the vertical bars denote the absolute value.
If 
and the percent error (an expression of the relative error) is
In words, the absolute error is the magnitude of the difference between the exact value and the approximation. The relative error is the absolute error divided by the magnitude of the exact value.
An error bound is an upper limit on the relative or absolute size of an approximation error.
Generalizations[edit]
These definitions can be extended to the case when 

Examples[edit]
Best rational approximants for π (green circle), e (blue diamond), ϕ (pink oblong), (√3)/2 (grey hexagon), 1/√2 (red octagon) and 1/√3 (orange triangle) calculated from their continued fraction expansions, plotted as slopes y/x with errors from their true values (black dashes)
- v
- t
- e
As an example, if the exact value is 50 and the approximation is 49.9, then the absolute error is 0.1 and the relative error is 0.1/50 = 0.002 = 0.2%. Another example would be if, in measuring a 6 mL beaker, the value read was 5 mL. The correct reading being 6 mL, this means the percent error in that particular situation is, rounded, 16.7%.
The relative error is often used to compare approximations of numbers of widely differing size; for example, approximating the number 1,000 with an absolute error of 3 is, in most applications, much worse than approximating the number 1,000,000 with an absolute error of 3; in the first case the relative error is 0.003 and in the second it is only 0.000003.
There are two features of relative error that should be kept in mind. Firstly, relative error is undefined when the true value is zero as it appears in the denominator (see below). Secondly, relative error only makes sense when measured on a ratio scale, (i.e. a scale which has a true meaningful zero), otherwise it would be sensitive to the measurement units. For example, when an absolute error in a temperature measurement given in Celsius scale is 1 °C, and the true value is 2 °C, the relative error is 0.5, and the percent error is 50%. For this same case, when the temperature is given in Kelvin scale, the same 1 K absolute error with the same true value of 275.15 K gives a relative error of 3.63×10−3 and a percent error of only 0.363%. Celsius temperature is measured on an interval scale, whereas the Kelvin scale has a true zero and so is a ratio scale. Thus the relative error is not very meaningful.
Instruments[edit]
In most indicating instruments, the accuracy is guaranteed to a certain percentage of full-scale reading. The limits of these deviations from the specified values are known as limiting errors or guarantee errors.[2]
See also[edit]
- Accepted and experimental value
- Condition number
- Errors and residuals in statistics
- Experimental uncertainty analysis
- Machine epsilon
- Measurement error
- Measurement uncertainty
- Propagation of uncertainty
- Quantization error
- Relative difference
- Round-off error
- Uncertainty
References[edit]
- ^ Golub, Gene; Charles F. Van Loan (1996). Matrix Computations – Third Edition. Baltimore: The Johns Hopkins University Press. p. 53. ISBN 0-8018-5413-X.
- ^ Helfrick, Albert D. (2005) Modern Electronic Instrumentation and Measurement Techniques. p. 16. ISBN 81-297-0731-4
External links[edit]
- Weisstein, Eric W. «Percentage error». MathWorld.
From Wikipedia, the free encyclopedia
For broader coverage of this topic, see Approximation.
Graph of 

The approximation error in a data value is the discrepancy between an exact value and some approximation to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value).
An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm).
In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm.
Formal definition[edit]
One commonly distinguishes between the relative error and the absolute error.
Given some value v and its approximation vapprox, the absolute error is
where the vertical bars denote the absolute value.
If 
and the percent error (an expression of the relative error) is
In words, the absolute error is the magnitude of the difference between the exact value and the approximation. The relative error is the absolute error divided by the magnitude of the exact value.
An error bound is an upper limit on the relative or absolute size of an approximation error.
Generalizations[edit]
These definitions can be extended to the case when 

Examples[edit]
Best rational approximants for π (green circle), e (blue diamond), ϕ (pink oblong), (√3)/2 (grey hexagon), 1/√2 (red octagon) and 1/√3 (orange triangle) calculated from their continued fraction expansions, plotted as slopes y/x with errors from their true values (black dashes)
- v
- t
- e
As an example, if the exact value is 50 and the approximation is 49.9, then the absolute error is 0.1 and the relative error is 0.1/50 = 0.002 = 0.2%. Another example would be if, in measuring a 6 mL beaker, the value read was 5 mL. The correct reading being 6 mL, this means the percent error in that particular situation is, rounded, 16.7%.
The relative error is often used to compare approximations of numbers of widely differing size; for example, approximating the number 1,000 with an absolute error of 3 is, in most applications, much worse than approximating the number 1,000,000 with an absolute error of 3; in the first case the relative error is 0.003 and in the second it is only 0.000003.
There are two features of relative error that should be kept in mind. Firstly, relative error is undefined when the true value is zero as it appears in the denominator (see below). Secondly, relative error only makes sense when measured on a ratio scale, (i.e. a scale which has a true meaningful zero), otherwise it would be sensitive to the measurement units. For example, when an absolute error in a temperature measurement given in Celsius scale is 1 °C, and the true value is 2 °C, the relative error is 0.5, and the percent error is 50%. For this same case, when the temperature is given in Kelvin scale, the same 1 K absolute error with the same true value of 275.15 K gives a relative error of 3.63×10−3 and a percent error of only 0.363%. Celsius temperature is measured on an interval scale, whereas the Kelvin scale has a true zero and so is a ratio scale. Thus the relative error is not very meaningful.
Instruments[edit]
In most indicating instruments, the accuracy is guaranteed to a certain percentage of full-scale reading. The limits of these deviations from the specified values are known as limiting errors or guarantee errors.[2]
See also[edit]
- Accepted and experimental value
- Condition number
- Errors and residuals in statistics
- Experimental uncertainty analysis
- Machine epsilon
- Measurement error
- Measurement uncertainty
- Propagation of uncertainty
- Quantization error
- Relative difference
- Round-off error
- Uncertainty
References[edit]
- ^ Golub, Gene; Charles F. Van Loan (1996). Matrix Computations – Third Edition. Baltimore: The Johns Hopkins University Press. p. 53. ISBN 0-8018-5413-X.
- ^ Helfrick, Albert D. (2005) Modern Electronic Instrumentation and Measurement Techniques. p. 16. ISBN 81-297-0731-4
External links[edit]
- Weisstein, Eric W. «Percentage error». MathWorld.
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
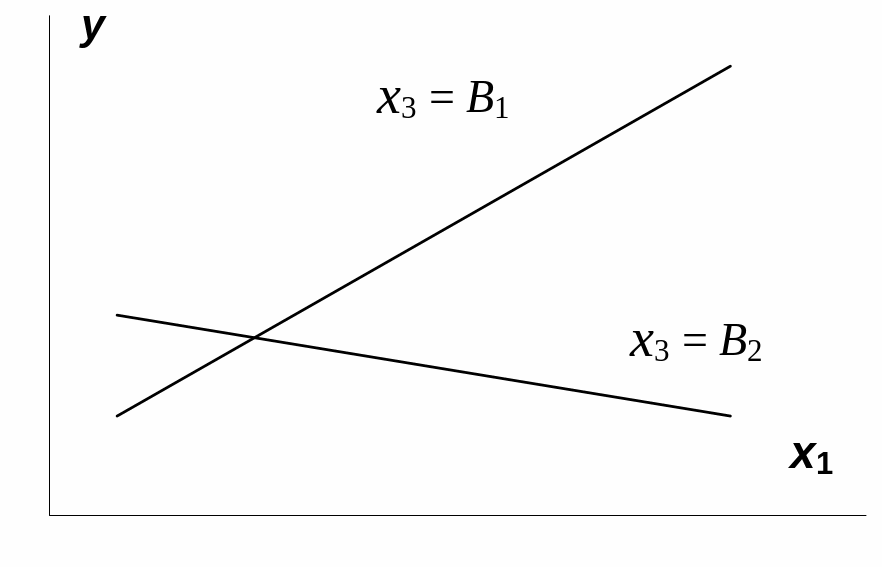
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текст урока с работающими фрагментами расчетов в файле uroki-approksimacii.xls
Ошибка аппроксимации — один из наиболее часто возникающих вопросов при применении тех или иных методов аппроксимации исходных данных. Есть разного рода ошибки аппроксимации:
— ошибки, связанные с погрешностями исходных данных;
— ошибки, связанные с несоответствием аппроксимирующей модели структуре аппроксимируемых данных.
В Excel есть хорошо разработанная функция Линейн, предназначенная для обработки данных и аппроксимаций, в которой задействован отлаженный математический аппарат. Для того, чтобы иметь о ней представление, обратимся (через F1) к описательной части этой разработки, которую приводим с сокращениями и некоторыми изменениями обозначений.
ЛИНЕЙН
Расчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
y=a+b1*x1+b2*x2+…bn*xn
Синтаксис:
ЛИНЕЙН(y;x;конст;статистика)
Массив y — известные значения y.
Массив x — известные значеня x. Массив x может содержать одно или несколько множеств переменных.
Конст — это логическое значение, которое указывает, требуется ли, чтобы свободный член a был равен 0.
Если аргумент конст имеет значение ИСТИНА, 1 или опущено, то a вычисляется обычным образом. Если аргумент конст имеет значение ЛОЖЬ или 0, то a полагается равным 0.
Статистика — это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА или 1, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ, 0 или опущена, то функция ЛИНЕЙН возвращает только коэффициенты и свободный член.
Дополнительная регрессионая статистика:
se1,se2,…,sen — стандартные значения ошибок для коэффициентов b1,b2,…,bn.
sea — стандартное значение ошибки для постоянной a (sea = #Н/Д, если конст имеет значение ЛОЖЬ).
r2 — коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y. Для получения информации о том, как вычисляется r2, см. «Замечания» в конце данного раздела.
sey — стандартная ошибка для оценки y.
F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет.
df — степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.
ssreg — регрессионая сумма квадратов.
ssresid — остаточная сумма квадратов.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Выборочную информацию из функции можно получить через функцию ИHДЕКС, например:
Y-пересечение (свободный член):
ИНДЕКС(ЛИНЕЙН(y;x);2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов. Затем Microsoft Excel подсчитывает сумму квадратов разностей между фактическими значениями y и средним значением y, которая называется общей суммой квадратов (регрессионая сумма квадратов + остаточная сумма квадратов). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными.
Заметьте, что значения y, предсказанные с помощью уравнения регрессии, возможно не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Пример 1 Наклон и Y-пересечение
ЛИНЕЙН({1;9;5;7};{0;4;2;3}) равняется {2;1}, наклон = 2 и y-пересечение = 1.
Использование статистик F и R2
Можно использовать F-статистику, чтобы определить, является ли результат с высоким значение r2 случайным. Если F-наблюдаемое больше, чем F-критическое, то взаимосвязь между переменными имеется. F-критическое можно получить из таблицы F-критических значений в любом справочнике по математической статистике. Для того, чтобы найти это значение, используя односторонний тест, положим величину Альфа (величина Альфа используется для обозначения вероятности ошибочного вывода о том, что имеется сильная взаимозависимость) равной 0,05, а для числа степеней свободы (обозначаемых обычно v1 и v2), положим v1 = k = 4 и v2 = n — (k + 1) = 11 — (4 + 1) = 6, где k — это число переменных, а n — число точек данных. Из таблицы справочника F-критическое равно 4,53. Наблюдаемое F-значение равно 459,753674 (это значение получено в опущенном нами примере), что заметно больше чем F-критическое значение 4,53. Следовательно, полученное регрессионное уравнение полезно для предсказания искомого результата.
[c.18]
Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии.
[c.29]
Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора.
[c.29]
Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации.
[c.30]
Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%.
[c.39]
Чем продолжительнее период, по данным которого построены модели, тем меньше темп роста ошибки аппроксимации при прочих равных условиях. Следовательно, чем короче период упреждения, тем короче следует брать и период анализа, и, наоборот, при долгосрочном планировании необходимо использовать максимально возможную продолжитель-
[c.64]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%.
[c.90]
Средняя ошибка аппроксимации
[c.94]
Средняя ошибка аппроксимации……,…….
[c.95]
В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4).
[c.144]
Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации.
[c.145]
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D).
[c.151]
Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости.
[c.152]
После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]
Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%.
[c.123]
Подобное обоснование является приблизительным и нуждается в дальнейшем уточнении с помощью ошибки аппроксимации.
[c.50]
Наибольшее значение ошибки аппроксимации свидетельствует о том, что оцениваемая модель дает наиболее адекватное описание формы взаимосвязи. Причем ошибка аппроксимации не должна превышать 0,2, или 20%.
[c.52]
Подставляя последовательно значения времени /, получим теоретические уровни товарооборота. Ошибка аппроксимации для прямолинейной формы тренда составит [c.184]
Далее рассчитывается ошибка аппроксимации для функции тренда в виде параболы второго порядка по формуле [c.187]
Для повышения надежности прогноза потребности в нефтепродуктах по управлению в целом и определения границ его достоверности на всех этапах прогнозирования предусматривается проведение верификации. При верификации принимаются в расчет не все частные прогнозы, а только те из них, которые удовлетворяют требованиям статистической надежности, дают наименьшую ошибку аппроксимации, подтверждаются проверкой ретроспективным методом и дают результаты, близкие к фактическим значениям за последний год ретроспективного периода. Для облегчения проведения расчетов по алгоритму (рис. 7) на каждом этапе прогнозирования (кратко-, средне- и долгосрочный прогнозы) составляются подсобные таблицы по форме 010107 (табл. 6).
[c.63]
Очевидно, что ошибки аппроксимации носят непериодический характер. В противном случае нужно было бы повторить всю процедуру, используя в качестве исходной выборки эти ошибки, и повторять ее до тех пор, пока не будут выделены все значимые гармоники.
[c.137]
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
[c.6]
Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических [c.6]
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели тесноты связи — индекс корреляции рху и среднюю ошибку аппроксимации 7, [c.13]
А = 8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.
[c.15]
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
[c.16]
Это означает, что 52% вариации заработной латы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации [c.18]
Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.
[c.32]
Оцените качество модели. Для этого а) определите ошибку аппроксимации t б) найдите показатель тесноты связи прибыли с исследуемым в мо-
[c.33]
Оцените с помощью средней ошибки аппроксимации качество уравнений.
[c.38]
Оцените качество уравнений с помощью средней ошибки аппроксимации.
[c.42]
Оцените качество уравнения через среднюю ошибку аппроксимации.
[c.92]
Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений.
[c.166]
СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ
[c.87]
Параметры моделей и выбор формы связи, определяющие уровень затрат в зависимости от значений отобранных факторов, вычисляются по методике, изложенной в работе [51]. Затем исследуется характер изменения случайных отклонений (ошибки аппроксимации) по каждому НГДУ отдельно. Если обнаружится определенная закономерность их изменений, то вычисляется функция их изменения во времени, и далее плановый
[c.68]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Дальнейший анализ выглядит чаще как моделирование взаимосвязей и оценка тесноты взаимозависимости (корреляционно-регрессионный анализ). Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Это относительная ошибка аппроксимации, средняя квадратическая ошибка аппроксимации (6ОСТ) (чем они меньше, тем лучше уравнение) и коэффициент множественной детерминации (R2) или коэффициент множественной корреляции (R) (чем ближе он к 1, тем более вероятность, что уравнение регрессии носит совершенно случайный характер). Для проверки значимости используют F-критерий с распределением Фишера.
[c.670]
Для более широкого освещения этой темы см. Приближение .
График (синий) с его линейной аппроксимацией (красный) при a = 0. Ошибка аппроксимации — это зазор между кривыми, и она увеличивается для значений x дальше от 0.
Ошибка аппроксимации в некоторых данных является расхождение между точным значением и некоторым приближением к ней. Ошибка аппроксимации может возникнуть по следующим причинам:
- измерения в данном не является точным из — за инструменты. (например, точное показание листа бумаги составляет 4,5 см, но, поскольку линейка не использует десятичные дроби, вы округлите его до 5 см.) или
- приближения
В математической области численного анализа, то устойчивость численная из алгоритма показывает, как ошибка распространяются по алгоритму.
Формальное определение
Обычно различают относительную ошибку и абсолютную ошибку.
Учитывая некоторое значение v и его приближение v приблизительно, абсолютная ошибка составляет
где вертикальные полосы обозначают абсолютное значение . Если относительная погрешность составляет
и ошибка процентов является
На словах абсолютная ошибка — это величина разницы между точным значением и приближением. Относительная ошибка — это абсолютная ошибка, деленная на величину точного значения. Ошибка в процентах — это относительная ошибка, выраженная в 100 единицах.
Граница ошибки — это верхний предел относительного или абсолютного размера ошибки аппроксимации.
Обобщения
Эти определения могут быть расширены на случай, когда и являются n -мерными векторами, путем замены абсолютного значения на n -норму .
Примеры
Наилучшие рациональные аппроксимации для π (зеленый круг), e (синий ромб), ϕ (продолговатый розовый), (√3) / 2 (серый шестиугольник), 1 / √2 (красный восьмиугольник) и 1 / √3 (оранжевый треугольник) вычисленные из их разложений в непрерывную дробь, построенные как наклоны y / x с ошибками от их истинных значений (черные штрихи)
- v
- т
- е
Например, если точное значение равно 50, а приближение — 49,9, тогда абсолютная ошибка составляет 0,1, а относительная ошибка составляет 0,1 / 50 = 0,002 = 0,2%. Другой пример: если при измерении стакана на 6 мл считанное значение будет 5 мл. Правильное показание составляет 6 мл, это означает, что процентная погрешность в данной конкретной ситуации округляется до 16,7%.
Относительная ошибка часто используется для сравнения приближений чисел разного размера; например, приближение числа 1000 с абсолютной ошибкой 3 в большинстве приложений намного хуже, чем приближение числа 1000000 с абсолютной ошибкой 3; в первом случае относительная погрешность составляет 0,003, а во втором — всего 0,000003.
Следует иметь в виду две особенности относительной ошибки. Во-первых, относительная ошибка не определена, когда истинное значение равно нулю, как оно указано в знаменателе (см. Ниже). Во-вторых, относительная погрешность имеет смысл только при измерении по шкале отношений (т. Е. Шкале с истинным значимым нулем), в противном случае она была бы чувствительна к единицам измерения. Например, когда абсолютная погрешность измерения температуры по шкале Цельсия составляет 1 ° C, а истинное значение — 2 ° C, относительная погрешность составляет 0,5, а погрешность в процентах составляет 50%. В том же случае, когда температура дана в шкале Кельвина, та же абсолютная ошибка 1 К с тем же истинным значением 275,15 К дает относительную ошибку 3,63 × 10 — 3 и ошибку в процентах всего лишь 0,363%. Температура Цельсия измеряется по шкале интервалов, тогда как шкала Кельвина имеет истинный ноль, как и шкала отношений.
Инструменты
В большинстве индикаторных приборов точность гарантируется до определенного процента от полной шкалы. Пределы этих отклонений от указанных значений известны как предельные ошибки или гарантийные ошибки.
Смотрите также
- Принятое и экспериментальное значение
- Относительная разница
- Неопределенность
- Анализ экспериментальной неопределенности
- Распространение неопределенности
- Ошибки и неточности в статистике
- Ошибка округления
- Ошибка квантования
- Погрешность измерения
- Погрешность измерения
- Машина эпсилон
Рекомендации
Внешние ссылки
- Вайсштейн, Эрик В. «Ошибка в процентах» . MathWorld .
Для более широкого освещения этой темы см. Приближение .
График (синий) с его линейной аппроксимацией (красный) при a = 0. Ошибка аппроксимации — это зазор между кривыми, и она увеличивается для значений x дальше от 0.
Ошибка аппроксимации в некоторых данных является расхождение между точным значением и некоторым приближением к ней. Ошибка аппроксимации может возникнуть по следующим причинам:
- измерения в данном не является точным из — за инструменты. (например, точное показание листа бумаги составляет 4,5 см, но, поскольку линейка не использует десятичные дроби, вы округлите его до 5 см.) или
- приближения
В математической области численного анализа , то устойчивость численная из алгоритма показывает , как ошибка распространяются по алгоритму.
Формальное определение
Обычно различают относительную ошибку и абсолютную ошибку.
Учитывая некоторое значение v и его приближение v приблизительно , абсолютная ошибка составляет
где вертикальные полосы обозначают абсолютное значение . Если относительная погрешность составляет
и ошибка процентов является
На словах абсолютная ошибка — это величина разницы между точным значением и приближением. Относительная ошибка — это абсолютная ошибка, деленная на величину точного значения. Ошибка в процентах — это относительная ошибка, выраженная в 100 единицах.
Граница ошибки — это верхний предел относительного или абсолютного размера ошибки аппроксимации.
Обобщения
Эти определения могут быть расширены на случай, когда и являются n -мерными векторами , путем замены абсолютного значения на n -норму .
Примеры
Наилучшие рациональные аппроксимации для π (зеленый круг), e (синий ромб), ϕ (продолговатый розовый), (√3) / 2 (серый шестиугольник), 1 / √2 (красный восьмиугольник) и 1 / √3 (оранжевый треугольник) вычисленные из их разложений в непрерывную дробь, построенные как наклоны y / x с ошибками от их истинных значений (черные штрихи)
- v
- т
- е
Например, если точное значение равно 50, а приближение — 49,9, тогда абсолютная ошибка составляет 0,1, а относительная ошибка составляет 0,1 / 50 = 0,002 = 0,2%. Другой пример: если при измерении стакана на 6 мл считанное значение будет 5 мл. Правильное показание составляет 6 мл, это означает, что процентная погрешность в данной конкретной ситуации округляется до 16,7%.
Относительная ошибка часто используется для сравнения приближений чисел разного размера; например, приближение числа 1000 с абсолютной ошибкой 3 в большинстве приложений намного хуже, чем приближение числа 1000000 с абсолютной ошибкой 3; в первом случае относительная погрешность составляет 0,003, а во втором — всего 0,000003.
Следует иметь в виду две особенности относительной ошибки. Во-первых, относительная ошибка не определена, когда истинное значение равно нулю, как оно указано в знаменателе (см. Ниже). Во-вторых, относительная погрешность имеет смысл только при измерении по шкале отношений (т. Е. Шкале с истинным значимым нулем), в противном случае она была бы чувствительна к единицам измерения. Например, когда абсолютная погрешность измерения температуры по шкале Цельсия составляет 1 ° C, а истинное значение — 2 ° C, относительная погрешность составляет 0,5, а погрешность в процентах составляет 50%. В том же случае, когда температура дана в шкале Кельвина , та же абсолютная ошибка 1 К с тем же истинным значением 275,15 К дает относительную ошибку 3,63 × 10 — 3 и ошибку в процентах всего лишь 0,363%. Температура Цельсия измеряется по шкале интервалов , тогда как шкала Кельвина имеет истинный ноль, как и шкала отношений.
Инструменты
В большинстве индикаторных приборов точность гарантируется до определенного процента от полной шкалы. Пределы этих отклонений от указанных значений известны как предельные ошибки или гарантийные ошибки.
Смотрите также
- Принятое и экспериментальное значение
- Относительная разница
- Неопределенность
- Анализ экспериментальной неопределенности
- Распространение неопределенности
- Ошибки и неточности в статистике
- Ошибка округления
- Ошибка квантования
- Погрешность измерения
- Погрешность измерения
- Машина эпсилон
Рекомендации
Внешние ссылки
- Вайсштейн, Эрик В. «Ошибка в процентах» . MathWorld .
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.

Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текст урока с работающими фрагментами расчетов в файле uroki-approksimacii.xls
Ошибка аппроксимации — один из наиболее часто возникающих вопросов при применении тех или иных методов аппроксимации исходных данных. Есть разного рода ошибки аппроксимации:
— ошибки, связанные с погрешностями исходных данных;
— ошибки, связанные с несоответствием аппроксимирующей модели структуре аппроксимируемых данных.
В Excel есть хорошо разработанная функция Линейн, предназначенная для обработки данных и аппроксимаций, в которой задействован отлаженный математический аппарат. Для того, чтобы иметь о ней представление, обратимся (через F1) к описательной части этой разработки, которую приводим с сокращениями и некоторыми изменениями обозначений.
ЛИНЕЙН
Расчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
y=a+b1*x1+b2*x2+…bn*xn
Синтаксис:
ЛИНЕЙН(y;x;конст;статистика)
Массив y — известные значения y.
Массив x — известные значеня x. Массив x может содержать одно или несколько множеств переменных.
Конст — это логическое значение, которое указывает, требуется ли, чтобы свободный член a был равен 0.
Если аргумент конст имеет значение ИСТИНА, 1 или опущено, то a вычисляется обычным образом. Если аргумент конст имеет значение ЛОЖЬ или 0, то a полагается равным 0.
Статистика — это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА или 1, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ, 0 или опущена, то функция ЛИНЕЙН возвращает только коэффициенты и свободный член.
Дополнительная регрессионая статистика:
se1,se2,…,sen — стандартные значения ошибок для коэффициентов b1,b2,…,bn.
sea — стандартное значение ошибки для постоянной a (sea = #Н/Д, если конст имеет значение ЛОЖЬ).
r2 — коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y. Для получения информации о том, как вычисляется r2, см. «Замечания» в конце данного раздела.
sey — стандартная ошибка для оценки y.
F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет.
df — степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.
ssreg — регрессионая сумма квадратов.
ssresid — остаточная сумма квадратов.
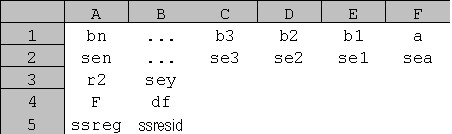
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Выборочную информацию из функции можно получить через функцию ИHДЕКС, например:
Y-пересечение (свободный член):
ИНДЕКС(ЛИНЕЙН(y;x);2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов. Затем Microsoft Excel подсчитывает сумму квадратов разностей между фактическими значениями y и средним значением y, которая называется общей суммой квадратов (регрессионая сумма квадратов + остаточная сумма квадратов). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными.
Заметьте, что значения y, предсказанные с помощью уравнения регрессии, возможно не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Пример 1 Наклон и Y-пересечение
ЛИНЕЙН({1;9;5;7};{0;4;2;3}) равняется {2;1}, наклон = 2 и y-пересечение = 1.
Использование статистик F и R2
Можно использовать F-статистику, чтобы определить, является ли результат с высоким значение r2 случайным. Если F-наблюдаемое больше, чем F-критическое, то взаимосвязь между переменными имеется. F-критическое можно получить из таблицы F-критических значений в любом справочнике по математической статистике. Для того, чтобы найти это значение, используя односторонний тест, положим величину Альфа (величина Альфа используется для обозначения вероятности ошибочного вывода о том, что имеется сильная взаимозависимость) равной 0,05, а для числа степеней свободы (обозначаемых обычно v1 и v2), положим v1 = k = 4 и v2 = n — (k + 1) = 11 — (4 + 1) = 6, где k — это число переменных, а n — число точек данных. Из таблицы справочника F-критическое равно 4,53. Наблюдаемое F-значение равно 459,753674 (это значение получено в опущенном нами примере), что заметно больше чем F-критическое значение 4,53. Следовательно, полученное регрессионное уравнение полезно для предсказания искомого результата.