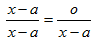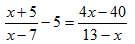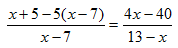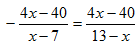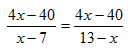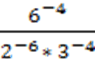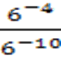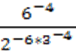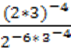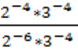Математические софизмы
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Атеев А.С. 1Самарина Е.А. 1
1МБОУ «ООШ № 12» Асбестовского городского округа
Самофалова В.В. 1
1МБОУ «ООШ № 12»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
1. Введение
Математика — один из наших любимых школьных предметов. Он нам нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.
Тема нашей работы «Софизмы в нашей жизни». Мы выбрали эту тему для своего проекта не случайно. Как-то вечером папа задал мне вопрос: «Саша, а ты знаешь, что 6 = 7? Мне стало интересно. Папа с легкостью доказал это равенство.
Вот как это было: 6=7.
Запишем верное равенство: 42 +12 — 54 = 49 +14 – 63.
Вынесем общий множитель за скобки: 6(7 + 2 – 9) = 7(7 + 2 – 9)
Разделим обе части на общий множитель (7 + 2 – 9).
Получим, что 6 = 7 , что и требовалось доказать. Где ошибка? Ведь этого быть не может. Папа сказал, что есть такое понятия, как софизм. Так я определился с темой проекта. Катя сама выбрала тему из списка, который был предложен учителем математики. Для нее понятие софизм тоже было неизвестно, поэтому она решила узнать, что означает это незнакомое и интересное слово.
В процессе работы мы выяснили, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой (например, 34 =7), так и то, что прямой угол равен тупому.
Эта тема сейчас актуальна, потому что софизм — это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад.
Цель: узнать, что такое софизмы и научиться находить ошибку в софизмах.
Задачи:
1. Познакомиться с историей софизмов.
2. Узнать, какие бывают софизмы. Классификация софизмов.
3. Понять, как найти ошибку в софизмах?
4. Разбор софизмов.
5. Составить анкету для обучающихся, познакомить одноклассников с результатами работы.
6. Составить рекомендации для нахождения ошибок в софизмах.
Гипотеза: софизмы — тренировка для ума.
Объект и предмет исследования: софизмы
Методы исследования:
1. Анализ литературы и информации, полученной из Интернет источников
2. Обсуждение темы с учителем, родными и одноклассниками
3. Анкетирование одноклассников
4. Анализ и обобщение полученных данных.
2. Теоретическая часть
Что такое софизмы?
Софизм (от греч. — мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами.
2.2. История возникновения софизмов
Мы изучили историю возникновения софизмов. Софистика – это искусство ведения спора. Она вошла в моду в Греции в V веке до нашей эры. Имея в этом выгоду или просто интерес, многие умные и хитрые люди строго логически доказывали, что черное – это белое, истина – это ложь, добро – это зло и т.д. Так появились софизмы – формально кажущиеся правильными, но по существу ложными умозаключениями. Эти рассуждения могут быть истинны в каждой отдельной части, но неверные в целом.
Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку, ухищрение или головоломку. Речь идет о «доказательстве», направленном на формально – логическое установление абсурдного положения. В основном математические софизмы строятся на неверном словоупотреблении, на неточности формулировок, на скрытом выполнении невозможных действий, на незаконных обобщениях.
Систематический анализ софизмов был дан впервые Аристотелем (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т.е. в мышлении. Каков бы ни был софизм, он обязательно содержит замаскированные ошибки. Часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применения теорем, формул и правил.
Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.
Софист – это:
1. Человек, прибегающий к софизмам для доказательства заведомо неверных мыслей, положений.
2. В древней Греции первоначальный мудрец, знаток, потом платный учитель философии, красноречия, искусства спора, а также — философ, расходившийся с общепринятыми взглядами в вопросах религии и морали и обвинявшийся противниками в пользовании софизмами.
Наиболее серьезную роль сыграли математические софизмы, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элеи. Например, одна из них: «В каждый момент времени летящая стрела неподвижна. Значит, она неподвижна во все моменты времени, и ее движение никогда не сможет начаться».
В истории развития математики софизмы способствовали повышению строгости в рассуждениях и более глубокому пониманию понятий и методов математики.
2.3. Классификация ошибок в софизмах
Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.
Софисты в своих рассуждениях использовали разные ошибки, такие как:
Логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство. Но закон Моисеев потерял свою силу, следовательно, воровство не запрещено», или «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа;
Терминологические ошибки – неправильное употребление слов или построение предложения. Например, «Все углы треугольника равны 180 градусам» в смысле «Сумма углов треугольника равна 180 градусам».
Ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные!
Практическая часть
3.1. Разбор математических софизмов
Рассмотрим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Математические софизмы делятся на 4 вида: арифметические, алгебраические, геометрические, логические. Мы рассмотрим некоторые из них.
Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Дважды два – пять (2 * 2 = 5)
Доказательство:
Пусть исходное соотношение — очевидное равенство:
4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой части (1) равенства, и мы получим:
4*(1:1)=5*(1:1) (2)
Разложим число 4 на произведение 2 *2
(2*2)* (1:1)=5*(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в в частном, множитель можно выносить либо из суммы, либо из разности.
Один рубль не равен ста копейкам
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: необходимо переходить к единым единицам измерения.
Софизм «5 = 6»
Докажем, что 5 =6. С этой целью возьмем числовое равенство 35 + 10- 45 = 42 + 12 — 54. Вынесем общий множитель левой и правой части за скобки. Получим 5(7 + 2 — 9) = 6 (7 + 2 — 9). Разделим обе части этого равенства на общий множитель (7 + 2 — 9). Получаем 5=6. В чем ошибка?
Ошибка: нельзя делить на равенство (7 + 2 — 9), т. к. (7 + 2 — 9)= 0. Ма знаем еще из начальной школы, что на 0 делить нельзя.
Таки образом, можно доказать равенство любых разных двух чисел.
Софизм «Пропавший рубль»
Три подруги зашли в кафе выпить по чашке кофе7 Выпили. Официант принес им счет на 30 рублей. Подруги заплатили по 10 рублей и вышли. Однако хозяин кафе решил сделать скидку посетительницам, сказав что кофе стоит 25 рублей. Официант взял деньги и побежал доганять подруг, но пока он бежал, подумал, что им будет трудно делить 5 рублей, ведь их трое, поэтому решил отдать им по 1 рублю, а 2 рубля оставить себе. Так и сделал.
Что же получилось? Подруги заплатили по 9 рублей. 9 . 3 = 27 рублей, да 2 рубля осталось у официанта. А где же еще 1 рубль?
Ошибка. Задача сформулирована так, чтобы запутать читателя. Подруги заплатили 27 рублей, из этой суммы 25 рублей осталось у хозяина кафе, а 2 рубля у официанта. И никакого пропавшего рубля!
Логические софизмы
Софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Приведем некоторые примеры:
Полный стакан равен пустому
Рассмотрим стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану наполовину пустому.
Увеличивая обе части равенства вдвое, получим, что стакан полный равен
стакану пустому. Где ошибка?
Ясно, что приведенное рассуждение неверно, так как в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации его применение бессмысленно, т.к. пустое увеличить вдвое не возможно.
Софизм учебы
Данным софизмом является песенка, сочиненная английскими студентами:
The more you study, the more you know
The more you know, the more you forget
The more you forget, the less you know
The less you know, the less you forget
The less you forget, the more you know
So why study?
Перевод:
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Это стихотворение можно смело назвать логическим софизмом!
Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
Софизм «Загадочное исчезновение» (Приложение 1). У нас есть произвольный прямоугольник на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?
Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.
Примеры софизмов приведены в Приложении 2.
Работая над проектом, мы составили рекомендации по нахождению ошибок в софизмах (Приложение 3).
3.2. Анкетирование
Мы провели анкетирование среди обучающихся 7 классов на знание софизмов. В анкетировании приняло участие 40 человек. Были заданы следующие вопросы:
1. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы «Два равно трём»?
«Да» – 24 человека, 60 %
2. Знакомо ли вам понятие «софизм»?
«Да» — 10 человек, 25 %
3. Хотелось ли вам познакомиться с софизмами?
«Да» — 36 человек, 90 %.
Анкетирование показало, что немногим ребятам известно понятие «софизм». 90 % обучающихся хотели бы больше узнать о софизмах. Мы выступим перед ребятами с нашим проектом.
Заключение
Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться. К концу работы над проектом ошибки стали находиться быстрее. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свою речь.
Вообще, решение софизмов – интересное и познавательное занятие. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Работая над проектом, мы составили рекомендации по разбору софизмов (Приложение 3). Наш проект будет полезен людям, которые начинают работать с софизмами с целью развития свих интеллектуальных способностей.
Мы считаем, наш проект актуален и имеет практическое применение. Задачи выполнены, цель достигнута.
Решение софизмов тренируют наш мозг, то есть наша гипотеза верна.
Действительно, софизмы являются тренировкой для ума.
Информационные источники
«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.
«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
Т.Н. Михеева. Софизмы
«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.
«Парадоксы науки». Автор: А.К.Сухотин. Издательство «Молодая гвардия», 1978 г.
Приложение 1
«Загадочное исчезновение»
Приложение 2
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Девушка — не человек
Доказательство от противного. Допустим, девушка – человек. Девушка – молодая, значит девушка – молодой человек. Молодой человек – это парень. Противоречие. Значит девушка — не человек.
Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.
Разговор софиста и любителя спорить
Софист: “Может ли мёд быть сладким и несладким одновременно?”
Любитель: “нет”
Софист: “ А мёд сладкий?”
Любитель: “Да”
Софист: “А мёд желтый?”
Любитель: “Да”
Софист: “А жёлтый — значит сладкий?”
Любитель: “Нет”
Софист: “Значит мёд сладкий и несладкий одновременно!”
Не знаешь то, что знаешь
— Знаешь ли ты то, о чём я хочу тебя спросить?
— Нет.
— Знаешь ли ты, что добродетель есть добро?
— Знаю.
— Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.
Примеры геометрических софизмов, которые можно услышать на уроке геометрии:
— Смежные углы равны 180 градусам;
— Накрест лежащие углы равны.
Приложение 3
Рекомендации по нахождению ошибок в софизмах
Внимательно прочитать условие предложенной вам задачи.
Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
Установить темы, которые отражены в софизме. Обучающиеся, учителя привыкли, что задания, предлагаемые в учебнике, не содержат ошибок в условии, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
Воспроизвести вслух точные формулировки утверждений. Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие.
Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности. Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма.
Проверять преобразования. После каждого перехода проверить полученный результат обратным действием. Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».
Просмотров работы: 12722
Математические софизмы
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Атеев А.С. 1Самарина Е.А. 1
1МБОУ «ООШ № 12» Асбестовского городского округа
Самофалова В.В. 1
1МБОУ «ООШ № 12»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
1. Введение
Математика — один из наших любимых школьных предметов. Он нам нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.
Тема нашей работы «Софизмы в нашей жизни». Мы выбрали эту тему для своего проекта не случайно. Как-то вечером папа задал мне вопрос: «Саша, а ты знаешь, что 6 = 7? Мне стало интересно. Папа с легкостью доказал это равенство.
Вот как это было: 6=7.
Запишем верное равенство: 42 +12 — 54 = 49 +14 – 63.
Вынесем общий множитель за скобки: 6(7 + 2 – 9) = 7(7 + 2 – 9)
Разделим обе части на общий множитель (7 + 2 – 9).
Получим, что 6 = 7 , что и требовалось доказать. Где ошибка? Ведь этого быть не может. Папа сказал, что есть такое понятия, как софизм. Так я определился с темой проекта. Катя сама выбрала тему из списка, который был предложен учителем математики. Для нее понятие софизм тоже было неизвестно, поэтому она решила узнать, что означает это незнакомое и интересное слово.
В процессе работы мы выяснили, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой (например, 34 =7), так и то, что прямой угол равен тупому.
Эта тема сейчас актуальна, потому что софизм — это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад.
Цель: узнать, что такое софизмы и научиться находить ошибку в софизмах.
Задачи:
1. Познакомиться с историей софизмов.
2. Узнать, какие бывают софизмы. Классификация софизмов.
3. Понять, как найти ошибку в софизмах?
4. Разбор софизмов.
5. Составить анкету для обучающихся, познакомить одноклассников с результатами работы.
6. Составить рекомендации для нахождения ошибок в софизмах.
Гипотеза: софизмы — тренировка для ума.
Объект и предмет исследования: софизмы
Методы исследования:
1. Анализ литературы и информации, полученной из Интернет источников
2. Обсуждение темы с учителем, родными и одноклассниками
3. Анкетирование одноклассников
4. Анализ и обобщение полученных данных.
2. Теоретическая часть
Что такое софизмы?
Софизм (от греч. — мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами.
2.2. История возникновения софизмов
Мы изучили историю возникновения софизмов. Софистика – это искусство ведения спора. Она вошла в моду в Греции в V веке до нашей эры. Имея в этом выгоду или просто интерес, многие умные и хитрые люди строго логически доказывали, что черное – это белое, истина – это ложь, добро – это зло и т.д. Так появились софизмы – формально кажущиеся правильными, но по существу ложными умозаключениями. Эти рассуждения могут быть истинны в каждой отдельной части, но неверные в целом.
Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку, ухищрение или головоломку. Речь идет о «доказательстве», направленном на формально – логическое установление абсурдного положения. В основном математические софизмы строятся на неверном словоупотреблении, на неточности формулировок, на скрытом выполнении невозможных действий, на незаконных обобщениях.
Систематический анализ софизмов был дан впервые Аристотелем (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т.е. в мышлении. Каков бы ни был софизм, он обязательно содержит замаскированные ошибки. Часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применения теорем, формул и правил.
Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.
Софист – это:
1. Человек, прибегающий к софизмам для доказательства заведомо неверных мыслей, положений.
2. В древней Греции первоначальный мудрец, знаток, потом платный учитель философии, красноречия, искусства спора, а также — философ, расходившийся с общепринятыми взглядами в вопросах религии и морали и обвинявшийся противниками в пользовании софизмами.
Наиболее серьезную роль сыграли математические софизмы, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элеи. Например, одна из них: «В каждый момент времени летящая стрела неподвижна. Значит, она неподвижна во все моменты времени, и ее движение никогда не сможет начаться».
В истории развития математики софизмы способствовали повышению строгости в рассуждениях и более глубокому пониманию понятий и методов математики.
2.3. Классификация ошибок в софизмах
Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.
Софисты в своих рассуждениях использовали разные ошибки, такие как:
Логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство. Но закон Моисеев потерял свою силу, следовательно, воровство не запрещено», или «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа;
Терминологические ошибки – неправильное употребление слов или построение предложения. Например, «Все углы треугольника равны 180 градусам» в смысле «Сумма углов треугольника равна 180 градусам».
Ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные!
Практическая часть
3.1. Разбор математических софизмов
Рассмотрим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Математические софизмы делятся на 4 вида: арифметические, алгебраические, геометрические, логические. Мы рассмотрим некоторые из них.
Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Дважды два – пять (2 * 2 = 5)
Доказательство:
Пусть исходное соотношение — очевидное равенство:
4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой части (1) равенства, и мы получим:
4*(1:1)=5*(1:1) (2)
Разложим число 4 на произведение 2 *2
(2*2)* (1:1)=5*(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в в частном, множитель можно выносить либо из суммы, либо из разности.
Один рубль не равен ста копейкам
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: необходимо переходить к единым единицам измерения.
Софизм «5 = 6»
Докажем, что 5 =6. С этой целью возьмем числовое равенство 35 + 10- 45 = 42 + 12 — 54. Вынесем общий множитель левой и правой части за скобки. Получим 5(7 + 2 — 9) = 6 (7 + 2 — 9). Разделим обе части этого равенства на общий множитель (7 + 2 — 9). Получаем 5=6. В чем ошибка?
Ошибка: нельзя делить на равенство (7 + 2 — 9), т. к. (7 + 2 — 9)= 0. Ма знаем еще из начальной школы, что на 0 делить нельзя.
Таки образом, можно доказать равенство любых разных двух чисел.
Софизм «Пропавший рубль»
Три подруги зашли в кафе выпить по чашке кофе7 Выпили. Официант принес им счет на 30 рублей. Подруги заплатили по 10 рублей и вышли. Однако хозяин кафе решил сделать скидку посетительницам, сказав что кофе стоит 25 рублей. Официант взял деньги и побежал доганять подруг, но пока он бежал, подумал, что им будет трудно делить 5 рублей, ведь их трое, поэтому решил отдать им по 1 рублю, а 2 рубля оставить себе. Так и сделал.
Что же получилось? Подруги заплатили по 9 рублей. 9 . 3 = 27 рублей, да 2 рубля осталось у официанта. А где же еще 1 рубль?
Ошибка. Задача сформулирована так, чтобы запутать читателя. Подруги заплатили 27 рублей, из этой суммы 25 рублей осталось у хозяина кафе, а 2 рубля у официанта. И никакого пропавшего рубля!
Логические софизмы
Софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Приведем некоторые примеры:
Полный стакан равен пустому
Рассмотрим стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану наполовину пустому.
Увеличивая обе части равенства вдвое, получим, что стакан полный равен
стакану пустому. Где ошибка?
Ясно, что приведенное рассуждение неверно, так как в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации его применение бессмысленно, т.к. пустое увеличить вдвое не возможно.
Софизм учебы
Данным софизмом является песенка, сочиненная английскими студентами:
The more you study, the more you know
The more you know, the more you forget
The more you forget, the less you know
The less you know, the less you forget
The less you forget, the more you know
So why study?
Перевод:
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Это стихотворение можно смело назвать логическим софизмом!
Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
Софизм «Загадочное исчезновение» (Приложение 1). У нас есть произвольный прямоугольник на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?
Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.
Примеры софизмов приведены в Приложении 2.
Работая над проектом, мы составили рекомендации по нахождению ошибок в софизмах (Приложение 3).
3.2. Анкетирование
Мы провели анкетирование среди обучающихся 7 классов на знание софизмов. В анкетировании приняло участие 40 человек. Были заданы следующие вопросы:
1. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы «Два равно трём»?
«Да» – 24 человека, 60 %
2. Знакомо ли вам понятие «софизм»?
«Да» — 10 человек, 25 %
3. Хотелось ли вам познакомиться с софизмами?
«Да» — 36 человек, 90 %.
Анкетирование показало, что немногим ребятам известно понятие «софизм». 90 % обучающихся хотели бы больше узнать о софизмах. Мы выступим перед ребятами с нашим проектом.
Заключение
Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться. К концу работы над проектом ошибки стали находиться быстрее. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свою речь.
Вообще, решение софизмов – интересное и познавательное занятие. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Работая над проектом, мы составили рекомендации по разбору софизмов (Приложение 3). Наш проект будет полезен людям, которые начинают работать с софизмами с целью развития свих интеллектуальных способностей.
Мы считаем, наш проект актуален и имеет практическое применение. Задачи выполнены, цель достигнута.
Решение софизмов тренируют наш мозг, то есть наша гипотеза верна.
Действительно, софизмы являются тренировкой для ума.
Информационные источники
«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.
«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
Т.Н. Михеева. Софизмы
«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.
«Парадоксы науки». Автор: А.К.Сухотин. Издательство «Молодая гвардия», 1978 г.
Приложение 1
«Загадочное исчезновение»
Приложение 2
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Девушка — не человек
Доказательство от противного. Допустим, девушка – человек. Девушка – молодая, значит девушка – молодой человек. Молодой человек – это парень. Противоречие. Значит девушка — не человек.
Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.
Разговор софиста и любителя спорить
Софист: “Может ли мёд быть сладким и несладким одновременно?”
Любитель: “нет”
Софист: “ А мёд сладкий?”
Любитель: “Да”
Софист: “А мёд желтый?”
Любитель: “Да”
Софист: “А жёлтый — значит сладкий?”
Любитель: “Нет”
Софист: “Значит мёд сладкий и несладкий одновременно!”
Не знаешь то, что знаешь
— Знаешь ли ты то, о чём я хочу тебя спросить?
— Нет.
— Знаешь ли ты, что добродетель есть добро?
— Знаю.
— Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.
Примеры геометрических софизмов, которые можно услышать на уроке геометрии:
— Смежные углы равны 180 градусам;
— Накрест лежащие углы равны.
Приложение 3
Рекомендации по нахождению ошибок в софизмах
Внимательно прочитать условие предложенной вам задачи.
Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
Установить темы, которые отражены в софизме. Обучающиеся, учителя привыкли, что задания, предлагаемые в учебнике, не содержат ошибок в условии, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
Воспроизвести вслух точные формулировки утверждений. Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие.
Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности. Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма.
Проверять преобразования. После каждого перехода проверить полученный результат обратным действием. Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».
Просмотров работы: 10450
Ошибки, «прячущиеся» в софизмах
Убедительность
на первый взгляд многих софизмов, их
«логичность» связана с хорошо
замаскированной ошибкой. Софизмы
обязательно содержат одну или несколько
логических ошибок.
При
разборе софизмов выделяются основные
ошибки:
-
Деление
на 0; -
Неправильные
выводы из равенства дробей; -
Неправильное
извлечение квадратного корня из квадрата
выражения; -
Нарушения
правил действия с величинами; -
Проведение
преобразований над математическими
объектами, не имеющими смысла; -
Неравносильный
переход от одного неравенства к другому; -
Выводы и вычисления
по неверно построенным чертежам;
Софизмы в Древней Греции.
«Людям,
которые желают идти верной дорогой,
важно также знать и об отклонениях».
Аристотель
Софистов
в Древней Греции называли мудрецами,
но это были мудрецы особого рода. Их
истина не интересовала. Они были, как
правило, платными “учителями мудрости”.
Их нанимали политики для того, чтобы, в
частности, переспорить оппонентов на
собрании, а также для того, чтобы выиграть
судебное дело. Софисты славились своим
умением представить черное белым, белое
черным. Они могли сегодня упорно
доказывать какой-либо тезис, а уже завтра
с таким же рвением антитезис.
Будучи
в большинстве случаев глубоко образованными
людьми, они не столько передавали
ученикам знания из различных областей
науки, сколько стремились научить их
владеть искусством словесных состязаний.
Чтобы выйти победителем в словесном
поединке, софисты часто пользовались
тем, что противник недостаточно глубоко
знает предмет, о котором идет речь,
недостаточно внимателен и наблюдателен,
и поэтому не в состоянии отличить ложь
от истины. В результате словесного
поединка противник должен был согласиться
с доводами софиста и признать себя
побежденным, хотя истина, казалось, была
на его стороне.
Но
суть деятельности софистов много больше,
чем простое обучение искусству
красноречия. Они обучали и просвещали
древнегреческий народ, старались
способствовать достижению нравственности,
присутствия духа, способности ума
ориентироваться во всяком деле. Но
софисты не были учеными. Умение, которое
должно было быть достигнуто с их помощью,
заключалось в том, что человек учился
иметь в виду многообразные точки зрения.
-
Вот
один из древних софизмов («рогатый»): «Что
ты не терял, то имеешь. Рога ты не терял.
Значит, у тебя рога».
Так все ли утверждения математики верны?
Вот
один из наиболее известных софизмов:
«Дважды два — пять!»
Рассмотрим
верное равенство:
16 — 36 = 25 — 45
Прибавим
к левой и правой части 81/4:
16 — 36 + 81/4 = 25
— 45 + 81/4
Преобразуем
выражение:
4*4 — 2*4*9/2 + (9/2)*(9/2) = 5*5 — 2*5*9/2 +
(9/2)*(9/2)
Теперь
можно заметить, что в левой и правой
части выражения записаны произведения
вида:
a²-2ab+b², то есть, квадрат разности:
(a-b) ². В нашем случае слева a=4, b=9/2, а справа
a=5, b=9/2.
Поэтому
перепишем выражение в виде квадратов
разности:
(4 — 9/2) ² = (5 — 9/2) ²
А
следовательно,
4 — 9/2 = 5 — 9/2
И
наконец, получаем долгожданное равенство:
4
= 5 или, 2*2 = 5
Где
ошибка?
Разбор
софизма:
Если
равны квадраты чисел,то не факт что
равны сами числа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Как найти ошибку в софизме? Примеры софизмов Подготовил Бакушкин Иван Как найти ошибку в софизме? Зачастую найти ошибку в софизме очень сложно. К тому же не существовал алгоритм нахождения ошибки в софизме. Но я, проанализировав софизмы, составил алгоритм, который может помочь в нахождении ошибки во многих софизмах.
(Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат, получается, из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки) (Ученики, учителя привыкли, что задания, предполагаемые в учебнике, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения) (Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие) (Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма) (Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам») (Работать блоками. Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока. Удобнее проследить за одним блоком, чем за целым преобразованием) Примеры софизмов
Сто сорок да сто сорок будет двести сорок. TranslateПеревод a. Женщина=Время*Деньги a. Время=Деньги a. Женщина=Деньги*Деньги b. Женщина=Деньги в квадрате c. Деньги- это и есть все ваши проблемы: d. Деньги=Корень из проблем i. Из этого следует: ii. Женщина=Корень из проблем в квадрате Вывод: Женщина=ПРОБЛЕМЫ Земля, Марс ит. д. — круглые. Значит, все планеты круглые. Апельсин тоже круглый, значит апельсин – планета. Движущийся предмет должен дойти до половины своего пути прежде, чем он достигнет его конца. Затем он должен пройти половину оставшейся половины, затем половину этой четвертой части и т.д. до бесконечности. Предмет будет постоянно приближаться к конечной точке, но так никогда ее не достигнет. Можно доказать, что учителя и ученики целый год ничего не делают. Для простоты будем считать, что в году 360 дней, из них 52 воскресных дня. Если не считать других выходных дней, останется 308 учебных дней. Ночью школа не работает, следовательно, половина количества суток пропадает, остается 154 учебных дня. В большинстве школ занятия продолжаются только до полудня, вследствие чего учебное время уменьшается вдвое. Получаем 77 учебных дней. Будем считать, что на каникулы выпадает только 60 дней, тогда для занятий останется всего 17 дней в году. Чем больше учишься, тем больше знаешь. Чем больше знаешь, тем больше забываешь. Чем больше забываешь, тем меньше знаешь. Чем меньше знаешь, тем меньше забываешь. Но чем меньше забываешь, тем больше знаешь. Так для чего учиться? Возьмем уравнение х-а = 0 Разделив обе его части на х-а, получим Откуда сразу же получаем требуемое равенство 1=0 Ошибка заключается в том, что на 0 делить нельзя (1). Рассмотрим уравнение Оно может быть решено следующим образом. Приведя левую часть уравнения к общему знаменателю, будем иметь Откуда следует или Поскольку числители дробей в левой и правой частях уравнения равны, то для того чтобы имело место равенство обеих частей уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким образом, приходим к равенству 7=13 Ошибка состоит в том, что область допустимых значений исходного уравнения (1) состоит из всех значений переменой х кроме х=7, х=13. В этом софизме неявно подразумевается, что равенство(2) является не уравнением, а тождеством равным при любых значениях х, что неверно. Поэтому утверждение софизма не имеет места. Возьмем верное равенство: 1 р. = 100 к., Возведем его по частям в квадрат, получим: 1 р. = 10000 к. Таким образом, один рубль не равен ста копейкам. (Ошибка: умножение величины на себя не имеет смысла, в квадрат возводятся только числа). Найти ошибку в рассуждении: Имеем верное числовое равенство: 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5 или . (Ошибка: ошибка допущена в левой и правой частях тождества 4:4=5:5 при вынесении общего множителя за скобки.) |
ГБОУ РХ СПО Хакасский политехнический колледж
Реферат
по теме:
Софизмы и парадоксы
в математике
Работу выполнила:
Шишигина Ирина,
студентки 2 курса гр. ЭП-21
Преподаватель:
Овчарук Любовь Павловна
Абакан 2015
Содержание
1. Введение……………………………………………………………………….3
2. Цели и задачи…………….…………………………..…….…………….….4
3. Понятие софизма…………..………………………..……..………….………4
4. Экскурс в историю…………………………………………………….….…5
5. Математические софизмы ……………………………………………….…6
- Алгебраические софизмы………..………………………………..……6
- «Один рубль не равен ста копейкам» …………………….………..…7
- « Если “a” больше “b”, то “a” всегда больше, чем “2b”»………….…8
- Геометрические софизмы ……………………………………………..8
- «Через точку на прямую можно опустить два перпендикуляра» ….8
- Арифметические софизмы……………………………………..………8
- «Дважды два равно пять» …………………………………………… 9
- Логические софизмы ……………………………………………….…. 9
- Многообразие парадоксов и их причины ………………..…………… .10
6.1 Парадокс Банаха – Тарского ……………………………………… 10
6.2 Задача о треугольнике ………………………………………….…. 10
6.3 Парадокс бесконечно малых величин ……………………………. 11
6.4 Парадокс изобретателя ……………………………..……………… 11
7. Заключение ………………………………………………………………..13
8. Литература…………………………………………………………….……13
ВВЕДЕНИЕ
Наверняка каждый человек хоть раз в жизни слышал подобную фразу: «Дважды два равно пяти» На самом деле, таких примеров можно привести много, но что все они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь шутка???
Именно эти вопросы мы хотим рассмотреть в нашей работе Математические софизмы
«Предмет математики настолько серьезен,
что полезно не упускать случая
сделать его немного занимательным»
Б. Паскаль
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Софизм — это то же надувательство, только выполненное намного изящнее и незаметнее, за что мы его и любим. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в софизмах выполняют «запрещенные» действия или не учитываются условия применимости теорем, формул и правил.
Софизмы имеют четкое логическое объяснение. Кроме того, с математическими софизмами мы встречаемся намного чаще, чем с обычными.
Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики и, кроме того, показывает, что математика – это живая наука. Надеемся, что наш проект будет интересен и принесёт пользу ребятам.
Актуальность выбранной темы заключается в том, что:
- Наше общество развивается большими темпами.
- Для развития производства требуются техники, инженеры, ученые, знания которых базируются на точных науках: математике, физике, химии.
- И эти науки надо не только знать, но и понимать.
Мы считаем, что софизмы развивают логику мышления, помогают лучше усвоить и разобраться в математике, прививают навыки правильного мышления.
Поэтому мы выбрали эту тему.
Основная гипотеза проекта
Если неточно знать формулировки теорем, математические формулы, правила и условия, при которых они выполняются, а также не анализировать построение чертежа к геометрической задаче, то можно получить абсурдные результаты, противоречащие общепринятым представлениям.
Цель нашей работы:
Познакомиться с софизмами, показать значимость математических софизмов
при изучении математики, показать как получаются абсурдные выводы. Важно четко понимать допущенные ошибки, иначе софизмы будут бесполезны.
Задачи:
- дать определение понятиям «софизм» и «парадокс», узнать в чём их отличие;
- классифицировать различные виды софизмов;
- понять, как найти ошибку в софизмах;
- составить компьютерную презентацию.
Методы исследования:
- Анкетирование;
- Анализ и контроль полученных результатов, классификация софизмов;
- Демонстрация полученных результатов в презентации;
- Выступление на конференции.
«Понятие софизма. Исторические сведения»
Понятие софизма
Софизм — (от греческого sophisma – уловка, ухищрение, выдумка, головоломка),
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного.
Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Разбор софизмов, прежде всего, развивает логическое мышление.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, и довольно тонкие ошибки.
Понимание ошибок в софизме помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
Мы проанализировали софизмы и выделили типичные ошибки в софизмах. Это:
- запрещенные действия,
- неточное использование условий теорем, формул и правил,
- ошибочный чертеж,
- опора на ошибочные умозаключения.
Нередко, ошибки, которые допускают в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах.
Основные создатели софизмов – древнегреческие ученые-философы, но, тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах.
Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.
Работая над проектом, мы обнаружили интересную формулу успешности софиста!*
Успешность софизма определяется несколькими составляющими:
a + b + c + d + e + f и определяется величиной этой суммы, где (a + с + е) составляет показатель силы диалектика, (b + d + f) есть показатель слабости его жертвы.
- а — отрицательные качества лица (нет развития способности управлять вниманием).
- b — положительные качества лица (способность активно мыслить)
- с — аффективный элемент в душе искусного диалектика
- d — качества, которые пробуждаются в душе жертвы софиста и омрачают в ней ясность мышления
- е — категоричность тона, не допускающего возражения, определённая мимика
- f — пассивность слушателя.
Экскурс в историю
Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества(5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространение мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия.
Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения.
* эту формулу нашли в Интернете на сайте http://pptonline.ru/slide/related/page/13/count/100/id/101563/category/1/cpages/10
Исторически сложилось, что с понятием софизма связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста- представить наихудший аргумент как наилучший путем хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. В Греции софистами называли и простых ораторов.
Известнейший ученый и философ Сократ поначалу был софистом, активно участвовал в спорах и обсуждениях софистов, но вскоре стал критиковать их учение. Такому же примеру последовали и его ученики (Ксенофонт и Платон).
Философия Сократа была основана на том, что мудрость приобретается с общением, в процессе беседы. Учение Сократа было устным, его и по сей день считают самым мудрым философом.
Что касается самих софизмов, то, пожалуй, самым популярным на тот момент в Древней Греции был софизм Евбулида : «Что ты не терял, ты имеешь. Рога ты не терял. Значит у тебя рога». Единственная неточность, которую возможно было допустить, то это — двусмысленность высказывания. Данная постановка фразы является нелогичной, но логика возникла намного позже, благодаря Аристотелю, поэтому, если бы фраза строилась так: «Все, что ты не терял. . .», то вывод стал бы логически безупречным.
Математические софизмы
Разбор и решение нестандартных математических задач помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам.
Однако следует помнить, что в математике важна аккуратность. Каждый шаг от одной логической конструкции к другой должен быть точным, тщательно выверенным. Один неверный переход может привести не просто к неточности, а к большой ошибке.
Мы предлагаем Вам вместе с нами попытаться разобраться с этим.
В нашей работе мы рассмотрим три типа математических софизмов: алгебраические, геометрические и арифметические.
- Алгебраические софизмы
Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
- «Один рубль не равен ста копейкам»
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е.
Если a=b,
c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
перемножая эти равенства почленно, получим
10 р.=100000 коп. (3)
и, наконец, разделив последнее равенство на 10 получим, что
1 р.=10 000 коп.
таким образом, один рубль не равен ста копейкам.
Где ошибка???
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство
10 р. =100 000 к . ,
которое после деления на 10 дает
1 р. = 10 000 коп.,
а не равенство 1р=10 000 к, как это записано в условии софизма.
Извлекая квадратный корень из равенства1 р. = 10 000 коп. получаем верное равенство 1р.=100 коп.
2) « Если “a” больше “b”, то “a” всегда больше, чем “2b”»
Возьмем два произвольных положительных числа a и b, такие, что a > b. Умножив это неравенство на b, получим новое неравенство ab > b·b, а отняв от обеих его частей a·a, получим неравенство ab-a·a > b·b — a·a, которое равносильно следующему:
a(b-a) > (b+a)(b-a). (1)
После деления обеих частей неравенства (1) на b-a получим, что
a > b+a (2),
А прибавив к этому неравенству почленно исходное неравенство a> b, имеем 2a >2b+a, откуда a > 2b. Итак, если a > b, то a > 2b.
Где ошибка?
Ошибка совершена при переходе от равенства (1) к (2). Т.к. a > b, то b — a<0, следовательно, при делении неравенства (1) на b – a, мы должны поменять знак неравенства на противоположный.
- Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
- «Через точку на прямую можно опустить два перпендикуляра»
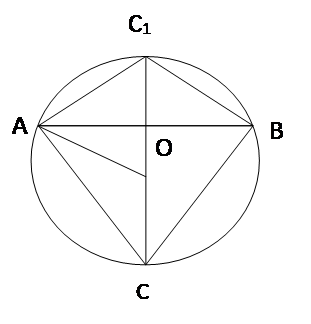
Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС.
На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках
Е и Д. Соединим точки Е и Д прямыми с точкой В.
Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ перпендикулярна АС и ВД перпендикулярна АС.
Через точку В проходят два перпендикуляра к прямой АС.
Где ошибка?
Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит из одной точки на прямой нельзя опустить два перпендикуляра.
- Арифметические софизмы.
Арифметика — (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
- «Дважды два — пять!»
Возьмем в качестве исходного соотношения следующее очевидное равенство: 4:4= 5:5
После вынесения за скобки общего множителя из каждой части равенства
будем иметь:
4∙(1:1)=5∙(1:1)
или
(2∙2)(1:1)=5(1:1)
Наконец, зная, что 1:1=1, мы из предыдущего получаем:
2∙2=5
Где ошибка?
Нельзя выносить множитель за скобки так, как было сделано. 4∙(1:1)=5∙(1:1)
Можно так 4 (1:4) и 5 (1:5).
Логические софизмы
Кроме математических софизмов, существует множество других. Понять абсурдность таких утверждений проще, но от этого они не становятся менее интересными. Очень многие софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными.
Полупустое и полуполное
«Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное».
Не знаешь то, что знаешь
«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Многообразие парадоксов и их причины
Парадоксы – это неожиданные утверждения, противоречащие здравому смыслу или общепризнанным научным теориям. Очень часто их рассматривают как ошибки, хотя в большинстве случаев они таковыми не являются. Обычно парадоксы построены на логически верных заключениях, но их противоречивый результат не является преднамеренным (этим они отличаются от софизмов). Парадоксы известны науке уже более двух тысяч лет. В античные времена были описаны многие парадоксы и для некоторых из них ученые до сих пор не могут найти объяснения и решения. Открываются парадоксы и в наши дни. Обычно подобные открытия сопровождаются кризисами в науке, разрушением старых, проверенных временем теорий и попытками создать новые, которые способны объяснить появившиеся противоречия. Парадоксы присутствуют везде – и в повседневной жизни, и в науке. Практически в каждой научной области исследования существуют свои парадоксы.
Парадоксы обнажают глубинные течения познавательного процесса. Возвещая о назревшем неблагополучии в науке, они вместе с этим решительно продвигают ее вперед и именно тем, что приносят новые, еще более парадоксальные идеи.
Парадоксы математические
Существуют парадоксы в математике. И вот, действительно, самое парадоксальное — это то, что в математике вообще есть парадоксы.
1. Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям. Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике)
2. Задача о треугольнике.
Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.
Разгадка простая: первый треугольник немного «вогнут», а второй — слегка выпуклый. В этом можно убедиться, сравнив наклон гипотенузы синего и жёлтого кусочков: у жёлтого наклон = 0.375, а у синего — 0.4. Получается, что общие площади верхнего и нижнего треугольников всё-таки различаются, а разница как раз составляет одну клетку!
3. Парадокс бесконечно малых величин
Математический кризис в этой области существовал в период XVII — XVIII веков.
Бесконечно малые — это переменные величины, стремящиеся к нулю, или, если быть точнее, к пределу, равному нулю. Проблема состояла в их туманном понимании: то они рассматриваются как числа равные нулю, то как ему неравные. Причем, при таком подходе, люди рассматривали их как постоянные величины. Тогда из этого названия таких величин следует, что бесконечное является чем-то завершенным.
Кризис перестал быть таковым после создания теории пределов в начале XIX века французским математиком Огюстеном Луи Коши (1789 — 1857). С того момента бесконечно малые величины рассматриваются как постоянно изменяющиеся, а не постоянные, стремящиеся к пределу, но никогда его не достигающие. Постоянно изменяющиеся числа!
4. Парадокс изобретателя
Ситуация, когда доказать более сильное утверждение легче, чем более слабое, и называется парадоксом изобретателя. Он был известен еще и древним мыслителям, но придумал это название в начале XX века венгерский математик Д. Пойа, сказав о парадоксе следующие слова: «Легче доказать более сильную теорему, чем более слабую». Этот парадокс существует не только в математике, но и в других областях, в том числе и в жизненных ситуациях. Такое же название (и по праву) получили ситуации, когда решить более общую задачу легче, чем более узкую. Прием, позволяющий это сделать, заключается в том, чтобы свести задачу к более общей, относительно которой исходная задача будет являться лишь частным случаем. Приведу один пример:
В III веке до н. э. тиран города Сиракузы Гиерон поручил своему подданному и близкому родственнику Архимеду определить, не подмешано ли к его золотой короне, изготовленной ювелирами, менее благородное серебро. Эту частную задачу Архимед смог решить лишь как общую (т.к. о химическом анализе тогда еще и не помышляли; к тому же корону разрушать было нельзя), выявив закон «подъемной силы», то есть силы Архимеда, действующей на погруженное в жидкость тело.
Таким же образом появились на свет в математике интегральное (выросшее из изобретенного древнегреческим математиком Евдоксом Книдским (около 408 — около 355 до н. э.) метода «исчерпывания») и дифференциальное (когда Лейбниц Готфрид Вильгельм (1646 — 1716) долго бился на задачей проведения касательной к кривой в заданной точке, сведя ее к проведению секущей через две бесконечно близкие точки) исчисления, в науке изобретена пастеризация и многое-многое другое.
Заключение.
О математических софизмах и парадоксах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые софизмы и парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день.
Математические софизмы – это лишь часть одного большого течения. Поиск заключенных в софизме ошибок, ясное понимание их причин ведет к осмысленному изучению математики. Обнаружение и анализ ошибки, заключенной в софизме, очень часто оказывается более поучительным, чем просто разбор решений «безошибочных» задач. Эффектная демонстрация «доказательства» явно неверного результата, демонстрация того, к какой нелепице приводит пренебрежение каким-либо математическим правилом, и последующий поиск и разбор ошибки, позволяют понять и «закрепить» математическое правило или утверждение.
Некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли нам разобраться, откуда же все-таки началась история софизмов.
Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научится искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Прослеживая историю математики, можно сказать, что во все времена математику спасала какая-нибудь новая идея. Она придавала математике строгость, восстанавливая ее авторитет. Поэтому не стоит бояться парадоксов, ибо они являются двигателями науки.
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Помимо основных целей, поставленных в начале работы, мы преследовали еще одну: прикосновение к тому, с чем сталкивались наши далекие предки, к теме, которая имеет исторические корни. Нами были рассмотрены примеры наиболее известных софизмов и парадоксов.
В процессе работы над проектом мы столкнулись с софизмами, в которых не смогли разобраться из-за недостаточного багажа знаний по математике. Мы будем пополнять знания на уроках математики, и вернемся к этим вопросам. Поэтому тема нашей работы далеко не исчерпана. Мы рассмотрели лишь некоторые, самые известные примеры софизмов. На самом деле их намного больше. Мы продолжим изучение этой темы в будущем.
А закончить я бы хотела словами А. Д. Александрова «Математика учит точности мысли, подчинению логике доказательства, понятию строго обоснованной истины, а всё это формирует личность, пожалуй, больше, чем музыка».
Список литературы
1. А. Г. Мадера, Д. А. Мадера «Математические софизмы», Москва, «Просвещение», 2003г.
2. Брадис В. М., Минковский В. Л., Харчева Л. К. «Ошибки в математических рассуждениях».
3. Перельман Я. И. «Занимательная математика».
4. Новосёлов М. М. «Абстракция множества парадокс Рассела». «Вопросы философии. 2003г. №7.
5. Аменицкий Н. «Математические развлечения и любопытные приёмы мышления. М.,1912г.
6. Горячев Д. Н., Воронец А. Н. «Задачи, вопросы и софизмы для любителей математике», М., 1966.
7. Лямин А. А. «Математические парадоксы и интересные задачи», М., (1911г.) 2010 г.
8.http://www.peterlife.ru/download%20free%20online/humanities/fl _5_a5.htm
9. http://www.tmn.fio.ru/works/60x/306/06_2.htm
10.http://www.golovolomka.hobby.re/books/gardner/gotcha/ch2/02.html
Софизмы в математике
Секция: Математические науки.
Автор: Шеметова Анастасия, Глазунова Екатерина, 8 класс
МБОУ «СОШ №18».
Научный руководитель: Лукьянова Ольга Георгиевна, учитель
математики МБОУ «СОШ №18».
Г. Миасс
Челябинская
область
Оглавление
Введение
I.
Софизм и история его возникновения
1.1. Софизм и софистика
1.2. Экскурс в историю
II.
Математические софизмы и их классификация
2.1. Софизмы и типичные ошибки в
них
2.2. Математические софизмы
2.3. Разбор математических
софизмов
2.4. Логические софизмы
2.5. Источники софизмов
III. «Софизмы из наших школьных тетрадей»
Заключение
Список литературы
Приложение 1.
Приложение 2. Арифметические софизмы
Приложение 3. Алгебраические софизмы
Приложение 4. Геометрические софизмы
В
математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.
И. Ньютон
Введение
У ученых есть такое свойство — поставят в
тупик все человечество, а потом целое поколение или даже несколько поколений с
трудом из него выбираются, проявляя чудеса изобретательности и изворотливости.
И одним из средств не только учёных, но и любознательных остроумных людей,
любящих ставить окружающих в тупик, является «софизм». Нас заинтересовал факт
глубокой древности зарождения софизмов и популярности их у ученых.
Актуальность: Наверное,
каждый человек хоть раз в жизни слышал фразу: «Дважды два равно пяти» или «Два
равно трем». Что они обозначают? Кто их выдумал? Имеют ли они какое-нибудь
логическое объяснение или же это лишь вымысел? Чтобы ответить на эти и подобные
им вопросы, мы в своей работе рассматриваем математические софизмы. Математический софизм – удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
Поэтому нам представляется актуальным изучение ошибок в софизмах, потому что их
понимание ведёт к пониманию математике в целом, помогает развивать логику и
навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее
осознал, а осознание ошибки предупреждает от ее повторения в дальнейших
математических рассуждениях.
Цель: изучение типичных ошибок, которые возникают у учащихся
в процессе изучения математики, их причин и способов предупреждения на примере
математических софизмов.
Задачи:
1.
изучить понятие софизма и историю его возникновения;
2.
рассмотреть виды софизмов и дать классификацию их ошибок;
3.
составить сборник разбора задач на софизмы по различным разделам
математики для 6 — 9 классов.
Гипотеза исследования: если в процессе обучения математике целенаправленно
и систематически организовывать работу учащихся над типичными ошибками, на
примере софизмов, то это будет способствовать повышению качества математической
подготовки учащихся.
I. Софизм и история его возникновения
1.1. Софизм и софистика
Софизм в
переводе с греческого означает дословно: уловка, выдумка или мастерство. Этим
термином называют утверждение, являющееся ложным, но не лишенным элемента
логики, за счет чего при поверхностном взгляде на него кажется верным.
Софизмы основаны на сознательном и преднамеренном обмане, нарушении логики.
Софизм — преднамеренная ошибка, совершаемая с целью запутать
противника и выдать ложное суждение за истинное.
Софистика –
направление философии, которое возникло в V — IV вв. до н.э. в Греции и
стало очень популярным в Афинах.
1.2. Экскурс в историю
Во
второй половине V века до н.э. в Греции появились софисты. Софистами называли
группу древнегреческих философов достигших большого искусства в логике. Они
появились во время становления демократии в Афинах и на подвластных Афинам
территориях. Софисты — это мудрецы, но мудрецы особого рода. Этих мудрецов
истина не интересовала. Они были, как правило, платными «учителями мудрости».
Их нанимали политики для того, чтобы организовать свою предвыборную компанию, в
частности, переспорить оппонентов на собрании, а также для того, чтобы выиграть
судебное дело. В Греции софистами называли и простых ораторов —
философов-учителей, задачей которых было научить своих учеников «мыслить,
говорить и делать». Одним из представителей
софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а
это и есть гражданское искусство» (приложение 1, рис. 1).
Чтобы выйти победителем в словесном
поединке, софисты часто пользовались тем, что противник недостаточно глубоко
знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен, и
поэтому не в состоянии отличить ложь от истины. В результате словесного
поединка противник должен был согласиться с доводами софиста и признать себя
побежденным, хотя истина, казалось, была на его стороне. Софизмы существуют и
обсуждаются более двух тысячелетий, причем острота их обсуждения не снижается с
годами. Если софизмы — всего лишь хитрости и словесные уловки, выведенные на
чистую воду еще Аристотелем, то долгая их история и устойчивый интерес к ним
непонятны. Однако софизмы существовали задолго до философов-софистов, а
наиболее известные и интересные были сформулированы позднее в сложившихся под
влиянием Сократа философских школах.(Приложение 1,рис.2)
Термин «софизм» впервые ввел Аристотель
(приложение 1, рис.3), охарактеризовавший софистику как мнимую, а не
действительную мудрость. К софизмам им были отнесены и «апории Зенона» (внешне парадоксальные рассуждения
на тему о движении и множестве), направленные
против движения и множественности вещей, и рассуждения собственно софистов, и
все те софизмы, которые открывались в других философских школах. Это говорит о
том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то
обычным для многих школ античной философии. Аристотель называл софизмом «мнимые
доказательства», в которых обоснованность заключения кажущаяся и обязана чисто
субъективному впечатлению, вызванному недостаточностью логического анализа.
Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана
с хорошо замаскированной ошибкой, с использованием, например, «неразрешённых»
или даже «запрещённых» правил или действий.
Современный софизм, основной задачей
которого является манипуляция общественным сознанием, существует в
многочисленных формах. Современные софисты, прежде всего, — специалисты по
пиару. Работа, которых заключается в навязывании обществу тех или иных
политических деятелей.
В обычном и распространенном понимании
софизм — это умышленный обман, основанный на нарушении правил. Но обман тонкий
и завуалированный. Цель софизма – выдать ложь за истину.
В нашей работе мы рассматриваем
математические софизмы.
II. Математические софизмы и их классификация
2.1. Софизмы и типичные ошибки в
них
Математический софизм — удивительное утверждение, в
доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
История математики полна неожиданных и
интересных софизмов, разрешение которых порой служило толчком к новым
открытиям. Математические софизмы приучают внимательно и настороженно
продвигаться вперед, тщательно следить за точностью формулировок, правильностью
записи чертежей, за законностью математических операций. Поиск и нахождение
ошибок в софизме способствует пониманию математики в целом и развивает
логическое мышление.
К типичным ошибкам
в софизмах относятся:
· запрещенные
действия;
· пренебрежение условиями
теорем, формул и правил;
· ошибочный чертеж;
· опора на ошибочные
умозаключения.
Нередко, ошибки,
допущенные в софизме, настолько умело скрыты, что даже опытный математик не
сразу их выявит. Именно в этом и проявляется связь математики и философии в
софизмах.
2.2. Математические софизмы
Математические
софизмы делятся на:
1. Арифметические софизмы — это числовые
выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Пример: « Дважды два — пять!».
Возьмем в качестве исходного соотношения
следующее очевидное равенство: 4:4= 5:5. После вынесения за скобки общего
множителя из каждой части равенства будем иметь: 4∙(1:1)=5∙(1:1)
или (2∙2)(1:1)=5(1:1) Наконец, зная, что 1:1=1, из соотношения 4(1:1)=5(1:1)
устанавливаем: 4=5, 2∙2=5.
Ошибка.
Распределительный закон умножения применяется
только для сложения и вычитания: ав + ас = а(в + с).
2. Алгебраические
софизмы —
намеренно скрытые ошибки в уравнениях и числовых выражениях.
Алгебра — один из больших разделов
математики, принадлежащий наряду с арифметикой и геометрией к числу старейших
ветвей этой науки. Задачи, а также методы алгебры отличаются от других отраслей
математики.
Приёмы
эти заключаются обычно в составлении и решении уравнений.
Пример: «Любое отрицательное число больше
положительного, имеющего то же абсолютное значение».
Этот софизм основан на очевидной истине:
«Если в равенстве числитель левой дроби больше знаменателя в n раз, то и в
правой части равенства соотношение внутри дроби будет таким же».
Напишем следующие равенства:
и
и
; т.е.
.
Другими словами, если в левой части
равенства + a > — a, то и в правой части равенства должно соблюдаться то же
соотношение.
Т.е. – a > + a.
Ошибка.
Чтобы получить из равенства +a > -a
равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить
знак неравенства (–a<+a).
3.Геометрические софизмы – это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость,
абсурд или противоречивое утверждение, связанное с геометрическими фигурами и
действиями над ними.
Пример: «Из точки на прямую можно
опустить два перпендикуляра.»
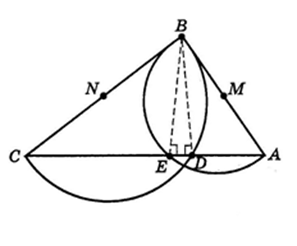
Другими словами, если в левой части
равенства + a > — a, то и в правой части равенства должно соблюдаться то же
соотношение.
Т.е. – a > + a.
Ошибка.
Чтобы получить из равенства +a > -a
равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить
знак неравенства (–a<+a).
3.Геометрические софизмы – это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость,
абсурд или противоречивое утверждение, связанное с геометрическими фигурами и
действиями над ними.
Пример: «Из точки на прямую можно
опустить два перпендикуляра.»
Рассмотрим
треугольник АВС.
Разделим стороны АВ и ВС пополам точками M
и N. На этих сторонах, как на диаметрах, опишем окружности с центрами в точках
M и N. Окружности пересекут сторону АС в точках D и E.
Углы
AEB и BDC опираются на диаметры АВ и ВС соответственно, значит они прямые.
Следовательно, отрезки BD и BE, исходящие
из точки В, будут перпендикулярны, стороне АС, следовательно, из точки В можно
опустить два перпендикуляра на сторону АС.
Ошибка.
Действительно, опустив из B перпендикуляр
на AC , получим два прямоугольных треугольника, гипотенузами которых будут
стороны BC и AB, и если вокруг этих треугольников описать окружности, их
гипотенузы будут диаметрами. Неправильный чертеж. Известно,
что окружности, построенные на двух сторонах треугольника как на диаметрах,
пересекаются в одной точке, лежащей на третьей стороне.
2.3. Разбор математических софизмов
В математических софизмов выделяются 6 основных
ошибок:
1. Деление на 0.
Софизм №1 «Пять равно шести».
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий
множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Ошибка.
При делении верного равенства
5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое
равенство можно делить только на число, отличное от 0.
Софизм №2 «Уравнение x-a=0 не имеет
корней».
Дано уравнение x –a = 0. Разделив обе
части этого уравнения на x-a, получим, что 1 = 0. Поскольку это равенство
неверное, то это означает, что исходное уравнение не имеет корней.
Ошибка.
Поскольку x = a – корень уравнения, то,
разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому
получили неверное равенство 1=0.(x—a=0 -на ноль делить нельзя).
2. Неправильные выводы из равенства дробей;
Софизм №3 «Отклонение от алгоритма может
привести к приобретению посторонних корней данного уравнения».
3. Неправильное извлечение квадратного корня из
квадрата выражения.
Софизм №4
3. Неправильное извлечение квадратного корня из
квадрата выражения.
Софизм №4 =
=
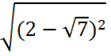
=2-
Ошибка.
При
вычислении квадратного корня 2-
Ошибка.
При
вычислении квадратного корня 2- < 0
=
=
=
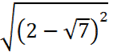
=ç2-
ç=
— 2
4. Нарушения правил действия с величинами.
Софизм №5 «Один метр не равен ста
сантиметрам».
Известно, что любые два равенства можно
перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d,
то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр =
100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно,
получим 10 метров = 100000 сантиметров и, разделив последнее равенство на 10,
получим, что 1 метр = 10000 сантиметров .
Ошибка.
Она состоит в нарушении правила действий
с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
«Один рубль не равен ста копейкам».
Возьмем верное равенство: 2р. = 200к. и
возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.
Ошибка.
Здесь надо вспомнить, что
возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не
величины.
5. Проведение преобразований над математическими
объектами, не имеющими смысла.
Софизм №6 «Два
неодинаковых натуральных числа равны между собой».
Решим систему двух уравнений:
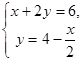
4. Нарушения правил действия с величинами.
Софизм №5 «Один метр не равен ста
сантиметрам».
Известно, что любые два равенства можно
перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d,
то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр =
100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно,
получим 10 метров = 100000 сантиметров и, разделив последнее равенство на 10,
получим, что 1 метр = 10000 сантиметров .
Ошибка.
Она состоит в нарушении правила действий
с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
«Один рубль не равен ста копейкам».
Возьмем верное равенство: 2р. = 200к. и
возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.
Ошибка.
Здесь надо вспомнить, что
возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не
величины.
5. Проведение преобразований над математическими
объектами, не имеющими смысла.
Софизм №6 «Два
неодинаковых натуральных числа равны между собой».
Решим систему двух уравнений:
.
Сделаем это
подстановкой у из 2-го уравнения в 1-е, получаем х+8-х=6, откуда
8=6.
Ошибка
Уравнение (2)
можно записать как х+2у=8, так, что исходная система запишется в виде: .
В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.
Графически это
означает, что прямые у=3-.
В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.
Графически это
означает, что прямые у=3- и у=4-
параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
6. Неравносильный переход от одного неравенства к
другому.
Софизм №7 «Если А
больше В, то А всегда больше, чем 2В».
Возьмем два произвольных
положительных числа А и В, такие, что А>В. Умножив это неравенство на В,
получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим
неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А).
(1)
После деления обеих частей
неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому
неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к
примеру, что из неравенства 6>5 следует, что 6>10.
Ошибка.
Здесь совершен неравносильный
переход от неравенства (1) к неравенству (2). Действительно, согласно условию А
> В, поэтому В – А < 0.Это означает, что обе части неравенства (1)
делятся на отрицательное число. Но согласно правилу преобразования неравенств
при делении или умножении неравенства на одно и то же отрицательное число знак
неравенства необходимо изменить на противоположный. С учетом сказанного из
неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к
которому почленно исходное неравенство В<А, получим просто исходное
неравенство А+В<В+2А.
7. Выводы и вычисления по неверно построенным чертежам;
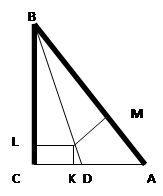
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
6. Неравносильный переход от одного неравенства к
другому.
Софизм №7 «Если А
больше В, то А всегда больше, чем 2В».
Возьмем два произвольных
положительных числа А и В, такие, что А>В. Умножив это неравенство на В,
получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим
неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А).
(1)
После деления обеих частей
неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому
неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к
примеру, что из неравенства 6>5 следует, что 6>10.
Ошибка.
Здесь совершен неравносильный
переход от неравенства (1) к неравенству (2). Действительно, согласно условию А
> В, поэтому В – А < 0.Это означает, что обе части неравенства (1)
делятся на отрицательное число. Но согласно правилу преобразования неравенств
при делении или умножении неравенства на одно и то же отрицательное число знак
неравенства необходимо изменить на противоположный. С учетом сказанного из
неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к
которому почленно исходное неравенство В<А, получим просто исходное
неравенство А+В<В+2А.
7. Выводы и вычисления по неверно построенным чертежам;
Софизм
№8 ∟С=90, ВД — биссектриса угла СВА, СК=КА, ОК перпендикулярна СА, О —
точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС.
∟С=90, ВД — биссектриса ∟ СВА,
СК=КА, ОК ^ СА, О —
точка пересечения прямых ОК и ВД, ОМ ^ АВ, ОL ^
ВС.
Имеем: D
LВО=D МВО, ВL = ВМ, ОМ = ОL = СК = КА,
D КОА=D ОМА (ОA- общая сторона, КА = ОМ, ∟ ОКА и
∟ ОМА — прямые), ∟ ОАК =
∟ МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и
потому ВА = ВС
Ошибка.
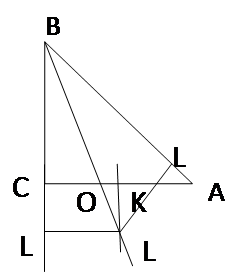 |
Рассуждения о
том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка
пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к
катету АС, находится вне треугольника АВС.
2.4. Логические софизмы
Один из видов
математических софизмов является логический софизм.
Пример № 1: «Полупустое или полуполное».
Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное
Ошибка.
Полупустое не является половиной чего либо
пустого, а является чем либо наполовину наполненным.
Пример
№2: «Когда
же учиться?»
1. По ночам занятий нет, половина суток свободна.
Остаётся: 365-182=183 дня. 2.
2. В школе ученики занимаются половину дня, значит, вторая
половина (или четвёртая часть суток) может быть свободна.
Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы
приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.
Итого остаётся 137-37=100 дней.
4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние
(7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.
5. Итак, школьники заняты в году 100-100=0 дней. Когда же
учиться?!
2.5. Источники софизмов
Источниками
софизмов может выступать терминология, которая используется во время спора.
Многие слова имеют несколько смыслов (доктор может быть врачом или же научным
сотрудником, имеющим ученую степень), за счет чего и происходит нарушение
логики. Софизмы в математике, например, основаны на изменении чисел путем
перемножения их и последующего сравнения исходных и полученных данных.
Неправильное ударение тоже может быть оружием софиста, ведь множество слов при
изменении ударения меняют и смысл. Построение фразы иногда очень запутанно,
как, например, «два умножить на два плюс пять». В данном случае непонятно
имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма
произведения двоек и пятерки.
Разбор и
решение любого рода математических задач, а в особенности нестандартных,
помогает развивать смекалку и логику. Математические софизмы относятся именно к
таким задачам.
III.
«Софизмы из наших школьных тетрадей»
Цель практической работы: проанализировать наши тетради для
контрольных работ по математике, выявить софизмы и найти ошибки, заключенные
в них.
Известная истина гласит «Умные люди учатся
на чужих ошибках». В математике приходится учиться, в основном, на собственных
ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и
полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.
С помощью задач,
содержащих противоречие в условии, можно предупредить ошибки учащихся,
связанные с работой над математическими объектами, которые не существуют при
заданных условиях. Если учащиеся решают задачу, работая с несуществующими
объектами, то происходит выход за границы применяемости теоремы, свойства и
т.д. Эти ошибки возникают по той причине, что большинство учебных задач
содержит информацию непротиворечивую и приводящую к единственному решению.
|
Софизм |
Ошибка |
|
№1 |
Рассуждения о
том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка
пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к
катету АС, находится вне треугольника АВС.
2.4. Логические софизмы
Один из видов
математических софизмов является логический софизм.
Пример № 1: «Полупустое или полуполное».
Полупустое есть то же, что и полуполное.
Если равны половины, значит, равны и целые. Следовательно, пустое есть то же,
что и полное
Ошибка.
Полупустое не является половиной чего либо
пустого, а является чем либо наполовину наполненным.
Пример
№2: «Когда
же учиться?»
1. По ночам занятий нет, половина суток свободна.
Остаётся: 365-182=183 дня. 2.
2. В школе ученики занимаются половину дня, значит, вторая
половина (или четвёртая часть суток) может быть свободна.
Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы
приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.
Итого остаётся 137-37=100 дней.
4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние
(7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.
5. Итак, школьники заняты в году 100-100=0 дней. Когда же
учиться?!
2.5. Источники софизмов
Источниками
софизмов может выступать терминология, которая используется во время спора.
Многие слова имеют несколько смыслов (доктор может быть врачом или же научным
сотрудником, имеющим ученую степень), за счет чего и происходит нарушение
логики. Софизмы в математике, например, основаны на изменении чисел путем
перемножения их и последующего сравнения исходных и полученных данных.
Неправильное ударение тоже может быть оружием софиста, ведь множество слов при
изменении ударения меняют и смысл. Построение фразы иногда очень запутанно,
как, например, «два умножить на два плюс пять». В данном случае непонятно
имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма
произведения двоек и пятерки.
Разбор и
решение любого рода математических задач, а в особенности нестандартных,
помогает развивать смекалку и логику. Математические софизмы относятся именно к
таким задачам.
III.
«Софизмы из наших школьных тетрадей»
Цель практической работы: проанализировать наши тетради для
контрольных работ по математике, выявить софизмы и найти ошибки, заключенные
в них.
Известная истина гласит «Умные люди учатся
на чужих ошибках». В математике приходится учиться, в основном, на собственных
ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и
полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.
С помощью задач,
содержащих противоречие в условии, можно предупредить ошибки учащихся,
связанные с работой над математическими объектами, которые не существуют при
заданных условиях. Если учащиеся решают задачу, работая с несуществующими
объектами, то происходит выход за границы применяемости теоремы, свойства и
т.д. Эти ошибки возникают по той причине, что большинство учебных задач
содержит информацию непротиворечивую и приводящую к единственному решению.
|
Софизм |
Ошибка |
|
|
№1 |
Неправильный
|
|
|
№2
|
||
|
№2
|
Нарушение |
Нарушение
|
|
|
|
|
|
№4
ОДЗ:
Умножим обе 2 Разложили 2 Разложили 2 = (x — 2) (2x + 1) (x — 2) (2x + 1) = x2 (x — 2) Разделим х — X2 -2x -1 =0 Д=4+4=8 X1= = (x — 2) (2x + 1) (x — 2) (2x + 1) = x2 (x — 2) Разделим х — X2 -2x -1 =0 Д=4+4=8 X1= X2=1- Корни Ответ: Корни Ответ: |
Ошибка: (x-2)(2x+1)=x2 (x-2) , на x-2произошла Верное x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х — x = 2 или x1=1 + |
Ошибка: (x-2)(2x+1)=x2 (x-2) , на x-2произошла Верное x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х — x = 2 или x1=1 + Уравнение 1 + Уравнение 1 + Но Ответ: Но Ответ: |
|
№5
|
||
|
№5
|
Верное |
Верное Ошибка: Ошибка: Правило: |
|
№6 Периметр треугольника равен 6, его стороны относятся как |
Задача провоцирует учащихся на то, чтобы дать ответ 2. При |
|
|
Правило: |
||
|
№6 Периметр треугольника равен 6, его стороны относятся как |
Задача провоцирует учащихся на то, чтобы дать ответ 2. При |
|
|
|
Известные элементы (радиус окружности и угол, образуемый |
Заключение
Исторические
сведения о софистике и софистах помогли нам разобраться, откуда же все-таки
началась история софизмов. Вначале мы думали, что софизмы бывают исключительно
математические. Причем в виде конкретных задач, но, начав исследование в этой
области, мы поняли, что софистика — это целая наука, а именно математические
софизмы — это лишь часть большого течения.
Разбор софизмов
развивает логическое мышление, помогает сознательному усвоению изучаемого
материала, воспитывая вдумчивость, наблюдательность, критическое отношение к
тому, что изучается. Кроме того, разбор софизмов увлекателен. Мы с большим
интересом воспринимали софизмы, чем труднее софизм, тем большее удовлетворение
доставляет его разбор. Порой сам попадаешься на уловки софиста.
Гипотеза, которую
мы ставили в начале работы «Если в процессе обучения математике целенаправленно и
систематически организовывать работу учащихся над типичными ошибками, на примере
софизмов, то это будет способствовать повышению качества математической подготовки
учащихся», подтвердилась.
Благодаря знанию
софизмов можно научиться искать ошибки в рассуждениях других, научится
грамотно строить свои рассуждения и логические объяснения. Когда ребенок раз
притронется к горячему предмету, то впоследствии он постарается этого не
делать. Он будет много осторожнее. Так, изучающий математику, впоследствии
проявит больше осторожности, чтобы не повторить осознанную ошибку. Значит, математические софизмы заставляют внимательно
и настороженно продвигаться вперед, тщательно следить за точностью
формулировок, правильностью записей и чертежей, за допустимостью обобщений, за
законностью выполняемых операций. Все это нужно и полезно. Только очень сухого
человека не может увлечь интересный софизм. Как приятно бывает обнаружить
ошибку в математическом софизме и тем как бы восстановить истину в ее правах.
Математические софизмы показали нам, как важно строго соблюдать правила и
формулировки теорем при логических умозаключениях.
Нам
было очень интересно работать над данной темой. Мы создали сборник «Софизмы из
наших школьных тетрадей».
Задания,
предложенные нами в работе, можно использовать как на уроках алгебры и
геометрии, так и на внеклассных мероприятиях.
Список
литературы
1. «Софисты»
под редакцией Б.С. Чернышева
2. «Софизмы. Алгебра.
Геометрия. Тригонометрия» под редакцией Т.Н. Михеевой
3. http://gamzatovasm.ru/node/88 — Алгебраические
софизмы
4. http://reshit.ru/sofizm — Геометрические
софизмы
5. http://sophisms.ucoz.ru/index/arifmeticheskie_sofizmy/0-6 — Арифметические софизмы
6. http://referatwork.ru/category/logika/view/131832_sofizmy — Логические софизмы
7. https://ru.wikipedia.org/wiki/Апории_Зенона — Апории Зенона
Приложения
Приложение 1.


Рис.
2 Сократ

Приложение 2.
Арифметические софизмы
1.
Верно ли равенство 7 = 8?
35 +
14 – 49 = 40 + 16 — 56
7(5 +
2 — 7)=8(5 + 2 — 7)
Следовательно,
7 = 8
Ошибка.
Обе части равенства разделили на (5 + 2 — 7),
но нарушено правило, что на «0» делить нельзя (5 + 2 – 7 = 0)
2.
Некто
утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы
последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же
чисел, но взятых в обратном порядке (от 1 до 9):
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2
Будем
последовательно вычитать числа второй строки из чисел первой. Например, так как
9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь
нетрудно установить,
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.
Итак,
45 – 45 = 45.
Ошибка состоит в том,
что занимаемую единицу возводили в ранг десятка.
3.Меньшее число больше, чем большее».
Очевидно,что7 > 5 и что – 8 = — 8
Тогда:7 – 8 > 5 — 8 или – 1 > — 3
Это не противоречит основному понятию об
отрицательных величина, на основании которого мы считаем меньшей ту
отрицательную величину, численное значение которой больше, и наоборот.
Умножим обе части последнего неравенства на (- 4).
Получим (-1)*(-4)>(-3)*(-4) или 4 > 12
Ошибка.
При умножении неравенства на отрицательное
число, знак неравенства изменяется на противоположный.
Приложение 3. Алгебраические софизмы
1.«Отрицательное число больше положительного».
Возьмем два положительных
числа а и с. Сравним два отношения: Рис. 3 Аристотель
Приложение 2.
Арифметические софизмы
1.
Верно ли равенство 7 = 8?
35 +
14 – 49 = 40 + 16 — 56
7(5 +
2 — 7)=8(5 + 2 — 7)
Следовательно,
7 = 8
Ошибка.
Обе части равенства разделили на (5 + 2 — 7),
но нарушено правило, что на «0» делить нельзя (5 + 2 – 7 = 0)
2.
Некто
утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы
последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же
чисел, но взятых в обратном порядке (от 1 до 9):
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2
Будем
последовательно вычитать числа второй строки из чисел первой. Например, так как
9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь
нетрудно установить,
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.
Итак,
45 – 45 = 45.
Ошибка состоит в том,
что занимаемую единицу возводили в ранг десятка.
3.Меньшее число больше, чем большее».
Очевидно,что7 > 5 и что – 8 = — 8
Тогда:7 – 8 > 5 — 8 или – 1 > — 3
Это не противоречит основному понятию об
отрицательных величина, на основании которого мы считаем меньшей ту
отрицательную величину, численное значение которой больше, и наоборот.
Умножим обе части последнего неравенства на (- 4).
Получим (-1)*(-4)>(-3)*(-4) или 4 > 12
Ошибка.
При умножении неравенства на отрицательное
число, знак неравенства изменяется на противоположный.
Приложение 3. Алгебраические софизмы
1.«Отрицательное число больше положительного».
Возьмем два положительных
числа а и с. Сравним два отношения: и
Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию:
Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию:
Но если в пропорции предыдущий член первого отношения больше последующего,
то предыдущий член второго отношения также больше своего последующего. В нашем
случае а > — с, следовательно, должно быть –а > с, т.е. отрицательное
число больше положительного.
Ошибка.
Данное свойство пропорции может оказаться неверным, если некоторые
члены пропорции отрицательны.
2. « Если
одно число больше другого, то эти числа равны»
Возьмем два
произвольных числа т и п, такие, что m > n , и другие три произвольных числа а, b и с, сумма которых
равна d, т.е. а + b + c = d. Умножив обе части этого равенства на n, а затем на
m, получим:
ma + mb + mc
= md, na + nb + nc = nd.
Сложив почленно равенства:
ma + mb + mc
= md и nd = na
+ nb + nc
получим: ma + mb + mc + nd = na + nc + nb + md.
Перенося здесь nd вправо, а md влево, имеем
ma + mb + mc
– md = na + nb + nc — nd.
Вынося слева число m, а справа число n за скобки,
придем к соотношению m (a + b + c — d) = n (a + b + c — d).
Разделив обе части последнего равенства на
(a + b + c — d), находим, что m = n.
Ошибка.
a + b + c – d =0, на ноль делить нельзя.
4.
«Любое число равно нулю»
Возьмем произвольное положительное число а и
рассмотрим сумму х бесконечного числа слагаемых, равных а: х = а + а + а + а +…
Очевидно, что мы можем представить эту сумму как х = а + (а + а + а +….) в
которой сумма, стоящая в скобках, также равна х как сумма бесконечного числа слагаемых,
равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0.
Ошибка допущена в равенстве (1) , в котором бесконечная сумма чисел
а обозначена конечным числом х.
4.
Решим систему двух
уравнений:
Сделаем это подстановкой у из 2го
уравнения в 1, получаем х + 8 — х = 6, откуда
8 = 6
Ошибка.
Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде:
Сделаем это подстановкой у из 2го
уравнения в 1, получаем х + 8 — х = 6, откуда
8 = 6
Ошибка.
Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде:
В этой системе
уравнений коэффициенты при переменных одинаковы, а правые части не равны между
собой, из этого следует, что система несовместна, т.е. не имеет ни одного
решения.
Графически это
означает, что прямые у=3 — и у = 4
— и у = 4
— параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
5. «Если “a” больше “b”, то “a” всегда больше,
чем “2b”»
Возьмем два
произвольных положительных числа a и b, такие, что a > b. Умножив это
неравенство на b, получим новое неравенство:
ab > bb, а отняв от обеих
его частей a·a, получим
неравенство:
ab—aa > bb — aa, которое
равносильно следующему: a(b—a) > (b+a)(b—a).(1)
После деления обеих частей неравенства (1)
на b—a получим, что a > b+a (2),
Прибавив к этому неравенству почленно
исходное неравенство a> b, имеем
2a >
2b + a,
откуда a > 2b.
Итак, если a > b, то a > 2b.
Ошибка совершена при
переходе от равенства (1) к (2).
Т.к. a > b, то b — a<0,
следовательно, при делении неравенства (1) на b – a, мы должны
поменять знак неравенства на противоположный.
6.«Единица равна двум»
Простым вычитанием легко убедиться в
справедливости равенства
1 — 3 = 4-6.
Добавив к обеим частям этого равенства
число 9/4, получим новое равенство
1 — 3 + 9/4 = 4 — 6
+ 9/4,
в котором, как нетрудно заметить, правая и
левая части представляют собой полные квадраты, т. е. (1 — 3/2)=(2 — 3/2)
Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство: 1 — 3/2
=2 — 3/2
откуда следует, что 1=2.
Ошибка.
По определению =(2 — 3/2)
Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство: 1 — 3/2
=2 — 3/2
откуда следует, что 1=2.
Ошибка.
По определению представляет собой некоторое
неотрицательное число, которое, будучи возведено в квадрат, даст х. Ясно, что
этому определению удовлетворяют два числа, а именно х и -х. Итак, если число х
неотрицательно (х ≥ 0), то= х; если же число х отрицательно (х<0), то есть число –х положительно, то
= х; если же число х отрицательно (х<0), то есть число –х положительно, то
= — x. Отсюда заключаем, что
(свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
7.
«Всякое
число равно своей половине.»
Запишем очевидное для любого числа a
тождество a2— a2= a2— a2,где
а — любое число.
Вынесем a в левой части за скобку,
а правую часть разложим на множители по формуле разности квадратов, получим
a(a – a) = (a + a)(a — a).
Разделив обе части на a — a, получим a = a + a, или a=2a.
Разделим на 2 и получим а
= а/2
Ошибка.
Мы делим обе части на ноль, а деление на
ноль запрещено
1. (свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
7.
«Всякое
число равно своей половине.»
Запишем очевидное для любого числа a
тождество a2— a2= a2— a2,где
а — любое число.
Вынесем a в левой части за скобку,
а правую часть разложим на множители по формуле разности квадратов, получим
a(a – a) = (a + a)(a — a).
Разделив обе части на a — a, получим a = a + a, или a=2a.
Разделим на 2 и получим а
= а/2
Ошибка.
Мы делим обе части на ноль, а деление на
ноль запрещено
1. , а длина всякой окружности равна ее
диаметру.
Построим
на отрезке МN как на диаметре окружность. Радиус окружности обозначим через . Тогда длина окружности будет
равна: . Тогда длина окружности будет
равна:
Поделим
MO и NO пополам точками
Поделим
MO и NO пополам точками и
и построим новые окружности с центрами в
этих точках радиусами и построим новые окружности с центрами в
этих точках радиусами .
Найдем
длины новых окружностей:
Сумма
их длин будет равна
Сумма
их длин будет равна
т.е.
равна длине большой окружности C.
Таким
же образом будем строить окружности и далее и находить сумму их длин.
Так,
сумма длин окружностей и
и
. и будет равна
Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны
Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны и т.д. При этом сумма длин всех этих
окружностей всегда будет равна .
Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна.
Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна.
С
другой стороны, сумма длин этих окружностей постоянна и равна , следовательно,
, следовательно,
Из
этого равенства получаем или, деля на
или, деля на
:
Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна
Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна . Пусть
— длина малой
окружности — длина малой
окружности,
— ее радиус. Как бы такая окружности ни была мала, всегда имеем или
или
Отсюда
видим, что эта бесконечно-малая окружность никогда не будет равна своему
диаметру ,
что следовало бы из результата софизма.
2.« Отрезки параллельных прямых, заключенные между сторонами
угла, равны»
Рассмотрим произвольный угол с
вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки
которых АВ и CD заключены между сторонами этого угла.
Как известно параллельные
прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ :
CE = BE : DE,
Откуда АЕ·DE = BE·CE
Умножив обе части последнего
равенства на отличную от нуля разность (АВ –CD), запишем
AE·DE·AB — AE·DE·CD = AE·DE·CD
— BE·CE·CD,
или
AB(AE·DE — BE·CE) = CD(AE·DE —
BE·CE)
Разделив обе части последнего равенства на (AE·DE — BE·CE), получим
равенство АВ=CD.
что следовало бы из результата софизма.
2.« Отрезки параллельных прямых, заключенные между сторонами
угла, равны»
Рассмотрим произвольный угол с
вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки
которых АВ и CD заключены между сторонами этого угла.
Как известно параллельные
прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ :
CE = BE : DE,
Откуда АЕ·DE = BE·CE
Умножив обе части последнего
равенства на отличную от нуля разность (АВ –CD), запишем
AE·DE·AB — AE·DE·CD = AE·DE·CD
— BE·CE·CD,
или
AB(AE·DE — BE·CE) = CD(AE·DE —
BE·CE)
Разделив обе части последнего равенства на (AE·DE — BE·CE), получим
равенство АВ=CD.
Ошибка.
AE·DE — BE·CE=0
3.Все треугольники равнобедренные.
Рассмотрим
произвольный ∆АВС (рис.2).
Проведем
в нем биссектрису угла B и серединный перпендикуляр к стороне АС. Точку их
пересечения обозначим через О.
Из
точки O опустим перпендикуляр OD на сторону АВ и перпендикуляр ОЕ на сторону
ВС. Очевидно, что ОА = ОС и OD = ОЕ. Но тогда ∆AOD = ∆СОЕ по катету и
гипотенузе. Поэтому ∟DAO = ∟ЕСО. В то же время ∟ОАС = ∟ОСА,
так как ∆АОС -равнобедренный.
Получаем:
∟ВАС = ∟DAO + ∟ОАС = ∟ЕСО + ∟ОСА = ∟ВСА
Итак, угол ВАС равен углу ВСА, поэтому ∆АВС — равнобедренный:
АВ=ВС.
Ошибка. При построения чертежа. Серединный перпендикуляр к
стороне и биссектриса противоположного ей угла для не равнобедренного
треугольника, пересекаются вне этого треугольника.
Приложение 4.
Логические софизмы.
1.
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше.
Значит, лекарств нужно принимать как можно больше».
Ошибка. При построения чертежа. Серединный перпендикуляр к
стороне и биссектриса противоположного ей угла для не равнобедренного
треугольника, пересекаются вне этого треугольника.
Приложение 4.
Логические софизмы.
1.
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше.
Значит, лекарств нужно принимать как можно больше».
2. Одна
песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+1
песчинка – тоже не куча. Следовательно, никакое число песчинок не образует кучу
песка. К этому парадоксу можно сделать следующий комментарий: метод полной
математической индукции нельзя применять, как показывает парадокс, к объёмно
неопределённым понятиям, каковым является понятие «куча песка».
3.
Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна
существовать курица, но ведь курица может вылупиться только из яйца, а значит,
первичным является именно оно.
3.
Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна
существовать курица, но ведь курица может вылупиться только из яйца, а значит,
первичным является именно оно.
4.«Может ли
всемогущий маг создать камень, который не сможет поднять?»
Если не может – значит, он не всемогущий.
Если может – значит, всё равно не всемогущий, т.к. он не может поднять это
камень.
6.В мире нет ни одного человека,
говорящего на моем языке; или короче: ни одного человека, говорящего; или еще
короче: ни одного человека.
6.В мире нет ни одного человека,
говорящего на моем языке; или короче: ни одного человека, говорящего; или еще
короче: ни одного человека.
Скачано с www.znanio.ru
|
Муниципальное бюджетное оБщеобразовательное учреждение «Центр образования №22 – Лицей искусств» г.Тула |
|
Математические софизмы |
|
Проект выполнила: ученица 10 В класса Юлина Карина Руководитель проекта: учитель математики Сватковская Е.А. |
Содержание:
Паспорт проекта.
Введение. Цели, задачи проекта.
-
Глава первая. Понятие софизма.
-
История софизмов.Виды софизмов.
-
Классы ошибок в софизмах.
-
-
Глава вторая. Виды математических софизмов:
-
логические софизмы.
-
алгебраические софизмы.
-
геометрические софизмы.
-
-
Глава третья. Как создать софизм?
-
Принципы, по которым составляются софизмы.
-
Создание своего софизма.
-
Заключение
Приложение
Введение.
Всем нам хоть раз в жизни встречались высказывания, такие как «Дважды два равно пять», «Два равно трем». Откуда взялись эти утверждения? Кто их придумал? Можно ли их объяснить или это просто выдумка?
В своей работе я хочу разобраться в вопросах, связанных с математическими софизмами. Математические софизмы, по моему мнению, интереснее других своей четкостью и логичностью объяснения. И мы сталкиваемся с ними намного чаще, чем с другими софизмами.
Софизмы заставляют нас думать в различных направлениях и рассматривать проблемы с разных сторон, анализируя небольшие детали. И еще, софизм – это обман, который не каждый сможет распознать, а, следовательно, люди обманывают друг друга с помощью софизмов. Так происходит и в наше время, и происходило тысячелетия назад.
Цель моего проекта — изучение математических софизмов
Задачи:
1.Найти, изучить и проанализировать информацию, полученную при изучении софизмов.
2. Изучить историю софизмов.
3.Рассмотреть виды софизмов, выявить ошибки в математических софизмах.
4. Разделить на классы математические софизмы.
5. Разобрать логику составления и решения математических софизмов.
6. Создать собственный софизм.
7. Привлечь интерес учащихся к урокам математики.
Объект проекта: софизмы.
Предмет проекта: математические софизмы.
В этой работе былииспользованы некоторые примеры алгебраических, геометрических, логических софизмов из книг «Что не так?» Львовского С.М., «Математические софизмы» Обреимова В.И., «Математические софизмы» А.Г. Мадеры, Д.А. Мадеры1. Так же из “Математической шкатулки” Ф.Ф. Нагибина, Е.С. Канина2 взяли историю развития математических софизмов.
Методы исследования: определение понятий, анализ и синтез.
Практическая значимость: Видеть и замечать неявные ошибки, акцентировать внимание на мелких деталях.Данный материал можно применять на факультативных занятиях, математическом кружке, чтобы привить интерес учащихся к математике.
Глава первая. Понятие софизма.
История возникновения софизмов.
Сам софизм был введен древнегреческим софистами в V в. до н.э. как пример обучения.Софисты были личными наёмными учителями и опирались на решение задач.
Аристотель не считал софизмы научным поиском истины, а «натаскиванием» и составил в книге «О софистических опровержениях» первую классификацию софизмов, выделив 13 видов софизмов, возникающих из-за двусмысленностей двоякого рода, 6, связанных с оборотами речи, и 7 паралогизмов или неправильно построенных рассуждений.
Аристотель софизмом называл «мнимые доказательства», убедительность многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой:
-
семантической: возникает за счёт нарушения однозначности мысли и приводит к смешению значений терминов;
-
логической: подмена основной мысли доказательства, принятие лжи за истину, несоблюдение допустимых способов рассуждения, использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах.
В истории математические софизмы играли существенную роль: уяснение ошибок в математических рассуждениях часто содействовало развитию математики.
Особенно поучительна в этом отношении аксиомао параллельных прямых Евклида. Звучит она так: через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной. На протяжении двух тысяч лет многие выдающиеся математики пытались это доказать, пытались это вывести из аксиом геометрии. Но попытки не увенчались успехом. Многочисленные «доказательства» оказались ошибочными. И все же они принесли огромную пользу в развитии геометрии: выяснились связи между разными теориями геометрии; тем самым была подготовлена почва для создания Неевклидовой геометрии.3
Виды софизмов
Существует довольно большое количество видов софизмов. Вот некоторые из них:
-
логические;
-
терминологические;
-
психологические;
-
интеллектуальные;
-
аффективные;
-
волевые;
-
математические;
-
исторические.
Классы ошибок в софизмах.
В софизмах ученые выделяют 3 класса ошибок:
1. Логические ошибки.
Так как вывод может быть выражен в силлогистической форме, то и любой софизм может сводиться к нарушению правил силлогизма. Наиболее часто к логическим софизмам приводят нарушения следующих правил:
-
вывод с отрицательной меньшей посылкой в первой фигуре: «Все люди суть разумные существа, жители планет не суть люди, следовательно, они не суть разумные существа»;
-
вывод с утвердительными посылками во второй фигуре: «Все, находящие эту женщину невинной, должны быть против наказания её; вы — против наказания её, значит, вы находите её невинной»;
-
вывод с общим заключением в третьей фигуре: «Закон Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно, воровство не запрещено».
2. Терминологические ошибки.
Больше всего распространены ошибки употребления среднего термина в большой и в меньшей посылке не в одинаковом значении.
Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы. Существует несколько классов терминологических ошибок:
-
ошибка омонимии;
-
ошибка сложения — когда разделительному термину придается значение собирательного;
-
ошибка разделения (обратная), когда собирательному термину дается значение разделительного;
-
ошибка ударения, когда подчёркивание повышением голоса в речи и курсивом в письме определенного слова или нескольких слов во фразе искажает её первоначальный смысл;
-
ошибка выражения, заключающаяся в неправильном или неясном для уразумения смысла построении фразы.
Более сложные софизмы происходят из неправильного построенного ряда доказательств, где ошибки являются тенью всего выражения.
3. Психологические ошибки.
Психологические причины софизмов бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.
4. Интеллектуальные причины.
Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софизму, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignavaratio). Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм: обозначим первые отрицательные качества через b, вторые соответствующие им положительные через а.
5. Аффективные причины.
Сюда относятся трусость в мышлении — боязнь опасных практических последствий, вытекающих от принятия известного положения; надежда найти факты, подтверждающие ценные для нас взгляды, побуждающая нас видеть эти факты там, где их нет, любовь и ненависть, прочно ассоциировавшиеся с известными представлениями. Желающий обольстить ум своего соперника софист должен быть не только искусным диалектиком, но и знатоком человеческого сердца, умеющим виртуозно распоряжаться чужими страстями для своих целей.
6. Волевые причины.
При обмене мнений мы воздействуем не только на ум и чувства собеседника, но и на его волю. Во всякой аргументации (особенно устной) есть элемент волевой — императивный — элемент внушения. Категоричность тона, не допускающего возражения, определенная мимика действуют неотразимым образом на лице, легко поддающихся внушению, особенно на массы, с другой стороны, пассивность слушателя особенно благоприятствует успешности аргументации противника. Логические, грамматические и психологические факторы теснейшим образом связаны между собой.
Таким образом, софизмы — довольно древнее понятие. Существует множество видов софизмов. Но всех их объединяют схожие «ошибки». Попытки разгадать математические софизмы приводят к более полному понятию математики.
Глава вторая. Виды математических софизмов.
1) Логические софизмы.
Начнем с небольшого английского софизма в качестве разминки:
The more you study – the more you know,
The more you know – the more you forget,
The more you forget – the less you know,
The less you know – the less you forget,
The less you forget – the more you know.
Why study?4
(Чем больше мы учим, тем больше знаем.
Чем больше мы знаем, тем больше забываем.
Чем больше мы забываем, тем меньше знаем.
Чем меньше мы знаем, тем меньше забываем.
Чем меньше забываем, тем больше знаем.
Зачем учиться?)
Следующий софизм довольно прост. Для начала познакомимся с одним занимательным парадоксом:
В один раз хозяину гостиницы с бесконечным, но счетным числом номеров, которые не были свободны, нужно было принять нового гостя. Хозяин нашел очень простой выход: он каждого из постояльцев переселил в комнату, номер которой был на единицу больше, чем номер прежней комнаты. В итоге, каждый обитатель n-й комнаты переехал в (n+1)-ю и освободил первую комнату для нового гостя. Как поступить хозяину, если к немуприедут бесконечно много гостей? Все также, хозяину просто требуется переместить всех прежних жильцов в (n*2) и разместить новых гостей в освободившиеся нечетные номера.Возможно ли, разместить новых гостей хозяину, при этом, не имея счетное количество комнат?
Во взятом нами софизмом рассказывается о хитром хозяине гостиницы, разместившем в девяти номерах десять гостей так, что каждому досталась одна комната:
Их было десять чудаков,
Тех спутников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
«Пусти, хозяин, ночевать,
Не будешь ты в убытке,
Нам только ночку переспать,
Промокли мы до нитки».
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
«Восьми гостям я предложу
Постели честь по чести,
А двум придется ночь проспать
В одной кровати вместе».
Лишь он сказал, и сразу крик,
От гнева красны лица.
Никто из всех десятерых
Не хочет потесниться.
Как охладить страстей тех пыл,
Умерить те волненья?
Но старый плут хозяин был
И разрешил сомненья.
Двух первых путников пока,
Чтоб не судили строго,
Просил пойти он в номер «А»
И подождать немного.
Спал третий в «Б», четвертый в «В»,
В «Г» спал всю ночь наш пятый,
В «Д», «Е», «Ж», «3» нашли ночлег
С шестого по девятый.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад Десятому герою.
Хоть много лет с тех пор прошло,
Неясно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами,
Понять, что, как и почему,
Вы постарайтесь сами.
В чем же тут ошибка? А все очень просто, мы просто забыли про десятого, точнее хозяин вернулся к первым двум, и отдал ключ одному из них, но поселил он девятерых и отдал, допустим, второму ключ от комнаты «И», но десятый тут никак не фигурирует.
4 рубля = 40000копейкам
Возьмем верное равенств:
2 рубля = 200 копейкам и возведем его по частям в квадрат.
Мы получим: 4 рубля = 40000 копейкам.5
В чем же ошибка? Вот в чем: возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.
Существует множество логических софизмов и можно найти даже такие у которых объяснение будет неоднозначным, вот пример такого:
«Учебная тревога»
Однажды командир Н-ской роты объявил солдатам следующее:
— В один из рабочих дней на следующей неделе в 5 часов утра у нас будет учебная тревога. Чтобы приблизить обстановку к боевой, эта тревога будет для вас неожиданной: пока ее не объявят, вы не будете знать, что она состоится именно в этот день.
Вечером того же дня рядовой Петров объяснял своим товарищам:
— Я все понял: никакой тревоги не будет, нам только голову морочат! Вот смотрите. В пятницу эту тревогу объявить не могут: ведь тогда уже в четверг вечером мы будем знать, что тревога будет именно в пятницу – другого-то дня не остается! А нам ведь объявили, что нам до последнего момента будет неизвестно, в какой день будет тревога, так что пятница исключается. Но могут ли объявить тревогу в четверг? Тоже нет! Ведь если в первые три дня тревоги не будет, то мы уже в среду вечером будем знать, что тревога будет в четверг или пятницу, а так как в пятницу ее объявить не могут, остается только четверг, и мы опять узнаем дату тревоги заранее, неожиданности не будет. Значит, остаются только понедельник, вторник и среда, но тут мы рассуждаем точно так же: в среду объявить тревогу невозможно, ну и так далее. Так что обойдемся без тревоги.
Рассуждение рядового Петрова всех убедило. Однако же в среду в пять утра по казарме разнеслось: «Рота, подъем! Тревога!». Как вы понимаете, для всех, включая рядового Петрова, это оказалось полной неожиданностью, так что все случилось в соответствии с тем, что объявил командир роты.
Но где же тогда ошибка в рассуждениях рядового Петрова?6
И правда, в чем же ошибся рядовой?
Есть два варианта «решения» этого вопроса.
Первое объяснение, заключается в том, что Петров ошибся в самом начале своих рассуждений. Ведь вполне возможно в пятницу провести тревогу. Во-первых, потому что есть те, кто так же, как и Петров, посчитают пятницу неудачным днем для проведения «неожиданной» тревоги. Люди, опирающиеся на этот вывод, предполагают, прохождение учения раньше пятницы. Во-вторых, есть среди нас те, которые не задумываются о следующем дне, так для них тревога будет тоже неожиданной.
Петров считает, что предсказуемое событие никак не может быть неожиданным. Но саму тревогу объявляет человек, а действия его точно предсказать невозможно. Можно предугадать действия компьютерной программы, зная ее исходный код и исходные данные. У человека же есть воля.
Есть и другое объяснение не с логической точки зрения, а с житейской. Одинаковые слова, иногда, имеют разные значения в зависимости от ситуации. В нашем случае слово «неожиданный» различно в значениях. Для Петрова, как было ранее сказано, важным было значение «предугадать». А вот командир не имел в виду, что солдаты не смогут предсказать дату и время тревоги. Смысл его речи был намного проще: лишь предупредить их о планирующейся тревоге, чтобы они готовились.
2) Алгебраические софизмы
4=5
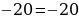
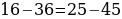
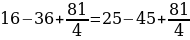
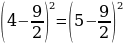
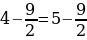
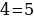
Ошибка: 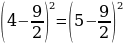
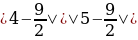
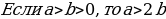
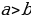
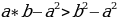
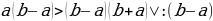
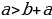
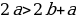
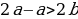
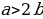
Ошибка: По условию 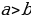
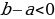
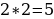
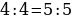
Вынесем за скобки общий множитель в каждой части:
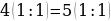
Числа в скобках равны, поэтому:
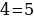
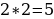
Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 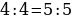
Отрицательноечисло больше положительного.
Возьмем два положительных числа a и b. Сравним два отношения: 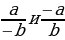
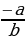
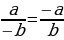
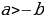
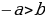
Ошибка заключается в том, что свойство (если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего) может оказаться неверным, если некоторые члены пропорции отрицательны.
Любое число равно числу, в два раза большему его.
Пусть 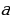
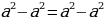
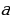
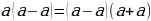
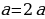
В уравнении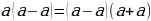
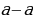
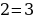
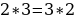
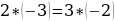
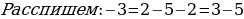
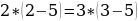
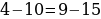
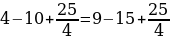
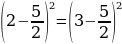
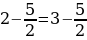
Увеличим обе части на 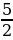
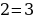
В чем же ошибка? Прибавляя к равным величинам равные, получаются равные суммы, но в этом случае величины не равны, посчитаем: 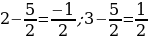
Следующий пример необычен тем, что он до сих пор не решен.
«Ахиллес никогда не догонит черепаху»
Древнегреческий философ Зенон доказывал, что Ахиллес, один из самых сильных и храбрых героев, осаждавших древнюю Трою, никогда не догонит черепаху, которая, как известно, отличается крайне медленной скоростью передвижения.
Вот примерная схема рассуждений Зенона:
Предположим, что Ахиллес и черепаха начинают движение одновременно, и Ахиллес стремится догнать черепаху. Примем для определённости, что Ахиллес движется в 10 раз быстрее черепахи, и что их отделяют друг от друга 100 шагов.
Когда Ахиллес пробежит расстояние в 100 шагов, отделяющие его от того места, откуда начала двигаться черепаха, то в этом месте он уже её не застанет, так как она пройдёт вперёд расстояние в 10 шагов. Когда Ахиллес пробежит и эти 10 шагов, то и там черепахи уже не будет, поскольку она успеет перейти на 1 шаг вперёд. Достигнув и этого места, Ахиллес опять не найдёт там черепахи, потому что она успеет пройти расстояние, равное 1/10 шага, и снова окажется несколько впереди его. Это рассуждение можно продолжать до бесконечности, и придётся признать, что быстроногий Ахиллес никогда не догонит медленно ползающую черепаху.
Где ошибка?
Софизм Зенона далек от своего конечного решения. Вот аспекты приведенные в книге Мадера А. Г., Мадера Д. А. «Математические софизмы»:
«Сначала определим время t, за которое Ахиллес догонит черепаху. Оно легко находится из уравнения a+vt=wt, где a – расстояние между Ахиллесом и черепахой до начала движения, v и w – скорости черепахи и Ахиллеса соответственно. Это время при принятых в софизме условиях (v=1 шаг/сек и w=10 шагов/сек) равно 11,111111… сек.
Другими словами, примерно через 11,1 сек. Ахиллес догонит черепаху.
Подойдём теперь к утверждениям софизма с точки зрения математики. Проследим логику Зенона. Предположим, что Ахиллес должен пройти столько же отрезков, сколько их пройдёт черепаха. Если черепаха до момента встречи с Ахиллесом пройдёт m отрезков, то Ахиллес должен пройти те же m отрезков плюс ещё один отрезок, который разделял их до начала движения. Следовательно, мы приходим к равенству m=m+1, что невозможно. Отсюда следует, что Ахиллес никогда не догонит черепаху.
Итак, путь, пройденный Ахиллесом, состоит из бесконечной последовательности отрезков, которые принимают бесконечный ряд значений.
Трудности, которые возникают при оперировании понятиями «непрерывного» и «бесконечного» до сих пор не определены, а разрешение противоречий, содержащихся в них, послужило более глубокому осмыслению основ математики».
Софизм Зенона справедлив в теории, но на практике не применим, довольно тяжело представить себе Ахиллеса, бегущего микроскопическое расстояние.7
3) Геометрические софизмы.
«Новое доказательство» теоремы Пифагора.
Возьмем прямоугольный треугольник с катетами 
и острым углом 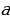
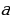

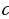
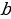

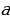
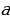
Имеем: 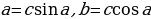
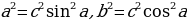
Просуммировав по частям эти равенства, получаем:
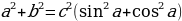
но
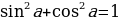
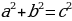
Здесь ошибка заключается в том, что формула 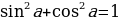
Ч
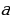
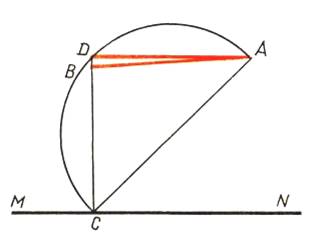
ерез точку, лежащую вне прямой, можно провести две прямые, параллельные данной прямой.
Дана пряма MN и вне ее точка A. Проведем через точку A прямую AB, параллельную прямой MN. Возьмем на MN некоторую точку C. На отрезке AC, как на диаметре, построим полуокружность. Пусть D – точка пересечения этой полуокружности с перпендикуляром к прямой MN, проходящим через точку C. Через точки A и D проведем прямую. Так как угол CDA прямой, а CD перпендикулярна MN, то AD – прямая, параллельная MN. Следовательно, через A проходят две прямые, параллельные прямой MN.
Ошибка: D принадлежит AB.
«Загадочный треугольник»
Дан прямоугольный треугольник 13*5 клеток, составленный из четырёх фигур.
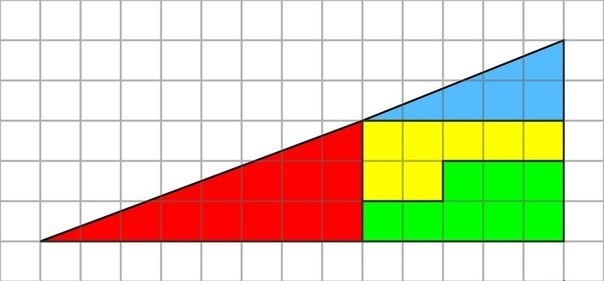
После перестановки фигур при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка (рис. 2). Но мы же понимаем, что такого быть не может.
Площади закрашенных фигур, конечно, равны между собой (обе по 32 клетки), однако, то, что визуально наблюдается как треугольники 13*5, на самом деле таковым не является, и имеет разные площади. То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура названа треугольником (на самом деле являющаяся вогнутым четырёхугольником). Это отчётливо заметно на рис. 2 – гипотенузы верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу(23 и 58), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Если нижние стороны этих треугольников параллельны, то гипотенузы в обоих треугольниках 13*5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем – наружу).Если наложить верхнюю и нижнюю фигуры 13*5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь. На рис. 3 этот параллелограмм приведён в верных пропорциях.
64=65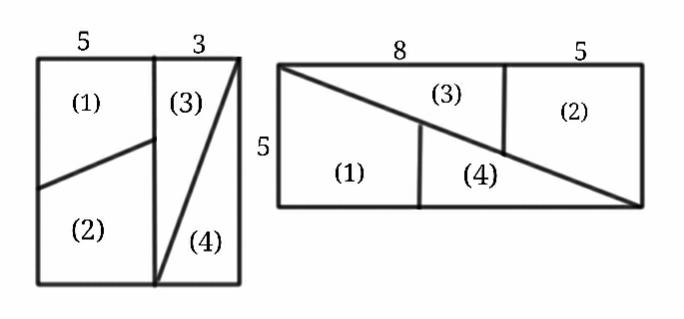
Квадрат со стороной, равной 8 единицам длины, разрезан на 4 части, как показано на рисунке выше. Из этих частей сложен прямоугольник. Основание этого прямоугольника оказалось равным 13 единицам длины, а высота – 5 единицам. Площадь исходного квадрата равна 64 квадратным единицам, а получившегося из него прямоугольника – 65 квадратным единицам. Значит, 64=65.
Ошибка: (1) и (4) части прямоугольника (отличного от квадрата) неплотно примыкают ко (2) и (3) частям его. Между ними образуется «щель» в виде вытянутого параллелограмма. Площадь этой щели как раз равна 1 квадратной единице.
Математические софизмы, какого бы вида они не были, всегда имеют логическое объяснение, и становятся сразу понятными, как только проанализировать их полностью. Даже имея некие «исключения» в виде неоднозначных и нерешенных софизмов, они все равно подтверждаются математическим путем.
Глава третья. Как создать софизм?
Принципы, по которым составляются софизмы.
Для начала берется какое-то равенство, неравенство, тождество,теорема или подчиняющееся логике выражение, и мы начинаем его менять — менять его стержень, подводя к использованию неправильных суждений. В математических софизмах это можно проворачивать согласно всем аксиомам, приведенным ниже.
Рассматривая каждый шаг преобразования, сможем найти «место» для ошибки. Хочу заметить, что большинство ошибок расположено в «спорных» случаях, в тех местах, где нужно помнить небольшие детали той или иной ситуации.
ОбреимовВ.И. в своей книге «Математические софизмы» обращается к следующим аксиомам:
-
Всякая величина равна самой себе;
-
Равные величины можно заменить равными;
-
Две величины, порознь равные третьей, равны между собой;
-
Если к равным величинам прибавить равные, то получатся равные суммы;
-
Если к равным величинам прибавить неравные, то получим неравные суммы, причем та сумма будет больше, которая получится от прибавления большей величины;
-
Если от равных величин отнимем равные, то получим равные разности;
-
Величина не измениться, если ее одновременно увеличить и уменьшить на одно и то же число:
-
Если равные величины умножить на равные же, то получим равные произведения;
-
Если равные величины помножить на неравные, то получим неравные произведения, причем то из произведений будет больше, которое поучится от умножения на большую величину;
-
Если равные величины разделим на равные, то получим равные частные;
-
Из двух отрицательных величин больше та, которой численное значение меньше;
-
Целое больше своей части;
-
Целое равно сумме всех своих частей;
-
Степени двух равных величин равны между собой;
-
Корни из двух равных величин равны между собой.8
Так же в его книге представлены общие «формулы», составления софизмов.
Логические софизмы — это какие-то истории, где рассуждения крутятся вокруг «стержня», который и является причиной рассуждений.
Создание своего софизма
Для начала стоит выбрать вид софизма. Я попробую взяться за алгебраические и логические софизмы.
Давайте начнем с алгебраических софизмов.
Возьмем один из софизмов, представленных ранее в части 2. Допустим, это будет софизм «Любое число равно числу, в два раза большему его». Первое, что мы можем сделать — это преобразовать конечный результат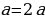
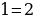
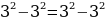
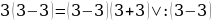
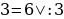
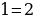
Мы получили новый софизм, ошибка которого заключается в том, что мы делим на (3-3), а эта скобка равна нулю = мы делим на ноль — чего делать, конечно же, нельзя.
Попробуем поиграть еще с одним софизмом.
Возьмем так же из части 2 софизм «2=3», но воспользуемся буквенным видом, представленном в книге «Математические софизмы» Обреимова В.И.9
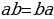















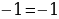
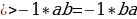
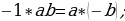
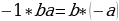
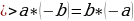
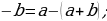
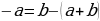
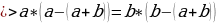
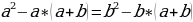
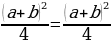
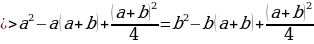
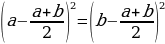
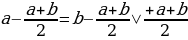
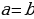
Теперь давайте в эту «формулу» подставим совершенно другие числа (не 2 и 3), пусть будет 5 и 7:
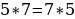
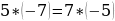
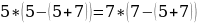
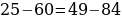
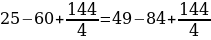
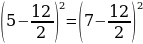
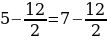
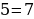
И вот наш «новый» софизм, основанный на уже имеющемся софизме.
Сейчас вам представиться софизм, который был самостоятельно составлен не из каких-то уже извесных «формул»:
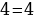
Разложим две части так, чтобы равенство было верным. И вычтем 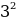
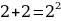
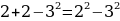
В левой стороне мы минус три возводим в квадрат, а в правой расскладываем по формуле разности квадратов:
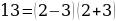
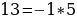
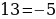
Ошибка в этом софизме довольно простая, но обычно многие ее допускают. Суть в том, что когда мы возводим в квадрат, минус в данном случае не принадлежит тройке, а играет роль именно знака.
Для логических софизмов нам нужно придумать логично-нелогичную сказку.
Вот первый вариант моей «сказки»:
На день рождения Оле подарили торт, разрезанный на двенадцать частей. К ней пришло пятеро друзей, она дала каждому по кусочку, следом пришли тетя, дядя, бабушка и дедушка, и ушло три человека. К тому времени подоспели еще пятеро гостей. И каждому досталось по кусочку. Но как такое может быть? Ведь кусочков было 12, а ели торт 15 человек.
В этом примере ошибка в том, что мы вернули три уже съеденых кусочка, такого, конечно же, не может быть.
И вот второй вариант, с теми же числами:
В концертном зале осталось двенадцать мест. Пришло шесть человек, они заняли свободные места, к первому звонку пришло еще четыре человека и вышло три. К началу концерта подоспели еще пять человек, сели на свободные места и три человека вернулись, заняв свои места. Вот так вот на твенадцати местах уместилось пятнадцать человек.
В этом случае можно рассуждать двояко либо кому-то правда не досталось места, либо же никто не говорил, какие именно пять человек пришли, но говориться, что три человека вернулись, то есть они могут быть в той пятерке, которая пришла.
Таким образом, для создания нового софизма нужно рассмотреть и понять уже известные нам. Но добиться чего-то совершенно нового очень и очень сложно.
Заключение.
Софизмы не новое понятие, пришедшее к нам от древнегреческих софистов. Ученные выделили ряд ошибок, на которых построенны софизмы.
Решение математических софизмов расширяет познание самой математики, ведь людой вид математических софизмов можно «решить» и зная ошибку ее не допустить в будущем.
Хотелось бы сказать пару слов о «создании» своего софизма.Во время работы над придумыванем софизма, мне было тяжело составить, что-то новое.
Занимаясь проектом, при решении задач на уроках я стала замечать места или случаи, где возможно было бы отклонится от правил. Не думаю, что те примеры можно считать за софизмы, ведь это просто ученические ошибки, но сама работа заставила меня видеть эти места.
Как выяснилось, малое количество людей знают, что такое софизм. Но старшие классы после объяснения лучше поняли принципы и смогли сами увидеть и указат ошибки (см. прил.).
Я считаю, что все мои цели и задачи, поставленные в начале работы, были достигнуты.
Приложение
Мне также было интересно, знают ли ученики разных возрастных категорий, что такое софизмы, и смогут ли они найти ошибки в математических, заведомо ложных, умозаключениях.
В рамках данного исследования ученикам 8 «Б» и 10 «В» классов (42 ученика) были предоставлены идентичные вопросники, включающие 3 вопроса:
1. Знакомо ли Вам понятие «софизм»? (Да/Нет)
2. Возьмём числовое равенство:
35+10-45=42+12-54.
Вынесем общие множители левой и правой частей за скобки.
Получим: 5(7+2-9)=6(7+2-9).
Разделим обе части этого равенства на общий множитель (заключенный в скобки).
Получаем 5=6.
Как Вы это объясните? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
3. Дано уравнение x-a=0.
Разделив обе части этого уравнения на x-a, получим, что 1=0.
Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Допущена ли здесь ошибка, и если да, то какая? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
Проанализировав ответы на вопросы, я получила следующие результаты:
1 вопрос: Знакомо ли Вам понятие «софизм»? (Да/Нет)
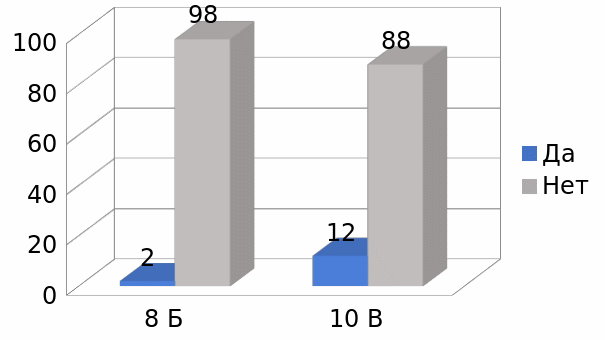
Из графика видно, что практически все ученики не знакомы с понятием софизма.
2 вопрос: Возьмём числовое равенство: 35+10-45=42+12-54.
Вынесем общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9).
Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5=6.
Как Вы это объясните? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
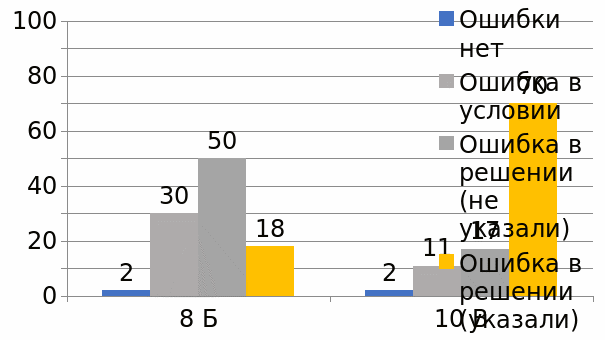
В этой задаче на внимательность нужно было найти конкретную математическую ошибку:7+2-9=0. На ноль делить нельзя.
С данной задачей справились 18% учеников 8 класса и 70%- 10 класса. При этом 50% восьмиклассников все же нашли наличие ошибки в решении, но не указали ее точно.
3 вопрос: Дано уравнение x-a=0.
Разделив обе части этого уравнения на x-a, получим, что 1=0.
Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Допущена ли здесь ошибка, и если да, то какая? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
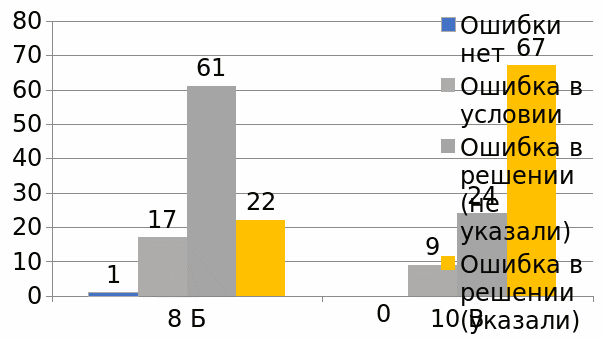
Ответом данной задачи было:
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.Верно на этот вопрос ответили 22% 8-классников и 67% 10-классников, при этом наличие ошибки отметили 100% учеников обоих классов, то есть явление софизма определили все!
Список литературы:
-
Игнатьев Е.И. Математическая смекалка. Занимательные задачи, игры фокусы, парадоксы – М., «Омега», 1994;
-
Нагибин Ф.Ф.,Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд.–М.: Издательство «Просвещение», 1988;
-
Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019;
-
Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. /А.Г.Мадера,Д.А. Мадера – М., Просвещение, 2003;
-
Обреимов В.Н.Математические софизмы — С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989.
1Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019; Обреимов В.Н. «Математические софизмы» — С.-Птербург Типография Ю.Н.Эрлик, Седовая, №9 1989; Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003
2Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд. – М.: Издательство «Просвещение», 1988.
3Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003.
4proza.ru
5Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд. – М.: Издательство «Просвещение», 1988.
6Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019
7Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003
8Обреимов В.Н. Математические софизмы — С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989
9Обреимов В.Н. Математические софизмы — С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989
Учительская газета, №45 от 6 ноября 2000. Читать номер
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям “очевидности”. Встречаются софизмы, содержащие и другие ошибки.
Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает необходимые в жизни навыки правильного мышления. Обнаружить ошибку в софизме – это значит осознать ее, а осознание ошибки предупреждает повторение ее в дальнейшем в других математических рассуждениях. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так и изучающий математику впоследствии проявит больше осторожности, чтобы не повторить осознанную ошибку.
Далее, что особенно важно, разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Когда изучающий математику разбирает софизм, он знает, что может попасть в западню, а поэтому старается обезвредить ее. Чтобы не попасть в ловушку, приходится очень внимательно продвигаться вперед и каждый шаг делать с большой осторожностью. Вопрос стоит так: кто кого подчинит себе, софизм ли разбирающего его, или наоборот. Значит, математические софизмы заставляют внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и полезно.
Наконец, разбор софизмов увлекателен. Только очень сухого человека не может увлечь интересный софизм. Как приятно бывает обнаружить ошибку в математическом софизме и тем как бы восстановить истину в ее правах. И чем труднее софизм, тем большее удовлетворение доставляет разбор его.
Если софизм “не поддается”, то надо обязательно обратиться за разъяснениями к учителю. Очень важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны и, может быть, даже вредны.
1. 4 руб. = 40000 коп. Возьмем верное равенство 2 руб. = 200 коп. и возведем его по частям в квадрат. Получится 4 руб. = 40000 коп. В чем ошибка?
2. 5 = 6. Попытаемся доказать, что 5 = 6. С этой целью возьмем числовое тождество: 35 + 10 – 45 = 42 + 12 – 54. Вынесем общие множители левой и правой частей за скобки. 5(7 + 2 – 9) = 6(7 + 2 – 9). Разделим обе части этого равенства на общий множитель. Получим 5 = 6. В чем ошибка?
3. 2 . 2 = 5. Найди ошибку в следующих рассуждениях. Имеем числовое тождество: 4 : 4 = 5 : 5. Вынесем за скобки в каждой части этого тождества общий множитель. Получим 4(1 : 1) = 5(1 : 1). Числа в скобках равны. Поэтому 4 = 5, или 2 . 2 = 5.
4. 2 = 3. Найди ошибку в следующем “доказательстве”. Разности 4 – 10 и 9 – 15 равны. К каждой из них прибавим одно и то же число 25/4, тогда получим равные числа, значит, 4 – 10 + 25/4 = 9 – 15 + 25/4. Это тождество можно переписать в таком виде: (2 – 5/2)2 = (3 – 5/2)2. Отсюда: 2 – 5/2 = 3 – 5/2, или 2 = 3.
5. 5 = 1. Желая доказать, что 5 = 1, будем рассуждать так. Из чисел 5 и 1 по отдельности вычтем одно и то же число 3. Получим числа 2 и -2. При возведении в квадрат этих чисел получаются равные числа 4 и 4. Значит, должны быть равны и исходные числа 5 и 1. Где ошибка?
6. 4 = 8. Возьмем систему уравнений:
2х + у = 8; х = 2 – у/2.
Решим эту систему способом подстановки. Получим: 4 – у + у = 8, т.е. 4 = 8. В чем здесь дело?
7. Все числа равны между собой. Попытаемся доказать, что все числа равны между собой. Пусть mn. Возьмем тождество: m2 – 2mn + n2 = n2 – 2nm + m2. Имеем (m – n)2 = (n – m)2. Отсюда m – n = n – m, или 2n = 2m, а значит, n = m. В чем ошибка?
8. Любое отличное от нуля число равно противоположному ему числу. Какая ошибка допущена в следующих рассуждениях? Возьмем произвольное, отличное от 0 число а. Обозначим его буквой х, х = а. Обе части этого равенства умножим на -4а. Получим -4ах = -4а2, или -4ах + 4а2 = 0. К обеим частям этого равенства прибавим х2. Получим х2 – 4ах + 4а2 = х2, или (х – 2а)2 = х2. Значит, х – 2а = х, но х = а, поэтому а – 2а = а, или
-а = а.
9. Любое число равно половине его. Возьмем два равных числа а и b, а = b. Обе части этого равенства умножим на а и затем вычтем из них по b2. Получим а2 – b2 = аb – b2, или (а + b) (а – b) = b(а – b). Отсюда а + b = b, или а + а = а, так как b = а. Значит, 2а = а, или а = а/2. Какая ошибка допущена в этих рассуждениях?
10. Отрицательное число больше положительного. Возьмем два положительных числа а и b. Сравним два отношения: а/-b и -а/b. Они равны, так как каждое из них равно -а/b. Можем составить пропорцию: а/-b = -а/b. Но если в пропорции предыдущий член первого отношения больше последующего, то и предыдущий член второго отношения больше своего последующего. В нашем случае а > -b, следовательно, должно быть -а > b, т.е. отрицательное число больше положительного. В чем ошибка?
11. Любое число равно числу, в два раза большему его. Пусть а – какое угодно число. Возьмем тождество: а2 – а2 = а2 – а2. В левой части его вынесем а за скобки, а правую часть разложим на множители по формуле разности квадратов. Тогда получим: (а – а)а = (а – а) (а + а). Упростив это тождество, получим а = 2а. В чем здесь ошибка?
12. Любое число равно нулю. Найди ошибку в таком рассуждении. Каково бы ни было число а, справедливы равенства: (+а)2 = а2 и (-а)2 = а2. Следовательно, (+а)2 = (-а)2, а значит, +а = -а, или а + а = 0, но тогда 2а = 0 и поэтому а = 0.
Из книги Ф. Нагибина “Математическая шкатулка”.
Что
такое софизм?
Софизм — (от греческого sophisma – уловка,
ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее
какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение,
противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда
содержит одну или несколько замаскированных ошибок.
Софизм как приём обучения был
введён древнегреческими софистами в греческих полисах ок. V в. до н.э. —
профессиональными учителями, обучавшими знатную молодежь красноречию,
ораторскому мастерству и искусству публичных дебатов в целях подготовки к
политической или иной карьере. В отличие от философов, занимавшихся научными
изысканиями в русле методологии институализированных философских школ, софисты
были личными наёмными учителями и опирались на плюралистическую методологию,
нацеленную на решение задач.
Аристотель называл софизмом «мнимые доказательства», в которых обоснованность
заключения кажется верной и обязана чисто субъективному впечатлению, вызванному
недостаточностью логического или семантического анализа. Убедительность на
первый взгляд многих софизмов, их «логичность» обычно связана с хорошо
замаскированной ошибкой:
Софистами называли группу древнегреческих философов
4-5 века до н.э., достигших большого искусства в логике. В период падения нравов
древнегреческого общества появляются так называемые учителя красноречия,
которые целью своей деятельности считали и называли приобретение и
распространения мудрости, вследствие чего они именовали себя софистами.
Кроме математических софизмов, существует множество
других. Нелепость таких утверждений понять гораздо проще, но это не делает их
менее интересными. Многие софизмы представляют собой игру, которая опирается на
игру с выражениями без всякого смысла. Причем эта игра лишена смысла и цели.
Поэтому именно такие софизмы кажутся особенно несерьезными и детскими.
Приведем несколько известных софизмов:
«Один рубль не равен ста копейкам»
Известно, что любые два равенства можно перемножить
почленно, не нарушая при этом равенства, т. е. если а = b и c = d, то ac = bd.
Применим это положение к двум очевидным равенствам:
1 рубль = 100 копейкам
10 рублей = 1000 копеек
Перемножая эти равенства почленно, получим
10 рублей = 100 000 копеек
и разделив последнее равенство на 10, получим, что
1 рубль = 10 000 копеек
Из данного софизма получается, что один рубль не
равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении
правила действий с именованными величинами: все действия, совершаемые над
величинами, необходимо совершать также и над их размерностями.
Следующий софизм:
«Полупустое и полуполное»
«Полупустое есть то же, что и полу полное. Если равны
половины, значит, равны и целые. Следовательно, пустое есть то же, что и
полное».
Понятно, что приведенное рассуждение неверно, так как
в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации
его применение бессмысленно.
«Крокодил»
На берегу реки стоят мать
с ребёнком, вдруг к ним подплывает крокодил и затаскивает ребёнка в воду.
Безутешная мать просит вернуть её чадо, на что крокодил отвечает, что согласен
отдать его целым и невредимым, если женщина правильно ответит на его вопрос:
«Вернёт ли он её ребёнка?». Понятно, что у женщины два варианта ответа — да или
нет. Если она утверждает, что крокодил отдаст ей ребёнка, то всё зависит от
животного — посчитав ответ правдой, похититель отпустит ребёнка, если же он
скажет, что мать ошиблась, то ребёнка ей не видать, согласно всем правилам
договора.
Отрицательный ответ
женщины всё значительно усложняет — если он оказывается верным, похититель
должен выполнить условия сделки и отпустить дитя, но таким образом ответ матери
не будет соответствовать действительности. Чтобы обеспечить лживость такого
ответа, крокодилу нужно вернуть ребёнка матери, но это противоречит договору,
ведь её ошибка должна оставить чадо у крокодила.
Стоит отметить, что
сделка, предложенная крокодилом, содержит логическое противоречие, поэтому его
обещание невыполнимо. Автором этого классического софизма считается оратор,
мыслитель и политический деятель Коракс Сиракузский, живший в V-м веке до нашей
эры.
Парадоксы
Парадокс (греч.
«пара» — «против», «докса» — «мнение»)
близок к софизму. Но от
него он отличается тем, что это не преднамеренно полученный противоречивый
результат.
Парадокс — странное,
расходящееся с общепринятым мнением, высказывание, а также мнение,
противоречащее (иногда только на первый взгляд) здравому смыслу.
Парадокс — это
когда невозможное возможно. Суть парадоксального суждения заключается в том,
что начав его рассматривать и исследовать, вы постепенно найдете в нем логику,
здравое зерно и придете к умозаключению, что невозможное возможно. Для лучшего
понимания какого-либо термина необходимо обратиться к его антониму.
Таковым для парадокса является
слово ортодокс – что значит традиционность, постоянство, проверенность
Самый известный
парадокс это :
«Парадокс
Зенона об Ахиллесе и черепахе».
Ахиллес и черепаха движутся по прямой в одну и ту же
сторону, черепаха находится на расстоянии 1000 метров впереди Ахиллеса. Ахиллес
бежит в 10 раз быстрее, чем ползёт черепаха.
Ахиллес никогда не догонит черепаху.
«Доказательство»
Ахиллес никогда не догонит черепаху, ведь пока он
пробежит 1000 метров до того места, где находилась черепаха, та уже отползёт на
100 метров вперёд. Когда же Ахиллес пробежит и эти 100 метров, черепаха
отползёт ещё немного дальше. Это будет продолжаться бесконечно: каждый раз,
когда Ахиллес бежит до места, где была черепаха, она уже отползёт на некоторое
расстояние.
«Парадокс
лжеца»
Критянин Эпименид сказал:
«Все критяне лжецы».
Эпименид сам критянин. Следовательно, он лжец.
Но если Эпименид лгун, тогда его заявление, что все
критяне лгуны — ложно.
Значит, критяне не лгуны.
Между тем Эпименид, как определено условием, критянин,
следовательно, он не лгун, и поэтому его утверждение «все критяне
лгуны» — истинно.
«Парадокс девочки и мальчика»
В теории вероятностей есть
парадокс, который называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые
он был сформулирован американским математиком Мартином Гарднером в одном из
номеров журнала «Scientific American».
Учёные спорят над
парадоксом уже несколько десятилетий и существует несколько способов его
разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный
вариант. В семье есть двое детей и точно известно, что один из них — мальчик.
Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый
взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо
девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей
существует четыре возможных комбинации полов детей — две девочки, два мальчика,
старший мальчик и младшая девочка и наоборот — девочка старшего возраста и
мальчик младшего.
Первую можно исключить,
так как один из детей совершенно точно мальчик, но в таком случае остаются три
возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик —
один шанс из трёх.
ГБОУ РХ СПО Хакасский политехнический колледж
Реферат
по теме:
Софизмы и парадоксы
в математике
Работу выполнила:
Шишигина Ирина,
студентки 2 курса гр. ЭП-21
Преподаватель:
Овчарук Любовь Павловна
Абакан 2015
Содержание
1. Введение……………………………………………………………………….3
2. Цели и задачи…………….…………………………..…….…………….….4
3. Понятие софизма…………..………………………..……..………….………4
4. Экскурс в историю…………………………………………………….….…5
5. Математические софизмы ……………………………………………….…6
- Алгебраические софизмы………..………………………………..……6
- «Один рубль не равен ста копейкам» …………………….………..…7
- « Если “a” больше “b”, то “a” всегда больше, чем “2b”»………….…8
- Геометрические софизмы ……………………………………………..8
- «Через точку на прямую можно опустить два перпендикуляра» ….8
- Арифметические софизмы……………………………………..………8
- «Дважды два равно пять» …………………………………………… 9
- Логические софизмы ……………………………………………….…. 9
- Многообразие парадоксов и их причины ………………..…………… .10
6.1 Парадокс Банаха – Тарского ……………………………………… 10
6.2 Задача о треугольнике ………………………………………….…. 10
6.3 Парадокс бесконечно малых величин ……………………………. 11
6.4 Парадокс изобретателя ……………………………..……………… 11
7. Заключение ………………………………………………………………..13
8. Литература…………………………………………………………….……13
ВВЕДЕНИЕ
Наверняка каждый человек хоть раз в жизни слышал подобную фразу: «Дважды два равно пяти» На самом деле, таких примеров можно привести много, но что все они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь шутка???
Именно эти вопросы мы хотим рассмотреть в нашей работе Математические софизмы
«Предмет математики настолько серьезен,
что полезно не упускать случая
сделать его немного занимательным»
Б. Паскаль
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Софизм — это то же надувательство, только выполненное намного изящнее и незаметнее, за что мы его и любим. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в софизмах выполняют «запрещенные» действия или не учитываются условия применимости теорем, формул и правил.
Софизмы имеют четкое логическое объяснение. Кроме того, с математическими софизмами мы встречаемся намного чаще, чем с обычными.
Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики и, кроме того, показывает, что математика – это живая наука. Надеемся, что наш проект будет интересен и принесёт пользу ребятам.
Актуальность выбранной темы заключается в том, что:
- Наше общество развивается большими темпами.
- Для развития производства требуются техники, инженеры, ученые, знания которых базируются на точных науках: математике, физике, химии.
- И эти науки надо не только знать, но и понимать.
Мы считаем, что софизмы развивают логику мышления, помогают лучше усвоить и разобраться в математике, прививают навыки правильного мышления.
Поэтому мы выбрали эту тему.
Основная гипотеза проекта
Если неточно знать формулировки теорем, математические формулы, правила и условия, при которых они выполняются, а также не анализировать построение чертежа к геометрической задаче, то можно получить абсурдные результаты, противоречащие общепринятым представлениям.
Цель нашей работы:
Познакомиться с софизмами, показать значимость математических софизмов
при изучении математики, показать как получаются абсурдные выводы. Важно четко понимать допущенные ошибки, иначе софизмы будут бесполезны.
Задачи:
- дать определение понятиям «софизм» и «парадокс», узнать в чём их отличие;
- классифицировать различные виды софизмов;
- понять, как найти ошибку в софизмах;
- составить компьютерную презентацию.
Методы исследования:
- Анкетирование;
- Анализ и контроль полученных результатов, классификация софизмов;
- Демонстрация полученных результатов в презентации;
- Выступление на конференции.
«Понятие софизма. Исторические сведения»
Понятие софизма
Софизм — (от греческого sophisma – уловка, ухищрение, выдумка, головоломка),
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного.
Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Разбор софизмов, прежде всего, развивает логическое мышление.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, и довольно тонкие ошибки.
Понимание ошибок в софизме помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
Мы проанализировали софизмы и выделили типичные ошибки в софизмах. Это:
- запрещенные действия,
- неточное использование условий теорем, формул и правил,
- ошибочный чертеж,
- опора на ошибочные умозаключения.
Нередко, ошибки, которые допускают в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах.
Основные создатели софизмов – древнегреческие ученые-философы, но, тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах.
Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.
Работая над проектом, мы обнаружили интересную формулу успешности софиста!*
Успешность софизма определяется несколькими составляющими:
a + b + c + d + e + f и определяется величиной этой суммы, где (a + с + е) составляет показатель силы диалектика, (b + d + f) есть показатель слабости его жертвы.
- а — отрицательные качества лица (нет развития способности управлять вниманием).
- b — положительные качества лица (способность активно мыслить)
- с — аффективный элемент в душе искусного диалектика
- d — качества, которые пробуждаются в душе жертвы софиста и омрачают в ней ясность мышления
- е — категоричность тона, не допускающего возражения, определённая мимика
- f — пассивность слушателя.
Экскурс в историю
Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества(5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространение мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия.
Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения.
* эту формулу нашли в Интернете на сайте http://pptonline.ru/slide/related/page/13/count/100/id/101563/category/1/cpages/10
Исторически сложилось, что с понятием софизма связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста- представить наихудший аргумент как наилучший путем хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. В Греции софистами называли и простых ораторов.
Известнейший ученый и философ Сократ поначалу был софистом, активно участвовал в спорах и обсуждениях софистов, но вскоре стал критиковать их учение. Такому же примеру последовали и его ученики (Ксенофонт и Платон).
Философия Сократа была основана на том, что мудрость приобретается с общением, в процессе беседы. Учение Сократа было устным, его и по сей день считают самым мудрым философом.
Что касается самих софизмов, то, пожалуй, самым популярным на тот момент в Древней Греции был софизм Евбулида : «Что ты не терял, ты имеешь. Рога ты не терял. Значит у тебя рога». Единственная неточность, которую возможно было допустить, то это — двусмысленность высказывания. Данная постановка фразы является нелогичной, но логика возникла намного позже, благодаря Аристотелю, поэтому, если бы фраза строилась так: «Все, что ты не терял. . .», то вывод стал бы логически безупречным.
Математические софизмы
Разбор и решение нестандартных математических задач помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам.
Однако следует помнить, что в математике важна аккуратность. Каждый шаг от одной логической конструкции к другой должен быть точным, тщательно выверенным. Один неверный переход может привести не просто к неточности, а к большой ошибке.
Мы предлагаем Вам вместе с нами попытаться разобраться с этим.
В нашей работе мы рассмотрим три типа математических софизмов: алгебраические, геометрические и арифметические.
- Алгебраические софизмы
Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
- «Один рубль не равен ста копейкам»
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е.
Если a=b,
c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
перемножая эти равенства почленно, получим
10 р.=100000 коп. (3)
и, наконец, разделив последнее равенство на 10 получим, что
1 р.=10 000 коп.
таким образом, один рубль не равен ста копейкам.
Где ошибка???
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство
10 р. =100 000 к . ,
которое после деления на 10 дает
1 р. = 10 000 коп.,
а не равенство 1р=10 000 к, как это записано в условии софизма.
Извлекая квадратный корень из равенства1 р. = 10 000 коп. получаем верное равенство 1р.=100 коп.
2) « Если “a” больше “b”, то “a” всегда больше, чем “2b”»
Возьмем два произвольных положительных числа a и b, такие, что a > b. Умножив это неравенство на b, получим новое неравенство ab > b·b, а отняв от обеих его частей a·a, получим неравенство ab-a·a > b·b — a·a, которое равносильно следующему:
a(b-a) > (b+a)(b-a). (1)
После деления обеих частей неравенства (1) на b-a получим, что
a > b+a (2),
А прибавив к этому неравенству почленно исходное неравенство a> b, имеем 2a >2b+a, откуда a > 2b. Итак, если a > b, то a > 2b.
Где ошибка?
Ошибка совершена при переходе от равенства (1) к (2). Т.к. a > b, то b — a<0, следовательно, при делении неравенства (1) на b – a, мы должны поменять знак неравенства на противоположный.
- Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
- «Через точку на прямую можно опустить два перпендикуляра»
Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС.
На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках
Е и Д. Соединим точки Е и Д прямыми с точкой В.
Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ перпендикулярна АС и ВД перпендикулярна АС.
Через точку В проходят два перпендикуляра к прямой АС.
Где ошибка?
Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит из одной точки на прямой нельзя опустить два перпендикуляра.
- Арифметические софизмы.
Арифметика — (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
- «Дважды два — пять!»
Возьмем в качестве исходного соотношения следующее очевидное равенство: 4:4= 5:5
После вынесения за скобки общего множителя из каждой части равенства
будем иметь:
4∙(1:1)=5∙(1:1)
или
(2∙2)(1:1)=5(1:1)
Наконец, зная, что 1:1=1, мы из предыдущего получаем:
2∙2=5
Где ошибка?
Нельзя выносить множитель за скобки так, как было сделано. 4∙(1:1)=5∙(1:1)
Можно так 4 (1:4) и 5 (1:5).
Логические софизмы
Кроме математических софизмов, существует множество других. Понять абсурдность таких утверждений проще, но от этого они не становятся менее интересными. Очень многие софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными.
Полупустое и полуполное
«Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное».
Не знаешь то, что знаешь
«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».
Лекарства
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
Многообразие парадоксов и их причины
Парадоксы – это неожиданные утверждения, противоречащие здравому смыслу или общепризнанным научным теориям. Очень часто их рассматривают как ошибки, хотя в большинстве случаев они таковыми не являются. Обычно парадоксы построены на логически верных заключениях, но их противоречивый результат не является преднамеренным (этим они отличаются от софизмов). Парадоксы известны науке уже более двух тысяч лет. В античные времена были описаны многие парадоксы и для некоторых из них ученые до сих пор не могут найти объяснения и решения. Открываются парадоксы и в наши дни. Обычно подобные открытия сопровождаются кризисами в науке, разрушением старых, проверенных временем теорий и попытками создать новые, которые способны объяснить появившиеся противоречия. Парадоксы присутствуют везде – и в повседневной жизни, и в науке. Практически в каждой научной области исследования существуют свои парадоксы.
Парадоксы обнажают глубинные течения познавательного процесса. Возвещая о назревшем неблагополучии в науке, они вместе с этим решительно продвигают ее вперед и именно тем, что приносят новые, еще более парадоксальные идеи.
Парадоксы математические
Существуют парадоксы в математике. И вот, действительно, самое парадоксальное — это то, что в математике вообще есть парадоксы.
1. Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям. Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике)
2. Задача о треугольнике.
Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.
Разгадка простая: первый треугольник немного «вогнут», а второй — слегка выпуклый. В этом можно убедиться, сравнив наклон гипотенузы синего и жёлтого кусочков: у жёлтого наклон = 0.375, а у синего — 0.4. Получается, что общие площади верхнего и нижнего треугольников всё-таки различаются, а разница как раз составляет одну клетку!
3. Парадокс бесконечно малых величин
Математический кризис в этой области существовал в период XVII — XVIII веков.
Бесконечно малые — это переменные величины, стремящиеся к нулю, или, если быть точнее, к пределу, равному нулю. Проблема состояла в их туманном понимании: то они рассматриваются как числа равные нулю, то как ему неравные. Причем, при таком подходе, люди рассматривали их как постоянные величины. Тогда из этого названия таких величин следует, что бесконечное является чем-то завершенным.
Кризис перестал быть таковым после создания теории пределов в начале XIX века французским математиком Огюстеном Луи Коши (1789 — 1857). С того момента бесконечно малые величины рассматриваются как постоянно изменяющиеся, а не постоянные, стремящиеся к пределу, но никогда его не достигающие. Постоянно изменяющиеся числа!
4. Парадокс изобретателя
Ситуация, когда доказать более сильное утверждение легче, чем более слабое, и называется парадоксом изобретателя. Он был известен еще и древним мыслителям, но придумал это название в начале XX века венгерский математик Д. Пойа, сказав о парадоксе следующие слова: «Легче доказать более сильную теорему, чем более слабую». Этот парадокс существует не только в математике, но и в других областях, в том числе и в жизненных ситуациях. Такое же название (и по праву) получили ситуации, когда решить более общую задачу легче, чем более узкую. Прием, позволяющий это сделать, заключается в том, чтобы свести задачу к более общей, относительно которой исходная задача будет являться лишь частным случаем. Приведу один пример:
В III веке до н. э. тиран города Сиракузы Гиерон поручил своему подданному и близкому родственнику Архимеду определить, не подмешано ли к его золотой короне, изготовленной ювелирами, менее благородное серебро. Эту частную задачу Архимед смог решить лишь как общую (т.к. о химическом анализе тогда еще и не помышляли; к тому же корону разрушать было нельзя), выявив закон «подъемной силы», то есть силы Архимеда, действующей на погруженное в жидкость тело.
Таким же образом появились на свет в математике интегральное (выросшее из изобретенного древнегреческим математиком Евдоксом Книдским (около 408 — около 355 до н. э.) метода «исчерпывания») и дифференциальное (когда Лейбниц Готфрид Вильгельм (1646 — 1716) долго бился на задачей проведения касательной к кривой в заданной точке, сведя ее к проведению секущей через две бесконечно близкие точки) исчисления, в науке изобретена пастеризация и многое-многое другое.
Заключение.
О математических софизмах и парадоксах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые софизмы и парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день.
Математические софизмы – это лишь часть одного большого течения. Поиск заключенных в софизме ошибок, ясное понимание их причин ведет к осмысленному изучению математики. Обнаружение и анализ ошибки, заключенной в софизме, очень часто оказывается более поучительным, чем просто разбор решений «безошибочных» задач. Эффектная демонстрация «доказательства» явно неверного результата, демонстрация того, к какой нелепице приводит пренебрежение каким-либо математическим правилом, и последующий поиск и разбор ошибки, позволяют понять и «закрепить» математическое правило или утверждение.
Некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли нам разобраться, откуда же все-таки началась история софизмов.
Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научится искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Прослеживая историю математики, можно сказать, что во все времена математику спасала какая-нибудь новая идея. Она придавала математике строгость, восстанавливая ее авторитет. Поэтому не стоит бояться парадоксов, ибо они являются двигателями науки.
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
Помимо основных целей, поставленных в начале работы, мы преследовали еще одну: прикосновение к тому, с чем сталкивались наши далекие предки, к теме, которая имеет исторические корни. Нами были рассмотрены примеры наиболее известных софизмов и парадоксов.
В процессе работы над проектом мы столкнулись с софизмами, в которых не смогли разобраться из-за недостаточного багажа знаний по математике. Мы будем пополнять знания на уроках математики, и вернемся к этим вопросам. Поэтому тема нашей работы далеко не исчерпана. Мы рассмотрели лишь некоторые, самые известные примеры софизмов. На самом деле их намного больше. Мы продолжим изучение этой темы в будущем.
А закончить я бы хотела словами А. Д. Александрова «Математика учит точности мысли, подчинению логике доказательства, понятию строго обоснованной истины, а всё это формирует личность, пожалуй, больше, чем музыка».
Список литературы
1. А. Г. Мадера, Д. А. Мадера «Математические софизмы», Москва, «Просвещение», 2003г.
2. Брадис В. М., Минковский В. Л., Харчева Л. К. «Ошибки в математических рассуждениях».
3. Перельман Я. И. «Занимательная математика».
4. Новосёлов М. М. «Абстракция множества парадокс Рассела». «Вопросы философии. 2003г. №7.
5. Аменицкий Н. «Математические развлечения и любопытные приёмы мышления. М.,1912г.
6. Горячев Д. Н., Воронец А. Н. «Задачи, вопросы и софизмы для любителей математике», М., 1966.
7. Лямин А. А. «Математические парадоксы и интересные задачи», М., (1911г.) 2010 г.
8.http://www.peterlife.ru/download%20free%20online/humanities/fl _5_a5.htm
9. http://www.tmn.fio.ru/works/60x/306/06_2.htm
10.http://www.golovolomka.hobby.re/books/gardner/gotcha/ch2/02.html
Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа №8 г. Белорецк
муниципального района Белорецкий район
Республики Башкортостан
III МЕЖРЕГИОНАЛЬНАЯ НАУЧНО – ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ
«ЕВРОПА – АЗИЯ. ОТКРЫВАЯ ГОРИЗОНТЫ»
Направление исследования: «Математика»
Тема: «Математические софизмы»
Автор работы: Кривошеева Екатерина Игоревна, обучающаяся 6 А класса МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ
Руководитель: Лукманова Гульсина Хакимовна, учитель математики МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ
2018
Оглавление
Введение…………………………………………………………………..3 стр.
ГЛАВА 1 Исторические условия возникновения софизмов ………..…5 стр. 1.1 Понятие софизма. Из истории возникновения софизмов…….…5 стр. 1.2 Классификация математических софизмов.………..…………..……7 стр.
Выводы по главе 1…………………………………………………….8 стр.
ГЛАВА 2 Исследование в сфере учебной деятельности
2.1 Классификация ошибок и их причины….. ………………………9 стр.
2.2 Анализ ошибок учащихся по математике…………………….….9 стр.
Выводы по главе 2……………………………………………………10 стр.
Заключение…………………………………..……………………………11 стр.
Список источников литературы и интернет – ресурсов.………….…..12 стр. Приложение «Классификация математических софизмов с примерами » Приложение «Классификация ошибок и их причин» Приложение «Результаты исследования»
Приложение «Анализ ошибок учащихся по математике»
Приложение «Анкета»
Введение
«Правильно понятая ошибка — путь к открытию»
И. П. Павлов
Знаменитый комик Чарли Чаплин сказал: «Способность думать, подобно игре на скрипке или рояле, требует ежедневной практики». Невозможно с этим не согласиться! Мыслительная деятельность человека − своеобразный инструмент, пользуясь которым, можно добиться духовных, нравственных, научных высот. Такое понятие, как «софизм» бесспорно свидетельствует о блестяще развитом уме и логике владеющего им человека.
Актуальность исследования. Наше общество развивается большими темпами, и все больше требуются техники, инженеры, ученые, знания которых базируются на точных науках: математика, физика, химия. Но эти науки надо не только знать, но и понимать. Для лучшего усвоения математики существуют софизмы. Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме — это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.
Целью настоящей работы как раз является показать значимость математических софизмов при изучении математики, их роль в формировании полноценной личности, способной адаптироваться в условиях современного общества.
Гипотеза: если неточно знать формулировки определений, математические формулы, правила и условия, при которых они выполняются, а также не анализировать построение чертежа к геометрической задаче, то можно получить абсурдные результаты, противоречащие общепринятым представлениям.
Задачи исследования:
-
Узнать, что называют софизмами и выяснить исторические условия возникновения софизмов; выяснить, какие виды математических софизмов бывают;
-
Рассмотреть влияние софизмов в математике, проанализировать и классифицировать ошибки в работах учащихся по математике;
-
Научиться самой обосновывать свои ошибки и познакомить своих одноклассников с софизмами и показать, что они встречаются чаще, чем они думают, просто они об этом не задумываются.
Предмет исследования: математические софизмы.
Объект исследования: ошибки учащихся в работах по математике.
В ходе исследования решались следующие проблемные вопросы:
-
Как появились софизмы?
-
Какие виды математических софизмов бывают?
-
В каких заданиях и как делают «математические» ошибки учащиеся?
-
Как использование софизмов помогает в понимании математики?
-
Как научиться «видеть» ошибки?
Чтобы достичь своей цели, использовались такие методы исследования: изучение литературы, сбор информации, анкетирование учащихся, обработка данных, составление таблиц и диаграмм, просмотр сайтов в Интернете.
Практическая значимость: тема исследования я считаю, значима, так как понимание математики пригодится в жизни и в первую очередь для успешной учебы в школе, надо не только точно знать правила и формулы, но уметь находить свои ошибки и ошибочные рассуждения.
ГЛАВА 1 Исторические условия возникновения софизмов 1.1 Понятие софизма. Из истории софизмов.
Софизмы… Редко кто встречался с этим понятием в жизни.
В самом начале своей работы, мы выяснили, а знают ли другие школьники о софизмах. Поэтому провели с руководителем анкету, на вопросы которой ответили 40 учеников 6 классов. И я выяснила, что практически с понятием софизмов они не знакомы. Тогда мы привели примеры известных софизмов: «Дважды два равно пяти» или хотя бы: «Два равно трем». И снова лишь 17% опрошенных ответили, что слышали о них, 27 % — считают, что встречались с софизмами на уроках математики, 30 % считают, что в повседневной действительности встречаются с софизмами.
Так что же это такое?
Софизм — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.
Софизм — (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. (Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.)
Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.
Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашла ошибку в софизме, значит, ты ее осознала, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.
Софизмы появились в Древней Греции. Они тесно связаны с философской деятельностью софистов. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса.
Аристотель называл софизмами «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению.
Вот один из древних софизмов («рогатый»), приписываемый Эвбулиду: «Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога». Здесь маскируется двусмысленность большей посылки. Если она мыслится универсальной: «Всё, что ты не терял…», то вывод логически безупречен, но неинтересен, поскольку очевидно, что большая посылка ложна; если же она мыслится частной, то заключение не следует логически. Последнее, однако, стало известно лишь после того, как Аристотель создал логику.
Этапы возникновения софизмов
1. Первая в истории проба проведения «логической профилактики» в математике принадлежит гениальному древнегреческому математику — Эвклиду. Он был автором первого из известных сборников математических софизмов и парадоксов (сборник «Псевдарий»).
2. Софистам идейно противостоял знаменитый греческий философ Сократ. Дискуссия между софистами и Сократом о существовании объективной истины зародилась приблизительно в V в. до н.э.
3. Наши дни: появление мысли о том, что человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искуснее замаскирована ошибка, тем больше удовлетворения приносит он тому, кто разгадал его, так как это — маленькое открытие и прекрасная школа, культура математических вычислений.
1.2 Классификация математических софизмов
Распределим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики.
В этом разделе работы я рассмотрю три типа математических софизмов: алгебраические, геометрические и арифметические (Приложение 1)
Арифметические софизмы — числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Пример: «Число, которое равно другому числу, и больше его, и меньше одновременно».
Алгебраические софизмы — намеренно скрытые ошибки в уравнениях и числовых выражениях. Пример: «Дважды два равно пяти».
Геометрические софизмы — это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними. Пример: «Спичка вдвое длиннее телеграфного столба».
Выводы по главе 1
Софизмы есть смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.
Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика — это целая наука, а именно математические софизмы — это лишь часть одного большого течения.
Очень важно, чтобы человек умел выявлять свои и чужие ошибки, учился избегать их.
ГЛАВА 2 Исследование в сфере учебной деятельности
2.1 Классификация ошибок и их причин.
Основные ошибки в математических софизмах (Приложение 2)
-
Деление на 0;
-
Неправильные выводы из равенства дробей;
-
Неправильное извлечение квадратного корня из квадрата выражения;
-
Нарушения правил действия с именованными величинами;
-
Путаница с понятиями “равенства” и “эквивалентность” в отношении множеств;
-
Не правильное использование теорем;
-
Проведение преобразований над математическими объектами, не имеющими смысла;
-
Неравносильный переход от одного неравенства к другому;
-
Выводы и вычисления по неверно построенным чертежам;
-
Ошибки, возникающие при операциях с бесконечными рядами и предельным переходом.
2.2 Анализ ошибок учащихся по математике
Чтобы показать и подтвердить значимость софизмов в жизни, мы провели исследовательскую работу в сфере учебной деятельности (Приложение 3, 5).
Данная работа была направлена: на развитие умения находить ошибку, анализировать и устранять ее; на развитие логического мышления; на формирование математической грамотности учащихся.
Исследование проводилось среди учащихся шестых классов. В 6 Б классе был проведен урок – презентация, посвященный алгебраическим софизмам по теме «Распределительное свойство умножения», а в 6 А данного урока не проводилось. Затем по этой теме была проведена самостоятельная работа. По итогам самостоятельных работ средние баллы в каждом из классов разошлись. В 6 Б классе средний балл был равен – 3,4, а в 6 А классе – 3,2. Только два учащихся (10%) 6 Б класса допустили ошибку по данной теме, когда в 6 А ошибки допустили 4 человека (21%). Все полученные данные мы оформили в виде диаграмм (приложение 3), которые наглядно показали нам различия по уровню усвоения темы самостоятельной. Таким образом, проанализировав полученные результаты, мы сделали вывод, что ученики, разобравшие варианты возможных ошибок, научились находить и устранять их. Ученики, не получившие данной информации, допустили различные ошибки по данной теме.
Также в своей работе мы провели анализ ошибок в работах учащихся 6 классов по математике. Как я уже отмечала ранее, неточное знание формулировок, правил и условий, при которых эти правила выполняются, приводят учащихся к неправильным, а иногда и абсурдным результатам.
В настоящем исследовании рассмотрели некоторые ошибки из контрольных работ обучающихся по математике (приложение 4).
Выводы по главе 2:
По результатам анализа ошибок, допущенных учащимися 6 классов в тестовых работах по математике, можно сделать вывод, что поверхностное изучении теории (а чаще её незнание) приводит к абсурдным результатам. Софизмы наглядно показывают, почему это происходит.
Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.
Заключение
Исследовать софизмы действительно очень интересно и необычно. Порой сама попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научиться грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку.
В своей работе мы доказали, что софизмы являются не просто интеллектуальным мошенничеством, а важным двигателем человеческой мысли. Показали практическое применение софизмов и их актуальность и в наше время. Мы рассмотрели математические софизмы с точки зрения их важности для изучения математики. Вот почему имеет первостепенное значение глубокое изучение школьной математики. И математические софизмы вам покажут, как важно строго соблюдать правила и формулировки теорем при логических умозаключениях.
«Решайте задачи и не бойтесь трудностей. Преодоление их вам доставит не только глубокое удовлетворение, но и большую радость, так как «в математике есть своя красота, как в поэзии и музыке» (Н.Е.Жуковский).
«Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным». Б. Паскаль
Список источников литературы и интернет ресурсов:
-
Ахманов А.С., Логическое учение Аристотеля, М., 1960г.
-
Брадис В.М., Минковский В.Л., Еленев Л.К., Ошибка в математических рассуждениях, 3 изд., М., 1967г.
-
Брутян Г., Паралогизм, софизм и парадокс//Вопросы философии, 1959г. № 1 с. 56-66.
-
Гарднер Мартин. Математические головоломки и развлечения.М.: Оникс, 1994г.
-
Глейзер Г.И. История математики в школе. М.:Просвещение, 1982г.
-
Кордемский Б.А. Великие жизни в математике. М.:Просвещение, 1995г.
-
Р.Курант, Г.Роббинс. Что такое математика? М.-.МЦНМО, 2004
-
Морозов И.А., О научном значении математических софизмов// Известия научного института им. П.Ф.Лесгафта, Пг., 1919г., с. 193-207.
-
Л.Ф.Пичурин. За страницами учебника алгебры. М. -.Просвещение, 1991г.
-
Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.
-
Софизмы http://sophisms.ucoz.ru/index/geometricheskie_sofizmy/0-9 (15.10.18г)
-
Софизмы http://sofizmy.narod.ru/ (20.10.18г)
Приложение 1
Классификация математических софизмов с примерами
Алгебраические софизмы. Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Приведем примеры таких софизмов.
1. «Сочетательное и переместительное свойства алгебраической суммы не имеют места» Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е. S=1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 +… (1)
И попробуем найти значение этой суммы. Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е. S=1 — (1 — 1) — (1 — 1) -…=1 – 0 – 0 — …= 1
Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда S= -1 +1 – 1 + 1 – 1 + 1 — …= -1 +(1-1)+(1-1)+…=-1+0+0+…= -1.
Итак, по-разному переставляя слагаемые суммы (1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых, а сочетательное и переместительное свойства алгебраической суммы не имеют места.
Где ошибка??? Данное свойство суммы может оказаться неверным, если некоторые члены суммы сгруппированы иначе.
2. «Дважды два равно пяти»
Имеем числовое равенство (верное): 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5, или 2 * 2=5.
Где ошибка? Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4:4=5:5.
3. «Отрицательное число больше положительного»
Возьмем два положительных числа а и с. Сравним два отношения:
а: (-с) и -а : с
Они равны, так как каждое из них равно –(а:с). Можно составить пропорцию:
а: (-с) = (-а) : с
Но, если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего.
В нашем случае а -с, следовательно, должно быть -ас, т.е. отрицательное число больше положительного.
Где ошибка??? Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.
« Спичка вдвое длиннее телеграфного столба»
Пусть а дм— длина спички и b дм — длина столба. Разность между b и a обозначим через c . Имеем b — a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b2 — ab = ca + c2. Вычтем из обеих частей bc. Получим: b2— ab — bc = ca + c2 — bc, или b(b — a — c) = — c(b — a — c), откуда b = — c, но c = b — a, поэтому b = a — b, или a = 2b.
Где ошибка??? В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.
Арифметические софизмы. Арифметика — (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы? Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Приведем примеры таких софизмов.
1. « 4 руб. = 40000 коп.» Возьмём верное равенство: 2руб.=200 коп. и возведём его по частям в квадрат. Мы получим: 4 руб.=40 000 коп. В чем ошибка?
В чем ошибка? Возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.
2.«Один рубль не равен ста копейкам»
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1) 10р.=10*100коп.(2)
перемножая эти равенства почленно, получим 10 р.=100000 коп. (3)
и, наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам.
Где ошибка??? Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 р. =100 000 к . , которое после деления на 10 дает
1 р. = 10 000 коп., (*) а не равенство 1р=10 000 к, как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство 1р.=100 коп.
-
«Число, равное другому числу, одновременно и больше, и меньше его»
Возьмем два произвольных положительных равных числа А и В и напишем для них следующие очевидные неравенства:
А-В и В-В. (1) Перемножив оба этих неравенства почленно, получим неравенство А*ВВ*В, а после его деления на В, что вполне законно, ведь В0, придем к выводу, что АВ. (2) Записав же два других столь же бесспорных неравенства В-А и А-А (3)
Аналогично предыдущему получим, что В*АА*А, а разделив на А0, придем к неравенству АВ. (4) Итак, число А, равное числу В, одновременно и больше, и меньше его.
Где ошибка??? Здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств.
Проделаем правильные преобразования неравенств. Запишем неравенство (1) в виде А+В0, В+В0. Левые части этих неравенств положительны, следовательно, умножая почленно оба эти неравенства (А+В)(В+В)0, или А-В, что представляет собой просто верное неравенство.
Аналогично предыдущему, записывая неравенства (3) в виде (В+А)0, А+А0, получим просто верное неравенство В-А.
Приложение 2
Классификация ошибок и их причин
Логические ошибки. Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может быть сведён к нарушению правил силлогизма. (Силлогизм — тонкий, хитрый ход (для подтверждения или доказательства чего-либо)).
Терминологические ошибки. Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы (всякое quaternio terminorum предполагает такое словоупотребление);
В устную речь математиками введены такие слова как «сумма», «произведение», «разность». Так — сумма произведения два на два и пятерки, а — удвоенная сумма двух и пяти.
Более сложные софизмы проистекают из неправильного построения целого сложного хода доказательств, где логические ошибки являются замаскированными неточностями внешнего выражения. Всякое беспорядочное следование мыслей представляет частный случай этой ошибки.
Психологические причины. Бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма поэтому предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.
Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софизму, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignava ratio) и т. п. Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм.
Аффективные причины ошибок. Сюда относятся трусость в мышлении — боязнь опасных практических последствий, вытекающих от принятия известного положения; надежда найти факты, подтверждающие ценные для нас взгляды, побуждающая нас видеть эти факты там, где их нет, любовь и ненависть, прочно ассоциировавшиеся с известными представлениями, и т. д. Желающий обольстить ум своего соперника софист должен быть не только искусным диалектиком, но и знатоком человеческого сердца, умеющим виртуозно распоряжаться чужими страстями для своих целей
Волевые причины. При обмене мнений мы воздействуем не только на ум и чувства собеседника, но и на его волю. Во всякой аргументации (особенно устной) есть элемент волевой — императивный — элемент внушения. Категоричность тона, не допускающего возражения, определённая мимика и т. п. () действуют неотразимым образом на лиц, легко поддающихся внушению, особенно на массы. С другой стороны, пассивность (
) слушателя особенно благоприятствует успешности аргументации противника. Таким образом, всякий софизм предполагает взаимоотношение между шестью психическими факторами:
. Успешность софизма определяется величиной этой суммы, в которой
составляет показатель силы диалектика,
есть показатель слабости его жертвы. Прекрасный психологический анализ софистики даёт Шопенгауэр в своей «Эристике» (перев. кн. Д. Н. Цертелева). Само собой разумеется, что логические, грамматические и психологические факторы теснейшим образом связаны между собой; поэтому софизм, представляющий, например, с логической точки зрения quaternio ter.
Приложение 3
Результаты исследования
Средний балл выполнения самостоятельной работы
в 6 классах
Диаграмма 1 Средний балл выполнения самостоятельной работы
в 6 классах
Классификация ошибок в работах учащихся 6 классов
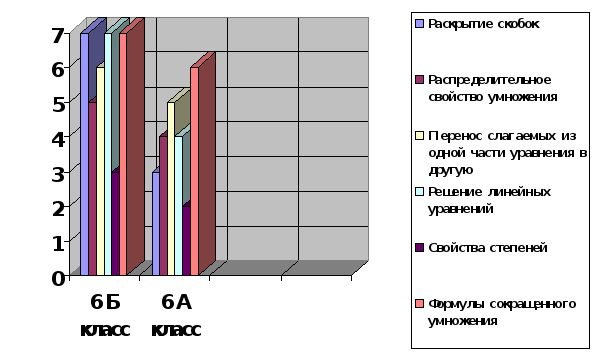
Приложение 4
Анализ ошибок учащихся по математике
6 класс Выражения, тождества, уравнения
1.Ученики знают распределительное свойство умножения относительно сложения и вычитания.
Правило: а(b + с) = ab + ас а(b — с) = аb — ас.
Ошибки: — 2(а + 4) = -2а + 8; — 2(а — 4) = -2а — 8.
«Минус» и «плюс» в формулах сыграли плохую роль после того, как ученики познакомились с отрицательными числами. Надо быть внимательными.
2.Правила раскрытия скобок все знают, а при применении забывают и выполняют его только для первого слагаемого.
Правило: + (а -b + с) = а — b + с; -(а-b- с) = -а + b — с.
Ошибки: — (5a + b- х) =-5а+ b- х.
3.Правило переноса слагаемых из одной части уравнения в другую.
Правило: при переносе слагаемых из одной части уравнения в другую их знаки меняются на противоположные. 5х — 7 = 2x + 9;
Ошибки: 5х + 2x = 9 — 7.
4.Решение линейного уравнения. Привычка из начальной школы большее число делить на меньшее «заставляет» при решении уравнений учащихся совершать ошибку, а надо всего то знать правило нахождения неизвестного множителя или правило деления обеих частей уравнения на одно и то же, отличное от нуля число. Правило ах = b; (а не равно 0) х = Ошибки: 6х =2; х = 3
5. Правило: при раскрытии скобок с применением распределительного свойства умножения нужно каждое слагаемое умножить на число.
2х — 5(х + 2) = 2х — 5х — 10;
Ошибки: 2х — 5(х + 2) = 2х — 5х +10.
Приложение 5
Анкета (Перед уроком – презентацией)
- Укажите ваш возраст.
- Укажите ваш пол.
- Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем»?
- Знакомо ли вам понятие «Софизм»?
(После урока – презентации)
- Постарайся дать определение этого понятия самостоятельно.
- Надо ли знакомить учащихся на уроках с софизмами?
- Как ты думаешь, для чего нужны софизмы?
- Хотел бы ты больше узнать о софизмах?
- Как ты считаешь, какую роль для тебя может сыграть более глубокое знакомство с софизмами?
26