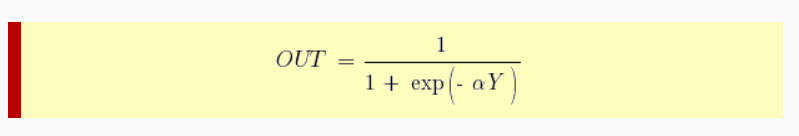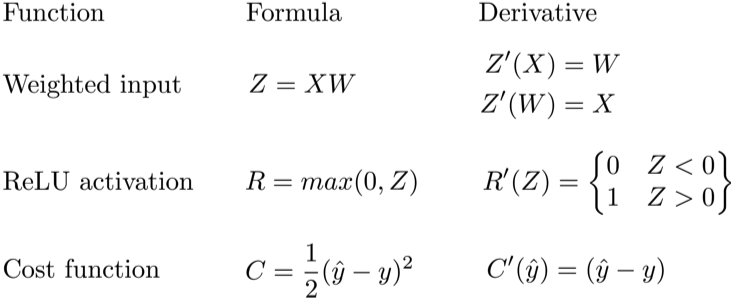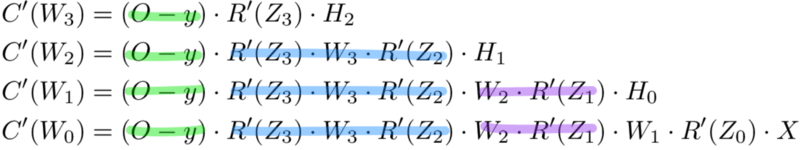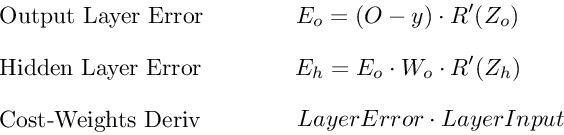Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
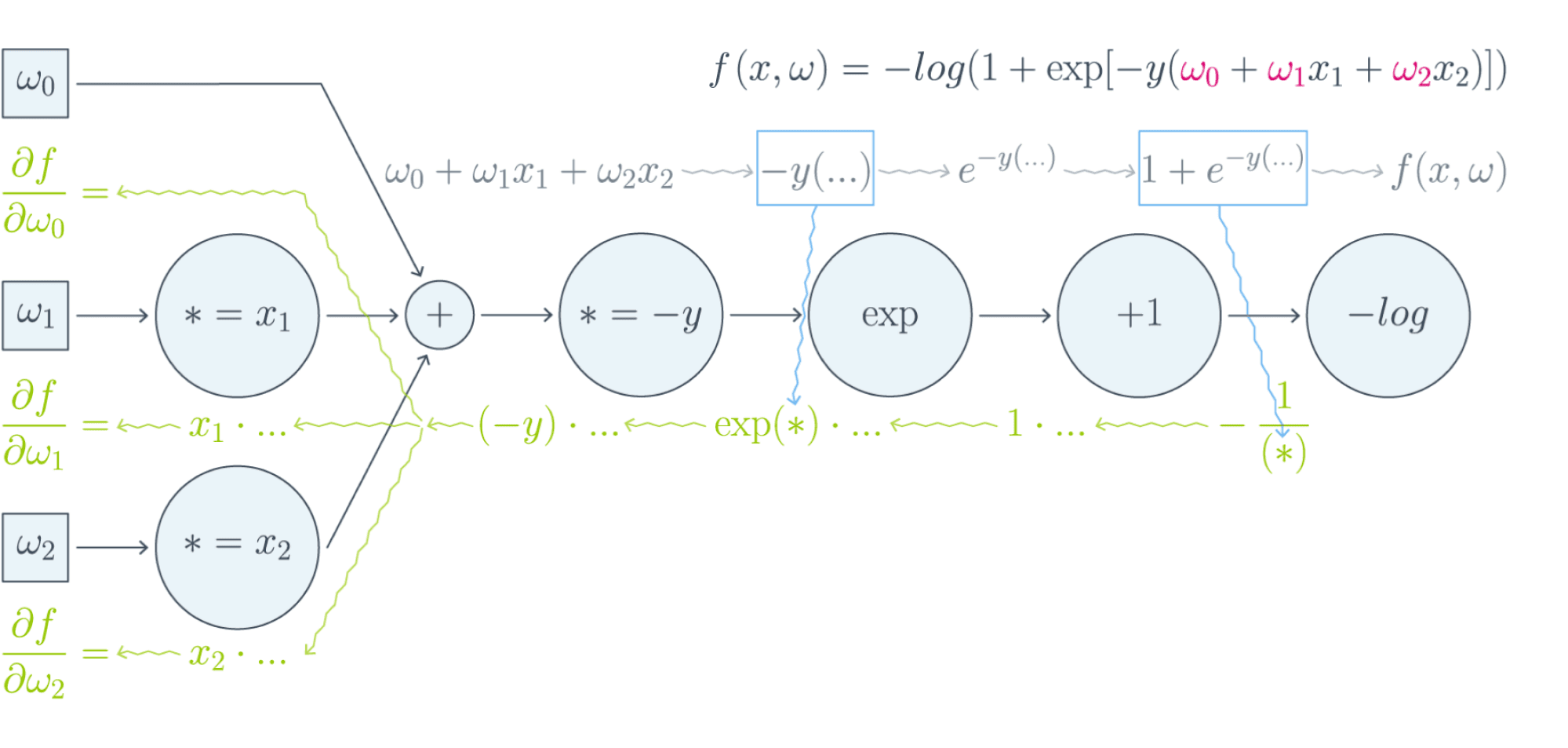
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
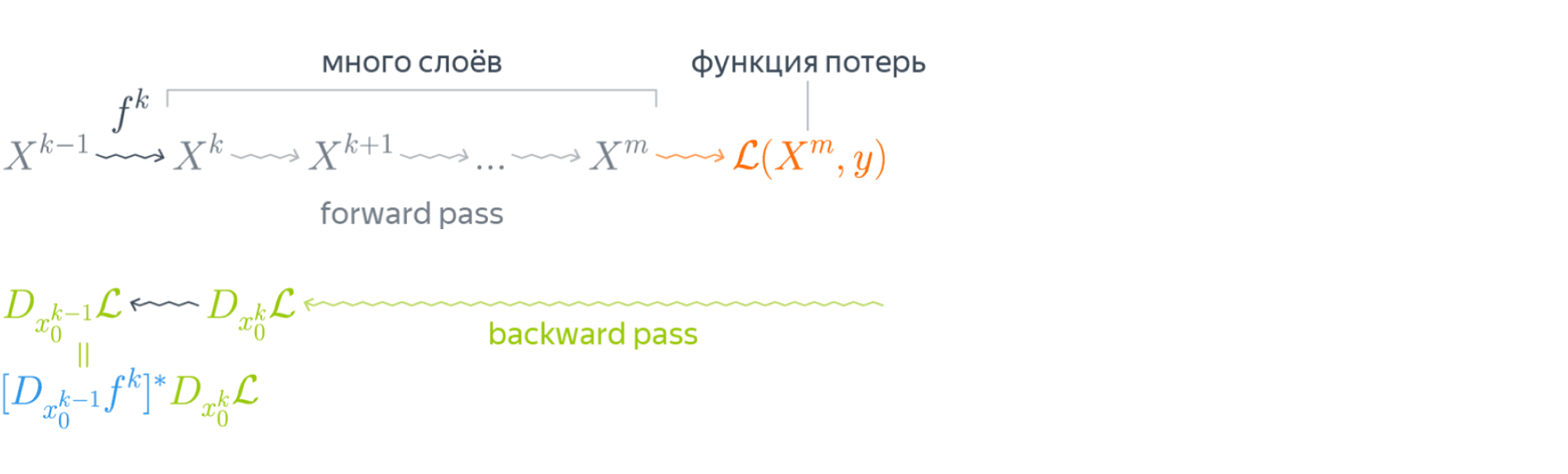
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
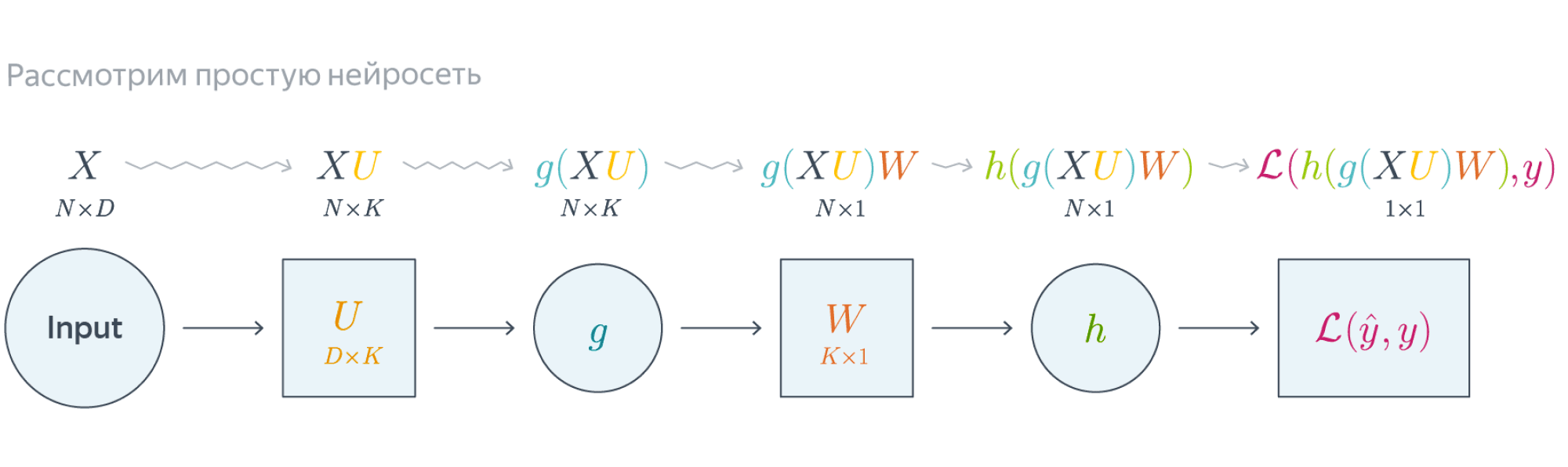
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
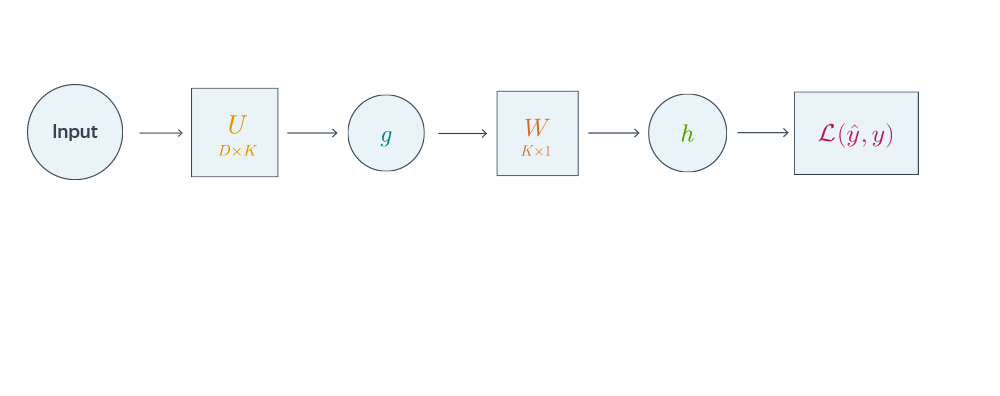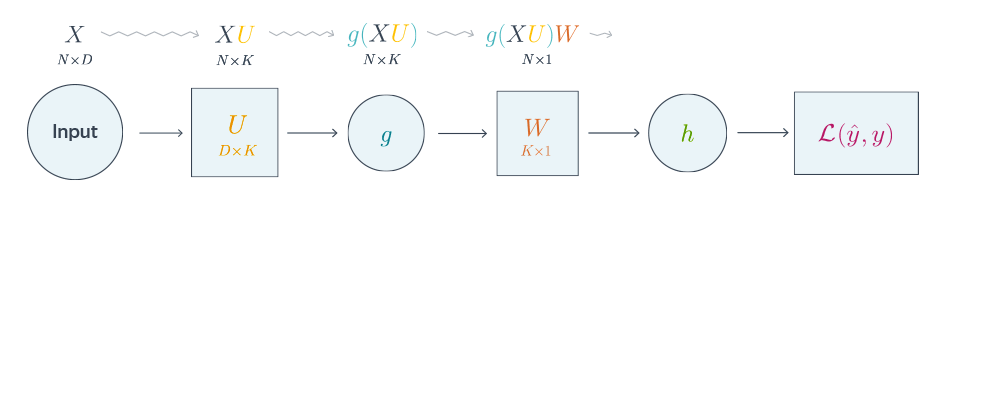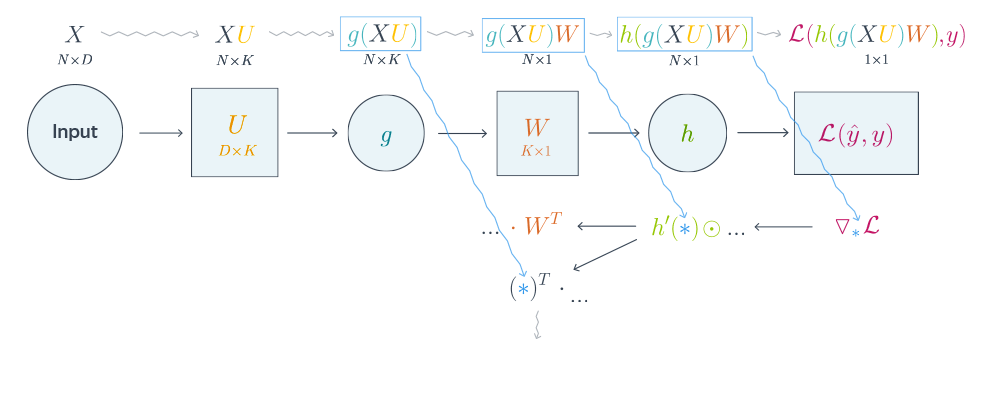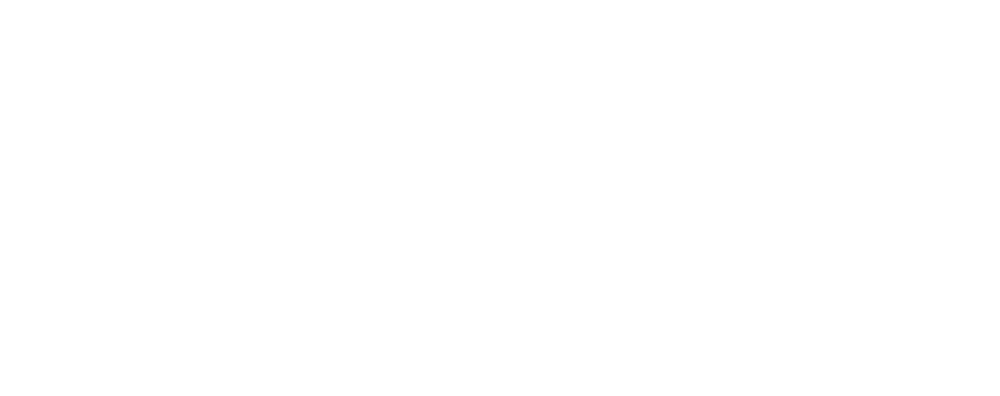
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
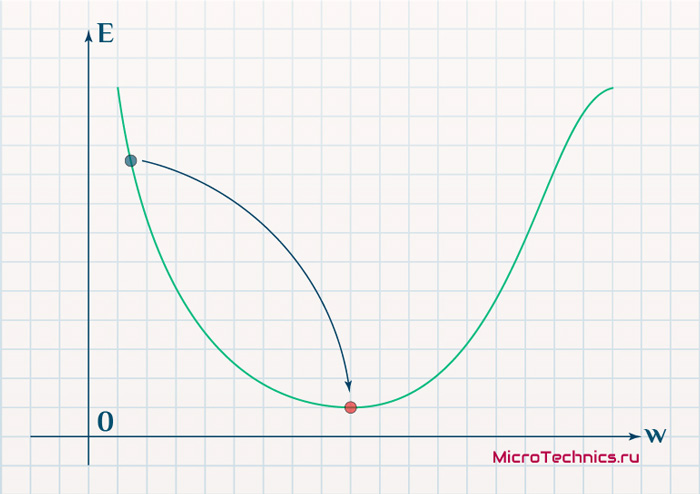
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
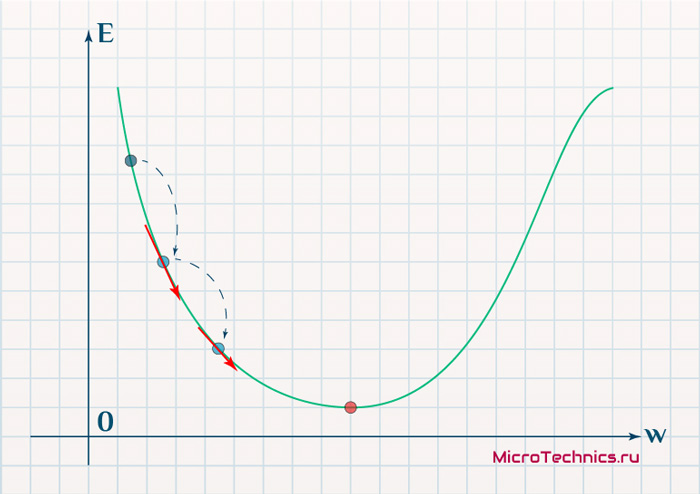
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
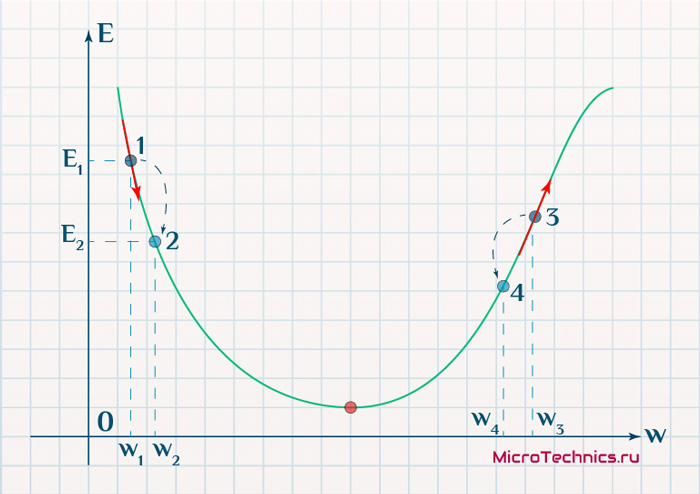
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
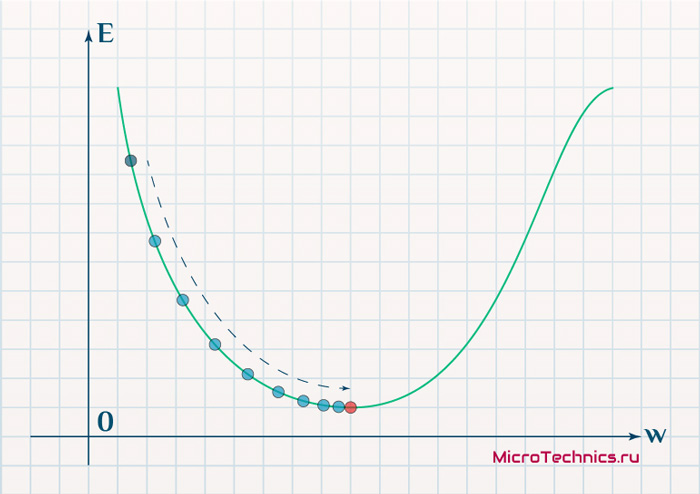
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
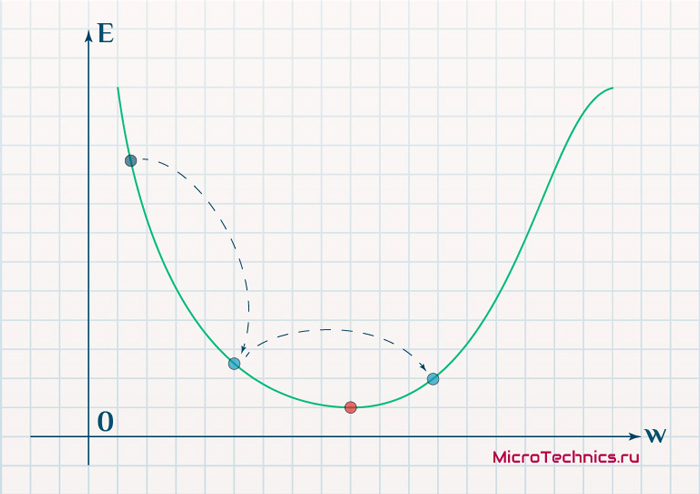
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
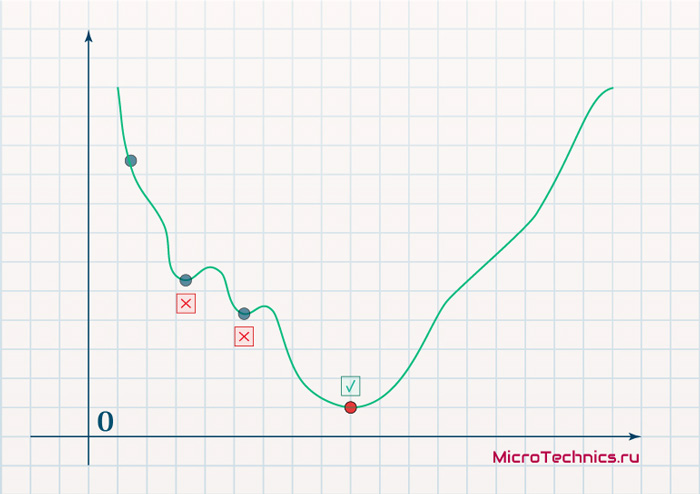
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
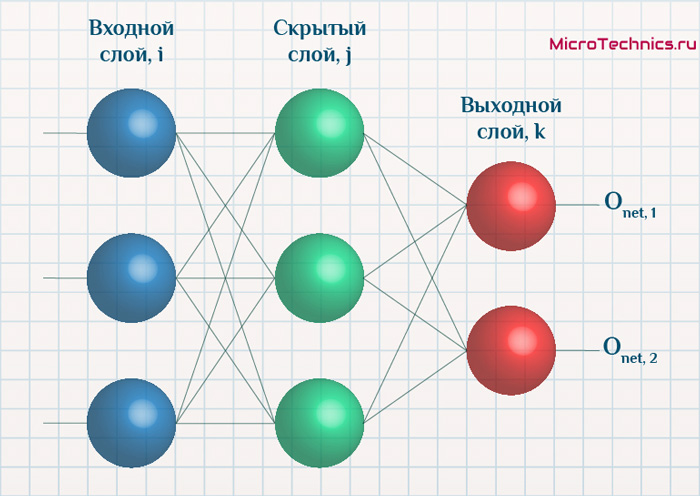
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
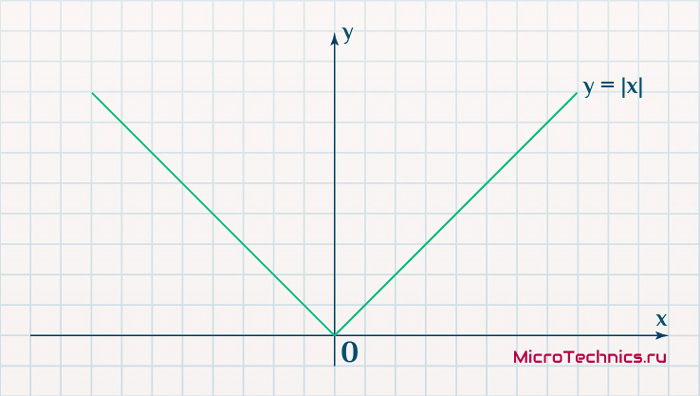
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
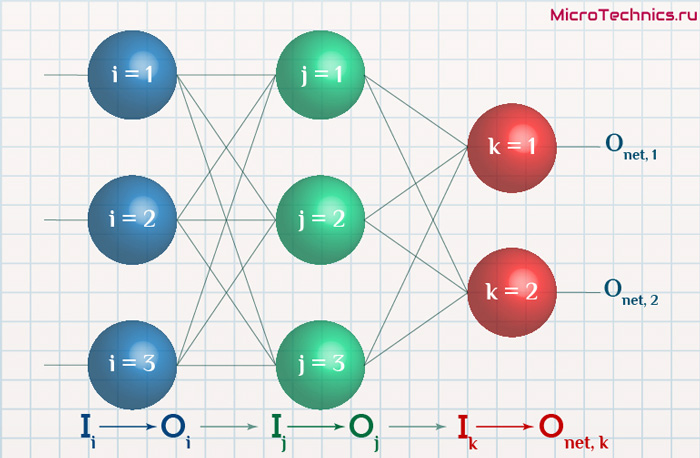
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
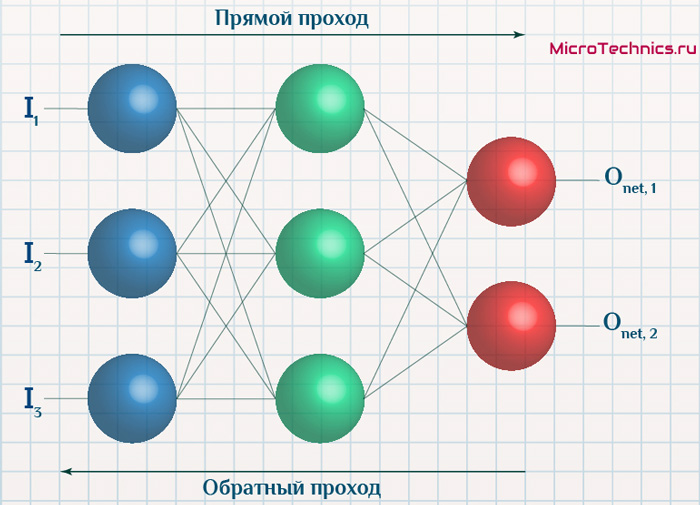
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
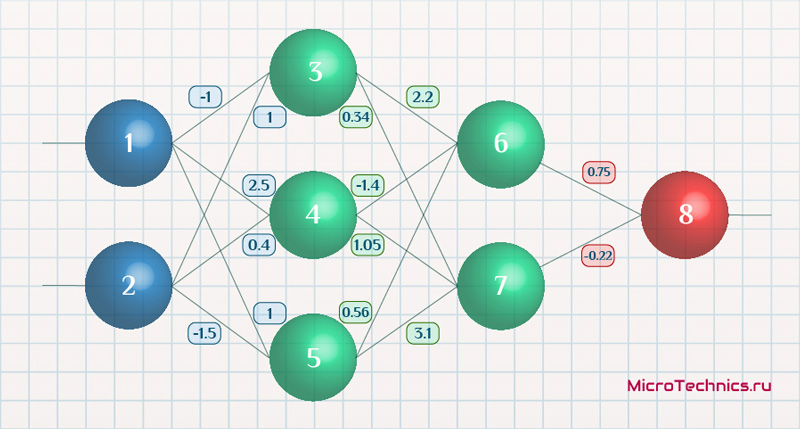
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
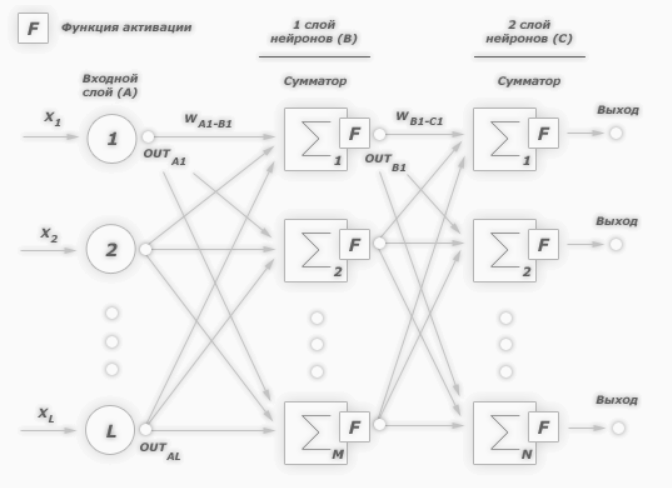
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
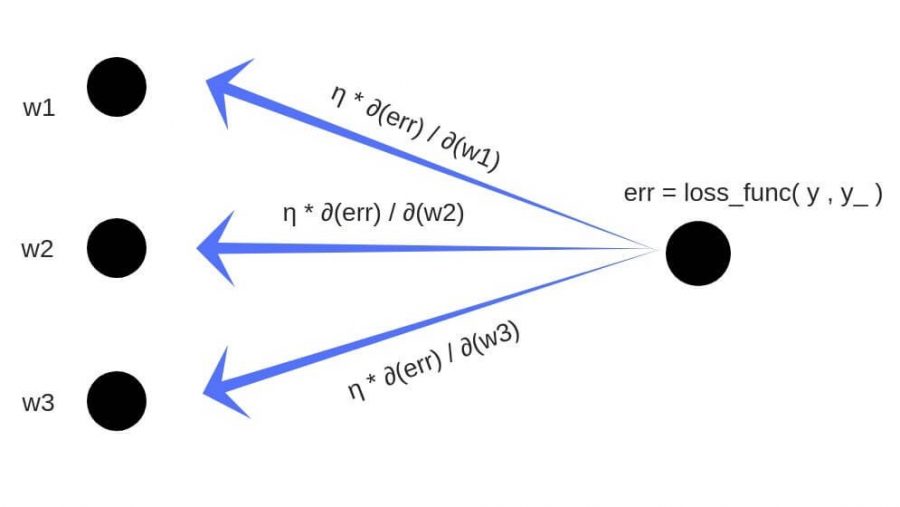
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Обновление правила цепочки
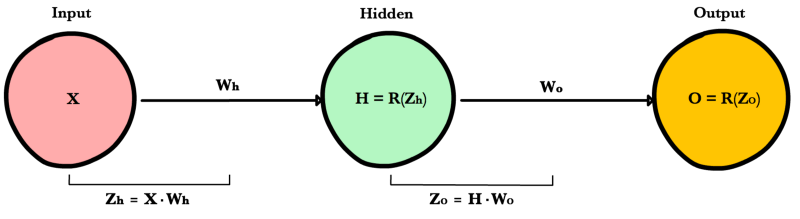
Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:
f(x)=A(B(C(x)))
A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:
f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)
Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.
f′(B)=f′(A)⋅A′(B)
Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.
Применение правила цепочки
Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:
Cost=C(R(Z(XW)))
Используя правило цепочки, мы легко можем найти производную потери относительно веса W.
C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X
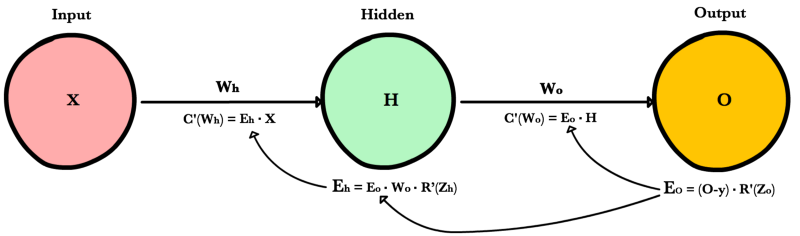
Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:
Какова производная от потери по Wo?
C′(WO)=C′(y^)⋅y^′(ZO)⋅Z′O(WO)=(y^−y)⋅R′(ZO)⋅H
А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.
C′(Wh)=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Zh)⋅Z′h(Wh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)⋅X
И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?
C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)
Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных. Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?
Сохранение работы с мемоизацией
Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.
Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?
Ошибка выходного слоя
Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети? Тогда производная такова:
C′(Zo)=(y^−y)⋅R′(Zo)
Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:
Eo=(y^−y)⋅R′(Zo)
Ошибка скрытого слоя
Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.
C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)
Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:
Eh=Eo⋅Wo⋅R′(Zh)
Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.
Производная потерь по любому весу
Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.
C′(WO)=(y^−y)⋅R′(ZO)⋅H
Мы знаем, что можем заменить первую часть уравнением для ошибки выходного слоя Eh. H представляет собой активацию скрытого слоя.
C′(Wo)=Eo⋅H
Таким образом, чтобы найти производную потерь по любому весу в нашей сети, мы просто умножаем ошибку соответствующего слоя на его вход (выход предыдущего слоя).
C′(w)=CurrentLayerError⋅CurrentLayerInput
Примечание: вход относится к активации с предыдущего слоя, а не к взвешенному входу, Z.
Подводя итог
Вот последние 3 уравнения, которые вместе образуют основу обратного распространения.
Вот процесс, визуализированный с использованием нашего примера нейронной сети выше:
Обратное распространение: пример кода
def relu_prime(z): if z > 0: return 1 return 0 def cost(yHat, y): return 0.5 * (yHat - y)**2 def cost_prime(yHat, y): return yHat - y def backprop(x, y, Wh, Wo, lr): yHat = feed_forward(x, Wh, Wo) # Layer Error Eo = (yHat - y) * relu_prime(Zo) Eh = Eo * Wo * relu_prime(Zh) # Cost derivative for weights dWo = Eo * H dWh = Eh * x # Update weights Wh -= lr * dWh Wo -= lr * dWo
Содержание
- Введение
- 1. Отличительные особенности сверточных нейронных сетей
- 1.1. Сверточный слой
- 1.2. Подвыборочный слой
- 2. Принципы обучения нейронов сверточных слоев
- 3. Построение сверточной нейронной сети
- 3.1. Базовый класс нейронов
- 3.1.1. Прямой проход
- 3.1.2. Расчет градиента ошибки
- 3.2. Элемент подвыборочного слоя
- 3.2.1. Прямой проход
- 3.2.2. Расчет градиента ошибки
- 3.3. Элемент сверточного слоя
- 3.4. Создание класса сверточной нейронной сети
- 3.4.1. Конструктор класса сверточной нейронной сети
- 3.4.2. Метод прямого прохода сверточной нейронной сети
- 3.4.3. Метод обратного прохода сверточной нейронной сети
- 4. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Продолжая тему нейронных сетей, предлагаю рассмотреть принципы работы и построения сверточных нейронных сетей (Convolutional Neural Network). Данный вид нейронных сетей широко применяется в задачах распознования объектов на фото и видеоизображениях. Считается, что сверточные нейронные сети устойчивы к изменению масштаба, смене ракурса и прочим пространственным искажениям изображения. Их архитектура позволяет одинаково успешно находить объекты в любом месте сцены. Применительно к трейдингу, с использованием сверточных нейронных сетей хочу улучшить детектирование торговых паттернов на ценовом графике.
1. Отличительные особенности сверточных нейронных сетей
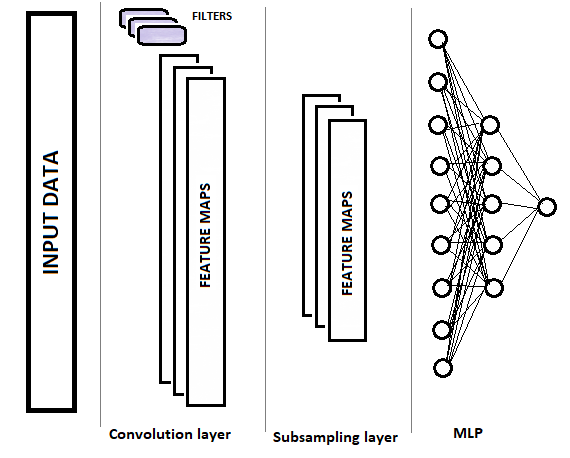
В сверточных сетях, по сравнению с полносвязным перцептроном, добавляются 2 новых вида слоев: сверточный(фильтр) и подвыборочный (субдискретизирующий). Чередуясь, указанные слои призваны выделить основные компоненты и отсеять шумы в исходных данных с параллельным понижением размерности (объема) данных, которые в последующем передаются на вход полносвязного перцептрона для принятия решения. Графически структура сверточной нейронной сети представлена на рисунке ниже. В зависимости от решаемых задач допускается последовательное использование нескольких групп из чередующихся сверточного и подвыборочного слоев.
1.1. Сверточный слой
За распознавание объектов в массиве исходных данных отвечает сверточный слой (Convolution layer). В данном слое осуществляются последовательные операции математической свертки исходных данных с небольшим шаблоном (фильтром), выступающими в качестве ядра свертки.
Свёртка — операция в функциональном анализе, которая при применении к двум функциям f и g возвращает третью функцию, соответствующую взаимокорреляционной функции f(x) и g(-x). Операцию свёртки можно интерпретировать как «схожесть» одной функции с отражённой и сдвинутой копией другой.(Wikipedia)
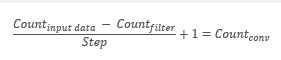
Иными словами, сверточный слой осуществляет поиск шаблонного элемента во всей исходной выборке. При этом на каждой итерации шаблон сдвигается по массиву исходных данных с заданным шагом, который может быть от «1» до размера шаблона. Если величина шага смещения меньше размера шаблона, то такая свертка называется с перекрытием.
В результате операции свертки получаем массив признаков, показывающих «схожесть» исходных данных с искомым шаблоном на каждой итерации. Для нормализации данных используются функции активации. Размер полученного массива будет меньше массива исходных данных, количество таких массивов равно количеству шаблонов (фильтров).
Немаловажен для нас и тот факт, что сами шаблоны не задаются при проектировании нейронной сети, а подбираются в процессе обучения.
1.2. Подвыборочный слой
Следующий, подвыборочный слой используется для снижения размерности массива признаков и фильтрации шумов. Применение данной итерации обусловлено предположением, что наличие сходства исходных данных с шаблоном первично, а точные координаты признака в массиве исходных данных не столь важны. Это позволяет решать проблему масштабирования, т.к. допускает некую вариативность расстояния между искомыми объектами.
На данном этапе происходит уплотнение данных путем сохранения максимального или среднего значения в пределах заданного «окна». Таким образом, сохраняется только одно значение для каждого «окна» данных. Операции осуществляются итерационно со смещением окна на заданный шаг при каждой новой итерации. Уплотнение данных выполняется отдельно для каждого массива признаков.
Довольно часто применяются подвыборочные слои с окном и шагом равным 2, что позволяет вдвое снизить размерность массива признаков. Но в практике допускается и использование большего размера окна, а также итерации уплотнения могут осуществляться как с перекрытием (величина шага меньше размера окна), так и без.
На выходе подвыборочного слоя получаем массивы признаков меньшей размерности.
В зависимости от сложности решаемых задач, после подвыборочного слоя возможно использование еще одну или несколько групп из сверточного и подвыборочного слоя. Принципы их построения и функциональность соответствуют описанным выше. В общем же случае, после одной или нескольких групп свертка + уплотнения массивы полученных признаков по всем фильтрам собираются в единый вектор и подаются на вход многослойного перцептрона для принятия решения нейронной сетью (о построение многослойного перцептрона рассказано в первой части данного цикла статей).
2. Принципы обучения нейронов сверточных слоев
Обучение сверточных нейронных сетей отсуществляется уже известным из предыдущих публикаций методом обратного распространения ошибки. Данный метод относится к методам обучения с учителем и заключается в спуске градиента ошибки от выходного слоя нейронов, через скрытые слои к входному слою нейронов с корректировкой весовых коэффициентов в сторону антиградиента.
Об обучении многослойного перцептрона я уже рассказывал в первой статье этого цикла, поэтому не буду останавливаться. Рассмотрим обучение нейронов подвыборочного и сверточного слоев.
В подвыборочном слое градиент ошибки считается для каждого элемента в массиве признаков по аналогии с градиентами нейронов полносвязного перцепртрона. Алгоритм передачи градиента на предыдущий слой зависит от применяемой операции уплотнения. Если берется только максимальное значение, то и весь градиент передается на нейрон с максимальным значением (для остальных элементов в пределах окна уплотнения устанавливается нулевой градиент). Если же используется операция усреднения в пределах окна, то и градиент равномерно распределяется на все элементы в пределах окна.
Т.к. в операции уплотнения не используются весовые коэффициенты, то и в процессе обучения ничто не корректируется.
Немного сложнее происходят вычисления при обучении нейронов сверточного слоя. Градиент ошибки рассчитывается для каждого элемента массива признаков и спускается к соответствующим нейронам предыдущего слоя. В основе процесса обучения сверточного слоя лежат операции свертки и обратной свертки.
Для передачи градиента ошибки от подвыборочного слоя к сверточному, сначала дополняются края массива градиентов ошибок, полученных от подвыборочного слоя, нулевыми элементами и затем производится свертка полученного массива с ядром свертки, развернутым на 180°. На выходе получаем массив градиентов ошибок размером равным массиву входных данных, в котором индексы градиентов будут соответствовать индексу корреспондирующего нейрона, предшествующего сверточному слою.
Для получения дельт весовых коэффициентов осуществляется свертка матрицы входных значений с матрицей градиентов ошибок данного слоя, развернутой на 180°. На выходе получим массив дельт с размером равным ядру свертки. Полученные дельты нужно скорректировать на производную функции активации сверточного слоя и коэффициент обучения. После чего, весовые коэффициенты ядра свертки изменяются на величину скорректированных дельт.
Наверное, звучит довольно сложно для понимания. Попробуем прояснить данные моменты при подробном рассмотрении кода.
3. Построение сверточной нейронной сети
Как уже было сказана выше, сверточная нейронная сеть будет состоять из 3-х типов нейронных слоев (сверточный, подвыборочный и полносвязный) с отличительными классами нейронов и различными функциями для прямого и обратного прохода. В тоже время, нам нужно объединить все нейроны в единую сеть и организовать вызов именно того метода обработки данных, который соответствует обрабатываемому нейрону. На мой взгляд, наиболее простой способ организовать данный процесс с помощью функционала наследования классов и виртуализации функций.
Вначале построим структуру наследования классов.
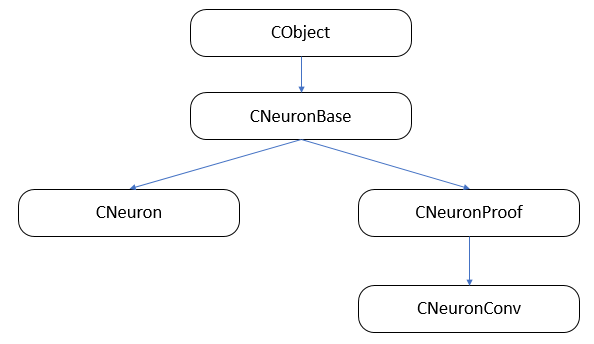
3.1. Базовый класс нейронов.
В первой статье мы создали класс слоя CLayer наследником класса CArrayObj, который является классом динамического массива для хранения ссылок на объекты класса CObject. Следовательно, все нейроны у нас должны унаследоваться от данного класса. На базе класса CObject создадим базовый класс CNeuronBase. В теле класса объявим общие для всех типов нейронов переменные и создадим шаблоны основных методов. Все методы класса объявлены виртуальными для возможности последующего переопределения.
class CNeuronBase : public CObject { protected: double eta; double alpha; double outputVal; uint m_myIndex; double gradient; CArrayCon *Connections; virtual bool feedForward(CLayer *prevLayer) { return false; } virtual bool calcHiddenGradients( CLayer *&nextLayer) { return false; } virtual bool updateInputWeights(CLayer *&prevLayer) { return false; } virtual double activationFunction(double x) { return 1.0; } virtual double activationFunctionDerivative(double x) { return 1.0; } virtual CLayer *getOutputLayer(void) { return NULL; } public: CNeuronBase(void); ~CNeuronBase(void); virtual bool Init(uint numOutputs, uint myIndex); virtual void setOutputVal(double val) { outputVal=val; } virtual double getOutputVal() { return outputVal; } virtual void setGradient(double val) { gradient=val; } virtual double getGradient() { return gradient; } virtual bool feedForward(CObject *&SourceObject); virtual bool calcHiddenGradients( CObject *&TargetObject); virtual bool updateInputWeights(CObject *&SourceObject); virtual bool Save( int const file_handle); virtual bool Load( int const file_handle) { return(Connections.Load(file_handle)); } virtual int Type(void) const { return defNeuronBase; } };
Названия переменных и методов соответствуют описанным ранее. Предлагаю рассмотреть методы feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) и updateInputWeights(CObject *&SourceObject), так как в указанных методах осуществляется диспетчеризация по работе с полносвязными и сверточными слоями.
3.1.1. Прямой проход.
Метод feedForward(CObject *&SourceObject) вызывается при прямом проходе для вычисления результирующего значения нейрона. При прямом проходе в полносвязных слоях каждый нейрон берет значения всех нейронов предыдущего слоя и, соответственно, на вход должен получить весь предыдущий слой. В сверточных и подвыборочных слоях на вход нейрона подается только часть данных, относящаяся к данному фильтру. В рассматриваемом методе выбор алгоритма осуществляется на основании типа класса, полученного в параметрах.
В начале проверяем действительность ссылки на объект, полученной в параметрах метода.
bool CNeuronBase::feedForward(CObject *&SourceObject) { bool result=false; if(CheckPointer(SourceObject)==POINTER_INVALID) return result;
Так как внутри оператора выбора нельзя объявлять экземпляры классов, подготовим шаблоны заранее.
CLayer *temp_l; CNeuronProof *temp_n;
Далее в операторе выбора проверим тип полученного в параметрах объекта. Если мы получили ссылку на слой нейронов, то предыдущий слой является полносвязным и, следовательно, вызовем метод для работы с полносвязными слоями (подробно описано в первой статье). Если же мы имеем дело с нейроном сверточного или подвыборочного слоя, то сначала мы получим слой выходных нейронов данного фильтра и затем воспользуемся методом обработки полносвязного слоя, передав ему в параметрах слой нейронов текущего фильтра с сохранением результата отработки в переменную result (подробнее о строении нейронов сверточного и подвыборочного слоев будет рассказано ниже). После отработки выходим из метода с передачей результата работы.
switch(SourceObject.Type()) { case defLayer: temp_l=SourceObject; result=feedForward(temp_l); break; case defNeuronConv: case defNeuronProof: temp_n=SourceObject; result=feedForward(temp_n.getOutputLayer()); break; } return result; }
3.1.2. Расчет градиента ошибки.
По аналогии с прямым проходом создан диспетчер для вызова функции расчета градиента ошибки на скрытых слоях нейронной сети сalcHiddenGradients(CObject *&TargetObject). Структура построения и логика метода аналогична описанному выше. Сначала проверяем действительность полученной ссылки. Затем объявляем переменные для хранения ссылок на соответствующие объекты. И в функции выбора по типу полученного объекта выбираем нужный метод. Отличия начинаются если в параметрах передана ссылка на элемент сверточного или подвыборочного слоя. Расчет градиента ошибки через такие нейроны отличается и распространяется не на все нейроны предыдущего слоя, а только в пределах окна выборки. Поэтому, расчет градиента перенесен в эти нейроны в метод calcInputGradients. При этом есть отличия в методах для расчета по слою или для конкретного нейрона. Следовательно, требуемый метод вызывается в зависимости от типа объекта из которого вызывается.
bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject) { bool result=false; if(CheckPointer(TargetObject)==POINTER_INVALID) return result; CLayer *temp_l; CNeuronProof *temp_n; switch(TargetObject.Type()) { case defLayer: temp_l=TargetObject; result=calcHiddenGradients(temp_l); break; case defNeuronConv: case defNeuronProof: switch(Type()) { case defNeuron: temp_n=TargetObject; result=temp_n.calcInputGradients(GetPointer(this),m_myIndex); break; default: temp_n=GetPointer(this); temp_l=temp_n.getOutputLayer(); temp_n=TargetObject; result=temp_n.calcInputGradients(temp_l); break; } break; } return result; }
Диспетчер updateInputWeights(CObject *&SourceObject) для обновления весовых коэффициентов построен по принципам описанным выше. С подробным кодом метода можно ознакомиться во вложении.
3.2. Элемент подвыборочного слоя.
Основным кирпичиком подвыборочного слоя выступает класс CNeuronProof, который наследуется от ранее описанного базового класса CNeuronBase. При проработке архитектуры было принято решение о создании в подвыборочном слое одного экземпляра такого класса на каждый фильтр. В связи с этим вводятся дополнительные переменные iWindow и iStep для хранения размера окна уплотнения и шага сдвига, соответственно. Также добавляем внутренний слой нейронов для хранения массивов признаков, градиентов ошибок и, при необходимости, весовых коэффициентов для передачи признаков в полносвязный перцептрон. И добавим метод для получения ссылки на внутренний слой нейронов по запросу.
class CNeuronProof : public CNeuronBase { protected: CLayer *OutputLayer; int iWindow; int iStep; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients( CLayer *&nextLayer); public: CNeuronProof(void){}; ~CNeuronProof(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int output_count); virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients( CLayer *prevLayer) ; virtual bool calcInputGradients( CNeuronBase *prevNeuron, uint index) ; virtual bool Save( int const file_handle) { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle)); } virtual bool Load( int const file_handle) { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle)); } virtual int Type(void) const { return defNeuronProof; } };
Не забываем переопределить логику работы для объявленных в базовом классе виртуальных функций.
3.2.1. Прямой проход.
Метод feedForward предназначен для отсеивания шумов и понижения размерности массива признаков. В описываемом решении для уплотнения данных используется функция арифметического среднего. Рассмотрим детальнее код метода. Вначале метода проверим актуальность полученной ссылки на предыдущий слой нейронов.
bool CNeuronProof::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Затем организуем цикл по перебору всех нейронов полученного в параметрах слоя с заданным шагом.
int total=prevLayer.Total()-iWindow+1; CNeuron *temp; for(int i=0;(i<=total && result);i+=iStep) {
В теле цикла создадим вложенный цикл для подсчета суммы выходных значений нейронов предыдущего слоя в пределах заданного окна уплотнения.
double sum=0; for(int j=0;j<iWindow;j++) { temp=prevLayer.At(i+j); if(CheckPointer(temp)==POINTER_INVALID) continue; sum+=temp.getOutputVal(); }
После подсчета суммы обратимся к соответствующему нейрону внутреннего слоя хранения результирующих данных и запишем в его результирующее значение отношение полученной суммы к размеру окна, что и составит среднее арифметическое для текущего окна уплотнения.
temp=OutputLayer.At(i/iStep); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setOutputVal(sum/iWindow); } return true; }
По завершении перебора всех нейронов завершаем работу метода.
3.2.2. Расчет градиента ошибки.
Для расчета градиента ошибки в данном классе создана два метода: calcHiddenGradients и calcInputGradients. Первый собирает данные о градиентах ошибки последующего слоя и считает градиент для элементов текущего слоя. Второй на основе данных полученных в первом методе распределяет ошибку по элементам предыдущего слоя.
В начале метода calcHiddenGradients, как обычно, проверим действительность полученной в параметрах ссылки. Дополнительно проверим состояния внутреннего слоя нейронов.
bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer) { if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0) return false;
Далее в цикле переберем все нейроны внутреннего слоя и вызовем метод по подсчету градиента ошибки.
gradient=0; int total=OutputLayer.Total(); CNeuron *temp; for(int i=0;i<total;i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); } return true; }
Хочу обратить внимание, что данный метод правильно отрабатывает, если далее следует полносвязный слой нейронов. Если далее следует сверточный или подвыборочный слой необходимо использовать метод calcInputGradients нейрона последующего слоя.
В параметрах метод calcInputGradients получает ссылку на предыдущий слой. И мы сразу, в начале метода, проверяем действительность данной ссылки состояние внутреннего слоя нейронов.
bool CNeuronProof::calcInputGradients(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Затем проверяем тип первого элемента полученного в параметрах слоя. В случае, если полученная ссылка указывает на подвыборочный или сверточный слой, то запросим ссылку на внутренний слой нейронов, соответствующего фильтра.
if(prevLayer.At(0).Type()!=defNeuron) { CNeuronProof *temp=prevLayer.At(m_myIndex); if(CheckPointer(temp)==POINTER_INVALID) return false; prevLayer=temp.getOutputLayer(); if(CheckPointer(prevLayer)==POINTER_INVALID) return false; }
Далее организуем цикл по перебору всех нейронов предыдущего слоя с обязательной проверкой действительность ссылки на обрабатываемый нейрон.
CNeuronBase *prevNeuron, *outputNeuron; int total=prevLayer.Total(); for(int i=0;i<total;i++) { prevNeuron=prevLayer.At(i); if(CheckPointer(prevNeuron)==POINTER_INVALID) continue;
Определим на какие нейроны внутреннего слоя влияет обрабатываемый нейрон.
double prev_gradient=0; int start=i-iWindow+iStep; start=(start-start%iStep)/iStep; double stop=(i-i%iStep)/iStep+1;
В цикле посчитаем градиент ошибки для обрабатываемого нейрона и сохраним полученный результат. После перебора всех нейронов предыдущего слоя завершаем работу метода.
for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++) { outputNeuron=OutputLayer.At(out); if(CheckPointer(outputNeuron)==POINTER_INVALID) continue; prev_gradient+=outputNeuron.getGradient()/iWindow; } prevNeuron.setGradient(prev_gradient); } return true; }
Аналогичным образом построен метод с аналогичным названием для подсчета градиента отдельного нейрона. Отличие заключается в исключении внешнего цикла по перебору нейронов. Вместо него идет обращение по порядковому номеру нейрона.
Так как в подвыборочном слое не используются весовые коэффициенты, то и метод их обновления можно опустить. Или, как вариант, для сохранения унификации структуры классов нейронов можно создать пустой метод, который при вызове будет возвращать значение true.
С полным кодом всех методов и функций можно ознакомиться во вложении.
3.3. Элемент сверточного слоя.
Для построения сверточного слоя будем использовать объекты класса CNeuronConv, которые будут наследоваться от класса CNeuronProof. В качестве функции активации для данного типа нейронов я выбрал параметрическую ReLU. Данная функция более легкая для расчета, по сравнению с гиперболическим тангенсом, используемым в нейронах полносвязного перцептрона. Для ее расчета введем дополнительную переменную param.
class CNeuronConv : public CNeuronProof { protected: double param; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual double activationFunction(double x); virtual bool updateInputWeights(CLayer *&prevLayer); public: CNeuronConv() : param(0.01) { }; ~CNeuronConv(void) { }; virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; virtual double activationFunctionDerivative(double x); virtual int Type(void) const { return defNeuronConv; } };
Методы прямого и обратного прохода построены по алгоритмам аналогичным класса CNeuron Proof. Отличия заключаются только в использовании функции активации и весовых коэффициентов. Поэтому не вижу причин для их детального рассмотрения. Разберем метод корректировки весовых коэффициентов updateInputWeights.
В параметрах метод получает ссылку на предшествующий слой нейронов и мы сразу проверяем действительность полученной ссылки и состояние внутреннего слоя.
bool CNeuronConv::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Далее, создаем цикл по перебору всех весовых коэффициентов и, разумеется, после получения ссылки на объект очередной связи проверяем ее действительность.
CConnection *con; for(int n=0; n<iWindow && !IsStopped(); n++) { con=Connections.At(n); if(CheckPointer(con)==POINTER_INVALID) continue;
После этого считаем свертку массива входных данных с массивом градиентов ошибок внутреннего слоя, развернутого на 180°. Для этого организовываем цикл по перебору всех элементов внутреннего слоя и умножению на элементы массива входных данных по схеме:
- первый элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на последний элемент массива градиента ошибок.
- второй элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на предпоследний элемент массива градиента ошибок.
- и т.д. до элемент с индексом равным количеству элементов в массиве внутреннего слоя со сдвигом на количество шагов равных порядковому номеру весового коэффициента умножается на первый элемент массива градиента ошибок.
Полученные произведения суммируем.
double delta=0; int total_i=OutputLayer.Total(); CNeuron *prev, *out; for(int i=0;i<total_i;i++) { prev=prevLayer.At(n*iStep+i); out=OutputLayer.At(total_i-i-1); if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) continue; delta+=prev.getOutputVal()*out.getGradient(); }
Рассчитанная сумма произведений и является базой для корректировки весовых коэффициентов. Корректируем весовые коэффициенты с учетом заданной скорости обучения.
con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); } return true; }
После корректировки всех весовых коэффициентов выходим из метода.
Класс CNeuron подробно описан в первой статье данного цикла и практически не изменился, поэтому разрешите не останавливаться на нем в этой статье.
3.4. Создание класса сверточной нейронной сети.
Теперь, когда созданы все кирпичики можно приступать к строительству дома — создадим класс сверточной нейронной сети, который объединит все типы нейронов в четкую структуру и организует работу нашей нейронной сети. Первый вопрос, который возникает при создании данного класса — это как мы будем задавать требуемую структуру сети. В полносвязный перцептрон мы передавали массив элементов в котором указывали количество нейронов в каждом слое. Сейчас же нам нужно больше информации для генерации нужного слоя сети. Создадим небольшой класс CLayerDescription для описания построения слоя. Данный класс не содержит никаких методов (кроме конструктора и деструктора), а включает только переменные для указания типа нейронов в слое, количество таких нейронов, размер окна и шага для нейронов сверточного и подвыборочного слоев. В параметрах же конструктора класса сверточной нейронной сети мы будем передавать ссылку на массив классов с описанием слоев.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void){}; int type; int count; int window; int step; }; CLayerDescription::CLayerDescription(void) : type(defNeuron), count(0), window(1), step(1) {}
Рассмотрим структуру класса сверточной нейронной сети CNetConvolution. Данный класс содержит:
- layers — массив слоев;
- recentAverageError — текущая ошибка сети;
- recentAverageSmoothingFactor — фактор усреднения ошибки;
- CNetConvolution — конструктор класса;
- ~CNetConvolution — деструктор класса;
- feedForward — метод прямого прохода;
- backProp — метод обратного прохода;
- getResults — метод для получения результатов последнего прямого прохода;
- getRecentAverageError — метод для получения текущей ошибки сети;
- Save и Load — методы для сохранения и загрузки ранее созданной и обученной сети.
class CNetConvolution { public: CNetConvolution(CArrayObj *Description); ~CNetConvolution(void) { delete layers; } bool feedForward( CArrayDouble *inputVals); void backProp( CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals) ; double getRecentAverageError() { return recentAverageError; } bool Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); static double recentAverageSmoothingFactor; virtual int Type(void) const { return defNetConv; } private: CArrayLayer *layers; double recentAverageError; };
Наименование методов и алгоритмы построения аналогичны описанным ранее для полносвязного перцептрона в первой статье данного цикла. Остановимся только на основных методах класса.
3.4.1. Конструктор класса сверточной нейронной сети.
Рассмотрим конструктор класса. В параметрах конструктор получает ссылку на массив описаний слоев для построения сети. Соответственно, проверяем действительность полученной ссылки, определяем количество слоев для построения и создаем новый экземпляр массива слоев.
CNetConvolution::CNetConvolution(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
int total=Description.Total();
if(total<=0)
return;
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
Далее объявляем внутренние переменные.
CLayer *temp; CLayerDescription *desc=NULL, *next=NULL, *prev=NULL; CNeuronBase *neuron=NULL; CNeuronProof *neuron_p=NULL; int output_count=0; int temp_count=0;
На этом подготовительный этап закончен и приступаем непосредственно к цикличности генерации слое нейронной сети. В начале цикла считываем информацию о текущем и последующем слоях.
for(int i=0;i<total;i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL;
Подсчитаем количество выходных связей для слоя и создадим новый экземпляр класса нейронного слоя. Обратите внимание, что количество связей на выходе слоя указываем только перед полносвязным слоем, в противном случае указываем нулевое значение. Это связано с тем, что сверточные нейроны сами хранят входные весовые коэффициенты, а подвыборочный слой их вообще не использует.
int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count); temp=new CLayer(outputs);
Далее в цикле идет генерация нейронов с разделением алгоритма по типу нейронов в создаваемом слое. Для полносвязных слоев осуществляется создание нового экземпляра нейрона и его инициализация. Обратите внимание, что для полносвязных слоев создается на один нейрон больше, чем указано в описании. Данный нейрон будет использоваться в качестве байесовского смещения.
for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++) { switch(desc.type) { case defNeuron: neuron=new CNeuron(); if(CheckPointer(neuron)==POINTER_INVALID) { delete temp; delete layers; return; } neuron.Init(outputs,n); break;
Для сверточного слоя создадим новый экземпляр нейрона. Посчитаем количество выходных элементов на основании информации о предыдущем слое и инициализируем только-что созданный нейрон.
case defNeuronConv: neuron_p=new CNeuronConv(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break;
Аналогичный алгоритм применяется для нейронов подвыборочного слоя.
case defNeuronProof: neuron_p=new CNeuronProof(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break; }
После объявления и инициализации нейрона добавляем его в нейронный слой.
if(!temp.Add(neuron)) { delete temp; delete layers; return; } neuron=NULL; }
По завершению цикла генерации нейронов очередного слоя добавляем слой в хранилище. После генерации всех слоев выходим из метода.
if(!layers.Add(temp)) { delete temp; delete layers; return; } } return; }
3.4.2. Метод прямого прохода сверточной нейронной сети.
Вся работа нейронной сети организована в методе прямого прохода feedForward. В параметрах данный метод получает исходные данные для анализа (в нашем случае это информация с ценового графика и используемых индикаторов). Первым делом проверяем действительность полученной ссылки на массив данных и состояние инициализации нейронной сети.
bool CNetConvolution::feedForward(CArrayDouble *inputVals) { if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1) return false;
Затем объявляем вспомогательные переменные и переносим полученные внешние данные на входной слой нейронной сети.
CLayer *previous=NULL; CLayer *current=layers.At(0); int total=MathMin(current.Total(),inputVals.Total()); CNeuronBase *neuron=NULL; for(int i=0;i<total;i++) { neuron=current.At(i); if(CheckPointer(neuron)==POINTER_INVALID) return false; neuron.setOutputVal(inputVals.At(i)); }
После загрузки исходных данных в нейронную сеть запускаем цикл последовательно перебора нейронных слоев от входа нейронной сети к ее выходу.
CObject *temp=NULL; for(int l=1;l<layers.Total();l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false;
Внутри запущенного цикла для каждого слоя запускаем вложенный цикл по перебору всех нейронов слоя с пересчетом их значений. Обратите внимание, что для полносвязных нейронных слоев не пересчитывается значение на последнем нейроне. Как уже говорилось выше, он используется в качестве байесовского смещения, и мы будем использовать только его весовой коэффициент.
total=current.Total(); if(current.At(0).Type()==defNeuron) total--; for(int n=0;n<total;n++) { neuron=current.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false;
Далее выбор метода зависит от типа нейронов предыдущего слоя. Для полносвязных слоев вызовем метод прямого распространения с указанием в параметрах ссылки на предыдущий слой.
if(previous.At(0).Type()==defNeuron) { temp=previous; if(!neuron.feedForward(temp)) return false; continue; }
Если ранее был сверточный или подвыборочный слой, то посмотрим на тип пересчитываемого нейрона. Для нейрона полносвязного слоя соберем внутренние слои всех нейронов предыдущего слоя в единый слой и затем вызовем метод прямого распространения текущего нейрона с указанием в параметрах ссылки на суммарный слой нейронов.
if(neuron.Type()==defNeuron) { if(n==0) { CLayer *temp_l=new CLayer(total); if(CheckPointer(temp_l)==POINTER_INVALID) return false; CNeuronProof *proof=NULL; for(int p=0;p<previous.Total();p++) { proof=previous.At(p); if(CheckPointer(proof)==POINTER_INVALID) return false; temp_l.AddArray(proof.getOutputLayer()); } temp=temp_l; } if(!neuron.feedForward(temp)) return false; if(n==total-1) { CLayer *temp_l=temp; temp_l.FreeMode(false); temp_l.Shutdown(); delete temp_l; } continue; }
По завершении цикла перебора всех нейронов такого слоя нужно удалить объект суммарного нейрона. При этом нам нужно удалить объект слоя без удаления объектов нейронов, содержащихся в данном слое, т. к. эти же объекты и далее будут использоваться в наших сверточных и подвыборочных слоях. Для этого установим флаг m_free_mode в состояние false и только потом удалим объект.
Если же перед нами элемент сверточного или подвыборочного слоя, то вызовем метод прямого распространения с передачей в параметрах ссылки на предыдущий элемент соответствующего фильтра.
temp=previous.At(n); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!neuron.feedForward(temp)) return false; } } return true; }
После перебора всех нейронов и слоев выходим из метода.
3.4.3. Метод обратного прохода сверточной нейронной сети.
Обучение нейронной сети осуществляется в методе обратного прохода backProp. В нем реализован метод обратного распространения ошибки от выходного слоя нейронной сети к ее входам. Следовательно, в параметрах данный метод получает фактические данные.
В начале метода проверяем действительность ссылки на объект эталонных значений.
void CNetConvolution::backProp(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return;
Затем, посчитаем среднеквадратичную ошибку на выходе прямого прохода нейронной сети от фактических данных и рассчитаем градиенты ошибки нейронов выходного слоя.
CLayer *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal(); error+=delta*delta; neuron.calcOutputGradients(targetVals.At(n)); } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
Следующим шагом организуем цикл с перебором всех слоев нейронной сети в обратном порядке, в котором запустим вложенный цикл с перебором всех нейронов соответствующего слоя для пересчета градиентов ошибок нейронов в скрытых слоях.
CNeuronBase *neuron=NULL; CObject *temp=NULL; for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CLayer *hiddenLayer=layers.At(layerNum); CLayer *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped(); ++n) {
Как и при прямом проходе, выбор нужного метода обновления градиентов ошибок осуществляется на основании анализа типов текущего нейрона и нейронов последующего слоя. Если далее следует полносвязный слой нейронов, то вызываем метод calcHiddenGradients анализируемого нейрона с передачей в параметрах ссылки на объект последующего слоя нейронной сети.
neuron=hiddenLayer.At(n); if(nextLayer.At(0).Type()==defNeuron) { temp=nextLayer; neuron.calcHiddenGradients(temp); continue; }
Если же далее следует сверточный или подвыборочный слой, то в таком случае проверяем тип текущего нейрона. Для полносвязного нейрона организуем цикл по перебору всех фильтров последующего слоя с запуском пересчета градиента ошибки по каждому фильтру для данного нейрона и суммируем полученные градиенты. В случае, когда текущий слой также является сверточный или подвыборочный, определим градиент ошибки по соответствующему фильтру.
if(neuron.Type()==defNeuron) { double g=0; for(int i=0;i<nextLayer.Total();i++) { temp=nextLayer.At(i); neuron.calcHiddenGradients(temp); g+=neuron.getGradient(); } neuron.setGradient(g); continue; } temp=nextLayer.At(n); neuron.calcHiddenGradients(temp); } }
После обновления всех градиентов запустим аналогичные циклы с той же логикой разветвления для обновления весовых коэффициентов нейронов. После обновления весов выходим из метода.
for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CLayer *layer=layers.At(layerNum); CLayer *prevLayer=layers.At(layerNum-1); total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0); int n_conv=0; for(int n=0; n<total && !IsStopped(); n++) { neuron=layer.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return; if(neuron.Type()==defNeuronProof) continue; switch(prevLayer.At(0).Type()) { case defNeuron: temp=prevLayer; neuron.updateInputWeights(temp); break; case defNeuronConv: case defNeuronProof: if(neuron.Type()==defNeuron) { for(n_conv=0;n_conv<prevLayer.Total();n_conv++) { temp=prevLayer.At(n_conv); neuron.updateInputWeights(temp); } } else { temp=prevLayer.At(n); neuron.updateInputWeights(temp); } break; default: temp=NULL; break; } } } }
С полным кодом всех методов и классов можно ознакомиться во вложении.
4. Тестирование
Для проверки работы сверточной нейронной сети был взят советник классификации из второй статьи данного цикла. Напомню, перед нейронной сетью стоит задача предсказания фрактала на текущей свече. Для этого на вход нейронной сети подается информация о формациях N последних свечей и данные 4-х осцилляторов за тот же период.
В сверточном слое нашей новой нейронной сети мы создадим 4 фильтра, которые будут искать паттерны в совокупности данных о формации свечи и показаниях осцилляторов на анализируемой свече. Окно и шаг фильтров будут соответствовать количеству данных на описание одной свечи. Иными словами, мы сравним всю информацию о каждой свече с неким паттерном и вернем значение сходимости. Такой подход позволит нам при необходимости дополнять исходные данные новой информацией о свечах (включение дополнительных индикаторов для анализа и т. д.) без существенной потери производительности.
В подвыборочном слое мы уменьшим размер массива признаков и сгладим результаты путем усреднения данных.
В самом советнике потребовались минимальные изменения. Это изменение класса нейронной сети при объявлении переменных и создании экземпляра.
CNetConvolution *Net;
Также изменения были внесены в части задании структуры нейронной сети в функции OnInit. Для тестирования была использована сеть с одним сверточным и одним подвыборочным слоем и 4-мя фильтрами в каждом. Структура полносвязных слоев осталась без изменений (сделано намеренно для оценки влияния сверточных слоев на работу всей сети).
Net=new CNetConvolution(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError()); CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; int filters=4; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronConv; desc.window=12; desc.step=12; if(!Topology.Add(desc)) return INIT_FAILED; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronProof; desc.window=3; desc.step=2; if(!Topology.Add(desc)) return INIT_FAILED; int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=n; desc.type=defNeuron; result=(Topology.Add(desc) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; } desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNetConvolution(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED; dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
В остальном код советника остался без изменений.
Тестирование проводилось на паре EURUSD период H1. В одном терминале на разных графиках одного инструмента одновременно было запущено 2 советника: со сверточной и полносвязной нейронной сетью. Параметры полносвязных слоев сверточной нейронной сети аналогичны полносвязной сети второго советника, т. е. к ранее построенной сети мы только добавили сверточный и подвыборочный слои.
Тестирование показала небольшой прирост производительности в сверточной нейронной сети. Несмотря на добавление двух слоев, по результатам 24 эпох среднее время обучения одной эпохи сверточной нейронной сети составило 2 часа 4 минуты, а полносвязной сети 2 часа 10 минут.
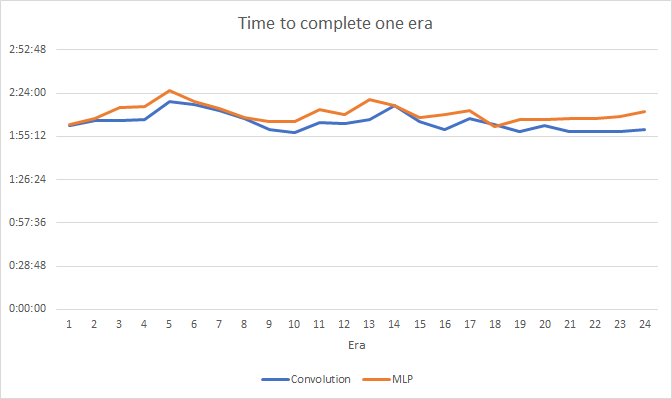
При этом сверточная нейронная сеть показывает немногим лучшие результаты по погрешности предсказания и «попадании в цель».
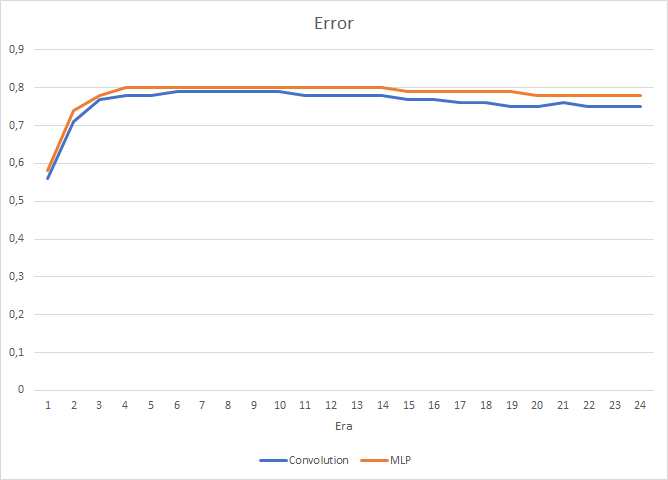
Визуально можно заметить, что на графике сверточной нейронной сети сигналы появляются реже, но ближе к цели.
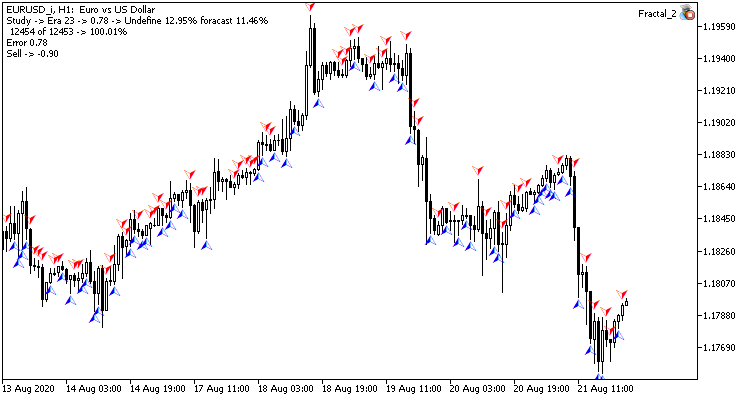
Заключение
В данной статье мы рассмотрели возможность использование сверточных нейронных сетей на финансовых рынках. И тестирование показывает, что их использование позволяет улучшить результаты работы полносвязной нейронной сети. В частности, это может быть связано с предварительной обработкой данных, подаваемых на вход полносвязного перцептрона. В сверточном и подвыборочном слоях осуществляется фильтрация данных от шума, что позволяет повысить качество исходных данных и, как результат, качество работы нейронной сети. А снижение размерности помогает уменьшить количество связей перцептрона с исходными данными, что дает прирост в производительности.
Ссылки
- Нейросети — это просто
- Нейросети — это просто (Часть 2): обучение и тестирование сети
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Fractal.mq5 | Советник | Советник с нейронной сетью регрессии (1 нейрон в выходном слое) |
| 2 | Fractal_2.mq5 | Советник | Советник с нейронной сетью классификации (3 нейрона в выходном слое) |
| 3 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети (перцептрона) |
| 4 | Fractal_conv.mq5 | Советник | Советник со сверточной нейронной сетью классификации (3 нейрона в выходном слое) |