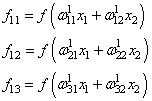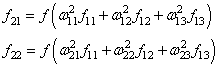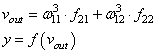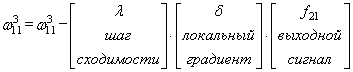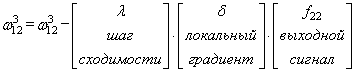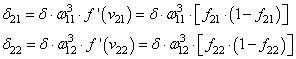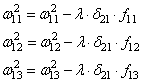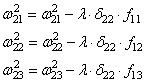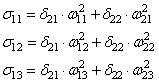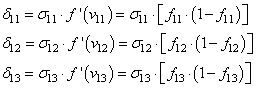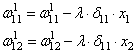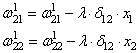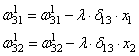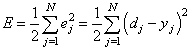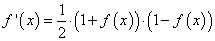Время на прочтение
8 мин
Количество просмотров 514K
О чём статья
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
l1 = 1/(1+np.exp(-(np.dot(X,syn0))))
l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))
l2_delta = (y - l2)*(l2*(1-l2))
l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
syn1 += l1.T.dot(l2_delta)
syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
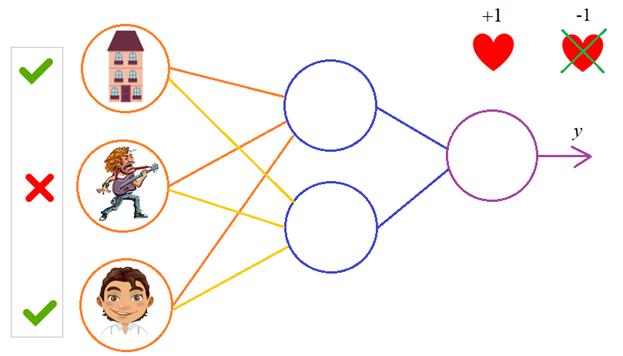
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
# Сигмоида
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
# набор входных данных
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# выходные данные
y = np.array([[0,0,1,1]]).T
# сделаем случайные числа более определёнными
np.random.seed(1)
# инициализируем веса случайным образом со средним 0
syn0 = 2*np.random.random((3,1)) - 1
for iter in xrange(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# насколько мы ошиблись?
l1_error = y - l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1,True) # !!!
# обновим веса
syn0 += np.dot(l0.T,l1_delta) # !!!
print "Выходные данные после тренировки:"
print l1
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
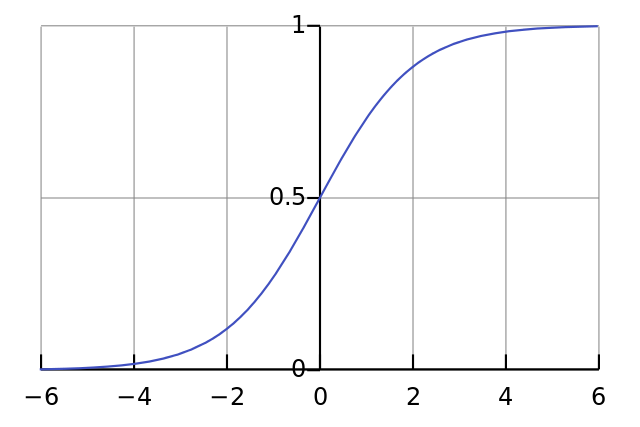
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y - l1
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
nonlin(l1,True)
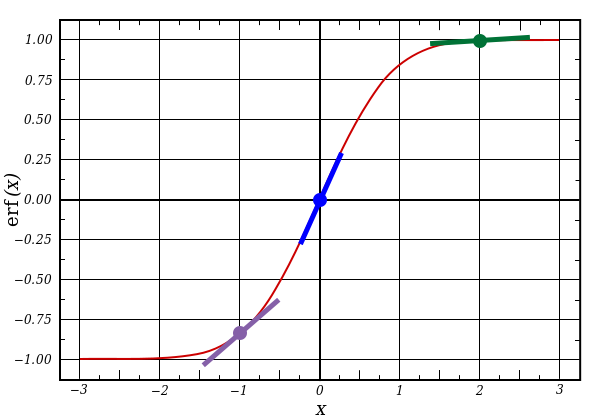
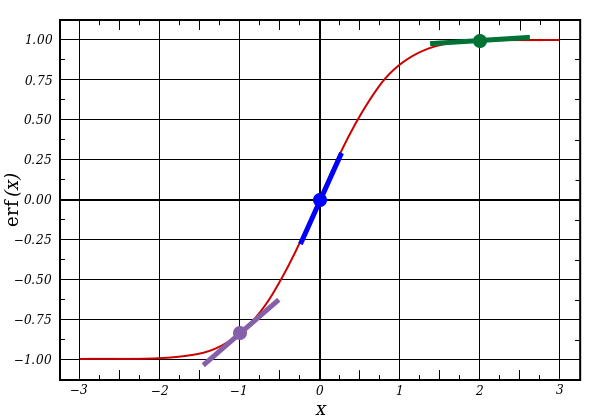
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
Полное выражение: производная, взвешенная по ошибкам
l1_delta = l1_error * nonlin(l1,True)
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
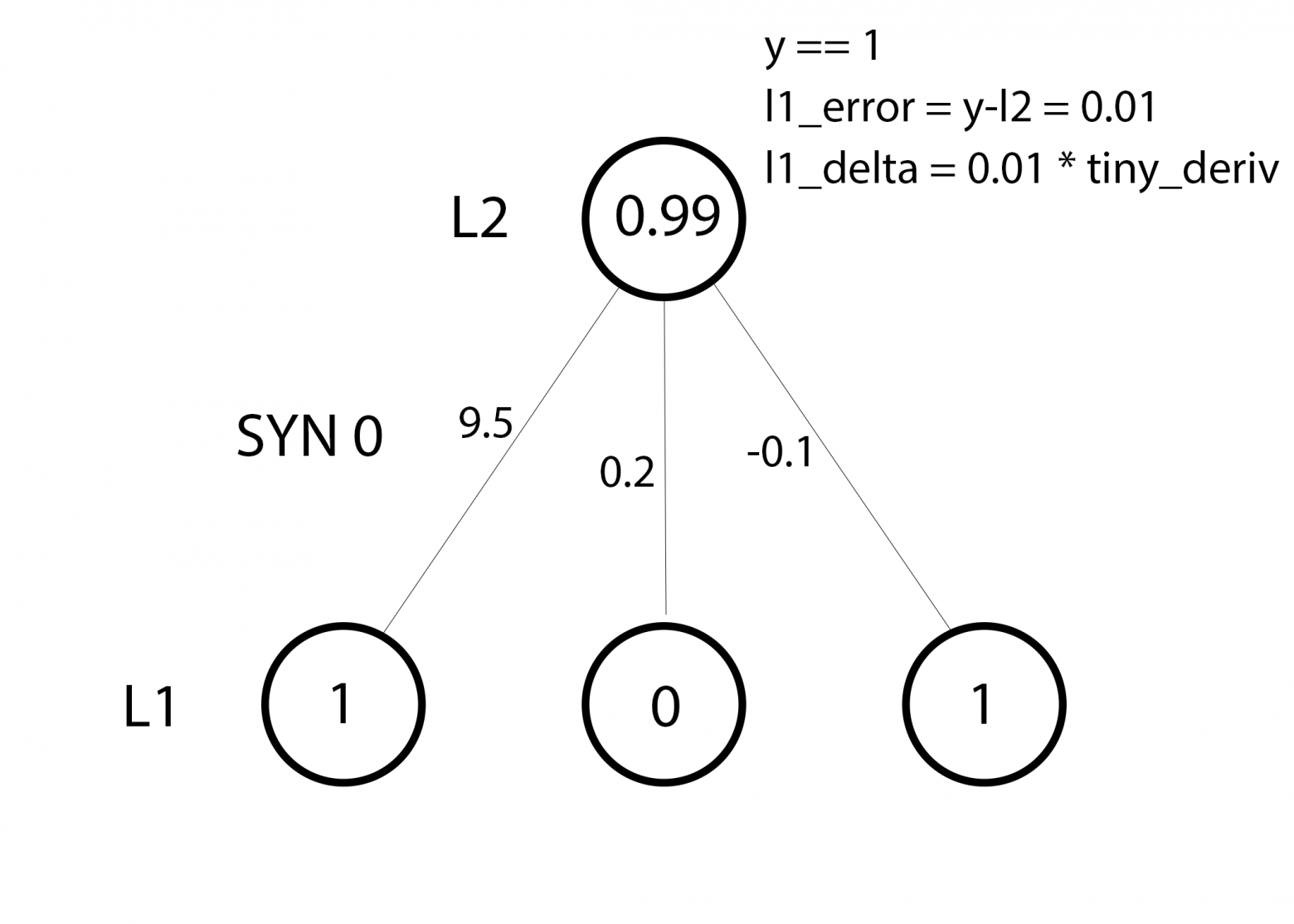
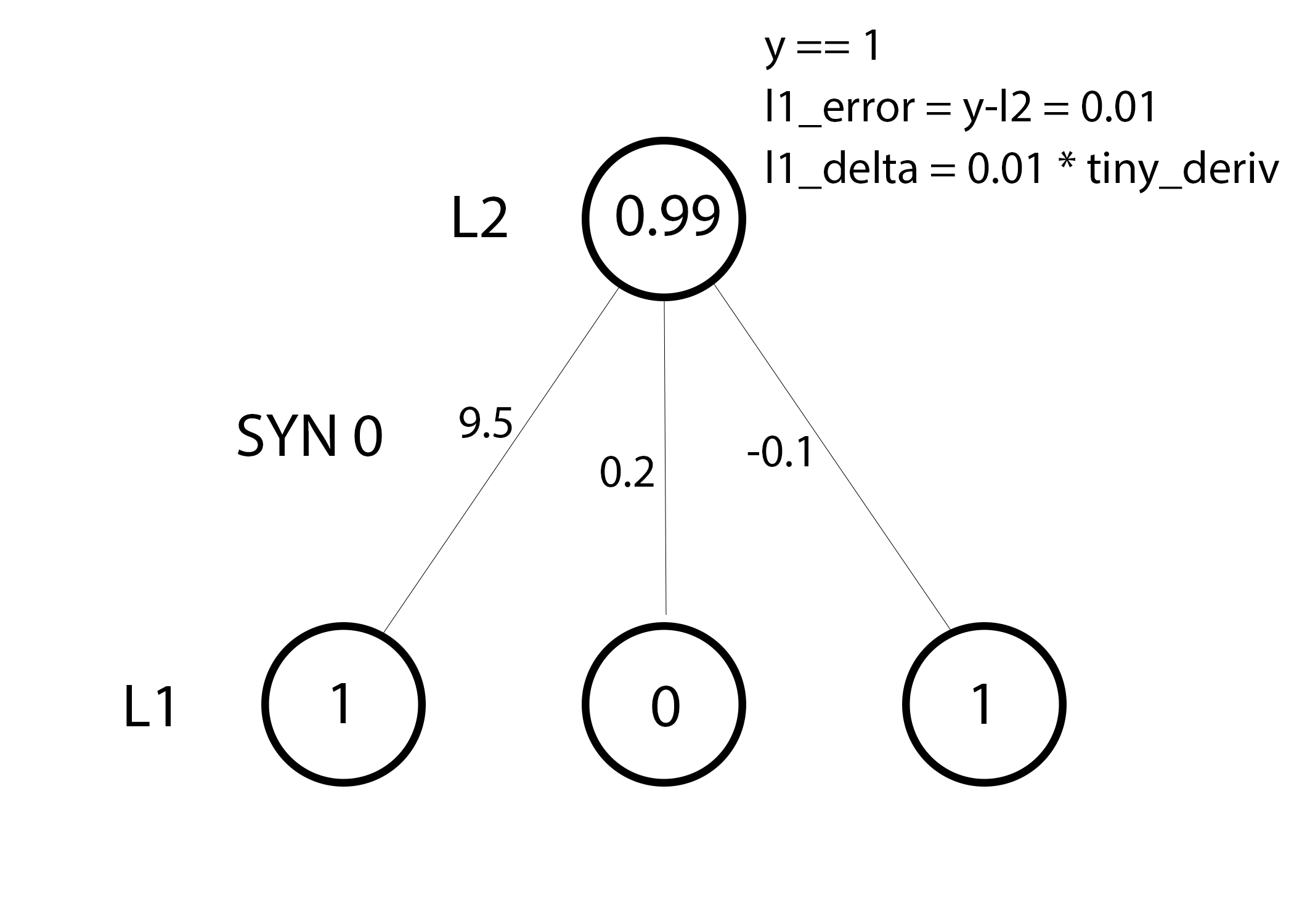
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
weight_update = input_value * l1_delta
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
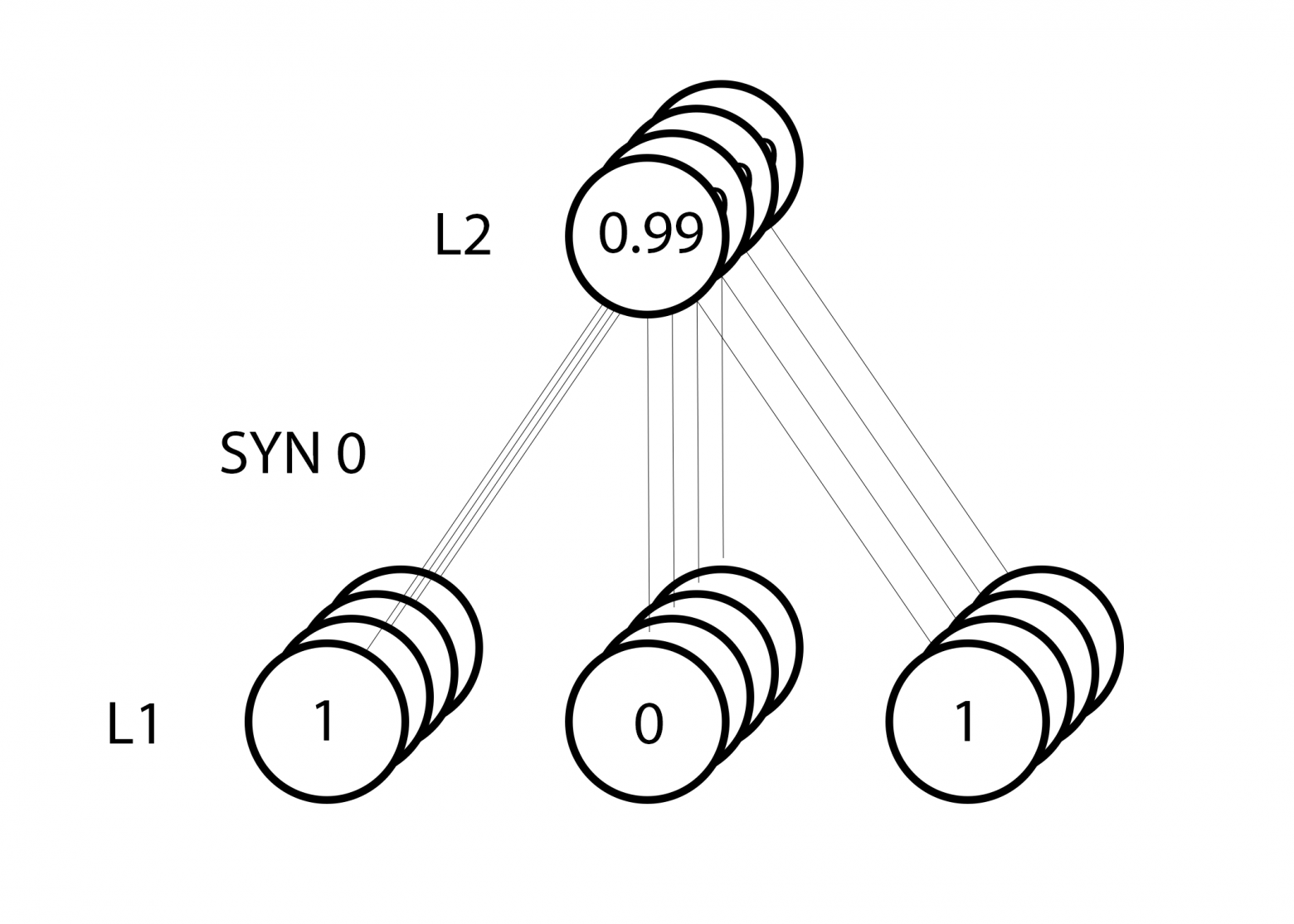
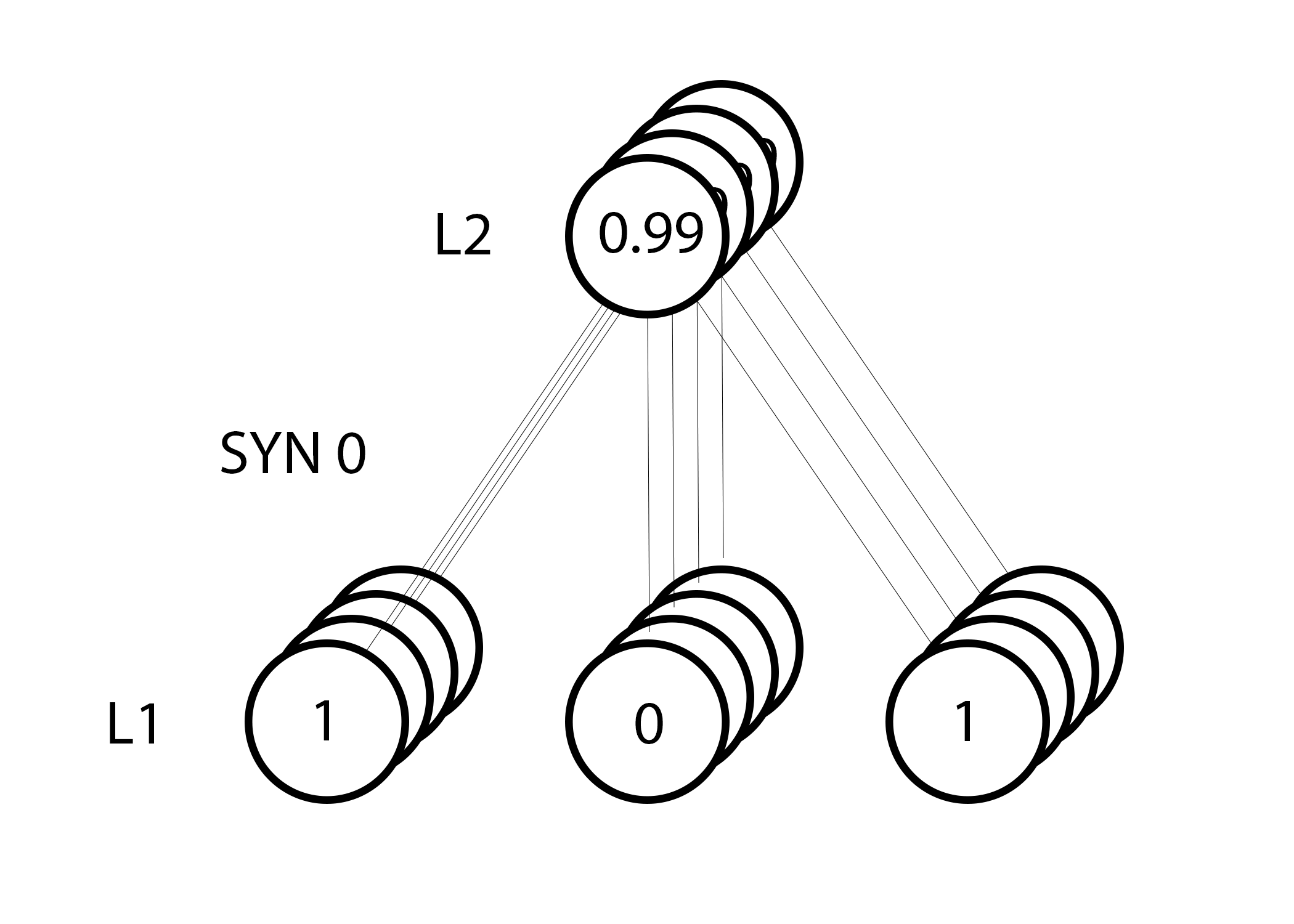
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
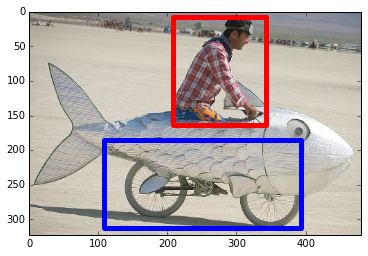
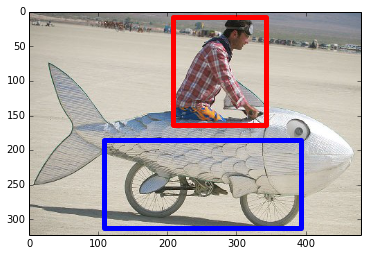
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
Стратегия
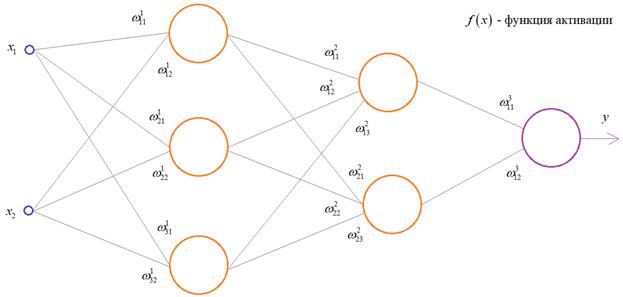
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# случайно инициализируем веса, в среднем - 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# проходим вперёд по слоям 0, 1 и 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# как сильно мы ошиблись относительно нужной величины?
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
# в какую сторону нужно двигаться?
# если мы были уверены в предсказании, то сильно менять его не надо
l2_delta = l2_error*nonlin(l2,deriv=True)
# как сильно значения l1 влияют на ошибки в l2?
l1_error = l2_delta.dot(syn1.T)
# в каком направлении нужно двигаться, чтобы прийти к l1?
# если мы были уверены в предсказании, то сильно менять его не надо
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Перевод
Ссылка на автора
Алгоритм обратного распространения — это классическая искусственная нейронная сеть с прямой связью.
Эта техника до сих пор используется для тренировки большого глубокое обучение сетей.
В этом руководстве вы узнаете, как реализовать алгоритм обратного распространения с нуля с помощью Python.
После завершения этого урока вы узнаете:
- Как переадресовать входные данные для вычисления выходных данных.
- Как распространять ошибки и обучать сеть.
- Как применить алгоритм обратного распространения к реальной задаче прогнозного моделирования.
Давайте начнем.
- Обновление ноябрь 2016: Исправлена ошибка в функции activ (). Спасибо Алекс!
- Обновление январь / 2017: Изменено вычисление fold_size в cross_validation_split (), чтобы оно всегда было целым числом. Исправляет проблемы с Python 3.
- Обновление январь / 2017: Обновлена небольшая ошибка в update_weights (). Спасибо, Томаш!
- Обновление апрель / 2018: Добавлена прямая ссылка на набор данных CSV.
- Обновление Авг / 2018: Протестировано и обновлено для работы с Python 3.6.
Описание
В этом разделе дается краткое введение в алгоритм обратного распространения и набор данных семян пшеницы, которые мы будем использовать в этом руководстве.
Алгоритм обратного распространения
Алгоритм обратного распространения — это контролируемый метод обучения для многослойных сетей прямой связи из области искусственных нейронных сетей.
Прямые нейронные сети вдохновлены обработкой информации одной или нескольких нейронных клеток, называемых нейронами. Нейрон принимает входные сигналы через свои дендриты, которые передают электрический сигнал в тело клетки. Аксон передает сигнал в синапсы, которые являются связями аксона клетки с дендритами другой клетки.
Принцип обратного распространения заключается в моделировании заданной функции путем изменения внутренних весовых коэффициентов входных сигналов для получения ожидаемого выходного сигнала. Система обучается с использованием метода контролируемого обучения, где ошибка между выходными данными системы и известным ожидаемым выходным значением представляется системе и используется для изменения ее внутреннего состояния.
Технически алгоритм обратного распространения — это метод обучения весов в многослойной нейронной сети с прямой связью. Как таковой, он требует, чтобы сетевая структура была определена из одного или нескольких уровней, где один уровень полностью связан со следующим уровнем. Стандартная сетевая структура — это один входной слой, один скрытый слой и один выходной слой.
Обратное распространение можно использовать как для задач классификации, так и для задач регрессии, но в этом руководстве мы сосредоточимся на классификации.
В задачах классификации наилучшие результаты достигаются, когда сеть имеет один нейрон в выходном слое для каждого значения класса. Например, проблема 2-классовой или двоичной классификации со значениями классов A и B. Эти ожидаемые результаты должны быть преобразованы в двоичные векторы с одним столбцом для каждого значения класса. Например, [1, 0] и [0, 1] для A и B соответственно. Это называется горячим кодированием.
Набор данных семян пшеницы
Набор данных семян включает в себя прогнозирование видов с учетом измерений семян из разных сортов пшеницы.
Есть 201 записей и 7 числовых входных переменных. Это проблема классификации с 3 выходными классами. Шкала для каждого числового входного значения варьируется, поэтому может потребоваться некоторая нормализация данных для использования с алгоритмами, которые взвешивают входные данные, такие как алгоритм обратного распространения.
Ниже приведен образец первых 5 строк набора данных.
15.26,14.84,0.871,5.763,3.312,2.221,5.22,1
14.88,14.57,0.8811,5.554,3.333,1.018,4.956,1
14.29,14.09,0.905,5.291,3.337,2.699,4.825,1
13.84,13.94,0.8955,5.324,3.379,2.259,4.805,1
16.14,14.99,0.9034,5.658,3.562,1.355,5.175,1При использовании алгоритма нулевого правила, который прогнозирует наиболее распространенное значение класса, базовая точность задачи составляет 28,095%.
Вы можете узнать больше и загрузить набор данных семян из UCI Хранилище Машинного Обучения,
Загрузите набор данных seed и поместите его в текущий рабочий каталог с именем файлаseeds_dataset.csv,
Набор данных представлен в формате табуляции, поэтому его необходимо преобразовать в CSV с помощью текстового редактора или программы для работы с электронными таблицами.
Обновите, загрузите набор данных в формате CSV напрямую:
- Скачать набор данных семян пшеницы
Руководство
Этот урок разбит на 6 частей:
- Инициализировать сеть.
- Вперед Распространять.
- Ошибка обратного распространения.
- Сеть поездов.
- Предсказать.
- Пример набора данных семян.
Эти шаги обеспечат основу, необходимую для реализации алгоритма обратного распространения с нуля и применения его к собственным задачам прогнозного моделирования.
1. Инициализировать сеть
Давайте начнем с чего-то простого, создания новой сети, готовой к обучению.
Каждый нейрон имеет набор весов, которые необходимо поддерживать. Один вес для каждого входного соединения и дополнительный вес для смещения. Нам нужно будет хранить дополнительные свойства для нейрона во время обучения, поэтому мы будем использовать словарь для представления каждого нейрона и сохранять свойства по именам, таким как ‘веса‘Для весов.
Сеть организована в слои. Входной слой на самом деле просто строка из нашего набора обучающих данных Первый настоящий слой — это скрытый слой. Затем следует выходной слой, который имеет один нейрон для каждого значения класса.
Мы организуем слои как массивы словарей и будем рассматривать всю сеть как массив слоев.
Хорошей практикой является инициализация весов сети небольшими случайными числами. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1.
Ниже приведена функция с именемinitialize_network ()это создает новую нейронную сеть, готовую к обучению. Он принимает три параметра: количество входов, количество нейронов в скрытом слое и количество выходов.
Вы можете видеть, что для скрытого слоя мы создаемn_hiddenнейроны и каждый нейрон в скрытом слое имеетn_inputs + 1веса, один для каждого входного столбца в наборе данных и дополнительный для смещения.
Вы также можете видеть, что выходной слой, который подключается к скрытому слою, имеетn_outputsнейроны, каждый сn_hidden + 1веса. Это означает, что каждый нейрон в выходном слое соединяется (имеет вес) с каждым нейроном в скрытом слое.
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return networkДавайте проверим эту функцию. Ниже приведен полный пример, который создает небольшую сеть.
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
seed(1)
network = initialize_network(2, 1, 2)
for layer in network:
print(layer)Запустив пример, вы можете увидеть, что код распечатывает каждый слой по одному. Вы можете видеть, что скрытый слой имеет один нейрон с 2 входными весами плюс смещение. Выходной слой имеет 2 нейрона, каждый с 1 весом плюс смещение.
[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}]
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]Теперь, когда мы знаем, как создать и инициализировать сеть, давайте посмотрим, как мы можем использовать ее для вычисления результата.
2. Вперед Распространение
Мы можем вычислить выход из нейронной сети, распространяя входной сигнал через каждый уровень, пока выходной уровень не выведет свои значения.
Мы называем это продвижением вперед.
Это метод, который нам понадобится для генерации прогнозов во время обучения, который необходимо будет исправить, и это метод, который нам понадобится после обучения сети для прогнозирования новых данных.
Мы можем разбить распространение вперед на три части:
- Активация нейронов.
- Передача нейронов.
- Вперед Распространение.
2.1. Активация нейронов
Первым шагом является вычисление активации одного нейрона с учетом входных данных.
Входными данными может быть строка из нашего обучающего набора данных, как в случае со скрытым слоем. Это также могут быть выходы от каждого нейрона в скрытом слое, в случае выходного слоя.
Активация нейрона рассчитывается как взвешенная сумма входов. Очень похоже на линейную регрессию.
activation = sum(weight_i * input_i) + biasкудавесвес сети,входявляется входом,яэто индекс веса или ввода исмещениеэто специальный вес, который не имеет входных данных для умножения (или вы можете думать, что входные данные всегда равны 1,0).
Ниже приведена реализация этого в функции с именемактивировать (), Вы можете видеть, что функция предполагает, что смещение является последним весом в списке весов. Это помогает здесь и позже сделать код легче для чтения.
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activationТеперь давайте посмотрим, как использовать активацию нейронов.
2.2. Нейрон Трансфер
Как только нейрон активирован, нам нужно перенести активацию, чтобы увидеть, что на самом деле представляет собой выход нейрона.
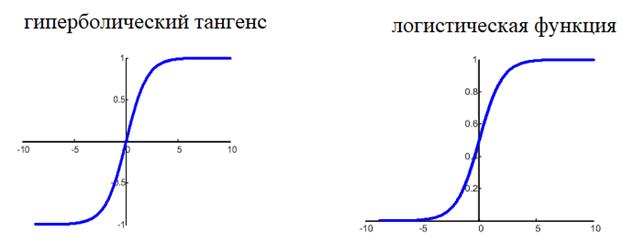
Различные передаточные функции могут быть использованы. Традиционно использовать функция активации сигмовидной кишки, но вы также можете использовать танх (тангенс гиперболический) функция для передачи выходов. Совсем недавно передаточная функция выпрямителя был популярен в крупных сетях глубокого обучения.
Функция активации сигмоида выглядит как S-образная форма, ее также называют логистической функцией. Он может принимать любое входное значение и производить число от 0 до 1 на S-кривой. Это также функция, из которой мы можем легко рассчитать производную (наклон), которая понадобится нам позже при ошибке обратного распространения.
Мы можем передать функцию активации с помощью функции сигмоида следующим образом:
output = 1 / (1 + e^(-activation))кудаеявляется основанием натуральных логарифмов (Номер Эйлера).
Ниже приведена функция с именемперечислить()который реализует сигмовидное уравнение.
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))Теперь, когда у нас есть кусочки, давайте посмотрим, как они используются.
2,3. Прямое распространение
Вперед, распространение входных данных просто.
Мы работаем через каждый слой нашей сети, вычисляя выходы для каждого нейрона. Все выходы из одного слоя становятся входами для нейронов на следующем слое.
Ниже приведена функция с именемforward_propagate ()это реализует прямое распространение для ряда данных из нашего набора данных с нашей нейронной сетью.
Вы можете видеть, что выходное значение нейрона хранится в нейроне с именем ‘выход«. Вы также можете увидеть, что мы собираем выходные данные для слоя в массиве с именемnew_inputsэто становится массивомвходныеи используется в качестве входных данных для следующего слоя.
Функция возвращает выходные данные из последнего слоя, также называемого выходным слоем.
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputsДавайте соединим все эти части и протестируем прямое распространение нашей сети.
Мы определяем нашу сеть, встроенную одним скрытым нейроном, который ожидает 2 входных значения, и выходной слой с двумя нейронами.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# test forward propagation
network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]]
row = [1, 0, None]
output = forward_propagate(network, row)
print(output)Выполнение примера распространяет входной шаблон [1, 0] и выдает выходное значение, которое печатается. Поскольку выходной слой имеет два нейрона, мы получаем список из двух чисел в качестве вывода.
Фактические выходные значения на данный момент просто бессмыслица, но затем мы начнем изучать, как сделать веса в нейронах более полезными.
[0.6629970129852887, 0.7253160725279748]3. Ошибка обратного распространения
Алгоритм обратного распространения назван по способу обучения весов.
Ошибка рассчитывается между ожидаемыми выходами и выходами, передаваемыми по сети. Эти ошибки затем распространяются в обратном направлении через сеть от выходного уровня к скрытому слою, назначая вину за ошибку и обновляя веса по мере их появления.
Математика для ошибки обратного распространения коренится в исчислении, но мы останемся на высоком уровне в этом разделе и сосредоточимся на том, что рассчитывается и как, а не почему расчеты принимают эту конкретную форму.
Эта часть разбита на две части.
- Передача Производная.
- Ошибка обратного распространения.
3.1. Производная передача
Учитывая выходное значение от нейрона, нам нужно вычислить его наклон.
Мы используем передаточную функцию сигмоида, производную которой можно рассчитать следующим образом:
derivative = output * (1.0 - output)Ниже приведена функция с именемtransfer_derivative ()который реализует это уравнение.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)Теперь посмотрим, как это можно использовать.
3.2. Ошибка обратного распространения
Первым шагом является вычисление ошибки для каждого выходного нейрона, это даст нам наш сигнал ошибки (вход) для распространения в обратном направлении по сети.
Ошибка для данного нейрона может быть рассчитана следующим образом:
error = (expected - output) * transfer_derivative(output)кудаожидаемыйявляется ожидаемым выходным значением для нейрона,выходэто выходное значение для нейрона иtransfer_derivative ()вычисляет наклон выходного значения нейрона, как показано выше.
Этот расчет ошибки используется для нейронов в выходном слое. Ожидаемое значение — это само значение класса. В скрытом слое все немного сложнее.
Сигнал ошибки для нейрона в скрытом слое рассчитывается как взвешенная ошибка каждого нейрона в выходном слое. Подумайте об ошибке, связанной с перемещением весов выходного слоя к нейронам в скрытом слое.
Обратно распространяющийся сигнал ошибки накапливается и затем используется для определения ошибки для нейрона в скрытом слое следующим образом:
error = (weight_k * error_j) * transfer_derivative(output)кудаerror_jэто сигнал ошибки отJй нейрон в выходном слое,weight_kэто вес, который соединяетКТретий нейрон к текущему нейрону и выход — это выход для текущего нейрона.
Ниже приведена функция с именемbackward_propagate_error ()который реализует эту процедуру.
Вы можете видеть, что сигнал ошибки, рассчитанный для каждого нейрона, хранится с именем «delta». Вы можете видеть, что слои сети перебираются в обратном порядке, начиная с выхода и работая в обратном направлении. Это гарантирует, что нейроны в выходном слое сначала рассчитывают значения «дельта», которые нейроны в скрытом слое могут использовать в последующей итерации. Я выбрал имя «дельта», чтобы отразить изменение, которое ошибка вносит в нейрон (например, дельта веса).
Вы можете видеть, что сигнал ошибки для нейронов в скрытом слое накапливается от нейронов в выходном слое, где скрыт номер нейронаJтакже индекс веса нейрона в выходном слоенейрон [грузики ‘] [J],
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])Давайте соберем все части вместе и посмотрим, как это работает.
Мы определяем фиксированную нейронную сеть с выходными значениями и распространяем ожидаемый выходной шаблон. Полный пример приведен ниже.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# test backpropagation of error
network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]]
expected = [0, 1]
backward_propagate_error(network, expected)
for layer in network:
print(layer)При выполнении примера печатается сеть после обратного распространения ошибки. Вы можете видеть, что значения ошибок рассчитываются и сохраняются в нейронах для выходного слоя и скрытого слоя.
[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'delta': -0.0005348048046610517}]
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095], 'delta': -0.14619064683582808}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763], 'delta': 0.0771723774346327}]Теперь давайте использовать обратное распространение ошибки для обучения сети.
4. Сеть поездов
Сеть обучается с использованием стохастического градиентного спуска.
Это включает в себя несколько итераций представления обучающего набора данных в сеть и для каждой строки данных, передавая входные данные, распространяя ошибку в обратном направлении и обновляя веса сети.
Эта часть разбита на две части:
- Обновление весов.
- Сеть поездов.
4.1. Обновление весов
Как только ошибки рассчитаны для каждого нейрона в сети с помощью метода обратного распространения, описанного выше, их можно использовать для обновления весов.
Веса сети обновляются следующим образом:
weight = weight + learning_rate * error * inputкудавесзаданный вес,learning_rateэто параметр, который вы должны указать,ошибкаошибка, рассчитанная по процедуре обратного распространения для нейрона ивходэто входное значение, вызвавшее ошибку
Та же процедура может использоваться для обновления веса смещения, за исключением того, что нет входного термина или входное значение является фиксированным значением 1,0.
Скорость обучения определяет, насколько изменить вес, чтобы исправить ошибку. Например, значение 0,1 обновит вес на 10% от суммы, которую он мог бы обновить. Предпочтительными являются малые скорости обучения, которые вызывают более медленное обучение в течение большого количества итераций обучения. Это увеличивает вероятность того, что сеть найдет хороший набор весов на всех уровнях, а не самый быстрый набор весов, которые минимизируют ошибку (так называемая преждевременная сходимость).
Ниже приведена функция с именемupdate_weights ()который обновляет весовые коэффициенты для сети с учетом входной строки данных, скорости обучения и предполагает, что прямое и обратное распространение уже выполнено.
Помните, что вход для выходного слоя представляет собой набор выходов из скрытого слоя.
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']Теперь мы знаем, как обновить вес сети, давайте посмотрим, как мы можем сделать это многократно.
4.2. Сеть поездов
Как уже упоминалось, сеть обновляется с использованием стохастического градиентного спуска.
Это включает в себя первый цикл для фиксированного числа эпох и в каждой эпохе обновление сети для каждой строки в наборе обучающих данных.
Поскольку обновления производятся для каждого шаблона обучения, этот тип обучения называется онлайн-обучением. Если ошибки были накоплены за период до обновления весов, это называется периодическим обучением или пакетным градиентным спуском.
Ниже приведена функция, которая реализует обучение уже инициализированной нейронной сети с заданным набором обучающих данных, скоростью обучения, фиксированным числом эпох и ожидаемым количеством выходных значений.
Ожидаемое количество выходных значений используется для преобразования значений класса в обучающих данных в одно горячее кодирование. Это двоичный вектор с одним столбцом для каждого значения класса, чтобы соответствовать выходу сети. Это необходимо для расчета ошибки для выходного слоя.
Вы также можете видеть, что ошибка квадрата суммы между ожидаемым выходом и выходом сети накапливается каждую эпоху и печатается. Это полезно для отслеживания того, насколько сеть изучает и совершенствует каждую эпоху.
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))Теперь у нас есть все для обучения сети. Мы можем собрать пример, который включает в себя все, что мы видели до сих пор, включая инициализацию сети и обучение сети на небольшом наборе данных.
Ниже приведен небольшой надуманный набор данных, который мы можем использовать для тестирования нашей нейронной сети.
X1 X2 Y
2.7810836 2.550537003 0
1.465489372 2.362125076 0
3.396561688 4.400293529 0
1.38807019 1.850220317 0
3.06407232 3.005305973 0
7.627531214 2.759262235 1
5.332441248 2.088626775 1
6.922596716 1.77106367 1
8.675418651 -0.242068655 1
7.673756466 3.508563011 1Ниже приведен полный пример. Мы будем использовать 2 нейрона в скрытом слое. Это проблема двоичной классификации (2 класса), поэтому в выходном слое будет два нейрона. Сеть будет обучаться в течение 20 эпох со скоростью обучения 0,5, что является высоким показателем, потому что мы готовим так мало итераций.
from math import exp
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))
# Test training backprop algorithm
seed(1)
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
n_inputs = len(dataset[0]) - 1
n_outputs = len(set([row[-1] for row in dataset]))
network = initialize_network(n_inputs, 2, n_outputs)
train_network(network, dataset, 0.5, 20, n_outputs)
for layer in network:
print(layer)При запуске примера сначала выводится ошибка квадрата суммы в каждую эпоху обучения. Мы можем видеть тенденцию уменьшения этой ошибки с каждой эпохой.
После обучения распечатывается сеть с отображением изученных весов. Также все еще в сети находятся выходные и дельта-значения, которые можно игнорировать. Мы могли бы обновить нашу функцию обучения, чтобы удалить эти данные, если мы хотим.
>epoch=0, lrate=0.500, error=6.350
>epoch=1, lrate=0.500, error=5.531
>epoch=2, lrate=0.500, error=5.221
>epoch=3, lrate=0.500, error=4.951
>epoch=4, lrate=0.500, error=4.519
>epoch=5, lrate=0.500, error=4.173
>epoch=6, lrate=0.500, error=3.835
>epoch=7, lrate=0.500, error=3.506
>epoch=8, lrate=0.500, error=3.192
>epoch=9, lrate=0.500, error=2.898
>epoch=10, lrate=0.500, error=2.626
>epoch=11, lrate=0.500, error=2.377
>epoch=12, lrate=0.500, error=2.153
>epoch=13, lrate=0.500, error=1.953
>epoch=14, lrate=0.500, error=1.774
>epoch=15, lrate=0.500, error=1.614
>epoch=16, lrate=0.500, error=1.472
>epoch=17, lrate=0.500, error=1.346
>epoch=18, lrate=0.500, error=1.233
>epoch=19, lrate=0.500, error=1.132
[{'weights': [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], 'output': 0.029980305604426185, 'delta': -0.0059546604162323625}, {'weights': [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], 'output': 0.9456229000211323, 'delta': 0.0026279652850863837}]
[{'weights': [2.515394649397849, -0.3391927502445985, -0.9671565426390275], 'output': 0.23648794202357587, 'delta': -0.04270059278364587}, {'weights': [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], 'output': 0.7790535202438367, 'delta': 0.03803132596437354}]Как только сеть обучена, мы должны использовать ее для прогнозирования.
5. Предсказать
Делать прогнозы с помощью обученной нейронной сети достаточно просто.
Мы уже видели, как распространять входной шаблон для получения выходного сигнала. Это все, что нам нужно сделать, чтобы сделать прогноз. Мы можем непосредственно использовать выходные значения как вероятность того, что шаблон принадлежит каждому выходному классу.
Возможно, было бы более полезно превратить этот вывод в четкое предсказание класса. Мы можем сделать это, выбрав значение класса с большей вероятностью. Это также называется функция arg max,
Ниже приведена функция с именемпредсказать, ()который реализует эту процедуру. Возвращает индекс в выходных данных сети, который имеет наибольшую вероятность. Предполагается, что значения класса были преобразованы в целые числа, начиная с 0.
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))Мы можем соединить это с нашим кодом выше для входного распространения и с нашим небольшим надуманным набором данных, чтобы проверить предсказания с уже обученной сетью. Пример жестко кодирует сеть, обученную на предыдущем шаге.
Полный пример приведен ниже.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Test making predictions with the network
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}],
[{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]]
for row in dataset:
prediction = predict(network, row)
print('Expected=%d, Got=%d' % (row[-1], prediction))При выполнении примера выводится ожидаемый результат для каждой записи в наборе обучающих данных, за которым следует четкое предсказание, сделанное сетью.
Это показывает, что сеть достигает 100% точности в этом небольшом наборе данных.
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1Теперь мы готовы применить наш алгоритм обратного распространения к реальному набору данных.
6. Набор данных семян пшеницы
В этом разделе применяется алгоритм обратного распространения к набору данных семян пшеницы.
Первым шагом является загрузка набора данных и преобразование загруженных данных в числа, которые мы можем использовать в нашей нейронной сети. Для этого мы будем использовать вспомогательную функциюload_csv ()загрузить файл,str_column_to_float ()преобразовать строковые числа в числа с плавающей запятой иstr_column_to_int ()преобразовать столбец класса в целочисленные значения.
Входные значения различаются по масштабу и должны быть нормализованы в диапазоне от 0 до 1. Обычно рекомендуется нормализовать входные значения в диапазоне выбранной передаточной функции, в данном случае сигмоидальной функции, которая выводит значения в диапазоне от 0 до 1. .dataset_minmax ()а такжеnormalize_dataset ()вспомогательные функции были использованы для нормализации входных значений.
Мы оценим алгоритм с использованием k-кратной перекрестной проверки с 5-кратным увеличением. Это означает, что 201/5 = 40,2 или 40 записей будут в каждом сгибе. Мы будем использовать вспомогательные функцииevaluate_algorithm ()оценить алгоритм с перекрестной проверкой иaccuracy_metric ()рассчитать точность прогнозов.
Новая функция с именемback_propagation ()был разработан для управления приложением алгоритма Backpropagation, сначала инициализируя сеть, обучая ее на наборе обучающих данных, а затем используя обученную сеть, чтобы делать прогнозы на тестовом наборе данных.
Полный пример приведен ниже.
# Backprop on the Seeds Dataset
from random import seed
from random import randrange
from random import random
from csv import reader
from math import exp
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
stats = [[min(column), max(column)] for column in zip(*dataset)]
return stats
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)-1):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Backpropagation Algorithm With Stochastic Gradient Descent
def back_propagation(train, test, l_rate, n_epoch, n_hidden):
n_inputs = len(train[0]) - 1
n_outputs = len(set([row[-1] for row in train]))
network = initialize_network(n_inputs, n_hidden, n_outputs)
train_network(network, train, l_rate, n_epoch, n_outputs)
predictions = list()
for row in test:
prediction = predict(network, row)
predictions.append(prediction)
return(predictions)
# Test Backprop on Seeds dataset
seed(1)
# load and prepare data
filename = 'seeds_dataset.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# normalize input variables
minmax = dataset_minmax(dataset)
normalize_dataset(dataset, minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.3
n_epoch = 500
n_hidden = 5
scores = evaluate_algorithm(dataset, back_propagation, n_folds, l_rate, n_epoch, n_hidden)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))Была построена сеть с 5 нейронами в скрытом слое и 3 нейронами в выходном слое. Сеть была подготовлена для 500 эпох с темпом обучения 0,3. Эти параметры были найдены с небольшой пробой и ошибкой, но вы можете сделать это намного лучше.
При выполнении примера выводится средняя точность классификации для каждого сгиба, а также средняя производительность по всем сгибам.
Вы можете видеть, что обратное распространение и выбранная конфигурация достигли средней точности классификации около 93%, что значительно лучше, чем алгоритм нулевого правила, который немного лучше, чем точность 28%.
Scores: [92.85714285714286, 92.85714285714286, 97.61904761904762, 92.85714285714286, 90.47619047619048]
Mean Accuracy: 93.333%расширения
В этом разделе перечислены расширения к учебнику, которые вы можете изучить.
- Параметры алгоритма настройки, Попробуйте большие или меньшие сети, обученные дольше или короче. Посмотрите, сможете ли вы улучшить производительность набора данных seed.
- Дополнительные методы, Поэкспериментируйте с различными методами инициализации веса (такими как небольшие случайные числа) и различными передаточными функциями (такими как tanh).
- Больше слоев, Добавьте поддержку для большего количества скрытых слоев, обученных так же, как один скрытый слой, используемый в этом руководстве.
- регрессия, Измените сеть так, чтобы в выходном слое был только один нейрон, и чтобы было предсказано реальное значение. Выберите регрессионный набор данных для практики. Линейная передаточная функция может использоваться для нейронов в выходном слое, или выходные значения выбранного набора данных могут быть масштабированы до значений между 0 и 1.
- Пакетный градиентный спуск, Измените процедуру обучения с онлайн на пакетный градиентный спуск и обновляйте веса только в конце каждой эпохи.
Вы пробовали какие-либо из этих расширений?
Поделитесь своим опытом в комментариях ниже.
Обзор
В этом руководстве вы узнали, как реализовать алгоритм обратного распространения с нуля.
В частности, вы узнали:
- Как переслать распространение входа для расчета выхода сети.
- Как обратно распространять ошибки и обновлять вес сети.
- Как применить алгоритм обратного распространения к реальному набору данных.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Background
Backpropagation is a common method for training a neural network. There is no shortage of papers online that attempt to explain how backpropagation works, but few that include an example with actual numbers. This post is my attempt to explain how it works with a concrete example that folks can compare their own calculations to in order to ensure they understand backpropagation correctly.
Backpropagation in Python
You can play around with a Python script that I wrote that implements the backpropagation algorithm in this Github repo.
Backpropagation Visualization
For an interactive visualization showing a neural network as it learns, check out my Neural Network visualization.
Additional Resources
If you find this tutorial useful and want to continue learning about neural networks, machine learning, and deep learning, I highly recommend checking out Adrian Rosebrock’s new book, Deep Learning for Computer Vision with Python. I really enjoyed the book and will have a full review up soon.
Overview
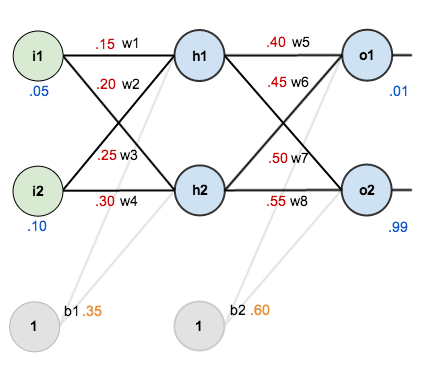
For this tutorial, we’re going to use a neural network with two inputs, two hidden neurons, two output neurons. Additionally, the hidden and output neurons will include a bias.
Here’s the basic structure:
In order to have some numbers to work with, here are the initial weights, the biases, and training inputs/outputs:
The goal of backpropagation is to optimize the weights so that the neural network can learn how to correctly map arbitrary inputs to outputs.
For the rest of this tutorial we’re going to work with a single training set: given inputs 0.05 and 0.10, we want the neural network to output 0.01 and 0.99.
The Forward Pass
To begin, lets see what the neural network currently predicts given the weights and biases above and inputs of 0.05 and 0.10. To do this we’ll feed those inputs forward though the network.
We figure out the total net input to each hidden layer neuron, squash the total net input using an activation function (here we use the logistic function), then repeat the process with the output layer neurons.
Total net input is also referred to as just net input by some sources.
Here’s how we calculate the total net input for :
We then squash it using the logistic function to get the output of :
Carrying out the same process for we get:
We repeat this process for the output layer neurons, using the output from the hidden layer neurons as inputs.
Here’s the output for :
And carrying out the same process for we get:
Calculating the Total Error
We can now calculate the error for each output neuron using the squared error function and sum them to get the total error:
Some sources refer to the target as the ideal and the output as the actual.
The is included so that exponent is cancelled when we differentiate later on. The result is eventually multiplied by a learning rate anyway so it doesn’t matter that we introduce a constant here [1].
For example, the target output for is 0.01 but the neural network output 0.75136507, therefore its error is:
Repeating this process for (remembering that the target is 0.99) we get:
The total error for the neural network is the sum of these errors:
The Backwards Pass
Our goal with backpropagation is to update each of the weights in the network so that they cause the actual output to be closer the target output, thereby minimizing the error for each output neuron and the network as a whole.
Output Layer
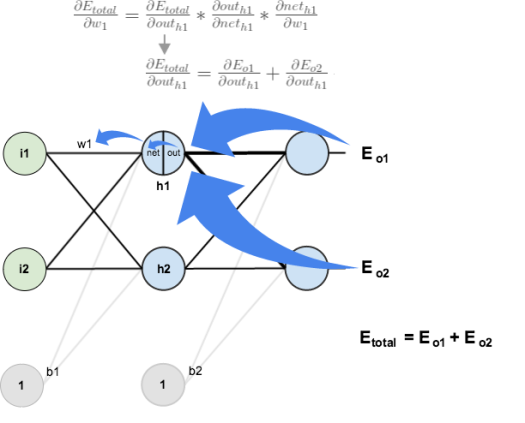
Consider . We want to know how much a change in
affects the total error, aka
.
is read as “the partial derivative of
with respect to
“. You can also say “the gradient with respect to
“.
By applying the chain rule we know that:
Visually, here’s what we’re doing:
We need to figure out each piece in this equation.
First, how much does the total error change with respect to the output?
is sometimes expressed as
When we take the partial derivative of the total error with respect to , the quantity
becomes zero because
does not affect it which means we’re taking the derivative of a constant which is zero.
Next, how much does the output of change with respect to its total net input?
The partial derivative of the logistic function is the output multiplied by 1 minus the output:
Finally, how much does the total net input of change with respect to
?
Putting it all together:
You’ll often see this calculation combined in the form of the delta rule:
Alternatively, we have and
which can be written as
, aka
(the Greek letter delta) aka the node delta. We can use this to rewrite the calculation above:
Therefore:
Some sources extract the negative sign from so it would be written as:
To decrease the error, we then subtract this value from the current weight (optionally multiplied by some learning rate, eta, which we’ll set to 0.5):
We can repeat this process to get the new weights ,
, and
:
We perform the actual updates in the neural network after we have the new weights leading into the hidden layer neurons (ie, we use the original weights, not the updated weights, when we continue the backpropagation algorithm below).
Hidden Layer
Next, we’ll continue the backwards pass by calculating new values for ,
,
, and
.
Big picture, here’s what we need to figure out:
Visually:
We’re going to use a similar process as we did for the output layer, but slightly different to account for the fact that the output of each hidden layer neuron contributes to the output (and therefore error) of multiple output neurons. We know that affects both
and
therefore the
needs to take into consideration its effect on the both output neurons:
Starting with :
We can calculate using values we calculated earlier:
And is equal to
:
Plugging them in:
Following the same process for , we get:
Therefore:
Now that we have , we need to figure out
and then
for each weight:
We calculate the partial derivative of the total net input to with respect to
the same as we did for the output neuron:
Putting it all together:
You might also see this written as:
We can now update :
Repeating this for ,
, and
Finally, we’ve updated all of our weights! When we fed forward the 0.05 and 0.1 inputs originally, the error on the network was 0.298371109. After this first round of backpropagation, the total error is now down to 0.291027924. It might not seem like much, but after repeating this process 10,000 times, for example, the error plummets to 0.0000351085. At this point, when we feed forward 0.05 and 0.1, the two outputs neurons generate 0.015912196 (vs 0.01 target) and 0.984065734 (vs 0.99 target).
If you’ve made it this far and found any errors in any of the above or can think of any ways to make it clearer for future readers, don’t hesitate to drop me a note. Thanks!
And while I have you…
In addition to dabbling in data science, I run Preceden timeline maker, the best timeline maker software on the web. If you ever need to create a high level timeline or roadmap to get organized or align your team, Preceden is a great option.
В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Код
|
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): l1 = 1/(1+np.exp(—(np.dot(X,syn0)))) l2 = 1/(1+np.exp(—(np.dot(l1,syn1)))) l2_delta = (y — l2)*(l2*(1—l2)) l1_delta = l2_delta.dot(syn1.T) * (l1 * (1—l1)) syn1 += l1.T.dot(l2_delta) syn0 += X.T.dot(l1_delta) |
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
|
Вход Выход 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0 |
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import numpy as np # Сигмоида def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1—f(x)) return 1/(1+np.exp(—x)) # набор входных данных X = np.array([ [0,0,1], [0,1,1], [1,0,1], [1,1,1] ]) # выходные данные y = np.array([[0,0,1,1]]).T # сделаем случайные числа более определёнными np.random.seed(1) # инициализируем веса случайным образом со средним 0 syn0 = 2*np.random.random((3,1)) — 1 for iter in xrange(10000): # прямое распространение l0 = X l1 = nonlin(np.dot(l0,syn0)) # насколько мы ошиблись? l1_error = y — l1 # перемножим это с наклоном сигмоиды # на основе значений в l1 l1_delta = l1_error * nonlin(l1,True) # !!! # обновим веса syn0 += np.dot(l0.T,l1_delta) # !!! print «Выходные данные после тренировки:» print l1 |
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
|
def nonlin(x,deriv=False): |
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
|
X = np.array([ [0,0,1], … |
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
|
y = np.array([[0,0,1,1]]).T |
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
|
syn0 = 2*np.random.random((3,1)) – 1 |
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
|
for iter in xrange(10000): |
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
|
l1 = nonlin(np.dot(l0,syn0)) |
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
|
(4 x 3) dot (3 x 1) = (4 x 1) |
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
|
l1_delta = l1_error * nonlin(l1,True) |
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
Полное выражение: производная, взвешенная по ошибкам
|
l1_delta = l1_error * nonlin(l1,True) |
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
|
syn0 += np.dot(l0.T,l1_delta) |
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
|
weight_update = input_value * l1_delta |
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
import numpy as np def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1—f(x)) return 1/(1+np.exp(—x)) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) np.random.seed(1) # случайно инициализируем веса, в среднем — 0 syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): # проходим вперёд по слоям 0, 1 и 2 l0 = X l1 = nonlin(np.dot(l0,syn0)) l2 = nonlin(np.dot(l1,syn1)) # как сильно мы ошиблись относительно нужной величины? l2_error = y — l2 if (j% 10000) == 0: print «Error:» + str(np.mean(np.abs(l2_error))) # в какую сторону нужно двигаться? # если мы были уверены в предсказании, то сильно менять его не надо l2_delta = l2_error*nonlin(l2,deriv=True) # как сильно значения l1 влияют на ошибки в l2? l1_error = l2_delta.dot(syn1.T) # в каком направлении нужно двигаться, чтобы прийти к l1? # если мы были уверены в предсказании, то сильно менять его не надо l1_delta = l1_error * nonlin(l1,deriv=True) syn1 += l1.T.dot(l2_delta) syn0 += l0.T.dot(l1_delta) |
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
|
l1_error = l2_delta.dot(syn1.T) |
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Источник
На предыдущих
занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их,
исходя из определенных математических соображений. Это можно сделать, когда
сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной
подбор становится попросту невозможным и возникает задача нахождения весовых
коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из
распространенных подходов к обучению заключается в последовательном
предъявлении НС векторов наблюдений и последующей корректировки весовых
коэффициентов так, чтобы выходное значение совпадало с требуемым:
|
weight_update = input_value * l1_delta |
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
import numpy as np def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1—f(x)) return 1/(1+np.exp(—x)) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) np.random.seed(1) # случайно инициализируем веса, в среднем — 0 syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): # проходим вперёд по слоям 0, 1 и 2 l0 = X l1 = nonlin(np.dot(l0,syn0)) l2 = nonlin(np.dot(l1,syn1)) # как сильно мы ошиблись относительно нужной величины? l2_error = y — l2 if (j% 10000) == 0: print «Error:» + str(np.mean(np.abs(l2_error))) # в какую сторону нужно двигаться? # если мы были уверены в предсказании, то сильно менять его не надо l2_delta = l2_error*nonlin(l2,deriv=True) # как сильно значения l1 влияют на ошибки в l2? l1_error = l2_delta.dot(syn1.T) # в каком направлении нужно двигаться, чтобы прийти к l1? # если мы были уверены в предсказании, то сильно менять его не надо l1_delta = l1_error * nonlin(l1,deriv=True) syn1 += l1.T.dot(l2_delta) syn0 += l0.T.dot(l1_delta) |
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
|
l1_error = l2_delta.dot(syn1.T) |
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Источник