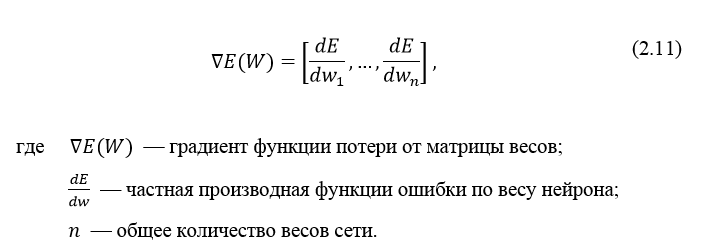Перевод
Ссылка на автора
В этой статье вы узнаете, как можно обучить нейронную сеть с помощью обратного распространения и стохастического градиентного спуска. Теории будут подробно описаны, и приведен подробный пример расчета, где обновляются как веса, так и смещения.
Это вторая часть в серии статей:
- Часть 1: Фонд,
- Часть 2: градиентный спуск и обратное распространение,
- Часть 3: Реализация в Java,
- Часть 4: лучше, быстрее, сильнее,
- Часть 5. Обучение сети чтению рукописных цифр,
- Дополнительный 1: Как я увеличил точность на 1% за счет увеличения данных,
- Дополнительно 2: Детская площадка MNIST,
Я предполагаю, что вы прочитали последнюю статью и что у вас есть хорошее представление о том, как нейронная сеть можетпреобразованиеданные. Если последняя статья требовала хорошего воображения (размышления о подпространствах в нескольких измерениях), эта статья, с другой стороны, будет более требовательной с точки зрения математики. Готовьтесь: бумага и ручка. Тихая комната. Тщательная мысль. Хороший ночной сон. Время, выносливость и усилие. Он утонет.
Контролируемое обучение
В прошлой статье мы пришли к выводу, что нейронную сеть можно использовать в качестве настраиваемой векторной функции. Мы корректируем эту функцию путем изменения весов и смещений, но их трудно изменить вручную. Их часто слишком много, даже если бы их было меньше, тем не менее было бы очень трудно получить хорошие результаты вручную.
Прекрасно то, что мы можем позволить сети настроить это самостоятельно, обучив сеть. Это можно сделать разными способами. Здесь я опишу то, что называетсяконтролируемое обучение, В этом типе обучения у нас есть набор данных, который былпомечены —у нас уже есть ожидаемый результат для каждого входа в этом наборе данных. Это будет наш учебный набор данных. Мы также гарантируем, что у нас есть маркированный набор данных, на котором мы никогда не обучаем сеть. Это будет наш тестовый набор данных, который будет использоваться для проверки того, насколько хорошо классифицируется обученная сеть.невидимые данные,
При обучении нашей нейронной сети мы подаем образец за образцом из набора обучающих данных по сети, и для каждого из них мы проверяем результат. В частности, мы проверяем, насколько результат отличается от того, что мы ожидали (ярлык). Разница между тем, что мы ожидали, и тем, что мы получили, называется стоимостью (иногда это называетсяошибкаилипотеря). Стоимость говорит нам, насколько правильной или неправильной была наша нейронная сеть в конкретном образце. Эту меру можно затем использовать для незначительной настройки сети, чтобы она была менее ошибочной при следующем поступлении этого образца через сеть.
Существует несколько различных функций стоимости, которые можно использовать (см. этот список например).
В этой статье я буду использовать функцию квадратичной стоимости:
(Иногда это также пишется с константой 0,5 впереди, что сделает его немного чище, когда мы его дифференцируем. Мы будем придерживаться версии выше.)
Возвращаясь к нашему примеру из часть 1,
Если бы мы ожидали:
… и получил …
… Стоимость будет:
Поскольку функция стоимости написана выше, размер ошибки явно зависит от выхода сети и ожидаемого значения. Если бы мы вместо этого определяли стоимость в терминах введенного значения (которое, конечно, детерминировано связано с выходными данными, если мы также учитываем все веса, смещения и какие функции активации были использованы), мы могли бы вместо этого написать:
C = C (y, exp) = C (W, b, Sσ, x, exp)— то есть стоимость является функциейWвосьмерокбiases, набор функций активации, входИксиехрectation.
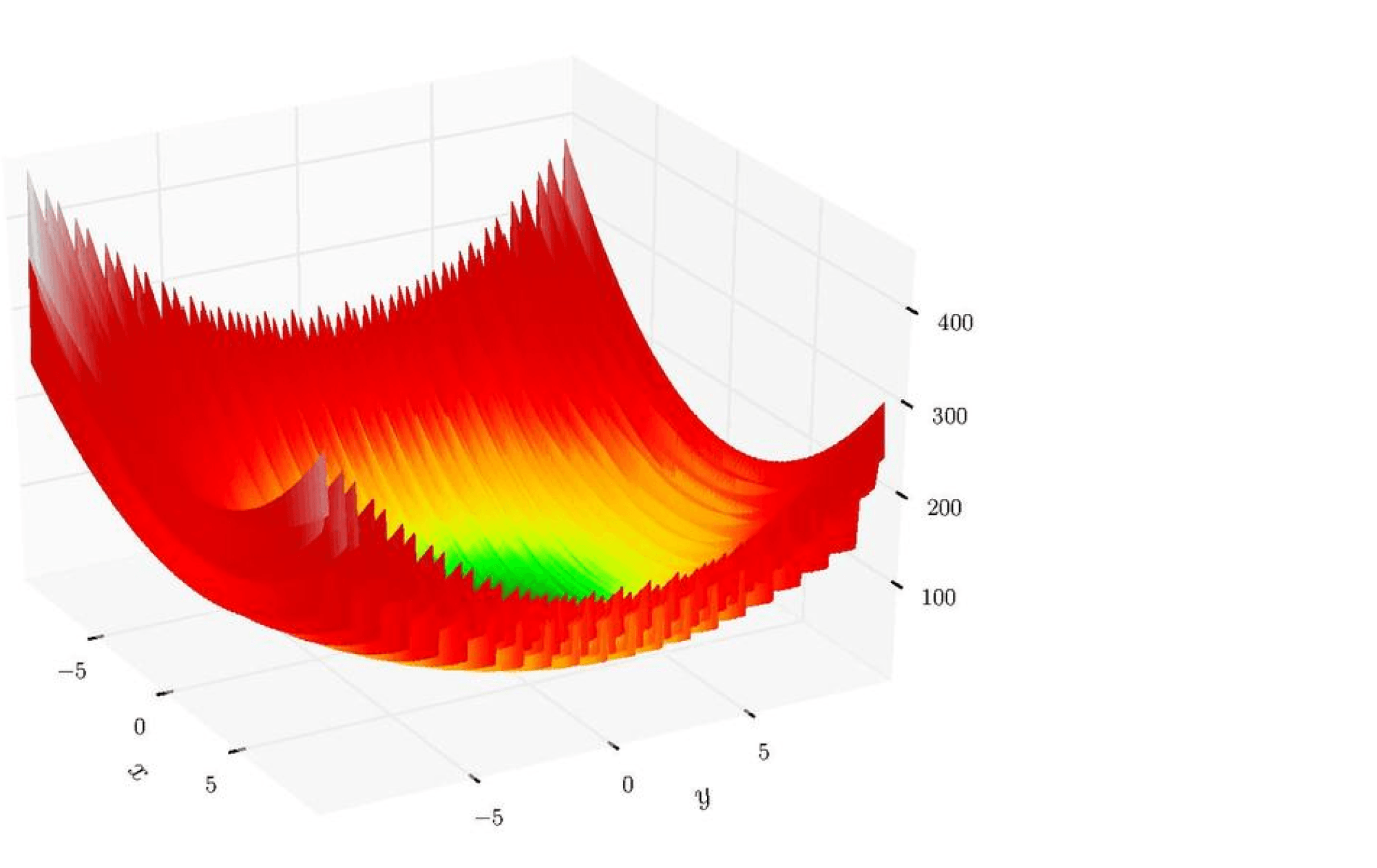
Стоимость — это всего лишь скалярное значение для всего этого ввода. Поскольку функция непрерывна и дифференцируема (иногдакусочно дифференцируемыйНапример, при использовании ReLU-активаций) мы можем представить непрерывный ландшафт холмов и долин для функции стоимости. В более высоких измерениях этот пейзаж трудно визуализировать, но только с двумя весамиW₁ иWMight это может выглядеть примерно так:
Предположим, мы получили именно то значение стоимости, которое указано красной точкой на изображении (на основе толькоW₁ иWThat в этом упрощенном случае). Наша цель сейчас — улучшить нейронную сеть. Если бы мы могли снизить стоимость, нейронная сеть была бы лучше в классификации наших помеченных данных. Желательно, чтобы мы нашлиглобальный минимумфункции стоимости в этом ландшафте. Другими словами:самая глубокая долина из них всех, Это трудно, и нет никаких явных методов для такой сложной функции, как нейронная сеть. Тем не менее, мы можем найтиместный минимумс помощью итеративного процесса под названием градиентный спуск. Локального минимума может быть достаточно для наших нужд, и если нет, мы всегда можем скорректировать дизайн сети, чтобы получить новый ценовой ландшафт для локального и итеративного исследования
Градиентный спуск
Из исчисления с несколькими переменными мы знаем, что градиент функции ∇f в конкретной точке будет касательным к поверхности вектором, указывающим направление, в котором функция увеличивается наиболее быстро. И наоборот, отрицательный градиент -∇f будет указывать в направлении, где функция уменьшается быстрее всего. Этот факт мы можем использовать для расчета новых весовW⁺ от наших текущих весовW:
В уравнении вышеηэто просто небольшая константа, называемая скоростью обучения. Эта константа говорит нам, какую часть вектора градиента мы будем использовать для изменения текущего набора весов на новые. Если выбран слишком маленький, веса будут корректироваться слишком медленно, и наша конвергенция к локальному минимуму займет много времени. Если установлено слишком высокое, мы можем промахнуться и пропустить (или получить бодрое не сходящееся итеративное поведение).
Все вещи в уравнении выше — это просто матричная арифметика. Нам нужно внимательнее рассмотреть градиент функции стоимости относительно весов:
Как вы видите, нас пока не интересует конкретная скалярная стоимость, C, анасколько изменяется функция Costкогда вес меняется (рассчитывается один за другим),
Если мы расширим аккуратную векторную форму (уравнение 1), это будет выглядеть так:
Хорошая вещь об использовании градиента состоит в том, что он будет корректировать те веса, которые больше всего нуждаются в большем изменении, и веса, которые меньше нуждаются в изменении меньше. Это тесно связано с тем, что вектор отрицательного градиента указывает точно в направлении максимального спуска. Чтобы увидеть это, пожалуйста, еще раз взгляните на упрощенное изображение ландшафта функции стоимости выше и попытайтесь визуализировать разделение вектора красного градиента на векторы его компонентов вдоль осей.
Идея градиентного спуска работает так же хорошо в N измерениях, хотя это трудно визуализировать. Градиент покажет, какие компоненты нужно изменить больше, а какие нужно изменить меньше, чтобы уменьшить функцию C.
До сих пор я только что говорил о весах. Как насчет предубеждений? Что ж, те же рассуждения справедливы и для них, но вместо этого мы вычисляем (что проще):
Теперь пришло время посмотреть, как мы можем вычислить все эти частные производные для весов и смещений. Это приведет нас на более волосатую территорию, так что пристегнитесь. Чтобы разобраться во всем этом, сначала нам нужно слово о …
нотация
В остальной части этой статьи интенсивные обозначения. Множество символов и букв, которые вы увидите, это просто индексы, чтобы помочь нам отслеживать, на какой слой и на нейрон я ссылаюсь. Не позволяйте этим индексам делать математические выражения пугающими. Указатели призваны помочь и сделать его более точным. Вот краткое руководство о том, как их читать:
Также обратите внимание на то, что вход в нейрон был названZв прошлой статье (что довольно распространено), но был изменен наяВот. Причина в том, что мне легче запомнить это какядля вводаа такжеодля вывода,
обратное распространение
Самый простой способ описать, как рассчитать частные производные, это посмотреть на один конкретный вес:
Мы также увидим, что есть небольшая разница в том, как обрабатывать частную производную, если этот конкретный вес связан с последним выходным слоем или если он связан с любым из предыдущих скрытых слоев.
Последний слой
Теперь рассмотрим один весвесʟв последнем слое:
Наша задача — найти:
Как описано в прошлой статье, есть несколько шагов между весом и функцией стоимости:
- Мы умножаем вес на результат предыдущего слоя и добавляем смещение. Результатом является входяʟк нейрону.
- этояʟзатем подается через функцию активацииσ, производя выход из нейронаоʟ₁
- Наконец этооʟ₁используется в функции стоимости.
Справедливо сказать, что это трудно рассчитать …
… просто глядя на это.
Однако, если мы разделим его на три этапа, которые я только что описал, все станет намного проще. Поскольку эти три шага являются цепочечными функциями, мы могли бы отделить их производную, используя правило цепочки из исчисления:
На самом деле эти три частных производных оказывается простым для вычисления:
Это означает, что у нас есть все три фактора, необходимые для расчета
Другими словами, теперь мы знаем, как обновить все веса в последнем слое.
Давайте поработаем в обратном направлении отсюда.
Скрытые слои
Теперь рассмотрим один весвесʜв скрытом слое перед последним слоем:
Наша цель — найти:
Мы продолжаем, как мы делали в последнем слое Цепное правило дает нам:
Два первых фактора те же, что и раньше, и решает следующее:
- выход из предыдущего слоя и…
- производная функции активации соответственно.
Тем не менее, фактор …
… немного сложнее. Причина в том, что изменениеоʜочевидно, изменяет вход для всех нейронов в последнем слое и, как следствие, изменяет функцию стоимости в гораздо более широком смысле по сравнению с тем, когда нам просто нужно было заботиться об одном выходе из одного нейрона последнего слоя (я проиллюстрировал это, сделав соединения шире на изображении выше).
Чтобы решить эту проблему, нам нужно разделить частную производную функции общей стоимости на каждый вклад последнего слоя.
… Где каждый термин описывает, насколько изменяется Стоимость, когдаоʜизменяется, но только для той части сигнала, которая направляется через этот определенный выходной нейрон.
Давайте проверим этот единственный термин для первого нейрона. Опять же, это станет немного понятнее, если мы разделим его с помощью правила цепочки:
Давайте посмотрим на каждый из них:
Давайте на мгновение остановимся и позволим всему этому погрузиться.
Подводя итог тому, что мы только что узнали:
- Чтобы узнать, как обновить конкретный вес в скрытом слое, мы берем частную производную стоимости в терминах этого веса.
- Применяя правило цепочки, мы получаем три фактора, два из которых мы уже знаем, как рассчитать.
- Третьим фактором в этой цепочке является взвешенная сумма произведения двух факторов, которые мы уже рассчитали в последнем слое.
- Это означает, что мы можем вычислить все веса в этом скрытом слое так же, как мы делали в последнем слое, с той лишь разницей, что мы используем уже вычисленные данные из предыдущего слоя вместо производной функции стоимости.
С вычислительной точки зрения это очень хорошая новость, поскольку мы зависим только от вычислений, которые мы только что сделали (только последний слой), и нам не нужно проходить глубже, чем это. Это иногда называютдинамическое программированиечто часто является радикальным способом ускорить алгоритм, когда динамический алгоритм найден.
И так как мы зависим только от общих вычислений в последнем слое (в частности, мы не зависим от функции стоимости), мы можем теперь идти назад, слой за слоем. Ни один скрытый слой не отличается от любого другого в плане того, как мы рассчитываем вес обновлений. Мы говорим, что мы даем стоимость (илиошибкаилиубыток)backpropagate. Когда мы достигаем первого слоя, мы готовы. В этот момент мы имеем частные производные для всех весов в уравнении (уравнение 1) и готовы сделать наш шаг градиентного спуска вниз в ландшафте функции стоимости.
И вы знаете, что: это все.
Эй, подождите … Уклоны !?
Хорошо, я вас слышу. На самом деле они следуют той же схеме. Разница лишь в том, чтопервый срокв производной цепочке выражения последнего слоя и скрытого слоя будут иметь вид:
… вместо того
Поскольку вход в нейроноʜ ·весʟ+ бчастная производная этого по отношению кбпросто равно 1. Итак, где мы в весовом случае умножили цепочку на выходные данные последнего слоя, мы просто игнорируем выходные данные в случае смещения и умножаем на единицу.
Все остальные расчеты идентичны. Вы можете думать о смещениях как о более простом подмножестве вычислений веса. Тот факт, что изменение смещений не зависит от выхода из предыдущего нейрона, на самом деле имеет смысл. Смещения добавляются «со стороны» независимо от данных, поступающих по проводам к нейрону.
Пример
Из моего недавнего спуска в страну обратного распространения я могу себе представить, что приведенное выше прочтение может быть довольно полезным. Не будь парализован. На практике это довольно просто, и, вероятно, все становится яснее и проще для понимания, если проиллюстрировать это на примере.
Давайте опираться на пример из Часть 1: Фонд:
Давайте начнем свес₅:
Собирая данные из прямого прохода в часть 1 и используя данные из приведенного выше примера расчета стоимости, мы рассчитаем фактор за фактором. Также давайте предположим, что у нас есть скорость обученияη= 0,1 для этого примера.
Аналогично мы можем вычислить все остальные параметры в последнем слое:
Теперь мы перемещаем один слой назад и фокусируемся навес₁:
Еще раз, выбирая данные из прямого прохода в часть 1 и используя данные сверху, это просто для расчета фактор за фактором.
Из расчетов в последнем слое:
Теперь у нас есть все и, наконец, можно найтивес₁:
Таким же образом мы можем вычислить все остальные параметры в скрытом слое:
Это оно Мы успешно обновили весы и смещения во всей сети!
Санитарная проверка
Давайте проверим, что сеть теперь ведет себя немного лучше на входе
х = [2, 3]
Когда мы в первый раз пропустили этот вектор через сеть, мы получили вывод
у = [0,712257432295742, 0,533097573871501]
… и стоимость+0,19374977898811957,
Теперь, после того, как мы обновили веса, мы получаем вывод
у = [0,7187729999291985 0,523807451860988]
… и стоимость+0,18393989144952877,
Обратите внимание, что оба компонента слегка сместились в сторону того, что мы ожидали [1, 0,2], и что общая стоимость сети теперь ниже.
Повторное обучение сделает его еще лучше!
Следующая статья показывает, как это выглядит в коде Java. Когда вы будете готовы к этому, пожалуйста, погрузитесь в: Часть 3: Реализация в Java,
Обратная связь приветствуется!
Первоначально опубликовано на machinelearning.tobiashill.se 4 декабря 2018 г.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
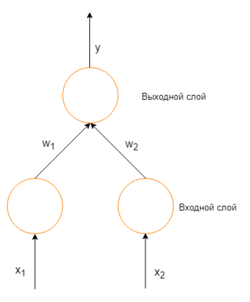
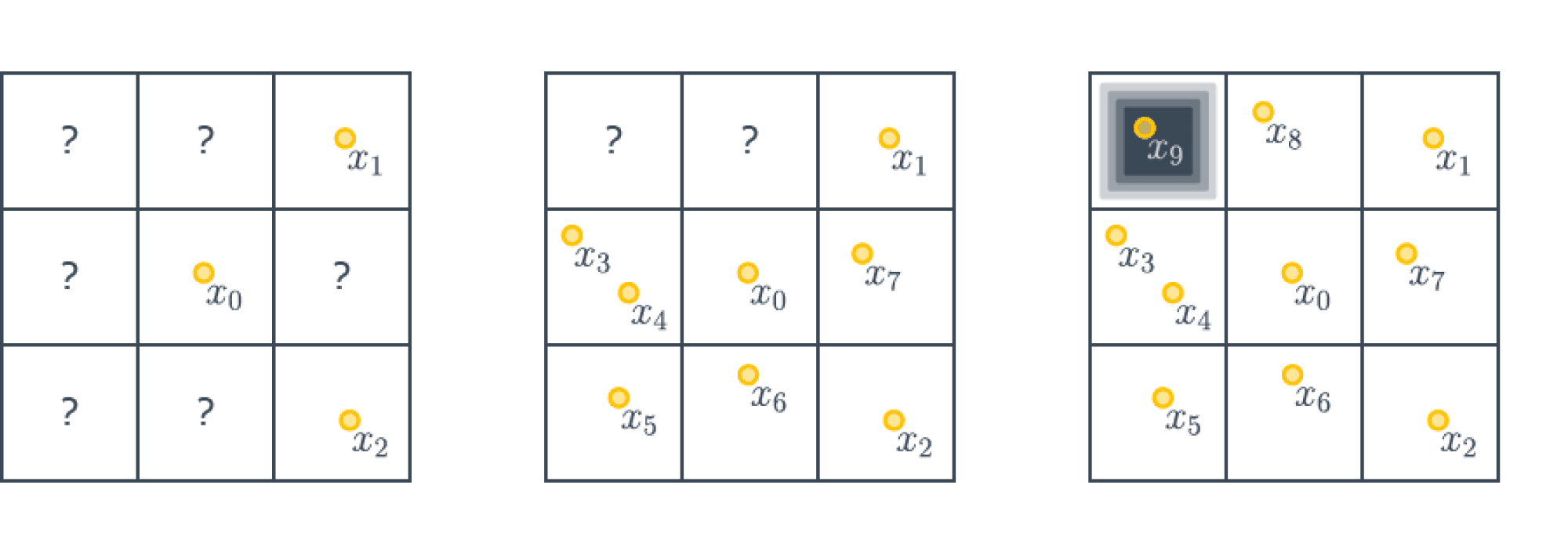
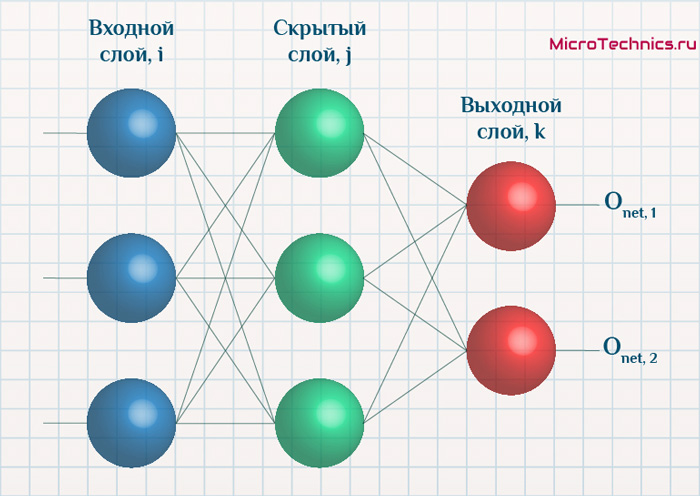
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
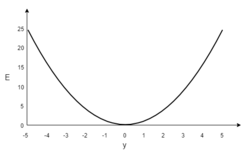
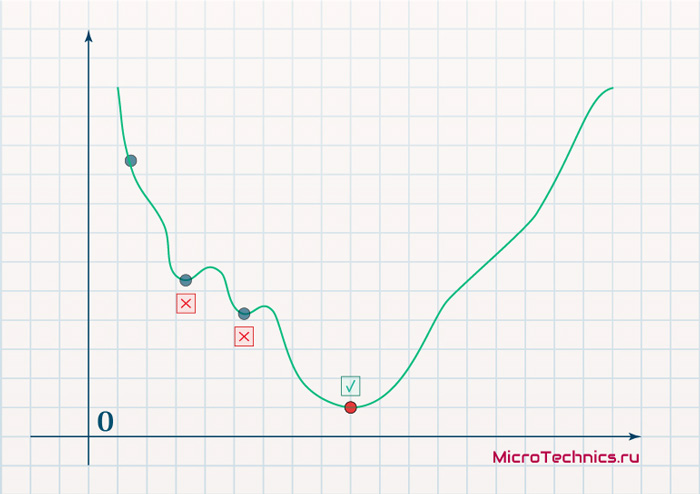
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
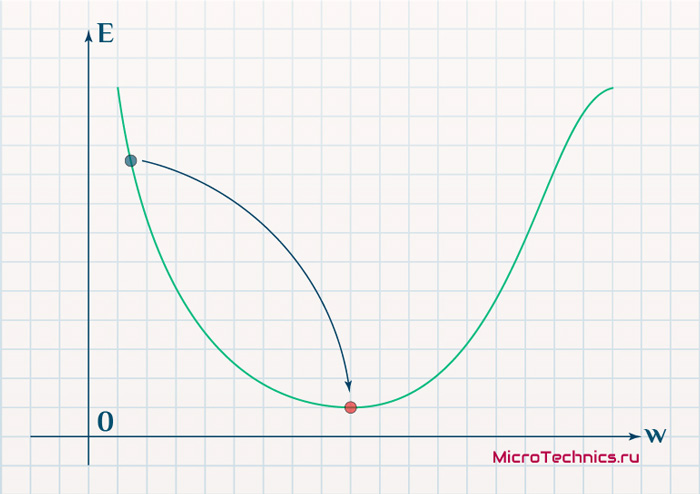
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
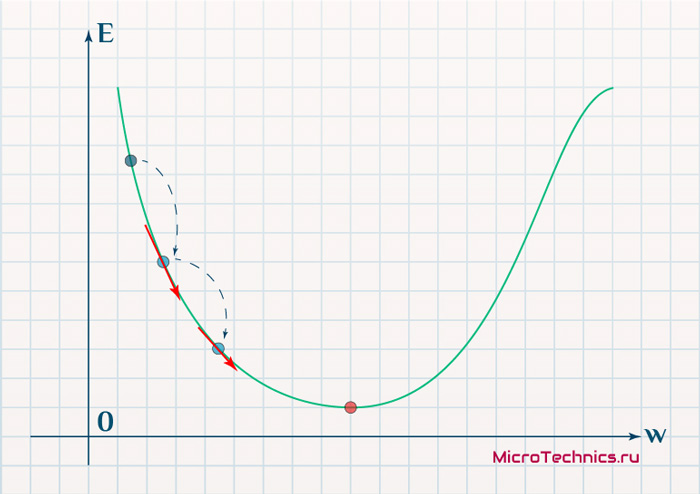
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
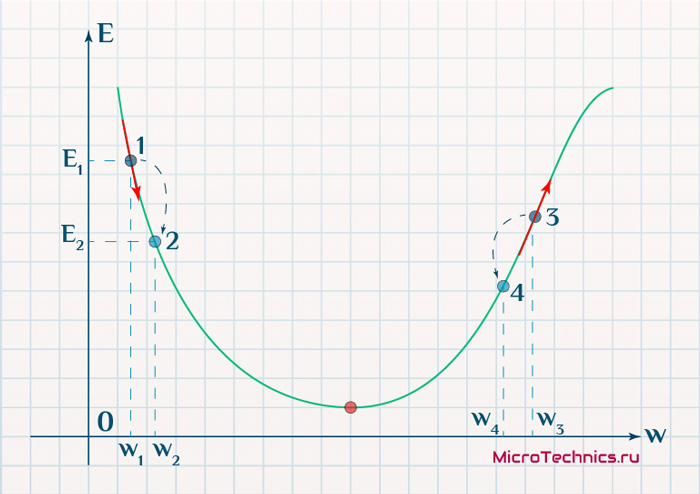
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
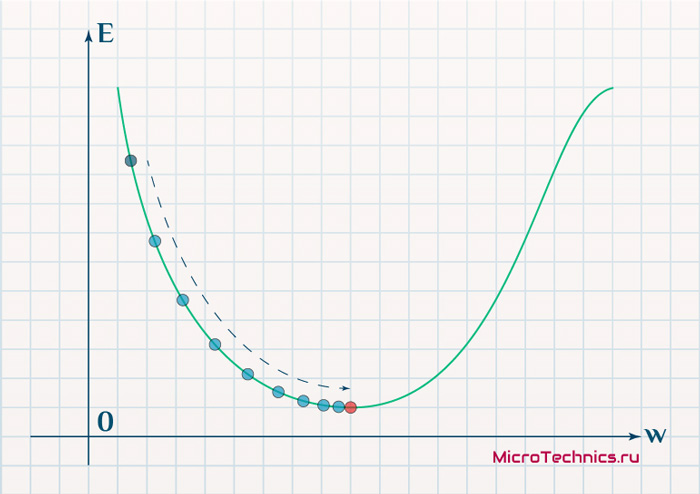
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
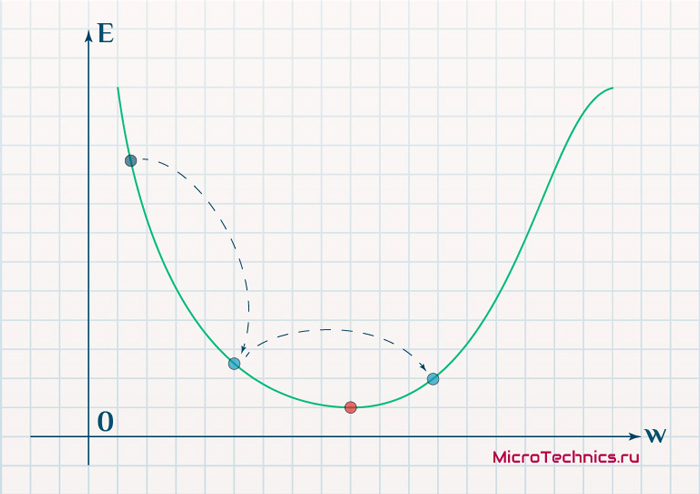
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
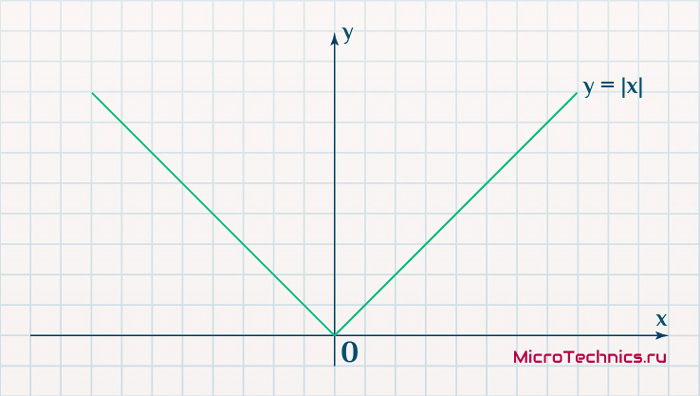
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
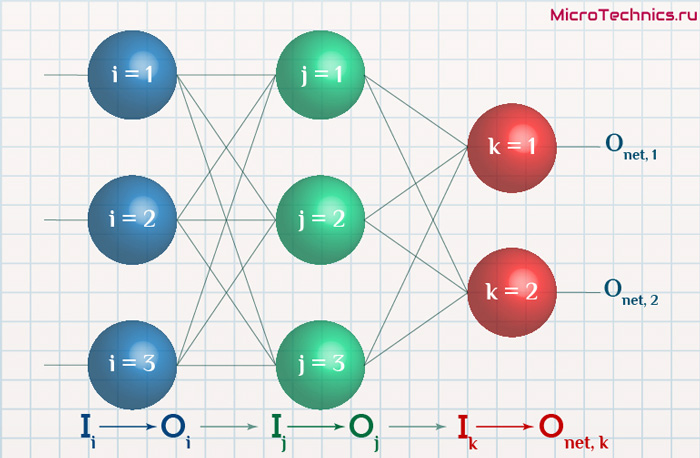
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
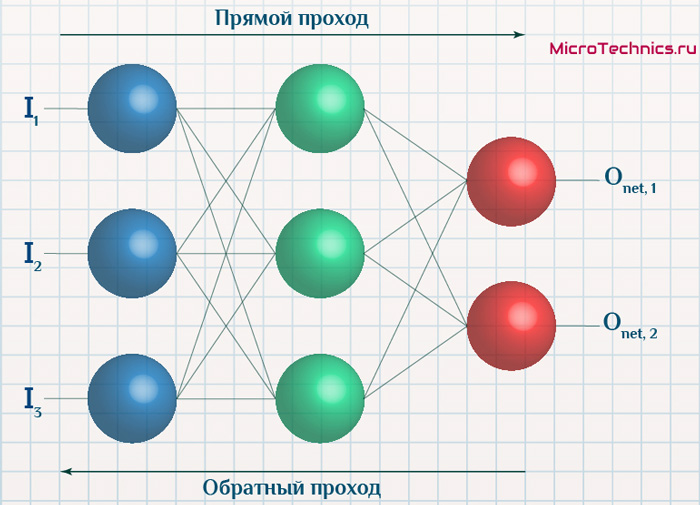
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
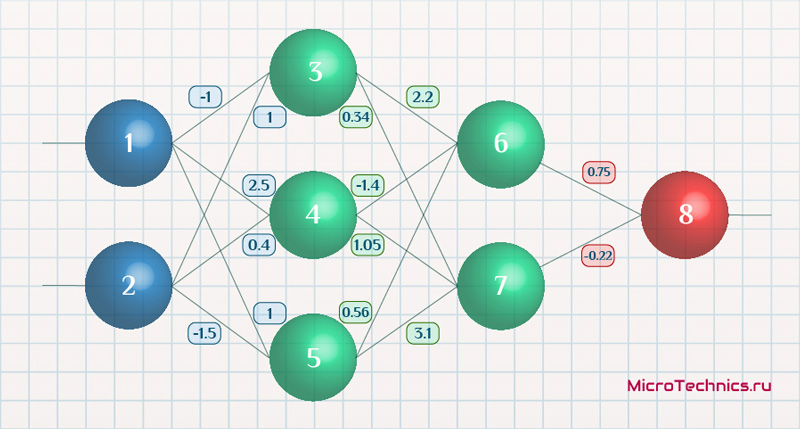
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Время на прочтение
5 мин
Количество просмотров 82K
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:
Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:
Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:
Выход каждого нейрона j является значением активационной функции

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.
Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:
Ошибка нейрона 
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:
Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
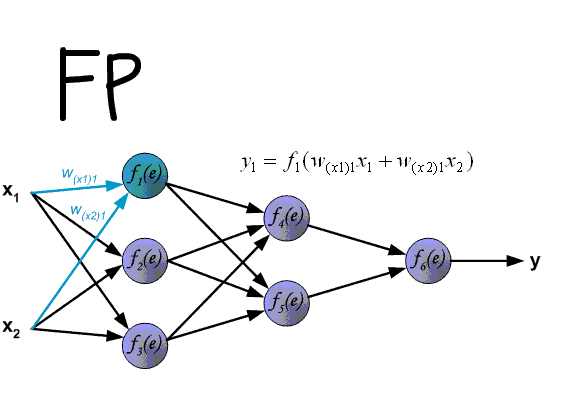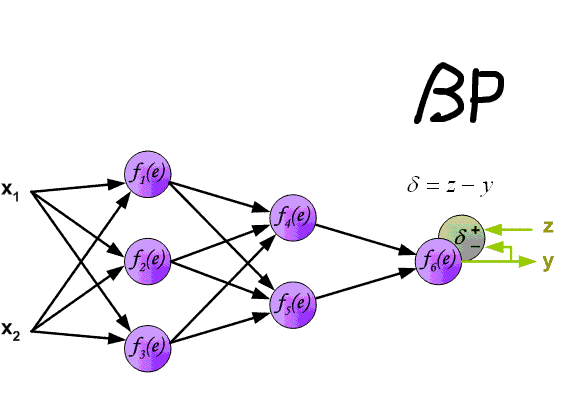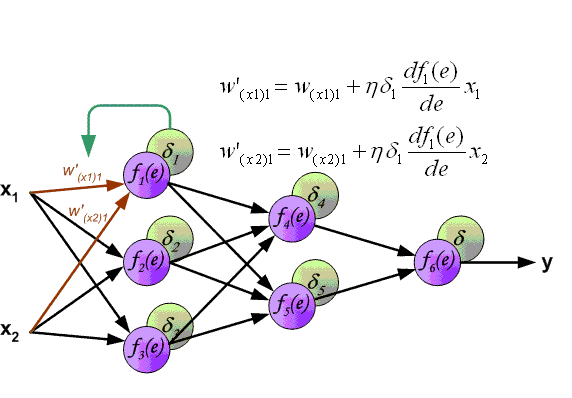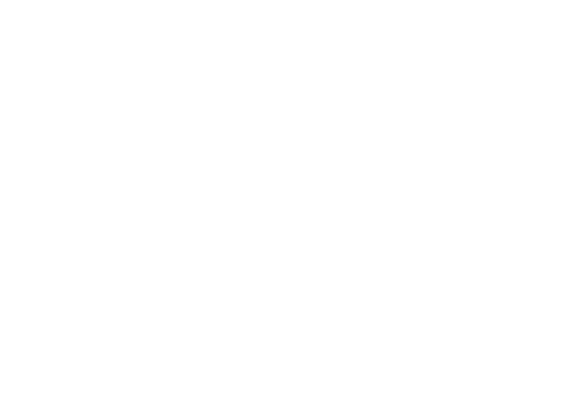
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
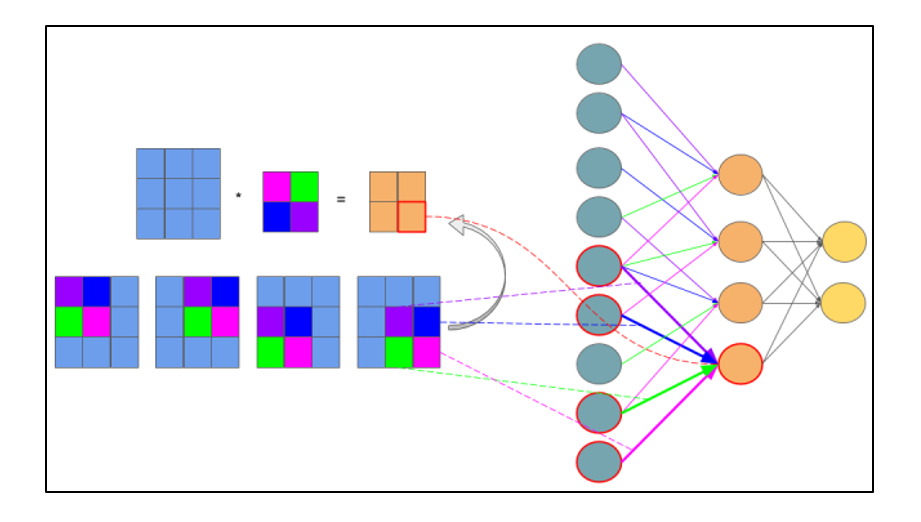
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
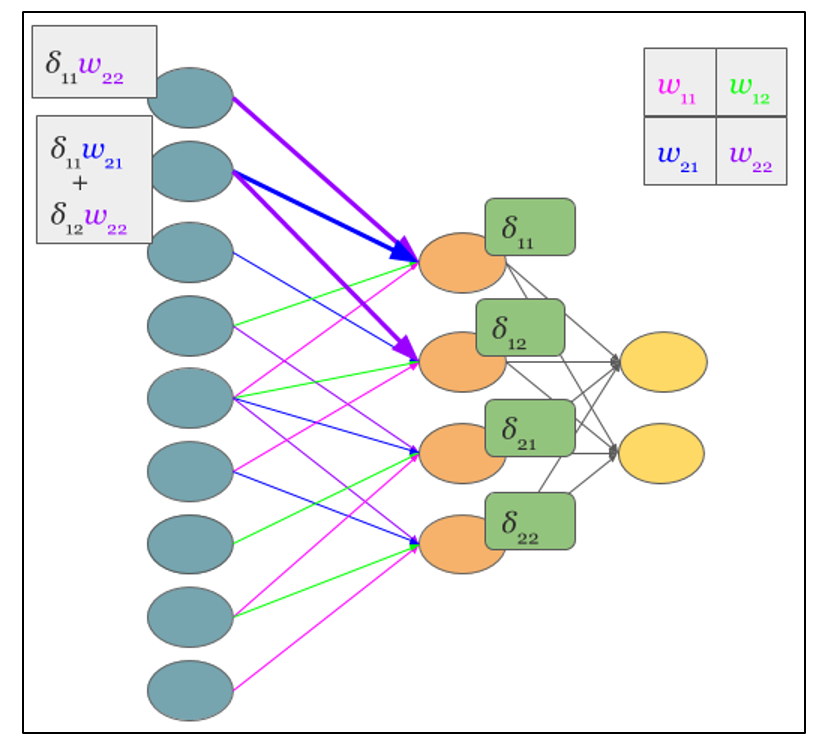
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.
Рисунок 2.10 — Результат операции обратной свертки
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Введение
Зачастую задачи машинного обучения формулируются таким образом, что «веса» модели, которую мы строим, возникают, как решение оптимизационной задачи. В качестве VIP-примера рассмотрим задачу линейной регрессии:
$$
Vert y — Xw Vert_2^2 to min_w,
$$
По сути, мы получили чистейшую задачу квадратичной оптимизации. В чем особенность конкретно этой задачи? Она выпуклая.
Для интересующихся определением.
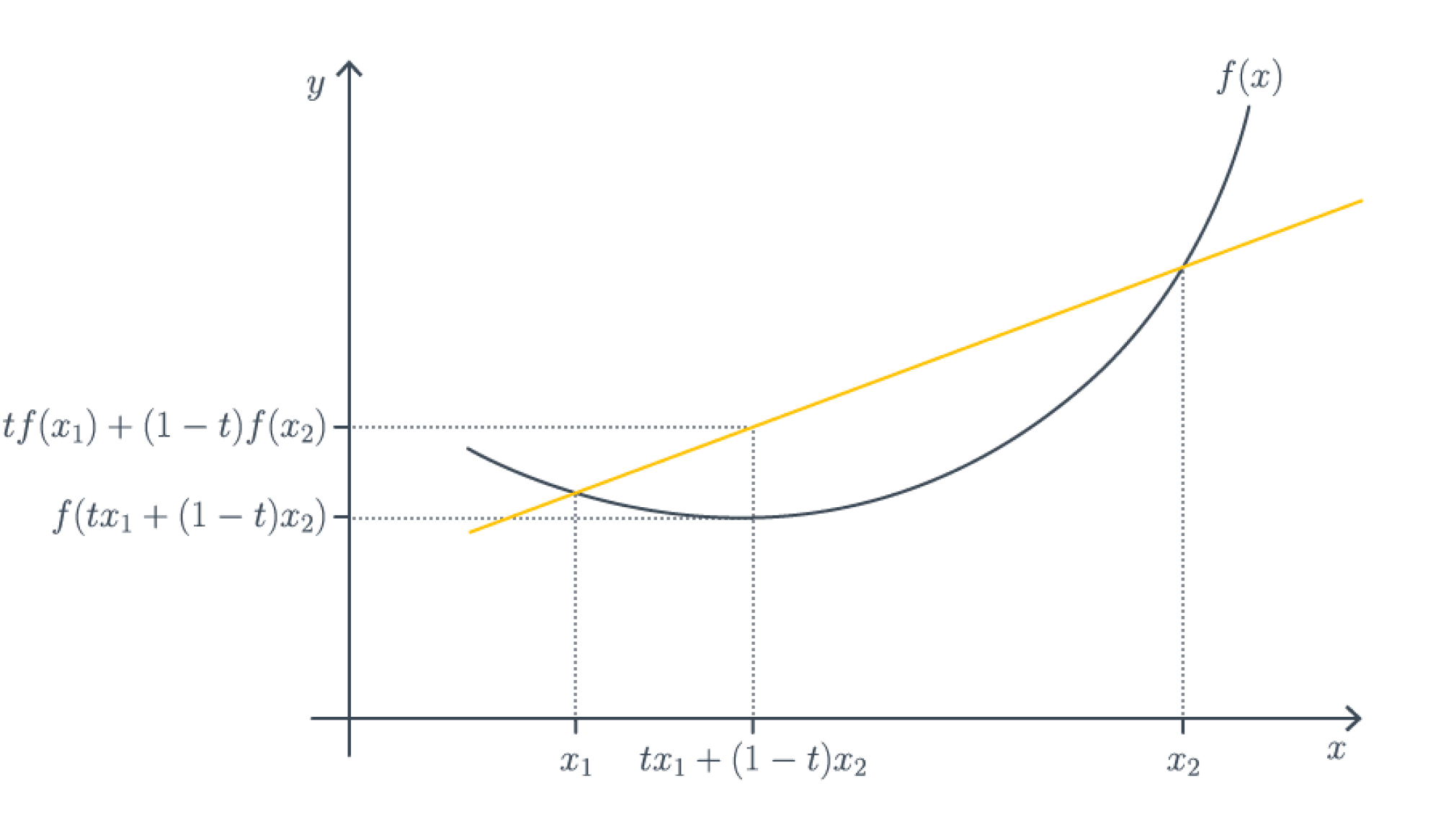
Функция $f colon mathbb{R}^d to mathbb{R}$ является (нестрого) выпуклой (вниз), если для любых $x_1,x_2 in mathbb{R}^d$ верно, что
$$
forall t in [0,1] : f(tx_1 + (1-t)x_2) leq t f(x_1) + (1-t) f(x_2).
$$
Чтобы запомнить, в какую сторону неравенство, всегда полезно рисовать следующую картинку с графическим определением выпуклой функции.
Эквивалентное определение, если функция достаточно гладкая – гессиан неотрицательно определен в любой точке, то есть в каждой точке функция хорошо приближается параболоидом ветвями вверх. Отсюда по критерию минимальности второго порядка автоматически следует, что всякая точка локального оптимума является точкой локального минимума, то есть локальных максимумов и сёдел в выпуклом мире попросту не существует.
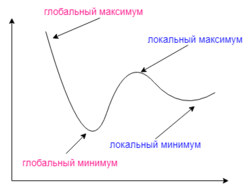
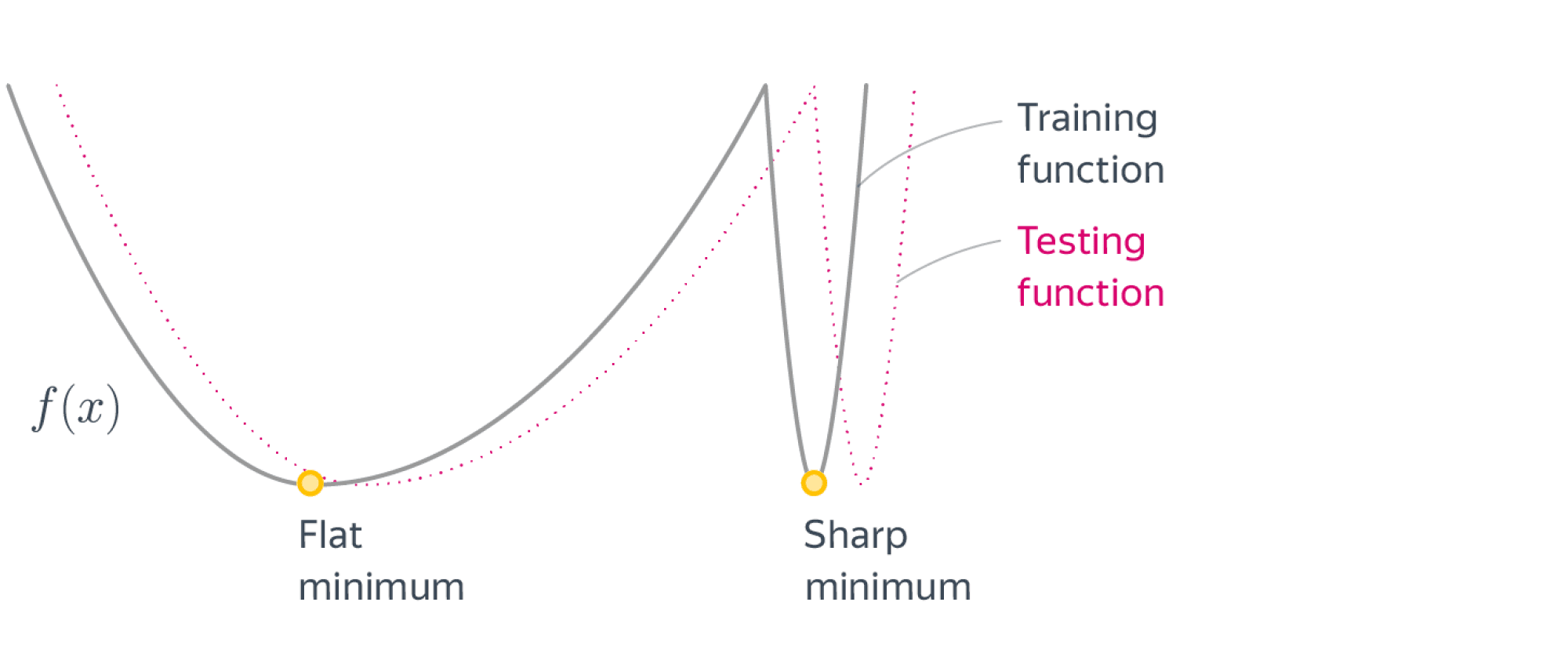
Важное свойство выпуклых функций – локальный минимум автоматически является глобальным (но не обязательно единственным!). Это позволяет избегать уродливых ситуаций, которые с теоретической точки зрения могут встретиться в невыпуклом случае, например, вот такой:
Теорема (No free lunch theorem) Пусть $A$ – алгоритм оптимизации, использующий локальную информацию (все производные в точке). Тогда существует такая невыпуклая функция $f colon [0,1]^d to [0,1]$, что для нахождения глобального минимума на квадрате $[0,1]^d$ с точностью $frac{1}{m}$ требуется совершить хотя бы $m^d$ шагов.
Для интересующихся доказательствами.
Будем строить наш контрпример, пользуясь принципом сопротивляющегося оракула (или рассуждениями с противником, кому как привычнее называть).
Разделим нашу область на подкубики размера $1/m times ldots times 1/m$. Зададим функцию следующим образом – она будет тождественно равна $1$ на всех кубиках, кроме одного, в середине которого будет точка с значением $0$ (мы не специфицируем, как значение будет гладко «снижаться» до $0$; можно построить кусочно-линейную функцию, а потом сгладить её).
А именно поставим ноль в тот кубик, который наш алгоритм оптимизации $A$ посетит последним. Так как кубиков у нас $m^d$, то алгоритм должен всегда совершить как минимум $m^d$ шагов, попробовав все кубики. Итого у нас следующая картинка ($m=3, d=2$):
Отметим дополнительно, что полученный контрпример можно сделать какой угодно гладкости (но не аналитическим).
Мы видим, что в общем случае без выпуклости нас ожидает полное разочарование. Ничего лучше перебора по сетке придумать в принципе невозможно. В выпуклом случае же существуют алгоритмы, которые находят глобальный минимум за разумное время.
Встречаются ли в жизни функции невыпуклые? Повсеместно! Например, функция потерь при обучении нейронных сетей, как правило, не является выпуклой. Но отсюда не следует, что любой алгоритм их оптимизации будет обязательно неэффективным: ведь «контрпример» из теоремы довольно специфичен. И, как мы увидим, оптимизировать невыпуклые функции очень даже возможно.
Найти глобальный минимум невыпуклой функции – очень трудная задача, но зачастую нам хватает локального, который является, в частности, стационарной точкой: такой, в которой производная равна нулю. Все теоретические результаты в случае невыпуклых задач, как правило, касаются поиска таких точек, и алгоритмы тоже направлены на их отыскание.
Этим объясняется и то, что большинство алгоритмов оптимизации, придуманных для выпуклого случая, дословно перешли в невыпуклый. Теоретическая причина в следующем: в выпуклом случае поиск стационарной точки и поиск минимума – буквально одна и та же задача, поэтому то, что хорошо ищет минимум в выпуклом случае, ожидаемо будет хорошо искать стационарные точки в невыпуклом. Практическая же причина в том, что оптимизаторы в библиотеках никогда не спрашивают, выпуклую ли им функцию подают на вход, а просто работают и работают хорошо.
Внимательный читатель мог возразить на моменте подмены задачи: подождите-ка, мы ведь хотим сделать функцию как можно меньше, а не стационарную точку искать какую-то непонятную. Доказать в невыпуклом случае тут, к сожалению, ничего невозможно, но на практике мы снова используем алгоритмы изначально для выпуклой оптимизации. Почему?
Причина номер 1: сойтись в локальный минимум лучше, чем никуда. Об этом речь уже шла.
Причина номер 2: в окрестности локального минимума функция становится выпуклой, и там мы сможем быстро сойтись.
Причина номер 3: иногда невыпуклая функция является в некотором смысле «зашумленной» версией выпуклой или похожей на выпуклую. Например, посмотрите на эту картинку (функция Леви):
У этой функции огромное количество локальных минимумов, но «глобально» она кажется выпуклой. Что-то отдаленно похожее наблюдается и в случае нейронных сетей. Нашей задачей становится не скатиться в маленький локальный минимум, который всегда рядом с нами, а в большую-большую ложбину, где значение функции минимально и в некотором смысле стабильно.
Причина номер 4: оказывается, что градиентные методы весьма часто сходятся именно к локальным минимумам.
Сразу отметим важную разницу между выпуклой и невыпуклой задачами: в выпуклом случае работа алгоритма оптимизации не очень существенно зависит от начальной точки, поскольку мы всегда скатимся в точку оптимума. В невыпуклом же случае правильно выбранная точка старта – это уже половина успеха.
Теперь перейдём к разбору важнейших алгоритмов оптимизации.
Градиентный спуск (GD)
Опишем самый простой метод, который только можно придумать – градиентный спуск. Для того, чтобы его определить, вспомним заклинание из любого курса матанализа: «градиент – это направление наискорейшего локального возрастания функции», тогда антиградиент – это направление наискорейшего локального убывания.
Для интересующихся формализмом.
Воспользуемся формулой Тейлора для $Vert h Vert = 1$ (направления спуска):
$$
f(x + alpha h) = f(x) + alpha langle nabla f(x), h rangle + o(alpha).
$$
Мы хотим уменьшить значение функции, то есть
$$
f(x) + alpha langle nabla f(x), h rangle + o(alpha) < f(x).
$$
При $alpha to 0$ имеем $langle nabla f(x), Delta x rangle leq 0$. Более того, мы хотим наискорешйшего убывания, поэтому это скалярное произведение хочется минимизировать. Сделаем это при помощи неравенства Коши-Буняковского:
$$
langle nabla f(x), h rangle geq — Vert nabla f(x) Vert_2 Vert h Vert_2 = Vert nabla f(x) Vert_2.
$$
Равенство в неравенстве Коши-Буняковского достигается при пропорциональности аргументов, то есть
$$
h = — frac{nabla f(x)}{Vert nabla f(x) Vert_2}.
$$
$$tag*{$blacksquare$}$$
Тогда пусть $x_0$ – начальная точка градиентного спуска. Тогда каждую следующую точку мы выбираем следующим образом:
$$
x_{k+1} = x_k — alpha nabla f(x_k),
$$
где $alpha$ – это размер шага (он же learning rate). Общий алгоритм градиентного спуска пишется крайне просто и элегантно:
x = normal(0, 1) # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
h = grad_f(x) # вычисляем направление спуска
x -= alpha * h # обновляем значение в точке
Эту схему в приложении к линейной регрессии можно найти в главе про линейные модели.
После всего этого начинаются тонкости:
- А как вычислять градиент?
- А как выбрать размер шага?
- А есть ли какие-то теоретические оценки сходимости?
Начнем разбирать вопросы постепенно. Для вычисления градиентов современный человек может использовать инструменты автоматического дифференцирования. Идейно, это вариация на тему алгоритма обратного распространения ошибки (backpropagation), ведь как правило человек задает функции, составленные из элементарных при помощи умножений/делений/сложений/композиций. Такой метод реализован во всех общих фреймворках для нейронных сетей (Tensorflow, PyTorch, Jax).
Но, вообще говоря, возникает некоторая тонкость. Например, расмотрим задачу линейной регрессии. Запишем её следующим образом:
$$
f(w) = frac{1}{N} sum_{i=1}^N (w^top x_i — y_i)^2.
$$
Видим, что слагаемых суммарно $N$ – размер выборки. При $N$ порядка $10^6$ и $d$ (это количество признаков) порядка $10^4$ вычисление градиента за $O(Nd)$ становится жутким мучением. Но если от $d$ избавиться без дополнительных предположений (например, о разреженности) нельзя, то с зависимостью от $N$ в каком-то смысле удастся разделаться при помощи метода стохастического градиентного спуска.
Хранение градиентов тоже доставит нам проблемы. У градиента столько же компонент, сколько параметров у модели, и если мы имеем дело с глубокой нейросетью, это даст значительные затраты дополнительной памяти. Хуже того, метод обратного распространения ошибки устроен так, что нам приходится помнить все промежуточные представления для вычисления градиентов. Поэтому вычислить градиент целиком невозможно ни для какой нормальной нейросети, и от этой беды тоже приходится спасаться с помощью стохастического градиентного спуска.
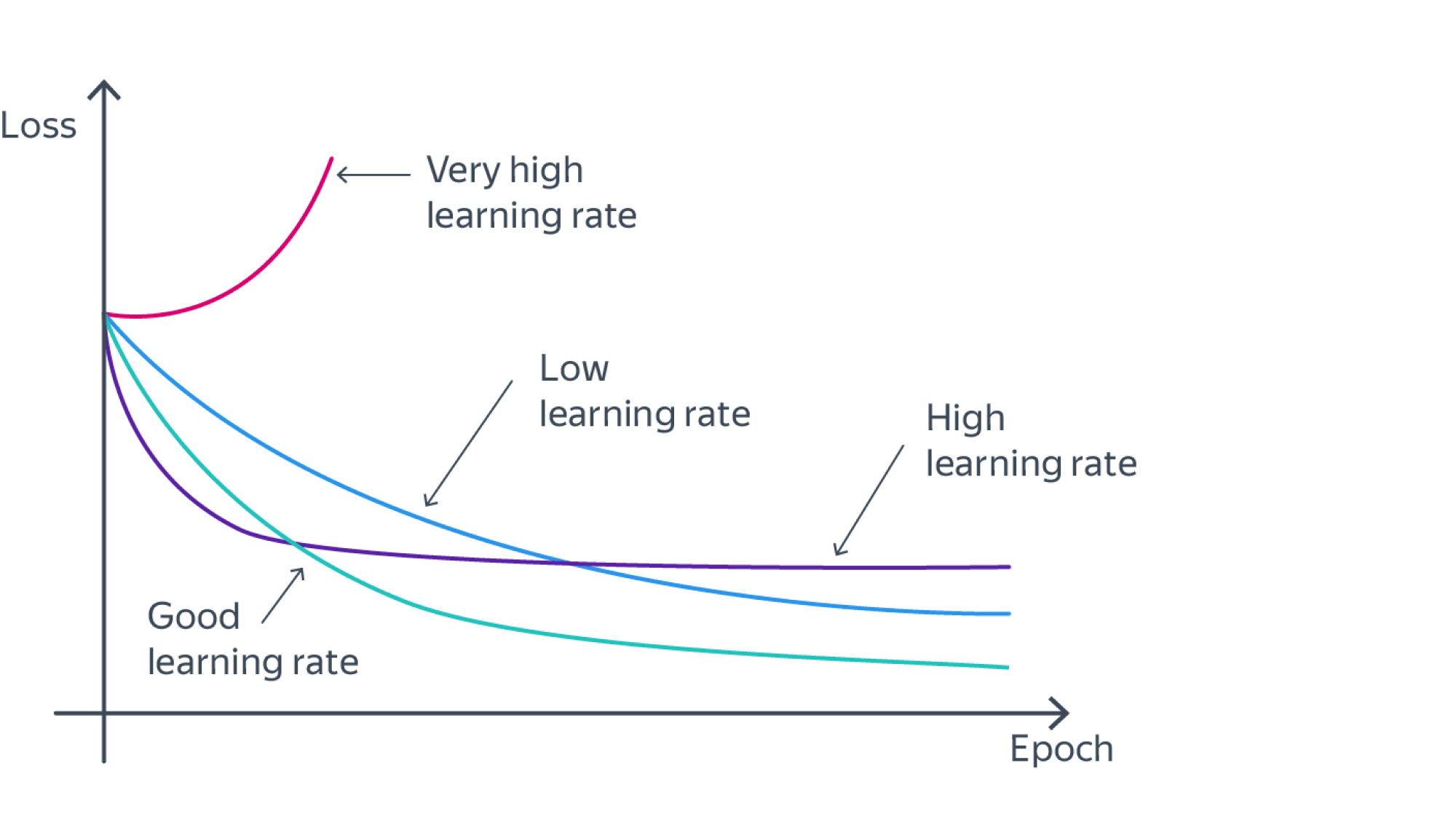
Теперь перейдем к размеру шага. Теория говорит о том, что если функция гладкая, то можно брать достаточно маленький размер шага, где под достаточно маленьким подразумевается $alpha leq frac1L$, где $L$ – некоторая константа, которая зависит от гладкости задачи (так называемая константа Липшица). Вычисление этой константы может быть задачей сложнее, чем изначальная задача оптимизации, поэтому этот вариант нам не годится. Более того, эта оценка крайне пессимистична – мы ведь хотим размер шага как можно больше, чтобы уменьшить функцию как можно больше, а тут мы будем изменять все очень мало.
Существует так называемый метод наискорейшего спуска: выбираем размер шага так, чтобы как можно сильнее уменьшить функцию:
$$
alpha_k = argmin_{alpha geq 0} f(x_k — alpha nabla f(x_k)).
$$
Одномерная оптимизация является не сильно сложной задачей, поэтому теоретически мы можем её совершать (например, методом бинарного/тернарного поиска или золотого сечения), можно этот шаг также совершать неточно. Но сразу стоит заметить, что это можно делать, только если функция $f$ вычислима более-менее точно за разумное время, в случае линейной регрессии это уже не так (не говоря уже о нейронных сетях).
Также есть всевозможные правила Армихо/Гольдштейна/Вульфа и прочее и прочее, разработанные в давние 60-е, и для их проверки требуется снова вычислять значения функции в точке. Желающие могут посмотреть на эти условия на википедии. Про более хитрые вариации выбора шагов мы поговорим позже, но сразу стоит сказать, что эта задача довольно сложная.
По поводу теории: сначала скажем что-то про выпуклый случай.
В максимально общем выпуклом случае без дополнительных предположений оценки для градиентного спуска крайне и крайне пессимистичные: чтобы достичь качества $varepsilon$, то есть
$$vert f(x_k) — f(x^*) vertleq varepsilon $$
достаточно сделаеть $O(R^2/varepsilon^2)$ шагов, где $R^2$ — это расстояние от $x_0$ до $x^*$. Выглядит очень плохо: ведь чтобы достичь точности $10^{-2}$, необходимо сделать порядка $10^4$ шагов градиентного спуска. Но на практике такого не происходит, потому что на самом деле верны разные предположения, дающие более приятные свойства. Для контраста, укажем оценку в случае гладкой и сильно выпуклой в точке оптимума функции: за $k$ шагов будет достигнута точность
$$
Oleft( minleft{R^2 exp
left(-frac{k}{4kappa}right), frac{R^2}{k} right}right),
$$
где $kappa$ – это так называемое число обусловленности задачи. По сути, это число измеряет, насколько линии уровня функции вытянуты в окрестности оптимума.
Морали две:
- Скорость сходимости градиентного спуска сильно зависит от обусловленности задачи;
- Также она зависит от выбора хорошей точки старта, ведь везде входит расстояние от точки старта до оптимума.
В качестве ссылки на доказательство укажем на работу Себастиана Стича, где оно довольно простое и общее.
В невыпуклом же случае все куда хуже с точки зрения теории: требуется порядка $O(1/varepsilon^2)$ шагов в худшем случае даже для гладкой функции, где $varepsilon$ – желаемая точность уменьшения нормы градиента.
Стохастический градиентный спуск (SGD)
Теперь мы попробуем сэкономить в случае регрессии и подобных ей задач. Будем рассматривать функционалы вида
$$
f(x) = sum_{i=1}^N mathcal{L}(x, y_i),
$$
где сумма проходится по всем объектам выборки (которых может быть очень много). Теперь сделаем следующий трюк: заметим, что это усреднение – это по сути взятие матожидания. Таким образом, мы говорим, что наша функция выглядит как
$$
f(x) = mathbb{E}[mathcal{L}(x, xi)],
$$
где $xi$ равномерно распределена по обучающей выборке. Задачи такого вида возникают не только в машинном обучении; иногда встречаются и просто задачи стохастического программирования, где происходит минимизация матожидания по неизвестному (или слишком сложному) распределению.
Для функционалов такого вида мы также можем посчитать градиент, он будет выглядеть довольно ожидаемо:
$$
nabla f(x) = mathbb{E} nabla mathcal{L}(x, xi).
$$
Будем считать, что вычисление матожидания напрямую невозможно.
Новый взгляд из статистики дает возможность воспользоваться классическим трюком: давайте подменим матожидание на его несмещенную Монте-Карло оценку. Получается то, что можно назвать стохастическим градиентом:
$$
tilde nabla f(x) = frac{1}{B} sum_{i=1}^B nabla mathcal{L}(x, xi_i).
$$
Говоря инженерным языком, мы подменили вычисление градиента по всей выборке вычислением по случайной подвыборке. Подвыборку $xi_1,ldots,xi_B$ часто называют (мини)батчем, а число $B$ – размерном батча.
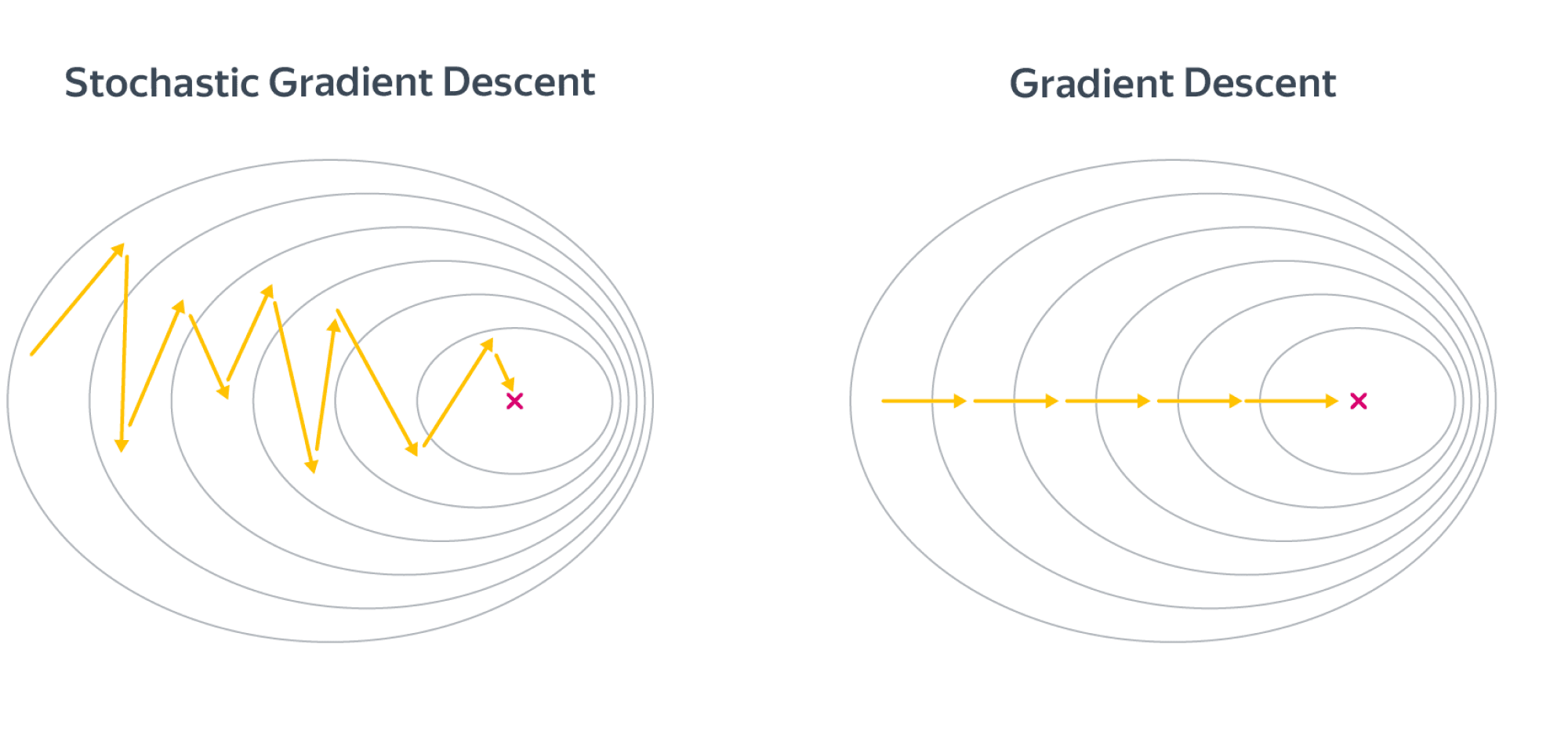
По-хорошему, наука предписывает нам каждый раз независимо генерировать батчи, но это трудно с вычислительной точки зрения. Вместо этого воспользуемся следующим приёмом: сначала перемешаем нашу выборку (чтобы внести дополнительную случайность), а затем будем рассматривать последовательно блоки по $B$ элементов выборки. Когда мы просмотрели всю выборку – перемешиваем еще раз и повторяем проход. Очередной прогон по обучающей выборке называется эпохой. И, хотя, казалось бы, независимо генерировать батчи лучше, чем перемешивать лишь между эпохами, есть несколько результатов, демонстрирующих обратное: одна работа и вторая (более новая); главное условие успеха – правильно изменяющийся размер шага.
Получаем следующий алгоритм, называемый стохастическим градиентным спуском (stochastic gradient descent, SGD):
x = normal(0, 1) # инициализация
repeat E times: # цикл по количеству эпох
for i = 0; i <= N; i += B:
batch = data[i:i+B]
h = grad_loss(batch).mean() # вычисляем оценку градиента как среднее по батчу
x -= alpha * h
Дополнительное удобство такого подхода – возможность работы с внешней памятью, ведь выборка может быть настолько большой, что она помещается только на жёсткий диск. Сразу отметим, что в таком случае $B$ стоит выбирать достаточно большим: обращение к данным с диска всегда медленнее, чем к данным из оперативной памяти, так что лучше бы сразу забирать оттуда побольше.
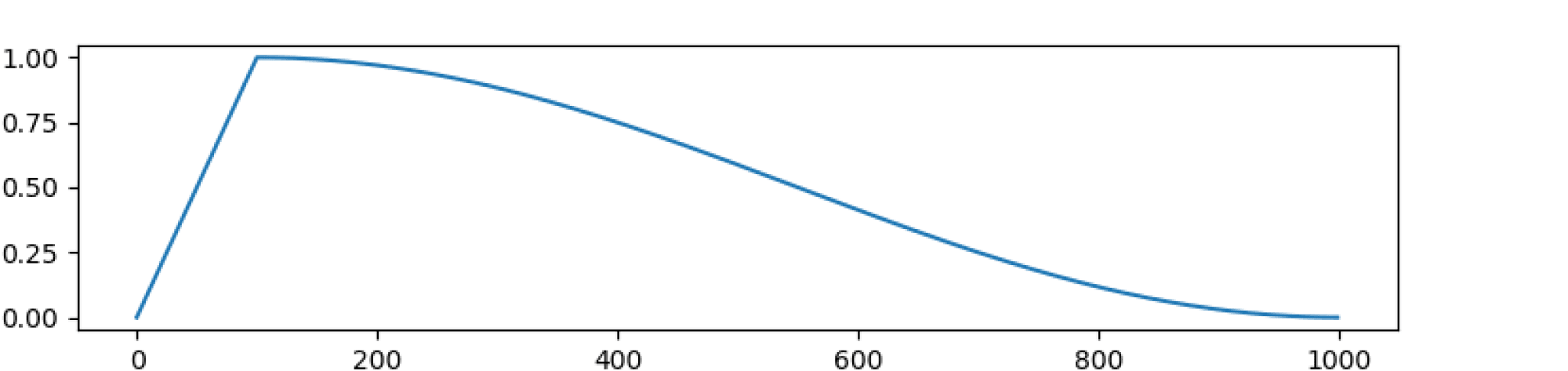
Поскольку стохастические градиенты являются лишь оценками истинных градиентов, SGD может быть довольно шумным:
Поэтому если вы обучаете глубокую нейросеть и у вас в память влезает лишь батч размером с 2-4 картинки, модель, возможно, ничего хорошего не сможет выучить. Аппроксимация градиента и поведение SGD может стать лучше с ростом размера батча $B$ – и обычно его действительно хочется подрастить, но парадоксальным образом слишком большие батчи могут порой испортить дело (об этом дальше в этой главе!).
Теоретический анализ
Теперь перейдем к теоретической стороне вопроса. Сходимость SGD обеспечивается несмещенностью стохастического градиента. Несмотря на то, что во время итераций копится шум, суммарно он зачастую оказывается довольно мал.
Теперь приведем оценки. Сначала, по традиции, в выпуклом случае. Для выпуклой функции потерь за $k$ шагов будет достигнута точность порядка
$$
Oleft( minleft{R^2 exp
left(-frac{k}{4kappa} right)+ frac{sigma^2}{mu k}, frac{R^2}{k} + frac{sigma^2 R}{sqrt{k}} right}right),
$$
где $sigma^2$ – это дисперсия стохградиента, а $mu$ – константа сильной выпуклости, показывающая, насколько функция является «не плоской» в окрестности точки оптимума. Доказательство в том же препринте С. Стича.
Мораль в следующем: дисперсия стохастического градиента, вычисленного по батчу размера $B$ равна $sigma_0^2/B$, где $sigma_0^2$ – это дисперсия одного градиента. То есть увеличение размера батча помогает и с теоретической точки зрения.
В невыпуклом случае оценка сходимости SGD просто катастрофически плохая: требуется $O(1/varepsilon^4)$ шагов для того, чтобы сделать норму градиента меньше $varepsilon$. В теории есть всевозможные дополнительные способы снижения дисперсии с лучшими теоретическими оценками (Stochastic Variance Reduced Gradient (SVRGD), Spider, etc), но на практике они активно не используются.
Использование дополнительной информации о функции
Методы второго порядка
Основной раздел.
Постараемся усовершенствовать метод стохастического градиентного спуска. Сначала заметим, что мы используем явно не всю информацию об оптимизируемой функции.
Вернемся к нашему VIP-примеру линейной регресии с $ell_2$ регуляризацией:
$$
Vert y — Xw Vert_2^2 + lambda Vert w Vert_2^2 to min_w.
$$
Эта функция достаточно гладкая, и может быть неплохой идеей использовать её старшие производные для ускорения сходимости алгоритма. В наиболее чистом виде этой философии следует метод Ньютона и подобные ему; о них вы можете прочитать в соответствующем разделе. Отметим, что все такие методы, как правило, довольно дорогие (исключая L-BFGS), и при большом размере задачи и выборки ничего лучше вариаций SGD не придумали.
Проксимальные методы
Основной раздел.
К сожалению, не всегда функции такие красивые и гладкие. Для примера рассмотрим Lasso-регресию:
$$
Vert y — Xw Vert_2^2 + lambda Vert w Vert_1 to min_w.
$$
Второе, не гладкое слагаемое резко ломает все свойства этой задачи: теоретически оценки для градиентного спуска становятся гораздо хуже (и на практике тоже). С другой стороны, регуляризационное слагаемое устроено очень просто, и эту дополнительную структурную особенность можно и нужно эксплуатировать. Методы решения задачи вида
$$
f(x) + h(x) to min_x,
$$
где $h$ – простая функция (в некотором смысле), а $f$ – гладкая, называются методами композитной оптимизации. Глубже погрузиться в них можно в соответствующем разделе, посвященном проксимальным методам.
Использование информации о предыдущих шагах
Следующая претензия к методу градиентного спуска – мы не используем информацию о предыдущих шагах, хотя, кажется, там может храниться что-то полезное.
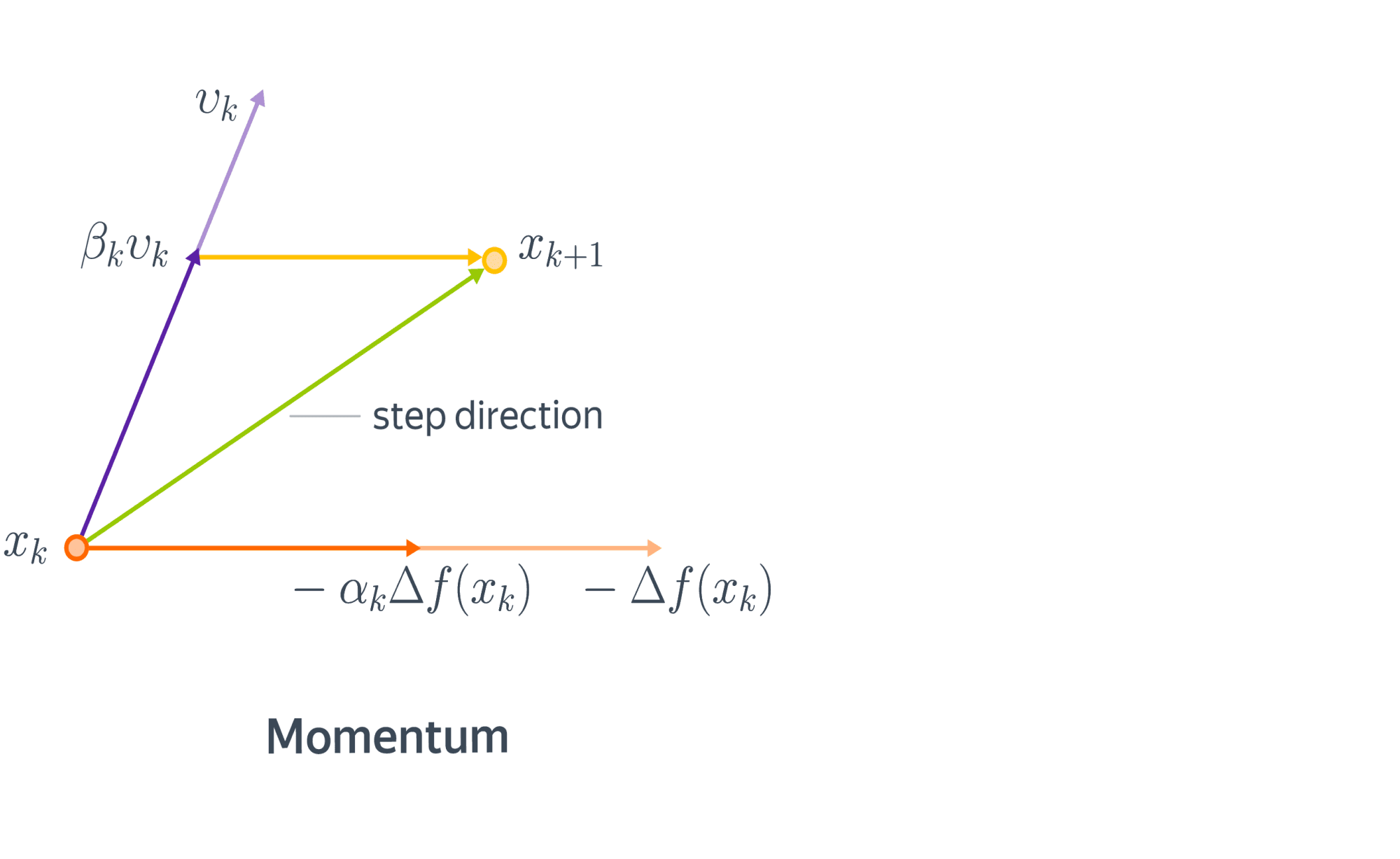
Метод инерции, momentum
Начнем с физической аналогии. Представим себе мячик, который катится с горы. В данном случае гора – это график функции потерь в пространстве параметров нашей модели, а мячик – её текущее значение. Реальный мячик не застрянет перед небольшой кочкой, так как у него есть некоторая масса и уже накопленный импульс – некоторое время он способен двигаться даже вверх по склону. Аналогичный прием может быть использован и в градиентной оптимизации. В англоязычной литературе он называется Momentum.
С математической точки зрения, мы добавляем к градиентному шагу еще одно слагаемое:
$$
x_{k+1} = x_k — alpha_k nabla f(x_k) + color{red}{beta_k (x_k — x_{k-1})}.
$$
Сразу заметим, что мы немного усугубили ситуацию с подбором шага, ведь теперь нужно подбирать не только $alpha_k$, но и $beta_k$. Для обычного, не стохастического градиентного спуска мы можем адаптировать метод наискорейшего и получить метод тяжелого шарика:
$$
(alpha_k, beta_k) = argmin_{alpha,beta} f(x_k — alpha nabla f(x_k) + beta (x_k — x_{k-1})).
$$
Но, увы, для SGD это работать не будет.
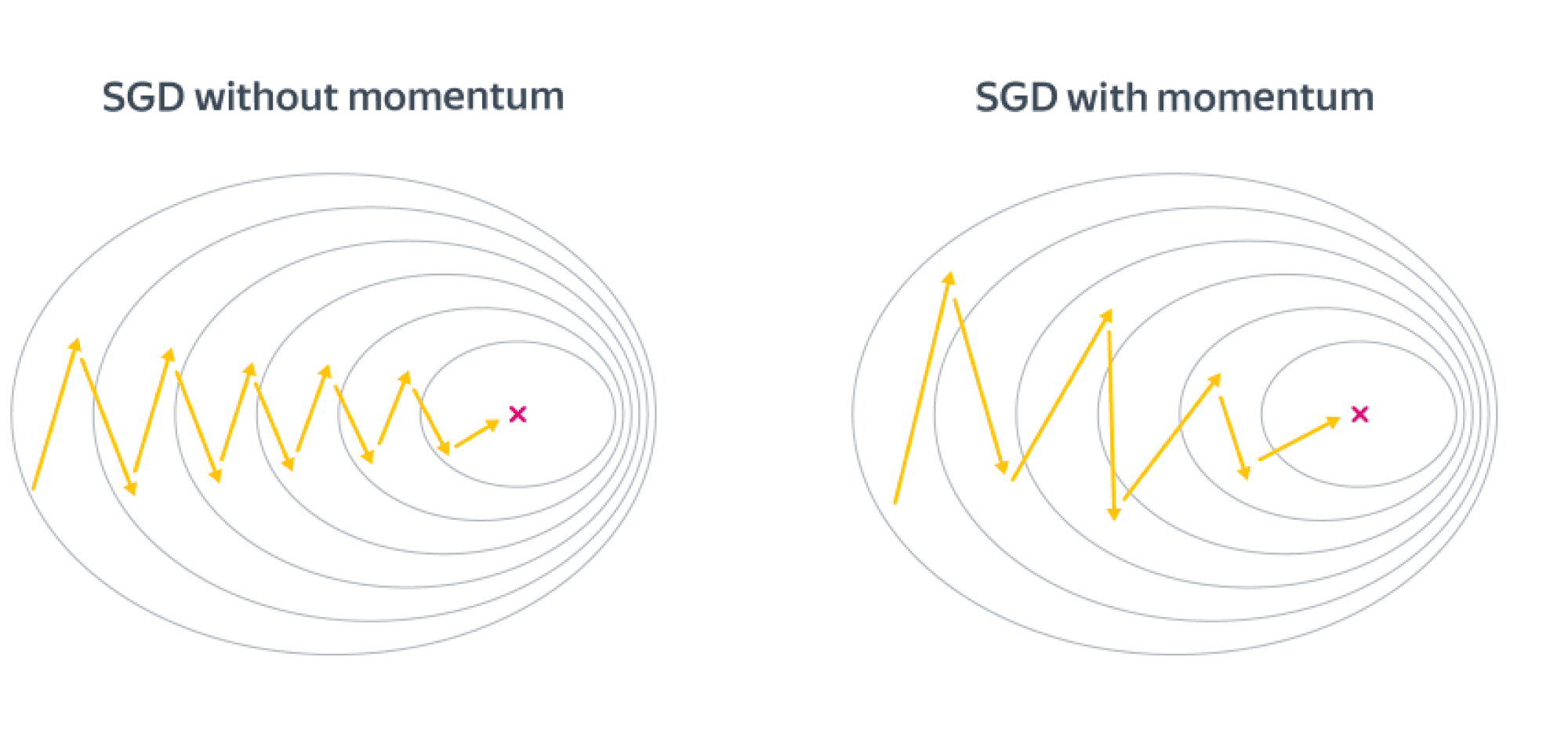
Выгода в невыпуклом случае от метода инерции довольно понятна – мы будем пропускать паразитные локальные минимумы и седла и продолжать движение вниз. Но выгода есть также и в выпуклом случае. Рассмотрим плохо обусловленную квадратичную задачу, для которой линии уровня оптимизируемой функции будут очень вытянутыми эллипсами, и запустим на SGD с инерционным слагаемым и без него. Направление градиента будет иметь существенную вертикальную компоненту, а добавление инерции как раз «погасит» паразитное направление. Получаем следующую картинку:
Также удобно бывает представить метод моментума в виде двух параллельных итерационных процессов:
$$begin{align}
v_{k+1} &= beta_k v_k — alpha_k nabla f(x_k)
x_{k+1} &= x_k + v_{k+1}.
end{align}
$$
Accelerated Gradient Descent (Nesterov Momentum)
Рассмотрим некоторую дополнительную модификацию, которая была предложена в качестве оптимального метода первого порядка для решения выпуклых оптимизационных задач.
Можно доказать, что в сильно выпуклом и гладком случае найти минимум с точностью $varepsilon$ нельзя быстрее, чем за
$$
Omegaleft( R^2expleft(-frac{k}{sqrt{kappa}}right) right)
$$
итераций, где $kappa$ – число обусловленности задачи. Напомним, что для обычного градиентного спуска в экспоненте у нас был не корень из $kappa$, а просто $kappa$, то есть, градиентный спуск справляется с плохой обусловленностью задачи хуже, чем мог бы.
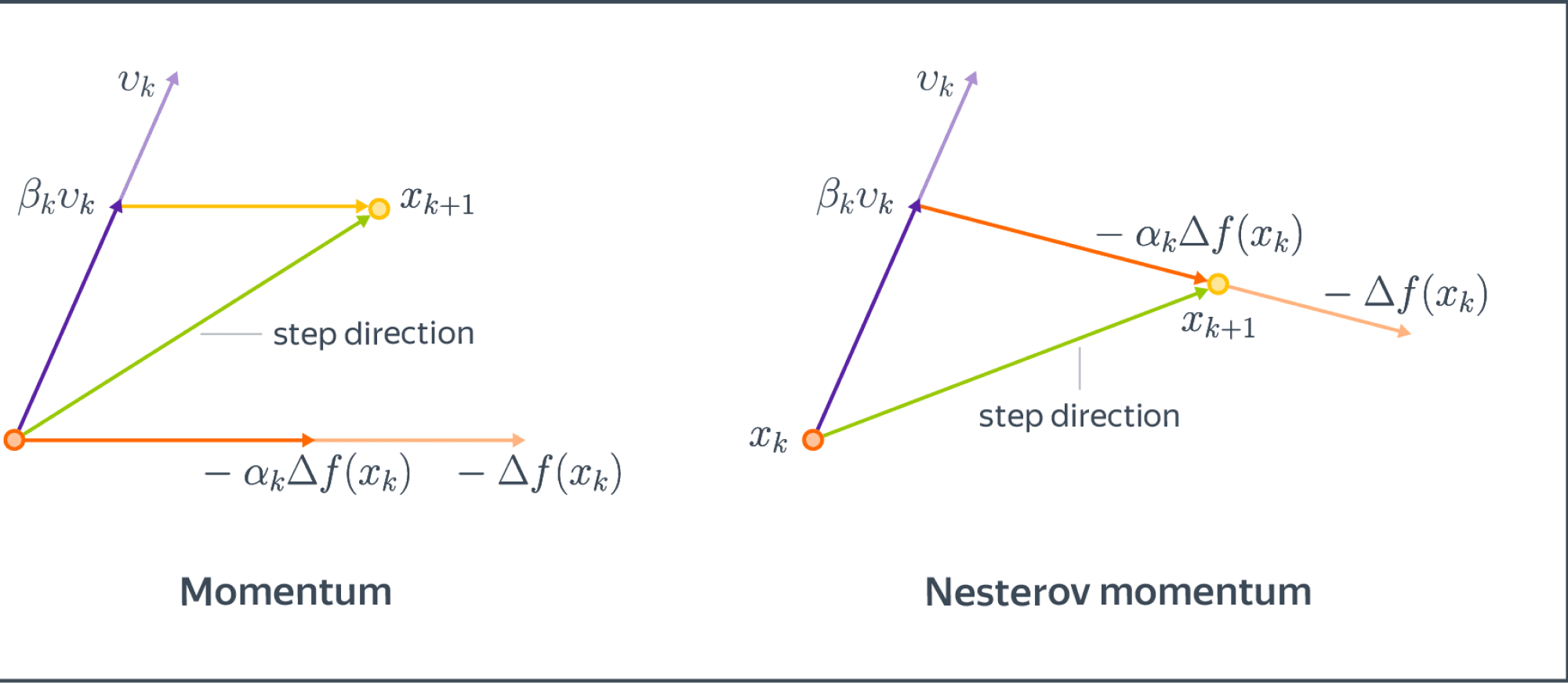
В 1983 году Ю.Нестеровым был предложен алгоритм, имеющий оптимальную по порядку оценку. Для этого модифицируем немного моментум и будем считать градиент не в текущей точке, а как бы в точке, в которую мы бы пошли, следуя импульсу:
$$begin{align}
v_{k+1} &= beta_k v_k — alpha_k nabla f(color{red}{x_k + beta_k v_k})
x_{k+1} &= x_k + v_{k+1}
end{align}
$$
Сравним с обычным momentum:
Комментарий: иногда упоминается, что Nesterov Momentum «заглядывает в будущее» и исправляет ошибки на данном шаге оптимизации. Конечно, никто не заглядывает в будущее в буквальном смысле.
В работе Нестерова были предложены конкретные (и довольно магические) константы для импульса, которые получаются из некоторой еще более магической последовательности. Мы приводить их не будем, поскольку мы в первую очередь заинтересованы невыпуклым случаем.
Nesterov Momentum позволяет значительно повысить устойчивость и скорость сходимости в некоторых случаях. Но, конечно, он не является серебряной пулей в задачах оптимизации, хотя в выпуклом мире и является теоретически неулучшаемым.
Также отметим, что ускоренный метод может напрямую примениться к проксимальному градиентному спуску. В частности, применение ускоренного метода к проксимальному алгоритму решения $ell_1$ регрессии (ISTA) называется FISTA (Fast ISTA).
Общие выводы:
- Добавление momentum к градиентному спуску позволяет повысить его устойчивость и избегать маленьких локальных минимумов/максимумов;
- В выпуклом случае добавление моментного слагаемого позволяет доказуемо улучшить асимптотику и уменьшить зависимость от плохой обусловленности задачи.
- Идея ускорения применяется к любым около-градиентным методам, в том числе и к проксимальным, позволяя получить, например, ускоренный метод для $ell_1$-регрессии.
Адаптивный подбор размера шага
Выше мы попытались эксплуатировать свойства градиентного спуска. Теперь же пришел момент взяться за больной вопрос: как подбирать размер шага? Он максимально остро встаёт в случае SGD: ведь посчитать значение функции потерь в точке очень дорого, так что методы в духе наискорейшего спуска нам не помогут!
Нужно действовать несколько хитрее.
Adagrad
Рассмотрим первый алгоритм, который является адаптацией стохастического градиентного спуска. Впервые он предложен в статье в JMLR 2011 года, но она написана в очень широкой общности, так что читать её достаточно сложно.
Зафиксируем $alpha$ – исходный learning rate. Затем напишем следующую формулу обновления:
$$begin{align}
G_{k+1} &= G_k + (nabla f(x_k))^2
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} nabla f(x_k).
end{align}
$$
Возведение в квадрат и деления векторов покомпонентные. По сути, мы добавляем некоторую квазиньютоновость и начинаем динамически подбирать размер шага для каждой координаты по отдельности. Наш размера шага для фиксированной координаты – это какая-то изначальная константа $alpha$ (learning rate), деленная на корень из суммы квадратов координат градиентов плюс дополнительный параметр сглаживания $varepsilon$, предотвращающий деление на ноль. Добавка $varepsilon$ на практике оставляется дефолтными 1e-8 и не изменяется.
Идея следующая: если мы вышли на плато по какой-то координате и соответствующая компонента градиента начала затухать, то нам нельзя уменьшать размер шага слишком сильно, поскольку мы рискуем на этом плато остаться, но в то же время уменьшать надо, потому что это плато может содержать оптимум. Если же градиент долгое время довольно большой, то это может быть знаком, что нам нужно уменьшить размер шага, чтобы не пропустить оптимум. Поэтому мы стараемся компенсировать слишком большие или слишком маленькие координаты градиента.
Но довольно часто получается так, что размер шага уменьшается слишком быстро и для решения этой проблемы придумали другой алгоритм.
RMSProp
Модифицируем слегка предыдущую идею: будем не просто складывать нормы градиентов, а усреднять их в скользящем режиме:
$$begin{align}
G_{k+1} &= gamma G_k + (1 — gamma)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} nabla f(x_k).
end{align}
$$
Такой выбор позволяет все еще учитывать историю градиентов, но при этом размер шага уменьшается не так быстро.
Общие выводы:
- Благодаря адаптивному подбору шага в современных оптимизаторах не нужно подбирать последовательность $alpha_k$ размеров всех шагов, а достаточно выбрать всего одно число – learning rate $alpha$, всё остальное сделает за вас сам алгоритм. Но learning rate все еще нужно выбирать крайне аккуратно: алгоритм может либо преждевременно выйти на плато, либо вовсе разойтись. Пример приведен на иллюстрации ниже.
Объединяем все вместе…
Adam
Теперь покажем гвоздь нашей программы: алгоритм Adam, который считается решением по умолчанию и практически серебряной пулей в задачах стохастической оптимизации.
Название Adam = ADAptive Momentum намекает на то, что мы объединим идеи двух последних разделов в один алгоритм. Приведем его алгоритм, он будет немного отличаться от оригинальной статьи отсутствием коррекций смещения (bias correction), но идея останется той же самой:
$$begin{align}
v_{k+1} &= beta_1 v_k + (1 — beta_1) nabla f(x_k)
end{align}
$$
$$begin{align}
G_{k+1} &= beta_2 G_k + (1 — beta_2)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} v_{k+1}.
end{align}
$$
Как правило, в этом алгоритме подбирают лишь один гиперпараметр $alpha$ – learning rate. Остальные же: $beta_1$, $beta_2$ и $varepsilon$ – оставляют стандартными и равными 0.9, 0.99 и 1e-8 соответственно. Подбор $alpha$ составляет главное искусство.
Зачастую, при начале работы с реальными данными начинают со значения learning rate равного 3e-4. История данного значения достаточно забавна: в 2016 году Андрей Карпатый (Andrej Karpathy) опубликовал шутливый пост в Twitter.
После чего сообщество подхватило эту идею (до такой степени, что иногда число 3e-4 называют Karpathy constant).
Обращаем ваше внимание, что при работе с учебными данными зачастую полезно выбирать более высокий (на 1-2 порядка) начальный learning rate (например, при классификации MNIST, Fashion MNIST, CIFAR или при обучении языковой модели на примере поэзии выбранного поэта).
Также стоит помнить, что Adam требует хранения как параметров модели, так и градиентов, накопленного импульса и нормировочных констант (cache). Т.е. достижение более быстрой (с точки зрения количества итераций/объема рассмотренных данных) сходимости требует больших объемов памяти. Кроме того, если вы решите продолжить обучение модели, остановленное на некоторой точке, необходимо восстановить из чекпоинта не только веса модели, но и накопленные параметры Adam. В противном случае оптимизатор начнёт сбор всех своих статистик с нуля, что может сильно сказаться на качестве дообучения. То же самое касается вообще всех описанных выше методов, так как каждый из них накапливает какие-то статистики во время обучения.
Интересный факт: Adam расходится на одномерном контрпримере, что совершенно не мешает использовать его для обучения нейронных сетей. Этот факт отлично демонстрирует, насколько расходятся теория и практика в машинном обучении. В той же работе предложено исправление этого недоразумения, но его активно не применяют и продолжают пользоваться «неправильным» Adamом потому что он быстрее сходится на практике.
AdamW
А теперь давайте добавим $ell_2$-регуляризацию неявным образом, напрямую в оптимизатор и минуя адаптивный размер шага:
$$begin{align}
v_{k+1} &= beta_1 v_k + (1 — beta_1) nabla f(x_k)
end{align}
$$
$$begin{align}
G_{k+1} &= beta_2 G_k + (1 — beta_2)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — left( frac{alpha}{sqrt{G_{k+1} + varepsilon}} v_{k+1} color{red}{ + lambda x_{k}} right).
end{align}
$$
Это сделано для того, чтобы эффект $ell_2$-регуляризации не затухал со временем и обобщающая способность модели была выше. Оставим ссылку на одну заметку про этот эффект. Отметим, впрочем, что этот алгоритм особо не используется.
Практические аспекты
Расписания
Часто learning rate понижают итеративно: каждые условные 5 эпох (LRScheduler в Pytorch) или же при выходе функции потерь на плато. При этом лосс нередко ведет себя следующим схематичным образом:
Помимо этого используют другие варианты «расписаний» для learning rate. Из часто применяемых неочевидных лайфхаков: сначала сделать warmup, то есть увеличивать learning rate, а затем начать постепенно понижать. Использовалось в известной статье про трансформеры. В ней предложили следующую формулу:
$$
lr = d^{-0.5}_{rm{model}} cdot min(step_ num^{-0.5}, step_ num cdot warmup_ steps^{-1.5}).
$$
По сути, первые $warmup_ steps$ шагов происходит линейный рост размера шага, а затем он начинает уменьшаться как $1/sqrt{t}$, где $t$ — число итераций.
Есть и вариант с косинусом из отдельной библиотеки для трансформеров.
В этой же библиотеке можно также почерпнуть идею рестартов: с какого-то момента мы снова включаем warmup, увеличивая размер шага.
Большие батчи
Представим ситуацию, что мы хотим обучить свою нейронную на нескольких GPU. Одно из решений выглядит следующим образом: загружаем на каждую видеокарту нейронную сеть и свой отдельный батч, вычисляем стохастические градиенты, а затем усредняем их по всем видеокартам и делаем шаг. Что плохого может быть в этом?
По факту, эта схема в некотором смысле эквивалентна работе с одним очень большим батчем. Хорошо же, нет разве?
На самом деле существует так называемый generalization gap: использование большого размера батча может приводить к худшей обобщающей способности итоговой модели. О причине этого эффекта можно поспекулировать, базируясь на текущих знаниях о ландшафтах функций потерь при обучении нейронных сетей.
Больший размер батча приводит к тому, что оптимизатор лучше «видит» ландшафт функции потерь для конкретной выборки и может скатиться в маленькие «узкие» паразитные локальные минимумы, которые не имеют обобщающий способности — при небольшом шевелении этого ландшафта (distributional shift c тренировочной на тестовую выборку) значение функции потерь резко подскакивает. В свою очередь, широкие локальные минимумы дают модель с лучшей обобщающей способностью. Эту идею можно увидеть на следующей картинке:
Иными словами, большие батчи могут приводить к переобучению, но это можно исправить правильным динамическим подбором learning rate, как будет продемонстрировано далее. Сразу отметим, что совсем маленькие батчи – это тоже плохо, с ними ничего не получится выучить, так как каждая итерация SGD знает слишком мало о ландшафте функции потерь.
LARS
Мы рассмотрим нестандартный оптимизатор для обучения нейронных сетей, которого нет в Pytorch по умолчанию, но который много где используется: Layer-wise Adaptive Rate Scaling (LARS). Он позволяет эффективно использовать большие размеры батчей, что очень важно при вычислении на нескольких GPU.
Основная идея заключена в названии – нужно подбирать размер шага не один для всей сети или каждого нейрона, а отдельный для каждого слоя по правилу, похожему на RMSProp. По сравнению с оригинальным RMSProp подбор learning rate для каждого слоя дает большую стабильность обучения.
Теперь рассмотрим формулу пересчета: пусть $w_l$ – это веса слоя $l$, $l < L$. Параметры алгоритма: базовый learning rate $eta$ (на который запускается расписание), коэффициент инерции $m$, коэффециент затухания весов $beta$ (как в AdamW).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
lr = eta * norm(w[l]) / (norm(g_l) + beta * norm(w[l])) # Вычислеяем learning rate для текущего слоя
v[l] = m * v[l] + lr * (g_l + beta * w[l]) # Обновляем momentum
w[l] -= v[l] # Делаем градиентный шаг по всему слою сразу
w_prev = w # Обновляем веса
LAMB
Этот оптимизатор введен в статье Large Batch Optimization For Deep Learning и является идейным продолжателем LARS, более приближенным к Adam, чем к обычному RMSProp. Его параметры – это параметры Adam $eta, beta_1, beta_2, varepsilon$, которые беруется как в Adam, а также параметр $lambda$, который отвечает за затухание весов ($beta$ в LARS).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
m[l] = beta_1 * m[l] + (1 - beta_1) * g_l # Вычисляем моментум
v[l] = beta_2 * v[l] + (1 - beta_2) * g_l # Вычисляем новый размер шага
m[l] /= (1 - beta_1**t) # Шаг для уменьшения смещения из Adam
v[l] /= (1 - beta_2**t)
r[l] = m[l] / sqrt(v[l] + eps) # Нормируем моментум как предписывает Adam
lr = eta * norm(w[l]) / norm(r[l] + llambda * w[l]) # Как в LARS
w[l] = w[l] - lr * (r[l] + llambda * w[l]) # Делаем шаг по моментуму
w_prev = w # Обновляем веса
Усреднение
Теперь снова заглянем в теорию: на самом деле, все хорошие теоретические оценки для SGD проявляются, когда берётся усреднение по точкам.
Этот эффект при обучении нейронных сетей был исследован в статье про алгоритм SWA. Суть очень проста: давайте усреднять веса модели по каждой $c$-й итерации; можно считать, что по эпохам. В итоге, веса финальной модели являются усреднением весов моделей, имевщих место в конце каждой эпохи.
В результате такого усреднения сильно повышается обобщающая способность модели: мы чаще попадаем в те самые широкие локальные минимумы, о которых мы говорили в разделе про большие батчи. Вдохновляющая картинка из статьи прилагается:
На второй и третьей картинке изображено сравнение SGD и SWA при обучении нейронной сети (Preactivation ResNet-164 on CIFAR-100) при одной и той же инициализации.
На первой же картинке изображено, как идеологически должен работать SWA. Также мы видим тут демонстрацию эффекта концентрации меры: после обучения стохастический градиентный спуск становится случайным блужданием по области в окрестности локального минимума. Если, например, предположить, что итоговая точка – это нормальное распределение с центром в реальном минимуме в размерности $d > 10^6$, то все эти точки с большой вероятности будут находиться в окрестности сферы радиуса $sqrt{d}$. Интуитивную демонстрацию многомерного нормального распределения можно увидеть на следующей картинке из книги Р.Вершинина «High-Dimensional Probability» (слева в размерности 2, справа в большой размерности):
Поэтому, чтобы вычислить центральную точку этой гауссианы, усреднение просто необходимо, по такому же принципу работает и SWA.
Предобуславливание
Теперь мы снова обратимся к теории: скорость сходимости градиентного спуска (даже ускоренного) очень сильно зависит от числа обусловленности задачи. Разумной идеей будет попытаться использовать какие-то сведения о задаче и улучшить этот показатель, тем самым ускорив сходимость.
В теории, здесь могут помочь техники предобуславливания. Но, к сожалению, попытки наивно воплотить эту идею приводят к чему-то, похожему на метод Ньютона, в котором нужно хранить большую-большую матрицу для обучения больших моделей. Способ обойти эту проблему рассмотрели в статье о методе Shampoo, который использует то, что веса нейронной сети зачастую удобно представлять как матрицу или даже многомерный тензор. Таким образом, Shampoo можно рассматривать как многомерный аналог AdaGrad.